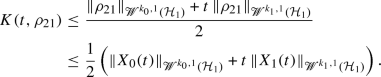Abstract
Various quantum analogues of the central limit theorem, which is one of the cornerstones of probability theory, are known in the literature. One such analogue, due to Cushen and Hudson, is of particular relevance for quantum optics. It implies that the state in any single output arm of an n-splitter, which is fed with n copies of a centred state \(\rho \) with finite second moments, converges to the Gaussian state with the same first and second moments as \(\rho \). Here we exploit the phase space formalism to carry out a refined analysis of the rate of convergence in this quantum central limit theorem. For instance, we prove that the convergence takes place at a rate \(\mathcal {O}\left( n^{-1/2}\right) \) in the Hilbert–Schmidt norm whenever the third moments of \(\rho \) are finite. Trace norm or relative entropy bounds can be obtained by leveraging the energy boundedness of the state. Via analytical and numerical examples we show that our results are tight in many respects. An extension of our proof techniques to the non-i.i.d. setting is used to analyse a new model of a lossy optical fibre, where a given m-mode state enters a cascade of n beam splitters of equal transmissivities \(\lambda ^{1/n}\) fed with an arbitrary (but fixed) environment state. Assuming that the latter has finite third moments, and ignoring unitaries, we show that the effective channel converges in diamond norm to a simple thermal attenuator, with a rate \(\mathcal {O}\Big (n^{-\frac{1}{2(m+1)}}\Big )\). This allows us to establish bounds on the classical and quantum capacities of the cascade channel. Along the way, we derive several results that may be of independent interest. For example, we prove that any quantum characteristic function \(\chi _\rho \) is uniformly bounded by some \(\eta _\rho <1\) outside of any neighbourhood of the origin; also, \(\eta _\rho \) can be made to depend only on the energy of the state \(\rho \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Central Limit Theorem (CLT) is one of the cornerstones of probability theory. This theorem and its various extensions have found numerous applications in diverse fields including mathematics, physics, information theory, economics and psychology. Any limit theorem becomes more valuable if it is accompanied by estimates for rates of convergence. The Berry–Esseen theorem (see e.g. [1]), which gives the rate of convergence of the distribution of the scaled sum of independent and identically distributed (i.i.d.) random variables to a normal distribution, thus provides an important refinement of the CLT.
The first results on quantum analogues of the CLT were obtained in the early 1970s by Cushen and Hudson [2], and Hepp and Lieb [3, 4]. The approach of [3] was generalised by Giri and von Waldenfels [5] a few years later. These papers were followed by numerous other quantum versions of the CLT in the context of quantum statistical mechanics [6,7,8,9,10,11,12,13,14], quantum field theory [15,16,17], von Neumann algebras [18, 19], free probability [20], noncommutative stochastic processes [21] and quantum information theory [22,23,24]. For a more detailed list of papers on noncommutative or quantum central limit theorems (QCLT), see for example [19, 25] and references therein. A partially quantitative central limit theorem for unsharp measurements has been obtained in [26].
An important pair of non-commuting observables is the pair (x, p) of canonically conjugate operators, which obey Heisenberg’s canonical commutation relations (CCR) \([x,p] = i I\), where I denotes the identity operator.Footnote 1 These observables could be, for example, the position and momentum operators of a quantum particle, or the so-called position and momentum quadratures of a single-mode bosonic field, described in the quantum mechanical picture by the Hilbert space  – the space of square integrable functions on \({\mathbb {R}}\). The corresponding annihilation and creation operators are constructed as
– the space of square integrable functions on \({\mathbb {R}}\). The corresponding annihilation and creation operators are constructed as  and
and  . When expressed in terms of \(a,a^\dag \), the CCR take the form \([a,a^\dag ]=I\).
. When expressed in terms of \(a,a^\dag \), the CCR take the form \([a,a^\dag ]=I\).
Quantum states are represented by density operators, i.e. positive semi-definite trace class operators with unit trace. A state \(\rho \) of a continuous variable quantum system is uniquely identified by its characteristic function, defined for all \(z \in \mathbb {C}\) by  . The special class of Gaussian states comprises all quantum states whose characteristic function is the (classical) characteristic function of a normal random variable on \(\mathbb {C}\).Footnote 2 Exactly as in the classical case, a quantum Gaussian state is uniquely defined by its mean and covariance matrix.
. The special class of Gaussian states comprises all quantum states whose characteristic function is the (classical) characteristic function of a normal random variable on \(\mathbb {C}\).Footnote 2 Exactly as in the classical case, a quantum Gaussian state is uniquely defined by its mean and covariance matrix.
Cushen and Hudson [2] proved a quantum CLT for a sequence of pairs of such canonically conjugate operators \(\{(x_n, p_n): n=1,2,\ldots \}\), with each pair acting on a distinct copy of the Hilbert space  . More precisely, they showed that sequences that are stochastically independent and identically distributed, and have finite covariance matrix and zero mean with respect to a quantum state \(\rho \) (given by a density operator on
. More precisely, they showed that sequences that are stochastically independent and identically distributed, and have finite covariance matrix and zero mean with respect to a quantum state \(\rho \) (given by a density operator on  ), are such that their scaled sums converge in distribution to a normal limit distribution [2, Theorem 1].
), are such that their scaled sums converge in distribution to a normal limit distribution [2, Theorem 1].
Their result admits a physical interpretation in terms of a passive quantum optical element known as the n-splitter. This can be thought of as the unitary operator \(U_{n\text {-split}}\) that acts on n annihilation operators of n independent optical modes as \(U_{n\text {-split}}\, a_j\, U_{n\text {-split}}^\dag = \sum _{k} F_{jk} a_k\), where  is the discrete Fourier transform matrix. Passivity here means that \(U_{n\text {-split}}\) commutes with the canonical Hamiltonian of the field, i.e. \(\left[ U_{n\text {-split}},\, \sum \nolimits _j a_j^\dag a_j\right] =0\). When n identical copies of a state \(\rho \) are combined by means of an n-splitter, and all but the first output modes are traced away, the resulting output state is called the n -fold quantum convolution of \(\rho \), and denoted by \(\rho ^{\boxplus n}\). This nomenclature is justified by the fact that the characteristic function \(\chi _{\rho \, \boxplus \, \sigma }\) of two states \(\rho \) and \(\sigma \) is equal to the product of the characteristic functions of \(\rho \) and \(\sigma \), a relation analogous to that satisfied by characteristic functions of convolutions of classical random variables. Observe state \(\rho ^{\boxplus n}\) can also be obtained as the output of a cascade of \(n-1\) beam splitters with suitably tuned transmissivities \(\lambda _j = j/(j+1)\) for \(j=1,2, \ldots n-1\) (see Fig. 1a).
is the discrete Fourier transform matrix. Passivity here means that \(U_{n\text {-split}}\) commutes with the canonical Hamiltonian of the field, i.e. \(\left[ U_{n\text {-split}},\, \sum \nolimits _j a_j^\dag a_j\right] =0\). When n identical copies of a state \(\rho \) are combined by means of an n-splitter, and all but the first output modes are traced away, the resulting output state is called the n -fold quantum convolution of \(\rho \), and denoted by \(\rho ^{\boxplus n}\). This nomenclature is justified by the fact that the characteristic function \(\chi _{\rho \, \boxplus \, \sigma }\) of two states \(\rho \) and \(\sigma \) is equal to the product of the characteristic functions of \(\rho \) and \(\sigma \), a relation analogous to that satisfied by characteristic functions of convolutions of classical random variables. Observe state \(\rho ^{\boxplus n}\) can also be obtained as the output of a cascade of \(n-1\) beam splitters with suitably tuned transmissivities \(\lambda _j = j/(j+1)\) for \(j=1,2, \ldots n-1\) (see Fig. 1a).
Cushen and Hudson’s result is that if \(\rho \) is a centred state (i.e. with zero mean) and has finite second moments, its convolutions \(\rho ^{\boxplus n}\) converge to the Gaussian state \(\rho _\mathrm {\scriptscriptstyle G}\) with the same first and second moments as \(\rho \) in the limit \(n\rightarrow \infty \) (Theorem 3). In [2, Theorem 1], the convergence is with respect to the weak topology of the Banach space of trace class operators, which translates to pointwise convergence of the corresponding characteristic functions, by a quantum analogue of Levy’s lemma that is also proven in [2]. This in turn implies that the convergence actually is with respect to the strong topology, i.e. in trace norm (see [27], or [28, Lemma 4]).
In this paper, we focus on the framework proposed by Cushen and Hudson, and provide a refinement of their result by deriving estimates for the associated rates of convergence. We consider a quantum system composed of m modes of the electromagnectic field, each modelled by an independent quantum harmonic oscillator, so that the corresponding Hilbert space becomes  . The main contribution of this paper consists of estimates on rate of convergence of \(\rho ^{\boxplus n}\) to the ‘Gaussification’ \(\rho _\mathrm {\scriptscriptstyle G}\) of \(\rho \), obtained under suitable assumptions on \(\rho \) – typically, the finiteness of higher-order moments. In analogy with the classical case, we refer to our Theorems 6 and 7 as quantum Berry–Esseen theorems. Our estimates are given in the form of bounds on the Schatten p-norms (for \(p=1\) and 2) of the difference \((\rho ^{\boxplus n} - \rho _\mathrm {\scriptscriptstyle G})\) in the limit of large n, as well as bounds on the relative entropy of \(\rho ^{\boxplus n}\) with respect to \(\rho _\mathrm {\scriptscriptstyle G}\) in the same limit.
. The main contribution of this paper consists of estimates on rate of convergence of \(\rho ^{\boxplus n}\) to the ‘Gaussification’ \(\rho _\mathrm {\scriptscriptstyle G}\) of \(\rho \), obtained under suitable assumptions on \(\rho \) – typically, the finiteness of higher-order moments. In analogy with the classical case, we refer to our Theorems 6 and 7 as quantum Berry–Esseen theorems. Our estimates are given in the form of bounds on the Schatten p-norms (for \(p=1\) and 2) of the difference \((\rho ^{\boxplus n} - \rho _\mathrm {\scriptscriptstyle G})\) in the limit of large n, as well as bounds on the relative entropy of \(\rho ^{\boxplus n}\) with respect to \(\rho _\mathrm {\scriptscriptstyle G}\) in the same limit.
We also show that the assumption of finiteness of the second moments cannot be removed from the Cushen–Hudson theorem. Namely, we construct a simple example of a single-mode quantum state \(\sigma \) such that \({\text {Tr}}\big [\sigma \, (a a^\dag )^{1-\delta }\big ]\) is finite for all \(\delta >0\) (and infinite for \(\delta =0\)), yet \(\sigma ^{\boxplus n}\) does not converge to any quantum state as \(n\rightarrow \infty \).
As an application, we propose and study a new model of optical fibre, represented as a cascade of n beam splitters, each with transmissivity \(\lambda ^{1/n}\) and fed with a fixed environment state \(\rho \), which is assumed to have bounded energy and thermal Gaussification. Such a model may be relevant to the mathematical modelisation of a channel running across an integrated optical circuit [29, 30]. We are able to show that for \(n\rightarrow \infty \) the cascade channel converges in diamond norm, up to irrelevant symplectic unitaries, to a thermal attenuator channel with transmissivity \(\lambda \) and the same photon number as that of the environment state \(\rho \). Furthermore, an extension of our results to the non-i.i.d. setting allows us to bound the rate of convergence in terms of the diamond norm distance. Finally, combining existing continuity bounds on entropies and energy-constrained channel capacities [31, 32], obtained by Winter [33, 34] and Shirokov [35, 36], with the known formulae expressing or estimating energy-constrained classical [37, 38] and quantum [39,40,41,42,43,44,45] capacities of thermal attenuator channels, we derive bounds on the same capacities for the cascade channel.
Finally, along the way we derive several novel results concerning quantum characteristic functions, which we believe to be of independent interest. First, we prove the simple yet remarkable fact that convolving any two quantum states (i.e. mixing them in a 50 : 50 beam splitter) always results in a state with non-negative Wigner function (Lemma 16). This allows us to interpret the quantum central limit theorem as a result on classical random variables, in turn enabling us to transfer techniques from classical probability theory to the quantum setting. Secondly, we derive new decay bounds on the behaviour of the quantum characteristic function both at the origin and at infinity. For instance, we prove that for any m-mode quantum state \(\rho \) and for any \(\varepsilon >0\) there exists a constant \(\eta =\eta (\rho ,\varepsilon )<1\) such that \(|\chi _\rho (z)|\le \eta (\rho ,\varepsilon )\) for all \(z\in \mathbb {C}^m\) with \(|z|\ge \varepsilon \) (Proposition 14). Moreover, we show that such a constant can be made to depend only on the second moments of the state, assuming they are finite (Proposition 15). As an explicit example, consider a single-mode state \(\rho \) with mean energy E. We then prove that \(|\chi _\rho (z)| \le 1 - \frac{c}{E^{2}}\) for all z with \(|z| \ge \frac{C}{\sqrt{E}}\), where c, C are universal constants. Note that any such bound must depend on the energy, as one can construct a sequence of highly squeezed Gaussian states for which the modulus of the characteristic function approaches one at any designated point in phase space (Example 2).
Layout of the paper: In Sect. 2 we introduce the notation and definitions used in the paper. In Sect. 3 we recall the Cushen and Hudson quantum central limit theorem. Our main results are presented in Sect. 4. The rest of the paper is devoted to the proofs of these results. We start with the novel properties of quantum characteristic functions (Sect. 5), which lie at the heart of our approach. Then, in Sect. 6 we prove our quantum Berry–Esseen theorems. Section 7 is devoted to the discussion of the optimality and sharpness of our results. In Sect. 8 we apply our quantitative non-i.i.d. extension of the Cushen–Hudson theorem to an optical fibre subject to non-Gaussian environment noise. The paper contains a technical appendix (Appendix A) that makes the connection between moments and the regularity of the quantum characteristic function and shows that our definition of moments induces a canonical family of interpolation spaces.
2 Notation and Definitions
In this section, we fix the basic notations used in the paper, and introduce the necessary definitions.
2.1 Mathematical notation
Let  denote a separable Hilbert space, and let
denote a separable Hilbert space, and let  denote the set of bounded linear operators acting on
denote the set of bounded linear operators acting on  . Let
. Let  denote the set of quantum states of a system with Hilbert space
denote the set of quantum states of a system with Hilbert space  , that is the set of density operators \(\rho \) (positive semi-definite, i.e. \(\rho \ge 0\), trace class operatorsFootnote 3 with unit trace) acting on
, that is the set of density operators \(\rho \) (positive semi-definite, i.e. \(\rho \ge 0\), trace class operatorsFootnote 3 with unit trace) acting on  . We denote by
. We denote by  the Schatten p-norm, defined as \(\Vert X\Vert _{p}=\left( {\text {Tr}}|X|^p\right) ^{1/p}\). The Schatten p -class
the Schatten p-norm, defined as \(\Vert X\Vert _{p}=\left( {\text {Tr}}|X|^p\right) ^{1/p}\). The Schatten p -class  is the Banach subspace of
is the Banach subspace of  formed by all bounded linear operators whose Schatten p-norm is finite. We shall hereafter refer to
formed by all bounded linear operators whose Schatten p-norm is finite. We shall hereafter refer to  as the set of trace class operators, to the corresponding norm \(\Vert \cdot \Vert _1\) as the trace norm, and to the induced distance (e.g. between quantum states) as the trace distance. The case \(p=2\) is also special, as the norm \(\Vert \cdot \Vert _2\) coincides with the Hilbert–Schmidt norm.
as the set of trace class operators, to the corresponding norm \(\Vert \cdot \Vert _1\) as the trace norm, and to the induced distance (e.g. between quantum states) as the trace distance. The case \(p=2\) is also special, as the norm \(\Vert \cdot \Vert _2\) coincides with the Hilbert–Schmidt norm.
Let A, B be positive semi-definite operators defined on some domains  . According to [46, Definition 10.15], we write that \(A\ge B\) if and only if \({{\,\mathrm{Dom}\,}}\left( A^{1/2}\right) \subseteq {{\,\mathrm{Dom}\,}}\left( B^{1/2}\right) \) and
. According to [46, Definition 10.15], we write that \(A\ge B\) if and only if \({{\,\mathrm{Dom}\,}}\left( A^{1/2}\right) \subseteq {{\,\mathrm{Dom}\,}}\left( B^{1/2}\right) \) and  for all \(|\psi >\in {{\,\mathrm{Dom}\,}}\left( A^{1/2}\right) \). Now, let A be a positive semi-definite operator, and let \(\rho \) be a quantum state with spectral decomposition
for all \(|\psi >\in {{\,\mathrm{Dom}\,}}\left( A^{1/2}\right) \). Now, let A be a positive semi-definite operator, and let \(\rho \) be a quantum state with spectral decomposition  . We define the expected value of A on \(\rho \) as
. We define the expected value of A on \(\rho \) as

with the convention that \({\text {Tr}}[\rho A]=+\infty \) if the above series diverges or if there exists an index i such that \(p_i>0\) and \(|e_i>\notin {{\,\mathrm{Dom}\,}}\left( A^{1/2}\right) \). To extend this definition to a generic densely defined self-adjoint operator X on  , it is useful to consider its decomposition \(X=X_+-X_-\) into positive and negative part [46, Example 7.1]. We will say that X has finite expected value on \(\rho \) if \(|e_i>\in {{\,\mathrm{Dom}\,}}\big (X_+^{1/2}\big )\cap {{\,\mathrm{Dom}\,}}\big (X_-^{1/2}\big )\) for all i such that \(p_i>0\), and moreover the two series \(\sum _i p_i \big \Vert X_\pm ^{1/2} |e_i>\big \Vert ^2\) both converge. In this case, we call
, it is useful to consider its decomposition \(X=X_+-X_-\) into positive and negative part [46, Example 7.1]. We will say that X has finite expected value on \(\rho \) if \(|e_i>\in {{\,\mathrm{Dom}\,}}\big (X_+^{1/2}\big )\cap {{\,\mathrm{Dom}\,}}\big (X_-^{1/2}\big )\) for all i such that \(p_i>0\), and moreover the two series \(\sum _i p_i \big \Vert X_\pm ^{1/2} |e_i>\big \Vert ^2\) both converge. In this case, we call

the expected value of X on \(\rho \). Clearly, given two operators \(A\ge B\ge 0\), we have that \({\text {Tr}}[\rho A]\ge {\text {Tr}}[\rho B]\).
For two real sequences \(\left( a_n(\lambda )\right) _n,\, \left( b_n(\lambda )\right) _n\) that depend on some parameter \(\lambda \), we write \(a_n(\lambda ) = \mathcal {O}_\lambda \left( b_n(\lambda )\right) \) if there exists a constant \(c_\lambda >0\) that only depends on \(\lambda \) such that \(|a_n(\lambda )|\le c_\lambda |b_n(\lambda )|\) holds in the limit \(n\rightarrow \infty \). We also write \(a_n(\lambda ) =\mathcal O_{\lambda }\left( b_n(\lambda )^{\infty }\right) \) if for every \(N \in \mathbb {N}\) we have that \(a_n(\lambda ) =\mathcal O_{\lambda }\left( b_n(\lambda )^{N}\right) \).
For an n-linear tensor \(A:\times _{i=1}^n \mathbb C^m \rightarrow \mathbb C^k\), we write  if the vector we apply the tensor to is the same in every component. For functions f, we sometimes abuse the notation by denoting the norm of this function as \(\Vert f(z) \Vert \) instead of
if the vector we apply the tensor to is the same in every component. For functions f, we sometimes abuse the notation by denoting the norm of this function as \(\Vert f(z) \Vert \) instead of  We denote with \(*\) the entry-wise complex conjugation, with \(\intercal \) the standard transposition of vectors, and with \(\dag \) the combination of the two.
We denote with \(*\) the entry-wise complex conjugation, with \(\intercal \) the standard transposition of vectors, and with \(\dag \) the combination of the two.
For partial derivatives with respect to complex variables \(z,z^*\) we write \(\partial _z\) and \(\partial _{z^*}.\) Consider an m-dimensional multi-index \(\alpha = (\alpha _1, \alpha _2,\ldots ,\alpha _m)\) with \(| \alpha | = \alpha _1 + \alpha _2 + \cdots + \alpha _m\). Then  and analogously for \(z^*\). The total derivatives of order k of a function \(f:\mathbb C^{m} \rightarrow \mathbb C\) we denote by
and analogously for \(z^*\). The total derivatives of order k of a function \(f:\mathbb C^{m} \rightarrow \mathbb C\) we denote by  We then recall the definition of the Fréchet derivative for functions \(f:\mathbb {C}^m \rightarrow \mathbb {C}\) such that
We then recall the definition of the Fréchet derivative for functions \(f:\mathbb {C}^m \rightarrow \mathbb {C}\) such that  and therefore
and therefore
with  . Let \(C_0(\mathbb {C}^m)\) denote the space of continuous functions \(f:\mathbb {C}^m \rightarrow \mathbb {C}\) that tend to zero as \(|z| \rightarrow \infty \), where for \(z\in \mathbb {C}^m\) we set
. Let \(C_0(\mathbb {C}^m)\) denote the space of continuous functions \(f:\mathbb {C}^m \rightarrow \mathbb {C}\) that tend to zero as \(|z| \rightarrow \infty \), where for \(z\in \mathbb {C}^m\) we set

We write \(C_c^{\infty }(\mathbb {C}^m)\) to denote the space of smooth and compactly supported functions on \(\mathbb {C}^m\). For some open set \(\Omega \subseteq \mathbb {C}^m\) with closure \(\bar{\Omega }\), a function \(f:\bar{\Omega } \rightarrow \mathbb {C}\), and a non-negative integer \(k\in \mathbb {N}_0\), we denote by \(C^k(\bar{\Omega })\) the space of functions for which the norm

is finite. Here, \(\alpha ,\beta \in \mathbb {N}_0^m\) are multi-indices. When \(k\ge 0\) is not an integer, we define instead

This extension allows us to consider the normed spaces \(C^k\big (\bar{\Omega }\big )\) for all \(k\ge 0\). Typically, we will deal with the case where \(\Omega \) is bounded, so that \(C^k\big (\bar{\Omega }\big )\) is in fact a Banach space. Finally, \(L^2(\Omega )\) will denote the space of equivalence classes of measurable functions \(f:\Omega \rightarrow \mathbb {C}\) whose \(L^2\) norm  is finite.
is finite.
2.2 Definitions
2.2.1 Quantum information with continuous variables
In this paper, we focus on continuous variable quantum systems. The Hilbert space of a set of m harmonic oscillators, in this context called ‘modes’, is the space  of square-integrable functions on \({\mathbb {R}}^m\). Let \(x_j,p_j\) be the canonical position and momentum operators on the \(j^{\text {th}}\) mode. The m annihilation and creation operators, denoted by
of square-integrable functions on \({\mathbb {R}}^m\). Let \(x_j,p_j\) be the canonical position and momentum operators on the \(j^{\text {th}}\) mode. The m annihilation and creation operators, denoted by  and
and  (\(j=1,\ldots , m\)), satisfy the commutation relations
(\(j=1,\ldots , m\)), satisfy the commutation relations
where I is the identity on  . An m-mode quantum state \(\rho \) is said to be centred if
. An m-mode quantum state \(\rho \) is said to be centred if

i.e. if all expected values of the canonical operators on \(\rho \), defined according to (2), vanish. For an m-tuple of non-negative integers \(n = (n_1,\ldots , n_m)\in \mathbb {N}_0^m\), the corresponding Fock state is defined by  , where
, where  denotes the (multi-mode) vacuum state. In what follows, we often consider \(m=1\).
denotes the (multi-mode) vacuum state. In what follows, we often consider \(m=1\).
The (von Neumann) entropy of a quantum state \(\rho \) is defined as

which is well defined although possibly infinite.Footnote 4 The relative entropy between two states \(\rho \) and \(\sigma \) is usually written as follows [47]

Again, the above expression is well defined and possibly infinite [48].Footnote 5
For two Hilbert spaces  , a quantum channel
, a quantum channel  is a completely positive, trace-preserving linear map. For a linear map
is a completely positive, trace-preserving linear map. For a linear map  , we define its diamond norm as
, we define its diamond norm as

where the supremum is over all non-zero trace class operators X on  .
.
Consider a quantum system with Hilbert space  , governed by a Hamiltonian H, which is taken to be a positive (possibly unbounded) operator on
, governed by a Hamiltonian H, which is taken to be a positive (possibly unbounded) operator on  . The energy of a state
. The energy of a state  is the quantity \({\text {Tr}}[\rho H]\in {\mathbb {R}}_+\cup \{+\infty \}\) defined as in (1).
is the quantity \({\text {Tr}}[\rho H]\in {\mathbb {R}}_+\cup \{+\infty \}\) defined as in (1).
Given two Hilbert spaces  and
and  , a Hamiltonian H on
, a Hamiltonian H on  , and some energy bound
, and some energy bound  , the corresponding energy-constrained classical capacity of a channel
, the corresponding energy-constrained classical capacity of a channel  is given by [31, 49,50,51,52]
is given by [31, 49,50,51,52]

where it is understood that the Hamiltonian \(H^{(n)}\) on  is given by
is given by  , where \(H_j\) acts on the \(j^{\text {th}}\) tensor factor, and tensor products with the identity operator are omitted for notational simplicity. With the same notation, one can also define the energy-constrained quantum capacity of \(\mathcal {N}\), given by [32, 34, 53,54,55]
, where \(H_j\) acts on the \(j^{\text {th}}\) tensor factor, and tensor products with the identity operator are omitted for notational simplicity. With the same notation, one can also define the energy-constrained quantum capacity of \(\mathcal {N}\), given by [32, 34, 53,54,55]

where  is the partial trace over the entirely arbitrary ancillary Hilbert space
is the partial trace over the entirely arbitrary ancillary Hilbert space  . In this paper we are interested in the simple case
. In this paper we are interested in the simple case  and
and  , so that there is a natural choice for H, namely, the canonical Hamiltonian
, so that there is a natural choice for H, namely, the canonical Hamiltonian

of m modes. In this case, we will omit the subscripts and simply write the energy-constrained capacities as \(\mathcal {C}\left( \mathcal {N}, E\right) \) and \(\mathcal {Q}\left( \mathcal {N}, E\right) \).
2.2.2 Phase space formalism
We define the displacement operator \(\mathcal {D}(z)\) associated with a complex vector \(z\in \mathbb {C}^m\) as
Thus, \(\mathcal {D}(z)\) is a unitary operator and satisfies \(\mathcal {D}(z)^\dag =\mathcal {D}(-z)\) and
valid for all \(z,w\in \mathbb {C}^m\).
Let \(H_{{\text {quad}}} = \sum _{j,k} \left( X_{jk} a_j^\dag a_k + Y_{jk} a_j a_k + Y_{jk}^* a_j^\dag a_k^\dag \right) \), where \(X=X^\dag \) is an \(m\times m\) Hermitian matrix, and \(Y=Y^\intercal \) is an \(m\times m\) complex symmetric matrix. The unitaries \(e^{-iH_{{\text {quad}}}}\) generated by such Hamiltonians, and products thereof,Footnote 6 are called symplectic unitaries, because they induce a symplectic linear transformation at the phase space level \((z_R, z_I)\in {\mathbb {R}}^{2m}\), where  and
and  [56, 57]. A symplectic unitary is called passive if it commutes with the number operator \(\sum _j a_j^\dag a_j\), which happens whenever the generating Hamiltonian \(H_{\text {quad}}\) satisfies \(Y=0\). A passive symplectic unitary V acts on annihilation operators as \(Va_j V^\dag = \sum _k U_{jk} a_k\), where U is an \(m\times m\) unitary matrix.
[56, 57]. A symplectic unitary is called passive if it commutes with the number operator \(\sum _j a_j^\dag a_j\), which happens whenever the generating Hamiltonian \(H_{\text {quad}}\) satisfies \(Y=0\). A passive symplectic unitary V acts on annihilation operators as \(Va_j V^\dag = \sum _k U_{jk} a_k\), where U is an \(m\times m\) unitary matrix.
For trace class operators  , the quantum characteristic function
, the quantum characteristic function  is given by
is given by

Conversely, the operator T can be reconstructed from \(\chi _T\) via the weakly defined identity
Observe that the adjoint \(T^\dag \) of T satisfies \(\chi _{T^\dag }(z)=\chi _T(-z)^*\) for all \(z\in \mathbb {C}^m\), so that T is self-adjoint if and only if \(\chi _T(-z)\equiv \chi _T(z)^*\). The characteristic function \(\chi _T\) of a trace class operator T is bounded and uniformly continuous [58, § 5.4]. If T is positive semi-definite (e.g. if T is a density operator), then \(\max _{\alpha } |\chi _T(\alpha )| = \chi _T(0)={\text {Tr}}[T]\).
We write \(|\psi _f>\) to denote the pure state corresponding to the wave function \(f\in {L}^2({\mathbb {R}}^m)\), so that the corresponding rank-one state  has the following characteristic function:
has the following characteristic function:
where as usual \(z = z_R + i z_I\).
The Fourier transform of the characteristic function is known as the Wigner function. For a trace class operator T, the Wigner function is given by [59, Eq. (4.5.12) and (4.5.19)]


Observe that \(W_{T^\dag }(z)=W_T(z)^*\), so that T is self-adjoint if and only if \(W_T(z)\in {\mathbb {R}}\) for all \(z\in \mathbb {C}^m\). From (21) it is not difficult to see that \(|W_T(z)|\le \frac{2^m}{\pi ^m} \Vert T\Vert _1\), where \(\Vert T\Vert _1={\text {Tr}}|T|\) reduces to 1 when T is a density operator. By taking the Fourier transform of (19), one can show that
Moreover, the energy of any density matrix, \(\rho \), can be obtained as a phase space integral
The displacement operator \(\mathcal {D}(z)\) induces a translation or displacement of the Wigner function as follows, hence the nomenclature:
The map \(T\mapsto \chi _T\), defined for trace class operators T in (17), extends uniquely to an isomorphism between the space of Hilbert–Schmidt operators and that of square-integrable functions \({L}^2(\mathbb {C}^m)\). In fact, the quantum Plancherel theorem guarantees that this is also an isometry, namely
and therefore
Henceforth, we refer to (26) as the quantum Plancherel identity.
Gaussian states on  are the density operators
are the density operators  such that \(W_\rho (z)\) is a Gaussian probability distribution on the real space \((z_R, z_I)\in {\mathbb {R}}^{2m}\) and are uniquely defined by their first and second moments. A particularly simple example of a single-mode Gaussian state is a thermal state with mean photon number \(N\in [0,\infty )\), given by
such that \(W_\rho (z)\) is a Gaussian probability distribution on the real space \((z_R, z_I)\in {\mathbb {R}}^{2m}\) and are uniquely defined by their first and second moments. A particularly simple example of a single-mode Gaussian state is a thermal state with mean photon number \(N\in [0,\infty )\), given by

The thermal state is the maximiser of the entropy among all states with a fixed maximum average energy:

for all \(N\ge 0\), where the function g is defined by

The characteristic function and Wigner function of the thermal state evaluate to [59, Eq. (4.4.21) and (4.5.31)]
respectively, so that \(\tau _N\) is easily seen to be a centred Gaussian state.
2.3 Moments
Definition 1
(Standard Moments). An m-mode quantum state \(\rho \) is said to have finite standard moments of order up to k, for some \(k\in [0,\infty )\), if

where \(H_m\) is the canonical Hamiltonian (14), and the above trace is defined as in (1).
Remark
The above condition is fairly easy to check once the matrix representation of \(\rho \) in the Fock basis is given. Namely, resorting to (1) and exchanging the order of summation for infinite series with non-negative terms, we see that (31) is equivalent to
where as usual \(|n|=\sum \nolimits _j n_j\).
Given \(k>0\) and \(m\in \mathbb {N}\), we can also define, by analogy with classical harmonic analysis, the m -mode bosonic Sobolev space of order k as follows

where as usual  . Here, we set
. Here, we set

with the canonical Hamiltonian on m modes being defined by (14). For density operators \(\rho \) it holds, using monotone convergence and cyclicity of the trace, that

where  is the indicator function of the interval [0, E].
is the indicator function of the interval [0, E].
It is well known that the characteristic function of any classical random variable with finite moments of order up to k (with k being a positive integer) is continuously differentiable k times everywhere. We can draw inspiration from this fact to devise an alternative way to introduce moments, relying on the regularity of the quantum characteristic function, in the quantum setting as well. We refer to moments defined in this manner as phase space moments.
Definition 2
( Phase space moments). An m-mode quantum state \(\rho \) is said to have finite phase space moments of order up to k, for some \(k\in [0,\infty )\), if

for some \(\varepsilon >0\), where  is the Euclidean ball of radius \(\varepsilon \) centred in 0, and the norm on the space \(C^{k}\left( B(0,\varepsilon )\right) \) is defined by (5) and (6).
is the Euclidean ball of radius \(\varepsilon \) centred in 0, and the norm on the space \(C^{k}\left( B(0,\varepsilon )\right) \) is defined by (5) and (6).
In complete analogy with the classical case, finiteness of standard moments implies local differentiability of the characteristic function, and hence finiteness of phase space moments. See Theorem 9 of Sect. 4.
However, the converse is not true in general. This is not surprising, as the same phenomenon is observed for classical random variables. In fact, a famous example by Zygmund [60] shows the existence of classical random variables with continuously differentiable characteristic function whose first absolute moments do not exist. We can swiftly carry over his example to the quantum realm, e.g. by considering a particular displaced vacuum state  . One can show that its characteristic function is \(\chi _\rho (z)=e^{-|z|^2}\sum _{n=2}^\infty \frac{\cos (2n z_I)}{n^2\log n}\), which turns out to be continuously differentiable everywhere [60]. However,
. One can show that its characteristic function is \(\chi _\rho (z)=e^{-|z|^2}\sum _{n=2}^\infty \frac{\cos (2n z_I)}{n^2\log n}\), which turns out to be continuously differentiable everywhere [60]. However,
which implies that \(\rho \) has no finite first-order moments (see Lemma 24).
In spite of the above counterexample, we show in Theorem 28 that at least if k is an even integer, then the existence of \(k^{\text {th}}\) order phase space moment implies the existence of the \(k^{\text {th}}\) order standard moment. Again, this is in total analogy with the classical case [61, Theorem 1.8.16].
Remark. Due to the above, for even k, we simply use the word moment in the statements of our theorems, instead of differentiating between standard moments and phase space moments.
2.4 Quantum convolution
A beam splitter with transmissivity \(\lambda \in [0,1]\) acting on two sets of m modes is a particular type of a passive symplectic unitary, which we express asFootnote 7

where \(a_j\) and \(b_j\) (\(j=1,\ldots , m\)) are the creation operators of the first and second sets of modes, respectively. Its action on annihilation operators can be represented as follows
Accordingly, displacement operators are transformed by
The beam splitter unitary can be used to define the following (\(\lambda \)-dependent) quantum convolution: for two m-mode quantum states \(\rho ,\sigma \) and \(\lambda \in [0,1]\), their (\(\lambda \)-dependent) quantum convolution is given by the state \(\rho \boxplus _\lambda \sigma \) which is defined according to [62] as

In terms of characteristic functions, this definition corresponds to
It is not difficult to verify that for all symplectic unitaries V and all \(\lambda \in [0,1]\), the beam splitter unitary \(U_\lambda \) of (34) satisfies \(\left[ V \otimes V,\ U_\lambda \right] = 0\). In particular,
for any state \(\sigma \). Also, using (35) it can be shown that the mean photon number of a quantum convolution is just the convex combination of those of the input states, i.e.
where the canonical Hamiltonian is defined by (14).
For all m-mode quantum states \(\sigma \) and all \(\lambda \in [0,1]\), we can use the corresponding convolution to define a quantum channel  , whose action is given by
, whose action is given by

When \(\sigma =\tau _N\) is a thermal state (with mean photon number N), the channel  is called a thermal attenuator channel. Its action, obtained by combining (38) and (30), is given by
is called a thermal attenuator channel. Its action, obtained by combining (38) and (30), is given by

For the thermal attenuator channel, the energy-constrained classical capacity (defined in (12)) can be shown to reduce to can be shown to be given by [37, 38]
where g is given by (29).
In what follows, we will be interested in the symmetric quantum convolutions \(\rho _1\boxplus \cdots \boxplus \rho _n\), iteratively defined for a positive integer n and states \(\rho _1, \ldots , \rho _n\), by the relations  and
and

We will also use the shorthand

In terms of characteristic and Wigner functions, we can also write
Here, \(\star \) denotes convolution, which is defined for n functions \(f_1,\ldots , f_n:\mathbb {C}^m\rightarrow {\mathbb {R}}\) by

Equation (46) shows that the quantum characteristic function of the symmetric quantum convolution satisfies the same scaling property as a sum of classical i.i.d. (independent and identically distributed) random variables. The important special case \(\rho _i\equiv \rho \) of (46) for all \(i \in \{i,2,\ldots ,n\}\), on which we will focus most of our efforts, reads
Iterating (39), using (44), shows that
holds for all symplectic unitaries V.
3 Cushen and Hudson’s Quantum Central Limit Theorem
In [2], Cushen and Hudson proved the following quantum mechanical analogue of the central limit theorem, which is the starting point of our study.
Theorem 3
[2, Theorem 1] . Let  be a centred m-mode quantum state with finite second moments. Then the sequence \((\rho ^{\boxplus n})_{n\in \mathbb {N}}\) converges weakly to the Gaussian state \(\rho _\mathrm {\scriptscriptstyle G}\) of same first and second moments as \(\rho \):
be a centred m-mode quantum state with finite second moments. Then the sequence \((\rho ^{\boxplus n})_{n\in \mathbb {N}}\) converges weakly to the Gaussian state \(\rho _\mathrm {\scriptscriptstyle G}\) of same first and second moments as \(\rho \):

where  is the set of bounded operators on
is the set of bounded operators on  .
.
Remark
The state \(\rho _\mathrm {\scriptscriptstyle G}\) is commonly called the Gaussification of \(\rho \).
In fact, the proof of Theorem 3 relies on the equivalence between weak convergence of states and pointwise convergence of their characteristic functions. More precisely, the following holds:
Lemma 4
([27, Lemma 4.3] and [28, Lemma 4]). Let \((\rho _n)_{n\in \mathbb {N}}\) be a sequence of density operators on  . The following are equivalent:
. The following are equivalent:
-
\((\rho _n)_{n\in \mathbb {N}}\) converges to a density operator in the weak operator topology, namely, it holds that
 for all
for all 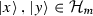 ;
; -
\((\rho _n)_{n\in \mathbb {N}}\) converges in trace distance to a trace class operator;
-
the sequence \((\chi _{\rho _n})_{n\in \mathbb {N}}\) of characteristic functions converges pointwise to a function that is continuous at 0.
Together, the above lemma and Theorem 3 allow us to conclude the following seemingly stronger convergence:
Theorem 5
Under the assumptions of Theorem 3, we have that
4 Main Results
The main objective of this paper is to refine Theorem 5 of the previous section in the following directions:
-
First, in the case in which the state \(\rho \) satisfies the conditions of the Cushen–Husdon theorem, we provide quantitative bounds on the rate at which the sequence of states \((\rho ^{\boxplus n})_{n\in \mathbb {N}}\) converges to \(\rho _\mathrm {\scriptscriptstyle G}\), under the assumption of finiteness of certain phase space moments of \(\rho \). We also show how finiteness of phase space moments is implied by finiteness of the corresponding standard moments, the latter having the advantage of being a more easily verifiable condition. Moreover, we show that finiteness of even integer phase space moments implies finiteness of even integer standard moments (Sect. 4.1).
-
Secondly, we provide an example to show that the assumption that the second moments be finite in the Cushen–Hudson theorem cannot be weakened (Sect. 4.2).
-
Thirdly, we extend our results to the non-i.i.d. setting, i.e. we consider a scaling in the quantum convolution different from (44). This allows us to analyse the propagation of states through cascades of beam splitters with varying transmissivities (Sect. 4.3).
-
Finally, we provide a precise asymptotic analysis of the behaviour of quantum characteristic functions at zero and at infinity (Sect. 4.4).
4.1 Quantitative bounds in the QCLT
In this section, we state our results on rates of convergence in the Cushen–Hudson quantum central limit theorem. We call them quantum Berry–Esseen theorems, as is customary in the literature. Our first theorem provides convergence rates \(\mathcal O\left( n^{-1/2}\right) \) in the quantum central limit theorem under a fourth-order moment condition. The rate of convergence is boosted to \(\mathcal O\left( n^{-1}\right) \) if the third derivative of the characteristic function at zero vanishes:
Theorem 6
(Quantum Berry–Esseen theorem; High regularity). Let \(\rho \) be a centred m-mode quantum state with finite fourth-order phase space moments. Then, the convergence in the quantum central limit theorem in Hilbert–Schmidt norm satisfies
Here, \(M_4'=M'_4(\rho ,\varepsilon )\) is the moment defined in (33), and \(\varepsilon >0\) is sufficiently small. Moreover, if \(D^3\chi _{\rho }(0)= 0\) then the convergence is at least with rate \(\mathcal {O}_{M_4'}\left( n^{-1}\right) \).
The proof of Theorem 6 is provided in Sect. 6. In the next Theorem, we weaken the assumption on the moments of the state \(\rho \), which leads to a slower rate of convergence.
Theorem 7
(Quantum Berry–Esseen theorem; Low regularity). Let \(\rho \) be a centred m-mode quantum state with finite \((2+\alpha )\)-order phase space moments, where \(\alpha \in (0,1]\). The convergence in the quantum central limit theorem in Hilbert–Schmidt norm is given by
Here, \(M_{2+\alpha }'=M'_{2+\alpha }(\rho ,\varepsilon )\) is the phase space moment defined in (33), and \(\varepsilon >0\) is sufficiently small.
The proof of Theorem 7 is provided in Sect. 6. The variable \(\alpha \) allows us to obtain a convergence rate under the assumption of finiteness of phase space moments of order all the way down to 2 (excluded), which is the assumption required in the Cushen–Hudson QCLT. The above results can further be used to find convergence rates in other, statistically more relevant, distance measures:
Corollary 8
(Convergence in trace distance and relative entropy). Assume that an m-mode quantum state \(\rho \) has finite third-order phase space moments. Then,
where \(M_3'=M'_3(\rho ,\varepsilon )\) is defined in (33), and \(\varepsilon >0\) is sufficiently small. The above rates are replaced by \(\mathcal {O}_{M'_{2+\alpha }}\left( n^{-\alpha /(2m+2)}\right) \) when \(\rho \) only satisfies the conditions of Theorem 7.
The proof of this Corollary is given in Sect. 6.
Remark
(Condition on the existence of moments). The error bounds in Theorems 6 and 7 are stated in terms of assumptions on the phase space moments \(M'_k\) given by (33), of the state. It is possible to bound the phase space moments \(M'_k\) directly in terms of the standard moments \(M_k\) defined in (31). This is stated in the following Theorem, whose proof is given in Appendices A–C
Theorem 9
Let \(k\in [0,\infty )\), m a positive integer, and \(\varepsilon >0\) be given. Then every m-mode quantum state with finite standard moments of order up to k also has finite phase space moments of the same order. More precisely, there is a constant \(c_{k,m}(\varepsilon )<\infty \) such that
Conversely, if the characteristic function is 2k times totally differentiable at \(z=0\) for some integer k, then the \(2k^{\text {th}}\) standard moment is finite as well.
The importance of Theorem 9 for us comes from the fact that most of our proofs rest upon local differentiability properties of the characteristic function. While mathematically useful, such properties have no direct physical meaning and may be hard to verify in practice. Instead, the condition of finiteness of higher-order standard moments, as given in Definition 1, bears a straightforward physical meaning, related to the properties of the photon number distribution of the state, and is often easier to verify.
The key to proving Theorem 9 for fractional k lies in an interpolation argument. To state it precisely, we briefly recall some basic facts about real interpolation theory (see [63] for more details): given two Banach spaces  and
and  , and a parameter \(0\le \theta \le 1\), define the K -function as follows:
, and a parameter \(0\le \theta \le 1\), define the K -function as follows:

and derive from this the function \(\Phi _{\theta } (K(X)) = \sup _{t>0} t^{-\theta }K(t,X).\) The real interpolation spaces, parametrised by \(\theta \in (0,1)\), are then defined as

Now, given two couples of Banach spaces  and
and  , and a map
, and a map  such that
such that  and
and  are bounded, the map
are bounded, the map  is bounded and:
is bounded and:

We want to apply this to the map \(\rho \mapsto \chi _\rho \).
The following interpolation result for density operators then holds:
Proposition 10
Let \(k_1 \ge k_0 \ge 0\) be real numbers. The m -mode bosonic Sobolev spaces  and
and  form a compatible couple such that for any m-mode quantum state \(\rho \) and \(\theta \in (0,1)\) the real interpolation norm satisfies
form a compatible couple such that for any m-mode quantum state \(\rho \) and \(\theta \in (0,1)\) the real interpolation norm satisfies

The proof of Proposition 10 is stated in Appendix B.
4.2 Optimality of convergence rates and necessity of finite second moments in the QCLT
The results stated in the previous section lead naturally to the following questions:
(i) Can the assumption of finiteness of second moments in the Cushen–Hudson theorem be weakened?
(ii) Are the convergence rates of Theorems 6 and 7 and Corollary 8 optimal?
We start by answering the first question in the negative: there exists a state with finite moments of all orders \(2(1-\delta )\) (for \(\delta >0\)) for which neither Theorem 3 nor Theorem 5 holds.
Proposition 11
Consider the one-mode state  with wave function
with wave function

Then: (a) \(\psi _f\) is centred; (b) \(M_{2(1-\delta )}(\psi _f) =<\psi _f|(a a^\dag )^{1-\delta }|\psi _f> <\infty \) for all \(\delta >0\); yet (c) the sequence  does not converge to any quantum state. Hence, the assumption of finiteness of second moments in the Cushen–Hudson QCLT (Theorems 3 and 5) cannot be weakened.
does not converge to any quantum state. Hence, the assumption of finiteness of second moments in the Cushen–Hudson QCLT (Theorems 3 and 5) cannot be weakened.
The proof of the above proposition is given in Sect. 7.
We now come to the second question (ii) regarding tightness of the estimates in Theorems 6 and 7 and Corollary 8. In Sect. 7 below, we study several explicit examples and provide convincing numerical evidence that our estimates are indeed tight, at least as far as the Hilbert–Schmidt convergence rates are concerned. Our findings are summarised as follows.
-
We start by looking at the pure state \(|\psi>=(|0>+|3>)/\sqrt{2}\), with density matrix
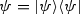 and thermal Gaussification \(\psi _\mathrm {\scriptscriptstyle G}= \tau _{3/2}\). Our findings indicate that \(\left\| \psi ^{\boxplus n} - \psi _\mathrm {\scriptscriptstyle G}\right\| _2 \sim c\, n^{-1/2}\), in the sense that the ratio between the two sides tends to 1 as \(n\rightarrow \infty \), for some absolute constant c (Example 5 and Fig. 4). Hence, the \(\mathcal O(n^{-1/2})\) convergence rate of Theorem 7 is attained.
and thermal Gaussification \(\psi _\mathrm {\scriptscriptstyle G}= \tau _{3/2}\). Our findings indicate that \(\left\| \psi ^{\boxplus n} - \psi _\mathrm {\scriptscriptstyle G}\right\| _2 \sim c\, n^{-1/2}\), in the sense that the ratio between the two sides tends to 1 as \(n\rightarrow \infty \), for some absolute constant c (Example 5 and Fig. 4). Hence, the \(\mathcal O(n^{-1/2})\) convergence rate of Theorem 7 is attained. -
Next, we focus on the second estimate of Theorem 6, and show that it is also tight. Namely, we compute the differences \(\left\| \psi ^{\boxplus n} - \psi _\mathrm {\scriptscriptstyle G}\right\| _\zeta \) for the simple case of a single-photon state
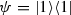 and for \(\zeta =1,2\), and find numerical evidence that again \(\left\| \psi ^{\boxplus n} - \psi _\mathrm {\scriptscriptstyle G}\right\| _\zeta \sim c\, n^{-1}\) for some absolute constant c (Example 4 and Fig. 4). This shows that the \(\mathcal O(n^{-1})\) convergence rate stated in Theorem 6, under the assumption that \(D^3\chi _\rho (0)=0\), is also attained.
and for \(\zeta =1,2\), and find numerical evidence that again \(\left\| \psi ^{\boxplus n} - \psi _\mathrm {\scriptscriptstyle G}\right\| _\zeta \sim c\, n^{-1}\) for some absolute constant c (Example 4 and Fig. 4). This shows that the \(\mathcal O(n^{-1})\) convergence rate stated in Theorem 6, under the assumption that \(D^3\chi _\rho (0)=0\), is also attained.
4.3 Applications to capacity of cascades of beam splitters with non-Gaussian environment
We now discuss applications of our results to the study of channels that arise naturally in the analysis of lossy optical fibres. We model a physical fibre of overall transmissivity \(\lambda \) as a cascade of n beam splitters, in each of which the signal state \(\omega \) is mixed via an elementary beam splitter of transmissivity \(\lambda ^{1/n}\) with a fixed state \(\rho \), modelling the environmental noise (Fig. 2). Each step corresponds to the action of the channel  (cf. the definition (41)), so that the whole cascade can be represented by the n-fold composition
(cf. the definition (41)), so that the whole cascade can be represented by the n-fold composition  . Note that this is in general a non-Gaussian channel, albeit it is Gaussian dilatable [28, 64]. We are interested in the asymptotic expression of the output state
. Note that this is in general a non-Gaussian channel, albeit it is Gaussian dilatable [28, 64]. We are interested in the asymptotic expression of the output state  as the number n tends to infinity, as a function of the input state \(\omega \). In other words, we want to study the asymptotic channel
as the number n tends to infinity, as a function of the input state \(\omega \). In other words, we want to study the asymptotic channel  .
.
At this point, it should not come as a surprise that such a channel exists and coincides with \(\mathcal {N}_{\rho _\mathrm {\scriptscriptstyle G},\,\lambda }\).
Before we see why, let us justify why the above model may be relevant to applications. The recently flourishing field of integrated quantum photonics sets as its goal that of implementing universal quantum computation on miniaturised optical chips [29, 30, 65, 66]. A quantum channel that runs across such a circuit is susceptible to noise generated by other active elements of the same circuit, e.g. single-photon sources. While we expect such noise to be far from thermal, it may become so in the limit \(n\rightarrow \infty \) of many interactions. In a regime where n is finite, albeit large, our setting will thus be the appropriate one. The forthcoming Corollary 13 allows us to study the classical and quantum capacity of the effective channel in such a regime.
Let us note in passing that the cascade architecture we are investigating now, in spite of some apparent resemblance, is different from that depicted in Fig. 1b. While we regard the former as more operationally motivated, the latter is mathematically convenient, as the transmissivities are tuned in such a way as to yield the symmetric convolution \(\rho ^{\boxplus n}\) at the output.
Theorem 12
(Approximation of thermal attenuators channels by cascades of beam splitters). Let \(\rho \) be a centred m-mode quantum state with finite third-order phase space moments \(M_3'\), cf. (33), and denote by \(\rho _\mathrm {\scriptscriptstyle G}\) its Gaussification. Then,

where \(\Vert \cdot \Vert _{\diamond }\) stands for the diamond norm (11).
One can further make use of the recently derived continuity bounds under input energy constraints [33,34,35,36] in order to find bounds on capacities of the cascade channel  in the physically relevant case where the Gaussification \(\rho _\mathrm {\scriptscriptstyle G}\) of \(\rho \) is a thermal state.Footnote 8
in the physically relevant case where the Gaussification \(\rho _\mathrm {\scriptscriptstyle G}\) of \(\rho \) is a thermal state.Footnote 8
Corollary 13
Consider a single-mode quantum state \(\rho \) with finite third-order phase space moments \(M_3'\) (cf. (33)) and thermal Gaussification \(\rho _\mathrm {\scriptscriptstyle G}=\tau _N\) as in (27). Then, for \(\lambda \in [0,1]\), mean photon number  , and some input energy \(E>0\), the energy-constrained classical and quantum capacity of the cascade channel
, and some input energy \(E>0\), the energy-constrained classical and quantum capacity of the cascade channel  relative to the canonical Hamiltonian \(a^\dag a\) satisfy
relative to the canonical Hamiltonian \(a^\dag a\) satisfy

and

where  (as in (29)), and \(\mathcal {Q}\big (\mathcal {E}_{N,\lambda }, E\big )\) is the quantum capacity of the thermal attenuator.Footnote 9
(as in (29)), and \(\mathcal {Q}\big (\mathcal {E}_{N,\lambda }, E\big )\) is the quantum capacity of the thermal attenuator.Footnote 9
The remainder terms are such that
for some constant \(C=C(M_3')\) and all sufficiently large \(n\ge n_0\left( \lambda E +(1-\lambda ) N, M_3'\right) \).
The proofs of Theorem 12 and Corollary 13 are postponed to Sect. 8.
4.4 New results on quantum characteristic functions
In this subsection we state our refined asymptotic analysis of the decay of quantum characteristic functions that we employ in the proofs of our main theorems. For arbitrary quantum states, we have the following asymptotic result on the quantum characteristic function at infinity. It states that the quantum characteristic function can, in absolute value, only attain the value one at zero and decays to zero at infinity. Both these properties do not hold for general classical random variables, see Sect. 5.2.
Proposition 14
The quantum characteristic function of an m-mode quantum state \(\rho \) is a continuous function that is arbitrarily small in absolute value outside of a sufficiently large compact set, i.e. \(\chi _{\rho }\) belongs to the Banach space \(C_0(\mathbb \mathbb {C}^{m})\) of asymptotically vanishing functions. Moreover, for any \(\varepsilon >0\) we have
where  denotes a Euclidean ball of radius \(\varepsilon \) centred at the origin.
denotes a Euclidean ball of radius \(\varepsilon \) centred at the origin.
The proof of Proposition 14 is given in Sect. 5.2. Interestingly, we can obtain a much more refined asymptotic on the decay of quantum characteristic functions if we assume that the state has finite second order moments.
Proposition 15
Let \(\rho \) be an m-mode state with finite average energy  , where we have explicitly accounted for the non-zero energy of the vacuum state. Then, for all \(z\in \mathbb {C}^m\) and all \(\delta \in [0,1]\) it holds that
, where we have explicitly accounted for the non-zero energy of the vacuum state. Then, for all \(z\in \mathbb {C}^m\) and all \(\delta \in [0,1]\) it holds that
5 New Results on Quantum Characteristic Functions: Proofs
Quantum characteristic functions constitute a central tool in our approach. Therefore, the first step in our path towards the quantum Berry–Esseen theorems is to prove the results stated in Sect. 4.4. The structure of this section is as follows:
-
Quantum–classical correspondence: We derive a quantum–classical correspondence of the central limit theorems by showing that the quantum convolution of two arbitrary density operators naturally induces a classical random variable (Sect. 5.1).
-
Decay bounds: We derive new decay estimates and asymptotic properties of the quantum characteristic function at infinity (Sect. 5.2).
5.1 Quantum–Classical Correspondence
In this section we show that the quantum convolution \(\rho \boxplus \sigma \) of any two states \(\rho \) and \(\sigma \) has a non-negative Wigner function. While the mathematics behind this is known (see e.g. [67, Proposition (1.99)], [2, Proposition 5], and [68, Eq. (8)]), we believe that its physical implications have not been appreciated to the extent they deserve.
Lemma 16
Let \(\rho \) and \(\sigma \) be arbitrary m-mode quantum states. Then the Wigner function of their convolution \(\rho \boxplus \sigma \) defined by (37), with \(\lambda =1/2,\) is given by
where  is the unitary and self-adjoint operator that implements a phase space inversion (in the sense of Eq. (61) below). In particular,
is the unitary and self-adjoint operator that implements a phase space inversion (in the sense of Eq. (61) below). In particular,
Proof
We start by verifying that J actually corresponds to a phase space inversion, in the sense that
for all m-mode quantum states \(\rho \) and all \(z\in \mathbb {C}^m\). This follows from the easily verified fact that \(J a_j J=-a_j\) for all j, which also implies that \(J\mathcal {D}(z)J = \mathcal {D}(-z)\). In fact, using (21) we find that
We now compute

In 1, we use the convolution property for the Wigner function in (47),where in 2 we just write out the convolution of several functions as in (48). In 3 we then first flip phase space variables according to (61) and use the displacement operator in 4 to translate them by \(\sqrt{2}z\), cf(24). Finally, in 5 we use the quantum Plancherel identity (25) to transform the integral over Wigner functions in a trace over density operators.
(24)
The above equalities are labelled by the equation numbers corresponding to the identities that justify them. \(\quad \square \)
Remark
It is not difficult to see that \(\lambda =1/2\) is the only special value for which Lemma 16 can hold, i.e. such that \(W_{\rho \, \boxplus _\lambda \sigma } (z)\ge 0\) for all m-mode states \(\rho ,\sigma \) and for all \(z\in \mathbb {C}^m\). To see why, consider the case where \(m=1\) and \(\rho ,\sigma \) are the first two Fock states. The action of the beam splitter unitary on the annihilation operators, as expressed by (35), leads to the identity  . Using the expression for the Wigner function of Fock states [59, Eq. (4.5.31)], we see that
. Using the expression for the Wigner function of Fock states [59, Eq. (4.5.31)], we see that
Hence, \(W_{|0> <0|\, \boxplus _\lambda |1> <1|}(0)<0\) as soon as \(0\le \lambda < 1/2\). For \(1/2<\lambda \le 1\), we arrive at the same conclusion by looking at the state  , obtained by sending \(\lambda \mapsto 1-\lambda \).
, obtained by sending \(\lambda \mapsto 1-\lambda \).
We proceed by showing how the above result bridges the gap between classical and quantum central limit theorems. We now fix an m-mode quantum state \(\rho \), and notice that \(\rho ^{\boxplus 2n} = (\rho \boxplus \rho )^{\boxplus n}\). Consider the probability density function  , where positivity holds by (60). Let X be a random variable with density \(f_X\). The mean and covariance matrix of X coincide with those of \(\rho \boxplus \rho \), which are in turn the same as those of \(\rho \). Hence, at the level of Gaussifications, \(f_\mathrm {\scriptscriptstyle G}= W_{\rho _\mathrm {\scriptscriptstyle G}}\). We write for an i.i.d. family of random variables \(X_i\) with law \(f_X\)
, where positivity holds by (60). Let X be a random variable with density \(f_X\). The mean and covariance matrix of X coincide with those of \(\rho \boxplus \rho \), which are in turn the same as those of \(\rho \). Hence, at the level of Gaussifications, \(f_\mathrm {\scriptscriptstyle G}= W_{\rho _\mathrm {\scriptscriptstyle G}}\). We write for an i.i.d. family of random variables \(X_i\) with law \(f_X\)

where 1 follows from (47) and 2 follows from the change of variables \(u\mapsto \sqrt{n}u.\) This implies by applying the classical and quantum Plancherel identities (26) that
which shows that the QCLT is equivalent to a certain CLT for classical i.i.d. random variables. The problem with this approach is that the right classical tool to use here would be an estimate on the rate of convergence of \((X_1+\cdots +X_n)/\sqrt{n}\) to the normal variable \(X_\mathrm {\scriptscriptstyle G}\) with respect to the \({L}^2\) norm. However, it is known that convergence fails to hold in general, and even under some finiteness of moments assumption there does not seem to be a readily available result in the literature, that is powerful enough to be successfully employed here. Therefore, we do not pursue this route further here.
5.2 Decay estimates on the quantum characteristic function
Before studying the rate of convergence in the quantum central limit theorem, we show that quantum characteristic functions have the so-called strict non-lattice property. To motivate this property, we start by recalling some basic properties of characteristic functions from classical probability theory.
The characteristic function \(\chi _X^{\text {cl}}\) of a classical random variable X always attains the value one at zero. However, it can also attain the value one, in absolute value, at any other point. The random variables that exhibit this latter behaviour are precisely those that are lattice-distributed;Footnote 10 see also [69, Section 3.5]. Examples include the Dirac, Bernoulli, geometric and Poisson distributions.
Knowing that \( \left| \chi ^{\text {cl}}_X(t) \right| <1\) for all values \(t\ne 0\) however does not imply that \(\limsup _{t \rightarrow \infty } \left| \chi ^{\text {cl}}_X(t) \right| <1\). This latter condition is known as the strict non-lattice property of a random variable. An example of a non-lattice distributed random variable which does not satisfy the strict non-lattice property is as follows.
Example 1
([69, Section 3.5]). Consider an enumeration of the positive rationals \(q_1,q_2,\ldots \in \mathbb {Q}_{+}\) with \(q_i \le i\) and a non-lattice random variable X defined by
The random variable X is then given by
which simplifies to
Let \(q_i=\frac{p_i}{r_i}\) where \(p_i \in \mathbb Z\) and \(r_i \in \mathbb N_0,\) by considering times \(t_n=2\pi \prod _{i=1}^n r_i\) for arbitrarily large n, one has \(\limsup _{t \rightarrow \infty } \left| \chi ^{\text {cl}}_X(t) \right| =1.\)
We now show the surprising fact that quantum characteristic functions do not exhibit this somewhat pathological behaviour. Instead, for any quantum state \(\rho \) it holds that \(\limsup _{\vert z \vert \rightarrow \infty } \left| \chi _{\rho }(z) \right| =0\), as the proof of Proposition 14 below shows.
Proof of Proposition 14
Thanks to the spectral theorem and by the dominated convergence theorem, it suffices to prove that \(\lim _{|z|\rightarrow \infty } \chi _{\psi _f}(z)=0\) for all wave function \(f\in {L}^2({\mathbb {R}}^m)\), where  , and \(|\psi _f>\) is the pure state with wave function f. We rephrase this as the requirement that \(\chi _{\psi _f}\) belongs to the Banach space \(C_0\left( \mathbb {C}^m\right) \), where the norm on \(C_0\left( \mathbb {C}^m\right) \) is the supremum norm.
, and \(|\psi _f>\) is the pure state with wave function f. We rephrase this as the requirement that \(\chi _{\psi _f}\) belongs to the Banach space \(C_0\left( \mathbb {C}^m\right) \), where the norm on \(C_0\left( \mathbb {C}^m\right) \) is the supremum norm.
We consider smooth compactly supported functions f first. For such functions, the claim follows by combining (i) Eq. (19); (ii) the fact that f is normalised, i.e. \(\int d^mx |f(x)|^2=1\); and (iii) the Riemann–Lebesgue lemma. For general \(f \in {L}^2({\mathbb {R}}^m)\), the result then follows by a density argument: for an arbitrary \(f \in {L}^2({\mathbb {R}}^m)\) there is a sequence of smooth and compactly supported functions \(f_n \in C_c^{\infty }({\mathbb {R}}^m)\) converging to \(f \in {L}^2({\mathbb {R}}^m)\), so that

Since \(C_0(\mathbb {C}^m)\) is a Banach space and \(\chi _{\psi _{f_n}} \in C_0(\mathbb {C}^m)\), this implies that also the limit \(\chi _{\psi _f} \in C_0(\mathbb {C}^m)\). Thus, to complete the proof of (58) it suffices to show that for every \({\varepsilon }>0\) and any \(z \in \mathbb {C}^m \backslash B(0,\varepsilon )\) one has that \(\left| \chi _{\psi _f}(z) \right| <1.\) If this were not the case, then \(|\psi _f>\) would be an eigenvector of the displacement operator \(\mathcal {D}(z)\). This is well known to be impossible, see e.g. [28, Lemma 10]. \(\quad \square \)
For a given state \(\rho \) and some fixed \(\varepsilon >0\), Proposition 14 tells us that there exists a constant \(\eta (\rho ,\varepsilon )<1\) such that \(\max _{z\in \mathbb {C}^m\setminus B(0,\varepsilon )} \left| \chi _\rho (z)\right| \le \eta (\rho ,\varepsilon )\) (cf. (58)). However, the problem of characterising the quantity \(\eta (\rho ,\varepsilon )\) in terms of some physically meaningful property of the state \(\rho \) remains. To this end, a natural candidate turns out to be the energy of the state. To see why this is the case, consider the following simple example.
Example 2
(Squeezed states). For every \(z\in \mathbb {C}^m\) and every \(\delta \in (0,1)\) there is a (Gaussian) state \(\rho _\mathrm {\scriptscriptstyle G}\) of mean photon number \({\text {Tr}}\left[ \rho _\mathrm {\scriptscriptstyle G}H_m \right] \le \frac{t^2}{8 \ln \frac{1}{1-\delta }} - \frac{1}{4}\) such that \(\left| \chi _{\rho _\mathrm {\scriptscriptstyle G}}(z)\right| \ge 1-\delta \).
To see that this is the case, up to the application of passive symplectic unitaries, it suffices to consider the case \(z=(t,0,\ldots , 0)\), where \(t>0\). Consider the ‘squeezed’ Gaussian state [70,71,72] defined by the characteristic function

where we set  . The mean photon number of \(\rho _\mathrm {\scriptscriptstyle G}\) is well known to be given by \({\text {Tr}}\left[ \rho _\mathrm {\scriptscriptstyle G}H_m \right] = \frac{1}{4} \left( \eta + \frac{1}{\eta }\right) - \frac{1}{2} \le \frac{1}{4\eta }-\frac{1}{4}\), where we used the fact that \(\eta \le 1\).
. The mean photon number of \(\rho _\mathrm {\scriptscriptstyle G}\) is well known to be given by \({\text {Tr}}\left[ \rho _\mathrm {\scriptscriptstyle G}H_m \right] = \frac{1}{4} \left( \eta + \frac{1}{\eta }\right) - \frac{1}{2} \le \frac{1}{4\eta }-\frac{1}{4}\), where we used the fact that \(\eta \le 1\).
The above example shows that any estimate on \(\eta (\rho ,\varepsilon )\) can be reasonably expected to depend on the energy. We now show that our preliminary work on the quantum–classical correspondence allows us to derive a general upper estimate for \(|\chi _\rho (z)|\) at any designated point \(z\in \mathbb {C}^m\) in terms of the energy of the state \(\rho \). For this purpose, we draw upon some important mathematical results from the well-developed theory of classical characteristic functions. Proposition 15, whose proof we present now, implies e.g. that for a one-mode state \(\rho \), we can take \(\eta (\rho ,\varepsilon ) = 1 - \frac{c}{E}\, \min \left\{ {\varepsilon }^2, \frac{C}{E}\right\} \), where E is the energy of \(\rho \), and c, C are universal constants.
Proof of Proposition 15
Denoting as usual with |z| the Euclidean norm (4) of \(z\in \mathbb {C}^m\), we write the following chain of inequalities.

Here, 1 is an application of the quantum convolution rule (cf. the \(n=2\) case of (49)). In 2 we introduced the classical random vector \(X(\rho \boxplus \rho )\) taking values in \(\mathbb {C}^m\), with probability distribution given by the Wigner function \(W_{\rho \, \boxplus \, \rho }\), which is everywhere non-negative by Lemma 16. The inequality in 3, which is the non-trivial one, follows from [61, Corollary 2.7.2]: we set  , with the latter estimate coming from (21), and \(\alpha =2\), so that
, with the latter estimate coming from (21), and \(\alpha =2\), so that

also, we substituted \(m\mapsto 2m\), because our phase space \(\mathbb {C}^m\) has real dimension 2m; finally, we used the well-known formula \(\Gamma (m+1/2) = \sqrt{\pi }\, 2^{-m} (2m-1)!!\), where \((\cdot )!!\) is the bi-factorial. Lastly, the inequality in 4 is just an application of the elementary estimate \(\sqrt{1-x}\le 1-\frac{x}{2}\) for \(0\le x <1\). \(\quad \square \)
Remark
In [61, Section 2.7], several other estimates for \(\left| \chi _X^{\text {cl}}(t)\right| \) are derived. While we decided to stick to the simplest one, as it is already very instructive, it is possible to substantially improve over it, e.g. by resorting to non-isotropic estimates (cf. for instance [61, Theorem 2.7.14]). Notably, our quantum–classical correspondence allows us to translate all of these inequalities to the quantum setting, up to an irrelevant factor of 1/2 in the associated constants (see step 4 in the above proof). We do not pursue this approach further, though we want to stress that it immediately leads to a plethora of further results.
6 Quantitative Bounds in the QCLT: Proofs
In this section, we provide proofs of the convergence rates in our quantum Berry–Esseen theorems. We also provide proofs of some of the statements in Sect. 4.3 on the convergence rate for cascades of beam splitters converging to thermal attenuator channels.
Outline of this section:. To fix ideas, we give a high-level outline of our proofs:
-
Williamson form: We apply a suitable symplectic unitary to the state, so as to make the Hessian of its characteristic function diagonal and larger than the identity. Subsequently, we use the quantum Plancherel identity to express the difference of the convolved state and its Gaussification in Hilbert–Schmidt norm as a difference of quantum characteristic functions in \({L}^2\) norm (Sect. 6.1).
-
Local-tail decomposition: We then split the integral of the \({L}^2\) norm of the difference of the quantum characteristic functions of the convolved state and the Gaussification of the original state into a regime around zero (Lemma 17), in which we can control the behaviour of the quantum characteristic function by its Taylor expansion, and a tail-regime in which we estimate the difference using Proposition 14. The error in the Taylor expansion is controlled by the phase space moments of the state, cf. Lemma 18.
-
Hilbert–Schmidt convergence: We implement the above ideas to prove Theorems 6 and 7, and Proposition 22 (Sect. 6.2).
-
Trace norm and entropic convergence: We then use the preservation of the boundedness of the second moment under quantum convolutions to obtain a quantitative estimate of convergence in trace distance, employing Markov’s inequality and the Gentle Measurement Lemma [73], and in relative entropy, using entropic continuity bounds [33] (Sect. 6.3).
-
Convergence rates for cascades of beam splitters: In the final subsection, we prove the results claimed in Sect. 4.3, namely convergence rates for cascades of beam splitters converging to thermal attenuator channels (Sect. 8).
6.1 Preliminary steps
6.1.1 Williamson form
Let \(\rho \) be a centred m-mode quantum state with finite second moments, as in the Cushen–Hudson theorem. It is known that one can find a symplectic unitary V and numbers \(\nu _1,\ldots , \nu _m\ge 1\) such that

satisfies
With a slight abuse of terminology, we will call \(\rho '\) the Williamson form of \(\rho \) [74]. Bringing a state to its Williamson form allows us to assume that (i) the smallest eigenvalue of its covariance matrix is at least one. Also, (ii) the transformation in (63) does not change the first moments of the state, so that if \(\rho \) is centred then \(\rho '\) remains centred. Finally, (iii) the same unitary V brings not only \(\rho \) but also its Gaussification \(\rho _\mathrm {\scriptscriptstyle G}\) to their Williamson forms simultaneously, so that
holds as well. Thanks to the covariance of the quantum convolution with respect to symplectic unitaries (50), we see that
Combining this with the quantum Plancherel identity (26) yields
In short, when estimating any unitarily invariant distance of \(\rho ^{\boxplus n}\) from its limit \(\rho _\mathrm {\scriptscriptstyle G}\), we can assume without loss of generality that all states are in their Williamson forms. When the Hilbert–Schmidt norm is employed, we can compute the distance as an \({L}^2\) norm at the level of characteristic functions, or equivalently at that of Wigner functions.
6.1.2 Local-tail decomposition
We continue with an important technical lemma that reduces the convergence in the quantum central limit theorem to the behaviour of the quantum characteristic function around zero.
Lemma 17
Let \(\rho \) be an m-mode quantum state with finite second-order phase space moment. Without loss of generality, we assume that \(\rho \) is centred and in Williamson form, and that its Gaussification \(\rho _\mathrm {\scriptscriptstyle G}\) has characteristic function as in (65). Then for every \(\varepsilon >0\) we have that
as \(n\rightarrow \infty \). If \(\rho \) has also finite third-order phase space moments, then
where the Fréchet derivative of \(\chi _\rho \) is defined by (3).
Proof
The first identity (68) follows along the lines of the second one (69) and so we focus on verifying the latter. Using the quantum Plancherel identity (26) and the relation (46), we apply the triangle inequality and split the integration domain into two disjoint sets such that
The last term on the rightmost side of (70) can be estimated explicitly using spherical coordinates. Namely, combining the fact that the coefficients appearing in the Williamson form satisfy \(\nu _j\ge 1\) with the bound \(\left| D^3\chi _{\rho }(0)\left( z^{\times 3}\right) \right| \le \left\| D^3\chi _{\rho }(0) \right\| |z|^3\), we obtain that
where we used that \(\int _0^{\infty }dr\, e^{-r^2} r^{2m+5}= \frac{\Gamma (m+3)}{2}\), and recalled the expression \({\text {vol}}\left( \mathbb S^{N-1}\right) =\frac{2\pi ^{N/2}}{\Gamma (N/2)}\) for the volume of the \((N-1)\)-sphere. Furthermore, the second-to-last term in (70) can be shown to be exponentially small. In fact,

where in 1 we use that \((a+b)^2 \le 2(a^2+b^2)\), in 2 we use that
and in (3) we changed variables in the first integral to \(u:=\frac{z}{\sqrt{n}}\). Finally, in 4, we used that the \(L^2\) norm of the characteristic function is at most one and switched to spherical coordinates to compute the second integral. In 5, instead, we estimated \(e^{-r^2}< e^{-\frac{\varepsilon ^2}{2}\, n} e^{-\frac{r^2}{2}}\) for \(r>\sqrt{n}\,\varepsilon \). Note that the first addend goes to zero faster than any inverse power of n for \(n\rightarrow \infty \) by Proposition 14. The second decays exponentially, essentially because the integral is bounded in n (in fact, it tends to 0 as \(n\rightarrow \infty \)). This concludes the proof. \(\quad \square \)
The first term on the right-hand side of (69) features an explicit dependence on n, while the second decays faster than any inverse power of n. Therefore, all that is left to do is to estimate the third term, which can be done by looking at the behaviour of the characteristic function in a neighbourhood of the origin. The first step in this direction, rather unsurprisingly, involves a Taylor expansion of \(\chi _\rho \) around 0. In the subsequent lemma we record various important estimates of this sort, which will play a key role in the proofs of our quantum Berry–Esseen theorems.
Lemma 18
For \(\varepsilon >0\) and \(k\in [0,\infty )\), let \(\rho \) be an m-mode state with finite phase space moments of order up to k (namely, with the notation of Definition 2, assume that \(M'_k(\rho ,\varepsilon )<\infty \)). Then for all \(z\in \mathbb {C}^m\) with \(|z|\le \sqrt{n}\, \varepsilon \) it holds that

In particular, if \(\rho \) is centred and in Williamson form,
depending on what phase space moments are finite. In (73), we assumed that \(\alpha \in (0,1)\).
The estimate in (71) follows immediately from using Hölder continuity of the derivative.
6.2 Proofs of convergence rates in Hilbert–Schmidt distance
We start with the proof of Theorem 6 assuming fourth-order moments.
Proof of Theorem 6
By the discussion in Sect. 6.1.1, we can assume that \(\rho \) is in Williamson form, namely, that its characteristic function satisfies (64), with \(\nu _1,\ldots , \nu _m\ge 1\). Since \(M'_2(\rho ,\varepsilon )\) is monotonically non-decreasing in \(\varepsilon \), for any fixed \(\mu \in (0,2)\) we can chose \(\varepsilon >0\) small enough so that for any  it holds that
it holds that
Looking at (72), this implies that \(2\left| 1-\chi _\rho \left( \tfrac{z}{\sqrt{n}} \right) \right| \le \mu \). Now, for \(x\in \mathbb {C}\) with \(|x|<2\) define the function

Substituting \(x=2\left( 1-\chi _\rho \left( \tfrac{z}{\sqrt{n}} \right) \right) \), we then have that
where to deduce the last inequality we observed that \(|x|\le \mu \) implies that \(|a(x)|\le a(\mu )\). Then, thanks to (78) and (74), an application of the triangle inequality yields
where for fixed m the constant \(C_1\) depends only on \(M'_3\) (remember that \(M'_2\le M'_3\) by construction). Using again (78) but now in conjunction with (75), by a swift application of the triangle inequality we see that

where for fixed m the constant \(C_2\) depends only on \(M'_4\) (remember that \(M'_2\le M'_4\) by construction). We now estimate

Here, 1 follows simply by the triangle inequality. In 2, we (i) observed that \(\left| e^u - (1+u)\right| \le |u|^2 e^{|u|}\); (ii) operated the substitution \(u=\log \left( \chi _\rho \left( \tfrac{z}{\sqrt{n}}\right) ^n\right) + \frac{1}{2} \sum _j \nu _j |z_j|^2\); (iii) noted that \({\mathbb {R}}\ni x\mapsto x^2 e^x\) is a monotonically increasing function; and (iv) used the fact – proved in (79) – that \(|u|\le \frac{C_1 |z|^3}{\sqrt{n}}\). Finally, in 3 we remembered that \(|z|\le \sqrt{n}\, \varepsilon \) and assumed that \(\varepsilon >0\) is small enough so that \(\varepsilon C_1\le \frac{1}{4}\). Now, since \(\nu _1,\ldots , \nu _m\ge 1\), we can rephrase the above estimate as
Upon integration, (82) naturally yields an upper bound for the second term on the right-hand side of (69). We obtain that

The justification of the above steps goes as follows: in 4 we switched to spherical coordinates; in 5 we performed the change of variables  ; in 6 we computed the gamma integrals, also remembering that \({\text {vol}}\left( \mathbb {S}^{2m-1}\right) = \frac{2\pi ^m}{(m-1)!}\); finally, the constant \(C_3\) introduced in 7 depends – for fixed m – only on \(M'_4\) (note that \(M'_3\le M'_4\) by construction). The proof of the first claim is completed once one inserts (83) into (69). In particular, if \(D^3\chi _{\rho }(0) = 0\) we see that the convergence rate is \(\mathcal O_{M'_4}\left( n^{-1}\right) \). This proves also the second claim. \(\quad \square \)
; in 6 we computed the gamma integrals, also remembering that \({\text {vol}}\left( \mathbb {S}^{2m-1}\right) = \frac{2\pi ^m}{(m-1)!}\); finally, the constant \(C_3\) introduced in 7 depends – for fixed m – only on \(M'_4\) (note that \(M'_3\le M'_4\) by construction). The proof of the first claim is completed once one inserts (83) into (69). In particular, if \(D^3\chi _{\rho }(0) = 0\) we see that the convergence rate is \(\mathcal O_{M'_4}\left( n^{-1}\right) \). This proves also the second claim. \(\quad \square \)
We continue with the proof of the low-regularity QCLT that assumes finiteness of phase space moments of order up to \(2+\alpha \), for some \(\alpha \in (0,1]\).
Proof of Theorem 7
We just deal with the case where \(\alpha \in (0,1)\). As above, we start by fixing \(\mu \in (0,2)\) and choosing a sufficiently small \(\varepsilon >0\) so that for any  the inequality (76) holds. By a similar estimate as in (79), but now leveraging (73) instead of (74), we have that for any \(z\in B\left( 0,\sqrt{n}\, \varepsilon \right) \)
the inequality (76) holds. By a similar estimate as in (79), but now leveraging (73) instead of (74), we have that for any \(z\in B\left( 0,\sqrt{n}\, \varepsilon \right) \)
where the constant \(C_4\) introduced in the last line depends only on \(M'_{2+\alpha }\) (note that \(M'_2\le M'_{2+\alpha }\)).

Here, in 1 we used the elementary estimate \(\left| e^u - 1\right| \le |u| e^{|u|}\), together with the observation that the function \({\mathbb {R}}\ni x\mapsto x e^x\) is monotonically increasing. In 2 we used the fact that \(|z|\le \sqrt{n}\, \varepsilon \), and chose \(\varepsilon >0\) sufficiently small so that \(\varepsilon ^{\alpha } C_4\le \frac{1}{4}\). Combining the above estimate with the fact that \(\nu _1,\ldots , \nu _m\ge 1\) yields
which upon integration in turn leads to

Here, in 3 we switched to spherical coordinates; in 4 we operated the change of variables  and computed the gamma integrals; the constant introduced in 5 depends, for fixed \(\alpha \), only on \(M'_{2+\alpha }\). Inserting (86) into the right-hand side of (69) completes the proof. \(\quad \square \)
and computed the gamma integrals; the constant introduced in 5 depends, for fixed \(\alpha \), only on \(M'_{2+\alpha }\). Inserting (86) into the right-hand side of (69) completes the proof. \(\quad \square \)
6.3 Convergence in trace distance and relative entropy
In this section, we further use the assumption of finiteness of the second moments of the state in order to find convergence rates in trace distance and in relative entropy.
Proof of Corollary 8
The hypothesis implies in particular that \(\rho \) has finite phase space moments of the second order. By Theorem 28, this amounts to saying that \(\rho \) has also finite standard moments of the second order, that is, that \({\text {Tr}}\left[ \rho H_m \right] \le E<\infty \). Iterating (40) and passing to the limit, we see that in fact
Now, for any \(E'>0\), denote by \(P_{E'}\) the projection onto the finite dimensional subspace generated by the eigenvectors of the canonical Hamiltonian \(H_m\) of eigenvalue less than \(E'\). Then, by Markov’s inequality, for any \({\varepsilon }>0\),
From the so-called ‘gentle measurement lemma’ [73, Lemma 9], we have that
Then,
The result follows after optimising over \({\varepsilon }>0\). In particular, if \(\left\| \rho ^{\boxplus n}-\rho _\mathrm {\scriptscriptstyle G}\right\| _2=\mathcal {O}\left( n^{-\alpha }\right) \), we find that \(\left\| \rho ^{\boxplus n}-\rho _\mathrm {\scriptscriptstyle G}\right\| _1=\mathcal {O}\left( n^{-\frac{\alpha }{m+1}}\right) \).
We now turn to the proof of the convergence in relative entropy. Observe that, since \(\rho ^{\boxplus n}\) and \(\rho _\mathrm {\scriptscriptstyle G}\) share the same first and second moments, \({\text {Tr}}\left[ \rho ^{\boxplus n}\log \rho _\mathrm {\scriptscriptstyle G}\right] ={\text {Tr}}\left[ \rho _\mathrm {\scriptscriptstyle G}\log \rho _\mathrm {\scriptscriptstyle G}\right] \) and thus \(D\left( \rho ^{\boxplus n}\big \Vert \rho _\mathrm {\scriptscriptstyle G}\right) = S\left( \rho _\mathrm {\scriptscriptstyle G}\right) - S\left( \rho ^{\boxplus n}\right) \). The result follows directly from [33, Lemma 18]. \(\quad \square \)
7 Optimality of Convergence Rates and Necessity of Finite Second Moments in the QCLT: Proofs
In this section we discuss the optimality of our results in two different directions:
-
First, we provide examples of states \(\rho \) that do not have finite second moments and for which \(\rho ^{\boxplus n}\) does not converge to any quantum state. This shows the necessity of the assumptions on finite second moments in the Cushen–Hudson Theorem (Sect. 7.1).
-
Secondly, we provide examples of explicit states which saturate our convergence rates in Theorems 6 and 7 (Sect. 7.2).
7.1 Failure of convergence for states with unbounded energy
We now show that the assumption of finiteness of second moments in Theorems 3 and 5 cannot be weakened, e.g. by replacing it with finiteness of some lower-order moments. Some examples of states with undefined moments that do not satisfy Theorems 3 and 5 can be obtained by drawing inspiration from probability theory. For instance, remembering that a classical Cauchy-distributed random variable does not satisfy the central limit theorem, we construct the following example.
Example 3
(Cauchy-based wave function). Consider the pure state \(|\psi _f>\) with wave function  . The characteristic function of this state can be computed thanks to (19), which in this case evaluates to
. The characteristic function of this state can be computed thanks to (19), which in this case evaluates to
The absolute value of this characteristic function is illustrated in Fig. 3.
Example of the modulus of a quantum characteristic function, taken from Example 3, with heavy tails in a single direction
We then find the pointwise limit \(\lim _{n \rightarrow \infty } \chi _{|\psi _f> <\psi _f|}\left( z/\sqrt{n}\right) ^n = \delta _{z,0}\) which again is not continuous at 0 and hence is not the characteristic function of any quantum state.
The main drawback of the above state is that it does not have even first order moments. We can fix this by considering a slightly more sophisticated example. To proceed further, we first need to recall a well-known integral representation of fractional matrix powers.
Lemma 19
([46, Proposition 5.16]). For all \(r\in (0,1)\), all positive (possibly unbounded) operators A, and all \(|\psi >\in {{\,\mathrm{Dom}\,}}\left( A^{1/2}\right) \), we have that
where all functions of A are defined by means of its spectral decomposition.
Proof of Proposition 11
The state is clearly centred, for instance because the wave function is symmetric under inversion \(x\mapsto -x\). We proceed to prove claim (b). Note that, since \(x^2+p^2=I+ 2a^\dagger a\ge I\), \(2 a a^\dag = x^2+p^2 + I \le 2(x^2+p^2)\), where  is the momentum operator. We now apply the operator inequality \((A+B)^{r} \le A^{r} + B^{r}\), which can be shown to hold for all \(r \in [0,1]\) and all positive (possibly unbounded) self-adjoint operators A, B. To prove this explicitly in the non-trivial case where \(r\in (0,1)\), we apply (87) to \(A+B\). For a generic \(|\psi >\in {{\,\mathrm{Dom}\,}}\left( A^{r/2}\right) \cap {{\,\mathrm{Dom}\,}}\left( B^{r/2}\right) \), we obtain that
is the momentum operator. We now apply the operator inequality \((A+B)^{r} \le A^{r} + B^{r}\), which can be shown to hold for all \(r \in [0,1]\) and all positive (possibly unbounded) self-adjoint operators A, B. To prove this explicitly in the non-trivial case where \(r\in (0,1)\), we apply (87) to \(A+B\). For a generic \(|\psi >\in {{\,\mathrm{Dom}\,}}\left( A^{r/2}\right) \cap {{\,\mathrm{Dom}\,}}\left( B^{r/2}\right) \), we obtain that
where the inequality in the above derivation follows e.g. from [46, Corollary 10.13]. Now, setting \(A=x^2\), \(B=p^2\) and \(r=1-\delta \), we obtain that
Computing the expectation value on \(|\psi _f>\) yields
where the last step is by explicit computation. This proves (b). We now move on to (c). For this we evaluate the characteristic function of the convolution  on the purely imaginary line. For \(t\in {\mathbb {R}}\), using (19) we obtain that
on the purely imaginary line. For \(t\in {\mathbb {R}}\), using (19) we obtain that
were \(K_1\) is a modified Bessel function of the second kind, and the last equality follows from (54) and [75, Eq. (9.6.25)]. Therefore, for any fixed \(t > 0\) it holds that
where we have used the expansion in [75, Eq. (9.6.53)] (see also [75, Eq. (6.3.2) and (9.6.7)]). Since \(\chi _{|\psi _f> <\psi _f|^{\boxplus \, n}}(0)=1\) for all n because \(|\psi _f>\!<\psi _f|^{\boxplus \, n}\) is a valid quantum state, the sequence of functions \(\chi _{|\psi _f> <\psi _f|^{\boxplus \, n}}\) does not possess a continuous limit. Hence, it cannot converge to the characteristic function of any quantum state. This proves (c).
\(\square \)
7.2 Optimality of the convergence rates
The following two examples show that the bounds stated in Theorems 6 and 7 are indeed saturated. Both examples consist of states constructed using the Fock basis. The construction of examples saturating the bounds in Theorems 6 and 7 is motivated by the following Proposition.
Proposition 20
Let \(\rho \) be a one-mode density operator satisfying the assumptions of Theorem 6 and also \(<i| \rho |j> =0\) for \(|i-j| \in \left\{ 1,3 \right\} \). Then the state \(\rho ^{\boxplus n}\) converges at least with rate \(\mathcal {O}\left( n^{-1}\right) \) to its Gaussification
In particular, every density operator satisfying the assumptions of Theorem 6 that is diagonal in the Fock basis achieves a \(\mathcal O(n^{-1})\) rate.
Proof of Proposition 20
By Theorem 6 it suffices to show that \(D^3\chi _{\rho }(0)=0\) under the assumptions of the Proposition. We start by recalling that any density operator \(\rho \) has an expansion into the Fock basis such that

Hence, we find for the characteristic function that
Using a finite-rank approximation of the density operator \(\rho \), it suffices then by Theorem 9 to analyse the component-wise derivatives in (89). The functions \(\chi _{|i> <j|}\) are explicitly given by [59, Eq. (4.4.46) and (4.4.47)]
Here,  are the associated Laguerre polynomials. By assumption, it suffices to consider the case where \(|i-j|\) is even or \(\vert i-j \vert \) is odd and at least 5. We find that by writing the characteristic function in the form
are the associated Laguerre polynomials. By assumption, it suffices to consider the case where \(|i-j|\) is even or \(\vert i-j \vert \) is odd and at least 5. We find that by writing the characteristic function in the form  for some suitable function \(H_{ji}\), as in (90), that for the different possible third derivatives, we have
for some suitable function \(H_{ji}\), as in (90), that for the different possible third derivatives, we have
Therefore, the only possible non-zero contribution to the third derivative of the quantum characteristic function \(\chi _{\rho }\) at zero could be due to terms that contain either one or three derivatives of functions \(H_{ji}\) evaluated at zero.
If \(|i-j| \ge 4\) then z and \(z^*\) appear in (90) with a joint power of at least 4; thus, this term’s contribution necessarily has to vanish. It suffices therefore to consider the case where \(\vert i-j \vert =2\). If \(H_{ji}\) is only differentiated once, then it is clear that this derivative has to vanish at zero, since \(z,z^*\) appear with a joint power of at least two.
If \(H_{ji}\) is differentiated three times, then the term \(|z|^{2}\) causes the derivative to vanish at zero unless this term is differentiated precisely two times. This, however, implies that the Laguerre polynomial is differentiated exactly once. However, by the chain rule any first order derivative of the term \(L_j^{\vert j-i \vert }(\vert z\vert ^2)\) vanishes at the origin. This concludes the proof. \(\quad \square \)
The following example shows that the \(\mathcal O(n^{-1})\) convergence rate stated in Proposition 20, under the assumption that \(D^3\chi _\rho (0)=0\), is in fact attained.
Example 4
(\(\mathcal O(n^{-1})\)-rate). By Proposition 20 we can take  to obtain a convergence rate of at least \(\mathcal O(n^{-1})\) in the QCLT. That the \(\mathcal O(n^{-1})\) rate is actually attained is illustrated in the right figure in Fig. 4. The \(\mathcal O(n^{-1})\) rate is saturated both in Hilbert–Schmidt and trace norm.
to obtain a convergence rate of at least \(\mathcal O(n^{-1})\) in the QCLT. That the \(\mathcal O(n^{-1})\) rate is actually attained is illustrated in the right figure in Fig. 4. The \(\mathcal O(n^{-1})\) rate is saturated both in Hilbert–Schmidt and trace norm.
The following example shows that the \(\mathcal O(n^{-1/2})\) convergence rate of Theorem 7 is attained.
Example 5
(\(\mathcal O(n^{-1/2})\)-rate). Consider the stateFootnote 11
Its characteristic function is explicitly given by (90)
Now, since \(<0|\rho |3>\ne 0\) we see that the condition of Proposition 20 does not hold. One verifies directly that \(\chi _\rho (z) = 1 - 2 |z|^2 + o\left( |z|^2\right) \), so that \(\rho \) is already in Williamson form (cf. (64)). Letting \(\Phi (z) = e^{-2|z|^2}\), we then find that \(\left\| {\chi }_{\rho } - \Phi \right\| _{{L}^2(\mathbb R^2)}\) converges with rate \(n^{-1/2}\), see Fig. 4.
This plot shows the expressions \(cn^{\alpha } \Vert \rho ^{\boxplus n}-\rho \Vert \) for a constant \(c>0\) such that \(\lim _{n \rightarrow \infty }cn^{\alpha } \Vert \rho ^{\boxplus n}-\rho \Vert =1.\) The left figure shows that the \(\mathcal O(1/\sqrt{n})\) convergence rate is sharp (Theorem 7) by using the state from Example 5. The right figure shows that we can obtain a rate \(\mathcal O(1/n)\) if \(D^3 \chi _{\rho }(0)=0\) (Theorem 6) by using the state from Example 4. In both figures we write \(\rho ^n\) for \(\rho ^{\boxplus n}\)
The following example shows that the \(\mathcal {O}(n^{-\alpha /2})\) convergence rate of Theorem 7 is attained at least for \(\alpha =1/2\).
Example 6
Consider the probability density function p on \({\mathbb {R}}\) given by

Its Fourier transform reads

where \(K_\nu (z)\) is again the modified Bessel function of the second kind, and (91) follows from [75, Eq. (9.6.25)]. Define the single-mode quantum state

where

is a so-called coherent state [76,77,78,79]. The characteristic function of \(\rho \) can be easily computed as
which leads us to
On the other hand, a little thought confirms that \(\rho \) has vanishing first moments and second moments given by \({\text {Tr}}[\rho x^2]=9/2\) and \({\text {Tr}}[\rho p^2] = 1/2\). Its Gaussification then reads

We also observe that: (a) \(\rho \) has finite standard moments of order up to \(5/2-\delta \), for all \(\delta >0\); but (b) it has no well-defined phase space moments (nor standard moments) of order 5/2.
To prove claim (a), start by setting  . Assuming that \(\delta \le 1/2\) so that \(\beta \ge 1\), for all \(t\in {\mathbb {R}}\) we have that
. Assuming that \(\delta \le 1/2\) so that \(\beta \ge 1\), for all \(t\in {\mathbb {R}}\) we have that

where 1 is just the definition of coherent state, 2 comes from the concavity of the function \(x\mapsto x^{\beta -1}\) and from the fact that \(q_n = \frac{t^{2n}e^{-t^2}}{n!}\) is a probability distribution over \(\mathbb {N}\), and finally in 3 we used the formula \(\sum _{n=0}^\infty \frac{x^n}{n!}(n+1) = (1+x)e^x\). From the above calculation we now deduce that
as claimed.
To prove claim (b), it suffices to use [75, Eq. (9.6.10) and (9.6.11)] in order to write \(z^\nu K_\nu (z) = A(z) + z^{2\nu } \ln (z)\, B(z)\), with \(\nu >0\), A, B analytic functions, and \(B(0)\ne 0\). Setting \(\nu =5/4\) shows that the phase space moment of \(\rho \) of order 5/2, as constructed in Definition 2, is not well defined, formally \(M'_{5/2}(\rho ,\varepsilon )=+\infty \) for all \(\varepsilon >0\).
We now present numerical evidence hinting at the fact that \(\left\| \rho ^{\boxplus n} - \rho _\mathrm {\scriptscriptstyle G}\right\| _2 = \mathcal {O}(n^{-1/4})\) for our choice of \(\rho \). Note that
The above integral can be evaluated numerically to a high degree of precision. Plotting the function \(-\ln \left\| \rho ^{\boxplus n} - \rho _\mathrm {\scriptscriptstyle G}\right\| _2\) against \(\ln n\) shows that \(\left\| \rho ^{\boxplus n} - \rho _\mathrm {\scriptscriptstyle G}\right\| _2\) decays as \(\mathcal {O}(n^{-1/4})\), cf. Figure 5. By what we have learnt above, Theorem 7 predicts a convergence at least as fast as \(\mathcal {O}(n^{-1/4+\delta })\) for every fixed \(\delta >0\), and is therefore tight at least for \(\alpha =1/2\).
8 Cascade of Beam Splitters: Proofs
In this section, we prove the results claimed in Sect. 4.3, namely convergence rates for cascades of beam splitters converging to thermal attenuator channels.
8.1 Generalities of the cascade channels
In order to study the convergence of the cascade channel, we start by proving the following elementary equivalence.
Lemma 21
For an m-mode quantum state \(\rho \), some \(\lambda \in [0,1]\), and a positive integer n, consider the cascade channel  (cf. (41)). One has that
(cf. (41)). One has that

where the effective environment state \(\rho (\lambda ,n)\) is defined via its characteristic function

Proof
We proceed by induction. The case \(n=1\) follows from (38). Let us assume that the claim holds for \(n-1\), so that

By setting \(\mu =\lambda ^{(n-1)/n}\) we see that

Since  , composition with the \(n^{\text {th}}\) copy of the channel
, composition with the \(n^{\text {th}}\) copy of the channel  yields
yields

which proves (93) and (94). Finally, one can also verify by induction that
where  , so that \(\rho (\lambda , n)\) is a legitimate quantum state for all \(\lambda \in [0,1]\) and all n. \(\quad \square \)
, so that \(\rho (\lambda , n)\) is a legitimate quantum state for all \(\lambda \in [0,1]\) and all n. \(\quad \square \)
8.2 On the effective environment state
Thanks to Lemma 21, the study of the cascade channel  boils down to that of the iteratively convolved state \(\rho (\lambda , n)\) of (94). Since such a convolution is not symmetric (cf. (49)), to proceed further we need to extend our quantum Berry–Esseen results to a non-i.i.d. scenario. Note that the classical central limit theorem has indeed been extended to sequences of independent, non-identically distributed random variables [1, 80], and even to sequences of correlated random variables [81]. Rates of convergence for the former case can be found for instance in [82] (see e.g. Theorem 13.3 of [82]).
boils down to that of the iteratively convolved state \(\rho (\lambda , n)\) of (94). Since such a convolution is not symmetric (cf. (49)), to proceed further we need to extend our quantum Berry–Esseen results to a non-i.i.d. scenario. Note that the classical central limit theorem has indeed been extended to sequences of independent, non-identically distributed random variables [1, 80], and even to sequences of correlated random variables [81]. Rates of convergence for the former case can be found for instance in [82] (see e.g. Theorem 13.3 of [82]).
Proposition 22
Let \(\rho \) be a centred m-mode quantum state with finite second-order phase space moments. Then the sequence of quantum states \(\rho (\lambda ,n)\) defined via (94) converges to the Gaussification \(\rho _\mathrm {\scriptscriptstyle G}\) of \(\rho \) in trace norm. Moreover, if \(\rho \) has finite third-order phase space moments then
Here, \(M_3'=M'_3(\rho ,\varepsilon )\) is defined by (33), and \(\varepsilon >0\) is sufficiently small.
Proof
The argument is a variation of that used to prove Theorem 7 in Sect. 6.2. First of all, reasoning as in Sect. 6.1.1, we can assume without loss of generality that \(\rho \) is in its Williamson form. To simplify the notation, we introduce the re-scaled vectors  , where \(\ell \in \{1,\ldots , n\}\). Then clearly \(\chi _{\rho (\lambda ,n)}(z) = \prod _{\ell =1}^n \chi _\rho \left( w_\ell \right) \). Note that \(\left| w_\ell \right| \le \sqrt{\frac{\log \left( 1/\lambda \right) }{n(1-\lambda )}}\,|z|\); substituting \(z\mapsto w_\ell \) into (72) and (74), we see that whenever \(|z|\le \sqrt{\frac{n(1-\lambda )}{\log \left( 1/\lambda \right) }}\, \varepsilon \) it holds that
, where \(\ell \in \{1,\ldots , n\}\). Then clearly \(\chi _{\rho (\lambda ,n)}(z) = \prod _{\ell =1}^n \chi _\rho \left( w_\ell \right) \). Note that \(\left| w_\ell \right| \le \sqrt{\frac{\log \left( 1/\lambda \right) }{n(1-\lambda )}}\,|z|\); substituting \(z\mapsto w_\ell \) into (72) and (74), we see that whenever \(|z|\le \sqrt{\frac{n(1-\lambda )}{\log \left( 1/\lambda \right) }}\, \varepsilon \) it holds that
We start by choosing \(\varepsilon >0\) small enough so that (76) holds for some \(\mu \in (0,2)\). We can now mimic the calculations in (79), obtaining

Here, in 1 we observed that \(\sum _{\ell =1}^n \frac{1-\lambda ^{1/n}}{1-\lambda }\,\lambda ^{\frac{\ell -1}{n}} = 1\) and applied the triangle inequality. To deduce 2, instead, we proceeded as for (78). Namely, on the first addend we used the identity \(\log \left( 1-\frac{x}{2}\right) + \frac{x}{2} = -\frac{x^2}{4}\, a(x)\) satisfied by the function a(x) defined by (77), we set \(x = 2\left( 1-\chi _\rho \left( w_\ell \right) \right) \), we noted that \(|x|\le \mu \) implies that \(|a(x)|\le a(\mu )\), and lastly we employed (98). The second addend, instead, has been estimated thanks to (99). Finally, for fixed m the constant introduced in 3 depends only on \(M'_3\) and \(\lambda \) (again, \(M'_2\le M'_3\) by construction).
Proceeding as usual, we continue to estimate

Note that in 4 we applied the elementary inequality \(\left| e^u-1\right| \le |u|e^{|u|}\), observed that \({\mathbb {R}}\ni x\mapsto x e^x\) is a monotonically increasing function, and leveraged the bound in (100). In 5, instead, we wrote \(\frac{C_6 |z|^3}{\sqrt{n}}\le C_6\, \sqrt{\frac{1-\lambda }{\log \tfrac{1}{\lambda }}}\, \varepsilon \, |z|^2\le \frac{1}{4} |z|^2\), where the last estimate holds provided that \(\varepsilon >0\) is small enough.
Remembering that \(\nu _1,\ldots , \nu _m\ge 1\), we can massage the above relation so as to get
Now, we can repeat the steps that led to (68). We obtain that

The justification of the above steps is as follows. The estimate in 6 is just an application of the triangle inequality. In 7 we used (101) and the elementary fact that \(|u+v|^2\le 2|u|^2+2|v|^2\) on the second addend. As for 8, we: (i) performed the integral and introduced a constant \(C_7\) that depends on m only on the first addend; (ii) decomposed \(\chi _{\rho (\lambda , n)}(z) = \chi _\rho (w_1) \cdot \prod _{\ell =2}^n \chi _\rho (w_\ell )\) on the second; and (iii) used the fact that \(e^{-\sum _j \nu _j |z_j|^2}\le e^{-|z|^2}< e^{-\frac{\varepsilon ^2}{2}\, n} e^{-\frac{1}{2} |z|^2}\) in the prescribed range on the third. Finally, in 9 we noted that if \(|z|>\sqrt{n}\,\varepsilon \) then eventually in n
for all \(\ell \in \{1,\ldots , n\}\); moreover, we used the fact that \(\int d^{2m} u\, |\chi _\rho (u)|^2\le 1\) to evaluate the integral in the second addend.
Since the second term in the rightmost side of (102) decays faster than any inverse power of n as \(n\rightarrow \infty \) thanks to Proposition 14, the proof of (96) is complete. Lastly, (97) follows similarly to Corollary 8. \(\quad \square \)
8.3 Approximating cascade channels
With this convergence at hand, we provide a quantitative bound on the approximation of thermal attenuator channels by cascades of beam splitters (with possibly non-Gaussian environment states). Recall that, to an environment state \(\rho \) one can associate an attenuator channel  of transmissivity \(0\le \lambda \le 1\). The following simple lemma is crucial to convert the above state approximation result (Proposition 22) into a statement about approximations of attenuator channels.
of transmissivity \(0\le \lambda \le 1\). The following simple lemma is crucial to convert the above state approximation result (Proposition 22) into a statement about approximations of attenuator channels.
Lemma 23
Given any two m-mode quantum states \(\rho _1\) and \(\rho _2\), and some \(\lambda \in [0,1]\), the corresponding channels defined as in (41) satisfy
Proof
Let R be any reference system, and let  be a state on the bipartite system AR. Then
be a state on the bipartite system AR. Then
where the inequality stems from the monotonicity of trace distance under quantum channels. \(\quad \square \)
With this lemma at hand, we are ready to prove Theorem 12.
Proof of Theorem 12
Recall from Lemma 21 that  , where \(\rho (\lambda ,n)\) is the state with characteristic function given by (94). Applying Lemma 23 and Proposition 22, we have that
, where \(\rho (\lambda ,n)\) is the state with characteristic function given by (94). Applying Lemma 23 and Proposition 22, we have that

concluding the proof. \(\quad \square \)
Proof of Corollary 13
We now move on to Corollary 13. Let us start by proving the statement on quantum capacities, namely (56) and (57). Our aim is to apply [34, Theorem 9] to the two channels  and \(\mathcal {N}_{\rho _\mathrm {\scriptscriptstyle G},\lambda }=\mathcal {E}_{N,\lambda }\), for the special case \(m=1\) (cf. (42)). We set
and \(\mathcal {N}_{\rho _\mathrm {\scriptscriptstyle G},\lambda }=\mathcal {E}_{N,\lambda }\), for the special case \(m=1\) (cf. (42)). We set

where the energy-constrained diamond norm is defined with respect to the canonical Hamiltonian, namely the number operator \(H=a^\dag a\) (see [36, Eq. (2)] and [34, Eq. (2)]). Note that \(\varepsilon _n = \mathcal {O}_{M_3'}\left( n^{-1/4}\right) \) by Theorem 12.
The input–output energy relations can be easily determined for both channels thanks to (95) and (40), which together show that \({\text {Tr}}\left[ \rho (\lambda , n)\, a^\dag a \right] = {\text {Tr}}\left[ \rho \, a^\dag a\right] = N = {\text {Tr}}\left[ \tau _N a^\dag a\right] \). One obtains that

This means that we can set \(\alpha =\lambda \) and \(E_0=(1-\lambda )N\), and hence \(\widetilde{E}=\lambda E+(1-\lambda )N\), in [34, Theorem 9]. We obtain that

Here, in step 1 we applied [34, Theorem 9] together with the formula \(S(\tau _N)=g(N)\) (see (28) and (29)); the inequality in 2 holds eventually in n for some universal constant \(c \le 57 + 24 \log e\), as can be seen by combining the bounds \(g(x)\le \log (x+1)+\log e\) (tight for large x) and \(g(x)\le -2x\log x\) (valid for sufficiently small x); finally, in 3 we used the fact that \(\varepsilon _n\le C(M_3')\, n^{-1/4}\) eventually in n by the already proven Theorem 12, together with the observation that \(x\mapsto -x\log x\) is an increasing function for sufficiently small \(x>0\).
To complete the first part of the proof we need to estimate the classical capacity of  in terms of that of the thermal attenuator \(\mathcal {E}_{N,\lambda }\) of (42), in turn given by (43). Although we could use the estimates in [34], we prefer to resort to the tighter ones provided in [36]. We obtain that
in terms of that of the thermal attenuator \(\mathcal {E}_{N,\lambda }\) of (42), in turn given by (43). Although we could use the estimates in [34], we prefer to resort to the tighter ones provided in [36]. We obtain that

The inequality in 4 is an application of [36, Proposition 6]. To see why, let us re-write the result of Shirokov [36, Proposition 6] for one-mode channels and with respect to the canonical Hamiltonian as
Here, \(\mathcal {N}_i\) (\(i=1,2\)) are two quantum channels with \(\frac{1}{2} \left\| \mathcal {N}_1-\mathcal {N}_2\right\| _{\diamond E}\le \epsilon \), we picked \(E'\) such that \(\sup _{\rho :\, {\text {Tr}}[\rho \, a^\dag a]\le E} {\text {Tr}}\left[ \mathcal {N}_i(\rho )\, a^\dag a\right] \le E'\), the function \(r_\epsilon \) is defined by  , and
, and  is the binary entropy. Setting
is the binary entropy. Setting  , \(\mathcal {N}_2=\mathcal {E}_{N,\lambda }\), we see that \(E'=\lambda E+(1-\lambda ) N\) (cf. (104) and [36, Eq. (21)]); choosing \(t=1/2\) and hence \(r_\varepsilon (t) \le r_1(t) = r_1(1/2) = 5/2\) yields the above relation 4, as claimed. The inequality in 5 holds for all sufficiently large n and for some absolute constant \(c'\le 15\). Finally, 6 is analogous to 3 above. \(\quad \square \)
, \(\mathcal {N}_2=\mathcal {E}_{N,\lambda }\), we see that \(E'=\lambda E+(1-\lambda ) N\) (cf. (104) and [36, Eq. (21)]); choosing \(t=1/2\) and hence \(r_\varepsilon (t) \le r_1(t) = r_1(1/2) = 5/2\) yields the above relation 4, as claimed. The inequality in 5 holds for all sufficiently large n and for some absolute constant \(c'\le 15\). Finally, 6 is analogous to 3 above. \(\quad \square \)
Remark
Let us stress that the threshold in n above which the inequalities in the above proof hold true depends on both \(\lambda E+(1-\lambda )N\) and \(M_3'\) (which dictates the rate of convergence of \(\varepsilon _n\rightarrow 0\)). Although this is a minor point from the point of view of the mathematical derivation, it may be important for applications.
Remark
An analytical formula for the quantum capacity of the thermal attenuator that appears in Corollary 13 is currently not known. The best lower bound to date reads [45, Eq. (9)]
where

The best upper bound to date, instead, can be obtained by combining the results of [40, Eq. (23)–(25)] (see also [41, Section 8]) with those of [44, Theorem 9] and [43, Theorem 46], in turn derived by refining a technique introduced in [42]. We look at the case where \(\lambda \ge \frac{N+1/2}{N+1}\), because below that value of \(\lambda \) the channel \(\mathcal {E}_{N,\lambda }\) becomes 2-extendable [83] (that is, anti-degradable [84,85,86]) and therefore \(\mathcal {Q}\left( \mathcal {E}_{N,\lambda }, E\right) =0\).



Notes
Throughout this paper we set \(\hbar = 1\).
The characteristic function of a complex-valued random variable X is defined by
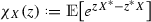 .
.That is, operators
 for which
for which 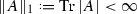 .
.One way to define it is via the infinite sum \(S(\rho ) = \sum _i (- p_i \log p_i)\), where
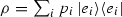 is the spectral decomposition of \(\rho \). Since all terms of this sum are non-negative, the sum itself can be assigned a well-defined value, possibly \(+\infty \).
is the spectral decomposition of \(\rho \). Since all terms of this sum are non-negative, the sum itself can be assigned a well-defined value, possibly \(+\infty \).To define it one considers the infinite sum
 , where
, where  and
and  are the spectral decompositions of \(\rho \) and \(\sigma \), respectively. As detailed in [48], the convexity of \(x\mapsto x\log x\) implies that all terms of this sum are non-negative, which makes the expression well defined.
are the spectral decompositions of \(\rho \) and \(\sigma \), respectively. As detailed in [48], the convexity of \(x\mapsto x\log x\) implies that all terms of this sum are non-negative, which makes the expression well defined.While not all products of unitaries of the form \(e^{-iH_{{\text {quad}}}}\) can be written as a single exponential, two such factors always suffice. See [56, p.37], combined with [56, Propositions 2.12, 2.18, and 2.19] and with the observation that the exponential Lie map of the unitary group is surjective.
Tensor products are omitted here.
These are discrete random variables with probability distributions supported on a lattice.
We use states \(|0>\) and \(|3>\) rather than \(|0>\) and \(|1>\) because the latter choice does not lead to a centred state.
References
Feller, W.: An Introduction to Probability Theory and Its Applications, vol. II, 2nd edn. Wiley, New York (1971)
Cushen, C.D., Hudson, R.L.: A quantum-mechanical Central Limit theorem. J. Appl. Probab. 8(3), 454–469 (1971)
Hepp, K., Lieb, E.H.: Phase-transitions in reservoir-driven open systems with applications to lasers and superconductors. Helv. Phys. Acta 46(5), 573–603 (1974)
Hepp, K., Lieb, E.H.: On the superradiant phase transition for molecules in a quantized radiation field: the Dicke Maser model. Ann. Phys. 76(2), 360–404 (1973)
Giri, N., von Waldenfels, W.: An algebraic version of the Central Limit theorem. Z. Wahrscheinlichkeitstheorie verw. Gebiete 42(2), 129–134 (1978)
Goderis, D., Vets, P.: Central limit theorem for mixing quantum systems and the CCR-algebra of fluctuations. Commun. Math. Phys. 122(2), 249–265 (1989)
Goderis, D., Verbeure, A., Vets, P.: About the mathematical theory of quantum fluctuations. Leuven University Press, Leuven, Belgium (1989)
Matsui, T.: Bosonic Central Limit Theorem for the one-dimensional XY model. Rev. Math. Phys. 14(07n08), 675–700 (2002)
Cramer, M., Eisert, J.: A quantum Central Limit Theorem for non-equilibrium systems: exact local relaxation of correlated states. New J. Phys. 12(5), 055020 (2010)
Goderis, D., Verbeure, A., Vets, P.: About the exactness of the linear response theory. Commun. Math. Phys. 136(2), 265–283 (1991)
Jakšić, V., Pautrat, Y., Pillet, C.-A.: Central Limit Theorem for locally interacting Fermi gas. Commun. Math. Phys. 285(1), 175–217 (2009)
Arous, G.B., Kirkpatrick, K., Schlein, B.: A central limit theorem in many-body quantum dynamics. Commun. Math. Phys. 321(2), 371–417 (2013)
Brandão, F.G.S.L., Cramer, M.: Equivalence of statistical mechanical ensembles for non-critical quantum systems (2015)
Brandão, F.G.S.L., Gour, G.: Reversible framework for quantum resource theories. Phys. Rev. Lett. 115, 070503 (2015)
Dereziński, J.: Boson free fields as a limit of fields of a more general type. Rep. Math. Phys. 21(3), 405–417 (1985)
Streater, R.F.: Entropy and the Central Limit Theorem in quantum mechanics. J. Phys. A 20(13), 4321–4330 (1987)
Michoel, T., Nachtergaele, B.: Central Limit Theorems for the large-spin asymptotics of quantum spins. Probab. Theory Relat. Fields 130(4), 493–517 (2004)
Goderis, D., Verbeure, A., Vets, P.: Non-commutative central limits. Probab. Theory Related Fields 82(4), 527–544 (1989)
Jakšić, V., Pautrat, Y., Pillet, C.-A.: A quantum central limit theorem for sums of independent identically distributed random variables. J. Math. Phys. 51(1), 015208 (2010)
Voiculescu, D.V., Dykema, K.J., Nica, A.: Free Random Variables, CRM Monograph Series. American Mathematical Society, Providence (1992)
Accardi, L., Lu, Y.G.: Quantum central limit theorems for weakly dependent maps. II. Acta Math. Hungar. 63(3), 249–282 (1994)
Hayashi, M.: Quantum Information: An Introduction. Springer, Berlin Heidelberg (2006)
Hayashi, M.: Quantum estimation and the Quantum Central Limit theorem. Am. Math. Soci. Transl. Ser. 2(227), 95–123 (2009)
Campbell, E.T., Genoni, M.G., Eisert, J.: Continuous-variable entanglement distillation and noncommutative central limit theorems. Phys. Rev. A 87, 042330 (2013)
Lenczewski, R.: Quantum Central Limit Theorems, pp. 299–314. Springer, Boston (1995)
Dimi, A., Daki, B.: On the central limit theorem for unsharp quantum random variables. New J. Phys. 20, 063051 (2018)
Davies, E.B.: Quantum stochastic processes. Commun. Math. Phys. 15(4), 277–304 (1969)
Lami, L., Sabapathy, K.K., Winter, A.: All phase-space linear bosonic channels are approximately Gaussian dilatable. New J. Phys. 20(11), 113012 (2018)
Carolan, J., Harrold, C., Sparrow, C., Martín-López, E., Russell, N.J., Silverstone, J.W., Shadbolt, P.J., Matsuda, N., Oguma, M., Itoh, M., Marshall, G.D., Thompson, M.G., Matthews, J.C.F., Hashimoto, T., O’Brien, J.L., Laing, A.: Universal linear optics. Science 349(6249), 711–716 (2015)
Rohde, P.P., Dowling, J.P.: The on-ramp to the all-optical quantum information processing highway. Science 349(6249), 696 (2015)
Holevo, A.S., Shirokov, M.E.: Continuous ensembles and the capacity of infinite-dimensional quantum channels. Theory Probab. Its Appl. 50(1), 86–98 (2006)
Wilde, M.M., Qi, H.: Energy-constrained private and quantum capacities of quantum channels. IEEE Trans. Inf. Theory 64(12), 7802–7827 (2018)
Winter, A.: Tight uniform continuity bounds for quantum entropies: conditional entropy, relative entropy distance and energy constraints. Commun. Math. Phys. 347(1), 291–313 (2016)
Winter, A.: Energy-constrained diamond norm with applications to the uniform continuity of continuous variable channel capacities (2017). arXiv:1712.10267
Shirokov, M.E.: Tight uniform continuity bounds for the quantum conditional mutual information, for the Holevo quantity, and for capacities of quantum channels. J. Math. Phys. 58(10), 102202 (2017)
Shirokov, M.E.: On the energy-constrained diamond norm and its application in quantum information theory. Prob. Inform. Transm. 54(1), 20–33 (2018)
Giovannetti, V., García-Patrón, R., Cerf, N.J., Holevo, A.S.: Ultimate classical communication rates of quantum optical channels. Nat. Photonics 8(10), 796–800 (2014)
Giovannetti, V., Holevo, A.S., García-Patrón, R.: A solution of Gaussian optimizer conjecture for quantum channels. Commun. Math. Phys. 334(3), 1553–1571 (2015)
Holevo, A.S., Werner, R.F.: Evaluating capacities of bosonic Gaussian channels. Phys. Rev. A 63, 032312 (2001)
Pirandola, S., Laurenza, R., Ottaviani, C., Banchi, L.: Fundamental limits of repeaterless quantum communications. Nat. Commun. 8(1), 15043 (2017)
Wilde, M.M., Tomamichel, M., Berta, M.: Converse bounds for private communication over quantum channels. IEEE Trans. Inf. Theory 63(3), 1792–1817 (2017)
Rosati, M., Mari, A., Giovannetti, V.: Narrow bounds for the quantum capacity of thermal attenuators. Nat. Commun. 9(1), 4339 (2018)
Sharma, K., Wilde, M.M., Adhikari, S., Takeoka, M.: Bounding the energy-constrained quantum and private capacities of phase-insensitive bosonic Gaussian channels. New J. Phys. 20(6), 063025 (2018)
Noh, K., Albert, V.V., Jiang, L.: Quantum capacity bounds of Gaussian thermal loss channels and achievable rates with Gottesman–Kitaev–Preskill codes. IEEE Trans. Inf. Theory 65(4), 2563–2582 (2019)
Noh, K., Pirandola, S., Jiang, L.: Enhanced energy-constrained quantum communication over bosonic Gaussian channels. Nat. Commun. 11(1), 457 (2020)
Schmuedgen, K.: Unbounded Self-adjoint Operators on Hilbert Space. Springer, Dordrecht (2012)
Umegaki, H.: Conditional expectation in an operator algebra. IV. Entropy and information. Kodai Math. Sem. Rep. 14(2), 59–85 (1962)
Lindblad, G.: Entropy, information and quantum measurements. Commun. Math. Phys. 33(4), 305–322 (1973)
Holevo, A.S.: On capacity of a quantum communications channel. Probl. Pered. Inform. 15(4):3–11 (1979). (English translation: Probl. Inf. Transm. 15(4):247–253)
Hausladen, P., Jozsa, R., Schumacher, B., Westmoreland, M., Wootters, W.K.: Classical information capacity of a quantum channel. Phys. Rev. A 54, 1869–1876 (1996)
Schumacher, B., Westmoreland, M.D.: Sending classical information via noisy quantum channels. Phys. Rev. A 56, 131–138 (1997)
Holevo, A.S.: The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 44(1), 269–273 (1998)
Lloyd, S.: Capacity of the noisy quantum channel. Phys. Rev. A 55, 1613–1622 (1997)
Shor, P.: Lecture Notes. MSRI Workshop on Quantum Computation (2002)
Devetak, I.: The private classical capacity and quantum capacity of a quantum channel. IEEE Trans. Inf. Theory 51(1), 44–55 (2005)
de Gosson, M.A.: Symplectic Geometry and Quantum Mechanics. Operator Theory: Advances and Applications. Birkhäuser, Basel (2006)
Serafini, A.: Quantum Continuous Variables: A Primer of Theoretical Methods. CRC Press, Taylor & Francis Group (2017)
Holevo, A.S.: Probabilistic and Statistical Aspects of Quantum Theory. Publications of the Scuola Normale Superiore, Scuola Normale Superiore (2011)
Barnett, S., Radmore, P.M.: Methods in Theoretical Quantum Optics Oxford Series in Optical and Imaging Sciences. Clarendon Press, Oxford (2002)
Zygmund, A.: A remark on characteristic functions. Ann. Math. Stat. 18(2), 272–276 (1947)
Ushakov, N.G.: Selected Topics in Characteristic Functions. Modern Probability and Statistics. de Gruyter, Berlin (2011)
König, R., Smith, G.: The entropy power inequality for quantum systems. IEEE Trans. Inf. Theory 60(3), 1536–1548 (2014)
Bergh, J., Löfström, J.: Interpolation Spaces: An Introduction, vol. 223. Springer, Berlin (2012)
Sabapathy, K.K., Winter, A.: Non-Gaussian operations on bosonic modes of light: photon-added Gaussian channels. Phys. Rev. A 95, 062309 (2017)
O’Brien, J.L., Furusawa, A., Vučković, J.: Photonic quantum technologies. Nat. Photonics 3(12), 687–695 (2009)
Politi, A., Matthews, J.C.F., Thompson, M.G., O’Brien, J.L.: Integrated quantum photonics. IEEE J. Sel. Top. Quantum Electron. 15(6), 1673–1684 (2009)
Folland, G.B.: Harmonic Analysis in Phase Space. Princeton University Press, Princeton (1989)
Jagannathan, R., Simon, R., Sudarshan, E.C.G., Vasudevan, R.: Dynamical maps and nonnegative phase-space distribution functions in quantum mechanics. Phys. Lett. A 120(4), 161–164 (1987)
Durrett, R.: Probability: Theory and Examples. Cambridge Series in Statistical and Probabilistic Mathematics, 5th edn. Cambridge University Press, Cambridge (2019)
Kennard, E.H.: Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 44(4), 326–352 (1927)
Stoler, D.: Equivalence classes of minimum uncertainty packets. Phys. Rev. D 1, 3217–3219 (1970)
Yuen, H.P.: Two-photon coherent states of the radiation field. Phys. Rev. A 13, 2226–2243 (1976)
Winter, A.: Coding theorem and strong converse for quantum channels. IEEE Trans. Inf. Theory 45(7), 2481–2485 (1999)
Williamson, J.: On the algebraic problem concerning the normal forms of linear dynamical systems. Am. J. Math. 58(1), 141–163 (1936)
Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Applied mathematics series. Dover Publications, Mineola (1965)
Schrödinger, E.: Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschaften 14(28), 664–666 (1926)
Klauder, J.R.: The action option and a Feynman quantization of spinor fields in terms of ordinary c-numbers. Ann. Phys. (N.Y) 11(2), 123–168 (1960)
Glauber, R.J.: Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963)
Sudarshan, E.C.G.: Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 10, 277–279 (1963)
Lindeberg, J.W.: Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung. Math. Z. 15(1), 211–225 (1922)
Bryc, W.: A remark on the connection between the large deviation principle and the central limit theorem. Statist. Probab. Lett. 18(4), 253–256 (1993)
Bhattacharya, R.N., Rao, R.R.: Normal approximation and asymptotic expansions, vol. 64. SIAM, Philadelphia (1986)
Lami, L., Khatri, S., Adesso, G., Wilde, M.M.: Extendibility of bosonic Gaussian states. Phys. Rev. Lett. 123, 050501 (2019)
Devetak, I., Shor, P.W.: The capacity of a quantum channel for simultaneous transmission of classical and quantum information. Commun. Math. Phys. 256(2), 287–303 (2005)
Caruso, F., Giovannetti, V., Holevo, A.S.: One-mode bosonic Gaussian channels: a full weak-degradability classification. New J. Phys. 8(12), 310 (2006)
Wolf, M.M., Pérez-García, D., Giedke, G.: Quantum capacities of bosonic channels. Phys. Rev. Lett. 98, 130501 (2007)
Geršgorin, S.: Über die Abgrenzung der Eigenwerte einer Matrix. Izv. Akad. Nauk. S.S.S.R 7, 749–754 (1931)
Varga, R.S.: Geršgorin and his circles. Springer, Berlin (2010)
Bourin, J.-C., Lee, E.-Y.: Unitary orbits of Hermitian operators with convex or concave functions. Bull. Lond. Math. Soc. 44(6), 1085–1102 (2012)
Acknowledgements
ND would like to thank M. Jabbour for helpful discussions. LL acknowledges financial support from the European Research Council under the Starting Grant GQCOP (grant no. 637352) and from Universität Ulm; he is also grateful to V. Giovannetti, A. Holevo and K. Sabapathy for discussions on Lemma 16, and to M.B. Plenio and M. Wilde for sharing their thoughts on our model of optical fibre. SB thanks G. Baverez for interesting discussions on stable laws and gratefully acknowledges support by the EPSRC grant EP/L016516/1 for the University of Cambridge CDT, the CCA. CR acknowledges financial support from the TUM university Foundation Fellowship and by the DFG cluster of excellence 2111 (Munich Center for Quantum Science and Technology).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H.-T. Yau
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Standard Moments Versus Phase Space Moments: The Integer Case
In this appendix we prove that a state with finite standard moments of order up to k also has finite phase space moments of order up to k, i.e. Theorem 10. More precisely, we show that its characteristic function is differentiable k times, and that there are constants \(c_{k,m}(\varepsilon )<\infty \) such that the standard moments and phase space moments, defined by (31) and (33), respectively, satisfy \(M'_k(\rho ,\varepsilon )\le c_{k,m}(\varepsilon ) M_k(\rho )\) for all m-mode quantum states \(\rho \). We start with the following lemma.
Lemma 24
For all positive integers m and real numbers \(k\in [0,\infty )\), there is a universal constant \(d_{k,m}>0\) such that
where  and
and  are the position and momentum quadratures of the \(j^{\text {th}}\) mode.
are the position and momentum quadratures of the \(j^{\text {th}}\) mode.
Proof
First of all, it suffices to consider the one-mode case. Indeed, assume that \((a a^\dag )^{k/2}\ge d_k (|x|^k + |p|^k)\) for some \(d_k>0\). Then, leveraging the fact that the operators \(a_j a_j^\dag \) commute with each other, and employing standard inequalities between p-norms, we deduce that
Therefore, from now on we look at the one-mode case only. The vector space  of states with a finite expansion in the Fock basis is a core for both \(\left( a a^\dag \right) ^{k/2}\), as well as \(|x|^k\) and \(|p|^k\). Thus, it suffices for us to prove the inequality (A1) on states in \(V_m\).
of states with a finite expansion in the Fock basis is a core for both \(\left( a a^\dag \right) ^{k/2}\), as well as \(|x|^k\) and \(|p|^k\). Thus, it suffices for us to prove the inequality (A1) on states in \(V_m\).
It is enough to show that \((a a^\dag )^{k/2} \ge d_k |x|^k\) for some constants \(d_k>0\), as the other inequality \((a a^\dag )^{k/2} \ge d_k |p|^k\) is obtained by performing a phase space rotation of an angle \(\pi /2\), i.e. by conjugating both sides by the unitary operator \(e^{i\frac{\pi }{2}\, a a^\dag }\).
We now prove that the inequality \((a a^\dag )^{k/2}\ge d_k |x|^k\) holds for some \(d_k>0\) on all vectors in \(V_m\). Write \(k = 2r h\), where \(r\in (0,1]\) and  . Since the function \(A\mapsto A^r\) is well known to be operator monotone [46, Proposition 10.14], it suffices to show that \((a a^\dag )^{h}\ge d_h x^{2h}\) for all non-negative integers \(h\in \mathbb {N}_0\). To this end, let us take advantage of our restriction to states with a finite expansion in the Fock basis. Defining \(\Pi _N\) as the projector onto the span of the first \(N+1\) Fock states (from 0 to N), we have to show that
. Since the function \(A\mapsto A^r\) is well known to be operator monotone [46, Proposition 10.14], it suffices to show that \((a a^\dag )^{h}\ge d_h x^{2h}\) for all non-negative integers \(h\in \mathbb {N}_0\). To this end, let us take advantage of our restriction to states with a finite expansion in the Fock basis. Defining \(\Pi _N\) as the projector onto the span of the first \(N+1\) Fock states (from 0 to N), we have to show that

where the inequality now involves only matrices. Thanks to Gershgorin’s circle theorem [87, 88], in order to show that \(A_N\) is positive semi-definite, it suffices to prove that \(A_N\) is diagonally dominant, i.e. that for all N and \(0\le n\le N\) the inequality
holds true. Writing down the left-hand side yields

Here, in 1 we extended the sum over \(n'\) to all values that yield a non-vanishing result, i.e. those that satisfy \(|n-n'|\le 2h\). In 2 we used the canonical commutation relations (7) to expand
In 3 we applied standard estimates for factorials: for example, when \(n\le n'\le n+2h\) we used the fact that \(n^\ell \sqrt{\frac{n'!}{n!}}\le n^\ell (n')^{(n'-n)/2}\le (n')^{\ell +(n'-n)/2}\le (n')^{2h}\le (n+2h)^{2h}\); moreover, we defined  . Finally, 4 follows by choosing e.g. \(d_h^{-1}=(2h+1)^{h} F_h\). Since (A2) holds for all n, we conclude that \(A_N\ge 0\) for all N, which completes the proof. \(\quad \square \)
. Finally, 4 follows by choosing e.g. \(d_h^{-1}=(2h+1)^{h} F_h\). Since (A2) holds for all n, we conclude that \(A_N\ge 0\) for all N, which completes the proof. \(\quad \square \)
Remark
The inequality in Lemma 24 depends critically on the special properties of the canonical operators. In fact, there is no universal constant \(d_k>0\) that makes the general relation \((A+B)^k\ge d_k\left( A^k+B^k\right) \) true for all positive matrices \(A,B\ge 0\). To see why this is the case, it suffices to consider two pure states  and
and  . Setting
. Setting  , it can be shown that the minimal eigenvalue of \((A+B)^k\) is \(\lambda ^k\), while that of \(A^k+B^k=A+B\) is clearly \(\lambda \). By Weyl’s principle, the conjectured matrix inequality would imply that \(\lambda ^k\ge d_k \lambda \) for all \(\lambda \in [0,1]\), absurd.
, it can be shown that the minimal eigenvalue of \((A+B)^k\) is \(\lambda ^k\), while that of \(A^k+B^k=A+B\) is clearly \(\lambda \). By Weyl’s principle, the conjectured matrix inequality would imply that \(\lambda ^k\ge d_k \lambda \) for all \(\lambda \in [0,1]\), absurd.
Proposition 25
Let \(k\ge 0\) and \(m\ge 1\) be integers; also, let \(\varepsilon >0\) be given. Then, there is a constant \(c_{k,m}(\varepsilon )<\infty \) such that every m-mode quantum state \(\rho \) with finite k-moments \(M_k(\rho )\), as defined by (31), also satisfies
In particular, according to (33), \(\rho \) has finite phase space moments of order up to k.
Proof
Let \(\rho \) be an m-mode quantum state. We start by considering the modified state  that is obtained by convolving it with the (multi-mode) vacuum state according to the rule (37) (for \(\lambda =1/2\)). A first important observation is that the moments of \(\sigma \) and \(\rho \) are related. Namely,
that is obtained by convolving it with the (multi-mode) vacuum state according to the rule (37) (for \(\lambda =1/2\)). A first important observation is that the moments of \(\sigma \) and \(\rho \) are related. Namely,
To see why, we pick a multi-index \(n\in \mathbb {N}_0^m\) and evaluate the \(n^{\text {th}}\) diagonal entries of \(\sigma \) with respect to the Fock basis. We obtain that

Here, in 1 we introduced the dephasing operator in the Fock basis, whose action is given by  . In 2 we observed that \(\Delta (\omega \boxplus \delta ) = \Delta (\omega )\boxplus \delta \) for all m-mode quantum states \(\omega \) whenever \(\delta =\Delta (\delta )\) is already diagonal in the Fock basis. To show this, first exploit linearity and factorisation of \(\Delta \) to reduce to the one-mode case. Then, use the representation \(\Delta (X)=\int _0^{2\pi } \frac{d\varphi }{2\pi }\, e^{i \varphi \, a^\dag a} X\, e^{-i \varphi a^\dag a}\), valid for bounded X and where the integrals are as usual weakly converging, and remember that \(e^{i\varphi \left( a^\dagger a+b^\dag b\right) }=e^{i\varphi a^\dagger a} \otimes e^{i\varphi b^\dag b}\) is a function of the total Hamiltonian and thus commutes with the action of the beam splitter. The identity in 3 follows from the formula
. In 2 we observed that \(\Delta (\omega \boxplus \delta ) = \Delta (\omega )\boxplus \delta \) for all m-mode quantum states \(\omega \) whenever \(\delta =\Delta (\delta )\) is already diagonal in the Fock basis. To show this, first exploit linearity and factorisation of \(\Delta \) to reduce to the one-mode case. Then, use the representation \(\Delta (X)=\int _0^{2\pi } \frac{d\varphi }{2\pi }\, e^{i \varphi \, a^\dag a} X\, e^{-i \varphi a^\dag a}\), valid for bounded X and where the integrals are as usual weakly converging, and remember that \(e^{i\varphi \left( a^\dagger a+b^\dag b\right) }=e^{i\varphi a^\dagger a} \otimes e^{i\varphi b^\dag b}\) is a function of the total Hamiltonian and thus commutes with the action of the beam splitter. The identity in 3 follows from the formula

for the convolution of a Fock state with the vacuum. Here, \(\ell ,\ell '\in \mathbb {N}_0^m\) are multi-indices, ordered entry-wise, and  . The above expression can be obtained easily e.g. by first reducing to the one-mode case, and then by induction on \(\ell \), employing the relations (35). Computing the \(k^{\text {th}}\) moment of \(\sigma \) then yields
. The above expression can be obtained easily e.g. by first reducing to the one-mode case, and then by induction on \(\ell \), employing the relations (35). Computing the \(k^{\text {th}}\) moment of \(\sigma \) then yields

Here, 4 and 7 follow from the representation in (32); in 5 we rearranged a double series of non-negative terms, and in 6 we observed that for a given \(\ell \in \mathbb {N}_0^m\) the coefficients  form a probability distribution over the set of multi-indices \(n\in \mathbb {N}_0^m\) with \(n\le \ell \). This proves that the \(k^{\text {th}}\) moments of \(\sigma \) are upper bounded by those of \(\rho \).
form a probability distribution over the set of multi-indices \(n\in \mathbb {N}_0^m\) with \(n\le \ell \). This proves that the \(k^{\text {th}}\) moments of \(\sigma \) are upper bounded by those of \(\rho \).
The state \(\sigma \) is also useful because its characteristic function is a close relative of that of \(\rho \). Namely, according to (38) we have that \(\chi _\sigma (z) = \chi _\rho (z/\sqrt{2})\, e^{-\Vert z\Vert ^2/4}\), and hence
for some constants \(g_{k,m}(\varepsilon )\). Thus, it suffices to find a suitable upper estimate for the norm \(\left\| \chi _\sigma \right\| _{C^{k}\left( B(0,\varepsilon )\right) }\). By Lemma 16, the Fourier transform of \(\chi _\sigma \), i.e. the Wigner function \(W_\sigma \) of \(\sigma \), is everywhere non-negative. Hence, \(\chi _\sigma \) can be seen as the characteristic function of a classical random variable Z over \(\mathbb {C}^m\), with probability density function \(W_\sigma \). If we show that Z has finite absolute moments of order k, then thanks to [61, Theorem 1.8.15] we deduce that \(\chi _\sigma \) is k-fold differentiable everywhere, and since
for all multi-indices \(\alpha ,\beta \in \mathbb {N}_0^m\), we in fact have that

Therefore, we now look at the quantity \(L_k(\sigma )\). For a vector \(u=u_R+ i u_I\in \mathbb {C}^m\), with \(u_R,u_I\in {\mathbb {R}}^m\), we observe that
Thus,

In the above derivation, the identity in 8 can be verified by first reducing to the case of a pure \(\sigma \), which can be done by linearity and by multiple applications of Tonelli’s theorem, and by subsequently remembering that for a pure state \(|\psi _f>\) with wave function \(f\in L^2({\mathbb {R}}^m)\) it holds e.g. that \(\int d^m u_I\, W_{|\psi _f> <\psi _f|}(u) = \sqrt{2} \left| f(\sqrt{2}\, u_R)\right| ^2\). The inequality in 9 is just an application of Lemma 24. Finally, in 10 we introduced a suitable constant \(c'_{k,m}\ge 1\).
Combining the above estimate with (A4), (A6), and (A3), we deduce that

which concludes the proof. \(\quad \square \)
Appendix B: Standard Moments Versus Phase Space Moments: The Fractional Case
In the last section, we showed that the \(k^{\text {th}}\) phase space moment was controlled by the \(k^{\text {th}}\) standard moment in the case of an integer constant k.
Here, we show that this fact still holds when k is a positive real number by an interpolation argument. In principle, we could conclude this fact from the setting of Proposition 25, using that for \(L^p(w_0)\) spaces with weight function \(w_0\) and \(L^p(w_1)\) spaces with weight function \(w_1\), the real interpolation spaces [63, Theorem 5.4.1] satisfy
where \(w_{\theta }:=w_0^{1-\theta }w_1^{\theta }\). This would allow us to extend the estimate in (A5) to fractional powers as well. However, we want to establish the stronger result that shows that the moments themselves naturally induce an interpolating family of normed spaces. That is, we show the following:
Proposition 26
Let \(\rho \) be an m-mode quantum state and \(k\ge 0\). If \({\text {Tr}}\left[ \rho \left( \sum \nolimits _{j} a_ja_j^\dagger \right) ^{k/2}\right] <\infty \), then \(\Vert \chi _\rho \Vert _{C^k(B(0,{\varepsilon }))}<\infty \) for some \({\varepsilon }>0\). Moreover,
for some constant \(C_{\varepsilon }>0\).
We have seen in Appendix 8.3 that the map \(\rho \mapsto \chi _\rho \) is bounded from  to \(C^k(B(0,{\varepsilon }))\) for any k integer. Since the spaces \(C^k(B(0,{\varepsilon }))\) form an interpolation family, meaning that for any \(k_0,k_1\in \mathbb {N}_0\) with \(k_1:=k_0+1\), \(C^{(1-\theta ) k_0+\theta k_1}(B(0,{\varepsilon }))=(C^{k_0}(B(0,{\varepsilon })),C^{k_1}(B(0,{\varepsilon })))_\theta \), we have from the previously mentioned interpolation method that
to \(C^k(B(0,{\varepsilon }))\) for any k integer. Since the spaces \(C^k(B(0,{\varepsilon }))\) form an interpolation family, meaning that for any \(k_0,k_1\in \mathbb {N}_0\) with \(k_1:=k_0+1\), \(C^{(1-\theta ) k_0+\theta k_1}(B(0,{\varepsilon }))=(C^{k_0}(B(0,{\varepsilon })),C^{k_1}(B(0,{\varepsilon })))_\theta \), we have from the previously mentioned interpolation method that

for some positive constant \(C_{\varepsilon }\) that comes from the bounds derived in Sect. 8.3 for \(k_0\) and \(k_1\). It only remains to prove that the interpolated norms  can further be bounded above by \(\Vert \rho \Vert _{\mathcal {W}^{(1-\theta )k_0+\theta k_1,1}}\). First, we recall a useful technical lemma [89, Lemma 3.4].
can further be bounded above by \(\Vert \rho \Vert _{\mathcal {W}^{(1-\theta )k_0+\theta k_1,1}}\). First, we recall a useful technical lemma [89, Lemma 3.4].
Lemma 27
Let \(T= \begin{pmatrix} T_{11} &{} T_{21} \\ T_{21}^\dagger &{} T_{22} \end{pmatrix}\) be a positive semi-definite trace class operator such that \(T_{11}:\mathbb {C}^d \rightarrow \mathbb {C}^d\), then
Proof of Proposition 26
We provide the proof only for \(m=1\), since the general case follows similarly. First, observe that
First, we restrict attention to states \(\rho \) that are orthogonal in the Fock basis. We then write \(\Pi _E\) for the spectral projection onto the Fock states of energy at most E, that is  . Next, we fix two parameters \(0\le k_0\le k_1\) and introduce the quantity \(\gamma _n:= (n+1)^{(k_1-k_0)/2}\), fix a parameter \(t>0\), define \(N_0(t) \in \mathbb N\) such that
. Next, we fix two parameters \(0\le k_0\le k_1\) and introduce the quantity \(\gamma _n:= (n+1)^{(k_1-k_0)/2}\), fix a parameter \(t>0\), define \(N_0(t) \in \mathbb N\) such that
the two operators
and \(\rho \equiv \rho _{{\text {diag}}}(t):=X_0(t)+X_1(t).\) Using these two operators we start estimating

where \(\alpha _n=\delta _{n > N_0(t)}\) and \(\beta _n =\delta _{n \le N_0(t)}\) with Kronecker delta \(\delta \). Thus, we obtain for the norm  the upper bound
the upper bound

We now recall that for \(\gamma _n \le t^{-1}\) we have \(\alpha _n=0\) and \(\beta _n=1\) such that
For \(\gamma _n > t^{-1}\) we have \(\alpha _n=1\) and \(\beta _n=0\) such that
Thus, in either case, we have the estimate

This shows that for arbitrary density operators

To extend the bound to a density operator \(\rho \) that is not diagonal in the Fock basis, and not only for the diagonal \(\rho _{{\text {diag}}}(t) \), we partition \(\rho \) as
and a self-adjoint diagonal operator \(S^{(k)}(t):={\text {diag}}\left( S_1^{(k)}(t),S_2^{(k)}(t) \right) \) where \(S_1^{(k)}(t):= \Pi _{N_0(t)}(aa^{\dagger })^{k/4}\Pi _{N_0(t)}\) and \(S_2^{(k)}(t):=(I-\Pi _{N_0(t)})(aa^{\dagger })^{k/4}(I-\Pi _{N_0(t)}).\) This implies that
Let then \(S_1^{(k)}(t):= \Pi _{N_0(t)}(aa^{\dagger })^{k/4}\Pi _{N_0(t)}\) and \(S_2^{(k)}(t):=(I-\Pi _{N_0(t)})(aa^{\dagger })^{k/4}(I-\Pi _{N_0(t)}).\) The previous Lemma 27 then shows that
From here, we examine three cases separately:
-
Case 1: \(\Vert T_{11}^{(k_1)} \Vert _1 \ge \Vert T_{22}^{(k_1)} \Vert _1.\) In this case, we find from choosing \(X_0:=\rho _{21}\) and \(X_1:=0\) in (53)

-
Case 2: \(\Vert T_{22}^{(k_0)} \Vert _1 \ge \Vert T_{11}^{(k_0)} \Vert _1\) In this case, we find from choosing \(X_0:=0\) and \(X_1:=\rho _{21}\) in (53)

-
Case 3: \(\Vert T_{22}^{(k_0)} \Vert _1 \le \Vert T_{11}^{(k_0)} \Vert _1\) and \(\Vert T_{22}^{(k_1)} \Vert _1 \ge \Vert T_{11}^{(k_1)} \Vert _1\) In this case, we find from choosing \(X_0=\rho _{21}/2\) and \(X_1= \rho _{21}/2\) in (53) that
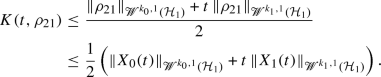 (B3)
(B3)
Hence, we have altogether that

which implies that

The result follows from the interpolation bound (B1).
\(\square \)
Appendix C: Standard Moments Versus Phase Space Moments: A Partial Converse
We now show that at least for even integers k, the existence of \(k^{\text {th}}\) order phase space moments implies the existence of standard moments of the same order.
Theorem 28
Let \(\rho \) be an m-mode quantum state such that its characteristic function \(\chi _{\rho }\) is 2k times totally differentiable at \(z=0\) for some integer k, then the \(2k^{\text {th}}\) standard moment is finite as well.
Proof
For simplicity, we restrict attention to \(m=1\). Let  and
and  be two Hamiltonians, and consider the spectral decomposition of the density operator
be two Hamiltonians, and consider the spectral decomposition of the density operator  . Then, there exist unique probability measures \(\mu _{e_i}\) such that
. Then, there exist unique probability measures \(\mu _{e_i}\) such that
We then define the new probability measure  such that
such that
We now proceed with an induction argument. Start by noting that for \(k=0\) the result holds. For \(k \ge 1\), define the auxiliary function \(\varphi :\mathbb {R} \rightarrow \mathbb {C}\) as

which is by assumption 2k times differentiable at zero and let \(u(t)=\mathfrak {R}\varphi (t)\). Then, u is also 2k times differentiable at zero. Since \(\varphi ^{2k}(0)\) exists, for \(t \in (-\varepsilon , \varepsilon )\), with sufficiently small \(\varepsilon >0\), the function \(t \mapsto \varphi ^{(2k-1)}(t)\) exists and is continuous.
We record that Taylor’s formula implies that for \(t \in (-\varepsilon ,\varepsilon )\)
where odd derivatives vanish at zero, since u is even.
We then define a positive continuous function \(f_k: {\mathbb {R}}\rightarrow [0,\infty )\) with \(f_k(0)=1\) and for \(t\ne 0\) as

From Taylor’s formula above we obtain the following estimate for t sufficiently small

Then, we have from Fatou’s lemma
Using integration by parts and standard estimates only, it is straightfroward to verify that the finiteness of both \({\text {Tr}}\left[ \rho \,H_{{{\text {lin}}}^{\pm }}^{2k}\right] \) implies the finiteness of \({\text {Tr}}\left[ \rho (aa^{\dagger })^{k}\right] \). \(\quad \square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Becker, S., Datta, N., Lami, L. et al. Convergence Rates for the Quantum Central Limit Theorem. Commun. Math. Phys. 383, 223–279 (2021). https://doi.org/10.1007/s00220-021-03988-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-03988-1




 for all
for all 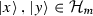 ;
;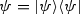 and thermal Gaussification
and thermal Gaussification 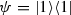 and for
and for 



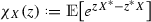 .
.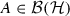 for which
for which 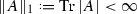 .
.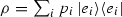 is the spectral decomposition of
is the spectral decomposition of  , where
, where  and
and  are the spectral decompositions of
are the spectral decompositions of  .
.