Abstract
In this paper, we consider a non-linear fourth-order evolution equation of Cahn–Hilliard-type on evolving surfaces with prescribed velocity, where the non-linear terms are only assumed to have locally Lipschitz derivatives. High-order evolving surface finite elements are used to discretise the weak equation system in space, and a modified matrix–vector formulation for the semi-discrete problem is derived. The anti-symmetric structure of the equation system is preserved by the spatial discretisation. A new stability proof, based on this structure, combined with consistency bounds proves optimal-order and uniform-in-time error estimates. The paper is concluded by a variety of numerical experiments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper studies non-linear fourth-order evolution equations of Cahn–Hilliard-type on evolving surfaces with prescribed surface velocity. The nonlinearities and their derivatives are only assumed to satisfy locally Lipschitz-type assumptions. The Cahn–Hilliard-type equation is formulated as a system of second-order equations, exhibiting an anti-symmetric structure:
The semi-discretisation of the system by high-order evolving surface finite elements, cf. [15, 27], preserves this anti-symmetric structure, which is utilised to prove a convergence result, via a new stability proof exploiting this structure. Optimal-order uniform-in-time error estimates in the \(L^2\) and \(H^1\) norms (depending on the \(\nabla _{\Gamma (t)} u\)-dependence of the nonlinearities) for both solution variables are proved.
Cahn and Hilliard first described an equation modelling phase separation processes in [9]. Since then it found many applications in an evolving surface setting as well: [40] investigates the asymptotic limit, and the effect of a mobility term leading to a degenerate Cahn–Hilliard equation. In [5] a discretisation of a coupled Cahn–Hilliard/Navier–Stokes system for lipid bilayer membranes is studied. In [41] the authors simulated lateral phase separation and coarsening in biological membranes by comparing surface Cahn–Hilliard and surface Allen–Cahn equations using unfitted finite elements. In [42] a model of lateral phase separation in a two component material surface is presented. In [43] a model for phase transitions on deforming surfaces is studied using isogeometric finite elements. For singular non-linearities, well-posedness and global-in-time existence results are established in the recent preprint [8]. A review of the planar case is found, e.g. in [21].
The Cahn–Hilliard equation on a stationary surface with boundary was first investigated by Du et al. [13]. They study a full discretisation of the Cahn–Hilliard equation with homogeneous Dirichlet boundary conditions, and prove optimal-order error estimates in the \(L^2\) norm for u, using linear finite elements.
Elliott and Ranner were the first to consider the Cahn–Hilliard equation on a closed evolving surface with a prescribed velocity in [22]. They proved optimal-order uniform-in-time error estimates in the \(L^2\) and \(H^1\) norms for the concentration difference and optimal-order \(L^2\)-in-time error estimates in the \(L^2\) and \(H^1\) norms for the chemical potential using a discretisation by linear evolving surface finite elements. Using a new stability proof, the results of this paper improve the error estimates for the chemical potential from optimal-order \(L^2\)-in-time to optimal-order uniform-in-time estimates.
In [41, 42] phase separation on dynamic membranes was approximated by a mixed finite difference–finite element discretisation of the Cahn–Hilliard equation on evolving surfaces.
The main results of this paper are stability and optimal-order uniform-in-time semi-discrete error estimates for the evolving surface non-linear Cahn–Hilliard-type equations: (a) in the \(H^1\) norm if the nonlinearities depend on u and \(\nabla _{\Gamma }u\), requiring at least quadratic finite elements, and (b) both in the \(L^2\) and \(H^1\) norms if both nonlinearities are independent of the surface gradient, using finite elements of degree \(k \ge 1\). Convergence is proved via a new stability estimate and showing consistency of the semi-discretisation.
The rather general model (1.1) includes the Cahn–Hilliard equation with proliferation terms [37, equation (3.1)], with advection terms on the surface cf. [34], the generalised Cahn–Hilliard-type equation of Cherfils et al. [10, equation (1.7)], see also [14, 38] and the reference therein for theoretical results, and the generalised Cahn–Hilliard equation from [26], etc. To correct mesh deformations of the evolving discrete surface arbitrary Lagrangian–Eulerian (ALE) methods have been proposed and analysed, see, e.g. [20, 33], the correcting advection-like term with the tangential ALE velocity also fit into the framework of (1.1).
Another main contribution of the paper is a new stability proof based on multiple energy estimates (summarised in Fig. 1). The main idea is to exploit the anti-symmetric structure of the second-order system corresponding to the Cahn–Hilliard(-type) equation. The generality of the stability proof can also be seen through the related results in [25, 29]. A further advantage of this stability proof, is that we strongly expect it to translate to proving stability and convergence of full discretisations using linearly implicit backward difference formulae. This is, however, beyond the scope of this paper.
In the presented stability analysis, the difference between the Ritz map of the exact solution and the numerical solution is estimated in terms of defects and their time derivatives. To account for initial errors in the chemical potential, a modification of the semi-discrete system is required. The stability proof uses energy estimates, performed in the matrix–vector formulation, and utilises the anti-symmetric structure of the error equations, testing the error equations with the errors and also with their time derivatives. The stability analysis was first developed for Willmore flow in [29]. A uniform-in-time \(L^\infty \) bound for the numerical solution is key to estimate the non-linear term. It is obtained from the time-uniform \(H^1\) norm error bounds using an inverse estimate and exists for a small time due to a continuous initial function. The stability proof is independent of geometric errors.
In the consistency analysis the \(L^2\) norms of the defects and their time derivatives are estimated. The bounds use geometric error estimates, including interpolation and Ritz map error estimates, bounds on the discrete surface velocity, and geometric approximation errors for high-order evolving surface finite elements, see [27].
The paper is structured as follows. In Sect. 2, based on the papers [15, 22], the weak formulation for the Cahn–Hilliard equation on evolving surfaces is derived as a system of equations. In Sect. 3 the evolving surface finite element method is used to discretise this system of equations in space. The obtained semi-discrete problem is written as a matrix–vector formulation. In Sect. 4 the novel error estimates proved in this work are stated and discussed in comparison to the existing results by Elliott and Ranner [22]. Section 5 contains the stability part of the proof. Section 6 treats the consistency part of the proof. In Sect. 7 the two parts are combined to prove the main result. In Sect. 8 a full discretisation to the problem is given, cf. [1, 2]. In Sect. 9 the theoretical results are complemented by numerical experiments.
2 Cahn–Hilliard equation on evolving surfaces
In the following we consider a smoothly evolving closed surface \(\Gamma (t)\subset \mathbb {R}^{d+1}\), with \(d = 1,2\), for \(0 \le t \le T\). The initial surface \(\Gamma (0) = \Gamma ^0\) is given (and at least \(C^2\)), and it evolves with the given and sufficiently smooth velocity v. The surface \(\Gamma (t)\) is given as the image of a smooth mapping \(X\,{:}\,\Gamma ^0 \times [0,T] \rightarrow \mathbb {R}^{d+1}\), by \(\Gamma (t)= \{X(p,t) \mid p \in \Gamma ^0 \}\). The embedding X and the velocity v satisfy the ordinary differential equation (ODE):
Let \(\nu \) denote the unit outward normal vector to \(\Gamma (t)\). Then the surface (or tangential) gradient on \(\Gamma (t)\), of a function \(u : \Gamma (t)\rightarrow \mathbb {R}\), is denoted by \(\nabla _{\Gamma (t)} u\), and is given by \(\nabla _{\Gamma (t)} u = \nabla {\bar{u}} -( \nabla {\bar{u}} \cdot \nu ) \nu \) (the surface gradient is independent of the extension \({\bar{u}}\) into a small neighbourhood of \(\Gamma (t)\)), while the Laplace–Beltrami operator on \(\Gamma (t)\) is given by \(\Delta _{\Gamma (t)} u = \nabla _{\Gamma (t)} \cdot \nabla _{\Gamma (t)} u\). Moreover, \(\partial ^{\bullet }u\) denotes the material derivative of u, i.e. \(\partial ^{\bullet }u(\cdot ,t) = {\mathrm{d}}/ {\mathrm{d}}t (u(X(\cdot ,t),t)) = \partial _t {\bar{u}}(\cdot ,t) + v \cdot \nabla \bar{u}(\cdot ,t)\). The space–time manifold will be denoted by \(\mathcal {G}_T= \cup _{t \in [0,T]} \Gamma (t)\times \{t\}\). For more details on these notions we refer to [12, 15, 16, 27].
In this paper we consider the general non-linear Cahn–Hilliard-type equation on evolving surfaces. It is a second-order system of partial differential equations for scalar functions \(u, w: \mathcal {G}_T\rightarrow \mathbb {R}\) given by
with continuous (and sufficiently regular) initial condition \(u(\cdot ,0) = u^0\) on the initial surface \(\Gamma ^0\). The scalar functions \(f,g:\mathbb {R}\times \mathbb {R}^d \rightarrow \mathbb {R}\) and their derivatives \(\partial _i f, \partial _i g\) are only assumed to be locally Lipschitz continuous. A typical example is a double-well potential, i.e. for the Cahn–Hilliard equation sets \(f(u) = 0\) and \(g(u) = \frac{1}{4}((u^2 - 1)^2)'\). In this case, the solution \(u \in [-1,1]\) models the concentration of surfactant fluids, with \(u=\pm 1\) indicating the pure occurrences of each, cf. [9].
The classical Cahn–Hilliard equation on a stationary surface \(\Gamma \) can be derived as the \(H^{-1}(\Gamma )\) gradient flow of the Ginzburg–Landau energy
cf. [22, Remark 2.1]. In [22] it is stated, that to obtain a gradient flow on an evolving surface, a model for the surface velocity v is needed, leading to a coupled system for u and v. In the evolving surface case, \(w = - \Delta _{\Gamma (t)} u + f(u)\) (with \(f = F'\)) is the variation of the evolving surface Ginzburg–Landau energy, see [40].
2.1 Weak formulation
On the evolving surface \(\Gamma (t)\) we recall the definition of standard Sobolev spaces \(L^2(\Gamma (t))\), and \(H^1(\Gamma (t))\) and its high-order variants, endowed with their usual norms, see [15, 17]. We also refer to [3, 4] for the definition of space–time function spaces.
The weak formulation of the Cahn–Hilliard system (2.2) reads: Find \(u(\cdot ,t) \in H^1(\Gamma (t))\) with a continuous-in-time material derivative \(\partial ^{\bullet }u(\cdot ,t) \in L^2(\Gamma (t))\) and \(w(\cdot ,t) \in H^1(\Gamma (t))\) such that for all test functions \(\varphi ^u(\cdot ,t) \in H^1(\Gamma (t))\) and \(\varphi ^w(\cdot ,t) \in H^1(\Gamma (t))\)
with initial data \(u(\cdot ,0) = u_0\) on \(\Gamma ^0\).
It is important to note here that the anti-symmetric structure of the above systems (2.2) and (2.4) will serve as a key property which will be heavily used in the stability analysis.
Using the Leibniz formula [15], an equivalent weak form reads as: Find \(u(\cdot ,t) \in H^1(\Gamma (t))\) with a continuous-in-time material derivative \(\partial ^{\bullet }u(\cdot ,t) \in L^2(\Gamma (t))\) and \(w(\cdot ,t) \in H^1(\Gamma (t))\) such that for all test functions \(\varphi ^u(\cdot ,t) \in H^1(\Gamma (t))\), with \(\partial ^{\bullet }\varphi ^u(\cdot ,t) = 0\), and \(\varphi ^w(\cdot ,t) \in H^1(\Gamma (t))\)
We note that as solution spaces for the weak problems one can equivalently use space–time Hilbert spaces, as it was done in [22, Definition 2.1] (denoted, e.g. by \(L^\infty _{H^1}\) and \(L^2_{H^1}\) therein). For more details on these spaces we refer to [3, 4, 23].
2.2 Abstract formulation
We will use the time-dependent bilinear forms, cf. [16, 17], for any \(u, \varphi \in H^1(\Gamma (t))\):
We further define \(a^*(t;\cdot ,\cdot ) := a(t;\cdot ,\cdot ) + m(t;\cdot ,\cdot )\). All bilinear forms are symmetric in u and \(\varphi \), m and \(a^*\) are positive definite, while a is positive semi-definite. Whenever it is possible, without confusion, we will omit the omnipresent time-dependence of the bilinear forms and write \(m(\cdot ,\cdot )\) instead of \(m(t;\cdot ,\cdot )\).
We note here that the bilinear forms directly generate the (semi-)norms, for any \(u \in H^1(\Gamma (t))\):
The weak formulation (2.4) is rewritten, using the bilinear forms from above, as
and (2.5) is rewritten as
The transport formula for the above bilinear forms, [17, Remark 3.3], is used later on, and reads, for any \(u(\cdot ,t), \varphi (\cdot ,t) \in L^2(\Gamma (t))\) with \(\partial ^{\bullet }u(\cdot ,t), \partial ^{\bullet }\varphi (\cdot ,t) \in L^2(\Gamma (t))\) for all \(0\le t\le T\):
3 Semi-discretisation on evolving surfaces
For the numerical solution of the above examples we consider a high-order evolving surface finite element method. In the following, from [12, 15, 16, 27], we briefly recall the construction of the discrete evolving surface, the high-order evolving surface finite element space, the lift operation, and the discrete bilinear forms, etc., which are used to discretise the Cahn–Hilliard equation of Sect. 2.
3.1 Evolving surface finite elements
The smooth initial surface \(\Gamma (0)\) is approximated by a k-order interpolating discrete surface, (a continuous, piecewise polynomial interpolation of \(\Gamma (0)\) of degree k over a reference element), denoted by \(\Gamma _h(0) := \Gamma _h^k(0)\), with vertices \(p_j \in \Gamma (0)\), \(j=1,\ldots ,N\), and is given by the (high-order) triangulation, with maximal mesh width h. In the following, we refer to \(\Gamma _h\) as a triangulation, and to the Lagrange points \(p_j\) as nodes. More details and the properties of such a discrete high-order initial surface are found in [12, Section 2] and [27, Section 3].
The triangulation of the surface \(\Gamma (t)\), denoted by \(\Gamma _h(t):= \Gamma _h^k(t)\), is obtained by integrating the ODE (2.1) (with the known velocity v) from time 0 to t for all the nodes \(p_j\) of the initial (high-order) triangulation. The nodes \(x_j(t)\) are on the exact surface \(\Gamma (t)\) for all times. The discrete surface \(\Gamma _h(t)\) remains to be an interpolation of \(\Gamma (t)\) for all times. We always assume that the evolving (high-order) triangles are forming an admissible triangulation of the surface \(\Gamma (t)\), which includes quasi-uniformity, and that the discrete surface is not a global double covering, cf. Section 5.1 of [15]. For more details (e.g. on time-uniformity of geometric bounds) we refer to [27, Section 3].
The discrete tangential gradient on the discrete surface \(\Gamma _h(t)\), of a function \(\varphi _h: \Gamma _h(t)\rightarrow \mathbb {R}\), is given by \(\nabla _{\Gamma _h(t)} \varphi _h = \nabla { {\bar{\varphi }}_h} - (\nabla { {\bar{\varphi }}_h} \cdot \nu _h) \nu _h\), understood in an element-wise sense, with \(\nu _h\) denoting the normal to \(\Gamma _h(t)\). (The discrete tangential gradient is independent of the arbitrary smooth extension \({\bar{\varphi }}_h\) onto a small neighbourhood of \(\Gamma _h(t)\).)
The high-order evolving surface finite element space \(S_h(t)\nsubseteq H^1(\Gamma (t))\) on \(\Gamma _h(t)\) is spanned by continuous, piecewise linear nodal basis functions on \(\Gamma _h(t)\) satisfying for each node \((x_j(t))_{j=1}^N\)
The finite element space is given as
The discrete velocity \(V_h\) of the surface \(\Gamma _h(t)\) is the evolving surface finite element interpolation of the surface velocity v of \(\Gamma (t)\), i.e.
The discrete material derivative is, for \(0 \le t \le T\), given by
independent of \({\bar{\varphi }}_h\) as an arbitrary smooth extension of \(\varphi _h\) onto a small neighbourhood of \(\Gamma _h (t)\). The key transport property of basis functions derived in Proposition 5.4 in [15], is
3.2 Lift
Following [12, 15], we define the lift operator \(\cdot ^\ell \) to compare functions on \(\Gamma _h(t)\), with a sufficiently small \(h \le h_0\) (such that \(\Gamma _h(t)\) is in a sufficiently small neighbourhood of \(\Gamma (t)\)), with functions on \(\Gamma (t)\). For functions \(\varphi _h:\Gamma _h(t)\rightarrow \mathbb {R}\), we define the lift as
where \(y=y(x,t) \in \Gamma (t)\) is the unique point on \(\Gamma (t)\) with \(x-y\) orthogonal to the tangent space \(T_y\Gamma (t)\). The inverse lift \(\varphi ^{-\ell }:\Gamma _h(t)\rightarrow \mathbb {R}\) denotes a function whose lift is \(\varphi :\Gamma (t)\rightarrow \mathbb {R}\). Finally, the lifted finite element space is denoted by \(S_h^\ell (t)\), and is given as
3.3 Discrete bilinear forms
The time-dependent discrete bilinear forms on \(S_h(t)\), i.e. the discrete counterparts of m, a and g, are given, for any \(u_h,\varphi _h \in S_h(t)\), by
As in the continuous case we let \(a_h^*(t;\cdot ,\cdot ) := a_h(t;\cdot ,\cdot ) + m_h(t;\cdot ,\cdot )\). The discrete bilinear forms, clearly inherit the properties of their continuous counterparts, such as the transport formula (2.9), see, e.g. [17, 27].
As in the continuous case, the discrete bilinear forms directly generate the discrete (semi-)norms, for any \(u_h \in S_h(t)\),
According to [12, 15], the discrete norms and their continuous counterparts are h-uniformly equivalent, for any \(\varphi _h \in S_h(t)\) and \(1 \le q \le \infty \),
3.4 Semi-discrete problem
The semi-discrete problem corresponding to the Cahn–Hilliard equation (2.4) reads: Find a solution \(u_h(\cdot ,t) \in S_h(t)\) with continuous-in-time discrete material derivative \(\partial ^{\bullet }_h u_h(\cdot ,t) \in S_h(t)\) and \(w_h(\cdot ,t) \in S_h(t)\) such that for all test functions \(\varphi _h^u(\cdot ,t) \in S_h(t)\) and \(\varphi _h^w(\cdot ,t) \in S_h(t)\)
with given initial data \(u_h(\cdot ,0) = u_h^0\) on \(\Gamma _h^0\).
Equivalently, the semi-discrete problem corresponding to the weak form (2.5), using the discrete version of the transport formula (2.9) for (3.7a), reads: Find a solution \(u_h(\cdot ,t) \in S_h(t)\) with continuous-in-time discrete material derivative \(\partial ^{\bullet }_h u_h(\cdot ,t) \in S_h(t)\) and \(w_h(\cdot ,t) \in S_h(t)\) such that for all test functions \(\varphi _h^u(\cdot ,t) \in S_h(t)\) with \(\partial ^{\bullet }_h \varphi _h^u =0\) and \(\varphi _h^w(\cdot ,t) \in S_h(t)\)
again, with given initial data \(u_h(\cdot ,0) = u_h^0\) on \(\Gamma _h^0\).
By a direct modification of the proof of Theorem 3.1 in [22] (based on standard ODE theory), we obtain that the above semi-discrete problem is well-posed, and the discrete material derivatives of both solution components are continuous in time, i.e. the nodal values of the semi-discrete solution are both \(C^1\) in time. Therefore, for a given \(u_h(\cdot ,0) = u_h^0\), the initial value \(w_h(\cdot ,0) = w_h^0\) is obtained by solving the elliptic problem (3.7b) (or (3.8b)) at time \(t = 0\).
3.5 Matrix–vector formulation
We collect the nodal values of \(u_h(\cdot ,t) = \sum _{j=1}^N u_j(t)\phi _j(\cdot ,t) \in S_h(t)\) and \(w_h(\cdot ,t) = \sum _{j=1}^N w_j(t)\phi _j(\cdot ,t) \in S_h(t)\), the solution pair of the semi-discrete problem (3.7), into the vectors \({{\mathbf {u}}}(t)= (u_1(t),\ldots ,u_N (t)) \in \mathbb {R}^N\) and \({{\mathbf {w}}}(t)= (w_1(t),\ldots ,w_N (t)) \in \mathbb {R}^N\). We define the time-dependent matrices, the mass and stiffness matrix, corresponding to the bilinear forms \(m_h\) and \(a_h\), respectively, and the non-linear terms involving f and g:
We further define the matrix corresponding to the bilinear form \(a_h^*\):
We also note that, via the transport property (3.3), the time derivative of the mass matrix is given by
The discrete material derivative of any surface finite element function \(u_h(\cdot ,t) \in S_h(t)\), with nodal values \({{\mathbf {u}}}(t)\), again by using the transport property (3.3) of the basis functions and the product rule, is given by
Thus, the nodal values of \(\partial ^{\bullet }_h u_h\) are given by the vector \(\dot{{\mathbf {u}}}(t)\).
The finite element semi-discretisation of the Cahn–Hilliard equation (3.7) then reads:
The anti-symmetric structure of (3.11), which is shared with (2.2) and (3.7), is recognised best in the rewritten form:
In order to exploit this favourable structure, the stability analysis will use the matrix–vector system (3.11).
For computations, it is however more advantageous to use the equivalent matrix–vector formulation
where the surface velocity \(V_h\) does not appear directly, as compared to the term with \(\dot{{\mathbf {M}}}(t)\) in (3.11).
The \(C^1\)-regularity results stated after (3.8) translate to the modified system as well: the solutions \({{\mathbf {u}}}(t)\) and \({{\mathbf {w}}}(t)\) are both in \(C^1(0,T;\mathbb {R}^N)\).
3.6 A modified problem
The initial value \({{\mathbf {u}}}(0)\) is chosen suitably, on the other hand the initial value \({{\mathbf {w}}}(0)\) is obtained, from the second equation of the system (3.11), or equivalently (3.12). Our error analysis requires the errors in both initial values to be \(O(h^{k+1})\) in the \(H^1(\Gamma _h)\) norm. For \({{\mathbf {u}}}\) this is achieved using the Ritz map of \(u^0\) (in which case the initial error in \({{\mathbf {u}}}\) will vanish), however, such an error estimate is still not feasible for \({{\mathbf {w}}}\). Instead we transform the second equation such that the initial error in \({{\mathbf {w}}}\) also vanishes, in exchange for a time-independent (and small) inhomogeneity.
To obtain optimal-order error estimates we modify the equation (3.11b) (and equivalently (3.12b) as well) using a time-independent correction term. Let \(\bar{{{\mathbf {w}}}}(0) \in \mathbb {R}^N\) denote the solution obtained from (3.11b) at time \(t = 0\), and let \({{\mathbf {w}}}^*(0) \in \mathbb {R}^N\) contain the nodal values of the Ritz map of w(0), and set
The second equation is then modified, such that the system (3.11) reads:
Similarly, the equivalent system (3.12) is modified to:
The semi-discrete finite element formulations (3.7) and (3.8) are modified accordingly.
We recall that the solutions of the modified semi-discrete problems (3.14) and (3.15) are both \(C^1\) in time.
The initial value \({{\mathbf {w}}}(0)\) is obtained by solving the elliptic problem (3.14b) at \(t = 0\), which, via (3.13) and (3.11b), yields
The advantage of the modified system is, that the errors in the initial data for \({{\mathbf {w}}}\) are included into the problem similarly to a residual term, which allows for a feasible weaker norm estimate of this term (in fact we will show later, that it is a defect term). Note that for the linear case, this is nothing else but shifting the solutions to a particular initial value using a constant inhomogeneity.
4 Error estimates
We next state a new convergence result for the evolving surface finite element semi-discretisation of polynomial degree \(k \ge 1\) if the nonlinearities only depend on u, and of degree \(k \ge 2\) if they also depend on \(\nabla _{\Gamma }u\). In the theorem below, and in the remainder of this work, these two cases will be referred to as (a) and (b), respectively.
Theorem 4.1
Let u and w be the weak solutions of the Cahn–Hilliard equation on an evolving surface (2.2), and assume that they satisfy the regularity conditions (4.1).
Then, there exists an \(h_0 > 0\) such that for all \(h \le h_0\) the errors between the solutions u and w and the evolving surface finite element solutions \(u_h\) and \(w_h\) of degree k, with nodal vectors solving the modified system (3.15), and choosing the Ritz map of \(u^0\) for the initial value \(u_h(\cdot ,0)\), satisfy the optimal-order uniform-in-time error estimates in both variables, for \(0 \le t \le T\):
(a) For general nonlinearities f and g depending on \((u,\nabla _{\Gamma }u)\), for at least quadratic finite elements \(k \ge 2\):
whereas the material derivative of the error in u satisfies
(b) If the nonlinearities are both independent of \(\nabla _{\Gamma }u\), then for any \(k\ge 1\):
whereas the material derivative of the error in u satisfies
The constant \(C > 0\) is independent of h and t, but depends on the bounds of the Sobolev norms of the solution u and w, on the surface evolution, and on the length of the time interval T.
Sufficient regularity conditions on \(u=u(\cdot ,t )\) and \(w=w(\cdot ,t)\) required by Theorem 4.1 are:
Our result proves uniform -in-time error estimates in the \(H^1\) and \(L^2\) norms (in both cases (a) and (b)) for the error in u and w and for the errors in the material derivatives of u (only sub-optimal in (a)).
The classical Cahn–Hilliard equation (with a double-well potential) is naturally recovered in case (b), and slightly improves the result of [22, Theorem 5.1], proving a new time uniform estimate for the chemical potential.
Comparing our regularity assumptions to [22, Theorem 5.1]: The spatial \(H^{k+1}(\Gamma (t))\) regularity assumptions (4.1) are required since we are using isoparametric evolving surface finite elements of degree k, whereas the assumptions on (further) material derivatives and the \(L^\infty \)-type and regularity assumptions on u and w, and \(\partial ^{\bullet }v\) (4.1) are required to obtain the uniform-in-time error estimates, via the new stability proof presented below.
Theorem 4.1 is proved by studying the questions of stability and consistency. The consistency of the algorithm is shown by proving high-order estimates for the defects (the error obtained by inserting the Ritz map of the exact solutions into the method), which are obtained by using geometric and approximation error estimates for high-order evolving surface finite elements from [27], which combines techniques of [12, 15, 17].
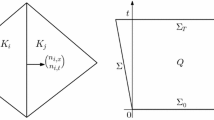
The main issue in the proof is stability, i.e. a mesh independent, uniform-in-time bound of the errors in terms of the defects. The main idea of the stability proof was originally developed for Willmore flow [29], and it relies on energy estimates that exploit the anti-symmetric structure of the Cahn–Hilliard equation, see (2.2), (3.7), and (3.14). The basic idea of the stability proof is concisely sketched in Fig. 1. In order to estimate the non-linear terms, a key issue in the stability proof is to ensure that the \(W^{1,\infty }\) norm of the error in u remains bounded. The uniform-in-time \(H^1\) norm error bounds together with an inverse estimate provide a bound in the \(W^{1,\infty }\) norm. Similarly, it is also possible to show such a \(W^{1,\infty }\) norm bound for the error in w, provided by our uniform-in-time \(H^1\) norm bounds in both u and w.
5 Stability
5.1 Preliminaries
This section is dedicated to the definition of a few concepts, such as the comparison of various quantities on different discrete surfaces and a generalised Ritz map, which are all used throughout the stability analysis.
The finite element matrices \({{\mathbf {M}}}(t)\), \({{\mathbf {A}}}(t)\), and \({{\mathbf {K}}}(t)\) induce (semi-)norms which correspond to discrete Sobolev (semi-)norms:
for any vector \({{\mathbf {w}}}\in \mathbb {R}^N\) corresponding to the finite element function \(w_h \in S_h(t)\).
From [30, Lemma 4.6] we recall the following estimates for the time derivatives of the mass and stiffness matrix, and, additionally, we prove that they also hold for the second order time derivatives.
Lemma 5.1
For all vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in \mathbb {R}^N\) we have
where the constant \(c > 0\) is independent of h, but depends on the surface velocity v.
Proof
The first two estimates were shown in Lemma 4.6 of [30].
We prove the estimate (5.2c) for the second derivative of the mass matrix. For fixed vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in \mathbb {R}^N\) corresponding to discrete functions \(w_h(\cdot ,t), z_h(\cdot ,t) \in S_h(t)\) (for \(0 \le t \le T\)), we have \(\partial ^{\bullet }_h w_h(\cdot ,t) = \partial ^{\bullet }_h z_h(\cdot ,t) = 0\) by the transport property (3.3), see (3.10). Using the discrete version of the Leibniz formula [15, Lemma 2.2] or [17, Lemma 4.2] twice, we obtain
We remind here that the discrete spatial differential operators, and hence the integrals, are understood in an element-wise sense.
To estimate the first integral we recall how to interchange surface differential operators with the material derivative [18, Lemma 2.6]. For discrete differential operators they read:
understood element-wise, for \(w_h:\Gamma _h(t)\rightarrow \mathbb {R}\) and \(w_h:\Gamma _h(t)\rightarrow \mathbb {R}^3\), respectively. Then, the second formula from (5.3) is used to estimate the first integral, together with the bounds on the discrete velocity \(V_h\). The boundedness of \(V_h\) is implied by the sufficient regularity of the velocity v, and recalling that \(V_h\) is the interpolation of v, cf. (3.1), see Lemma 6.2 or [6, Lemma 3.1.6]. We altogether obtain
The second integral is directly bounded by
The estimate for the stiffness matrix is shown by analogous arguments, now using the interchange formula [28, Equation (7.27)], and the analogous version of (5.3) for the first order differential operator appearing in the transport formula for the stiffness matrix [17, Lemma 4.2, (4.18)]. \(\square \)
5.2 Error equations and defects
Before turning to the stability analysis, let us define a Ritz map of the exact solution onto the evolving surface finite element space, from [27, 35] we recall the definition of a time-dependent Ritz map on evolving surfaces: \(R_h : H^1(\Gamma (t)) \rightarrow S_h^\ell (t)\), (here we do not include the velocity term of [35]).
Let \(u(\cdot ,t) \in H^1(\Gamma (t))\) for \(0 \le t \le T\) be arbitrary. Then, the Ritz map is defined through \({\widetilde{R}}_h (t)u \in S_h(t)\) which satisfies, for all \(\varphi _h \in S_h (t)\),
The Ritz map is then defined as the lift of \(\widetilde{R}_h(t)\), i.e. \(R_h(t)u = ({\widetilde{R}}_h(t)u)^\ell \in S_h^\ell (t)\). We will often suppress the omnipresent time-dependency of the Ritz map. In [35] it was shown that the above Ritz map is well-defined, error estimates for the high-order evolving surface FEM were shown in [27], and are recalled in Lemma 6.4. We note, that the Ritz map used here differs from the one used by Elliott and Ranner in [22], and the references therein, as it involves the bilinear form \(a^*\) instead of a together with the average condition.
Let us consider now the (unlifted) Ritz map of the exact solutions u and w of (2.2), which are denoted by
whose nodal values are collected into the vectors
The nodal vectors of the Ritz maps of the exact solutions satisfy the system (3.11) only up to some defects \({{\mathbf {d}}}_{{\mathbf {u}}}(t)\) and \({{\mathbf {d}}}_{{\mathbf {w}}}(t)\) in \(\mathbb {R}^N\), corresponding to the finite element functions \(d_h^u(\cdot ,t)\) and \(d_h^w(\cdot ,t)\) in \(S_h(t)\):
The errors between the nodal values of the semi-discrete solutions and of the Ritz maps of the exact solutions are denoted by \({{\mathbf {e}}}_{{\mathbf {u}}}(t)= {{\mathbf {u}}}(t)- {{\mathbf {u}}}^*(t)\) and \({{\mathbf {e}}}_{{\mathbf {w}}}(t)= {{\mathbf {w}}}(t)- {{\mathbf {w}}}^*(t)\) in \(\mathbb {R}^N\). By subtracting (5.5) from (3.14) we obtain that the errors \( {{\mathbf {e}}}_{{\mathbf {u}}}\) and \({{\mathbf {e}}}_{{\mathbf {w}}}\) (corresponding to the functions \(e_{u_h}\) and \(e_{w_h} \in S_h(t)\)) satisfy the following error equations:
with zero initial values \({{\mathbf {e}}}_{{\mathbf {u}}}(0) = 0\) and \({{\mathbf {e}}}_{{\mathbf {w}}}(0) = 0\). Both initial values indeed vanish by construction: for \({{\mathbf {e}}}_{{\mathbf {u}}}(0)\) recall that we choose \({{\mathbf {u}}}(0)\) to be the nodal values of the Ritz map of \(u^0\) and \({{\mathbf {u}}}^*(t)\) contains the nodal values of the Ritz map of u for all t, while for \({{\mathbf {e}}}_{{\mathbf {w}}}(0)\) we have \({{\mathbf {w}}}(0) = {{\mathbf {w}}}^*(0)\) by the construction (3.16).
Since the initial values also satisfy (5.6b) at \(t = 0\), we obtain the useful expression
5.3 Stability bounds
Proposition 5.2
Suppose there exists a constant \(c > 0\) independent of h and t such that the defects are bounded for a \(\kappa \ge 2\) by
Furthermore, suppose that for all \(0\le t \le T\) the Ritz maps \(u_h^* = {\widetilde{R}}_h u\) and \(w_h^* = {\widetilde{R}}_h w\) satisfy the bounds \(\Vert u_h^*(\cdot ,t)\Vert _{W^{1,\infty }(\Gamma _h(t))} \le M\) and \(\Vert w_h^*(\cdot ,t)\Vert _{W^{1,\infty }(\Gamma _h(t))} \le M\).
Then, there exists \(h_0 > 0\) such that the following error bound holds for \(h \le h_0\) and \(0 \le t \le T\):
The constant \(C > 0\) is independent of t and h, but depends exponentially on the final time T.
In Sect. 6, Proposition 6.7, we show that the defects are in fact bounded as \(O(h^{k+1})\).
Proof
The proof is based on energy estimates, and its basic idea is very similar to that of [29]. Proving uniform-in-time \(H^1\) norm error estimates is essential for handling the non-linear term, which is done by deriving a \(W^{1,\infty }\) norm bound for the errors using an inverse estimate.
In order to achieve a uniform-in-time stability bound, two sets of energy estimates are required. These energy estimates strongly exploit the anti-symmetric structure of (2.2). (i) In the first one, an energy estimate is proved for \({{\mathbf {e}}}_{{\mathbf {u}}}\), but comes with a critical term involving \(\dot{{\mathbf {e}}}_{{\mathbf {u}}}\). (ii) The second estimate uses the time derivative of (5.6b), leads to a bound of this critical term and also to a uniform-in-time bound for \({{\mathbf {e}}}_{{\mathbf {w}}}\). The combination of these two energy estimates gives the above stability bound. The structure and basic idea of the proof is sketched in Fig. 1.
Sketch of the structure of the energy estimates for the stability proof. In the diagram \({{\mathbf {r}}}_1\) and \({{\mathbf {r}}}_2\) denote the right-hand sides of (5.6a) and (5.6b). (Note that, after time differentiation, the term \({{\mathbf {R}}}_2\) not only contains the time derivative of \({{\mathbf {r}}}_2\), but other terms involving derivatives of matrices as well.)
In order to handle the non-linear terms we first prove the stability bound on a time interval where the \(W^{1,\infty }\) norm of \(e_{u_h}\) is small enough, and then show that this time interval can be enlarged up to T.
In the following c and C are generic constants that take different values on different occurrences. Whenever it is possible, without confusion, we omit the argument t of time-dependent vectors but not of time-dependent matrices. By \(\varrho _j> 0\) we will denote small numbers, used in Young’s inequalities for different absorptions, and hence we will often incorporate h independent multiplicative constants into those, yet unchosen, factors.
We start by stating that there exists a maximal time \(0 < t^* \le T\) such that, for all \(t \le t^*\),
Since \(e_{u_h}(\cdot ,0) = 0\) and since \(u_h\) and \(u_h^*\), respectively their spatial derivatives \(\nabla _{\Gamma _h} u_h\) and \(\nabla _{\Gamma _h} u_h^*\) are continuous in time, we directly infer that \(t^* > 0\).
Thus, by the assumption that the Ritz maps of the exact solutions satisfy \(\Vert u_h^*(t)\Vert _{W^{1,\infty }(\Gamma _h(t))}, \Vert w_h^*(t)\Vert _{W^{1,\infty }(\Gamma _h(t))} \le M\), with a finite constant \(M>0\), we obtain the following bound for the numerical solution:
for all \(0 \le t \le t^*\) and for \(h \le h_0\) sufficiently small, and similarly for \(w_h\). Thus, for \(f \in C(\mathbb {R}\times \mathbb {R}^d)\)
for all \(0 \le t \le t^*\) and \(h \le h_0\) sufficiently small. We first prove the stated stability bound for \(0 \le t \le t^*\), and then show that indeed \(t^*\) coincides with T.
Energy estimate (i): We take the first error equation (5.6a) and test it with \({\mathbf {e}_{\mathbf {u}}}\), while the second one (5.6b) is tested by \({\mathbf {e}_{\mathbf {w}}}\), to obtain
By adding the two equations, and by the symmetry of \({{\mathbf {A}}}\), we eliminate the mixed term \({{\mathbf {e}}}_{{\mathbf {u}}}^T{{\mathbf {A}}}(t){\mathbf {e}_{\mathbf {w}}}\), and obtain
Using the product rule and symmetry of \({{\mathbf {M}}}\) we rewrite the first term as
which altogether yields
Similarly, we test (5.6a) by \({\mathbf {e}_{\mathbf {w}}}\) and (5.6b) by \({\dot{\mathbf {e}}_{\mathbf {u}}}\), now a subtraction leads to cancelling the mixed term \({{\mathbf {e}}}_{{\mathbf {w}}}^T{{\mathbf {M}}}(t){\dot{\mathbf {e}}_{\mathbf {u}}}\), and again by the product rule and the symmetry of \({{\mathbf {A}}}\), we obtain
Taking the linear combination of the above equalities yields
The terms on the right-hand side are now estimated separately.
The terms involving time derivatives of matrices are estimated using Lemma 5.1, by
For the non-linear terms, using (5.11) and the local-Lipschitz property of f, we obtain
where L is the local Lipschitz constant of f, and we similarly obtain
The defect terms are estimated by the Cauchy–Schwarz inequality, as
The terms involving the correction term \({\varvec{\vartheta }}\) are bounded similarly as the defect terms. Using equality (5.7) and the norm equivalence in time [19, Lemma 4.1] (to change the time from 0 to t), we obtain
Altogether, by the combination of the estimates (5.14)–(5.17) with (5.13), by multiple Young’s inequalities (with \(\varrho _0 > 0\) chosen later on) and by absorptions to the left-hand side, we obtain
Integrating from 0 to \(t \in (0,t^*]\), and using that \({\mathbf {e}_{\mathbf {u}}}(0) = 0\), we obtain the first energy estimate:
Note that if we do not use the Ritz map for the initial value for \(u_h\), the error \(\Vert {{\mathbf {e}}}_{{\mathbf {u}}}(0)\Vert _{{{\mathbf {K}}}(0)}^2\) would not vanish on the right-hand side. This \(H^1\) norm error however cannot be bounded with the sufficient order. Furthermore, note the critical term, with \(\Vert {\dot{\mathbf {e}}_{\mathbf {u}}}(s)\Vert _{{{\mathbf {K}}}(s)}\), on the right-hand side, which cannot be bounded or absorbed in any direct way.
Energy estimates (ii) To control the critical term on the right-hand side of (5.20) we will now derive an energy estimate, which includes this term on the left-hand side. To this end, we first differentiate the second equation of (5.6) with respect to time (note that the time-independent \({\varvec{\vartheta }}\) vanishes), and, after rearranging the terms, we obtain the following system:
Testing the error equation system (5.21) twice, similarly as before in Part (i), would not lead to a feasible energy estimate, but to a bound which includes a new critical term \({\dot{\mathbf {e}}_{\mathbf {u}}}\). The issue is avoided by separating the two estimates for the error equations, (ii.a) and (ii.b), and then taking their weighted combination in (ii.c), (ii.a). We test (5.21a) by \({\dot{\mathbf {e}}_{\mathbf {u}}}\) and (5.21b) by \({\mathbf {e}_{\mathbf {w}}}\), adding the two equations together to cancel the mixed term \({\dot{\mathbf {e}}_{\mathbf {u}}}^T{{\mathbf {A}}}(t){\mathbf {e}_{\mathbf {w}}}\), and using the product rule as before, we obtain
The right-hand side terms are again estimated separately. The ones in the first line are bounded, using Lemma 5.1, by
The first non-linear term is estimated as in (5.15)–(5.16c) whereas the second non-linear term occurs differentiated with respect to time. Therefore, with the help of the transport formula (2.9) we compute, omitting the omnipresent argument t,
Let us first estimate the most challenging second term. Inserting
\({\mp } \int _{\Gamma _h(t)}{\partial _2 g\big (u_h, \nabla _{\Gamma _h (t)} u_h\big ) \,{\partial ^{\bullet }}_h\, \nabla _{\Gamma _h (t)} u_h^* \, e_{w_h}}\) we bound II by
using the first interchange formula from (5.3), the local Lipschitz property of \(\partial _2 g\) together with (5.12), and the bounds on \(V_h\) obtained by interpolation error estimates (for details, see [6, Lemma 3.1.6]).
The second term is now estimated analogously, by adding and subtracting, but not requiring the interchange steps, these yield
using the local Lipschitz property of \(\partial _1 g\) together with (5.12). Furthermore, for the third term we directly obtain
using the local Lipschitz property of g together with (5.12). Altogether, the estimates for I–III yield
The defect terms are bounded, similarly as before, by
Altogether, by plugging in (5.23)–(5.25) into (5.22), then using Young’s inequalities (with a small number \(\varrho _1>0\)), we obtain the first energy estimate of this part:
(ii.b) We now test (5.21a) by \({{\dot{\mathbf {e}}_{\mathbf {w}}}}^T\) and (5.21b) by \({\dot{\mathbf {e}}_{\mathbf {u}}}^T\), then subtracting the second from the first equation to cancel the mixed term \({{\dot{\mathbf {e}}_{\mathbf {w}}}}^T{{\mathbf {M}}}(t){\dot{\mathbf {e}}_{\mathbf {u}}}\) and using the product rule again we obtain
The terms are again estimated separately. The terms with time derivatives of matrices on the right-hand sides of (5.27) are bounded, using Lemma 5.1, by
The differentiated non-linear term is bounded, similarly to (5.24), by
with a particular constant \(c_0 > 0\) (independent of h, but depending on \(F''\), viz. on the constant in (5.24)). The defect terms are bounded, similarly as before, by
Let us highlight that it is not possible to directly estimate the terms containing \({{\dot{\mathbf {e}}_{\mathbf {w}}}}(t)\) in their current form, because there is no term on the left-hand side to absorb them. Therefore, we first rewrite them using the product rule, and estimate them using Lemma 5.1, to obtain
Altogether, by plugging in (5.31)–(5.30) into (5.27), then using Young’s inequalities (with a small number \(\varrho _2>0\)), we obtain the second energy estimate of this part:
(ii.c) We now take the weighted combination of the energy estimates from (ii.a) and (ii.b): multiplying the estimate (5.26) by \(\frac{3 c_0}{4 \varrho _3}\) and adding it to the estimate (5.32). Collecting the terms and directly absorbing the term \(c_0 \Vert {\dot{\mathbf {e}}_{\mathbf {u}}}\Vert _{{{\mathbf {M}}}(t)}^2\) on the right-hand side of (5.32) to the left-hand side, (and choosing \(\varrho _1,\varrho _2,\varrho _3>0\) small enough for absorption of the \(\Vert {\dot{\mathbf {e}}_{\mathbf {u}}}\Vert _{{{\mathbf {K}}}(t)}^2\) terms from the left-hand side to the right-hand side), we obtain
Integrating the above inequality (5.33) from 0 to \(t \le t^*\), and then dividing by \(\min \big \{\frac{c_0}{2 \varrho _3},\frac{1}{2} \big \}\), yields
We estimate the newly obtained non-integrated terms on the right-hand side using Lemma 5.1, Cauchy–Schwarz and Young’s inequalities, the estimate for the non-linear term (5.16a), a further absorption, and using that \({{\mathbf {e}}}_{{\mathbf {u}}}(0)\) and \({{\mathbf {e}}}_{{\mathbf {w}}}(0)\) are zero, we then obtain
with a \(c_1 > 0\). This energy estimate now contains the (previously) critical term \({\dot{\mathbf {e}}_{\mathbf {u}}}\) on the left-hand side. Without the construction in Sect. 3.6 the initial values for \({{\mathbf {w}}}\) would not vanish and a term \(\Vert {\mathbf {e}_{\mathbf {w}}}(0)\Vert _{{{\mathbf {K}}}(0)}^2\) would remain on the right-hand side. This \(H^1\) norm error however cannot be bounded with the sufficient order.
Combining the energy estimates: We now take again a \(c_1\)-weighted linear combination (in order to absorb the term \(c_1 \Vert {\mathbf {e}_{\mathbf {u}}}\Vert _{{{\mathbf {K}}}(t)}^2\)) of the two energy estimates (5.20) and (5.34), to obtain
By choosing \(\varrho _0\) small enough, the first term (previously the critical term) on the left-hand side is now absorbed. This enables us to use Gronwall’s inequality, which then yields the stated stability estimate on \([0,t^*]\).
Now, it only remains to show that, in fact, \(t^* = T\), for h sufficiently small. The proved stability bound (for \(0 \le t \le t^*\)) together with the assumed defect bounds (5.8) imply
By an inverse estimate, see, e.g. [7, Theorem 4.5.11], we have, for \(0 \le t \le t^*\),
for sufficiently small h. Therefore, the bound (5.10) is extended beyond \(t^*\), which contradicts the maximality of \(t^*\) unless we already have \(t^* = T\). We hence proved the stability bound (5.9) over [0, T], and completed the proof. \(\square \)
Remark 5.3
The dimensional assumptions \(\Gamma (t)\subset \mathbb {R}^{d+1}\) for \(d = 1,2\) are not entirely restrictive. For a higher dimensional surface, the argument (5.36) can be repeated for a \(\kappa \) sufficiently large, that is requiring a finite element basis of sufficiently high order, depending on the dimension d.
6 Consistency
Before we turn to proving consistency of the spatial semi-discretisation and to the proof of Theorem 4.1, we collect some preparatory results: error estimates of the nodal interpolations on the surface, for the Ritz map, and some results which estimate various geometric errors. Most of these results were shown in [12, 17, 27].
Let us briefly recall our assumptions on the evolving surface and on its discrete counterpart, from Sects. 2 and 3.1: \(\Gamma (t)\) is a closed smooth (at least \(C^2\)) surface in \(\mathbb {R}^{d+1}\) with \( d\le 3\), evolving with the surface velocity v, with regularity \(v(\cdot ,t),\partial ^{\bullet }v(\cdot ,t) \in W^{k+1,\infty }(\Gamma (t))\) uniformly in time. The discrete surface \(\Gamma _h(t)\) is a k-order interpolation of \(\Gamma (t)\) at each time, and therefore its velocity \(V_h\) is the nodal interpolation of v on \(\Gamma _h(t)\), see (3.1) and Sect. 3.1.
6.1 Geometric errors
6.1.1 Interpolation error estimates
The following result gives estimates for the error in the interpolation. Our setting follows that of Section 2.5 of [12].
Let us assume that the surface \(\Gamma (t)\) is approximated by the interpolation surface \(\Gamma _h(t)\) of order k. Then for any \(u \in H^{k+1}(\Gamma (t))\), there is a unique k-order surface finite element interpolation \({\widetilde{I}}_h u \in S_h(t)\), furthermore we set \(({\widetilde{I}}_h u)^\ell = I_h u\).
Lemma 6.1
For any \(u(\cdot ,t)\in H^{k+1}(\Gamma (t))\) for all \(0 \le t \le T\). The surface interpolation operator \(I_h\) of order k satisfies the following error estimates, for \(u = u(\cdot ,t)\) and for \(0 \le t \le T\),
with a constant \(c > 0\) independent of h and t, but depending on v and \(\mathcal {G}_T\).
6.1.2 Discrete surface velocities
This section gives a definition of a discrete velocity on the exact surface \(\Gamma (t)\) associated to \(V_h\), and explores approximation results for the discrete velocities. The following result, recalled from [6, Lemma 3.1.6], shows boundedness of the discrete velocity \(V_h\), using the fact that it is the interpolation of v. The proof is based on the interpolation error estimate Lemma 6.1 and the interchange formulas (5.3).
Lemma 6.2
Assume that v and \(\partial ^{\bullet }v\) are in \(W^{{k+1},\infty }(\Gamma (t))\). Then, for \(h \le h_0\) sufficiently small, the following bounds hold:
where the constant \(c > 0\) is independent of h and t, but depends on \(\mathcal {G}_T\).
To \(V_h\) we associate a discrete surface (or material) velocity of \(\Gamma (t)\), denoted by \(v_h\). It is the surface velocity of the lifted material points \(y(t)= (x(t))^\ell \in \Gamma (t)\). The edges of a lifted element evolve with this velocity \(v_h\), which is not the interpolation of v in \(S_h^\ell (t)\). For more details we refer to [17, Definition 4.3] and [16, Section 5.4].
Here we recall an explicit formula for \(v_h\): for \(x(t)\in \Gamma _h(t)\) with \(y(t)= x^\ell (t)\),
with \(y(t)= y(x(t),t) \in \Gamma (t)\) denoting the lift of \(x(t)\in \Gamma _h(t)\), cf. Section 3.2, i.e. the unique solution to \(x(t)= y(x(t),t) + d(x(t),t) \, \nu (y(x(t),t),t)\). For an explicit formula using \(V_h\) and a distance function we refer to [17, equation (4.7)].
Apart from the original material derivative \(\partial ^{\bullet }\) on \(\Gamma (t)\), a discrete material derivative associated to the velocity \(v_h\) is also defined on \(\Gamma (t)\), see [17, equation (4.9)], for \(\varphi (\cdot ,t): \Gamma (t)\rightarrow \mathbb {R}\) (element-wise) by
where \({\bar{\varphi }}(\cdot ,t)\) is an extension into a small neighbourhood of \(\Gamma (t)\). That is we have the following three different material derivatives:
We note here that it will be always clear from the context whether the discrete material derivative \(\partial ^{\bullet }_h\) is meant on \(\Gamma (t)\) associated to \(v_h\), or on \(\Gamma _h(t)\) associated to \(V_h\).
From [27, Lemma 5.4] we recall high-order error bounds between the velocity \(v_h\) of the lifted material points and the surface velocity v (for the case \(k=1\), and without material derivative, \(l = 0\), we refer to [17]).
Lemma 6.3
The difference between the continuous velocity v and the discrete velocity \(v_h\) on \(\Gamma (t)\) is estimated by
for \(l \ge 0\), with a constant \(c_l > 0\) independent of h and t, but depending on the surface velocity v.
Since we need to establish a bound for the discrete material derivatives of both defects \(d_u\) and \(d_w\), we recall some transport formulas from [17, Lemma 4.2] (for any sufficiently regular functions):
These formulas will help us to derive equations for \(\partial ^{\bullet }_h d_u\) and \(\partial ^{\bullet }_h d_w\) and are often used in the proofs in Sect. 6.1.4. The two transport formulae on \(\Gamma (t)\), (2.9) and (6.3a), arise by interpreting \(\Gamma (t)\) as a continuous surface with velocity v, and as the union of curved elements (the lifted elements of \(\Gamma _h(t)\)) with velocity \(v_h\), see (6.1), respectively. We will use them analogously to [17, Section 7].
6.1.3 Error estimates for the generalised Ritz map
From [27, Theorem 6.3 and 6.4] we recall that the generalised Ritz map (5.4) satisfies the following optimal high-order error estimates.
Lemma 6.4
Let \(u : \mathcal {G}_T\rightarrow \mathbb {R}\) such that \(u(\cdot ,t)\) and \((\partial ^{\bullet })^{(j)} u(\cdot ,t)\in H^{k+1}(\Gamma (t))\) for all \(0 \le t \le T\) and \(j=1,\ldots ,l\), for some \(l \in {{\mathbb {N}}}\). Then, the error in the generalised Ritz map (5.4) satisfies the bounds, for \(0 \le t \le T\) and for \(h \le h_0\) with sufficiently small \(h_0\),
where the constant \(c>0\) is independent of h and t, but depends on \(\mathcal {G}_T\).
6.1.4 Geometric approximation errors
The time dependent bilinear forms m, r and their discrete counterparts \(m_h,r_h\), from (2.6) and (3.5), respectively, satisfy the following high-order geometric approximation estimates, see [27, Lemma 5.6].
Lemma 6.5
Let \(z_h, \varphi _h \in S_h(t)\) arbitrary with lifts \(z_h^\ell , \varphi _h^\ell \in S_h^\ell (t)\). Then, for all \(h \le h_0\) with \(h_0\) sufficiently small, the following estimates hold
where the constant \(c > 0\) is independent of h and t, but depends on \(\mathcal {G}_T\).
Similar results hold for the errors in the bilinear form a, cf. [27, Lemma 5.6], but these are not used herein. The previous estimates also hold for any functions in \(L^2(\Gamma _h(t))\). Therefore, the proof of the previous lemma implies
respectively for g. Let \(\mu _h\) denote the quotient of the measures on \(\Gamma (t)\) and \(\Gamma _h(t)\). In [27, Lemma 5.2] it is shown that the following estimates hold:
Below we present and prove a new geometric approximation estimate which relates time derivatives of r and \(r_h\).
Lemma 6.6
Let \(z_h, \varphi _h \in S_h(t)\) be arbitrary with \(\partial ^{\bullet }_h z_h, \partial ^{\bullet }_h \varphi _h \in S_h(t)\), with their corresponding lifts in \(S_h^\ell (t)\). Then, for all \(h \le h_0\) with \(h_0\) sufficiently small, the following estimate holds
where the constant \(c > 0\) is independent of h and t, but depends on the surface velocity v.
Proof
Although, this lemma was first proved in [6, Lemma 3.1.8], due to its importance we present it here in full detail.
We start by differentiating the integral transformation
with respect to time using the transport formulae (6.3), to obtain
Using \(\partial ^{\bullet }_h (z_h^\ell ) = (\partial ^{\bullet }_h z_h)^\ell \), see [17, Lemma 4.1], we obtain
In particular, for \(\partial ^{\bullet }_h z_h\) in the role of \(z_h\), and with the use of the geometric estimate for the surface measure \(\Vert \partial ^{\bullet }_h \mu _h\Vert _{L^\infty } \le c h^{k+1}\) (6.6) we obtain the estimate
and with \(\partial ^{\bullet }_h \varphi _h\) in the role of \(\varphi _h\),
Differentiating equation (6.8) with respect to time, using (6.3), yields
Computing the derivatives on the left-hand side then leads to
The pairs in the first two lines on the right-hand side are already estimated above, while the last term is estimated by the geometric estimate \(\Vert \partial ^{\bullet }_h \mu _h\Vert _{L^\infty } \le c h^{k+1}\) (6.6). To estimate the remaining derivative term, we first compute the time derivative by (6.3b) and then estimate each term to obtain
using the geometric error estimate \(\Vert (\partial ^{\bullet }_h)^{(2)} \mu _h\Vert _{L^\infty } \le c h^{k+1}\) (6.7).
Altogether, by triangle inequalities and by combining the above estimates, we obtain
where we have used the bounds on the discrete velocity from Lemma 6.2, and the geometric estimate \(\Vert 1 - \mu _h\Vert _{L^{\infty }} \le c h^{k+1}\) (6.5). \(\square \)
6.2 Defect bounds
In this section we prove bounds for the defects and for their time derivatives, i.e. we prove that condition (5.8) of Proposition 5.2 is indeed satisfied.
Proposition 6.7
Let u, w solve the Cahn–Hilliard equation on an evolving surface (2.2). Furthermore, let u, w and the continuous surface velocity v be sufficiently smooth, e.g. satisfying (4.1). Then, for all \(h \le h_0\) sufficiently small, and for all \(t \in [0,T]\):
(a) For general nonlinearities f and g the defects are bounded as
(b) If f and g are both independent of \(\nabla _{\Gamma }u\), then the above estimates in (6.9) are improved to \(O(h^{k+1})\).
The constant \(c > 0\) is independent of h and t, but depends on the bounds on Sobolev norms of u, w and the surface velocity v.
Proof
The Ritz map (5.4) of the exact solutions u and w satisfies the discrete problem only up to some defects, \(d_u(\cdot ,t)\in S_h(t)\) and \(d_w(\cdot ,t)\in S_h(t)\), defined in (5.5). Rewriting these equations using the bilinear form notation from (2.6), we thus have, for an arbitrary \(\varphi _h \in S_h(t)\),
Upon subtracting the corresponding equations for the exact solution (2.5) with \(\varphi =\varphi _h^\ell \) and applying the transport formula (6.3a) (with \(\partial ^{\bullet }_h \varphi _h^\ell = 0\)), from the equations in (6.10), and then adding and subtracting some terms in order to apply the definition of the Ritz map \(\widetilde{R}_h\) (5.4), we obtain the following two equations satisfied by the defects \(d_u\) and \(d_w\):
We now estimate the defects and their material derivatives in the \(L^2(\Gamma (t))\) norm by bounding each pair on the right-hand sides of the above equations separately, using the geometric estimates from the previous subsection and using similar techniques as in [17, 27]. Since throughout the proofs most norms are on \(\Gamma (t)\), we will omit these below and write \(L^2\), \(H^{k+1}\) instead of \(L^2(\Gamma (t))\), \(H^{k+1}(\Gamma (t))\), etc.
Bound for \(d_u\): For the pair in the first line, we add and subtract terms to obtain
where we have used Lemma 6.5 together with the fact that \(\partial ^{\bullet }_h (z_h^\ell ) = (\partial ^{\bullet }_h z_h)^\ell \) ( [17, Lemma 4.1]) and the Ritz map error bound Lemma 6.4. The Ritz map error estimate is again used to show the bound \(\Vert \partial ^{\bullet }_h R_h u\Vert _{L^2} \le c ( \Vert u\Vert _{H^{k+1}} + \Vert \partial ^{\bullet }u\Vert _{H^{k+1}} )\).
By the same techniques, we prove the following bound for \(II_u\):
The third term \(III_u\) is estimated using similar arguments as before, by Lemma 6.5, Lemma 6.4, and the boundedness of \(v_h\) (proved using Lemma 6.3),
The fourth term \(IV_u\) including the non-linearity is estimated using the above techniques, and in addition, due to the (locally Lipschitz continuous) non-linear terms f and g, requires a \(W^{1,\infty }\) bound on the Ritz map, which we obtain by
with \(k - d/2\ge 0\), using an inverse estimate [7, Theorem 4.5.11], interpolation error bounds Lemma 6.1, and for the last term the (sub-optimal) interpolation error estimate of [12, Proposition 2.7] (with \(p=\infty \)). We then estimate, using
Note in particular that the only term in all of the above consistency estimates which is of order \(O(h^k)\) is the last term in (6.16), which is due to the presence of \(\nabla _{\Gamma }u\) in the nonlinearity.
The estimates (6.12)–(6.16) together, using the norm equivalence (3.6), and the definition of the \(L^2\) norm, in general for \(f(u,\nabla _{\Gamma }u)\), yields
If f is independent of \(\nabla _{\Gamma }u\), then by the note after (6.16), the defect estimate improves to
Bound for \(\partial ^{\bullet }_h d_u\): We start by differentiating the defect equation for \(d_u\) (6.11a) with respect to time. Using that \(\partial ^{\bullet }_h\varphi _h = \partial ^{\bullet }_h (\varphi _h^\ell ) = 0\), we obtain
The first term is immediately bounded, using Lemma 6.2, the Cauchy–Schwarz inequality and (6.17), by
The terms differentiated in time are estimated separately, using analogous techniques as before.
For the first term, by the transport formulas (6.3a) and (6.3b), we obtain
where for the inequality we used the arguments used to show (6.12) and (6.14).
By the same arguments, for the second term we obtain the bound
By the time differentiation of the third term, using the transport formulas (6.3a) and (6.3b), we obtain
The pair in the third line is estimated by previous arguments just as before, by
The remaining pair in the rectangular brackets is estimated by similar ideas as above, adding and subtracting intermediate terms, using the geometric approximation estimate from Lemma 6.6, Ritz map error estimates Lemma 6.4 and bounds on expressions with \(v_h\) (shown using Lemma 6.3 with \(l = 0\) and 1), and Lemma 6.2:
For the time derivative of the fourth term using
we obtain
Similarly to (6.15) we obtain a \(W^{1,\infty }\) bound of the material derivative of the Ritz map, see also the proof of Proposition 7.1 in [28], which we need for the next two estimates. The first term is estimated as
using (6.4). The second one additionally uses the interchange formulas (5.3) to obtain
The third one is bounded, similarly to (6.16), by
The combination of the estimates (6.18)–(6.23), using the norm equivalence (3.6), yields for a general \(f(u,\nabla _{\Gamma }u)\):
If f is independent of \(\nabla _{\Gamma }u\), then we obtain
Bound for \(d_w\): The \(L^2\) norm of the defect \(d_w\) (6.11b) is estimated by the same techniques by which the bound (6.13) was shown.
By similar techniques as before, and using (6.4) together with (6.15) the pairs for \(d_w\) are estimated analogously. The bounds for \(I_w\) and \(II_w\) are straightforward using the arguments above for \(d_u\), while \(III_w\) is bounded, similarly to (6.16), using the local Lipschitz continuity of g, by
Again, note the only \(O(h^k)\)-term in (6.26).
We altogether obtain the estimate, for the general case \(g(u,\nabla _{\Gamma }u)\):
Similarly as before, if g is independent of \(\nabla _{\Gamma }u\), the above estimate improves to
Bound for \(\partial ^{\bullet }_h d_w\): Just as for \(\partial ^{\bullet }_h d_u\), we differentiate the expression (6.11b) with respect to time. Using again \(\partial ^{\bullet }_h\varphi _h = \partial ^{\bullet }_h (\varphi _h^\ell ) = 0\), we obtain
The first term is estimated using (6.27), while the remaining terms are bounded similarly to (6.20) and (6.23) (using (6.15)).
Altogether, we obtain, for a general \(g(u,\nabla _{\Gamma }u)\):
while, if g is independent of \(\nabla _{\Gamma }u\) we obtain
\(\square \)
Remark 6.8
If the non-linearities are depending only linearly on \(\nabla _{\Gamma }u\), e.g. an advective term \(f(u,\nabla _{\Gamma }u) = {\tilde{f}}(u) + \varvec{w} \cdot \nabla _{\Gamma }u\), then the defects (although do not fall into case (b)) can still be bounded as \(O(h^{k+1})\). This requires the use of individually modified Ritz maps, whose definition includes this linear \(\nabla _{\Gamma }u\)-depending term. Such Ritz maps have been already used and analysed in [35, Definition 8.1], and [29].
7 Proof of Theorem 4.1
Proof of Theorem 4.1
We combine the stability bound of Proposition 5.2, and the consistency estimates of Proposition 6.7.
The errors are split as follows
upon recalling that \(u_h^* = \widetilde{R}_h u\) and \(w_h^* = \widetilde{R}_h w\).
The first terms in each error are directly and similarly bounded by error estimates for the Ritz map Lemma 6.4 – uniformly in time – by
The second terms are the errors \(e_{u_h}\), \(e_{w_h}\) and \(\partial ^{\bullet }_h e_{u_h}\), therefore bounded by the combination of the stability estimate (5.9) and the consistency estimates Proposition 6.7 (a) and (b), for the two respective cases of \(\nabla _{\Gamma }u\) dependency. In Proposition 5.2 the \(W^{1,\infty }\) norm assumption on \(u_h^* = \widetilde{R}_h u\) was proved in (6.15). Altogether, we obtain
where \(j = k\) in case (a), and \(j = k+1\) in case (b).
By combining the above estimates we obtain the stated error estimates in parts (a) and (b) of Theorem 4.1. \(\square \)
8 Full discretisation via linearly implicit backward difference formulae
We recall the matrix–vector formulation from (3.15):
As a time discretisation, we consider the linearly implicit s-step backward differentiation formulae (BDF). For a step size \(\tau >0\), and with \(t_n = n \tau \le T\), the discretised time derivative is determined by
while the non-linear term uses an extrapolated value, and reads as:
We determine the approximations to the variables \({{\mathbf {u}}}^n\) to \({{\mathbf {u}}}(t_n)\) and \({{\mathbf {w}}}^n\) to \({{\mathbf {w}}}(t_n)\) by the fully discrete system of linear equations, for \(n \ge s\),
which is used for the upcoming numerical experiments. The starting values \({{\mathbf {u}}}^i\) and \({{\mathbf {w}}}^i\) (\(i=0,\ldots ,s-1\)) are assumed to be given. They can be precomputed using either a lower order method with smaller step sizes, or an implicit Runge–Kutta method.
The method is determined by its coefficients, given by \(\delta (\zeta )=\sum _{j=0}^s \delta _j \zeta ^j=\sum _{\ell =1}^s \frac{1}{\ell }(1-\zeta )^\ell \) and \(\gamma (\zeta ) = \sum _{j=0}^{s-1} \gamma _j \zeta ^j = (1 - (1-\zeta )^s)/\zeta \). The classical BDF method is known to be zero-stable for \(s\le 6\) and to have order s; see [24, Chapter V]. This order is retained by the linearly implicit variant using the above coefficients \(\gamma _j\); cf. [1, 2].
The anti-symmetric structure of the system is preserved, and is observed in (8.3). Since the idea of energy estimates, using the G-stability theory of Dahlquist [11] and the multiplier technique of Nevanlinna & Odeh [39], can be transferred to linearly implicit BDF full discretisations (up to order 5), we strongly expect that Proposition 5.2 translates to the fully discrete case, and so does the convergence result Theorem 4.1. This is strengthened by the successful application of these techniques to the analogous linearly implicit backward difference methods applied to evolving surface PDEs: [32, 33, 36] showing optimal-order error bounds for various problems on evolving surfaces. The method was also analysed for various geometric surface flows, for \(H^1\)-regularised surface flows [31], and for mean curvature flow [28], both proving optimal-order error bounds for full discretisations.
9 Numerical experiments
We performed numerical experiments, using (8.3), for the classical non-linear Cahn–Hilliard equation on an evolving surface, hence our results are easily compared to those in the literature, in particular [22]. We report on the following experiments:
-
We perform a convergence test for the non-linear Cahn–Hilliard equation with the linear evolving surface FEM and BDF methods of various order, to illustrate the convergence rates of Theorem 4.1. We would like to note here that [22] only presents errors and EOCs for a linear problem (using the linearly implicit Euler method).
-
We perform the same experiment as Elliott and Ranner in [22, Section 6.2], i.e. we report on the evolution of the Ginzburg–Landau energy along the surface evolution for the non-linear Cahn–Hilliard equation with \(\varepsilon = 0.1\) using the first and second order BDF methods.
-
We perform a numerical experiment that reports on the effects of \(\varvec{\vartheta }\) and using the Ritz map as initial value.
In the numerical experiments we use the classical Cahn–Hilliard equation on an evolving surface (2.2) with the double-well potential, hence the non-linear terms are \(f(u) = 0\) and \(g(u) = \frac{1}{4}((u^2 - 1)^2)' = u^3 - u\). With an arbitrary \(0< \varepsilon < 1\), formulated as a system the problem reads:
with an extra inhomogeneity \(b (\cdot ,t) : \Gamma (t)\rightarrow \mathbb {R}\), chosen such that the exact solution is known to be \(u(x,t) = e^{-6t} x_1 x_2\), while w is also explicitly known through the second equation of (9.1). The surface \(\Gamma (t)\) evolves time-periodically from a sphere into an ellipsoid and back. In particular the surface is given as the zero level set of a distance function:
with \(a(t)= 1 + 0.25\sin (2 \pi t)\). The initial surface \(\Gamma (0) = \Gamma ^0\) is the unit sphere. The surface evolution is computed using the ODE for the positions (2.1), with
For the numerical experiments the ODE was solved numerically by the classical 4th order Runge–Kutta method with the smallest time step size present in the experiment.
Various numerical experiments have been carried out using the same evolving surface, in particular also for the Cahn–Hilliard equation by Elliott and Ranner [22], and for other problems as well, see, for instance [15, 36].
The initial value \(u_h^0\) is the interpolation of the exact initial value \(u_0\). For high-order BDF methods the required additional starting values \(u_h^i\) (for \(i=1,\ldots ,q-1\)) are taken as the interpolation of the exact values, if they exist, as well or are otherwise computed using a cascade of steps performed by the preceding lower order method.
9.1 Convergence experiments
The following convergence experiments are illustrating the convergence rates stated by Theorem 4.1. In these experiments we have used the parameter \(\varepsilon = 0.5\). The final time is \(T=1\), the time discretisations use a sequence of time step sizes \(\tau = 0.2 \times 2^{-i}\) for \(i=1,\ldots ,7\), and a sequence of initial meshes with (roughly quadrupling) degrees of freedom as reported in the figures.
In Figs. 2, 3, 4 and 5 we report on the \(L^\infty (L^2)\) norm errors (left) and \(L^\infty (H^1)\) norm errors (right) between the numerical and exact solution for both variables u and w, i.e. the plots show the errors
where the norms are understood as
For the first order BDF method, Fig. 2 shows logarithmic plots of the errors against the mesh width h, the lines marked with different symbols correspond to different time step sizes. We also report on temporal convergence in Fig. 3, where the roles are reversed, the errors are plotted against the time step size \(\tau \), and the lines with different markers correspond to different mesh refinements.
In Fig. 2 we can observe two regions: a region where the spatial discretisation error dominates, matching to the order of convergence of our theoretical results of Theorem 4.1 (note the reference lines), and a region, with small mesh widths, where the temporal discretisation error dominates (the error curves flatten out). For the \(H^1\) norm we observe better spatial convergence rates as the predicted \(O(h^k)\), (probably due to the smoothness of the exact solution). For Fig. 3, the same description applies, but with reversed roles. Although, we do not study convergence of full discretisations, the classical order of the BDF methods is observed. We note here, that flat error curves, which were completely dominated by a discretisation error, were not plotted.
Figures 4 and 5 report on the same plots, but for the third order BDF method. Again, both the spatial and temporal convergence, as shown by the figures, are in agreement with the theoretical convergence results of Theorem 4.1 and with the classical orders of the BDF methods (note the reference lines).
The plots for time convergence, Figs. 3 and 5, are supporting our claim that Theorem 4.1 can be extended for full discretisations with linearly implicit BDF methods, which is left to a subsequent work.
9.2 The Ginzburg–Landau energy
The numerical experiments in [22, Section 6.2] reporting on the Ginzburg–Landau energy were repeated here for high-order BDF methods.
We again consider the non-linear Cahn–Hilliard equation (9.1), with \(\varepsilon = 0.1\) and with \(b = 0\) on the same evolving surface \(\Gamma (t)\) as before, but with \(a(t)= 1 + 0.25\sin (10 \pi t)\), and with initial value
This setting is the same as in [22, Section 6.2].
In Figs. 6 and 7 we report on the time evolution of the Ginzburg–Landau energy (until \(T=0.2\) and \(T=1\)) of the BDF2/linear ESFEM discretisation. In both plots we have used the time step size \(\tau = 10^{-4}\) (the same as [22, Section 6.2]), and eight different mesh refinement levels (higher numbering denotes finer meshes). The meshes are not nested refinements of a single coarse grid. The coarsest mesh has 54 while the finest has 10,146 nodes.
As it was pointed out by Elliott and Ranner [22] “the energy does not decrease monotonically along solutions”, see Fig. 6, and as they predicted the solutions converge to a time-periodic solution, the periodicity in their energies is nicely observed in Fig. 7.
9.3 The effect of \(\varvec{\vartheta }\)
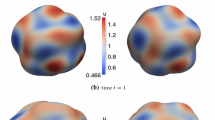
We report on the effect of \(\varvec{\vartheta }\) by presenting the computed numerical solution obtained from the scheme (3.12) and (3.15) with the interpolation and the Ritz map as initial values, respectively.
We again use the evolving ellipsoid example with \(a(t)= 1 + 0.5\sin (\frac{2 \pi t}{5})\), cf. (9.2) and an initial sphere of radius \(R = 5\), while the starting value is \(u^0 = \frac{225}{56{,}693}(x_1 + x_1^2x_2^2x_3)\) (such that \(\max |u^0| = 1\)). The discrete initial values are the interpolation of \(u^0\) for (3.12) and the Ritz map (5.4) of \(u^0\) for (3.15). The nodal vector \(\varvec{\vartheta }\) and the Ritz map are each obtained by solving an elliptic problem.
Figure 8 presents the numerical solutions with the two different discrete initial values, without (left) and with \(\varvec{\vartheta }\) (right), for different times \(t = 0, 1, 2, 3, 5\), computed on a mesh with 4098 nodes and using a time step size \(\tau = 0.0125\).
References
Akrivis, G., Li, B., Lubich, C.: Combining maximal regularity and energy estimates for time discretizations of quasilinear parabolic equations. Math. Comput. 86(306), 1527–1552 (2017)
Akrivis, G., Lubich, C.: Fully implicit, linearly implicit and implicit–explicit backward difference formulae for quasi-linear parabolic equations. Numer. Math. 131(4), 713–735 (2015)
Alphonse, A., Elliott, C.M., Stinner, B.: An abstract framework for parabolic PDEs on evolving spaces. Port. Math. 72(1), 1–46 (2015)
Alphonse, A., Elliott, C.M., Stinner, B.: On some linear parabolic PDEs on moving hypersurfaces. Interfaces Free Bound. 17(2), 157–187 (2015)
Barrett, J.W., Garcke, H., Nürnberg, R.: Finite element approximation for the dynamics of fluidic two-phase biomembranes. ESAIM Math. Model. Numer. Anal. 51(6), 2319–2366 (2017)
Beschle, C.: Error estimates for the Cahn–Hilliard equation on evolving surfaces. University of Tübingen, Master thesis (2019)
Brenner, S.C., Scott, R.: The Mathematical Theory of Finite Element Methods, vol. 15. Springer, Berlin (2008)
Caetano, D., Elliott, C.M.: Cahn–Hilliard equations on an evolving surface. Eur. J. Appl. Math. 32(5), 937–1000 (2021)
Cahn, J., Hilliard, J.: Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28(2), 258–267 (1958)
Cherfils, L., Miranville, A., Zelik, S.: On a generalized Cahn–Hilliard equation with biological applications. Discrete Contin. Dyn. Syst. Ser. B 19(7), 2013–2026 (2014)
Dahlquist, G.: G-stability is equivalent to A-stability. BIT 18(4), 384–401 (1978)
Demlow, A.: Higher-order finite element methods and pointwise error estimates for elliptic problems on surfaces. SIAM J. Numer. Anal. 47(2), 805–827 (2009)
Du, Q., Ju, L., Tian, L.: Finite element approximation of the Cahn–Hilliard equation on surfaces. Comput. Methods Appl. Mech. Eng. 200(29–32), 2458–2470 (2011)
Duan, N., Zhao, X.: Global existence of a generalized Cahn–Hilliard equation with biological applications. arXiv:1712.02989 (2017)
Dziuk, G., Elliott, C.M.: Finite elements on evolving surfaces. IMA J. Numer. Anal. 27(2), 262–292 (2007)
Dziuk, G., Elliott, C.M.: Finite element methods for surface PDEs. Acta Numer. 22, 289–396 (2013)
Dziuk, G., Elliott, C.M.: \(L^2\)-estimates for the evolving surface finite element method. Math. Comput. 82(281), 1–24 (2013)
Dziuk, G., Kröner, D., Müller, T.: Scalar conservation laws on moving hypersurfaces. Interfaces Free Bound. 15(2), 203–236 (2013)
Dziuk, G., Lubich, C., Mansour, D.: Runge–Kutta time discretization of parabolic differential equations on evolving surfaces. IMA J. Numer. Anal. 32(2), 394–416 (2012)
Elliott, C., Venkataraman, C.: Error analysis for an ALE evolving surface finite element method. Numer. Methods Partial Differ. Equ. 31(2), 459–499 (2015)
Elliott, C.M.: The Cahn–Hilliard model for the kinetics of phase separation. In: Mathematical Models for Phase Change Problems (Óbidos, 1988), volume 88 of Internat. Ser. Numer. Math., pp. 35–73. Birkhäuser, Basel (1989)
Elliott, C.M., Ranner, T.: Evolving surface finite element method for the Cahn–Hilliard equation. Numer. Math. 129(3), 483–534 (2015)
Elliott, C.M., Ranner, T.: A unified theory for continuous-in-time evolving finite element space approximations to partial differential equations in evolving domains. IMA J. Numer. Anal. 41, 1696–1845 (2020)
Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II.: Stiff and Differential—Algebraic Problems, 2nd edn. Springer, Berlin (1996)
Harder, P., Kovács, B.: Error estimates for the Cahn–Hilliard equation with dynamic boundary conditions. IMA J. Numer. Anal. (2021). https://doi.org/10.1093/imanum/drab045
Khain, E., Sander, L.M.: Generalized Cahn–Hilliard equation for biological applications. Phys. Rev. E 77(5), 051129 (2008)
Kovács, B.: High-order evolving surface finite element method for parabolic problems on evolving surfaces. IMA J. Numer. Anal. 38(1), 430–459 (2018)
Kovács, B., Li, B., Lubich, C.: A convergent evolving finite element algorithm for mean curvature flow of closed surfaces. Numer. Math. 143(4), 797–853 (2019)
Kovács, B., Li, B., Lubich, C.: A convergent evolving finite element algorithm for Willmore flow of closed surfaces. Numer. Math. 149(3), 595–643 (2021)
Kovács, B., Li, B., Lubich, C., Power Guerra, C.: Convergence of finite elements on an evolving surface driven by diffusion on the surface. Numer. Math. 137(3), 643–689 (2017)
Kovács, B., Lubich, C.: Linearly implicit full discretization of surface evolution. Numer. Math. 140(1), 121–152 (2018)
Kovács, B., Power Guerra, C.: Error analysis for full discretizations of quasilinear parabolic problems on evolving surfaces. NMPDE 32(4), 1200–1231 (2016)
Kovács, B., Power Guerra, C.: Higher order time discretizations with ALE finite elements for parabolic problems on evolving surfaces. IMA J. Numer. Anal. 38(1), 460–494 (2018)
Liu, J., Dedè, L., Evans, J.A., Borden, M.J., Hughes, T.J.R.: Isogeometric analysis of the advective Cahn–Hilliard equation: spinodal decomposition under shear flow. J. Comput. Phys. 242, 321–350 (2013)
Lubich, C., Mansour, D.: Variational discretization of wave equations on evolving surfaces. Math. Comput. 84(292), 513–542 (2015)
Lubich, C., Mansour, D., Venkataraman, C.: Backward difference time discretization of parabolic differential equations on evolving surfaces. IMA J. Numer. Anal. 33(4), 1365–1385 (2013)
Miranville, A.: The Cahn–Hilliard equation and some of its variants. AIMS Math. 2(3), 479 (2017)
Miranville, A.: Existence of solutions to a Cahn–Hilliard type equation with a logarithmic nonlinear term. Mediterr. J. Math. 16(1), 18 (2019)
Nevanlinna, O., Odeh, F.: Multiplier techniques for linear multistep methods. Numer. Funct. Anal. Optim. 3, 377–423 (1981)
O’Connor, D., Stinner, B.: The Cahn–Hilliard equation on an evolving surface. arXiv:1607.05627 (2016)
Yushutin, V., Quaini, A., Majd, S., Olshanskii, M.: A computational study of lateral phase separation in biological membranes. Int. J. Numer. Methods Biomed. Eng. 35(3), 3181 (2019)
Yushutin, V., Quaini, A., Olshanskii, M.: Numerical modeling of phase separation on dynamic surfaces. J. Comput. Phys. 407, 109–126 (2020)
Zimmermann, C., Toshniwal, D., Landis, C.M., Hughes, T.J.R., Mandadapu, K.K., Sauer, R.A.: An isogeometric finite element formulation for phase transitions on deforming surfaces. Comput. Methods Appl. Mech. Eng. 351, 441–477 (2019)
Acknowledgements
We thank Christian Lubich for helpful discussions, in particular on initial values. We would like to thank two Referees whose comments have helped us to improve the presentation of the paper. The manuscript was partially written when Balázs Kovács had been working at the University of Tübingen. We gratefully acknowledge their support. The work of Cedric Aaron Beschle is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 251654672—TRR 161. The work of Balázs Kovács is supported by Deutsche Forschungsgemeinschaft—Project-ID 258734477—SFB 1173, and by the Heisenberg Programme of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 446431602.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beschle, C.A., Kovács, B. Stability and error estimates for non-linear Cahn–Hilliard-type equations on evolving surfaces. Numer. Math. 151, 1–48 (2022). https://doi.org/10.1007/s00211-022-01280-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01280-5