Skip to main content
SpringerLink
Log in

The loop-linking number of line arrangements

  • Published:
Mathematische Zeitschrift Aims and scope Submit manuscript

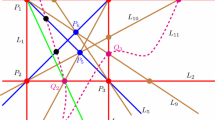
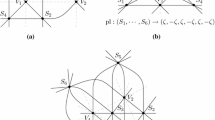
Abstract

In his Ph.D. thesis, Cadegan-Schlieper constructs an invariant of the embedded topology of a line arrangement which generalizes the \(\mathcal {I}\)-invariant introduced by Artal, Florens and the author. This new invariant is called the loop-linking number in the present paper. We refine the result of Cadegan-Schlieper by proving that the loop-linking number is an invariant of the homeomorphism type of the arrangement complement. We give two effective methods to compute this invariant, both are based on the braid monodromy. As an application, we detect an arithmetic Zariski pair of arrangements with 11 lines whose coefficients are in the 5th cyclotomic field. Furthermore, we also prove that the fundamental groups of their complements are not isomorphic; it is the Zariski pair with the fewest number of lines which have this property. We also detect an arithmetic Zariski triple with 12 lines whose complements have non-isomorphic fundamental groups. In the appendix, we give 29 combinatorial types which lead to similar ordered arithmetic Zariski pairs of 11 lines. To conclude this paper, we give a additivity theorem for the union of arrangements. This first allows us to prove that the complements of Rybnikov’s arrangements are not homeomorphic, and then leads us to a generalization of Rybnikov’s result. Lastly, we use it to prove the existence of homotopy-equivalent lattice-isomorphic arrangements which have non-homeomorphic complements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. We should also mention here the refinement obtained by Jiang and Yau [25] who proved that the homeomorphism type of the complement determines the intersection lattice.

  2. This name arises from the work of Zariski who pioneered the study of the topology of equisingular curves [40, 41]. In particular, he constructed the first example of two irreducible curves of degree 6 which have the same local singularities and non-isomorphic fundamental groups.

  3. In the general case of algebraic plane curves, a Zariski pair is said to be arithmetic if the equations of their arrangements are conjugated in a Galois field. Such pairs have been extensively studied by authors like Degtyarev, Oka, Shimada or Tokunaga. Note that the Zariski pairs of arrangements given in [4, 19] are arithmetic.

  4. The boundary manifold is the boundary of a regular tubular neighborhood of \(\bigcup _{L\in \mathcal {A}}L\). It is a graph 3-manifold determined by the combinatorics of \(\mathcal {A}\). This manifold has been studied in [13].

  5. See [34] for more details about complex reflection groups.

  6. The ordered (resp. oriented) topological type of \(\mathcal {A}\) is the class of homeomorphism of \(\mathbb {C}\mathbb {P}^2\) which fixes \(\bigcup _{L\in \mathcal {A}}L\) and respects a fixed complete order on \(\mathcal {A}\) (resp. the global orientation of \(\mathbb {C}\mathbb {P}^2\) and the local orientation of the meridians).

  7. If \(\mathcal {A}\) is a pencil then its topology is combinatorially determined.

  8. It is compact, orientable, irreducible, and has an embedded incompressible surface.

  9. Note that this isomorphism between the ordered combinatorics is unique.

  10. To lighten the notation a sub-arrangement \(\mathcal {A}_P=\{L_{i_1},\ldots ,L_{i_m}\}\) is denoted by \(\{i_1,\ldots ,i_m\}\).

  11. The braids \(B_{ {(P\rightarrow L)} }\) are given as tuple of integer \((i_1,\ldots ,i_k)\), where a positive integer i in the tuple indicates a positive crossing between the strands number i and \(|i+1|\); while a negative i indicates a negative crossing between strands numbers |i| and \(|i|+1\). The singular points \(P_{i_1,\ldots , i_m}\) are expressed as the tuple \([i_1,\dots ,i_m]\).

  12. A wiring diagram of \(\mathcal {M}_2\) (resp. \(\mathcal {M}_4\)) can be obtained from the one of \(\mathcal {M}_3\) (resp. \(\mathcal {M}_1\)) by the inversion of the sign of the virtual crossings.

  13. This can be viewed as a consequence of Theorem 5.5 presented below.

  14. We consider the orders given by the indices, i.e. \(L^k_i< L^k_j \Leftrightarrow i<j\).

  15. A more detailed list with the equations of the realizations and the automorphism groups is given in the first version of this paper available at arXiv:2004.03550.

References

  1. Artal, E.B., Martín-Morales, J., Cogolludo-Agustín, J.I.: Triangular curves and cyclotomic Zariski tuples. Collect. Math. 71, 427–441 (2020)

    Article  MathSciNet  Google Scholar 

  2. Arvola, W.A.: The fundamental group of the complement of an arrangement of complex hyperplanes. Topology 31(4), 757–765 (1992)

    Article  MathSciNet  Google Scholar 

  3. Bartolo, E.A., Ruber, J.C., Augustín, J.I.C.: Essential coordinate components of characteristic varieties. Math. Proc. Camb. Philos. Soc. 136(2), 287–299 (2004)

    Article  MathSciNet  Google Scholar 

  4. Bartolo, E.A., Ruber, J.C., Agustín, J.I.C., Buzunáriz, M.M.: Topology and combinatorics of real line arrangements. Compos. Math. 141(6), 1578–1588 (2005)

    Article  MathSciNet  Google Scholar 

  5. Bartolo, E. A., Ruber, J.C., Agustín, J.I.C., Buzunáriz, M.Á.M.: Invariants of combinatorial line arrangements and Rybnikov’s example. In: Singularity theory and its applications. Papers from the 12th MSJ International Research Institute of the Mathematical Society of Japan, Sapporo, Japan, September 16–25, 2003, pp. 1–34. Mathematical Society of Japan, Tokyo (2006)

  6. Bartolo, E. A., Cogolludo, J.I., Tokunuga, H.: A survey on Zariski pairs. In: Algebraic geometry in East Asia—Hanoi 2005. Proceedings of the 2nd International Conference on Algebraic Geometry in East Asia, Hanoi, Vietnam, October 10–14, 2005, pp. 1–100. Mathematical Society of Japan, Tokyo (2008)

  7. Bartolo, E.A., Cogolludo-Agustín, J.I., Guerville-Ballé, B., Marco-Buzunáriz, M.: An arithmetic Zariski pair of line arrangements with non-isomorphic fundamental group. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 111(2), 377–402 (2017)

    Article  MathSciNet  Google Scholar 

  8. Bartolo, E.A., Florens, V., Guerville-Ballé, B.: A topological invariant of line arrangements. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 17(3), 949–968 (2017)

    MathSciNet  MATH  Google Scholar 

  9. Bartolo, E.A., Guerville-Ballé, B., Viu-Sos, J.: Fundamental groups of real arrangements and torsion in the lower central series quotients. Exp. Math. 29(1), 28–35 (2020)

    Article  MathSciNet  Google Scholar 

  10. Brieskorn, E., Knörrer, H.: Plane algebraic curves. In: Transl. from the German by John Stillwell, vol. VI, 721, pp. DM 98.00. Birkhäuser, Basel (1986)

  11. Buzunáriz, M.Á.M.: A description of the resonance variety of a line combinatorics via combinatorial pencils. Graphs Comb. 25(4), 469–488 (2009)

    Article  MathSciNet  Google Scholar 

  12. Cadegan-Schlieper, W.: On the geometry and topology of hyperplane complements associated to complex and quaternionic reflection groups. PhD thesis, University of California-Los Angeles (2018)

  13. Cohen, D.C., Suciu, A.I.: The boundary manifold of a complex line arrangement. In: Proceedings of the Conference on Groups, Homotopy and Configuration Spaces, University of Tokyo, Japan, July 5–11, 2005 in Honor of the 60th Birthday of Fred Cohen, pp. 105–146. Geometry & Topology Publications, Coventry (2008)

  14. Cohen, D.C., Suciu, A.I.: The braid monodromy of plane algebraic curves and hyperplane arrangements. Comment. Math. Helv. 72(2), 285–315 (1997)

    Article  MathSciNet  Google Scholar 

  15. Falk, M., Randell, R.: On the homotopy theory of arrangements. II. In: Arrangements—Tokyo 1998. Proceedings of a workshop on mathematics related to arrangements of hyperplanes, Tokyo, Japan, July 13–18, 1998. In honor of the 60th birthyear of Peter Orlik, pp. 93–125. Kinokuniya Company Ltd., Tokyo (2000)

  16. Fan, K.-M.: Direct product of free groups as the fundamental group of the complement of a union of lines. Mich. Math. J. 44(2), 283–291 (1997)

    Article  MathSciNet  Google Scholar 

  17. Florens, V., Guerville-Ballé, B., Marco-Buzunariz, M.A.: On complex line arrangements and their boundary manifolds. Math. Proc. Camb. Philos. Soc. 159(2), 189–205 (2015)

    Article  MathSciNet  Google Scholar 

  18. Goodman, J.E.: Proof of a conjecture of Burr, Grünbaum, and Sloane. Discrete Math. 32, 27–35 (1980)

    Article  MathSciNet  Google Scholar 

  19. Guerville-Ballé, B.: An arithmetic Zariski 4-tuple of twelve lines. Geom. Topol. 20(1), 537–553 (2016)

    Article  MathSciNet  Google Scholar 

  20. Guerville-Ballé, B.: Multiplicativity of the \(\cal{I}\)-invariant and topology of glued arrangements. J. Math. Soc. Japan 70(1), 215–227 (2018)

    Article  MathSciNet  Google Scholar 

  21. Guerville-Ballé, B.: Topology and homotopy of lattice isomorphic arrangements. Proc. Am. Math. Soc. 148, 2193–2200 (2020)

    Article  MathSciNet  Google Scholar 

  22. Guerville-Ballé, B., Viu-Sos, J.: Configurations of points and topology of real line arrangements. Math. Ann. 374(1–2), 1–35 (2019)

    Article  MathSciNet  Google Scholar 

  23. Haken, W.: Ein Verfahren zur Aufspaltung einer 3-Mannigfaltigkeit in irreduzible 3- Mannigfaltigkeiten. Math. Z. 76, 427–467 (1961)

    Article  MathSciNet  Google Scholar 

  24. Haken, W.: Theorie der Normalflächen. Ein Isotopiekriterium für den Kreisknoten. Acta Math. 105, 245–375 (1961)

    Article  MathSciNet  Google Scholar 

  25. Jiang, T., Yau, S.S.-T.: Topological invariance of intersection lattices of arrangements in \(\mathbb{CP}^ 2\). Bull. Am. Math. Soc. New Ser. 29(1), 88–93 (1993)

    Article  Google Scholar 

  26. MacLane, S.: Some interpretations of abstract linear dependence in terms of projective geometry. Am. J. Math. 58, 236–240 (1936)

    Article  MathSciNet  Google Scholar 

  27. Moishezon, B.G.: Stable branch curves and braid monodromies. Algebraic geometry. In: Proceedings Conference, Chicago Circle 1980. Lecture Notes in Mathematics, vol. 862, pp. 107–192 (1981)

  28. Nazir, S., Yoshinaga, M.: On the connectivity of the realization spaces of line arrangements. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 11(4), 921–937 (2012)

    MathSciNet  MATH  Google Scholar 

  29. Neumann, W.D.: A calculus for plumbing applied to the topology of complex surface singularities and degenerating complex curves. Trans. Am. Math. Soc. 268, 299–343 (1981)

    Article  MathSciNet  Google Scholar 

  30. Orlik, P., Solomon, L.: Combinatorics and topology of complements of hyperplanes. Invent. Math. 56, 167–189 (1980)

    Article  MathSciNet  Google Scholar 

  31. Orlik, P., Terao, H.: Arrangements of hyperplanes, vol. 300. Springer, Berlin (1992)

    Book  Google Scholar 

  32. Rybnikov, G.L.: On the fundamental group of the complement of a complex hyperplane arrangement. Funct. Anal. Appl. 45(2), 137–148 (2011)

    Article  MathSciNet  Google Scholar 

  33. Salvetti, M.: Arrangements of lines and monodromy of plane curves. Compos. Math. 68(1), 103–122 (1988)

    MathSciNet  MATH  Google Scholar 

  34. Shephard, G.C., Todd, J.A.: Finite unitary reflection groups. Can. J. Math. 6, 274–304 (1954)

    Article  MathSciNet  Google Scholar 

  35. Suciu, A.I.: Hyperplane arrangements and Milnor fibrations. Ann. Fac. Sci. Toulouse Math. (6) 23(2), 417–481 (2014)

    Article  MathSciNet  Google Scholar 

  36. Waldhausen, F.: Eine Klasse von 3-dimensionalen Mannigfaltigkeiten. I, II. Invent. Math. 3, 308–333 (1967)

    Article  MathSciNet  Google Scholar 

  37. Waldhausen, F.: On irreducible \(3\)-manifolds which are sufficiently large. Ann. Math. (2) 87, 56–88 (1968)

    Article  MathSciNet  Google Scholar 

  38. Westlund, E.: The boundary manifold of an arrangement. PhD thesis, University of Wisconsin-Madison (1997)

  39. Ye, F.: Classification of moduli spaces of arrangements of nine projective lines. Pac. J. Math. 265(1), 243–256 (2013)

    Article  MathSciNet  Google Scholar 

  40. Zariski, O.: On the problem of existence of algebraic functions of two variables possessing a given branch curve. Am. J. Math. 51, 305–328 (1929)

    Article  MathSciNet  Google Scholar 

  41. Zariski, O.: On the irregularity of cyclic multiple planes. Ann. Math. (2) 32, 485–511 (1931)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

During this work the author have been supported, first by the postdoctoral grant #2017/15369-0 of the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), second by the Polish Academy of Sciences, and third by JSPS KAKENHI Grant Number JP17H06128. The author would like to thank J. Viu-Sos for all their rewarding discussions and all his remarks/comments which greatly contributed to improve the quality of this article. He is also grateful to E. Hollen for her efficient and careful proofreading of this manuscript.

Author information

Authors and Affiliations

  1. Institute of Mathematics for Industry, Kyushu University, Fukuoka, Japan

    Benoît Guerville-Ballé

Authors
  1. Benoît Guerville-Ballé
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Benoît Guerville-Ballé.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Values for the arrangements \(\mathcal {M}_i\)

1.1 Generator of \({{\,\mathrm{TLG}\,}}(C,\mathbb {Z}/5\mathbb {Z})\)

The generator \(\Lambda _0\) of \({{\,\mathrm{TLG}\,}}(C,\mathbb {Z}/5\mathbb {Z})\) is given by the following characters \(\lambda _{ {(P\rightarrow L)} }\).

figure c

1.2 The upper-linking numbers of \(\mathcal {M}_1\)

The values of the upper-linking numbers of the braid \(B_{ {(P\rightarrow L)} }\) are given below. The values denoted with a \(=^*\) symbol have been simplified using the property \(\sum _{L\in \mathcal {A}} m_L = 0\).

figure d

Appendix B: List of arithmetic Zariski pairs with 11 lines

Each one of following combinatoricsFootnote 15 admits four realizations Galois conjugated in the 5th cyclotomic fields and its tensor linking groups with coefficients in \(\mathbb {Z}/5\mathbb {Z}\) is isomorphic to \(\mathbb {Z}/5\mathbb {Z}\). Furthermore, their realizations can be distinguished using the loop-linking number. The following list has been obtained using a computer-aid checking of all the lines combinatorics with 11 lines. First, we listed the combinatorics which admits a non-trivial tensor linking group with coefficients in \(\mathbb {Z}/p\mathbb {Z}\) for \(p=5,7,9,11\). Then, we determined the moduli-space of each of these combinatorics, and for the one which have several connected-components, we computed their loop-linking numbers. To our knowledge and our computations, the following list together with the examples obtained from the ordered Zariski pair of Sect. 4.1 and the one of [19], is the complete list of the combinatorics which leads to an arithmetic Zariski pair with 11 lines that can be detected by the loop-linking number with coefficient in \(\mathbb {Z}/p\mathbb {Z}\) for \(p=5,7,9,11\).

$$\begin{aligned} C_1=\big \{&\{1, 2\}, \{1, 3, 4, 5\}, \{1, 6, 8\}, \{1, 7, 11\}, \{1, 9, 10\}, \{2, 3, 6, 7\}, \{2, 4, 11\}, \{2, 5, 10\}\\&\{2, 8, 9\}, \{3, 8, 11\}, \{3, 9\}, \{3, 10\}, \{4, 6, 9\}, \{4, 7\}, \{4, 8\}, \{4, 10\}, \{5, 6\}, \{5, 7\}\\&\{5, 8\}, \{5, 9, 11\}, \{6, 10\}, \{6, 11\}, \{7, 8, 10\}, \{7, 9\}, \{10, 11\} \big \} \\&\\ C_2=\big \{&\{1, 2, 3\}, \{1, 4\}, \{1, 5, 7, 8\}, \{1, 6, 9\}, \{1, 10, 11\}, \{2, 4, 5, 6\}, \{2, 7, 11\}, \{2, 8\}, \{2, 9, 10\}\\&\{3, 4, 9\}, \{3, 5\}, \{3, 6, 8\}, \{3, 7\}, \{3, 10\}, \{3, 11\}, \{4, 7, 10\}, \{4, 8, 11\}, \{5, 9, 11\}\\&\{5, 10\}, \{6, 7\}, \{6, 10\}, \{6, 11\}, \{7, 9\}, \{8, 9\}, \{8, 10\} \big \} \\&\\ C_3=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 6, 10\}, \{2, 5, 8\}, \{2, 7\}, \{2, 9, 11\}\\&\{3, 4, 7\}, \{3, 5\}, \{3, 6, 11\}, \{3, 8\}, \{3, 9\}, \{3, 10\}, \{4, 8, 11\}, \{4, 9\}, \{5, 6, 9\}, \{5, 7\}\\&\{5, 10\}, \{5, 11\}, \{6, 8\}, \{7, 8, 10\}, \{7, 9\}, \{7, 11\}, \{9, 10\} \big \} \\&\\ C_4=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 6, 10\}, \{2, 5, 8\}, \{2, 7, 9\}\\&\{2, 11\}, \{3, 4, 7\}, \{3, 5\}, \{3, 6, 11\}, \{3, 8\}, \{3, 9\}, \{3, 10\}, \{4, 8, 11\}, \{4, 9\}, \{5, 6, 9\}\\&\{5, 7\}, \{5, 10\}, \{5, 11\}, \{6, 8\}, \{7, 8, 10\}, \{7, 11\}, \{9, 10\}, \{9, 11\} \big \} \\&\\ C_5=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8\}, \{2, 5, 6\}, \{2, 7, 9, 10\}\\&\{2, 11\}, \{3, 4, 10\}, \{3, 5\}, \{3, 6, 9\}, \{3, 7\}, \{3, 8, 11\}, \{4, 6, 11\}, \{4, 7\}, \{4, 9\}, \{5, 7, 8\}\\&\{5, 9\}, \{5, 10\}, \{5, 11\}, \{6, 8\}, \{6, 10\}, \{7, 11\}, \{8, 10\}, \{9, 11\} \big \} \\&\\ C_6=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8, 10\}, \{2, 5\}, \{2, 6, 9\}, \{2, 7, 11\}\\&\{3, 4, 6\}, \{3, 5\}, \{3, 7\}, \{3, 8, 11\}, \{3, 9\}, \{3, 10\}, \{4, 7, 9\}, \{4, 11\}, \{5, 6, 11\}, \{5, 7\}\\&\{5, 8\}, \{5, 9, 10\}, \{6, 8\}, \{6, 10\}, \{7, 8\}, \{7, 10\}, \{9, 11\} \big \} \\&\\ C_7=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8, 10\}, \{2, 5\}, \{2, 6, 11\}, \{2, 7, 9\}\\&\{3, 4, 7\}, \{3, 5\}, \{3, 6, 8\}, \{3, 9\}, \{3, 10\}, \{3, 11\}, \{4, 6\}, \{4, 9, 11\}, \{5, 6, 9\}, \{5, 7, 10\}\\&\{5, 8\}, \{5, 11\}, \{6, 10\}, \{7, 8\}, \{7, 11\}, \{8, 11\}, \{9, 10\} \big \} \\&\\ C_8=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8, 10\}, \{2, 5\}, \{2, 6, 11\}, \{2, 7, 9\}\\&\{3, 4, 9\}, \{3, 5, 6\}, \{3, 7\}, \{3, 8\}, \{3, 10\}, \{3, 11\}, \{4, 6\}, \{4, 7, 11\}, \{5, 7\}, \{5, 8, 11\}\\&\{5, 9\}, \{5, 10\}, \{6, 8\}, \{6, 9, 10\}, \{7, 8\}, \{7, 10\}, \{9, 11\} \big \} \\&\\ C_9=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8, 10\}, \{2, 5, 6\}, \{2, 7\}, \{2, 9, 11\}\\&\{3, 4, 7\}, \{3, 5\}, \{3, 6, 9\}, \{3, 8\}, \{3, 10\}, \{3, 11\}, \{4, 6, 11\}, \{4, 9\}, \{5, 7\}, \{5, 8\}\\&\{5, 9, 10\}, \{5, 11\}, \{6, 8\}, \{6, 10\}, \{7, 8, 11\}, \{7, 9\}, \{7, 10\} \big \} \\&\\ C_{10}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8, 10\}, \{2, 5, 6\}, \{2, 7\}, \{2, 9, 11\}\\&\{3, 4, 7\}, \{3, 5\}, \{3, 6, 9\}, \{3, 8\}, \{3, 10\}, \{3, 11\}, \{4, 6, 11\}, \{4, 9\}, \{5, 7, 8\}, \{5, 9, 10\}\\&\{5, 11\}, \{6, 8\}, \{6, 10\}, \{7, 9\}, \{7, 10\}, \{7, 11\}, \{8, 11\} \big \} \\&\\ C_{11}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 8, 10\}, \{2, 5, 6\}, \{2, 7, 9\}\\&\{2, 11\}, \{3, 4, 7\}, \{3, 5\}, \{3, 6, 11\}, \{3, 8\}, \{3, 9\}, \{3, 10\}, \{4, 6\}, \{4, 9, 11\}, \{5, 7, 8\}\\&\{5, 9\}, \{5, 10\}, \{5, 11\}, \{6, 8\}, \{6, 9, 10\}, \{7, 10\}, \{7, 11\}, \{8, 11\} \big \} \\&\\ C_{12}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 10\}, \{2, 5, 6, 8\}, \{2, 7\}, \{2, 9, 11\}\\&\{3, 4, 6, 11\}, \{3, 5\}, \{3, 7, 9\}, \{3, 8\}, \{3, 10\}, \{4, 7, 8\}, \{4, 9\}, \{5, 7\}, \{5, 9, 10\}, \{5, 11\}\\&\{6, 9\}, \{6, 10\}, \{7, 10\}, \{7, 11\}, \{8, 10\}, \{8, 11\} \big \} \\&\\ C_{13}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10, 11\}, \{2, 4, 10\}, \{2, 5, 9, 11\}, \{2, 6\}, \{2, 7, 8\}\\&\{3, 4, 7\}, \{3, 5, 8\}, \{3, 6, 11\}, \{3, 9\}, \{3, 10\}, \{4, 6, 8\}, \{4, 9\}, \{4, 11\}, \{5, 6\}, \{5, 7\}\\&\{5, 10\}, \{6, 9, 10\}, \{7, 9\}, \{7, 10\}, \{7, 11\}, \{8, 10\}, \{8, 11\} \big \} \\&\\ C_{14}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 4, 6, 11\}, \{2, 5, 9\}, \{2, 7, 10\}\\&\{2, 8\}, \{3, 4, 7\}, \{3, 5\}, \{3, 6\}, \{3, 8\}, \{3, 9, 11\}, \{3, 10\}, \{4, 8, 9\}, \{4, 10\}, \{5, 6, 10\}\\&\{5, 7\}, \{5, 8\}, \{5, 11\}, \{6, 9\}, \{7, 9\}, \{7, 11\}, \{8, 10, 11\} \big \} \\&\\ C_{15}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 8, 10\}, \{1, 7, 9\}, \{1, 11\}, \{2, 4, 6\}, \{2, 5, 9, 11\}, \{2, 7, 8\}\\&\{2, 10\}, \{3, 4, 7\}, \{3, 5, 10\}, \{3, 6, 11\}, \{3, 8\}, \{3, 9\}, \{4, 8, 9\}, \{4, 10\}, \{4, 11\}, \{5, 6\}\\&\{5, 7\}, \{5, 8\}, \{6, 7\}, \{6, 9\}, \{7, 10, 11\}, \{8, 11\}, \{9, 10\} \big \} \\&\\ C_{16}=\big \{&\{1, 2, 3\}, \{1, 4, 5\}, \{1, 6, 10\}, \{1, 7, 11\}, \{1, 8, 9\}, \{2, 4, 6\}, \{2, 5, 7\}, \{2, 8, 10\}, \{2, 9, 11\}\\&\{3, 4\}, \{3, 5, 9\}, \{3, 6\}, \{3, 7, 8\}, \{3, 10\}, \{3, 11\}, \{4, 7, 10\}, \{4, 8, 11\}, \{4, 9\}, \{5, 6, 11\}\\&\{5, 8\}, \{5, 10\}, \{6, 7\}, \{6, 8\}, \{6, 9\}, \{7, 9\}, \{9, 10\}, \{10, 11\} \big \} \\&\\ C_{17}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 6\}, \{1, 7\}, \{1, 8, 10\}, \{1, 9, 11\}, \{2, 4, 7\}, \{2, 5, 8, 9\}, \{2, 6, 11\}\\&\{2, 10\}, \{3, 4, 9\}, \{3, 5\}, \{3, 6, 10\}, \{3, 7\}, \{3, 8\}, \{3, 11\}, \{4, 8\}, \{4, 10, 11\}, \{5, 7, 10\}\\&\{5, 11\}, \{6, 7\}, \{6, 8\}, \{6, 9\}, \{7, 8, 11\}, \{7, 9\}, \{9, 10\} \big \} \\&\\ C_{18}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 6\}, \{1, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 4, 7, 9\}, \{2, 5, 8\}, \{2, 6\}, \{2, 10, 11\}\\&\{3, 4, 11\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{3, 8, 10\}, \{3, 9\}, \{4, 8\}, \{4, 10\}, \{5, 7\}, \{5, 9, 11\}\\&\{5, 10\}, \{6, 7, 10\}, \{6, 8, 11\}, \{6, 9\}, \{7, 11\}, \{8, 9\} \big \} \\&\\ C_{19}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 6\}, \{1, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 4, 7, 9\}, \{2, 5, 11\}, \{2, 6, 8\}\\&\{2, 10\}, \{3, 4\}, \{3, 5, 10\}, \{3, 6\}, \{3, 7, 11\}, \{3, 8\}, \{3, 9\}, \{4, 8\}, \{4, 10, 11\}, \{5, 7\}\\&\{5, 8, 9\}, \{6, 7, 10\}, \{6, 9\}, \{6, 11\}, \{8, 10\}, \{8, 11\}, \{9, 11\} \big \} \\&\\ C_{20}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 6\}, \{1, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 4, 9, 11\}, \{2, 5, 10\}, \{2, 6, 8\}\\&\{2, 7\}, \{3, 4, 7\}, \{3, 5\}, \{3, 6\}, \{3, 8, 9\}, \{3, 10, 11\}, \{4, 8\}, \{4, 10\}, \{5, 7, 11\}, \{5, 8\}\\&\{5, 9\}, \{6, 7, 10\}, \{6, 9\}, \{6, 11\}, \{7, 9\}, \{8, 10\}, \{8, 11\} \big \} \\&\\ C_{21}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 6\}, \{1, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 4, 11\}, \{2, 5, 7, 9\}, \{2, 6\}, \{2, 8, 10\}\\&\{3, 4, 10\}, \{3, 5, 11\}, \{3, 6, 8\}, \{3, 7\}, \{3, 9\}, \{4, 7\}, \{4, 8, 9\}, \{5, 8\}, \{5, 10\}, \{6, 7, 11\}\\&\{6, 9\}, \{6, 10\}, \{7, 10\}, \{8, 11\}, \{9, 11\}, \{10, 11\} \big \} \\&\\ C_{22}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 7\}, \{1, 6, 9\}, \{1, 8, 11\}, \{1, 10\}, \{2, 4, 6, 8\}, \{2, 5, 10\}, \{2, 7, 11\}\\&\{2, 9\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7, 10\}, \{3, 8, 9\}, \{3, 11\}, \{4, 9, 10\}, \{4, 11\}, \{5, 6\}\\&\{5, 8\}, \{5, 9, 11\}, \{6, 7\}, \{6, 10, 11\}, \{7, 8\}, \{7, 9\}, \{8, 10\} \big \} \\&\\ C_{23}=\big \{&\{1, 2, 3\}, \{1, 4, 5, 7\}, \{1, 6, 10\}, \{1, 8\}, \{1, 9, 11\}, \{2, 4, 6, 8\}, \{2, 5, 11\}, \{2, 7\}, \{2, 9, 10\}\\&\{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7, 11\}, \{3, 8, 10\}, \{3, 9\}, \{4, 9\}, \{4, 10, 11\}, \{5, 6\}, \{5, 8, 9\}\\&\{5, 10\}, \{6, 7, 9\}, \{6, 11\}, \{7, 8\}, \{7, 10\}, \{8, 11\} \big \} \\&\\ C_{24}=\big \{&\{1, 2, 3, 4\}, \{1, 5, 6\}, \{1, 7, 8\}, \{1, 9\}, \{1, 10, 11\}, \{2, 5\}, \{2, 6, 10\}, \{2, 7, 9\}, \{2, 8, 11\}\\&\{3, 5, 7\}, \{3, 6\}, \{3, 8\}, \{3, 9, 10\}, \{3, 11\}, \{4, 5\}, \{4, 6, 7\}, \{4, 8, 9\}, \{4, 10\}, \{4, 11\}\\&\{5, 8, 10\}, \{5, 9, 11\}, \{6, 8\}, \{6, 9\}, \{6, 11\}, \{7, 10\}, \{7, 11\} \big \} \\&\\ C_{25}=\big \{&\{1, 2, 3, 4\}, \{1, 5, 6\}, \{1, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 5, 7\}, \{2, 6, 9\}, \{2, 8, 11\}, \{2, 10\}\\&\{3, 5\}, \{3, 6, 8\}, \{3, 7, 9\}, \{3, 10\}, \{3, 11\}, \{4, 5\}, \{4, 6, 10\}, \{4, 7, 11\}, \{4, 8\}, \{4, 9\}\\&\{5, 8, 10\}, \{5, 9, 11\}, \{6, 7\}, \{6, 11\}, \{7, 10\}, \{8, 9\}, \{10, 11\} \big \} \\&\\ C_{26}=\big \{&\{1, 2, 3, 4\}, \{1, 5, 6\}, \{1, 7, 8\}, \{1, 9, 10\}, \{1, 11\}, \{2, 5, 9\}, \{2, 6, 7\}, \{2, 8, 11\}, \{2, 10\}\\&\{3, 5, 7\}, \{3, 6\}, \{3, 8, 9\}, \{3, 10\}, \{3, 11\}, \{4, 5\}, \{4, 6, 9\}, \{4, 7, 11\}, \{4, 8\}, \{4, 10\}\\&\{5, 8, 10\}, \{5, 11\}, \{6, 8\}, \{6, 10, 11\}, \{7, 9\}, \{7, 10\}, \{9, 11\} \big \} \\&\\ C_{27}=\big \{&\{1, 2, 3, 4\}, \{1, 5, 6\}, \{1, 7, 10\}, \{1, 8, 9\}, \{1, 11\}, \{2, 5, 7\}, \{2, 6, 8\}, \{2, 9, 10\}, \{2, 11\}\\&\{3, 5, 9\}, \{3, 6, 11\}, \{3, 7\}, \{3, 8\}, \{3, 10\}, \{4, 5\}, \{4, 6, 7\}, \{4, 8, 11\}, \{4, 9\}, \{4, 10\}\\&\{5, 8, 10\}, \{5, 11\}, \{6, 9\}, \{6, 10\}, \{7, 8\}, \{7, 9, 11\}, \{10, 11\} \big \} \\&\\ C_{28}=\big \{&\{1, 2, 4\}, \{1, 3, 5\}, \{1, 6, 7\}, \{1, 8, 9\}, \{1, 10\}, \{1, 11\}, \{2, 3\}, \{2, 5, 6\}, \{2, 7, 8\}, \{2, 9, 10\}\\&\{2, 11\}, \{3, 4, 7\}, \{3, 6, 8\}, \{3, 9, 11\}, \{3, 10\}, \{4, 5, 9\}, \{4, 6, 10\}, \{4, 8\}, \{4, 11\}\\&\{5, 7, 11\}, \{5, 8\}, \{5, 10\}, \{6, 9\}, \{6, 11\}, \{7, 9\}, \{7, 10\}, \{8, 10, 11\} \big \} \\&\\ C_{29}=\big \{&\{1, 2, 5\}, \{1, 3, 7\}, \{1, 4, 8\}, \{1, 6, 9\}, \{1, 10, 11\}, \{2, 3, 9\}, \{2, 4, 10\}, \{2, 6, 8\}, \{2, 7, 11\}\\&\{3, 4, 6\}, \{3, 5, 10\}, \{3, 8, 11\}, \{4, 5, 7\}, \{4, 9, 11\}, \{5, 6\}, \{5, 8\}, \{5, 9\}, \{5, 11\}, \{6, 7\}\\&\{6, 10\}, \{6, 11\}, \{7, 8\}, \{7, 9\}, \{7, 10\}, \{8, 9\}, \{8, 10\}, \{9, 10\} \big \} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guerville-Ballé, B. The loop-linking number of line arrangements. Math. Z. 301, 1821–1850 (2022). https://doi.org/10.1007/s00209-021-02953-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00209-021-02953-x

Mathematics Subject Classification

Search

Navigation