Abstract
We give an algebraic criterion for the existence of projectively Hermitian–Yang–Mills metrics on a holomorphic vector bundle E over some complete non-compact Kähler manifolds \((X,\omega )\), where X is the complement of a divisor in a compact Kähler manifold and we impose some conditions on the cohomology class and the asymptotic behaviour of the Kähler form \(\omega \). We introduce the notion of stability with respect to a pair of (1, 1)-classes which generalizes the standard slope stability. We prove that this new stability condition is both sufficient and necessary for the existence of projectively Hermitian–Yang–Mills metrics in our setting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The celebrated Donaldson–Uhlenbeck–Yau theorem [8, 28] says that on a compact Kähler manifold \((X,\omega )\), an irreducible holomorphic vector bundle E admits a Hermitian–Yang–Mills (HYM) metric if and only if it is \(\omega \)-stable. After this pioneering work, there have been several results aiming to generalize this to non-compact Kähler manifolds [1, 15, 19, 21, 22, 25]. A key issue is to understand what role stability plays on the existence of projectively Hermitian–Yang–Mills (PHYM) metrics. An interesting special case in the non-compact setting is when (X, E) both can be compactified, i.e. X is the complement of a divisor in a compact Kähler manifold \(\,\overline{\!{X}}\) and E is the restriction of a holomorphic vector bundle \(\,\overline{\!{E}}\) on \(\,\overline{\!{X}}\), and when the Kähler metric has a known asymptotic behaviour. Under these assumptions, one wants to build a relation between the existence of PHYM metrics on E and some algebraic data on \(\,\overline{\!{E}}\). In this paper, we prove a result in this setting.
Let \(\,\overline{\!{X}}\) be an n-dimensional (\(n\ge 2\)) compact Kähler manifold, D be a smooth divisor and \(X=\,\overline{\!{X}}\backslash D\) denote the complement of D in \(\,\overline{\!{X}}\). Let \(\,\overline{\!{E}}\) be a holomorphic vector bundle on \(\,\overline{\!{X}}\), which we always assume to be irreducible unless otherwise mentioned. Let E,  denote its restriction to X and D respectively. Suppose the normal bundle \(N_D\) of D in \(\,\overline{\!{X}}\) is ample. On X we consider complete Kähler metrics \(\omega \) satisfying Assumption 1 (see Sect. 2 for a precise definition). Roughly speaking, we assume that \(\omega \) is asymptotic to certain model Kähler metrics given explicitly on the punctured disc bundle of \(N_D\) and there is a decomposition \(\omega =\omega _0+\sqrt{-1}\partial {\bar{\partial }}\varphi \), where \(\omega _0\) is a smooth closed (1,1)-form on \(\,\overline{\!{X}}\) vanishing when restricted to D, \(\varphi \) is a smooth function on X. Typical examples satisfying these assumptions are Calabi–Yau metrics on the complement of an anticanonical divisor of a Fano manifold and its generalizations [13, 14, 27] (see Sect. 6.2 for a sketch).
denote its restriction to X and D respectively. Suppose the normal bundle \(N_D\) of D in \(\,\overline{\!{X}}\) is ample. On X we consider complete Kähler metrics \(\omega \) satisfying Assumption 1 (see Sect. 2 for a precise definition). Roughly speaking, we assume that \(\omega \) is asymptotic to certain model Kähler metrics given explicitly on the punctured disc bundle of \(N_D\) and there is a decomposition \(\omega =\omega _0+\sqrt{-1}\partial {\bar{\partial }}\varphi \), where \(\omega _0\) is a smooth closed (1,1)-form on \(\,\overline{\!{X}}\) vanishing when restricted to D, \(\varphi \) is a smooth function on X. Typical examples satisfying these assumptions are Calabi–Yau metrics on the complement of an anticanonical divisor of a Fano manifold and its generalizations [13, 14, 27] (see Sect. 6.2 for a sketch).
To state our theorem, we need two ingredients: the existence of a good initial hermitian metric on E and the definition for stability with respect to a pair of classes. The following lemma is proved in Sect. 4.
Lemma 1.1
If  is \(c_1(N_D)\)-polystable, then there is a hermitian metric \(H_0\) on E satisfying:
is \(c_1(N_D)\)-polystable, then there is a hermitian metric \(H_0\) on E satisfying:
-
(1)
there is a hermitian metric \(\,\overline{\!{H}}_0\) on \(\,\overline{\!{E}}\) and a function \(f\in C^{\infty }(X)\) such that \(H_0={e}^f\,\overline{\!{H}}_0\),
-
(2)
\(|\Lambda _{\omega }F_{H_0}|=O(r^{-N_0})\), where r denotes the distance function to a fixed point induced by the metric w and \(N_0\) is the number in Assumption 1–(3).
We call \(H_0\) conformal to a smooth extendable metric if it satisfies the first condition in Lemma 1.1. A key feature we use in this paper is that the induced metic on \(\textrm{End}(E)\) is conformally invariant with respect to metrics on E. Therefore the two hermitian metrics \(H_0\) and \(\,\overline{\!{H}}_0\) induce the same metric on \(\textrm{End}(E)\) and this is the norm used in Lemma 1.1-(2). Then naturally (following [25]) one wants to find a PHYM metric in the following set
Here we use \(\sqrt{-1}{{\mathfrak {s}}}{{\mathfrak {u}}}(E,H_0)\) to denote the subbundle of \(\textrm{End}(E)\) consisting of the trace-free and self-adjoint endomorphisms with respect to \(H_0\). Though \(H_0\) in general is not unique, we will show that if we fix the induced metric on \(\det E\), then the set \({\mathcal {P}}_{H_0}\) is uniquely determined as long as \(H_0\) satisfies conditions in Lemma 1.1 (see Proposition 4.7).
Next we define stability with respect to a pair of (1,1)-classes, which generalizes the standard slope stability defined for Kähler classes in [16, Chapter 5]. In the following, we use \(\mu _{\alpha }(S)\) to denote the slope of a torsion-free coherent sheaf with respect to a class \(\alpha \in H^{1,1}(M)\) on a compact Kähler manifold M (see Sect. 3.2 for a more detailed discussion), i.e.
Definition 1.2
Let M be a compact Kähler manifold, \(\alpha ,\beta \in H^{1,1}(M)\) be two classes, E be a holomorphic vector bundle over M. We say E is \((\alpha ,\beta )\)-stable if every coherent reflexive subsheaf S of E with \(0<\text {rank}(S)<\text {rank}(E)\) satisfies either of the following conditions:
-
(a)
\(\mu _{\alpha }(S)< \mu _{\alpha }(E)\), or
-
(b)
\(\mu _{\alpha }(S)= \mu _{\alpha }(E)\) and \(\mu _{\beta }(S)<\mu _{\beta }(E)\).
The main result of this paper is
Theorem 1.3
Let \(\omega =\omega _0+dd^c\varphi \) be a Kähler metric satisfying the Assumption 1 in Sect. 2. Suppose  is \(c_1(N_D)\)-polystable and \({\mathcal {P}}_{H_0}\) is defined by (1.1). Then there exists a unique \(\omega \)-PHYM metric in \({\mathcal {P}}_{H_0}\) if and only if \(\,\overline{\!{E}}\) is \(\left( c_1(D),[\omega _0]\right) \)-stable.
is \(c_1(N_D)\)-polystable and \({\mathcal {P}}_{H_0}\) is defined by (1.1). Then there exists a unique \(\omega \)-PHYM metric in \({\mathcal {P}}_{H_0}\) if and only if \(\,\overline{\!{E}}\) is \(\left( c_1(D),[\omega _0]\right) \)-stable.
By the definition of \((\alpha ,\beta )\)-stability in Definition 1.2, we have the following consequence.
Corollary 1.4
Suppose \(\omega \) and \(\,\overline{\!{E}}\) satisfy the conditions in Theorem 1.3. Then we have
-
(1)
suppose \([\omega _0]=0\), then there exists a unique \(\omega \)-PHYM metric in \({\mathcal {P}}_{H_0}\) if and only if \(\,\overline{\!{E}}\) is \(c_1(D)\)-stable.
-
(2)
if
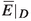 is \(c_1(N_D)\)-stable, then there exists a unique \(\omega \)-PHYM in \({\mathcal {P}}_{H_0}\).
is \(c_1(N_D)\)-stable, then there exists a unique \(\omega \)-PHYM in \({\mathcal {P}}_{H_0}\).
Now let us give a brief outline for the proof of Theorem 1.3. For the “if” direction, we follow the argument in [19, 25] by solving Dirichlet problems on a sequence of domains exhausting X. A key issue here is to prove a uniform \(C^0\)-estimate. For this we rely on a weighted Sobolev inequality in [27, Proposition 2.1] and Lemma 5.4 which builds a relation between weakly holomorphic projection maps over X and coherent subsheaves over \(\,\overline{\!{X}}\). For the “only if” direction, we use integration by parts to show that the curvature form on E can be used to compute the degree of \(\,\overline{\!{E}}\) with respect to \([\omega _0]\) (see Lemma 5.3). For both directions, the asymptotic behaviour of the Kähler metric \(\omega \) plays an essential role.
Then let us compare Theorem 1.3 with some results existing in the literature. In [25] and [19], by assuming some conditions on the base Kähler manifold \((X,\omega )\) and an initial hermitian metric on E, it was proved that for an irreducible vector bundle E the existence of a PHYM metric is equivalent to a stability condition called analytic stability. In our case, since we assume that E has a compactification \(\,\overline{\!{E}}\) on \(\,\overline{\!{X}}\), the existence of good initial metrics is guaranteed by the polystablity assumption of  . Moreover the stability we used in Theorem 1.3 is for \(\,\overline{\!{E}}\) which is purely algebraic, i.e. independent of choice of metrics. In [1], for asymptotically conical Kähler metrics on X, it was proved that if
. Moreover the stability we used in Theorem 1.3 is for \(\,\overline{\!{E}}\) which is purely algebraic, i.e. independent of choice of metrics. In [1], for asymptotically conical Kähler metrics on X, it was proved that if  is \(c_1(N_D)\)-polystable, then there exists PHYM metrics on E. No extra stability condition is needed in this case. Therefore the necessity of stability conditions depends on the geometry of \((X,\omega )\) at infinity. Another typical example for such a phenomenon is the problem for the existence of bounded solutions of the Poisson equation on noncompact manifolds. See Sect. 6.1 for a brief discussion.
is \(c_1(N_D)\)-polystable, then there exists PHYM metrics on E. No extra stability condition is needed in this case. Therefore the necessity of stability conditions depends on the geometry of \((X,\omega )\) at infinity. Another typical example for such a phenomenon is the problem for the existence of bounded solutions of the Poisson equation on noncompact manifolds. See Sect. 6.1 for a brief discussion.
The paper is organized as follows. In Sect. 2, we discuss the assumptions on the Kähler manifold \((X,\omega )\) and prove a weighted mean value inequality for nonnegative almost subharmonic functions. In Sect. 3, we give a brief review of some standard results for hermitian holomorphic vector bundles and give a detailed discussion on \((\alpha ,\beta )\)-stability used in Theorem 1.3. In Sect. 4, Lemma 1.1 is proved and we also show that the assumption in Lemma 1.1 is necessary. In Sect. 5, we prove Theorem 1.3 and give an example which does not satisfy the stability assumption. In Sect. 6.1, we discuss some other results on the existence of PHYM metrics. In Sect. 6.2, we discuss some Calabi–Yau metrics satisfying Assumption 1. In Sect. 6.3, we prove a counterpart of Theorem 1.3 in a different setting where \(\,\overline{\!{X}}\) is a compact Kähler surface and \(c_1(N_D)\) is trivial. In Sect. 6.4, we discuss some problems for further study.
1.1 Notations and conventions
-
\(d^c=\frac{\sqrt{-1}}{2}(-\partial +{\bar{\partial }})\), so \(dd^c=\sqrt{-1}\partial {\bar{\partial }}\).
-
\(\Delta =\sqrt{-1}\Lambda {\bar{\partial }}\partial \), so in local normal coordinates \(\Delta f=-\sum _{i=1}^{n}\frac{\partial ^2f}{\partial z_i\partial \bar{z_i}}\).
-
\(B_r(p)\) denotes the geodesic ball centered at p with radius r and if the basepoint p is clear from the context, we will just write it as \(B_r\).
-
In this paper, we identify a holomorphic vector bundle with the sheaf formed by its holomorphic sections.
-
When we integrate on a Riemannian manifold (M, g), typically we will omit the volume element \(d V_g\).
-
Let \((M,\omega )\) be a Kähler manifold and (E, H) be a hermitian holomorphic vector bundle over M. We use \(C^{\infty }(M,E)\) to denote smooth sections of E;
$$\begin{aligned} W^{k,p}(M,E;\omega ,H)\, (\text {respectively} W_{loc}^{k,p}(M,E;\omega ,H)) \end{aligned}$$to denote sections of E which are \(W^{k,p}\) (respectively \(W_{loc}^{k,p}\)) with respect to the metric \(\omega \) and H. If bundles or metrics are clear from the text, we will omit them.
2 On the asymptotic behaviour of \(\omega \)
As mentioned in the introduction, the asymptotic behaviour of the Kähler metric on the base manifold is crucial to make the argument in this paper work. In this section we will discuss these assumptions. Let \(\,\overline{\!{X}}\) be an n-dimensional (\(n\ge 2\)) compact Kähler manifold, D be a smooth divisor and \(X=\,\overline{\!{X}}\backslash D\) denote the complement of D in \(\,\overline{\!{X}}\). Let \(L_D\) denote the holomorphic line bundle determined by D.
From now on, we assume the normal bundle of D, i.e. \(N_D=L_D|_D\) is ample unless otherwise mentioned. Then we know that \(c_1(D)\) is nef and big. We fix a hermitian metric \(h_D\) on \(N_D\) such that
is a Kähler form on D, where \(\Theta _{h_D}\) denotes the curvature of \(h_D\). Let \({\mathcal {D}}\) (respectively \({\mathcal {C}}\)) denote the (respectively punctured) disc bundle of \(N_D\) under the metric \(h_D\), i.e.
We are mainly interested in the region where \(|\xi |_{h_D}\) is small, which will be viewed as a model of X at infinity. Then we have a well-defined positive smooth function on \({\mathcal {C}}\)
such that \(\sqrt{-1}\partial {\bar{\partial }}t=\omega _D\), where using the obvious projection map \(p:{\mathcal {C}}\rightarrow D\), we view \(\omega _D\) as a form on \({\mathcal {C}}\). Then for every smooth function \(F:(0,\infty )\longrightarrow {\mathbb {R}}\) with \(F'>0\) and \(F''>0\),
defines a Kähler form on \({\mathcal {C}}\). Let \(g_{F}\) denote the corresponding Riemannian metric and \(r_{F}\) denote the induced distance function to a fixed point p.
We need a diffeomorphism to identify a neighborhood of D in \(N_D\) with a neighborhood of D in \(\,\overline{\!{X}}\). For this, we use the following definition introduced by Conlon and Hein in [6, Definition 4.5].
Definition 2.1
An exponential-type map is a diffeomorphism \(\Phi \) from a neighborhood of D in \(N_D\) to a neighborhood of D in \(\,\overline{\!{X}}\) such that
-
(1)
\(\Phi (p)=p\) for all \(p\in D\),
-
(2)
\(d\Phi _p\) is complex linear for all \(p\in D\),
-
(3)
\(\pi (d\Phi _p(v))=v\) for all \(p\in D\) and \(v\in N_{D,p}\subset T^{1,0}_pN_D\), where \(\pi \) denotes the projection \(T^{1,0}_p\,\overline{\!{X}}\rightarrow T^{1,0}_p\,\overline{\!{X}}/T^{1,0}_pD=N_{D,p}\).
Now we can state the assumptions for the Kähler metric \(\omega \) on X. We consider a special class of potentials:
Assumption 1
Let \(\omega \) be a Kähler form on X and g be the corresponding Riemannian metric. We assume that
-
(1)
the sectional curvature of g is bounded,
-
(2)
\(\omega \) can be written as \(\omega _0+\sqrt{-1}\partial {\bar{\partial }}\varphi \), where \(\varphi \) a smooth function on X and \(\omega _0\) is a smooth (1, 1)-form on \(\,\overline{\!{X}}\) with \(\omega _0|_D=0\),
-
(3)
there exists an exponential-type map \(\Phi \) from a neighborhood of D in \(N_D\) to a neighborhood of D in \(\,\overline{\!{X}}\) and a potential \(F\in {\mathcal {H}}\) such that
$$\begin{aligned} \left| \Phi ^*(\omega )-\omega _{F}\right| _{g_{F}}=O(r_F^{-N_0}) \text { for some number }\, N_0\ge 8. \end{aligned}$$(2.5)
Remark 2.2
There are (lots of) other potentials F besides those given in (2.4) making the argument in this paper work, but for simplicity of the statement and some computations we only consider potentials in \({\mathcal {H}}\). The order in (2.5) is not optimal either and again we just choose the number 8 for a neat statement. From now on, unless otherwise mentioned, \(N_0\) denotes the number in (2.5).
Here are the main properties we will use for Kähler metrics defined by the potentials in \({\mathcal {H}}\). For simplicity of notation, we omit the subscript for the dependence on F.
Proposition 2.3
For the Kähler metric defined by a potential \(F=At^a\in {\mathcal {H}}\), we have
-
(1)
The metric is complete as \(|\xi |_{h_D}\rightarrow 0\),
-
(2)
\(r\sim t^{\frac{a}{2}}\),
-
(3)
\(\textrm{Vol}(B_r(p))\sim r^{2n(1-\frac{1}{a})}\),
-
(4)
if \(\theta \) is a smooth form on \({\mathcal {D}}\) with \(\theta |_D=0\), then \(\left| \theta \right| _g=O(e^{-\delta t})\) for some \(\delta >0\).
Conditions (1)–(3) follow directly from (2.3) and (2.4). Condition (4) can be proved directly by doing computation in local coordinates on \({\mathcal {D}}\) as in [14, Section 3]. For completeness and later reference, we include some details.
Proof of (4):
We choose local holomorphic coordinates \({\underline{z}}=\{z_i\}_{i=1}^{n-1}\) on the smooth divisor D and fix a local holomorphic trivialization \(e_0\) of \(N_D\) with \(|e_0|_{h_D}=e^{-\psi }\), where \(\psi \) is a smooth function on D satisfying \(\sqrt{-1}\partial {\bar{\partial }}\psi =\omega _D\). Then we get local holomorphic coordinates \(\{z_1,\ldots ,z_{n-1},w\}\) on \({\mathcal {C}}\) by writing a point \(\xi =we_0({\underline{z}})\). Then in these coordinates we can write (2.3) as
Then it is easy to check the following estimates:
Then (4) follows directly from (2.7). \(\square \)
Remark 2.4
Actually, from the proof of Proposition 2.3-(4), we can give an effective lower bound for \(\delta \). For example, for 2-forms, \(\delta \) can be chosen to be any positive number sufficiently close to (and less than) 1/2. However \(\delta >0\) is sufficient for our later use.
Remark 2.5
Although not needed in this paper, we mention that following the computation in [27, Section 4] or [3, Section 3], we can show that \(\Vert Rm\Vert \le C r^{2(\frac{1}{a}-1)}\).
In Assumption 1, we only assume the asymptotics of the Kähler forms. To get the asymptotic behaviour of the corresponding Riemannian metrics, we need to show that the complex structure of \(\,\overline{\!{X}}\) and \({\mathcal {D}}\) are also close to each other (with respect to the metric \(g_F\)). When D is an anticanonical divisor, the following result is proved in [14, Proposition 3.4]. For a general smooth divisor D, the author learned the following proof from Song Sun.
Lemma 2.6
Let \(J_{{\mathcal {D}}}\) and  denote the complex structure on \({\mathcal {D}}\) and \(\,\overline{\!{X}}\) respectively. And \(\Phi ^*J_{\,\overline{\!{X}}}:=d\Phi \circ J_{\,\overline{\!{X}}}\circ (d\Phi )^{-1}\) denote the pullback of \(J_{\,\overline{\!{X}}}\) under an exponential-type map \(\Phi \). Then we have
denote the complex structure on \({\mathcal {D}}\) and \(\,\overline{\!{X}}\) respectively. And \(\Phi ^*J_{\,\overline{\!{X}}}:=d\Phi \circ J_{\,\overline{\!{X}}}\circ (d\Phi )^{-1}\) denote the pullback of \(J_{\,\overline{\!{X}}}\) under an exponential-type map \(\Phi \). Then we have
Proof
Since \(d\Phi _p\) is complex linear for all \(p\in D\), we know \(\Phi ^*J_{\,\overline{\!{X}}}-J_{{\mathcal {D}}}\) is smooth section of \(\textrm{End}(T{\mathcal {D}})\) vanishing on D. But this is not enough to get the bound claimed in (2.8). We will use the integrability of \(\Phi ^*J_{\,\overline{\!{X}}}\) and property (3) in Definition 2.1. In the following, we ignore the pull-back notation.
Around a fixed point in D we can choose local holomorphic coordinates \(\left\{ w,z_1 \ldots , z_{n-1}\right\} \) of the total space of \(N_{D}\) so that the zero section is given by \(w=0\). Then we can write for \(\alpha =1, \ldots , n-1\) that
where \(P_{\alpha }\) and \(Q_{\alpha \beta }\) are linear functions of w and \(\,\overline{\!{w}}\), i.e. there are smooth functions \(p_{\alpha }\) and \(p_{\,\overline{\!{\alpha }}}\) of \(\{z_i\}\) such that  and a similar expression for \(Q_{\alpha \beta }\). There are no type (1, 0) vectors in the linear term of the right hand side because \(J_{\,\overline{\!{X}}}^2=-\textrm{id}\). Since \(J_{\,\overline{\!{X}}}\) is integrable, we know that
and a similar expression for \(Q_{\alpha \beta }\). There are no type (1, 0) vectors in the linear term of the right hand side because \(J_{\,\overline{\!{X}}}^2=-\textrm{id}\). Since \(J_{\,\overline{\!{X}}}\) is integrable, we know that
is still of type (1, 0) with respect to \(J_{\,\overline{\!{X}}}\), which coincides with \(J_{{\mathcal {D}}}\) when restricted to D. Therefore
By the property (2) and (3) in Definition 2.1 and the following standard exact sequence of the holomorphic vector bundles on D
we know that on D, the \(d\,\overline{\!{z}}_{\alpha }\) component of \({\bar{\partial }}_{J_{\,\overline{\!{X}}}}\partial _{w}\) is tangential to D. Note that by definition we have \({\bar{\partial }}_{J_{\,\overline{\!{X}}}}\partial _{w}={\mathcal {L}}_{\partial _{w}}J_{\,\overline{\!{X}}}\), therefore we know that
Since on D, the \(d\,\overline{\!{z}}_{\alpha }\) component of \({\bar{\partial }}_{J_{\,\overline{\!{X}}}}\partial _{w}\) is tangential to D, we obtain \(p_{\,\overline{\!{\alpha }}}=0\). So we have for \(\alpha =1,\ldots , n-1\)
Now on \({\mathcal {D}}\) we consider the local basis of holomorphic vector fields (with respect to \(J_{{\mathcal {C}}}\)):
and correspondingly \(\bar{e}_{n}, \bar{e}_{\alpha }\) the conjugate vector fields, and \(e^{n}, e^{\alpha }\) the dual frame etc. Then we can write
where i, j range from \(1, \ldots , n, {\overline{1}}, \ldots , \bar{n}\). Then (2.9) implies that we have \(\left| J_{i}^{j}\right| =O\left( \left| w\right| \right) \) for all i, j. Then the lemma follows from the explicit expression of the Kähler metric on \({\mathcal {D}}\), see (2.7). \(\square \)
From the assumption (2.5) on the Kähler form and (2.8) on the complex structure asymptotics, we obtain that for the corresponding Riemannian metric
It is also useful to write down the Riemannian metric \(g_F\) explicitly in real coordinates. Note that the set \(\left\{ \xi \in N_D:\left| \xi \right| _{h_D}<1\right\} \) is diffeomorphic to \(\mathbb {R_{+}}\times Y\), where Y is a smooth \((2n-1)\)-dimensional \(S^1\) bundle over D. Let \(F(t)=At^a\in {\mathcal {H}}\). Then we can write the Riemannian metric \(g_{F}\) as follows
where \(g_D\) is the corresponding Riemannian metric for \(\omega _D\) and \(\theta \) is a connection 1-form on Y such that \(d\theta =\omega _D\).
From the asymptotic of the Riemannian metric tensor (2.11), the explicit expression of the Riemannian metric \(g_F\) in (2.12) and conditions in Assumption 1, one can directly show the following result.
Lemma 2.7
Suppose \((X,\omega ,g)\) satisfy Assumption 1, then
-
(1)
the volume growth of g is at most 2, i.e. there exists a constant \(C>0\) such that Vol(\(B_R(p))\le CR^2\) for all R sufficiently large.
-
(2)
for large numbers \(K,\alpha =2\) and \(\beta =\frac{4}{a}-2\), \((X,\omega )\) is of \((K,\alpha ,\beta )\)-polynomial growth as defined in [27, Definition 1.1],
-
(3)
if \(\theta \) is a smooth form on \(\,\overline{\!{X}}\) vanishing when restricted to D, then
$$\begin{aligned} \left| \theta \right| _{g}=O(r^{-N_0}). \end{aligned}$$
That (M, g) is of \((K,\alpha ,\beta )\)-polynomial growth is important for us since we need the weighted Sobolev inequality in [27, Proposition 2.1] to prove a weighted mean value inequality in the next subsection.
2.1 A weighted mean value inequality
In this subsection, using a weighted Sobolev inequality in [27], we prove a weighted mean value inequality for nonnegative functions which are almost subharmonic. This is important when we run Simpson’s argument to get a uniform \(C^0\)-estimate. As usual, r denotes the distance function to a fixed base point induced by a Riemannian metric.
Lemma 2.8
Let (X, g) be a Riemannian manifold which is of \((K,\alpha ,\beta )\)-polynomial growth as defined in [27]. Let u be a nonnegative compactly supported Lipschitz function satisfying \(\Delta u \le f\) in the weak sense. Suppose that \(|f|=O(r^{-N})\), for some \(N\ge 2+\alpha +\beta \), then there exist \(C_i=C_i(n, N)\) such that
Proof
The following argument is the standard Moser iteration with the help of the weighted Sobolev inequality in [27, Proposition 2.1].
Let \(\gamma =\frac{2n+1}{2n-1}\). Note that we have \(\int u^p\Delta u\ \le \int u^pf\) for any \(p\ge 1\). Integration by parts and using that \(|f|=O(r^{-N})\), we have
Let \(d\mu =(1+r)^{-N}dV_g\) and without loss of generality, we may assume \(d\mu \) has total mass 1. Then the weighted Sobolev inequality shows that
Applying the triangle inequality and Hölder inequality, we get
Let \(p_i=\gamma ^i\), \(i=0,1,\ldots \). We have for any i
Either there exists a sequence of \(p_{i_j}\rightarrow \infty \) such that \(\int u^{p_{i_j}}d \mu \le 1\), which implies that \(\Vert u\Vert _{L^{\infty }}\le 1\), or there exists a smallest \(i_0\) such that and \(\int u^{p_{i}}d\mu > 1\) for \(i\ge i_0\). In the second case, we have
Iterating gives that
\(\square \)
2.2 The assumption on the degree a
The only reason why we need to assume \(a\le \frac{n}{n-1}\) is that the volume growth of the corresponding Riemannian metric is at most 2. In fact we have the following easy but useful degree vanishing property for Riemannian manifolds with at most quadratic volume growth.
Lemma 2.9
Let (M, g) be a complete Riemannian manifold with volume growth order at most 2. Let \(u\in C^{\infty }(M)\) satisfying \(|\nabla u|\in L^2\) and \(\Delta u\in L^1\), then
Proof
By the Cauchy–Schwarz inequality and the assumption on the volume growth, we have
Therefore there is a sequence \(R_i\rightarrow \infty \) such that \(\int _{\partial B_{R_i}}|\nabla u|\ dS\rightarrow 0\). Since \(\Delta u\) is integrable, \(\int _{M} \Delta u \ dV_{g}=\lim _{i\rightarrow \infty }\int _{B_{R_i}} \Delta u\ dV_g \) for any sequence \(R_i\) going to infinity. Using Stokes’ theorem, we have
\(\square \)
2.3 Assumption on \(\Phi \) and \(\omega \)
By Proposition 2.3 and the assumption on the decomposition of \(\omega =\omega _0+\sqrt{-1}\partial {\bar{\partial }}\varphi \), we know that (2.5) is equivalent to say that
Writing \(\Phi ^*(\sqrt{-1}\partial {\bar{\partial }}\varphi )-\omega _{F}\) as \(d(\Phi ^*d^c\varphi -d^cF)\) and integrating this exact 2-form, we can show the following result, whose proof is similar to that given in [14, Lemma 3.7].
Lemma 2.10
There exists a real 1-form \(\eta \) outside a compact set of \({\mathcal {C}}\) with
such that
Proof
Choose a cut-off function \(\chi \) which equals 1 on \(\{0<|\xi |_{h_D}< \delta \}\)and 0 on \(\{|\xi |_{h_D}> 2\delta \}\) for some \(\delta >0\). Let
And it suffices to write \(\theta =d\eta \) with \(|\eta |_{g_F}=O(r_{F}^{-N_0+1+\frac{2}{a}})\).
We identify \({\mathcal {C}}\) with \(\mathbb {R_{+}}\times Y\) in such a way that the Riemannian metric \(g_F\) can be written as \(dr^2+g_r\), where r is the coordinate function on \({\mathbb {R}}_{+}\) and \(g_r\) is a metric on \(\{r\} \times Y^{2n-1}\) that depends on r. Then \(\theta \) is supported on the region \(\{r>r_0\}\) for some \(r_0>0\). Then there exist a 1-form \(\alpha \) and a 2-form \(\beta \) supported on the region \(\{r>r_0\}\) such that \(\partial _{r}\lrcorner \alpha =0\) and \(\partial _{r}\lrcorner \beta =0\)
Then we define
\(\theta \) is closed, therefore \(d\alpha +\partial _r\beta =0\) and then one can directly check that \(\theta =d\eta \). Since \(dr\wedge \alpha \) is perpendicular to \(\beta \) and we assumed \(|\theta |_{g_F}=O(r_F^{-N_0})\), we obtain that \(|\alpha |_{g_F}=O(r_F^{-N_0})\). Fix a smooth background Riemannian metric \({\bar{g}}\) on Y. Then from (2.12) and (2.11), we obtain the following estimate
Then the estimate for \(|\eta |_{g_F}\) follows from a direct computation. \(\square \)
Remark 2.11
A similar argument can be applied to \(dd^c\varphi \) directly on X (using Assumption 1) and we obtain that there exists a cut-off function \(\chi \) supported on a compact set and a smooth real 1-form \(\psi \) supported outside a compact set satisfying \(|\psi |=O(r^{1+\frac{1}{a}})\) such that
This is quite useful when we want to integrate by parts on X.
We assumed that \(\omega _0\) is a closed (1,1)-form on \(\,\overline{\!{X}}\) and vanishes when restricted to D. In particular, \(\int _{\,\overline{\!{X}}}c_1(D)\wedge \omega _0^{n-1}=0\). Then by the Lelong–Poincaré formula, we obtain the following.
Lemma 2.12
Let \(S\in H^0(\,\overline{\!{X}},L_D)\) be a defining section of D and h be any smooth hermitian metric on \(L_D\). Let \(f=\log |S|^2_h\), then we have
3 Hermitian holomorphic vector bundles
Firstly let us recall the definition of projectively Hermitian–Yang–Mills metrics. Given a hermitian metric H on a holomorphic vector bundle E, there is a unique connection compatible with these two structures and it is called the Chern connection of (E, H). Let \(F_H\) denote the curvature of the Chern connection and we call it the Chern curvature of (E, H). Let E be a holomorphic vector bundle on a Kähler manifold \((X,\omega )\). A hermitian metric H is called an \(\omega \)-projectively Hermitian–Yang–Mills metric (\(\omega \)-PHYM) if
Accordingly the Chern connection is called an \(\omega \)-PHYM connection if (3.1) is satisfied. A hermitian metric H is called an \(\omega \)-Hermitian–Yang–Mills (\(\omega \)-HYM) metric if
for some constant \(\lambda \). We also use the notation \(F^{\perp }_H\) to denote the trace-free part of the curvature form, i.e. \(F_H^{\perp }=F_H-\frac{\text {tr}(F_H)}{\text {rank}(E)}\textrm{id}_E\). Then (3.1) is equivalent to say \(\Lambda _{\omega }F^{\perp }_H=0\).
Remark 3.1
Note that the PHYM property is conformally invariant, i.e. if a hermitian metric \(H_0\) satisfies (3.1), then \(H=H_0e^f\) also satisfies (3.1) for every smooth function f. Moreover to get a HYM metric from a PHYM metric, it suffices to solve a Poisson equation, which is always solvable for a constant \(\lambda \) such that \(\int _X(\text {tr}(\Lambda _{\omega }F_H)-\lambda )\omega ^n=0\) when M is compact.
3.1 Basic differential inequalities
Let E be a holomorphic vector bundle and H, K be two hermitian metrics on E, then we have an endomorphism h defined by
We will write this as \(H=Kh\) and \(h=K^{-1}H\) interchangeably. Note that h is positive and self-adjoint with respect to both H and K. Let \(\partial _H\) and \(\partial _K\) denote the (1, 0) part of the Chern connection determined by H and K respectively. By abuse of notation, we use the same notation to denote the induced connection on \(\textrm{End}( E)\). Simpson showed that
Lemma 3.2
[25] Let \(H=Kh\), then we have
-
(1)
\(\partial _H=\partial _K+h^{-1}\partial _K(h)\);
-
(2)
\(\Delta _{K}h=h\sqrt{-1}(\Lambda F_H-\Lambda F_K)+\sqrt{-1}\Lambda {\bar{\partial }}(h) h^{-1}\partial _K(h)\) where \(\Delta _K=\sqrt{-1}\Lambda {\bar{\partial }}\partial _K\);
-
(3)
\(\Delta \log \textrm{tr}(h) \le 2\left( \left| \Lambda F_{H}\right| _{H}+\left| \Lambda F_{K}\right| _{K}\right) \).
Moreover in (2) and (3), if \(\det (h)=1\) then the curvatures can be replaced by the trace-free curvatures \(F^{\perp }\).
3.2 Slope stability
If \( \left| \text {tr}(\Lambda _{\omega }F_H)\right| \in L^1\), the \(\omega \)-degree of (E, H) and \(\omega \)-slope of (E, H) are defined to be
Now let us assume M is compact. Integration by parts shows that the degree defined above is independent of the metric H and only depends on the cohomology class of \([\omega ]\in H^2(X,{\mathbb {R}})\), i.e. by the Chern–Weil theory,
Moreover for any coherent subsheaf S of E, one can define its \(\omega \)-degree as follows (see [16, Chapter 5]). It is shown that \(\det S:=(\wedge ^rS)^{**}\) is a line bundle, where r is the rank of S and define
As before we define \(\mu _{\omega }(S)\), the \(\omega \)-slope of S, to be \(\frac{\deg _{\omega }(S)}{\text {rank}(S)}\). Note that for the definition of \(\omega \)-degree and \(\omega \)-slope, we do not need \(\omega \) to be a Kähler form at all, and a real closed (1, 1)-form is enough. That is for every real closed (1, 1)-form \(\alpha \), we can define
The slope \(\mu _{\alpha }(S)\) is defined similarly as before and we will use the notation \(\mu (S,\alpha )\) and \(\mu _{\alpha }(S)\) interchangeably.
We have the following definition which generalizes the standard slope stability defined for Kähler classes in [16, Chapter 5].
Definition 3.3
Let M be a compact Kähler manifold, \(\alpha ,\beta \in H^{1,1}(M)\) be two cohomology classes, E be a holomorphic vector bundle over M.
-
(1)
We say E is \(\alpha \)-stable if for every coherent reflexive subsheaf S of E with \(0<\text {rank}(S)<\text {rank}(E)\), we have \(\mu _{\alpha }(S)<\mu _{\alpha }(E)\); E is \(\alpha \)-polystable if it is the direct sum of stable vector bundles with the same \(\alpha \)-slope; E is \(\alpha \)-semistable if for every coherent reflexive subsheaf S of E with \(0<\text {rank}(S)<\text {rank}(E)\), we have \(\mu _{\alpha }(S)\le \mu _{\alpha }(E)\);.
-
(2)
We say E is \((\alpha ,\beta )\)-stable if every coherent reflexive subsheaf S of E with \(0<\text {rank}(S)<\text {rank}(E)\) satisfies either of the following conditions:
-
(a)
\(\mu _{\alpha }(S)< \mu _{\alpha }(E)\), or
-
(b)
\(\mu _{\alpha }(S)= \mu _{\alpha }(E)\) and \(\mu _{\beta }(S)<\mu _{\beta }(E)\).
-
(a)
From the definition, we know that if \(\beta =0\), then E is \((\alpha ,\beta )\)-stable if and only if it is \(\alpha \)-stable; if E is \(\alpha \)-stable, then it is \((\alpha ,\beta )\)-stable for any class \(\beta \). In applications, typically the first class \(\alpha \) has some positivity. For example, in our Theorem 1.3, \(\alpha =c_1(D)\) is nef and big.
Remark 3.4
For every coherent subsheaf S of a holomorphic vector bundle E, we have an exact sequence of sheaves:
where \(S^{**}/S\) is a torsion sheaf and supports on an analytic set with codimension at least 2. Then by [16, Section 5.6], we know \(\det S=\det (S^{**})\). In particular, we know that E is \(\alpha \)-stable (respectively \((\alpha ,\beta )\)-stable) if and only if the conditions in (1) (respectively (2)) hold for every coherent subsheaf of E.
3.3 Coherent subsheaves and weakly holomorphic projection maps
Let (E, H) be a hermitian holomorphic vector bundle over a Kähler manifold \((M,\omega )\). Suppose S is a coherent subsheaf of E, since E is torsion-free, then S is torsion free and hence locally free outside \(\Sigma \) which is a closed analytic set of codimension at least 2. Moreover on \(X\backslash \Sigma \) we have an induced orthogonal projection map \(\pi =\pi ^H_S\) satisfying
Outside the singular set \(\Sigma \), the Chern curvature of \((S,H|_S)\) is related to the Chern curvature (E, H) by
Let us mention a result in current theory:
Theorem 3.5
[10] Let \(\Sigma \) be a closed analytic subset of codimension at least 2 in a Kähler manifold \((M,\omega )\). Assume T is a closed positive current on \(M\backslash \Sigma \) of bidegree (1, 1), i.e a (1, 1)-form with distribution coefficients, then the mass of T is locally finite in a neighborhood of \(\Sigma \). More precisely, every \(p\in \Sigma \) has a neighborhood \(U\subseteq M\) such that
Applying the above theorem to \(\text {tr}(\sqrt{-1}\partial \pi \wedge {\bar{\partial }}\pi )\), one gets
In general, an element \(\pi \in W^{1,2}_{loc}(M,\textrm{End}( E);\omega ,H)\) is said to be a weakly holomorphic projection map if it satisfies (3.4) almost everywhere. By the discussion above, we know that for a coherent subsheaf S of E, \(\pi _{S}^H\) is a weakly holomorphic projection map. A highly nontrivial result due to Uhlenbeck and Yau [28] is that the converse is also true (see also [24]).
Theorem 3.6
[28] Suppose there is a weakly holomorphic projection map \(\pi \), then there exists a coherent subsheaf S of E such that \(\pi =\pi ^H_{S}\) almost everywhere.
If X is compact, \(\deg _{\omega }(S)\) defined in (3.3) can be computed using the curvature form \(F_{S,H}\). The following result is well-known, see [16, Section 5.8]. We include a simple proof using Theorem 3.5.
Proposition 3.7
Let (E, H) be a hermitian holomorphic vector bundle over a compact Kähler manifold \((M,\omega )\) and S be a coherent subsheaf of E. Then
where \(\deg _{\omega }(S)\) and \(F_{S,H}\) are defined in (3.3) and (3.5) respectively.
Proof
Let r denote the rank of S. Since S is a subsheaf of E, there is a natural sheaf homomorphism
Note that \(\Phi \) is only injective on \(M\backslash \Sigma \) in general. Let \(\wedge ^rH\) denote the metric on \(\wedge ^r E\) induced from H, then \(\Phi ^*(\wedge ^rH)\) defines a singular hermitian metric on \((\wedge ^rS)^{**}\) which is smooth outside \(\Sigma \) and whose curvature form is equal to \(\text {tr}(F_{S,H})\). Since \(\Phi \) is a holomorphic bundle map, by choosing a local holomorphic basis of \((\wedge ^rS)^{**}\) and \(\wedge ^r E\), it is easy to show that \(\Phi ^*(\wedge ^rH)=fK\), where K is a smooth hermitian on \((\wedge ^rS)^{**}\), the function f is positive smooth outside \(\Sigma \) and converge to 0 polynomially along \(\Sigma \).
Then by Theorem 3.5, it suffices to prove the following: for every smooth positive function f on \(M\backslash \Sigma \) satisfying \(\Delta \log f\in L^1\), and \(|f|=O(\textrm{dist}(\cdot , \Sigma )^{k})\) for some k one has
Note that \(|\log f|\in L^2\), then (3.8) follows from the Cauchy–Schwarz inequality and existence of good cut-off functions. More precisely, since \(\Sigma \) has real codimension at least 4, it is well-known that there exists a sequence of cut-off functions \(\chi _{\epsilon }\) such that \(1-\chi _{\epsilon }\) is supported in the \(\epsilon \)-neighborhood of \(\Sigma \) and we have uniform \(L^2\) bound on \(\Delta \chi _{\epsilon }\).
We briefly describe a construction of these cut-off functions. Let s be a regularized distance function to \(\Sigma \) in the sense that \(s:M\rightarrow {\mathbb {R}}_{\ge 0}\) is smooth and satisfies that there exist positive constants \(C_k\) such that
The existence of such a regularized distance function can be derived from [26, Theorem 2 on page 171]. After a rescaling, we may assume \(s<1\) on M. For every \(\epsilon >0\), let \(\rho _{\epsilon }\) be a smooth function which is equal to one on the interval \((-\infty , \varepsilon ^{-1})\) and zero on \((2+\varepsilon ^{-1}, \infty )\). Moreover we can have \(|\rho ^{\prime }_{\epsilon }|+|\rho ^{\prime \prime }_{\epsilon }|\le 10\). Then we define
and we can directly check they satisfy the desired properties. \(\square \)
Motivated by the above result, Simpson [25] uses the right hand side of (3.7) to define an analytic \(\omega \)-degree of a coherent subsheaf on a noncompact Kähler manifold. Typically one needs to assume \(|\Lambda _{\omega }F_H|\in L^1\) to ensure the first term of (3.5) is integrable. Then the degree of a coherent subsheaf is either a finite number or \(-\infty \) depending on whether \(|{\bar{\partial }}\pi |\in L^2\). In general, this analytic degree depends on the choice of the background metric H. And a key observation in this paper is that when E has a compactification and H is conformal to a smooth extendable hermitian metric, this analytic degree does have an algebraic interpretation, see Lemmas 5.3 and 5.4.
3.4 Dirichlet problem
We have the following important theorem of Donaldson:
Theorem 3.8
[9] Given a hermitian holomorphic vector bundle \((E,H_0)\) over \((Z,\omega )\) which is a compact Kähler manifold with non-empty boundary \(\partial Z\), there is a unique hermitian metric H on E such that
-
(1)
\(H|_{\partial Z}=H_0|_{\partial Z}\),
-
(2)
\(\sqrt{-1}\Lambda _{\omega }F_H=0\).
As observed in [19], one can do conformal changes to H to fix the induced metric on \(\det E\) and still have it to be a projectively Hermitian–Yang–Mills metric.
Proposition 3.9
[19] Given a hermitian holomorphic vector bundle \((E,H_0)\) over \((Z,\omega )\) which is a compact Kähler manifold with boundary, there is a unique hermitian metric H on E such that
-
(1)
\(H|_{\partial Z}=H_0|_{\partial Z}\) and \(\det H=\det H_0\),
-
(2)
\(\sqrt{-1}\Lambda _{\omega }F_H^{\perp }=0\),
3.5 Donaldson functional for manifolds with boundary
Next we recall Simpson’s construction [25] for Donaldson functional. We follow the exposition in [19, Subsection 2.5] and focus on compact Kähler manifolds with boundary.
Let \((Z,\omega )\) be a compact Kähler manifold with boundary, \((E,H_0)\) be a hermitian holomorphic vector bundle. Let b be a smooth section of \(\textrm{End}(E)\) which is self-adjoint with respect to \(H_0\). Then for any smooth function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) and \(\Phi :{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) respectively, we can define
as follows: at each point \(p\in Z\), choose an orthonormal basis \(\{e_i\}\) of E such that \(b(e_i)=\lambda _ie_i\). Let \(\{e_i^{\vee }\}\) denote its dual basis, then set
Recall that for any two hermitian metrics \(H_1\) and \(H_2\), there is a smooth section s of \(\textrm{End}( E)\), which is self-adjoint with respect to both \(H_1\) and \(H_2\) such that \(H_2=H_1e^s\) and \(\det H=\det H_0\) if and only if \(\text {tr}(s)=0\). Let \({\mathcal {P}}_{H_0}\) denote the space of hermitian metrics H of E such that
Let \(\Psi (\lambda _1,\lambda _2)\) denote the smooth function
Then put
Mochizuki proved the following important result
Theorem 3.10
[19] If \(H\in {\mathcal {P}}_{H_0}\) is an \(\omega \)-PHYM metic, then \({\mathcal {M}}_{\omega }(H_0,H)\le 0\).
3.6 Bando–Siu’s interior estimate
The following result shows that to get a local uniform bound for a sequence of PHYM metrics, it suffices to have a uniform \(C^0\)-bound.
Theorem 3.11
[2, 15] Let \( B_2(p)\subseteq (M,\omega )\) be a geodesic ball of radius 2 contained in a Kähler manifold such that  is compact. Let \((E,H_0)\) be a hermitian holomorphic vector bundle over \(B_2(p)\). Suppose \(H=H_0e^s\) is an \(\omega \)-PHYM metric with \(\text {tr}(s)=0\), then for any \(k\in {\mathbb {N}}\) and \(p\in (1,\infty )\) there exists a smooth function \({\mathcal {F}}_{k,p}\) which vanishes at the origin and depends only on the geometry of \(B_2(p)\) such that
is compact. Let \((E,H_0)\) be a hermitian holomorphic vector bundle over \(B_2(p)\). Suppose \(H=H_0e^s\) is an \(\omega \)-PHYM metric with \(\text {tr}(s)=0\), then for any \(k\in {\mathbb {N}}\) and \(p\in (1,\infty )\) there exists a smooth function \({\mathcal {F}}_{k,p}\) which vanishes at the origin and depends only on the geometry of \(B_2(p)\) such that
4 Existence of a good initial metric
In this section, we continue to use notations in Sect. 2 and always assume the Kähler metric on X satisfies the Assumption 1. We begin by working on the model space \(({\mathcal {C}},\omega _{{\mathcal {C}}})\), where \(\omega _{{\mathcal {C}}}=dd^c F(t)\) for some potential \(F(t)\in {\mathcal {H}}\). Using the explicit expression of \(\omega _{{\mathcal {C}}}\) in (2.3), it is easily to show that
Lemma 4.1
Let E be a holomorphic vector bundle on D and \(p^*(E)\) be its pull back to \({\mathcal {C}}\). Suppose \(H_D\) is a metric on E satisfying \(\sqrt{-1}\Lambda _{\omega _D}F_{H_D}=\lambda \textrm{id}_E\) for some constant \(\lambda \), then \(H=e^{-\frac{\lambda }{n-1} \log |\xi |^2_{h_D}}\) \( p^*(H_D)\) defines a metric on \(p^*(E)\) satisfying \(\sqrt{-1}\Lambda _{\omega _{{\mathcal {C}}}}F_H=0\).
Remark 4.2
If \(n=2\), the metric H actually is a flat metric on \(p^*(E)\).
Let \(\,\overline{\!{E}}\) be a holomorphic vector bundle on \({\mathcal {D}}\). We still use p to denote the projection map from \({\mathcal {D}}\) to D. Then we can compare the holomorphic structure on \(\,\overline{\!{E}}\) and \(p^*(\,\overline{\!{E}}|_D)\) as follows. In a neighborhood of D, which we may assume to be \({\mathcal {C}}\), we fix a bundle map \(\Phi :\,\overline{\!{E}}\rightarrow p^*(\,\overline{\!{E}}|_D)\) such that \(\Phi |_D\) is the canonical identity map and \(\Phi \) is an isomorphism as maps between complex vector bundles. Then \(\Phi \) pulls back the holomorphic structure on \(p^*(\,\overline{\!{E}}|_D)\) to \(\,\overline{\!{E}}\). Now we have two holomorphic structures on \(\,\overline{\!{E}}\) and denote them by \({\bar{\partial }}_1\) and \({\bar{\partial }}_2\). Then the difference
is a smooth section of \({\mathcal {A}}^{0,1}(\textrm{End}( \,\overline{\!{E}}))\) and is 0 when restricted to D. Locally near a point in D, choose holomorphic coordinates \(\{z_1,\ldots ,z_{n-1},w\}\) such that \(D=\{w=0\}\). Using these coordinates, \(\beta \) can be written as \(f_i\text {d}{\bar{z}}^i+h\text {d}{\bar{w}}\) where \(f_i\) and h are smooth sections of \(\textrm{End}( \,\overline{\!{E}})\) and \(f_i|_{w=0}=0\).
Now suppose we have a Hermitian metric H on  , then via \(\Phi \) we view it as a metric on \(\,\overline{\!{E}}|_{{\mathcal {C}}}\). Let \(\partial _i\) denote the (1, 0) part of the Chern connection determined by \({\bar{\partial }}_i\) and H. Then one can check that
, then via \(\Phi \) we view it as a metric on \(\,\overline{\!{E}}|_{{\mathcal {C}}}\). Let \(\partial _i\) denote the (1, 0) part of the Chern connection determined by \({\bar{\partial }}_i\) and H. Then one can check that
where \(\beta ^{*_H}\) denote the smooth section of \({\mathcal {A}}^{1,0}(\textrm{End}( \,\overline{\!{E}}))\) obtained from \(\beta \) by taking the metric adjoint for the \(\textrm{End}( \,\overline{\!{E}})\) part and taking conjugate for the 1-form part. Locally \(\mu =f_i^{*_H}\text {d}z^i+h^{*_H}\text {d}w\). Since H is only defined over \({\mathcal {C}}\), a priori \(f^{*_H}\) and \(h^{*_H}\) are only defined on \({\mathcal {C}}\). Note that the operator \(*_H\) is conformally invariant with respect to the choice of metric H, so if \(H= e^f\,\overline{\!{H}}\) for some function \(f\in C^{\infty }({\mathcal {C}})\) and metric \(\,\overline{\!{H}}\) on \(\,\overline{\!{E}}\), \(f_i^{*_H}\) and \(h^{*_H}\) are smooth sections over \({\mathcal {D}}\). Then we can compute the difference of curvatures for \(({\bar{\partial }}_1,H)\) and \(({\bar{\partial }}_2, H)\):
where we abuse notation to use the same symbol \(\partial \) and \({\bar{\partial }}\) to denote the induced connection on \(\textrm{End}( \,\overline{\!{E}})\). Again note that the induced metric (and hence the Chern connection) on \(\textrm{End}( \,\overline{\!{E}})\) is conformally invariant for metrics H on \(\,\overline{\!{E}}\). Therefore \(F_{{\bar{\partial }}_2,H}-F_{{\bar{\partial }}_1,H}\) is a smooth \(\textrm{End}( \,\overline{\!{E}})\) valued (1, 1)-form over \({\mathcal {D}}\) and \(i^*_D(F_{{\bar{\partial }}_2,H}-F_{{\bar{\partial }}_1,H})=0\). Then by Proposition 2.3, we obtain there exists a \(\delta >0\),
Combining this and the previous lemma, we proved that
Proposition 4.3
Let \(\,\overline{\!{E}}\) be a holomorphic vector bundle on \({\mathcal {D}}\). Suppose there is a metric \(H_D\) on \(\,\overline{\!{E}}|_D\) satisfying \(\sqrt{-1}\Lambda _{\omega _D}F_{H_D}=\lambda \textrm{id}\) for some constant \(\lambda \), then there is a Hermitian metric H on \(\,\overline{\!{E}}|_{{\mathcal {C}}}\) satisfying:
-
(1).
there is a hermitian metric \(\,\overline{\!{H}}\) on \(\,\overline{\!{E}}\) and a function \(f\in C^{\infty }({\mathcal {C}})\) such that \(H=e^f\,\overline{\!{H}}\), and
-
(2).
\(|\Lambda _{\omega _{{\mathcal {C}}}}F_{H}|=O( e^{-\delta t})\) for some \(\delta >0\).
Motivated by this, we can give the proof of the Lemma 1.1.
Proof of Lemma 1.1
By the Donaldson–Uhlenbeck–Yau theorem there exists a hermitian metric \(H_D\) on  such that
such that
Extend \(H_D\) smoothly to get a hermitian metric \(\,\overline{\!{H}}_0\) on \(\,\overline{\!{E}}\). Using the diffeomorphism \(\Phi \) given in the Assumption 1-(3) we get a positive smooth function on X by abuse of notations stilled denoted by t, which is equal to \((\Phi ^{-1})^{*}t\) outside a compact set on X.
Define a hermitian metric on E using
Then we claim that
From the construction, \(F_{H_0}=F_{\,\overline{\!{H}}_0}-\frac{\lambda dd^c t}{n-1}\textrm{id}\), where \(F_{\,\overline{\!{H}}_0}\) is smooth bundle valued (1,1)-form on \(\,\overline{\!{X}}\). Recall that for a 2 form \(\theta \),
Since we assume that \(|\Phi ^*(\omega )-\omega _{{\mathcal {C}}}|=O(r^{-N_0})\), then (4.4) will follow from the following estimate on \({\mathcal {C}}\): there exist a \(\delta >0\) such that
By (2.8) and (2.10), we can easily show that there exists a \(\delta >0\) such that
Using the same argument as we did before Proposition 4.3, we can show that there exists a \(\delta >0\) such that
Then (4.5) follows from (4.2), (4.6) and (4.7). \(\square \)
Remark 4.4
Recall that we use \(S\in H^0(\,\overline{\!{X}},L_D)\) to denote a defining section of D. Then from the definition of t, we know that there exists a smooth hermitian metric h on \(L_D\) such that \(t=-\log |S|_{h}^2\).
Remark 4.5
From the above discussion, we also obtain that \(|F_{H_0}|=O(r^{1-a})\). In general, we can not expect a higher decay order for the full curvature tensor \(F_{H_0}\) since it has non-vanishing component along the directions tangential to D, but if \(n=2\) we actually proved that

From the proof given above, the assumption that \(E|_D\) is \(c_1(N_D)\)-polystable is used crucially to have a good initial metric \(H_0\) satisfying (1) and (2) in Lemma 1.1, which both are important for the proof. We show the assumption that \(E|_D\) is \(c_1(N_D)\)-polystable is also necessary subject to the conditions in Lemma 1.1. More precisely, we have that
Proposition 4.6
Suppose there is a Hermitian metric \(H_0\) on E satisfying:
-
(1).
\(|\Lambda _{\omega }F_{H_0}|=O(r^{-N_0})\), where as before \(N_0\) is the number in (2.5), and
-
(2).
there is a hermitian metric \(\,\overline{\!{H}}_0\) on \(\,\overline{\!{E}}\) and a function \(f\in C^{\infty }(X)\) such that \(H_0=e^f\,\overline{\!{H}}_0\).
Then \(\,\overline{\!{H}}_0|_D\) defines a PHYM metric with respect to \(\omega _D\in c_1(N_D)\), i.e, \(\,\overline{\!{E}}|_D\) is \(c_1(N_D)\)-polystable.
Proof
By these two assumptions, we have \(\left| \sqrt{-1}\Lambda _{\omega }F_{\,\overline{\!{H}}_0}+\Delta _{\omega }f \textrm{id} \right| =O(r^{-N_0})\). In particular the trace-free part of \(\Lambda _{\omega }F_{\,\overline{\!{H}}_0}\) decays like \(r^{-N_0}\). Since
is a smooth bundle valued (1,1)-form on \(\,\overline{\!{X}}\), its pull-back under \(\Phi \) to \({\mathcal {D}}\) is a smooth bundle valued 2-form satisfying that its restriction to D is of type (1,1) and
From the explicit expression of the Kähler form \(\omega _{F}\) in (2.3) and the assumption on the potential F in Assumption 1, we know that
\(\square \)
Next we can show that the set \({\mathcal {P}}_{H}\) defined in (1.1) is unique if we fix the induced metric on the determinant line bundle. More precisely, we have
Proposition 4.7
Suppose we have two metrics \(H_0\) and \(H_1\) satisfying the condition (1) and (2) in Lemma 1.1 and \(\det H_0=\det H_1\), then
In particular, there exists a constant \(C>0\) such that \(C^{-1}H_0\le H_1\le CH_0\).
Proof
By condition (1) in Lemma 1.1, we know that there are smooth hermitian metrics \(\,\overline{\!{H}}_0\) and \(\,\overline{\!{H}}_1\) and smooth functions \(f_0\) and \(f_1\) on X such that for \(i=0,1\)
And by doing a conformal change, we may assume \(\det \,\overline{\!{H}}_0=\det \,\overline{\!{H}}_1\). Let \(h=\,\overline{\!{H}}_0^{-1}\,\overline{\!{H}}_1\). Since \(\det H_0=\det H_1\), we have
From the proof of Proposition 4.6, we know that \(\,\overline{\!{H}}_i|_D\) are PHYM. By the uniqueness of PHYM metrics on compact Kähler manifolds, we know that
where \(\nabla \) denotes the induced connection on \(\textrm{End}(\,\overline{\!{E}})\) from the Chern connection on \((\,\overline{\!{E}},\,\overline{\!{H}}_0)\). From this and noting that \(H_0\) is conformal to an extendable metric, we can check directly that
Then from the definition of \({\mathcal {P}}_{H_0}\), we obtain that \({\mathcal {P}}_{H_0}={\mathcal {P}}_{H_1}.\) \(\square \)
5 Proof of the main theorem
We first prove a lemma on the degree vanishing property.
Lemma 5.1
Let \((X^n, \omega )\) be a complete Kähler manifold and \(\beta \) be a d-closed (k, k) form with \(\displaystyle \int _{X} |\beta |\omega ^n\) finite for some \(1\le k\le n-1\). Suppose \(\omega =d\eta \) for some smooth 1-form \(\eta \) with \(|\eta |=O(r)\), then \(\displaystyle \int \beta \wedge \omega ^{n-k}=0\).
Proof
Fix a base point \(p\in X\) and let \(\rho _R\) be a smooth cut-off function which is 1 on \(B_R(p)\), 0 outside \(B_{2R}(p)\) and \(|\nabla \rho _R|\le \frac{C}{R}\) where C is a constant independent of R. Integrating by parts, we have the following
which is bounded by \(C\int _{B_{2R}(p)\backslash B_R(p)}\left| \beta \right| \omega ^n\). And this term tends to 0 as \(R\rightarrow \infty \) since \(|\beta | \in L^1\). \(\square \)
From now on, we assume \(\omega =\omega _0+dd^c\varphi \) is a Kähler form satisfying the Assumption 1 in Sect. 2. Note that we only proved that \(dd^c\varphi =d\psi \) for a smooth form \(\psi \) with \(|\psi |=O(r^{1+\frac{1}{a}})\) (see Remark 2.11). Therefore we can not apply Lemma 5.1 directly. Typically we have a definite decay order for \(|\beta |\), so we can still use integration by parts to show some degree vanishing properties. More precisely, we have
Lemma 5.2
Let \(\beta \) be a d-closed (k, k) form for some \(1\le k\le n-1\), satisfying \(|\beta |=O(r^{-N_0})\). Then
Proof
By a similar integration by part argument as in the proof of Lemma 5.1, it suffices to show that
This follows from the facts that \(|\beta |=O(r^{-N_0})\), \(|\psi |=O(r^{1+\frac{1}{a}})\) and the volume growth order of \(\omega \) is at most 2. \(\square \)
The following two lemmas are crucial for us since they relate information on \(\,\overline{\!{X}}\) and that on X.
Lemma 5.3
Let \(H_0\) be the metric constructed in Lemma 1.1. One has the following equality:
Proof
Firstly, recall that
By the construction in Lemma 1.1, we know that \(|\Lambda _{\omega }\text {tr}(F_{H_0})|=O(r^{-N_0})\). Since the volume growth order of \(\omega \) is at most 2, we know that \(\Lambda _{\omega }\text {tr}(F_{H_0})\) is absolutely integrable. Therefore the left hand side of (5.3) is well-defined.
By the Chern-Weil theory, for any smooth hermitian metric \(\,\overline{\!{H}}_0\) on  we have
we have
By the construction (4.3), \(H_0=e^{Ct} \) \( \,\overline{\!{H}}_0\) for some constant C and t defined in Sect. 4. Moreover by Remark 4.4, \(t=-\log |S|^2_h\) for some smooth hermitian metric on \(L_D\). By Lemma 2.12, we obtain that \(\int _X dd^ct\wedge \omega _0^{n-1}=0\). So we have
Using (5.2) and \(\omega =\omega _0+dd^c \varphi \), to prove (5.1), it suffices to show that for any \(k=1,\ldots ,n-1\),
Case 1. \(1\le k\le n-2\). Since \(\omega _0\) vanishes when restricted to D, by Lemma 2.7, we know that \(|\omega _0|=O(r^{-N_0})\). Combining this with Remark 4.5, we know that \(\text {tr}(F_{H_0})\wedge \omega _0^{n-1-k}\) is a closed \((n-k,n-k)\)-form with decay order at least \(r^{-N_0}\). Therefore Lemma 5.2 implies that its integral is 0.
Case 2. \(k=n-1\). If \(n=2\), then by (4.8) we can still apply Lemma 5.2. If \(n\ge 3\), note that though \(|\Lambda _{\omega }\text {tr}(F_{H_0})|=O(r^{-N_0})\), \(|\text {tr}(F_{H_0})|\) is not in \(L^1\) in general. So we can not apply Lemma 5.2 directly. Instead we shall use the asymptotic behaviour of \(\text {tr}(F_{H_0})\) obtained from the construction. Integrating by parts and pulling back via \(\Phi \), we know that
Then by (2.5), Lemma 2.10 and the assumption \(N_0>8\), we obtain that the right hand side of the above equality equals
By (4.6) and (4.7), we know that it equals
Note that when restricted to the level set of t,
Therefore \(\left( p^*\text {tr}(F_{\,\overline{\!{H}}_0})-\frac{\lambda \text {rank}(E)}{n-1} dd^ct\right) \wedge (dd^cF(t))^{n-2}=0\) by (4.2). \(\square \)
Lemma 5.4
Suppose \(\,\overline{\!{E}}|_D\) is \(c_1(N_D)\)-polystable and let \(H_0\) be the metric constructed in Lemma 1.1.
-
(1).
Let \(\,\overline{\!{S}}\) be a coherent reflexive subsheaf of \(\,\overline{\!{E}}\). If \(\,\overline{\!{S}}|_D\) is locally free and a splitting factor of \(\,\overline{\!{E}}|_D\), then \({\bar{\partial }}\pi _S^{H_0}\in L^2(X;\omega , H_0)\).
-
(2).
Let \(\pi \in W^{1,2}_{loc}(X,\,\overline{\!{E}}^*\otimes \,\overline{\!{E}};\omega ,H_0)\) be a weakly holomorphic projection map. If \({\bar{\partial }}\pi \in L^2(X;\omega ,H_0)\), then there exists a coherent reflexive subsheaf \(\,\overline{\!{S}}\) of \(\,\overline{\!{E}}\) such that \(\pi =\pi ^{H_0}_S\) a.e. and \(\,\overline{\!{S}}|_D\) is a splitting factor of \(\,\overline{\!{E}}|_D\).
Proof
A crucial point here is that \(H_0\) is conformal to a smooth extendable metric \(\,\overline{\!{H}}_0\). In particular, for a coherent subsheaf S of E, the projections induced by \(H_0\) and \(\,\overline{\!{H}}_0\) are the same. Note that by [4, Lemma 3.23 and Remark 3.25], for every coherent reflexive subsheaf \(\,\overline{\!{S}}\) of \(\,\overline{\!{E}}\), \(\,\overline{\!{S}}|_D\) is torsion free and can be naturally viewed as a subsheaf of \(\,\overline{\!{E}}|_D\).
(1) Let \(\pi =\pi _{\,\overline{\!{S}}}^{\,\overline{\!{H}}_0}\). Then \(\pi \) is smooth in a neighborhood of D and \({\bar{\partial }}\pi |_D=0\) by assumption. Note that \(\pi _S^{H_0}=\pi |_X\), so it suffices to show \({\bar{\partial }}\pi \in L^2(X,\omega , \,\overline{\!{H}}_0)\). Fix small balls \(U_i\) of \(\,\overline{\!{X}}\) covering D such that there are holomorphic coordinates \(\{z_1,\ldots ,z_{n-1},w\}\) on each \(U_i\) with \(D\cap U_i=\{w=0\}\) and \(\,\overline{\!{E}}\) is trivial on each ball \(U_i\). Under these coordinates and trivializations we can write
where we view \({\bar{\partial }}_z \pi \) and \({\bar{\partial }}_w \pi \) as matrices of smooth functions and \({\bar{\partial }}_z \pi |_{w=0}=0\). So we have \(|{\bar{\partial }}_z\pi |\le C|w|\) and \(|{\bar{\partial }}_w\pi |\le C\). Then the result follows from the explicit estimate given in (2.7).
(2) Given a projection map \(\pi \in W^{1,2}_{loc}(X,\,\overline{\!{E}}^*\otimes \,\overline{\!{E}};\omega ,H_0)\) with \( {\bar{\partial }}\pi \in L^2(X;\omega ,H_0)\), we first prove the following:
Claim
\(\pi \in W^{1,2}(\,\overline{\!{X}};\omega _{\,\overline{\!{X}}}, \,\overline{\!{H}}_0)\) for a fixed (hence any) smooth Kähler metric \(\omega _{\,\overline{\!{X}}}\) on \(\,\overline{\!{X}}\).
Since \(|\pi |_{\,\overline{\!{H}}_0}\le 1\) and by [7, Lemma 7.3], it suffices to show \({\bar{\partial }}\pi \in L^2(\,\overline{\!{X}}; \omega _{\,\overline{\!{X}}}, \,\overline{\!{H}}_0)\). By (2.8) and (2.11), we may assume in local coordinates around D the Kähler metric \(\omega \) is exactly given by the model space. We choose local holomorphic coordinates \({\underline{z}}=\{z_i\}_{i=1}^{n-1}\) on the smooth divisor D and fix a local holomorphic trivialization \(e_0\) of \(N_D\) with \(|e_0|_{h_D}=e^{-\psi }\), where \(\psi \) is a smooth function on D satisfying \(\sqrt{-1}\partial {\bar{\partial }}\psi =\omega _D\). Then we get local holomorphic coordinatea \(\{z_1,\ldots ,z_{n-1},w\}\) on \({\mathcal {C}}\) by writing a point \(\xi =we_0({\underline{z}})\). Choose a basis of (0, 1)-forms \(\text {d}{\bar{z}}_1 \ldots \text {d}{\bar{z}}_{n-1}, \frac{\text {d}{\bar{w}}}{{\bar{w}}}-{\bar{\partial }}_{z_i} \psi \text {d}{\bar{z}}_i\). Then we can write
where \(f_i\) and h are sections of \(\textrm{End}(E)\). Notice that \(d{\bar{z}}_i\) is perpendicular to the \(\frac{\text {d}{\bar{w}}}{{\bar{w}}}-{\bar{\partial }}_{z_i} \psi \text {d}{\bar{z}}_i\). Since \({\bar{\partial }}\pi \) is in \(L^2\) with respect to \(\omega \), by (2.7) we know that

Then we know that \(f_i-h{\bar{\partial }}_{z_i}\psi ,\ \frac{h}{{\bar{w}} }\) are all \(L^2\)-integrable with respect to the Lebesgue measure. Therefore the claim is proved:
Then Uhlenbeck–Yau’s result (Theorem 3.6) implies that there exists a coherent subsheaf \(\,\overline{\!{S}}\) of \(\,\overline{\!{E}}\) such that \(\pi =\pi ^{\,\overline{\!{H}}_0}_{\over S}\) outside the singular set of \(\,\overline{\!{S}}\). Taking the double dual, we may assume \(\,\overline{\!{S}}\) is reflexive. By the integrability condition (5.5), \({\bar{\partial }}\pi _{\over S}^{\,\overline{\!{H}}_0}|_D=0\), which means that \(\,\overline{\!{S}}|_D\) is a splitting factor of \(\,\overline{\!{E}}|_D\) since \(\,\overline{\!{E}}|_D\) is polystable. \(\square \)
Now we are ready to prove the main theorem. We decompose it into two propositions.
Proposition 5.5
Suppose there exists an \(\omega \)-PHYM metric H in \({\mathcal {P}}_{H_0}\), then \(\,\overline{\!{E}}\) is \(\left( c_1(D),[\omega _0]\right) \)-stable.
Proof
Suppose there is a reflexive subsheaf \(\,\overline{\!{S}}\) of \(\,\overline{\!{E}}\) with \(0< \text {rank}(\,\overline{\!{S}})< \text {rank}(\,\overline{\!{E}})\) such that \(\mu (\,\overline{\!{S}},c_1(D))\ge c_1(\,\overline{\!{E}},c_1(D))\), we need to show that \(\mu (\,\overline{\!{S}}, [\omega _0])<\mu (\,\overline{\!{E}}, [\omega _0])\). By [18] for any coherent refelxive sheaf \({\mathcal {E}}\) on \(\,\overline{\!{X}}\), we have
(When \({\mathcal {E}}\) is a vector bundle, this follows from the fact that the first Chern class \(c_1(D)\) is the Poincaré dual of the homology class defined by the divisor D. For a general reflexive sheaf, the key point is to show that \(c_1({\mathcal {E}})|_D=c_1({\mathcal {E}}|_D)\) using the fact that \({\mathcal {E}}\) is locally free outside an analytic set of (complex) codimension at least 3.) Therefore we have
By assumption, \(\,\overline{\!{E}}|_D\) is \(c_1(N_D)\)-polystable, so (5.6) implies that \(\,\overline{\!{S}}|_D\) is locally free and is a splitting factor of \(\,\overline{\!{E}}|_D\). Then by Lemma 5.4, we have
Claim
\({\bar{\partial }}\pi _S^H\in L^2(X;\omega ,H_0)=L^2(X;\omega ,H)\).
For simplicity of notation, in the following we omit the dependence on S. By the definition of \({\mathcal {P}}_{H_0}\) and \(H\in {\mathcal {P}}_{H_0}\), we know that \(H=H_0 e^s\) with \(\left\| s\right\| _{L^{\infty }}+\left\| {\bar{\partial }}s\right\| _{L^2}<\infty \). The claim follows directly from the following pointwise inequality (outside the singular set \(\Sigma \) of S)
where C is a constant independent of points and all the norms are with respect to \(H_0\). Let \(r_0\), r denote the rank of S and E respectively. Near any given point \(p\in X\backslash \Sigma \), we can find a local holomorphic basis \(\{e_1,\ldots ,e_{r_0},e_{r_0+1},\ldots ,e_r\}\) of E such that
In the following we use Einstein summation convention and use i, j to denote numbers from 1 to r, \(\alpha ,\beta \) to denote numbers from 1 to \(r_0\). Under this basis \(\pi ^{H_0}\) can be written as
where we view \(H_0=(H_{0,ij})=(\left<e_i,e_j\right>_{H_0})\) as a matrix and \({\widetilde{H}}_0=({\widetilde{H}}_{0,\alpha \beta })=(\left<e_{\alpha },e_{\beta }\right>_{H_0})\) as a submatrix of \(H_0\). Then
Similarly, \(\pi ^H\) can be written as \(e_{\alpha }^{\vee }\otimes e_{\alpha }+H_{i\beta }{\widetilde{H}}^{\beta \alpha }e_i^{\vee }\otimes e_{\alpha }\). Note that as a matrix \(H=H_0h\), where h is the matrix representation of \(e^s\) under the basis \(\{e_i\}_{i=1}^r\). Since \(\left\| s\right\| _{L^{\infty }}<\infty \), we have
which gives (5.7).
Let \(\pi =\pi ^H_S\). Using the Chern–Weil formula and the fact that \(H\in {\mathcal {P}}_{H_0}\) is PHYM, we have
and consequently is \(L^1\).
Claim
Assume this for a moment, then by Lemma 5.3, we know that
and equality holds if and only if \({\bar{\partial }}\pi =0\). Suppose \({\bar{\partial }}\pi =0\). Since \(\left| \pi \right| _{\,\overline{\!{H}}_0}=\left| \pi \right| _{H_0}\le C\left| \pi \right| _H\le C\). Again by [7, Lemma 7.3], there is a global holomorphic section of \(\textrm{End}(\,\overline{\!{E}})\), which is still denoted by \(\pi \), such that \(\pi =\pi ^H_S\) a.e. and \(\pi ^2=\pi \). Note that since \(\text {rank}(\pi )=\text {tr}(\pi )\) is real valued and holomorphic, it follows that \(\text {rank}\pi \) is a constant. Thus \(\,\overline{\!{E}}\) holomorphically splits as the direct sum of \(\ker \pi \) and \(\Im \pi \), which contradicts with our assumption that \(\,\overline{\!{E}}\) is irreducible. Therefore we prove that
Proof of the claim: since \(H\in {\mathcal {P}}_{H_0}\), we have
for a bounded real valued smooth function u with \(|\nabla u|\in L^2\). By Lemma 2.9,
By the same argument in Lemma 5.3, we can show
Hence we complete the proof of the claim. \(\square \)
Proposition 5.6
Let \(H_0\) be the metric constructed in Lemma 1.1. Suppose \(\,\overline{\!{E}}\) is \(\left( c_1(D),{[\omega _0]}\right) \)-stable, then there exists a unique \(\omega \)-PHYM metric H in \({\mathcal {P}}_{H_0}\).
Proof
Uniqueness is easy, for convenience we will review the argument. Suppose we have two \(\omega \)-PHYM metrics \(H_1\), \(H_2\in {\mathcal {P}}_{H_0}\). Let \(h=H_1^{-1}H_2\). By the definition of \({\mathcal {P}}_{H_0}\), we know that \(\det h=1\) and h is both bounded from above and below and \(|{\bar{\partial }}h| \in L^2\). Then by taking the trace of the differential equality in Lemma 3.2-(2), we get
By Lemma 2.9,
Therefore \({\bar{\partial }}h=0\) and since h is self-adjoint with respect to \(H_i\), it is parallel with respect to the Chern connection determined by \(({\bar{\partial }},H_i)\). Then its eigenspaces give a holomorphic decomposition of \(\,\overline{\!{E}}\) which contradicts the assumption that \(\,\overline{\!{E}}\) is irrducible unless h is a multiple of identity map. Since \(\det h=1\), it must be that h is the identity map, i.e. \(H_1=H_2\).
For the existence part, we follow Simpson and Mochizuki’s argument [19, 25]. For completeness, we include some details. Let \(\{X_i\}\) be an exhaustion of X by compact domains with smooth boundary and we solve Dirichlet problems on every \(X_i\) using Donaldson’s theorem (Theorem 3.8). Then we have a sequence of PHYM metrics \(H_i\) on \(E|_{X_i}\) such that \(H_i|_{\partial X_i}=H_0|_{\partial X_i}\) and \(\det H_i=\det H_0\). Let \(s_i\) be the endomorphism determined by \(H_i=H_0h_i=H_0e^{s_i}\). Then we have \(s_i|_{\partial X_i}=0\) and \(\text {tr}(s_i)=0\).
We argue by contradiction to prove a uniform \(C^0\)-estimate for \(s_i\). First note that by Lemma 3.2, \(e^{s_i}\) satisfies the elliptic differential inequality
Therefore \(\text {tr}(e^{s_i})\) satisfies the weighted mean value inequality in Lemma 2.8. Since \(\text {tr}(e^{s_i})\) and \(|s_i|\) are mutually bounded, we know that \(|s_i|\) also satisfies the weighted mean value inequality (2.13). Lemma 2.8 plays an essential role since it ensures that after normalization we can have a nontrivial limit in \(W^{1,2}_{loc}\). Suppose there is a sequence \(s_i\) such that \(\sup _{X_i}| s_i|_{H_0}\rightarrow \infty \) as \(i\rightarrow \infty \). Then by Lemma 2.8, we obtain
Let \(u_i=l_i^{-1}s_i\). Then by Lemma 2.8 again we obtain there is a constant C independent of i such that
where the norms are with respect to the back ground metric \(H_0\). Then following Simpson’s argument, we can show that
Lemma 5.7
After passing to a subsequence, \(u_i\) converge weakly in \(W^{1,2}_{loc}\) to a nonzero limit \(u_{\infty }\). The limit \(u_{\infty }\) satisfies the following property: if \(\Phi : {\mathbb {R}} \times {\mathbb {R}} \rightarrow {\mathbb {R}}\) is a positive smooth function such that \(\Phi \left( \lambda _{1}, \lambda _{2}\right) <\left( \lambda _{1}-\lambda _{2}\right) ^{-1}\) whenever \(\lambda _{1}>\lambda _{2}\), then
Proof
By Theorem 3.10
By the definition of \(\Psi \) in (3.9), we know that as \(l \rightarrow \infty , l \Psi \left( l \lambda _{1}, l \lambda _{2}\right) \) increases monotonically to \(\left( \lambda _{1}-\lambda _{2}\right) ^{-1}\) if \(\lambda _{1}>\lambda _{2}\) and \(\infty \) if \(\lambda _{1} \le \lambda _{2}\). Fix a \(\Phi \) as in the statement of the lemma. We know that for all \(A>0\) there exists \(l_A\) such that if \(|\lambda _i|\le A\) and \(l>l_A\), then we have
Since sup \(\left| u_{i}\right| \) are bounded, its eigenvalues are also bounded. Then by (5.11) and (5.12), we obtain that for i sufficiently large
Again since \(\sup |u_i|\) is bounded we can find \(\Phi \) satisfying the assumption in the lemma and \(\Phi (u_i)=c_0\) for all i, where \(c_0\) a fixed small positive number. Then by (5.13) and the construction of \(H_0\), there exists a positive constant C such that
Therefore by a diagonal sequence argument and after passing to a subsequence we may assume \(u_i\) converge weakly in \(W^{1,2}_{loc}\) to a limits \(u_{\infty }\) with \(\int _X|{\bar{\partial }}u_{\infty }|^2\le C\). We claim that \(u_{\infty }\ne 0\). Indeed by (5.9), there exists a compact set \(K\subseteq X\) independent of i such that
Since on compact sets the embedding from \(W^{1,2}\) to \(L^1\) is compact, after taking the limit, we get \(\int _K|u_{\infty }|(1+r)^{-N}\ge \frac{1}{2}\). In particular \(u_{\infty }\ne 0\).
Next we prove (5.10). By the uniform boundedness of \(u_i\), the \(O(r^{-N_0})\) decay property of \(|\Lambda F_{H_0}|\) and the nonnegativity of the second term of the left hand side in (5.13), we know that there exists \(\epsilon _i\rightarrow 0\) such that for any \(j\ge i\), we have
Note that \(\left<\Phi \left( u_{j}\right) \left( {\bar{\partial }}u_{j}\right) , {\bar{\partial }}u_{j}\right>_{H_0}=|\Phi ^{\frac{1}{2}}(u_j)({\bar{\partial }}u_j)|_{H_0}^2.\) By [25, Proposition 4.1], we know that on each fixed \(X_i\), \(\Phi ^{\frac{1}{2}}(u_j)\rightarrow \Phi ^{\frac{1}{2}}(u_{\infty })\) in \(\textrm{Hom}\left( L^{2}, L^{q}\right) \text{ for } \text{ any } q<2\). Since \({\bar{\partial }}u_j\) converge weakly in \(L^2(X_i)\) to \({\bar{\partial }}u_{\infty }\), we obtain that \(\Phi ^{\frac{1}{2}}(u_j)({\bar{\partial }}u_j)\) converge weakly to \(\Phi ^{\frac{1}{2}}(u_{\infty })({\bar{\partial }}u_{\infty })\) in \(L^q(X_i)\) for any \(q<2\). Then we know that for any \(q<2\),
Let \(q\rightarrow 2\), we obtain
Letting \(i\rightarrow \infty \), the inequality (5.10) is proved. \(\square \)
Simpson’s argument in [25, Lemma 5.5 and Lemma 5.6] can be applied verbatim to the infinite volume case, so we have
Lemma 5.8
[25] Let \(u_{\infty }\) be a limit obtained in the previous lemma. Then we have
-
(1)
The eigenvalues of \(u_{\infty }\) are constant and not all equal.
-
(2)
Let \(\Phi : {\mathbb {R}} \times {\mathbb {R}} \longrightarrow (0, \infty )\) be a \(C^{\infty }\)-function such that \(\Phi \left( \lambda _{i}, \lambda _{j}\right) =0\) if \(\lambda _{i}>\lambda _{j}\). Then \(\Phi \left( u_{\infty }\right) \left( \bar{\partial } u_{\infty }\right) =0\).
Let \(\lambda _1 \le \lambda _2\le \cdots \le \lambda _{\text {rank}(E)}\) denote the eigenvalues of \(u_{\infty }\). Let \(\gamma \) be an open interval between the eigenvalues (since eigenvalues of \(u_{\infty }\) are not all equal by the previous lemma, there exists such a nonempty interval). We choose a \(C^{\infty }\)-function \(p_{\gamma }: {\mathbb {R}} \longrightarrow (0, \infty )\) such that \(p_{\gamma }\left( \lambda _{i}\right) =1\) if \(\lambda _{i}<\gamma \), and \(p_{\gamma }\left( \lambda _{i}\right) =0\) if \(\lambda _{i}>\gamma \). Set \(\pi _{\gamma }:=p_{\gamma }\left( u_{\infty }\right) \), see Sect. 3.5 for the definition. Then one can easily show that [19, 25]
-
(1)
\(\pi _{\gamma }^2=\pi _{\gamma }\), \((\textrm{id}-\pi _{\gamma })\circ \pi _{\gamma } =0\) and \(\pi _{\gamma }\) is self-adjoint with respect to \(H_0\).
-
(2)
\(\int _X|{\bar{\partial }}\pi _{\gamma }|^2<\infty \).
Moreover using (5.10), Simpson proved that
Lemma 5.9
[25] There exists at least one \(\gamma \) such that
By Lemma 5.4, we get a filtration of \(\,\overline{\!{E}}\) by coherent reflexive subsheaves \(\,\overline{\!{S}}_i\) whose restrictions to D are splitting factors of \(\,\overline{\!{E}}|_D\). Since we assume that \(\,\overline{\!{E}}|_D\) is \(c_1(N_D)\)-polystable, we know that for every i
Then again by [18], we have
Note that Lemma 5.9 is equivalent to the statement that there exists at least one \(\,\overline{\!{S}}_i\) such that
Then by Lemma 5.3,
which contradicts with the \((c_1(D),{[\omega _0]})\)-stability assumption. Therefore we do have a uniform \(C^0\)-estimate for \(s_i\).
Bando–Siu’s interior regularity result Theorem 3.11 can be applied to get local uniform estimate for all derivatives of \(s_i\). Then we can take limits to get a smooth section \(s\in \textrm{End}( E)\), which is self-adjoint with respect to \(H_0\) and \(\text {tr}(s)=0\) and more importantly
Then we use Mochizuki’s argument in [19, Section 2.8] to show that
Indeed taking the trace of the equality in Lemma 3.2-( 2) and noting that \(H_i=H_0h_i\) is PHYM, we have
Since \(\det h_i=1\) and \(h_i|_{\partial X_i}=\textrm{id}\), we know that \(\nabla _{\nu _i}\text {tr}(h_i)\le 0\), where \(\nu _i\) denotes the outward unit normal vector of \(\partial X_i\). Integrating (5.16) over \(X_i\) and using Stoke’s theorem in the left hand side, we obtain
Since we have uniform \(C^0\)-estimate for \(s_i=\log h_i\), there exist constants \(C_1\) and \(C_2\) independent of i such that
Let \(i\rightarrow \infty \), we have \(\int _X|{\bar{\partial }}s|^2\le C_2\). \(\square \)
On the stability condition. Note that global semistability is known [18], if we assume the restriction to D is semistable. There do exist irreducible holomorphic vector bundles which are polystable when restricted to D but not globally stable, even under more restrictive assumptions that \(\,\overline{\!{X}}\) is Fano and \(D\in |K_{\,\overline{\!{X}}}^{-1}|\).
Example 5.10
Recall that for holomorphic vector bundles S, Q over a complex manifold M, all exact sequences \(0\rightarrow S\rightarrow E\rightarrow Q\rightarrow 0\) of holomorphic vector bundles are classified by elements \(\beta \in H^1(M,\textrm{Hom}(Q,S))\) and in particular the exact sequence splits holomorphically if and only if the corresponding element \(\beta =0\). Now taking M to be \({{\mathbb {C}}}{{\mathbb {P}}}^1\times {{\mathbb {C}}}{{\mathbb {P}}}^1\), D to be a smooth anticanonical divisor. Then \(c_1(D)\) is a Kähler class and D itself is an elliptic curve. Choose \(\textrm{Hom}(Q,S)=L=p_1^*({\mathcal {O}}(2))\otimes p_2^*({\mathcal {O}}(-2))\). Then by the Künneth’s formula, \(\dim H^1(M,L)=3\). Note that \(\deg (L|_D)=0\), which by Serre duality implies \(\dim H^1(D,L)=\dim H^0(D,L^*)\le 1\). So there exists a class \(\beta \in H^1(M,L)\) corresponding to a non-splitting exact sequence of holomorphic vector bundles whose restriction to D splits as a direct sum of two line bundles with the same degree. Therefore E itself is not \(c_1(D)\)-stable but \(E|_D\) is \(c_1(N_D)\)-polystable. Such an E is irreducible, because if \(E=L_1 \oplus L_2\), then \(\deg (L_i,c_1(D))=\deg (L_i|_D)=0\) since \(E|_D\) is polystable of degree 0, which implies that S has to be one of the \(L_i\) and Q is the other one. This contradicts with the construction of E.
6 Discussion
6.1 More results on the existence of PHYM metrics
By Donaldson’s theorem on the solvability of Dirichlet problem (Theorem 3.8), the elliptic differential inequality (Lemma 3.2-(3)), the maximal principle and Bando–Siu’s interior estimate (Theorem 3.11), we get the following well-known existence result.
Theorem 6.1
Let \((M,\omega ,g)\) be a complete Kähler manifold, E be a holomorphic vector bundle on M. Suppose there exists a smooth hermitian metric \(H_0\) on E such that the equation
admits a positive solution u. Then there exists a smooth hermitian metric \(H=H_{0}e^s\) satisfying
Moreover, if u is bounded and \(|\Lambda F_{H_0}|\in L^1\) then \(|{\bar{\partial }}s|\in L^2\).
There are many examples for which (6.1) has a positive solution and even bounded solutions [1, 21, 23].
-
(1)
Suppose (M, g) is asymptotically conical and \(|\Lambda F_{H_0}^{\perp }|=O(r^{-2-\epsilon })\) for some \(\epsilon >0\), then (6.1) admits a solution u with \(|u|=O(r^{-\epsilon })\).
-
(2)
Suppose (M, g) is non-parabolic (i.e admits a positive Green’s function) and \(|\Lambda F_{H_0}^{\perp }|\in L^1\), then (6.1) admits a positive solution.
-
(3)
Suppose (M, g) has nonnegative Ricci curvature, \(|\Lambda F_{H_0}^{\perp }|=O(r^{-2})\) and
$$\begin{aligned} \frac{1}{\textrm{Vol}(B_r)}\int _{B_r} |\Lambda F_{H_0}^{\perp }|=O(r^{-2-\epsilon }), \end{aligned}$$for some \(\epsilon >0\), then (6.1) admits a bounded solution. In particular, if (M, g) has nonnegative Ricci curvature, volume growth order greater than 2, \(|\Lambda F_{H_0}^{\perp }|=O(r^{-2})\) and \(|\Lambda F_{H_0}^{\perp }|\in L^1\), then (6.1) admits a bounded solution.
Theorem 6.1 can not be applied to \((X,\omega ,g)\) satisfying Assumption 1 since we do not know whether (6.1) admits a positive solution (for this volume growth order at most 2 is a key issue). And actually Theorem 1.3 tells us that there are some obstructions for the existence of \(\omega \)-PHYM metrics which are mutually bounded with the initial metric.
Such a phenomenon also appears when we seek a bounded solution for the Poisson equation
on a complete noncompact Riemannian manifold (M, g) with nonnegative Ricci curvature. Suppose f is compactly supported for simplicity, then we know that
-
(1)
if the volume growth order is greater than 2, i.e. there is a constant \(c>0\) such that \(\textrm{Vol}(B_r)\ge c r^{2+\epsilon }\) for some \(\epsilon >0\), then (6.2) admits a bounded solution. (Since by Li–Yau [17], (M, g) admits a positive Green’s function which is \(O(r^{-\epsilon })\) at infinity, a bounded solution of (6.2) is obtained by the convolution with the Green’s function.)
-
(2)
if the volume growth order does not exceed 2, i.e. there is a constant \(C>0\) such that \(\textrm{Vol}(B_r)\le C (r+1)^{2}\), then (6.2) admits a bounded solution if and only if \(\int _Mf=0\). (For the “if” direction, see [11, Theorem 1.5]. For the “only if” direction, suppose we have a bounded function u and a compactly supported function f such that \(\Delta u=f\). Then by Cheng–Yau’s gradient estimate [5], we obtain \(|\nabla u|\le \frac{C}{r}\) for some \(C>0\) independent of r. Multiplying u both sides in (6.2) and integrating by parts, we obtain that \(|\nabla u|\in L^2\). Then Lemma 2.9 implies \(\int _Mf=0\).)
Next we discuss another result whose proof is similar to the proof of Theorem 1.3. Let  be an n-dimensional (\(n\ge 2\)) compact Kähler manifold, D be a smooth divisor. Let
be an n-dimensional (\(n\ge 2\)) compact Kähler manifold, D be a smooth divisor. Let  denote the restriction of
denote the restriction of  to D and \(X=\,\overline{\!{X}}\backslash D\) denote the complement of D in \(\,\overline{\!{X}}\). Let \(L_D\) be the line bundle determined by D and \(S\in H^0(\,\overline{\!{X}},L_D)\) be a defining section of D. Fix a hermitian metric h on \(L_D\). Then after scaling h, the function \(t=-\log |S|_h^2\) is smooth and positive on X. For any smooth function \(F:(0,\infty )\longrightarrow {\mathbb {R}}\) with
\(|F'(t)|\rightarrow 0\) as
\(t\rightarrow \infty \) and
\(F''(t)\ge 0\) there exists a large constant A such that
to D and \(X=\,\overline{\!{X}}\backslash D\) denote the complement of D in \(\,\overline{\!{X}}\). Let \(L_D\) be the line bundle determined by D and \(S\in H^0(\,\overline{\!{X}},L_D)\) be a defining section of D. Fix a hermitian metric h on \(L_D\). Then after scaling h, the function \(t=-\log |S|_h^2\) is smooth and positive on X. For any smooth function \(F:(0,\infty )\longrightarrow {\mathbb {R}}\) with
\(|F'(t)|\rightarrow 0\) as
\(t\rightarrow \infty \) and
\(F''(t)\ge 0\) there exists a large constant A such that

is a Kähler form on X. By scaling
 we may assume
\(A=1\). One can easily check that
\(\omega \) is complete is and only if
\(\int _{1}^{\infty } \sqrt{F''}=\infty \) and it always has finite volume. In the following, we always assume the function F satisfies
\(|F'(t)|\rightarrow 0\) as
\(t\rightarrow \infty \) and
\(F''(t)\ge 0\). Then we can state assumptions on
\(\omega \).
we may assume
\(A=1\). One can easily check that
\(\omega \) is complete is and only if
\(\int _{1}^{\infty } \sqrt{F''}=\infty \) and it always has finite volume. In the following, we always assume the function F satisfies
\(|F'(t)|\rightarrow 0\) as
\(t\rightarrow \infty \) and
\(F''(t)\ge 0\). Then we can state assumptions on
\(\omega \).
Assumption 2
Let \(\omega \) be the Kähler form defined by (6.3) and g be the corresponding Riemannian metric. We assume that
-
(1)
the sectional curvature of g is bounded.
-
(2)
\(C^{-1}t^{-2+\epsilon }\le F''(t)\le C\) for some constant \(C,\epsilon >0\) and t sufficiently large.
A consequence of these assumptions is that (X, g) is complete and of \((K,\alpha ,\beta )\)-polynomial growth defined in [27, Definition 1.1], so we can use the weighted Sobolev inequality as we did for the proof of Lemma 2.8.
Let \(\,\overline{\!{E}}\) be an irreducible holomorphic vector bundle on \(\,\overline{\!{X}}\) such that \(\,\overline{\!{E}}|_D\) is \(\omega _D\)-polystable. Then by Donaldson–Uhlenbeck–Yau theorem, there exists a hermitian metric \(H_D\) on \(\,\overline{\!{E}}|_D\) such that

Extend \(H_D\) smoothly to get a smooth hermitian metric \(H_0\) on \(\,\overline{\!{E}}\). Then by (6.4) and Assumption 2-(2), one can easily show that
Lemma 6.2
There exists a \(\delta >0\) such that \(|\Lambda _{\omega } F_{H_0}^{\perp }|=O(e^{-\delta t})\).
Then we have the following result
Theorem 6.3
Suppose \((X,\omega )\) satisfies Assumption 2 and  is
is  -polystable. Let \(H_0\) be a hermitian metric as above and
-polystable. Let \(H_0\) be a hermitian metric as above and  be defined by (1.1). Then there exists an \(\omega \)-PHYM metric in
be defined by (1.1). Then there exists an \(\omega \)-PHYM metric in  if and only if
if and only if  is
is  -stable.
-stable.
Using the argument in Proposition 5.5, the “only if” direction follows from Lemma 2.9 and the following lemma.
Lemma 6.4
For every smooth closed (1,1)-form \(\theta \) on \(\,\overline{\!{X}}\), we have

Proof
Firstly note that since there exists a positive number \(c>0\) such that
 and
\(\int \omega ^n<\infty \), the left hand side of (6.5) is well-defined. Therefore it suffices to show that for any
\(1\le k\le n-1\)
and
\(\int \omega ^n<\infty \), the left hand side of (6.5) is well-defined. Therefore it suffices to show that for any
\(1\le k\le n-1\)

Let \(S_{\epsilon }\) denote the level set \(\{|S|_h=\epsilon \}\). By integration by part, it suffices to show that

Case 1.
\(k=1\). Note that with respect to the smooth back ground metric
 ,
\(\textrm{Vol}(S_{\epsilon })=O(\epsilon )\) and
\(|d^c F|\le C|F'(t)|\epsilon ^{-1}\) on
\(S_{\epsilon }\). Then (6.6) follows from the assumption that
\(|F'|\rightarrow 0\) as
\(t\rightarrow \infty \).
,
\(\textrm{Vol}(S_{\epsilon })=O(\epsilon )\) and
\(|d^c F|\le C|F'(t)|\epsilon ^{-1}\) on
\(S_{\epsilon }\). Then (6.6) follows from the assumption that
\(|F'|\rightarrow 0\) as
\(t\rightarrow \infty \).
Case 2. \(2\le k\le n-1\). Then (6.6) follows from the fact that \(|F'(t)|\rightarrow 0\) as \(t\rightarrow \infty \) and \(d^ct\wedge d^c t=0\). \(\square \)
For the “if” direction, the argument in Proposition 5.6 applies. We will not give the details and just point out the following two observations which make the argument work in this setting. The key points are
-
(1)
Assumption 2 and Lemma 6.2 ensure that we can apply the weighted mean value inequality proved in Lemma 2.8.
-
(2)
We have
 since
since
 for some
\(c>0\), therefore by Uhlenbeck–Yau’s theorem (Theorem 3.6) a weakly projection map
\(\pi \) of E over X with
\(|{\bar{\partial }}\pi |\in L^2(X,\omega )\) defines a coherent torsion free sheaf
\(\,\overline{\!{S}}\) of
\(\,\overline{\!{E}}\).
for some
\(c>0\), therefore by Uhlenbeck–Yau’s theorem (Theorem 3.6) a weakly projection map
\(\pi \) of E over X with
\(|{\bar{\partial }}\pi |\in L^2(X,\omega )\) defines a coherent torsion free sheaf
\(\,\overline{\!{S}}\) of
\(\,\overline{\!{E}}\).
6.2 Calabi–Yau metrics satisfying Assumption 1
As mentioned in the Introduction, there do exist interesting Kähler metrics satisfying the Assumption 1, which contain Calabi–Yau metrics on the complement of an anticanonical divisor of a Fano manifold and its generalizations [13, 14, 27]. We will call them Tian–Yau metrics. Here we give a sketch for the construction of these Calabi–Yau metrics and refer to [13]-Section 3 for more details.
Let \(\,\overline{\!{X}}\) be an n-dimensional ( \(n\ge 2\)) projective manifold, \(D\in |K^{-1}_{\,\overline{\!{X}}}|\) be a smooth divisor and \(X=\,\overline{\!{X}}\backslash D\) be the complement of D in \(\,\overline{\!{X}}\). Suppose that the normal bundle of D in \(\,\overline{\!{X}}\), \(N_D=K^{-1}_{\,\overline{\!{X}}}|_D\) is ample. Fixing a defining section \(S\in H^0(\,\overline{\!{X}}, K^{-1}_{\,\overline{\!{X}}})\) of the divisor D whose inverse can be viewed as a holomorphic volume form \(\Omega _X\) on X with a simple pole along D. Let \(\Omega _D\) be the holomorphic volume form on D given by the residue of \(\Omega _X\) along D. Using Yau’s theorem [29], there is a hermitian metric \(h_D\) on \(K^{-1}_{\,\overline{\!{X}}}|_D\) such that its curvature form is a Ricci-flat Kähler metric \(\omega _D\) with

by rescaling S if necessary. One can show that the hermitian metric \(h_D\) extends to a global hermitian metric \(h_{\,\overline{\!{X}}}\) on \(K^{-1}_{\,\overline{\!{X}}}\) such that its curvature form is nonnegative and positive in a neighborhood of D.
By glueing a smooth positive constant on a compact set, we get a global positive smooth function z which is equal to \((-\log |S|^2_{h_{\,\overline{\!{X}}}})^{\frac{1}{n}}\) outside a compact set. For any \(A\in {\mathbb {R}}\), we denote \(h_A=h_{\,\overline{\!{X}}}e^{-A}\) and \(v_A=\frac{n}{n+1}(-\log |S|_{h_A}^2)^{\frac{n+1}{n}}\), which is viewed as a smooth function defined outside a compact set on X.
We denote by \(H^2_{c,+}(X)\) the subset of \(\textrm{Im} (H^2_c(X, \mathbb R)\rightarrow H^2(X,\mathbb R))\) consisting of classes \({\mathfrak {k}}\) such that \(\int _Y{\mathfrak {k}}^p>0\) for any compact analytic subset Y of X of pure dimension \(p>0\).
Then Hein–Sun–Viaclovsky–Zhang proved the following result.
Theorem 6.5
[13] For every class \({\mathfrak {k}} \in H_{c,+}^{2}(X)\), there is a unique Kähler metric \(\omega \in {\mathfrak {k}} \) such that
-
(1)
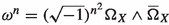 , and
, and -
(2)
\(|\nabla ^l_{\omega }(\omega -\sqrt{-1}\partial {\bar{\partial }}v_A)|_{\omega }=O\left( e^{-\delta z^{\frac{n}{2}}}\right) \) for some \(\delta ,A>0\) and all \(l\ge 0\).
And from the construction in [13]-Section 3, we have the decomposition \(\omega =\omega _0+dd^c\varphi \), where \(\omega _0\) is a smooth (1,1)-form on \(\,\overline{\!{X}}\) vanishing when restricted to D. And by Theorem 6.5 and the estimate in [14, Proposition 3.4], one can directly check that these Kähler metrics satisfy Assumption 1.
Remark 6.6
It was proved in [14] that Tian–Yau metrics \(\omega _{TY}\) can be realized as the rescaled pointed Gromov–Hausdorff limits of a sequence of Calabi–Yau metrics \(\omega _k\) on a K3 surface. We expect that \(\omega _{TY}\)-PHYM connections we obtained in this paper give models for the limits of \(\omega _k\)-HYM connections on the K3 surface.
6.3 On the ampleness assumption of the normal bundle \(N_D\)
In this subsection, we first explain why we assume the normal bundle of D is ample and then discuss the case where the normal bundle is trivial on compact Kähler surfaces.
Let us start with a question. Suppose we have a nontrivial class \(\alpha \) in \(H^{1,1}(\,\overline{\!{X}})\) and  a smooth divisor, when does
a smooth divisor, when does
hold for every coherent reflexive sheaf \({\mathcal {E}}\) on \(\,\overline{\!{X}}\) ? A sufficient condition is that
In order to have the above equality, a natural (possibly the only reasonable) choice is that \(\alpha =c_1(D)\).
To make the argument in this paper work, we also need the following property: if a vector bundle F on D is polystable with respect to \(\alpha |_D\) and S is a coherent subsheaf of F with the same \(\alpha |_D\)-degree as F, then S is a vector bundle and is a splitting factor of F. (Note that this does not follow from the definition since \(\alpha |_D\) may not be a Kähler class. For example if \(\alpha |_D\) is 0, then definitely it does not satisfy this property.) In general in order to have this property, we need \(\alpha |_D\) to be a Kähler class. This is one of the reasons why we assume that the normal bundle of D is ample, i.e. \(c_1(D)|_D\) is a Kähler class. Another reason is that by assuming \(N_D\) is ample, on the punctured disc bundle \({\mathcal {C}}\) we have explicit exact Kähler forms, which give models of the Kähler forms on X.
However if \(\,\overline{\!{X}}\) is a compact complex surface, in which case the divisor D now is a smooth Riemann surface, then the property mentioned above always holds. Note that on a Riemann surface D, the slope of a vector bundle is canonically defined and independent of the choice of cohomology classes on D.
Lemma 6.7
Let \(\,\overline{\!{X}}\) be a compact Kähler surface and D be a smooth divisor. Suppose \(\,\overline{\!{E}}|_D\) is polystable. Let \(\,\overline{\!{S}}\) be a coherent reflexive subsheaf of \(\,\overline{\!{E}}\). Then \(\mu (\,\overline{\!{S}},c_1(D))=\mu (\,\overline{\!{E}},c_1(D))\) if and only if \(\,\overline{\!{S}}|_D\) is a splitting factor of \(\,\overline{\!{E}}|_D\).
Using this, most of the arguments in Sect. 5 can be modified to work for divisors D with \(c_1(N_D)=0\) in complex dimension 2. In the following, we assume \(c_1(N_D)=0\) in \(H^2(D,{\mathbb {R}})\). Then it is easy to see that \(c_1(D)\) is nef and by the global \(\partial {\bar{\partial }}\)-lemma on D, we know that there exists a hermitian metric \(h_D\) on \(N_D\) with vanishing curvature. Let \(L_D\) be the line bundle determined by D and \(S\in H^0(\,\overline{\!{X}},L_D)\) be a defining section of D. Then we can extend \(h_D\) smoothly to get a smooth hermitian metric h on \(L_D\) and after a rescaling, we may assume that \(t=-\log |S|_h^2\) is positive on X. In this case, we can consider (at least) all monomials potentials with degree greater than 1
Assumption 3
Let \(\omega \) be a Kähler form on X and g be the corresponding Riemannian metric. We assume that
-
(1)
the sectional curvature of g is bounded.
-
(2)
the form \(\omega \) can be written as \(\omega _0+\sqrt{-1}\partial {\bar{\partial }}F(t)\) for some \(F\in {\mathcal {H}}\), where \(\omega _0\) is a smooth closed (1,1)-form on \(\,\overline{\!{X}}\).
Suppose \((X,\omega ,g)\) satisfies Assumption 3, then we have the following consequences:
-
the Riemannian metric g is complete and has volume growth order at most 2,
-
(X, g) is of \((K,2,\beta )\)-polynomial growth as defined in [27, Definition 1.1] for some positive constants K and \(\beta \).
Let \(\,\overline{\!{E}}\) be an irreducible holomorphic vector bundle over \(\,\overline{\!{X}}\) such that \(\,\overline{\!{E}}|_D\) is polystable with degree 0. Then by Donaldson–Uhlenbeck–Yau theorem (for Riemann surfaces this was first proved by Narasimhan and Seshadri [20]), there exists a hermitian metric \(H_D\) on \(\,\overline{\!{E}}|_D\) such that
Since D is a Riemann surface, this is equivalent to say that \(H_D\) gives a flat metric on \(\,\overline{\!{E}}|_D\), i.e.
Extending \(H_D\) smoothly to get a hermitian metric \(H_0\) on \(\,\overline{\!{E}}\) then by (6.9) and the proof of Lemma 1.1, we know that \(H_0\) is already a good initial metric in the following sense:
Then we have the following result, whose proof is essentially the same as that for Theorem 1.3. We just point out the difference.
Theorem 6.8
Suppose \((X,\omega )\) satisfies Assumption 3 and  flat. Let \(H_0\) be a hermitian metric as above and \({\mathcal {P}}_{H_0}\) be defined by (1.1). Then there exists an \(\omega \)-PHYM metric in
flat. Let \(H_0\) be a hermitian metric as above and \({\mathcal {P}}_{H_0}\) be defined by (1.1). Then there exists an \(\omega \)-PHYM metric in  if and only if \(\,\overline{\!{E}}\) is
if and only if \(\,\overline{\!{E}}\) is  -stable.
-stable.
The argument in Sect. 5 can be applied if Lemma 5.3 still holds. The analog of Lemma 5.3 in this case is the following lemma, for which we need to assume \(\,\overline{\!{E}}|_D\) is flat.
Lemma 6.9
Suppose \((X,\omega )\) satisfies Assumption 3 and \(\,\overline{\!{E}}|_D\) is flat. Let \(H_0\) be a hermitian metric as above. Then we have the following equality:
Proof
By Chern–Weil theory, it suffices to show that
The argument in Lemma 2.10 can be used again to show that there exists a cut-off function \(\chi \) supported on a compact set and a smooth 1-form \(\psi \) supported outside a compact set such that
Moreover \(|\psi |\) grows at most in a polynomial rate of r. Then (6.11) follows from integration by parts and (6.10). \(\square \)
Example 6.10
Let \(\,\overline{\!{X}}={{\mathbb {C}}}{{\mathbb {P}}}^1\times D\), where D is a compact Riemann surface. Then \(D=\{\infty \}\times D\) is a smooth divisor with trivial normal bundle. Fix a Kähler form \(\omega _D\) on D and also view it as a form on \({{\mathbb {C}}}{{\mathbb {P}}}^1\times D\) via the pull-back of the obvious projection map. Note that up to a scaling \([\omega _D]\in c_1({{\mathbb {C}}}{{\mathbb {P}}}^1)\) in \(H^{1,1}(\,\overline{\!{X}})\). We can consider asymptotically cylindrical metrics on \(X={\mathbb {C}}\times D\) given by the Kähler forms
where z denotes the coordinate function on \({\mathbb {C}}\) and \(\varphi =\Phi ''\) is a positive smooth function defined on \({\mathbb {R}}\) such that \(\varphi (t)=e^{t}\) when t is sufficiently negative and \(\varphi (t)=1\) for t sufficiently positive. Then one can easily check that \((X,\omega )\) satisfies Assumption 3 with \(F(t)=t^2\). Let \(\,\overline{\!{E}}\) be an irreducible holomorphic vector bundle on \({{\mathbb {C}}}{{\mathbb {P}}}^1\times D\) such that \(\,\overline{\!{E}}|_D\) is flat. Then by Theorem 6.8, we know that
Similar examples as in Example 5.10 show that the condition \(\left( c_1(D),c_1({{\mathbb {C}}}{{\mathbb {P}}}^1)\right) \)-stability is non-trivial. More specifically, let D be a Riemann surface with genus \(g\ge 1\) and \(k\ge 2\) be an integer. Then similar argument as in Example 5.10 shows that there exists a non-splitting extension
whose restriction to D splits. Then one can easily check that E is irreducible and not \(\left( c_1(D),c_1({{\mathbb {C}}}{{\mathbb {P}}}^1)\right) \)-stable.
6.4 Some problems for further study
Let \((X,\omega )\) satisfy the Assumption 1. As illustrated by Theorem 6.5 it is more natural to assume a stronger condition on the background Kähler metric \(\omega \). More precisely, we assume that in (2.5) the right hand side is replaced by \(O(e^{-\delta _0 r^{\alpha _0}})\) for some \(\delta _0, \alpha _0 >0\) and we also have the same bound for higher order derivatives. Under these assumptions and motivated by the result of Hein [12] for solutions of complex Monge–Ampère equations, we make the following conjecture.
Conjecture 1
The solution s obtained in Proposition 5.6 decays exponentially, i.e \(|\nabla ^k s|=O(e^{-\delta r^{\alpha }})\) for some \(\delta , \alpha >0\) and all \(k\ge 0\).
Note that the key issue is to prove that |s| decays exponentially, since all of the higher order estimates will follows form standard elliptic estimates.
It is also an interesting problem to study the notion of \((\alpha ,\beta )\)-stability. From the definition, we have the following consequence:
Proposition 6.11
Let \(\alpha ,\beta \in H^{1,1}(M)\) be two classes on a compact Kähler manifold M. Suppose \(\alpha \in H^2(M,{\mathbb {Z}})\) and \(\alpha \wedge \beta =0\). Then a holomorphic vector bundle E is \((\alpha ,\beta )\)-stable if and only if E is \(\alpha \)-semistalbe and there exists an \(\epsilon _0>0\) such that \(\alpha +\epsilon \beta \)-stable for all \(0<\epsilon < \epsilon _0\).
It is natural to consider the following problem. Let \(\,\overline{\!{E}}\) be a \((c_1(D),[\omega _0])\)-stable holomorphic vector bundle on \(\,\overline{\!{X}}\). Then by Proposition 6.11, we know that \(\,\overline{\!{E}}\) is \([\omega _0]+\epsilon ^{-1}c_1(D)\)-stable for \(\epsilon \) positive and sufficiently small. Donaldson–Uhlenbeck–Yau theorem says that for every Kähler form \(\omega \) in \([\omega _0]+\epsilon ^{-1}c_1(D)\), there exists an \(\omega \)-Hermitian–Yang–Mills metric on \(\,\overline{\!{E}}\). In our setting, it is natural to consider the following Kähler forms
where \(\theta _{\epsilon }\) is a closed nonnegative (1,1)-form in \(c_1(D)\), supported and positive in an \(\epsilon \)-neighborhood of D and \(\chi _{\epsilon }\) is a cut-off function which equals 1 outside an \(\epsilon \)-neighborhood of D and 0 in a smaller neighborhood of D. The Kähler forms are chosen such that
Conjecture 2
Suppose \(\,\overline{\!{E}}|_D\) is \(c_1(N_D)\)-polystable and \((c_1(D),[\omega _0])\)-stable. Let \(H_{\epsilon }\) denote the Hermitian–Yang–Mills metric on \(\,\overline{\!{E}}\) with respect to the Kähler form \(\omega _{\epsilon }\). Then there exists smooth functions \(f_{\epsilon }\) on X such that
where H is the hermitian metric constructed in Theorem 1.3.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Bando, S.: Einstein–Hermitian Metrics on Non-compact Kähler Manifolds. CRC Press, Boca Raton (2020)
Bando, S., Siu, Y.-T.: Stable sheaves and Einstein–Hermitian metrics. In: Geometry and Analysis on Complex Manifolds: Festschrift for Professor S Kobayashi’s 60th Birthday, pp. 39–50. World Scientific (1994)
Stable sheaves and Einstein-Hermitian metrics: Bando, S., Siu, Y.-T. Stable Sheaves Einstein-Hermitian Metrics 39, 39–50 (1994)
Chen, X., Sun, S.: Singularities of Hermitian–Yang–Mills connections and Harder-Narasimhan–Seshadri filtrations. Duke Math. J. 169(14), 2629–2695 (2020)
Yuen Cheng, S., Yau, S.-T.: Differential equations on Riemannian manifolds and their geometric applications. Commun. Pure Appl. Math. 28(3), 333–354 (1975)
Conlon, R.J., Hein, H.-J.: Asymptotically conical Calabi–Yau metrics on quasi-projective varieties. Geom. Funct. Anal. 25(2), 517–552 (2015)
Demailly, J.-P.: Complex analytic and differential geometry. Citeseer (1997)
Donaldson, S.K.: Anti self-dual Yang–Mills connections over complex algebraic surfaces and stable vector bundles. Proc. Lond. Math. Soc. 3(1), 1–26 (1985)
Donaldson, S.K.: Boundary value problems for Yang–Mills fields. J. Geom. Phys. 8(1–4), 89–122 (1992)
Harvey, R.: Removable singularities for positive currents. Am. J. Math. 96(1), 67–78 (1974)
Hein, H.-J.: Weighted Sobolev inequalities under lower Ricci curvature bounds. Proc. Am. Math. Soc. 139(8), 2943–2955 (2011)
Hein, H.-J.: Gravitational instantons from rational elliptic surfaces. J. Am. Math. Soc. 25(2), 355–393 (2012)
Hein, H.-J., Sun, S., Viaclovsky, J., Zhang, R.: Gravitational instantons and del Pezzo surfaces. arXiv preprint arXiv:2111.09287 (2021)
Hein, H.-J., Sun, S., Viaclovsky, J., Zhang, R.: Nilpotent structures and collapsing Ricci-flat metrics on the K3 surface. J. Am. Math. Soc. 35(1), 123–209 (2022)
Jacob, A., Walpuski, T.: Hermitian–Yang–Mills metrics on reflexive sheaves over asymptotically cylindrical Kähler manifolds. Commun. Partial Differ. Equ. 43(11), 1566–1598 (2018)
Kobayashi, S.: Differential Geometry of Complex Vector Bundles. Princeton University Press, Princeton (2014)
Li, P., Tung Yau, S.: On the parabolic kernel of the Schrödinger operator. Acta Math. 156, 153–201 (1986)
Mistretta, E.C.: A remark on stability and restrictions of vector bundles to hypersurfaces. Boletín de la Sociedad Matemática Mexicana 27(2), 1–7 (2021)
Mochizuki, T.: Kobayashi-Hitchin correspondence for analytically stable bundles. Trans. Am. Math. Soc. 373(1), 551–596 (2020)
Narasimhan, M.S., Seshadri, C.S.: Stable and unitary vector bundles on a compact Riemann surface. Ann. Math. 82, 540–567 (1965)
Ni, L.: The Poisson equation and Hermitian–Yang–Mills metrics on holomorphic vector bundles over complete noncompact Kähler manifolds. Indiana Univ. Math. J. 51, 679–704 (2002)
Ni, L., Ren, H.: Hermitian–Yang–Mills metrics for vector bundles on complete Kähler manifolds. Trans. Am. Math. Soc. 353(2), 441–456 (2001)
Ni, L., Shi, Y., Tam, L.-F.: Poisson equation, Poincaré–Lelong equation and curvature decay on complete Kähler manifolds. J. Differ. Geom. 57(2), 339–388 (2001)
Popovici, D.: A simple proof of a theorem by Uhlenbeck and Yau. Math. Z. 250(4), 855–872 (2005)
Simpson, C.T.: Constructing variations of Hodge structure using Yang–Mills theory and applications to uniformization. J. Am. Math. Soc. 1, 867–918 (1988)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions, vol. 2. Princeton University Press, Princeton (1970)
Tian, G., Yau, S.T.: Complete Kähler manifolds with zero Ricci curvature. I. J. Am. Math. Soc. 3(3), 579–609 (1990)
Uhlenbeck, K., Yau, S.-T.: On the existence of Hermitian–Yang–Mills connections in stable vector bundles. Commun. Pure Appl. Math. 39(S1), S257–S293 (1986)
Yau, S.-T.: On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampére equation, I. Commun. Pure Appl. Math. 31(3), 339–411 (1978)
Acknowledgements
The author wants to express his deep and sincere gratitude to his advisor Song Sun, for the patient guidance, inspiring discussions and valuable suggestions. He is grateful to Charles Cifarelli for careful reading of the draft and numerous useful suggestions, to Sean Paul for his interest, and to the anonymous referee for comments and suggestions. The author is partially supported by NSF grant DMS-1810700 and NSF grant DMS-2004261.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J. Hermitian–Yang–Mills connections on some complete non-compact Kähler manifolds. Math. Ann. 390, 4535–4575 (2024). https://doi.org/10.1007/s00208-024-02849-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-024-02849-1



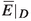 is
is  since
since
 for some
for some
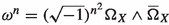 , and
, and