Cannon–Thurston maps for ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats

Abstract

Mahan Mitra (Mj) proved Cannon–Thurston maps exist for normal hyperbolic subgroups of a hyperbolic group (Mitra in Topology, 37(3):527–538, 1998). We prove that Cannon–Thurston maps do not exist for infinite normal hyperbolic subgroups of non-hyperbolic ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats with respect to the visual boundaries. We also show Cannon–Thurston maps do not exist for infinite infinite-index normal ${{\,\textrm{CAT}\,}}(0)$ subgroups with isolated flats in non-hyperbolic ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats. We obtain a structure theorem for the normal subgroups in these settings and show that outer automorphism groups of hyperbolic groups have no purely atoroidal $\mathbb {Z}^2$ subgroups.

1 Introduction

Cannon–Thurston maps, named after the seminal work of Cannon and Thurston in the setting of hyperbolic 3-manifolds, allow one to combine two far-reaching approaches in geometric group theory: the study of the boundaries of a group and the study of the collection of subgroups of a group. Cannon and Thurston [14] proved if M is a closed fibered hyperbolic 3-manifold with fiber a closed surface $\Sigma$, then there is a continuous surjective map from the visual boundary of the surface subgroup $\partial {\widetilde{\Sigma }}\cong \partial \mathbb {H}^2 \cong S^1$ to the visual boundary of the 3-manifold group $\partial {\widetilde{M}} \cong \partial \mathbb {H}^3 \cong S^2$ that extends the inclusion ${\widetilde{\Sigma }} \hookrightarrow {\widetilde{M}}$ between the universal covers.

The study of group boundaries is especially fruitful in the presence of hyperbolic or non-positive curvature. Gromov [25] proved every hyperbolic group G admits a visual boundary, which is unique up to G-equivariant homeomorphism and which yields a compactification of any Cayley graph for G constructed with respect to a finite generating set. A similar theorem was obtained by Hruska–Kleiner [29] for ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats. ${{\,\textrm{CAT}\,}}(0)$ spaces with isolated flats, roughly speaking, are negatively curved away from a collection of isometrically embedded Euclidean flats and share common features with $\delta$-hyperbolic spaces [27, 29,30,31]. In this paper, we establish a striking distinction between these classes of groups in terms of Cannon–Thurston maps.

The Cannon–Thurston map for hyperbolic groups $H \le G$ is the continuous map $\partial H \rightarrow \partial G$ that extends the inclusion from a Cayley graph for H into a Cayley graph for G given by choosing a finite generating set for H and extending it to a finite generating set for G, when such a continuous extension exists. Generalizing to include groups acting on ${{\,\textrm{CAT}\,}}(0)$ spaces, orbit maps between ${{\,\textrm{CAT}\,}}(0)$ model spaces yield a natural notion of inclusion from a subgroup to a group. The Cannon–Thurston map is, again, defined as a continuous H-equivariant extension of this inclusion to the visual boundaries of the model spaces. See Sect. 2.5 for details.

Mitra (Mj) [40], generalizing work of Cannon–Thurston, proved Cannon–Thurston maps exist for normal hyperbolic subgroups of a hyperbolic group. We prove this result does not extend to the setting of ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats, which in this paper have by definition a non-empty collection of flats and are thus non-hyperbolic.

Theorem 5.3

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and let $H \triangleleft G$ be an infinite hyperbolic normal subgroup. Then the Cannon–Thurston map does not exist for (H, G).

We prove an analogous theorem when the normal subgroup is also ${{\,\textrm{CAT}\,}}(0)$ with isolated flats.

Theorem 5.6

Let $H \triangleleft G$ be ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats and suppose that H is an infinite, infinite-index normal subgroup of G. Then the Cannon–Thurston map does not exist for (H, G).

We obtain a structure theorem for the normal subgroups that arise in the theorems above. If H is a torsion-free infinite-index hyperbolic normal subgroup of a hyperbolic group G, then combined work of Mosher [44], Paulin [49], Rips–Sela [50], and Bestvina–Feighn [3] proves that H is a free product of finitely many finitely generated free groups and surface groups. See [39] for a brief explanation. We prove a similar, but necessarily weaker (see Example 3.4), decomposition theorem in the setting of ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats. We state the result below in the simpler setting that the normal subgroup H is torsion-free; for the full statement, see Sect. 3.

Special Case of Theorem 3.3

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and let $H \triangleleft G$ be an infinite-index torsion-free normal subgroup that is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Then $H \cong F_r * H_1 \ldots * H_n$, where $r,n \ge 0$, $F_r$ denotes the free group of rank r, and $H_i$ is either a closed surface group, a free abelian group, or a 1-ended group that is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats and whose JSJ decomposition over elementary subgroups does not contain any rigid vertex groups.

Cannon–Thurston maps are known to exist for certain group pairs in the theorems above with respect to another well-studied boundary. Hruska–Kleiner [29] proved if G is a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats and ${\mathcal {P}}$ is the collection of maximal virtually abelian subgroups of G, then $(G, {\mathcal {P}})$ forms a relatively hyperbolic group pair. Bowditch [8] showed the pair $(G, {\mathcal {P}})$ has a well-defined boundary, now called the Bowditch boundary and denoted $\partial (G, {\mathcal {P}})$. The ${{\,\textrm{CAT}\,}}(0)$ visual boundary contains spheres which arise as the visual boundary of flats, while these spheres are collapsed to points in the Bowditch boundary; see work of Tran [57]. Pal [48, Theorem 3.11] proved the existence of the Cannon–Thurston map for $H \triangleleft G$ with respect to the Bowditch boundaries in the case that the group H is hyperbolic relative to a nontrivial subgroup $H_1$, the group G is hyperbolic relative to $N_G(H_1)$ and weakly hyperbolic relative to $H_1$, and G preserves cusps; see also [7, 42]. Under these assumptions, the quotient group is also known to be hyperbolic by work of Mj–Sardar [46]. We remark that the natural peripheral structure on a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats described above may contain more than one subgroup.

Two motivating questions regarding Cannon–Thurston maps are

• (1) For which groups $H \le G$ and for which boundaries does the Cannon–Thurston map exist?

• (2) If the Cannon–Thurston map exists, what is its structure? Can this structure be applied to better understand groups and their boundaries?

The focus of this paper is the first question above, though we were inspired by results regarding the second. Namely, a prototypical example of a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats is the fundamental group of a mapping torus of a pseudo-Anosov homeomorphism of a surface with negative Euler characteristic and one boundary component. These groups are examples of free-by-cyclic groups $F_n \rtimes \mathbb {Z}$ and act freely and cocompactly on truncated hyperbolic 3-space [47, 56]. For hyperbolic extensions of free groups, there is a powerful theory of Cannon–Thurston maps that continues to be developed and applied [1, 15, 34, 39, 40]. Thus, we aimed to understand whether these results generalize to the ${{\,\textrm{CAT}\,}}(0)$ setting. Our main theorems suggest that generalizations must be studied with respect to the Bowditch boundary.

Background on Cannon–Thurston maps is given in the survey of Mj [41]. The first example of a hyperbolic group pair for which the Cannon–Thurston map does not exist was given by Baker–Riley [9]; see also [43, 45].

Remark 1.1

Every finitely presented group has a Morse boundary that is well-defined up to homeomorphism, as shown by Cordes [11], who generalized the contracting boundary construction of Charney–Sultan [13]. The Morse boundary captures hyperbolic-like behavior of a group and coincides with the visual boundary if the group is hyperbolic and the contracting boundary if the group is ${{\,\textrm{CAT}\,}}(0)$. For background, see [12]. Suppose $H \triangleleft G$, where H is an infinite hyperbolic group and G is a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats. We prove that the Cannon–Thurston map does not exist for the pair (H, G) with respect to their Morse boundaries; see Proposition 5.5.

1.1 Method of proof

If $H \triangleleft G$ is an infinite hyperbolic normal subgroup of a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, we find a dynamical obstruction to the existence of the Cannon–Thurston map. To illustrate our methods, we begin by presenting a special case. Let $G = \left\langle a,b \right\rangle \rtimes _{\phi } \left\langle t \right\rangle$, where $\phi$ is an automorphism of the rank-two free group $\left\langle a,b \right\rangle$ given by $\phi (a) = aba$ and $\phi (b) = ba$. Then $G = \left\langle a,b,t \, | \, t^{-1}at = aba, t^{-1}bt = ba \right\rangle$ is the fundamental group of a mapping torus of a pseudo-Anosov homeomorphism of a surface of genus one with one boundary component. The group G is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats and $H = \left\langle a,b \right\rangle$ is a hyperbolic normal subgroup of G. The commutator element $[a,b] \le H$ commutes with the element $t \in G$. By the Flat Torus Theorem [5, Theorem II.7.1], if G acts properly and cocompactly by isometries (i.e., geometrically) on a ${{\,\textrm{CAT}\,}}(0)$ space X, then the element [a, b] stabilizes a flat $F \subset X$ on which it acts by translation. Hence, the element [a, b] acts trivially on its boundary $\partial F \subset \partial X$. Since $[a,b] \in H$ has infinite order, the element acts by North-South dynamics on $\partial H$ (see Definition 2.2). This difference in dynamics proves a (continuous H-equivariant) Cannon–Thurston map cannot exist.

More generally, we prove in Proposition 5.2 that if $H \triangleleft G$ is an infinite hyperbolic normal subgroup of a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, then there exists an infinite-order element of H which acts by translation on a flat in any ${{\,\textrm{CAT}\,}}(0)$ space on which the group G acts geometrically. To prove Proposition 5.2, we analyze the outer automorphism group of the normal hyperbolic subgroup and apply the following theorem.

Theorem 4.5

Let H be a hyperbolic group. Then there does not exist a purely atoroidal subgroup of ${{\,\textrm{Out}\,}}(H)$ isomorphic to $\mathbb {Z}^2$.

The proof of Theorem 4.5 relies on two graph of groups decompositions associated to a hyperbolic group G, a Stallings–Dunwoody decomposition of G as a finite graph of groups with finite edge groups and vertex groups that have at most one end and the JSJ decomposition of the non-Fuchsian one-ended factors in the Stallings–Dunwoody decomposition. As these graph of groups decompositions have aspects invariant under outer automorphisms, the proof reduces to the case that the hyperbolic group is virtually a closed surface group or virtually a free group. The surface group case follows from work of McCarthy [38]. The main tool we use in the free group case is the work of Feighn–Handel [19].

If $H \triangleleft G$ are both ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats, and H is an infinite-index subgroup, then it is possible that an element of H acts by North-South dynamics on $\partial H$, and acts by translation on a flat in a ${{\,\textrm{CAT}\,}}(0)$ model space for G. In this case, our previous dynamical arguments (see Lemma 5.1) prove the Cannon–Thurston map does not exist. However, there are examples in which this is not the case; see Example 3.4 and Fig. 1. In these situations, we employ a different strategy of proof: we show there are sequences of elements in the subgroup H so that the corresponding orbit points converge to the same point in $\partial H$, but converge to different points in the boundary of a flat in $\partial G$. For example, with $H \triangleleft G$ as in the beginning of this subsection, the sequences $[a,b]^n$ and $[a,b]^n\phi ^n(a) = [a,b]^nt^nat^{-n}$ converge to the same point in $\partial H$. However, these sequences converge to different points in $\partial G = \partial X$ as the sequence $[a,b]^nt^nat^{-n}$ approximates the diagonal in the flat in X stabilized by [a, b] and t. The theory of closest-point projections for relatively hyperbolic group pairs of Druţu–Sapir [16] and Sisto [53] constitutes an important tool in our analysis.

2 Preliminaries

2.1 Visual boundary

Definition 2.1

Let X be a proper geodesic metric space which is hyperbolic or ${{\,\textrm{CAT}\,}}(0)$. The visual boundary of X, denoted $\partial X$, is the set of equivalence classes of geodesic rays in X, where two rays $c_1,c_2:[0,\infty ) \rightarrow X$ are equivalent if there exists a constant D so that $d(c_1(t),c_2(t)) \le D$ for all $t \in [0,\infty )$.

There is a natural topology on $X \cup \partial X$ called the cone topology. With respect to this topology, both $\partial X$ and $X \cup \partial X$ are compact Hausdorff spaces whenever X is proper. An isometry of X induces a homeomorphism of $\partial X$. See [5, 33] for details. For the remainder of the paper, we assume that the hyperbolic and ${{\,\textrm{CAT}\,}}(0)$ spaces we consider are proper geodesic metric spaces (thus locally compact and complete).

Definition 2.2

(North-South dynamics) If Z is a topological space, then $g \in {{\,\textrm{Homeo}\,}}(Z)$ acts with North-South dynamics if g fixes two distinct points $z_-, z_+ \in Z$ and for any open sets $U,V \subset Z$ with $z_- \in U$ and $z_+ \in V$ there exists an integer N so that $g^n(Z - U) \subset V$ and $g^{-n}(Z-V) \subset U$ for all $n \ge N$.

Some authors refer to this as uniform North-South dynamics as opposed to pointwise North-South dynamics (see for instance [37]). We adopt this definition as it corresponds to the sources for Theorems 2.4 and 2.6 , however let us record for the sake of completeness that the notions coincide for the spaces of interest to us:

Proposition 2.3

Let Z be a compact Hausdorff space and let $g \in {{\,\textrm{Homeo}\,}}(Z)$ have distinct fixpoints $z_-$ and $z_+$. The following are equivalent

• (1) For all $z \in Z$, if $z \ne z_-$ then $\lim _{n \rightarrow \infty } g^n z = z_+$ and if $z \ne z_+$ then $\lim _{n \rightarrow \infty } g^{-n} z = z_-$.

• (2) For all open sets $U \ni z_-$ and $V \ni z_+$ there exists an integer n such that $g^n(Z - U) \subset V$ and $g^{-n}(Z-V) \subset U$.

• (3) g acts with North-South dynamics.

If Z is moreover assumed metrizable, then (1) $\implies$ (3) can also be deduced from [28, Theorem 1].

Proof

The implication (3) $\implies$ (2) is immediate and formal; we see that (3) $\implies$ (1) by unpacking the definition and using the Hausdorff property to select an appropriate neighborhood. We deduce (3) from the following common weakening of (1) and (2): suppose that for all $z \ne z_-$ and open $V \ni z_+$ there exists $n \ge 0$ such that $g^n z \in V$, and similarly for all $z \ne z_+$ and open $U \ni z_-$ there exists $m \ge 0$ such that $g^{-m} z \in U$.

Let $U \ni z_-$ and $V \ni z_+$ be open. We will show there exists $N = N_+$ such that $g^n (Z - U) \subset V$ for all $n \ge N_+$; we similarly get such an $N_-$ in the other direction, thus satisfying the definition of North-South dynamics by taking $\max \{ N_+, N_- \}$. Assume without loss of generality that $U \cap V = \emptyset$ (as taking smaller U and V only makes satisfying the definition harder and the two fixpoints have disjoint neighborhoods since Z is Hausdorff); this implies that $gU \cap gV = \emptyset$ so we can go one step further and use $U \cap gU$ in place of U to assume that U is disjoint from $V \cup gV$. We first consider pushing ‘south’: our assumption tells us precisely that $Z - \{z_+\} = \cup _{m = 0}^\infty g^m U$. Since Z is compact and $V \ni z_+$ is open, we conclude that $Z - V$ is compact and thus has a finite subcover of the form $\cup _{m = 0}^M g^m U$.

We set $V_0 = V \cap g V \cap \dots \cap g^{M-1} V$ and claim that $g V_0 \subset V_0$. Indeed, if this were not the case there would be some $z \in g V \cap g^2 V \cap \dots \cap g^M V$ with $z \not \in V_0$, which would force $z \not \in V$, or in other words $z \in Z - V \subset \cup _{m=0}^M g^m U$. This now gives a contradiction, as either $z \in U$ so that $z \notin gV$ or $z \in g^m U$ for some $1 \le m \le M$ and thus $z \not \in g^m V$.

Since $V_0 \ni z_+$ is open our original assumption (now pushing ‘north’) tells us that $Z - \{ z_- \} = \cup _{n=0}^\infty g^{-n} V_0$. Again we appeal to compactness, this time of $Z - U$, to see that $Z - U \subset V_0 \cup g^{-1} V_0 \cup \dots \cup g^{-N} V_0$ for some N. As $g V_0 \subset V_0$ we have $V_0 \subset g^{-1} V_0$ and so on by induction so that in fact $Z - U \subset g^{-N} V_0$, that is, $g^N (Z-U) \subset V_0$. Thus for any $n \ge N$ we have $g^n (Z-U) = g^{n-N} g^N (Z-U) \subset g^{n-N} V_0 \subset V_0 \subset V$ as required. $\square$

Theorem 2.4

[21, Théorème 8.16] [25, 8.1.G] If H is a hyperbolic group and $a \in H$ is an element of infinite order, then a acts by North-South dynamics on $\partial H$.

Definition 2.5

Let X be a ${{\,\textrm{CAT}\,}}(0)$ space, and let $h \in {{\,\textrm{Isom}\,}}(X)$ be a loxodromic element. The element h is called a rank-one isometry of X if there exists an axis for h which does not bound an isometrically embedded copy of a Euclidean half-plane.

Theorem 2.6

[2, Lemma III.3.3] Let X be a proper ${{\,\textrm{CAT}\,}}(0)$ space and let g be an isometry of X. If g has rank one, then g acts on $\partial X$ with North-South dynamics.

2.2 ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats

Definition 2.7

Let X be a ${{\,\textrm{CAT}\,}}(0)$ space. For $k \ge 2$, a k-flat in X is an isometrically embedded copy of Euclidean space $\mathbb {E}^k$.

Definition 2.8

Let X be a ${{\,\textrm{CAT}\,}}(0)$ space, and suppose a group G acts geometrically on X. The space X has the isolated flats property if X is not quasi-isometric to $\mathbb {E}^n$ and there is a non-empty G-invariant collection of flats ${\mathcal {F}}$, of dimension at least two, such that the following conditions hold:

• (1) There exists a constant $D < \infty$ such that each flat in X lies in the D-tubular neighborhood of some $F \in {\mathcal {F}}$.

• (2) For every $\rho < \infty$ there exists $\kappa (\rho )<\infty$ such that for any two distinct flats $F,F' \in {\mathcal {F}}$, ${{\,\textrm{diam}\,}}(N_\rho (F) \cap N_\rho (F')) <\kappa (\rho )$.

If a group G is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats if G acts geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space with the isolated flats property.

Remark 2.9

By definition, a ${{\,\textrm{CAT}\,}}(0)$ space with isolated flats contains a non-trivial flat of dimension at least two. By [29, Lemma 3.1.2], a ${{\,\textrm{CAT}\,}}(0)$ group G with isolated flats has a non-trivial free abelian subgroup of rank at least two. Thus, if $H \le G$ is hyperbolic, then H has infinite-index in G.

The following theorem collects the results of work of Hruska–Kleiner [29] relevant to this paper. We refer the reader to [29] for additional background.

Theorem 2.10

[29, Theorems 1.2.1, 1.2.2] Let X be a ${{\,\textrm{CAT}\,}}(0)$ space, and let G be a group acting geometrically on X.

• (1) The following are equivalent.

  • (a) The space X has the isolated flats property.

  • (b) The space X is relatively hyperbolic with respect to a family of flats ${\mathcal {F}}$.

  • (c) The group G is a relatively hyperbolic group with respect to a collection of virtually abelian subgroups of rank at least two.

• (2) If the space X has the isolated flats property, then the visual boundary $\partial X$ is a group invariant of G.

Lemma 2.11

Let G act geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X with isolated flats. If $g \in G$ has infinite order, then either g acts by translation on a flat in X or g has rank-one.

Proof

Suppose the element g does not have rank one. Then an axis for g bounds a half-flat $F_0$ in X. By Theorem 2.10, the space X is hyperbolic relative to a family of flats, so this half-flat $F_0$ must be contained in a bounded neighborhood of a flat F in X. Let $\ell$ be an axis for g. The endpoints $\alpha ^+, \alpha ^-$ of the line $\ell$ lie in the boundary of the half-flat $F_0$ in $\partial X$, and hence lie in the boundary of the flat F in $\partial X$. By work of Tran [57, Main Theorem], there is a G-equivariant continuous map $\pi : \partial X\rightarrow \partial (G, {\mathcal {P}})$, where $\partial (G, {\mathcal {P}})$ denotes the Bowditch boundary for G defined with respect to the peripheral structure given by Hruska–Kleiner in Theorem 2.10. Moreover, there exists a parabolic fixed point $z \in \partial (G,{\mathcal {P}})$ so that $\pi (\partial F) = z$. Since g fixes $\alpha ^+$ and $\alpha ^-$, the element g fixes $\pi (\alpha ^{\pm }) = z \in \partial (G, {\mathcal {P}})$. Thus, by work of Bowditch [8] (see also [32, Section 3]), the element g is contained in a conjugate of a peripheral subgroup of G. Thus, g is contained in a virtually abelian subgroup of G of rank at least two; hence, g acts by translation on a flat in X by the Flat Torus Theorem [5, Corollary II.7]. $\square$

Lemma 2.12

Let G be ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. If $A \times B \le G$ and A and B are infinite, then A and B are virtually abelian.

Proof

By the Flat Torus Theorem [5, Theorem II.7.1], every infinite-order element of A has an axis that spans a flat with an axis of every infinite-order element of the subgroup B. Thus if $a,a' \in A$ and $b \in B$ are infinite, then an axis for b is contained in a flat F stabilized by $\left\langle a,b \right\rangle$ and an axis for b is contained in a flat $F'$ stabilized by $\left\langle a',b \right\rangle$. As in the proof of Lemma 2.11, there is a continuous G-equivariant map $\pi : \partial X \rightarrow \partial (G, {\mathcal {P}})$. Since an axis for b is contained in the flats F and $F'$, there exists a parabolic point $z \in \partial (G, {\mathcal {P}})$ so that $\pi (F) = \pi (F') = z$ and the elements a, $a'$, and b stabilize z by [57, Main Theorem]. Thus, by work of Bowditch [8], the elements a and $a'$ belong to the same conjugate of a peripheral subgroup of G. Thus, A is virtually abelian. Similarly, B is virtually abelian. $\square$

2.3 Stallings–Dunwoody and JSJ decompositions

To describe the structure of normal subgroups, we apply the Stallings–Dunwoody and JSJ decomposition theories. We recall the relevant statements below. For background on graphs of groups, see [52, 55]. The graph of groups decomposition given in the next theorem is called a Stallings–Dunwoody decomposition of G.

Theorem 2.13

[17, 54] If G is a finitely presented group, then G splits as a finite graph of groups with finite edge groups and vertex groups that have at most one end.

Remark 2.14

If the group G has one end, then the graph of groups decomposition given by the above theorem is trivial. This is the case in particular when G has a finitely generated, infinite, infinite-index normal subgroup (as is the set up of Theorems 5.3 and 5.6), since an infinite-ended group cannot have such a subgroup. This was proved by Karrass–Solitar; it is a special case of [35, Theorem 10] when G is an amalgam and of [36, Theorem 9] when G is an HNN extension. (Alternatively, appealing to more modern technology, infinite-ended groups have positive first $L^2$-Betti number, which is an obstruction to having such a subgroup).

Lemma 2.15

Let $H_v$ be a one-ended vertex group in a Stallings–Dunwoody decomposition of a finitely presented group H, and let $\phi \in {{\,\textrm{Out}\,}}(H)$. Then there exists $m \ge 1$ so that $\phi ^m([H_v]) = [H_v]$.

Proof

Let T and $T'$ be the Bass–Serre trees of two Stallings–Dunwoody decompositions of H. We claim that T and $T'$ have the same one-ended vertex stabilizers up to conjugation.

To prove the claim, let $H_1, \ldots , H_n \le H$ and $H_1', \ldots H_m' \le H$ be representatives of one-ended vertex stabilizers of T/H and $T'/H$, respectively. Since $H_i$ is one-ended, the subgroup $H_i$ fixes a unique vertex of the tree $T'$. Thus $H_i \le gH_j'g^{-1}$ for some $g \in H$ and $1 \le j \le m$. Similarly, the group $gH_j'g^{-1}$ is one-ended, so $gH_j'g^{-1} \le h H_k h^{-1}$ for some $h \in H$ and $1 \le k \le n$. Thus, $H_i \le gH_jg^{-1} \le hH_kh^{-1}$. The subgroups $H_i$ and $hH_kh^{-1}$ fix unique vertices in the tree T, so $H_i=H_k$. Therefore, for every $1\le i \le n$, there exists $j \in \{1, \ldots , m\}$ such that $[H_i] = [H_j']$ and vice versa, concluding the proof of the claim.

Let $H_v$ be a one-ended vertex stabilizer of the tree T and let $T' = T\cdot \phi$. Since T and $T'$ have the same one-ended vertex stabilizers, there exists an $m \ge 1$ such that $\phi ^m([H_v]) = [H_v]$. $\square$

Remark 2.16

Lemma 2.15 is a specific instance of a general fact mentioned by Guirardel–Levitt [24, Introduction]: Two G-trees belonging to the same deformation space over a class of subgroups ${\mathcal {A}}$ have the same vertex stabilizers, provided one restricts to the vertex groups not in ${\mathcal {A}}$.

The graph of groups decomposition for a hyperbolic group or a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats provided by the next two theorems is called the JSJ decomposition of G over two-ended or elementary subgroups, respectively. For 1-ended hyperbolic groups that are not Fuchsian, we use the language due to Bowditch [6]; see [24] for background on JSJ decompositions. We note that there are various uses of the term “elementary” in the literature. To avoid confusion, we reserve the term in this paper for the JSJ theory (see Definition 2.21), and write the assumptions explicitly in other cases.

Definition 2.17

A Fuchsian group is a finitely generated group that is not finite or two-ended and acts properly discontinuously on the hyperbolic plane. A cocompact Fuchsian group is a Fuchsian group that acts cocompactly on the hyperbolic plane. In particular, a cocompact Fuchsian group is virtually a closed surface group, the fundamental group of a closed surface.

Definition 2.18

[6] A bounded Fuchsian group is a Fuchsian group that is convex cocompact (i.e., it acts cocompactly on the convex hull of its limit set in $\mathbb {H}^2$) but is not virtually a closed surface group. The convex core of the quotient is a compact orbifold with non-empty boundary consisting of a disjoint union of compact 1-orbifolds. The peripheral subgroups are the maximal two-ended subgroups which project to the fundamental groups of the boundary 1-orbifolds. A hanging Fuchsian subgroup H of a group is a virtually-free quasi-convex subgroup together with a collection of peripheral two-ended subgroups, which arise from an isomorphism of H with a bounded Fuchsian group. A full quasi-convex subgroup of a group G is a quasi-convex subgroup that is not a finite-index subgroup of any strictly larger subgroup of G.

Theorem 2.19

[6, Thm 0.1] Let G be a one-ended hyperbolic group that is not Fuchsian. There is a canonical JSJ decomposition of G as the fundamental group of a graph of groups such that each edge group is 2-ended and each vertex group is either (1) 2-ended; (2) maximal hanging Fuchsian; or, (3) a maximal quasi-convex subgroup not of type (2). These types are mutually exclusive, and no two vertices of the same type are adjacent. Every vertex group is a full quasi-convex subgroup. Moreover, the edge groups that connect to any given vertex group of type (2) are precisely the peripheral subgroups of that group.

Remark 2.20

The JSJ decomposition due to Bowditch is constructed via the topology of the visual boundary of the hyperbolic group G. It follows from construction that any automorphism of G induces an isomorphism of the Bass–Serre tree of the JSJ decomposition.

For many relatively hyperbolic groups $(G, {\mathcal {P}})$, there is also a canonical JSJ decomposition due to Guirardel–Levitt [22] which is invariant under the subgroup of ${{\,\textrm{Out}\,}}(G)$ that preserves the set of conjugacy classes of the peripheral subgroups of G. Denote this subgroup by ${{\,\textrm{Out}\,}}(G, {\mathcal {P}})$. We state their results in the special case of a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats. In this special case, ${{\,\textrm{Out}\,}}(G, {\mathcal {P}}) = {{\,\textrm{Out}\,}}(G)$ because the set of peripheral subgroups is the set of maximal abelian subgroups of G which is preserved by every automorphism.

Definition 2.21

Let G be hyperbolic relative to a finite collection ${\mathcal {P}}= \{P_1, \ldots , P_k\}$. A subgroup of G is elementary if it is either contained in a conjugate of some $P_i \in {\mathcal {P}}$ or if it is infinite, virtually cyclic, and not contained in any $P_i \in {\mathcal {P}}$.

Theorem 2.22

[22, Theorem 4][23, Section 3] Let G be hyperbolic relative to ${\mathcal {P}}$, a collection of maximal virtually abelian subgroups of rank at least two. Also suppose G is one-ended. Then there is an elementary JSJ tree for G relative to ${\mathcal {P}}$ which is invariant under ${{\,\textrm{Out}\,}}(G)$. The vertex groups in the JSJ decomposition have one of four types: (0.a) rigid; (0.b) maximal hanging Fuchsian; (1.a) maximal parabolic: conjugate to a $P_i \in {\mathcal {P}}$; and (1.b) maximal loxodromic: maximal virtually cyclic subgroup of G and not contained in a $P_i \in {\mathcal {P}}$. Vertex groups of type (0.*) are only adjacent to vertex groups of type (1.*).

Notation 2.23

Let G be a one-ended group that is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, and let T be the JSJ tree for G given by either Theorem 2.19 or Theorem 2.22, respectively. Let ${{\,\textrm{Out}\,}}^0(G) \le {{\,\textrm{Out}\,}}(G)$ denote the outer automorphisms of G that act trivially on the graph T/G. The subgroup ${{\,\textrm{Out}\,}}^0(G)$ has finite index in the group ${{\,\textrm{Out}\,}}(G)$.

A key feature of the JSJ decompositions considered in this paper is that outer automorphisms in ${{\,\textrm{Out}\,}}^0(G)$ “restricted to” rigid vertex groups have finite-order. This fact is made more precise as follows.

Remark 2.24

[23, Section 2.6] Let G be a one-ended group that is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, and let T be the JSJ tree for G. For a vertex v of T/G, there is a map $\rho _v :{{\,\textrm{Out}\,}}^0(G) \rightarrow {{\,\textrm{Out}\,}}(G_v)$ given as follows: choose a representative ${\tilde{v}}$ of v in T that is stabilized by $G_v$. For $\phi \in {{\,\textrm{Out}\,}}^0(G)$, choose a representative $\Phi$ of $\phi$ such that the induced map on T fixes ${\tilde{v}}$. Then $\rho _v(\phi )$ is represented by the restriction of $\Phi$ to $G_v$. We say $\rho _v(\phi )$ is the restriction of $\phi$ to $G_v$.

Theorem 2.25

[3, 49] Let G be hyperbolic, and let $G_v \le G$ be a vertex group of type (3) in Theorem 2.19. Suppose $\phi \in {{\,\textrm{Out}\,}}^0(G)$, and let $\phi '$ be the restriction of $\phi$ to $G_v$. Then $\phi '$ has finite order.

Theorem 2.26

[23, Proposition 4.1] Let G be ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, and let $G_v \le G$ be a vertex group of type (0.a) in Theorem 2.22. Suppose $\phi \in {{\,\textrm{Out}\,}}^0(G)$, and let $\phi '$ be the restriction of $\phi$ to $G_v$. Then $\phi '$ has finite order.

2.4 Limit set

Definition 2.27

Let a group G act by isometries on a hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ space X, and let $x \in X$. The limit set of G defined at x, denoted $\Lambda _x G$, is the set of accumulation points in $\partial X$ of the G-orbit of x in the space X.

In many natural situations the limit set does not depend on the choice of basepoint:

Lemma 2.28

If G acts properly discontinuously and cocompactly by isometries on a proper hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ space X, and $x,y \in X$, then $\Lambda _xG = \Lambda _yG$.$\square$

Lemma 2.29

[26, Proof of Lemma 5.2] Let X be a proper ${{\,\textrm{CAT}\,}}(0)$ space, and let $G \le {{\,\textrm{Isom}\,}}(X)$ be a subgroup so that G does not fix a point on $\partial X$. Then for every $x \in X$, $\Lambda _xG$ is the unique minimal closed nonempty G-invariant subset of $\partial X$.$\square$

Lemma 2.30

Let G act geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X with isolated flats. If $H \triangleleft G$ is infinite, then $H \le {{\,\textrm{Isom}\,}}(X)$ contains a rank-one isometry of X.

Proof

The subgroup H contains an infinite-order element h. Indeed, the group G satisfies the Strong Tits Alternative: every subgroup of G is either finitely generated virtually abelian or contains a free subgroup of rank two [29, Theorem 1.2.2]. By Theorem 2.10, the group $(G, {\mathcal {P}})$ forms a relatively hyperbolic group pair, where ${\mathcal {P}}$ is a collection of virtually abelian subgroups of G of rank at least two. The peripheral subgroups of G are almost malnormal [18, Section 3.3], so $H \not \subset P_i$ for any $P_i \in {\mathcal {P}}$. Thus, either H is two-ended or contains a free subgroup of rank two. So, H contains an infinite-order element h.

By Lemma 2.11, we may assume the element h acts by translation on a flat in X. So, $h \in P_i^{g_0}$, a conjugate of a peripheral subgroup $P_i$ of G. Consider $g \in G \backslash P_i^{g_0}$. Then $ghg^{-1} \in P_i^{gg_0}$, a different conjugate of a peripheral subgroup of G. Since $H \triangleleft G$, the element $ghg^{-1} = h' \in H$. We can ensure that the product $hh'$ does not stabilize a flat in X. Indeed, the elements h and $h'$ act elliptically on the JSJ tree for G given by Theorem 2.22 (since G is one-ended, see Remark 2.14), and we can choose the conjugating element g to translate the fixed points of h far enough that h and $h'$ fix disjoint sets of vertices. So, their product acts as a loxodromic on the tree, and is thus not contained in a peripheral subgroup. By Lemma 2.11, the element $hh'$ has rank one. $\square$

Lemma 2.31

Let G act geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X with isolated flats. If $H \triangleleft G$ is a normal subgroup, then $\Lambda _xH = \Lambda _xG$ for all $x \in X$.

Proof

Suppose a group G acts geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X with isolated flats, and let $x \in X$. Let $H \triangleleft G$ be a normal subgroup. Since ${{\,\textrm{Stab}\,}}(g\cdot \Lambda _xH) = g {{\,\textrm{Stab}\,}}(\Lambda _xH) g^{-1} \supset gHg^{-1} = H$ for all $g \in G$, the set $g \cdot \Lambda _xH$ is H-invariant for all $g \in G$.

We first show that $g \cdot \Lambda _xH = \Lambda _x H$ for all $g \in G$. The subgroup H contains a rank-one isometry $h \in H$ by Lemma 2.30. Let $h^{\infty } = \lim _{n \rightarrow \infty } h^n\cdot x \in \Lambda _xH$. Then the sequence $\{h^n \cdot gh^{\infty }\}_{n \in \mathbb {N}}$ converges to $h^{\infty }$ by North-South dynamics, unless $g \cdot h^\infty = h^{-\infty }$. In the general case since $g \cdot \Lambda _xH$ is closed and H-invariant we have the limit $h^\infty \in g \cdot \Lambda _xH$, so in either case $g \cdot \Lambda _xH \cap \Lambda _x H \ne \emptyset$. By Lemma 2.29, the set $\Lambda _xH$ is the smallest closed H-invariant set in $\partial X$. Since $g \cdot \Lambda _xH \cap \Lambda _x H \ne \emptyset$ and $g \cdot \Lambda _xH$ is closed and H-invariant, $g \cdot \Lambda _xH = \Lambda _xH$. Therefore, the set $\Lambda _xH \subset \Lambda _xG$ is closed and G-invariant. Thus, Lemma 2.29 implies $\Lambda _xH = \Lambda _xG$. $\square$

2.5 Cannon–Thurston map

Morally, the Cannon–Thurston map for $H \hookrightarrow G$ should be an extension of the subgroup inclusion to the boundary, as it is in the hyperbolic case. To define the boundary of a ${{\,\textrm{CAT}\,}}(0)$ group G we however need a ${{\,\textrm{CAT}\,}}(0)$ model space X on which it acts. Rather than develop a theory of the compactification $G \cup \partial X$, which would enable a definition of Cannon–Thurston maps simply ‘extending the group inclusion to the boundary’, we exploit the convenience afforded by the identification of the limit set $\Lambda _x G$ with the boundary $\partial X$ and make the following definition.

Definition 2.32

(Cannon–Thurston map) Let $H \le G$ such that H acts geometrically on Y and G acts geometrically on X, where X and Y are hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ spaces. Let $x \in X$ and $y \in Y$. A Cannon–Thurston map for the pair $(H \curvearrowright Y, G \curvearrowright X)$ is the map $f :\partial Y \rightarrow \partial X$ defined by

$$\begin{aligned} f\left( \lim _{i \rightarrow \infty } h_i \cdot y\right) =\lim _{i \rightarrow \infty } h_i \cdot x, \end{aligned}$$

provided f is well-defined and continuous. Being well-defined means that $f(\xi )$ does not depend on the choice of the sequence of group elements $h_i \in H$ such that $\underset{i \rightarrow \infty }{\lim } h_i \cdot y = \xi$.

Remark 2.33

If $H \le G$ are hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, then the choice of model spaces X and Y does not affect the existence of the Cannon–Thurston map for the pair $H \le G$. This follows from the fact that the visual boundary is a quasi-isometry invariant for hyperbolic groups [25] and a group invariant for the ${{\,\textrm{CAT}\,}}(0)$ with isolated flats case [29, Corollary 4.1.9]. Thus, we may define a Cannon–Thurston map for the pair (H, G). Note that the example of Croke–Kleiner [10] shows that without the isolated flats assumption, ${{\,\textrm{CAT}\,}}(0)$ groups do not in general have a well-defined boundary. This is critical, since for such an example, with G acting on X and Y with $\partial X \not \cong \partial Y$, there cannot exist Cannon–Thurston maps for both of the pairs $(G \curvearrowright X, G \curvearrowright Y)$ and $(G \curvearrowright Y, G \curvearrowright X)$ because the compositions would have to be the identity maps on $\partial X$ and $\partial Y$ implying $\partial X \cong \partial Y$.

Remark 2.34

By definition, the Cannon–Thurston map is H-equivariant.

If H and G are hyperbolic groups and H is a quasi-convex subgroup of G, then the Cannon–Thurston map exists for the pair (H, G) by [21]. Hruska–Kleiner prove an analogous statement in the setting of ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats [29, Theorem 4.1.8].

3 The structure of normal subgroups

Notation 3.1

Let $1 \rightarrow H \rightarrow G \xrightarrow {p} Q \rightarrow 1$ be a short exact sequence of groups. This sequence induces a homomorphism $\phi : Q \rightarrow {{\,\textrm{Out}\,}}(H)$. If $q \in Q$, let $\phi _q = \phi (q)$. If $A \le G$ is a subgroup, let [A] denote the conjugacy class of A in G.

Lemma 3.2

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and suppose $H \triangleleft G$ is a normal subgroup of infinite-index such that H is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Then the following hold.

• (1) Let $q \in Q$ be an infinite order element and $H' \le H$. If $\phi _q \in {{\,\textrm{Out}\,}}(H)$ restricts to an outer automorphism $\phi _q' \in {{\,\textrm{Out}\,}}(H')$, then the group G contains a subgroup isomorphic to the semi-direct product $H' \rtimes _{\phi _q'} \mathbb {Z}$.

• (2) The group $Q = G/H$ contains an element of infinite-order.

• (3) If $q \in Q$ has infinite order, then the element $\phi _q \in {{\,\textrm{Out}\,}}(H)$ has infinite order.

Proof

We first prove (1). By assumption there exists $g \in G$ with $p(g) = q$ such that $H'^g = H'$ inducing $\phi _q' \in {{\,\textrm{Out}\,}}(H')$. An elementary argument proves the subgroup $\left\langle H', g \right\rangle \le G$ is isomorphic to the group $H' \rtimes _{\phi _q'} \mathbb {Z}$.

To prove (2), suppose first that H is hyperbolic. By [29, Lemma 3.1.2], for every flat $F \subset X$, there exist elements $a,b \in {{\,\textrm{Stab}\,}}_G(F)$ with $\left\langle a,b \right\rangle \cong \mathbb {Z}^2$. Since H is hyperbolic, the images p(a) and p(b) in the quotient $p:G \rightarrow Q$ cannot both be finite; otherwise, H would contain an abelian subgroup of rank two.

Suppose now that H is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Let $G' \le G$ be a maximal-rank free abelian subgroup of G; the rank n of $G'$ is at least two. Suppose G acts geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X. The quotient space X/G contains an n-torus T with fundamental group $G'$. The infinite-index subgroup $H \le G$ yields an infinite cover X/H of X/G. Consider the full pre-image of T in X/H. This pre-image need not be connected and will not be compact. The pre-image of the torus could fail to be compact if either the pre-image has infinitely many compact components, or if the pre-image contains a component that is not compact. However, the pre-image cannot contain infinitely many compact n-torus components since H has finitely many conjugacy classes of rank-n free abelian subgroups by [29, Lemma 3.1.2].

To prove (3), suppose $q \in Q$ is an element of infinite order. There exists $g \in G$ with $p(g) = q$. The subgroup $\left\langle H, g \right\rangle \le G$ is isomorphic to the group $H \rtimes _{\phi _q} \mathbb {Z}$ by (1). If $\phi _q$ has finite order, then this semi-direct product is virtually a product $H \times \mathbb {Z}$. Since G is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, Lemma 2.12 forces H to be virtually abelian, and since H is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, it must then in fact be virtually cyclic. However, by Lemma 2.31, the group H is not two ended. Thus, the element $\phi _q$ has infinite order. $\square$

The next theorem characterizes the isomorphism types of normal subgroups that are either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats in a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats.

Theorem 3.3

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and let $H \triangleleft G$ be an infinite-index normal subgroup that is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Let ${\mathcal {H}}$ be a Stallings–Dunwoody decomposition of H. If $H_v \le H$ is a one-ended vertex group of ${\mathcal {H}}$, then $H_v$ is either

• (1) virtually a closed surface group, or

• (2) virtually abelian, or

• (3) hyperbolic and the JSJ decomposition of $H_v$ over 2-ended subgroups given by Theorem 2.19 does not contain vertex groups of type (3), or

• (4) a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats whose JSJ decomposition over elementary subgroups given by Theorem 2.22 does not contain any vertex groups of type (0.a).

Proof

Suppose $H_v$ is neither virtually a closed surface group, nor virtually abelian. We first show that $H_v$ is either hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Since $H_v$ is a vertex group of a splitting of H over finite groups, a Cayley graph of $H_v$ quasi-isometrically embeds in a Cayley graph of H. Therefore, if H is hyperbolic, then $H_v$ is also hyperbolic. Suppose now that H is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. By [30, Theorem 1.3], the subgroup $H_v$ is a ${{\,\textrm{CAT}\,}}(0)$ group. By Theorem 2.10, the group H is hyperbolic relative to the collection of its maximal virtually abelian subgroups. Thus, the coned-off Cayley graph of H with respect to these subgroups is hyperbolic [18]. By [16, Theorem 8.29], $H_v$ is hyperbolic relative to subgroups of the form $H_v \cap gP_ig^{-1}$, where $g \in G$ and $P_i$ is a peripheral subgroup of H. If $H_v$ does not contain a $\mathbb {Z}^2$ subgroup, then we claim that $H_v$ is hyperbolic. Indeed, the subgroup $H_v$ does not intersect any $\mathbb {Z}^2$ subgroup non-trivially. Thus, no vertex of the quasi-isometrically embedded Cayley graph of $H_v$ gets coned-off. Hence, the subgroup $H_v$ is hyperbolic. Otherwise, $H_v$ is hyperbolic relative to virtually abelian subgroups, and hence by Theorem 2.10, the subgroup $H_v$ is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats.

By Lemma 3.2, there exists an element $q \in Q = G/H$ of infinite order which induces an infinite-order outer automorphism $\phi _q \in {{\,\textrm{Out}\,}}(H)$. Also, by Lemma 2.15, there exists an $m \ge 1$ such that $\phi _q^m([H_v]) = [H_v]$ for the one-ended vertex group $H_v$.

Suppose the subgroup $H_v$ is hyperbolic. By Theorem 2.19, there is a canonical JSJ decomposition for $H_v$. Suppose towards a contradiction that the JSJ decomposition for $H_v$ contains a vertex group $H_v^i$ of type (3). We prove there exists $n \ge 1$ such that $\phi _q^n$ restricts to an infinite-order element of ${{\,\textrm{Out}\,}}(H_v^i)$ to produce a contradiction to Theorem 2.25. As explained in Section 2.3, there exists $\ell \ge 1$ so that the restriction $\phi _q^{m\ell }|_{H_v} \in {{\,\textrm{Out}\,}}(H_v)$ preserves the vertex groups in the JSJ decomposition of $H_v$, yielding a further restriction to the rigid vertex group $H_v^i$ of $H_v$, an element $\psi = \phi _q^{m\ell }|_{H_v^i} \in {{\,\textrm{Out}\,}}(H_v^i)$. Thus $H_v^i \rtimes _{\psi } \mathbb {Z}$ is a subgroup of G. Since $H_v^i$ is not isomorphic to $\mathbb {Z}$, this outer automorphism is infinite by Lemma 3.2(1) and Lemma 2.12, contradicting Theorem 2.25.

If the subgroup $H_v$ is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, then analogous arguments, using Theorem 2.22 and Theorem 2.26, prove $H_v$ has no vertex groups of type (0.a). $\square$

Example 3.4

If $Y_f$ is the mapping torus of a homeomorphism $f: Y \rightarrow Y$ of a space Y, then $\pi _1(Y) \triangleleft \pi _1(Y_f)$ is an infinite-index normal subgroup. The following list provides examples of normal subgroups of various types as in Theorem 3.3.

• (a) Let $\Sigma$ be a connected surface with non-empty boundary and negative Euler characteristic. Let $\Psi :\Sigma \rightarrow \Sigma$ be a pseudo-Anosov homeomorphism of $\Sigma$ that fixes the boundary components of $\Sigma$ pointwise, and let $Y_{\Psi }$ denote the corresponding mapping torus. By work of Thurston [47, 56], $\pi _1(Y_{\Psi })$ acts by isometries on hyperbolic 3-space with quotient a finite-volume hyperbolic 3-manifold M with torus cusps. Let $M_\Psi$ denote the manifold M truncated at its cusps so $\pi _1(M_\Psi ) \cong \pi _1(Y_{\Psi })$. By [5, Theorem II.11.27] and [31, Proposition 9.1], the universal cover $\widetilde{M_\Psi }$ is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Ruane [51] proved the ${{\,\textrm{CAT}\,}}(0)$ boundary of $\widetilde{M_\Psi }$ is homeomorphic to the Sierpinski carpet.

• (b) Suppose $\Sigma _1, \ldots , \Sigma _k$ and $\Psi _1, \ldots , \Psi _k$ are surfaces and pseudo-Anosov maps as in (a) for $k \ge 2$. Let Y be the union of the surfaces $\Sigma _i$ glued along their boundary components by homeomorphisms in some configuration so that each boundary component is glued to at least one other, and let $\Psi :Y \rightarrow Y$ be a homeomorphism so that $\Psi |_{\Sigma _i} = \Psi _i$. Then the mapping torus $Y_{\Psi }$ is the union of truncated 3-manifolds $M_{\Psi _1}, \ldots , M_{\Psi _k}$ glued together along their boundary tori. As above, the universal cover of $Y_{\Psi }$ is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Depending on k and the gluing configuration, the space Y is either a closed surface of negative Euler characteristic or a one-ended hyperbolic group whose JSJ decomposition does not contain any rigid vertex groups.

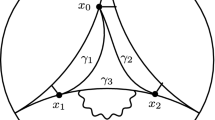
• (c) Let $\Sigma$ be a closed connected surface of negative Euler characteristic, and let $f_\Sigma :\Sigma \rightarrow \Sigma$ be a pseudo-Anosov homeomorphism that fixes a point $x \in \Sigma$. Let T denote the k-torus, and let $f_T:T \rightarrow T$ be the identity map. Let Y be the wedge of $\Sigma$ and T, where $x \in \Sigma$ is identified to a point on T, and let $f: Y \rightarrow Y$ be a homeomorphism so that $f|_{\Sigma } = f_{\Sigma }$ and $f|_T = f_T$. Then the universal cover of the mapping torus is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats, and $\pi _1(Y) = \pi _1(\Sigma ) * \mathbb {Z}^k$ is a normal ${{\,\textrm{CAT}\,}}(0)$ subgroup with isolated flats. See Figure 1.

Example 3.5

The following example does not arise from a mapping torus of a homeomorphism of a 2-complex. Let $H = {\mathcal {A}}* {\mathcal {B}}* \pi _1(\Sigma )$, where ${\mathcal {A}}\cong \mathbb {Z}^k$ and ${\mathcal {B}}\cong \mathbb {Z}^\ell$ with $k, \ell \ge 2$, and $\Sigma$ is a closed hyperbolic surface. The group H is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. Let $w \in \pi _1(\Sigma )$ be a non-trivial element and $\Phi$ an automorphism of $\pi _1(\Sigma )$ induced by a pseudo-Anosov homeomorphism of $\Sigma$. Let

$$\begin{aligned} G= \Biggl \langle \begin{array}{c|cc} &{} tat^{-1} = a &{} \forall a \in {\mathcal {A}}\\ {\mathcal {A}}, {\mathcal {B}}, \pi _1(\Sigma ), t &{} tbt^{-1}=w^{-1}bw &{}\forall b \in {\mathcal {B}}\\ &{} tct^{-1} = \Phi (c) &{} \forall c \in \pi _1(\Sigma ) \\ \end{array} \Biggr \rangle . \end{aligned}$$

Since $G = \left\langle {\mathcal {A}}, t \right\rangle *_{\left\langle t \right\rangle } \Big ( \left\langle \pi _1(\Sigma ), wt \right\rangle *_{\left\langle wt \right\rangle } \left\langle {\mathcal {B}}, wt \right\rangle \Big )$, the group G is ${{\,\textrm{CAT}\,}}(0)$ by [5, Proposition II.11.17]. The group G is the fundamental group of a space obtained by gluing a $(k+1)$-torus $T_k$ and an $(\ell +1)$-torus $T_{\ell }$ to a closed hyperbolic 3-manifold $M_{\Phi }$ so that essential simple closed curves on $T_k$ and $T_{\ell }$ are glued to disjoint geodesic essential simple closed curves in $M_{\Phi }$. Thus, the group G is ${{\,\textrm{CAT}\,}}(0)$ with isolated flats.

4 The outer automorphism group of a hyperbolic group

Definition 4.1

Let $\Gamma$ be a group. An outer automorphism $\phi \in {{\,\textrm{Out}\,}}(\Gamma )$ is atoroidal if no positive power of $\phi$ preserves the conjugacy class of any infinite-order element in $\Gamma$. A subgroup $K \le {{\,\textrm{Out}\,}}(\Gamma )$ is purely atoroidal if every infinite order element of K is atoroidal.

Proposition 4.2

There does not exist a purely atoroidal subgroup of ${{\,\textrm{Out}\,}}(F_r)$ isomorphic to $\mathbb {Z}^2$.

Remark 4.3

Feighn–Handel [19] classify abelian subgroups of ${{\,\textrm{Out}\,}}(F_r)$ up to finite index, and our proof of Proposition 4.2 below relies on their analysis. Given an element $\phi \in {{\,\textrm{Out}\,}}(F_r)$, Feighn–Handel define an abelian subgroup $D(\phi )$ called the disintegration subgroup of $\phi$; an example is given in this remark. They prove that for every abelian subgroup $A \le {{\,\textrm{Out}\,}}(F_r)$ there exists $\phi \in A$ so that $D(\phi ) \cap A$ has finite index in A. The techniques in the following proof are not used elsewhere in this paper, so we refer the reader to the work of Feighn–Handel [19, 20] for additional background, motivation, and definitions.

The disintegration subgroup of an outer automorphism of the free group is motivated by the disintegration of a mapping class group element. If $\psi$ is an element of the mapping class group of a surface $\Sigma$, then by Thurston’s classification theorem there exists a corresponding decomposition of the surface $\Sigma$ into a disjoint union of subsurfaces $\Sigma _i$, which either are annuli or have negative Euler characteristic. There exists a homeomorphism $h :\Sigma \rightarrow \Sigma$ representing $\psi$ such that for each annulus, $h|_{\Sigma _i}$ is a non-trivial Dehn twist, and for the other subsurfaces, $h|_{\Sigma _i}$ is either a pseudo-Anosov homeomorphism or the identity. Suppose the subsurfaces are numbered such that $h|_{\Sigma _i}$ is not the identity for $1 \le i \le n$. For $1 \le i \le n$, let $h_i :\Sigma \rightarrow \Sigma$ agree with h on $\Sigma _i$ and be the identity on $\Sigma - \Sigma _i$. The disintegration of $\psi$ is the abelian group generated by $\{h_i \, | \, 1 \le i \le n\}$.

A (rotationless) outer automorphism has a normal form given by a topological representative $g :G \rightarrow G$ called a completely split train track map of a finite graph G. The graph G decomposes as a disjoint union of subgraphs called strata, and g restricted to a non-zero stratum is either exponentially growing, non-exponentially growing, or the identity. However, unlike surface homeomorphisms, these strata might not be invariant under g. The disintegration process determines certain invariant subgraphs of G and defines an abelian group $D(\phi )$. For example, let $\phi$ be the atoroidal outer automorphism with a completely split train track representative on a 6-petaled rose with edges labeled $\{a,b,c,d,e,f\}$ given by

$$\begin{aligned} g: a \mapsto ac , b \mapsto a, c \mapsto b, d \mapsto df, e \mapsto d, f \mapsto e. \end{aligned}$$

The group $D(\phi )$ is isomorphic to $\mathbb {Z}^2$ and is generated by

$$\begin{aligned}&g_1: a \mapsto ac , b \mapsto a, c \mapsto b, d \mapsto d, e \mapsto e, f \mapsto f, \\&g_2: a \mapsto a , b \mapsto b, c\mapsto c, d \mapsto df, e \mapsto d, f \mapsto e. \end{aligned}$$

In particular, $D(\phi )$ is not purely atoroidal.

Proof of Proposition 4.2

Assume towards a contradiction $A \cong \mathbb {Z}^2$ is a purely atoroidal subgroup of ${{\,\textrm{Out}\,}}(F_r)$. By [19, Theorem 7.2], there exists an element $\phi \in A$ such that $D(\phi ) \cap A$ is a finite-index subgroup of A, where $D(\phi )$ is the disintegration subgroup of $\phi$. We will analyze the subgroup $D(\phi )$ to obtain an element $\psi \in D(\phi ) \cap A$ that is not purely atoroidal.

Let $f :G \rightarrow G$ be a completely split train track representative of $\phi$. Then G has a filtration $G_1 \subset G_2 \subset \ldots \subset G_K$, where each filtration element $G_i$ is an f-invariant subgraph for $1 \le i \le K$. Let the stratum $H_i$ be the closure of $G_i - G_{i-1}$. The element $\phi$ is atoroidal, so the graph G has no closed indivisible Nielsen paths, (quasi)-exceptional paths, or non-fixed non-exponentially growing edges. Thus, each stratum has one of three types: (i) exponentially growing, (ii) fixed non-exponentially growing, or (iii) zero stratum.

The B-graph used to define $D(\phi )$ in this setting has vertex set in one-to-one correspondence with the exponentially growing stratum of G. There is an edge $\{H_i, H_j\}$ in the B-graph for $i >j$ if there exists an edge $e_i \subset H_i$ so that $f(e_i)$ intersects $H_j$ in a certain way; see [19, Definition 6.3]. By definition of $D(\phi )$, the rank of $D(\phi )$ gives a lower bound to the number of components of the B-graph. Thus, the B-graph has components $B_1, \ldots , B_k$ with $k \ge 2$. Let $B_1$ denote the component of the B-graph containing $H_r$, the exponentially growing stratum in G with the smallest value of r. Let $X_1 \subset G$ be the union of the exponentially growing stratum in $B_1$ and their associated zero stratum. Let $X_1' = X_1 \cup G_r$. Since $H_r$ is exponentially growing, $H_r$ is connected and $G_r$ is not a forest. Hence, the rank of $\pi _1(X_1')$ is at least one.

Since the subgraph $X_1$ contains an exponentially growing stratum, there exists a nontrivial lamination $\Lambda$ associated to $X_1$. The lamination $\Lambda$ is stabilized by $D(\phi )$, and there is a corresponding Perron–Frobenius stretch factor homomorphism $PF_{\Lambda } :D(\phi ) \cap A \rightarrow \mathbb {Z}$. Since $D(\phi ) \cap A \cong \mathbb {Z}^2$, the kernel has rank at least one, so there exists a non-trivial element $\psi \in D(\phi ) \cap A$ that does not stretch $\Lambda$. By definition of $D(\phi )$, the element $\psi$ is the identity on $X_1$. Moreover, since $X_1'$ is the union of $X_1$ and a collection of fixed non-exponentially growing edges, the element $\psi$ fixes $X_1'$. Since $X_1'$ has rank at least one, the element $\psi$ is not atoroidal, a contradiction. $\square$

Corollary 4.4

If H is a finitely generated virtually free group, then there does not exist a purely atoroidal subgroup of ${{\,\textrm{Out}\,}}(H)$ isomorphic to $\mathbb {Z}^2$.

Proof

Suppose there exists a purely atoroidal subgroup $A = \left\langle \phi , \psi \right\rangle \cong \mathbb {Z}^2 \subset {{\,\textrm{Out}\,}}(H)$. We will use this subgroup to construct a purely atoroidal $\mathbb {Z}^2$ subgroup in the outer automorphism group of a free group, contradicting Proposition 4.2.

Let $F_r \le H$ be a free subgroup of finite index N in H. Since H is finitely generated, there are finitely many subgroups of a given index. Therefore, we can take $F_r$ to be a characteristic subgroup of H (for instance, the intersection of all free subgroups of a given finite index). We fix a choice $\Phi ,\Psi \in {\text {Aut}}(H)$ of representatives of $\phi$ and $\psi$, respectively. Since $F_r$ is characteristic we can take the restrictions $\Phi ' = \Phi |_{F_r}$, $\Psi ' = \Psi |_{F_r} \in {{\,\textrm{Aut}\,}}(F_r)$ with images $\phi ', \psi ' \in {{\,\textrm{Out}\,}}(F_r)$.

We claim there exists $M > 0$ such that $[\phi '^M, \psi '] = 1 \in {{\,\textrm{Out}\,}}(F_r)$. Let us fix some notation: the commutator bracket $[x, y] := x y x^{-1} y^{-1}$ and our (outer) automorphisms act on the left so we likewise make our inner automorphisms act by conjugation on the left, that is, $i_k(g) := k g k^{-1}$ for $g, k \in F_r$, and similarly define conjuation in ${\text {Aut}}(F_r)$. This has the consequence that $i_k i_{k'} = i_{k k'}$ and that $i_k^\phi = \phi i_k \phi ^{-1} = i_{\phi (k)}$. Since $\phi$ and $\psi$ are commuting elements of ${{\,\textrm{Out}\,}}(H)$, there exists $h \in H$ such that $[\Phi , \Psi ] = i_h$. In general the identity $[x^n, y] = [x, y]^{x^{n-1}} \dots [x, y]^x [x, y]$ holds, so we compute that $[\Phi ^n, \Psi ] = i_{h_n}$ where $h_n = \Phi ^{n-1}(h) \dots \Phi (h) h$. Now we need to show that for some $M > 0$ we have $h_M \in F_r$. Note that $h_{n+1} = \Phi (h_n) h$. Let ${\overline{h}}_n$ be the image of $h_n$ in $H / F_r$. Since $F_r$ is characteristic, $\Phi$ induces ${\overline{\Phi }} \in {{\,\textrm{Aut}\,}}(H / F_r)$ and ${\overline{h}}_{n+1} = {\overline{\Phi }}({\overline{h}}_n) {{\overline{h}}}$. The mapping $g \mapsto {\overline{\Phi }}(g) h$ is a bijection of the finite set $H / F_r$, so it is periodic. Since ${\overline{h}}_0 = 1$, there exists $M > 0$ with ${\overline{h}}_M = 1$, that is, $h_M \in F_r$.

Thus, after replacing $\phi$ with $\phi ^M$ if necessary, we have a homomorphism $A \rightarrow {{\,\textrm{Out}\,}}(F_r)$ defined by $\phi \mapsto \phi ', \psi \mapsto \psi '$, which sends every outer automorphism $\theta$ to the outer automorphism $\theta '$ given by restricting some lift of $\theta$. Every non-trivial $\theta \in A$ is atoroidal in ${{\,\textrm{Out}\,}}(H)$ and therefore $\theta '$ is atoroidal in ${{\,\textrm{Out}\,}}(F_r)$ (since conjugacy in $F_r$ is a finer equivalence relation than conjugacy in H). This gives both that the homomorphism $A \rightarrow {{\,\textrm{Out}\,}}(F_r)$ is injective and that its $\mathbb {Z}^2$ image is purely atoroidal. $\square$

Theorem 4.5

Let H be a hyperbolic group. Then there does not exist a purely atoroidal subgroup of ${{\,\textrm{Out}\,}}(H)$ isomorphic to $\mathbb {Z}^2$.

Proof

Without loss of generality, we may assume H is infinite, and not virtually $\mathbb {Z}$. Suppose there exists a purely atoroidal subgroup $A = \left\langle \phi , \psi \right\rangle \cong \mathbb {Z}^2 \le {{\,\textrm{Out}\,}}(H)$.

Suppose first that the group H is one-ended. Since centralizers of pseudo-Anosov homeomorphisms, which are also the atoroidal homeomorphisms of a surface, are virtually cyclic [38], we conclude by an analogous argument to that in the proof of Corollary 4.4 that the group H is not Fuchsian. By [49], the group H splits over a 2-ended subgroup since the outer automorphism group of H is infinite. Thus, the group H has a non-trivial JSJ decomposition containing a 2-ended vertex group $H_v$. Up to passing to a finite-index subgroup, the group A preserves $[H_v]$, a contradiction.

Now suppose H is infinite-ended. Let ${\mathcal {H}}$ be a Stallings–Dunwoody splitting of H over finite groups. Since H is not virtually free by Corollary 4.4, there exists a one-ended vertex group $H_v$ of ${\mathcal {H}}$. By Lemma 2.15, there exist $m, n \ge 1$ such that $\phi ^m([H_v]) = [H_v]$ and $\psi ^n([H_v]) = [H_v]$. Let $N=mn$. We first claim that $\left\langle \phi ^N|_{H_v}, \psi ^N|_{H_v} \right\rangle$ is an abelian subgroup of ${{\,\textrm{Out}\,}}(H_v)$. To see this, let $\Psi , \Phi \in {{\,\textrm{Aut}\,}}(H)$ be representatives of $\psi$ and $\phi$, respectively, such that $\Psi ^N(H_v) = H_v$, $\Phi ^N(H_v) = H_v$, and the commutator $[\Phi ^N, \Psi ^N]$ is an inner automorphism given by some $h \in H$. Then $[\Phi ^N, \Psi ^N](H_v) = H_v = hH_vh^{-1}$. The subgroup $H_v$ fixes a unique vertex v of the Bass–Serre tree corresponding to ${\mathcal {H}}$, and $hH_vh^{-1}$ fixes a unique vertex $h\cdot v$. Thus, $v = h\cdot v$, so $h \in H_v$. Therefore, $\phi ^N$ and $\psi ^N$ restrict to commuting outer automorphisms of $H_v$. Now, $\left\langle \phi ^N|_{H_v}, \psi ^N|_{H_v} \right\rangle$ is a purely atoroidal subgroup of ${{\,\textrm{Out}\,}}(H_v)$ isomorphic to $\mathbb {Z}^2$. The argument from the previous paragraph yields a contradiction. $\square$

5 The nonexistence of Cannon–Thurston maps

5.1 Hyperbolic normal subgroups

To prove that Cannon–Thurston maps do not exist for hyperbolic normal subgroups of a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, we use the following criterion.

Lemma 5.1

Let $H \le G$ such that H acts geometrically on Y and G acts geometrically on X, where X and Y are hyperbolic or ${{\,\textrm{CAT}\,}}(0)$ spaces. If there exists an element $h \in H$ so that

• (1) h acts by North-South dynamics on $\partial Y$;

• (2) h acts by translation on a flat $F \subset X$; and

• (3) $\partial F \subset \Lambda _xH \subset \partial X$,

then the Cannon–Thurston map does not exist for (H, G).

Proof

Suppose there exists such an element h and let its fixed points on $\partial Y$ be denoted $h^{\pm \infty }$. Suppose towards a contradiction that the Cannon–Thurston map ${\hat{\iota }}:\partial Y \rightarrow \partial X$ exists. Since the Cannon–Thurston map is H-equivariant (Remark 2.34), $\Lambda _xH \subset {\hat{\iota }}(\partial Y)$. By equivariance, for every point $x = {\hat{\iota }}(y)$ in ${\hat{\iota }}(\partial Y)$ distinct from ${\hat{\iota }}(h^{\pm \infty })$, we have $\lim _{n \rightarrow \infty } h^n x = \lim _{n \rightarrow \infty } {\hat{\iota }}( h^n y) = {\hat{\iota }}(h^{+ \infty }) \ne x$, so the action of h on ${\hat{\iota }}(\partial Y)$ has at most two fixed points. However, h acts by translations on the flat F; hence, h acts trivially on $\partial F \subset \Lambda _xH \subset {\hat{\iota }}(\partial Y)$, a contradiction. $\square$

Proposition 5.2

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and let $H \triangleleft G$ be a hyperbolic normal subgroup. Then there exists an infinite order element $h \in H$ which acts by translation on a flat under any geometric action of G on a ${{\,\textrm{CAT}\,}}(0)$ space X.

Proof

Consider any subgroup $A \le G$ with $A \cong \mathbb {Z}^2$; such a subgroup exists by our definition of isolated flats requiring the set of flats to be non-empty together with [29, Lemma 3.1.2], a converse to the Flat Torus Theorem. We claim that some infinite order $h \in H$ lies in a $\mathbb {Z}^2$ subgroup of G, which implies the proposition by the standard Flat Torus Theorem. If $A \cap H \ne 1$ then we are done, so suppose $A \cap H = 1$. Consider the map $A \rightarrow {{\,\textrm{Out}\,}}(H)$ coming from conjugation in G. If it has kernel, then there exists some non-trivial $g \in A$ and some $h_0 \in H$ such that $h^g = h^{h_0}$ for all $h \in H$. If not, then its image is isomorphic to $\mathbb {Z}^2$ and thus cannot be purely atoroidal by Theorem 4.5, so there is some non-trivial $g \in A$ and some infinite order $h \in H$ such that $h^g = h^{h_0}$ for some $h_0 \in H$. In either case there is some infinite order $h \in H$ commuting with $g h_0^{-1}$. Since $A \cap H = 1$ we see that g has infinite order in the quotient G/H and thus no non-zero power of $g h_0^{-1}$ is in H, so $\langle h, g h_0^{-1} \rangle \cong \mathbb {Z}^2$. $\square$

Theorem 5.3

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and let $H \triangleleft G$ be an infinite hyperbolic normal subgroup. Then the Cannon–Thurston map does not exist for (H, G).

Proof

By Proposition 5.2, there exists an infinite-order element $h \in H$ which acts by translation on a flat in X. Since H is hyperbolic, the element h acts by North-South dynamics on $\partial H$ by Theorem 2.4. By Lemma 2.31, ${\hat{\iota }}(\partial H) = \partial G \cong \partial X$. Thus, the hypotheses of Lemma 5.1 are satisfied, and the Cannon–Thurston map does not exist. $\square$

The above results imply that the Cannon–Thurston map for the pair (H, G) also does not exist with respect to their Morse boundaries, $\partial _MH$ and $\partial _MG$. In this setting, we define the Cannon–Thurston map as before.

Definition 5.4

Let $H \le G$ so that H acts geometrically on Y and G acts geometrically on X, where X and Y are proper geodesic metric spaces. Let $x \in X$ and $y \in Y$. A Cannon–Thurston map for the pair (H, G) with respect to their Morse boundaries is the map $f :\partial _M Y \rightarrow \partial _M X$ defined by

$$\begin{aligned} f\left( \lim _{i \rightarrow \infty } h_i \cdot y\right) =\lim _{i \rightarrow \infty } h_i \cdot x, \end{aligned}$$

provided f is well-defined and continuous.

Proposition 5.5

Let G be a ${{\,\textrm{CAT}\,}}(0)$ group with isolated flats, and let $H \triangleleft G$ be an infinite hyperbolic normal subgroup. Then the Cannon–Thurston map does not exist for (H, G) with respect to their Morse boundaries.

Proof

Suppose H acts geometrically on a proper geodesic metric space Y, and suppose the group G acts geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X. There exists an infinite-order element $h \in H$ that acts by translation on a flat in X by Proposition 5.2. Let $y \in Y$, and let $x \in X$ be a point in the aforementioned flat stabilized by h. Since H is hyperbolic and $h \in H$ has infinite-order, the sequence $\{h^n \cdot y\}_{n \in \mathbb {N}}$ converges to a point in $\partial H \cong \partial _MH$. However, the sequence $\{h^n \cdot x\}_{n \in \mathbb {N}}$ converges to a point in the boundary of a flat in X, and hence does not converge to a point in $\partial _MG$. Thus, the Cannon–Thurston map does not exist for the pair (H, G) with respect to their Morse boundaries. $\square$

5.2 Normal ${{\,\textrm{CAT}\,}}(0)$ subgroups with isolated flats

Theorem 5.6

Let $H \triangleleft G$ be ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats and suppose that H is an infinite, infinite-index normal subgroup of G. Then the Cannon–Thurston map does not exist for (H, G).

Proof

Suppose H and G act geometrically on Y and X, respectively, where Y and X are ${{\,\textrm{CAT}\,}}(0)$ spaces with isolated flats. The structure of the normal subgroup H is guaranteed by Theorem 3.3. By Lemma 5.1 and Lemma 2.11, we may assume that the only infinite-order elements of H that stabilize a flat in X lie in a conjugate of a (peripheral) free abelian subgroup of H of rank at least two. Let $y \in Y$ and $x \in X$. To prove the Cannon–Thurston map does not exist, we will exhibit sequences $\{h_n\}_{n \in \mathbb {N}}, \{h'_n\}_{n \in \mathbb {N}} \subset H$ so that

$$\begin{aligned} \lim _{n \rightarrow \infty } h_n \cdot y= & {} \lim _{n \rightarrow \infty } h'_n \cdot y \in \partial Y. \end{aligned}$$

(1)

$$\begin{aligned} \lim _{n \rightarrow \infty } h_n \cdot x\ne & {} \lim _{n \rightarrow \infty } h'_n \cdot x \in \partial X. \end{aligned}$$

(2)

Fig. 1

On the left, the universal cover of the wedge of a torus and the surface $\Sigma$ is homotopic to Y, the union of countably many copies of the Euclidean and hyperbolic planes attached to each other along line segments. On the right, the space ${\overline{X}}$ is the union of a 3-torus and the mapping torus of a pseudo-Anosov homeomorphism $\phi :\Sigma \rightarrow \Sigma$ glued to each other along a circle. The universal cover X is the union of countably many copies of $\mathbb {E}^3$ and $\mathbb {H}^3$ glued to each other along lines. The groups $H = \pi _1({\overline{Y}})$ and $G = \pi _1({\overline{X}})$ are ${{\,\textrm{CAT}\,}}(0)$ with isolated flats. The Cannon–Thurston map from $\partial H$ to $\partial G$ does not exist because the orbit points corresponding to the sequences $\{a^n\}$ and $\{a^n\phi _*^n(b) = a^nt^nbt^{-n}\}$ converge to the same point $\alpha \in \partial Y \cong \partial H$, but converge to different points in $\partial X \cong \partial G$. Indeed, the geodesic in X from the basepoint to $a^nt^nbt^{-n}$ passes through the R-neighborhood of $a^nt^n$ for some R independent of n

Let ${\mathcal {H}}$ be a Stallings–Dunwoody splitting of H. Since H is not virtually free, there exists a one-ended vertex group in ${\mathcal {H}}$.

Case 1: ${\mathcal {H}}$ has a one-ended vertex group which is a virtually abelian subgroup.

We first define the sequences $\{h_n\}_{n \in \mathbb {N}},\{h_n'\}_{n \in \mathbb {N}} \subset H$. An example appears in Figure 1. Let ${\mathcal {A}}' \le H$ denote a one-ended vertex group of ${\mathcal {H}}$ that is virtually abelian. Let ${\mathcal {A}}\le {\mathcal {A}}'$ be a finite-index subgroup isomorphic to $\mathbb {Z}^k$ for some $k \ge 2$. By Lemma 3.2, there is an infinite-order element $q \in Q = G/H$ that induces an infinite-order outer automorphism $\phi _q \in {{\,\textrm{Out}\,}}(H)$. By Lemma 2.15, there exists $m \ge 1$ such that $\phi _q^m([{\mathcal {A}}']) = [{\mathcal {A}}']$. Up to passing to a further power if necessary, we may assume that $\phi _q^m([{\mathcal {A}}]) = [{\mathcal {A}}]$. By Lemma 3.2, the group G contains a subgroup isomorphic to the group ${\mathcal {A}}\rtimes _{\phi _q^m} \mathbb {Z}$, which is solvable. By the Solvable Subgroup Theorem [5, Theorem II.7.8], this solvable subgroup is virtually abelian. Thus, after possibly passing to a power, the element $\phi _q^m$ restricted to ${\mathcal {A}}$ is the identity. Therefore, there exists $t \in G$ with $p(t) = q^m$, where $p:G \rightarrow Q$ is the quotient map, and so that $\phi _q^{mn}(h) = t^nht^{-n} = h$ for all $h \in {\mathcal {A}}$ and $n \in \mathbb {Z}$.

Since the group H is not virtually abelian, there exists an infinite order element $h_0 \in H \setminus {\mathcal {A}}'$. The subgroup $\left\langle {\mathcal {A}}', h_0 \right\rangle \le H$ is also not virtually abelian. Indeed, if $\left\langle {\mathcal {A}}', h_0 \right\rangle$ were virtually abelian, and hence one-ended, then this group would act elliptically on any tree on which it acts with finite edge stabilizers including in particular the Bass–Serre tree for ${\mathcal {H}}$, on which it would fix the same vertex as ${\mathcal {A}}'$, a contradiction. We claim that $h_0$ does not commute with any power of t. Indeed, in this case, $\left\langle {\mathcal {A}}', h_0 \right\rangle \oplus \left\langle t^k \right\rangle$ would be a subgroup of G, contradicting Lemma 2.12.

Consider the elements $t^nh_0t^{-n}$ for $n \in \mathbb {N}$. Fix a point p in the flat stabilized by ${\mathcal {A}}$ in Y. Choose $a_n \in {\mathcal {A}}$ so that $d(a_n\cdot p, t^nh_0t^{-n}\cdot p)$ is minimized, and among such $a_n \in {\mathcal {A}}$, $d(a_n \cdot p, p)$ is maximized. If the length $|a_n|<D$ for all $n \in \mathbb {N}$ and some $D \ge 0$, let $h_1 \in {\mathcal {A}}$ be an arbitrary infinite-order element and let $h_n = h_1^n$. Otherwise, after choosing an infinite subsequence (we will abuse notation and continue to write $n \in \mathbb {N}$ rather than $n_k, k \in \mathbb {N}$), we have $|a_n| \rightarrow \infty$ as $n \rightarrow \infty$ so that $\{a_n\cdot p\}_{n \in \mathbb {N}}$ converges to a point $\alpha$ in the visual boundary of the flat in Y stabilized by ${\mathcal {A}}$, by compactness of $Y \cup \partial Y$, and $\{a_nt^n \cdot x\}$ converges to a point in the boundary of the flat in X stabilized by $\left\langle {\mathcal {A}}, t \right\rangle$. Let $h_n = a_n$. In both cases, let $h_n' = h_nt^nh_0t^{-n}$.

To show (1), suppose $F \subset Y$ is a flat stabilized by ${\mathcal {A}}$, and let $y \in F$. Consider the geodesic segment $\gamma _n$ in Y connecting $id \cdot y$ to $h_n'\cdot y = h_nt^nh_0t^{-n} \cdot y = h_na_nw_n \cdot y.$ In the case that $h_n = h_1^n \in {\mathcal {A}}$ and the length of $a_n$ is bounded by $D\ge 0$, the geodesic $\gamma _n$ passes through the $D'$-neighborhood of the point $h_1^n\cdot y$ for all $n \in \mathbb {N}$ and some $D' \ge 0$. Thus, $h_n\cdot y$ and $h_n'\cdot y$ converge to the same point in $\partial Y$. Otherwise, $h_n = a_n$ and $h_n' = a_na_nw_n$, and, similarly, $h_n\cdot y$ and $h_n'\cdot y$ converge to the same point in $\partial Y$.

To prove (2), we will show $\lim _{n \rightarrow \infty } h'_n \cdot x = \lim _{n \rightarrow \infty } h_nt^n \cdot x$. Suppose the basepoint $x \in X$ lies in the flat $F_0$ stabilized by $\mathbb {Z}^{k+1} \cong \left\langle {\mathcal {A}}, t \right\rangle \le G$. For all $n \in \mathbb {N}$, the points $h_nt^n\cdot x$ lie in the flat $F_0$. Let $F_n \subset X$ denote the flat containing the point $h_nt^nh_0t^{-n} \cdot x$. That is, $F_n = h_nt^nh_0\cdot F_0$. By assumption, $h_0$ does not commute with any non-trivial element of the subgroup $\left\langle {\mathcal {A}},t \right\rangle$. Therefore, in the language of Definition 2.8, the flats $F_0$ and $F_n$ lie in tubular neighborhoods of distinct flats in ${\mathcal {F}}\subset X$. For $S \subset X$, let $\pi _{F_0}(S)$ denote the almost projection [16, 53] of S to $F_0$: the set of points of $F_0$ whose distance from S is less than $d(S,F_0) + 1$. The subspace $\pi _{F_0}(F_n)$ has bounded diameter by [53, Theorem 2.14]. For all $n \in \mathbb {N}$ we have $d(h_nt^n\cdot x, \pi _{F_0}(F_n)) = d(h_1t\cdot x, \pi _{F_0}(F_1))$ so in particular these distances are uniformly bounded. Therefore, by [53, Lemma 1.15], there exists $R>0$ so that the geodesic connecting x to $h_nt^nh_0t^{-n}\cdot x$ passes through $B_R(h_nt^n\cdot x)$ for all $n \in \mathbb {N}$. Thus, $\lim _{n \rightarrow \infty } h'_n \cdot x = \lim _{n \rightarrow \infty } h_nt^n \cdot x \ne \lim _{n \rightarrow \infty } h_n \cdot x$, as desired.

Case 2: No vertex group of ${\mathcal {H}}$ is isomorphic to a virtually abelian group.

In this case, there exists $H_1 \le H$, a one-ended vertex group in the Stallings–Dunwoody decomposition of H so that the elementary JSJ decomposition of $H_1$ contains a maximal virtually abelian vertex group ${\mathcal {A}}_H$. In addition, there exists a maximally hanging Fuchsian vertex group $H_v$ adjacent to ${\mathcal {A}}_H$. As in Case 1, there exists an infinite-order element $q \in Q$ which yields an infinite-order outer automorphism $\phi _q \in {{\,\textrm{Out}\,}}(H)$ so that $\phi _q([{\mathcal {A}}_H])= [{\mathcal {A}}_H]$ and $\phi _q([H_v]) = [H_v]$. Since $H_v$ is a maximal hanging Fuchsian group, it contains a finite-index subgroup $H_{\Sigma }$ isomorphic to $\pi _1(\Sigma )$, where $\Sigma$ is a surface with negative Euler characteristic and non-empty boundary. After passing to a power, we may also assume $\phi _q([H_{\Sigma }]) = [H_{\Sigma }]$. As above, there exists $t' \in G$ so that $p(t') = q$ and $t'ht'^{-1} = h$ for all $h \in {\mathcal {A}}_H$; and, for all $h \in H_v$, there exists $w \in H$ and $h' \in H_v$ so that $t'ht'^{-1} = wh'w^{-1}$. There exists an infinite-order element $\alpha \in {\mathcal {A}}_H \cap H_v$ since these vertex groups are adjacent. After taking a power, we may assume that $\alpha \in H_{\Sigma }$. Thus, $w \in {\mathcal {A}}_H$, and there exists $t \in G$ so that $p(t) = q$ and $tht^{-1} = h$ for all $h \in {\mathcal {A}}_H$, and for all $h \in H_v$, there exists $h' \in H_v$ so that $tht^{-1} = h'$. Let $h_n = \alpha ^n$ and let $h_n' = \alpha ^nt^nh_0t^{-n}$ for $n \in \mathbb {N}$, where $\alpha$ is as defined above, and $h_0$ is an arbitrary element of $H_{\Sigma }$.

To prove (1), observe that $t^nh_0t^{-n} = \Phi ^n(h_0)$, where we may assume that $\Phi \in {{\,\textrm{Aut}\,}}(F_n)$ is a fully irreducible automorphism induced by a pseudo-Anosov homeomorphism of $\Sigma$. Indeed, if $\Phi$ is not induced by a pseudo-Anosov, then $\Phi$ fixes the homotopy class of a curve $\beta$ on $\Sigma$. Then the element $\beta$ stabilizes a flat in X but does not stabilize a flat in Y. Hence by Lemma 2.11 and Theorem 2.6, the element $\beta$ acts by North-South dynamics on Y. Thus by Lemma 5.1 the Cannon–Thurston map does not exist. So, the automorphism $\Phi$ is induced by a pseudo-Anosov homeomorphism. By [4, Proposition 1.6] the sequence $\Phi ^n(h_0)$ converges to a leaf $\ell$ in the Bestvina-Feighn-Handel lamination $\Lambda _{\Phi }$, which is a closed, $F_n$-invariant subset of $\partial ^2 F_n$. Here $\partial ^2 F_n$ is the quotient of $(\partial F_n \times \partial F_n$ minus the diagonal) by the flip action. A lift of $\alpha$ to a Cayley graph of $\mathbb {F}_n$ determines a leaf in $\partial ^2 F_n$ corresponding to $\alpha$. By [4, Proposition 1.8], the leaf $\ell$ has bounded overlap with any lift of $\alpha$. This implies there exists a uniform bound on the overlap between any geodesic in $\{[y, \Phi ^n(h_0) \cdot y]\}_{n \in \mathbb {N}}$ and any geodesic in $\{[y, \alpha ^m \cdot y]\}_{m \in \mathbb {Z}}$. Thus, $\lim _{n \rightarrow \infty } h_n\cdot y = \lim _{n \rightarrow \infty } h_n' \cdot y$.

The proof of (2) is analogous to the proof of (2) in Case 1. $\square$

Remark 5.7

Suppose $H \triangleleft G$ are ${{\,\textrm{CAT}\,}}(0)$ groups with isolated flats and G acts geometrically on a ${{\,\textrm{CAT}\,}}(0)$ space X. Suppose, as in the proof above, the only infinite-order elements of H that stabilize a flat in X lie in a conjugate of a (peripheral) free abelian subgroup of H of rank at least two. The proof of Theorem 5.6 extends to show there are, in fact, countably many sequences that converge to the same point in $\partial H$, but converge to pairwise distinct points in $\partial G$. Indeed, as defined in the proof above, consider the sequences $\{h_n\}_{n \in \mathbb {N}}$ and $\{h_{n,k}' = h_nt^{kn}h_0t^{-kn}\}_{n \in \mathbb {N}}$ for a fixed $k \in \mathbb {N}$. Then, for $k \ne k'$, the sequences $\{h'_{n,k}\}$ and $\{h'_{n,k'}\}$ converge to the same point in $\partial H$, but converge to rays with different slopes in a flat in X, and hence converge to different points in $\partial G$.