Abstract
The Milnor number \(\mu _f\) of a holomorphic function \(f :({\mathbb {C}}^n,0) \rightarrow ({\mathbb {C}},0)\) with an isolated singularity has several different characterizations as, for example: 1) the number of critical points in a morsification of f, 2) the middle Betti number of its Milnor fiber \(M_f\), 3) the degree of the differential \({\text {d}}f\) at the origin, and 4) the length of an analytic algebra due to Milnor’s formula \(\mu _f = \dim _{\mathbb {C}}{\mathcal {O}}_n/{\text {Jac}}(f)\). Let \((X,0) \subset ({\mathbb {C}}^n,0)\) be an arbitrarily singular reduced analytic space, endowed with its canonical Whitney stratification and let \(f :({\mathbb {C}}^n,0) \rightarrow ({\mathbb {C}},0)\) be a holomorphic function whose restriction f|(X, 0) has an isolated singularity in the stratified sense. For each stratum \({\mathscr {S}}_\alpha \) let \(\mu _f(\alpha ;X,0)\) be the number of critical points on \({\mathscr {S}}_\alpha \) in a morsification of f|(X, 0). We show that the numbers \(\mu _f(\alpha ;X,0)\) generalize the classical Milnor number in all of the four characterizations above. To this end, we describe a homology decomposition of the Milnor fiber \(M_{f|(X,0)}\) in terms of the \(\mu _f(\alpha ;X,0)\) and introduce a new homological index which computes these numbers directly as a holomorphic Euler characteristic. We furthermore give an algorithm for this computation when the closure of the stratum is a hypersurface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Summary of results
The Milnor number \(\mu _f\) is one of the central invariants of a holomorphic function
with isolated singularity. It has—among others—the following characterizations, cf. [29, Chapter 7] and [1, Chapter 2].
-
1)
It is the number of Morse critical points in a morsification \(f_\eta \) of f.
-
2)
It is equal to the middle Betti number of the Milnor fiber
$$\begin{aligned} M_f = B_\varepsilon \cap f^{-1}(\{\delta \}), \quad \varepsilon \gg \delta >0. \end{aligned}$$ -
3)
It is the degree of the map
$$\begin{aligned} \frac{1}{|{\text {d}}f|} {\text {d}}f :\partial B_\varepsilon \rightarrow S^{2n-1} \end{aligned}$$for some choice of a Hermitian metric on \(({\mathbb {C}}^n,0)\).
-
4)
It is the length of the Milnor algebra
$$\begin{aligned} {\mathcal {O}}_n / {\text {Jac}}(f), \end{aligned}$$where \({\text {Jac}}(f) = \langle \frac{\partial f}{ \partial x_1},\dots ,\frac{\partial f}{\partial x_n} \rangle \) is the Jacobian ideal of f.
In this note we consider the more general setup of an arbitrary reduced complex analytic space \((X,0) \subset ({\mathbb {C}}^n,0)\) and a holomorphic function \(f :({\mathbb {C}}^n,0) \rightarrow ({\mathbb {C}},0)\), whose restriction f|(X, 0) to (X, 0) has an isolated singularity in the stratified sense. To this end, we will assume that (X, 0) is endowed with a complex analytic Whitney stratification \(S = \{ {\mathscr {S}}_\alpha \}_{\alpha \in A}\) with finitely many connected strata \({\mathscr {S}}_\alpha \). There always exists a Milnor fibration for the restriction f|(X, 0) of any function f to (X, 0), regardless of whether or not f|(X, 0) has isolated singularity; see [23], or [14]. Denote the corresponding Milnor fiber by
where X is a suitable representative, \(B_\varepsilon \) a ball of radius \(\varepsilon \) centered at the origin in \({\mathbb {C}}^n\), and \(\varepsilon \gg \delta > 0\) sufficiently small.
We introduce invariants \(\mu _f(\alpha ;X,0)\) of f|(X, 0)—see Definition 5—which generalize the classical Milnor number simultaneously in all of these four characterizations. Let \(X_\alpha = \overline{ {\mathscr {S}}_\alpha }\) be the closure of the stratum \({\mathscr {S}}_\alpha \) and \(d(\alpha )\) its (complex) dimension. Then for every \(\alpha \in A\) the number \(\mu _f(\alpha ;X,0)\) is
-
1’)
the number of Morse critical points on the stratum \({\mathscr {S}}_\alpha \) in a morsification of f. For the definition of morsifications in this context see Sect. 3.1.
-
2’)
the number of direct summands for \(\alpha \) in the homology decomposition of the Milnor fiber \(M_{f|(X,0)}\), see Proposition 1.
-
3’)
the Euler obstruction \({\text {Eu}}^{{\text {d}}f}\left( X_\alpha ,0 \right) \) of the 1-form \({\text {d}}f\) on \((X_\alpha ,0)\), see Definition 8 and Corollary 3.
-
4’)
the derived homological index
$$\begin{aligned} \mu _f(\alpha ;X,0) = (-1)^{d(\alpha )} \cdot \chi \left( {\mathbb {R}} \nu _* \left( {{\tilde{{\varOmega }}}}^\bullet _{\alpha }, \nu ^* {\text {d}}f \wedge - \right) _0 \right) , \end{aligned}$$i.e. the Euler characteristic of a finite complex of coherent \({\mathcal {O}}_X\)-modules, cf. Theorem 1 and Corollary 4.
A similar discussion for the generalizations of 1)–3) has been carried out by Seade et al. in [30]. The study of homology decomposition for the Milnor fiber has been initiated by Siersma [31] in the case that not only f|(X, 0) but also the space (X, 0) itself has isolated singularity. See also the closely related bouquet decomposition of the Milnor fiber [33] due to Tibăr and the article [28] by Massey for a decomposition similar to Proposition 1 in terms of hypercohomology of constructible sheaves. The definition of the Euler obstruction of a 1-form goes back to MacPherson [27], but can also be adapted from the analogous notion for vector fields as described in [2] by Brasselet et al. We will use the definition by Ebeling and Gusein-Zade from [8].
Contrary to those previous topological considerations for the generalizations of 1)–3), we will describe the Euler obstructions \({\text {Eu}}^{{\text {d}}f}(X_\alpha ,0)\) as an analytic invariant in Theorem 1. This allows us to also generalize the characterization 4) of the Milnor number to 4’). For the particular case when \(\overline{{\mathscr {S}}_\alpha }\) is a hypersurface, an algorithm for the computation of the numbers \(\mu _f(\alpha ;X,0)\) as a homological index is given in Sect. 5.
Example 1
The following example illustrates the setup considered in this article. Let \(X \subset {\mathbb {C}}^3\) be the Whitney umbrella given by the equation \(h = y^2-xz^2 = 0\) and endowed with the stratification
This stratification is known to satisfy the Whitney conditions A and B (Fig. 1).
As a function \(f :{\mathbb {C}}^3 \rightarrow {\mathbb {C}}\) with isolated singularity on (X, 0) we consider
Note that f does not have isolated singularity on \({\mathbb {C}}^3\). Its restriction f|X to X, however, has only isolated critical points in the stratified sense (cf. Definitions 1 and 2 below) at the points
In particular, there are no critical points of the restriction \(f|{\mathscr {S}}_1 = -x^2\) of f to the first stratum \({\mathscr {S}}_1 \cong {\mathbb {C}}^*\) since \(0 \notin {\mathscr {S}}_1\). It will become clear later, why we label the last two of these points with indices 6 and 7. We will usually have to neglect these points, since we are interested in the local behaviour of f on the germ (X, 0) of X at the origin \(0 \in {\mathbb {C}}^3\). As we shall see in Example 2, we have
for the restriction f|(X, 0) at this point.
2 Background and motivation
Suppose the function f, the space (X, 0), and its stratification have been chosen as in 1’) to 4’) from Sect. 1. An application of [30, Proposition 2.3] by Seade et al. shows that
where \({\text {Eu}}_f\left( \overline{{\mathscr {S}}}_\alpha ,0\right) \) is the Euler obstruction of the function f on \((\overline{{\mathscr {S}}}_\alpha ,0)\) from [2]. It is defined as follows.
Let \(\nu :{{\tilde{X}}} \rightarrow X\) be the Nash transformation of (X, 0). Then there always exists a continuous alteration v of the gradient vector field \({\text {grad}}f\) on \(({\mathbb {C}}^n,0)\) which is tangent to the strata of (X, 0), and a lift \(\nu ^* v\) of v to the Nash bundle \({{\tilde{T}}}\) on \({{\tilde{X}}}\). Over the link \(K = \partial B_\varepsilon \cap X\) of (X, 0) this lift is well defined as a non-zero section in \({{\tilde{T}}}\) up to homotopy. Now \({\text {Eu}}_f(X,0)\) is the obstruction to extending \(\nu ^* v\) as a nowhere vanishing section to the interior of \({{\tilde{X}}}\). The same procedure can then be applied to the closure of a stratum \((\overline{{\mathscr {S}}_\alpha },0)\) in place of (X, 0).
Based on this notion, Seade et al. discuss a generalization of 1)–3) in [30] which is similar to the one presented here. To understand how our approach came about to also include 4), i.e. Milnor’s formula, we have to consider the article [30] in the context of a series of papers by various authors on different indices of vector fields and 1-forms on singular varieties. A thorough survey of the results from that time is [9].
One of these indices—the GSV index of a vector field—is particularly close to the idea of the Euler obstruction. The GSV index was first defined in [13, Definition 2.1 ii)] for the following setup:
Let \((X,0) = (g^{-1}(\{0\}),0) \subset ({\mathbb {C}}^{n+1},0)\) be an isolated hypersurface singularity and v the germ of a vector field on \(\left( {\mathbb {C}}^{n+1},0 \right) \) which has an isolated zero at the origin and is tangent to (X, 0). The GSV index \({\text {Ind}}_{GSV}(v,X,0)\) of v on (X, 0) is the obstruction to extending the section v|K as a \(C^\infty \)-section of the tangent bundle from the link \(K = X\cap \partial B_\varepsilon \) to the interior of the Milnor fiber \(B_\varepsilon \cap g^{-1}(\{\delta \})\). Here we deliberately identify the link K with the boundary \(\partial B_\varepsilon \cap g^{-1}(\{\delta \})\) of the Milnor fiber and the section v|K with its image under this identification.
In [12], Gómez-Mont introduces the homological index of a vector field v on (X, 0) as above in order to obtain an algebraic formulaFootnote 1 for the GSV index. The homological index is defined as \({\text {Ind}}_{\hom }(v,X,0) = \chi ({\varOmega }^\bullet _{X,0}, v)\), i.e. the Euler characteristic of the complex
where \({\varOmega }^p_{X,0}\) denotes the module of universally finite Kähler differentials on (X, 0) and v is the homomorphism given by contraction of a differential form with the vector field v. Later on in his article, Gómez-Mont generalizes the GSV index in the obvious way to the setting of an arbitrary complex space (X, 0) with an isolated singularity and a fixed smoothing \(X'\) of (X, 0). He proves in [12, Theorem 3.2] that
with \(k(X,X')\) a constant depending only on (X, 0) and the chosen smoothing, but independent of the vector field v. This is an important intermediate step for the computation of the GSV index from the homological index, but it remains to determine the constant \(k(X,X')\).
For an isolated hypersurface singularity \((X,0) = (g^{-1}(\{0\}),0)\) and its canonical smoothing \(X' = B_\varepsilon \cap g^{-1}(\{\delta \})\), \(\varepsilon \gg \delta >0\) this is done in [12, Section 3.2]: in this case \(k(X,X') = 0\) so that the homological index and the GSV index really coincide. In the general case, however, the constant \(k(X,X')\) is a non-trivial invariant of the singularity and its smoothing.
From our point of view, the main novelty in the approach by Gómez-Mont was the introduction of derived geometry in this setting and its comparison with topological invariants in Eq. (2). To prove it, he uses the fact that both indices obey the law of conservation of number which states, roughly speaking, that the total number of indices is preserved under small perturbations of the vector field. For the GSV index this is immediate from the definition since it only depends on the homotopy class of the non-zero section v|K on the boundary. For the homological index \({\text {Ind}}_{\hom }(v,X,0)\) this follows from a result in [11] which states that, more generally, the law of conservation of number holds for the holomorphic Euler characteristic of a complex of coherent sheaves with finite dimensional cohomology under arbitrary small perturbations of the (co-)boundary maps. The complex \(({\varOmega }_{X,0}^\bullet , v)\) in (1) with perturbations of v is a particular instance of this situation and, hence, for suitable representatives and \({{\tilde{v}}}\) sufficiently close to v one has
To conclude the proof of Eq. (2), observe that at smooth points \(p \in X_{{\text {reg}}}\) the GSV index and the homological index coincide so that any deformation of v to some \({{\tilde{v}}}\) necessarily changes the two indices at the origin by the same amount. Consequently, the difference of these two indices is a locally constant function in v. The general claim then follows from the fact that for the choice of a sufficiently small ball \(B_\varepsilon \) around the origin, the set of those vector fields on \(B_\varepsilon \cap X\) with an isolated zero on (X, 0) form an open and connected set in the Banach space of continuous vector fields on \(B_\varepsilon \cap X\) which are holomorphic in the interior, cf. [12, Theorem 3.2].
In this article, we will not be dealing with vector fields, but with holomorphic 1-forms.Footnote 2 This is more natural in the context of morsifications and it has several further advantages. For example, we can drop the tangency conditions to (X, 0) which we had to impose on a vector field. It is straightforward—and even easier—to also define the Euler obstruction \({\text {Eu}}^\omega (X,0)\) of a 1-form \(\omega \) with isolated zero on (X, 0): again, let \(\nu :{{\tilde{X}}} \rightarrow X\) be the Nash transformation. Then there is a natural pullback \(\nu ^* \omega \) of \(\omega \) to a section of the dual of the Nash bundle and this section does not vanish on \(\nu ^{-1}(\partial B_\varepsilon \cap X)\) whenever \(\omega \) has an isolated zero on (X, 0) in the stratified sense. The Euler obstruction of such an \(\omega \) on (X, 0) is the obstruction to extending \(\nu ^* \omega \) as a nowhere vanishing section to the interior of \({{\tilde{X}}}\).
There is a natural notion of the homological index for a 1-form \(\omega \) with isolated zero on any purely n-dimensional complex analytic space (X, 0) with isolated singularity. In [10], Ebeling et al. define
where \(\left( {\varOmega }^\bullet _{X,0}, \omega \wedge - \right) \) is the complex

with differential given by the exterior multiplication with \(\omega \). Note that in case \((X,0) \cong ({\mathbb {C}}^n,0)\) is smooth and \(\omega = {\text {d}}f\) is the differential of a function f with isolated singularity on (X, 0), the homological index coincides with the classical Milnor number. This is due to the fact that the complex (3) is the Koszul complex in the partial derivatives \(\frac{\partial f}{\partial x_i}\) of f which is known to be a free resolution of the Milnor algebra for an isolated hypersurface singularity.
When (X, 0) has isolated singularity, there is no immediate interpretation for the homological index of \(\omega \) in terms of previously known invariants. However, it is relatively easy to see with the same reasoning as for indices of vector fields that the difference
is also a constant, independent of the 1-form \(\omega \). Again, both invariants satisfy the law of conservation of number. Suppose we have chosen a suitable representative X of (X, 0) and a sufficiently small ball \(B_\varepsilon \). Then for any holomorphic 1-form \(\omega '\) on X which has only isolated zeroes on the smooth part \(X_{{\text {reg}}}\) of X and which is sufficiently close to the original 1-form \(\omega \), we have
This holds because, again, \({\text {Eu}}^{\omega '}(X,p) = {\text {Ind}}_{\hom }(\omega ', X,p)\) at smooth points \(p \in X_{{\text {reg}}}\) so that the difference of these two indices at the origin is a locally constant function of \(\omega \). A similar reasoning as for the homological index for vector fields above can now be made to conclude that \(k'(X,0)\) is well defined invariant of (X, 0).
The formula (4) can only be used to compute \({\text {Eu}}^\omega (X,0)\) from the homological index \({\text {Ind}}_{\mathrm {ind}}(\omega ,X,0)\) up to the constant \(k'(X,0)\) which is a sort of “residual homological index”. Since this invariant of (X, 0) is unknown in general, we propose a modification of the homological index in Sect. 4 which directly computes the Euler obstruction, i.e. for which the residual homological index always vanishes by construction. This new index will be based on the Nash transformation \(\nu :{{\tilde{X}}} \rightarrow X\) of (X, 0), the complex of sheaves \(\left( {\tilde{{\varOmega }}}^\bullet , \nu ^* \omega \wedge - \right) \) on \({{\tilde{X}}}\), and the derived pushforward of this complex along the proper map \(\nu \). It will therefore be called the derived homological index and it is in general different from the homological index defined in [10] and also harder to compute. However, the derived homological index has the further advantage that it is defined for arbitrarily singular spaces (X, 0).
3 Generalizations of the Milnor number
We briefly recall the necessary definitions of singularity theory on stratified spaces, cf. [24]. Let \(U \subset {\mathbb {C}}^n\) be an open domain, \(X \subset U\) a closed, reduced complex analytic set, and \(f :U \rightarrow {\mathbb {C}}\) a holomorphic function.
Definition 1
Suppose \(S = \{ {\mathscr {S}}_\alpha \}_{\alpha \in A}\) is a complex analytic Whitney stratification of X. A point \(p \in X\) is a regular point of f|X in the stratified sense, if it is a regular point of the restriction \(f|{\mathscr {S}}_\alpha \) of f to the stratum \({\mathscr {S}}_\alpha \) containing p.
The existence of complex analytic Whitney stratifications was shown by Hironaka [21]. In [26, Corollaire 6.1.8] Lê and Teissier constructed a canonical Whitney stratification for reduced, equidimensional complex analytic spaces, and in [32] it was shown that this stratification is minimal. Whenever one of these strata consists of several components, we shall in the following consider each one of these components as a stratum of its own and—unless otherwise specified—use this stratification on any given reduced equidimensional complex analytic space X.
Definition 2
We say that f has an isolated singularity at (X, p), if there exists a neighborhood \(U'\) of p such that all points \(x \in U' \cap X \setminus \{p\}\) are regular points of f in the stratified sense for the canonical Whitney stratification of X.
We give a brief definition of the Milnor fibration of f|(X, p) in this setting, cf. [24, Paragraphe (3.3) and Lemme 3.5]. Let \(B_\varepsilon \) be the ball of radius \(\varepsilon \) around p in \({\mathbb {C}}^n\). There exists \(\varepsilon _0>0\) such that for every \(\varepsilon _0 \ge \varepsilon >0\) the intersections \(\partial B_\varepsilon \cap X\) is transversal in the stratified sense, see e.g. [14, Part I, Section 1.4], [6], or [5]. Since f is a stratified submersion on (X, 0) away from the origin, the central fiber \(X \cap f^{-1}(\{f(p)\})\) is again Whitney stratified by the intersections of the strata of X with \(f^{-1}(\{f(p)\})\). We can apply the same arguments so that also \(\partial B_\varepsilon \cap X \cap f^{-1}(\{f(p)\})\) is a stratified transverse intersection for all \(\varepsilon _0\ge \varepsilon >0\). Fix one such \(\varepsilon = \varepsilon _0 >0\). Applying Thom’s isotopy lemma, we find that for sufficiently small \(\varepsilon \gg \delta >0\) the restriction of f
is a proper \(C^0\)-fiber bundle over the punctured disc \(D_\delta ^* \subset {\mathbb {C}}\) of radius \(\delta >0\) around f(p): the Milnor fibration of f|(X, p). The fiber
is unique up to homeomorphism and thus an invariant of f|(X, p).
3.1 Morsifications
For functions on stratified spaces the simplest singularities are the stratified Morse critical points. They generalize the classical Morse critical points of a holomorphic function in the sense that every function f with an isolated singularity on (X, p) can be deformed to a function with finitely many stratified Morse critical points on X, cf. Corollary 2. Thus, they are the basic building blocks for the study of isolated singularities on stratified spaces.
Definition 3
(cf. [14, Section 2.1]) A point \(p \in {\mathscr {S}}_\alpha \subset X\) is a stratified Morse critical point of f|X if
-
i)
the point p is a classical Morse critical point of the restriction \(f|{\mathscr {S}}_\alpha \) of f to the stratum \({\mathscr {S}}_\alpha \).
-
ii)
the differential \({\text {d}}f(p)\) of f at \(p \in {\mathbb {C}}^n\) does not annihilate any limiting tangent spaces \(T \subset T_p {\mathbb {C}}^n\) from other adjacent strata \({\mathscr {S}}_\beta \) of X at p.
Consider a point \(p \in U\) and the germ \(f :({\mathbb {C}}^n,p) \rightarrow ({\mathbb {C}},f(p))\) of f at p. An unfolding of f at p is a map germ
such that \(f= f_0\). It is clear that whenever \(p\in X\), any unfolding of f induces an unfolding \(F|(X,p)\times ({\mathbb {C}},0)\) of f|(X, p).
Definition 4
Let \((X,p) \subset ({\mathbb {C}}^n,p)\) be a reduced complex analytic space and \(f :({\mathbb {C}}^n,p) \rightarrow ({\mathbb {C}},f(p))\) a holomorphic function with isolated singularity on (X, p). An unfolding F of f induces a morsification of f|(X, p), if there exists an open neighborhoods \(V \subset {\mathbb {C}}^n\) of p and an open disc \(T \subset {\mathbb {C}}\) around the origin such that \(f_t|X\) has only Morse critical points in \(X \cap V\) for all \(0 \ne t \in T\).
For the existence of morsifications and the density of Morse functions in the stratified setting see for example [14]. We will usually take \(f_t(x) = f(x) - t \cdot l(x)\) for a generic linear form \(l \in {\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}})\), cf. [25] and Corollary 2.
We may choose the open neighborhood V in Definition 4 to be an open Milnor ball \(B_\varepsilon \) for f|(X, p). Then for \(t = \eta \ne 0\) sufficiently small, all Morse critical points of \(f_\eta \) on \(X \cap B_\varepsilon \) arise from the original singularity of \(f_0\) at \(0 \in X\) and we can count the number of Morse critical points of \(f_\eta \) on each stratum \({\mathscr {S}}_\alpha \) in \(X \cap B_\varepsilon \).
Definition 5
We define the numbers \(\mu _f(\alpha ;X,0)\) of f|(X, p) to be the number of Morse critical points on the stratum \({\mathscr {S}}_\alpha \) in a morsification of f|(X, p).
These numbers clearly depend on the choice of the stratification. However, it follows from [30, Proposition 2.3], that they do not depend on the choice of the morsification F|(X, p) of f|(X, p). This fact will also be a consequence of Theorem 1.
Example 2
We continue with Example 1. As a morsification of f|(X, 0) we may choose
Clearly, \(\mu _f(0;X,0) = 1\), because \({\mathscr {S}}_0\) is a one-point stratum and any such point is a critical point of a function in the stratified sense.
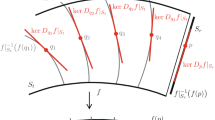
The real picture of the polar curves from Example 2 for the morsification of f on the regular locus of X; visualized as hyperplane sections together with the critical points of \(f_t\) for \(t=1\)
On \({\mathscr {S}}_1\) the function \(f_\eta \) has exactly one Morse critical point for \(\eta \ne 0\) (not pictured in Fig. 2). This can be verified by classical methods: note that \(X_1 = \overline{{\mathscr {S}}_1}\) is smooth and the restriction of f to \(X_1\) is an ordinary \(A_1\) singularity. The given morsification is moving this critical point from \(x=0\) to \(x=-t/2\) so that for \(t\ne 0\) it really lies in the stratum \({\mathscr {S}}_1\).
In order to compute \(\mu _f(2;X,0)\) let
be the global curve of critical points of \(f_t\) on the regular part \(X_{{\text {reg}}} = {\mathscr {S}}_2\) of the whole affine variety \(X \subset {\mathbb {C}}^3\). Using a computer algebra system, one can verify that the critical points of \(f_t\) on (X, 0) sweep out seven branches in \({\varGamma }\) under the variation of t. Five of these branches
pass through the origin \(0 \in {\mathbb {C}}^3\), i.e. they arise from the critical point of f on (X, 0). Note that \({\varGamma }_{4,5}(t)\) does not have real coordinates for \(t \in {\mathbb {R}}\setminus \{0\}\) so that these branches do not appear in the real picture in Fig. 2. However, their behaviour is symmetric to what happens with the real branches \({\varGamma }_{2,3}(t)\). Each one of these branches corresponds to a Morse critical point of \(f_t\) on \({\mathscr {S}}_2 \subset X\) and we drew them as dots in Fig. 2 for \(t=1\). Thus we have
The remaining two branches
are swept out from the points \(p_6\) and \(p_7\) and do not contribute to the number \(\mu _f(2;X,0)\) of f|(X, 0) at the origin. They lay on the horizontal component of the polar curve in the lower half of Fig. 2.
3.2 Homology decomposition for the Milnor fiber
The Milnor fiber \(M_{f|(X,0)}\) of a holomorphic function f on a complex analytic space \((X,0) \subset ({\mathbb {C}}^n,0)\) is by construction a topologically stable object: by virtue of Thom’s Isotopy Lemma, small perturbations of the defining equation f do not alter \(M_{f|(X,0)}\) up to homeomorphism. Consequently, in a morsification \(F = (f_t,t)\) of f|(X, 0) we may identify the Milnor fiber \(M_{f|(X,0)}\)
and the generic fiber \(B_\varepsilon \cap X \cap f_\eta ^{-1}(\{\delta \})\) of \(f_\eta \) for suitable choices of \(\varepsilon \gg \delta \gg \eta > 0\). For the previous example this is illustrated in the first two pictures of Fig. 3.
The classical theory of morsifications (see e.g. [1]) can be generalized to this setting using stratified Morse theory [14, Part II]. This leads to the following homology decomposition for the Milnor fiber:
Proposition 1
Let \((X,0) \subset ({\mathbb {C}}^n,0)\) be a complex analytic space, \(S = \{{\mathscr {S}}_\alpha \}_{\alpha \in A}\) a complex analytic Whitney stratification of X with connected strata, \({\mathcal {L}}(X,{\mathscr {S}}_\alpha )\) the complex link of X along the stratum \({\mathscr {S}}_\alpha \), \(C({\mathcal {L}}(X, {\mathscr {S}}_\alpha ))\) the real cone over it,
a holomorphic function with an isolated singularity on (X, 0) in the stratified sense, and \(M_{f|(X,0)}\) its Milnor fiber on X. Then the reduced homology of the Milnor fiber decomposes as
where \(d(\alpha ) = \dim ( {\mathscr {S}}_\alpha )\) is the complex dimension of the stratum \({\mathscr {S}}_\alpha \) and \(\mu _f(\alpha ;X,0)\) the number of Morse critical points on \({\mathscr {S}}_\alpha \) in a morsification of f.
Proposition 1 shows that the characterizations 1’) and 2’) of the numbers \(\mu _f(\alpha ;X,0)\) in Sect. 1 coincide. We will give a proof below, but first discuss some relations of Proposition 1 with various other results.
For f and (X, 0) as in Proposition 1 the vanishing Euler characteristic of f|(X, 0) is defined to be the reduced topological Euler characteristic of the Milnor fiber \({\overline{\chi }}\left( M_{f|(X,0)} \right) \). Now the homology decomposition provides a formula for this invariant as a linear combination of the numbers \(\mu _f(\alpha ;X,0)\):
Corollary 1
In the same setup as in Proposition 1 the vanishing Euler characteristic of f|(X, 0) is
Note that the coefficients \((-1)^{d(\alpha )-1} \cdot (1 - \chi ( {\mathcal {L}}(X, {\mathscr {S}}_\alpha )))\) depend only on the germ (X, 0), but not on the function f.
Remark 1
When (X, 0) is smooth, this formula reduces to the equality \({\overline{\chi }}(M_f) = \mu _f\) of the classical Milnor number and the reduced Euler characteristic of the Milnor fiber.
In the case where (X, 0) is equidimensional of dimension d with an isolated singularity at the origin, the right hand side has two summands:
The first one corresponds to the zero-dimensional stratum \({\mathscr {S}}_0 = \{0\} \subset X\) and the other one to the stratum \({\mathscr {S}}_1 = X_{{\text {reg}}}\) of smooth points of X. Since \({\mathscr {S}}_0\) is only a point, the number \(\mu _f(0;X,0)\) is always equal to one and \({\mathcal {L}}(X,\{0\})\) is the classical complex link of (X, 0). We wrote \(\mu _f(X,0)\) for the only other number of Morse critical points, omitting the index \(\alpha \) of the stratum.
We will see later on in Corollary 3 that \(\mu _f(X,0)\) equals \({\text {Eu}}^{{\text {d}}f}(X,0)\) and then Corollary 1 recovers a formula from [8, Proposition 4]:
See also the discussion of the relation with the Lê-Greuel formula in Example 4 below for the case that (X, 0) is an isolated complete intersection singularity.
Remark 2
We may also relate Corollary 1 to some results from [8] around the radial index for continuous 1-forms \(\omega \) with isolated singularity on (X, 0) as defined by Ebeling and Gusein-Zade in [10, Definition 2.1] and [8, Section 1]. Suppose (X, 0) is equidimensional of complex dimension d. Then according to [8, Theorem 3] the (complex) radial index of the 1-form \({\text {d}}f\) is
Substituting this into Corollary 1 we recover the formula from [8, Theorem 4]
in the special case where the 1-form \(\omega \) is of the form \({\text {d}}f\) for some function f.
Proof of Proposition 1
Choose \(\varepsilon > 0\) sufficiently small so that the squared distance function to the origin \(r^2 : {\mathbb {C}}^n \rightarrow {\mathbb {R}}_{\ge 0}\) does not have any critical points in the ball \(B_\varepsilon \) neither on X nor on \(X \cap f^{-1}(\{0\})\). After shrinking \(\varepsilon >0\) once more, if necessary, we may assume that the space \(B_\varepsilon \cap X \cap f^{-1}(\{0\})\) is a deformation retract of \(B_\varepsilon \cap X \cap f^{-1}(D_\delta ) \) for sufficiently small \(\varepsilon \gg \delta > 0\). In particular, the space \(B_\varepsilon \cap X \cap f^{-1}(D_\delta )\) is contractible.
Its boundary \(\partial ( B_\varepsilon \cap X \cap f^{-1}(D_\delta ))\) is topologically stable under small perturbations of f. So is the Milnor fiber
In any unfolding \(F = (f_t,t)\) of f we may therefore identify the pairs
for sufficiently small \(\varepsilon \gg \delta \gg \eta >0\).
After modifying \(f_\eta \) a little more we may assume that all critical values \(\{c_i\}_{i=1}^N\) of \(f_\eta \) are distinct points in the disc \(D_\delta \). Choose non-intersecting differentiable paths \(\gamma _i:[0,1] \rightarrow D_\delta \) from \(\delta \) to \(c_i\) and let \(\gamma _i([0,1])\) be its image in \(D_\delta \). By virtue of Thom’s First Isotopy Lemma, the map
is a \(C^0\)-fiber bundle away from the points \(c_i\) and the space \(B_\varepsilon \cap X \cap f_\eta ^{-1}(D_\delta )\) retracts onto \(f_\eta ^{-1}\left( \bigcup _{i=1}^N \gamma _i([0,1]) \right) \).
Along each path \(\gamma _i\), one attaches a so called thimble to \(B_\varepsilon \cap X \cap f_\eta ^{-1}(\{\delta \}) \cong M_{f|(X,0)}\). This thimble is given by the product of the tangential and the normal Morse datum of \(f_\eta \) at the critical point \(p_i\) over \(c_i\). See [14] for a definition of these. Altogether, we obtain
This finishes the proof of Proposition 1. \(\square \)
Remark 3
The existence of a homology decomposition as in (6) also follows from the bouquet decomposition of the Milnor fiber due to Tibăr [33] which is stronger in the sense that it holds on a homotopy level. But since its proof is not built on morsifications, it is a priori not clear that in general the numbers which play the corresponding role of the \(\mu _f(\alpha ;X,0)\) in the resulting homology decomposition coincide with the number of Morse critical points in a morsification. The interplay of Proposition 1 with Tibăr’s bouquet decomposition will be studied in a forthcoming note.
Example 3
We continue with Example 2. For \(t=1\) the critical point of the morsified function \(f_{1}\) on \({\mathscr {S}}_1\) is \((-1/2,0,0)^T\). On \({\mathscr {S}}_2 \subset X\) they are
The complex links \({\mathcal {L}} ( X, {\mathscr {S}}_\alpha )\) of X along the different strata are the following.
For \({\mathscr {S}}_0 = \{0\}\), it is the complex link of the Whitney umbrella (X, 0) itself, which is known to be the nodal cubic. Hence \(\mathcal (X,{\mathscr {S}}_0) \cong _{\mathrm {ht}} S^1\) is homotopy equivalent to a circle.
Along \({\mathscr {S}}_1\) the normal slice of X consists of two complex lines meeting transversally. The complex link is therefore a pair of points \({\mathcal {L}}(X,{\mathscr {S}}_1) \cong \{ q_1, q_2 \}\).
For the third stratum \({\mathscr {S}}_2\), the normal slice is a single point and the complex link is empty. We adapt the convention that the real cone over the empty set \(C(\emptyset ) = \{pt\}\) is the vertex pt of the cone (Fig. 4).
The homology decomposition for the Milnor fiber thus reads
where we write \({\mathbb {Z}}[e]\) for a shift of \({\mathbb {Z}}\) by e in the homological degree. In combination with the bouquet decomposition theorem from [33], we may even infer that \(M_{f|(X,0)}\) is homotopy equivalent to a bouquet of seven circles.
At this point it is apt to compare our results to the well known Lê-Greuel formulas for isolated complete intersection singularities [16, 22]. As we will see, the numerical invariants considered there are in general different from our numbers \(\mu _f(\alpha ;X,0)\).
Example 4
Suppose \(h = x^2+y^2-z^2\) so that \(X = \{h=0\} \subset {\mathbb {C}}^3\) is the double cone and let
Then both (X, 0) and \((X \cap f^{-1}(\{0\}),0)\) are isolated complete intersection singularities with Milnor fibers \(M_{h|({\mathbb {C}}^n,0)}\) and \(M_{f|(X,0)}\), respectively. It is well known that these Milnor fibers are homotopy equivalent to a bouquet of spheres of real dimension d equal to their complex dimensions, cf. [19], and we obtain the numbers
i.e. the classical Milnor numbers of the ICIS.
If we were to compute these numbers using the Lê-Greuel formulas, [22, Theorem 3.7.1] and [16, Korollar 5.5], we would proceed as follows. For suitable representatives we consider the restriction of the function f to the Milnor fiber \(M_{h|({\mathbb {C}}^3,0)}\), i.e. the canonical smoothing of (X, 0). We may choose a small, generic perturbation \({{\tilde{f}}}\) of f which has only Morse critical points on \(M_{h|({\mathbb {C}}^3,0)}\) and deliberately identify \(M_{f|(X,0)}\) with the subspace
for some \(1 \gg |\delta | > 0\). A part of the long exact sequence of the pair
\(\left( M_{h|({\mathbb {C}}^3,0)}, M_{f|(X,0)} \right) \) then reads
and it is easy to see using Morse theory that the term in the middle is a free \({\mathbb {Z}}\)-module of rank r equal to the number of Morse critical points of \({{\tilde{f}}}\) on \(M_{h|({\mathbb {C}}^3,0)}\).
Now \(b_{h|({\mathbb {C}}^3,0)} = 1\) can be deduced directly from Milnor’s classical formula. According to [16, Korollar 5.5], the number r can be computed as the length of an algebra:
By the last term we mean the \(2\times 2\)-minors of the Jacobian matrix of h and f. Then the exact sequence above yields \(b_{f|(X,0)} = 5\).
Let us now compute the homology of \(M_{f|(X,0)}\) along the lines of Proposition 1. The difference is that we do not consider a morsification of f on the smoothing of (X, 0), but on the singular space itself. We choose this morsification to be
and one finds that \(f_t\) has Morse critical points on the two-dimensional stratum \({\mathscr {S}}_2 := X_{{\text {reg}}}\) at only four points
Thus, \(\mu _f(2;X,0) = 4\) in this example and there is a free direct summand of rank 4 in the homology decomposition (6) of \(M_{f|(X,0)}\).
The part of the decomposition of \(H_1(M_{f|(X,0)})\) that is yet missing stems from the critical point of \(f_t\) on the zero dimensional stratum \({\mathscr {S}}_0 = \{0\}\) of X at the origin. It is now easy to see that the complex link \({\mathcal {L}}(X,\{0\})\) is nothing but the Milnor fiber of the restriction of the function h to the hyperplane \(\{x=0\}\) and therefore homotopy equivalent to a single sphere of dimension 1.
Altogether, this again yields \(H_2(M_{f|(X,0)}) \cong {\mathbb {Z}}\oplus {\mathbb {Z}}^4\) to be free of rank 5, but with an additional decomposition of this homology group as a direct sum. Note, however, that this decomposition depends on the particular choice of the space (X, 0) and the function f or—equivalent to that—it depends on the particular regular sequence (h, f). It is not an invariant of the ICIS \((X \cap f^{-1}(\{0\}),0) \subset ({\mathbb {C}}^3,0)\) since the latter is defined by the ideal \(\langle h, f \rangle \) which could also be given by any other set of generators.
Also note that in this example, the homological index as it was defined by W. Ebeling, S. Gusein-Zade, and J. Seade is in fact
due to [10, Theorem 3.2 (iii)]. That means, similar to the GSV index [12], it measures the number of critical points of a perturbation \({{\tilde{f}}}\) of the function f on the smoothing of (X, 0) and might therefore be better suited for the study of functions on isolated hypersurface and complete intersection singularities.
3.3 The Euler obstruction of a 1-form
In [30, Proposition 2.3], J. Seade et al. proved that
for the top dimensional stratumFootnote 3\({\mathscr {S}}_\gamma \). The Euler obstruction of a function is defined using the gradient vector field \({\text {grad}}f\). For the purposes of this note, it is more natural to consider the 1-form \({\text {d}}f\) and its canonical lift to the dual \({\tilde{{\varOmega }}}^1\) of the Nash bundle as we will describe below. This provides the notion of the Euler obstruction \({\text {Eu}}^{{\text {d}}f}(X,0)\) of the 1-form \({\text {d}}f\) on (X, 0), as was first defined by Ebeling and Gusein-Zade in [8]. In this section, we will follow their example and also consider the slightly more general case of an arbitrary 1-form \(\omega \) on (X, 0).
Throughout this section, we let \(U \subset {\mathbb {C}}^n\) be an open domain and \(X \subset U\) a reduced, complex analytic space. Suppose that X is equidimensional of dimension d. On the set of nonsingular points \(X_{{\text {reg}}}\) we can consider the map
taking any point p to the class of its tangent space \(T_p X\) as a subspace of \(T_p {\mathbb {C}}^n\) by means of the embedding of X.
Definition 6
The Nash transformation of X is the complex analytic closure of the graph
together with its projections

The restriction of the tautological bundle on \(U \times {\text {Grass}}(d,n)\) to \({{\tilde{X}}}\) will be referred to as the Nash bundle \({\tilde{T}}\). The dual bundle will be denoted by \({\tilde{{\varOmega }}}^1\).
For the dual of the Nash bundle there is a natural notion of pullback of 1-forms on X which is defined as follows. We can think of a point \((p,V) \in {\tilde{X}}\) as a pair of a point \(p\in X\) and a limiting tangent space V from \(X_{{\text {reg}}}\) at p. The space V can be considered both as a subspace of \(T_p {\mathbb {C}}^n\) and as the fiber of the Nash bundle \({\tilde{T}}\) at the point (p, V). Let us denote by \(\langle \cdot , \cdot \rangle \) the canonical pairing between a vector space and its dual. For a 1-form \(\omega \) on \({\mathbb {C}}^n\), a limiting tangent space V at p and a vector \(v \in V\) we define
Here we consider v as a point in the fiber of the Nash bundle over the point \((p,V) \in {\tilde{X}}\) on the left hand side and as a vector in \(V \subset T_p {\mathbb {C}}^n\) on the right hand side.
In order to define the Euler obstruction of a 1-form, we need to adapt Definitions 1 and 3 in this setup. Since for 1-forms there is no associated Milnor fibration, we may drop the assumption that the stratification of X satisfies Whitney’s condition B.
Definition 7
Let \(\omega \) be a holomorphic 1-form on \(U\subset {\mathbb {C}}^n\) and suppose \(S = \{ {\mathscr {S}}_\alpha \}_{\alpha \in A}\) is a complex analytic stratification of \(X\subset U\) satisfying Whitney’s condition A. We say that \(\omega |(X,p)\) is nonzero at a point \(p\in X\) in the stratified sense if \(\omega \) does not vanish on the tangent space \(T_p {\mathscr {S}}_\beta \) of the stratum \({\mathscr {S}}_\beta \) containing p. We say that a 1-form \(\omega \) on U has an isolated zero on (X, p), if there exists an open neighborhood \(U'\) of p such that \(\omega \) is nonzero on X in the stratified sense at every point \(x \in U' \cap X\setminus \{p\}\).
If in the following we do not specify a stratification, we again choose S to be the canonical Whitney stratification for a reduced, equidimensional complex analytic space X.
It is an immediate consequence of the Whitney’s condition A that at every point \(p\in X\) such that the restriction \(\omega |{\mathscr {S}}_\alpha \) of \(\omega \) to the stratum \({\mathscr {S}}_\alpha \) containing p is non-zero, also the pullback \(\nu ^* \omega \) is non-zero at any point \((p,V) \in \nu ^{-1}(\{p\})\) in the fiber of \(\nu :{\tilde{X}} \rightarrow X\) over p. In particular, \(\nu ^* \omega \) is a nowhere vanishing section on the preimage of a punctured neighborhood \(U'\) of p whenever \(\omega \) has an isolated zero on (X, p) in the stratified sense.
Definition 8
(cf. [8]) Let \((X,p) \subset ({\mathbb {C}}^n,p)\) be an equidimensional, reduced, complex analytic space of dimension d and \(\omega \) the germ of a 1-form on \(({\mathbb {C}}^n,p)\) such that \(\omega |(X,p)\) has an isolated zero in the stratified sense. The Euler obstruction \({\text {Eu}}^\omega (X,p)\) of \(\omega \) on (X, p) is defined as the obstruction to extending \(\nu ^* \omega \) as a nowhere vanishing section of the dual of the Nash bundle from the preimage \(\nu ^{-1}( \partial B_\varepsilon \cap X )\) of the real link \(\partial B_\varepsilon \cap X\) of (X, p) to the interior of \(\nu ^{-1}( B_\varepsilon \cap X)\) of the Nash transform. More precisely, it is the value of the obstruction class
of the section \(\nu ^*\omega \) on the fundamental class of the pair
\(\left( \nu ^{-1}(B_\varepsilon \cap X), \nu ^{-1}(\partial B_\varepsilon \cap X )\right) \):
As we shall see below, the Euler obstruction of a 1-form \(\omega \) with isolated singularity on (X, p) counts the zeroes on \(X_{{\text {reg}}}\) of a generic deformation \(\omega _\eta \) of \(\omega \). In the case \(\omega = {\text {d}}f\) for some function f with isolated singularity on (X, p), these zeroes correspond to Morse critical points of \(f_\eta \) on \(X_{{\text {reg}}}\) in an unfolding. We have seen before that these are not the only critical points of \(f_\eta \).
Definition 9
Suppose \(S = \{ {\mathscr {S}}_\alpha \}_{\alpha \in A}\) is a complex analytic stratification of X satisfying Whitney’s condition A. A point \(p \in X\) is a simple zero of \(\omega |X\), if the following holds. Let \({\mathscr {S}}_\beta \) be the stratum containing p and \(\sigma ( \omega |{\mathscr {S}}_\beta )\) the section of the restriction \(\omega |{\mathscr {S}}_\beta \) as a submanifold of the total space of the vector bundle \({\varOmega }^1_{{\mathscr {S}}_\beta }\). Denote the zero section by \(\sigma (0)\).
-
i)
The intersection of \(\sigma (\omega |{\mathscr {S}}_\beta )\) and the zero section
$$\begin{aligned} \sigma ( \omega |{\mathscr {S}}_\beta ) \pitchfork _p \sigma (0) \end{aligned}$$in the vector bundle \({\varOmega }^1_{{\mathscr {S}}_\beta }\) on \({\mathscr {S}}_\beta \) is transverse at p.
-
ii)
\(\omega \) does not annihilate any limiting tangent space V from a higher dimensional stratum at p.
Whenever \(\omega = {\text {d}}f\) for some holomorphic function f, this reduces precisely to the definition of a stratified Morse critical point p of f|X, Definition 3.
Analogous to morsifications we define an unfolding of a 1-form \(\omega \). Since \({\varOmega }^1_{U}\) is trivial, we can consider \(\omega \) as a holomorphic map \(U \rightarrow {\mathbb {C}}^n\). An unfolding of \(\omega \) is then given by a holomorphic map germ
Proposition 2
Any 1-form \(\omega \) with an isolated zero on (X, p) admits an unfolding \(W = (\omega _t,t)\) as above on some open sets \(U' \times T\) such that for a sufficiently small ball \(B_\varepsilon \subset U'\) around p and an open subset \(0 \in T' \subset T\) one has
-
i)
\(X\cap B_\varepsilon \) retracts onto the point p,
-
ii)
\(\omega = \omega _0\) on \(U'\) and \(\omega \) has an isolated zero on \(X \cap U'\),
-
iii)
for every \(t \in T'\), \(t \ne 0\), the 1-form \(\omega _t\) has only simple isolated zeroes on \(X \cap B_\varepsilon \) and is nonzero on \(X \cap U'\) at all boundary points \(x \in X \cap \partial B_\varepsilon \).
Moreover, \(\omega _t\) can be chosen to be of the form \(\omega _t = \omega - t \cdot {\text {d}}l\) for a linear form \(l \in {\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}})\).
Definition 10
We define the multiplicity \(\mu ^\omega ( \alpha ; X,p)\) of \(\omega |(X,p)\) to be the number of simple zeroes of \(\omega _t\) on \({\mathscr {S}}_\alpha \) for \(t \ne 0\) in an unfolding as in Proposition 2.
Again, we clearly have \(\mu _f(\alpha ;X,p) = \mu ^{{\text {d}}f}(\alpha ;X,p)\) in the case where \(\omega = {\text {d}}f\) is the differential of a function f with isolated singularity on (X, p). As a straightforward consequence we obtain:
Corollary 2
For a holomorphic function \(f :U \rightarrow {\mathbb {C}}\) with an isolated singularity in the stratified sense at (X, p) a morsification \(F = (f_t,t)\) of f|(X, p) can be chosen to be of the form
for a linear form \(l \in {\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}})\).
A statement similar to Corollary 2 has been proven by Lê in [25]. In order to be self-contained, we include a proof of our version for morsifications of 1-forms.
Proof of Proposition 2
We will show using Bertini-Sard-type methods that there exists a dense set \({\varLambda }\subset {\mathbb {P}}({\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}))\) of admissible lines such that the linear form l in Proposition 2 can be chosen to be an arbitrary non-zero linear form with \([l] \in {\varLambda }\).
For a fixed \(\alpha \) let \(X_\alpha = \overline{{\mathscr {S}}_\alpha }\) be the closure of the stratum \({\mathscr {S}}_\alpha \), \(d(\alpha )\) its dimension, and \(\nu :{\tilde{X}}_\alpha \rightarrow X_\alpha \) its Nash transform. Denote the fiber of \(\nu \) over the point \(p \in X\) by E. Since the question is local in p, we may restrict our attention to arbitrary small open neighborhoods of E of the form \(\nu ^{-1}(U')\) for some open set \(U' \ni p\). Set
and let \(\pi :N \rightarrow {\tilde{X}}_\alpha \) and \(\rho :N \rightarrow {\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}})\) be the two canonical projections. It is easy to see that N has the structure of a principle \({\mathbb {C}}^{n-d(\alpha )}\)-bundle over \({\tilde{X}}_\alpha \). In particular, the open subset \({{\mathscr {S}}}_\alpha ' = (\nu \circ \pi )^{-1}({\mathscr {S}}_\alpha ) \subset N\) is a complex manifold of dimension n.
Let \({\varPhi }:N \dashrightarrow {\mathbb {P}}({\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}))\) be the rational map sending a point \((x,V,\varphi )\) to the class \([\varphi ] \in {\mathbb {P}}({\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}))\). Since \(\omega \) had an isolated zero on (X, p), this map is regular on the dense open subset \(N\setminus (\pi \circ \nu )^{-1}(\{p\})\) which in particular contains \({\mathscr {S}}'_\alpha \). In order to work with regular and proper maps, we may resolve the indeterminacy of \({\varPhi }\) and obtain a commutative diagram

Suppose \(L \in {\mathbb {P}}({\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}))\) is a regular value of \({\hat{{\varPhi }}}|\hat{{\mathscr {S}}}_\alpha \), then \({\hat{{\varPhi }}}^{-1}(\{L\}) \cap \hat{{\mathscr {S}}}_\alpha \) is a smooth complex analytic curve. If we let \(C \subset N\) be the image in N of its analytic closure in \({\hat{N}}\), then evidently \(\rho |C :C \rightarrow L\) is a finite, branched covering at \(0 \in L\). It follows a posteriori from the Curve Selection Lemma that \(\rho \) is a submersion at every point \((x,V,\varphi ) \in C \cap {\mathscr {S}}'_\alpha \) in a neighborhood of E. An inspection of the differential of \(\rho \) at such a point \((x,V,\varphi )\) reveals that the transversality requirement i) in Definition 9 is satisfied for the 1-form \(\omega - {\text {d}}\varphi \) at x. Conversely, this means that for every nonzero linear form \(l \in L\) and every sufficiently small \(t \ne 0\) the 1-form \(\omega - t \cdot {\text {d}}l\) has only isolated zeroes at those points \(x \in {\mathscr {S}}_\alpha \), for which \((x, V, t\cdot l) \in C\). Repeating this process for every stratum, we obtain a dense set \({\varLambda }_1 \subset {\mathbb {P}}({\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}))\) of pre-admissible lines.
In order to verify also the requirement ii) in Definition 9, we proceed as follows. Let \(Y_\alpha = X_\alpha \setminus {\mathscr {S}}_\alpha \) be the union of limiting strata of \({\mathscr {S}}_\alpha \) and \(\tilde{Y}_\alpha \), \(Y'_\alpha \), and \(\hat{Y}_\alpha \) their preimages in \({\tilde{X}}_\alpha \), N, and \({\hat{N}}\), respectively. These three spaces might have rather difficult geometry, but evidently \(\dim {\hat{Y}}_\alpha < \dim {\hat{N}} = n\) and the map \({\hat{Y}}_\alpha \rightarrow Y_\alpha \) is surjective.
There exists a dense subset \({\varLambda }_2 \subset {\mathbb {P}}({\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}))\) such that the restriction \({\hat{{\varPhi }}}|{\hat{Y}}_\alpha \) has at most discrete fibers over \({\varLambda }_2\). To see this, we may for example stratify \({\hat{Y}}_\alpha \) by finitely many locally closed complex submanifolds \(M_i\) and choose \({\varLambda }_2\) as the set of all regular values of \({\hat{{\varPhi }}}| M_i\). Since \(\dim M_i \le \dim {\hat{Y}}_\alpha < n\), the fiber \({\hat{Q}} = ({\hat{{\varPhi }}}|{\hat{Y}}_\alpha )^{-1}(L)\) of a point \(L \in {\varLambda }_2\) is discrete and so is its image \(Q \subset N\), because \({\hat{N}} \rightarrow N\) is proper. This means that for a given \(l \in L\) there are only finitely many preimages \((x,V,l) \in \rho ^{-1}(L)\), i.e. the set of points \(x \in X\), for which \(\omega - {\text {d}}l\) annihilates a limiting tangent space V at x is finite in a neighborhood of p. We may choose \(U'\) and \(B_\varepsilon \) sufficiently small to avoid those points.
To conclude the proof set \({\varLambda }= {\varLambda }_1 \cap {\varLambda }_2\), choose a linear form \(0 \ne l \in L\) for some \(L \in {\varLambda }\) and adjust the choices of \(U'\) and \(B_\varepsilon \) accordingly. Since \(\partial B_\varepsilon \cap X\) is compact there will be no zeroes of \(\omega _t = \omega - t \cdot {\text {d}}l\) on the boundary for small variations of t and \(T'\) can be chosen so that this holds for all \(t \in T'\). \(\square \)
We are now prepared to show equivalence of 1’) and 3’), in parallel to [30, Proposition 2.3].
Proposition 3
For every 1-form \(\omega \) on U with an isolated zero on (X, p) we have
where \(X_\alpha = \overline{{\mathscr {S}}_\alpha }\) is the closure of the stratum \({\mathscr {S}}_\alpha \).
Proof
Choose a representative
of an unfolding of \(\omega |(X,p)\) and a ball \(B_\varepsilon \subset U'\) as in Proposition 2. The Euler obstruction of \(\omega \) at \((X_\alpha ,p)\) depends only on its obstruction class
Being a homotopy invariant, this class does not change under small perturbations and it is therefore evident from the definitions that for every \(\eta \in T\) and every \(\alpha \in A\) one has
We may therefore select one \(\eta \ne 0\) and use \(\omega _\eta \) instead of \(\omega \) to compute the Euler obstruction. The evaluation of the obstruction class counts the number of zeroes of \(\omega _\eta \). Observe that by construction, \(\nu ^* \omega \) is nonzero at any point \((x,V) \in {\tilde{X}}_\alpha \setminus \nu ^{-1}({\mathscr {S}}_\alpha )\), because \(\omega _\eta \) does not annihilate any limiting tangent space V at x. Thus, the zeroes of \(\nu ^* \omega _\eta \) are located in \(\nu ^{-1}( {\mathscr {S}}_\alpha )\). At every such zero \((x,V) \in \nu ^{-1}({\mathscr {S}}_\alpha )\) of \(\omega _\eta \) the intersection of \(\sigma (\omega _\eta |{\mathscr {S}}_\alpha )\) and the zero section in \({\varOmega }^1_{{\mathscr {S}}_\alpha }\) is transverse with positive orientation and therefore contributes an increment of 1 to the Euler obstruction. Consequently, \({\text {Eu}}^\omega (X_\alpha ,p)\) coincides with \(\mu ^\omega (\alpha ; X,p)\). \(\square \)
Corollary 3
Whenever \(f :U \rightarrow {\mathbb {C}}\) is a holomorphic function with isolated singularity on (X, p), we have
Example 5
We continue with Example 3. For \(\alpha = 0\) the real link of \((\overline{{\mathscr {S}}_0},0)\) is empty and the Euler obstruction is 1 by convention.
In the case \(\alpha = 1\) the closure \(X_1 = \overline{{\mathscr {S}}}_1\) of the stratum \({\mathscr {S}}_1\) is already a smooth line. Consequently, the Nash transformation \(\nu :{\tilde{X}}_1 \rightarrow X_1\) is an isomorphism and \({\tilde{{\varOmega }}}^1\) coincides with the usual sheaf of Kähler differentials. In this case, the Euler obstruction of \({\text {d}}f\) on \((X_1,0)\) coincides with the degree of the map
Since \(0 \in X_1\) is a classical Morse critical point, \({\text {d}}f\) has a simple, isolated zero on \((X_1,0)\) and therefore
In this particular case of a function on a complex line, the computation of the Euler obstruction reduces to Rouché’s theorem.
For \(\alpha = 2\) we really need to work with the Nash transformation and the morsification \(F=(f_t,t)\) of f|(X, 0). To this end, we identify \({\text {Grass}}(2,3)\) with its dual Grassmannian \({\text {Grass}}(1,3) \cong {\mathbb {P}}^2\) via
In homogeneous coordinates \((s_0:s_1:s_2)\) of \({\mathbb {P}}^2\) the rational map \({\varPhi }\) from (7) is given by the differential of h:
The equations for \({\tilde{X}} \subset {\mathbb {P}}^2 \times {\mathbb {C}}^3\) are rather complicated, but they simplify in the canonical charts of \({\mathbb {P}}^2 \times {\mathbb {C}}^3\). We will consider the chart \(s_0 \ne 0\), leaving the computations in the other charts to the reader. The equations for \({\tilde{X}}\) read
In particular, we can use \((z,s_1)\) as coordinates on \({\tilde{X}} \cap \{ s_0 \ne 0 \} \cong {\mathbb {C}}^2\). The exceptional set \(E \subset {\tilde{X}}\), i.e. the set of points \(q\in {\tilde{X}}\), at which \(\nu :{\tilde{X}} \rightarrow X\) is not a local isomorphism, is the preimage of the x-axis in \({\mathbb {C}}^3\). In the above coordinates it is given by
Let \({\mathcal {O}}(-1)\) be the (relative) tautological bundle on \({\mathbb {P}}^2 \times {\mathbb {C}}^3\). The dual bundle \({\mathcal {O}}(1)\) has a canonical set of global sections \(e_0,e_1,e_2\) in correspondence with the homogeneous coordinates \((s_0:s_1:s_2)\). With these choices the differential of \(f_t = y^2 - (x-z)^2 - t(x+2z)\) pulls back to
We consider \(\nu ^* {\text {d}}f_t\) as a section in \({\tilde{{\varOmega }}}^1\), the dual of the Nash bundle \({\tilde{T}}\). Note that \({\tilde{T}}\) appears as part of the Euler sequence

on \({\tilde{X}}\). The standard trivialization of \({\tilde{T}}\) in the chart \(s_0 \ne 0\) is given by the sections
and therefore the zero locus of \(\nu ^* {\text {d}}f_t\) on \({\tilde{X}}\) is given by the equations \(\nu ^*{\text {d}}f_t(v_1) = \nu ^* {\text {d}}f_t(v_2) = 0\). Substituting all the above expressions we obtain
It is easy to see that for \(t = 0\) the exceptional set \(E = \{z=0\}\) is contained in the zero locus of \(\nu ^* {\text {d}}f_0\). In particular, the zero locus is non-isolated and we can not use \(\nu ^* {\text {d}}f_0\) to compute the Euler obstruction as in the proof of Proposition 3.
For \(\eta \ne 0\), however, the zero locus of \(\nu ^* {\text {d}}f_\eta \) consists of only finitely many points. A primary decomposition reveals that there are seven branches
in the local coordinates \((z,s_1)\) of \({\tilde{X}}\). They are precisely taken to the corresponding branches \({\varGamma }_i(t)\) from Example 2 by \(\nu \). Again, only the first five of them have limit points close to \(\nu ^{-1}(\{0\})\) for \(t \rightarrow 0\), i.e. only the first five branches contribute to \({\text {Eu}}^{{\text {d}}f}(X,0)\) for sufficiently small \(\varepsilon \gg \eta >0\). Therefore,
as anticipated.
Remark 4
Definition 10 and Proposition 2 suggest yet another interpretation of the numbers \(\mu ^\omega (\alpha ;X,p)\), namely as microlocal intersection numbers—a point of view which has also been used in [28]. For a stratum \({\mathscr {S}}_\alpha \) of X and its closure \(X_\alpha \) one can define the conormal cycle of \({\mathscr {S}}_\alpha \) as
This is an analytic subvariety of the total space of the vector bundle \({\varOmega }^1_U\). So is the section \(\sigma (\omega )\) of \(\omega \) on U. In this context, Proposition 2 appears as a moving lemma, which puts the two varieties in a general position. Clearly, the local intersection multiplicity \(\left( {\varLambda }_\alpha \circ \sigma (\omega )\right) \) of the two varieties at \((p,0) \in {\varOmega }^1_U\) coincides with \(\mu ^\omega (\alpha ;X,p) = {\text {Eu}}^\omega (X_\alpha ,p)\). See also [2, Corollary 5.4].
4 The Euler obstruction as a homological index
Throughout this section let again \(U \subset {\mathbb {C}}^n\) be an open domain and \(X \subset U\) a closed, equidimensional, reduced, complex analytic space.
For a holomorphic function \(f :U \rightarrow {\mathbb {C}}\) with an isolated singularity on X at a point \(p\in X\), Proposition 3 and Corollary 3 suggest the following interpretation of the Euler obstruction: in a morsification \(F = (f_t,t)\) of f|(X, p) the singularities of f|(X, p) become Morse critical points on the regular strata \({\mathscr {S}}_\alpha \). In this sense, a morsification separates the singularities of the function f|(X, p) from the singularities of the space (X, p) itself. The Euler obstructions \({\text {Eu}}^{{\text {d}}f}\left( X_\alpha ,p\right) \) of \({\text {d}}f\) on the closures \(X_\alpha = \overline{{\mathscr {S}}}_\alpha \) of the strata know the outcome of this separation beforehand and even without a given concrete morsification. A particular, but remarkable consequence of these considerations is that \({\text {Eu}}^{{\text {d}}f}(X_\alpha ,p) = 0\) for all \(\alpha \in A\) whenever f does not have a singularity on (X, p)—independent of the singularities of the germ (X, p) itself.
Suppose for the moment that also the space (X, p) has itself only an isolated singularity so that the homological index \({\text {Ind}}_{\hom }({\text {d}}f, X,p)\) as in [10] is defined. The comparison of \({\text {Eu}}^{{\text {d}}f}(X,p)\) with \({\text {Ind}}_{\hom }({\text {d}}f, X, p)\) is based on the fact that both the Euler obstruction and the homological index satisfy the law of conservation of number and that they coincide at Morse critical points. In an arbitrary unfolding \(F = (f_t,t)\) of f|(X, p) we can therefore use both the Euler obstruction and the homological index to count the number of Morse critical points on \(X_{{\text {reg}}}\) arising from f|(X, p). But for a fixed unfolding parameter \(t = \eta \) only the Euler obstruction \({\text {Eu}}^{{\text {d}}f_\eta }(X,p)\) can be used to measure whether \(f_\eta \) is still singular at (X, p) or whether all singularities of f have left from the point p for \(t = \eta \ne 0\). If the latter is the case—as for example in a morsification—the homological index \({\text {Ind}}_{\hom }({\text {d}}f_{\eta },X,p)\) is
The number \(k'(X,p)\) is an invariant of the space (X, p), but unknown in general. Therefore, the homological index \({\text {Ind}}_{\hom }({\text {d}}f,X,p)\) can not be used to count the number of Morse critical points on \(X_{{\text {reg}}}\) in a morsification; it only separates the singularities of the function f from the singularities of X up to an unknown quantity.
We return to the more general setting of an arbitrarily singular \(X \subset U\). Suppose \(\omega \) is a holomorphic 1-form on U and let \(p\in X\) be a point for which \(\omega \) has an isolated zero on (X, p). Then \({\text {Eu}}^\omega (X_\alpha ,p)\) is counting the number of simple zeroes on \({\mathscr {S}}_\alpha \) close to p in a generic perturbation \(\omega _\eta \) of \(\omega \). It is evident from the construction that we may restrict our attention to the case where \(X = X_\alpha = \overline{{\mathscr {S}}}_\alpha \) is irreducible and reduced and we only need to consider isolated zeroes of \(\omega _\eta \) on \(X_{{\text {reg}}}\). Translating the previous discussion to this setting we see that—conversely—a homological index \(I(\omega ,X,p)\) has to coincide with the Euler obstruction \({\text {Eu}}^\omega (X,p)\) whenever the following two conditions are met:
- \((\dagger )\):
-
\(I(\omega ,X,p)\) coincides with \({\text {Eu}}^\omega (X,p)\) at any smooth point p of X.
- \((\ddagger )\):
-
For every singular point p of X one has
$$\begin{aligned} I(\omega ,X,p) = 0 \end{aligned}$$whenever \(\omega \) is a 1-form such that \(\omega |(X,p)\) is nonzero or has at most a simple zero at p in the stratified sense.
It is therefore worthwhile to investigate once again the structural reasons as to why \((\dagger )\) is satisfied for \({\text {Ind}}_{\hom }(\omega ,X,p)\) at smooth points and why \({\text {Eu}}^{\omega }(X,p) = 0\) whenever \(\omega \) has at most a simple zero on X at a point p on a lower dimensional stratum. We will exploit these reasons for the construction of the derived homological index in Theorem 1 which then satisfies \((\dagger )\) and \((\ddagger )\) simultaneously.
The fact that the homological index of a 1-form \(\omega \) with an isolated zero at a smooth point \((X,p) \cong ({\mathbb {C}}^n,p)\) coincides with its Euler obstruction and its topological index is based on the following observation. In local coordinates \(x_1,\dots ,x_n\) of (X, p), the complex (3) becomes a Koszul complex on the local ring \({\mathcal {O}}_{X,p}\) in the components of \(\omega = \sum _{i=1}^n \omega _i {\text {d}}x_i\). Since \({\mathcal {O}}_{X,p}\) is Cohen-Macaulay and the zero locus of \(\omega \) is isolated, the \(\omega _i\) must form a regular sequence on \({\mathcal {O}}_{X,p}\) and the following lemma applies, cf. [4, Corollary 1.6.19].
Lemma 1
Let \((R, {\mathfrak {m}})\) be a Noetherian local ring, \(M = R^r\) a free module, \(v = \left( v_1,\dots ,v_r\right) ^T \in M\) an element and

the Koszul complex associated to v. We consider \(R = \bigwedge ^0 M\) to be situated in degree zero, \(M = \bigwedge ^1 M\) in degree one, etc.
-
i)
Whenever \((v_1,\dots ,v_r)\) is a regular sequence on R as an R-module, then (9) is exact except for the last step where we find
$$\begin{aligned} H^r\left( K^\bullet (v,R) \right) = R / \langle v_1,\dots ,v_r\rangle . \end{aligned}$$ -
ii)
Whenever \(v \notin {\mathfrak {m}} M\), the Koszul complex is exact.
Consequently, \({\text {Ind}}_{\hom }(\omega ,X,p) = \dim _{{\mathbb {C}}} {\mathcal {O}}_{X,p}/\langle \omega _1,\dots ,\omega _n\rangle \) at a smooth point p of X and this evaluates to 1 on simple zeroes of \(\omega \). Part ii) of this lemma explains why the homological index of \(\omega \) is zero at all smooth points where \(\omega \) does not vanish.
From this viewpoint, the difficulty in comparing the Euler obstruction of a 1-form \(\omega \) at a singular point p of X with its homological index at p stems from the fact that the restriction \(\omega |(X,p)\) is not anymore an element of a free module, but of the module of Kähler differentials \({\varOmega }_{X,p}^1\). The key idea is to address this issue by replacing \({\varOmega }^1_{X,p}\) and \(\omega \) with the Nash bundle \({\tilde{{\varOmega }}}^1\) and the section \(\nu ^* \omega \). In order to work with finite \({\mathcal {O}}_X\)-modules we need to consider the derived pushforward of the associated bundles. The following Lemma establishes the requirement \((\ddagger )\) for the derived homological index in Theorem 1 as motivated from Lemma 1 ii).
Lemma 2
Let \(U \subset {\mathbb {C}}^n\) be an open domain, \(X\subset U\) an irreducible and reduced closed analytic subspace of dimension d, and \(\nu :{\tilde{X}} \rightarrow X\) its Nash transformation. For any point \(p \in X\) the stalk at p of the complex of sheaves
is exact, whenever \(\omega \) does not annihilate any limiting tangent space V from \(X_{{\text {reg}}}\) at p.
Proof
The statement that \(\omega \) does not annihilate any limiting tangent space V of a top-dimensional stratum at p is equivalent to saying that \(\nu ^{*}\omega \) is nonzero at every point \((p,V) \in {\tilde{X}}\) in the fiber \(\nu ^{-1}(\{p\})\) of the Nash transformation over p. If \(\nu ^* \omega \) is nonzero then, according to Lemma 1 ii), the complex of sheaves

is exact along \(\nu ^{-1}( \{ p\})\) and therefore quasi-isomorphic to the zero complex. Consequently, also the stalk at p of the derived pushforward of this complex has to vanish. \(\square \)
Theorem 1
Suppose \(U \subset {\mathbb {C}}^n\) is an open domain, \(X \subset U\) a reduced, equidimensional complex analytic subspace of dimension d, endowed with a complex analytic stratification satisfying Whitney’s condition A. Let \(\omega \) be a holomorphic 1-form on U with an isolated zero on X in the stratified sense at a point p. Then
where \(\nu :{\tilde{X}} \rightarrow X\) is the Nash transformation and \(({\tilde{{\varOmega }}}^\bullet , \nu ^*\omega \wedge - )\) is the complex of coherent sheaves on \({\tilde{X}}\) given by the exterior powers of the Nash bundle and multiplication with \(\nu ^*\omega \).
Corollary 4
Let \((X,p) \subset ({\mathbb {C}}^n,p)\) be a reduced complex analytic space with a complex analytic Whitney stratification \(S = \{{\mathscr {S}}_\alpha \}_{\alpha \in A}\). Suppose
is a holomorphic function with an isolated singularity on (X, p). For \(\alpha \in A\) let \(\nu :{\tilde{X}}_\alpha \rightarrow X_\alpha \) be the Nash transformation of the closure \(X_\alpha = \overline{ {\mathscr {S}}_\alpha }\) and \({\tilde{{\varOmega }}}^k_\alpha \) the k-th exterior power of the dual of the Nash bundle on \({\tilde{X}}_\alpha \). Then
Proof
We may apply Theorem 1 to the space \(X_\alpha = \overline{{\mathscr {S}}_\alpha }\) and the restriction of the 1-form \({\text {d}}f\) to it. \(\square \)
Proof of Theorem 1
The sheaves in the complex \({\mathbb {R}} \nu _* ({\tilde{{\varOmega }}}^\bullet , \nu ^* \omega \wedge - )\) are finite \({\mathcal {O}}_n\)-modules since the morphism \(\nu \) is proper. By assumption, \(\omega \) has an isolated zero on (X, p) in the stratified sense and hence Lemma 2 implies that the cohomology of this complex is supported at the origin. In particular, its Euler characteristic is finite.
Suppose \(W = (\omega _t,t)\) is an unfolding of \(\omega |(X,p)\) as in Proposition 2 and—possibly after shrinking U—let
be a suitable representative thereof. Denote by \(\pi :U \times T \rightarrow T\) the projection to the parameter t. The unfolding of \(\omega \) induces a family of complexes of sheaves \(\left( {\tilde{{\varOmega }}}^\bullet , \nu ^* \omega _t \wedge -\right) \) on the Nash transform \({\tilde{X}}\) and hence also on the derived pushforward. This furnishes a complex of coherent sheaves
on \(U \times T\) which becomes a family of complexes over T via the projection \(\pi \). Clearly, every sheaf \(R^k \nu _* {\tilde{{\varOmega }}}^r\) is \(\pi \)-flat. We may apply the main result of [12]: there exist neighborhoods \(p \in U' \subset U\) and \(0 \in T' \subset T\) such that for every \(\eta \in T'\) we have
i.e. the Euler characteristic satisfies the law of conservation of number.
Suppose \(U', T'\) and \(B_\varepsilon \) have also been chosen as in Proposition 2 and fix \(\eta \in T'\), \(\eta \ne 0\). By construction, \(\omega _\eta \) has only simple, isolated zeroes on the interior of \(X \cap B_\varepsilon \) and none on the boundary.
Whenever \(x \in (X \setminus X_{{\text {reg}}}) \cap B_\varepsilon \) is such a point, at which \(\omega _\eta \) has a simple zero outside \(X_{{\text {reg}}}\), the restriction of \(\omega _\eta \) to any limiting tangent space V of \(X_{{\text {reg}}}\) at x is nonzero and consequently
according to Lemma 2.
Whenever \(x \in X_{{\text {reg}}} \cap B_\varepsilon \) is a point with a simple zero of \(\omega _\eta \) at x we find the following. The Nash transformation \(\nu \) is a local isomorphism around x and therefore
is the Koszul complex on the modules \({\varOmega }^k_{X,x}\). Lemma 1 allows us to compute the Euler characteristic
The statement now follows from the principle of conservation of number. \(\square \)
5 Explicit computations for a function on a singular hypersurface
The following section will be phrased in purely algebraic terms. This is due to the fact that the complex numbers do not form a computable field and also the ring of convergent power series is often unavailable in computer algebra systems for symbolic computations. For these reasons, we will assume that both \((X,0) \subset ({\mathbb {C}}^n,0)\) and either f or \(\omega \) as in Theorem 1 or Corollary 4 are algebraic and defined over some finite extension field K of \({\mathbb {Q}}\). More generally, we will work with proper maps

of algebraic spaces and coherent algebraic sheaves \({\mathcal {F}}\) on \({\tilde{X}}\) which are given in terms of some finitely presented, graded module M over the ring
In our applications in Sect. 5.2 the map \(\pi \) will be the projection of the Nash transformation and \({\mathcal {F}}\) should be thought of as one of the exterior powers of the dual of the Nash bundle.
It is well known that for any coherent algebraic sheaf \({\mathcal {F}}\) on \({\tilde{X}}\) the sheaves \(R^p\pi _*({\mathcal {F}})\) are \({\mathcal {O}}_{X}\)-coherent. Let \({\mathcal {O}}_{X}^h\), \({\mathcal {O}}_{{\tilde{X}}}^h\), and \({\mathcal {F}}^h\) be the respective analytifications. Grauert’s theorem on direct images [15] assures that also the direct images \(R^p\pi _*({\mathcal {F}}^h)\) are \({\mathcal {O}}_X^h\)-coherent and using Čech cohomology we obtain a natural morphism of cohomology sheaves
for every p.
Whenever \({\mathcal {F}}\) is given by a graded module M as above, one can express the higher direct images of \({\mathcal {F}}\) in terms of the cohomology of the relative twisting sheaves \({\mathcal {O}}(-w)\) on \({\mathbb {P}}^r \times ({\mathbb {C}}^n,0)\) (cf. Propositions 4, Proposition 5 below) and vice versa for the respective analytifications. Now the formal completions of the rings
are isomorphic and so are the formal completions of
for all p and w.
In the particular cases we will be considering, the sheaf \({\mathcal {F}}\)—or, more generally, a complex of sheaves \({\mathcal {F}}^\bullet \)—will always be of a form such that the modules \(R^p \pi '_*{\mathcal {F}}\) and \(R^p \pi '_*({\mathcal {F}}^h)\), or, respectively, the cohomology sheaves of \({\mathbb {R}}\pi '_* {\mathcal {F}}^\bullet \) and \({\mathbb {R}}\pi '_*({\mathcal {F}}^\bullet )^h\), have at most isolated support at the origin. Thus, in either one of the settings the canonical maps to the formal completions of the cohomology modules are isomorphisms of vector spaces and it follows that the comparison morphisms \(\varepsilon \) above are isomorphisms in this case as well. With the given restrictions on \({\mathcal {F}}\) or \({\mathcal {F}}^\bullet \), we may therefore carry out all the computations of the Euler characteristics of the coherent analytic sheaves derived from \({\mathcal {F}}^h\) or \(({\mathcal {F}}^\bullet )^h\) on \(X^h\) in the purely algebraic setting over the field K.
Example 6
We continue with Example 5 and prepare for the explicit computation. As previously discussed, the only interesting stratum of X is \({\mathscr {S}}^2= X_{{\text {reg}}}\). To compute the number \(\mu _f(2;X,0)\) we will describe a complex of graded S-modules representing \(({\tilde{{\varOmega }}}^\bullet ,\nu ^* {\text {d}}f\wedge -)\). We set \(A = {\mathbb {C}}[x,y,z]\), \(S= A[s_0,s_1,s_2]\) and consider S as a homogeneous coordinate ring of \({\mathbb {P}}^2_A\) over A. The ideal \(J\subset S\) of homogeneous equations for the Nash transform \({\tilde{X}}\) is obtained from the equations for the total transform by saturation: denote by L the ideal of \(2\times 2\)-minors of the matrix
Over \(X_{{\text {reg}}}\) these equations describe the graph of the rational map \({\varPhi }\) underlying the Nash blowup (7). Now
where \(\langle y,z\rangle \) is the ideal defining the singular locus of X on which \({\varPhi }\) is not defined.
Let \(Q^p\) be the module representing \(\bigwedge ^p {\mathcal {Q}}\) with \({\mathcal {Q}}\) the tautological quotient bundle on \({\mathbb {P}}^2_A\). A graded, free resolution of the \(Q^p\) is given by appropriate shifts of the Koszul complex in the s-variables. Let
be the tautological section. Together with
we obtain the following double complex.

For every q the module \(M^q\) representing the restriction \(\bigwedge ^q {\tilde{{\varOmega }}}^1\) of \({\mathcal {Q}}^q\) to \({\tilde{X}}\) is given by \(Q^q \otimes S/J\). The complex of sheaves \(({\tilde{{\varOmega }}}^\bullet , \nu ^*{\text {d}}f\wedge -)\) on \({\tilde{X}}\) is thus represented by the complex of graded modules
As we shall see in the next section, Proposition 5, we can compute the derived pushforward \({\mathbb {R}}\nu _*({\tilde{{\varOmega }}}^\bullet , \nu ^* {\text {d}}f\wedge -)\) via a truncated Čech-double-complex on the complex of modules \((M^\bullet , \nu ^* {\text {d}}f \wedge - )\).
5.1 Derived pushforward on relative projective space
Let A be a commutative Noetherian ring. We set \(S = A[s_0,\dots ,s_{r}]\) and consider S as a graded A-algebra. On the geometric side let
be the associated projection. Let \({\mathcal {O}}= {\tilde{S}}\) be the structure sheaf of \({\mathbb {P}}^r_A\) and \({\mathcal {O}}(-w)\) the relative twisting sheaves for \(w \in {\mathbb {Z}}\). Given a finitely generated graded S-module M let \({\tilde{M}}\) be the corresponding of \({\mathcal {O}}\)-modules on \({\mathbb {P}}^r_A\). We will first describe how to compute \({\mathbb {R}}\pi _* ({\tilde{M}})\) as a complex of finitely generated A-modules up to quasi-isomorphism and then generalize these results for complexes of finite, graded S-modules \((M^\bullet ,D^\bullet )\) and their associated complexes of sheaves on \({\mathbb {P}}^r_A\).
To this end, we may use Čech cohomology with respect to the canonical open covering of \({\mathbb {P}}^r_A\). For a graded S-module M let
These modules are not finitely generated over S, but they have a natural structure as a direct limit of finite S-modules given by the submodules
The Čech complex on M is obtained from \({\check{C}}^p(M)\) and the differentials \({\check{{\text {d}}}}\, :{\check{C}}^p(M) \rightarrow {\check{C}}^{p+1}(M)\) taking an element
to the element in \({\check{C}}^{p+1}(M)\) with its \((j_{0},\dots ,j_{p+1})\)-th component given by
As usual, the hat \(\hat{\cdot }\) indicates that the index is to be omitted. We will write
for the p-th cohomology of the Čech complex on a module M and its truncations.
The modules \(S(-w)\) and the corresponding twisting sheaves \({\mathcal {O}}(-w)\) have a well known cohomology, see [20, Chapter III.5]. We deliberately identify
and set
The last term has a structure as a direct limit of S-modules via the maps
The pairing of monomials
provides us with an identification
for all \(w \in {\mathbb {Z}}\). Note that this pairing is compatible with the natural S-module structure on both sides.
Proposition 4
Let M be a graded S-module and

an exact complex. Let \(\left( \bigoplus _{i_\bullet =1}^{r_\bullet } E(w_{\bullet ,i_\bullet }), D^\bullet \right) \) be the complex with the S-module \(\bigoplus _{i_{-k}=1}^{r_{-k}} E(w_{-k,i_{-k}})\) as in (14) in cohomological degree \(-k\) and \(D^k\) the differentials induced by the same differentials as those in \(K^\bullet \). Then there is a short exact sequence

and isomorphisms
for \(0 < p \le r\).
Proof
The statements follow from a diagram chase in the double complex (15). Note that in (15) all columns but the last one are exact by construction. The same holds for all rows but the first one. Since taking cohomology commutes with direct sums, the complex
is identical with the last column of (15), while the first row is the Čech complexon M. \(\square \)

We can use Proposition 4 to describe \({\mathbb {R}}\pi _* ({\tilde{M}})\) as a complex of finite A-modules. Choose any
and let
be the inclusions of finite S-modules as before. The restriction on the choice of d assures that the degree zero part of every \(E(-w_{-k,i_{-k}})\) is fully contained in the image of \({\varPsi }^{-k}_d\). Consequently, the homomorphism of complexes in degree zero
is an isomorphism of complexes of finite A-modules.
In other words, there is a short exact sequence of free finite A-modules

and isomorphisms
for \(0 < p \le r\).
In terms of Čech-cohomology this implies the following. We may replace every Čech complex \({\check{C}}^\bullet (K^{-p})\) in (15) by its truncation \({\check{C}}^\bullet _{\le d}( K^{-p} )\) and restrict to the degree zero strands in each term. Another diagram chase reveals a quasi-isomorphism
as complexes of finite A-modules.
Proposition 5
Let \(M^\bullet \) be a bounded complex of finitely generated, graded S-modules and \(K^{\bullet ,q} \overset{\varepsilon }{\longrightarrow } M^q\) a graded free resolution of every \(M^q\) with
Choose \(d \ge \max \left\{ w_{-p,q,i_{-p,q}} : M^q \ne 0, -p > -r-1 \right\} -r\). Then \({\mathbb {R}} \pi _*( {\tilde{M}}^\bullet )\) is quasi-isomorphic to the degree zero part of the total complex of the double complex \(C_{\le d}^{\bullet ,\bullet }\) with terms \(C_{\le d}^{p,q} = {\check{C}}^{p}_{\le d}( M^q)\):
Proof
The right derived pushforward of a single sheaf \({\tilde{M}}\) on \({\mathbb {P}}^r_A\) is usually defined via injective resolutions of \({\tilde{M}}\) and it is well known that the resulting complex is quasi-isomorphic to the Čech complex on \({\tilde{M}}\) for the affine covering above. For a complex of sheaves \({\tilde{M}}^\bullet \) the derived pushforward can be computed as the total complex of a double complex \(I^{\bullet ,\bullet }\) of injective sheaves which forms an injective resolution of \({\tilde{M}}^\bullet \). There is a corresponding spectral sequence identifying this total complex with the total complex of the Čech double complex for \({\tilde{M}}^\bullet \) up to quasi isomorphism analogous to the case of a single sheaf. The result now follows from (16): On the first page of the spectral sequence of the Čech double complex \({\check{C}}^\bullet (M^\bullet )\) we may replace each term \(H^p( {\check{C}}^\bullet (M^q))\) with the truncation \(H^p( {\check{C}}^\bullet _{\le d}(M^\bullet ))\). \(\square \)
5.2 An algorithm for the derived homological index
Let \((X,0) \subset ({\mathbb {C}}^n,0)\) be a reduced algebraic hypersurface defined over some finite extension K of \({\mathbb {Q}}\) and \(\omega \) an algebraic 1-form with an isolated zero on (X, 0) in the stratified sense and defined over the same field. We briefly describe how to use Proposition 5 in order to compute the Euler obstruction \({\text {Eu}}^\omega (X,0)\) as in (11) from Theorem 1.
Set \(A = K[x_1,\dots ,x_n]_{\langle x_1,\dots ,x_n\rangle }\) and let \(S = A[s_1,\dots ,s_n]\) be the graded ring in the s-variables. Let J be the homogeneous ideal of S defining the Nash transform \({\tilde{X}} \subset {\mathbb {P}}^{n-1}\times ({\mathbb {C}}^n,0)\) and \(M^q\) the graded modules presenting the duals of the exterior powers of the Nash bundle \({\tilde{{\varOmega }}}^q\) on \({\tilde{X}}\) joint with the morphisms given by the pullbacks \(\nu ^*\omega \) as in Example 6. To compute the Euler obstruction \({\text {Eu}}^\omega (X,0)\) as a homological index we proceed as follows.
-
1)
We compute a partial graded free resolution of every one of the \(M^q\) using standard bases and a mixed ordering whose first block is graded and global in the s-variables and whose second block is local in the x-variables, cf. [17].
-
2)
From this we obtain the bound d on the pole order for the Čech double complex and we can build the truncated Čech double complex \({\check{C}}^\bullet _{\le d}(M^\bullet )\) as a double complex of finite S-modules.
-
3)
The degree-0-strands of \({\check{C}}^\bullet _{\le d}(M^\bullet )\) are finite A-modules generated by monomials in the s-variables. We can choose generators and relations accordingly and extract the induced matrices for \(\nu ^*\omega \wedge -\) and the maps of the Čech complexes over A from the corresponding maps defined over S.
-
4)
Since \(\omega \) had an isolated zero, the cohomology of the resulting total complex must be finite over K. We can proceed by the usual standard basis methods for the computation of Euler characteristics.
These computations apply in particular to the case \(X = \overline{{\mathscr {S}}_\alpha }\) and \(\omega = {\text {d}}f\) as in Corollary 4.
Remark 5
Note that in Proposition 5 we do not need to compute a quasi-isomorphism of \(M^\bullet \) with a complex of free S-modules by means of a double complex, but only resolutions of the individual terms \(M^q\). With a view towards the application of Proposition 5 for the computation of (11) this entails that the number d can be chosen once and for all for a given space (X, 0) and then used for every 1-form \(\omega \) with an isolated zero on (X, 0).
Example 7
We continue with Example 6 and compute \(\mu _f(2;X,0)\) by means of Formula (12) in Corollary 4. The algorithm above has been implemented in the computer algebra system Singular [7] and the computations were carried out over the rings

with a mixed ordering and the ring

with a local ordering.
As a first step, we need to determine the bound d in Proposition 5 and therefore compute graded resolutions of the modules \(M^q\) in Example 6. The shifts \(w_{p,i_p}\) as in Proposition 5 are gathered in Table 1 where we write \(w^k\) whenever the shift w appears exactly k times among the generators of the respective module.
We deduce from Table 1 that choosing \(d=2\) is sufficient for our computations and proceed to assemble the truncated Čech double complex with terms
This complex now takes the form

with the horizontal maps being induced by exterior multiplication with \(\nu ^* {\text {d}}f\) on the first factor and the vertical maps by the Čech differentials on the second factor of the respective tensor products. Note that these maps are both merely those of the Koszul complex in the components of \(\nu ^* {\text {d}}f\) and the sequence \((s_0^2, s_1^2, s_2^2)\), respectively.
The associated total complex is again a complex of finite S-modules. The number of generators of the modules involved is listed in the second row of Table 2. In order to extract the degree-0-part, i.e. the corresponding complex of A-modules, we choose the appropriate monomial bases in the s-variables. As the reader can see from the third row of Table 2, this immediately pushes the number of generators and the size of the involved matrices towards sizes which are impossible to treat without the aid of a computer. Nevertheless, the computations are feasible and a modern desktop computer takes only fractions of a second to compute the cohomology of this complex. The result is
where we write \(h^k(\cdot )\) for the vector space dimension of the k-th homology of a complex. Comparing this with Formula (12) confirms the result: \(\mu _f(2;X,0) = 5\).
We conclude this section with two more remarks.
Remark 6
As the previous example suggests, it is essential to use mixed orderings with a local block for the affine variables for the computation of the homological index. Indeed, if one chooses a global ordering on the variables x, y, z, one will obtain the value 7 for \(k=2\) in (17), i.e. one again also counts the two critical points of f on X away from the origin.
Remark 7
In this section we have restricted ourselves to the case of a function f on a hypersurface \((X,0) \subset ({\mathbb {C}}^n,0)\). The reason for this is that in this case the Grassmannian involved in the computation of the Nash blowup can be identified with \({\mathbb {P}}^{n-1}\) and there is a well established theory and notation for the twisting sheaves \({\mathcal {O}}(-e)\) and their cohomology. Theoretically, it would also be possible to do similar computations for varieties (X, 0) of arbitrary codimension c in \(({\mathbb {C}}^n,0)\) by means of the Plücker embedding
In practice, however, this introduces a very inconvenient amount of homogeneous variables and new equations coming from the Plücker relations. Furthermore, the description of the tautological bundle over the Grassmannian and its cohomology in terms of the twisting sheaves is more complicated for general c. This leads us to exclude the general case from our discussion for now.
Data availability
No datasets were generated or analysed during the current study.
Notes
Algebraic formulae for the GSV index of v on (X, 0) were also given in [13], but only under the additional assumption that v was also tangent to all fibers of f.
Or, in case (X, 0) is reducible, the union of the top dimensional strata.
References
Arnold, V., Gusein-Zade, S., Varchenko, A.: Singularities of Differentiable Maps, vol. II. Birkhäuser, Basel (1985)
Brasselet, J.P., Massey, D., Parameswaran, A.J., Seade, J.: Euler obstruction and defects of functions on singular varieties. J. Lond. Math. Soc. (2) 70(1), 59–76 (2004)
Brasselet, J.P., Schwartz, M.H.: Sur les classes de Chern d’un ensemble analytique complexe. Astérisque 82–83, 93–147 (1981)
Bruns, W., Herzog, J.: Cohen–Macaulay Rings. Cambridge University Press, Cambridge (1993)
Burghelea, D., Verona, A.: Local homological properties of analytic sets. Manuscr. Math. 7, 55–66 (1972). https://doi.org/10.1007/BF01303536
Cheniot, D.: Sur les sections transversales d’un ensemble stratifié. C. R. Acad. Sci. Paris Sér. A-B 275, A915–A916 (1972)
Decker, W., Greuel, G.M., Pfister, G., Schönemann, H.: Singular 4-1-2—a computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2019)
Ebeling, W., Gusein-Zade, S.: Radial index and Euler obstruction of a 1-form on a singular variety. Geom. Dedic. 113, 231–241 (2005)
Ebeling, W., Gusein-Zade, S.M.: Indices of vector fields and 1-forms on singular varieties. Global Aspects of Complex Geometry, pp. 129–169. Springer, Berlin (2006)
Ebeling, W., Gusein-Zade, S.M., Seade, J.: Homological index for 1-forms and a Milnor number for isolated singularities. Int. J. Math. 15(9), 895–905 (2004)
Giraldo, L., Gómez-Mont, X.: A law of conservation of number for local Euler characteristics. Contemp. Math. 311, 251–259 (2002)
Gómez-Mont, X.: An algebraic formula for the index of a vector field on a hypersurface with an isolated singularity. J. Algebr. Geom. 7(4), 731–752 (1998)
Gómez-Mont, X., Seade, J., Verjovsky, A.: The index of a holomorphic flow with an isolated singularity. Math. Ann. 291(4), 737–751 (1991)
Goresky, M., MacPherson, R.: Stratified Morse Theory. Springer, Berlin (1988)
Grauert, H.: Ein theorem der analytischen Garbentheorie und die Modulräume komplexer Strukturen. Publ. Math. IHES 5, 233–292 (1960)
Greuel, G.: Der Gauss-Manin-Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten. Math. Ann. 214, 235–266 (1975)
Greuel, G.M., Pfister, G.: A Singular Introduction to Commutative Algebra. Springer, Berlin (2002)
Greuel, G.M., Stussak, C., Urbannek, M., Meyer, H.: Surfer, software for visualization of real algebraic surfaces. https://imaginary.org/program/surfer
Hamm, H.: Lokale topologische Eigenschaften komplexer Räume. Math. Ann. 191, 235–252 (1972)
Hartshorne, R.: Algebraic Geometry. Springer, Berlin (1977)
Hironaka, H.: Stratification and flatness. In: Holm, P. (ed.) Real and Complex Singularities, pp. 199–265. Nordic Summer School/NAVF, Olso (1977)
Lê, D.T.: Calculation of Milnor number of isolated singularity of complete intersection. Funct. Anal. Appl. 8(2), 127–131 (1974)
Lê, D.T.: Some remarks on relative monodromy. In: Proceedings of Ninth Nordic Summer School/NAVF Symposium on Mathematics, Oslo 1976, pp. 397–403 (1977)
Lê, D.T.: Le concept de singularité isolée de fonction analytique. Complex Analytic Singularities, Advanced Studies in Pure Mathematics, vol. 8, pp. 215–227. North-Holland, Amsterdam (1987)
Lê, D.T.: Complex analytic functions with isolated singularities. J. Alg. Geom 1(1), 83–100 (1992)
Lê, D.T., Teissier, B.: Variétés polaires locales et classes de Chern des variétés singulières. Ann. Math. (2) 114(3), 457–491 (1981)
MacPherson, R.D.: Chern classes of singular algebraic varieties. Ann. Math. 100, 423–432 (1974)
Massey, D.: A little microlocal Morse theory. Math. Ann. 321, 275–294 (2001)
Milnor, J.: Singular Points of Complex Hypersurfaces. Princenton University Press, Princenton (1968)
Seade, J., Tibăr, M., Verjovsky, A.: Milnor numbers and Euler obstruction. Bull. Braz. Math. Soc. 36, 2 (2005)
Siersma, D.: A Bouquet theorem for the Milnor fiber. J. Alg. Geom. 4, 51–66 (1995)
Teissier, B.: Variétés polaires. II. Multiplicités polaires, sections planes, et conditions de Whitney. Algebraic geometry (La Rábida, 1981). Lecture notes in mathematics, vol. 961, pp. 314–491. Springer, Berlin (1982)
Tibăr, M.: Bouquet decomposition of the Milnor fibre. Topology 35, 227–241 (1995)
Acknowledgements
The author is indebted to J. Seade for discussions on the homological index, the law of conservation of number, and Euler obstructions. These conversations took place at the meeting ENSINO V at João Pessoa, Brazil in July 2019 and the author wishes to also thank the organizers A. Menegon Neto, J. Snoussi, M. da Silva Pereira, and M. F. Zanchetta Morgado for the opportunity to give a course on determinantal singularities together with M.A.S. Ruas. Thanks also go to J. Schürmann for encouraging discussions during the conference “Non-isolated singularities and derived geometry” at Cuernavaca, Mexico the same year. Most of the work on this article was carried out while being employed at the Institut für Mathematik at the Johannes Gutenberg Universität Mainz. The pictures for the examples were produced using the software “Surfer” [18].
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there is no conflict of interest.
Additional information
Communicated by Thomas Schick.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zach, M. A generalization of Milnor’s formula. Math. Ann. 382, 901–942 (2022). https://doi.org/10.1007/s00208-021-02223-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-021-02223-5