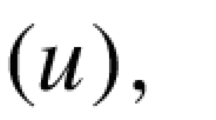On the Gibbons’ conjecture for equations involving the p-Laplacian

Abstract

In this paper we prove the validity of Gibbons’ conjecture for the quasilinear elliptic equation $-\Delta _p u = f(u)$ on $\mathbb {R}^N.$ The result holds true for $(2N+2)/(N+2)< p < 2$ and for a very general class of nonlinearity f.

1 Introduction

In this work we are concerned with the study of qualitative properties of weak solutions of class $C^1$ to the quasilinear elliptic equation

where we denote a generic point of ${\mathbb {R}}^N$ by $(x',y)$ with $x'=(x_1,x_2, \ldots , x_{N-1}) \in \mathbb {R}^{N-1}$ and $y=x_N \in \mathbb {R}$, $p>1$ and $N > 1$. The nonlinear function f will be assumed to satisfy the following assumptions :

$$\begin{aligned} {(h_f)} \qquad {\left\{ \begin{array}{ll} f \in C^1([-1,1]), \quad f(-1)= f(1)=0, &{} \\ f_+'(-1)<0, \quad f'_-(1)<0, &{} \\ {\mathcal {N}}_f:=\{t \in [-1,1] \ | \ f(t)=0\} \,\, {\text{ is } \text{ a } \text{ finite } \text{ set. }} &{} \end{array}\right. } \end{aligned}$$

A very special case covered by our assumptions is the well-known semilinear Allen–Cahn equation

$$\begin{aligned} -\Delta u =u(1-u^2)\quad \text {in}\,\, {\mathbb R}^N, \end{aligned}$$

(1.1)

for which the following conjecture has been stated

Gibbons’ conjecture [5] Assume $N>1$ and consider a bounded solution $u \in C^2({\mathbb R}^N)$ of (1.1) such that

$$\begin{aligned} \lim _{x_N\rightarrow \pm \infty }u(x',x_N)=\pm 1, \end{aligned}$$

uniformly with respect to $x'$. Then, is it true that

$$\begin{aligned} u(x)=\tanh \left( \frac{x_N-\alpha }{\sqrt{2}} \right) , \end{aligned}$$

for some $\alpha \in {\mathbb R}$?

Gibbons’ conjecture was proven independently and with different methods by [2, 3, 10, 11] (see also [12] for further results in the semilinear scalar case and [17] for a result on related semilinear elliptic systems. The case of a uniformly elliptic fully nonlinear operator and the one of the fractional laplacian are treated in [18] (see also [19]).

Here we study Gibbons’ conjecture for the quasilinear equation (${\mathcal P}$). To the best of our knowledge, there are no general results in this framework. This lack of results is mainly due to the fact that, unlike the semilinear case, when working with the singular operator $-\Delta _p(\cdot )$, both the weak and the strong comparison principles might fail. This (possible) failure being caused either by the presence of critical points or by the fact that the nonlinearity f changes sign. Those difficulties are even more magnified by the fact that we are facing a problem on an unbounded domain, the entire euclidean space $\mathbb {R}^N.$ Also, in the pure quasilinear case, $p\ne 2$, we cannot exploit the usual arguments and tricks related to the linearity of the Laplace operator. Despite all those problems and difficulties, we are able to study and solve the quasilinear version of Gibbons’ conjecture by making use of the celebrated moving planes method which goes back to the papers of Alexandrov [1] and Serrin [25] (see also [4, 20]).

Our main result is the following

Theorem 1.1

Assume $N > 1$, ${(2N+2)}/{(N+2)}< p < 2$ and let $u \in C^1(\mathbb {R}^N)$ be a weak solution of $({\mathcal P})$, such that

$$\begin{aligned} |u|\le 1 \qquad {\text{ on }}\quad \mathbb {R}^N \end{aligned}$$

and

$$\begin{aligned} \lim _{y \rightarrow + \infty } u(x',y) = 1 \quad \text {and} \quad \lim _{y \rightarrow - \infty } u(x',y) =-1, \end{aligned}$$

(1.2)

uniformly with respect to $x' \in \mathbb {R}^{N-1}$. If f fulfills ($h_f$), then u depends only on y and

$$\begin{aligned} \partial _{y} u > 0 \quad \text {in} \quad \mathbb {R}^N. \end{aligned}$$

(1.3)

To get our main result, we first prove a new weak comparison principle for quasilinear equations in half-spaces and then we exploit it to start the moving plane procedure at infinity in the y-direction. Then, by a delicate analysis based on the use of the techniques developed in [7, 8] and [14,15,16], the translation invariance of the considered problem and the method introduced in [10], we obtain the monotonicity of the solution in all the directions of the upper hemi-sphere $\mathbb {S}^{N-1}_+:=\{\nu \in \mathbb {S}^{N-1}_+ \ | \ (\nu , e_N) \}$. This result, in turn, will provide the desired one-dimensional symmetry result as well as the strict monotonicity.

The paper is organized as follows: In Sect. 2 we recall the definition of weak solution of (${\mathcal P}$), as well as some results about the strong maximum principle and the comparison principles for nonlinear equations involving the p-Laplace operator. In Sect. 3 we prove a new weak comparison principle in half-spaces. In Sect. 4 we prove the monotonicity of the solution in the y-direction, exploiting the moving plane procedure. In Sect. 5 we prove the one-dimensional symmetry and the strict monotonicity of the solution.

2 Strong maximum principles and strong comparison principles for quasilinear elliptic equations

The aim of this section is to recall some results about the strong comparison principles and the strong maximum principles for quasilinear elliptic equations that will be used several times in the proof of our main theorem. To this end we first recall the definition of weak solution for the quasilinear equation $-\Delta _p u = f(u)$.

Definition 2.1

Let $\Omega$ be an open set of $\mathbb {R}^N$, $N\ge 1$. We say that $u \in C^1(\Omega )$ is a weak subsolution to

$$\begin{aligned} -\Delta _p u = f(u) \quad \text {in} \quad \Omega \end{aligned}$$

(2.1)

if

$$\begin{aligned} \int _{\Omega } |\nabla u|^{p-2}(\nabla u, \nabla \varphi ) \, dx \, \le \int _{\Omega } f(u) \varphi \, dx \qquad \forall \varphi \in C_c^\infty (\Omega ), \, \varphi \ge 0. \end{aligned}$$

(2.2)

Similarly, we say that $u \in C^1(\Omega )$ is a weak supersolution to (2.1) if

$$\begin{aligned} \int _{\Omega } |\nabla u|^{p-2} (\nabla u, \nabla \varphi ) \, dx \, \ge \int _{\Omega } f(u) \varphi \, dx \qquad \forall \varphi \in C_c^\infty (\Omega ), \, \varphi \ge 0. \end{aligned}$$

(2.3)

Finally, we say that $u \in C^1(\Omega )$ is a weak solution of equation (2.1), if (2.2) and (2.3) hold. Sometimes for brevity, we shall use the term ‘solution’ to indicate a weak solution to the considered problem.

The first result that we are going to present is the classical strong maximum principle due to Vazquez [28] (see also the book of Pucci and Serrin [22])

Theorem 2.2

(Strong Maximum Principle and Höpf’s Lemma, [22, 28]) Let $u \in C^1(\Omega )$ be a non-negative weak solution to

$$\begin{aligned} -\Delta _p u + c u^q = g \ge 0 \quad \text {in} \quad \Omega \end{aligned}$$

with $1<p<+\infty$, $q\ge p-1$, $c \ge 0$ and $g \in L^\infty _{loc} (\Omega )$. If $u \ne 0$, then $u>0$ in $\Omega$. Moreover for any point $x_0 \in \partial \Omega$ where the interior sphere condition is satisfied, and such that $u \in C^1(\Omega ) \cup \{x_0\}$ and $u(x_0) = 0$ we have that $\partial _\nu u>0$ for any inward directional derivative (this means that if y approaches $x_0$ in a ball $B \subseteq \Omega$ that has $x_0$ on its boundary, then $\lim _{y \rightarrow x_0} \frac{u(y)-u(x_0)}{|y-x_0|}>0)$.

It is very simple to guess that in the quasilinear case, maximum and comparison principles are not equivalent; for this reason we need also to recall the classical version of the strong comparison principle for quasilinear elliptic equations

Theorem 2.3

(Classical Strong Comparison Principle, [6, 22])

Let $u,v \in C^1(\Omega )$ be two solutions to

$$\begin{aligned} -\Delta _p w = f(w) \qquad \text {in} \quad \Omega \end{aligned}$$

(2.4)

such that $u \le v$ in $\Omega$, with $1<p<+\infty$ and let ${\mathcal {Z}} =\{x \in \Omega \ | \ |\nabla u (x)| + |\nabla v (x)| = 0\}$. If $x_0 \in \Omega \setminus {\mathcal {Z}}$ and $u(x_0)=v(x_0)$, then $u=v$ in the connected component of $\Omega \setminus {\mathcal {Z}}$ containing $x_0$.

For the proof of this result we suggest [6]. The main feature of Theorem  2.3 is that it holds far from the critical set. Now we present a result which holds true, under stronger assumptions, on the entire domain $\Omega$.

Theorem 2.4

(Strong Comparison Principle, [7, 23]) Let $u,v\in C^1(\overline{\Omega })$ be two solutions to (2.4), where $\Omega$ is a bounded domain of ${\mathbb {R}}^N$ and $\frac{2N+2}{N+2}<p<+\infty$. Assume that at least one of the following two conditions $(f_u)$,$(f_v)$ holds:

$({{\varvec{f}}}_{{\varvec{u}}})$::

either

$$\begin{aligned} f(u(x)) >0 \quad \text{ in }\quad \overline{\Omega } \end{aligned}$$

(2.5)

or

$$\begin{aligned} f(u(x)) <0 \quad \text{ in }\quad \overline{\Omega }; \end{aligned}$$

(2.6)

$({{\varvec{f}}}_{{\varvec{v}}})$::

either

$$\begin{aligned} f(v(x)) >0 \quad \text{ in }\quad \overline{\Omega } \end{aligned}$$

(2.7)

or

$$\begin{aligned} f(v(x)) <0 \quad \text{ in }\quad \overline{\Omega }. \end{aligned}$$

(2.8)

Suppose furthermore that

$$\begin{aligned} u\le v\quad \text{ in }\quad \Omega . \end{aligned}$$

(2.9)

Then $u\equiv v$ in $\Omega$ unless

$$\begin{aligned} u<v\quad \text{ in }\quad \Omega . \end{aligned}$$

(2.10)

Proof

The proof of this result follows by the same arguments in [7, 15, 23, 24]. Note in fact that under the assumption (${{\varvec{f}}}_{{\varvec{u}}}$) or (${{\varvec{f}}}_{{\varvec{v}}}$), it follows that $|\nabla u|^{-1}$ or $|\nabla v|^{-1}$ has the summability properties exposed by Theorem 3.1 in [24]. Then the weighted Sobolev inequality is in force, see e.g. Theorem 8 in [15].

Now, it is sufficient to note that the Harnack comparison inequality given by Corollary 3.2 in [7] holds true, since the proof it is only based on the weighted Sobolev inequality.

Finally it is standard to see that the Strong Comparison Principle follows by the weak comparison Harnack inequality (that it is based on the Moser-iteration scheme [21, 27]), see Theorem 1.4 in [7]. $\square$

Let us now recall that the linearized operator at a fixed solution w of (2.4), $L_w(v,\varphi )$ (with weight $\rho =|\nabla w|^{p-2}$), is well defined in the set $\hat{\Omega }:=\Omega \setminus \{x\in \Omega \ | \ |\nabla w|=0 \}$ for every smooth functions $v\in C^1(\hat{\Omega })$ and $\varphi \in C_c^1(\hat{\Omega })$ by

$$\begin{aligned} \begin{aligned} L_w(v, \varphi )&\equiv \int _{\hat{\Omega }} |\nabla w|^{p-2}(\nabla v, \nabla \varphi )+(p-2) |\nabla w|^{p-4}(\nabla w, \nabla v)(\nabla w, \nabla \varphi )\\ {}&\quad - f'(w)v \varphi \, dx . \end{aligned} \end{aligned}$$

(2.11)

Here below we recall two versions of the strong maximum principle for the linearized equation (2.15) that we shall use in our proofs. The first result holds far from the critical set:

Theorem 2.5

(Classical Strong Maximum Principle for the Linearized Operator, [22]) Let $u\in C^1(\overline{\Omega })$ be a solution to problem (2.4), with $1<p<+\infty$. Let $\eta \in \mathbb {S}^{N-1}$ and let us assume that for any connected domain $\Omega ' \subset \Omega \, \setminus$ $\{x \in \Omega \ | \ |\nabla u (x)| = 0\}$

$$\begin{aligned} \partial _\eta u\ge 0 \quad \text {in} \quad \Omega '. \end{aligned}$$

(2.12)

Then $\partial _\eta u \equiv 0$ in $\Omega '$ unless

$$\begin{aligned} \partial _\eta u> 0 \quad \text {in} \quad \Omega '. \end{aligned}$$

(2.13)

Next we recall a more general result which holds true on the entire domain $\Omega$ under the same assumptions of Theorem  2.4. To this end we have to define the linearized operator (2.11) at a fixed solution w of (2.4) in the whole domain $\Omega$. We point out that under the hypothesis (2.16) or (2.17), thanks to [24, Theorem 3.1], the weight $\rho =|\nabla w|^{p-2} \in L^1(\Omega )$ if $p>(2N+2)/(N+2)$. Hence $L_w(v,\varphi )$, is well defined, for every v and $\varphi$ in the weighted Sobolev space $H^{1,2}_\rho (\Omega )$ with¹$\rho =|\nabla w|^{p-2}$ by

$$\begin{aligned} \begin{aligned} L_w(v, \varphi )&\equiv \int _\Omega |\nabla w|^{p-2}(\nabla v, \nabla \varphi )+(p-2) |\nabla w|^{p-4}(\nabla w, \nabla v)(\nabla w, \nabla \varphi )\\ {}&\quad - f'(w)v \varphi \, dx . \end{aligned} \end{aligned}$$

We point out that the linearized operator is also well defined if $v\in L^2(\Omega )$, $|\nabla w|^{p-2}\nabla v\in L^2(\Omega )$ and $\varphi \in W^{1,2}(\Omega )$.

Finally $v \in H^{1,2}_\rho (\Omega )$ is a weak solution of the linearized operator if

$$\begin{aligned} L_w(v, \varphi )=0 \qquad {\forall \varphi \in H^{1,2}_{0,\rho }(\Omega )}. \end{aligned}$$

(2.15)

For future use we recall that, as it follows by the regularity results in [8, 23, 24], the directional derivatives of the solution $\partial _{\eta } u$ ($\eta \in \mathbb {S}^{N-1}$) belong to the weighted Sobolev space $H^{1,2}_{\rho }(\Omega )$ and fulfill (2.15). Moreover (from [8, 23, 24]), it follows also that $|\nabla u|^{p-2}\nabla u\in W^{1,2}_{loc}(\Omega )$ so that if $\varphi \in W^{1,2}_{c}(\Omega )$ (with compact support), the linearized operator $L_w(\partial _{\eta } u, \varphi )$ is still well defined.

Theorem 2.6

(Strong Maximum Principle for the Linearized Operator, [7, 23]) Let $u\in C^1(\Omega )$ be a solution to problem (2.4), with $\frac{2N+2}{N+2}<p<+\infty$. Assume that either

$$\begin{aligned} f(u(x)) >0 \quad \text{ in }\quad \overline{\Omega } \end{aligned}$$

(2.16)

or

$$\begin{aligned} f(u(x)) <0 \quad \text{ in }\quad \overline{\Omega }. \end{aligned}$$

(2.17)

If $\eta \in \mathbb {S}^{N-1}$ and $\partial _\eta u \ge 0$ in $\Omega$, then either $\partial _\eta u \equiv 0$ in $\Omega$ or $\partial _\eta u>0$ in $\Omega$.

We conclude this section by the following

Remark 2.7

Here we want to point out the following two properties satisfied by any weak solution of class $C^1$ to (${\mathcal P}$), with $1< p <2,$ and such that $\vert u \vert \le 1$ on $\mathbb {R}^N$. They will be used several times throughout the paper.

• Since $p<2$, we have that : either $|u|<1$ on $\mathbb {R}^N$ or $u\equiv \pm 1$ on $\mathbb {R}^N$. To see this, let us define the function $w=1-u$. It follows that w is a non-negative weak solution of class $C^1$ to

  $$\begin{aligned} -\Delta _p w = g(w) \quad \text {in} \,\, \mathbb {R}^N, \end{aligned}$$

  with $g(w):= -f(1-w)$. Moreover $g\in C^1([0,2])$ (see assumptions ${(h_f)}$ in the Introduction) and in particular it is a Lipschitz-continuous function on the interval [0, 2] with $g(1)=0$. Since $p<2$, it is therefore possible to find a constant $c > 0$ such that

  $$\begin{aligned} -\Delta _p w + c w^{p-1}=g(w)+ c w^{p-1}\ge 0 \qquad \textit{in} \quad {\mathbb R}^N. \end{aligned}$$

  By Theorem  2.2, it follows that either $w \equiv 0$ in ${\mathbb R}^N$ or $w>0$ in ${\mathbb R}^N,$ that is, either $u \equiv 1$ on ${\mathbb {R}}^N$ or $u < 1$ on ${\mathbb {R}}^N.$ Once $u < 1$ on ${\mathbb {R}}^N$ we can apply the same argument to the non-negative function $w = u+1$ to get: either $u \equiv -1$ on ${\mathbb {R}}^N$ or $u > - 1$ on ${\mathbb {R}}^N.$ As claimed.

• By classical regularity results [9, 26] and since $\Vert f(u)\Vert _{L^{\infty }({\mathbb R}^N)} \le \Vert f \Vert _{L^{\infty }([-1,1])}$ (here we have used the assumption $\Vert u \Vert _{L^{\infty }({\mathbb R}^N)} \le 1$), we deduce that : given $R \in (0,1)$ there exist $\alpha \in (0,1)$ and $C>0$, depending only on N, p, R and $\Vert f \Vert _{L^{\infty }([-1,1])}$, so that

  $$\begin{aligned} \Vert \nabla u\Vert _{L^{\infty }({\mathbb R}^N)}\le & {} C, \end{aligned}$$

  (2.18)
  $$\begin{aligned} \vert \nabla u(x) - \nabla u(y) \vert\le & {} C \left( \frac{\vert x-y\vert }{R}\right) ^{\alpha }, \end{aligned}$$

  (2.19)

  for every $x_0\in \mathbb {R}^N$ and any $x,y \in B_R(x_0).$ In particular, $u \in C^{1,\alpha }(\mathbb {R}^N)$ and

  $$\begin{aligned} \Vert u \Vert _{C^{1,\alpha }({\mathbb {R}}^N)} \le C_0, \end{aligned}$$

  for some constant $C_0>0$ depending only on N, p and $\Vert f \Vert _{L^{\infty }([-1,1])}$. Indeed, taking $R={1}/{2}$, we get $\Vert \nabla u\Vert _{L^{\infty }({\mathbb R}^N)}\le C(\frac{1}{2})$ by (2.18). Therefore, if $\vert x - y \vert < 1,$ we have $\vert u(x) - u(y) \vert \le C(\frac{1}{2}) \vert x-y \vert \le C(\frac{1}{2})\vert x -y \vert ^{\alpha }$ while, if $\vert x - y \vert \ge 1,$ we clearly have $\vert u(x) - u(y) \vert \le 2 \Vert u \Vert _{L^{\infty }({\mathbb {R}}^N)} \le 2 \Vert u \Vert _{L^{\infty }({\mathbb {R}}^N)} \vert x -y \vert ^{\alpha } \le 2 \vert x -y \vert ^{\alpha }$. Hence the $\alpha$-Hölder seminorm $[u]_{0,\alpha ,{\mathbb {R}}^N} \le \max \{2, C(\frac{1}{2})\}$. Furthermore, if $\vert x - y \vert < 1,$ then $x,y \in B_{\frac{1}{2}}(x_0)$, where $x_0$ is the middle point of the segment joining x and y. We can then apply (2.19) to get $\vert \nabla u(x) - \nabla u(y) \vert \le 2^{\alpha } C(\frac{1}{2}) \vert x-y \vert ^{\alpha } \le 2C(\frac{1}{2}) \vert x-y \vert ^{\alpha }.$ Finally, if $\vert x -y \vert \ge 1$, then $\vert \nabla u(x) - \nabla u(y) \vert \le 2 \Vert \nabla u \Vert _{L^{\infty }({\mathbb {R}}^N)} \le 2 C(\frac{1}{2}) \vert x-y \vert ^{\alpha }.$ Hence $[\nabla u]_{0,\alpha ,{\mathbb {R}}^N} \le 2 C(\frac{1}{2}).$ The desired claims follow.

3 Preliminary results

In this section we shall denote by $\Sigma$ any (affine) open half-space of $\mathbb {R}^N$ of the form

$$\begin{aligned} \Sigma := {\mathbb {R}}^{N-1}\times (a,b), \end{aligned}$$

where either $a=-\infty$ and $b\in {\mathbb R}$, or $a\in {\mathbb R}$ and $b=+\infty$.

We also recall some known inequalities which will be used in this section. For any $\eta , \eta ' \in {\mathbb {R}}^N$ with $|\eta |+|\eta '|>0$ there exists positive constants $C_1, C_2, C_3$ depending only on p such that

$$\begin{aligned} \begin{aligned}{}[|\eta |^{p-2}\eta -|\eta '|^{p-2}\eta '][\eta - \eta ']&\ge C_1 (|\eta |+|\eta '|)^{p-2}|\eta -\eta '|^2, \\ \\ \Vert \eta |^{p-2}\eta -|\eta '|^{p-2}\eta '|&\le C_2 (|\eta |+|\eta '|)^{p-2}|\eta -\eta '|,\\\\ \Vert \eta |^{p-2}\eta -|\eta '|^{p-2}\eta '|&\le C_3 |\eta -\eta '|^{p-1} \quad \text{ if }\quad 1 < p \le 2. \end{aligned} \end{aligned}$$

(3.1)

The first result that we need is a weak comparison principle between a subsolution and a supersolution to (${\mathcal P}$) ordered on the boundary of some open half-space $\Sigma$ of $\mathbb {R}^N$. We prove the following

Proposition 3.1

Assume $N>1, \, p>1$ and $f\in C^1({\mathbb R})$. Let $u, v \in C^{1, \alpha }_{loc}(\overline{\Sigma })$ such that $|\nabla u|, |\nabla v| \in L^\infty ({\Sigma })$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle -\Delta _p u \le f(u) &{}\quad \text {in}\,\, \Sigma ,\\ \displaystyle -\Delta _p v \ge f(v) &{}\quad \text {in}\,\, \Sigma ,\\ \displaystyle u \le v &{}\quad \text {on}\,\,\partial \Sigma , \end{array}\right. } \end{aligned}$$

(3.2)

where $\Sigma$ is the open half-space ${\mathbb {R}}^{N-1}\times (-\infty ,b).$ Moreover, let us assume that there are $\delta >0$, sufficiently small, and $L>0$ such that

$$\begin{aligned}&f'(t)<- L\quad \text {in} \quad [-1,-1+\delta ], \end{aligned}$$

(3.3)

$$\begin{aligned}&-1 \le u \le -1 + \delta \quad \text {in} \quad \Sigma . \end{aligned}$$

(3.4)

Then

$$\begin{aligned} u \le v \quad \text {in} \,\,\Sigma . \end{aligned}$$

(3.5)

The same result is true if $\Sigma = {\mathbb {R}}^{N-1}\times (a, +\infty )$ and (3.3) and (3.4) are replaced by

$$\begin{aligned} f'(t)<- L\quad \text {in} \quad [1-\delta ,1] \quad \text {and} \quad 1-\delta \le v \le 1 \quad \text {in} \quad \Sigma . \end{aligned}$$

Proof

We prove the result when (3.3) and (3.4) are in force. The other case is similar.

We distinguish two cases:

Case 1 $1<p <2$. We set

$$\begin{aligned} \psi :=w^\alpha \varphi _R^{\alpha +1}, \end{aligned}$$

(3.6)

where $\alpha >1$, $R >0$ large, $w:=(u-v)^+$ and $\varphi _R$ is a standard cutoff function such that $0\le \varphi _R \le 1$ on $\mathbb {R}^N$, $\varphi _R = 1$ in $B_R$, $\varphi _R = 0$ outside $B_{2R}$, with $|\nabla \varphi _R| \le 2/R$ in $B_{2R} \setminus B_R$. Let us define ${\mathcal {C}}(2R):=\Sigma \cap B_{2R} \cap \text {supp} (\omega )$. First of all we notice that $\psi \in W^{1,p}_0({\mathcal {C}}(2R))$. By density arguments we can take $\psi$ as test function in (2.2) and (2.3), so that, subtracting we obtain

$$\begin{aligned} \begin{aligned}&\alpha \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla w) w^{\alpha -1} \varphi _R^{\alpha +1} \, dx \\&\le - (\alpha +1) \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla \varphi _R) w^\alpha \varphi _R^{\alpha +1} \, dx\\&\ \ \ \ + \int _{{\mathcal {C}}(2R)} [f(u)-f(v)] w^\alpha \varphi _R^{\alpha +1} \, dx\,. \end{aligned} \end{aligned}$$

(3.7)

From (3.7), using (3.1) and noticing that f is decreasing in $[-1,-1+{\delta }]$, we obtain

$$\begin{aligned} \begin{aligned}&\alpha C_1 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 w^{\alpha -1} \varphi _R^{\alpha +1} \, dx \\&\quad \le \alpha \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla w) w^{\alpha -1} \varphi _R^{\alpha +1} \, dx \\&\quad \le - (\alpha +1) \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla \varphi _R) w^\alpha \varphi _R^\alpha \, dx\\&\qquad + \int _{{\mathcal {C}}(2R)} f'(\xi ) (u-v)^+w^\alpha \varphi _R^{\alpha +1} \, dx\,\\&\quad \le (\alpha +1) C_3 \int _{{\mathcal {C}}(2R)} |\nabla w|^{p-1} |\nabla \varphi _R| w^\alpha \varphi _R^\alpha \, dx - L\int _{{\mathcal {C}}(2R)} (u- v)^+w^\alpha \varphi _R^{\alpha +1} \, dx, \end{aligned} \end{aligned}$$

(3.8)

where $\xi$ is some point that belongs to (v, u). Hence, recalling also that $|\nabla u|, |\nabla v| \in L^\infty ({\Sigma })$, we deduce

$$\begin{aligned} \begin{aligned}&\alpha C_1 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 w^{\alpha -1} \varphi _R^{\alpha +1} \, dx\\&\quad \le (\alpha +1) C_3 \int _{{\mathcal {C}}(2R)} |\nabla w|^{p-1} |\nabla \varphi _R| w^\alpha \varphi _R^\alpha \, dx -L\int _{{\mathcal {C}}(2R)} w^{\alpha +1} \varphi _R^{\alpha +1} \, dx \\&\quad \le (\alpha +1) C \int _{{\mathcal {C}}(2R)} |\nabla \varphi _R| w^\alpha \varphi _R^\alpha \, dx - L\int _{{\mathcal {C}}(2R)} w^{\alpha +1} \varphi _R^{\alpha +1} \, dx \end{aligned} \end{aligned}$$

(3.9)

where $C=C(p, \Vert \nabla u\Vert _{L^\infty ({\Sigma })},\Vert \nabla v\Vert _{L^\infty ({\Sigma })})$. Exploiting the weighted Young inequality with exponents $\alpha +1$ and ${(\alpha +1)}/{\alpha }$ in (3.9), we obtain

$$\begin{aligned} \begin{aligned}&\alpha C_1 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 w^{\alpha -1} \varphi _R^{\alpha +1} \, dx\\&\quad \le \frac{C}{\sigma ^{\alpha +1}} \int _{{\mathcal {C}}(2R)} |\nabla \varphi _R|^{\alpha +1} \, dx+ \alpha C \sigma ^{\frac{\alpha +1}{\alpha }}\int _{{\mathcal {C}}(2R)} w^{\alpha +1} \varphi _R^{\alpha +1}\, dx \\&\qquad -L\int _{{\mathcal {C}}(2R)} w^{\alpha +1} \varphi _R^{\alpha +1} \, dx \\&\quad \le \frac{C}{\sigma ^{\alpha +1}} \int _{{\mathcal {C}}(2R)} |\nabla \varphi _R|^{\alpha +1} \, dx+ \left( \alpha C\sigma ^{\frac{\alpha +1}{\alpha }} - L\right) \int _{{\mathcal {C}}(2R)} w^{\alpha +1} \varphi _R^{\alpha +1}\, dx\\&\quad \le \frac{2^{\alpha +1}C}{\sigma ^{{\alpha +1}}R^{\alpha -(N-1)}} + \left( \alpha C\sigma ^{\frac{\alpha +1}{\alpha }} -L \right) \int _{{\mathcal {C}}(2R)} w^{\alpha +1} \varphi _R^{\alpha +1} \, dx. \end{aligned} \end{aligned}$$

Now taking $\alpha > N-1$, if we choose $\sigma =\sigma (p,\alpha , L,N, \Vert \nabla u\Vert _{L^\infty ({\Sigma })},\Vert \nabla v\Vert _{L^\infty ({\Sigma })})>0$ sufficiently small so that

$$\begin{aligned} \alpha C\sigma ^{\frac{\alpha +1}{\alpha }} -L < 0, \end{aligned}$$

we obtain

$$\begin{aligned} \int _{{\mathcal {C}}(R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 w^{\alpha -1} \, dx \le \frac{\tilde{C}}{\alpha \sigma ^{{\alpha +1}}R^{\alpha -(N-1)}}. \end{aligned}$$

(3.10)

Passing to the limit in (3.10) for $R \rightarrow + \infty$, by Fatou’s Lemma we have

$$\begin{aligned} \int _{\Sigma } \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 w^{\alpha -1} \, dx \le 0. \end{aligned}$$

This implies that $u \le v$ in $\Sigma$.

Case 2 $p \ge 2$. We set

$$\begin{aligned} \psi :=w \varphi _R^2, \end{aligned}$$

(3.11)

where $R >0$, $w:=(u-v)^+$ and $\varphi _R$ is the standard cutoff function defined above. First of all we notice that $\psi \in W^{1,p}_0(B_{2R})$. Let us define ${\mathcal {C}}(2R):=\Sigma \cap B_{2R} \cap \text {supp} (\omega )$. By density arguments we can take $\psi$ as test function in (2.2) and (2.3), so that, subtracting we obtain

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla w) \varphi _R^2 \, dx \\&\quad \le - 2 \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla \varphi _R) w \varphi _R \, dx\\&\qquad + \int _{{\mathcal {C}}(2R)} [f(u)-f(v)] w \varphi _R^2 \, dx\,. \end{aligned} \end{aligned}$$

(3.12)

From (3.12), using (3.1) and that $f'(u) \le -L$ in $[-1,-1+\delta ]$, we obtain

$$\begin{aligned} \begin{aligned}&C_1 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \varphi _R^2 \, dx \\&\quad \le \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla w) \varphi _R^2 \, dx \\&\quad \le - 2 \int _{{\mathcal {C}}(2R)} (|\nabla u|^{p-2} \nabla u - |\nabla v|^{p-2} \nabla v, \nabla \varphi _R) w \varphi _R \, dx\\&\qquad +\int _{{\mathcal {C}}(2R)} f'(\xi ) (u-v)^+w \varphi _R^2 \, dx\,\\&\quad \le 2 C_2 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w| \ |\nabla \varphi _R| w \varphi _R \, dx \\&\qquad - L \int _{{\mathcal {C}}(2R)} (u- v)^+w \varphi _R^2 \, dx, \end{aligned} \end{aligned}$$

(3.13)

where $\xi$ is some point that belongs to (v, u). Using in (3.13) the weighted Young inequality (and the fact that $|\nabla u|, |\nabla v| \in L^\infty ({\Sigma })$), we obtain

$$\begin{aligned} \begin{aligned}&C_1 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \varphi _R^2 \, dx \\&\quad \le 2 C_2 \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{\frac{p-2}{2}} |\nabla w| \left( |\nabla u| + |\nabla v|\right) ^{\frac{p-2}{2}} |\nabla \varphi _R| w \varphi _R \, dx \\&\qquad - L \int _{{\mathcal {C}}(2R)} w^2 \varphi _R^2 \, dx\\&\quad \le C_2 \sigma \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \, dx \\&\qquad + \frac{C_2}{\sigma } \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla \varphi _R|^2 w^2 \varphi _R^2 \, dx \\&\qquad - L \int _{{\mathcal {C}}(2R)} w^2 \varphi _R^2 \, dx.\\&\quad \le C_2 \sigma \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \, dx \\&\qquad + \left( \frac{C}{\sigma R^2} - L\right) \int _{{\mathcal {C}}(2R)} w^2 \varphi _R^2 \, dx, \end{aligned} \end{aligned}$$

(3.14)

where $C=C(p, \Vert \nabla u\Vert _{L^\infty ({\Sigma })},\Vert \nabla v\Vert _{L^\infty ({\Sigma })})$ is a positive constant. Hence, up to redefine the constants, we have

$$\begin{aligned} \begin{aligned} \int _{{\mathcal {C}}(R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \, dx&\le C\sigma \int _{{\mathcal {C}}(2R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \, dx \\&\ \ \ + \frac{1}{C_1}\left( \frac{C}{\sigma R^2} - L\right) \int _{{\mathcal {C}}(2R)} w^2 \varphi _R^2 \, dx. \end{aligned} \end{aligned}$$

(3.15)

Now we set

$$\begin{aligned} \displaystyle {\mathcal {L}}(R):=\int _{{\mathcal {C}}(R)} \left( |\nabla u| + |\nabla v|\right) ^{p-2} |\nabla w|^2 \, dx. \end{aligned}$$

By our assumption,$|\nabla u|, |\nabla v| \in L^\infty (\Sigma )$, it follows that ${\mathcal {L}}(R) \le \dot{C} R^N$ for every $R>0$ and for some $\dot{C}=\dot{C}(p, \Vert \nabla u\Vert _{L^\infty ({\Sigma })},\Vert \nabla v\Vert _{L^\infty ({\Sigma })})$. Moreover, in equation (3.15), we take $\sigma =\sigma (p, N, \Vert \nabla u\Vert _{L^\infty ({\Sigma })},\Vert \nabla v\Vert _{L^\infty ({\Sigma })})>0$ sufficiently small so that $C\sigma < {1}/{2^N}$. Finally we fix $R_0 >0$ such that

$$\begin{aligned} \displaystyle \frac{C}{\sigma R^2} - L < 0 \end{aligned}$$

for every $R \ge R_0$. Therefore by (3.15) we deduce that

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}(R) \le \vartheta {\mathcal {L}}(2R) &{}\quad \forall R \ge R_0\\ {\mathcal {L}}(R) \le \dot{C} R^N &{}\quad \forall R \ge R_0, \end{array}\right. } \end{aligned}$$

(3.16)

where $\displaystyle \vartheta :=C\sigma <1/2^N$. By applying Lemma 2.1 in [14] it follows that ${\mathcal {L}}(R)=0$ for all $R \ge R_0$. Hence $u \le v$ in $\Sigma$. $\square$

Let us recall a weak comparison principle in narrow domains that will be an essential tool in the proof of Theorem 1.1.

Theorem 3.2

[16] Let $1<p<2$ and $N>1$. Fix $\lambda _0 > 0$ and $L_0>0$. Consider $a,b \in \mathbb {R}$, with $a < b$, $\tau , \epsilon > 0$ and set

$$\begin{aligned} \Sigma _{(a,b)}:= \mathbb {R}^{N-1} \times (a,b). \end{aligned}$$

Let $u,v \in C^{1,\alpha }_{loc}(\overline{\Sigma }_{(a,b)})$ such that $\Vert u\Vert _\infty + \Vert \nabla u\Vert _\infty \le L_0$, $\Vert v\Vert _\infty + \Vert \nabla v\Vert _\infty \le L_0$, f fulfills $({{\varvec{h}}_{\varvec{f}}})$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _p u \le f(u) &{}\quad \text {in} \ \Sigma _{(a,b)} \\ -\Delta _p v \ge f(v) &{} \quad \text {in} \ \Sigma _{(a,b)} \\ u \le v &{}\quad \text {on} \ \partial {\mathcal {S}}_{(\tau , \epsilon )}, \\ \end{array}\right. } \end{aligned}$$

(3.17)

where the open set ${\mathcal {S}}_{(\tau , \epsilon )} \subseteq \Sigma _{(a,b)}$ is such that

$$\begin{aligned} {\mathcal {S}}_{(\tau , \epsilon )} = \bigcup _{x' \in \mathbb {R}^{N-1}} I_{x'}^{\tau , \epsilon }, \end{aligned}$$

and the open set $I_{x'}^{\tau , \epsilon } \subseteq \{x'\} \times (a,b)$ has the form

$$\begin{aligned} I_{x'}^{\tau , \epsilon } = A_{x'}^\tau \cup B_{x'}^\epsilon , \; \text {with} \; |A_{x'}^\tau \cap B_{x'}^\epsilon | = \emptyset \end{aligned}$$

and, for $x'$ fixed, $A_{x'}^\tau , B_{x'}^\epsilon \subset (a,b)$ are measurable sets such that

$$\begin{aligned} A^\tau _{x'}| \le \tau \quad \text {and} \quad B_{x'}^\epsilon \subseteq \{x_N \in \mathbb {R}\ | \ |\nabla u(x',x_N)|< \epsilon , \ |\nabla v (x',x_N)| < \epsilon \}. \end{aligned}$$

Then there exist

$$\begin{aligned} \tau _0=\tau _0(N,p,a,b,L_0)>0 \end{aligned}$$

and

$$\begin{aligned} \epsilon _0=\epsilon _0(N,p,a,b,L_0)>0 \end{aligned}$$

such that, if $0< \tau < \tau _0$ and $0< \epsilon < \epsilon _0$, it follows that

$$\begin{aligned} u \le v \quad \text {in} \,\,{\mathcal {S}}_{(\tau , \epsilon )}. \end{aligned}$$

The proof of this result is contained in [16, Theorem 1.6], where the authors proved the same result for a more general class of operators and nonlinearities and also in the presence of a first order term.

4 Monotonicity with respect to $x_N$

The purpose of this section consists in showing that all the non-trivial solutions u to (${\mathcal P}$) that satisfies (1.2) are increasing in the $x_N$ direction. Since in our problem the right hand side depends only on u, it is possible to define the following set

$$\begin{aligned} {\mathcal {Z}}_{f(u)}:= \{ x \in \mathbb {R}^N \ | \ u(x) \in {\mathcal {N}}_f\}. \end{aligned}$$

Without any a priori assumption on the behaviour of $\nabla u$, the set ${\mathcal {Z}}_{f(u)}$ may be very wild, see Fig. 1.

Fig. 1

The set ${\mathcal {Z}}_{f(u)}$

We state now the main result of this paragraph in the following

Proposition 4.1

Under the assumptions of Theorem 1.1, we have that

$$\begin{aligned} \partial _{x_N} u \ge 0 \quad \text {in} \,\, \mathbb {R}^N \qquad \text {and} \qquad \partial _{x_N} u > 0 \quad \text {in} \,\, \mathbb {R}^N\setminus {\mathcal {Z}}_{f(u)}. \end{aligned}$$

(4.1)

Proposition 4.1 will be proved at the end of Sect. 4 using different preliminary results. To this end we start by proving a lemma that we will use repeatedly in the sequel of the work.

Let us define the upper hemisphere

$$\begin{aligned} \mathbb {S}^{N-1}_+:=\{\nu \in \mathbb {S}^{N-1} \ | \ (\nu , e_N)>0\}. \end{aligned}$$

(4.2)

Lemma 4.2

Let ${\mathcal U}$ a connected component of ${\mathbb R}^N\setminus {\mathcal {Z}}_{f(u)}$, $\eta \in \mathbb {S}^{N-1}_+$ and let us assume that $\partial _\eta u\ge 0$ in ${\mathcal U}$. Then

$$\begin{aligned} \partial _\eta u> 0\quad \text {in}\,\,{\mathcal U}. \end{aligned}$$

Proof

Using Theorem  2.6 we deduce that either $\partial _\eta u> 0$ in ${\mathcal U}$ or $\partial _\eta u\equiv 0$ in ${\mathcal U}$. For contradiction, assume that $\partial _\eta u \equiv 0$ in ${\mathcal U}$. Pick $P_0 \in {\mathcal U}$ and let us define

$$\begin{aligned} r(t)=P_0+t\eta , \quad t\in {\mathbb {R}} \end{aligned}$$

and

$$\begin{aligned} t_0=\inf \left\{ t\in {\mathbb R}\,:\, r(\vartheta ) \in {\mathcal U}, \; \forall \vartheta \in (t,0]\right\} . \end{aligned}$$

(4.3)

We note that the infimum in (4.3) is well defined, since by definition the connected component ${\mathcal U}$ is an open set, and that $t_0 \in [-\infty , 0)$.

In the case $t_0=-\infty$, we deduce that $u(P_0)=-1$. Indeed u is constant on r(t) for $t\in (-\infty , 0]$ (recall that $\partial _\eta u \equiv 0$ in ${\mathcal U}$) and (1.2) holds. But this is a contradiction, see Remark  2.7.

In the case $t_0>-\infty$, we deduce that $r(t_0)\in {\mathcal {Z}}_{f(u)}$ and therefore $f(u(r(t_0)))=f(u(P_0+t_0\eta ))=0$. But u is constant on r(t) for $t_0\le t\le 0$, which implies that $f(u(P_0))=f(u(P_0+t_0\eta ))=0$, namely $P_0\in {\mathcal {Z}}_{f(u)}$. The latter clearly contradicts the assumption $P_0 \in {\mathcal U}$. Therefore $\partial _\eta u> 0$ in ${\mathcal U}$ as desired. $\square$

Some arguments used in the proofs of the results of this section, are based on a nontrivial modification of the moving plane method. Let us recall some notations. We define the half-space $\Sigma _\lambda$ and the hyperplane $T_\lambda$ by

$$\begin{aligned} \begin{aligned} \Sigma _\lambda := \{x \in \mathbb {R}^N \ | \ x_N < \lambda \},\ \quad \quad T_\lambda&:= \partial \Sigma _\lambda = \{x \in \mathbb {R}^N \ | \ x_N = \lambda \} \end{aligned} \end{aligned}$$

(4.4)

and the reflected function $u_\lambda (x)$ by

$$\begin{aligned} u_\lambda (x) = u_\lambda (x',x_N):= u(x', 2\lambda -x_N) \quad \text {in}\,\, {\mathbb R}^N. \end{aligned}$$

We also define the critical set ${\mathcal {Z}}_{\nabla u}$ by

$$\begin{aligned} {\mathcal {Z}}_{\nabla u}:=\{x \in \mathbb {R}^N \ | \ \nabla u(x) = 0 \}. \end{aligned}$$

(4.5)

The first step in the proof of the monotonicity is to get a property concerning the local symmetry regions of the solution, namely any $C \subseteq \Sigma _\lambda$ such that $u \equiv u_\lambda$ in C.

Having in mind these notations we are able to prove the following:

Proposition 4.3

Under the assumption of Theorem 1.1, let us assume that u is a solution to $({\mathcal P})$ satisfying (1.2), such that

• (i) u is monotone non-decreasing in $\Sigma _\lambda$ and

• (ii) $u \le u_\lambda$ in $\Sigma _\lambda$.

Then $u < u_\lambda$ in $\Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)}$.

Proof

By (1.2), given $0<\delta _0<1$ there exists $M_0=M_0(\delta _0)>0$, with $\lambda >-M_0$, such that $u(x)=u(x',x_N)<-1+\delta _0$ in $\{x_N<- M_0\}$ and $u_\lambda (x)=u(x',2\lambda -x_N)>1-\delta _0$ in $\{x_N<- M_0\}$. We fix $\delta _0$ sufficiently small such that $f'(u)<-L$ in $\{x_N<- M_0\}$, for some $L>0$. Arguing by contradiction, let us assume that there exists $P_0 =(x_0',x_{N,0}) \in \Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)}$ such that $u(P_0)=u_\lambda (P_0)$. Let $\mathcal {U}_0$ the connected component of $\Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)}$ containing $P_0$. By Theorem 2.4, since $u(P_0)=u_\lambda (P_0)$, we deduce that ${\mathcal U}_0$ is a local symmetry region, i.e. $u\equiv u_\lambda$ in $\mathcal {U}_0$.

We notice that, by construction, $u < u_\lambda$ in $\Sigma _{-M_0}$, since $u(x)<-1+\delta _0$ and $u_\lambda (x)=u(x',2\lambda - x_N) > 1-\delta _0$ in $\Sigma _{-M_0}$. Since $\mathcal {U}_0$ is an open set of $\Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)}$ (and also of $\mathbb {R}^N$) there exists $\rho _0=\rho _0(P_0)>0$ such that

$$\begin{aligned} B_{\rho _0}(P_0) \subset \mathcal {U}_0. \end{aligned}$$

(4.6)

Fig. 2

The slided ball $B_{\rho _0}(P_0)$

We can slide $B_{\rho _0}$ in ${\mathcal U}_0$, towards to $-\infty$ in the y-direction and keeping its centre on the line $\{x'=x'_0\}$ (see Fig. 2), until it touches for the first time $\partial {\mathcal {U}}_0$ at some point $z_0\in {\mathcal {Z}}_{f(u)}$. In Fig. 3, we show some possible examples of first contact point with the set ${\mathcal {Z}}_{f(u)}$.

Fig. 3

The first contact point $z_0$

Now we consider the function

$$\begin{aligned} w_0(x):=u(x)-u(z_0) \end{aligned}$$

and we observe that $w_0(x) \ne 0$ for every $x \in B_{\rho _0}(\hat{P}_0)$, where $\hat{P}_0$ is the new centre of the slided ball. In fact, if this is not the case there would exist a point $\bar{z} \in B_{\rho _0}(\hat{P}_0)$ such that $w_0(\bar{z})=0$, but this is in contradiction with the fact that ${\mathcal {U}}_0 \cap {\mathcal {Z}}_{f(u)}= \emptyset$. We have to distinguish two cases. Since $p < 2$ and f is locally Lipschitz, we have that

• Case 1 If $w_0(x) > 0$ in $B_{\rho _0}(\hat{P}_0)$, then

  $$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _p w_0 \le C w_0^{p-1} &{} \quad \text {in} \ B_{\rho _0}(\hat{P}_0)\\ w_0>0 &{} \quad \text {in} \ B_{\rho _0}(\hat{P}_0)\\ w(z_0)=0 &{} \quad z_0 \in \partial B_{\rho _0}(\hat{P}_0), \end{array}\right. } \end{aligned}$$

  where C is a positive constant.

• Case 2 If $w_0(x) < 0$ in $B_{\rho _0}(\hat{P}_0)$, setting $v_0 = - w_0$ we have

  $$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _p v_0 \le C v_0^{p-1} &{} \quad \text {in} \ B_{\rho _0}(\hat{P}_0)\\ v_0>0 &{} \quad \text {in} \ B_{\rho _0}(\hat{P}_0) \\ v_0(z_0)=0 &{} \quad z_0 \in \partial B_{\rho _0}(\hat{P}_0), \end{array}\right. } \end{aligned}$$

  where C is a positive constant.

In both cases, by the Höpf boundary lemma (see e.g. [22, 28]), it follows that $|\nabla w(z_0)|=|\nabla u (z_0)| \ne 0$.

Using the Implicit Function Theorem we deduce that the set $\{u=u(z_0)\}$ is a smooth manifold near $z_0$. Now we want to prove that

$$\begin{aligned} u_{x_N}(z_0)> 0 \end{aligned}$$

and actually that the set $\{u=u(z_0)\}$ is a graph in the y-direction near the point $z_0$. By our assumption we know that $u_{x_N}(z_0):=u_y(z_0) \ge 0$. According to [7, 8] (see also Sect. 2), the linearized operator of (${\mathcal P}$) is well defined

$$\begin{aligned} L_u(u_y, \varphi )\equiv & {} \int _{\Sigma _\lambda } [|\nabla u|^{p-2} (\nabla u_y, \nabla \varphi ) + (p-2) |\nabla u|^{p-4} (\nabla u, \nabla u_y)(\nabla u, \nabla \varphi )] \, dx \nonumber \\&- \int _{\Sigma _\lambda } f'(u) u_y \varphi \, dx \end{aligned}$$

(4.7)

for every $\varphi \in C^1_c(\Sigma _\lambda )$. Moreover $u_y$ satisfies the linearized equation (2.15), i.e.

$$\begin{aligned} L_u(u_y, \varphi ) =0 \quad \forall \varphi \in C^1_c(\Sigma _\lambda ). \end{aligned}$$

(4.8)

Let us set $z_0=(z_0',y_0)$. We have two possibilities: $u_y(z_0)=0$ or $u_y(z_0)>0$.

Claim: We show that the case $u_y(z_0)=0$ is not possible.

If $u_y(z_0)=0$, then $u_y(x) \equiv 0$ in all $B_{\hat{\rho }}(z_0)$ for some positive ${\hat{\rho }}$; to prove this we use the fact that $|\nabla u(z_0)|\ne 0$, $u\in C^{1,\alpha }$ and that Theorem  2.5 holds.

By construction of $z_0$ there exists $\varepsilon _1 >0$ such that every point $z \in {\mathcal {S}}_1 := \{(z'_0,t) \in \mathcal {U}_0 : y_0< t < y_0+ \varepsilon _1\}$ has the following properties:

• (1) $z \in \overline{\mathcal {U}_0}$, since the ball is sliding along the segment ${\mathcal {S}}_1$;

• (2) $z \not \in \partial {\mathcal {U}}_0$, since $z_0$ is the first contact point with $\partial {\mathcal {U}}_0$.

In particular, for every $z \in {\mathcal {S}}_1$ we have

$$\begin{aligned} z \in \overline{\mathcal {U}_0} \setminus \partial \mathcal {U}_0 = \mathcal {U}_0. \end{aligned}$$

(4.9)

Since $|\nabla u(z_0)|\ne 0$ and $u\in C^{1,\alpha }$, by Theorem  2.5 it follows that there exists $0< \varepsilon _2 < \varepsilon _1$ such that

$$\begin{aligned} u_y(x)=0 \quad \forall x \in B_{\varepsilon _2}(z_0). \end{aligned}$$

Let us consider ${\mathcal {S}}_2:=\{(z'_0,t) \in \mathcal {U}_0 : y_0< t < y_0+ \varepsilon _2\}$; by definition ${\mathcal {S}}_2 \subset {\mathcal {S}}_1$ and every point of ${\mathcal {S}}_2$ belongs also to ${\mathcal {Z}}_{f(u)}$, since $u(z)=u(z_0)$ for every $z \in {\mathcal {S}}_2$ and $z_0 \in {\mathcal {Z}}_{f(u)}$ by our assumptions. But this gives a contradiction with (4.9).

From what we have seen above, we have $|\nabla u (z_0)| \ne 0$ and hence there exists a ball $B_r(z_0)$ where $|\nabla u (x)| \ne 0$ for every $x \in B_r(z_0)$. By Theorem  2.3 it follows that $u \equiv u_\lambda$ in $B_r(z_0)$ namely $u \equiv u_\lambda$ in a neighborhood of the point $z_0\in \partial {\mathcal U}_0$. Since $u_y (z_0)>0$ and ${\mathcal {N}}_f$ is finite

$$\begin{aligned} B_r(z_0)\cap \left( (\Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)})\setminus {\mathcal {U}}_0\right) \ne \emptyset \end{aligned}$$

and $u_y(x) >0$ in $B_r(z_0)$, as consequence, the set $\{u=u(z_0)\}$ is a graph in the y-direction in a neighborhood of the point $z_0$. Now we have to distinguish two cases:

• Case 1 $u(z_0)=\min [\mathcal {N}_f\setminus \{-1\}].$ Define the sets

  $$\begin{aligned} {\mathcal {C}}_1:= \{x\in {\mathbb R}^N \,:\, x'\in \left( B_r(z_0) \cap \{y:=y_0\} \right) \quad \text {and}\quad u(x)<u(z_0) \} \end{aligned}$$
  $$\begin{aligned} {\mathcal {C}}_2:= B_r(z_0) \cup ( (B_r(z_0) \cap \{y:=y_0\}) \times (-\infty , y_0)) \end{aligned}$$

  and

  $$\begin{aligned} {\mathcal {C}}={\mathcal {C}}_1\cap {\mathcal {C}}_2. \end{aligned}$$

  We observe that ${\mathcal {C}}$ is an open unbounded path-connected set (actually a deformed cylinder), see Fig. 4. Since $f(u(z_0))$ has the right sign, by Theorem  2.4 it follows that $u\equiv u_\lambda$ in ${\mathcal C}$ and this in contradiction with the uniform limit conditions (1.2).

• Case 2 $u(z_0)>\min [{\mathcal {N}}_f\setminus \{-1\}]$. In this case the open ball $B_r(z_0)$ must intersect another connected component (i.e. $\not \equiv {\mathcal {U}}_0$) of $\Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)}$, such that $u \equiv u_\lambda$ in a such component, see Fig. 5. Here we used the fact that near the (new) first contact point, the corresponding level set is a graph in the y-direction. Now, it is clear that repeating a finite number of times the argument leading to the existence of the touching point $z_0$, we can find a touching point $z_m$ such that

  $$\begin{aligned} u(z_m)=\min [{\mathcal {N}}_f\setminus \{-1\}]. \end{aligned}$$

  The contradiction then follows exactly as in Case 1.

Fig. 4

Case 1: $u(z_0)=\min [\mathcal {N}_f\setminus \{-1\}]$

Fig. 5

Case 2: $u(z_0)>\min [{\mathcal {N}}_f\setminus \{-1\}]$

Hence $u < u_\lambda$ in $\Sigma _\lambda \setminus {\mathcal {Z}}_{f(u)}$. $\square$

To prove Proposition 4.1 we need the following result:

Lemma 4.4

Under the assumption of Theorem 1.1, let u be a solution to $({\mathcal P})$. Then there exist $M_0=M_0(p,f, N, \Vert \nabla u\Vert _{L^{\infty }(\mathbb {R^N})})>0$ sufficiently large such that for every $M\ge M_0$ there exits a constant $C^*=C^*(M)>0$ such that

$$\begin{aligned} {|\nabla u|\ge \partial _{x_N} u \ge C^*> 0 \quad \text {in} \; \{-M-1<x_N < -M+1\}.} \end{aligned}$$

(4.10)

Proof

Performing the moving plane procedure, using (1.2) and ($h_f$), by the Proposition 3.1 with $v=u_\lambda$ and $\Sigma =\Sigma _\lambda$, we infer that there exists a constant $M_0=M_0(p,f, N, \Vert \nabla u\Vert _{L^{\infty }(\mathbb {R^N})})>0$ such that $\partial _{x_N} u \ge 0$ in $\{x_N < -M_0+1\}$. Now we can assume

$$\begin{aligned} {\mathcal {Z}}_{f(u)} \cap \{x_N < -M_0+1\} = \emptyset , \end{aligned}$$

then by Theorem 2.6 it follows that $\partial _{x_N} u > 0$ in $\{x_N < -M_0+1\}$, since the case $\partial _{x_N} u = 0$ would imply a contradiction, i.e. $u(x)=-1$ in $\{x_N < -M_0+1\}$ . We observe that in particular it holds $|\nabla u| \ge \partial _{x_N} u>0$ in $\{-M_0-1<x_N<-M_0+1\}$. We want to prove that for all $M\ge M_0$, there exists $C^*=C^*(M)>0$ such that $\partial _{x_N} u \ge C^*>0$ in $\{-M-1<x_N<-M+1\}$.

Arguing by contradiction let us assume that there exists a sequence of point $P_n=(x'_n,x_{N,n})$, with $-M-1<x_{N,n}<-M+1$ for every $n \in \mathbb {N}$, such that $\partial _{x_N} u (P_n) \rightarrow 0$ as $n \rightarrow + \infty$ in $\{-M-1<x_N<-M+1\}$. Up to subsequences, let us assume that

$$\begin{aligned} x_{N,n} \rightarrow \bar{x}_N \; \text {with} \; -M-1 \le \bar{x}_N \le -M+1. \end{aligned}$$

Let us now define

$$\begin{aligned} \tilde{u}_n(x',x_N):=u(x'+x'_n, x_N) \end{aligned}$$

so that $\Vert \tilde{u}_n\Vert _\infty = \Vert u \Vert _\infty \le 1$. By the second claim of Remark 2.7, we have that

$$\begin{aligned} \Vert \tilde{u}_n\Vert _{C^{1,\alpha }(\mathbb {R}^N)} \le C_0 \end{aligned}$$

for some $0< \alpha < 1$. By Ascoli’s Theorem we have

$$\begin{aligned} \tilde{u}_n \overset{C^{1,\alpha '}_{loc}(\mathbb {R}^N)}{\longrightarrow } \tilde{u} \end{aligned}$$

up to subsequences, for $\alpha ' < \alpha$. By construction $\partial _{x_N} \tilde{u} \ge 0$ and $\partial _{x_N} \tilde{u} (0,\bar{x}_N) = 0$, hence by Theorem 2.5 it follows that $\partial _{x_N}\tilde{u} = 0$ in $\{-M-1<x_N<-M+1\}$ and therefore $\partial _{x_N}\tilde{u} = 0$ in all $\{(x',x_n)\,:\,x_N<-M+1\}$ by Theorem 2.6, since ${\mathcal {Z}}_{f(u)} \cap \{x_N < -M_0+1\} = \emptyset$. This gives a contradiction (by Theorem 2.5) with the fact that $\displaystyle \lim _{x_N\rightarrow -\infty }u(x',x_N)=-1$ (this implies that $\displaystyle \lim _{x_N\rightarrow -\infty } \tilde{u}(x',x_N)=-1$ ), see Remark 2.7. $\square$

With the notation introduced above, we set

$$\begin{aligned} \Lambda := \{\lambda \in \mathbb {R}\ | \ u \le u_t \; \text {in} \ \Sigma _t \; \forall t < \lambda \}. \end{aligned}$$

(4.11)

Note that, by Proposition  3.1 (with $v=u_t)$, it follows that $\Lambda \ne \emptyset$, hence we can define

$$\begin{aligned} \bar{\lambda }:= \sup \Lambda . \end{aligned}$$

(4.12)

Moreover it is important to say that by the continuity of u and $u_\lambda$, it follows that

$$\begin{aligned} u \le u_{\bar{\lambda }} \quad \text {in} \; \Sigma _{\bar{\lambda }}. \end{aligned}$$

The proof of the fact that $u(x',x_N)$ is monotone increasing in the $x_N$-direction in the entire space ${\mathbb R}^N$ is done once we show that $\bar{\lambda }= + \infty$. To do this we assume by contradiction that $\bar{\lambda }< + \infty$, and we prove a crucial result, which allows us to localize the support of $(u-u_{\bar{\lambda }})^+$. This localization, that we are going to obtain, will be useful to apply the weak comparison principle given by Proposition  3.1 and Theorem  3.2.

Proposition 4.5

Under the assumption of Theorem 1.1, let u be a solution to $({\mathcal P})$. Assume that $\bar{\lambda }< + \infty$ (see (4.12)) and set

$$\begin{aligned} W_\varepsilon :=(u-u_{\bar{\lambda }+ \varepsilon }) \chi _{\{x_N \le \bar{\lambda }+ \varepsilon \}}. \end{aligned}$$

Let $M,\kappa >0$ be such that $M>2|\bar{\lambda }|$. Then for all $\mu \in (0, (\bar{\lambda }+M)/2)$ there exists $\bar{\varepsilon }> 0$ such that for every $0< \varepsilon < \bar{\varepsilon }$

$$\begin{aligned} \text {supp }\, W^+_\varepsilon \subset \{x_N \le -M\} \cup \{ \bar{\lambda }- \mu \le x_N \le \bar{\lambda }+ \varepsilon \} \cup \{ |\nabla u| \le \kappa \}. \end{aligned}$$

(4.13)

Proof

Assume by contradiction that (4.13) is false, so that there exists $\mu >0$ in such a way that, given any $\bar{\varepsilon }>0$, we find $0<\varepsilon \le \bar{\varepsilon }$ so that there exists a corresponding $x_\varepsilon = (x'_\varepsilon , x_{N, \varepsilon })$ such that

$$\begin{aligned} u(x'_\varepsilon , x_{N, \varepsilon }) \ge u_{\bar{\lambda }+ \varepsilon } (x'_\varepsilon , x_{N, \varepsilon }), \end{aligned}$$

with $x_\varepsilon = (x'_\varepsilon , x_{N, \varepsilon })$ belonging to the set

$$\begin{aligned} \{(x',x_N)\in {\mathbb R}^N\,:\,M< x_{N, \varepsilon } < \bar{\lambda }- \mu \} \end{aligned}$$

and such that $|\nabla u(x_\varepsilon )| \ge \kappa$.

Taking $\bar{\varepsilon }= {1}/{n}$, then there exists $\varepsilon _n \le 1/n$ going to zero, and a corresponding sequence

$$\begin{aligned} x_n = (x'_n, x_{N,n}) = (x'_{\varepsilon _n}, x_{N, \varepsilon _n}) \end{aligned}$$

such that

$$\begin{aligned} u(x'_n, x_{N, n}) \ge u_{\bar{\lambda }+ \varepsilon _n} (x'_n, x_{N, n}) \end{aligned}$$

with $-M< x_{N,n} < \bar{\lambda }- \mu$. Up to subsequences, let us assume that

$$\begin{aligned} x_{N,n} \rightarrow \bar{x}_N \; \text {with} \; -M \le \bar{x}_N \le \bar{\lambda }- \mu . \end{aligned}$$

Let us define

$$\begin{aligned} \tilde{u}_n(x',x_N):=u(x'+x'_n, x_N) \end{aligned}$$

so that $\Vert \tilde{u}_n\Vert _\infty = \Vert u \Vert _\infty \le 1$. By the second claim of Remark  2.7, we have that

$$\begin{aligned} \Vert \tilde{u}_n\Vert _{C^{1,\alpha }(\mathbb {R}^N)} \le C_0 \end{aligned}$$

for some $0< \alpha < 1$. By Ascoli’s Theorem we have

$$\begin{aligned} \tilde{u}_n \overset{C^{1,\alpha '}_{loc}(\mathbb {R}^N)}{\longrightarrow } \tilde{u} \end{aligned}$$

up to subsequences, for $\alpha ' < \alpha$. By construction it follows that

• $\tilde{u} \le \tilde{u}_{\bar{\lambda }} \quad \text {in} \ \Sigma _{\bar{\lambda }}$;

• $\tilde{u}(0,\bar{x}_N) = \tilde{u}_{\bar{\lambda }} (0, \bar{x}_N)$;

• $| \nabla \tilde{u}(0, \bar{x}_N)| \ge \kappa$.

Since $|\nabla \tilde{u} (0, \bar{x}_N)| \ge \kappa$ there exists $\rho >0$ and a ball $B_\rho (0,\bar{x}_N) \subset \Sigma _{\bar{\lambda }}$ such that $|\nabla u(x)| \ne 0$ for every $x \in B_\rho (0,\bar{x}_N)$. Now, if $\tilde{u}(0,\bar{x}_N) \in {\mathcal {Z}}_{f(u)}$, since $\tilde{u}$ is non constant in $B_\rho (0,\bar{x}_N)$, there exists $P_0 \in B_\rho (0,\bar{x}_N)$ such that $u(P_0) \not \in {\mathcal {Z}}_{f(u)}$. By Theorem  2.3 it follows that

$$\begin{aligned} \tilde{u} \equiv \tilde{u}_{\bar{\lambda }} \quad \text {in}\,\, B_\rho (0,\bar{x}_N). \end{aligned}$$

(4.14)

On the other hand, by Proposition 4.3 it follows that

$$\begin{aligned} \tilde{u} < \tilde{u}_{\bar{\lambda }} \qquad \text {in} \,\,\Sigma _{\bar{\lambda }} \setminus {\mathcal {Z}}_{f(u)}. \end{aligned}$$

This gives a contradiction with (4.14). Hence we have (4.13). $\square$

Proof of Proposition  4.1

Let us assume by contradiction that $\bar{\lambda }<+\infty$, see (4.12). Let $\hat{M}>0$ be such that Proposition  3.1 and Lemma  4.4 apply. Let $C^*=C^*(\hat{M})$ be the constant given in Lemma  4.4. By Proposition  4.5 (choose $M=4 \hat{M}+1$ there, redefining $\hat{M}$ if necessary) we have that

$$\begin{aligned} \text {supp }\, W^+_\varepsilon \subset \{x_N \le -4\hat{M}-1\} \cup \{-4\hat{M} +1\le x_N \le \bar{\lambda }+ \varepsilon \}, \end{aligned}$$

(4.15)

where $W_\varepsilon :=(u-u_{\bar{\lambda }+ \varepsilon }) \chi _{\{x_N \le \bar{\lambda }+ \varepsilon \}}$. In particular, to get (4.15), we choose $\kappa$ in Proposition 4.5 such that $2\kappa =C^*$. Then we deduce that

$$\begin{aligned} u\le u_{\bar{\lambda }+\varepsilon }\,\,\text {in}\,\, \{(x,x_N)\in {\mathbb R}^N\,:\ -4\hat{M} -1<x_N<-4\hat{M} +1\}. \end{aligned}$$

(4.16)

Using (4.16), we can apply Proposition  3.1 in $\{x_N < -4\hat{M}-1\}$ and therefore, together Lemma  4.4 and Proposition  4.5, we actually deduce

$$\begin{aligned} \text {supp }\, W^+_\varepsilon \subset \{-4\hat{M} +1\le x_N \le \bar{\lambda }+ \varepsilon \}. \end{aligned}$$

In particular, if we look to (4.13), we deduce that $\text {supp }\, W^+_\varepsilon$ must belong to the set

$$\begin{aligned} A:=\left\{ \{ \bar{\lambda }- \mu \le x_N \le \bar{\lambda }+ \varepsilon \} \cup \{ |\nabla u| \le \kappa \}\right\} \cap \left\{ x_N\ge -4\hat{M} +1\right\} . \end{aligned}$$

We now apply Theorem  3.2 in the set A. Let us choose (in Theorem 3.2)

$$\begin{aligned} L_0=1+\Vert \nabla u\Vert _{L^{\infty }({\mathbb {R}}^N)} \end{aligned}$$

and take $\tau _0=\tau _0(p,\bar{\lambda }, \hat{M}, N, L_0)>0$ and $\epsilon _0=\epsilon _0(p,\bar{\lambda }, \hat{M}, N, L_0)>0$ as in Theorem  3.2. Let $\mu , \varepsilon$ in Proposition  4.5 such that $2(\mu +\varepsilon )< \tau _0$ and let us redefine $\kappa$ eventually such that $\kappa :=\min \{C^*/2, \epsilon _0\}$. We finally apply Theorem  3.2 concluding that actually $W_\varepsilon ^+=0$ in the set A. This gives a contradiction, in view of the definition (4.12) of $\bar{\lambda }$. Consequently we deduce that $\bar{\lambda }=+\infty$. This implies the monotonicity of u, that is $\partial _{x_N} u \ge 0$ in $\mathbb {R}^N$. By Theorem  2.6, it follows that

$$\begin{aligned} \partial _{x_N} u > 0 \quad \text {in} \, \mathbb {R}^N \setminus {\mathcal {Z}}_{f(u)}, \end{aligned}$$

since by Lemma  4.2, the case $\partial _{x_N} u\equiv 0$ in some connected component, say ${\mathcal U}$, of $\mathbb {R}^N \setminus {\mathcal {Z}}_{f(u)}$ can not hold. $\square$

5 1-Dimensional symmetry

In this section we pass from the monotonicity in $x_N$ to the monotonicity in all the directions of the upper hemisphere $\mathbb {S}^{N-1}_+$ defined in (4.2). We refer to [10] for the case of the Laplacian operator, where in the proof the linearity of the operator was crucial. Here we have to take into account the singular nature and the nonlinearity of the operator p-Laplacian.

Lemma 5.1

Under the same assumption of Theorem 1.1, given $\rho >0$ and $k>0$, we define

$$\begin{aligned} \Sigma _k^\rho :=\{x \in \mathbb {R}^N \ | -k< x_N < k\} \cap \{|\nabla u| > \rho \}. \end{aligned}$$

Assume $\eta \in \mathbb {S}^{N-1}_+$ and suppose that

$$\begin{aligned} \partial _\eta u \ge 0\quad \text {in}\,\, {\mathbb R}^N \quad \text {and} \quad \partial _\eta u> 0\quad \text {in}\,\, {\mathbb R}^N\setminus {\mathcal {Z}}_{f(u)}. \end{aligned}$$

(5.1)

Then, there exists an open neighbourhood ${\mathcal O}_\eta$ of $\eta$ in $\mathbb {S}^{N-1}_+$, such that

$$\begin{aligned} \partial _\nu u = (\nabla u, \nu ) > 0 \quad \text {in} \, \, \Sigma _k^\rho , \end{aligned}$$

(5.2)

for every $\nu \in {\mathcal O}_\eta$.

Proof

Arguing by contradiction let us assume that there exist two sequences $\{P_m\}~\in {\mathbb R}^N$ and $\{\nu _m\} \in \mathbb {S}^{N-1}_+$ such that, for every $m \in \mathbb {N}$ we have that $P_m=(x'_m,x_{N,m}) \in \Sigma _k^\rho$, $|(\nu _m, \eta ) -1 | < 1/m$ and $\partial _{\nu _m}u(P_m) \le 0$. Since $-k< x_{N,m} < k$ for every $m \in \mathbb {N}$, then up to subsequences $x_{N,m} \rightarrow \bar{x}_N$. Now, let us define

$$\begin{aligned} \tilde{u}_m(x', x_N):=u(x'+x'_m, x_N) \end{aligned}$$

so that $\Vert \tilde{u}_m\Vert _\infty = \Vert u \Vert _\infty \le 1$. By the second claim of Remark 2.7, we have that

$$\begin{aligned} \Vert \tilde{u}_m\Vert _{C^{1,\alpha }(\mathbb {R}^N)} \le C_0. \end{aligned}$$

By Ascoli’s Theorem, via a standard diagonal process, we have, up to subsequences

$$\begin{aligned} \tilde{u}_m \overset{C^{1,\alpha '}_{loc}(\mathbb {R}^N)}{\longrightarrow } \tilde{u}, \end{aligned}$$

for some $0<\alpha '< \alpha$.

By uniform convergence and (5.1) it follows that

$$\begin{aligned} \partial _{\eta } \tilde{u}(0,\bar{x}_N) = 0\quad \text {and}\quad | \nabla \tilde{u}(0, \bar{x}_N)| \ge \rho . \end{aligned}$$

• If $P_0:=(0,\bar{x}_N) \in {\mathcal {Z}}_{f(\tilde{u})}$, since $|\nabla \tilde{u} (0, \bar{x}_N)| \ge \rho$, then there exists a ball $B_r(P_0)$ such that $|\nabla \tilde{u} (x)| \ne 0$ for every $x \in B_r(P_0)$. By Theorem 2.5, applied having in mind that $|\nabla \tilde{u} (x)| \ne 0$ in $B_r(P_0)$, it follows that $\partial _{\eta } \tilde{u} (x) = 0$ for every $x \in B_r(P_0)$. In particular $\partial _{\eta } \tilde{u} (x) = 0$ for every $x \in B_r(P_0) \cap \left( \Sigma _k^\rho \setminus {\mathcal {Z}}_{f(\tilde{u})} \right)$, hence by Theorem 2.6 we deduce that $\partial _{\eta } \tilde{u} \equiv 0$ in the connected component ${\mathcal U}$ of $\Sigma _k^\rho \setminus {\mathcal {Z}}_{f(\tilde{u})}$ containing $B_r(P_0)$ (possibly redefining r), but this is in contradiction with Lemma 4.2.

• If $P_0 \in \Sigma _k^\rho \setminus {\mathcal {Z}}_{f(\tilde{u})}$ by Theorem 2.6 it follows that $\partial _{\eta } \tilde{u} > 0$ in the connected component of $\mathbb {R}^N \setminus {\mathcal {Z}}_{f(\tilde{u})}$ containing the point $P_0$. Indeed the case $\partial _{\eta } \tilde{u} \equiv 0$ in the connected component of $\mathbb {R}^N \setminus {\mathcal {Z}}_{f(\tilde{u})}$ containing $P_0$ can not hold since Lemma 4.2.

Hence we deduce (5.2). $\square$

Having in mind the previous lemma, now we are able to prove the monotonicity in a small cone of direction around $\eta$ in the entire space.

Proposition 5.2

Under the assumption of Theorem 1.1, assume $\eta \in \mathbb {S}^{N-1}_+$ such that ${\partial _\eta u}>0$ in ${\mathbb R}^N\setminus {\mathcal {Z}}_{f(u)}$. Then, there exists an open neighbourhood ${\mathcal O}_\eta$ of $\eta$ in $\mathbb {S}^{N-1}_+$, such that

$$\begin{aligned} \partial _\nu u = u_\nu \ge 0 \quad \text {in} \,\, \mathbb {R}^N \quad \text {and} \quad \partial _\nu u = u_\nu > 0\quad \text {in} \,\, \mathbb {R}^N \setminus {\mathcal {Z}}_{f(u)}, \end{aligned}$$

(5.3)

for every $\nu \in {\mathcal O}_\eta$.

Proof

We fix $\tilde{\delta }>0$ and let $k=k(\tilde{\delta })>0$ be such that $u < -1 + \tilde{\delta }$ in $\{x_N< -k\}$, $u > 1- \tilde{\delta }$ in $\{x_N>k\}$ and (3.3) holds in $\{|x_N| > k\}$. By Lemma  5.1 it follows that for all $\rho >0$ one has

$$\begin{aligned} \text {supp}\, (u_\nu ^-) \subseteq \left( \{|x_N|\ge k\} \cup \left( \{-k<x_N<k\}\cap \{|\nabla u|\le \rho \}\right) \right) . \end{aligned}$$

For simplicity of exposition we set

$$\begin{aligned} A:=\{|x_N|\ge k\}\quad \text {and} \quad D:=\left( \{-k<x_N<k\}\cap \{|\nabla u|\le \rho \}\right) . \end{aligned}$$

Our claim is to show that $u_\nu ^-=0$ in $A \cup D$. In order to do this we split the proof in two part.

Step 1. We show that $u_\nu ^-=0$ in A.

We set

$$\begin{aligned} \varphi :=(u_\nu ^-)^\alpha \varphi _R^{2} \chi _{\mathcal {A}(2R)} \end{aligned}$$

(5.4)

where $\alpha >1$, $R >0$ large, ${\mathcal {A}}(2R):=A \cap B_{2R}$ and $\varphi _R$ is a standard cutoff function such that $0\le \varphi _R \le 1$ on $\mathbb {R}^N$, $\varphi _R = 1$ in $B_R$, $\varphi _R = 0$ outside $B_{2R}$, with $|\nabla \varphi _R| \le 2/R$ in $B_{2R} \setminus B_R$. First of all we notice that $\varphi$ belongs to $W^{1,2}_0(\mathcal {A}(2R))$ (we remark that by the regularity results [8, 23, 24] it follows that $u\in W^{2,2}_{loc}({\mathbb R}^N)$, if $p<3$). To see this, use the definition of $\varphi _R$ and note that by Lemma  4.4 and Lemma  5.1, it follows that $u_\nu ^-=0$ on the hyperplanes $|x_N|=k$, namely on $\partial A$.

According to [7, 8] (see also Sect. 2) the linearized operator is well defined

$$\begin{aligned} \begin{aligned} L_u(u_\nu , \varphi )&\equiv \int _{\mathbb {R}^N} [|\nabla u|^{p-2} (\nabla u_\nu , \nabla \varphi ) + (p-2)&\!\!|\nabla u|^{p-4} (\nabla u, \nabla u_\nu )(\nabla u, \nabla \varphi )] \, dx \\&\quad - \int _{\mathbb {R}^N} f'(u) u_\nu \varphi \, dx \end{aligned} \end{aligned}$$

(5.5)

for every $\varphi \in W^{1,2}_{c}({\mathbb R}^N)$. Moreover it satisfies the following equation

$$\begin{aligned} L_u(u_\nu , \varphi ) =0 \quad \forall \varphi \in W^{1,2}_{c}({\mathbb R}^N). \end{aligned}$$

(5.6)

Taking $\varphi \in W^{1,2}_0(\mathcal {A}(2R))\cap W^{1,2}_{c}({\mathbb R}^N)$ defined in (5.4) in the previous equation, we obtain

$$\begin{aligned} \begin{aligned}&\alpha \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} (\nabla u_\nu , \nabla u_\nu ^-) (u_\nu ^-)^{\alpha -1} \varphi _R^2\\&\qquad + 2 \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} (\nabla u_\nu , \nabla \varphi _R) (u_\nu ^-)^\alpha \varphi _R \\&\qquad +\alpha (p-2) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-4} (\nabla u, \nabla u_\nu )(\nabla u, \nabla u_\nu ^-) (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx \\&\qquad + 2 (p-2) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-4} (\nabla u, \nabla u_\nu )(\nabla u, \nabla \varphi _R) (u_\nu ^-)^\alpha \varphi _R \, dx \\&\quad = \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx \end{aligned} \end{aligned}$$

(5.7)

Making some computations we obtain

$$\begin{aligned} \begin{aligned}&\alpha \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx\\&\quad = -2 \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} (\nabla u_\nu ^-, \nabla \varphi _R) (u_\nu ^-)^\alpha \varphi _R \, dx\\&\qquad +\alpha (2-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-4} (\nabla u, \nabla u_\nu ^-)^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx \\&\qquad + 2 (2-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-4} (\nabla u, \nabla u_\nu ^-)(\nabla u, \nabla \varphi _R) (u_\nu ^-)^\alpha \varphi _R \, dx \\&\qquad + \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx \\&\quad \le \alpha (2-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx \\&\qquad +2(3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-| \ |\nabla \varphi _R| (u_\nu ^-)^\alpha \varphi _R \, dx\\&\qquad + \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2\, dx. \end{aligned} \end{aligned}$$

(5.8)

Now it is possible to rewrite (5.8) as follows

$$\begin{aligned} \begin{aligned}&\alpha (p-1)\int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx\\&\quad \le 2(3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-| \ |\nabla \varphi _R| (u_\nu ^-)^\alpha \varphi _R \, dx\\&\qquad + \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx. \end{aligned} \end{aligned}$$

(5.9)

Exploiting the weighted Young inequality we obtain

$$\begin{aligned} \begin{aligned}&\alpha (p-1)\int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx\\&\quad \le 2(3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^\frac{p-2}{2} |\nabla u_\nu ^-| \ (u_\nu ^-)^\frac{\alpha -1}{2} |\nabla u|^\frac{p-2}{2} |\nabla \varphi _R| (u_\nu ^-)^\frac{\alpha +1}{2} \varphi _R \, dx\\&\qquad + \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx\\&\quad \le \sigma (3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx\\&\qquad + \frac{3-p}{\sigma } \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla \varphi _R|^2 (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx\\&\qquad + \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx. \end{aligned} \end{aligned}$$

(5.10)

Since $u_\nu =(\nabla u, \nu )$, where $\Vert \nu \Vert =1$, we have

$$\begin{aligned} \begin{aligned}&\alpha (p-1)\int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx\\&\quad \le \sigma (3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx\\&\qquad + \frac{3-p}{\sigma } \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-1} |\nabla \varphi _R|^2 (u_\nu ^-)^\alpha \varphi _R^2 \, dx\\&\qquad + \int _{{\mathcal {A}}(2R)} f'(u) (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx\\&\quad \le \sigma (3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx\\&\qquad + \hat{C} \int _{{\mathcal {A}}(2R)} |\nabla \varphi _R|(u_\nu ^-)^\alpha \varphi _R^2 |\nabla \varphi _R| \, dx\\&\qquad - L \int _{{\mathcal {A}}(2R)} (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx, \end{aligned} \end{aligned}$$

(5.11)

where we used (3.3) and where $\hat{C}:={3-p}/{\sigma } \Vert \nabla u\Vert ^{p-1}_\infty$. Exploiting the Young inequality with exponents $({\alpha +1})/{\alpha }$ and $\alpha +1$ we obtain

$$\begin{aligned} \begin{aligned}&\alpha (p-1)\int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \varphi _R^2 \, dx\\&\quad \le \sigma (3-p) \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx\\&\qquad + \frac{\hat{C}}{\alpha +1}\int _{{\mathcal {A}}(2R)} |\nabla \varphi _R|^{\alpha +1} \, dx \\&\qquad + \frac{\hat{C}(\alpha +1)}{\alpha } \int _{{\mathcal {A}}(2R)} |\nabla \varphi _R|^{\frac{\alpha +1}{\alpha }} (u_\nu ^-)^{\alpha +1} \varphi _R^{2 \frac{\alpha +1}{\alpha }} \, dx\\&\qquad - L \int _{{\mathcal {A}}(2R)} (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx, \end{aligned} \end{aligned}$$

(5.12)

Since $|\nabla \varphi _R| \le 2/R$ in $B_{2R} \setminus B_R$, $0 \le \varphi _R \le 1$ in $\mathbb {R}^N$ and $\varphi _R=1$ in $B_R$, we obtain

$$\begin{aligned} \begin{aligned} \int _{{\mathcal {A}}(R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx&\le \vartheta \int _{{\mathcal {A}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx\\&\quad + \frac{1}{\alpha (p-1)}\left( \frac{\hat{C}(\alpha +1)}{\alpha R^\frac{\alpha +1}{\alpha }}- L \right) \\&\quad \times \int _{{\mathcal {A}}(2R)} (u_\nu ^-)^{\alpha +1} \varphi _R^2 \, dx,\\&\quad + \frac{\bar{C}}{R^{\alpha -(N-1)}}, \end{aligned} \end{aligned}$$

(5.13)

where $\vartheta :={\sigma (3-p)}/{\alpha (p-1)}$ and $\bar{C}: = {2\hat{C}}/{\alpha (\alpha +1)(p-1) }$. Now we fix $\alpha >0$ such that $\alpha >N-1$, $\sigma >0$ sufficiently small such that $\vartheta < 2^{-N}$ and finally $R_0>0$ such that $\displaystyle {\hat{C}(\alpha +1)}/{\alpha R^\frac{\alpha +1}{\alpha }}- L < 0$. Having in mind all these fixed parameters let us define

$$\begin{aligned} {\mathcal {L}}(R):= \int _{{\mathcal {A}}(R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\alpha -1} \, dx. \end{aligned}$$

It is easy to see that ${\mathcal {L}}(R) \le C R^N$. By (5.13) we deduce that holds

$$\begin{aligned} {\mathcal {L}}(R) \le \vartheta {\mathcal {L}}(2R) + \frac{\bar{C}}{R^{\alpha - (N-1)}} \end{aligned}$$

for every $R \ge R_0$. By applying Lemma 2.1 in [14] it follows that ${\mathcal {L}}(R)=0$ for all $R \ge R_0$. Hence passing to the limit we obtain that $u_\nu ^-=0$ in A.

Step 2. $u_\nu ^-=0$ in D.

Let us denote by $B'$ the $(N-1)$ dimensional ball in $\mathbb {R}^{N-1}$ and $\psi _R(x',x_N)=\psi _R(x')\in C_c^\infty ({\mathbb R}^{N-1})$ is a standard cutoff function such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi _R \equiv 1, &{}\quad \text { in } B^{'}(0,R) \subset {\mathbb {R}}^{N-1},\\ \psi _R \equiv 0, &{}\quad \text { in } {\mathbb {R}}^{N-1} \setminus B^{'}(0,2R),\\ |\nabla \psi _R | \le \frac{2}{R}, &{}\quad \text { in } B^{'}(0, 2R) \setminus B^{'}(0,R) \subset {\mathbb {R}}^{N-1}. \end{array}\right. } \end{aligned}$$

(5.14)

Let us define the cylinder

$$\begin{aligned} {\mathcal {C}}(R):=\left\{ (x',x_N)\in {\mathbb R}^N\,:\, \{x \in \mathbb {R}^N \ | -k< x_N < k\}\cap \overline{\{B^{'}(0,R)\times {\mathbb {R}}\}} \right\} . \end{aligned}$$

We set

$$\begin{aligned} \psi :=(u_\nu ^-)^\beta \psi _R^{2} \chi _{{\mathcal {C}}(2R)} \end{aligned}$$

(5.15)

where $\beta >1$. First of all we notice that $\psi$ belongs to $W^{1,2}_0({\mathcal {C}}(2R))$ by (5.14) and since $u_\nu ^-=0$ on $\partial A$ (as above, see Lemmas 4.4 and 5.1). Recalling (5.5) we have also in this case that

$$\begin{aligned} L_u(u_\nu , \psi ) =0 \quad \forall \psi \in W^{1,2}_{c}({\mathbb R}^N). \end{aligned}$$

(5.16)

Taking $\psi \in W^{1,2}_0({\mathcal {C}}(2R))\cap W^{1,2}_{c}({\mathbb R}^N)$ defined in (5.15) in the previous equation, we obtain

$$\begin{aligned} \begin{aligned}&\beta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} (\nabla u_\nu , \nabla u_\nu ^-) (u_\nu ^-)^{\beta -1} \psi _R^2\, dx\\&\qquad + 2 \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} (\nabla u_\nu , \nabla \psi _R) (u_\nu ^-)^\beta \psi _R \, dx\\&\qquad +\beta (p-2) \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-4} (\nabla u, \nabla u_\nu )(\nabla u, \nabla u_\nu ^-) (u_\nu ^-)^{\beta -1} \psi _R^2 \, dx \\&\qquad + 2 (p-2) \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-4} (\nabla u, \nabla u_\nu )(\nabla u, \nabla \varphi _R) (u_\nu ^-)^\beta \psi _R \, dx \\&\quad = \int _{{\mathcal {C}}(2R)} f'(u) (u_\nu ^-)^{\beta +1} \psi _R^2 \, dx. \end{aligned} \end{aligned}$$

(5.17)

Repeating verbatim the same argument of (5.8), (5.9) and (5.10), starting by (5.17) we obtain

$$\begin{aligned} \begin{aligned}&\beta (p-1) \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\beta -1} \psi _R^2 \, dx\\&\quad \le \sigma (3-p)\int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx\\&\qquad + \frac{(3-p)}{\sigma }\int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla \psi _R|^2(u_\nu ^-)^{\beta +1} \psi _R^2 \, dx\\&\qquad + \int _{{\mathcal {C}}(2R)} f'(u) (u_\nu ^-)^{\beta +1} \psi _R^2 \, dx. \end{aligned} \end{aligned}$$

(5.18)

Since $u_\nu =(\nabla u, \nu )$ and $|\nabla u| \le \rho$ in ${\mathcal {C}}(2R)$ we have

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\beta -1} \psi _R^2 \, dx \\&\quad \le \vartheta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx\\&\qquad + \hat{C} \rho ^{p-1} \int _{{\mathcal {C}}(2R)} |\nabla \psi _R|^2(u_\nu ^-)^{\beta } \psi _R^2 \, dx\\&\qquad + C_k \int _{{\mathcal {C}}(2R)} (u_\nu ^-)^{\beta +1} \psi _R^2 \, dx. \end{aligned} \end{aligned}$$

(5.19)

where $\vartheta := {\sigma (3-p)}/{\beta (p-1)}$, $\hat{C}:={(3-p)}/{\sigma \beta (p-1)}$ and $\tilde{C}:={\Vert f'\Vert _{L^\infty ((-1,1))}}{\beta (p-1)}$. Exploiting the Young inequality with exponents $({\beta +1})/{\beta }$ and $\beta +1$ we obtain

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\beta -1} \psi _R^2 \, dx\\&\quad \le \vartheta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx\\&\qquad + \frac{\hat{C} \rho ^{p-1}}{\beta +1}\int _{{\mathcal {C}}(2R)} |\nabla \psi _R|^{\beta +1} \, dx \\&\qquad + \frac{\hat{C} \rho ^{p-1}(\beta +1)}{\beta } \int _{{\mathcal {C}}(2R)} |\nabla \psi _R|^{\frac{\beta +1}{\beta }} (u_\nu ^-)^{\beta +1} \psi _R^{2 \frac{\beta +1}{\beta }} \, dx\\&\qquad + \tilde{C} \int _{{\mathcal {C}}(2R)} (u_\nu ^-)^{\beta +1} \psi _R^2 \, dx. \end{aligned} \end{aligned}$$

(5.20)

Since $|\nabla \psi _R| \le 2/R$ in $B'_{2R} \setminus B'_R$, $0 \le \psi _R \le 1$ in $\mathbb {R}^N$ and $\psi _R=1$ in $B'_R$, we obtain

$$\begin{aligned}&\int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\beta -1} \psi _R^2 \, dx \\&\quad \le \vartheta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx + \bar{C}_{R}\\&\quad \times \int _{{\mathcal {C}}(2R)} (u_\nu ^-)^{\beta +1} \psi _R^2 \, dx + \frac{2^{\beta +1}\hat{C} \rho ^{p-1}}{(\beta +1) R^{\beta -(N-2)}}\\&\quad \le \vartheta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx+ \bar{C}_{R}\\&\quad \times \int _{B'(0,2R)} \left( \int _{-k}^{k} \left[ (u_\nu ^-)^\frac{\beta +1}{2} \right] ^2 \, dx_N \right) \psi _R^2(x') \, dx' \\&\qquad + \frac{2^{\beta +1}\hat{C} \rho ^{p-1}}{(\beta +1) R^{\beta -(N-2)}}\\&\quad \le \vartheta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx+ \bar{C}_{R} C_p(k)^2 \frac{(\beta +1)^2}{4}\\&\quad \times \int _{{\mathcal {C}}(2R)} |\partial _{x_N} u_\nu ^- |^2(u_\nu ^-)^{\beta -1} \psi _R^2 \, dx + \frac{2^{\beta +1}\hat{C} \rho ^{p-1}}{(\beta +1) R^{\beta -(N-2)}}\\&\quad \le \vartheta \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 \ (u_\nu ^-)^{\beta -1} \, dx\\&\qquad + \bar{C}_{R} C_p(k)^2 \frac{(\beta +1)^2}{4} \rho ^{2-p} \int _{{\mathcal {C}}(2R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\beta -1} \psi _R^2 \, dx\\&\qquad + \frac{2^{\beta +1}\hat{C} \rho ^{p-1}}{(\beta +1) R^{\beta -(N-2)}}, \end{aligned}$$

with $\bar{C}_{R}:={\hat{C} \rho ^{p-1}(\beta +1)}/{\beta R^\frac{\beta +1}{\beta }} + \tilde{C}$. We point out that in (5.21) we used a Poincaré inequality in the set $[-k,k]$ (denoting with $C_p$ the associated constant) together with the fact that $\psi _R=\psi _R(x')$.

Finally we choose $\beta >0$ such that $\beta >N-2$, $\vartheta >0$ sufficiently small such that $\vartheta < 2^{-N+1}$ and $\rho >0$ sufficiently small such that

$$\begin{aligned} \bar{C}_{R} C_p(k)^2 \frac{(\beta +1)^2}{2} \rho ^{2-p} < 1. \end{aligned}$$

Having in mind all these fixed parameters let us define

$$\begin{aligned} {\mathcal {L}}(R):= \int _{{\mathcal {C}}(R)} |\nabla u|^{p-2} |\nabla u_\nu ^-|^2 (u_\nu ^-)^{\beta -1} \, dx. \end{aligned}$$

It is easy to see that ${\mathcal {L}}(R) \le C R^{N-1}$. By (5.21) (up to a redefining of the constant involved) we deduce that

$$\begin{aligned} {\mathcal {L}}(R) \le \vartheta {\mathcal {L}}(2R) + \frac{C}{R^{\beta - (N-2)}} \end{aligned}$$

(5.21)

holds for every $R > 0$. By applying Lemma 2.1 in [14] it follows that ${\mathcal {L}}(R)=0$ for all $R >0$. Since $p<2$, passing to the limit in (5.21), we deduce that for a.e. $x\in D$

$$\begin{aligned} \text {either } u_\nu ^-(x)=0,\qquad \text {or } |\nabla u_\nu ^-(x)|=0. \end{aligned}$$

(5.22)

This actually implies that $u_\nu ^-(x)=0$ in D. Indeed let us suppose that would exist a point $P\in D$ such that $u_\nu ^-(P)\ne 0$. Let us consider the connected component ${\mathcal U}$ of $D\setminus \{x\in D\,\,:\,\, u_\nu ^-(x)=0\}$ containing P. By the continuity of $u_\nu ^-$, it follows that $u_\nu ^-=0$ on the boundary $\partial {\mathcal U}$. On the other hand $u_\nu ^-$ must be constant in ${\mathcal U}$ (since by (5.22) $|\nabla u_\nu ^-|=0$ there) .This is a contradiction.

By this two step we deduce that $u_\nu \ge 0$ in $\mathbb {R}^N$. Finally by Lemma  4.2 we get (5.3). $\square$

Proof of Theorem  1.1

Using Proposition  4.1 we get that the solution is monotone increasing in the y-direction and this implies that $\partial _y u\ge 0$ in ${\mathbb R}^N$. In particular we have $\partial _y u> 0$ in ${\mathbb R}^N\setminus {\mathcal {Z}}_{f(u)}$ by (4.1). By Proposition  5.2, actually we obtain that the solution is increasing in a cone of directions close to the y-direction. This allows us to show that in fact, for $i=1,2,\cdots ,N-1$, $\partial _{x_i}u=0$ in ${\mathbb R}^N$, just exploiting the arguments in [10] (see also [17]). We provide the details for the sake of completeness. Let $\Omega$ be the set of the directions $\eta \in {\mathbb {S}}^{N-1}_+$ for which there exists an open neighborhood ${\mathcal {O}}_\eta \subset {\mathbb {S}}^{N-1}_+$ such that

$$\begin{aligned} \partial _\nu u = u_\nu \ge 0 \quad \text {in} \,\, \mathbb {R}^N \quad \text {and} \quad \partial _\nu u = u_\nu > 0\quad \text {in} \,\, \mathbb {R}^N \setminus {\mathcal {Z}}_{f(u)}, \end{aligned}$$

for every $\nu \in {\mathcal {O}}_\eta$. The set $\Omega$ is non-empty, since $e_N \in \Omega$, and it is also open by Proposition  5.2. Now we want to show that it is also closed. Let $\bar{\eta }\in {\mathbb {S}}^{N-1}_+$ and let us consider the sequence $\{ \eta _n\}$ in $\Omega$ such that $\eta _n \rightarrow \bar{\eta }$ as $n \rightarrow +\infty$ in the topology of ${\mathbb {S}}^{N-1}_+$. Since by our assumptions $\partial _{\eta _n} u \ge 0$ in $\mathbb {R}^N$, passing to the limit we obtain that $\partial _{\bar{\eta }} u \ge 0$ in $\mathbb {R}^N$. By Lemma  4.2 it follows that $\partial _{\bar{\eta }} u > 0$ in $\mathbb {R}^N \setminus {\mathcal {Z}}_{f(u)}$. By Proposition  5.2 there exists an open neighborhood ${\mathcal {O}}_{\bar{\eta }}$ such that (5.3) is true for every $\nu \in {\mathcal {O}}_{\bar{\eta }}$; hence $\bar{\eta }\in \Omega$ and this implies that $\Omega$ is also closed. Now, since ${\mathbb {S}}_+^{N-1}$ is a path-connected set, we have that $\Omega ={\mathbb {S}}_+^{N-1}$. Then there exists $v\in C^{1,\alpha }_{loc}({\mathbb R})$ such that $u(x',y)=v(y)$. Now we prove (1.3). We proceed by contradiction. Let us assume that there exists $b \in {\mathcal {Z}}_{f(u)}$ $\setminus \{ -1,1 \}$ such that $v'(b)=0$. Then, by $u_y \ge 0$, the level set $\{v=v(b)\}$ must be a bounded closed interval (possibly reduced to a single point), i.e., there exist $\alpha , \beta \in \mathbb {R}$ with $\alpha \le \beta$ such that

$$\begin{aligned} \{v=v(b)\}=[\alpha , \beta ]. \end{aligned}$$

Therefore, by Höpf’s Lemma, we have that $v'(\beta )>0$. The latter clearly implies that $\{v=v(b)\}=\{\beta \} = \{b\}$ and so $v'(b)>0$, which is in contradiction with our initial assumption. Hence we deduce that $\partial _y u>0$ in ${\mathbb R}^N$, concluding the proof. $\square$