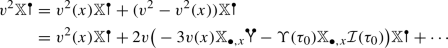A Priori Bounds for the $\Phi ^4$ Equation in the Full Sub-critical Regime

Abstract

We derive a priori bounds for the $\Phi ^4$ equation in the full sub-critical regime using Hairer’s theory of regularity structures. The equation is formally given by

where the term $+\infty \phi$ represents infinite terms that have to be removed in a renormalisation procedure. We emulate fractional dimensions $d<4$ by adjusting the regularity of the noise term $\xi$, choosing $\xi \in C^{-3+\delta }$. Our main result states that if $\phi$ satisfies this equation on a space–time cylinder $D= (0,1) \times \{ |x| \leqslant 1 \}$, then away from the boundary $\partial D$ the solution $\phi$ can be bounded in terms of a finite number of explicit polynomial expressions in $\xi$. The bound holds uniformly over all possible choices of boundary data for $\phi$ and thus relies crucially on the super-linear damping effect of the non-linear term $-\phi ^3$. A key part of our analysis consists of an appropriate re-formulation of the theory of regularity structures in the specific context of (*), which allows us to couple the small scale control one obtains from this theory with a suitable large scale argument. Along the way we make several new observations and simplifications: we reduce the number of objects required with respect to Hairer’s work. Instead of a model $(\Pi _x)_x$ and the family of translation operators $(\Gamma _{x,y})_{x,y}$ we work with just a single object $(\mathbb {X}_{x, y})$ which acts on itself for translations, very much in the spirit of Gubinelli’s theory of branched rough paths. Furthermore, we show that in the specific context of (*) the hierarchy of continuity conditions which constitute Hairer’s definition of a modelled distribution can be reduced to the single continuity condition on the “coefficient on the constant level”.

1 Introduction

The theory of regularity structures was introduced in Hairer’s groundbreaking work [23] and has since been developed into an impressive machinery [6, 8, 12] that systematically yields existence and uniqueness results for a whole range of singular stochastic partial differential equations from mathematical physics. Examples include the KPZ equation [15, 22], the multiplicative stochastic heat equation [26], as well as reversible Markovian dynamics for the Euclidean $\Phi ^4$ theory in three dimensions [23], in “fractional dimension $d<4$” [6], for the Sine-Gordon model [13, 28], for the Brownian loop measure measure on a manifold [7] and for the $d = 3$ Yang–Mills theory [11].

A serious limitation of this theory so far is that these existence and uniqueness results only hold for a short time, and this existence time typically depends on the specific realisation of the random noise term in the equation. Most applications are furthermore limited to a compact spatial domain such as a torus. The reason for this limitation is that the whole machinery is set up as the solution theory for a mild formulation in terms of a fixed-point problem, and that specific features of the non-linearity, such as damping effects or conserved quantities, are not taken into account. With this method, global-in-time solutions can only be obtained in special situations, for example if all non-linear terms are globally Lipschitz [24] or if extra information on an invariant measure is available [14, 25].

This article is part of a programme to derive a priori bounds within the regularity structures framework in order to go beyond short time existence and compact spatial domains. We focus on the $\Phi ^4$ dynamics which are formally given by the stochastic reaction diffusion equation

$$\begin{aligned} (\partial _t-\Delta )\phi =-\phi ^3+\xi , \end{aligned}$$

(1.1)

where $\xi$ is a Gaussian space–time white noise over $\mathbb {R}\times \mathbb {R}^{d}$. A priori bounds for this equation have recently been derived by several groups for the two dimensional case $d=2$ [32, 34] and the more difficult case $d=3$ [2, 18, 19, 30, 31]. In this article we obtain bounds throughout the entire sub-critical regime, formally dealing with all “fractional dimensions” up to (but excluding) the critical dimension $d=4$. Here we follow the convention of [6] to emulate fractional dimensions $d<4$ by adjusting the regularity assumption on $\xi$, and assuming that it can only be controlled in a distributional parabolic Besov–Hölder space of regularity $-3+\delta$ for an arbitrarily small $\delta >0$. Connecting back to the $\Phi ^4$ dynamics driven by space–time white noise, $\delta = 0-$ mimics the scaling of the equation with $d=4$ and $\delta = 1/2-$ gives us back equation with $d=3$.

Our analysis is based the method developed in the $d=3$ context in [30] where it was shown that if $\phi$ solves (1.1), on a parabolic cylinder, say on

$$\begin{aligned} D=(0,1)\times \{|x|<1\}, \end{aligned}$$

(1.2)

where $|x| = \max \{ |x_1|, \ldots , |x_d| \}$ denotes the supremum norm on $\mathbb {R}^d$, then it can be bounded on any smaller cylinder $D_R = (R^2,1) \times \{|x|<1-R\}$ only in terms of the distance R and the realisation of $\xi$ when restricted to a small neighbourhood of D. This bound holds uniformly over all possible choices for $\phi$ on the parabolic boundary of D, thus leveraging on the full strength of the non-linear damping term $-\phi ^3$. This makes the estimate extremely useful when studying the large scale behaviour of solutions, because given a realisation of the noise, any local function of the solution (for example a localised norm or testing against a compactly supported test-function) can be controlled in a completely deterministic way by objects that depend on the noise realisation on a compact set, without taking the behaviour of solution elsewhere into account.

Our main result is the exact analogue valid throughout the entire sub-critical regime.

Theorem 1.1

(Theorem 9.1 below) Let $\delta \in (0, \frac{1}{2})$ and let $\xi$ be of regularity $-3+\delta$. Let $\{ \mathbb {X}_{\bullet } \tau :\tau \in \mathcal {W}, \mathcal {V}\}$ be a local product lift of $\xi$.

Let $\phi$ solve

$$\begin{aligned} (\partial _t-\Delta )\phi =-\phi ^{\circ _{\mathbb {X}}3}+\xi \quad \text {on}\quad D, \end{aligned}$$

(1.3)

where $\phi ^{\circ _{\mathbb {X}}3}$ refers to the renormalised cube sub-ordinate to $\mathbb {X}$.

Then $v:= \phi - \sum _{\tau \in \mathcal {W}} \mathbb {X}_{\bullet } \mathcal {I}(\tau )$ satisfies

$$\begin{aligned} \Vert v\Vert _{D_R}\leqslant C\max \Big \{\frac{1}{R},[\mathbb {X};\tau ]^\frac{1}{\delta m_{\scriptscriptstyle \Xi }(\tau )}, \tau \in \mathcal {T}_{\Delta }, m_{\scriptscriptstyle \Xi }\ne 0 \Big \} \end{aligned}$$

uniformly in the choice of the local product, where $\Vert \bullet \Vert _{D_R}$ denotes the supremum norm on $D_R$ and $m_{\scriptscriptstyle \Xi }(\tau )$ is the number of noises in $\tau$, and the set of trees $\mathcal {T}_{\Delta }$ is defined in (4.2).

Here the “local product” denotes a finite number of functions/distributions $\mathbb {X}_{\bullet } \tau$, each of which is constructed as a polynomial of degree $m_{\scriptscriptstyle \Xi }(\tau )$ in $\xi$, see Sect. 3. Local products correspond to models [23, Definition 2.17] in the theory of regularity structures, but we use them slightly differently and hence prefer a different name and notation. The functions / distributions $\mathbb {X}_{\bullet } \tau$ are indexed by two sets $\mathcal {W}$ and $\mathcal {V}$. Here $\mathcal {W}$ contains the most irregular terms so that after their subtraction the remainder v can be bounded in a positive regularity norm. The semi-norms $[\mathbb {X};\tau ]$ are defined in (5.11) and they correspond to the order bounds on models [23, Equation (2.15)]. The renormalised cube sub-ordinate to a local product is defined in Definition 7.1. This notion corresponds exactly to the reconstruction with respect to a model / local product $\mathbb {X}_{\bullet }$ of the abstract cube in [23].

When analysing an equation within the theory of regularity structures, one proceeds in two steps: in a probabilistic step a finite number of terms in a perturbative approximation of the solution are constructed - these terms are referred to as the model already mentioned above. The terms in this expansion are just as irregular as $\phi$ itself, and their construction a priori poses the same problem to define non-linear operations. However, they are given by an explicit polynomial expression of the Gaussian noise $\xi$ and they can thus be analysed using stochastic moment calculations. It turns out that in many situations the necessary non-linear operations on the model can be defined despite the low regularity due to stochastic cancellations. However, this construction does require renormalisation with infinite counterterms.

In the second analytic step the remainder of the perturbative expansion is bounded. The key criterion for this procedure to work is a scaling condition, which is called sub-criticality in [23], and which corresponds to super-renormalisability in Quantum Field Theory. This condition states, roughly speaking, that on small scales the non-linearity is dominated by the interplay of noise and linear operator. As mentioned above, in the context of (1.1) this condition is satisfied precisely for $\xi \in C^{-3+\delta }$ if $\delta >0$. Sub-criticality ensures that only finitely many terms in the expansion are needed to yield a remainder that is small enough to close the argument.

It is important to note that while subcriticality ensures that the number of terms needed in the model is finite, this number can still be extremely large and typically diverges as one approaches the threshold of criticality. A substantial part of [6, 8, 12] is thus dedicated to a systematic treatment of the algebraic relations between all of these terms and their interaction, as well as the effect of renormalising the model on the original equation. The local-in-time well posedness theory for (1.1) for all sub-critical $\xi \in C^{-3+\delta }$, which was developed in [6], was one of the first applications of the complete algebraic machinery.

The three dimensional analysis in [30] was the first work that used regularity structures to derive a priori bounds. All of the previous works mentioned above [2, 18, 19, 31] were set in an alternative technical framework, the theory of paracontrolled distributions developed in [20]. These two theories are closely related: both theories were developed to understand the small scale behaviour of solutions to singular SPDEs, and both separate the probabilistic construction of finitely many terms in a perturbative expansion from the deterministic analysis of a remainder. Furthermore, many technical arguments in the theory of regularity structures have a close correspondent in the paracontrolled distribution framework. However, up to now paracontrolled distributions have only been used to deal with equations with a moderate number of terms in the expansion (for example (1.1) for $d \leqslant 3$ [10] or the KPZ equation [21]). Despite efforts by several groups (see for example [3, 4]) this method has not yet been extended to allow for expansions of arbitrary order. Thus for some of the most interesting models mentioned above, for example the Sine-Gordon model for $\beta ^{2}$ just below $8\pi$, the reversible dynamics for the Brownian loop measure on a manifold, the three-dimensional Yang–Mills theory, or the $\Phi ^4$ model close to critical dimension considered here, even a short time existence and uniqueness theory is currently out of reach of the theory of paracontrolled distributions.

The analysis in [30] was based on the idea that the large and small scale behaviour of solutions to singular SPDEs should be controlled by completely different arguments: for large scales the irregularity of $\xi$ is essentially irrelevant and bounds follow from the strong damping effect of the non-linearity $-\phi ^3$. The small scale behaviour is controlled using the smoothing properties of the heat operator. This philosophy was implemented by working with a suitably regularised equation which could be treated with a maximum principle and by bounding the error due to the regularisation using regularity structures.

However, this analysis did not make use of the full strength of the regularity structure machinery. In fact, the three-dimensional $\Phi ^4$ equation is by now considered as one of the easiest examples of a singular SPDE, because the model only contains a moderate number of terms, only five different non-trivial products need to be defined using stochastic arguments and only two different divergences must be renormalised. The interplay of these procedures is not too complex and no advanced algebraic machinery is needed to deal with it. Instead, in [30] the few algebraic relations were simply treated explicitly “by hand". The main contribution of the present article is thus to implement a similar argument when the number of terms in the model is unbounded, thus combining the analytic ideas from [30] with the algebraic techniques [6, 8]. For this it turns out to be most convenient to re-develop the necessary elements of the theory of regularity structures in the specific context of (1.1), leading to bounds that are tailor-made as input for the large-scale analysis.

Along the way, we encounter various serious simplifications and new observations which are interesting in their own right:

• As already hinted at in Theorem 1.1 we make systematic use of the “generalised Da Prato–Debussche trick” [6, 14]. This means that instead of working with $\phi$ directly, we remove the most irregular terms of the expansion leading to a function valued remainder. This was already done in [6] but only in order to avoid a technical problem concerning the initial conditions. For us the remainder v is the more natural object, observing that for all values of $\delta >0$ it solves an equation of the form

  $$\begin{aligned} (\partial _t-\Delta )v&=-v^3 + \cdots \end{aligned}$$

  (1.4)

  where $\ldots$ represents a large number of terms (the number diverges as $\delta \downarrow 0$) which involve renormalised products of either 1, v or $v^2$ with various irregular “stochastic terms”. For each $\delta >0$, v takes values in a positive regularity Hölder norm (that is it is a function) and so an un-renormalised damping term $-v^3$ appears on the right hand side. Of course, the Hölder regularity of v is not enough to control many of the products appearing in $\ldots$, and a local expansion of v is required to control these terms. However, we are able to show that for each fixed value of $\delta$ all of these terms are ultimately of lower order relative to $(\partial _t-\Delta )v$ and $v^3$.

• One of the key ideas in the theory of regularity structures is positive renormalisation and the notion of order. For most of the analysis, the functions/distributions from the model need to be centered around a base-point x, that is one works with functions/distributions that depend on the usual “running variable” as well as on the base-point. In Hairer’s work, these objects are denoted by $\Pi _x$. A good description of their behaviour under a change of base-point x is key to the analysis, and in Hairer’s framework this is encoded in a family of translation operators $\Gamma _{x,y}$. There is a close relationship between these $\Pi _{x}$ and $\Gamma _{x,y}$ maps and some generic identities relating them were found in [5]. Our observation is that - at least in the context of Equation (1.4)—most of the matrix entries for $\Gamma _{x,y}$ coincide with entries for $\Pi _x$ evaluated at y. Therefore we can work with just a single object $\mathbb {X}_{\bullet }$ (corresponding to $\mathbf {\Pi }$ in [23]) and its re-centered version $\mathbb {X}_{\bullet ,\bullet }$ that acts on itself for translation. A price to pay for this is that some care is needed for trees that involve derivatives. With this choice our framework is highly reminiscent of Gubinelli’s work on branched rough paths [17], the only real difference being the introduction of some (linear) polynomials, first order derivatives, and the flexibility to allow for non-canonical products.

• As in [23] we use the model/local product to build a local approximation of v around any base-point x. This takes the form

  $$\begin{aligned} v(y) \approx \sum _{\tau \in \mathcal {V}} \Upsilon _x(\tau ) \mathbb {X}_{y,x} \mathcal {I}(\tau ), \end{aligned}$$

  with a well-controlled error as y approaches x. In order to use this local expansion to control non-linearities two key analytic ingredients are needed: the first is the order bound discussed above, and the second is a suitable continuity condition on the coefficients $\Upsilon _x(\tau )$. In [23] these conditions are encoded in a family of model-dependent semi-norms, which make up the core of the definition of a modelled distribution [23, Definition 3.1]. It turns out however, that the coefficients $\Upsilon _x(\tau )$ that appear in the expansion of the solution v are far from generic: up to signs and combinatoric factors they can only be either 1, v(x), $v(x)^2$, or $v_{\textbf{X}}(x)$ (a generalised derivative of v). Furthermore, there is a simple criterion (Lemma 6.8) to see which of these is associated to a given tree $\tau$. This fact was already observed in [6] and was called coherence there. Here we observe that the various semi-norms in the definition of a modelled distribution are in fact all truncations of the single continuity condition on the first coefficient $\Upsilon (\textbf{1}) = v$. This observation is key for our analysis, as this particular semi-norm is precisely the output of our Schauder Lemma.

• Our deterministic theory cleanly separates the issues of positive and negative renormalisation in the context of (1.1). Indeed, we can derive a priori bounds under extremely general assumptions on the specific choice of the local product $\mathbb {X}$ which seems quite a bit larger and simpler than the space of models given in [8]. The key information contained in $\mathbb {X}$ is how certain a priori unbounded products should be interpreted. Our definition of a local product allows for these interpretations to be completely arbitrary! We can then always define the centered version of $\mathbb {X}$ (or path) and the only assumption where the various functions interact is in the assumption that these centered products satisfy the correct order bound. We do however include a Sect. 8 in which we introduce a specific class of local products for which the renormalised product $\phi ^{\circ _{\mathbb {X}} 3}$ appearing in (1.3) is still a local polynomial in $\phi$ and its spatial derivatives. Our approach in this section is to apply a recursive negative renormalisation that commutes with positive renormalisation, similar to [5]. Finally, the class of local products described in Sect. 8 also contains local products that correspond to the BPHZ renormalised model [8, 12].

1.1 Conventions

Throughout we will work with functions/distributions defined on (subsets of) $\mathbb {R}\times \mathbb {R}^{d}$ for an arbitrary $d \geqslant 1$. We measure regularity in Hölder-type norms that reflect the parabolic scaling of the heat operator. For example, we set

$$\begin{aligned} d((t,x),(\bar{t}, \bar{x}))=\max \Big \{\sqrt{|t-\bar{t}|},|x-\bar{x}|\Big \}, \end{aligned}$$

(1.5)

and for $\alpha \in (0,1)$, we define the (local) Hölder semi-norm $[\bullet ]_\alpha$ accordingly as

$$\begin{aligned}{}[u]_\alpha :=\sup _{d(z,\bar{z})<1}\frac{|u(z)-u(\bar{z})|}{d(z,\bar{z})^\alpha }. \end{aligned}$$

(1.6)

Distributional norms, that is Hölder type norms for negative regularity $\alpha <0$ play an important role throughout. These norms are defined in terms of the behaviour under convolution with rescaled versions of a suitable compactly supported kernel $\Psi$. For example, for $\alpha <0$ we set

$$\begin{aligned}{}[\xi ]_{\alpha }=\sup _{L\leqslant 1} \Big \Vert (\xi )_L \Big \Vert L^{-\alpha }, \end{aligned}$$

(1.7)

where $\Vert \bullet \Vert$ refers to the supremum norm on $\mathbb {R}\times \mathbb {R}^{d}$ and the operator $(\bullet )_L$ denotes convolution with a compactly supported smooth kernel $\Psi _L(x)=L^{-d-2}\Psi \Big ( \frac{x_0}{L^2}, \frac{\bar{x}}{L} \Big )$, where $x=(x_0,\bar{x})$. Just as in [30] we work with a specific choice of $\Psi$, but this is only relevant in the proof of the Reconstruction Theorem, Lemma A.1. These topics are discussed in detail in Appendix A.

In the case of space–time white noise, the quantity in (1.7) is almost surely not finite, but our analysis only depends on the noise locally: a space–time cut-off can be introduced. Throughout the paper we also make the qualitative assumption that $\xi$ and all other functions are smooth. This corresponds to introducing a regularisation of the noise term $\xi$ (for example by convolution with a regularising kernel at some small scale—in field theory this is called an ultra-violet cut-off). This is very convenient, because it allows to avoid unnecessary discussions about how certain objects have to be interpreted and in which sense partial differential equations hold. We stress however that our main result, Theorem 9.1, is a bound only in terms of those low-regularity norms (Definition 5.7) which can be controlled when the regularisation is removed in the renormalisation procedure. Even though all functions involved are smooth, we will freely use the term “distribution” to refer to a smooth function that can only be bounded in a negative regularity norm.

2 Overview

As stated in the introduction a large part of our analysis consists of a suitable re-formulation of elements of the theory of regularity structures. The key notions we require are local products, the renormalised product sub-ordinate to a local product, as well as the relevant norms that permit us to bound these renormalised products. We start our exposition with an overview over these notions and how they are interconnected. The exposition in this section is meant to be intuitive and rather “bottom up”. The actual analysis begins in Sect. 3.

2.1 Subcriticality

The starting point of our analysis is a simple scaling consideration: assume $\phi$ solves

$$\begin{aligned} (\partial _t-\Delta )\phi = - \phi ^3 + \xi \end{aligned}$$

(2.1)

for $\xi \in C^{-3+\delta }$. Schauder theory suggests that the solution $\phi$ is not better than $C^{-1 + \delta }$. In this low regularity class no bounds on $\phi ^3$ are available, but as we will see below, the notion of product we will work with has the property that negative regularities add under multiplication. Therefore we will obtain a control on (a renormalised version of) $\phi ^3$ as a distribution in $C^{-3+3\delta }$. Despite this very low regularity, for $\delta >0$, the term $\phi ^3$ is still more regular than the noise $\xi$. This observation is the core of Hairer’s notion of sub-criticality (see [23, Assumption 8.3]) and suggests that the small-scale behaviour of $\phi$ and $\phi ^3$ can ultimately be well understood by building a perturbative expansion based on the linearised equation.

2.2 Trees

We follow Hairer’s convention to index the terms in this expansion by a set of trees. This is not only a convenient notation that allows to organise which term corresponds to which operation, but also allows for an efficient organisation of the relations between these terms. We furthermore follow the convention to view trees as abstract symbols which form the basis of a finite-dimensional vector space. The trees are built from a generator symbol $\Xi$ (which represents the noise $\xi$ and graphically are the leaves of the tree) followed by applying the operator $\mathcal {I}(\cdot )$ (which represents to solving the heat equation and graphically corresponds to the edges of the tree) and taking products of trees (which represents to some choice of point-wise product and graphically corresponds to joining two trees at their root). To carry out the localisation procedure, discussed in Sect. 2.4 below, along with $\Xi$, additional generators $\{\textbf{1},\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$ are used in our construction of trees.

We associate concrete meaning to trees via an operator $\mathbb {X}_{\bullet }$ which we call a “local product”, see Definition 3.8. Even though this may seem somewhat bulky initially, it turns out to be extremely convenient as the concrete definition of $\mathbb {X}_{\bullet }$ on the same tree may change during the renormalisation procedure and because, the local product also appears in a centered form denoted by $\mathbb {X}_{\bullet , \bullet }$; see Sect. 2.6 below.

2.3 Subtracting the most irregular terms

The first step of our analysis consists of subtracting a finite number of terms from $\phi$ to obtain a remainder v which is regular enough to be bounded in a positive Hölder norm. The regularity analysis in Sect. 2.1 suggests that the regularity of $\phi$ can be improved by removing $\xi$ from the right hand side of (2.1). We introduce the first graph, $\mathcal {I}(\Xi )$ or graphically , and impose that $\mathbb {X}_{\bullet }$ acts on this symbol yielding a function that satisfies

(2.2)

We set so that $\tilde{v}$ solves

(2.3)

Of course the problem of controlling the cube of a distribution of regularity $-1+\delta$ has not disappeared, but instead of $\phi ^3$ one now has to control and . At this point one has to make use of the fact that is known much more explicitly than the solution $\phi$, and can thus be analysed using explicit covariance calculations. We do not discuss these calculations here, but rather view these products as part of the given data: we introduce two additional symbols $\mathcal {I}(\Xi ) \mathcal {I}(\Xi ) \mathcal {I}(\Xi )$ or graphically , and similarly $\mathcal {I}(\Xi ) \mathcal {I}(\Xi )$ or and assume that $\mathbb {X}$ acts on these additional symbols yielding distributions which are controlled in $C^{-3+3\delta }$ and $C^{-2+2\delta }$. We stress that only the control on these norms enters the proof of our a priori bound, and no relation to needs to be imposed (see however Sect. 8 below). Instead of (2.3) we thus consider

(2.4)

Note that the most irregular term on the right hand side is so that we can expect $\tilde{v} \in C^{-1+3\delta }$ that is we have gained $2 \delta$ differentiability with respect to $\phi$. We mention at this point, that we will always work with interior Schauder regularity estimates permitting us to largely avoid having to deal with estimating the behaviour near the boundary. For $\delta >\frac{1}{3}$ (which corresponds to dimensions “$d< 3 \frac{1}{3}$”) $\tilde{v}$ is thus controlled in a positive order Hölder norm. For smaller $\delta$ we proceed to subtract an additional term to again remove the most irregular term from the right hand side as above. We define a new symbol $\mathcal {I}( \mathcal {I}(\Xi ) \mathcal {I}(\Xi ) \mathcal {I}(\Xi ))$ or graphically , postulate that $\mathbb {X}_{\bullet }$ acts on this symbol yielding a distribution which solves

(2.5)

and define a new remainder which takes values in $C^{-1+5 \delta }$. In general, for any $\delta >0$ we denote by $\mathcal {W}$ the set of trees of order $< -2$ (for these trees, order is the same as the regularity of the local product on this tree. Below, in Sect. 2.6 we will encounter additional trees for which these notions differ) and define

$$\begin{aligned} v := \phi - \sum _{w \in \mathcal {W}} (-1)^{\frac{m(w)-1}{2}} \mathbb {X}_{\bullet } \mathcal {I}(\tau ), \end{aligned}$$

(2.6)

where $m(w)$ denotes the number of “leaves” of the tree w (all trees in $\mathcal {W}$ have an odd number of leaves, see Sect. 3). Then v takes values in a Hölder space of positive regularity. The remainder equation then turns into

$$\begin{aligned} (\partial _t-\Delta )v&=-v^3\\&\quad -3\sum _{w\in \mathcal {W}} (-1)^{\frac{m(w)-1}{2}} v^2 \mathbb {X}_\bullet \mathcal {I}(w)\nonumber \\&\quad -3\sum _{w_1,w_2\in \mathcal {W}} (-1)^{\frac{m(w_1) + m(w_2)-2}{2}} v \mathbb {X}_\bullet ( \mathcal {I}(w_1) \mathcal {I}(w_2)) \nonumber \\&\quad -\sum _{\begin{array}{c} w_1,w_2,w_3\in \mathcal {W}\\ \mathcal {I}(w_1) \mathcal {I}(w_2) \mathcal {I}(w_3) \notin \mathcal {W} \end{array}}(-1)^{\frac{m(w_1) + m(w_2) + m(w_3)-3}{2}} \mathbb {X}_\bullet (\mathcal {I}(w_1) \mathcal {I}(w_2) \mathcal {I}(w_3)) .\nonumber \end{aligned}$$

(2.7)

For the constraint in the last sum, note that if $\tau = \mathcal {I}(w_1) \mathcal {I}(w_2) \mathcal {I}(w_3) \in \mathcal {W}$, one would have removed $\mathcal {I}(\tau )$ from the remainder v in (2.6).

We stress that the structure of this equation is always the same in the sense that $(\partial _t-\Delta )v =-v^3$ is perturbed by a large number of irregular terms (the number actually diverges as $\delta \rightarrow 0$). Bounding these irregular terms forces us to introduce additional trees as we will see below, but ultimately we will show that all of these terms are of lower order with respect to $(\partial _t-\Delta )v =-v^3$.

2.4 Iterated fFreezing of coefficients

We now discuss the remainder equation (2.7) in more detail, writing it as

(2.8)

where we are isolating the most irregular terms in each of the three sums appearing on the right hand side of (2.7). The most irregular term in the sum on the second line of (2.7) is and the most irregular term in the third line is . For the last line, the precise form of the most irregular term depends on $\delta$ and there could be multiple terms of the same low regularity. Here we just keep track of one of them, simply denote it by $\mathbb {X}_\bullet \tau _{0}$ and also leave the combinatorial prefactor $\Upsilon (\tau _{0})$ implicit. We remark that $\mathbb {X}_\bullet \tau _{0}$ is always a distribution of regularity $C^{-2+\kappa }$ for some $\kappa \in (0, 2 \delta )$. To simplify the exposition we disregard all of the (many) additional terms hidden in the ellipses $\ldots$ for the moment.

We recall the standard multiplicative inequality

$$\begin{aligned} \Vert f g \Vert _{C^{-\beta }} \lesssim \Vert f \Vert _{C^\alpha } \Vert g \Vert _{C^{-\beta }} \end{aligned}$$

for $\alpha , \beta >0$ which holds if and only if $\alpha - \beta >0$. In view of the regularity we would thus require $v \in C^\gamma$ for $\gamma > 2-2\delta$ in order to have a classical interpretation of the product on the right hand side of (2.8). Unfortunately, v is much more irregular: it is governed by the irregularity of the term $\mathbb {X}_\bullet \tau _{0}$ of regularity $C^{-2+\kappa }$ on the right hand side of the equation, and therefore by Schauder theory we can only expect v to be of class $C^\kappa$.

The solution to overcome this difficulty presented in [23] amounts to an “iterated freezing of coefficient” procedure to obtain a good local description of v around a fixed base-point: we fix a space–time point x and rewrite the third, and most irregular term on the right hand side of (2.8) as

(2.9)

and use this to rewrite the equation (2.8) as

(2.10)

where we have introduced new symbols and $\mathcal {I}( \tau _{0})$ and postulated that $\mathbb {X}$ acts on these symbols to yield a solution of the inhomogeneous heat equation with right hand sides and $\mathbb {X}_{\bullet } \tau _{0}$. The worst term on the right hand side is now so that the left hand side can at best be of regularity $2\delta$. However, near the base-point we can use the smallness of the pre-factor $|v(\bullet ) - v(x)| \lesssim [v]_\kappa d(\bullet , x)^\kappa$ to get the better estimate

(2.11)

where have used the short-hand notation

(2.12)

This bound in turn can now be used to get yet a better approximation in (2.9): we write

(2.13)

At this point two additional non-classical products appear in the second and third term on the right hand side, and as before they are treated as part of the assumed data: we introduce two additional symbols and $\mathcal {I}(\tau _{0})\mathcal {I}(\Xi ) \mathcal {I}(\Xi )$ and assume that $\mathbb {X}$ acts on these symbols yielding distributions which we interpret as playing the roles of the products and . Similarly, we introduce the base-point dependent versions as

(2.14)

Our full prescription defining basepoint dependent trees will require the algebraic framework given in Sect. 4, but for now we motivate the formulae above as follows - for products of trees we only need to recenter “branches” of positive degree. For instance, the first line above can be written .

With these recenterings defined, (2.13) becomes re-interpreted as

(2.15)

The last two terms on the right hand side can now again be moved to the left hand side of the equation suggesting that near x we can improve the approximation (2.10) of v(y) by considering

(2.16)

where

(2.17)

with the improved estimate $|\tilde{U}(y,x)| \lesssim d(y,x)^{4\delta +\kappa }$, thus gaining another $2\delta$ with respect to U(y, x).

The whole procedure can now be iterated: in each step an improved approximation of v is plugged into the product which in turn yields an even better local approximation of v near x. At some point, additional terms have to be added:

• In order to get a local description of order $>1$, “generalized derivatives” $v_{\textbf{X}_i}$ of v appears, that is a term $\sum _{i=1}^d v_{\textbf{X}_i}(x)(y_i - x_i)$ has to be included.

• The term on the right hand side of the remainder equation (2.8) has regularity $-1+\delta$, so once one wishes to push the expansion of v to a level $>1+\delta$, one also has to “freeze the coefficient” $v^2$, that is write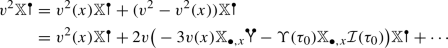

  

  leading to additional terms on the left hand side.

• Of course, the various terms which were hidden in $\ldots$ in (2.8) above have to be treated in a similar way leading to (many) additional terms in the local description of v.

Ultimately, we iterate this scheme until we have a local description an order $\gamma$, that has to satisfy $\gamma > 2-2\delta$. The threshold is determined by the product : namely is of regularity $-2+2\delta$ and the constraint is that $\gamma -2 +\delta$ has to be positive. Note that this corresponds exactly to the regularity of v that would be classically required to control .

2.5 Renormalised products

The previous discussion thus suggests that we have a Taylor-like approximation of v near the base-point x

$$\begin{aligned} v(y) \approx v(x) + \sum _{i=1}^d v_{\textbf{X}_i}(x) \cdot (y_i-x_i) + \sum _{\tau \in \mathcal {V}_{\textsc {prod}}} \Upsilon _{x}(\tau ) \mathbb {X}_{y,x}\mathcal {I}(\tau ) \end{aligned}$$

(2.18)

for coefficients $\Upsilon _{x}$ and with an error that is controlled by $\lesssim d(x,y)^{\gamma }$. Here $\mathcal {V}_{\textsc {prod}}$ denotes the set of trees appearing in the recursive construction described above. We unify our notation by also writing the first two terms with “trees” and set

$$\begin{aligned} \mathbb {X}_{y,x} \mathcal {I}(\textbf{1})&= 1 \mathbb {X}_{y,x} \mathcal {I}(\textbf{X}_i)&= y_i - x_i\\ \Upsilon _{x}(\textbf{1})&= v(x) \Upsilon _{x}(\textbf{X}_i )&= v_{\textbf{X}_i} (x) , \end{aligned}$$

thus permitting to rewrite (2.18) as

$$\begin{aligned} v(y) \approx \sum _{\tau \in \mathcal {V}} \Upsilon _{x}(\tau ) \mathbb {X}_{y,x}\mathcal {I}(\tau ), \end{aligned}$$

(2.19)

where $\mathcal {V}=\mathcal {V}_{\textsc {prod}}\cup \{\textbf{1},\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$.

Of course, up to now our reasoning was purely formal, because it relied on all of the ad hoc products of singular distributions that were simply postulated along the way. We now turn this formal reasoning into a definition of the products sub-ordinate to the choices in the local product $\mathbb {X}$. More precisely, we define renormalised products such as

(2.20)

Our main a priori bound in Theorem 9.1 holds for the remainder equation interpreted in this sense, under very general assumptions on the local product $\mathbb {X}$. However, under these very general assumptions it is not clear (and in general not true) that the renormalised products are in any simple relationship to the usual products. In Sect. 8 we discuss a class of local products for which the renormalised products can be re-expressed as explicit local functionals of usual products. In particular, for those local products we always have

for real parameters $a,b,c, d_i$. This class of local products contains the examples that can actually be treated using probabilistic arguments.

2.6 Positive renormalisation and order

One of the key insights of the theory of regularity structures is that the renormalised products defined above can be controlled quantitatively in a process called reconstruction, and the most important ingredient for that process are the definitions of suitable notions of regularity / continuity for the local products $\mathbb {X}$ and the coefficients $\Upsilon$. We start with the local products.

The base-point dependent or centered versions of the local product, $\mathbb {X}_{y,x}$ that appear naturally in the expansions above (for example in (2.12), (2.14), (2.17)) are in fact much more than a notational convenience. The key observation is that their behaviour as the running argument y approaches the base-point x is well controlled in the so-called order bound. For defined in (2.12) we have

(2.21)

which amounts to the Hölder regularity of . The order bounds become more interesting in more complex examples: for defined in (2.17) we have

(2.22)

The remarkable observation here is that the function is itself only of regularity $2\delta$, so that this estimate expresses that the second term exactly compensates the roughest small scale fluctuations. The exponent $4\delta$ is defined as the order of the tree simply denoted by . Analogously, for the tree defined in (2.14) we have the order exceeding the regularity of the distribution which is only $-2+2\delta$, the same as the regularity of . As these quantities are distributions the order bound now has to be interpreted by testing against the rescaled kernel $\Psi _T$

(2.23)

This notion of order of trees has the crucial property that it behaves additive under multiplication - just like the regularity of distributions discussed above. This property is what guarantees that for sub-critical equations the number of trees with order below any fixed threshold is always finite.

2.7 Change of base-point

As sketched in the discussion above, the base-point dependent centered local products $\mathbb {X}_{\bullet , \bullet }$ are defined recursively from the un-centered ones. For what follows, a good algebraic framework to describe the centering operation and the behaviour under the change of base-point is required. It turns out that both operations can be formulated conveniently using a combinatorial operation called the coproduct $\Delta$ (note that this $\Delta$ has nothing to do with the Laplace operator, it will always be clear from the context which object we refer to). This coproduct associates to each tree a finite sum of couples $(\tau ^{(1)}, \tau ^{(2)})$ where $\tau ^{(1)}$ is a tree and $\tau ^{(2)}$ is a finite list of trees. Equivalently, the coproduct can be seen as a linear map

$$\begin{aligned} \Delta :\mathcal {T}_{\Delta }\rightarrow \textrm{Vec}(\mathcal {T}_{\Delta }) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}}), \end{aligned}$$

where $\mathcal {T}_{\Delta }$ and $\mathcal {T}_{\textrm{cen}}$ are sets of tree that we will define later (see (4.2) for the former and Sect. 4.3 for the latter), $\textrm{Vec}(A)$ is the free vector space generated by the set A, respectively, and $\textrm{Alg}(A)$ is the free non-commutative unital algebra generated by A (that is, $\textrm{Alg}(A)$ consists of linear combinations of words in elements of A, where the product on words is concatenation and the unit is given by the empty word).

This coproduct is defined recursively, reflecting exactly the recursive positive renormalisation described above in Sect. 2.4. For example

so that for example the first definitions of (2.12) and (2.16) turn into

that is the different terms in the coproduct correspond to the different terms appearing in the positive renormalisation, and for each pair $\tau ^{1} \otimes \tau ^{2}$, the first tree $\tau ^{1}$ corresponds to the “running variable y” and $\tau ^{2}$ to the value of the base-point. Here $\mathbb {X}_{x}^\textrm{cen}: \textrm{Alg}(\mathcal {T}_{\textrm{cen}}) \rightarrow \mathbb {R}$ is a multiplicative map that associates to a given $\tau \in \mathcal {T}_{\textrm{cen}}$ a corresponding quantity for recentering about x. These quantities can be defined recursively to match this definition for example

This way of codifying the relation between the centered and un-centered local products is useful, for example when analysing the effect of the renormalisation procedure (Sect. 8) but even more importantly they give an efficient way to describe how $\mathbb {X}_{y,x}$ behave under change of base-point. It turns out that we obtain the remarkable formula for all $\tau \in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$

$$\begin{aligned} \mathbb {X}_{y,z}(\tau ) = (\mathbb {X}_{y,\bar{z}} \otimes \mathbb {X}_{\bar{z},z}) \Delta \tau , \end{aligned}$$

(2.24)

that is the centered object $\mathbb {X}_{y,z}$ acts on itself as a translation operator!

2.8 Continuity of coefficients

With this algebraic formalism in hand, we are now ready to describe the correct continuity condition on the coefficients. This continuity condition is formulated in terms of the concrete realisation of the local product, in that an “adjoint” of the translation operator appears. In order to formulate it, we introduce another combinatorial notation $C_+(\bar{\tau },\tau )$, which is defined recursively to ensure that

$$\begin{aligned} \Delta \mathcal {I}(\tau )=\sum _{\bar{\tau }\in \mathcal {V}\cup \mathcal {W}}\mathcal {I}(\bar{\tau })\otimes C_+(\bar{\tau },\tau ). \end{aligned}$$

We argue below that the correct family of semi-norms for the various coefficients $\Upsilon (\tau )$ is given by

$$\begin{aligned} \sup _{d(x,y) \leqslant 1} \frac{1}{d(x, y)^{\gamma -|\tau |} } \left| \Upsilon _{x}(\tau ) -\sum _{ \begin{array}{c} \bar{\tau } \in \mathcal {V}\\ |\bar{\tau } | < \gamma \end{array}} \Upsilon _{y}(\bar{\tau }) \mathbb {X}_{y,x} C_+(\tau , \bar{\tau }) \right| . \end{aligned}$$

(2.25)

The Reconstruction Theorem (see Lemma A.1 for our formulation) implies that the renormalised products (2.20) can be controlled in terms of the semi-norms (2.25) and the order bounds (for example (2.23)). Reconstruction takes as input the whole family of semi-norms (2.25), but it turns out that in our case, it suffices to deal with a single semi-norm on the coefficients: the coefficients $\Upsilon _{x}(\tau )$ that appear in the recursive freezing of coefficients described in Sect. 2.4 are far from arbitrary. It is very easy to see that (up to combinatorial coefficients and signs) the only possible coefficients we encounter are v, $v^2$, $v_\textbf{X}$, and 1. It then turns out that all of the semi-norms (2.25) are in fact truncations of the single continuity condition on the coefficient v itself. This semi-norm can then be easily seen to be

$$\begin{aligned} \sup _{d(x,y) \leqslant 1} \frac{1}{d(x, y)^{\gamma }} \left| v(x) - \sum _{ \begin{array}{c} \tau \in \mathcal {V}\\ | \tau | < \gamma \end{array}} \Upsilon _{y}(\tau ) \mathbb {X}_{y,x} \mathcal {I}(\tau ) \right| , \end{aligned}$$

(2.26)

which measures precisely the quality of the approximation (2.19) at the starting point of this discussion.

2.9 Outline of paper

A large part of this article is concerned with providing the details of the arguments sketched above in a streamlined ”top-down” way: The set of trees, their order and local products are defined in Sect. 3, while Sect. 4 provides a systematic treatment of combinatorial properties of the coproduct. The centering of local products and the change of base point formula (2.24) are discussed in Sect. 5, while Sect. 6 contains the detailed discussion of the coefficients $\Upsilon$ sketched above in Sect. 2.5. The renormalised products in the spirit of (2.20) are defined in Sect. 7. As already announced above, Sect. 8 contains the discussion of a special class of local products, for which the renormalised product can be expressed in a simple form. The actual large-scale analysis only starts in Sect. 9, where the main result is announced. This section also contains a detailed outline of the strategy of proof. The various technical Lemmas that constitute this proof can then be found in Sect. 10. Finally, we provide two appendices in which some known results are collected: Appendix A discusses norms on spaces of distributions in the context of the reconstruction theorem. Appendix B collects different variants of classical Schauder estimates.

3 Tree Expansion and Local Products

The objects we refer to as trees will be built from

• a set of generators $\{\textbf{1},\textbf{X}_{1},\ldots , \textbf{X}_{d},\Xi \}$, which can be thought of as the set of possible types of leaf nodes of the tree

• applications of an operator $\mathcal {I}$, $\tau \mapsto \mathcal {I}(\tau )$ adds a new root vertex to $\tau$ which is connected to the old root by an edge,

• a tree product, which joins roots of trees at a common node.

As an example, we have

In particular, when drawing our trees pictorially we decorate the leaf nodes with a $\bullet$ for an instance of $\Xi$, 0 for an instance of $\textbf{1}$, and $j \in \{1,\ldots ,d\}$ for an instance of $\textbf{X}_{j}$. Notice that we do not decorate internal (non-leaf) nodes and have the root node at the bottom.

Our tree product is non-commutative which in terms of our pictures means that we distinguish between the ways a tree can be embedded in the plane. For example, the following trees are treated as distinct from the trees above:

Remark 3.1

We work with a non-commutative tree product to remove nearly all combinatorial factors from key algebraic relations in our framework, this greatly simplifies their statements and proofs.

Whenever we map trees over to concrete functions and or distributions this mapping will treat identically any two trees that coincide when one imposes commutativity of the tree product.

We say a tree $\tau$ is planted if it is of the form $\tau = \mathcal {I}(\tilde{\tau })$ for some other tree $\tilde{\tau }$, some examples would be

We take a moment to describe the intuition behind these trees. The symbol $\Xi$ will represent the driving noise, we will often call nodes of type $\Xi$ noise leaves/nodes. Regarding the operator $\mathcal {I}$, when applied to trees different from $\{\textbf{1},\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$, $\mathcal {I}$ will represent solving the heat equation, that is

$$\begin{aligned} \text {``}(\partial _{t} - \Delta ) \mathcal {I}(\tau ) = \tau \text {''}. \end{aligned}$$

However, we think of the trees as algebraic objects so such an equation is only given here as a mnemonic and will be made concrete when we associate functions to trees in Sect. 3.2.

The symbols $\{\textbf{1},\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$ themselves will not correspond to any analytic object, but the trees $\{\mathcal {I}(\textbf{1}),\mathcal {I}(\textbf{X}_{1}),\ldots ,\mathcal {I}(\textbf{X}_{d})\}$ will play the role of the classical monomials, that is $\mathcal {I}(\textbf{1})$ corresponds to 1 and $\mathcal {I}(\textbf{X}_{j})$ corresponds to the monomial $z_{j}$.

Remark 3.2

Encoding polynomials as branches of a tree instead of the standard convention of treating them as node decorations is more consistent with our non-commutative approach - for example we want to treat

$$\begin{aligned} \mathcal {I}(\tau _1) \mathcal {I}(\tau _2) \mathcal {I}(\textbf{X}_1)\quad \text {and}\quad \mathcal {I}(\tau _1) \mathcal {I}(\textbf{X}_1) \mathcal {I}(\tau _2)\; \end{aligned}$$

as different trees. If we treated $\textbf{X}_{1}$ as a decoration at the root of the tree then both trees would be the same. This convention is also compatible with viewing every unplanted tree as a tree product of three factors, and in later inductive algebraic arguments it is convenient to think of the $\{\textbf{1},\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$ as leaves.

We define $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ to be the smallest set of trees containing $\{\textbf{1},\textbf{X}_{1},\ldots , \textbf{X}_{d},\Xi \} \subset \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ and such that for every $\tau _{1}, \tau _{2}, \tau _{3} \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ one also has $\mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$. The trees in $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}{\setminus } \{\textbf{1}, \textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$ will be used to write expansions for the right hand side of (1.1). We remark that non-leaf nodes in $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ have three offspring, for instance $\mathcal {I}(\Xi )^{2}\mathcal {I}(\textbf{1}) \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ but . However, the three different permutations of $\mathcal {I}(\Xi )^{2}\mathcal {I}(\textbf{1})$ will play the role of that did in expressions like (2.4), and as an example of how this simplifies our combinatorics we remark that this allows us to forget about the “3” that appears in (2.4).

We also define a corresponding set of planted trees $\mathcal {T}_{\textsc {LHS}}^{\textsc {all}}= \{ \mathcal {I}(\tau ): \tau \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}\}$. The planted trees in $\mathcal {T}_{\textsc {LHS}}^{\textsc {all}}$ will be used to describe an expansion of the solution $\phi$ to (1.1).

At certain points of our argument the roles of the planted trees of $\mathcal {T}_{\textsc {LHS}}^{\textsc {all}}$ and the unplanted trees of $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ will be quite different. For this reason we will reserve the use of the greek letter $\tau$ (and $\bar{\tau }$, $\tilde{\tau }$, etc.) for elements of $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$. If we want to refer to a tree that could belong to either $\mathcal {T}_{\textsc {LHS}}^{\textsc {all}}$ or $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ we will use the greek letter $\sigma$.

3.1 The order of a tree and truncation

We give a recursive definition of the order $|\cdot |$ on $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}\cup \mathcal {T}_{\textsc {LHS}}^{\textsc {all}}$ as follows. Given $\mathcal {I}(\tau ) \in \mathcal {T}_{\textsc {LHS}}^{\textsc {all}}$ we set $|\mathcal {I}(\tau )| = |\tau | +2$. Given $\tau \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ we set

$$\begin{aligned} |\tau |:= {\left\{ \begin{array}{ll} -2, &{} \tau =\textbf{1}, \\ -1, &{} \tau =\textbf{X}_{i}, i \in \{1,\ldots ,d\}\\ -3+\delta , &{} \tau =\Xi ,\\ \sum _{i=1}^{3} |\mathcal {I}(\tau _{i})| = 6+\sum _{i=1}^3|\tau _i|, &{} \tau =\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3). \end{array}\right. } \end{aligned}$$

The values of $-2$ and $-1$ for homogeneities of the trees $\textbf{1}$ and $\textbf{X}_{i}$ may seem a bit odd but this is just due to the convention that it is $\mathcal {I}(\textbf{1})$ and $\mathcal {I}(\textbf{X}_{i})$ that actually play the role of the classical monomials and we want $|\mathcal {I}(\textbf{1})| = 0$ and $|\mathcal {I}(\textbf{X}_{i})| = 1$.

It will be helpful throughout this article to have notation for counting the number of occurrences of a certain leaf type in a tree. We define the functions $m_{\textbf{1}},\ m_{\textbf{x}_{i}},\ m_{\scriptscriptstyle \Xi }: \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}\rightarrow \mathbb {Z}_{\geqq 0}$ which count, on any given tree, the number of occurrences of $\textbf{1}$, $\textbf{X}_{i}$ and $\Xi$ as leaves in the tree.

We also set $m_{\textbf{x}}= \sum _{i=1}^{d} m_{\textbf{x}_{i}}$ for the function that returns the total number of $\{\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$ leaves and $m=m_{\textbf{1}}+m_{\textbf{x}}+m_{\scriptscriptstyle \Xi }$ which returns the total number of leaves of the given tree.

One can easily check that, for $\tau \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$,

$$\begin{aligned} |\tau |=-3+m_{\scriptscriptstyle \Xi }(\tau )\delta +m_{\textbf{1}}(\tau )+2m_{\textbf{x}}(\tau )\;. \end{aligned}$$

(3.1)

We will only work with a finite set of trees in our analysis, and we clarify the different roles that they play in our construction by organizing them into various subsets. We define the following subsets of $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$:

$$\begin{aligned} \begin{aligned} \textrm{Poly}&:= \{\textbf{X}_{1},\ldots ,\textbf{X}_{d},\textbf{1}\},\\ \mathcal {W}&:= \{\tau \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}:\ |\tau | < -2\},\ \mathcal {W}_{\textsc {prod}}:= \mathcal {W}{\setminus } \{\Xi \},\\ \mathcal {V}&:= \{\tau \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}},\; -2 \leqslant |\tau | \leqslant 0\},\ \mathcal {V}_{\textsc {prod}}:= \mathcal {V}{\setminus } \textrm{Poly}. \end{aligned} \end{aligned}$$

As a mnemonic, $\mathcal {W}_{\textsc {prod}}$ (resp $\mathcal {V}_{\textsc {prod}}$), is the set of those trees in $\mathcal {W}$ (resp $\mathcal {V}$) which are themselves the tree product of three planted trees.

The infinite sets $\mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$ and $\mathcal {T}_{\textsc {LHS}}^{\textsc {all}}$ will not appear in what follows and we instead work with the finite subsets

$$\begin{aligned} \mathcal {T}_{\textsc {RHS}}:= \mathcal {W}\cup \mathcal {V}_{\textsc {prod}}\quad \text {and}\quad \mathcal {T}_{\textsc {LHS}}:= \mathcal {I}(\mathcal {T}_{\textsc {RHS}}) \cup \mathcal {I}(\textrm{Poly}), \end{aligned}$$

(3.2)

where above and in what follows we write $\mathcal {I}(A) = \{\mathcal {I}(\tau ):\ \tau \in A\}$.

We now describe the roles of the sets $\textrm{Poly}$, $\mathcal {W}$, and $\mathcal {V}$ introduced above.

The set $\mathcal {W}$ consists of those trees that appear in our expansion of the right hand side of (1.1) that have the lowest orders. When “subtracting the most irregular terms” as described in Sect. 2.3 we will be subtracting the trees of $\mathcal {I}(\mathcal {W})$ which are all of negative order themselves. In particular, the trees of $\mathcal {W}$ will appear in tree expansions for the right hand side of (1.1) but will not appear by themselves on the right hand side of the remainder equation. Other than possibly requiring renormalisation, the trees of $\mathcal {W}_{\textsc {prod}}$ behave simply in our algebraic framework because they do not require any recentering. We will see that they appear with a constant coefficient in our expansion of the right hand side of (1.1) and do not include any of the generators in $\textrm{Poly}$. The letter chosen for this set refers to the fact that these trees are seen in the more classical “Wild expansion” for the right hand side of (1.1), that is a naive iterative perturbation expansion.

On the other hand, the trees of $\mathcal {V}_{\textsc {prod}}$ will appear on the right hand side of expansions of both (1.1) and the remainder equation (hence why we call it $\mathcal {V}$). We do not include $|\tau | > 0$ in $\tau \in \mathcal {V}_{\textsc {prod}}$ since we only need to expand the right hand side of the remainder equation up to order 0.

While the trees in $\mathcal {V}$ are less singular than those in $\mathcal {W}$, they behave more complicated in our algebra - in particular all the trees in $\mathcal {V}_{\textsc {prod}}$ will require recentering.

Our remainder will then be described by an expansion in terms of trees of $\mathcal {I}(\mathcal {V})$ As mentioned earlier, the trees of $\textrm{Poly}$ will not, by themselves, play a role in our expansions, but in our expansion of the remainder the trees in $\mathcal {I}(\textrm{Poly})$ will come with unknown, space–time dependent coefficients which we think of as “generalised derivatives”and the trees in $\mathcal {I}(\mathcal {V})$ come with coefficients which are monomials in these generalised derivatives.

Assumption 3.3

For the rest of the paper, we treat $\delta > 0$ as fixed, and assume, without loss of generality for the purposes of our main theorem, that $\delta$ has been chosen so that $\{|\tau |: \tau \in \mathcal {W}\cup \mathcal {V}_{\textsc {prod}}\}$ does not contain any integers.

We have the following straightforward lemma.

Lemma 3.4

The sets $\mathcal {W}$ and $\mathcal {V}$ are both finite.

Proof

From the formula (3.1), one can see that $\tau \in \mathcal {W}$ if and only if $m_{\textbf{1}}(\tau )=m_{\textbf{x}}(\tau )=0$ and $m_{\scriptscriptstyle \Xi }(\tau )<\delta ^{-1}$. Similarly for $\tau \in \mathcal {V}_{\textsc {prod}}$, one has

$$\begin{aligned} (m_{\textbf{1}}(\tau ),m_{\textbf{x}}(\tau ))\in \{(0,0),(1,0),(2,0),(0,1)\}, \end{aligned}$$

and $m_{\scriptscriptstyle \Xi }(\tau )<\delta ^{-1}(3-m_{\textbf{1}}(\tau )-2m_{\textbf{x}}(\tau ))$. $\square$

Remark 3.5

Clearly Lemma 3.4 would be false for $\delta = 0$, that is when the equation is critical.

We also have the following lemma describing the trees in $\mathcal {W}_{\textsc {prod}}$.

Lemma 3.6

For any $\tau \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}\setminus \{\Xi \}$, $|\tau | \geqq -3 + 3\delta > |\Xi | = -3 + \delta$. Moreover, for any $w \in \mathcal {W}_{\textsc {prod}}$, one has

$$\begin{aligned} w = \mathcal {I}(w_{1})\mathcal {I}(w_{2})\mathcal {I}(w_{3}) \end{aligned}$$

(3.3)

where $w_{1},w_{2},w_{3} \in \mathcal {W}$.

Proof

The first statement about $|\tau |$ is a simple consequence of (3.1) and the constraint that $m_{\scriptscriptstyle \Xi }(\tau ) \geqq 3$. For the second statement, we write $w = \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3})$ with $\tau _{1},\tau _{2},\tau _{3} \in \mathcal {T}_{\textsc {RHS}}^{\textsc {all}}$. Then we have, by bounding the orders of $\tau _{2}$ and $\tau _{3}$ from below,

$$\begin{aligned} |w| = 6 + |\tau _{1}| + |\tau _{2}| + |\tau _{3}| \geqq |\tau _{1}| + 2 \delta . \end{aligned}$$

Then, the condition that $|w| \leqq -2$ forces $|\tau _{1}| < -2$ so we have $\tau _{1} \in \mathcal {W}$ and clearly the same argument applies for $\tau _{2},\tau _{3}$. $\square$

Our various tree expansions will be linear combinations of trees in $\mathcal {T}_{\textsc {RHS}}$ or $\mathcal {T}_{\textsc {LHS}}$ and we define tree products of such linear combinations by using linearity. However, here we implement a truncation convention that will be in place for the rest of the paper. Namely, given $\sigma _{1},\sigma _{2},\sigma _{3} \in \mathcal {T}_{\textsc {LHS}}$ if $|\sigma _{1}| + |\sigma _{2}| + |\sigma _{3}| > 0$, we enforce that

$$\begin{aligned} \sigma _{1} \sigma _{2} \sigma _{3} := 0\;. \end{aligned}$$

(3.4)

Imposing (3.4) is important for analytic reasons (since one doesn’t expect infinite tree expansions to converge). in fact, the key algebraic identities for coproducts we prove (such as Lemma 4.5) hold whether or not one makes the truncation (3.4), which is a consequence of how our coproducts behave with respect to degrees (see (4.7)).

In particular, with these conventions an important identity for us will be

$$\begin{aligned} \Big ( \sum _{ \tau \in \mathcal {V}\cup \mathcal {W}} \mathcal {I}(\tau ) \Big )^{3} = \sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}} \tau \;. \end{aligned}$$

(3.5)

Above, on the left, the $(\bullet )^{3}$ indicates a three-fold tree product. To verify the identity above, note that for $\tau _{1},\tau _{2},\tau _{3} \in \mathcal {V}\sqcup \mathcal {W}$, one has $\tau = \mathcal {I}(\tau _1) \mathcal {I}(\tau _2) \mathcal {I}(\tau _3) \in \tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$ if and only if $|\tau | > 0$. The non-commutativity of the tree product means we see no combinatorial coefficients in (3.5).

3.2 Local products

In this section we begin to specify how trees are mapped into analytic expressions. Our starting point for this will be what we call a local product and will be denoted by $\mathbb {X}$. Each local product $\mathbb {X}$ should be thought of as a (minimal) description of how products of planted trees should be interpreted at a concrete level.

We will view local products as being defined on a relatively small set of trees and then canonically extended to all of $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$ (and in the sequel, to larger sets of trees that will appear).

Definition 3.7

We define $\mathcal {Q}\subset \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$ to consist of all trees

$$\begin{aligned} \tau = \mathcal {I}(\tau _{1}) \mathcal {I}(\tau _{2}) \mathcal {I}(\tau _{3}) \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}, \end{aligned}$$

satisfying the following properties:

• $\tau _{1},\tau _{2},\tau _{3} \not \in \{\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$.

• At most one of the trees $\tau _{1},\tau _{2},\tau _{3}$ is equal to $\textbf{1}$.

Note that $\mathcal {W}_{\textsc {prod}}\subset \mathcal {Q}$. The set $\mathcal {Q}$ includes all “non-trivial” products of trees, namely those corresponding to classically ill-defined products of distributions. Our philosophy is that once a local product $\mathbb {X}$ is specified on the noise $\Xi$ and all these non-trivial products then we are able to define all other products that appear in our analysis—see the section immediately following. Describing a minimal set of data as above will be useful when we describe the renormalisation of local products in Sect. 8.3.

We impose the first of the two constraints stated above because multiplication by the tree $\mathcal {I}(\textbf{X}_{i})$ corresponds to multiplication of a distribution/function by $z_{i}$ which is always well-defined—so we enforce that this product is not deformed. We impose the second of the two constraints above since a tree of the form $\mathcal {I}(\textbf{1})\mathcal {I}(\tau )\mathcal {I}(\textbf{1})$ (or some permutation thereof) does not represent a new non-trivial product because the factors $\mathcal {I}(\textbf{1})$ corresponds to the the classical monomial 1.

There is a natural equivalence relation $\sim$ on $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$ where $\tau \sim \tau '$ if and only if $\tau$ and $\tau '$ are the same modulo non-commutativity. More precisely, $\sim$ is the smallest equivalence relation on $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$ with the properties that $\tau \sim \bar{\tau } \rightarrow \mathcal {I}(\tau ) \sim \mathcal {I}(\bar{\tau })$ and, for any permutation $\theta$ on three elements, $\sigma _{1} \sigma _{2} \sigma _{3} \sim \sigma _{\theta (1)}\sigma _{\theta (2)}\sigma _{\theta (3)}$.

Definition 3.8

A local product is a map $\mathbb {X}: \mathcal {Q}\cup \{\Xi \} \rightarrow C^{\infty }(\mathbb {R}\times \mathbb {R}^{d})$, which we write $\tau \mapsto \mathbb {X}_{\bullet }\tau$.

We further enforce that if $\tau , \bar{\tau } \in \mathbb {X}$ satisfy $\tau \sim \bar{\tau }$ then $\mathbb {X}_{\bullet } \tau = \mathbb {X}_{\bullet } \bar{\tau }$.

3.3 Extension of local products

We now describe how any local product $\mathbb {X}$ is extended to $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$, this procedure will involve induction in $m_{e}(\sigma ) + m_{\textbf{x}}(\sigma )$ where $m_{e}(\sigma )$ is the number of edges of $\sigma$.

We start by defining, for any function $f: \mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$, $(\mathcal {L}^{-1}f)$ to be the unique bounded solution u of

$$\begin{aligned} (\partial _t-\Delta )u =\rho f. \end{aligned}$$

(3.6)

where $\rho$ is a smooth cutoff function with value 1 in a neighbourhood of the parabolic cylinder D (defined in (1.2) above) and vanishes outside of $\{z;\ d(z,0)<2\}$.

We now describe how we extend $\mathbb {X}$ to $\mathcal {V}_{\textsc {prod}}{\setminus } \mathcal {Q}$. If $\tau = \mathcal {I}(\tau _{1}) \mathcal {I}(\tau _{2}) \mathcal {I}(\tau _{3}) \in \mathcal {V}_{\textsc {prod}}{\setminus } \mathcal {Q}$ then precisely one of the following conditions holds

• (1) Exactly one of the $\tau _{1}$, $\tau _{2}$, $\tau _{3}$ belong to the set $\{\textbf{X}_{i}\}_{i=1}^{d}$.

• (2) Two of the factors $\tau _{1},\tau _{2},\tau _{3}$ are equal to $\textbf{1}$.

In the first case above we can assume without loss of generality that $\tau _{1} = \textbf{X}_{i}$, then we set

$$\begin{aligned} \mathbb {X}_{z} \tau = z_{i} \mathbb {X}_{z}(\mathcal {I}(\textbf{1}) \mathcal {I}(\tau _{2}) \mathcal {I}(\tau _{3})). \end{aligned}$$

In the second case above we can assume without loss of generality that $\tau _{1} = \tau _{2} = \textbf{1}$, then we set

$$\begin{aligned} \mathbb {X}_{z} \tau = (\mathcal {L}^{-1} \mathbb {X}_{\bullet } \tau _{3})(z). \end{aligned}$$

Next we extend any local product $\mathbb {X}$ to $\mathcal {T}_{\textsc {LHS}}$ by setting, for any $\mathcal {I}(\tau ) \in \mathcal {T}_{\textsc {LHS}}$,

$$\begin{aligned} \mathbb {X}_{z}\mathcal {I}(\tau ) = {\left\{ \begin{array}{ll} z_{i} &{} \text { if}\quad \tau = \textbf{X}_{i}\\ 1 &{} \text { if}\quad \tau = \textbf{1}\\ (\mathcal {L}^{-1} \mathbb {X}_{\bullet }\tau )(z) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(3.7)

Finally, we extend by linearity to allow $\mathbb {X}$ to act on linear combinations of elements of $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$. Adopting the language of rough path theory and regularity structures, given smooth noise $\xi :\mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ we say a local product $\mathbb {X}$ is a lift of $\xi$ if $\mathbb {X}_{z}\Xi = \xi (z)$. Without additional constraints lifts are not unique.

Definition 3.9

We say a local product $\mathbb {X}$ is multiplicative if, for every

$$\begin{aligned} \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) \in \mathcal {Q},\end{aligned}$$

one has

$$\begin{aligned} \mathbb {X}_{z} \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) = \mathbb {X}_{z} \mathcal {I}(\tau _{1}) \mathbb {X}_{z} \mathcal {I}(\tau _{2}) \mathbb {X}_{z} \mathcal {I}(\tau _{3})\;, \end{aligned}$$

(3.8)

where on the right hand side we are using the extension of $\mathbb {X}$ to planted trees.

The following lemma is then straightforward to prove.

Lemma 3.10

Given any smooth $\xi :\mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ there is a unique multiplicative lift of $\xi$ into a local product, up to the choice of cut-off function $\rho$.

Multiplicative local products will not play a special role in our analysis but we will use them at several points to compare our solution theory for (1.1) to the classical solution theory.

4 The Coproduct

As discussed in Sect. 2.4, local products $\mathbb {X}_{\bullet }$ enter in our analysis in a centered form which depends on the choice of a basepoint x. The construction of these centered objects is given in Sect. 5. As a preliminary step, in this section we define a combinatorial operation on trees, called the coproduct, which plays a central role in this construction.

4.1 Derivative edges

For trees $\sigma$ with $|\sigma | \in (1,2)$ we will need the centering procedure to generate first order Taylor expansions in spatial directions. In order to encode these derivatives at the level of our algebraic symbols we introduce a new set of edges $\mathcal {I}^{+}_{i}, i=1\ldots d$ and also define the sets of trees

$$\begin{aligned} \mathcal {V}_{> 1}= & {} \{ \tau \in \mathcal {V}_{\textsc {prod}}: -1< |\tau | < 0\}, \end{aligned}$$

(4.1)

$$\begin{aligned} \mathcal {T}_{\Delta }=: & {} \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}\cup \big \{ \mathcal {I}^{+}_{i}(\tau ): 1 \leqq i \leqq d,\ \tau \in \mathcal {V}_{> 1}\cup \{\textbf{X}_{i}\} \big \}. \end{aligned}$$

(4.2)

As a mneumonic, $\mathcal {T}_{\Delta }$ is the set of trees on which we will apply $\Delta$. Given $1 \leqq i \leqq d$ and $\tau \in \mathcal {V}_{> 1}\cup \{\textbf{X}_{i}\}_{i=1}^{d}$, we also call $\mathcal {I}_{i}^{+}(\tau )$ a planted tree. The order of these new planted trees introduced here is given by $|\mathcal {I}_i^+(\tau )|=|\tau |+1$. We also adopt the shorthand that, for $1 \leqq i \leqq d$,

$$\begin{aligned} \mathcal {I}^{+}_{i}(\textbf{X}_{j}) = 0 \quad \text {for}\quad j\not = i, \mathcal {I}^{+}_{i}(\textbf{1}) = 0,\quad \text {and}\quad \mathcal {I}^{+}_{i}(\tau ) = 0\quad \text {for all}\quad \tau \in \mathcal {V}_{\textsc {prod}}\setminus \mathcal {V}_{> 1}. \end{aligned}$$

We emphasise that these new edges will only ever appear as the bottom edge of a planted tree. Graphically we distinguish these edges by writing an index by them. For example,

At an analytic level, the role of $\mathcal {I}^{+}_{i}(\textbf{X}_{j})$ is the same as that of $\mathcal {I}(\textbf{1})$ but distinguishing these symbols will be important - see Remark 6.11.

4.2 Algebras and vector spaces of trees

We now give some notation for describing the codomain of our coproduct $\Delta$. Given a set of trees T we write $\textrm{Vec}(T)$ for the vector space (over $\mathbb {R}$) generated by T.

Given a set of planted trees T we write $\textrm{Alg}(T)$ for the unital non-commutative algebra (again over $\mathbb {R}$) generated by T. We will distinguish between the tree product introduced in Sect. 3 and the product that makes $\textrm{Alg}(T)$ an algebra, calling the the latter product the “forest product” (note that the truncation (3.4) is applied for the tree product but not the forest product). While both the tree product and forest product are non-commutative, the roles they play are quite different—see Remark 4.2

We will write $\cdot$ to denote the forest product when using algebraic variables for trees, that is given $\sigma , \tilde{\sigma } \in T$, we write $\sigma \cdot \tilde{\sigma }$ for the forest product of $\sigma$ and $\tilde{\sigma }$. As a real vector space $\textrm{Alg}(T)$ is spanned by products $\sigma _{1} \cdot \sigma _{2} \cdots \sigma _{n}$ with $\sigma _{1},\ldots ,\sigma _{n} \in T$. We call such a product $\sigma _{1} \cdot \sigma _{2} \cdots \sigma _{n}$ a “forest”. The unit for the forest product is given by the “empty” forest and is denoted by 1.

Graphically, we will represent forest products just by drawing the corresponding planted trees side by side, for instance writing

4.3 Coproduct

We define another set of trees

$$\begin{aligned} \mathcal {T}_{\textrm{cen}}:= \mathcal {I}(\mathcal {V}) \cup \{ \mathcal {I}_{i}^{+}(\tau ): \tau \in \mathcal {V}_{> 1}\cup \{\textbf{X}_{i}\}, 1 \leqq i \leqq d\}\;. \end{aligned}$$

(4.3)

As a mnemonic, $\mathcal {T}_{\textrm{cen}}$ are the trees that are used to implement recentering. Our coproduct will be a map

$$\begin{aligned} \Delta : \mathcal {T}_{\Delta }\rightarrow \textrm{Vec}(\mathcal {T}_{\Delta }) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}}). \end{aligned}$$

Our definition of $\Delta$ will be recursive. The base cases of this recursive definition are the trees in $w\in \mathcal {W}$ and planted trees $\mathcal {I}(w),\; w\in \mathcal {W}$, and the elementary trees $\mathcal {I}(\textbf{1})$, $\mathcal {I}(\textbf{X}_i)$ and $\mathcal {I}^+_i(\textbf{X}_i)$:

$$\begin{aligned}&\Delta \mathcal {I}(\textbf{1}) = \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\textbf{1}),\\&\Delta \mathcal {I}(\textbf{X}_{i}) = \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\textbf{X}_{i}) + \mathcal {I}(\textbf{X}_{i}) \otimes \mathcal {I}_{i}^{+}(\textbf{X}_{i}),\nonumber \\&\Delta \mathcal {I}^{+}_{i}(\textbf{X}_{i}) = \mathcal {I}^{+}_{i}(\textbf{X}_{i}) \otimes \mathcal {I}^{+}_{i}(\textbf{X}_{i}),\nonumber \\&\Delta w= w \otimes 1,\ \Delta \mathcal {I}(w) = \mathcal {I}(w) \otimes 1,\ w\in \mathcal {W}.\nonumber \end{aligned}$$

(4.4)

Note that in the last line, the 1 appearing is the unit element in the algebra and should not be mistaken for $\textbf{1}\in \textrm{Poly}$. The first and third definitions are compatible with the fact that $\mathcal {I}(\textbf{1})$ and $\mathcal {I}^{+}_{i}(\textbf{X}_{i})$ are represent the constant function 1, and so the coproduct acts trivially on them. For the second line we note that to recenter a linear monomial, one subtracts the same monomial evaluated at the basepoint (the first term on the RHS) while the second term gives the monomial evaluated on the active space–time argument (the $\mathcal {I}^{+}_{i}(\textbf{X}_{i})$ being a way to represent the constant 1 again, see Remark 6.11). Finally, the last line of (4.4) comes from the fact that trees $\mathcal {W}$, as they are built up iteratively from smaller trees, never involve trees of positive degree - from the algebraic point of view they behave just like the noise $\Xi$.

The recursive part of our definition is then given by

$$\begin{aligned}&\Delta \mathcal {I}(\tau )=\mathcal {I}(\textbf{1})\otimes \mathcal {I}(\tau )+ \mathcal {I}(\textbf{X}_{i})\otimes \mathcal {I}^{+}_{i}(\tau )\nonumber +(\mathcal {I}\otimes \textrm{Id})\Delta \tau ,\ \tau \in \mathcal {V}_{\textsc {prod}},\\&\Delta \mathcal {I}^{+}_{i}(\tau ) = \mathcal {I}^{+}_{i}(\textbf{X}_{i}) \otimes \mathcal {I}^{+}_{i}(\tau ) + (\mathcal {I}^{+}_{i} \otimes \textrm{Id}) \Delta \tau , \tau \in \mathcal {V}_{> 1},\\&\Delta (\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3)) =\Delta (\mathcal {I}(\tau _1))\Delta (\mathcal {I}(\tau _2))\Delta (\mathcal {I}(\tau _2)),\nonumber \\&\quad \mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3) \in \mathcal {V}_{\textsc {prod}},\nonumber \end{aligned}$$

(4.5)

where, on the right hand side of the last line above we are referring to the natural product $[\textrm{Vec}(\mathcal {T}_{\textsc {LHS}}) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})]^{\otimes 3} \rightarrow \textrm{Vec}(\mathcal {T}_{\textsc {RHS}}) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$. This product is just given by setting

$$\begin{aligned} \bigotimes _{i=1}^{3} (\mathcal {I}(\tau _{i}) \otimes a_{i}) \mapsto \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) \otimes (a_{1}\cdot a_{2}\cdot a_{3}) \;, \end{aligned}$$

(4.6)

and then extending by linearity. We also make note of the fact that, in the first and second lines of (4.5), we are using our convention of Einstein summation - since i does not appear on the left hand side then the i on the right hand side is summed from 1 to d.

In the first (resp. second) line of (4.5), the first two terms (resp. first term) on the RHS recenter the outermost integration, while the last term RHS recursively attempts to recenter earlier integrations.

We also note that a term $\sigma ' \otimes f$ appears in the expansion of $\Delta \sigma$ then one has

$$\begin{aligned} |\sigma '| \leqq |\sigma |\quad \text {and}\quad |\sigma | = |\sigma '| + |f|. \end{aligned}$$

(4.7)

One can verify that it is indeed the case that $\Delta$ maps $\mathcal {T}_{\Delta }$ into $\textrm{Vec}(\mathcal {T}_{\Delta }) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$ by checking inductively, using (4.4) for the bases cases and (4.5) for the inductive step. We also have the following lemma on how $\Delta$ acts on subsets of $\mathcal {T}_{\Delta }$.

Lemma 4.1

For $X = \mathcal {T}_{\textsc {LHS}},\; \mathcal {T}_{\textsc {RHS}},\; \mathcal {V}_{\textsc {prod}}\,$ or $\mathcal {T}_{\textrm{cen}}$ the map $\Delta$ maps X into $\textrm{Vec}(X) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$.

Proof

The first two statements are immediate consequences of our definitions. We turn to proving the third statement, where we proceed by induction in the number of edges of $\tau \in \mathcal {V}$. The base case(s) where $\tau$ has three edges are easily verified by hand. For the inductive step, we write $\tau = \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3})$. Now, if $\tau _{1},\tau _{2},\tau _{3} \in \mathcal {W}$ one can check that the last line of (4.5) gives us that $\Delta \tau = \tau \otimes 1$ and we are done. On the other hand, if we have $\tau _{i} \in \mathcal {V}$ for some i then $\Delta \mathcal {I}(\tau ) \in \textrm{Vec}(\mathcal {I}(\mathcal {V})) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$ and so we are done by combining the last line of (4.5) with (3.3).

Finally, the fourth statement is immediate by inspection for planted trees $\mathcal {T}_{\textrm{cen}}\setminus \mathcal {I}(\mathcal {V}_{\textsc {prod}})$ while for planted trees in $\mathcal {I}(\mathcal {V}_{\textsc {prod}})$ it follows from using the third statement for $\tau$ in the first line of (4.5). $\square$

We extend $\Delta$ to sums of trees of linearity, so that $\Delta : \textrm{Vec}(\mathcal {T}_{\Delta }) \rightarrow \textrm{Vec}(\mathcal {T}_{\Delta }) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$.

Remark 4.2

The two products we have introduced on trees, the tree product and the forest product, play different roles in our framework: the tree product represents a point-wise product of functions/distributions which may not be defined canonically. Therefore we do not enforce that local products act multiplicatively with respect to the tree product. On the other hand, any map on trees that is applied to a forest is extended multiplicatively - we do not allow for any flexibility in how forest products are interpreted at a concrete level. In particular, the trees in the forests that $\Delta$ produces in the right factor of its codomain are all of non-negative order and should be thought of as being associated to products of base-point dependent constants rather than a point-wise product of space–time functions/distributions.

Example 4.3

We show one pictorial example. The value of our parameter $\delta$ influences the definition of the set $\mathcal {V}_{\textsc {prod}}$ and whether $\mathcal {I}^{+}_{i}(\tau )$ vanishes or not for $\tau \in \mathcal {V}_{\textsc {prod}}$, therefore most non-trivial computations of $\Delta$ we would present are valid only for a certain range of the parameter $\delta$.

For the example we present below, we restrict to $\frac{3}{7}>\delta >\frac{1}{3}$ and therefore . We then have, using Einstein’s convention for the index $i\in \{1,\ldots ,d\}$ (when an index i appears twice on one side of an equation, it means a summation over $i=1\ldots d$)

Now we have , along with and

Putting this all together gives

We show now the example of an unplanted tree in the case $\delta <\frac{1}{3}$ and therefore . On the other hand, we always have . With Einstein’s convention for the index $j\in \{1,\ldots ,d\}$

Remark 4.4

The last formula in (4.5) for $\tau \in \mathcal {V}_{\textsc {prod}}$ is also valid for $\tau \in \mathcal {W}_{\textsc {prod}}$ where it is trivial. The first formula of (4.5) can also be extended to $\tau \in \mathcal {V}$ if one adopts the convention that $\Delta \textbf{X}_{i} = \Delta \textbf{1}= 0$. We chose not to do this since the trees of $\textrm{Poly}$ do not, by themselves, play a role in our algebraic expansions and analysis except when they appear in a larger tree.

We extend $\Delta$ to forests of planted trees by setting $\Delta 1 = 1 \otimes 1$ and, for any forest $\sigma _{1} \cdots \sigma _{n}$, $n \geqq 1$,

$$\begin{aligned} \Delta ( \sigma _{1} \cdots \sigma _{n}) = (\Delta \sigma _{1}) \cdots (\Delta \sigma _{n}), \end{aligned}$$

where on the right hand side we use the forest product to multiply all the factors components-wise. We extend to sums of forests of planted trees by additivity so that $\Delta : \textrm{Alg}(\mathcal {T}_{\textsc {LHS}}) \rightarrow \textrm{Alg}(\mathcal {T}_{\textsc {LHS}}) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$ and, by Lemma 4.1, we also have that $\Delta$ maps $\textrm{Alg}(\mathcal {T}_{\textrm{cen}})$ into $\textrm{Alg}(\mathcal {T}_{\textrm{cen}}) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$.

While a single application of $\Delta$ will be used for centering objects around a basepoint, we will see in Sect. 5 that a double application of $\Delta$ will be used for describing the behaviour when changing this basepoint. This is our reason for also defining $\Delta$ on the planted trees of $\mathcal {T}_{\textrm{cen}}\setminus \mathcal {T}_{\textsc {LHS}}$. It will be important below to know that the two ways of “applying $\Delta$ twice” agree, this is encoded in the following lemma:

Lemma 4.5

$\Delta$ satisfies a co-associativity property: for any $\sigma \in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$,

$$\begin{aligned} (\Delta \otimes \textrm{Id}) \Delta \sigma = (\textrm{Id}\otimes \Delta ) \Delta \sigma \;, \end{aligned}$$

(4.8)

where both sides are seen as elements of $\textrm{Vec}(\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}}) \otimes \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$.

Proof

We argue by induction in the size of $\sigma$. The cases where $\sigma = \mathcal {I}(\textbf{1})$, or $\mathcal {I}(\textbf{X}_{i})$ are straightforward to check. Note that by multiplicativity of $\Delta$ with respect to the tree product it suffices to establish the inductive step for $\sigma = \mathcal {I}(\tau )$ for some $\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$. The case where $\tau \in \mathcal {W}_{\textsc {prod}}$ is trivial so we walk through the verification of the identity when $\tau \in \mathcal {V}_{\textsc {prod}}$. On the left we have

$$\begin{aligned} (\Delta \otimes \textrm{Id}) \Delta \mathcal {I}(\tau )&= (\Delta \otimes \textrm{Id}) \Big [ \mathcal {I}(\textbf{1})\otimes \mathcal {I}(\tau )+ \mathcal {I}(\textbf{X}_{i})\otimes \mathcal {I}^{+}_{i}(\tau ) +(\mathcal {I}\otimes \textrm{Id})\Delta \tau \Big ]\\&= \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\tau ) + \mathcal {I}(\textbf{X}_{i}) \otimes \mathcal {I}_{i}^{+}(\textbf{X}_{i}) \otimes \mathcal {I}^{+}_{i}(\tau ) \\&\quad + \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\textbf{X}_{i}) \otimes \mathcal {I}^{+}_{i}(\tau ) + \mathcal {I}(\textbf{1}) \otimes \big ( (\mathcal {I}\otimes \textrm{Id}) \Delta \tau \big )\\&\quad + \mathcal {I}(\textbf{X}_{j}) \otimes \big ( (\mathcal {I}_{j}^{+} \otimes \textrm{Id}) \Delta \tau \big ) + (\mathcal {I}\otimes \textrm{Id}\otimes \textrm{Id}) (\Delta \otimes \textrm{Id}) \Delta \tau . \end{aligned}$$

On the right we have

$$\begin{aligned} ( \textrm{Id}\otimes \Delta ) \Delta \mathcal {I}(\tau )&= (\textrm{Id}\otimes \Delta ) \Big [ \mathcal {I}(\textbf{1})\otimes \mathcal {I}(\tau )+ \mathcal {I}(\textbf{X}_{i})\otimes \mathcal {I}^{+}_{i}(\tau ) +(\mathcal {I}\otimes \textrm{Id})\Delta \tau \Big ]\\&= \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\tau ) + \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\textbf{X}_{j}) \otimes \mathcal {I}^{+}_{j}(\tau )\\&\quad + \mathcal {I}(\textbf{1}) \otimes \big ( (\mathcal {I}\otimes \textrm{Id}) \Delta \tau \big ) + \mathcal {I}(\textbf{X}_{i}) \otimes \mathcal {I}_{i}^{+}(\textbf{X}_{i}) \otimes \mathcal {I}^{+}_{i}(\tau )\\&\quad + \mathcal {I}(\textbf{X}_{i}) \otimes \big ( (\mathcal {I}_{i}^{+} \otimes \textrm{Id}) \Delta \tau \big ) + (\mathcal {I}\otimes \textrm{Id}\otimes \textrm{Id}) (\textrm{Id}\otimes \Delta ) \Delta \tau . \end{aligned}$$

All the terms in the expression for the left and right hand sides can be immediately matched except for the very last terms, but these are seen to be identical by using our induction hypothesis, which is

$$\begin{aligned} (\textrm{Id}\otimes \Delta ) \Delta \tau = (\Delta \otimes \textrm{Id}) \Delta \tau . \end{aligned}$$

$\square$

4.4 Useful relations on trees

We introduce two (reflexive and antisymmetric) relations on unplanted trees $\mathcal {T}_{\textsc {RHS}}$, which we denote $\leqslant$ and $\subset$.

Definition 4.6

Given $\bar{\tau }, \tau \in \mathcal {T}_{\textsc {RHS}}$ we have $\bar{\tau } \leqslant \tau$ if and only if one can obtain $\tau$ from $\bar{\tau }$ by replacing occurrences of the generators $\textbf{1}$ in $\bar{\tau }$ with appropriately chosen trees $\tau _1,\ldots \tau _{m_{\textbf{1}}(\bar{\tau })}\in \mathcal {T}_{\textsc {RHS}}$ and, for every $1 \leqq i \leqq d$, occurrences of $\textbf{X}_{i}$ with trees $\tau _{1},\ldots ,\tau _{m_{\textbf{X}_{i}(\bar{\tau })}} \in \mathcal {T}_{\textsc {RHS}}{\setminus }\{\textbf{1}, \textbf{X}_j,j\ne i\}$.

Example 4.7

We give two pictorial examples:

Definition 4.8

Given $\bar{\tau }, \tau \in \mathcal {T}_{\textsc {RHS}}$ we have $\bar{\tau } \subset \tau$ if and only if $\bar{\tau } = \tau$ or $\bar{\tau }$ appears in the inductive definition of $\tau$, that is the expression $\mathcal {I}(\bar{\tau })$ should appear at some point when one writes out the full algebraic expression for $\tau$.

Example 4.9

We give an example below.

We also use the notation < and $\subsetneq$ to refer to the non-reflexive (strict) relations corresponding to $\leqq$ and $\subset$.

One can get an intuition of how the coproduct works with the idea of cutting branches: on the left-hand side of $\Delta \tau$ we have trees $\bar{\tau }\leqslant \tau$, and on the right-hand side, we have the trees $\mathcal {I}(\tilde{\tau })$ or $\mathcal {I}^+_i(\tilde{\tau })$ where $\tilde{\tau }\subset \tau$ has been cut from $\tau$ to obtain $\bar{\tau }$. We formalise this in the following section.

4.5 Another formula for $\Delta$

Given $\tau \in \mathcal {T}_{\textsc {RHS}}$, one can think of $\Delta \tau$ as a linear combination of terms where one sums over ways to “chop off” planted subtrees of $\tau$ of positive order, which each term being a tensor product of the “pruned tree” with a forest of “cuttings”.

In this section we will start by going the other direction - given another tree $\bar{\tau } \in \mathcal {T}_{\textsc {RHS}}$ we will define a forest $C_{+}(\bar{\tau },\tau )$ of planted trees that consists of the cuttings that must have been chopped off from $\tau$ by $\Delta$ to be left with $\bar{\tau }$ as the pruned tree. If it is not possible to obtain $\bar{\tau }$ from $\tau$ then one will have $C_{+}(\bar{\tau },\tau ) = 0$. With this intuitive picture in place, we now turn to giving precise definitions.

We write $\mathcal {F}_{\textrm{cen}}$ for the collection of all finite, non-commutative words in $\mathcal {T}_{\textrm{cen}}$, including the empty word. In particular, $\mathcal {F}_{\textrm{cen}}$ is a vector space basis for $\textrm{Alg}(\mathcal {T}_{\Delta })$. We define a map $C_+: \mathcal {T}_{\textsc {RHS}}\times \mathcal {T}_{\textsc {RHS}}\rightarrow \mathcal {F}_{\textrm{cen}} \sqcup \{0\}$ recursively. The recursion is given in the following table:

Table 1 This table gives a recursive definition of $C_+(\bar{\tau }, \tau )$

Here $p_+$ is the projection on trees of positive order. In particular, for $\delta <1$, one has $p_+\mathcal {I}(\Xi ),\ \mathcal {I}^{+}_{i}(\Xi ) =0$. Note also that $C_+(\Xi ,\Xi )=1$, which is the unit element in the algebra of trees, not to be mistaken for $\textbf{1}$.

Example 4.10

We give two pictorial examples

and

We explain how this can be understood in the language of “cuts”. There are three types of cutting procedures that can be applied to a tree $\sigma$.

• (1) One cuts an $\mathcal {I}$-branch and takes the attached planted tree, leaving behind an $\mathcal {I}(\textbf{1})$.

• (2) One cuts an $\mathcal {I}$ branch and takes the attached planted tree, with its “trunk” becoming a derivative $\mathcal {I}^{+}_{k}$, and leaving behind a $\mathcal {I}(\textbf{X}_{k})$. Note that this only occurs when one the tree $\tau \subset \sigma$ attached to this $\mathcal {I}$ branch belongs to $\mathcal {V}_{> 1}$.

• (3) One cuts an $\mathcal {I}_{i}^{+}$ branch (which must be the trunk of $\sigma$) and takes the all of $\sigma$, leaving behind an $\mathcal {I}_{i}^{+}(\textbf{X}_{i})$.

If $\delta > \frac{1}{3}$, the tree is obtained from by performing the first type of cut on the leftmost and rightmost $\mathcal {I}$ branches of connected to the root, leaving behind .

In the second example, one performs the second type of cut on the rightmost $\mathcal {I}$ branch connected to the root of , generating an $\mathcal {I}_{j}^{+}$ trunk on the planted tree taken and leaving behind an $\mathcal {I}(\textbf{X}_{j})$ on .

Some immediate properties of these forests $C_{+}(\tau ,\bar{\tau })$ are given in the following lemma:

Lemma 4.11

Let $\tau , \bar{\tau } \in \mathcal {T}_{\textsc {RHS}}$. Then we have

$$\begin{aligned} C_+(\bar{\tau },\tau )&\ne 0\Rightarrow \bar{\tau } \leqslant \tau ,\\ \mathcal {I}(\tau ')&\in C_+(\bar{\tau },\tau )\quad \text {or}\quad \mathcal {I}^+_i(\tau ')\in C_+(\bar{\tau },\tau )\Rightarrow \tau '\subset \tau \nonumber . \end{aligned}$$

(4.9)

Under the assumption that $C_+(\bar{\tau },\tau )\ne 0$ we have

$$\begin{aligned} m_{\scriptscriptstyle \Xi }(\tau )&=m_{\scriptscriptstyle \Xi }(\bar{\tau })+m_{\scriptscriptstyle \Xi }(C_+(\bar{\tau },{\tau }))\quad m_{\textbf{1}}(\bar{\tau })+m_{\textbf{x}}(\bar{\tau })=\sharp (C_+(\bar{\tau },\tau )),\\ m_{\textbf{1}}(\tau )&=m_{\textbf{1}}(C_+(\bar{\tau },\tau )),\quad m_{\textbf{x}}(\tau )=m_{\textbf{x}}(C_+(\bar{\tau },\tau ))\nonumber , \end{aligned}$$

(4.10)

where $\sharp (C_+(\bar{\tau },\tau ))$ is the number of trees in $C_+(\bar{\tau },\tau )$ (including multiplicity) and we extend the functions $m_{\textbf{1}},\; m_{\textbf{x}}$ and $m_{\scriptscriptstyle \Xi }$ to forests of the planted trees by summing over the individual planted trees in the forest.

The next lemma finally gives the expression of the coproduct $\Delta$ in terms of $C_+$. This expression is used throughout the paper without explicit reference to this lemma.

Lemma 4.12

For any $\tau \in \mathcal {V}\cup \mathcal {W}$,

$$\begin{aligned} \Delta \mathcal {I}(\tau ) = \sum _{\bar{\tau }\in \mathcal {V}\cup \mathcal {W}}\mathcal {I}(\bar{\tau }) \otimes C_+(\bar{\tau },\tau ). \end{aligned}$$

(4.11)

In particular, one has the formulae

$$\begin{aligned} \Delta \mathcal {I}(\tau ) = {\left\{ \begin{array}{ll} \mathcal {I}(\tau ) \otimes 1 &{} \text {if}\quad \tau \in \mathcal {W}\;,\\ \sum _{\bar{\tau }\in \mathcal {V}}\mathcal {I}(\bar{\tau })\otimes C_+(\bar{\tau },\tau ) &{} \text {if}\quad \tau \in \mathcal {V}\;. \end{array}\right. } \end{aligned}$$

(4.12)

Moreover, for any $\tau \in \mathcal {T}_{\textsc {RHS}}$,

$$\begin{aligned} \Delta \tau =\sum _{\bar{\tau }\in \mathcal {V}\cup \mathcal {W}}\bar{\tau }\otimes C_+(\bar{\tau },\tau ) = \tau \otimes 1 + \sum _{ \bar{\tau }\in \mathcal {V}\atop \bar{\tau } \not = \tau } \bar{\tau }\otimes C_+(\bar{\tau },\tau )\;. \end{aligned}$$

(4.13)

Proof

We prove (4.12) by induction, with the base cases given by $\tau \in \textrm{Poly}\cup \mathcal {W}$ which we check now:

$$\begin{aligned} \Delta \mathcal {I}(\textbf{1})=\mathcal {I}(\textbf{1})\otimes \mathcal {I}(\textbf{1})\quad \text {and}\quad C_+(\bar{\tau },\textbf{1})=\mathcal {I}(\textbf{1})\delta _{\{\bar{\tau }=\textbf{1}\}}. \end{aligned}$$

Since $\mathcal {I}^+_j(\textbf{X}_i)=0$ for $j\ne i$, we also have $\Delta \mathcal {I}(\textbf{X}_i)=\mathcal {I}(\textbf{1})\otimes \mathcal {I}(\textbf{X}_i)+\mathcal {I}(\textbf{X}_i)\otimes \mathcal {I}^+_i(\textbf{X}_i)$ and $C_+(\bar{\tau },\textbf{X}_i)=\mathcal {I}(\textbf{X}_i)\delta _{\{\bar{\tau }=\textbf{1}\}}+\mathcal {I}^+_i(\textbf{X}_i)\delta _{\{\bar{\tau }=\textbf{X}_i\}}.$

Finally, for $\tau =w\in \mathcal {W}$, we have to show that the sum in the right-hand side of (4.11) contains only one term. Indeed, for any $w'\leqslant w$, we also have $w'\in \mathcal {W}$, hence $|\mathcal {I}(w')|<0$ and $C_+(\bar{\tau },w)=\delta _{\{\bar{\tau }=w\}}$.

We now prove the inductive step for $\tau =\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3)\in \mathcal {V}_{\textsc {prod}}$, with the induction hypothesis $\Delta \mathcal {I}(\tau _k)=\sum _{\bar{\tau }_k}\mathcal {I}(\bar{\tau }_k)\otimes C_+(\bar{\tau }_k,\tau _k),$ for $k=1,2,3.$ We have that $C_+(\textbf{1},\tau )=p_+\mathcal {I}(\tau )=\mathcal {I}(\tau )$ since $\tau \in \mathcal {V}_{\textsc {prod}}$ and $C_+(\textbf{X}_i,\tau )=\mathcal {I}^+_i(\tau )=\mathcal {I}^+_i(\tau )\delta _{\{\tau \in \mathcal {V}_{> 1}\}}$, and from the definition of $\Delta$, we have

$$\begin{aligned} \Delta \mathcal {I}(\tau )&=\mathcal {I}(\textbf{1})\otimes \mathcal {I}(\tau )+\mathcal {I}(\textbf{X}_i)\otimes \mathcal {I}^+_i(\tau )\\&\quad +\sum _{\bar{\tau }_1,\bar{\tau }_2,\bar{\tau }_3}\mathcal {I}(\mathcal {I}(\bar{\tau }_1)\mathcal {I}(\bar{\tau }_2)\mathcal {I}(\bar{\tau }_3))\otimes C_+(\bar{\tau }_1,\tau _1)C_+(\bar{\tau }_2,\tau _2)C_+(\bar{\tau }_3,\tau _3). \end{aligned}$$

Furthermore, for any $\bar{\tau }\leqslant \tau \in \mathcal {V}_{\textsc {prod}}$, we have that either $\bar{\tau }=\tau$ or $m_{\textbf{1}}(\bar{\tau })+m_{\textbf{x}}(\bar{\tau })\geqslant 1$ therefore $|\bar{\tau }|\geqslant -2$. Hence the sum can be restricted to trees $\bar{\tau }=\mathcal {I}(\mathcal {I}(\bar{\tau }_1)\mathcal {I}(\bar{\tau }_2)\mathcal {I}(\bar{\tau }_3))\in \mathcal {V}_{\textsc {prod}}$. This concludes the proof of (4.11)

Finally, we prove (4.13). This is immediate if $\tau = \mathcal {W}$, otherwise one has $\tau = \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) \in \mathcal {V}_{\textsc {prod}}$ and one obtains the desired result by combining (4.12) and the multiplicativity of $\Delta$ with respect to the tree product as described in the last line of (4.5). $\square$

5 From Local Products to Paths

5.1 Definition of paths and centerings

For any choice of local product $\mathbb {X}$, we will define two corresponding families of maps, a path $(\mathbb {X}_{z,x}:\mathcal {T}_{\Delta }\rightarrow \mathbb {R};\ z,x\in \mathbb {R}\times \mathbb {R}^{d})$ and a centering $(\mathbb {X}^\textrm{cen}_z: \mathcal {T}_{\textrm{cen}}\rightarrow \mathbb {R};\ z\in \mathbb {R}\times \mathbb {R}^{d})$ where $\mathcal {T}_{\textrm{cen}}$ is defined in (4.3).

Both the path and the centering are defined through an inductive procedure that intertwines these two families of maps.

One particular aim of our definitions will be to allow us to obtain the formula

$$\begin{aligned} \mathbb {X}_{z,x} \mathcal {I}(\tau ) = (\mathbb {X}_{z} \otimes \mathbb {X}^{\textrm{cen}}_{x}) \Delta \mathcal {I}(\tau ) \quad \text {for any}\quad \tau \in \mathcal {V}_{\textsc {prod}}, \end{aligned}$$

(5.1)

where we are extending $\mathbb {X}^{\textrm{cen}}_{x}$ to act on forests of planted trees by multiplicativity.

As we discussed in Sect. 2, we define

$$\begin{aligned} \mathbb {X}_{z,x}\mathcal {I}(\textbf{1}):=1\quad \text {and}\quad \mathbb {X}_{z,x}\mathcal {I}(\textbf{X}_i):=z_i-x_i, \end{aligned}$$

(5.2)

and

$$\begin{aligned} \mathbb {X}_{z,x} \tau := \mathbb {X}_{z} \tau ,\quad \mathbb {X}_{z,x} \mathcal {I}(\tau ) := \mathbb {X}_{z} \mathcal {I}(\tau ) \quad \text {for any}\quad \tau \in \mathcal {W}. \end{aligned}$$

(5.3)

With our definition (5.3) it is immediate that (5.1) holds for $\tau \in \mathcal {W}$. For $\tau \in \mathcal {V}_{\textsc {prod}}$ we define

$$\begin{aligned} \mathbb {X}_{z,x}\mathcal {I}(\tau ) := \mathcal {L}^{-1}(\mathbb {X}_{\bullet , x}\tau )(z) - \mathcal {L}^{-1}(\mathbb {X}_{\bullet , x}\tau )(x) - \mathbb {1}_{\tau \in \mathcal {V}_{> 1}} (z_{i} - x_{i}) \nu ^{(i)}_{\tau }(x)\;, \end{aligned}$$

(5.4)

for which one must take as input the definition of $\mathbb {X}_{\bullet ,x}\tau$ and

$$\begin{aligned} \nu _{\tau }(x) = (\nu ^{(i)}_{\tau }(x))_{i=1}^{d} := \nabla ( \mathcal {L}^{-1}(\mathbb {X}_{\bullet ,x}\tau ))(z) |_{z=x}\;, \end{aligned}$$

(5.5)

where $\nabla$ denotes the spatial gradient. For the centering we will define

$$\begin{aligned} \begin{aligned} \mathbb {X}^{\textrm{cen}}_{x} \mathcal {I}(\textbf{1})&:= 1, \quad \mathbb {X}^{\textrm{cen}}_{x} \mathcal {I}(\textbf{X}_i):=-x_i,\quad \mathbb {X}^{\textrm{cen}}_{x}\mathcal {I}^{+}_{i}(\textbf{X}_{i}):= 1,\\ \mathbb {X}^{\textrm{cen}}_{x} \mathcal {I}(\tau )&:= -\mathcal {L}^{-1}(\mathbb {X}_{\bullet , x}\tau )(x) + {\mathbb {1}}_{\tau \in \mathcal {V}_{> 1}}x_i \nu ^{(i)}_{\tau }(x)\quad \text {for any}\quad \tau \in \mathcal {V}_{\textsc {prod}},\\ \mathbb {X}^{\textrm{cen}}_{x} \mathcal {I}_{i}^{+}(\tau )&:= -\nu _{\tau }^{(i)}(x) \quad \text {for any}\quad \tau \in \mathcal {V}_{> 1}. \end{aligned} \end{aligned}$$

(5.6)

The formulae above are inductive, we remark that for $\tau \in \mathcal {V}_{\textsc {prod}}$ one needs to be given $\mathbb {X}_{\bullet ,y}\tau$ in order to define $\mathbb {X}^{\textrm{cen}}_{y}\mathcal {I}(\tau )$ and, if $\tau \in \mathcal {V}_{> 1}$, that same input is needed to define $\mathbb {X}^{\textrm{cen}}_{y}\mathcal {I}^{+}_{i}(\tau )$. Note that since $1 \in \textrm{Alg}(\mathcal {T}_{\textrm{cen}})$ is the “empty product” we have $\mathbb {X}^{\textrm{cen}}_{x} 1 = 1$.

Finally, to handle the tree products that appear in the remainder equation we define

$$\begin{aligned} \mathbb {X}_{z,x} \tau := (\mathbb {X}_{z} \otimes \mathbb {X}_{x}^{\textrm{cen}}) \Delta \tau \quad \text {for all}\quad \tau \in \mathcal {V}_{\textsc {prod}}. \end{aligned}$$

(5.7)

Again, the formula above is an inductive definition - a sufficient condition for specifying the right hand side above is that we already know $\mathbb {X}_{\bullet ,x}$ for every $\bar{\tau } \in \mathcal {V}_{\textsc {prod}}$ for $\bar{\tau } \subsetneq \tau$.

Remark 5.1

Note that if (5.7) is extended to $\tau \in \mathcal {W}$ it agrees with the definition given in (5.3).

Lemma 5.2

If one adopts the inductive set of definitions (5.2), (5.4), (5.3), and (5.6), to determine the path on $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$ and the centering on $\mathcal {T}_{\textrm{cen}}$ then (5.1) holds for every $\tau \in \mathcal {V}\cup \mathcal {W}$.

Proof

The fact that (5.1) holds for every $\tau \in \mathcal {W}\cup \mathcal {I}(\mathcal {W}) \cup \mathcal {I}(\textrm{Poly})$ is immediate. Now suppose that $\tau \in \mathcal {V}_{\textsc {prod}}$, we can then rewrite (5.4) as

$$\begin{aligned} \mathbb {X}_{z,x}\mathcal {I}(\tau )= \mathcal {L}^{-1}(\mathbb {X}_{\bullet , x}\tau )(z)-{\mathbb {1}}_{\tau \in \mathcal {V}_{> 1}} z_{i}\nu ^{(i)}_{\tau }(x)+\mathbb {X}^\textrm{cen}_x\mathcal {I}(\tau ). \end{aligned}$$

We also have

$$\begin{aligned} \begin{aligned} \mathcal {L}^{-1}(\mathbb {X}_{\bullet , x}\tau )(z)&= \mathcal {L}^{-1}[(\mathbb {X}_{\bullet }\otimes \mathbb {X}_x^\textrm{cen}) \Delta \tau ](z)\\&= [(\mathcal {L}^{-1}\mathbb {X}_{\bullet }\cdot )(z)\otimes \mathbb {X}_x^\textrm{cen}] \Delta \tau \\&= (\mathbb {X}_{z} \otimes \mathbb {X}_x^\textrm{cen}) (\mathcal {I}\otimes \textrm{Id}) \Delta \tau . \end{aligned} \end{aligned}$$

The desired claim follows upon observing that

$$\begin{aligned} \begin{aligned} -{\mathbb {1}}_{\tau \in \mathcal {V}_{> 1}}z_{i}\nu _{\tau }^{(i)}(x)&= (\mathbb {X}_z \otimes \mathbb {X}^\textrm{cen}_x)(\mathcal {I}(\textbf{X}_{i}) \otimes \mathcal {I}_{i}^{+}(\tau )),\quad \\ \text {and}\quad \mathbb {X}^\textrm{cen}_x\mathcal {I}(\tau ) =&(\mathbb {X}_z \otimes \mathbb {X}^{\textrm{cen}}_{x})( \mathcal {I}(\textbf{1}) \otimes \mathcal {I}(\tau ))\;. \end{aligned} \end{aligned}$$

$\square$

At this point we have finished the inductive definition of the path on the trees of $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$ and of the centering on the trees of $\mathcal {T}_{\textrm{cen}}$. What is left is to define the path on the trees of $\{ \mathcal {I}^{+}_{i}(\tau ): 1 \leqq i \leqq d,\ \tau \in \mathcal {V}_{> 1}\cup \{\textbf{X}_{i}\}\}$.

In keeping with our convention of thinking of $\mathcal {I}^{+}_{i}(\textbf{X}_{i})$ as acting like $\mathcal {I}(\textbf{1})$ for all analysis, we set

$$\begin{aligned} \mathbb {X}_{z,x}\mathcal {I}^{+}_{i}(\textbf{X}_i):= 1. \end{aligned}$$

Our definition for the action of a path $\mathbb {X}_{\bullet ,\bullet }$ on a tree $\mathcal {I}_{i}^{+}(\tau )$ for $\tau \in \mathcal {V}_{> 1}$ is motivated by the fact that such trees are not really part of our tree expansions but instead only appear in order to encode change of base-point operations.

In particular, $\mathbb {X}_{u,x}\mathcal {I}_{i}^{+}(\tau )$ will play a role in how we relate centering at u versus centering at x and the identity we will be aiming for is Chen’s relation (5.10).

The key identity we would like to hold is that, for any $z,x \in \mathbb {R}\times \mathbb {R}^{d}$,

$$\begin{aligned} \mathbb {X}^{\textrm{cen}}_{x} \mathcal {I}^{+}_{i}(\tau ) = \big ( \mathbb {X}^{\textrm{cen}}_{z} \otimes \mathbb {X}_{z,x} \big ) \Delta \mathcal {I}^{+}_{i}(\tau ). \end{aligned}$$

(5.8)

Note that in the above equation we are using our convention of extending $\mathbb {X}_{z,x}$ to forests of planted trees by multiplicativity.

Expanding the action of $\Delta$ in (5.8) gives us an inductive procedure for defining $\mathbb {X}_{\bullet ,\bullet }\mathcal {I}^{+}_{i}(\tau )$ for $\tau \in \mathcal {V}_{> 1}$. Namely, we will define, for any $\tau \in \mathcal {V}_{> 1}$,

$$\begin{aligned} \begin{aligned} \mathbb {X}_{z,x}\mathcal {I}^{+}_{i} (\tau )&:= \mathbb {X}^{\textrm{cen}}_{x}\mathcal {I}^{+}_{i}(\tau ) - (\mathbb {X}^{\textrm{cen}}_{z}\circ \mathcal {I}^{+}_{i} \otimes \mathbb {X}_{z,x}) \Delta \tau \\&=-\nu _{\tau }^{(i)}(x) + \sum _{ \bar{\tau } \in \mathcal {V}_{> 1}} \nu _{\bar{\tau }}^{(i)}(z) \mathbb {X}_{z,x} C_{+}(\bar{\tau },\tau ). \end{aligned} \end{aligned}$$

(5.9)

We then see that, in order to define $\mathbb {X}_{z,x} \mathcal {I}_{i}^{+}(\tau )$ it suffices to have defined $\mathbb {X}_{\bullet ,x}(\tau )$, $\mathbb {X}_{\bullet ,x}(\bar{\tau })$ for every $\bar{\tau } \in \mathcal {V}_{\textsc {prod}}$ with $\bar{\tau } < \tau$, along with $\mathbb {X}_{z,x}\mathcal {I}(\tilde{\tau })$ and $\mathbb {X}_{z,x}\mathcal {I}_{i}^{+}(\tilde{\tau })$ for every $\tilde{\tau } \subsetneq \tau$.

Remark 5.3

We take a moment to draw parallels between our definitions and those found in the theory of regularity structures. Those unfamiliar with the theory of regularity structures can skip this remark.

In our context, the local product $\mathbb {X}_{z}$ plays the role of the “un-recentered” $\varvec{\Pi }(\bullet )(z)$ map in the theory of regularity structures.

The corresponding path $\mathbb {X}_{z,x}$ sometimes plays the role of the map $(\Pi _{x}\bullet )(z)$ and sometimes plays a role more analogous to $\gamma _{z,x}(\bullet )$ where $\gamma _{z,x}$ is as in [23, Section 8.2], that is it is the character that defines $\Gamma _{z,x}$.

• For $\sigma \in \mathcal {W}\cup \mathcal {I}(\mathcal {W})$ the path $\mathbb {X}_{z,x}\sigma$ plays the role of $(\Pi _{x}\sigma )(z)$ or equivalently $(\varvec{\Pi }\sigma )(z)$.

• For $\tau \in \mathcal {V}_{\textsc {prod}}$,

  • $\mathbb {X}_{z,x}\tau$ plays the role of $(\Pi _{x}\tau )(z)$.

  • $\mathbb {X}_{z,x}\mathcal {I}(\tau )$ plays the role of $(\Pi _{x}\mathcal {I}(\tau ))(z)$ and $\gamma _{z,x}(\mathcal {I}(\tau ))$. In particular these two quantities are the same and in our context this means that the definition (5.4) is actually compatible with the formula (5.8) - see (5.12).

• For $\tau \in \mathcal {V}_{> 1}$ and $1 \leqq i \leqq d$, $\mathbb {X}_{z,x}\mathcal {I}_{i}^{+}(\tau )$ plays the role of $\gamma _{z,x}(\mathcal {I}_{i}(\tau ))$ which in general has a different value than $(\Pi _{x}\mathcal {I}_{i}(\tau ))(z)$. This is why we cannot define $\mathbb {X}_{z,x}\mathcal {I}_{i}^{+}(\tau )$ with some formula that is analogous to (5.4).

5.2 Properties of paths and centerings

The first property we will investigate is Chen’s relation.

Definition 5.4

We say a local product satisfies Chen’s relation on $\sigma \in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$ if, for every $z,u,x \in \mathbb {R}\times \mathbb {R}^{d}$,

$$\begin{aligned} (\mathbb {X}_{z,u} \otimes \mathbb {X}_{u,x}) \Delta \sigma = \mathbb {X}_{z,x} \sigma \;. \end{aligned}$$

(5.10)

Remark 5.5

We use Chen’s relation to study the change of base-point operation for tree expansions, and the sole role of $\mathcal {I}_{i}^{+}(\tau )$ for $\tau \in \mathcal {V}_{> 1}$ is to describe this procedure.

Therefore we are not interested in Chen’s relation (5.10) for the case where $\sigma = \mathcal {I}_{i}^{+}(\tau )$ and instead $\mathcal {I}_{i}^{+}(\tau )$ plays the role of an intermediate object in the expansion of (5.10).

The following lemma is straightforward because of the trivial structure of the coproduct in those cases:

Lemma 5.6

Any local product automatically satisfies Chen’s relation on every $\sigma \in \mathcal {W}\cup \mathcal {I}(\mathcal {W}) \cup \mathcal {I}(\textrm{Poly}) \cup \{ \mathcal {I}_{i}^{+}(\textbf{X}_{i}) \}_{i=1}^{d}$.

We also define semi-norms to capture our notion of order bounds, using the convolution with an approximation of unity denoted by $(\cdot )_L$ as introduced in equation (1.7).

Definition 5.7

Given a local product $\mathbb {X}$ and $\sigma \in \mathcal {T}_{\Delta }$, we define

(5.11)

We say $\mathbb {X}$ satisfies an order bound on $\sigma$ if $[\mathbb {X}; \sigma ] < \infty$.

For any forest of planted trees $\sigma _{1} \cdots \sigma _{n}$, $n \in \mathbb {Z}_{\geqq 0}$, we write

$$\begin{aligned}{}[\mathbb {X}; \sigma _{1} \cdots \sigma _{n}]:= \prod _{j=1}^{n} [\mathbb {X}; \sigma _{j}]. \end{aligned}$$

We also write $[\mathbb {X}; 0]:= 0$.

Remark 5.8

We note that for any $\sigma \in \mathcal {I}(\textrm{Poly}) \cup \{\mathcal {I}_{i}^{+}(\textbf{X}_{i})\}_{i=1}^{d}$ we have the bound $[\mathbb {X}; \sigma ] \lesssim 1$ uniformly over local products $\mathbb {X}$.

Since we are working in the smooth setting, it is also true that any local product $\mathbb {X}$ satisfies an order bound on $\tau \in \mathcal {T}_{\textsc {RHS}}$ (and $\mathcal {I}(\tau ) \in \mathcal {I}(\mathcal {W})$). However, it is not obvious and in general not true, that these bounds remain finite, when one passes to the rough limit, where $\xi$ is genuinely only a $C^{-3+\delta }$ distribution. In the application to stochastic PDE, these bounds can be controlled in the limit, but this requires additional probabilistic arguments as well as a renormalisation procedure.

Since we have Lemma 5.6 we now verify that our definitions automatically guarantee that any local product satisfies Chen’s relation on any $\tau \in \mathcal {I}(\mathcal {V}) \cup \mathcal {V}_{\textsc {prod}}$.

We now turn to showing the desired statements about Chen’s relation.

5.2.1 Proving Chen’s Relation

It is useful to introduce a stronger, partially factorized version of Chen’s relation.

Definition 5.9

Given $\mathcal {I}(\tau ) \in \mathcal {I}(\mathcal {V})$ we say a local product $\mathbb {X}$ satisfies the strong Chen’s relation on $\mathcal {I}(\tau )$ if, for every $x,y \in \mathbb {R}^{d}$, one has the identity

$$\begin{aligned} \begin{aligned} \mathbb {X}^{\textrm{cen}}_{y} \mathcal {I}(\tau ) =&\big ( \mathbb {X}^{\textrm{cen}}_{x} \otimes \mathbb {X}_{x,y} \big )\Delta \mathcal {I}(\tau ). \end{aligned} \end{aligned}$$

(5.12)

We remark that it is trivial to check that any local product satisfies strong Chen’s relation on $\mathcal {I}(\tau ) \in \mathcal {I}(\textrm{Poly})$. The following lemma is half of our inductive step for proving Chen’s relation.

Lemma 5.10

Suppose a local product $\mathbb {X}$ satisfies Chen’s relation on $\tau \in \mathcal {V}_{\textsc {prod}}$, then $\mathbb {X}$ satisfies strong Chen’s relation on $\mathcal {I}(\tau )$.

Proof

Expanding both sides of (5.12) gives

$$\begin{aligned} \begin{aligned}&\mathcal {L}^{-1} \big ( \mathbb {X}_{\bullet ,y} \tau \big )(y) + y_{j} \mathbb {X}^{\textrm{cen}}_{y} \mathcal {I}_{j}^{+}(\tau )\\&\quad =\mathcal {L}^{-1}(\mathbb {X}_{\bullet ,y} \tau )|^{y}_{x} + (y_{i} - x_{i}) \mathbb {X}_{y}^{\textrm{cen}} \mathcal {I}^{+}_{i}(\tau )\\&\qquad + x_{k} \big ( \mathbb {X}_{y}^{\textrm{cen}} \mathcal {I}^{+}_{k}(\tau ) - \sum _{\tilde{\tau } \in \mathcal {V}_{\textsc {prod}}} (\mathbb {X}_{x}^{\textrm{cen}} \mathcal {I}^{+}_{k}(\tilde{\tau })) \mathbb {X}_{x,y}C_{+}(\tilde{\tau },\tau ) \big )\\&\qquad - \sum _{\tilde{\tau } \in \mathcal {V}_{\textsc {prod}}} \big ( \mathbb {X}_{x}^{\textrm{cen}}\mathcal {I}(\tilde{\tau }) \big ) \big ( \mathbb {X}_{x,y} C_{+}(\tilde{\tau },\tau ) \big ) \end{aligned} \end{aligned}$$

(5.13)

Each of the three lines on the right hand side above come from one of the three terms on the right hand side of the first line of (4.5).

Doing the explicit cancellations lets us simplify (5.13) to

$$\begin{aligned} \begin{aligned} 0&=\mathcal {L}^{-1}(\mathbb {X}_{\bullet ,y}\tau )(x) + x_{k} \sum _{\tilde{\tau } \in \mathcal {V}_{\textsc {prod}}} (\mathbb {X}_{x}^{\textrm{cen}} \mathcal {I}^{+}_{k}(\tilde{\tau })) \mathbb {X}_{x,y}C_{+}(\tilde{\tau },\tau )\\&\quad + \sum _{\tilde{\tau } \in \mathcal {V}_{\textsc {prod}}} \big ( \mathbb {X}_{x}^{\textrm{cen}}\mathcal {I}(\tilde{\tau }) \big ) \big ( \mathbb {X}_{x,y} C_{+}(\tilde{\tau },\tau ) \big ) \end{aligned} \end{aligned}$$

(5.14)

We then obtain (5.14) by using our assumption on Chen’s relation for $\tau$ to write

$$\begin{aligned} \begin{aligned}&\mathcal {L}^{-1}(\mathbb {X}_{\bullet ,y}\tau )(x) = \mathcal {L}^{-1}\Big ( (\mathbb {X}_{\bullet ,x} \otimes \mathbb {X}_{x,y}) \Delta \tau \Big )(x)\\&\quad = \sum _{\tilde{\tau } \in \mathcal {V}_{\textsc {prod}}} \big ( \mathcal {L}^{-1}\mathbb {X}_{\bullet ,x}(\tilde{\tau })\big )(x) \big ( \mathbb {X}_{x,y}C_{+}(\tilde{\tau },\tau ) \big )\;, \end{aligned} \end{aligned}$$

and then recalling that for any $\tilde{\tau }$ in the above sum one has

$$\begin{aligned} \mathcal {L}^{-1}(\mathbb {X}_{\bullet ,x}\tilde{\tau }\big )(x) = - \mathbb {X}_{x}^{\textrm{cen}}\mathcal {I}(\tilde{\tau }) - x_{k} \mathbb {X}_{x}^{\textrm{cen}}\mathcal {I}_{k}^{+}(\tilde{\tau }). \end{aligned}$$

$\square$

The following lemma is the second half of our inductive step:

Lemma 5.11

Fix $\tau \in \mathcal {V}_{\textsc {prod}}$ and suppose $\mathbb {X}$ is a local product satisfying the strong Chen property on $\mathcal {I}(\bar{\tau })$ for every $\bar{\tau } \subsetneq \tau$. Then $\mathbb {X}$ satisfies Chen’s relation on $\tau$.

Proof

We have

$$\begin{aligned} \begin{aligned} ( \mathbb {X}_{x,y} \otimes \mathbb {X}_{y,z}) \Delta \tau&= ( \mathbb {X}_{x} \otimes \mathbb {X}_{y}^{\textrm{cen}} \otimes \mathbb {X}_{y,z}) (\Delta \otimes \textrm{Id}) \Delta \tau \\&= ( \mathbb {X}_{x} \otimes \mathbb {X}_{y}^{\textrm{cen}} \otimes \mathbb {X}_{y,z}) (\textrm{Id}\otimes \Delta ) \Delta \tau \\&= ( \mathbb {X}_{x} \otimes \mathbb {X}_{z}^{\textrm{cen}}) \Delta \tau \\&= \mathbb {X}_{x,z} \tau \;. \end{aligned} \end{aligned}$$

In the first equality we used our identity (5.7) for $\mathbb {X}_{x,y}$ and in the second we used the co-associativity property of Lemma 4.5.

For the third equality we used the fact that $\Delta$ is multiplicative over forests of planted trees so we can use either Lemma 5.10 or (5.8) for the planted trees that appear in the forests that appear on the right factor of $\Delta \tau$. Fix $\tilde{\tau } \not \in \{\textbf{1}, \textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$. Then for any $\mathcal {I}(\bar{\tau }) \in C_{+}(\tilde{\tau },\tau )$ one has $\bar{\tau } \subsetneq \tau$ so one can use Lemma 5.10 for these factors. For the factors $\mathcal {I}^{+}_{i}(\bar{\tau }) \in C_{+}(\tilde{\tau },\tau )$ one can just use (5.8). $\square$

Putting together these two lemmas for our inductive step, combined with Lemma 5.6 which gives us the base cases for our induction, we arrive at the following proposition.

Proposition 5.12

Any local product $\mathbb {X}$ satisfies Chen’s relation on $\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$.

6 Modelled Distribution

With the definition of local products and their associated paths in place, we now show how to use them to give a good local approximation to the solution v of the remainder equation. As explained above in (2.19), we seek a local approximation to v of the form

$$\begin{aligned} v(y) \approx&\; \mathbb {X}_{y,x} \Theta (x) = \sum _{\tau \in \mathcal {V}} \Theta _{x}(\tau ) \mathbb {X}_{y,x} \mathcal {I}(\tau ) \end{aligned}$$

(6.1)

for suitable coefficients $\Theta \in C^{\infty }(\mathbb {R}\times \mathbb {R}^{d}; \textrm{Vec}(\mathcal {V}) )$ (which we interchangeably view as a map $\Theta : \mathcal {V}\rightarrow C^{\infty }$ taking $\tau \mapsto \Theta _{\bullet }(\tau )$) and with an error of order $\lesssim d(x,y)^\gamma$. In this section we first introduce a family of seminorms that measure the regularity of the coefficient map $\Theta$ and that ultimately permit to bound renormalised products. Subsequently, we turn to a specific choice of coefficients $\Theta$ (denoted by $\Upsilon$, see Definition 6.7) which arise in “freezing of coefficient procedure” described in Sect. 2.4. The main result of this section, Theorem 6.12, shows a close connection between the various seminorms for this specific choice of coefficient.

In order to motivate the regularity condition we rewrite equation 6.1 for another base-point $\bar{x}$ (but for the same argument y)

$$\begin{aligned} v(y) \approx&\sum _{\bar{\tau } \in \mathcal {V}} \Theta _{\bar{x}}(\bar{\tau }) \mathbb {X}_{y,\bar{x}} \mathcal {I}(\bar{\tau }) , \end{aligned}$$

(6.2)

then use Chen’s relation (5.10) and Lemma 4.12 in the form

$$\begin{aligned} \mathbb {X}_{y,\bar{x}} \mathcal {I}(\bar{\tau }) = \sum _{\tau \in \mathcal {V}} \mathbb {X}_{y,x} \mathcal {I}(\tau ) \mathbb {X}_{x,\bar{x}} C_+(\tau , \bar{\tau }) \end{aligned}$$

to rewrite the right hand side of (6.2) and compare the resulting expression to (6.1), arriving at

$$\begin{aligned} \left| \sum _{\tau \in \mathcal {V}} \left( \Theta _{x}(\tau ) -\sum _{\bar{\tau } \in \mathcal {V}} \Theta _{\bar{x}}(\bar{\tau }) \mathbb {X}_{x,\bar{x}} C_+(\tau , \bar{\tau }) \right) \mathbb {X}_{y,x} \mathcal {I}(\tau ) \right| \lesssim d(x,y)^\gamma + d(\bar{x},y)^\gamma . \end{aligned}$$

(6.3)

Specialising this inequality to those y for which $d(\bar{x},y) \approx d (x,y) \approx d(x,\bar{x}) \approx d$ yields the estimate

$$\begin{aligned} \left| \sum _{\tau \in \mathcal {V}} \left( \Theta _{x}(\tau ) -\sum _{\bar{\tau } \in \mathcal {V}} \Theta _{\bar{x}}(\bar{\tau }) \mathbb {X}_{x,\bar{x}} C_+(\tau , \bar{\tau }) \right) \mathbb {X}_{y,x} \mathcal {I}(\tau ) \right| \lesssim d^\gamma . \end{aligned}$$

(6.4)

In view of the the order bound (5.11)

$$\begin{aligned} | \mathbb {X}_{y,x} \mathcal {I}(\tau ) | \lesssim d^{|\tau |+2}, \end{aligned}$$

the following definition is natural:

Definition 6.1

Let $\mathbb {X}_{\bullet }$ be a local product and $\mathbb {X}_{\bullet , \bullet }$ be the path constructed from $\mathbb {X}_{\bullet }$. Then for $\Theta \in C^{\infty }(\mathbb {R}\times \mathbb {R}^{d}; \textrm{Vec}(\mathcal {V}) )$ for $\tau \in \mathcal {V}$ and $0<\gamma <2$ we define

$$\begin{aligned} U_{\gamma -2}^\tau (y,x) := \Theta _{y}(\tau ) -\sum _{\underset{|\bar{\tau }|<\gamma -2}{\bar{\tau } \in \mathcal {V}} } \Theta _{x}(\bar{\tau }) \mathbb {X}_{y,x} C_+(\tau , \bar{\tau }), \end{aligned}$$

(6.5)

and the seminorm

$$\begin{aligned}{}[U^\tau ]_{ \gamma -|\tau |-2 } := \sup _{d(x,y) \leqq 1} \frac{1}{d(x, y)^{\gamma -|\tau |-2} } \big | U_{\gamma -2}^\tau (y,x) \big |. \end{aligned}$$

(6.6)

It is important to observe that the semi-norm $[U^\tau ]_{ \gamma -|\tau |-2 }$ involves the coefficients, $\Theta _{\bar{\tau }}$ as well as the paths $\mathbb {X}_{\bullet , \bullet }$ on all symbol $\bar{\tau }$ for which $C_+(\tau , \bar{\tau })$ does not vanish, and that all of these trees $\bar{\tau }$ satisfy $\tau \leqslant \bar{\tau }$. Also, for $\tau = \textbf{1}$, in view of the identity $C_+(\textbf{1}, \bar{\tau }) = \bar{\tau }$ and $| \textbf{1}|=-2$ the quantity $[U^\textbf{1}]_{ \gamma }$ measures exactly the size of the error in the expression (6.1) at the beginning of this discussion.

Remark 6.2

The definition of the semi-norm corresponds exactly to Hairer’s definition of a modelled distribution, [23, Definition 3.1]. In Hairer’s notation the expression $| U_{\gamma -2}^\tau (y,x) |$ becomes

$$\begin{aligned} \Vert \Theta (x) - \Gamma _{xy}\Theta (y) \Vert _{\mathcal {I}(\tau )}. \end{aligned}$$

The following lemma relates the notion of classical derivative with the generalised derivatives that appear in the modeled distribution:

Lemma 6.3

Let $1< \gamma < 2$. Fix a local product $\mathbb {X}$ and $\Theta \in C^{\infty }(\mathbb {R}\times \mathbb {R}^{d}; \textrm{Vec}(\mathcal {V}) )$. Then, for $1 \leqq i \leqq d$,

$$\begin{aligned} \Theta _{x}(\textbf{X}_{i}) = \partial _{i} \left( \Theta _{y}(\textbf{1}) - \sum _{\bar{\tau } \in \mathcal {V}_{\textsc {prod}}\atop |\bar{\tau }| < -1} \Theta _{x}(\bar{\tau }) \mathbb {X}_{y,x}C_{+}(\textbf{1},\bar{\tau }) \right) \Big |_{y=x}\;, \end{aligned}$$

(6.7)

where the partial derivative $\partial _i$ acts in the variable y.

Proof

Note that by assumption we have that that $|U^{\textbf{1}}_{\gamma - 2}(y,x)|\lesssim d(y,x)^{\gamma }$ and since $\gamma > 1$ it follows that

$$\begin{aligned} \big ( \partial _i U^{\textbf{1}}_{\gamma - 2}(y,x) \big )\big |_{y=x} = 0 . \end{aligned}$$

We obtain the desired result by plugging in the definition of $U^{\textbf{1}}_{\gamma -2}(y,x)$ and recalling that

$$\begin{aligned} \begin{aligned} \big ( \partial _{i} \mathbb {X}_{y,x}C_{+}(\textbf{1},\textbf{1}) \big ) \big |_{y=x}&= \big ( \partial _{i} \mathbb {X}_{y,x}\mathcal {I}(\textbf{1}) \big ) \big |_{y=x} = 0,\\ \big ( \partial _{i} \mathbb {X}_{y,x}C_{+}(\textbf{1},\textbf{X}_{j}) \big ) \big |_{y=x}&= \big ( \partial _{i} \mathbb {X}_{y,x}\mathcal {I}(\textbf{X}_{j}) \big ) \big |_{y=x} = \delta _{\{j = i\}},\\ \text {and } \big ( \partial _{i} \mathbb {X}_{y,x}C_{+}(\textbf{1},\bar{\tau }) \big ) \big |_{y=x}&= 0\quad \text {for}\quad \bar{\tau } \in \mathcal {V}_{\textsc {prod}}\quad \text {with}\quad |\bar{\tau }| > -1. \end{aligned} \end{aligned}$$

In the last statement we are using that $|\mathbb {X}_{y,x}C_{+}(\textbf{1},\bar{\tau })| \lesssim d(y,x)^{|\bar{\tau }| + 2}$. $\square$

Remark 6.4

While all of our analysis is performed in the smooth setting, we remark that conclusion of Lemma 6.3 also holds in the limit to the rough setting if, for $U^{\textbf{1}}_{\gamma -2}(y,x)$ defined as in (6.5), we have $[U^\textbf{1}]_{\gamma } < \infty$.

We now introduce some short-hand notation that will be very useful in the following calculations. First, for a given local product $\mathbb {X}$, for $\Theta \in C^{\infty }(\mathbb {R}\times \mathbb {R}^{d}; \textrm{Vec}(\mathcal {V}) )$ and $\gamma \in (0,2)$ we denote by

$$\begin{aligned} V_\gamma (y,x):=\sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V},}}\Theta _x(\tau )\mathbb {X}_{y,x}\mathcal {I}(\tau ) \;. \end{aligned}$$

(6.8)

We also introduce a truncated “square” and a “spatial derivative”:

$$\begin{aligned} V_\gamma ^2(y,x)&:=\sum _{\underset{|\tau _1|+|\tau _2|<\gamma -4}{\tau _1,\tau _2\in \mathcal {V},}}\Theta _x(\tau _1)\Theta _x(\tau _2)\mathbb {X}_{y,x}\mathcal {I}(\tau _1)\mathbb {X}_{y,x}\mathcal {I}(\tau _2)\;, \end{aligned}$$

(6.9)

$$\begin{aligned} V^{\partial ,i}_\gamma (y,x)&:=\sum _{\underset{|\tau |<\gamma -1}{\tau \in \mathcal {V}_{> 1},}}\Theta _x(\tau )\mathbb {X}_{y,x}\mathcal {I}^+_i(\tau )\;. \end{aligned}$$

(6.10)

Note that due to the choice of index set $V_\gamma ^2(y,x)$ does not coincide with the point-wise square $(V_\gamma (y,x))^2$. $V_{\gamma }^{\partial ,i}$ can be thought of as a term by term derivative of $V_\gamma$, mapping $\mathcal {I}(\tau ) \mapsto \mathcal {I}^{+}_{i}(\tau )$, where we recall that $\mathcal {I}_{i}^{+}(\tau ) = 0$ if $\mathcal {V}\setminus \mathcal {V}_{> 1}$.

Recalling the definition (6.5) specialised to $\tau = \textbf{X}_i$ as well as the identity $C_+(\textbf{X}_i, \tau ) = \mathcal {I}^+_i(\tau )$ for $\tau \in \mathcal {V}_{> 1}$ and $=0$ otherwise (see Table 1) we have the identity

$$\begin{aligned} U_\gamma ^{\textbf{X}_i}(y,x) = \Theta _y(\textbf{X}_i) - V_{\gamma -1}^{\partial ,i}(y,x). \end{aligned}$$

(6.11)

A first nice observation is a control for the “three point continuity operator” for $V_\gamma$ (the left-hand side of (6.12) below) in terms of the $U_{\gamma -2}^\tau$ and $\mathbb {X}_{\bullet , \bullet }$. This “three point continuity operator” corresponds exactly to Gubinelli’s $\delta$ operator [16, 17]. In our calculations this quantity is needed to bound derivatives (see (6.17) below) and as input to the Schauder lemmas presented in Sect. B.

Lemma 6.5

Let $\mathbb {X}_{\bullet }$ be a local product. Let $\Theta \in C^{\infty }(\mathbb {R}\times \mathbb {R}^{d}; \textrm{Vec}(\mathcal {V}) )$ and let V be defined as in (6.8). Then for any space–time points $x,y,z \in \mathbb {R}\times \mathbb {R}^{d}$ we have

$$\begin{aligned} \nonumber&V_\gamma (z,x) - V_\gamma (z,y)+ V_\gamma (y,y)-V_\gamma (y,x) \\&\quad = - \sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V}\setminus \{ \textbf{1}\},}} U^{\tau }_{\gamma -2} (y,x) \, \mathbb {X}_{z,y} \mathcal {I}(\tau ) \;. \end{aligned}$$

(6.12)

Proof

We re-organise the terms on the left hand side of (6.12) to write

$$\begin{aligned} \nonumber&V_\gamma (z,x) -V_\gamma (z,y) + V_\gamma (y,y) - V_\gamma (y,x)\\ \nonumber&\quad = \sum _{\underset{|\bar{\tau }|<\gamma -2}{\bar{\tau }\in \mathcal {V},}} \Theta _x(\bar{\tau }) \big (\mathbb {X}_{z,x}\mathcal {I}(\bar{\tau })- \mathbb {X}_{y,x}\mathcal {I}( \bar{\tau } ) \big ) \\&\qquad -\sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V},}} \Theta _y(\tau ) \big ( \mathbb {X}_{z,y}\mathcal {I}(\tau ) - \mathbb {X}_{y,y}\mathcal {I}(\tau ) \big ). \end{aligned}$$

(6.13)

We use Chen’s relation (5.10) for the terms in the first sum on the right hand

$$\begin{aligned} \mathbb {X}_{z,x}\mathcal {I}(\bar{\tau })- \mathbb {X}_{y,x}\mathcal {I}( \bar{\tau })&=\sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V}}} \big (\mathbb {X}_{z,y}\mathcal {I}(\tau ) -\mathbb {X}_{y,y}\mathcal {I}(\tau ) \big ) \mathbb {X}_{y,x}C_+(\tau ,\bar{\tau }) \;. \end{aligned}$$

Plugging this into the first term on the right hand side of (6.13), exchanging the summation in $\tau$ and $\bar{\tau }$ gives

$$\begin{aligned}&V_\gamma (z,x) -V_\gamma (z,y) + V_\gamma (y,y) - V_\gamma (y,x)\\&\quad =\sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V},}}\Big (\big ( \mathbb {X}_{z,y}\mathcal {I}(\tau ) - \mathbb {X}_{y,y}\mathcal {I}(\tau ) \big ) \big (\sum _{\underset{|\bar{\tau }|<\gamma -2}{\bar{\tau }\in \mathcal {V},}} \Theta _x(\bar{\tau }) \mathbb {X}_{y,x}C_+(\tau ,\bar{\tau } ) - \Theta _y(\tau )\big )\Big ). \end{aligned}$$

Finally, noting that $\mathbb {X}_{z,y}\mathcal {I}(\textbf{1}) -\mathbb {X}_{y,y}\mathcal {I}(\textbf{1})= 0$ and $\mathbb {X}_{y,y}\mathcal {I}(\tau ) = 0$ for $\tau \in \mathcal {V}{\setminus }\{ \textbf{1}\}$ leads to the desired expression (6.12). $\square$

The next lemma gives relations between V, $V^2$ and $V^{\partial ,i}$. These will be used heavily in Sect. 10.

Lemma 6.6

Truncation: for $0<\beta<\gamma <2$, $V_{\gamma -\beta }$ is a truncation of $V_\gamma$

$$\begin{aligned} \nonumber \Theta _y(\textbf{1})-V_\gamma (y,x)&=\Theta _y(\textbf{1})-V_{\gamma -\beta }(y,x) \\&\quad -\sum _{\gamma -\beta -2\leqslant |\tau |<\gamma -2}\Theta _x(\tau )\mathbb {X}_{y,x}\mathcal {I}(\tau )\;. \end{aligned}$$

(6.14)

Multiplication: for $0<\gamma <1$, $V^2_\gamma$ is a truncation of $(V_\gamma )^2$:

$$\begin{aligned} \Theta _y(\textbf{1})^2-V^2_{\gamma }(y,x)&=\Theta _y(\textbf{1})(\Theta _y(\textbf{1})-V_{\gamma }(y,x))\end{aligned}$$

(6.15)

$$\begin{aligned}&\quad +\sum _{-2\leqslant |\tau |<\gamma -2}\Theta _x(\tau )\mathbb {X}_{y,x}\mathcal {I}(\tau )\\&\quad (\Theta _y(\textbf{1})-V_{\gamma -|\tau |-2}(y,x)).\nonumber \end{aligned}$$

(6.16)

Derivative: To control derivatives we use the following reorganisation of Lemma 6.5: for $1<\gamma <2$ we have

$$\begin{aligned}&V_\gamma (z,x) - V_\gamma (z,y) + V_\gamma (y,y) -V_\gamma (y,x)\\&\quad +\sum _{i=1}^d \big (\Theta _y(\textbf{X}_i) - V_{\gamma -1}^{\partial ,i}(y,x)\big )(y-z)_i\nonumber = -\sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V}_{\textsc {prod}},}} U^{\tau }_{\gamma -2} (y,x) \, \mathbb {X}_{z,y} \mathcal {I}(\tau ). \end{aligned}$$

(6.17)

This last identity (6.17) will be combined with Lemma A.3 to give a bound on $V^{\partial ,i}$ below.

Proof

The first two identities are immediate. In the third one, we use the identity (6.11) and rewrite the term corresponding to $\tau =\textbf{X}_i$, for which $\mathbb {X}_{z,y}\textbf{X}_i=(y-z)_i$. $\square$

We introduce in the following definition a coefficient map $\Upsilon$ depending on some real valued functions $v_\textbf{1}$ and $v_{\textbf{X}_i}$, $i=1\ldots d$, on $\mathbb {R}\times \mathbb {R}^{d}$:

Definition 6.7

Given real parameters $v_\textbf{1},\ v_{\textbf{X}_i},\ i=1\ldots d$ and $\tau \in \mathcal {V}\sqcup \mathcal {W}$ we set

$$\begin{aligned} \Upsilon (\tau )[v_\textbf{1},v_\textbf{X}] :={\left\{ \begin{array}{ll} v_\textbf{1}, &{} \tau =\textbf{1}, \\ v_{\textbf{X}_{i}}, &{} \tau =\textbf{X}_{i},\\ 1, &{} \tau =\Xi ,\\ -\prod _{i=1}^3\Upsilon (\tau _i)[v_\textbf{1},v_\textbf{X}], &{} \tau =\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3), \end{array}\right. } \end{aligned}$$

(6.18)

where we adopt, above and in what follows, the notation convention $v_{\textbf{X}} = (v_{\textbf{X}_{i}})_{i=1}^{d}$. We may omit the parameters $[v_\textbf{1},v_\textbf{X}]$ from the notation when there is no possible confusion, We usually work in the case where $v_{\textbf{1}}$ and $v_{\textbf{X}}$ are functions of spacetime $\mathbb {R}\times \mathbb {R}^{d}$ in which case we use the shorthand: $\Upsilon (\tau )[v_\textbf{1}(z),v_\textbf{X}(z)]=:\Upsilon _z(\tau )$.

We extend $\Upsilon$ to planted trees, in particular we set $\Upsilon (\mathcal {I}(\tau )):= \Upsilon (\tau )$ for $\tau \in \mathcal {W}\cup \mathcal {V}$ and $\Upsilon (\mathcal {I}^+_i(\tau ))= \Upsilon (\tau )$ for $\tau \in \mathcal {V}_{> 1}\cup \{\textbf{X}_{i}\}_{i=1}^{d}$. We also extend $\Upsilon$ to forests of planted trees by multiplicativity.

We give an explicit formula for $\Upsilon$ in the next lemma.

Lemma 6.8

$$\begin{aligned} \Upsilon (\tau )[v_\textbf{1},v_\textbf{X}]=(-1)^{\frac{m(\tau )-1}{2}} v_\textbf{1}^{m_{\textbf{1}}(\tau )} \prod _{i=1}^{d}v_{\textbf{X}_{i}}^{m_{\textbf{x}_{i}}(\tau )}. \end{aligned}$$

Proof

We prove this by induction in $m(\tau )$, the base cases being immediate from the first three lines of (6.18). For the inductive step, write $\tau = \mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3)$ and observe that

$$\begin{aligned} \Upsilon (\tau )[v_\textbf{1},v_\textbf{X}] = -\prod _{j=1}^3\Upsilon (\tau _j)[v_\textbf{1},v_\textbf{X}] = - \prod _{j=1}^{3} (-1)^{\frac{m(\tau _j)-1}{2}} v_\textbf{1}^{m_{\textbf{1}}(\tau )} \prod _{i=1}^{d}v_{\textbf{X}_{i}}^{m_{\textbf{x}_{i}}(\tau _j)}. \end{aligned}$$

The first equality is the last line of (6.18) and the second equality comes from the inductive hypothesis. The result then follows since $m(\tau ) = \sum _{j=1}^{3} m(\tau _j)$ and the same is true of $m_{\textbf{x}_{i}}$. $\square$

Note that since we only consider trees of negative order, we always have $m_{\textbf{1}}(\tau )+2m_{\textbf{x}}(\tau )<3$. In particular only $\pm v_{\textbf{1}}$, $\pm v_\textbf{1}^2$, $\pm v_{\textbf{X}_i}$ or $\pm 1$ can appear and these possibilities correspond, respectively, to $m_{\textbf{1}}(\tau ) = 1$, $m_{\textbf{1}}(\tau ) = 2$, $m_{\textbf{x}_{i}}(\tau ) = 1$, and $m_{\textbf{1}}(\tau ) = m_{\textbf{x}}(\tau ) = 0$.

Assumption 6.9

For the remainder of the paper, we will always assume that the coefficient map $\Theta \in C^{\infty }(\mathbb {R}\times \mathbb {R}^{d}; \textrm{Vec}(\mathcal {V}) )$ is of the form

$$\begin{aligned} \Theta _{z}(\bullet ) = \Upsilon (\bullet )[v_{\textbf{1}}(z),v_{\textbf{X}}(z)] = \Upsilon _{z}(\bullet ) \text { for some }v_\textbf{1},\ v_{\textbf{X}}\;. \end{aligned}$$

(6.19)

We enforce the relation (6.19) for the rest of the article, in particular this is implicit in any use of the notation $U^\tau$.

The following identities are the main motivation behind our definition of $\Upsilon$:

Lemma 6.10

One has

$$\begin{aligned} - \Big ( \sum _{\tau \in \mathcal {V}\cup \mathcal {W}} \Upsilon (\tau ) \mathcal {I}(\tau ) \Big )^{3} = \sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}} \Upsilon (\tau ) \tau \;. \end{aligned}$$

(6.20)

We also have for any $\tau \in \mathcal {V}, \ \bar{\tau }\in \mathcal {V}_{\textsc {prod}}$ such that $C_+(\tau ,\bar{\tau })\ne 0$,

$$\begin{aligned} \Upsilon (\bar{\tau })=(-1)^\frac{m(\tau )-1}{2}\Upsilon (C_+(\tau ,\bar{\tau })), \end{aligned}$$

(6.21)

where $\Upsilon$ acts on forests multiplicatively.

Proof

For the equality (6.20), we recall the bijective correspondence $(\tau ^{1},\tau ^{2},\tau ^{3}) \mapsto \tau$ between $\tau _{1},\tau _{2},\tau _{3} \in \mathcal {V}\sqcup \mathcal {W}$ and $\tau = \mathcal {I}(\tau _1) \mathcal {I}(\tau _2) \mathcal {I}(\tau _3) \in \tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$. The result then follows by combining this with the last line of (6.18).

The identity (6.21) follows from Lemma 6.8 and Lemma 4.11. $\square$

Remark 6.11

The coproduct plays a central role in algebraically encoding the terms that appear in our centering procedure, but the precise choices (4.4) and (4.5) were motivated by (4.8) and (4.10).

The key content of (4.10) is that for any $\tau \in \mathcal {V}$ and any $\sigma \otimes \sigma _{1} \cdots \sigma _{n}$ appearing in the expansion of $\Delta \mathcal {I}(\tau )$, the precise number of $\textbf{X}_{i}$ and $\textbf{1}$ generators appearing in the forest $\sigma _{1} \cdots \sigma _{n}$ and in $\tau$ coincide. This in turn is needed for the crucial relation (6.21). For this reason we have to work with the different algebraic objects $\mathcal {I}(\textbf{1})$, $\mathcal {I}_{i}^{+}(\textbf{X}_{i})$, and the empty forest 1 - even though all these symbols are treated identically at an analytic level.

For instance, one might be tempted to set $\Delta \mathcal {I}(\textbf{1}) = \mathcal {I}(\textbf{1}) \otimes 1$ but this would break (4.10) since the number of $\textbf{1}$’s in the empty forest 1 is zero while the number in $\textbf{1}$ is one. Similarly, one cannot include $\mathcal {I}(\textbf{X}_{i}) \otimes \textbf{1}$ or $\mathcal {I}(\textbf{X}_{i}) \otimes \mathcal {I}(\textbf{1})$ in the expansion of $\Delta \mathcal {I}(\textbf{X}_{i})$. Finally, we have to write the term $\mathcal {I}_{i}^{+}(\textbf{X}_{i}) \otimes \mathcal {I}_{i}^{+}(\tau )$ in the second line of (4.5) instead of, say, $\mathcal {I}(\textbf{1}) \otimes \mathcal {I}_{i}^{+}(\tau )$, because of our earlier choices and (4.8).

The key result of this section is the observation that under the structure assumption described in Remark 6.9, all continuity conditions are controlled by the condition on $\textbf{1}$ and $\textbf{X}_i$. This follows from the bounds established in Lemma 6.6 and the following theorem which uses the structure of $\Upsilon$.

Theorem 6.12

For $\tau \in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$, the quantity $U_{\gamma }^\tau (y,x)$ takes the following form

$$\begin{aligned} U^\tau _\gamma (y,x)={\left\{ \begin{array}{ll} (-1)^\frac{m(\tau )-1}{2}(v_\textbf{1}(y)-V_{\gamma -|\tau |}(y,x)) &{} \text {if}\quad m_{\textbf{1}}(\tau ) = 1,\\ (-1)^\frac{m(\tau )-1}{2}(v_\textbf{1}(y)^2-V^2_{\gamma -|\tau |}(y,x)) &{} \text {if}\quad m_{\textbf{1}}(\tau ) = 2,\\ (-1)^\frac{m(\tau )-1}{2}(v_{\textbf{X}_i}(y)-V^{\partial ,i}_{\gamma -|\tau |}(y,x)) &{} \text {if}\quad m_{\textbf{x}_{i}}(\tau )=1,\\ 0 &{} \text {if}\quad m_{\textbf{1}}(\tau ), m_{\textbf{x}}(\tau ) = 0. \end{array}\right. } \end{aligned}$$

(6.22)

Proof

From Lemma 6.10, we have

$$\begin{aligned}\Upsilon (\bar{\tau }) C_+(\tau , \bar{\tau })=(-1)^\frac{m(\tau )-1}{2}\Upsilon (C_+(\tau ,\bar{\tau }))C_+(\tau , \bar{\tau }).\end{aligned}$$

This allows to write:

$$\begin{aligned} U^\tau _\gamma (y,x)=\Upsilon _y(\tau )-(-1)^{\frac{m(\tau )-1}{2}}\sum _{|\bar{\tau }|<\gamma }\Upsilon _x(C_+(\tau ,\bar{\tau }))\mathbb {X}_{y,x}C_+(\tau ,\bar{\tau }). \end{aligned}$$

We can use Lemma 4.11 to study the different cases:

• If $m_{\textbf{1}}(\tau ) = 1$ and $C_+(\tau ,\bar{\tau })\ne 0$ then there exists a unique $\tilde{\tau }\in \mathcal {V}$ such that $C_+(\tau ,\bar{\tau })=\mathcal {I}(\tilde{\tau })$. Conversely, for each $\tilde{\tau }\in \mathcal {V}$ with $|\tilde{\tau }|<\gamma -|\tau |-2$, there exists a unique $\bar{\tau }\in \mathcal {V}$ with $|\bar{\tau }|<\gamma -2$ such that $C_+(\tau ,\bar{\tau })=\mathcal {I}(\tilde{\tau })$. Indexing the sum over this $\tilde{\tau }$ gives the expression of $V_{\gamma -|\tau |}$.

• If $m_{\textbf{x}_{i}}(\tau ) = 1$ and $C_+(\tau ,\bar{\tau })\ne 0$ then there exists a unique $\tilde{\tau }\in \mathcal {V}$ such that $C_+(\tau ,\bar{\tau })=\mathcal {I}^+_i(\tilde{\tau })$. Indexing the sum over this $\tilde{\tau }$ gives the expression of $V^{\partial ,i}_{\gamma -|\tau |}$.

• If $m_{\textbf{1}}(\tau ) = 2$ and $C_+(\tau ,\bar{\tau })\ne 0$ then there exists a unique non-commutative couple $(\tilde{\tau }_1,\tilde{\tau }_2)\in \mathcal {V}^2$ such that $C_+(\tau ,\bar{\tau })=\mathcal {I}(\tilde{\tau }_1)\cdot \mathcal {I}(\tilde{\tau }_2)$. Indexing the sum over these $\tilde{\tau }_1,\tilde{\tau }_2$ gives the expression of $V^{2}_{\gamma -|\tau |}$, using also the multiplicative action of $\mathbb {X}$ on forests of planted trees.

We finally see that we get the correct order using the fact that $|\tau |+|C(\tau ,\bar{\tau })| = |\bar{\tau }|$. $\square$

Lemma 6.3 above showed that the continuity condition on a modelled distribution enforces the relation (6.7) between the coefficients $\Theta _{z}(\textbf{X}_{i})$ and the other coefficients. Since we are now imposing the structural condition (6.19), we see that all the left hand side of (6.7) is given by $v_{\textbf{X}_i}(x)$ and the right hand side of (6.7) has no dependence on $v_{\textbf{X}}(x)$ - therefore the continuity condition combined with (6.19) determines $v_{\textbf{X}}(x) = (v_{\textbf{X}_i}(x))_{i=1}^{d}$ as a function of $v_{\textbf{1}}$ and the local product $\mathbb {X}$ along with associated derivatives. For future use we encode this as a map $(v_{\textbf{1}},\mathbb {X}) \mapsto \mathcal {D}^{\mathbb {X}}_iv_{\textbf{1}} = v_{\textbf{X}_{i}}$.

Definition 6.13

Given a local product $\mathbb {X}$ and a smooth function $v:\mathbb {R}\times \mathbb {R}_x^{d} \rightarrow \mathbb {R}$ we define $\mathcal {D}^{\mathbb {X}}v = (\mathcal {D}^{\mathbb {X}}_{i}v)_{i=1}^{d}$, $\mathcal {D}^{\mathbb {X}}_{i}v:\mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ by setting, for $1 \leqq i \leqq d$,

$$\begin{aligned} (\mathcal {D}^{\mathbb {X}}_{i}v)(x) = \sum _{\bar{\tau } \in \mathcal {V}_{\textsc {prod}}\atop |\bar{\tau }| < -1} \Upsilon _{x}(\bar{\tau }) \big ( \partial _{i} \mathbb {X}_{y,x}C_{+}(\textbf{1},\bar{\tau }) \big ) \big |_{y=x} - \partial _{i}v(y)\big |_{y=x} , \end{aligned}$$

where the partial derivatives above acts in the dummy variable y and the $\Upsilon _{x}(\cdot )$ coefficients above are defined using the parameter $v(x)=v_{\textbf{1}}(x)$. Note that we do not need to specify a parameter $v_{\textbf{X}}(x)$ for the $\Upsilon _{x}$ map above since every $\bar{\tau }$ appearing in this sum satisfies $m_{\textbf{x}}(\bar{\tau }) = 0$.

7 Renormalised Products of Tree Expansions

In this section we define renormalised “point-wise” products, taking as input a local product and tree expansions. Fix some smooth noise $\xi$ and let $\mathbb {X}$ be a lift of $\xi$. Upon fixing the choice of $\mathbb {X}$ we will arrive at an analogue of equation (1.1) which we now describe. The solution to this yet to be identified equation will be written in the form

$$\begin{aligned} \nonumber \phi (z)&= v(z) + \sum _{\tau \in \mathcal {W}} (-1)^\frac{m(\tau )-1}{2} \mathbb {X}_{z}\mathcal {I}(\tau ) \\ \nonumber&= \sum _{\tau \in \mathcal {W}\cup \{ \textbf{1}\} } \Upsilon _z(\tau ) \mathbb {X}_{z,z}\mathcal {I}(\tau ) \\&= \sum _{\tau \in \mathcal {W}\cup \mathcal {V}} \Upsilon _z(\tau ) \mathbb {X}_{z,z}\mathcal {I}(\tau )\;. \end{aligned}$$

(7.1)

Above, in passing from the first to second line, we have used the definition of $\Upsilon$ on $\mathcal {W}$ in Lemma 6.8 as well as the fact that $\mathbb {X}_{z,z} \mathcal {I}(\tau ) = \mathbb {X}_z \mathcal {I}(\tau )$ for $\tau \in \mathcal {W}$. In passing to the last line we used the simple observation that for $\tau \in \mathcal {V}\setminus \{ \textbf{1}\}$, $\mathbb {X}_{z,z} \mathcal {I}(\tau ) = 0$. This trivially gives the identity

$$\begin{aligned} \phi ^3(z) \nonumber&= \sum _{\tau _1, \tau _2, \tau _3 \in \mathcal {W}\cup \mathcal {V}} \Upsilon _z(\tau _1) \Upsilon _z(\tau _2)\Upsilon _z(\tau _3) \mathbb {X}_{z,z}\mathcal {I}(\tau _1) \mathbb {X}_{z,z}\mathcal {I}(\tau _2) \mathbb {X}_{z,z}\mathcal {I}(\tau _3) \\&= - \sum _{\tau _1, \tau _2, \tau _3 \in \mathcal {W}\cup \mathcal {V}} \Upsilon _z(\mathcal {I}(\tau _1) \mathcal {I}(\tau _2)\mathcal {I}(\tau _3) ) \mathbb {X}_{z,z}\mathcal {I}(\tau _1) \mathbb {X}_{z,z}\mathcal {I}(\tau _2) \mathbb {X}_{z,z}\mathcal {I}(\tau _3) \;. \end{aligned}$$

(7.2)

The renormalisation now consists of replacing each of the point-wise products $\mathbb {X}_{z,z}\mathcal {I}(\tau _1) \mathbb {X}_{z,z}\mathcal {I}(\tau _2) \mathbb {X}_{z,z}\mathcal {I}(\tau _3)$ which in general we do not control by the terms $\mathbb {X}_{z,z}\mathcal {I}(\tau _1) \mathcal {I}(\tau _2)\mathcal {I}(\tau _3)$ which we control by assumption. The following definition extends this idea to more general expansions:

Definition 7.1

Fix a local product $\mathbb {X}$. Suppose we are given, for $1 \leqq i \leqq 3$, smooth functions $\theta ^{(i)}(z):\mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ and $\Theta ^{(i)}:\mathbb {R}\times \mathbb {R}^{d} \rightarrow \textrm{Vec}(\mathcal {T}_{\textsc {LHS}})$ with

$$\begin{aligned} \theta ^{(i)}(z) = \mathbb {X}_{z,z}\Theta ^{(i)}(z) = \sum _{\tau \in \mathcal {V}\cup \mathcal {W}} \Theta ^{(i)}_{z}(\tau ) \mathbb {X}_{z,z}\mathcal {I}(\tau )\;. \end{aligned}$$

(7.3)

Then, we define

$$\begin{aligned} \begin{aligned}&(\theta ^{(1)} \circ _{\mathbb {X}} \theta ^{(2)} \circ _{\mathbb {X}} \theta ^{(3)})(z)\\&\quad =\sum _{ \tau = \mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}} \Theta ^{(1)}_{z}(\tau _{1}) \Theta ^{(2)}_{z}(\tau _{2}) \Theta ^{(3)}_{z}(\tau _{3}) \mathbb {X}_{z,z} \tau . \end{aligned} \end{aligned}$$

(7.4)

In the case where there is a single function $\theta ^{(i)} = \theta$ and a single corresponding tree expansion $\Theta ^{(i)} = \Theta$ then we just write $\theta ^{\circ _{\mathbb {X}}3}$ for the left hand side of (7.4).

We adopt the convention that when $\theta ^{(i)}(z) = \mathbb {X}_{z,z} \mathcal {I}(\tau ) = \mathbb {X}_{z} \mathcal {I}(\tau )$, where $\tau \in \mathcal {W}$, appears as a factor in a local product, we will implicitly take $\Theta ^{(i)}(z) = \mathcal {I}(\tau )$. We remark that, with the generality we allow in the definition of local products, there is no reason to expect that $(\theta ^{(1)} \circ _{\mathbb {X}} \theta ^{(2)} \circ _{\mathbb {X}} \theta ^{(3)})(z)$ is given by some polynomial in the functions $\theta ^{(i)}(z)$ and their spatial derivatives. However, a trivial case where there is such a correspondence is in the case of a multiplicative local product in which case one clearly has $(\theta ^{(1)} \circ _{\mathbb {X}} \theta ^{(2)} \circ _{\mathbb {X}} \theta ^{(3)})(z) = \theta ^{(1)}(z)\theta ^{(2)}(z)\theta ^{(3)}(z)$.

Remark 7.2

An important observation about the importance of these tree expansions is the following. In (7.3), the contribution on the two right hand sides from $\tau \in \mathcal {V}\setminus \{\textbf{1}\}$ vanishes due to the order bound for any local product.

Similarly, if the local product $\mathbb {X}$ is multiplicative then none of the terms involving either $\tau _{1}$ or $\tau _{2}$ or $\tau _{3} \in \mathcal {V}$ contribute to the value of the renormalised product.

However, if the $\mathbb {X}$ is not multiplicative then it can certainly be the case that these terms from $\tau \in \mathcal {V}{\setminus } \{\textbf{1}\}$ contribute to the value of the renormalised product even though they do not contribute to the value of the $\theta ^{(i)}(z)$. At the same time, in the end we only need to keep products of trees $\mathcal {I}(\tau _{1})\mathcal {I}(\tau _2)\mathcal {I}(\tau _{3})$ with $|\mathcal {I}(\tau _{1})\mathcal {I}(\tau _2)\mathcal {I}(\tau _{3})| < 0$ in our analysis of renormalised products. This motivates our truncation convention for tree products described at the end of Sect. 3.1.

We can now specify the equations we obtain a priori bounds for.

Definition 7.3

Fix a local product $\mathbb {X}$. Then we say the solution of the $\Phi ^4$ equation driven by $\mathbb {X}$ is a smooth function $\phi :\mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ solving

$$\begin{aligned} (\partial _t-\Delta )\phi = \phi ^{\circ _{\mathbb {X}} 3} + \xi \;. \end{aligned}$$

(7.5)

Here we write $\xi = \mathbb {X}_{z}\Xi$ and the tree expansion $\Phi$ for $\phi$ used to define $\phi ^{\circ _{\mathbb {X}} 3}$ is defined by

$$\begin{aligned} \Phi (z) = \sum _{\tau \in \mathcal {V}\cup \mathcal {W}} \Upsilon _{z}(\tau ) \mathcal {I}(\tau ), \end{aligned}$$

where $\Upsilon$ is defined as in Definition 6.7 and the parameter $v_{\textbf{1}}(z)$ is given by

$$\begin{aligned} v_{\textbf{1}}(z)= \phi (z) - \sum _{\tau \in \mathcal {W}} \Upsilon _{z}(\tau ) \mathbb {X}_{z}\mathcal {I}(\tau )\;, \end{aligned}$$

(7.6)

while we set parameter $v_{\textbf{X}} = \mathcal {D}^{\mathbb {X}}v_{\textbf{1}}$ as given in Definition 6.13.

Definition 7.4

Fix a local product $\mathbb {X}$. We say that a smooth function $v:\mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ solves the $\Phi ^4$-remainder equation driven by $\mathbb {X}$ if it satisfies

$$\begin{aligned} \begin{aligned} (\partial _t-\Delta )v&= - \Big ( v^{3} + 3 \sum _{\tau \in \mathcal {W}} (-1)^{\frac{m(\tau )-1}{2}} v \circ _{\mathbb {X}} v \circ _{\mathbb {X}} \mathbb {X}_{\bullet }\mathcal {I}(\tau )\\&\quad +3 \sum _{\tau _{1},\tau _{2} \in \mathcal {W}} (-1)^{\frac{m(\tau _1) + m(\tau _2)-2}{2}} v \circ _{\mathbb {X}} \mathbb {X}_{\bullet }\mathcal {I}(\tau _1) \circ _{\mathbb {X}} \mathbb {X}_{\bullet }\mathcal {I}(\tau _2)\\&\quad - \sum _{ \tau _{1},\tau _{2},\tau _{3} \in \mathcal {W}\atop |\tau _{1}| + |\tau _{2}| + |\tau _{3}| > -8} (-1)^{\frac{m(\tau _1) + m(\tau _2) + m(\tau _3)-3}{2}} \mathbb {X}_{\bullet }\mathcal {I}(\tau _{1})\mathcal {I}(\tau _{2})\mathcal {I}(\tau _{3}) \Big ). \end{aligned} \end{aligned}$$

(7.7)

Here, the tree expansion that governs v is given by

$$\begin{aligned} V(z) = \sum _{\tau \in \mathcal {V}} \Upsilon _{z}(\tau ) \mathcal {I}(\tau )\; \end{aligned}$$

where $\Upsilon _{z}$ is defined as in Definition 6.7 using the function v(z) and the parameters $v_{\textbf{1}} = v$ and $v_{\textbf{X}} = \mathcal {D}^{\mathbb {X}}v$.

The following statement is then straightforward.

Lemma 7.5

There is a one to one correspondence between solutions in the sense of Definition 7.3 to those of Definition 7.4, the correspondence is given by taking $\phi$ which is a solution in the sense Definition 7.3 and mapping it to $v = v_{\textbf{1}}$ which will be a solution in the sense of (7.6).

8 A Useful Class of Local Products

This section is somewhat orthogonal to the main result of this paper. Here we present a particular subset of local products which are defined in terms of recursive procedure that guarantees that the renormalised product appearing in (7.5) is a local polynomial in $\phi$ and its derivatives. This class of local products also includes those that satisfy the necessary uniform stochastic estimates in order to go to the rough setting, namely the BPHZ renormalisation of [8, 12]—see also Remark 9.8.

8.1 Another derivative edge

Our class of local products will, for $\delta$ sufficiently small, allow the renormalised product $\phi ^{\circ _{\mathbb {X}} 3}$ to involve spatial derivatives $\partial _{i}\phi$ for $1 \leqq i \leqq d$.

To describe the generation of these derivatives in terms of operations on trees we will introduce yet another set of edges $\{\mathcal {I}^{-}_{i}\}_{i=1}^{d}$ and another set of planted trees

$$\begin{aligned} \mathcal {T}_{\textsc {LHS}}^{-}= \mathcal {T}_{\textsc {LHS}}\cup \big \{ \mathcal {I}^{-}_{i}(\tau ): \tau \in \mathcal {T}_{\textsc {RHS}}, 1 \leqq i \leqq d\} \; \cup \{ \mathcal {I}^{+}_{i}(\textbf{X}_{i}): 1 \leqq i \leqq d\}. \end{aligned}$$

We also adopt the notational convention that

$$\begin{aligned} \mathcal {I}^{-}_{i}(\textbf{X}_{i}) = \mathcal {I}^{+}_{i}(\textbf{X}_{i}),\;\mathcal {I}^{-}_{i}(\textbf{1}) = 0, \quad \text {and}\quad \mathcal {I}^{-}_{i}(\textbf{X}_{j}) = 0\quad \text {if}\quad i \not = j. \end{aligned}$$

Both the new set of edges $\{\mathcal {I}^{-}_{i}\}_{i=1}^{d}$ and the set of edges $\{\mathcal {I}^{+}_{i}\}_{i=1}^{d}$ introduced in Sect. 4 should be thought of as representing a spatial derivative of a solution to a heat equation. However these two sets of edges play different roles in our argument: a symbol $\mathcal {I}^{+}_{i}(\tau )$ for $\tau \in \mathcal {V}_{> 1}$ is used to describe centering terms while the terms $\mathcal {I}^{-}_{i}(\tilde{\tau })$ for $\tilde{\tau } \in \mathcal {T}_{\textsc {RHS}}$ are only used for derivatives generated by our choice of renormalisation procedure - our original non-linearity $-\phi ^3$ didn’t include derivatives of $\phi$ but if our renormalisation produced a new term involving $\partial _{i} \phi$ (which could occur) then these symbols $\mathcal {I}^{-}_{i}(\tilde{\tau })$ are needed to model this term.

In particular, since the renormalised product associated to a local product $\mathbb {X}$ is defined in terms of the path built from it, it will be useful to extend this path to act on such $\mathcal {I}_{i}^{-}(\tilde{\tau })$ trees and the natural action to choose here will be different than the action of the path on $\mathcal {I}_{i}^{+}(\tau )$ trees.

Another difference between these two sets of derivative edges is that while we adopted the convention that, for any $\tau \in \mathcal {T}_{\textsc {RHS}}{\setminus } \mathcal {V}_{> 1}$, one has $\mathcal {I}^{+}_{i}(\tau ) = 0$. We do not adopt the same convention for $\mathcal {I}^{-}_{i}(\tau )$.

For convenience we will treat the symbols $\mathcal {I}_{i}^{-}(\textbf{X}_{i})$ and $\mathcal {I}^{+}_{i}(\textbf{X}_{i})$ as the same and also adopt the convention that $\mathcal {I}_{i}^{-}(\textbf{1}) = 0$. We also extend our notion of order to $\mathcal {T}_{\textsc {LHS}}^{-}$ by setting, for $\tau \in \mathcal {T}_{\textsc {RHS}}$, $|\mathcal {I}_{i}^{-}(\tau )|=|\tau |+1$.

We extend any local product $\mathbb {X}$ to the new trees we have added in $\mathcal {T}_{\textsc {LHS}}^{-}$ by setting, for $1 \leqq i \leqq d$,

$$\begin{aligned} \mathbb {X}_{z} \mathcal {I}_{i}^{-}(\tau )= {\left\{ \begin{array}{ll} \partial _{i} (\mathcal {L}^{-1} \mathbb {X}_{\bullet }\tau )(z)&{} \text {if}\quad \tau \in \mathcal {T}_{\textsc {RHS}},\\ 1 &{} \text {if}\quad \tau = \textbf{X}_{i}. \end{array}\right. } \end{aligned}$$

(8.1)

8.2 Operations on $\mathcal {I}_{i}^{-}$ trees

Given a local product $\mathbb {X}$, we extend the corresponding path to $\mathcal {I}_{i}^{-}$ trees by setting, for any $\tau \in \mathcal {T}_{\textsc {RHS}}$ and $1 \leqq i \leqq d$,

$$\begin{aligned} \mathbb {X}_{z,w} \mathcal {I}^{-}_{i}(\tau ) = \big ( \mathbb {X}_{z} \otimes \mathbb {X}^{\textrm{cen}}_{w} \big ) \Delta \mathcal {I}^{-}_{i}(\tau ). \end{aligned}$$

(8.2)

where we extend the formulae of (4.5) by setting, for $1 \leqq i \leqq d$,

$$\begin{aligned} \begin{aligned} \Delta \mathcal {I}^{-}_{i}(\tau ) = (\mathcal {I}^{-}_{i} \otimes \textrm{Id}) \Delta \tau + \mathcal {I}^{+}_{i}(\textbf{X}_{i}) \otimes \mathcal {I}^{+}_{i}(\tau ),\quad \tau \in \mathcal {T}_{\textsc {RHS}}. \end{aligned} \end{aligned}$$

Remark 8.1

We remark that our convention that $\mathcal {I}_{i}^{-}(\textbf{X}_{i}) = \mathcal {I}^{+}_{i}(\textbf{X}_{i})$ also seems natural since this guarantees (4.8) holds for $\sigma$ of the form $\mathcal {I}_{i}^{-}(\tau )$, but this observation will not play any role in our argument.

We then have the following easy lemma.

Lemma 8.2

Let $\mathbb {X}$ be a local product, then for any $1 \leqq i \leqq d$ and $\tau \in \mathcal {W}\sqcup \mathcal {V}$, one has

$$\begin{aligned} \partial _{i} \mathbb {X}_{z,w}\mathcal {I}(\tau ) = \mathbb {X}_{z,w}\mathcal {I}^{-}_{i}(\tau )\quad \text {for any}\quad \tau \in \mathcal {W}\cup \mathcal {V}, \end{aligned}$$

(8.3)

where the derivative $\partial _{i}$ above acts in the variable z. In particular, one has

$$\begin{aligned} \mathbb {X}_{z,z}\mathcal {I}^{-}_{i}(\tau ) = 0 \quad \text {if}\quad |\mathcal {I}^{-}_{i}(\tau )| > 0. \end{aligned}$$

(8.4)

Moreover, if $\Theta : \mathcal {V}\rightarrow C^{\infty }$ has the property that, for some $1< \gamma <2$, we have $[U^{\textbf{1}}]_{\gamma } < \infty$ (where $U^{\textbf{1}}_{\gamma -2}$ is defined as in (6.5)) then we have that

$$\begin{aligned} \partial _{i} \Theta _{z}(\textbf{1}) = \sum _{\tau \in \mathcal {V}\atop |\tau | \leqq -1} \Theta _{z}(\tau ) \mathbb {X}_{z,z}\mathcal {I}^{-}_{i}(\tau ). \end{aligned}$$

(8.5)

Proof

The first statement (8.3) is a straightforward computation using (8.3) and (8.1) and (8.2). The second statement (8.4) then follows from the first one and the order bound $[\mathbb {X}: \mathcal {I}(\tau )]$ for such $\tau$.

Finally, the third statement (8.5) follows immediately from combining (8.3) and Lemma 6.3. $\square$

8.3 A recipe for local products

With this notation in hand, our recipe for building a local product $\mathbb {X}$ will be to first specify the smooth function $\mathbb {X}_{z}\Xi$ and then inductively define, for $\tau \in \mathcal {Q}$ (recall that $\mathcal {Q}$ was defined in Definition 3.7),

$$\begin{aligned} \mathbb {X}_{z} \tau = \mathbb {X}_{z} R \tau \end{aligned}$$

(8.6)

where $R: \mathcal {Q}\rightarrow \textrm{Alg}(\mathcal {T}_{\textsc {LHS}}^{-})$, and on the right hand side, we apply $\mathbb {X}_{z}$ multiplicatively over the planted trees appearing in the forests of $\textrm{Alg}(\mathcal {T}_{\textsc {LHS}}^{-})$ and use the cnventions of Sect. 3.3 and (8.2) to reduce the right-hand side to evaluating $\mathbb {X}_{z}$ on $\mathcal {V}\cup \mathcal {W}$. For this to be a well-defined way to construct local products the map R must satisfy the following two criteria.

• For the induction (8.6) to be closed, it is natural to enforce that R should have a triangular structure in that, for any $\tau \in \mathcal {Q}$, any planted tree appearing in a forest appearing in $R\tau$ should be of the form $\mathcal {I}(\tilde{\tau })$ or $\mathcal {I}^{-}_{i}(\tilde{\tau })$ with $\tilde{\tau }$ strictly fewer edges than $\tau$.

• In order for $\mathbb {X}_{z}$ to be invariant under permutations of non-commutative tree products it also natural to enforce that R behaves well with respect to reordering, namely that $\tau \sim \tau '$, where $\sim$ is the equivalence relation defined in Sect. 3.2, then $R \tau \sim R \tau '$ (where we extend $\sim$ to linear combinations of trees in the natural way).

If we have a map R as above and use it to build a local product $\mathbb {X}$ using (8.6) then we say $\mathbb {X}$ is built from R.

For what follows it is useful to define the map $q_{F}$ which takes tree products to forest products, namely $q_{F}$ maps $\mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}\ni \mathcal {I}(\tau _{1}) \mathcal {I}(\tau _{2}) \mathcal {I}(\tau _{3}) \mapsto \mathcal {I}(\tau _{1}) \cdot \mathcal {I}(\tau _{2}) \cdot \mathcal {I}(\tau _{3}) \in \textrm{Alg}(\mathcal {T}_{\textsc {LHS}})$.

Remark 8.3

One possible choice for a renormalisation operator $R_{\textrm{mult}}$ is setting, for each $\tau \in \mathcal {Q}$, $R_{\textrm{mult}}\tau = q_{F} \tau$. If one uses $R_{\textrm{mult}}$ to build a local product $\mathbb {X}$ then it follows that $\mathbb {X}$ is a multiplicative local product.

However, in order to allow more flexibility than a multiplicative local product but still make it easy to show that that the product $\phi ^{\circ _{\mathbb {X}} 3}$ in (7.5) admits a nice formula, we impose a structural assumption on the operator R.

This assumption can be expressed in terms of a slightly modified version of our earlier defined coproduct.

8.4 A modified coproduct and local renormalisation operators

The modified coproduct is defined with a map $C_-$, modification of $C_+$. $C_-:(\bar{\tau },\tau )\in (\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}})^{2} \rightarrow \mathcal {F}$ is given by the table below.

Table 2 This table gives a recursive definition of $C_-(\bar{\tau }, \tau )$. Possible values of $\tau$ are displayed in the first column, while possible values of $\bar{\tau }$ are shown in the first row

The difference between $C_+$ and $C_-$ is the removal of the projection on positive planted trees. Similarly, we never assume that $\mathcal {I}^-_i(\tau )=0$ if $\tau \not \in \tilde{\mathcal {V}}$. $C_-$ also satisfies Lemma 4.11, with the first implication in (4.9) being an equivalence in this case.

The next lemma, which follows in an immediate way from the definition of our sets of trees $\mathcal {V}$ and $\mathcal {W}$, will be useful when we try to drive an explicit formula for $\phi ^{\circ _{\mathbb {X}} 3}$.

Lemma 8.4

For any fixed $\bar{\tau } \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$,

$$\begin{aligned}&p_{\leqslant 0}\sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}} C_{-}(\bar{\tau },\tau ) \\&={\left\{ \begin{array}{ll} \big ( \sum _{\tau \in \mathcal {W}} \mathcal {I}(\tau ) + \mathcal {I}(\textbf{1}) \big )&{}\text {if}\quad m_{\textbf{1}}(\bar{\tau }) = 1\;,\\ \big ( \sum _{\tau \in \mathcal {W}} \mathcal {I}(\tau ) + \mathcal {I}(\textbf{1}) \big ) \cdot \big ( \sum _{\tau \in \mathcal {W}} \mathcal {I}(\tau ) + \mathcal {I}(\textbf{1}) \big ) &{} \text {if}\quad m_{\textbf{1}}(\bar{\tau }) = 2\;,\\ \sum _{\tau \in \mathcal {V}\cup \mathcal {W}\atop |\tau | \leqq -1} \mathcal {I}_{i}^{-}(\tau ) &{} \text {if}\quad m_{\textbf{x}_{i}}(\bar{\tau }) = 1\;. \end{array}\right. } \end{aligned}$$

Above, $p_{\leqslant }: \textrm{Alg}(\mathcal {T}_{\textsc {LHS}}^{-}) \rightarrow \textrm{Alg}(\mathcal {T}_{\textsc {LHS}}^{-})$ is the projection that annihilates any forest of planted trees that contains a planted tree of strictly positive degree.

Definition 8.5

Given a map $r: \mathcal {Q}\rightarrow \mathbb {R}$ such that r is invariant under permutations we define a corresponding map $R:\mathcal {Q}\rightarrow \textrm{Alg}(\mathcal {T}_{\textsc {LHS}}^{-})$ by defining

$$\begin{aligned} R(\tau )= q_{F} \tau +\sum _{\tau '\in \ \mathcal {Q}}r(\tau ')C_-(\tau ',\tau )\;. \end{aligned}$$

(8.7)

Note that counterterm maps r and local renormalisation operators R determine each other uniquely.

We then immediately have

Lemma 8.6

Let R be a local renormalisation operator..

Given a local product $\mathbb {X}$ built from R, the formula (8.6) defining $\mathbb {X}$ for $\tau \in \mathcal {Q}$ actually also holds as an identity for $\tau \in \mathcal {V}_{\textsc {prod}}{\setminus } \mathcal {Q}$ where R is itself is extended to $\mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$ by applying the formula (8.7).

Suppose we are given a $\mathbb {X}$ built from R. Then the formula (8.6) allows us to compute the action of $\mathbb {X}_{\bullet }$ on any element $\tau \in \mathcal {V}\cup \mathcal {W}$ in terms of its actions on simpler trees. However, the starting formula for $\phi ^{\circ _{\mathbb {X}} 3}$ involves the action of the corresponding path $\mathbb {X}_{z,z}$. Therefore in order to work out an explicit formula for $\phi ^{\circ _{\mathbb {X}} 3}$ it would be good to have an analog of (8.6) for paths $\mathbb {X}_{\bullet ,\bullet }$ instead of just the underlying local product $\mathbb {X}_{\bullet }$. Heuristically the idea for getting such a formula is showing that the action of a local renormalisation operator will “commute” with our centering operations. To this end we have the following lemma.

Lemma 8.7

Let R be a local renormalisation operator. Then one has, for any $\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$, the identity

$$\begin{aligned} \Delta R \tau = (R \otimes \textrm{Id}) \Delta \tau \;. \end{aligned}$$

(8.8)

Proof

$$\begin{aligned} \Delta R(\tau )= \Delta q_{F}\tau + \sum _{\bar{\bar{\tau }}\in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}}r(\bar{\bar{\tau }})\Delta C_-(\bar{\bar{\tau }},\tau ). \end{aligned}$$

We split the sum above depending on $m_{\textbf{1}}(\bar{\bar{\tau }})$ and $m_{\textbf{x}}(\bar{\bar{\tau }})$, for $\bar{\bar{\tau }}\leqslant \tau$. If $m_{\textbf{1}}(\bar{\bar{\tau }})=m_{\textbf{x}}(\bar{\bar{\tau }})=0$, then $C_-(\bar{\bar{\tau }},\tau )=\delta _{\{\tau =\bar{\bar{\tau }}\}}.$

If $m_{\textbf{1}}(\bar{\bar{\tau }})=1$, then we have $C_-(\bar{\bar{\tau }},\tau )=\mathcal {I}(\sigma )$ where $\sigma \subset \tau$ and

$$\begin{aligned} \Delta \mathcal {I}(\sigma )=\sum _{\tilde{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}}\mathcal {I}(\tilde{\tau })\otimes C_+(\tilde{\tau },\tilde{\sigma }). \end{aligned}$$

For each element $\tilde{\tau }$ in this sum, we define a corresponding $\bar{\tau }$ by replacing the occurrence of $\sigma$ in $\tau$ identified above by $\tilde{\tau }$. We have $\bar{\bar{\tau }}\leqslant \bar{\tau }\leqslant \tau$ and by the inductive formulas,

$$\begin{aligned} \mathcal {I}(\tilde{\tau })=C_-(\bar{\bar{\tau }},\bar{\tau }) \end{aligned}$$

and

$$\begin{aligned} C_+(\tilde{\tau },\tilde{\sigma })=C_+(\bar{\tau },\tau ). \end{aligned}$$

The following picture is a representation of $\tau$ and the relation between its different subtrees, for one choice of $\tilde{\tau }$, to give an intuition of the proof in blue is $C_+(\tilde{\tau },\tilde{\sigma })=C_+(\bar{\tau },\tau )$, which in this example is a product of two planted trees:

If $m_{\textbf{x}}(\bar{\bar{\tau }})=1$, the same holds by replacing $\mathcal {I}$ by $\mathcal {I}^-_i$ in the argument.

If $m_{\textbf{1}}(\bar{\bar{\tau }})=2$, then we write $C_-(\bar{\bar{\tau }},\tau )=\mathcal {I}(\sigma _1)\cdot \mathcal {I}(\sigma _2)$ where $\sigma _i\subset \tau$ and for $i=1,2$,

$$\begin{aligned} \Delta \mathcal {I}(\sigma _i)=\sum _{\tilde{\tau }_i\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}}\mathcal {I}(\tilde{\tau }_i)\otimes C_+(\tilde{\tau }_i,\tilde{\sigma }_i). \end{aligned}$$

For each element $\tilde{\tau }_1$ and $\tilde{\tau }_2$, we define $\bar{\tau }$ by replacing $\sigma _i$ by $\tilde{\tau }_i$ in $\tau$. We have $\bar{\bar{\tau }}\leqslant \bar{\tau }\leqslant \tau$ and by the inductive formulas,

$$\begin{aligned} \mathcal {I}(\tilde{\tau }_1)\cdot \mathcal {I}(\tilde{\tau }_2)=C_-(\bar{\bar{\tau }},\bar{\tau }) \end{aligned}$$

and

$$\begin{aligned} C_+(\tilde{\tau }_1,\tilde{\sigma }_1)\cdot C_+(\tilde{\tau }_2,\tilde{\sigma }_2)=C_+(\bar{\tau },\tau ). \end{aligned}$$

In all the cases discussed, we can index the sum induced by the coproduct in terms of $\bar{\tau }$ instead of $\tilde{\tau }$ or $\tilde{\tau }_1,\tilde{\tau }_2$. Permutation of that sum with the sum over $\bar{\bar{\tau }}$ then gives

$$\begin{aligned} \Delta R(\tau )&=\Delta q_{F} \tau +\sum _{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}}(\sum _{\bar{\bar{\tau }}\in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}}r(\bar{\bar{\tau }}) C_-(\bar{\bar{\tau }},\bar{\tau }))\otimes C_+(\bar{\tau },\tau )\\&=\sum _{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}}( q_{F} \bar{\tau }+\sum _{\bar{\bar{\tau }}\in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}}r(\bar{\bar{\tau }}) C_-(\bar{\bar{\tau }},\bar{\tau }))\otimes C_+(\bar{\tau },\tau )\\&= \sum _{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}}R(\bar{\tau })\otimes C_+(\bar{\tau },\tau )\\&=(R\otimes \textrm{Id})\Delta \tau \;, \end{aligned}$$

where above we adopt the convention that $r(\tau ') = 0$ if $\tau ' \not \in \mathcal {Q}$. $\square$

With this identity we can now give an analog of (8.6) for our paths.

Lemma 8.8

Suppose that the local product $\mathbb {X}$ was built from an local renormalisation map R. Then, for any $x,y \in \mathbb {R}^{d}$, and tree $\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}$ one has

$$\begin{aligned} \mathbb {X}_{x,y} \tau = \mathbb {X}_{x,y} R \tau , \end{aligned}$$

(8.9)

where on the right hand side we extend $\mathbb {X}_{x,y}$ to forests of planted trees multiplicatively.

Proof

Our proof is by induction in the size of $\tau$. The bases cases where $m_{\tau } = 3$ are straightforward to check by hand. For the inductive step, we note that one has

$$\begin{aligned}{} & {} \mathbb {X}_{x,y} \tau = (\mathbb {X}_{x} \otimes \mathbb {X}^{\textrm{cen}}_y) \Delta \tau = (\mathbb {X}_{x}R \otimes \mathbb {X}^{\textrm{cen}}_y) \Delta \tau \\{} & {} \quad = (\mathbb {X}_{x} \otimes \mathbb {X}^{\textrm{cen}}_y) \Delta R\tau = \mathbb {X}_{x,y} R\tau , \end{aligned}$$

where in the second equality we used Lemma 8.6 and in the third equality we used Lemma 8.7. $\square$

Remark 8.9

We describe how the renormalisation of $\Phi ^4_3$ (which in our setting corresponds to fixing $\delta = 1/2-$ with Gaussian noise) used in previous works such as [33] corresponds to a choice of a local renormalisation operator R.

We define $\mathcal {Q}_{{\textrm{wick}}}$ to be the three different elements of $\mathcal {V}_{\textsc {prod}}$ obtained by permuting the tree product in $\mathcal {I}(\textbf{1})\mathcal {I}(\Xi )^{2}$, that is,

$$\begin{aligned} \mathcal {Q}_{{\textrm{wick}}} = \{\mathcal {I}(\textbf{1})\mathcal {I}(\Xi )^{2},\mathcal {I}(\Xi )\mathcal {I}(\textbf{1})\mathcal {I}(\Xi ),\mathcal {I}(\Xi )^{2}\mathcal {I}(\textbf{1})\}, \end{aligned}$$

and we similarly define $\mathcal {Q}_{{\textrm{sunset}}}$ to be the collection of the 9 different elements of $\mathcal {V}_{\textsc {prod}}$ which are obtained by permutations of the tree product in

(The word sunset is used to make a connection with the QFT literature for $\phi ^4_3$, the corresponding divergent Feynman graph consists of two vertices of degree three which can be drawn as a “sunset”.) There are nine elements because there are three different orders for each of the two tree products appearing in this tree, for instance one also has

$$\begin{aligned} \mathcal {I}\big (\mathcal {I}(\textbf{1})\mathcal {I}(\Xi )^{2}\big )\mathcal {I}(\Xi )^{2} \in \mathcal {Q}_{{\textrm{sunset}}}. \end{aligned}$$

The corresponding counterterm map r is given by

$$\begin{aligned} r(\tau ) = {\left\{ \begin{array}{ll} - C_{{\textrm{wick}}} &{} \text {if}\quad \tau \in \mathcal {Q}_{{\textrm{wick}}},\\ - C_{{\textrm{sunset}}} &{} \text {if}\quad \tau \in \mathcal {Q}_{{\textrm{sunset}}},\\ 0 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

where one has

$$\begin{aligned} \begin{aligned} C_{{\textrm{wick}}}&= \mathbb {E}[(\mathcal {L}^{-1}\xi )(0)^2].\\ C_{{\textrm{sunset}}}&=\mathbb {E}[\theta (0)\mathcal {L}^{-1}\theta (0)], \end{aligned} \end{aligned}$$

where $\xi$ is our (regularised) noise, P is the space–time Green’s function for the heat kernel and $\theta$ is defined by

$$\begin{aligned} \theta (z)=(\mathcal {L}^{-1}\xi )(z)^2-\mathbb {E}[(\mathcal {L}^{-1}\xi )(0)^2]=(\mathcal {L}^{-1}\xi )(z)^2-C_{{\textrm{wick}}}. \end{aligned}$$

The promised local renormalisation operator is then given by building R from r as in (8.7).

As an example, we compute

8.5 Formula for the rRenormalised cube

The next proposition gives the explicit formulae for our renormalised product that promised at the beginning of this section.

Proposition 8.10

Let $\mathbb {X}$ be built from a local renormalisation operator R.

Fix smooth functions $v_{\textbf{1}}, v_{\textbf{X}_{1}},\ldots ,v_{\textbf{X}_{d}}: \mathbb {R}\times \mathbb {R}^{d} \rightarrow \mathbb {R}$ and let

$$\begin{aligned} \Phi (z) = \sum _{\tau \in \mathcal {V}\cup \mathcal {W}} \Upsilon _{z}(\tau ) \mathcal {I}(\tau ) \end{aligned}$$

where $\Upsilon$ is defined in terms of the parameters $v_{\textbf{1}}$ and $v_{\textbf{X}}$, and

$$\begin{aligned} \phi (z) = \mathbb {X}_{z,z}\Phi (z) = \Upsilon _{z}(\textbf{1}) + \sum _{\tau \in \mathcal {W}} \Upsilon (\tau ) \mathbb {X}_{z}\mathcal {I}(\tau )\;. \end{aligned}$$

Moreover, suppose that, for some $1< \gamma < 2$, if $U^{\textbf{1}}_{\gamma -2}$ as in (6.5) with $\Theta _{\bullet }(\cdot ) = \Upsilon _{\bullet }(\cdot )|_{\mathcal {V}}$, we have that $[U^{\textbf{1}}]_{\gamma } < \infty$.

Then, if we define $\phi ^{\circ _{\mathbb {X}} 3}$ as in Definition 7.1 using $\Theta$ as our tree expansion for $\phi$, we then have

$$\begin{aligned} \phi ^{ \circ _{\mathbb {X}} 3}(z) = \phi ^3(z) - r_1 - r_\Phi \phi (z) - r_{\Phi ^2}\phi ^2(z) - \sum _{i=1}^{d} r_{\partial _{i}\Phi } \partial _{i}\phi (z), \end{aligned}$$

(8.10)

where

$$\begin{aligned} \begin{aligned} r_1&= \sum _{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}, \atop m_{\textbf{1}}(\bar{\tau }) + m_{\textbf{x}}(\bar{\tau })=0}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }),\quad r_\Phi =\sum _{\underset{m_{\textbf{1}}(\bar{\tau })=1}{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}}}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }), \\ r_{\Phi ^2}&=\sum _{\underset{m_{\textbf{1}}(\bar{\tau })=2}{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}}}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }) ,\quad r_{\partial _{i}\Phi }=\sum _{m_{\textbf{x}_{i}}(\bar{\tau })=1 \atop \bar{\tau }\in \mathcal {V}_{\textsc {prod}}}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }). \end{aligned} \end{aligned}$$

(8.11)

Here $r: \mathcal {Q}\rightarrow \mathbb {R}$ is the map from which R is built.

Proof

We have

$$\begin{aligned} \begin{aligned} \phi ^{\circ _{\mathbb {X}}3}(z)&= \sum _{\tau _{1}, \tau _{2},\tau _{3} \in \mathcal {V}\cup \mathcal {W}_{\textsc {prod}}} \Upsilon _{z}(\tau _{1}) \Upsilon _{z}(\tau _{2}) \Upsilon _{z}(\tau _{3}) \mathbb {X}_{z,z} \mathcal {I}(\tau _{1}) \mathcal {I}(\tau _{2}) \mathcal {I}(\tau _{3})\\&= \sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}} \Upsilon _{z}(\tau ) \mathbb {X}_{z,z}\tau \\&= \sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}} \Upsilon _{z}(\tau ) \mathbb {X}_{z,z}R\tau \\&= \sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}}\Upsilon _{z}(\tau )( \mathbb {X}_{z,z}q_{F}\tau +\sum _{\bar{\tau }\in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}}r(\bar{\tau }) \mathbb {X}_{z,z}C_-(\bar{\tau },\tau ))\;, \end{aligned} \end{aligned}$$

where the first equality follows from the definition of renormalised local products, the second equality comes from Lemma 6.10, and the third equality comes from Lemma 8.8.

By appealing to Lemma 6.10 once more, we can rewrite the first term of the last line above as

$$\begin{aligned} \begin{aligned} - \mathbb {X}_{z,z}q_{F} \sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}}\Upsilon _{z}(\tau )\tau&= \mathbb {X}_{z,z}q_{F} \left( \sum _{\tau \in \mathcal {V}\cup \mathcal {W}}\Upsilon _{z}(\tau )\mathcal {I}(\tau ) \right) ^{3}\\&= \left( \sum _{\tau \in \mathcal {V}\cup \mathcal {W}}\Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}(\tau ) \right) ^{3} = \phi ^{3}(z)\;. \end{aligned} \end{aligned}$$

By using Lemma 8.4 (note that $\mathbb {X}_{z,z}p_{\leqq 0} = \mathbb {X}_{z,z}$ on $\textrm{Alg}(\mathcal {T}_{\textsc {LHS}}^{-})$) followed by equation (6.21), and using the fact that $\mathbb {X}_{z,z}\sigma =0$ if $|\sigma |>0$, we have

$$\begin{aligned}&\sum _{\tau \in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}}\Upsilon _z(\tau )\sum _{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}}r(\bar{\tau })\mathbb {X}_{z,z}C_-(\bar{\tau },\tau )\\&\quad =\sum _{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}\cup \mathcal {W}_{\textsc {prod}}, \atop m_{\textbf{1}}(\bar{\tau }) + m_{\textbf{x}}(\bar{\tau }) =0}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }) 1 \nonumber \\&\qquad +\sum _{\underset{m_{\textbf{1}}(\bar{\tau })=1}{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}}}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }) \sum _{\tau \in \{\textbf{1}\} \cup \mathcal {W}} \Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}(\tau )\nonumber \\&\qquad +\sum _{\underset{m_{\textbf{1}}(\bar{\tau })=2}{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}}}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }) \big ( \sum _{\tau \in \{\textbf{1}\} \cup \mathcal {W}} \Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}(\tau ) \big )^{ 2} \nonumber \\&\qquad + \sum _{i=1}^{d} \sum _{\underset{m_{\textbf{x}_{i}}(\bar{\tau })=1}{\bar{\tau }\in \mathcal {V}_{\textsc {prod}}}}(-1)^\frac{m(\bar{\tau })-1}{2}r(\bar{\tau }) \sum _{\tau \in \mathcal {V}\cup \mathcal {W}\atop |\tau | \leqq -1} \Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}^{-}_{i}(\tau ) \nonumber . \end{aligned}$$

(8.12)

We then obtain the desired result by observing that, for the second and third terms on the right hand side above,

$$\begin{aligned} \sum _{\tau \in \{\textbf{1}\} \cup \mathcal {W}} \Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}(\tau ) = \Upsilon _{z}(\textbf{1}) + \sum _{\tau \in \mathcal {W}} \Upsilon _{z} \mathbb {X}_{z} \mathcal {I}(\tau ) = \phi (z) \end{aligned}$$

and, for the third term on the right hand side above, we have, for $1 \leqq i \leqq d$,

$$\begin{aligned} \begin{aligned} \sum _{\tau \in \mathcal {V}\cup \mathcal {W}\atop |\tau | \leqq -1} \Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}^{-}_{i}(\tau ) =&\sum _{\tau \in \mathcal {W}} \Upsilon (\tau )\mathbb {X}_{z}\mathcal {I}_{i}^{-}(\tau ) + \sum _{\tau \in \mathcal {V}\atop |\tau | \leqq -1} \Upsilon _{z}(\tau )\mathbb {X}_{z,z}\mathcal {I}^{-}_{i}(\tau )\\ =&\sum _{\tau \in \mathcal {W}} \Upsilon _{z}(\tau ) \partial _{i}\mathbb {X}_{z}\mathcal {I}(\tau ) + \partial _{i}\Upsilon _{z}(\textbf{1}) = \partial _{i}\phi (z)\;. \end{aligned} \end{aligned}$$

For the first equality of the second line above we used Lemma 8.2 - in particular, (8.5) - with $\Theta _{\bullet }(\cdot ) = \Upsilon _{\bullet }(\cdot )|_{\mathcal {V}}$. $\square$

Remark 8.11

Under the assumptions of Proposition 8.10 one can also show that each one of the renormalised products in (7.7) can also be expressed in terms of local polynomials of v(z), $\{\partial _{i}v(z)\}_{i=1}^{d}$, and $\{\mathbb {X}_{z}\mathcal {I}(\tau ): \tau \in \mathcal {W}\}$.

However, we refrain from doing this because the index sets for the summations that define the analogs of the constants (8.11) become quite complicated.

Remark 8.12

Returning to the example of $\Phi ^4_3$ described in Remark 8.9, one then sees that $r_{\partial _{i}\Phi } = r_{\Phi ^{2}} = r_{1} = 0$ for all $1 \leqq i \leqq d$ and

$$\begin{aligned} r_{\Phi } = \sum _{\tau \in \mathcal {Q}_{{\textrm{wick}}}} (-1)^{\frac{3-1}{2}} (-C_{{\textrm{wick}}}) + \sum _{\tau \in \mathcal {Q}_{{\textrm{sunset}}}} (-1)^{\frac{5-1}{2}} (-C_{{\textrm{sunset}}}) = 3C_{{\textrm{wick}}} - 9C_{{\textrm{sunset}}}. \end{aligned}$$

9 Main Result

9.1 Statement of main theorem

We recall the definition of the parabolic cylinders D and $D_R$:

$$\begin{aligned} D=(0,1)\times \{|x|<1\},\quad D_R=(R^2,1) \times \{|x|<1-R\} \end{aligned}$$

We introduce the parabolic ball of center $z=(t,x)$ and radius R in the metric d (defined in (1.5)), looking only into the past:

$$\begin{aligned} B(z,R)=\{\bar{z}=(\bar{t},\bar{x})\in \mathbb {R}\times \mathbb {R}^d, d(z,\bar{z})<R,\bar{t}<t\}. \end{aligned}$$

(9.1)

Note that for $R'<R\leqslant 1$ we have $D_{R'}+B(0,R-R')\subset D_R$.

We denote by $\Vert \cdot \Vert$ the $L^\infty$ norm on the whole space $\mathbb {R}\times \mathbb {R}^d$ and for any open set $\Vert \cdot \Vert _B$ is the $L^\infty$ norm of the restriction of the function to B.

Theorem 9.1

There exists a constant C such that if v solves the $\Phi ^4$ remainder equation driven by a local product $\mathbb {X}$, in the sense of Definition 7.4, pointwise on D, then

$$\begin{aligned} \Vert v\Vert _{D_R}\leqslant C\max \Big \{\frac{1}{R},[\mathbb {X};\tau ]^\frac{1}{\delta m_{\scriptscriptstyle \Xi }(\tau )}, \tau \in \mathcal {T}_{\Delta }, m_{\scriptscriptstyle \Xi }(\tau )\ne 0\Big \}. \end{aligned}$$

(9.2)

Recall that the set of trees $\mathcal {T}_{\Delta }$ is defined in (4.2).

This theorem generalises to an arbitrary bounded domain $\tilde{D}$ in the following way: our construction of local products in (3.6) is adapted to the choice of domain D through the cut-off function $\rho$. This should be replaced by a cut-off function that has value 1 on a 1-enlargement of $\tilde{D}$, and vanishes on a 2 enlargement of the set. Then for every point in $\tilde{D}$, one can obtain a bound depending only on the path by applying a translated version of the theorem, for R sufficiently small.

Remark 9.2

One could work harder to prove that the order bounds on $\mathcal {V}_{\textsc {prod}}\cup \mathcal {T}_{\textsc {RHS}}$ imply the order bounds on all other trees. However this requires global Schauder estimates and the exact statements we would need are not easy to find in the literature we instead state an estimate in terms of all order bounds.

The following corollary is a reformulation of this theorem following from Definition 7.3.

Corollary 9.3

There exists a constant C such that if $\phi$ is a pointwise solution to equation (7.5) driven by a local product $\mathbb {X}$ in D, then for $v=\phi -\sum _{w\in \mathcal {W}}\Upsilon (w)\mathbb {X}\mathcal {I}(w)$, the bound (9.2) holds.

The next result is a particular case of the local product introduced in Sect. 8. It follows from Proposition 8.10.

Corollary 9.4

Let R be a local renormalisation operator, and $\mathbb {X}$ be the local product built from R. There exists a constant C such that if $\phi$ is a pointwise solution to

$$\begin{aligned} (\partial _t-\Delta )\phi =-\phi ^3(z) + r_1 + r_\Phi \phi (z) + r_{\Phi ^2}\phi ^2(z) + \sum _{i=1}^{d} r_{\partial _{i}\Phi } \partial _{i}\phi (z) + \xi , \end{aligned}$$

(9.3)

in D, where the coefficients $r_1,\ r_\Phi ,\ r_{\Phi ^2}$ and $r_{\partial _{i}}$ are given by (8.11), then for $v=\phi -\sum _{w\in \mathcal {W}}\Upsilon (w)\mathbb {X}\mathcal {I}(w)$, the bound (9.2) holds.

The typical application of these results concerns paths $\mathbb {X}$, which are constructed from a Gaussian noise $\xi$. One can, for example, take a spacetime white noise $\bar{\xi }$ over $\mathbb {R}\times \mathbb {R}^4$ and set

$$\begin{aligned} \xi := (1- \Delta )^{-\frac{\bar{\delta }}{2}} \bar{\xi } \end{aligned}$$

(9.4)

for $\bar{\delta } >\delta$. In this case, for any given tree $\tau$ the quantity $[\mathbb {X};\tau ]$ is in the (inhomogeneous) Wiener chaos of order $m_{\scriptscriptstyle \Xi }(\tau )$. In particular, one gets for some $\lambda >0$,

$$\begin{aligned} \mathbb {E}[\exp (\lambda [\mathbb {X};\tau ]^\frac{2}{m_{\scriptscriptstyle \Xi }(\tau )})]<\infty . \end{aligned}$$

(9.5)

The methodology developed in [12] (essentially - see Remark 9.8) establishes (9.5) for (9.4). We then have the following corollary:

Corollary 9.5

Let $\mathbb {X}$ satisfy the bound (9.5). If v is a pointwise solution to the remainder equation driven by a local product $\mathbb {X}$ on D, according to Definition 7.4 then there exists a constant $\bar{\lambda }>0$ such that

$$\begin{aligned} \mathbb {E}[\exp (\bar{\lambda }\Vert v\Vert _{D_\frac{1}{2}}^{2\delta })]<\infty . \end{aligned}$$

Remark 9.6

The results presented here also imply a bound for the corresponding elliptic equation in dimension $6-$, that is

$$\begin{aligned} \Delta \phi =\phi ^3-\xi \quad x \in \mathbb {R}^6, \end{aligned}$$

where $\xi$ is a 6-dimensional white noise which is slightly regularized (for example by applying $(1-\Delta )^{-\frac{\bar{\delta }}{2}}$ for an arbitrary $\bar{\delta }>0$). The four and five dimensional versions of this equation where recently studied in [1, 18]. Our Corollaries 9.4 and 9.5 can be applied directly, if $\phi$ is viewed as a stationary solution of the parabolic equation (that is with $\partial _t \phi =0$).

Remark 9.7

One of the main motivations to study the stochastic quantisation equation in $d=1,2,3$ is as a tool to access the invariant measure with formal density

$$\begin{aligned} \mu (d \phi ) \propto \exp \Big ( - 2 \int _{\mathbb {R}^d} |\nabla \phi |^2 + \frac{1}{4} \phi ^4 -\cdots dx \Big ) \end{aligned}$$

(9.6)

where as above the $\ldots$ represents infinite counter-terms that need to be removed. While our equation (1.1) is the natural extension to fractional dimension from the PDE point of view, it is less natural in this context.

If $\xi$ is chosen as in (9.4), then, since the noise is white in time, at least formally (1.1) defines a strong Feller process and our estimates can be used to prove the existence of an invariant measure. However, this measure does not have an expression akin to (9.6) and it is also not expected to be reflection positive.

In the literature a different way to emulate the $\Phi ^4$ measures close to criticality has been proposed: In [9] the random fields over $\mathbb {R}^3$ with formal density

$$\begin{aligned} \mu (d \phi ) \propto \exp \Big ( - 2 \int _{\mathbb {R}^3} ( |\nabla |^{\frac{3}{4}+\delta } \phi )^2 + \frac{1}{4} \phi ^4 dx -\cdots \Big ) \end{aligned}$$

are studied and shown to have interesting infrared behaviour. The natural stochastic quantisation equation for this model is

$$\begin{aligned} (\partial _t + (- \Delta )^{\frac{3}{4} + 2 \delta } ) \phi = - \phi ^3 + \cdots + \xi , \end{aligned}$$

(9.7)

where $\xi$ is now a space–time white noise over $\mathbb {R}\times \mathbb {R}^3$. Just as (1.1), this equation approaches the threshold of criticality as $\delta \downarrow 0$. It would be interesting to investigate if our methods can be adapted to deal with (9.7). While we expect that the local theory developed in Sects. 3–8 should still apply, our large scale theory does depend on the specific form of the heat operator. The main challenges would be to find appropriate replacement for the localised Schauder estimate, Lemma A.2, and in particular for our version of the maximum principle, Lemma 9.9 (see [29, Lemma 5] for a Schauder estimate for a non-local operator using the same strategy of proof as we use).

Remark 9.8

We take a moment to give more detail about comparing the results of [8, 12] within regularity structures and the setting of the present article.

The first point is that, at an algebraic level, the space of models obtained by deforming the canonical model using the reduced renormalisation group of [8] is certainly compatible with Definition 8.5 - in order to go from a renormalised model to the corresponding local product one just chooses the counterterm map r in (8.7) to be the same as the corresponding renormalisation character in [8].

Regarding the stochastic estimates, we would need estimates on the “BPHZ local product” on our trees $\tau \in \mathcal {W}_{\textsc {prod}}\sqcup \mathcal {V}_{\textsc {prod}}$. One immediate difference in our setting is that in [12] the “integration” that defines planted trees given by a convolution with a translation invariant kernel. In our setting the integration procedure corresponds to solving a heat equation, possibly with space–time boundary conditions, so that our local products are not space–time stationary. One approach to controlling trees with boundary conditions in terms of the stationary trees of [12] could be extending some of the methods of [27].

Putting this difference aside (that is putting ourselves in the stationary setting), if we took $\xi$ as in (9.4) then the desired estimates would follow from checking the three “power-counting”’ conditions of [12, Thm 2.15] for every tree.

The first of the three power counting conditions is an integrability condition for when $\tau$ “contracts” with other noises (different from the noises that sit on $\tau$’s leaves). The integrability condition is that, given any collection of noises A such that the sum of the number of noises in $\tau$ and in A is even, one should have

$|\tau |$ + (total degree of the noises in A) + $(d+2) \times$ (number of noises in A) $> 0$.

The second of these power counting conditions imposes that removing a noise from any tree $\tau$ (in our language, replacing an instance of $\mathcal {I}(\Xi )$ in $\tau$ with $\mathcal {I}(\textbf{1})$) should always result in a tree of positive degree.

The third of these power counting conditions imposes that we must have $\deg (\tau ) > -(d+2)/2$, this guarantees that the stochastic object associated to $\tau$ has a finite variance (diverging variances cannot be renormalized with the additive renormalizations one usually performs in path-wise approaches to singular SPDE).

For our present situation in which we only have one type of noise, the second condition is a consequence of subcriticality (if it failed for some $\tau$, then one would have $\deg (\tau ) < \deg (\Xi )$.

We now turn to the third condition, for which the worst tree is $\tau = \mathcal {I}(\Xi )^3$. The fact that this is the worst tree can be argued by sub-criticality since any larger tree is obtained by replacing instances of $\Xi$ in $\tau$ with other trees, which can only increase the degree.

The third condition requires us to also fix the dimension of space. Note that one cannot apply [12, Thm 2.15] for arbitrarily small $\delta > 0$ and $d \leqq 3$, this is because one could then arrange for $|\mathcal {I}(\Xi )^3| < - (d+2)/2$.

Therefore, in order to take $\delta > 0$ arbitrarily small one would need to take $d \geqq 4$, but in this case we can prove even stronger versions of the first and third conditions: for every $\tau \in \mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}$, one has $|\tau | + |\Xi | > -d -2$ and $|\tau | > -(d+2)/2$.

9.2 Proof of Theorem 9.1

We start the proof by specifying further the norms that we are using. We often work with norms which only depend on the behaviour of functions / distributions on a fixed subset of time–space: if $B\subset \mathbb {R}\times \mathbb {R}^d$ is a bounded set, then the addition of a subscript B such as $[U^\tau ]_{\alpha ,B}$ means that the corresponding supremum is restricted to variables in B. The use of a third index r as in $[U^\tau ]_{\alpha ,B,r}$ indicates that the supremum is restricted to z and $\bar{z}$ at distance at most r from each other. Similarly for a function of two variable, $\Vert \cdot \Vert _{B,r}$ is the norm restricted to $z,\bar{z}\in B$ with $d(z,\bar{z})\leqslant r$.

We remind the reader that the letter $\tau$ always refers to an unplanted tree. In particular, sums indexed by $|\tau |\in J$ for an interval J only refer to unplanted trees of that order. Planted trees will be explicitly denoted by $\mathcal {I}(\tau )$.

We recall the remainder equation

$$\begin{aligned} (\partial _t-\Delta )v&=-v^3-3\sum _{w\in \mathcal {W}}\Upsilon (w)v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w)\\&\quad -3\sum _{w_1,w_2\in \mathcal {W}}\Upsilon (w_1)\Upsilon (w_2)v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2)\\&\quad +\sum _{\tau \in \partial \mathcal {W}}\Upsilon (\tau )\mathbb {X}_\bullet \tau . \end{aligned}$$

Here we have introduced $\partial \mathcal {W}=\{\tau \in \mathcal {V},\tau =\mathcal {I}(w_1)\mathcal {I}(w_2)\mathcal {I}(w_3),w_i\in \mathcal {W}\}$. Note that the product $v^3$ does not need to be expressed using the renormalised product $\circ _\mathbb {X}$ since v is of positive regularity. All the factors $\Upsilon$ are just combinatorial factors $\pm 1$ which is why we omitted the subscript variable y. Also recall that the path $\mathbb {X}$ is built to respect the equivalence relation $\sim$ given in Sect. 3.2 which is why we can combine terms giving the two factors of 3 above.

The first thing we do is to convolve this equation with the kernel $\Psi _L$ introduced in Sect. 1.1 (see also Appendix A), and we obtain

$$\begin{aligned} (\partial _t-\Delta )v_L&=-v_L^3+(v_L^3-(v^3)_L)-3\sum _{w\in \mathcal {W}}\Upsilon (w)(v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L\end{aligned}$$

(9.8)

$$\begin{aligned}&\quad -3\sum _{w_1,w_2\in \mathcal {W}}\Upsilon (w_1)\Upsilon (w_2)(v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))_L\\&\quad -\sum _{\tau \in \partial \mathcal {W}}\Upsilon (\tau )(\mathbb {X}_\bullet \tau )_L.\nonumber \end{aligned}$$

(9.9)

We are going to use the following version of the maximum principle for this equation:

Lemma 9.9

For some $R \in [0,1)$, let u be continuous on $\overline{D_R}$ and $C^2$ in $D_R$ and satisfy point-wise in $D_R$:

$$\begin{aligned} (\partial _t-\Delta )u=-u^3+g \end{aligned}$$

(9.10)

there g is a bounded function. We have, the following point-wise bound on u, for all $(t,x)\in D_R$:

$$\begin{aligned}&| u(x,t) | \\ \nonumber&\leqslant C\max \Big \{\frac{1}{\min \{\sqrt{t-R},((1-R)-x_i),((1-R)+x_i),i=1,2,3\}},\Vert g\Vert ^\frac{1}{3}\Big \} \end{aligned}$$

(9.11)

for some constant $C=C(d)>0$,

The statement for $R=0$ is taken directly from [30, Lemma 2.7], and the proof can be found there. The adaptation to $R>0$ is immediate.

To apply this lemma, we need bounds on the commutator,

$$\begin{aligned}|(v^3)_L-(v_L)^3|\lesssim \Vert v\Vert ^2[v]_\alpha L^\alpha ,\end{aligned}$$

as well as quantities of the type

$$\begin{aligned} (\mathbb {X}_{\bullet }\tau )_L(x)\text { where }\tau \in \partial \mathcal {W}, \end{aligned}$$

which are bounded by $[\tau ]_{|\tau |}L^{|\tau |}\leqslant [\tau ]_{|\tau |} L^{-3+\delta m_{\scriptscriptstyle \Xi }(\tau )}$, in view of (3.1). The following two products will require more work:

$$\begin{aligned} (v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L\text { with }w\in \mathcal {W}\end{aligned}$$

(9.12)

and

$$\begin{aligned} (v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))_L\text { with }w_1,w_2\in \mathcal {W}. \end{aligned}$$

(9.13)

The proof of Theorem 9.1 proceeds recursively by deriving bounds on $\Vert v \Vert _{D_{R_n}}$ for suitable $R_n$. Throughout the recursion it is convenient to remove the dependence on the various norms $[\mathbb {X};\tau ]$ by working under the following domain-dependent assumption:

Assumption 9.10

Let $D'$ be a domain and let $c>0$. We assume that, for all $\tau \in \mathcal {T}_{\Delta }$ with $m_{\scriptscriptstyle \Xi }\ne 0$,

$$\begin{aligned}{}[\mathbb {X};\tau ]\leqslant c\Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau )}. \end{aligned}$$

(9.14)

With this set-up, we proceed to prove the next lemmas to control the two products (9.12) and (9.13). We extend the notation $m_{\scriptscriptstyle \Xi }$ to sums of trees linearly. The functions $m_{\textbf{1}}, m_{\textbf{x}}$ and $m$ will also be extended similarly.

Lemma 9.11

Assume that Assumption 9.10 holds for some domain $D'$ and that $x \in \mathbb {R}\times \mathbb {R}^d$ and $0<L\leqslant 1$ are such that $B(x,L) \subseteq D'$. Then, for $w_1,w_2\in \mathcal {W}$, there exists an $\varepsilon >0$ such that, for $J=[-2,-6-|w_1|-|w_2|+\varepsilon )$,

$$\begin{aligned}&\left| (v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))_L(x)- \sum _{|\tau |\in J}\left( \Upsilon _x(\tau )\mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\right) _L(x)\right| \nonumber \\&\quad \lesssim c\sum _{|\tau |\in J}\Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)}[U^\tau ]_{-6-|w_1|-|w_2|-|\tau |+\varepsilon , B(x,L)}L^\varepsilon . \end{aligned}$$

(9.15)

We also have, for $|\tau |\in J$,

$$\begin{aligned}&\left| \Upsilon _x(\tau )\left( \mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\right) _L(x)\right| \\&\quad \leqslant c\Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau )+\delta m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)} |v_\textbf{X}(x) |^{m_{\textbf{x}}(\tau )}L^{6+|\tau |+|w_1|+|w_2|}\nonumber . \end{aligned}$$

(9.16)

Lemma 9.12

Assume that Assumption 9.10 holds for some domain $D'$ and that $x \in \mathbb {R}\times \mathbb {R}^d$ and $0 < L\leqslant 1$ are such that, $B(x,L) \subseteq D'$. Then for $w\in \mathcal {W}$, there exists $\varepsilon >0$ such that for $\tilde{J}=\{(a,b)\in [-2,-1]^2, a+b<-6-|w|+\varepsilon \}$,

$$\begin{aligned}&\Big |(v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L(x\nonumber )\\&\quad -\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\Big (\mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\Big )_L(x)\Big |\\&\quad \lesssim c\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)}[U^{\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi )}]_{-6-|w|-|\tau _1|-|\tau _2|+\varepsilon , B(x,L)}L^\varepsilon .\nonumber \end{aligned}$$

(9.17)

We also have, for $(|\tau _1|,|\tau _2|)\in \tilde{J}$,

$$\begin{aligned}&\Big |\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\Big (\mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\Big )_L(x)\Big |\\&\quad \leqslant c\Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau _1+\tau _2)+\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)}L^{6+|\tau _1|+|\tau _2|+|w|}.\nonumber \end{aligned}$$

(9.18)

In both of these lemmas, the existence of the $\varepsilon$ follows from the following remark:

Remark 9.13

Our choice of $\delta$ is such that $\mathcal {I}(\textbf{1})\mathcal {I}(\textbf{1})\mathcal {I}(\textbf{1})$ is the only tree of order 0. Therefore for any non-trivial product, the sum can be indexed over trees $\tau$ of order $|\tau |<\varepsilon$, for some $\varepsilon >0$. The renormalised product is therefore described up to positive order $\varepsilon$.

Remark 9.14

(On the exponents of $\Vert v \Vert$) The interval J in Lemma 9.11 (resp. the set $\tilde{J}$ in Lemma 9.12) are chosen precisely in a way to guarantee that all trees $\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2)$ on the right hand sides of (9.15) and (9.16) (resp. $\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w)$ in (9.17) and (9.18)) have negative order. Recalling the relation (3.1), that connects $|\tau |$ with $m_{\scriptscriptstyle \Xi }(\tau )$, $m_{\textbf{1}}(\tau )$, $m_{\textbf{x}}(\tau )$, this results in the restriction

$$\begin{aligned} m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)\delta +m_{\textbf{1}}(\tau )+2m_{\textbf{x}}(\tau ) < 3, \end{aligned}$$

(9.19)

(resp. $\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)+ m_{\textbf{1}}(\tau _1+\tau _2) <3$) limiting the exponents of $\Vert v\Vert _{D'}$ that can appear on the right hand sides of (9.15) and (9.16) (resp. (9.17) and (9.18)). This restriction of exponents is crucial for our argument, because powers $<3$ of $\Vert v \Vert$ can be reabsorbed during the arguments using the exponent $\frac{1}{3}$ on the right hand side of (9.11).

Applying the Schauder Lemma A.1 yields the following estimates:

Lemma 9.15

Let $D' = D_R$ for some $R>0$. Let Assumption 9.10 hold for some $c>0$ small enough (chosen in (10.14) and (10.16)), then for $d_0=\Vert v\Vert _{D'}^{-1}$ we have

$$\begin{aligned} \sup _{d\leqslant d_0}d^\gamma [V]_{\gamma ,D'_d,d}\lesssim \Vert v\Vert _{D'} +c\sup _{d\leqslant d_0}d\Vert v_\textbf{X}\Vert _{D'_d}. \end{aligned}$$

(9.20)

In particular, for $R \in (0, \frac{1}{2})$, we also have

$$\begin{aligned} \sup _{d\leqslant d_0}d\Vert v_\textbf{X}\Vert _{D'_d}\lesssim \Vert v\Vert _{D'}, \end{aligned}$$

(9.21)

and (9.20) becomes

$$\begin{aligned} \sup _{d\leqslant d_0}d^{\gamma -\beta -|\tau |+m_{\textbf{x}}(\tau )}[U^\tau ]_{\gamma -\beta -|\tau |,D'_d,d}\lesssim \Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau )+m_{\textbf{x}}(\tau )}. \end{aligned}$$

(9.22)

Here $D'_d = \{ x :B(x,d) \subseteq D' \}$ denotes the set of interior points of $D'$ with distance $\leqslant d$ from the boundary.

A few more computations allow for the closing of this argument.

Lemma 9.16

Let $D' = D_R$ for some $R \in (0,\frac{1}{2})$. There exists a $\lambda >0$ such that if Assumption 9.10 holds for some $c>0$ small enough (determined by the previous Lemma 9.15 and by (10.22)) we have

$$\begin{aligned} \Vert v\Vert _{{D'}_{\lambda \Vert v\Vert _{D'}^{-1}}}\leqslant \frac{\Vert v\Vert _{D'}}{2}. \end{aligned}$$

(9.23)

Here, as before $D'_{\lambda \Vert v\Vert _{D'}^{-1}}$ denotes the set of interior points of $D'$ with distance $\geqslant \lambda \Vert v\Vert _{D'}^{-1}$ from the boundary, that is $D_{R+\lambda \Vert v\Vert _{D'}^{-1}}$.

The final proof of the main theorem relies on an iteration of this result. We define a finite sequence $0=R_0<\cdots <R_N=\frac{1}{2}$ by setting

$$\begin{aligned} R_{n+1}-R_n=\lambda \Vert v\Vert _{D_{R_n}}^{-1}, \end{aligned}$$

as long as the $R_{n+1}$ defined that way stay less than $\frac{1}{2}$. We terminate this algorithm once it would produce $R_{n+1}\geqslant \frac{1}{2}$ in which case we set $R_N=R_{n+1}=\frac{1}{2}$. Note that $\Vert v\Vert _{D_{R_n}}^{-1}$ is increasing so the sequence necessarily terminates after finitely many steps.

We now prove that Theorem 9.1 holds for all $d=R_n, n=0,\ldots ,N$. First, if Assumption 9.10 fails for a $k = 0,1,2, \ldots , n$, there exists a $\tau \in \mathcal {T}_{\textsc {RHS}}$ such that

$$\begin{aligned} \Vert v \Vert _{D_{R_n}} \leqslant \Vert v \Vert _{D_{R_k}} \leqslant \Big ( \frac{[\mathbb {X};\tau ]}{c} \Big )^{\frac{1}{\delta m_{\scriptscriptstyle \Xi }(\tau )}}. \end{aligned}$$

Otherwise, applying Lemma 9.16 for $D'=D_{R_k}$ gives the bounds for smaller and smaller boxes yields

$$\begin{aligned} \Vert v\Vert _{D_{R_{k+1}}}\leqslant \frac{\Vert v\Vert _{D_{R_k}}}{2}, \end{aligned}$$

and hence, for $k<n$, $\Vert v\Vert _{D_{R_n}}\leqslant \Vert v\Vert _{D_{R_k}}2^{k-n}$, which implies that

$$\begin{aligned} R_n=\sum _{k=0}^{n-1}R_{k+1}-R_k=\sum _{k=0}^{n-1}\lambda \Vert v\Vert _{D_{R_k}}^{-1}\leqslant \lambda \Vert v\Vert _{D_{R_{n-1}}}^{-1}\sum _{k=0}^{n-1}2^{k-n+1}\lesssim \Vert v\Vert _{D_{R_{n-1}}}^{-1}, \end{aligned}$$

This implies that for any $R\in (R_{n-1},R_n)$, $\Vert v\Vert _{D_R}\leqslant \Vert v\Vert _{D_{R_{n-1}}}\lesssim R_n^{-1}\leqslant R^{-1}$, which proves the theorem in that case.

If the end-point is $R_N=\frac{1}{2}$, we either have $R_{N-1}>\frac{1}{4}$ or $R_N-R_{N-1}>\frac{1}{4}$. In both cases $\Vert v\Vert _{D_{R_{N-1}}}\lesssim R_{N-1}^{-1}\lesssim 1$.

10 Proof of the Intermediate Results

10.1 A technical lemma

We first quantify the expansions given in equations (6.8), (6.9) and (6.10), used now with $\Theta =\Upsilon$.

$$\begin{aligned} \nonumber [V]_{\alpha }&=\sup _{x,y}\frac{|v_\textbf{1}(x)-V_\alpha (y,x)|}{d(x,y)^\alpha },\\ [V^2]_{\alpha }&=\sup _{x,y}\frac{|v_\textbf{1}(x)^2-V^2_\alpha (y,x)|}{d(x,y)^\alpha },\\ \nonumber [V^{\partial ,i}]_{\alpha }&=\sup _{x,y}\frac{|v_{\textbf{X}_i}(x)-V^{\partial ,i}_\alpha (y,x)|}{d(x,y)^\alpha }. \end{aligned}$$

(10.1)

For any domain D, we denote the restriction of this norm to $x,y\in D$ by adding the subscript D. A second subscript d may be added when we restrict to x, y satisfying $d(x,y)<d$.

Using Theorem 6.12 we have the identities

(10.2)

Using Lemma 6.6 and the Assumption 9.10 to replace all order bounds on trees in this lemma by powers of $\Vert v\Vert _{D'}$, we get the following general bound for the norm of U. The bound in the case of $m_{\textbf{x}}(\tau )=1$ is a straightforward application of Lemma A.3.

Lemma 10.1

Under the Assumption 9.10, for any $\tau \in \mathcal {V}$, and $0<\beta<\gamma <2$,

(10.3)

10.2 Proof of Lemma 9.11

Take $w_1,w_2\in \mathcal {W}$. From Definition 7.1, there exists $\varepsilon >0$ such that, for $J=[-2,-6-|w_1|-|w_2|+\varepsilon )$,

$$\begin{aligned}&(v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))_L(x)\\&\quad =\sum _{|\tau |\in J}\Big (\Upsilon _\bullet (\tau )\mathbb {X}_{\bullet ,\bullet }(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\Big )_L(x).\nonumber \end{aligned}$$

(10.4)

We know J is the right interval even though we have a longer expansion of v because the unplanted trees of positive homogeneity vanish in our formalism. This corresponds to $|\tau |+|w_1|+|w_2|+6<0$, and Remark 9.13 tells us that this expansion is the same to positive level $\varepsilon$, for $\varepsilon >0$ small enough.

We prove estimate  (9.15) by using the reconstruction Lemma A.1. Define $F(y,x)=\sum _{|\tau |\in J}\Upsilon _{x}(\tau )\mathbb {X}_{y,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))$, and we aim to bound a suitable regularisation of $F(y,x) - F(x,x)$. Lemma A.1 and Assumption 9.10 imply the desired estimate  (9.15) as soon as the following identity is established:

$$\begin{aligned}&\Big | \int \Psi _l(x_2-y)(F(y,x_1)-F(y,x_2))dy \Big |\\&\nonumber \quad \leqslant \sum _{|\tau |\in J}[\mathbb {X};\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2)][U^\tau ]_{-6-|w_1|-|w_2|-|\tau |+\varepsilon ,B(x,L)}\\&\nonumber \quad \times l^{6+|w_1|+|w_2|+|\tau |}d(x_1,x_2)^{-6-|w_1|-|w_2|-|\tau |+\varepsilon }\;. \end{aligned}$$

(10.5)

By multiplicativity of the coproduct, and since $w_1,w_2\in \mathcal {W}$, we first note that for $\bar{\tau } \in \mathcal {V}$

$$\begin{aligned} \Delta (\mathcal {I}(\bar{\tau })\mathcal {I}(w_1)\mathcal {I}(w_2))&=\Delta \mathcal {I}(\bar{\tau })\Delta \mathcal {I}(w_1)\Delta \mathcal {I}(w_2)\\&=\sum _{-2\leqslant |\tau |\leqslant |\bar{\tau }|}\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2)\otimes C_+(\tau ,\bar{\tau }). \end{aligned}$$

Using Chen’s relation, we have

$$\begin{aligned} F(y,x_1)&=\sum _{|\bar{\tau }|\in J}\Upsilon _{x_1}(\bar{\tau })\mathbb {X}_{y,x_1}(\mathcal {I}(\bar{\tau })\mathcal {I}(w_1)\mathcal {I}(w_2))\\&=\sum _{|\bar{\tau }|\in J}\Upsilon _{x_1}(\bar{\tau })\sum _{|\tau |\in J}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\mathbb {X}_{x_2,x_1}C_+(\tau ,\bar{\tau })\\&=\sum _{|\tau |\in J}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\sum _{|\bar{\tau }|\in J}\Upsilon _{x_1}(\bar{\tau }) \mathbb {X}_{x_2,x_1}C_+(\tau ,\bar{\tau }). \end{aligned}$$

Therefore,

$$\begin{aligned}&F(y,x_1)-F(y,x_2)\\&=\sum _{|\tau |\in J}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\Big (\sum _{|\bar{\tau }|\in J}\Upsilon _{x_1}(\bar{\tau })\mathbb {X}_{x_2,x_1}C_+(\tau ,\bar{\tau })-\Upsilon _{x_2}(\tau )\Big )\\&=-\sum _{|\tau |\in J}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))U_{-6-|w_1|-|w_2|-|\tau |+\varepsilon }^\tau (x_2,x_1)\\ \end{aligned}$$

which proves (10.5) and thus (9.15).

The bound (9.16) is simply the order bound on the trees, which can be expressed as:

$$\begin{aligned} |\Upsilon _x(\tau )&\Big (\mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\Big )_L(x)|\\&\nonumber \leqslant |v(x)| ^{m_{\textbf{1}}(\tau )} |v_\textbf{X}(x) |^{m_{\textbf{x}}(\tau )}[\mathbb {X};\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2)]L^{6+|\tau |+|w_1|+|w_2|}\\&\nonumber \overset{\text {Ass. 9.10}}{\leqslant }c\Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau )+\delta m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)} |v_\textbf{X}(x)|^{m_{\textbf{x}}(\tau )}L^{6+|\tau |+|w_1|+|w_2|}. \end{aligned}$$

(10.6)

10.3 Proof of Lemma 9.12

Take $w\in \mathcal {W}$. From Definition 7.1 and Remark 9.13, there exists $\varepsilon >0$ such that for $\tilde{J}=\{(a,b)\in [-2,-1]^2, a+b<-6-|w|+\varepsilon \}$,

$$\begin{aligned} \nonumber&(v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L(x) \\&=\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\Big (\Upsilon (\tau _1)\Upsilon (\tau _2)\mathbb {X}_{\bullet ,\bullet }(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\Big )_L(x). \end{aligned}$$

(10.7)

We know J is the right domain even though we have a longer expansion for v because unplanted trees of positive order vanish in our setting.

We prove the bound (9.17). Define

$$\begin{aligned} F(y,x)=\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\Upsilon _{x}(\tau _1)\Upsilon _{x}(\tau _2)\mathbb {X}_{y,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w)), \end{aligned}$$

and we aim to bound a suitable regularisation of $F(y,x)-F(x,x)$. Lemma A.1 and Assumption 9.10 implies the desired bound as soon as the following bound is established:

$$\begin{aligned} \nonumber&\Big | \int \Psi _l(x_2-y)(F(y,x_1)-F(y,x_2))dy \Big |\\&\nonumber \quad \leqslant \sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}[\mathbb {X};\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w)][U^{\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi )}]_{-6-|w|-|\tau _1|-|\tau _2|+\varepsilon , B(x,L)}\\&\quad l^{6+|\tau _1|+|\tau _2|+|w|}d(x_1,x_2)^{-6-|w|-|\tau _1|-|\tau _2|+\varepsilon } \end{aligned}$$

(10.8)

By multiplicativity of the coproduct, and since $w\in \mathcal {W}$, we first note that for $(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}$,

$$\begin{aligned} \Delta (\mathcal {I}(\bar{\tau }_1)\mathcal {I}(\bar{\tau }_2)\mathcal {I}(w))&=\Delta \mathcal {I}(\bar{\tau }_1)\Delta \mathcal {I}(\bar{\tau }_2)\Delta \mathcal {I}(w)\\&=\sum _{\underset{-2\leqslant |\tau _1|\leqslant |\bar{\tau }_1|}{-2\leqslant |\tau _2|\leqslant |\bar{\tau }_2|}}\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w)\otimes C_+(\tau _1,\bar{\tau }_1) C_+(\tau _2,\bar{\tau }_2). \end{aligned}$$

Using Chen’s relation, we have

$$\begin{aligned}&F(y,x_1)=\sum _{(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}} \Upsilon _{x_1}(\bar{\tau }_1) \Upsilon _{x_1}(\bar{\tau }_2) \mathbb {X}_{y,x_1}(\mathcal {I}(\bar{\tau }_1)\mathcal {I}(\bar{\tau }_2)\mathcal {I}(w))\\&=\sum _{(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}}\Upsilon _{x_1}(\bar{\tau _1}) \Upsilon _{x_1}(\bar{\tau _2})\\&\quad \times \sum _{\underset{-2\leqslant |\tau _1|\leqslant |\bar{\tau }_1|}{-2\leqslant |\tau _2|\leqslant |\bar{\tau }_2|}} \mathbb {X}_{y,x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\mathbb {X}_{x_2,x_1}( C_+(\tau _1,\bar{\tau }_1) C_+(\tau _2,\bar{\tau }_2))\\&=\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}} \mathbb {X}_{y,x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\\&\quad \times \sum _{(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}} \Upsilon _{x_1}(\bar{\tau }_1)\Upsilon _{x_1}(\bar{\tau }_2)\mathbb {X}_{x_2,x_1}( C_+(\tau _1,\bar{\tau }_1) C_+(\tau _2,\bar{\tau }_2)). \end{aligned}$$

In the following computation, we introduce a mock $\Upsilon (\Xi )$, which is just a factor $-1$, and $C_+(\Xi ,\Xi )=1$ to make explicit that the structure of the terms appearing here is that of $U^{\tilde{\tau }}_\beta$ for some $\tilde{\tau }$ and $\beta$.

$$\begin{aligned}&F(y,x_1)-F(y,x_2) =\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\\&\quad \times \Big (\sum _{(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}}\Upsilon _{x_1}(\bar{\tau }_1)\Upsilon _{x_1}(\bar{\tau }_2)\mathbb {X}_{x_2,x_1}( C_+(\tau _1,\bar{\tau }_1) C_+(\tau _2,\bar{\tau }_2))-\Upsilon _{x_2}(\tau _1)\Upsilon _{x_2}(\tau _2)\Big )\\&\quad =\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\times \Big (\Upsilon _{x_2}(\tau _1)\Upsilon _{x_2}(\tau _2)\Upsilon _{x_2}(\Xi )\\&\qquad -\sum _{(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}}\Upsilon _{x_1}(\bar{\tau }_1)\Upsilon _{x_1}(\bar{\tau }_2)\Upsilon _{x_1}(\Xi )\mathbb {X}_{x_2,x_1}( C_+(\tau _1,\bar{\tau }_1) C_+(\tau _2,\bar{\tau }_2)C_+(\Xi ,\Xi ))\Big )\\&\quad =\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\times \Big (\Upsilon _{x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi ))\\&\qquad -\sum _{(|\bar{\tau }_1|,|\bar{\tau }_2|)\in \tilde{J}}\Upsilon _{x_1}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi ))\mathbb {X}_{x_2,x_1}( C_+(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi ),\mathcal {I}(\bar{\tau }_1)\mathcal {I}(\bar{\tau }_2)\mathcal {I}(\Xi ))\Big )\\&\quad =\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\mathbb {X}_{y,x_2}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))U^{\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi )}_{-3+\delta -|w|+\varepsilon } (x_2,x_1), \end{aligned}$$

which proves (10.8) and thus (9.17).

The bound (9.18) is directly the order bound on the trees, which can be expressed as:

$$\begin{aligned}&|\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\Big (\mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\Big )_L(x)|\\&\quad \nonumber \leqslant |v(x) |^{m_{\textbf{1}}(\tau _1+\tau _2)}[\mathbb {X};\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w)]L^{6+|\tau _1|+|\tau _2|+|w|}\\&\quad \nonumber \overset{\text {Ass. 9.10}}{\leqslant }c\Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau _1+\tau _2)+\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)}L^{6+|\tau _1|+|\tau _2|+|w|}. \end{aligned}$$

(10.9)

Note that here the term $v_\textbf{X}$ does not appear since $\tilde{J}$ does not contain any homogeneities higher than 1.

10.4 Proof of Lemma 9.15

For $\gamma \in (2-2\delta ,2)$ we have

$$\begin{aligned} (\partial _t-\Delta )_y V_\gamma (y,x)=\sum _{-2<|\tau |<\gamma -2}\Upsilon _{x}(\tau )\mathbb {X}_{yx}(\tau ). \end{aligned}$$

We write trees in this sum as $\tau =\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\tau _3)$. The first remark we make is that if $|\tau _i|\geqslant -2$ for $i=1,2,3$, then $|\tau |\geqslant 0>\gamma -2$. We also remark that for $w\in \mathcal {W}$, $\Upsilon _x(w)$ is independent of x and for $\tau \in \partial \mathcal {W}$, $\mathbb {X}_{yx}\tau$ is also independent of x. Therefore, accounting for symmetries with the factor 3, we get:

$$\begin{aligned}&(\partial _t-\Delta )_y V_\gamma (y,x)\\&\quad =-3\sum _{w\in \mathcal {W}}\Upsilon _{y}(w)\sum _{|\tau _1|+|\tau _2|<\gamma -8-|w|}\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\mathbb {X}_{y,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\\&\qquad -3\sum _{w_1,w_2\in \mathcal {W}}\Upsilon _{y}(w_1)\Upsilon _{y}(w_2)\sum _{|\tau |<\gamma -8-|w_1|-|w_2|}\Upsilon _x(\tau )\mathbb {X}_{y,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\\&\qquad +\sum _{\tau \in \partial \mathcal {W}}\Upsilon _y(\tau )\mathbb {X}_{y,y}\tau . \end{aligned}$$

Using the remainder equation, we have:

$$\begin{aligned}&(\partial _t-\Delta )(v-V_\gamma (\cdot ,x))(y)=-v^3(y)\\&\quad -3\sum _{w\in \mathcal {W}}\Upsilon _y(w)\Big ((v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_y\mathcal {I}(w))(y)\\&\quad -\sum _{|\tau _1|+|\tau _2|<\gamma -8-|w|}\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\mathbb {X}_{y,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\Big )\\&\quad -3\sum _{w_1,w_2\in \mathcal {W}}\Upsilon _y(w_1)\Upsilon _y(w_2)\Big ((v\circ _\mathbb {X}\mathbb {X}_y\mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_y\mathcal {I}(w_2))(y)\\&\quad -\sum _{|\tau |<\gamma -8-|w_1|-|w_2|}\Upsilon _x(\tau )\mathbb {X}_{y,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\Big ). \end{aligned}$$

We need to bound this after integration against $\Psi _{L_1}(z-y)dy$ for $z\in B(x,L_2)$, for $x\in D'_{2d}$, for $L_1<\frac{d}{2}$ and $L_2<\frac{d}{4}$ to apply the Schauder Lemma A.1. We first have:

$$\begin{aligned} |(v^3)_{L_1}(z)|\leqslant \Vert v\Vert ^3_{D'}. \end{aligned}$$

If $F(y,x)= \sum _{|\tau _1|+|\tau _2|<\gamma -8-|w|}\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\mathbb {X}_{y,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))$, then the Lemma 9.12 gives a bound on $(v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w)-F(\bullet ,z))_{L_1}(z)$, and from equation (10.8) we have a bound on $(F(\bullet ,x)-F(\bullet ,z))_{L_1}(z)$. Together with Assumption 9.10, these give

$$\begin{aligned}&\Big |\Big ((v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))\\&\qquad -\sum _{|\tau _1|+|\tau _2|<\gamma -8-|w|}\Upsilon _x(\tau _1)\Upsilon _x(\tau _2)\mathbb {X}_{\cdot ,x}(\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(w))\Big )_{L_1}(z)\Big |\nonumber \\ \lesssim&\quad c\sum _{|\tau _1|+|\tau _2|<\gamma -8-|w|}[U^{\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi )}]_{-6-|w|-|\tau _1|-|\tau _2|+\varepsilon ,D'_d,d}\nonumber \\&\quad \times \Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)}(L_1^\varepsilon + L_1^{6+|\tau _1|+|\tau _2|+|w|}d(x,z)^{-6-|w|-|\tau _1|-|\tau _2|+\varepsilon })\nonumber . \end{aligned}$$

(10.10)

Similarly with $F(y,x)=\sum _{|\tau |<\gamma -8-|w_1|-|w_2|}\Upsilon _x(\tau )\mathbb {X}_{y,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))$, Lemma 9.11 gives a bound on $(v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))-F(\bullet ,z))_{L_1}(z))$ and from Equation (10.5), we have a bound on $(F(\bullet ,x)-F(\bullet ,z))_{L_1}(z)$. Together with Assumption 9.10, these give

$$\begin{aligned}&\Big |\Big (v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2)\\&\qquad -\sum _{|\tau |<\gamma -8-|w_1|-|w_2|}\Upsilon _x(\tau )\mathbb {X}_{\bullet ,x}(\mathcal {I}(\tau )\mathcal {I}(w_1)\mathcal {I}(w_2))\Big )_L(z)\Big |\nonumber \\&\quad \lesssim c\sum _{|\tau |<\gamma -8-|w_1|-|w_2|}[U^\tau ]_{-6-|w_1|-|w_2|-|\tau |+\varepsilon ,D'_d,d}\nonumber \\&\quad \times \Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)}(L^\varepsilon +L^{6+|w_1|+|w_2|+|\tau |}d(x,z)^{-6-|w_1|-|w_2|-|\tau |+\varepsilon }).\nonumber \end{aligned}$$

(10.11)

We also need the three-point continuity. It is a consequence of Lemma 6.5, and can be quantified, for $x\in D'_d$, for $y\in B(x,\frac{d}{4})$, for $z\in B(y,\frac{d}{4})$, as

$$\begin{aligned}&|V_\gamma (z,x) - V_\gamma (z,y)+ V_\gamma (y,y)-V_\gamma (y,x)+V^i_\gamma (y,x)(z_i-y_i)|\\&\leqslant \sum _{\underset{\tau \ne \textbf{X}}{-2<|\tau |<\gamma -2}} [ U^{\tau }]_{\gamma -2-|\tau |,D'_\frac{d}{2},\frac{d}{2}} d(y,x)^{\gamma -2-|\tau |} \, [\mathbb {X}; \mathcal {I}(\tau )]d(z,y)^{|\tau |+2}\nonumber \\&\overset{\text {Ass. 9.10}}{\leqslant } c\sum _{\underset{\tau \ne \textbf{X}}{-2<|\tau |<\gamma -2}} \Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau )}[ U^{\tau }]_{\gamma -2-|\tau |,D'_\frac{d}{2},\frac{d}{2}} d(y,x)^{\gamma -2-|\tau |} \, d(z,y)^{|\tau |+2}.\nonumber \end{aligned}$$

(10.12)

Finally, in order to apply Lemma A.1 for $v-V_\gamma (\cdot ,x))(y)$ in the role of U(y, x) we write using first the definition (6.8) of $V_\gamma$, Lemma 6.8, and then Assumption 9.10 to get

$$\begin{aligned} \sup _{d \leqslant d_0} \Vert v - V_\gamma \Vert _{D'_d,d}&\leqslant \Vert v \Vert _{D'} + \sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V},}} \Vert \Upsilon _{\bullet }(\tau ) \Vert _{D'} [\mathbb {X}; \mathcal {I}(\tau )]d_0^{|\tau |+2}\\&\leqslant \Vert v \Vert _{D'} + c \sum _{\underset{|\tau |<\gamma -2}{\tau \in \mathcal {V},}} d_0^{|\tau |+2} \Vert v_\textbf{1}\Vert _{D'}^{m_{\textbf{1}}(\tau )+\delta m_{\scriptscriptstyle \Xi }(\tau )} \Vert v_{\textbf{X}} \Vert _{D'}^{m_{\textbf{x}}(\tau )} . \end{aligned}$$

We now notice that all the term appearing in (10.10),(10.11) and (10.12) have a common structure. By replacing the homogeneities by their expressions in terms of $\delta m_{\scriptscriptstyle \Xi }$ for the trees in $\mathcal {W}$, and relabelling $\tau =\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi )$ in (10.10), we get, after application of Lemma A.1,

$$\begin{aligned} \sup _{d\leqslant d_0}d^\gamma [V]_{\gamma ,D'_d,d}&\lesssim \sup _{d\leqslant d_0}d^2\Vert v\Vert _{D'}^3\\&\quad +c\sup _{a,b,\tau }\sup _{d\leqslant d_0}\Big (d^{b}\Vert v\Vert _{D'_d}^{a+\delta m_{\scriptscriptstyle \Xi }(\tau )}[U^{\tau }]_{b-2-a-|\tau |,D'_d,d}\Big )\nonumber \\&\quad + \Vert v \Vert _{D'} + c\sup _{\tau } d_0^{|\tau |+2} \Vert v_\textbf{1}\Vert _{D'}^{m_{\textbf{1}}(\tau )+\delta m_{\scriptscriptstyle \Xi }(\tau )} \Vert v_{\textbf{X}} \Vert _{D'}^{m_{\textbf{x}}(\tau )} \nonumber , \end{aligned}$$

(10.13)

where $[V]_{\gamma ,D'_d,d}$ is as defined in (10.1) with the supremum taken over $x,y \in D'_d$ with $d(x,y) \leqslant d$ and where the supremum is taken over a finite subset of

$$\begin{aligned} \{(a,b,\tau )\in \mathbb {R}_+^2\times \mathcal {T}_{\textsc {RHS}},a\geqslant 0\;, b\geqslant \gamma \;, b-2-a-|\tau |< \gamma \}. \end{aligned}$$

We apply the Lemma 10.1 to the second part.

We see now that if we take

$$\begin{aligned} d_0=\Vert v\Vert _{D'}^{-1}\;, \end{aligned}$$

(10.14)

then there exists a value of $c_0<1$ such that for any $0<c<c_0$, the occurrences of $[V]_{\gamma ,D'_d,d}$ can be absorbed into the left-hand side, and the other terms also simplify: if $m_{\textbf{x}}(\bar{\tau })=1$, we bound

$$\begin{aligned}d^{|\bar{\tau }|+2}\Vert v\Vert _{D'}^{m_{\textbf{1}}(\bar{\tau })+\delta m_{\scriptscriptstyle \Xi }(\bar{\tau })}\Vert v_\textbf{X}\Vert _{D'_d}^{m_{\textbf{x}}(\bar{\tau })}\leqslant d^{-1+2m_{\textbf{x}}(\bar{\tau })}\Vert v_\textbf{X}\Vert _{D'_d}^{m_{\textbf{x}}(\bar{\tau })}=d\Vert v_\textbf{X}\Vert _{D'_d},\end{aligned}$$

and if $m_{\textbf{x}}(\bar{\tau })=0$,

$$\begin{aligned}d^{|\bar{\bar{\tau }}|+2}\Vert v\Vert _{D'}^{m_{\textbf{1}}(\bar{\tau })+\delta m_{\scriptscriptstyle \Xi }(\bar{\tau })}=d^{-1+m_{\textbf{1}}(\bar{\tau })+\delta m_{\scriptscriptstyle \Xi }(\bar{\tau })}\Vert v\Vert _{D'}^{m_{\textbf{1}}(\bar{\tau })+\delta m_{\scriptscriptstyle \Xi }(\bar{\tau })}\leqslant \Vert v\Vert _{D'}.\end{aligned}$$

This gives (9.20).

We now prove the bound on $\Vert v_\textbf{X}\Vert _{D'_d}$. For that we take $\varepsilon$ small enough such that there is no tree of regularity between 1 and $1+\varepsilon$. Then we can apply Lemma A.3 with $\kappa =1+\varepsilon$ but with $U(x,y)=\sum _{-2\leqslant |\tau |<-1}\Upsilon _x(\tau )\mathbb {X}_{yx}\mathcal {I}(\tau )$. We get

$$\begin{aligned} \Vert v_\textbf{X}\Vert _{D'_d}\lesssim d^\varepsilon [V]_{1+\varepsilon ,D'_d,d}+d^{-1} \Vert U\Vert _{D'_d,d}. \end{aligned}$$

In applying Lemma A.3, the fact that $R \in (0,1/2)$ guarantees we have a interior cone condition on $D'_{d}$ with $r_{0} = d$ for any $d \leqq d_{0}$.

We have by Assumption 9.10

$$\begin{aligned} d^{-1} \Vert U\Vert _{D'_d,d}\lesssim \sum _{n}d^{n-2}\Vert v\Vert _{D'}^{n}, \end{aligned}$$

and from (10.3)

$$\begin{aligned} d^\varepsilon [V]_{1+\varepsilon ,D'_d,d}\lesssim d^{\gamma -1} [V]_{\gamma ,D'_d,d} +c\sum _{n,m}d^{n+2m-2}\Vert v\Vert _{D'_d}^{n}\Vert v_\textbf{X}\Vert _{D'_d}^m, \end{aligned}$$

where the sum ranges over a finite set of indices $n\geqslant 0$ and $m\in \{0,1\}$. We have, assuming $d_0 = \Vert v\Vert _{D'}^{-1}$,

$$\begin{aligned} \sup _{d\leqslant d_0}d\Vert v_\textbf{X}\Vert _{D'_d}\lesssim \sup _{d\leqslant d_0}\Big ( d^{\gamma } [V]_{\gamma ,D'_d,d} +c(\Vert v\Vert _{D'}+d\Vert v_\textbf{X}\Vert _{D'_d})\Big ). \end{aligned}$$

If we take c small enough, depending on the constant implicit in $\lesssim$, for some constant $C>0$ we have

$$\begin{aligned} \sup _{d\leqslant d_0}d\Vert v_\textbf{X}\Vert _{D'_d}\leqslant C\sup _{d\leqslant d_0}\Big ( [V]_{\gamma ,D'_d,d} d^{\gamma }+\Vert v\Vert _{D'}\Big ). \end{aligned}$$

(10.15)

Together with (9.20), this gives, for a constant c small enough,

$$\begin{aligned} \sup _{d\leqslant d_0}d^\gamma [V]_{\gamma ,D'_d,d}\lesssim \Vert v\Vert _{D'}. \end{aligned}$$

(10.16)

10.5 Proof of Lemma 9.16

We apply the Lemma 9.9 to the convolved equation (9.8), on the domain $D'$.

$$\begin{aligned} \Vert v\Vert _{D'_{d+d'}}&\lesssim \max \Big \{{d'}^{-1},\quad \Vert (v^3)_L-v_L^3\Vert _{D'_{d}}^{\frac{1}{3}},\quad \Vert (\mathbb {X}_{\bullet }\tau )_L\Vert _{D'_d}^{\frac{1}{3}} ,\quad \tau \in \partial \mathcal {W},\nonumber \\&\quad \Vert (v\circ _\mathbb {X}\mathbb {X}_{\bullet }\mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_{\bullet }\mathcal {I}(w_2))_L\Vert _{D'_d}^{\frac{1}{3}},\; w_i\in \mathcal {W},\\&\quad \Vert (v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L\Vert _{D'_d}^{\frac{1}{3}}, \; w\in \mathcal {W},\quad \Vert v-v_L\Vert _{D'_{d+d'}}\Big \} .\nonumber \end{aligned}$$

(10.17)

We have, for $d>L$,

$$\begin{aligned} \nonumber \Vert (v^3)_L-v_L^3\Vert _{D'_{d}}&\lesssim \Vert v\Vert ^2_{D'_{d-L}}[v]_{\alpha ,{D'_{d-L}},L}L^\alpha \quad \text {and} \\ \Vert v-v_L\Vert _{D'_{d+d'}}&\leqslant [v]_{\alpha ,{D'_{d-L}},L}L^\alpha , \end{aligned}$$

(10.18)

and for $\alpha$ small enough, we have, by Lemma 9.15, $[v]_{\alpha ,{D'_{d-L}},L}\lesssim {(d-L)}^{-\alpha }\Vert v\Vert _{D'}$.

From Lemma 9.11 we get, for $w_1,w_2\in \mathcal {W}$,

$$\begin{aligned}&\Vert (v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))_L\Vert _{D'_d}\\&\quad \lesssim c\sum _{|\tau |\in J}\Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)}\Big ([U^\tau ]_{-6-|w_1|-|w_2|-|\tau |+\varepsilon ,D'_{d-L},d}L^\varepsilon \\&\qquad +\Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau )}\Vert v_\textbf{X}\Vert _{D'_{d-L}}^{m_{\textbf{x}}(\tau )}L^{6+|\tau |+|w_1|+|w_2|}\Big )\nonumber . \end{aligned}$$

From Lemma 9.12 we get, for $w\in \mathcal {W}$,

$$\begin{aligned}&\Vert (v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L\Vert _{D'_d}\\&\lesssim c\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)}\Big ([U^{\mathcal {I}(\tau _1)\mathcal {I}(\tau _2)\mathcal {I}(\Xi )}]_{-6-|w|-|\tau _1|-|\tau _2|+\varepsilon ,D'_{d-L},d}L^\varepsilon \\&\quad +\Vert v\Vert _{D'}^{m_{\textbf{1}}(\tau _1+\tau _2)}L^{6+|\tau _1|+|\tau _2|+|w|}\Big ). \end{aligned}$$

Using Lemma 9.15 and setting $d=\Vert v\Vert _{D'}^{-1}$ and $L=\frac{d}{k}$ for some $k\geqslant 2$ gives, for $w_1,w_2\in \partial \mathcal {W}$,

$$\begin{aligned} \Vert (v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_1)\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w_2))_L\Vert _{D'_d}\lesssim c\Vert v\Vert _{D'}^3K(w_1,w_2,k) \;, \end{aligned}$$

(10.19)

where

$$\begin{aligned} K(w_1,w_2,k)=\sum _{|\tau |\in J}\Big (k^{-\varepsilon }+k^{3-\delta m_{\scriptscriptstyle \Xi }(\tau +w_1+w_2)-m_{\textbf{1}}(\tau )-2m_{\textbf{x}}(\tau )}\Big ), \end{aligned}$$

and for $w\in \mathcal {W}$,

$$\begin{aligned} \Vert (v\circ _\mathbb {X}v\circ _\mathbb {X}\mathbb {X}_\bullet \mathcal {I}(w))_L\Vert _{D'_d}\lesssim c\Vert v\Vert _{D'}^3K'(w,k) \end{aligned}$$

(10.20)

where

$$\begin{aligned} K'(w,k)=\sum _{(|\tau _1|,|\tau _2|)\in \tilde{J}}\Big (k^{-\varepsilon }+k^{3-\delta m_{\scriptscriptstyle \Xi }(\tau _1+\tau _2+w)-m_{\textbf{1}}(\tau _1+\tau _2)} \Big ). \end{aligned}$$

Finally, for $\tau \in \partial \mathcal {W}$, we get from Assumption 9.10 that

$$\begin{aligned} \Vert (\mathbb {X}\tau )_L\Vert _{D'_d}\lesssim c L^{-3+\delta m_{\scriptscriptstyle \Xi }(\tau )}\Vert v\Vert _{D'}^{\delta m_{\scriptscriptstyle \Xi }(\tau )}=c\Vert v\Vert _{D'}^3k^{3-\delta m_{\scriptscriptstyle \Xi }(\tau )}. \end{aligned}$$

(10.21)

With (10.18), (10.19), (10.20) and (10.21), the bound (10.17) becomes

$$\begin{aligned} \Vert v\Vert _{D'_{\Vert v\Vert _{D'}^{-1}+R}}&\lesssim \max \Big \{R^{-1},\quad k^{-\frac{\alpha }{3}}\Vert v\Vert _{D'},\quad c^\frac{1}{3}\Vert v\Vert _{D'} k^{1-\frac{\delta m_{\scriptscriptstyle \Xi }(\tau )}{3}} ,\; \tau \in \partial \mathcal {W},\nonumber \\&\quad c^\frac{1}{3}\Vert v\Vert _{D'}K(w_1,w_2,k)^\frac{1}{3},\; w_1,w_2\in \mathcal {W}, \\&\quad c^\frac{1}{3}\Vert v\Vert _{D'}K'(w,k)^\frac{1}{3},\; w\in \mathcal {W},\quad k^{-\alpha }\Vert v\Vert _{D'},\Big \}.\nonumber \end{aligned}$$

(10.22)

We see that we can now choose $k>2$ large enough and then $c<c_0$, as well as $R=(\lambda -1) \Vert v\Vert _{D'}^{-1}$ for $\lambda$ large enough such that (10.22) becomes

$$\begin{aligned} \Vert v\Vert _{{D'}_{\lambda \Vert v\Vert _{D'}^{-1}}}\leqslant \frac{\Vert v\Vert _{D'} }{2}. \end{aligned}$$

(10.23)

Appendices

Reconstruction Lemma

In this section, we present the result that is essential for the proof of Lemmas 9.11 and 9.12, allowing us to define a function given its local description. It is inspired from [23, Proposition 3.28]. We show here a localised result that was introduced in [30]. We also reproduce the short proof here. It depends strongly on a specific choice of kernel to measure the regularity, which we construct hereafter.

We fix a non-negative smooth function $\Phi$ with support in B(0, 1), symmetric in space, with $\Phi (x)\in [0,1]$ for all $x\in \mathbb {R}\times \mathbb {R}^d$ and with integral 1. Setting $\Phi _L(t,x)=L^{-{d+2}}\Phi (\frac{t}{L^2},\frac{x}{L})$, we now define $\Psi _{L,n}= \Phi _{L2^{-1}}*\Phi _{L2^{-2}}*\cdots *\Phi _{L2^{-n}}$ and $\Psi _L=\lim _{n\rightarrow \infty }\Psi _{L,n}$ so that $\Psi _L=\Phi _\frac{L}{2}*\Psi _\frac{L}{2}$. $\Psi _L$ and $\Psi _{L,n}$ are non-negative and smooth, symmetric in space and with supports contained in B(0, L) and $B(0,(1-2^{-n})L)$. We define the operator $(\cdot )_L$ by convolution with $\Psi _L$, and $(\cdot )_{L,n}$ by convolution with $\Psi _{L,n}$ for $n\geqslant 1$. $(\cdot )_{L,0}$ is the identity. Since $\Psi _{L,n+m}=\Psi _{L,n}*\Psi _{L2^{-n},m}$, we have

$$\begin{aligned} (\cdot )_{L,n+m}=((\cdot )_{L2^{-n},m})_{L,n}. \end{aligned}$$

(A.1)

Taking m to infinity in this, or equivalently noticing that $\Psi _L=\Psi _{L,n}*\Psi _{L2^{-n}}$, we have the desired relation between dyadic scales

$$\begin{aligned} (\cdot )_L=((\cdot )_{L2^{-n}})_{L,n}. \end{aligned}$$

(A.2)

Lemma A.1

(Reconstruction) Let $\gamma >0$ and A be a finite subset of $(-\infty ,\gamma ]$. Let $L\in (0,1)$ and $x\in \mathbb {R}\times \mathbb {R}^d$. For a continuous function $F :B(x,L)^2 \rightarrow \mathbb {R}$ assume that for all $\beta \in A$ there exist constants $C_\beta >0$ and $\gamma _\beta \geqslant \gamma$ such that for all $l\in (0,L)$, for all $x_1,x_2\in B(x,L-l)$

$$\begin{aligned} \Big | \int \Psi _l(x_2-y)(F(y,x_1)-F(y,x_2))dy \Big |\leqslant \sum _{\beta \in A}C_\beta d(x_1,x_2)^{\gamma _\beta -\beta }l^\beta . \end{aligned}$$

(A.3)

Then $f:y\mapsto F(y,y)$ satisfies

$$\begin{aligned} \Big | \int \Psi _L(x-y)(F(y,x)-f(y))dy \Big |\lesssim \sum _{\beta \in A}C_\beta L^{\gamma _\beta }, \end{aligned}$$

(A.4)

where “$\lesssim$” represents a bound up to a multiplicative constant depending only on $\gamma$ and A.

In the proof we will use the following notations for f a function of one variable and F a function of two variables:

$$\begin{aligned}{}[F,(\cdot )_L](x)&=\int \Psi _L(x-y)F(y,x)dy. \end{aligned}$$

(A.5)

Proof

This is the only place where our particular choice of convolution kernel is crucial. This allows us to use the following factorisation:

$$\begin{aligned}&\Big |[F,(\cdot )_{L2^{-n}}](x_1)-\Big ([F,(\cdot )_{L2^{-n-1}}]\Big )_{L2^{-n},1}(x_1)\Big |\\&\quad =\Big |\int \int \Psi _{L2^{-n-1}}(x_2-y)\Phi _{L2^{-n-1}}(x_1-x_2)(F(y,x_1)-F(y,x_2))dydx_2\Big |\\&\quad \leqslant \sum _{\beta \in A}C_\beta \int \Phi _{L2^{-n-1}}(x_1-x_2)d(x_1,x_2)^{\gamma _\beta -\beta }(L2^{-n-1})^\beta dx_2\\&\quad \leqslant \sum _{\beta \in A}C_\beta (L2^{-n-1})^{\gamma _\beta }. \end{aligned}$$

Using the specific property of the kernels $\Phi$ and $\Psi$ once more, we get the telescopic sum

$$\begin{aligned} \Big |[F,(\cdot )_L]-\big ([F,(\cdot )_{L2^{-N}}]\big )_{L,N-1} \Big |&=\Big |\sum _{n=0}^N\Big ([F,(\cdot )_{L2^{-n}}]-\big ([F,(\cdot )_{L2^{-n-1}}]\big )_{L2^{-n},1}\Big )_{L,n}\Big |\\&\leqslant \sum _{n=0}^N\sum _{\beta \in A}C_\beta (L2^{-n-1})^{\gamma _\beta }\lesssim \sum _{\beta \in A}C_\beta L^{\gamma _\beta }, \end{aligned}$$

where the constant in ”$\lesssim$” depends only on $\gamma$ (in particular not on N). By continuity $([F,(\cdot )_{L2^{-N}}]\big )_{L,N-1}$ converges to $(f)_L$ as $N \rightarrow \infty$ thus proving the lemma. $\square$

In the definition of local product for a planted tree, we solve the heat equation with a cut-off function. The following lemma justifies that for a smooth cut-off, this does not change the order bound.

Schauder Lemmas

We start by introducing a few norms. For $\alpha \in (0,1)$, we define the Hölder semi-norm $[.]_\alpha$

$$\begin{aligned}{}[f]_\alpha :=\sup _ {z\ne \bar{z}\in \mathbb {R}\times \mathbb {R}^d}\frac{|f(z)-f(\bar{z})|}{d(z,\bar{z})^\alpha }. \end{aligned}$$

(B.1)

For $\alpha \in (1,2)$, we define the Hölder semi-norm $[.]_\alpha$

$$\begin{aligned}{}[f]_\alpha :=\sup _{\begin{array}{c} z \ne \bar{z} \in \mathbb {R}\times \mathbb {R}^d\\ z= (t,x); \; \bar{z} = (\bar{t}, \bar{x}) \end{array}}\frac{|f(z)-f(\bar{z})-\nabla f(z).(x-\bar{x})|}{d(z,\bar{z})^\alpha }, \end{aligned}$$

(B.2)

where $\nabla$ refers to the spatial gradient.

We will often deal with functions $F(z,\bar{z})$ of two variables generalising the increments of $f(z) - f(\bar{z})$ in (B.2) above. In this case we define, for $\alpha \in (1,2)$,

$$\begin{aligned}{}[F]_\alpha :=\sup _{\begin{array}{c} z\in \mathbb {R}\times \mathbb {R}^d\\ z =(t,x) \end{array}}\inf _{\nu (z)\in \mathbb {R}^d}\sup _{\begin{array}{c} \bar{z}\in \mathbb {R}\times \mathbb {R}^d\setminus \{z\} \\ \bar{z} = (\bar{t}, \bar{x}) \end{array}}\frac{|F(\bar{z},z)-\nu (z).(x-\bar{x})|}{d(z,\bar{z})^\alpha }. \end{aligned}$$

(B.3)

The infimum over functions $\nu$ is attained when $\nu (z)$ is the spatial gradient in the second coordinate of F at point (z, z). We use the same conventions as in Sect. 9.2 for localised versions of such norms. In all this section, "$\lesssim$" denotes a bound that holds up to a multiplicative constant that only depends on $\kappa$ and A when relevant. The localised Schauder estimate is taken from [30, Lemma 2.11] and its proof can be found there.¹

Lemma A.1

Let $1<\kappa <2$ and $A\subset (-\infty ,\kappa ]$ be finite. Let U be a bounded function of two variables defined on a domain $D\times D$ such that $U(x,x)=0$ for all x. Let $d_0>0$ and assume that for any $0<d\leqslant d_0$ and $L_1\leqslant \frac{d}{4}$ there exists a constant $M^{(1)}_{D_d,L_1}$ such that for all base-points $x\in D_d$ and length scales $L_2\leqslant L_1$, it holds that

$$\begin{aligned} L_2^2\Vert (\partial _t-\Delta )U_{L_2}(\cdot ,x)\Vert _{B(x,L_1)}\leqslant M^{(1)}_{D_d,{L_1}}\sum _{\beta \in A}L_2^\beta {L_1}^{\kappa -\beta }. \end{aligned}$$

(B.4)

Assume furthermore, that for $L_1 \leqslant \frac{d}{2},L_2\leqslant \frac{d}{4}$ there exists a constant $M^{(2)}_{D_d,L_1,L_2}$ such that, for any $x\in D_d$ and $y\in B(x,L_1)$, there exists $\lambda (y,x) = (\lambda ^{(i)}(y,x))_{i=1}^{d} \in \mathbb {R}^d$ such that, for any $z\in B(y,L_2)$, the following “three-point continuity” holds:

$$\begin{aligned} \begin{aligned} |U(z,x)-U(y,x)-U(z,y)&-(z_{i} - y_{i}) \lambda ^{(i)}(y,x)|\\&\leqslant M^{(2)}_{D_d,L_1,L_2}\sum _{\beta \in A}d(y,x)^\beta d(z, y)^{\kappa -\beta }. \end{aligned} \end{aligned}$$

(B.5)

Additionally, define

$$\begin{aligned} M^{(1)}:=\sup _{d\leqslant d_0}d^\kappa M^{(1)}_{D_d,\frac{d}{2}},\quad \text {and}\quad M^{(2)}:=\sup _{d\leqslant d_0}d^\kappa M^{(2)}_{D_d,\frac{d}{2},\frac{d}{4}}. \end{aligned}$$

Then

$$\begin{aligned} \sup _{d\leqslant d_0}d^\kappa [U]_{\kappa ,D_d,d}\lesssim M^{(1)}+M^{(2)} +\sup _{d\leqslant d_0}\Vert U\Vert _{D_d,d}. \end{aligned}$$

(B.6)

The following lemma, taken from [30, Corollary 2.12], gives bounds on the derivative:

Lemma A.2

Let $\kappa > 1$ and $U\in C^{\kappa }(\mathbb {R}\times \mathbb {R}^{d})$ then, for the optimal function $\nu$ in (B.3), for any $r\in (0,\infty )$,

$$\begin{aligned} \Vert \nu \Vert \lesssim r^{\kappa -1}[U]_{\kappa } + r^{-1} \Vert U\Vert \;. \end{aligned}$$

(B.7)

Suppose, furthermore, that there exists a constant M and, for all $x,y \in \mathbb {R}\times \mathbb {R}^{d}$, a vector $\lambda (y,x) = (\lambda ^{(i)}(y,x))_{i=1}^{d} \in \mathbb {R}^d$ such that for any $z \in \mathbb {R}\times \mathbb {R}^{d}$ one has the three-point continuity bound

$$\begin{aligned} |U(z,x) -U(y,x) -U(z,y) -(z_{i} - y_{i})\lambda ^{(i)}(y,x)| \leqslant M \sum _{\beta \in A} d(y,x)^\beta d(z, y)^{\kappa -\beta }\;. \end{aligned}$$

(B.8)

Then, if we write $f(z,w) = (f^{(i)}(z,w))_{i=1}^{d}$ where $f^{(i)}(z,w) = \nu ^{(i)}(z) - \nu ^{(i)}(w) + \lambda ^{(i)}(z,w)$, one has

$$\begin{aligned}{}[f]_{\kappa -1}\lesssim [U]_{\kappa }+M\;. \end{aligned}$$

(B.9)

A localised version of this lemma is as follows:

Lemma A.3

Assume that D satisfies a spatial interior cone condition with parameters $r_0>0$ and $\beta \in (0,1)$, that is for all $r\in [0,r_0]$, for all $x\in D$, for any vector $\theta = (\theta ^{(i)})_{i=1}^{d}\in \mathbb {R}^{d}$, there exists $y\in D$ such that $d(x,y)=r$ and

$$\begin{aligned} \Big |\sum _{i=1}^{d} \theta ^{(i)} (y_{i} - x_{i}) \Big |\geqslant \beta d(x,y) |\theta |. \end{aligned}$$

Let $\kappa > 1$ and $U\in C^{\kappa }$ then, for the optimal function $\nu$ in (B.3) and for all $r\in [0,r_0]$, we have the bound

$$\begin{aligned} \beta \Vert \nu \Vert _{D} \leqslant r^{\kappa -1}[U]_{\kappa ,D} + r^{-1} \Vert U\Vert _{D,r}\;. \end{aligned}$$

(B.10)

Suppose furthermore that there exists a constant M and, for all $x,y \in D$, a vector $\lambda (y,x) = (\lambda ^{(i)}(y,x))_{i=1}^{d} \in \mathbb {R}^d$ such that for any $z \in D$ one has the the three-point continuity bound

$$\begin{aligned} |U(z,x) -U(y,x) -U(z,y) -(z_{i} - y_{i})\lambda ^{(i)}(y,x)| \leqslant M \sum _{\beta \in A} d(y,x)^\beta d(z, y)^{\kappa -\beta }\;. \end{aligned}$$

(B.11)

Then, if we write $f(z,w) = (f^{(i)}(z,w))_{i=1}^{d}$ where $f^{(i)}(z,w) = \nu ^{(i)}(z) - \nu ^{(i)}(w) + \lambda ^{(i)}(z,w)$, one has, for every $r \in [0,r_{0}]$,

$$\begin{aligned}{}[f]_{\kappa -1,D}\lesssim [U]_{\kappa ,D}+M+r^{-\kappa }\Vert U\Vert _{D,r}\;. \end{aligned}$$

(B.12)

Symbolic Index

In this appendix, we collect the most used symbols of the article, together with their meaning and the page where they were first introduced.

Symbol	Meaning	Page
$d(\cdot ,\cdot )$	Parabolic distance between space–time points $z,\bar{z} \in \mathbb {R}\times \mathbb {R}^{d}$	6
$\Xi$	The abstract noise	15
$\textrm{Poly}$	The set $\{\textbf{1},\textbf{X}_{1},\ldots ,\textbf{X}_{d}\}$	17
$\mathcal {W}$	Unplanted trees with $|\tau | < -2$	17
$\mathcal {W}_{\textsc {prod}}$	Set of product trees in $\mathcal {W}$, namely $\mathcal {W}\setminus \{\Xi \}$	17
$\mathcal {V}$	Unplanted trees with $|\tau | \in [-2,0]$, includes $\textrm{Poly}$	17
$\mathcal {V}_{\textsc {prod}}$	Set of product trees in $\mathcal {V}$, namely $\mathcal {V}\setminus \textrm{Poly}$	17
$\mathcal {T}_{\textsc {RHS}}$	Unplanted trees on right hand side of $\phi$ equation, $\mathcal {T}_{\textsc {RHS}}= \mathcal {W}\cup \mathcal {V}_{\textsc {prod}}$	17
$\mathcal {T}_{\textsc {LHS}}$	Planted trees in expansion of $\phi$, $\mathcal {T}_{\textsc {LHS}}= \mathcal {I}(\mathcal {T}_{\textsc {RHS}}) \cup \mathcal {I}(\textrm{Poly})$	17
$\mathcal {V}_{> 1}$	$\{\tau \in \mathcal {V}_{\textsc {prod}}: |\tau | > 1\}$	20
$\mathcal {T}_{\Delta }$	$\mathcal {T}_{\textsc {RHS}}\cup \mathcal {T}_{\textsc {LHS}}\cup \mathcal {T}_{\textrm{cen}}$, where our coproduct is defined	20
$\mathcal {T}_{\textrm{cen}}$	Planted trees that only appear for centering	21
$\mathcal {I}$	Edge of a tree corresponding to heat kernel	15
$\mathcal {I}_+^{(i)}$	Edge for derivative of heat kernel for positive renormalisation	20
$\mathcal {I}_-^{(i)}$	Edge for derivative of heat kernel for negative renormalisation	40
$[\bullet ]_{\alpha }$	Hölder seminorm of index $\alpha$	63
$[\mathbb {X};\bullet ]$	Seminorm for the local product $\mathbb {X}$ applied to a tree	30
$\Vert \bullet \Vert$	$L^\infty$ norm	48
$\mathbb {X}_\bullet$	Local product	20
$\mathbb {X}^{\textrm{cen}}_\bullet$	Centering map	27
$\mathbb {X}_{\bullet ,\bullet }$	Local path	27
$\rho$	Cut-off function used to define local product	19
$\leqslant ,\subset$	Relations on trees	24
$m(\tau )$	Number of leaves in a tree $\tau$	17
$m_{\scriptscriptstyle \Xi }$	Number of noise leaves in a tree $\tau$	17
$m_{\textbf{x}}$	Number of $\{\textbf{X}_{i}\}_{i=1}^{d}$ leaves in a tree $\tau$	17
$m_{\textbf{1}}$	Number of $\textbf{1}$ leaves in a tree $\tau$	17
$|\bullet |$	Order of a tree	17
$\delta$	Noise is regularity $C^{-3-\delta }$, $\delta > 0$	2
D	$(0,1)\times \{|x|<1\}$	2
$D_R$	$(R^2,1) \times \{|x|<1-R\}$	2
$\Delta$	Coproduct	20
$C_+$	Cut map for coproduct	25
$C_-$	Cut map for modified coproduct	42
$\mathcal {R}$	Renormalisation operator	42
$\circ _\mathbb {X}$	Renormalised product of tree expansion	39
$(\bullet )_L$	Convolution with the kernel $\Psi _L$	7
$\Psi _L$	Smooth compactly supported kernel, rescaled at length L	7
$\Upsilon$	Coefficient map for solutions to equation	35
$V_\gamma$	Expansion of the remainder solution to level $\gamma$	34
$V^2_\gamma$	Expansion of square of remainder solution to level $\gamma$	34
$V^{((i)}_\gamma$	Expansion of derivative of the remainder solution to level $\gamma$	34
$U^{\tau }_\gamma$	Expansion of the local approximation on level $\tau$	33