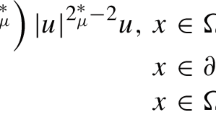Abstract
In this paper, we consider the sharp thresholds of blow-up and global existence for the nonlinear Schrödinger–Choquard equation
We derive some finite time blow-up results. Due to the failure of this equation to be scale invariant, we obtain some sharp thresholds of blow-up and global existence by constructing some new estimates. In particular, we prove the global existence for this equation with critical mass in the \(L^{2}\)-critical case. Our obtained results extend and improve some recent results.
Similar content being viewed by others
1 Introduction
In this paper, we study the sharp threshold of blow-up and global existence for the nonlinear Schrödinger–Choquard equation
where \(\psi (t,x):[0,T^{*})\times \mathbb{R}^{N} \rightarrow \mathbb{C}\) and \(0< T^{*}\leq \infty \), \(N\geq 3\), \(\psi _{0} \in H^{1}\), \(\lambda _{1},\lambda _{2} \in \mathbb{R}\), \(0< p_{1}< \frac{4}{N-2}\), \(1+\frac{\alpha }{N}< p_{2}<1+\frac{2+\alpha }{N-2}\), \(I_{\alpha }: \mathbb{R}^{N}\rightarrow \mathbb{R}\) is the Riesz potential defined by
where Γ is the Gamma function and \(\max \{0,N-4\}<\alpha <N\).
When \(\lambda _{2}=0\), Eq. (1.1) is the classical Schrödinger equation which appears in various areas of physics, such as nonlinear plasmas and nonlinear optics; see [2, 18]. This class of equations received a great deal of attention from mathematicians see [2, 18]. Particularly, from scaling invariance of (1.1) with \(\lambda _{2}=0\), Weinstein [19] and Zhang [21] obtained the sharp threshold of blow-up and global existence for the \(L^{2}\)-critical nonlinearity and \(L^{2}\)-supercritical nonlinearity, respectively.
When \(\lambda _{1}=0\), \(0<\alpha <N\) and \(1+\frac{\alpha }{N}< p_{2}<\frac{N+ \alpha }{N-2}\), under the assumption that the local well-posedness holds for (1.1), Chen and Guo [3] derived the existence of blow-up solutions and the instability of standing waves. When \(0<\alpha <N\) and \(1+\frac{\alpha }{N}< p_{2}<1+\frac{2+\alpha }{N}\), Squassina et al. in [1] studied the soliton dynamics of (1.1) under the assumption that the solution ψ of (1.1) is in \(C([0,\infty ),H^{2})\cap C^{1}((0,\infty ),L^{2})\). The dynamical properties of blow-up solutions have been investigated in [11]. In [8], Feng and Yuan systematically studied the Cauchy problem (1.1) for general \(\max \{0,N-4\}< \alpha <N\) and \(2\leq p_{2}<\frac{N+\alpha }{N-2}\). More precisely, they studied the local well-posedness, global existence, the existence of blow-up solutions and the dynamics of blow-up solutions. The sharp threshold of global existence and blow-up, the instability of standing wave of (1.1) with \(\lambda _{1}=0\) and a harmonic potential have been investigated in [5].
From the local well-posedness of (1.1) with \(\lambda _{1}=0\) or \(\lambda _{2}=0\), for small initial data \(\psi _{0}\), the solution \(\psi (t)\) to (1.1) exists globally, and the solution \(\psi (t)\) may blow up for some large initial data. Hence, whether there are some sharp thresholds of global existence and blow-up for (1.1) is a very interesting problem. In particular, the sharp thresholds of global existence and blow-up for nonlinear Schrödinger equations are pursued strongly in [2, 4, 6, 7, 9, 12–24]. However, in these papers, the scale invariance plays an important role in the study of the sharp threshold of blow-up and global existence. When \(\lambda _{1}\neq 0\) and \(\lambda _{2}\neq 0\), there is no any scaling invariance for Eq. (1.1). Therefore, the study of the sharp threshold of blow-up and global existence for (1.1) with \(\lambda _{1}\neq 0\) and \(\lambda _{2}\neq 0\) is of particular interest.
To study this problem, we mainly use the idea of Zhang and Zhu [22], where they studied sharp criteria for the Davey–Stewartson system
Due to the failure of (1.1) to be scale invariant, motivated by the idea in [22], we must construct some new estimates to establish some sharp thresholds of blow-up and global existence for (1.1). We will derive sharp thresholds of blow-up and global existence for (1.1) in the following three cases: (i) \(\lambda _{1}<0\) and \(\lambda _{2}<0\); (ii) \(\lambda _{1}>0\) and \(\lambda _{2}<0\); (iii) \(\lambda _{1}<0\) and \(\lambda _{2}>0\). However, the authors in [22] only studied sharp criteria for (1.2) with \(\lambda _{1}<0\) and \(\lambda _{2}<0\). Therefore, we extend and improve these sharp thresholds for the Davey–Stewartson system to the Schrödinger–Choquard equation. In particular, we can prove the global existence for this equation with critical mass in the \(L^{2}\)-critical case.
This paper is organized as follows: in Sect. 2, we recall some preliminaries. In Sect. 3, we will derive some sufficient conditions on existence of blow-up solutions. In Sect. 4, we will derive some sharp thresholds of blow-up and global existence for (1.1) by constructing some new estimates. Section 5 is a concluding section.
2 Preliminaries
In order to study the sharp threshold of blow-up and global existence for (1.1), we first make the following assumption about the local well-posedness of (1.1).
Assumption 1
Let \(\psi _{0} \in H^{1}\), \(0< p_{1}< \frac{4}{N-2}\) and \(1+\frac{\alpha }{N}< p_{2}<1+\frac{2+\alpha }{N-2}\) with \(N\geq 3\). Then, there exist \(T^{*}>0\) and a unique maximal solution \(u\in C([0,T^{*}),H^{1})\). In addition, if \(T^{\ast }< \infty \), then \(\| \psi (t)\| _{H^{1}}\rightarrow \infty \) as \(t\uparrow T^{\ast } \). Moreover, the solution \(\psi (t)\) satisfies
for all \(0\leq t< T^{*}\), where \(E(\psi (t))\) is defined by
Remark
When \(0< p_{1}<\frac{4}{N-2}\) and \(2\leq p_{2}<1+\frac{2+ \alpha }{N-2}\), this assumption can be easily proved by Strichartz’s estimates and a fixed point argument; see [2, 8]. When \(1+\frac{\alpha }{N}< p_{2}<2\), we deduce from the Hardy–Littlewood–Sobolev inequality that \(\int _{\mathbb{R}^{N}} (I _{\alpha }\ast |\psi |^{p_{2}})|\psi |^{p_{2}}\,dx\) is well-defined for \(\psi \in H^{1}\). Thus, we assume that the local well-posedness of (1.1) holds for \(\frac{N+\alpha }{N}< p_{2}<2\). However, we cannot prove this result since the nonlinearity \((I_{\alpha }\ast |\psi |^{p _{2}})|\psi |^{p_{2}-2}\psi \) is singular when \(\frac{N+\alpha }{N}< p _{2}<2\). Consequently, the case of \(\frac{N+\alpha }{N}< p_{2}<2\) will be the object of a future investigation.
By the same argument as that in [2], we can easily derive the following lemma.
Lemma 2.1
Let\(\psi _{0} \in \varSigma :=\{u\in H^{1}, xu\in L^{2}\}\), and the solution\(\psi (t)\)to (1.1) exists on the interval\([0,T^{*})\). Then, \(\psi (t) \in \varSigma \)for all\(t\in [0,T^{*})\). Moreover, let\(F(t)=\int _{\mathbb{R}^{N}} |x\psi (t,x)|^{2}\,dx\), then
and
Finally, we recall two important Gagliardo–Nirenberg type inequalities; see [8, 19].
Lemma 2.2
([19])
LetQbe the ground state solution of the following elliptic equation:
Then, the optimal constant in the Gagliardo–Nirenberg inequality,
is
In particular, in the\(L^{2}\)-critical case, i.e., \(p=\frac{4}{N}\), \(C_{*}=\frac{p+2}{2\|Q\|_{L^{2}}^{p}}\).
Lemma 2.3
([8])
LetRbe the ground state solution of the following elliptic equation:
The best constant in the Gagliardo–Nirenberg type inequality
is
In particular, in the\(L^{2}\)-critical case, i.e., \(p=1+\frac{2+ \alpha }{N}\), \(C^{*}=p\|R\|_{L^{2}}^{2-2p}\).
This inequality has been extended to the fractional case; see [10].
Finally, we recall the following compactness lemma is vital in the proof of global existence; see [7].
Lemma 2.4
Let\(N\geq 2\), \(0< p<\frac{4}{N-2}\). Let\(\{u_{n}\}\)be a bounded sequence in\(H^{1}\)such that
Then there exist a sequence\((x_{n})_{n\geq 1}\)in\(\mathbb{R}^{N}\)and\(U \in H^{1}\setminus \{0\}\)such that up to a subsequence,
3 The existence of blow-up solutions
In this section, we will derive the sufficient conditions about existence of blow-up solutions.
Theorem 3.1
Let\(\psi _{0}\in \varSigma \), \(\lambda _{1}<0\), \(h_{0}:=\operatorname{Im} \int _{\mathbb{R}^{N}} \bar{\psi }_{0}x\nabla \psi _{0}\,dx>0\)and\(\frac{4}{N}< p_{1}< \frac{4}{N-2}\)with\(N\geq 3\). Then, the solution\(\psi (t)\)of (1.1) blows up in each of the following three cases:
- (1)
\(\lambda _{2}>0\), \(1+\frac{\alpha }{N}< p_{2}<1+\frac{Np_{1}+2\alpha }{2N}\), and\(E(\psi _{0})<0\);
- (2)
\(\lambda _{2}<0\), \(1+\frac{2+\alpha }{N}< p_{2}<1+\frac{Np_{1}+2 \alpha }{2N}\), and\(E(\psi _{0})<0\);
- (3)
\(\lambda _{2}<0\), \(1+\frac{\alpha }{N}< p_{2}\leq 1+ \frac{2+\alpha }{N}\), and\(E(\psi _{0})+C\|\psi _{0}\|_{L^{2}}^{\frac{2Np _{1}+2p_{1}\alpha -4Np_{2}+4N+4\alpha }{Np_{1}-2Np_{2}+2N+2\alpha }}<0\)for some constantC.
More precisely, there is\(T^{*}\in (0, C\frac{\|x\psi _{0}\|_{L ^{2}}^{2}}{y_{0}} ]\)such that
Proof
In the following, we will prove \(F'(t)<0\) and \(F''(t)<0\) for all \(t\in [0,T^{*})\). More precisely, we will prove that
for some constant \(c>0\), where \(h(t)\) is defined by (2.4). Thus, it follows from (2.5) that \(F''(t)<0\) for all \(t\in [0,T^{*})\). This shows that \(F(t)\) is concave and the solution \(\psi (t)\) of (1.1) blows up. Indeed, it follows from \(y(0)=y_{0}>0\) that \(h(t)>h(0)>0\) for all \(t>0\). On the other hand, we deduce from Hölder’s inequality that
for all \(t\in [0,T^{*})\). This implies
We deduce from (3.1) and (3.2) that
This shows that there is \(T^{*}\in (0, \frac{\|x \psi _{0}\|_{L ^{2}}^{2}}{cy_{0}} ]\) such that \(\|\nabla \psi (t)\|_{L^{2}} \rightarrow \infty \) as \(t\rightarrow T^{*}\).
Case (i): \(\lambda _{2}>0\), \(Np_{1}>2Np_{2}-2N-2\alpha \), and \(E(\psi _{0})<0\). We deduce from (2.5), (2.2), and our assumptions that
This implies that (3.1) holds.
Case (ii): \(\lambda _{2}<0\), \(Np_{1}+2N+2\alpha >2Np_{2}\), \(p_{2}>1+\frac{ \alpha +2}{N}\) and \(E(\psi _{0})<0\). We deduce from (2.5), (2.2), and our assumptions that
This implies that (3.1) holds.
Case (iii): \(\lambda _{2}<0\), \(1+\frac{\alpha }{N}< p_{2}\leq 1+\frac{2+ \alpha }{N}\), and \(E(\psi _{0})+C\|\psi _{0}\|_{L^{2}}^{\frac{2Np_{1}+2p _{1}\alpha -4Np_{2}+4N+4\alpha }{Np_{1}-2Np_{2}+2N+2\alpha }}<0\) for some constant C.
We deduce from \(p_{1}>\frac{4}{N}\) that there is a constant ε such that \(p_{1}>\frac{2(2+\varepsilon )}{N}\). Let \(\theta :=\frac{2(2+\varepsilon )}{p_{1}N}<1\). Therefore, it follows from (2.2) and our assumptions that
Applying Young’s inequality, we have
Therefore, we can choose \(\delta >0\) enough small such that
which implies
Therefore, if \(Np_{1}\theta E+C(\delta )\frac{|\lambda _{2}|\theta (Np _{1}-2p_{2}N+2N+2\alpha )}{2p_{2}}\|\psi _{0}\|_{L^{2}}^{\frac{2Np_{1}+2p _{1}\alpha -4Np_{2}+4N+4\alpha }{Np_{1}-2Np_{2}+2N+2\alpha }}<0\), then
This implies that (3.1) holds. □
4 Sharp conditions of blow-up and global existence
From the local well-posedness of the nonlinear Schrödinger–Choquard equation, for small initial data \(\psi _{0}\), the solution \(\psi (t)\) to (1.1) exists globally, and the solution \(\psi (t)\) may blow up for some large initial data. Therefore, whether there are some sharp thresholds of global existence and blow-up for (1.1) is a very interesting problem. For Eq. (1.1), there are two nonlinearities and there is no scaling invariance, which are the main difficulties. We obtain the following sharp conditions of blow-up and global existence for (1.1) by constructing some new estimates.
4.1 \(L^{2}\)-Critical case
Theorem 4.1
Let\(\psi _{0}\in H^{1}\), \(\lambda _{1}=-1\), \(\lambda _{2}=1\), \(p_{1}=\frac{4}{N}\)and\(1+\frac{\alpha }{N}< p_{2}<1+ \frac{2+\alpha }{N}\). Assume thatQis the ground state solution of (2.6). Then, we have the following sharp threshold mass of blow-up and global existence.
- (i)
If\(\|\psi _{0}\|_{L^{2}}\leq \|Q\|_{L^{2}}\), then the solution of (1.1) exists globally.
- (ii)
If the initial data\(\psi _{0}=c\rho ^{\frac{N}{2}} Q(\rho x)\)satisfies\(|x|\psi _{0}\in L^{2}\), where the complex numbercsatisfying\(|c|> 1\), and the real number\(\rho >0\), then the solutionψof (1.1) with initial data\(\psi _{0}\)blows up in finite time.
Proof
(i) We firstly consider the case \(\|\psi _{0}\|_{L^{2}}<\|Q\|_{L^{2}}\). It follows from (2.3) and (2.7) that
Due to \(\|\psi _{0}\|_{L^{2}}<\|Q\|_{L^{2}}\), we find that \(\|\nabla \psi (t)\|_{L^{2}}\) is uniformly bounded for all time t. Therefore, (i) follows from the conservation of mass and Proposition 2.1.
When \(\|\psi _{0}\|_{L^{2}}=\|Q\|_{L^{2}}\), if the solution \(\psi (t)\) of (1.1) blows up in finite time, then there exists \(T^{*}>0\) such that \(\lim_{t\rightarrow T^{*}}\|\nabla \psi (t)\|_{L^{2}}=\infty \). Set
Let \(\{t_{n}\}_{n=1}^{\infty }\) be an any time sequence such that \(t_{n}\rightarrow T^{*}\), \(\rho _{n}:=\rho (t_{n})\) and \(v_{n}(x):=v(t _{n},x)\). Then, the sequence \(\{v_{n}\}\) satisfies
Observe that
Thus, we deduce from the Gagliardo–Nirenberg inequality (2.10) and \(1+\frac{\alpha }{N}< p_{2}<1+\frac{2+\alpha }{N}\) that
This, together with (4.2) implies that \(\int _{\mathbb{R}^{N}} |v _{n}(x)|^{p_{1}+2}\,dx\rightarrow (2/N+1)\|\nabla Q\|_{L^{2}}^{2}\). Thus, we deduce from (4.1) that there exist a subsequence, still denoted by \(\{v_{n}\}\), and \(u\in H^{1}\backslash \{0\}\) such that
for some \(\{x_{n}\}\subseteq \mathbb{R}^{N}\). This implies that there exists \(C_{0}>0\) such that
On the other hand, we deduce from (2.7) and \(\|\psi (t)\|_{L^{2}}= \|\psi _{0}\|_{L^{2}}=\|Q\|_{L^{2}}\) that
for all \(t\in [0,T^{*})\). This implies that
for all \(t\in [0,T^{*})\). We consequently obtain
which is a contradiction with (4.3). Thus, the solution \(\psi (t)\) of (1.1) exists globally.
(ii) Since \(|x|\psi _{0}\in L^{2}\), \(J(t)=\int _{\mathbb{R}^{N}} |x \psi (t,x)|^{2}\,dx\) is well-defined, and it follows from Lemma 2.1 that
By the definition of initial data \(\psi _{0}(x)=c\rho ^{\frac{N}{2}} Q( \rho x)\) and the Pohoz̆aev identity for Eq. (2.6), i.e., \(\frac{1}{2}\|\nabla Q\|_{L^{2}}^{2}=\frac{1}{p_{1}+2}\|Q\|^{p_{1}+2} _{L^{p_{1}+2}}\), we deduce that
Thanks to \(Np_{2}-N-\alpha <2\), we can take ρ large enough such that
It follows from (4.4) that \(F''(t)<16 E(\psi _{0}) < 0\). By the standard concave argument, the solution ψ of (1.1) with the initial data \(\psi _{0}\) blows up in finite time. □
4.2 \(L^{2}\)-Supercritical case
Theorem 4.2
Let\(\lambda _{1}=\lambda _{2}=-1\), \(p_{1}>\frac{4}{N}\), and\(\psi \in C([0,T^{*}),H^{1})\)be a solution of (1.1). Then we have the following sharp criteria of blow-up and global existence for (1.1).
- (1)
\(\|\psi _{0}\|_{L^{2}}<\|R\|_{L^{2}}\), \(p_{2}=1+\frac{2+\alpha }{N}\), and\(E(\psi _{0})< \frac{Np_{1}-4}{2Np_{1}} (1 -\frac{\| \psi _{0} \|^{2p_{2}-2}_{L^{2}}}{\|R\|^{2p_{2}-2}_{L^{2}}} )y_{0}^{2}\). If\(\|\nabla \psi _{0}\|_{L^{2}}< y_{0}\), then the solution\(\psi (t)\)of (1.1) exists globally; If\(\|\nabla u_{0}\|_{L^{2}}>y_{0}\), then the solution\(\psi (t)\)of (1.1) blows up, whereRis the ground state solution of (2.9) with\(p=1+\frac{2+\alpha }{N}\), \(y_{0}\)is defined by (4.8).
- (2)
\(1+\frac{\alpha +2}{N}< p_{2}<1+\frac{Np_{1}+2\alpha }{2N}\)and\(E(\psi _{0})<\frac{Np_{2}-N-\alpha -2}{2(Np_{2}-N-\alpha )}y_{1}^{2}\). If\(\|\nabla \psi _{0}\|_{L^{2}}< y_{1}\), then the solution\(\psi (t)\)of (1.1) exists globally; If\(\|\nabla \psi _{0}\|_{L^{2}}>y_{1}\), then the solution\(\psi (t)\)of (1.1) blows up, where\(y_{1}\)is the unique positive solution of the equation\(f(y)=0\)and\(f(y)\)is defined in (4.13) with\(1+\frac{\alpha +2}{N}< p_{2}<1+\frac{Np_{1}+2 \alpha }{2N}\).
- (3)
\(1+\frac{Np_{1}+2\alpha }{2N}< p_{2}<1+\frac{2+\alpha }{N-2}\)and\(E(\psi _{0})<\frac{Np_{1}-4}{2Np_{1}}y_{2}^{2}\). If\(\|\nabla \psi _{0}\|_{L^{2}}< y_{2}\), then the solution\(\psi (t)\)of (1.1) exists globally; If\(\|\nabla \psi _{0}\|_{L^{2}}>y_{2}\), then the solution\(\psi (t)\)of (1.1) blows up, where\(y_{2}\)is the unique positive solution of the equation\(f(y)=0\)and\(f(y)\)is defined in (4.13) with\(1+\frac{Np_{1}+2\alpha }{2N}< p_{2}<1+\frac{2+\alpha }{N-2}\).
Proof
Case (1): \(p_{2}=1+\frac{2+\alpha }{N}\). First, we deduce from (2.7) and (2.10) that
where \(C_{*}\) and \(C^{*}\) are defined by (2.8) and (2.11), respectively, \(h(y)\) is defined by
By a simple computation, we find that \(h(y)\) is continuous on \([0,\infty )\) and
By the assumption \(\|\psi _{0}\|_{L^{2}}<\|R\|_{L^{2}}\), \(1-\frac{C ^{*}}{p_{2}}\| \psi _{0}\|^{2p_{2}-2}_{L^{2}}>0\). Thus, the equation \(h'(y)=0\) has a unique positive root:
This implies that \(h(y)\) is increasing on the interval \([0,y_{0})\), decreasing on the interval \([y_{0},\infty )\) and
By (2.2) and \(E(\psi _{0})< h(y_{0})\), we have
Now, we claim that if \(\|\nabla \psi _{0}\|_{L^{2}}< y_{0}\), then \(\|\nabla \psi (t)\|_{L^{2}}< y_{0}\), for all \(t\in [0,T^{*})\). This implies the solution \(\psi (t)\) of (1.1) exists globally. Let us prove this result by contradiction. If not, by the continuity of \(\|\nabla \psi (t)\|_{L^{2}}\), there exists \(t_{0}\in [0,T^{*})\) such that \(\|\nabla \psi (t_{0})\|_{L^{2}}=y_{0}\). Thus, \(h(\|\nabla \psi (t_{0})\|_{L^{2}})=h(y_{0})=h_{\max }\). Moreover, taking \(t=t_{0}\) in (4.10), it follows that
which is a contradiction. Thus, the solution \(\psi (t)\) of (1.1) exists globally.
On the other hand, if \(\|\nabla \psi _{0}\|_{L^{2}}>y_{0}\), by the same argument, it follows that \(\|\nabla \psi (t)\|_{L^{2}}>y_{0}\) for all \(t\in [0,T^{*})\). Thus, by (2.2), (2.5), (2.7), and the assumption \(E(\psi _{0})< \frac{Np_{1}-4}{2Np_{1}} (1 -\frac{ \| \psi _{0}\|^{2p_{2}-2}_{L^{2}}}{\|R\|^{2p_{2}-2}_{L^{2}}} )y _{0}^{2}\), we deduce that
Therefore, by the classical argument for Schrödinger equations, the solution \(\psi (t)\) of (1.1) blows up.
Case (2): \(1+\frac{\alpha +2}{N}< p_{2}<1+\frac{Np_{1}+2\alpha }{2N}\) and \(E(\psi _{0})<\frac{Np_{2}-N-\alpha -2}{2(Np_{2}-N-\alpha )}y_{1}^{2}\). Similarly, we define a function \(g(y)\) on \([0,\infty )\) by
Thus, it follows that \(E(\psi (t))\geq g(\|\nabla \psi (t)\|_{L^{2}})\), \(g(y)\) is continuous on \([0,\infty )\) and
Next, we define a function \(f(y)\) by
For the equation \(f(y)=0\), there is a unique positive solution \(y_{1}\). Indeed, by the assumption \(1+\frac{\alpha +2}{N}< p_{2}<1+\frac{Np _{1}+2\alpha }{2N}\), for \(y>0\), we have
which implies that \(f(y)\) is decreasing on \([0,\infty )\). Due to \(f(0)=1\), there exists a unique \(y_{1}>0\) such that \(f(y_{1})=0\). Therefore, we have
This implies that \(g(y)\) is increasing on \([0,y_{1})\), decreasing on \((y_{1},+\infty )\) and
On the other hand, we deduce from (2.2) and the assumption \(E(u_{0})<\frac{Np_{2}-N-\alpha -2}{2(Np_{2}-N-\alpha )}y_{1}^{2}\) that
By the same argument as Case (1), we find that if \(\|\nabla \psi _{0}\| _{L^{2}}< y_{1}\), then, for all \(t\in [0,T^{*})\), \(\|\nabla \psi (t)\| _{L^{2}}< y_{1}\), which implies the solution \(\psi (t)\) of (1.1) exists globally.
And if \(\|\nabla \psi _{0}\|_{L^{2}}>y_{1}\), by the same way, it follows that \(\|\nabla \psi (t)\|_{L^{2}}>y_{1}\) for all \(t\in [0,T^{*})\). Thus, it follows from (2.2) and (2.5) that
This implies that the solution of (1.1) blows up.
Case (3): \(1+\frac{Np_{1}+2\alpha }{2N}< p_{2}<1+\frac{2+\alpha }{N-2}\) and \(E(\psi _{0})<\frac{Np_{1}-4}{2Np_{1}}y_{2}^{2}\). By the same argument as Case (2), we have
where \(y_{2}\) is the unique positive solution of (4.13). Thus, we deduce from (2.2) and the assumption \(E(\psi _{0})<\frac{Np _{1}-4}{2Np_{1}}y_{2}^{2}\) that
By the same argument as Case (1), we find that if \(\|\nabla \psi _{0}\| _{L^{2}}< y_{1}\), then, for all \(t\in [0,T^{*})\), \(\|\nabla \psi (t)\| _{L^{2}}< y_{1}\), which implies the solution \(\psi (t)\) of (1.1) exists globally.
And if \(\|\nabla \psi _{0}\|_{L^{2}}>y_{2}\), in the same way, it follows that \(\|\nabla \psi (t)\|_{L^{2}}>y_{2}\) for all \(t\in [0,T^{*})\). Thus, it follows from (2.2) and (2.5) that
This implies that the solution \(\psi (t)\) of (1.1) blows up. □
Theorem 4.3
Let\(\lambda _{1}=1\), \(\lambda _{2}=-1\), \(1+\frac{Np_{1}+2\alpha }{2N}< p _{2}<1+\frac{2+\alpha }{N-2}\), and\(E(\psi _{0})< \frac{Np_{2}-N- \alpha -2}{2(Np_{2}-N-\alpha )}x_{0}^{2}\), and\(\psi \in C([0,T^{*}),H ^{1})\)be a solution of (1.1). If\(\|\nabla \psi _{0}\|< x_{0}\), then the solution\(\psi (t)\)of (1.1) exists globally; If\(\|\nabla \psi _{0}\|>x_{0}\), then the solution\(\psi (t)\)of (1.1) blows up, where\(x_{0}\)is defined by (4.21).
Proof
Applying (2.10), it follows that
where the \(C^{*}\) are defined by (2.11) and
By a simple computation, we find that the unique positive solution \(x_{0}\) of \(f'(x)=0\) is given by
This implies that f is increasing on \((0,x_{0})\) and decreasing on \((x_{0},\infty )\). By a simple computation, it follows that
By (2.2) and the assumption \(E(\psi _{0})< f(x_{0})\), it follows that
If \(\|\nabla \psi _{0}\|_{L^{2}}< x_{0}\), it follows from the continuity argument that \(\|\nabla \psi (t)\|_{L^{2}}< x_{0}\) for all \(t\in [0,T ^{*})\). Therefore, the solution \(\psi (t)\) of (1.1) exists globally.
If \(\|\nabla \psi _{0}\|_{L^{2}}>x_{0}\), we deduce from the continuity argument that \(\|\nabla \psi (t)\|_{L^{2}}>x_{0}\) for all \(t\in [0,T ^{*})\). We choose \(\delta >0\) small enough so that
This implies that
Thus, we deduce from (2.2), (2.5) and (4.22) that
Therefore, by the classical argument for Schrödinger equations, the solution \(\psi (t)\) of (1.1) blows up. □
Theorem 4.4
Let\(\lambda _{1}=-1\), \(\lambda _{2}=1\), \(1+\frac{\alpha +2}{N}< p_{2}<1+\frac{Np _{1}+2\alpha }{2N}\), and\(E(\psi _{0})< \frac{Np_{2}-N-\alpha -2}{2(Np _{2}-N-\alpha )}x_{0}^{2}\), and\(\psi \in C([0,T^{*}),H^{1})\)be a solution of (1.1). If\(\|\nabla \psi _{0}\|< x_{1}\), then the solution\(\psi (t)\)of (1.1) exists globally; If\(\|\nabla \psi _{0}\|>x _{1}\), then the solution\(\psi (t)\)of (1.1) blows up, where\(x_{1}\)is defined by (4.25).
Proof
Applying (2.7), it follows that
where the \(C_{*}\) are defined by (2.8) and
By a simple computation, we find that the unique positive solution \(x_{1}\) of \(f'(x)=0\) is given by
This implies that f is increasing on \((0,x_{1})\) and decreasing on \((x_{1},\infty )\). By a simple computation, it follows that
By (2.2) and the assumption \(E(\psi _{0})< f(x_{1})\), it follows that
If \(\|\nabla \psi _{0}\|_{L^{2}}< x_{1}\), it follows from the continuity argument that \(\|\nabla \psi (t)\|_{L^{2}}< x_{1}\) for all \(t\in [0,T ^{*})\). Therefore, the solution \(\psi (t)\) of (1.1) exists globally.
If \(\|\nabla \psi _{0}\|_{L^{2}}>x_{1}\), we deduce from the continuity argument that \(\|\nabla \psi (t)\|_{L^{2}}>x_{1}\) for all \(t\in [0,T ^{*})\). We can choose \(\delta >0\) small enough so that
This implies that
Thus, we deduce from (2.2), (2.5) and (4.26) that
Therefore, by the classical argument for Schrödinger equations, the solution \(\psi (t)\) of (1.1) blows up. □
5 Conclusions
In this paper, we obtain some sharp thresholds of blow-up and global existence for the nonlinear Schrödinger–Choquard equation. We firstly obtain some sufficient conditions about existence of blow-up solutions. Due to the loss of scaling invariance for this equation, we derive some sharp thresholds of blow-up and global existence by constructing some new estimates. In particular, we prove the global existence for this equation with critical mass in the \(L^{2}\)-critical case.
References
Bonanno, C., d’Avenia, P., Ghimenti, M., Squassina, M.: Soliton dynamics for the generalized Choquard equation. J. Math. Anal. Appl. 417, 180–199 (2014)
Cazenave, T.: Semilinear Schrödinger Equations. Courant Lecture Notes in Mathematics, vol. 10. NYU, CIMS, Am. Math. Soc., Providence (2003)
Chen, J., Guo, B.: Strong instability of standing waves for a nonlocal Schrödinger equation. Phys. D, Nonlinear Phenom. 227, 142–148 (2007)
Dinh, D., Feng, B.: On fractional nonlinear Schrödinger equation with combined power-type nonlinearities. Discrete Contin. Dyn. Syst. 39, 4565–4612 (2019)
Feng, B.: Sharp threshold of global existence and instability of standing wave for the Schrödinger–Hartree equation with a harmonic potential. Nonlinear Anal., Real World Appl. 31, 132–145 (2016)
Feng, B.: On the blow-up solutions for the fractional nonlinear Schrödinger equation with combined power-type nonlinearities. Commun. Pure Appl. Anal. 17, 1785–1804 (2018)
Feng, B.: On the blow-up solutions for the nonlinear Schrödinger equation with combined power-type nonlinearities. J. Evol. Equ. 18, 203–220 (2018)
Feng, B., Yuan, X.: On the Cauchy problem for the Schrödinger–Hartree equation. Evol. Equ. Control Theory 4, 431–445 (2015)
Feng, B., Zhang, H.: Stability of standing waves for the fractional Schrödinger–Choquard equation. Comput. Math. Appl. 75, 2499–2507 (2018)
Feng, B., Zhang, H.: Stability of standing waves for the fractional Schrödinger–Hartree equation. J. Math. Anal. Appl. 460, 352–364 (2018)
Genev, H., Venkov, G.: Soliton and blow-up solutions to the time-dependent Schrödinger–Hartree equation. Discrete Contin. Dyn. Syst., Ser. S 5, 903–923 (2012)
Guo, Q., Zhu, S.: Sharp threshold of blow-up and scattering for the fractional Hartree equation. J. Differ. Equ. 264, 2802–2832 (2018)
Holmer, J., Roudenko, S.: A sharp condition for scattering of the radial 3d cubic nonlinear Schrödinger equation. Commun. Math. Phys. 67, 282–435 (2008)
Leng, L., Li, X., Zheng, P.: Sharp criteria for the nonlinear Schrödinger equation with combined nonlinearities of power-type and Hartree-type. Appl. Anal. 96, 2846–2851 (2017)
Li, X., Zhang, J., Lai, S., Wu, Y.: The sharp threshold and limiting profile of blow-up solutions for a Davey–Stewartson system. J. Differ. Equ. 250, 2197–2226 (2011)
Saanouni, T.: Remarks on the inhomogeneous fractional nonlinear Schrödinger equation. J. Math. Phys. 57, 081503 (2016)
Saanouni, T.: A note on the fractional Schrödinger equation of Choquard type. J. Math. Anal. Appl. 470, 1004–1029 (2019)
Sulem, C., Sulem, P.L.: The Nonlinear Schrödinger Equation. Springer, Berlin (1999)
Weinstein, M.I.: Nonlinear Schrödinger equations and sharp interpolation estimates. Commun. Math. Phys. 87, 567–576 (1983)
Yang, L., Li, X., Wu, Y., Louis, C.: Global well-posedness and blow-up for the Hartree equation. Acta Math. Sci. Ser. B Engl. Ed. 37, 941–948 (2017)
Zhang, J.: Sharp conditions of global existence for nonlinear Schrödinger and Klein–Gordon equations. Nonlinear Anal. 48, 191–207 (2002)
Zhang, J., Zhu, S.: Sharp blow-up criteria for the Davey–Stewartson system in \(\mathbb{R}^{3}\). Dyn. Partial Differ. Equ. 8, 239–260 (2011)
Zhu, S.: Blow-up solutions for the inhomogeneous Schrödinger equation with \(L^{2}\) supercritical nonlinearity. J. Math. Anal. Appl. 409, 760–776 (2014)
Zhu, S.: On the Davey–Stewartson system with competing nonlinearities. J. Math. Phys. 57, 031501 (2016)
Acknowledgements
The author would like to thank the referees for their pertinent comments and valuable suggestions.
Availability of data and materials
Not applicable.
Funding
This paper is supported by the National Natural Science Foundation of China (No. 11601435).
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that no competing interests exist.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Feng, B. Sharp thresholds of blow-up and global existence for the Schrödinger equation with combined power-type and Choquard-type nonlinearities. Bound Value Probl 2019, 195 (2019). https://doi.org/10.1186/s13661-019-01310-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-019-01310-6