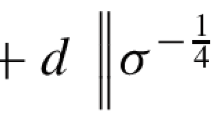Abstract
We prove that every GNS-symmetric quantum Markov semigroup on a finite dimensional matrix algebra satisfies a modified log-Sobolev inequality. In the discrete time setting, we prove that every finite dimensional GNS-symmetric quantum channel satisfies a strong data processing inequality with respect to its decoherence free part. Moreover, we establish the first general approximate tensorization property of the relative entropy. This extends the famous strong subadditivity of the quantum entropy (SSA) of two subsystems to the general setting of two subalgebras. All three results are independent of the size of the environment and hence satisfy the tensorization property. They are obtained via a common, conceptually simple method for proving entropic inequalities via spectral or \(L_2\)-estimates. As an application, we combine our results on the modified log-Sobolev inequality and approximate tensorization to derive tight bounds for local generators.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Results
Relative entropy is a fundamental information measure that has been widely used in probability, statistics and information theory. It was first introduced by Kullback and Leibler [52] for probability distributions (also called KL-divergence), and later extended by Umegaki [79] to the noncommutative setting for quantum states. For two quantum states with density matrices \(\rho \) and \(\sigma \), the relative entropy of \(\rho \) with respect to \(\sigma \) is defined as
where \({\text {tr}}\) is the matrix trace. When \(\rho \) and \(\sigma \) share a same eigenbasis, (1) recovers the KL-divergence for two (discrete) probability densities. In both classical and quantum cases, \(D(\rho \Vert \sigma )\) measures how well the classical or quantum state \(\rho \) can be distinguished from \(\sigma \) by statistical or quantum-mechanical experiments [13, 43, 65]. In this work, we study several related inequalities of the quantum relative entropy which have direct applications in quantum information theory and quantum many-body systems. Some of our results also yield new insights in the classical cases for probability distributions.
1.1 Modified Logarithmic Sobolev Inequality
The logarithmic Sobolev inequality is a functional inequality that was first introduced by Gross in his study of quantum field theory [40] as an equivalent formulation of hypercontractivity [64]. Over the past several decades, logarithmic Sobolev inequalities have been intensively studied for their applications in analysis, probability and information theory (see e.g. the [41, 54] and the references therein). Let \((\Omega ,\mu )\) be a probability space and \(({\mathcal {T}}_t:L_\infty (\Omega ,\mu )\rightarrow L_\infty (\Omega ,\mu ))_{t\ge 0}\) be a Markov semigroup with the unique invariant measure \(\mu \). The semigroup \(({\mathcal {T}}_t)_{t\ge 0}\) is said to satisfy the \(\alpha \)-logarithmic Sobolev inequality (in short, \(\alpha \)-LSI) for \(\alpha >0\) if
for any real function f in the domain of \({\mathcal {L}}\), where \({\mathcal {L}}\) is the generator of the semigroup, i.e. \({\mathcal {T}}_t=e^{t{\mathcal {L}}}\). It is well-known that the logarithmic Sobolev inequality admits a (weaker) variant formulation, called modified logarithmic Sobolev inequality, which is directly related to the relative entropy. The semigroup \(({\mathcal {T}}_t)_{t\ge 0}\) is said to satisfy the \(\alpha \)-modified logarithmic Sobolev inequality (in short, \(\alpha \)-MLSI ) for \(\alpha >0\) if, for any probability density \(f\ge 0\) with \(\int f \mathrm{d}\mu =1\),
The left hand side is the (classical) entropy functional \(\text {Ent}(f):=\int f\ln f \mathrm{d}\mu \). The \(\alpha \)-MLSI (2) is equivalent to
which means that the entropy of the system decays exponentially. This entropic convergence property is a powerful tool to derive mixing times for the semigroup.
The main purpose of this work is to study modified logarithmic Sobolev inequalities for quantum Markov semigroups. Quantum Markov semigroups are noncommutative generalizations of Markov semigroups where the underlying function spaces are replaced by matrix algebras or operator algebras. Let \({\mathcal {H}}\) be a finite dimensional Hilbert space and let \({\mathcal {B}}({\mathcal {H}})\) be the bounded operators on \({\mathcal {H}}\). A quantum Markov semigroup (QMS) \(({\mathcal {P}}_t: {\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}}))_{t\ge 0}\) is a continuous semigroup of completely positive trace preserving maps. Such continuous-time families of quantum channels model the Markovian evolution of dissipative open quantum systems. In recent years, the connection between logarithmic Sobolev inequalities and other functional inequalities, such as hypercontractivity, Poincaré inequality and transport cost inequalities, have been largely extended to quantum Markov semigroup (see [21, 22, 29, 50, 66, 74]). Some of these works found direct applications in quantum information and quantum computational complexity (see e.g. [11, 16, 63]).
Despite the rich connections to many aspects of quantum Markov processes, logarithmic Sobolev inequalities in the quantum framework are missing one key property—the tensorization property. For two classical Markov semigroups \(({\mathcal {S}}_t)_{t\ge 0}\) and \(({\mathcal {T}}_t)_{t\ge 0}\), if each semigroup satisfies \(\alpha \)-MLSI, then \(({\mathcal {S}}_t\otimes {\mathcal {T}}_t)_{t\ge 0}\) also satisfies \(\alpha \)-MLSI [14] with the same constant \(\alpha \). Tensorization is a powerful property that allow us to obtain MLSI for large, composite systems in terms of the dynamics on smaller subsystems, which is a technique that was already used by Gross in his very first work on the logarithmic Sobolev inequality. Nevertheless, the tensor stability of MLSI fails for general (non-ergodic) quantum Markov semigroups [17, Proposition 4.21]. The lack of tensorization property is a common difficulty in quantum information (see e.g. the super-additivity of the channel capacity [42, 75]). On the other hand, it was discovered in [37] that the tensorization property is satisfied with a stronger definition of MLSI: a quantum Markov semigroup \(({\mathcal {P}}_t: {\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}}))_{t\ge 0}\) is said to satisfy the \(\alpha \)-complete modified logarithmic Sobolev inequality (in short, \(\alpha \)-CMLSI) if for any \(n\ge 1\), the amplification \({\mathcal {P}}_t\otimes {\text {id}}_{n}\) satisfies \(\alpha \)-MLSI, where \({\text {id}}_{n}\) is the identity map on an n-dimensional quantum system. Our first main result shows that such tensor stable modified log-Sobolev inequalities generically hold in finite dimensions.
Theorem 1.1
Let \(({\mathcal {P}}_t)_{t\ge 0}\) be a quantum Markov semigroup and assume \(({\mathcal {P}}_t)_{t\ge 0}\) is GNS-symmetric to some full-rank invariant state \(\sigma \). Denote \(\displaystyle E_*=\lim \nolimits _{t\rightarrow \infty }{\mathcal {P}}_{t*}\) as the limit of the pre-adjoint map, which gives the projection onto the fixed point space of \({\mathcal {P}}_{t*}\). Then for all \(n\in {\mathbb {N}}\) and all states \(\rho \in {\mathcal {B}}({\mathcal {H}}\otimes {\mathbb {C}}^n)\),
where \(D(\cdot \Vert \cdot )\) denotes the relative entropy and the constant \(\alpha \) satisfies
Here \(\lambda \) is the spectral gap of the generator \({\mathcal {L}}\) of the QMS and \(C_{{\text {cb}}}(E_*)\) is the complete Pimsner–Popa index of the map \(E_*\).
We refer to Section 3 for details concerning the spectral gap and GNS symmetry, and to Section 2 for the index \(C_{{\text {cb}}}(E_*)\). We emphasise that Theorem 1.1 asserts that there exists an exponential decay rate \(\alpha \) for the relative entropy independent of \(n\in {\mathbb {N}}\), and which holds not only for the semigroup \(({\mathcal {P}}_t)_{t\ge 0}\) itself but also for its amplifications \(({\mathcal {P}}_t\otimes {\text {id}}_{n})_{t\ge 0}\) coupling it to an environment system \({\mathbb {C}}^n\). This definition was introduced in [37], and proved to satisfy the tensorization property: whenever two quantum Markov semigroups satisfy \(\alpha \)-CMLSI, their tensor product satisfies \(\alpha \)-CMLSI. Later, Li, Junge and LaRacuente [56] proved that the heat semigroup of Riemannian manifolds of positive curvature and all classical (continuous-time) finite Markov chains satisfy CMLSI. Using the noncommutative curvature lower bound introduced in [21, 29], CMLSI was obtained for heat semigroup on all compact Riemannian manifolds and some examples from operator algebras [17, 18]. Despite the constant progress on this topic in the recent years, the problem of the positivity of the CMLSI constant for finite dimensional QMS has been left open. Here, Theorem 1.1 finally provides a positive answer to the question via a relatively simple proof.
1.2 Strong Data Processing Inequality
One key property behind the widespread applications of the quantum relative entropy is the data processing inequality. It states that the relative entropy is non-increasing under the action of a quantum channel \(\Phi \) (complete positive trace perserving map). Namely, for all states \(\rho \) and \(\sigma \),
As the relative entropy is a measure of distinguishability, the data processing inequality asserts that two states can not become more distinguishable after applying a same channel to them. First proved by Lindblad [60] and Uhlmann [78], the data processing inequality for the relative entropy has been largely refined and improved in recent years (e.g. [23, 48, 62]). As discussed in [12, 44, 55, 63], one natural refinement of the inequality consists in asking when the contraction of the relative entropy observed in (4) can be strict, i.e. whether there exists a constant \(c<1\) such that
This question has been intensively studied for classical channels and more general entropies (see e.g. [3, 26, 32, 33, 59, 71, 73] and the references therein) under the name strong data processing inequality (SDPI). In the quantum setting, despite progresses on some special cases [44, 63], the existence of a contractive coefficient for general channels in (5) remains open. Our second main result is the following strong data processing inequality as a discrete time analog of Theorem 1.1:
Theorem 1.2
(c.f. Corollary 4.3) Let \(\Phi :{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}})\) be a quantum channel. Suppose \(\Phi \) is GNS-symmetric to a full-rank invariant state \(\sigma =\Phi (\sigma )\). Then there exists an explicit constant \(c<1\) such that for any \(n\in {\mathbb {N}}\) and all bipartite states \(\rho \in {\mathcal {D}}({\mathcal {H}}\otimes {\mathbb {C}}^n)\),
where \(E_*\) is the projection onto the decoherence-free space of \(\Phi \).
We refer to Section 4 for the definition of \(E_*\) and remark that the constant c explicitly depends on the index \(C_{{\text {cb}}}(E_*)\) and an \(L_2\)-condition \(\lambda :=\parallel \! \Phi -E_*:L_2\rightarrow L_2 \! \parallel _{}\). The above inequality (CSDPI) implies a discrete time entropy decay. Moreover, the inequality (CSDPI) again gives a uniform control for all amplifications \(\Phi \otimes {\text {id}}_n\), which is the reason that we call it complete strong data processing inequality (CSDPI). These improvements over the standard data processing inequality have applications to quantum state preparation and quantum channel capacities [9, 19]. For instance, similarly to CMLSI, CSDPI admits tensorization: if two quantum channels \(\Phi \) and \(\Psi \) satisfy CSDPI with contraction coefficient \(c<1\), so does \(\Phi \otimes \Psi \). Also, thanks to its “completeness”, Theorem 1.2 implies a concrete estimate on the convergence \(\Phi ^n \rightarrow \Phi ^n\circ E_*\) in terms of the diamond norm.
1.3 Approximate Tensorization of Relative Entropy
The data processing inequality is closely related to another celebrated inequality in quantum information theory, namely the strong subadditivity (SSA). SSA can be equivalently stated in terms of relative entropies as follows: for any tripartite state \(\rho ^{ABC}\),
here \(\frac{\mathbbm {1}_{AB}}{d_{AB}}\) is the completely mixed state on AB whereas \(\rho ^C\) denotes the reduced density on C (and similarly for the other terms). SSA was long known in classical information theory, and proved by Lieb and Ruskai [58] for the quantum entropy. Later Petz [68] proved SSA in a very general setting: given any four matrix subalgebras \({\mathcal {N}}\subset {\mathcal {N}}_1,{\mathcal {N}}_2\subset {\mathcal {M}}\), and corresponding projections \(E_1,\,E_2,\,E_{\mathcal {N}}\) from \({\mathcal {M}}\) onto \({\mathcal {N}}_1,\,{\mathcal {N}}_2\) and \({\mathcal {N}}\), for all states \(\rho \) on \({\mathcal {M}}\), it holds that
as long as \(E_1\circ E_2=E_2\circ E_1=E_{\mathcal {N}}\). This last commutation relation is usually referred to as a “commuting square” condition and was introduced by Popa [72].
Although the commuting square gives a nice characterization of SSA, SSA-type inequalities are also desired when the “commuting square” condition is not fully satisfied. For instance, in the context of classical lattice spin systems, where the projections are conditional expectations onto different regions of the lattice with respect to a given Gibbs measure, the commuting square condition corresponds to the infinite temperature regime [8]. To assess the finite temperature regime, (6) has to be modified in the following way [24, 27]: there exists a constant \(c >1\) such that, for all states \(\rho \),
where the constant c is some measure of the violation of the commutation relation \(\Vert E_1\circ E_2-E_{\mathcal {N}}\Vert \) in some appropriate norm. This inequality, called approximate tensorization of the relative entropy, was used in the classical case (i.e. when all algebras are commutative) in the study of logarithmic Sobolev inequalities for lattice spin system [24]. In the quantum setting, a weaker bound to (7) was derived in [8] with a further additive error term vanishing on classical states. However, the question of finding general bounds like (7) without the additive error term was left unresolved. Our third main theorem answers this question.
Theorem 1.3
Let \({\mathcal {N}}\subset {\mathcal {N}}_1,{\mathcal {N}}_2\subset {\mathcal {M}}\) be four finite dimensional von Neumann algebras. Let \(E_1,\,E_2,\,E_{\mathcal {N}}\) be the corresponding projections from \({\mathcal {M}}\) onto \({\mathcal {N}}_1,\,{\mathcal {N}}_2\) and \({\mathcal {N}}\) such that \(E_{\mathcal {N}}\circ E_{1}=E_{\mathcal {N}}\circ E_{2}=E_{\mathcal {N}}\). Then there exists an explicit constant \(c_{{\text {cb}}}\) such that, for any \(n\in {\mathbb {N}}\) and all states \(\rho \in {\mathcal {M}}\otimes {\mathcal {B}}({\mathbb {C}}^n)\), we have
We refer to Theorems 5.1 and Corollary 5.4 for concrete estimates on the constant \(c_{{\text {cb}}}\). All of the three results above rely on a common conceptually simple tool, namely a two-sided estimate of the relative entropy via the so-called Bogoliubov-Kubo-Mori Fisher information (see Lemma 2.2 in Section 2 for more details). The Bogoliubov-Kubo-Mori Fisher information is closely related to a special case of monotone Riemannian metric on the state space studied in [55, 69] and a quantum \(\chi _2\)-divergence studied in [82]. This allows us to approach each of the three above entropic inequalities via corresponding spectral gap conditions. Given the simplicity of our approach, we believe it will also prove useful in the study of other entropic inequalities.
1.4 Applications and Examples
Based on the above results, we exploit the approximate tensorization estimate from Theorem 1.3 to get tighter bounds on the optimal CMLSI constant for quantum Markov semigroups (QMS) relevant to the communities of mathematical physics and quantum information theory. For a QMS \(({\mathcal {P}}_t=e^{t{\mathcal {L}}})_{t\ge 0}\) with the generator \({\mathcal {L}}\), we denote by \(\alpha _{{\text {CMLSI}}}({\mathcal {L}})\) the largest constant \(\alpha \) satsisfying (CMLSI) in Theorem 1.1. In Section 6, we restrict our analysis to the class of symmetric QMS, that is QMS symmetric to the trace inner product or equivalently the maximally mixed state. The generators of these semigroups admit a simple form as a sum of double commutators with self-adjoint operators \(\{a_k\}\):
Using approximate tensorization, we obtain the following improved CMLSI constant for symmetric QMS:
Theorem 1.4
(c.f. Corollary 6.3) For a symmetric generator \({\mathcal {L}}\) given as above,
where \(d_{\mathcal {H}}\) is the dimension of the underlying Hilbert space, and \(\lambda :=\min _k \lambda ({\mathcal {L}}_{a_k})\) is the minimum spectral gap of any of the generators \({\mathcal {L}}_{a_k}(\rho )=[a_k,[a_k,\rho ]]\).
Note that the above bound is asymptotically better than Theorem 1.1 because the index is \(C_{{\text {cb}}}(E_*)=d_{\mathcal {H}}^2\) for primitive semigroups.
Example 1.5
Consider the quantum Markov semigroups induced by sub-Laplacians of the special unitary group \({\text {SU}}(2)\) on its irreducible representations:
Here \(X_m\) (resp. \(Y_m\)) is the spin-\(\frac{m-1}{2}\) representation of the Pauli X matrix (resp. Y-matrix). In contrast to the induced semigroup of the standard Laplace-Beltrami operator \(\Delta =X^2+Y^2+Z^2\) the CMLSI constant of \({\mathcal {L}}^H_m\) is not accessible from the corresponding classical Markov semigroup due to the lack of curvature lower bound in the sub-Riemannian setting. With help of numerics, we obtain that
uniformly for all \(m\ge 2\).
In Section 6.2, we focus on symmetric semigroups which bare a locality structure inherited from a graph. More precisely, given a finite graph \(G=(V,E)\), we consider the n-fold tensor product \({\mathcal {H}}_V:=\bigotimes _{v\in V}{\mathcal {H}}_v\) of a finite dimensional local Hilbert space \({\mathcal {H}}\), namely, an n-qudit system for \(d=\dim ({\mathcal {H}})\). The Lindblad operators are supported on the edges \(e\in E\) of the graph
where for any edge \(e\in (v,w)\in E\) and any \(j\in J^{(e)}\), the local Lindblad operator \(L^{(e)}_j\) acts trivially on subsystems other than \({\mathcal {H}}_{v}\otimes {\mathcal {H}}_{w}\). We call (10) a subsystem Lindbladian, which means that the global dynamics consists of local interactions on subsystems of adjacent vertices. This gives a general model of 2-local interacting quantum lattice spin systems. Using approximate tensorization again, we provide a lower bounds on the CMLSI constant for the global Lindbladian \({\mathcal {L}}_G\) based on the local Lindbladians \({\mathcal {L}}_e\).
Theorem 1.6
(c.f. Theorem 6.6) Let \(G=(V,E)\) be a finite, connected graph of maximum degree \(\gamma \) and let \({\mathcal {L}}_G\) be a symmetric subsystem Lindbladian of the form (10). Denote by \(E_e\) the projection onto the kernel of the local Lindbladian \({\mathcal {L}}_e\). Then
where \(\alpha _{{\text {CMLSI}}}({\mathcal {L}}_e)\) is the \({\text {CMLSI}}\) constant of \({\mathcal {L}}_e\), and \(\lambda ({\widetilde{{\mathcal {L}}}}_G)\) is the spectral gap of the generator \({\widetilde{{\mathcal {L}}}}_G:=\sum _{e\in E}E_e-{\text {id}}\).
Here the index C can be chosen as either the complete Pimsner–Popa index [70] of the algebra \({\mathcal {N}}\) of fixed points of the evolution, or the inverse minimal eigenvalue of the Choi state of the projection map \(\displaystyle E_G:=\lim _{t\rightarrow \infty }e^{t{\mathcal {L}}_G}\). The index C can be thought of as what replaces the size of the graph in the case of classical graph Laplacians. In particular, for expander graphs, our bound gives
We exemplify our bound on the random transposition model.
Example 1.7
(Random transposition) Motivated by the classical random transposition model in [14, 35], we introduce the quantum nearest neighbor random transposition via the local Lindbladian on an edge \((i,j)\in E\) given by
where \(S_{i,j}:{{\mathcal {H}}_{i}\otimes {\mathcal {H}}_{j}}\rightarrow {\mathcal {H}}_{i}\otimes {\mathcal {H}}_{j}\) is the swap unitary gate between vertex i and j. Then the global Lindbladian \({\mathcal {L}}_G^{{\text {NNRT}}}:= \sum _{e\in E}{\mathcal {L}}_{e}\) is generated by local random swaps on \(|V|=n\) qudits. In this case, we find that
where \(\lambda ({\mathcal {L}}_G^{{\text {NNRT}}})\) is the spectral gap and the factorial n! is the size of the permutation group \({\mathcal {S}}_n\). This presents an exponential improvement over the bounds from Theorem 1.1, where the constant was controlled by the inverse size of the group \((n!)^{-1}\).
The rest of the paper is organized as follows: in the next section, we review some preliminary definitions and prove our key lemma. Section 3 is devoted to the proof of Theorem 1.1, which is our first main result on the complete modified log-Sobolev inequality. In Section 4, we prove the complete strong data processing inequality of Theorem 1.2. The approximate tensorization results are discussed in Section 5. Section 6 provides the improved CMSLI constant of Theorem 1.4 for symmetric quantum Markov semigroups. In Section 6.2, we discuss examples from subsystem Lindbladians. We end the paper with some discussion on questions that remain open. We remark that although we restrict our discussion to finite dimensions, the general results in Sections 3, 4, and 5 can be extended to (trace) symmetric maps in the setting of finite von Neumann algebras, as long as the index \(C_{{\text {cb}}}(E)\) is finite and the corresponding spectral gap condition is satisfied. For more examples and applications, we invite the interested reader to consult a longer version of the present article available at [39].
Notations. We denote \({\mathcal {H}}\) as a Hilbert space, \({\mathcal {B}}({\mathcal {H}})\) as the bounded operators on \({\mathcal {H}}\), and \({\mathcal {M}}\subset {\mathcal {B}}({\mathcal {H}})\) as a von Neumann subalgebra. We write “\({\text {tr}}\)” for the standard matrix trace, \(\langle \cdot ,\cdot \rangle _{{\text {HS}}}\) for the trace inner product and \(\parallel \! \cdot \! \parallel _{2}\) for the Hilbert–Schmidt norm. The corresponding Hilbert–Schmidt space (resp. trace class operators) is denoted by \({\mathcal {T}}_2({\mathcal {H}})\) (resp. \({\mathcal {T}}_1({\mathcal {H}})\)). Operators will be denoted by capital letters \(A,X,Y,\ldots \), and states or density operators are denoted by Greek letters \(\rho ,\sigma ,\omega ,\ldots \). Sometimes we will also use lowercase letters to emphasize their belonging to a subalgebra. We write \(A^\dagger \) for the adjoint of an operator \(A\in {\mathcal {B}}({\mathcal {H}})\), and \(\Phi ^*\) (or \(\Phi _*\)) for the adjoint (or pre-adjoint) of a map \(\Phi :{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}})\). The identity operator on \({\mathcal {H}}\) is denoted as \(\mathbbm {1}_{{\mathcal {H}}}\) and the identity map on a von Neumann subalgebra \({\mathcal {M}}\subseteq {\mathcal {B}}({\mathcal {H}})\) is \({\text {id}}_{{\mathcal {M}}}\). We also denote the dimension of \({\mathcal {H}}\) by \(d_{\mathcal {H}}={\text {dim}}({\mathcal {H}})\). Given two maps \(\Phi ,\Psi :{\mathcal {M}}\rightarrow {\mathcal {M}}\) on a von Neumann subalgebra \({\mathcal {M}}\subseteq {\mathcal {B}}({\mathcal {H}})\), we write \(\Phi \le _{{\text {cp}}} \Psi \) if \(\Psi -\Phi \) is completely positive. Given a subalgebra \({\mathcal {N}}\subset {\mathcal {M}}\), we will use \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) for a conditional expectation onto \({\mathcal {N}}\) and write \(C(E_{{\mathcal {N}}})\) for the corresponding Pimsner–Popa index (see Section 2). We will also write \(C(E_{{\mathcal {N}}})=C_\tau ({\mathcal {M}}:{\mathcal {N}})\) where \(\tau \) is the special operator (17) uniquely determined by \(E_{{\mathcal {N}}}\). When \(E_{{\mathcal {N}}}\) is trace preserving and \(\tau =\frac{1}{d_{H}}\), we omit \(\tau \) and write the original Pimsner–Popa index as \(C({\mathcal {M}}:{\mathcal {N}})\).
2 Preliminaries
2.1 Relative Entropy and Conditional Expectation
Throughout the paper, we will consider \({\mathcal {H}}\) to be a finite dimensional Hilbert space. We say that an operator \(\rho \in {\mathcal {B}}({\mathcal {H}})\) is a state (or density operator) if \(\rho \ge 0\) and \({\text {tr}}(\rho )=1\). We denote by \({\mathcal {D}}({\mathcal {H}})\) the set of states on \({\mathcal {H}}\). A quantum channel \(\Phi : {\mathcal {T}}_1({\mathcal {H}})\rightarrow {\mathcal {T}}_1({\mathcal {H}})\) (or more generally, \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\)) is a completely positive trace preserving map. With slight abuse of notation, we will often write \(\Psi (\rho ):=(\Psi \otimes {\text {id}}) (\rho )\) for a bipartite state \(\rho \in {\mathcal {D}}({\mathcal {H}}\otimes {\mathbb {C}}^n)\) and a quantum channel \(\Psi :{\mathcal {T}}_1({\mathcal {H}})\rightarrow {\mathcal {T}}_1({\mathcal {H}})\). For two states \(\rho \) and \(\sigma \), their relative entropy is defined as
where \({{\,\mathrm{supp}\,}}(\rho )\) (resp. \({{\,\mathrm{supp}\,}}(\sigma )\)) is the support projection of \(\rho \) (resp. \(\sigma \)).
Let \({\mathcal {N}}\subseteq {\mathcal {M}}\subseteq {\mathcal {B}}({\mathcal {H}})\) be two von Neumann subalgebras. Recall that a conditional expectation onto \({\mathcal {N}}\) is a completely positive unital map \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) satisfying that
-
(i)
for all \(a \in {\mathcal {N}}\), \(E_{\mathcal {N}}(a)=a\)
-
(ii)
for all \(a,b\in {\mathcal {N}},X\in {\mathcal {B}}({\mathcal {H}})\), \(E_{\mathcal {N}}(aXb)=aE_{\mathcal {N}}(X)b\).
We denote by \(E_{{\mathcal {N}}*}\) its adjoint map with respect to the trace inner product, i.e.
For a state \(\rho \), the relative entropy with respect to the conditional expectation \(E_{{\mathcal {N}}*}\) is given by
where the infimum is always attained by \(E_{{\mathcal {N}}*}(\rho )\). We note that \(D(\rho \Vert E_{{\mathcal {N}}*}(\rho ))\) depends not only on the subalgebra \({\mathcal {N}}\), but also on the conditional expectation \(E_{{\mathcal {N}}}\), which is not unique for a subalgebra \({\mathcal {N}}\). Indeed, for any \(\sigma \) satisfying \(E_{{\mathcal {N}}*}(\sigma )=\sigma \), we have the chain rule (see [46, Lemma 3.4])
Hence the infimum is attained if and only if \(D(E_{{\mathcal {N}}*}(\rho )\Vert \sigma )=0\). More explicitly, a finite dimensional von Neumann (sub)algebra can always be expressed as a direct sum of matrix algebras with multiplicity, i.e.
Denote \(P_i\) as the projection onto \({\mathcal {H}}_i\otimes {\mathcal {K}}_i\). There exists a family of density operators \(\tau _i\in {\mathcal {D}}({\mathcal {K}}_i)\) such that
where \({\text {tr}}_{{\mathcal {K}}_i}\) is the partial trace with respect to \({\mathcal {K}}_i\). A state \(\sigma \) satisfies \(E_{{\mathcal {N}}*}(\sigma )=\sigma \) if and only if
for some density operators \(\sigma _i\in {\mathcal {D}}({\mathcal {H}}_i)\) and a probability distribution \(\{p_i\}_{i=1}^n\). We denote \({\mathcal {D}}(E_{\mathcal {N}}):=\{\sigma \in {\mathcal {D}}({\mathcal {H}}) | \sigma =E_{{\mathcal {N}}*}(\sigma )\}\) as the subset of states that are invariant under \(E_{{\mathcal {N}}*}\). For any \(\sigma \in {\mathcal {D}}(E_{\mathcal {N}})\) and all \(X\in {\mathcal {M}}\),
2.2 Subalgebra Index and Max-relative Entropy
Let \({\mathcal {M}}\subset {\mathcal {B}}({\mathcal {H}})\) be a finite dimensional von Neumann algebra and let \({\mathcal {N}}\subset {\mathcal {M}}\) be a subalgebra of \({\mathcal {M}}\). The trace preserving conditional expectation \(E_{{\mathcal {N}},{\text {tr}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) is defined so that, for any \( X\in {\mathcal {M}}\) and \( Y\in {\mathcal {N}}\),
\(E_{{\mathcal {N}},{\text {tr}}}\) is self-adjoint and corresponds to taking \(\displaystyle \tau _i=d_{{\mathcal {K}}_i}^{-1}\mathbbm {1}_{{\mathcal {K}}_i}\) in (13). We recall the definition of the index associated to the algebra inclusion \({\mathcal {N}}\subset {\mathcal {M}}\),
where the supremum in \(C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\) is taken over all finite dimensional matrix algebras \({\mathbb {M}}_n\). The index \(C({\mathcal {M}}:{\mathcal {N}})\) was first introduced by Pimsner and Popa in [70] for the connection to subfactor index and Connes entropy, and the completely bounded version \(C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\) was studied in [38]. In particular, it was proved in [38, Theorem 3.9] that \(C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\) is indeed some completely bounded norm (see (69) in “Appendix B”).
These indices are closely related to the notion of maximal relative entropy. Recall that for two states, \(\rho ,\omega \), their maximal relative entropy is [28]
Indeed,
For all finite dimensional inclusion \({\mathcal {N}}\subset {\mathcal {M}}\), the index \(C({\mathcal {M}}:{\mathcal {N}})\) is explicitly calculated in [70, Theorem 6.1] (hence also for \(C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\)). In particular, for \({\mathcal {M}}={\mathcal {B}}({\mathcal {H}})\) and \({\mathcal {N}}=\bigoplus _{i=1}^n {\mathcal {B}}({\mathcal {H}}_i)\otimes {\mathbb {C}}\mathbbm {1}_{{\mathcal {K}}_i}\),
For example, if we take \({\mathcal {D}}\subset {\mathcal {B}}({\mathcal {H}})\) to be the subalgebra of diagonal matrices and \({\mathbb {C}}\) as the multiple of identity
In this paper, we will also consider the index for a general conditional expectation \(E_{{\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) (see e.g [51] for more information). For a conditional expectation \(E_{{\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) onto \({\mathcal {N}}\), we define
Here, we recall that \({\mathbb {M}}_n\) is the n-dimensional matrix algebra and \(E_{{\mathcal {N}}}\otimes {\text {id}}_{{\mathbb {M}}_n}\) is a conditional expectation from \({\mathcal {M}}\otimes {\mathbb {M}}_n\rightarrow {\mathcal {N}}\otimes {\mathbb {M}}_n\). Note that given the subalgebra \({\mathcal {N}}\), \(E_{{\mathcal {N}}}\) and \(E_{{\mathcal {N}}*}\) are uniquely determined by any invariant state \(\sigma \in {\mathcal {D}}(E_{{\mathcal {N}}})\), or equivalently the densities \(\{\tau _i\}\) in (13). Indeed, denoting
we have
In particular, \(E_{{\mathcal {N}}}\) is faithful if and only if \(\tau \) is full-rank. By definition, the Pimsner–Popa index \(C({\mathcal {M}}:{\mathcal {N}})\) is the special case for the trace perserving condition expectation \(C(E_{{\mathcal {N}},{\text {tr}}})\). In the later discussion, we will often use the alternative notation
Since \(\tau \) commutes with \({\mathcal {N}}\),
where \(\mu _{{\text {min}}}(\tau )=\min _{i}\mu _{\min }(\tau _i)\) is the minimal eigenvalue of \(\tau \). Hence in finite dimensions, both \(C(E_{{\mathcal {N}}})\) and \(C_{{\text {cb}}}(E_{{\mathcal {N}}})\) are finite if and only if \(E_{{\mathcal {N}}}\) is faithful. Moreover, for any invariant state \(\sigma \in {\mathcal {D}}(E_{\mathcal {N}})\), by the obvious bound \(\sigma \le \tau \), we also have
2.3 A Key Lemma
We shall now discuss the key lemma that will be repeatedly used in the later sections. Given a density operator \(\rho \in {\mathcal {D}}({\mathcal {H}})\), we define the multiplication operator
\(\Gamma _\rho \) is a positive operator on the Hilbert–Schmidt space \({\mathcal {T}}_2({\mathcal {H}}):=L_2({\mathcal {B}}({\mathcal {H}}),{\text {tr}})\) and hence induces a weighted \(L_2\)-norm (semi-norm if \(\rho \) is not full-rank) defined for \(X\in {\mathcal {B}}({\mathcal {H}})\) as

We denote by \(L_2(\rho )\) the corresponding \(L_2\)-space. For a full-rank density \(\rho \), the inverse operator of \(\Gamma _\rho \) is given by
which is the double operator integral for the difference quotient of \(f(t)=\ln t\) and operator \(\rho \) (see e.g. [21]). We denote by slight abuse of notations the corresponding weighted \(L_2\)-norm as

and the corresponding \(L_2\) space as \(L_2(\rho ^{-1})\). Note that the definition \(\parallel \! \cdot \! \parallel _{\rho ^{-1}}\) does not amount to plugging in the inverse operator \(\sigma =\rho ^{-1}\) into the definition of \(\parallel \! \cdot \! \parallel _{\sigma }\) in (21). Namely, in our notations \(\parallel \! X \! \parallel _{\rho ^{-1}}\ne \parallel \! X \! \parallel _{\sigma }\) for \(\sigma =\rho ^{-1}\). The inverse weighted norm \(\parallel \! \cdot \! \parallel _{\rho ^{-1}}\) is closely related to the quantum \(\chi ^2\)-divergence introduced in [77, Defnition 1] for the logarithmic function. It is easy to see that
Lemma 2.1
If \(\rho \le c\,\sigma \) for any two states \(\rho ,\sigma \) and some \(c>0\), then, for any \(X\in {\mathcal {B}}({\mathcal {H}})\) and all \(\mu _1,\mu _2>0\),
In particular, \(\parallel \! X \! \parallel _{\sigma ^{-1}}\le c\parallel \! X \! \parallel _{\rho ^{-1}}\).
Proof
This is a standard comparison. Using cyclicity of the trace and the fact that \(t\mapsto t^{-1}\) is operator anti-monotone,
In the last equality, we used the change of variable \(r\rightarrow \frac{r}{c}\). \(\square \)
Our key lemma is a two-sided estimate of \(D(\rho \Vert \sigma )\) via the inverse weighted norm.
Lemma 2.2
Let \(\rho \) and \(\sigma \) be two full-rank density operators and suppose \(\rho \le c\,\sigma \) for some \(c>0\). Then
where \(\displaystyle k(c)=\frac{c\ln c-c+1}{(c-1)^2}\). Note that \(k(c)\le 1/2\) for \(c\ge 1\).
Proof
For the lower bound, we consider \(\rho _t:=(1-t)\sigma +t\rho , t\in [0,1]\) and the function \(f(t)=D(\rho _t\Vert \sigma )\). We have \(f(0)=0\), \(f(1)=D(\rho \Vert \sigma )\) and the derivatives
Note that \(f'(0)= 0\) and \(\rho _t\le (ct+(1-t))\sigma \). We have for the lower bound
where we used Lemma 2.1 and
The upper bound is a special case of [77, Proposition 6]. Here we present a different proof using a method similar to our lower bound. Note that \(\rho _t=(1-t)\sigma +t\rho \ge (1-t)\sigma \). Then,
\(\square \)
Remark 2.3
Note that the upper bound does not require the assumption \(\rho \le c\,\sigma \).
Now given a conditional expectation \(E_{\mathcal {N}}:{{\mathcal {M}}}\rightarrow {\mathcal {N}}\), it follows immediately from the above that for any state \(\rho \) and \(\rho _{{\mathcal {N}}}=E_{{\mathcal {N}}*}(\rho )\),
where \(C(E_{{\mathcal {N}}})\) is the index defined in (16). We also have an variant of the lower bound with another weighting state.
Lemma 2.4
Let \(\rho \), \(\sigma \) and \(\omega \) be three full-rank density operators and suppose \(\rho ,\sigma \le c\,\omega \) for some \(c>0\). Then
Proof
Take \(\rho _t=(1-t)\sigma +t\rho , t\in [0,1]\). By the assumption and Lemma 2.1, we have \(\rho _t\le c\,\omega \) and hence
for each t. Therefore,
\(\square \)
2.4 Detailed Balance
We shall now discuss the detailed balance condition and its connection to the spectral gap. Given a full-rank state \(\sigma \) and \(0\le s\le 1\), we define the multiplication operator
\(\Gamma _{\sigma ,s}\) is a positive operator on the Hilbert–Schmidt space and induces the following weighted inner product
We denote by \(L_2(\sigma ,s)\) the corresponding \(L_2\) space. A map \(\Phi ^*:{\mathcal {M}}\rightarrow {\mathcal {M}}\) is self-adjoint with respect to \(\langle \cdot ,\cdot \rangle _{\sigma ,s}\) if
where \(\Phi \) is the adjoint of \(\Phi ^*\) for the trace inner product. Denote
as the modular generator, modular operator, and modular automorphism group of \(\sigma \) respectively. It was proved in [21, Theorem 2.9] that under the assumption \(\Phi ^*(a^\dagger )=(\Phi ^*(a))^\dagger \), \(\Phi ^*\) is self-adjoint with respect to \(\langle \cdot ,\cdot \rangle _{\sigma ,s}\) for some \(s\ne 1/2\) if and only if \(\Phi ^*\) commutes with \(\Delta _\sigma \) and is self-adjoint for \(s=1/2\), and hence \(\Phi ^*\) is self-adjoint with respect to \(\langle \cdot ,\cdot \rangle _{\sigma ,s}\) for all \(s\in [0,1]\). We say that a map \(\Phi ^*\) satisfies \(\sigma \)-DBC (detailed balance condition) if \(\Phi ^*\) is self-adjoint with respect to \(\langle \cdot ,\cdot \rangle _{\sigma ,1}\). Note that
Thus, we also have \(\Gamma _{\sigma }\circ \Phi ^*=\Phi \circ \Gamma _{\sigma } \) and hence \(\Gamma _{\sigma }^{-1}\circ \Phi =\Phi ^{*}\circ \Gamma _{\sigma }^{-1} \) if \(\Phi ^*\) satisfies the \(\sigma \)-DBC.
Let \(E_{{\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) be a conditional expectation. It can be readily seen that \(E_{{\mathcal {N}}}\) satisfies the \(\sigma \)-DBC condition for all \(\sigma \in {\mathcal {D}}(E_{\mathcal {N}})\) (invariant state satisfying \(\sigma =E_{{\mathcal {N}}*}(\sigma )\)). Hence
In particular, \(E_{{\mathcal {N}}}\) is the projection onto \({\mathcal {N}}\) for the \(L_2\)-norms \(\parallel \! \cdot \! \parallel _{\sigma ,s}\) for any \(s\in [0,1]\) and \(\parallel \! \cdot \! \parallel _{\sigma }\), for all \(\sigma \in {\mathcal {D}}(E_{\mathcal {N}})\). Indeed, for any \(X\in {\mathcal {M}}\),

Now, let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel and \({\mathcal {N}}\) be the multiplicative domain of \(\Phi ^*\). Then,
There always exists an invariant state \(\sigma \) such that \(\Phi (\sigma )=\sigma \). The next lemma shows that if \(\Phi ^*\) satisfy \(\sigma \)-DBC, then \(\Phi ^*\) restricted to \({\mathcal {N}}\) is a \(*\)-involution.
Lemma 2.5
Let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel and let \({\mathcal {N}}\) be the multiplicative domain of \(\Phi ^*\). Then,
-
(i)
There exists an invariant state \(\sigma \) such that \(\Phi (\sigma )=\sigma \)
If, in addition, \(\sigma \) is full-rank and \(\Phi ^*\) satisfies \(\sigma \)-\({\text {DBC}}\),
-
(ii)
\(\Phi ^*\) is a contraction on \(L_2(\sigma ,s)\) for any \(s\in [0,1]\) and \(L_2(\sigma )\). \(\Phi ^*\) restricted to \({\mathcal {N}}\) is a \(*\)-isomorphism and an \(L_2\)-isometry on \(L_2(\sigma ,s)\) for all \(s\in [0,1]\), as well as on \(L_2(\sigma )\).
-
(iii)
Let \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) be the conditional expectation such that \(E_{{\mathcal {N}}*}(\sigma )=\sigma \). Then
$$\begin{aligned} \Phi ^*\circ E_{{\mathcal {N}}}= E_{{\mathcal {N}}} \circ \Phi ^*, (\Phi ^*)^2\circ E_{{\mathcal {N}}}=E_{{\mathcal {N}}}\circ (\Phi ^*)^2= E_{{\mathcal {N}}}. \end{aligned}$$
Proof
(i) Viewing \(\Phi \) as a linear map, \(\Phi \) has eigenvalue 1 because \(\Phi ^*(\mathbbm {1})=\mathbbm {1}\). Since \(\Phi \) preserves self-adjointness, we have an operator \(a=a^\dagger \) such that \(\Phi (a)=a\). Let \(a_+\) (resp. \(a_-\)) be the positive (resp. negative) part of a. We have \(\Phi (a)=\Phi (a_+)-\Phi (a_-)=a\). Because \(\Phi \) is positive and trace preserving, \(\Phi (a_+)\) and \(\Phi (a_-)\) are positive and
We show that this implies \(\Phi (a_+)=a_+\) and \(\Phi (a_-)=a_-\), which proves (i). Indeed, let \(b_1\) and \(b_2\) be any two positive operators such that
Then by duality, there exists a self-adjoint operator \(-1\le X\le 1\) such that
This implies that \({{\,\mathrm{supp}\,}}(b_1)\) is contained in the spectrum projection of X for eigenvalue \(+1\) and similarly \({{\,\mathrm{supp}\,}}(b_2)\) is contained in the spectrum projection of X for eigenvalue \(-1\). Hence \({{\,\mathrm{supp}\,}}(b_1)\) and \({{\,\mathrm{supp}\,}}(b_2)\) are mutually orthogonal, which implies \(b_+=b_1\) and \(b_-=b_2\). The result follows after choosing \(b=\Phi (a)\) with \(b_1=\Phi (a_+)\), \(b_2=\Phi (a_-)\), \(b_+=\Phi (a)_+\) and \(b_-=\Phi (a)_-\). For (ii), consider, for \(X\in {\mathcal {M}}\),
In the above inequality, we used the Kadison–Schwarz inequality and the second to last equality follows from \(\Phi (\sigma )=\sigma \). Note that \(\alpha _{s}({\mathcal {N}})={\mathcal {N}}\) for any \(s\in {\mathbb {C}}\). Then for any \(X\in {\mathcal {N}}\), \(\Phi ^*(\alpha _{i\frac{1-s}{2}}(X)^\dagger )\Phi ^*(\alpha _{i\frac{1-s}{2}}(X))=\Phi ^*(\alpha _{i\frac{1-s}{2}}(X)^\dagger \alpha _{i\frac{1-s}{2}}(X))\) and the above inequality becomes an equality. This proves (ii) for \(L_2(\sigma ,s)\) for all \(s\in [0,1]\). The assertion for \(L_2(\sigma )\) follows by integration. For (iii), we first note that, for any \(X\in {\mathcal {N}}\), \((\Phi ^*)^2(X)=X\). Indeed,
This further implies that \(\Phi ^*(X)\in {\mathcal {N}}\) is in the multiplicative domain because
Also, \(\Phi ^*\) is invariant on the orthogonal complement of \({\mathcal {N}}\) because, for any \(Y\in {\mathcal {M}}\),
This completes the proof. \(\square \)
We see from the above lemma that under \(\sigma \)-DBC, \(\Phi ^*\) is a self-adjoint contraction on \(L_2(\sigma ,s)\) (also \(L_2(\sigma )\)), and \({\mathcal {N}}\) is the union of the eigenspace of \(\Phi ^*\) for eigenvalue 1 and \(-1\). The eigenspace for eigenvalue 1 is the fixed point space of \(\Phi ^*\), which is a subalgebra \({\mathcal {F}}\subset {\mathcal {N}}\). For each invariant state \(\sigma =\Phi (\sigma )\), we have \(\sigma =E_{{\mathcal {F}}*}(\sigma )\). In finite dimensions, there always exists \(0<\varepsilon <1\) such that
which is a spectral gap condition. The next lemma shows that this spectral gap condition is independent of \(s\in [0,1]\) and of the choice of invariant state \(\sigma \).
Lemma 2.6
Let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel and \(\Phi ^*\) be its adjoint. Suppose \(\Phi ^*\) satisfy \(\sigma \)-\({\text {DBC}}\) for some full-rank invariant state \(\sigma \) such that \(\Phi (\sigma )=\sigma \). Then,
-
(i)
\((\Phi ^*)^2\) satisfies \(\rho \)-\({\text {DBC}}\) for all states \(\rho \in {\mathcal {D}}(E_{\mathcal {N}})\) and \(\Phi ^*\) satisfies \(\rho \)-\({\text {DBC}}\) for all invariant states \(\rho \).
-
(ii)
For each full-rank state \(\rho \in {\mathcal {D}}(E_{\mathcal {N}})\), denote \(\lambda (\rho ,s)=\parallel \! \Phi ^*({\text {id}}-E_{{\mathcal {N}}}):L_2(\rho ,s)\rightarrow L_2(\Phi (\rho ),s) \! \parallel _{}^2\). Then for all \(s\in [0,1]\)
$$\begin{aligned}\lambda (\rho ,s)=\lambda (\sigma ,1). \end{aligned}$$ -
(iii)
For each full-rank state \(\rho \in {\mathcal {D}}(E_{\mathcal {N}})\), denote \(\lambda (\rho ):=\parallel \! \Phi ^*({\text {id}}-E_{{\mathcal {N}}}):L_2(\rho )\rightarrow L_2(\Phi (\rho )) \! \parallel _{}^2\). Then
$$\begin{aligned}\lambda (\rho )&:=\parallel \! \Phi ({\text {id}}-E_{{\mathcal {N}}*}):L_2(\rho ^{-1})\rightarrow L_2(\Phi (\rho )^{-1}) \! \parallel _{}\\&= \parallel \! \Phi ^*({\text {id}}-E_{{\mathcal {N}}}):L_2(\rho )\rightarrow L_2(\Phi (\rho )) \! \parallel _{}= \lambda (\sigma ,1)=\lambda (\sigma ).\end{aligned}$$
Proof
By Lemma 2.5, \((\Phi ^*)^2|_{{\mathcal {N}}}\) is the identity map and we have the module property
Note that for any two states \(\rho ,\sigma \in {\mathcal {D}}(E_{\mathcal {N}})\), \(\rho ^{-s}\sigma ^{s}\in {\mathcal {N}}\) for any \(s\in {\mathbb {C}}\). Therefore, we have for all \(s\in [0,1]\),
This shows \((\Phi ^*)^2\) satisfies \(\rho \)-DBC. Now consider a state \(\rho \) such that \(\Phi (\rho )=\rho \). Because both \(\rho ,\sigma \in {\mathcal {D}}(E_{\mathcal {F}})\), we have \(\rho ^{-s}\sigma ^{s}\in {\mathcal {F}}\) for any \(s\in {\mathbb {C}}\). Then it follows from the same argument above that \(\Phi ^*\) satisfies \(\rho \)-DBC. For (ii), we denote \(\iota =\Phi ^*|_{{\mathcal {N}}}\) to be the involution \(\Phi ^*\) restricted to \({\mathcal {N}}\). Note that for any \(s\in {\mathbb {C}}\), it can be verified by the finite dimensional direct sum structure in (13) that
where \(\rho \circ \iota =\Phi (\rho )\). For a mean zero element \(Y=X-E_{\mathcal {N}}(X)\),
where \(Y_0= \Gamma _{\sigma ,s}^{-1/2}\Gamma _{\rho ,s}^{1/2}(Y)\) is also a mean zero element in \({\mathcal {N}}^\perp \). Moreover,
where we used (25) in the first line. This proves \(\lambda (\rho ,s)=\lambda (\sigma ,s)\) for each s. For the independence of s, we have, for \(r\in [0,1]\),
where \(\alpha _{i\frac{r-s}{2}}(Y)=\alpha _{i\frac{r-s}{2}}(X-E_{{\mathcal {N}}}(X))=\alpha _{i\frac{r-s}{2}}(X)-E_{{\mathcal {N}}}(\alpha _{i\frac{r-s}{2}}(X))\) is also in \({\mathcal {N}}^\perp \). Moreover,
For (iii), the inequality \(\lambda (\rho )\le \lambda (\sigma ,1)\) follows from integrating the \(\langle \cdot ,\cdot \rangle _{\rho ,s}\) inner product to obtain \(\langle \cdot ,\cdot \rangle _{\rho }\). The equality \(\lambda (\sigma ,1)=\lambda (\sigma )\) follows from the fact that the map \(\Phi ^*({\text {id}}-E_{{\mathcal {N}}})\) is self-adjoint with respect to both \(\langle \cdot ,\cdot \rangle _\sigma \) and \(\langle \cdot ,\cdot \rangle _{\sigma ,s}\) for any \(s\in [0,1]\). Then the quantity \(\parallel \! \Phi ^*({\text {id}}-E_{{\mathcal {N}}}) \! \parallel _{}\), which is equal to the maximal eigenvalue of \(\Phi ^*({\text {id}}-E_{{\mathcal {N}}})\), is independent of the choice of Hilbert space norm \(\Vert \cdot \Vert \). We note that, by (25),
and
This implies \(\Gamma _{\Phi (\rho )}\circ \Phi ^*({\text {id}}-E_{{\mathcal {N}}})\circ \Gamma _{\rho }^{-1}=\Phi ({\text {id}}-E_{{\mathcal {N}}*}) \), and hence
Moreover, since both \(\sigma \) and \(\rho \) are invariant to \(\Phi ^2\), we have by (ii),
This verifies (iii). \(\square \)
3 Modified Logarithmic Sobolev Inequalities
In this section, we prove the complete modified logarithmic Sobolev inequality (CMLSI) for quantum Markov semigroups on finite dimensional matrix algebras. The argument is a simple application of the key estimates in Section 2.3. Let \({\mathcal {M}}\subset {\mathcal {B}}({\mathcal {H}})\) be a finite dimensional von Neumann algebra. A quantum Markov semigroup (QMS) \(({\mathcal {P}}_t)_{t\ge 0}:{\mathcal {M}}\rightarrow {\mathcal {M}}\) is a continuous parameter semigroup of completely positive, unital maps such that \({\mathcal {P}}_0={\text {id}}_{\mathcal {M}}\) and \({\mathcal {P}}_s\circ {\mathcal {P}}_t ={\mathcal {P}}_{s+t}\) for all \(s,t\ge 0\). Such a semigroup is characterised by its generator, called the Lindbladian \({\mathcal {L}}\), which is defined as
so that \({\mathcal {P}}_t={\text {e}}^{t{\mathcal {L}}}\) for all \(t\ge 0\). A QMS is said to be primitive if it admits a unique full-rank invariant state \(\sigma \). In this section, we consider semigroups \({\mathcal {P}}_t:{\mathcal {M}}\rightarrow {\mathcal {M}}\) on a finite dimensional von Neumann algebra \({\mathcal {M}}\) and exclusively study QMS that satisfy the following detailed balance condition with respect to some (possibly non-unique) full-rank invariant state \(\sigma \): if, for any \(X,Y\in {\mathcal {M}}\) and any \(t\ge 0\),

then we say that a semigroup \({\mathcal {P}}_t\) is GNS-symmetric if \({\mathcal {P}}_t\) satisfies \(\sigma \)-DBC for a full-rank invariant state \(\sigma \). It was proved (see [21, 61]) that for a GNS-symmetric QMS \(({\mathcal {P}}_t:{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}}))_{t\ge 0}\) on \({\mathcal {B}}({\mathcal {H}})\), its generator \({\mathcal {L}}\) can be written as
Here \(A_j\in {\mathcal {B}}({\mathcal {H}})\) and \(\omega _j\) are some real parameters such that for any invariant state \(\sigma \), \(\Delta _{\sigma }(A_j):=\sigma A_j\,\sigma ^{-1}={\text {e}}^{-\omega _j}A_j\). Very recently, this result was extended by Wirth [80] to all uniform continuous semigroups \(({\mathcal {P}}_t:{\mathcal {M}}\rightarrow {\mathcal {M}})_{t\ge 0}\) on a von Neumann algebra \({\mathcal {M}}\). Since we focus on finite dimensions, all the (continuous) semigroups considered in this paper admit the above Lindbladian form (26). Moreover, there exists a conditional expectation \({E}_{{\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {F}}\) onto the fixed point algebra \({\mathcal {F}}=\{X\in {\mathcal {M}}|[A_{j},X]=0\forall j\}\) such that [34]
We are interested in the exponential convergence to this limit in terms of relative entropy. Recall that the entropy production (sometimes also referred as Fisher information) for a state \(\rho \in {\mathcal {D}}({\mathcal {M}})\) is defined as
which is the opposite of the derivative of the relative entropy with respect to the equilibrium state. Here and in what follows, \({\mathcal {L}}_*\) (resp. \({\mathcal {P}}_{t*}\) and \(E_{{\mathcal {F}}*}\)) denotes the adjoint maps of the generator \({\mathcal {L}}\) (resp. semigroup map \({\mathcal {P}}_{t}\) and conditional expectation \(E_{{\mathcal {F}}}\)). We say that a QMS \({\mathcal {P}}_{t}:{\mathcal {M}}\rightarrow {\mathcal {M}}\) satisfies the modified logarithmic Sobolev inequality (MLSI) with \(\alpha >0\) if, for any \(\rho \in {\mathcal {D}}({\mathcal {M}})\),
The best constant \(\alpha \) achieving this bound is called the modified logarithmic Sobolev constant of the semigroup, and is denoted by \(\alpha _{{\text {MLSI}}}({\mathcal {L}})\). It turns out that this inequality is equivalent to the following exponential decay of relative entropy;
We also consider the complete modified logarithmic Sobolev inequality (CMLSI), which requires
to hold for all states \(\rho \) on \({\mathcal {M}}\otimes {\mathcal {B}}({\mathcal {H}})\) and any finite dimensional Hilbert space \({\mathcal {H}}\) as a reference system (or even \({\mathcal {B}}({\mathcal {H}})\) replaced by a finite von Neumann algebra). We denote the best constant \(\alpha \) achieving (MLSI) as \(\alpha _{{\text {CMLSI}}}({\mathcal {L}})\). In [46], it was shown that the proof of the positivity of \(\alpha _{{\text {CMLSI}}}\) for all GNS-symmetric quantum Markov semigroups can be reduced to that for (trace) symmetric quantum Markov semigroups, that is to those for which \({\mathcal {L}}={\mathcal {L}}_*\). However, the problem of the positivity of the CMLSI constant for symmetric QMS has been left open despite considerable work delved on that topic in the recent years (see e.g. [17, 18, 37, 81]). Here, we provide a positive answer to the question via a simple application of our key estimates from Section 2.3.
First, we recall that the Dirichlet form associated to \({\mathcal {L}}\) takes the following simple form [21, Section 5]: for any invariant state \(\sigma =E_{{\mathcal {F}}*}(\sigma )\),
where \(\partial _j(X):=[A_j,X]\). We denote
Then the entropy production associated to \({\mathcal {L}}\) can be written as (see [46, Lemma 2.3])
where, for any \(X\in {\mathcal {M}}\),
We denote the kernels corresponding to the inner products \(\Vert .\Vert _{\sigma ,\omega _j}\) and \(\Vert .\Vert _{\sigma ^{-1},\omega _j}\) by \(\Gamma _{\sigma ,\omega _j}\) and \(\Gamma _{\sigma ^{-1},\omega _j}\), respectively.
Lemma 3.1
The following relation holds for any full-rank state \(\sigma \):
Moreover, whenever \(\sigma =E_{{\mathcal {F}}*}(\sigma )\),
Proof
The first identity follows from Lemma 5.8 in [21]. The proof of the second identity follows by direct computation using the commutation relation \(\sigma A_j={\text {e}}^{-\omega _j}A_j\sigma \). \(\square \)
We recall that the spectral gap \(\lambda ({\mathcal {L}})\) of the Lindbladian \({\mathcal {L}}\) is characterized as
for a given full-rank invariant state \(\sigma \).
Lemma 3.2
Suppose \({\mathcal {P}}_t\) is GNS-symmetric to a full-rank invariant state \(\sigma =E_{{\mathcal {F}}*}(\sigma )\). Then the infimum in (33) is independent of the choice of the full-rank invariant state \(\sigma \).
Proof
By assumption the generator \({\mathcal {L}}\) is symmetric with respect to the GNS inner product (\(\sigma \)-DBC), which also implies self-adjointness with respect to the inner products \(\langle .,.\rangle _\sigma \) (cf. [21, Theorem 2.9]). Moreover, self-adjointness with respect to the GNS inner product is independent of the invariant state chosen. Therefore, \({\mathcal {L}}\) is self-adjoint with respect to \(\langle .,.\rangle _\sigma \) for any full-rank invariant state \(\sigma \). Now, the spectral gap (33) is the difference between the smallest eigenvalue (here, 0) and the second smallest eigenvalue of \(-{\mathcal {L}}\), hence a quantity independent of the inner product with respect to which \({\mathcal {L}}\) is self-adjoint, which allows us to conclude. \(\square \)
We are now ready to prove Theorem 1.1, which is the main theorem of this section.
Theorem 3.3
Any GNS-symmetric quantum Markov semigroup on a finite dimensional von Neumann algebra \({\mathcal {M}}\) satisfies the complete modified logarithmic Sobolev inequality. More precisely, given such a QMS \(({\mathcal {P}}_t={\text {e}}^{t{\mathcal {L}}}:{\mathcal {M}}\rightarrow {\mathcal {M}})_{t\ge 0}\) with fixed point algebra \({\mathcal {F}}\), the following bound holds true:
Similarly, the modified logarithmic Sobolev inequality constant is controlled by
Proof
The proof of the upper bounds is standard and can be found in [6, 50], so we focus on the lower bounds. We first provide a bound on the MLSI constant. For this we use the upper bound in Lemma 2.2 that, for \(X:=\Gamma _{E_{{\mathcal {F}}*}(\rho )}^{-1}(\rho )\),
where \(\lambda ({\mathcal {L}})\) is the spectral gap of \({\mathcal {L}}\). Next, we have, by (29), that
For the above equality (1), we used the inverse relation (31); in (2) we used the relation (32); (3) is an application of Lemma 2.1 with the weights \(\mu _1:={\text {exp}}({-\frac{\omega _j}{2}})\) and \(\mu _2:={\text {exp}}({\frac{\omega _j}{2}})\); finally (4) follows from (30). The proof of CMLSI (34) follows the exact same steps, up to replacing the constant \(C_{\tau }({\mathcal {M}}:{\mathcal {F}})\) by its completely bounded version \(C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {F}})\). \(\square \)
Remark 3.4
The above theorem applies for the derivation triples introduced in Carlen-Maas’s work [22] as well as the symmetric quantum Markov semigroup on finite von Neumann algebra considered in [17, 25, 30] whenever the index \(C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {F}})\) is finite. Nevertheless, \(C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {F}})=C({\mathcal {M}}:{\mathcal {F}})=+\infty \) whenever \({\mathcal {M}}\) is infinite dimensional and \({\mathcal {F}}\) is finite dimensional, which limits its applicability in infinite dimensional settings. In infinite dimensions, other tools like curvature have been introduced to obtain CMLSI (see [17, 18, 56, 81]).
Remark 3.5
When \({\mathcal {M}}:={\mathcal {B}}({\mathcal {H}})\) and the semigroup is primitive, comparison to the logarithmic Sobolev constant \(\alpha _{{\text {LSI}}}\) combined with standard interpolation inequalities provide the following bounds for \(\alpha _{{\text {MLSI}}}\) [20, 50, 66]:
The lower bound can be compared with the one provided in (35) together with (19) and (15) to give that
Clearly, the lower bounds in (36) are asymptotically tighter. However, we emphasise that our bounds (37) are the first generic non-trivial lower bounds for non-primitive QMS, and the CMLSI bound are independent of the size of the environment and hence stable under tensorization, which is even new for primitive semigroup. For classical Markov semigroups (equivalently, graph Laplacians of a weighted graph), (37) gives an alternative CMLSI bounds to the one proved in [56]. In Sects. 6 and 6.2, we will use the approximate tensorization bounds, which is the subject of Section 5, to derive bounds on the CMLSI constant that are sharper than (37) above. As we will see, in some cases, the CMLSI lower bounds can scale similarly to the LSI bounds in the primitive setting. It remain opens whether the CMLSI constant admits asymptotic bounds better than \({\mathcal {O}}(d_{\mathcal {H}}^{-2})\lambda ({\mathcal {L}})\) in general.
4 Strong Data Processing Inequalities
In this section, we study the complete strong data processing inequality for a quantum channel, which is a discrete time analog of CMLSI. We recall the definition of the weighted \(L_2\)-norm corresponding to a full-rank state \(\omega \):
If \(X=\rho -\omega \) for some other state \(\rho \),
is a special case of the quantum \(\chi _2\)-divergence studied in [82]. It is known that \(\chi _2\) also satisfies the data processing inequality: for a quantum channel \(\Phi \),
Indeed, the data processing inequality of relative entropy follows from (38) and the argument used in Lemma 2.2. We shall now discuss how to control relative entropy contraction coefficients by their \(\chi _2\) analogues.
Let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel and \(\Phi ^*\) be the adjoint map of \(\Phi \). We denote by \({\mathcal {N}}\) the multiplicative domain of \(\Phi ^*\). Suppose \(\Phi \) admits a full-rank invariant state \(\sigma \) and \(\Phi \) satisfies \(\sigma \)-DBC. Then by Lemma 2.5, \(\Phi ^*\) restricted to \({\mathcal {N}}\) is a \(*\)-isomorphism. Denote by \(E:{\mathcal {M}}\rightarrow {\mathcal {N}}\) the \(\sigma \)-preserving condition expectation and by \(E_*\) its pre-adjoint on \({\mathcal {M}}_*\). For a full-rank state \(\omega \), we have discussed the following \(L_2\)-contraction constant in Lemma 2.6:
Equivalently, \(\lambda (\omega )\) gives the contraction coefficient of \(\chi _2\):
Here the supremum is over all state \(\rho \ne \omega \) with \(E_*(\rho )=E_*(\omega )\), and we restrict our optimization to states \(\rho \) and \(\omega \) with the same “mean” (also called decoherence free part) given by the map \(E_*\). This is because if \({\mathcal {N}}\ne {\mathbb {C}}\mathbbm {1}\) is not trivial, then for any two invariant states \(\sigma ,\sigma '\in {\mathcal {D}}({\mathcal {N}})\),
and hence \(\lambda (\sigma )=1\) for any invariant state \(\Phi (\sigma )=\sigma \).
The next theorem is a quantum analog of [73, Theorem 3.4] which shows that the \(\chi _2\) contraction coefficient implies local strong data processing inequality.
Theorem 4.1
Let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel that admits some full-rank invariant state \(\sigma =\Phi (\sigma )\). Let \(\omega \) be a full-rank state and denote \(\lambda (\omega ):=\parallel \! \Phi ({\text {id}}-E_*):L_2(\omega ^{-1})\rightarrow L_2(\Phi (\omega )^{-1}) \! \parallel _{}^2\). Then, for any state \(\rho \) with \(E_*(\omega )=E_*(\rho )\),
where c is a constant such that
Here \( C(\rho :\omega ):=\inf \{C | \rho \le C \,\omega \}\) and \(c(C,\lambda )\) is an explicit function such that \(c(C,\lambda )<1\) whenever \(\lambda <1\). In particular, for any state \(\rho \), \(c\,(C(\rho :\omega ),\lambda (\omega ))\le c\,(\mu _{\min }(\omega )^{-1},\lambda (\omega ))\) where \(\mu _{\min }(\omega )\) is the minimum eigenvalue of \(\omega \).
Proof
We first show the lower bound. Write \(\lambda \equiv \lambda (\omega )\). Let \(\rho \) be a state with \(E_*(\rho )=E_*(\omega )\). Take the linear interpolation of states \(\omega _t:=(1-t)\,\omega +t\,\rho , t\in [0,1]\). Now assume \(\Phi \) satisfies (39) for \(c>0\). We have
since \(E_*(\omega _t)=E_*(\omega )\). Consider the function \(f(t)= c\, D(\omega _t\Vert \omega )-D(\Phi (\omega _t)\Vert \Phi (\omega ))\). Taking derivatives, we have \(f(0)=f'(0)=0\) and [55]
Note that \(f''(0)\ge 0\), because \(f(t)\ge 0\) for \(t\in [0,\varepsilon ]\). Therefore,
This proves the lower bound
For the upper bound, denote \(\rho _t=t\rho +(1-t)\,\omega \) and \(g(t)=D(\rho _t\Vert \omega )-D(\Phi (\rho _t)\Vert \Phi (\omega ))\). We have \(g(0)=g'(0)=0\), and
It follows from (38) (see also [55, Example 2]) that \(g''(t)\ge 0\). Using Lemma 2.1 and the definition of \(\lambda (\omega )\), we also have that
where \(C=\inf \{C |\rho \le C\, \omega \}\). Thus, we have, for \(t_0:=\frac{1-\lambda ^2}{1+\lambda ^2(C-1)}\),
Denote \(\displaystyle a(s):=\int _0^s \frac{1}{1+(C-1)t}-\frac{\lambda ^2}{1-t}\, \mathrm{d}t= \frac{\ln (1+(C-1)s)}{C-1}+\lambda ^2\ln (1-s)\). Since \(g'(0)=0\), we have \(g'(s)\ge a(s)\parallel \! \rho -\omega \! \parallel _{\omega ^{-1}}^2\) if \(s\le t_0\) and \(g'(s)\ge a(t_0)\parallel \! \rho -\omega \! \parallel _{\omega ^{-1}}^2\) if \(s\ge t_0\). Denote
We have
where the last inequality follows from Lemma 2.2. The SDPI constant is then upper bounded by
It is clear from the derivation that c as a function depending on C and \(\lambda \) satisfies
Then the last assertion follows from \(\rho \le \mathbbm {1}\le \mu _{\min }(\omega )^{-1}\omega \). \(\square \)
Next, we consider strong data processing inequality for a quantum channel \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) with respect to its decoherence free states \({\mathcal {D}}(E_{\mathcal {N}})\). We say \(\Phi \) satisfies a \(\alpha \)-strong data processing inequality (\(\alpha \)-SDPI) for some \(0<\alpha <1\) if for any state \(\rho \in {\mathcal {D}}({\mathcal {H}})\),
We say that \(\Phi \) satisfies the \(\alpha \)-complete strong data processing inequality (\(\alpha \)-CSDPI) for some \(0<\alpha <1\) if, for any \(n\in {\mathbb {N}}\) and all bipartite states \(\rho \in {\mathcal {D}}({\mathbb {M}}_n({\mathcal {M}}))\),
where \({\text {id}}_n\) denotes the identity channel on the matrix algebra \({\mathbb {M}}_n\). We denote the best (smallest) constant achieving SDPI (41) (resp. CSDPI (41)) as \(\alpha _{{\text {SDPI}}}(\Phi )\) (resp. as \(\alpha _{{\text {CSDPI}}}(\Phi )\)). The advantage of the CSDPI constant is that it is stable under tensorization.
Proposition 4.2
Let \(\Phi _1:{\mathcal {M}}_{1*}\rightarrow {\mathcal {M}}_{1*}\) and \(\Phi _2:{\mathcal {M}}_{2*}\rightarrow {\mathcal {M}}_{2*}\) be two quantum channel. Denote \(E_j:{\mathcal {M}}_j\rightarrow {\mathcal {N}}_j, j=1,2\) as the condition expectation onto the multiplicative domain of \(\Phi _j^*\) respectively. Then
Namely, for any \(n\ge 1\) and states \(\rho \in {\mathcal {D}}({\mathcal {M}}_1\otimes {\mathcal {M}}_2\otimes {\mathbb {M}}_n)\)
Proof
The proof is a natural application of the data processing inequality. For ease of notations, we argue for \(n=1\) as the case for general \(n\ge 1\) follows the same argument. Note that for \(j=1,2\), \(\Phi _j\circ E_{j*}= E_{j*}\circ \Phi _j\). Write \(\alpha _1:=\alpha _{{\text {CSDPI}}}(\Phi _1)\) and \(\alpha _2:=\alpha _{{\text {CSDPI}}}(\Phi _2)\). We have
where in the second equality and the last inequality, we used the chain rule (12) and the second last inequality uses data processing inequality for the map \({\text {id}}\otimes \Phi _2\) and \(\Phi _1\otimes {\text {id}}\), respectively. \(\square \)
As an application of Theorem (4.1), we have \(\alpha _{{\text {SDPI}}}(\Phi )\) and \(\alpha _{{\text {CSDPI}}}(\Phi )\) are two-sided bounded by the spectral gap in finite dimensions.
Corollary 4.3
Let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel and \({\mathcal {N}}\) be the multiplicative domain of \(\Phi ^*\). Assume that \(\Phi ^*\) satisfies the \(\sigma \)-\({\text {DBC}}\) for some full-rank invariant state \(\sigma =\Phi (\sigma )\). Denote the spectral gap \(\lambda (\Phi ):=\parallel \! \Phi ^*({\text {id}}-E_{{\mathcal {N}}}):L_2(\sigma )\rightarrow L_2(\sigma ) \! \parallel _{}^2<1\). There exists an explicit constant \( c\,(C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {N}}),\lambda )<1\) such that
The same estimate holds for \(\alpha _{{\text {SDPI}}}(\Phi )\) simply replacing \(C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\) by \(C_{\tau }({\mathcal {M}}:{\mathcal {N}})\).
Proof
We have shown in Lemma 2.6 that \(\lambda (\Phi )=\lambda (\sigma )\) and \(\lambda (\sigma )\ge \lambda (\rho )\) for all decoherence free state \(\omega \in {\mathcal {D}}(E_{{\mathcal {N}}*})\). Then (44) follows from Theorem 4.1 and the fact that \(\rho \le C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {N}}) E_{{\mathcal {N}}*}(\rho )\) for any \(\rho \in {\mathcal {D}}({\mathcal {H}}\otimes {\mathbb {C}}^n)\). \(\square \)
Remark 4.4
For a primitive unital quantum channel \(\Phi :{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}})\), it was proved in [63] that
where \(\alpha _{{\text {LSI}}}(\Phi ^*\Phi -{\text {id}})\) is the log-Sobolev constant of the map \(\Phi ^*\Phi -{\text {id}}\) seen as the generator of a quantum Markov semigroup. This is generically better than the bounds found in Corollary 4.3. Nevertheless, our results give explicit SDPI constants for general non-egordic GNS-symmetric quantum channels, independently of the size of the environment. Moreover, the CSDPI constant satisfies the tensorization property.
5 Approximate Tensorization
In this section, we consider the approximate tensorization of the relative entropy in a general setting. Let \({\mathcal {M}}\) be a finite dimensional von Neumann algebra equipped with a faithful trace \({\text {tr}}\). Let \({\mathcal {N}}_1,{\mathcal {N}}_2\subset {\mathcal {M}}\) be two subalgebras of \({\mathcal {M}}\) and \({\mathcal {N}}={\mathcal {N}}_1 \cap {\mathcal {N}}_2\). Let \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) and \(E_i:{\mathcal {M}}\rightarrow {\mathcal {N}}_i,i=1,2\), be conditional expectations such that \(E_{{\mathcal {N}}}\circ E_i=E_{{\mathcal {N}}}\). If \(\rho \) is a state that satisfies \(E_{{\mathcal {N}}*}(\rho )=\rho \), then
Namely, every \(E_{{\mathcal {N}}}\) invariant state is both \(E_1\) and \(E_2\) invariant. Denote that \(\rho _{\mathcal {N}}=E_{{\mathcal {N}}*}(\rho )\) and \(\rho _i=E_{i*}(\rho ), i=1,2\). We are interested in the following approximate tensorization property:
It was proved in [36, Corollary 2.3] that the constant c equals to 1 if and only if \(E_1\) and \(E_2\) form a commuting square, i.e. \(E_1\circ E_2=E_2\circ E_1=E_{{\mathcal {N}}}\). Using the chain rule \(D(\rho \Vert \rho _{\mathcal {N}})=D(\rho \Vert \rho _i)+D(\rho _i\Vert \rho _{\mathcal {N}})\), the inequality (45) is equivalent to the entropic uncertainty relation
where \(\alpha = \displaystyle \frac{c}{2c-1}>1/2\). Take \(\rho (t)=t\rho +(1-t)\rho _{{\mathcal {N}}}\) and the function
Then we have \(f(0)=f'(0)=0\) and
so a necessary condition for (46) and, equivalently, (45), is that for any state \(\rho \),
In particular, if we choose \(\rho =\rho _1=E_{1*}(\rho )\), we have
Because \(1/2< \alpha \le 1\), for \(\lambda =\frac{1-\alpha }{\alpha }\) this can be reformulated as the \(L_2\)-clustering condition
Since \(E_{2}\circ E_{1}\) is the identity on \({\mathcal {N}}\) and satisfies the \(\rho _{{\mathcal {N}}}\)-DBC condition, the above definition is independent of the choice of invariant state \(\rho _{\mathcal {N}}\) (see Lemma 2.6, also [8, Theorem 2]). Note that in finite dimensions, the constant \(\lambda \) is always strictly less than 1, otherwise there would exist a nonzero \(X\notin {\mathcal {N}}\) such that \(E_{1}(X)=X,E_2(X)=X\) and hence \(X\in {\mathcal {N}}\), which leads to a contradiction. We now show that the \(L_2\)-clustering condition is also a sufficient condition for (45).
Theorem 5.1
Let \(\sigma \in {\mathcal {D}}(E_{\mathcal {N}})\). Denote \(\parallel \! E_{1}\circ E_{2} -E_{{\mathcal {N}}}:L_2(\sigma )\rightarrow L_2(\sigma ) \! \parallel _{}=\lambda <1\) as the \(L_2\)-clustering constant. Then for any state \(\rho \),
where
-
(i)
the constant c satisfies
$$\begin{aligned} \frac{1}{1-\lambda ^2}\le c\le \frac{2\,C_{\tau }({\mathcal {M}}:{\mathcal {N}})}{(1-\lambda )^2}\,; \end{aligned}$$(48) -
(ii)
if, in addition, \(\lambda <\frac{1}{\sqrt{2}}\),
$$\begin{aligned}&c\le 1+\Big (\frac{\lambda }{1-\lambda }+\frac{\lambda ^2}{1-2\lambda ^2}\Big )\,C_{\tau }({\mathcal {M}}:{\mathcal {N}}). \end{aligned}$$(49)
Similarly, for any \(n\in {\mathbb {N}}\) and all states \(\rho \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathbb {M}}_n)\), we have
where \(c_{{\text {cb}}}\) satisfies either (48) or (49) after replacing \(C_{\tau }({\mathcal {M}}:{\mathcal {N}})\) by \(C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\).
Proof
The lower bound was proven at the beginning of the section, so we focus on the upper bound. Note that \(E_1,E_2\) and \(E_{\mathcal {N}}\) are all projections on \(L_2(\rho _{{\mathcal {N}}})\). For a state \(\rho \), we write \(\rho _{12}=E_{1*} E_{2*}(\rho )\) and \(\rho _{21}=E_{2*} E_{1*}(\rho )\). By the \(L_2\)-clustering condition
Moreover, since \(E_{1*},E_{2*}\) and \(E_{{\mathcal {N}}*}\) are projections on \(L_2(\rho _{\mathcal {N}}^{-1})\),
where the last line follows from (51). Namely, we have
Now, using Lemma 2.2,
where \(\rho _1(t)=t\rho +(1-t)\rho _1\) and \(\rho _2(t)=t\rho +(1-t)\rho _2\). As in Lemma 2.2, for \(i=1,2\) \(\displaystyle D(\rho \Vert \rho _i)=\int _0^1 \int _{0}^s \parallel \! \rho -\rho _i \! \parallel _{\rho _i(t)}^2\mathrm{d}t\mathrm{d}s\). Then, integrating the above inequality, we have
which proves (i). For (ii), by the chain rule ([46, Lemma 3.4]), we have
and similarly,
It suffices to estimate the error term \( {\text {tr}}(\rho _{1}(\ln \rho _{12}-\ln \rho _{{\mathcal {N}}}))\) and \({\text {tr}}(\rho _{2}(\ln \rho _{21}-\ln \rho _{{\mathcal {N}}}))\). Recall the integral identity that for positive \(A,B> 0\)
Thus, by Cauchy–Schwarz inequality and Lemma 2.2,
Similarly,
Note that by the \(L_2\)-clustering condition,
Thus
Therefore, for \(\lambda < \frac{1}{\sqrt{2}}\), by Lemma 2.4,
\(C_1=C_\tau ({\mathcal {N}}_1:{\mathcal {N}})\), and \(C_2=C_\tau ({\mathcal {N}}_2:{\mathcal {N}})\). On the other hand, denoting
we have
where \(C_{\max }:=\max \{C_\tau ({\mathcal {N}}_1:{\mathcal {N}}),C_\tau ({\mathcal {N}}_2:{\mathcal {N}}),C_{\tau }({\mathcal {M}}:{\mathcal {N}}_1),C_{\tau }({\mathcal {M}}:{\mathcal {N}}_2)\}\le C_\tau ({\mathcal {M}}:{\mathcal {N}})\). Therefore, we have
follows after rearranging the terms in the outer bounds and a last use of the data processing inequality. The proof of (50) follows the exact same lines after replacing \(C_{\tau }({\mathcal {M}}:{\mathcal {N}})\) by \(C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\) . \(\square \)
Remark 5.2
By using \(\rho _{i}(t)=t\rho +(1-t)\rho _i\le \big (tC_\tau ({\mathcal {M}}:{\mathcal {N}})+(1-t)C_\tau ({\mathcal {N}}_i:{\mathcal {N}})\big )\rho _{\mathcal {N}}\), the constant c in (i) can be improved to
where \(\displaystyle K(c_1,c_2):=\frac{c_1\ln c_1-c_1+c_2}{(c_1-c_2)^2}\). \(c_{{\text {cb}}}\). For (ii), as shown in the proof, the constant \(C_\tau ({\mathcal {M}}:{\mathcal {N}})\) in (ii) can be improved to
The same remark holds for \(c_{{\text {cb}}}\) in both cases.
The above theorem gives the equivalence of \(L_2\)-clustering condition and complete approximate tensorization \(c_{{\text {cb}}}\) given finite index. Moreover, the (ii) above recovers the optimal constant \(c=1\) in the case of commuting squares (\(\lambda =0\)).
In the classical literature [24, 27], approximate tensorization constants were found under the strong condition of smallness of the norm \(\parallel \! E_1\circ E_2-E_{\mathcal {N}}:L_1\rightarrow L_\infty \! \parallel _{}\) instead of the \(L_2\)-condition \(\parallel \! E_1\circ E_2-E_{\mathcal {N}}:L_2\rightarrow L_2 \! \parallel _{}\) that we use. In that setting, the approximate tensorization constants obtained in Theorem 5.1 are not tight because the Pimsner–Popa indices coincide with the dimension bounds for the \(L_1\rightarrow L_\infty \) norm. Quantum extensions using \(L_1\rightarrow L_\infty \) cluster condition were recently found in [8], however they yield additive error terms in generic noncommutative situations, e.g. when the algebra \({\mathcal {N}}\) is not trivial. This generalization however was found fruitful in deriving the positivity of the MLSI constant for some classes of Gibbs samplers in [19], where the multiplicative constant could be related to the notion of clustering of correlations in the equilibrium Gibbs state. There, the analysis could be reduced to the case of states \(\rho \) for which the additive error vanishes. However, the problem of the vanishing of the additive constant for general states remained open.
After the preprint submission of a preliminary version of the present paper, LaRacuente in [53] introduced a method based on our Lemma 2.2 to find asymptotically tight approximate tensorization constants. The main idea from [53] resides in an application of the map \((E_1\circ E_2)^k\) in order to control the \(L_1\rightarrow L_\infty \) norm via \(\Vert (E_1\circ E_2)^k-E_{\mathcal {N}}:L_2(\sigma )\rightarrow L_2(\sigma )\Vert =\lambda ^k\), at the cost of having to multiply the approximate tensorization constant by k. Our next two results can be interpreted as a merging of these different contributions to improve the tightness of the approximate tensorization constant. We first start with a theorem which generalizes the original results of [24, 27] without the additive error terms found in [8], at the cost of having to replace the \(L_1\rightarrow L_\infty \) condition by the completely bounded version of it. Although the condition is closer to that of [53], our proof is arguably more straightforward and resembles the ones of [8, 19, 24, 27].
Theorem 5.3
Let \({\mathcal {N}}\subset {\mathcal {M}}\) be a finite dimensional von Neumann subalgebra and \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) be a conditional expectation. Let \(\Phi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) be a quantum channel such that \(\Phi ^*\) is GNS-symmetric to a full-rank \(E_{\mathcal {N}}\)-invariant states and satisfies \(\Phi ^*\circ E_{\mathcal {N}}=E_{\mathcal {N}}\circ \Phi ^*=E_{\mathcal {N}}\). Suppose, for some \(0<\varepsilon <\sqrt{2\ln 2-1}\), that
where the inequalities hold in completely positive order. Then, for all \(n\in {\mathbb {N}}\) and states \(\rho \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathbb {M}}_n)\),
Proof
Let \(\rho \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathbb {M}}_n)\) and \(\rho _{\mathcal {N}}:=E_{{\mathcal {N}}*}(\rho )\). Then,
for \(A:=\exp (\ln \Phi ^2(\rho )-\ln \rho _{\mathcal {N}}+\ln \rho )\). Here the last inequality follows from the positivity of the relative entropy. Using Lieb’s triple matrix inequality (see [57, Theorem 7]),
Then, by the GNS-symmetry of \(\Phi ^*\),
where (1) arises from the basic inequality \(\ln (x)\le x-1\) and the trace preserving property of \(\Phi \) and \(E_{{\mathcal {N}}*}\). Now, since \(\Phi ^*\ge _{{\text {cp}}} (1-\varepsilon )E_{{\mathcal {N}}}\), there exists a quantum channel \(\Psi :{\mathcal {M}}_*\rightarrow {\mathcal {M}}_*\) such that \(\Phi =(1-\varepsilon )E_{{\mathcal {N}}*}+\varepsilon \Psi \). Therefore,
where (2) comes from Lemma 2.2 and the fact that \(\Phi ^*\le (1+\varepsilon )E_{{\mathcal {N}}}\), so that
The result follows after rearranging the terms in the last inequality. \(\square \)
The above theorem can be used to derive approximate tensorization bounds. We are grateful to Chi-Fang Chen for pointing out that the approximate tensorization constant in the older version can be improved with a factor \(\frac{1}{m}\).
Corollary 5.4
Let \({\mathcal {N}}_1,\ldots ,{\mathcal {N}}_m\subset {\mathcal {M}}\) be finite dimensional von Neumann subalgebras of \({\mathcal {B}}({\mathcal {H}})\), and let \({\mathcal {N}}=\cap _{i=1}^m {\mathcal {N}}_i\). Let \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) and \(E_i:{\mathcal {M}}\rightarrow {\mathcal {N}}_i\) be some corresponding conditional expectations. Suppose for some full-rank \(E_{\mathcal {N}}\)-invariant state \(\sigma =E_{{\mathcal {N}}*}(\sigma )\), \(\sigma =E_{i*}(\sigma )\) for each i. Then for \(\Phi ^*=\frac{1}{m}\sum _{i=1}^mE_i\), we have that, for all \(n\in {\mathbb {N}}\) and all states \(\rho \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathbb {M}}_n)\),
whenever \(0<\varepsilon < \sqrt{2\ln (2)-1}\) and k satisfies
If, additionally, \(E_i\) and \(E_{\mathcal {N}}\) are trace preserving conditional expectations, we have that for all \(n\in {\mathbb {N}}\) and all state \(\rho \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathbb {M}}_n)\),
where \(\lambda :=\Vert \Phi -E_{\mathcal {N}}:L_2({\text {tr}})\rightarrow L_2({\text {tr}})\Vert \) and \(\lceil s \rceil \) denotes the smallest integer greater than or equal to s.
Proof
Equation (53) is a direct consequence of Theorem 5.3 and successive applications of convexity of the relative entropy and the chain rule [53, Lemma 3.2],
In the case when all \(E_i\) and E are trace preserving, we prove in “Appendix A” that \(\varepsilon \) can be chosen as (see Lemma A.1)
for k large enough so that the condition (54) is satisfied. Therefore, we can choose \(\varepsilon \le \sqrt{\ln 2-\frac{1}{2}}\) and \(1-\varepsilon ^2(2\ln (2)-1)^{-1}\ge 1/2\) by taking
Then (55) follows from (53). \(\square \)
Remark 5.5
Although the bound (53) does not recover the exact tensorization for commuting conditional expectations, it has the merit over our other bounds to be independent of the index \(C_{\tau ,{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})\). In Section 6, we use the bound (55) to derive sharper CMLSI constants than Theorem 3.3 for several examples.
Remark 5.6
Another natural choice is \(\Phi ^*=\prod _{i=1}^m E_i\), where the product can be interpreted with any order. Indeed, by the chain rule,
By a similar argument as to that above, we obtain the approximate tensorization
with \(\lambda _p:=\parallel \! \prod _{i=1}^m E_i-E_{{\mathcal {N}}} \! \parallel _{}\). Let us also denote \(\lambda _s:=\parallel \! \frac{1}{m}\sum _{i=1}^m E_i-E_{{\mathcal {N}}} \! \parallel _{}\). By the detectability lemma [4], we have
where \(\lambda _E=m-m\lambda _s\) is the spectral gap of \(\sum _{i}\mathbbm {1}-E_i\) and g is the integer such each \(E_i\) commute with all but at most g \(E_j\)’s. Then when \(\lambda _E\rightarrow 0\) is small, the approximate tensorization constant from \(\Phi ^*=\prod _{i=1}^m E_i\) is always weaker than the one from \(\Phi ^*=\frac{1}{m}\sum _{i=1}^m E_i\).
6 Applications and Examples
6.1 Symmetric Lindbladians
In this section, we use the approximate tensorization results of Section 5 to give tighter bounds on the CMLSI constant for generators \({\mathcal {L}}\) which can be expressed as a summation of a family of generators
For simplicity, here we only consider symmetric generators. We say that a generator \({\mathcal {L}}:{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}})\) is symmetric if
Hence, \({\mathcal {L}}={\mathcal {L}}_*\), \({\mathcal {P}}_t={\mathcal {P}}_{t*}\) and the conditional expectations \(E=E_*\) are all trace symmetric (or equivalently, \({\mathcal {P}}_t\) is GNS-symmetric with respect to the completely mixed state \(\frac{\mathbbm {1}}{d_{\mathcal {H}}}\)). In this case, we do not distinguish \({\mathcal {P}}_t\) (resp. E and \({\mathcal {L}}\)) from its predual \({\mathcal {P}}_{t*}\) (resp. \(E_*\) and \({\mathcal {L}}_*\)) because one can identify \({\mathcal {B}}({\mathcal {H}})\cong {\mathcal {B}}({\mathcal {H}})_*\) via the Hilbert–Schmidt inner product in finite dimensions. The main idea here consists in using the approximate tensorization of the CMLSI constant.
Proposition 6.1
Let \(({\mathcal {L}}_{k}:{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}}))_{k=1}^m\) be a family of symmetric generators and \({\mathcal {L}}=\sum _{k=1}^m{\mathcal {L}}_{k}\). Denote E, resp. \(E_k\), as the conditional expectation onto the kernel of \({\mathcal {L}}\), resp. \({\mathcal {L}}_{k}\). Then the CMLSI constants of \({\mathcal {L}}\) and \({\mathcal {L}}_k\) satisfy
where C satisfies the complete approximate tensorization
Moreover, denote \(\lambda ({\mathcal {L}}_{k})\) as the spectral gap of \({\mathcal {L}}_{k}\) and \(\lambda _E\) as the spectral gap of \({\mathcal {L}}_E=\sum _{k}(E_k-{\text {id}})\). Then,
where \(C_{{\text {cb}}}(E)\) is the index of E and \(\lambda :=1-\frac{\lambda _E}{m}\).
Proof
For any state, we have
Here the first inequality above uses the assumption (56), and the last line uses the linearity of the entropy production (27). For the second assertion, we denote \({\mathcal {N}}\) as the range of E, which coincides with the kernel of \({\mathcal {L}}\). Then \(\frac{1}{m}\sum _{k}E_k-E\) is a positive contraction supported on \(L_2({\mathcal {N}})^\perp \subset L_2({\mathcal {B}}({\mathcal {H}}))\). Since
we have
Then the approximate tensorization constant (57) follows from using \(\Psi =\frac{1}{m}\sum _{k}E_k\) in Corollary 5.4. \(\square \)
Remark 6.2
The above proposition can be extended to a family of generator \({\mathcal {L}}_k\) that are GNS-symmetric to a common full rank state \(\sigma \). Indeed, the content in “Appendix B” can be extended to state preserving conditional expectations (see [7, Section 5]), hence Corollary (55) and the above Proposition 6.1 also extend to that setting. Nevertheless, the symmetric setting is sufficient for the examples discussed in this section.
We now illustrate the above bound on several examples. First, we note that, due to symmetry, the Lindbladian (26) takes a simple form
where \(a_1,\ldots ,a_m\in {\mathcal {B}}({\mathcal {H}})\) form a family of self-adjoint operators. Let us first consider a single term in the generator
for a self-adjoint \(a\in {\mathcal {B}}({\mathcal {H}})\). Let \(a=\sum _{i=1}^n\kappa _i P_i\) be the spectral decomposition of a, where \(P_i\) is the spectral projection with respect to the eigenvalue \(\kappa _i\). One calculates that
Then \({\mathcal {L}}_a\) generates the semigroup
which is a Schur multiplier semigroup (also called generalized dephasing semigroup). The invariant subalgebra \({\mathcal {N}}_a=\oplus _{i=1}^n {\mathcal {B}}(P_i{\mathcal {H}})\) and the indices are
Viewing \({\mathcal {L}}_a\) as a self-adjoint operator on \(L_2({\mathcal {B}}({\mathcal {H}}),{\text {tr}})\), \(P_i{\mathcal {B}}({\mathcal {H}})P_j\) corresponds to the eigenspace associated to the eigenvalue \(-(\kappa _i-\kappa _j)^2\). Thus the norm and spectral gap of \({\mathcal {L}}_a\) are
It was proved in [17, Theorem 4.23] that Schur multiplier semigroups admit the following estimates on their CMLSI constant (note that our normalization of the CMLSI constants differs with [17] by a factor of 2):
Moreover, for a commuting family \(\{a_1,\ldots ,a_m\}\), the Lindbladian \({\mathcal {L}}(\rho )= -\sum _{k=1}^m[a_k,[a_k,\rho ]]\) also generates a Schur multiplier semigroup and the above estimate (59) remains valid.
Applying Proposition 6.1, we extend the above estimate to general Lindbladians of the form \({\mathcal {L}}=\sum _{k}{\mathcal {L}}_{a_k}\) for not necessarily commuting operators \(a_k\).
Corollary 6.3
Let \(({\mathcal {P}}_t=e^{{\mathcal {L}}t}:{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}}))_{t\ge 0}\) be a symmetric quantum Markov semigroup, and let its generator be given by
Denote \(E_{\mathcal {N}}\), resp. \(E_k\), as the conditional expectation onto the kernel of \({\mathcal {L}}\), resp. that of \({\mathcal {L}}_{a_k}\). Denote \(\lambda ({\mathcal {L}}_{a_k})\) as the spectral gap of \({\mathcal {L}}_{a_k}\) and \(\lambda _E\) as the spectral gap of \({\mathcal {L}}_E=\sum _{k}(E_k-{\text {id}})\). Then,
where \(d={\text {dim}}({\mathcal {H}})\) and \(\lambda :=1-\frac{\lambda _E}{m}\).
Remark 6.4
For the spectral gap, we have that, for each k,
Also, the spectral gap of \({\mathcal {L}}_E=\sum _{i}E_i-{\text {id}}\) satisfies
because \({\text {id}}-E_k\ge -\parallel \! {\mathcal {L}}_{a_k}:L_2\rightarrow L_2 \! \parallel _{}^{-1}{\mathcal {L}}_{a_k}\) and \(\parallel \! {\mathcal {L}}_{a_k}:L_2\rightarrow L_2 \! \parallel _{}\le \parallel \! {\mathcal {L}}:L_2\rightarrow L_2 \! \parallel _{}\), since each generator \({\mathcal {L}}_{a_k}\) is a non-positive operator in the \(L_2\) sense. Therefore the constant obtained in Theorem 6.3 can be further estimated by
Thus, in general, the constant obtained in Corollary 6.3 has better asymptotics in terms of the dimension d than that of Theorem 3.3. We note that this approach does not apply to GNS-symmetric Lindbladians because in general the decomposition (58) in terms of Schur multipliers is not available.
Example 6.5
We now illustrate Theorem 6.3 for transference semigroups from the sub-Laplacian on \({\text {SU}}(2)\). We refer to [37, Section 4.2] for the transference technique for quantum Markov semigroups. Let \({\text {SU}}(2)\) be the special unitary group on \({\mathbb {C}}^2\). Denote
as the anti-selfadjoint Pauli matrices. Then
which is isomorphic to the 3-sphere \({\mathbb {S}}^3\). Its Lie algebra is the anti-selfadjoint matrix space
equipped with the Lie bracket relations
The canonical bi-invariant Riemannian metric on \({\text {SU}}(2)\) admits \(\{X,Y,Z\}\) as an orthonormal basis. The representation theory of \({\text {SU}}(2)\) gives the well-known spin structure of quantum mechanics, where any irreducible representation of \({\text {SU}}(2)\) is indexed by an integer \(m\in {\mathbb {N}}^+\). Let \(\eta _m:\mathfrak {s}\mathfrak {u}(2)\rightarrow i({\mathbb {M}}_{m})_{{\text {sa}}}\) be the Lie algebra homomorphism induced by the m-th irreducible representation, and let \(\{{|{j}\rangle }| j=1,\ldots ,m \}\) be the eigenbasis of \(\eta _m(Z)\). Denote that \(X_m:=\eta _m(X)\), and similarly for \(Y_m\) and \(Z_m\) as short notations. Under the normalization of (60),
For each irreducible representation, one can consider quantum Markov semigroups transferred from the heat semigroup \((e^{\Delta t})_{t\ge 0}\) on \({\text {SU}}(2)\), which is given by the Casimir operator
It follows from the complete Bakry-Emery Theorem [56, Theorem 4.3] that the heat semigroup has \(\alpha _{{\text {CMLSI}}}(\Delta )\ge 2\) because its Ricci curvature is 1. Therefore, the transferred Lindbladian on \({\mathbb {M}}_{m}\)
admits a uniform CMLSI constant \(\alpha _{{\text {CMLSI}}}({\mathcal {L}}_m^\Delta )\ge 2\) by transference principle [37, Proposition 4.7]. Here we consider the canonical sub-Laplacian on \({\text {SU}}(2)\) given by
It is known (see e.g. [10]) that \(\Delta _H\) is hypoelliptic and generates a classical Markov semigroup \((e^{\Delta _H t})_{t\ge 0}\); its transferred Lindbladian on \({\mathbb {M}}_m\) is given by
Although the CMLSI constant for the sub-Laplacian \(\Delta _H\) is currently still unknown (MLSI is known from hypercontractivity), we can use approximate tensorization to obtain a uniform lower bound on \(\alpha _{{\text {CMLSI}}}({\mathcal {L}}_{m}^{H})\) for each m.
It suffices to consider \(m\ge 3\). Denote \({\mathcal {X}}\) and \({\mathcal {Y}}\) as the kernel of \({\mathcal {L}}_{X_m}(\cdot )=[X_m,[X_m,\cdot ]]\) (resp. \({\mathcal {L}}_{Y_m}\)). Since both \(X_m\) and \(Y_m\) have distinct spectrum \(\{m-1,m-3,m-5,\ldots ,-(m-1)\}\), \({\mathcal {X}}\) and \({\mathcal {Y}}\) are subalgebra generated by \(X_m\) and \(Y_m\) respectively. Then the conditional expectation \(E_{\mathcal {X}}\) (resp. \(E_{\mathcal {Y}}\)) are the pinching map
where \(\{{|{x_i}\rangle }\}\) and \(\{{|{y_j}\rangle }\}\) are the eigenbasis of \(X_m\) and respectively \(Y_m\). Also denote \(E_{\mathbb {C}}:={\text {tr}}(.)m^{-1}\mathbbm {1}\) the conditional expectation onto \({\mathbb {C}}1\). Note that it is sufficient to consider the map \(E_{\mathcal {X}}E_{\mathcal {Y}}-E_{{\mathbb {C}}}:{\mathcal {B}}({\mathcal {H}}_A)\rightarrow {\mathcal {B}}({\mathcal {H}}_A)\) from its support \({\mathcal {Y}}\) to the range \({\mathcal {X}}\), which is given by the matrix
Therefore, we have that
Since all the eigenvectors \(\{{|{x_i}\rangle }\}\) and \(\{{|{y_j}\rangle }\}\) are explicit, one can numerically see that the constant \(\lambda \) in Corollary 5.4 satisfies \(\lambda <1/5\). Combining Corollary 5.4 and Lemma A.1, we get the approximate tensorization
for \(c=2(1-\frac{1}{25}(2\ln 2-1)^{-1})^{-1}\approx 2.231<\frac{9}{4}\). Furthermore, since both \(X_m\) and \(Y_m\) have integer spectrum, they can be transferred from the Laplace operator \(\Delta _{\mathbb {T}}\) on the unit torus \({\mathbb {T}}\). Then by transference and [17, Theorem 4.12] (note that our normalization differs by a factor of 2),
for each m. Therefore we obtain the dimension-free numerical bound
which is obviously tighter than the dimension dependent estimate from Theorem 3.3 (\({\mathcal {L}}_m^H\) has a uniform spectral gap 1 for all m by transference, see [10, Proposition 3.1]). It remains open whether the sub-Laplacian \(\Delta _H\) itself satisfies CMLSI.
6.2 Subsystem Lindbladians
In this subsection, we consider symmetric Markov semigroups whose Lindblad operators act on edges of a given graph. Such generators have been extensively studied for functional inequalities in the classical setting. (see e.g. [76] and the references therein). Here, we use (i) the CMLSI constants found in Theorem 3.3 to control the local interaction in combination with (ii) the sharpening of the approximate tensorization constant found in Section 6 to derive asymptotically tight lower bounds on the CMLSI constant for various models of relevance.
Let \(G:=(V,E)\) be a finite, connected and undirected graph with vertex set V, of cardinality \(|V|=n\), and edge set \(E:=\{(v,w)\in V\times V:\,v\sim w\}\). We recall that the degree \({\text {deg}}(v)\) of a vertex \(v\in V\) is the number of edges that are incident to v. Moreover, G is said to be \(\gamma \)-regular if all vertices \(v\in V\) have same degree \(\gamma \). Important examples include finite groups through the scope of their Cayley graphs. Given a graph \(G:=(V,E)\), the graph Laplacian \(\Delta _G\) acting on the function spaces \(\{f| f:V\rightarrow {\mathbb {C}} \}\) is defined as
where \(\Delta _G\) is a negative semi-definite matrix on \(l_2(V)\), which generates the heat semigroup \(T_t=e^{\Delta _G t}\) on \(l_\infty (V)\). Note that here we choose \(\Delta _G\) to be negative to match our convention for quantum Lindbladians. The spectral gap is defined as the gap between the largest and second largest eigenvalues of \(\Delta _G\).
Here we consider a quantum Markov semigroup with the locality structure of \(G=(V,E)\) consists in introducing a local evolution on the n-fold tensor product \({\mathcal {H}}_V:=\bigotimes _{v\in V}{\mathcal {H}}_v\) of a given finite dimensional local Hilbert space \({\mathcal {H}}\), namely, an n-qudit system for \(d=\dim ({\mathcal {H}})\). The Lindblad operators are supported on the edges \(e\in E\) as
where for any edge \(e=(v,w)\) and \(\{L^{(e)}_j\}_{j\in J^{(e)}}\) are the family of local Lindblad operators that act trivially on subsystems other than \({\mathcal {H}}_{v}\otimes {\mathcal {H}}_{w}\). We call (62) a subsystem Lindbladian. In what follows, we denote by \({\mathcal {M}}_V:={\mathcal {B}}({\mathcal {H}}_V)\) (resp. \({\mathcal {M}}_e:={\mathcal {B}}({\mathcal {H}}_{v}\otimes {\mathcal {H}}_w)\)) the algebra of operators on which \({\mathcal {L}}_G\) (resp. \({\mathcal {L}}_e\) for \(e=(v,w)\in E\)) acts. We also denote by \(E_e\) ( resp. \(E_G\)) the conditional expectation projecting onto the kernel of \({\mathcal {L}}_e\) for \(e\in E\) (resp, of \({\mathcal {L}}_G\)). Finally, we introduce the indices
and \(c_G\) as the minimum non-zero eigenvalue of the Choi-Jamiolkowski state \(J_{E_G}\) of \(E_{G}\). It is also useful to introduce the generator
As previously discussed, the lower bounds on the complete modified logarithmic Sobolev constant derived in Theorem 3.3 are asymptotically not tight when the total dimension is large. For instance, in the case of a primitive semigroup on n-qudit systems, the completely bounded Pimsner–Popa index is equal to \(d^{n}\), where d is the dimension of the local Hilbert space \({\mathcal {H}}\). This gives lower bounds on the CMLSI constant of a subsystem Lindbladian that are exponentially small in the number of vertices. In the next theorem, we essentially leverage the locality structure of \({\mathcal {L}}_G\) to provide exponentially tighter bounds by combining Theorem 3.3, Corollary 5.4, Lemma A.1 and the detectability lemma [1, 2, 4, 49].
Theorem 6.6
Let \(G=(V,E)\) be a finite, connected, undirected graph with maximum degree \(\gamma \), and let \({\mathcal {L}}_G\) be a symmetric subsystem Lindbladian of the form (62). Then, for all \(m\in {\mathbb {N}}\) and any state \(\rho \in {\mathcal {D}}({\mathcal {H}}_V\otimes {\mathbb {C}}^{\otimes m})\),
where \(C:=\min \{C_G,c_G^{-1}\}\) and \(\lambda ({\widetilde{{\mathcal {L}}}}_G)\) is the spectral gap of \({\widetilde{{\mathcal {L}}}}_G\). Moreover, the \({\text {CMLSI}}\) constant for the generator \({\mathcal {L}}_G\) satisfies
As a consequence, whenever \(\lambda ({\widetilde{{\mathcal {L}}}}_G)\) is uniformly lower bounded by a constant independent of |V|, \(\alpha _{{\text {CMLSI}}}({\widetilde{{\mathcal {L}}}}_G)=\Omega \Big (\frac{1}{\ln (C)}\Big )\), hence recovering the asymptotics of classical expanders.
Proof
We first establish (63): by Remark 5.6, the approximate tensorization constant of the family \(\{E_e\}_{e\in E}\) of conditional expectations can be upper bounded by the constant 4k, where k is the integer such that
for \(\varepsilon := \sqrt{\ln (2)-\frac{1}{2}}\). Here the ordering in the product \(\prod _{e\in E}\,E_e\) is arbitrary. Next, we have from Lemmas A.1 and A.2 in “Appendix A” that k can be chosen as
Finally, the \(L_2\)-constant \(\lambda \) can be controlled by the gap of the generator \({\widetilde{{\mathcal {L}}}}_G\) using the detectability Lemma from [4, Corollary 3]:
Here \(\gamma \) is the maximum degree of the graph. We then use Theorem 3.3 to further lower bound \(\alpha _{{\text {CMLSI}}}({{\mathcal {L}}}_e)\) in terms of the spectral gap \(\lambda ({\mathcal {L}}_e)\) and corresponding index \(C_e\).
\(\square \)
Remark 6.7
A sequence of \(\gamma \)-regular graphs \(\{G_i=(V_i,E_i)\}_{i\in {\mathbb {N}}}\) of increasing size with \(\lim _{i} |V_i|=+\infty \) is called a family of expander graphs if there exists \(\lambda _0>0\) such that the spectral gaps \(\lambda (\Delta _{G_i})\ge \lambda _0\) uniformly for all i [45]. Modified logarithmic Sobolev inequalities for such generators have been widely considered in the classical literature, (see e.g. the survey [14]). In the limit \(i\rightarrow \infty \), using Corollary 5.4 for the average map \(\Phi =\frac{1}{|E|}\sum _{e}E_e\) instead of resorting to the detectability Lemma for the product map \(\Phi =\prod _{e\in E}\,E_e\) would lead to a similar bound:
In [15, Remark 5.6], it was shown that the MLSI constant of a random walk on an expander graph G of degree \(\gamma \) satisfies that
Since, for these graphs, \(C=\ln |G|\), the above estimates show that our lower bounds recover the right dependence on |G| up to multiplicative constants.
6.3 Random Permutations
We now illustrate the bounds derived in Theorem 6.6 on random permutations models. We consider quantum Markov semigroups introduced in [9, Section IV.D] which represent the action of a random transposition gate applied to two registers i, j on the n qudit system \({\mathcal {H}}_V={\mathcal {H}}^{\otimes n}\) with \(\dim ({\mathcal {H}})=d\). Let \(G=(V,E)\) be a finite graph with \(|V|=n\). Denote the swap gate \(S_{i,j}\) acting on registers of vertex i and j as
for any two \(|\psi \rangle ,|\varphi \rangle \in {\mathcal {H}}\). The generator of the quantum nearest neighbour random transposition model [9, Section IV.D] is defined as
for \(e=(i,j)\). The above generator can simply be understood as that of the natural action of the permutation group \({\mathcal {S}}_n\) on \({\mathcal {H}}_V={\mathcal {H}}^{\otimes n}\), which allows transitions between random adjacent registers connected by edges. In other words, \({\mathcal {L}}^{{\text {NNRT}}}_G\) is the subsystem Lindbladian of the graph \(G=(V,E)\) with the local Lindbladian \({\mathcal {L}}_e\) at edge \((i,j)\in E\).
Corollary 6.8
Let \(G=(V,E)\) be a connected finite graph and let \({\mathcal {L}}_{{\text {NNRT}}}^G\) be the generator of the quantum nearest neighbour random transposition model defined as above. Then
where \(\gamma \) is the maximal degree of G and \(\lambda ({\mathcal {L}}^{{\text {NNRT}}}_G)\) is the spectral gap.
Proof
We first note that, for each edge,
where \(E_{i,j}(\rho )=\frac{1}{2}(S_{i,j}\rho S_{i,j}+\rho )\) is a conditional expectation onto the symmetric space on \({\mathcal {H}}_{i}\otimes {\mathcal {H}}_j\). The maps \(E_{i,j}\) are implemented by the self-adjoint unitaries \(S_{i,j}\). Then by [81, Theorem 5.1], the local CMLSI constant \(\alpha _{{\text {CMLSI}}}({\mathcal {L}}_e)=2\). Given the bound derived in Theorem 6.6, it suffices to calculate the index \(C_G:=C_{{\text {cb}}}({\mathcal {B}}({\mathcal {H}}_V):{\mathcal {N}})\), where \({\mathcal {N}}\) is the fixed point subalgebra of \({\mathcal {L}}^{{\text {NNRT}}}_G\). Since G is connected, then \(\{\sigma _{i,j}\ |\ (i,j)\in E \}\) is a generating set for \({\mathcal {S}}_n\). Thus \({\mathcal {N}}\) is the commutant of the representation
As discussed in Example A.4 of “Appendix A”, the index is
where \(m_i\) is the dimension of irreducible representation \(\pi _i\) and the summation is over all irreducible representations in the decomposition of \(\pi =\oplus _{i}\pi _i\otimes {\text {id}}_{{n_i}}\). By the expression provided in (14), we know all irreducible representations (up to unitary equivalent) are contained in \(\pi \). Then, by the Schur–Weyl Theorem,
\(\square \)
The quantum random transposition model above corresponds to a classical random transposition on the permutation group \({\mathcal {S}}_n\) on \([n]:=\{1,\ldots , n\}\). Indeed, consider the classical generator \(\Delta _{{\mathcal {S}}_n}^G\) on \({\mathcal {S}}_n\),
where \(\sigma _{ij}\in {\mathcal {S}}_{n}\) is the 2-permutation switching i and j. One can verify that \({\mathcal {L}}^{{\text {NNRT}}}_G\) is the transferred generator of \(\Delta _{{\mathcal {S}}_n}^G\), which is the the graph Laplacian \(\Delta _{{\mathcal {S}}_n}^G\) of the Cayley graph of \({\mathcal {S}}_n\) with generating set \(\{\sigma _{ij}\ | \ (i,j)\in E \}\).
For a general graph \(G=(V,E)\), the transference goes through the graph Laplacian \(\Delta _{{\mathcal {S}}_n}^G\) of the Cayley graph of \({\mathcal {S}}_n\) with generating set \(\{\sigma _{ij}\ | \ (i,j)\in E \}\). When a sharp estimate for \(\alpha _{{\text {CMLSI}}}(\Delta _{{\mathcal {S}}_n})\) is missing, our Theorem 6.6 can provide tighter bounds than transference. It was proved in [56] that for a graph Laplacian \(\Delta _G\),
where \(\gamma \) is the maximum degree of G. Here, we have \(V={\mathcal {S}}_n\) with \(|{\mathcal {S}}_n|=n!\) growing exponentially. This exponential growth also appears if we use Theorem 3.3,
since \(C_{{\text {cb}}}(l_\infty ({\mathcal {S}}_n);{\mathbb {C}})=|{\mathcal {S}}_n|=n!\). Compared with these, Theorem 6.6 gives a lower bound on the CMLSI constant for \({\mathcal {L}}^{{\text {NNRT}}}_G\) that has exponentially better dependence of \(|G|=n\) (and is also independent of \(d=\dim ({\mathcal {H}})\)).
7 Discussion and Open Problems
We end our paper by discussing some open problems. Theorem 3.3 proves that any GNS-symmetric quantum Markov semigroup \(({\mathcal {P}}_{t}:{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}}))_{t\ge 0}\) on a finite dimensional Hilbert space \({\mathcal {H}}\) satisfies the complete modified log-Sobolev inequality (CMLSI) with constant
where \({\mathcal {L}}\) is the generator and \(E=\lim _{t} {\mathcal {P}}_t\). In the primitive case (unique invariant state), \(C_{{\text {cb}},\tau }(E)\sim d^2\) with \(d=\dim ({\mathcal {H}})\). On the other hand, it was proven that, for a primitive semigroup with invariant state \(\sigma \),
where \(\alpha _{{\text {MLSI}}}\) is the optimal constant for the modified log-Sobolev inequality and \(\alpha _{{\text {LSI}}}\) is the optimal constant for the \(L_2\)-log-Sobolev inequality (LSI), which is known to be equivalent to hypercontractivity [66]. Here \(\mu _{\min }(\sigma )\) is the minimal eigenvalue of \(\sigma \) and \(\ln (\mu _{\min }(\sigma )^{-1})\sim \ln d\). Our lower bound on \(\alpha _{{\text {CMLSI}}}\) controls any amplification \({\mathcal {P}}_{t}\otimes {\text {id}}_{{\mathbb {M}}_n}\), in contrast with \(L_2\)-log-Sobolev inequality/hypercontractivity bound which fails for \({\mathcal {P}}_{t}\otimes {\text {id}}_{{\mathbb {M}}_n}\) for any \(n>1\). It remains open whether the bound (66) can be improved asymptotically.
Problem 7.1
Does there exist a general lower bound on the \({\text {CMLSI}}\) constant of the form \(\alpha _{{\text {CMLSI}}}({\mathcal {L}})\ge \lambda ({\mathcal {L}})\, {\mathcal {O}}(\ln d)^{-1}\)?
Our second question concerns the strong data processing inequality (SDPI). It was proven in [63] that for a primitive unital quantum channel \(\Phi \),
where \(\alpha _{{\text {LSI}}}(T^*T-{\text {id}})\) is the LSI constant of the map \(T^*T-{\text {id}}\) seen as the generator of a QMS. This combined with (66) gives upper bounds on SDPI constant for primitive unital channel. Nevertheless, since LSI generally fails for non-primitive semigroups, this approach does not apply to CSDPI. In order to find better (C)SDPI constant, we propose the following question:
Problem 7.2
Can we find a lower bound on \(\alpha _{{\text {SDPI}}}(\Phi )\) in terms of the modified log-Sobolev constant \(\alpha _{{\text {MLSI}}}(\Phi ^*\Phi -{\text {id}})\) for any non-primitive quantum channel \(\Phi \)?
For classical Markov chains, such a result was obtained in [31]. Note that in general \(2\alpha _{{\text {MLSI}}}({\mathcal {L}})\ge \alpha _{{\text {LSI}}}({\mathcal {L}})\), so a positive answer to Problem 7.2 would be stronger than (68). Moreover, combined with our Theorem 3.3, such a positive solution would also give a lower estimate on the CSDPI constant in terms of the spectral gap and the index.
Recall that our SDPI constant \(\alpha _{{\text {SDPI}}}\) is defined as the optimal constant \(0\le \alpha \le 1\) such that
for any state \(\rho \). Here \(E_*(\rho )\) is the decoherence free part of the state \(\rho \) in the sense that for a GNS symmetric channel \(\Phi \), \(\Phi ^2\circ E_*(\rho )=E_*(\rho )\) and \(\displaystyle \lim _{n\rightarrow \infty }\parallel \! \Phi ^n(\rho )-\Phi ^n\circ E_*(\rho ) \! \parallel _{}=0\). This is a natural choice analogous to MLSI. Nevertheless, the data processing inequality asserts that \(D(\Phi (\rho )\Vert \Phi (\sigma ))\le D(\rho \Vert \sigma )\) for any two states \(\rho \) and \(\sigma \). Indeed, in Theorem 4.1, we prove that for a state \(\omega \), the best local constant \(\alpha '(\sigma )\), which satisfies
for all states \(\rho \) with \(E_*(\rho )=E_*(\omega )\), can be two-sided controlled by the corresponding \(\chi _2\) contraction coefficient. (Here the restriction \(E_*(\rho )=E_*(\omega )\) is needed because without it the constant \(\alpha (\omega )\) would often be trivially equal to 1). It is then natural to ask whether for a quantum channel \(\Phi \), there is a non-trivial upper bound on \(\alpha (\omega )\) uniformly in \(\omega \). Namely,
Problem 7.3
For a finite dimensional quantum channel \(\Phi \), does there exist a constant \(\alpha '(\Phi )<1\) such that
for all states \(\rho ,\sigma \) with \(E_*(\rho )=E_*(\omega )\)?
Such a constant \(\alpha '(\Phi )\) leads to a stronger notion of contraction than our definition of \(\alpha _{{\text {SDPI}}}\); it is closer to the classical strong data processing inequality studied in [71, 73], which was proven to be equivalent to the contraction coefficient of (classical) \(\chi _2\)-divergence. Note that, by our Theorem 4.1, it also suffices to show that there is a global contraction coefficient on the quantum \(\chi _2\) divergence
for all states \(\sigma \).
References
Aharonov, D., Arad, I., Landau, Z., Vazirani, U.: The detectability lemma and quantum gap amplification. In: Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, pp. 417–426, 2009
Aharonov, D., Arad, I., Landau, Z., Vazirani, U.: Quantum Hamiltonian complexity and the detectability lemma. arXiv preprint arXiv:1011.3445, 2010
Ahlswede, R., Gács, P.: Spreading of sets in product spaces and hypercontraction of the Markov operator. Ann. Probab. 4, 925–939, 1976
Anshu, A., Arad, I., Vidick, T.: Simple proof of the detectability lemma and spectral gap amplification. Phys. Rev. B 93(20), 205142, 2016
Baillet, M., Denizeau, Y., Havet, J.-F.: Indice d’une espérance conditionnelle. Compositio Mathematica 66(2), 199–236, 1988
Bardet, I.: Estimating the decoherence time using non-commutative functional inequalities. arXiv preprint arXiv:1710.01039, 2017
Bardet, I., Capel, Á., Gao, L., Lucia, A., Pérez-García, D., Rouzé, C.: Entropy decay for davies semigroups of a one dimensional quantum lattice. arXiv preprint arXiv:2112.00601, 2021
Bardet, I., Capel, A., Rouzé, C.: Approximate tensorization of the relative entropy for noncommuting conditional expectations. arXiv preprint arXiv:2001.07981, 2020
Bardet, I., Junge, M., Laracuente, N., Rouze, C., Franca, D.S.: Group transference techniques for the estimation of the decoherence times and capacities of quantum Markov semigroups. IEEE Trans. Inf. Theory 67(5), 2878–2909, 2021
Baudoin, F., Bonnefont, M.: The subelliptic heat kernel on \(\operatorname{SU}(2)\): representations, asymptotics and gradient bounds. Mathematische Zeitschrift 263(3), 647–672, 2009
Beigi, S., Datta, N., Rouzé, C.: Quantum reverse hypercontractivity: its tensorization and application to strong converses. Commun. Math. Phys. 376(2), 753–794, 2020
Berta, M., Sutter, D., Walter, M.: Quantum Brascamp–Lieb dualities. arXiv preprint arXiv:1909.02383, 2019
Blahut, R.: Hypothesis testing and information theory. IEEE Trans. Inf. Theory 20(4), 405–417, 1974
Bobkov, S., Tetali, P.: Modified log-Sobolev inequalities, mixing and hypercontractivity. In: Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, pp. 287–296, 2003
Bobkov, S.G., Tetali, P.: Modified logarithmic Sobolev inequalities in discrete settings. J. Theor. Probab. 19(2), 289–336, 2006
Brandao, F.G., Harrow, A.W., Horodecki, M.: Local random quantum circuits are approximate polynomial-designs. Commun. Math. Phys. 346(2), 397–434, 2016
Brannan, M., Gao, L., Junge, M.: Complete logarithmic Sobolev inequalities via Ricci curvature bounded below I. arXiv preprint arXiv:2007.06138, 2020
Brannan, M., Gao, L., Junge, M.: Complete logarithmic Sobolev inequalities via Ricci curvature bounded below II. arXiv preprint arXiv:2007.06138, 2020
Capel, Á., Rouzé, C., França, D. S.: The modified logarithmic Sobolev inequality for quantum spin systems: classical and commuting nearest neighbour interactions. arXiv preprint arXiv:2009.11817, 2020
Carbone, R., Martinelli, A.: Logarithmic Sobolev inequalities in non-commutative algebras. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 18(02), 1550011, 2015
Carlen, E.A., Maas, J.: Gradient flow and entropy inequalities for quantum Markov semigroups with detailed balance. J. Funct. Anal. 273(5), 1810–1869, 2017
Carlen, E.A., Maas, J.: Non-commutative calculus, optimal transport and functional inequalities in dissipative quantum systems. J. Stat. Phys. 178(2), 319–378, 2020
Carlen, E.A., Vershynina, A.: Recovery map stability for the data processing inequality. J. Phys. A Math. Theor. 53(3), 035204, 2020
Cesi, F.: Quasi-factorization of the entropy and logarithmic Sobolev inequalities for Gibbs random fields. Probab. Theory Relat. Fields 120(4), 569–584, 2001
Cipriani, F.: Dirichlet forms and Markovian semigroups on standard forms of von Neumann algebras. J. Funct. Anal. 147(2), 259–300, 1997
Csiszár, I.: Information-type measures of difference of probability distributions and indirect observation. Studia Scientiarum Mathematicarum Hungarica 2, 229–318, 1967
Dai Pra, P., Paganoni, A.M., Posta, G., et al.: Entropy inequalities for unbounded spin systems. Ann. Probab. 30(4), 1959–1976, 2002
Datta, N.: Min-and max-relative entropies and a new entanglement monotone. IEEE Trans. Inf. Theory 55(6), 2816–2826, 2009
Datta, N., Rouzé, C.: Relating relative entropy, optimal transport and Fisher information: a quantum HWI inequality. In: Annales Henri Poincaré, pp. 1–36. Springer, 2020
Davies, E.B., Lindsay, J.M.: Non-commutative symmetric Markov semigroups. Mathematische Zeitschrift 210(1), 379–411, 1992
Del Moral, P., Ledoux, M., Miclo, L.: On contraction properties of Markov kernels. Probab. Theory Relat. Fields 126(3), 395–420, 2003
Dobrushin, R.L.: Central limit theorem for nonstationary Markov chains. I. Theory Probab. Appl. 1(1), 65–80, 1956
Dobrushin, R.L.: Central limit theorem for nonstationary Markov chains. II. Theory Probab. Appl. 1(4), 329–383, 1956
Frigerio, A., Verri, M.: Long-time asymptotic properties of dynamical semigroups on W\(^*\)-algebras. Mathematische Zeitschrift 180(3), 275–286, 1982
Gao, F., Quastel, J., et al.: Exponential decay of entropy in the random transposition and Bernoulli–Laplace models. Ann. Appl. Probab. 13(4), 1591–1600, 2003
Gao, L., Junge, M., LaRacuente, N.: Unifying entanglement with uncertainty via symmetries of observable algebras. arXiv preprint arXiv:1710.10038, 2017
Gao, L., Junge, M., LaRacuente, N.: Fisher information and logarithmic Sobolev inequality for matrix-valued functions. In: Annales Henri Poincaré, vol. 21, pp. 3409–3478. Springer, 2020
Gao, L., Junge, M., LaRacuente, N.: Relative entropy for von Neumann subalgebras. Int. J. Math. 31(06), 2050046, 2020
Gao, L., Rouzé, C.: Complete entropic inequalities for quantum Markov chains. arXiv preprint arXiv:2102.04146v3, 2021
Gross, L.: Hypercontractivity and logarithmic Sobolev inequalities for the Clifford–Dirichlet form. Duke Math. J. 42(3), 383–396, 1975
Gross, L.: Hypercontractivity, logarithmic Sobolev inequalities, and applications: a survey of surveys. Diffus. Quantum Theory Radic. Elem. Math. 47, 45–73, 2014
Hastings, M.B.: Superadditivity of communication capacity using entangled inputs. Nat. Phys. 5(4), 255–257, 2009
Hiai, F., Petz, D.: The proper formula for relative entropy and its asymptotics in quantum probability. Commun. Math. Phys. 143(1), 99–114, 1991
Hiai, F., Ruskai, M.B.: Contraction coefficients for noisy quantum channels. J. Math. Phys. 57(1), 015211, 2016
Hoory, S., Linial, N., Wigderson, A.: Expander graphs and their applications. Bull. Am. Math. Soc. 43(4), 439–561, 2006
Junge, M., LaRacuente, N., Rouzé, C.: Stability of logarithmic Sobolev inequalities under a noncommutative change of measure. arXiv preprint arXiv:1911.08533, 2019
Junge, M., Parcet, J.: Mixed-Norm Inequalities and Operator Space\( L_p \)Embedding Theory. American Mathematical Society, 2010
Junge, M., Renner, R., Sutter, D., Wilde, M. M., Winter, A.: Universal recovery maps and approximate sufficiency of quantum relative entropy. In: Annales Henri Poincaré, vol. 19, pp. 2955–2978. Springer, 2018
Kastoryano, M.J., Brandao, F.G.: Quantum Gibbs samplers: the commuting case. Commun. Math. Phys. 344(3), 915–957, 2016
Kastoryano, M.J., Temme, K.: Quantum logarithmic Sobolev inequalities and rapid mixing. J. Math. Phys. 54(5), 052202, 2013
Kosaki, H.: Type III Factors and Index Theory, vol. 43. Research Institute of Mathematics, Global Analysis Research Center, Seoul, 1998
Kullback, S., Leibler, R.A.: On information and sufficiency. Ann. Math. Stat. 22(1), 79–86, 1951
LaRacuente, N.: Quasi-factorization of quantum relative entropy for subalgebras with scalar intersection. arXiv preprint arXiv:1912.00983, 2019
Ledoux, M.: Analytic and geometric logarithmic Sobolev inequalities. Journées équations aux dérivées partielles, pp. 1–15, 2011
Lesniewski, A., Ruskai, M.B.: Monotone Riemannian metrics and relative entropy on noncommutative probability spaces. J. Math. Phys. 40(11), 5702–5724, 1999
Li, H., Junge, M., LaRacuente, N.: Graph Hörmander systems. arXiv preprint arXiv:2006.14578, 2020
Lieb, E.H.: Convex trace functions and the Wigner–Yanase–Dyson conjecture. Les rencontres physiciens-mathématiciens de Strasbourg-RCP25, 19, 0–35, 1973
Lieb, E.H., Ruskai, M.B.: Proof of the strong subadditivity of quantum-mechanical entropy. Les rencontres physiciens-mathématiciens de Strasbourg-RCP25, 19, 36–55, 1973
Liese, F., Vajda, I.: On divergences and informations in statistics and information theory. IEEE Trans. Inf. Theory 52(10), 4394–4412, 2006
Lindblad, G.: Completely positive maps and entropy inequalities. Commun. Math. Phys. 40(2), 147–151, 1975
Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48(2), 119–130, 1976
Müller-Hermes, A., Reeb, D.: Monotonicity of the quantum relative entropy under positive maps. In: Annales Henri Poincaré, vol. 18, pp. 1777–1788. Springer, 2017
Müller-Hermes, A., Stilck França, D., Wolf, M.M.: Entropy production of doubly stochastic quantum channels. J. Math. Phys. 57(2), 022203, 2016
Nelson, E.: The free Markoff field. J. Funct. Anal. 12(2), 211–227, 1973
Ogawa, T., Nagaoka, H.: Strong converse and Stein’s lemma in quantum hypothesis testing. In: Asymptotic Theory of Quantum Statistical Inference: Selected Papers, pp. 28–42. World Scientific, 2005
Olkiewicz, R., Zegarlinski, B.: Hypercontractivity in noncommutative \({L}_p\) spaces. J. Funct. Anal. 161(1), 246–285, 1999
Paschke, W.L.: Inner product modules over \(\cal{B}\)*-algebras. Trans. Am. Math. Soc. 182, 443–468, 1973
Petz, D.: On certain properties of the relative entropy of states of operator algebras. Mathematische Zeitschrift 206(1), 351–361, 1991
Petz, D.: Monotone metrics on matrix spaces. Linear Algebra Appl. 244, 81–96, 1996
Pimsner, M., Popa, S.: Entropy and index for subfactors. Annales scientifiques de l’École Normale Supérieure, Ser. 4 19(1), 57–106, 1986
Polyanskiy, Y., Wu, Y.: Strong data-processing inequalities for channels and Bayesian networks. In: Carlen, E.A., Madiman, M., Werner, E.M. (eds.) Convexity and Concentration, pp. 211–249. Springer, 2017
Popa, S.: Orthogonal pairs of *-subalgebras in finite von Neumann algebras. J. Oper. Theory 9, 253–268, 1983
Raginsky, M.: Strong data processing inequalities and \({\Phi }\)-Sobolev inequalities for discrete channels. IEEE Trans. Inf. Theory 62(6), 3355–3389, 2016
Rouzé, C., Datta, N.: Concentration of quantum states from quantum functional and transportation cost inequalities. J. Math. Phys. 60(1), 012202, 2019
Smith, G., Yard, J.: Quantum communication with zero-capacity channels. Science 321(5897), 1812–1815, 2008
Stroock, D.W., Zegarlinski, B.: The equivalence of the logarithmic Sobolev inequality and the Dobrushin–Shlosman mixing condition. Commun. Math. Phys. 144(2), 303–323, 1992
Temme, K., Kastoryano, M.J., Ruskai, M.B., Wolf, M.M., Verstraete, F.: The \(\chi _2\)-divergence and mixing times of quantum Markov processes. J. Math. Phys. 51(12), 122201, 2010
Uhlmann, A.: Relative entropy and the Wigner–Yanase–Dyson–Lieb concavity in an interpolation theory. Commun. Math. Phys. 54(1), 21–32, 1977
Umegaki, H.: Conditional expectation in an operator algebra, iv (entropy and information). In: Kodai Mathematical Seminar Reports, vol. 14, pp. 59–85. Department of Mathematics, Tokyo Institute of Technology, 1962
Wirth, M.: Christensen–Evans theorem and extensions of GNS-symmetric quantum Markov semigroups. arXiv preprint arXiv:2203.00341, 2022
Wirth, M., Zhang, H.: Complete gradient estimates of quantum Markov semigroups. arXiv preprint arXiv:2007.13506, 2020
Wolf, M.M.: Quantum channels & operations: Guided tour. Lecture notes available at http://www-m5.ma.tum.de/foswiki/pubM, 5, 2012
Acknowledgements
Cambyse Rouzé is supported by a Junior Researcher START Fellowship from the MCQST as well as by the Alexander von Humboldt fellowship. Cambyse Rouzé is grateful to Daniel Stilck França, Angela Capel and Ivan Bardet for stimulating discussions. Cambyse Rouzé and Li Gao particularly thank Daniel Stilck França for very useful comments on a preliminary version of the paper. Li Gao thanks Marius Junge and Haojian Li for helpful discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Mouhot.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Completely Positive Order Relations from Norm Estimates
Appendix A: Completely Positive Order Relations from Norm Estimates
In this appendix, we provide two generic strategies to derive the order relations needed in Theorem 5.3 in the case of symmetric generators. Our first method is a variant of [37, Lemma 3.15] (see also [53, Corollary 1.8]). Let \({\mathcal {M}}\) be a finite dimensional von Neumann algebra equipped with trace \(\tau \) and let \({\mathcal {N}}\subset {\mathcal {M}}\) be a von Neumann subalgebra. Note that we do not fix the normalization of \(\tau \) at this point. For \(p\ge 1\), the space of p-integrable operators in \({\mathcal {M}}\) is denoted by \(L_p({\mathcal {M}},\tau )\equiv L_p(\tau )\), with associated norm
We also need the notion of an amalgamated \(L_p\) norm [47]: for \(1\le p\le \infty \) the \(L_\infty ^p({\mathcal {N}}\subset {\mathcal {M}})\) norm of \(X\in {\mathcal {M}}\) is given by
where the supremum is taken over \(a,b\in {\mathcal {N}}\) with \(\parallel \! a \! \parallel _{2p}=\parallel \! b \! \parallel _{2p}=1\). Its operator space structure is given by (see [38, Appendix])
It was proved in [38, Theorem 3.9] that
Let \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) be the trace preserving conditional expectation onto \({\mathcal {N}}\). Recall that there exists a module basis \(\{\xi _i\}_{i=1}^n\in {\mathcal {M}}\) satisfying ( [67, Theorem 3.15], see also [5, Conséquence 1.8]):
where \(p_i\in {\mathcal {N}}\) are some projections. Also recall that \(\Phi :{\mathcal {M}}\rightarrow {\mathcal {M}}\) is a \({\mathcal {N}}\)-bimodule map if \(\Phi (aXb)=a\Phi (X)b\) for all \(a,b\in {\mathcal {N}}\) and \(X\in {\mathcal {M}}\). We have \(\Phi \circ E_{\mathcal {N}}=E_{{\mathcal {N}}}\) if \(\Phi \) is unital and \(E_{{\mathcal {N}}}\circ \Phi = E_{{\mathcal {N}}}\) if \(\Phi \) is trace preserving. For a \({\mathcal {N}}\)-bimodule map \(\Phi \), we have by [37, Lemma 3.12]
Next, we define the module Choi operator of a bi-modular map \(\Phi \) as
where \(l_2^n\) denotes the space of n-dimensional vectors with associated norm
and \(\{{|{i}\rangle }\}_{i=1}^n\) is a fixed orthonormal basis in \(l_2^n\). Thus \(\Phi \) and \(\chi _\Phi \) determine each other because for each \(x\in {\mathcal {M}}\), we have a unique decomposition \(x=\sum _{i}\xi _i x_i \) with \(x_i\in {\mathcal {N}}\) satisfying \(p_ix_i=x_i\). Indeed, we have \(x_i=E_{\mathcal {N}}(\xi _i^\dagger x)\). Moreover, \(\Phi \) is completely positive if and only if \(\chi _\Phi \) is a positive operator in \({\mathcal {B}}(l_2^n)\otimes {\mathcal {M}}\). Indeed, for any finite family \(y_1,\ldots ,y_m\in {\mathcal {M}}\), we assume the decomposition \(y_j=\sum _{l}\xi _l x_{jl}\) with \(x_{jl}\in {\mathcal {N}}\). Then
from which the equivalence claimed directly follows. We also recall [37, Lemma 3.14] that for a \({\mathcal {N}}\)-bimodule map \(\Phi \),
We are now ready to state and prove the first main Lemma of this section:
Lemma A.1
Let \({\mathcal {N}}\subset {\mathcal {M}}\) be a von Neumann subalgebra and let \(E_{\mathcal {N}}:{\mathcal {M}}\rightarrow {\mathcal {N}}\) be the corresponding trace preserving conditional expectation. Let \(\Phi :{\mathcal {M}}\rightarrow {\mathcal {M}}\) be a \({\mathcal {N}}\)-bimodule map.
-
(i)
if \(\parallel \! \chi _\Phi -\chi _{E_{\mathcal {N}}} \! \parallel _{{\mathcal {B}}((l_2^n))\otimes {{\mathcal {M}}}}{}\le \varepsilon < 1\), then
$$\begin{aligned} (1-\varepsilon )E_{{\mathcal {N}}}\le _{{\text {cp}}} \Phi \le _{{\text {cp}}} (1+\varepsilon ) E_{{\mathcal {N}}} \ . \end{aligned}$$ -
(ii)
if \(\Phi \) is a \(\tau \)-symmetric quantum channel and \(\lambda :=\parallel \! \Phi -E_{\mathcal {N}}:L_2({\mathcal {M}},\tau )\rightarrow L_2({\mathcal {M}},\tau ) \! \parallel _{}<1\), then for \(k>\frac{\ln C_{{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})}{-\ln \lambda }\),
$$\begin{aligned} (1-\varepsilon )E_{\mathcal {N}}\le _{{\text {cp}}} \Phi ^k\le _{{\text {cp}}} (1+\varepsilon )E_{\mathcal {N}}\end{aligned}$$for \(\varepsilon =\lambda ^kC_{{\text {cb}}}({\mathcal {M}}:{\mathcal {N}})<1 \).
Proof
For (i) we first observe that the Choi operator of \(E_{{\mathcal {N}}}\)
is a projection. By the assumption \(\parallel \! \chi _\Phi -\chi _{E_{\mathcal {N}}} \! \parallel _{{\mathcal {B}}((l_2^n))\otimes {{\mathcal {M}}}}{}\le \varepsilon <1\), we may write \(\chi _{E_{\mathcal {N}}}-\chi _\Phi =\alpha -\beta \) with \(\displaystyle 0\le \alpha ,\beta \le \varepsilon \). Let \(\{y_1,\ldots ,y_m\}\) be a finite family of elements in \( {\mathcal {M}}\) with decomposition \(y_j=\sum _{l}\xi _l x_{jl}\) with \(x_{jl}=p_jx_{jl}\in {\mathcal {N}}\), and denote \(Y=\sum _{j}{|{1}\rangle }{\langle {j}|}\otimes y_j\). Then,
Since \(0\le \alpha \le \varepsilon \),
and similarly for \(\beta \). Thus we showed that
for any \(Y=\sum _{j}{|{1}\rangle }{\langle {j}|}\otimes y_j\), which proves (i) because any \(X\ge 0\) in \({\mathbb {M}}_m\otimes {\mathcal {M}}\) can be written as a sum \(X=\sum _{j}Y_j^\dagger Y_j\) of such Y’s.
For (ii), we first observe that since \(\Phi \) is trace perserving and unital, we have by bimodule property that \(\Phi \circ E_{\mathcal {N}}=E_{\mathcal {N}}\circ \Phi = E_{{\mathcal {N}}}\) and hence \((\Phi -E_{{\mathcal {N}}})^k=\Phi ^k-E_{{\mathcal {N}}}\). Then, we can use identity (71) between the \(L_\infty \) norm of the module Choi operator of \(\Phi ^k\) and its \(L_\infty ^1\) norm, so that:
where we also used (69) and (70). Then the assertion (ii) follows from (i). \(\square \)
The next main result of the present appendix is an approach to obtain \({\text {cp}}\) orders which follows the idea of [16, Appendix A]. Here, we restrict ourselves to the algebra \({\mathcal {M}}={\mathcal {B}}({\mathcal {H}})\) and take \(\tau :={\text {tr}}\) to be the standard matrix trace. Given a map \(\Phi :{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {B}}({\mathcal {H}})\), the standard (normalized) Choi-Jamiolkowski matrix \(J_\Phi \) is
where \({|{\psi }\rangle }=\frac{1}{\sqrt{d_{\mathcal {H}}}}\sum _{i}{|{i}\rangle }{|{i}\rangle }\) is the maximally entangled state on \({\mathcal {H}}\otimes {\mathcal {H}}\). It is well-known that \(J_\Phi \ge 0\) if and only if \(\Phi \) is completely positive, and \(J_\Phi \) is a state if and only if \(\Phi \) is a quantum channel.
Lemma A.2
Let \(E_{{\mathcal {N}}}:{\mathcal {B}}({\mathcal {H}})\rightarrow {\mathcal {N}}\) be the trace preserving conditional expectation onto a subalgebra \({\mathcal {N}}\). Let \(\Phi :{\mathcal {T}}_1({\mathcal {H}})\rightarrow {\mathcal {T}}_1({\mathcal {H}})\) be a quantum channel such that \(\Phi \circ E_{{\mathcal {N}}}=E_{{\mathcal {N}}}\circ \Phi =E_{{\mathcal {N}}}\). Suppose \(J_{E_{\mathcal {N}}}\ge C_E^{-1} P\) for some \(C_E>0\) where P is the support projection of \(J_{E_{\mathcal {N}}}\).
-
(i)
If \(J_\Phi \) has support \(P_{\Phi }\le P\) and for some \(0\le \varepsilon <1\)
$$\begin{aligned} \Vert J_\Phi -J_{E_{{\mathcal {N}}}}\Vert _{\infty }\le \varepsilon \, C_E^{-1}\, , \end{aligned}$$then
$$\begin{aligned} (1-\varepsilon )E_{\mathcal {N}}\le _{{\text {cp}}} \Phi \le _{{\text {cp}}} (1+\varepsilon )E_{\mathcal {N}}. \end{aligned}$$ -
(ii)
If for each k, \(J_{\Phi ^k}\) has support projection P and \(\lambda :=\parallel \! \Phi -E_{{\mathcal {N}}}:L_2({\mathcal {B}}({\mathcal {H}}),{\text {tr}})\rightarrow L_2({\mathcal {B}}({\mathcal {H}}),{\text {tr}}) \! \parallel _{}<1\). Then for \(k> \frac{\ln (C_E)}{-\ln (\lambda )}\),
$$\begin{aligned} (1-\varepsilon )E_{\mathcal {N}}\le _{{\text {cp}}} \Phi ^k\le _{{\text {cp}}} (1+\varepsilon )E_{\mathcal {N}},\end{aligned}$$where \(\varepsilon =\lambda ^k\,C_E<1\).
Proof
If \(J_\Phi \) has support \(P_\Phi \le P\), then
Similarly,
Thus we have
which implies (i). For (ii), we note that the maximally entangled state \({|{\psi }\rangle }{\langle {\psi }|}\) is a pure state, so that
Then assertion (ii) follows from (i). \(\square \)
We end this appendix by comparing the approaches proposed in Lemmas A.1 and A.2 in two cases.
Example A.3
(Trivial subalgebra) Consider the trivial subalgebra \({\mathbb {C}}1\subset {\mathcal {B}}({\mathcal {H}})\). Then for \(\dim ({\mathcal {H}})=d\),
Example A.4
(Unitary Representations of compact groups) Let G be a compact group and let \(\pi :G\rightarrow {\mathcal {B}}({\mathcal {H}})\) be a unitary representation. The fixed point space for the conjugation action \(\alpha :G\curvearrowright {\mathcal {B}}({\mathcal {H}})\) defined as \(\alpha _g(x)=\pi (g)x\pi (g)^\dagger \) is \({\mathcal {N}}=\pi (G)'=\{x\in {\mathcal {B}}({\mathcal {H}})\ |\ x\pi (g)=\pi (g)x\ \}\), that is the commutant of the representation. Suppose \(\pi \) admits the decomposition \(\pi =\oplus _{i\in {\text {Irr}}(G)}\big (\pi _{i}\otimes {\text {id}}_{n_i}\big )\) as a direct sum of irreducible representations \(\pi _i:G\rightarrow {\mathbb {M}}_{m_i}\) with multiplicity \(n_i\). Then \({\mathcal {N}}= \oplus _{i\in {\text {Irr}}(G)}\big ({\mathbb {C}}\mathbbm {1}_{m_i}\otimes {\mathbb {M}}_{n_i}\big )\) is a direct sum of matrix algebras \({\mathbb {M}}_{n_i}\) with multiplicity \(m_i\). The trace preserving conditional expectation is
where \({\text {tr}}_{m_i}(x)={\text {tr}}(x)\frac{\mathbbm {1}}{m_i}\) is the partial trace map and \({\text {id}}_{n_i}\) is the identity map on \({\mathbb {M}}_{n_i}\). The Choi-Jamiolkowski state of \(E_{{\mathcal {N}}}\) is
where \(\mathbbm {1}_{m_i}\in {\mathbb {M}}_{m_i}\) is the identity operator and \({|{\psi _{n_i}}\rangle }=\frac{1}{\sqrt{n_i}}\sum _{j=1}^{n_i}{|{j}\rangle }{|{j}\rangle }\) is the maximally entangled state in \({\mathbb {M}}_{n_i}\otimes {\mathbb {M}}_{n_i}\). The support projection is
Then \(J_{E_{{\mathcal {N}}}}\ge C_E^{-1} P\) for
On the other hand, the cb-index is
In particular, when G is a finite group and \(\pi _L: G\rightarrow {\mathcal {B}}(l_2(G))\) is its the left regular representation, we have by Schur–Weyl Theorem that \(n_i=m_i\) and
where \({\mathcal {N}}\) is isomorphic to the group algebra \({\mathbb {C}}G\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, L., Rouzé, C. Complete Entropic Inequalities for Quantum Markov Chains. Arch Rational Mech Anal 245, 183–238 (2022). https://doi.org/10.1007/s00205-022-01785-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-022-01785-1