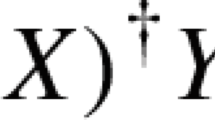The Decoherence-Free Subalgebra of Gaussian Quantum Markov Semigroups

Abstract

We demonstrate a method for finding the decoherence-free subalgebra ${\mathcal {N}}({\mathcal {T}})$ of a Gaussian quantum Markov semigroup on the von Neumann algebra ${\mathcal {B}}(\Gamma (\mathbb {C}^d))$ of all bounded operator on the Fock space $\Gamma (\mathbb {C}^d)$ on $\mathbb {C}^d$. We show that ${\mathcal {N}}({\mathcal {T}})$ is a type I von Neumann algebra $L^\infty (\mathbb {R}^{d_c};\mathbb {C}){\overline{\otimes }}{\mathcal {B}}(\Gamma (\mathbb {C}^{d_f}))$ determined, up to unitary equivalence, by two natural numbers $d_c,d_f\le d$. This result is illustrated by some applications and examples.

1 Introduction

Quantum channels and quantum Markov semigroups (QMS) describe the evolution of an open quantum system subject to noise because of the interaction with the surrounding environment. Couplings to external degrees of freedom typically lead to decoherence. Gaussian quantum channels and Markov semigroups play a key role because several models are based on linear couplings of bosonic systems to other bosonic systems with quadratic Hamiltonians. As a result, the time evolution is then determined by a Gaussian channel in the discrete time case and Markov semigroup in the time continuous case.

Decoherence-free subalgebras determine observables whose evolution is not affected by noise and play a fundamental role not only in the analysis of decoherence (see [2, 4, 7, 22, 26, 27] and the references therein) but also in the study of the structure of QMSs (see [18]).

The case of a norm-continuous QMS $({\mathcal {T}}_t)_{t\ge 0}$ has been extensively studied ([13, 18] and the references therein). The generator is represented in a GKLS form ${\mathcal {L}}(x)={\text {i}}[H,x]-(1/2)\sum _{\ell }\left( L_\ell ^*L_\ell x - 2L_\ell ^*L_\ell x + x L_\ell ^*L_\ell \right)$ for some bounded operators $L_\ell , H$ with H self-adjoint and the decoherence-free subalgebra is characterized as the commutant of operators $L_\ell ,L_\ell ^*$ and their iterated commutators with H ([13] Proposition 2.3).

Gaussian QMSs arise in several relevant models and form a class with a rich structure with a number of explicit formulas ([1, 10, 20, 31]), yet they are not norm-continuous. However, it is known that their generators can be written in a generalized GKLS form with operators $L_\ell$ that are linear (see (2.7)) and H quadratic (see (2.6)) in boson creation and annihilation operators $a_j,a^{\dagger }_k$ ([11, 29]). As a consequence, operators $L_\ell ,L_\ell ^*$ and their iterated generalized commutators with H are linear in boson creation and annihilation operators $a_j,a^{\dagger }_k$.

In this paper we consider Gaussian QMS on the von Neumann algebra ${\mathcal {B}}(\Gamma (\mathbb {C}^d))$ of all bounded operators on the Boson Fock space on $\mathbb {C}^d$ and characterize their decoherence-free subalgebras as generalized commutants of these iterated generalized commutators (Theorem 3.2). Indeed, we show that it suffices to consider iterated commutators up to the order $2d-1$. Moreover, we prove (Theorem 3.7) that the decoherence-free subalgebra is a type I von Neumann algebra $L^\infty (\mathbb {R}^{d_c};\mathbb {C}){\overline{\otimes }}{\mathcal {B}}(\Gamma (\mathbb {C}^{d_f}))$ determined, up to unitary equivalence, by two natural numbers $d_c,d_f\le d$. This conclusion is illustrated by some examples and a detailed analysis of the case of a Gaussian QMS with a single operator $L_\ell$.

The symplectic structure on $\mathbb {C}^d$ plays a fundamental role in the origin of von Neumann algebras of the type $L^\infty (\mathbb {R}^{d_c};\mathbb {C})$ as possible decoherence-free subalgebras determined by generalized commutants via Araki’s duality theorem. Moreover, even if at a purely algebraic level Theorem 3.2 looks like a natural generalization of the norm continuous case, several difficulties arise from unboundedness of operators $L_\ell$ and H and, as a consequence, unboundedness of the generator ${\mathcal {L}}$ of the QMS ${\mathcal {T}}$. The defining property (3.1) of ${\mathcal {N}}({\mathcal {T}})$ involves an operator x and the product $x^*x$, but, even if x belongs to the domain of the generator of the QMS ${\mathcal {T}}$, there is no reason why $x^*x$ should (see e.g. [17]) therefore one has to work with quadratic forms. Domain problems arising from generalized commutators have to be carefully handled because one needs to make sense of generalized commutations such as $x[H,L_\ell ]\subseteq [H,L_\ell ]x$ and $\mathrm {e}^{{\text {i}}t H}x\mathrm {e}^{-{\text {i}}t H} L_\ell \subseteq L_\ell \, \mathrm {e}^{{\text {i}}t H}x\mathrm {e}^{-{\text {i}}t H}$ for $x\in {\mathcal {N}}({\mathcal {T}})$.

The decoherence-free subalgebra of a QMS with unbounded generator was also characterized in [14]. In that paper the result was obtained thorugh several technical assumptions (that hold in the case of Gaussian semigroups) and using a dilation of the QMS via quantum stochastic calculus. The proof we give here (Appendix B) is simpler because it does not appeal to these assumptions and is more direct because it does not use quantum stochastic calculus.

The paper is organized as follows. In Sect. 2 we introduce Gaussian QMS, present their construction by the minimal semigroup method (see [16]), prove well-definedness (conservativity or identity preservation) applying the sufficient condition of [9] and show the explicit formula for the action on Weyl operators (Theorem 2.4). Proofs, that can be obtained from applications of standard methods, are collected in Appendix A. Section 3 contains the main results of the paper. We first recall the definition of decoherence-free subalgebra. Then we prove its characterization for a Gaussian QMS (Theorem 3.2 with proof in Appendix B). Finally we prove the structure result Theorem 3.7. Applications and examples are presented in Sect. 4.

2 Gaussian QMSs

In this section we introduce our class of Gaussian semigroups starting from their generators and fix some notation. Let ${\mathsf {h}}$ be the Fock space ${\mathsf {h}}=\Gamma (\mathbb {C}^d)$ which is isometrically isomorphic to $\Gamma (\mathbb {C})\otimes \cdots \otimes \Gamma (\mathbb {C})$ with canonical orthonormal basis $(e(n_1,\ldots ,n_d))_{n_1,\ldots ,n_d\ge 0}$ (with $e(n_1,\ldots ,n_d)=e_{n_1}\otimes \ldots \otimes e_{n_d}$). Let $a_j, a_j^{\dagger }$ be the creation and annihilation operator of the Fock representation of the d-dimensional Canonical Commutation Relations (CCR)

$$\begin{aligned} a_j\,e(n_1,\ldots ,n_d)= & {} \sqrt{n_j}\ e(n_1,\ldots ,n_{j-1},n_j-1,\ldots ,n_d),\\ a_j^{\dagger }\,e(n_1,\ldots ,n_d)= & {} \sqrt{n_j+1}\ e(n_1,\ldots ,n_{j-1},n_j+1,\ldots ,n_d), \end{aligned}$$

The CCRs are written as $[a_j,a_k^{\dagger }]=\delta _{jk}\mathbb {1}$, where $[\cdot ,\cdot ]$ denotes the commutator, or, more precisely, $[a_j,a_k^{\dagger }]\subseteq \delta _{jk}\mathbb {1}$ because the domain of the operator in the left-hand side is smaller.

For any $g\in \mathbb {C}^d$, define the exponential vector e(g) associated with g by

$$\begin{aligned} e_g=\sum _{n\in \mathbb {N}^d}\frac{g_1^{n_1}\cdots g_d^{n_d}}{\sqrt{n_1!\cdots n_d!}}\,e(n_1,\ldots ,n_d) \end{aligned}$$

Creation and annihilation operators with test vector $v\in \mathbb {C}^d$ can also be defined on the total set of exponential vectors (see [28]) by

$$\begin{aligned} a(v)e_g=\langle v,g \rangle e_g, \quad a^{\dagger }(v)e_g=\frac{\mathrm {d}}{\mathrm {d}\varepsilon }e_{g+\varepsilon u}|_ {\varepsilon =0} \end{aligned}$$

for all $u\in \mathbb {C}^d$. The unitary correspondence $\Gamma (\mathbb {C}^d)\mapsto \Gamma (\mathbb {C})\otimes \cdots \otimes \Gamma (\mathbb {C})$

$$\begin{aligned} e_g\mapsto \sum \limits _{n_1\ge 0,\ldots , n_d\ge 0}\frac{g_1^{n_1}\ldots g_d^{n_d}}{\sqrt{n_1!\ldots n_d!}} \,e_{n_1}\otimes \ldots \otimes e_{n_d} \end{aligned}$$

allows one to establish the identities

$$\begin{aligned} a(v)=\sum \limits _{j=1}^d{\overline{v}}_ja_j, \quad a^{\dagger }(u)=\sum \limits _{j=1}^d u_ja_j^{\dagger } \end{aligned}$$

for all $u^{\mathrm{T}}=[u_1,\ldots ,u_d],v^{\mathrm{T}}=[v_1,\ldots ,v_d]\in \mathbb {C}^d$.

The above operators are obviously defined on the linear manifold D spanned by the elements $(e(n_1,\ldots ,n_d))_{n_1,\ldots ,n_d\ge 0}$ of the canonical orthonormal basis of ${\mathsf {h}}$ that turns out to be an essential domain for all the operators considered so far. This also happens for quadrature operators

$$\begin{aligned} q(u) = \left( a(u)+a^{\dagger }(u)\right) /\sqrt{2}\qquad u\in \mathbb {C}^d \end{aligned}$$

(2.1)

that are symmetric and essentially self-adjoint on the domain D by Nelson’s theorem on analytic vectors ([30] Th. X.39 p. 202). The linear span of exponential vectors also turns out to be an essential domain for operators q(u) for the same reason. If the vector u has real (resp. purely imaginary) components one finds position (resp. momentum) operators and the commutation relation $[q(u),q(v)]\subseteq {\text {i}}\Im \langle u, v\rangle \mathrm{1l}$ (where $\Im$ and $\Re$ denote the imaginary and real part of a complex number). Momentum operators, i.e. quadratures $q({\text {i}}r)$ with $r\in \mathbb {R}^d$ are also denoted by $p(r)=\sum _{1\le j\le d} r_j p_j$ where $p_j={\text {i}}(a^{\dagger }_j-a_j)/\sqrt{2}$. In a similar way we write $q(r)=\sum _{1\le j\le d} r_j q_j$ with $q_j=q(e_j)=(a^{\dagger }_j+a_j)/\sqrt{2}$.

Another set of operators that will play an important role in this paper are the Weyl operators, defined on the exponential vectors via the formula

$$\begin{aligned} W(z)e_g=\mathrm {e}^{-\parallel z\parallel ^2/2-\langle z,g \rangle }e_{z+g}\quad z,g\in \mathbb {C}^d. \end{aligned}$$

By this definition $\langle W(z)e_f,W(z)e_g\rangle = \langle e_f,e_g\rangle$ for all $f,g\in \mathbb {C}^d$, therefore W(z) extends uniquely to a unitary operator on ${\mathsf {h}}$. Weyl operators satisfy the CCR in the exponential form, namely, for every $z,z^\prime \in \mathbb {C}^d$,

$$\begin{aligned} W(z)W(z^\prime ) = \text {e}^{-{\text {i}}\Im \left\langle z , z^\prime \right\rangle } W(z+z^\prime ). \end{aligned}$$

(2.2)

It is well-known that W(z) is the exponential of the anti self-adjoint operator $-{\text {i}}\sqrt{2}\, q({\text {i}}z)$

$$\begin{aligned} W(z) = \mathrm {e}^{-{\text {i}}\sqrt{2}\, q({\text {i}}z)} = \mathrm {e}^{z a^{\dagger }-{\overline{z}}a}. \end{aligned}$$

(2.3)

Finally, we recall here two relevant properties that are valid on D and on suitable dense domains

$$\begin{aligned} \left[ \,a(v),W(z)\,\right] = \langle v, z\rangle W(z), \qquad \left[ \,a^{\dagger }(v),W(z)\,\right] =\langle z, v\rangle W(z). \end{aligned}$$

(2.4)

A QMS ${\mathcal {T}}=({\mathcal {T}}_t)_{t\ge 0}$ is a $\hbox {weakly}^*$-continuous semigroup of completely positive, identity preserving, $\hbox {weakly}^*$-continuous maps on ${\mathcal {B}}({\mathsf {h}})$. The predual semigroup ${\mathcal {T}}_*= ({\mathcal {T}}_{*t})_{t\ge 0}$ on the predual space of trace class operators on ${\mathsf {h}}$ is a strongly continuous contraction semigroup.

Gaussian QMSs can be defined in various equivalent ways. Here we introduced them through their generator because it is the object we are mostly concerned with. The pre-generator, or form generator, of a Gaussian QMSs can be represented in a generalized (since operators $L_\ell , H$ are unbounded) Gorini–Kossakowski–Lindblad-Sudarshan (GKLS) form (see [29] Theorems 5.1, 5.2 and also [11, 32])

$$\begin{aligned} {\mathcal {L}}(x) = {\text {i}}\left[ H, x\right] -\frac{1}{2}\sum _{\ell =1}^m \left( L_\ell ^*L_\ell \, x - 2 L_\ell ^* x L_\ell + x\, L_\ell ^*L_\ell \right) . \end{aligned}$$

(2.5)

where $1 \le m \le 2d$, and

$$\begin{aligned} H&= \sum _{j,k=1}^d \left( \Omega _{jk} a_j^{\dagger } a_k + \frac{\kappa _{jk}}{2} a_j^{\dagger } a_k^{\dagger } + \frac{\overline{\kappa _{jk}}}{2} a_ja_k \right) + \sum _{j=1}^d \left( \frac{\zeta _j}{2}a_j^{\dagger } + \frac{\bar{\zeta _j}}{2} a_j \right) , \end{aligned}$$

(2.6)

$$\begin{aligned} L_\ell&= \sum _{k=1}^d \left( \overline{v_{\ell k}} a_k + u_{\ell k}a_k^{\dagger }\right) = a(v_{\ell \bullet }) + a^{\dagger } (u_{\ell \bullet }), \end{aligned}$$

(2.7)

$\Omega :=(\Omega _{jk})_{1\le j,k\le d} = \Omega ^*$ and $\kappa := (\kappa _{jk})_{1\le j,k\le d}= \kappa ^{\mathrm{T}} \in M_d(\mathbb {C})$, are $d\times d$ complex matrices with $\Omega$ Hermitian and $\kappa$ symmetric, $V=(v_{\ell k})_{1\le \ell \le m, 1\le k\le d}, U=(u_{\ell k})_{1\le \ell \le m, 1\le k\le d} \in M_{m\times d}(\mathbb {C})$ are $m\times d$ matrices and $\zeta =(\zeta _j)_{1\le j\le d} \in \mathbb {C}^d$. The notation $v_{\ell \bullet }$ and $u_{\ell \bullet }$ refers to vectors in $\mathbb {C}^d$ obtained from the $\ell$-th row of the corresponding matrices.

We exclude the case where the pre-generator ${\mathcal {L}}$ reduces to the Hamiltonian part ${\text {i}}[H,x]$ and so we suppose that one among matrices V, U is non-zero. An application of Nelson’s theorem on analytic vectors ([30] Th. X.39 p. 202) shows that H, as an operator with domain D, is essentially selfadjoint. In addition, operators $L_\ell$ are closable therefore we will identify them with their closure.

It can be shown (see [29] Theorems 5.1, 5.2) that a QMS ${\mathcal {T}}$ is Gaussian if maps ${\mathcal {T}}_{*t}$ of the predual semigroup ${\mathcal {T}}_*$ preserve Gaussian states or, still in an equivalent way, maps ${\mathcal {T}}_t$ act explicitly on Weyl operators (Theorem 2.4 below).

Clearly, ${\mathcal {L}}$ is well defined on the dense (not closed) sub-$^*$-algebra of ${\mathcal {B}}({\mathsf {h}})$ generated by rank one operators $|\xi \rangle \langle \xi '|$ with $\xi ,\xi '\in D$ because all operator compositions make sense. However, since the operators $H,L_\ell$ are unbounded, the domain of ${\mathcal {L}}$ is not the whole of ${\mathcal {B}}({\mathsf {h}})$. For this reason we look at it as a pre-generator and describe in detail its extension to a generator of a QMS by the minimal semigroup method (Theorem 2.3 below).

Remark

The above generalized GKLS form is the most general with operators $L_\ell$ which are first order polynomials in $a_j,a^{\dagger }_j$ and the self-adjoint operator H which is a second order polynomial in $a_j,a^{\dagger }_j$. Indeed, in the case where $L_\ell$ are as above plus a multiple of the identity operator, exploiting non uniqueness of GKLS representations (see [28], section 30) one can always apply a translation and reduce himself to the previous case.

We choose the minimum number of operators $L_\ell$ (also called Kraus operators), namely the parameter m.

Definition 2.1

A GKLS representation of ${\mathcal {L}}$ is mimimal if the number m in (2.5) is minimal.

A GKLS representation is minimal if and only if the following condition on V and U, that will be in force throughout the paper, holds.

Proposition 2.2

The pre-generator ${\mathcal {L}}$ has a minimal GKLS representation if and only if

$$\begin{aligned} {\mathrm{ker}}\left( V^{*}\right) \cap {\mathrm{ker}}\left( U^{\mathrm{T}}\right) =\{0\}. \end{aligned}$$

(2.8)

Proof

A GKLS respesentation (2.5) is minimal GKLS if and only if the set $\{\mathbb {1},L_1,\ldots , L_m\}$ consists of linearly independent operators (see [28], Theorem 30.16), namely, $\alpha _0\mathbb {1}+\sum _{\ell =1}^m\alpha _{\ell }L_{\ell }=0$ for $\alpha _0,\alpha _\ell \in \mathbb {C}$ implies $\alpha _{\ell }=0$ for $\ell =0,1,\ldots ,m$. This identity is equivalent to

$$\begin{aligned} \alpha _0\mathbb {1}+\sum _{j=1}^d(V^*\alpha )_ja_j+\sum _{j=1}^d(U^{\mathrm{T}}\alpha )_ja_j^{\dagger }=0. \end{aligned}$$

Since $\left\{ \mathbb {1}, a_1, a_1^{\dagger },\dots , a_d, a_d^{\dagger }\right\}$ is a linearly independent set, the last equation is equivalent to $\alpha \in {\mathrm{ker}}(V^*),\alpha \in {\mathrm{ker}}(U^{\mathrm{T}}),\alpha _0=0$ and the proof is complete. $\square$

For all $x\in {\mathcal {B}}({\mathsf {h}})$ consider the quadratic form with domain $D\times D$

$$\begin{aligned} \begin{aligned} {\texttt {\pounds }}(x) [\xi ',\xi ]&= {\text {i}}\left\langle H\xi ' , x\xi \right\rangle - {\text {i}}\left\langle \xi ' , x H\xi \right\rangle \\&- \frac{1}{2} \sum _{\ell =1}^m \left( \left\langle \xi ' , xL_\ell ^*L_\ell \xi \right\rangle -2\left\langle L_\ell \xi ' , xL_\ell \xi \right\rangle + \left\langle L_\ell ^* L_\ell \xi ' , x \xi \right\rangle \right) \end{aligned} \end{aligned}$$

(2.9)

We postpone to the Appendix the construction of the unique Gaussian QMS with pre-generator (2.5) and state here the final result.

Theorem 2.3

There exists a unique QMS, ${\mathcal {T}}=({\mathcal {T}}_t)_{t\ge 0}$ such that, for all $x\in {\mathcal {B}}({\mathsf {h}})$ and $\xi ,\xi '\in D$, the function $t\mapsto \left\langle \xi ' , {\mathcal {T}}_t (x) \xi \right\rangle$ is differentiable and

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} \left\langle \xi ' , {\mathcal {T}}_t (x) \xi \right\rangle = {\texttt {\pounds }}({\mathcal {T}}_t(x)) [\xi ',\xi ] \qquad \forall \, t\ge 0. \end{aligned}$$

The domain of the generator consists of $x\in {\mathcal {B}}({\mathsf {h}})$ for which the quadratic form ${\texttt {\pounds }}(x)$ is represented by a bounded operator.

Weyl operators do not belong to the domain of the generator of ${\mathcal {T}}$ because a straightforward computation (see, for instance, Appendix A Sect. 4.5) shows that the quadratic form ${\texttt {\pounds }}(x)$ is unbounded. In spite of this we have the following explicit formula (see [11, 32])

Theorem 2.4

Let $({\mathcal {T}}_{t})_{t\ge 0}$ be the quantum Markov semigroup with generalized GKLS generator associated with $H,L_\ell$ as above. For all Weyl operator W(z) we have

$$\begin{aligned} {\mathcal {T}}_t(W(z)) = \exp \left( -\frac{1}{2}\int _0^t \Re \left\langle \mathrm {e}^{sZ}z , C \mathrm {e}^{sZ}z \right\rangle \mathrm {d}s +{\text {i}}\int _0^t \Re \left\langle \zeta , \mathrm {e}^{sZ}z \right\rangle \mathrm {d}s \right) W\left( \mathrm {e}^{tZ}z\right) \end{aligned}$$

(2.10)

where the real linear operators Z, C on $\mathbb {C}^d$ are

$$\begin{aligned} Zz= & {} \left[ \left( \overline{ U^*U - V^*V}\right) /2 + {\text {i}}\Omega \right] z + \left[ \left( U^TV - V^T U\right) /2 + {\text {i}}\kappa \right] \overline{z} \end{aligned}$$

(2.11)

$$\begin{aligned} Cz= & {} \left( \overline{ U^*U + V^*V}\right) z + \left( U^TV + V^T U\right) \overline{z} \end{aligned}$$

(2.12)

We refer to Sect. 4.5 for the proof.

3 Structure of ${\mathcal {N}}({\mathcal {T}})$

The decoherence-free subalgebra (see [2, 7, 13, 14]) of ${\mathcal {T}}$ is defined as

$$\begin{aligned} {\mathcal {N}}({\mathcal {T}})= \left\{ x\in {\mathcal {B}}({\mathsf {h}}) \mid {\mathcal {T}}_t(x^*x)={\mathcal {T}}_t(x^*){\mathcal {T}}_t(x), \ {\mathcal {T}}_t(x x^*)={\mathcal {T}}_t(x){\mathcal {T}}_t(x^*), \, \forall t\ge 0 \right\} . \end{aligned}$$

(3.1)

This is the biggest sub von Neumann algebra of ${\mathcal {B}}({\mathsf {h}})$ on which maps ${\mathcal {T}}_t$ act as $^*$-homorphisms by the following known facts (see e.g. Evans [15] Th. 3.1).

Proposition 3.1

Let ${\mathcal {T}}$ be a QMS on ${\mathcal {B}}({\mathsf {h}})$ and let ${{\mathcal {N}}}({\mathcal {T}})$ be the set defined by (3.1). Then:

• 1. ${{\mathcal {N}}}({\mathcal {T}})$ is ${\mathcal {T}}_t$-invariant for all $t\ge 0$,

• 2. For all $x\in {{\mathcal {N}}}({\mathcal {T}})$ and all $y\in {\mathcal {B}}({\mathsf {h}})$ we have ${\mathcal {T}}_t(x^*y)={\mathcal {T}}_t(x^*){\mathcal {T}}_t(y)$ and ${\mathcal {T}}_t(y^*x)={\mathcal {T}}_t(y^*){\mathcal {T}}_t(x)$,

• 3. ${\mathcal {N}}({\mathcal {T}})$ is a von Neumann subalgebra of ${\mathcal {B}}({\mathsf {h}})$.

The decoherence-free subalgebra of a QMS with a bounded generator, i.e. written in a GKLS form with bounded operators $H,L_\ell$ instead of (2.7), (2.6) is the commutator of the set of operators $\delta ^{n}_H(L_\ell ), \delta ^{n}_H(L_\ell ^*)$ with $\ell =1,\dots , m,\, n\ge 0$ where $\delta _H(x)=[H,x]$.

Generators of Gaussian QMSs are represented in a generalized GKLS form with unbounded operators $L_\ell , H$, but ${\mathcal {N}}({\mathcal {T}})$ can be characterized in a similar way considering generalized commutatant of a set of unbounded operators. We recall that, the generalized commutant of an unbounded operator L is the set of bounded operators x for which $xL\subseteq Lx$, namely Lx is an extension of xL.

We begin our investigation on ${\mathcal {N}}({\mathcal {T}})$ by the following

Theorem 3.2

The decoherence-free subalgebra of a Gaussian QMS with generator in a generalized GKLS form associated with operators $L_\ell ,H$ as in (2.7),(2.6) is the generalized commutant of linear combinations of operators

$$\begin{aligned} \delta ^{n}_H(L_\ell ), \quad \delta ^{n}_H(L_\ell ^*) \qquad \ell =1,\dots , m,\ 0\le n\le 2d-1 \end{aligned}$$

(3.2)

where $\delta _H(x)=[H,x]$ denotes the generalized commutator and $\delta ^n_H$ denotes its n-th iterate. Moreover ${\mathcal {T}}_t(x)= \mathrm {e}^{{\text {i}}t H} x\, \mathrm {e}^{-{\text {i}}t H}$ for all $t\ge 0$ and $x\in {\mathcal {N}}({\mathcal {T}})$.

We defer the proof to Appendix B. Here we give an example to show that inequality $n\le 2d-1$ is sharp.

Example

Consider the Gaussian QMS with only one operator $L_\ell$, i.e. $m=1$ and

$$\begin{aligned} L_1=p_1, \qquad H = q^2_d + \sum _{j=1}^{d-1} p_{j+1}q_j \end{aligned}$$

Compute

$$\begin{aligned} \delta _H(L_1)= {\text {i}}p_2, \quad \delta ^2_H(L_1)=-p_3,\, ...,\, \ \delta ^{d-1}_H(L_1)={\text {i}}^{d-1}p_d, \quad \delta ^{d}_H(L_1)={\text {i}}^{d}q_d \end{aligned}$$

therefore $\delta ^{d+1}_H(L_1)={\text {i}}^{d+1} q_{d-1}$. Iterating commutators we see that $\delta ^{d+k}_H(L_1)$ is proportional to $q_{d-k}$ so that, for $k=d-1$ one gets $q_1$. Clearly, for all k with $0\le k \le d-1$

$$\begin{aligned} \left\{ \, \delta ^j_H(L_1),\, \delta ^j_H(L^*_1)\,\mid \, j\le d+k \,\right\} ' \end{aligned}$$

which is isomorphic to $L^\infty (\mathbb {R}^{d-1-k};\mathbb {C})$ (i.e. measurable functions of momentum operators $p_1,\dots ,p_{d-1+k}$). Summing up, if we consider $2d-1$ iterated commutators we get all $p_j,q_j$ and ${\mathcal {N}}({\mathcal {T}})$ is trivial by the irreducibility of the Weyl representation of CCR.

In the sequel we provide a simpler characterization of ${\mathcal {N}}({\mathcal {T}})$ in terms of real subspaces of $\mathbb {C}^d$ and find its structure. In order to make clear the thread of the discussion, we omit technicalities related with unbounded operators that can be easily fixed because D is an essential domain for operators involved in our computations and we concentrate on the algebraic aspect. A straightforward computation yields

$$\begin{aligned} {[}H,L_\ell ] = \sum _{i=1}^d\left( \left( \Omega u_{\ell \bullet }-\kappa {\overline{v}}_{\ell \bullet }\right) _i a^{\dagger }_i -\left( {\overline{\Omega }}{\overline{v}}_{\ell \bullet } -{\overline{\kappa }} u_{\ell \bullet } \right) _i a_i\right) +\frac{\langle \zeta ,u_{\ell \bullet }\rangle - \langle v_{\ell \bullet },\zeta \rangle }{2}\mathrm{1l}. \end{aligned}$$

Therefore the set of operators of which we have to consider the generalized commutant, thanks to the CCR, is particularly simple and contains only linear combinations of creation and annihilation operators together with a multiple of the identity $\mathrm{1l}$ that plays no role.

Now notice that each linear combination of creation and annihilation operators is uniquely determined by a pair v, u of vectors in $\mathbb {C}^{d}$ representing coefficients of annihilation and creation operators so that, for example, the operator $L_\ell$ in (2.7) and its adjoint $L_\ell ^*$ are determined by

$$\begin{aligned} L_\ell =\sum _{j=1}^d\left( {\overline{v}}_{\ell j} a_j + u_{\ell j} a^{\dagger }_j \right) \rightsquigarrow \left[ \begin{array}{c} {\overline{v}}_{\ell \bullet } \\ u_{\ell \bullet } \end{array}\right] , \; L_\ell ^*=\sum _{j=1}^d\left( {\overline{u}}_{\ell j} a_j + v_{\ell j} a^{\dagger }_j \right) \rightsquigarrow \left[ \begin{array}{c} {\overline{u}}_{\ell \bullet } \\ v_{\ell \bullet } \end{array}\right] \end{aligned}$$

In a similar way, after computing commutators,

$$\begin{aligned} {[}H,L_\ell ]\rightsquigarrow \left[ \begin{array}{cc} -\Omega ^T &{} {\overline{\kappa }} \\ -\kappa \ &{} \Omega \end{array}\right] \left[ \begin{array}{c} {\overline{v}}_{\ell \bullet } \\ u_{\ell \bullet } \end{array}\right] , \qquad [H,L_\ell ^*]\rightsquigarrow \left[ \begin{array}{cc} -\Omega ^T &{} {\overline{\kappa }} \\ -\kappa \ &{} \Omega \end{array}\right] \left[ \begin{array}{c} {\overline{u}}_{\ell \bullet } \\ v_{\ell \bullet } \end{array}\right] \end{aligned}$$

Denote by $\mathbb {H}$ the above $2d\times 2d$ matrix (built by four $d\times d$ matrices)

$$\begin{aligned} \mathbb {H} =\left[ \begin{array}{cc} -\Omega ^T &{} {\overline{\kappa }} \\ -\kappa \ &{} \Omega \end{array}\right] \end{aligned}$$

and let ${\mathcal {V}}$ be the real subspace of $\mathbb {C}^{2d}$ generated by vectors

$$\begin{aligned} \mathbb {H}^{\ n}\left[ \begin{array}{c} {\overline{v}}_{\ell \bullet } \\ u_{\ell \bullet } \end{array}\right] , \qquad \mathbb {H}^{\ n}\left[ \begin{array}{c} {\overline{u}}_{\ell \bullet } \\ v_{\ell \bullet } \end{array}\right] \end{aligned}$$

(3.3)

with $\ell =1,\dots , m$ and $0\le n \le 2d-1$.

The above remarks allow us to associate with elements of (3.2) a set of vectors in $\mathbb {C}^{2d}$ and characterize the generalized commutant of (3.2) in a purely algebraic way.

Lemma 3.3

An operator $x \in {\mathcal {B}}({\mathsf {h}})$ belongs to ${\mathcal {N}}({\mathcal {T}})$ if and only if it belongs to the generalized commutant of

$$\begin{aligned} \left\{ \,q({\text {i}}w)\,\mid \, w \in {\mathcal {M}}\,\right\} \end{aligned}$$

(3.4)

where

$$\begin{aligned} {\mathcal {M}} = {\mathrm{Lin}}_\mathbb {R}\left\{ \, {\text {i}}(v+u), v-u\,\mid \, [{\overline{v}},u ]^{\mathrm{T}} \in {\mathcal {V}}\,\right\} \subset \mathbb {C}^d. \end{aligned}$$

(3.5)

Proof

By the above remarks we know that the operators in the set (3.2) are linear combination of annihilation and creation operators up to a multiple of the identity operator and the generalized commutant of (3.2) coincides with the generalized commutant of

$$\begin{aligned} \left\{ \, a(v) + a^{\dagger } (u)\, \mid \, [{\overline{v}}, u]^{\mathrm{T}} \in {\mathcal {V}}\, \right\} . \end{aligned}$$

(3.6)

To conclude the proof we just need to show that the commutants of (3.4) and (3.6) are the same. Notice at first that if $[{\overline{v}},u]^{\mathrm{T}} \in {\mathcal {V}}$ also $[{\overline{u}},v]^{\mathrm{T}} \in {\mathcal {V}}$, indeed if $\delta _H^n(L_\ell ) = a(v)+ a^{\dagger }(u)$ then $\delta _H^n (L_\ell ^*)= (-1)^n\delta _H^n(L_\ell )^* = (-1)^n \left( a(u)+ a^{\dagger }(v) \right)$ on the domain D. Now from (2.1) we obtain

$$\begin{aligned} \sqrt{2}\,q({\text {i}}(u-v))&= {\text {i}}\left( a(v) + a^{\dagger }(u) \right) -{\text {i}}\left( a(u) + a^{\dagger }(v)\right) , \\ \sqrt{2}(a(v)+a^{\dagger }(u))&= q(v+u) - {\text {i}}q({\text {i}}(u-v)). \end{aligned}$$

Therefore every element of (3.4) is a linear combination of elements of (3.6) and viceversa, concluding the proof. $\square$

In order to describe the structure of the decoherence-free subalgebra we recall now some useful definitions and properties of symplectic spaces. At first note that $\mathbb {C}^d$ equipped with the real scalar product $\Re \langle \cdot , \cdot \rangle$ is a real Hilbert space. Considering instead $\Im \langle \cdot , \cdot \rangle$ we obtain a bilinear, antisymmetric (i.e. $\Im \langle z_1, z_2 \rangle = - \Im \langle z_2, z_1 \rangle$, for all $z_1, z_2 \in \mathbb {C}^d$) and non-degenerate (i.e. $\Im \langle z_1, z_2 \rangle = 0$ for all $z_2 \in \mathbb {C}^d$ implies $z_1=0$) form also called a symplectic form. We now recall the following definitions.

Definition 3.4

Let $M \subset \mathbb {C}^d$ a real linear subspace.

• 1. M is a symplectic space if $\Im \langle \cdot ,\cdot \rangle$ is non degenerate when restricted to elements of M.

• 2. Two elements $z_1, z_2$ of M are called symplectically orthogonal if they satisfy $\Im \langle z_1,z_2 \rangle =0$.

• 3. Let $M_1 \subset M$ be a real linear subspace. We call symplectic complement of $M_1$ in M, and denote it by ${M_1}'$, the set

  $$\begin{aligned} M' = \left\{ \, z \in M \,\mid \, \Im \langle z,m \rangle = 0 \quad \forall m \in M_1\, \right\} . \end{aligned}$$

• 4. $M_1$ is an isotropic subspace if $M_1 \subset M_1'$.

• 5. $M_1$ is a symplectic subspace if $M_1$ is a symplectic space (i.e. the symplectic form $\Im \langle \cdot ,\cdot \rangle$ is non degenerate when restricted to elements of $M_1$).

In order to fix some of the concepts in the above definition we provide the following

Example

Consider $M=\mathbb {C}^d$ which is a symplectic space and let $(e_j)_{j=1}^d$ be its canonical complex orthonormal basis. Clearly $(e_j, {\text {i}}e_j)_{j=1}^d$ is an orthonormal basis for $\mathbb {C}^d$ considered as a real Hilbert space. Consider now a vector $e_j$ for a fixed index j. It is orthogonal to all other elements of the basis with respect to the real scalar product $\Re \langle \cdot , \cdot \rangle$, however it is symplectically orthogonal to all other elements of the basis except for ${\text {i}}e_j$.

Consider now $M_1 = {\mathrm{Lin}}_\mathbb {R} \{ e_1, {\text {i}}e_1 \}$ and $M_2= {\mathrm{Lin}}_\mathbb {R} \{ e_2 \}$, which are real linear subspaces of $\mathbb {C}^d$. It is easy to see that

$$\begin{aligned} {M_1}' = {\mathrm{Lin}}_\mathbb {R} \{ e_2, {\text {i}}e_2, \dots , e_d, {\text {i}}e_d\}, \quad {M_2}' = {\mathrm{Lin}}_\mathbb {R} \{ e_1, {\text {i}}e_1, e_2, e_3, {\text {i}}e_3, \dots , e_d, {\text {i}}e_d\}. \end{aligned}$$

In particular $M_2 \subset M_2'$ hence it is an isotropic subspace, while $M_1$ is a symplectic subspace.

Eventually it is worth noticing that not all symplectic subspaces of M are also complex subspaces; from here the need to consider real vector spaces. Indeed, consider $M_3= {\mathrm{Lin}}_\mathbb {R} \{ e_1 + e_2, {\text {i}}e_1\}$. It is easy to prove that $M_3$ is a symplectic subspace of M but it is not a complex subspace, since $e_1 = (-{\text {i}}) {\text {i}}e_1 \not \in M_3$.

The previous example although seemingly simple is actually quite representative of what happens in the general case. In analogy with classical linear algebra most complicated situations can be simplified performing a change of basis through a homomorphism. We provide here the analogous definition for symplectic spaces.

Definition 3.5

Let $M_1, M_2 \subset \mathbb {C}^d$ be symplectic spaces. We say $B:M_1 \rightarrow M_2$ is a symplectic transformation if it is a real linear map and moreover

$$\begin{aligned} \Im \langle Bz_1, Bz_2 \rangle = \Im \langle z_1, z_2 \rangle , \quad \forall z_1,z_2 \in M_1. \end{aligned}$$

We say B is a Bogoliubov transformation or symplectomorphism if it is an invertible symplectic transformation.

Next Proposition collects all the properties of symplectic spaces we need (see [6] for a comprehensive treatment)

Proposition 3.6

Let $M \subset \mathbb {C}^d$ be a symplectic space and let $(e_j)_{j=1}^d$ be the canonical complex orthonormal basis of $\mathbb {C}^d$.

• 1. There exists a symplectomorphism B

  $$\begin{aligned} B : M \rightarrow {\mathrm{Lin}}_\mathbb {R} \{ e_1, {\text {i}}e_1 , \dots , e_{d_1}, {\text {i}}e_{d_1} \} \end{aligned}$$

  In particular $\dim _\mathbb {R} M = 2 d_1$.

• 2. If $M_1 \subset M$ is a real linear subspace of M then $M_1$ is also a symplectic subspace if and only if $M_1 \cap {M_1}' = \{ 0 \}$.

• 3. If $M_1$ is an isotropic subspace with $d_1 = \dim _\mathbb {R} M_1$ then there exists a symplectomorphism B such that

  $$\begin{aligned} B : M_1 \rightarrow {\mathrm{Lin}}_\mathbb {R} \{ e_1, \dots , e_{d_1}\}. \end{aligned}$$

We give a proof in Appendix C for self-containedness.

For all subset ${\mathcal {M}}$ of $\mathbb {C}^d$ we denote by ${\mathcal {W}}({\mathcal {M}})$ the von Neumann algebra generated by Weyl operators W(z) with $z\in {\mathcal {M}}$. H. Araki’s Theorem 4 p. 1358 in [3], sometimes referred to as duality for Bose fields, (see also [25] Theorem 1.3.2 (iv) for a proof with our notation), up to a constant in the symplectic from and also [21] Theorem 1.1) shows that the commutant of ${\mathcal {W}}({\mathcal {M}})$ is ${\mathcal {W}}({\mathcal {M}}')$. Applying this result we can prove the following

Theorem 3.7

The decoherence-free subalgebra ${\mathcal {N}}({\mathcal {T}})$ is the von Neumann subalgebra of ${\mathcal {B}}({\mathsf {h}})$ generated by Weyl operators W(z) such that z belongs to the sympletic complement of (3.5). Moreover, up to unitary equivalence,

$$\begin{aligned} {\mathcal {N}}({\mathcal {T}}) = L^\infty (\mathbb {R}^{d_c};\mathbb {C})\,{\overline{\otimes }}\,{\mathcal {B}}(\Gamma (\mathbb {C}^{d_f})) \end{aligned}$$

(3.7)

for a pair of natural numbers $d_c,d_f\le d$.

The subscript f (resp. c) stands for full (resp. commutative).

Proof

By Lemma 3.3 any $x\in {\mathcal {N}}({\mathcal {T}})$ satisfies $x \, q({\text {i}}w)\subseteq q({\text {i}}w)\, x$ for all $w\in {\mathcal {M}}$. Therefore, for all real number r, $x (\mathrm{1l}+{\text {i}}r q({\text {i}}w))\subseteq (\mathrm{1l}+ {\text {i}}r q({\text {i}}w))x$ and, right and left multiplying by the resolvent $(\mathrm{1l}+{\text {i}}r q({\text {i}}w))^{-1}$ which is a bounded operator

$$\begin{aligned} (\mathrm{1l}+ {\text {i}}r q({\text {i}}w))^{-1}x = x (\mathrm{1l}+{\text {i}}r q({\text {i}}w))^{-1}. \end{aligned}$$

Iterating n times and considering $r=1/n$ we find

$$\begin{aligned} \left( \mathrm{1l}+ {\text {i}}q({\text {i}}w)/n\right) ^{-n}x = x \left( \mathrm{1l}+ {\text {i}}q({\text {i}}w)/n\right) ^{-n} \end{aligned}$$

and, taking the limit as n goes to $+\infty$, by the Hille-Yosida theorem ([5] Theorem 3.1.10 p.371) we have

$$\begin{aligned} W(w)x&=\mathrm {e}^{-{\text {i}}q({\text {i}}w)}x =\lim _{n\rightarrow \infty }\left( \mathrm{1l}+ {\text {i}}q({\text {i}}w)/n\right) ^{-n}x \\&= x \lim _{n\rightarrow \infty }\left( \mathrm{1l}+ {\text {i}}q({\text {i}}w)/n\right) ^{-n} = x W(w) \end{aligned}$$

and so x belongs to ${\mathcal {W}}({\mathcal {M}})'$ which coincides with ${\mathcal {W}}({\mathcal {M}}')$ by Araki’s Theorem 4 in [3].

Conversely, if z belongs to the symplectic complement of ${\mathcal {M}}$, then from (2.4) and (2.1) we have $W(z)q({\text {i}}w)e_g=q({\text {i}}w)W(z)e_g$ for all $w\in {\mathcal {M}}$ and $g\in \mathbb {C}^d$. Since the linear span of exponential vectors is an essential domain for $q({\text {i}}w)$, for all $\xi \in {\mathrm{Dom}}(q({\text {i}}w))$ there exists a sequence $(\xi _n)_{n\ge 1}$ in ${\mathcal {E}}$ such that $(q({\text {i}}w)\xi _n)_{n\ge 1}$ converges to $q({\text {i}}w)\xi$. It follows that $(q({\text {i}}w)W(z)\xi _n)_{n\ge 1}$ converges and, since $q({\text {i}}w)$ is closed, $W(z)\xi$ belongs to ${\mathrm{Dom}}(q({\text {i}}w))$ and $W(z)q({\text {i}}w)\xi =q({\text {i}}w)W(z)\xi$, namely $q({\text {i}}w)W(z)$ is an extension of $W(z)q({\text {i}}w)$. Therefore W(z) belongs to the generalized commutant of all $q({\text {i}}w)$ with $w\in {\mathcal {M}}$ and therefore to ${\mathcal {N}}({\mathcal {T}})$ by Lemma 3.3.

In order to prove (3.7) consider ${\mathcal {M}}^c:= {\mathcal {M}} \cap {\mathcal {M}}'$ which is a real linear subspace of both ${\mathcal {M}}$ and ${\mathcal {M}}'$. Consider now ${\mathcal {M}}^r$ and ${\mathcal {M}}^f$ as the real linear complement of ${\mathcal {M}}^c$ in ${\mathcal {M}}$ and ${\mathcal {M}}'$ respectively, i.e.

$$\begin{aligned} {\mathcal {M}} = {\mathcal {M}}^c \oplus {\mathcal {M}}^r, \qquad {\mathcal {M}}' = {\mathcal {M}}^c \oplus {\mathcal {M}}^f. \end{aligned}$$

(${\mathcal {M}}^c \perp {\mathcal {M}}^r$ and ${\mathcal {M}}^c \perp {\mathcal {M}}^f$, more precisely, they are orthogonal with respect to the real part of the scalar product). We will show that ${\mathcal {M}}^f$ is a symplectic subspace of $\mathbb {C}^d$ and that it is symplectically orthogonal to both ${\mathcal {M}}^c$ and ${\mathcal {M}}^r$. Suppose $z \in {\mathcal {M}}^f$ is such that $\Im \langle z, z_f \rangle =0$ for all $z_f \in {\mathcal {M}}^f$. By construction $\Im \langle z, z_c \rangle =0$ for all $z_c \in {\mathcal {M}}^c={\mathcal {M}} \cap {\mathcal {M}}'$. Therefore

$$\begin{aligned} \Im \langle z, m \rangle = 0, \quad \forall m \in {\mathcal {M}}', \end{aligned}$$

since ${\mathcal {M}}' = {\mathcal {M}}^c \oplus {\mathcal {M}}^f$. Therefore $z \in {\mathcal {M}}''={\mathcal {M}}$, but then

$$\begin{aligned} z \in {\mathcal {M}} \cap {\mathcal {M}}' \cap {\mathcal {M}}^f = {\mathcal {M}}^c \cap {\mathcal {M}}^f = \{0 \}. \end{aligned}$$

Hence ${\mathcal {M}}^f$ is a symplectic subspace. Eventually, ${\mathcal {M}}^f \subset {\mathcal {M}}'$ and ${\mathcal {M}}={\mathcal {M}}'' \subset ({\mathcal {M}}^f)'$. In particular ${\mathcal {M}}^f$ is symplectically orthogonal to both ${\mathcal {M}}^r, {\mathcal {M}}^c$. Let $d_c = \dim _\mathbb {R} {\mathcal {M}}^c$ and $2d_f= \dim _\mathbb {R} {\mathcal {M}}^f$ which is even by Proposition 3.6 1. Still by Proposition 3.6 we can find a symplectomorphism B such that

$$\begin{aligned} B : {\mathcal {M}}' \rightarrow {\mathrm{Lin}}_\mathbb {R} \{ e_1, \dots , e_{d_c} \} \oplus {\mathrm{Lin}}_\mathbb {R}\{ e_{d_c+1}, {\text {i}}e_{d_c+1}, \dots , e_{d_c+d_f}, {\text {i}}e_{d_c+d_f}\}, \end{aligned}$$

where $(e_j)_{j=1}^{d_c+d_f}$ is the canonical complex orthonormal basis of $\mathbb {C}^{d_c+d_f}$. Eventually, since symplectic transformation in finite dimensional symplectic spaces are always implemented by unitary transformations on the Fock space (see [12] Theorem 3.8), we obtain the final result. $\square$

Remark

An analogous argument to the proof of the previous theorem allows us to show that also ${\mathcal {M}}^r$ is a symplectic subspace which is symplectically orthogonal to both ${\mathcal {M}}^c$ and ${\mathcal {M}}^f$. If $2d_r=\dim _\mathbb {R} {\mathcal {M}}^r$, in total analogy with the proof, we can always find a symplectomorphism such that

$$\begin{aligned} {\mathcal {M}} \cup {\mathcal {M}}' \simeq \mathbb {C}^{d_r} \oplus {\mathcal {M}}^c \oplus \mathbb {C}^{d_f}, \end{aligned}$$

where ${\mathcal {M}}_c$ is the real subspace of $\mathbb {C}^{d_c}$ generated by $\{e_1, \dots , e_{d_c}\}$. In particular, after the unitary transformation associated with the symplectic transformation, we have

$$\begin{aligned} {\mathcal {W}}({\mathcal {M}} \cup {\mathcal {M}}') = {\mathcal {B}}(\Gamma (\mathbb {C}^{d_r})) {\overline{\otimes }} L^\infty (\mathbb {R}^{d_c} ; \mathbb {C}) {\overline{\otimes }} {\mathcal {B}}(\Gamma (\mathbb {C}^{d_f})). \end{aligned}$$

Remark

It is worth noticing here that a QMS with ${\mathcal {N}}({\mathcal {T}})$ as in (3.7) does not necessarily admit a dilation with $d_c$ classical noises because the corresponding Kraus operators $L_\ell$ could be normal but not self-adjoint (see Sect. 4.2 for an example) and so one may find obstructions to dilations with classical noises as shown in [19].

Corollary 3.8

The decoherence-free subalgebra ${\mathcal {N}}({\mathcal {T}})$ is generated by Weyl operators W(z) with z belonging to real subspaces of ${\mathrm{ker}}(C)$ that are Z-invariant.

Proof

By Theorem 3.7 it suffices to show that z belongs to the symplectic complement ${\mathcal {M}}'$ of (3.5) if and only if it belongs to a real subspace of ${\mathrm{ker}}(C)$ that is Z-invariant.

If z belongs to ${\mathcal {M}}'$ then $W(z)\in {\mathcal {N}}({\mathcal {T}})$ and ${\mathcal {T}}_t(W(z))= \mathrm {e}^{{\text {i}}t H} W(z)\, \mathrm {e}^{-{\text {i}}t H}$ for all $t\ge 0$. Comparison with (2.10) yields

$$\begin{aligned} \mathrm {e}^{{\text {i}}t H}&W(z)\, \mathrm {e}^{-{\text {i}}t H} \\&= \exp \left( -\frac{1}{2}\int _0^t \Re \left\langle \mathrm {e}^{sZ}z, C \mathrm {e}^{sZ}z\right\rangle \mathrm {d}s +{\text {i}}\int _0^t \Re \left\langle \zeta , \mathrm {e}^{sZ}z\right\rangle \mathrm {d}s \right) W\left( \mathrm {e}^{tZ}z\right) . \end{aligned}$$

Unitarity of both left and right operators implies $\Re \left\langle \mathrm {e}^{sZ}z, C \mathrm {e}^{sZ}z\right\rangle =0$ for all $s\ge 0$ and $\mathrm {e}^{sZ}z$ belongs to ${\mathrm{ker}}(C)$ for all $s\ge 0$, namely, in an equivalent way, z and also Zz (by differentiation) belong to ${\mathrm{ker}}(C)$.

Conversely, if z belongs to a real subspace of ${\mathrm{ker}}(C)$ that is Z-invariant, then $\mathrm {e}^{sZ}z$ also belongs to that subset for all $s\ge 0$. The explicit formula (2.10) shows that

$$\begin{aligned} {\mathcal {T}}_t(W(z))=\exp \left( {\text {i}}\int _0^t \Re \left\langle \zeta , \mathrm {e}^{sZ}z\right\rangle \mathrm {d}s \right) W\left( \mathrm {e}^{tZ}z\right) \end{aligned}$$

therefore

$$\begin{aligned} {\mathcal {T}}_t(W(z)^*){\mathcal {T}}_t(W(z))= \mathrm {e}^{{\text {i}}t H} W(z)^*W(z)\, \mathrm {e}^{-{\text {i}}t H} =\mathrm{1l}={\mathcal {T}}(W(z)^*W(z)) \end{aligned}$$

and, in the same way, ${\mathcal {T}}_t(W(z)){\mathcal {T}}_t(W(z)^*)={\mathcal {T}}(W(z)W(z)^*)$. It follows that $W(z)\in {\mathcal {N}}({\mathcal {T}})$ and z belongs to the symplectic complement of (3.5) by Theorem 3.7. $\square$

The following corollary shows that we can perform a unitary transformation of the Fock space in order to reduce the number of creation and annihilation operators that appear in the Kraus’ operators.

Corollary 3.9

There exists a unitary transformation U of the Fock space such that

$$\begin{aligned} U L_\ell U^* = \sum _{j=1}^{d_r+d_c} ({\overline{v}}_j a_j + u_j a^{\dagger }_j) \end{aligned}$$

Proof

It suffices to consider the transformation obtained in the Remark after Theorem 3.7. Indeed each Kraus operator corresponds to a vector $[{\overline{v}}, u]^{\mathrm {T}} \in {\mathcal {V}}$ which in turn corresponds to two generators in the subspace ${\mathcal {M}}$. Performing the symplectomorphism in the cited Remark we have

$$\begin{aligned} {\mathcal {M}} \simeq \mathbb {C}^{d_r} \oplus {\mathcal {M}}^c \end{aligned}$$

which has dimension $2d_r + d_c$. In particular if U is the unitary transformation that implements this symplectomorphism $U L_\ell U^*$ will depend at most from $d_r+ d_c$ modes. $\square$

Example

One may wonder if H can also be written in a special form in the new representation of the CCR, for example as the sum of two self-adjoint operators, one depending only on $b_{1},b^{\dagger }_{1},\dots ,b_{d_r+d_c},b^{\dagger }_{d_r+d_c}$ and the other depending only on $b_{d_r+d_c+1},b^{\dagger }_{d_r+d_c+1},\dots ,b_{d},b^{\dagger }_{d}$. This happens when ${\mathcal {N}}({\mathcal {T}})$ is a countable sum of type I factors (see [13]) but not in the case of Gaussian QMSs with $d_c>0$ as shows this example.

Let $d=2$, $m=1$ and

$$\begin{aligned} L = q_1, \qquad H = q_1 p_2. \end{aligned}$$

Clearly, by Theorem 3.2, ${\mathcal {N}}({\mathcal {T}})$ is the algebra $L^\infty (\mathbb {R};\mathbb {C}){\overline{\otimes }}{\mathcal {B}}(\Gamma (\mathbb {C}))$ but H is the product of two operators depending on different coordinates.

4 Applications

In this section we present two examples to illustrate the admissible structures of decoherence-free subalgebras of a Gaussian QMS on ${\mathcal {B}}(\Gamma (\mathbb {C}^d))$ with $d\ge 2$ and the application to an open system of two bosons in a common environment (see Ref. [8]). We begin by considering the case of only one noise operator.

4.1 The Case One L, $H=N$

The operators (2.7) and (2.6) are the closure of operators defined on D

$$\begin{aligned} L=\sum _{j=1}^d\left( {\overline{v}}_j a_j + u_j a^{\dagger }_j\right) , \qquad H=\sum _{j=1}^d a_j^{\dagger } a_j \end{aligned}$$

(4.1)

(either v or u is nonzero). We compute recursively

$$\begin{aligned} \delta ^{2n+1}_H(L) = \sum _{j=1}^d\left( u_j a^{\dagger }_j-{\overline{v}}_j a_j\right) , \qquad \delta ^{2n}_H(L) = L \end{aligned}$$

for all $n\ge 0$, and, in the same way, $\delta ^{2n+1}_H(L^*) = \sum _{j=1}^d\left( v_j a^{\dagger }_j-{\overline{u}}_j a_j\right)$, $\delta ^{2n}_H(L^*) = L^*$. It follows that ${\mathcal {M}}'$ is the symplectic complement of

$$\begin{aligned} {\mathrm{Lin}}_{\mathbb {R}}\left\{ \, v-u, v+u, {\text {i}}(v+u),{\text {i}}(v-u)\,\right\} ={\mathrm{Lin}}_{\mathbb {R}}\left\{ \, v, u, {\text {i}}v ,{\text {i}}u\,\right\} ={\mathrm{Lin}}_{\mathbb {C}}\left\{ \, v, u \,\right\} . \end{aligned}$$

Thus ${\mathcal {M}}'$ is the orthogonal (for the complex scalar product) of the complex linear subspace generated by v and u, it is a complex subspace of $\mathbb {C}^d$ and

$$\begin{aligned} {\mathcal {N}}({\mathcal {T}}) = \left\{ \, W(z)\,\mid \, z\in {\mathcal {M}}'\,\right\} ={\mathcal {B}}(\Gamma ({\mathcal {M}}')). \end{aligned}$$

If v, u are linearly independent, then the complex dimension of ${\mathcal {M}}'$ is $d-2$, and ${\mathcal {N}}({\mathcal {T}})$ is isomorphic to ${\mathcal {B}}(\Gamma (\mathbb {C}^{d-2}))$.

4.2 The Case One L, $H=0$

Let L be as in (4.1). If $H=0$, then $\delta _H =0$. In particular

$$\begin{aligned} {\mathcal {M}} = {\mathrm{Lin}}_{\mathbb {R}} \{ v-u,u-v, {\text {i}}(v+u), {\text {i}}(u+v) \} = {\mathrm{Lin}}_{\mathbb {R}} \{ v-u, {\text {i}}(v+u) \} \end{aligned}$$

and, since both v and u cannot be zero in our framework, $\dim _\mathbb {R} {\mathcal {M}}$ is either 1 or 2. If it is equal to 1 (first case), clearly ${\mathcal {M}}\cap {\mathcal {M}}'={\mathcal {M}}$ and ${\mathcal {M}}^r=\{0\}$ therefore $d_c=1$ and $d_r=0$. It follows that $d_f=d-1$ and ${\mathcal {N}}({\mathcal {T}})$ is a von Neumann algebra unitarily equivalent to $L^\infty (\mathbb {R}; \mathbb {C} ) {\overline{\otimes }} {\mathcal {B}}(\Gamma (\mathbb {C}^{d-1}))$. If $\dim _\mathbb {R} {\mathcal {M}}=2$ then, since ${\mathcal {M}}^r$ is a symplectic space, its real dimension must be even and so we distinguish two cases: $d_r=0,d_c=2$ (second case) and $d_r=1, d_c=0$ (third case). If $d_c=2$, again ${\mathcal {M}}\cap {\mathcal {M}}'={\mathcal {M}}$, and ${\mathcal {N}}({\mathcal {T}})$ is a von Neumann algebra $L^\infty (\mathbb {R}^2; \mathbb {C} ) {\overline{\otimes }} {\mathcal {B}}(\Gamma (\mathbb {C}^{d-2}))$.

If $d_c=0,d_r=1$, then $d_f=d-1$ and ${\mathcal {N}}({\mathcal {T}})$ is a von Neumann algebra ${\mathcal {B}}(\Gamma (\mathbb {C}^{d-1}))$. This classification is summarized by Table 1 in which the last column labeled “L” contains possible choices of the operator L that realize each case.

Table 1 ${\mathcal {N}}({\mathcal {T}})$ that can arise with one L and $H=0$

In the last part of the section we will characterize each case by just looking directly at the operator L instead of computing ${\mathcal {M}}$.

Suppose L is self-adjoint. In this case ${\mathcal {V}}$ is composed of only one vector which is of the form $[{\overline{v}},v]^{\mathrm{T}}$. Therefore ${\mathcal {M}}= {\mathrm{Lin}}_\mathbb {R} \{ {\text {i}}v\}$ and $d_c=1$, while $d_r=0$ ($1^{\mathrm{st}}$ case).

Consider now instead the case L normal but not self-adjoint. An explicit computation shows that $0 = [L, L^*] = \Vert v \Vert ^2 - \Vert u \Vert ^2$ on D. This condition shows that ${\mathcal {M}} = {\mathcal {M}}\cap {\mathcal {M}}'$ since

$$\begin{aligned} \Im \langle v-u,{\text {i}}(v+u) \rangle = \Vert v \Vert ^2 - \Vert u \Vert ^2=0. \end{aligned}$$

Moreover $u \ne v$ since L is not self-adjoint, hence $d_c=2$ ($2^{\mathrm{nd}}$ case). If L is not even normal (i.e. $\Vert v \Vert ^2 \ne \Vert u \Vert ^2$) then by the previous calculations $d_c=0$ and $d_r=1$ ($3^{\mathrm{rd}}$ case).

Summing up: the 1$^{\mathrm{st}}$ case arises when L is self-adjoint, the case 2$^{\mathrm{nd}}$ case arises when L is normal but not self-adjoint and the 3$^{\mathrm{rd}}$ case arises when L is not normal or, equivalently $\Vert v \Vert ^2 \ne \Vert u \Vert ^2$.

In the last case it can be shown that when $\Vert v \Vert ^2 > \Vert u \Vert ^2$ (resp. $\Vert v \Vert ^2 < \Vert u \Vert ^2$) there exists a Bogoliubov transformation changing L to a multiple of the annihilation operator $a_1$ (resp. creation operator $a^{\dagger }_1$).

4.3 Two Bosons in a Common Bath

The following model for the open quantum system of two bosons in a common environment has been considered in Ref. [8]. Here $d=2$ and H is as in equation 2.6 with $\kappa =\zeta =0$. The completely positive part of the GKLS generator ${\mathcal {L}}$ is

$$\begin{aligned} \frac{1}{2}\sum _{j,k=1,2} \gamma ^{-}_{jk}\, a^{\dagger }_j X a_k + \frac{1}{2}\sum _{j,k=1,2} \gamma ^{+}_{jk}\, a_j X a^{\dagger }_k \end{aligned}$$

(4.2)

where $(\gamma ^{\pm }_{jk})_{j,k = 1,2}$ are positive definite $2\times 2$ matrices.

Note that, by a change of phase $a_1\rightarrow \mathrm {e}^{{\text {i}}\theta _1} a_1$, $a^{\dagger }_1\rightarrow \mathrm {e}^{-{\text {i}}\theta _1} a^{\dagger }_1$, $a_2\rightarrow \mathrm {e}^{{\text {i}}\theta _2} a_2$, $a^{\dagger }_2\rightarrow \mathrm {e}^{-{\text {i}}\theta _2} a^{\dagger }_2$, we can always assume that $(\gamma ^{-}_{jk})_{j,k = 1,2}$ is real symmetric. Write the spectral decomposition

$$\begin{aligned} \gamma ^{\pm } = \lambda _{\pm }|\varphi ^{\pm }\rangle \langle \varphi ^{\pm }| + \mu _{\pm }|\psi ^{\pm }\rangle \langle \psi ^{\pm }| \end{aligned}$$

where the vectors $\varphi ^{-},\psi ^{-}$ have real components. Rewrite the first term of (4.2) as

$$\begin{aligned} \sum _{j,k=1,2} \gamma ^{-}_{jk}\, a^{\dagger }_j X a_k&= \lambda _{-}\sum _{j,k=1,2} \varphi ^{-}_j \varphi ^{-}_k \, a^{\dagger }_j X a_k + \mu _{-}\sum _{j,k=1,2} \psi ^{-}_j \psi ^{-}_k \, a^{\dagger }_j X a_k\\&= \lambda _{-}\left( \sum _{j=1,2} \varphi ^{-}_j \, a^{\dagger }_j\right) X \left( \sum _{k=1,2}\varphi ^{-}_k a_k\right) \\&+ \mu _{-}\left( \sum _{j=1,2} \psi ^{-}_j \, a^{\dagger }_j\right) X \left( \sum _{k=1,2}\psi ^{-}_k a_k\right) \end{aligned}$$

and write in a similar way the second term of (4.2)

$$\begin{aligned} \sum _{j,k=1,2} \gamma ^{+}_{jk}\, a_j X a^{\dagger }_k&= \lambda _{+}\left( \sum _{j=1,2} \overline{\varphi ^{+}}_j \, a_j\right) X \left( \sum _{k=1,2}\varphi ^{+}_k a^{\dagger }_k\right) \\&+ \mu _{+}\left( \sum _{j=1,2} \overline{\psi ^{+}}_j \, a_j\right) X \left( \sum _{k=1,2}\psi ^{+}_k a^{\dagger }_k\right) \end{aligned}$$

We can represent ${\mathcal {L}}$ in a generalized GKLS form with a number of Kraus operators $L_\ell$ depending on the number of strictly positive eigenvalues among $\lambda _{\pm },\mu _{\pm }$.

$$\begin{aligned} L_1 = \lambda _{-}^{1/2} \sum _{k=1,2} \varphi _k^{-} a_k&\qquad&L_2 = \mu _{-}^{1/2} \sum _{k=1,2} \psi _k^{-} a_k \\ L_3 = \lambda _{+}^{1/2} \sum _{k=1,2}\varphi _k^{+} a^{\dagger }_k&\qquad&L_4 = \mu _{+}^{1/2} \sum _{k=1,2}\psi _k^{+} a^{\dagger }_k \end{aligned}$$

Relabelling if necessary, we can always assume $0\le \lambda _{-} \le \mu _{-}$ and $0\le \lambda _{+} \le \mu _{+}$.

We begin our analysis by considering the case where $H=0$.

If $\lambda _{-}>0$ (or $\lambda _{+}>0$) then there are four vectors v, u in the defining set of ${\mathcal {M}}$ namely

$$\begin{aligned} {\mathcal {M}} = {\mathrm{Lin}}_{\mathbb {R}}\left\{ \, \varphi ^{-}, \psi ^{-}, {\text {i}}\varphi ^{-}, {\text {i}}\psi ^{-} \,\right\} \quad (\mathrm{or\ } = {\mathrm{Lin}}_{\mathbb {R}}\left\{ \, \varphi ^{+}, \psi ^{+}, {\text {i}}\varphi ^{+}, {\text {i}}\psi ^{+} \,\right\} ) \end{aligned}$$

thus ${\mathcal {M}}'=\{0\}$ and ${\mathcal {N}}({\mathcal {T}}) = \mathbb {C}\mathrm{1l}$.

Suppose now that $\lambda _{+}=\lambda _{-}=0$ and $\mu _{-},\mu _{+}>0$ so that there are only two Kraus operators, the above $L_2$ and $L_4$ and

$$\begin{aligned} {\mathcal {M}} = {\mathrm{Lin}}_{\mathbb {R}}\left\{ \,\psi ^{-}, \psi ^{+}, {\text {i}}\psi ^{-}, {\text {i}}\psi ^{+} \,\right\} . \end{aligned}$$

It follows that, if $\psi ^{-}, \psi ^{+}$ are $\mathbb {R}$-linearly independent, we have again ${\mathcal {M}}=\mathbb {C}^2$ whence ${\mathcal {M}}'=\{0\}$ and ${\mathcal {N}}({\mathcal {T}}) = \mathbb {C}\mathrm{1l}$. Otherwise, if $\psi ^{+}$ is a real non-zero multiple of $\psi ^{-}$, then, as $\psi ^{\pm }$ and ${\text {i}}\psi ^{\pm }$ are $\mathbb {R}$-linearly independent, the real dimension of ${\mathcal {M}}$ and ${\mathcal {M}}'$ is two, ${\mathcal {M}}\cap {\mathcal {M}}'=\{0\}$ so that ${\mathcal {N}}({\mathcal {T}})$ is isomorphic to ${\mathcal {B}}(\Gamma (\mathbb {C}))$.

It is not difficult to see that, in any case, the dimension of ${\mathcal {M}}$ cannot be 1 or 3 (because creation and annihilation operator always appear separately in different Kraus operators L, never in the same).

Summarizing: ${\mathcal {N}}({\mathcal {T}})$ is non-trivial and isomorphic to ${\mathcal {B}}(\Gamma (\mathbb {C}))$ if and only if $\gamma ^{+}$ and $\gamma ^{-}$ are rank-one and commute.

Finally, if we consider a non-zero H, it is clear that ${\mathcal {N}}({\mathcal {T}})$ is always trivial unless $\gamma ^{+}$ and $\gamma ^{-}$ are rank-one, commute and their one-dimensional range is an eigenvector for $\Omega$ and $\Omega ^T$.

Appendices

Appendix A: Construction of Gaussian QMSs From the GKLS Generator

In this section we outline how one can construct the minimal quantum dynamical semigroup associated with operators $H, L_\ell$ and following [16], Section 3.3. The first step is to prove that the closure of the operator G

$$\begin{aligned} G = -\frac{1}{2} \sum _{\ell =1}^m L_\ell ^* L_\ell -{\text {i}}H \end{aligned}$$

(4.3)

defined on the domain D generates a strongly continuous contraction semigroup. To this end we recall the result due to Palle E.T. Jorgensen (see [23], Theorem 2).

Theorem 4.1

Let G be a dissipative linear operator on a Hilbert space ${\mathsf {h}}.$ Let $(D_n)_{n\ge 1}$ be an increasing family of closed subspaces of ${\mathsf {h}}$ whose union is dense in ${\mathsf {h}}$ and contained in the domain of G and let $P_{D_n}$ be the orthogonal projection of ${\mathsf {h}}$ onto $D_n.$ Suppose that there exists an integer $n_0$ such that $GD_n\subset D_{n+n_0}$ for all $n\ge 1$. Then the closure ${\overline{G}}$ generates a strongly continuous contraction semigroup on ${\mathsf {h}}$ and $\cup _{n\ge 1}D_n$ is a core for ${\overline{G}}$, if there exists a sequence $(c_n)_{n\ge 1}$ in $\mathbb {R}_+$ such that $|| GP_{D_n} - P_{D_n}GP_{D_n}||\le c_n$ for all n and

$$\begin{aligned} \sum \limits _{n=1}^{\infty }c_n^{-1}=\infty \end{aligned}$$

We are now able to prove the following proposition.

Proposition 4.2

The operator ${\overline{G}}$ is the infinitesimal generator of a strongly continuous contraction semigroup on ${\mathsf {h}}$ and D is a core for this operator.

Proof

We apply Theorem 4.1 with $D_n$ the linear manifold spanned by vectors $e(n_1,\ldots ,n_d)$ with $n_1+\ldots +n_d\le n$. Clearly $D=\cup _{n\ge 1}D_n$. The operator G is obviously densely defined and dissipative. Therefore it is closable (see e.g. [5], Lemma 3.1.14) and its closure, denoted ${\overline{G}}$ is dissipative. Clearly, by the explicit form of the action of creation and annihilation operators on vectors $e(n_1,\ldots ,n_d)$, the operator G maps $D_n$ into $D_{n+2}$ for all $n\ge 0$.

A straightforward computation using (4.3) yields

$$\begin{aligned} (GP_{D_n} - P_{D_n}GP_{D_n}) = -\left( \frac{1}{2}\sum _{k,j=1}^d \left( \sum _{\ell =1}^m v_{\ell k} u_{\ell j} +{\text {i}}\kappa \right) a^{\dagger }_k a^{\dagger }_j +\frac{{\text {i}}}{2} \sum _{k=1}^d \zeta _k a^{\dagger }_k\right) P_{D_n}, \end{aligned}$$

namely the non-zero part is the one involving only creations. Let us fix $u=\sum _{|\alpha |\le n} r_{\alpha }e_{\alpha }$ a vector in $D_n$, where $\alpha =(\alpha (1),\ldots ,\alpha (d))$ is a multi-index, $|\alpha |=\alpha (1)+\ldots +\alpha (d)$, and the vector $e_{\alpha }^{\mathrm{T}}=(e_{\alpha (1)},\ldots ,e_{\alpha (d)})$. Clearly $a^{\dagger }_j u \in D_{n+1}$ and

$$\begin{aligned} \left\| a^{\dagger }_j u \right\| ^2 \le \sum _{|\alpha |\le n} \left| r_{\alpha } \right| ^2 \left( \alpha (j) +1 \right) \left\| e_{\alpha +1_j} \right\| ^2 \le (n+1) \left\| u \right\| ^2. \end{aligned}$$

Therefore we have also

$$\begin{aligned} \left\| a^{\dagger }_j a^{\dagger }_k u \right\| ^2 \le (n+2) \left\| a^{\dagger }_k u \right\| ^2 \le (n+2)(n+1)\left\| u \right\| ^2 \le (n+2)^2\left\| u \right\| ^2. \end{aligned}$$

This means that

$$\begin{aligned} \left\| (GP_{D_n} - P_{D_n}GP_{D_n}) u \right\|&\begin{aligned}\le \frac{1}{2}\sum _{j,k=1}^d&\left\| \left[ \sum _\ell \left( {\overline{v}}_{\ell \bullet }\right) ^* u_{\ell \cdot } +{\text {i}}\kappa \right] _{jk} a^{\dagger }_j a^{\dagger }_ku \right\| \\&+ \sum _{j=1}^d \left\| \zeta _j a^{\dagger }_j u \right\| \end{aligned}\\&\le c(n+2) \left\| u \right\| /2 \end{aligned}$$

with $c>0$ a constant that does not depend on n. Eventually, since the series $\sum _{n\ge 1} (n+2)^{-1}$ diverges, we can apply Theorem 4.1 and the proposition is proved. $\square$

A similar argument allows us to prove the following

Proposition 4.3

The closure $\Phi$ of the operator $\sum _{1\le \ell \le m}L_\ell ^*L_\ell$ defined on the domain D is essentially self-adjoint.

Let us denote by G also the closure of the operator G to simplify the notation. Using standard arguments, the operators $L_{\ell }$ can be extended to the domain of G and further extended to the domain

$$\begin{aligned} \left\{ \,u\in {\mathsf {h}}\,\mid \, u=\sum _{\alpha }r_{\alpha }e_{\alpha },\sum _{\alpha }|\alpha | \,|r_{\alpha }|^2<\infty \,\right\} , \end{aligned}$$

where $\alpha =(\alpha (1),\ldots ,\alpha (d))$ is a multi-index, $|\alpha |=\alpha (1)+\ldots +\alpha (d)$, and the vector $e_{\alpha }=(e_{\alpha (1)},\ldots ,e_{\alpha (d)})$.

In the next section we will show that the minimal semigroup is identity preserving and so it is a well defined QMS, whose predual semigroup is trace preserving.

1.1 Conservativity

We will establish conservativity by applying the Chebotarev-Fagnola sufficient condition (see [9] , [16] section 3.5). More precisely, we will apply the following result:

Theorem 4.4

Suppose that:

• 1. the operator G is the infinitesimal generator of a strongly continuous contraction semigroup $(P_t)_{t\ge 0}$ in ${\mathsf {h}}$,

• 2. the domain of the operators $(L_\ell )_{\ell \ge 1}$ contains the domain of G and, for every $u\in D(G)$, we have

  $$\begin{aligned} \langle u,Gu\rangle +\langle Gu,u\rangle +\sum \limits _\ell \langle L_\ell u,L_\ell u\rangle =0, \end{aligned}$$

• 3. there exists a self-adjoint operator C with domain coinciding with the domain of G and a core D for C with the following properties

  • (a) $L_\ell (D)\subset D(C^{1/2})$ for all $\ell \ge 1$,

  • (b) there exists a self-adjoint operator $\Phi$ such that

    $$\begin{aligned} -2\Re \langle u,Gu\rangle =\langle u,\Phi u\rangle \le \langle u,C u\rangle \end{aligned}$$

    for all $u\in D$,

  • (c) there exists a positive constant b such that the inequality

    $$\begin{aligned} 2\Re \langle Cu,Gu\rangle +\sum _{\ell \ge 1}\langle C^{1/2}L_\ell u,C^{1/2}L_\ell u\rangle \le b\langle u,C u\rangle \end{aligned}$$

    holds for every $u\in D.$

Then the minimal quantum dynamical semigroup is Markov.

In order to check the above conditions one should proceed with computations on quadratic forms. However, these are equivalent to algebraic computations of the action of the formal generator $\pounds$ on first and second order polynomials is $a_j,a^{\dagger }_j$ therefore we will go on with algebraic computations so as to reduce the clutter of the notation.

Lemma 4.5

It holds

$$\begin{aligned} 2\pounds (a_k)&= a^{\dagger } \left( \left( U^{\mathrm{T}}V-V^{\mathrm{T}}U-2\mathrm {i}\kappa \right) _{k \bullet }\right) +a \left( \left( U^*U-V^*V+2\mathrm {i}{\overline{\Omega }}\right) _{k\bullet } \right) - \mathrm {i}\zeta _k\mathbb {1}, \\ 2\pounds (a_k^{\dagger })&= a \left( \left( U^{\mathrm{T}}V-V^{\mathrm{T}}U-2\mathrm {i}\kappa \right) _{k \bullet }\right) +a^{\dagger } \left( \left( U^*U-V^*V+2\mathrm {i}{\overline{\Omega }}\right) _{k\bullet } \right) + \mathrm {i}\overline{\zeta _k}\mathbb {1}. \end{aligned}$$

Proof

First write

$$\begin{aligned} \pounds _0(X):={\mathcal {L}}(X) - {\text {i}}[H,X] =\frac{1}{2}\sum _{\ell =1}^m\left( L_\ell ^*[X,L_\ell ] +[L_\ell ^*,X]L_\ell \right) . \end{aligned}$$

By the CCR one has

$$\begin{aligned} {[}a_k,L_\ell ]&=\sum _{j=1}^d [a_k,u_{\ell j}a_j^{\dagger }]=u_{\ell k}\mathbb {1}, \\ {[}L_\ell ^*,a_k]&=[a_k^{\dagger },L_\ell ]^* =\sum _{j=1}^d {[}a_k^{\dagger },{\overline{v}}_{\ell j}a_j]^*=-v_{\ell k}\mathbb {1} \end{aligned}$$

Therefore we obtain that

$$\begin{aligned} \pounds _0(a_k)=\frac{1}{2}\sum _{\ell =1}^m\left\{ \left( \sum _{j=1}^d v_{\ell j}a_j^{\dagger }+{\overline{u}}_{\ell j}a_j\right) u_{\ell k}-v_{\ell k}\left( \sum _{j=1}^d{\overline{v}}_{\ell j}a_j+u_{\ell j}a_j^{\dagger }\right) \right\} . \end{aligned}$$

and

$$\begin{aligned} {[}H,a_k]=-\frac{{\text {i}}\zeta _k}{2}\mathbb {1}-\sum _{j=1}^d\left( \Omega _{kj}a_j+\kappa _{kj} a_j^{\dagger }\right) . \end{aligned}$$

which both lead to

$$\begin{aligned} \pounds (a_k)&= \mathrm {i} [H,a_k]+\pounds _0 (a_k)\\&= -\frac{\zeta _k}{2}\mathbb {1}-\mathrm {i}\sum _{j=1}^d\left( \Omega _{kj}a_j+\kappa _{kj} a_j^{\dagger }\right) \\&\quad + \frac{1}{2}\sum _{\ell =1}^m\left\{ \left( \sum _{j=1}^d v_{\ell j}a_j^{\dagger }+{\overline{u}}_{\ell j}a_j\right) u_{\ell k}-v_{\ell k}\left( \sum _{j=1}^d{\overline{v}}_{\ell j}a_j+u_{\ell j}a_j^{\dagger }\right) \right\} \end{aligned}$$

Using the last equality and $\pounds (a_k^{\dagger })=\pounds (a_k)^*$ concludes the proof. $\square$

The following formula is verified for any generator $\pounds$ of a QMS:

Lemma 4.6

For all $X,Y\in {\mathcal {B}}({\mathsf {h}})$

$$\begin{aligned} \pounds (XY)= X\pounds (Y)+\pounds (X) Y +\sum _{\ell =1}^m [L_\ell ,X^*]^*[L_\ell ,Y]. \end{aligned}$$

(4.4)

Proof

Let $\pounds _0(X)=-(1/2)\sum _{\ell =1}^m\left( L_\ell ^*L_\ell X-2L_\ell ^*XL_\ell +XL_\ell ^*L_\ell \right)$ then we can write $\pounds _0(XY)-X\pounds _0(Y)-\pounds _0(X)Y$ as

$$\begin{aligned}&\sum _{\ell =1}^m\left( -\frac{1}{2}L_\ell ^*L_\ell XY+L_\ell ^*XYL_\ell -\frac{1}{2}XYL_\ell ^*L_\ell \right) \\&\quad +\sum _{\ell =1}^m\left( \frac{1}{2}XL_\ell ^*L_\ell Y-XL_\ell ^*YL_\ell +\frac{1}{2}XYL_\ell ^*L_\ell \right) \\&\quad +\sum _{\ell =1}^m\left( \frac{1}{2}L_\ell ^*L_\ell XY-L_\ell ^*XL_\ell Y+\frac{1}{2}XL_\ell ^*L_\ell Y\right) \\&\quad = \sum _{\ell =1}^m \left( L_\ell ^*XYL_\ell + XL_\ell ^*L_\ell Y -XL_\ell ^*YL_\ell - L_\ell ^*XL_\ell Y\right) \\&\quad =\sum _{\ell =1}^m \left( [L_\ell ^*,X]YL_\ell -[L_\ell ^*,X]L_\ell Y \right) = \sum _{\ell =1}^m \left( [L_\ell ,X^*]^*\, [L_\ell ,Y] \right) \end{aligned}$$

Recalling the usual commutator property $[H,XY]=[H,X]Y+X[H,Y]$, we find then

$$\begin{aligned} \pounds (XY)-X\pounds (Y)-\pounds (X)Y = \pounds _0(XY)-X\pounds _0(Y)-\pounds _0(X)Y. \end{aligned}$$

This completes the proof. $\square$

As a final step towards proving conservativity via Theorem 4.4, we prove the following

Proposition 4.7

Let $C=\sum \limits _{k=1}^d a_ka_k^{\dagger }$. There exist a constant $b>0$ such that $\pounds (C)\le b C$

Proof

By Lemmas 4.5 we have that

$$\begin{aligned} \pounds (a_k) = \sum _{j=1}^d \left( w_{kj}a^{\dagger }_j+z_{kj}a_j\right) -\frac{\mathrm {i}\zeta _k}{2}\mathbb {1}, \quad \pounds (a_k^{\dagger }) = \sum \limits _{j=1}^d \left( {\overline{w}}_{kj}a_j+{\overline{z}}_{kj}a_j^{\dagger }\right) +\frac{\mathrm {{\text {i}}}{\overline{\zeta }}_k}{2}\mathbb {1} \end{aligned}$$

for some complex numbers $w_{kj},z_{kj}, \zeta _j$. While, by Lemma 4.6, we get

$$\begin{aligned} \pounds (a_k a_k^{\dagger })&= -\mathrm {i}{\overline{\zeta }}_k a_k/2 + \sum _{j=1}^d\left( {\overline{w}}_{kj}a_ka_j+{\overline{z}}_{kj}a_ka_j^{\dagger }\right) \\&+ \mathrm {i}\zeta _k a^{\dagger }_k/2 + \sum _{j=1}^d\left( w_{kj}a_j^{\dagger }a_k^{\dagger }+z_{kj}a_ja_k^{\dagger } \right) +\Vert v_{\bullet k} \Vert ^2\mathbb {1}\\&= \sum _{j=1}^d\left( {\overline{z}}_{kj}a_ka_j^{\dagger }+z_{kj}a_ja_k^{\dagger } +{\overline{w}}_{kj}a_ka_j+w_{kj}a_j^{\dagger }a_k^{\dagger }\right) \\&+ \frac{\mathrm {i}}{2}\left( \zeta _k a_k^{\dagger } -{\overline{\zeta }}_ka_k\right) +\Vert v_{\bullet k} \Vert ^2\mathbb {1} \end{aligned}$$

Note that for each k, j

$$\begin{aligned} |a_j^{\dagger }-z_{kj}a_k^{\dagger }|^2=a_ja_j^{\dagger }+|{z}_{jk}|^2 a_ka_k^{\dagger } -{\overline{z}}_{kj}a_ka_j^{\dagger }-z_{kj}a_ja_k^{\dagger }\ge 0, \end{aligned}$$

it follows that

$$\begin{aligned} {\overline{z}}_{kj}a_ka_j^{\dagger }+z_{kj}a_ja_k^{\dagger }\le a_ja_j^{\dagger }+|{z}_{jk}|^2 a_ka_k^{\dagger } \end{aligned}$$

(4.5)

and, in the same way

$$\begin{aligned} {\overline{w}}_{kj}a_ka_j+w_{kj}a_k^{\dagger }a_j\le |w_{kj}|^2a_ka_k^{\dagger }+a_ja_j^{\dagger }. \end{aligned}$$

(4.6)

Finally, from

$$\begin{aligned} |a_k^{\dagger }+\mathrm {i}{\overline{\zeta }}_k\mathbb {1}|^2 =a_ka_k^{\dagger }+|\zeta _k|^2\mathbb {1}-\mathrm {i}\zeta _k a_k^{\dagger }+\mathrm {i}{\overline{\zeta }}_k a_k\ge 0 \end{aligned}$$

it follows that

$$\begin{aligned} \mathrm {i}\zeta _ka_k^{\dagger }-\mathrm {i}{\overline{\zeta }}_ka_k\le a_ka_k^{\dagger }+|\zeta _k|^2\mathbb {1}. \end{aligned}$$

(4.7)

By (4.5),(4.6), and (4.7)

$$\begin{aligned} \pounds (C)\le \left( 3 d\max _{1\le k\le d}\left( 1+\sum _{j=1}^d(|z_{kj}|^2+|w_{kj}|^2)\right) C +\sum _{j=1}^d\left( |\zeta _j|^2+\Vert v_{\bullet j} \Vert ^2\right) \mathbb {1}\right) \end{aligned}$$

since $C\ge d\mathbb {1}$ then $\pounds (C)\le b C$ with

$$\begin{aligned} b=\max \left\{ 3d\max _{1\le k\le d}\left( \sum \sum _{j=1}^d(|z_{kj}|^2 +|w_{kj}|^2)\right) , \sum _{j=1}^d\left( |\zeta _j|^2+\Vert v_{\bullet j} \Vert ^2\right) \,\right\} . \end{aligned}$$

$\square$

We can eventually state the result on conservativity.

Theorem 4.8

The minimal QDS semigroup generated by the pre-generator (2.5) with H, $L_\ell$ given by (2.6),(2.7) is Markov.

Proof

We apply Theorem 4.4 with the operator C given by

$$\begin{aligned} {\mathrm{Dom}}(C) = \left\{ u=\sum _\alpha u_\alpha e(\alpha ) \,\mid \, \sum _\alpha |\alpha |^2 |u_\alpha |^2 < \infty \,\right\} , \qquad Cu = \sum _{j=1}^d a_j a_j^{\dagger } u . \end{aligned}$$

Conditions 1 and 2 are satisfied by definition and by Proposition 4.2. For condition 3 one can choose D as in the proof of Proposition 4.2. In this way (a) is easily satisfied, while (c) follows from Proposition 4.7. The operator $\Phi$ is the self-adjoint extension of $\sum _\ell L_\ell ^*L_\ell$ (defined on the domain D) and is second-order polynomial in $a, a^{\dagger }$. Inequalities like (4.6) and (4.5) allows one to show that $\Phi$ is majorized by a suitable multiple of C. Replacing C with this suitable multiple the proof is completed by Proposition 4.7. $\square$

1.2 Proof of Theorem 2.4

Following the proof of Theorem 2 in [1] let us start by derivating (2.10) at $t=0$. Using

$$\begin{aligned} \frac{{\text {d}}}{{\text {dt}}} W(\mathrm {e}^{tZ}z)\Big |_{t=0}= W(z) \sum _{j=1}^d \left( (Zz)_j a_j^{\dagger } - (\overline{Zz})_ja_j + \frac{1}{2} \left( \overline{z_j}(Zz)_j - (\overline{Zz})_jz_j \right) \right) \end{aligned}$$

(with respect to the norm topology) one has ${\mathcal {L}}(W(z))= W(z) Y(z)$, where Y(z) corresponds to the operator

$$\begin{aligned} \sum _{j=1}^d\left( (Zz)_j a_j^{\dagger } - (\overline{Zz})_ja_j + \frac{1}{2} \left( \overline{z_j}(Zz)_j - (\overline{Zz})_jz_j \right) \right) - \frac{1}{2}\Re \left\langle z , Cz \right\rangle + {\text {i}}\Re \left\langle \zeta , z \right\rangle . \end{aligned}$$

Now instead let us rewrite the GKLS pre-generator as

$$\begin{aligned} {\mathcal {L}}(W(z)) = {\text {i}}\left[ H , W(z) \right] +\frac{1}{2} \sum _{\ell =1}^m \left( L_\ell ^* \left[ W(z) , L_\ell \right] + \left[ L_\ell ^* , W(z) \right] L_\ell \right) . \end{aligned}$$

Recalling that $\Omega =\Omega ^*, \kappa =\kappa ^{\mathrm{T}}$ and from (2.4) one gets

$$\begin{aligned} \left[ W(z) , L_\ell \right] = - W(z) \left( \overline{V}z + U\overline{z} \right) _\ell , \quad \left[ L_\ell ^* , W(z) \right] = W(z)\left( V\overline{z} + \overline{U}z\right) _\ell \end{aligned}$$

and so

$$\begin{aligned} \left[ H , W(z) \right]&= W(z)\left[ a\left( \Omega z + \kappa \overline{z} \right) + a^{\dagger } \left( \Omega z + \kappa \overline{z} \right) \right] \\&+\left( \frac{1}{2} \left\langle z , \Omega z + \kappa \overline{z} \right\rangle + \frac{1}{2} \overline{\left\langle z , \Omega z + \kappa \overline{z} \right\rangle } + \Re \left\langle \zeta , z \right\rangle \right) W(z) \end{aligned}$$

At last one finds

$$\begin{aligned} \sum _{\ell =1}^m\left[ L_\ell ^* , \left[ W(z) , L_\ell \right] \right]&= -\sum _{\ell =1}^mW(z) \left( \overline{V}z + U\overline{z}\right) _\ell \left( V\overline{z} + \overline{U}z\right) _\ell \\&= -W(z)\left( \left\langle z , \overline{V^*V} z + V^{\mathrm{T}}U \overline{z} \right\rangle + \overline{\left\langle z , \overline{U^*U}z + U^{\mathrm{T}}V \overline{z} \right\rangle }\right) . \end{aligned}$$

Using the previous results one finds that ${\mathcal {L}}(W(z)) = W(z) X(z)$ for some operator X(z) which is explicitly given by

$$\begin{aligned} X(z) =&a^{\dagger } \left( \left( \frac{\overline{U^*U - V^*V}}{2} + {\text {i}}\Omega \right) z + \left( \frac{ U^{\mathrm{T}}V - V^{\mathrm{T}} U}{2} + {\text {i}}\kappa \right) \overline{z} \right) \\&-a \left( \left( \frac{\overline{U^*U - V^*V}}{2} +{\text {i}}\Omega \right) z + \left( \frac{U^{\mathrm{T}}V-V^{\mathrm{T}}U}{2} + {\text {i}}\kappa \right) \overline{z} \right) \\&+ \frac{1}{2} \left\langle z , {\text {i}}\Omega z + {\text {i}}\kappa \overline{z} \right\rangle - \frac{1}{2} \overline{\left\langle z , {\text {i}}\Omega z + {\text {i}}\kappa \overline{z} \right\rangle } + {\text {i}}\Re \left\langle \zeta , z \right\rangle \\&- \frac{1}{2} \left( \left\langle z , \overline{V^*V} z + V^{\mathrm{T}}U \overline{z} \right\rangle + \overline{\left\langle z , \overline{U^*U}z + U^{\mathrm{T}}V \overline{z} \right\rangle }\right) . \end{aligned}$$

Since X(z) and Y(z) must coincide for every $z\in \mathbb {C}^d$ the proof of Theorem 2.4 is complete.

Appendix B: Characterization of ${\mathcal {N}}({\mathcal {T}})$

In this section we derive the characterization of ${\mathcal {N}}({\mathcal {T}})$ in terms of iterated commutators. We begin by illustrating the idea of the proof in the case where the operators $L_\ell$ and H are bounded. For all $x,y\in {\mathcal {B}}({\mathsf {h}})$, recall the formula (4.4) from Lemma 4.6. Note that, if $x\in {\mathcal {N}}({\mathcal {T}})$ and y is arbitrary then, since ${\mathcal {T}}_t(y^*x)={\mathcal {T}}_t(y^*){\mathcal {T}}_t(x)$ by Proposition 3.1 1, taking the derivative at $t=0$ we get ${\mathcal {L}}(y^*x) = {\mathcal {L}}(y^*)x+ y^*{\mathcal {L}}(x)$, therefore

$$\begin{aligned} \sum _{\ell =1}^m[L_\ell ,y]^*[L_\ell , x] =0. \end{aligned}$$

(4.8)

If the operators $L_\ell$ are bounded, we are allowed to take $x=y$, then $[L_\ell ,x]=0$ for all $\ell$. Moreover, since $x^*$ also belongs to ${\mathcal {N}}({\mathcal {T}})$, taking the adjoint of $[L_\ell ,x^*]=0$, x also commutes with all the operators $L_\ell ^*$ and ${\mathcal {L}}(x)={\text {i}}[H,x]$. Clearly, since ${\mathcal {N}}({\mathcal {T}})$ is ${\mathcal {T}}_t$-invariant, ${\mathcal {L}}(x)=\lim _{t\rightarrow 0}({\mathcal {T}}_t(x)-x)/t$ belongs to ${\mathcal {N}}({\mathcal {T}})$. Therefore $[L_\ell ,[H,x]]=0$ for all $\ell$ and, by the Jacobi identity

$$\begin{aligned} \left[ \,x,[H,L_\ell ]\,\right] = -\left[ \,H,[L_\ell ,x]\,\right] - \left[ \,L_\ell ,[x,H]\,\right] = 0. \end{aligned}$$

In this way, one can show inductively that x commutes with the iterated commutators (3.2).

If the operators $L_\ell ,H$ are unbounded, one has to cope with several problems. The operator ${\mathcal {L}}$ is unbounded and, even if we choose x, y in the domain of ${\mathcal {L}}$, it is not clear whether $y^*x$ belongs to the domain of ${\mathcal {L}}$ (see [17]). Multiplication of generalized commutators $[L_\ell ,y]$ $[L_\ell ,x]$ may not be defined. If we choose a “nice” $y\in {\mathrm{Dom}}({\mathcal {L}})$ then it is not clear whether we can take $x=y$ because we do not know a priori if our “nice” y belongs to ${\mathcal {N}}({\mathcal {T}})$.

We begin the analysis of ${\mathcal {N}}({\mathcal {T}})$ by a few preliminary lemmas.

Lemma 4.9

The following derivative exists with respect norm topology for all $z\in \mathbb {C}$

$$\begin{aligned} \frac{ \mathrm {d}}{\mathrm {d}t}{\mathcal {T}}_t(W(z))e_g\Big |_{t=0} = G^* W(z)e_g + \sum _{\ell =1}^m L_\ell ^* W(z) L_\ell e_g + W(z) G e_g \end{aligned}$$

Proof

The right-hand side operator $G^* W(z) + \sum _{\ell =1}^m L_\ell ^* W(z) L_\ell + W(z) G$ is unbounded (for $z\not =0$) therefore W(z) does not belong to the domain of ${\mathcal {L}}$ but we can consider the quadratic form $\pounds (W(z))$ on $D\times D$. Differentiability of functions $t\mapsto \left\langle \xi ',{\mathcal {T}}_t(x)\xi \right\rangle$ also holds for $\xi ,\xi '$ in the linear span of exponential vectors. Therefore, for all such $\xi$, we have (Theorem 2.3)

$$\begin{aligned} \left\langle \xi , \left( {\mathcal {T}}_t(W(z))-W(z)-t\pounds (W(z))\right) e_g \right\rangle = \int _0^t \left\langle \xi , \pounds ({\mathcal {T}}_s(W(z)) - W(z)) e_g \right\rangle \mathrm {d}s. \end{aligned}$$

Recalling that ${\mathcal {T}}_s(W(z)) =\varphi _z(s)W(\mathrm {e}^{sZ}z)$ as in (2.10) for a complex valued function $\varphi$ such that $\lim _{s\rightarrow 0} \varphi _z(s)=1$, the right-hand side integrand can be written as

$$\begin{aligned} \left( \varphi _z(s)-1\right) \left\langle \xi , \pounds (W(\mathrm {e}^{sZ}z)) e_g \right\rangle + \left\langle \xi , \pounds (W(\mathrm {e}^{sZ}z)-W(z)) e_g \right\rangle \end{aligned}$$

A long but straightforward computation shows the function

$$\begin{aligned} s\mapsto \pounds (W(\mathrm {e}^{sZ}z)-W(z)) e_g \end{aligned}$$

is continuous vanishing at $s=0$ and the function $s\mapsto \pounds (W(\mathrm {e}^{sZ}z)) e_g$ is bounded with respect to the Fock space norm. Therefore, taking suprema for $\xi \in \Gamma (\mathbb {C}^d)$, $\Vert \xi \Vert =1$, we find the inequalities

$$\begin{aligned} \left\| \left( {\mathcal {T}}_t(W(z))-W(z)-t\pounds (W(z))\right) e_g\right\|&\le \int _0^t \left| \varphi _z(s)-1\right| \left\| \pounds (W(\mathrm {e}^{sZ}z)) e_g\right\| \mathrm {d}s\\&\quad + \int _0^t \left\| \pounds (W(\mathrm {e}^{sZ}z)-W(z)) e_g\right\| \mathrm {d}s \end{aligned}$$

The conclusion follows dividing by t and taking the limit as $t\rightarrow 0^+$. $\square$

Lemma 4.10

Let $x\in {\mathcal {N}}({\mathcal {T}})$. For all exponential vectors $e_g,e_f$ and all Weyl operators W(z) we have

$$\begin{aligned} \sum _{\ell =1}^m\left\langle \left[ L_\ell , W(-z)\right] e_g, x L_\ell \, e_f\right\rangle = \sum _{\ell =1}^m\left\langle L_\ell ^*\left[ L_\ell , W(-z)\right] e_g, x \, e_f\right\rangle . \end{aligned}$$

(4.9)

Proof

If $x\in {\mathcal {N}}({\mathcal {T}})$, then, for all $g,f,z\in \mathbb {C}^d$ and $t\ge 0$ we have

$$\begin{aligned} \langle e_g,({\mathcal {T}}_t(W(z)x)&-W(z)x)e_f\rangle = \left\langle e_g,\left( {\mathcal {T}}_t(W(z)){\mathcal {T}}_t(x)-W(z)x\right) e_f\right\rangle \\&= \left\langle e_g,\left( {\mathcal {T}}_t(W(z))-W(z)\right) x\,e_f\right\rangle + \left\langle e_g, W(z) \left( {\mathcal {T}}_t(x)-x\right) e_f\right\rangle \\&+ \left\langle \left( {\mathcal {T}}_t(W(-z))-W(-z)\right) e_g, \left( {\mathcal {T}}_t(x)-x\right) e_f\right\rangle \end{aligned}$$

By Lemma 4.9 means the norm limit

$$\begin{aligned} \lim _{t\rightarrow 0^+}\frac{ ({\mathcal {T}}_t(W(-z))-W(-z))e_g}{t} \end{aligned}$$

exists, therefore $\sup _{t>0}t^{-1}\Vert {\mathcal {T}}_t(W(-z))-W(-z))e_g\Vert <+\infty$. Moreover

$$\begin{aligned} \left\| \left( {\mathcal {T}}_t(x)-x\right) e_f\right\| ^2= & {} \left\langle e_f, \left( {\mathcal {T}}_t(x^*)-x^*\right) \left( {\mathcal {T}}_t(x)-x\right) e_f \right\rangle \\\le & {} \left\langle e_f, \left( {\mathcal {T}}_t(x^*x)- x^*{\mathcal {T}}_t(x) -{\mathcal {T}}_t(x^*)x+x^*x\right) e_f \right\rangle \end{aligned}$$

which tends to 0 as $t\rightarrow 0^+$ by $\hbox {weak}^*$ continuity of ${\mathcal {T}}_t$. As a result

$$\begin{aligned} \lim _{t\rightarrow 0^+} t^{-1}\left\langle e_g,\left( {\mathcal {T}}_t(W(z))-W(z)\right) \left( {\mathcal {T}}_t(x)-x\right) e_f\right\rangle =0, \end{aligned}$$

therefore

$$\begin{aligned} \lim _{t\rightarrow 0^+}t^{-1}\langle e_g,({\mathcal {T}}_t(W(z)x)-W(z)&x)e_f\rangle = \lim _{t\rightarrow 0^+}t^{-1} \left\langle e_g, W(z) \left( {\mathcal {T}}_t(x)-x\right) e_f\right\rangle \\&+ \lim _{t\rightarrow 0^+}t^{-1}\left\langle \left( {\mathcal {T}}_t(W(-z))-W(-z)\right) e_g,x\,e_f\right\rangle \end{aligned}$$

and we get

$$\begin{aligned}&\left\langle G e_g,W(z)x\, e_f\right\rangle +\sum _{\ell =1}^m \left\langle L_\ell e_g, W(z)x L_\ell e_f\right\rangle +\left\langle e_g, W(z)x\, Ge_f\right\rangle \\&\quad = \left\langle \left( G^* W(-z) + \sum _\ell L_\ell ^* W(-z) L_\ell + W(-z)G\right) e_g,x\,e_f\right\rangle \\&\quad + \left\langle GW(-z)e_g, x e_f\right\rangle +\sum _{\ell =1}^m\left\langle L_\ell W(-z)e_g, x L_\ell e_f\right\rangle +\left\langle W(-z)e_g, x G e_f\right\rangle . \end{aligned}$$

The first term in the left-hand side cancels with the third term in right-hand side and last terms in both sides cancel as well. Noting that

$$\begin{aligned} G^* W(-z)e_g+GW(-z)e_g=-\sum _\ell L_\ell ^*L_\ell W(-z)e_g \end{aligned}$$

adding the first and fourth terms in the right-hand side, we find

$$\begin{aligned} \sum _{\ell =1}^m \left\langle L_\ell e_g, W(z)x L_\ell e_f\right\rangle&= \sum _{\ell =1}^m \left[ \left\langle L_\ell ^* W(-z) L_\ell e_g,x\,e_f\right\rangle +\left\langle L_\ell W(-z)e_g, x L_\ell e_f\right\rangle \right] \\&- \sum _{\ell =1}^m \left\langle L_\ell ^*L_\ell W(-z)e_g, x e_f\right\rangle . \end{aligned}$$

Rearranging terms we get (4.9) which is a weak form of identity (4.8). $\square$

The following lemma serves to get (4.9) for each $\ell$ fixed without summation, taking advantage of the arbitrarity of z.

Lemma 4.11

For all $\ell _\bullet \in \{\, 1,2,\dots , d\,\}$ fixed there exists $z\in \mathbb {C}^d$ such that

$$\begin{aligned} \sum _{j=1}^d \left( {\overline{v}}_{i j}z_j+u_{i j} {\overline{z}}_j\right) = \delta _{i, \ell _\bullet } =\left\{ \, \begin{array}{cl} 1 &{} {\textit{ if }} \ i= \ell _\bullet \\ 0 &{} {\textit{ if }} \ i\not = \ell _\bullet \end{array} \right. \end{aligned}$$

Proof

Note that ${\overline{V}}z+U{{\overline{z}}}$ arises from the map composition

$$\begin{aligned} \begin{array}{cccc} \quad J_c &{} &{} \left[ \,{\overline{V}}\,|\,U\,\right] &{} \\ z \ \rightarrow &{} \left[ \begin{array}{c} z \\ {\overline{z}}\end{array} \right] &{} \longrightarrow &{} {\overline{V}}z+U{{\overline{z}}} \\ \end{array} \end{aligned}$$

Let $(\phi _\ell )_{1\le \ell \le m}$ be an orthonormal basis of $\mathbb {C}^m$. We look for a $z\in \mathbb {C}^m$ solving the real linear system

$$\begin{aligned} \left[ \,{\overline{V}}\,|\,U\,\right] J_c\, z = \phi _{\ell _\bullet } \end{aligned}$$

Since

$$\begin{aligned} {\mathrm{Ran}}\left( \left[ {\overline{V}}\,|\,U\,\right] J_c\right) = {\mathrm{ker}}\left( \left[ {\overline{V}}\,|\,U\,\right] J_c)^{\mathrm{T}}\right) ^\perp = {\mathrm{ker}}\left( J_c^{\mathrm{T}}\left[ {\overline{V}}\,|\,U\,\right] ^{\mathrm{T}}\right) ^\perp , \end{aligned}$$

$J_c$ is one-to-one and, by the minimality assumption (2.8)

$$\begin{aligned} {\mathrm{ker}}\left( \left[ {\overline{V}}\,|\,U\,\right] ^{\mathrm{T}}\right) = {\mathrm{ker}}\left( \left[ \begin{array}{c}V^*\\ U^{\mathrm{T}}\end{array}\right] \right) ={\mathrm{ker}}\left( V^*\right) \cap {\mathrm{ker}}\left( U^{\mathrm{T}}\right) =\{0\}, \end{aligned}$$

we find ${\text {Ran}}\left( \left[ {\overline{V}}\,|\,U\,\right] J_c\right) =\mathbb {C}^m$ and the proof is complete. $\square$

Proposition 4.12

The decoherence-free subalgebra $x\in {\mathcal {N}}({\mathcal {T}})$ is contained in the generalized commutant of the operators $L_\ell ,L_\ell ^*$  $1\le \ell \le m$.

Proof

For a Weyl operator W(z) we have

$$\begin{aligned} {[}L_\ell ,W(z)] = \sum _{j=1}^d\left[ {\overline{v}}_{\ell j} a_j + u_{\ell j}a^{\dagger }_j, W(z)\right] = \sum _{j=1}^d\left( {\overline{v}}_{\ell j}z_j+u_{\ell j} {\overline{z}}_j\right) W(z). \end{aligned}$$

and (4.9) becomes

$$\begin{aligned}&\sum _{\ell =1}^m\sum _{j=1}^d\left( {\overline{v}}_{\ell j}z_j+u_{\ell j} {\overline{z}}_j\right) \left\langle W(-z)e_g, x L_\ell e_f\right\rangle \\&\quad = \sum _{\ell =1}^m\sum _{j=1}^d\left( {\overline{v}}_{\ell j}z_j+u_{\ell j} {\overline{z}}_j\right) \left\langle L_\ell ^* W(-z) e_g, x e_f\right\rangle . \end{aligned}$$

By Lemma 4.11, choosing some special $z_\ell \in \mathbb {C}^d$, we find

$$\begin{aligned} \left\langle W(-z_\ell )e_g, x L_\ell e_f\right\rangle = \left\langle L_\ell ^* W(-z_\ell ) e_g, x e_f\right\rangle \end{aligned}$$

for all $g,f\in \mathbb {C}^d$ and all $\ell$. Therefore, by the arbitrarity of g and the explicit action of Weyl operators on exponential vectors

$$\begin{aligned} \left\langle e_w, x L_\ell e_f\right\rangle = \left\langle L_\ell ^* e_w, x e_f\right\rangle \end{aligned}$$

for all $w,f\in \mathbb {C}^d$ and all $\ell$. Since exponential vectors form a core for $L_\ell ^*$ and $L_\ell$ is closed, this implies that $x e_f$ belongs to the domain of $L_\ell$ and $L_\ell x e_f = xL_\ell e_f$, namely $xL_\ell \subseteq L_\ell x$.

Replacing x with $x^*$ we find $x^*L_\ell \subseteq L_\ell x^*$ and standard results on the adjoint of products of operators (see e.g. [24] 5.26 p. 168) lead to the inclusions

$$\begin{aligned} x L_\ell ^* \subseteq \left( L_\ell x^*\right) ^* \subseteq \left( x^*L_\ell \right) ^* =L_\ell x^*. \end{aligned}$$

It follows that x belongs to the generalised commutant of the set of Kraus operators, namely $\left\{ \,L_\ell ,L_\ell ^*\,\mid \, 1\le \ell \le m\,\right\}$. $\square$

Lemma 4.13

The domain ${\mathrm{Dom}}(N^{n/2})$ is $\mathrm {e}^{{\text {i}}t H}$-invariant for all $t\in \mathbb {R}$ and there exists a constant $c_n>0$ such that

$$\begin{aligned} \left\| (N+\mathrm{1l})^{n/2} \mathrm {e}^{{\text {i}}t H} \xi \right\| ^2 \le \mathrm {e}^{c_n |t|} \left\| (N+\mathrm{1l})^{n/2} \xi \right\| ^2 \end{aligned}$$

(4.10)

for all $\xi \in {\mathrm{Dom}}(N^{n/2})$.

Proof

Consider Yosida approximations of the identity operator $(\mathrm{1l}+\epsilon (N+\mathrm{1l}) )^{-1}$ for all $\epsilon >0$ and bounded approximations $X_\epsilon =(N+\mathrm{1l})^n(\mathrm{1l}+\epsilon (N+\mathrm{1l}) )^{-n}$ of the n-the power of $N+\mathrm{1l}$. Note that, the domain D is invariant for these operators and also H invariant. For all $u\in D$, setting $v_\epsilon = (\mathrm{1l}+\epsilon N )^{-n}u$ we have

$$\begin{aligned} \left\langle u, (X_\epsilon H - H X_\epsilon )u \right\rangle = \left\langle v_\epsilon , ((N+\mathrm{1l})^n H (\mathrm{1l}+\epsilon N )^n - (\mathrm{1l}+\epsilon N )^n H (N+\mathrm{1l})^n)v_\epsilon \right\rangle \end{aligned}$$

Compute

$$\begin{aligned}&\left( (N+\mathrm{1l})^n H (\mathrm{1l}+\epsilon (N+\mathrm{1l}) )^n - (\mathrm{1l}+\epsilon (N+\mathrm{1l}) )^n H (N+\mathrm{1l})^n\right) \\&\quad = \sum _{k=0}^n\left( {\begin{array}{c}n\\ k\end{array}}\right) \epsilon ^k ((N+\mathrm{1l})^n H (N+\mathrm{1l})^k - (N+\mathrm{1l})^k H (N+\mathrm{1l})^n) \\&\quad = \sum _{k=0}^n\left( {\begin{array}{c}n\\ k\end{array}}\right) \epsilon ^k (N+\mathrm{1l})^k [(N+\mathrm{1l})^{n-k}, H\,] (N+\mathrm{1l})^k \end{aligned}$$

and noting that the commutator $[(N+\mathrm{1l})^{n-k}, H]$ is a polynomial in $a_j,a^{\dagger }_k$ of order $2(n-k)$. This implies that we can find a constant $c_n$ such that $|\langle u', [(N+\mathrm{1l})^{n-k},H]u'\rangle | \le c_n \Vert (N+\mathrm{1l})^{(n-k)/2} u'\Vert ^2$ (for $u'\in D$) and so we get the inequality

$$\begin{aligned} \left| \left\langle u, X_\epsilon H u \right\rangle - \left\langle Hu, X_\epsilon u \right\rangle \right|&\le c_n \sum _{k=0}^n\left( {\begin{array}{c}n\\ k\end{array}}\right) \epsilon ^k \left\langle v_\epsilon , (N+\mathrm{1l})^{n+k}v_\epsilon \right\rangle \\&= c_n \left\langle v_\epsilon , (N+\mathrm{1l})^n(\mathrm{1l}+\epsilon (N+\mathrm{1l}) )^nv_\epsilon \right\rangle \\&= c_n \left\langle u, X_\epsilon u \right\rangle . \end{aligned}$$

The above inequality extends to $u\in {\mathrm{Dom}}(H)$ by density.

Now, for all $u\in {\mathrm{Dom}}(H)$ and $t\ge 0$, we have

$$\begin{aligned} \left\| X_\epsilon ^{1/2} \mathrm {e}^{{\text {i}}t H} u\right\| ^2&-\left\| X_\epsilon ^{1/2} u \right\| ^2 = \int _0^t \frac{\mathrm {d}}{\mathrm {d}s}\left\| X_\epsilon ^{1/2} \mathrm {e}^{{\text {i}}s H} u \right\| ^2\, \mathrm {d}s \\&= {\text {i}}\int _0^t \left( \left\langle \mathrm {e}^{{\text {i}}s H} u, X_\epsilon H \mathrm {e}^{{\text {i}}s H} u\right\rangle -\left\langle H\mathrm {e}^{{\text {i}}s H} u, X_\epsilon \mathrm {e}^{{\text {i}}s H} u\right\rangle \right) \mathrm {d}s \\&\le c_n \int _0^t \left\| X_\epsilon ^{1/2} \mathrm {e}^{{\text {i}}s H}u\right\| ^2 \mathrm {d}s. \end{aligned}$$

Gronwall’s lemma implies and a similar argument for $t<0$ yield

$$\begin{aligned} \left\| X_\epsilon ^{1/2} \mathrm {e}^{{\text {i}}t H} u \right\| ^2 \le \mathrm {e}^{c_n |t|} \left\| X_\epsilon ^{1/2} u \right\| ^2 \end{aligned}$$

for all $t\in \mathbb {R}$. Considering $u\in D$ and taking the limit as $\epsilon$ goes to zero we get (4.10) for $\xi \in D$ and, finally for $\xi \in {\mathrm{Dom}}(N^{n/2})$ because D is a core for $N^{n/2}$. $\square$

Lemma 4.14

For all j there exists $M_d(\mathbb {C})$ valued analytic functions ${\mathsf {H}}^{-},{\mathsf {H}}^{+}$ such that

$$\begin{aligned} \mathrm {e}^{-{\text {i}}t H}\, a_j\, \mathrm {e}^{{\text {i}}t H} \xi = \sum _{k=1}^d \left( {\mathsf {H}}^{-}_{jk}(t)\,\mathrm {e}^{-{\text {i}}t H}\, a_k\, \mathrm {e}^{{\text {i}}t H}\xi + {\mathsf {H}}^{+}_{jk}(t)\,\mathrm {e}^{-{\text {i}}t H}\, a_k^{\dagger } \mathrm {e}^{{\text {i}}t H} \xi \right) \end{aligned}$$

for all $t\in \mathbb {R}$, $\xi \in {\mathrm{Dom}}(N)$.

Proof

For all $\xi ',\xi \in {\mathrm{Dom}}(N)$ we have

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} \left\langle \xi ', \mathrm {e}^{-{\text {i}}t H}\, a_j\, \mathrm {e}^{{\text {i}}t H}\xi \right\rangle&= \lim _{s\rightarrow 0} \frac{1}{s}\left\langle \xi ', \left( \mathrm {e}^{-{\text {i}}(t+s) H}\, a_j\, \mathrm {e}^{{\text {i}}(t+s) H} -\mathrm {e}^{-{\text {i}}t H}\, a_j\, \mathrm {e}^{{\text {i}}t H}\right) \xi \right\rangle \\&= \lim _{s\rightarrow 0} s^{-1} \left\langle \left( \mathrm {e}^{{\text {i}}(t+s) H}- \mathrm {e}^{{\text {i}}t H}\right) \xi ', a_j\, \mathrm {e}^{{\text {i}}t H}\xi \right\rangle \\&+ \lim _{s\rightarrow 0} s^{-1} \left\langle a_j^{\dagger }\mathrm {e}^{{\text {i}}t H}\xi ', \left( \mathrm {e}^{{\text {i}}(t+s) H}- \mathrm {e}^{{\text {i}}t H}\right) \xi \right\rangle \\&= \left\langle {\text {i}}H \mathrm {e}^{{\text {i}}t H}\xi ', a_j\, \mathrm {e}^{{\text {i}}t H}\xi \right\rangle + \left\langle a_j^{\dagger }\, \mathrm {e}^{{\text {i}}t H}\xi ', {\text {i}}H\mathrm {e}^{{\text {i}}t H}\xi \right\rangle . \end{aligned}$$

Now, for all $u,v\in D$ we have

$$\begin{aligned} \left\langle {\text {i}}H v, a_j u\right\rangle + \left\langle a_j^{\dagger } v , {\text {i}}H u \right\rangle = -{\text {i}}\left\langle v, [H,a_j] u\right\rangle = \sum _{k=1}^d \left( c^{-}_{jk} \left\langle v, a_k u\right\rangle + c^{+}_{jk}\left\langle v, a^{\dagger }_k u\right\rangle \right) \end{aligned}$$

for some complex constants $c^{-}_{jk},c^{+}_{jk}$. The left-hand and right-hand side make sense for $u,v\in {\mathrm{Dom}}(N)$, therefore they can be extended by density and so

$$\begin{aligned}&\frac{\mathrm {d}}{\mathrm {d}t} \left\langle \xi ', \mathrm {e}^{-{\text {i}}t H}\, a_j\, \mathrm {e}^{{\text {i}}t H}\xi \right\rangle \\&\quad = \sum _{k=1}^d \left( c^{-}_{jk} \left\langle \xi ', \mathrm {e}^{-{\text {i}}t H}\, a_k\, \mathrm {e}^{{\text {i}}t H} \xi \right\rangle + c^{+}_{jk}\left\langle \xi ', \mathrm {e}^{-{\text {i}}t H}\, a^{\dagger }_k \mathrm {e}^{{\text {i}}t H} \xi \right\rangle \right) \end{aligned}$$

for all $\xi ',\xi \in {\mathrm{Dom}}(N)$. Considering the conjugate we find a differential equation for $\left\langle \xi ', \mathrm {e}^{-{\text {i}}t H}\, a_j^{\dagger }\, \mathrm {e}^{{\text {i}}t H}\xi \right\rangle$ an so we get a linear system of 2d differential equations with constant coefficients. The solution of the system yields analytic functions ${\mathsf {H}}^{-},{\mathsf {H}}^{+}$ as blocks of the exponential of a $2d\times 2d$ matrix. $\square$

Proof of Theorem 3.2

Let $G_0$ be the self-adjoint extension of $-\sum _{\ell =1}^d L_\ell ^*L_\ell /2$. By Proposition 4.12, for all $y\in {{\mathcal {N}}}({\mathcal {T}})$ and all $v,u\in {\mathrm{Dom}}(N)$, we have

$$\begin{aligned}&\left\langle G_0 v, y u \right\rangle +\sum _{\ell =1}^m \left\langle L_\ell v, y L_\ell u \right\rangle + \left\langle v, y G_0 u \right\rangle \\&\quad = -\frac{1}{2}\sum _{\ell = 1}^m\left( \left\langle L_\ell ^*L_\ell v, y u \right\rangle -2\left\langle L_\ell v, y L_\ell u \right\rangle +\left\langle v, y L_\ell ^*L_\ell u \right\rangle \right) \\&\quad = -\frac{1}{2}\sum _{\ell = 1}^m\left( \left\langle L_\ell ^* y^* L_\ell v, u \right\rangle -2\left\langle L_\ell v, y L_\ell u \right\rangle +\left\langle v, L_\ell ^* y L_\ell u \right\rangle \right) = 0 \end{aligned}$$

because $L_\ell ^* y^*$ and $L_\ell ^* y$ are extensions of $y^*L_\ell ^*$ and $y L_\ell ^*$ respectively, namely $\pounds (x)={\text {i}}[H,x]$ (as a quadratic form).

Now, recalling that ${{\mathcal {N}}}({\mathcal {T}})$ is ${\mathcal {T}}_s$-invariant by Proposition 3.1 1. for all $v,u\in {\mathrm{Dom}}(N)$ also $\mathrm {e}^{-{\text {i}}(t-s)H}v$ and $\mathrm {e}^{-{\text {i}}(t-s)H}u$ belong to the domain of N by Lemma 4.13, we have

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}s} \left\langle \mathrm {e}^{-{\text {i}}(t-s)H}v, {\mathcal {T}}_s(x) \mathrm {e}^{-{\text {i}}(t-s)H}u \right\rangle =0 \end{aligned}$$

which implies

$$\begin{aligned} {\mathcal {T}}_t(x) = \mathrm {e}^{{\text {i}}t H}\, x\, \mathrm {e}^{-{\text {i}}t H}. \end{aligned}$$

From ${\mathcal {T}}_t$-invariance of ${{\mathcal {N}}}({\mathcal {T}})$ it follows that also $\mathrm {e}^{{\text {i}}tH}\,x\,\mathrm {e}^{-{\text {i}}tH}$ belongs to the generalized commutant of the operators $L_\ell , L_\ell ^*$ ($\ell \ge 1$).

Since ${\mathrm{Dom}}(N)$ is $\mathrm {e}^{{\text {i}}t H}$-invariant by Lemma 4.13, replacing $\xi \in {\mathrm{Dom}}(N)$ by $\mathrm {e}^{{\text {i}}t H}\xi \in {\mathrm{Dom}}(N)$ and left multiplying by $\mathrm {e}^{-{\text {i}}t H}$ the identity $\mathrm {e}^{{\text {i}}t H}x\,\mathrm {e}^{-{\text {i}}t H}L_\ell \xi =L_\ell \, \mathrm {e}^{{\text {i}}t H} x\, \mathrm {e}^{-{\text {i}}t H}\xi$ becomes

$$\begin{aligned} x\,\mathrm {e}^{-{\text {i}}t H}L_\ell \, \mathrm {e}^{{\text {i}}t H}\xi =\mathrm {e}^{-{\text {i}}t H}L_\ell \, \mathrm {e}^{{\text {i}}t H} x\, \xi \end{aligned}$$

Taking the scalar product with two exponential vectors and differentiating n times at $t=0$ the identity

$$\begin{aligned} \left\langle v, x\, \mathrm {e}^{-{\text {i}}t H}\, L_\ell \, \mathrm {e}^{{\text {i}}t H}u\right\rangle = \left\langle \mathrm {e}^{-{\text {i}}t H}\, L_\ell ^*\, \mathrm {e}^{{\text {i}}t H} v, x u \right\rangle \end{aligned}$$

with $u,v\in {\mathrm{Dom}}(N)$, we get

$$\begin{aligned} \left\langle v, x\, \delta ^n_H (L_\ell ) u\right\rangle = \left\langle \delta ^n_H (L^*_\ell ) v, x u \right\rangle . \end{aligned}$$

Since iterated commutators $\delta ^n_H (L_\ell )$ are first order polynomials in $a_j,a^{\dagger }_k$, this means that x belongs to the generalized commutant of $\delta ^n_H (L_\ell )$. The same argument applies to generalized commutators of $\delta ^n_H (L_\ell ^*)$ for all $\ell \ge 1$, $n\ge 0$.

Conversely, if x belongs to the generalized commutant of operators $\delta ^n_H (L_\ell )$, $\delta ^n_H (L_\ell ^*)$ for all $\ell \ge 1$, $0 \le n\le 2d-1$, recall that each one of these generalized commutators is a first order polynomial in $a_j,a^{\dagger }_k$ and so determines two vectors (coefficients of creation and annihilation operators) ${\overline{v}},u\in \mathbb {C}^d$ and, eventually, a vector $[{\overline{v}},u]^{\mathrm{T}}\in \mathbb {C}^{2d}$. Let ${\mathcal {V}}_n$ be the complex linear subspace of $\mathbb {C}^{2d}$ determined by vectors in $\mathbb {C}^{2d}$ corresponding to generalized commutators of order less or equal than n. Clearly, ${\mathcal {V}}_n\subseteq {\mathcal {V}}_{n+1}$ for all n and so the dimensions $\hbox {dim}_{\mathbb {C}}({\mathcal {V}}_n)$ form a non decreasing sequence of natural numbers bounded by 2d. Moreover, if $\hbox {dim}_{\mathbb {C}}({\mathcal {V}}_n)=$ $\hbox {dim}_{\mathbb {C}}({\mathcal {V}}_{n+1})$, then ${\mathcal {V}}_n={\mathcal {V}}_{n+1}$ and so

$$\begin{aligned} \delta ^{n+1}_H (L_\ell )&= \sum _{m=0}^n \left( z_m\delta _H^{(m)}(L_\ell ) +w_m\delta _H^{(m)}(L_\ell ^*) \right) + \eta _n\mathrm{1l}, \\ \delta ^{n+1}_H (L_\ell ^*)&= \sum _{m=0}^n (-1)^{m}\left( {\overline{w}}_m\delta _H^{(m)}(L_\ell ) +{\overline{z}}_m\delta _H^{(m)}(L_\ell ^*) \right) + {\overline{\eta }}_n\mathrm{1l}, \end{aligned}$$

for some $z_1,\dots ,z_n,w_1,\dots ,w_n,\eta _n\in \mathbb {C}$. Iterating, it turns out that the linear part in creation and annihilation operators of $\delta ^{n+m}_H (L_\ell )$ and $\delta ^{n+m}_H (L_\ell )$ depends on vectors in ${\mathcal {V}}_{n}$ for all $m\ge 0$. It follows that, starting from a value $n_0\ge 1$ (corresponding to the zero order commutators $L_\ell$ and $L_\ell ^*$), the sequence of dimensions has to increase at least by 1 before reaching the maximum value. As a consequence, this is attained in at most $2d-1$ steps.

Summarizing, if x belongs to the generalized commutant of operators $\delta ^n_H (L_\ell )$, $\delta ^n_H (L_\ell ^*)$ for all $\ell \ge 1$, $0 \le n\le 2d-1$, then it belongs to generalized commutant of these operators for all $n\ge 0$. By Lemma 4.14, we can consider the analytic function on $\mathbb {R}$

$$\begin{aligned} t\mapsto \left\langle \xi ', x\, \mathrm {e}^{-{\text {i}}tH}L_\ell \,\mathrm {e}^{{\text {i}}tH}\xi \right\rangle - \left\langle \mathrm {e}^{-{\text {i}}tH}L_\ell ^*\,\mathrm {e}^{{\text {i}}tH}\xi ', x\, \xi \right\rangle \end{aligned}$$

for all $\xi ,\xi '\in D$. The n-th derivative at $t=0$ is $(-{\text {i}})^n$ times

$$\begin{aligned} \left\langle \xi ', x\, \delta ^{n}_H (L_\ell )\xi \right\rangle - \left\langle \delta ^{n}_H (L_\ell ^*)\xi ', x\, \xi \right\rangle = 0 \end{aligned}$$

for all $n\ge 0$ because x belongs to the generalized commutant of operators $\delta ^n_H (L_\ell )$. The same argument shows that x belongs to the generalized commutant of operators $\delta ^n_H (L_\ell ^*)$. Applying Theorem 4.1 of [14] (with $C=N$ and keeping in mind that $[G,C],[G^*,C]$ are second order polynomials in $a_j,a^{\dagger }_k$, therefore relatively bounded with respect to C whence with respect to $C^{3/2}$) it follows that ${\mathcal {T}}_t(x)=\mathrm {e}^{{\text {i}}tH}x\,\mathrm {e}^{-{\text {i}}tH}$.

The same conclusion holds for $x^*$ and $x^*x$ because they belong to the generalized commutant of operators $\delta ^n_H (L_\ell ),\delta ^n_H (L_\ell ^*)$. Therefore $x\in {\mathcal {N}}({\mathcal {T}})$ and the proof is complete. $\square$

Appendix C: Proof of Proposition 3.6

Proof

Statement 2. readily follows by noticing that if $z \in M_1$ is such that $\Im \langle z, z_1 \rangle =0$ for all $z_1 \in M_1$, then $z \in M_1 \cap {M_1}'$. Therefore $\Im \langle \cdot , \cdot \rangle$ is non-degenerate when restricted to $M_1$ if and only if $M_1 \cap {M_1}' = \{0 \}$.

We now prove the first one on the existence of the symplectomorphism for M. The first step in this proof is an adaptation of the Gram-Schmidt procedure to symplectic spaces. Consider $z_1 \in M$ with $z_1 \ne 0$ and observe that there exists $z \in M$ such that $\Im \langle z_1, z \rangle \ne 0$, otherwise the symplectic form would be degenerate on M. We can now set $z_2 = {z}/{ \Im \langle z_1, z \rangle }$, so that $\Im \langle z_1, z_2 \rangle = 1$. Let $M_1 = {\mathrm{Lin}}_\mathbb {R} \{ z_1, z_2 \}$ we now show that $\dim _\mathbb {R} M_1 = 2$ and

$$\begin{aligned} M = M_1 \oplus {M_1}', \end{aligned}$$

where both $M_1$ and ${M_1}'$ are symplectic spaces. Clearly if $z_1, z_2$ were linearly dependent we would have $z_1 = sz_2$ for some $s \in \mathbb {R}$ and then $\Im \langle z_1, z_2 \rangle = 0$ which contradicts the construction of $z_2$. Again since $\Im \langle z_1, z_2 \rangle \ne 0$ we have $M_1 \cap {M_1}' = \{ 0 \}$ and $M_1$ is a symplectic subspace for what we proved at the beginning. Moreover if $z_1 \in M_1$ we can write

$$\begin{aligned} z = (z + \Im \langle z, z_1 \rangle z_2 - \Im \langle z, z_2 \rangle z_1 ) + (\Im \langle z, z_2 \rangle z_1 - \Im \langle z , z_1 \rangle z_2), \end{aligned}$$

where it holds

$$\begin{aligned} z + \Im \langle z, z_1 \rangle z_2 - \Im \langle z, z_2 \rangle z_1 \in {M_1}', \quad \Im \langle z, z_2 \rangle z_1 - \Im \langle z , z_1 \rangle z_2 \in M_1, \end{aligned}$$

hence we have proved $M= M_1 \oplus {M_1}'$. Eventually ${M_1}'$ is a symplectic space since it holds ${M_1}'' = M_1$ and ${M_1}'' \cap {M_1}' = \{0\}$. Note also that $\dim _\mathbb {R} {M_1}' \ne 1$ otherwise the symplectic form would be degenerate on it.

We can now repeat the same reasoning starting with the symplectic space ${M_1}'$ in order to obtain $z_3,z_4 \in {M_1}'$ such that $\Im \langle z_3, z_4 \rangle =1$ and setting $M_2 = {\mathrm{Lin}}_\mathbb {R} \{ z_3, z_4 \}$ we have

$$\begin{aligned} M = M_1 \oplus M_2 \oplus {M_2}', \end{aligned}$$

where $M_1, M_2, {M_2}'$ are symplectic spaces with $\dim _\mathbb {R} M_j =2$ and $\dim _\mathbb {R} {M_2}' \ne 1$. Notice that they are also pairwise symplectically orthogonal, since both $M_2, {M_2}' \subset {M_1}'$. Since the remainder space ${M_j}'$ has always dimension different from 1 we can iterate this process until we get ${M_j}'=\{0\}$. When the procedure stops we have a sequence $M_1, \dots , M_{d_1}$ of mutually (symplectically) orthogonal symplectic spaces, with $M_j = {\mathrm{Lin}}_\mathbb {R} \{ z_{2j}, z_{2j+1}\}$, $\Im \langle z_{2j},z_{2j+1} \rangle =1$. Clearly $2d_1 = \dim _\mathbb {R} M$ and this concludes the first step of the proof.

In order to conclude the proof of this point is sufficient to construct the symplectomorphism via

$$\begin{aligned} B z_{2j} = e_j, \quad Bz_{2j+1} = {\text {i}}e_j. \end{aligned}$$

Eventually for the symplectomorphism of $M_1 \subset M$ an isotropic subset, consider $\{ z_1, \dots , z_{d_1} \}$ a real linear basis of $M_1$ with $d_1 = \dim _\mathbb {R} M_1$. Since $M_1$ is isotropic we have

$$\begin{aligned} \Im \langle z_j, z_k \rangle = 0 \quad \forall j,k=1, \dots , d_1. \end{aligned}$$

This proves 2. In order to prove 3. it suffices to define

$$\begin{aligned} B z_j = e_j, \end{aligned}$$

to get a symplectomorphism B. $\square$