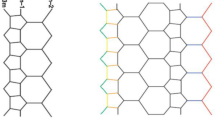
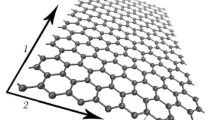
Abstract
Carbon nanotubes are modeled as point configurations and investigated by minimizing configurational energies including two- and three-body interactions. Optimal configurations are identified with local minima and their fine geometry is fully characterized in terms of lower-dimensional problems. Under moderate tension, we prove the existence of periodic local minimizers, which indeed validates the so-called Cauchy–Born rule in this setting.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Agrawal, P.M., Sudalayandi, B.S., Raff, L.M., Komandur, R.: Molecular dynamics (MD) simulations of the dependence of C-C bond lengths and bond angles on the tensile strain in single-wall carbon nanotubes (SWCNT). Comput. Mater. Sci. 41, 450–456 (2008)
Allinger, N.L.: Molecular Structure: Understanding Steric and Electronic Effects from Molecular Mechanics. Wiley, New York (2010)
Arroyo, M., Belytschko, T.: Continuum mechanics modeling and simulation of carbon nanotubes. Meccanica 40, 455–469 (2005)
Bajaj, C., Favata, A., Podio-Guidugli, P.: On a nanoscopically-informed shell theory of single-wall carbon nanotubes. Eur. J. Mech. A Solids 42, 137–157 (2013)
Braides, A., Lew, A., Ortiz, M.: Effective cohesive behavior of layers of interatomic planes. Arch. Ration. Mech. Anal. 180, 151–182 (2006)
Brenner, D.W.: Empirical potential for hydrocarbons for use in stimulating the chemical vapor deposition of diamond films. Phys. Rev. B 42, 9458–9471 (1990)
Brook, B.R., Bruccoleri, R.E., Olafson, B.D., States, D.J., Swaminathan, S., Karplus, M.: CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4, 187–217 (1983)
Budyka, M.E., Zyubina, T.S., Ryabenko, A.G., Lin, S.H., Mebel, A.M.: Bond lengths and diameters of armchair single-walled carbon nanotubes. Chem. Phys. Lett. 407, 266–271 (2005)
Cao, G.X., Chen, X.: The effects of chirality and boundary conditions on the mechanical properties of single-wall carbon nanotubes. Int. J. Solid. Struct. 44, 5447–5465 (2007)
Charlier, J.-C., Lambin, Ph: Electronic structure of carbon nanotubes with chiral symmetry. Phys. Rev. B 57, R15037 (1998)
Clark, M., Cramer III, R.D., Van Opdenbosch, N.: Validation of the general purpose tripos 5.2 force field. J. Comput. Chem. 10, 982–1012 (1989)
Clayden, J., Greeves, N., Warren, S.G.: Organic Chemistry. Oxford University Press, Oxford (2012)
Conti, S., Dolzmann, G., Kirchheim, B., Müller, S.: Sufficient conditions for the validity of the Cauchy-Born rule close to \(SO(n)\). J. Eur. Math. Soc. (JEMS) 8, 515–530 (2006)
Cox, B.J., Hill, J.M.: Exact and approximate geometric parameters for carbon nanotubes incorporating curvature. Carbon 45, 1453–1462 (2007)
Cox, B.J., Hill, J.M.: Geometric structure of ultra-small carbon nanotubes. Carbon 46, 711–713 (2008)
Davoli, E., Piovano, P., Stefanelli, U.: Wulff shape emergence in graphene. Math. Models Methods Appl. Sci. 26(12), 2277–2310 (2016)
Demczyk, B.G., et al.: Direct mechanical measurement of the tensile strength and elastic modulus of multiwalled carbon nanotubes. Mater. Sci. Eng. A 334, 173–178 (2002)
Dresselhaus, M.S., Dresselhaus, G., Saito, R.: Carbon fibers based on \(\text{C}_{60}\) ad their symmetry. Phys. Rev. B 45(11), 6234–6242 (1992)
Dresselhaus, M.S., Dresselhaus, G., Saito, R.: Physics of carbon nanotubes. Carbon 33, 883–891 (1995)
Li, W.E.D.: On the crystallization of 2D hexagonal lattices. Commun. Math. Phys. 286(3), 1099–1140 (2009)
Ming, W.E.P.: Cauchy-Born rule and the stability of crystalline solids: dynamic problems. Acta Math. Appl. Sin. Engl. Ser. 23, 529–550 (2007)
Ming, W.E.P.: Cauchy-Born rule and the stability of crystalline solids: static problems. Arch. Ration. Mech. Anal. 183, 241–297 (2007)
Jorio, A., Dresselhaus, G., Dresselhaus, M.S. (Eds.).: Carbon Nanotubes Advanced Topics in the Synthesis, Structure, Properties and Applications, Topics in Applied Physics, vol. 111. Springer, New York, 2011
El Kass, D., Monneau, R.: Atomic to continuum passage for nanotubes: a discrete Saint-Venant principle and error estimates. Arch. Ration. Mech. Anal. 213, 25–128 (2014)
Ericksen, J.L.: On the Cauchy-Born rule. Math. Mech. Solids 13, 199–220 (2008)
Ericksen, J.L.: The Cauchy and Born hypotheses for crystals. In: Phase Transformations and Material Instabilities in Solids (Madison, Wis., 1983), vol. 52, pp. 61–77, Publ. Math. Res. Center Univ. Wisconsin. Academic Press, Orlando, 1984
Farmer, B., Esedoḡlu, S., Smereka, P.: Crystallization for a Brenner-like potential. Commun. Math. Phys. 349, 1029–1061 (2017)
Favata, A., Podio-Guidugli, P.: A new CNT-oriented shell theory. Eur. J. Mech. A/Solids 35, 75–96 (2012)
Favata, A., Micheletti, A., Podio-Guidugli, P.: A nonlinear theory of prestressed elastic stick-and-spring structures. J. Eng. Sci. 80, 4–20 (2014)
Favata, A., Podio-Guidugli, P.: A shell theory for carbon nanotube of arbitrary chirality. In: Shell and Membrane Theories in Mechanics and Biology. Advanced Structured Materials, vol. 45, pp. 155–167. Springer, Cham, 2015
Favata, A., Micheletti, A., Podio-Guidugli, P., Pugno, N.M.: Geometry and self-stress of single-wall carbon nanotubes and graphene via a discrete model based on a 2nd-generation REBO potential. J. Elast. 125, 1–37 (2016)
Friedrich, M., Piovano, P., Stefanelli, U.: The geometry of \(C_{60}\): a rigorous approach via molecular mechanics. SIAM J. Appl. Math. 76, 2009–2029 (2016)
Friedrich, M., Schmidt, B.: An atomistic-to-continuum analysis of crystal cleavage in a two-dimensional model problem. J. Nonlinear Sci. 24, 145–183 (2014)
Friedrich, M., Schmidt, B.: An analysis of crystal cleavage in the passage from atomistic models to continuum theory. Arch. Ration. Mech. Anal. 217, 263–308 (2015)
Friesecke, G., James, R.D., Müller, S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55, 1461–1506 (2002)
Friesecke, G., Theil, F.: Validity and failure of the Cauchy-Born hypothesis in a two-dimensional mass-spring lattice. J. Nonlinear Sci. 12, 445–478 (2002)
Geim, A.K., Novoselov, K.S.: The rise of graphene. Nat. Mater. 6, 183–191 (2007)
van Gunsteren, W.F., Berendsen, H.J.C.: Groningen Molecular Simulation (GROMOS) Library Manual. BIOMOS b.v, Groningen (1987)
Gupta, A., Sakthivela, T., Seal, S.: Recent development in 2D materials beyond graphene. Progr. Mat. Sci. 73, 44–126 (2015)
Han, F., Azdoud, Y., Lubineau, G.: Computational modeling of elastic properties of carbon nanotube/polymer composites with interphase regions. Part I: micro-structural characterization and geometric modeling. Comput. Mater. Sci. 81, 641–651 (2014)
Iijima, S.: Helical microtubules of graphitic carbon. Nature 354, 56–58 (1991)
James, R.D.: Objective structures. J. Mech. Phys. Solids 54, 2354–2390 (2006)
Jiang, H., Zhang, P., Liu, B., Huans, Y., Geubelle, P.H., Gao, H., Hwang, K.C.: The effect of nanotube radius on the constitutive model for carbon nanotubes. Comput. Mater. Sci. 28, 429–442 (2003)
Jindal, V.K., Imtani, A.N.: Bond lengths of armchair single-walled carbon nanotubes and their pressure dependence. Comput. Mater. Sci. 44, 156–162 (2008)
Jishi, R.A., Dresselhaus, M.S., Dresselhaus, G.: Symmetry properties and chiral carbon nanotubes. Phys. Rev. B 47, 166671–166674 (1993)
Kanamitsu, K., Saito, S.: Geometries, electronic properties, and energetics of isolated single-walled carbon nanotubes. J. Phys. Soc. Jpn. 71(2), 483–486 (2002)
Krishnan, A., Dujardin, E., Ebbesen, T.W., Yianilos, P.N., Treacy, M.M.J.: Young's modulus of single-walled nanotubes. Phys. Rev. B 58, 14013–14019 (1998)
Kroto, H.W., Heath, J.R., O'Brien, S.C., Curl, R.F., Smalley, R.E.: C 60: buckminsterfullerene. Nature 318, 162–163 (1985)
Kroto, H.W.: The stability of the fullerenes \(C_n\), with \(n=24, 28, 32, 36, 50, 60\) and \(70\). Nature 329, 529–531 (1987)
Kurti, J., Zolyomi, V., Kertesz, M., Sun, G.: The geometry and the radial breathing model of carbon nanotubes: Beyond the ideal behaviour. New J. Phys. 5, 1–21 (2003)
Lazzaroni, G., Stefanelli, U.: Chain-like ground states in three dimensions. In preparation, 2017
Lee, R.K.F., Cox, B.J., Hill, J.M.: General rolled-up and polyhedral models for carbon nanotubes. Fuller. Nanotub. Carbon Nanostruct. 19, 726–748 (2011)
Lewars, E.G.: Computational Chemistry, 2nd edn. Springer, New York (2011)
Li, X., Yang, W., Liu, B.: Bending induced rippling and twisting of multiwalled carbon nanotubes. Phys. Rev. Lett. 98, 205502–205505 (2007)
Mainini, E., Murakawa, H., Piovano, P., Stefanelli, U.: Carbon-nanotube geometries: analytical and numerical results. Discrete Contin. Dyn. Syst. Ser. S 10, 141–160 (2017)
Mainini, E., Murakawa, H., Piovano, P., Stefanelli, U.: Carbon-nanotube geometries as optimal configurations. Multiscale Model. Simul. 15(4), 1448–1471 (2017)
Mainini, E., Stefanelli, U.: Crystallization in carbon nanostructures. Commun. Math. Phys. 328(2), 545–571 (2014)
Mannix, A.J., Kiraly, B., Hersma, M.C., Guisiger, N.P.: Synthesis and chemistry of elemental 2D materials. Nat. Rev. Chem. 1, 14 (2017)
Mas-Ballesté, R., Gómez-Navarro, C., Gómez-Herrero, J., Zamora, F.: 2D materials: to graphene and beyond. Nanoscale 3, 20 (2011)
Mayo, S.L., Olafson, B.D., Goddard, W.A.: DREIDING: a generic force field for molecular simulations. J. Phys. Chem. 94, 8897–8909 (1990)
Morris, J.E., Iniewski, K.: Graphene, carbon nanotubes, and nanostructures: techniques and applications. CRC Press, Boca Raton (2013)
Novoselov, K.S., et al.: Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005)
Poncharal, P., Wang, Z.L., Ugarte, D., de Heer, W.A.: Electrostatic deflections and electro-mechanical resonances of carbon nanotubes. Science 283, 1513–1516 (1999)
Rappé, A.K., Casewit, C.L.: Molecular Mechanics Across Chemistry. University Science Books, Sausalito, CA (1997)
Rochefort, A., et al.: Electrical and mechanical properties of distorted carbon nanotubes. Phys. Rev. B 60, 13824–13830 (1999)
Ru, C.Q.: Axially compressed buckling of a doublewalled carbon nanotube embedded in an elastic medium. J. Mech. Phys. Solids 49, 1265–1279 (2001)
Schmidt, B.: On the derivation of linear elasticity from atomistic models. Netw. Heterog. Media 4, 789–812 (2009)
Stefanelli, U.: Stable carbon configurations. Boll. Unione Mat. Ital 9(10), 335–354 (2017)
Stillinger, F.H., Weber, T.A.: Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 8, 5262–5271 (1985)
Tersoff, J.: New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 37, 6991–7000 (1988)
Treacy, M.M.J., Ebbesen, T.W., Gibson, J.M.: Exceptionally high Young's modulus observed for individual carbon nanotubes. Nature 381, 678–680 (1996)
Tuukkanen, S., et al.: Stretching of solution processed carbon nanotube and graphene nanocomposite films on rubber substrates. Synth. Met. 191, 28–35 (2014)
Wang, X., Wang, X., Xiao, J.: A non-linear analysis of the bending modulus of carbon nanotubes with rippling deformations. Compos. Struct. 69, 315–321 (2005)
Warner, J.H., Young, N.P., Kirkland, A.I., Briggs, G.A.D.: Resolving strain in carbon nanotubes at the atomic level. Nat. Mater. 10, 958–962 (2011)
Weiner, P.K., Kollman, P.A.: AMBER: Assisted model building with energy refinement. A general program for modeling molecules and their interactions. J. Comput. Chem. 2, 287–303 (1981)
Yakobson, B.I., Brabec, C.J., Bernholc, J.: Nanomechanics of carbon tubes: instabilities beyond linear response. Phys. Rev. Lett. 76, 2511–2514 (1996)
Yu, M.-F., Files, B.S., Arepalli, S., Ruoff, R.S.: Tensile loading of ropes of single wall carbon nanotubes and their mechanical properties. Phys. Rev. Lett. 84, 5552–5555 (2000)
Zanzotto, G.: On the material symmetry group of elastic crystals and the Born rule. Arch. Ration. Mech. Anal. 121, 1–36 (1992)
Zhang, D.-B., Dumitric̆a, T.: Elasticity of ideal single-walled carbon nanotubes via symmetry-adapted tight-binding objective modeling. Appl. Phys. Lett. 93, 031919 (2008)
Zhao, X., Liu, Y., Inoue, S., Jones, R.O., Ando, Y.: Smallest carbon nanotube is \(3\)Å in diameter. Phys. Rev. Lett. 92(12), 125502 (2004)
Acknowledgements
Open access funding provided by Austrian Science Fund (FWF). M.F. acknowledges support from the Alexander von Humboldt Stiftung. E.M. acknowledges support from the Austrian Science Fund (FWF) project M 1733-N20. P. P. acknowledges support from the Austrian Science Fund (FWF) project P 29681, and from the Vienna Science and Technology Fund (WWTF), the City of Vienna, and the Berndorf Private Foundation through Project MA16-005. U.S. acknowledges support from the Austrian Science Fund (FWF) projects P 27052, I 2375, and F 65 and from the Vienna Science and Technology Fund (WWTF) through project MA14-009. The authors would like to acknowledge the kind hospitality of the Erwin Schrödinger International Institute for Mathematics and Physics, where part of this research was developed under the frame of the thematic program Nonlinear Flows.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by A. Braides
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Friedrich, M., Mainini, E., Piovano, P. et al. Characterization of Optimal Carbon Nanotubes Under Stretching and Validation of the Cauchy–Born Rule. Arch Rational Mech Anal 231, 465–517 (2019). https://doi.org/10.1007/s00205-018-1284-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-018-1284-7