Myopic and farsighted stability in network formation games: an experimental study

Abstract

We test the performance of myopic and farsighted stability concepts in a network formation experiment with a stream of payoffs and relatively unstructured link formation process. A subtle treatment variation demonstrates clearly the power of myopic stability concepts in precisely identifying the set of the most stable networks. However, we also find support for the predictions of farsighted concepts of stability, especially those that assume players’ pessimism about the eventual outcome of a deviation. This is the first study to demonstrate that there exist environments where farsighted stability concepts identify empirically stable networks that are not identified by myopic concepts. Thus, myopic stability concepts are not necessarily sufficient to predict all stable outcomes in empirical applications.

1 Introduction

Network interactions involving a regular flow of payoffs feature in many social and economic environments. For example, the export profits of a firm, a bank’s risk exposure and associated returns, and the number of papers published by academic researchers depend, respectively, on the network of trade partners (Chaney 2014), the credit and debit relationships among banks (Iori et al. 2008; Martinez-Jaramillo et al. 2014), and the constellation of co-authors (Liu et al. 2011; Ozel 2012) in place at a given point in time. The importance attached to social and professional networks is shown by the popularity of websites such as LinkedIn, Xing, and ResearchGate. The prevalence of situations in which people and firms are concerned with benefits and losses that they derive from their ongoing relationships makes it desirable to understand which network structures in these environments are stable and thus likely to be observed.

Many theories have been proposed to predict the stable outcomes of network formation games. As the relationships we are interested in are those where “it takes two to tango”, we restrict attention to theories that assume bilateral, or pairwise link formation, where links require the consent of both parties to form, and can be broken unilaterally. Within this approach, we focus on the large and prominent group of cooperative stability concepts, which analyse network stability by describing the conditions that stable networks should satisfy and do not rely on a particular network formation protocol. As we describe in more detail later, these stability concepts can be broadly divided into three classes, assuming myopic, farsighted, or cautious farsighted behaviour. The purpose of this study is to identify which of these classes of concepts best describes the outcomes of network formation in an environment with a flow of payoffs, focusing on the empirical relevance of farsighted and cautious farsighted concepts.¹

We compare the predictive power of pairwise myopic, farsighted, and cautious farsighted stability concepts in a laboratory experiment, implementing two different three-player network formation games. The experiment has three important features. First, it is novel in that it enables the clear identification of farsighted behaviour by having networks which are predicted to be farsightedly but not myopically stable. Secondly, reflecting the real-world applications mentioned above, subjects in our experiment are paid for all intermediate steps of network formation rather than only for the final network. Finally, our subjects interact in an essentially unstructured manner. In particular, they are able to suggest and agree to links at any point in time. This is both a closer representation of the situations we are interested in, which do not involve strict timing or ordering of actions, and more in the spirit of the cooperative concepts we focus on. Allowing continuous adjustment of links also prevents players from failing to reach a desired network simply because of the miscoordination that may arise from more structured approaches.

Overall, our experimental results suggest that if one is concerned with only the most stable networks, myopic concepts perform best in our environment; however, if one wishes to identify all networks which have the potential to be stable, then cautious farsighted concepts should be considered. We now describe these findings in more detail.

The most stable networks are those predicted by myopic stability concepts, that is, concepts in which players are assumed to consider only the immediate payoff consequences of adding or deleting a link they may be involved in and do not take into account possible chains of other players’ reactions.² Networks that are identified as myopically stable exhibit strong empirical stability according to two measures: they often lasted the full duration of a game, and once they were in place, on average they remained in place for at least one more time period with very high probability.

We also find clear evidence of the stability of networks identified by concepts that assume farsighted behaviour. Farsightedness means that players take into account the chains of reactions that might follow after their own initial deviation.³ The most stable networks, discussed above, are not only myopically but also farsightedly stable (for convenience we will refer to these networks as myopically stable, but one should bear in mind that they are also farsightedly stable). However, farsighted stability concepts predict additional networks. Although these additional networks do not exhibit as high a degree of stability as those identified by myopic concepts, they are the only other networks that were regularly observed to last entire games, and once in place, to be significantly more likely to remain than not.

Theoretical concepts can make two types of errors: failing to predict a network which turns out to be stable and predicting networks which are not empirically stable. Thus, we can further compare the value of myopic and farsighted concepts by studying which concepts predict exactly the set of empirically stable networks. We find that this depends on the strictness of one’s definition of empirical stability. We define the strictness of a stability definition according to the minimum probability with which a type of network must remain in place in order to be classified as stable. We find a range of probabilities where myopic concepts precisely identify the set of stable networks; however, for a range of lower probabilities, it is two of the cautious farsighted concepts—the largest farsightedly consistent set (Page et al. 2005) and the cautious path stable set (Teteryatnikova 2018)—that predict exactly the empirically stable networks. Cautious farsighted concepts assume that players will not add or delete a link if there is any possibility of eventually ending up worse off than in the status quo. All other considered stability concepts either predicted stability for networks that were not empirically stable, or classed as unstable networks that were, in fact, empirically stable. Thus, if one wants to identify only networks which have a high likelihood of showing strong stability in a repeated payoff setting, myopic concepts are best, but if one wishes to identify all networks which have the potential to be stable, cautious farsighted concepts are preferable.

The relatively stronger stability of myopically stable networks is highlighted by a subtle difference between the two network formation games used in the experiment. In the first game, the complete network is, in theory, myopically stable, while the one-link networks are farsightedly but not myopically stable.⁴ In the second game, we change only the payoffs of the unstable two-link networks, but in such a way that the one-link networks become myopically stable and the complete network only (cautious) farsightedly stable. This change in payoffs of an unstable intermediate network leads to a complete reversal in observed stability: the vast majority of stable networks in the first game are complete networks, with a small but non-negligible number of stable one-link networks; in the second game, the bulk of stable outcomes are one-link networks, with relatively few stable complete networks.

Interestingly, the difference in stability between farsightedly and myopically stable networks becomes smaller as subjects become more experienced. While all theoretically stable types of networks become more stable in later rounds, this effect is stronger for the farsightedly stable networks. This may reflect the greater difficulty in understanding the benefits of remaining in such networks.

The primary advantage of using a laboratory experiment rather than a field study is that we know the precise payoffs associated with each network; in an empirical study, it may be difficult to observe not only payoffs, but even which networks are in place at a given time. Furthermore, our relatively simple experimental setting gives the best chance of observing farsighted behaviour by maximizing the possibility for subjects to fully understand the environment and the likely consequences of their actions. Although external validity may be questioned, testing theoretical predictions in such a simplified setting is useful as the stability concepts we consider are general, and should apply equally in the laboratory as in the outside world. Thus, if a concept is not useful in explaining behaviour in the simplified laboratory environment, it is also unlikely to have predictive power in more complex “real-life” applications. Conversely, the findings regarding farsighted stability in our experiment reveal that myopic concepts will not in general capture all empirically stable networks.

There is a small but growing experimental literature on “pure” network formation games such as ours, where payoffs are derived directly from the network structure rather than from further interactions between linked players.⁵ These kinds of games are used to focus on network stability and not risk confounds with behaviour in unrelated interactions. Among these, the most similar to ours in terms of design are Burger and Buskens (2009) and Van Dolder and Buskens (2014), both of which involve payments at regular intervals and link formation in continuous time.⁶ Both papers consider only myopic pairwise stability, which they find to be predictive in the network games they implement. The latter paper also identifies farsighted behaviour in the sense that groups often move from a myopically stable network if a more efficient myopically stable network can eventually be formed. Moreover, in line with our results, they find that fairness concerns do not significantly influence behaviour.

Other experiments examining cooperative pairwise stability in pure network formation games include Pantz (2006), Carrillo and Gaduh (2012) and Kirchsteiger et al. (2016).⁷ Unlike our experiment, in all of these only one final network is paid, and the games are played with a strict timing of moves. Only Kirchsteiger et al. (2016) explicitly considers farsighted stability. They find that farsightedly stable networks tend to arise, but only if not too great a degree of farsightedness is required. Because in the games we implement stable networks are at most two steps apart, we are unable to comment on the limited farsightness they identify. Our design, however, more clearly shows the importance of farsighted stability concepts for two reasons. Firstly, for the particular definition of farsightedness in Kirchsteiger et al. (2016), all farsightedly stable networks are also myopically stable. In contrast, the broader range of stability concepts we consider allowed us to have networks that are only farsightedly stable. Secondly, their farsightedly stable networks are also Pareto dominant among all stable networks, while our theoretically stable networks are all equally efficient.

In our experiment we use cooperative theories to provide predictions about which networks will exhibit stability. We are aware that many of these theories are not formally defined for environments with dynamic payoffs, and we do not claim that our experiment is a strict test of any theory. However, we argue that it is reasonable to use them for generating hypotheses in our setting, as the intuition underlying most of these concepts tends to be dynamic in nature. For example, networks that are pairwise (myopically) stable according to Jackson and Wolinsky (1996) are justified as being stable because any deviation would incur an immediate cost, and networks that are farsightedly stable are such because chains of deviations may incur costs. A further reason for using cooperative concepts in a repeated payoff environment is given by Nash et al. (2012) who follow the same approach for a repeated multilateral bargaining game: in their game, as in ours, almost any outcome can be supported as a subgame-perfect Nash equilibrium, so cooperative theories are required to make useful predictions.⁸ Other recent papers using a similar methodology include Berninghaus et al. (2006), Burger and Buskens (2009), Tremewan and Vanberg (2016), and Van Dolder and Buskens (2014).⁹

The paper proceeds as follows: Sect. 2 discusses the theoretical stability concepts we consider and their predictions for the two network formation games we implement in the experiment; Sects. 3 and 4 describe our laboratory experiment and the results; finally, Sect. 5 concludes. Additional tables, formal theoretical definitions and experiment instructions are provided in appendices.

2 Experimental games and theoretical stability concepts

In this section we first describe the two network formation games played in the experiment. We then introduce the relevant theoretical stability concepts and explain their different predictions in the experimental games. Because we discuss a large number of concepts, some of which involve lengthy technical definitions, in the main text we provide only a rough intuition of why each prediction arises. Formal definitions are provided in “Appendix B”. We emphasize here that the purpose of this experiment is not to differentiate between each of the myriad theoretical stability concepts that have been proposed in the literature—this would require a huge number of treatments given the number of concepts and the overlap in many of their predictions. We attempt only to differentiate between three broad classes of concepts, namely those based on myopic, farsighted, and cautious farsighted behaviour. We have a particular interest in the last two classes, which have received the least attention in the empirical literature.

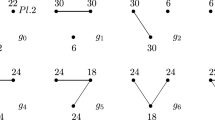
The network formation games we implement in our experiment are shown in Fig. 1. Each game consists of the set of all possible networks for the three-player case. These are the empty network (where no links have formed), three one-link networks, three two-link networks, and the complete network (where all three links are formed). For convenience of exposition, we define $G_j^i$ as the network, or set of networks, in Game i with j links, for $i\in \left\{ I,II\right\}$ and $j\in \left\{ 0,\ldots ,3\right\}$. Nodes of a network represent players and links indicate bilateral relationships between players. The payoff of a player in each network is represented by a number next to the corresponding node. In both games these payoffs are anonymous, in the sense that all players in a symmetric position receive the same payoff—both within each network and across networks of the same type. Given this feature, Fig. 1 shows just one representative one-link network and one representative two-link network. Moreover, in all networks, apart from the empty network, the sum of players’ payoffs is identical, which makes these networks equally efficient and hence, rules out efficiency concerns as an explanation of behaviour.¹⁰

We chose this setting with three players and anonymous allocation of payoffs to keep things as simple as possible and maximize the chances that subjects in our experiment fully understand the environment. This is particularly important in view of our interest in testing for the possible existence of farsighted behaviour in network formation, which requires subjects to understand not only the payoff structure of the games, but also chains of others’ reactions. We recognize that identifying farsighted behaviour in this relatively simple environment does not imply that it will be observed to the same extent with larger networks. However, we think it important to establish that environments where farsighted concepts bring added value to myopic concepts do exist.¹¹ Conversely, not finding farsighted behaviour in our simple games would be clear evidence that myopic concepts are sufficient.

As is most relevant to our experiment, we confine attention to the cooperative pairwise theory of network formation, where creation of a link requires the consent of both involved players, while severance of a link is a unilateral decision of either player involved in the link.¹² This theory focuses on characterizing the outcome rather than the process of network formation, leaving the process itself largely undefined or unstructured.¹³ Among the cooperative pairwise concepts, two main approaches have been proposed in the literature.

Fig. 1

Experimental games: Game I (above) and Game II (below)

The first approach assumes that players behave myopically, in the sense that their decision to add or delete a link is guided completely by payoffs that can be obtained immediately after making the change. In particular, players do not take into account that others might react to their actions by adding or deleting some other links, which might eventually lower or increase the payoffs of the original individual(s). The most well-known concept within this approach is pairwise stability, or PWS (Jackson and Wolinsky 1996), and its set-valued version, the pairwise myopically stable set, or PWMS (Herings et al. 2009).¹⁴ According to Jackson and Wolinsky (1996), a network is considered pairwise (myopically) stable if no individual player can immediately benefit from deleting one of her links, and no pair of individuals can benefit from forming a link. It is easy to see that this holds only for the complete network in Game I ($G_3^I$) and for each of the one-link networks in Game II ($G_1^{II}$).¹⁵

The second approach to cooperative pairwise stability assumes that players are farsighted and take into account the chains of reactions that might follow after their own move. Almost all pairwise farsighted stability concepts rely on the idea that players form or sever links based on the improvement that an eventual stable network offers relative to the current network. These include the pairwise farsightedly stable set (PWFS), von Neumann–Morgenstern pairwise farsightedly stable set (vN-MFS), largest pairwise consistent set (LPWC), all defined in Herings et al. (2009), and the largest farsightedly consistent set (LFC) introduced in Page et al. (2005).¹⁶ Following an alternative approach, the cautious path stable set, or CPS (Teteryatnikova 2018), assumes that players add or delete links taking into account not only the payoff associated with a final stable network, but also payoffs from intermediate networks.

The predictions of these farsighted stability concepts in our experimental games can be intuitively understood as follows. In Game I, all pairwise farsighted concepts identify the one-link networks ($G_1^I$) and the complete network ($G_3^I$) as stable. For example, the one-link networks are farsightedly stable because although either of the linked players could achieve a short-term gain by forming a link with the third player, they do not do so as they foresee that the other two players would then have an incentive to form the last link, leaving them with a payoff of 22 rather than 30. Making a change in a one-link network therefore “guarantees” that the eventual payoff of a linked player who forms a second link will be worse. Similarly, in the complete network, cutting a link “guarantees” that the player’s payoff will not improve: in this case even the short-term payoff of the player is worse than in the complete network ($17<22$).

The same certainty regarding the negative consequences of a link change clearly exists for each one-link network in Game II ($G_1^{II}$), as 30 is the maximum payoff players can achieve, and so these networks are stable under all farsighted concepts. However, in the complete network of Game II ($G_3^{II}$), deleting a link may or may not eventually decrease a player’s payoff, depending on the subsequent action chosen by the player with two links remaining, who now has an incentive to cut a further link. If the link that is deleted at this second step is with the original player, she will be worse off; however, if it is with the third player, she will be better off. The possibility of an eventual payoff improvement as a result of cutting a link in the complete network makes this network unstable according to many farsighted concepts of stability (PWFS, vN-MFS). It is only when players are sufficiently cautious or pessimistic about future network changes that they prefer to avoid the risk and do not delete a link in the complete network.¹⁷ This intuition is captured by such concepts of stability as LPWC, LFC and CPS, which identify the complete network as stable.

In summary, in Game I all pairwise myopic and farsighted concepts of stability identify the complete network ($G_3^I$) as stable; in addition, all farsighted concepts identify one-link networks ($G_1^I$) as stable. In Game II, on the contrary, all myopic and farsighted concepts of stability identify one-link networks ($G_1^{II}$) as stable; in addition, the cautious farsighted concepts identify the complete network ($G_3^{II}$) as stable. These predictions of different farsighted and myopic stability concepts in both games are summarized in Table 1, and more detail is provided by Table 8 in “Appendix B”.¹⁸ For simplicity, in the following we will refer to the network which is stable only under cautious farsighted concepts ($G_3^{II}$) as cautious farsighted (cFS), those which are stable under all farsighted but not myopic concepts of stability ($G_1^I$) as farsightedly stable (FS), and we will refer to networks that are myopically stable ($G_3^I$ and $G_1^{II}$) as pairwise stable (PWS), keeping in mind that they are also farsightedly stable.

In addition to the networks that we describe as FS and cFS, each of the two-link networks is also identified as stable by one of the farsighted concepts: PWFS in Game I and LPWC in Game II. The reason has to do with the details of both concepts’ definitions, which we leave for “Appendix B”. Inspecting the payoffs of the games, and as discussed further in “Appendix B”, it is intuitively unlikely that these networks will exhibit stability. Thus, we do not refer to these networks as farsightedly stable.

Table 1 Summary of predictions

3 Experimental design

In this section we first describe the playing screen, the manner in which subjects interacted, and further procedural details. We then describe our strategy of identifying which networks are empirically stable and of comparing the relative validity of different stability concepts in our setting.

3.1 Experimental procedures

On the playing screen, subjects saw themselves represented as a green circle at the bottom of the screen and the other two players as blue circles at the top. Links could be formed between two players in the following way. A subject could indicate they were willing to form a link with another player by clicking on the appropriate blue dot, resulting in a pink arrow pointing towards the other player. Clicking again would undo this action. If two players had both clicked on each other, then a link was formed and shown in red. Links could be broken by either of the parties clicking on the other, leaving a pink arrow pointing towards the player who had broken the link. All of these actions could be taken at any time and were immediately observed by the other two players.

Payoffs were made at one-second intervals according to the network described by the red links.¹⁹ Each player’s per-second payoffs were displayed next to their circle. Each game lasted 30 s: we chose this duration as a compromise between lasting long enough for stable networks to emerge, but short enough that boredom was unlikely to motivate subjects to leave otherwise stable networks. We refer to each 30 s game as a “round”. The total points accrued were displayed and updated throughout the round, as was the number of seconds remaining.

The playing screen seen by subjects is shown in the instructions in the “Appendix E”. A video of a sample round can be viewed at http://homepage.univie.ac.at/james.tremewan/Research/network.mp4.

Before commencing the paid rounds, subjects completed a detailed tutorial familiarizing them with the interface and played three practice rounds with payoffs different from those in the games of interest. Throughout the experiment subjects were able to consult a handout showing the per-second payoff of every player in each of 8 possible networks of every game. Each session consisted of 20 incentivized rounds with groups randomly rematched after each round.²⁰ The type of network in place at the beginning of each round was randomly determined. More precisely, one quarter of games began in the empty network, one quarter in one of the three one-link networks, one quarter in one of the three two-link networks, and one quarter in the complete network.

The experiments were programmed in Z-tree (Fischbacher 2007) and took place at the Vienna Center for Experimental Economics. For each game, four sessions were conducted, each consisting of 18 subjects divided into two matching groups. This gives us a total of 8 independent observations per game, and 16 in total. One randomly chosen period was paid, with every 45 points exchanged for 1 Euro. Sessions lasted approximately one hour.

3.2 Predictions

The identification of networks as empirically stable requires an absolute definition of stability. Strictly speaking, the theories suggest that a stable network, once entered, will remain in place with probability one. However, given the inevitable noise in human behaviour, this criterion is too strict. We define a type of network as being stable with respect to ${\bar{q}}$ if such a network that is in place for a given payment remains in place for the next payment with probability greater than some fixed probability ${\bar{q}}$:²¹

Definition 1

A type of network is stable with respect to probability${\bar{q}}$ if, conditional upon being paid in the current period, the probability of it being paid in the next period is greater than ${\bar{q}}$.

Higher values of ${\bar{q}}$ represent more strict definitions of stability. The value of ${\bar{q}}$ that should be considered in a given application will depend on what one considers sufficiently “stable” in that context. Note that this definition controls for the probability with which a network is reached. That is, we are primarily interested in the stability of networks once they have arisen, rather than the frequency with which they occur.

Let q be the proportion of paid networks of type $G_j^i$ that remain in place for the next payment: we consider there to be statistical evidence that network $G_j^i$ is stable according to Definition 1 if we can reject the null hypothesis $H_0: q \le {\bar{q}}$.

Which networks are determined to be stable clearly depends on the value chosen for ${\bar{q}}$. In the results section, we first identify the networks which are stable for ${\bar{q}}=0.5$ (Sect. 4.3). We view this as a minimal criterion for stability, under which networks are more likely to remain in place than not. We then show how this set of networks changes as the requirement for stability becomes more strict (i.e. as ${\bar{q}}$ increases to one).

Each theoretical stability concept divides the set of all networks into those which are stable and those which are unstable, as shown in Sect. 2. Rather than formally define a hypothesis for each concept, it is more straightforward to identify the networks which are stable, and compare this set of empirically stable networks to the sets that are predicted theoretically. For a concept to be validated in our setting, the empirically and theoretically stable sets should coincide precisely. Thus, theories can be rejected either for failing to predict networks which turn out to be empirically stable, or predicting networks to be stable when they are not.²²

We are also interested in whether networks that are myopically stable are more stable than those that require farsighted behaviour. We therefore compare the relative stability of each type of network, predicting that networks identified by myopic concepts are more stable than those predicted only by the cognitively more demanding farsighted concepts.

4 Results

We begin this section by giving a descriptive overview of the data before proceeding to formal statistical tests. The first set of tests are relative, comparing the stability of different types of networks. The second set of tests ask whether or not each type of network is “stable” using the absolute definition of stability described in the previous section (Definition 1). Finally, we consider learning by comparing network stability in the first and second halves of the experiment and look at transitions between networks.

4.1 Data overview

To give a full picture of the raw data, in the initial descriptive analysis we focus on the simplest statistic capturing the stability of a network, the duration of a network. We measure the duration of a network as the number of payments that occur between when the network is formed and when a different network becomes the basis for payment.²³ We regard the one-second period between payments as non-binding negotiation, so, for example, if a link is broken and reformed between payments, we do not consider the second network to be new. We refer to the number of consecutive payments of a given network as its duration in periods.

The duration and frequencies of each type of network in each game are displayed in Figs. 2 and 3. To accommodate the large number of networks of short duration while keeping visible differences in the distributions of more stable networks, the data are split between durations of $\le 5$ and $>5$ periods. Summary statistics of the different types of networks are given in Table 2.

The PWS networks ($G_3^I$ and $G_1^{II}$) clearly display the greatest stability, often lasting upwards of 15 seconds. The FS networks $G_1^I$ and the cFS network $G_3^{II}$ also often last more than half the periods of a game, but much less frequently than the PWS networks. By contrast, distributions of $G_2^I$ (identified by PWFS) and $G_2^{II}$ (identified by LPWC) do not possess these long tails, and there is only one round in which one of these two types of networks lasts longer than half the game. The empty networks occur rarely, and seldom last more than two seconds. As the only networks observed to last entire games, it is already clear that $G_3^I$, $G_1^{II}$, $G_1^I$, and $G_3^{II}$ display a potential for strong stability, which the other networks do not.²⁴

Fig. 2

Duration and frequency of networks (Game I)

Fig. 3

Duration and frequency of networks (Game II)

Table 2 Summary statistics

4.2 Comparative stability

We turn now to formal statistical tests. Table 3 reports the proportions of paid networks of each type that are also paid in the subsequent period, along with standard errors clustered by matching group. These proportions disaggregated by matching group can be found in “Appendix D” (Table 9).

Table 3 Proportion of paid networks that are also paid in the subsequent period (q)

As can be seen in Table 3, changing the payoffs attached to the two-link network from those in Game I to those in Game II has no significant impact on the stability of the empty network or the two-link networks themselves. However, it increases the probability of remaining in the one-link network by 0.21 ($p<0.01$) as it becomes PWS and decreases the probability of remaining in the complete network by 0.13 ($p<0.05$) as it becomes only cFS. Thus, we find a strong treatment effect, with the PWS networks apparently more stable than either the FS or cFS networks.

To compare the stability of networks within a game, we regress the probability of remaining in the current network on the different types of networks, with the two-link network as the comparison group. Table 4 presents the results of linear probability models,²⁵ the first column using data from only Game I, the second from only Game II, and the third pooling the data from both games. Because in the final regression we want a variable for all pairwise stable networks, the dummy variable PWS takes the value one for networks in $G_3^I$ and $G_1^{II}$. In line with the notation introduced earlier, we label the dummy variables indicating $G_I^I$ and $G_3^{II}$ as FS and cFS, respectively.

As can be seen from the first column of Table 4, the networks in Game I can be ranked from least to most stable as empty, two-link, one-link (FS), complete (PWS), with all relationships significant ($p<0.01$). The second column reports the results for Game II, ranking the networks from least to most stable as empty, two-link, complete (cFS), one-link (PWS), with all relationships strongly significant ($p<0.01$) apart from the last, with the one-link network being only weakly more stable than the complete ($p=0.068$).

Table 4 Probability of remaining in current network

The last column of Table 4 addresses the possibility that the stability of the complete network is due in part to the fact that it represents an equal share of the surplus to all players and thus may be focal, or appeal to subjects with fairness concerns. To test this, we pool the data from the two games and include as a regressor a dummy for being a complete network. This controls for fairness concerns because the coefficient on the dummy variable for the complete network in Game II (cFS) now represents extra stability given by factors other than factors shared with the complete network in Game I. As can be seen from the final column of Table 4, the coefficient on the complete network dummy is insignificant and close to zero, whereas all the findings from the previous two regressions are unchanged. We are therefore confident that the stability of the complete networks is not due to focality or fairness concerns.

4.3 Absolute stability

We now test whether each type of network is stable according to the absolute measure of stability proposed in Definition 1 (Sect. 3.2). We first identify which networks are stable for what we consider a minimal requirement for stability, ${\bar{q}}=0.5$, that is a network is more likely to remain in place than not. With empirical probabilities of remaining in the same network of 0.92 and 0.89, respectively, the PWS networks in both games ($G_3^I$ and $G_1^{II}$) are found to be stable according to one-tailed t-tests ($p<0.01$). The equivalent probabilities for the FS network ($G_1^I$) and the cFS network ($G_3^{II}$) are 0.68 and 0.79, both significantly greater than 0.5 ($p<0.05$ and $p<0.01$, respectively).

The empty networks in both games and the two-link networks in Game I are less likely to remain in place than be left, so cannot be stable according to our definition. The probability of remaining in the two-link networks in Game II is 0.52, but this is not significantly greater than 0.5 ($p=0.3$).

Comparing the set of networks that are empirically stable according to these tests to the sets identified by different theoretical stability concepts, we can see that only two of the cautious farsighted concepts, CPS and LFC, identify them precisely: in Game I, myopic concepts do not include the stable $G_1^I$, and the farsighted PWFS contains the unstable $G_2^I$; in Game II, none of the myopic and simple farsighted concepts (PWS, PWMS, PWFS, vN-MFS) contain the stable $G_3^{II}$, while the cautious farsighted LPWC identifies the unstable $G_2^{II}$.

Figure 4 shows how the set of stable networks varies as the criterion for stability becomes stricter. For each value of ${\bar{q}}\in \left[ 0.5,1\right]$ we show the networks that are identified as stable at the 5% level, i.e. where we can reject the hypothesis that a type of network remains in place with probability less than or equal to ${\bar{q}}$.

Fig. 4

Sets of networks which are stable with respect to ${\bar{q}}\in \left[ 0.5,1\right]$. A network $G_j^i$ which remains in place with empirical probability q is considered stable if $H_0: q \le {\bar{q}}$ is rejected with $p<0.05$

For ${\bar{q}}\in \left[ 0.5,0.56\right]$, there is no change in the set of stable networks. For ${\bar{q}}\in \left[ 0.56,0.70\right]$, $G_1^I$ is no longer stable, and none of the theoretical concepts we consider precisely identify the remaining three networks. For ${\bar{q}}\in \left[ 0.70,0.84\right]$, the only stable networks are those identified by PWS. For ${\bar{q}}\in \left[ 0.84,0.87\right]$, only $G_3^I$ is stable, which is again not the prediction of any theory, and for ${\bar{q}}>0.87$, no network can be categorized as stable.

4.4 Learning

We now consider how the stability of networks changes as subjects gain more experience. To that end, we compare the first and last ten rounds of the experiment. First of all, we note that all the results from the preceding two subsections hold when looking exclusively at either early or late rounds (details available on request). Table 5 shows the probability of remaining in each of the networks in the first and last 10 rounds, and the difference between the two.

The empty networks become slightly less stable over time with the probabilities of remaining in place reduced by 4 p.p. and 3 p.p. in Games I and II, respectively, while the equivalent probabilities for the two-link networks are almost unchanged. None of these differences are statistically significant. The PWS networks in both games increase in stability, by 5 p.p. in Game I and 2 p.p. in Game II, with the former difference marginally significant ($p<0.1$). Stability increases substantially for both the FS (11 p.p.) and cFS (8 p.p.) networks; however, only the former is statistically significant ($p<0.05$).

Thus, it appears in general that networks that are identified theoretically as stable increase in stability as subjects become more experienced. This is particularly evident for the farsighted stability concepts (although this difference in differences is not statistically significant in either game).

Table 5 Proportion of paid networks that are also paid in the subsequent period (q)

4.5 Transitions

While the main interest of this paper is the stability of individual networks, and our measure of stability controls for the probability that a network arises, it is of interest to see how transition probabilities influence the frequency of different networks. Tables 6 and 7 show the transition probabilities between paid network types for Games I and II, respectively. (More detail can be found in Tables 10 and 11 in “Appendix D”, which disaggregate the one and two-link networks.)²⁶

Table 6 Transitions (row to column): Game I

Table 7 Transitions (row to column): Game II

The vast majority of transitions involve the addition or deletion of a single link. The only notable exception to this are transitions in both games from the empty network, of which 20% jump directly to a two-link network, or occasionally the complete network; subjects are understandably in a hurry to escape the inefficient outcome. The small discrepancy between the figures in Table 3 and the proportion of one-link to one-link and two-link to two-link transitions is due to the small number of cases where a link is deleted and another added within a second so that there is a transition between two distinct networks of the same type.

The most interesting transitions are those from the two-link networks. In each game, transitions from a two-link network can either be to a PWS or a (c)FS network. Transitions to the PWS network follow an improving path and are immediately beneficial to any party connected to the altered link, whereas transitions to the FS and cFS networks involve an immediate loss to one of the parties. The myopically attractive transitions to the PWS are substantially more common than transitions in the other direction: in Game I, 33% of transitions are to the PWS complete network compared to 16% to a FS one-link network; in Game II, 33% of transitions are to a PWS one-link network compared to 9% to the cFS complete network. As one quarter of all games begin in two-link networks, this goes some way to explaining the greater frequency of PWS networks relative to FS networks (see Table 2). The fact that the difference in frequencies is smaller in Game I, where the one-link network is FS, is most likely due to our first observation that transitions typically involve only the addition or deletion of a single link: a majority of the quarter of games that begin in an empty network pass through a one-link network. Thus, the nature of transitions favours the occurrence of both PWS and one-link networks.²⁷

One may also wonder if subgroups of players manage to coordinate in two-step transitions in order to improve their payoffs. The only time in our games when it is possible to observe this kind of coordination is when two players in a complete network each break their link with the third player and increase their payoffs from 22 to 30. We can look for evidence of such coordination by looking at all two-step transitions from the complete to two-link to one-link networks. There are two types of these sequences, depending on whether the second player to break a link does so with the third player, or with the player who broke the first link. In the former case, the first player benefits (the two players coordinate), whereas in the latter, the first player receives a lower payoff (coordination fails).

We find that in only 42% of such sequences in Game I and 45% in Game 2 does the player who breaks the first link benefit. The fact that these proportions differ little from 50% makes it impossible to determine the relative importance of the possible mechanisms underlying these numbers: for example, all the second players may be choosing randomly; alternatively half may be coordinating (e.g. by reciprocating the opportunity provided by the first player), while the other half are motivated by inequity aversion and choose to punish the first player for deviating from an equal payoff network. However, the observation that deviating from a complete network more often than not involves a loss may explain the increase in stability of these networks over time, as noted in Sect. 4.4.

5 Conclusion

We find that the most stable networks in two experimental network formation games with flows of payoffs are those identified by myopic stability concepts. The evidence comes in three forms: firstly, they remain in place for the whole duration of games with greatest frequency; secondly, comparing results across games we see that networks with identical structure and payoffs are significantly more stable when they are theoretically myopically stable; finally, within each game, they are the networks that when entered are most likely to remain in place for the next period.

While myopically stable networks are clearly the most stable, we also find convincing evidence of farsighted behaviour. Both farsighted and cautious farsighted networks (that are not at the same time myopically stable) exhibit stability, in that they have the potential to last the full 30 s of a round, and also in that once they are in place, they are significantly more likely to remain than not. They are also significantly more stable than all networks that in theory are neither myopically nor farsightedly stable.

By comparing stability in the first and last ten rounds of the experiment, we find that stability of all theoretically stable networks increases over time. Moreover, it increases by more for farsightedly stable networks. Therefore, subjects’ experience leads to a less significant difference in stability between farsightedly and myopically stable networks.

Considering which concepts most precisely identify the set of all stable networks, we find that this depends on the strictness of one’s empirical definition of stability. The strictness of a definition depends on the probability with which a type of network must remain in place in order to be classified as stable, with stricter definitions requiring higher values of this probability. We find that myopic concepts precisely identify the set of stable networks for a range of high probabilities, but for definitions which are not so strict they fail to identify all stable networks. For a range of less strict definitions, it is the two cautious farsighted concepts that predict exactly the empirically stable networks.

We conclude that the appropriateness of myopic versus farsighted concepts of stability in predicting outcomes of network interactions which involve a regular flow of payoffs depends on the purpose of the prediction. If the aim is to predict the outcomes that are most likely to arise, the myopic concepts perform best, as they identify the networks that are most consistently and strongly stable. If on the other hand, the aim is to identify the full range of outcomes that may achieve stability, or if a weaker definition of stability is acceptable, then the concepts that perform best are farsighted and assume pessimism regarding final outcomes. While the importance of farsighted stability may not generalize to all settings, for example games where longer chains of reactions need to be anticipated, our experiment proves the existence of environments where myopic concepts do not suffice.

Appendices

A Experimental games and predictions

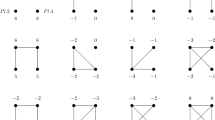
All eight possible networks in each of our two experimental games are presented on Figs. 5 and 6.

Fig. 5

Game I

Fig. 6

Game II

In these figures $g_0$ denotes the empty network, $g_1$, $g_2$ and $g_3$ are one-link networks, $g_4$, $g_5$ and $g_6$ are two-link networks, and $g_7$ is the complete network. Using this notation, Table 8 describes theoretical predictions of different stability concepts in both games, extending the summary provided by Table 1.

Table 8 Detailed summary of predictions

B Formal definitions

In this section we formally define theoretical concepts of stability discussed in the paper. While the application of the defined concepts to our experimental games is rather straightforward, technical details for some of the concepts are also explained below. The remaining details are available from the authors.

Let $Y_i(g)$ be a payoff that player i obtains in a network g, and let the set of all possible networks on n nodes be denoted by ${\mathbb {G}}$. If players i and j are linked in the network g, this is denoted by $ij\in g$; otherwise, $ij\notin g$. Networks obtained by adding or deleting a link ij to/from an existing network g are denoted by $g+ij$ and $g-ij$, respectively.

Following Jackson and Wolinsky (1996), a network g is defined to be pairwise stable, or PWS, if no player can immediately benefit from deleting one of her links, and no pair of players can benefit from forming a link.

Definition 2

Network $g\in {\mathbb {G}}$ is pairwise stable if

• (i) for all $ij\in g$, $Y_i(g)\ge Y_i(g-ij)$ and $Y_j(g)\ge Y_j(g-ij)$, and

• (ii) for all $ij\notin g$, if $Y_i(g)< Y_i(g+ij)$ then $Y_j(g)>Y_j(g+ij)$.

The definition of the pairwise myopically stable set of networks, or PWMS (Herings et al. 2009), requires introducing a myopic improving path first. It is a finite sequence of networks that can emerge when players form or sever links based on the improvement that the immediately resulting network offers them relative to the current network. Formally, the definition in Herings et al. (2009) states that a myopic improving path from a network g to a network $g^{\prime }\ne g$ is a finite sequence of networks $g_1,\ldots ,g_K$ with $g_1=g$ and $g_K=g^{\prime }$ such that for any $1\le k\le K-1$ either

• (i) $g_{k+1}=g_k-ij$ for some ij such that $Y_i(g_{k+1})>Y_i(g_k)$ or $Y_j(g_{k+1})>Y_j(g_k)$, or

• (ii) $g_{k+1}=g_k+ij$ for some ij such that $Y_i(g_{k+1})>Y_i(g_k)$ and $Y_j(g_{k+1})\ge Y_j(g_k)$.

If there exists a myopic improving path from g to $g^{\prime }$, this is denoted by $g\mapsto g^{\prime }$, and for any network g, $M(g)=\{g^{\prime }\in {\mathbb {G}}| g\mapsto g^{\prime } \}$. In terms of this notation, a pairwise myopically stable set can be defined as follows.

Definition 3

A set of networks $G\subseteq {\mathbb {G}}$ is pairwise myopically stable if

• (i) $\forall$$g\in G$,

  • (ia) $\forall ij\notin g$ such that $g+ij\notin G$, $\left( Y_i(g+ij), Y_j(g+ij)\right) =\left( Y_i(g), Y_j(g)\right)$ or $Y_i(g+ij)< Y_i(g)$ or $Y_j(g+ij)< Y_j(g)$,

  • (ib) $\forall ij\in g$ such that $g-ij\notin G$, $Y_i(g-ij)\le Y_i(g)$ and $Y_j(g-ij)\le Y_j(g)$,

• (ii) $\forall$$g^{\prime }\in {\mathbb {G}}{\setminus } G$$M(g^{\prime })\bigcap G \ne \emptyset$,

• (iii) $\forall G^{\prime }\subsetneq G$ at least one of conditions (ia), (ib), (ii) is violated by $G^{\prime }$.

Simply put, a set of networks G is PWMS if (i) all possible myopic pairwise deviations from any network $g\in G$ to a network outside the set are deterred by the threat of ending worse off or equally well off, (ii) there exists a myopic improving path from any network outside the set leading to some network in the set, and (iii) there is no proper subset of G satisfying conditions (i) and (ii).

The definition of the pairwise farsightedly stable set of networks, or PWFS (Herings et al. 2009), corresponds to the one of a pairwise myopically stable set with myopic deviations and myopic improving paths replaced by farsighted deviations and farsighted improving paths. A farsighted improving path is a sequence of networks, where in each network a player or players making a change may not gain immediately but they improve their payoff in the final network. Namely, a farsighted improving path from a network g to a network $g^{\prime }\ne g$ is a finite sequence of networks $g_1,\ldots ,g_K$ with $g_1=g$ and $g_K=g^{\prime }$ such that for any $1\le k\le K-1$ either

• (i) $g_{k+1}=g_k-ij$ for some ij such that $Y_i(g_K)>Y_i(g_k)$ or $Y_j(g_K)>Y_j(g_k)$, or

• (ii) $g_{k+1}=g_k+ij$ for some ij such that $Y_i(g_K)>Y_i(g_k)$ and $Y_j(g_K)\ge Y_j(g_k)$.

If there exists a farsighted improving path from g to $g^{\prime }$, this is denoted by $g\rightarrow g^{\prime }$, and for a given network g, $F(g)=\{g^{\prime }\in {\mathbb {G}}| g\rightarrow g^{\prime } \}$. Using this notation, Herings et al. (2009) defines a pairwise farsightedly stable set of networks as follows.

Definition 4

A set of networks $G\subseteq {\mathbb {G}}$ is pairwise farsightedly stable if

• (i) $\forall$$g\in G$,

  • (ia) $\forall ij\notin g$ such that $g+ij\notin G$, $\exists g^{\prime }\in F(g+ij)\bigcap G$ such that $\left( Y_i(g^{\prime }), Y_j(g^{\prime })\right) =\left( Y_i(g), Y_j(g)\right)$ or $Y_i(g^{\prime })< Y_i(g)$ or $Y_j(g^{\prime })< Y_j(g)$,

  • (ib) $\forall ij\in g$ such that $g-ij\notin G$, $\exists g^{\prime }, g^{\prime \prime }\in F(g-ij)\bigcap G$ such that $Y_i(g^{\prime })\le Y_i(g)$ and $Y_j(g^{\prime \prime })\le Y_j(g)$,

• (ii) $\forall$$g^{\prime }\in {\mathbb {G}}{\setminus } G$$F(g^{\prime })\bigcap G \ne \emptyset$,

• (iii) $\forall G^{\prime }\subsetneq G$ at least one of conditions (ia), (ib), (ii) is violated by $G^{\prime }$.

Intuitively, and following Herings et al. (2009) on p. 532, a set of networks G is PWFS if (i) all possible pairwise deviations from any network $g\in G$ to a network outside G are deterred by a credible threat of ending worse off or equally well off, (ii) there exists a farsighted improving path from any network outside the set leading to some network in the set, and (iii) there is no proper subset of G satisfying conditions (i) and (ii). Applying this definition to the two network formation games that we implement in our experiment, we obtain multiple predictions. In particular, in Game I, apart from the PWFS set that includes all one-link networks and the complete network, there are a number of PWFS sets that contain two-link networks. For example, $G=\{g_4,g_5,g_7\}$ is PWFS because (i) all external pairwise deviations from any network in G are deterred by a possibility of returning to the starting network, (ii) from the empty and from each of the one-link networks, there exists a short farsighted improving path to either $g_4$ or $g_5$, and from the two-link network $g_6$ there exists a one-step improving path to $g_7$, (iii) no proper subset of G satisfies (i) and (ii). The fact that one-link networks are not stable, while two-link networks are stable according to some of the PWFS predictions is counterintuitive. Indeed, even though there exists an improving path from any one-link network to one of the two-link networks in G, farsighted individuals should foresee that the process of network formation will not stop there, as from each of the two-link networks another simple improving deviation leads to the complete network, where the payoff of every player is 22 rather than 30.

Another pair of farsighted stability concepts discussed by Herings et al. (2009) are the von Neumann–Morgenstern pairwise farsightedly stable set, or vN-MFS, and the largest pairwise consistent set, or LPWC. They are based on the original definition of the von Neumann–Morgenstern stable set (von Neumann and Morgenstern 1944) and the largest consistent set (Chwe 1994).

Definition 5

A set of networks $G\subseteq {\mathbb {G}}$ is von Neumann–Morgenstern pairwise farsightedly stable if (i) $\forall$$g\in G$$F(g)\bigcap G=\emptyset$, and (ii) $\forall$$g^{\prime }\in {\mathbb {G}}{\setminus } G$$F(g^{\prime })\bigcap G\ne \emptyset$.

Simply put, a set of networks G is vN-MFS if no farsighted improving path exists between any pair of networks in G, and from any network outside the set, there is a farsighted improving path leading to some network in G.

The largest pairwise consistent set contains any pairwise consistent set. Here, rather than define the pairwise consistent set, we introduce the LPWC set directly via the iterative procedure that is commonly used to construct it.²⁸ The set is given by the intersection of sets $\{Z_k\}_{k\ge 1}$, where each $Z^k$ ($k=1,2,\ldots$) is inductively defined as follows: let $Z^0\equiv {\mathbb {G}}$ and $g\in Z^{k-1}$ belongs to $Z^k$ with respect to Y if

• (ia) $\forall ij\notin g$$\exists g^{\prime }\in Z^{k-1}$, where $g^{\prime }=g+ij$ or $g^{\prime }\in F(g+ij)$ such that $\left( Y_i(g^{\prime }), Y_j(g^{\prime })\right) =\left( Y_i(g), Y_j(g)\right)$ or $Y_i(g^{\prime })< Y_i(g)$ or $Y_j(g^{\prime })< Y_j(g)$,

• (ib) $\forall ij\in g$$\exists g^{\prime }, g^{\prime \prime }\in Z^{k-1}$, where $g^{\prime }=g-ij$ or $g^{\prime }\in F(g-ij)$, and $g^{\prime \prime }=g-ij$ or $g^{\prime \prime }\in F(g-ij)$, such that $Y_i(g^{\prime })\le Y_i(g)$ and $Y_j(g^{\prime \prime })\le Y_j(g)$.

The resulting LPWC set requires that both external and internal pairwise deviations are deterred. It assumes that players are sufficiently cautious and irrespective of whether they are in the network within or outside the stable set, consider all possible improving paths that might be followed after a deviation. Applying the above procedure to our experimental games, we find that in Game II it identifies all, apart from the empty network, as LPWC. Intuitively the reason why one-link networks and the complete network are stable is the same as explained in the main text (Sect. 2). Furthermore, two-link networks are stable because (ia) adding a link in a two-link network reduces the payoffs of both involved players (or leaves them unchanged if the same link is deleted again), and (ib) deleting a link in a two-link network may lead—via a certain farsighted improving path from one-link to two-link to another one-link network—to the reduction of the initially deviating player’s payoff ($6<18$). However, that specific improving path from one-link to two-link to another one-link network requires that the intermediate network payoffs do not matter to players (and that when a link is added, only one player must strictly improve her final payoff, and the other only weakly). Indeed, a player with payoff 30 in a one-link network who adds a link at the first step of that improving path obtains payoff 18 in the intermediate, two-link network before regaining 30 in another one-link network (after deleting the second link). We note that the same path is not improving according to alternative cautious farsighted stability concepts—CPS and LFC—which assume that payoffs in intermediate networks matter to players at least marginally (CPS) or that links can only be added when both players can strictly improve their payoff in the final network (LFC).

We now define these two alternative cautious farsighted stability concepts: cautious path stable set, or CPS (Teteryatnikova 2018), and the largest farsightedly consistent set, or LFC (Page et al. 2005). The former requires first defining path payoffs and surely improving path.

For any player i a path payoff is a function that specifies the payoff $\pi _i(P)$ that player i obtains on any path, or sequence of networks P. For example, this could be a simple arithmetic average of payoffs in all networks of the sequence, or a sum with exponential discounting. The path payoff function allows defining an improving path of networks as a sequence where every link is added or deleted based on the improvement that the remainder of the path offers to player(s) relative to staying in the status quo network for the same number of steps. Moreover, when players are sufficiently cautious, they change links in the network according to not just an improving but a surely improving path. An improving path is called surely improving relative to a (stable) set G if whenever a link is added or deleted, the involved player(s) prefer any improving path that starts after the link is added or deleted and leads to a network in G to staying in the current network for the same number of steps. Then the CPS set is defined as a minimal set which satisfies the property that for any network outside the set there exists a surely improving path relative to G leading to some network in the set.

Definition 6

A set of networks $G\in {\mathbb {G}}$ is cautious path stable if (i) $\forall$$g^{\prime }\in {\mathbb {G}}{\setminus } G$ there exists a surely improving path relative to G that leads to G, and (ii) $\forall$$G^{\prime }\subsetneq G$ violates condition (i).

The CPS set is also shown to satisfy internal stability: for any pair of networks in the set, there does not exist a surely improving path (relative to G) between them. Therefore, the definition of the CPS set is conceptually similar to the one of the vN-MFS set, but it considers path payoffs instead of final network payoffs and surely improving paths instead of “simple” improving paths. Clearly, predictions of CPS depend on the exact specification of the path payoff function. In the two experimental games of this paper, the predictions are calculated under the assumption that players’ path payoffs are defined by the arithmetic average of payoffs in all networks of the path. The details of deriving these predictions are provided in Teteryatnikova (2018).

Finally, the largest farsightedly consistent set, or LFC (Page et al. 2005) in case of two-player coalitions and pairwise approach to link formation can be defined using a slightly different notion of a farsightedly improving deviation. Unlike most of the farsighted concepts considered above, it assumes that whenever a link is added, both involved players must strictly improve their payoff in a final network (but as usual, when a link is deleted, just one of the involved players must improve her payoff). Let us denote by ${\overline{F}}(g)$ a set of networks that can be reached through a sequence of such improving deviations starting from network g. As any such sequence is also farsightedly improving in “old” sense, we have that ${\overline{F}}(g)\subseteq F(g)$. Then the farsightedly consistent set of networks and the LFC set, which is the largest such set, can be defined as follows:

Definition 7

A set of networks $G\subseteq {\mathbb {G}}$ is farsightedly consistent if $\forall$$g\in G$,

• (ia) $\forall ij\notin g$, $\exists g^{\prime }\in G$, where $g^{\prime }=g+ij$ or $g^{\prime }\in {\overline{F}}(g+ij)\bigcap G$, such that $Y_i(g^{\prime })\le Y_i(g)$ or $Y_j(g^{\prime })\le Y_j(g)$,

• (ib) $\forall ij\in g$, $\exists g^{\prime }, g^{\prime \prime }\in G$, where $g^{\prime }=g-ij$ or $g^{\prime }\in {\overline{F}}(g-ij)\bigcap G$, and $g^{\prime \prime }=g-ij$ or $g^{\prime \prime }\in {\overline{F}}(g-ij)\bigcap G$, such that $Y_i(g^{\prime })\le Y_i(g)$ and $Y_j(g^{\prime \prime })\le Y_j(g)$.

The LFC set is the farsightedly consistent set that contains any farsightedly consistent set.

Thus, a set of networks is largest farsightedly consistent if it is the largest set for which given any network in the set and any deviation from that network (to a network in- or outside the set), there exists an improving path leading to some network in the set where the initially deviating player(s) is not better off and possibly worse off.

C Non-cooperative network formation game

In this section we consider a non-cooperative network formation game that can be viewed as an approximation of the game played in our experiment. Namely, we study a finitely repeated version of the one-shot simultaneous-move game of Myerson (1991). At each stage, three players simultaneously choose which players they want to be connected to (if any) and a link is formed whenever both involved players choose each other. This game is played repeatedly 30 times (the 30 payoffs at one-second intervals in the experiment) under the assumption that past actions are perfectly observable. Below we provide a formal description of this game and present a simple argument showing that the repeated play of any network in both of our experimental treatments can arise as a subgame-perfect Nash equilibrium.²⁹

Using formal notation, the stage game in normal form is $G=(A_1,A_2,A_3; f_1,f_2,f_3)$, where $A_i$ is an action space of player i and $f_i$ is i’s stage-game payoff function. The action space of each player includes a choice of not linking to anyone, linking to both other players and linking to just one of them. For example, $A_1=\left\{ \emptyset , \{2,3\}, \{2\},\{3\}\right\}$. Thirty repetitions of this stage game result in a new game, $G^{30}$, and player i’s payoff in this game is given by the sum of her payoffs in each round:³⁰

$$\begin{aligned} F_i(a)=\sum _{t=1}^{30}f_i(a^t), \end{aligned}$$

where $a^t$ is the action profile of players at stage t and $a=\{a^t\}_{t=1}^{30}$. A strategy of player i in the game $G^{30}$ is a specification of an action at date 1, and thereafter an action at each date t conditional on any conceivable history of play, up to and including date $t-1$.

As in the static network formation game of Myerson (1991), multiple Nash equilibria arise in this finitely repeated game. In particular, below we show that with payoff specification of Game I, there exists a subgame-perfect equilibrium where each network is played repeatedly for 30 rounds, and with payoff specification of Game II, there exists a subgame-perfect equilibrium where each network is played repeatedly for either 29 or 30 rounds. Thus, all eight networks in both of our experimental treatments can be considered as stable according to equilibrium predictions of this non-cooperative game.

Note that in Game I any network can arise as a Nash equilibrium outcome of the stage game. For example, the empty network is an equilibrium outcome if none of the players proposes any links, and any two-link network is an equilibrium outcome if one player chooses to link with both other players, while they choose to link only with that player but not with each other. Given such choices, no player has an incentive to unilaterally change her own action. Then, as playing a Nash equilibrium of the stage game in every round is always a subgame-perfect equilibrium of a repeated game, we obtain that in Game I, any network played repeatedly for 30 rounds can arise as a subgame-perfect Nash equilibrium.

Similarly, in Game II the empty network and each of the one-link networks can be supported as a Nash equilibrium outcome of the stage game, and there exists a subgame-perfect Nash equilibrium of the repeated game where each of these networks emerges in all 30 rounds. The two-link and complete networks, on the other hand, are not Nash equilibria of the stage game as at least one of the players has an incentive to unilaterally delete one link. However, it is easy to show that there exists a subgame-perfect equilibrium of the repeated game where each of these networks arises in the first 29 rounds followed by a one-link network in the last round.

Consider the two-link network $g_5$ in Fig. 6, where Player 2 has two links. The following strategy profile supports the emergence of this network in the first 29 rounds of the game (and one-link network in the last round) as a subgame-perfect Nash equilibrium.³¹ In each of the first 29 rounds, if no deviation has taken place, Player 2 chooses to link with Players 1 and 3, while Players 1 and 3 choose to link with Player 2 but not with each other. In the last round, Player 2 links only with one player, say Player 1, and Player 1 links only with Player 2 (Player 3 can do anything). If at any round $t\in \{1,\ldots ,29\}$, a player i deviates to a different action, then from date $t+1$ onward (until and including the last round) the other two players punish the deviator by proposing a link to each other but not to i. Given such strategies, only Player 2 may have an incentive to deviate and only at $t\in \{1,\ldots ,29\}$: by proposing a link to one player instead of two, she would increase her immediate payoff from 18 to 30. However, in all subsequent rounds her payoff would be 6, irrespective of own actions. This makes even her best deviation, at round 29 (with only one round of punishment) unprofitable as $30+6<18+30$. Moreover, a deviation off the equilibrium path is not beneficial either as the “punishing” players obtain their best possible payoff. Thus, the described strategy profile is a subgame-perfect Nash equilibrium.

Similarly, the complete network can be supported in the first 29 rounds as a subgame-perfect equilibrium if the following strategy profile is played. At any $t\in \{1,\ldots ,29\}$ each player chooses to link with two other players, and at $t=30$ Player 2 links randomly with Player 1 or 3, choosing each of them with probability 0.5, while Players 1 and 3 choose to link only with Player 2 but not with each other (a one-link network is formed). A deviation by player i at any $t\in \{1,\ldots ,29\}$ is punished by the other two players choosing to link with each other but not with i in the remaining rounds of the game. Given such strategy profile, an incentive to deviate may only exist at $t\in \{1,\ldots ,29\}$, as deleting a link in the complete network (that is, choosing to link with one instead of two players) increases player’s immediate payoff from 22 to 24. However, due to the subsequent punishment, even the best possible deviation—where Player 1 or Player 3 proposes just one link at $t=29$ – is not profitable because $24+6<22+(30\cdot 0.5+6\cdot 0.5)$. Thus, neither on or off the equilibrium path do players have an incentive to deviate, which means that our strategy profile is a subgame-perfect Nash equilibrium.

These findings demonstrate the existence of multiple Nash equilibria, where all networks in Games I and II are identified as stable. Moreover, this would not change even if we modelled precisely the games implemented in the laboratory by allowing moves in continuous time. Because no payoffs occur between seconds, it is easy to see that there exist equilibria in this new game where at the times of payoffs players choose actions as described in the various equilibria above and they keep choosing these same actions continuously throughout the subsequent second until the next payoff instance. This would result in equilibria where all networks of both games last the whole 30 or 29 s. Note that in this sense, cooperative concepts employed in our experiment offer a refinement of Nash equilibria by identifying a more narrow set of stable networks.³²

D Experimental results

see Tables 9, 10, 11.

Table 9 Probability of remaining in current network by matching group

Table 10 Transitions (row to column): Game I

Table 11 Transitions (row to column): Game II

E Instructions

[ONSCREEN]

Before the experiment begins there will be a short tutorial and three practice games to make sure everybody understands how points can be earned.

The points that are distributed in these three practice rounds will not affect your final payment.

Please click “Continue” to proceed to the tutorial.

[PRINTED]

Please read and follow these instructions. Text in italics describes things you should do onscreen. If you have a question, raise your hand and someone will come to help you as soon as possible.

• In each round of this experiment you will be interacting with two other people using the screen you can see on your monitor.

• You are represented by the green dot, and the other two players by the blue dots.

• Links may be formed between two players in the following way:

  • You can indicate that you are willing to form a link with another person by clicking on their blue dot.

  • Clicking on them again indicates you are no longer willing to form a link with them.

  • You can click on a person as many times as you like, switching back and forth between being willing to form a link with them or not.

  • If two people have both clicked on each other then a link is formed and it is shown in red.

  • A link can be formed between to people only if both of them want it to be formed.

  • If only one of the people has shown they are willing to form a link then it is shown in pink.

• On the screen in front of you the two other people have formed a link, and the person on your right has indicated they are willing to form a link with you.

  • Click on the blue dot on the left and see how the line turns pink. Click again and see how it becomes white again.

  • Click on the blue dot on the right and see how the line turns red. Click again and see how it becomes pink again.

  • Notice that nothing you can do will change the colour of the line between the other two people. Whether or not that link is formed depends only on their decisions.

• Every second, you and the two other people will earn points. The number of points per second earned by each person is shown in red next two their dot.

• The number of points each person earns per second depends on which links are formed at that point in time.

• These numbers will vary from round to round and will be shown to you before each round begins. The numbers for the screen you see in front of you are described in the following diagram:

• Click on the two other people and see how the numbers in red change, and how they relate to the diagram. Notice that it doesn’t make a difference if a line is white or pink; the numbers change only if a link is formed or broken (i.e. becomes red, or changes from red to pink).

• In the practice rounds and real interactions the screen will look slightly different. An example is shown below:

• As mentioned before, points will be earned every second. The total number of points you have earned so far in a round will be shown at the top left of the screen as shown in the picture “Your Point”). This number will increase every second by the red number below the green dot.

• Each round lasts for 30 s. The number of seconds left will shown at the top right.

• WHEN YOU HAVE UNDERSTOOD THESE INSTRUCTIONS, PLEASE CLICK THE BUTTON ON YOUR COMPUTER SCREEN.

[ONSCREEN]

Please answer the following questions relating to the picture shown in the handout.

Click “Continue” when you have answered all questions.

How many points are you earning per second?

How many points is the person on your left earning per second?

How many points have you earned so far this round?

How many seconds are left before the round ends?

[New Screen]

You have answered all the questions correctly.

Before the real experiment begins there will be three practice rounds.

These practice rounds will not affect your final payment.

The purpose of these practice rounds is for you to learn how these interactions work. You should use them to experiment and learn how links are formed and how they relate to the payoffs. Do not worry about earning a lot of points because they do not count!

The points associated with each practice round are shown on your handout.

If you have any questions, please raise your hand and someone will come to help you as soon as possible.

Otherwise please click “Continue” and wait for the other participants to finish the Tutorial.

The first practice round is about to begin.

Check the payoffs described in Fig. 1 of your printed instructions. These are the payoffs that are relevant for the practice rounds.

Click OK when you are ready to begin.

[New Screen]

The first practice round is about to begin.

Check the payoffs described in Fig. 1 of your printed instructions. These are the payoffs that are relevant for the practice rounds.

[New Screen]

Click OK when you are ready to begin.

The practice rounds are now over.

You will now be handed the diagrams which describe the payoffs for the first real rounds.

[New Screen]

You will now play a game similar to the one in the tutorial but with different payoffs.

Please look at the diagram you have just been given to see how the points you earn will depend on the links that are formed.

You will play this game 20 times. The links that have been already formed at the beginning of the game will be randomly determined each time.

After each time you will be randomly rematched with new participants. This means it is unlikely you will be playing with exactly the same people as in the previous round.

When all games have been played, one game will be randomly chosen to determine how much you will be paid. All participants will be paid for the same game. For every 90 points you earn in that game you will be paid 2 Euros.

When you are ready to start, please click “Continue”.