Mixed equilibria in Tullock contests

Abstract

Any symmetric mixed-strategy equilibrium in a Tullock contest with intermediate values of the decisiveness parameter (“$2<R<\infty$”) has countably infinitely many mass points. All probability weight is concentrated on those mass points, which have the zero bid as their sole point of accumulation. With contestants randomizing over a non-convex set, there is a cost of being “halfhearted,” which is absent from both the lottery contest and the all-pay auction. Numerical bid distributions are generally negatively skewed and exhibit, for some parameter values, a higher probability of ex-post overdissipation than the all-pay auction.

1 Introduction

Even after several decades, the game-theoretic analysis of Tullock’s (1980) model of a political contest is still incomplete. Indeed, Nash equilibria in either pure or mixed strategies have been described explicitly only for a range of lower values of the decisiveness parameter (Pérez-Castrillo and Verdier 1992; Nti 1999), and for the limit case of the all-pay auction (Hillman and Samet 1987; Hillman and Riley 1989; Baye et al. 1996), but not so for intermediate values. As has been widely acknowledged, this lack of a game-theoretic prediction is undesirable, in particular because the resulting constraints on the decisiveness parameter do not have a proper economic motivation.¹

For the case of intermediate values of the decisiveness parameter (“$2<R<\infty$”), in which a pure-strategy Nash equilibrium does not exist, Baye et al. (1994) proved the existence of a symmetric mixed-strategy Nash equilibrium with complete rent dissipation, and subsequently approximated the limit distribution by calculating equilibria of rent-seeking games with finite strategy spaces. Building on those results, Alcade and Dahm (2010) showed that many contests of intermediate decisiveness allow a mixed-strategy equilibrium that shares important statistics with the equilibrium of the corresponding all-pay auction.² However, a more structural understanding of the limit distribution remained elusive. For example, it was not known whether the limit distribution is continuous as in the case of the all-pay auction, or a finite collection of mass points as in Che and Gale’s (2000) analysis of difference-form contests, or something completely different. Moreover, numerical calculations based on contests with finite strategy spaces have tended to offer only rather low-resolution images of the limit distribution.³

The present paper addresses these issues by deriving new structural properties of mixed-strategy Nash equilibria in the rent-seeking game. Specifically, it is shown that any symmetric mixed-strategy equilibrium in the Tullock contest of intermediate decisiveness entails countably infinitely many mass points. Moreover, all probability weight is concentrated on these mass points. Finally, the mass points form a discrete set in the strategy space and accumulate only at the zero bid, which itself is played with probability zero.⁴

These findings are potentially important because they imply that the equilibrium prediction for intermediate values of the decisiveness parameter differs structurally (even though not necessarily statistically) from the tractable cases that have been studied more frequently in the literature. For illustration, consider the equilibrium payoff function in a two-player contest, i.e., the expected payoff of a contestant as a function of her own expenditure, assuming that the other contestant adheres to the equilibrium strategy (see Fig. 1). For various intermediate values of $R$, it can be seen that there are many local strict maxima that all lead to the same expected payoff of zero. It turns out that infinitely many of these local maxima receive positive mass in the equilibrium distribution. Thus, contrasting both the pure-strategy equilibrium in the lottery contest and the continuous mixed-strategy equilibrium in the all-pay auction, the equilibrium bid distribution for intermediate values of the decisiveness parameter has a non-convex support.⁵

Fig. 1

Equilibrium payoff functions in the two-player Tullock contest

The main tools for proving the results of this paper are taken from the realm of complex analysis. It is shown that the equilibrium payoff function allows a complex-analytic extension to an open connected subset of the complex numbers $\mathbb {C} =\{x+\sqrt{-1}y:x,y\in \mathbb {R} \}$ that encompasses the real interval $(0,\infty )$.⁶ But any non-constant function that is analytic over an open connected subset of the complex numbers has a discrete set of zeros. Since all expenditure levels in the support of a mixed equilibrium strategy necessarily yield the same expected payoff, this implies that all positive bids used in an equilibrium strategy must be isolated points of the support, which is the key ingredient of the equilibrium analysis.⁷

The remainder of the paper is structured as follows. The necessary material from complex analysis is reviewed in Sect. 2. In Sect. 3, the discreteness result is stated and proved. The equilibrium characterization can be found in Sect. 4. Section 5 offers numerical illustrations. Concluding remarks are collected in Sect. 6. An Appendix describes the numerical approach that has been used to calculate examples of bid distributions.

2 Background on analytic functions

This section recalls some concepts and results from complex analysis. For further details and proofs, the reader is referred to any textbook on the topic, such as Conway (1978).

Here is the definition of a complex-analytic function.

Definition 2.1

A complex-valued function $f$ is complex-analytic in an open set $U\subseteq \mathbb {C}$ if, at any point $z_{0}\in U$, there is a power series $\sum _{m=0}^{\infty }\alpha _{m}(z-z_{0})^{m}$ in $z$ around $z_{0}$, with coefficients $\alpha _{m}\in \mathbb {C}$ for $m=0,1,2,\ldots$, that converges to $f(z)$ for all $z$ in a neighborhood $V\subseteq U$ of $z_{0}$.

A zero of a complex-valued function $f$ is a point $z$ in the domain of $f$ such that $f(z)=0$. The following result says that the zeros of a non-constant complex-analytic function on an open connected set necessarily form a discrete set.

Lemma 2.2

If $f$ is a complex-analytic function on an open connected set $U\subseteq \mathbb {C}$ and if there is a sequence of distinct points $z_{1},z_{2},\ldots$ in $U$ with $z_{0}=\lim _{n\rightarrow \infty }z_{n}\in U$ and such that $f(z_{n})=0$ for $n=1,2,\ldots$, then $f(z)=0$ for all $z\in U$.

The following two standard results in complex analysis serve as the main technical tools to show that the equilibrium payoff function in the rent-seeking game allows an analytic extension to some complex domain that contains the interval $(0,\infty )$.

Lemma 2.3

(Cauchy’s Theorem) Let $f$ be a complex-analytic function on the open set $U\subseteq \mathbb {C}$. Then,

$$\begin{aligned} {\displaystyle \oint _{\xi }} f(z)dz=0 \end{aligned}$$

(1)

for every closed rectifiable curve $\xi$ that is homotopic to zero in $U$.

Lemma 2.4

(Morera’s Theorem) Let $f$ be a continuous complex-valued function on the open set $U\subseteq \mathbb {C}$. Suppose that Eq. (1) holds for every triangular path $\xi$ in $U$. Then, $f$ is complex-analytic in $U$.

3 The support of mixed equilibria in the Tullock contest

In the sequel, I will discuss only the simple example of a two-player rent-seeking game.⁸ Each player $i=1,2$ chooses a level of expenditure $x_{i}\ge 0$. For a fixed value of the parameter $R\ge 0$, player $i$’s payoff in the rent-seeking game is given by

$$\begin{aligned} \Pi _{i}(x_{i},x_{j})=\dfrac{x_{i}^{R}}{x_{i}^{R}+x_{j}^{R}}-x_{i}, \end{aligned}$$

(2)

where $j\ne i$, and the ratio is interpreted as $\frac{1}{2}$ if the denominator vanishes.

Recall the following facts about the equilibrium set of this game. For $0\le R\le 2$, there is a symmetric pure-strategy Nash equilibrium in which each agent invests $\frac{R}{4}$. For $2<R<\infty$, however, there does not exist a pure-strategy equilibrium. Instead, there is a symmetric mixed-strategy equilibrium with complete rent dissipation.⁹

The following lemma collects those properties of Tullock’s “ impact function” that are relevant for the discreteness result stated further below.

Lemma 3.1

For any finite $R\ge 0$, the function $h(x_{i})=x_{i}^{R}$ allows a complex-analytic extension $\widehat{h}$ to an open neighborhood $H$ of $(0,\infty )$ in $\mathbb {C}$. Moreover, $h(x_{i})>0$ for any $x_{i}>0$.

Proof

Denoting by $\ln z_{i}$ the principal value of the complex logarithm, the mapping $\widehat{h}(z_{i})=\exp (R\cdot \ln z_{i})$ is complex-analytic on the half-plane $H=\{z_{i}\in \mathbb {C} :\mathrm{Re }(z_{i})>0\}$. Clearly, $\widehat{h}(x_{i})=h(x_{i})$ for any $x_{i}>0$. This proves the first claim. The second claim is obvious. $\square$

Fix now some parameter value $R$ and take some symmetric mixed-strategy equilibrium $\mu ^{*}$ of the rent-seeking game with decisiveness $R$. The following result provides some information about the support $S^{*}$ of $\mu ^{*}$.

Theorem 3.2

$S^{*}\cap (0,\infty )$ is discrete and allows only the zero bid as a potential accumulation point.

Proof

Choose some complex-analytic extension $\widehat{h}$ of $h$ to an open neighborhood $H$ of $(0,\infty )$ in $\mathbb {C}$. It is claimed first that, for any $\varepsilon \in (0,1)$, there is some $\delta =\delta (\varepsilon )>0$ such that the complex-valued function

$$\begin{aligned} \widetilde{\Pi }_{i}(z_{i},x_{j})=\frac{\widehat{h}(z_{i})}{\widehat{h} (z_{i})+x_{j}^{R}}-z_{i} \end{aligned}$$

(3)

is well-defined and bounded on $U(\varepsilon ,\delta )\times \mathbb {R}_{+}$, where

$$\begin{aligned} U(\varepsilon ,\delta )=\left\{ z_{i}\in \mathbb {C} :\varepsilon <\mathrm{Re }z_{i}<\frac{1}{\varepsilon }\text {, }\left| \mathrm{Im }z_{i}\right| <\delta \right\} \end{aligned}$$

(4)

is the rectangular domain that is illustrated in Fig. 2.

Fig. 2

Construction of the domain $U(\varepsilon ,\delta )$

To prove this claim, take some $\varepsilon \in (0,1)$. On the non-empty compact interval $I_{\varepsilon }=[\varepsilon ,\frac{1}{\varepsilon }]$, the continuous function $h$ assumes a minimum value $M=M(\varepsilon )>0$.¹⁰ Given that $H$ is an open set, there exists, for any $x_{i}\in I_{\varepsilon }$, a small disc $D(x_{i})=\{z_{i}\in \mathbb {C} :\left| z_{i}-x_{i}\right| <\delta _{1}(x_{i})\}$ of radius $\delta _{1}(x_{i})>0$ around $x_{i}$ such that $D(x_{i})\subseteq H$. Moreover, since the function $\widehat{h}$ is continuous, $\delta _{1}(x_{i})$ may be chosen sufficiently small such that $\mathrm{Re }(\widehat{h}(z_{i}))>\frac{M}{2}$ for any $z_{i}\in D(x_{i})$. Exploiting now the compactness of $I_{\varepsilon }$ once more, there are finitely many $x_{i}^{1},\ldots ,x_{i} ^{\nu }\in I_{\varepsilon }$ such that the open discs $D(x_{i}^{1} ),\ldots ,D(x_{i}^{\nu })$ cover $I_{\varepsilon }$. Clearly, it may be assumed without loss of generality that $x_{i}^{1}<\ldots <x_{i}^{\nu }$, as illustrated in Fig. 2. But then, any two neighboring discs $D(x_{i}^{v_0}),D(x_{i}^{\nu _{0}+1})$, for $\nu _{0}=1,\ldots ,\nu -1$, have a non-empty open intersection. Moreover, $x_{i}^{1}-\delta _{1}(x_{i}^{1})<\varepsilon$ and $x_{i}^{\nu }+\delta _{1}(x_{i}^{\nu })>\frac{1}{\varepsilon }$. Hence, for any sufficiently small $\delta$, the set $U(\varepsilon ,\delta )$ is covered by the discs $D(x_{i} ^{1}),\ldots ,D(x_{i}^{\nu })$. In particular, $\mathrm{Re }(\widehat{h} (z_{i}))>\frac{M}{2}$ for any $z_{i}\in U(\varepsilon ,\delta )$. It follows that, for $\delta$ sufficiently small, the function $\widetilde{\Pi }_{i}$ is indeed well-defined and bounded on $U(\varepsilon ,\delta )\times \mathbb {R} _{+}$. To prove the theorem, consider now the complex-valued equilibrium payoff function

$$\begin{aligned} \overline{\Pi }_{i}(z_{i})=\int \widetilde{\Pi }_{i}(z_{i},x_{j})d\mu ^{*}(x_{j})\text {.} \end{aligned}$$

(5)

Because the integrand is bounded on $U(\varepsilon ,\delta )\times \mathbb {R} _{+}$ as well as continuous in $z_{i}$ over $U(\varepsilon ,\delta )$ for any $x_{j}\ge 0$, and because $\mu ^{*}$ has a compact support, the Lebesgue’s Dominated Convergence Theorem implies that $\overline{\Pi }_{i}$ is continuous on $U(\varepsilon ,\delta )$. To show that $\overline{\Pi }_{i}$ is even complex-analytic in $U(\varepsilon ,\delta )$, consider an arbitrary triangular path $\xi$ in $U(\varepsilon ,\delta )$. Then, for any $x_{j}\ge 0$, since $U(\varepsilon ,\delta )$ is contractible and $\widetilde{\Pi }_{i}(\cdot ,x_{j})$ is complex-analytic in $U(\varepsilon ,\delta )$, Cauchy’s Theorem implies that

$$\begin{aligned} {\displaystyle \oint _{\xi }} \widetilde{\Pi }_{i}(z_{i},x_{j})dz_{i}=0\text {.} \end{aligned}$$

(6)

Integrating over $\mu ^{*}$ yields

$$\begin{aligned} \int \left( {\displaystyle \oint _{\xi }} \widetilde{\Pi }_{i}(z_{i},x_{j})dz_{i}\right) d\mu ^{*}(x_{j})=0\text {.} \end{aligned}$$

(7)

Since $\mu ^{*}$ has a compact support, and $\widetilde{\Pi }_{i}$ is bounded on $U(\varepsilon ,\delta )\times \mathbb {R} _{+}$, one may exchange the order of integration in Eq. (7), so that

$$\begin{aligned} {\displaystyle \oint _{\xi }} \left( \int \widetilde{\Pi }_{i}(z_{i},x_{j})d\mu ^{*}(x_{j})\right) dz_{i}=0. \end{aligned}$$

(8)

But $\xi$ was arbitrary, so that Morera’s Theorem implies that $\overline{\Pi }_{i}$ is indeed analytic in the complex domain $U(\varepsilon ,\delta )$. Moreover, $\overline{\Pi }_{i}$ is non-constant in $U(\varepsilon ,\delta )$ for $\varepsilon$ sufficiently small because $\overline{\Pi }_{i}(x_{i})\le 1-x_{i}$ for any $x_{i}\ge 0$. Take now any $x_{i}^{*}\in S^{*}$ such that $x_{i}^{*}>0$. For $\varepsilon$ sufficiently small, $x_{i}^{*}$ is an interior point of $I_{\varepsilon }$. Since $x_{i}^{*}$ is a best response to $\mu ^{*}$, one has $\overline{\Pi }_{i}(x_{i}^{*})-\Pi ^{*}=0$, where $\Pi ^{*}$ denotes the expected equilibrium payoff. By Lemma 2.2, there is an open neighborhood $\widehat{V}$ of $x_{i}^{*}$ in $U(\varepsilon ,\delta )$ such that $x_{i}^{*}$ is the only zero of $\overline{\Pi }_{i}-\Pi ^{*}$ in $\widehat{V}$. But then, $\widetilde{V}=\widehat{V}\cap \mathbb {R} _{++}$ is an open neighborhood of $x_{i}^{*}$ in the strategy set $\mathbb {R}_{+}$ such that $x_{i}^{*}$ is the only best response to $\mu ^{*}$ in $\widetilde{V}$. $\square$

4 Equilibrium characterization

By Theorem 3.2, any symmetric Nash equilibrium $\mu ^{*}$ of the rent-seeking game has the property that the intersection of its support $S^{*}$ with $(0,\infty )$ is discrete and allows only the zero bid as a potential accumulation point. Thus, either $S^{*}$ is finite, or the zero bid is an accumulation point of $S^{*}$. For $R>2$, however, it will be shown below that the origin necessarily is an accumulation point of $S^{*}$.¹¹ It is also shown that for $R\le 2$, there are no symmetric mixed-strategy equilibria in addition to the well-known pure-strategy equilibrium.

As before, I will restrict attention to the simplest of all cases and leave any discussion to Sect. 6.

Theorem 4.1

In any symmetric equilibrium of the two-player rent-seeking game with $2<R<\infty$, the support of the distribution of expenditure levels has the zero bid as an accumulation point. Thus, the equilibrium is characterized by a sequence of mass points

$$\begin{aligned} y_{1}>y_{2}>\ldots >0\textit{,} \end{aligned}$$

(9)

chosen with respective positive probabilities $q_{1}\textit{,}q_{2}\textit{,}\ldots$, so that $\lim _{k\rightarrow \infty }y_{k}=0$ and $\sum _{k=1}^{\infty }q_{k}=1$. Moreover,

$$\begin{aligned} \sum _{k=1}^{\infty }\frac{q_{k}y_{K}^{R}}{y_{K}^{R}+y_{k}^{R}}-y_{K}&=0\text {, }\end{aligned}$$

(10)

$$\begin{aligned} \sum _{k=1}^{\infty }\frac{q_{k}Ry_{K}^{R-1}y_{k}^{R}}{(y_{K}^{R}+y_{k}^{R})^{2}}-1&=0\text {,} \end{aligned}$$

(11)

for any integer $K\ge 1$. Finally, there are no non-degenerate mixed-strategy equilibria for $R\le 2$.

Proof

Suppose that the zero bid is not an accumulation point of $S^{*}$. Then, using Theorem 3.2, $S^{*}$ is discrete and compact, hence finite. Let $y_{1}>y_{2}>\ldots >y_{L}$ be the mass points of the equilibrium bid distribution, used with respective probabilities $q_{1},\ldots ,q_{L}$, where ${\textstyle \sum _{k=1}^{L}} q_{k}=1$. From the first-order condition at $y_{L}$,

$$\begin{aligned} \sum _{k=1}^{L}\frac{q_{k}Ry_{L}^{R-1}y_{k}^{R}}{(y_{L}^{R}+y_{k}^{R})^{2}}=1, \end{aligned}$$

(12)

one obtains

$$\begin{aligned} \sum _{k=1}^{L}\frac{2y_{k}^{R}}{y_{L}^{R}+y_{k}^{R}}\frac{q_{k}y_{L}^{R}}{y_{L}^{R}+y_{k}^{R}}-y_{L}=\frac{2-R}{R}y_{L}. \end{aligned}$$

(13)

But since $y_{k}\ge y_{L}$ for $k=1,\ldots ,L$, it follows that

$$\begin{aligned} \sum _{k=1}^{L}\frac{q_{k}y_{L}^{R}}{y_{L}^{R}+y_{k}^{R}}-y_{L}\le \frac{2-R}{R}y_{L}. \end{aligned}$$

(14)

Thus, for $R>2$, bidding $y_{L}$ yields a negative expected payoff in equilibrium, which is impossible. The contradiction shows that the origin is necessarily an accumulation point of $S^{*}$. To prove Eq. (10), one notes that

$$\begin{aligned} \Pi ^{*}=\sum _{k=1}^{\infty }\frac{q_{k}y_{K}^{R}}{y_{K}^{R}+y_{k}^{R}}-y_{K}, \end{aligned}$$

(15)

for any index $K\ge 1$, where $\Pi ^{*}$ is the expected equilibrium payoff, as before. Taking the limit $K\rightarrow \infty$, and subsequently exchanging the sum and the limit via the Lebesgue’s Dominated Convergence Theorem, implies then that $\Pi ^{*}=0$. Finally, it is shown that there are no non-degenerate mixed-strategy equilibria for $R\le 2$. Indeed, by Theorem 3.2, any symmetric equilibrium bid distribution consists of discretely located mass points $\{y_{k}\}_{k=1}^{L}$ that are chosen with probabilities $\{q_{k}\}_{k=1}^{L}$, where $L\le \infty$. Consider now the first-order condition at $y_{1}$, i.e.,

$$\begin{aligned} \sum _{k=1}^{L}\frac{q_{k}Ry_{1}^{R-1}y_{k}^{R}}{(y_{1}^{R}+y_{k}^{R})^{2}}-1=0. \end{aligned}$$

(16)

Arguing as above, this implies

$$\begin{aligned} \sum _{k=1}^{L}\frac{q_{k}y_{1}^{R}}{y_{1}^{R}+y_{k}^{R}}-y_{1}\ge \frac{2-R}{R}y_{1}\text {,} \end{aligned}$$

(17)

where the inequality is strict if $L>1$. Hence, for $R\le 2$, rent dissipation would be imperfect in any non-degenerate mixed-strategy equilibrium. As pointed out above, however, $\Pi ^{*}>0$ is feasible only if the zero bid is not an accumulation point of $S^{*}$. Thus, $L$ is finite. Noting now that the left-hand side of inequality (14) is equal to the left-hand side of inequality (17), it follows that, indeed, $L=1$.¹² Thus, any symmetric equilibrium in the two-player Tullock contest with $R\le 2$ is necessarily in pure strategies. $\square$

The equilibrium description provided by Theorem 4.1 contrasts with both the unique (pure-strategy) Nash equilibrium in the lottery contest and the unique (mixed-strategy) equilibrium in the all-pay auction. As already explained in the Introduction, the peculiar nature of the mixed-strategy equilibria in the Tullock contest is caused by the non-convexity of the relevant best-response set, which is illustrated by Fig. 1. Intuitively, the suboptimality of bids placed, e.g., strictly between bids $y_{1}$ and $y_{2}$, captures a cost of being “halfhearted” in the sense that such positive bids are too low to be effective against a decisive action by the opponent, but at the same time too high as a measured defense against speculative underbidding.

5 Numerical illustrations

5.1 Solving the infinite system

While Theorem 4.1 clarifies the structure of the mixed-strategy equilibrium in the Tullock contest, it is also desirable to learn more about the specific values of the parameters $y_{k}$ and $q_{k}$. Since an explicit solution of Eqs. (10–11) is not readily available, I truncated the infinite system and solved the resulting finite system numerically.¹³ Parameter values obtained along these lines, rounded to the fourth digit, are shown in Table 1. As can be seen, for $R$ kept fixed, the probability weight $q_{k}$ is generally declining in $k$. Moreover, as $R$ increases, the probability distribution becomes more dispersed and stretched out over a larger range, with any two neighboring mass points moving more closely together. In sum, this may be seen as refining somewhat an earlier description given by Baye et al. (1994).¹⁴

Table 1 Numerical bid distributions

5.2 Higher moments of the bid distributions

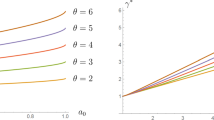
Figure 3 exhibits the first four moments of the numerical bid distribution. As the right-upper panel illustrates, the skewness of the bid distribution is generally negative for $R>2$, in contrast to the corresponding case of the all-pay auction. Moreover, with variance increasing and skewness vanishing for higher $R$, a higher degree of decisiveness seems to foster speculative underbidding.

Fig. 3

Moments of the numerical bid distributions

5.3 Overdissipation

Figure 4 shows the probability of ex-post overdissipation, $\Delta (R)$, as a function of $R$. Somewhat unexpectedly, $\Delta (R)$ exceeds, for some values of $R$, the probability of ex-post overdissipation in the all-pay auction, which is 0.5 (Baye et al. 1999). In fact, $\Delta (R)$ approaches unity for $R$ close to $2$. These possibilities are obviously related to the discreteness of the equilibrium bid distribution.

Fig. 4

The probability of ex-post overdissipation

6 Concluding remarks

While Theorem 3.2 has been stated and proved only for symmetric equilibria in the two-player Tullock contest, it reflects a more general fact. Indeed, it is not hard to see that the proof extends to settings with more than two players, heterogeneous valuations, and alternative impact functions.¹⁵

Similarly, variants of Theorem 4.1 can be derived for other classes of contests. In particular, the arguments made above extend to the case of symmetric equilibria in Tullock contests with $N\ge 2$ players, where then non-degenerate mixed-strategy equilibria exist if and only if $R>N/(N-1)$.

Starting from Theorem 4.1, one may also obtain an explicit characterization of all-pay auction equilibria constructed by Alcade and Dahm (2010) in contests with heterogeneous valuations. For example, if $N\ge 2$ contestants possess respective valuations $v_{1},\ldots ,v_{N}$, where $v_{1}\ge v_{2}\ge \ldots \ge v_{N}>0$, then player 1 randomizes over infinitely many positive mass points $\{y_{k}v_{2}\}_{k=1}^{\infty }$ with probabilities $\{q_{k}\}_{k=1}^{\infty }$, player 2 randomizes over $\{0\}\cup \{y_{k}v_{2}\}_{k=1}^{\infty }$ with probabilities $1-v_{2}/v_{1}$ and $\{q_{k}v_{2}/v_{1}\}_{k=1}^{\infty }$, while players $3,\ldots ,N$ remain inactive. The characterization of the symmetric two-player equilibrium thereby sheds light also on the structure of equilibria in more general contests.

Appendix: Numerical approach

To calculate numerical bid distributions in the symmetric two-player Tullock contest, one focuses on conditions (10–11) for indices $K\le K^{\max }$ and stipulates that $y_{k}=0$ for $k>K^{\max }$. Pursuing this route leads to a system of equations

$$\begin{aligned}&\sum _{k=1}^{K-1}\frac{q_{k}y_{K}^{R}}{y_{K}^{R}+y_{k}^{R}}+\frac{q_{K}}{2}+\sum _{k=K+1}^{K^{\max }}\frac{q_{k}y_{K}^{R}}{y_{K}^{R}+y_{k}^{R}} +\sum _{k=K^{\max }+1}^{\infty }q_{k}-y_{K} =0\text {, }\end{aligned}$$

(18)

$$\begin{aligned}&\sum _{k=1}^{K-1}\frac{q_{k}Ry_{K}^{R-1}y_{k}^{R}}{(y_{K}^{R}+y_{k}^{R})^{2} }+\frac{q_{K}R}{4y_{K}}+\sum _{k=K+1}^{K^{\max }}\frac{q_{k}Ry_{K}^{R-1} y_{k}^{R}}{(y_{K}^{R}+y_{k}^{R})^{2}}-1 =0, \end{aligned}$$

(19)

where $K=1,\ldots ,K^{\max }$. Using the relationship

$$\begin{aligned} \frac{q_{K}}{2}+\sum _{k=K^{\max }+1}^{\infty }q_{k}=1-\sum _{k=1}^{K-1} q_{k}-\frac{q_{K}}{2}-\sum _{k=K+1}^{K^{\max }}q_{k}, \end{aligned}$$

(20)

Equation (18) may be rewritten as

$$\begin{aligned} 1-\sum _{k=1}^{K-1}q_{k}+\sum _{k=1}^{K-1}\frac{q_{k}y_{K}^{R}}{y_{K}^{R} +y_{k}^{R}}-\frac{q_{K}}{2}-\sum _{k=K+1}^{K^{\max }}\frac{q_{k}y_{k}^{R}}{y_{K}^{R}+y_{k}^{R}}-y_{K}=0\text {.} \end{aligned}$$

(21)

Solving now Eqs. (19) and (21) separately for $q_{K}$ yields the simplified system

$$\begin{aligned} q_{K}&=2(1-\sum _{k=1}^{K-1}q_{k}-y_{K}+\alpha _{K}(y_{K})-\beta _{K} (y_{K}))\end{aligned}$$

(22)

$$\begin{aligned}&=\frac{4y_{K}}{R}(1-\alpha _{K}^{\prime }(y_{K})+\beta _{K}^{\prime } (y_{K})), \end{aligned}$$

(23)

for $K=1,\ldots ,K^{\max }$, where the functions

$$\begin{aligned} \alpha _{K}(x)&=\sum _{k=1}^{K-1}\frac{q_{k}x^{R}}{x^{R}+y_{k}^{R}},\end{aligned}$$

(24)

$$\begin{aligned} \beta _{K}(x)&=\sum _{k=K+1}^{K^{\max }}\frac{q_{k}y_{k}^{R}}{x^{R}+y_{k} ^{R}}, \end{aligned}$$

(25)

may be seen as error terms with respective derivatives $\alpha _{K}^{\prime }(x)$ and $\beta _{K}^{\prime }(x)$.

Ignoring all error terms in (22–23) generates useful initial values for approximate solution vectors $\{y_{k}\}_{k=1}^{K^{\max }}$ and $\{q_{k}\}_{k=1}^{K^{\max }}$. In explicit terms, these initial values are $y_{K}=\frac{R(R-2)^{K-1}}{(R+2)^{K}}$ and $q_{K}=\frac{4(R-2)^{K-1} }{(R+2)^{K}}$, for $K=1,\ldots ,K^{\max }$, as can be verified using a straightforward induction argument. Approximate solutions can then be improved locally at the $K$-th mass point, for any $K=1,\ldots ,K^{\max }$, by solving (22–23) numerically for “updated” values $\widetilde{y}_{K}$ and $\widetilde{q}_{K}$ of $y_{K}$ and $q_{K}$. To ensure a cumulative probability of one, any updated probability vector $(q_{1},\ldots q_{K-1},\widetilde{q}_{K},q_{K+1},\ldots ,q_{K^{\max }},1-\sum _{k=1}^{K^{\max }}q_{k})$ was multiplied through with $1/(1-q_{K} +\widetilde{q}_{K})$. To generate the data for this paper, a Visual Basic macro executed about 40 round-robin iterations of such updating, where $K^{\max }=14$. For any considered value of $R>2$, the procedure always converged to the same distribution, regardless of changes made to initial conditions.