Abstract
Monitoring the time-variable geopotential identifies the mass redistribution across the Earth and reveals, e.g., climate change and availability of water resources. The features of interest are characterized by spatial and temporal scales accessible only through space missions. Among the most important gravity missions are GRACE (2002–2017), its successor GRACE-FO (since 2018), and GOCE (2009–2013), which all sense the Earth’s gravity field via the geopotential derivatives. We investigate the geopotential estimation through frequency comparisons between orbiting clocks by means of the Doppler-canceling technique, describing the clocks’ behavior in the Earth’s gravitational field via Einstein’s general relativity. The novelty of this approach lies in measuring gravity by sensing the geopotential itself. The proof of principle for the measurement is achieved through an innovative mission scenario: for the first time, the observations are collected by a probing clock in LEO. We show gravity solutions obtained by simulating an estimation problem via our proposed architecture. The results suggest that we can conceivably retrieve the geopotential coefficients with accuracy comparable to the GRACE measurement concept by employing clocks with stabilities of order \({10}^{-18}\). Presently, terrestrial clocks can routinely attain fractional frequency stabilities of \({10}^{-18}\), whereas spaceborne clocks are still at the \({10}^{-15}\) level. While our findings are promising, further analysis is needed to obtain more realistic indications on the feasibility of an actual mission, whose realization will be possible when clock technology reaches the required performance. The goal is for the technique investigated in this study to become a future staple for gravity field estimation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Earth’s gravity field is constantly varying as the masses responsible for the generation of the field shift around, both above and below the surface, due to exchanges between land, groundwater, oceans, and atmosphere. The measurement of gravity allows us to study the processes that shape our planet (Cambiotti et al. 2020; Chen et al. 2019; Ghobadi-Far et al. 2020; Girotto and Rodell 2019; Tapley et al. 2019; Velicogna and Wahr 2006a, b). The observation of the mass redistribution on Earth at a global scale was fulfilled only with the advent of space missions. The Challenging Minisatellite Payload (CHAMP) was the first mission dedicated to monitoring the Earth’s gravity (Reigber et al. 2000). The two most recent missions that significantly contributed to the improvement in our knowledge of the geopotential are the Gravity Recovery and Climate Experiment (GRACE), along with GRACE Follow-On (GRACE-FO), and the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE).
GRACE (Tapley et al. 2004a) consisted of two identical satellites in the same orbital plane separated by \(\approx 220 {\text{km}}\). The measurement, represented by the inter-satellite range, was accomplished with low–low satellite–satellite tracking (LL-SST) via a micrometer level K-Band ranging (KBR) system. With this technique, GRACE produced monthly models of the Earth’s time-varying gravity of unprecedented accuracy. GRACE-FO (Pie et al. 2021) has the same working principle as GRACE but, in addition to the microwave interferometer, the relative distance is also obtained by a laser ranging interferometer (LRI). GRACE and GRACE-FO observe gravity through gravimetry, since they measure the integral effects on the twin satellites of the accelerations given by the gradient of the geopotential \(U\). Hence, they are sensitive to the first derivatives of \(U\).
GOCE (Rummel et al. 2011) was the first satellite gravity gradiometry (SGG) mission, whose goal was to accurately map the static part of the Earth’s gravity field (Brockmann et al. 2014). Inserted into a Sun-synchronous orbit at an altitude of \(\approx 250 {\text{km}}\) and equipped with active drag-free control, it determined the geoid height at the \({\text{cm}}\) level with spatial resolution of \(100 {\text{km}}\) thanks to three orthogonally mounted one-axis gradiometers placed at the satellite’s center of mass. The measurement, based on the principle of differential accelerometry, was obtained after a complex filtering process (Schuh 2003). The resulting observable consisted of a square matrix of dimension \(3\) containing the gravity gradients. Thus, GOCE sensed the second derivatives of \(U\).
GRACE/GRACE-FO and GOCE provide examples of the techniques devised to monitor Earth’s gravity and bring benefits to society in the form of practical applications (Pail et al. 2015; van der Meijde et al. 2015), e.g., quantification of changes in water storage on land, ice mass loss, global sea level rise, and oceans’ circulation. Therefore, it is of the utmost importance that we research new methods for observing gravity that would allow us to improve our knowledge of the geopotential and discern those features of the mass transport on Earth that were previously undetected.
1.1 Background and earlier works
In this paper, we investigate the estimation of the geopotential \(U\) by means of the frequency shift (FS) to which electromagnetic signals traveling in the Earth’s gravitational field are subjected. Mathematically, this phenomenon is described by the general theory of relativity (GR) published by Albert Einstein in 1915 (Einstein 1997). One of the three tests of GR suggested by Einstein is indeed the redshift of spectral lines, which is a test of the principle of equivalence (EP) that guided him in his formulation of GR. A major progress in the experimental evidence of the redshift was provided by Pound and Rebka (1960). In the meantime, discussions about the empirical validation of the EP by comparing a clock on Earth with a clock on an artificial satellite had appeared (Hoffmann 1957; Jenkins 1969; Refsdal 1962; Singer 1956). Hafele and Keating (1972) flew four cesium beam atomic clocks on commercial jet flights and, comparing them to clocks on the ground, found the accrued time differences to agree reasonably well with the predicted GR values.
Later, using a two-way communication system for the implementation of the Doppler-canceling (DC) technique (Kleppner et al. 1970), the GP-A experiment confirmed the EP by measuring the FS between a terrestrial hydrogen maser and a similar clock placed on a rocket (Vessot and Levine 1979; Vessot et al. 1980). By now, the EP has been extensively tested with a wide variety of methods, largely space-based, among which the comparison of atomic clocks still plays an important role (Abuter et al. 2018; Asenbaum et al. 2020; Ashby et al. 2018; Delva et al. 2018; Hermann et al. 2018; Litvinov et al. 2018; Touboul et al. 2022; Voisin et al. 2020; Will 2014). Yet, GR is not regarded as the ultimate theory of gravitation because of its incompatibility with quantum mechanics (QM), and violations of its underlying EP are expected when accurate enough tests will be possible (Damour 2012).
In light of the wealth of tests, it is reasonable to view GR as correct and approach the problem of inferring \(U\) by utilizing precise frequency standards. In fact, this is one of the tasks of chronometric geodesy (Delva and Geršl 2017; Delva et al. 2019). Then, it is logical to explore the application of chronometric geodesy in space by measuring the FS of signals exchanged between distant clocks in motion relative to each other within the Earth’s gravity field and thus calculate the geopotential difference \(\Delta U\) between the clocks’ locations. The fundamental relation allowing us to deduce \(U\) is the gravitational part of the FS, which is explicitly caused by \(\Delta U\).
In recent years, there have been studies about using the FS to compute \(\Delta U\) between two arbitrary points on Earth (Shen et al. 2011) and between a transmitter in low Earth orbit (LEO) and a ground receiver (Mayrhofer and Pail 2012). Subsequently, Shen et al. (2016, 2017) simulated experiments in which they measured \(U\) at a ground station and \(\Delta U\) between two ground stations by means of the FS of transmitted signals via one or more satellites. They employed the FS calculated through the DC technique, that is, the Doppler-canceled FS (Ashby 1998; Blanchet et al. 2001), which will be referred to as DCFS hereafter. Afterward, Müller et al. (2018) carried out, via an error propagation tool, an accuracy assessment of the Earth’s global gravity field recovery by means of DCFS measurements. In their mission scenario, the signals were continuously exchanged between perfect terrestrial clocks and a spaceborne clock with a frequency stability of \(10^{ - 18}\) in a polar LEO of \(250 {\text{km}}\) altitude. They concluded that, for such a gravity field determination, the position and velocity of the spaceborne clock must be known with very high precisions. Furthermore, real experiments have been conducted where \(\Delta U\) between two ground clocks was obtained utilizing existing satellite links (Shen et al. 2019; Wu et al. 2020).
Müller and Wu (2020) evaluated the sensitivity to Earth’s gravity of simulated cold atom interferometry (CAI) gradiometers and clocks observables. Either by direct laser link or via relay satellites in higher orbit, they compared the frequency between a target clock in LEO and a network of clocks on the ground, inferring \(\Delta U\) from the measured FS. The measurement uncertainty was assumed to be between \(10^{ - 19}\) and \(10^{ - 17}\), and they modeled the frequency instability of the clocks with white noise. Migliaccio et al. (2023) and Rossi et al. (2023) examined a mission providing measurements of the Earth’s gravity field and its temporal variations in which satellites, orbiting in a GRACE-like formation, carry on board CAI gradiometers and clocks. Frequency comparisons between adjacent satellites produce the \(\Delta U\) values through optical links. They modeled the clocks’ measurement errors as white noise with zero mean and standard deviation of a few parts in \(10^{18}\). Lastly, Shen et al. (2023) investigated the geopotential recovery via DCFS measurements between a clock in LEO and clocks in geosynchronous equatorial orbit (GEO). They modeled the frequency instability, assumed to be in the range from \(10^{ - 17}\) to \(10^{ - 13}\), with white noise and random walk. Despite differences in method, in Sect. 6 we will compare our results to the solutions from the studies cited in this paragraph obtained with clocks’ observables only.
1.2 Goal of this study
We consider an estimation problem whose objective is to determine the time-variable gravity field of the Earth by means of DCFS measurements. We do not contemplate gradiometric measurements at this stage, since they have already been considered in some of the aforementioned works. We propose to monitor the global gravity variations by recovering the average gravity during a monthly sampling interval. For a well-conditioned solution, it is necessary to collect a global set of measurements within the defined estimation interval. In order to attain global coverage of the Earth, we simulate a mission scenario where the DCFS observables are collected along the trajectory of a satellite-borne clock, placed in a circular polar LEO at an altitude \(h \cong 500 {\text{km}}\). Subsequently, we utilize the resulting DCFS spatial sampling in the implementation of the estimation process to solve for the spherical harmonic coefficients (SHC) of the series representation of the geopotential \(U\). Our approach consists in computing the observables between the clock in LEO, which we denote as the probing clock \(A\), and reference clocks \(B\) placed in GEO (Giuliani 2022). The innovation of our mission design consists in the fact that the DCFS measurements are collected by clock \(A\), which probes Earth’s gravity. The main objective of this work is to provide a proof of concept for the mission under consideration and identify the necessary frequency stability of the clocks to produce satisfactory gravity solutions. Although we use a number of simplifying assumptions, our simulation accounts for the significant effect of the imperfect knowledge of \(A\)’s orbit on the quality of the solution. Because the gravitational part of the DCFS is caused by the geopotential difference \(\Delta U\) between the locations of the clocks involved, the measurement is sensitive to \(U\) itself.
The paper is organized as follows. Section 2 summarizes the role played by clocks in chronometric geodesy together with their level of performance, providing a background to infer the required technological advancement for the proposed gravity mission based on our findings. In Sect. 3, we introduce the GR metric tensor in the Geocentric Celestial Reference System (GCRS) and provide formulations for the time transfer and the DCFS. We also calculate the consequences of non-gravitational forces on the time kept by a clock. In Sect. 4, after some preliminary considerations, we describe the architecture of the gravity mission and the objectives of the simulation. Section 5 outlines the numerical implementation of the estimation process, explaining the employed kinematical approach. In Sect. 6, we show and interpret the results for the SHC obtained by solving the estimation problem. Finally, Sect. 7 contains the conclusions, including a discussion of how we can improve on the present analysis. The assumptions adopted throughout the study are stated in the appropriate sections. In the following, the reader interested in greater detail is referred to Giuliani (2022).
2 Clocks and chronometric geodesy
Currently, optical clocks (OC) are the best frequency standards available. Given adequate averaging times, stationary OC can routinely reach a fractional frequency stability of \(10^{ - 18}\) (Kolkowitz and Ye 2021; Ludlow et al. 2015; McGrew et al. 2018). Campaigns using transportable OC (TOC) have demonstrated uncertainties of \(1.9 \times 10^{ - 15}\) over \(90 {\text{km}}\) (Grotti et al. 2018) and \(4.3 \times 10^{ - 18}\) across a \(450 {\text{m}}\) vertical separation (Takamoto et al. 2020). The realization of space-qualified clocks is more complicated, although microgravity could improve the performance of some atomic clocks. Global Navigation Satellite System (GNSS) satellites carry microwave clocks (MC) with instabilities in the \(10^{ - 15}\) range between \(10^{4} \) and \(10^{6} {\text{s}}\) (Hollberg 2021). The Cold Atom Clock Experiment in Space (CACES) mission succeeded in operating a laser-cooled rubidium clock on the Tiangong space station (Liu et al. 2018) with a stability close to \(3 \times 10^{ - 13}\) at \(1 {\text{s}}\). The Deep Space Atomic Clock (DSAC) mission validated a mercury trapped-ion clock for independent navigation, showing a stability of \(\approx 3 \times 10^{ - 15}\) at \(23 {\text{d}}\), an estimated drift of \(\approx 3 \times 10^{ - 16} /{\text{d}}\), and low sensitivity to changes in radiation, temperature, and magnetic fields (Burt et al. 2021). Scheduled to be launched to the International Space Station (ISS) in the near future, the Atomic Clock Ensemble in Space (ACES) mission (Cacciapuoti and Salomon 2011) will carry a clock based on samples of laser-cooled cesium atoms and an active hydrogen maser, generating a time scale with instability and inaccuracy of a few parts in \(10^{16}\) (Heß et al. 2011). The Space Optical Clocks (SOC) and SOC2 projects (Bongs et al. 2015) aim at installing an OC, presumably based on bosonic strontium (Origlia et al. 2018), on the ISS targeting an instability below \(10^{ - 15}\) at \(1 {\text{s}}\) and an inaccuracy below \(5 \times 10^{ - 17}\).
The working principle of chronometric geodesy (CG), which has numerous purposes (Bjerhammar 1985; Bondarescu et al. 2015; Mehlstäubler et al. 2018; Müller et al. 2018; Tanaka and Katori 2021), is to convert the FS between separated clocks on the Earth’s surface into gravity potential (geopotential \(U\) plus centrifugal potential) differences. The high sensitivity of OC allows for the implementation of CG and the accurate determination of \(\Delta U\) (a FS of \(10^{ - 18}\) corresponds to a height difference of \(\approx 1 {\text{cm}}\) near the Earth). Furthermore, with precise knowledge of the clocks’ positions, \(\Delta U\) profiles can be employed for gravity field recovery. The basic idea of the geopotential estimation by means of satellite-borne clocks, which is the focus of the present study, is to apply CG in space. Demonstration of geopotential mapping via the gravitational FS is one of the tasks of ACES, whose main goal is to test fundamental physics including searching for violations of the EP. The necessary links for distant clocks comparisons can be accomplished in different ways (Riehle 2017) and, usually, are not a limiting factor for time and frequency transfer (TFT). On the Earth’s surface, OC can be connected through telecommunication fibers (Lisdat et al. 2016; Takano et al. 2016). When the clocks are in motion, the signals have to be exchanged through free space (Bergeron et al. 2019; Bodine et al. 2020; Shen et al. 2022).
Free-space comparisons by means of satellite links are carried out by either reception of signals from GNSS satellites or two-way techniques (Bauch 2015). Global Positioning System (GPS) measurements of radio frequency code and microwave carrier phase can be combined through precise point positioning (PPP) techniques to reach uncertainties of \(\approx 10^{ - 15}\) at \(1 {\text{d}}\) and close to \(10^{ - 16}\) at \(30 {\text{d}}\) (Petit et al. 2015). Furthermore, the Integer-PPP (IPPP) technique allowed to obtain an uncertainty of \(10^{ - 16}\) between \(3 \) and \(5 {\text{d}}\) across two laboratories \(270 {\text{km}}\) apart, achieving a low-\(10^{ - 17}\) regime at above \(10 {\text{d}}\) (Petit et al. 2017). The two-way satellite TFT (TWSTFT) technique, which compares clocks by exchanging microwave signals via telecommunication satellites in GEO, has uncertainty of \(\approx 10^{ - 15}\) at \(1 {\text{d}}\) over \(2080 {\text{km}}\) (Huang et al. 2016), improving to a few parts in \(10^{16}\) beyond \(2 \times 10^{3} {\text{s}}\) over \(9000 {\text{km}}\) using the carrier phase (Fujieda et al. 2014). The MicroWave Link (MWL) instrument, which will be employed by ACES to compare the clocks on board the ISS with ground clocks, has a projected instability below \(10^{ - 16}\) at \(1 {\text{d}}\) and \(\approx 2 \times 10^{ - 17}\) at \(10 {\text{d}}\) (Schäfer and Feldmann 2016). The experimental European Laser Timing (ELT) optical link, an evolution of the time transfer by laser link (T2L2), will also be part of ACES.
3 Relativistic theory
3.1 Post-Newtonian metric tensor of the GCRS
The relativistic formulation utilized in this paper is based on the framework suggested by the IAU 2000 Resolutions B1.3–B1.5 (International Astronomical Union 2000; Soffel et al. 2003), which was established by two formalisms. One is due to Kopeikin (1988, 1990), Brumberg and Kopeikin (1989), Brumberg (1991), and Klioner and Voinov (1993), whereas the other was developed by Damour et al. (1991, 1992, 1993, 1994). In the following, we adopt the notation according to which greek and latin indices, respectively, can take on the values from \(0\) to \(3\) and \(1\) to \(3\); we use the Einstein summation convention for repeated indices. All our calculations will be carried out in the GCRS, whose coordinates are \(x^{\mu } = \left( {ct x y z} \right)\), where \(t\) is the Geocentric Coordinate Time (TCG) and \(c\) is the speed of light in vacuum. TCG differs from the Terrestrial Time (TT) by a constant rate (Petit and Luzum 2010): their difference is equal to \({\text{TCG}} - {\text{TT}} = \left[ {L_{G} /\left( {1 - L_{G} } \right)} \right]\left( {{\text{JD}}_{{{\text{TT}}}} - {\text{T}}_{0} } \right) \times 86400 {\text{s}}\), where \(L_{G} = 6.969290134 \times 10^{ - 10}\) is a defining constant, \({\text{JD}}_{{{\text{TT}}}}\) is the TT Julian date, and \({\text{T}}_{0} = 2443144.5003725\).
The main quantity that needs to be defined is the metric tensor \(g_{\mu \nu }\) of the GCRS. Imposing the harmonic coordinate conditions and modeling the Earth as a non-relativistic perfect fluid (Will 2018) the post-Newtonian metric tensor, including terms up to order \(c^{ - 2}\), can be written as
where the Kronecker delta \(\delta_{ij}\) (\(\delta_{ij} = 1\) if \(i = j\) and \(0\) otherwise) represents the metric tensor of Euclidean space. In the International Terrestrial Reference System (ITRS), related to the GCRS by a rotation (Petit and Luzum 2010), the gravitational potential \(U\) in Eq. 1 can be expanded outside the Earth as (Heiskanen and Moritz 1967)
where \(r\) is the radius, \(\lambda\) the longitude, and \(\phi\) the latitude, \(l\) is the degree and \(m\) the order, \(\overline{P}_{lm}\) is the fully normalized Legendre associated function, \(\overline{S}_{lm}\) and \(\overline{C}_{lm}\) are the fully normalized SHC, and \(GM\) and \(R\) are the Earth’s gravitational parameter and equatorial radius.
3.2 Coordinate time transfer
For a massless particle like the photon, the mathematical treatment is simplified by using the geometrical optics assumption (Landau and Lifshitz 1975; Misner et al. 2017), valid for electromagnetic waves with sufficiently high frequency. This allows us to idealize the wave as a light ray with direction of propagation determined by the wave vector \(k^{\mu } = dx^{\mu } /d\vartheta\), where \(\vartheta\) is an independent parameter varying along the ray. Since \(k^{\mu } k_{\mu } = 0\), the null geodesic equation governing the photon’s motion in curved spacetimes (Weinberg 1972) can be manipulated to obtain the covariant equations of motion, with which it is possible to work out the photon’s trajectory onto its orbital plane and produce an expression for the time of flight as a function of the radius (Blanchet et al. 2001).
Let us suppose that an electromagnetic signal \(\psi\) is transmitted from a clock \(B\) at \(t_{B}\) and received by clock \(A\) at \(t_{A}\). The position \(\vec{x} = \left( {x y z} \right)\), velocity \(\vec{v} = d\vec{x}/dt\), acceleration \(\vec{a} = d\vec{v}/dt\), and geopotential \(U\) of \(A\) and \(B\) are denoted by \(\vec{x}_{A}\), \(\vec{v}_{A}\), \(\vec{a}_{A}\), and \(U_{A}\) and \(\vec{x}_{B}\), \(\vec{v}_{B}\), \(\vec{a}_{B}\), and \(U_{B}\). We can compute the coordinate time transfer, i.e., \(t_{BA} = t_{A} - t_{B}\), through the time of flight formula. The result contains the Newtonian contribution of order \(c^{ - 1}\) plus a relativistic correction of order \(c^{ - 3}\) known as Shapiro time delay (Shapiro 1964). However, the expression of \(t_{BA}\) includes quantities referred to \(t_{B}\) as well as \(t_{A}\): it is convenient to rewrite \(t_{BA}\) so that only \(t_{A}\) is involved. This can be achieved by a Taylor expansion around \(t_{A}\) of the quantities at \(t_{B}\) which, to order \(c^{ - 3}\), leads to (Giuliani 2022)
where \({\overrightarrow{d}}_{BA}={\overrightarrow{x}}_{A}\left({t}_{A}\right)-{\overrightarrow{x}}_{B}\left({t}_{A}\right)\) is the instantaneous distance vector, \({d}_{BA}=\left|{\overrightarrow{d}}_{BA}\right|\), \({r}_{A}=\left|{\overrightarrow{x}}_{A}\left({t}_{A}\right)\right|\), and \({r}_{B}=\left|{\overrightarrow{x}}_{B}\left({t}_{B}\right)\right|\). The second and fourth terms on the right-hand side are indicated as Sagnac corrections of order \({c}^{-2}\) and \(c^{ - 3}\).
3.3 One-way FS
The velocities of clocks \(A\) and \(B\) and the different values of \(U\) at their respective locations will cause a FS of the signal \(\psi\) as it travels along its path from \(B\) to \(A\). As far as the gravitational FS is concerned, only the relative FS between two points can be measured by clocks: the absolute FS at a point cannot be detected since the clock’s frequency standards and the phenomenon being observed are equally affected by gravitation (Weinberg 1972). To calculate the one-way (1W) FS, we introduce the wave surface \(S\) (Fock 1964; Synge 1960), upon which the phase \(\Phi\) of the propagating wave takes on everywhere the same constant value and whose equation can be written as \(S = h\Phi /2\pi\) (\(h\) is an infinitesimal constant, e.g., Planck constant). \(\Phi\) varies solely in the direction of propagation of the wave, i.e., the normal \(k_{\mu } = S_{,\mu }\) to \(S\). Let us suppose that an observer, with proper time \(\tau\) and four-velocity \(U^{\mu } = dx^{\mu } /d\tau\), intersects the surfaces of the signal \(\psi\) and, after moving by \(dx^{\mu }\), experiences a change \(dS = h\). Since this corresponds to a change in \(\Phi\) by \(2\pi\), it follows that the elapsed \(d\tau\) necessarily coincides with the period of the wave, whose frequency is then \(f = d\tau^{ - 1}\).
Applying this reasoning to both \(A\) and \(B\) , we obtain \(f_{A}\) and \(f_{B}\), which designate \(\psi\)’s frequency as observed by \(A\) at \(t_{A}\) and \(B\) at \(t_{B}\). We remark that, although \(f_{A}\) and \(f_{B}\) are both reciprocals of proper time intervals, \(f_{B}\) is the actual proper frequency of \(\psi\) (what would be observed if the source were at rest in flat spacetime). We denote this proper frequency as \(\tilde{f}\) and substitute \(f_{B}\) with \(\tilde{f}\). Moreover, we assume that all clocks adopt the same \(\tilde{f}\) as fundamental frequency to generate signals and perform time and frequency comparisons. For instance, \(\tilde{f}\) would be the frequency standard provided by the transition upon which the clock is based. Then, the 1WFS is the ratio \(f_{A} /\tilde{f}\), which can be computed by means of the line element \(c^{2} d\tau^{2} = - g_{\mu \nu } dx^{\mu } dx^{\nu }\) and Eq. 3 (Blanchet et al. 2001). The final expression can be further expanded in powers of \(c^{ - 1}\) (Giuliani 2022): to order \(c^{ - 2}\), it becomes
where \({\widehat{n}}_{BA}={\overrightarrow{r}}_{BA}/{r}_{BA}\), \({\overrightarrow{r}}_{BA}={\overrightarrow{x}}_{A}\left({t}_{A}\right)-{\overrightarrow{x}}_{B}\left({t}_{B}\right)\), \({r}_{BA}=\left|{\overrightarrow{r}}_{BA}\right|\), \(\Delta \overrightarrow{v}={\overrightarrow{v}}_{A}\left({t}_{A}\right)-{\overrightarrow{v}}_{B}\left({t}_{B}\right)\), \({v}_{A}=\left|{\overrightarrow{v}}_{A}\left({t}_{A}\right)\right|\), \({v}_{B}=\left|{\overrightarrow{v}}_{B}\left({t}_{B}\right)\right|\), and \(\Delta U={U}_{A}\left({t}_{A}\right)-{U}_{B}\left({t}_{B}\right)\). The second term on the right-hand side involves the Doppler shift (DS) of order \({c}^{-1}\) and could cause either a redshift or a blueshift. The last two terms of order \({c}^{-2}\) are a consequence of the gravitational and special-relativistic time dilations, respectively, and always give rise to a blueshift.
3.4 Necessity to eliminate the DS of order \({{\varvec{c}}}^{-1}\)
We cannot employ the 1WFS to retrieve the SHC (Müller et al. 2018; Shen et al. 2016). To show this, we assess the errors with which the quantities in the 1WFS equation must be known to determine \(\Delta U\) with sufficient accuracy (Giuliani 2022). Propagating the uncertainties (assumed to be independent and random) on Eq. 4, we get
The first equality relates the measurement error to the instrumentation error. The latter is assumed to be caused by the fractional frequency instability of the clocks \(A\) and \(B\), supposed identical and given by \(\delta {f}_{A}/{f}_{A}=\delta {f}_{B}/{f}_{B}=\delta f/\widetilde{f}\). We immediately find that the constraint on the DS is several orders of magnitude smaller than what is presently attainable with precise orbit determination (POD). In fact, using \(\delta f/\widetilde{f}={10}^{-18}\) and equating the left-hand side to the first term on the right-hand side, we calculate \(\delta \left({\widehat{n}}_{BA}\bullet \Delta \overrightarrow{v}\right)\lesssim 4.2\times {10}^{-10} \text{m}/\text{s}\). If we instead suppose to have access to any component of the velocities with a precision \(\delta v={10}^{-6} \text{m}/\text{s}\), the corresponding DS error is \(\approx 4.7\times {10}^{-15}\), which would completely dominate over the measurement error. On the other hand, the errors from the third and fourth terms do not represent a limitation. Therefore, it is clear that we must necessarily eliminate the DS of order \({c}^{-1}\). Lastly, \(\delta f/\widetilde{f}={10}^{-18}\) yields the uncertainty \(\delta \left(\Delta U\right)\approx 1.3\times {10}^{-1} {\text{m}}^{2}/{\text{s}}^{2}\).
3.5 Two-way FS
Let us consider the case where clock \(A\) initially emits the signal \(\psi \) of frequency \(\widetilde{f}\) , whereas clock \(B\), upon reception, transponds \(\psi \) back to \(A\). It is important that \(\psi \) is transponded coherently: \(B\) employs \(\widetilde{f}\) to determine \(\psi \)’s frequency \({f}_{B}\), which will be the same frequency of the signal (a replica of the received \(\psi \)) transmitted back to \(A\). We assume that \(B\) can instantaneously transpond \(\psi \): \({t}_{B}\) represents the instant when \(B\) receives and transponds \(\psi \). Finally, \(\psi \) will have frequency \({f}_{A}\) when received by \(A\). Thus, the 1WFS to which \(\psi \) is subjected during each leg will compound, indicating the resulting effect as two-way (2W) FS. To derive the 2WFS, we must multiply out the two 1WFS. Equation 4 directly applies to \({f}_{A}/{f}_{B}\) of the second leg (where \(A\) refers to the instant of final reception). Nevertheless, we have to swap \(A\) and \(B\) to obtain \({f}_{B}/\widetilde{f}\) for the leg from \(A\) to \(B\) (where \(A\) refers to the instant of initial transmission). The need to distinguish which instant each subscript \(A\) refers to can be removed with a Taylor expansion of the quantities evaluated at the initial transmission around the instant of final reception, which we indicate without confusion as \({t}_{A}\). Then, computation of the 2WFS (Giuliani 2022) to order \({c}^{-2}\) produces
where all quantities can be defined as above keeping in mind the meaning of \({t}_{A}\) and \({t}_{B}\) in this context. As we can see, the DS of order \({c}^{-1}\) is twice that of Eq. 4. Moreover, at this level of approximation, we note the vanishing of the gravitational FS and the appearance of a term including the acceleration \({\overrightarrow{a}}_{A}\) of \(A\) at \({t}_{A}\).
3.6 Formulation of the DCFS
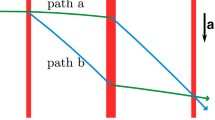
The DC technique (Kleppner et al. 1970; Vessot and Levine 1979) consists in combining Eqs. 4 and 6 with the goal to eliminate the DS of order \({c}^{-1}\) and yield the DCFS. To this purpose, we suppose the two sequences of events illustrated in Fig. 1 to occur. Firstly, clock \(A\) transmits a signal \({\psi }_{1}\) to clock \(B\), which coherently transponds \({\psi }_{1}\) back to \(A\). Secondly, \(B\) transmits an additional signal \({\psi }_{2}\), independent of \({\psi }_{1}\), to \(A\). Also, we make the following two assumptions: \(B\) simultaneously receives/transponds \({\psi }_{1}\) (we neglect the transponder delay) and transmits \({\psi }_{2}\) at \({t}_{B}\); \({\psi }_{1}\) and \({\psi }_{2}\) travel along the same path from \(B\) to \(A\) and are received by \(A\) at the final instant \({t}_{A}\). With this understanding, the definitions of the quantities in the formulae for the 1WFS of \({\psi }_{2}\) and the 2WFS of \({\psi }_{1}\) are still valid. Upon reception, \(A\) can then compute the DCFS which, to order \({c}^{-3}\), takes the form (Ashby 1998; Blanchet et al. 2001; Giuliani 2022)
where \(\overrightarrow{\nabla }{U}_{A}=\left({U}_{A,x} {U}_{A,y} {U}_{A,z}\right)\) is the gradient of \({U}_{A}\) (rotated from the ITRS to the GCRS) and \({\overrightarrow{j}}_{A}=d{\overrightarrow{a}}_{A}/dt\) is the jerk of \(A\), both evaluated at \({t}_{A}\). The first two terms of order \({c}^{-2}\) in parentheses on the right-hand side represent the general-relativistic FS: they are, respectively, the gravitational FS and special-relativistic redshift. The third term, involving \({\overrightarrow{a}}_{A}\), was introduced by the Taylor expansion about \({t}_{A}\). Equation 7 is the measurement employed to recover the Earth’s gravity field in the estimation problem. From a theoretical point of view, it is essential that both \(A\) and \(B\) are syntonized to \(\widetilde{f}\) if the DCFS measurement is to provide truthful information about the geopotential. In particular, \(A\) must produce \({\psi }_{1}\) of frequency \(\widetilde{f}\) and determine the FS of the received \({\psi }_{1}\) and \({\psi }_{2}\) by comparing them against \(\widetilde{f}\), whereas \(B\) must rely on \(\widetilde{f}\) to coherently transpond \({\psi }_{1}\) and produce \({\psi }_{2}\) of frequency \(\widetilde{f}\).
Let us consider the probing clock \(A\) in LEO and a reference clock \(B\) in GEO. At closest approach, the value of the terms of order \({c}^{-2}\) on the right-hand side of Eq. 7 is, respectively, \(\approx 5.4\times {10}^{-10}\), \(\approx -3.7\times {10}^{-10}\), and \(\approx -3.3\times {10}^{-9}\). Instead, for geometries where the clocks and the Earth’s center of mass form a right triangle (similar to the configuration just before the visibility between the two clocks is lost), the same terms can amount to \(\approx 5.4\times {10}^{-10}\), \(\approx -6.4\times {10}^{-10}\), and \(\approx 6.4\times {10}^{-10}\). The terms of order \({c}^{-3}\) are about \({10}^{-5}\) times smaller. Due to the clocks’ orbits, the gravitational FS coincides with a blueshift and, unlike the special-relativistic redshift, is approximately constant. In contrast, the acceleration term can cause either a redshift or a blueshift according to the sign of \({\overrightarrow{r}}_{BA}\bullet {\overrightarrow{a}}_{A}\). We remark that the DCFS was derived without accounting for perturbations from other solar system bodies and Earth’s solid and ocean tides. Also, the coordinate part of the FS was computed modeling the Earth as a monopole (the effect of \({C}_{20}\) does not exceed \(4\times {10}^{-17}\)). Hence, the accuracy level of Eq. 7 is \(5\times {10}^{-17}\) (Blanchet et al. 2001). In the Earth’s vicinity, the terms of order \({c}^{-4}\) do not exceed a few parts in \({10}^{19}\) (Wolf and Petit 1995).
Lastly, ignoring terms of order \({c}^{-3}\) in Eq. 7 and propagating the uncertainties, we get
The first equality relates the measurement error to the instrumentation error, which is assumed to be caused by the instability \(\delta f/\widetilde{f}\) of \(A\) and \(B\). Taking \(\delta f/\widetilde{f}={10}^{-18}\), the measurement error is \(\approx 1.7\times {10}^{-18}\). Instead, utilizing \(\delta v={10}^{-6} \text{m}/\text{s}\) for the uncertainty of the velocity components for both clocks \(A\) and \(B\), the contribution from the second term on the right-hand side is at most \(\approx 1.7\times {10}^{-19}\) and therefore does not represent a limitation. Conversely, \(\Delta U\) and \({\overrightarrow{r}}_{BA}\bullet {\overrightarrow{a}}_{A}\) can be computed with an uncertainty of \(\approx 1.1\times {10}^{-1} {\text{m}}^{2}/{\text{s}}^{2}\). However, what can be accomplished with a certain \(\delta f/\widetilde{f}\) in terms of the uncertainty with which we can recover the SHC can only be evaluated by simulating an estimation problem.
3.7 Influence of non-gravitational forces
A clock in the Earth’s proximity will be acted upon by non-gravitational (NG) forces \({f}_{NG}^{\mu }\) which modify the relation between its proper time \(\tau \) and \(t\) (Weinberg 1972). To quantify this effect, we differentiate \({g}_{\mu \nu }{U}^{\mu }{U}^{\nu }\) with respect to \(\tau \), where \({U}^{\mu }\) is the clock’s four-velocity, and employing the clock’s equations of motion, we find (Giuliani 2022)
where \(m\) is the clock’s rest mass. It follows that the line element formula \({c}^{2}{d\tau }^{2}=-{g}_{\mu \nu }{dx}^{\mu }{dx}^{\nu }\) ceases to be valid and must be adjusted by a term \(\mathcal{D}\) which considers the influence of \({f}_{NG}^{\mu }/m\) along the clock’s trajectory. For clock \(A\), supposing the non-gravitational acceleration to be opposite to the velocity and to have magnitude \(\approx {10}^{-7} \text{m}/{\text{s}}^{2}\), and using \({g}_{\mu \nu }\) given by Eq. 1, yields \({\mathcal{D}}/c^{2} \approx - 3.4 \times 10^{ - 20} s^{ - 1} \times \Delta t\), where \(\Delta t\) represents the elapsed time. For \(\Delta t\approx 3\times {10}^{3} \text{s}\), the contribution of \(\mathcal{D}/{c}^{2}\) reaches the accuracy of Eq. 7. For simplicity, in the following, we assume the spacecrafts carrying the clocks to be equipped with a drag-free control system to counteract the non-gravitational forces: the total \({f}^{\mu }\) vanishes and the clocks travel along a geodesic. Therefore, we can regard the equations provided in Sect. 3 as correct. The alternative would be to rewrite the equations including \(\mathcal{D}\) and suppose that its effect can be accounted for by measuring \({f}_{NG}^{\mu }/m\) with precise onboard accelerometers.
4 Concept of the simulated gravity mission
4.1 Preliminary theoretical considerations
The method employed to detect gravity characterizes the region of the geopotential spectrum that can be retrieved more effectively. For instance, GRACE/GRACE-FO and GOCE provide more accurate gravity models at the low-to-mid and mid-to-high degrees of \(U\), respectively. Moreover, the components of the gravity field of degree \(l\) decrease as \({r}^{-\left(l+1\right)}\) away from the geocenter, with each spatial derivative producing an additional factor \({r}^{-1}\). Since the proposed estimation technique observes \(U\) directly, we expect the DCFS measurement to somewhat mitigate the altitude attenuation and potentially improve the knowledge of the lower degrees of the spectrum, i.e., the longer spatial wavelengths capturing most of the geopotential time-variability we are primarily attempting to recover.
The gravity signal produced by the SHC experienced by the probing clock \(A\) contains frequencies of twice per orbit and higher (we set the degree \(1\) SHC equal to zero, consistent with the assumption that the geocenter coincides with the GCRS origin). Consequently, the error in the computation of the DCFS measurement due to the uncertainty in the SHC will have the same frequencies. The orbit error, i.e., the imperfect knowledge of the position and velocity of the clocks, is mainly due to errors in the clocks’ initial conditions, in the SHC, and in the force model. Hence, the orbit error largely contributes to the DCFS error with a frequency of once per orbit, or equivalently \(1\) CPR (cycle-per-revolution), but it generates components both of higher and lower frequencies as well (the \(1\) CPR error is about three and six orders of magnitude, respectively, greater than the errors due to \({C}_{20}\) and the rest of the SHC).
Considering the previous remarks, we selected a LEO of altitude \(h\cong 500 \text{km}\) for \(A\), which should provide a good balance between mission duration and quality of the solutions. Also, in order to capture the time-variable geopotential, we chose to estimate a square gravity field of maximum degree \(l\) and order \(m\) given by \(d=60\). Then, the half-wavelength spatial resolution of the field is \(\pi R/d\cong 334 \text{km}\). The duration of the sampling interval \({t}_{s}\) with which the DCFS measurements are collected should be based on \(d\) in order for the field’s resolution and the size of the sampled region to be comparable. Thus, we chose \({t}_{s}=40 \text{s}\) which, when multiplied by the speed of \(A\), yields \({v}_{A}{t}_{s}\cong 305 \text{km}\). A longer \({t}_{s}\) could possibly limit the observability of the SHC of higher degree even further, since their influence would be averaged out.
Furthermore, we can state that the DCFS error components of frequency \(1\) CPR and lower are outside our bandwidth of interest. This is because the components of the gravity signal necessary for the determination of \(U\), i.e., those generated by the SHC, have frequencies of \(2\) CPR and higher. To this regard, the signal produced by a reference clock \(B\) in GEO is outside the bandwidth of interest, even though \(B\) is influenced by the SHC too. In fact, because of its high altitude and almost fixed location with respect to the Earth, \(B\) cannot be used as a probing clock. Then, its gravity signature in the DCFS observable, which will have frequencies much lower than \(2\) CPR since \(B\) is slowly moving, can be considered outside the useful bandwidth. In the following, we are going to make the simplifying assumption that the effects whose contributions are outside the bandwidth of interest can be ignored.
4.2 Mission architecture and objectives
The SHC represent global features of the Earth’s gravity field and estimating the geopotential \(U\) and its temporal variations by means of DCFS measurements from space demands assembling a coherent global data set: a circular polar LEO for the probing clock \(A\) is the only possibility. Then, to have a high signal-to-noise ratio we must maximize the terms of order \({c}^{-2}\) in Eq. 7 containing the SHC, i.e., \(\Delta U\) and \({\overrightarrow{r}}_{BA}\bullet {\overrightarrow{a}}_{A}\). Large magnitudes can simply be achieved by placing \(A\) and the reference clocks \(B\) at great radial distances, implying that \(B\) must be either on the Earth’s surface or in orbits of sufficiently higher altitude. In order to compare the two scenarios, we computed \(\Delta U/{c}^{2}\) values for a few SHC (Giuliani 2022): while this provides only an indication we infer that, to place the clocks \(B\) in orbit, the latter must be at least a GEO for this configuration to be competitive. Conversely, the magnitude of \({\overrightarrow{r}}_{BA}\bullet {\overrightarrow{a}}_{A}/{c}^{2}\) can become up to \(\cong 70\) times greater with respect to \(B\) on the ground.
We must also consider that, besides requiring a continuous link between \(A\) and \(B\) during \({t}_{s}\), the DCFS observables need to be collected consecutively. With \(B\) on the ground, each pass of \(A\) lasts \(\cong 10 \text{min}\). Hence, either we have a dense network of clocks on the Earth’s surface or, more reasonably, employ a few ground clocks and utilize satellite links. The latter’s downside is the further complication of the DCFS measurement concept. Instead, with \(B\) in GEO, two clocks would be enough for the uninterrupted visibility of \(A\): each clock could directly exchange signals with \(A\) for extended periods, and the DCFS observables can be obtained without relay satellites.
An additional element to consider is the neutral and non-neutral atmosphere. The troposphere represents the main source of systematic error in the lower part, whereas the ionosphere plays the major role from \(\cong 50 \text{km}\). The atmosphere will cause a certain \(1\) W signal delay which can be largely compensated for by the DC technique, permitting a drastic cancelation of the error (Kleppner et al. 1970). The maximum magnitude of the fractional FS induced by the troposphere and ionosphere, respectively, in the DCFS measurement realized with microwave signals between a ground clock and a clock on a GPS orbit is \(\approx 9.5\times {10}^{-19}\) and \(\approx 2.7\times {10}^{-18}\) (Shen et al. 2017). With \(B\) on the ground and using satellite links, the increased complexity would arguably make the error cancellation more difficult to attain and the signals propagate through the entire troposphere. Furthermore, the ionospheric refraction depends on the signal’s frequency and, employing two frequency bands, it is possible to apply an additional correction (Montenbruck and Gill 2000). Optical or higher frequency links, presumably utilized in the future, are going to decrease the ionospheric effect but also introduce a dependency on weather conditions in the troposphere. With \(B\) in GEO, the latter problem can be mitigated by discarding signals traveling close to the Earth. Moreover, the ionospheric FS in the DCFS measurement for signals whose altitude is always greater than \(500 \text{km}\) does not exceed \(\approx {10}^{-19}\) (Shen et al. 2023).
Another important factor consists of systematic effects, due to the action of exterior bodies (mainly the Sun and the Moon) and Earth’s dynamics, which subject clocks on the Earth’s surface to time-variable FS (Voigt et al. 2016). The solid tides, which have semi-diurnal and diurnal dominant components but also a permanent part, produce a maximum FS amplitude of \(\approx 4.7\times {10}^{-17}\). The contribution from ocean tides, whose dominant components are semi-diurnal and diurnal, does not exceed \(\approx 1.4\times {10}^{-17}\) close to the coast. The solid and ocean tides induced by polar motion, which is mostly described by an annual motion plus a motion of period \(433 \text{d}\), yield maximum amplitudes of \(\approx 4.5\times {10}^{-19}\) and \(\approx 1.1\times {10}^{-19}\), respectively. The tides due to length of day (LOD) variations, which occur over a wide range of temporal scales, contribute less than \(\approx 4.5\times {10}^{-20}\). The FS amplitude arising from pressure loading of the atmospheric tides generated by solar heating, with dominant semi-diurnal and diurnal waves, does not exceed \(\approx 3.3\times {10}^{-19}\). The direct effect of the exterior bodies, which instead increases with the distance from the Earth, is also responsible for tidal variations in the rate of clocks.
Non-tidal mass redistributions in the atmosphere, oceans, and hydrosphere cause FS whose amplitudes are up to, respectively, \(\approx 5.6\times {10}^{-19}\), \(\approx 2.2\times {10}^{-18}\), and \(\approx 1.7\times {10}^{-18}\); these effects occur both at short (from hours to days) and seasonal scales. Secular contributions from sea level variations and glacial isostatic adjustment (GIA) are at most \(\approx 1.1\times {10}^{-18}/\text{y}\) and \(\approx 1.7\times {10}^{-18}/\text{y}\), respectively. Furthermore, there exist perturbations originating from other geodynamical processes, tectonic motion, etc. (Wolf and Petit 1995). The influence of seismic events and volcanism is very localized and the associated FS amounts to less than \({10}^{-16}\). Vertical movements of the Earth’s crust and human activity, which are localized and have time scales longer than a year, contribute to less than \({10}^{-16}\). Episodic effects, like storm surges and droughts, can reach \(\approx {10}^{-18}\) (Müller et al. 2018).
With \(B\) on the ground, a large number of time-variable effects need to be modeled to compute the FS correctly. Conversely, the influence of geophysical processes is greatly diminished in GEO, whose gravitational environment is less affected by perturbations and noise (the effect of exterior bodies is easier to model), although the physical environment is harsher and more difficult to control in space. Finally, the primary part of \(U\), i.e., the static component, should be modeled with the necessary accuracy. With \(B\) in GEO, the static part of \({U}_{B}\) can be expressed as in Eq. 2. Instead, with \(B\) on the ground, the gravity potential is the sum of \({U}_{B}\) and the centrifugal potential: its representation becomes more complex (Petit and Luzum 2010) and the local value can be determined with limited accuracy (Pavlis and Weiss 2017). For example, the GNSS plus geoid approach is able to provide the gravity potential with an uncertainty between \(2.2\) and \(3.3\) parts in \({10}^{18}\) (Voigt et al. 2016). Additionally, irregularities in the Earth’s rotation, like precession, nutation, etc., cause further time-varying FS which are not of gravitational nature: their daily and yearly components can reach amplitudes of a few parts in \({10}^{16}\) (Fateev et al. 2015). Table 1 summarizes the fractional FS discussed so far as well as those relevant to the comparison between clocks \(A\) and \(B\).
Considering the previous remarks, we adopted the scenario depicted in Fig. 2 for our simulations (Giuliani 2022). In particular, we placed three reference clocks, labeled \(B1\), \(B2\), and \(B3\), in GEO with angular separation of \(120^\circ \). The probing clock \(A\) performs the DCFS measurements in a nearly circular and nearly polar (\(89^\circ \) inclination) LEO with an initial altitude \(h\) of \(500 \text{km}\). In this configuration, the line of sight between \(A\) and at least one reference clock is unobstructed at any instant, with two reference clocks being visible most of the time. The period during which a reference clock is within the field of view of \(A\) is indicated as an arc. Then, the DCFS observables are collected by \(A\) with sampling interval \({t}_{s}=40 \text{s}\) employing the pairs composed by \(A\) and each of the available \(B1\), \(B2\), and \(B3\) for the duration of the corresponding arcs. In Fig. 2, the measurements are being realized by the pairs \(A\)-\(B1\) and \(A\)-\(B3\), while the line of sight of \(A\)-\(B2\) is obstructed by the Earth. To ensure adequate spatial sampling, we chose a mission length of \(1\) month, during which Earth’s gravity is continuously monitored. We emphasize that the novelty of our architecture lies in the DCFS measurements being performed by the probing clock, which differs from what was done in Shen et al. (2023). This improves the dependency of Eq. 7 on the SHC, since the magnitude of \({\overrightarrow{r}}_{BA}\bullet {\overrightarrow{a}}_{A}\) can be up to \(\cong 10\) times greater than \(\Delta U\).
The main objective of our simulations is to provide a proof of principle for a gravity mission dedicated to the estimation of the time-variable geopotential via the DCFS observable. In order to assess the theoretical performance of the measurement and eliminate spurious effects, we employ a somewhat simplified mission scenario. Specifically, we assume the time-variable gravity to be negligible for \(B1\), \(B2\), and \(B3\). Next, we assume that the atmospheric error can be ignored and that the stability of the links does not constitute a limiting factor. Nevertheless, we consider the presence of the orbit error and attempt to remove its effect on the gravity solutions.
From a technological point of view, building a space-qualified clock that operates at the fundamental frequency \(\widetilde{f}\) with the necessary accuracy and reaches the required stability \(\delta f/\widetilde{f}\) in an averaging time not longer than \({t}_{s}\) is arguably the greatest challenge. In this study, we do not address the technology problem and assume that such clocks exist. In fact, a corollary goal of the simulations is to determine which \(\delta f/\widetilde{f}\) would allow us to obtain a satisfactory solution, and thus the needed metrology advancements, while keeping other aspects, e.g., POD methods, at the current performance level. Moreover, we suppose that the necessary infrastructure to accomplish the mission with the proposed configuration is in place. To this regard, we assume that the signal processing does not introduce errors and that the DCFS measurement error is solely due to the instrumentation error \(\delta f/\widetilde{f}\) affecting the clocks. We can envisage a future network of ultra-stable frequency standards in GEO whose purposes would be the realization of reference systems, worldwide time and frequency distribution, and GNSS augmentation (Levine 2002). We can think of \(B1\), \(B2\), and \(B3\) as part of this network, which would help to leverage the costs of the mission. Also, \(A\) could use the disseminated time to tag the DCFS observables.
5 Numerical implementation of the estimation problem
5.1 Computation of orbits and DCFS measurements
For LEO below \(4000 \text{km}\), Earth’s time-variable gravity causes FS with amplitude of some parts in \({10}^{18}\) (Wolf and Petit 1995). Ideally, the signals we are not interested in, like the tides, are modeled with the required accuracy such that the remaining effects on the probing clock \(A\) are exclusively due to the phenomena we want to recover, e.g., variations in continental water storage, ice mass loss, and consequences of climate change. For simplicity, we assume the probing clock \(A\) to be under the influence of only the static part of the geopotential \(U\) and ignore all the time-variable contributions, including those from the exterior bodies. This does not prevent our study from assessing how well the DCFS measurement can determine the gravity signal of interest. In fact, the latter is described by the temporal evolution of the low-degree SHC, which can be tracked with consecutive gravity field solutions. Therefore, what matters is to demonstrate that the measurement can produce a solution in which the aforementioned SHC are retrieved with sufficient accuracy. On the other hand, the direct effect of the exterior bodies, which causes FS of amplitude \(\approx {10}^{-17}\) for \(A\), is outside our bandwidth of interest.
Additionally, our assumptions lead to the Newtonian equations of motion for \(A\) in the GCRS:
where a dot means differentiation with respect to \(t\). Note that we set \({\overrightarrow{a}}_{A}=\overrightarrow{\nabla }{U}_{A}\) since, as stated at the end of SubSect. 3.7, we assume clock \(A\) to be equipped with a drag-free control system. \(A\)’s orbit was generated through the numerical integration of Eq. 10 (Giuliani 2022). Instead, as discussed in SubSect. 4.1, the gravity signals of the slowly moving reference clocks \(B1\), \(B2\), and \(B3\) contain low frequencies which are outside the bandwidth of interest. Thus, we assumed the reference clocks to have constant geopotential and fixed position in the ITRS: their orbit in the GCRS was obtained by transforming from the ITRS to the GCRS. Regarding this transformation, needed to compute \(\overrightarrow{\nabla }{U}_{A}\) in Eqs. 7 and 10 as well, we considered only the Earth’s rotation and supposed the angular velocity vector to be directed along the \(z\) axis of the GCRS, with a constant rotation period equal to a sidereal day. Also, we assumed the trajectory of a clock to describe the motion of its center of mass and that clocks have negligible size.
Next, we calculated the arcs between \(A\) and \(B1\), \(B2\), and \(B3\). During the considered month, the number of arcs for the pairs \(A\)-\(B1\), \(A\)-\(B2\), and \(A\)-\(B3\), respectively, was \(443\), \(442\), and \(443\). For each pair, \(\cong 350\) arcs were in the range from \(3000\) to \(3500 \text{s}\), \(\cong 25\) from \(3500\) to \(4000 \text{s}\), and \(\cong 70\) from \(6000\) to \(7500 \text{s}\). Within each arc between \(A\) and any of the reference clocks, each DCFS observable was computed by \(A\) through Eq. 7 at the instant indicated as \({t}_{A}\) (\({\overrightarrow{j}}_{A}\) was computed numerically). Consequently, the collection of the observables with sampling interval \({t}_{s}\) generated a \({t}_{A}\) time series, with each \({t}_{s}\) being centered around its \({t}_{A}\). In particular, because the effect of the terms included in Eq. 7 builds up during the \(40 \text{s}\) sampling interval thus determining the measured value of the DCFS observable at the end of the \(40 \text{s}\), we let each time instant labeling a measurement coincide with the middle point of the corresponding sampling interval. Regarding \({\overrightarrow{x}}_{B}\) and \({\overrightarrow{v}}_{B}\) of the involved reference clock, we first calculated \({t}_{BA}\) via Eq. 3 and then applied a Taylor expansion of the quantities referred to \({t}_{B}\) around \({t}_{A}\) to the required accuracy (Giuliani 2022). Combining all the reference clocks, the total number of observations was \(122150\). Note that the measurements for which the exchanged signals attained an altitude below \(250 \text{km}\) were discarded.
5.2 Kinematical approach
5.2.1 Estimation theory
Because we are employing a kinematical approach, we actually have two estimation problems (Giuliani 2022): fitting the trajectory of clock \(A\) through orbit determination and retrieving the SHC, which involve the nonlinear equations represented by, respectively, Eqs. 10 and 7. Each problem was investigated using a linearized weighted least squares estimation method (Tapley et al. 2004b). In this formulation, we employ an observation equation to estimate the quantities represented in a state vector. The true state vector contains the values we want to recover while the nominal state vector contains the starting values. Also, with each observation is associated an error. The linearization is carried out around the nominal state vector and involves the partial derivatives of the observable with respect to the estimated parameters. The solution consists of the best estimate of the deviation between the true and nominal state vectors at a specified initial epoch, together with the variance–covariance matrix of the estimation error. The solution is then used to update the nominal state vector and the process is repeated until convergence is reached. The variance–covariance matrix was not employed in the iteration process but was only used to calculate the formal errors associated with the estimated parameters at each iteration.
The first estimation problem, i.e., the orbit determination for clock \(A\), was accomplished for each of the \(1328\) arcs. In this case, the state vector is composed by \({\overrightarrow{x}}_{A}\) and \({\overrightarrow{v}}_{A}\), with the initial epoch being the beginning of the corresponding arc. The observables consist of simulated kinematic measurements of \({\overrightarrow{x}}_{A}\) via a GNSS receiver sampled at \(1 \text{s}\), generated by integrating Eq. 10 utilizing the true initial conditions and the true gravity field to obtain the true \({\overrightarrow{x}}_{A}\) and \({\overrightarrow{v}}_{A}\) for the arc and then adding the observation error \({\sigma }_{pos}\) to \({\overrightarrow{x}}_{A}\). \({\sigma }_{pos}\) is the uncertainty of the measurements, which we assumed to be white Gaussian (representative of the actual noise affecting this type of position measurements). Instead, by integrating the equations of motion using the nominal initial conditions of the arc and the nominal gravity field, we obtain the nominal \({\overrightarrow{x}}_{A}\) and \({\overrightarrow{v}}_{A}\). We emphasize that the GNSS position observables are used to determine both the position and velocity of \(A\), which together constitute \(A\)’s orbit. We identify the orbit error as the difference between the nominal and the true orbits. In the end, we have a set of \(1328\) fitted nominal initial conditions which, when used to integrate Eq. 10 with the nominal gravity field, provide the nominal trajectory of \(A\). We remark that the orbit fit represents the best dynamical trajectory while the nominal SHC are kept fixed.
In the main estimation problem, concerned with the computation of the gravity field solution, the state vector is the set of SHC while the observation equation is the DCFS measurement. The true and nominal gravity fields were GRACE models taken 6 months apart: their difference, consisting of seasonal signal at the \(\text{cm}\) level in geoid height, allows us to assess the measurement ability to recover the true field with little a priori knowledge. The maximum degree \(l\) and order \(m\) of the estimated field were \(d=60\) (we employed the same expansion for Eqs. 7 and 10) with the state vector having \({d}^{2}+2d-3=3717\) components. Also, we assumed the SHC to be constant during the month in which the mission occurs, so that the estimated deviation is not referred to any specific initial epoch. Utilizing the true field and the true trajectory of \(A\) in Eq. 7, we get the true observables, from which the observed (\(O\)) observables can be obtained by adding the observation error. Instead, the nominal field and the nominal trajectory yield the computed (\(C\)) observables. The residuals \(O-C\) appearing in the linearized observation equation form a vector with \(122150\) components. Along with the \(C\) observables, we calculated the partial derivatives as well (Giuliani 2022), which can be written as
Noticeably, the DCFS measurement is sensitive to \(U\) but also to the first derivatives of \(U\). In fact, the SHC are explicitly contained in \(\Delta U\) and \({\overrightarrow{a}}_{A}\) at order \({c}^{-2}\), and again in \(\Delta U\), \({\overrightarrow{a}}_{A}\), and \(\overrightarrow{\nabla }{U}_{A}\) at order \({c}^{-3}\). After the best estimate of the deviation was obtained, it was used to update the SHC in the nominal state vector whose value, upon convergence, represents the gravity solution. We emphasize that this approach is kinematical since the nominal trajectory of \(A\) is fixed while the SHC are estimated.
Regarding the uncertainty of the DCFS observable, we assumed the measurement error \({\sigma }_{obs}=\delta {\left(\Delta f/\widetilde{f}\right)}_{DC}\) to be caused by the clock instrumentation error. This is characterized by internal stochastic noise processes and systematic errors (Riley and Howe 2008). The latter, given by frequency drifts, environmental effects, aging, etc., are outside the bandwidth of interest and, for simplicity, are not included. We further assumed that such clocks, able to attain their best performance within \({t}_{s}\), reach a flicker floor (Hollberg 2021) after which their stability does not improve. Therefore, we considered only flicker noise (Kasdin and Walter 1992) as the source of the frequency instability \(\delta f/\widetilde{f}\) of the clocks. Lastly, since the influence of the clocks \(B1\), \(B2\), and \(B3\) is outside the bandwidth of interest, we did not account for their contribution to the measurement error: the orbits and geopotentials of the reference clocks, obtained as described in SubSect. 5.1, were regarded as the known true values.
5.2.2 Description of the simulations
Our simulations can be divided into two groups (Giuliani 2022). In the first group, denoted case 1, we evaluated the ability of the DCFS observable to recover the true gravity field in the presence of measurement error alone by estimating the SHC using only the true trajectory of clock \(A\). Following the red part of the diagram in Fig. 3, we integrated the true trajectory of \(A\), determined the arcs, and collected the true observables to which we added flicker noise with variance \({\sigma }_{obs}^{2}\) to obtain the measured observables \(O\). In the last step, we calculated the \(C\) observables and the partial derivatives by utilizing the nominal gravity field and again the true trajectory of \(A\), and then computed the solution. Hence, we did not perform orbit determination to obtain the nominal trajectory of \(A\) but instead we always employed the true trajectory of \(A\), ensuring that there is no contribution from the orbit error in the residuals and the partial derivatives. Experiments were carried out with \({\sigma }_{obs}={10}^{-15}\), \({10}^{-17}\) and \({10}^{-19}\).
The results were illustrated by plotting (the square root of) the degree difference variance (DDV) on a logarithmic scale versus \(l\), computed as
where \({\overline{C} }_{lm}\) and \({\overline{S} }_{lm}\) are the true SHC, \(\widehat{{\overline{C}}}_{lm}\) and \(\widehat{{\overline{S}}}_{lm}\) are the estimated field, and \(R\) is used to convert to geoid height. A DDV plot is a way to display the true error of the solution, i.e., the distance between the true and estimated gravity fields. Additionally, some results were visualized via triangular plots, where the magnitude of the true error for each SHC is shown in a color plot utilizing a logarithmic scale. Triangular plots can also be created for the formal error associated with \(\widehat{{\overline{C}}}_{lm}\) and \(\widehat{{\overline{S}}}_{lm}\), which is obtained when solving the estimation process.
In the second group of simulations, denoted case 2, we accomplished the orbit determination for clock \(A\) in order to addressed the orbit error, which affects both the residuals and the partial derivatives. To assess its effect, the blue part of the diagram in Fig. 3 was also involved: we added white noise with zero mean and variance \(\sigma_{pos}^{2}\) to the true trajectory of \(A\) to simulate kinematic GNSS position measurements. In the next step, these measurements were used to fit \(A\)’s nominal trajectory, integrated employing the nominal gravity field. Subsequently, thanks to the fitted nominal trajectory and the nominal field, we obtained the \(C\) observables and computed the gravity solution (last step of the red part of the diagram). We carried out only the experiment with \(\sigma_{pos} = 10^{ - 2} {\text{m}}\), which is in line with the performance currently available from POD. The results were illustrated by means of a DDV plot.
In the remainder of case 2, we attempted to remove the orbit error by applying the feedback loop depicted by the dashed arrows in Fig. 3: the computed solution was adopted as the next nominal gravity field utilized to fit the nominal trajectory of \(A\) again, with which another solution was then recomputed, and so forth. The idea is that fitting the nominal trajectory with an improved gravity field should reduce the orbit error, in turn leading to a better solution. The results were displayed via the DDV plots of successive iterations (iteration \(0\) designates the first time going through the data). The check for convergence was implemented by visually comparing the DDV plots of consecutive iterations: if the method did not produce further refinements, the process was stopped.
6 Gravity field solutions
The results for case 1, in which there is no orbit error, are illustrated in Fig. 4. The distance of the nominal field from the true field is shown by the dashed black line. As expected, the error of the solutions increases with degree \(l\), with the trend becoming approximately linear after several degrees. Eventually, the error dominates, implying that the SHC of highest degree are not well-determined. Going from cases 1(a–c), the improvement in the quality of the solutions reflects the decrease in \(\sigma_{obs}\). Nevertheless, we found that a further improvement from the same decrement in \(\sigma_{obs}\) is prevented by numerical limitations due to the double precision format used to represent numbers on a computer. As we can see, solution 1(a) is not able to recover the SHC and is actually farther from the true field than it is the nominal field. Solution 1(b) successfully retrieves the SHC only for degrees below about \(20\). Instead, solution 1(c) recovers the full geopotential spectrum (this is also confirmed by the post-fit residuals, in which the leftover gravity signature agrees with \(\sigma_{obs}\)). Since the improvement is proportional to the DCFS measurement performance we can state that, to monitor the time-variable gravity signal described by the lower degrees, we need \(\sigma_{obs}\) to be at most around a few parts in \(10^{18}\). Our findings prove that the DCFS measurement holds the necessary gravitational information and is effective in retrieving the geopotential, which was the goal of this study.
DDV plots of the gravity solutions with respect to the true field for Case 1 (Giuliani 2022)
Finally, for a meaningful comparison with the performance of the GRACE measurement concept, we included in Fig. 4 the pre-mission GRACE baseline (National Research Council 1997). This was obtained under simplifying assumptions similar to those employed in our analysis: only error in the range-rate measurement modeled as white noise at the level of \(5 \times 10^{ - 7} {\text{m}}/{\text{s}}\) was considered. We can see that, to estimate the geopotential and its temporal variability as accurately as GRACE, \(\sigma_{obs}\) must not be greater than about \(10^{ - 18}\). We must also keep in mind that, by virtue of the first equality of Eq. 8, the realization of a certain \(\sigma_{obs}\) necessitates clocks with frequency stability given by \(\delta f/\tilde{f} = \sigma_{obs} /\sqrt 3\).
Comparing our results to Fig. 10 (a) of Müller and Wu (2020), who placed the probing clock in a GRACE orbit, the reference clocks on the ground, and simulated data for \(1\) month with \(5 {\text{s}}\) sampling interval, we note that their solutions produced with the same noise level of our 1(b) and (c) basically coincide with the latter for the first few degrees but start to diverge afterward, suggesting that the scenario with the reference clocks in GEO could be advantageous as the degree increases. Regarding Migliaccio et al. (2023), their Fig. 6 indicates that, to generate a solution that roughly matches the performance of our 1(b), they had to resort to a Bender configuration (Bender et al. 2008) with six clocks (three clocks on each of two orbits having altitudes below \(400 {\text{km}}\) and inclinations, respectively, of \(89^\circ\) and \(66^\circ\)), a \(1000 {\text{km}}\) distance between adjacent clocks, data spanning \(1\) month with \(1 {\text{s}}\) sampling interval, and a noise level of \(10^{ - 18}\). Moreover, it is important to stress that a significant difference between our measurement equation and those utilized by Müller and Wu (2020) and Migliaccio et al. (2023) is the presence of the third term in parentheses on the right-hand side of Eq. 7 containing \(\vec{a}_{A}\) to order \(c^{ - 2}\).
In Fig. 5, we provide the triangular plots for solution 1(c) to show the true error and the formal estimation error for each of the individual SHC. The true error, illustrated in Fig. 5(a), increases with the degree like in Fig. 4, confirming that the DCFS measurement is more sensitive to the longer wavelengths of the gravity spectrum. We also observe that, starting from about degree \(25\), the error increases when moving along the order \(m\) toward the sectorial (\(l = m\)) SHC by keeping \(l\) fixed. This behavior might be a consequence of the chosen sampling interval \(t_{s} = 40 {\text{s}}\) and could improve by decreasing the latter. Instead, Fig. 5(b) visualizes the formal error, which increases with \(l\) but is approximately uniform across \(m\).
The results for case 2 are presented in Fig. 6. We took case 1(c), plotted with a continuous black line, as our DCFS measurement baseline and introduced the orbit error by employing the fitted nominal trajectory. As we can see, the error for solution 2(a) is less than that of the initial nominal field, with the two curves joining at the end. However, the orbit error causes 2(a) to be worse than 1(c) by more than one order of magnitude and up to two orders of magnitude for the lowest degrees. Between cases 2(a) and (b), there is a general improvement across all degrees. Going from 2(b) to (f), the error keeps decreasing but the reduction is less pronounced with each iteration, with no clear improvement between 2(e) and (f) at degrees \(2\), \(3\), and \(4\). We also note that, among the low degrees, the highest error occurs for all iterations at degree \(3\), which is the maximum of the dashed black line as well. Moreover, for degrees above about \(35\), the improvement is very small from 2(b) to (c) and practically negligible from 2(c) to (f). We report that, for case 2(a), the orders of magnitude of the position and velocity error, respectively, are \(10^{ - 2} {\text{m}}\) and \(10^{ - 5} {\text{m}}/{\text{s}}\) , whereas for case 2(f), they are \(10^{ - 3} {\text{m}}\) and \(10^{ - 6} {\text{m}}/{\text{s}}\). Clearly, even with \(\sigma_{obs} = 10^{ - 19}\), the residual orbit error due to \(\sigma_{pos} = 10^{ - 2} {\text{m}}\) does not permit a significant improvement beyond the gravity solution 2(f). This is also confirmed by the post-fit residuals which, for case 2(f), still have an approximate order of magnitude of ten times \(\sigma_{obs}\). As a consequence of the orbit error limitation, we did not iterate any further.
DDV plots of the gravity solutions with respect to the true field for Case 2 (\(\sigma_{pos} = 10^{ - 2} {\text{m}}\), \(\sigma_{obs} = 10^{ - 19}\)) (Giuliani 2022)
7 Conclusions and future prospects
The fundamental result of this paper is the proof of principle for a space mission dedicated to the determination of the Earth’s gravity field and its time-variability by means of the DCFS measurement. Our gravity field solutions were computed with an innovative mission architecture: three reference clocks are placed in GEO while the DCFS observables are collected by a probing clock in LEO. We conclude that the initial evaluation of the concept is promising and that the SHC can be effectively recovered, especially at the large spatial scales of interest. Significantly, we found that, under similar conditions, the performance of the DCFS measurement is comparable to that of the GRACE measurement concept for a measurement error \(\sigma_{obs} = 10^{ - 18}\). Moreover, as shown by Fig. 4, scaling \(\sigma_{obs}\) by a certain factor causes the same change in the quality of the solution as well. Nevertheless, our kinematical approach was unsuccessful in eliminating the orbit error. In the following, we will briefly look at three main aspects of our analysis that can be improved.
The first aspect has to do with the relaxation of the simplifying assumptions to achieve a realistic simulation and assess the feasibility of an actual mission. The effects that we ignored because they are outside our bandwidth of interest have to be included and properly addressed. Because of uncertainties in the background models, the high frequency time-variable gravity signals that need to be modeled will introduce errors whose influence on the solution quality has to be evaluated. The effects of the atmosphere on the measurement have to be considered and it is crucial to employ a better error model for clocks. A complete treatment of the non-gravitational forces would require, besides their inclusion in the accelerations appearing in all the previous equations, also the modification of the relativistic frequency shift equations, as noted in SubSect. 3.7. Then, their role as a source of error, whether utilizing a drag-free control system or onboard accelerometers, has to be analyzed. To accomplish a meaningful analysis, a detailed description of both the DCFS observable and the clocks dynamics is indispensable: we must account for all the involved factors at the necessary level of accuracy.
The second aspect regards the estimation method. To better reflect the effect of the various observational and dynamical model errors, a fully dynamical approach, in which the SHC together with the initial position and velocity of the probing clock are part of the same state vector \({\mathcal{X}}\), should be implemented (Tapley et al. 2004b). In particular, this would permit the computation of the gravity solution and fitting the nominal trajectory at the same time, simultaneously adjusting the SHC and the initial conditions at each iteration: ideally, this would reduce a large part of the orbit error, increasing the solution quality, and enhance the SHC observability. The assumption that the reference clocks have constant geopotential and fixed position in the ITRS needs to be removed as well. Another improvement would be represented by the introduction of additional parameters in \({\mathcal{X}}\) whose task is to absorb specific error sources such as the dominant \(1\) CPR orbit error, clock frequency drifts, instrumentation biases, etc. Furthermore, the required precision for the knowledge of position and velocity of the orbiting clocks should be investigated utilizing state-of-the-art POD.
The third aspect concerns the series of elements that can be controlled to reach an optimal measurement architecture. For instance, we proved observability with an adequate number of samples. However, it is essential to identify the minimum number of measurements in order to obtain a satisfactory gravity solution. Subsequently, the sampling interval \(t_{s}\) can be changed to determine the time it takes to collect the necessary number of samples and to find their appropriate spatial distribution. We can also experiment with the number of probing clocks and inspect their ideal orbit configurations, e.g., altitude, inclination, and eccentricity. By altering the spatial sampling and modifying the time span of the solutions, it is then possible to tackle issues such as spatial and temporal aliasing. Moreover, there are additional elements we can vary, such as the length of the arcs and the maximum degree \(l\) and order \(m\) for the expansion in SHC of the estimated Earth’s gravity field. Additional efforts are also required to identify the optimal constellation of the clocks and to explore possible alternative configurations to that employed in this work, e.g., a scenario in which all the clocks being compared are in LEO.
Finally, the mission described in this study can only be accomplished with the required technological advancements. Arguably, building space-qualified clocks able to attain a frequency stability consistent with the measurement error within \(t_{s}\) is the most difficult challenge. Furthermore, setting up the network of clocks, particularly the reference clocks in GEO, is in itself a demanding and costly endeavor. An incentive would be to employ the clocks in GEO primarily for time and frequency dissemination. Indeed, improving the knowledge of the gravity field, especially the low-degree SHC, would in turn benefit the accuracy of time scales. Also, the performance of the electronic instrumentation involved in the realization of the DCFS measurement has to be considered. For instance, it is crucial to characterize how delays in signal processing would affect the quality of the solution.
Once the simulation of a realistic mission scenario is carried out via the dynamical approach, it will represent a more accurate indication of the actual efficacy of a future gravity mission in sensing the geopotential \(U\) and its time-variability. It would also provide the possibility to objectively assess whether the DCFS measurement is generally competitive with the established gravimetry and gradiometry techniques in determining Earth’s gravity and if the former could be complementary to and combined with the latter. Moreover, comparing the results with methods whose ability to recover \(U\) is more effective in the low-degree region of the gravity spectrum will be important (Meyer et al. 2019; Shabanloui et al. 2023). In summary, based on the results of this initial investigation, our conclusion is that space-based observation of gravity by means of clocks, besides its conceptual elegance, holds the potential to ultimately lead to a paradigm shift for missions dedicated to the geopotential estimation: relativistic effects will not be treated as corrections anymore but will assume the central role of observable.
Data availability
The GRACE gravity field models employed as the true and nominal gravity fields and the gravity field solutions generated in this study are available from the corresponding author upon request.
References
Abuter R, Amorim A, Anugu N et al (2018) Detection of the gravitational redshift in the orbit of the star S2 near the galactic centre massive black hole. A&a 615:L15. https://doi.org/10.1051/0004-6361/201833718
Asenbaum P, Overstreet C, Kim M, Curti J, Kasevich MA (2020) Atom-interferometric test of the equivalence principle at the level. Phys Rev Lett 125:191101. https://doi.org/10.1103/PhysRevLett.125.191101
Ashby N, Parker TE, Patla BR (2018) A null test of general relativity based on a long-term comparison of atomic transition frequencies. Nature Phys 14:822–826. https://doi.org/10.1038/s41567-018-0156-2
Ashby N (1998) Testing relativity with a laser-cooled cesium clock in space. In: Proceedings of the 1998 IEEE International Frequency Control Symposium (Cat. No.98CH36165), pp 320–328 https://doi.org/10.1109/FREQ.1998.717923
Bauch A (2015) Time and frequency comparisons using radiofrequency signals from satellites. C R Physique 16:471–479. https://doi.org/10.1016/j.crhy.2015.02.006
Bender PL, Wiese DN, Nerem RS (2008) A possible dual-GRACE mission with 90 degree and 63 degree inclination orbits. In: Proceedings of the 3rd International Symposium on Formation Flying, Missions and Technologies, ESA Symposium Proceedings, SP-654 jILA Pub, Vol 8161, pp 1665–1669
Bergeron H, Sinclair LC, Swann WC, Khader I, Cossel KC, Cermak M, Deschênes J-D, Newbury NR (2019) Femtosecond time synchronization of optical clocks off of a flying quadcopter. Nat Commun 10:1819. https://doi.org/10.1038/s41467-019-09768-9
Bjerhammar A (1985) On a Relativistic Geodesy. Bull Géod 59:207–220. https://doi.org/10.1007/BF02520327
Blanchet L, Salomon C, Teyssandier P, Wolf P (2001) Relativistic theory for time and frequency transfer to order. A&a 370:320–329. https://doi.org/10.1051/0004-6361:20010233
Bodine MI, Deschênes J-D, Khader IH et al (2020) Optical atomic clock comparison through turbulent air. Phys Rev Research 2:033395. https://doi.org/10.1103/PhysRevResearch.2.033395
Bondarescu R, Schärer A, Lundgren A, Hetényi G, Houlié N, Jetzer P, Bondarescu M (2015) Ground-based optical atomic clocks as a tool to monitor vertical surface motion. Geophys J Int 202:1770–1774. https://doi.org/10.1093/gji/ggv246
Bongs K, Singh Y, Smith L et al (2015) Development of a strontium optical lattice clock for the SOC mission on the ISS. C R Physique 16:553–564. https://doi.org/10.1016/j.crhy.2015.03.009
Brockmann JM, Zehentner N, Höck E, Pail R, Loth I, Mayer-Gürr T, Schuh W-D (2014) EGM_TIM_RL05: an independent geoid with centimeter accuracy purely based on the GOCE mission. Geophys Res Lett 41:8089–8099. https://doi.org/10.1002/2014GL061904
Brumberg VA (1991) Essential relativistic celestial mechanics. CRC Press, Boca Raton. https://doi.org/10.1201/9780203756591
Brumberg VA, Kopeikin SM (1989) Relativistic theory of celestial reference frames. In: Kovalevsky J, Mueller II, Kolaczek B (eds) Reference frames in astronomy and geophysics. Kluwer Academic Publishers, Dordrecht, pp 115–141. https://doi.org/10.1007/978-94-009-0933-5
Burt EA, Prestage JD, Tjoelker RL, Enzer DG, Kuang D, Murphy DW, Robison DE, Seubert JM, Wang RT, Ely TA (2021) Demonstration of a trapped-ion atomic clock in space. Nature 595:43–47. https://doi.org/10.1038/s41586-021-03571-7
Cacciapuoti L, Salomon C (2011) Atomic clock ensemble in space. J Phys: Conf Ser 327:012049. https://doi.org/10.1088/1742-6596/327/1/012049
Cambiotti G, Douch K, Cesare S, Haagmans R, Sneeuw N, Anselmi A, Marotta AM, Sabadini R (2020) On earthquake detectability by the next-generation gravity mission. Surv Geophys 41:1049–1074. https://doi.org/10.1007/s10712-020-09603-7
Chen J, Tapley BD, Seo K-W, Wilson CR, Ries JC (2019) Improved quantification of global mean ocean mass change using GRACE satellite gravimetry measurements. Geophys Res Lett 46:13984–13991. https://doi.org/10.1029/2019GL085519
Damour T (2012) Theoretical aspects of the equivalence principle. Class Quantum Grav 29:184001. https://doi.org/10.1088/0264-9381/29/18/184001
Damour T, Soffel M, Xu C (1991) General-relativistic celestial mechanics. I. Method and definition of reference systems. Phys Rev D 43:3273–3307. https://doi.org/10.1103/PhysRevD.43.3273
Damour T, Soffel M, Xu C (1992) General-relativistic celestial mechanics. II. Translational equations of motion. Phys Rev D 45:1017–1044. https://doi.org/10.1103/PhysRevD.45.1017
Damour T, Soffel M, Xu C (1993) General-relativistic celestial mechanics. III. Rotational equations of motion. Phys Rev D 47:3124–3135. https://doi.org/10.1103/PhysRevD.47.3124
Damour T, Soffel M, Xu C (1994) General-relativistic celestial mechanics. IV. Theory of satellite motion. Phys Rev D 49:618–635. https://doi.org/10.1103/PhysRevD.49.618
Delva P, Geršl J (2017) Theoretical tools for relativistic gravimetry, gradiometry and chronometric geodesy and application to a parameterized post-Newtonian metric. Universe 3:24. https://doi.org/10.3390/universe3010024
Delva P, Puchades N, Schönemann E, Dilssner F, Courde C, Bertone S, Gonzalez F, Hees A, Le Poncin-Lafitte C, Meynadier F, Prieto-Cerdeira R, Sohet B, Ventura-Traveset J, Wolf P (2018) Gravitational redshift test using eccentric Galileo satellites. Phys Rev Lett 121:231101. https://doi.org/10.1103/PhysRevLett.121.231101
Delva P, Denker H, Lion G (2019) Chronometric geodesy: methods and applications. In: Puetzfeld D, Lämmerzahl C (eds) Relativistic geodesy. Springer, Cham, pp 25–85. https://doi.org/10.1007/978-3-030-11500-5_2
Einstein A (1997) The field equations of gravitation. The collected papers of Albert Einstein, vol 6. Princeton University Press, Princeton, pp 117–120
Fateev VF, Kopeikin SM, Pasynok SL (2015) Effect of irregularities in the earth’s rotation on relativistic shifts in frequency and time of earthbound atomic clocks. Meas Tech 58:647–654. https://doi.org/10.1007/s11018-015-0769-0
Fock V (1964) The theory of space, time and gravitation. Pergamon Press, Oxford. https://doi.org/10.1016/C2013-0-05319-4
Fujieda M, Piester D, Gotoh T, Becker J, Aida M, Bauch A (2014) Carrier-phase two-way satellite frequency transfer over a very long baseline. Metrologia 51:253–262. https://doi.org/10.1088/0026-1394/51/3/253
Ghobadi-Far K, Han S-C, Allgeyer S, Tregoning P, Sauber J, Behzadpour S, Mayer-Gürr T, Sneeuw N, Okal E (2020) GRACE gravitational measurements of tsunamis after the 2004, 2010, and 2011 great earthquakes. J Geod 94:65. https://doi.org/10.1007/s00190-020-01395-3
Girotto M, Rodell M (2019) Terrestrial water storage. In: Maggioni V, Massari C (eds) Extreme hydroclimatic events and multivariate hazards in a changing environment. Elsevier, Amsterdam, pp 41–64. https://doi.org/10.1016/B978-0-12-814899-0.00002-X
Giuliani S (2022) Theory and application of extremely precise frequency standards on low Earth orbit to the determination of geopotential time-variability. Dissertation, The University of Texas at Austin. https://repositories.lib.utexas.edu/handle/2152/117733
Grotti J, Koller S, Vogt S et al (2018) Geodesy and metrology with a transportable optical clock. Nature Phys 14:437–441. https://doi.org/10.1038/s41567-017-0042-3
Hafele JC, Keating RE (1972) Around-the-world atomic clocks: observed relativistic time gains. Science 177:168–170. https://doi.org/10.1126/science.177.4044.168
Heiskanen WA, Moritz H (1967) Physical geodesy. W. H Freeman and Company, San Francisco
Herrmann S, Finke F, Lülf M et al (2018) Test of the gravitational redshift with Galileo satellites in an eccentric orbit. Phys Rev Lett 121:231102. https://doi.org/10.1103/PhysRevLett.121.231102
Heß MP, Stringhetti L, Hummelsberger B et al (2011) The ACES mission: system development and test status. Acta Astronaut 69:929–938. https://doi.org/10.1016/j.actaastro.2011.07.002
Hoffmann B (1957) General relativistic red shift and the artificial satellite. Phys Rev 106:358–359. https://doi.org/10.1103/PhysRev.106.358
Hollberg L (2021) Atomic clocks for GNSS. In: Morton YTJ, van Diggelen F, Spilker JJ Jr, Parkinson BW, Lo S, Gao G (eds) Position, navigation, and timing technologies in the 21st century. Wiley, Hoboken, pp 1497–1519. https://doi.org/10.1002/9781119458555
Huang Y-J, Fujieda M, Takiguchi H, Tseng W-H, Tsao H-W (2016) Stability improvement of an operational two-way satellite time and frequency transfer system. Metrologia 53:881–890. https://doi.org/10.1088/0026-1394/53/2/881
Petit G, Luzum B (2010) IERS conventions. IERS Technical Note No. 36. Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main. https://www.iers.org/SharedDocs/Publikationen/EN/IERS/Publications/tn/TechnNote36/tn36.pdf. Accessed 22 July 2023
International Astronomical Union (2000) IAU 2000 resolutions. XXIVth General Assembly, Manchester, UK, 2000. https://www.iau.org/static/resolutions/IAU2000_French.pdf. Accessed 22 July 2023
Jenkins RE (1969) A satellite observation of the relativistic Doppler shift. Astron J 74:960–963. https://doi.org/10.1086/110889
Kasdin NJ, Walter T (1992) Discrete simulation of power law noise. In: Proceedings of the 1992 IEEE Frequency Control Symposium, pp 274–283 https://doi.org/10.1109/FREQ.1992.270003
Kleppner D, Vessot RFC, Ramsey NF (1970) An orbiting clock experiment to determine the gravitational red shift. Astrophys Space Sci 6:13–32. https://doi.org/10.1007/BF00653616
Klioner SA, Voinov AV (1993) Relativistic theory of astronomical reference systems in closed form. Phys Rev D 48:1451–1461. https://doi.org/10.1103/PhysRevD.48.1451
Kolkowitz S, Ye J (2021) Precision timekeeping: optical atomic clocks. In: Singh SC (ed) Guo C. Handbook of laser technology and applications, CRC Press, Boca Raton pp, pp 139–156. https://doi.org/10.1201/9781003130123
Kopeikin SM (1988) Celestial coordinate reference systems in curved space-time. Celest Mech 44:87–115. https://doi.org/10.1007/BF01230709
Kopeikin SM (1990) Theory of relativity in observational radio astronomy. Soviet astronomy, vol 34. American Institute of Physics, College Park, pp 5–10
Landau LD, Lifshitz EM (1975) The classical theory of fields, 4th edn. Elsevier, Amsterdam
Levine J (2002) Time and frequency distribution using satellites. Rep Prog Phys 65:1119–1164. https://doi.org/10.1088/0034-4885/65/8/201
Lisdat C, Grosche G, Quintin N et al (2016) A clock network for geodesy and fundamental science. Nat Commun 7:12443. https://doi.org/10.1038/ncomms12443
Litvinov DA, Rudenko VN, Alakoz AV et al (2018) Probing the gravitational redshift with an earth-orbiting satellite. Phys Lett A 382:2192–2198. https://doi.org/10.1016/j.physleta.2017.09.014
Liu L, Lü D-S, Chen W-B et al (2018) In-orbit operation of an atomic clock based on laser-cooled 87Rb atoms. Nat Commun 9:2760. https://doi.org/10.1038/s41467-018-05219-z
Ludlow AD, Boyd MM, Ye J, Peik E, Schmidt PO (2015) Optical Atomic Clocks. Rev Mod Phys 87:637–701. https://doi.org/10.1103/RevModPhys.87.637
Mayrhofer R, Pail R (2012) Future satellite gravity field missions: feasibility study of post-Newtonian method. In: Pacino MC, Marti U, Kenyon S (eds) Geodesy for planet earth iag Symposia. Springer, Berlin Heidelberg, pp 231–238. https://doi.org/10.1007/978-3-642-20338-1_28
McGrew WF, Zhang X, Fasano RJ, Schäffer SA, Beloy K, Nicolodi D, Brown RC, Hinkley N, Milani G, Schioppo M, Yoon TH, Ludlow AD (2018) Atomic clock performance enabling geodesy below the centimetre level. Nature 564:87–90. https://doi.org/10.1038/s41586-018-0738-2
Mehlstäubler TE, Grosche G, Lisdat C, Schmidt PO, Denker H (2018) Atomic clocks for geodesy. Rep Prog Phys 81:064401. https://doi.org/10.1088/1361-6633/aab409
Meyer U, Sosnica K, Arnold D, Dahle C, Thaller D, Dach R, Jäggi A (2019) SLR, GRACE and Swarm gravity field determination and combination. Remote Sens 11:956. https://doi.org/10.3390/rs11080956
Migliaccio F, Reguzzoni M, Rosi G, Braitenberg C, Tino GM, Sorrentino F, Mottini S, Rossi L, Koç Ö, Batsukh K, Pivetta T, Pastorutti A, Zoffoli S (2023) The MOCAST+ study on a quantum gradiometry satellite mission with atomic clocks. Surv Geophys 44:665–703. https://doi.org/10.1007/s10712-022-09760-x
Misner CW, Thorne KS, Wheeler JA (2017) Gravitation. Princeton University Press, Princeton
Montenbruck O, Gill E (2000) Satellite orbits. Springer, Berlin, Heidelberghttps://doi.org/10.1007/978-3-642-58351-3
Müller J, Wu H (2020) Using quantum optical sensors for determining the earth’s gravity field from space. J Geod 94:71. https://doi.org/10.1007/s00190-020-01401-8
Müller J, Dirkx D, Kopeikin SM, Lion G, Panet I, Petit G, Visser PNAM (2018) High performance clocks and gravity field determination. Space Sci Rev 214:5. https://doi.org/10.1007/s11214-017-0431-z
National Research Council (1997) Satellite gravity and the geosphere: contributions to the study of the solid Earth and its fluid envelopes. The National Academies Press, Washington, DC. https://doi.org/10.17226/5767
Origlia S, Pramod MS, Schiller S, Singh Y, Bongs K, Schwarz R, Al-Masoudi A, Dörscher S, Herbers S, Häfner S, Sterr U, Lisdat C (2018) Towards an optical clock for space: compact, high-performance optical lattice clock based on bosonic atoms. Phys Rev A 98:053443. https://doi.org/10.1103/PhysRevA.98.053443
Pail R, Bingham R, Braitenberg C, Dobslaw H, Eicker A, Güntner A, Horwath M, Ivins E, Longuevergne L, Panet I, Wouters B (2015) IUGG expert panel (2015) science and user needs for observing global mass transport to understand global change and to benefit society. Surv Geophys 36:743–772. https://doi.org/10.1007/s10712-015-9348-9
Pavlis NK, Weiss MA (2017) A re-evaluation of the relativistic redshift on frequency standards at NIST, Boulder, Colorado, USA Metrologia 54: 535–548https://doi.org/10.1088/1681-7575/aa765c
Petit G, Arias F, Panfilo G (2015) International atomic time: status and future challenges. C R Physique 16:480–488. https://doi.org/10.1016/j.crhy.2015.03.002
Petit G, Leute J, Loyer S, Perosanz F (2017) Sub 10−16 frequency transfer with IPPP: recent results. In: 2017 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS), pp 784–787 https://doi.org/10.1109/FCS.2017.8089035
Pie N, Bettadpur SV, Tamisiea M, Krichman B, Save H, Poole S, Nagel P, Kang Z, Jacob G, Ellmer M, Fahnestock E, Landerer FW, McCullough C, Yuan D-N, Wiese DN (2021) Time variable Earth gravity field models from the first spaceborne laser ranging interferometer. J Geophys Res 126:e2021JB022392. https://doi.org/10.1029/2021JB022392
Pound RV, Rebka GA Jr (1960) Apparent weight of photons. Phys Rev Lett 4:337–341. https://doi.org/10.1103/PhysRevLett.4.337
Refsdal S (1962) Rate difference between a clock in an artificial satellite and a clock on Earth. Phys Rev 127:977–978. https://doi.org/10.1103/PhysRev.127.977
Reigber C, Lühr H, Schwintzer P (2000) Status of the CHAMP mission. In: Rummel R, Drewes H, Bosch W, Hornik H (eds) Towards an integrated global geodetic observing system (IGGOS), IAG symposia. Springer, Berlin Heidelberg, pp 63–65
Riehle F (2017) Optical clock networks. Nat Photon 11:25–31. https://doi.org/10.1038/nphoton.2016.235
Riley WJ, Howe D (2008) Handbook of frequency stability analysis. NIST Special Publication 1065. https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication1065.pdf. Accessed 22 July 2023
Rossi L, Reguzzoni M, Koç Ö, Rosi G, Migliaccio F (2023) Assessment of gravity field recovery from a quantum satellite mission with atomic clocks and cold atom gradiometers. Quantum Sci Technol 8:014009. https://doi.org/10.1088/2058-9565/aca8cc
Rummel R, Yi W, Stummer C (2011) GOCE Gravitational Gradiometry. J Geod 85:777–790. https://doi.org/10.1007/s00190-011-0500-0
Schäfer W, Feldmann T (2016) Perspectives of time and frequency transfer via satellite. J Phys: Conf Ser 723:012038. https://doi.org/10.1088/1742-6596/723/1/012038
Schuh W-D (2003) The processing of band-limited measurements; filtering techniques in the least squares context and in the presence of data gaps. Space Sci Rev 108:67–78. https://doi.org/10.1023/A:1026121814042
Shabanloui A, Wu H, Müller J (2023) Estimation of temporal variations in the earth’s gravity field using novel optical clocks onboard of low Earth orbiters. In: Shabanloui A, Wu H, Müller J (eds) International Association of Geodesy Symposia. Springer, Berlin Heidelberg. https://doi.org/10.1007/1345_2023_220
Shapiro II (1964) Fourth test of general relativity. Phys Rev Lett 13:789–791. https://doi.org/10.1103/PhysRevLett.13.789
Shen W, Ning J, Liu J, Li J, Chao D (2011) Determination of the geopotential and orthometric height based on frequency shift equation. Nat Sci 3:388–396. https://doi.org/10.4236/ns.2011.35052
Shen Z, Shen W-B, Zhang S (2016) Formulation of geopotential difference determination using optical-atomic clocks onboard satellites and on ground based on Doppler cancellation system. Geophys J Int 206:1162–1168. https://doi.org/10.1093/gji/ggw198
Shen Z, Shen W-B, Zhang S (2017) Determination of gravitational potential at ground using optical-atomic clocks on board satellites and on ground stations and relevant simulation experiments. Surv Geophys 38:757–780. https://doi.org/10.1007/s10712-017-9414-6
Shen W-B, Sun X, Cai C, Wu K, Shen Z (2019) Geopotential determination based on a direct clock comparison using two-way satellite time and frequency transfer. Terr Atmos Ocean Sci 30:21–31. https://doi.org/10.3319/TAO.2018.07.09.02
Shen Q, Guan J-Y, Ren J-G et al (2022) Free-space dissemination of time and frequency with instability over km. Nature 610:661–666. https://doi.org/10.1038/s41586-022-05228-5
Shen Z, Shen W, Xu X, Zhang S, Zhang T, He L, Cai Z, Xiong S, Wang L (2023) A method for measuring gravitational potential of satellite’s orbit using frequency signal transfer technique between satellites. Remote Sens 15:3514. https://doi.org/10.3390/rs15143514
Singer SF (1956) Application of an artificial satellite to the measurement of the general relativistic “red shift.” Phys Rev 104:11–14. https://doi.org/10.1103/PhysRev.104.11
Soffel M, Klioner SA, Petit G et al (2003) The IAU 2000 resolutions for astrometry celestial mechanics and metrology in the relativistic framework explanatory supplement. Astron J 126:2687–2706. https://doi.org/10.1086/378162
Synge JL (1960) Relativity: the general theory. North-Holland Publishing Company, Amsterdam
Takamoto M, Ushijima I, Ohmae N, Yahagi T, Kokado K, Shinkai H, Katori H (2020) Test of general relativity by a pair of transportable optical lattice clocks. Nat Photonics 14:411–415. https://doi.org/10.1038/s41566-020-0619-8
Takano T, Takamoto M, Ushijima I, Ohmae N, Akatsuka T, Yamaguchi A, Kuroishi Y, Munekane H, Miyahara B, Katori H (2016) Geopotential measurements with synchronously linked optical lattice clocks. Nat Photon 10:662–666. https://doi.org/10.1038/nphoton.2016.159
Tanaka Y, Katori H (2021) Exploring potential applications of optical lattice clocks in a plate subduction zone. J Geod 95:93. https://doi.org/10.1007/s00190-021-01548-y
Tapley BD, Bettadpur SV, Ries JC, Thompson PF, Watkins MM (2004a) GRACE measurements of mass variability in the Earth system. Science 305:503–505. https://doi.org/10.1126/science.1099192
Tapley BD, Watkins MM, Flechtner F et al (2019) Contributions of GRACE to understanding climate change. Nat Clim Chang 9:358–369. https://doi.org/10.1038/s41558-019-0456-2
Tapley BD, Schutz BE, Born GH (2004b) Statistical orbit determination elsevier, Amsterdamhttps://doi.org/10.1016/B978-0-12-683630-1.X5019-X
Touboul P, Métris G, Rodrigues M et al (2022) MICROSCOPE mission: final results of the test of the equivalence principle. Phys Rev Lett 129:121102. https://doi.org/10.1103/PhysRevLett.129.121102
van der Meijde M, Pail R, Bingham R, Floberghagen R (2015) GOCE data, models, and applications: a review. Int J Appl Earth Obs Geoinf 35:4–15. https://doi.org/10.1016/j.jag.2013.10.001
Velicogna I, Wahr J (2006a) Measurements of time-variable gravity show mass loss in Antarctica. Science 311:1754–1756. https://doi.org/10.1126/science.1123785
Velicogna I, Wahr J (2006b) Acceleration of Greenland ice mass loss in spring 2004. Nature 443:329–331. https://doi.org/10.1038/nature05168
Vessot RFC, Levine MW (1979) A test of the equivalence principle using a space-borne clock. Gen Relat Gravit 10:181–204. https://doi.org/10.1007/BF00759854
Vessot RFC, Levine MW, Mattison EM, Blomberg EL, Hoffman TE, Nystrom GU, Farrel BF, Decher R, Eby PB, Baugher CR, Watts JW, Teuber DL, Wills FD (1980) Test of relativistic gravitation with a space-borne hydrogen maser. Phys Rev Lett 45:2081–2084. https://doi.org/10.1103/PhysRevLett.45.2081
Voigt C, Denker H, Timmen L (2016) Time-variable gravity potential components for optical clock comparisons and the definition of international time scales. Metrologia 53:1365–1383. https://doi.org/10.1088/0026-1394/53/6/1365
Voisin G, Cognard I, Freire PCC, Wex N, Guillemot L, Desvignes G, Kramer M, Theureau G (2020) An improved test of the strong equivalence principle with the pulsar in a triple star system. A&a 638:A24. https://doi.org/10.1051/0004-6361/202038104
Weinberg S (1972) Gravitation and cosmology. John Wiley & Sons Inc, New York
Will CM (2014) The confrontation between general relativity and experiment. Living Rev. https://doi.org/10.12942/lrr-2014-4
Will CM (2018) Theory and experiment in gravitational physics. Cambridge University Press, Cambridge. https://doi.org/10.1017/9781316338612
Wolf P, Petit G (1995) Relativistic theory for clock syntonization and the realization of geocentric coordinate times. A&a 304:653–661
Wu K, Shen Z, Shen W, Sun X, Cai C, Wu Y (2020) A preliminary experiment of determining the geopotential difference using two hydrogen atomic clocks and TWSTFT technique. Geodesy Geodynam 11:229–241. https://doi.org/10.1016/j.geog.2020.03.006
Acknowledgements
The authors acknowledge the Texas Advanced Computing Center (TACC) at the University of Texas at Austin for providing the computational resources to implement the research and produce the results described in this study. We want to thank Richard Matzner for his suggestions to make the theoretical exposition of relativity clearer. We are grateful to Brian Gunter and three additional anonymous reviewers for providing valuable feedback that allowed the improvement of the manuscript. This work was sponsored by NASA under contract 80NSSC22K0325.
Author information
Authors and Affiliations
Contributions
SG, BDT, and JCR conceptualized the research and designed the work. SG reviewed the relativistic theory, developed the software, and performed the computations. BDT, JCR, and SG analyzed and interpreted the results. SG prepared the first draft of the manuscript and produced the figures; BDT and JCR provided critical comments and suggestions for the revisions. SG, BDT, and JCR approved the final version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no financial or non-financial interests to disclose that are relevant to the content of this article.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Giuliani, S., Tapley, B.D. & Ries, J.C. Determination of the time-variable geopotential by means of orbiting clocks. J Geod 98, 50 (2024). https://doi.org/10.1007/s00190-024-01868-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-024-01868-9