Sentinel-6 Michael Freilich precise orbit determination using PODRIX and TriG receiver measurements

Abstract

The Sentinel-6 Michael Freilich altimetry mission flies two GNSS receivers: a primary multi-GNSS (GPS plus Galileo) PODRIX receiver and a GPS-only TriG receiver. Each of these receivers is independently capable of supporting the precise orbit determination (POD) requirement for < 1.5 cm radial rms error. In this study, we characterize the performance of single-receiver solutions and evaluate the benefits of a combined TriG and PODRIX orbit solution. The availability of both sets of receiver observations revealed a 10 mm in-track difference between orbit solutions derived independently from TriG and PODRIX tracking data. Based on satellite laser ranging (SLR) residuals, this bias has been isolated to an apparent inconsistency between the estimated TriG receiver clock and observation time-tags of approximately 1.3 $\mu \hbox {s}$, which is equivalent to a common range error of roughly 400 m in the TriG observations. After applying this calibration, the TriG and PODRIX displayed similar performance in terms of orbit overlap precision. PODRIX-Galileo observations showed lower code and phase tracking residual rms values compared to the GPS observations. Overall, processing the calibrated TriG and PODRIX observations separately results in highly accurate orbit solutions with radial orbit accuracies better than 1 cm rms as indicated by one-way SLR residual rms of 7.2 mm or better for each solution. Orbit solution accuracy is slightly improved by processing both TriG and PODRIX observations together, resulting in one-way SLR residual rms of 7.0 mm.

1 Introduction

Satellite altimetry plays a critical role in both climate science and oceanography (Le Traon et al. 2019). The Sentinel-6 Michael Freilich (MF) spacecraft, launched in November 2020, is the latest in a 30-year series of space-based reference ocean altimeters to measure global sea surface height. Primarily designed to measure global ocean sea surface height and provide continuity of service, it builds on the success of previous ocean-monitoring missions beginning with TOPEX/Poseidon in 1992 (Fu et al. 1994) and followed by the Jason-1/2/3 series of spacecraft (Ménard et al. 2003; Lambin et al. 2010; Vaze et al. 2010). Together, these missions provided valuable insights into ocean currents, sea-level rise and other oceanographic phenomena (Donlon et al. 2021a). Each of these satellites has occupied the same reference orbit with an inclination of 66 degrees, an altitude of 1339–1356 km and an orbital period of 112 min, resulting in a repeat ground track of 9.9 days. The reference orbit was designed to avoid aliasing of the dominant tidal frequencies into the altimetry data (Parke et al. 1987).

Like its predecessors, Sentinel-6 MF is a multi-national satellite mission that serves as the current reference altimeter mission for global sea surface height, against which other altimetry missions such as CryoSat-2 (Wingham et al. 2006) and Sentinel-3 (Donlon et al. 2012) are calibrated. The Sentinel-6 MF payload includes the Poseidon-4 Ku/C-band synthetic aperture radar altimeter that provides high precision altimetry measurements and a multi-frequency Advanced Microwave Radiometer for Climate (AMR-C) to correct for delay caused by atmospheric water vapor (Donlon et al. 2021a). The accuracy of satellite-based altimetry is highly dependent on orbit knowledge, with radial orbit errors mapping directly into the sea surface height estimates. To support the precise orbit determination (POD) radial accuracy requirement of < 1.5 cm (rms) (Donlon et al. 2021b), Sentinel-6 MF is equipped with four independent tracking systems: a Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) receiver (Auriol and Tourain 2010), a laser retroreflector array for ground-based satellite laser ranging (SLR), a redundant pair of multi-GNSS (GPS plus Galileo) PODRIX receivers developed by RUAG, which is the primary GNSS POD instrument (Montenbruck et al. 2021; Peter et al. 2022; ESA 2023), and a GPS-only TriG receiver from NASA’s Jet Propulsion Laboratory (JPL) that supports POD and radio occultation measurements (Tien et al. 2010, 2012).

Sentinel-6 MF is a unique mission in that it flies two fully independent, and simultaneously active, geodetic GNSS receivers in low Earth orbit (LEO). This configuration presents an opportunity to study and characterize a multi-receiver, multi-GNSS constellation POD solution. The performance of the combined solution can be compared and contrasted with the performance of each receiver alone and between solutions based on either the GPS or Galileo observations. The configuration of Sentinel-6 MF acts as an orbiting geodetic observatory, linking four separate tracking systems in GPS, Galileo, DORIS and SLR. As described by Haines et al. (2015), having a single space platform with multiple geodetic tracking systems could enable better realizations of the terrestrial reference frame along with improved gravity recovery. While the primary goal of this study is to understand and characterize the POD associated with the TriG and PODRIX, it is important to highlight the additional benefits that Sentinel-6 MF could provide for geodetic science.

Montenbruck et al. (2021) demonstrated highly accurate POD solutions for Sentinel-6 MF with a consistency of 1 cm between the PODRIX-GPS-only and Galileo-only solutions when compared to the solutions using the full set of GPS and Galileo observations. Additional PODRIX derived solutions were described by Peter et al. (2022) and Zandbergen et al. (2022) where it was found that the Galileo-only solutions performed better than the GPS-only solutions, but when combined, the two performed as well or better than either alone. Each of the previous studies noted the Galileo observations had lower residual rms and better ambiguity fixing statistics.

This paper builds upon results from Conrad et al. (2023), where TriG-only POD solutions for Sentinel-6 MF were shown to have radial orbits accuracies better than 1 cm, as inferred by independent SLR data. In this paper, we estimate Sentinel-6 MF orbit solutions using all observations from both the PODRIX and Trig receivers, both independently and together. Section 2 provides an overview of the two receivers and tracking modes as well as the available data after editing. This is followed by a brief description of the background models, POD processing strategy and in-flight antenna calibration estimation. Next, Sect. 3 provides a description of the observed in-track bias between the TriG and PODRIX, and the calibration of the TriG observations to resolve it. Section 4 provides an overview of the results for six solutions; TriG-only, TriG-only with 10-degree elevation mask, PODRIX-GPS-only, PODRIX-Galileo-only, PODRIX-GPS plus Galileo (referred to as PODRIX from here on) and TriG plus PODRIX (referred to as combined from here on). A Trig-only solution with a 10-degree elevation mask is included in our analysis as a direct comparison to the PODRIX receiver which only tracks down to 10-degree elevation. The results examine the estimated antenna calibrations from in-flight data, internal metrics—consisting of post-fit residual rms and orbit precision as measured by differences between neighboring daily orbit solutions, and ambiguity resolution statistics. Finally, the orbit accuracy of each solution is evaluated through the use of independent SLR measurements which are withheld from the POD solutions.

2 Methods

2.1 Sentinel-6 MF instrumentation

The primary Sentinel-6 MF GNSS POD instrument is a redundant pair of multi-GNSS (GPS and Galileo) PODRIX receivers from RUAG, each capable of tracking up to a combined total of 18 GPS and Galileo satellites (Montenbruck et al. 2021; Peter et al. 2022). Only one of the two PODRIX receivers is typically active at a given time. A secondary NASA JPL TriG receiver with support for radio occultation measurements also provides POD quality GPS observations, tracking up to 12 satellites (Tien et al. 2010, 2012). The TriG does not enforce any limitations on tracking based on elevation, but the PODRIX employs a 10-degree receiver elevation mask. Table 1 shows the various signals available on Sentinel-6 MF and their corresponding RINEX 3.05 (receiver independent exchange format-version 3.05) observation codes (Romero 2020). The current PODRIX tracking configuration includes a mix of legacy and modern GPS observations on the L1 and L2 frequency bands, along with those from Galileo on E1 and E5a bands. With this extensive measurement set, Sentinel-6 MF facilitates the comparison of solutions using newer signals against the legacy observations, which have an extensive, well-established record for POD.

Table 1 GNSS observation types available on Sentinel-6 MF. TriG observations are derived from P(Y) (along with C/A on L1) tracking while the PODRIX tracks P(Y) on Block IIR satellites and C/A and L2C for Blocks IIR-M, IIF and GPS IIIA

During this study, the TriG is configured to track the GPS C1C/C1W/C2W pseudorange along with L1C/L1W/L2W carrier signals. The PODRIX tracks both GPS and Galileo signals. For GPS, the C1C/C1W/C2W pseudorange and L1C/L2W carrier phase are tracked for the Block IIR satellites, but C1C/C2L pseudorange and L1C/L2L carrier phase are tracked for Blocks IIR-M, IIF and GPS IIIA satellites which transmit the modernized L2L signal. For Galileo signals, the C1C/C5Q pseudorange and L1C/L5Q phase signals are tracked. Note: The L1C signals are used for both the TriG and PODRIX-GPS ionosphere-free phase combinations.

We use the rapid orbit, clock and wide-lane products that are estimated based on 1W/2W observations for GPS and 1C/5Q for Galileo from the JPL International GNSS Service analysis center (Dietrich et al. 2018). The TriG produces the C1W/C2W pseudoranges, which are consistent with the clock product, so no corrections based on observation type are necessary. The same is true for the PODRIX-Galileo C1C/C5Q pseudoranges. On the other hand, the PODRIX C1C/C2L measurements must be corrected for differential code biases (DCB) that exist between the different pseudorange signals. DCBs are the result of hardware delays between different codes and can occur on both transmitters and receivers. Uncorrected DCBs degrade the wide-lane ambiguity resolution, which is the first step for single-receiver ambiguity resolution (Bertiger et al. 2010b). Before processing, several corrections have been applied to the PODRIX RINEX files. The first is a calibration by the manufacturer of temperature-dependent pseudorange corrections which account for receiver-based biases between C1C–C1W and C2L–C2W pseudorange observations as described by Montenbruck et al. (2021). In this study, the authors also estimated an additional empirical correction to the L2L phase measurement of 0.075 cycles from a short baseline test with the redundant PODRIX receiver. This phase offset is likely due to differences in the PODRIX tracking hardware between L2W and L2C. Finally, GPS satellite-specific DCB corrections are applied to the PODRIX-GPS C1C and C2L observations to bring them in-line with the GPS C1W and C2W observations for which the clock and wide-lane bias products are derived. More detail on the DCB corrections applied for this study is provided in Appendix A.

2.2 Data overview

TriG pseudorange and phase observations are downlinked at 1 Hz. The PODRIX phase observations are also available at 1 Hz, but the code observations are sent only once per 10 s. Prior to orbit estimation, raw measurements are screened for outliers and flagged for phase breaks. Continuous phase arcs shorter than 10-minutes are discarded. The remaining phase and pseudorange measurements are, respectively, decimated and carrier smoothed to 5 min. Within the filter, the phase data are weighted 100 times higher than the pseudorange. For the time period spanning 2021-06-30 to 2022-12-31, Fig. 1 shows the total combined TriG and PODRIX observations after data editing. Over this time period, the TriG contributes 40.5% and the PODRIX 59.5%. For the PODRIX observations, 8.7% are GPS C1W/C2W, 46.1% GPS C1C/C2L and 45.2% Galileo. In the receiver frame, approximately 35% of TriG observations are below 20-degree elevation, while fewer than 24% of PODRIX observations are below this threshold due to the 10-degree elevation mask. In the transmitter frame, more than half of all TriG observations occur at boresight angles between 14 and 17 degrees. The PODRIX-Galileo on the other hand has only about 30% of observations above 14 degrees with a maximum of 15 degrees. This is due not only to the 10-degree mask, but also the higher altitude of the Galileo constellation.

Fig. 1

Number of observations after editing from 2021-06-30 to 2022-12-31 as a function of receiver elevation (left) and transmitter boresight (right) for TriG C1W/C2W (blue), PODRIX-GPS C1W/C2W (orange), PODRIX-GPS C1C/C2L (green) and PODRIX-Galileo C1C/C5Q (red). The left panel also shows all PODRIX observations from both GPS and Galileo (purple)

Fig. 2

Number of satellites tracked at each epoch from 2021-06-30 to 2022-12-31 for PODRIX-GPS C1W/C2W (orange), PODRIX-GPS C1C/C2L (green), PODRIX-Galileo C1C/C5Q (red), TriG C1W/C2W (blue), ant total PODRIX (purple)

Figure 2 shows the percentage of epochs with a given number of tracked satellites. The median tracked is 9 for the TriG, 1 for the PODRIX-GPS C1W/C2W, 6 for PODRIX-GPS C1C/C2L and 6 for PODRIX-Galileo resulting in a combined total of 13. The TriG tracks eight satellites or more 91.7% of the time, while the PODRIX tracks eight or more observations 99.0% of the time. By combining the GPS and Galileo constellations, the PODRIX shows an increase in the median number tracked by 4 transmitters compared to the TriG, despite its 10-degree elevation mask. However, because the TriG tracks down to zero degrees, it provides a benefit to the overall viewing geometry. In terms of the number of measurements possible, the multi-constellation tracking provides a clear advantage.

2.3 Orbit background models

We use JPL’s GipsyX/RTGx software (Bertiger et al. 2020) with the models listed in Table 2 for all precise orbit determination solutions.

Table 2 Measurement and POD models applied in GipsyX/RTGx

A macromodel combined with measured spacecraft attitude is used to compute the drag forces, and solar radiation pressure (SRP) forces are applied from a composite SRP table as estimated by Conrad et al. (2022). The drag model incorporates the DTM-2000 empirical thermosphere model (Bruinsma et al. 2003) to estimate the atmospheric density from the F10.7 cm solar flux and Kp geomagnetic indices. Radiation pressure forces for both Earth albedo (Knocke et al. 1988) and visible solar (Milani et al. 1987) are applied. The geopotential is computed using the GRACE time-variable CNES/GRGS RL04 Earth gravity models up to degree and order 200 (Lemoine et al. 2019). Gravitational effects from the solid Earth and pole tides conform to update 1.3.0 of the IERS Conventions (Petit and Luzum 2010) released in 2019 (https://iers-conventions.obspm.fr/conventions_material.php). More importantly, the pole tide model adopts the linear mean pole from Ries and Desai (2017) and the ocean pole tide from Desai et al. (2015). Ocean tides use a GOT4.8a model (Ray 2013) which is modified to account for geocenter motion (Desai and Ray 2014) and implemented using the convolution formalism of Desai and Yuan (2006). Third-body gravitational effects are included using the JPL DE421 planetary and lunar ephemeris (Folkner et al. 2009).

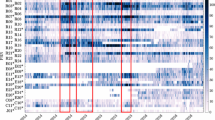
GPS satellite ephemerides, clock solutions, wide-lane phase bias information, and Earth orientation parameters all come from the JPL International GNSS Service (IGS) Analysis Center multi-GNSS Rapid products (Dietrich et al. 2018). The IGS14 transmitter phase center offset (PCO) and phase variation (PV) calibrations from igs14_2196.atx (Rebischung and Schmid 2016) are applied with the exception of the GPS IIIA transmitters which uses the estimated extension from Conrad et al. (2023) to accommodate observations with transmitter boresight angles above 14 degrees. Finally, while the PODRIX-GPS and Galileo observations share a common clock bias contribution from the receiver, there exists an inter-system bias between the observable clock solutions. Also, as noted previously (Montenbruck et al. 2021; Peter et al. 2022), there are small glitches (2–3 cm) which can occur in either the GPS or Galileo phase observations and are absorbed by the clock solution. These glitches can be seen most easily in the GPS/Galileo clock solution differences (Fig. 3). This effect confounds the estimation of a constant inter-signal bias, as it would degrade the ambiguity resolution. For this reason, separate clock biases are estimated for the TriG, PODRIX-GPS and PODRIX-Galileo observation sets.

Fig. 3

Receiver clock bias for PODRIX-Galileo (blue) and PODRIX-GPS (orange) and solution differences from 2022-01-22

2.4 Orbit solution strategy

Table 3 POD estimation strategy within GipsyX/RTGx

Our solutions adopt a reduced-dynamic POD approach with single-receiver ambiguity resolution (Bertiger et al. 2010b). The POD solution is an iterative process. A reference trajectory is first constructed from a dynamic fit to the on-board navigation solution. Next, three dynamic passes are processed estimating a drag coefficient and constant amplitude once-per-orbit empirical accelerations in the cross-track and in-track directions. Each subsequent pass adopts the previously estimated dynamic parameters as the a priori values. A reduced-dynamic pass follows the dynamic passes, with constant empirical accelerations, estimated stochastically, in the radial and in-track directions, as well as stochastic once-per-orbit accelerations in the cross-track and in-track directions. The once-per-orbit accelerations apply nominal values as estimated in the final dynamic pass. The parameterizations are summarized in Table 3 including the stochastic update intervals and correlation times. These reduced-dynamic and ambiguity-resolved solutions are the basis for the final accuracy assessment using independent SLR observations.

2.5 Receiver antenna calibrations

For Sentinel-6 MF, there are two independent active receivers, each with a separate physical antenna. In addition, despite the fact that the PODRIX-GPS and PODRIX-Galileo observations share an antenna, they require separate calibrations due to the different linear observation combinations and associated IGS14 transmitter calibrations. This results in a total of three antenna calibrations.

The Sentinel-6 MF PODRIX and TriG receiver antenna calibrations are estimated from daily solutions generated from 24-hour dynamic orbit estimates. Outliers are first be removed as they can significantly influence the receiver antenna calibration especially for bins with low measurement density. This is done using a dynamic solution with a priori PVs to simply detect the outliers. With these observations excluded, a new dynamic orbit solution is estimated that also simultaneously estimates corrections to the a priori two-dimensional receiver antenna calibration. The estimated antenna calibration correction is defined for discrete bins of 3 degrees in elevation and 4 degrees in azimuth for elevations below 51 degrees. Above this, the azimuth bin spacing is variable to account for lower measurement density at higher elevations. Table 4 shows the antenna calibration estimation strategy.

It is important for each orbit solution to ensure that the antenna calibrations for both the code and the phase are estimated in a manner that is consistent with the receiver observations under study. For example, the TriG POD solutions use an antenna calibration that is estimated using only TriG observations, whereas for the combined antenna calibration, the TriG, PODRIX-GPS and PODRIX-Galileo corrections to the pre-launch calibrations are simultaneously estimated together in a single solution.

Table 4 POD estimation strategy for antenna calibrations

Fig. 4

Ionosphere-free phase combination pre-launch antenna calibrations used for a priori calibration

To initialize the in-flight antenna calibration, we begin with the pre-launch antenna calibrations for each Sentinel-6 MF antenna as shown in Fig. 4. While there are only two physical antennas (not counting the redundant PODRIX antenna), three separate pre-launch calibrations are applied: TriG-GPS, PODRIX-GPS and PODRIX-Galileo. The physical antennas for both receivers are very similar, and so the phase variations are relatively consistent between the three pre-launch calibrations. Each contains a z-offset to align the calibrations to the antenna reference point, about 91 mm for TriG and PODRIX-GPS and 77 mm for PODRIX-Galileo. For comparative purposes, Fig. 5 shows the same pre-launch antenna calibrations but with the mean z-offset removed. The PODRIX-Galileo pre-launch calibration, which uses the same antenna as the PODRIX-GPS, shows slightly smaller PVs than both GPS calibrations due to the use of the E5 signal instead of the L2 signal used for GPS.

Fig. 5

Ionosphere-free phase combination pre-launch antenna calibrations with mean z-offset removed

Our antenna calibration values are described using azimuth measured clockwise from 0 to 360 degrees and elevation from 0 to 90 degrees in the antenna frame, which is closely aligned with the spacecraft body-x/y/z frame. The 0-degree azimuth direction corresponds to the positive antenna-y direction (body +x), 90-degree azimuth to the antenna-x direction (body +y) and 90-degree elevation to the positive antenna-z direction (body -z). The calibration values are then added to the range model after bilinear interpolation to the observation azimuth and elevation.

Given the attitude of Sentinel-6 MF, it is difficult to resolve a mean PCO from the phase variations relative to the antenna reference point for the in-track (aligned with spacecraft body-x direction) direction. This same issue has previously been observed in estimation of the horizontal PCOs for GNSS satellites during periods when the spacecraft attitude aligns the body x- or y-axis with the in-track direction (Schmid et al. 2007; Huang et al. 2022). When estimating antenna offsets, this essentially decouples the antenna location from the center of mass under the constraint that the offset is fixed across the entire solution arc. It is possible for the center of mass to be offset in the in-track direction without creating any inconsistency with the observations or dynamical models. Because the Sentinel-6 MF antenna offset in the body-x direction is aligned with the in-track direction, it is similarly difficult to observe. For this reason, we also choose to constrain the PCO of the antenna calibration correction in the body-x direction to zero. We also constrain the entire antenna calibration correction such that the mean of all bins above 30-degree elevation is set to zero. The choice of 30 degrees is intended to prevent low elevation multipath and noise from influencing the constraint. When multiple calibrations are being estimated together, the x-offset constraint is applied to only one antenna calibration. This allows for any observable baseline between the calibrations to be retained. For the PODRIX, the Galileo calibration x-offset is chosen to be constrained to zero, whereas for the combined, the TriG calibration is constrained.

3 TriG/PODRIX in-track bias correction

Before processing a combined solution, we compared TriG-based solutions to separately processed PODRIX-GPS and PODRIX-Galileo orbit solutions. The applied background models and estimation strategies were the same for all three solutions. The following comparisons show the differences between 30-hour reduced-dynamic solutions applying the pre-flight antenna calibrations. Figure 6 shows the distribution of the orbit differences across 550 days. Small radial differences of a few millimeters exist between GPS and Galileo solutions. This is likely due to inconsistencies between the pre-flight calibrations and the applied transmitter calibrations. The offsets in the cross-track differences are also small, below 0.5 mm. The in-track differences, however, show a consistent offset of about 10 mm between the two receiver solutions, regardless of the constellation used with the PODRIX. While this in-track difference does not have a significant impact on altimetry, it is important to identify the source for better understanding the behavior of each receiver.

Fig. 6

Daily mean component differences between PODRIX-GPS and TriG solutions (blue), PODRIX-Galileo and TriG (orange) and PODRIX-Galileo and PODRIX-GPS for radial (left), cross-track (middle) and in-track (right) components from 2021-06-30 to 2022-12-31. Note: the violin plots show a mirrored kernel density plot along the y-axis, and the bars represent the location of the maximum, mean and minimum of the data set

The approximately 10 mm shift between the TriG and PODRIX is consistent with the observed baseline shift as reported by Desai et al. (2022) and Montenbruck et al. (2022). The observed differences between solutions is relative, and it could potentially be due to one or both receivers. In order to determine the cause, the first step is to determine which receiver is the source of the relative bias. To do this, we examined the SLR residuals from each orbit solution in the above comparisons for systematic body-frame errors. These offsets will map into the SLR measurements based on observation azimuth and elevation in the spacecraft body frame using

$$\begin{aligned} SLR_{res}= & {} X_{off}cos(el)cos(az) + Y_{off}cos(el)sin(az) \nonumber \\{} & {} + Z_{off}sin(el) \end{aligned}$$

(1)

We can estimate the offsets using a least squares approach with the resulting offsets being in the same frame as the SLR observation azimuth and elevation, which in this case is the spacecraft body frame. Because of the yaw-fixed attitude, these offsets will be highly correlated with the orbit frame. The least squares fit produces a body x-offset, which corresponds roughly to an in-track offset of 8.5 mm for TriG orbit solutions that is not present in either of the PODRIX solutions as shown in Table 5. Timing errors in the SLR observations could also map into an in-track error at the few mm level (Arnold et al. 2019), but the TriG in-track offset is larger than would be expected. Given that the PODRIX body-x offsets are much smaller, this indicates the TriG as the dominant source of the relative in-track bias.

Table 5 Spacecraft body-x/y/z offsets estimated from the SLR residuals. These are correlated with the orbit in-track (body-x), cross-track (body-y) and radial (body-z) directions

An in-track/body-x error such as the one seen here can be caused by something physical, such as an error in the antenna reference point (or center of mass), or timing errors. The yaw-fixed attitude of Sentinel-6 MF can make distinguishing these two effects difficult. However, during several periods of low beta angle, Sentinel-6 MF was commanded to perform a yaw-flip maneuver (180-degree yaw bias for $\sim$ 4 days) to support POD activities related to resolving the estimated antenna calibration y-offsets (ESA 2023). These 180-degree yaw flips allow for separating physical (body-fixed) offsets from in-track offsets caused by timing errors. As shown in more detail later, this bias appears to be caused by a timing error.

Receiver timing errors change the observed pseudorange in two ways: a bias across all observations from the receiver clock and a range-rate effect related to time-tag errors. For a given transmitter and receiver pair and ignoring ionosphere, multipath, and measurement noise, the observed pseudorange is

$$\begin{aligned} \rho = c(t_{rx}^r-t_{tx}^t) \end{aligned}$$

(2)

where $\rho$ is the pseudorange, c is the speed of light, $t_{rx}^r$ is the receiver clock time at time of reception, and $t_{tx}^t$ is the transmitter clock time at time of transmission. This can be rewritten in terms of the geometric range and the receiver and transmitter clock biases relative to GNSS time ($t_{GNSS}$) as

$$\begin{aligned} \rho = r + \delta t_{rx}^r(c-\dot{\rho }) - c\delta t_{tx}^t \end{aligned}$$

(3)

where

$$\begin{aligned} \delta t_{rx}^r= & {} t_{GNSS}^r - t_{rx}^r \end{aligned}$$

(4)

$$\begin{aligned} \delta t_{tx}^t= & {} t_{GNSS}^t - t_{tx}^t \end{aligned}$$

(5)

Equation 3 models the expected pseudorange by incorporating both the bias and time-tag effects under the assumption that the time-tag bias is only due to the receiver clock offset relative to $t_{GNSS}$. It should be noted that modeling the time-tag in this way will have very little effect on the estimated clock bias. This is due to the fact that c is much larger than $\dot{\rho }$. However, given the high range rates for a LEO spacecraft of more than 6000 m/s, it will have a significant impact on the expected pseudorange. The TriG receiver clock bias is often larger than 100 $\mu$s which could potentially result in over half a meter difference in the modeled vs observed pseudorange without this correction.

The pseudorange as modeled in Eq. 3 works well, but as mentioned before, assumes that the time-tag offset is consistent with the receiver clock offset. If this assumption does not hold true, either because of an added range bias (clock-like bias but no effect on time-tag) or a time-tag offset (from some source other than the receiver clock), then it will produce an error in the modeled pseudorange that is absorbed by an in-track offset when the position of the spacecraft is estimated. This in-track offset is proportional to the receiver velocity and the timing error.

Fig. 7

Daily range bias estimates across 550 days (left) for the TriG (Blue) and PODRIX-GPS (orange) and the daily estimated differences (right)

When the pseudorange is modeled using Eq. 3, it is not possible to separate a pure range bias from a pure time-tag bias. Consider the case where the pseudorange contains a time-tag bias, $\tau$,

$$\begin{aligned} \rho = r + \delta t_{rx}^r(c-\dot{\rho }) + \tau \dot{\rho } + \ldots \end{aligned}$$

(6)

This can be easily transformed into an equivalent statement, but with a range bias using the following,

$$\begin{aligned} \rho&= r + \delta t_{rx}^r(c-\dot{\rho }) + \tau \dot{\rho } + \tau c - \tau c + \ldots \end{aligned}$$

(7)

$$\begin{aligned}&= r + \delta t_{rx}^r(c-\dot{\rho }) - \tau (c-\dot{\rho }) + \tau c + \ldots \end{aligned}$$

(8)

$$\begin{aligned}&= r + (\delta t_{rx}^r - \tau )(c-\dot{\rho }) + \tau c + \ldots \end{aligned}$$

(9)

Estimation of either a constant range bias or time-tag bias allows for the separation of the clock bias and the time-tag. In practice, it is easier to estimate a constant range bias over the entire solution arc and an independent white noise receiver clock bias at each epoch.

To test this hypothesis, a constant range bias was estimated for a combined TriG and PODRIX 30-hour reduced-dynamic orbit solution with applied pre-launch antenna calibrations and ambiguity resolution. Daily range biases were estimated for both the TriG and PODRIX-GPS observations but not for PODRIX-Galileo. Figure 7 (left) shows the daily estimated range bias values across 1.5 years. Both solutions have a similar pattern in the time history with the TriG showing a large offset relative to the PODRIX-Galileo observations. Meanwhile, the PODRIX-GPS observations have a relatively small offset with respect to the PODRIX-Galileo observations, as might be expected. However, recall from Fig. 3 that the PODRIX-GPS and Galileo observations show relative clock offsets of a few meters. The differences between the TriG and PODRIX-GPS solutions show a relatively consistent offset. The mean offset weighted by the formal error over the entire time-span results in a range bias estimate for the TriG of $405 \pm 64~\hbox {m}$ and for the PODRIX-GPS of $-38 \pm 54~\hbox {m}$.

The SLR residual indication of a relative bias of about 9.5 mm between the TriG and PODRIX is consistent with the absolute range bias of 405 m or equivalent to a time-tag inconsistency of $1.35~\mu \hbox {s}$. Given the orbital velocity of Sentinel-6 MF ($\sim 7000~\hbox {m/s}$), a time-tag error of $1.35~\mu \hbox {s}$ produces roughly 9.5 mm of displacement consistent with the observed bias between the TriG and PODRIX. The source of this error is unclear, but determination of the exact cause is beyond the scope of this study. Thus, for the remainder of this analysis, all TriG solutions simply apply a fixed range bias of 405 m to the pseudorange observations.

4 Results

The results presented here cover 550 days from June 30, 2021, to December 31, 2022. An evaluation of six different 30-hour, reduced-dynamic orbit solutions with ambiguity resolution are examined and compared: a TriG-only solution, a TriG-only solution with 10-degree elevation mask, a PODRIX-GPS-only solution, a PODRIX-Galileo-only solution, a PODRIX-GPS plus Galileo solution, and a TriG plus PODRIX combined solution. Each solution uses an in-flight antenna calibration estimated from consistent methodology. The solutions are evaluated for consistency using post-fit residual rms, orbit overlaps and ambiguity resolution statistics. Finally, the orbit accuracy for each solution is assessed with independent SLR observations.

Fig. 8

Correction to the pre-launch antenna calibration for the TriG (left), PODRIX-GPS (middle) and PODRIX-Galileo (right)

Table 6 Antenna offsets [body-x, body-y, body-z] computed from corrections relative to the pre-launch calibrations

4.1 Antenna calibration

Figure 8 shows the estimated in-flight PV corrections for each antenna calibration in the combined solution. Because mean spacecraft body-x/y/z offsets can be absorbed in the PVs, it is useful to examine how these offsets have changed relative to the nominal pre-launch antenna calibration. Table 6 lists the mean body-x/y/z offsets contained within each set of PV corrections. At the scale in Fig. 8, each separate antenna calibration appears very similar, and so only the results from the combined solution are shown. The antenna offsets within each calibration are consistent across the different solutions. GPS phase calibration corrections have very similar z-offsets of about 20 mm whereas PODRIX-Galileo has a -12 mm z-offset. For the combined solution, constraining the TriG x-offset to zero results in a small offset of about 1 mm in both the PODRIX calibrations. This may be the result of a small baseline difference or possibly related to the estimated range bias for the TriG. Nevertheless, it is quite small.

Offsets of 5–9 mm are present in the y-component for all three antenna calibrations but with opposite signs for the TriG and PODRIX. Similar offsets were observed by Desai et al. (2022) and Montenbruck et al. (2022) who suggested a spurious yaw bias of roughly 0.4 degrees in the measured satellite attitude could provide an explanation. To test the sensitivity of the orbit solutions to a yaw shift, we compared TriG-based orbit solutions with and without a 0.4-degree yaw bias across all of 2021. Each of the two solutions had a separate antenna calibration estimated in a manner consistent with the applied quaternions. The orbit differences are very small, with typical daily rms differences of 0.03, 0.04 and 0.08 mm, respectively, for radial, cross-track and along track. While the application of a yaw bias does reduce the y-offsets in the antenna calibration for Sentinel-6 MF, it has a negligible effect on the orbit solution when the antenna calibration is consistent with the applied attitude.

4.2 Internal metrics

Each orbit solution is first evaluated using a set of internal metrics comprising the daily post-fit residual rms to test for goodness of fit. Next, a comparison of the orbit overlap difference rms is used to assess the orbit solution precision and consistency.

Fig. 9

Distribution of the daily ionosphere-free phase residual rms statistics from the combined solution computed separately for TriG L1C/L2W, TriG >10-deg L1C/L2W, PODRIX-GPS L1W/L2W, PODRIX-GPS L1C/L2L and PODRIX-Galileo L1C/L5Q

Fig. 10

Distribution of the daily ionosphere-free code residual rms statistics from the combined solution computed separately for TriG C1W/C2W, TriG >10-deg C1W/C2W, PODRIX-GPS C1W/C2W, PODRIX-GPS C1C/C2L and PODRIX-Galileo C1C/C5Q

Table 7 Post-fit residual rms in terms of the mean ± the standard deviation of the daily statistics

Figures 9 and 10 show the distribution of the combined solution phase and code daily residual rms from 30-hour reduced-dynamic orbit solutions with ambiguity resolution. The mean of the daily rms ± the overall standard deviation is shown in Table 7. The TriG residuals are larger overall due to tracking down to zero degrees which increases the number of noisy observations which occur at low elevations. When applying a 10-degree mask to the TriG, as is done for the PODRIX, the observations with the highest measurement noise are removed. This results in phase residuals that are slightly smaller than the PODRIX-GPS. The PODRIX-Galileo phase and code residuals are smaller than any of the GPS with less variability overall. The PODRIX-GPS code observations are nearly 20 cm smaller than the TriG even accounting for the 10-degree mask. Also, the PODRIX C1W/C2W observations have a similar rms to the C1C/C2L observations. The C1C/C2L residuals do exhibit a different distribution in Fig. 10 which could possibly be related the residual receiver DCBs between C1W/C2W and C1C/C2L.

Fig. 11

Daily overlap difference rms for radial (left), cross-track (middle) and in-track (right) from Sentinel-6 MF ambiguity-resolved reduced-dynamic orbit solutions for six cases: (1) TriG, (2) TriG >10-deg, (3) PODRIX-GPS, (4) PODRIX-Galileo, (5) PODRIX, (6) Combined

The orbit solution precision can be evaluated using orbit overlaps. From the 30-hour solution arcs, this results in 6 h of overlap between each daily solution. Using only the central four hours to avoid edge effects, a single rms value for the radial, cross-track, and in-track directions is computed from the daily component differences. Figure 11 shows the distribution of the daily rms statistics after $5\sigma$ outlier removal. All solutions exhibit very good precision with the TriG and PODRIX solutions showing very similar performance. The PODRIX-Galileo solution has slightly higher mean overlap rms and the most variability from day-to-day. Combining all observations into a single solution produces the most consistent overlap statistics with decreases in the mean overlap rms as well as in the daily variability across the solution time span as shown in Table 8. The most notable improvement is for the in-track overlap which seems to benefit the most from the increase in observations. This is evident in both the PODRIX and the combined solutions. It is interesting to note, however, that applying a 10-degree elevation mask to the TriG did not degrade the solution precision. This is likely due to removal of the noisy low-elevation observations.

Table 8 Overlap difference rms in terms of the mean ± the standard deviation of the daily statistics after $5\sigma$ outlier removal

The slightly poorer performance of the PODRIX-Galileo compared to the other solutions may be due to a few factors. It is possible that performance may be degraded by the IGS14 calibrations and potentially lower accuracy orbit and clock products. This could be tested by applying the newer IGS20 calibrations to evaluate this effect. It is also possible that the Galileo ambiguity resolution may play a factor and is discussed in more detail in the next section.

4.3 Ambiguity resolution

Each of the daily reduced-dynamic POD solutions implement single-receiver ambiguity resolution (Bertiger et al. 2010b). The phase ambiguity biases are fixed using a wide-lane bias product estimated from a ground station network. This allows for the formation of double differences with the LEO receiver. The narrow-lane ambiguities are fixed based only on resolved wide-lane double differences that pass a confidence threshold and distance to the nearest integer test. The resulting constraints are not a linearly independent set of double differences, but rather applied from all possible double-difference combinations. Because of this, constrained ambiguities are then applied within the filter smoother using a confidence weight of 10 cm. The ambiguity-resolved solution is then iterated 10 times as described by Bertiger et al. (2010b).

Fig. 12

Daily solution percent of wide-lane samples fixed to within 10 centi-cycles (left), and the constrained double differences as a percentage of the total possible for six solutions: (1) TriG tracking data (blue), (2) TriG tracking data > 10 degrees (orange), (3) PODRIX-GPS tracking data (green), (4) PODRIX-Galileo tracking data (red), (5) PODRIX tracking data (purple), (6) TriG plus PODRIX tracking data (brown)

Figure 12 shows the wide-lane statistics from the ambiguity resolution process. The wide-lane resolution for the TriG has a relatively low percentage of samples fixed to within 10 centi-cycles with an overall mean of 40.3%. The PODRIX-GPS and Galileo, on the other hand, perform much better at 59.4% and 84.8%, respectively. Because only passes with acceptable wide-lane criteria are constrained, a similar pattern is observed in the constrained double differences as a percentage of the total possible. For the TriG, the cause of the poor wide-lane resolution is uncertain, but may be related to the large code residual rms observed earlier. It is interesting to note that the TriG does show a small benefit to the fixing statistics when the 10-degree elevation mask is applied.

Fig. 13

Total number of daily applied constraints (left) and the overall mean narrow-lane (right) samples resolved to within 10 centi-cycles of an integer after each iteration from 2021-06-30 to 2022-12-31 for six solutions: (1) TriG tracking data (blue), (2) TriG tracking data > 10 degrees (orange), (3) PODRIX-GPS tracking data (green), (4) PODRIX-Galileo tracking data (red), (5) PODRIX tracking data (purple), (6) TriG plus PODRIX tracking data (brown)

Figure 13 (left) shows the daily total number of double-difference passes which are constrained in the 30-hour solution arc. Despite the lower fixing statistics for the TriG, it has a similar number of constraints applied as the PODRIX-GPS which is likely due to the higher number of tracked GPS transmitters for the TriG. Galileo on the other hand, despite having the highest fixing percentage, has significantly fewer applied constraints. The reason for this is likely related to the wide-lane bias product containing far fewer stations for Galileo than for GPS and so fewer double differences are possible. In the combined solution, the applied constraints are dominated by the GPS double differences.

The overall average narrow-lane resolution as a function of iteration is shown in Fig. 13 (right). Like the wide-lane, the TriG percentage of narrow-lane samples resolved to less than 10 centi-cycles is the lowest across all iterations. The lower narrow-lane fixing rate for the TriG is also evident in the combined solution. This poorer fixing rate is due to a number of fixed ambiguities which appear to be in error by a half-integer. This half-integer error has also been observed by Bertiger et al. (2010a). Given that the ambiguity resolution is applied with a soft constraint, it does not appear to have a significant effect on the orbit solution.

Fig. 14

SLR residual rms (left) and bias (right) as a function of boresight angle

4.4 Independent SLR residuals

To evaluate the orbit accuracy, we consider independent SLR observations (Pearlman et al. 2019). Station positions are modeled in the ITRF2014 reference frame and include seasonal geocenter motion (Altamimi et al. 2016). Only a set of high performing SLR stations, with one-way residual biases below 5 mm for the entire data set, are considered to evaluate the Sentinel-6 MF orbit solutions. These include the following six stations: Greenbelt, Maryland; Graz, Austria; Herstmonceux, the UK; Mt Stromlo, Australia; Yarragadee, Australia; and Wettzell, Germany. For this analysis, station residual biases are not removed from the observations. SLR range corrections are applied based on line-of-sight azimuth and elevation in the laser retroreflector array (LRA) frame using the tabulated model from Mercier and Couhert (2016). After $5\sigma$ filtering, Fig. 14 shows the SLR one-way residual rms in the left panel, and the overall bias in the right panel. Table 9 shows a comparison of the overall statistics from each orbit solution. Here, we can see that all orbit solutions have relatively similar rms values between 7.0 mm and 7.5 mm. The SLR residual rms below 45-degree off-nadir angle (high station elevation) in the LRA frame of 6.8 mm or lower for all solutions and indicates radial accuracies better than 1 cm.

Table 9 Comparison of the overall rms, bias and rms below 45-degree off-nadir angle

Table 10 Spacecraft body-x/y/z offsets estimated from the SLR residuals. These are correlated with the orbit in-track (body-x), cross-track (body-y) and radial (body-z) directions

From the SLR residuals, mean body-x/y/z offset, correlated with the radial, cross-track and in-track directions, can be computed using a least squares approach with Eq. 1 as shown in Table 10. We see that all offsets are below 3 mm, and the application of the range bias on the TriG solution has effectively removed the body-x bias as previously observed. The Body-y/z offsets are consistent between each solution with relative differences being smaller than 0.2 mm. The body-z/radial offset will be correlated with the overall biases seen in the right panel of Fig. 14 which are related to both the station biases and potentially errors in the applied range bias correction. Removal of a global bias for all observations does remove the observed body-z offset but would produce an overly optimistic estimate of any potential radial bias which may arise from force modeling errors. The body-y/cross-track offsets are more difficult to explain. One potential explanation would be a body-y error in the spacecraft center of mass or the LRA spacecraft reference location. Another potential explanation is the uncertainty in the station positions. Because the Sentinel-6 MF attitude is roughly yaw-fixed and the orbit is inclined 66 degrees, errors in the station positions relative to the geocenter which are aligned with the Earth’s axis will map into the cross-track direction and appear as a body-y bias. The yaw bias proposed by Desai et al. (2022) and Montenbruck et al. (2022) is unlikely to be the primary cause of the body-y offsets observed in the SLR residuals. As mentioned earlier, there is very little change to the center of mass location between orbit solutions with and without the yaw bias applied. However, there will be a shift in the location of the LRA in the orbit frame when applying the yaw bias. With the proposed yaw bias of 0.4 degrees, this will shift the location of the LRA roughly 2.7 mm in the in-track direction and 0.6 mm in the cross-track direction. The yaw bias will manifest primarily as a body-x offset in the SLR residuals. Application of the yaw bias will affect the SLR residuals for each solution in the same way, so it will not fundamentally alter the conclusions presented here.

5 Summary

Sentinel-6 MF is the first operational science platform in LEO that flies multiple active receivers and also tracks GPS plus Galileo observations. After estimation of antenna calibrations, orbit solutions derived from TriG and PODRIX observations were assessed for precision and accuracy. Both the TriG and PODRIX observations are capable of producing highly accurate orbit solutions which meet the mission requirement for a radial rms error less than 1.5 cm.

The ability to compare the TriG and PODRIX solutions revealed a range bias of approximately 400 m in the TriG observations. Correcting for this removed a systematic bias in the in-track direction as revealed by the SLR residual analysis where a reduction from 8.3 mm to 7.1 mm is observed. This improvement is due to both the in-track bias correction as well as the applied antenna calibration. When including the TriG and PODRIX observations in a single solution, this results in the most precise orbit solutions as evidenced by orbit overlaps and SLR residual rms.

The TriG and PODRIX receivers show similar performance in terms of orbit overlaps and fits to withheld SLR observations. For each receiver, some additional improvement is possible. Of the two receivers, the TriG had the poorest daily wide-lane ambiguity resolution. Further investigation may provide a means to improve the wide-lane ambiguity resolution and examine the effect on the orbit solutions. For the PODRIX, the use of multi-code GPS signals complicates the ambiguity resolution due to the presence of DCBs that must be accounted for in a way that is consistent with the current wide-lane products. This is evident in the lower wide-lane resolution and percentage of fixed double differences for the GPS observations compared to Galileo. Despite this, the Galileo solutions performed slightly worse in terms of orbit overlaps and SLR residuals compared to GPS. This contrasts with previous work by (Peter et al. 2022) and (Zandbergen et al. 2022) which observed slightly better orbit performance for the PODRIX-Galileo only solutions when compared to PODRIX-GPS only solutions. The reason for better PODRIX-GPS solutions in this study is likely due to a few factors. The first is the use of Galileo IGS14 transmitter calibrations, orbit and clock product and significantly fewer available double-difference combinations in the wide-lane bias product. The second is the application of our empirical DCB estimates which improved the ambiguity resolution for the PODRIX-GPS solution. As the Galileo orbit, clock and wide-lane products mature, its contributions to LEO-based science missions will continue to grow.

Differential code bias correction

Fig. 15

Post-fit pseudorange rms (left) and wide-lane ambiguity resolution (right) as a function of percentage of samples fixed to within 10 centi-cycles of an integer for a given C1C and C2L offset. The values applied to SVN-50 observations are marked with a red X

Table 11 Estimated DCB corrections for the PODRIX-GPS C1C and C2L observations. Corrections are additive to the observations to make them consistent with C1W and C2W observations

Fig. 16

Comparison of estimated PODRIX C1C–C1W and C2L–C2W Differential code biases to those estimated by DLR (Montenbruck et al. 2014)

Fig. 17

Post-fit pseudorange residuals (left panel) and distance to nearest integer from the wide-lane double differences (right panel) from 2022-01-02 for three cases: (1) No DCB corrections applied (blue), (2) Applied DCB corrections from DLR, (3) DCB corrections estimated from PODRIX observations

Because a subset of the PODRIX-GPS signals observe the C1W/C2W pseudoranges, which are consistent with the wide-lane bias product, they can serve as a reference against which the remaining C1C–C1W and C2L–C2W biases can be estimated. This was done by first fixing TriG reduced-dynamic orbit solutions. Then, biases were applied to the C1C and C2L observations across a range of ±0.5 m in 0.05 m steps for each frequency. The C1W/C2W observations, along with a single C2L transmitter, were fit to the fixed orbit solutions estimating only the receiver clock, phase biases and resulting wide-lane ambiguity resolution statistics. This produced a total of 441 solutions for each C2L transmitter. Finally, the C1C and C2L bias values were chosen based on the intersection of the most successful wide-lane ambiguity resolution and the lowest post-fit pseudorange residual rms. This was done for all L2C transmitters on two separate days, 2021-06-30 and 2022-05-29, and the average bias from these two days was applied to all observations across a time span of 1.5 years. By estimating transmitter specific biases in this way, they will also absorb any receiver DCBs. Because the receiver DCBs are the same across all transmitters, this will affect the overall level of the biases, but not the relative differences between transmitters. Figure 15 shows an example of the results for space vehicle number (SVN) 50 from 2021-06-30. Applying these biases greatly improves the overall wide-lane ambiguity resolution. Table 11 lists the applied DCB values estimated from this method.

Figure 16 shows the empirically estimated DCBs compared to published weekly values from Deutsches Zentrum für Luft- und Raumfahrt (DLR) (Montenbruck et al. 2014) for 2022-01-02. While some estimates are close to the DLR values, others have differences larger than 30 cm. When applying DCBs from both the DLR published values and the estimated DCBs to the PODRIX observations, it can be seen that there is a large decrease in post-fit residuals as shown in Fig. 17. However, there is very little improvement in the wide-lane double differences for the DLR DCB application, which in an ideal case would be integer values. The reason for this may be related to a couple of factors. The first being that the biases are not part of the same orbit and clock product from which the wide-lane bias values are derived. The second is likely related to how the biases are estimated. As can be seen in the right panel in Fig. 15, there are many sets of biases that will minimize the residuals. As described by Montenbruck et al. (2014), to separate out the receiver and transmitter biases, which are estimated together, a zero mean condition is applied to the transmitters. This constraint, while producing biases that are consistent with a transmitter clock product based on GPS P(Y) observations, will not necessary produce biases which are consistent with the wide-lane bias product when signals are mixed in a single receiver. For this reason, we apply the empirically estimated DCBs listed in Table 11 for all PODRIX-GPS C1C and C2L observations.