Full-Bayes GNSS-A solutions for precise seafloor positioning with single uniform sound speed gradient layer assumption

Abstract

A systematic analysis methodology for precise seafloor positioning using the GNSS-A has been constructed and implemented in the open-source software GARPOS. It introduces a linearized perturbation field model for extraction of the 4-dimensional sound speed variation, and solves the perturbation parameters simultaneously with the seafloor position based on the empirical Bayes approach. Although it can provide the solutions stably and almost analytically, it has less expandability when imposing additional nonlinear constraint parameters in the observation equation. Even though such parameters can be optimized by applying some information criteria, information on the details of the joint posterior probability would be lost and only the conditional posterior can be estimated. To overcome the above limitations, we implemented full-Bayes estimation using the Markov-Chain Monte Carlo algorithm. This approach can not only help evaluate the dependency of the existing constraint parameters on the seafloor position, but also let us discuss the effects of the additionally imposed constraints. We imposed a constraint under the assumption that a temporally-variable gradient layer steadily lies at a certain depth in the observation scale (typically < 10 km × 10 km, < 1 day). This models the cases with temperature gradients due to a large-scale structure such as the Kuroshio current or internal waves with long-wavelength. The constraint narrows the posterior of the horizontal position and provides a better solution for many datasets, especially in the Nankai Trough region. For the other datasets, the constraint emphasized bias errors, which can also provide information on the possibility of instrumental and modelling errors.

1 Introduction

In this century, space-based geodetic techniques have reached the seafloor covered with thousands of meters of ocean, by combining the Global Navigation Satellite System (GNSS) and undersea acoustic ranging techniques, i.e., the GNSS-A (Spiess 1985). Repeated GNSS-A observations have detected crustal deformation in the source regions of megathrust earthquakes, for example, for steady interseismic movements (e.g., Gagnon et al. 2005; Fujita et al. 2006; Watanabe et al. 2015; Yokota et al. 2016), for instantaneous response to earthquakes (e.g., Kido et al. 2006, 2011; Tadokoro et al. 2006; Sato et al. 2011), for postseismic transient deformation (e.g., Watanabe et al. 2014, 2021; Tomita et al. 2017; Honsho et al. 2019), and for episodic velocity changes due to slow slip events (Yokota and Ishikawa 2020). Such findings for seismic cycles in subduction zones were realized by the improvements of the GNSS-A observation and analysis techniques to achieve centimeter-scale positioning on the seafloor.

The Japan Coast Guard (JCG) has been constructing and operating the Seafloor Geodetic Observation Array (SGO-A) for detecting crustal deformation in the seismogenic zone along the Japan Trench and the Nankai Trough since 2000 (Fig. 1). In the SGO-A project, the JCG installed four seafloor acoustic mirror transponders for each site, and periodically collects thousands of round-trip travel time data along pre-determined track lines using their survey vessels (Fig. 1a; e.g., Ishikawa et al. 2020).

Fig. 1

a Schematics of GNSS-A observation (after Watanabe et al. 2020) and b locations of SGO-A sites (red and yellow circles). Currents (wide lines) and a mixed water region (encircled by the purple oval) are schematically shown based on Yasuda et al. (1996)

The GNSS-A observation system is an integrated system consisting of a GNSS antenna/receiver, surface and seafloor acoustic instruments, and a gyro sensor. Among the various error sources in the system, it is essential to properly estimate and correct the influence of underwater sound speed variation for precise GNSS-A positioning. In the first stage of in-situ applications of GNSS-A observation, Spiess et al. (1998) estimated the horizontal position of the array of multiple seafloor acoustic transponders with a precision of several centimeters. They collected the acoustic travel time data from the sea surface directly above the center of the transponder array, and cancelled the effects of the time-dependent sound speed perturbation by neglecting the vertical displacement. Osada et al. (2003) estimated the temporal variation of sound speed by comparing the residuals of travel time data. Kido (2007) suggested a method to estimate the horizontal gradient of sound speed using five transponders. Kido et al. (2008) also introduced a variable of vertical delay to represent the sound speed variation.

Obana et al. (2000) took a different approach to estimate the 3-dimensional position of a single transponder, by using the least squares method for the acoustic travel time data with various slant ranges. They only used the measured sound speed profiles, resulting in a precision of 10–20 cm. Yamada et al. (2002) numerically investigated the effect of the sound speed variation on the ranging. To cancel the bias errors including the effects of the sound speed variation, Xu et al. (2005) performed a theoretical work to develop the method with single- and double-differencing techniques. Fujita et al. (2006) developed the method to iteratively estimate the seafloor position and temporal variation of sound speed to achieve the detection of horizontal crustal deformation in a precision of 1 cm/year. On the other hand, Ikuta et al. (2008) applied the simultaneous estimation of the seafloor position and sound speed variation. They determined the coefficients of B-spline function (e.g., de Boor 1978) for the temporal variation of sound speed with the penalized least squares method. However, they determined the degree of smoothness not statistically, but just practically. For data acquisition, Sato et al. (2013) showed the importance of well-distributed acoustic ranging data from actual observation datasets, which had been realized by mounting the transducer on the hull of vessels.

In the latter half of 2010s, researchers improved the positioning accuracy by implementing models that express a sound speed field with spatial inclinations (e.g., Yasuda et al. 2017; Honsho et al. 2019; Yokota et al. 2019), instead of a horizontally stratified sound speed field. Based on those existing formulations, Watanabe et al. (2020) constructed a new GNSS-A observation model by introducing the idea of a perturbation field. The perturbation field, expressed as a function of time and acoustic instrument positions, generally covers all of the spatio-temporally varying terms, though most of which are assumed as spatio-temporal variations of the sound speed structure in the ocean. They implemented the GNSS-A model with a linearized perturbation field, which essentially includes the existing sound speed field models (e.g., Yasuda et al. 2017; Honsho et al. 2019; Yokota et al. 2019), into an open-source software “GARPOS” (the latest version is v1.0.1; Watanabe et al. 2022a). GARPOS solves the seafloor positions along with the smoothened time-dependent coefficients in the perturbation field model, by taking an empirical Bayes approach.

Specifically, the perturbation field in GARPOS corresponds to the perturbation in the sound speed structure. Watanabe et al. (2020) imposed a constraint that the perturbation field changes smoothly. In their scheme, the degrees of roughness for the components of the perturbation field are controlled by hyperparameters, which are deterministically selected by minimizing the Akaike Bayesian information criterion (ABIC; Akaike 1980). Simultaneously, they also introduced the assumption of correlations among the data errors, by referencing the case of the Synthetic Aperture Radar interferometry (InSAR) data (e.g., Fukahata and Wright 2008). The correlations reflect the characteristics of GNSS-A error sources which are mainly from the ocean environment. Because the ocean environment largely changes with each observation visit, GARPOS optimizes the shape of variance–covariance matrix for each dataset, unlike many other papers where only the scale factors for the variance–covariance matrix were estimated (e.g., Koch and Kusche 2002; Fukuda and Johnson 2008). This assumption contributes to the successful choice of appropriate smoothing hyperparameters, leading to avoid overfits of the perturbation field’s coefficients to the data. It is also noted that this resolved the problem mentioned in Ikuta et al. (2008), where the statistical criteria cannot work well.

GARPOS, which provides more stable positioning solutions than the former solver, is now regularly used for the routine GNSS-A analysis of the SGO-A. It contributed to precisely tracing time-variable seafloor movements (e.g., Watanabe et al. 2021). It can also extract information on the underwater sound speed structure from the perturbation term, e.g., the horizontally inclined sea-water temperature caused by the Kuroshio warm current, as discussed by Yokota et al. (2022) and Watanabe et al. (2020). The systematic extraction of oceanographic information by GNSS-A, i.e., the GNSS-A oceanography, provides a new technique for measurement in the ocean.

However, GARPOS provides perturbation parameters that cannot be interpreted as a realistic oceanographic structure for some datasets. Such solutions can be improved by imposing constraints on the perturbation field based on a proper structure (Yokota et al. 2022). For example, when there is a global-scale current, the sound speed structure is fully described with a horizontally inclined layer in one direction. Such a constraint requires nonlinear model parameters in the observation equation. GARPOS, taking the semi-analytical approach to solve the model parameters, has limitations in expandability in imposing such nonlinear constraints. One practical solution for this problem is to select the appropriate values for those parameters deterministically by maximizing the marginal likelihood with the repeated forward calculations, based on the scheme of empirical Bayes. However, it is difficult to search those parameters exhaustively.

In addition, for further discussions on GNSS-A such as the evaluations of positioning errors, it is necessary to consider how the uncertainty in the estimation of constraint parameters affects the positions. It is also important to obtain the posterior distributions for parameters which reflect the efficiency or appropriateness of the assumed models for each dataset, because the underwater environment is highly variated with observation visits and we typically have insufficient information on it. Furthermore, it is not obvious that the posterior distribution can be approximated with a normal distribution, which leads to worse estimations when applying the maximum likelihood estimation or maximum a posteriori estimation (Watanabe 2018). For these purposes, this empirical Bayes method also has limitations in estimating the posterior distributions of relevant parameters or the marginal probability of positions with respect to the other parameters. For those reasons, a new scheme is required to adequately impose the constraints and evaluate their effects on the GNSS-A analysis.

For these purposes, i.e., (1) to adequately impose the constraints which makes the observation equation nonlinear, (2) to evaluate the effects of all parameters in stochastic models, and (3) to directly estimate the shape of posterior distribution for seafloor position, we expanded the formulation of GARPOS based on the full-Bayes approach, and implemented it into a software using the Markov-Chain Monte Carlo (MCMC) method to directly estimate the joint posterior distribution for the positions and the other parameters. This contributes to the evaluation of inter-parameter correlations, of appropriateness or efficiency of assumed models, and of positioning precision as a marginal distribution. We then imposed additional nonlinear constraints on the perturbation field, i.e., the situation where the sound speed is fully described with a horizontally inclined structure in one direction, which approximately reflects the large-scale oceanographic structure. We also prepared a hybrid model where a small bias for the spatial gradient of a perturbation field was allowed, to loosen the above constraint. Those new models were tested with actual GNSS-A datasets collected in different waters.

2 Formulation

2.1 Definitions for GNSS-A variables and observation equation

This section introduces the definition of the GNSS-A observation equation proposed by Watanabe et al. (2020) with some updates. In the GNSS-A, we solve the problem to determine the positions of the seafloor transponders, ${\varvec{X}\!_{j}}$, where $j$ denotes the serial number of transponders, from the observed acoustic round-trip travel time, ${{\varvec{T}}}^{o}$, between the sea-surface transducer and the seafloor transponder, as

$$ \begin{array}{*{20}c} {{\varvec{T}}^{o} = {\varvec{T}}^{c} \left( {{\varvec{P}}\left( t \right),{\varvec{X}}\!_{j} ,V\left( {e,n,u,t} \right)} \right) + \varvec{\epsilon},} \\ \end{array} $$

(1)

where ${\varvec{T}}^{c}$, ${\varvec{P}}\left( t \right)$, $V\left( {e,n,u,t} \right)$, and $\varvec{\epsilon}$ denote the calculated travel time, the sea-surface transducer position, the sound speed structure, and the observation error vector, respectively. Although ${\varvec{T}}^{c}$ can be fully calculated by ray-tracing based on Snell’s law, we cannot obtain the complete expression of $V\left( {e,n,u,t} \right)$. Therefore, Watanabe et al. (2020) took an approach to divide the effects of the 4-dimensional sound speed variation, i.e., $V\left( {e,n,u,t} \right)$, into a horizontally stratified static reference profile, i.e., $V_{0} \left( u \right)$, and a perturbation. This leads to the following travel time expression:

$$ \begin{aligned} &T_{i}^{c} \left( {{\varvec{P}}\left( {t = t_{{i_{ + } }} ,t_{{i_{ - } }} } \right), {\varvec{X}\!_{j}} ,V\left( {e,n,u,t} \right)} \right)\\ &\quad = \exp \left( { - \gamma_{i} } \right) \cdot \tau_{i} \left( {{\varvec{P}}\left( {t = t_{{i_{ + } }} ,t_{{i_{ - } }} } \right),{\varvec{X}\!_{j}} ,V_{0} \left( u \right)} \right), \end{aligned} $$

(2)

where $t_{{i_{ + } }}$, $t_{{i_{ - } }}$, $\gamma_{i}$, and $\tau_{i}$ denote the transmission and reception times of acoustic signals at the sea-surface transducer, the perturbation term, and the reference travel time under the reference sound speed profile ${V}_{0}\left(u\right)$, respectively. The term $\mathrm{exp}\left(-{\gamma }_{i}\right)$ is selected to easily relate ${\gamma }_{i}$ to the sound speed perturbation. As shown by Watanabe et al. (2020), when $\left|{\gamma }_{i}\right|\ll 1$ is satisfied, $\left(1+{\gamma }_{i}\right)\overline{{V }_{0}}$, where $\overline{{V }_{0}}$ is an average of ${V}_{0}\left(u\right)$, approximately denotes the average sound speed along the ith acoustic path. The perturbation term can be considered as a value extracted from a scalar perturbation field depending on time and the acoustic instrument positions, i.e., $\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)$, as follows:

$${\gamma }_{i}\equiv \frac{1}{2}\sum\limits_{{{t}_{l}\in\left\{{t}_{{i}_{+}},{t}_{{i}_{-}}\right\}}}\Gamma \left({t}_{l}, {\varvec{P}}\left({t}_{l}\right),\boldsymbol{ }{{\varvec{X}}}\!_{j}\right).$$

(3)

With this general $\Gamma$-formulation, all perturbations including the random error can be fully covered in principle when $\Gamma$ has a sufficiently large degree of freedom (also see Sect. 3.1). The practical problem is to find out the reasonable and realistic expression of $\Gamma$, avoiding overfitting to the high-frequency noise. Watanabe et al. (2020) took an assumption of continuity and simplicity of the perturbation field $\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)$ to express the perturbation field as a linear system with respect to ${\varvec{P}}$ and ${\varvec{X}}$, as follows:

$$\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)\equiv {\alpha }_{0}\left(t\right)+{\boldsymbol{\alpha }}_{1}\left(t\right)\cdot \frac{{\varvec{P}}}{{L}^{*}}+{\boldsymbol{\alpha }}_{2}\left(t\right)\cdot \frac{{\varvec{X}}}{{L}^{*}},$$

(4.1)

where ${L}^{*}$ denotes a characteristic length for the observation scale, and the temporal variations of each coefficient are expanded using a linear basis set as

$$\begin{array}{c}\left\{\begin{array}{l}{\alpha }_{0}\left(t\right)=\sum\nolimits_{k=0}^{{K}_{a}}{a}_{k}^{\langle 0\rangle }{\Phi }_{k}^{\langle 0\rangle }\left(t\right)\\ {\boldsymbol{\alpha }}_{1}\left(t\right)=\sum\nolimits_{k=0}^{{K}_{b}} \left({a}_{k}^{\langle 1E\rangle }{\Phi }_{k}^{\langle 1E\rangle }\left(t\right),\boldsymbol{ }{a}_{k}^{\langle 1N\rangle }{\Phi }_{k}^{\langle 1N\rangle }\left(t\right), 0\right)\\ {\boldsymbol{\alpha }}_{2}\left(t\right)=\sum\nolimits_{k=0}^{{K}_{c}} \left({a}_{k}^{\langle 2E\rangle }{\Phi }_{k}^{\langle 2E\rangle }\left(t\right),\boldsymbol{ }{a}_{k}^{\langle 2N\rangle }{\Phi }_{k}^{\langle 2N\rangle }\left(t\right), 0\right)\end{array}\right., \end{array}$$

(4.2)

where ${a}_{k}^{\langle \cdot \rangle }$ are the coefficients of the $k$th basis function, ${\Phi }_{k}^{\langle \cdot \rangle }\left(t\right)$, for each term named $\langle \cdot \rangle$ and $E$ and $N$ in $\langle \cdot \rangle$ denote the eastward and northward components of the vector, respectively. In GARPOS, the B-spline functions (e.g., de Boor 1978) are taken for the basis. The vertical components of ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$ are set to zero because both ${\varvec{P}}$ and ${\varvec{X}}$ hardly vary in the vertical direction. For simplification, we compile these coefficients into a vector ${\varvec{a}}$, and call it “perturbation coefficients”, hereafter.

In the present study, we take the rigid-array constraint formerly introduced by Watanabe et al. (2020) based on Matsumoto et al. (2008), where the local deformation within the transponder array is assumed to be sufficiently small so that the same array geometry can be used throughout all the observation visits. Under this assumption, ${{\varvec{X}}}_{j}$ can be expressed with a 3-dimensional vector ${\varvec{x}}$, denoting the parallel displacement of the transponder array. Hence, we define the observation equation in logarithmic form as follows:

$$\begin{aligned}\mathrm{log}\left({T}_{i}^{o}/{T}^{*}\right)&=\mathrm{log}\left({\tau }_{i}\left({\varvec{x}}|\overline{{{\varvec{X}}}\!_{j}},{\varvec{P}},{V}_{0}\right)/{T}^{*}\right) -{\gamma }_{i}\left({\varvec{a}}|\overline{{{\varvec{X}}}\!_{j}},{\varvec{P}}\right)+{e}_{i} \end{aligned}$$

(5)

for the $i$th acoustic signal, where ${T}^{*}$, $\overline{{{\varvec{X}} }\!_{j}}$, and ${e}_{i}$ denote the characteristic travel time, the relative positions of each transponder and the observation error, respectively. The variables on the left and right sides of the vertical bar indicate the estimators and the observables, respectively. Because ${\varvec{\gamma}}$, as defined by Eqs. (3) and (4), is linear with respect to ${\varvec{a}}$, we can rewrite the observation equation in a simpler form as

$${\varvec{d}}={\varvec{f}}\left({\varvec{x}}\right)+G{\varvec{a}}+{\varvec{e}},$$

(6)

where ${d}_{i}=\mathrm{log}\Big({T}_{i}^{o}/{T}^{*}\Big)$, ${f}_{i}\left({\varvec{x}}\right)=\mathrm{log}\Big({\tau }_{i}\Big({\varvec{x}}|\overline{{{\varvec{X}} }\!_{j}},{\varvec{P}},{V}_{0}\Big)/{T}^{*}\Big)$, and $G{\varvec{a}}=-{\varvec{\gamma}}\left({\varvec{a}}|\overline{{{\varvec{X}}}\!_{j}},{\varvec{P}}\right)$. Note that ${\varvec{P}}$ is derived from the GNSS antenna position, the gyro data, and the local-tie vector of the transducer to the GNSS antenna in the gyro’s rectangular coordinates (called the “ATD offset” in Watanabe et al. 2020). Although the ATD offset can be estimated from well-distributed data, we do not solve it in the present study.

2.2 Bayesian formulation

When solving the observation equations, constraints or assumptions are usually imposed. As far as parameters in the stochastic model are concerned, they can be typically estimated by using the standard variance and covariance estimation (VCE) methods such as Helmert’s VCE method, maximum likelihood, least-squares and minimum norm unbiased quadratic method (Koch 1999; Helmert 1907; Pukelsheim 1976; Rao and Kleffe 1988). For nonlinear VCE, Teunissen and Amiri-Simkooei (2008) introduced the least-squares procedure by means of the Gauss–Newton iteration method.

In the present study, we apply a Bayesian approach to seafloor geodesy. More precisely, we follow the formulation of Watanabe et al. (2020), which will be briefly outlined in this section. To solve the observation equation, Watanabe et al. (2020) took an approach based on Bayesian estimation, by introducing several parameters that control the data error variance–covariance such as correlation time scale, and the prior constraints for model parameters such as smoothness constraints. Here, these additional parameters in stochastic models are compiled into a vector, ${\varvec{\theta}}$, for generality of the formulation.

In the Bayesian formulation, all parameters are given as the probability distributions, and the posterior probability density function (pdf), $p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)$, is calculated using Bayes’ theorem as

$$p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)=\frac{p\left({\varvec{d}}|{\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)}{p\left({\varvec{d}}\right)},$$

(7)

where $p\left({\varvec{d}}\right)$ and $p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)$ are a marginal pdf for data that can be considered as a constant in this problem, and a prior pdf, respectively. By taking the reasonable assumptions that the priors for ${\varvec{x}}$ and ${\varvec{\theta}}$ are independent, i.e., $p\left({\varvec{x}},{\varvec{\theta}}\right)=p\left({\varvec{x}}\right)p\left({\varvec{\theta}}\right)$, and that the prior for ${\varvec{a}}$ does not depend on ${\varvec{x}}$, i.e., $p\left({\varvec{a}}|{\varvec{x}},{\varvec{\theta}}\right)=p\left({\varvec{a}}|{\varvec{\theta}}\right)$, one obtains

$$p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)=\frac{p\left({\varvec{x}}\right)p\left({\varvec{\theta}}\right)}{p\left({\varvec{d}}\right)}p\left({\varvec{d}}|{\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)p\left({\varvec{a}}|{\varvec{\theta}}\right).$$

(8)

For the simplicity, we assume that the observation error ${\varvec{e}}$ follows a Gaussian distribution with a variance–covariance of ${\Sigma }_{d}\left({\varvec{\theta}}\right)$, as Watanabe et al. (2020). In that case, the likelihood function for the observation equation is expressed as

$$\begin{aligned} & p\left({\varvec{d}}|{\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)={\left(2\pi \right)}^{-\frac{n}{2}}{\left|{\Sigma }_{d}\left({\varvec{\theta}}\right)\right|}^{-\frac{1}{2}} \\ &\quad \mathrm{exp}\left[-\frac{1}{2}{\left({\varvec{d}}-{\varvec{f}}\left({\varvec{x}}\right)-G{\varvec{a}}\right)}^{\rm{T}}\right. \left.{{\Sigma }_{d}\left({\varvec{\theta}}\right)}^{-1}\left({\varvec{d}}-{\varvec{f}}\left({\varvec{x}}\right)-G{\varvec{a}}\right)\right],\end{aligned}$$

(9)

where $n$ and $\left|{\Sigma }_{d}\left({\varvec{\theta}}\right)\right|$ are the number of data and the determinant of ${\Sigma }_{d}\left({\varvec{\theta}}\right)$, respectively (Watanabe et al. 2020). In general, ${\Sigma }_{d}\left({\varvec{\theta}}\right)$ may have finite non-diagonal components. Because acoustic ranging data are collected while a ship is sailing, the data have both spatial and temporal biases in the short term. This will lead to correlations in the data error vector ${\varvec{e}}$. Specifically, the data for similar acquisition timing tend to be affected by similar error sources in the ocean because they have similar acoustic paths. This was quantified with the non-diagonal components of ${\Sigma }_{d}\left({\varvec{\theta}}\right)$, as already discussed by Watanabe et al. (2020). They showed the importance of setting the finite non-diagonal components of ${\Sigma }_{d}\left({\varvec{\theta}}\right)$ to suppress overfitting. We take over their expression, where the data error covariance is controlled by three parameters in stochastic models, i.e., $\left[{\sigma }^{2},{\mu }_{t},{\mu }_{MT}\right]\in{\varvec{\theta}}$, as follows:

$$\begin{aligned}{\Sigma }_{d}\left({\sigma }^{2},{\mu }_{t},{\mu }_{MT}\right)={\sigma }^{2}{\Sigma }_{d}^{0}\left({\mu }_{t},{\mu }_{MT}\right)\end{aligned}$$

(10.1)

and

$${\Sigma_{d_{ij}}^{0}}\left({\mu }_{t},{\mu }_{MT}\right)=\left\{ \begin{array}{c}\begin{aligned}& \qquad\mathrm{exp}\left(-\frac{\left|{t}_{i}-{t}_{j}\right|}{{\mu }_{t}}\right) \,{\mathrm {if}}\, {\mathrm{the}} \, {\mathrm{transponders} }\, {\mathrm{for}} \,{i} \,{\mathrm{and}} \,{j}\, {\mathrm{are}}\, {\mathrm{the}}\, \;{\mathrm{same}} \\ &{\mu }_{MT}\mathrm{exp}\left(-\frac{\left|{t}_{i}-{t}_{j}\right|}{{\mu }_{t}}\right) {\mathrm{for}}\, {\mathrm{others}}\end{aligned}\end{array}\right.. $$

(10.2)

The values of ${\mu }_{t}$ and ${\mu }_{MT}$ control the correlation time scale for the ranging observation and the inter-transponder correlation, respectively. Because the correlation between the observation errors cannot be independently obtained from the specifications of the GNSS-A observation system, these parameters should be estimated from each dataset. Note that this expression was taken over from Fukahata and Wright (2008).

Regarding $p\left({\varvec{a}}|{\varvec{\theta}}\right)$, Watanabe et al. (2020) imposed the prior constraint that the temporal changes of the perturbation coefficients are smooth, to suppress overfitting to the data. By defining the roughness in a quadratic form with a positive-semidefinite matrix $H\left({\varvec{\theta}}\right)$, the constraint is expressed as follows:

$$\begin{array}{c}p\left({\varvec{a}}|{\varvec{\theta}}\right)={\left(2\pi \right)}^{-\frac{h}{2}}{\Vert {\Lambda }_{H}\left({\varvec{\theta}}\right)\Vert }^{\frac{1}{2}}\cdot \mathrm{exp}\left[-\frac{1}{2}{{\varvec{a}}}^{{\rm{T}}}H\left({\varvec{\theta}}\right){\varvec{a}}\right],\end{array}$$

(11)

where $h$ and $\Vert {\Lambda }_{H}\left({\varvec{\theta}}\right)\Vert$ are the rank of $H\left({\varvec{\theta}}\right)$ and the absolute value of the product of non-zero eigenvalues of $H\left({\varvec{\theta}}\right)$, respectively. Specifically, we can compose the following definition:

$$\begin{array}{c}{{\varvec{a}}}^{{\rm{T}}}H\left({\varvec{\theta}}\right){\varvec{a}}=\sum\limits_{l\in\{0,1E,1N,2E,2N\}}\displaystyle \int_{t}{{\nu }_{l}^{-2}\left(\frac{{\partial }^{2}{\alpha }_{l}\left(t\right)}{\partial {t}^{2}}\right)}^{2}dt,\end{array}$$

(12)

where $\nu_l^{2}\in\boldsymbol{\theta}\quad(l\in\{0,1E,1N,2E,2N\})$ are the hyperparameters denoting the degree of contribution from each component, respectively. We also take ${\nu }_{1}^{2}\equiv {\nu }_{1E}^{2}/{\nu }_{0}^{2}={\nu }_{1N}^{2}/{\nu }_{0}^{2}$ and ${\nu }_{2}^{2}\equiv {\nu }_{2E}^{2}/{\nu }_{0}^{2}={\nu }_{2N}^{2}/{\nu }_{0}^{2}$, and use the same knot vectors for five coefficients for easier implementation. Thus, the concrete expression of ${\varvec{\theta}}$ defined here is ${\varvec{\theta}}\ni \left[{\sigma }^{2},{\mu }_{t},{\mu }_{MT},{\nu }_{0}^{2},{\nu }_{1}^{2},{\nu }_{2}^{2}\right]$. The contents of ${\varvec{\theta}}$ may be changed with the assumed models introduced in Sect. 3.

2.3 Estimation methods

2.3.1 Empirical Bayes approach (conventional)

To estimate the seafloor transponder positions, Watanabe et al. (2020) took an approach based on the empirical Bayes estimation (called the “EB solution” hereafter). In their approach, the values of ${\varvec{\theta}}$ are deterministically selected by maximizing the marginal likelihood, as follows:

$$\begin{array}{c}\widehat{{\varvec{\theta}}}={\text{argmax}}_{\varvec{\theta}}\left(\displaystyle\iint p\left({\varvec{d}}|{\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)d{\varvec{x}}d{\varvec{a}}\right).\end{array}$$

(13)

This approach only estimates the conditional posterior pdf, i.e., $p\left({\varvec{x}},{\varvec{a}}|{\varvec{d}},\widehat{{\varvec{\theta}}}\right)$, as an approximation with a normal distribution. The concrete derivation for the existing GARPOS is shown by Watanabe et al. (2020). Note that this selection procedure is actually the same as the ABIC-based approach because the dimension of ${\varvec{\theta}}$ does not change with the models in the previous study.

2.3.2 Full-Bayes approach

In the present study, we use stochastic sampling methods such as Markov-Chain Monte Carlo (MCMC), for the efficient estimation of the joint posterior, $p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)$ (e.g., Fukuda and Johnson 2008). It is also an important advantage of the full-Bayes estimation that it can directly estimate the posterior pdf of all parameters, which cannot be accessed by the empirical Bayes approach. MCMC also has an advantage in expandability for further works such as in cases where the assumption of a non-Gaussian likelihood function for $p\left({\varvec{d}}|{\varvec{x}},{\varvec{a}},{\varvec{\theta}}\right)$ is required instead of Eq. (9), unlike the assumptions used in many papers (e.g., Koch and Kusche 2002; Fukuda and Johnson 2008). Actually, acoustic measurements in the GNSS-A possibly have discrete ambiguities in the unit of wavelength of carrier waves (0.1 ms in our configuration), like a cycle slip in GNSS. This would require multimodal likelihood functions for error distribution. The expandability of MCMC would be helpful to survey such features.

In the case where a Gaussian distribution is used for the likelihood function as Eq. (9) as assumed in Watanabe et al. (2020), we can largely reduce the dimension of MCMC samples analytically by using the marginalized pdf with respect to ${\varvec{a}}$, as follows:

$$\begin{array}{c}p\left({\varvec{x}},{\varvec{\theta}}|{\varvec{d}}\right)=\displaystyle\int p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)d{\varvec{a}}. \end{array}$$

(14)

Because the observation equation is linear with respect to ${\varvec{a}}$, the integral can be theoretically calculated. From Eqs. (8), (9), and (11), one obtains

$$\begin{aligned}p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)&=\frac{p\left({\varvec{x}}\right)p\left({\varvec{\theta}}\right)}{p\left({\varvec{d}}\right)}{\left(2\pi \right)}^{-\frac{n+h}{2}}{\left|{\Sigma }_{d}\left({\varvec{\theta}}\right)\right|}^{-\frac{1}{2}}\\ & \quad \times {\Vert {\Lambda }_{H}\left({\varvec{\theta}}\right)\Vert }^{\frac{1}{2}}\mathrm{exp}\left[-\frac{1}{2}s\left({\varvec{a}};{\varvec{d}},{\varvec{x}},{\varvec{\theta}}\right)\right],\end{aligned}$$

(15.1)

where

$$\begin{aligned} & s\left({\varvec{a}};{\varvec{d}},{\varvec{x}},{\varvec{\theta}}\right) ={\left({\varvec{d}}-{\varvec{f}}\left({\varvec{x}}\right)-G{\varvec{a}}\right)}^{{\rm{T}}}{{\Sigma }_{d}\left({\varvec{\theta}}\right)}^{-1} \\ &\quad \left({\varvec{d}}-{\varvec{f}}\left({\varvec{x}}\right)-G{\varvec{a}}\right)+{{\varvec{a}}}^{{\rm{T}}}H\left({\varvec{\theta}}\right){\varvec{a}}.\end{aligned}$$

(15.2)

By integrating Eq. (15.1) with respect to ${\varvec{a}}$, we obtain the concrete expression of the marginal pdf, as follows:

$$\begin{aligned}p\left({\varvec{x}},{\varvec{\theta}}|{\varvec{d}}\right)&=\frac{p\left({\varvec{x}}\right)p\left({\varvec{\theta}}\right)}{p\left({\varvec{d}}\right)}{\left(2\pi \right)}^{-\frac{n+h}{2}}{\left|{\Sigma }_{d}\left({\varvec{\theta}}\right)\right|}^{-\frac{1}{2}} {\Vert {\Lambda }_{H}\left({\varvec{\theta}}\right)\Vert }^{\frac{1}{2}}\\ & \quad \times \int \mathrm{exp}\left[-\frac{1}{2}s\left({\varvec{a}};{\varvec{d}},{\varvec{x}},{\varvec{\theta}}\right)\right]d{\varvec{a}}.\end{aligned}$$

(16)

We can rewrite Eq. (15.2) by completing the square, as

$$\begin{array}{c}s\left({\varvec{a}};{\varvec{d}},{\varvec{x}},{\varvec{\theta}}\right)=s\left({{\varvec{a}}}^{\boldsymbol{*}}\right)+{\left({\varvec{a}}-{{\varvec{a}}}^{*}\right)}^{{\rm{T}}}{C\left({\varvec{\theta}}\right)}^{-1}\left({\varvec{a}}-{{\varvec{a}}}^{*}\right),\end{array}$$

(17.1)

where ${{\varvec{a}}}^{\boldsymbol{*}}$ and $C\left({\varvec{\theta}}\right)$ correspond to the maximum likelihood solution and its variance–covariance, respectively, for the given ${\varvec{x}}$ and ${\varvec{\theta}}$. Specifically, they can be written as follows:

$$\begin{array}{c}{{\varvec{a}}}^{\boldsymbol{*}}=C\left({\varvec{\theta}}\right){G}^{{\rm{T}}}{{\Sigma }_{d}\left({\varvec{\theta}}\right)}^{-1}\left({\varvec{d}}-{\varvec{f}}\left({\varvec{x}}\right)\right),\end{array}$$

(17.2)

$$\begin{array}{c}C\left({\varvec{\theta}}\right)={\left({G}^{{\rm{T}}}{{\Sigma }_{d}\left({\varvec{\theta}}\right)}^{-1}G+H\left({\varvec{\theta}}\right)\right)}^{-1}.\end{array}$$

(17.3)

Therefore, by calculating the integral in Eq. (16) using Eq. (17.1), one obtains

$$\begin{aligned}p\left({\varvec{x}},{\varvec{\theta}}|{\varvec{d}}\right)&=\frac{p\left({\varvec{x}}\right)p\left({\varvec{\theta}}\right)}{p\left({\varvec{d}}\right)}{\left(2\pi \right)}^{-\frac{n+h-m}{2}}{\left|{\Sigma }_{d}\left({\varvec{\theta}}\right)\right|}^{-\frac{1}{2}} {\Vert {\Lambda }_{H}\left({\varvec{\theta}}\right)\Vert }^{\frac{1}{2}}{\left|C\left({\varvec{\theta}}\right)\right|}^{\frac{1}{2}} \\ &\quad \times \mathrm{exp}\left[-\frac{1}{2}s\left({{\varvec{a}}}^{\boldsymbol{*}}\left({\varvec{d}},{\varvec{x}},{\varvec{\theta}}\right)\right)\right] \end{aligned},$$

(18)

where $m$ and $\left|C\left({\varvec{\theta}}\right)\right|$ are the rank and the determinant of $C\left({\varvec{\theta}}\right)$, respectively. Although we can also reduce the scale parameter ${\sigma }^{2}$ by analytically marginalizing out using an inverse gamma distribution as the prior pdf (e.g., Koch and Kusche 2002), it remains in the MCMC sample vector because it would little contribute to the improvement on the computational speed.

3 Models for the perturbation field

In this section, we first show the physical meaning of the perturbation field $\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)$ defined as Eq. (4), and then suggest several constraints on it by taking the oceanographic features into account. The key subject in the $\Gamma$-formulation is to appropriately model the perturbation due to the sound speed structure for a reasonable sound speed correction in the GNSS-A.

3.1 Interpretation of the perturbation field $\Gamma$

From the definition in Eq. (2), the perturbation term ${\gamma }_{i}$ is introduced to cover the effects of (i) the spatio-temporal variations of the sound speed from the reference profile. However, in general, it is also affected by other perturbations, such as (ii) random errors in acoustic travel time measurement, (iii) bias errors in acoustic instruments and integrated systems including artificial errors, and (iv) the kinematic positioning error for the sea surface GNSS observation.

When considering perturbation sources sufficiently correlated with $t$, ${\varvec{P}}$, and ${\varvec{X}}$ for a reasonable construction of the parametric model for $\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)$ as Eq. (4), the effects from (i) the spatio-temporal variations of the sound speed with respect to the reference profile should be taken into account. Almost all the other perturbation sources are either sufficiently random, correctable with a well-arranged dataset, or unable to be corrected within a single dataset. It should be noted that this $\Gamma$-formulation still possibly affected by (iv) the GNSS positioning error containing the relatively short-term (shorter than the observation and sufficiently longer than the shot interval) random-walk type noise, though on the order of centimeter (e.g., Watanabe et al. 2017).

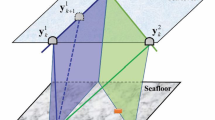
In the $\Gamma$-formulation, it is easy to relate the perturbation field to the effect of the sound speed variation. Because $\left(1+{\gamma }_{i}\right)\overline{{V }_{0}}$ approximately denotes the average sound speed along the acoustic path as mentioned in Sect. 2.1, the function $\overline{{V }_{0}}\Gamma$ can also be considered as the sound speed anomaly field (Fig. 2). In the linearized form as Eq. (4), $\overline{{V }_{0}}{\alpha }_{0}$ is interpreted as a spatially uniform perturbation from the reference profile (the second terms of the right-hand side of Fig. 2, as the 0th-order residual structure), and $\overline{{V }_{0}}{\boldsymbol{\alpha }}_{1}$ and $\overline{{V }_{0}}{\boldsymbol{\alpha }}_{2}$ correspond to the spatial gradients of residual sound speed structure projected onto the sea surface and seafloor, respectively (the gray-shaded area in Fig. 2, as the 1st-order residual structure).

Fig. 2

Schematic diagrams of holographic projection onto coefficients of linearized perturbation field for simplified cases with a large scale oceanographic structure and b water intrusion. In the expression of $\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)$, the actual sound speed structure is estimated separately for the horizontally-stratified reference profile, the spatially-uniform time-dependent perturbation (the 0th-order residual structure), and the horizontal gradient terms (the 1st-order residual structure). The 1st-order residual structure is estimated by projecting to two parameters ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$ on a sea surface and a seafloor, respectively. The figure is updated from Yokota et al. (2022)

3.2 Model “m100”: no constraint

Firstly, we define a model without any additional constraint on the $\Gamma$-formulation, named as model “m100” (the number means the model version in the software, i.e., model version 1.0.0). This model solves two gradient components, ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$ independently. This is the same formulation defined by Watanabe et al. (2020), and provides the same constraint as the conventional GARPOS. This model has a parameter vector as ${{\varvec{\theta}}}_{\mathrm{m}100}\equiv \left[{\sigma }^{2},{\mu }_{t},{\mu }_{MT},{\nu }_{0}^{2},{\nu }_{1}^{2},{\nu }_{2}^{2}\right]$.

3.3 Model “m101”: single gradient layer assumption

To add constraints on $\Gamma$, it is important to understand which is the dominant or plausible sound speed structure in the GNSS-A observation scale (typically < 10 km × 10 km, as shown in Fig. 1a). Specifically, in the cases with large-scale structure such as the Kuroshio current or with internal waves having a long wavelength (left-hand side of Fig. 2a), the 1st-order residual structures can be approximately expressed as structures with a single gradient layer at a certain depth (the third terms on the right-hand side of Fig. 2a).

Such cases lead to identical directions for the gradient components, and their ratio, i.e., $\kappa \left(t\right)\equiv \left|{\boldsymbol{\alpha }}_{1}\left(t\right)\right|/\left|{\boldsymbol{\alpha }}_{2}\left(t\right)\right|$, gives the characteristic depth of the gradient layer. When the acoustic ray bending due to the refraction is sufficiently negligible, the travel time perturbation from the residual structure is equivalent to the perturbation from the structure where a thin layer of a uniform gradient lies at a certain depth, ${d}_{c}$:

$$\begin{array}{c}{d}_{c}\left(t\right)={\left(1+\kappa \left(t\right)\right)}^{-1}D,\end{array}$$

(19)

where $D$ denotes the water depth at the site (see Appendix A for the derivation). This setting provides a more general expression than that for the models suggested by Yasuda et al. (2017) and Honsho et al. (2019), where a uniform gradient layer lies in the shallow portion from the sea surface to a certain depth, ${d}_{0}$. With the proposed thin-layer model, ${d}_{0}$ in the conventional models can be written as ${d}_{0}=2{d}_{c}$.

We assume that the large-scale oceanographic structure in the observation area does not change during a GNSS-A observation visit, though the strength or direction of the gradient can vary. For example, this reflects oceanographic conditions dominated by a steady strong current or internal waves with long wavelengths (Fig. 2a). This assumption is implemented by setting ${d}_{c}\left(t\right)$ as a constant, i.e., $\kappa \left(t\right)={\kappa }_{0}$, where ${\kappa }_{0}$ is constant through the observation. By simultaneously estimating the posterior of ${\kappa }_{0}$, we can obtain the solution under the situation where a temporally-variable gradient layer steadily lies at a certain depth.

As naively tested by Yokota et al. (2022) with conventional GARPOS, the positioning accuracy is often improved by constraining $\kappa \left(t\right)$ as a constant. They used a primitive two-step approach: the ratio of ${\boldsymbol{\alpha }}_{1}$ to ${\boldsymbol{\alpha }}_{2},$ i.e., ${\kappa }_{0}$, is extracted from the conventional GARPOS result (the 1st step), and then ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$ are solved for the given ${\kappa }_{0}$ (the 2nd step). Different from their strategy, the proposed method, where ${\kappa }_{0}$ is included in the parameter vector ${\varvec{\theta}}$, has advantages in estimating the joint posterior pdf.

Under this assumption, the perturbation field is written as,

$$\begin{array}{c}{\Gamma }_{101}\left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)\equiv {\alpha }_{0}\left(t\right)+{\boldsymbol{\alpha }}_{1}\left(t\right)\cdot \frac{{\varvec{P}}}{\displaystyle{L}^{*}}+{\kappa }_{0}{\boldsymbol{\alpha }}_{1}\left(t\right)\cdot \frac{{\varvec{X}}}{\displaystyle{L}^{*}}\end{array}$$

(20)

and the model parameter vector ${\varvec{a}}$ is contracted to

$$\begin{array}{c}{{\varvec{a}}}^{{\rm{T}}}=\left[{{{\varvec{a}}}^{\langle 0\rangle }}^{{\rm{T}}},{{{\varvec{a}}}^{\langle 1E\rangle }}^{{\rm{T}}},{{{\varvec{a}}}^{\langle 1N\rangle }}^{{\rm{T}}}\right]. \end{array}$$

(21)

According to the above modification, the penalty term defined in Eq. (12) is also redefined as

$$\begin{array}{c}{{\varvec{a}}}^{{\rm{T}}}{H}_{101}\left({\varvec{\theta}}\right)\varvec{a}=\displaystyle \sum\limits_{l\in\{ 0, 1E, 1N\}}\int_{t}{{\nu }_{l}^{-2}\left(\frac{{\partial }^{2}{\alpha }_{l}\left(t\right)}{\partial {t}^{2}}\right)}^{2}dt,\end{array}$$

(22)

This model version is called “m101” hereafter. It should be noted that this model is expected to be applicable not only for seas with strong currents but also in other situations because it results in applying a simpler fit for noisy or complicated sound speed structures. This model has a parameter vector as ${{\varvec{\theta}}}_{\mathrm{m}101}\equiv \left[{\sigma }^{2},{\mu }_{t},{\mu }_{MT},{\nu }_{0}^{2},{\nu }_{1}^{2},{\kappa }_{0}\right]$.

3.4 Model “m102”: single gradient layer with offset of ${\boldsymbol{\alpha }}_{2}$

According to Yokota et al. (2022), some of the GNSS-A datasets showed deterioration of the positioning accuracy when the two-step single gradient constraint was applied. This is considered to be partly because of the inadequateness of the applied assumption. For example, in cases where the steady background gradient structure due to both currents and large internal waves are dominant, two or more gradient layers can exist with different directions at different depths. Such cases, where an additional spatio-temporally steady gradient layer coexists with the spatially steady but temporally variable single gradient layer, can be expressed by adding an offset to either ${\boldsymbol{\alpha }}_{1}$ or ${\boldsymbol{\alpha }}_{2}$, i.e., ${\boldsymbol{\alpha }}_{2}\left(t\right)\equiv {\kappa }_{0}{\boldsymbol{\alpha }}_{1}\left(t\right)+\delta {\boldsymbol{\alpha }}_{2}$. $\delta {\boldsymbol{\alpha }}_{2}$ denotes the residual for the m101 model. In the cases where the single gradient layer assumption is appropriate, $\delta {\boldsymbol{\alpha }}_{2}$ should be reduced to zero. Although $\delta {\boldsymbol{\alpha }}_{2}$ can be a function of time, we assume it to be a constant in the time domain.

To solve the observation equation with this constraint, we can use the following perturbation field:

$$\begin{array}{c}{\Gamma }_{102}\left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)\equiv {\alpha }_{0}\left(t\right)+{\boldsymbol{\alpha }}_{1}\left(t\right)\cdot \frac{{\varvec{P}}}{{\displaystyle {L}}^{*}}+\left({\kappa }_{0}{\boldsymbol{\alpha }}_{1}\left(t\right)+\delta {\boldsymbol{\alpha }}_{2}\right)\cdot \frac{{\varvec{X}}}{{\displaystyle {L}}^{*}} \end{array}$$

(23)

and the model parameter vector ${\varvec{a}}$ as

$$\begin{array}{c}{{\varvec{a}}}^{{\rm{T}}}=\left[{{{\varvec{a}}}^{\langle 0\rangle }}^{{\rm{T}}},{{{\varvec{a}}}^{\langle 1E\rangle }}^{{\rm{T}}},{{{\varvec{a}}}^{\langle 1N\rangle }}^{{\rm{T}}},{\delta {\boldsymbol{\alpha }}_{2}}^{{\rm{T}}}\right]. \end{array}$$

(24)

To suppress the absolute value of $\delta {\boldsymbol{\alpha }}_{2}$, we added a penalty term to Eq. (22) as follows:

$${{\varvec{a}}}^{{\rm{T}}}{H}_{102}\left({\varvec{\theta}}\right){\varvec{a}}=\displaystyle \sum\limits_{l\in \{0, 1E,1N\}}\int_{t}{{\nu }_{l}^{-2}\left(\frac{{\partial }^{2}{\alpha }_{l}\left(t\right)}{\partial {t}^{2}}\right)}^{2}dt{+}{\rho }_{2}^{2}{\left({\delta \boldsymbol{\alpha }}_{2}\right)}^{2},$$

(25)

where ${\rho }_{2}^{2}\in{\varvec{\theta}}$ is a hyperparameter denoting the degree of the penalty due to the absolute value of $\delta {\boldsymbol{\alpha }}_{2}$. This model version is called “m102” hereafter. This model has a parameter vector as ${{\varvec{\theta}}}_{\mathrm{m}102}\equiv \left[{\sigma }^{2},{\mu }_{t},{\mu }_{MT},{\nu }_{0}^{2},{\nu }_{1}^{2},{\kappa }_{0},{\rho }_{2}^{2}\right]$.

4 Data and methods

4.1 GNSS-A data

To discuss the effects of the proposed constraints on seafloor positioning, we processed the GNSS-A data obtained at several SGO-A sites (red circles in Fig. 1b). We selected two SGO-A sites from each of the off-Shikoku/Kii and the off-Tohoku regions, i.e., TOS2 and KUM2, and FUKU and MYGI, respectively. Table 1 shows the specifications of the GNSS-A data we used. Because the seafloor transponders are battery-powered instrument, they are regularly replaced, typically about every 10 years. To avoid possible bias errors due to the misestimation of relative positions for old/new transponder sets, we used the GNSS-A data obtained for the same transponder set in the present study. The data used in the present study are available from Japan Coast Guard (2022).

Table 1 Locations and observation periods of the GNSS-A observation sites used in the present study

In the off-Shikoku region (for TOS2), where the strong Kuroshio current regularly flows eastward (shown as a broad purple band in Fig. 1b), a uni-directional oceanographic structure perpendicular to the current tends to be dominant. In the off-Kii region (for KUM2), the Kuroshio current usually flows eastward, except during periods when the Kuroshio meanders (shown as broken bold band in Fig. 1b). In contrast, in the off-Tohoku region (for FUKU and MYGI), mixing of warm and cold currents easily generates a more complicated oceanographic structure with, e.g., multiscale eddies.

4.2 Sampling from posterior distribution

When considering the prior $p\left({\varvec{x}}\right)$ in Eq. (18) as a uniform distribution, meaning no constraint on the position, we obtain the following likelihood function:

$$\begin{aligned} p\left( {{\varvec{x}},{\varvec{\theta}}{|}{\varvec{d}}} \right) &= c \cdot p\left( {\varvec{\theta}} \right)\left| {\Sigma_{d} \left( {\varvec{\theta}} \right)} \right|^{{ - \frac{1}{2}}}|| \Lambda_{H} \left( {\varvec{\theta}} \right)||^{\frac{1}{2}} \left| {C\left( {\varvec{\theta}} \right)} \right|^{\frac{1}{2}} \\ & \quad \exp \left[ { - \frac{1}{2}s\left( {{\varvec{a}}^{*} \left( {{\varvec{d}},{\varvec{x}},{\varvec{\theta}}} \right)} \right)} \right],\end{aligned} $$

(26)

where $c$ is a constant depending on the selected model and dataset. Technically, the term $p\left({\varvec{\theta}}\right)$ should be a sufficiently broad distribution, or it can be used to avoid numerical instability such as rank deficiency due to the divergence of relevant parameters. It can also be used to restrict the parameter values, such as ${\sigma }^{2}>0$, and $0\le {\mu }_{MT}\le 1$. For this implementation, we transformed these variables by using the logarithmic or logit functions (the left column in Table 2). In the present study, we tentatively use the Gaussian distributions with sufficiently large variances as the prior pdf of these transformed parameters.

Table 2 Standard deviations of proposal distribution for each parameter in the MCMC sampling

We obtained the samples from $p\left({\varvec{x}},{\varvec{\theta}}|{\varvec{d}}\right)$, with the Metropolis–Hastings algorithm (Hastings 1970). In this algorithm, MCMC sample series, ${{\varvec{z}}}_{k}={\left[{{\varvec{x}}}_{k}^{{\rm{T}}},{{\varvec{\theta}}}_{k}^{{\rm{T}}}\right]}^{{\rm{T}}}$, are generated from an arbitrary proposal distribution, $p\left({{\varvec{z}}}_{k-1}|{{\varvec{z}}}_{k}\right)$, as follows: (1) Choose an arbitrary value for ${{\varvec{z}}}_{0}$ as an initial sample. (2) Pick a candidate for the $k$th sample ($k\ge 1$), ${\varvec{z}}\boldsymbol{^{\prime}}={\left[{{\varvec{x}}}^{\boldsymbol{^{\prime}}T},{{{\varvec{\theta}}}^{\boldsymbol{^{\prime}}}}^{{\rm{T}}}\right]}^{{\rm{T}}}$, from the proposal distribution. (3) Calculate the ratio of likelihood to the previous sample, i.e., $r= p\left({{\varvec{x}}}^{\prime},{\varvec{\theta}}^{\prime}|{\varvec{d}}\right)/p\left({{\varvec{x}}}_{k-1},{{\varvec{\theta}}}_{k-1}|{\varvec{d}}\right)$. (4) Compare the value $r$ with a value randomly generated from a uniform distribution $u\in \left[\mathrm{0,1}\right]$. (5) If $r\ge u$, set ${{\varvec{z}}}_{k}=\boldsymbol{ }{\varvec{z}}\boldsymbol{^{\prime}}$ (the candidate is accepted). If $r<u$, set ${{\varvec{z}}}_{k}={{\varvec{z}}}_{k-1}$ (the candidate is rejected).

The newly developed MCMC solver named “GARPOS-MCMC v.1.0.0,” is available in the Zenodo repository (Watanabe et al. 2022b). For the proposal distribution $p\left({{\varvec{z}}}_{k-1}|{{\varvec{z}}}_{k}\right)$, we selected a Gaussian distribution. The specifications for the proposal distribution and sampling are summarized in Table 2. Initial values and proposal distributions for the parameters were selected by trial and error, with reference to the results of conventional EB solutions, for earlier convergence. We obtained 50,000 MCMC samples at a sampling rate of 50 but dumped the first 25,000 samples as a burn-in period.

5 Results

All outputs of GARPOS-MCMC, including the sample series, distributions, and the 2.5th, 25th, 50th, 75th, and 97.5th percentiles for each dataset are stored in the Zenodo repository (Watanabe et al. 2022c). Examples of these percentiles for the posterior distributions for the parameters are summarized in Table 3. Figures 3 and 4 show examples of the series and the distributions of MCMC samples, respectively. Note that the ranges of the axes in Fig. 3 vary in each panel, to clearly show the behavior of the MCMC sample convergence. The MCMC sample series in the m100 model (e.g., Fig. 3a) rapidly converges to a certain distribution (typically less than 2000 samples). In contrast, the sample series in the m101 (e.g., Fig. 3b) and m102 (e.g., Fig. 3c) models for several datasets show multimodality in the smoothing hyperparameters. One of the most significant cases is the dataset “MYGI.1910.meiyo_m4,” which is shown in Figs. 3 and 4. The multimodality in such cases was caused by the indivisibility of ${\alpha }_{0}\left(t\right)$ and ${\boldsymbol{\alpha }}_{1}\left(t\right)$ in the single surface-unit configuration, which comes from the dependency of the surface position ${\varvec{P}}\left(t\right)$ on time. Nonetheless, almost all of the datasets including such cases show approximately unimodal distributions of seafloor positions, which were determined on the order of centimeters (e.g., Table 3 and Fig. 4).

Table 3 Examples of the 2.5th, 25th, 50th, 75th, and 97.5th percentiles of the MCMC sample distributions for the dataset named “TOS2.1305.kaiyo_k4” and “MYGI.1910.meiyo_m4”

Fig. 3

Examples of MCMC sample series for datasets named “TOS2.1305.kaiyo_k4” and “MYGI.1910.meiyo_m4,” solved with the a m100, b m101, and c m102 models

Fig. 4

Examples of MCMC sample distributions for datasets named “TOS2.1305.kaiyo_k4” and “MYGI.1910.meiyo_m4,” solved with the a m100, b m101, and c m102 models. The values of correlation coefficients are shown in the upper triangular part of the matrix

To survey the effects of the uncertainty of the smoothing hyperparameters on the seafloor positions, we plotted the histograms of the correlation coefficients between each component of the seafloor position and each parameter for all datasets (Fig. 5). Figure 5 clearly shows that all of the datasets have little correlation between the seafloor position components and the smoothing hyperparameters. The smoothing hyperparameters are strongly independent of the seafloor positions, indicating that the multimodalities in the smoothing hyperparameters shown in the tests (e.g., Fig. 3b, c) are trivial in seafloor positioning.

Fig. 5

Histograms of correlation coefficients between each component of seafloor position and other parameters for all the dataset solved with the a m100, b m101, and c m102 models

For the discussion of the correlations among the seafloor positions and the perturbation coefficients, it is useful to generate a Monte Carlo sample from the joint posterior $p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)$. Because the conditional posterior distribution of the perturbation coefficients for each MCMC sample is given as a normal distribution, i.e., $p\left({\varvec{a}}|{\varvec{d}},{\varvec{x}},{\varvec{\theta}}\right)\sim N\left({{\varvec{a}}}^{\boldsymbol{*}},C\left({\varvec{\theta}}\right)\right)$, a Monte Carlo sample from the posterior $p\left({\varvec{x}},{\varvec{a}},{\varvec{\theta}}|{\varvec{d}}\right)$ can be artificially generated by adding a vector ${\varvec{a}}$ sampled from $N\left({{\varvec{a}}}^{\boldsymbol{*}},C\left({\varvec{\theta}}\right)\right)$. Figure 6 shows examples of the posterior distribution of the seafloor position, ${\varvec{x}}$, and the averages of perturbation coefficients in the dimension of sound speed, i.e., $\overline{{V }_{0}}\overline{{\alpha }_{0}}$, $\overline{{V }_{0}}\overline{{\alpha }_{1\mathrm{E}}}$, $\overline{{V }_{0}}\overline{{\alpha }_{1\mathrm{N}}}$, $\overline{{V }_{0}}\overline{{\alpha }_{2\mathrm{E}}}$, and $\overline{{V }_{0}}\overline{{\alpha }_{2\mathrm{N}}}$, for the m100 solutions. Figure 7 shows histograms of the correlation coefficients between each component of the seafloor position and each of the averaged perturbation coefficients. All datasets (see also figures in the Zenodo repository; Watanabe et al. 2022c) show strong positive correlations ($>0.6$) between the value of ${\boldsymbol{\alpha }}_{2}$ and the horizontal position in the m100 solutions (Fig. 7a). In contrast, slightly weaker negative correlations were typically shown both between the value of ${\alpha }_{0}$ and the vertical position, and between the value of ${\boldsymbol{\alpha }}_{1}$ and the horizontal position.

Fig. 6

Examples of artificially sampled posterior distributions for m100 solutions among seafloor positions and averages of perturbation coefficients in dimension of sound speed, for datasets named “TOS2.1305.kaiyo_k4” and “MYGI.1910.meiyo_m4.” The values of correlation coefficients are shown in the upper triangular part of the matrix

Fig. 7

Histograms of correlation coefficients between each component of seafloor positions and averaged perturbation coefficients for all datasets solved with the a m100, b m101, and c m102 models

As shown in Fig. 7b, the correlation between the horizontal position components and the corresponding components of ${\boldsymbol{\alpha }}_{2}$ significantly weakened especially in the m101 solutions, compared to the m100 solutions. The connection of ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$ by the parameter ${\kappa }_{0}$ in the m101 model contributed to a decrease in the independency of the estimation of the horizontal parameters. This is also indicated by the tendency of a larger correlation between ${\kappa }_{0}$ and the horizontal position (Fig. 5b). In the m101 model, additional information related to ${\boldsymbol{\alpha }}_{1}$ is used for the determination of ${\boldsymbol{\alpha }}_{2}$, which results in a shift of the horizontal position.

Compared to the m101 solutions, the m102 solutions have almost the same or smaller correlation between ${\kappa }_{0}$ and the horizontal position (Fig. 5b and c). This means that the parameter ${\kappa }_{0}$ controlled the horizontal position along with ${\boldsymbol{\alpha }}_{2}$ in both models, but that the m102 model can suppress the effect of constraints depending on the data’s suitability to the m101 model’s assumption, as designed.

As the end products of the GNSS-A seafloor positioning, the time series of seafloor displacements for each SGO-A site are given in Figs. 8, 9, 10 and 11. Panels in the figures show the solutions derived with the three suggested models and the conventional EB solutions (Japan Coast Guard 2022), aligned to the International Terrestrial Reference Frame 2014 (ITRF2014). The m100 solutions are almost consistent with the EB solutions, including the ranges of 95% confidence intervals. Both the m101 and m102 solutions show differences from the m100 solutions in the horizontal component, as explained above.

Fig. 8

Time series of array-center displacement at TOS2 derived from the m100 (blue histograms), m101 (red histograms), and m102 (orange histograms) models, aligned to ITRF2014. EB solutions are also shown as green circles with 3-sigma error bars in panel (a)

Fig. 9

Time series of array-center displacement at KUM2 derived from the m100 (blue histograms), m101 (red histograms), and m102 (orange histograms) models, aligned to ITRF2014. EB solutions are also shown as green circles with 3-sigma error bars in panel (a)

Fig. 10

Time series of array-center displacement at FUKU derived from the m100 (blue histograms), m101 (red histograms), and m102 (orange histograms) models, aligned to ITRF2014. EB solutions are also shown as green circles with 3-sigma error bars in panel (a)

Fig. 11

Time series of array-center displacement at MYGI derived from the m100 (blue histograms), m101 (red histograms), and m102 (orange histograms) models, aligned to ITRF2014. EB solutions are also shown as green circles with 3-sigma error bars in panel (a)

6 Discussion and conclusions

The m100 solutions provided distributions almost consistent with the EB’s normal distributions (Figs. 8, 9, 10 and 11). This is because the position parameters have little correlation with the other parameters in the m100 solutions, as shown in the MCMC sample distributions (Figs. 4a and 5a). This is the same for the EB solutions, as generally discussed in the previous study (Watanabe et al. 2020). Among the parameters, little correlation is shown, except ${\sigma }^{2}$ and ${\mu }_{t}$ (Fig. 4a). These parameters should have a positive correlation when the eigenvalues of ${\Sigma }_{d}$ is conserved, by definition.

The marginal probability for horizontal positions for the m101 solutions generally showed a narrower distribution than that for the m100 solutions (Figs. 8, 9, 10 and 11). The horizontal positions are correlated with the characteristic depth of the gradient layer, i.e., ${\kappa }_{0}$, which worked as an additional constraint as discussed in Sect. 5. This will also lead to the inconsistency in full-Bayes and empirical Bayes solutions under the m101 constraint, different from the m100 constraint. When selecting ${\kappa }_{0}$ to be a certain value as a point estimation, the conditional probability, i.e., the m101-based EB solution, will provide a narrower distribution than the marginal probability estimated from the MCMC method. This is an important advantage of the full-Bayes MCMC, for the flexible implementation of various constraints. To the contrary, all tested models return almost the same posterior pdf for the vertical position. This is because the spatial gradient components, i.e., ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$, correlate only slightly with the vertical position (Figs. 6 and 7), so that ${\kappa }_{0}$ was unable to control the vertical position.

From the viewpoint of stabilizing the position time series, the smoothness of the horizontal displacement time series was improved, although with some outliers (Figs. 8, 9, 10 and 11). Those outliers might have been affected by the over-simplification of a complicated actual sound speed structure, or biases in instruments and systems that became obvious due to the decrease of degree of freedom.

The m102 solutions provided the approximate superposition of the m100 and m101 solutions (Figs. 8, 9, 10 and 11). In some datasets, the m102 model seemed to correct the adverse effect of the m101 model, especially for observations in Mar 2016 and Nov 2016 at TOS2, in Oct 2016 at KUM2, and in Dec 2017 at FUKU. In contrast, although the m101 solutions improved the positioning stability compared to the m100 solutions, some m102 results showed restoration to the relatively worse m100 solutions, e.g., in Nov 2017 and Aug 2018 at KUM2, and in Jun 2016 at MYGI. This is possibly caused by some system bias errors leading to the misestimation of the ${\boldsymbol{\alpha }}_{2}$ component, which strongly correlates with the horizontal position. It is important to robustly estimate the offset of ${\boldsymbol{\alpha }}_{2}$, regardless of its error sources.

The m101 model is considered to be more suitable for sites located in waters affected by the steady and strong Kuroshio current, i.e., in the Nankai Trough region (TOS2 and KUM2; Fig. 1b). For TOS2, the m102 method appropriately corrected the outliers in the m101 solutions and provided a smoother time series than that for the other models, though the outliers might be caused by system biases rather than the complicated sound speed structure. Meanwhile, the m102 solutions at KUM2 became more unstable than the m101 solutions especially in the eastward component. In the cases of KUM2, it is considered that the misestimation of $\delta {\boldsymbol{\alpha }}_{2}$, possibly due to system biases, caused the deterioration of positioning accuracy.

For FUKU and MYGI located in the eastern off-Tohoku region where small eddies due to seasonal mixing of warm and cold currents tend to be generated (Fig. 1b), it is expected that the m101 assumption is less applicable. This will require a case-by-case selection for the appropriate models depending on additional information on oceanographic states during each GNSS-A observation.

As discussed above, the full-Bayes formulation in GARPOS-MCMC can improve the implementation of flexible priors for better solutions that adequately extract typical oceanographic features, or also for further evaluation of system biases. Moreover, the m101 solutions for several datasets had larger position biases in the displacement time series, not all of which were corrected in the m102 solutions. This means that the offset $\delta {\boldsymbol{\alpha }}_{2}$ not only reflected more complicated actual sound speed structures as designed, but also could be contaminated by other system errors. By extending this discussion, instrumental errors and modeling errors are possibly divided even within a single dataset with appropriate parameterization and various modeling realized by a flexible MCMC method. This clarifies future subjects and targets for improvement of GNSS-A accuracy.

By parameterizing the corresponding bias, instrumental errors such as system-specific biases can be quantified from the data. Furthermore, we can easily expand the algorithm to apply a non-Gaussian likelihood function instead of Eq. (9), for the further surveys on the characteristics of the GNSS-A’s acoustic measurements. For the modeling errors, regardless of the dominant oceanographic features, researchers can improve the positioning stability by carefully selecting the constraints on the perturbation field, $\Gamma \left(t, {\varvec{P}},\boldsymbol{ }{\varvec{X}}\right)$, from additional information. In those ways, GARPOS-MCMC has the potential to be a basic platform for the further improvement of analysis techniques to develop more precise GNSS-A seafloor geodesy and oceanography.

Appendix A

In this appendix, we show the constraints imposed on the gradient components, ${\boldsymbol{\alpha }}_{1}$ and ${\boldsymbol{\alpha }}_{2}$, for the cases where the residual sound speed structure contains only a single uniform sound speed gradient layer at a certain depth.

First, the reference travel time for the horizontally-stratified reference sound speed profile ${V}_{0}\left(u\right)$ is obtained by integrating the reference slowness along the acoustic path, as follows:

$$\tau =\int \frac{ds}{{V}_{0}\left(s\right)}.$$

(A1)

We then consider the sound speed structure where a perturbation is added to the reference profile along the path, i.e., $V\left(e,n,u\right)={V}_{0}\left(u\right)+\delta \upsilon \left(s\right)$. If we assume that $\delta \upsilon \ll {V}_{0}$ is satisfied, which also leads to the assumption that refraction due to the perturbation term is negligible, the travel time $T$ can be calculated as

$$\begin{aligned}\frac{T}{\tau }=\frac{1}{\tau }\int \frac{ds}{{V}_{0}\left(u\right)+\delta \upsilon \left(s\right)}\cong 1-\frac{1}{\tau }\int \frac{\delta \upsilon \left(s\right)ds}{{{V}_{0}\left(u\right)}^{2}}.\end{aligned}$$

(A2)

We define the sound speed anomaly for each path, $\overline{\delta V }$, using the path length $S=\int ds$ and the average reference sound speed $\overline{{V }_{0}}=S/\tau$, as, $\overline{\delta V }=S/T-\overline{{V }_{0}}$. From equation (A2), we obtain

$$\begin{aligned}\overline{\delta V }= \overline{{V }_{0}}\left({\left(1-\frac{1}{\tau }\int \frac{\delta \upsilon \left(s\right)ds}{{{V}_{0}\left(u\right)}^{2}}\right)}^{-1}-1\right)\cong \frac{{\overline{{V }_{0}}}^{2}}{S}\int \frac{\delta \upsilon \left(s\right)ds}{{{V}_{0}\left(u\right)}^{2}}.\end{aligned}$$

(A3)

For the easier interpretation, we consider a toy model where the ${V}_{0}\left(u\right)$ is uniform so that ${V}_{0}\left(u\right)=\overline{{V }_{0}}$ is satisfied. Under this assumption, the acoustic ray path is a geometrically straight line connecting ${\varvec{X}}$ and ${\varvec{P}}$, and Eq. (A4) is simplified to

$$\begin{aligned}\overline{\delta V}\cong \frac{1}{S }\int \delta \upsilon \left(s\right)ds. \end{aligned}$$

(A4)

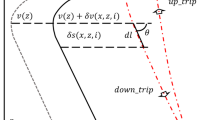
Here, we consider the 2-dimensional case for the sound speed perturbation with a single uniform gradient layer that lies on ${d}_{c}-{d}_{L}/2<z<{d}_{c}+{d}_{L}/2$ in a site with a uniform water depth, $D$, as shown in Fig. 

Fig. 12

Schematics of effects of uniform gradient layer lying at given depth, in case where refraction can be sufficiently negligible. (a) Case where the gradient layer has a finite thickness. (b) Case where the gradient layer has an infinitesimal thickness, but has the same consequence as case (a). This figure was adapted from Yokota et al. (2022)

12a, i.e., $\delta \upsilon \left(s\right)=x{\zeta }_{0}\mathrm{rect}\left(\left(z-{d}_{c}\right)/{d}_{L}\right)$, with ${\zeta }_{0}$ and rect$\left(z\right)$ denoting a constant and the rectangular function, respectively. In this case, the gradient field can be written as $\zeta \left(z\right)={\zeta }_{0}\mathrm{rect}\left(\left(z-{d}_{c}\right)/{d}_{L}\right)$. Setting the depression angle of ${\varvec{X}}=\left({x}_{X},D\right)$ seen from ${\varvec{P}}=\left({x}_{P},0\right)$ as $\phi$, i.e., $S\,\mathrm{cos}\; \phi ={x}_{X}-{x}_{P}$, the sound speed anomaly can be calculated as

$$\begin{array}{c}\overline{\delta V}\cong \frac{\displaystyle{\zeta }_{0}{x}_{0}{x}_{c}}{\displaystyle{x}_{X}-{x}_{P}}, \end{array}$$

(A5)

where

$${x}_{0}=\left({x}_{X}-{x}_{P}\right)\frac{{d}_{L}}{D},$$

(A5.1)

$${x}_{c}=\frac{{d}_{c}}{D}{x}_{X}+\left(1-\frac{{d}_{c}}{D}\right){x}_{P}.$$

(A5.2)

Therefore, we obtain

$$\overline{\delta V}\cong {\zeta }_{0}\frac{{d}_{L}}{D}\left(1-\frac{{d}_{c}}{D}\right)P+{\zeta }_{0}\frac{{d}_{L}}{D}\frac{{d}_{c}}{D}X.$$

(A6)

Recalling that $\overline{{V }_{0}}\Gamma$ is comparable with $\overline{\delta V }$ (Sect. 3.1), we obtain

$${d}_{c}=\frac{1}{1+{\kappa }_{0}}D,$$

(A7)

which is identical to Eq. (19). In addition, we can easily derive the relationship as, $\left|{\boldsymbol{\alpha }}_{1}\right|\propto \left|{\boldsymbol{\alpha }}_{2}\right|\propto {\zeta }_{0}{d}_{L}$. This derivation also shows that the strength of the gradient, $\zeta$, and the thickness of the gradient layer, ${d}_{L}$, are non-separable in this formulation. For example, when taking an infinitesimally small value for ${d}_{L}$, the perturbation is written as $\delta \upsilon \left(s\right)=x{\zeta }_{0}\delta \left(z-{d}_{c}\right)$, where $\delta \left(z\right)$ denotes the Dirac delta function (Fig. 12b).