Centimeter-level-precision seafloor geodetic positioning model with self-structured empirical sound speed profile

Abstract

In-field Sound Speed Profile (SSP) measurement is still indispensable for achieving centimeter-level-precision Global Navigation Satellite System (GNSS)-Acoustic (GNSS-A) positioning in current state of the art. However, in-field SSP measurement on the one hand causes a huge cost and on the other hand prevents GNSS-A from global seafloor geodesy especially for real-time applications. We propose an Empirical Sound Speed Profile (ESSP) model with three unknown temperature parameters jointly estimated with the seafloor geodetic station coordinates, which is called the 1st-level optimization. Furthermore, regarding the sound speed variations of ESSP we propose a so-called 2nd-level optimization to achieve the centimeter-level-precision positioning for monitoring the seafloor tectonic movement. Long-term seafloor geodetic data analysis shows that, the proposed two-level optimization approach can achieve almost the same positioning result with that based on the in-field SSP. The influence of substituting the in-field SSP with ESSP on the horizontal coordinates is less than 3 mm, while that on the vertical coordinate is only 2–3 cm in the standard deviation sense.

Introduction

Global Navigation Satellite System (GNSS)-Acoustic (GNSS-A) positioning technique has become a vital tool for seafloor geodesy and crustal deformation applications of submarine offshore regions (Bürgmann & Chadwell, 2014; Iinuma et al., 2021). GNSS-A positioning technique was pioneered by Fred Spiess (Spiess, 1985; Spiess et al., 1998) and further developed for more than two decades (Chadwell & Sweeney, 2010; Chadwell et al., 1997). Regional seafloor geodetic networks were established in the past (Poutanen & Rózsa, 2020; Yang et al., 2020) and had provided key observations for constraining tectonic motion, crustal deformation and the earthquake cycle (Gagnon & Chadwell, 2007; Gagnon et al., 2005; Iinuma et al., 2021; Kido et al., 2006; Sato et al., 2011). GNSS-A technique achievements made in the past are on the one hand from observation scheme advances (Kido et al., 2008; Sato et al., 2013; Spiess et al., 1998) and on the other hand from acoustic positioning model improvements (Asada & Yabuki, 2006; Fujita et al., 2006; Spiess, 1980; Watanabe et al., 2020; Yang & Qin, 2020; Yokota et al., 2019). Nowadays, terrestrial geodesy has greatly facilitated low-cost and real-time positioning and near-real-time atmosphere state sensing due to positioning model advances (Torge & Müller, 2012), but this has not been achieved in seafloor geodesy. One of important reasons for this is that the high-precision seafloor geodetic positioning seriously relies on the Sound Speed Profile (SSP) measurement in field.

The sound speed structure of the ocean water prominently varies from the depth, spatial location and the time (Yokota et al., 2022). Although several global ocean environment observation plans have been in operation (Hayes et al., 1991; Stammer et al., 2003; Zeng et al., 2016), e.g., Array for Real-time Geostrophic Oceanography (Argo) and Transparent Ocean Plan (TOP) (Wu et al., 2020), the current resolution of ocean environment observations, e.g., the Argo observations having a temporal resolution of several days (Roemmich et al., 2009), cannot satisfy the high-precision seafloor geodetic positioning demands; and therefore an in-field Reference SSP (RSSP) measurement is still required. The sound speed can be directly measured or derived from the Conductivity-Temperature-Depth (CTD) profiler measurement (Wilson & Wayne, 1960). However, it is still unrealistic to conduct a high-resolution Sound Speed Field (SSF) measurement for GNSS-A positioning because of the huge cost; and therefore GNSS-A positioning technique in the current state of the art adopts a RSSP to perform the seafloor geodetic positioning (Watanabe et al., 2020). For this, the positioning model requires a strong resist ability to remedy the sound speed variation effect of the RSSP.

The acoustic positioning is seriously affected by the sound speed variations (Kido et al., 2008), which is very familiar to the atmosphere variation affecting GNSS positioning (Chen & Herring, 1997). Inspired by this, the Nadir Total Delay (NTD) model which is analogous to the zenith total delay in GNSS was proposed recently (Honsho & Kido, 2017; Honsho et al., 2019). This idea developed in the GNSS-A positioning can be also found in analyzing the sound speed variation for GNSS-A measurements (Kido et al., 2008). Besides NTD model, a generalized GNSS-A positioning model was also developed to correct the effect of the sound speed variation (Watanabe et al., 2020; Yokota et al., 2022). However, this kind of methods can extract only the sound speed variation relative to the in-field SSP.

In fact, the sound speed variation effect was very early studied by the GNSS-A and SSP observations in Hawaii (Osada et al., 2003). Then, the temporal variation inversion based on the RSSP was developed to eliminate this kind of effect (Fujita et al., 2004, 2006; Matsumoto et al., 2008). For more precisely characterizing the sound speed variation, the inversion method based on a 3-order B-spline model was developed in the past (Ikuta et al., 2008), and then Yokota et al. (2019) advanced this method by extracting the first-order and second-order horizontal sound speed gradients to represent more sound speed variation details (Yasuda et al., 2017). Note that, the above-mentioned inversion methods are based on the RSSP. In fact, the sound speed inversion without using the RSSP was also developed in the past (Chen, 2014). Recently, a self-constraint positioning method without the assistance of in-field SSP has also been developed (Zhao et al., 2022). However, without using the in-field SSP it is still hard to achieve a desirable positioning accuracy, e.g., the positioning error of the above self-constraint positioning method is up to 0.54 m. Precise positioning models without the assistance of in-field SSP still need to be developed to reduce the in-field SSP measurement cost, which is the vitally meaningful not only for facilitating the low-cost large-scale and even global seafloor geodesy but also for achieving the real-time seafloor geodetic applications, like nowadays mature GNSS geodesy.

This contribution is to develop a Self-structured Empirical SSP (SESSP) approach to achieve centimeter-precision-level seafloor geodetic three-dimensional positioning. In "Three-parameter empirical SSP" section, a three-parameter Empirical Temperature Profile (ETP) model is proposed to structure an Empirical Sound Speed Profile (ESSP) by using the Del Grosso’s sound speed formula. In "Two-level optimizations on ESSP" section, a novel GNSS-A positioning model based two-level optimizations is proposed, of which the 1st-level optimization is to fix the ETP model parameters, and the 2nd-level optimization is to finally achieve high-precision location regarding the sound speed variations relative to ESSP. In "Experiment results and tests" section, the proposed models are verified by the long-term seafloor geodetic array observations.

Three-parameter empirical SSP

The horizontal sound speed stratification can be expressed as an exponential SSP with unknowns for applying much of the World’s oceans (Munk, 1974). Besides, an empirical bilinear SSP $c_{{{\text{BP}}}} (u,{\varvec{p}}_{{{\text{BP}}}} )$ with four unknown parameters was also proposed and applied in the seafloor geodetic positioning, that is Chen (2014)

$$c_{{{\text{BP}}}} (u,{\varvec{p}}_{{{\text{BP}}}} ) = \left\{ {\begin{array}{*{20}l} {v_{{\text{s}}} + g_{{\text{u}}} u} \hfill & {0 \le u < u_{{\text{b}}} } \hfill \\ {v_{{\text{b}}} + g_{{\text{d}}} (u - u_{{\text{b}}} )} \hfill & {u_{{\text{b}}} \le u} \hfill \\ \end{array} } \right.$$

(1)

where $u$ is the depth, ${\varvec{p}}_{{{\text{BP}}}} = \left( {\begin{array}{*{20}c} {v_{{\text{s}}} } & {g_{{\text{u}}} } & {g_{{\text{d}}} } & {u_{{\text{b}}} } \\ \end{array} } \right)$ is the unknown parameter vector, $v_{{\text{s}}}$ is the surface sound speed, $u_{{\text{b}}}$ is the bilinear break depth, $v_{{\text{b}}}$ is the sound speed corresponding to the depth $u_{{\text{b}}}$, and $g_{{\text{u}}}$ and $g_{{\text{d}}}$ are the piecewise gradients of the bilinear function. The unknown parameters can be estimated jointly with the seafloor geodetic station coordinates.

Chen (2014) pointed out that $v_{{\text{s}}}$ and $u_{{\text{b}}}$ were treated knowns for the facilitation of surface sound speed measurement, but this is not so practical in some cases. Note that there are a series of equivalent profiles that can be used to obtain almost the same positioning result (Sun et al., 2019; Zielinski & Geng, 1999), i.e., this is an ill-posed problem widely existed in nonlinear inversion. To obtain a meaningful solution, we should impose a prior information on ${\varvec{p}}_{{{\text{BP}}}}$ with a certain uncertainty, see the Table 3. For solving this problem, we however present a novel ESSP by Del Grosso sound speed formula with an ETP as follow

$$T_{{{\text{ETP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} ) = \user2{\tau p}_{{{\text{ETP}}}} = T_{{\text{m}}} + \Delta T{\text{e}}^{{ - \frac{u}{{u_{0} }}}}$$

(2)

where ${\varvec{p}}_{{{\text{ETP}}}} = \left( {T_{{\text{m}}} \, \Delta T} \right)^{{\text{T}}}$ is an unknown parameter vector of ETP to be jointly estimated with the seafloor geodetic station coordinates, ${\varvec{\tau}} = \left( {T_{{\text{m}}} \;{\text{e}}^{{ - u/u_{0} }} } \right)$ is the corresponding coefficient matrix, $T_{{\text{m}}}$ represents the intermediate overmeasurement, $\Delta T$ represents the temperature difference between the sea-surface and sea-bottom, $u_{0}$ represents the depth of the thermocline, see Fig. 1. The $u_{0}$ and $T_{{\text{m}}}$ can be statistically induced from the long-term ocean environment observations and thereby we can impose prior constraints on the parameter estimation.

Fig. 1

Illustration on the empirical temperature profile

As shown in Fig. 1, the three parameters $T_{{\text{m}}}$, $\Delta T$ and $u_{0}$ to be estimated are the control parameters of the ETP shape. Note that the deep-sea bottom water temperature is generally very stable, for which it is convenient to impose a priori knowledge or constraint on the model parameter $T_{{\text{m}}}$. Besides, the deep-sea water temperature will decrease 1–2 °C per 1000 m, which might also be useful to characterize the ETP. Then, substituting ETP (2) and the average salinity S = 35‰ into the Del Grosso formula (Grosso, 1974; Wong & Zhu, 1995), we can establish an ESSP as

$$c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} ) = \beta_{{\text{C}}} + \beta_{{\text{P}}} + \beta_{{\text{T}}} ({\varvec{p}}_{{{\text{ETP}}}} )$$

(3)

where $c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )$ is ESSP,

$$\beta_{{\text{C}}} = {\text{C}}_{{\text{c}}} + {\text{C}}_{{{\text{s}}(1)}} S + {\text{C}}_{{{\text{s}}(2)}} S^{2}$$

(4)

is a constant associated with the salinity S, ${\text{C}}_{{\text{c}}}$ is the constant term in the Del Grosso formula,

$$\begin{aligned} \beta_{{\text{P}}} & = {\text{C}}_{{\text{s(2)p(2)}}} S^{2} P^{2} + {\text{C}}_{{\text{p(1)}}} P + {\text{C}}_{{\text{p(2)}}} P^{2} + {\text{C}}_{{\text{p(3)}}} P^{3} \\ & {\text{ = C}}_{{\text{p(1)}}} P + {\text{(C}}_{{\text{s(2)p(2)}}} S^{2} + {\text{C}}_{{\text{p(2)}}} )P^{2} + {\text{C}}_{{\text{p(3)}}} P^{3} \\ & = {\text{C}}_{{\text{p(1)}}} P + {\text{C}}_{{\text{d(1)}}} P^{2} + {\text{C}}_{{\text{p(3)}}} P^{3} \\ \end{aligned}$$

(5)

is the sound speed variation associated with the pressure P which is recommended to use the Leroy’s formula as Leroy and Parthiot (1998)

$$P = 1.0052405(1 + 5.28 \times 10^{ - 3} \sin^{2} \varphi )u + 2.36 \times 10^{ - 6} u^{2}$$

(6)

where $\varphi$ is the latitude,

$$\begin{aligned} \beta_{{\text{T}}} ({\varvec{p}}_{{{\text{ETP}}}} ) & = {\text{C}}_{{\text{t(1)}}} T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(2)}}} T_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(3)}}} T_{{{\text{ETP}}}}^{3} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & + {\text{C}}_{{{\text{tp}}}} PT_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(3)p}}} PT_{{{\text{ETP}}}}^{3} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{tp(2)}}} P^{2} T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(2)p(2)}}} P^{2} T_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{tp(3)}}} P^{3} T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & + {\text{C}}_{{{\text{st}}}} ST_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{st(2)}}} ST_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{{\text{stp}}}} SPT_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{s(2)tp}}} S^{2} PT_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & = ({\text{C}}_{{\text{t(1)}}} + {\text{C}}_{{{\text{st}}}} S)T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + (({\text{C}}_{{{\text{tp}}}} + {\text{C}}_{{{\text{stp}}}} S + {\text{C}}_{{\text{s(2)tp}}} S^{2} )P + {\text{C}}_{{\text{t(1)p(2)}}} P^{2} + {\text{C}}_{{\text{t(1)p(3)}}} P^{3} )T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & + {\text{ (C}}_{{\text{st(2)}}} S + {\text{C}}_{{\text{t(2)}}} {)}T_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(2)p(2)}}} P^{2} T_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & + {\text{C}}_{{\text{t(3)}}} T_{{{\text{ETP}}}}^{3} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(3)p}}} PT_{{{\text{ETP}}}}^{3} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & = {\text{C}}_{{\text{d(2)}}} T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) + ({\text{C}}_{{\text{d(3)}}} P + {\text{C}}_{{\text{t(1)p(2)}}} P^{2} + {\text{C}}_{{\text{t(1)p(3)}}} P^{3} )T_{{{\text{ETP}}}} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & + {\text{C}}_{{\text{d(4)}}} T_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(2)p(2)}}} P^{2} T_{{{\text{ETP}}}}^{2} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ & + {\text{C}}_{{\text{t(3)}}} T_{{{\text{ETP}}}}^{3} ({\varvec{p}}_{{{\text{ETP}}}} ) + {\text{C}}_{{\text{t(3)p}}} PT_{{{\text{ETP}}}}^{3} ({\varvec{p}}_{{{\text{ETP}}}} ) \\ \end{aligned}$$

(7)

is the sound speed variation determined by the water temperature T and the temperature-depth mixture terms.

With S = 35‰, we can then figure out the coefficients of Eqs. (3), (4), (5), (7) and they are given in Table 1 for facilitating the calculation. Finally, for an arbitrary latitude specified we can figure out the ESSP by employing the data in Table 1.

Table 1 ESSP coefficients

As the proposed ESSP regards the sound speed variation with hydrostatic pressure of the water that implied in the Leroy’s formula and the water temperature’s exponential decaying characteristic with the depth that implied in the proposed empirical temperature profile, it is more meaningful and accurate to perform the SSP inversion result. We can also use other sound speed formulae to structure the ESSP complying with their applicable conditions, e.g., Wilson formula (Wilson, 1960) and Chen-Millero formula (Chen & Millero, 1977). In the following section, we will propose an optimization approach to determine the model parameters of ETP (2).

Two-level optimizations on ESSP

Overall Scheme

Next, we will conduct a joint estimation of ESSP parameters and the seafloor geodetic station coordinates by employing the 1st-level optimization as shown in Fig. 2, which is called as sound speed self-structured empirical SSP approach for its independence on the in-field SSP measurement.

Fig. 2

Overall scheme of the two-level optimization

As shown in Fig. 2, the 1st-level optimization is performed in the context of the ray-tracing positioning procedure while the 2nd-level one is performed by B-splines for characterizing acoustic delay caused by the sound speed variations relative to ESSP.

The 1st-level optimization

GNSS-A positioning is achieved by a combination of the sea-surface GNSS positioning with the precise acoustic round-trip time measurement from the sea-surface acoustic transducer to the seafloor acoustic transponder (Asada & Yabuki, 2006). Due to the horizontal density stratification of the ocean, the seafloor geodetic positioning generally uses the ray-tracing positioning model. For taking place of the high-cost in-field SSP measurement, we use ESSP $c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )$ to perform a joint estimation of ${\varvec{p}}_{{{\text{ETP}}}}$ and the seafloor geodetic coordinates. This time that the GNSS-A positioning model reads

$$T_{{{\text{obs}},i}} = T_{i} \left( {{\varvec{X}},c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )} \right) + \varepsilon_{{{\text{T}},i}}$$

(8)

where $T_{{{\text{obs}},i}}$ is the ith round-trip time observation, ${\varvec{X}}$ is the seafloor transponder coordinate vector to be estimated, $\varepsilon_{{{\text{T}},i}}$ is the random error of observation. $T_{i} = T_{{{\text{s}},i}} + T_{{{\text{r}},i}}$ represents calculated the ith round-trip time,

$$T_{J,i} \, = \, \int_{{u_{\text{X}} }}^{{u_{\text{x}}^{J} }} {\frac{1}{{\cos \beta_{i} (u)}}\frac{1}{{c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )}}{\text{d}}u} \quad J \in \{\text{s},\text{r}\}$$

(9)

is one half of the round-trip travelling time calculated by the Two Dimensional (2D) ray-tracing model (Spiess, 1980), $u_{{\text{x}}}^{J} ,u_{{\text{X}}}$ are depths of the transducer and transponder, respectively. Note that, horizontal coordinates of transponder are implied in the incident angle $\beta_{i} (u)$ of the ith ray calculated by the inversion of the eigenray (Yang et al., 2021).

For n observations we have an over-determined vector-form observation equation ${\varvec{T}}_{{{\text{obs}}}} = {\varvec{T}}\left( {{\varvec{X}},c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )} \right) + {\varvec{\varepsilon}}_{{\text{T}}}$ solved by the nonlinear least squares (LS) criterion reads:

$$\mathop {\min }\limits_{{{\varvec{p}}_{{{\text{ETP}}}} }} \, g_{1} ({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ): = {\varvec{V}}^{{\text{T}}} ({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ){\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}(\varvec{X},{\varvec{p}}_{{{\text{ETP}}}} )$$

(10)

where $g_{1}$ is the weighted sum of the squared residuals, ${\varvec{V}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ): = {\varvec{T}}_{{{\text{obs}}}} - {\varvec{T}}\left( {{\varvec{X}},c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )} \right)$ is the residual vector, and ${\varvec{\varSigma}}_{\text{L}}^{{}} = {\varvec{P}}^{ - 1} \sigma_{0}^{2}$ and $\sigma_{0}^{2}$ are the variance of observations and prior unit weight variance, respectively. ${\varvec{P}} = {\text{diag}}(p_{1} ,p_{2} , \ldots ,p_{n} )$ is the weight matrix of observations where $p_{i} = (\sin (e_{i} ))^{2}$ is the weight of the ith observation and $e_{i}$ is the corresponding elevation angle, respectively. Hereafter, we however adopt an equal weight matrix to simplify the discussion, i.e., $p_{i} = 1$. To obtain LS solution we get the following first-order partial derivatives of $g_{1} \left( {{\varvec{X}},{\varvec{p}}_{\text{ETP}} } \right)$, that is

$${\varvec{h}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ) = \left( {\begin{array}{*{20}c} {\partial g_{1} /\partial {\varvec{X}}} \\ {\partial g_{1} /\partial {\varvec{p}}_{{{\text{ETP}}}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {{\varvec{A}}^{\text{T}} ({\varvec{X}}){{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} )} \hfill \\ {{\varvec{B}}_{{}}^{\text{T}} ({\varvec{p}}_{{{\text{ETP}}}} ){{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} )} \hfill \\ \end{array} } \right)$$

(11)

where

$${\varvec{A}}({\varvec{X}}) = \frac{{\partial {\varvec{T}}}}{{\partial {\varvec{X}}}} = \left( {\begin{array}{*{20}c} {\sum\limits_{{J \in \{ {\text{s}},{\text{r}}\} }} {\frac{{\partial T_{J,1} }}{{\partial {\varvec{X}}}}} } \\ {\sum\limits_{{J \in \{ {\text{s}},{\text{r}}\} }} {\frac{{\partial T_{J,2} }}{{\partial {\varvec{X}}}}} } \\ \vdots \\ {\sum\limits_{{J \in \{ {\text{s}},{\text{r}}\} }} {\frac{{\partial T_{J,n} }}{{\partial {\varvec{X}}}}} } \\ \end{array} } \right) = c_{{\text{X}}}^{ - 1} \left( {\begin{array}{*{20}c} {\sum\limits_{{J \in \{ {\text{s}},{\text{r}}\} }} {\left( {\begin{array}{*{20}c} {\sin \alpha_{J,1} \sin \beta_{J,1} } & {\cos \alpha_{J,1} \sin \beta_{J,1} } & {\cos \beta_{J,1} } \\ \end{array} } \right)} } \\ {\sum\limits_{{J \in \{ {\text{s}},{\text{r}}\} }} {\left( {\begin{array}{*{20}c} {\sin \alpha_{J,2} \sin \beta_{J,2} } & {\cos \alpha_{J,1} \sin \beta_{J,2} } & {\cos \beta_{J,2} } \\ \end{array} } \right)} } \\ \vdots \\ {\sum\limits_{{J \in \{ {\text{s}},{\text{r}}\} }} {\left( {\begin{array}{*{20}c} {\sin \alpha_{J,n} \sin \beta_{J,n} } & {\cos \alpha_{J,n} \sin \beta_{J,n} } & {\cos \beta_{J,n} } \\ \end{array} } \right)} } \\ \end{array} } \right)$$

(12)

is the Jacobian matrix of the nonlinear observation about the coordinate vector, $c_{{\text{X}}}^{{}}$ is the sound speed at the depth of the transponder, $\alpha_{J,i} ,\beta_{J,i}$ are the azimuth angle and incident angle of the ith ray, respectively.

$${\varvec{B}}({\varvec{p}}_{{{\text{ETP}}}} ) = \frac{{\partial {\varvec{T}}}}{{\partial {\varvec{p}}_{{{\text{ETP}}}} }} = \frac{{\partial {\varvec{T}}}}{{\partial c_{{{\text{ESSP}}}} }}\frac{{\partial c_{{{\text{ESSP}}}} }}{{\partial {\varvec{p}}_{{{\text{ETP}}}} }}$$

(13)

is the first-order derivative of the round-trip time ${\varvec{T}}$ about ${\varvec{p}}_{{{\text{ETP}}}}$. ${\varvec{B}}({\varvec{X}})$ is hardly analytically given but it can be numerically solved. Then, vanishing ${\varvec{h}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} )$, i.e., we have

$$\left\{ {\begin{array}{*{20}c} {{\varvec{A}}^{\text{T}} ({\varvec{X}}){\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ) = 0} \\ {{\varvec{B}}_{{}}^{\text{T}} ({\varvec{p}}_{{{\text{ETP}}}} ){\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}({\varvec{X}},{\varvec{p}}_{\text{ETP}} ) = 0} \\ \end{array} } \right.$$

(14)

that can be used to obtain the LS solution. With initial values ${\varvec{X}}_{0} ,{\varvec{p}}_{{{\text{ETP}}(0)}}^{{}}$, if $g^{\prime\prime}_{1} ({\varvec{X}}_{0} ,{\varvec{p}}_{{{\text{ETP}}(0)}}^{{}} )$ is positively defined, then LS solution can be locally solved by Newton’s method with the second-order partial derivative of $g_{1} ({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} )$, that reads (Xue et al., 2014):

$$\left( \begin{gathered} {\varvec{X}}_{k + 1} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k + 1}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} {\varvec{X}}_{k} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k}} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}l} {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} +{\varvec{\varGamma}}_{{\text{X}}} } \hfill & {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} } \hfill \\ {{\varvec{B}}_{k}^{\text{T}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } \hfill & {{\varvec{B}}_{k}^{\text{T}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} +{\varvec{\varGamma}}_{{\text{p}}} } \hfill \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} } \\ {{\varvec{B}}_{k}^{\text{T}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} } \\ \end{array} } \right)$$

(15)

where ${\varvec{A}}_{k}^{{}} : = {\varvec{A}}({\varvec{X}}_{k} )$, ${\varvec{B}}_{k}^{{}} : = {\varvec{B}}({\varvec{p}}_{{{\text{ETP}},k}} )$, ${\varvec{V}}_{k} : = {\varvec{V}}({\varvec{X}}_{k} ,{\varvec{p}}_{{{\text{ETP}},k}} )$ and k is the iteration index,

$${\varvec{\varGamma}}_{{\text{X}}} = \sum\limits_{i = 1}^{n} {V_{i} ({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} )p_{i} \sigma_{0}^{ - 2} {\varvec{S}}_{i} ({\varvec{X}})}$$

(16)

in which ${\varvec{S}}_{i} ({\varvec{X}}) = \partial {\varvec{a}}_{i}^{\text{T}} ({\varvec{X}})/\partial {\varvec{X}}$ is the first-order derivative of the ith row ${\varvec{a}}_{i} ({\varvec{X}})$ of ${\varvec{A}}({\varvec{X}})$, i.e., the Hessian matrix of the round-trip time $T_{i} ({\varvec{X}})$ about ${\varvec{X}}$,

$${\varvec{\varGamma}}_{{\text{p}}} = \sum\nolimits_{i = 1}^{n} {V_{i} {(}{\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} {)}p_{i} \sigma_{0}^{ - 2} {\varvec{Q}}}_{i} ({\varvec{p}}_{{{\text{ETP}}}} )$$

(17)

in which ${\varvec{Q}}_{i} {(}{\varvec{p}}_{{{\text{ETP}}}} {)} = \partial {\varvec{b}}_{i}^{{\text{T}}} {(}{\varvec{p}}_{{{\text{ETP}}}} {)/}\partial {\varvec{p}}_{{{\text{ETP}}}}$ is the first-order derivative of the ith row ${\varvec{b}}_{i} {(}{\varvec{X}}{)}$ of ${\varvec{B}}({\varvec{p}}_{{{\text{ETP}}}} {)}$, i.e., the Hessian matrix of the round-trip time ${\varvec{T}}_{i} ({\varvec{p}}_{{{\text{ETP}}}} )$ about ${\varvec{p}}_{{{\text{ETP}}}}$. Note that, ${\varvec{\varGamma}}_{{\text{X}}}$ and ${\varvec{\varGamma}}_{{\text{p}}}$ can be ignored for long-distance or small-residual cases, and at this time we recommend using Gauss–Newton iterative formula as

$$\left( \begin{gathered} {\varvec{X}}_{k + 1} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k + 1}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} {\varvec{X}}_{k} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k}} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}c} {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } & {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} } \\ {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } & {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} } \\ {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} } \\ \end{array} } \right)$$

(18)

which is recommended to be terminated under the condition $\mathop {\max }\limits_{i = 1,2, \ldots ,S} \left( {\left\| {{\varvec{X}}_{i,k + 1} - {\varvec{X}}_{i,k} } \right\|} \right) < \delta$ where $\delta$ is a sufficient small positive value, i is the index of the S seafloor geodetic stations. It is generally necessary to introduce a certain number of constraints on partial parameters to stabilize the iteration or to obtain a meaningful solution.

Next, we impose a priori constraints on ${\varvec{p}}_{{{\text{ETP}}}}$. The first a priori constraint can be structured by the temperature stability of the seawater-bottom, that is

$$T_{{\text{b}}} = T_{{{\text{ETP}}}} (u_{{\text{X}}} ,{\varvec{p}}_{{{\text{ETP}}}} ) + \varepsilon_{{\text{b}}}^{{}}$$

(19)

where $u_{{\text{X}}}$ is the depth of the seafloor geodetic station, the error $\varepsilon_{{\text{b}}}^{{}}$ represents the uncertainty of the a priori seawater-bottom temperature. Note that because deep-sea temperature is generally quite stable, the average temperature of the seawater bottom can be easily obtained by global ocean environment observations.

Let ${\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}}$ be the variance of $T_{{\text{b}}}$, we can structure the following LS criterion

$$\min \quad{g}_{1} ({\varvec{Z}}){\mathbf{ = }}{\varvec{V}}^{{\text{T}}} ({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ){\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ) + (T_{{\text{b}}} - \user2{\tau p}_{{{\text{ETP}}}} )^{{\text{T}}} {(}{\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}} )^{ - 1} (T_{{\text{b}}} - \user2{\tau p}_{{{\text{ETP}}}} )$$

(20)

where ${\varvec{Z}} = ({\varvec{X}}^{{\text{T}}} \quad {\varvec{p}}_{{{\text{ETP}}}}^{{\text{T}}} )^{{\text{T}}}$ is the parameter vector to be estimated. Omitting the deduction, we can obtain the Gauss–Newton iterative formula as

$$\left( \begin{gathered} {\varvec{X}}_{k + 1} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k + 1}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} {\varvec{X}}_{k} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k}} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}l} {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } \hfill & {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} } \hfill \\ {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } \hfill & {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} + {\varvec{\tau}}^{{\text{T}}} {(}{\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}} {)}_{{}}^{ - 1} {\varvec{\tau}}} \hfill \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}l} {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} } \hfill \\ {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} + {(}{\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}} {)}_{{}}^{ - 1} (T_{{\text{b}}} - \user2{\tau p}_{{{\text{ETP}},k}} )} \hfill \\ \end{array} } \right)$$

(21)

which is recommended to use the same termination condition. It is generally hard to obtain a global or meaningful solution of the problem without an effective initial value.

For most cases an arbitrary guess value of the unknown ${\varvec{p}}_{{{\text{ETP}}}}$ is sufficient to start the iteration, but we still recommend using a coarse grid search approach to obtain a robust initial value. Let ${\varvec{p}}_{{{\text{ETP}}(0)}}$ and ${\varvec{\varSigma}}_{{\text{p}}}^{{{\text{ETP}}}}$ be the initial value and the variance of ${\varvec{p}}_{{{\text{ETP}}}}$, respectively, at this time we can structure the following LS criterion

$$\begin{aligned} \min \quad g_{1} ({\varvec{Z}}) & {\mathbf{ = }}{\varvec{V}}^{{\text{T}}} ({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ){\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}({\varvec{X}},{\varvec{p}}_{{{\text{ETP}}}} ) + (T_{{\text{b}}} - \user2{\tau p}_{{{\text{ETP}}}} )^{{\text{T}}} {(}{\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}} )_{{}}^{ - 1} (T_{{\text{b}}} - \user2{\tau p}_{{{\text{ETP}}}} ) \\ & \quad + ({\varvec{p}}_{{{\text{ETP}}(0)}} - {\varvec{p}}_{{{\text{ETP}}}} )^{{\text{T}}} {(}{\varvec{\varSigma}}_{{\text{p}}}^{{{\text{ETP}}}} )_{{}}^{ - 1} ({\varvec{p}}_{{{\text{ETP}}(0)}} - {\varvec{p}}_{{{\text{ETP}}}} ) \\ \end{aligned}$$

(22)

Omitting the deduction, we can write out the Gauss–Newton iterative formula as

$$\left( \begin{gathered} {\varvec{X}}_{k + 1} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k + 1}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} {\varvec{X}}_{k} \hfill \\ {\varvec{p}}_{{{\text{ETP}},k}} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}l} {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } \hfill & {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} } \hfill \\ {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{A}}_{k}^{{}} } \hfill & {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{B}}_{k}^{{}} + {\varvec{\tau}}^{{\text{T}}} {(}{\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}} {)}_{{}}^{ - 1} {\varvec{\tau}} + ({\varvec{\varSigma}}_{{\text{p}}}^{{{\text{ETP}}}} )_{{}}^{ - 1} } \hfill \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}l} {{\varvec{A}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} } \hfill \\ {{\varvec{B}}_{k}^{{\text{T}}}{\varvec{\varSigma}}_{{\text{L}}}^{ - 1} {\varvec{V}}_{k} + {(}{\varvec{\varSigma}}_{{\text{T}}}^{{\text{b}}} {)}_{{}}^{ - 1} (T_{{\text{b}}} - \user2{\tau p}_{{{\text{ETP}},k}} ) + ({\varvec{\varSigma}}_{{\text{p}}}^{{{\text{ETP}}}} )_{{}}^{ - 1} ({\varvec{p}}_{{{\text{ETP}}(0)}} - {\varvec{p}}_{{{\text{ETP}},k}} )} \hfill \\ \end{array} } \right)$$

(23)

The sea-surface temperature has a great fluctuation throughout the year, and thereby we recommend a very loose constraint on the parameter $\Delta T$.

It is notable that Newton-type methods are of local convergence and may seriously suffer from ill-posedness of the problem, e.g., the non-uniqueness of the nonlinear parameter $u_{0}$, and therefore it is recommended to be found out by a grid search method. In fact, the LS solution $\hat{\user2{Z}}$ of (23) can be treated as a function about the variable $u_{0}$ because of $\tau (u_{0} ) = \left( {T_{{\text{m}}} \quad {\text{e}}^{{ - u/u_{0} }} } \right)$ and it is denote as $\hat{\user2{Z}}(u_{0} )$.

The algorithm is given in Fig. 3.

Fig. 3

1st-level optmization algorithm

Note that $T_{{\text{m}}} ,\Delta T$ are linear parameters for (2) but they are nonlinear parameters both for (3) and (8), and therefore must be iteratively solved.

The 2nd-level optimization

Next, we will take the ESSP $c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )$ derived from the 1st-level optimization as a RSSP $c_{0} (u)$ to conduct the precise positioning. Regarding the N and E direction variations and temporal variation of the sound speed, we can express the Four Dimensional (4D) SSF $c(n,e,u,t)$ to be the form as

$$c(n,e,u,t) = c_{0} (u) + k_{{\text{t}}} (u,t)t + k_{{\text{n}}} (u,t)n + k_{{\text{e}}} (u,t)e$$

(24)

where $c_{0} (u): = c_{{{\text{ESSP}}}} (u,{\varvec{p}}_{{{\text{ETP}}}} )$ is the ESSP obtained from the 1st-level optimization, $k_{{\text{n}}} (u,t),k_{{\text{e}}} (u,t),k_{{\text{t}}} (u,t)$ are sound speed gradients of the SSF relative to RSSP.

It is very familiar to the sound speed inversion in the 1st-level optimization that the spatiotemporal sound speed gradients can be jointly estimated with the seafloor geodetic coordinates. With “Appendix 1” we can directly write out the positioning model regarding the three sound speed gradients, that is

$$\begin{aligned} T_{{{\text{obs}}}} & = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\left( {\cos \beta } (u)\right)^{ - 1} c_{0}^{ - 1} (u){\text{d}}u} \\ & \quad - m_{{\text{t}}} Z_{{\text{t}}} (t,p_{{\text{t}}} ) - m_{{\text{n}}} Z_{{\text{n}}} (t,{\varvec{p}}_{{\text{n}}} ) - m_{{\text{e}}} Z_{{\text{e}}} (t,{\varvec{p}}_{{\text{e}}} ) - m_{{{\text{n}}^{\prime } }} Z_{{{\text{n}}^{\prime } }} (t,p_{{{\text{n}}^{\prime } }} ) - m_{{{\text{e}}^{\prime } }} Z_{{{\text{e}}^{\prime } }} (t,{\varvec{p}}_{{{\text{e}}^{\prime } }} ) + \varepsilon_{{\text{T}}} \\ \end{aligned}$$

(25)

where t is the travel time observation,

$$\left\{ {\begin{array}{*{20}l} {m_{{\text{t}}} = (\cos z)^{ - 1} } \hfill \\ {m_{{\text{n}}} = (\cos z)^{ - 1} \tan z\cos \alpha } \hfill \\ {m_{{\text{e}}} = (\cos z)^{ - 1} \tan z\sin \alpha } \hfill \\ {m_{{{\text{n}}^{\prime } }} = (\cos z)^{ - 1} \tan z^{\prime}\cos \alpha^{\prime}} \hfill \\ {m_{{{\text{e}}^{\prime } }} = (\cos z)^{ - 1} \tan z^{\prime}\sin \alpha^{\prime}} \hfill \\ \end{array} } \right.$$

(26)

is the mapping function, $z$ and $\alpha$ are the zenith angle and azimuth angle of the sea-surface platform observed at the seafloor geodetic station, respectively; $z^{\prime}$ and $\alpha^{\prime}$ are the zenith angle and azimuth angle observed at the seafloor geodetic network array center, respectively.

$$\left\{ {\begin{array}{*{20}l} {Z_{{\text{t}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{t \, k_{{\text{t}}} (u,t)}}{{c_{0}^{2} (u)}}{\text{d}}u} } \hfill \\ {Z_{{\text{n}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{n}}} (u,t)u}}{{c_{0}^{2} (u)}}{\text{d}}u} } \hfill \\ {Z_{{\text{e}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{e}}} (u,t)u}}{{c_{0}^{2} (u)}}{\text{d}}u} } \hfill \\ {Z_{{{\text{n}}^{\prime } }} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{n}}} (u,t)u_{{\text{X}}} }}{{c_{0}^{2} (u)}}{\text{d}}u} } \hfill \\ {Z_{{{\text{e}}^{\prime } }} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{e}}} (u,t)u_{{\text{X}}} }}{{c_{0}^{2} (u)}}{\text{d}}u} } \hfill \\ \end{array} } \right.$$

(27)

are the five zenith delays, $\lambda (u) = (\cos z)^{ - 1} \cos (\beta (u))$ can be defined as the measure of the ray bending degree. To characterize the five time-varying zenith delay parameters $Z_{K} (t),K \in \left\{ {t,n,e,n^{\prime},e^{\prime}} \right\}$, the following B-splines

$$Z_{K} (t,{\varvec{p}}_{K} ) = \sum\limits_{q = 0}^{{Q_{K} }} {p_{K,q} \varPhi_{K,q,k} } (t)\quad K \in \{ t,n,e,n^{\prime},e^{\prime}\}$$

(28)

are recommended, ${\varvec{p}}_{K} = \left( {p_{K,1} ,p_{K,2} , \ldots ,p_{K,Q(K)} } \right)$ is the unknown model parameter vector to be estimated, ${\varvec{p}}_{K,q}$ is the coefficient of the qth k-degree B-spine basis function $\Phi_{K,q,k} (t)$. This indicates the observation time span is split into $L_{J} = (Q_{J} - k + 1)$ intervals of which the knots span is $S_{K} = S_{{{\text{all}}}} /L_{J}$ where $S_{{{\text{all}}}}$ is the observation time span. If it is not especially specified, the subscript $k$ will be omitted in the following discussion.

At this stage, considering the smooth nature of the physical ocean process signal, we can conduct a series of 2-order smooths on the sound speed variations, and therefore we can alternatively use the optimization criterion as follow

$$\mathop {\min }\limits_{{{\varvec{X}},\varvec{p}_{K} }} \quad g({\varvec{X}},{\varvec{p}}_{K} ): = {\varvec{V}}^{\text{T}} ({\varvec{X}},{\varvec{p}}_{K} ){\varvec{PV}}({\varvec{X}},{\varvec{p}}_{K} ) + \sum\limits_{{ \, K \in \{ t,n,e,n^{\prime},e^{\prime}\} }} {\left\| {Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} )} \right\|_{{}}^{2} }$$

(29)

where $Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} )$ is the second-order derivative of $Z_{K} (t,{\varvec{p}}_{K} )$ about the time,

$$\left\| {Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} )} \right\|_{{}}^{2} = \lambda_{K}^{2} \int_{{t_{1} }}^{{t_{2} }} {(Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} ))^{2} {\text{d}}t}$$

(30)

is the squared norm of the estimated signal $Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} )$, where $t_{1}$ and $t_{2}$ are the starting time and end time of the observation, respectively, which is defined by the inner product $\left\langle {f_{i} (t),f_{j} (t)} \right\rangle = \int {f_{i} (t)\lambda_{K} f_{j} (t){\text{d}}t}$ of $f_{i} (t)$ and $f_{j} (t)$, $\lambda_{K}^{2}$ is the scale factor of the space specified by the above inner produce, which can be defined as

$$\lambda_{K}^{2} = \sigma_{0,K}^{ - 2}$$

(31)

where $\sigma_{0,K}^{2}$ represents the variance of the random signal $Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} )$.

To connect the minimization (29) with the normal form (20) of LS with constraints, we can rewrite (30) into the form as

$$\left\| {Z^{\prime\prime}_{K} (t,{\varvec{p}}_{K} )} \right\|_{{}}^{2} = ({\mathbf{0}}^{\text{T}} - {\varvec{p}}_{K}^{\text{T}} )(\Sigma_{\text{p}}^{K} )_{{}}^{ - 1} ({\mathbf{0}} - {\varvec{p}}_{K}^{{}} )$$

(32)

where

$$({\varvec{\varSigma}}_{{\text{p}}}^{K} )_{{}}^{ - 1} = {\varvec{P}}_{{\text{p}}}^{K} \sigma_{0,K}^{ - 2}$$

(33)

of which

$${\varvec{P}}_{\text{p}}^{K} = \left( {\begin{array}{*{20}c} {\left( {\varPhi^{\prime\prime}_{K,1} (t),\varPhi^{\prime\prime}_{K,1} (t)} \right)} & {\left( {\varPhi^{\prime\prime}_{K,1} (t),\varPhi^{\prime\prime}_{K,2} (t)} \right)} & \cdots & {\left( {\varPhi^{\prime\prime}_{K,1} (t),\varPhi^{\prime\prime}_{K,Q(K)} (t)} \right)} \\ {\left( {\varPhi^{\prime\prime}_{K,2} (t),\varPhi^{\prime\prime}_{K,1} (t)} \right)} & {\left( {\varPhi^{\prime\prime}_{K,2} (t),\varPhi^{\prime\prime}_{K,2} (t)} \right)} & \cdots & {\left( {\varPhi^{\prime\prime}_{K,2} (u),\varPhi^{\prime\prime}_{K,Q(K)} (t)} \right)} \\ \vdots & \vdots & {} & \vdots \\ {\left( {\varPhi^{\prime\prime}_{K,Q(K)} (t),\varPhi^{\prime\prime}_{K,1} (t)} \right)} & {\left( {\varPhi^{\prime\prime}_{K,Q(K)} (t),\varPhi^{\prime\prime}_{K,2} (t)} \right)} & \cdots & {\left( {\varPhi^{\prime\prime}_{K,Q(K)} (u),\varPhi^{\prime\prime}_{K,Q(K)} (t)} \right)} \\ \end{array} } \right)$$

(34)

is the weight matrix. Then, Omitting the deduction, we can immediately write out the Gauss–Newton solution of (29). To save the space, we write the Gauss–Newton solution only with the first three zenith delays, that is

$$\left( \begin{gathered} {\varvec{X}}_{k + 1} \hfill \\ {\varvec{p}}_{{{\text{N}},k + 1}} \hfill \\ {\varvec{p}}_{{{\text{E}},k + 1}} \hfill \\ {\varvec{p}}_{{{\text{t}},k + 1}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} {\varvec{X}}_{k} \hfill \\ {\varvec{p}}_{{{\text{N}},k}} \hfill \\ {\varvec{p}}_{{{\text{E}},k}} \hfill \\ {\varvec{p}}_{{{\text{t}},k}} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}c} {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{A}}_{k}^{{}} } & {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{N}}}^{{}} } & {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{E}}}^{{}} } & {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{t}}}^{{}} } \\ {{\varvec{M}}_{{\text{N}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{A}}_{k}^{{}} } & {{\varvec{M}}_{{\text{N}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{N}^{{}} + ({\varvec{\varSigma}}_{{\text{p}}}^{{\text{N}}} )_{{}}^{ - 1} } & {{\varvec{M}}_{{\text{N}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{E}}}^{{}} } & {{\varvec{M}}_{{\text{N}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{t}}}^{{}} } \\ {{\varvec{M}}_{{\text{E}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{A}}_{k}^{{}} } & {{\varvec{M}}_{{\text{E}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{N}}}^{{}} } & {{\varvec{M}}_{{\text{E}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{E}}}^{{}} + ({\varvec{\varSigma}}_{{\text{p}}}^{{\text{E}}} )_{{}}^{ - 1} } & {M_{{\text{E}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{t}}}^{{}} } \\ {{\varvec{M}}_{{\text{t}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{A}}_{k}^{{}} } & {{\varvec{M}}_{{\text{t}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{N}}}^{{}} } & {{\varvec{M}}_{\text{t}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{E}}}^{{}} } & {{\varvec{M}}_{{\text{t}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{M}}_{{\text{t}}}^{{}} + ({\varvec{\varSigma}}_{{\text{p}}}^{{\text{t}}} )_{{}}^{ - 1} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {{\varvec{A}}_{k}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{V}}_{k} } \\ \begin{gathered} {\varvec{M}}_{{\text{N}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{V}}_{k} - ({\varvec{\varSigma}}_{{\text{p}}}^{{\text{N}}} )_{{}}^{ - 1} {\varvec{p}}_{{{\text{N}},k}} \hfill \\ {\varvec{M}}_{{\text{E}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{V}}_{k} - ({\varvec{\varSigma}}_{{\text{p}}}^{{\text{E}}} )_{{}}^{ - 1} {\varvec{p}}_{{{\text{E}},k}} \hfill \\ {\varvec{M}}_{{\text{t}}}^{\text{T}}{\varvec{\varSigma}}_{\text{L}}^{ - 1} {\varvec{V}}_{k} - ({\varvec{\varSigma}}_{{\text{p}}}^{{\text{t}}} )_{{}}^{ - 1} {\varvec{p}}_{{{\text{t}},k}} \hfill \\ \end{gathered} \\ \end{array} } \right)$$

(35)

where ${\varvec{M}}_{K}^{{}}$ is the design matrix of the parameter ${\varvec{p}}_{K}$. The above formula can be easily extended for estimating the five zenith delays. Note that hyperparameter $\sigma_{0,K}^{2}$ might be optimally determined by the cross-test method or AIC criterion, but hereafter we set them to be zeros.

Experiment results and tests

Experimental data

The test adopts Japanese seafloor geodetic network array MYGI to verify the proposed GNSS-A positioning models. The observation span of the opened MYGI station data is from 2011 to 2020, having 35 repeated observations. The long-term displacement time series solution facilitates the positioning accuracy verification based on the fact the station has a linear motion trend with the tectonic movement of the plate (Fig. 4).

Fig. 4

MYGI station location

We take the GNSS-Acoustic Ranging combined POsitioning Solver (GARPOS V1.0.0) software output as an external reference solution to evaluate the propose models. The GARPOS software adopts the recommended default parameter settings.

1st-level optimization results

Prior temperatures from Argo observation

We collected Argo observations around MYGI within an area of 110,889 km², lying within the interval [(142.9167° ± 1.5°) E, (38.0833° ± 1.5°) N], from March 28, 2011 to June 15, 2020, see Fig. 5. It shows that the sea-surface temperature has a very large fluctuation, but the seawater bottom temperature is very stable. It is also hard to precisely fix the thermocline depth which lies within the interval (300 m 500 m).

Fig. 5

MYGI surrounding Argo observations from 2011 to 2020

The depth of MYGI station plots about 1727.8 m. the probability distribution of seawater bottom temperature at this depth in Fig. 6. It shows that, the mean of the seawater bottom temperature is 2.15 $^\circ{\rm C}$ and STD is 0.09 $^\circ{\rm C}$. Therefore, we adopt the 1st-level optimization parameter settings in Table 2. The same method is used to analyze the seawater bottom sound speed.

Fig. 6

Seawater temperature distribution at the depth 1727.8 m

Table 2 Parameter settings of 1st-level optimization on ESSP

The parameter settings of 1st-level optimization on bilinear SSP are given in Table 3. We impose lose constraints on the surface sound speed and the two sound speed gradients. Like constraining the bottom water temperature of ESSP, the bottom sound speed is imposed with a tight constraint 1486.62 m/s with the STD 0.01 m/s.

Table 3 Parameter settings of 1st-level optimization on bilinear SSP

SSP inversion precision analysis

The SSP inversion results are compared with the in-field SSP and they are given in Fig. 7. It shows that the SSP inversions can overall characterize the shape of the in-field SSP, but it is hard to precisely fit the sea-surface sound speed. To precisely reflect the SSP inversion precision we adopt three piece-wise statistics, see Fig. 8.

Fig. 7

SSP inversion results from 1st-level optimization

Fig. 8

Piece-wise statistics for SSP inversion precision

Figure 8 shows that both for the bilinear SSP and ESSP the sound speed inversion precision increases with the depth, e.g., for the proposed ESSP, the mean bias and STD of the inversion sound speed in deepwater are 0.085 m/s and 2.448 m/s respectively, but those in the shallow water are up to 2.455 m/s and 10.862 m/s respectively. Table 4 shows that the inversion precision of proposed ESSP is overall better than that of the bilinear SSP even though the bilinear SSP has a relatively small bias for whole water column. Note that it is hard to avoid a bias in the inversion SSP relative to the in-field SSP.

Table 4 Mean bias and STD of the inversion SSP

Positioning precision analysis

We adopt the Argo SSP nearby MYGI station and the inversion SSPs to perform the positioning. Taking the positioning result based on the in-field SSP as a reference, we can then figure out the positioning errors caused by the substitutions of the in-field SSP and they given in Fig. 9. It shows that the Argo SSP solution has a relatively large positioning error especially in the vertical direction, but the solutions based on the inversion SSPs are almost same with each other.

Fig. 9

Solutions of Argo SSP, bilinear SSP and ESSP

The bias and STD of the positioning error series in Fig. 9 are figured out and they are given in Table 5. It shows that both the proposed ESSP solution and bilinear SSP can achieve decimeter-level-precision positioning, e.g., the positional error of the proposed ESSP solution for each coordinate component doesn’t exceed 0.4 m, but there are biases 0.003 m and − 0.016 m in E direction and N direction, respectively. The vertical bias of proposed ESSP solution is smaller than that of the bilinear SSP solution and they are − 0.219 m and − 0.260 m, respectively, but their horizontal biases can be considered at the same order for centimeter-precision-level positioning. Although the bilinear SSP inversion precision is significantly lower than that the proposed ESSP, both the bilinear SSP solution and the proposed ESSP solution possess almost the same residual with the in-field SSP solution, see Fig. 10. This indicates that the two inversion SSPs are approximately equivalent to each other for the geodetic positioning application. This also shows that imposing a prior knowledge about the sound speed on the inversion is vitally important to obtain a meaningful SSP inversion solution.

Table 5 Positioning error comparison of the solutions based on different SSPs

Fig. 10

1st-level optimization residuals of different SSP solutions

2nd-level optimization results

We use the parameter settings in Table 6 for performing the 2nd-level optimization. Note that the positioning accuracy may be further improved by optimally selecting the knots span $S_{{\text{t}}} ,S_{{{\text{NEU}}}}$ and the smooth factor $\sigma_{K}^{ - 2}$.

Table 6 Parameter settings for 2nd-level optimization

The above empirical parameter settings listed in Table 6 will be further validated in following page.

The positioning results based on the 2nd-level optimization are given in Fig. 11. It shows that the E and N coordinate biases existing in the 1st-level optimization have been removed at a great extent.

Fig. 11

Comparison of 1st-level and 2nd-level optimizations

Table 7 shows that the horizontal precision of 2nd-level optimization for ESSP is better than 3 mm, while the vertical precision is better than 3 cm. The horizontal positioning accuracy of ESSP is very close to that of bilinear SSP, but vertical STD of ESSP solution is 0.0238 m which is significantly smaller than that 0.0433 m of bilinear SSP solution. Further considering the positioning error of the reference solution based on the in-field SSP, we can draw the conclusion that the proposed two-level optimization approach can achieve almost the same horizontal positioning precision with that based on in-field SSP. This conclusion becomes more solid when making a comparison among the 2nd-level optimization residuals of different SSP solutions as shown in Fig. 12. It also shows that the residuals are sharply shrunk after applying the 2nd optimization, compare to Fig. 9. A special attention on an existing bias about 1 cm in the vertical direction needs to be paid in future studies.

Table 7 Accuracy comparison of 1st-level optimization and 2nd-level optimization

Fig. 12

2nd-level optimization residuals of different SSP solutions

Long-term displacement time series analysis

Let ${\overline{\varvec {X}}}_{j}$ be the undetermined array geometry to perform the rigid-array fixed solution, $\Delta {\varvec {X}}^{\left( \kappa \right)}$ be the positional difference of the array center for kth-epoch observation, and they can be determined by solving the equation as (Watanabe et al., 2020):

$$\left\{ {\begin{array}{*{20}l} {{\varvec{X}}_{j}^{\left( \kappa \right)} = \delta_{j}^{\left( \kappa \right)} {\overline{\varvec{X}}}_{j} + \delta_{j}^{\left( \kappa \right)} \Delta {\varvec{X}}^{\left( \kappa \right)} } \hfill & {\left( {j = 1, \ldots ,w\text{ ; }\kappa = 1, \ldots ,\eta } \right)} \hfill \\ {0 = \sum\limits_{\kappa = 1}^{\eta } {\Delta {\varvec{X}}^{\left( \kappa \right)} } } \hfill & {} \hfill \\ \end{array} } \right.$$

(36)

where, if the transponder j is used in $\kappa$th observation, $\delta_{j}^{\left( \kappa \right)} = 1$. In addition, $\delta_{j}^{\left( \kappa \right)} = 0$. where w and $\eta$ are the number of transponders and epochs, respectively, and ${\varvec {X}}_{j}^{\left( \kappa \right)}$ denotes the transponders’ position at the kth-epoch.

The long-term displacement time series obtained by (36) is plotted in Fig. 13. The GARPOS solution time series based on in-field SSP as an external reference is also plotted in Fig. 13 for conducting the comparison. Then, we can use the linear model x(t) = x₀ + vt + e where x is the displacement time series and v is the velocity to fit the displacement time series to verify the proposed approach. The LS fitting residual as an estimation of the observation error e can be then used to evaluate the positioning precision.

Fig. 13

GARPOS solution and the proposed 2nd-level optimization solution

Figure 13 shows that the proposed 2nd-level optimization approach can produce almost the same station movement trend as the GARPOS solutions, and more detailed information about the time series residuals is given in Table 8.

Table 8 Displacement time series analysis results

Table 8 shows that the largest difference among the station velocities along E, N, U directions is about 5.5 mm/a and it happens in the U direction. The horizontal displacement time series residual STDs of proposed models are close to that of GARPOS model. The influence of the substitution of the in-field SSP with the self-structured ESSP on the station velocity estimation are 0.0, 0.4 and − 1.4 mm/a in E, N, U directions, respectively, which can be ignored in applying GNSS-A to the seafloor geodesy in the current state of the art. We can draw almost the same conclusion for apply the bilinear SSP to the seafloor geodetic positioning. It is a very interesting but important that for seafloor geodetic positioning at centimeter precision and long-term tectonic displacement monitoring in-field SSP measurements might be unnecessary. However, as an extra product the SSP inversion should keep its physical meaning by imposing a prior knowledge, such as the hydrostatic pressure of the water and the water temperature’s exponential decaying characteristic with the depth.

Remarks and conclusions

High-cost in-field SSP measurements have prevented GNSS-A from global seafloor geodesy, especially for real-time applications. The proposed self-structured SSP (SSSP) approach is a useful way to facilitate GNSS-A for conducting the large-scale and even global seafloor geodetic positioning.

The overall shape of the in-field SSP can be characterized by the proposed three-parameter empirical temperature profile by performing a joint estimation of the three parameters with the seafloor geodetic coordinates. However, the global optimal solution of the thermocline depth parameter is hard to be obtained in the context of the Gauss–Newton method because of its non-uniqueness and local convergence, and therefore the grid search method is recommended to be used. The seawater bottom temperature might also face with ill-posed problems, but fortunately the seawater bottom temperature prior constraint can be easily structured by the history ocean environment observations or by the current ocean temperature knowledge because of its stability.

The inaccuracy of the self-structured SSP can be almost completely absorbed by the proposed 2nd-level optimization such that it can achieve almost the same positioning result as that based on the in-field SSP. The influence of substituting the in-field SSP with the proposed SSSP on the horizontal positioning is less than 3 mm while that on the vertical positioning is better than 3cm in the STD sense. The influence of the substitution of the in-field SSP with the self-structured SSP on the station velocity estimation are further reduced to be omitted for applying GNSS-A to the seafloor geodesy in current state of the art. Sound speed inversion accuracy of the proposed SSSP is more accurate than the bilinear SSP and this leads to a more accurate vertical positioning precision.

Appendix 1: Seafloor geodetic positioning models with five acoustic zenith delays

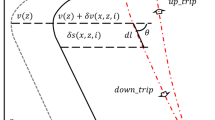
As shown in Fig. 14, without loss of generality, let the origin of NEU coordinate system be the centroid of the seafloor geodetic network array, let the RSSP $c_{0} (u)$ be at $(n_{0} = 0,e_{0} = 0,t_{0} = 0)$, the first-order Taylor series expansion of SSF $c(n,e,u,t)$ at $(n_{0} = 0,e_{0} = 0,t_{0} = 0)$ reads

$$c(n,e,u,t) = c_{0} (u) + k_{{\text{n}}} (u,t)n + k_{{\text{e}}} (u,t)e + k_{{\text{t}}} (u,t)t$$

(37)

where $k_{{\text{n}}} (u,t): = k_{{\text{n}}} (0,0,u,t)$, $k_{{\text{e}}} (u,t): = k_{{\text{e}}} (0,0,u,t)$, $k_{{\text{t}}} (u,t): = k_{{\text{t}}} (0,0,u,t)$ are the partial derivatives about the variable n, e and t, respectively, which represent the gradients of SSF.

Fig. 14

Seafloor geodetic network geometry

As shown in Fig. 14, let $\alpha^{\prime}$ and $z^{\prime}$ are the azimuth angle and zenith angle of the surface transducer position x, ${\varvec{X}}$ is the seafloor transponder coordinate vector to be estimated, $u_{{\text{X}}}$ be the depth of the seafloor geodetic station, then SSP at the position x can be expressed as

$$\begin{aligned} c^{\prime}_{0} (u,t) & = c_{0} (u){ + }k_{{\text{t}}} (u,t)t + n_{{\text{x}}} k_{{\text{n}}} (u,t) + e_{{\text{x}}} k_{{\text{e}}} (u,t) \hfill \\ & = c_{0} (u){ + }k_{{\text{t}}} (u,t)t + u_{{\text{X}}} \tan (z^{\prime})(\cos (\alpha^{\prime})k_{{\text{n}}} (u,t) + \sin (\alpha^{\prime})k_{{\text{e}}} (u,t)) \hfill \\ \end{aligned}$$

(38)

The acoustic range signal travelling time is determined by the SSP along the ray. With SSP $c^{\prime}_{0} (u,t)$ at the surface transducer position, we can figure out SSP along the ray. The horizontal gradient of SSF is very small and therefore the sound speed along the ray can be approximated by that along the Line of Sight (LOS). Then, let $\alpha$ and $z$ are the azimuth angle and zenith angle of the ray observed at the seafloor transponder position x, at arbitrary depth u, we have

$$c(LOS) = c^{\prime}_{0} (u,t) + u\tan (z)(\cos (\alpha )k_{{\text{n}}} (u,t) + \sin (\alpha )k_{{\text{e}}} (u,t))$$

(39)

For approximating the ray travelling time function $T = \int_{L} {c^{ - 1} (L){\text{d}}s}$ where L is the ray trajectory, with the Taylor series approximation $(y + {\text{d}}y)^{ - 1} = y^{ - 1} - y^{ - 2} {\text{d}}y$ we have

$$\begin{aligned} T \, & = \int_{L} {c^{ - 1} (L)\text{d}s} \approx \int_{L} {c^{ - 1} (LOS)\text{d}s} \\ & { = }\int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {(\cos \beta (u))^{ - 1} c^{ - 1} (LOS)\text{d}u} \\ & \approx \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {(\cos \beta (u))^{ - 1} c_{0}^{ - 1} (u)\text{d}u} \, - D_{{\text{t}}} (t) - \tan (z)(\cos (\alpha )D_{{\text{n}}} (t) + \sin (\alpha )D_{{\text{e}}} (t)) \\ & \quad - \tan (z^{\prime})(\cos (\alpha^{\prime})D_{{{\text{n}^{{\prime}}}}} (t) + \sin (\alpha^{\prime})D_{{{\text{e}^{{\prime}}}}} (t)) \\ \end{aligned}$$

(40)

where

$$\left\{ \begin{gathered} D_{{\text{t}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\frac{1}{\cos \beta (u)}\frac{{tk_{{\text{t}}} (u,t)}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ D_{{\text{n}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\frac{1}{\cos \beta (u)}\frac{{uk_{{\text{n}}} (u,t)}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ D_{{\text{e}}} \text{(}t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\frac{1}{\cos \beta (u)}\frac{{uk_{{\text{e}}} (u,t)}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ D_{{{\text{n}^{{\prime}}}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\frac{1}{\cos \beta (u)}\frac{{u_{{\text{X}}} k_{{\text{n}}} (u,t)}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ D_{{{\text{e}^{{\prime}}}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\frac{1}{\cos \beta (u)}\frac{{u_{{\text{X}}} k_{{\text{e}}} (u,t)}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ \end{gathered} \right.$$

(41)

are the acoustic delays along LOS. To counterbalance the ray incident angle $\beta (u)$ involved in (41), introducing the azimuthal auqengle z and then we can rewrite the model (40) into the form as follow

$$T_{{\text{obs}}} { = }\int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {(\cos \beta (u))^{ - 1} c_{0}^{ - 1} (u)\text{d}u} \, - m_{{\text{t}}} Z_{{\text{t}}} (t) - m_{{\text{n}}} Z_{{\text{n}}} (t) - m_{{\text{e}}} Z_{{\text{e}}} (t) - m_{{{\text{n}^{{\prime}}}}} Z_{{{\text{n}^{{\prime}}}}} (t) - m_{{{\text{e}^{{\prime}}}}} Z_{{{\text{e}^{{\prime}}}}} (t){ + }\varepsilon_{\text{T}}$$

(42)

where $T_{{{\text{obs}}}}$ is the observed value of round-trip time, $\varepsilon_{{\text{T}}}$ is the random error of observation.

$$\left\{ {\begin{array}{*{20}l} {m_{{\text{t}}} = (\cos z)^{ - 1} } \hfill \\ {m_{{\text{n}}} = (\cos z)^{ - 1} \tan z\cos \alpha } \hfill \\ {m_{{\text{e}}} = (\cos z)^{ - 1} \tan z\sin \alpha } \hfill \\ {m_{{{\text{n}}^{\prime } }} = (\cos z)^{ - 1} \tan z^{\prime}\cos \alpha^{\prime}} \hfill \\ {m_{{{\text{e}}^{\prime } }} = (\cos z)^{ - 1} \tan z^{\prime}\sin \alpha^{\prime}} \hfill \\ \end{array} } \right.$$

(43)

is the zenithal mapping function,

$$\left\{ \begin{gathered} Z_{{\text{t}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{t \, k_{{\text{t}}} (u,t)}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ Z_{{\text{n}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{n}}} (u,t)u}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ Z_{{\text{e}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{e}}} (u,t)u}}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ Z_{{{\text{n}^{{\prime}}}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{n}}} (u,t)u_{{\text{X}}} }}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ Z_{{{\text{e}^{{\prime}}}}} (t) = \int_{{u_{{\text{X}}} }}^{{u_{{\text{x}}} }} {\lambda^{ - 1} (u)\frac{{k_{{\text{e}}} (u,t)u_{{\text{X}}} }}{{c_{0}^{2} (u)}}\text{d}u} \hfill \\ \end{gathered} \right.$$

(44)

where $\lambda (u) = (\cos z)^{ - 1} \cos \beta (u) \approx 1$ such that $Z_{*} (t)$ can represent the zenith delay unrelated to the time-varying of LOS. The above proposed model is different from the GARPOS model which adopts a default multiplicative compensation on the RSSP as

$$\begin{aligned} T({\varvec{x}})& = \int_{{u_{{\text{X}}} }}^{{u_{{\varvec{x}}} }} {\frac{1}{c(u,t)}\text{d}s} \\ & = \int_{{u_{{\text{X}}} }}^{{u_{{\varvec{x}}} }} {\frac{1}{{{\varGamma} (t)c_{0} (u)}}\text{d}s} = {{\varGamma}^{-1}} (t)\int_{{u_{{\text{X}}} }}^{{u_{{\varvec{x}}} }} {\frac{1}{{c_{0} (u)}}\text{d}s} = {{\varGamma}^{-1}} (t)T_{0} ({\varvec{x}}) \end{aligned}$$

(45)

where ${\varGamma} (t)$ is a time-varying factor to characterize SSP variation, $T_{0} ({\varvec{x}})$ is the travel time calculated by the RSSP, $T({\varvec{x}})$ is the travel time calculated by the time-varying SSP. To deal with the multiplicative compensation, we can follow the GARPOS approach taking logarithms on both sides of the observation $T_{{{\text{obs}}}} = {\varGamma} ^{-1}\left( t \right)T_{0} \left( {\varvec{x}} \right) + \varepsilon$, that is

$$\ln T_{{\text{obs}}} = \ln T_{0} ({\varvec{x}}) + \ln {\varGamma}^{-1} (t) + \varepsilon^{\prime}$$

(46)

Assuming ${\varGamma}^{-1} (t) = e^{\gamma (t)}$, we can have

$$\ln T_{\text{obs}} = \ln T_{0} ({\varvec{x}}) + \gamma (t) + \varepsilon^{\prime}$$

(47)

where $\varepsilon^{\prime}$ is the observation error vector, $\gamma (t)$ is the correction coefficient, which can be parameterized by a B-spline about the time. Further considering the horizontal gradient of sound speed, GARPOS finally adopts

$$\gamma (t) = \gamma_{0} \left( t \right) + \gamma_{1} \left( t \right) \cdot \user2{P^{\prime}} + \gamma_{2} \left( t \right) \cdot \user2{X^{\prime}}$$

(48)

where $\user2{P^{\prime}}$ is horizontal coordinate under the NEU coordinate system centered on specific original point which is the mean coordinates of transducer positions during the whole surveying session. $\user2{X^{\prime}}$ is horizontal coordinate under the NEU coordinate system centered on specific original point which is the mean coordinates of seafloor transponder array positions.