1 Introduction

Knowledge of the satellite antenna phase center offsets (PCOs) is a prerequisite for precise applications of Global Navigation Satellite Systems (GNSSs). Within the International GNSS Service (IGS, Johnston et al. 2017), the satellite antenna PCO is defined as the vector from the center of mass to the mean phase center (Rothacher and Schmid 2010). The horizontal components X and Y refer to a plane parallel to the antenna panel. The Z-direction is perpendicular to that plane and nominally points toward the center of the Earth (Montenbruck et al. 2015). Elevation- and azimuth-dependent deviations from the mean center are considered as phase center variations (PCVs).

Due to initial lack of manufacturer values or estimated PCOs, conventional PCO values were used for the European GNSS Galileo in the IGS antenna model igs08.atx since July 2015 (Schmid 2015). These values were obtained from approximate dimensions of the satellite body (Montenbruck et al. 2014). Steigenberger et al. (2016) estimated PCOs of Galileo from the ionosphere-free linear combination of E1 and E5a observations. They obtained horizontal and vertical PCOs for three groups of satellites: in-orbit validation (IOV) satellites, full operational capability (FOC) satellites, and FOC satellites in eccentric orbit (FOCe). The estimates of two different analysis centers (ACs) agreed on the level of 1 and 3.5 cm for the X- and Y-PCOs and about 10 cm for the Z-PCOs. These block-specific PCO estimates were incorporated in igs08.atx in September 2016 (Schmid 2016).

Satellite-specific pre-launch manufacturer calibrations of the Galileo IOV and FOC PCOs and PCVs were published in December 2016 (Romero 2016) and October 2017 (Martinez 2017), respectively. They are available from the European GNSS Service Center of the European Union Agency for the Space Programme (EUSPA 2022) and updated as soon as new Galileo satellites are declared operational. They comprise frequency-specific values for the E1 (1575.42 MHz), E5a (1176.45 MHz), E5b (1207.14 MHz), E5 (1191.795 MHz), and E6 (1278.75 MHz) frequency bands. These values are included in the IGS antenna model igs14.atx since October 2017 (Villiger 2017).

Galileo orbit and clock products (Steigenberger et al. 2015) are computed by the ACs of the multi-GNSS pilot project (MGEX, Montenbruck et al. 2017) of the IGS on a regular basis. All these products refer to the ionosphere-free linear combination of E1 and E5a observations. This selection is attributed to the fact that early Galileo receivers were only capable of tracking these two frequencies, which are interoperable with GPS L1 and L5. However, an increasing number of IGS stations nowadays also provide E5b and E6 observations. The tracking of the E5 AltBOC signal is still limited and therefore not considered in this study.

During the preparation of the 3rd IGS reprocessing campaign (repro3), multi-frequency calibrations for a limited set of commonly used receiver antennas were made available (Villiger 2019a, b). These calibrations were either performed in an anechoic chamber (Villiger et al. 2020) or in the field with a robot (Wübbena et al. 2019). They allow for a consistent processing of all Galileo observations, whereas earlier analysis had to substitute the receiver antenna calibrations for the lower L-band (E5a, E5b, E5, E6) by GPS L2 (1227.60 MHz) values.

The joint availability of multi-frequency receiver and satellite antenna calibrations enables for the first time a determination of the terrestrial scale with GNSS. The Galileo-based results of Villiger et al. (2020) showed a scale offset of 1 ppb w.r.t. ITRF2014 (Altamimi et al. 2016) for the E1/E5a ionosphere-free linear combination. However, they also found a discrepancy of 0.38 ppb between receiver antenna calibrations obtained in an anechoic chamber and those from robot calibrations.

For BeiDou-3, a recent study by Zajdel et al. (2022) revealed notable frequency-specific inconsistencies between observed and manufacturer-calibrated satellite antenna PCOs in the B1, B2, and B3 bands. This finding served as a motivation for a detailed investigation of Galileo antenna PCOs across the various frequency bands. To analyze the consistency of the Galileo satellite antenna ground calibrations, PCO values are estimated from ionosphere-free linear combinations of E1/E5a, E1/E5b, and E1/E6 observations. The global network comprises about 150 stations supporting all four frequencies and equipped with fully calibrated receiver antennas. Details of the PCO estimation are discussed in Sect. 3. The stability of the estimated PCOs is evaluated and they are compared to the pre-flight manufacturer calibrations as well as the latest IGS antenna model igs20.atx in Sect. 4.

2 ITRF scale and igs20.atx

The scale of the International Terrestrial Reference Frame (ITRF) is defined by the space geodetic techniques Very Long Baseline Interferometry (VLBI) and Satellite Laser Ranging (SLR). For the most recent release ITRF2020, the scale difference between both techniques is 0.15 ppb (Altamimi et al. 2022). The combined IGS solution used as GNSS input for ITRF2020 was computed in the framework of the 3rd IGS reprocessing campaign (Rebischung 2021). Altogether 10 ACs contributed to repro3. Three of them processed only GPS, one GPS + GLONASS, one GPS + Galileo, and five GPS + GLONASS + Galileo. For Galileo, all analysis centers except for TU Graz (TUG) utilized the ionosphere-free linear combination of E1 and E5a. TUG processed all Galileo frequencies together in a so-called raw approach (Strasser 2022).

Due to the incorporation of Galileo observations, the IGS contribution to ITRF2020 might have been incorporated into the scale realization for the first time. However, the scale of the IGS combined contribution for ITRF2020 showed a scale offset of 0.68 ppb w.r.t. the combined VLBI and SLR scale and a scale drift of 0.018 ppb/a (Altamimi et al. 2022). Due to these large discrepancies, the GNSS technique was ultimately excluded from the ITRF2020 scale realization.

As a consequence, a systematic offset of 1-2 dm between the manufacturer-calibrated Galileo PCOs and the estimated ones is expected when fixing the scale to ITRF2020. Subject to proper consistency of the manufacturer calibrations, this offset should be purely frame-related and not depend on the choice of a specific frequency or signal combination in the Galileo orbit determination and PCO estimation. Therefore, we only consider differences between individual frequency pairs in the subsequent consistency analysis. In particular, consistency of PCO calibrations across frequency bands is important for multi-frequency precise point positioning and timing applications utilizing three or even four frequencies (e.g., Duong et al. 2019; Psychas et al. 2021; Zhang and Pan 2022). Such applications are expected to grow in the near future in view of the provision of multi-frequency correction data by the Galileo high accuracy service (Fernandez-Hernandez et al. 2022).

In order ensure consistency of the IGS products with the ITRF2020 scale, the available manufacturer antenna calibrations were shifted in Z-direction for all frequencies when generating the igs20.atx antenna model (Rebischung et al. 2022). For GPS III, the Z-PCO correction amounts to +8.9 cm. The Galileo IOV satellite E102 showed a different behavior than the other IOV and FOC satellites. Therefore, a dedicated offset of +1.5 cm was applied. For all the other Galileo satellites, the Z-PCOs were shifted by +15.6 cm.

Fig. 1
figure 1

Stations used for the estimation of satellite antenna PCOs

Full size image

3 PCO estimation

Galileo PCOs within this study are estimated from a global network of IGS tracking stations. The station selection is based on the following criteria:

  • availability of multi-frequency receiver antenna calibration

  • Galileo E1/E5a/E5b/E6 and GPS L1/L2 tracking

  • availability of ITRF2020 station coordinates

  • global coverage.

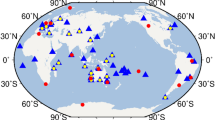
The selected network of 148 tracking stations is shown in Fig. 1. The data interval covers one year, namely July 1, 2021, until June 30, 2022. Ionosphere-free linear combinations of GPS L1/L2 and Galileo E1/E5a, E1/E5b, E1/E6 are processed with the NAPEOS software (Springer 2009). GPS observations are included to strengthen the common estimation parameters and reduce system-specific systematic errors. Daily global solutions are computed including the estimation of station coordinates, troposphere zenith delays, receiver and satellite clocks, inter-system biases, Earth rotation parameters, satellite orbits, and finally PCOs. Solar radiation pressure of the Galileo satellites is modeled with a box-wing model based on satellite metadata (EUSPA 2022). To account for deficiencies of this model, five parameters of the Empirical CODE Orbit Model (ECOM, Beutler et al. 1994) are estimated on top. Z-PCO estimates are highly correlated with the terrestrial scale as well as satellite antenna PCVs. Therefore, the scale of the ground network used for PCO estimation is heavily constrained to ITRF2020 and the Galileo PCVs are fixed to the manufacturer values (EUSPA 2022). GPS satellite antenna PCVs are fixed to the IGS repro3 antenna model, while GPS PCOs are freely adjusted.

Table 1 Statistics of the PCO estimation from different linear combinations.
Full size table

Table 1 lists selected statistical properties of the different solutions. The mean observation number per day is highest for the E1/E5a and E1/E5b linear combinations and differs by 8.3‰ for E1/E6. The median phase residuals are on the level of 1 cm. E1/E6 shows slightly higher phase residuals compared to E1/E5a and E1/E5b but a significant increase in pseudorange residuals of 43% compared to E1/E5a. The latter impact the PCO estimation only indirectly via the widelane ambiguity resolution with the Melbourne-Wuebbena combination (Melbourne 1985; Wübbena 1985) using carrier-phase and pseudorange observations for baselines up to 6000 km. The main reason for these increased residuals is the amplified noise of the E1/E6 ionosphere-free linear combination compared to E1/E5a or E1/E5b due to a smaller separation of the two frequencies (Duan et al. 2023).

The formal errors of the PCO estimates only differ on the few tenth of a millimeter level. However, they are larger by a factor of two for the Y-PCOs compared to the X-PCOs due to geometry-related effects discussed in Schmid et al. (2007). The time series of horizontal PCO estimates show a significant dependence on the elevation of the Sun above the orbital plane (\(\beta \)-angle) affecting the estimates themselves as well as their formal errors. These systematic effects are introduced by correlations with the orbital elements (Schmid et al. 2007) and have to be considered when computing mean PCO values.

Fig. 2
figure 2

Horizontal satellite antenna PCOs of different ionosphere-free linear combinations: a E1/E5a, b E1/E5b, c E1/E6. IOV: in-orbit validation; FOC: full operational capability; FOCe: FOC in eccentric orbit (E201 and E202)

Full size image
Fig. 3
figure 3

Horizontal satellite antenna PCO differences between manufacturer calibrations and estimated values. Results for different ionosphere-free linear combinations are shown: a E1/E5a, b E1/E5b, c E1/E6. The light colors indicate the IOV satellites

Full size image

4 PCO estimation results

4.1 Horizontal PCOs

In order to minimize the impact of the systematic errors discussed in the previous section, the daily PCO estimates are weighted with their formal errors for computing mean horizontal PCO values. These mean values as well as the manufacturer calibrations for the E1/E5a, E1/E5b, and E1/E6 ionosphere-free linear combination are shown in Fig. 2.

The first two Galileo FOC satellites (E201 and E202) were accidentally inserted in an erroneous orbit (Steigenberger and Montenbruck 2017). The circularization of these orbits consumed a notable amount of fuel, which introduced a shift in the center-of-mass of these satellites. As the PCOs refer to the center-of-mass, this can be clearly seen in the shifted X-PCO values of these two spacecraft. The estimated Galileo IOV PCOs show a larger scatter compared to the FOC satellites, in particular for the E1/E6 linear combination.

The differences of the estimated and calibrated absolute values from Fig. 2 are plotted in Fig. 3. A systematic shift of about +1 cm in X-direction can be seen for all linear combinations. In Y-direction, no such discrepancy is present. The standard deviations of the horizontal Galileo FOC PCO differences are 4 mm for the X-component and 3 mm for the Y-component. No significant differences can be seen for various linear combinations. The IOV satellites have a larger scatter, in particular for the E1/E6 combination.

In order to assess the impact of a 1 cm X-PCO shift on the estimated parameters, two solutions were computed to generate precise orbit and clock products. An E1/E5a solution with the horizontal manufacturer PCOs serves as reference. This solution is compared to a second solution generated with all FOC X-PCOs shifted by \({-1}\) cm. The estimated satellite positions and clock offsets of the two solutions differ on the one-centimeter level with a STD of 5 mm. The two sets of orbit and clock products were used as input for a precise point point positioning (PPP, Zumberge et al. 1997) using the same antenna calibrations applied in the product generation. The estimated station coordinates differ on the few tenth of a millimeter level. Therefore, the systematic difference between estimated and calibrated X-PCOs is considered to be negligible for end-users of the precise Galileo orbit and clock products.

Fig. 4
figure 4

Horizontal PCO differences between ionosphere-free linear combinations: a E1/E5a − E1/E5b, b E1/E5a − E1/E6. The red ellipses are obtained from the mean formal errors of individual PCO estimates (see Table 1) by error propagation and indicate the expected scatter of PCO differences between frequency pairs in case of purely uncorrelated errors

Full size image
Fig. 5
figure 5

Differences between estimated and calibrated Z-PCOs: a E1/E5a, b E1/E5b, c E1/E6. The light colors indicate the IOV satellites. The error bars represent the standard deviation computed from the 1-year time series

Full size image

The origin of the systematic differences in the X-PCO is not known. Possible reasons include the impact of the satellite body on the in-orbit PCOs and correlations between solar radiation pressure parameters and PCOs. Based on Monjas et al. (2010) as well as the fact that the published PCOs refer to a mechanical reference point of the antenna element, we assume that the chamber calibrations were performed for the antenna panel only without being mounted on the satellite. Near-field effects of the satellite body as well as the mounting of a radio-transparent multi-layer insulation protecting the antenna from large temperature variations in space can introduce changes of the PCO.

Steigenberger et al. (2016) analyzed the impact of different solar radiation pressure (SRP) models on Galileo PCO estimation. They found that a sophisticated SRP modeling is essential for stable PCO results. A box-wing model in combination with a reduced set of empirical parameters resulted in the most stable results that could even further improved by constraining the direct SRP parameter D\(_0\). Although a box-wing a priori model is used in the current study, it cannot be excluded that this model might contribute to the systematic X-PCO differences due to correlations between D\(_0\) and the X-PCOs.

Fig. 6
figure 6

Z-PCO differences between ionosphere-free linear combinations: a E1/E5a − E1/E5b, b E1/E5a − E1/E6

Full size image

A further differencing step allows for the assessment of the internal consistency of the different sets of PCOs, namely the estimated PCOs and the calibrated PCOs. The E1/E5a ionosphere-free linear combination has been selected as reference. Differences of E1/E5b and E1/E6 w.r.t. that linear combination are illustrated in Fig. 4. The PCO differences of the manufacturer calibrations are on the level of only 0.5 to 1.1 mm for E1/E5b and 1.1 to 1.6 mm for E1/E6 in terms of RMS. The RMS values of the estimated PCO differences for the FOC satellites are slightly higher with 0.8 to 1.2 mm and 1.5 to 3.8 mm. The Galileo FOC PCO differences are well within their formal errors obtained by error propagation from the values in Table 1 and indicated by red ellipses in Fig. 4. However, most of the estimated Galileo IOV PCO differences are close to these formal errors or even exceed them.

4.2 Z-PCOs

The Z-PCO estimates of the Galileo IOV satellites range from 79 to 111 cm. For the FOC satellites, Z-PCOs between 85 and 115 cm are obtained. Figure 5 shows the Z-PCO differences for the three different linear combinations w.r.t. the calibrated PCOs. The anomalous behavior of the IOV satellite E102 already mentioned before is obvious. \(\varDelta \)Z of E102 differs by about 13 cm from the mean of the other active IOV satellites E101 and E103, see Table 2. The Z-PCO differences show an overall offset of 10 to 15 cm due to the scale inconsistency of ITRF2020 used for the PCO estimation and the manufacturer calibrations. The offsets of E1/E5a and E1/E5b differ by 1.2 cm on average over all satellites and by only 3 mm for the FOC satellites. E1/E6 shows differences of 3–4 cm compared to E1/E5a and E1/E5b. The scatter of the Galileo FOC Z-PCO estimates in terms of standard deviation is 2.2 cm, 2.4 cm, and 3.1 cm for E1/E5a, E1/E5b, and E1/E6, respectively.

Figure 6 illustrates the internal consistency of the estimated and calibrated PCO sets by differencing pairs of linear combinations as already done for the horizontal PCOs in Sect. 4.1. The differences of the estimated Z-PCOs show a higher scatter for the IOV satellites for E1/E5a−E1/E5b. The absolute values of the estimated inter-frequency PCO differences differ by up to 15 cm from the calibrated ones. The FOC satellites show a significantly higher consistency in Fig. 6a with a STD of 0.9 cm for the estimations and 0.6 cm for the calibrations. The E1/E5a−E1/E6 differences in Fig. 6b exhibit a larger scatter across the various satellites for both, the estimations as well as the calibrations, with STD values of 2.7 and 2.3 cm, respectively, for the FOC satellites.

According to Montenbruck et al. (2022), Z-PCO differences \(\varDelta \text {PCO}_{z}\) translate into station height changes \(\varDelta h\) with a ratio of

$$\begin{aligned} \alpha = \frac{\varDelta h}{\varDelta \text {PCO}_{z}}=-0.041 \end{aligned}$$
(1)

The numerical value of \(\alpha \) in Eq. 1 refers to the Galileo orbit height and a 10\(^\circ \) cutoff angle applied in the GNSS data analysis discussed in Sect. 3.

Table 2 Mean Z-PCO differences between estimated values and manufacturer calibrations for dedicated groups of satellites. The last two columns give the scale differences w.r.t. ITRF2020 at epoch 2022.0 obtained from \(\varDelta \)Z-PCO according to Eq. 1
Full size table

The right columns of Table 2 list scale differences corresponding to calibration inconsistencies for the various dual-frequency signal combinations. They were computed with Eq. 1 from the Z-PCO differences in the left columns. The scale difference of 0.73 ppb obtained for the E1/E5a linear combination agrees closely with the scale difference between ITRF2020 and the IGS repro3 solution of 0.68 ppb, see Sect. 2. The E1/E5b linear combination results in a slightly smaller scale differences, whereas E1/E6 gives a scale difference of almost 1 ppb.

For a comparison of the estimated PCOs with the igs20.atx antenna model, scale drifts have to be considered. The igs20.atx antenna model reproduces the ITRF2020 scale only for the reference epoch 2015.0. When used for other epochs, it introduces a drift of about +0.1 mm/a at the surface of the Earth (Rebischung et al. 2022) or, equivalently, +0.016 ppb/a. This corresponds to a Z-PCO-drift of \({-2.4}\) mm/a, see Fig. 7. The mean epoch of our PCO estimates is 2022.0 resulting in an expected scale bias or station height difference of 0.7 mm. Converted to a Z-PCO according to Eq. 1, a correction value of \({-1.7}\) cm is obtained.

Table 3 lists the mean Z-PCO differences between the estimates for different linear combinations and the igs20.atx PCOs after accounting for the scale drift correction. Although the anomalous behavior of E102 is already considered in igs20.atx by applying a different PCO correction value (see Sect. 2), this satellite still shows inconsistent Z-PCO differences compared to the other IOV satellites. They amount to 3–4 cm for E1/E5a and E1/E6 and even 10 cm for E1/E5b. The IOV satellites E101 and E102 show a Z-PCO difference consistency on the few millimeter level for E1/E5a and E1/E6 and one centimeter for E1/E5b compared to the FOC satellites. For E101 and E103 as well as the FOC satellites, a difference of about 4 cm can be seen between linear combinations of E1 and E5a/E5b and the E1/E6 linear combination. The standard deviations of the FOC satellites are on the 2 cm level for E1/E5a and with 3 cm slightly higher for E1/E6. For the FOC satellites, the Z-PCO differences given in Table 3 correspond to a scale difference of \({-0.15}\) ppb,\({-0.12}\) ppb, and +0.12 ppb for E1/E5a, E1/E5b, and E1/E6.

Fig. 7
figure 7

Relationship between TRF scale and Z-PCOs

Full size image

5 Summary and conclusions

Galileo satellite antenna phase center offsets have been estimated for the ionosphere-free linear combinations of E1/E5a, E1/E5b, and E1/E6. The Y-PCO estimates of the FOC satellites agree within their estimation precision with the manufacturer calibrations, whereas the X-PCOs show a systematic difference of about 1 cm. The differences of horizontal PCO estimates obtained from the various linear combinations are on the few millimeter level for the FOC satellites. The IOV satellites show larger differences of up to 2 cm. The Z-PCO estimates have a 10–16 cm discrepancy w.r.t. the manufacturer calibrations. This systematic offset is attributed to the scale inconsistency of the manufacturer calibrations and ITRF2020 used for the PCO estimation. Compared to the latest IGS antenna model igs20.atx consistent with ITRF2020, the Z-PCO differences amount to only ±2 cm.

Table 3 Mean Z-PCO differences for dedicated groups of satellites: estimated values and igs20.atx including scale drift correction. All values are given in cm
Full size table

The terrestrial scale realized by E1/E5a and E1/E5b observations of the FOC satellites using the respective manufacturer calibrations of the transmit antenna PCOs is consistent at the 0.03 ppb level. When using manufacturer-calibrated Galileo PCOs for realization of the terrestrial reference frame, use of the ionosphere-free linear combination of E1 and E6 observations would result in a scale difference of 0.25 ppb compared to use of the E1/E5a or E1/E5b combinations. Increased scale differences are also present for the IOV satellites, in particular for the E1/E5b observations. Nevertheless, the scale consistency of different Galileo frequencies is better by a factor of two compared to BDS-3 results of Zajdel et al. (2022). Furthermore, the internal Galileo scale consistency across different frequency bands is also almost a factor of three better than the current scale difference between GNSS and SLR/VLBI as seen in the ITRF2020. Proper understanding of manufacturer-calibrated GNSS transmit antenna PCOs and their impact on the terrestrial reference frame scale thus remains an important research topic for the future.