External gravitational field of a homogeneous ellipsoidal shell: a reference for testing gravity modelling software

Abstract

There are numerous applications in geodesy and other geo-sciences in which the gravitational potential effect or other functions of the potential are computed by forward modelling from a given mass distribution. Different volume discretisations, e.g. prisms, tesseroids or mass layers are used. In order to control the numerical realisation of the forward calculation in the practical application, e.g. in reduction tasks, these evaluation programs should be verified against rigorous analytical solutions. In this contribution, a closed analytical solution for the potential of an ellipsoidal shell as a test body is presented. Furthermore, we derive the respective closed formulae for the gravity vector and the gravity gradient tensor. Program implementations of the tesseroid approach are compared on the basis of this ellipsoidal mass arrangement. For the practical usage, fast-converging expansions in spherical harmonics are provided in addition. The derivation of the formulae is based on a closed solution of the potential of a homogeneous ellipsoid for computation points situated on the rotation axis, which then is extended to the external space.

1 Introduction

The determination of the gravity field of the Earth and its variation in time is one of the main tasks of Geodesy (Rummel et al. 2005). The most dominant spatial variations on the Earth’s surface and in external space close to the Earth are induced by the topographical, isostatic masses and hydrological mass variations. The modelling of these masses is generally performed by volume discretisations, reducing the shape of the volume elements to geometrically simple bodies such as rectangular prisms (Forsberg 1984; Nagy et al. 2000, 2002), polyhedrons (D’Urso 2014), spherical tesseroids (Anderson 1976; Heck and Seitz 2007; Grombein et al. 2013; Fukushima 2018; Marotta et al. 2019) or ellipsoidal prisms (Abd-Elmotaal and Kühtreiber 2021; Roussel et al. 2015). The precise computation of the gravitational field of the topographic and isostatic masses is still a numerical challenge, despite of the use of modern parallel computers with distributed kernels, since—due to the irregularity of these mass constituents—a huge amount of volume elements has to be used in the discretisation of the attracting masses. This applies in particular due to the continuing increase in the resolution of volume elements.

Efficient approaches have been developed in the past years for the accurate calculation of the gravitational potential and its functionals and have been implemented by suitable software. In order to control those approaches and the respective computer programs, the numerical results should be compared with and verified against analytical solutions, based on simple mass distributions. The most simple global mass distribution, approximating the Earth’s topography, is a spherical shell, which has often been applied in Geodesy for testing evaluation procedures and software (cf. Heck and Seitz 2007; Fukushima 2018). A massive spherical shell bounded by two concentric spheres produces a gravitational field that can be described by a closed analytical solution. However, a spherical shell creates a mathematically simple, isotropic gravitational field. Only the potential and its radial derivatives do not vanish and can therefore be tested in such a simple test embedding. By using Laplace’s equation, $V_\textrm{xx} = V_\textrm{yy} = - V_\textrm{zz}/2$ can be calculated indirectly in the isotropic case.

In the present paper, we propose an ellipsoidal massive shell bounded by two confocal ellipsoids of revolution as a more general and realistic test configuration. Using the ellipsoid instead of the isotropic spherical case leads to a much better approximation of the general shape of the Earth as it depends also on the horizontal position of the computation point. In addition to the derivatives in radial direction also the latitudinal and mixed gradients can be controlled by this ellipsoidal setting. Analytical solutions for the external gravitational potential of a homogeneous ellipsoid of revolution have been derived by various authors, e.g. by Kellogg (1929), Hobson (1931), MacMillan (1958) and Wang (1988). Any of these solutions refers to coordinate systems which are rather unfamiliar in Geodesy. The $\arctan$, $\sinh$, $\cosh$ functions used in these approaches are also very time-consuming in terms of numerical efforts.

In this paper, we derive solutions in spherical coordinates and elliptical coordinates which have not been published before, according to our knowledge. Furthermore, we follow a new innovative way of derivation: after having obtained a closed solution for the special case of a computation point on the positive z-axis, this result is extended to the complete external space of the ellipsoid by harmonic continuation. As a by-product, this procedure provides an illustration of the well-known Runge–Krarup theorem related to the validity of the spherical harmonic series. We prove that any homogeneous ellipsoid of revolution with the same total mass M (but different in density and volume) and the same linear eccentricity (but different semi-major axes) produces the same gravitational field at any computation point in external space.

While the solution in terms of spherical coordinates produces an infinite, but very fast-converging series in spherical harmonics, an alternative derivation in elliptical coordinates results in a finite series of ellipsoidal harmonics of degrees zero and two. However, in practice the series solution in spherical harmonics will be preferred due to its higher numerical effectivity. The computing times required in both cases are comparatively small. A significant advantage of the representation in spherical harmonics series expansion is the possibility of obtaining their spectral components and being able to use them for further investigations.

The structure of the paper is as follows: in Sect. 2, the geometrical properties of an ellipsoidal shell are explained, while the central Sect. 3 presents two approaches for the calculation of the gravitational potential of a solid homogeneous ellipsoid of revolution and an ellipsoidal shell, based on spherical and ellipsoidal harmonics. A new methodology for the analytical derivation of the mathematical expressions is presented.

Fig. 1

Confocal ellipsoids and the geometry of an ellipsoidal shell

Table 1 Parameters $a_i$, $b_i$ and $e_i^2$ based on $E=E_{GRS80} = a_0 e_0$

Section 4 contains numerical comparisons between several solution approaches, before a discussion of results and some conclusions finalise the paper. In an appendix, we provide the complete expressions for the gravity vector and the gravity gradient tensor (first- and second-order derivatives of the potential) in terms of spherical and elliptical coordinates, and investigate the convergence behaviour of the spherical harmonic series.

2 Geometry of an ellipsoidal shell

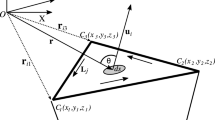
It is assumed that the ellipsoidal shell is situated between two concentric, confocal ellipsoids $\varepsilon _1$ with semi-axes $a_1$, $b_1$ and $\varepsilon _2$ with semi-axes $a_2$, $b_2$ having the same rotational axis (cf. Fig. 1). The attached Cartesian coordinate system is defined as follows: the z-axis is the rotation axis and the $(x,y)-$plane is the equatorial plane. For the dimensions of the two considered ellipsoids the relation $a_1 > a_2$ and $b_1 > b_2$ holds, this means that $\varepsilon _2$ is completely situated inside $\varepsilon _1$. External field means that the calculation point P is situated on or outside the ellipsoid $\varepsilon _1$.

Since both ellipsoids have been assumed as confocal, the linear eccentricity $E = \sqrt{a^2 - b^2}$ is the same for $\varepsilon _1$ and $\varepsilon _2$. Numerical values for the parameters $a_i$, $b_i$ and $e_i = E/a_i$ of various confocal ellipsoids are listed in Table 1, starting from the respective values of the Geodetic Reference System 1980 (Moritz 1980b), where $E_\textrm{GRS80}=521854.0097$ m.

3 Gravitational potential of a homogeneous ellipsoid and ellipsoidal shell

In this chapter, we will present two approaches for the calculation of the potential and its derivatives at points outside the ellipsoid. The first approach is based on representations in terms of spherical harmonics. The second approach is related to ellipsoidal harmonics. However, both representations describe the same gravitational field and lead to the same numerical values (besides rounding effects) for the potential and its derivatives outside the ellipsoid $\varepsilon _1$.

The derivation of the formulae relies on the following procedure: first, we derive a closed analytical solution for the special case of a computation point situated on the positive z-axis, the rotation axis of the ellipsoid. In a second step, this result is extended to computation points in the complete external space, using harmonic continuation by representations in terms of spherical and ellipsoidal harmonics. As a by-product, an illustration of the well-known Runge–Krarup theorem related to the validity of the spherical harmonic series in the spatial domain below the Brillouin sphere is provided.

The gravitational potential of a homogeneous ellipsoidal shell results from the difference of the external potential fields of the two confocal ellipsoids $\varepsilon _1$ and $\varepsilon _2$, due to the linear superposition principle of potentials.

3.1 Approach I: analytical expansion in spherical harmonics

The gravitational potential of an ellipsoidal shell with constant mass density $\rho$ can be expressed by Newton’s integral (Heiskanen and Moritz, 1967, (1–11))

$$\begin{aligned} V(P) = G \rho \iiint _{\Omega } \frac{1}{\ell (P,P^\prime )} \ \textrm{d}\Omega , \end{aligned}$$

(1)

at the computation point P outside the domain $\Omega$ containing the total mass M. $P^\prime \in \Omega$ is the running integration point. Newton’s gravitational constant is denoted by G. The Euclidean distance $\ell$ between P and $P^\prime$ can be expressed in Cartesian coordinates (x, y, z)

$$\begin{aligned} \ell = \ell (P,P^\prime ) = \sqrt{(x-x^\prime )^2 + (y-y^\prime )^2 + (z-z^\prime )^2} , \end{aligned}$$

(2)

or in geocentric spherical coordinates (r, $\vartheta$, $\lambda$)

$$\begin{aligned} \ell (P,P^\prime ) = \sqrt{r^2 + {r^\prime }^2 - 2rr^\prime \cos {\psi }} , \end{aligned}$$

(3)

or in cylindrical coordinates ($\eta$, $\zeta$, $\lambda$)

$$\begin{aligned} \ell (P,P^\prime ) = \sqrt{\eta ^2 + {\eta ^\prime }^2 - 2 \eta \eta ^\prime \cos (\lambda -\lambda ^\prime ) + (\zeta -\zeta ^\prime )^2} . \end{aligned}$$

(4)

The respective differential volume elements $\textrm{d}\Omega$ in the mentioned coordinate systems, which are used within this paper, are

$$\begin{aligned} \begin{aligned} \textrm{d}\Omega&= \textrm{d}x^\prime \textrm{d}y^\prime \textrm{d}z^\prime \,, \\ \textrm{d}\Omega&= {r^\prime }^2 \sin \vartheta ^\prime \textrm{d}\vartheta ^\prime \textrm{d}\lambda ^\prime \textrm{d}r^\prime \,, \\ \textrm{d}\Omega&= \eta ^\prime \textrm{d}\lambda ^\prime \textrm{d}\eta ^\prime \textrm{d}\zeta ^\prime \,. \end{aligned} \end{aligned}$$

(5)

The spherical distance $\psi$ between the position vectors of P and $P^\prime$ which occurs in Eq. (3) is defined by

$$\begin{aligned} \cos {\psi }(P,P^\prime ):= \cos {\vartheta } \cos {\vartheta ^\prime } + \sin {\vartheta } \sin {\vartheta ^\prime } \cos \left( \lambda ^\prime - \lambda \right) . \nonumber \\ \end{aligned}$$

(6)

3.1.1 Special case: gravitational potential of a homogeneous ellipsoid at $P \in z$-axis

First, let us consider a computation point P on the z-axis, with $z \ge b$ and $x_P=y_P=0$.

Fig. 2

Spherical and cylindrical coordinates

It is tempting to use spherical polar coordinates ($r, \vartheta , \lambda$) for the evaluation of the Newton integral (1), but this procedure leads to insurmountable difficulties in the integration process. As an alternative we prefer cylindrical coordinates ($\eta ^\prime ,\zeta ^\prime ,\lambda ^\prime$) for the position of the integration point $P^\prime$, where $\lambda ^\prime$ is the geographical longitude, $\eta ^\prime$ the distance from the rotation axis of the ellipsoid and $\zeta ^\prime$ the distance from the equatorial plane (see Fig. 2). The distance $\ell$ from the computation point to the integration point can be expressed in cylindrical coordinates by setting $\zeta _P \ge \max (\zeta ^\prime )$, $\eta =0$ in Eq. (4)

$$\begin{aligned} \ell (P,P^\prime ) = \sqrt{ {\eta ^\prime }^2 + (z - {\zeta ^\prime })^2} , \quad \hbox {with} \quad z \ge \max (\zeta ^\prime ) . \end{aligned}$$

(7)

Expressing Newton’s integral (1) by replacing the volume element $\textrm{d}\Omega$ in cylindrical coordinates (see Eq. (5)) results in the explicit form of Newton’s integral

$$\begin{aligned} V(P) = G \rho \mathop {\int }\limits _{\lambda ^\prime =0}^{2\pi } \mathop {\int }\limits _{\eta ^\prime =0}^{p(\zeta ^\prime )} \mathop {\int }\limits _{\zeta ^\prime =-b}^{+b} \frac{\eta ^\prime \textrm{d}\lambda ^\prime \textrm{d}\eta ^\prime \textrm{d}\zeta ^\prime }{\sqrt{ {\eta ^\prime }^2 + (z - {\zeta ^\prime })^2}} . \end{aligned}$$

(8)

The upper limit of $\eta ^\prime$ is the orthogonal distance of the ellipsoidal surface points from the z-axis, depending on $\zeta ^\prime$: $p(\zeta ^\prime )$, which can be derived from the equation of the ellipsoid.

From (Heck 2003)

$$\begin{aligned} \begin{aligned} \left( \frac{p}{a} \right) ^2 + \left( \frac{\zeta ^\prime }{b} \right) ^2&= 1 \\ p^2&= {x^\prime }^2 + {y^\prime }^2 \,, \end{aligned} \end{aligned}$$

(9)

results

$$\begin{aligned} p^2(\zeta ^\prime ) = a^2 \left( 1 - \frac{{\zeta ^\prime }^2}{b^2} \right) \,. \end{aligned}$$

(10)

Integration with respect to $\lambda ^\prime$ gives simply

$$\begin{aligned} \mathop {\int }\limits _{\lambda ^\prime =0}^{2\pi } \textrm{d}\lambda ^\prime = 2 \pi , \end{aligned}$$

(11)

while the integral with respect to $\eta ^\prime$ yields

$$\begin{aligned} \begin{aligned} V(P(z))&= 2 \pi G \rho \mathop {\int }\limits _{-b}^{+b} \left. \sqrt{ {\eta ^\prime }^2 + (z - {\zeta ^\prime })^2} \right| ^{p(\zeta ^\prime )}_{\eta ^\prime =0} \textrm{d}\zeta ^\prime \,, \\&= 2 \pi G \rho \mathop {\int }\limits _{-b}^{+b} \left[ \sqrt{ z^2 + a^2 - 2 z \zeta ^\prime - {e^\prime }^2 {\zeta ^\prime }^2 } - z + \zeta ^\prime \right] \textrm{d}\zeta ^\prime \,, \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} {e^\prime }^2 = \frac{a^2 - b^2}{b^2} \end{aligned}$$

(13)

is the square of the second numerical eccentricity. In the following, we also refer to the first numerical eccentricity e

$$\begin{aligned} e^2 = \frac{a^2 - b^2}{a^2} \end{aligned}$$

(14)

and the linear eccentricity E with

$$\begin{aligned} E^2 = a^2 - b^2 \,, \end{aligned}$$

(15)

related by the well-known formulae

$$\begin{aligned} \begin{aligned} (1 - e^2) (1 + {e^\prime }^2 )&= 1 \,, \\ a^2&= (1 + {e^\prime }^2 ) b^2 \quad \hbox {and} \\ E&= a e = b e^\prime \,. \end{aligned} \end{aligned}$$

(16)

Integration of Eq. (12) with respect to $\zeta ^\prime$, making use of Bronstein et al. (2008)

$$\begin{aligned} \begin{aligned} \int \sqrt{X} \textrm{d}x&= \frac{ (2\alpha x + \beta ) \sqrt{X}}{4 \alpha } + \\&\quad \frac{4\alpha \gamma - \beta ^2}{8\alpha } \left( - \frac{1}{\sqrt{-\alpha }} \arcsin \frac{2\alpha x + \beta }{\sqrt{-4\alpha \gamma + \beta ^2}} \right) \,, \end{aligned} \end{aligned}$$

(17)

where $X=\alpha x^2 + \beta x + \gamma$ and $\alpha <0$, yields

$$\begin{aligned} \begin{aligned} V(P(z)) =&\, 2 \pi G \rho \left\{ \frac{1}{2{e^\prime }^2} ({e^\prime }^2b + z) \sqrt{ z^2 + a^2 - 2 zb - {e^\prime }^2b^2 } \right. \\&-\frac{1}{2{e^\prime }^2} (-{e^\prime }^2b + z) \sqrt{ z^2 + a^2 + 2 zb - {e^\prime }^2b^2 } \\&-\frac{1}{2 {e^\prime }^3 } ({e^\prime }^2(z^2+a^2)+z^2) \left[ \arcsin \frac{ - {e^\prime }^2b - z }{\sqrt{ {e^\prime }^2(z^2+a^2) + z^2}} \right. \\&\left. \left. - \arcsin \frac{ {e^\prime }^2b - z }{\sqrt{ {e^\prime }^2(z^2+a^2) + z^2}} \right] - 2zb \right\} \,. \end{aligned} \end{aligned}$$

(18)

The difference between two $\arcsin$ terms, which occur in (18), can be expressed by

$$\begin{aligned} \arcsin x - \arcsin y = \arcsin \left( x \sqrt{1-y^2} - y \sqrt{1-x^2} \right) \,. \end{aligned}$$

Together with

$$\begin{aligned} \begin{aligned} \sqrt{ z^2 + a^2 - 2 zb - {e^\prime }^2b^2 }&= z - b \\ \sqrt{ z^2 + a^2 + 2 zb - {e^\prime }^2b^2 }&= z + b \end{aligned} \end{aligned}$$

yields after some tedious, but elementary manipulations

$$\begin{aligned} \begin{aligned} V(P(z))&= 2 \pi G \rho \frac{b}{e^2} \left[ \frac{ z^2 }{2 a e} \left( 1 + \frac{a^2 e^2}{z^2} \right) \arcsin \left( \frac{ 2 \frac{ae}{z} }{ 1 + \frac{a^2 e^2}{z^2}} \right) - z \right] \,. \end{aligned} \end{aligned}$$

(19)

Defining $x:= \frac{ae}{z}$ and using the relationship

$$\begin{aligned} \begin{aligned} \arctan x&= \frac{1}{2} \arcsin \frac{2x}{1+x^2} \end{aligned} \end{aligned}$$

result in

$$\begin{aligned} \begin{aligned} V(P(z))&= 2 \pi G \rho \frac{b}{e^2} \left[ \frac{ z^2 }{ a e } \left( 1 + \frac{a^2 e^2}{z^2} \right) \arctan \left( \frac{ae}{z} \right) - z \right] \,. \end{aligned} \end{aligned}$$

(20)

Finally, let us consider the total mass M of the homogeneous ellipsoid

$$\begin{aligned} \begin{aligned} M&= \frac{ 4 }{ 3 } \pi \rho a^2 b \end{aligned} \end{aligned}$$

(21)

resulting in the closed expression

$$\begin{aligned} \boxed { V(P(z)) = \frac{ 3 }{ 2 } \frac{{GM}}{ E } \left[ \frac{ z^2 }{ E^2 } \left( 1 + \frac{E^2}{z^2} \right) \arctan \left( \frac{E}{z} \right) - \frac{z}{E} \right] } \end{aligned}$$

(22)

(in consistency with Lambert (1961), after correction of Eq. (50) ibd.). Consult also the former paper of Lambert (1952).

For numerical reasons, a series expansion of Eq. (22) is preferable. Denoting $x:= \frac{E}{z}$, $|x| < 1$ and using

$$\begin{aligned} \begin{aligned} \arctan x = x - \frac{1}{3} x^3 + \frac{1}{5} x^5 - \frac{1}{7} x^7 + \dots , \end{aligned} \end{aligned}$$

the bracket $[\dots ]$ in (22) can be developed in

$$\begin{aligned} \begin{aligned} \frac{z}{x} (1+x^2) \arctan x - z&= 2z \left( \frac{x^2}{1\cdot 3} - \frac{x^4}{3\cdot 5} + \frac{x^6}{5\cdot 7} - \dots \right) \,, \end{aligned} \end{aligned}$$

resulting in the numerically fast-converging series expansion

$$\begin{aligned} \boxed { V(z) = \frac{{GM}}{ E } \sum ^\infty _{n=0} \frac{ 3 (-1)^n }{ (2n+1)(2n+3) } \left( \frac{E}{z} \right) ^{2n+1} \,. } \end{aligned}$$

(23)

For an evaluation point P outside the ellipsoid which is located on the (positive) z-axis, $z > b$ holds. It is straightforward that $E/z = be^\prime /z < e^\prime = 0.082\,094\,438$ (Moritz 1980b). This leads to $(E/z)^{2n+1} < 2\cdot 10^{-8}$ even for $n=3$ which indicates the very fast numerical convergence.

3.1.2 General case: gravitational potential at arbitrary points outside the ellipsoid

Expression (23) holds for any computation point on the positive z-axis (or on the negative z-axis if z is changed to |z|) for $z \ge b$. This equation can easily be extended to the whole space outside the ellipsoid, considering that V in the external space is a harmonic function, with rotational symmetry with respect to the z-axis and equatorial symmetry with respect to the $(x,y)-$plane:

$$\begin{aligned} \begin{aligned} V(r,\vartheta )&= \frac{{GM}}{ r } \left( 1 + \frac{c_2}{r^2} P_2(\cos \vartheta ) + \frac{c_4}{r^4} P_4(\cos \vartheta ) + \dots \right) \end{aligned} \end{aligned}$$

(24)

with unknown coefficients $c_{2n}$. $P_2$ and $P_4$ denote Legendre polynomials of degrees 2 and 4, depending on the polar distance $\vartheta$ (complement to geocentric latitude). Specifying this expression for points on the positive z-axis, i.e. $r=z$, $\vartheta =0$ yields

$$\begin{aligned} \begin{aligned} V(z)&= \frac{{GM}}{ z } \left( 1 + \frac{c_2}{z^2} + \frac{c_4}{z^4} + \frac{c_6}{z^6} + \dots \right) \end{aligned} \end{aligned}$$

(25)

which can be compared with the series expansion (23). Termwise comparison results in the coefficients $c_{2n}$

$$\begin{aligned} c_2 = - \frac{3}{3\cdot 5} E^2, \quad c_4 = + \frac{3}{5\cdot 7} E^4, \quad c_6 = - \frac{3}{7\cdot 9} E^6, \quad \dots \,. \end{aligned}$$

(26)

Thus, we obtain the final result for the gravitational potential of the homogeneous ellipsoid at any computation point outside the ellipsoid

$$\begin{aligned} \boxed { V(r, \vartheta ) = \frac{{GM}}{ E } \sum ^\infty _{n=0} \frac{ 3 (-1)^n }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n+1} P_{2n}(\cos \vartheta ) \,. } \end{aligned}$$

(27)

The terms of degree zero and two ($n=0$ and $n=1$) are consistent with the respective expressions by Moritz (1990, p. 36), approximately derived in a different context.

Remark 1

It is obvious from Eq. (27) that the potential of a homogeneous ellipsoid only depends on its total mass M and linear eccentricity E, not on any other ellipsoidal parameter. Thus, any homogeneous ellipsoid of revolution with the same mass M and the same linear eccentricity E (confocal ellipsoids) produces the same gravitational field at any point $P(r, \vartheta , \lambda )$ in the external (mass-free) space, i.e. outside of $\varepsilon _1$ (see Fig. 1).

Usually, the spherical harmonic expansion of the gravitational potential is scaled to a fixed radius $R > E$ (e.g. $R = a$, Brillouin sphere, or $R = b$, Bjerhammar sphere). For a mass distribution with rotational and equatorial symmetry, the standard expression is provided by the formula

$$\begin{aligned} \begin{aligned} V(r, \vartheta )&= \frac{{GM}}{ r } \sum _{n=0}^\infty \left( \frac{R}{r} \right) ^n V_{n} P_{n} (\cos \vartheta ) \,, \quad n \,\,\,\hbox {even}\,. \end{aligned} \end{aligned}$$

(28)

Since Eqs. (27) and (28) represent the same function, the Stokes’ coefficients $V_n$ in Eq. (28) can be analytically expressed as

$$\begin{aligned} \begin{aligned} V_n&= \frac{3 (-1)^{n/2}}{ (n+1)(n+3) } \left( \frac{E}{R} \right) ^{n} \,, \quad 0 \le n \,\,\,\hbox {even} \end{aligned} \end{aligned}$$

(29)

or in fully normalised coefficients

$$\begin{aligned} \boxed { \overline{V}_n = \frac{V_n}{\sqrt{2n+1}} = \frac{ 3 (-1)^{n/2} }{ (n+1)(n+3)\sqrt{2n+1} } \left( \frac{E}{R} \right) ^{n} \,, \quad 0 \le n \,\,\,\hbox {even} \,. } \end{aligned}$$

(30)

Numerical values for the fully normalised coefficients derived in Eq. (30) are listed in Table 2. They are based on the linear eccentricity $E_{GRS80}=521854.0097$ m and semi-major axis $a=R=6378137$ m of the Geodetic Reference System 1980 (GRS80) (Moritz 1980b).

Table 2 Fully normalised coefficients $\overline{V}_n$ based on GRS80 parameters $R=a$ and E (Moritz 1980b)

Remark 2

The construction of Eqs. (27) and (28) by the extension of the closed expression Eq. (22) from the z-axis to the external space can be considered as an illustration of the validity of the Runge property of harmonic functions, which in the present context is formulated by the Runge–Krarup theorem (Moritz, 1980a, p. 67 ff). Loosely spoken the Runge–Krarup theorem, applied to our case, guarantees that any harmonic function, regular outside the ellipsoid, can be approximated arbitrarily well by harmonic functions regular outside a sphere situated completely within the ellipsoid. Due to our constructive approach based on Eq. (24), we have extended the domain of harmonicity from the region outside a Brillouin sphere, enclosing the ellipsoid completely, to the larger region outside a Bjerhammar sphere, situated completely within the ellipsoid; as Eq. (27) shows, the radius of this internal sphere may be as small as $R=E$, the linear eccentricity of the ellipsoid. As a matter of fact, although the spherical harmonic series (27) and (28) converge in the domain outside the focal sphere $R=E$, they do not represent the potential inside the ellipsoid, which is not a harmonic function but fulfils the Poisson equation inside the masses. In contrast, the spherical harmonic series (27) and (28) represent the analytical (harmonic) continuation in the internal domain.

Based on Eq. (27), it is straightforward to develop the first and second derivatives of the potential at a point in the space outside the ellipsoid.

The first and second radial derivatives of the potential are

$$\begin{aligned}&\boxed { \frac{\partial V(r, \vartheta )}{\partial r} = \frac{{GM}}{ E^2 } \sum ^\infty _{n=0} \frac{ 3 (-1)^{n+1} }{ 2n+3 } \left( \frac{E}{r} \right) ^{2n+2} P_{2n}(\cos \vartheta ) \,, } \end{aligned}$$

(31)

$$\begin{aligned}&\boxed { \begin{aligned} \frac{\partial ^2 V(r, \vartheta )}{\partial r^2}&= \frac{GM }{ E^3 } \sum ^\infty _{n=0} 3 (-1)^{n+2} \frac{ 2n+2 }{ 2n+3 } \left( \frac{E}{r} \right) ^{2n+3} \\&\qquad P_{2n}(\cos \vartheta ) \,. \end{aligned}} \end{aligned}$$

(32)

A general representation of the radial derivative of any degree $k > 0$ is provided in Appendix A.3.

Applying the relation between the partial derivatives in spherical coordinates and Cartesian coordinates in a local topocentric system which are given in Tscherning (1976) or Grombein et al. (2013), we elaborated the components of the gravity vector and the gravity gradient tensor $g_i$ and $M_{ij}$ of the potential of a homogeneous ellipsoid of revolution. The expressions are compiled in Appendix A.1.

The gravitational potential and its derivatives at computation points on the surface of the ellipsoid can be calculated by inserting $r_E(\vartheta )$ for r in Eqs. (27), (31) and (32) (cf. Heck (2003))

$$\begin{aligned} \begin{aligned} r_E(\vartheta )&= a \sqrt{\frac{1 - \left( \frac{E}{a} \right) ^2 }{1 - \left( \frac{E}{a} \right) ^2 \sin ^2\vartheta } }\,. \end{aligned} \end{aligned}$$

(33)

3.1.3 Gravitational field of a homogeneous ellipsoidal shell

In the following, we will derive the gravity field of a homogeneous shell between two confocal ellipsoids of revolution.

Confocal ellipsoids $\varepsilon _1$ and $\varepsilon _2$ have the same linear eccentricity (see Fig. 1 and compare the definition in Eq. (15))

$$\begin{aligned} \begin{aligned} E&= \sqrt{a^2_i - b^2_i} = a_i e_i \,, \quad i=\{1,2\} \,, \quad a_1 > a_2 \,. \end{aligned} \end{aligned}$$

From Eqs. (27), (31) and (32), it is obvious that just the difference of the masses $M_1$ and $M_2$ has to be considered:

$$\begin{aligned} \begin{aligned} M_i&= \frac{4}{3} \pi \rho a^2_i b_i \,, \quad i=\{1,2\} \,, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} \Delta M&= M_1 - M_2 = \frac{4}{3} \pi \rho \left( a^3_1 \sqrt{1 - \left( \frac{E}{a_1} \right) ^2} - a^3_2 \sqrt{1 - \left( \frac{E}{a_2} \right) ^2} \right) \,. \end{aligned} \end{aligned}$$

(34)

With this premise, the final expression for the potential of a homogeneous ellipsoidal shell results in

$$\begin{aligned} \boxed { \begin{aligned} \Delta V(r, \vartheta )&= \frac{ G \Delta M }{ r } \sum ^\infty _{n=0} \frac{ 3 (-1)^n }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n} P_{2n}(\cos \vartheta ) \,, \\&\qquad E > 0 \,. \end{aligned}} \end{aligned}$$

(35)

It should be noted that the radial distance between two confocal ellipsoids is not constant. Figure 3 presents the variation of the thickness of the ellipsoidal shell from the pole to the equator, where $a_1$ corresponds to the semi-major axis of the GRS80 ellipsoid and $a_2 = a_1 - 10$ km. The maximum difference occurs at the pole with $d(\vartheta =0^\circ ) = 34$ m; see also Table 1.

Fig. 3

Variation of the thickness $d(\vartheta )$ of an ellipsoidal shell with $a_1 - a_2 = 10$ km

The lower bound $r_\textrm{LB}(\vartheta )$ of the shell is the ellipsoidal radius of the confocal ellipsoid $\varepsilon _2$

$$\begin{aligned} \begin{aligned} r_\textrm{LB}(\vartheta )&= r_\textrm{E} (\vartheta , a_2) = a_2 \sqrt{\frac{1 - \left( \frac{E}{a_2} \right) ^2 }{1 - \left( \frac{E}{a_2} \right) ^2 \sin ^2\vartheta } } \,, \end{aligned} \end{aligned}$$

(36)

and the upper bound $r_E(\vartheta )$ is defined in Eq. (33). Throughout this chapter, we fix the dimension of $\varepsilon _2$ by definition of the thickness of the ellipsoidal shell at the equator with $d = a_1 - a_2 > 0$. The latitude-dependent thickness of the ellipsoidal shell is sufficiently accurately approximated by

$$\begin{aligned} \begin{aligned} d(\vartheta )&= r_\textrm{E} (\vartheta ) - r_\textrm{LB}(\vartheta ) \ge d > 0 \,. \end{aligned} \end{aligned}$$

(37)

Elliptical ($u, \theta , \lambda$) and spherical ($r, \vartheta , \lambda$) coordinates, the dimensions of confocal ellipsoids as well as the thickness of the ellipsoidal shell are depicted in Fig. 4.

Fig. 4

Dimensions of confocal ellipsoids, elliptical, spherical and geodetic coordinates

The semi-major and semi-minor axis of the confocal ellipsoid $\varepsilon _1$ is denoted by a and b, and the semi-minor axis of any smaller confocal ellipsoid $\varepsilon _2$ is denoted by the elliptic coordinate u. The thickness $d(\vartheta )$ of the ellipsoidal layer can be computed from the difference of Eqs. (36) and (33). Its slight increase from the equator to the pole is visible in Fig. 3. At the equator $d(\vartheta =\pi /2)=d$ holds.

Figure 5 shows the contribution of each degree n to the potential, assuming $a_1 - a_2 = 10$ km. The rapid convergence of the series (35) is obvious. From the extremal numerical example (thickness of the shell is approx. 10 km, P on $\varepsilon _1$), the truncation error is less than $10^{-5}$ m$^2$ s$^{-2}$ if the series is expanded only up to degree $n=6$.

The radial derivative of the potential of a homogeneous shell between two confocal ellipsoids of revolution results from Eqs. (31) and (34) by the findings that the potential of the shell is only a function of the mass difference between the two confocal ellipsoids:

$$\begin{aligned} \boxed {\begin{aligned} \delta g(r, \vartheta )&= - \frac{\partial \Delta V(r, \vartheta )}{\partial r} = \frac{G \Delta M}{ r^2 } \sum ^\infty _{n=0} \frac{ 3 (-1)^n }{ 2n+3 }\\&\qquad \left( \frac{E}{r} \right) ^{2n} P_{2n}(\cos \vartheta ) \,, \quad E > 0 \,. \end{aligned}} \end{aligned}$$

(38)

In Fig. 6, the rapid convergence of the series (38) is obvious. From the extremal numerical example (thickness of the shell is approx. 10 km, P on $\varepsilon _1$), the truncation error is less than $10^{-6}$ mGal if the series is expanded only up to degree $n=6$. Even if the series is truncated after $n=4$, the approximation error is still below $10^{-3}$ mGal.

Fig. 5

Contributors to the series expansion for the gravitational potential of an ellipsoidal homogeneous shell, calculated on the surface of $\varepsilon _1$ along a meridian. $a_1 - a_2 = 10$ km, $\rho = 2670$ kg m$^{-3}$

Fig. 6

Contributors to the series expansion for the negative radial derivative of the gravitational potential of an ellipsoidal homogeneous shell, calculated on the surface of $\varepsilon _1$ along a meridian. $a_1 - a_2 = 10$ km, $\rho = 2670$ kg m$^{-3}$

3.2 Approach II: expansion in ellipsoidal harmonics

As an alternative to spherical harmonics the external gravitational potential of a mass distribution can be represented in ellipsoidal harmonics, which will be based on elliptical coordinates ($u, \theta , \lambda$). According to Heiskanen and Moritz (1967, p. 43), specified for a body with rotational and equatorial symmetry, which is independent on longitude $\lambda$, the potential can be expressed by the infinite series

$$\begin{aligned} \begin{aligned} V(u, \theta )&= \sum _{n=0}^\infty a_{2n} Q_{2n}\left( \dot{\iota } \frac{u}{E} \right) P_{2n} (\cos \theta ) \,, \end{aligned} \end{aligned}$$

(39)

where $\dot{\iota } = \sqrt{-1}$ is the imaginary unit and E is the linear eccentricity as defined in (15); $a_{2n}$ are complex-valued coefficients. For $n=0$ and $n=1$, the Legendre functions of second kind $Q_{2n}$ can be taken from Heiskanen and Moritz (1967, p. 66)

$$\begin{aligned} \begin{aligned} Q_0 \left( \dot{\iota } \frac{u}{E} \right)&= -\dot{\iota } \arctan \frac{E}{u} \\ Q_2 \left( \dot{\iota } \frac{u}{E} \right)&= \frac{\dot{\iota }}{2} \left[ \left( 1 + 3 \frac{u^2}{E^2}\right) \arctan \frac{E}{u} - 3\frac{u}{E} \right] \,. \end{aligned} \end{aligned}$$

(40)

For the derivation of the ellipsoidal harmonic coefficients $a_{2n}$, we use a procedure analogous to chapter 3.1; i.e. we first consider a computation point P situated on the z-axis and then generalise the result to the complete external space by harmonic extension.

For points on the rotational ($=z$) axis of the homogeneous ellipsoid of revolution $\theta =0^\circ$ holds. From this, it follows that for all Legendre polynomials $P_{2n}(\cos \theta )=1$ $\forall$ n holds. Furthermore, it is obvious that for the points P located on the rotational axis the coordinate z in the polar system of the point P is identical to u; thus, $u=z$.

Based on this new approach (ansatz), Eqs. (39) and (40) result in

$$\begin{aligned} \begin{aligned} \dot{\iota } V(z, \theta )&= a_{0} \arctan \frac{E}{z} - \frac{1}{2} a_2 \left[ \left( 1 + 3 \frac{z^2}{E^2}\right) \arctan \frac{E}{z} - 3\frac{z}{E} \right] + \dots \, . \end{aligned} \end{aligned}$$

(41)

Now, let us compare this expression with the closed form (22). It can easily be recognised that

$$\begin{aligned} \begin{aligned} a_{0}&= \dot{\iota } \frac{{GM}}{E} \,, \quad a_{2} = - \dot{\iota } \frac{{GM}}{E} \,, \quad a_{2n} = 0 \quad \forall \,\,\, n>1 \end{aligned} \end{aligned}$$

which can be inserted in (39) in order to obtain the development of the external potential in ellipsoidal harmonics:

$$\begin{aligned} \begin{aligned} V(u, \theta )&= \dot{\iota } \frac{{GM}}{E} \left\{ Q_0 \left( \dot{\iota } \frac{u}{E} \right) - Q_2 \left( \dot{\iota } \frac{u}{E} \right) P_{2} (\cos \theta ) \right\} \,. \end{aligned} \end{aligned}$$

(42)

Obviously, the ellipsoidal harmonic series is finite and is composed of degree 0 and 2 terms only. As a result, we get the gravitational potential of the homogeneous ellipsoid of revolution in the space outside the ellipsoid with semi-minor axis b and linear eccentricity E in closed form

$$\begin{aligned} \boxed { \begin{aligned} V(u, \theta )&= \frac{{GM}}{E} \left\{ \arctan \frac{E}{u} + \frac{1}{4} \left[ \left( 1 + 3 \frac{u^2}{E^2}\right) \arctan \frac{E}{u} - 3\frac{u}{E} \right] \right. \\&\qquad \left. \left( 3 \cos ^2 \theta - 1 \right) \right\} \,. \end{aligned}} \end{aligned}$$

(43)

In Appendix A.2, we present the partial derivatives of first and second order with respect to the elliptical coordinates u and $\theta$ and compose them into the components of the gravity vector and gravity gradient tensor with respect to the local triad ($-\theta , \lambda , u$), corresponding to a North/East/Up coordinate system. It is obvious that—although the formulae in elliptical coordinates are closed analytical expressions—in practical applications the fast-converging, truncated spherical harmonic series are more convenient and will be preferred due to their simpler programming feasibility. In addition, the representation in spherical harmonics provides information about the spectral content, which can be of great importance in practice.

In detail, the components of the gravity vector are

$$\begin{aligned}&\boxed { \begin{aligned} g_N&= \frac{3}{2} \frac{{GM}}{E} \frac{1}{\sqrt{u^2 + E^2 \cos ^2\theta }} \left[ \left( 1 + 3 \frac{u^2}{E^2}\right) \arctan \frac{E}{u} - 3\frac{u}{E} \right] \\&\qquad \sin \theta \cos \theta , \end{aligned}} \end{aligned}$$

(44)

$$\begin{aligned}&\boxed { g_L = 0 ,} \end{aligned}$$

(45)

$$\begin{aligned}&\boxed { \begin{aligned} g_U =&\, - \frac{{GM}}{E^2} \sqrt{\frac{u^2+E^2}{u^2 + E^2 \cos ^2\theta }} \left\{ \frac{E^2}{E^2+u^2}\right. \\&\left. -\left[ \frac{3u}{2E} \arctan \frac{E}{u} - 1 - \frac{1}{2}\frac{u^2}{E^2 + u^2} \right] \left( 3 \cos ^2 \theta - 1 \right) \right\} . \end{aligned}} \end{aligned}$$

(46)

Since the linear eccentricity E is the same for all confocal ellipsoids, the gravitational potential of a homogeneous ellipsoidal shell results from Eq. (43) by replacing the mass M by the mass $\Delta M$ of the shell, provided by Eq. (34).

On the surface of the homogeneous ellipsoid $(u=b)$, the expression (43) reduces to

$$\begin{aligned} \begin{aligned} V(u=b, \theta ) =&\frac{{GM}}{E} \left\{ \arctan \frac{E}{b} \right. \\&\left. + \frac{1}{4} \left[ \left( 1 + 3 \frac{b^2}{E^2}\right) \arctan \frac{E}{b} - 3\frac{b}{E} \right] \right. \\&\left. \left( 3 \cos ^2 \theta - 1 \right) \right\} \\ =&\, \frac{{GM}}{E} \left\{ \arctan (e^\prime )\right. \\&\left. +\, \frac{1}{2} \left[ \left( 1 + \frac{3}{e^{\prime 2}}\right) \arctan (e^\prime ) - \frac{3}{e^\prime } \right] P_{2}(\cos \theta )\right\} \,, \end{aligned} \end{aligned}$$

(47)

where $e^\prime = \frac{E}{b}$ denotes the second numerical eccentricity of the ellipsoid (see Eq. (16)). Similarly, the gravitational potential of an ellipsoidal shell results from Eq. (47) by replacing M by $\Delta M$, when b and $e^\prime$ are the parameters of the upper boundary surface containing the computation point.

Throughout this paper, geocentric spherical coordinates are denoted by r, $\vartheta$, $\lambda$ and elliptical coordinates by u, $\theta$, $\lambda$. In elliptical coordinates, a point P in space is fixed by the intersection of a confocal ellipsoid $u=\text {const.}$, a hyperboloid $\theta =\text {const.}$ and the meridian plane $\lambda =\text {const.}$ passing through P. Furthermore, geodetic (geographical) coordinates are denoted by h, $\varphi$, $\lambda$. The longitude $\lambda$ is identical in any coordinate system used. The “vertical” coordinates are accordingly r, u and the ellipsoidal height h in the case of geodetic coordinates. The geodetic latitude $\varphi$ of a point P on the surface of an ellipsoid of revolution is the angle between the ellipsoidal normal, which is running through P, and the projection of the ellipsoidal normal onto the equatorial plane (see Fig. 4).

For the transformation from spherical co-latitude (polar distance) $\vartheta$ to elliptical co-latitude $\theta$ at points on the surface of the ellipsoid, the relation

$$\begin{aligned} \begin{aligned} \cos \theta&= \frac{\cos \vartheta }{\sqrt{1 - e^2 \sin ^2 \vartheta }} = \sqrt{ \frac{1 +e^{\prime 2}}{ 1 + e^{\prime 2} \cos ^2 \vartheta } } \cos \vartheta \end{aligned} \end{aligned}$$

(48)

can be used, similarly for the transformation from geodetic latitude $\varphi$ to elliptical co-latitude $\theta$ the following relation holds:

$$\begin{aligned} \begin{aligned} \cos \theta&= \frac{\sin \varphi }{\sqrt{1 + e^{\prime 2} \cos ^2 \varphi }} = \sqrt{\frac{1 - e^2}{1 - e^2 \sin ^2 \varphi } } \sin \varphi \,. \end{aligned} \end{aligned}$$

(49)

Equations (48) and (49) result from the manipulation of (Heiskanen and Moritz, 1967, (1–103)) and (Heck, 2003, (3.35), (3.37)). The geodetic latitude $\varphi$, the spherical co-latitude $\vartheta$ and the elliptical co-latitude $\theta$ are related to each other by the following equations

$$\begin{aligned} \begin{aligned} \tan \vartheta&= \frac{1}{(1-e^2) \tan \varphi } \,, \\ \tan \theta&= \frac{1}{\sqrt{1 - e^2} \tan \varphi } \,, \\ \tan \theta&= \sqrt{1 - e^2} \tan \vartheta \,. \end{aligned} \end{aligned}$$

(50)

Remark 3

Equations (48) or (49) can easily be inserted in Eq. (47). Obviously, the gravitational potential on the surface of a homogeneous ellipsoid can be represented in closed analytical form not only in elliptical coordinates but also when geodetic or spherical latitudes are used.

4 Numerical comparisons

The formulae derived in Sect. 3 provide helpful analytical tools for testing algorithms and software in gravity field modelling. In Geodesy, a spherical shell has often been applied to testing software for calculating topographic gravity field functionals (cf. Heck and Seitz, 2007; Fukushima, 2018). However, a spherical shell creates a mathematically simple gravitational field that is independent from the horizontal position; in contrast, an ellipsoidal shell provides a more geo-realistic test setting which is also dependent on the geographical latitude because it takes the flattening of the Earth into account. As a very concrete practical consequence of modelling the test masses in the form of an ellipsoidal shell, not only the potential and its radial derivatives but also the latitude-dependent (and mixed ones with r) derivatives are different from zero, so that the software is also controllable for these functionals.

The massive ellipsoid or ellipsoidal shell can be discretised in various ways, as performed by different groups, resulting in numerical values for the potential and its derivatives (see, for example, Šprlák et al, 2020). By the derived analytical formulae, we have a means to check the performance of those approaches and software, in space as well as in frequency domain. Using a global discretization of an ellipsoidal topography, we demonstrate in Chapter 4.2 such a benchmark check related to the tesseroid approach according to Heck and Seitz (2007) and Grombein et al. (2013) which has been implemented in software used by different groups. Before, in Chapter 4.1, we validate the spherical harmonic expansion described in Chapter 3.1 with respect to the rigorous closed formula (43).

All numerical investigations are carried out for computation points $P_i$ running along a meridian at $\lambda _i =\Delta \vartheta /2 =$ constant with $0^\circ< \vartheta _i < \pi /2$, $\vartheta _i = \Delta \vartheta /2 + (i-1) \Delta \vartheta$. A step size of $\Delta \vartheta =5^\prime$ is chosen. $P_i(\vartheta _i,\lambda _i)$ is located on the surface of the ellipsoid $\varepsilon _1$. In all numerical investigations carried out, the Newtonian gravitation constant $G=6.6743 \cdot 10^{-11}$ m$^3$ kg$^{-1}$ s$^{-2}$ is used. The mass density is set to $\rho =2670$ kg m$^{-3}$ without restriction of generality.

Since the potential of an ellipsoidal shell and also its radial derivative are rotationally symmetrical, and there is equatorial symmetry too, this test setting is obvious and sufficiently general.

4.1 Spherical versus ellipsoidal harmonic expansion

In this chapter, the analytical representations developed in Sect. 3 for the potential of a homogeneous ellipsoidal shell in terms of spherical and ellipsoidal harmonics are compared numerically.

We compare the results given in Eqs. (30) and (35) with the exact closed solution in two terms based on ellipsoidal harmonics (47). To ensure that the evaluation of the potential is taken at the same points $P_i$ on the ellipsoid, the geocentric polar distance $\vartheta _i$ is converted to the elliptical co-latitude $\theta _i$ by the use of Eq. (48). Both latitude parameters are visualised in Fig. 4.

In Fig. 7, the difference between the potential of the ellipsoidal shell given in ellipsoidal harmonics and the series solution in spherical harmonics is provided for $N \in \{0,2,4,6,8,10\}$ in semi-logarithmic scale.

Fig. 7

Difference in potential between the solution in ellipsoidal and spherical harmonics of an ellipsoidal homogeneous shell, calculated on the surface of $\varepsilon _1$ along a meridian. $a_1 - a_2 = 10$ km, $\rho = 2670$ kg m$^{-3}$

Fig. 8

Difference in gravitational attraction between the solution in ellipsoidal and spherical harmonics of an ellipsoidal homogeneous shell, calculated on the surface of $\varepsilon _1$ along a meridian. $a_1 - a_2 = 10$ km, $\rho = 2670$ kg m$^{-3}$

The approximation error in spherical harmonics compared to the closed (exact) solution in ellipsoidal harmonics is as follows: for the potential, it is less than $10^{-5}$ m$^2$ s$^{-2}$ if the series is expanded only up to degree $N=6$, as can be seen in Fig. 7. For $N \ge 10$, the results are numerically identical indicated by the difference smaller than $10^{-9}$ m$^2$ s$^{-2}$ which primarily is due to rounding errors and corresponds to a relative accuracy of $10^{-14}$.

The difference in gravitational attraction between the solution in ellipsoidal (Eq. (38)) and spherical (Eq. (46)) harmonics of an ellipsoidal homogeneous shell of thickness $d = 10$ km and homogeneous density $\rho = 2670$ kg m$^{-3}$ is less than $10^{-3}$ mGal if the series is expanded only up to degree $N=6$. This can be seen in Fig. 8 indicated by the dashed lines. If $\delta g_\textrm{s}(N=20)$ is used as reference, the approximation error becomes much smaller (cf. Fig. 8 solid lines). From these results, it can be concluded that the closed solution faces some numerical limitations, rather than the solution in spherical harmonics.

Statistical values for the potential and gravitational attraction in ellipsoidal and spherical harmonics are provided in Table 3.

Table 3 Statistical values for the potential (m$^2$ s$^{-2}$) and gravitational attraction (mGal) in ellipsoidal and spherical harmonics

The equivalent representation of the potential and its attraction in spherical and elliptical coordinates (Eqs. (35), (43) and (38), (46), respectively) is confirmed by the identical numerical results (besides negligible numerical effects) presented in Figs. 7 and 8.

4.2 Tesseroid discretisation versus spherical harmonic expansion

Usually, a computational implementation of a spatial mass discretisation is validated against an analytical solution. Here, we apply extended spherical volume elements, called tesseroids. A spherical tesseroid is bounded by two meridians in East–West direction with geocentric longitudes $\lambda _1$ and $\lambda _2$. In North–South direction, the tesseroid is bounded by two concentric conical surfaces with opening angles $\vartheta _1=\pi /2-\varphi _1$ and $\vartheta _2=\pi /2-\varphi _2$. In the spherical case, the top and bottom bounding surfaces are spheres of radii $r_1=R$ and $r_2=R+d$. The spherical tesseroid is depicted in Fig. 9. An ellipsoidal tesseroid is bounded by the confocal ellipsoids $\varepsilon _1$ and $\varepsilon _2$, respectively, where the distance d between the bounding surfaces is latitude-dependent (Roussel et al. 2015).

Fig. 9

Geometry of a spherical tesseroid (Heck and Seitz 2007)

Routines for the computation of the gravitational field of a spherical tesseroid have been developed and tested in many studies (Marotta and Barzaghi 2017; Hirt et al. 2014; Grombein et al. 2013; Uieda et al. 2016). In Heck and Seitz (2007) and Fukushima (2018), the potential and the gravitational attraction (negative radial derivative) was validated against a spherical shell, using the closed formulae (Vaníček et al. (2001, 2004))

$$\begin{aligned} V^\textrm{shell}(r)&:= \frac{4}{3}\pi \rho \left( r_2^3 - r_1^3 \right) \frac{1}{r}, \quad r \ge r_2 > r_1, \end{aligned}$$

(51)

$$\begin{aligned} g^\textrm{shell}(r)&:= \frac{4}{3}\pi \rho \left( r_2^3 - r_1^3 \right) \frac{1}{r^2}, \quad r \ge r_2 > r_1. \end{aligned}$$

(52)

In the spherical case, the thickness of the shell is $H=d=r_2 - r_1$. $R=r_1=6368137$ m is the constant radius of the sphere on which the shell is elongated.

Already in Heck and Seitz (2007), it is pointed out that the spherical tesseroid formulae can also be used in an ellipsoidal arrangement. An ellipsoidal tesseroid can be approximated by a spherical one by using $r_1 = r_\textrm{E}(\varepsilon _2)$ and $r_2 = r_\textrm{E}(\varepsilon _1)$, respectively, referring Eq. (33) to the mean latitude $(\varphi _1 + \varphi _2)/2$.

Fig. 10

Approximation error for the gravitational potential of an ellipsoidal homogeneous shell, calculated on the surface of $\varepsilon _1$ along a meridian, when using tesseroids. $a_1 - a_2 = 10$ km, $\rho = 2670$ kg m$^{-3}$, $\Delta \varphi =\Delta \lambda =\{3^{\prime }$ (red), $2^{\prime }$ (blue), $1^{\prime }$ (green), $30^{\prime \prime }$ (black) }. The exact solution which the tesseroid evaluation is compared to, is calculated using Eq. (35) in spherical harmonics with a maximum degree of expansion $N=20$

In order to check the tesseroid approach in the ellipsoidal context, we have discretised an ellipsoidal shell between the confocal ellipsoids $\varepsilon _1$ and $\varepsilon _2$, using a grid size $\Delta \varphi =\Delta \lambda =30^{\prime \prime }$ and $a_1 - a_2 = 10$ km, identical with the tesseroid dimensions. The differences between the results of the tesseroid approach and the rigorous formulae for the potential and its radial derivative are presented in Figs. 10 and 11, showing the approximation error along a meridian on the upper boundary surface $\varepsilon _1$.

The absolute difference between the potential values calculated from Eq. (35) and the tesseroid method (Heck and Seitz 2007; Grombein et al. 2013) indicates that generally the tesseroid approach agrees better than $10^{-5}$ m$^2$ s$^{-2}$.

The maximal numerical discrepancy occurs at the pole and reaches an absolute value of 0.027 m$^2$ s$^{-2}$. Keep in mind, that at the poles, the tesseroids degenerate into triangular columns.

The same conclusions can be drawn for the radial derivative of the potential (gravity attraction). For the chosen numerical example ($a_1-a_2=d=10$ km, $\Delta \vartheta = \Delta \lambda =30^{\prime \prime }$, $h_P=0$ m), the numerical tesseroid solution agrees with Eq. (38) to an order of magnitude better than $10^{-6}$ mGal, besides in the direct vicinity of the poles. Both the analytical solution for the ellipsoidal shell and the gravity forward modelling by tesseroids—as well as the respective software implementations—are thus confirmed. This mutual confirmation is of course dependent on the used geometrical fineness of discretization of the ellipsoidal shell. In order to touch this important topic, which is not in the focus of this paper, the approximation errors obtained on a coarser discretisation with $\Delta \varphi \times \Delta \lambda =$ $\{3^{\prime } \times 3^{\prime }$, $2^{\prime } \times 2^{\prime }$, $1^{\prime } \times 1^{\prime }\}$ are presented in Figs. 10 and 11. The effect of the different discretisations can be clearly seen here. While the coarser discretisation leads to systematic deviations with a very smooth progression, the result with a discretisation of $30^{\prime \prime } \times 30^{\prime \prime }$ merely shows random behaviour. This is caused by rounding errors and reflects only numerical effects. In addition, this confirms that the used fine discretisation of $30^{\prime \prime } \times 30^{\prime \prime }$ is fine enough for our numerical investigations.

Fig. 11

Approximation error for the radial derivative of the potential of an ellipsoidal homogeneous shell, calculated on the surface of $\varepsilon _1$ along a meridian when using tesseroids. $a_1 - a_2 = 10$ km, $\rho = 2670$ kg m$^{-3}$, $\Delta \varphi =\Delta \lambda =\{3^{\prime }$ (red), $2^{\prime }$ (blue), $1^{\prime }$ (green), $30^{\prime \prime }$ (black) }. The exact solution which the tesseroid evaluation is compared to, is calculated using Eq. (38) in spherical harmonics with a maximum degree of expansion $N=20$

5 Conclusion

We have derived the external gravitational potential of a homogeneous ellipsoidal shell, bounded by two confocal ellipsoids of revolution, by solving the respective Newton integral in terms of spherical and elliptical coordinates, resulting in spherical and ellipsoidal harmonics. While the spherical harmonic representation produces a numerically fast-converging series for a global homogeneous ellipsoidal shell of, for example, 10 km thickness, which is used as an extreme case in the presented numerical investigations, the development in ellipsoidal harmonics consists of a finite series of degrees zero and two. As a matter of fact, both representations are theoretically equivalent, providing the same numerical results (up to rounding effects) if the spherical harmonic series is truncated at a suitable maximal degree. The series development in spherical harmonics enables the representation of the spectral components of the potential and the gradients, which may be considered as an advantage compared with the representation in ellipsoidal harmonics.

In Sects. 3.1 and 3.2, the derivation procedure starts from the solution of the Newton integral for computation points situated on the rotation axis, for which a closed analytical solution exists in spherical as well as in elliptical coordinates; in a second step, this solution is extended to the external space by harmonic continuation. The comparison between the rigorous finite ellipsoidal harmonic solution and the spherical harmonic expansion proves that the series expansion up to degree $n=6$ is sufficient for guaranteeing an approximation error less than $10^{-5}$ m$^2$ s$^{-2}$. This truncated series is easy to handle and contains only four terms. Thus, in practical applications the truncated spherical harmonic series will be preferred due to its higher numerical efficiency in comparison with the closed, but complicated analytical expressions in elliptical coordinates. The latter shows in the presented investigations some numerical problems, especially for the gravity gradient. The closed solution in elliptical coordinates consists only of two terms, but time-consuming arctan(x) function calls appear. Another disadvantage is that the spectral components cannot be used explicitly.

The derived formulae can be applied for testing and verification of computer programs and software implementations used for forward and inverse modelling in gravity field studies. In contrast to the often used isotropic test scenario based on a homogeneous spherical shell, the gravitational field of an ellipsoidal shell is also dependent on the horizontal position of the computation point, thus providing a more general control. As a matter of fact, with the presented ellipsoidal approach it is now possible to check also the gradients in latitudinal direction.

In Sect. 4.2, we have checked the well-established tesseroid approach (Heck and Seitz 2007; Grombein et al. 2013) and respective software by using a homogeneous ellipsoidal shell as test body representing the Earth’s topography. Discretising the ellipsoidal shell by tesseroidal volume elements of different sizes ($3^{\prime }$, $2^{\prime }$, $1^{\prime }$, $30^{\prime \prime }$) and summing up their contributions to the gravitational potential provide a numerical solution that has been compared with the rigorous analytical solution. In this way, the validity of the approach and the performance of the evaluation software could be proved. In the case of a 10 km-thick ellipsoidal shell and a discretisation of $30^{\prime \prime } \times 30^{\prime \prime }$, the agreement at a computation point on the ellipsoidal surface is generally better than $10^{-5}$ m$^2$ s$^{-2}$; the maximal discrepancy occurs at the poles, amounting to 0.027 m$^2$ s$^{-2}$, due to the degeneration of the tesseroids in the near zone to (quasi-)triangular elements. The results obtained with the coarser resolution clearly show the obvious dependency on the geometrical discretisation used. The latter is also an important outcome of the presented investigations. The derived solutions for potential and gravitational attraction for an ellipsoidal shell can be used to get a reliable statement on the results derived from DTMs of different resolutions.

In a similar way, the formulae derived in the paper may be used for checking other approaches and software (e.g. TC Software, Forsberg (1984); Forsberg and Tscherning (2014)), based on different discretisations, e.g. rectangular prisms (Nagy et al. 2000, 2002) or polyhedrons (D’Urso 2014).

Finally, also software for spherical harmonic analysis and synthesis can be controlled by the aid of the formulae derived in our paper.

Appendices

Appendices

1.1 A.1 Derivation of the gravity vector and gravity gradient tensor in spherical coordinates

Applying the relation between the partial derivatives in spherical coordinates and Cartesian coordinates in a local topocentric system which are given in Tscherning (1976) or Grombein et al. (2013), we elaborated the following expressions:

for the components of the gravity vector

$$\begin{aligned} g_{1} =-\frac{1}{r}\,\frac{\partial V}{\partial \vartheta }, \quad g_{2} =\frac{1}{r\sin {\vartheta }}\,\frac{\partial V}{\partial \lambda }, \quad g_{3} =\frac{\partial V}{\partial r} \,. \end{aligned}$$

(53)

and gravity gradients

$$\begin{aligned} M_{11}&=\frac{1}{r^2}\left( \frac{\partial ^2 V}{\partial \vartheta ^2} + r \frac{\partial V}{\partial r}\right) , \nonumber \\ M_{22}&=\frac{1}{r^2\sin ^2{\vartheta }}\left( \frac{\partial ^2 V}{\partial \lambda ^2} + \sin \vartheta \cos \vartheta \frac{\partial V}{\partial \vartheta } + r\sin ^2{\vartheta } \frac{\partial V}{\partial r} \right) , \nonumber \\ M_{33}&=\frac{\partial ^2 V}{\partial r^2}, \nonumber \\ M_{12}&=\frac{1}{r^2\sin {\vartheta }}\left( -\frac{\partial ^2 V}{\partial \vartheta \partial \lambda }+ \cot {\vartheta } \frac{\partial V}{\partial \lambda } \right) = M_{21},\nonumber \\ M_{13}&=\frac{1}{r}\left( -\frac{\partial ^2 V}{\partial \vartheta \partial r} + \frac{1}{r} \frac{\partial V}{\partial \vartheta }\right) = M_{31}, \nonumber \\ M_{23}&=\frac{1}{r\sin {\vartheta }}\left( \frac{\partial ^2 V}{\partial \lambda \partial r} - \frac{1}{r} \frac{\partial V}{\partial \lambda }\right) = M_{32} \,, \end{aligned}$$

(54)

we found the following expressions for the components of the gravity vector and the gravity gradient tensor $g_i$ and $M_{ij}$ of a homogeneous ellipsoid of revolution:

$$\begin{aligned}&\boxed { \begin{aligned} g_1&= -\frac{1}{r} \frac{\partial V(r, \vartheta )}{\partial \vartheta } = \frac{{GM}}{ E^2 } \sum ^\infty _{n=0} \frac{ (-1)^{n+1} }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n+2}\\&\qquad P^\prime _{2n}(\cos \vartheta ) \,, \end{aligned}} \end{aligned}$$

(55)

$$\begin{aligned}&\boxed { g_2 = \frac{1}{r \sin \vartheta } \frac{\partial V(r, \vartheta )}{\partial \lambda } = 0 \,, } \end{aligned}$$

(56)

$$\begin{aligned}&\boxed { g_3 = \frac{\partial V(r, \vartheta )}{\partial r}\,, \quad \quad \hbox {cf. Eq. } (31) \,, } \end{aligned}$$

(57)

$$\begin{aligned}&\boxed { \begin{aligned}M_{11}&= \frac{ 3\,GM}{ E^3 } \sum ^\infty _{n=0} \frac{ (-1)^n }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n+3}\\&\qquad \left[ P^{\prime \prime }_{2n} -(2n+1) P_{2n} \right] \,, \end{aligned}} \end{aligned}$$

(58)

$$\begin{aligned}&\boxed { \begin{aligned}M_{22}&= \frac{{GM}}{ E^3 } \sum ^\infty _{n=0} \frac{ (-1)^{n+1} }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n+3}\\&\qquad \left[ \cot \vartheta P^{\prime }_{2n} + (2n+1) P_{2n} \right] \,, \end{aligned}} \end{aligned}$$

(59)

$$\begin{aligned}&\boxed { M_{33} = V_{rr} =\frac{\partial ^2 V(r, \vartheta )}{\partial r^2} \,, \quad \quad \hbox {cf. Eq. } (32) \,, } \end{aligned}$$

(60)

$$\begin{aligned}&\boxed { M_{12} = V_{\vartheta \lambda } = 0 \,, } \end{aligned}$$

(61)

$$\begin{aligned}&\boxed { M_{13} = \frac{{GM}}{ E^3 } \sum ^\infty _{n=0} \frac{ (-1)^{n} }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n+3} 2n P^\prime _{2n} \,, } \end{aligned}$$

(62)

$$\begin{aligned}&\boxed { M_{23} = V_{\lambda r} = 0 \,. } \end{aligned}$$

(63)

The presented tensor elements $g_i$ and $M_{ij}$ can be considered as the physical coordinates of the tensors of first and second order (covariant derivatives). They refer to the topocentric left-handed reference frame with the orthonormal base vectors (northing, easting, up). The normalised base vectors are defined as:

$$\begin{aligned} \textbf{g}_1:= -\frac{1}{r} \frac{\partial \textbf{x}}{\partial \vartheta }, \quad \textbf{g}_2:= \frac{1}{r \sin \vartheta } \frac{\partial \textbf{x}}{\partial \lambda }, \quad \textbf{g}_3:= \frac{\partial \textbf{x}}{\partial r}, \end{aligned}$$

(64)

with the position vector $\textbf{x}_P$ of P and its geocentric distance $r=|\textbf{x}_P|$.

1.2 A.2 Derivation of the gravity vector and gravity gradient tensor in elliptical coordinates

In order to derive the gravity vector and gravity gradient tensor in elliptical coordinates, we are using the tensor calculus (cf. Klingbeil, 1966).

In an earth-fixed equatorial coordinate system with base vectors $\textbf{e}_i$, the Cartesian coordinates of a position vector of a computation point P are given in elliptical coordinates $\beta _k=\{\theta ,\lambda ,u\}$

$$\begin{aligned} \begin{aligned} x^{1}&= \sqrt{u^2 + E^2} \sin \theta \cos \lambda \,, \\ x^{2}&= \sqrt{u^2 + E^2} \sin \theta \sin \lambda \,, \\ x^{3}&= u \cos \theta \,. \end{aligned} \end{aligned}$$

(65)

The respective covariant base vectors are defined as

$$\begin{aligned} \textbf{g}_k = \textbf{e}_i \frac{\partial x^i}{\partial \beta _k} \,. \quad \quad \hbox {(Einstein's summation rule has been applied).} \end{aligned}$$

(66)

Applying (66) to (65), we get the covariant base vectors:

$$\begin{aligned} \begin{aligned} \textbf{g}_1 = \left( \begin{array}{c} c_1 \cos \lambda \\ c_1 \sin \lambda \\ - u \sin \theta \end{array} \right) \,, \quad \ \textbf{g}_2 = \left( \begin{array}{c} -c_2 \sin \lambda \\ c_2 \cos \lambda \\ 0 \end{array} \right) \,, \quad \textbf{g}_3 = \left( \begin{array}{c} c_3 \cos \lambda \\ c_3 \sin \lambda \\ \cos \theta \end{array} \right) \end{aligned} \end{aligned}$$

(67)

with the abbreviations $c_1=\sqrt{u^2 + E^2} \cos \theta$, $c_2 =\sqrt{u^2 + E^2} \sin \theta$ and $c_3=\frac{u}{\sqrt{u^2 + E^2}} \sin \theta$.

From this, we evaluate the covariant metric tensor $g_{ij} = \textbf{g}_i \otimes \textbf{g}_j$ as a dyadic product:

$$\begin{aligned} (g_{ij}) = \left( \begin{array}{ccc} u^2 + E^2 \cos ^2\theta &{} 0 &{} 0 \\ 0 &{} (u^2 + E^2) \sin ^2\theta &{} 0 \\ 0 &{} 0 &{} \frac{u^2 + E^2 \cos ^2\theta }{u^2 + E^2} \end{array} \right) , \nonumber \\ \end{aligned}$$

(68)

and its inverse, the contravariant metric tensor $g^{ij} = 1/g_{ij}$:

$$\begin{aligned} (g^{ij}) = \left( \begin{array}{ccc} \frac{1}{u^2 + E^2 \cos ^2\theta } &{} 0 &{} 0 \\ 0 &{} \frac{1}{(u^2 + E^2) \sin ^2\theta } &{} 0 \\ 0 &{} 0 &{} \frac{u^2 + E^2}{u^2 + E^2 \cos ^2\theta } \end{array} \right) . \end{aligned}$$

(69)

The Christoffel symbols are defined as

$$\begin{aligned} \Gamma _{\ell m}^k = \frac{1}{2} g^{kn} \left( g_{m n,\ell } + g_{n \ell ,m} - g_{\ell m,n} \right) \, \end{aligned}$$

(70)

and are elaborated based on (68) and (69):

$$\begin{aligned} \Gamma _{\ell m}^1= & {} \left( \begin{array}{ccc} \frac{-E^2\sin \theta \cos \theta }{u^2 + E^2 \cos ^2\theta } &{} 0 &{} \frac{u}{u^2 + E^2 \cos ^2\theta } \\ &{} \frac{-(u^2 + E^2)\sin \theta \cos \theta }{u^2 + E^2 \cos ^2\theta } &{} 0 \\ \hbox {sym} &{} &{} \frac{E^2\sin \theta \cos \theta }{(u^2+E^2)(u^2 + E^2 \cos ^2\theta )} \end{array} \right) , \end{aligned}$$

(71)

$$\begin{aligned} \Gamma _{\ell m}^2= & {} \left( \begin{array}{ccc} 0 &{} \tan \theta &{} 0 \\ &{} 0 &{} \frac{u}{u^2 + E^2} \\ \hbox {sym} &{} &{} 0 \end{array} \right) , \end{aligned}$$

(72)

$$\begin{aligned} \Gamma _{\ell m}^3= & {} \left( \begin{array}{ccc} \frac{-u(u^2 +E^2)}{u^2 + E^2 \cos ^2\theta } &{} 0 &{} \frac{-E^2\sin \theta \cos \theta }{u^2 + E^2 \cos ^2\theta } \\ &{} \frac{-u(u^2 + E^2)\sin ^2\theta }{u^2 + E^2 \cos ^2\theta } &{} 0 \\ \hbox {sym} &{} &{} \frac{ u E^2 \sin ^2\theta }{(u^2+E^2)(u^2 + E^2 \cos ^2\theta )} \end{array} \right) . \end{aligned}$$

(73)

Now, the covariant second derivatives of the potential in elliptical coordinates are:

$$\begin{aligned} V_{ik}&= \partial ^2_{ik} V - \Gamma _{ik}^n \ V_n \,, \end{aligned}$$

(74)

$$\begin{aligned} V_{11}&= \frac{\partial ^2 V}{\partial \theta ^2} + \frac{E^2\sin \theta \cos \theta }{u^2 + E^2 \cos ^2\theta } \frac{\partial V}{\partial \theta } + \frac{u(u^2 +E^2)}{u^2 + E^2 \cos ^2\theta } \frac{\partial V}{\partial u} \,, \end{aligned}$$

(75)

$$\begin{aligned} V_{12}&= 0 =V_{21} \,, \end{aligned}$$

(76)

$$\begin{aligned} V_{13}&= \frac{\partial ^2 V}{\partial \theta \partial u} \!-\! \frac{u}{u^2 \!+\! E^2 \cos ^2\theta } \frac{\partial V}{\partial \theta } \!+\! \frac{E^2\sin \theta \cos \theta }{u^2 \!+\! E^2 \cos ^2\theta } \frac{\partial V}{\partial u} = V_{31}\! \,, \end{aligned}$$

(77)

$$\begin{aligned} V_{22}&= \frac{(u^2 + E^2)\sin \theta }{u^2 + E^2 \cos ^2\theta } \left[ \cos \theta \frac{\partial V}{\partial \theta } + u \sin \theta \frac{\partial V}{\partial u} \right] \,, \end{aligned}$$

(78)

$$\begin{aligned} V_{23}&= 0 = V_{32} \,, \end{aligned}$$

(79)

$$\begin{aligned} V_{33}&= \frac{\partial ^2 V}{\partial u^2} - \frac{E^2\sin \theta }{(u^2+E^2)(u^2 + E^2 \cos ^2\theta )}\nonumber \\&\left[ \cos \theta \frac{\partial V}{\partial \theta } + u \sin \theta \frac{\partial V}{\partial u} \right] \nonumber \\&= \frac{\partial ^2 V}{\partial u^2} - \frac{E^2}{(u^2+E^2)^2} V_{22}\,. \end{aligned}$$

(80)

Finally, we get the physical components of the gravity vector and gravity gradient tensor in the left-handed local north-oriented frame (northing, longitudinal=easting, up) which is defined as $(N,L,U) \hat{=} (-\theta ,\lambda ,u)$.

The gravity vector elements are:

$$\begin{aligned} g_\textrm{N}&= - \frac{1}{\sqrt{u^2 + E^2 \cos ^2\theta }} \frac{\partial V}{\partial \theta } \,, \end{aligned}$$

(81)

$$\begin{aligned} g_\textrm{L}&= 0 \,,&\end{aligned}$$

(82)

$$\begin{aligned} g_\textrm{U}&= \sqrt{\frac{u^2+E^2}{u^2 + E^2 \cos ^2\theta }} \frac{\partial V}{\partial u} \,. \end{aligned}$$

(83)

The gravity gradient tensor elements are:

$$\begin{aligned} M_\textrm{NL}&= M_\textrm{LN} = M_\textrm{LU} = M_\textrm{UL} = 0\,, \end{aligned}$$

(84)

$$\begin{aligned} M_\textrm{NN}&= \frac{1}{u^2 + E^2 \cos ^2\theta } V_{11} \,, \end{aligned}$$

(85)

$$\begin{aligned} M_\textrm{LL}&= \frac{1}{(u^2 + E^2) \sin ^2\theta } V_{22} \,, \end{aligned}$$

(86)

$$\begin{aligned} M_\textrm{UU}&= \frac{u^2+E^2}{u^2 + E^2 \cos ^2\theta } V_{33} \,, \end{aligned}$$

(87)

$$\begin{aligned} M_\textrm{NU}&= -\frac{\sqrt{u^2+E^2}}{u^2 + E^2 \cos ^2\theta } V_{13} = M_\textrm{UN} \,. \end{aligned}$$

(88)

The Laplace equation $Lap V =\Delta V = M_\textrm{NN} + M_\textrm{LL} + M_\textrm{UU} = 0$ results from Equations (85), (86) and (87)

$$\begin{aligned} Lap V =&\, \Delta V = \frac{1}{u^2 + E^2 \cos ^2\theta } \nonumber \\&\left[ \frac{\partial ^2 V}{\partial \theta ^2} + \cot \theta \frac{\partial V}{\partial \theta } + (u^2 + E^2) \frac{\partial ^2 V}{\partial u^2} + 2u \frac{\partial V}{\partial u} \right] \,, \end{aligned}$$

(89)

in accordance with Heiskanen and Moritz (1967, p. 41, (1-105)).

The partial derivatives in elliptical coordinates required for the evaluation are as follows, starting from equation (43) for the potential:

$$\begin{aligned} \frac{\partial V(u, \theta )}{\partial u} =&\, - \frac{1}{2}\frac{{GM}}{E^2} \left\{ \frac{2 E^2}{E^2+u^2}\right. \nonumber \\&\left. -\left[ \frac{3u}{E} \arctan \frac{E}{u} - 2 - \frac{u^2}{E^2 + u^2} \right] \right. \nonumber \\&\left. \left( 3 \cos ^2 \theta - 1 \right) \right\} , \end{aligned}$$

(90)

$$\begin{aligned} \frac{\partial V(u, \theta )}{\partial \theta } =&\, -\frac{3}{2} \frac{{GM}}{E} \left[ \left( 1 + 3 \frac{u^2}{E^2}\right) \arctan \frac{E}{u} - 3\frac{u}{E} \right] \nonumber \\&\sin \theta \cos \theta , \end{aligned}$$

(91)

$$\begin{aligned} \frac{\partial ^2 V(u, \theta )}{\partial u^2} =&\, \frac{{GM}}{E^3} \left\{ \frac{2uE^3}{(E^2+u^2)^2}\right. \nonumber \\&\left. + \left[ \frac{3}{2} \arctan \frac{E}{u} - \frac{5uE^3 + 3u^3E}{2(E^2 + u^2)^2} \right] \right. \nonumber \\&\left. \left( 3 \cos ^2 \theta - 1 \right) \right\} , \end{aligned}$$

(92)

$$\begin{aligned} \frac{\partial ^2 V(u, \theta )}{\partial u \partial \theta } =&\, - 3 \frac{{GM}}{E^2} \left[ \frac{3u}{E} \arctan \frac{E}{u} - 2 - \frac{u^2}{E^2 + u^2} \right] \nonumber \\&\sin \theta \cos \theta , \end{aligned}$$

(93)

$$\begin{aligned} \frac{\partial ^2 V(u, \theta )}{\partial \theta ^2} =&\, -\frac{3}{2} \frac{{GM}}{E} \left[ \left( 1 + 3 \frac{u^2}{E^2}\right) \arctan \frac{E}{u} - 3\frac{u}{E} \right] \nonumber \\&( 2\cos ^2\theta -1) \,. \end{aligned}$$

(94)

Inserting the partial derivatives with respect to the elliptical coordinates (Eqs. (90)–(94)) into (85)–(88), we get the final result, the gravity gradient tensor expressed in elliptical coordinates:

$$\begin{aligned} M_\textrm{NN} =&\, -\frac{3}{2}\frac{{GM}}{E (u^2 + E^2 \cos ^2\theta )^2} \nonumber \\&\left\{ \left[ - \frac{u^2}{E^2} (E^2+3u^2) - \left( u^2 + E^2 - 6\frac{u^4}{E^2} \right) \cos ^2\theta \right. \right. \nonumber \\&\left. +\, 2 ( E^2 - 3u^2 )\cos ^4\theta \right] \arctan \frac{E}{u} \nonumber \\&\left. +\,2\frac{u^3}{E} + \frac{u}{E} (2E^2 - 3u^2 )\cos ^2 \theta - 3uE \cos ^4\theta ) \right\} \,, \end{aligned}$$

(95)

$$\begin{aligned} M_\textrm{LL} =&\, -\frac{3}{2}\frac{{GM}}{E^3} \left[ \arctan \frac{E}{u} - \frac{uE}{u^2 + E^2} \right] \,, \end{aligned}$$

(96)

$$\begin{aligned} M_\textrm{UU} =&\, \frac{3}{2}\frac{{GM}}{E} \frac{u^2+E^2}{u^2 + E^2 \cos ^2\theta } \nonumber \\&\left\{ \left[ \frac{3\cos ^2\theta }{E^2} - \frac{u^2 + E^2 \cos ^2\theta }{E^2(u^2+E^2)} \right] \arctan \frac{E}{u} \right. \nonumber \\&+\, \frac{2 uE}{(u^2+E^2)^2} \sin ^2\theta + \frac{u}{E(u^2+E^2)}(3\cos ^2\theta - 1) \nonumber \\&\left. -\,\frac{uE \sin ^2\theta }{(u^2+E^2)(u^2 + E^2 \cos ^2\theta )} \left( 1 - \frac{E^2 \sin ^2 \theta }{u^2+E^2} \right) \right\} \,, \end{aligned}$$

(97)

$$\begin{aligned} M_\textrm{NU} =&\, \frac{3}{2}\frac{{GM}}{E^2} \frac{\sqrt{u^2+E^2}}{u^2 + E^2 \cos ^2\theta } \sin \theta \cos \theta \nonumber \\&\left\{ \frac{3u}{E} \arctan \frac{E}{u} - 2 - \frac{u^2}{u^2+E^2} \right\} \,. \end{aligned}$$

(98)

1.3 A.3 Higher-order radial derivatives of the potential in spherical coordinates

Based on Eq. (27), the radial derivative of any degree $k > 0$ at a point in the space outside the ellipsoid can be expressed in the general formula:

$$\begin{aligned} \boxed { \begin{aligned}\frac{\partial ^k V(r, \vartheta )}{\partial r^k}&= \frac{ G M }{ E^{k+1} } \displaystyle \sum ^\infty _{n=0} \frac{(-1)^{n+k} \left[ \displaystyle \prod _{j=1}^{k}{(2n+j) } \right] }{ (2n+1)(2n+3) } \left( \frac{E}{r} \right) ^{2n+k+1}\\&\qquad P_{2n}(\cos \vartheta ) \,. \end{aligned}} \end{aligned}$$

(99)

The first and second radial derivatives are explicitly given in Eqs. (31) and (32).

1.4 A.4 Convergence of the infinite spherical harmonic series

The fast convergence of the potential coefficients can be derived analytically as shown in the following. Starting with Eq. (30), the analytical expression of the potential coefficients in the basis of spherical harmonics is:

$$\begin{aligned} \overline{V}_n =&\frac{V_n}{\sqrt{2n+1}} = \frac{ 3 (-1)^{n/2} }{ (n+1)(n+3)\sqrt{2n+1} } \left( \frac{E}{R} \right) ^{n} \,, \\ \quad&0 \le n \,\,\,\hbox {even} \,. \end{aligned}$$

We express the convergence as ratio between two consecutive coefficients $\overline{V}_{n}$ and

$$\begin{aligned} \begin{aligned} \overline{V}_{n+2}&= \frac{ 3 (-1)^{(n+2)/2} }{ (n+2+1)(n+2+3)\sqrt{2(n+2)+1} } \left( \frac{E}{R} \right) ^{n+2} \,, \\&= \frac{ 3 (-1)^{n/2}(-1) }{ (n+3)(n+5)\sqrt{2n+5} } \left( \frac{E}{R} \right) ^{n+2} \,, \\ \quad&0 \le n+2 \,\,\,\hbox {even} \,. \end{aligned} \end{aligned}$$

(100)

The ratio between $\overline{V}_{n+2}$ and $\overline{V}_{n}$ is given straightforward by

$$\begin{aligned} \begin{aligned} \frac{\overline{V}_{n+2}}{\overline{V}_{n}}&= \frac{ 3 (-1)^{n/2}}{3 (-1)^{n/2}(-1)} \frac{ (n+1)(n+3)}{(n+3)(n+5)} \frac{\sqrt{2n+1}}{\sqrt{2n+5} } \left( \frac{E}{R} \right) ^{n+2} \\ {}&\left( \frac{R}{E} \right) ^{n}\\&= - \frac{ n+1 }{ n+5 } \sqrt{ \frac{2n+1}{2n+5} } \left( \frac{E}{R} \right) ^{2} \,. \end{aligned} \end{aligned}$$

(101)

It can be seen that the magnitude of the n-dependent pre-factor in Eq. (101) is always smaller than one. If we assume that $\varepsilon _1$ is the surface of the Geodetic Reference System 1980 (Moritz 1980b), we set $R=a$, without loss of generality, and note that $E=ae$, the final expression of the convergence of the potential coefficients is given by:

$$\begin{aligned} \begin{aligned} \frac{\overline{V}_{n+2}}{\overline{V}_{n}}&\approx - e^2 \,. \end{aligned} \end{aligned}$$

(102)

The numerical behaviour of the coefficients expressing the potential of an ellipsoidal shell in spherical harmonics is clearly shown in Fig. 5. The rapid decay is obvious from the provided numbers in Table 2.