Exact closed-form expressions for the complete RTM correction

Abstract

We present exact, closed-form expressions for the complete RTM correction and the harmonic correction to disturbing potential, gravity disturbance, gravity anomaly, and height anomaly. They need to be applied in quasi-geoid modelling whenever data points are buried inside the masses after residual terrain model (RTM) reduction and analytically downward-continued functionals of the disturbing potential at the original locations of the data points are required. Compared to recent work of the authors published in this journal, no Taylor series enter the expressions and numerical instabilities of the harmonic downward continuation from the RTM surface to the Earth’s surface are avoided as are inaccuracies in the free-air upward continuation from the Earth’s surface to the RTM surface caused by a lack of precise information about higher-order derivatives of the disturbing potential. The new expressions can easily be implemented in any existing RTM software package and do not require additional computational resources. For two test areas located in western Norway and the Auvergne in France, we compute the complete RTM correction and the harmonic correction to the afore-mentioned functionals of the disturbing potential. Overall, all harmonic corrections are non-negative with maximum values of 1.54 $\textrm{m}^2/\textrm{s}^2$, 263.0 $\upmu$Gal, 263.9 $\upmu$Gal, and 15.7 m (Norway) and 1.55 $\textrm{m}^2/\textrm{s}^2$, 263.3 $\upmu$Gal, 263.3 $\upmu$Gal, and 15.8 cm (Auvergne) for disturbing potential, gravity disturbance, gravity anomaly, and height anomaly, respectively. The medians are 0.02 $\textrm{m}^2/\textrm{s}^2$, 33.6 $\upmu$Gal, 33.7 $\upmu$Gal, and 0.3 cm (Norway) and 0.01 $\textrm{m}^2/\textrm{s}^2$, 19.2 $\upmu$Gal, 19.2 $\upmu$Gal, and 0.1 cm (Auvergne). We also show that the nth Taylor polynomials used in the recent work of the authors published in this journal may have large remainders depending on the topography in the vicinity of the evaluation point no matter how n is chosen. Finally, we show that the commonly used expression for the harmonic correction to gravity anomaly introduced in 1981 is almost exact, though it was derived along a completely different line of reasoning. The errors do not exceed 49 $\upmu$Gal in both test areas. Moreover, the errors have a negligible impact on the computed height anomalies in one-centimetre quasi-geoid modelling, as the mean error does not exceed a few $\upmu$Gal in both test areas.

1 Introduction

The residual terrain model (RTM) reduction was introduced in Forsberg and Tscherning (1981) as a method to deal with topography in gravity field modelling. Basically, the RTM reduction aims at removing from the data the contribution of short-wavelengths topographic signals relative with respect to a smooth mean elevation surface, here referred to as the RTM surface. In this way, unwanted high-frequency topographic signals present in the data are largely removed depending among others on the quality and resolution of the topographic information (i.e. digital elevation model and/or bathymetry model, mass density model). After application of the RTM reduction, stations above the RTM surface are essentially in free-air while stations below the RTM surface are buried inside the masses. The latter implies that the RTM-reduced geopotential functionals at stations located below the RTM surface represent values inside the masses. Before these RTM-reduced internal geopotential functionals are used in quasi-geoid modelling, Forsberg and Tscherning (1981) suggested to apply a correction, referred to as the harmonic correction, which provides analytically downward-continued functionals at the original location of the data points.

The expression for the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981), though very simple to evaluate, was known to be an approximation, which at that time was sufficient as no high-resolution, precise digital elevation models were available. Forsberg and Tscherning (1981) did not derive expressions for the harmonic correction to other functionals of the disturbing potential. However, as far as disturbing potential and height anomaly are concerned, they argued that the corresponding harmonic corrections are likely very small and may be neglected in most cases. Since then, many attempts were made to address the problem of the harmonic correction (cf. Klees et al. 2022 for a review).

Recently, Klees et al. (2022) provided for the first time expressions for the harmonic correction to disturbing potential and height anomaly and improved expressions for the radial derivative of the disturbing potential. Using topographic data over a part of western Norway and the Auvergne in France, they computed and analysed the harmonic correction to these functionals. In fact, their expressions for the harmonic correction are also approximations, as they were based on nth Taylor polynomials. Based on an estimated upper bound of the remainders of the nth Taylor polynomials, ibid. suggested the choice $n=2$ for disturbing potential and height anomaly and $n=1$ for the radial derivative of the disturbing potential. Using the new expressions, they showed that in areas of strong topographic variations (e.g. around the Norwegian fjords), the differences with respect to the harmonic correction to gravity anomaly in Forsberg and Tscherning (1981) can be as large as 100 mGal. Moreover, as these differences do not average out over the data area, they may introduce significant long-wavelength errors in the computed quasi-geoid model. They also showed that the harmonic correction to disturbing potential and height anomaly only need to be applied in areas of strong topographic variations with peak values of 1 $\textrm{m}^2/\textrm{s}^2$ (disturbing potential) and 0.1 m (height anomaly) in the Norway and Auvergne test areas, whereas in the flat and hilly parts of these areas, they are mostly below 0.1 $\textrm{m}^2/\textrm{s}^2$ (disturbing potential) and 0.01 m (height anomaly).

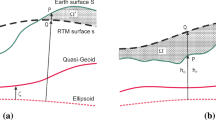
The approach suggested in Klees et al. (2022) allows to compute the complete RTM correction (i.e. the sum of RTM reduction and harmonic correction) to any linear functional of the disturbing potential. It involves four steps (cf. Fig. 1):

• 1. Masses inside the volume $\Omega ^+$ are removed, and the functional is corrected for the effect this has.

• 2. The functional obtained in step 1 is upward-continued in free air from its original location on the Earth’s surface to the RTM surface along the ellipsoidal normal.

• 3. Masses are added to the volume $\Omega ^-$ to obtain a constant mass density in $\Omega ^-$, and the functional from step 2 is corrected accordingly.

• 4. The functional obtained in step 3 is downward-continued analytically from the RTM surface to the original location on the Earth’s surface along the ellipsoidal normal providing an analytically downward-continued functional at the original location. This functional is ready to be used in quasi-geoid modelling.

Klees et al. (2022) used truncated Taylor series for the free-air upward continuation of step 2 and the analytic downward continuation of step 4, respectively. For each remainder, they provided upper bounds based on the exterior gravity field of a homogeneous mean Earth sphere. However, we will show in Appendix B using a simple example that the upper bounds provided in Klees et al. (2022) are not really upper bounds everywhere. In particular, in deep, narrow valleys, they may underestimate the magnitude of the remainders significantly. Consequently, some results and conclusions presented in Klees et al. (2022) became wrong and need to be corrected. Moreover, we also show in Appendix B that this problem is not solved by just increasing the order n of the Taylor polynomials. Therefore, we need another approach for step 2 and step 4, which does not involve Taylor series.

Fig. 1

Mass distribution of the Earth before (a) and after (b) RTM reduction

In this paper, we will provide exact, closed-form expressions for the complete RTM correction to disturbing potential, gravity disturbance, gravity anomaly, and height anomaly. They are easy to implement in any existing RTM software package and do not require additional computational resources. In Sect. 2, we will derive the exact, closed-form expression for disturbing potential. A key quantity arising in this expression is the harmonic downward continuation of the gravitational field of the masses added to volume $\Omega ^-$ (cf. Fig. 1) to the location of a data point, which, after step 3, is buried in the masses. An exact, closed-form expression for this harmonic downward continuation is derived in Sect. 3. The results of Sects. 2 and 3 are combined in Sect. 4 providing the final exact, closed-form expression for the complete RTM correction to disturbing potential and also its radial derivative. Likewise, exact, closed-form expressions are provided for gravity disturbance, gravity anomaly, and height anomaly using their relation with the disturbing potential. In Sect. 5, the new expressions will be applied to the two test areas already considered in Klees et al. (2022). Moreover, we will identify the results and conclusions in Klees et al. (2022) which are wrong due to the underestimation of the magnitude of the remainders of the nth Taylor polynomials used in step 2 and step 4 of the complete RTM correction approach. In Sect. 6, we close with a summary and some final remarks.

Fig. 2

Computation of $V^{-,\textrm{HDC}}_{\textrm{P}}$

2 Exact, closed-form expression for the complete RTM correction to disturbing potential

To derive the new expression for the complete RTM correction to disturbing potential, we start with the four-step procedure suggested in Klees et al. (2022), but use a more compact notation for a better readability.

Let T be the disturbing potential, P a point on the Earth’s surface, and Q the intersection of the ellipsoidal normal through P and the RTM surface (cf. Fig. 1). If P is located above the RTM surface, the complete RTM correction reduces to the RTM reduction introduced in Forsberg and Tscherning (1981). After RTM reduction, the point P is hanging in free-air inside the harmonic domain of the RTM-reduced disturbing potential. Here, we are only interested in points P, which are located below the RTM surface. These points are buried in the masses, which were added to the volume $\Omega ^-$ in step 3. We denote by $V^+$ the gravitational potential of the masses in $\Omega ^+$ and by $V^-$ the gravitational potential of the masses added to volume $\Omega ^-$ (cf. Fig. 1). Note that if our data area does not contain water surfaces, $\Omega ^-$ is mass-free before step 3 (cf. Fig. 2 and Table 1 in Klees et al. (2022)). Then, the masses added to $\Omega ^-$ in step 3 are identical to the masses in $\Omega ^-$ after step 3. The four-step procedure in Klees et al. (2022) proceeds as follows:

Table 1 Statistics of the complete RTM correction to gravity anomaly, Eq. (37), and height anomaly, Eq. (39) for the Norway test area (222, 892 evaluation points) and the Auvergne test area (95, 360 evaluation points). Only evaluation points located below the RTM surface were included

Step 1: Move the masses in $\Omega ^+$ to infinity and correct $T_{\tiny {\text{ P }}}$ for the gravitational effect this has:

$$\begin{aligned} T^+_{\tiny {\text{ P }}}:= T_{\tiny {\text{ P }}}- V^+_{\tiny {\text{ P }}}. \end{aligned}$$

(1)

Step 2: Upward continue in free-air $T^+_{\tiny {\text{ P }}}$ of Eq. (1) to the point Q on the RTM surface along the ellipsoidal normal through P:

$$\begin{aligned} T^+_{\tiny {\text{ Q }}}:= T^+_{\tiny {\text{ P }}}+\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}. \end{aligned}$$

(2)

Step 3: Add mass to the volume $\Omega ^-$ so that the mass density equals some pre-selected value and correct $T^+_{\tiny {\text{ Q }}}$ of Eq. (2) for the gravitational effect this has:

$$\begin{aligned} T^{\tiny {\text{ red }}}_\textrm{Q}:= T^+_{\tiny {\text{ Q }}}+ V^-_{\tiny {\text{ Q }}}. \end{aligned}$$

(3)

Step 4: Downward-continue harmonically $T^{\tiny {\text{ red }}}$ from point Q on the RTM surface to point P on the Earth’s surface along the ellipsoidal normal through P:

$$\begin{aligned} T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}:= T^{\tiny {\text{ red }}}_\textrm{Q}+\delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}. \end{aligned}$$

(4)

Note that the upper index “UC” in Eq. (2) and “HDC” in Eq. (4) means “free-air upward continuation” and “harmonic downward continuation”, respectively. When combining Eqs. (1)–(4), we can write $T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}$ as the difference between $T_{\tiny {\text{ P }}}$ and the complete RTM correction, denoted $(T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}$:

$$\begin{aligned} T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}&:= T_{\tiny {\text{ P }}}- (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}, \nonumber \\ (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&:= V^+_{\tiny {\text{ P }}}- V^-_{\tiny {\text{ Q }}}- (\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}+ \delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}). \end{aligned}$$

(5)

We find it important to mention that due to step 4, $T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}$ is different from $T^{\tiny {\text{ red }}}_{\textrm{P}}$, the value of $T^{\tiny {\text{ red }}}$ at P inside the masses. Remember that after step 3, $T^{\tiny {\text{ red }}}$ is actually harmonic outside the RTM surface (“actually” means we ignore that the DEM is just an approximation to the Earth’s surface and the density of the masses in $\Omega ^+$ and of the masses in $\Omega ^-$ (if there are any), are not exactly known). In step 4, $T^{\tiny {\text{ red }}}$ is harmonically downward-continued from point Q on the RTM surface through the masses to point P on the Earth’s surface, which gives $T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}$.

Using the definition of the RTM reduction according to Forsberg and Tscherning (1981),

$$\begin{aligned} (T)^{\tiny {\text{ RTM }}}_{\tiny {\text{ P }}}:= V^+_{\tiny {\text{ P }}}- V^-_{\tiny {\text{ P }}}, \end{aligned}$$

(6)

Equation (5) is re-written as

$$\begin{aligned} (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}= (T)^{\tiny {\text{ RTM }}}_{\tiny {\text{ P }}}- \Big [ V^-_{\tiny {\text{ Q }}}- V^-_{\tiny {\text{ P }}}+ (\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}+ \delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}) \Big ]. \end{aligned}$$

(7)

The term in brackets on the right-hand side of Eq. (7) is the exact expression for the harmonic correction, denoted $(T)^{\tiny {\text{ harm }}}_{\textrm{P}}$. Hence, we may write

$$\begin{aligned} (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}= (T)^{\tiny {\text{ RTM }}}_{\tiny {\text{ P }}}- (T)^{\tiny {\text{ harm }}}_{\textrm{P}}, \end{aligned}$$

(8)

with

$$\begin{aligned} (T)^{\tiny {\text{ harm }}}_{\textrm{P}}= V^-_{\tiny {\text{ Q }}}- V^-_{\tiny {\text{ P }}}+ (\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}+ \delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}). \end{aligned}$$

(9)

$V^-_{\tiny {\text{ P }}}$, which does not appear in the expression for the complete RTM correction appears by construction in the RTM reduction in Eq. (6) and the harmonic correction of Eq. (9). Note that $V^-_{\tiny {\text{ P }}}$ is the gravitational potential of the masses added to volume $\Omega ^-$ in step 3, evaluated at P. Though P is located inside the masses after step 3, P is also a point located on the boundary of the harmonic domain of the gravitational potential of the masses added to volume $\Omega ^-$.

In Klees et al. (2022), the effect of the free-air upward continuation (UC) from point P to point Q in step 2, $\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}$, and the effect of the harmonic downward continuation (HDC) from point Q to point P in step 4, $\delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}$, were considered separately. For each effect, a nth Taylor polynomial about P ($\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}$) and Q ($\delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}$) was used. In Appendix B, we have chosen a simple mass configuration to demonstrate that the remainder of each nth Taylor polynomial used in Klees et al. (2022) may introduce errors in the computed complete RTM correction, which are much larger than the upper bounds in Klees et al. (2022) suggest and also much larger than the measurement error. This applies in particular to the effect of the harmonic downward continuation, $\delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}$, at points P located in deep, narrow valleys, i.e. at locations where the complete RTM corrections attain large magnitudes. The remainder of the harmonic downward continuation in step 4 does not decrease when increasing n. Moreover, in deep, narrow valleys, the upward continuation in step 2 may also be prone of errors, because derivatives of the disturbing potential may differ significantly from their nominal values.

We will show that Taylor series for the upward continuation of step 2 and the harmonic downward continuation of step 4 can be avoided completely. To do so, we exploit the superposition principle of gravitating masses, which allows the combination of step 2 and step 4 into a single step, and provides closed-form expressions for the complete RTM correction. Key are three observations. First, the upward continuation of step 2 is done in free-air in the gravitational field $T^+$ (cf. Eq. (2)). Second, the point P is located on the boundary of the harmonic domain of $T^+$ as $T^+$ is the disturbing potential before masses are added to volume $\Omega ^-$. Third, the disturbing potential after step 3, i.e. after masses has been added to volume $\Omega ^-$, $T^{\tiny {\text{ red }}}= T^+ + V^-$, is harmonic outside the RTM surface. Hence, the continuity of $T^+$ across the boundary of the harmonic domain allows us to write

$$\begin{aligned} T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}= T^+_{\tiny {\text{ P }}}+ V^{-,\textrm{HDC}}_{\textrm{P}}, \end{aligned}$$

(10)

where $V^{-,\textrm{HDC}}_{\textrm{P}}$ is the harmonic downward continuation of the gravitational potential $V^-$ from its upper harmonic domain through the masses to point P. Using Eq. (10), the effect of the harmonic downward continuation of step 4, $\delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}$, can be written as

$$\begin{aligned} \delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}&= T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}- T^{\tiny {\text{ red }}}_\textrm{Q}= T^+_{\tiny {\text{ P }}}+ V^{-,\textrm{HDC}}_{\textrm{P}}- T^{\tiny {\text{ red }}}_\textrm{Q}\nonumber \\&= T^+_{\tiny {\text{ P }}}+ V^{-,\textrm{HDC}}_{\textrm{P}}- (T^+_{\tiny {\text{ Q }}}+ V^-_{\tiny {\text{ Q }}}) \nonumber \\&= (T^+_{\tiny {\text{ P }}}- T^+_{\tiny {\text{ Q }}}) + V^{-,\textrm{HDC}}_{\textrm{P}}- V^-_{\tiny {\text{ Q }}}\nonumber \\&= -\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}+ V^{-,\textrm{HDC}}_{\textrm{P}}- V^-_{\tiny {\text{ Q }}}. \end{aligned}$$

(11)

In Eq. (11), we move $\delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}$ to the left-hand side, which provides an expression for the joint effect of the free-air upward continuation of step 2 and the harmonic downward continuation of step 4:

$$\begin{aligned} \delta T^{\tiny {\text{ HDC }}}_{\tiny {\text{ Q } \rightarrow \text{ P }}}+ \delta T^{\tiny {\text{ UC }}}_{\tiny {\text{ P } \rightarrow \text{ Q }}}= V^{-,\textrm{HDC}}_{\textrm{P}}- V^-_{\tiny {\text{ Q }}}. \end{aligned}$$

(12)

Equation (12) is the first main result of this paper. The sum appears in both the expression for the complete RTM correction and the harmonic correction. Therefore, with Eq. (12) we may write for the complete RTM correction, $(T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}$, Eq. (8), and the harmonic correction, $(T)^{\tiny {\text{ harm }}}_{\textrm{P}}$, Eq. (9) at points P located below the RTM surface:

$$\begin{aligned} (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= V^+_{\tiny {\text{ P }}}- V^{-,\textrm{HDC}}_{\textrm{P}}, \end{aligned}$$

(13)

$$\begin{aligned} (T)^{\tiny {\text{ harm }}}_{\textrm{P}}&= V^{-,\textrm{HDC}}_{\textrm{P}}- V^-_{\tiny {\text{ P }}}. \end{aligned}$$

(14)

Equation (13) consists of two terms. The term $V^+_{\textrm{P}}$ is the gravitational potential at P of the masses in $\Omega ^+$. The term $V^{-,\textrm{HDC}}_{\textrm{P}}$ is the harmonic downward continuation to point P of the exterior gravitational potential of the masses added to volume $\Omega ^-$, where “exterior” refers to the region above the RTM surface.

The harmonic correction to disturbing potential of Eq. (14) also comprises two terms, one of them is $V^{-,\textrm{HDC}}_{\textrm{P}}$, which already appeared in Eq. (13). The other one, $V^-_{\tiny {\text{ P }}}$, is the gravitational potential at P of the masses added to volume $\Omega ^-$. Note that P is located on the lower boundary of the harmonic domain of $V^-$.

$V^+_{\tiny {\text{ P }}}$ and $V^-_{\tiny {\text{ P }}}$ are computed when computing the RTM reduction (cf. Eq. (6)). To do so, the volumes $\Omega ^+$ and $\Omega ^-$ are discretized using rectangular prisms and/or tesseroids. For prisms, a closed-form expression exists (cf. Nagy et al. 2001, 2002). For tesseroids, a truncated Taylor series is used (cf. Heck and Seitz 2007; Grombein et al. 2013).

3 The computation of $V^{-,\textrm{HDC}}_{\textrm{P}}$

$V^{-,\textrm{HDC}}_{\textrm{P}}$ plays a key role in the complete RTM correction and the harmonic correction according to Eqs. (13) and (14). In principle, it could be computed using an nth Taylor polynomial about Q. However, as shown in Appendix B, this does not provide an accurate enough approximation to $V^{-,\textrm{HDC}}_{\textrm{P}}$, in particular not in deep, narrow valleys, no matter how n is chosen. Finding a suitable, preferably closed-form expression for $V^{-,\textrm{HDC}}_{\textrm{P}}$ is not straightforward and requires some additional considerations.

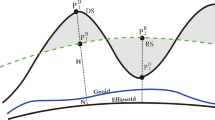
Suppose we cut out from $\Omega ^-$ a cylinder of radius R and height $\Delta h = h_\textrm{Q} - h_{\textrm{P}}$, and a symmetry axis identical to the line $Q-P$ (cf. Fig. 2). The volume cut out in this way is denoted $\Omega ^-_h$, the remaining volume is denoted $\delta \Omega ^-$, and the volume of the cylinder is denoted $\Omega _\textrm{c}$. Then,

$$\begin{aligned} \Omega ^- = \delta \Omega ^- + \Omega ^-_\textrm{h} = \delta \Omega ^- + \Omega _\textrm{c} + (\Omega ^-_\textrm{h} - \Omega _\textrm{c}). \end{aligned}$$

(15)

The difference $\Omega _\varepsilon := \Omega ^-_\textrm{h} - \Omega _\textrm{c}$ is the volume between i) the top of the cylinder and the RTM surface, and ii) the bottom of the cylinder and the Earth’s surface (cf. Fig 2). We find it important to mention here that we can make this difference arbitrarily small by choosing a small enough radius R. Now, according to the superposition principle of gravitating masses, we can write $V^{-,\textrm{HDC}}_{\textrm{P}}$ as the sum of the contribution of the masses in $\delta \Omega ^-$ and $\Omega ^-_\textrm{h}$, i.e.

$$\begin{aligned} V^{-,\textrm{HDC}}_{\textrm{P}}= \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\delta \Omega ^-} + \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega ^-_\textrm{h}}. \end{aligned}$$

(16)

Because P is located on the boundary of the harmonic domain of the masses in $\delta \Omega ^-$, the first term on the right-hand side of Eq. (16) is

$$\begin{aligned} \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\delta \Omega ^-} = \Big ( V_{\textrm{P}}^-\Big )_{\delta \Omega ^-} = V_{\textrm{P}}^- - \Big ( V^-_{\textrm{P}} \Big )_{\Omega ^-_\textrm{h}}. \end{aligned}$$

(17)

Note that $\Big ( V^-_{\textrm{P}} \Big )_{\Omega ^-_\textrm{h}}$ is the gravitational potential at point P of the masses which were cut out. Using Eqs. (41) and (43) in Appendix A, it is

$$\begin{aligned} \Big ( V^-_{\textrm{P}} \Big )_{\Omega ^-_\textrm{h}}&= \Big ( V^-_{\textrm{P}} \Big )_{\Omega _c} + \Big ( V^-_{\textrm{P}} \Big )_{\Omega _\varepsilon } \nonumber \\&= V_{z < 0}(R,\Delta h,-\Delta h) + \Big ( V^-_{\textrm{P}} \Big )_{\Omega _\varepsilon }, \end{aligned}$$

(18)

$$\begin{aligned} \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega ^-_\textrm{h}}&= \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega _c} + \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega _\varepsilon } \nonumber \\&= V_{z>0}(R,\Delta h,-\Delta h) + \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega _\varepsilon }. \end{aligned}$$

(19)

Inserting Eqs. (17)–(19) in Eq. (16), we find

$$\begin{aligned}{} & {} V^{-,\textrm{HDC}}_{\textrm{P}}{=} V^-_{\textrm{P}} {+} V_{z>0}(R,\Delta h,{-}\Delta h) {-} V_{z < 0}(R,\Delta h,{-}\Delta h) \nonumber \\{} & {} \quad {+} \Big ( \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega _\varepsilon } {-} \Big ( V^{-}_{\textrm{P}} \Big )_{\Omega _\varepsilon }\Big ). \end{aligned}$$

(20)

However, according to Eqs. (41) and (43) in Appendix A, it is

$$\begin{aligned} V_{z>0}(R,\Delta h,{-}\Delta h) {-} V_{z < 0}(R,\Delta h,{-}\Delta h) {=} 2\pi G \rho \Delta h^2 \nonumber \\ \end{aligned}$$

(21)

independent of R. Hence,

$$\begin{aligned} V^{-,\textrm{HDC}}_{\textrm{P}}{=} V^{-}_{\textrm{P}} {+} 2\pi G \rho \Delta h^2 {+} \Big \{ \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega _\varepsilon } {-} \Big ( V^{-}_{\textrm{P}} \Big )_{\Omega _\varepsilon }\Big \}.\nonumber \\ \end{aligned}$$

(22)

The size of the term $\{ \cdot \}$ on the right-hand side of Eq. (22) is controlled by the size of R. In particular,

$$\begin{aligned} \Big ( V^{-,\textrm{HDC}}_{\textrm{P}}\Big )_{\Omega _\varepsilon } - \Big (V^-_{\textrm{P}} \Big )_{\Omega _\varepsilon } \rightarrow 0,\; R \rightarrow 0. \end{aligned}$$

(23)

Hence, we can make this term arbitrarily small by choosing a sufficiently small R. At the same time, the right-hand side of Eq. (21) does not depend on R. Hence, when choosing a sufficiently small R, Eq. (22) is actually equal to

$$\begin{aligned} V^{-,\textrm{HDC}}_{\textrm{P}}= V^-_{\textrm{P}} + 2\pi G \rho \Delta h^2 \end{aligned}$$

(24)

and can be considered as being exact. Equation (24) is the second main result of this paper.

4 Exact, closed-form expressions

Using Eq. (24), we obtain the following expression for the complete RTM correction to disturbing potential, Eq. (13), and the harmonic correction to disturbing potential, Eq. (14):

$$\begin{aligned} (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= V^+_{\tiny {\text{ P }}}- V^-_{\tiny {\text{ P }}}- 2\pi G \rho \Delta h^2, \end{aligned}$$

(25)

$$\begin{aligned} (T)^{\tiny {\text{ harm }}}_{\textrm{P}}&= 2\pi G \rho \Delta h^2. \end{aligned}$$

(26)

Both equations are of closed-form and, as explained in Sect. 3, actually exact.

Following the same line of reasoning, we can easily find exact, closed-form expressions for the complete RTM correction and harmonic correction to the radial derivative of the disturbing potential. With

$$\begin{aligned} \partial _r V_{z>0}(R,\Delta h,-\Delta h) - \partial _r V_{z < 0}(R,\Delta h,-\Delta h) = -4\pi G \rho \Delta h. \end{aligned}$$

(e.g. Kadlec 2011 with the remark that in Eq. 2.52 of ibid. it must read $-h^2$ instead of $h^2$), which is also independent of R, we find

$$\begin{aligned} (\partial _r T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= \partial _r V^+_{\tiny {\text{ P }}}- \partial _r V^-_{\tiny {\text{ P }}}+ 4\pi G \rho \Delta h, \end{aligned}$$

(27)

$$\begin{aligned} (\partial _r T)^{\tiny {\text{ harm }}}_{\tiny {\text{ P }}}&= -4\pi G \rho \Delta h. \end{aligned}$$

(28)

To find similar expressions for the complete RTM correction and the harmonic correction to gravity disturbance, $\delta g$, gravity anomaly, $\Delta g$, and height anomaly, $\zeta$ is straightforward. First, we remember the relationship between these functionals and the disturbing potential (we use the spherical approximation for convenience):

$$\begin{aligned} \delta g&= - \partial _r T, \end{aligned}$$

(29)

$$\begin{aligned} \Delta g&= -\partial _r T - {2 \over r}\,T, \end{aligned}$$

(30)

$$\begin{aligned} \zeta&= {1 \over \gamma }\, T, \end{aligned}$$

(31)

where r is the spherical distance to and $\gamma$ the normal gravity at the telluroid point associated with the evaluation point. Second, we define

$$\begin{aligned} \delta g^+_{\textrm{P}}&:= -\partial _r V^+ \Big |_{\textrm{P}},\;\; \delta g^-_{\textrm{P}} := -\partial _r V^- \Big |_{\textrm{P}}, \end{aligned}$$

(32)

$$\begin{aligned} \Delta g^+_{\textrm{P}}&:= - \partial _r V^+\Big |_{\textrm{P}} - {2 \over r} V^+_{\textrm{P}},\;\; \Delta g^-_{\textrm{P}} := - \partial _r V^-\Big |_{\textrm{P}} - {2 \over r} V^-_{\textrm{P}} \end{aligned}$$

(33)

$$\begin{aligned} \zeta ^+_{\textrm{P}}&:= {1 \over \gamma } T^+_{\textrm{P}},\;\; \zeta ^-_{\textrm{P}} := {1 \over \gamma } T^-_{\textrm{P}}. \end{aligned}$$

(34)

Then, using Eqs. (25)–(28), we find:

$$\begin{aligned} (\delta g)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= \Big (\delta g^+_{\textrm{P}} - \delta g^-_{\textrm{P}}\Big ) - 4\pi G \rho \Delta h, \end{aligned}$$

(35)

$$\begin{aligned} (\delta g)^{\tiny {\text{ harm }}}_{\tiny {\text{ P }}}&= 4 \pi G \rho \Delta h, \end{aligned}$$

(36)

$$\begin{aligned} (\Delta g)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= \Big (\Delta g^+_{\textrm{P}} - \Delta g^-_{\textrm{P}}\Big ) - 4\pi G \rho \Delta h \Big ( 1 - {\Delta h \over r}\Big ), \end{aligned}$$

(37)

$$\begin{aligned} (\Delta g)^{\tiny {\text{ harm }}}_{\tiny {\text{ P }}}&= 4\pi G \rho \Delta h \Big ( 1 - {\Delta h \over r}\Big ), \end{aligned}$$

(38)

$$\begin{aligned} (\zeta )^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= \Big (\zeta ^+_{\textrm{P}} - \zeta ^-_{\textrm{P}}\Big ) - {2\pi G \rho \over \gamma } \Delta h^2, \end{aligned}$$

(39)

$$\begin{aligned} (\zeta )^{\tiny {\text{ harm }}}_{\tiny {\text{ P }}}&= {2\pi G \rho \over \gamma } \Delta h^2. \end{aligned}$$

(40)

We find it important to mention that in each of the Eqs. (35), (37), and (39) the term in brackets on the right-hand side is equal to the corresponding RTM reduction. In practice, only the expressions for the complete RTM correction are relevant. However, the expressions for the harmonic corrections are of interest if one is interested in the error of the harmonic corrections to gravity anomaly and gravity disturbance in Forsberg and Tscherning (1981) and (Klees et al. 2022) or in the magnitude of the harmonic correction to disturbing potential and height anomaly.

Remember that Eq. (38) is actually an exact expression for the harmonic correction to gravity anomaly. It differs from the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981) by just the term $-4\pi G \rho {\Delta h^2 \over r}$. For the Norway and Auvergne test areas (see Sect. 5), extreme tesseroid heights do not exceed 2000 m. Then, the term $4\pi G \rho {\Delta h^2 \over r}$ has a magnitude not exceeding 0.14 mGal when assuming a mass density $\rho = 2670$ kg/m$^3$. This result is very astonishing because the harmonic correction to gravity anomaly in Forsberg and Tscherning (1981) was derived along a completely different line of reasoning.

5 Application to the Norway and Auvergne test areas

We apply the expressions for the complete RTM correction and the harmonic correction to the Norway and Auvergne test areas. For details about these areas including statistics of the topography, we refer to Klees et al. (2022). Whereas (Klees et al. 2022) used a low-resolution and a high-resolution RTM surface, we will present the results for the low-resolution RTM surface, which (Klees et al. 2022) called RTM$_{36}$. RTM$_{36}$ mimics a reference gravity field complete to degree 300. It was computed as by applying a spherical Gaussian lowpass filter to the high-resolution DEM, which was truncated at its half width of $36'$. We find it important to mention that for the Norway test area, the evaluation points are the nodes of an $18^{\prime \prime } \times 18^{\prime \prime }$ grid, which formed a subgrid of the DEM, whereas for the Auvergne test area, the evaluation points are identical to the gravity stations.

Figure 3 shows a geographic rendition, Fig. 4 the histograms, and Table 1 some statistics of the complete RTM correction to gravity anomaly and height anomaly for the Norway and Auvergne test areas. Only evaluation points below the RTM surface have been included (222, 892 for the Norway test area, which corresponds to $28\%$ of all points; 95, 360 for the Auvergne test area, which corresponds to $71\%$ of all points). The corrections have large peak magnitudes of 377.2 mGal and 1.159 m (Norway test area) and 163.5 mGal and 2.128 m (Auvergne test area). The different topographic regimes in both test areas explain the differences in the complete RTM correction both in terms of spatial pattern, distribution, and range. The bi-model distribution of the complete RTM correction to height anomaly in the Auvergne test area can be explained by the distinguished topography with rather flat regions left to a line from south-west to north-east and moderate to high mountain ranges right to that line (cf. Fig. 6 in Klees et al. (2022)).

Fig. 3

Complete RTM correction to gravity anomaly and height anomaly in the Norway and Auvergne test areas. Shown are only the evaluation points which are located below the RTM surface

Fig. 4

Histograms of the complete RTM correction to gravity anomaly and height anomaly in the Norway and Auvergne test areas

We do not show corresponding information for gravity disturbances and disturbing potential. The reason why we left out the results for gravity disturbances is that the complete RTM correction does not differ much from that for gravity anomalies as the histogram of the differences in Fig. 5 reveals. In both test areas, the maximum difference is 48 $\upmu$Gal, and the median is below 1 $\upmu$Gal. The complete RTM correction to disturbing potential is not shown as it is actually a scaled complete RTM correction to height anomaly.

Fig. 5

Histogram of the differences between the complete RTM correction to gravity anomaly and gravity disturbance at evaluation points located below the RTM surface

Figures 6 and 7 show a geographic rendition and the histograms of the harmonic correction to gravity anomaly and height anomaly, respectively, for the Norway and the Auvergne test areas. Table 2 complements this information with some statistics of the harmonic corrections to disturbing potential, gravity disturbance, gravity anomaly, and height anomaly. All harmonic corrections are non-negative. Moreover, peak values of the harmonic correction to gravity anomaly and height anomaly are comparable in both test areas (263.9 mGal and 15.7 cm in the Norway test area versus 263.3 mGal and 15.8 cm in the Auvergne test area). However, there are significant differences in the distribution of the harmonic corrections with overall larger values in the Norway test area compared to the Auvergne test area (cf. Fig. 7). For instance, the $95\%$ percentiles are 161 mGal and 5.9 cm in the Norway test area compared to 72.7 mGal and 1.2 cm in the Auvergne test area.

Fig. 6

Harmonic correction to gravity anomaly and height anomaly in the Norway and Auvergne test areas

Fig. 7

Histograms of the harmonic correction to gravity anomaly and height anomaly in the Norway and Auvergne test areas

Table 2 Statistics of the harmonic correction to disturbing potential, Eq. (26), gravity disturbance, Eq. (36), gravity anomaly, Eq. (38), and height anomaly, Eq. (40) for the Norway test area (222, 892 evaluation points) and the Auvergne test area (95, 360 evaluation points). Note that the harmonic correction to gravity anomaly in Forsberg and Tscherning (1981) is identical to the harmonic correction to gravity disturbance, Eq. (36)

The majority ($60\%$ in the Norway test area and $89\%$ in the Auvergne test area) of the harmonic corrections to height anomaly do not exceed 0.5 cm. Only 25% (Norway) and $6\%$ (Auvergne) are larger than 1 cm, and only 5% are larger than 5.9 cm (Norway) and 1.2 cm (Auvergne). Values of several centimetres are only attained at a relatively low number of points. For instance, among the 222, 892 (Norway) and 95, 360 (Auvergne) evaluation points located below the RTM surface, there are only 13, 818 (Norway) and 651 (Auvergne) evaluation points with corrections exceeding 5 cm, and 2, 461 (Norway) and 188 (Auvergne) evaluation points with corrections exceeding 10 cm.

Differences between the harmonic correction to gravity anomaly and gravity disturbance are small as one can expect when comparing Eq. (38) with Eq. (36). The maximum difference is 49 $\upmu$Gal, and only 10% exceed 10 $\upmu$Gal in both test areas. These differences are at the same time identical to the approximation error of the harmonic correction to gravity anomaly in Forsberg and Tscherning (1981). The mean approximation error is just 3 $\upmu$Gal (Norway) and 0.9 $\upmu$Gal (Auvergne). Basically, a nonzero mean error of the harmonic correction to gravity anomaly in Forsberg and Tscherning (1981) may cause a bias in the computed height anomalies. The magnitude of the bias depends on the area covered by the biased gravity anomaly dataset. However, seen the small magnitude of the mean error, one can expect negligible biases if one aims at a one-centimetre quasi-geoid model. For instance, assuming that the size of the area is 500 $\times$ 500 $\hbox {km}^2$, a bias of 3 $\upmu$Gal causes a maximum height anomaly error of less than 1 mm (cf. Klees and Slobbe 2018). In reality, the bias is even smaller as it only occurs at stations which are located below the RTM surface.

6 Rectification of the results in Klees et al. (2022)

The harmonic correction to gravity disturbance and disturbing potential published in Klees et al. (2022) were computed using nth Taylor polynomials for step 2 and step 4 of the four-step procedure with $n=1$ for gravity disturbance and $n=2$ for disturbing potential. The upper bounds of the remainders of the nth Taylor polynomials provided in Klees et al. (2022) were estimated using a homogeneous spherical Earth. These upper bounds appeared to underestimate the magnitude of the remainders. Therefore, the statistics of the harmonic correction to gravity disturbance and disturbing potential in Klees et al. (2022) are not correct. This concerns in particular the extreme values and, correspondingly, the range. The largest errors are attained in deep, narrow valleys, which are numerous in the Norway test area and less frequent in the Auvergne test area. The same applies to the complete RTM correction in Klees et al. (2022), because ibid. computed it as sum of RTM reduction and harmonic correction. Here, we provide a rectification of the main results and conclusions in Klees et al. (2022):

• Klees et al. (2022) reported maximum errors of the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981) as large as the harmonic correction itself in extreme cases. This result is wrong. In reality, the error of the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981) is much smaller. Assuming a mass density in $\Omega ^-$ of 2670 $\hbox {kg m}^3$ and setting r in Eq. (38) equal to the mean radius of the Earth, $r = 6371$ km, the error in $\upmu$Gal is $-\,35.15 \Delta h^2_{\mathrm{[km]}}$, where $\Delta h$ is the tesseroid height. Hence, this error is very small. The harmonic correction in Forsberg and Tscherning (1981) is exact for gravity disturbances.

• Klees et al. (2022) reported harmonic corrections to gravity disturbance which may be negative at some locations. In reality, all harmonic corrections are non-negative.

• Klees et al. (2022) reported large nonzero mean errors for the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981), in particular for the Norway test area, which may bias the computed quasi-geoid model. This result is wrong. In reality, the mean errors for the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981) are very small in the Norway and Auvergne test areas, not exceeding a few $\upmu$Gal. The corresponding bias in the computed quasi-geoid model is negligible if one aims at a one-centimetre quasi-geoid model.

7 Summary and final remarks

We derived exact, closed-form expressions for the complete RTM correction and the harmonic correction to disturbing potential, gravity disturbance, gravity anomaly, and height anomaly using the four-step procedure suggested in Klees et al. (2022). The derivation was motivated by the fact that the expressions in Klees et al. (2022), which were based on the use of nth Taylor polynomials, appeared to be poor approximations for particular evaluation points and topographies. Particularly, the harmonic downward continuation in step 4 appeared to be unstable in some cases, which rendered the use of any nth Taylor polynomial useless, and required a Taylor-series-free approach. Key towards the new expressions was the observation that the free-air harmonic upward continuation in step 2 and the harmonic downward continuation in step 4 cancel out each other to a large extent; what is left is identical to a harmonic downward continuation in the gravitational field of the masses added to volume $\Omega ^-$. For this harmonic downward continuation, we derived exact, closed-form expressions for the disturbing potential and its radial derivative using the superposition principle of gravitating masses. This leads to surprisingly simple expressions for the complete RTM correction and the harmonic correction to disturbing potential, gravity disturbance, gravity anomaly, and height anomaly. Astonishing is the observation that the harmonic correction to gravity anomaly introduced in Forsberg and Tscherning (1981) is almost exact, with maximum errors in the two test areas not exceeding 49 $\upmu$ Gal. Even more, it is exact if interpreted as the harmonic correction to gravity disturbance. The new expressions for the complete RTM correction and the harmonic correction to disturbing potential, gravity disturbance, gravity anomaly and height anomaly are easy to implement in any existing RTM software package and do not require more resources than the computation of the harmonic correction to gravity anomaly suggested in Forsberg and Tscherning (1981).

Appendices

Appendix A

Here, we verify the expressions for the complete RTM correction and the harmonic correction derived in Sect. 4 using two synthetic mass distributions for which closed-form expressions for all relevant quantities of the four-step procedure in Klees et al. (2022) are known. Without loss of generality, we set the disturbing potential equal to the gravitational potential of the mass distribution and assume that the volume $\Omega ^+$ is free of masses, i.e. $V^+ = 0$ and $\partial _r V^+ = 0$.

First, we verify the expressions for the complete RTM correction and the harmonic correction to disturbing potential. The mass distribution is given by a large cylinder (radius $R_l$, height $h_l$, and constant mass density $\rho$) with a small cylinder (radius $R_s < R_l$, height $h_s < h_l$, and constant mass density $\rho$) cut out. The small cylinder represents $\Omega ^-$. The two cylinders share the same symmetry axis and are aligned along the top (see Fig. 8). In step 3 of the four-step procedure, the volume $\Omega ^-$ is filled with masses, which corresponds to putting back the small cylinder. Hence, $T^{\textrm{red}}$ is identical to the gravitational potential of the large cylinder. We use well-known expressions for the gravitational potential of a homogeneous cylinder for points located on the symmetry axis, which can be found in, e.g. Heiskanen and Moritz (1967) and (Kadlec 2011). In the following, we need to know the expression for the gravitational potential of a homogeneous cylinder (radius R, height h, constant mass density $\rho$) at three selected points on the symmetry axis: above the cylinder, inside the cylinder, and below the cylinder. We choose the symmetry axis as the z-axis, put the origin $z=0$ at the top of the cylinder, and assume that the positive z-axis points upwards (cf. Fig 9). Then (cf. Kadlec (2011)),

Fig. 8

Mass configuration

$$\begin{aligned} V_{\tiny {z>0}}(R,h,z)&= G \rho \pi \Big [ p - h^2 + h(l_h - 2z)\Big ], \end{aligned}$$

(41)

$$\begin{aligned} V_{\tiny {-h< z < 0}}(R,h,z)&= G \rho \pi \Big [ p - h^2 + h(l_h - 2z) - 2z^2\Big ], \end{aligned}$$

(42)

$$\begin{aligned} V_{z < -h}(R,h,z)&= G \rho \pi \Big [ p + h^2 + h(l_h + 2z)\Big ], \end{aligned}$$

(43)

where

$$\begin{aligned} l_h&= \sqrt{R^2 + (h+z)^2}, \end{aligned}$$

(44)

$$\begin{aligned} l_0&= \sqrt{R^2 + z^2}, \end{aligned}$$

(45)

$$\begin{aligned} p&= R^2 \ln \Big ( {l_h + h + z \over z + l_0}\Big ) + z(l_h - l_0). \end{aligned}$$

(46)

Moreover, due to the continuity of the gravitational potential in ${\mathcal {R}}^3$, it is

$$\begin{aligned} V(R,h,0)&{=} \lim _{z \rightarrow 0^{+}} V_{\tiny {z>0}}(R,h,z) \nonumber \\&{=} \lim _{z \rightarrow 0^{-}} V_{\tiny {{-}h< z < 0}}(R,h,z), \end{aligned}$$

(47)

$$\begin{aligned} V(R,h,{-}h)&{=} \lim _{z \rightarrow {-}h^{+}} V_{\tiny {{-}h< z< 0}}(R,h,z)\nonumber \\&{=} \lim _{z \rightarrow {-}h^{-}} V_{z < {-}h}(R,h,z). \end{aligned}$$

(48)

Point P and point Q are located on the symmetry axis with $z_{\textrm{P}} = -h_s$ and $z_\textrm{Q} = 0$, respectively. It is (remember that in our example there are no masses in $\Omega ^+$, i.e. $V^+ = 0 \Rightarrow T = T^+$):

$$\begin{aligned} T_{\tiny {\text{ P }}}&= V_{\tiny {-h_l< z < 0}}(R_l,h_l,-h_s) - V(R_s,h_s,-h_s), \end{aligned}$$

(49)

$$\begin{aligned} V^+_{\textrm{P}}&= 0, \end{aligned}$$

(50)

$$\begin{aligned} T^+_{\tiny {\text{ P }}}&= T_{\tiny {\text{ P }}}, \end{aligned}$$

(51)

$$\begin{aligned} T^+_{\tiny {\text{ Q }}}&= V(R_l,h_l,0) - V(R_s,h_s,0), \end{aligned}$$

(52)

$$\begin{aligned} T^{\tiny {\text{ red }}}_\textrm{Q}&= V(R_l,h_l,0), \end{aligned}$$

(53)

$$\begin{aligned} T^{\textrm{red}}_{\textrm{P}}&= V_{-h_l< z < 0}(R_l,h_l,-h_s), \end{aligned}$$

(54)

$$\begin{aligned} V^-_\textrm{Q}&= V(R_s,h_s,0), \end{aligned}$$

(55)

$$\begin{aligned} V^-_{\textrm{P}}&= V(R_s,h_s,-h_s) \end{aligned}$$

(56)

$$\begin{aligned} T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}&= V_{\tiny {z>0}}(R_l,h_l,-h_s). \end{aligned}$$

(57)

Note that $T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}$ is the harmonic downward continuation of $T^{\textrm{red}}$ from above the large cylinder to point P. From these equations, we can compute the complete RTM correction and the harmonic correction as

$$\begin{aligned} (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= T_{\tiny {\text{ P }}}- T^{\tiny {\text{ red,HDC }}}_{\textrm{P}}, \end{aligned}$$

(58)

$$\begin{aligned} (T)^{\tiny {\text{ harm }}}_{\textrm{P}}&= V^+_{\textrm{P}} - V^-_{\textrm{P}} - (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}. \end{aligned}$$

(59)

Equations (58) and (59) now need to be compared with the corresponding equations derived in Sect. 4, which for the given mass configuration are

$$\begin{aligned} (T)^{\tiny {\text{ cRTM }}}_{\tiny {\text{ P }}}&= - V^-_{\textrm{P}} -2\pi G \rho \Delta h^2, \end{aligned}$$

(60)

$$\begin{aligned} (T)^{\tiny {\text{ harm }}}_{\textrm{P}}&= 2\pi G \rho \Delta h^2. \end{aligned}$$

(61)

The results are shown in Table 3. They confirm that the expressions for the complete RTM correction and the harmonic correction to disturbing potential of Sect. 4 are correct.

Table 3 Key quantities of the four-step procedure for the computation of the complete RTM correction and harmonic correction to disturbing potential. All units in $\textrm{m}^2\ \textrm{s}^{-2}$. $R_l = 5000$ m, $h_l = 2000$ m, $\rho = 2670$ kg/m$^3$, $G = 6.67426 \cdot 10^{-11}$ m$^3$kg$^{-1}$s$^{-2}$

Next, we verify the expressions for the complete RTM correction and harmonic correction to the radial derivative of the disturbing potential. We consider a synthetic Earth, which is a homogeneous sphere of radius R and gravitational constant GM. The gravitational potential of the synthetic Earth is set equal to the disturbing potential. The RTM surface is assumed to be the surface $r = R + h$, where r is the radial distance from the centre of mass of the synthetic Earth. Hence, the volume $\Omega ^-$ is a spherical shell with inner radius R and outer radius $R + h$. In step 3 of the four-step procedure of Sect. 2, we fill the mass-free volume $\Omega ^-$ with mass of density $\rho$. Let the total mass in $\Omega ^-$ be denoted $M^-$. There are no masses in $\Omega ^+$, i.e. $\partial _r V^+=0 \Rightarrow \partial _r T_{\tiny {\text{ P }}}= \partial _r T^+_{\tiny {\text{ P }}}$. Note that $r_{\textrm{P}} = R$ and $r_\textrm{Q} = R+h$. Using afore-mentioned mass distributions, the following expressions apply:

$$\begin{aligned} \partial _r T_{\textrm{P}}^+&= \partial _r T_{\textrm{P}} - \partial _r V^+ = \partial _r T_{\textrm{P}} = {GM \over R^2}, \end{aligned}$$

(62)

$$\begin{aligned} \partial _r T_\textrm{Q}^+&= \partial _r T_{\textrm{P}}^+ + (\partial _r T)_{\textrm{P} \rightarrow \text{ Q }}^{\tiny \text{ UC }} = {GM \over (R+h)^2}, \end{aligned}$$

(63)

$$\begin{aligned} \partial _r T_\textrm{Q}^{\textrm{red}}&= \partial _r T_\textrm{Q}^+ + \partial _r V_\textrm{Q}^- = {G(M+M^-) \over (R+h)^2}, \end{aligned}$$

(64)

$$\begin{aligned} \partial _r T_{\textrm{P}}^{\textrm{red,HDC}}&= \partial _r T_\textrm{Q}^{\textrm{red}} + (\partial _r T)_{\tiny {\text{ Q } \rightarrow \text{ P }}}^{\tiny \text{ HDC }} = {G(M+M^-) \over R^2}, \end{aligned}$$

(65)

$$\begin{aligned} (\partial _r V)_{\textrm{P}}^{-,\textrm{HDC}}&= {GM^- \over R^2}. \end{aligned}$$

(66)

Using these expressions, we can compute the complete RTM correction, $(\partial _r T)_{\textrm{P}}^{\textrm{cRTM}}$ and the harmonic correction, $(\partial _r T)_{\textrm{P}}^{\textrm{harm}}$ as

$$\begin{aligned} (\partial _r T)_{\textrm{P}}^{\textrm{cRTM}}&= (\partial _r V)_{\textrm{P}}^+ - (\partial _r V)_{\textrm{P}}^{-,\textrm{HDC}} = - (\partial _r V)_{\textrm{P}}^{-,\textrm{HDC}}, \end{aligned}$$

(67)

$$\begin{aligned} (\partial _r T)_{\textrm{P}}^{\textrm{harm}}&= (\partial _r V)_{\textrm{P}}^{-,\textrm{HDC}} - \partial _r V_{\textrm{P}}^- = (\partial _r V)_{\textrm{P}}^{-,\textrm{HDC}} . \end{aligned}$$

(68)

Note that in the last equation, we used the fact that $\partial _r V_{\textrm{P}}^- = 0$. Remember that the radial derivative of the gravitational potential of a homogeneous spherical shell is continuous in ${\mathcal {R}}^3$ and zero inside the spherical shell.

Equations (67) and (68) need to be identical with the expressions for the complete RTM correction to $\partial _r T$, Eq. (27), and the harmonic correction to $\partial _r T$, Eq. (28), which are for the given mass configuration equal to (remember that $\partial _r V^+_{\textrm{P}} = 0$)

$$\begin{aligned} (\partial _r T)_{\textrm{P}}^{\textrm{cRTM}}&= 4\pi G\rho \Delta h, \end{aligned}$$

(69)

$$\begin{aligned} (\partial _r T)_{\textrm{P}}^{\textrm{harm}}&= -4\pi G\rho \Delta h, \end{aligned}$$

(70)

The results in Table 4 provide the evidence, that this is indeed so, i.e. the expressions for the complete RTM correction and the harmonic correction to the radial derivative of the disturbing potential of Sect. 4 are correct.

Table 4 Key quantities of the four-step procedure for the computation of the complete RTM correction and harmonic correction to the radial derivative of the disturbing potential. $GM = 3,986,004 418 \cdot 10^{14}$ m$^3$s$^{-2}$, $R = 6,371,000$ m, $\rho = 2670$ kg/m$^3$

Appendix B

We want to demonstrate that using a Taylor series for the harmonic downward continuation of step 4 as suggested in Klees et al. (2022) may be unstable in some cases with higher order terms increasing rapidly with alternating signs. Moreover, we show that using a nth Taylor polynomial with $n=1$ for gravity anomaly and gravity disturbance, and $n=2$ for disturbing potential and height anomaly as suggested in Klees et al. (2022) may provide poor approximations in some cases. This also implies that the upper bounds provided in Klees et al. (2022) are not correct. In particular, in deep, narrow valleys (i.e. in areas where harmonic corrections take up large values), they may underestimate the magnitude of the remainder significantly. Note that the problem is not solved automatically by computing the complete RTM correction, simply because the harmonic downward continuation in step 4 is also part of the complete RTM correction. Combining step 2 and step 4 also does not solve this problem, as an analytic downward continuation through the masses in $\Omega ^-$ also appears in the sum of step 2 and step 4. The solution to this problem, which was provided in Sect. 4 indeed solves this problem.

Fig. 9

Computation of $V^{-,\textrm{HDC}}_{\textrm{P}}$

We consider a single cylinder of radius R and height h (cf. Fig. 9). As in Appendix A, the z-axis is identical to the symmetry axis, the top of the cylinder is $z=0$ and the positive z-axis points upwards. Equations (41)–(43) describe the gravitational potential of the cylinder for points on the symmetry axis above, inside and below the cylinder, respectively. We consider the harmonic downward continuation of the gravitational potential $V_{\tiny {z>0}}(R,h,z)$ from a point Q on top of the cylinder (i.e. $z_\textrm{Q} = 0$) to a point P at the bottom of the cylinder (i.e. $z_{\textrm{P}} = -h)$. The harmonic downward continuation of the gravitational potential above the top of the cylinder to the point P is given by $V_{\tiny {z>0}}(R,h,z_{\textrm{P}})$. Klees et al. (2022) used the nth Taylor polynomial about $z = z_\textrm{Q} = 0$ to compute the harmonic downward continuation to point P as

$$\begin{aligned} V_{\textrm{P}}^{\textrm{HDC,n}}{} & {} = V_{\tiny {z>0}}(R,h,0) + \sum _{m=1}^n {1 \over m!}\lim _{z \rightarrow 0^+}\nonumber \\{} & {} \quad \Biggl ({\partial ^m V_{\tiny {z>0}}(R,h,z) \over \partial z^m}\Biggr ) (-h)^m. \end{aligned}$$

(71)

They claim that $n=2$ provides a sufficiently accurate approximation to $V_{\textrm{P}}^{\textrm{HDC}}$. We will show using the simple example of a homogeneous cylinder that $V_{\textrm{P}}^{\textrm{HDC,n}}$ may differ significantly from $V_{\textrm{P}}^{\textrm{HDC}}$ not only for $n=2$, but also for larger values of n.

Table 5 Harmonic downward continuation of the gravitational potential of a homogeneous cylinder (radius R, height h, mass density $\rho = 2670$ kg/m$^3$) to a point P at the bottom of the cylinder ($z_\textrm{P} = -h$) using an nth Taylor polynomial about Q. Gravitational potential in units of m$^2$/s$^2$

Table 5 shows the results for various choices of R, h, and n. Obviously, $V_{\textrm{P}}^{\textrm{HDC,n}}$ is a poor approximation to $V_{\textrm{P}}^{\textrm{HDC}}$ if h/R is large (e.g. column 2 and 3 in Table 5). If the ratio h/R decreases, the approximation error decreases with increasing n. An analysis of the term

$$\begin{aligned} \lim _{z \rightarrow 0^+}\Biggl ({\partial ^m V_{\tiny {z>0}}(R,h,z) \over \partial z^m} \Biggr ) (-h)^m \end{aligned}$$

(72)

in the Taylor series reveals that it comprises a factor $\Big ({h \over R}\Big )^{m-1}$, which dominates this term. Hence, for a cylinder, we can expect no convergence of $V_{\textrm{P}}^{\textrm{HDC,n}}$ if $h/R > 1$. On the other hand, if $h/R < 1$, $V_{\textrm{P}}^{\textrm{HDC,n}}$ may provide a good approximation to $V_{\textrm{P}}^{\textrm{HDC}}$ already for moderate values n.

For practical applications, this result implies that the harmonic downward continuation from Q on the RTM surface to P on the Earth’s surface using a nth Taylor polynomial does not provide a good approximation in deep, narrow valleys (the equivalent of $h/R > 1$ for a cylinder). Only if the width of the valley is greater than twice its depth (corresponding to $h/R < 1$ for the cylinder), the nth Taylor polynomial may provide a reasonable (relative error on the order of a few percent) approximation already for low n, e.g. $n=2$ as suggested in Klees et al. (2022). In general, however, a nth Taylor polynomial should not be used for the harmonic downward continuation $V_{\textrm{P}}^{\textrm{HDC}}$. The same applies to the analytic downward continuation of linear functionals of the disturbing potential such as gravity anomalies, gravity disturbances, and height anomalies.