Abstract
In this paper, we derive improved expressions for the harmonic correction to gravity and, for the first time, expressions for the harmonic correction to potential and height anomaly. They need to be applied at stations buried inside the masses to transform internal values into harmonically downward continued values, which are then input to local quasi-geoid modelling using least-squares collocation or least-squares techniques in combination with the remove-compute-restore approach. Harmonic corrections to potential and height anomaly were assumed to be negligible so far resulting in yet unknown quasi-geoid model errors. The improved expressions for the harmonic correction to gravity, and the new expressions for the harmonic correction to potential and height anomaly are used to quantify the approximation errors of the commonly used harmonic correction to gravity and to quantify the magnitude of the harmonic correction to potential and height anomaly. This is done for two test areas with different topographic regimes. One comprises parts of Norway and the North Atlantic where the presence of deep, long, and narrow fjords suggest extreme values for the harmonic correction to potential and height anomaly and corresponding large errors of the commonly used approximation of the harmonic correction to gravity. The other one is located in the Auvergne test area with a moderate topography comprising both flat and hilly areas and therefore may be representative for many areas around the world. For both test areas, two RTM surfaces with different smoothness are computed simulating the use of a medium-resolution and an ultra-high-resolution reference gravity field, respectively. We show that the errors of the commonly used harmonic correction to gravity may be as large as the harmonic correction itself and attain peak values in areas of strong topographic variations of about 100 mGal. Moreover, we show that this correction may introduce long-wavelength biases in the computed quasi-geoid model. Furthermore, we show that the harmonic correction to height anomaly can attain values on the order of a decimetre at some points. Overall, however, the harmonic correction to height anomaly needs to be applied only in areas of strong topographic variations. In flat or hilly areas, it is mostly smaller than one centimetre. Finally, we show that the harmonic corrections increase with increasing smoothness of the RTM surface, which suggests to use a RTM surface with a spatial resolution comparable to the finest scales which can be resolved by the data rather than depending on the resolution of the global geopotential model used to reduce the data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Local quasi-geoid modelling has become a routine task despite the fact that the mathematical theory is still incomplete (e.g., Sanso and Sideris 2013). Reducing the data for the contribution of a global geopotential model (GGM) and for the gravitational signal of the topography (and, if applicable, the bathymetry) appeared to be necessary to obtain an accurate local model. The former ensures that the long wavelengths have less energy, which makes it possible to ignore data far outside the area of interest when computing the local quasi-geoid model. The latter ensures that the energy of short wavelengths (ideally those which cannot be modelled) is significantly reduced, and the residual field, being harmonic in a larger domain, is smoother than the original one.
There are several types of topographic reduction, depending on the method used in local quasi-geoid modelling, see Tziavos and Sideris (2013) for a review. The subject of this study is the so-called residual terrain model (RTM) reduction, which has been introduced in (Forsberg and Tscherning 1981). This type of topographic reduction is part of the remove-compute-restore approach and frequently used in the framework of Molodensky’s theory of the quasi-geoid (Denker 2013; Tziavos and Sideris 2013). Given the fact that in local quasi-geoid modelling, the data are always reduced for the contribution of a GGM, the aim of the RTM correction is to reduce the data for the gravitational signal of the masses, which are not captured by the GGM. To do so, the real Earth’s topography (including bathymetry if applicable) is replaced by a smoother topography (the RTM topography), and the data are reduced for the gravitational effect of the mass deficit between the two topographies. In the past, this idea was implemented in different ways (cf., Forsberg and Tscherning 1981; Forsberg 1984; Denker and Wenzel 1986; Vermeer and Forsberg 1992; Hirt et al. 2014); see also the review paper (Tziavos and Sideris 2013).
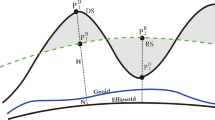
In this study, we follow the implementation in (Forsberg and Tscherning 1981). The body with RTM topography is referred to as the RTM-reduced earth and its surface is referred to as the RTM surface (cf. Fig. 1). A well-known conceptual problem of this implementation arises for data points located below the RTM surface, a situation frequently encountered in or close to areas of strong topographic variations. After RTM reduction, the gravity field functionals neither represent boundary values nor values inside the harmonic domain of the gravitational potential of the RTM-reduced earth. To address this conceptual problem, Forsberg and Tscherning (1981) suggested an additional correction to be applied to gravity anomalies at those stations, which they refer to as the harmonic correction. After RTM and harmonic correction have been applied, the reduced gravity anomalies are consistent with a harmonically downward continued gravitational potential of the RTM-reduced earth. The downward continuation is not done strictly, but comprises several approximations. The most important one is that for every buried data point the action of the masses encompassed in the RTM body is modelled as a Bouguer plate of a thickness equal to the vertical distance of the data point to the RTM surface. That is, to every data point a planar Bouguer plate is assigned with its own vertical position and thickness. The advantage of this simplification is that the harmonic correction can be computed easily (cf. Sect. 2). The downside is that errors in the reduced gravity anomalies are introduced, which among others, depend on the deviation of the RTM surface from a planar surface, in particular in some neighbourhood of the data point. The deviation depends on how the RTM surface has been constructed from a high-resolution model of the topography and bathymetry. A common approach is to apply a low-pass filter, and to relate the cut-off frequency of this filter to the maximum spherical harmonic degree of the GGM. Then, the higher the maximum degree is, the more the RTM surface differs from the surface of a Bouguer plate. Errors in the reduced gravity anomalies are also introduced if the Bouguer plate is replaced by a finite Bouguer plate, a spherical shell or a spherical cap. (e.g., Kadlec 2011). Forsberg and Tscherning (1981) do not apply a harmonic correction to disturbing potential or height anomaly (see also Forsberg 1984). They argue that if the RTM surface is smooth and does not differ much from a Bouguer plate in the neighbourhood of the station, the harmonic correction for potential and height anomaly are close to zero, and may be neglected.
The main objective of this paper is twofold. First, for stations located below the RTM surface, we derive new formulas for harmonically downward continued gravity and potential values referring to the RTM-reduced earth bounded by the RTM surface. Second, we use the new formulas and investigate (i) the approximation error of the harmonic correction to gravity as suggested in (Forsberg and Tscherning 1981), and (ii) the magnitude of the harmonic correction to potential and height anomaly, which were neglected until now. We do this numerically for two areas with different topographic regimes.
The paper is organised as follows. In Sect. 2, we briefly summarise and elaborate on the harmonic correction to gravity in (Forsberg and Tscherning 1981). In Sect. 3, we derive the new formulas and extract from them new expressions for the harmonic correction to gravity and potential and compare them with the harmonic correction in (Forsberg and Tscherning 1981). In Sect. 4, we describe the results of experiments, which aim at a verification of the formulas derived in Sect. 3, and a quantification of (i) the approximation error of the harmonic correction to gravity in (Forsberg and Tscherning 1981) and (ii) the magnitude of the harmonic corrections to potential and height anomaly. In Sect. 5, we provide a summary and some concluding remarks.
2 Harmonic correction of Forsberg and Tscherning
The RTM correction in (Forsberg and Tscherning 1981) reduces an Earth gravity field functional to the corresponding functional of a RTM-reduced earth, which is bounded by the RTM surface, s. A point \(P \in S\) located above the RTM surface hangs in free air whereas a point \(P \in S\) located below the RTM surface is buried inside the masses of the RTM-reduced earth (cf. Fig. 1). Hence, a reduced gravity field functional at a point \(P \in S\) located below the RTM surface represents a functional inside the masses of the RTM-reduced earth. The harmonic correction of (Forsberg and Tscherning 1981) aims at a transformation of this internal gravity field functional into a harmonically downward continued gravity field functional. Forsberg and Tscherning (1981) apply this transformation only to gravity.
Let \(P \in S\) be a point on the Earth’s surface (i.e., on the topography or the sea surface); let Q be the intersection of the ellipsoidal normal through P with the RTM surface, i.e., \(Q \in s\). As we assume that P is located below the RTM surface, the ellipsoidal height difference \(\Delta h = h_Q - h_P\) is positive. The transformation from an internal gravity value to a harmonically downward continued gravity value according to Forsberg and Tscherning (1981) is done in four steps (e.g., Gerlach 2003, p. 71).
Step 1 Add \(2\pi G \rho _0 \Delta h\) to the gravity at P, g(P). This corresponds to the removal of a Bouguer plate of thickness \(\Delta h\) and mass density \(\rho _0\), which is located on top of point P.
Step 2 Use a model of the free-air gravity gradient along the ellipsoidal normal through P, and upward continue gravity from \(P \in S\) to \(Q \in s\). This provides gravity at Q, g(Q).
Step 3 Restore the Bouguer plate of step 1; this increases g(Q) of step 2 with \(2\pi G \rho _0 \Delta h\). Note that steps 1 to 3 are comparable to the Poincaré and Prey reduction used in Helmert’s theory ( Heiskanen and Moritz 1967, Sect. 4.3).
Step 4 Downward-continue g(Q) of step 3 using the free-air gravity gradient of step 2. This provides a gravity value at P, which is consistent with a harmonically downward continued potential of the RTM-reduced earth with boundary s.
After step 4, gravity g(P) has increased with
Equation (1) is the harmonic correction to gravity in (Forsberg and Tscherning 1981). Note that although it is called a correction, it is added to the RTM-reduced gravity value to obtain a harmonically downward continued gravity value, whereas the RTM correction is subtracted from measured gravity. In this paper, we follow the sign convention in (Forsberg and Tscherning 1981) for the harmonic correction. The increase of Eq. (1) is twice the effect of a Bouguer plate of thickness \(\Delta h\) and density \(\rho _0\). The same result is obtained if in step 3 the Bouguer plate is not restored but condensed on an infinite plane through point P. This interpretation is used in (Forsberg and Tscherning 1981). Applying the same procedure to a height anomaly is meaningless as the gravitational potential of a Bouguer plate is not defined. However, Forsberg and Tscherning (1981) argue that if the RTM surface is smooth enough in some neighbourhood of the data point, the harmonic correction to potential (likewise to height anomaly) at this point is very small and may be neglected. Ignoring the harmonic correction to potential implies that no difference is made between the potential inside the masses and a harmonically downward continued potential.
Note that Eq. (1) still applies if the Bouguer plate is replaced by a spherical shell. This follows directly from the formulas derived in Kadlec (2011) and is a result of potential theory (Martinec 1998). However, in case of a spherical shell, the harmonic correction to height anomaly is well-defined and given by
where \(\gamma \) is normal gravity at P (cf. Kadlec 2011). Assuming \(\rho _0 = 2670\) kg/m\(^3\) and \(\Delta h=500\) m, this is about 2.8 cm, i.e., not negligible in cm-accuracy quasi-geoid modelling. The effect is below 1 cm if \(\vert \Delta h \vert < 300\) m. This simple example already indicates that depending on the situation, the harmonic correction to height anomaly may not be neglected.
The harmonic correction to gravity in (Forsberg and Tscherning 1981) is an approximation, and to our knowledge, the approximation error has not been investigated yet. A major conceptual weakness of this approximation is that the vertical position of the Bouguer plate differs per data point. Even if two data points are just a few kilometres apart, the vertical positions of the two Bouguer plates may differ by tens or hundreds of metres. This introduces inconsistencies in the reduced gravity values, in particular between neighboured data points.
There are several attempts in literature to address the conceptual weakness of the harmonic correction in (Forsberg and Tscherning 1981). For instance, Kadlec (2011) suggested to replace the (infinite) Bouguer plate by a finite one or a finite spherical shell (i.e., a spherical cap), and writes the RTM correction as the difference between the complete effect of the topography and the complete effect of the RTM topography. However, this does not provide gravity field functionals consistent with a harmonically downward continued potential field. Therefore, this idea should not be used in the context of local quasi-geoid modelling. Omang et al. (2012) suggested to upward continue inside the masses observed gravity field functionals to the RTM surface ignoring the horizontal components of the gravity gradient vector. After RTM reduction, the gravitational potential of the RTM-reduced earth fulfils Laplace’s equation, i.e., \(\Delta V(P) = -4 \pi G \rho _0\), and assuming vanishing horizontal gravity gradients, it is \(V_{zz} = -4 \pi G \rho _0\). Therefore, the upward continuation to the RTM surface changes gravity by \(- 4 \pi G \rho _0 \Delta h\). In this way, they obtain gravity field functionals at points on the RTM surface, and avoid the problem of a harmonic correction. The main disadvantage of this approach is that errors in the vertical gradient of gravity, specially due to variations of density, directly propagate into the upward continued gravity anomalies proportional to the height difference \(\Delta h\).
3 The complete RTM correction
Here, we follow a different approach for data points located below the RTM surface. The approach is applicable to all methods used in local quasi-geoid modelling which do not require data located on the boundary of the harmonic domain. The approach does not move terrestrial data to the RTM surface. This is important, because moving data from the Earth’s surface (land topography or sea surface) to the RTM surface may introduce significant errors in areas where the distance to the RTM surface is large (e.g., the Norwegian fjords) due to a lack of knowledge of the external potential field. This applies in particular to gravity anomalies due to uncertainties in the free-air vertical gravity gradient. Furthermore, the approach provides harmonically downward continued data referring to a RTM-reduced earth which is bounded by the RTM surface like the harmonic correction in (Forsberg and Tscherning 1981) does, but with a much higher accuracy and not limited to gravity anomalies. This aspect is very important if gravity data are combined with other gravity field functionals in local quasi-geoid modelling as only then the reduced datasets are consistent in the sense that they all refer to a harmonically downward continued field.
Intrinsically, the new equations not only comprise the RTM corrections but also improved harmonic corrections. We refer to them as the complete RTM corrections. The equations are derived for two types of gravity field functionals, i.e., for gravity g and potential W. Dividing the equation for W by the normal gravity at the telluroid point provides the equation for height anomaly. The derivation of the corresponding equations for other gravity field functionals is out of the scope of this study, but straightforward. We find it appropriate to note that for all other points (i.e., points located above the RTM surface), the complete RTM correction is identical to the RTM correction in (Forsberg and Tscherning 1981).
We assume that the data point P is located on the land topography or the sea surface. As before, a point Q is the intersection of the ellipsoidal normal through P with the RTM surface. \(\Omega \) denotes the volume between the Earth’s surface (i.e., the topography on land or the bathymetry at sea) and the RTM surface. The part of the volume \(\Omega \) that is located above the RTM surface is denoted \(\Omega ^+\); likewise, the volume below the RTM surface is denoted \(\Omega ^-\). The RTM-reduced earth is mass-free in volume \(\Omega ^+\) and is filled with masses of constant density \(\rho _0\) in volume \(\Omega ^-\), where \(\rho _0\) is commonly set equal to a mean crustal density (cf. Figs. 1, 2).
\(\delta V_\text {RTM}^+\) and \(\delta g_\text {RTM}^+\) denote the gravitational potential and gravitational strength, respectively, of the masses inside the volume \(\Omega ^+\). Likewise, \(\delta V_\text {RTM}^-\) and \(\delta g_\text {RTM}^-\) denote the gravitational potential and gravitational strength, respectively, of the masses added to the volume \(\Omega ^-\).
Note that when computing \(\delta g_\text {RTM}^+\), \(\delta g_\text {RTM}^-\), \(\delta V_\text {RTM}^+\), and \(\delta V_\text {RTM}^-\) we need to distinguish between the five cases depicted in Fig. 2 and listed in Table 1. Three of them require to compute two tesseroids per grid cell (Heck and Seitz 2007; Grombein et al. 2013).
3.1 Complete RTM correction for points located below the RTM surface
Let \(\delta g_\text {corr}(P)\) and \(\delta W_\text {corr}(P)\) be the complete RTM correction to measured gravity and potential, respectively. Then, we define the reduced gravity \(g_\text {red}(P)\) and reduced potential \(W_\text {red}(P)\) as
Note that \(g_\text {red}(P)\) and \(W_\text {red}(P)\) refer to a RTM-reduced earth, which is mass-free outside the RTM surface; moreover, they represent harmonically downward continued potential field functionals at points \(P \in S\) located below the RTM surface. Whenever convenient, the value of a function f at a point P is either written as f(P) or as \(f_P\). All equations are provided with error terms. The factors appearing in the error terms are derived for an isotropic potential field for which applies
The complete RTM correction requires four steps to be taken:
Step 1 Move the masses inside \(\Omega ^+\) to infinity and correct gravity and potential for the gravitational effect this has. If the effect on gravity is denoted \(\delta g_\text {RTM}^+(P)\) and the effect on potential is denoted \(\delta V_\text {RTM}^+(P)\), we obtain reduced values of gravity, \(g^+(P)\), and potential, \(W^+(P)\), respectively, i.e.,
Note that all evaluation points P are located on the Earth’s surface (land topography or sea surface), i.e., \(P \in S\) (cf. Figs. 1, 2).
Step 2 For points \(P \in S\) located below the RTM surface (i.e., points for which \(\Delta h = h_Q - h_P > 0\), where h is the ellipsoidal height), upward continue gravity and potential obtained in step 1 to the corresponding points \(Q \in s\); data at all other points \(P \in S\) are left unchanged:
where R is the mean radius of the Earth and \(\varepsilon = \frac{\Delta h}{R}\). Terms of the order of \({\mathcal {O}}(\varepsilon ^2)\) and \({\mathcal {O}}(\varepsilon ^3)\) are neglected in the expansion of gravity and potential, respectively. Note that \(\frac{\partial g^+}{\partial h}\) in Eq. (8) and \(\frac{\partial ^2 W^+}{\partial h^2}\) in Eq. (9) have step discontinuities across the surface bounding the masses. Therefore, it is appropriate to mention here that \(\frac{\partial g^+}{\partial h}\Big \vert _P\), \(\frac{\partial W^+}{\partial h}\Big \vert _P\) and \(\frac{\partial ^2 W^+}{\partial h^2}\Big \vert _P\) are free-air gradients which apply to a modified Earth which has no masses in \(\Omega ^+\), i.e.,
where \(P'\) is a point on the ellipsoidal normal through P with ellipsoidal height \(h_P + \delta \). Using the difference quotient, Eqs. (10) and (11) may be approximated by
respectively.
Step 3 Fill the volume \(\Omega ^-\) with mass so that the mass density equals \(\rho _0\), and correct gravity and potential for the gravitational effect this has (cf. Figs. 1, 2). For data that have been upward continued in step 2, the gravitational effect has to be computed at the points \(Q \in s\). If \(\delta g_\text {RTM}^-(Q)\) is the effect on gravity and \(\delta V_\text {RTM}^-(Q)\) the effect on potential, we obtain reduced values of gravity and potential, respectively, i.e.,
Note that for all other points, the reduced values of gravity and potential refer to points \(P \in S\).
Step 4 Perform a harmonic downward continuation of the data referring to points \(Q \in s\) (i.e., data that have been upward continued in step 2) to their original locations \(P \in S\) on the Earth’s surface (i.e., land topography or sea surface) along the ellipsoidal normal through P:
The gradients in the last two equation are free-air gradients which apply to a RTM-reduced earth bounded by the RTM surface, i.e.,
and \(Q'\) is a point on the ellipsoidal normal through Q with ellipsoidal height \(h_Q + \delta \). Hence, for points P located below the RTM surface, \(g_\text {red}(P)\) and \(W_\text {red}(P)\) represent harmonically downward continued quantities.
Inserting Eqs. (6), (8), and (14) into Eq. (16) yields
Likewise, inserting Eqs. (7), (9), and (15) into Eq. (17) yields
In Eq. (21), the term proportional to \(\Delta h\) can be simplified. To do so, we take the partial derivative with respect to h of Eqs. (14) and (8), respectively, and obtain,
Inserting the last equation into Eq. (21) gives
From Eq. (14),
which allows to simplify the error term of Eq. (24) and provides the final form of Eq. (21):
The term in brackets on the right-hand side of Eq. (26) is the complete RTM correction to gravity as defined in Eq. (3). Ignoring the error term provides the approximation
Norway test area: harmonic correction to gravity, \(\delta g_\text {harm}(P)\) (Eq. (37)), the difference between \(\delta g_\text {harm}(P)\) and the harmonic correction in (Forsberg and Tscherning 1981), \(\delta g_\text {harm}(P) - \delta g^{FT}_\text {harm}(P)\), and the harmonic correction to height anomaly, \(\delta \zeta _\text {harm}(P)\) (based on Eq. (41)). The areas where topography or sea surface is located above the RTM surface are shown in white
Equation (22) can be simplified. First, taking the first and second partial derivative of Eq. (15) with respect to h, we find
Inserting this result into Eq. (22) gives
A Taylor series expansion of \(W^+\) about P and Q, respectively, shows that in Eq. (29) the last term before the error term is of the order of \(4W^+(Q) {\mathcal {O}}(\varepsilon ^4)\), i.e., it can be neglected. Furthermore, the error term in Eq. (29) can be simplified. From Eq. (15), it follows that
hence,
which provides the final from the Eq. (22):
The term in brackets on the right-hand side of Eq. (32) is the complete RTM correction to potential as defined in Eq. (4). Ignoring the error term provides the approximation
We may achieve the same results within error in just three steps. This is shown in “Appendix A”.
3.2 Complete RTM correction for arbitrary data points
So far, we derived new formulas for the complete RTM correction for data points located below the RTM surface. For all other data points, the well-known RTM correction in (Forsberg and Tscherning 1981) applies. Hence, we obtain the following formulas for arbitrary data points \(P \in S\):
-
(i)
Gravity For gravity at a point \(P \in S\) with \(\Delta h = h_Q - h_P < 0\) (i.e., P is located above the RTM surface and therefore in free air after mass redistribution), the reduced value of gravity at this point is
$$\begin{aligned} \begin{aligned} g_\text {red}(P)&= g(P) - \Big [ \delta g_\text {RTM}^+(P)- \delta g_\text {RTM}^-(P)\Big ] \,, \quad \Delta h < 0 \,. \end{aligned} \end{aligned}$$(34)The term in brackets is identical to the RTM correction given in Forsberg and Tscherning (1981) (see also Forsberg and Tscherning (1997)). At a point \(P \in S\) with \(\Delta h = h_Q - h_P > 0\) (i.e., P is located inside the masses of the RTM-reduced earth), the reduced value of gravity up to terms \(3 \delta g_\text {RTM}^-(Q){\mathcal {O}}(\varepsilon ^2)\) is
$$\begin{aligned} g_\text {red}(P)&= g(P) - \Big [ \delta g_\text {RTM}^+(P)- \delta g_\text {RTM}^-(Q)+ {\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \Delta h \Big ] \,, \quad \nonumber \\&\quad \Delta h > 0 \,. \end{aligned}$$(35)We re-write Eq. (35) as
$$\begin{aligned} \begin{aligned} g_\text {red}(P)&= g(P) {-} \Big [ \delta g_\text {RTM}^+(P)- \delta g_\text {RTM}^-(P)\Big ] \\&\qquad \quad {+}\Big [ {-} \delta g_\text {RTM}^-(P)+ \delta g_\text {RTM}^-(Q)- {\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \Delta h\Big ], \ \Delta h {>} 0 \,. \end{aligned}\nonumber \\ \end{aligned}$$(36)The first two terms on the right-hand side of Eq. (36) represent a gravity value inside the masses of the RTM-reduced earth. Hence, the last term in brackets reduces this internal gravity value into a harmonically downward continued gravity value, i.e., it is the new formula for the harmonic correction to gravity:
$$\begin{aligned} \delta g_\text {harm}(P)&= - \delta g_\text {RTM}^-(P)+ \delta g_\text {RTM}^-(Q)\nonumber \\ {}&\quad - {\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \Delta h \,, \quad \Delta h > 0. \end{aligned}$$(37)Equation (37) is correct up to terms \(3 \delta g_\text {RTM}^-(Q){\mathcal {O}}(\varepsilon ^2)\).
-
(ii)
Potential For a point \(P \in S\) with \(\Delta h = h_Q - h_P < 0\), the reduced value of the potential is
$$\begin{aligned} \begin{aligned} W_\text {red}(P)&= W(P) - \Big [ \delta V_\text {RTM}^+(P)- \delta V_\text {RTM}^-(P)\Big ] \,, \quad \Delta h < 0 \,. \end{aligned} \end{aligned}$$(38)If \(P \in S\) with \(\Delta h = h_Q - h_P > 0\), the improved expression for the reduced potential up to terms \(\delta V_\text {RTM}^-(Q){\mathcal {O}}(\varepsilon ^3)\) is
$$\begin{aligned} W_\text {red}(P)&= W(P) - \Big [ \delta V_\text {RTM}^+(P)- \delta V_\text {RTM}^-(Q)- {\partial \delta V_\text {RTM}^-\over \partial h}\Big \vert _Q \nonumber \\&\quad \times (-\Delta h) - {1 \over 2} {\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q\,\Delta h^2 \Big ],\; \Delta h> 0 \,, \nonumber \\&= W(P) - \Big [ \delta V_\text {RTM}^+(P)- \delta V_\text {RTM}^-(Q)- \delta g_\text {RTM}^-(Q)\Delta h \nonumber \\&\quad - {1 \over 2} {\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q\,\Delta h^2 \Big ],\; \Delta h > 0 \,. \end{aligned}$$(39)Formally, Eq. (39) may be re-written as
$$\begin{aligned} W_\text {red}(P)= & {} W(P) - \Big [ \delta V_\text {RTM}^+(P)- \delta V_\text {RTM}^-(P)\Big ] \nonumber \\&+ \Big [ - \delta V_\text {RTM}^-(P)+ \delta V_\text {RTM}^-(Q)- {\partial \delta V_\text {RTM}^-\over \partial h}\Big \vert _Q \nonumber \\&\Delta h - {1 \over 2} {\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q\,\Delta h^2\Big ],\;\Delta h > 0 \,, \end{aligned}$$(40)where the second term in brackets is the new formula for the harmonic correction to potential, i.e.,
$$\begin{aligned} \delta V_\text {harm}&= - \delta V_\text {RTM}^-(P)+ \delta V_\text {RTM}^-(Q)- {\partial \delta V_\text {RTM}^-\over \partial h}\Big \vert _Q \,\Delta h \nonumber \\&\quad - {1 \over 2} {\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q\,\Delta h^2 \,, \quad \nonumber \\&\quad \Delta h > 0 \,. \end{aligned}$$(41)
Equation (41) is correct up to terms \(\delta V_\text {RTM}^-(Q){\mathcal {O}}(\varepsilon ^3)\).
Equations (37) and (41) involve the terms \({\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \Delta h\) and \({1 \over 2}{\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q \Delta h^2\), respectively. To obtain an idea about the magnitude of these terms, we consider a volume \(\Omega ^-\), which consists of a spherical cap of radius \(\psi _0\) and thickness \(\Delta h\). We locate the point Q at the top centre of the spherical cap to maximise the magnitude of the two terms. We use Eq. (2.134) on p. 50 of Kadlec (2011). If \(\psi _0 = 5^\prime \), \(\Delta h = 1000\) m, and the density contrast of the masses in \(\Omega ^-\) is 2670 kg/m\(^3\), we find a value of \({\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \thickapprox - {\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q= 0.012\) mGal/m. Hence, \({\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \Delta h = 12\) mGal, and \({1 \over 2}{\partial ^2 V_{RTM}^- \over \partial h^2}\Big \vert _Q \Delta h^2 = 0.06\) m\(^2\)/s\(^2\). The former is much larger than the accuracy of today’s gravity anomaly datasets; the latter is below the accuracy level achievable today in local gravity field modelling. If \(\Delta h\) is halved to \(\Delta h = 500\) m, the term \({\partial \delta g_\text {RTM}^-\over \partial h}\Big \vert _Q \Delta h\) reduces by a factor of four to about 3.0 mGal. This is still above the noise standard deviation of today’s terrestrial gravity anomaly datasets. From this, we expect that in moderate terrain, only the term \({1 \over 2}{\partial ^2 V_{RTM}^- \over \partial h^2}\Big \vert _Q \Delta h^2\) in Eq. (41) may be neglected.
3.3 Approximation error of the harmonic correction of Forsberg and Tscherning
The complete RTM correction according to Forsberg and Tscherning (1981), \(\delta g_\text {corr}^\text {FT}(P)\) and \( \delta W_\text {corr}^\text {FT}(P)\), respectively, is the sum of RTM correction and harmonic correction, with the understanding that the latter is only applied to gravity at points located below the RTM surface and is assumed to be zero for potential, i.e.,
where \(\Delta h = h_Q - h_P\), and \(\delta g^{FT}_\text {harm}(P)\) is the harmonic correction of Eq. (1) proposed in (Forsberg and Tscherning 1981).
If \(\Delta h > 0\), there is a difference between the complete RTM correction \(\delta g_\text {corr}(P)\) of Eq. (27) and \(\delta g_\text {corr}^\text {FT}(P)\) of Eq. (42). Assuming that the approximation error of \(\delta g_\text {corr}(P)\) is much smaller than that of \(\delta g_\text {corr}^\text {FT}(P)\) (this is confirmed by the numerical results of Sect. 4), we may refer to the difference as the approximation error of the harmonic correction to gravity in (Forsberg and Tscherning 1981):
Likewise, if \(\Delta h > 0\), there is a difference between the complete RTM correction to potential, \(\delta W_\text {corr}(P)\) of Eq. (33) and \(\delta W_\text {corr}^\text {FT}(P)\) of Eq. (43). This difference is equal to the new formula for the harmonic correction to potential as (Forsberg and Tscherning 1981) assumed that the harmonic correction to potential is negligible for smooth RTM surfaces:
4 Experiments
The experiments are divided into two parts. First, semi-analytical investigations are carried out to clarify the nature of the harmonic correction and to verify the equations derived in Sect. 3. Second, numerical investigations are carried out in two regions with the goal to quantify the approximation error of the harmonic correction to gravity and potential in Forsberg and Tscherning (1981). Here, we present the results of the numerical experiments; the semi-analytical experiments are presented in “Appendix B”.
Numerical experiments were done for two regions with different topographic regimes. The first region is located between \(1^\circ \)E–\(10^\circ \)E and \(56^\circ \)N–\(63^\circ \)N and comprises parts of Norway and the Atlantic ocean. Here, we expect significant approximation errors of the harmonic corrections to gravity and potential in Forsberg and Tscherning (1981) as height differences between the Earth’s surface and the RTM surface are large and change quickly, in particular around the fjords. The second region is located in the centre of France between \(1^\circ \)W–\(7^\circ \)E and \(43^\circ \)N–\(49^\circ \)N. This area is referred to as the Auvergne test area as it has been used in the past to compare different methods of local quasi-geoid modelling (cf. Duquenne 2006). It is a moderate mountainous area with heights varying from less than 150 m in the north-west where the Bassin de Paris starts to 1886 m at the Puy de Sancy in the middle south. In this test area, we expect smaller approximation errors of the harmonic correction to gravity in (Forsberg and Tscherning 1981) and smaller harmonic corrections to potential and height anomaly.
Each RTM surface is computed by applying a low-pass filter to the high-resolution digital topographic and bathymetric model (DTM). We use a spherical Gaussian low-pass filter, which is truncated at a spherical distance \(\psi _0\). The spherical distance \(\psi _0\) is also the distance at which the Gaussian filter has dropped to half of it maximum value. We refer to \(\psi _0\) as the radius of the Gaussian filter. We relate the choice of \(\psi _0\) to the maximum degree N of the GGM which is used to reduce the data for long-wavelength signals, as \(\psi _0 = {180^\circ \over N}\), i.e., \(\psi _0\) is set equal to the half-wavelength resolution of the GGM. This filter is in fact a weighted moving average filter, where the size of the window is equal to the half-wavelength resolution of the GGM and the weights are determined by the Gaussian. The filter operation is implemented in the frequency domain using a 2D planar FFT.
For each test area, two RTM surfaces with different smoothness were computed. The first one assumes that the data were reduced for the contribution of an ultra-high-resolution GGM complete to degree 2160 (e.g., EGM2008, Pavlis et al. 2012). The corresponding radius of the spherical Gaussian filter is \(\psi _0=5^\prime \). The second one assumes that the GGM is complete to degree 300 (e.g., Pail et al. 2011; Bruinsma et al. 2014; Förste et al. 2019); the corresponding radius of the spherical Gaussian filter is \(\psi _0=36^\prime \). We refer to the two RTM surfaces as \(\hbox {RTM}_5\) and \(\hbox {RTM}_{{36}}\), respectively.
Applying a low-pass filter to a local DTM causes edge effects along the boundaries of the DTM due to missing data. Therefore, RTM effects were always computed over a spherical patch which was smaller than the area of the DTM by one degree in all four directions.
In Sects. 4.2 and 4.4, we focus on the harmonic correction to gravity, potential, and height anomaly. An analysis of the individual contributors to the complete RTM correction to gravity and potential is provided in “Appendix C” for the Norway test area and in “Appendix D” for the Auvergne test area.
4.1 Norway test area
The DTM for the Norway test area is based on EuroDEM (Eurogeographics 2008) and has a half-wavelength resolution of \(2^{\prime \prime } \times 2^{\prime \prime }\). A characteristic feature of this area are the long, deep and narrow fjords. Hence, we can expect significant positive and negative height differences between the DTM and each of the two RTM surfaces. These height differences are referred to as RTM tesseroid heights (cf. Fig. 3). The RTM tesseroid heights range from \(-1404\) m to 1036 m for \(\hbox {RTM}_5\) and from \(-1825\) m to 1252 m for \(\hbox {RTM}_{{36}}\) (cf. Table 2); the corresponding RMS values are 139 m and 204 m, respectively. In the vicinity of extreme tesseroid heights, we can expect large approximation errors of the harmonic correction to gravity in (Forsberg and Tscherning 1981) and large harmonic corrections to potential and height anomaly.
4.2 Norway test area: harmonic correction
In the Norway test area, the harmonic correction was evaluated at the 800,000 nodes of an equal-angular \(18^{\prime \prime } \times 18^{\prime \prime }\) grid, which formed a subgrid of the DEM. About \(32\%\) (\(\hbox {RTM}_5\)) and \(29\%\) (\(\hbox {RTM}_{{36}}\)) of the evaluation points were located below the RTM surface. Figure 4 shows a geographic rendition of the improved harmonic correction to gravity and height anomaly, and the approximation error of the harmonic correction to gravity in (Forsberg and Tscherning 1981). It appears that their distributions are asymmetric with a one-sided long tail, which is the reason why we prefer percentiles and median above RMS, mean, and standard deviation in the summary statistics of Table 3.
Referring to Table 3, there are a few observations worth to be mentioned. First, the harmonic correction to gravity of Eq. (37) can be negative unlike the correction in Forsberg and Tscherning (1981). The latter is always non-negative, as it assumes that all masses of the RTM-reduced earth inside the volume \(Q^-\) are located above the level of the evaluation point. In reality, however, some masses in \(\Omega ^-\) may be located below that level. Overall, this reduces the magnitude of the harmonic correction, but may also lead to negative values at particular evaluation points in extreme situations (e.g., if the RTM surface has lows in the neighbourhood of the evaluation point). In the Norway test area this only happened for the smooth RTM surface, \(\hbox {RTM}_{{36}}\), at just \(0.03\%\) of the evaluation points. No negative values were noticed for the rougher \(\hbox {RTM}_5\) surface. We explain this by the fact that then the volume \(\Omega ^-\) is smaller so is the amount of mass added to this volume, and the effect of masses located below the level of the evaluation point and close-by is very small and not enough to make the harmonic correction negative.
Second, it is an over-simplification to state that the smoother the RTM surface the smaller the harmonic correction to gravity. For the Norway test area, all statistics of Table 3 point to a larger harmonic correction for the (smooth) \(\hbox {RTM}_{{36}}\) surface, compared to the (rough) \(\hbox {RTM}_5\) surface. This can be explained by the fact that for a smooth RTM surface, the volume \(\Omega ^-\) increases so does the amount of mass added to that volume resulting in larger harmonic corrections to gravity.
Third, the approximation error of the harmonic correction to gravity in Forsberg and Tscherning (1981) is very large in the Norway test area. It ranges from \(-126.9\) mGal to 13.1 mGal (\(\hbox {RTM}_5\)) and \(-284.8\) mGal to 191.5 mGal (\(\hbox {RTM}_{{36}}\)). Hence, the range of the approximation error of the harmonic correction to gravity in Forsberg and Tscherning (1981) is comparable to the range of the harmonic correction of Eq. (37). Most of the approximation errors are negative (about \(81\%\) for \(\hbox {RTM}_5\) and \(77\%\) for \(\hbox {RTM}_{{36}}\)), i.e., the harmonic correction to gravity in Forsberg and Tscherning (1981) is often too large. We explain this by the fact that Forsberg and Tscherning (1981) assumed that all masses of the RTM-reduced earth are located above the level of the evaluation point, whereas in reality there are also masses located below that level.
Fourth, the harmonic correction to height anomaly (likewise to potential) is non-negative for both \(\hbox {RTM}_5\) and \(\hbox {RTM}_{{36}}\), except a few points with slightly negative values of magnitudes not exceeding 0.1 cm. We explain this by the higher smoothness of this correction compared to the harmonic correction to gravity. This results in some cancellation of positive and negative contributions to the harmonic correction generated by the mass redistribution inside the volume \(\Omega ^-\) as also mass redistributions in areas further away from the evaluation point still contribute.
Fifth, the harmonic correction to height anomaly is not negligible as also indicated by the histogram of Fig. 5. Peak values are 7.8 cm (\(\hbox {RTM}_5\)) and 11.5 cm (\(\hbox {RTM}_{{36}}\)). About \(12\%\) (\(\hbox {RTM}_5\)) and \(23\%\) (\(\hbox {RTM}_{{36}}\)) of all harmonic corrections are larger than 1 cm, though the majority of \(77\%\) (\(\hbox {RTM}_5\)) and \(65\%\) (\(\hbox {RTM}_{{36}}\)) of the corrections are smaller than 0.5 cm. The \(95\%\) percentiles are 1.8 cm (\(\hbox {RTM}_5\)) and 4.4 cm (\(\hbox {RTM}_{{36}}\)). Whereas the former is comparable to the reported quality of the Baltic Region and Nordic Area (NKG2015) gravimetric quasi-geoid model of 1.5–1.8 cm (\(95\%\) confidence level) based on a comparison with GPS-levelling (cf. Eshagh and Berntsson 2019), the latter is significantly larger than the \(95\%\) confidence level.
Auvergne test area: harmonic correction to gravity, \(\delta g_\text {harm}\) of Eq. (37), the difference between \(\delta g_\text {harm}\) and the harmonic correction in Forsberg and Tscherning (1981), \(\delta g_\text {harm}- \delta g^{FT}_\text {harm}\), and the harmonic correction to height anomaly, \(\delta \zeta _\text {harm}\) (based on Eq. (41)). The areas where topography or sea surface is located above the RTM surface are shown in white
Sixth, the approximation error of the harmonic correction to gravity in Forsberg and Tscherning (1981) has a non-zero mean: \(-7.6\) mGal (\(\hbox {RTM}_5\)) and \(-10.2\) mGal (\(\hbox {RTM}_{{36}}\)). This introduces a bias in the reduced gravity anomalies when using the harmonic correction to gravity in Forsberg and Tscherning (1981). This bias introduces long-wavelength errors in the computed quasi-geoid model. When computing a correction surface in support of GNSS-levelling, most of the bias will be absorbed.
4.3 Auvergne test area
The DTM of the Auvergne test area is based on SRTM3 (Jarvis et al. 2008). It is given for an area of \(42^\circ \)N–\(50^\circ \)N and \(2^\circ \)W–\(8^\circ \)E at the nodes of a \(3^{\prime \prime } \times 3^{\prime \prime }\) grid. To reduce the computational costs, we use a data window covering an area of \(44^\circ \)N–\(49^\circ \)N and \(1^\circ \)W–\(7^\circ \)E. We still refer to this smaller area as the Auvergne test area (cf. Fig. 6a). Likewise, the data area was reduced accordingly comprising 133,615 of the original 244,009 gravity values. Different from the Norway test area, the RTM corrections were not computed at the nodes of an equal-angular grid but at the gravity stations.
The statistics of the DTM- and RTM-surfaces as well as of the tesseroid heights are given in Table 4.
4.4 Auvergne test area: harmonic correction
In the Auvergne test area, the harmonic correction had to be computed at about \(59\%\) (\(\hbox {RTM}_5\)) and \(71\%\) (\(\hbox {RTM}_{{36}}\)) of all evaluation points. These percentages are significantly larger compared to those for the Norway test area. As already found in Sect. 4.2, the smooth \(\hbox {RTM}_{{36}}\) surface increases the number of evaluation points which are located below the RTM surface, i.e., for which harmonic corrections need to be computed, in the Auvergne test area. Figure 7 shows a geographic rendition of the harmonic correction to gravity of Eq. (37) and height anomaly (based on Eq. (41)), and the approximation error of the harmonic correction to gravity in Forsberg and Tscherning (1981). The corresponding summary statistics are given in Table 5.
There are a few aspects which we would like to mention when comparing the results with those for the Norway test area presented in Sect. 4.2.
First, all harmonic corrections to gravity are non-negative; for the Norway test area, we found that at some evaluation points, the harmonic correction to gravity is negative for the relatively rough \(\hbox {RTM}_5\) surface, which we explained by strong variations of that surface in the neighbourhood of these points. Obviously, these extreme situations do not occur in the Auvergne test area as topographic variations in this area are not that extreme.
Second, the peak approximation error of the harmonic correction to gravity in Forsberg and Tscherning (1981) appears to be very large again with \(-118.5\) mGal (\(\hbox {RTM}_5\)) and \(-109.6\) mGal (\(\hbox {RTM}_{{36}}\)). However, the low \(95\%\) percentiles of the absolute approximation errors, which are 4.1 mGal (\(\hbox {RTM}_5\)) and 5.2 mGal (\(\hbox {RTM}_{{36}}\)), indicate, that there is only a small number of points where such extreme values occur.
Third, the statistics of the harmonic corrections to gravity and height anomaly are overall smaller in the Auvergne test area compared to the Norway test area. This is a consequence of the moderate topography in the Auvergne test area, which implies smaller tesseroid heights compared to the Norway test area. The harmonic corrections to height anomaly are very small, though the peak values of 10.9 cm (\(\hbox {RTM}_5\)) and 13.6 cm (\(\hbox {RTM}_{{36}}\)) are even larger than the peak values found in the Norway test area. The large peak values may be caused by the location of the gravity stations, which in the mountains often follow the roads; correspondingly, tesseroid heights at these stations may become pretty large (remember that in the Norway test area, the evaluation points are located on a equal-angular grid and are not related to gravity stations). However, larger harmonic corrections to height anomaly only occur at a very small number of gravity stations. This is supported by the histograms of Fig. 8. About \(98\%\) (\(\hbox {RTM}_5\)) and \(90\%\) (\(\hbox {RTM}_{{36}}\)) of all corrections are smaller than 0.5 cm and only \(1\%\) (\(\hbox {RTM}_5\)) and \(6\%\) (\(\hbox {RTM}_{{36}}\)) of all corrections are larger than 1 cm. The \(95\%\) percentiles are just 0.2 cm (\(\hbox {RTM}_5\)) and 1.1 cm (\(\hbox {RTM}_{{36}}\)) compared to 1.8 cm (\(\hbox {RTM}_5\)) and 4.4 cm (\(\hbox {RTM}_{{36}}\)) in the Norway test area. From this we conclude that the harmonic correction to height anomaly is not critical when computing a quasi-geoid model in the Auvergne test area. When looking at the published results of the Auvergne quasi-geoid test, standard deviations of the computed height anomalies based on a comparison with GPS-levelling data between 2.9 and 6.7 cm are reported; the median is 3.5 cm (Forsberg 2010). Only about \(0.2\%\) (\(\hbox {RTM}_5\)) and \(0.8\%\) (\(\hbox {RTM}_{{36}}\)) of the harmonic corrections for height anomaly are larger than this median.
Fourth, the harmonic correction to gravity in Forsberg and Tscherning (1981) introduces a bias in the reduced gravity anomalies as already observed in the Norway test area (cf. Sect. 4.2). However, in the Auvergne test area, the magnitude of the bias is much smaller: \(-0.87\) mGal (\(\hbox {RTM}_5\)) and \(-0.97\) mGal (\(\hbox {RTM}_{{36}}\)). Still, it will introduce a long-wavelength bias in the computed quasi-geoid model. A suitable chosen correction surface estimated from the differences between gravimetric and geometric height anomalies at a set of GNSS-levelling points will absorb most of the long-wavelength errors.
5 Summary and concluding remarks
We derived new (approximate) equations for the harmonic correction to gravity and potential which apply to points located below the RTM surface, and provide harmonically downward continued gravity and potential values referring to a RTM-reduced earth bounded by the RTM surface. We showed that the approximation error of the simple harmonic correction to gravity as suggested in Forsberg and Tscherning (1981) can be as large as the harmonic correction itself.
The new equations allow for the first time to compute the harmonic correction to potential and height anomaly. This is important if these types of gravity field functionals are used as data in local quasi-geoid modelling (e.g., Farahani et al. 2017; Slobbe et al. 2019). We showed that in both test areas, the harmonic correction to height anomaly can be larger than the target accuracy of today’s quasi-geoid models (i.e., one centimetre) with peak values close to or even exceeding the one decimetre level at some points. Overall, however, the results indicate that the harmonic correction to height anomaly may be critical mainly in areas with strong topographic variations like the Norway test area, whereas in flat or hilly areas such as large parts of the Auvergne test area, the one-centimetre threshold will only be exceeded at a few points.
We also showed that the choice of the RTM surface has a significant impact on the magnitude of the harmonic corrections. Overall, a smooth RTM surface provides larger harmonic corrections to gravity, potential, and height anomaly. Likewise, the errors of the harmonic correction to gravity in Forsberg and Tscherning (1981) increase with increasing smoothness of the RTM surface. Therefore, we do not recommend to use very smooth RTM surfaces. From a theoretical point of view there is no need to relate the resolution of the RTM surface (i.e., its smoothness) to the spatial resolution of the GGM used in data reduction. It is sufficient to choose the smoothness of the RTM surface such that the high-frequency signals in the gravity datasets that cannot be resolved for a given data distribution and accuracy are reduced as much as possible. For some areas of interest, this may allow the choice of rougher RTM surfaces.
One of the main concerns related to the harmonic correction to gravity in Forsberg and Tscherning (1981) is the bias this correction introduces in the reduced gravity anomalies. This bias causes long-wavelength errors in the computed quasi-geoid model.
The new equations for the harmonic correction to gravity and potential involve Taylor series expansions, and the dominant term of the remainder is of the order of \({\mathcal {O}}(\varepsilon ^2)\) and \({\mathcal {O}}(\varepsilon ^3)\), respectively. Using the results provided in Tables 2, 4, 6, and 7, we can estimate this term. For instance, the largest tesseroid height in the Norway test area is \(\Delta h = 1825\) m (cf. Table 2, \(\hbox {RTM}_{{36}}\)), hence \(\varepsilon = 2.9\cdot 10^{-4}\). When we combine this value with the largest value of \(\delta g_\text {RTM}^-(Q)\), which is 123.3 mGal (cf. Table 6), the dominant term of the remainder of Eq. (26) is \(3.1 \cdot 10^{-5}\) mGal. Likewise, the largest value of \(\delta V_\text {RTM}^-(Q)\) is 28.76 m\(^2\)/s\(^2\) (cf. Table 7, \(\hbox {RTM}_{{36}}\)); hence, the dominant term of the remainder of Eq. (32) is \(6.8 \cdot 10^{-10}\) m\(^2\)/s\(^2\). A comparison of these error estimates with the differences between the new harmonic corrections and the ones in Forsberg and Tscherning (1981) indicates how substantial the improvements are which the new harmonic corrections provide.
The complete RTM correction presented in this paper can easily be implemented in existing RTM software. The numerical complexity is about a factor of two higher than the traditional RTM correction in Forsberg and Tscherning (1981). In fact, the modified code has to be run twice; first, to compute the effect of removing the masses in the volume \(\Omega ^+\); second, to compute the effect of adding masses to the volume \(\Omega ^-\).
Finally, we would like to mention that the harmonic corrections to gravity, potential, and height anomaly must not be restored in the remove-compute-restore approach. They are only needed to transform values inside the masses into harmonically downward continued values and do not reflect mass re-distributions.
Data availability
The Auvergne dataset can be requested from the IAG International Service for the Geoid, https://www.isgeoid.polimi.it/. The digital elevation models for the Norway test area can be downloaded from https://eurogeographics.org/maps-for-europe/ (land topography) and https://www.gebco.net/ (bathymetry).
References
Bruinsma S, Förste C, Abrikosov O, Lemoine JM, Marty JC, Mulet S, Rio MH, Bonvalot S (2014) ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys Res Lett 41(21):7508–7514. https://doi.org/10.1002/2014GL062045
Denker H (2013) Regional gravity field modeling: theory and practical results. In: Xu G (ed) Sciences of Geodesy-II: innovations and future developments, Springer, Berlin, pp 185–291, https://doi.org/10.1007/978-3-642-28000-9_5
Denker H, Wenzel HG (1986) Recovery of short wavelength gravity field information from the topography by spectral filtering. In: Proceedings of international symposium on the definition of the Geoid, Instituto Geografico Militare Italiano, Florence, Italy, vol 1, pp 223–238
Duquenne H (2006) A data set to test geoid computation methods. In: Proceedings of 1st international symposium of the international gravity field service. Harita Dergisi, Istanbul, Turkey, Command of Mapping, pp 61–65
Eshagh M, Berntsson J (2019) On quality of nkg2015 geoid model over the Nordic countries. J Geod Sci 9:97–110
Eurogeographics (2008) Eurodem product description. https://eurogeographics.org/maps-for-europe/eurodem/, eurogeographics, Brussels, Belgium
Farahani H, Slobbe D, Klees R, Seitz K (2017) Impact of accounting for coloured noise in radar altimetry data on a regional quasi-geoid model. J Geod 91:97–112
Forsberg R (1984) A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling. Department of Geodetic Science and Surveying, Report 355, Ohio State University, Columbus, Ohio, USA
Forsberg R (2010) Geoid determination in the mountains using ultra-high resolution spherical harmonic models—the Auvergne case. In: Contadakis ME, et al (ed) The apple of the knowledge. In Honor of Professor Emeritus Demetrius N. Arabelos, Ziti Editions (ISBN:978-960-243-674-5), Thessaloniki
Forsberg R, Tscherning CC (1981) The use of height data in gravity field approximation by collocation. J Geophys Res 86(B9):7843–7854. https://doi.org/10.1029/JB086iB09p07843
Forsberg R, Tscherning CC (1997) Topographic effects in gravity field modelling for BVP. In: Sansò F, Rummel R (eds) Geodetic boundary value problems in view of the one centimeter geoid. Lecture Notes in Earth Sciences, vol 65. Springer, Berlin, pp 239–272. https://doi.org/10.1007/BFb0011707
Förste C, Abrikosov O, Bruinsma S, Dahle C, König R, Lemoine JM (2019) ESA’s release 6 GOCE gravity field model by means of the direct approach based on improved filtering of the reprocessed gradients of the entire mission (go_cons_gcf_2_dir_r6). Helmholz-Zentrum, Geoforschungszentrum (GFZ), Potsdam, Germany. https://doi.org/10.5880/ICGEM.2019.004
Gerlach C (2003) Zur Höhensystemumstellung und Geoidberechnung in Bayern. Deutsche Geodätische Kommission, Reihe C, Heft 571, DGK, München
Grombein T, Seitz K, Heck B (2013) Optimized formulas for the gravitational field of a tesseroid. J Geod 87(7):645–660. https://doi.org/10.1007/s00190-013-0636-1
Heck B, Seitz K (2007) A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J Geod 81(2):121–136. https://doi.org/10.1007/s00190-006-0094-0
Heiskanen WA, Moritz H (1967) Physical geodesy. W. H. Freeman & Co, New York
Hirt C, Kuhn M, Claessens S, Pail R, Seitz K, Gruber T (2014) Study of the earth’s short-scale gravity field using the ertm2160 gravity model. Comput Geosci 73:71–80. https://doi.org/10.1016/j.cageo.2014.09.001
Jarvis A, Reuter HI, Nelson A, Guevara E (2008) Hole-filled seamless SRTM data v4. International Centre for Tropical Agriculture (CIAT). http://srtm.csi.cgiar.org
Kadlec M (2011) Refining gravity field parameters by residual terrain modelling. Ph.D. Thesis, Faculty of Applied Sciences, University of West Bohemia, Pizen
Martinec Z (1998) Boundary-value problems for gravimetric determination of a precise geoid. Lecture notes in earth sciences, vol 73. Springer, Berlin
Omang OC, Tscherning CC, Forsberg R (2012) Generalizing the harmonic reduction procedure in residual topographic modeling. In: Sneeuw N, Novák P, Crespi M, Sansò F (eds) VII Hotine-Marussi Symposium on Mathematical Geodesy. Springer, Heidelberg, pp 233–238
Pail R, Bruinsma S, Migliaccio F, Förste C, Goiginger H, Schuh W, Höck E, Reguzzoni M, Brockmann J, Abrikosov O, Veicherts M, Fecher T, Mayrhofer R, Krasbutter I, Sansò F, Tscherning C (2011) First GOCE gravity field models derived by three different approaches. J Geod 85(11):819–843. https://doi.org/10.1007/s00190-011-0467-x
Pavlis N, Holmes S, Kenyon S, Factor J (2012) The development and evaluation of the earth gravitational model 2008 (EGM2008). J Geophys Res. https://doi.org/10.1029/2011JB008916
Sanso F, Sideris ME (2013) Geoid determination–theory and methods. Springer, Heidelberg
Slobbe D, Klees R, Farahani H, Huisman L, Alberts B, Voet P, de Doncker F (2019) The impact of noise in a grace/goce global gravity model on a local quasi-geoid. J Geophys Res 124:3219–3237
Tziavos IN, Sideris MG (2013) Topographic reductions in gravity and geoid modeling. In: Sansò F, Sideris MG (eds) Geoid determination: theory and methods. Springer, Berlin, pp 337–400. https://doi.org/10.1007/978-3-540-74700-0_8
Vermeer M, Forsberg R (1992) Filtered terrain effects: a frequency domain approach to terrain effect evaluation. Manuscr Geodaet 17:215–226
Acknowledgements
The authors would like to thank the state of Baden-Württemberg (Germany) and the Steinbuch Center for Computing at the Karlsruhe Institute of Technology for the allocation of computing time on the high performance parallel computer system bwunicluster.
Author information
Authors and Affiliations
Contributions
RK did the study conception, design, and most of the analytical work. KS did the coding, the numerical computations, and provided some minor contributions to the analytical work. The first draft of the manuscript was written by RK. Data analysis was done by RK, KS, and CS. All authors commented on previous versions of the manuscript, and read and approved the final manuscript.
Corresponding author
Appendices
Appendix A: Complete RTM correction: three-step procedure
In Sect. 3, we derived the equations for the complete RTM correction in four steps. Here, we suggest a three-step procedure and show analytically that from a theoretical point of view both provide the same results. The difference with respect to the four-step procedure is that points \(P \in S\) which are located below the RTM surface are upward continued (in the Earth’s gravity field) to the RTM surface before the masses in \(\Omega ^+\) are removed and masses are added to \(\Omega ^-\).
Three-step procedure
Step 1 Upward-continue data at points \(P \in S\) located below the RTM surface to the corresponding points \(Q \in s\) using the free-air vertical gravity gradient; all other data are left unchanged.
where the inner gradients are defined as
and \(P'\) is a point on the ellipsoidal normal through P with ellipsoidal height \(h_P + \delta \).
Step 2 Move the masses inside \(\Omega ^+\) to infinity assuming that their mass density is \(\rho _0\), and fill the volume \(\Omega ^-\) with mass to achieve a mass density of \(\rho _0\). Compute the effect this has on gravity and potential, respectively, at Q:
Step 3 Downward-continue harmonically the data that have been upward continued in step 1 to their original locations on the Earth’s surface (terrain or sea surface), i.e., from Q to P along the ellipsoidal normal through P:
where \({\partial g_\text {red}\over \partial h}\Big \vert _Q\) and \({\partial ^2 W_\text {red}\over \partial h^2}\Big \vert _Q\) are defined as in Eq. (18) and Eq. (20), respectively.
Inserting Eqs. (46) and (51) into Eq. (53), we find
Using the partial derivative of Eq. (51) with respect to h, we re-write Eq. (55) as
This is identical to Eq. (26), the result of the four-step procedure derived in Sect. 3.1.
Inserting Eqs. (47) and (52) into Eq. (54), and observing Eqs. (46) and (51), we find
Using the partial derivative of Eq. (52) with respect to h, we can simplify Eq. (57) to
This is identical to Eq. (32), the result of the four-step procedure derived in Sect. 3.1.
From a practical point of view, there is a minor difference between the four-step and the three-step procedure. This difference is in the upward continuation operation. Take as an example a measured gravity value. In the four-step procedure this gravity value has to be upward continued to the RTM surface using the free-air gravity gradient referring to a modified Earth which is mass-free inside \(\Omega ^+\) (step 2). In the three-step procedure, the upward continuation uses the free-air gravity gradient of the real Earth. Note that the gradient to be used in the upward continuation of the three-step procedure is likely rougher than the gravity gradient used in step 2 of the four-step procedure. The reason is that the removal of the masses inside \(\Omega ^+\) likely has a smoothing effect on the gravity gradient.
Appendix B: Semi-analytical experiments
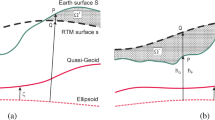
In the first semi-analytical example, we consider the Earth to be a non-rotating homogeneous sphere of radius R and constant density \(\rho \). The gravity measurement point P is located on the surface of that sphere, i.e., \(r_P=R\). The RTM-surface is assumed to be a sphere of radius \(r_Q = R + h\) as depicted in Fig. 9a. The complete RTM correction to gravity follows from applying Eq. (26) and neglecting terms of the order \({\mathcal {O}}(\varepsilon ^2)\):
For a spherical shell, a power series expansion yields
hence,
Inserting the last two expressions into Eq. (59) yields
With measured gravity at P,
we find
Gravity \(g_\text {red}(P)\) corresponds to the harmonically downward continued gravity of our RTM-reduced earth, which is a homogenous sphere of radius \(R+h\). Therefore, \(g_\text {red}(P)\) can easily be computed exactly. For this, we consider the difference between g(P) and \(g_\text {red}(P)\), which is caused by the mass \(M^- = \rho \Omega ^-\) of a spherical shell with inner radius R and outer radius \(R+h\), i.e.,
Hence,
If M denotes the mass of a homogenous sphere of radius R and density \(\rho \), the exact value of \(g_\text {red}(P)\) is
Equations (63) and (66) are identical up to terms \({\mathcal {O}}(\varepsilon ^2)\). This is less than 1 \(\mu \)Gal for any shell of thickness \(\vert h \vert < 9\) km. The application of the derived complete RTM reduction leads to a corrected gravity value at P, which is now a boundary value of the external gravity potential caused by the mass \(M^+ = M + M^- = {4 \over 3} \pi \rho (R+h)^3\). It is no longer an inner potential gradient and can be upward continued by the use of a free-air reduction. If necessary to apply, the free-air gradient is now based on \(M^+\). For the gravity potential of the RTM-reduced earth, we find
The correct analytical result of a homogeneous sphere with radius \(R+h\) and density \(\rho \) is
Equations (67) and (68) agree up to terms of \({\mathcal {O}}(\varepsilon ^4)\).
The second semi-analytical example uses a spherical cap with opening angle \(\psi _c\) to model the RTM-masses in the region \(\Omega ^-\) (see Fig. 9b). In this more specific example, the presented precise harmonic correction formulas are also confirmed analytically.
We assume that the Earth consists of a non-rotating homogeneous sphere of radius \(R+h\) with constant density \(\rho \) with a conical mass element with symmetry axis through P and opening angle \(\psi _c \le \pi \) removed (cf. Fig. 9b). The RTM-reduced earth, which results after the complete RTM correction has been applied, is a homogeneous sphere of radius \(R+h\). With this assumption it follows directly that \(r_P = R\), i.e., the point P is located on the sphere of radius R at a depths h below the RTM surface. For this geometry, it is
Hence, Eq. (35) reads
The analytical expressions for the gravity effect of a spherical cap, \(\delta g_Q^{sc}\), are given in Kadlec (2011, Eq. (2.106)) or Heck and Seitz (Eq. (54), 2007). Using the approximations \(\psi _c < 1^\circ \), \(\sin \psi _c \approx \psi _c\), \(\cos \psi _c \approx 1-\psi _c^2/2\), it is up to terms of \({\mathcal {O}}(\varepsilon ^2)\),
with the Euclidean distances
and the spherical distance \(\psi \) between the geocentric vectors of \(P\) and \(Q\),
For the last term of Eq. (73), we find ( Kadlec 2011, Eq. (2.134)) up to terms of \({\mathcal {O}}(\varepsilon ^2)\)
When inserting the last expressions into Eq. (73) the evaluations lead to the gravity value including the harmonic correction which is in accordance with the expected value (cf. Eq. (66)) on the approximation level of \({\mathcal {O}}(\varepsilon ^2)\).
For the potential the results of this thought experiment are based on Kadlec (2011, Eq. (2.98)) or Heck and Seitz (2007, Eq. (52)):
-
(i)
The gravity potential W(P) at a point \(P\in S\):
$$\begin{aligned} W(P) = \frac{4}{3} \pi G \rho R^2 + 2 \pi G \rho ((R+h)^2 - R^2) - \delta V_\text {RTM}^-\vert _P \,, \end{aligned}$$ -
(ii)
The expected value of the harmonically continued potential is
$$\begin{aligned} \begin{aligned} W^*\Big \vert _P&= \frac{4}{3} \pi G \rho \frac{\left( R + h\right) ^3}{R} \,, \\&= \frac{4}{3} \pi G \rho R^2 \left( 1 + 3 \frac{h}{R} + 3 \left( \frac{h}{R}\right) ^2 + \left( \frac{h}{R}\right) ^3 \right) \end{aligned} \end{aligned}$$ -
(iii)
Gravity potential at P after applying harmonic RTM reduction according Eq. (39):
$$\begin{aligned} W_\text {red}(P)&= W_P - \delta V_\text {corr}(P)= \frac{4}{3} \pi G \rho R^2 \left[ 1 + 3\frac{h}{R} \nonumber \right. \\&\left. \quad + 3\left( \frac{h}{R}\right) ^2 + {\mathcal {O}}(\varepsilon ^3)\right] \,. \end{aligned}$$(78) -
(iv)
Items (ii) and (iii) are equal on the approximation level \({\mathcal {O}}(\varepsilon ^3)\). The application of the derived harmonic RTM reduction leads to a corrected gravity potential at P, which is now a boundary value of the external gravity potential caused by the masses \(M^*\).
Norway test area: contributors to the complete RTM correction to gravity according to Eq. (27). Units in \(\mathrm{mGal}\). The contributors in Figures e and f are only computed at evaluation points which are located below the RTM surface
Norway test area: contributors to the complete RTM correction to potential according to Eq. (33). Units in \(\mathrm{m}^{2}\mathrm{s}^{-2}\). The contributors in Figures c, d, g, and h were only computed at evaluation points which are located below the RTM surface
Appendix C: Complete RTM correction for the Norway test area
Figures 10 and 11 show a geographic rendition of the contributors to the complete RTM correction to gravity and potential, respectively, in the Norway test area. The statistics of the contributors are presented in Table 6 for gravity and Table 7 for potential. All contributors have distributions with a long, one-sided tail. Therefore, Tables 6 and 7 show next to range, the \(25\%\), \(75\%\) and \(95\%\) percentiles and the median instead of mean, RMS and standard deviation. Both tables reveal that the complete RTM correction is dominated by the mass re-distribution related term, \(\delta g_\text {RTM}^+(P)- \delta g_\text {RTM}^-(Q)\) and \(\delta V_\text {RTM}^+(P)- \delta V_\text {RTM}^-(Q)\), respectively. Their contribution to the complete RTM correction is about \(75\%\) for gravity and about \(90\%\) for potential. Among the two remaining terms of the complete RTM correction to potential, which are only relevant at evaluation points located below the RTM surface, the term \({ \partial \delta V_\text {RTM}^-\over \partial h} \Big \vert _Q \,\Delta h\) is the largest; its range is 0.82 \({\mathrm{m}^2 \mathrm{s}^{-2}}\) (\(\hbox {RTM}_5\)) and 1.29 \({\mathrm{m}^2 \mathrm{s}^{-2}}\) (\(\hbox {RTM}_{{36}}\)). The term \(-{1 \over 2} {\partial ^2 \delta V_\text {RTM}^-\over \partial h^2}\Big \vert _Q\,\Delta h^2\) is indeed small as the rough estimate in Sect. 3.2 already indicated, but with a range of 0.25 \({\mathrm{m}^2 \mathrm{s}^{-2}}\) (\(\hbox {RTM}_5\)) and 0.35 \({\mathrm{m}^2 \mathrm{s}^{-2}}\) (\(\hbox {RTM}_{{36}}\)) still not negligible in cm-accuracy local quasi-geoid modelling.
Auvergne test area: contributors to the complete RTM correction to gravity according to Eq. (27). Units in \(\mathrm{mGal}\). The contributors in Figures e and f were only computed at evaluation points which are located below the RTM surface
Appendix D: Complete RTM correction for the Auvergne test area
Figures 12 and 13 show a geographic rendition of the contributors to the complete RTM correction to gravity and potential, respectively, over the Auvergne test area. The associated statistics are provided in Tables 8 and 9, respectively. The share of the mass redistribution related contributors to the complete RTM correction is comparable to the one found for the Norway test area, though in absolute terms, the contributors are a bit smaller now. When comparing the results for the two RTM surfaces, we notice again that the complete RTM correction and its contributors are larger for the smoother \(\hbox {RTM}_{{36}}\) surface compared to the rougher \(\hbox {RTM}_5\) surface for both gravity and potential.
Auvergne test area: contributors to the complete RTM correction to potential according to Eq. (33). Units in \(\mathrm{m}^{2}\mathrm{s}^{-2}\). The contributors in Figures e, f, g, and h were only computed at evaluation points which are located below the RTM surface
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klees, R., Seitz, K. & Slobbe, D.C. The RTM harmonic correction revisited. J Geod 96, 39 (2022). https://doi.org/10.1007/s00190-022-01625-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-022-01625-w