Abstract
Mass change inferences from GRACE and GRACE-FO typically involve, first, the preparation of spherical harmonic (SH) datasets on global gravity field changes and, second, their subsequent analysis that leads to mass change estimates. This study addresses the second step, which builds on SH input datasets that comprise the monthly gravity field solutions as well as amendments to low-degree components and subtraction or re-addition of certain modeled geophysical signals. A variety of methods have been developed to estimate mass changes from SH input datasets. It remains a challenge to assess and compare different methods adopted by different studies and to understand the mechanisms by which their results differ. Methods are often distinguished as belonging to either the inverse or direct approach. In the inverse approach, mass changes are estimated using a set of predefined spatial patterns. In the direct approach, surface mass density variations are integrated by using a predefined weight function, or sensitivity kernel. In this paper, we recall that sensitivity kernels are inherent not only to the direct approach. They are also inherent and may be made explicit, for inverse approaches. We prove that certain implementations of the direct and inverse approach have identical sensitivity kernels, and are therefore equivalent, under the condition that they rigorously incorporate the same signal and error covariance information. We present sensitivity kernels for the example of four different methods to estimate Greenland Ice Sheet mass changes. We discuss the sensitivity kernels in relation to the underlying differences in the methods. We propose to use sensitivity kernels as a means of communicating, assessing and comparing methods of mass change estimates. Once the sensitivity kernels associated to a method are made explicit, any user can readily investigate the method in terms of leakage effects, error propagation from the input SH datasets, or effects of the choice of the SH input datasets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The determination of mass changes within a specific area at the Earth surface (such as a drainage basin) is the most common application of satellite gravimetry realized by the Gravity Recovery And Climate Experiment (GRACE) and GRACE-Follow-On missions (Wouters et al. 2014; Tapley et al. 2019), both referred to as GRACE in the following. Typically, mass change estimates are obtained by analyzing GRACE-based spherical harmonic (SH) representations of gravity field variations. Methods of this analysis, and hence of SH-based GRACE mass change estimates, are the subject of this study. We do not address choices involved in the preparation of the SH datasets that are input to the mass change estimates. This preparation of SH input datasets (or ‘GRACE-based gravity field variations’) includes the generation of monthly GRACE gravity field solutions by GRACE Level-2 processing centers, amendments to the low-degree components of the solutions from additional data sources (Sun et al. 2016; Loomis et al. 2019, 2020) as well as subtraction or re-addition of certain modeled gravity field effect such as glacial isostatic adjustment or atmospheric and oceanic mass redistributions, respectively.
A variety of methods have been developed for mass change estimates from GRACE-based SH gravity field variations. These methods need to address effects of errors in the SH input datasets, notably the GRACE gravity field solutions, and effects due to the imposed limitations to spatial resolution. See Sect. 2.3 for a formal definition of the two effects (‘GRACE error effects’ and ‘leakage errors’) that follows Swenson and Wahr (2002) and for a pertinent discussion. Early methods directly modify the region function over which the SH input datasets are integrated after their conversion to a surface mass density representation. They hence follow a direct approach. The resulting weight function (also called sensitivity kernel, SK) can be represented in either the spatial or SH domain (Swenson and Wahr 2002). An alternative approach (referred to as inverse approach) consists in parametrizing expected mass changes by predefined patterns and fitting these patterns to GRACE-based gravity field variations or functionals thereof. Starting from early developments of this approach (Chen et al. 2006; Wouters et al. 2008; Forsberg and Reeh 2007; Horwath and Dietrich 2009; Jacob et al. 2012), many different variants have been developed for many applications.
In this paper we consider applications to mass changes of the Greenland Ice Sheet (GrIS) as an example. This choice is guided by the authors’ previous work and does not imply limitations of the theoretical framework of SKs. For the GrIS (as well as for the Antarctic Ice Sheet), an extensive assessment and comparison of different methods and different choices of the SH input datasets has been done on the level of the results by the Ice sheet Mass Balance Inter-comparison Exercise (IMBIE) studies (Shepherd et al. 2012, 2019). Shepherd et al. (2019) reported that different GRACE mass change estimates for the GrIS over 2005–2015 had a range of 104 Gt a\(^{-1}\) (i.e., approximately between – 189 and – 293 Gt a\(^{-1}\) (Extended Data Fig. 5, Shepherd et al. 2019)). The spread between results may be more substantial for single drainage basins (not addressed by IMBIE so far). For example, for ice drainage basin 4 in Southeast Greenland, Groh et al. (2019) reported a range of results between – 30 and – 78 Gt a\(^{-1}\), that is by more than a factor 2, across different methods.
A large part of such spread is due to different choices of the SH input datasets (including low-degree amendments and corrections for certain geophysical signals). Their effect has been investigated in detail by a number of studies (e.g., Barletta et al. 2013; Velicogna and Wahr 2013; Blazquez et al. 2018; Shepherd et al. 2019), mostly based on a single method of analyzing the SH input datasets.
Comparative assessments of different methods have been more challenging, unless the different methods (or different variants of a method) are implemented by the same investigator (e.g., Bonin and Chambers 2013; Ran et al. 2018). Such comparative assessment could be done in a coordinated action where different investigators apply their method to identical SH input datasets. Within the first IMBIE assessment (Shepherd et al. 2012) a preparatory experiment of this kind was conducted based on synthetic input SH datasets, but not published in detail. A similar, and more extensive, framework for a systematical comparison of different methods was implemented by Groh et al. (2019). The study imposed 27 synthetic test signals to each method. Results obtained with those test signals were compared to the synthetic truth in order to assess leakage effects induced by those test signals.
In this article we elaborate, illustrate and advocate SKs as a framework for the definition, assessment and comparison of SH-based GRACE mass change estimation methods. While SKs are quite obvious for the direct approach, they may be less obvious for the inverse approach. Few studies have calculated and visualized SKs for specific inverse approaches (e.g., Horwath and Dietrich 2009; Jacob et al. 2012; Tiwari et al. 2009; Joodaki et al. 2014; Mohajerani et al. 2018; Mohajerani et al. 2019). In Sect. 2 we elaborate a framework to express the SKs for a variety of methods following the direct or inverse approach. To illustrate the value of SKs, we implement four different estimation methods for GrIS mass changes. We express them by their inherent SKs and discuss these SKs in Sect. 3. We provide a concluding discussion in Sect. 4
Since many estimation methods can be fully described by their SKs, optimizing an estimation method can also be done by optimizing the SK itself. One of the four methods selected for illustration purposes in this paper uses this approach of directly optimizing the SK regarding a formal minimization of propagated GRACE solution errors and leakage errors. This method of tailored SKs was implemented at Technische Universität Dresden in the frame of the Antarctic Ice Sheet Climate Change Initiative (CCI) and the Greenland Ice Sheet CCI projects (Groh and Horwath 2021). We also show (in Sect. 2.7) the equivalence of the tailored SK method and the inverse method in the case that the same stochastic characterization of signal and error covariances is incorporated rigorously in the implementation of both methods.
2 Theory
2.1 Surface mass redistributions and their gravity field effect
Following Wahr et al. (1998), we model mass redistributions at the Earth surface in terms of anomalies of surface mass density (SMD) on a sphere, with units of mass per surface area (kg m\(^{-2}\)). SMD anomalies (with respect to some reference mass distribution) are denoted by \(\kappa (\vartheta ,\lambda )\equiv \kappa (\Omega )\), where the spherical position (colatitude \(\vartheta \) and longitude \(\lambda \)) is denoted by \(\Omega \). We expand \(\kappa (\Omega )\) into spherical harmonics according to
Here, \(\kappa _{nm}\) are the SH coefficients of \(\kappa (\Omega )\) and \(Y_{nm}(\Omega )\) are the fully normalized SH base functions of degree n and order \(\vert m \vert \) (Wahr et al. 1998; Horwath and Dietrich 2009) where positive and negative m indicate cosine and sine dependence on longitude, respectively. Changes in Earth’s gravitational potential V are expressed by the SH expansion
where r is the radial component of the spherical coordinates, GM is the product of the gravitational constant G and the Earth mass M, a is the semi-major axis of the Earth reference ellipsoid, and \(\Delta c_{nm}\) are the changes of the Stokes coefficients. The relation between surface mass changes \(\kappa \) on a thin surface mass layer of an elastic Earth and gravity field changes \(\Delta V\) is given in the SH domain by
where \(k'_n\) are the elastic load Love numbers (Wahr et al. 1998) which depend on the elastic Earth model.
2.2 A general form of SH-based GRACE mass change estimates
The GRACE satellite gravimetry mission provides time-variable (typically monthly) SH gravity field solutions. After their further modification (amendment of low-degree components, account for certain modeled gravity field variations) and after subtraction of a reference field, one obtains the SH input dataset to the further analysis, namely ‘observed’ Stokes coefficient anomalies \(\Delta c_{nm}^\text {\,obs}(t)\) for time t. They are restricted to the observed, finite part of the SH spectrum \(\{(n,m)\}_\text {obs}\) (with a total of N pairs (n, m)), and they include errors. The observed gravity field variations can be also expressed as equivalent ‘observed’ SMD anomalies \(\kappa _{nm}^\text {obs}(t)\) for \((n,m)\in \{(n,m)\}_\text {obs}\), by applying Eq. (3). Here we use \(\kappa _{nm}^\text {obs}\) not in the strict sense of being observed by GRACE alone but already including the effects of amendments to the GRACE solutions as recalled above in this paragraph.
Our target is to estimate \(\Delta m(t)\), i.e., integrated surface mass changes in a given region,
The region is described by its region function \(\vartheta (\Omega )\) defined as 1 inside the region and 0 outside. The expression \(\iint _{\Omega } \dots \textrm{d}\Omega \) is used to abbreviate the spherical integration \(\int _{\lambda =0}^{2\pi }\int _{\vartheta =0}^{\pi } \dots \sin \vartheta \, \textrm{d}\vartheta \, \textrm{d}\lambda \). In the SH domain, Eq. (4) becomes
where \(\vartheta _{nm}\) are the SH coefficients of \(\vartheta (\Omega )\) and \(\sum _{\{(n,m)\}_{\text {\,all}}}\) is an abbreviation for \(\sum _{n=0}^{\infty }\sum _{m=-n}^{n}\).
The estimation of mass changes \(\Delta m(t)\) from satellite gravimetry cannot apply Eq. (5) or (4) directly, in view of the spectral truncation and the errors inherent to \(\kappa _{nm}^\text {obs}\). Instead, we consider estimators \(\widehat{\Delta m}(t)\) of the general form
Here, the summation is only over the part of the SH spectrum covered by the GRACE-based SH input datasets, \(\{(n,m)\}_{\text {\,obs}}\). The coefficients \(\eta _{nm}\), with \((n,m)\in \{(n,m)\}_\text {obs}\) represent the SK of the mass change estimator in the SH domain. This SK defines the mass change estimator. The spatial representation of the sensitivity kernel is
With
the spatial representation of the estimator (Eq. 6) is
Hence, in the spatial domain, the SK \(\eta (\Omega )\) is the weight function applied for the integration of gravimetry-based SMD anomalies.
The term ‘sensitivity kernel’ (SK) is used here for \(\eta \) in either the spatial or SH domain. The same definition was used by e.g., Jacob et al. (2012); Mohajerani et al. (2018, 2019). The SK determines weights to be applied in an integration. It is not meant as the kernel of a convolution. Previous studies used alternative terms for the same concept. These terms include ‘averaging kernel’ (e.g., Swenson and Wahr 2002), ‘averaging function’ (e.g., Velicogna and Wahr 2006) or ‘weight function’ (e.g., Horwath and Dietrich 2009).
To simplify notations, we arrange \(\{\eta _{nm}: (n,m)\in \{(n,m)\}_\text {obs}\}\) in a column vector \({\varvec{\eta }}\) with N elements. Likewise, \(\{\kappa _{nm}^\text {obs}(t)\}\) and similar sets of SH coefficients are arranged in column vectors, annotated by bold-face symbols. Equation (6) then reads
The SH components of degree-1 and degree-0 deserve additional remarks. The degree-1 components of \(\kappa \) are generally different from zero. They are commonly determined either from a combination of GRACE and model assumptions or from satellite laser ranging (e.g., Sun et al. 2016). Here we assume they are part of the SH input dataset, that is, we subsume them under the observed components. The degree-0 component \(\kappa _{0,0}\) is zero if global mass conservation is implied for the considered mass redistributions. This is the case we address here. (The contrary case is briefly discussed in the sequence.) Hence, no changes of degree-0 are determined by the SH input dataset and \(\{(n,m)\}_{\text {\,obs}}\) excludes degree-0. The region function \(\vartheta \), by its original definition, has a non-zero global average and therefore includes a degree-0 component. However, since \(\kappa _{0,0}=0\), omission of this degree-0 component does not change the result of Eq. (5). Equivalently, subtraction of the global average from \(\vartheta \) does not change the result of Eq. (4). By the same reasoning, adding a degree-0 component to \(\eta \) does not change the results of Eqs. (6) and (9). We may therefore choose to add any degree-0 component to \(\eta \) if we want to illustrate how closely \(\eta \) can resemble \(\vartheta \) in adopting the values 1 and 0 inside and outside the given region, respectively. We note that in the more general case where the SH input dataset has a nonzero degree-0 component, the degree-0 component of \(\eta \) is meaningful and needs to be determined. This is the case, for instance, if the preparation of the SH input datasets includes the subtraction of a non-mass-conserving signal, such as due to atmospheric mass changes (Chen et al. 2019). However, the examples elaborated in this article assume \(\kappa _{0,0}=0\).
2.3 GRACE error effect and leakage error
Let \(\delta {\varvec{\kappa }}(t)\) denote the errors of \({\varvec{\kappa }}^\text {obs}(t)\) due to the errors of the SH input datasets. The effect of these errors on the mass change estimate (the ‘GRACE error effect’) is
The leakage error of the mass change estimate,
arises from the fact that the true SMD \(\kappa \) is integrated with the weight function \(\eta \) instead of \(\vartheta \). In the SH domain Eq. (12) reads
While in Eq. (13) \(\kappa _{nm}\) and \(\vartheta _{nm}\) are defined over the full SH spectrum, the definition of the SK \(\eta _{nm}\) was originally restricted to \(\{(n,m)\}_{\text {obs}}\) so that we set \(\eta _{nm}=0\) for \((n,m) \notin \{(n,m)\}_{\text {obs}}\).
By definition, the leakage error depends on the true signal (\(\kappa \)). The GRACE error effect depends on the errors of the SH input datasets (\(\delta {\varvec{\kappa }}\), limited to the spectral range they provide). It is worth mentioning that \(\delta {\varvec{\kappa }}\) may, in fact, include components that are related to the actual signal. Such errors may occur if details in the complex processing of level-1 data imply (possibly hidden) mechanisms of signal filtering or dampening (e.g., Meyer et al. 2015; Ditmar 2022). Such error components may be particularly difficult to include in a stochastic error characterization. In our framework, their effect on mass change estimates is subsumed under ‘GRACE error effects’. However, they may resemble leakage errors in the way how they depend on the actual signal.
2.4 The inverse approach
The basic idea of the inverse approach (or forward-modeling approach, or mascon approach) is to prescribe a finite set of mass redistribution patterns and to determine scaling factors for these patterns such that the sum of scaled patterns fits the GRACE data. Here we elaborate that inverse approaches can be expressed by SKs in the form of Eqs. (6), (9) and (10). For specific inverse approaches this has been elaborated previously (Horwath and Dietrich 2009; Jacob et al. 2012).
We prescribe a set \(\kappa ^i(\Omega )\) \((i=1,\dots ,u)\) of patterns of SMD anomalies. Each \(\kappa ^i(\Omega )\) may be expressed as a set of SH coefficients \(\kappa ^i_{nm}\), \((n,m)\in \{(n,m)\}_\text {\,all}\). We arrange \(\{\kappa _{nm}^i: (n,m)\in \{(n,m)\}_\text {\,obs}\}\) in vectors \({\varvec{a}}^i\). A simple realization of the inverse approach is to solve
for the scaling factors \(\beta _i(t)\) \((i=1,\dots ,u)\) that minimize the residual vector \({\varvec{\varepsilon }}\) in an ordinary least-squares sense. With the vectors \({\varvec{a}}^i\) assembled in a (N, u)-matrix \({\varvec{A}}\) and the numbers \(\beta _i(t)\) assembled in a vector \({\varvec{\beta }}(t)\), Eq. (14) reads
and the estimate for \({\varvec{\beta }}(t)\) is
In a region defined by the region function \(\vartheta (\Omega )\), the mass changes associated to the patterns \(\kappa ^i(\Omega )\) (\(i=1,\dots u\)) are
which we arrange in a vector \({\varvec{m}}\). The GRACE mass change estimate for that region is
By substituting \({\varvec{\hat{\beta }}}(t)\) with Eq. (16), we find
By comparing Eqs. (10) and (19), we identify the SK for this simple realization of the inverse approach as
A realization of the inverse approach requires the choice of patterns \(\kappa ^i(\Omega )\) and a number of additional choices, which may differ from the ones made above. Next, we address these choices and the modifications of Eq. (20) they imply.
(a) Where available error variances and covariances of the GRACE SH solutions can be accounted for in a generalized least-squares estimation. With \({\varvec{C}}_\text {obs}\) denoting the error covariance matrix of \({\varvec{\kappa }}^\text {obs}\), Eq. (15) is then replaced by
and the least squares estimate for \({\varvec{\beta }}(t)\) is
Note that error covariances are not available for all GRACE SH solutions and even if available likely realize an incomplete representation of the true error structure. However, in practice also an imperfect approximation of the GRACE error covariance can be used to account for errors in the GRACE SH solution.
(b) A filtered version of \({\varvec{\kappa }}^\text {obs}\) can replace the pseudo-observables \({\varvec{\kappa }}^\text {obs}\) used in Eq. (15). As a way of accounting for the GRACE error characteristics, isotropic Gaussian filters and non-isotropic destriping filters are popular choices, usually applied in the SH domain. Filtering can be expressed as a linear operation that transforms \({\varvec{\kappa }}^\text {obs}(t)\) into a new vector of pseudo-observables
with a square filter matrix \({\varvec{F}}\). In that case, filtered versions of the prescribed patterns of SMD anomalies
need to be employed in the inverse approach. Instead of Eq. (14), the observation equation then reads
and its ordinary least-squares solution is
(c) The pseudo-observables may be in fact any functionals of the gravity field variations observed by GRACE. For example, Wouters et al. (2008) and Schrama et al. (2014) chose SMD anomalies \(\kappa ^\text {obs}(\Omega _j,t)\) evaluated in the spatial domain at nodes \(\Omega _j\) \((j=1,\dots ,J)\) of a grid defined regionally or globally, respectively. Forsberg and Reeh (2007) and Barletta et al. (2013) chose the effect of surface mass changes on gravity at satellite height, again evaluated at grid nodes \(\Omega _j\). Any such pseudo-observables can be expressed as a linear functional of the observed gravity field changes \(\Delta c^\text {obs}_{nm}\), and likewise of \(\kappa ^\text {obs}_{nm}\). Hence, the pseudo-observables arranged in a vector \({\varvec{y}}^\text {obs}\) can be written as
with a (J, N)-matrix \({\varvec{G}}\). The prescribed patterns \({\varvec{a}}^i\) need to be mapped likewise into the same pseudo-observables
The observation equation then reads
and its ordinary least-squares solution is
All choices of pseudo-observables and of ways to account for GRACE solution errors discussed so far lead to the general relation
where the weight matrix \({\varvec{P}}\) is either the unity matrix \({\varvec{I}}\), \({\varvec{C}}_\text {obs}^{-1}\), \({\varvec{F}}^{\textsf{T}}{\varvec{F}}\) or \({\varvec{G}}^{\textsf{T}}{\varvec{G}}\). Likewise, \({\varvec{P}}\) can be derived for more general choices. For example, a sequence of filtering the GRACE data and transforming it into some spatial-domain gravity field functional leads to \({\varvec{P}} = ({\varvec{GF}})^{\textsf{T}}{\varvec{GF}}\).
(d) A regularization may be applied to stabilize the inversion. In other words, a-priori information about the variance-covariance structure of the expected mass redistributions can be introduced. This can be done by using a covariance matrix of \({\varvec{\beta }}\),
in pseudo-observation equations
where \({\varvec{\varepsilon }}_\text {pat} = -{\varvec{\beta }}\) is the vector of residuals. By including these additional observation equations, the least-squares solution becomes
with \({\varvec{R}} = {\varvec{C}}_{\text {pat}}^{-1}\).
By substituting Eq. (31) into Eq. (18), we identify that the SK \({\varvec{\eta }}\) for any variant of the inverse approach discussed here has the form
or
2.5 The regional integration approach
From the start of GRACE mass change applications until today, mass change estimators have been realized by directly defining the SK (cf. \(\eta (\Omega )\) in Eq. 9). This approach is referred to as regional integration approach, or direct approach. Typically, the SK was defined in a heuristic manner by modifying the region function. For example, the original region was extended or diminished by a buffer zone to avoid leakage, it was smoothed to dampen GRACE error effects and it was sometimes scaled subsequently for further leakage prevention. Examples include work by Velicogna and Wahr (2006) and Horwath and Dietrich (2009) for ice sheets, Johnson and Chambers (2013) and Chen et al. (2018) for global ocean mass and Famiglietti et al. (2011) for terrestrial water storage.
2.6 Regional integration approach with tailored sensitivity kernels
The pioneering study by Swenson and Wahr (2002) already laid out a formal optimization of the SK based on covariance information for both geophysical signal and GRACE errors. Here we elaborate such a formalism for our purpose. We seek for a sensitivity function \({\varvec{\eta }}\) that minimizes, in a least-squares sense—the sum of leakage errors and propagated GRACE errors. An example of this method includes the work by Groh and Horwath (2021) for the Antarctic ice sheet.
For the ease of presenting the basic ideas, in this subsection we neglect the SH components outside \(\{(n,m)\}_{\text {obs}}\). We show in Appendix A that this neglection does not change the expression of the tailored SK derived here (Eq. 44) .
We express the leakage effect (Eq. 13) in vector notation as
where \({\varvec{\vartheta }}\) and \({\varvec{\kappa }}\) contain the SH coefficients \(\vartheta _{nm}\) and \(\kappa _{nm}\), respectively, with \((n,m)\in \{(n,m)\}_\text {obs}\).
Let \({\varvec{C}}_\kappa \) denote the covariance matrix of the (true) SMD anomalies \({\varvec{\kappa }}\). Its propagation through Eq. (34) gives the variance of the leakage effect,
Likewise, propagating the GRACE error covariance matrix \({\varvec{C}}_\text {obs}\) through Eq. (11) gives the variance of the GRACE error effect,
We solve for the SK \({\varvec{\eta }}\) that minimizes \(\text{ Var }(\delta m^\text {leak}+\delta m^\text {obs})\), which equals \(\text{ Var }(\delta m^\text {leak})+\text{ Var }(\delta m^\text {obs})\) as we assume that the two errors are uncorrelated. Hence, \({\varvec{\eta }}\) must fulfill
The derivatives of Eqs. (35) and (36) are
and their substitution into Eq. (37) leads to
We may express any signal covariance matrix \({\varvec{C}}_\kappa \) as
where the annotations \({\varvec{A}}\) and \({\varvec{C}}_\text {pat}\) are intentional repetitions from Sect. 2.4: \({\varvec{A}}\) is a matrix with each column holding the SH coefficients of a pattern of SMD anomalies; \({\varvec{C}}_\text {pat}\) is the covariance matrix of amplitudes (scaling factors) of these patterns. Indeed, Eq. (41) is a useful form of composing signal covariance information (e.g., by prescribing geographical signal patterns) or of decomposing a given covariance matrix (e.g., through an eigenvector, or empirical orthogonal function, decomposition). Then, Eq. (40) reads
We define the vector
which contains the mass changes in the region of interest associated to the patterns assembled by the columns of \({\varvec{A}}\) (cf. Eq. 17). Then we finally get
To discuss the tailored SK approach in the context of previous work we recall that it adopts the concept by Swenson and Wahr (2002) to minimize the total error of regionally integrated mass changes. On a similar line of development, Kusche (2007), Klees et al. (2008) and Wu et al. (2009) elaborated on filtering for GRACE anomaly fields (referred to as optimal filtering in the following) that incorporate signal and error covariance information to minimize, in a global least-squares sense, the combined effect of GRACE solution errors and signal distortion. While the resulting spatially continuous filtered fields are invaluable for illustrations in maps, quantification of mass changes necessarily involves the additional step of regional integration. The transpose of \(({\varvec{C}}_\kappa + {\varvec{C}}_\text {obs})^{-1} {\varvec{C}}_\kappa \) (cf. Eq. 40) is a representation of the optimal filter matrix in the sense of Kusche (2007), Klees et al. (2008) and Wu et al. (2009). Hence, the SK expressed by Eq. (40) corresponds to the concatenation of an optimal filtering of the GRACE field and subsequent integration with the unfiltered region function. We note that some previous studies on optimal filtering proposed deviating approaches for the subsequent estimate of regional integrals. Wu et al (2009, their Section 3) proposed to modify the filtering in adaption to the target integration region. Siemes et al. (2013) applied a buffering of the region function and a rescaling of the integration result. This implies that some realizations of optimal filtering may not be considered actually optimal for subsequent integration over a given target region. We take this note as an argument for optimizing, in a single coherent scheme, the estimate of the target magnitude, which is regionally integrated mass change.
Our way of expressing signal covariance information through a set of prescribed patterns (Eq. 41) lends itself to studies with a regional focus (such as for Greenland, as addressed in Sect. 3) which make up a large portion of GRACE applications. Scientists interested in a particular region typically have knowledge and datasets on the expected regional signal patterns and amplitudes that are more specific and detailed than similar information for the rest of the globe at the scientist’s disposal. Such specifically regional information is also particularly relevant for leakage considerations in regionally-oriented GRACE mass change studies. Hence, by incorporating more detailed signal covariance information for the region of study, scientists can ‘tailor’ their method to their signal of interest. The term ‘tailored sensitivity kernel’ might be suitable to convey this concept of refraining from any global optimality despite the formal optimization involved.
2.7 Proposition on the equivalence of approaches
The following proposition holds: The SKs from the inverse approach (Eq. 33) and the tailored SK approach (Eq. 44) are equal if the inverse approach uses \({\varvec{P}} = {\varvec{C}}_\text {obs}^{-1}\) and \({\varvec{R}} = {\varvec{C}}_\text {pat}^{-1}\) and if both approaches use the same defining elements \({\varvec{C}}_\text {obs}\), \({\varvec{A}}\) and \({\varvec{C}}_\text {pat}\). In other words, the direct approach and the inverse approach are equivalent if they rigorously incorporate the same signal covariance and error covariance information.
Indeed, the stated equality
can be verified by multiplying both sides with \(({\varvec{A}} {\varvec{C}}_\text {pat} {\varvec{A}}^{\textsf{T}}+ {\varvec{C}}_\text {obs})\) from left and with \(\left( {{\varvec{A}}}^{\textsf{T}}{\varvec{C}}_\text {obs}^{-1}{\varvec{A}} + {\varvec{C}}_{\text {pat}}^{-1} \right) \) from right. After this equivalent transformation, both sides become \({\varvec{A}} {\varvec{C}}_\text {pat} {\varvec{A}}^{\textsf{T}}{\varvec{C}}_\text {obs}^{-1}{\varvec{A}} + {\varvec{A}}\).
We have elaborated earlier in Sect. 2.4 that inverse methods are particular realizations of the regional integration approach so that they can be analyzed and interpreted from the viewpoint of either the inverse approach or the regional integration approach. Now we see that, conversely, the regional integration approach, if realized through tailored SKs, corresponds to a particular realization of the inverse approach. Tailored SK estimates, too, can therefore be interpreted from the viewpoint of either the inverse approach or the regional integration approach.
3 Application
3.1 Methods implemented in this study
We derive, discuss and compare SKs and mass change results from four different methods of mass change estimates for the GrIS. These four methods adopt characteristics from previous studies. However, we implemented these methods ourselves in the framework of this study. Our intention is not to reproduce the methods of previous studies in detail but to implement them in a way that facilitates comparison. We limited the number of implemented methods in this study to four but the same concept also applies to many other methods, notably inverse methods that do not explicitly consider SKs in their original design (see Method II and III). Our implementation of the four methods, referred to as ’Method I – IV’ in the following, is described in more detail below. The methods cover the inverse and the regional integration approach and differ in their choice of patterns \({\varvec{a}}^i\), pseudo-observables \({\varvec{y}}^\text {obs}\) and filtering. An overview is given in Table 1. The methods are adapted such that the patterns \({\varvec{a}}^i\) can be aggregated to integrated mass changes of the same 8 drainage basins (Zwally et al. 2012) shown in Fig. 1. The involved patterns are visualized in Fig. 2. All methods use the same input GRACE SH solutions with degree \(n\le 90\) so that SKs are computed for \(\{(n, m)\}_\text {obs}=\{(n, m): 1 \le n \le 90\}\).
Greenland drainage basins (colored) from Zwally et al. (2012). The dashed line represents the 2000 m elevation contour
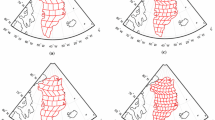
Patterns in the region around Greenland used in our implementation of the four different methods. a, b Patterns for Methods I and II, respectively, represented by colored areas. c, d Patterns for Method III and IV, respectively, represented by individual dots. In the later analysis they are aggregated to basins represented by colors. Note that Methods I and IV use globally distributed patterns not restricted to the region shown
Method I Method I is based on the inverse method by Jacob et al. (2012). Patterns and observables are defined in the SH domain. Each pattern (or mascon) corresponds to a constant SMD anomaly in a distinct area. We defined 31 such patterns for the GrIS, different from those used by Jacob et al. (2012), by subdividing the GrIS basins along the 2000 m elevation line and along further lines (Fig. 2a). In addition, we defined 81 patterns associated to glaciated areas outside the GrIS. Smoothing is done by a Gaussian filter with a half-width radius of 200 km. The smoothed patterns are then fitted to the smoothed surface mass density anomalies from GRACE. The SK in the general form of Eq. (33) has the weight matrix
which arises from the discussion in Sect. 2.4 (b). The diagonal matrix \({\varvec{F}}_\text {G}\) contains the filter coefficients of the Gaussian filter. No regularization is required for this method.
Method II Method II is based on the inverse method by Wouters et al. (2008) and Schrama and Wouters (2011). It performs the fitting in the spatial domain. The fitting is done by a formal least-squares minimization, as done by Schrama and Wouters (2011) while Wouters et al. (2008) used an iterative approximative minimization. Patterns are defined by uniform SMD anomalies in distinct areas (Fig. 2b). They are filtered and fitted to filtered GRACE-based SMD anomalies evaluated on grid nodes. Schrama and Wouters (2011) investigated the use of several basin configurations and ultimately chose a representation by nine basins (they split eight basins, different from those used here, by the 2000 m elevation contour and merged the parts above 2000 m to one basin). For comparability to the other methods, we chose a 16-basin representation for the GrIS (eight basins split by a 2000 m elevation contour). For the surrounding regions (within the map domain of Fig. 2), we defined patterns for the four ice covered regions of Ellesmere Island, Baffin Island, Iceland and Svalbard as well as for 15 additional patterns covering the surrounding ocean and landmasses (Wouters et al. 2008, Supp.). We applied a Gaussian filter with a half-width radius of 200 km. To express the kernel of this method in the general form of Eq. (33), the weight matrix has to include the mapping of the patterns in \({\varvec{A}}\) into the spatial domain as discussed in Sect. 2.4 (c):
The matrix \({\varvec{G}}_\text {SHS}\) expresses the spherical harmonic synthesis and consists of SH basis functions \({\varvec{Y}}_{nm}^{\textsf{T}}(\Omega )\) for each grid node. Unlike Schrama and Wouters (2011) we did not use a form of regularization as given in Eq. (31).
Method III Method III is based on the inverse method by Forsberg and Reeh (2007), Barletta et al. (2013) and Forsberg et al. (2017). Pseudo-observables in this method are gravity changes at GRACE orbit altitude. Patterns of mass changes are defined as point masses on the Earth surface. More precisely, the pseudo-observables were evaluated over a grid at 400 km altitude from the GRACE Stokes coefficient anomalies after subtracting the elastic load deformation effect and applying a DDK5 filter (Kusche 2007). The point masses were placed on equal-area nodes with a radius of 20.2 km per node over the GrIS and other ice covered regions nearby (see Fig. 2c) and expressed in the SH domain (Pollack 1973). Following Barletta et al. (2013), we included a complementary solution area to account for non-ice signals like land hydrology or errors in the ocean models. For this purpose we defined additional patterns within a sector around Greenland (the map domain of Fig. 2) separated from the patterns of ice mass changes by a gap of 550 km. According to the formalism of Sect. 2.4, the mapping of the SH representation of SMD changes to the pseudo-observables and the filtering are expressed in the weight matrix
The mapping is split into the conversion from coefficients of SMD to Stokes coefficients (Eq. 3) (\({\varvec{G}}_{\kappa \text {2s}}\)), the subtraction of the elastic load deformation effect (\({\varvec{G}}_\text {def}\)), the conversion to SH coefficients of gravity at orbit altitude (\({\varvec{G}}_\text {gorb}\)) and the synthesis into the spatial domain (\({\varvec{G}}_\text {SHS}\)). The filtering with the non-isotropic DDK5 filter is realized by the non-diagonal matrix \({\varvec{F}}_\text {DDK}\). A regularization is required for this method to stabilize the inversion. The matrix \({\varvec{R}}\) in Eq. (33) was set to the diagonal matrix \(\lambda ^2 {\varvec{I}}\). We empirically derived the regularization factor \(\lambda ^2\) as 2.0 \(\times \) 10\(^{-42}\) starting with an approximation formula from Press et al. (2002). We note that unlike Forsberg and Reeh (2007) we did not directly use Newton’s law of gravitation to compute the gravitational attraction of the point masses. Instead, we used the general form of Eq. (33) with the matrix \({\varvec{A}}\) holding the SH coefficients of SMD anomalies associated to point masses. This enables us to use one weight matrix \({\varvec{P}}\) (Eq. 48) that consistently describes the mapping and filtering of both the patterns and the observations, including their truncation to \(\{(n, m)\}_\text {obs}\).
Method IV Method IV uses the regional integration approach (Eq. 10) with tailored SKs (Sect. 2.6). Unlike for the first three methods, here the SKs are determined directly (Eq. 44). We derived SKs fulfilling Eq. (37) for a set of regions that actually correspond to grid cells of a dense polar-stereographic grid with a spatial resolution of 50 km \(\times \) 50 km covering the GrIS. The kernels for the entire GrIS, a particular drainage basin (as in Fig. 1) or any other region of interest can be derived by adding up the SKs of all grid cells defining these regions. Groh and Horwath (2021) describe the details of a realization of the tailored SK approach for Antarctic ice masses. Its realization for GrIS mass changes is outlined in the following.
To express the leakage variance through Eqs. (35) and (41), we defined patterns by means of point masses located at the nodes of a dense 50 km \(\times \) 50 km grid (890 nodes), both for GrIS and surrounding glaciated regions, and at the nodes of a coarser (1.4 \(\times \) 10\(^4\) km\(^2\)), globally defined icosahedron grid elsewhere (35863 nodes, Fig. 2d). The pattern predefined for the targeted grid cells ensures the minimization of leakage-out. Hence, the corresponding entry in \({\varvec{m}}\) in Eq. (44) equals the mass of the point mass. All remaining patterns are included to minimize leakage-in, requiring the elements of \({\varvec{m}}\) to be zero for these patterns. The amplitudes of the predefined patterns are expressed through their signal covariance matrix \({\varvec{C}}_\text {pat}\). A constant signal standard deviation of 400 mm was assumed for all patterns on the dense grid, which reflects the order of magnitude of ice mass changes. The standard deviation for all patterns on the coarser grid was set to 33.6 mm. The essential choice here is about the ratio between the signal standard deviations associated to the two types of patterns (near-field ice and far-field). The ratio of about 12 adopted here reflects that a larger mass variability is expected for the ice-covered regions in Greenland and its vicinity than for their surroundings. This ratio was found appropriate after testing different choices in simulation experiments of the kind described by Groh et al. (2019). No spatial correlations between the patterns were accounted for, yielding a diagonal signal covariance matrix \({\varvec{C}}_\text {pat}\). In terms of the notation of the inverse approach (Eq. 33), this means that additional information were introduced through a diagonal matrix
We expressed the variance of the GRACE error effect through a covariance matrix \({\varvec{C}}_\text {obs}\) according to Eq. (36). Hence, when expressed in terms of the inverse approach (Eq. 33) the weight matrix is
We derived \({\varvec{C}}_\text {obs}\) based on the empirical covariance of residuals of unfiltered surface density anomaly coefficients with respect to a model of temporal changes consisting of a linear component and harmonic components (Groh and Horwath 2021). Since such residuals still contain geophysical signals on lower SH degrees, error variances and covariances were not considered for SH degree \(\le 35\) and were downweighted by a factor that changes gradually from zero at degree 35 to one at degree 55. The covariance matrix obtained in this way was finally scaled to define \({\varvec{C}}_\text {obs}\). The scaling factor was set to 0.1, which was found appropriate after testing different choices in simulation experiments of the kind described by Groh et al. (2019). This scaling effectively controls the relative weights between the leakage requirement and GRACE error requirement imposed by \({\varvec{C}}_\kappa \) and \({\varvec{C}}_\text {obs}\) in Eq. (40). It is justified not only because the imposed magnitude of the signal covariance is somewhat arbitrary. More importantly, the GRACE error requirement (just as the leakage requirement) needs to accommodate signals at different temporal scales, including long-term linear trends. While the empirical GRACE error covariance matrix applies for monthly anomalies, smaller error covariances apply at longer time-scales.
3.2 GRACE releases and auxiliary data
We applied the methods described in Sect. 3.1 to Level-2 GRACE monthly gravity-field solutions of Release 06 provided by the Center for Space Research (CSR RL06) (Bettadpur 2018; Save 2019). We made use of 206 monthly solutions up to a SH degree \(n_\text {max} = {90}\), spanning the interval from 2002-04 to 2020-07. We added degree-1 coefficients derived by combining the monthly solutions and assumptions on ocean mass redistribution (Swenson et al. 2008; Bergmann-Wolf et al. 2014; Sun et al. 2016). These degree-1 series are similar to those provided in TN-13 by the GRACE/GRACE-FO Science Data System. We replaced \(C_{2,0}\) coefficients with estimates based on satellite laser ranging provided in TN-14 (Loomis et al. 2019). We replaced \(C_{3,0}\) coefficients by TN-14 values for the time period starting from October 2016 in response to the GRACE and GRACE-FO accelerometer instrument issues (Loomis et al. 2020). We removed linear trends due to glacial isostatic adjustment by using the model by Caron et al. (2018).
3.3 Results
We examine the SKs and the mass change estimates of our implementation of four different methods outlined in Sect. 3.1. We take the whole GrIS and two of its drainage basins (Basin 7 and 4) as example target regions. For other drainage basins, results are shown in the supplementary material.
The mass change time series are shown in Fig. 3. Linear trends (computed by fitting a quadratic polynomial together with annual and semiannual sinusoids) are also quoted. For the whole GrIS as a target region (Fig. 3a), the time series are very similar across the four methods. They agree in representing seasonal signals as well as specific events like an increased melt in 2019 (Sasgen et al. 2020). The linear trends over 2002-04–2020-07 vary across methods between – 251 and – 263 Gt a\(^{-1}\), that is, by about 5 %. For Basin 7 (Fig. 3b) the time series from different methods differ in their smoothness and, accordingly, in how much a seasonal signal can be distinguished. Specific events like the melt in 2019 appear in all four time series but with different magnitudes. The trend varies by up to 20 %. It amounts to – 37.9 Gt a\(^{-1}\) for Method I and is less negative by 3.7–6.2 Gt a\(^{-1}\) for the other methods. For Basin 4 (Fig. 3c) the time series differ most. Differences in smoothness are much more pronounced than for Basin 7. Time series are smoothest for Method III and IV and by far most noisy for Method I. Trends are very different across methods. They range from – 30 to – 70 Gt a\(^{-1}\) and thereby differ by a factor of more than 2.
For our presentation of SKs in Figs. 4 and 5, we add a degree-0 component to each SK, as indicated in the figures. As discussed in Sect. 2.2, this has no effect on the mass change estimator represented by the SK but may facilitate comparison to the region functions \(\vartheta \). The degree-0 component is derived empirically in the spatial domain after synthesizing the SK over the whole globe. We mask out the sector around Greenland (the map domain of Fig. 2) and take the median value of the remaining grid as the degree-0 component.
Figure 4a–d shows regional maps of the SKs for the whole GrIS. The SKs resemble the shape of the region function in that they are close to 1.0 over the GrIS and decrease to values close to 0.0 outside the GrIS. Unlike for the region function, this decrease is slow and smooth. The four methods differ in how fast the SKs decrease and how much they over- and undershoot the values of 1.0 and 0.0 in the GrIS domain and outside, respectively. The SK of Method III decreases the smoothest, while the SKs of Method II and IV show the steepest decrease. In turn, they exhibit over- and undershoots. Specifically, for Method II the SK stays negative over extended ocean areas, going below – 0.2 in some places, while over the GrIS itself it partly exceeds 1.2.
For Basin 7 (Fig. 4e–h) all four SKs roughly resemble the smoothed and rescaled region function. Inside the basin the SKs for Method I, II and IV overshoot to more than 1.6, while the SK of Method III does not reach 1.0 and appears to be smoother, overall. The decrease of the SK across the basin boundary is steepest for Method I and II. In turn, it is followed by prominent undershoots (below – 0.3 for Method II) in adjacent ice drainage basins. All SKs decrease less steeply in the direction of the ocean than in the direction of the adjacent ice sheet basins.
For Basin 4 (Fig. 4i–l) with its narrow, elongated shape, the SKs have peculiar features and differ substantially across methods. For Method III and IV the SKs have similar characteristics as for Basin 7 but their apex is offset from the basin center to the adjacent ocean resulting in values smaller than 1.0 over most of the drainage basin itself. The under- and overshoots for both methods are larger than for basin 7. Method III undershoots up to – 0.4 in the ocean west to southern Greenland while Method IV undershoots up to – 0.3 in the ocean between Greenland and Iceland and overshoots up to 0.2 in the ocean west to southern Greenland. For Method II, the apex is offset to the northern margin of the drainage basin where it has values as large as 2.2. The SK decreases steeply within the basin and attains values around 0.0 in its southern part in the transition into an undershoot in southwest Greenland. Another undershoot in the ice drainage basin north of Basin 4 is as negative as – 0.7. For Method I, the SK resembles the region function quite well within the target Basin 4, with values between 1.4 in its center and 0.5 at its edges. However, it has extreme under- and overshoots outside Basin 4. Three undershoots on the GrIS itself reach values down to – 0.5 to – 1.0. In the ocean west and east to Greenland an overshoot and an undershoot, respectively, have extrema as large as + 3.5 and – 2.8.
Same as Fig. 4 but in a global representation of the sensitivity kernels
Global maps of the SKs are shown in Fig. 5. In the far field they deviate little from 0.0. The different patterns of these deviations are highlighted by the color scale limited to \(\pm \,{0.011}\).
For all three target regions, the SKs for Method IV have a checkered pattern of global oscillations. The oscillations have strong amplitudes in the region around Greenland that decrease to a steady level in the mid- and low-latitudes. The amplitudes increase again close to Antarctica. For Method I and II oscillations appear as ringing centered in Greenland with highest amplitudes in the Basin 4 SK and lowest amplitudes in the GrIS SK (barely discernible in Fig. 5b). For Method III, instead, the global deviations from zero adopt a hemispherical pattern with predominantly positive values on the hemisphere centered in Greenland and negative values on the opposite hemisphere. Distinct north–south stripes within the geographic longitudes of Greenland are another unique feature of the Method III SKs.
For Method I, glaciated areas around the globe stand out with values at the adopted \(C_{0,0}\) values (hence they would be zero if \(C_{0,0}\) was omitted). These are the areas where Method I co-estimates mass changes. For Method II, a region around Greenland stands out with particularly large SK variations different from the oscillations elsewhere. This region (best discernible in Fig. 5b,f) is the sector around Greenland (the map domain of Fig. 2) where Method II prescribes the regionally limited mass change patterns (cf. Fig. 2)
Degree amplitudes of the SKs are shown in Fig. 6. For the GrIS (Fig. 6a), they peak around degree 7 to 10 for all four methods and decrease quickly for higher degrees. For Basin 4 and 7 (Fig. 6b, c) they peak at higher degrees and are overall quite different between the four methods. For Method IV there is a distinct maximum around degree 40. For Method III the degree amplitudes at high degrees (above 35) are by far lowest among the four methods.
3.4 Interpretation
Hereafter, we interpret the observed SK properties and their differences in view of the differences between the underlying methods of mass change estimates.
All methods build on a set of prescribed patterns of surface mass change. By each pattern, a requirement is imposed on the SK to avoid leakage from this pattern. We refer to it as ‘leakage requirement’. The tailored SK approach makes this requirement explicit. The inverse approach likewise ensures that the mass changes associated to the prescribed patterns are correctly inferred insofar as it correctly estimates the amplitudes of these patterns. The leakage requirement exclusively refers to the finite set of prescribed patterns. The way how this requirement shapes the SK in detail therefore depends on the prescription of patterns. Methods I and II prescribe patterns such that each pattern is associated to a specific area (‘areal pattern’) and has a constant non-zero SMD in this area and zero SMD outside this area. (Omission of the degree-0 component leads to the subtraction of the global mean, so that outside the specific area the patterns attain a slightly non-zero constant value.) The leakage requirement for such a pattern means that on average over the area, the SK is 1 (or 0) in the case that the area is within (or outside, respectively) the target region of the mass change estimate. From the point of view of the leakage requirement for areal patterns over- and undershoots of the SK within the area are harmless as long as they compensate each other within the area. Methods III and IV define point mass patterns. The leakage requirement then requires the SK to be 1 (or 0) at each point mass position inside (or outside) the target region and does not allow for a compensation between under- and overshoots.
A second requirement on the SK is to avoid the propagation of GRACE errors on the mass change estimate. We refer to it as ‘GRACE error requirement’. Roughly speaking, this requires smoothness of the SK. This may be in conflict with the leakage requirement. In the tailored SK formalism, this GRACE error requirement is imposed through the GRACE error covariance matrix (or some imperfect approximation thereof). In the inverse approaches, the weight matrix \({\varvec{P}}\) can be regarded as a way to account for the GRACE error characteristics. For example, Method I incorporates the Gaussian filter weights in \({\varvec{P}}\) (Eq. 46). The resemblance between the degree dependence of the Gaussian filter weights and the degree dependence of the inverse GRACE error degree amplitudes makes \({\varvec{P}}\) a robust approximation of \({\varvec{C}}_\text {obs}^{-1}\).
A relative weighting between the leakage requirement and the GRACE error requirement can be done by relative scaling between \({\varvec{C}}_\text {pat}\) and \({\varvec{C}}_\text {obs}\) in the notation of the tailored SK approach implemented by Method IV, or between \({\varvec{P}}\) and \({\varvec{R}}\) (if present) in the notation of the inverse approach. The absence of \({\varvec{R}}\) in Method I can be interpreted as a priority to the leakage requirement. Method II and III likewise realize some compromise between the two requirements. However, it is less accessible from the tailored SK point of view how this compromise is attained because the elements \({\varvec{P}}\) and \({\varvec{R}}\) (if present) deviate considerably from the conditions imposed in the proposition of Sect. 2.7.
For the entire GrIS as a target region (Fig. 4a–d), differences between the SKs from the four methods appear primarily in the adjacent ocean domain. We attribute these differences to the different definition of ocean mass change patterns made by the different methods. For Method I, there are no explicitly defined patterns of ocean mass change. The requirement of reaching zero outside the GrIS is therefore not reinforced by additional requirements of reaching zero inside specific areas. This leads to a smooth transition towards zero outside the GrIS that is accelerated only by nearby patterns of land ice change in the Canadian Arctic. For Method II, oceanic mass change patterns are defined as areal patterns within a sector around Greenland. This requires that the SK is zero on average over each of the considered ocean areas. This requirement leads to a steep decrease of the SK from the GrIS towards the ocean domain and negative values in large parts of the ocean sub-regions which compensate the positive values close to the GrIS. For Method III and IV, ocean patterns are prescribed as point masses so that the leakage requirement means to bring the SK close to zero at every individual point mass position. For Method IV, undershooting occurs anyway in result of the steep decrease of the SK from 1.0 to 0.0 in conjunction with the smoothness requirement. For Method III, the SK decrease is more gentle, partly because oceanic patterns are not defined close to Greenland so that non-zero SK values are not penalized there. The fact that leakage requirements associated to ice sheet patterns are stronger than leakage requirements associated to oceanic patterns also explains why for the GrIS as a whole (Fig. 4a–d) all SKs are consistently very close to 1.0 all over the ice sheet.
The SKs for a single basin like Basin 7 (Fig. 4e–h) illustrate how the different prescription of ice versus ocean mass change patterns affect the SK shape. The SKs tend to decrease more steeply towards the adjacent ice sheet basins than towards the ocean because the defined ice sheet patterns impose stronger leakage requirements than the oceanic patterns. Indeed, for Methods I and III no oceanic patterns are defined close to Greenland. For Method II, positive SK values in the near-Greenland ocean may be compensated by negative values further away as discussed above. For Method IV, patterns over the ocean are given a lower weight in \({\varvec{C}}_\text {pat}\) than patterns over the GrIS.
The peculiarities of Basin 4 SKs (Fig. 4i–l) underline the potentially strong impact of details of the pattern definitions. For Method I, the parametrization is done by separate patterns for the northern and southern part of the basin (cf. Fig. 2a). Therefore, the SK has to be close to 1.0 on average over the northern part and southern part separately. In consequence, it is close to 1.0 all over Basin 4. The tight requirements within the basin entail the large under- and overshoots elsewhere. In contrast to Method I, the Method II SK varies extremely between the north and the south of Basin 4. Even so, its average over the basin is close to 1.0. Since the two areal patterns prescribed for this basin (cf. Fig. 2b) stretch over the north-south range of the basin, the SK still fulfills the related leakage requirement despite its extreme variations. For Method III, the offset of the SK apex into the ocean is enabled by the absence of patterns over the ocean domain in the 550 km buffer zone, that is, by the absence of any leakage requirement for this zone. The SK of Method IV represents a compromise with only small under- and overshoots, a smaller offset of the apex into the ocean and a closer resemblance to the region function of the basin.
Large under- and overshoots that appear for single basin SKs (such as for Basin 4 with Method I) do not appear to the same degree for the GrIS SK, that is, the sum of the individual basins’ SKs. The individual basins’ under- and overshoots are compensated for by similar, but opposite, under- and overshoots of other basins’ SKs. For the case of the Method I SK for Basin 4, the compensation is mostly by the SK of Basin 6 (see Fig. S3 in the supplementary material).
Some remarkable differences between Method III and the other methods seen in the global representation of SKs (Fig. 5) can be related to the choice of pseudo-observables and of filtering. We attribute the hemispherical features of the Method III SKs to the choice of pseudo-observables. Gravity at orbit height, evaluated regionally, cannot separate mass changes in the far field from mass changes in Greenland itself. Hence, far-field mass changes affect the Greenland mass change estimates, and this is reflected in non-zero SK values in the far field. In contrast, Methods I, II and IV establish a more localized link between the target quantity and the pseudo-observables, both being some representation of SMD anomalies. Moreover, the SKs of Method III are by far the smoothest among the four methods. We attribute this to the regularization applied to stabilize the estimation of point masses from the pseudo-observables, where the pseudo-observables arise from upward continuation, hence smoothing, of the surface mass changes. The distinct north-south stripes in the SKs of Method III are most likely a consequence of the involved DDK filtering.
The checkered global pattern of the Method IV SKs (Fig. 5d, h, l) associated to the degree amplitude maxima around degree 40 (Fig. 6) can be attributed to the empirical, and incomplete, GRACE error covariance information incorporated by this method. By Eq. (44), \({\varvec{\eta }}\) is determined as a compromise between two conflicting requirements: avoid leakage errors (and hence include high-degree SH components) and avoid the propagation of GRACE errors (and hence dampen high-degree components). Since the requirement on GRACE errors becomes effective only between degree 35 and 55, the spectral content of \({\varvec{\eta }}\) peaks in this band.
The differences seen between the SKs are also reflected in the mass change time series. The GrIS SKs for the four methods are very similar over the GrIS itself. They differ more substantially in the adjacent ocean domain. Since SMD variations are smaller in the ocean domain than in the GrIS domain, these SK differences have only small effects on the mass change time series. For the individual basins, the SKs show larger differences among the methods and also deviate more substantially from the actual region functions. This certainly causes leakage effects which are different among the methods and cause differences between the resulting ice mass trends. For example, for Basin 4, the Method II SK amounts to 2.2 in the north of the basin and thereby over-weights known pronounced mass losses of glaciers in this region (e.g., Brough et al. 2019; Khan et al. 2020). The same mass losses are under-weighted by Methods III and IV with SK values of 0.6–0.7 compared to 2.2 for Method II. This difference contributes to the Basin 4 trend being more negative from Method II than from Method III and IV. The small-scale, large-amplitude features of the Method I SK for Basin 4 involve substantial amplitudes of SH components up to \(n_\text {max} = 90\) (cf. Fig. 6c). This leads to an increased propagation of GRACE solution errors and hence an increased noise in the mass change time series. The smoothness of the SKs for Method III and IV, in contrast, entails lowest noise levels for the Basin 4 mass change time series from these methods. However, in the summation of the individual basins’ time series to the GrIS time series, the noise contents compensate each other. This corresponds to the compensation among small-scale under- and overshoots of the SKs as discussed above.
4 Discussion and conclusions
Mass change estimates from GRACE SH solutions by different studies differ for a number of reasons. The reasons include not only the methods applied to the SH input datasets but also the choices related to these input datasets, such as the GRACE SH solutions, the treatment of low-degree coefficients, or geophysical corrections like for glacial isostatic adjustment. This has complicated attempts to compare the methods in isolation and to attribute part of the differences between results to differences between the methods. Therefore, such attempts have been limited (e.g., Groh et al. 2019; Bonin and Chambers 2013; Ran et al. 2018). In addition to experiments with prescribed choices of input GRACE solutions and corrections, the intercomparison study by Groh et al. (2019) also imposed the participants to apply their processing chain to synthetic input data in order to specifically assess the leakage error. The synthetic input data represented different test signals in the format of GRACE SH solutions. Differences between the results and the known synthetic ”truth” revealed the leakage error associated to the test signals. However, the number of test signals was limited to 27 to reduce the effort for the participants to reasonable levels, which may have limited the significance of the derived leakage error statistics. Even so, the effort for the participating groups was considerable and not all were able to contribute to this part of the intercomparison.
The availability of SKs as elaborated in this study not only makes mass change estimates easy to reproduce, but also boosts opportunities for method assessments and method intercomparisons. Any scientist can apply a given SK to any test signal to perform specific leakage assessments by evaluating Eq. (12). Likewise, the propagation of errors of the input GRACE solutions can be assessed by evaluating Eq. (11) for particular error samples or by propagating an error covariance matrix through Eq. (11). Likewise, the effect of any change in the SH input datasets (such as input GRACE solutions or applied corrections for solid-Earth processes) can be immediately evaluated through Eq. (10). Effects of changing the SH input data can be easily separated from effects of changing the method of analyzing this SH input data. The former effects correspond to a change of \({\varvec{\kappa }}^\text {obs}\) in Eq. (10), while the latter correspond to a change of \({\varvec{\eta }}\).
The value of SKs applies to any target region and target signal of surface mass redistribution, beyond the GrIS example elaborated here. In fact, applications to hydrological drainage basins, where the signals in neighboring basins may differ substantially in the phase of their seasonality or in other temporal characteristics, may particularly benefit from a simple access to method comparisons.
These opportunities of method assessment and comparison apply to inverse methods just as they do for direct methods. In particular, leakage effects have not always been obvious for inverse methods since such methods may formally attribute GRACE observations to mass redistribution patterns with precise geographic delineation. The expression of inverse methods by SKs clarifies that the concept of leakage applies anyway. Leakage is unavoidable due to either the incompleteness of the set of prescribed patterns or the necessity of regularization.
The design of a specific method of mass change estimates usually involves many details and intermediate steps, such as the choice and implementation of prescribed patterns, the derivation of pseudo-observables, a discretization in the spatial domain, a stabilization of the inversion. Moreover, the implementation of a method involves specific algorithms and software tools. Therefore, a reproduction of such a design and implementation is laborious or even impossible based on published information. However, the mathematical essence of a method is given by the associated SK. Therefore, for many purposes, assessments and comparisons of methods do not need to reproduce the whole processing chain but may start from the associated SKs.
We illustrated the SK concept by presenting and discussing SKs associated to four different methods. In Sect. 2.7 we showed that the SKs from the direct approach and the inverse approach are equal if they rigorously incorporate the same signal covariance and error covariance information. For the four implemented methods this condition is not met since none of them incorporate the same stochastic information, i.e., they differ in their explicit or implicit assumption on signal and error covariances as described in Sect. 3.1. As a result the presented SKs exhibit remarkable differences across methods, which are the reason for differences in the resulting mass change time series. Some of the SK features, such as the extreme overshoots and undershoots in Fig. 4i, j, the global patterns in Fig. 5c, g, k, or the distinct global oscillation in Fig. 5d, h, l may be surprising and may be indicative of unexpected leakage effects. This underlines the value of making SKs explicit, assessing them and sharing them.
We provide the SKs derived in this article online at http://dx.doi.org/10.25532/OPARA-196. We will also provide SKs for the CCI GMB products of Greenland and Antarctica based on the tailored SK method at https://data1.geo.tu-dresden.de/.
While the four implementations adopt methods introduced by previous studies referred to in Sect. 3.1, we did not intend to precisely reproduce their methods. Therefore, the SKs discussed here are not identical to their SKs. We also note that the study by Jacob et al. (2012) underlying our Method I did not aim at resolving mass changes of individual drainage basins.
The presented SK framework involves some limiting assumptions made for simplicity, which may be released in order to arrive at more general SK frameworks. Three directions of generalization are worth mentioning. First, we represent mass variations in terms of SMDs on a sphere. Chao (2016) and Vishwakarma et al. (2022) elaborated on the caveat that mass redistributions in the Earth’s interior, such as due to glacial isostatic adjustment, have to be considered separately and on how a glacial isostatic adjustment correction should avoid physical inconsistencies. Li et al. (2017) and Ditmar (2018) proposed to replace the sphere by a reference ellipsoid as a more accurate representation of the Earth surface and elaborated the pertinent ellipsoidal corrections.
Second, we have formulated SKs as being time-independent. It is obvious how time dependence can be implemented. Methods that adapt to time-dependent GRACE error characteristics (e.g., Horvath et al. 2018) may be accommodated in this way. It is important to note that such error-adaptive methods pose additional challenges for leakage assessment. While leakage effects are usually conceived as effects of some actual temporal mass changes, time-variable SKs would induce leakage effects even in the absence of mass changes. This can be seen in the symmetry between \(\kappa \) and \(\eta - \vartheta \) in Eq. (12).
Third, the SK concept may be generalized to be applicable to data-adaptive methods. Such methods include data-adaptive filtering (e.g., Schrama et al. 2007) or data-adaptive leakage correction (e.g., Vishwakarma et al. 2017). In that case, the expression of the estimator as a linear operator (Eq. 6) would need to be reconsidered. Similar generalizations apply if GRACE data is combined with additional observations, such as satellite altimetry over the ice sheet (Forsberg et al. 2017; Kappelsberger et al. 2021) or over the ocean (Rietbroek et al. 2016) or GNSS-based solid-Earth surface deformations (Kusche and Schrama 2005). In such cases, the sensitivity of mass change estimates to the GRACE-based input depends on those additional observations and the relative weights that arise for the different observation types. In fact, for inverse problems with multiple datasets, assessments of the sensitivity to the individual input data may be particularly valuable, as it may not be clear beforehand what information is really provided from which dataset (e.g., Kusche and Schrama 2005).
In the quest for an optimal GRACE mass estimation method, tailored SKs are designed to minimize the total error variance, in line with previous investigations on optimal estimators (Swenson and Wahr 2002; Wu et al. 2009). We have shown (Sect. 2.7) that the tailored SK method is equivalent to an inverse method that employs the same covariance information on both the mass redistribution signals and the GRACE errors. Hence, such an inverse method possesses the same optimality property as the tailored SK method. One may argue that, in turn, inverse methods that do not incorporate covariance information this way are not optimal. This argument, however, can be immediately weakened by noting that in practice complete covariance information (on both signal and GRACE error) is not available and therefore none of the methods presented here can be considered optimal for a statistical point of view. Estimates that are formally non-optimal might be more robust against the incompleteness of covariance information employed. The quest for best methods of GRACE mass change estimates is not concluded by far.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/s00190-022-01697-8. It includes extended versions of Fig. 3 – 6 including all eight ice drainage basins and a table of the empirically determined degree-0 terms used for presentation of the sensitivity kernels.
Data Availability Statement
The SKs presented in this study for all four methods and all eight drainage basins are available at the TU Dresden Open Access Repository and Archive (http://dx.doi.org/10.25532/OPARA-196).
References
Barletta VR, Sørensen LS, Forsberg R (2013) Scatter of mass changes estimates at basin scale for Greenland and Antarctica. Cryosphere 7(5):1411–1432. https://doi.org/10.5194/tc-7-1411-2013
Bergmann-Wolf I, Zhang L, Dobslaw H (2014) Global eustatic sea-level variations for the approximation of geocenter motion from GRACE. J Geodetic Sci 4:1. https://doi.org/10.2478/jogs-2014-0006
Bettadpur S (2018) UTCSR level-2 processing standards document for level-2 product release 0006, v5.0. Technical report, Center for Space Research, The University of Texas at Austin, Austin
Blazquez A, Meyssignac B, Lemoine J et al (2018) Exploring the uncertainty in GRACE estimates of the mass redistributions at the Earth surface: implications for the global water and sea level budgets. Geophys J Int 215(1):415–430. https://doi.org/10.1093/gji/ggy293
Bonin J, Chambers D (2013) Uncertainty estimates of a GRACE inversion modelling technique over Greenland using a simulation. Geophys J Int 194(1):212–229. https://doi.org/10.1093/gji/ggt091
Brough S, Carr JR, Ross N et al (2019) Exceptional Retreat of Kangerlussuaq Glacier, East Greenland, between 2016 and 2018. Front Earth Sci. https://doi.org/10.3389/feart.2019.00123
Caron L, Ivins ER, Larour E et al (2018) GIA model statistics for GRACE hydrology, cryosphere, and ocean science. Geophys Res Lett. https://doi.org/10.1002/2017GL076644
Chao BF (2016) Caveats on the equivalent water thickness and surface mascon solutions derived from the GRACE satellite-observed time-variable gravity. J Geod 90(9):807–813. https://doi.org/10.1007/s00190-016-0912-y
Chen JL, Wilson CR, Blankenship DD et al (2006) Antarctic mass rates from GRACE. Geophys Res Lett 33(L11):502. https://doi.org/10.1029/2006GL026369
Chen JL, Tapley B, Save H et al (2018) Quantification of ocean mass change using Gravity Recovery and Climate Experiment, satellite altimeter, and Argo floats observations. J Geophys Res Solid Earth 123(11):10212–10225. https://doi.org/10.1029/2018JB016095
Chen J, Tapley B, Seo KW et al (2019) Improved quantification of global mean ocean mass change using GRACE satellite gravimetry measurements. Geophys Res Lett 46(23):13984–13991. https://doi.org/10.1029/2019GL085519
Ditmar P (2018) Conversion of time-varying Stokes coefficients into mass anomalies at the Earth’s surface considering the Earth’s oblateness. J Geod 92(12):1401–1412. https://doi.org/10.1007/s00190-018-1128-0
Ditmar P (2022) How to quantify the accuracy of mass anomaly time-series based on GRACE data in the absence of knowledge about true signal? J Geod. https://doi.org/10.1007/s00190-022-01640-x
Famiglietti JS, Lo M, Ho SL et al (2011) Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys Res Lett. https://doi.org/10.1029/2010GL046442
Forsberg R, Reeh N (2007) Mass change of the Greenland Ice Sheet from GRACE. In: Proceedings of the 1st international symposium of the IGFS, Harita Dergisi, Ankara, pp 454–458
Forsberg R, Sørensen L, Simonsen S (2017) Greenland and Antarctica ice sheet mass changes and effects on global sea level. Surv Geophys 38(1):89–104. https://doi.org/10.1007/s10712-016-9398-7
Groh A, Horwath M (2021) Antarctic ice mass change products from GRACE/GRACE-FO using tailored sensitivity kernels. Remote Sens 13(9):1736. https://doi.org/10.3390/rs13091736
Groh A, Horwath M, Horvath A et al (2019) Evaluating GRACE mass change time series for the Antarctic and Greenland ice sheet-methods and results. Geosciences 9(10):415. https://doi.org/10.3390/geosciences9100415
Horvath A, Murböck M, Pail R et al (2018) Decorrelation of GRACE time variable gravity field solutions using full covariance information. Geosciences 8(9):323. https://doi.org/10.3390/geosciences8090323
Horwath M, Dietrich R (2009) Signal and error in mass change inferences from GRACE: the case of Antarctica. Geophys J Int 177(3):849–864. https://doi.org/10.1111/j.1365-246X.2009.04139.x
Jacob T, Wahr J, Pfeffer WT et al (2012) Recent contributions of glaciers and ice caps to sea level rise. Nature 482:514–518. https://doi.org/10.1038/nature10847
Johnson GC, Chambers DP (2013) Ocean bottom pressure seasonal cycles and decadal trends from GRACE Release-05: ocean circulation implications. J Geophys Res Oceans 118(9):4228–4240. https://doi.org/10.1002/jgrc.20307
Joodaki G, Wahr J, Swenson S (2014) Estimating the human contribution to groundwater depletion in the Middle East, from GRACE data, land surface models, and well observations. Water Resour Res 50(3):2679–2692. https://doi.org/10.1002/2013WR014633
Kappelsberger MT, Strößenreuther U, Scheinert M et al (2021) Modeled and observed bedrock displacements in North-East Greenland using refined estimates of present-day ice-mass changes and densified GNSS measurements. J Geophys Res Earth Surf 126(4):e2020JF005,860. https://doi.org/10.1029/2020JF005860
Khan SA, Bjørk AA, Bamber JL et al (2020) Centennial response of Greenland’s three largest outlet glaciers. Nat Commun. https://doi.org/10.1038/s41467-020-19580-5
Klees R, Revtova EA, Gunter BC et al (2008) The design of an optimal filter for monthly GRACE gravity models. Geophys J Int 175:417–432
Kusche J (2007) Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J Geod 81(11):733–749. https://doi.org/10.1007/s00190-007-0143-3
Kusche J, Schrama E (2005) Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J Geophys Res 110(B09):409. https://doi.org/10.1029/2004JB003556
Li J, Chen J, Li Z et al (2017) Ellipsoidal correction in GRACE surface mass change estimation. J Geophys Res Solid Earth. https://doi.org/10.1002/2017JB014033
Loomis BD, Rachlin KE, Luthcke SB (2019) Improved Earth oblateness rate reveals increased ice sheet losses and mass-driven sea level rise. Geophys Res Lett 46(12):6910–6917. https://doi.org/10.1029/2019GL082929
Loomis BD, Rachlin KE, Wiese DN et al (2020) Replacing GRACE/GRACE-FO C30 with satellite laser ranging: impacts on Antarctic Ice Sheet mass change. Geophys Res Lett 47:e2020GL088,306. https://doi.org/10.1029/2019GL085488
Meyer U, Jäggi A, Beutler G et al (2015) The impact of common versus separate estimation of orbit parameters on GRACE gravity field solutions. J Geod 89(7):685–696. https://doi.org/10.1007/s00190-015-0807-3
Mohajerani Y, Velicogna I, Rignot E (2018) Mass loss of Totten and Moscow University Glaciers, East Antarctica, using regionally optimized GRACE Mascons. Geophys Res Lett 45(14):7010–7018. https://doi.org/10.1029/2018GL078173
Mohajerani Y, Velicogna I, Rignot E (2019) Evaluation of regional climate models using regionally optimized GRACE Mascons in the Amery and Getz ice shelves Basins, Antarctica. Geophys Res Lett. https://doi.org/10.1029/2019GL084665
Pollack HN (1973) Spherical harmonic representation of the gravitational potential of a point mass, a spherical cap, and a spherical rectangle. J Geophys Res 78(11):1760–1768. https://doi.org/10.1029/JB078i011p01760
Press W, Teukolsky S, Vetterling W et al (2002) Numerical recipes in C. The art of scientific computing. Cambridge University Press, Second Edition
Ran J, Ditmar P, Klees R (2018) Optimal mascon geometry in estimating mass anomalies within Greenland from GRACE. Geophys J Int 214(3):2133–2150. https://doi.org/10.1093/gji/ggy242
Rietbroek R, Brunnabend SE, Kusche J et al (2016) Revisiting the contemporary sea-level budget on global and regional scales. Proc Natl Acad Sci USA 113(6):1504–1509. https://doi.org/10.1073/pnas.1519132113
Sasgen I, Wouters B, Gardner AS et al (2020) Return to rapid ice loss in Greenland and record loss in 2019 detected by the GRACE-FO satellites. Commun Earth Environ 1:1. https://doi.org/10.1038/s43247-020-0010-1
Save H (2019) CSR level-2 processing standards document for level-2 product release 06, v1.1. Technical report, Center for Space Research, The University of Texas at Austin, Austin
Schrama EJO, Wouters B (2011) Revisiting Greenland ice sheet mass loss observed by GRACE. J Geophys Res 116(B2):B02407. https://doi.org/10.1029/2009JB006847
Schrama EJO, Wouters B, Lavallée DA (2007) Signal and noise in Grav- ity Recovery and Climate Experiment (GRACE) observed surface mass variations. J Geophys Res 112(B08):407. https://doi.org/10.1029/2006JB004882
Schrama EJO, Wouters B, Rietbroek R (2014) A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from GRACE data. J Geophys Res Solid Earth 119(7):6048–6066. https://doi.org/10.1002/2013JB010923
Shepherd A, Ivins ER (2012) A reconciled estimate of ice-sheet mass balance. Science 338(6111):1183–1189. https://doi.org/10.1126/science.1228102
Shepherd A, Ivins E, Rignot E et al (2019) Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature. https://doi.org/10.1038/s41586-019-1855-2
Siemes C, Ditmar P, Riva REM et al (2013) Estimation of mass change trends in the Earth’s system on the basis of GRACE satellite data, with application to Greenland. J Geod 87(1):69–87. https://doi.org/10.1007/s00190-012-0580-5
Sun Y, Riva REM, Ditmar P (2016) Optimizing estimates of annual variations and trends in geocenter motion and J\(_{2}\) from a combination of GRACE data and geophysical models. J Geophys Res Solid Earth 121(11):8352–8370. https://doi.org/10.1002/2016JB013073
Swenson S, Wahr J (2002) Methods for inferring regional surface- mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J Geophys Res 107(B9):2193. https://doi.org/10.1029/2001JB000576
Swenson S, Chambers D, Wahr J (2008) Estimating geocenter variations from a combination of GRACE and ocean model output. J Geophys Res B113(B08):410. https://doi.org/10.1029/2007JB005338
Tapley BD, Watkins MM, Flechtner F et al (2019) Contributions of GRACE to understanding climate change. Nat Clim Change 9(5):358–369. https://doi.org/10.1038/s41558-019-0456-2
Tiwari VM, Wahr J, Swenson S (2009) Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys Res Lett. https://doi.org/10.1029/2009GL039401
Velicogna I, Wahr J (2006) Measurements of time-variable gravity show mass loss in Antarctica. Science 311(5768):1754–1756. https://doi.org/10.1126/science.1123785
Velicogna I, Wahr J (2013) Time-variable gravity observations of ice sheet mass balance: precision and limitations of the GRACE satellite data. Geophys Res Lett 40(12):3055–3063. https://doi.org/10.1002/grl.50527
Vishwakarma BD, Horwath M, Devaraju B et al (2017) A data-driven approach for repairing the hydrological catchment signal damage due to filtering of GRACE products. Water Resour Res 53(11):9824–9844. https://doi.org/10.1002/2017WR021150
Vishwakarma B, Horwath M, Groh A et al (2022) Accounting for GIA signal in GRACE products. Geophys J Int 228(3):2056–2060. https://doi.org/10.1093/gji/ggab464
Wahr J, Molenaar M, Bryan F (1998) Time variability of the Earth’s gravity field: hydrological and oceanic effects and their possible detection using GRACE. J Geophys Res 103(B12):30205–30229. https://doi.org/10.1029/98JB02844
Wouters B, Chambers D, Schrama EJO (2008) GRACE observes small-scale mass loss in Greenland. Geophys Res Lett 35(L20):501. https://doi.org/10.1029/2008GL034816
Wouters B, Bonin J, Chambers D et al (2014) GRACE, time-varying gravity, earth system dynamics and climate change. Rep Prog Phys 77(11):116801. https://doi.org/10.1088/0034-4885/77/11/116801
Wu X, Blom RG, Ivins ER et al (2009) Improved inverse and probabilistic methods for geophysical applications of GRACE gravity data. Geophys J Int 177(3):865–877. https://doi.org/10.1111/j.1365-246X.2009.04141.x
Zwally HJ, Giovinetto MB, Beckley MA et al (2012) Antarctic and Greenland drainage systems. GSFC Cryospheric Sciences Laboratory. https://earth.gsfc.nasa.gov/cryo/data/polar-altimetry/antarctic-and-greenland-drainage-systems
Acknowledgements
We are grateful to three anonymous reviewers, the associate editor Brian Gunter and the editor-in-chief Jürgen Kusche for their detailed comments that helped to improve the original manuscript. We thank the German Space Operations Center (GSOC) of the German Aerospace Center (DLR) for providing continuously and nearly 100% of the raw telemetry data of the twin GRACE satellites.
Funding
Open Access funding enabled and organized by Projekt DEAL. The work of TD was funded by the German Research Foundation (DFG, Grant SCHE 1426/28-1) and the German Federal Ministry of Education and Research (BMBF) (Project Greenland Ice Sheet/Ocean Interaction GROCE, Grant No. 03F0855C). The work of AG was funded by the European Space Agency through the Climate Change Initiative (CCI) projects Antarctic Ice Sheet CCI and CCI+ (Contract Numbers 4000112227/15/I-NB and 4000126813/19/I-NB), Greenland Ice Sheet CCI and CCI+ (contract numbers 4000112228/15/I-NB and 4000126523/19/I-NB) and Sea-level Budget Closure CCI (contract number 4000119910/17/I-NB) as well as by funds of the German Federal Ministry of Education and Research (BMBF) (project Greenland Ice Sheet/Ocean Interaction, GROCE, Grant no. 03F0778G). The work of EB was partly funded by DFG (Grant SCHE 1426/26-1) within the Priority Programme SPP 1158 ”Antarctic Research with Comparative Investigations in Arctic Ice Areas”.
Author information
Authors and Affiliations
Contributions
MH conceptualized the study. MH, AG, TD, and EB developed the methodology. AG and TD developed and adapted the software. TD conducted the formal analysis. TD and EB conducted the investigation. TD did the visualization. TD wrote the original draft for Chapters 1,3,4; MH wrote the original draft for Chapter 2. All authors contributed to the manuscript review and editing.
Corresponding author
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix A: Tailored sensitivity formalism with account for unobserved parts of the SH spectrum
Appendix A: Tailored sensitivity formalism with account for unobserved parts of the SH spectrum
In Sect. 2.6 we have neglected the parts of the SH spectrum outside \(\{(n,m)\}_\text {obs}\) when expressing leakage by Eq. (34) and when approximating relation (17) by Eq. (43).
We now include SH contributions up to an arbitrarily high level. While the vector \({\varvec{\kappa }}\) by definition contains \(\kappa _{nm}\) restricted to \(\{(n,m)\}_\text {obs}\), we supplement this vector by a vector \({\varvec{\kappa }}_\text {h}\) that contains the missing \(\kappa _{nm}\) up to a sufficiently high level of degree and order. Likewise, we supplement \({\varvec{\vartheta }}\) by \({\varvec{\vartheta }}_\text {h}\) and \({\varvec{A}}\) by \({\varvec{A}}_\text {h}\).
Instead of approximating the leakage error by Eq. (34), we now write
that is, we now include the leakage of signal components that are outside the spectrum resolved by GRACE. Instead of Eqs. (35) and (38) we find
In the last equation, we may do the replacement
That is, \({\varvec{m}}\) is defined as the mass change associated to SMD patterns that are defined in a spatial resolution not restricted to the GRACE resolution. This definition is now fully consistent with the definition of \({\varvec{m}}\) made by Eq. (17) in the context of the inverse approach.
The minimum condition (37), after insertion of Eqs. (A3) (A4) and (39), leads to the same SK expression (44) as derived in Sect. 2.6.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Döhne, T., Horwath, M., Groh, A. et al. The sensitivity kernel perspective on GRACE mass change estimates. J Geod 97, 11 (2023). https://doi.org/10.1007/s00190-022-01697-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-022-01697-8