1 Introduction

Since the launch of the Gravity Recovery and Climate Experiment (GRACE) satellite mission in 2002, satellite gravimetry became the primary tool to study mass transport in the Earth’s system at the global and regional scale. This is the only technique that can directly sense mass re-distribution both at the Earth’s surface and at any depth inside the Earth. Thanks to that, GRACE data have substantially contributed to a quantitative analysis of various processes that accompany the climate change (Wouters et al. 2014; Tapley et al. 2019). This includes estimating the mass balance of ice sheets and mountain glaciers (Velicogna and Wahr 2005; Luthcke et al. 2006; Chen et al. 2006; Ramillien et al. 2008; Van den Broeke et al. 2009; Pritchard et al. 2011; Shepherd et al. 2012; Jacob et al. 2012; Siemes et al. 2013; Shepherd et al. 2020) and monitoring mass transport of hydrological origin (see Güntner 2008; Ramillien et al. 2008; Jiang et al. 2014; Reager et al. 2016, as well as references therein). Furthermore, satellite gravimetry turned out to be very valuable for an observation of groundwater storage changes (Rodell et al. 2009; Tiwari et al. 2009; Tangdamrongsub et al. 2017; Frappart and Ramillien 2018). Other applications of GRACE data are oceanography (Chambers et al. 2004; Han et al. 2005; Cazenave et al. 2009; Killett et al. 2011; Bonin and Chambers 2011; Chambers and Schröter 2011; Saynisch et al. 2015); studies of the Glacial Isostatic Adjustment (GIA) and mantle viscosity (Simon et al. 2017; Rovira-Navarro et al. 2020; Sun and Riva 2020), as well as an assessment of co-seismic and post-seismic mass transport associated with large earthquakes (Han et al. 2006, 2010, 2011, 2016).

The primary Level-2 data product extracted from GRACE observations is a collection of gravity field solutions, each of which is composed of a set of spherical harmonic coefficients up to a certain maximum degree (Heiskanen and Moritz 1967). These solutions are typically provided with one-month sampling interval, which implies that each solution represents the mean gravity field in the corresponding month. Those solutions can be used as input to estimate, for instance, mass anomalies at the Earth’s surface (Wahr et al. 1998; Ditmar 2018). The latter estimates are used for a further analysis in most of GRACE applications. An exception is studies related to the solid Earth, when mass transport of interest takes place deep inside the Earth, so that an estimation of mass anomalies at the Earth’s surface becomes unphysical.

Time-series of GRACE monthly solutions are offered by three official data processing centers: the Center of Space Research (CSR) of the university of Texas at Austin (Bettadpur 2018); the German Research Centre for Geosciences (GFZ) in Potsdam (Germany) (Dahle et al. 2018); and the Jet Propulsion Laboratory (JPL) of the California Institute of Technology (Yuan 2018). A number of other research groups also produce their own solutions (we will return to that point in Sect. 2). Methodologies and background models exploited by all those groups are different, so that the quality of the solutions produced at different groups is not the same as well. In order to select the best solution time-series or to ensure the optimal combination of solutions from different groups, end users need to know how the quality of different solutions compares.

As it was pointed out by Meyer et al. (2019) and Chen et al. (2021), there are two widely used approaches to quantify the noise level in GRACE-based mass anomaly estimates: (i) to consider the difference between those estimates and a signal model or (ii) to compare the solutions from different groups with each other.

A commonly used signal model exploited in the first approach is composed of a seasonal variability and a linear trend. Such a model reflects the typical behavior of mass transport in the Earth’s system. The seasonal variability can be approximated by (co-)sinusoidal functions with the annual period. To account for deviations of the actual seasonal cycle from an annual (co-)sinusoidal curve, (co-)sinusoidal functions of the semi-annual period are frequently added. For instance, this allows for a better approximation of the seasonal cycle in polar areas, where snow mass slowly accumulates in the autumn, winter, and early spring, and then rapidly declines in late spring and early summer. Each of the functions forming the signal model is scaled with a factor, which can be estimated from GRACE data themselves. Such an approach is particularly successful in the areas where the signals in GRACE-based solutions are small, such as oceans. However, most of GRACE data users are interested in the geographical regions where the signals are not small. In that case, such an approach may severely overestimate the noise level in the solutions, since deviations of the actual signal from the signal model rather reflect natural irregularities of mass transport than errors in GRACE solutions. Of course, one may extrapolate the errors observed over the oceans onto the region of interest. However, such a procedure assumes that the errors are sufficiently homogeneous. It cannot detect signal-related errors, such as an improper signal scaling or a temporal offset of the produced estimates.

The other approach is to analyze the differences between alternative GRACE solution time-series. This can be done either by considering the differences between individual time-series and the mean one (Meyer et al. 2019) or by an estimation of noise variances of individual time-series using the three-cornered hat method (Gray and Allan 1974; Chen et al. 2021). This approach is, however, not free from weak points either. It is important to keep in mind that mass anomaly time-series from different groups stem from the same raw GRACE measurements and, therefore, may share errors that propagate from those measurements into mass anomaly estimates. Then, noise levels in the computed mass anomalies may be underestimated. On the other hand, if one of the time-series does not share the “common” errors with the others (e.g., due to the usage of a regularization), deviations of that time-series from the others may be interpreted as errors. Then, the noise level in the most accurate solutions will be overestimated, so that those solutions will be mistakenly seen as noisier than the other solutions.

Here, we present a novel empirical technique to assess errors in GRACE-based mass anomaly time-series. The technique does not require knowledge of true signal and, therefore, is applicable all over the globe. Our intention is to make the results more accurate and objective, as compared to those from the traditionally used techniques, which are addressed above. The proposed technique stems from the methodology proposed earlier by Ditmar et al. (2018). According to that methodology, a tailored regularization is applied to an unconstrained GRACE-based mass anomaly time-series. Variance component estimation (VCE) (Koch and Kusche 2002) is exploited to split the total data variance into signal variance and noise variance. In the examples presented by Ditmar et al. (2018), that methodology demonstrated a very good performance. A later analysis showed, however, that an automatized application of that methodology at each particular node of a global grid may lead to unsatisfactory results at some locations. In particular, this concerns the locations where signal shows an erratic behavior, so that VCE fails to split the total data variance into signal variance and noise variance properly. Therefore, we have developed the methodology by Ditmar et al. (2018) further. Firstly, we decided to analyze the solution time-series from different groups simultaneously, which facilitates a proper separation of the signal variance from noise variances. Secondly, we have analyzed various regularization functionals in order to select the one that yields the best results. The list of considered regularization functionals includes conventional Tikhonov regularization functionals of different orders, the one proposed by Ditmar et al. (2018), as well as a novel regularization functional, which can be seen as a modification of the latter one.

To demonstrate the performance of the developed technique and to select the best performing regularization functional, we perform lake tests. In these tests, we use the “true” mass anomalies caused by water level variations in large lakes (those variations are routinely measured by satellite altimetry missions). We fit the “true” mass anomalies with those extracted from GRACE solutions. In doing so, we co-estimate a number of additional parameters in the “GRACE-altimetry” differences in order to absorb the impact of nuisance signals. In the first instance, this concerns a co-estimation of seasonal variability, which may reflect, among others, steric variations of water levels. The residual time-series obtained in this way are interpreted as realizations of noise in the GRACE-based estimates. Then, the “true” noise Standard Deviations (StD) are compared with those obtained with VCE after an application of various regularization functionals, which allows us to identify the best performing one.

In these lake tests, we estimate, among others, the optimal scaling to be applied to the “true” mass anomalies in order to match the GRACE-based ones. This allows us to assess signal damping in different GRACE solution time-series. To quantify this signal damping, we introduce the term “signal retaining.” The more a signal is damped, the less the signal retaining is. An absent signal is characterized by zero retaining. Furthermore, the estimated damping of signals in the GRACE solutions is compared with the expected one. The latter is the result of truncating the infinite spherical harmonic series associated with a unit water mass variation in a given lake at a certain degree \(L_{\max }\). This maximum degree is specified consistently with the maximum degree in the analyzed GRACE solutions. Then, we introduce the “relative signal retaining” as the ratio of the observed retaining and the expected one. By comparing relative signal retainings of different solution time-series, we are able to compare the latter ones in terms of signal damping: both for individual lakes and in average.

Ultimately, we apply the developed methodology to compare noise levels in various GRACE solution time-series all over the globe. We consider both the solutions from the official GRACE data processing centers and solutions offered by other groups.

The structure of the manuscript is as follows. In Sect. 2, we present the analyzed GRACE solution time-series. In Sect. 3, we discuss in detail the adopted procedures. The section starts from the lake tests. In particular, we present there the considered regularization functionals—both known from literature and the proposed one. In addition, we address in that section the empirical procedure exploited to estimate noise levels in GRACE solutions globally. In Sect. 4, we present the obtained results. Again, the section starts from lake tests. Among others, we select the most efficient regularization functionals and compare different GRACE solutions in terms of signal damping. In the second part of the section, we present results of the global comparison of different GRACE solutions in terms of errors in mass anomaly estimates. Finally, Sects. 5 and 6 are left for a discussion and conclusions, respectively.

2 GRACE data

2.1 Considered solution time-series

In this study, we analyze time-series of monthly GRACE solutions complete to degree 60 in the time interval from Feb. 2003 to Mar. 2016. Furthermore, a preliminary analysis showed that a number of GRACE time-series show abnormally high noise levels in Jan.-Feb. 2015. Therefore, it was decided to exclude these two months from the analysis as outliers.

In principle, our goal is to consider as many solution time-series as possible. At the same time, we find it important that the considered time-series consist of exactly the same sets of months in order to ensure a fair comparison of them. This implies that the gaps allowed in each of the considered time-series should either be dictated by an incomplete availability of raw GRACE data or coincide with the months defined as outliers; additional gaps must be absent or, at least, reduced to minimum.

On the basis of these criteria, we have identified eight GRACE monthly solution time-series (Table 1). It is worth noticing that not all of them are free from additional gaps. XISM time-series lacks a solution for Oct. 2010, whereas HUST time-series lacks the month of Dec. 2015. In addition, four out of the eight time-series lack May 2015. For the sake of consistency, all the solutions for these three months are ignored, even if many time-series do contain them. Ultimately, all the considered time-series are comprised of 139 consistently selected monthly solutions.

Table 1 GRACE monthly solution time-series considered in this study
Full size table

Seven of the considered time-series are composed of unconstrained solutions. Only the GRGS solutions are regularized. Noteworthy, the GRGS solutions are the only solutions that were originally computed up to a degree higher than 60 (namely, 90). We have truncated them at degree 60 in order to make them consistent with the others. Inclusion of these solutions into the comparison allows us to quantify the effects of the regularization adopted in the production of the solutions. This concerns, on the one hand, the suppression of noise and, on the other hand, signal damping. Noteworthy, GRGS solutions are the only solutions that are provided with a 10-day sampling interval (though each solution reflects a weighted average of mass anomalies within a 30-day interval). To ensure a better temporal consistency with the other solutions, we consider every third solution from the GRGS time-series; each of the selected solutions represents approximately the same time interval as the solutions in the other time-series (i.e., one calendar month).

2.2 Initial processing and preliminary analysis

All the GRACE solutions lack the degree-1 coefficients. Furthermore, the \(C_{2,0}\) coefficients in those solutions are relatively inaccurate, so that they are typically replaced with alternative estimates from other sources. In our case, the estimates of both degree-1 and \(C_{2,0}\) coefficients were produced by Sun et al. (2016), who used as input a combination of CSR GRACE coefficients of higher degrees/orders with the Ocean Bottom Pressure (OBP) estimates provided by the AOD1B RL06 data product (Dobslaw et al. 2016).

The considered solutions are presented in terms of geoid heights per degree in Fig. 1. Each of the presented curves represents the rms average over all the 139 months under consideration. The curves show a divergence above degree 20, which mostly reflects differences in noise levels of the considered solutions. The GRSG solutions seem to be the most accurate ones, which is explained by the fact that they are regularized. As far as unconstrained solutions are concerned, ITSG and CSR solutions show the lowest noise levels, whereas noise in XISM and HUST solutions seems to be the highest. A more in-depth analysis of these solutions is presented in the further sections.

Fig. 1
figure 1

The solutions considered in this study, in terms of geoid height per degree. Each of the curves represents the rms average over all the 139 months under consideration

Full size image

3 Methodology

3.1 Lake tests: direct estimation of signal retaining and noise in GRACE solutions

Using mass variations in large lakes and mediterranean seas to quantify noise levels in GRACE solutions is not a new idea. For instance, Swenson and Wahr (2007) used for that purpose Caspian Sea, Liu et al. (2010) Lake Victoria, and Yildiz et al. (2011) Black Sea. Furthermore, Fenoglio-Marc et al. (2012) considered in their analysis Mediterranean and Black Seas, whereas Loomis and Luthcke (2017) addressed mass variations in four seas: Mediterranean, Black, Red, and Caspian. In the latter case, independent estimates of mass variations in the seas were also used for a calibration of GRACE solutions.

In our study, five lakes have been selected. Two of them are located in non-tropical areas: the Caspian Sea (the largest lake on Earth) and Lake Ladoga (the largest lake of Europe). Three other lakes are located in Africa: Victoria (the largest lake of Africa) and Tanganyika near the equator, as well as Lake Nasser in the northern part of the continent (the smallest one of the five). Further information about the considered lakes can be found in Table 2.

Table 2 The lakes considered in the lake tests
Full size table

At least two out of the five considered lakes are subject to anthropogenic impacts. One of them is Lake Nasser, which was artificially formed in 1960s, after a construction of the Aswan High Dam across the River Nile. The outflow from the Lake Nasser is almost fully controlled by that dam (Eldardiry and Hossain 2019). Lake Victoria is man-regulated as well. In particular, an over-abstraction of lake water by a downstream power station in 2003–2006 resulted in a water level decline of approximately 0.6 m (Sutcliffe and Petersen 2007).

Remarkably, all the considered lakes are characterized by significant inter-annual variability (Fig. 2). In particular, this concerns Lake Nasser, where the peak-to-peak amplitude of resulting water volume anomalies reaches \(\sim 43\) km\(^3\) (Longuevergne et al. 2013). As a result, all these lakes generate a sufficiently strong inter-annual signal, which is clearly sensed by GRACE. This allows us to focus on inter-annual water level/mass variations, as it is explained below.

Fig. 2
figure 2

Inter-annual variations of water levels in the lakes under consideration, as they are derived from satellite altimetry data. Seasonal variations with the annual and semi-annual periods are subtracted. Variations in Lake Nasser are additionally reduced by 80% (i.e., scaled with factor 0.2), so that their range in the plot is more consistent with those of the other lakes

Full size image

To conduct the tests, we convert each monthly set of spherical harmonic coefficients into mass anomalies in terms of Equivalent Water Heights (EWH). The mass anomalies are computed at the Earth surface, which is approximated by the WGS84 ellipsoid. To that end, we apply the methodology proposed by Wahr et al. (1998), which was modified by Ditmar (2018) in order to take into account the Earth’s oblateness. Finally, the mean mass anomaly within the territory of a given lake is computed.

The obtained mass anomaly time-series (defined in terms of EWH) is compared with a water level time-series based on satellite altimetry data. The latter time-series is subject to an empirical scaling in order to account for signal damping in GRACE solutions. Importantly, GRACE data may contain nuisance signals caused by hydrological processes around the lake. Since the spatial resolution of GRACE is limited, the latter signals cannot be separated from the signal of the lake itself. Around Lake Ladoga and Caspian Sea, for instance, such signals may be triggered to a large extent by an accumulation of snow in winter. To reduce the nuisance hydrological signals, we make use of the version 2.1 data product from the Global Land Data Assimilation System (GLDAS) (Rodell et al. 2004). We extract monthly mass anomalies (in terms of equivalent water depths) associated with snow cover, soil moisture, and canopy. These mass anomalies are converted into spherical harmonic coefficients in the degree range from 1 to 60, so that these anomalies become spectrally consistent with the exploited GRACE data. Then, the long-term mean per coefficient is subtracted consistently with GRACE data. Finally, the resulting spherical harmonic coefficients are subtracted from the GRACE-based ones.

Furthermore, we take into account that both altimetry and GRACE data may contain residual nuisance signals, which are absent in the counterpart dataset. This concerns not only GRACE data, but also altimetry data, which may contain a steric signal (particularly, due to thermal expansion of water in the lake). To account for residual nuisance signals in both altimetry and gravimetry datasets, we limit the compared signals to inter-annual variations. To that end, we simultaneously estimate the lake signal scaling and parameters of an empirical seasonal signal, represented by (co-)sinusoidal functions of the annual and semi-annual periods. It will be shown in Sect. 5 that this approach ensures a sufficient mitigation of steric signal.

In addition, we optionally co-estimate a linear trend in the data. We will return to this point a bit later.

As soon as the time-series under consideration are understood as continuous functions of time, the functional model adopted to estimate the unknown parameters can be written as follows:

$$\begin{aligned}&C_1 + C_2 \sin \omega t + C_3 \cos \omega t + C_4 \sin 2 \omega t + C_5 \cos 2 \omega t\nonumber \\&\qquad + \{C_6 \, t\}_{\mathrm{optional}} \, + E \, h(t) = d (t) + e(t), \end{aligned}$$
(1)

where \(C_1, \ldots C_5\) are the unknown coefficients characterizing a constant bias and seasonal nuisance signals in the input datasets; \(C_6\) is an optionally co-estimated parameter characterizing a linear trend, h(t) is the altimetry-based time-series of water level variations in the lake, E is an unknown scaling coefficient, d(t) is the GRACE-based time-series of mean mass anomalies within the lake in terms of EWH, and \(\omega = \frac{2\pi }{1 \, \text{ yr }}\). The primary goals of the analysis are to quantify: (i) signal retaining, which is characterized by the scaling coefficient E, and (ii) data noise e(t), which is defined as the misfit between the GRACE data d(t) and the reconstructed signal in the left-hand side of Eq. (1).

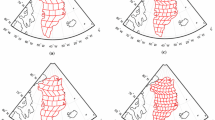
An ideal mass anomaly time-series of infinite spatial resolution would be characterized by unit signal retaining. A lower value of signal retaining reflects, in the first instance, the omission error caused by limiting the GRACE solutions to a certain maximum spherical harmonic degree \(L_{\max }\). For a given lake and a pre-defined \(L_{\max }\), it is easy to compute the expected signal retaining that reflects the omission error alone. To that end, we consider a “lake mask”—a synthetic signal that is equal to 1 inside the lake contour and equal to 0 outside. Then, this signal is low-pass filtered by computing the associated spherical harmonic coefficients from degree 1 to \(L_{\max }=60\), which are used to restore the signal in the spatial domain. After that, the expected signal retaining \(E_{\mathrm{exp}}\) is calculated as the mean mass anomaly within the lake contour. The values \(E_{\mathrm{exp}}\) computed in this way for the five considered lakes are reported in the last column of Table 2. Obviously, the larger a lake, the larger the associated signal retaining. This is an expected result, since a small lake area does not allow one to capture the associated signal properly; the rest of the signal “leaks” outside the lake contour. This effect is illustrated with Fig. 3, which shows the low-pass filtered lake masks for the Caspian Sea and Lake Ladoga.

Fig. 3
figure 3

Low-pass filtered lake masks of the Caspian Sea (top) and Lake Ladoga (bottom). A lake mask is defined as a function which is equal to 1 inside the lake contour and to 0 outside it. Filtering is performed by retaining the coefficients of degrees from 1 to 60 in the spherical harmonic expansion of the lake mask

Full size image

Knowledge of the expected signal retaining allows us to compute the relative retaining \(\varepsilon \), which is defined as the ratio of the actual and expected retainings:

$$\begin{aligned} \varepsilon = E/E_{\text{ exp }}. \end{aligned}$$
(2)

We find this quantity more informative than the actual retaining E, since it allows one to immediately see if signal damping in a given solution can be explained purely by the omission error or there are also some other factors that play a role. Furthermore, the computation of relative retaining values facilitates a comparison of signal damping for different lakes.

Misfit e(t), which is interpreted as noise in GRACE data, is represented in terms of its Standard Deviation (StD). This information is used to quantify the accuracy of different GRACE solution time-series. Furthermore, knowledge of this noise StD allows us to quantify the formal errors in the unknown parameters in Eq. (1), including the signal retaining E. Importantly, the latter formal error \(\sigma _{\mathrm{E}}\) is used to decide whether the linear trend (i.e., parameter \(C_6\)) is to be co-estimated or not. Namely, we look for the option that leads to a smaller formal error \(\sigma _{\mathrm{E}}\). In principle, the co-estimation of an additional parameter makes the normal matrix associated with Eq. (1) more ill-conditioned, which may result in an increase of the formal errors in all the unknown parameters. On the other hand, an elimination of parameter \(C_6\) from the list of unknowns may increase the misfit e(t), particularly if GRACE data contain a strong trend signal, which is absent in altimetry data. This may also result in an increase of the estimated formal errors in the unknown parameters. Having compared the two options, we have found that smaller formal errors \(\sigma _{\mathrm{E}}\) for lakes Ladoga and Nasser are typically obtained when linear trend is co-estimated. For the other three lakes, the preferred option is elimination of \(C_6\) from the list of unknowns. We stick to this choice in all the lake tests presented below.

Presence of a nuisance linear trend in GRACE data over Lake Ladoga can be explained by a relatively strong GIA signal there, since that lake is located at the periphery of Fennoscandia. A pronounced nuisance trend in GRACE data over Lake Nasser is likely caused by a long-term water loss in the adjacent Nubian Aquifer (Ahmed and Abdelmohsen 2018).

3.2 Quantification of noise with variance component estimation: selection of the regularization functional

The lake tests allow us to quantify noise level over only a few geographical locations. Therefore, a different approach is to be applied if noise level is to be estimated globally. To that end, we propose to combine various mass anomaly time-series at a given location into a single regularized time-series. At this point, we are interested not in the final product, but in the estimated noise level in each of the input time-series, for which purpose VCE is used (Koch and Kusche 2002; Ditmar et al. 2018).

Assuming that errors in the analyzed mass anomaly time-series are neither cross-correlated nor correlated in time, one may combine several mass anomaly time-series by minimizing the following objective function:

$$\begin{aligned} \Phi [\mathbf {x}]= & {} \frac{1}{\sigma _1^2} \sum _i \left( x_i - d_i^{(1)} \right) ^2 + \cdots \frac{1}{\sigma _n^2} \sum _i \left( x_i - d_i^{(n)} \right) ^2\nonumber \\&\quad + \frac{1}{\sigma _s^2} \Omega [\mathbf {x}], \end{aligned}$$
(3)

where \(d_i^{(k)}\) is the mass anomaly in the ith month derived from the kth input time-series, n is the number of analyzed time-series, \(\sigma _k^2\) is the unknown error variance of the kth mass anomaly time-series, \(\sigma _s^2\) is the unknown signal variance, \(\Omega [\mathbf {x}]\) is a regularization functional, and \(x_i\) (\(i=1, 2,\ldots \)) is the regularized mass anomaly time-series to be estimated. VCE allows us to estimate both noise variances \(\sigma _k^2\) and signal variance \(\sigma _s^2\), though only noise variances are of interest in this study, since they are used to estimate noise StD \(\sigma _k\) (\(k=1,\ldots n\)).

To facilitate an optimal isolation of noise in each particular input time-series (and, therefore, to ensure a good estimation of the associated noise variance), the most appropriate regularization functional is to be used. In this study, we consider four different regularization functionals known from literature, as well as a new one. Furthermore, we consider also a minimization of the of objective function \(\Phi [\mathbf {x}]\) without a regularization (“NoReg” case: \(\Omega [\mathbf {x}]=0\)).

The regularization functionals under consideration are applied to quantify noise in mass anomaly time-series over all five lakes. The results are compared with the noise StD estimates extracted from the misfits e(t) between GRACE and altimetry data (cf. Sect. 3.1). In this way, we select the regularization functional(s) that yield the most consistent results.

For the sake of simplicity, the mass anomaly time-series is represented below as a continuous function of time x(t), which is defined in the time interval \(\left[ t_{\mathrm{beg}}; \, t_{\mathrm{end}} \right] \). Of course, finite-difference analogs of the presented regularization functionals are adopted in practice.

3.2.1 Tikhonov regularization

Three of the five considered regularization functionals represent a well-known Tikhonov regularization. This type of regularization aims at minimizing the unknown function itself or/and its derivatives (Tikhonov and Arsenin 1977). In our study, we consider the following implementations of the Tikhonov regularization:

  • Zero-order Tikhonov (Tikh-0) regularization, which minimizes the magnitude of the unknown function x(t) itself:

    $$\begin{aligned} \Omega [x] = \int \limits _{t_{\mathrm{beg}}}^{t_{\mathrm {end}}} \left[ x(t)\right] ^2 \, \text{ d }t. \end{aligned}$$
    (4)

    This approach prevents the occurrence of large peaks, since the unknown function is forced to be as close to zero as possible.

  • First-order Tikhonov (Tikh-1) regularization, when the first derivative of the unknown function is minimized:

    $$\begin{aligned} \Omega [x] = \int \limits _{t_{\mathrm{beg}}}^{t_{\mathrm {end}}} \left[ \dot{x}(t)\right] ^2 \, \text{ d }t. \end{aligned}$$
    (5)

    In this way, the occurrence of large discontinuities is prevented, since the unknown function is force to be as smooth as possible.

  • Second-order Tikhonov (Tikh-2) regularization, when the second derivative of the unknown function is minimized:

    $$\begin{aligned} \Omega [x] = \int \limits _{t_{\mathrm{beg}}}^{t_{\mathrm {end}}} \left[ \ddot{x}(t)\right] ^2 \, \text{ d }t. \end{aligned}$$
    (6)

    This type of regularization prevents the occurrence of sharp changes in the trend, since those changes would result in large values of the second derivative of x(t).

3.2.2 Minimization of month-to-month year-to-year double differences

One more regularization functional considered in this study minimizes the so-called month-to-month year-to-year double differences (MYDD). If, as before, the mass anomaly time-series are considered as continuous functions, MYDD regularization functional can be written as follows:

$$\begin{aligned} \Omega [x] = \int \limits _{t_{\mathrm{beg}} + 1 \text{ yr }}^{t_{\mathrm{end}}} \left[ \dot{x}(t) - \dot{x}(t-1 \, \text{ yr})\right] ^2 \, \text{ d }t. \end{aligned}$$
(7)

It was designed by Ditmar et al. (2018) specifically for the optimal handling of mass-anomaly time-series. Those time-series typically demonstrate a pronounced seasonal cycle. As soon as the minimized quantity is a year-to-year difference of the unknown function rather than the function itself, all the signals that show an annual periodicity escape the penalization. As a result, the bias triggered by regularization is reduced. Importantly, a seasonal signal in a given year is frequently offset with respect to the one in the previous year due to the presence of inter-annual variability or a secular trend. In order to take this effect into account, Ditmar et al. (2018) proposed to minimize the year-to-year differences of not the unknown function itself, but of its time-derivative. It was proved in that publication that the MYTD regularization does not penalize signals composed of an annual periodic term and a linear trend.

It is worth mentioning that the rate of seasonal mass gains/losses typically reflects climate-related processes, such as precipitation, water runoff (including meltwater runoff), and evapotranspiration. As soon as the climate conditions do not change from year to year, the associated mass gains and losses follow the same annual cycle and, therefore, escape the penalization applied by the MYDD regularization. For this reason, Ditmar et al. (2018) interpreted the MYDD regularization as the one tailored for climate stationarity.

The MYDD regularization has already demonstrated a good performance in the analysis of mass anomaly time-series in different geographical regions: Greenland (Ditmar et al. 2018; Ran et al. 2018; Guo et al. 2018, 2020), Tonlé Sap basin in Cambodia (Ditmar et al. 2018), Mississippi River basin (Guo et al. 2018), and Amazon River basin (Guo et al. 2020). Furthermore, it was successfully used to calibrate the error covariance matrices of degree-1 and \(C_{20}\) spherical harmonic coefficients estimated from a combination of GRACE-based monthly solutions and an ocean bottom pressure model (Sun et al. 2017).

3.2.3 Novel regularization functional

In the course of preliminary studies, a comparison of Tikh-1 and Tikh-2 regularizations showed that the former regularization is frequently inferior in the context of mass anomaly time-series. This was interpreted as an evidence that mass anomalies typically show a smooth behavior in the time domain: large month-to-month differences are unlikely not only in terms of mass anomalies themselves, but also in terms of their time-derivatives. Therefore, the Tikh-2 regularization, which penalizes sharp changes in mass anomaly time-derivatives, does a better job in separating noise from signal. This brings up an idea to switch from the first-order to the second-order time-derivative also in the context of year-to-year differences. Like the MYDD minimization, such an approach will not penalize a seasonal cycle. On the other hand, it inherits the benefits of the Tikh-2 regularization (as compared to Tikh-1) by penalizing sharp changes in time-derivatives (as soon as those changes do not show an annual periodicity). Assuming that the minimized time-series is a continuous function, one can write the resulting regularization functional as follows:

$$\begin{aligned} \Omega [x] = \int \limits _{t_{\mathrm{beg}} + 1 \text{ yr }}^{t_{\mathrm{end}}} \left[ \ddot{x}(t) - \ddot{x}(t-1 \, \text{ yr})\right] ^2 \, \text{ d }t. \end{aligned}$$
(8)

It is easy to demonstrate that the class of signals not penalized by this regularization functional is even wider than in the MYDD case: such signals may be composed of not only an annual periodic term and a linear trend, but also of an acceleration (i.e., quadratic) term.

As soon as a finite-difference analog of the functional given by Eq. (8) is considered, it can be represented as a minimization of month-to-month year-to-year triple differences (MYTD). This is because the finite-difference analog of the second time derivative is a month-to-month double difference. A further computation of year-to-year differences ultimately results in triple-differences. In what follows, acronym “MYTD” is used to denote this type of regularization.

3.3 Empirical estimation of noise in GRACE-based mass anomalies over the entire Earth’s surface

As soon as the best empirical strategy to assess noise levels in GRACE-based mass anomalies is defined, we apply this strategy to analyze the time-series under consideration globally. Importantly, we find an analysis of unconstrained solutions “as they are” not very informative in this context. Most of the solutions suffer from random noise, which increases with the spherical harmonic degree (cf. Fig. 1). As a result, most of unconstrained solutions in the spatial domain suffer from high-frequency noise, which by far exceeds signals of interest. It is easy to assess the level of that noise, but that information is of little interest, since in practice this noise is largely filtered out. Therefore, we find it more practical to apply a low-pass filter prior to the analysis. To that end, we use a Gaussian filter of 400-km half-width (Wahr et al. 1998). We note that a Gaussian filter is isotropic, so that its impact is independent of the geographical location. This guarantees that spatial variations in the quality of a given GRACE model reflect only the behavior of the model itself, and not properties of the filter. For the sake of consistency, the GRGS solutions are also filtered in this way, even though those solutions are regularized by design, so that high-frequency noise there is largely suppressed.

As before, the mass anomalies in the spatial domain are computed taking into account the Earth’s oblateness Ditmar (2018). We do so per node of a global equiangular \(1^{\circ } \times 1^{\circ }\) grid. Each grid node is analyzed independently of the others.

4 Results

4.1 Estimation of noise and signal retaining in GRACE-based estimates of mass anomalies over the selected lakes

As it is explained in Sect. 3.1, the focus of the lake tests is a comparison of GRACE-based mass anomaly time-series (in terms of EWH) with water levels variations based on altimetry data. To begin with, we made a visual comparison of those time-series. In that comparison, we downscaled the altimetry-based water level variations by applying the expected signal retaining \(E_{\mathrm{exp}}\) (see the last column in Table 2). In this way, signal damping in the GRACE solutions due to the omission error is accounted for. For instance, Fig. 4 presents a comparison of GRACE-based and altimetry-based time-series for the Caspian sea. It is remarkable that most of the GRACE solutions are able to reproduce water level variations in the Caspian Sea rather accurately, even though no filtering was applied to them. The mass anomaly time-series for the remaining four lakes can be seen as a Supplementary material (Figs. S1–S4).

Fig. 4
figure 4

GRACE-based mass anomaly time-series (in terms of EWH) versus altimetry-based water level variations in the Caspian Sea. The latter variations are downscaled with the factor of 0.687, the expected signal retaining \(E_{\mathrm{exp}}\) for the Caspian Sea (cf. Table 2). In this way, signal damping in the GRACE solutions due to the omission error is accounted for. Each of the panels presents only four GRACE-based time-series to make each time-series better visible

Full size image

Lake tests allow us to quantify noise in the GRACE-based mass anomaly time-series for the five considered lakes (Fig. 5). The regularized GRGS solutions show the lowest noise levels over all the lakes, followed by unconstrained ITSG and CSR solutions. Noise in the HUST and XISM solutions is the highest. The remaining three time-series (GFZ, JPL, and WHU) are in-between. Thus, the obtained results are consistent with the findings based on the plot of geoid heights per degree (see Fig. 1 and the associated discussion in Sect. 2.2).

Fig. 5
figure 5

Estimated standard deviations of noise in the GRACE-based mass anomaly time-series for the five considered lakes

Full size image
Table 3 Mean values of the estimated noise StD and weighted mean values of the relative signal retaining for the eight GRACE mass anomaly time-series under consideration. Both quantities are the result of averaging over all five considered lakes
Full size table

Next, we estimate the relative signal retainings with Eq. (2), see Fig. 6. It shows that the estimates for the Caspian Sea are always less than 100%. This as an evidence that the signal triggered by water level variations in the Caspian Sea is somewhat damped in all the considered GRACE solutions. At the same time, some GRACE-based time-series show relative signal retainings above 100% (particularly, for lakes Nasser and Tanganyika). It would be probably unfair to attribute this excess solely to errors in the relative retaining estimates (which are shown in Fig. 6 with error bars). Most probably, this excess can be explained by the presence of nuisance signals in GRACE data, which correlate with the signal of interest. Over lake Tanganyika, those nuisance signals likely reflect residual mass variations of hydrological origin that occur around the lake and are absorbed neither by GLDAS nor by the additional terms in Eq. (1). Due to a limited spatial resolution of GRACE data, these signals inevitably leak into the estimated mass variations within the lake contour. Over Lake Nasser, an abnormally large signal in GRACE data can also be explained by an expansion of the lake area as the water level there increases. As a result, the actual increase in the water mass there is larger than the one assumed by a fixed lake geometry. All this means that the estimates of the relative signal retaining must be treated with a caution, since they may systematically underestimate signal damping in GRACE data (except for the Caspian Sea). Nevertheless, it is still instructive to compare relative signal retainings obtained for different GRACE time-series with each other.

Fig. 6
figure 6

Relative signal retainings of the GRACE-based mass anomaly time-series for the five considered lakes, as computed with Eq. (2). The error bars indicate the formal errors of the obtained estimates

Full size image

To facilitate this comparison, we have computed the weighted mean values of the relative signal retaining on the basis of all five lakes (see the third column in Table 3). To make a comparison of the GRACE solutions more informative, we present also the mean values of the estimated noise StD, which are based on the five lakes under consideration (second column in Table 3). One can see that ITSG and HUST time-series are characterized by the maximum signal retaining. Remarkably, the ITSG solutions show also the lowest noise level among all the unconstrained solutions. As it is already noticed above, noise in the regularized GRGS solutions is even lower. Nevertheless, relative signal retaining in these solutions is relatively poor: in average, it is by 15% lower than in the ITSG solutions. The CSR solutions show a slightly higher noise level than the ITSG solutions. At the same time, signal retaining in the CSR solutions is lower by \(\sim 9\%\). The lowest signal retaining is demonstrated by the XISM solutions: by 26% lower than that of the ITSG solutions. The remaining three GRACE time-series (JPL, GFZ, and WHU) show about the same signal retaining as the CSR time-series (by 6-9% lower that of the ITSG solutions), but suffer from higher noise (about 2 times higher than that in the ITSG solutions).

4.2 Selection of the regularization functional

As it is explained in Sect. 3.2, we propose to use VCE to estimate noise in each GRACE mass anomaly time-series globally, including the locations where the true signal is not known. In order to fine-tune the noise estimation procedure, the most appropriate regularization functional is to be selected. To that end, we compare the altimetry-based noise StD estimates, which are already presented in the previous section, with the VCE-based estimates computed in the presence of various types of regularization (as well as without a regularization at all). As an example, Fig. 7 presents such a comparison for the Caspian Sea. It is easy to see that the absence of a regularization (“NoReg” case), the zero-order Tikhonov regularization (“Tikh-0”) and the first-order Tikhonov regularization (“Tikh-1”) result in relatively large discrepancies with respect to altimetry-based estimates. The largest discrepancies are observed for the regularized GRGS model. We interpret this as an indication that this model likely lacks noise patterns that are shared by the other models, which are unconstrained. Then, systematic deviations of this model from the others are attributed by VCE to noise in GRGS model. In other words, in the absence of a regularization or when the regularization is sub-optimal, GRGS model is seen as “too good to be truth.” On the other hand, the other three regularizations—the second-order Tikhonov regularization (“Tikh-2”), minimization of month-to-month year-to-year double differences (“MYDD”), and minimization of month-to-month year-to-year triple differences (“MYTD”)—result in noise estimates that are close to the altimetry-based ones.

Fig. 7
figure 7

Comparison of noise StD estimates for various GRACE-based mass anomaly time-series over the Caspian Sea. Solid lines indicate the estimates obtained with VCE, when either one of five regularization functionals is used or no regularization is applied at all. Dashed lines show the noise Std estimates obtained from a comparison with altimetry data, as reported in Sect. 4.1 (cf. Fig. 5)

Full size image

To make the differences between the performance of the considered regularization functionals better visible, we calculate the ratios of the two noise StD estimates, \(\sigma _k^{ \mathrm {(VCE)}}/\sigma _k^{\mathrm {(Altimetry)}}\) (see Fig. 8a). Furthermore, we compute for each GRACE model and each regularization functional the mean ratio over all five lakes (Fig. 8b). In addition, both panels in Fig. 8 present the mean ratios over all eight GRACE models (dashed lines) and the associated standard deviations (reddish shadowing). On the basis of these results, as well as similar results obtained for the other lakes individually (not shown), we have come up with the following findings:

Fig. 8
figure 8

The ratios of noise StD estimates \(\sigma _k^{ \mathrm {(VCE)}}/\sigma _k^{\mathrm {(Altimetry)}} \times 100\%\) obtained for different GRACE mass anomaly time-series with different regularization functionals (or without a regularization). The results are presented for the Caspian Sea (top panel) and as the mean values over the five lakes under consideration (bottom panel). The dashed lines present the mean ratios over all eight GRACE time-series. The reddish shadowing indicates the associated standard deviations. The reddish shadowing in the bottom panel reflects the variability of the results obtained for individual lakes (not that of the mean values over the five lakes)

Full size image

  • In the case of an unconstrained GRACE model, VCE typically underestimates noise StD. In the absence of a regularization (the worst-case scenario), this underestimation may reach \(\sim 30\%\).

  • Tikh-2, MYDD, and (particularly) MYTD regularizations make VCE-based estimates much more realistic (in the case of unconstrained GRACE models, the underestimation, if present, does not exceed 10–15%).

  • The larger the noise level, the better the VCE-based estimates. For instance, accuracy of the HUST and XISM models can be properly quantified with any regularization (or in the absence of it).

  • In almost all cases, inaccuracies of the VCE procedure do not affect the ranking of models (the most accurate time-series remains the most accurate one in every scenario).

From all this, we conclude that VCE can indeed be used to estimate noise StD in GRACE-based mass anomaly time-series when the true signal is not known. In doing so, it is advisable to use a regularization. The MYTD regularization seems to be the most appropriate for that purpose. This is because (i) the obtained estimates are, in average, closest to the true ones (even though noise StD may still be underestimated, this underestimation is the smallest); and (ii) variability of the obtained estimates is the smallest as well (i.e., all the time-series are underestimated by a more or less the same factor).

At the same time, we note that the VCE-based estimates obtained for regularized solutions must be treated with a caution. Those solutions show a somewhat anomalous behavior. The noise StD under- (or over-) estimation in that case may be significantly larger than for unconstrained solutions. Furthermore, MYTD regularization is not necessarily yields the best result in that case; other regularization techniques (e.g., Tikh-2) may look preferable. Thus, the usage of several regularization techniques may be recommended to assess the performance of regularized solutions more objectively.

Fig. 9
figure 9

Noise StD estimated with VCE in the presence of MYTD regularization. The results are shown for mass anomaly time-series based on GRACE solutions from CSR, JPL, and GFZ

Full size image
Fig. 10
figure 10

Same as Fig. 9, but for ITSG and GRGS solutions

Full size image
Fig. 11
figure 11

Same as Fig. 9, but for WHU, HUST, and XISM solutions. Mind a different color scale, as compared to Figs. 9 and 10

Full size image

4.3 Empirical estimation of noise in GRACE data over the entire Earth’s surface

Inspired by the findings of the previous section, we apply VCE to estimate the accuracy of all eight GRACE models globally. In the first instance, the MYTD regularization is used. The obtained results are presented in Figs. 9, 10 and 11. For completeness, we have repeated the computations using the MYDD and Tikh-2 regularization functionals. The maps obtained in the latter two cases are not presented, since they are rather similar to those produced with the MYTD regularization (apart from some differences in the overall noise levels). Furthermore, we compute the global RMS averages of noise StD estimates (Table 4). In spite of the concerns expressed in the previous section, the choice of regularization has only a minor impact onto the obtained results, so that we consider the obtained estimates as sufficiently robust.

First of all, we see that behavior of noise in the unconstrained solutions is, in general, consistent with the earlier findings: noise levels of the ITSG and CSR solutions are the lowest, whereas those of the HUST and XISM solutions are the highest. It is interesting to notice that XISM solutions show a higher noise level than HUST solutions, whereas is was vice versa for most of the lakes considered above (cf. Fig. 5). We attribute this to the impact of 400-km Gaussian filter, which has suppressed noise at the highest spherical harmonic degrees. As a result, noise at intermediate degrees becomes dominant, and this noise is apparently higher just in the XISM solutions (see also Fig. 1).

Observed spatial variations in the noise levels of the unconstrained solutions are, to a large extent, also not unexpected. These variations reveal a well-known dependence of noise level on geographical latitude: the noise level is highest in the equatorial areas and lowest near the poles. This can be explained by variations of the density of observations (which is highest in the polar areas), as well as by variations in the anisotropy of the measurement sensitivity (which is highest near the equator).

At the same time, some of the solutions show a clear increase in the noise level at certain geographical locations. For the CSR solutions, for instance, such locations are: (i) Foxe Basin (to the north from the Hudson Bay); (ii) the northwest coast of Australia; and (iii) Filchner-Ronne Ice Shelf (cf. the top panel in Fig. 9). At the latter location, JPL and GFZ solutions show an increased noise level as well. Most probably, these features can be attributed to inaccuracies in the background models of ocean tides. This is consistent with the findings of Kvas et al. (2019), who extracted from different GRACE monthly solutions the signal with a period of 161 days—the alias period of the semi-diurnal \(S_2\) tide (Ray and Luthcke 2006). As soon as the accuracy of the adopted ocean tide model is reduced at a particular location, residual \(S_2\) tide signals there alias into the time-series of GRACE monthly solutions, showing up as a 161-day signal at those locations. In the analysis of Kvas et al. (2019), the JPL and GFZ solutions showed a clear presence of the 161-day signal at the the Filchner-Ronne Ice Shelf, whereas the CSR solutions demonstrated a pronounced 161-day signal at all three aforementioned locations (see Fig. 6 in that publication). We find it remarkable that the methodology we have proposed reveals such features in GRACE monthly solutions without using any information about alias periods of ocean tides.

In WHU and HUST solutions (see the top and middle panels in Fig. 11, respectively), the set of locations with an increased noise level includes: (i) Gulf of Carpentaria; (ii) Gulf of Thailand + the western part of the South China Sea; and (iii) East Siberian Sea + Chukchi Sea. This can be explained by the usage of relatively old background models of tidal and non-tidal mass transport in the ocean (EOT11a and AOD1B RL05, respectively).

Finally, regularized GRGS solutions (the bottom panel in Fig. 10) show an increased noise level in multiple mediterranean seas and coastal areas of the World Ocean, the most pronounced spots being visible at: (i) an extended region in South-East Asia, stretching from the Gulf of Thailand through the western part of the South China Sea into the Java Sea; (ii) Arafura Sea + Gulf of Carpentaria; (iii) Red Sea; (iv) Black Sea; (v) Yellow Sea; (vi) Kara Sea; (vii) Bering Sea; and (viii) Baltic Sea + North Sea. It is unlikely that those features can be attributed to the exploited ocean tide model, FES2014, since the other solutions using a similar model (GFZ and JPL) do not contain those features. Therefore, the most likely reason is the exploitation of TUGO model of non-tidal mass transport in the ocean, which is a unique feature of the GRGS solutions. It is also interesting to notice that the overall noise level in the GRGS solutions is not as low as could be expected from the lake test presented in the previous sections. The most likely explanation is, again, the low-pass filtering, which suppresses high-frequency noise in the unconstrained solutions. As a result, the comparison is mostly focused now on the intermediate degree range, where the benefits of a regularization are limited (cf. Fig. 1).

It may look surprising that the ITSG solutions hardly show an increased noise level over the ocean, even though the AOD1B RL06 background model exploited in their production is not very accurate at some locations. Those inaccuracies resulted, for instance, in an increased noise level in the Argentine Basin, as it was revealed by Kvas et al. (2019) (see Fig. 4 in their publication). In our case, however, this and other inaccuracies of the AOD1B RL06 data product manifest themselves as signal in the GRACE solutions rather than as noise (see Fig. S5 in the Supplementary material). In order to shed light on this outcome, we present four selected mass anomaly time-series at the point within the Argentine Basin where the estimated signal RMS is maximum (Fig. S6). The figure shows that all four mass anomaly time-series, which reflect errors in the de-aliasing products, are very similar. This is in spite of the fact that they are based on three different de-aliasing products: AOD1B RLO6 (CSR, ITSG), TUGO (GRGS), and AOD1B RLO5 (WHU). This implies that all three dealiasing products probably lack the actual signals within the Argentine Basin. Then, their errors are similar because they are close to the actual signal—the signal restored in the GRACE-based mass anomalies. As a result, the Argentine Basin is identified as an area of an increased signal variance, and not as an area of an increased noise variance.

5 Discussion

The primary focus of this study is an optimal methodology to assess noise levels in GRACE-based mass anomaly time-series in the absence of knowledge about the true signal. As it is mentioned in Sect. 1, two approaches that are widely used for that purpose are (i) comparison of a GRACE time-series with a signal model, which is typically extracted from the GRACE data themselves (e.g., as a combination of seasonal variations and a linear trend) or (ii) comparison of alternative GRACE time-series with the mean one. Both approaches are not perfect. The first approach may overestimate noise when the true signal is more complicated than the signal model assumes. The second approach may underestimate noise if the alternative time-series suffer from similar noise realizations, which originate from errors in raw GRACE data. On the other hand, the second approach may overestimate noise in a particular time-series if that time-series is much less noisy than the alternative ones (e.g., due to the usage of a regularization).

Table 4 Global RMS values of noise StD estimates obtained with VCE (in cm EWH). The results are shown for mass anomaly time-series based on all eight GRACE solutions under consideration. The results are obtained with three different regularization techniques (Tikh-2, MYDD, and MYTD)
Full size table

With this study, we propose a novel technique, which is based on computing an optimal combination of alternative time-series in the presence of a regularization. To find the optimal weights associated with individual time-series, VCE is used. In this way, noise variance (and, therefore, noise StD) for each of the time-series is estimated. Such a technique can be seen as a hybrid technique, which contains some features of both commonly used ones. In the extreme case when only one time-series is analyzed, usage of a certain regularization functional can be seen as an implicit introduction of a signal model. For instance, the MYDD regularization was developed under the assumption that the true signal is primarily a combination of a seasonal signal and a linear trend (cf. Sect. 3.2). At the same time, the proposed technique is expected to suffer less in that case from a noise overestimation than the commonly used technique that exploits a signal model explicitly. This is because even the penalized data component (i.e., the difference between the data and the signal model) is not considered entirely as noise. In the other extreme case when a regularization is absent, the proposed technique becomes somewhat similar to a comparison of alternative GRACE time-series with their mean. But also in that case, the proposed technique is expected to produce better results, since it computes not the plain mean, but the weighted mean, taking into account different noise levels in the input time-series.

Fig. 12
figure 12

The ratios of noise StD estimates \(\sigma _k^{ \mathrm {(VCE)}}/\sigma _k^{\mathrm {(Altimetry)}} \times 100\%\) obtained for different GRACE mass anomaly time-series and different lakes using the MYTD regularization

Full size image

Of course, even the usage of a statistically optimal procedure cannot guarantee that the noise levels are estimated exactly. The scenario of a particular concern is noise shared by all the time-series under consideration. If this noise contains components that are identical to mass transport signals, the contribution of those components to the total noise StD will remain basically “invisible,” so that the total noise levels will be underestimated. In order to assess to what extent such concerns are justified, we have made a further analysis of the results obtained in the lake tests with the recommended MYTD regularization. We explicitly compare the “actual” (i.e., the altimetry-based) noise levels \(\sigma _k^{\mathrm {(Altimetry)}}\) with the VCE-based estimates \(\sigma _k^{\mathrm {(VCE)}}\) over all the five considered lakes (Fig. 12). This comparison shows that the proposed VCE-based procedure is able to estimate the noise level in unconstrained GRACE solutions rather accurately: in all cases it is very close to the altimetry-based estimate (deviations stay in the range between \(-10\) and 5%). As far as regularized GRGS solutions are concerned, the proposed procedure indeed underestimates their noise level by 10–30%. However, since this underestimation is observed for only one time-series, its mechanism must be totally different. We believe that it can be explained by the fact that the application of a regularization inevitably introduces a bias into results of a data inversion. In our context, this means that the regularized monthly solutions likely suffer from an increased signal leakage, which also contributes to their total error budget. However, stochastic properties of the leaked signal are definitely different from those of random noise. For instance, the leaked signal likely shows significant correlations in the time domain (in line with the original mass transport signal). Therefore, it is not surprising that the adopted VCE procedure, which assumes white noise in all the input data time-series, may underestimate noise in the GRGS solutions.

In addition, the results presented in Fig. 12 allow us to address the concern about a possible overestimation of noise level when a solution time-series deviates from the others not because it suffers from an increased noise level, but because it is very good and partly lacks noise shared by all the other time-series. According to Fig. 12, the proposed procedure may indeed overestimate noise level in high-quality solutions. More specifically, this effect is likely observed for the ITSG solutions over 3 lakes out of five (Caspian Sea, Nasser, and Victoria). However, this overestimation does not exceed 5%. We believe that such a minor overestimation will have little effect when noise levels in different GRACE solution time-series are compared.

Since hydrological signals mostly show a seasonal variability, one may pose a question about the need to apply the GLDAS-based reduction of hydrological signals in the lake tests. To answer that question, we have also repeated the lake tests without applying that reduction. It turns out that this reduction has only a minor effect onto the estimated levels of noise in GRACE-based mass anomalies. In average, it reduced the estimated standard deviations of noise by not more than 2 mm, as one can see from a comparison of the 2nd and 4th columns in Table 3. As a consequence, an elimination or not elimination of hydrological signals does not change any inferences based on the noise level estimates, including the finding that the MYTD regularization ensures the best quality of noise estimation. These results show that our noise estimates are sufficiently insensitive to signals of hydrological origin which are described by the GLDAS model. This concerns temporal variations in the shallow soil moisture variations, snow cover, and interception. On the other hand, GLDAS does not cover other types of hydrological signals, such as those due to water level variations in open water bodies, deep soil moisture variations in the presence of a thick vadose zone, as well as variations in the groundwater level. Therefore, it cannot be excluded that the remaining hydrological signals still have an impact on the obtained noise estimates. In particular, Lake Nasser is a point of concern in view of water exchange between the lake and the surrounding Nubian Sandstone Aquifer System. As it was shown by Abdelmohsen et al. (2020), a recharge of the aquifer system manifests itself as a progression of a water front away from the lake, reaching distances of up to 700 km in about four months. As a result, GRACE-based estimates of the total water storage display an increasing phase delay with the distance from the lake. To analyze the potential impact of this phenomenon onto the estimates of noise in GRACE data, an additional test was done. In that test, the altimetry data over Lake Nasser were artificially advanced by applying a time offset of 1, 2, 3, or 4 months. The resulting estimates of noise StD are shown in supplementary Fig. S7. As can be easily seen, an attempt to advance altimetry data results in a noticeable increase in the noise StD estimates for three GRACE time-series: GRGS (by up to 41.5%), ITSG (by up to 6.3%), and JPL (by up to 2.4%). The estimates for the remaining GRACE time-series are almost unaffected (the differences are within \(\pm \, 2\%\)). From this, we conclude that the water mass variations associated with the re-charge of the aquifer system around Lake Nasser are likely minor, as compared to mass variations within the lake itself. Thus, we fail to find any evidences that the noise estimates obtained in the lake tests on the basis of altimetry data suffer from unaccounted hydrological signals.

At the same time, subtraction of GLDAS signals has affected the signal retaining for some of the considered lakes. As one can see from a comparison of Fig. 6 and supplementary Fig. S8, this subtraction has reduced significantly the relative signal retaining for the lakes Ladoga and Tanganyika, and slightly for Lake Victoria. As a result, the mean relative signal retaining over 5 lakes is reduced by 1–2% (cf. the third and the last columns in Table 3). This implies that mass variations of hydrological origin around the considered lakes may be strongly correlated with water mass variations in the lakes themselves. If those signals are not corrected for, they may leak inside the territory of the lake, so that signal damping in GRACE solutions is partly compensated. This finding is consistent with our explanation in Sect. 4.1 regarding the relative signal retaining exceeding 100% for Lake Tanganyika: this phenomenon is likely caused by residual hydrological signals that are not captured by GLDAS and correlate with water mass variations in the lake.

Another point that we have not discussed yet is the potential impact of the steric component of water level variations in the considered lakes. This signal is predominantly caused by thermal expansion of lake water. Such a signal is expected to be particularly pronounced in the Caspian Sea due to a large difference between water temperatures in summer and winter (\(> 25^{\circ }\)C), in combination with a large lake area (so that the altimetry-based signal is to be scaled with factor \(\sim 0.69\), which is relatively large, cf. Table 2). To quantify the effect of that signal in Caspian Sea, we partly follow the approach of Swenson and Wahr (2007). We assume that this signal can be represented by a homogeneous thermal expansion of the mixed layer, the thickness of which is set equal to 28.1 m. As far as the coefficient of thermal expansion \(\alpha \) is concerned, we refrain from setting it to a constant value, since that approximation would be too coarse: this coefficient strongly depends on temperature, becoming even negative at temperatures near \(0\,^{\circ }\)C. We consider the dependence of \(\alpha \) on temperature in line with (Sverdrup et al. 1942), assuming the mean water salinity of 12.5‰ (Terziev et al. 1992). Time-series of monthly water temperatures in the Caspian Sea were downloaded from the catalogue provided by the Coordinating Committee of Hydrometeorology of the Caspian Sea (CASPCOM). Eight stations have been selected, from which an uninterrupted time-series over the entire time interval under consideration is available (Aktau, Derbent, Fort Shevchenko, Izberg, Kulaly, Makhachkala, Peshnoy, and Tyuleniy island). Then, the mean water temperature variations over the selected stations are computed and converted into steric water level variations in the Caspian Sea. Ultimately, the long-term mean of that signal is computed and subtracted consistently with GRACE data. The resulting time-series is shown as a green curve in supplementary Fig. S9. Obviously, the steric signal demonstrates a clear seasonal periodicity. Since the annual and semi-annual component of that signal are not used in the evaluation of GRACE data in the lake tests, we have subtracted those components (see the black curve in Fig. S9). The resulting signal is small (\(\hbox {RMS} = 0.5\) cm). Then, it is not surprising that the total inter-annual sea level variations (blue curve in Fig. S9) and the steric-corrected ones (red curve) are very close. Furthermore, an attempt to use steric-corrected water level variations in the Caspian Sea instead of those extracted from altimetry data directly results in very similar estimates of noise level in GRACE data: the obtained noise StD is changed by not more than 0.05 cm. Similar results are obtained after increasing the thickness of the mixed layer to 40 m. An attempt to decrease the thickness of the mixed layer to 15 m or less reduces the effect of steric correction even further. As far as the other lakes are concerned, the contribution of the steric signal to the estimated noise levels in GRACE data would be even smaller. This is primarily due to a further reduction of the expected signal retaining for those lakes (Table 2).

Concerning the estimates of the relative signal retaining, the effect of steric signal is expected to be small as well. For example, application of the steric correction in the Caspian Sea case changes the estimated relative signal retaining by not more than 0.05% (provided that the thickness of the mixed layer is set to 28.1 m). Such a change is at least an order of magnitude smaller than the errors in our estimates of relative signal retaining (cf. Table 3).

Thus, we can safely conclude that steric water level variations in the considered lakes have not affected the obtained results.

6 Conclusions

A novel technique is proposed to estimate noise levels in GRACE-based mass anomaly time-series in the absence of knowledge about the true signal. The tests conducted on the basis of five selected lakes confirmed the efficiency of the proposed technique. Furthermore, it was demonstrated that a regularization is an important element of it. Is was also shown that the performance of the proposed technique is affected by the choice of the regularization functional. The best results were obtained with the novel MYTD regularization. This is a finite-difference analog of the regularization functional that minimizes year-to-year differences between the values of the second time-derivative of the unknown function. Of course, one may expect the best performance of this regularization when the actual signal is such that it is not penalized at all. As it is mentioned in Sect. 3.2.3, such a signal may consists of an annual periodic term, a linear trend, and an acceleration term. On the other hand, the lake tests have demonstrated that this regularization functional remains efficient also when the actual signals show a large interannual variability (including the ones of an anthropogenic origin).

The developed technique allowed us to quantify noise StD for the mass anomaly time-series based on GRACE solutions from eight different data processing centers. The analysis was performed globally, including the areas where the signals are large and not known from independent sources. It was found, in particular, that ITSG and CSR solutions show the best performance, in terms of global RMS values of noise levels.

Apart from the well-known dependence of errors on latitude, we have identified problematic geographical areas for many of the considered solution time-series. Those problematic areas typically occur in the mediterranean seas and coastal areas of the ocean. Most probably, they are caused by an imperfectness of the background models exploited to compute and subtract rapid mass transport signals of tidal and non-tidal origin.

The aforementioned lake tests allowed us also to compare the signal damping in different GRACE solutions. It was found that ITSG and HUST solutions suffer from the least signal damping (let noise in the latter solutions be high). Signal in most of the other unconstrained solutions turned out to be damped by 6–9%, as compared to ITSG solutions. A likely reason is a partial absorption of gravity field signals in the course of gravity field modeling, when the authors co-estimated additional parameters in an attempt to reduce the impact of low-frequency errors in the raw GRACE data (such as errors in accelerometer data).

One of the GRACE models we considered—from GRGS—consists of regularized solutions. In general, noise in those solutions turned out to be comparable to that in the best unconstrained solutions or even lower. Still, we would advise to use GRGS solutions with some caution. As the conducted lake tests have shown, those solutions damp signals more than unconstrained solutions (in the conducted tests, the signals are damped in average by 15%, as compared to ITSG solutions).

We believe that the proposed technique may become a useful tool to assess the quality of mass transport estimates based on satellite gravimetry data. In particular, we envision its usage for the analysis of: (i) GRACE solutions produced by more groups; (ii) GRACE solutions of the next release; and (iii) solutions based on the data from other satellite gravimetry missions (in the first instance, GRACE Follow-On mission).