1 Introduction

One of the key challenges of modern volcanology is to identify and characterize the ongoing state of activity of volcanoes, through recognition of meaningful changes in observable parameters. This helps to increase the efficiency of hazard mitigation plans, thus reducing the impact of eruptive events on the populations that live in the vicinity of active volcanoes. The joint use of different geophysical, geochemical and volcanological parameters allows to improve the possibilities of volcano monitoring, thus enhancing the quality of the models that are used to understand the driving processes of eruptive events (Acocella et al. 2016; Alparone et al. 2011; Bonaccorso et al. 2011a, b, c; Carbone et al. 2015; Hajian et al. 2019).

Volcanic unrest is often accompanied by surface deformation and gravity changes (Berrino et al. 1992; Battaglia et al. 2003; Bonforte et al. 2007, 2017; Greco et al. 2016; Carbone et al. 2017). Accordingly, high-precision gravity and ground deformation measurements are increasingly performed to monitor active and quiescent volcanoes. They allow discovery of magma transfers across the feeding systems of active volcanoes (Bonaccorso et al. 2011a; Del Negro et al. 2013), changes in the amount of exsolved volatiles in magma reservoirs (Carbone et al. 2015) and changes in the rate of fracturing of the hosting medium (Carbone et al. 2009, 2014; Greco et al. 2010). Gravity and ground deformation measurements complement each other, thus providing a more complete information on the processes driving the phases of unrest (Battaglia et al. 2008; Bonforte et al. 2007).

At Mt. Etna volcano (Italy), gravity and ground deformation measurements have been accomplished since the eighties, either individually or jointly (Budetta et al. 1989; Obrizzo et al. 2004; Puglisi et al. 2004; Bonaccorso et al. 2011a; Alparone et al. 2013), allowing to shed light on the volcanic processes in the shallow and intermediate plumbing system of the volcano (Bonforte et al. 2007; 2017; Carbone and Greco 2007; Carbone et al. 2015; Del Negro et al. 2013; Greco et al. 2016).

Gravity changes associated with volcanic processes occur over a wide range of time scales, from minutes to years and with magnitude between a few and a few hundred µGal (1 µGal = 10−8 ms−2). High-precision instruments are necessary to detect such small signals and both time‐lapse surveys, along networks of stations, and continuous measurements, at single points, are carried out. Time lapse surveys can be carried out with relative (spring) gravimeters, that measure gravity differences over space, between pairs of stations, or by absolute gravimeters, capable of measuring the actual value of the gravitational acceleration at the observation point (Carbone et al. 2017; Greco et al. 2012).

In order to accurately measure small gravity changes due to volcanic processes (few µGal), repeated absolute gravity (AG) measurements have been performed at Mt. Etna (Italy) using the IMGC-02 (D’Agostino et al. 2008) and the Microg LaCoste FG5#238 gravimeters, since 2007 and 2009, respectively (Pistorio et al. 2011; Greco et al. 2012, 2015). Even though the use of absolute gravimeters on active volcanoes implies many difficulties (e.g. transport of the instrumentation, power supply at sites where mains electricity is not available), AG measurements may successfully replace or supplement relative gravity surveys, which often require a significant effort to mitigate the effect of instrumental drift and tares (Rymer 1989). The availability of absolute measurements in points very close to active volcanic structures provides accurate information on the changes related to magmatic processes.

At Mt. Etna, ground deformation measurements were first performed using the Electronic Distance Measurement (EDM) technique (Puglisi et al. 2004; Alparone et al. 2013) that has been later replaced by Global Positioning System (GPS), gradually evolved to Global Navigation Satellite Systems (GNSS). While EDM measurements were able to provide changes in the distances between pairs of points, GPS measurements provide the 3D position of a point on the surface. Continuous GPS measurements are carried out at Mt. Etna across a network that includes about 40 stations (Bruno et al. 2012). Time lapse surveys are also accomplished (at least once per year) to obtain a more detailed picture of the ground deformation pattern on a denser network, including several benchmarks in the most active areas.

Even considering the long history of gravity measurements at Mt Etna, a 10-year-long dataset of absolute gravity measurements, collected at one of the most active volcanoes in the world, is unprecedented and in itself exceptional, especially if one considers that: (i) high-quality measurements were collected by moving and installing absolute gravimeters, engineered for quiet laboratory conditions, in the harsh environments that characterize the summit zone of the volcano; (ii) the data allow to coherently track also small gravity changes occurring over time scales of years. Furthermore, through comparison with correlated ground deformation data, we reveal a mechanism of long-term magma accumulation and discharge, involving a strong “mass excess”.

Here, we present the results obtained through the joint analysis of repeated AG and GPS measurements at Mt. Etna over a 10-year-long interval, during which the volcano displayed a lively eruptive activity, with several lava fountain events and intense Strombolian activity from the summit craters. We demonstrate that the joint study of gravity and GPS data is crucial for better understanding the driving volcanic processes, drawing conclusions behind the volcanic activity, which couldn’t be reached if only one of the two dataset was available.

2 Review of Mt. Etna activity during 2009 to 2018

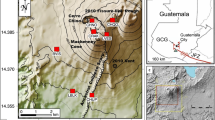
After the 2008–2009 flank eruption (Napoli et al. 2008), Mt. Etna (Fig. 1a) remained largely quiescent until 2010. Explosive activity resumed on 11 January 2011 from a pit on the east flank of the South-East Crater (SEC), one of the four summit craters of Mt. Etna (Fig. 1b). Between January 2011 and December 2013, 44 lava fountaining episodes (Fig. 1c) occurred from this vent (Calvari et al. 2018). Among these, only 4 episodes took place during the first half of 2011, while, since July, 13 events occurred in slightly more than 100 days (early July to late October 2011). Other clusters of closely spaced events occurred between early March and late May 2012 (5 events in 75 days), between mid-February and late April 2013 (13 events in less than 70 days; Cannata et al. 2015; Spampinato et al. 2015; Bruno et al. 2016), between late October and early December 2013 (6 events in less than 40 days). Between the two phases of closely spaced lava fountains in 2012 and early 2013, mild and intermittent eruptive activity occurred from the Bocca Nuova (BN) summit crater (Fig. 1b), between July and October 2012. As a consequence of this activity, a cinder cone and a lava flow field formed within the Bocca Nuova crater (Cannata et al. 2015; Slatcher et al. 2015; Spampinato et al. 2015). It is worth noting that, during the lava fountain on 26 October 2013, another summit crater (the North-East Crater (NEC); Fig. 1b) erupted simultaneously with the SEC (Fig. 1d).

Fig. 1
figure 1

a sketch map of the eastern side of Sicily showing the position of Mt. Etna and the CTA absolute gravity station, in the town of Catania, which is used as reference; b the active craters in the summit zone of Mt. Etna (VOR, Voragine; BN, Bocca Nuova; NEC, North-East Crater; SEC, South-East Crater; NSEC, New South-East Crater); c the January 5, 2012 eruption, one of the numerous lava fountaining episodes from the NSEC of Mt. Etna; d twin volcanic plumes on October 26, 2013 from NSEC (on the left of the photo) and from SEC (on the right of the photo). Photos (c) and (d): credit by Boris Behncke, INGV—Osservatorio Etneo

Full size image

The accumulation of the ballistics emitted during the 44 lava fountaining episodes led to the formation of a new cinder cone (the NSEC), which grew on the east flank of the SEC. After the 2011–2013 NSEC lava fountains, the eruptive activity switched to moderate lava effusion from the NSEC, during January-April and July–August 2014. On 28 December 2014, a further lava fountain episode occurred from the NSEC, bringing the number of events to 45 (Bonforte and Guglielmino 2015).

During 2011–2014, a total volume of ∼150 × 106 m3 (pyroclastics products plus lava flows) erupted from the NSEC through lava fountain episodes (De Beni et al. 2015). Due to the high frequency of explosive episodes, the average eruption rate in this period is close to the rate observed during longer-term major effusive eruptions (Aloisi et al. 2018).

In January 2015, ash plume emissions started from the Voragine crater (VOR). Explosive activity from this crater increased in intensity and became almost regular since 27 October. It climaxed with two sequences of 4 and 3 events from the Voragine crater (VOR) on 3–5 December 2015 (Vulpiani et al. 2016) and on 18–21 May 2016, respectively, bringing to a total of 52 the episodes of lava fountaining from Mt. Etna’s summit craters during January 2011 to May 2016. The lava fountains of 3–5 December 2015 rank among the most violent that have occurred at Mt. Etna in the last two decades (Aloisi et al. 2017; Bonaccorso and Calvari 2017). After the major explosive events in May 2016, volcanic activity subsided for a few months. Strombolian eruptions and lava flows took place at the end of January 2017 and the activity intensified at the end of February 2017, with several lava flows issued from a new vent in the saddle between NSEC and SEC, until the end of April 2017. During June 2017-August 2018, fumarolic activity persisted at several locations in the crater area, and, on a few occasions, minor ash emissions were observed.

3 Mt. Etna’s gravity and geodetic monitoring networks

A network for relative gravity measurements has been operated at Mt. Etna since 1986 (Budetta et al. 1989, 1999). The network has evolved over the years and it currently consists of 71 benchmarks, covering an area of about 400 km2. LaCoste and Romberg model D and Scintrex CG-3 M/CG-5 gravimeters have been utilized to perform the relative measurements (Budetta and Carbone 1998; Carbone et al. 2009; Greco et al. 2014).

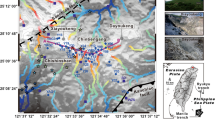
To achieve a balance between quality and efficiency in gravity measurements, we have investigated the applicability of absolute gravity measurements for volcano monitoring purposes. The first 4 stations for absolute measurements at Mt. Etna were installed in 2007, along a North–South profile crossing the summit craters, at elevations between about 1700 and 2850 m a.s.l. (SLN, MNT, PDN and PPR; Fig. 2). Another station was installed far from the summit active craters, in the facilities of INGV–OE (town of Catania, 50 m a.s.l.; CTA in Fig. 1a), intended as primary reference station. In 2009, we added 7 more stations (GAL, MSC, MSP, GPA, SES, CPC, CVE; Fig. 2), arranged as a ring around the volcano at elevations between 1150 and 2000 m a.s.l. (Greco et al. 2012, 2015).

Fig. 2
figure 2

Sketch map of Mt. Etna showing the positions of the stations for absolute gravity measurements (blue triangles) and the benchmarks for GPS measurements (red circles). The yellow circles highlight the absolute gravity stations and GPS benchmarks whose data are shown in Fig. 4

Full size image

Currently, the network for AG measurements includes, besides CTA, 11 stations, evenly distributed around the volcano edifice (Fig. 2). An absolute gravity station consists of a facility with a proper installation surface and providing protection to the instrumentation against ambient factors. Indeed, the main constraint when defining the position of a new absolute gravity station on Mt. Etna is the presence of a facility to house the instrumentation. Even though absolute measurements are time-consuming (with a FG5, each measurement requires about 8–10 h to complete), the data quality is significantly improved with respect to the use of spring-type gravimeters. In order to check the performance of the absolute gravimeter, we conducted repeated measurements at CTA station (mostly at the beginning and at the end of each survey at Mt. Etna), where FG5#238 is usually maintained. We obtained a good reproducibility of the absolute measurements at this station, with uncertainties on each measurement ranging between 2.5 and 7.8 μGal. The standard deviation of 31 measurements, carried out during 2009 to 2018, is 3.2 μGal (Fig. 3). FG5#238 is also routinely checked against other absolute gravimeters, in the framework of international and regional inter-comparisons. The results provided by FG5#238 were consistent with the Key Comparison Values (Jiang et al. 2012; Greco et al. 2015; Newell et al. 2017; Pálinkáš et al. 2017; Falk et al. 2020). Absolute gravimeters are compared for the purpose of assuring their reliability and ensure the traceability of measurements to the SI units. On the other hand, comparisons are also essential for long-term absolute measurements in geodesy and geophysics to insure the consistency of the observations over a time period of decades.

Fig. 3
figure 3

Top: The FG5#238 absolute gravimeter during a measurement session at CTA station in the town of Catania (see Fig. 1a for the location of CTA station). The coordinates of the station, its elevation, the averaged value of g during the 2009–2018 interval, the combined averaged uncertainty (± 4.3 μGal) and the standard deviation of 31 measurements (3.2 μGal) are also reported. Bottom: Absolute gravity values at CTA (Catania) station during 2009–2018 period, collected with the Micro-g LaCoste FG5#238 absolute gravimeter. The values of g are referred to an elevation of 1.2169 m from the ground, corresponding to the distance between the ground and the effective position of free-fall for FG5#238. The error bars represent the combined uncertainty

Full size image

The whole Mt. Etna’s gravity network is occupied every summer. More frequent measurements are carried out through relative spring gravimeters across same elements of the network (almost monthly along an East–West profile; Carbone et al. 2009; Greco et al. 2010; Del Negro et al. 2013; Bonforte et al. 2017), or during eruptive events.

Ground deformation monitoring of Mt. Etna started in the 70’s and has evolved ever since, in both networks and methods. Upgrades to the GPS network for repeated measurements have been accomplished also considering the opportunity of having the benchmarks in the same position as (or within close distance from) those used to perform gravity and other geophysical measurements (Puglisi et al. 2004). Most of the gravity and GPS benchmarks are co-located or within a few meters (Bonforte et al. 2007), with the exception of some sites where the distance is of the order of a few hundred meters. The whole GPS network (about 80 benchmarks) is surveyed at least once every year. Here, we present data from 22 GPS benchmarks (Fig. 2), of which 11 are co-located with absolute gravity stations, 5 lie on the summit area and 6 are located on sites not or slightly affected by the east flank seaward sliding (Bonforte et al. 2011). Measurements are usually performed during the summer, when, due to the lack of snow cover, the summit stations can be reached. Data are analysed jointly with data from the 40 continuously running GPS stations, in order to obtain information about the changes during the period between two subsequent campaigns at a higher space resolution (Bonforte et al. 2008). Additional surveys may also be carried out along parts of the periodic network, during eruptive or seismic crises, in order to improve the time resolution of the data (Bonforte et al. 2013, 2017). On rare occasions, GPS measurements could not be performed at sites where absolute gravity measurements were carried out (e.g. due to the dense vegetation that masks the GPS satellite signal). In these cases, the information on ground deformation was retrieved using data from the other closer GPS benchmarks.

4 Repeated absolute gravity and GPS measurements

Between 2009 and 2018, we conducted almost yearly AG campaigns at Mt. Etna, using the FG5#238 free-fall gravimeter. In addition to AG measurements, vertical gravity gradient (VGG) measurements were performed using a spring relative instrument. More frequent AG measurements were carried out at SLN, CVE and CTA stations (Fig. 2). At SLN and CVE almost monthly relative gravity data were also collected through a spring gravimeter, which were employed to improve the time resolution of the changes observed through AG measurements. The averaged combined uncertainty estimated for all the gravity measurements is 7.1 μGal.

The gravity changes likely due to volcanic processes are obtained after correcting the data for effects of Earth tides and polar motion, in compliance with the International Earth Rotation and Reference Systems Service (IERS) conventions 2010 (Petit and Luzum, 2010). The effect of atmospheric mass variations is also removed using the standard barometric admittance factor of − 0.3 µGal/hPa (Merriam, 1992).

Usually, absolute gravity measurements are referred to a specific height above the station (from the ground) that mainly depends on the gravimeter type. Converting a measure taken at the real instrumental height into the corresponding value at any other height above the station needs accurate determination of the VGG. Since we used gravity data collected with both relative and absolute gravimeters, thus at different heights from the ground, to compare them, we used the local VGGs, measured using Scintrex relative gravimeters, to refer the relative gravity measurements to the common height of 1.2169 m (corresponding to the effective distance between the ground and the effective position of free-fall for FG5; Niebauer et al. 1995; Timmen 2003).

GPS measurements are conducted using multi-frequency GPS receivers in static mode on self-centring benchmarks. The latter is designed to eliminate setup errors and allow the maximum accuracy and repeatability of the measurements (Bonforte et al. 2016). The software used for processing GPS data is the last available version of a commercial survey data processing provided by Trimble® (Trimble Business Center). The overall procedure is the same used for geodetic surveys on Sicilian volcanoes (Bonforte and Puglisi 2006; Bonforte and Guglielmino, 2008). GPS data are post-processed by using precise final ephemerides and precise antenna calibration models provided by IGS (Bonforte et al. 2013). To obtain the precise positioning of each GPS station, more than 20,000 baselines are usually processed when measuring the whole network and final solutions show 2–3 mm errors for the horizontal components and 3–4 mm for the vertical ones.

Both gravity and geodetic surveys were carried out in the same season of the year (late-spring to early-summer), thus minimizing seasonal effects due to the different water content in the subsoil.

5 Absolute gravity and elevation changes during the 2009–2018 period

AG values are corrected for local changes in elevation through the corresponding GPS data, using the experimental vertical gradient of gravity measured at each absolute station. Height-corrected absolute gravity time-series from five key stations of the network (Fig. 2) are presented in the left side of Fig. 4, while the corresponding elevation time-series from the GPS benchmarks closest to the five gravity stations are shown in the right side of the same figure.

Fig. 4
figure 4

Left: absolute gravity time series from five key stations of the network (marked with yellow circles in Fig. 2); the error bars indicate the combined uncertainty. Right: elevation time series from the five GPS benchmarks closest to the above key gravity stations. The black curves are low-pass filters, with cut-off period of about 3 years, applied to the time series. The vertical red dashed lines mark the Nov-2011—Oct-2014 interval, which was selected for data modelling (see Sect. 6). On top of both sides of the figure, the red points and the green bar mark phases of eruptive activity

Full size image

Both gravity and elevation time series show an increase/decrease cycle throughout 2009 to 2014 (Fig. 4a). In particular, a phase of gravity increase and uplift occurred between 2009 and late 2011, followed by a phase of gravity decrease and subsidence, between late 2011 and late 2014. This cycle affects the whole volcano edifice, with stronger variations mostly observed at the station closer to the summit craters (e.g. PDN and EPDN in Fig. 4).

To better evidence the increase/decrease cycle throughout the gravity and elevation data, we low-pass filter (cut-off period of 3 years) the time series from all available stations, after linear interpolation is applied to oversample the data at constant rate (1 day). The filtered time series are shown as black curves in Fig. 4. As for gravity, the increase and decrease phases reach a maximum amplitude (about + 50 and -70 µGal, respectively) at PDN station (Fig. 4). Besides being stronger, the 2011–2014 decrease phase displays a more coherent pattern over space than the previous increase phase, as evidenced in Fig. 5. The patterns of the inflation and deflation phases during 2009 to 2014 have similar characteristics, even though the filtered amplitudes of the elevation changes during the inflation phase are more evenly distributed than the amplitudes of the corresponding gravity changes (Fig. 5). During the subsidence phase, a maximum filtered amplitude of about -6 cm is reached at the stations closest to the summit craters (Fig. 5b).

Fig. 5
figure 5

Absolute height-corrected gravity changes (red arrows) and vertical deformation (yellow arrows) observed during 2009 to 2011 (a) and 2011 to 2014 (b). All changes are obtained using the low-pass filtered time series (cut-off period of about 3 years) from each observation point

Full size image

After 2014, absolute gravity data were collected only at a few stations of the network and that explains why the three upper time-series in the left side of Fig. 4 provide information relevant only to the 2009–2014 interval. Hence, while the 2009–2014 cycle is well described by the available gravity data, from 2015 onwards, the available AG measurements do not allow to describe the gravity changes with adequate space and time resolution. The general pattern of the gravity changes during 2015 to 2018 can be retrieved using the data acquired at Serra La Nave (SLN) and Casa del Vescovo (CVE) stations, where almost yearly AG and ground deformation data were integrated with more frequent relative gravity measurements (Fig. 4). However, only qualitative inferences can be made on the data from only two stations, that could also reflect local effects, rather than being representative of the behaviour of the entire volcano.

6 Gravity and elevation changes during 2011 to 2014: data modelling

The fact that during 2009–2014 the residual gravity changes (i.e. after correction for the free air effect) share the same increase/decrease pattern of vertical ground deformation (Fig. 4) indicates that the contribution to the observed gravity changes from the underground mass redistributions exceed the contribution due to the vertical displacement of the observation points (Battaglia et al. 2008).

To gain insight into the bulk mass and volume changes over the studied interval, we model gravity variation and deformation using analytical solutions. As reported in the previous section and shown in Fig. 5, the 2011–2014 phase of deflation and gravity decrease is characterized by slightly stronger amplitudes and more coherent patterns over space than the previous phase of uplift and gravity increase (2009–2011). Accordingly, to infer the characteristics of the pressure and mass sources, we invert deformation and residual gravity changes during 2011–2014. Given the similarity, in terms of time development, spatial pattern and amplitude of the changes between the phases of uplift/gravity increase and deflation/gravity decrease, we assume that the processes driving the observed changes during the whole considered interval (2009–2014) developed within the same source volumes and that similar mass and volume changes were involved during the two sub-intervals, with opposite sign.

Deformation and residual gravity changes are inverted separately, to produce independent models and avoid possible bias from forcing the solutions to share the same position.

Residual gravity changes are inverted to constrain the source location and associated mass change. The low-pass filtered time-series of residual gravity changes (Fig. 5) from the 11 available absolute stations are used to evaluate the changes during 2011–2014. As a forward model, we consider the gravitational attraction of a spherical body of finite size and mass, which is identical to that of a point source with the same mass (Battaglia and Hill, 2009). The spherical shape involves the minimum number of model parameters and was utilized not to over-interpreting the relatively sparse available data. The best fit to the measured gravity changes is calculated through performing a minimization of the sum of absolute deviations (SAD), with respect to the involved parameters (location of the source model and mass change). To avoid possible convergence on local minima, the optimum solution is uniformly searched in a 6.5 × 6.5 × 6.5 km3 volume around and beneath the summit craters. Results are shown in Fig. 6, as the location probability density (obtained from the inverse of the SAD values) within the search domain. The optimum mass-source model is centred slightly east of the summit craters (white star in Fig. 6a), at a depth of about 5 km b.s.l. (Fig. 6b). The mass decrease during 2011–2014 is modelled as − 7 × 1011 kg and the RMS error between observed and calculated (best-fit) gravity changes is 5 µGal (Fig. 7).

Fig. 6
figure 6

(a) and (b) Mass source location probability on the horizontal and vertical (E-W trending) planes cutting the best-fit position (white star). At each node of the search grid, the location probability is obtained as the inverse of the sum of absolute deviations between observed and calculated gravity changes (see text). The black star marks the projection, on the same planes, of the best-fitting pressure source. (c) and (d) Pressure source location probability on the horizontal and vertical (E-W trending) planes cutting the best-fit position (black star). At each node of the search grid, the location probability is obtained as the inverse of the sum of absolute deviations between observed and calculated vertical deformatios (see text). The white star marks the projection, on the same planes, of the best-fitting mass source

Full size image
Fig. 7
figure 7

Observed and calculated gravity changes versus horizontal distance from the source. The RMS error between observed and calculated (best-fit) gravity changes is 5 µGal

Full size image

The source of ground deformation is constrained through inversion of the vertical component of the GPS observations. The reason for disregarding the horizontal components of the deformation is that, over time-scales of years, they are dominated by the gravitational spreading of Mt. Etna’s volcano edifice (Urlaub et al. 2018). This is shown by Aloisi et al. (2018), who analysed surface area changes recorded at intermediate altitude on the west flank of Mt. Etna, during 2009–2017. They showed that, even though areal dilatation/contraction cycles occur over time scales of months, there is a general dilatation trend, leading to an area increase of about 30 ppm, across the whole considered interval.

The low-pass filtered vertical deformation time-series from 22 GPS stations (Fig. 5) are used to create the database of changes during 2011–2014, which then become the input to the inversion scheme. The latter involves a finite spherical magma body as the forward model of the pressure source, which is described through the analytical solution of McTigue (1987). Also in this case, the optimum solution is achieved through minimizing the SADs, while the source location probability is defined in the whole search domain (Panels c and d of Fig. 6). The optimum pressure-source model lies beneath the summit craters, at a depth of about 4700 m (black star in Fig. 6). The best solution involves a bulk volume decrease of 8*106 m3. The RMS error between observed and calculated (best-fit) elevation changes is 1.2 cm (Fig. 8).

Fig. 8
figure 8

Observed and calculated elevation changes versus horizontal distance from the source. The RMS error between observed and calculated (best-fit) elevation changes is 1.2 cm

Full size image

A comparison between the results obtained through the inversion of the gravity and deformation data shows that the mass and pressure sources occupy similar positions. In particular, the location probability maps show that each source is placed in a position where the probability of finding the other one is high (Fig. 6). This observation implies that the deformation and gravity changes during the studied period are, most likely, different effects of the same overall source processes.

7 Gravity and elevation changes during 2015 to 2018

After the cycle of gravity increase and uplift, followed by gravity decrease and subsidence, during the interval between 2009 and 2014, a new phase of moderate uplift started in early 2016 and continued throughout 2018 (Fig. 4). Weak positive elevation changes (mostly less than 2 cm) were observed at most stations, but without a clearly defined spatial pattern.

After 2014, absolute gravity measurements were performed only at SLN and CVE stations (see Sect. 5 and Fig. 4). Data from the two stations highlight a relatively fast gravity increase (late 2014 to early-2016), which reached an amplitude of about 50 μGal at SLN (Fig. 4), followed by an overall gravity decrease until the end of the period considered in the present study.

Within the limits of the available data, we can conclude that the coupled behaviour of gravity and elevation changes which characterized the 2009–2014 interval did not continue after 2014. This could indicate a different behaviour of the volcano, which is indeed reflected in the different eruptive styles characterizing the years before and after early 2015.

8 Discussion

Residual absolute gravity measurements between 2009 and late 2014 highlight a cycle of gravity increase (2009–2011) and decrease (2011–2014), accompanied by synchronous ground elevation changes following the same pattern of increase (uplift) and decrease (subsidence; see Fig. 4). Inversion of residual gravity and deformation data during the 2011–2014 decrease phase indicates that, overall, the mass and pressure sources share a similar position beneath the summit area of the volcano, at a depth of ~ 5 km b.s.l. (Fig. 6). This suggests that, within the measurement and model uncertainty, the observed gravity changes and deformation are triggered by processes occurring in the same source volume. The latter is a well-known storage zone at intermediate depth (e.g. Bonforte et al. 2008; Aloisi et al. 2018). Nevertheless, while the inversion of vertical deformation points to a bulk volume decrease of 8*106 m3, a conservative estimate of the volume change from residual gravity variations is 250*106 m3, assuming a magma density of 2700 kg m−3. Hence, even though the sources of deformation and gravity changes roughly coincide, the volume change inferred from the deformation is only 3% of the volume change inferred from residual gravity variations.

This kind of discrepancy was found at other volcanoes, like Piton de la Fournaise (La Réunion; Bonvalot et al. 2008), Askja and Krafla (Iceland; de Zeeuw-van Dalfsen et al. 2005, 2006) and Kīlauea (Hawaii, Johnson et al. 2010). Residual gravity changes measured between 2009 and 2012 inside Kīlauea Caldera were accompanied by surface displacements of the same area. Modelling results indicated that the sources of deformation and gravity changes coincided, but the volume change inferred from deformation was only 8–9% of the volume changes inferred from residual gravity variations. Bagnardi et al. (2014) reviewed different processes able to produce bulk mass change without the expected corresponding volume change. Those include compression/decompression of the magma in the reservoir, substitution of the resident magma with magma having different density, and filling/empting of void space.

Residual gravity changes pointing to the involvement of bulk volumes larger than expected from the associated ground deformation were observed at Mt. Etna on different occasions (e.g. Budetta et al. 1999; Carbone et al. 2003, 2008; Greco et al. 2016) and they were explained through mechanisms similar to those proposed by Bagnardi et al. (2014).

Currenti (2014) reviewed observations from Mt. Etna during September 1994 to October 1995 (Budetta et al. 1999) as a case study to show, through finite element modelling, that the source geometry may also play a significant role in controlling the relationship between gravity changes and ground deformation occurring at volcanoes. In particular, for ellipsoidal sources, the ratio of gravity change to vertical deformation may be higher than predicted by the Mogi model, leading to the possible development of major gravity changes without significant deformation. However, this is especially true in the case of relatively shallow sources.

According to Bonafede and Ferrari (2009), the magma stored in a reservoir (assumed spherical) can undergo a volume contraction/expansion (ΔVin) equal to:

$${\Delta V}_{in}={V}_{0}\Delta p{\beta }_{m} ,$$
(1)

where V0 is total volume of the reservoir, Δp is the pressure change and βm is the compressibility of the resident magma. It also holds that the outwards volume expansion/contraction of the reservoir (ΔVout) is (Bonafede and Ferrari, 2009):

$${\Delta V}_{\mathrm{out}}={V}_{0}\Delta p\frac{3}{4\mu } ,$$
(2)

where μ is the rigidity modulus of the host medium. The overall volume change (ΔVm), occurring when new magma is injected to or withdrawn from the reservoir, is (Bonafede and Ferrari 2009):

$${\Delta V}_{m}={\Delta V}_{\mathrm{out}}+{\Delta V}_{\mathrm{in}}={\Delta V}_{\mathrm{out}}\left(1+\frac{4\mu {\beta }_{m}}{3}\right) ,$$
(3)

Our results point to a value of the ratio between ΔVm (volume deduced from residual gravity) and ΔVout (volume deduced from ground deformation) on the order of 30, implying that:

$$1+\frac{4\mu {\beta }_{m}}{3}\approx 30; { \beta }_{m}\approx \frac{22}{\mu }$$
(4)

Assuming a standard value for μ of 25 GPa and assuming that the observed ΔVm / ΔVout ratio is due solely to shrinking of the magma inside the reservoir, from [4] we obtain βm ≈ 0.9 GPa−1. Compressibility of degassed basalts at crustal depths is in the range 0.06–0.1 GPa−1 (Rivalta and Segall, 2008), thus, about an order of magnitude lower than the above result. However, βm can reach higher values (up to 3 GPa−1), in the case of volatile-rich magmas stored at depths of > 3 km (Kilbride et al. 2016). Indeed, at Mt. Etna, CO2 is thought to become exsolved at considerable depth (p > 200 MPa; Moretti et al. 2018), implying that there could be a significant amount of volatiles in the magma reservoir at the inferred source depth of ~ 5 km.

Magma compressibility could thus explain, at least in part, the discrepancy between magma volumes deduced from gravity and ground deformation data.

Filling/empting of void space by magma was also invoked to explain the occurrence of gravity changes with minor deformation at Mt. Etna (Rymer et al. 1993) and other volcanoes (e.g. Johnson et al. 2010). However, due to the increasing confining pressure, it is unlikely that open space may persist at depths of more than a few km beneath the surface, implying that this mechanism is more effective in producing gravity changes when the mass source is located at shallow depths.

Progressive replacement of resident magma by magma having a different density is another mechanism that may lead to gravity changes not accompanied by the expected deformation. Bagnardi et al. (2014) suggested that sustained gas emission may lead to substitution of gas-rich magma in a bulk reservoir by outgassed magma sinking to deeper levels of the plumbing system. The resulting density increase within the reservoir induces a gravity change without any important volume change of the reservoir itself.

This mechanism could have acted during the first part of the 2009–2011 interval, when only sustained degassing occurred from the summit craters of Mt. Etna (Mattia et al. 2015), possibly leading to a densification of the inferred mass source at ~ 5 km b.s.l. Successively, when eruptive activity resumed from the summit craters, the recycling mechanism could have become progressively less efficient, eventually favouring the switch from density increase to decrease within the bulk reservoir.

Overall, gravity and vertical deformation data during 2009–2011 image a recharge phase, whereby most of the new material coming from below was stocked in the reservoir at intermediate depth through shrinking of the resident magma (left panel of Fig. 9). This view is supported by the findings of Paonita et al. (2016), who observed a marked increase in 3He/4He during early 2010 to early 2012. The latter was interpreted as due to a recharge event in a magma chamber at ~ 8 km depth. Recycling of outgassed, denser magma sinking from shallower levels, could have contributed to enhance the ratio of gravity change to vertical deformation during the 2009–2011 interval (left panel of Fig. 9).

Fig. 9
figure 9

Summary cartoon (not to scale) showing the inferred processes during 2009 to 2014. Left: during the 2009–2011 recharge phase, magma input from deep portions of the plumbing system caused pressure increase in a reservoir at about 5 km b.s.l. This led to bulk volume increase and density (mass) increase by magma compression. In turn, these processes caused the observed inflation and gravity increase. Right: since 2011, magma outflow from the reservoir at ~ 5 km depth towards shallower levels of the plumbing system progressively exceeded the influx of magma from below. This led to the intense eruptive activity during 2011–2014 and the switch from pressure increase to decrease within the reservoir at ~ 5 km depth, which promoted bulk volume reduction, thus the observed subsidence, and decompression-related density decrease, observed at the surface as gravity decrease. Transient pressure and mass changes probably occurred in the shallower storage zone described by Bonforte et al. (2008) and Bonaccorso et al. (2011a), but over time-scales too short to be resolved by the gravity and GPS measurements in the focus of the present study

Full size image

Conversely, gravity decrease and subsidence during 2011 to 2014 are indicative of discharge from the reservoir at ~ 5 km b.s.l. (right panel of Fig. 9). We suppose that, during this interval, the influx of magma to the reservoir from below was much smaller than the outflow towards shallower levels of the plumbing system, which promoted bulk volume reduction (subsidence) and decompression-related (increase in the volume fraction of exsolved gas) density, thus gravity, decrease. The abrupt reduction in the 3He/4He signal during the first half of 2012 (Paonita et al. 2016) would suggest an overpressure decrease much faster than deduced from gravity and vertical deformation data (Fig. 4). This discrepancy could depend on the different depths of the storage regions imaged by the geochemical and geophysical data, where different, though related, processes could have taken place.

Within the limits of the available temporal resolution, the start of the gravity decrease and subsidence phase coincided with, or immediately followed, the resumption of sustained eruptive activity from the summit craters during the second half of 2011 (Fig. 4), when a sequence of closely spaced lava fountains (5–10 days between successive events) occurred (Behncke et al. 2014). Until late 2014, ∼150*106 m3 of material was emitted only through lava fountains from the NSEC (De Beni et al. 2015), which, taking into account that eruptive activity other than lava fountaining took place during the same interval, represents a minimum estimate of the total volume outputted by the volcano. Nevertheless, the above estimate, though lower, is still on the same order of magnitude as the volume deduced from inversion of the gravity decrease. These observations suggest that most magma inferred to have left the storage zone at ~ 5 km b.s.l., between 2011 and 2014, fed the eruptive activity from the summit craters of Mt. Etna during the same interval.

9 Concluding remarks

The availability of absolute gravity data from 11 points, at elevations of between 1150 and 2850 m on the slopes of Mt. Etna, allows to consistently track changes up to a few tens of μGals occurring over multi-year time scales, since 2009. That is not always possible with the more widely utilized relative (spring) gravimeters, since, in order to compare data acquired during different measurement campaigns, each campaign must be related to a reference outside the active area, assumed to be unaffected by volcano-related gravity changes (Carbone et al. 2017). Especially over long time scales (several months to years), this may introduce significant errors, since possible variations at the reference station(s), due to man-made, hydrological, and other effects, will be propagated through the entire network. Furthermore, changes in the instrumental drift rate and tares (Rymer 1989) during a measurement campaign with a spring device will significantly increase the error budget.

The analysis of absolute gravity and ground elevation changes during 2009 to 2014 allows to recognize a long-term cycle of charge and discharge, occurring in a reservoir beneath the summit area of Mt. Etna, at depth of about 5 km b.s.l. (Fig. 9). In particular, the patterns of gravity and ground elevation changes indicate that, since 2009, thanks to the high (gas-enhanced) compressibility of the resident magma, this storage zone accommodated a large amount of new magma coming from deeper levels, before magma was transferred to shallower portions of the feeder system. Consideration of the eruptive activity during the studied period suggests that magma transfer to shallower levels started in early 2011, when the first episodes of lava fountaining in the 2011–2013 sequence occurred from the NSEC (Calvari et al. 2018). The emplacement of this upward mass transfer, likely associated with a reduced influx to the inferred storage zone at intermediate depth from below, progressively led to the switch from positive to negative gravity and ground elevation changes. Starting from the second half of 2011, when a cluster of closely-spaced lava fountains occurred (July to October 2011; Behncke et al. 2014), gravity decrease and subsidence (Fig. 5) indicate that the storage zone at 5 km b.s.l. was undergoing volume reduction and decompression-related density decrease (Fig. 9). This regime continued throughout the following ~ 2 years as the magma lost from the storage zone at intermediate depth fed the eruptive activity until late 2014.

Results of previous studies (Bonforte et al. 2008; Bonaccorso et al. 2011a) suggest that magma transfer from the storage at intermediate depth to a shallower part of the feeding system, located at about sea level, occurs prior to each Strombolian eruption or lava fountain event. Indeed, the shallow storage system is not able to accommodate large amounts of magma, implying that a tight overall balance between refilling and erupted magma is maintained (Bonaccorso et al. 2013; Bonforte et al. 2021). This view explains why long-term gravity and elevation changes are dominated by the effects of processes occurring in the storage zone at intermediate depth: possible effects linked to transitory disequilibrium in the shallower reservoir likely occur over time-scales too short to be resolved by the absolute gravity and GPS measurements in the focus of the present study.

We provide a further evidence of the great potential of joint gravity and ground deformation studies to enhance our understanding of how volcanoes work. Repeated absolute gravity measurements allowed to unambiguously track a long-term recharge phase, involving a much larger amount of magma than one would have inferred from considering only the associated ground elevation changes. The accumulated magma fed volcanic activity during the subsequent ~ 2-year phase of discharge. Our results thus have important implications for the long-term volcanic hazard assessment and encourage the execution of absolute/hybrid gravity measurements (Greco et al. 2012) to complement ground deformation monitoring at volcanoes where bulk mass redistributions may develop over time scales of months to years.