Bayesian modelling of piecewise trends and discontinuities to improve the estimation of coastal vertical land motion

Abstract

One of the major sources of uncertainty affecting vertical land motion (VLM) estimations are discontinuities and trend changes. Trend changes are most commonly caused by seismic deformation, but can also stem from long-term (decadal to multidecadal) surface loading changes or from local origins. Although these issues have been extensively addressed for Global Navigation Satellite System (GNSS) data, there is limited knowledge of how such events can be directly detected and mitigated in VLM, derived from altimetry and tide-gauge differences (SATTG). In this study, we present a novel Bayesian approach to automatically and simultaneously detect such events, together with the statistics commonly estimated to characterize motion signatures. Next to GNSS time series, for the first time, we directly estimate discontinuities and trend changes in VLM data inferred from SATTG. We show that, compared to estimating a single linear trend, accounting for such variable velocities significantly increases the agreement of SATTG with GNSS values (on average by 0.36 mm/year) at 339 globally distributed station pairs. The Bayesian change point detection is applied to 606 SATTG and 381 GNSS time series. Observed VLM, which is identified as linear (i.e. where no significant trend changes are detected), has a substantially higher consistency with large-scale VLM effects of glacial isostatic adjustment (GIA) and contemporary mass redistribution (CMR). The standard deviation of SATTG (and GNSS) trend differences with respect to GIA+CMR trends is by 38% (and 48%) lower for time series with constant velocity compared to variable velocities. Given that in more than a third of the SATTG time series variable velocities are detected, the results underpin the importance to account for such features, in particular to avoid extrapolation biases of coastal VLM and its influence on relative sea-level-change determination. The Bayesian approach uncovers the potential for a better characterization of SATTG VLM changes on much longer periods and is widely applicable to other geophysical time series.

1 Introduction

Understanding and estimating vertical land motion (VLM) is critical to quantify and interpret the rates of coastal relative sea level change (RSLC). Next to the absolute sea level change (ASLC), with a current global rate of about 3 mm/year (Cazenave et al. 2018), VLM substantially influences regional relative sea level change with rates in the same order of magnitude as the ASLC itself. VLM uncertainties are thus also a major contributor to the error budget of RSLC (Wöppelmann and Marcos 2016; Santamaría-Gómez et al. 2017). VLM is caused by various processes, such as the Glacial Isostatic Adjustment (GIA) (Peltier 2004), surface loading changes (e.g. due to ice and water mass changes (Farrell 1972; Riva et al. 2017; Frederikse et al. 2020), tectonic and volcanic activity (Riddell et al. 2020; Houlié and Stern 2017; Serpelloni et al. 2013), human impacts such as groundwater pumping (e.g. Wada et al. 2012; Kolker et al. 2011), or other local effects caused by erosion or dam building, for instance. In order to determine the impact of VLM on either contemporary or projected RSLC, a general assumption is that the regional VLM is constant over decadal to centennial time scales, which is valid for VLM excited by processes such as GIA. However, natural processes, in particular seismic activity, or nonlinear deformation due to surface mass changes (Frederikse et al. 2020), but also instrumental issues can hinder the assessment of the linear component of VLM. Therefore, we develop a novel approach, to detect discontinuities and potential significant trend changes in VLM data. The unsupervised (automatic) identification of such events is useful to mitigate discontinuities and can also serve as a decision-making tool for the treatment of nonlinear time-dependent VLM.

Most of global VLM observations stem from the Global Navigation Satellite Systems (GNSS) or from differences of absolute (satellite altimetry—SAT) and relative sea level (tide gauge—TG) measurements (SATTG). With the increasing availability of altimetry data (in time), as well as with an enhanced performance of coastal altimetry, the latter method (SATTG) has been steadily developed and applied over the last two decades (e.g. Cazenave et al. 1999; Nerem and Mitchum 2003; Kuo et al. 2004; Pfeffer and Allemand 2016; Wöppelmann and Marcos 2016; Kleinherenbrink et al. 2018; Oelsmann et al. 2021). SATTG VLM estimates are particularly valuable, because they complement GNSS-based VLM at the coastlines. Nevertheless, linear VLM rates from GNSS are more accurate (0.6 mm/year, (Santamaría-Gómez et al. 2014)) than those from SATTG (1.2–1.8 mm/year, (Kleinherenbrink et al. 2018; Pfeffer and Allemand 2016)). Ideally, they should be one order of magnitude less than contemporary rates of absolute sea level change, which is in the range of 1–3 mm/year (Wöppelmann and Marcos 2016).

These reported accuracy estimates are based on the assumption that VLM is linear. However, GNSS and SATTG time series, whose records are typically shorter than three decades, are not always suitable to estimate a long-term linear component of VLM. They may be affected by variable velocities at shorter timescales, which are most commonly caused by earthquakes and their associated post-seismic crustal deformation (e.g. Klos et al. 2019), but can also have other natural or human-related origins. Kolker et al. (2011), for instance, found significant subsidence trend changes (in the order of several mm/year) at TGs in the Gulf of Mexico, which were attributed to subsurface fluid withdrawal. Cazenave et al. (1999) reported that also volcanic activity can cause discontinuities and trend changes, based on the analysis of SATTG time series. Besides these geophysical origins, about one-third of discontinuities detected in GNSS time series could be attributed to instrumental issues, such as antenna changes (Gazeaux et al. 2013).

While discontinuity detection has been extensively addressed for GNSS data (Blewitt et al. 2016; Klos et al. 2019), to our knowledge, there exists no study which adequately tackles the problem of directly estimating discontinuities in SATTG time series. Wöppelmann and Marcos (2016), for example, manually rejected time series, which were potentially affected by variable velocities. Klos et al. (2019), on the other hand, utilized GNSS data to correct SATTG VLM estimates that were strongly influenced by tectonic activity. Thus, an improved and independent characterization of SATTG time series is crucial, because SATTG observations have the potential to substantially expand scarce VLM estimates derived from GNSS time series, which also usually cover a shorter time span than the SATTG observations (Wöppelmann and Marcos 2016). Therefore, we develop a Bayesian model to automatically and simultaneously detect change points (cp), caused by discontinuities and trend changes, as well as other common time-series features of SATTG observations. We apply our method to a global set of 606 SATTG pairs and 381 coastal GNSS stations and show that our approach better aligns SATTG and GNSS trends. The latter is demonstrated by comparing our results at 339 GNSS/SATTG co-located stations globally distributed. The method can be potentially valuable for GNSS time-series analysis, in particular with regard to the unsupervised detection of discontinuities or significant trend changes.

The awareness of discontinuities and other nonlinear behaviour in time series, as well as the demand for accurate position and velocity estimates from GNSS data, have led to the development of a wide range of semi- to fully automatic discontinuity detection tools, e.g. Vitti (2012), Gallagher et al. (2013), Goudarzi et al. (2013), Kowalczyk and Rapinski (2018) or Klos et al. (2019). Some discontinuity-detection approaches feature deterministic models (including, e.g. rate, annual cycle and noise formulations), as well as step functions to model discontinuities in time series (He et al. 2017; Klos et al. 2019). Montillet et al. (2015), for instance, investigated different approaches to detect single discontinuities at specified epochs using linear-least squares. Another approach of discontinuity detection is Hector (Bos et al. 2013a; Montillet and Bos 2020), which utilizes Maximum Likelihood Estimation (MLE) to determine trends and noise parameters. Discontinuities are identified in an iterative manner until the Bayesian information criterion (BIC, Schwarz 1978) reaches a predefined threshold (Bos and Fernandes 2016). As an alternative to modelling trends and discontinuities explicitly, Wang et al. (2016) presented a state-space model and singular spectrum analysis, which provides a better approximation of time-varying nonsecular trends or annual cycle amplitudes, than the MLE method. Another nonparametric method is MIDAS (Median Interannual Difference Adjusted for Skewness, Blewitt et al. (2016)), which is a variant of a Theil–Sen trend estimator and is capable to robustly mitigate discontinuities in the data for linear trend estimation. Many other solutions for discontinuity detection exist, which are more thoroughly described in, e.g. Gazeaux et al. (2013) or He et al. (2017).

In a comparative research study, Gazeaux et al. (2013) analysed the capability of 25 different algorithms to detect discontinuities in synthetically generated data. They found, however, that manual screening still outperformed the best candidate among the solutions. Trends derived from semiautomated approaches were shown to still be biased in the order of ± 0.4 mm/year, as a result of undetected discontinuities in the data. Given this accuracy limitation, improving automatic discontinuity detection is thus subject of ongoing research and leads to steady development of the algorithms, see, e.g. He et al. (2017).

The discontinuity detection with standard approaches like linear least-squares becomes particularly difficult for an increasing number of discontinuities with unknown epoch. In addition, as highlighted by Wang et al. (2016), site movements are not necessarily strictly linear and can be affected by time-varying movements. Thus, it is critical to also detect discontinuities in the form of the onset of trend changes or post-seismic deformation to evaluate the validity of a strictly linear secular motion. Commonly applied algorithms, such as MIDAS, for instance, do not yet account for such time-series features. Another central challenge for discontinuity and trend change detection is the appropriate identification of the stochastic properties of the time series. This is especially problematic for SATTG time series, as their associated noise amplitudes are usually one order of magnitude larger than in GNSS data.

To our knowledge, none of the existing methods have been applied or tested to detect an arbitrary number of discontinuities and/or trend changes in SATTG time series. More generally, it is currently unknown to what extent variable velocities caused by dynamics such as seismic events can be (automatically) detected in SATTG time series, given the high noise levels in the data. To fill this gap, we present in this paper a new algorithm called DiscoTimeS (Discontinuities in Time Series), which simultaneously estimates the number of discontinuities, the associated magnitudes of discontinuities and piecewise linear trends together with other time series features, such as the annual cycle and noise properties. With the implementation of this method, we seek to answer the following research questions:

• To what extent can we automatically detect change points in SATTG time series?

• How does piecewise determination of trends in SATTG data improve its comparability with GNSS data?

• How can we exploit the detection and mitigation of trend changes to obtain more robust linear VLM estimates?

To cope with the extensive number of parameters, we use a Bayesian framework and generate inferences with Markov chain Monte Carlo (MCMC) methods. MCMC methods are capable to deal with highly complex models and were already successfully applied by Olivares and Teferle (2013) to estimate noise model components in GNSS data. Although not yet tested, these methods could also be adapted to SATTG time series. The framework allows to assess the empirical probability distribution of a set of multiple unknown parameters such as the epoch and the number of change points in the data. The appropriate analysis of the empirical probability distribution is a key element for the automated detection of discontinuities and trend changes.

We describe the datasets, i.e. synthetic, GNSS and SATTG time series, as well as GIA VLM data in Sect. 2. The Bayesian model formulation and set-up are presented in Sect. 3. In Sect. 4.1, we evaluate the model performance using synthetic SATTG and GNSS data. Section 4.2 provides examples of physical origins of trend changes and substantiates the necessity to detect them. In Sect. 4.3, we analyse 339 time series of co-located SATTG and GNSS stations and discuss the implications of discontinuity detection in SATTG time series. Finally, in Sect. 4.4 we demonstrate how mitigating discontinuities can enhance the agreement of VLM observations with VLM from GIA and contemporary mass redistribution (CMR). We show that these results are also consistent with trend estimates derived with MIDAS. We discuss the advantages, caveats and potential applications of our method in Sect. 5.

2 Data

To answer our research questions and to test our method, we apply the Bayesian model to VLM time series from GNSS and SATTG, as well as to synthetically generated data. We use multi-mission altimetry data, combined with most recent (until 2020) TG observations from PSMSL (Permanent Service for Mean Sea Level, Holgate et al. 2013). We compare SATTG trend estimates with global VLM estimates of GIA and the nonlinear effect of CMR.

2.1 SATTG observations

Previous studies have inferred VLM either from direct differences of SAT and TG observations, or from networks of TGs and ASL from altimetry using different interpolation techniques (Santamaría-Gómez et al. 2014; Montillet et al. 2018; Hawkins et al. 2019). In this research, we analyse VLM time series which are derived from SATTG differences according to the recipe in Oelsmann et al. (2021). In order to increase the quality and quantity of altimetry data close to the coast, we use dedicated choices in terms of range and corrections needed to estimate sea surface height (see Table 1). We use along-track altimetry data of the missions ERS-2, Envisat, Saral, Topex, Jason1 to Jason3, their extended missions and Sentinel 3A and 3B. All these missions provide continuous altimetry time series over 25 years (1995–2020). For all missions, satellite orbits in the ITRF2014 (Altamimi et al. 2016b) are used. To reduce systematic differences between the different missions, the tailored altimetry data is cross-calibrated using the global multi-mission crossover analysis (MMXO) (Bosch and Savcenko 2007; Bosch et al. 2014).

Table 1 Applied models and geophysical corrections for estimating sea surface heights

We use monthly TG data from PSMSL. At every TG, we select 20% of the highest correlated data within a radius of 300 km. This selection confines a region of coherent sea-level variations, which is called Zone of Influence (ZOI). Using these highly correlated altimetry observations, we reduce the discrepancies w.r.t. the TG observations and simultaneously enhance the temporal density of altimetry data, because several altimetry tracks are combined. This has the effect of reducing the uncertainty and increasing the accuracy of SATTG trends. A relatively large selection radius of 300 km is chosen, because previous studies found along-shore correlation length scales up to 1000 km (e.g. Hughes and Meredith 2006). We also showed in a previous study (Oelsmann et al. 2021) that VLM is consistent in a ZOI, even if VLM is computed from distant (up to 300 km) but highly correlated sea-level anomalies. Correlations are computed based on detrended and deseasoned SAT and TG data. When combining the individual mission time series and monthly PSMSL data, the along-track data are averaged and decimated to monthly means to match the frequency of TG observations. The correlations are computed independently for missions which share the same nominal track. We spatially average the along-track data in the ZOI and compute the differences between their monthly averages and the TG data. Furthermore, the following data selection criteria are applied: We omit time series where the multi-mission, monthly SAT time series (averaged in the ZOI) present a correlation with the TG data lower than 0.7 (i.e. $\sim$ 10th percentile of all data) and a root-mean-square (RMS) error higher than 5.5 cm ($\sim$ 90th percentile of all data). We only use SATTG time series with a minimum of 150 months of valid data, which yields a number of 606 remaining SATTG estimates.

2.2 GNSS data

The GNSS time series are obtained from the Nevada Geodetic Laboratory (NGL) of the University of Nevada (Blewitt et al. 2016, http://geodesy.unr.edu, accessed on 1 September, 2020). Because we directly compare segments of linear trends from SATTG and GNSS time series, we require sufficiently long periods of data. Therefore, we only use time series with minimum lengths of 6 years and with at least 3 years years of valid observations. Additionally, based on the uncertainty estimates provided by MIDAS, we reject GNSS time series with a trend uncertainty larger than 2 mm/year. This prevents us from using very noisy GNSS data. Finally, we select the closest GNSS station within a 50-km radius to a TG. Because the monthly SATTG time series have a lower resolution than the GNSS time series, we downsample the latter daily time series to weekly averages (similarly as in Olivares-Pulido et al. 2020), which also reduces computational time of the fitting procedure.

2.3 Synthetic data of sensitivity experiments

In order to evaluate the performance of our method, we apply the model to synthetic time series which mimic the properties of real SATTG and GNSS time series and include discontinuities (in form of offsets) and trend changes.

The modelled time-series features are a trend, a harmonic annual cycle and a noise term. All time series have a duration of 20 years and 5% missing values. We define the time-series properties (i.e. annual cycle and noise amplitudes) according to the analysis of the 606 SATTG time series and 381 GNSS time series, which were analysed using the Bayesian Model DiscoTimeS and Maximum Likelihood Estimation (Bos et al. 2013a).

We apply a seasonal component to model annual surface mass loading variations affecting VLM, such as hydrological or atmospheric loading (e.g. Glomsda et al. 2020; Ray et al. 2021). In contrast to the GNSS data, annual variations in SATTG data can, however, also stem from discrepancies in the observations of the different techniques. As we show in the following, these non-geophysical deviations can have much larger amplitudes than those obtained from GNSS data and also influence the noise characteristics.

Several studies affirmed that a combination of white noise (WN) and power law noise (PL) is most appropriate to describe stochastic properties of GNSS time series (e.g. Williams 2008; Langbein 2012). For the synthetic GNSS time series, we create PL + WN noise, using similar properties as found for 275 GNSS vertical position time series by Santamaría-Gómez et al. (2011). We use a spectral index of $-0.9$, which is close to flicker noise process, and amplitudes of 2 mm/year and 6 mm/year$^{-\mathrm{k/4}}$ for white and coloured noise, respectively. To study the impact of the noise type on the change point detection, we also analyse synthetic GNSS data with less realistic AR1 noise.

Although several studies (Royston et al. 2018; Bos et al. 2013b) investigated noise properties of altimetry and TG SL time series, there is no consensus on which noise model is most appropriate for SATTG time series. Thus, we determine the noise characteristics of the data using an autoregressive process AR1 and a PL + WN noise model (with the Hector Software, Bos et al. 2013a). The Bayesian Information Criterion (BIC, Schwarz 1978) is slightly more in favour of the AR1 noise model compared to the PL + WN process. Therefore, we decide to apply the AR1 noise model for SATTG data.

We adopt different magnitudes of the annual cycle, the AR1 coefficient and the white noise amplitude according to median values, which are estimated from SATTG and GNSS time series (derived from fitting them with the Bayesian Model), as defined in Table 2. The noise and annual cycle amplitudes are 6–7 times larger for SATTG than for GNSS time series. It is expected that this behaviour strongly influences the range of discontinuities and trend changes to be detectable by the algorithm. Therefore, in the sensitivity experiments, we take these different noise properties into account by testing the detectability of different discontinuity-to-noise ratios, instead of absolute values of discontinuities.

Table 2 Synthetic time-series features

Fig. 1

Examples of synthetic height time series (mm) generated for the sensitivity experiments. The upper (lower) row shows time series which imitate VLM observations from GNSS-PLWN (and SATTG). The different lines exemplify variations of the discontinuity-to-noise ratio (a, d), the trend change magnitudes in mm/year (b, e), as well as of variations in the number of change points and the magnitudes of the discontinuities and trend changes (c, f). In the discontinuity (a, d) and the trend change experiments (b, e), the change point is located in the centre of the time series. In c and f, change points are randomly distributed

Table 3 Set-up of the sensitivity experiments

We perform three experiments in which we vary (1) only the discontinuity-to-noise-ratio, (2) the trend and (3) the number of change points, together with discontinuities and trends. The full set-up is described in Table 3. Figure 1a exemplifies time series of the experimental set-ups for different parameters.

The change point for the first two experiments is set in the centre of the time series. These experiments are conducted to assess the sensitivity of the algorithm to detect single discontinuities and trend changes for different noise amplitudes in the data. The third experiment is built to reveal how different numbers of change points might affect the trend estimation.

We vary the discontinuity-to-noise ratio and the trend change with a stepsize of 0.5 mm/year. For every step and every tested number of change points (in the change point experiment), we generate 10 different synthetic series and model fits.

2.4 GIA and CMR estimates

We use the GIA solution from Caron et al. (2018), which is based on 128,000 forward models. The likelihood of parameters, which describe the Earth structure and ice history, was estimated from an inversion of GPS and relative sea level data within a Bayesian framework. The GIA estimate represents the expectation of the most likely GIA signal. Formal uncertainty estimates were directly inferred from the Bayesian statistics.

Next to GIA-related long-term surface deformations, we take into account the effects of ongoing changes in terrestrial water storage as well as mass changes in glaciers and ice sheets causing elastic responses of the Earth, which can result in variable vertical velocities (e.g. Riva et al. 2017; Frederikse et al. 2019). These responses to CMR are not captured by GIA models and only partially detected by GNSS data due to the relative shortness of the record lengths. Frederikse et al. (2019) showed that associated time-varying solid Earth deformations can lead to significantly different trends in the order of mm/years depending on the time period considered during the last two decades. Therefore, we supplement VLM estimates from GIA with CMR-related land motions according to Frederikse et al. (2020). This estimate is based on a combination of GRACE (Gravity Recovery and Climate Experiment, Tapley et al. 2004) and GRACE-FO (Gravity Recovery and Climate Experiment Follow-On, Kornfeld et al. 2019) observations during 2003–2018, as well as process model estimates, observations and reconstructions for the period 1900–2003. To correct SATTG and GNSS VLM estimates with CMR, we compute linear trends of CMR over the same time spans of observation and add them to the GIA trend estimates.

3 Methods

3.1 DiscoTimeS: a Bayesian model for change point detection

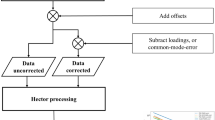
Our overarching goal is to detect the most common time-series features in GNSS and SATTG data using a single comprehensive model. The major components considered in this study are discontinuities o(t) (abrupt changes in height), trends g(t), a seasonal term seas and a noise term $\eta$, which can also be identified in Fig.  2:

$$\begin{aligned} y(t) = o(t) + g(t) + seas + \eta \end{aligned}$$

(1)

Here y(t) denotes either GNSS or SATTG observations at time t and is described with a set of unknown parameters $\varTheta$, which define the motion components (see Sect. 3.3 and Table 4 for a full description of $\varTheta$). The discontinuities o(t) and trend components g(t) are assumed to change with time. Disruptions can occur in form of abrupt jumps, changes in trends, the onset of post-seismic deformation or a combination of such events. Thus, the time-dependent components are piecewise estimated over individual segments of the time series. These segments depend on the number of change points and the time (epoch) when they occur (hereafter called change point position), which are unknown parameters $\varTheta$ of the model, as well. We aim to simultaneously estimate the most likely number n and position of change points $s_j$, together with the other terms describing the motion signatures.

Fig. 2

Bayesian model fit for a SATTG time series and b GNSS time series observed at co-located stations in Kujiranami (Japan). The discontinuity and trend change in 2011 are similarly detected in SATTG and GNSS data. Observed height changes [m] are shown in orange together with 1000 randomly drawn realizations from different chains in green (shading in the background). The blue lines illustrate the posterior means of the selected best chain (see Appendix B). The blue shading denotes the $2\sigma$ confidence intervals (CI) of this model. Detected change points are marked by the dashed vertical lines. The grey dotted lines confine the segments of the time series ($sattg_1, sattg_2$), which are compared with the GNSS piecewise trends (colour figure online)

3.2 Deterministic and stochastic model components

In the following, we summarize how the deterministic components, discontinuities, trend changes and the seasonal cycle are defined. Suppose that the linear motion at the beginning of the time series is defined by a base trend k. The time series is divided by n change points at positions $s_j$ (with $j=1,..., n$). After every change point, the base trend is updated by an incremental trend change $h_j$. This can be described as a cumulative sum of all trend adjustments over time $k + \sum _{j: t > s_j} h_j$. Taylor and Letham (2018) used $k + \mathbf {a}(t)^T\mathbf {h}$ ($= k +\sum _{j=1}^{n} a(t)_j h_j$) as an alternative representation using the Heaviside step function $\mathbf {a}(t) \in 0,1$.

Thus, we obtain a segmented step function for the trend component. Multiplication of this trend function with time would, however, introduce discontinuities at the change point positions, which are proportional to the trend change: $\gamma = s_j h_j$. Hence, the full representation of the trend component must be corrected for these discontinuities as follows:

$$\begin{aligned} g(t) = (k + \mathbf {a}(t)^T \mathbf {h})t - \mathbf {a}(t)^T {\varvec{\gamma }}. \end{aligned}$$

(2)

In agreement with trend changes, arbitrary discontinuities (i.e. offsets) can occur after every change point. Such ‘segment discontinuities’ are parameterized in a similar way as in Eq. (2):

$$\begin{aligned} o(t) = o + \mathbf {a}(t)^T \mathbf {p}. \end{aligned}$$

(3)

Here o is again the base offset and $\mathbf {p}$ is a vector of length n, which comprises the discontinuity adjustments after every $s_j$.

For simplicity, we implement a time-invariant seasonal component (i.e. without interannual variations), which describes the seasonal cycle as monthly multi-year averages. The twelve multi-year monthly means are contained in the vector $\mathbf {m}$. Thus, the seasonal component is:

$$\begin{aligned} seas= \mathbf {x}(t)^T\mathbf {m}, \end{aligned}$$

(4)

with $\mathbf {x}(t) \in 0,1$:

$$\begin{aligned} x_i(t)= {\left\{ \begin{array}{ll} 1, &{} \text {if } month \, (t) = i\\ 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

Finally, the noise $\eta$ in Eq. (1) is approximated as a first-order autoregressive process AR(1). We emphasize that the presented model set-up explicitly allows for trend changes, which are, however, usually constrained in other applications. These include, for example, the computation of reference frames (ITRF2014 (Altamimi et al. 2016a) and DTRF2014 (Seitz et al. 2021)), or existing trend-estimators like MIDAS. In Sect. 4.2, we discuss several geophysical processes, which generate trend changes and hamper the determination of secular trends. These examples underline the advantages of detecting trend changes, which can otherwise lead to misinterpretations of estimated secular rates.

3.3 Bayesian parameter estimation

The resulting model consists of a multitude of unknown model parameters, which is particularly influenced by the arbitrary number of change points and related properties (e.g. epoch, magnitude of discontinuity). Thus, given the high complexity of our problem, we use Bayesian MCMC methods (e.g. Brooks et al. 2011) to approximate the full posterior probability distribution of the model parameters $P(\theta |y)$.

For every parameter in $\varTheta$, we formulate our prior beliefs of their probability distributions $P(\varTheta$), which are then updated during the sampling process. Such an assignment of $P(\varTheta )$ is exemplified using the two most influential parameters in our model, which are the number n and the position $s_j$ of change points. Note that n sets the size of the parameter vectors, for example, of the vector containing the trend increments. Thus, for $n = 0$, we do not estimate any trend change or discontinuity, for instance. The number of change points is approximated with multiple ($n_{max}$) discrete Bernoulli distributions, which generate samples between 1 (change point detected, with probability q) and 0 (no change point detected, probability $1-q$) for every possible change point. A change point is switched on when the probability q exceeds 0.5. The position of the change points $\mathbf {s}$ is assumed to be normally distributed. Their mean values $\varvec{\mu }_{\mathbf {s}}$ are drawn from a random uniform distribution U(t) (hyperprior, i.e. a probability distribution of the hyperparameters $\varvec{\mu }_{\mathbf {s}}$ of the prior distribution) spanning the time period of observations:

$$\begin{aligned} \mathbf {s} \sim {\mathcal {N}}(\varvec{\mu }_{\mathbf {s}},\,\varvec{\sigma }_{{\textbf {s}}^{{\textbf {2}}}}) \text { with } \varvec{\mu }_{\mathbf {s}} \sim U(t) \text { and } t \in [t_1, T] \end{aligned}$$

(6)

The positive autocorrelation coefficient $\phi$ and the white noise amplitude $\sigma _{w}^2$ are both drawn from halfnormal distributions with $\sigma _\phi$ and $\hat{\sigma }_{w}$, respectively. Finally, we approximate all the other parameters, the trend and discontinuities $o,\mathbf {p},k,\mathbf {h}$ and the monthly means $\mathbf {m}$ with normal distributions. Hence, we obtain the following set of unknown parameters of the model: $\varTheta = (\mathbf {q},\varvec{\mu }_{\mathbf {s}},\mu _o,\varvec{\mu }_{\mathbf {p}}, \mu _k, \varvec{\mu }_{\mathbf {h}},\varvec{\mu }_{\mathbf {m}},\varvec{\sigma }_{\mathbf {s}},\sigma _o, \varvec{\sigma }_{\mathbf {p}},\sigma _k,\varvec{\sigma }_{\mathbf {h}}, \sigma _\phi , \hat{\sigma }_{w},\varvec{\sigma }_{\mathbf {m}})$. As can be seen, the complexity of the model is set by the number of change points. For example, if two change points are detected, there are 2 ($\mu _o, \mu _k$) + 12 ($\varvec{\mu }_{\mathbf {m}}$)+ 2*4 ($\mathbf {q},\varvec{\mu }_{\mathbf {s}},\varvec{\mu }_{\mathbf {p}},\varvec{\mu }_{\mathbf {h}},$) + 2 $\sigma _\phi ,\hat{\sigma }_{w}$ = 24 different parameters to be estimated.

In addition to the type of probability distribution $P(\varTheta$), we also specify initial values of the associated distribution parameters. Here, we make use of prior knowledge of common GNSS and SATTG time-series characteristics, to improve the parameter estimation. As an example, we set $\mathbf {q}_0 = 0.1$ as the initial values for the probability (i.e. 10%) of a change point to occur (at the beginning of initialization). Thus, we define a so-called informative prior for $\mathbf {q}_0$, which expresses specific knowledge of the expectation of a change point to occur. We also define other initial settings, which are more thoroughly explained in Appendix A. Table 4 summarizes the complete model set-up and initial assumptions. Note that these initial values are set for the normalized time series.

Table 4 Overview of model components, parameters and prior distributions

We use different MCMC samplers to generate inferences about the desired target distribution $P(\theta |y)$. For all continuous variables, we use the state-of-the-art No-U-Turn (NUTS) sampler (Hoffman and Gelman 2014). For the binary variables $\mathbf {q}$, which control the occurrence of change points, we use a Metropolis-within-Gibbs step method (e.g. van Ravenzwaaij et al. 2018). In order to enhance the robustness of the parameter estimates, we generate an ensemble consisting of eight independent Markov Chains, whose initial conditions are perturbed within the limits of the aforementioned described prior distributions. Every chain features 8000 iterations, which is found to be sufficient for individual chains to achieve convergence of the parameters (according to the convergence diagnostic by Geweke (1992)). As an example of the required computing capacities, fitting a 20-year-long weekly sampled GNSS time series takes on average four hours using four cores with two hyperthreads per core.

Figure 2 shows independent model fits of SATTG and GNSS time series. Next to the observations (red), we show randomly selected draws from the eight different Markov chains (green), as well as the posterior mean of trends and discontinuities from the ensemble (blue), which is identified as the best chain. Vertical dashed lines indicate detected change points.

The example shows that, depending on the characteristics of the time series, the Markov chains may behave very differently. While in the case of SATTG there is almost no spread (green line), for the GNSS example it is very large (green background shading). The latter is an example of ’multimodality’, a central problem when using discrete variables (Brooks et al. 2011). We utilize different Bayesian model selection criteria (see Appendix B), which provide a measure of model fit and complexity, to select a single best-performing chain among the ensemble members. The successful approximation of the observations by the depicted chain selection in Fig. 2b underpins that exploiting several independent chains is of paramount importance for parameter estimation.

4 Results

4.1 Sensitivity experiments with synthetic data

The sensitivity experiments are performed to investigate (1) the accuracy of the trend estimation (in the presence of discontinuities and trend changes) as well (2) as the accuracy of the discontinuity epoch. For this purpose, we simulate different time series (with different noise properties) and gradually vary time-series parameters such as the magnitude of the discontinuity, the trend change, or the number of change points (see Sect. 2.3). Figure 3 summarizes the results for the synthetic GNSS data with PL and AR1 noise (first and second row), as well as for the SATTG time series (last row). In columns 1–3, we illustrate the accuracy of trend estimation expressed by the absolute deviations of the estimated trends (of the individual ensembles) from the known (prescribed) linear trends (see Appendix C); column 4 shows the change point detection-rate.

We compare the absolute deviations of the estimated piecewise trends $\varDelta$PW (in green), with the deviations of trends, computed without accounting for any discontinuities in the data, i.e. the deviations of single linear trends ($\varDelta$LIN, in red). Figure 3 shows that these deviations are linearly dependent on the magnitude of the discontinuity or the trend change. These statistics are compared to the deviations of trends, which are obtained, when piecewise trends are computed over the known individual time-series segments ($\varDelta$LIN (discontinuity known), blue line). The latter represents the theoretical best trend estimate, given the noise of the data.

We observe that the Bayesian $\varDelta$PW estimates in the discontinuity and the trend experiments (Fig. 3 first and second column) generally outperform the linear trend estimates $\varDelta$LIN. With increasing discontinuity or trend change, the accuracy of the Bayesian estimates remains almost constant, while the linear trend deviations $\varDelta$LIN are naturally increasing, in particular with increasing offset magnitude. There is, however, a notable dependency of the $\varDelta$PW deviations on the noise type and noise amplitudes. The accuracy of trend estimates is much lower for GNSS data with a PL noise model, than for the AR1 noise. In the latter case (AR1 model, Fig. 3e, f), the $\varDelta$PW deviations are practically identical to the theoretically best achievable deviations, while for the GNSS-PLWN experiments deviations between 0.25–0.5 mm/year are found (Fig. 3a, b). Hence, the higher low-frequency variability in the GNSS-PLWN data strongly influences the general accuracy level of trend estimation and has a higher impact than the magnitude of the offset.

Fig. 3

Accuracy of trend estimates and detection rates based on the sensitivity experiments with synthetic data. Results are provided for the discontinuity (first column), trend (second column) and change point (third and fourth columns) sensitivity experiments. Each row shows statistics for different time-series types: GNSS+PLWN (first row), GNSS-AR1 (second row) and SATTG time series (last row). In columns 1–3, we show absolute (weighted) deviations of piecewise ($\varDelta$PW , green) and linear trend ($\varDelta$LIN, red) estimates with respect to the piecewise simulated (known) trends of the synthetic time series. The linear trends are computed with least squares without accounting for discontinuities. The blue line ($\varDelta$LIN) corresponds to linear trend estimates which are computed over the known time-series segments, i.e. here we assume the discontinuities are known. Solid lines and shadings indicate the mean and 95% confidence bounds of the different fits per tested parameter. In c, g and k the magenta lines show $\varDelta$PW deviations when only SATTG (GNSS) segments with a length over 8 (3) years are used. A discontinuity-to-noise ratio of 1 is equivalent to 3.2 mm (GNSS) and 20 mm (SATTG). In the change point experiments, the magnitudes of the discontinuities are randomly drawn from an uniform distribution covering values within the twofold–fivefold of the white noise amplitudes. In the last column, we show true- and false-positive detection rates (TP and FP) for the change point sensitivity experiment (colour figure online)

In accordance with the differences induced by the noise model type, also the noise amplitudes influence the accuracy of trend estimates. The $\varDelta$PW trend deviations of the simulated SATTG time series (Fig. 3i, j), which have much higher noise amplitudes than the GNSS-AR1 data, range in the order of 0.5–1.5 mm/year. Still, the estimated piecewise trends are only slightly worse than the theoretical best achievable trend estimates and consistently better than the $\varDelta$LIN deviations. This underpins that the model can significantly improve the accuracy of trend estimation ($\varDelta$PW) by mitigating unknown discontinuities or trend changes.

In the change point experiments (Fig. 3c, g k), different numbers of change points with random epoch and magnitudes of discontinuities and trend changes were simulated. The experiments confirm the dependence of the accuracy of trend estimates on noise model type and amplitudes as found for the single discontinuity and trend experiments. Here, higher trend deviations are found for the experiment with synthetic GNSS data and PL noise w.r.t. the AR1 noise model.

We simulate up to 4 change points and we observe that the model performances slightly deteriorate as the number of change points increase (Fig. 3c, g, k). Accordingly, performances are expected to further decrease with a much larger number of change points, if the duration of the time series remains the same. This is likely caused by the reduced length of the remaining time-series segments. For example, with four equally distributed change points, each segment would only have a length of 4 years (for a 20-year-long time series). At the given noise levels of the time series, a 4-year-long SATTG time series would, however, have a trend uncertainty of more than 5 mm/year (even without accounting for autocorrelated noise). The large noise amplitudes and their effect on trend uncertainty therefore set a natural lower bound for accurate trend estimation when using short segments of SATTG or GNSS time series. A lower trend accuracy is thus less a sign of low model performance, but rather caused by the large uncertainties of the piecewise trends. The magenta curves in Fig. 3c, g, k illustrate how the $\varDelta$PW trend deviations are influenced when only longer time series are used. Here, we set the minimum required length of the SATTG (GNSS) time series to 8 (3) years, which corresponds to trend uncertainties of $\sim$ 2 mm/year uncertainty. For both time-series types, SATTG and GNSS, this entails better accuracy and a reduction in the number of extreme deviations as shown by the narrower uncertainty bands, which represent the spread of the different fits per parameter. Therefore, we also apply these criteria of minimum segment lengths (i.e. 8 years for SATTG and 3 years for GNSS) for the real data applications.

The performance of the discontinuity detection is also evaluated by means of the false-positive (FP) and true-positive (TP) detection rates for the different experimental set-ups (see Fig. 3d, h, l). A change point is correctly detected when the prescribed change point position is within the confidence bounds (95%) of the 2 $\sigma$ uncertainties of the estimated change point position. The TP detection rate is defined as the proportion of change points that are correctly detected (w.r.t. the number of prescribed change points). Detected change points that do not correspond to the prescribed ones are accounted in the FP detection rate, which indicates over/misfitting of the data.

The TP detection (FP detection) rate for the GNSS-PLWN time series is lower (higher) than for the associated GNSS-AR1 time series (Fig. 3d, h). These results reflect the differences in the performances based on the accuracy of the trend estimates. In particular, the increased FP rate for GNSS-PLWN time series consolidates that simultaneously estimating discontinuities and trend changes in the presence of PL noise remains a key challenge for discontinuity detection. Interannual variations (in GNSS-PLWN series) are likely to be overfit or misinterpreted, for example, by fitting discontinuities or trend changes. This can explain the better performance for GNSS-AR1 time series, which feature little low-frequency variability. Also, the generally high TP detection rate for SATTG shows that differences in the noise amplitude are less influential than the type of the noise itself.

Overall, we obtain relatively high TP detection rates (50–100%), compared to previously reported statistics by Gazeaux et al. (2013), where the highest reported TP rate was in the order of 40%. On average, 223 out of 270 prescribed change points are correctly detected in the cp-experiments. Differences in the experimental set-up, as well as in the definition of the TP detection rate, can explain these disparities. For example, in the change point experiments, discontinuities have a minimum size of two times the white noise amplitude. In Gazeaux et al. (2013), the magnitudes of the discontinuities were drawn from a Pareto distribution, which includes smaller discontinuities than applied in the presented experiments. Also the definition of the detection-rate differs across the studies, considering that in this study the estimated epoch uncertainties are used as a temporal tolerance and Gazeaux et al. (2013) set a constant 5-day tolerance window around a change point. There exist also general differences in the time-series noise-amplitudes and temporal resolutions. With the focus on discontinuity detection in SATTG time series, it should be noted that the accuracy of epoch estimation in SATTG data strongly decreases compared to GNSS data, given the low monthly resolution as well as the high noise levels in the data.

In summary, the synthetic experiments verify that DiscoTimeS improves the accuracy of those trend estimates that are impaired by unidentified discontinuities. Hence, in the following chapters we apply the algorithm to real data and test to what extent DiscoTimeS can be utilized as an unsupervised discontinuity-detector.

Fig. 4

Vertical land motion time series from GNSS observations and contemporary mass redistribution (CMR). The first row depicts earthquake-affected stations from Alaska (a), Chile (b) and Japan (c, d). The second row illustrates time series from stations near or at the coast of the Gulf of Mexico, influenced by local processes causing variable velocities. The last row shows station time series in Iceland (i, j) and Alaska (k, l), which correlate on decadal time scales with CMR (j and l, blue lines). Note that a trend of 13 mm/year was subtracted from the JNU1 station. We show observations in orange, the model estimate of piecewise trends in blue (with 2 $\sigma$ confidence intervals and dashed lines for detected change points) and the trend estimate from MIDAS in grey (a–h) (colour figure online)

4.2 Detecting discontinuities and trend changes in SATTG and GNSS data

The premise of this study is that VLM cannot only be disturbed by abrupt changes in height, but can also exhibit trend changes on decadal time scales, which hamper an unbiased assessment of secular trends. The detection of significant trend changes can provide valuable information about the reliability of extrapolating the VLM at the considered station. To further substantiate the existence and physical justification of such nonsecular VLM, we show GNSS observations together with piecewise trend estimates, as well as the single linear trend estimates by MIDAS (which is a robust estimator of a single trend).

Figure 4 depicts three physical mechanisms that can influence the linearity of VLM. The majority of trend changes in VLM observations can be attributed to earthquakes, see Fig. 4a–d. These examples are useful to understand the limitations of established methods (like MIDAS), which do not incorporate possible trend changes. In such cases, an estimation of trend changes can be applied as a preprocessing step before fitting the data with adequate models including terms of post-seismic deformation, for instance.

Fig. 5

Vertical land motion time series from SATTG (top row) and GNSS (bottom row) pairs. a Station in Sakamoto Asamushi, Aomori, Japan, b station in Mossel Bay, South Africa, c station in La Palma, Spain. Next to the observations (orange line), we show the model mean fit in green (in the background), the model mean without the annual cycle in blue lines and finally the 2 $\sigma$ confidence intervals of the fit with blue shadings. The positions of change points are marked by the vertical dashed lines. The time series show pronounced discontinuities in SATTG observations, which are partially also observed in the GNSS time series (colour figure online)

Next to earthquakes, VLM can also be affected by more localized processes as highlighted by the time series in the second row (e–h) of Fig. 4. The associated GNSS stations are all located in the Gulf of Mexico, near Houston. In this zone, VLM exhibits a relatively large spatial and temporal variability (0–10 mm/year subsidence), which is influenced by extraction of hydrocarbons, groundwater withdrawal, land reclamation and sedimentation, (Letetrel et al. 2015; Kolker et al. 2011). Such processes likely also affect the selected GNSS stations. The station velocities in Fig. 4e, f indicate that averaged linear trends might not be entirely representative of a secular trend, given the detected variability in trends over different periods of time. The closely located stations DEN1 and DEN3 (with a distance of 2 km) also show a trend change around the end of year 2015, which is also not reported in the station metadata. Hence, we assume that local VLM explains the consistency of the signal in both stations. As in the previous examples, it is not straightforward to derive a secular trend in such cases.

The third mechanism that contributes to potential trend changes is nonlinear surface deformation due to mass loading changes. In the last row of Fig. 4, we show stations located in high northerly latitudes (AKUR in Iceland and JNU1 in Alaska), which are most likely affected by present-day ice mass changes (on top of secular GIA VLM). In Fig. 4i, k, we show the GNSS observations and the model estimates of piecewise trends. Next to them, we show surface deformation time series due to CMR from Frederikse et al. (2020) in panels Fig. 4j, l, with the same GNSS time series in the background. The CMR data indicate subtle trend changes on subdecadal time scales, which are qualitatively also reflected by the GNSS data. Frederikse et al. (2020) provided evidence that decadal VLM variations due to CMR changes can significantly influence GNSS station velocities in the order of millimeters per year. This is particularly critical when VLM is derived from short time series.

Evident physical origins motivate the identification of trend changes in GNSS and SATTG data. Thus, in the following section we investigate whether accounting for trend changes can improve the agreement of trends over individual periods between independent techniques.

4.3 Comparison of piecewise and linear SATTG trends with piecewise GNSS trends

We compare piecewise trends from SATTG and GNSS data at 339 globally distributed station pairs, which have a maximum distance of 50 km. The trends are computed with the same model settings (of the deterministic and noise components) for both time series. Figure 5 displays time series at three stations that exemplify the increased consistency of the estimations in SATTG and GNSS time series when using the DiscoTimeS approach.

Figure 5a (corresponding to a station located in Japan) and Fig. 5b (corresponding to a station located in Mossel Bay, South Africa) show an almost coincident position of the largest discontinuity detected. In the first case, we can detect the discontinuity caused by the Tōhoku Earthquake in 2011. Due to the related crustal deformation, the northern parts of the Tohoku region were affected by land uplift (Imakiire and Koarai 2012), as can also be seen by the instantaneous $\sim$4 cm uplift in both time series shown in Fig. 5a. The subsequent post-seismic deformation is approximated by a range of piecewise trend segments in the GNSS time series. In the SATTG time series, these subtle post-seismic signals are below the detection limits due to the larger noise amplitude of the data (see upper panel in Fig. 5a), and consequently a single trend is estimated. Due to the strong instantaneous earthquake-induced land uplift, most of the concurrent change points (in GNSS and SATTG data) are found in Japan. Figure 5b shows a change in the zero position of the TG (in Mossel Bay), which is in agreement with a height change in the GNSS time series. The origin of the shift in the SATTG time series (or accordingly the TG) is unclear, because it is not documented in the station metadata. The automated detection of the discontinuity is thus crucial to estimate accurate VLM trends and can facilitate and support the manual inspection of discontinuities.

Figure 5c shows height changes in time series of La Palma, a region that is affected by volcanic activity. We observe high variability in the SATTG time series over the period 1997–2008. The trend in the latter segment of SATTG aligns much better with the GNSS data over the same period than the variations before. Identification of such variability can be a very useful information for investigations focused on SL trends based on TG observations. This example also underpins the importance of analysing such effects in SATTG time series directly, considering that we often have limited information from GNSS over the full period of observation, as is the case at this particular location.

Despite the abundance of time series, which are affected by both, discontinuities and trend changes, in the majority of cases discontinuities are not necessarily associated with a trend change (such as in Fig. 5b or in the GNSS time series in Fig. 5c). In order to mitigate such inappropriate trend changes, we apply a significance check. At every detected discontinuity, we test whether the trend differences between consecutive time-series segments are significant, given the combined trend uncertainties of the segments. Trend uncertainties of every time segments are recomputed, while the estimated discontinuity epochs and magnitudes of discontinuities are held constant. Otherwise, trend uncertainties would be influenced by the estimated epoch and discontinuity uncertainties. The re-computation of the trend uncertainties is performed with DiscoTimeS, without allowing for change points and with appropriate noise models for the respective time-series types. We use an AR1 model for SATTG and a PLWN model for GNSS data, assuming a constant spectral index of $-0.9$. Note, that in the model configuration, which incorporates the estimation of discontinuities, a AR1 noise model is used for both time-series types. We iterate the test over all time-series segments, which also allows to identify multiple non-significant trend changes. Finally, for all neighbouring segments with no significant trend changes, we remove the detected discontinuities and recompute the trends over the combined segments. We apply this significance test for the following statistical comparison of SATTG and GNSS trends.

Fig. 6

Comparison of the piecewise trend deviations $\varDelta$PW with the single linear trend deviations $\varDelta$LIN. The trend deviations are the absolute weighted deviations from the piecewise GNSS trends as described by Eqs. (7) and (8) in Appendix C. We subtract the $\varDelta$PW from the $\varDelta$LIN deviations at every individual station pair. Therefore, a positive difference indicates an improvement by using the Bayesian model compared to estimating a single linear trend from a SATTG time series, and vice versa. The differences are grouped by the number of detected change points in the SATTG time series, as well as by the maximum allowed distance between GNSS and TG stations

To what extent the Bayesian piecewise trend estimation improves trend estimates from SATTG (w.r.t. GNSS data) is depicted by Fig. 6 and Table 5. Here, positive values of the differences of trend deviations $\varDelta$LIN and $\varDelta$PW indicate an improvement when using the Bayesian change point detection, i.e. a better consistency between GNSS and SATTG is ensured. The differences are grouped by the number of detected change points in SATTG time series. We additionally sorted the data by the maximum allowed distance of a TG-GNSS pair. In 227 of the cases, the model detects no change points in the data. Here, the deviations of trend estimates are equal for both $\varDelta$LIN and $\varDelta$PW. This means that we model purely linear motions over the full period in both cases.

When one or two change points are detected, the piecewise trend estimation outperforms the linear trend estimation with mean improvement of 0.48 mm/year (21.7%) for one detected change point and an improvement of 0.46 mm/year (17.5%) for two detected change points. The percentage of improvements refers to the absolute deviations of trends as also listed in Table 5.

There are only nine cases where more than two change points are detected. Here, the scatter of trend differences using the piecewise estimation decreases compared to the linear estimates. This could be due to the increased fragmentation of the data and shortness of the time-series segments. Such small number of samples (9), however, hinders a robust assessment of the significance of improvement/deterioration. In general, the lower consistency achieved in such cases suggests a careful treatment of SATTG piecewise trends with more than two detected change points for the given record lengths.

Table 5 Comparison of the piecewise trend deviations $\varDelta$PW with single linear trend deviations $\varDelta$LIN (as deviations from the piecewise GNSS trends)

To test the significance of the improvement when at least one change point is detected (i.e. $n > 0$), we apply ordinary bootstrapping (see, e.g., Storch and Zwiers 1999). Based on the given differences of $\varDelta$LIN$-\varDelta$PW (with $n > 0$), we generate 10,000 random sets with replacements, using the same number of sample size for each set (i.e. 112 VLM differences). We compute the mean of these bootstrapped sets, which yields an empirical probability distribution of the mean and its 95% confidence intervals (i.e. the 2.5 and 97.5% percentiles). The obtained mean of $+0.36$ [0.02, 0.7] mm/year shows that in general the improvement by fitting piecewise trends is significant.

Fig. 7

Geographical distribution of trend differences (between $\varDelta$LIN and $\varDelta$PW). Positive values indicate an improvement in the agreement of SATTG and GNSS VLM in mm/year. a The global distribution; b Europe and c Japan and South Korea. In the regional maps the scatter points of absolute values larger than 0.5 mm/year are scaled by the square root of their magnitudes

The geographical distribution of the differences (mm/year) between $\varDelta$LIN and $\varDelta$PW is illustrated in Fig. 7. Improvement (deterioration) with respect to a linear trend estimation is indicated with red (blue), and the circles sizes are scaled by their absolute values. The largest improvement occurs in regions with pronounced tectonic activity, in particular in Japan (Fig. 7c).

Fig. 8

Trend differences between a single linear SATTG estimates, b time-averaged piecewise GNSS trend estimates and c MIDAS trend estimates and VLM from GIA (red) and GIA+CMR (blue). The 606 single linear SATTG trend estimates are grouped into a set where no change point was detected ($n=0$, 380 cases) and at least one change point was detected ($n > 1$, 226 cases). The GNSS data are grouped into sets in which the weighted standard deviation of the trend changes in a single time series is below or above 0.4 mm/year. This value represents the median of all standard deviations for the 381 GNSS stations. Trend differences are up to twice as large as for SATTG and GNSS VLM observations which are characterised as ‘variable’ VLM (colour figure online)

An improvement (in the order of $\sim$ 1–2 mm/year) is also observed in regions with less tectonic activity, which are nearly randomly distributed over the globe. This indicates that a non-negligible part of the stations are also affected by other (local) phenomena, which are potentially more difficult to detect and less likely to be known than those related to earthquakes.

Another area of improvement is the East Australian coast. Frederikse et al. (2019) showed that this region is affected by variable velocities due to CMR. Vertical solid Earth crustal deformation rates were shown to vary from $\sim$0.5 mm/year in 2002–2009 to $-1.5$ mm/year in 2009–2017. This could be an explanation for a better agreement of the piecewise SATTG and GNSS trends in this area. For this comparison, SATTG and GNSS data are intentionally not corrected for CMR to test how associated variable velocities can be detected by DiscoTimeS.

In some cases, DiscoTimeS trend estimates yield larger deviations compared to the single linear trend estimates. Some of these cases are located in Great Britain (Fig. 7b) and Japan (Fig. 7c). There are various possible reasons which might explain such degradation. One factor could be the relatively large allowed maximum distance of 50 km between the GNSS and TG stations. The comparability of piecewise trend estimates with GNSS could be severely reduced, when the VLM dynamics are caused by very localized events. In such a case, a smooth long-term linear trend might better fit to a distant GNSS estimate. Indeed, when only allowing for a maximum distance of 1 km, some of those cases can be mitigated and the improvements by using piecewise trend estimates increases further (Fig. 6).

Next to differential VLM at GNSS and TG stations caused by highly localised VLM, it should be emphasised that errors in the altimetry data or mismatches between SAT and TG SL observations still represent the largest error sources. This is also governed by the accuracy of altimetry SL observations in the coastal zone, which is influenced by a large variety of factors, for example, the applied corrections and adjustments (e.g. tidal corrections), but also local conditions such as complex coastlines or islands, which can perturb the backscattered radar signal. Next to deviations in the observed oceanic SL signals, the associated non-physical noise in SATTG VLM time series can thus lead to an erroneous detection of discontinuities, which should therefore be carefully inspected.

4.4 Exploiting knowledge of variable velocities to increase consistency of SATTG and GNSS VLM estimates with VLM from GIA and CMR

One important contribution of DiscoTimeS is its ability for qualitatively labelling the vertical land motion as ‘constant’ or ‘variable’. While trend uncertainty is a good statistical measure to quantify a possible range of trend changes, it is, however, less suited as a measure to resolve a possible time-dependent variable velocities. Therefore, we also investigate how we can exploit the information on the segmentation and trend changes in the SATTG and GNSS time series to increase their agreement with large-scale VLM features such as GIA (and CMR). We use the estimated number of change points to detect potentially nonlinear motion in SATTG time series. For GNSS data, where more discontinuities ($n > 0$ in 92% of the cases, i.e. 688 in total) are detected, we allow for a possible small rate of change in the trends (< 0.4 mm/year), such that the overall motion is still labelled as ’constant’. This threshold corresponds to the median weighted standard deviation of piecewise trends within a times series, $std(pw\_gnss)$, of all GNSS data. To substantiate the results, we complement the analysis by comparing estimated GNSS trends with those computed with MIDAS (Blewitt et al. 2016).

Figure 8 and Table 6 show the differences of single linear SATTG trends w.r.t. GIA and GIA+CMR estimates. The linear SATTG trends are grouped according to whether change points are detected by the model or not. Linear SATTG trends agree much better with the large-scale VLM, when the model detects no change points, i.e. when it characterises the motion over the full period as ’linear’. The agreement with GIA+CMR VLM, which is quantified by the standard deviation of the differences, is almost 40% (1.22 mm/year) better for the case of no detected change points. We obtain the best agreement when also including the CMR correction compared to using the GIA estimate only.

Still, the standard deviation of the differences of SATTG trends and the combined GIA+CMR effect (1.95 mm/year) as well as the median bias of trends (0.59) are relatively large. Such high discrepancies can be caused by local VLM, which is constant but not represented by either the GIA model nor the CMR effect. There is, for example, a strong outlier with a deviation from GIA+CMR of almost 18.2 mm/year when no change point is detected (Fig. 8a). The derived SATTG time series (from a TG in Elfin Cove, Alaska) is associated with a very steady uplift motion (of 21 mm/year), which is not captured by the combined GIA+CMR effect. Overall, despite these cases of local but highly constant VLM, excluding the SATTG estimates associated with variable velocities strongly improves the agreement of SATTG and GIA+CMR on a global scale.

Table 6 Statistics of trend differences of linear SATTG trends (computed with least-squares without accounting for change points) and GNSS with respect to GIA/GIA+CMR VLM estimates

We obtain similar results from the analogous analysis comparing GNSS and GIA+CMR effects. Here, we compare the weighted averaged piecewise trends (estimated with DiscoTimeS), as well as the MIDAS trends with GIA+CMR VLM estimates. The trend differences are sorted according to the standard deviation of trend changes within a time series as detected by DiscoTimeS. Trend differences w.r.t. large-scale GIA+CMR VLM are strongly reduced for time series with minor trend changes ($\hbox {std} < 0.4$ mm/year), compared to time series where a high standard deviation in trend changes is detected (see Fig. 8b and Table 6 second section). As for SATTG VLM estimates, the combined GIA+CMR effect improves the comparability compared to the sole GIA VLM correction.

These findings are also supported by the analysis of MIDAS trends, which are grouped according to the same criteria as the piecewise DiscoTimeS estimate. The standard deviation of the differences of trends w.r.t. to GIA (or GIA+CMR) is consistent with the statistics obtained by the DiscoTimeS estimates (Table 6). Based on these statistics, the performances of DiscoTimeS in terms of trend estimation are at the same level of MIDAS, also when a significant nonlinear behaviour is detected. The results not only underline the benefit of detecting trend changes to spot significant variable velocities, but also substantiates the validity of DiscoTimeS for mitigating discontinuities. In essence, the significantly increased consistency with GIA+CMR estimates substantiates the successful detection and characterization of variable velocities in both GNSS and SATTG time series.

5 Discussion and concluding remarks

We present a new approach to automatically and simultaneously estimate discontinuities, trend changes, seasonality and noise properties in geophysical time series. With the focus on VLM, we demonstrate the versatility and adaptability of the Bayesian model and its application for SATTG and GNSS data. The major aim of the model development is to further improve the detectability of variable velocities, than it is currently achievable by state-of-the-art algorithms. Although we strongly focus on coastal VLM for relative sea-level estimation, we highlight that the model promises a much wider application range, especially in geodesy, for detecting discontinuities in time series of space-geodetic techniques or climate and sea-level sciences in an automated mode.

We use sensitivity experiments to understand the impact of discontinuities and trend changes on trend accuracy and detection limits for time series of different noise properties. The analyses show that the accuracy of trend estimates and the detection rates are influenced by the noise characteristics (noise type and magnitudes), as well as by time series parameters such as the number of simulated change points. The accuracy of linear trends estimated over very short periods decreases according to the growing uncertainties. Therefore, we set 3 and 8 years as minimum required segment lengths for GNSS and SATTG observations, respectively. Using these constraints, DiscoTimeS consistently outperforms linear trend estimates, also for time series with multiple change points, discontinuities and trend changes. Differences between estimated and prescribed trends are in the order of 0.3–0.5 mm/year for synthetic GNSS data simulated using PLWN noise, < 0.1 mm/year for GNSS data simulated using AR1 noise and within a range of 0.5–1.5 mm/year for SATTG data.

The results show that PL noise has a significant impact on the accuracy of trend estimates, as well as on the detection rates of change points. This implicates that PL noise can represent an ambiguity for the model, which causes difficulties to discriminate between noise and discontinuity or trend change and can potentially lead to overfitting of the data. The discussion on the role of PL noise for discontinuity detection was also raised by (Gazeaux et al. 2013). They highlighted that Hector (Bos and Fernandes 2016), as the only algorithm to take into account PL noise, yielded a lower FP rate (i.e. was less likely to overfit the data), but had also a reduced TP rate. Thus, further developments are required to better disentangle discontinuities in the presence of low-frequency noise and to find a compromise between over- and underfitting of the data, which ultimately depends on the user requirements. Because we analyse time series with an unknown number of discontinuities and additionally trend changes (and PL-noise), which substantially increases the complexity of the problem and thus the uncertainties of the estimates, the model estimates should be carefully reviewed and interpreted by the user.

We use sensitivity experiments to understand the detection limits of discontinuities and trend changes for time series of different noise properties. The analyses show that the ability to detect different magnitudes of discontinuities and trend changes strongly depends on the signal-to-noise ratio and the temporal resolution of the data. The model accurately detects discontinuities in the order of 3–4 mm and $\sim$ 1 mm/year trend changes in synthetic GNSS time series (with white noise amplitudes of 3.2 mm and a duration of 20 years). The detection limit for discontinuities for much noisier SATTG-type time series (20 mm white noise amplitudes) is one order of magnitude larger with about $\sim$4 cm. In case of trend changes in SATTG time series, the accuracy of detecting the exact position of discontinuities in time series is decreased. However, the determination of the magnitude of the trend change itself is still about three times more accurate than estimates obtained from single linear trend fits. The results also point towards the necessity of setting a lower limit of time series length, over which piecewise linear trends are estimated. The accuracy of linear trends estimated over very short periods decreases according to the growing uncertainties. Therefore, we set 3 (8) years as minimum required segment lengths for GNSS (SATTG) observations. Using these constraints, the model consistently outperforms linear trend estimates, also for time series with multiple change points, discontinuities and trend changes.

We apply the model to globally distributed coastal VLM data, consisting of 381 GNSS and 606 SATTG observations using the same model settings. The comparison of piecewise estimated GNSS and SATTG trends at 339 co-located station shows a higher agreement of the trends by 0.36 mm/year compared to linear SATTG estimates, when change points are detected in SATTG time series. The improvement is 0.48 mm/year (21.7%) and 0.46 (17.4%) for one (two) detected change points in the SATTG time series.

The fact that we obtain significant improvements in the comparability of GNSS and SATTG trends when accounting for variable velocities, supports the possibility to assess the time dependency of SATTG VLM at locations where no GNSS stations are available. This is crucial, because SATTG time series usually cover much longer periods of observations than GNSS data. The model also enables the characterization of the ’linearity’ of the VLM, as shown by the much higher consistency of GNSS and SATTG trends with GIA+CMR, for time series which are identified as ’linear’ VLM. This could also generally support a more systematic selection of GNSS VLM data to constrain GIA models (e.g. Caron et al. 2018).

Despite the progress in taking a step towards a fully automated discontinuity detection (see also previous developments, e.g. Gazeaux et al. 2013), the model estimates should still be carefully reviewed in view of the variety of factors and inadequate model assumptions, which can still compromise the model results. One central challenge is the correct identification of the stochastic noise properties in the presence of change points, which can strongly influence the change point detection rate. We show, for example, that PL noise still leads to a higher ambiguity (and overfitting) in the detection of change points than noise models without low-frequency components. In addition, differences between SAT and TG data, which can either be caused by physical or instrumental issues, can also result in an erroneous discontinuity-detection. Such time series should therefore be carefully inspected by the user. Another remaining caveat is that the parametrization of post-seismic relaxation with piecewise incremental trends is a simplification of the process and can be better described by using a relaxation model. These limitations should be considered, when applying the presented method as an unsupervised discontinuity and trend change detection tool for preprocessing data.

Appendices

Appendices

Model initialization

Before estimating the parameters, time series are normalized, such that the same prior assumptions are valid for both SATTG and GNSS data. Compared to SATTG time series GNSS data have much lower noise amplitudes, so without normalization the prior of, e.g., $\sigma _{w}$, would need to be set individually. We normalize the data by the median of their 2-year running-standard-deviation, hereinafter called $\sigma _{obs}$. With this approach we avoid that extreme discontinuities (in particular present in GNSS data), which present orders of magnitudes larger than the ’true noise amplitude’ influence the normalization. We also subtract the offset of the first observation from the data.

Next to the initial probability of $\mathbf {q}_0$, which is explained in Sect. 3.3, several other parameters need to be initialized. The maximum number $n_{max}$ of possible detectable change points is set to 5. The initial AR(1) noise parameter (i.e. the lag-one autocorrelation coefficient) are set to $\sigma _\phi = 0.4$ and $\hat{\sigma }_{w} = 1$. The white noise standard deviation is thus consistent with the standard deviation of the normalized data. In case the PLWN model is applied we set $\hat{\sigma }_{w} = 0.2,\hat{\sigma }_{pl} = 1$. To reduce the complexity of the model, the spectral index is not estimated but prescribed to $\kappa = -0.9$, which generates a noise process close to Flicker Noise. For the trend parameters, we also use informative priors: We set $\sigma _k$ and $\varvec{\sigma }_{\mathbf {h}}$ to 1. Note that this value corresponds to $\sim 1 \sigma _{obs}/year$, and is thus in the order of mm/year to cm/year (for GNSS or SATTG time series). This is another crucial prior assumption, which is based on knowledge of typical physical magnitudes of VLM. The definition primarily avoids that large shifts in the time series would be compensated in form of large VLM rates, but rather be approximated by discontinuities. For the discontinuities, we use noninformative priors with $\sigma _o$ and $\varvec{\sigma }_{\mathbf {p}}$ of 20 (which can be translated to 20 standard deviations). The exact initial change point positions are randomly drawn from the aforementioned uniform distribution, the prior standard deviation ${\varvec{\sigma }}$ is set to 5 years. The multi-year monthly means $\varvec{\mu }_{\mathbf {m}}$ are set to 0 with $\varvec{\sigma }_{\mathbf {m}}$=1.

For very obvious and easily detectable discontinuities in the data (in particular in GNSS time series), knowledge of such events can support the model initialization and generally speed up the computation. We therefore incorporate the position and magnitudes of discontinuities $\varvec{\mu }_{\mathbf {s}}$ and $\varvec{\mu }_{\mathbf {p}}$ in the initial conditions, which are detected when absolute consecutive differences are 15 times larger than the median of all consecutive differences. In general, such events are only recognized for some GNSS stations.

Model selection strategies

There are several options to compare and evaluate different Bayesian models (Gelman et al. 2013). As an objective measure to compare different individual model realizations, we take into account the out-of-sample predictive accuracy of a model. Here, the Pareto-smoothed importance sampling leave-one-out cross-validation (PSIS-LOO) introduced by (Vehtari et al. 2017) is applied, which provides an approximation of the predictive accuracy (loo) and a simulated estimate of the effective number of parameters (p-loo) of the model. In theory, in the cross-validation (CV) approach the data is split into training sets, on which the model is trained, as well as holdout sets from which the predictive accuracy is computed. (Vehtari et al. 2017) developed an efficient method to compute LOO using the existing simulation draws in order to avoid re-fitting of the full time series. As an example, the estimates of piecewise trends and discontinuities (blue) in Fig. 2 stem in both cases (SATTG and GNSS) from the ensemble member with the best CV-score.

Using CV (or other criteria such as WAIC (widely applicable information criterion) or DIC (deviance information criterion)) to select a single best-performing realization, can however lead to overfitting of the data and introduce a significant selection bias (Piironen and Vehtari 2017), even though the CV-score might indicate the best predictive accuracy among the realizations. Piironen and Vehtari (2017) show that, for example, CV-based model selection is especially vulnerable to overfitting at smaller sample sizes, which might thus also have a significant influence for our application where SATTG time series have much lower samples (resolution) than the GNSS data. They underpin that Bayesian Model Averaging yields better results and is substantially less prone to overfitting than single model selection based on CV.

Therefore, we take into account the averaged number of estimated change points ${\overline{n}}$ over all model candidates, as a simplified variant of Bayesian Model Averaging. Note, that even if two realizations estimated the same number of change points, the estimated change point positions and dependent parameters might still significantly deviate. For this reason, we can not average over all parameters and only use ${\overline{n}}$ as ensemble average information.

In total we define three selection options, to identify which is the best solution for SATTG and GNSS time series. In the first case, $best_{loo}$, we select the model with the highest predictive accuracy. Secondly, we select the model with the highest predictive accuracy from the candidates where $n = {\overline{n}}$. This selection is called $\overline{best_{loo}}$ and represents a less optimistic choice than $best_{loo}$. Finally, as the most conservative selection scheme, we use the model with the lowest effective number of parameters $\overline{lowest_{p-loo}}$. Note, that this is not necessarily equivalent to the model with the lowest number of change points. The estimated effective number of parameters is also reduced, for example, when there is no significant trend change after a change point and $\mathbf {h}$ becomes zero.

The comparison of SATTG and GNSS piecewise trends in Sect. 4.3 reveals that the highest agreement of piecewise trends is achieved when selecting SATTG ensemble member based on $\overline{lowest_{p-loo}}$ and GNSS chains based on $\overline{best_{loo}}$. We obtain similar results when using $best_{loo}$ to select the best GNSS realization. The fact that we obtain best results when we choose the chain with the lowest number of effective parameters for SATTG ($\overline{lowest_{p-loo}}$), indicates that using $best_{loo}$ instead might lead to overfitting of the data, as also discussed by Piironen and Vehtari (2017). The necessity to apply different selection schemes is most likely caused by the general differences in noise properties of the different techniques, combined with the different sample sizes of the observations. SATTG data could especially be vulnerable to overfitting in cases when change points are detected due to discrepancies of SAT and TG data, which are not attributable to local VLM dynamics or equipment changes.

Piecewise and linear trend validation

For either synthetic or real data, we investigate how the performance of piecewise trend estimation agrees with the fit of a linear trend estimate computed using linear least square estimation. We compare the deviations of piecewise estimated trends with the deviations of a linear trend fit with respect to the known (prescribed) trends of the synthetic time series. Similarly, we analyse the deviations of piecewise SATTG trends and deviations of linear SATTG trends with respect to the piecewise GNSS trends. Note that in the latter case we consider the piecewise GNSS trends as the ground truth, which are also estimated with the Bayesian model. With the real data application, we aim to answer our research questions, i.e. to which extent variable velocities can be detected in SATTG time series and what improvements or benefits are obtained by using this approach.

Figure 2 exemplifies how the piecewise SATTG and the piecewise GNSS trends are compared and matched with each other. The two SATTG trend segments to be compared with GNSS are indicated by $sattg_1$ and $sattg_2$. Every piecewise SATTG trend is matched with the piecewise GNSS trend which is estimated over the same period. In case that one SATTG trend segment is compared to several piecewise GNSS trends $pw\_gnss_i$, the latter are again averaged and weighted by the fraction of the length of the GNSS segment $l_i$ relative to the overlap period of SATTG and GNSS segments.

Thus, for $n > 0$ we obtain several piecewise SATTG and GNSS trend differences for a single station pair. In order to derive a single trend difference estimate for a SATTG-GNSS pair, we average these absolute piecewise trend differences again by weighting them by the time of the individual overlap periods as given in Eq. (7). This procedure yields absolute trend differences, which are both based on piecewise SATTG and GNSS trends and hereinafter called $\varDelta PW$.

$$\begin{aligned} \varDelta PW = \frac{\sum _{i=1}^{n} |(pw\_sattg_i - pw\_gnss_i)| l_i}{\sum _{i=1}^{n}l_i} \end{aligned}$$

(7)

In a similar way, we compute $\varDelta LIN$ to analyse the differences between single linear SATTG $lin\_sattg_i$ and piecewise GNSS trend estimates, as shown in Eq. (8)

$$\begin{aligned} \varDelta LIN = \frac{\sum _{i=1}^{n} |(lin\_sattg_i - pw\_gnss_i)| l_i}{\sum _{i=1}^{n}l_i} \end{aligned}$$

(8)

The example of the real data trend comparison can also be transferred to the sensitivity experiments. Here, the piecewise SATTG fit can be thought of as the synthetic data fit and the piecewise GNSS trends are representative for the known piecewise trends of the synthetic data.