Strategy for the realisation of the International Height Reference System (IHRS)

Abstract

In 2015, the International Association of Geodesy defined the International Height Reference System (IHRS) as the conventional gravity field-related global height system. The IHRS is a geopotential reference system co-rotating with the Earth. Coordinates of points or objects close to or on the Earth’s surface are given by geopotential numbers C(P) referring to an equipotential surface defined by the conventional value W₀ = 62,636,853.4 m² s⁻², and geocentric Cartesian coordinates X referring to the International Terrestrial Reference System (ITRS). Current efforts concentrate on an accurate, consistent, and well-defined realisation of the IHRS to provide an international standard for the precise determination of physical coordinates worldwide. Accordingly, this study focuses on the strategy for the realisation of the IHRS; i.e. the establishment of the International Height Reference Frame (IHRF). Four main aspects are considered: (1) methods for the determination of IHRF physical coordinates; (2) standards and conventions needed to ensure consistency between the definition and the realisation of the reference system; (3) criteria for the IHRF reference network design and station selection; and (4) operational infrastructure to guarantee a reliable and long-term sustainability of the IHRF. A highlight of this work is the evaluation of different approaches for the determination and accuracy assessment of IHRF coordinates based on the existing resources, namely (1) global gravity models of high resolution, (2) precise regional gravity field modelling, and (3) vertical datum unification of the local height systems into the IHRF. After a detailed discussion of the advantages, current limitations, and possibilities of improvement in the coordinate determination using these options, we define a strategy for the establishment of the IHRF including data requirements, a set of minimum standards/conventions for the determination of potential coordinates, a first IHRF reference network configuration, and a proposal to create a component of the International Gravity Field Service (IGFS) dedicated to the maintenance and servicing of the IHRS/IHRF.

1 Introduction

A current main objective of Geodesy is the implementation of an integrated global geodetic reference system that simultaneously supports the consistent determination and monitoring of the Earth’s geometry, rotation, and gravity field changes with high accuracy worldwide (IAG 2017). This objective is in accordance with the resolution adopted by the United Nations General Assembly on a Global Geodetic Reference Frame (GGRF-UN) for Sustainable Development (A/RES/69/266) on February 26, 2015. During the last decades, a huge progress in the realisation of the International Celestial Reference System (ICRS, Ma and Feissel 1997) and the International Terrestrial Reference System (ITRS, Petit and Luzum 2010) has been achieved. The definition, realisation, and maintenance of these two systems guarantee a globally unified geometric reference frame with reliability at the centimetre level. An equivalent high-precision gravity field-related global height system is missing. Most countries today use regional or local height systems, which have been implemented individually, applying in general diverse procedures. At present, there are some hundred local and regional physical height systems in use. They refer to local sea surface levels, are usually stationary (do not consider variations in time), and realise different physical height types (orthometric or normal heights), and their combination in a global frame presents uncertainties at the metre level. The geodetic data depending on them (e.g. physical heights, gravity anomalies, geoid models, digital terrain models, etc.) are usable in limited geographical areas only, and their global combination or with satellite-based data (especially Global Navigation Satellite Systems’ (GNSS) positioning) shows discrepancies with magnitudes much higher than the accuracy required today.

An accurate, consistent and well-defined global vertical reference system that is in accordance with the increased precision of modern observational techniques and is capable of supporting the present needs of science and society regarding geo-referenced data of high resolution has yet to be established as an international standard (IAG 2017). The International Association of Geodesy (IAG), as the organisation responsible for the advancement of the science of Geodesy, introduced in 2015 the International Height Reference System (IHRS) as the conventional gravity field-related global height system (see IAG Resolution No. 1 (2015) in Drewes et al. 2016). The theoretical foundations for the definition of the IHRS are described in Ihde et al. (2017). Based on this work, this study concentrates on the strategy for the realisation of the IHRS; i.e. the implementation of the International Height Reference Frame (IHRF). Given that a reference frame realises a reference system physically by a solid materialisation of points or observing instruments, and mathematically by the determination of coordinates referring to that reference system (Drewes 2009), this study considers four main aspects: (1) methods for the determination of IHRF physical coordinates (e.g. geopotential numbers referring to the conventional reference W₀ value); (2) standards and conventions needed to ensure consistency between the definition and the realisation of the reference system; (3) station selection for the IHRF reference network; and (4) Operational infrastructure to guarantee a reliable and long-term sustainability of the IHRS/IHRF.

Accordingly, Sect. 2 summarises the definition of the IHRS. Sections 3–5 concentrate on the determination and accuracy assessment of IHRF coordinates based on the existing resources: global gravity models of high resolution (GGM-HR in Sect. 3), regional gravity field modelling (Sect. 4), and existing physical height systems (Sect. 5). These sections also provide a description of current limitations and possibilities of improvement in the coordinate determination using each method. The outcome of this analysis is presented in two parts: Sect. 6 proposes the standards and conventions identified as the minimum requirements for the determination of IHRF coordinates. It includes a standardised strategy for the treatment of the permanent tide in the determination of IHRF coordinates in the mean-tide system. Section 7 recommends the strategy for the implementation of the IHRF, which covers (1) the determination and evaluation of IHRF coordinates depending on the data availability; (2) improvement of the input data required for the determination of IHRF coordinates; (3) the criteria for the IHRF station selection; and (4) the usability and long-term sustainability of the IHRF. The paper finishes with an outlook about the activities to be faced in the near future.

2 International height reference system: IHRS

The definition of the IHRS is based on the following fundamental conventions (see IAG Resolution No. 1 (2015) in Drewes et al. 2016; Ihde et al. 2017):

• (a) The vertical reference level is an equipotential surface of the Earth’s gravity field with the geopotential value W₀ = 62,636,853.4 m² s⁻². W₀ is understood to be the gravity potential of the geoid or the geoidal potential value.

• (b) The vertical potential coordinate is the difference −ΔW(P) between the potential W(P) of the Earth’s gravity field at a point P, and the geoidal potential value W₀. This potential difference ‐ΔW(P) is also designated as the geopotential number C(P):

  $$C\left(P\right)=-\Delta W\left(P\right)={W}_{0}-W\left(P\right)$$

  (1)

• (c) The spatial reference of the position P for the potential W(P) = W(X_P) is given by the coordinate vector X_P = X(P) in the ITRS.

• (d) Parameters, observations, and data should be related to the mean tidal system/mean crust.

• (e) The unit of length is the metre and the unit of time is the second of the International System of Units (SI).

Convention (a) defines the one of the infinite number of equipotential surfaces to which the vertical coordinate −ΔW(P) or C(P) refers; i.e. it defines the global vertical datum. As the reference value W₀ is conventionally adopted (i.e. it is known) and it is assumed to be stationary (Sánchez et al. 2016), the potential value W(P) is considered as a primary coordinate of the IHRF. Since only potential differences can be measured and not the potential itself, the determination of absolute potential values W(P) from observational data is only possible after introducing adequate constraints. The main constraint is that the gravitational potential V must vanish at infinity; i.e. V∞ = 0. Consequently, this so-called regularity condition is also a basic convention for the definition and realisation of the IHRS.

Convention (c) W(P) = W(X_P) makes evident that the IHRS is founded on the combination of a geometric component given by X and a physical component given by the determination of W at X. Coordinates of a point attached to the solid surface of the Earth include station positions X(P), W(P) (or C(P)) and their variation with time, i.e. Ẋ(P), Ẇ(P) (or Ċ(P)). The station positions are regularised in the sense that high-frequency time variations are removed by conventional corrections and they represent a quasi-static state. The coordinate time-derivatives Ẋ(P), Ẇ(P), Ċ(P) usually describe secular (linear) changes and they are known as station velocities. X is to be defined in the ITRS, and it follows the standards, conventions, and procedures outlined by the International Earth Rotation and Reference Systems’ Service IERS (Petit and Luzum 2010) for the computation of the International Terrestrial Reference Frame (ITRF). The determination of ITRF coordinates is well described in the existing literature (e.g. Altamimi et al. 2016; Seitz et al. 2016), and it is not further considered in this paper. For practical purposes, coordinates X can be converted to ellipsoidal coordinates latitude (φ), longitude (λ), and ellipsoidal height (h) and the geopotential numbers C(P) may be converted to a physical height (dynamic, orthometric, or normal height). In this paper, we use normal heights (H*) when metric units are needed. The reference ellipsoid is the GRS80 (Moritz 2000). It is utilised to infer any quantity requiring ellipsoid parameters or a normal gravity field.

Convention (d) introduces the mean-tide system to support the geodetic monitoring of geophysical phenomena governed by fluids within the System Earth. For instance, the sea level change monitoring is performed in the mean-tide system, because removing the direct or indirect effects of the permanent tide misrepresents the real water motion and does not allow a reliable quantification and modelling of the sea level change. This occurs not only in oceanographic applications, but also in hydrographic and geophysical fluid studies. In other words, the global change occurs in the mean-tide system and the IHRF should provide a consistent reference in monitoring it. Convention (d) means that parameters, observations, and data relate to the mean tidal system/mean crust. However, given that gravity field modelling is not possible in the mean-tide system (because the gravity potential would not be a harmonic function), it is agreed that the data processing is performed in the tide-free or zero-tide system, and then, at the very end of the process, the IHRF coordinates are converted to the mean-tide system (see Sect. 6.2). Input data and intermediate products should continue primarily referring to the tide system in which they are given.

According to Ihde et al. (2017), the accuracy of the IHRF potential numbers (Eq. 1) should ideally be at the same level of accuracy as the coordinates X. Currently, the target accuracy is ± 3 mm in the vertical station positions and ± 0.3 mm a⁻¹ in the vertical station velocities. This would correspond to about ± 3 × 10⁻² m² s⁻² and ± 3 × 10⁻³ m² s⁻²a⁻¹ for the potential coordinates W(P) and Ẇ(P), respectively. These values seem to be unrealistic under the available resources (see next sections). Therefore, for the moment, we concentrate on determining static potential values (without considering time variations) and evaluating the possibility of reaching an accuracy around ± 0.1 m² s⁻² (equivalent to ± 1 cm in height). In this study, we consider three options for the determination of potential differences referring to the IHRS: (1) using global gravity models of high resolution (GGM-HR); (2) using regional gravity field (geoid or quasi-geoid) models; and (3) the unification (transformation) of the existing physical height systems into the IHRS.

3 Determination of IHRF-related potential differences using global gravity models of high resolution

The most pragmatic way to solve Eq. (1) would be a direct computation of W(P) by introducing the ITRF coordinates of any point into the harmonic expansion equation representing a GGM-HR. The advances in the satellite gravimetry, especially GRACE (Tapley et al. 2004) and GOCE (Drinkwater et al. 2003), allow accuracies of about ± 0.2 m² s⁻² (corresponding to a vertical position accuracy of ± 2 cm) at long (up to degree 70) and medium (up to degree 200) gravity signal wavelengths; i.e. at a maximum spatial resolution of 100 km (Rummel et al. 2002). At this resolution, the mean global omission error of the GGMs is estimated to be ± 30 cm to ± 40 cm. Therefore, the GGM satellite-only component has necessarily to be extended or be refined with surface (terrestrial/marine/airborne/satellite altimetry) gravity data. The Earth Gravitational Model 2008 (EGM2008) was the first model providing spherical harmonic degree and order up to 2159, and additional coefficients extending to degree 2190 and order 2159; see Pavlis et al. (2012, 2013). This model was released before the availability of GOCE data and including only four years of GRACE data. However, it has been the basis for the computation of the high degrees (> 360) in recent GGM-HRs like EIGEN-6C4 (spherical degree 2190, Förste et al. 2015), GECO (spherical degree 2190, Gilardoni et al. 2016), and SGG-UGM-1 (spherical degree 2159, Liang et al. 2018). Current efforts concentrate on improving the surface gravity data set in order to release a new EGM (labelled as EGM2020) including also complete sets of GRACE and GOCE data (Barnes 2019). In addition, ongoing studies explore the combination of the usual gravity observables (satellite and surface gravity) with synthetic gravity data inferred from detailed topographic models to increase the GGM-HR resolution. For instance, the model XGM2019e (Zingerle et al. 2019) provides a resolution up to degrees 5399 and 5540 in the ellipsoidal and the spherical spectrum, respectively.

The reliability of the GGMs is usually assessed by comparison of geoid heights inferred from the GGMs and from levelling points co-located with GNSS positioning; see e.g. Gruber et al. (2011), Fecher et al. (2017), and Gruber and Willberg (2019). To account for systematic effects (biases or tilts) in the levelling data, the mean difference between both geoid data sets is removed and a planar correction surface is applied to the GNSS/levelling-based geoid. The root-mean-square (RMS) error of the remaining differences indicates how well the GGM-based geoid fits to the GNSS/levelling-based geoid. These RMS values reflect a combination of levelling errors, GNSS ellipsoidal height errors, GGM commission error, and GGM omission error. As it is very difficult to separate these error components, ascertaining the real uncertainty of the GGM-HR seems to be not feasible yet. However, if the same GNSS/levelling data set is used for evaluating different GGMs, it is possible to assess the improvement of the GGMs with respect to each other. As an example, Gruber and Willberg (2019) demonstrate that 80% of the differences between the EGM2008 and recent GGM-HRs reflect the contribution of GOCE data to the determination of the geoid medium wavelengths. They also conclude that the availability of new surface gravity data sets is responsible for about 20% of the differences of the recent GGM-HRs with respect to EGM2008 in a global average. Rummel et al. (2014) found that the expected accuracy of a GGM-HR-based geoid was about ± 4 cm to ± 6 cm in well-surveyed regions, and about ± 20 cm to ± 40 cm with extreme cases of ± 1 m in sparsely surveyed regions. Five years later, based on reprocessed GOCE data, longer GRACE data series, and GNSS/levelling data of better quality, Gruber and Willberg (2019) demonstrate that recent GGM-HR may reach an accuracy around ± 2 cm in well-developed regions with smooth topography (like Germany). In sparsely surveyed regions or areas with strong topography gradients, the uncertainty of about ± 20 cm to ± 40 cm remains (see as example the analysis for Brazil in Gruber and Willberg 2019).

Figure 1a–c compares the normal heights inferred from the models EIGEN-6C4 (degree 2190), GECO (degree 2190), and SGG-UGM-1 (degree 2159) at a set of 162 ITRF stations distributed worldwide. We compute the potential values pointwise using the three models, we subtract the reference potential W₀ (see item (a) in Sect. 2), and we convert the potential differences to normal heights using the GRS80 normal gravity field. Then, we compare the normal height values with respect to the arithmetic mean of the three models. While all terrestrial and altimetry data contained in GECO and SGG-UGM-1 are identical to EGM2008, EIGEN-6C4 contains updated altimetry data over the oceans (DTU10 altimetry, Andersen 2010) and EGM2008 data on the continents. Additionally, the satellite-only component of SGG-UGM-1 considers exclusively GOCE data, GECO combines the satellite-only component of EGM2008 with GOCE-TIM5 (Brockmann et al. 2014), and EIGEN-6C4 includes 10 years of GRACE data (GRGS-RL03-v2, Bruinsma et al. 2010), GOCE-DIR5 (Bruinsma et al. 2013), and 25 years of satellite laser ranging observations to LAGEOS. As the high-degree components of the three models are based on the EGM2008, we could expect similar omission error values. In this way, the discrepancies shown in Fig. 1a–c are mainly caused by the different satellite data included in each model and the different strategies applied in the data processing and spectral combination for the estimation of the harmonic coefficients. The standard deviations values (STDs) vary from ± 2.8 cm to ± 3.8 cm and the pointwise differences reach up to 28 cm. With this experiment, we cannot state which model is better or worse. We are only showing that depending on the model, the vertical coordinate at the same point can diverge up to ± 10 cm in North America and Europe and more than ± 30 cm in areas with strong topography gradients and few terrestrial gravity data like in the western part of South America.

Fig. 1

Comparison of the global gravity models (a) EIGEN-6C4 (degree 2190), (b) GECO (degree 2190), and (c) SGG-UGM-1 (degree 2159) in terms of normal heights with respect to the mean model. Potential values are obtained pointwise using the three models, the reference potential W₀ is subtracted, the potential differences are converted to normal heights, and normal height differences with respect to the arithmetic mean of the three models are computed

The ultra-high-resolution model XGM2019e (Zingerle et al. 2019) combines the satellite-only model GOCO06S (degree 300, Kvas et al. 2019) with DTU13 altimetry-derived gravity data (Andersen et al. 2015), an improved data set of 15′ × 15′ mean surface gravity anomalies, and synthetic gravity data based on the Earth2014 model (Hirt and Rexer 2015). The mean surface gravity anomalies are provided by the United States National Geospatial-Intelligence Agency (NGA) and contain significant improvements in the land gravity data distribution and quality, especially in South America, Africa, Asia, and Antarctica. A description of these data can be found in Fecher et al. (2017) or Pail et al. (2018). The contribution of the new surface gravity data is evident in Fig. 2, which compares the normal heights inferred from XGM2019e up to degree 5540 with the arithmetic mean of the three models mentioned previously (see Fig. 1). The smallest differences (less than ± 1 cm) are located in those regions with well-distributed terrestrial gravity data sets included in EGM2008 (see Pavlis et al. 2012, 2013), while the largest differences (from ± 20 cm to ± 30 cm) occur in remote islands, the Andes, and in the South Atlantic, close to Antarctica.

Fig. 2

Comparison of normal heights inferred from the global gravity model XGM2019e (degree 5540) with the mean value of the normal heights obtained from EIGEN-6C4 (degree 2190), GECO (degree 2190), and SGG-UGM-1 (degree 2159). These differences are mainly attributable to the contribution of surface gravity data posterior to EGM2008 and the gravity synthetic effects inferred from the Earth2014 topography model. (Mean value: 0.5 cm, STD: ± 8.2 cm, Min: − 30.5 cm, Max: 31.0 cm)

Table 1 summarises the statistics of XGM2019e (degree 5540) compared to EGM2008 (degree 2190), EIGEN-6C4 (degree 2190), GECO (degree 2190), SGG-UGM-1 (degree 2159), and XGM2016 (degree 719) in terms of normal heights at the 162 ITRF stations used in this work. These differences largely reflect the advancements in the global gravity field modelling: higher resolution, more observations, better approaches (or models) for the removal or correction of systematic effects in the measurements, homogenisation of processing standards, improved combination and error analysis strategies, redundancy in the data analysis, powerful computation facilities to handle large datasets, etc. A consequence of these improvements is for instance the frequent release of new satellite-only GGMs based on updated reprocessed GRACE and GOCE data combined with kinematic orbits of satellite missions launched for purposes different from gravimetry, like satellite laser ranging or satellite radar altimetry. Indeed, since the launch of the first GRACE mission in 2002, about 70 satellite-only gravity models (up to degree 300) have been released (see Ince et al. 2019). While new satellite measurements, standards and processing strategies can be assimilated very quickly to produce improved satellite-based gravity models, the assimilation of new surface gravity data poses still a big challenge. A first milestone in the determination of GGMs with high degrees was the model EGM96 up to degree 360 (Lemoine et al. 1998). The following high-degree model (EGM2008) was released 12 years later in 2008 (Pavlis et al. 2012, 2013). After this, six models representing a modification of EGM2008 have been published that make use of improved satellite data from GRACE and GOCE, but include the high degrees of EGM2008. Quite recently, in 2017, it was possible to compute the upgraded GGM GOCO05c (degree 720, Fecher et al. 2017), which considers NGA’s 15′ × 15′ mean gravity anomalies inferred from new and improved terrestrial gravity data posterior to EGM2008. This model is understood as the predecessor of XGM2016 (Pail et al. 2018) and XGM2019e (Zingerle et al. 2019), which are based on exactly the same set of surface gravity anomalies. The next expected GGM-HR is the EGM2020 (Barnes 2019), which should include in addition to the latest GRACE and GOCE data releases, an updated and improved data set of 5′ × 5′ mean surface gravity anomalies.

Table 1 Statistics of XGM2019e (degree 5540) compared to EGM2008 (degree 2190), EIGEN-6C4 (degree 2190), GECO (degree 2190), SGG-UGM-1 (degree 2159), and XGM2016 (degree 719) in terms of normal heights at 162 ITRF stations globally distributed

The GGMs available at the IAG International Centre for Global Earth Models (ICGEM, Ince et al. 2019) make evident that while satellite-only GGMs are released with an averaged frequency of three months, the surface gravity dataset included in GGM-HRs can be updated more or less every 10 years (only three times from 1996 to 2017). The assimilation of surface gravity data in the computation of GGM-HRs is not a question of data processing abilities or capabilities. It is a consequence of the restricted accessibility to existing gravity databases and the high costs associated with gravimetric surveys, which are usually carried out over long time-consuming field campaigns with big human efforts, leaving large data gaps especially in areas of limited access like high mountains, deserts, swamps, or jungles. An effective alternative to increase quality and data distribution is the airborne gravity as it is being done in the USA within the project GRAV-D (Gravity for the Redefinition of the American Vertical Datum, https://www.ngs.noaa.gov/GRAV-D/index.shtml). A main objective of GRAV-D is to increase the availability of airborne-based surface gravity data towards the determination of a 1-cm geoid in the US main land and territories. For that matter, the corresponding US agencies have been performing airborne gravimetric surveys during the last decade systematically. The estimated costs reach 39 million US dollars, showing that this technique is very expensive and may not be massively applied in less developed regions, where terrestrial data are of very bad quality or not available. Exactly those regions benefit at maximum from the satellite gravity missions, since these are the only data source able to provide new gravity field information. This benefit may be further extended with the use of synthetic gravity signal inferred from topographic models as proposed by Zingerle et al. (2019). Nonetheless, the GGM-HR medium and short wavelengths (about degree 250–2000) in such areas are fill-in data predicted from topographic models with a nominal mass density value and they do not necessarily represent the actual gravity signal.

One possibility of improving the reliability of the vertical coordinate is the combination of GGMs with surface gravity data of high resolution following the remove–compute–restore (RCR) procedure (Tscherning 1986; Schwarz et al. 1990). In the RCR procedure, the short (topography) and long (GGM) wavelengths are removed from the observations, then the residual quantities are used for the gravity field modelling (e.g. determination of the disturbing potential), and at the very end of the process, the short and long wavelength contributions are restored again in terms of potential values. While the satellite-only component of the GGMs ensures the realisation of a common reference level for all regions/countries around the world, the local/regional surface gravity measurements increase the resolution provided by the GGMs and contribute to coming closer to the accuracy goal in the computation of the W(P) values. In the following, we call this combination regional gravity field modelling of high resolution and it is based on the procedures applied for the determination of regional geoid or quasi-geoid models.

4 Determination of IHRF-related potential differences based on regional gravity field modelling of high resolution

The fundamental approach for the regional gravity field modelling is the geodetic boundary value problem (GBVP). It may be formulated in different ways depending on the unknowns (potential and boundary surface) and the gravity field observables available to specify the boundary conditions. The mostly used formulations are the scalar-free GBVP (potential and vertical position of the boundary surface unknown, horizontal position of the observables available) and the fixed GBVP (potential unknown, boundary surface known, coordinate vectors X of the observables available); see e.g. Koch and Pope (1972), Sacerdote and Sansò (1986), Heck (1989, 2011), Sansò (1995). The usual boundary condition is the magnitude of the gravity vector obtained from gravimetry, which is converted to gravity disturbances for solving the fixed GBVP, or to gravity anomalies for solving the scalar-free GBVP. Nonetheless, additional observables like geopotential numbers, gravity potential gradients, or deflections of the vertical may be included. As the existing gravity databases mainly contain gravity anomalies with latitude and longitude values, the scalar-free GBVP is the formulation most applied presently. However, the intensive use of GNSS opens today the possibility of a direct application of the fixed GBVP. A main limitation is that, while recent gravimetric surveys provide gravity values with ITRF positions, big efforts are necessary for the reliable transformation of the historical terrestrial gravity anomalies to gravity disturbances due to missing metadata and the use of regional/local horizontal and vertical datums for geo-referencing the gravity values (see e.g. Grombein et al. 2015).

Given that the boundary conditions (i.e. the gravity field observables) depend in a nonlinear way on the unknown gravity potential function, the solution of any GBVP requires the linearisation of the observation equations. This is done by introducing a known reference potential field (usually the normal gravity field of a level ellipsoid) and by describing unknowns and gravity observables as relative quantities with respect to that reference field. Additionally, in the case of the scalar-free GBVP, a reference (or approximation) surface has to be adopted. If the Earth’s surface is assumed as boundary surface, the reference surface is the telluroid (theory of Molodensky). If the boundary surface is an equipotential surface, the reference surface is a level ellipsoid (theory of Stokes). In this case, the equipotential surface acting as boundary surface is that equipotential surface with the same potential (W₀) as the normal potential (U₀) on the ellipsoid: W = W₀ = U₀. The unknown potential function is then the disturbing potential T = W − U. The solution of the GBVP in regional gravity modelling is usually given in terms of integral formulas. They allow a pointwise determination of the disturbing potential and are easily adaptable to the available surface gravity data coverage and quality. The integral kernels (acting as weighting functions on the boundary conditions when being modified) differ depending on the formulation of the GBVP; we talk about the Stokes function for the scalar-free GBVP, and about the Hotine or Koch function for the fixed GBVP (for details, see e.g. Hofmann-Wellenhof and Moritz 2005, Chapter 8). Alternative approaches to the integral formulas are the least-squares collocation (LSC, e.g. Forsberg and Tscherning 1981; Tscherning 1985, 1993, 2013), and more recently, spherical radial basis functions (SRBF, e.g. Schmidt et al. 2007; Bentel et al. 2013; Lieb et al. 2015). Independently of the approach applied to solve the GBVP, a common strategy is the RCR procedure (Tscherning, 1986; Schwarz et al. 1990).

The practical application of the RCR procedure demands some modifications of the GBVP formulations in accordance with the available data. Essential aspects are the adaptation of the integral kernels (Stokes or Hotine functions) to ensure the appropriate spectral transfer of the residual gravity field signal (see a detailed discussion in e.g. Featherstone 2013; Hirt 2011), the method to estimate and remove the topographic effects (Forsberg 1984, 1997; Forsberg and Tscherning 1997), and the selection of the most appropriate integration radius around the computation point (Forsberg and Featherstone 1998). This leads to a very large variety of possibilities to solve the GBVP, and each possibility produces different results (i.e. different disturbing potential values at the same computation point). However, the regional gravity field modelling plays a main role in the determination of potential values as IHRF coordinates because (1) regional/local geoid modellers have access to surface gravity data sets that are not available for the determination of GGM-HR; and (2) new regional/local gravity surveys can be easily assimilated for the computation of updated regional/local (quasi-)geoid models, leading to updated/improved potential values. In this way, we are convinced that national/regional experts on gravity field modelling should be involved in the establishment of the IHRF in their regions, as they have the best possible data for the computation of the IHRF potential values. The challenge is, however, to assess the consistency between the large variety of strategies, methods, and approximations utilised in the regional (quasi-)geoid computation as described above. Thus, it is necessary to find a way to separate how much of the results depend on the method and how much they depend on the input data. One possibility would be to process all regional gravity sets using the same strategy, reductions, and approximations. Nevertheless, a centralised computation of the potential values (as the IERS does with the ITRF coordinates) is complicated due to the restricted accessibility to surface gravity data. Additionally, to set up a unified/standard procedure may not be suitable, since regions with different characteristics require particular approaches (e.g. modification of kernel functions, size of integration caps, geophysical reductions for glacial isostatic adjustment, etc.). The alternative is to standardise as much as possible to get as similar and compatible results as possible with the different methods.

To assess the repeatability of the results provided by different approaches utilised in the solution of the GBVP and to identify a set of basic standards to ensure a minimum consistency between them, a computation experiment based on the same input data and different processing strategies was performed over two years (2017–2019). More than 40 colleagues grouped in fourteen computation teams supported this initiative and delivered individual solutions obtained following their own computation procedures and using their own software. This experiment was called the Colorado experiment (Wang et al. 2021) as the input data are distributed over this region. The main objectives were (1) the determination of geoid and quasi-geoid models and potential values, and (2) the comparison of the individual solutions among each other and with GNSS data co-located with terrestrial gravity and levelling of high precision. The comparison of the individual contributions among each other allows to identify discrepancies between processing strategies, while the comparison with the GNSS/levelling data permits to assess the reliability of the individual contributions using independent data of high quality. For this experiment, the United States National Geodetic Survey (NGS) provided terrestrial gravity data, airborne gravity, and a digital terrain model covering the area between latitudes 35° N–40° N and longitudes 110° W–102° W. The gravity data comprise about 60,000 terrestrial gravity values and 48 flight lines with GRAV-D airborne data (Damiani, 2011) for block MS05 (https://www.ngs.noaa.gov/GRAV-D/data_ms05.shtml). The digital terrain model corresponds to a corrected version of SRTM v4.1 (Jarvis et al. 2008) with a spatial resolution of 3″ × 3″. In this corrected version, elevations were fixed for spikes and voids in the Colorado region (Ahlgren et al. 2018). The Colorado data were distributed together with a document summarising a minimum set of basic requirements (standards) for the computations (Sánchez et al. 2018). The GNSS, gravity, and levelling surveys used for the validation of the results were performed under the Geoid Slope Validation Survey 2017 (GSVS17, VanWestrum et al. 2021). The GSVS17 profile runs from the East to the West along 350 km over flat areas and mountain regions with strong vertical gradients. It is composed of 223 benchmarks with a mean distance of 1.6 km. The levelling data were adjusted in terms of geopotential numbers under minimum constraint conditions with respect to the final benchmark 223. These geopotential numbers are further converted to orthometric heights and normal heights for the evaluation of gravimetric geoid and quasi-geoid models (see details in VanWestrum et al. 2021). Wang et al. (2021) describe in detail the data provided by NGS for the Colorado experiment and summarise the comparison of the geoid and quasi-geoid models delivered by the different contributing groups. In this work, we concentrate on the determination and evaluation of the potential differences with respect to the IHRS W₀ reference value. This analysis is a main input to define the strategy for the implementation of the IHRF described in Sects. 6 and 7.

4.1 Recovering potential values from (quasi-)geoid models

The determination of station potential values W(P) is straightforward if the disturbing potential T(P) is known:

$$W\left(P\right)=U\left(P\right)+T\left(P\right).$$

(2)

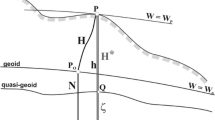
U(P) is the normal potential of the reference ellipsoid. For the realisation of the IHRS, the potential values W(P) must be determined at the reference stations; i.e. at the Earth’s surface and not at the geoid. Consequently, consistency with the approach used for the estimation of the disturbing potential should be ensured. By applying the fixed GBVP or the scalar-free GBVP following Molodensky’s theory, the disturbing potential is determined at the point P on the Earth’s surface (Fig. 3) and the estimation of W(P) is straightforward. When Stokes’ theory is followed, the disturbing potential is determined at the point P₀ on the geoid (inside the Earth’s topographic masses, see Fig. 3) and an upward continuation is necessary to estimate W(P) on the Earth’s surface. This upward continuation must be consistent with the hypotheses applied to reduce the gravity values from the Earth’s surface to the geoid. We prefer, therefore, to start from the quasi-geoid or disturbing potential at the Earth’s surface and then to infer the potential values W(P). If the preference of the regional gravity field modelling experts is to compute the geoid first, we recommend to transform geoid undulations (N) to height anomalies ($\zeta$) and then to infer the potential values W(P). The transformation from N to $\zeta$ must also be consistent with the hypotheses applied for the geoid computation. The usual term based on the Bouguer anomaly (see Eqs. 8–115 in Hofmann-Wellenhof and Moritz 2005) is not sufficiently accurate. Refined approximations like those proposed by Flury and Rummel (2009) or Sjӧberg (2010) are needed to decrease the degradation of achievable precision introduced by this transformation (see Sect. 4.4).

Fig. 3

Heights and reference surfaces (modified from Sánchez et al. 2018)

Potential values W(P) can be recovered from a solution of the fixed or scalar-free GBVP after Molodensky using:

$$W\left(P\right)=U\left(P\right)+T\left(P\right)=U\left(P\right)+\left({T}_{0}+\sum_{n=2}^{\infty }{T}_{n}\left(P\right)\right),$$

(3)

or

$$W\left(P\right)=U\left(P\right)+\zeta\left(P\right)\cdot\upgamma +\Delta {W}_{0}.$$

(4)

U(P) and γ are the GRS80 normal potential and gravity value, respectively, and ζ is the height anomaly. The sum of terms in parenthesis in Eq. (3) represents the disturbing potential in a linear, spherical, and constant radius approximation, which for a point with the geocentric co-latitude θ and longitude λ is given by (Hofmann-Wellenhof and Moritz 2005, Eq. 2–328):

$$T\left(\theta ,\right)={T}_{0}+{T}_{1}\left(\theta ,\right)+\sum_{n=2}^{\infty }{T}_{n}\left(\theta ,\right).$$

(5)

${T}_{1}\left(\theta ,\lambda\right)=0$, since the first-degree coefficients (C₁ = C₁₁ = S₁₁ = 0) are assumed to be zero to align the Earth’s centre of masses with the origin of the geometric coordinate system (ITRS/ITRF). The zero-degree term T₀ includes the difference between the values employed by the GGM and reference ellipsoid for the geocentric gravitational constant GM (cf. Eqs. 2–330, Hofmann-Wellenhof and Moritz 2005):

$$ \begin{aligned} T_{0} & = \frac{1}{{r_{P} }}\left( {GM_{GGM} - GM_{GRS80} } \right) \\ & = \frac{1}{{r_{P} }}\left( {3.986 004 415 \times 10^{14} \,{\text{m}}^{3} \,{\text{s}}^{ - 2} - 3.986 00 \times 10^{14} \,{\text{m}}^{3} \,{\text{s}}^{ - 2} } \right) \\ \end{aligned} $$

(6)

r_p is the geocentric radial distance of the computation point P.

ΔW₀ in Eq. (4) is the difference between the conventional reference potential value W₀ and the potential U₀ on the reference ellipsoid:

$$ \Delta W_{0} = W_{0} - U_{0} = 62,636,853.4\,{\text{m}}^{2} \,{\text{s}}^{ - 2} - 62,636,860.850\,{\text{m}}^{2} \,{\text{s}}^{ - 2} = - 7.45\,{\text{m}}^{2} \,{\text{s}}^{ - 2} . $$

(7)

A rigorous analytical solution in closed form of any GBVP demands a harmonic, linear, spherical, and constant radius approximation of the observation equations (see Eq. (5)). This means: masses outside the boundary surface, nonlinear terms, ellipsoidal terms, and topographic terms in the boundary conditions are mathematically removed or neglected. With every level of approximation, artificial errors are introduced to the boundary conditions (which are already influenced by the observation errors) and the accuracy of the estimated values for the unknown potential degrades. In view of the present accuracy requirements, these effects cannot be neglected in precise gravity field modelling, and thus, they have to be considered by appropriate processing strategies or reductions. Consequently, it is expected that the disturbing potential values (Eq. 5) are at least corrected by atmospheric effects, topographic effects, and ellipsoidal effects. In a very general classification, these effects can be considered (1) at the observation level before solving the GBVP; (2) as corrections to be added to the estimated disturbing potential after solving the GBVP; (3) by modifying the integral kernels contained in the GBVP formulation; or (4) by the combination of (1), (2) and (3). The way to remove these effects is a part of the processing strategy and it is usually up to the gravity field modellers. A special case is the handling of the permanent tide effects. To solve the GBVP, masses outside the boundary surface have usually to be removed; i.e. the input data have to be given in the non-tidal (tide-free) or the zero-tide system. However, to be consistent with the IHRS definition, the IHRF geopotential number must be given in the mean-tide system. Consequently, we recommend to calculate the geopotential in the tide-free or zero-tide system and then to transform it to the mean-tide at the end of the computation procedure (see Sect. 6.2). This keeps the computations consistent with the gravity/geoid work in the tide-free or zero-tide system without introducing an unwanted amount of new transformations or corrections. For the particular case of the Colorado experiment, we use the tide-free system because the gravity data, geometric coordinates, and GNSS/levelling data provided by NGS are in the tide-free system. If everything is consistent, this should not influence the comparison of results.

4.2 Comparison of geopotential numbers recovered from the (quasi-)geoid models delivered to the Colorado experiment

In total, fourteen working groups delivered solutions to the Colorado experiment (see Wang et al. 2021). From these fourteen solutions, thirteen include absolute potential values at the benchmarks of the GSVS17 profile. “Appendix 1” summarises the main characteristics of the processing strategies utilised in each solution and provides bibliography for every computation if further reading is desired. The individual solutions are identified with sequence numbers that are used for the comparisons described in this and the next sections. In a very general description, it can be mentioned that solutions 1, 2, 3, 4, 5, 6, 7, 8, and 11 solve the scalar-free GBVP after Molodensky’s theory; solutions 9 and 10 solve the fixed GBVP; and solutions 12 and 13 solve the scalar-free GBVP after Stokes’ theory. For the comparison, the geoid undulations of models 12 and 13 are converted to height anomalies applying the usual Bouguer anomaly-based term before estimating the potential values with Eq. (4). A refined estimation of geopotential values from model 13 including the terrain correction to take into account the deviation of the topography from the Bouguer plate is presented in Sect. 4.4. In this study, the comparison between the solutions is performed in terms of IHRS-based geopotential numbers (see Eq. 1); i.e. the reference value W₀ is subtracted from the pointwise potentials. Afterwards, the individual geopotential number sets are compared with each other and with the potential differences obtained from levelling in combination with terrestrial gravimetry along the GSVS17 profile.

For the comparison of the solutions, mean geopotential numbers are computed and removed from the pointwise values. Here, we group the solutions according to the main data processing characteristics. One group covers the solutions based on the scalar-free GBVP after Molodenky’s theory using fast Fourier transform (FFT) integration and a Wong–Gore (or similar) modification of the integral kernel (solutions 1, 2, 3, and 4; Fig. 4a). A second group considers the solutions based on the scalar-free GBVP after Molodenky’s theory with a least-squares modification of Stokes’ formula with additive corrections (solutions 5, 6, 7, and 8; Fig. 4b). The next group comprises the solutions based on least-squares collocation (solutions 10 and 11) and spherical radial basis functions (solution 9); see Fig. 4c. It should be noted here that solutions 9 and 10 solve the fixed GBVP and solution 11 the scalar-free GBVP after Molodenky’s theory. The last group contains the solutions based on the scalar-free GBVP after Stokes’ theory (solutions 12 and 13; Fig. 4d). As mentioned, in this case the potential values are inferred after converting the geoid undulations to height anomalies. Table 2 shows the comparison statistics between the individual geopotential number sets and the mean values.

Fig. 4

Geopotential number differences with respect to the mean value (model-mean) at the 223 GSVS17 benchmarks. Solutions are grouped according to the main data processing approach

Table 2 Geopotential number differences with respect to the mean value (model − mean) at the 223 GSVS17 benchmarks, units (m² s⁻²)

The individual solutions agree within ± 0.09 m² s⁻² and ± 0.23 m² s⁻² (equivalent to ± 0.009 m and ± 0.023 m) in terms of standard deviation with respect to the mean value. The solutions 9 and 10, based on the fixed GBVP, present STD values less than ± 0.10 m² s⁻² (± 0.010 m). Solutions 3, 4 and 5 agree at the ± 0.13 m² s⁻² (± 0.013 m) STD level. The overall differences range from − 0.86 m² s⁻² (− 0.088 m) for solution 2 to + 0.77 m² s⁻² (+ 0.079 m) for solution 12. Figure 4a–d clearly shows that the divergences between the individual solutions have a high correlation with the topography. In general, the largest residuals occur at or near the highest peaks (3292.75 m at benchmark No. 86 and 2843.33 m at benchmark No. 196). As most of the solutions (except solutions 9 and 10) model the terrain effects using SRTM v.4.1 data, it is evident that these discrepancies are mainly caused by the handling of the topography effects in the individual processing strategies. Indeed, the two most similar solutions (9 and 10 in Fig. 4c) apply the same strategy and the same topographic models dV_ell_Earth2014 (Rexer et al. 2016) and ERTM2160 (Hirt et al. 2014) for the terrain effects. The pointwise differences with respect to the mean value between these two models vary from − 0.21 to + 0.09 m² s⁻² (− 0.021 m to 0.009 m). Models 2 (Fig. 4a), 8 (Fig. 4b), 12 (Fig. 4d), and 13 (Fig. 4d) present the largest residuals (up to about ± 0.60 m² s⁻² or ± 0.061 m). The other models differ from the mean in a narrow band from − 0.30 to + 0.30 m² s⁻² (− 0.030 m to + 0.030 m) except for a few spikes.

These results are in agreement with the findings of Wang et al. (2021), who compare 1′ × 1′ geoid and quasi-geoid models for the whole Colorado area and pointwise height anomalies and geoid undulations at the 223 GSVS17 benchmarks. While the standard deviations of the height anomaly differences along the GSVS17 profile vary from ± 0.010 m to ± 0.034 m, the standard deviations of the geoid undulation differences vary from ± 0.016 m to ± 0.036 m. By comparing the models over the complete area, the quasi-geoid differences with respect to mean model present STD values from ± 0.015 m to ± 0.028 m; the geoid model comparison presents STD between ± 0.021 m and to ± 0.056 m.

4.3 Comparison of model-based with levelling-based potential differences

The comparison described in Sect. 4.2 highlights the differences between the various data processing strategies applied within the Colorado experiment. To assess the reliability of the solutions, we compare their potential differences (in the following called model-based potentials C_mod) with the potential differences inferred from high-precise levelling and gravity corrections along the GSVS17 profile (in the following called levelling-based potentials C_lev); see details about the levelling data processing in VanWestrum et al. (2021). For the objective of this study, we compare model-based (C_mod) and levelling-based (C_lev) potential differences in two ways: (1) between consecutive benchmarks:

$$\Delta {C}_{i,i+1}=\left({C}_{{\mathrm{mod}},i}-{C}_{{\mathrm{mod}},i+1}\right)-\left({C}_{{\mathrm{lev}},i}-{C}_{{\mathrm{lev}},i+1}\right),$$

(8)

and (2) between all possible baseline lengths (d_ij) of the GVSV17 profile:

$$\Delta {C}_{i,j}=\left({C}_{{\mathrm{mod}},i}-{C}_{{\mathrm{mod}},j}\right)-\left({C}_{{\mathrm{lev}},i}-{C}_{{\mathrm{lev}},j}\right);$$

(9)

i and j are the indexes of the GSVS17 benchmarks and d_ij is the distance in [km] along the levelling path between each pair of points. The d_ij values are grouped in 15 class intervals varying from 15 to 108 km. The varying length of the class intervals is needed to ensure that at least 2000 benchmark pairs are available per class. The RMS values of the ΔC_ij differences (Eq. 9) for each interval indicate the consistency between the model-based and levelling-based potential values as a function of the distance. The comparisons in Eqs. (8) and (9) are also performed using the potential values inferred from the GGMs considered in Sect. 3. In addition to EGM2008, EIGEN-6C4, GECO, SGG-UGM-1, XGM2016, and XGM2019, we include the potential values obtained after combining XGM2016 up to degree 719 with the topographic model dV_ell_Earth2014 (Rexer et al. 2016) from degree 720 to degree 2159, and the residual terrain model ERTM2160 (Hirt et al. 2014) from degree 2160 to degree ~ 80000 (equivalent to a spatial resolution of 250 m). This combination is achieved using the same SRBF-based processing strategy applied in solution 9 (see Liu et al. 2020).

Table 3 summarises the statistics obtained from Eq. (8). The results for the GGM-HR are quite homogeneous; the RMS values are around ± 0.11 m² s⁻² (0.011 m) and the range of the differences vary from 0.53 m² s⁻² (0.053 m) for the XGM2016 + dV_ell_Earth2014 + ERTM2160 combined model up to 0.76 m² s⁻² (0.076 m) for the models including EGM2008 data for the high-degree harmonics. The consecutive station differences for the regional solutions vary from − 0.33 m² s⁻² (− 0.033 m) to + 0.29 m² s⁻² (+ 0.029 m), except for the models 6, 8, 12, and 13 that present difference ranges from 0.86 m² s⁻² (0.088 m) to 1.55 m² s⁻² (0.158 m). These values are larger than those obtained from the GGM-HR. The RMS values for the regional solutions are in the ± 0.07 m² s⁻² (± 0.007 m) to ± 0.10 m² s⁻² (± 0.010 m) range, except solutions 6 and 8, which reach ± 0.16 m² s⁻² (± 0.016 m). It should be noted that the mean distance between two consecutive benchmarks is about 1.6 km, which is close to the grid spacing (about 1.5 km) of the 1′ × 1′ geoid/quasi-geoid solutions. In other words, these solutions do not contain the geopotential spatial features smaller than the grid spacing. Consequently, it appears that the RMS values in Table 3 largely reflect the combined effect of omission and commission errors of the regional and GGM-HR models for this short baseline. The regional models show slightly smaller scatter than the GGH-HR models due to the relatively higher spatial resolution.

Table 3 Consecutive benchmark differences between the model-based (C_mod) and the levelling-based geopotential numbers (C_lev) along the GSVS17 profile, units (m² s⁻²)

Figure 5 shows the standard deviation of all 13 regional solutions for each respective (i, i + 1) pair plotted versus the ellipsoidal height. The smallest standard deviation values (± 0.02 to ± 0.04 m² s⁻², equivalent to ± 0.002 to ± 0.004 m) occur where the topography is smooth (benchmarks 110–170). They increase with the roughness of topography, occurring the largest values (larger than ± 0.15 m² s⁻² or ± 0.015 m) at the strongest topographic gradients. This shows that the large scatter is associated with the rough topography where the omission error tends to be large, and the topography effects are treated quite differently among the 13 solutions. Consequently, a challenge (or limitation) in the determination of model-based geopotential numbers is a better modelling of terrain effects.

Fig. 5

Discrepancies between the model-based (C_mod) and levelling-based (C_lev) potential differences between consecutive benchmarks (i, i + 1) along the GSVS17 profile (cf. Eq. 8). Standard deviation of all 13 regional solutions is plotted versus the ellipsoidal height. The largest standard deviation values occur at the strongest topographic gradients

Table 4 and Fig. 6 present the RMS values obtained from the baseline-length depending comparison (Eq. 9). Italics in Table 4 highlight the smallest value at every baseline-length interval. The RMS values for the geopotential differences inferred from GGM-HR vary from ± 0.32 m² s⁻² (± 0.030 m) to ± 0.93 m² s⁻² (± 0.095 m); the EGM2008 model showing the largest ones. The improvement of the EIGEN-6C4, GECO, and SGG-UGM-1 RMS values in comparison with EGM2008 can be explained by the contribution of GOCE data to the satellite-only component of these models. The newer XGM2016, XGM2019, and the combined XGM2016 + dV_ell_Earth2014 + ERTM2160 models fit in a similar way the levelling-based potential differences between 63 and 202 km, presenting the best RMS values at the 122–145 km interval. The large RMS values (around 0.60 m² s⁻² or 0.060 m) of these models at distances between 15 and 60 km may be a consequence of the low resolution (15′ × 15′) of the mean surface gravity anomalies included in the determination of the XGM models. These anomalies lack gravity information finer than 15′ × 15′, causing an omission error, which apparently cannot completely be solved by the synthetic gravity data inferred from topography models. Remember that EGM2008 contains 5′ × 5′ (or denser) mean surface gravity anomalies, and these anomalies are transferred to the high degrees of the models EIGEN-6C4, GECO, and SGG-UGM-1. The angled pattern described by the RMS values of XGM2016, XGM2019, and the combined XGM2016 + dV_ell_Earth2014 + ERTM2160 model suggests that they fit the levelling-based potential differences at some frequencies only. For instance, the RMS values at the intervals 63–81 km and 122–145 km are better than the values for the intervals 81–101 km and 101–122 km. This could be produced by un-modelled high frequencies or artefacts contained in the topography-based synthetic gravity signal. This should be investigated in the near future.

Table 4 RMS values obtained of the baseline-length depending comparison between model-based (C_mod) and levelling-based (C_lev) potential differences (see Eq. (9)), units (m² s⁻²)

Fig. 6

Baseline-length depending comparison between model-based (C_mod) and levelling-based (C_lev) potential differences (see Eq. (9)). a Comparison of the regional solutions; b comparison of the GGM-HRs

Regarding the regional solutions, the RMS values vary from ± 0.12 to ± 0.78 m² s⁻² (± 0.012 m to ± 0.080 m). While solutions 3 and 7 (with RMS values less than ± 0.30 m² s⁻² or ± 0.030 m) fit best the levelling-based geopotential differences up to distances of about 120 km, solution 13 shows a better agreement for the distances from 120 to 350 km. All solutions (except 1, 6, 8, and 12) agree at an RMS level of ± 0.20 to ± 0.40 m² s⁻² (± 0.020 m to ± 0.040 m) for distances varying between 30 and 150 km. At larger distances (from 150 to 350 km), the consistency between all models is better than ± 0.70 m² s⁻² (± 0.071 m). One could assume that the decrease in the RMS values with the distance is caused by the levelling error accumulation and that an unidentified tilt in the levelling line misrepresents this comparison. However, solution 13 does not present this behaviour. One possibility of the difference could be the parametrisation/modification of the integration kernels for the spectral combination of the different gravity data sources (global models, regional surface gravity, topography effects). This has to be investigated in a next iteration of this study. Figure 6 shows that the solutions based on the high-resolution gravity modelling fit better the levelling-based potential differences than the GGM-HR models. Solutions 6 and 8 present worse RMS values than the other regional solutions; however, they are at the same RMS level of the best-fitting GGM-HRs.

4.4 Comparison of potential differences inferred from different approximations to convert the geoid to the quasi-geoid

In Sect. 4.1, we mentioned that when the potential values W(P) are to be inferred from a geoid model, an upward continuation from the point P₀ on the geoid to the point P on the Earth’s surface is necessary (see Fig. 3 for the position of P₀ and P). We also emphasised that the upward continuation should be consistent with the hypotheses applied for the geoid computation. To explore the influence of this conversion on the potential values, we applied two different approximations to recover the potential values W(P) from the geoid undulations delivered by solution 13 (Huang and Véronneau 2013). The first approximation (Eq. 10) corresponds to the usual Bouguer anomaly-based term for the conversion between N and ζ, which is consistent with the Helmert orthometric heights (cf. Hofmann-Wellenhof and Moritz 2005, Eq. (4–33)). This approximation is used for the comparisons described in the previous sections. The second approximation (Eq. 11) takes into account the deviation of the topography from the Bouguer plate around P:

$$ W\left( P \right) = W_{0} - \left( {h - N} \right) \cdot \overline{g}\quad {\text{with}}\quad \overline{g} = g\left( P \right) + 0.424 \times 10^{ - 6} \cdot \left( {h - N} \right) \left[ {{\text{m}}^{2} \,{\text{s}}^{ - 2} } \right] $$

(10)

$$ W\left( P \right) = W_{0} - \left( {h - N} \right) \cdot \overline{g}\quad {\text{with}}\quad \overline{g} = g\left( P \right) + 0.424 \times 10^{ - 6} \cdot \left( {h - N} \right) + TC\, \left[ {{\text{m}}^{2} \,{\text{s}}^{ - 2} } \right] $$

(11)

W₀ = 62,636,853.4 m²s^–2. h is the ellipsoidal height (provided by NGS). N is the geoid undulation interpolated from the 1′ × 1′ geoid model at the GSVS17 benchmarks. g(P) is the gravity value at each benchmark (this value is interpolated from the terrestrial gravity data set provided by NGS). The factor 0.424 × 10^–6 refers to an average density of topographic masses of ρ = 2,670 kg m⁻³ (see e.g. Hofmann-Wellenhof and Moritz 2005, Eq. (4–31)). TC stands for the terrain correction, and it is estimated following Sects. 3.4 and 4.3 of Hofmann-Wellenhof and Moritz (2005) and using the SRTM v.4.1 model evenly at seven points between the geoid and topography. The potential differences between both approximations present a mean value of − 0.16 m² s^–2 (corresponding to − 0.016 m) and vary from − 0.60 m² s^–2 (–0.060 m) to + 0.27 m² s^–2 (+ 0.027 m). Figure 7 displays these differences together with the topographic profile of the GSVS17 test points. It should be noted that the peaks in the comparison of solution 13 with the mean geopotential numbers (see Fig. 4d) are similar to the peaks of the differences between the two sets of solution 13 geopotential values but with opposite signs. When comparing these two approximations with the levelling-based potential differences (C_lev) using Eq. (9), it is evident that considering the topographic correction makes the estimation of the potential differences between the geoid and topography more accurate, thus increasing the agreement between the model-based and the levelling-based potential differences (see Fig. 8). A further analysis is needed to compare different approaches for the conversion between N and $\zeta$.

Fig. 7

Differences after recovering potential values from a geoid model using different approximations for the upward continuation of the potential from the geoid surface to the Earth’s surface

Fig. 8

Baseline-length depending comparison between model-based (C_mod) and levelling-based (C_lev) potential differences (see Eq. 9). Coloured lines represent the model-based potential values recovered from solution 13 after using different approximations for the upward continuation of the potential from the geoid surface to the Earth’s surface. The light blue lines represent the other 12 solutions (cf. Fig. 6a)

5 Vertical datum unification of existing physical height systems into the IHRS

The existing physical height reference frames have been established by means of precise levelling referring to local vertical datums W_0l, usually realised by the mean sea level determined at arbitrarily selected tide gauges. The local geopotential numbers C_l(P)

$${C}_{l}\left(P\right)={W}_{0l}-W\left(P\right)$$

(12)

can be converted to IHRF geopotential numbers C^IHRF(P), if the difference δW_0l between the local W_0l and the global W₀ reference levels is known:

$$ C^{IHRF} \left( P \right) = \left( {W_{0} - W_{0l} } \right) + C_{l} \left( P \right) = \delta W_{0l} + C_{l} \left( P \right)\quad {\text{with}}\quad \delta W_{0l} = W_{0} - W_{0l} . $$

(13)

An estimation of δW_0l is possible by adding it to the observation equations of a GBVP. In this case, the scalar-free GBVP is preferred because the gravity anomalies depend on the level difference between P and Q (for the Molodensky approach) or between P₀ and Q₀ (for the Stokes approach); see Fig. 3. Thus, the level W_0l is implicit in the boundary conditions and it can be handled as an additional unknown. As the number of unknowns increases, additional observations are required. In this case, ellipsoidal heights h determined with GNSS at the levelling points with physical (orthometric H or normal H*) heights are used to constrain the values of δW_0l to the discrepancies between ([h − H]− N) or ([h − H*]− ζ). For details about the formulation of the extended GBVP equation observations, please refer to e.g. Rummel and Teunissen (1988), Heck and Rummel (1990), Xu and Rummel (1991), Gatti et al. (2012) and Sideris (2014). Empirical examples can be found in e.g. Rummel et al. (2014), Willberg et al. (2017), Vergos et al. (2018); or Sánchez and Sideris (2017). In the first three examples, the contribution of GOCE data to the height system unification is evaluated. In the latter, the vertical datum unification of the North American and South American height systems into the IHRS is discussed.

It is clear that the estimation of δW_0i depends on the combination of levelling-based physical heights, ellipsoidal heights, and high-resolution gravity field modelling (regional geoid or quasi-geoid models). Therefore, according to Sánchez and Sideris (2017), to get δW_0i values as reliable as possible, the numerical evaluation of the extended GBVP must be performed at geodetic stations of highest quality that refer to the same ITRF and are connected to the local vertical datum by means of first-order precise levelling (in combination with gravity). The scalar-free GBVP after Molodensky’s theory is preferred to minimise uncertainties caused by discrepancies between the hypotheses introduced to compute gravity anomalies at the geoid. Additionally, the input data should be standardised; for instance, geometric and physical heights should refer to the same epoch and be given in the same tide system used in the determination of the regional (quasi-)geoid. However, the reliability of the vertical datum unification depends on the limitations of the regional gravity field modelling (see the evaluation of the Colorado experiment results in Sect. 4 or in Wang et al. (2021)); and the characteristics of the existing height systems (see, e.g.; Sánchez 2012; Angermann et al. 2016, Chapter 4.6), in particular the long-distance accumulation of systematic errors in levelling. A possibility to improve the results is an iterative approach: once a first estimation of δW_0i is available, the height-related observables (geopotential numbers, terrestrial gravity anomalies) are re-computed and used to iterate the GBVP solution. This loop should be repeated until sub-mm differences are obtained between consecutive iterations. With the final values of δW_0i, the local geopotential numbers can be referred to the global IHRS W₀ using Eq. (13). It should be noted that in the usual practice, the δW_0i values are added to the local (quasi-)geoid models to support the so-called GNSS/levelling technique at national or regional scales. For the transformation of the local height systems to the IHRF, the δW_0i have to be added to the local physical heights (or geopotential numbers). The relative accuracy between the IHRF geopotential numbers at levelling points will depend on the accuracy of the levelling itself; it would be very high between consecutive points and may suffer from the accumulation of systematic errors over long distances. The absolute accuracy of the IHRF geopotential numbers based on the vertical datum unification will depend on the accuracy of the input data considered for the determination of the δW_0i values. According to Rummel et al. (2014) or Sánchez and Sideris (2017), this accuracy may reach mean values from around ± 0.5 m² s⁻² (± 5 cm) in well-surveyed regions up to some decimetres (± 4.0 m² s⁻², equivalent to 40 cm) in sparsely surveyed regions. To improve the reliability of the vertical datum unification, it is very important to increase the accuracy and quality of the input data needed for the determination of δW_0i (see Sánchez and Sideris 2017). As the vertical datum unification is largely discussed in the existing literature, no further details are presented here.

6 Standards and conventions for the determination of IHRF coordinates

6.1 Basic standards

One key objective of the Colorado experiment is the identification of standards and conventions to ensure consistency between different computation methods as far as possible. Although some standardisation issues are still open (see Sect. 7.1), we have identified the following set of basic standards and conventions (cf. Sánchez et al. 2018):

6.1.1 Degree-zero

As long as IAG does not release a new geodetic reference system (GRS), GRS80 should be used for the regional (quasi-)geoid computation; i.e. for the computation of gravity anomalies, disturbing potential, ellipsoidal coordinates, geoid heights, height anomalies, etc. A zero-degree correction has then to be added to get to the latest GM value and to the conventional reference value W₀ (IAG Resolution 1, 2015). The zero-degree term for the disturbing potential is given by Eq. (6). Accordingly, the zero-degree term for the geoid and the quasi-geoid is:

$${N}_{0}=\frac{\left({GM}_{GGM}-{GM}_{GRS80}\right)}{{r}_{{P}_{0}}\cdot {\upgamma }_{{Q}_{0}}}- \frac{\Delta {W}_{0}}{{\upgamma }_{{Q}_{0}}}$$

(14)

$${\zeta}_{0}=\frac{\left({GM}_{GGM}-{GM}_{GRS80}\right)}{{r}_{P}\cdot {\upgamma }_{Q}}- \frac{\Delta {W}_{0}}{{\upgamma }_{Q}}$$

(15)

Please see Fig. 3 for the position of P, Q, P₀ and Q₀, and Eq. (7) for the value of ΔW₀. In this way, to compute the geoid or the quasi-geoid, the GBVP should be solved starting with degree two and then Eq. (14) or Eq. (15) should be added. In the Colorado experiment, the degree-zero term and the use of the WGS84 ellipsoid caused large differences among the first-iteration of geoid and quasi-geoid solutions. These discrepancies were reduced at the second iteration, when the computation groups adopted these conventions (Wang et al. 2021).

6.1.2 Mass centre convention

As mentioned in Eq. (5), the first-degree coefficients (C₁ = C₁₁ = S₁₁ = 0) are assumed to be zero to align the Earth’s centre of masses with the origin of the geometric coordinate system (ITRS/ITRF). The misalignment between the geocentre and the ITRF origin can be considered at the millimetre level according to the transformation from ITRF2014 to ITRF2008 at epoch 2010.0 (see Table 4 in Altamimi et al. 2016). The secular ITRF origin variation rate with respect to the geocentre is believed less than 1 mm a⁻¹. Thus, this assumption meets the sub-centimetre requirement.

6.1.3 Correction of uncertainties caused by the approximations needed to solve GBVP

As mentioned in Sect. 4, it is expected that the disturbing potential values obtained after solving the GBVP in a harmonic, linear, spherical, and constant radius approximation (see Eq. 5) are corrected by the effects removed before the computation. This means, at least, atmospheric effects, topographic effects, and ellipsoidal effects should be restored. Until now, there was lack of a convention on considering atmospheric effects while the topographic and ellipsoidal effects are generally taken into account.

6.2 Treatment of the permanent tide in the realisation of the IHRS

The GBVP can be solved with gravity field observables in the tide-free (non-tidal) or zero-tide system. Mean-tide gravity cannot be used as it includes the time average of the tide-generating potential generated by masses outside the boundary surface. These masses must be removed; otherwise, the disturbing potential T would not be a harmonic function. According to the IAG Resolution No. 16, 1983 (Tscherning 1984), the zero-tide system is to be used for the Earth’s gravity field and crust modelling. (For the crust, the zero-tide and the mean-tide systems are the same.) However, both systems, the tide-free and the zero-tide, are presently in use for gravity and crust. For the determination of IHRF geopotential numbers, we recommend to perform the computations in the zero-tide system and, afterwards, to convert the zero-tide potential coordinates to the mean-tide system.

In agreement with the IERS Conventions (e.g. Luzum and Petit, 2010), the time average W_T of the tide-generating potential is adopted to be:

$${W}_{T}\left(r,\, \phi \right)=A\cdot {\left(\frac{r}{a}\right)}^{2}\cdot \left({\mathrm{sin}}^{2}\,\phi -\frac{1}{3}\right)={A}^{^{\prime}}\cdot {\left(\frac{r}{a}\right)}^{2}\cdot {P}_{2}\left(\mathrm{sin}\, \phi\right)=A^{\prime\prime}\cdot {\left(\frac{r}{a}\right)}^{2}\cdot \stackrel{-}{{P}_{2}}\left(\mathrm{sin}\, \phi \right),$$

(16)

with $A=-2.9166\, {\mathrm{m}}^{2}\,{\mathrm{s}}^{-2}$, ${A}^{^{\prime}}=\frac{2}{3}A=-1.9444\, {\mathrm{m}}^{2}\,{\mathrm{s}}^{-2}$, $A^{\prime\prime}=\frac{A{^{\prime}}}{\sqrt{5}}=-0.86956\, {\mathrm{m}}^{2}\,{\mathrm{s}}^{-2}$. ${P}_{2}\left(\cdot \right)$ is the second-degree Legendre polynomial. $\stackrel{-}{{P}_{2}}\left(\cdot \right)$ is the second-degree fully normalised Legendre polynomial. The scaling parameter $a=\mathrm{6,378,137} \mathrm{m}$ is the GRS80 semi-major axis. r and $\phi$ are the geocentric radius and latitude, respectively. According to Ihde et al. (2008) and Mäkinen (2021), the factor A in Eq. (16) differs less than 0.0001 m² s⁻² from the corresponding term (known as M₀S₀) in the most recent time-harmonic expansions of the tide-generating potential by Hartmann and Wenzel (1995), Roosbeek (1996) and Kudryavtsev (2004, 2007).

${W}_{T}\left(r,\, \phi\right)$ can be written as a function of geodetic latitude φ and ellipsoidal height h over the GRS80 ellipsoid (Ihde et al. 2008; Sacher et al. 2009; Mäkinen, 2021):

$${\stackrel{-}{W}}_{T}\left(\varphi ,h\right)=\left(1+\frac{2h}{a}\right)\cdot \left(0.9722-2.8841\cdot {\mathrm{sin}}^{2} \varphi -0.0195\cdot {\mathrm{sin}}^{4} \varphi \right) \left[{\mathrm{m}}^{2}{\mathrm{s}}^{-2}\right].$$

(17)

This formula is valid at all points of the terrestrial topography. The maximum contribution (e.g. at the highest mountains) of the coefficient $\frac{2h}{a}=0.31\times {10}^{-6} {\mathrm{m}}^{-1}\cdot h$ to Eq. (17) is on the topography of the Earth less than 0.003 m²s^–2 (equivalent to 0.3 mm in height).

Geopotential numbers in the zero-tide system C_ZT are defined by

$${C}_{ZT}={W}_{0}-{W}_{ZT},$$

(18)

where W_ZT is the zero-tide potential. The generic definition of mean-tide geopotential numbers is

$${C}_{MT}={W}_{0}-\left({W}_{ZT}+{W}_{T}\right)={C}_{ZT}-{W}_{T},$$

(19)

In Eq. (19), the height dependence of W_T (first term in Eq. (17)), though small, would cause practical and theoretical difficulties if it were actually incorporated in a height system (Mäkinen 2017, 2019, 2021). Therefore, in the definition of the IHRF geopotential numbers ${C}^{IHRF}$, the height dependent W_T is conventionally replaced by W_T0, the value of W_T at the mean-tide geoid. Thus,

$${C}^{IHRF}:={C}_{ZT}-{W}_{T0}.$$

(20)

Since the distance between the geoid and the ellipsoid is maximally around 100 m, W_T0 in Eq. (20) can be calculated from W_T at the GRS80 ellipsoid

$${W}_{T0}\approx {\stackrel{-}{W}}_{T}\left(\varphi ,0\right)=0.9722-2.8841\cdot {\mathrm{sin}}^{2} \varphi -0.0195\cdot {\mathrm{sin}}^{4} \varphi \left[{\mathrm{m}}^{2}{\mathrm{s}}^{-2}\right].$$

(21)

In this manner, ${C}^{IHRF}$ is obtained from C_ZT using the datum-surface type transformation of Eq. (20) and the definition of ${C}^{IHRF}$ is similar to the mean-tide geopotential numbers used in national and continental levelling networks (Mäkinen 2017, 2019, 2021).

Equations (19) and (20) mean that the strategy to determine IHRF geopotential numbers ${C}^{IHRF}$ is to solve the GBVP in the zero-tide system to obtain the zero-tide potential W_ZT, then to calculate the zero-tide geopotential number C_ZT with Eq. (18), and finally, to get ${C}^{IHRF}$ from the zero-tide geopotential number using Eqs. (20) and (21). Since the height dependence of W_T has been eliminated in the definition of the IHRF geopotential numbers in Eq. (20), standard methods apply in the calculation of orthometric heights, normal heights and dynamic heights from ${C}^{IHRF}$ (see, e.g.; Hofmann-Wellenhof and Moritz 2005, Chapter 4).

For the solution of the GBVP in the zero-tide system, the GGM should be given in the zero-tide system and be evaluated at mean-tide = zero-tide coordinates (X^MT). As the ITRF coordinates are given in the conventional tide-free system (X^NT), the mean-tide positions have to be restored. The IERS Conventions provide correction formulas to be added to the 3-D Cartesian coordinates (see Eq. (7.14a) and Eq. (7.14b), Sect. 7.1.1.2 in Petit and Luzum 2010). They are given with a precision of 0.1 mm. Ihde et al. (2008) added a decimal to give the precision 0.01 mm. The radial component (positive outwards) is

$$\left[-120.61+0.12\cdot {P}_{2}\left(\mathrm{sin}\, \phi \right)\right]{\cdot P}_{2}\left(\mathrm{sin}\,\phi \right)\, \left[\mathrm{mm}\right],$$

(22)

and the transverse component (positive northwards) is

$$\left[-25.21-0.06\cdot {P}_{2}\left(\mathrm{sin}\,\phi\right)\right]\cdot \mathrm{sin}\,2\phi\,\left[\mathrm{mm}\right].$$

(23)

Equations (22) and (23) are the components of the vector $\Delta \overrightarrow{r}$ to be added to the ITRF tide-free positions (X^NT) to get mean-tide = zero-tide positions (X^MT).

Regarding the GGM, the coefficient of second-degree C₂₀ dominates the tidal system and defines in which tide system the potential is obtained. Some GGMs provide the coefficient C₂₀ in the tide-free (non-tidal) system $\left({C}_{20}^{NT}\right)$; other GGMs provide it in the zero-tide system $\left({C}_{20}^{ZT}\right)$. Their relationship is given by

$${C}_{20}^{ZT}={C}_{20}^{NT}+{k}_{20}\cdot \frac{{r}_{0}}{GM}\cdot {A}^{^{\prime}}\cdot {\left(\frac{{r}_{0}}{a}\right)}^{2}$$

(24)

where k₂₀ is the conventional Love number (k₂₀ = 0.30190, see Petit and Luzum 2010), GM is the geocentric gravitational constant, and r₀ is the distance scaling factor used in the generation of the tide-free GGM. The parameters A’ and a refer to Eq. (16). In practice, we can assume ${\left(\frac{{r}_{0}}{a}\right)}^{2}\approx 1$ with sufficient accuracy.

As mentioned above, we recommend to transform tide-free input quantities (GGM and coordinates) to the zero-tide and to solve the GBVP in the zero-tide system. However, many analysts prefer to solve the GBVP in the tide-free system. For the purposes of the IHRF, the tide-free GBVP results are considered intermediate computation products (W_prov) only. They do not have a conventional IHRF status, already because they depend on the specific tide-free reductions contained in the input quantities. Corrections must be added to W_prov to obtain the zero-tide potential W_ZT. If everything is done correctly, the obtained W_ZT will be the same as in an originally zero-tide computation.

If the potential is calculated with a tide-free GGM, the correction ${\Delta W}^{GGM}$ should be added to obtain the zero-tide potential. In spherical coordinates, this correction is given by:

$${\Delta W}^{GGM}\left(r,\, \phi \right)={k}_{20}\cdot {A}^{^{\prime}}\cdot {\left(\frac{{r}_{0}}{a}\right)}^{2}\cdot {\left(\frac{{r}_{0}}{r}\right)}^{3}\cdot {P}_{2}\left(\mathrm{sin}\, \phi\right),$$

(25)

where we can again assume ${\left(\frac{{r}_{0}}{a}\right)}^{2}\approx 1$. In ellipsoidal coordinates (with r₀ = 6,378,136.55 m, IERS Conventions 2010), this correction corresponds to:

$${\Delta}{\stackrel{-}{W}}^{GGM}\left(\varphi ,h\right)={k}_{20}\cdot \left(1-\frac{3h}{a}\right)\cdot \left(0.9722-2.8673\cdot {\mathrm{sin}}^{2} \varphi -0.0690\cdot {\mathrm{sin}}^{4} \varphi \right) \left[{\mathrm{m}}^{2}{\mathrm{s}}^{-2}\right].$$

(26)

If the position of the computation point is given in ITRF tide-free coordinates, the correction ${\Delta W}^{ITRF}$ must be added to obtain the potential at the mean-tide = zero-tide position:

$${\Delta W}^{ITRF}\left(\varphi \right)\approx \left(-{\gamma}_{0}\left(\varphi \right)\right)\cdot {h}_{T}\left(\varphi \right)=-0.5901+1.7475\cdot {\mathrm{sin}}^{2} \varphi +0.0273\cdot {\mathrm{sin}}^{4} \varphi \left[{\mathrm{m}}^{2}{\mathrm{s}}^{-2}\right],$$

(27)

γ₀ is the normal gravity at the ellipsoid surface and h_T(φ) is the projection of the vector $\Delta \overrightarrow{r}$ (see Eq. 22 and Eq. 23) on the ellipsoidal normal (see Ihde et al. 2008; Mäkinen 2021):

$${h}_{T}\left(\varphi \right)=60.34-179.01\cdot {\mathrm{sin}}^{2} \varphi -1.82\cdot {\mathrm{sin}}^{4} \varphi\,\left[\mathrm{mm}\right].$$

(28)

Equation (27) is accurate only to 0.01 m² s⁻², but it can be rescaled using (g/γ₀) pointwise to have an accuracy of 0.0001 m² s⁻² (Mäkinen 2021). g is the actual gravity at the computation point. In spherical coordinates, ${\Delta W}^{ITRF}$ can be obtained as a correction surface simply by computing the difference between the evaluation of the GGM at the mean-tide station positions (X^MT) [i.e. corrected by Eqs. (22) and (23)] and at the original tide-free positions (X^NT); see Mäkinen (2021).

The zero-tide geopotential is then obtained by summing the corrections of Eqs. (26) and (27):

$${W}_{ZT}={W}_{prov}+{\Delta W}^{ITRF}+{\Delta} {\stackrel{-}{W}}^{GGM}$$

(29)

W_prov is the intermediate potential product without the corrections. Depending on the computation scheme used to solve the GBVP (see Fig. 9), none or only one of the corrections in Eq. (29) may be required. If both corrections are needed, they can be combined setting h = 0 and k₂₀ = 0.30190 (IERS Conventions 2010) in Eq. (26):

Fig. 9

Scheme for the determination of IHRF geopotential values after solving the GBVP in the zero-tide system or in the tide-free (non-tidal) system. ${C}_{20}^{ZT}$: GGM coefficient of second degree in the zero-tide system; ${C}_{20}^{NT}$: GGM coefficient of second degree in the tide-free system; X^NT: ITRF position in the conventional tide-free system, X^MT: ITRF position in the mean-tide = zero-tide system, W_prov: intermediate potential value; W_ZT: zero-tide potential; C_ZT: geopotential value in the zero-tide system; ${C}^{IHRF}$: IHRF geopotential number (in the mean-tide system); ${\Delta\stackrel{-}{W}}^{GGM}$ and ${\Delta W}^{ITRF}$: corrections to the intermediate potential values to obtain the zero-tide potential (see Eqs. 26, 27, and 30)

$${\Delta W}^{ITRF}+{\Delta} {\stackrel{-}{W}}^{GGM}=-0.2966+0.8819\cdot {\mathrm{sin}}^{2}\varphi +0.0065\cdot {\mathrm{sin}}^{4} \varphi \left[{\mathrm{m}}^{2}{\mathrm{s}}^{-2}\right].$$

(30)

Finally, the zero-tide geopotential number (Eq. 18) is computed using $W_{ZT}$ from Eq. (29) and the IHRF mean-tide geopotential number ${C}^{IHRF}$ is obtained with Eq. (20).

More information about the formulas in this section and their background can be found in Mäkinen (2021). Reviews about the treatment of the permanent tide in Geodesy are provided by Ekman (1989, 1996), and Mäkinen and Ihde (2009), among others.

7 A first strategy for the establishment of the IHRF

The establishment of the IHRF demands a reference network and the determination of IHRF geopotential values at the stations belonging to that reference network. In this section, we concentrate on the action plans needed for the computation of suitable IHRF coordinates based on the analysis described in Sects. 3–5; the basic criteria for the IHRF station selection; and a proposal about the organisational and operational infrastructure required to ensure the long-term sustainability, availability, and reliability of the IHRF.

7.1 Strategy for the determination and evaluation of IHRF coordinates depending on the data availability

In Sect. 2, we mentioned that the overall target accuracy for the stationary IHRF physical coordinates (geopotential numbers referring to the conventional W₀ value) is ± 3 × 10⁻² m² s⁻² (about ± 0.003 m). However, as this accuracy is very optimistic, we concentrate for the moment on evaluating the possibility of reaching an accuracy at the ± 0.1 m² s⁻² (± 0.010 m) level. According to the experimental results in this study and other related studies, we can classify the determination of potential values in three main scenarios:

• (a) Regions without (or with very few) surface gravity data,

• (b) Regions with some surface gravity data, but with poor data coverage or unknown data quality,

• (c) Regions with good surface gravity data coverage and quality.

The only option to determine potential values in regions with poor or inexistent surface gravity data (scenario (a)) is the use of GGM-HRs. We can expect mean accuracy values around the ± 4 m² s⁻² (± 0.4 m) level as this accuracy is guaranteed by the satellite component of the GGM. In comparison with EGM2008, it is possible to increase the accuracy about 30%, if the GGM-HRs consider GRACE and GOCE data, as well as new surface data or synthetic gravity signals inferred from topographic models (see Table 4 and Fig. 6). Since the new model EGM2020 will include much more new surface gravity data than the GGMs considered in this study, it is expected that the gravity signal in previous poorly covered regions would be better represented, reaching an accuracy level around ± 1 m² s⁻² (± 0.1 m). However, this depends on the distribution of the new gravity data sets included in EGM2020, as they contribute to improve the GGM accuracy only in the covered regions; i.e. new gravity data sets over Europe or the USA will hardly contribute to improving the gravity signal in Africa. For this improvement, it would be necessary to collect and to include in the EGM2020 new gravity data sets in Africa. In any way, it should be clear that, if no regional gravity data are available to be included in a GGM-HR or to determine a regional gravity field model, the best possible accuracy for the IHRF coordinates will be around ± 4 m² s⁻² (± 0.4 m), or even worse in regions with strong topography gradients. So far, this is what we can get. However, to avoid multiple potential values provided by different GGM-HRs at the same point (see Sect. 3), it is necessary to select one GGM-HR as reference model for the computation of the IHRF coordinates at stations located in regions belonging to scenario (a). Improved GGM-HR can be taken into consideration, when a new solution for the IHRF is released (see Sect. 7.3).

In regions belonging to scenarios (b) and (c), the IHRF coordinates are to be determined using the high-resolution regional gravity field modelling; i.e. the solution of a GBVP based on the combination of satellite gravity data (GGM), surface gravity data, and topographic effects. The essential difference between these two scenarios is the gravity data distribution and quality. While in scenario (c) it is possible to infer the potential values from precise (quasi-)geoid regional models (like in the Colorado experiment), in scenario (b) the reliability of the existing (quasi-)geoid models is poor and additional gravity surveys around the IHRF reference stations may be performed to increase the accuracy of the geopotential numbers computed at those specific stations. This is like a pointwise improvement of the regional gravity field modelling. The recommendation is to perform gravity surveys around the IHRF station(s) with a spatial resolution between 2 and 4 km (depending on the relief) and within a radius between 100 and 200 km. These data are then used to solve a GBVP estimating the disturbing potential at the IHRF station(s). This recommendation is just to improve the accuracy of the potential coordinates at the IHRF stations. If a (quasi-)geoid model of high resolution is needed; e.g. for practical GNSS/levelling, then the gravity data distribution and coverage should be extended to the complete area of interest and not only around the IHRF stations. In the pointwise determination of potential values, possible truncation errors caused by the omission of the gravity field signal outside the 100 km to 200 km radius around the IHRF station should be minimised by employing a GGM to model the long wavelengths of the gravity field. Similarly, special care should be given to possible low frequency errors rising from poorly modelled terrain effects; therefore, these effects should be estimated using a topography model extended by at least 40% to 50% of the area covered by the gravity data in all directions. To detect and assess the magnitude of these possible errors, it is necessary to have supplementary, independent data for the evaluation of the potential differences, the best option here being the levelling with gravity reductions co-located with GNSS positioning. This evaluation may be done in an absolute and in a relative way. The evaluation of (quasi-)geoid models is based on the discrepancies of absolute heights [h − H − N]. Hence, we call it absolute way of comparison. The absolute comparison is influenced by the different reference levels of the existing height systems and the accumulation of systematic errors in levelling over a long distance, which demand some data manipulations to obtain reliable comparison results. One way to reduce this is the comparison of potential differences inferred from the GBVP-based (or GGM-based) potential values with the potential differences obtained from levelling (corrected by gravity effects) at various lengths of baselines; see Tables 3 and 4 and Figs. 5 and 6. In the Colorado experiment, we use a 350-km-long levelling line, which seems to be appropriate to identify systematic biases of low degree. However, the extension of the levelling line(s) for the evaluation of the gravity field models may be shorter (or longer) in regions with smoother (or stronger) topography. Of course, if gravity surveys are possible and GNSS/levelling co-location points are available, IHRF stations belonging to scenario (a) can be handled as scenario (b) stations.

Scenario (c) represents the regions with very good conditions like those evaluated in the Colorado experiment. Here, not only the input data are of high quality, but also the colleagues processing the data have large experience in the regional gravity field modelling. Therefore, the results delivered by 13 different processing procedures present a quite good agreement, and they suggest that the ± 0.1 m² s⁻² (± 0.010 m) accuracy level could be reachable in the next future. From the analysis described in Sect. 4, we identify the spectral combination of the input gravity data and the modelling of terrain effects as the main sources of discrepancy between the Colorado solutions. In this frame, we present in the following some considerations aiming at reducing possible differences caused by these two aspects.

Regarding the spectral combination, when surface gravity data are to be combined with a GGM, the very accurate long wavelength gravity signal provided by satellite gravimetry (GRACE, GOCE) should be retained, and the surface gravity data should mainly contribute to the shorter wavelengths. To achieve spectral consistency, the integral kernels needed to solve the GBVP have to be accordingly modified to optimise the spectral transition from the satellite-only GGM to the surface gravity anomalies. Otherwise, the results (e.g. the disturbing potential) will present long wavelength distortions. In the Colorado experiment, different strategies are applied to modify the Stokes function, and they deliver different results for the same points (see Fig. 4). For instance, solutions based on a Wong–Gore kernel modification present pointwise discrepancies up to 1.2 m² s⁻² (0.12 m); solutions based on a least-squares modification with additive corrections present discrepancies up to 1 m² s⁻² (0.1 m). A standardisation of the spectral transition would definitely improve the agreement between different regional gravity field models. However, this seems to be inappropriate as the choice of the spectral transition depends on the quality of the surface gravity data in the area of study. With surface gravity data of low precision, the satellite-only GGM should be utilised up to higher degrees, and vice versa. Thus, the spectral transition should be tuned to the regional/local situation, and this aspect is lost with a fixed standardisation. On the other hand, to select one kernel modification as standard (for instance, the Wong–Gore modification) would close the door for other methods like stochastic kernel modifications (spectral modification, least-squares modification) and to LSC and SRBF approaches, which, according to the Colorado experiment results, have proved to be suitable for the precise regional gravity field modelling. Taking these arguments into account, a standard in this regard could be expressed in such a way that the satellite-only GGM should be fully trusted up to certain degree (for instance, 180), and it should not be trusted at all (approximately) above another higher degree (for instance, 250). Complementary, there should be a gradual transition in between. However, the selection of low and high modification degrees may vary from region to region depending not only on the surface gravity data quality and coverage, but also on the GNSS/levelling data used for the evaluation of the different kernel modifications. Thus, a standardisation in this regard seems to be also unfeasible. Here we mention the use of a satellite-only GGM to avoid uncertainties produced by possible long-wavelength systematic biases contained in the surface gravity data employed for the determination of GGM of higher degree. However, a combined GGM could be also used, if the GGM constrains the low-degree components and the maximum kernel modification degree is chosen so that the satellite signal dominates the disturbing potential below the chosen limit. A significant advantage of using a combined GGM is reducing edge effects and truncation errors.

Ihde et al. (2017) propose to select a certain (conventional) satellite-only GGM together with a specified maximum degree for the IHRS realisation. The main argument for this is of course that the resulting regional models will become more consistent. An argument against is the fact that satellite-only GGMs are frequently updated (more for data reprocessing matters than for availability of new data, see Sect. 3), and regional/national gravity field models will almost certainly be computed using the best model available at the time of computation. An alternative could be to update the specified IHRS satellite-only GGM with specified maximum degree every now and then. This can be done for every new IHRF release (see Sect. 7.3).

Regarding the handling of topographic effects, the most applied procedure is the residual terrain model (RTM) reduction (see e.g. Forsberg 1984; Forsberg and Tscherning 1981, 1997). It has the advantage that the effects of the short gravity field wavelengths are to be evaluated up to some distance from the computation point, as the effects for zones at larger distances are assumed to be negligibly small. The effects of the masses between the topographic surface and a smooth reference elevation surface are usually determined using a prism integration of either positive or negative mass density, normally 2,670 kg m⁻³ as agreed in the Colorado experiment. Other mass density values can be also regionally taken into account (see e.g.Denker 2013), especially if synthetic gravity data are used to improve the gravity signal. The results, however, depend on the resolution of the topography model (for the selection of the prism size), the resolution of the reference elevation surface, the distance between the computation point and the prisms, and the so-called harmonic correction. This correction is necessary for those points below the reference elevation surface (inside the masses), where the potential is not harmonic. Although some approximations exist to estimate this harmonic correction, it is still a critical aspect of the RTM procedure and has to be further studied (e.g. Forsberg and Tscherning 1997; Omang et al. 2012; Rexer et al. 2018). In the Colorado experiment, different elevation models (SRTM V4.1 and Earth2014) and different parameters (prism size, reference topography resolution, harmonic corrections, integration radii, computation approach) have been applied, and for the moment, we are not able to conclude how much these differences are responsible for the discrepancies between the results provided by the contributing solutions. Thus, the handling (and results) of the topographic effects within the Colorado experiment has to be further analysed. We suspect that the large variety of options to be considered in the RTM computation will surely prevent us from introducing a standardisation in this regard. Consequently, our recommendation is to identify the best RTM configuration by contrasting the results with supplementary, independent data, being precise levelling co-located with GNSS the best option.

7.2 Strategy to improve the input data required for the determination of IHRF coordinates

To achieve everywhere similar accuracy in the determination of IHRF geopotential numbers as that obtained in the Colorado experiment, it is necessary to reproduce as much as possible the data distribution and quality available for that experiment. It is clear that the GGMs cover the complete Earth and are usable worldwide. To assess their reliability, commission errors may be inferred from the covariance matrix usually published with the GGM coefficients (see Ince et al. 2019), and omission errors can be predicted using the variance model of Tscherning and Rapp (1974) or Kaula (1966). However, as these error estimations are very optimistic, it is recommended to perform some comparisons with levelling of high precision co-located with GNSS.

For the surface gravity data and terrain models, it is necessary to follow the same criteria applied for the determination of (quasi-)geoid models of high resolution. The main general requirements are:

• (a) The most important aspect is to fill gravity data gaps, initially around of the sites selected to be IHRF reference stations, and ideally over the complete region/country requiring a precise (quasi-)geoid model.

• (b) The required resolution for the surface gravity data is around 2–4 km depending on the relief (in mountain areas the gravity observations have to be closer than in flat areas). A good possibility to increase the data coverage (especially on the top of the mountains or in remote areas like jungles or deserts) is airborne gravimetry; however, this technique is very expensive and it may not be available everywhere. On the other hand, relative terrestrial gravimetry is very time-consuming, and thus, also expensive.

• (c) Homogeneously distributed gravity points around the IHRF reference stations up to 100–200 km (~ 1°–2°) are desired. These gravity data may exist or have to be observed. If old gravity data sets are used, they should be checked, especially for systematic errors and quality of the height. Considering that the elevation models used to estimate the topographic effects are given in the ITRF, the quality of the gravity points’ horizontal coordinates also plays an important role in areas with strong topographic gradients. In many cases, the old gravity values refer to local geodetic datums, which present displacements up to 500 m with respect to the ITRF. This may represent a vertical dislocation of several hundred metres between gravity points and terrain model (e.g. the Andes or the Himalaya) and the RTM corrections may be misrepresented by large systematic effects. According to Denker (2013), the minimum required accuracies for gravity values and coordinates should be about ± 0.15 mGal for gravity, 0.3 m for heights, and 1.0 m for the horizontal coordinates. To minimise systematic errors of low degree in the gravity data sets, the gravity reference network underlying the regional gravimetry should include or be connected to absolute gravity reference stations.

• (d) The best and most expensive alternative is of course to make new gravity measurements, which should be well connected to a reliable modern gravity reference frame, preferably to the new International Gravity Reference Frame (IGRF, Wziontek et al. 2021). The positions of the new gravity data should be determined with GNSS.

• (e) For the modelling of terrain effects, topographic models should have spatial resolutions of about 100 m (or better) in mountainous areas and about 1000 m (or better) in flat areas. In this regard, if national or regional topography models of high resolution are not available, global models of public domain like SRTM or Earth2014 may be used. However, some evaluations are required to fill data gaps and to check gross errors in the same way that Ahlgren et al. (2018) did for the Colorado area.

7.3 Strategy for the IHRF station selection

According to Ihde et al. (2017), the reference frame realising the IHRS should be based on a worldwide homogeneously distributed set of reference stations including a core network and regional/national densifications. The core network has to be well materialised and maintained to ensure sustainability and long-term stability of the reference frame. The regional and national densifications are to provide local accessibility to the global frame. The IHRF reference network should be.

• (a) co-located with fundamental geodetic observatories (Appleby et al. 2015) and reference stations of the IGRF (Wziontek et al. 2021) to support the connection between geometrical (geocentric Cartesian coordinates X) and physical (potential W and gravity g) reference systems, as well as with the time realisation (reference clocks);

• (b) materialised by GNSS continuously operating reference stations to monitor and detect deformations of the reference frame; in this case, stations belonging to the ITRF and the regional reference frames like SIRGAS, EPN, APREF, etc., are preferred;

• (c) connected with the existing vertical reference frames to facilitate the vertical datum unification into the IHRF;

• (d) well surveyed with availability of surface gravity data around the IHRF reference stations for high-resolution gravity field modelling (i.e. precise estimation of W).

Based on these criteria, a preliminary station selection for the IHRF was performed including primarily the core stations of the Global Geodetic Observing System (GGOS; Appleby et al. 2015), ITRF sites with at least two co-located space techniques (VLBI, SLR, DORIS and GNSS), and GNSS stations belonging to the fiducial network of the International GNSS Service (IGS, Johnston et al. 2017). Afterwards, regional and national experts were asked to evaluate whether the preliminary selected sites are suitable to be included in the IHRF (mainly if gravity data are available or if there are possibilities to survey them), and to propose additional geodetic sites to improve the density and distribution of the IHRF stations in their regions/countries. After the feedback from the regional/national experts, the first approximation to the IHRF reference network is based on about 170 stations (Fig. 10; Sánchez and Barzaghi 2020). Currently, this station selection is regularly refined in agreement with changes/updates of other geodetic reference frames (ITRF and IGRF and their densifications). This network is the basis for the determination of a preliminary IHRF solution as next step in the implementation of the IHRS. Afterwards, regular updates of the IHRF, probably synchronised with the release of new ITRF solutions, should be implemented to take account for new stations, coordinate changes with time (Ẋ, Ẇ), and improvements in the estimation of X and W (new observations, better standards, better models, better computation algorithms, etc.).

Fig. 10

IHRF reference network (as of October 2020)

Regional and national densifications of the global IHRF reference network may be established in accordance with the particular local needs and the distribution of the GNSS reference stations. Main requirement is however the availability of surface gravity data of high quality. If regional (quasi-)geoid models of high resolution are available, an IHRF reference station may be installed every 50 km or 100 km. If the region is not well surveyed and additional efforts are necessary to collect surface gravity data, the mean distance between IHRF stations may be increased up to 500 km. According to Sect. 7.1, the IHRF physical coordinates should be based on the gravity field modelling of high resolution. If it is not possible, the adopted GGM-HR may be used. For higher resolutions and applications requiring accuracies at the millimetre level, high-precise levelling is recommended. In the case, the nearest IHRF station (or stations) should be used as fiducial point to process the levelling data. In this way, levelling would be utilisable at short distances (up to about 100 km), where the accumulation of systematic errors is not a critical issue. Large levelling networks covering entire countries would not continue being necessary. This option is of course a decision of the national agencies responsible for the geodetic reference frame matters. The regional and national IHRF densifications would refer to a specific IHRF release, including station positions referring to a certain epoch and station position variations with time. This is the same procedure used for the release of updated versions of the ITRF.

7.4 Strategy to ensure the usability and long-term sustainability of the IHRF

In scientific applications, the ITRF is the best available platform for the determination of geometric coordinates (positions, trajectories, velocities). It is well accepted and widely used. In practical and non-geodetic applications, the ITRF is automatically accepted and used by everyone employing GNSS techniques and ITRF-based satellite orbits. Regional and national densifications of the ITRF have been necessarily established, because GNSS is today the primary technique applied for the establishment of geometric reference frames. Discussions about a gravity field-based world height system or global vertical reference system like the IHRS started 30 years ago, but its realisation became possible for the first time after GRACE and GOCE. However, the accuracy of physical coordinates (geopotential numbers) based on the gravity field modelling (GGM or solution of the GBVP) is one to two levels worse than in the ITRF. In applications requiring high accuracy, geodetic levelling continues being the appropriate technique. Consequently, to achieve a wide acceptance of the IHRS/IHRF, the accuracy of IHRF physical coordinates has to be drastically improved. In the best case, the IHRF will be involuntarily accepted and used by everyone using GNSS in combination with a consistent gravity field (geopotential) model of high resolution. Nevertheless, the existing physical height systems will most probably continue in daily use, while the IHRS/IHRF will be utilisable in global change studies and transnational/transregional applications requiring the consistent connection of the local height systems.

To ensure the maintenance and availability of the IHRF on a long-term basis, it is necessary to install an operational and organisational infrastructure, being the IGFS the self-evident hosting organisation. For instance, one of the main lessons learned of the Colorado experiment is the necessity of assessing the reliability of the IHRF geopotential numbers estimated by national/regional experts contributing to the establishment of the IHRS. This assessment may be performed in different ways (see green boxes in Fig. 11):

• (a) By installing auxiliary stations close to the core IHRF stations connected by levelling of high precision to have independent data to compare the potential differences obtained with the GBVP solution, in a similar way like the GSVS2017 profile (see Sect. 4.3).

• (b) By ensuring redundancy in the computation of IHRF geopotential numbers. For this purpose, the IGFS could install IHRF analysis centres or associates that are able to determine geopotential numbers using input data provided by the national/regional computation centres, and then, IGFS and local results can be compared.

• (c) By calibration of the computation methods used by national/regional experts. For this purpose, the national/regional experts determine potential values using a certain set of input data and their results are compared with results obtained by other processing approaches (like in the Colorado experiment). In this case, test input data and results should be managed by the IGFS.

In addition to the evaluation of the IHRF coordinates, the operational infrastructure for the IHRS/IHRF has to take care of (cf. Fig. 11):

• (a) Maintenance of the IHRF reference network in accordance with the GGOS Bureau of Networks and Observations (GGOS-BNO), which keeps the updated GGOS core site catalogue, and the coordinators of the reference networks for the ITRF, IGRF, and their regional densifications, usually kept by the IAG regional sub-commissions for reference frames and gravity field modelling. This activity should be faced by the IHRF reference network coordination (see blue boxes in Fig. 11).

• (b) Maintenance of a catalogue with the conventions and standards needed for the IHRF. This should consider a harmonisation with the conventions and standards kept by the GGOS Bureau of Products and Standards (GGOS-BPO), the IERS Conventions (for the determination of the ITRF), and the standards applied in the IGRF and the global gravity field modelling. This task should be carried out by the IHRF conventions’ coordination (see pink boxes in Fig. 11).

• (c) The national/regional agencies/entities contributing to the realisation of the IHRF in their regions may be declared as IHRF national/regional computation centres (dark blue box in Fig. 11). The input data would then be provided by existing IAG gravity field services and local data centres; e.g. GGM are provided by ICGEM and surface gravity data are provided by the Bureau Gravimétrique International (BGI) and refined/complemented with gravity data available at local data centres. In a similar way, one can proceed with digital elevation models (see violet box in Fig. 11).

• (d) In an ideal data flow scheme, the national/regional IHRF computation centres would provide the IGFS with the following products (cyan box in Fig. 11): potential values at the IHRF reference stations; vertical datum unification parameters (to transform the existing local height systems to the IHRF); mean gravity anomalies or disturbances (without violating data confidentiality but contributing to the determination of improved GGMs); and regional (quasi-)geoid models of high resolution. The mean gravity anomalies (or disturbances) and the (quasi-)geoid models would be then managed by BGI and the International Service for the Geoid (ISG), respectively. For the combination of the regional/national solutions, validation, storage, management, and servicing of potential values at IHRF stations and vertical datum parameters, the IGFS would have to establish a new element, which could be called IHRF product centre (see magenta boxes in Fig. 11).

Fig. 11

IHRF realisation, maintenance, and servicing within the IGFS

8 Closing remarks

On the basis of this paper, we realise that the implementation of a global reference system for physical heights as the IHRS is a big challenge and requires the support of a wide scientific community. Thus, the installation of the IHRS/IHRF is only possible within a global and well-structured organisation like the IAG. A lot of work is required. A source of inspiration is the ITRF. If we compare the initial version of the ITRF (ITRF0; Boucher and Altamimi 1989) with the most recent one (ITRF2014; Altamimi et al. 2016), the huge improvement is evident. The ITRF0 included station positions only (station velocities were taken from a geological-geophysical plate tectonic model), there were as many coordinate sets for each station as unsolicited analysis centres processing that station, the conversion to ellipsoidal coordinates used arbitrary values for the ellipsoid constants (the GRS80 was not always considered), station positions presented a precision from ± 11 to ± 60 mm, etc. The ITRF2014 is totally different: standardised computation, various processing and combination centres, station positions, and motions with accuracy at the millimetre level. Following this example, we are confident that once we have implemented a first approximation to the IHRF, it can be improved by considering more and more details that at the beginning may represent unsolvable obstacles.

In the near future, we aim at comparing the Colorado results at different stages of the computation. In this study, we compare the potential values inferred from the very final (quasi-)geoid models. In the next iteration, we have to examine in detail the treatment of input data and especially, the processing of the airborne gravity data, the handling of terrain effects, and the relative weighting of GGM, terrestrial gravity data, and airborne gravity data. We need to quantify how much of the discrepancies between the solutions is related to the treatment of the data, and how much is related to the different approaches. The latter is of particular importance if we go for a worldwide distributed processing of potential data (i.e. national/regional processing centres computing IHRF physical coordinates). This should be complemented with appropriate strategies for error analysis and validation to infer reliable accuracy values for the potential coordinates. Simultaneously, we will compute an initial quasi-stationary solution for the IHRF reference network shown in Fig. 10 following the strategy described in Sect. 7.1. Once this quasi-stationary solution is available, we have to identify a suitable methodology for the determination and modelling of the potential coordinate changes with time.

Appendix 1. Processing strategies utilised in the Colorado experiment

In the following, we provide the main characteristics of the (quasi-)geoid models contributing to the Colorado experiment (cf. Wang et al. 2021, Appendix 2). They are identified with sequence numbers that are used in the comparisons presented in Sect. 4.

• Solution 1: Computed at the School of Earth and Planetary Sciences, Curtin University (Curtin), Perth, Australia. Processing details in Claessens and Filmer (2020). Scalar-free GBVP after Molodenky’s Theory using 1D-FFT Stokes integration with deterministically modified integral kernel based on GNSS/levelling data. RCR procedure with the GGM xGEOID17B (Wang et al. 2017), terrestrial and airborne gravity and topography reductions based on the SRTM v.4.1 model.

• Solution 2: Computed at the Technical University of Denmark (DTU), Copenhagen, Denmark. Processing details in Forsberg and Tscherning (1981), Forsberg (1987), and Forsberg and Featherstone (1998). Scalar-free GBVP after Molodenky’s Theory using spherical FFT with a Wong–Gore modified Stokes function for a low-wavelength cut-off transition band at harmonic degrees 180–190. RCR procedure with the GGM XGM2016 (up to degree 360), terrestrial and airborne gravity, and RTM terrain reductions from an averaged 9″ SRTM digital elevation model.

• Solution 3: Computed at the National Geodetic Survey (NGS), Silver Spring, MD, USA. Processing details in Wang et al. (2020). Scalar-free GBVP after Molodensky’s Theory with a Wong–Gore modification of the Stokes function. RCR procedure with the GGM xGEOID17B, terrestrial and airborne gravity, and topography reductions based on the SRTM v.4.1 model.

• Solution 4: Computed at the Laboratory of Gravity Field Research and Applications, Department of Geodesy and Surveying, Aristotle University of Thessaloniki (AUTh), Greece. Processing details in Grigoriadis et al. (2021). Scalar-free GBVP after Molodensky’s Theory with a 1D-FFT Stokes integration using a Wong–Gore kernel modification based on GNSS/levelling data. RCR procedure with the GGM XGM2016 (up to degree 719), terrestrial and airborne gravity, and RTM terrain reductions from the model SRTM v.4.1 using the spectral approach proposed in Rexer et al. (2016).

• Solution 5: Computed at the Chinese Academy of Surveying and Mapping (CASM), Beijing, China. Processing details in Jiang and Wang (2016). Scalar-free GBVP after Molodensky’s Theory using a least-squares modification of Stokes’ formula with additive corrections (LSMSA) algorithm (Sjöberg 2003, 2005). RCR procedure using the GGM GOCO05S (Mayer-Gürr et al. 2015) and terrestrial and airborne gravity.

• Solution 6: Computed at the Istanbul Technical University, Gravity Research Group (ITU), Istanbul, Turkey. Processing details in Işık et al. (2021). Scalar-free GBVP after Molodensky’s Theory using an unbiased version of least-squares modification of Stokes’ formula with additive corrections (LSMSA) algorithm (Sjöberg 2003). RCR procedure using the GGM XGM2016 (up to degree 719) and terrestrial and airborne gravity.

• Solution 7: Computed at the University of Gävle, Lantmäteriet (Swedish mapping, cadastral and land registration authority) and Royal Institute of Stockholm (KTH), Sweden. Processing details in Ågren et al. (2009). Scalar-free GBVP after Molodensky’s Theory with a least-squares modification of Stokes’ formula with additive corrections (LSMSA). RCR procedure using the GGM GOCO05S (up to degree 240) and terrestrial and airborne gravity.

• Solution 8: Computed at the New Technologies for the Information Society, University of West Bohemia, Pilsen, Czech Republic and the Faculty of Geodesy, University of Zagreb, Zagreb, Republic of Croatia (NTIS-GEOF). Processing details in Varga et al. (2021). Scalar-free GBVP after Molodensky’s Theory with a least-squares modification of Stokes’ formula with additive corrections (LSMSA). RCR procedure using the GGM XGM2016 (up to degree 500) and terrestrial and airborne gravity.

• Solution 9: Computed at the Deutsches Geodätisches Forschungsinstitut, Technical University of Munich (DGFI-TUM), Germany. Processing details in Liu et al. (2020). Fixed GBVP with spherical radial basis functions (SRBF). RCR with the GGM XGM2016, terrestrial and airborne gravity, and topography effects from the models dV_ELL_Earth2014 and ERTM2160.

• Solution 10: Computed at the Institute of Astronomical and Physical Geodesy (IAPG), Technical University Munich, Germany. Processing details in Willberg et al. (2019, 2020). Fixed GBVP with a one-step residual least-squares collocation, including full covariance information from the GGM. RCR procedure using XGM2018 (a slightly modified version of XGM2016), terrestrial and airborne gravity, and the models dV_ELL_Earth2014 and ERTM2160 for the topographic induced gravity.

• Solution 11: Computed at the Politecnico di Milano (Polimi), Italy. Processing details in Grigoriadis et al. (2021). Scalar-free GBVP after Molodensky’s Theory using LSC. RCR procedure with the GGM XGM2016 (up to degree 719), terrestrial and airborne gravity, and RTM terrain reductions from the model SRTM v.4.1 using the spectral approach proposed in Rexer et al. (2016).

• Solution 12: Computed at the Geospatial Information Authority of Japan (GSI), Tsukuba, Japan. Processing details in Matsuo and Forsberg (2021). Scalar-free GBVP after Stokes’ Theory using Helmert’s second method of condensation of the topography and the hybrid Meissl-Molodensky modified spheroidal Stokes kernel. RCR procedure with the GGM XGM2016 (up to degree 719), terrestrial and airborne gravity, and a RTM correction based on the SRTM v.4.1 model. Transformation from N to $\zeta$ using the Bouguer anomaly-based term.

• Solution 13: Computed at the Canadian Geodetic Survey (CGS), Nature Resources Canada, Ottawa, Canada. Processing details in Huang and Véronneau (2013). Scalar-free GBVP after Stokes’ Theory with a modified degree-banded Stokes kernel. Spectral combination of the GGM xGEOID17B (up to degree 150 from where it goes into transition with the surface gravity data up to degree 210) and terrestrial and airborne gravity (between degrees 210 and 790 with smooth transition at each end) with SRTM v4.1 model (to complete the geoid frequencies up to degree 10,800). Transformation from N to $\zeta$ applying the usual the Bouguer anomaly-based term and a refined approximation including the terrain correction to the Bouguer plate (see Sect. 4.4).