Abstract
Currently, Global Navigation Satellite Systems (GNSS) do not contribute to the realization of origin and scale of combined global terrestrial reference frame (TRF) solutions due to present system design limitations. The future Galileo-like medium Earth orbit (MEO) constellation, called “Kepler”, proposed by the German Aerospace Center DLR, is characterized by a low Earth orbit (LEO) segment and the innovative key features of optical inter-satellite links (ISL) delivering highly precise range measurements and of optical frequency references enabling a perfect time synchronization within the complete constellation. In this study, the potential improvements of the Kepler constellation on the TRF origin and scale are assessed by simulations. The fully developed Kepler system allows significant improvements of the geocenter estimates (realized TRF origin in long-term). In particular, we find improvements by factors of 43 for the Z and of 8 for the X and Y component w. r. t. a contemporary MEO-only constellation. Furthermore, the Kepler constellation increases the reliability due to a complete de-correlation of the geocenter coordinates and the orbit parameters related to the solar radiation pressure modeling (SRP). However, biases in SRP modeling cause biased geocenter estimates and the ISL of Kepler can only partly compensate this effect. The realized scale enabling all Kepler features improves by 34% w. r. t. MEO-only. The dependency of the estimated satellite antenna phase center offsets (PCOs) upon the underlying TRF impedes a scale realization by GNSS. In order to realize the network scale with 1 mm accuracy, the PCOs have to be known within 2 cm for the MEO and 4 mm for the LEO satellites. Independently, the scale can be realized by estimating the MEO PCOs and by simultaneously fixing the LEO PCOs. This requires very accurate LEO PCOs; the simulations suggest them to be smaller than 1 mm in order to keep scale changes below 1 mm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Origin and scale together with orientation are the datum defining parameters of global terrestrial reference systems (TRS). The origin is defined in the long-term mean center of mass for the whole Earth’s system (solid Earth and fluid envelope). The SI (Système International d’unités) meter is the unit of length and the scale is consistent with the Geocentric Coordinate Time (TCG). The orientation coincides with the orientation defined by the Bureau International de l’Heure (BIH) at the reference epoch 1984.0 (IERS Conventions 2010, Petit and Luzum 2010). The realization of the TRS is the terrestrial reference frame (TRF), for which the datum has to be properly realized by the space geodetic techniques.
Global TRFs are usually determined by a combination of four space geodetic techniques: Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), Global Navigation Satellite Systems (GNSS), Satellite Laser Ranging (SLR), and Very Long Baseline Interferometry (VLBI). Since each technique has particular strengths and weaknesses resulting in a different sensitivity and suitability for the TRF-defining parameters (Sillard and Boucher 2001), only two techniques contribute currently to the datum realization, that are SLR and VLBI.
The origin of the International Terrestrial Reference Frame (ITRF) is realized by SLR alone and the scale by SLR and VLBI. The unambiguous direct SLR measurements have a high sensitivity to the geocenter which is in long-term the realized origin of the ITRF. Furthermore, the non-gravitational forces have much less impact on the SLR satellites with their cannonball shape than on GNSS satellites, e.g., Meindl et al. (2013). However, it should be mentioned that special attention has to be given to range biases, satellite center-of-mass errors and signature effects affecting the SLR measurements as well as to the rather inhomogeneous global station distribution. In addition to the unique strength of VLBI to determine all Earth orientation parameters, the scale can be considered as unambiguous. The celestial reference frame of VLBI provides a stable space segment consisting of only two angles (right ascension and declination of extra-galactic radio sources) with no distance measurements to the space targets or between them. It is therefore independent of the gravitational parameter GM (G—gravitational constant, M—mass of the Earth), which has direct impact on the scale of any satellite technique. In recent ITRF solutions, including the latest ITRF2014 (Altamimi et al. 2016), GNSS and DORIS do not contribute to the realization of the origin and the scale. Nevertheless, DORIS and especially GNSS are essential for the densification of the global networks and for the combination of all four techniques.
The absolutely essential requirements of 1 mm accuracy and 1 mm/decade long-term stability specified by the Global Geodetic Observing System (GGOS, Gross et al. 2009) are not fulfilled yet. The current estimated origin accuracy of ITRF2014 is 3 mm w. r. t. ITRF2008 (Altamimi et al. 2011) and the scale shows a discrepancy between SLR and VLBI of 1.37 ppb (\(\sim \) 9 mm on the Earth’s surface) (Altamimi et al. 2016). In view of the next realization, the planned ITRF2020, there have been continuous and promising efforts to reduce the scale discrepancy between SLR and VLBI, due to, e.g., refined range bias handling in the SLR estimation process (Appleby et al. 2016; Luceri et al. 2019) and the modeling of the gravitational deformation of the VLBI telescopes (Sarti et al. 2011; Nothnagel et al. 2019).
Nevertheless, it would be desirable to have another independent technique besides SLR and VLBI for comparison and validation of TRFs. GNSS is indeed a good choice due to its excellent global station network and many satellites providing a large number of continuous observations. GNSS is, like SLR, a dynamic technique since the satellites orbit around the center of mass of the Earth’s system enabling direct access to the geocenter. The information inherent in the observations, e.g., their sensitivity to geocenter motion, should be fully exploited and redundant information, potentially leading to over-constrained solutions should be avoided, in order to get a proper minimum constraint network solution (Sillard and Boucher 2001; Kotsakis 2012; Glaser et al. 2015). However, there are some limitations currently preventing GNSS from contributing to the origin and scale realization of global combined TRFs.
Concerning the geocenter estimation by GNSS, Männel and Rothacher (2017) summarized five major limitations: the higher orbital height compared to, e.g., LAGEOS (SLR), the estimation of epoch-wise clock offsets, the existence of carrier-phase ambiguities, the estimation of tropospheric zenith delays and the uncertainties in the solar radiation pressure modeling.
Previous studies have shown that GNSS is able under certain conditions to realize origin and scale of a TRF, especially in long-term (Heflin et al. 2002; Rülke et al. 2008; Dach et al. 2014; Glaser et al. 2015). The sensitivity of GPS/GNSS to the geocenter estimation can be improved by the inclusion of LEO (low Earth orbit) satellites as demonstrated by, e.g., König et al. (2005) using CHAMP, GRACE and SAC-C, Haines et al. (2015) using GRACE and TOPEX/Poseidon, Kuang et al. (2015) simulating different LEO orbital configurations, Männel and Rothacher (2017) combining four LEO satellites (GRACE-A, GRACE-B, OSTM/Jason-2 and GOCE), Kuang et al. (2019) using in addition the accelerometer data of GRACE and Couhert et al. (2020) using Jason-2. The common estimation of station and satellite clock offsets for every epoch and tropospheric parameters is according to Rebischung et al. (2014) a major limitation, and a GNSS without the need to estimate clock offsets would most probably facilitate an accurate geocenter estimation. Furthermore, the estimated GNSS geocenter coordinates show artifacts on the harmonics of the draconitic year (e.g., Ray et al. 2008) due to remaining systematics in the modeled GNSS orbits (Rebischung et al. 2016), especially in the solar radiation pressure modeling (Meindl et al. 2013, 2015; Rodriguez-Solano et al. 2014; Glaser et al. 2015). A possible contribution of DORIS to the TRF origin was investigated by, e.g., Couhert et al. (2018).
Concerning the scale, GPS/GNSS does not contribute to the ITRF scale since present satellite antenna phase center offsets (PCOs) were derived with a fixed ITRF and are, therefore, intrinsically dependent on the SLR and VLBI scale (Schmid et al. 2007). Previous studies, e.g., Zhu et al. (2003) and Cardellach et al. (2007), provided a relation to express the dependency of the scale and the PCO of the GPS satellites. Moreover, it is possible to realize an independent scale by estimating antenna pattern of the GNSS satellites, for instance by transferring this information via LEO satellites such as GRACE and TOPEX/Poseidon (Haines et al. 2015; Männel 2016) or via calibrated antenna pattern for Galileo from the GSA (European GNSS Agency) (Rebischung 2019; Villiger et al. 2020). The realization of the network scale by GNSS is currently under investigation within the reprocessing effort of the International GNSS Service (IGS, Johnston et al. 2017) (Antenna Working Group) as contribution to the ITRF2020. It yet has to be decided how GNSS will contribute to the scale realization of ITRF2020.
In this study, the potential of a future GNSS constellation on the origin and scale of global TRFs is investigated by simulations. Simulation studies are the only possibility to assess the impact of future developments of the GNSS technique on the TRF. The future constellation called “Kepler”Footnote 1 (Günther 2018) is introduced in Sect. 2.1 and the simulation setup including the different scenarios in Sect. 2.2. In Sect. 3.1 the improvements in origin, in Sect. 3.2 the improvements in scale, and in Sect. 3.3 in other parameters such as Earth rotation parameters are discussed by the future Kepler constellation w. r. t. contemporary GNSS, e.g., Galileo.
2 Method
2.1 Future GNSS constellation “Kepler”
The future GNSS constellation Kepler is characterized by the innovative features of two-way optical inter-satellite links (ISL) and optical frequency references. This effort is related to the Helmholtz funded project called ADVANTAGEFootnote 2 (Advanced Technologies for Navigation and Geodesy, Giorgi et al. 2019b) which is a joint effort of the German Aerospace Center DLR and the German Research Center for Geosciences GFZ. The overall project goal is to establish an architecture for a future space infrastructure for navigation and geodesy.
The Kepler constellation consists of 24 medium Earth orbit (MEO, semi-major axis: 29600 km) satellites in three orbital planes (inclination of 56\(^\circ \)), similar to Galileo in its final operational capability, and six LEO satellites (semi-major axis: 7600 km) in two perpendicular near-polar planes (inclination of 89.7\(^\circ \)). A sketch of the constellation is presented in Fig. 1. The MEO satellites transmit legacy L-band signals.
The two-way optical ISL enable very precise and unambiguous inter-satellite range measurements for time synchronization within the complete constellation and support precise orbit determination. Optical frequency references are cavity-stabilized lasers, which are already used on the GRACE-FO (Gravity Recovery and Climate Experiment Follow-On) mission (Thompson et al. 2011; Dahl et al. 2017; Abich et al. 2019), and ultra-stable optical clocks carried on the LEO satellites. The frequency references are used to generate a very stable composite system time common for all satellites. The offset between the system time and the ground time scale (e.g., UTC) will be known or can be estimated with very high precision. It enables a significant reduction or even an entire elimination (fixing to known values) of the satellite clock parameters in the estimation process.
The ISL connect all MEO satellites in one orbital plane and the LEO and the MEO satellites in different orbital planes according to an ISL scheduler. The ISL scheduler is based on different constraints defined by DLR. For further information about the Kepler constellation the interested reader is referred to Giorgi et al. (2019a, 2019b).
2.2 Simulations
Simulations were performed by utilizing the software EPOS-OC (Zhu et al. 2004) which was extended to facilitate the simulation and processing of the ISL for complex satellite constellations such as Kepler. The simulated observations are based on white noise different for the various observation types. The standard deviations of the white noise process (normally distributed random uncertainties with zero mean), see Table 1, used in the simulations are based on typical post fit RMS values from processing of real ground and LEO data. The phase measurements on the LEO satellites are usually more accurate than on the ground. White noise is usually deployed in such kind of simulations and the level of white noise in GNSS simulations is similar to, e.g., Dach et al. (2015) with 500 mm for code and 2 mm in phase and Kuang et al. (2015) with 500 mm for code and 65 mm for phase.
The precise orbit determination was performed for 1-day arcs. All the MEO and LEO satellite orbits were processed in a common adjustment applying the dynamic approach. In the simulations the code and phase hardware delays are assumed to be known (calibrated). 124 globally distributed ground stations constitute the network. The analysis period covers 10 days. This is sufficiently long in order to generate a reliable TRF (station positions only), but short enough to keep processing times at an acceptable level. The focus of this study is to investigate the impact of various simulation scenarios on different parameters. In order to get conclusions about the time variations, we will extend in further studies our simulation time span to at least three years to reliably estimate station velocities.
In the recovery step, the simulated observations were evaluated in a precise orbit and parameter estimation process with EPOS-OC. Based on that, daily normal equation systems (NEQs) were setup for six simulation scenarios as given in Table 2. The simulation scenarios were defined to assess the individual contribution of the ISL, the LEO satellites, and the known (fixed) clocks on the TRF origin and scale. Starting from the MEO-only constellation, which is like the Galileo constellation, the MEO ISL are added, then the LEOs, then the ISL between the MEOs and the LEOs, and finally the satellite clocks are fixed to simulate the effect of known clocks with an accuracy better than the carrier phase noise, and do not have to be estimated. The last scenario features the full Kepler constellation. It should be mentioned that the fixing of satellite clocks facilitates an initial assessment of the complete features of the Kepler constellation.
Prior to the combination of the daily NEQs, parameters such as orbital elements, tropospheric parameters, clocks and ambiguities (float solution) were pre-eliminated. The ambiguities of all the MEO and LEO satellites were solved as float solutions. The effect of fixed ambiguities was not analyzed within this study. For instance, Brockmann (1997) found an improvement by a factor of 3 in the Z component of the geocenter in case of an ambiguity-fixed w.r.t. an ambiguity-float solution. The daily NEQs were stacked, and finally station positions, geocenter coordinates and Earth rotation parameters (ERPs) were estimated. No-net rotation and no-net translation conditions were imposed to 39 datum stations following the simulation approach by Glaser et al. (2019). The scale was assessed by Helmert transformations w. r. t. the true simulated values.
Since uncertainties in the solar radiation pressure (SRP) modeling impede an accurate origin realization by MEO-only GNSS (Meindl et al. 2013; Arnold et al. 2015), we investigated the impact of mismodeling of SRP. The empirical CODE (Center for Orbit Determination in Europe) orbit model (ECOM) consisting of nine parameters was used, Beutler et al. (1994) and Springer et al. (1999):
in a Sun-fixed system with D in the direction towards the Sun, Y perpendicular to this direction along the solar panels, and B completes the right-handed system and with the constant biases \(D_0,Y_0,B_0\), the harmonics \(D_{[C,S]}, Y_{[C,S]}, B_{[C,S]}\), and the argument of latitude u of the satellites. The five parameter ECOM, where \(D_0,Y_0,B_0,B_C,B_S\) are estimated, is commonly used. In the simulations, all ECOM parameters are based on values derived from a real GPS data analysis over 14 days (April 30–May 13, 2017) of one GPS satellite (PRN03) provided by the IGS, see Table 3. In the recovery, the nine ECOM parameters were either fixed to true simulated values (perfect SRP modeling) or fixed to values biased by 1\(\sigma \) for all the satellites (SRP mismodeling).
It should be mentioned, that the nine parameter ECOM has been further developed. For instance, Arnold et al. (2015) showed that the new extended ECOM (“ECOM2”) results in more reliable geocenter estimates in Z direction. It is expected to use analytical models such as box-wing models for the Kepler constellation, as already done for the Galileo satellites. Rodriguez-Solano et al. (2014) showed that draconitic errors can significantly be reduced in the estimated parameters such as geocenter coordinates by using an adjustable box-wing model. As shown by, e.g., Bury et al. (2019), so-called hybrid models, where a priori box-wing models are introduced and three constant biases only are estimated, result in smaller formal errors of the geocenter Z component and stabilize the solution. In our simulations, the setup with ECOM is sufficient for the purpose of assessing the impact of biased SRP ECOM parameters on the geocenter estimates. The simulated ECOM values were fixed in the recovery, whereby the five ECOM parameters \(D_0, Y_0, B_0, B_C, B_S\) of the “reduced ECOM” (Springer et al. 1999) were biased by 1\(\varvec{\sigma }\) (see Table 3). The standard deviations, presented in Table 3, represent the scatter of the estimated values over the 14 days time period and are assumed to be realistic for this snapshot. The assumption of estimating ECOM5 parameters, instead of the full ECOM9, seems justified since it will be not necessary to estimate the full set of empirical orbit parameters if box-wing models are available. Currently in orbit modeling it is preferred to use physical instead of empirical orbit models as far as it is possible. The metadata have been released for Galileo with surface properties allowing for the generation of satellite models, such as the box-wing model.
The SRP modeling of the LEO satellites was based on cannonball models and assumed to be perfect in this study. Other main orbit perturbations within the LEO orbit determination such as atmospheric drag, albedo, and time-variable gravity field were modeled and recovered in the same way; therefore no mismodeling was simulated. More information about the orbit determination and different LEO modeling errors of the Kepler constellation can be found in Michalak et al. (2020).
3 Results
3.1 Origin
The estimated geocenter coordinates were first evaluated by their standard deviations (i.e., formal errors) over the entire simulation period for the six different simulation scenarios (Table 2) in case of perfect models (no SRP mismodeling). As shown in Fig. 2, the extension of the constellation significantly improves the precision of the estimated geocenter coordinates, especially in Z direction. Due to the addition of the ISL between the MEO satellites within one orbital plane the precision improves by a factor of 13 in Z and 2.5 in X and Y w. r. t. the MEO-only case. This improvement is more than the expected improvement due to the larger number of observations, see Table 5 column “exp.”. The addition of just the LEO satellites to the MEO constellation significantly improves the geocenter estimation from GNSS as well which is in concert with previous studies, e.g., Haines et al. (2015); Kuang et al. (2015); Männel and Rothacher (2017). We find very similar improvements as in the MEO-MEO ISL scenario by a factor of 2.5 in X and Y and even by 14 in Z for the MEO plus LEO constellation w. r. t. MEO-only. The orbital and observation geometry is improved by LEO satellites with higher inclinations, resulting in significant improvements in the formal errors of the Z component of the geocenter as already demonstrated by Kuang et al. (2015, Fig. 8). The six LEO satellites of the Kepler system are in two perpendicular planes with an inclination of 89.9\(^\circ \), which improves the sensitivity of Z in the geocenter, in addition to the 24 MEO satellites with an inclination of 56\(^\circ \) (Galileo-like). Finally, the full Kepler constellation with all ISL (between MEO as well as MEO and LEO satellites) and perfectly synchronized clocks shows improvements in the geocenter estimates by a factor of 43 in Z and by 8 for X and Y w. r. t. the MEO-only constellation.
Standard deviations of estimated geocenter coordinates (GCC) in X, Y, Z direction in case of different simulation scenarios, see Table 2
Correlations for geocenter estimates in X, Y, Z and parameters of ECOM in case of different scenarios (Table 2) for one day and one satellite (other days and satellites show the same pattern)
A correlation analysis between the estimated geocenter coordinates in X, Y, Z direction and the nine ECOM parameters was performed, the correlations for all six scenarios are presented in Fig. 3. The geocenter shows large correlations with the SRP parameters in the usual GNSS constellation, the MEO-only case. The largest correlation can be found between the Z coordinate of the geocenter and the constant bias \(D_0\) in the direction towards the Sun of the SRP model, which is in accordance with Meindl et al. (2013). Based on consideration on orbital perturbations they identify the major limitation in the estimability of the geocenter by GNSS in the high correlation between the \(D_0\) parameter and geocenter in Z direction. In our simulations, the scenario with the ISL between the MEO satellites already reduces the correlation between the geocenter estimates and the ECOM parameters significantly up to a complete de-correlation. Therefore, the Kepler constellation will allow a complete de-correlation of the SRP and the geocenter parameters resulting in a more reliable estimation of the origin of the reference frame.
Estimated geocenter coordinates in X, Y, Z over 10 days in case of biased solar radiation pressure modeling (ECOM5 parameters are biased by 1\(\sigma \) for all satellites) and different simulation scenarios (Table 2). Mean values and standard deviations in brackets
The systematic effect of biased SRP parameters on the geocenter coordinates was assessed and the resulting geocenter coordinates are illustrated in Fig. 4. All the simulated ECOM values were fixed in the recovery, whereby the five ECOM parameters \(D_0, Y_0, B_0, B_C, B_S\) of the “reduced ECOM” (Springer et al. 1999) were biased by \(1\sigma \) (see Table 3). The biased ECOM5 model by \(1\sigma \) results in biased geocenter coordinates of up to \(-8.1\) mm in Z direction in the MEOs + ISL\(_{\text {MEO}}\) scenario. The biased geocenter coordinates presented here are only caused by an offset introduced in the SRP modeling and not by the insensitivity of the GNSS technique to the origin. The biased ECOM can be partly compensated by the addition of the LEO satellites with perfectly simulated SRP modeling. The full Kepler constellation still shows biased geocenter coordinates of about 3 mm in X and 5 mm in Z direction. It seems that in this case the ISL do not improve the estimated geocenter coordinates. The very precise ISL observations stabilize the orbit by partly suppressing the other observations, also in the case of biased orbits. Highest priority should be always to improve the orbit modeling, and then the Kepler features such as the ISL result in an improved parameter estimation like the geocenter. It should be noted that the values of ECOM used in the simulations are average values over 14 days of real observations. They represent a certain state and are assumed to be time-invariant in this short period of time investigated in this study. In reality the ECOM parameters are time dependent since the elevation of the Sun changes w. r. t. the orbital plane in the quasi-inertial frame. With the SRP mismodeling of the MEO satellites of a certain state in our simulations (snapshot) it can be seen that the perfect LEO orbits can partly absorb the SRP bias of the MEO satellites but the ISL cannot. It can be expected that a longer time span, e.g., of at least one year, will not change the conclusions presented in this study.
3.2 Scale
The quality of the scale realization of the Kepler constellation was assessed by the so-called “reference system effect” described in Sillard and Boucher (2001). They define three factors of the quality of the frame realization: the observation technique, the tracking network, and the analysis process. The last two factors were constant in our simulations, only the technique setup changed within the six simulation scenarios. All improvements in the scale can be, therefore, attributed to the amendments of the Kepler system w. r. t. the standard GNSS constellation. The resulting standard deviations of the realized scale in case of the different scenarios with perfect models are presented in Fig. 5 and the respective improvements w. r. t. the MEO-only constellation in Table 4. Here, in all scenarios the PCOs were fixed to their true values, no bias was introduced (perfect modeling). By extending the constellation, we find an improvement in the standard deviations of the realized scale. The fully-developed Kepler constellation shows the largest improvement by 34%. The Kepler constellation with the LEO satellites, the ISL between the MEO and LEO satellites and the perfect time synchronization is the most beneficial for the network scale realization. The scenarios with the ISL between the MEO satellites already show an improvement of 19%.
Standard deviations of realized scale in case of different scenarios, see Table 2
Network scale change [mm] on the Earth’s surface for different simulation scenarios (Table 2) and z-PCO bias of 2 cm for all MEO satellites
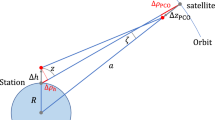
The impact of biased satellite PCOs on the scale was evaluated assuming initially perfectly calibrated ground antennas. Since the scale of the implied frame is sensitive to the Z direction of the satellite PCOs (hereinafter z-PCO), we focus on that particular component. The bias was introduced in the adjustment in addition to the a priori PCOs used in the simulations. First, a bias of 2 cm in the z-PCO of all the MEO satellites was introduced and all PCOs (MEO and LEO) were fixed, that means, satellite PCOs were not estimated as unknown parameters. The resulting network scale change on the Earth’s surface in case of the six simulation scenarios is depicted in Fig. 6. In the MEO-only scenario a scale change of about 0.9 mm (0.14 ppb) was found, which is in accordance with the relation provided by Zhu et al. (2003) (scale change [ppb] \(=\) 7.8 \(\cdot \) \(\varDelta z\)-PCO [m]). Amongst the simulation scenarios, the smallest scale difference was found for the MEO + LEO solution. The addition of the LEO satellites improves the overall orbital geometry of the constellation and seems to stabilize the solution. The MEO-only case shows the largest scale change due to the biased PCO. Compared to the MEO + LEO scenario, the solutions with the very precise ISL show a larger scale change due to biased PCO. The ISL connect the MEO satellites within one orbital plane and the MEO and LEO satellites of different planes. The ground network, which is needed to derive the network scale, is connected only via GNSS which refers directly to the z-PCO. In the MEO + LEO case the LEO orbit seems to absorb most of the MEO z-PCO bias. However, in case of the ISL more of the PCO bias propagates to the scale. The very precise ISL measurements create a stiff constellation by fixing the distance between MEO and LEO satellites and the biases get less absorbed by the orbital parameters.
Network scale change [mm] on the Earth’s surface for different simulation scenarios (Table 2) and z-PCO bias of 1 cm for all LEO satellites
In a next setup, a smaller bias of 1 cm in the z-PCOs of the LEO satellites was introduced and all PCOs were fixed. The z-PCOs of the MEO constellation were introduced without any bias in this case. The LEO z-PCO bias of 1 cm is presented in view of a final network scale change of less than 1 mm towards the GGOS goals. The resulting network scale change is presented in Fig. 7. The MEO + LEO solution without the Kepler ISL shows the largest scale change of 2.3 mm. The network scale is more sensitive to the quality of the LEO PCOs compared to the quality of the MEO PCOs due to the lower LEO orbits. Comparing with the other scenarios with the ISL, the scale changes get significantly reduced below 0.1 mm for the full Kepler constellation.
Focusing on MEO + LEO constellations, which are already in orbit unlike the proposed Kepler constellation, one can ask how accurately do the LEO PCOs need to be known for a change in the network scale below 1 mm in view of GGOS? To answer this question, we introduced different biases in the LEO z-PCOs and fixed all PCOs (no estimation of PCOs). The resulting scale changes in case of the MEO + LEO scenario and the different LEO z-PCO biases of \(-[10,5,4,3,1]\) mm are depicted in Fig. 8. Therefore, to achieve a network scale accurate to the 1-mm level, the LEO \(\varDelta z\)-PCOs need to be known with an uncertainty of 4 mm or better. Based on various solutions, we derived an approximated relation (“rule of thumb”) for the MEO plus LEO constellation: scale change [mm] \(=\) 0.22 \(\cdot \varDelta z\)-PCO [mm], similar to the one for the MEO-only constellation provided by Zhu et al. (2003) and confirmed by our simulations.
In all results presented so far, the PCO were not estimated. Therefore, in principle, no independent network scale can be realized by GNSS due to the current intrinsic dependency to the fixed ITRF scale based on VLBI and SLR. In order to realize an independent network scale by GNSS, the MEO satellite PCOs have to be freely estimated within the adjustment together with station coordinates or to rely on their calibration on ground before launch. The estimation can be done, for instance in a MEO plus LEO constellation by fixing the LEO satellite PCOs and transferring this information to the MEO satellites. However, in this case the estimated MEO satellite PCOs and the consequent network scale completely rely on the fixed LEO satellite PCOs. To assess the impact of probable biases in the LEO satellite PCOs within an estimation of MEO PCO and other parameters, small LEO PCO biases of \(-[10,5,1,0.8,0.7,0.5,0]\) mm were introduced in the MEO + LEO constellation and the resulting scale change is shown in Fig. 9. It is important to note, that in this case, the LEO \(\varDelta z\)-PCO needs to be known with an accuracy of 0.7 mm or better, in order to realize the network scale accurate to 1 mm. It is in agreement with an experiment with real data, where Huang et al. (2020) found a 2.7 cm shift in the terrestrial scale after adding an artificial bias of \(+3\) cm on the LEO PCO when processing GNSS observations tracked by Swarm.
3.3 Other parameters
The precision of other estimated parameters such as station positions and Earth rotation parameters are presented in Table 5 for the sake of completeness. The station positions improve by up to 8% on average for the full Kepler constellation w. r. t. the MEO-only constellation. The relative improvement in the formal errors of the different scenarios w. r. t. MEO-only is very similar in all Cartesian and local coordinate components. Therefore, only an average value of the improvements is provided. That improvement is below the expected (up to 13%) that stems from the additional observations (LEO satellites, ISL), see Table 5 column “exp.”. In further studies the impact of the same number of observations and estimated parameters in every simulation scenario can be investigated, e.g., by replacing one type of observation by another and adapting the stochastic model accordingly.
Standard deviations of estimated Earth rotation parameters \(x_p, y_p\) and UT1-UTC in case of different scenarios, see Table 2
The improvements in the ERP go well beyond the expected improvements; 63% and 64% for x-pole and y-pole and 85% for UT1-UTC for the full Kepler constellation w. r. t. the MEO-only case. It should be mentioned that the ERP were setup as continuous piece-wise linear parameters once per day at midnight. UT1-UTC was estimated by GNSS due to fixing of the first value of the satellite arc. Comparing the different simulation scenarios, the largest leap in precision for all ERP by a single Kepler feature can be attributed to the addition of the ISL between the MEO satellites, see also Fig. 10. In case of the determination of the ERP the very precise ISL seem beneficial due to more stable orbits and a more stiff constellation. It is an important result since GNSS is the primary technique to determine polar motion.
The standard deviation \(s_0\) of the unit weight provides a quality criteria of the adjustment. In case of all scenarios, \(s_0\) is very similar and close to 1 (as introduced a priori) demonstrating an equal quality of the solutions, even by the extension of the constellation with new additional observations (optical ISL, LEO satellites). It ensures to directly compare our six simulation scenarios from a statistical point of view. In addition, \(s_0\) should get smaller in case of every simulation scenario towards the full Kepler constellation due to the larger degree of freedom (DOF \(=\) “number of observation minus number of unknowns”). The MEO + LEO scenario has the smallest \(s_0\) of all scenarios. However, the scenario MEO + ISL\(_{\text {MEO}}\) shows a larger \(s_0\) than the MEO-only case indicating that the functional and stochastic model might not yet be perfectly suited.
4 Summary and conclusions
Due to system-specific characteristics, e.g., the necessary estimation of epoch-wise satellite clocks, and remaining orbital model uncertainties, e.g., of the solar radiation pressure, GNSS do currently not contribute to the origin and scale realization of ITRF2014 but it might become possible in the future.
A future GNSS constellation “Kepler” is proposed by the German Aerospace Center DLR featuring in addition to a Galileo-like MEO-only constellation, six LEO satellites in two polar planes as well as precise optical ISL and optical frequency references (Giorgi et al. 2019b). Since the accuracy requirements of GGOS on global TRFs have not been achieved yet, it is worth investigating the impact of the proposed Kepler constellation on the origin and scale realization. An ensemble of simulation scenarios with an extension of the standard Galileo constellation by the innovative Kepler features, LEO satellites in the constellation, precise ISL between the satellites and perfectly known clocks, was set up to assess the individual contribution of these system-specific characteristics.
In case of the geocenter, all simulation scenarios employing the individual Kepler features result in improvements in the estimated geocenter coordinates, especially in the Z component of the geocenter, w. r. t. a MEO-only constellation. It is of special importance since the Z direction is usually considered to be the weakest geocenter component. Primarily, the individual contribution of the ISL between the MEO satellites and the addition of the LEO satellites succeed in this improvement by factors of 13 and 14 in Z and 2.5 in X and Y, respectively. The complete Kepler constellation will clearly improve the precision of the estimated geocenter by factors of 43 in Z and of 8 for X and Y w. r. t. a Galileo-like MEO-only constellation. These improvements go well beyond the expected improvement due to the larger number of observations of the full Kepler constellation w. r. t. MEO-only. Furthermore, the Kepler constellation facilitates a complete de-correlation of the geocenter coordinates and the SRP model parameters improving the reliability of the estimated geocenter. The individual contribution of the ISL between the MEO satellites in addition to the MEO-only constellation is already very promising for that. As already shown by, e.g., Meindl et al. (2013), a MEO-only constellation shows a high correlation between the geocenter and the ECOM parameters of the SRP modeling. Therefore, uncertainties in the SRP modeling lead to limitations in the estimation of the geocenter by current GNSS. The impact of SRP mismodeling was evaluated by introducing biases of 1\(\sigma \) to the reduced ECOM resulting in biased geocenter coordinates of about 4 mm in the MEO-only case and of up to 8.1 mm in the scenario with the MEO plus the MEO ISL. The Kepler features as well as the complete constellation can only partly compensate for this mismodeling. Therefore, special emphasis in the utilization of an innovative future constellation like Kepler has to be placed upon the reduction of remaining uncertainties in the precise orbit modeling, especially of the SRP.
The scale realization can be improved by the Kepler constellation by up to 34% w. r. t. the state-of-the-art, that is MEO-only, suggested by the standard deviations of the realized scale employing the approach of Sillard and Boucher (2001). The impact of probable uncertainties in the satellite PCOs on the network scale was investigated by introducing biased z-PCOs on the MEO and LEO satellites. We find that the z-PCOs have to be better than 2 cm in case of the MEO and better than 4 mm in case of the LEO satellites to realize a network scale to be better than 1 mm in view of GGOS. In these solutions all satellite PCO were fixed to their a priori values which are intrinsically linked to the applied ITRF. Therefore, such a network scale depends so far on the VLBI and SLR scale. An independent scale realization by GNSS is possible for instance in a MEO plus LEO constellation by estimating the MEO z-PCOs and simultaneously fixing the LEO PCOs, e.g., done by Haines et al. (2015) and Männel (2016). For this purpose, the LEO z-PCOs need to be known very precisely and our simulations suggest that they have to be better than 1 mm for a scale change below 1 mm. It might be a challenging task for pre-launch calibrations and requires special emphasis when relying on the LEO z-PCO for the scale realization by GNSS. Special attention should be also given to the risk of multipath effects of the LEO antenna.
Additionally, significant improvements in the estimated ERP (63% in \(x_p\), 64% in \(y_p\), 85% in UT1-UTC) were identified in case of the Kepler constellation in comparison to a standard Galileo constellation.
In general, the unique features of the Kepler constellation yield improvements in the estimated parameters, including the geocenter coordinates, and the network scale. As shown by the different simulation scenarios, the inclusion of the very precise ISL between the MEO satellites constitutes an important and valuable component of the Kepler constellation with regard to the TRF determination. The inclusion of LEO satellites for the TRF determination is already nowadays very beneficial, especially for the geocenter estimation due to the better orbital coverage. For instance, the Sentinel-3A/B satellites on two different orbital planes have similar inclinations but a lower altitude compared to Kepler. The Sentinel-3 satellites could be also used for co-location in space since they are equipped with SLR retroreflectors and GPS and DORIS receivers. For example, Strugarek et al. (2019) suggest to use SLR and GPS measurements to Sentinel-3A/3B for geocenter estimation. As shown in this study, the ISL as the innovative feature of Kepler between the MEOs, without LEOs, already result in a significant improvement in the geocenter estimation. Furthermore, the final Kepler constellation is one united system and will be processed accordingly which is different to a MEO + LEO constellation such as GNSS + GRACE.
The precise orbit determination of current and future GNSS constellations has to be in any case continuously improved by further reducing remaining systematics. Then, the potential of the innovative features employed by the Kepler constellation can be fully exploited.
Future studies comprise the refined satellite clock modeling towards most realistic simulations of the fully developed Kepler constellation. It might be also worth to study the effect of different satellite arc lengths within Kepler since, e.g., longer arcs can improve the solution of geocenter and ERP (Lutz et al. 2016) and decrease the correlation of orbital and tropospheric parameters with geocenter coordinates (Haines et al. 2015). The other space geodetic techniques will also be included to assess the benefit in multi-technique solutions like the ITRF towards the completion of the demanding GGOS requirements.
Data availability statement
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Abich K, Abramovici A, Amparan B, Baatzsch A, Okihiro BB, Barr DC, Bize MP, Bogan C, Braxmaier C, Burke MJ, Clark KC, Dahl C, Dahl K, Danzmann K, Davis MA, de Vine G, Dickson JA, Dubovitsky S, Eckardt A, Ester T, Barranco GF, Flatscher R, Flechtner F, Folkner WM, Francis S, Gilbert MS, Gilles F, Gohlke M, Grossard N, Guenther B, Hager P, Hauden J, Heine F, Heinzel G, Herding M, Hinz M, Howell J, Katsumura M, Kaufer M, Klipstein W, Koch A, Kruger M, Larsen K, Lebeda A, Lebeda A, Leikert T, Liebe CC, Liu J, Lobmeyer L, Mahrdt C, Mangoldt T, McKenzie K, Misfeldt M, Morton PR, Müller V, Murray AT, Nguyen DJ, Nicklaus K, Pierce R, Ravich JA, Reavis G, Reiche J, Sanjuan J, Schütze D, Seiter C, Shaddock D, Sheard B, Sileo M, Spero R, Spiers G, Stede G, Stephens M, Sutton A, Trinh J, Voss K, Wang D, Wang RT, Ware B, Wegener H, Windisch S, Woodruff C, Zender B, Zimmermann M (2019) In-orbit performance of the GRACE follow-on laser ranging interferometer. Phys Rev Lett 123(031):101. https://doi.org/10.1103/PhysRevLett.123.031101
Altamimi Z, Collilieux X, Métivier L (2011) ITRF2008: an improved solution of the international terrestrial reference frame. J Geodesy 85(8):457–473. https://doi.org/10.1007/s00190-011-0444-4
Altamimi Z, Rebischung P, Métivier L, Collilieux X (2016) ITRF2014: a new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J Geophys Res Solid Earth 121(8):6109–6131. https://doi.org/10.1002/2016JB013098
Appleby G, Rodríguez J, Altamimi Z (2016) Assessment of the accuracy of global geodetic satellite laser ranging observations and estimated impact on ITRF scale: estimation of systematic errors in LAGEOS observations 1993–2014. J Geod 90:1371–1388. https://doi.org/10.1007/s00190-016-0929-2
Arnold D, Meindl M, Beutler G, Dach R, Schaer S, Lutz S, Prange L, Sośnica K, Mervart L, Jäggi A (2015) CODE’s new solar radiation pressure model for GNSS orbit determination. J Geodesy 89(8):775–791. https://doi.org/10.1007/s00190-015-0814-4
Beutler G, Brockmann E, Gurtner W, Hugentobler U, Mervart L, Rothacher M (1994) Extended orbit modeling techniques at the CODE processing center of the international GPS service (IGS): theory and initial results. Manuscripta geodaetica 19:367–386
Brockmann E (1997) Combination of solutions for geodetic and geodynamic applications of the global positioning system (GPS), Geodätisch-geophysikalische Arbeiten in der Schweiz, vol 55. Schweizerische Geodätische Kommission. https://www.sgc.ethz.ch/sgc-volumes/sgk-55.pdf
Bury G, Zajdel R, Sośnica K (2019) Accounting for perturbing forces acting on Galileo using a box-wing model. GPS Solut 23(3):74. https://doi.org/10.1007/s10291-019-0860-0
Cardellach E, Elósegui P, Davis JL (2007) Global distortion of GPS networks associated with satellite antenna model errors. J Geophys Res Solid Earth 112(B7). https://doi.org/10.1029/2006JB004675
Couhert A, Mercier F, Moyard J, Biancale R (2018) Systematic error mitigation in DORIS-derived geocenter motion. J Geophys Res Solid Earth 123(11):10,142–10,161. https://doi.org/10.1029/2018JB015453
Couhert A, Delong N, Ait-Lakbir H, Mercier F (2020) GPS-based LEO orbits referenced to the earth’s center of mass. J Geophys Res Solid Earth 125(2):e2019JB018,293. https://doi.org/10.1029/2019JB018293
Dach R, Schaer S, Hugentobler U, Rodríguez-Solano C, Lutz S, Steigenberger P, Sośnica K, Meindl M, Beutler G, Jäggi A (2014) Estimating the geocenter from GNSS data. In: IGS Workshop— Celebrating 20 years of service, Pasadena, USA, June 23–27, 2014. http://stage.igs.org/assets/pdf/Workshop%202014%20-%20PY05%20-%20Dach%20-%202315%20-%20Estimating%20the%20geocenter%20from%20GNSS%20data.pdf
Dach R, Lutz S, Walser P, Fridez P (eds) (2015) Bernese GNSS software version 5.2. Astronomical Institute, University of Bern, Switzerland. http://www.bernese.unibe.ch/docs/DOCU52.pdf
Dahl C, Baatzsch A, Dehne M, Gilles F, Hager P, Herding M, Nicklaus K, Voss K, Abich K, Braxmaier C, Gohlke M, Guenther B, Sanjuan J, Zender B, Barranco GF, Görth A, Mahrdt C, Müller V, Schütze D, Stede G, Heinzel G (2017) Laser ranging interferometer on GRACE follow-on. In: Proceedings of international conference on space optics—ICSO’16, vol 10562. https://doi.org/10.1117/12.2297705
Giorgi G, Kroese B, Michalak G (2019a) Future GNSS constellations with optical inter-satellite links. Preliminary space segment analyses. In: 2019 IEEE Aerospace Conference, pp 1–13. https://doi.org/10.1109/AERO.2019.8742105
Giorgi G, Schmidt T, Trainotti C, Mata-Calvo R, Fuchs C, Hoque M, Berdermann J, Furthner J, Günther C, Schuldt T, Sanjuan J, Gohlke M, Oswald M, Braxmaier C, Balidakis K, Dick G, Flechtner F, Ge M, Glaser S, König R, Michalak G, Murböck M, Semmling M, Schuh H (2019b) Advanced technologies for satellite navigation and geodesy. Adv Space Res 64(6):1256–1273. https://doi.org/10.1016/j.asr.2019.06.010
Glaser S, Fritsche M, Sośnica K, Rodríguez-Solano CJ, Wang K, Dach R, Hugentobler U, Rothacher M, Dietrich R (2015) A consistent combination of GNSS and SLR with minimum constraints. J Geodesy 89(12):1165–1180. https://doi.org/10.1007/s00190-015-0842-0
Glaser S, König R, Neumayer KH, Nilsson T, Heinkelmann R, Flechtner F, Schuh H (2019) On the impact of local ties on the datum realization of global terrestrial reference frames. J Geodesy 93(5):655–667. https://doi.org/10.1007/s00190-018-1189-0
Gross R, Beutler G, Plag HP (2009) Integrated scientific and societal user requirements and functional specifications for the GGOS. In: Global geodetic observing system: meeting the requirements of a global society on a changing planet in 2020. Springer, Berlin, pp 209–224. https://doi.org/10.1007/978-3-642-02687-4_7
Günther C (2018) Kepler-satellite navigation without clocks and ground infrastructure. In: Proceedings of the 31st international technical meeting of the satellite division of the institute of navigation, Miami, Florida, September 2018, pp 849–856. https://doi.org/10.33012/2018.15997
Haines BJ, Bar-Sever YE, Bertiger WI, Desai SD, Harvey N, Sibois AE, Weiss JP (2015) Realizing a terrestrial reference frame using the Global Positioning System. J Geophys Res Solid Earth 120(8):5911–5939. https://doi.org/10.1002/2015JB012225
Heflin M, Argus D, Jefferson D, Webb F, Zumberge J (2002) Comparison of a GPS-defined global reference frame with ITRF2000. GPS Solut 6(1–2):72–75. https://doi.org/10.1007/s10291-002-0015-5
Huang W, Männel B, Brack A, Schuh H, Ge M (2020) Estimation of GPS transmitter antenna phase center offsets by integrating spacebased GPS observations. Adv Space Res (under review)
Johnston G, Riddell A, Hausler G (2017) The International GNSS Service. In: Teunissen PJ, Montenbruck O (eds) Springer handbook of global navigation satellite systems. Springer, Cham, pp 967–982. https://doi.org/10.1007/978-3-319-42928-1_33
König R, Reigber C, Zhu S (2005) Dynamic model orbits and Earth system parameters from combined GPS and LEO data. Adv Space Res 36(3):431–437. https://doi.org/10.1016/j.asr.2005.03.064
Kotsakis C (2012) Reference frame stability and nonlinear distortion in minimum-constrained network adjustment. J Geodesy 86(9):755–774. https://doi.org/10.1007/s00190-012-0555-6
Kuang D, Bar-Sever Y, Haines B (2015) Analysis of orbital configurations for geocenter determination with GPS and low-Earth orbiters. J Geodesy 89(5):471–481. https://doi.org/10.1007/s00190-015-0792-6
Kuang D, Bertiger W, Desai SD, Haines BJ, Yuan DN (2019) Observed geocenter motion from precise orbit determination of GRACE satellites using GPS tracking and accelerometer data. J Geodesy 93(10):1835–1844. https://doi.org/10.1007/s00190-019-01283-5
Luceri V, Pirri M, Rodríguez J, Appleby G, Pavlis EC, Müller H (2019) Systematic errors in SLR data and their impact on the ILRS products. J Geodesy 93(11):2357–2366. https://doi.org/10.1007/s00190-019-01319-w
Lutz S, Meindl M, Steigenberger P, Beutler G, Sośnica K, Schaer S, Dach R, Arnold D, Thaller D, Jäggi A (2016) Impact of the arc length on GNSS analysis results. J Geodesy 90(4):365–378. https://doi.org/10.1007/s00190-015-0878-1
Männel B (2016) Co-location of geodetic observation techniques in space. Geodätisch-geophysikalische Arbeiten in der Schweiz, vol 97. Schweizerische Geodätische Kommission. https://www.sgc.ethz.ch/sgc-volumes/sgk-97.pdf
Männel B, Rothacher M (2017) Geocenter variations derived from a combined processing of LEO- and ground-based GPS observations. J Geodesy 91(8):933–944. https://doi.org/10.1007/s00190-017-0997-y
Meindl M, Beutler G, Thaller D, Dach R, Jäggi A (2013) Geocenter coordinates estimated from GNSS data as viewed by perturbation theory. Adv Space Res 51(7):1047–1064. https://doi.org/10.1016/j.asr.2012.10.026
Meindl M, Beutler G, Thaller D, Dach R, Schaer S, Jäggi A (2015) A comment on the article “A collinearity diagnosis of the GNSS geocenter determination” by P. Rebischung, Z. Altamimi, and T. Springer. J Geodesy 89(2):189–194. https://doi.org/10.1007/s00190-014-0765-1
Michalak G, Glaser S, Neumayer KH, König R (2020) Precise orbit and Earth parameter determination supported by LEO satellites, inter-satellite links and synchronized clocks of a future GNSS. Adv Space Res (under review)
Nothnagel A, Holst C, Haas R (2019) A VLBI delay model for gravitational deformations of the Onsala 20 m radio telescope and the impact on its global coordinates. J Geodesy 93:2019–2036. https://doi.org/10.1007/s00190-019-01299-x
Petit G, Luzum B (eds) (2010) IERS Conventions (2010), IERS Technical Note, vol 36. Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt a. M., Germany
Ray J, Altamimi Z, Collilieux X, van Dam T (2008) Anomalous harmonics in the spectra of GPS position estimates. GPS Solut 12(1):55–64. https://doi.org/10.1007/s10291-007-0067-7
Rebischung P (2019) Preliminary tests regarding the inclusion of Galileo in IGS repro3. In: International GNSS service: analysis centre workshop 2019, April 15–17, 2019, Potsdam. https://s3-ap-southeast-2.amazonaws.com/igs-acc-web/igs-acc-website/workshop2019/Rebischung-IGSAC-2019.pdf
Rebischung P, Altamimi Z, Springer T (2014) A collinearity diagnosis of the GNSS geocenter determination. J Geodesy 88(1):65–85. https://doi.org/10.1007/s00190-013-0669-5
Rebischung P, Altamimi Z, Ray J, Garayt B (2016) The IGS contribution to ITRF2014. J Geodesy 90(7):611–630. https://doi.org/10.1007/s00190-016-0897-6
Rodriguez-Solano C, Hugentobler U, Steigenberger P, Bloßfeld M, Fritsche M (2014) Reducing the draconitic errors in GNSS geodetic products. J Geodesy 88(6):559–574. https://doi.org/10.1007/s00190-014-0704-1
Rülke A, Dietrich R, Fritsche M, Rothacher M, Steigenberger P (2008) Realization of the Terrestrial Reference System by a reprocessed global GPS network. J Geophys Res Solid Earth 113(B8). https://doi.org/10.1029/2007JB005231
Sarti P, Abbondanza C, Petrov L, Negusini M (2011) Height bias and scale effect induced by antenna gravitational deformations in geodetic VLBI data analysis. J Geodesy 85(1):1–8. https://doi.org/10.1007/s00190-010-0410-6
Schmid R, Steigenberger P, Gendt G, Ge M, Rothacher M (2007) Generation of a consistent absolute phase center correction model for GPS receiver and satellite antennas. J Geodesy 81(12):781–798. https://doi.org/10.1007/s00190-007-0148-y
Sillard P, Boucher C (2001) A review of algebraic constraints in terrestrial reference frame datum definition. J Geodesy 75(2):63–73. https://doi.org/10.1007/s001900100166
Springer TA, Beutler G, Rothacher M (1999) A new solar radiation pressure model for GPS satellites. GPS Solut 2(3):50–62. https://doi.org/10.1007/PL00012757
Strugarek D, Sośnica K, Arnold D, Jäggi A, Zajdel R, Bury G, Drozdzewski M (2019) Determination of global geodetic parameters using satellite laser ranging measurements to Sentinel-3 satellites. Remote Sens 11(19):2282. https://doi.org/10.3390/rs11192282
Thompson R, Folkner WM, de Vine G, Klipstein WM, McKenzie K, Spero R, Yu N, Stephens M, Leitch J, Pierce R, Lam TTY, Shaddock DA (2011) A flight-like optical reference cavity for GRACE follow-on laser frequency stabilization. In: 2011 Joint conference of the IEEE international frequency control and the European frequency and time forum (FCS) proceedings, pp 1–3. https://doi.org/10.1109/FCS.2011.5977873
Villiger A, Dach R, Schaer S, Prange L, Zimmermann F, Kuhlmann H, Wübbena G, Schmitz M, Beutler G, Jäggi A (2020) GNSS scale determination using calibrated receiver and Galileo satellite antenna patterns. J Geodesy 94(93). https://doi.org/10.1007/s00190-020-01417-0
Zhu S, Reigber C, König R (2004) Integrated adjustment of CHAMP, GRACE, and GPS data. J Geodesy 78(1–2):103–108. https://doi.org/10.1007/s00190-004-0379-0
Zhu SY, Massmann FH, Yu Y, Reigber C (2003) Satellite antenna phase center offsets and scale errors in GPS solutions. J Geodesy 76(11):668–672. https://doi.org/10.1007/s00190-002-0294-1
Acknowledgements
This work has been supported by the Helmholtz-Gemeinschaft Deutscher Forschungszentren e.V. under grant number ZT-0007 (ADVANTAGE, Advanced Technologies for Navigation and Geodesy). ADVANTAGE is a joint project of the German Aerospace Center (DLR) and the German Research Centre for Geosciences (GFZ) aiming at defining future systems for navigation, geodesy and metrology. The IGS (Johnston et al. 2017) is acknowledged for providing data used to derive the ECOM values for the simulations. The authors are very grateful for the detailed and valuable comments on the manuscript of three anonymous reviewers.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.G. defined the study. S.G., G.M. and H.N. generated and analyzed the data. All authors contributed to the analysis, interpretation, and discussion of the results. S.G. wrote the manuscript with major contributions by R.K., B.M. and G.M and inputs from all authors. All authors read and approved the final manuscript.
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Glaser, S., Michalak, G., Männel, B. et al. Reference system origin and scale realization within the future GNSS constellation “Kepler”. J Geod 94, 117 (2020). https://doi.org/10.1007/s00190-020-01441-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-020-01441-0