Measures of kurtosis: inadmissible for asymmetric distributions?

Abstract

Skewness and kurtosis are natural characteristics of a distribution. While it has long been recognized that they are more intrinsically entangled than other characteristics like location and dispersion, this has recently been made more explicit by Eberl and Klar (Stat Papers 65:415–433, 2024) with regard to orders of kurtosis. In this paper, we analyze the implications of this entanglement on kurtosis measures in general and for several specific examples. As a key finding, we show that kurtosis measures that are defined in the classical order-based way, which is analogous to measures of location, dispersion and skewness, do not exist. This raises serious doubts about the frequent application of such measures to skewed data. We then consider old and new proposals for kurtosis measures and evaluate under which additional conditions they measure kurtosis in a meaningful way. Some measures also allow more specific representations of the influence of skewness on the measurement of kurtosis than are available in a general setting. This works particularly well for a family of newly introduced density-based kurtosis measures.

1 Introduction

Pearson (1895) introduced the concept of kurtosis in the form of the fourth standardized moment. Contrary to location, dispersion and skewness, which can also be measured using (standardized) moments, it took a long time for kurtosis to be understood as a more general concept (Chissom 1970; Darlington 1970). Bickel and Lehmann (1975) defined a measure of kurtosis as a “suitable ratio” of two measures of scale or dispersion without going into more detail. In the same paper, a general approach for the definition of characteristics of probability distributions was laid out using stochastic orderings. This idea was picked up by Oja (1981), who incorporated work on convex transformations by van Zwet (1964) to define a class of stochastic orderings that can be used as foundation for the measurement of location, dispersion, skewness and kurtosis. His crucial property for a kurtosis measure $\kappa$ is that $F \preceq G$ for distribution functions F and G and a suitable stochastic order of kurtosis $\preceq$ implies $\kappa (F) \le \kappa (G)$. Here, the usual choice for the order $\preceq$ is $\le _s$, which means that the function $F \circ G^{-1}$ is concave-convex, where F and G are assumed to be continuous and strictly increasing. In the years since, a number of alternative kurtosis measures have been proposed. Most of them are based on quantiles (see, e.g., Ruppert 1987; Balanda and MacGillivray 1988; Moors 1988 and Jones et al. 2011) with a notable exception being a measure based on L-moments by Hosking (1989).

Kurtosis measures are frequently used in different fields of applications, ranging from environmental science to finance and insurance. Here, it is commonplace that these measures are applied to skewed distributions, see Cooper (2020) and López-Martín et al. (2022) for specific examples and Eberl and Klar (2024) for a broader overview. In contrast, it has long been established in the statistical literature that a major problem arising in the treatment of kurtosis is its intrinsic entanglement with skewness. This is already implied by the fact that the orders of kurtosis by van Zwet (1964) and Oja (1981) are only defined for symmetric distributions. More recently, Blest (2003) and Jones et al. (2011) have presented approaches to construct skewness-invariant measures of kurtosis that are based on moments and quantiles, respectively.

Eberl and Klar (2024) examine the relationship between skewness and orders of kurtosis, which work as a foundation for the measurement of kurtosis. There, the drawbacks of earlier approaches by MacGillivray and Balanda (1988) and Balanda and MacGillivray (1990) are pointed out and the compatibility of two major types of kurtosis orders with asymmetric distributions is analyzed in detail. The first order is a generalization of $\le _s$, and the second is $\le _3$, which is defined via $F \circ G^{-1}$ being convex of order three. This order is stronger than $\le _s$ and is a canonical choice in view of basic orders of location, dispersion and skewness. It is established that these kurtosis orders are not transitive for distributions with different skewness, which implies that these orders cannot be characterized by appropriate measures of kurtosis. In order to circumvent this problem, so-called transitivity sets are introduced that consist of equally skewed distributions and it is shown that the fundamental kurtosis order $\le _3$ is transitive on these sets.

In this paper, we examine and discuss the implications of these results for measures of kurtosis. Specifically, we show that no meaningful kurtosis measures exist that fulfil a slight modification of the usual order-based defining properties. This result follows directly from the non-transitivity of the aforementioned kurtosis orders shown by Eberl and Klar (2024). The emerging doubt as to whether kurtosis measures are still meaningful is then answered as follows: we consider a number of kurtosis measures considered in the literature as well as new proposals and analyze whether they are compatible with kurtosis orderings if they are restricted to transitivity sets. Subsequently, one of the first ideas concerning the systematic measurement of kurtosis by Bickel and Lehmann (1975), namely considering ratios of dispersion measures, is evaluated. The analysis of the kurtosis measures is concluded by a comparison of their numerical values for a few specific distributions as well as the proposal of empirical counterparts along with some of their asymptotic properties.

2 Kurtosis orders and transitivity sets

In this section, we summarize several definitions and results from Eberl and Klar (2024). Throughout the paper, we assume that all distribution functions are three times differentiable and have interval support. We also adopt the notation from Eberl and Klar (2024) as we denote the interior of the support of a distribution function F by $D_F$ and assume $f = F'$ to be strictly positive on $D_F$. The set of all distribution functions that satisfy these assumptions is denoted by $\mathcal {P}$. Furthermore, X always denotes a random variable with distribution function F.

The following definition is a modified version of those made by Oja (1981) and Eberl and Klar (2024) whereas the term relative inverse distributions function is adopted from Müller and Stoyan (2002).

Definition 1

Let $F, G \in \mathcal {P}$ and $k \in \mathbb {N}_0$.

• (a) The function

  $$\begin{aligned} R_{FG}: D_F \rightarrow D_G, \quad x \mapsto G^{-1}(F(x)) \end{aligned}$$

  is said to be the relative inverse distribution function (RIDF) from F to G. We also define the modification $\Delta _{FG}: D_F \rightarrow \mathbb {R}, x \mapsto R_{FG}(x) - x$.

• (b) F is said to precede G in the order of the k-th convex characteristic, denoted by $F \le _k G$, if $\Delta _{FG}^{(k)} \ge 0$ holds. Here, we assume that the k-th derivative $\Delta _{FG}^{(k)}$ of $\Delta _{FG}$ exists.

Note that, for $k \ge 2$, $F \le _k G$ is equivalent to $R_{FG}^{(k)} \ge 0$. For $k = 0, 1, 2$, the order of the k-th convex characteristic coincides with basic orders of location, dispersion and skewness: $\le _0$ is the usual stochastic order $\le _{st}$, $\le _1$ is the dispersive order $\le _{disp}$ and $\le _2$ is the convex transformation order $\le _c$ by van Zwet (1964) (see also Oja 1981). Although the kurtosis order $\le _3$ follows the same pattern, it is rarely mentioned in the literature. A much more popular kurtosis order is $\le _s$, which was proposed by van Zwet (1964) and subsequently utilized by Oja (1981) and Groeneveld and Meeden (1984), among others. It is defined in the following, along with a generalization by Eberl and Klar (2024).

Definition 2

Let $F, G \in \mathcal {P}$ and $t_0 \in \mathbb {R}$.

• (a) F is said to be less kurtotic than G  in concave-convex sense, denoted by $F \le _s G$, if

  $$\begin{aligned} R_{FG}''(x) {\left\{ \begin{array}{ll} \le 0, \quad &{}\text {if } \quad x < 0,\\ \ge 0, \quad &{}\text {if } \quad x > 0. \end{array}\right. } \end{aligned}$$

• (b) F is said to be less kurtotic than G  in the generalized concave-convex sense with threshold $t_0$, denoted by $F \le _{gs}^{t_0} G$, if there exists a $p_{FG} \in [0, 1]$ such that

  $$\begin{aligned} R_{FG}''(x) {\left\{ \begin{array}{ll} \le t_0, \quad &{}\text {if } \quad x < p_{FG},\\ \ge t_0, \quad &{}\text {if } \quad x > p_{FG}. \end{array}\right. } \end{aligned}$$

Eberl and Klar (2024) proved the following results concerning the relationship between the kurtosis orders and their transitivity properties. Define

$$\begin{aligned} \gamma _D^p: \mathcal {P}\rightarrow \mathbb {R}, \quad F \mapsto \frac{f'(F^{-1}(p))}{(f(F^{-1}(p))^2} \end{aligned}$$

for $p \in (0, 1)$, which satisfies the crucial property of a skewness measure as it preserves the convex transformation order $\le _2$ (see Eberl and Klar 2024). Furthermore, define $\mathcal {T}_{D, p}^t = \{F \in \mathcal {P}: \gamma _D^p(F) = t\}$ for $p \in (0, 1), t \in \mathbb {R}$. Note that $\mathcal {S}\subseteq \mathcal {T}_{D, 1/2}^{0}$ holds, where $\mathcal {S}$ denotes the subset of $\mathcal {P}$ containing all symmetric distributions.

Theorem 3

For $F, G \in \mathcal {P}$, $F \le _{gs}^{t_0} G$ for all $t_0 \in \mathbb {R}$ is equivalent to $F \le _3 G$.

Theorem 4

• (a) Neither the order $\le _3$ nor $\le _{gs}^{t_0}$ is transitive on $\mathcal {P}$ for any $t_0 \in \mathbb {R}$.

• (b) The order $\le _3$ is transitive on the set $\mathcal {T}_{D, p}^t$ for all $p \in (0, 1), t \in \mathbb {R}$.

3 Measures of kurtosis: (non-)existence

Contrary to kurtosis orders, measures of kurtosis are often applied to asymmetric distributions (see, e.g., Wheeler 1975; Hanook et al. 2013 and the references in Eberl and Klar 2024). Measures are mostly chosen based on historical relevance and ease of use, typically resulting in the fourth standardized moment. Since this practice obviously lacks rigour, we start out by giving a general framework for the definition of kurtosis measures. Let $\mathcal {Q}\subseteq \mathcal {P}$ be the subset of all distributions for which a given kurtosis measure candidate is defined. Oja (1981) called a mapping $\kappa : \mathcal {Q}\rightarrow \mathbb {R}$ a measure of kurtosis, if it satisfies the following two properties:

• (K1) $\kappa (a X + b) = \kappa (X)$ for all $a \in \mathbb {R}{\setminus } \{0\}, b \in \mathbb {R}$ and $F \in \mathcal {Q}$,

• (K2) $\kappa (F) \le \kappa (G)$ for all $F, G \in \mathcal {Q}$ such that $F \le _K G$ for some kurtosis order $\le _K$.

This definition is in line with that of measures of central location, dispersion and skewness as given by, e.g., Oja (1981). The crucial property is (K2), requiring that the measure preserves a certain order with respect to the relevant characteristic. However, an evaluation of kurtosis measures with respect to this property has only been done under the assumption of symmetry in the literature (van Zwet 1964, Ruppert 1987 or Hosking 1989).

Based on Eberl and Klar (2024), the order $\le _3$ seems to be superior to the generalized concave-convex order $\le _{gs}^{t_0}$ for three major reasons. First, while $\le _3$ is unambiguous, $\le _{gs}^{t_0}$ depends on the threshold $t_0$ for which there exists no obvious choice if the distribution is asymmetric. Second, $\le _3$ is stronger than $\le _{gs}^{t_0}$ for any threshold $t_0$, meaning that the former imposes a more fundamental requirement on corresponding kurtosis measures. Third, $\le _3$ is transitive if it is restricted to sets of constant density-based skewness, which could not be shown for $\le _{gs}^{t_0}$. The order $\le _3$ is also the kurtosis analogue of the fundamental orders $\le _0$, $\le _1$ and $\le _2$ for location, dispersion and skewness. However, by refining the counterexample for the general transitivity of $\le _3$ in Eberl and Klar (2024), we observe that even this most basic requirement for a kurtosis measure cannot be satisfied in a meaningful way. For that, define the strict version $\prec$ of any stochastic order $\preceq$ by $F \prec G$, if $F \preceq G$ and $G \not \preceq F$.

Theorem 5

• (a) There exists no mapping $\kappa : \mathcal {P}\rightarrow \mathbb {R}$ such that $F \le _3 G$ implies $\kappa (F) \le \kappa (G)$ and $F <_3 G$ implies $\kappa (F) < \kappa (G)$ for all $F, G \in \mathcal {P}$.

• (b) Let $t_0 \in \textrm{int}(R_{FG}''(D_F))$. There exists no mapping $\kappa : \mathcal {P}\rightarrow \mathbb {R}$ such that $F \le _{gs}^{t_0} G$ implies $\kappa (F) \le \kappa (G)$ and $F <_{gs}^{t_0} G$ implies $\kappa (F) < \kappa (G)$ for all $F, G \in \mathcal {P}$.

Proof

• (a) As in Example 5 in Eberl and Klar (2024), we consider the following distributions:

  $$\begin{aligned} F: [0, 1] \rightarrow [0, 1],&\quad t \mapsto t^3,\\ G: [0, 1] \rightarrow [0, 1],&\quad t \mapsto t,\\ H: [0, 1] \rightarrow [0, 1],&\quad t \mapsto 1 - \root 3 \of {1-t}. \end{aligned}$$

  Note that $F, G, H \in \mathcal {P}$. Eberl and Klar (2024) proved that $F \le _3 G$ and $G \le _3 H$ holds, but also $F \not \le _3 H$. Note that this does not imply $H \le _3 F$ as $\le _3$ is not a total relation. Now we assume that there exists a mapping $\kappa : \mathcal {P}\rightarrow \mathbb {R}$ that preserves the order $\le _3$. It follows that $\kappa (F) \le \kappa (G) \le \kappa (H)$. We now contradict this by showing $H \le _3 F$, which then implies $H <_3 F$ and $\kappa (H) < \kappa (F)$. To this end, it holds that

  $$\begin{aligned} R_{HF}(t): [0, 1] \rightarrow [0, 1], \quad t \mapsto F^{-1}(H(t)) = \left( 1 - (1-t)^{1/3} \right) ^{1/3}. \end{aligned}$$

  It follows that, for $t \in [0, 1]$,

  $$\begin{aligned} R_{HF}'(t)&= \tfrac{1}{9} \left( 1 - (1-t)^{1/3} \right) ^{-2/3} (1-t)^{-2/3},\\ R_{HF}''(t)&= \tfrac{2}{27} \left( 1 - (1-t)^{1/3} \right) ^{-2/3} (1-t)^{-5/3} - \tfrac{2}{81} \left( 1 - (1-t)^{1/3} \right) ^{-5/3} (1-t)^{-4/3},\\ R_{HF}'''(t)&= \tfrac{10}{81} \left( 1 - (1-t)^{1/3} \right) ^{-2/3} (1-t)^{-8/3} - \tfrac{4}{81} \left( 1 - (1-t)^{1/3} \right) ^{-5/3} (1-t)^{-7/3}\\&\quad + \tfrac{10}{729} \left( 1 - (1-t)^{1/3} \right) ^{-8/3} (1-t)^{-2}. \end{aligned}$$

  Now,

  $$\begin{aligned} H \le _3 F&\Leftrightarrow R_{HF}'''(t) \ge 0 \quad \forall t \in [0, 1] \\&\Leftrightarrow \tfrac{10}{81} \left( 1 - (1-t)^{1/3} \right) ^2 - \tfrac{4}{81} \left( 1 - (1-t)^{1/3} \right) (1-t)^{1/3}\\&\quad + \tfrac{10}{729} (1-t)^{2/3} \ge 0 \quad \forall t \in [0, 1]\\&\Leftrightarrow (1-t)^{2/3} - \tfrac{27}{17} (1-t)^{1/3} + \tfrac{45}{68} \ge 0 \quad \forall t \in [0, 1] \\&\Leftrightarrow \left( (1-t)^{1/3} - \tfrac{27}{34} \right) ^2 \ge - \left( \tfrac{3}{17} \right) ^2 \quad \forall t \in [0, 1]. \end{aligned}$$

  Since the last inequality is obviously true for all $t \in [0, 1]$, this concludes the proof.

• (b) Let $F_i$ denote the cdf of a Weibull distributed random variable with shape parameter $i>0$ and consider the triple $(F_j, F_k, F_\ell )$ with $2\ell < k$ and $\ell \in (\frac{j}{2}, j)$. It follows that the conditions $j \notin (k, 2k)$, $k \notin (\ell , 2 \ell )$ and $\ell \in (\frac{j}{2}, j)$ are satisfied. According to the consideration of the Weibull distribution in Section 4.1 of Eberl and Klar (2024), these three conditions are, in order, equivalent to $F_j \le _{gs}^{t_0} F_k$, $F_k \le _{gs}^{t_0} F_\ell$ and $F_\ell <_{gs}^{t_0} F_j$, thus concluding the proof by contradiction.

$\square$

Obviously, the statement of Theorem 5 is also valid if the set $\mathcal {P}$ is replaced by any other set of distributions that includes the three used for the counterexample or any other triple of distributions that poses an analogous contradiction.

Since there is an additional assumption made in Theorem 5, we cannot conclude that there is no kurtosis measure that satisfies property (K2) on a sufficiently rich set of distributions. This is due to the fact that the mapping $\kappa _T \equiv k$ for some $k \in \mathbb {R}$ is a trivial kurtosis measure which satisfies properties (K1) and (K2). Likewise, the mapping $\kappa _T \equiv 0$ is a measure of central location, dispersion and skewness. To exclude the trivial measure, property (K2) could be extended to

(K$2^\prime$):

$\kappa (F) \le \kappa (G)$ for all $F, G \in \mathcal {Q}$ such that $F \le _K G$ and $\kappa (F) < \kappa (G)$ for all $F, G \in \mathcal {Q}$ such that $F <_K G$ for some kurtosis order $\le _K$ with strict version $<_K$.

Then, Theorem 5 proves that there exist no kurtosis measures based on the kurtosis orders $\le _3$ or $\le _{gs}^{t_0}$. Furthermore, we can conclude that there exist no kurtosis measures based on any kurtosis order which is weaker than $\le _3$ in both the strict and non-strict version.

Since the proof of Theorem 5 is based upon the intransitivity of $\le _3$, the question arises how kurtosis measures behave on the transitivity sets of $\le _3$. However, that question needs to be addressed separately for each candidate, which is done in the following section. There, we focus on the fulfilment of (K2) for $\le _3$ and the generalized concave-convex order.

4 Measures of kurtosis: examples and properties

4.1 The standardized fourth moment

The earliest attempt at measuring kurtosis is attributed to Pearson (1895) and is given by the standardized fourth moment

$$\begin{aligned} \kappa _M: \mathcal {L}^{4} \rightarrow \mathbb {R}, \quad X \mapsto \mathbb {E}\left[ \left( \frac{X - \mu _X}{\sigma _X}\right) ^4\right] \end{aligned}$$

(denoted by $\beta _2$ by Pearson), where $\mathcal {L}^{n} \subseteq \mathcal {P}$ denotes the set of all distributions with finite n-th moment for $n \in \mathbb {N}$. Ever since, the concept of kurtosis and what it describes has been much discussed. However, its oldest measure is still its most prominent one and is often understood as synonymous with the notion of kurtosis itself (see, e.g., McAlevey and Stent 2018 or Crack 2022). The use of $\kappa _M$ as a kurtosis measure is in agreement with the use of the first three (standardized) moments as measures of central location, dispersion and skewness, respectively. The fourth moment, however, is the first that cannot be standardized with respect to a lower moment, namely the third one. The fact that $\kappa _M$ is not invariant to skewness (in terms of the standardized third moment $\gamma _M$) is reflected in the inequality

$$\begin{aligned} \kappa _M(X) \ge (\gamma _M(X))^2 + 1, \quad F \in \mathcal {L}^{4} \end{aligned}$$

(1)

(Pearson 1916, p. 432). The inequality states that a distribution that is strongly skewed in either direction necessarily has a higher kurtosis than less skewed distributions. For example, consider a normally distributed random variable Z. Since $\kappa _M(Z) = 3$, it is less kurtotic with respect to $\kappa _M$ than any random variable that is sufficiently skewed to satisfy $|\gamma _M(X)| > \sqrt{2}$ (like, e.g., $X \sim \textrm{Exp}(\lambda ), \lambda > 0$, with $\gamma _M(X) = 2$). Hence, distributions are generally not comparable with respect to $\kappa _M$ if they exhibit a large difference in skewness. For symmetric distributions, the measure $\kappa _M$ preserves the order $\le _s$ (van Zwet 1964, pp. 20–21). The fact that $\le _{gs}^0$ is generally weaker than $\le _3$ and equivalent to $\le _s$ for symmetric distributions gives the following result.

Theorem 6

If the mapping $\kappa _M$ is restricted to the domain $\mathcal {S}$, it satisfies property (K2) for the kurtosis orders $\le _3$ and $\le _{gs}^0$.

In fact, the result by van Zwet includes more than that: it states that every even standardized moment higher than the second satisfies property (K2) if restricted to symmetric distributions. This is related to the fact that the 2k-th moment, $k \ge 2$, can only be standardized with respect to the first two moments and not with respect to higher moments. Analogously, it is easy to show that the generalization of the standard deviation to $\root 2k \of {\mathbb {E}[(X-\mu _X)^{2k}]}$ is a measure of dispersion for all $k \ge 1$, since, contrary to the kurtosis measure, the dispersion is not standardized out of the measure. Because there is no way of standardizing with respect to kurtosis, the difference in terms of kurtosis is still represented in higher-order standardized even moments.

4.2 Quantile-based approaches to measuring kurtosis

Without any differentiability assumptions, convexity of order k can be defined based on differences: Oja (1981) considers determinants of matrices, while Eberl and Klar (2024) consider divided differences. Both approaches are equivalent (see, e.g., Nørlund 1926). The connection of quantile-based measures of location, dispersion and skewness with the corresponding orders of convex characteristics is best established using these difference-based definitions of convexity (see, e.g., Oja 1981). Thus, we also follow this approach for measures and orders of kurtosis. Usage of divided differences yields that $F \le _3 G$ is equivalent to

$$\begin{aligned} \frac{ \frac{G^{-1}(p_3)-G^{-1}(p_2)}{F^{-1}(p_3)-F^{-1}(p_2)} -\frac{G^{-1}(p_2)-G^{-1}(p_1)}{F^{-1}(p_2)-F^{-1}(p_1)} }{F^{-1}(p_3)-F^{-1}(p_1)} -\frac{ \frac{G^{-1}(p_2)-G^{-1}(p_1)}{F^{-1}(p_2)-F^{-1}(p_1)} -\frac{G^{-1}(p_1)-G^{-1}(p_0)}{F^{-1}(p_1)-F^{-1}(p_0)} }{F^{-1}(p_2)-F^{-1}(p_0)}&\ge 0 \end{aligned}$$

(2)

for all $0<p_0<p_1<p_2<p_3<1$. This equivalence has previously been established by Eberl and Klar (2024), who used it to define a quantile-based kurtosis functional. Contrary to a conventional measure, this functional quantifies the difference in kurtosis between two given distributions and allows the functional to be compatible with the order $\le _3$ in the sense that it is non-negative for arbitrary distribution functions F, G with $F \le _3 G$.

Here, we use (2) as a basis for conventional kurtosis measures. Since (2) cannot generally be rewritten in a way that is symmetric in F and G, we assume that F is a symmetric distribution function, and choose $0<\alpha<\eta <1/2$. Further, put $p_0=\alpha , p_1=\eta , p_2=1-\eta , p_3=1-\alpha$, and define $c = F^{-1}(\eta )-F^{-1}(\alpha ) = F^{-1}(1-\alpha )-F^{-1}(1-\eta )$ and $d=F^{-1}(1-\eta )-F^{-1}(\eta )$. Then, (2) takes the specific form

$$\begin{aligned} \frac{1}{c} \left( G^{-1}(1-\alpha )-G^{-1}(\alpha ) \right) - \left( \frac{2}{d}+\frac{1}{c} \right) \left( G^{-1}(1-\eta )-G^{-1}(\eta ) \right)&\ge 0. \end{aligned}$$

This is equivalent to

$$\begin{aligned} \frac{F^{-1}(1-\alpha )- F^{-1}(\alpha )}{ F^{-1}(1-\eta ) - F^{-1}(\eta ) }&\le \frac{G^{-1}(1-\alpha )-G^{-1}(\alpha )}{G^{-1}(1-\eta )-G^{-1}(\eta )}. \end{aligned}$$

(3)

As a consequence, for $0<\alpha<\eta <1/2$, the mapping

$$\begin{aligned} \kappa _Q^{\alpha , \eta }: \mathcal {P}\rightarrow \mathbb {R}, \quad F \mapsto \frac{F^{-1}(1-\alpha )- F^{-1}(\alpha )}{ F^{-1}(1-\eta ) - F^{-1}(\eta ) } \end{aligned}$$

(4)

preserves the order $\le _3$ on the subset $\mathcal {S} \subseteq \mathcal {P}$ of symmetric distributions. The same is true for the alternative mapping

$$\begin{aligned} \kappa _{QA}^{\alpha ,\eta }: \mathcal {P}\rightarrow \mathbb {R}, \quad F \mapsto \frac{F^{-1}(1-\alpha )-3F^{-1}(1-\eta )+3F^{-1}(\eta )-F^{-1}(\alpha )}{F^{-1}(1-\eta )-F^{-1}(\eta )}, \end{aligned}$$

which is structurally more similar to the kurtosis functional by Eberl and Klar (2024). $\kappa _{QA}^{\alpha ,\eta }(F) \le \kappa _{QA}^{\alpha ,\eta }(G)$ can be equivalently transformed into (3) by adding 3 on either side. As $\le _3$, $\le _{gs}^0$ is also preserved by both quantile-based measures, as the following result shows.

Theorem 7

Let $0<\alpha<\eta <1/2$. If the mappings $\kappa _Q^{\alpha , \eta }$ and $\kappa _{QA}^{\alpha , \eta }$ are restricted to the domain $\mathcal {S}$, they both satisfy property (K2) for the kurtosis orders $\le _3$ and $\le _{gs}^0$.

Proof

Let $F, G \in \mathcal {S}$ satisfy $F \le _{gs}^0 G$. It is sufficient to show $\kappa _Q^{\alpha , \eta }(F) \le \kappa _Q^{\alpha , \eta }(G)$. Since $R_{FG}$ is antisymmetric, it is concave on ${\text {supp}}(F) \cap (-\infty , 0]$ and convex on ${\text {supp}}(F) \cap [0, \infty )$. Because of $F^{-1}(\frac{1}{2}) = 0$, this is equivalent to

$$\begin{aligned} \frac{G^{-1}(p_2)-G^{-1}(p_1)}{F^{-1}(p_2)-F^{-1}(p_1)} -\frac{G^{-1}(p_1)-G^{-1}(p_0)}{F^{-1}(p_1)-F^{-1}(p_0)} {\left\{ \begin{array}{ll} \le 0 \quad &{}, \text { if } 0<p_0<p_1<p_2\le \tfrac{1}{2},\\ \ge 0 \quad &{}, \text { if } \tfrac{1}{2}\le p_0<p_1<p_2<1. \end{array}\right. }\nonumber \\ \end{aligned}$$

(5)

Because of the symmetry of F and G, one of the two inequalities is redundant and we limit ourselves to the upper inequality. By applying $p_0 = \alpha , p_1=\eta , p_2 = \tfrac{1}{2}$ to the upper part of (5), we obtain

$$\begin{aligned}&\frac{F^{-1}(1-\alpha ) - F^{-1}(\alpha )}{F^{-1}(1-\eta ) - F^{-1}(\eta )} = \frac{F^{-1}(\tfrac{1}{2}) - F^{-1}(\alpha )}{F^{-1}(\frac{1}{2}) - F^{-1}(\eta )} = \frac{F^{-1}(\eta ) - F^{-1}(\alpha )}{F^{-1}(\frac{1}{2}) - F^{-1}(\eta )} + 1\\&\qquad \le \frac{G^{-1}(\eta ) - G^{-1}(\alpha )}{G^{-1}(\frac{1}{2}) - G^{-1}(\eta )} + 1 = \frac{G^{-1}(\tfrac{1}{2}) - G^{-1}(\alpha )}{G^{-1}(\frac{1}{2}) - G^{-1}(\eta )} = \frac{G^{-1}(1-\alpha ) - G^{-1}(\alpha )}{G^{-1}(1-\eta ) - G^{-1}(\eta )} \end{aligned}$$

The outer identities follow from the symmetry of F and G, which yields $F^{-1}(1-\alpha ) - F^{-1}(\tfrac{1}{2}) = F^{-1}(\tfrac{1}{2}) - F^{-1}(\alpha )$ (and the same if F is replaced by G or $\alpha$ is replaced by $\eta$). $\square$

In fact, Theorem 7 is still true, if only the less kurtotic distribution F is assumed to be symmetric. This is already clear for $\le _3$ from the derivation of (3), but the following explanation for $\le _{gs}^0$ offers more insight into how that relates to the relationship between kurtosis and skewness.

Let $0<\alpha<\eta <\tfrac{1}{2}$ and $F \in \mathcal {S}, G \in \mathcal {P}$ with $F \le _{gs}^0 G$. Then, (5) still holds. By choosing $p_0=\alpha , p_1=\eta , p_2=\tfrac{1}{2}$ in the upper case of (5) and choosing $p_0=\tfrac{1}{2}, p_1=1-\eta , p_2=1-\alpha$ in the lower case, we obtain

$$\begin{aligned} \frac{G^{-1}(\tfrac{1}{2}) - G^{-1}(\alpha )}{G^{-1}(\frac{1}{2}) - G^{-1}(\eta )}&\ge \frac{F^{-1}(\tfrac{1}{2}) - F^{-1}(\alpha )}{F^{-1}(\frac{1}{2}) - F^{-1}(\eta )}\nonumber \\&= \frac{F^{-1}(1-\alpha ) - F^{-1}(\tfrac{1}{2})}{F^{-1}(1-\eta ) - F^{-1}(\frac{1}{2})} \le \frac{G^{-1}(1-\alpha ) - G^{-1}(\tfrac{1}{2})}{G^{-1}(1-\eta ) - G^{-1}(\frac{1}{2})}. \end{aligned}$$

(6)

Since $\kappa _Q^{\alpha , \eta }(F)$ and $\kappa _Q^{\alpha , \eta }(G)$ are weighted averages of the one-sided quantities in (6), it follows

$$\begin{aligned} \kappa _Q^{\alpha , \eta }(F)&\le \min \left\{ \frac{G^{-1}(\tfrac{1}{2}) - G^{-1}(\alpha )}{G^{-1}(\frac{1}{2}) - G^{-1}(\eta )}, \frac{G^{-1}(1-\alpha ) - G^{-1}(\tfrac{1}{2})}{G^{-1}(1-\eta ) - G^{-1}(\frac{1}{2})} \right\} \end{aligned}$$

(7)

$$\begin{aligned}&\le \frac{G^{-1}(\frac{1}{2}) - G^{-1}(\eta )}{G^{-1}(1-\eta ) - G^{-1}(\eta )} \frac{G^{-1}(\tfrac{1}{2}) - G^{-1}(\alpha )}{G^{-1}(\frac{1}{2}) - G^{-1}(\eta )}\nonumber \\&\quad + \frac{G^{-1}(1-\eta ) - G^{-1}(\frac{1}{2})}{G^{-1}(1-\eta ) - G^{-1}(\eta )} \frac{G^{-1}(1-\alpha ) - G^{-1}(\tfrac{1}{2})}{G^{-1}(1-\eta ) - G^{-1}(\frac{1}{2})}\nonumber \\&= \kappa _Q^{\alpha , \eta }(G). \end{aligned}$$

(8)

Inequality (7) is basically the same inequality that was used to prove Theorem 7 and its tightness is influenced by both F and G. However, the tightness of inequality (8) only depends on G with equality holding if G is symmetric, suggesting that an increase of asymmetry for G tends to decrease the tightness of the inequality $\kappa _Q^{\alpha , \eta }(F) \le \kappa _Q^{\alpha , \eta }(G)$.

The measures $\kappa _Q^{\alpha , \eta }$ and $\kappa _{QA}^{\alpha , \eta }$ have appeared quite often in the literature, see Ruppert (1987), Balanda and MacGillivray (1988), and Jones et al. (2011), where further references can be found. Specific choices of the parameters in the literature are $\eta =\frac{1}{4}$ and $\alpha =0.05$ or $\alpha =0.01$. Alternative parameter choices can be obtained through equidistant evaluation of the quantile function. For example, the quintile-based measure $\kappa _{QA}^{1/5,2/5}$ was introduced in Jones et al. (2011, p. 90), motivated by the analogy with Bowley’s skewness measure $\gamma _Q^{1/4}$, which takes second differences instead of third ones. Furthermore, Moors (1988, p. 26) defined the octile-based measure

$$\begin{aligned} M&= \frac{F^{-1}(\frac{7}{8})-F^{-1}(\frac{5}{8}) + F^{-1}(\frac{3}{8})-F^{-1}(\frac{1}{8})}{ F^{-1}(\frac{6}{8})-F^{-1}(\frac{2}{8})}. \end{aligned}$$

Noting

$$\begin{aligned} M&= \kappa _Q^{1/8,2/8}-\kappa _Q^{3/8,2/8} =\kappa _Q^{1/8,2/8} - \left( \kappa _Q^{2/8,3/8}\right) ^{-1}, \end{aligned}$$

it follows that M preserves the orders $\le _3$ and $\le _{gs}$ for symmetric distributions as well.

4.3 Density-based approaches to measuring kurtosis

In this section, we consider kurtosis measures based on the density and its derivatives. The proposed quantities at times bear a resemblance to those used in Critchley and Jones (2008), where a similar idea is addressed using a different approach.

Eberl and Klar (2024) showed that

$$\begin{aligned} \gamma _D^p: \mathcal {P}\rightarrow \mathbb {R}, \quad F \mapsto -\frac{f'(F^{-1}(p))}{(f(F^{-1}(p))^2} \end{aligned}$$

satisfies the crucial property of a skewness measure for all $p \in (0, 1)$, i.e. it preserves the order $\le _2$. In fact, it is easy to see that $R_{FG}''(x) \ge 0$ for all $x \in D_F$, and thereby also $F \le _2 G$, is equivalent to $\gamma _D^p(F) \le \gamma _D^p(G)$ for all $p \in (0, 1)$. The defining inequalities $\Delta _{FG}(x) \ge 0$ and $\Delta _{FG}'(x) \ge 0$ of the orders $\le _0$ and $\le _1$ of location and dispersion can be transformed in a similar way. By defining $\nu _D^p(F) = F^{-1}(p), p \in (0, 1),$ as a location measure and $\tau _D^p(F) = (f(F^{-1}(p)))^{-1}$ as a dispersion measure, it can be shown that $F \le _0 G$ is equivalent to $\nu _D^p(F) \le \nu _D^p(G)$ for all $p \in (0, 1)$ and that $F \le _1 G$ is equivalent to $\tau _D^p(F) \le \tau _D^p(G)$ for all $p \in (0, 1)$.

In order to use the same methodology for measures of kurtosis, we first calculate

$$\begin{aligned} R_{FG}'''(t)&= \left( \frac{1}{g(R_{FG}(t))}\right) ^5 \cdot \Big [ f''(t) (g(R_{FG}(t)))^4 - 3 f(t) f'(t) (g(R_{FG}(t)))^2 g'(R_{FG}(t))\\&\quad + 3 (f(t))^3 (g'(R_{FG}(t)))^2 - (f(t))^3 g(R_{FG}(t)) g''(R_{FG}(t)) \Big ]. \end{aligned}$$

Based on this, we find

$$\begin{aligned} F \le _3 G&\Leftrightarrow f''(t) (g(R_{FG}(t)))^4 - (f(t))^3 g(R_{FG}(t)) g''(R_{FG}(t))\nonumber \\&\; \ge 3 \left[ f(t) f'(t) (g(R_{FG}(t)))^2 g'(R_{FG}(t)) - (f(t))^3 (g'(R_{FG}(t))^2) \right] \ \forall t \in D_F \nonumber \\&\Leftrightarrow \frac{f''(t)}{(f(t))^3} - \frac{g''(R_{FG}(t))}{(g(R_{FG}(t)))^3} \ge 3 \frac{f'(t)}{(f(t))^2} \frac{g'(R_{FG}(t))}{(g(R_{FG}(t)))^2} - 3 \frac{(g'(R_{FG}(t)))^2}{(g(R_{FG}(t)))^4}\nonumber \\&\qquad \forall t \in D_F \nonumber \\&\Leftrightarrow \frac{f''(F^{-1}(p))}{(f(F^{-1}(p)))^3} - \frac{g''(G^{-1}(p))}{(g(G^{-1}(p)))^3} \nonumber \\&\; \ge 3 \frac{g'(G^{-1}(p))}{(g(G^{-1}(p)))^2} \left( \frac{f'(F^{-1}(p))}{(f(F^{-1}(p)))^2} - \frac{g'(G^{-1}(p))}{(g(G^{-1}(p)))^2} \right) \qquad \forall p \in (0, 1). \end{aligned}$$

(9)

By plugging in the definition of $\gamma _D^p, p \in (0, 1)$, $F \le _3 G$ is equivalent to

$$\begin{aligned} \frac{f''(F^{-1}(p))}{(f(F^{-1}(p)))^3} - \frac{g''(G^{-1}(p))}{(g(G^{-1}(p)))^3} \ge 3 \gamma _D^p(G) (\gamma _D^p(F) - \gamma _D^p(G)) \quad \forall p \in (0, 1). \end{aligned}$$

If we now assume that both F and G are symmetric, $\gamma _D^{1/2}(F) - \gamma _D^{1/2}(G) = 0$ holds for the specific choice $p = \frac{1}{2}$. In that case, $F \le _3 G$ implies

$$\begin{aligned} -\frac{f''(F^{-1}(\frac{1}{2}))}{(f(F^{-1}(\frac{1}{2})))^3} \le -\frac{g''(G^{-1}(\frac{1}{2}))}{(g(G^{-1}(\frac{1}{2})))^3}. \end{aligned}$$

This suggests that a reasonable choice for a density-based kurtosis measure is obtained as the special case $p = \frac{1}{2}$ from the following class of mappings

$$\begin{aligned} \kappa _D^p: \mathcal {P}\rightarrow \mathbb {R}, \quad F \mapsto -\frac{f''(F^{-1}(p))}{(f(F^{-1}(p)))^3}, \end{aligned}$$

(10)

where $p \in (0, 1)$. By plugging this into (9), we see that $F \le _3 G$ is equivalent to

$$\begin{aligned} \kappa _D^p(G) - \kappa _D^p(F) \ge 3 \gamma _D^p(G) (\gamma _D^p(F) - \gamma _D^p(G)) \quad \forall p \in (0, 1). \end{aligned}$$

(11)

Additionally, swapping the roles of F and G yields that $G \le _3 F$ is equivalent to

$$\begin{aligned} \kappa _D^p(G) - \kappa _D^p(F) \le 3 \gamma _D^p(F) (\gamma _D^p(F) - \gamma _D^p(G)) \quad \forall p \in (0, 1). \end{aligned}$$

(12)

Now, if $\kappa _D^p$ is heuristically understood to measure kurtosis and $\gamma _D^p$ is understood to measure skewness, this statement can be interpreted as follows: if two distributions are equally skewed, the right sides of both (11) and (12) vanish, meaning that the kurtosis comparison between F and G is centred around zero. G exhibits more kurtosis than F, if $\kappa _D^p(G) \ge \kappa _D^p(F)$, and vice versa, with both cdf’s being equivalent in terms of kurtosis, if the two quantities are equal. This behaviour can be summarized as follows.

Theorem 8

Let $t \in \mathbb {R}$ and $p \in (0, 1)$. If $F, G \in \mathcal {T}_{D, p}^t$ satisfy $F \le _3 G$, then $\kappa _D^p(F) \le \kappa _D^p(G)$.

It can be shown that $\kappa _D^p$ satisfies (K1), if and only if $p = \frac{1}{2}$. Thus, for any $t \in \mathbb {R}$, $\kappa _D^{1/2}$ restricted to the set $\mathcal {T}_D^t$ is a measure of kurtosis in the sense of (K1) and (K2). Note that $\mathcal {T}_D^0$ is a superset of $\mathcal {S}$.

However, the situation gets more complex if F and G differ in terms of skewness. Define $\ell _{FG}^p = 3 \gamma _D^p(G) (\gamma _D^p(F) - \gamma _D^p(G))$ as the lower limit for $F \le _3 G$ and $u_{FG}^p = 3 \gamma _D^p(F) (\gamma _D^p(F) - \gamma _D^p(G))$ as the upper limit for $G \le _3 F$, both for all $p \in (0, 1)$. Since

$$\begin{aligned} u_{FG}^p - \ell _{FG}^p = 3 (\gamma _D^p(F) - \gamma _D^p(G))^2 \ge 0, \end{aligned}$$

the centre of their comparison in terms of skewness extends to an interval of length $3 (\gamma _D^p(F) - \gamma _D^p(G))^2$. Hence, the bigger the difference in skewness is between the two distributions, the larger the interval that is associated with equivalence with respect to the kurtosis order $\le _3$. The aforementioned centre of the kurtosis comparison not only extends to an interval but also shifts, depending on the concrete values of $\gamma _D^p(F)$ and $\gamma _D^p(G)$ and, more specifically, on their signs. It is easy to see from the definitions that $\ell _{FG}^p$ and $u_{FG}^p$ have the same sign, if and only if $\gamma _D^p(F)$ and $\gamma _D^p(G)$ have the same sign. Note that $\ell _{FG}^p$ and $u_{FG}^p$ having the same sign means that $\kappa _D^p(F) = \kappa _D^p(G)$ for all $p \in (0, 1)$ implies $F <_3 G$ if this sign is negative and $G <_3 F$ if it is positive. Furthermore, 0 is contained in the interval $[\ell _{FG}^p, u_{FG}^p]$, around which the kurtosis comparison is centred, if and only if $\gamma _D^p(F)$ and $\gamma _D^p(G)$ have differing signs (including the case that either is zero).

Fig. 1

Graph of the difference of density-based kurtosis measures for the $\textrm{Weib}(1)$ and the $\textrm{Weib}(k)$-distribution

The interplay of the difference of kurtosis measures and the upper and lower limits with respect to the order $\le _3$ is considered in the following for the example of Weibull distributions.

Example 9

Let $X \sim \textrm{Weib}(1)$ with cdf F and let $Y \sim \textrm{Weib}(k)$ with cdf G for $k > 0$, where ${\text {Weib}}(k)$ denotes the Weibull distribution with shape parameter k and scale parameter 1. The difference $\kappa _D^p(G) - \kappa _D^p(F)$ for $p = \frac{1}{2}$ is plotted in Fig. 1 as a function of k. Additionally, the plot shows in red the lower and upper limits $\ell _{FG}^{1/2}$ and $u_{FG}^{1/2}$ from (11) and (12). All three graphs are obviously zero at $k = 1$ since $F = G$ holds in that case. For $1<k<2$, we have $\kappa _D^{1/2}(G) - \kappa _D^{1/2}(F) > u_{FG}^{1/2}$. This observation is in line with $F <_3 G$ holding for exactly those values of k as mentioned in Eberl and Klar (2024) because of the equivalence

$$\begin{aligned}&F <_3 G \Leftrightarrow F \le _3 G \text { and } G \not \le _3 F \Leftrightarrow \ \kappa _D^p(G) - \kappa _D^p(F) \ge \ell _{FG}^p \ \ \forall p \in (0, 1) \quad \text {and}\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \ \exists p_0 \in (0, 1): \ \kappa _D^{p_0}(G) - \kappa _D^{p_0}(F) > u_{FG}^{p_0}. \end{aligned}$$

(13)

In this case, the latter inequality holds for $p_0 = \frac{1}{2}$. The observation $\kappa _D^{1/2}(G) - \kappa _D^{1/2}(F) < \ell _{FG}^{1/2}$ for $\frac{1}{2}< k < 1$ is in accordance with the fact that $G <_3 F$ holds in a similar way. This is not immediately obvious from Fig. 1 but can be validated by rescaling the plot window. The fact that $\kappa _D^{1/2}(G) - \kappa _D^{1/2}(F) \in [\ell _{FG}^{1/2}, u_{FG}^{1/2}]$ holds for $k < \frac{1}{2}$ and $k>2$ is an implication of $F =_3 G$. For the same reason, $\kappa _D^p(G) - \kappa _D^p(F) \in [\ell _{FG}^p, u_{FG}^p]$ follows for all $p \in (0, 1)$.

Note that the family of Weibull distributions decreases in skewness with respect to $\le _2$ as k increases. Hence, the sign change of both $\ell _{FG}^{1/2}$ and $u_{FG}^{1/2}$ at $k=1$ stems from the fact that $\gamma _D^{1/2}(G) - \gamma _D^{1/2}(F)$ changes its sign from positive to negative. The additional sign change of $\ell _{FG}^{1/2}$ at $k \approx 3.26$ stems from $\gamma _D^{1/2}(G)$ changing sign. The Weibull distribution changes from right-skewed to left-skewed around that value of k with the exact value being determined by the utilized skewness measure.

Overall, (11) and (12) suggest that the comparison of distributions in terms of kurtosis has to account for possible differences in skewness. The same observation is made in Sects. 4.1 and 4.2. In the first case, the evidence comes in the form of the well-known inequality (1). In the second case, it is shown that the tightness of the inequality $\kappa _Q^{\alpha , \eta }(F) \le \kappa _Q^{\alpha , \eta }(G)$ is reduced if F or G are markedly skew or if they exhibit a large difference in skewness.

A similar statement can be made about the density-based measurement of kurtosis in this section. However, compared to the ideas from Sect. 4.2, the inequalities (11) and (12) represent the influence of skewness on the measurement of kurtosis in a more precise way. Since these inequalities also characterize the kurtosis order $\le _3$, this helps to understand why it is difficult to meaningfully apply the order to distributions with a significant difference in skewness.

Similarly to the quantile-based kurtosis functional $\kappa _{QF}^\alpha , \alpha \in (0, \frac{1}{2}),$ by Eberl and Klar (2024), which preserves the order $\le _3$ in the sense that $F \le _3 G$ implies $\kappa _{QF}^\alpha (F, G) \ge 0$, we can now define a density-based kurtosis functional by

$$\begin{aligned} \kappa _{DF}^p(F, G) = \kappa _D^p(G) - \kappa _D^p(F) - 3\gamma _D^p(G) \left( \gamma _D^p(F) - \gamma _D^p(G) \right) \end{aligned}$$

for all $p \in (0, 1)$. An advantage $\kappa _{DF}^p$ has over $\kappa _{QF}^\alpha$ is that it characterizes the order $\le _3$ in the sense that $F \le _3 G$ is equivalent to $\kappa _{DF}^p(F, G) \ge 0$ for all $p \in (0, 1)$. However, neither $\kappa _{DF}^p$ nor $\kappa _{QF}^\alpha$ is symmetric in their two arguments F and G.

Another connection between density- and quantile-based measures is that the former can be obtained as a limiting case of the latter. This is also true for corresponding measures of dispersion and skewness as discussed in the following remark.

Remark 10

Let $F \in \mathcal {P}$.

• (a) The canonical quantile-based measures of location are quantiles themselves, which can be seen as density-based measures of location, as stated in the beginning of this section.

• (b) The canonical quantile-based measure of dispersion is the interquantile distance (see, e.g., Müller and Stoyan 2002). In order to obtain a symmetric quantity, we define $\tau _Q^\alpha (F) = F^{-1}(1-\alpha ) - F^{-1}(\alpha ), \alpha \in (0, \frac{1}{2})$. Obviously, $\lim _{\alpha \nearrow \frac{1}{2}} \tau _Q^\alpha (F) = 0$ holds. In order to obtain a derivative, we multiply with a factor that only depends on $\alpha$ and not on F itself, which vanishes for $\alpha \nearrow \frac{1}{2}$. This yields

  $$\begin{aligned} \lim _{\alpha \nearrow \frac{1}{2}} \frac{1}{1 - 2\alpha } \cdot \tau _Q^\alpha (F)&= \lim _{\alpha \nearrow \frac{1}{2}} \frac{F^{-1}(1-\alpha ) - F^{-1}(\alpha )}{(1-\alpha ) - \alpha }\\&= \left( F^{-1}\right) '\left( \frac{1}{2}\right) = \frac{1}{f(F^{-1}(\frac{1}{2}))} = \tau _D(F). \end{aligned}$$

• (c) A quantile-based skewness measure that is structurally similar to the previously presented quantities is given by

  $$\begin{aligned} \gamma _D^\alpha (F) = \frac{F^{-1}(1-\alpha ) - 2 F^{-1}(\frac{1}{2}) + F^{-1}(\alpha )}{F^{-1}(1-\alpha ) - F^{-1}(\alpha )} \end{aligned}$$

  (see, e.g., Groeneveld and Meeden 1984). After multiplying with a similar $\alpha$-dependent factor as before, we now obtain the limiting value for $\alpha \nearrow \frac{1}{2}$ by rewriting the resulting term as the ratio of a second-order and a first-order difference quotient

  $$\begin{aligned} \lim _{\alpha \nearrow \frac{1}{2}} \frac{4}{1 - 2\alpha } \cdot \gamma _Q^\alpha (F)&= 4 \cdot \lim _{\alpha \nearrow \frac{1}{2}} \frac{\frac{F^{-1}(1-\alpha ) - 2 F^{-1}(\frac{1}{2}) + F^{-1}(\alpha )}{(1-2\alpha )^2}}{\frac{F^{-1}(1-\alpha ) - F^{-1}(\alpha )}{1-2\alpha }} = \frac{\left( F^{-1}\right) ''(\frac{1}{2})}{\left( F^{-1}\right) '(\frac{1}{2})}\\&= - \frac{f'(F^{-1}(\frac{1}{2}))}{(f(F^{-1}(\frac{1}{2})))^2} = \gamma _D(F), \end{aligned}$$

  where we used that

  $$\begin{aligned} \left( F^{-1}\right) ''(p) = \left( \frac{1}{f(F^{-1}(p))}\right) ' = -\frac{f'(F^{-1}(p))}{(f(F^{-1}(p)))^3} \end{aligned}$$

  for $p \in (0, 1)$.

• (d) The quantile-based kurtosis measure that seems to be most closely related to $\tau _Q^\alpha$ and $\gamma _Q^\alpha$ is $\kappa _{QA}^{\alpha , \eta }$ because it has a higher-order difference in its numerator. Because $\kappa _{QA}^{\alpha , \eta }$ is dependent upon two parameters $0<\alpha<\eta <\frac{1}{2}$, further assumptions have to be made to calculate a meaningful limit. In order to obtain a natural continuation of the previous limits, $\alpha$ and $\eta$ are chosen in such a way that the evaluation points of the quantile function are equidistant. Hence, we choose $\eta = \frac{1}{2}-\beta$ and $\alpha = \frac{1}{2} - 3\beta$ for a $\beta \in (0, \frac{1}{6})$, meaning that the distance between to neighbouring evaluation points is fixed to $2\beta$. After slightly altering the previously used rescaling factor, the following limit is obtained for $\beta \searrow 0$

  $$\begin{aligned} \lim _{\beta \searrow 0} \frac{2}{\beta ^2} \cdot \kappa _{QA}^{\frac{1}{2} - 3\beta , \frac{1}{2} - \beta }(F)&= 8 \cdot \lim _{\beta \searrow 0} \frac{\frac{F^{-1}(\frac{1}{2}+3\beta ) - 3 F^{-1}(\frac{1}{2}+\beta ) + 3 F^{-1}(\frac{1}{2} - \beta ) - F^{-1}(\frac{1}{2} - 3\beta )}{(2\beta )^3}}{\frac{F^{-1}(\frac{1}{2} + \beta ) - F^{-1}(\frac{1}{2} - \beta )}{2\beta }}\nonumber \\&= \frac{\left( F^{-1}\right) '''(\frac{1}{2})}{\left( F^{-1}\right) '(\frac{1}{2})} = -\frac{f''(F^{-1}(\frac{1}{2}))}{(f(F^{-1}(\frac{1}{2})))^3} + 3 \left( \frac{f'(F^{-1}(\frac{1}{2}))}{(f(F^{-1}(\frac{1}{2})))^2}\right) ^2\nonumber \\&= \kappa _D^{1/2}(F) + 3 (\gamma _D^{1/2}(F))^2. \end{aligned}$$

  (14)

  In contrast to the two previous parts, we do not obtain the already known density-based measure as the limiting value. However, if the limit above is defined as an alternative density-based kurtosis measure, most of the results concerning $\kappa _D$ can be replicated. Particularly, if we define

  $$\begin{aligned} \kappa _{DA}^p: \mathcal {P}\rightarrow \mathbb {R}, \quad F \mapsto \kappa _D^p(F) + 3 (\gamma _D^p(F))^2, \end{aligned}$$

  we obtain that $F \le _3 G$ is equivalent to

  $$\begin{aligned} \kappa _{DA}^p(G) - \kappa _{DA}^p(F) \ge 3 \gamma _D^p(F) (\gamma _D^p(G) - \gamma _D^p(F)) \quad \forall p \in (0, 1). \end{aligned}$$

  (15)

  This lower bound coincides with $\ell _{GF}^p$, the lower bound for the corresponding difference of measures $\kappa _D^p$ with the roles of F and G reversed. Therefore, $\kappa _{DA}^p$ also preserves the order $\le _3$, if F and G are equally skewed in the sense of $\gamma _D^p(F) = \gamma _D^p(G)$, or if one of the cdf’s (in this case F) is symmetric and $p = \frac{1}{2}$.

4.4 Expectile-based approaches to measuring kurtosis

Eberl and Klar (2022, 2023) presented methods for the quantification of dispersion and skewness using expectiles. Expectiles are generalized quantiles and possess a number of desirable quantities. In the cited papers, expectile-based measures of dispersion and skewness were defined analogously to the quantile-based measures $\tau _Q^\alpha$ and $\gamma _Q^\alpha$ in the present paper by simply substituting the quantile function for the corresponding expectile function. In the context of this paper, we denote these measures by $\tau _E^\alpha$ and $\gamma _E^\alpha$. Since the resulting quantities are at times difficult to analyze, their limits analogous to those obtained in Remark 10 were considered since they are easier to handle; they are given by $\tau _{EL}(X) = \mathbb {E}[|X - \mu _X|]$ (the mean absolute deviation) and by $\gamma _{EL}(F) = 2 F(\mu _F) - 1$. In this section, we proceed similarly for measures of kurtosis.

For any cdf $F \in \mathcal {L}^{1}$ with $e_F$ denoting the corresponding expectile function, we define an expectile-based kurtosis measure by

$$\begin{aligned} \kappa _E^{\alpha , \eta }(F) = \frac{e_F(1-\alpha ) - 3 e_F(1-\eta ) + 3 e_F(\eta ) - e_F(\alpha )}{e_F(1-\eta ) - e_F(\eta )}, \quad 0<\alpha<\eta <\frac{1}{2}. \end{aligned}$$

We use the analogue to $\kappa _{QA}^{\alpha , \eta }$ instead of the equivalent analogue to $\kappa _Q^{\alpha , \eta }$ because the former is better suited for determining its limiting value, as noted in Remark 10. In contrast to the expectile-based measures considered in Eberl and Klar (2022, 2023), the expectile kurtosis $\kappa _E^{\alpha , \eta }$ has the major problem that it is not known whether it preserves any kurtosis order on some subset of distributions like $\mathcal {S}$. Thus, its limiting value is needed to draw a connection to kurtosis orders. We consider the same limit as in (14) and replace the quantile function with the corresponding expectile function, yielding

$$\begin{aligned} \lim _{\beta \searrow 0} \frac{2}{\beta ^2} \cdot \kappa _E^{\frac{1}{2} - 3\beta , \frac{1}{2} - \beta }(F)&= 8 \cdot \lim _{\beta \searrow 0} \frac{\frac{e_F(\frac{1}{2}+3\beta ) - 3 e_F(\frac{1}{2}+\beta ) + 3 e_F(\frac{1}{2} - \beta ) - e_F(\frac{1}{2} - 3\beta )}{(2\beta )^3}}{\frac{e_F(\frac{1}{2} + \beta ) - e_F(\frac{1}{2} - \beta )}{2\beta }}\nonumber \\ {}&= \frac{\left( e_F\right) '''(\frac{1}{2})}{\left( e_F\right) '(\frac{1}{2})}. \end{aligned}$$

(16)

The first two derivatives of the expectile function $e_F$, evaluated at 1/2, are given by

$$\begin{aligned} e_F'(1/2)&= 2 \tau _{EL}(F),\\ e_F''(1/2)&= 8 \tau _{EL}(F) \cdot (2 F(\mu _F) - 1) \end{aligned}$$

(see Eberl and Klar 2022). To shorten the following calculations, we use the abbreviation $\delta _F = \tau _{EL}(F)$. The third derivative at 1/2 can be calculated similarly to the second, which utilizes the general form of the first derivative, given by

$$\begin{aligned} e_{F}'(\alpha ) = \frac{\mathbb {E}[| X-e_{F}(\alpha ) |]}{(1-\alpha )F(e_{F}(\alpha ))+\alpha \left( 1-F(e_{F}(\alpha ))\right) }, \quad \alpha \in (0, 1) \end{aligned}$$

(see Holzmann and Klar 2016). If we denote the numerator and the denominator by $u(\alpha )$ and $v(\alpha )$, respectively, we obtain

$$\begin{aligned} e_F'''(\tfrac{1}{2}) = \lim _{\alpha \nearrow \frac{1}{2}} \frac{u''(\alpha ) (v(\alpha ))^2 - 2 u'(\alpha ) v'(\alpha ) v(\alpha ) + 2 u(\alpha ) (v'(\alpha ))^2 - u(\alpha ) v''(\alpha ) v(\alpha )}{(v(\alpha ))^3}. \end{aligned}$$

This can be calculated using

$$\begin{aligned} u(\alpha )&= \mathbb {E}[|X - e_F(\alpha )|] {\mathop {\rightarrow }\limits ^{\alpha \rightarrow \frac{1}{2}}} \delta _F,\\ u'(\alpha )&= e_F'(\alpha ) (2 F(e_F(\alpha )) - 1) {\mathop {\rightarrow }\limits ^{\alpha \rightarrow \frac{1}{2}}} e_F'(\tfrac{1}{2}) (2F(\mu _F) - 1) = 2 \delta _F \gamma _{EL}(F),\\ u''(\alpha )&= e_F''(\alpha ) (2 F(e_F(\alpha )) - 1) + 2 (e_F'(\alpha ))^2 f(e_F(\alpha )) {\mathop {\rightarrow }\limits ^{\alpha \rightarrow \frac{1}{2}}} 8 \delta _F \left( (\gamma _T(F))^2 + \delta _F f(\mu _F) \right) \end{aligned}$$

and

$$\begin{aligned} v(\alpha )&= (1-\alpha ) F(e_F(\alpha )) + \alpha (1 - F(e_F(\alpha ))) {\mathop {\rightarrow }\limits ^{\alpha \rightarrow \frac{1}{2}}} \tfrac{1}{2},\\ v'(\alpha )&= (1 - 2F(e_F(\alpha ))) + (1-2\alpha ) f(e_F(\alpha )) e_F'(\alpha ) {\mathop {\rightarrow }\limits ^{\alpha \rightarrow \frac{1}{2}}} -\gamma _{EL}(F),\\ v''(\alpha )&= (1-2\alpha ) f'(e_F(\alpha )) (e_F'(\alpha ))^2 + (1-2\alpha ) f(e_F(\alpha )) e_F''(\alpha ) - 4 f(e_F(\alpha )) e_F'(\alpha )\\&{\mathop {\rightarrow }\limits ^{\alpha \rightarrow \frac{1}{2}}} - 8 f(\mu _F) \delta _F \end{aligned}$$

(see also Eberl and Klar 2022). Hence,

$$\begin{aligned} e_F'''(\tfrac{1}{2})&= 8 \left[ 2 \delta _F \left( (\gamma _{EL}(F))^2 + \delta _F f(\mu _F) \right) + 2 \delta _F (\gamma _{EL}(F))^2 + 2 \delta _F (\gamma _{EL}(F))^2 + 4 f(\mu _F) \delta _F^2 \right] \\&= 48 \delta _F \left( \delta _F f(\mu _F) + (\gamma _{EL}(F))^2 \right) . \end{aligned}$$

By plugging this into (16), we obtain the limiting expectile-based kurtosis measure

$$\begin{aligned} \lim _{\beta \searrow 0} \frac{2}{\beta ^2} \cdot \kappa _E^{\frac{1}{2} - 3\beta , \frac{1}{2} - \beta }(F)&= \frac{\left( e_F\right) '''(\frac{1}{2})}{\left( e_F\right) '(\frac{1}{2})} = \frac{48 \delta _F \left( \delta _F f(\mu _F) + (\gamma _{EL}(F))^2 \right) }{2 \delta _F}\\&= 24 \left( \delta _F f(\mu _F) + (\gamma _{EL}(F))^2 \right) . \end{aligned}$$

Disregarding the factor 24, we define the mapping

$$\begin{aligned} \kappa _{EL}: \mathcal {L}^{1} \rightarrow \mathbb {R}, \quad F \mapsto \tau _{EL}(F) \cdot f(\mu _F) + (\gamma _{EL}(F))^2. \end{aligned}$$

(17)

If we restrict that mapping to symmetric distributions, the second summand vanishes, as then, $\gamma _T(F) = 0$. In that case, $\kappa _{EL}$ satisfies the requirements for a kurtosis measure.

Theorem 11

If the mapping $\kappa _{EL}$ is restricted to the domain $\mathcal {S}$, it satisfies (K1) and (K2) for the kurtosis orders $\le _3$ and $\le _{gs}^0$.

Proof

Let $F \in \mathcal {S}$. We start by showing that $\kappa _{EL}$ satisfies (K1) in two steps. To prove that $\kappa _{EL}(aX+b) = \kappa _{EL}(X)$ for all $a>0$ and $b \in \mathbb {R}$, note that $\tau _{EL}(aX+b) = a \tau _{EL}(X)$ and

$$\begin{aligned} f_{aX+b}(\mathbb {E}[aX+b])&= \frac{1}{a} f\left( \frac{\mathbb {E}[aX+b] - b}{a}\right) = \tfrac{1}{a} f(\mu _F). \end{aligned}$$

For (K1), it remains to be shown that $\kappa _{EL}(-X) = \kappa _{EL}(X)$, which is implied by $\tau _{EL}(-X) = \tau _{EL}$ and $f_{-X}(\mathbb {E}[-X]) = f(-\mathbb {E}[-X]) = f(\mu _F)$.

Now, assume $F, G \in \mathcal {S}$ such that $F \le _{gs}^0 G$. Since $\kappa _{EL}$ satisfies (K1), it is invariant under shifts and rescaling, and we may assume without restriction that $\mu _F = \mu _G = 0$ and $f(\mu _F) = g(\mu _G)$. It follows from $F \le _{gs}^0 G$ as well as $F, G \in \mathcal {S}$ that $R_{FG}$ is concave on $(-\infty , 0] \cap D_F$ and convex on $[0, \infty ) \cap D_F$. Thus, $R_{FG}'(t) = f(t)/g(R_{FG}(t)), t \in D_F,$ is decreasing for $t\le 0$ and increasing for $t\ge 0$. Therefore, the function $R_{FG}'$ reaches its global minimum $f(\mu _F)/g(\mu _G) = f(0)/g(0) = 1$ at 0. (Since both F and G are symmetric, their medians and means coincide, yielding $R_{FG}(0) = 0$.) It follows that $R_{FG}'(t) \ge 1$ for all $t \in D_F$, which is equivalent to $F \le _1 G$. Since $\tau _{EL}$ is a dispersion measure (see Hürlimann 2002, p. 15), $\tau _{EL}(F) \le \tau _{EL}(G)$ holds, concluding the proof. $\square$

In fact, the result above holds for any mapping $\kappa : \mathcal {S} \rightarrow \mathbb {R}, F \mapsto \tau (F) f(\nu (F))$, where $\nu$ is an arbitrary measure of central location and $\tau$ is an arbitrary measure of dispersion. The second generalization is valid because the fact that $\tau _{EL}$ is a dispersion measure is the only property of $\tau _{EL}$ that is utilized in the proof of Theorem 11. The mean can be replaced by any other location measure since all location measures are equal on a symmetric distribution.

We make use of this flexibility by centring the kurtosis measure around the median instead of around the mean. The resulting mapping

$$\begin{aligned} \kappa _{EM}: \mathcal {L}^{1} \rightarrow \mathbb {R}, \quad F \mapsto \mathbb {E}[|X - F^{-1}(\tfrac{1}{2})|] \cdot f(F^{-1}(\tfrac{1}{2})), \end{aligned}$$

(18)

involves the mean absolute deviation around the median and preserves the order $\le _3$ under weaker assumptions.

Theorem 12

Let $t \in \mathbb {R}$. If $F, G \in \mathcal {T}_{D, 1/2}^t$ satisfy $F \le _3 G$, then $\kappa _{EM}(F) \le \kappa _{EM}(G)$.

Proof

Since $\kappa _{EM}$ is invariant to affine linear transformations (for analogous reasons as $\kappa _{EL}$ on $\mathcal {S}$), we can assume without restriction that $F^{-1}(\frac{1}{2}) = G^{-1}(\frac{1}{2}) = 0$ and $f(F^{-1}(\frac{1}{2})) = g(G^{-1}(\frac{1}{2}))$. According to Proposition 12 in Eberl and Klar (2024), 1/2 is a so-called inflection value for all pairs $F, G \in \mathcal {T}_{D, 1/2}^t$ with $F \le _3 G$, meaning that $R_{FG}$ is concave on $(-\infty , F^{-1}(1/2)] \cap {\text {supp}}(F)$ and convex on $[F^{-1}(1/2), \infty ) \cap {\text {supp}}(F)$. Noting $F^{-1}(1/2) = 0$ and that the mapping $F \mapsto \mathbb {E}[|X - F^{-1}(1/2)|]$ is also a dispersion measure (see Hürlimann 2002, p. 15), the remainder of the proof is analogous to that of Theorem 11. $\square$

4.5 Ratios of dispersion measures as measures of kurtosis

As mentioned in the introduction, one of the first attempts to construct kurtosis measures in a general way was made by Bickel and Lehmann (1975, pp. 469–470), where they announced to define a kurtosis measure as a ‘suitable’ ratio of two (possibly rescaled) dispersion measures. Of the measures we have discussed in Sect. 4, several fit this description.

The most obvious instance is the quantile-based measure $\kappa _Q^{\alpha , \eta }$, which is defined as a wider interquantile range divided by a more narrow interquantile range. Any interquantile range is by definition a measure of dispersion. The situation is similar for the expectile kurtosis $\kappa _E$, which is equivalent to a ratio of two interexpectile ranges $\tau _E$. While any interexpectile range is a dispersion measure (see Eberl and Klar 2023), the ratio could not be shown to preserve the order $\le _3$ on any notable subset of distributions.

Another example is the expectile limit measure around the median, which can be rewritten as

$$\begin{aligned} \kappa _{EM}(F) = \frac{\mathbb {E}[|X - F^{-1}(\tfrac{1}{2})|]}{\tau _D(F)}. \end{aligned}$$

Finally, the moment-based measure $\kappa _M$ is equivalent to the monotonically transformed

$$\begin{aligned} \root 4 \of {\kappa _M(F)} = \frac{\root 4 \of {\mathbb {E}[(X-\mu _F)^4]}}{\sigma _F}, \quad F \in \mathcal {L}^{4}. \end{aligned}$$

Here, two measures $\kappa _1$ and $\kappa _2$ are said to be equivalent, if $\kappa _1(F) \le \kappa _1(G)$ is equivalent to $\kappa _2(F) \le \kappa _2(G)$ for all cdf’s F and G. Since the generalized standard deviation $\root 2k \of {\mathbb {E}[(X-\mu _F)^{2k}]}$ is also a dispersion measure for all $k \in \mathbb {N}$ (see Sect. 4.1), $\root 4 \of {\kappa _M}$ is also a ratio of two dispersion measures. The other kurtosis measures in this work have no obvious representation as a ratio of two dispersion measures. Hence, while the rather vague definition from Bickel and Lehmann (1975) has some merit, it does not seem to coincide with the order-based approach.

A pattern can be observed for kurtosis measures that are ratios of two dispersion measures. In all cases, the dispersion measure in the numerator puts more emphasis on the tails of the distribution relative to the measure in the denominator, which focuses more on the centre of the distribution. This begs the question as to why these kinds of constructions tend to preserve the order $\le _3$, at least on the subset of symmetric distributions. While the notion of ’putting more emphasis on the tails’ seems to be too vague to obtain any general rigorous result explaining this behaviour, the proof of Theorem 11 is fairly instructive for this kind of situation. If $F, G \in \mathcal {S}, F \ne G$ satisfy $F \le _{gs}^0\,G$, then the function $R_{FG}'$ is decreasing up to 0 and increasing from there on. We now assume that the more centre-focused dispersion measures $\tau _C$ in the denominator satisfies $\tau _C(F) = \tau _C(G)$. If $\tau _C$ not only preserves the dispersive order $\le _1$ but also its strict version $<_1$, then neither $R_{FG}'>1$ nor $R_{FG}'<1$ is true. It follows that there exists a $t_0 \in D_F \cap [0, \infty )$ such that $R_{FG}'(t)>1$ holds for $|t| \ge t_0$. If the more tail-focused dispersion measure $\tau _T$ in the numerator is sufficiently similar to $\tau _C$, then $\tau _T(F) \le \tau _T(G)$ follows from the fact that the dispersions of F and G are similar around the centre (since $\tau _C(F) = \tau _C(G)$) and that F is more dispersed than G on the tails (since $R_{FG}'(t)>1$ for large absolute values of t). Overall, the mapping $F \mapsto \tau _T(F)/\tau _C(F)$ then preserves the concave-convex order $\le _{gs}^0$ and therefore also the order $\le _3$.

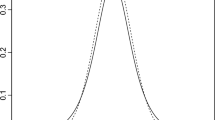
This similarity in the construction of a number of kurtosis measures strengthens the interpretation of the concept of kurtosis by Balanda and MacGillivray (1988), who describe kurtosis as “the location- and scale-free movement of probability mass from the shoulders of a distribution into its center and tails”. The density of a typical symmetric and unimodal distribution that is very kurtotic has a sharp peak in the centre, declines steeply away from it, and has fat tails. Thus, the dispersion of the distribution mostly lies far away from its centre. If a distribution exhibits little kurtosis, the shoulders of its density are very prominent compared to its centre and tails. Here, the dispersion of the distribution is mostly close to the centre. Overall, a centre-focused dispersion measure $\tau _C$ tends to take larger values for distributions with less kurtosis, and a tail-focused dispersion measure $\tau _T$ tends to take larger values for more kurtotic distributions. This is illustrated in Fig. 2.

4.6 Numerical comparison of the different kurtosis measures

Since measures of kurtosis are much more prevalent in applied sciences than in the mathematical literature, we briefly compare the numerical values of the measures considered in the previous subsections. For that, we use three families of distributions: Student’s t-distribution, the beta distribution and the sinh-arcsinh distribution. To simplify the notation, we denote $\kappa _Q = \kappa _Q^{0.05, 0.25}$, $\kappa _D = \kappa _D^{0.5}$ and $\kappa _E^{0.05, 0.25}$ throughout. Furthermore, note that $\kappa _{EL} = \kappa _{EM}$ holds for symmetric distributions.

First, we consider Student’s t-distribution, which is a classical example for a one-parameter familiy of symmetric distributions that varies in terms of kurtosis. The values of all six kurtosis measures analyzed in this paper are plotted in Fig. 3. Instead of $\kappa _E$ we consider $\kappa _E+3$, which is structurally equivalent to $\kappa _Q$ and always takes non-negative values. The different measures all behave similarly with large values and a steep decline for a small number of degrees of freedom. The curves then all flatten out as the parameter increases. The levels at which they flatten out as well as the exact shapes of the curves vary between the different measures. This can partly be explained by the fact that some of them are only defined for sufficiently high degrees of freedom.

Fig. 2

Illustration: the centre-focused dispersion measure $\tau _C$ is smaller for the more kurtotic distribution G in blue and larger for the less kurtotic distribution F in orange. The opposite is the case for the tail-focused dispersion measure $\tau _T$. (Here: $\tau _C = \tau _Q^{0.25}$ and $\tau _T = \tau _Q^{0.01}$)

Fig. 3

Values of the six considered kurtosis measures for Student’s t distribution $t_\nu$ with varying degrees of freedom $\nu > 0$

Next, we use the beta distribution, which depends on two shape parameters $\alpha , \beta > 0$. We consider the symmetric case $\alpha = \beta$, as well as $\alpha = 5\beta$, i.e. asymmetric, left-skewed distributions. The values of the kurtosis measures in both scenarios are shown in Fig. 4. The curves in the symmetric case behave similarly to those for the t-distribution as they all have a similar shape and mostly differ in scale and shift. The fact that the distribution becomes more kurtotic for increasing parameter values coincides with its visual perception. For small values of $\alpha$, $\kappa _D$ takes negative values because the density function is then left-curved at its center rather than right-curved as it usually is for symmetric unimodal distributions. In the asymmetric case, however, the six kurtosis measures behave very differently: some are increasing, some are decreasing and some are neither. This is because the skewness of the distribution interferes with the measurement of its kurtosis by introducing ambiguity.

Fig. 4

Values of the six considered kurtosis measures the beta distribution ${\text {B}}(\alpha , \beta )$ with varying shape parameters $\alpha , \beta > 0$

Finally, we consider the sinh-arcsinh distribution introduced by Jones and Pewsey (2009). A random variable X is said to be sinh-arcsinh-distributed with skewness parameter $\nu \in \mathbb {R}$ and (inverse) kurtosis parameter $\tau > 0$, if

$$\begin{aligned} Z = S_{\nu , \tau }(X) = \sinh (\tau \cdot {\text {arsinh}}(X) - \nu ) \end{aligned}$$

is standard normal. This distribution family is superior to other skewness-kurtosis-families for several reasons: its density, quantile function and moments can easily be calculated, it includes the standard normal distributions in the interior of the parameter space, and, most importantly, its kurtosis parameter exhibits strong invariance properties with respect to its skewness parameter (Eberl and Klar 2024). Besides the symmetric case $\nu =0$, we consider the asymmetric, right-skewed case of $\nu = 1$. The corresponding values of the kurtosis measures are plotted in Fig. 5. In the symmetric case, all kurtosis measures again behave similarly. As one would expect, all curves are decreasing. While the differences in the shapes of the curves are larger in the asymmetric case, all kurtosis measures except $\kappa _D$ are still decreasing as a function of $\tau$. This behaviour persists if the degree of skewness is increased further, and we conjecture that this is related to the fact that the skewness and kurtosis parameters of this distribution family are not entangled (see Eberl and Klar 2024, Theorem 23). The peculiar behaviour of the density-based kurtosis measure is explained by the fact that it evaluates the distribution only in a local way. For symmetric unimodal distributions, the density evaluated at the median (which then coincides with the mode) is right-curved, resulting in $\kappa _D > 0$. However, in the right-skewed case, the median is typically larger than the mode and then lies within a long left-curved area of the density, leading to $\kappa _D < 0$. In order to understand what information is actually conveyed by this value of the kurtosis measure, one has to take the values of the corresponding density-based skewness measure $\gamma _D$ into account in the sense of (11).

Fig. 5

Values of the six considered kurtosis measures for the sinh-arcsinh distribution ${\text {SAS}}(\nu , \tau )$ with varying skewness parameter $\nu \in \mathbb {R}$ and (inverse) kurtosis parameter $\tau > 0$

4.7 Empirical counterparts of the different measures of kurtosis

The asymptotic distribution of the empirical moment kurtosis, i.e. the fourth standardized empirical moment, can be found in Borroni and De Capitani (2022, Theorem 2). In the following, we briefly discuss the empirical counterparts of the remaining kurtosis measures. Details run along the lines of the corresponding skewness measures (Eberl and Klar 2020), and are omitted.

Let $X_1,\ldots ,X_n$ be independent and identically distributed random variables with $X_1\sim F$. Further, let $\hat{q}_p$ denote the empirical p-quantile. Then, for $0<\alpha<\eta <1/2$, the obvious plug-in estimator of $\kappa _Q^{\alpha , \eta }$ in (4) is $\hat{\kappa }_Q^{\alpha , \eta } = (\hat{q}_{1-\alpha }-\hat{q}_\alpha )/ (\hat{q}_{1-\eta }-\hat{q}_\eta )$, and standard arguments yield the asymptotic normality

$$\begin{aligned} \sqrt{n}\left( \hat{\kappa }_Q^{\alpha ,\eta }-\kappa _Q^{\alpha ,\eta }\right)&\overset{D}{\longrightarrow }\ N\left( 0,\sigma _{\kappa _Q}^2\right) , \end{aligned}$$

where $\sigma _{\kappa _Q}^2$ depends on $\alpha ,\eta$ and F. Similarly, one can construct plug-in estimators of $\kappa _{QA}^{\alpha ,\eta }$ and M.

For estimating $\kappa _D^{1/2}$ in (10), one needs estimates of the density f and its second derivative. This is commonly achieved by using a kernel density estimator $\hat{f}_h$ and its second derivative $\hat{f}_h''$, where h denotes the bandwidth. Then, a possible estimator is

$$\begin{aligned} \hat{\kappa }_D^{1/2} = -\hat{f}_h''( \hat{q}_{1/2}) / (\hat{f}_h( \hat{q}_{1/2})^3). \end{aligned}$$

Since the optimal bandwidth for estimation of the rth derivative is of order $n^{-1/(2r+5)}$, one can show that the AMISE converges to zero with rate $n^{-4/(2r+5)}$ (Scott 1992). Hence, very large sample sizes are necessary compared to the rate $n^{-1}$ for quantile-based measures to obtain a comparably accurate estimate.

Assuming a finite second moment and using the asymptotics of empirical expectiles (Holzmann and Klar 2016), it can be proved that the estimator $\hat{\kappa }_E^{\alpha ,\eta } = (\hat{e}_{1-\alpha } -3\hat{e}_{1-\eta } +3\hat{e}_{\eta } -\hat{e}_{\alpha }) / (\hat{e}_{1-\eta } -\hat{e}_{\eta })$ of $\kappa _E^{\alpha ,\eta }$ in () satisfies

$$\begin{aligned} \sqrt{n}\left( \hat{\kappa }_E^{\alpha ,\eta }-\kappa _E^{\alpha ,\eta }\right)&\overset{D}{\longrightarrow }\ N\left( 0,\sigma _{\kappa _E}^2\right) , \end{aligned}$$

where $\sigma _{\kappa _E}^2$ depends on $\alpha ,\eta$ and F. On the other hand, the plug-in estimator of $\kappa _{EL}$ in (17), given by

$$\begin{aligned} \hat{\kappa }_{EL} = \hat{f}_h(\bar{X}) \ \sum _{j=1}^n |X_j-\bar{X}|/n + \big (2F_n(\bar{X})-1\big )^2, \end{aligned}$$

again suffers from a rate of convergence slower than $n^{-1}$, but not to the same extent as $\hat{\kappa }_D^{1/2}$. The same remark applies to the plug-in estimator of $\kappa _{EM}$ in (18). In summary, estimators for all measures of kurtosis are readily available. Estimators involving the estimation of the density or its derivative need larger sample sizes. This concerns $\kappa _D^{1/2}$ in particular, which is why this measure should only be used for theoretical considerations.

5 Conclusion

As shown in this work, kurtosis measures in the traditional sense do not exist, due to the intrinsic entanglement between skewness and kurtosis. This implies that kurtosis cannot be measured in the same way as location, dispersion and skewness, and the same also holds for all higher convex characteristics. One possible solution to this problem is given by the kurtosis functional introduced by Eberl and Klar (2024), which quantifies the difference in kurtosis between two given distributions. Another approach, which allows the kurtosis of a single distribution to be quantified, is pursued throughout Sect. 4 of this paper by restricting kurtosis measures to transitivity sets of the order $\le _3$. However, most of the results are only valid if the measure is restricted to the specific transitivity set $\mathcal {S}$ of symmetric distributions. In particular, this is true for the moment- and quantile-based measures, the two most well-known quantities in the literature. The only kurtosis measures that preserve $\le _3$ on more general transitivity sets are $\kappa _D^p$ and $\kappa _{EM}$, both of which are computed by evaluating the density of the distribution in question. This makes it difficult to apply these measures to data.

Some of the results on the preservation of $\le _3$ by kurtosis measures on transitivity sets also shed some light on how notable differences in skewness influence the behaviour of these measures. An instructive example of this are formulas (11) and (12) on the relationship between the density-based measures of skewness and kurtosis. They can be interpreted as follows: as long as two distributions F and G are equally skewed, their kurtosis values are perfectly comparable. However, as the distributions start to differ in skewness, a window of indistinguishability in terms of kurtosis opens up. If the difference of the kurtosis values lies within this window, neither of the two distributions can be pointed out as being more kurtotic as $F =_3 G$ holds. If the two distributions are differently skewed in the same direction, zero is not even included in this window of indistinguishability. Thus, differences in skewness obscure the view on the comparison in terms of kurtosis.

Although the interaction with skewness is not equally explicit for other kurtosis measures, they do exhibit tendencies pointing in a similar direction. For the quantile-based measure $\kappa _Q^{\alpha , \eta }$, the kurtosis order is preserved by respective one-sided quantities that measure kurtosis on either side of the center of the distributions. However, the weights in their weighted average which gives the overall kurtosis measure are dependent on the skewness of the involved distributions. If the margin between the one-sided quantities is not wide enough relative to the skewness difference, no meaningful difference in terms of kurtosis can be established.

That considerable skewness in either direction interferes with the measurement of kurtosis is also represented in the fact that the square of a related skewness measure plays an additive role in a number of kurtosis measures. Obviously, this is the case in the well-known inequality between the moment-based measures of skewness and kurtosis. This is even more explicit in the kurtosis measures $\kappa _{DA}^p$ and $\kappa _{EL}$, where the closely related skewness measure features as a squared summand in the definition.

A goal in future research is to find a general approach to construct kurtosis measures in a way that incorporates the intrinsic influence of skewness. Similarly, a more rigorous foundation underlying the idea of kurtosis measures as ratios of dispersion measures and how this incorporates skewness would be desirable.