Abstract
Movement behaviour data are compositional in nature, therefore the logratio methodology has been demonstrated appropriate for their statistical analysis. Compositional data can be mapped into the ordinary real space through new sets of variables (orthonormal logratio coordinates) representing balances between the original compositional parts. Geometric rotation between orthonormal logratio coordinates systems can be used to extract relevant information from any of them. We exploit this idea to introduce the concept of pivoting balances, which facilitates the construction and use of interpretable balances according to the purpose of the data analysis. Moreover, graphical representation through ternary diagrams has been ordinarily used to explore time-use compositions consisting of, or being amalgamated into, three parts. Data dimension reduction techniques can however serve well for visualisation and facilitate understanding in the case of larger compositions. We here develop suitable pivoting balance coordinates that in combination with an adapted formulation of compositional partial least squares regression biplots enable meaningful visualisation of more complex time-use patterns and their relationships with an outcome variable. The use and features of the proposed method are illustrated in a study examining the association between movement behaviours and adiposity from a sample of Czech school-aged girls. The results suggest that an adequate strategy for obesity prevention in this group would be to focus on achieving a positive balance of vigorous physical activity in combination with sleep against the other daily behaviours.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Daily movement behaviour data are mostly examined in terms of their association with human health and wellbeing. They are usually reported as amounts of time spent in various activities during a certain time period of observation. When 24-h data are available, the partition is generally made in terms of sleep, sedentary behaviour (SB), and physical activity (PA) of different intensities: light (LPA), moderate (MPA) and vigorous (VPA). We denote the corresponding vector of variables as MB = (Sleep, SB, LPA, MPA, VPA). Time-use data are compositional in nature because they consist of co-dependent positive parts or fractions of a whole period of observation carrying relative information. This implies that the interest lies, not on the absolute values of the compositional parts, but on the ratios between them. As a consequence, the particular scale in which the time-use composition is measured (typically either hours/day, minutes/day or similar, or directly in percentages or proportions) is actually irrelevant. The logratio approach provides a consistent statistical methodology for the analysis of compositional data (Aitchison 1986; Pawlowsky-Glahn et al. 2015).
There has been an increasing awareness of the suitability of compositional methods to conduct statistical analysis in public health research. The basic concepts of compositional descriptive statistics, visualisation, and linear regression models based on orthonormal logratio (olr) coordinates (often referred to as isometric logratio (ilr) coordinates) in the context of time-use data were demonstrated in Chastin et al. (2015). Further studies followed applying those concepts and presenting other techniques within the logratio framework in the area (Dumuid et al. 2017a, 2017; Štefelová et al. 2018; McGregor et al. 2020; Pelclová et al. 2020). In relation to the work presented here, standard partial least squares (PLS) regression has been used to deal with the multicollinearity problem in raw 24-h movement behaviour data when investigating their relationship with a health parameter (e.g. Aadland et al. (2018)). This certainly allows to circumvent the technical issue; however, as with ordinary regression analysis omitting one category of time use for the same purpose, it still ignores the relative nature of time-use data entirely and focuses on the absolute information. This for example implies the assumption that potential benefits of increasing VPA are the same regardless of the initial condition of the individual. Within the compositional framework, time-use data are instead conceptualised as carriers of relative information where that and the interplay with the other time-use categories matter. Hence, PLS regression in this context, as it is equally the case for ordinary regression analysis and its robust alternatives (Štefelová et al. 2018), should be applied in logratio coordinates to account for these features (Hinkle and Rayens 1995; Gallo 2010; Kalivodová et al. 2015; Wang et al. 2010; Chen et al. 2021; Štefelová et al. 2021).
As for the graphical representation of time-use compositions, ternary diagrams are commonly used as a counterpart of scatterplots for ordinary data (Chastin et al. 2015). A ternary diagram is an equilateral triangle that allows to visualise 3-part compositions. In the context of the current work, the vertices represent the three time-use behaviours and the observed compositions are displayed by points. Those lying close to a vertex have higher percentages in the behaviour that is represented by that vertex, whereas points lying around the centre of the triangle have similar percentages in all three behaviours. Thus, the compositions are plotted at distances from the edges corresponding to their values in the respective compositional parts. However, similarly to the ordinary scatterplot, its practical usefulness is limited as the number of compositional parts increases, since only 3-part subsets (subcompositions) can be displayed at once. Thus, if we consider a 5-part MB composition, 10 ternary diagrams would be needed to visualise all possible combinations of 3-part subcompositions. Moreover, ternary diagrams display the original compositional data as standard (positive-constrained) observations, which could lead to biased conclusions in relation to the data structure and variability, specifically concerning groupings in the data and presence of outlying observations (Filzmoser et al. 2018), as the difference observed with the naked eye may not precisely correspond to the actual dissimilarity between observations. The reason is that compositions obey a particular geometry so-called Aitchison geometry (Pawlowsky-Glahn and Egozcue 2001; Billheimer et al. 2001) which, unlike the commonly assumed Euclidean real space geometry, accounts for their scale invariance and relative nature. The Aitchison geometry has Euclidean vector space structure and then enables to express compositional data in coordinates with respect to an orthonormal basis. Accordingly, it is possible to transfer the statistical processing of the data into the ordinary Euclidean real space while preserving the distances and angles of the original data. Such olr coordinate representation can thus be used for a visually reliable graphical representation (Pawlowsky-Glahn et al. 2015). Then, and even more in the case of larger compositions, data dimensionality reduction techniques such as compositional variants of principal components analysis (PCA) or PLS regression (with this latter considering the relationship with an outcome variable) can be used to obtain a more insightful visualisation of compositions through a biplot display based on their logratio coordinates.
Moreover, it is common in compositional data analysis to express the input data in a so-called balance coordinate system (another form of olr coordinates) (Egozcue and Pawlosky-Glahn 2005; Egozcue and Pawlowsky-Glahn 2019; Martín-Fernández 2019). Balance coordinates represent contrasts between two groups of parts of the composition and their particular expression depends on the orthonormal basis used as reference (one amongst infinitely many possible). Importantly, this can be tailored to some extent so that the collection of balances associated to it includes some contrast(s) which have a practical interpretation (see the sequential binary partition procedure described in Sect. 2). However, not all balances of interest in a study can be generally obtained from just one such a coordinate system. Consequently, often, several of the balances generated from a single orthogonal basis are meaningless for the practitioner, with this issue being more likely as the size of the composition at hand increases. This might have discouraged a wider adoption of balance coordinates within time-use epidemiology where, with just a few exceptions (see e.g. McGregor et al. (2020)), the so-called pivot coordinates approach (Fišerová and Hron 2011; Filzmoser et al. 2018) has been mostly applied so far (Dumuid et al. 2017; Štefelová et al. 2018; Dumuid et al. 2020). This later formally considers orthogonal rotations between olr coordinate systems so that the dominance of one behaviour relative to the others is sequentially isolated for statistical assessment.
The issues discussed above and the combination of the ideas around balance and pivot coordinates lead to the introduction here of the concept of pivoting balances and its implementation to facilitate a synthetic and meaningful graphical display of compositions and their relationships with outcome variables. This work thus enables the combination of balance-like coordinates into a same modelling and visualisation task, here PLS regression and biplot, including those that cannot be obtained from a single balance coordinate system. In particular, this is implemented with the objective of providing improved visualisation of complex time-use patterns in relation to adiposity. The method relies on the flexibility of the concept of pivot coordinates, which has been also exploited recently to define orthonormal pairwise logratio representations (Hron et al. 2021) and to implement weighted statistical analysis schemes (Hron et al. 2021). Firstly, we discuss compositional balances as a way to construct interpretable logratio coordinate representations of time-use compositions, considering the ordinal character of the wake-time components. Next, the basic ideas behind PLS regression and the associated biplot display are developed, including their extension to the compositional case based on the novel concept of pivoting balances. Finally, the proposed method is applied to examine the association between 24-h movement behaviours patterns and adiposity from a sample of Czech school-aged girls, particularly assessing how the distribution of time between behaviours relates to healthier conditions.
2 Balance coordinates for compositional data
Compositional data are essentially characterised by the scale invariance property (Pawlowsky-Glahn et al. 2015; Filzmoser and Hron 2019). This means that multiplying a composition by a positive constant does not alter the relative information conveyed by the (log)ratios between its parts. Scale invariance implies that compositional data are formally defined on a sample space consisting of equivalence classes of proportional vectors (Barcelól Vidal and Martín-Fernández 2016). This clashes with the direct application of ordinary statistical methods which assume data on an absolute scale obeying the standard Euclidean geometry of the real space. However, it has been shown that ordinary methods can still be applied after mapping of compositions into the real Euclidean space through e.g. olr coordinates (Egozcue et al. 2003; Egozcue and Pawlowsky-Glahn 2019; Martín-Fernández 2019). These olr coordinates are obtained with respect to an orthonormal basis in the Aitchison geometry of compositional data and facilitate transferring the statistical results back to the original sample space by inverse mapping (Egozcue et al. 2003).
Given a D-part composition \({\varvec{x}} = (x_1, \ldots , x_D)^\top\), a procedure known as sequential binary partition (SBP) can be applied to construct \(D-1\) (the actual degrees of freedom of a D-part composition) customised olr coordinates called (compositional) balances consisting of a real vector \({\varvec{b}} = ( b_1, \ldots , b_{D-1})^\top\) (Egozcue and Pawlosky-Glahn 2005). In the first step of the SBP process, the entire collection of compositional parts is split into two disjoint subsets, with each subset being summarised by the geometric mean of its components and going into the numerator and denominator respectively of a normalised logratio. This defines the first balance \(b_1\). The resulting subsets are sequentially further split in the same way until only one-part subsets remain, leading to the subsequent balances \(b_2, \ldots , b_{D-1}\).
The general formula for a balance coordinate is as follows:
where \(x^{+}_{j_{i}}\) and \(x^{-}_{j_{i}}\) refers to the parts selected for the numerator and denominator, respectively, in the jth balance while \(r_j\) and \(s_j\) stands for the respective number of parts in each subset; the vector \({\varvec{g}}_j\) represents rows of a \((D-1, D)\)-matrix of logcontrast coefficients \({\textbf{G}}\) with elements
It holds that \({\textbf{G}} {\textbf{G}}^\top = {\textbf{I}}_{D-1}\), where \({\textbf{I}}_{D-1}\) is the \((D-1)\)-dimensional identity matrix.
Balance coordinates are then usually interpreted, as their name indicates, in terms of a balance (contrast) between two subsets of components. The use of balances is particularly advantageous to define interpretable contrasts between parts of the composition according to the scientific questions of interest and based on domain-specific knowledge (e.g. active versus non-active behaviours (McGregor et al. 2020)).
Note that different partitions lead to different systems of balances but, as for any olr coordinate representation, they are orthogonal rotations of each other that simply represent the information in the composition in a different way (Egozcue and Pawlosky-Glahn 2005). So, given two different vectors of balances \({\varvec{b}} = {\textbf{G}} \ln {\varvec{x}}\) and \({\varvec{b}}^* = {\textbf{G}}^* \ln {\varvec{x}}\), it holds that \({\varvec{b}}^* = {\textbf{G}}^* {\textbf{G}}^\top {\varvec{b}}\).
A popular type of balances are the so-called pivot coordinates (Fišerová and Hron 2011), where one part (placed in the numerator) is set against the remaining ones (in the denominator). Note that the role of a single compositional part relative to all the others is highlighted in the first pivot coordinate. Thus, by placing one particular part each time in the numerator of the first pivot coordinate, we can construct D different olr coordinate systems and extract the first coordinate from each one of them. In more detail, denoting composition \({\varvec{x}}\) rearranged so that the lth part is put at the first place as \({\varvec{x}}^{(l)} = \left( x_{1}^{(l)}, \ldots , x_{D}^{(l)} \right) ^\top = (x_{l}, x_{1}, \ldots , x_{l-1}, x_{l+1}, \ldots , x_{D})^\top , \ l=1, \ldots , D\), the corresponding set of pivot coordinates given by a real vector \({\varvec{z}}^{(l)} = \left( z_{1}^{(l)}, \ldots , z_{D-1}^{(l)} \right) ^\top\) is constructed as
Note that the first pivot coordinate \(z_{1}^{(l)}\) isolates all the information about part \(x_l\) relative to the others. It is interesting to note the relationship between the set of first pivot coordinates \(z_{1}^{(1)}, \ldots , z_{1}^{(D)}\) and the well-known clr coefficients
Clr coefficients are not olr coordinates but coefficients with respect to a generating system on the simplex and lead a to singular covariance matrix (Aitchison 1986). It holds that \(c_l = \sqrt{(D-1)/D} \cdot z_1^{(l)}, \ l=1, \ldots , D\) and, therefore, \(z_{1}^{(1)} + \ldots + z_{1}^{(D)} = 0\). Moreover, for general balances, it holds that \({\varvec{b}} = {\textbf{G}} {\varvec{c}}\), which consequently also applies to pivot coordinates.
2.1 Pivoting balances and their use with movement behaviour compositions
Although the process described above based on pivot coordinates has been commonly used in practice (Filzmoser et al. 2018), it might not necessarily be the best strategy when there is a natural ordering across compositional parts, as we can understand for time-use compositions. A pivot coordinate associated with a part regarded within the ordering as an “intermediate level” could potentially aggregate logratios having opposite associations with the outcome variable. Then it seems reasonable to consider more general balances that represent relevant trade-offs between subsets of parts instead of just one against the others (McGregor et al. 2020). In particular, we are interested here in balances that take into consideration all the parts available and their order. That is, considering different first balances where each adds one more intense activity part into the subset in the numerator of the balance, and then investigate how these additions affect the results. It is not be possible to obtain all these balances from a single SBP by construction, and it requires to consider different olr coordinate systems instead. Hence, following a strategy analogous to the one used with pivot coordinates, we can consider L olr coordinate systems to construct desirable balances \({\varvec{b}}^{(l)} = \left( b_{1}^{(l)}, \ldots , b_{D-1}^{(l)} \right) ^\top\), with \(l=1,\ldots , L\) (the superscript here refers to the balance coordinate system considered), that in turn isolate a balance of interest in the first coordinates \(b_{1}^{(l)}\). Accordingly, we denote the respective matrix of logcontrast coefficients as \({\textbf{G}}^{(l)}\). The number of coordinate systems L to consider will depend on the specific data set. In the following, and because of its conceptual analogy with pivot coordinates, we will refer to the balances resulting from these coordinate systems as pivoting balances.
Focusing on our context of application, it is generally accepted that a higher health benefit is obtained from more physically demanding activities, but the role of sleep is less clear (Felsö et al. 2017), we suggest the following coordinate systems with different initial partitions into two subgroups. Starting with sleep against the rest of behaviours, the subset of parts in the numerator is subsequently enlarged from the least to the most intense activities; and vice versa, sleep in the numerator is subsequently accompanied by the other activities from the most to the least intense. The remaining three balances in each coordinate system are constructed arbitrarily by following the SBP rules. Thus, this gives rise to \(L=7\) coordinate systems with pivoting balances \({\varvec{b}}^{(l)} = \left( b_{1}^{(l)}, b_{2}^{(l)}, b_{3}^{(l)}, b_{4}^{(l)}\right) ^\top , \ l=1,\ldots , 7\). We give those coordinates of interest, i.e. \(b_{1}^{(1)}, \ldots , b_{1}^{(7)}\) , the symbolic notation Sleep_SB.LPA.MPA.VPA, Sleep.SB_LPA.MPA.VPA, Sleep.SB.LPA_MPA.VPA, Sleep.SB.LPA.MPA_VPA, Sleep.VPA_SB.LPA.MPA, Sleep.MPA.VPA_SB.LPA, and Sleep.LPA.MPA.VPA_SB (i.e. using an underscore to separate the parts in the numerator and the denominator of the logratio and a point symbol to split out the parts into the respective subgroup). Table 1 illustrates an exemplary SBP to obtain the required set of balances.
As for the interpretation, e.g. the balance Sleep_SB.LPA.MPA.VPA compares time spent in sleep relative to the average (computed by the geometric mean) of time spent in waking-time behaviours, Sleep.SB_LPA.MPA.VPA is a contrast of average time spent in inactive behaviours against average time spent in physical activities, and so on. Accordingly, positive values of the balance Sleep_SB.LPA.MPA.VPA mean dominance of sleep over the averaged contributions of the waking-time components, and vice versa. Similarly, positive values of the balance Sleep.SB_LPA.MPA.VPA implies a dominance of averaged contributions of inactive behaviours over averaged contributions of physical activity. Note that the reciprocal balances, i.e. the balances resulting from swapping the subsets of behaviours in the numerator and denominator of the logratio, differ only on the sign. Thus, the arrangement of the subsets of behaviours in the balance can be chosen accordingly to the intended interpretation.
The approach based on balances, where the groups are represented by the respective geometric means, can be compared with the case where the groups are characterized by amalgamation (summing) of parts in both groups, called summated logratios (Greenacre 2020). In principle, the idea of pivoting logratio coordinates as discussed above could be used with summated logratios as well, but the resulting coordinate systems would not be orthogonal rotations of each other anymore, which is a crucial requirement for the PLS regression modelling introduced below. Another important point is the difference in interpretation. While the parts in each group are amalgamated when using summated logratios, using balances instead implies that all possible logratios between parts from both groups are aggregated (Hron et al. 2020),
which honours the fact that all relevant information in compositional data is contained in (pairwise) logratios. Balances stress that each part has a role in the relationship with the response. Accordingly, when investigating the possible effect on the health outcome of changes in the balance as measured through the respective regression coefficient, for instance by increasing the value of the balance by one, such a change implies to multiply the parts aggregated by the geometric mean in the numerator of the balance by the same constant. Note that the result here involves the normalising constant of the balance which guarantees orthonormality. Alternatively, interpretation can be facilitated by omitting the normalising constants of the balances and considering binary instead of natural logarithms (Müller et al. 2018), so that the orthonormality of coordinates is relaxed to be orthogonality. In this case, an increase of one in the balance corresponds with each part in the numerator being doubled and, consequently, the values of all ratios whose logs are aggregated into the balance being doubled. For an interpretation in terms of e.g. min/day of a regression coefficient, say for the balance Sleep.VPA_SB.LPA.MPA, the coefficient would account for how the health outcome is changed when the time allocations to Sleep and VPA are doubled with respect to SB, LPA and MPA.
3 PLS regression and biplot
PLS regression enjoys wide popularity in areas such as chemometrics (Höskuldson 1988; Martens 2001), especially in the case where the number of explanatory variables is significantly larger than the number of observations. It aims to fit the relationship between response variable(s) and potentially many and/or highly correlated explanatory variables by finding a small number of uncorrelated latent factors that synthetize the relationship in lower dimensions. The underlying assumption is that the observed data are generated by a process driven by this small number of latent factors, also known as PLS components. The values on the PLS components (scores) are linear combinations of the explanatory variables with parameters (loadings) determined in such a way that they maximize the covariance between the response and the explanatory variables. Regression coefficients associated with the original explanatory variables can be deduced from the PLS components. Even if PLS regression is particularly useful for the analysis of high-dimensional data, it offers other features that make the method also appealing for datasets with a relatively small to moderate number of explanatory variables, as it is commonly the case of movement behaviour data. These include the capacity to handle multicollinearity and highly correlated explanatory variables, the ability to separate main information from noise, the no requirement of distributional assumptions for error terms and, what is particularly relevant for our purposes, the possibility to visualize data in low dimensions via a PLS biplot that, unlike common PCA biplots, takes into account the relationship between outcome and explanatory variables.
In this work we focus on PLS regression with just one response variable, commonly known as PLS1 in practice (in contrast with PLS2 used for the multivariate response case). Although meaning PLS1, for the sake of succinctness we will refer to just PLS in the following.
In order to describe PLS regression, we consider two data structures: a column vector \({\textbf{y}}\) of size n and a matrix \({\textbf{F}}\) of size \(n \times m\) called design matrix. The vector \({\textbf{y}}\) represents values of the response variable on n objects, whereas the columns of \({\textbf{F}}\) describe m explanatory variables measured on the same n objects. The data are assumed to be mean-centred. The aim of PLS is to find a linear relationship of the form
by estimating a vector \(\varvec{\beta }\) of m unknown regression coefficients. The vector \({\textbf{e}}\).0 represents an error term with n components. PLS decomposes the design matrix as
where \(\mathbf {E_{F}}\) is an error matrix, \({\textbf{T}}\) is a score matrix of size \(n \times a\), and \({\textbf{P}}\) is a loading matrix of size \(m \times a\), with a being the number of PLS components. This latter is usually selected based on cross-validated (CV) prediction performance assessed by root mean squared error of prediction (RMSEP) and coefficient of determination R\(^2\) (Varmuza and Filzmoser 2009). One procedure to determine the optimal number of PLS components is the randomisation test approach (van der Voet 1994). In brief, given a reference model chosen according to the absolute minimum in the CV curve, the procedure tests for the significance of increments of the squared prediction error from using models with fewer components. The selected model is the one with the smallest number of components that is not significantly worse than the reference model. In the following, \({\textbf{t}}_j\) and \({\textbf{p}}_j\), with \(\ j=1,\ldots ,a\), will denote the jth column of \({\textbf{T}}\) and \({\textbf{P}}\) respectively.
A number of numerical methods have been proposed to estimate the PLS model coefficients so that the covariance between the scores and the response is maximised. The NIPALS algorithm is a popular choice (Varmuza and Filzmoser 2009) and it can be summarised in the following steps.
For \(j=1,\ldots ,a\):
-
1.
\({\textbf{v}}_j = \dfrac{{\textbf{F}}_j^\top {\textbf{y}}}{\left( {\textbf{y}}^\top {\textbf{y}} \right) }\), with \({\textbf{F}}_1 = {\textbf{F}}\),
-
2.
\({\textbf{w}}_j = \dfrac{{\textbf{v}}_j}{\sqrt{{\textbf{v}}_j^\top {\textbf{v}}_j}}\),
-
3.
\({\textbf{t}}_j = {\textbf{F}}_j {\textbf{w}}_j\),
-
4.
\({\textbf{p}}_j = \dfrac{{\textbf{F}}_j^\top {\textbf{t}}_j}{\left( {\textbf{t}}_j^\top {\textbf{t}}_j \right) }\),
-
5.
\(u_j = \dfrac{{\textbf{y}}^\top {\textbf{t}}_j}{\left( {\textbf{t}}_j^\top {\textbf{t}}_j \right) }\),
-
6.
\({\textbf{F}}_{j+1} = {\textbf{F}}_j - {\textbf{t}}_j {\textbf{p}}_j^\top\).
The regression coefficients are then estimated by
where the matrix \({\textbf{W}}\) is formed by columns \({\textbf{w}}_j\), \({\textbf{P}}\) by columns \({\textbf{p}}_j\) and the column vector \({\textbf{u}}\) by elements \(u_j, \ j = 1, \ldots , a\).
The NIPALS algorithm, as well as most of the other popular methods for PLS regression (e.g. kernel or SIMPLS algorithms), produces uncorrelated scores (i.e. \({\varvec{t}}_j^\top {\varvec{t}}_k=\delta _{jk}\), for \(j,k=1,\dots ,a\), with \(\delta _{jk}\) being 1 if \(j=k\) and 0 otherwise) (Varmuza and Filzmoser 2009).
The individual statistical significance of the explanatory variables is determined by the bootstrap method. Denoting by \({\hat{\mu }}_{k}\), \({\hat{\sigma }}_{k}\), \({\hat{\gamma }}_{k (\alpha /2)}\) and \({\hat{\gamma }}_{k (1-\alpha /2)}\) respectively the bootstrap mean, standard deviation, and the \((\alpha /2)\)- and \((1-\alpha /2)\) quantiles of the coefficient estimate \({\hat{\beta }}_{k}\), \(k=1,\ldots ,m,\), over S bootstrap resamples; the estimated bootstrap standardised coefficients are computed as \({\hat{\mu }}_{k}/{\hat{\sigma }}_{k}\) and \(100(1-\alpha ) \%\) bootstrap confidence intervals for standardised coefficients as \(({\hat{\gamma }}_{k (\alpha /2)}/{\hat{\sigma }}_{k}, {\hat{\gamma }}_{k (1-\alpha /2)}/{\hat{\sigma }}_{k})\). The k-th explanatory variable is considered statistically significant (at statistical significance level \(\alpha\)) if the respective confidence interval does not include zero.
Finally, the two-dimensional PLS biplot displays scores and loadings corresponding to the first two PLS components (Oyedele and Gardner-Lubbe 2015). That is, the representation of the n observations (using points) is given by the rows of the matrix \({\textbf{T}}_{2}=({\textbf{t}}_1, {\textbf{t}}_2)\) and the representation of the m explanatory variables (using arrows from the origin) is given by the rows of the matrix \({\textbf{P}}_{2}=({\textbf{p}}_1, {\textbf{p}}_2)\). The scores represent the projection of the observations onto the space defined by the PLS components, while the loadings represent the effect of the explanatory variables on the directions of the projections. Therefore, a PLS biplot provides a single graphical representation of the observations alongside the explanatory variables which, unlike ordinary biplots based on PCA, accounts for the relationship with the response variables as said above. The observations in the direction of an arrow are characterised by higher values on the corresponding explanatory variable. The sign of the relationship with the outcome variables determines the direction of the arrow.
3.1 Compositional PLS regression and biplot based on pivoting balances
Where compositional explanatory variables are present, PLS regression is applied on an adequate logratio coordinate representation (Gallo 2010; Kalivodová et al. 2015; Wang et al. 2010). Unlike in previous literature, we do not represent compositional data in just one coordinate system and instead extend the concept of pivot coordinates to a more general setting as described in Sect. 2.1. This allows to generate directly balance logratio coordinates which are of interest in the study at hand.
We consider D-part composition alongside other q non-compositional covariates as explanatory variables, with the composition represented by pivoting balances, i.e. by balance coordinates \(b_{1}^{(l)}, \ldots , b_{D-1}^{(l)}\) from the lth coordinate systems, \(l=1,\ldots ,L\). Specifically, recall that the interest is in each of the first balances \(b_{1}^{(l)}\) that includes all the parts in the given arrangement (see Sect. 2.1). Then the following L regression models are considered:
where the vector \({\textbf{y}}\) stands for the values of the response variable and the columns of the matrix \({\textbf{F}}^{(l)}\) combine values on lth set of balances and q non-compositional covariates for the n observations. The vector \(\varvec{\beta }^{(l)} = \left( \beta _1^{(l)},\ldots , \beta _{D-1}^{(l)}, \beta _D, \ldots , \beta _{D-1+q} \right) ^\top\) is the corresponding vector of regression coefficients and \({\textbf{e}}\) is the error term. Following the PLS approach depicted above, from the model fit resulting from each of the L coordinate systems, the focus is on the coefficient estimate of the first balance \(b_{1}^{(l)}\). So the estimates of interest can be summarised in the vector \(\left( {\hat{\beta }}_1^{(1)}, \ldots , {\hat{\beta }}_1^{(D)}, {\hat{\beta }}_D, \ldots {\hat{\beta }}_{D-1+q} \right)\). Note that the coefficients associated with the non-compositional covariates are invariant to the specific choice of balances due to the orthogonality of the coordinate representation and linearity of PLS regression (Helland 2010). This property also leads to the fact that the decomposition of the matrix \({\textbf{F}}^{(l)}\) yields the same score matrix \({\textbf{T}}\) in each of the L models; although of course different first \(D-1\) rows of the matrix of loadings
are obtained from each model.
For the PLS biplot, we display only loadings corresponding to the first balance from each coordinate system and the loadings corresponding to non-compositional variables. That is, we use the matrix of scores corresponding to the first two PLS components \({\textbf{T}}_{2}=({\textbf{t}}_1, {\textbf{t}}_2)\) for the visualisation of the observations. Denoting by \({\textbf{P}}_{2}^{(l)}=({\textbf{p}}_1^{(l)}, {\textbf{p}}_2^{(l)})\) the matrix of loadings corresponding to the first two PLS components in the lth coordinate system, the first row of \({\textbf{P}}_{2}^{(l)}\) is used for the representation of the balance \(b_{1}^{(l)}\) with \(l=1, \ldots , L\); and the last q rows from any given \({\textbf{P}}_{2}^{(l)}\) are used to visualise the q non-compositional covariates. When interpreting the biplot, similarly to the case for PCA biplots (Kynčlová et al. 2016), we need to take into account that the loadings are generated from different PLS models. Then, observations in the direction of an arrow are characterised by higher (absolute) values on the corresponding balance (and hence by dominance of the parts in the numerator over those in the denominator of the logratio). Nevertheless, note that due to the way the PLS biplot is constructed, i.e. using first balances from different coordinate systems, the usual interpretation of the angles between arrows (loadings) in terms of degree of association between the corresponding balances would be misleading. For example, we cannot say that two balances are highly correlated based on the fact that their two arrows nearly overlap. However, in such a case, we can still refer to proximity between the balances, in the sense that having them pointing to the same direction indicates that they have a similar relationship with the response variable. This follows from the fact that the same scores are produced by all balance coordinate systems (as it is case for any olr coordinate system) and the corresponding matrices of loadings are orthogonal rotations of each other.
Building on such relationship between coordinate systems, a model can be fit in an arbitrary balance coordinate system and be used to obtain the regression coefficients and loadings for all the L models. Namely, it holds that
and
where \({\textbf{G}}^{(k)}\) and \({\textbf{G}}^{(l)}\) stand for the respective matrices of log-contrast coefficients.
Consequently, we can obtain results for all the L models from one model, where compositions are expressed in clr coefficients instead of balances (note that unlike for ordinary least squares (LS) regression, collinearity between clr variables is not a problem for PLS regression). The regression coefficient estimates and the loadings for the non-compositional covariates, as well as the matrix of scores, are the same for any of the L models using balances. Denoting the regression coefficient estimates for the clr coefficients by \({\hat{\beta }}_1^{\star }, \ldots , {\hat{\beta }}_{D}^{\star }\) and the elements in the first D rows of the loading matrix by \(p_{ij}^{\star }\), it holds that
and
Then, the relevant information about the L first balances can be obtained as
and the composed matrix of loadings, with \(a=2\) for 2-dimensional graphical representation, is
where
Finally, note that for pivot coordinates it holds that \({\hat{\beta }}_1^{(l)} = \sqrt{D/(D-1)} \cdot {\hat{\beta }}_l^{\star }\) and \(p_{j1}^{(l)} = \sqrt{D/(D-1)} \cdot p_{jl}^{\star }\), with \(\ l = 1, \ldots L\) and \(j=1,\ldots , a\). This is analogous to the case of loadings in principal component analysis (Kynčlová et al. 2016). The relationships between PLS regression results from different coordinate systems are examined in more detail in Appendix A.
4 Case study: examining the association of 24-h movement behaviours with adiposity
The association between the 24-h time-use composition MB = (Sleep,SB,LPA,MPA,VPA) and adiposity is investigated from a sample of 414 Czech school-aged girls. Fat mass (FM) is used as an adiposity-related indicator and was measured using multi-frequency bio-electrical impedance analysis (InBody 720, InBody Co., Seoul, Korea). The 24-h time-use data were collected using a wrist-worn tri-axial ActiGraph accelerometers (ActiGraph Corp., Pensacola, FL, USA) wGT3X-BT and GT9X Link for children and adolescents, respectively. Raw data were processed with the GGIR package (version 1.10-7) on the R system for statistical computing (Migueles et al. 2019). Time spent in SB, LPA, MPA and VPA was classified using cut-points for non-dominant wrist (SB: \(< 36\) mg; LPA: \(36-200\) mg; MPA: \(201-706\) mg; VPA \(\le 707\) mg, where mg stands for milli gravity-based acceleration units (Hildebrand et al. 2017)). The default algorithm guided by participants sleep log was used to detect sleep time (van Hees et al. 2015). Additionally, age and height were recorded. The age of the participants ranged from 8.1 to 19 years (with mean \(\pm\) standard deviation equal to \(13.8 \pm 2.9\) years). The height ranged from 117.7 to 181.9 cm (\(157.7 \pm 12.2\) cm). Fat mass ranged from 1.1 to 38.7 kg (\(12.5 \pm 6.6\) kg). The compositional mean for MB, computed as the vector of geometric means of its parts and re-scaled to be expressed in min/day, was (491.3, 676.0, 231.9, 38.2, 2.5). The study was approved by the Ethics Committee of the Faculty of Physical Culture, Palacký University Olomouc (reference number: 19/2017). It was conducted in accordance with the Ethical principles of the 1964 Declaration of Helsinki and its later amendments. Parents or guardians provided a written informed consent for the participation of their children in the study.
To gain a initial insight into the problem at hand, we can visualise the (centred) data using ternary diagrams. Instead of plotting all 10 possible combinations of 3-part subcompositions, we display the 3-part composition of sleep, SB and the amalgamated parts of PA; as well as the 3-part subcomposition consisting of the PA parts only (Fig. 2 in Appendix B). The data points are coloured according to the individuals’ fat mass. We can already observe some patterns from this limited visualisation. Particularly, it indicates that a higher proportion of time spent in SB is associated with higher fat mass, whereas the association points towards the opposite direction for VPA.
In the following, we illustrate how applying the proposed PLS regression biplot based on pivoting balances provides a more comprehensive view. As justified in Sect. 2.1, \(L=7\) regression models (3) are considered with FM (in log-scale) set as the response variable and the composition MB playing the role of explanatory variable, with this represented by sets of pivoting balances \(\left( b_{1}^{(l)}, b_{2}^{(l)}, b_{3}^{(l)}, b_{4}^{(l)}\right) , \ l=1,\ldots , 7\), resulting from seven balance coordinate systems. Naturally, fat mass depends on height and age (with these two being highly correlated for individuals in school age). Accordingly, age and height (both mapped into real space using a log-transformation) are put in as covariates in the models. PLS regression modelling is conducted as detailed in the previous section. Based on the randomised test approach, retaining the first two PLS components to produce the PLS biplot is considered adequate (CV RMSEP \(= 0.49\) and CV R\(^2 = 0.32\)). Thus, estimates of the regression coefficients are derived from the first two PLS components for each of the 7 regression models. Actually, following on the relationships between olr coordinate systems detailed in Sect. 3.1, a single model is fitted and all the other estimates are derived from this one.
Table 2 shows the bootstrap standardised regression coefficients estimated from 1000 bootstrap resamples (including the respective 95% bootstrap confidence intervals) for each of the first pivoting balances \(b_1^{(l)},\ l=1,\ldots ,7\), as indicated in Table 1, as well as for the additional covariates. Considering the usual \(5\%\) significance level threshold, statistically significant balances having a negative relationship with FM are the following: Sleep_SB.LPA.MPA.VPA, VPA_Sleep.SB.LPA.MPA, Sleep.VPA_SB.LPA.MPA, Sleep.MPA.VPA_SB.LPA and Sleep.LPA.MPA.VPA_SB. Thus, the significant balances are those including SB in the denominator and Sleep and/or VPA in the numerator whereas the non-significant include a confront Sleep against VPA. Thus, the results suggest that for obesity prevention (in school-aged girls) it would be beneficial to spend relatively less time sitting and more time sleeping and doing high-intense physical activity. Moreover, it is suggested that the two non-active behaviours (sleep and SB) have opposite associations with fat. That is, sleep, unlike SB, would play a positive role in fat reduction. Finally, both non-compositional covariates (age and height) are positively associated with FM as it would be expected.
It is worth mentioning that for this case study applying ordinary LS regression instead of PLS in a similar way (i.e. sequentially on the corresponding pivoting balance coordinate systems plus the covariates) leads to analogous final conclusions in terms of statistical significance for all the variables except for age, which is not identified as a relevant variable (see Table 5 in Appendix B). This counter-intuitive result is just a consequence of the high correlation between age and height, that is not well handled by LS regression but adequately so by using PLS instead.
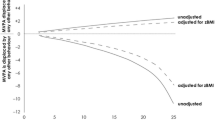
Furthermore, the construction of the PLS biplot based on the first pivoting balances (together with the non-compositional variables) from the seven coordinate systems provides further insight into what would be more recommendable movement behaviour patterns within the 24-h period associated with lower adiposity (Fig. 1). The first two PLS components explain \(92.22\%\) of the variance of the explanatory variables and \(33.32\%\) of the variance of the response variable (i.e. the corresponding coefficient of determination for this model is 0.3332). The arrows representing the variables are coloured according to the sign of their respective associations with the FM outcome (positive in red and negative in blue for statistically significant associations, grey for non-significant association). Note that extending the arrow of a balance backwards from the origin would represent the direction of increasing value of the corresponding reciprocal balance. A colour gradient is used to distinguish the points according to the individuals’ FM (in log-scale). The points are fairly well distinguished according to the relationships of the significant variables with the FM outcome along both PLS component axes. The arrows of the variables with significantly positive regression coefficients point roughly towards the top-right quadrant, which includes mainly individuals having higher fat mass. The variables with significantly negative regression coefficients point to opposite direction (i.e. roughly bottom-left quadrant), where the individuals with lower fat mass mostly concentrate. A few outlying cases are observed in the bottom-right quadrant, particularly two cases of lower fat mass corresponding to the very young individuals with low level of physical activity. We can see that the first PLS component is largely related to the relative amount of VPA, while the second one is determined rather by the relative amount of sleep (plus age and height). The balance that most clearly indicates the division between lower and higher fat mass is Sleep.VPA_SB.LPA.MPA. So increasing the ratios of both VPA and sleep to SB, LPA and MPA is an even better strategy for obesity prevention than only increasing VPA with respect to the other behaviours. From the results obtained via PLS regression and the associated biplot we can therefore draw the conclusion that VPA is the most beneficial behaviour for fat reduction, however enjoying enough sleep is also relevant. Furthermore, the most beneficial action would be to spend more time in these activities at the expense of sitting, whereas there is no meaningful evidence of a beneficial impact of lighter PA.
PLS biplot based on compositional balances from seven pivoting balance coordinate systems. The lighter the colour of the point, the higher the fat mass level of the corresponding individual. Statistically significant variables in positive (resp. negative) direction are coloured in red (resp. blue), grey colour indicates non-significant variables. The dashed lines indicate the origin for the first and second PLS component axes (PLS comp. 1 and PLS comp. 2). A \(92.22\%\) of the explanatory variables variance (resp. \(33.32\%\) of the response variable variance) is explained by the first two PLS components: \(88.50\%\) by PLS comp. 1 and \(3.72\%\) by PLS comp. 2 (resp. \(20.49\%\) by PLS comp.1 and \(12.83\%\) by PLS comp. 2)
4.1 Comparison with pivot coordinates and PCA
For comparison, we can also look at the results obtained from PLS regression performed on pivot coordinates (Table 6 and Fig. 3 in Appendix B; the notation has been simplified as there is no need to detail the parts in the denominator). The results indicate that only balances considered in the pivoting balances are significant, and the PLS biplot leads to similar conclusions. However, note that if e.g. increasing MPA was also beneficial for fat reduction, the pivot coordinate representing MPA against the geometric mean of the others (which also aggregates logratios to VPA and sleep) would hardly give this information. Instead, the balance Sleep.MPA.VPA_SB.LPA could provide it when compared to Sleep.VPA_SB.LPA.MPA. Furthermore, we can compare the resulting PLS biplots with appropriate PCA biplots (Figs. 4 and 5 in Appendix B). Note that the relationships between PCA scores and loadings from different coordinate systems are analogous to those in the PLS case. Here, the beneficial impact of VPA for obesity prevention is depicted, but the role of sleep is not that easily deduced.
4.2 Isotemporal substitution analysis
By performing isotemporal substitution analysis (Dumuid et al. 2017a), we can look at how reallocation of time (in absolute sense) from one behaviour to another would impact the outcome variable. Table 3 shows estimated change in FM associated with 1 min reallocation between movement behaviours. These estimates were computed as follows: (1) PLS regression coefficient estimates obtained from each bootstrap resample were used to compute the relative difference between the predicted FM from the reallocated mean composition and the FM from the original mean composition (with parts adding to \(\kappa = 24\) h); (2) the mean across bootstrap resamples was used as final estimate of the change (including a confidence interval based on the \((\alpha /2)\)- and \((1-\alpha /2)\) quantiles of the distribution).
At the usual \(5\%\) significance level, statistically significant changes were obtained for time reallocations between VPA and any of the remaining activities and for time reallocation between sleep and SB. Hence, this support the idea that obesity can be prevented by increasing VPA even at the expanse of sleep. Moreover, note that to compare e.g. the impact of a time exchange of SB and VPA against SB and sleep, we should take into account that, in relative terms, 1 min of VPA means something completely different than 1 min of sleep. That is, taking our mean composition as reference, that means \(40\%\) of VPA, whereas \(40\%\) of sleep is about 200 min. Estimating the change in FM for a 200-min reallocation from sleep to SB (respectively from SB to sleep) we obtain a \(31.17\% \ (20.35, 43.84)\%\) increase (respectively \(-20.72\% \ (-26.78, -13.69)\%\) decrease).
Therefore it seems reasonable to also examine the effect of relative time reallocations (something that in fact aligns with what pivoting balances are meant for). That is, looking at the difference in the outcome variable when, instead of a part \(x_j\), \(j=1,\ldots , D\), we consider \(R \cdot x_j\), with R being a proportional factor. Note that in order to have all the parts adding up to \(\kappa = 24\) h, the remaining parts \(x_k\), with \(k=1,\ldots , D\) and \(\ k\ne j\), need to be multiplied by \((\kappa - Rx_j)/(\kappa -x_j)\). In case that two parts \(x_i\) and \(x_j,\) with \(\ i, j =1,\ldots , D\) and \(\ i \ne j\), are multiplied by R, then the remaining parts \(x_k\), for \(\ k=1,\ldots , D\) and \(\ k\ne i,j\), need to be multiplied by \([\kappa - R(x_i+x_j)]/[\kappa -(x_i+x_j)]\), and so on for more parts. Using this procedure, Table 4 shows the results from increasing a part by \(10\%\), i.e. using \(R=1.1\), while the remaining parts are proportionally decreased. These results confirm that the relative increase in both VPA and sleep with respect to the remaining behaviours leads to even higher decrease in FM than only increasing VPA at the expense of the remaining behaviours.
5 Final remarks
This work introduces and demonstrates the potential of the new concept of pivoting balance coordinates. In combination with a tailored compositional PLS regression biplot display, we devise an advanced method to investigate and visualize movement behaviour patterns and their association with health outcomes. This type of low-dimensional representation becomes particularly relevant as the 24-h movement behaviours are increasingly described at a higher level of granularity thanks to the use of new accelerometer technologies. The proposed method combines advantages of the pivot coordinate and the balance coordinate logratio approaches to deal with compositional data. In particular, only those balances which are relevant for the analysis are considered and the mutual orthonormality of the coordinate systems allows to achieve a unique PLS solution. The user just needs to be aware that the pivoting balances come from different coordinate systems and adapt interpretation of their relationships accordingly.
The practical use of the method has been illustrated using a database about 24-h movement behaviour and adiposity in Czech school-aged girls. The findings stress the relevant role that time-use exchanges combining both VPA and sleep together can play in obesity prevention. The study emphasizes the relevance of considering all movement behaviours within the day, while accounting for their compositional character, to better understand the combined effects of movement behaviours in obesity within the paediatric population.
Building on previous developments, this work demonstrates the flexibility of the pivot coordinates approach (Hron et al. 2020). In principle, any logratio of interest (even beyond the concept of balances) can be set to occupy the pivotal position and be complemented by other coordinates to achieve orthonormality of the resulting olr coordinate system. We expect further methodological progress following this approach in the near future.
All computations in this work were performed on the R environment for statistical computing, (R Core Team 2021) using the packages compositions (van den Boogaart and Tolosana-Delgado 2008) and pls (Mevik and Wehrens 2007) for specific tasks. The computing routines implementing the proposed method are available at https://github.com/StefelovaN/Balance-based-PLS-biplot/.
References
Aadland E, Kvalheim O, Anderssen S, Resaland G, Andersen L (2018) The multivariate physical activity signature associated with metabolic health in children. Int J Behav Nutr Phys Act 15:77. https://doi.org/10.1186/s12966-018-0707-z
Aitchison J (1986) The statistical analysis of compositional data. Chapman & Hall, London. https://doi.org/10.1007/978-94-009-4109-0
Barceló Vidal C, Martín-Fernández J (2016) The mathematics of compositional analysis. Austrian J Stat 45(57). https://doi.org/10.17713/ajs.v45i4.142
Billheimer D, Guttorp P, Fagan W (2001) Statistical interpretation of species composition. J Am Stat Assoc 96(456):1205–1214. https://doi.org/10.1198/016214501753381850
Chastin S, Palarea-Albaladejo J, Dontje M, Skelton D (2015) Combined effects of time spent in physical activity, sedentary behaviors and sleep on obesity and cardio-metabolic health markers: A novel compositional data analysis approach. PLoS ONE 10:1–37. https://doi.org/10.1371/journal.pone.0139984
Chen J, Zhang X, Hron K (2021) Partial least squares regression with compositional response variables and covariates. J Appl Stat 48(16):3130–3149
Dumuid D, Pedišić Z, Stanford T, Martín-Fernández J, Hron K, Maher C, Lewis L, Olds T (2017b) The compositional isotemporal substitution model: a method for estimating changes in a health outcome for reallocation of time between sleep, physical activity and sedentary behaviour. Stat Methods Med Res 28:846–857. https://doi.org/10.1177/0962280217737805
Dumuid D, Stanford T, Olds T, Lewis L, Martín-Fernández J, Pedišić Z, Hron K, Katzmarzyk P, Barreira T, Broyles S, Chaput J, Fogelholm M, Hu G, Lambert E, Maia J, Sarmiento O, Standage M, Tremblay M, Tudor-Locke C, Maher C (2017a) Compositional data analysis for physical activity, sedentary time and sleep research. Stat Methods Med Res 27(12):3726–3738. https://doi.org/10.1186/s12889-018-5207-1
Dumuid D, Pedišić Z, Palarea-Albaladejo J, Martín-Fernández J, Hron K, Olds T (2020) Compositional data analysis in time-use epidemiology: What, why, how. Int J Environ Res Public Health 17:2220. https://doi.org/10.3390/ijerph17072220
Egozcue J, Pawlosky-Glahn V (2005) Groups of parts and their balances in compositional data analysis. Math Geol 37(7):795–828. https://doi.org/10.1007/s11004-005-7381-9
Egozcue J, Pawlowsky-Glahn V (2019) Rejoinder on: Compositional data: the sample space and its structure. TEST 28:658–663. https://doi.org/10.1007/s11749-019-00674-2
Egozcue J, Pawlowsky-Glahn V, Mateu-Figueras G, Barceló-Vidal C (2003) Isometric logratio transformations for compositional data analysis. Math Geol 35(3):279–300. https://doi.org/10.1023/A:1023818214614
Felsö R, Lohner S, Hollódy K, Erhardt E, Molnár D (2017) Relationship between sleep duration and childhood obesity: systematic review including the potential underlying mechanisms. Nutr Metab Cardiovasc Dis 27(9):751–761. https://doi.org/10.1016/j.numecd.2017.07.008
Filzmoser P, Hron K (2019) Comments on: Compositional data: the sample space and its structure. TEST 28:639–643. https://doi.org/10.1007/s11749-019-00671-5
Filzmoser P, Hron K, Templ M (2018) Applied compositional data analysis. Springer, Cham. https://doi.org/10.1007/978-3-319-96422-5
Fišerová E, Hron K (2011) On the interpretation of orthonormal coordinates for compositional data. Math Geosci 43(4):455–468. https://doi.org/10.1007/s11004-011-9333-x
Gallo M (2010) Discriminant partial least squares analysis on compositional data. Stat Model 10(1):41–56. https://doi.org/10.1177/1471082X0801000103
Greenacre M (2020) Amalgamations are valid in compositional data analysis, can be used in agglomerative clustering and their logratios have an inverse transformation. Appl Comput Geosci 5:100017. https://doi.org/10.1016/j.acags.2019.100017
Helland I (2010) Steps towards a unified basis for scientific models and methods. World Scientific, Singapore. https://doi.org/10.1142/7404
Hildebrand M, Hansen B, van Hees V, Ekelund U (2017) Evaluation of raw acceleration sedentary thresholds in children and adults. Scand J Med Sci Sports 27(12):1814–1823. https://doi.org/10.1111/sms.12795
Hinkle J, Rayens W (1995) Partial least squares and compositional data: problems and alternatives. Chemom Intell Lab Syst 30(95):159–172. https://doi.org/10.1016/0169-7439(95)00062-3
Höskuldson A (1988) PLS regression methods. J Chemom 2:211–228. https://doi.org/10.1002/cem.1180020306
Hron K, Engle M, Filzmoser P, Fišerová E (2020) Weighted symmetric pivot coordinates for compositional data with geochemical applications. Math Geosci. https://doi.org/10.1007/s11004-020-09862-5
Hron K, Coenders G, Filzmoser P, Palarea-Albaladejo J, Faměra M, Matys Grygar T (2021) Analyzing pairwise logratios revisited. Math Geosci 53(7):1643–1666
Hron K, Engle M, Filzmoser P, Fišerová E (2021) Weighted symmetric pivot coordinates for compositional data with geochemical applications. Math Geosci 53(4):655–674
Kalivodová A, Hron K, Filzmoser P, Najdekr L, Janečková H, Adam T (2015) PLS-DA for compositional data with application to metabolomics. J Chemom 29(1):21–28. https://doi.org/10.1002/cem.2657
Kynčlová P, Filzmoser P, Hron K (2016) Compositional biplots including external non-compositional variables. Statistics 50:1–17. https://doi.org/10.1080/02331888.2015.1135155
Martens H (2001) Reliable and relevant modelling of real world data: a personal account of the development of pls regression. Chemom Intell Lab Syst 58(2):85–95. https://doi.org/10.1016/S0169-7439(01)00153-8
Martín-Fernández J (2019) Comments on: Compositional data: the sample space and its structure. TEST 28(3):653–657
McGregor D, Palarea-Albaladejo J, PM D, Hron K, Chastin S, (2020) Cox regression survival analysis with compositional covariates: application to modelling mortality risk from 24-h physical activity patterns. Stati Methods Med Res 29(5):1447–1465. https://doi.org/10.1177/0962280219864125
Mevik BH, Wehrens R (2007) The pls package: Principal component and partial least squares regression in R. J Stat Softw 18(2):1–24. https://doi.org/10.18637/jss.v018.i02
Migueles J, Rowlands A, Huber F, Sabia S, van Hees V (2019) GGIR: A research community-driven open source R package for generating physical activity and sleep outcomes from multi-day raw accelerometer data. J Measur Phys Behav 2(3):188–196. https://doi.org/10.1123/jmpb.2018-0063
Müller I, Hron K, Fišerová E, Šmahaj J, Cakirpaloglu P, Vančáková J (2018) Interpretation of compositional regression with application to time budget analysis. Aust J Stat 47(2):3–19. https://doi.org/10.17713/ajs.v47i2.652
Oyedele O, Gardner-Lubbe S (2015) The construction of a partial least-squares biplot. J Appl Stat 42:1–12. https://doi.org/10.1080/02664763.2015.1043858
Pawlowsky-Glahn V, Egozcue J (2001) Geometric approach to statistical analysis on the simplex. Stoch Env Res Risk Assess 15(5):384–398. https://doi.org/10.1007/s004770100077
Pawlowsky-Glahn V, Egozcue J, Tolosana-Delgado R (2015) Modeling and analysis of compositional data. Wiley, Chichester. https://doi.org/10.1002/9781119003144
Pelclová J, Štefelová N, Dumuid D, Pedišić v, Hron K, Gába A, Olds T, Pechová J, Zając-Gawlak I, Tlučáková L, (2020) Are longitudinal reallocations of time between movement behaviours associated with adiposity among elderly women? A compositional isotemporal substitution analysis. Int J Obes 44(4):857–864. https://doi.org/10.1038/s41366-019-0514-x
Štefelová N, Dygrýn J, Hron K, Gába A, Rubín L, Palarea-Albaladejo J (2018) Robust compositional analysis of physical activity and sedentary behaviour data. Int J Environ Res Public Health 15(10):2248. https://doi.org/10.3390/ijerph15102248
Štefelová N, Palarea-Albaladejo J, Hron K (2021) Weighted pivot coordinates for partial least squares-based marker discovery in high-throughput compositional data. Stat Anal Data Min 14(4):315–330
van den Boogaart K, Tolosana-Delgado R (2008) “compositions’’: A unified r package to analyze compositional data. Comput Geosci 34(4):320–338. https://doi.org/10.1016/j.cageo.2006.11.017
van der Voet H (1994) Comparing the predictive accuracy of models using a simple randomization test. Chemom Intell Lab Syst 25(2):313–323. https://doi.org/10.1016/0169-7439(94)00084-V
vanHees V, Sabia S, Anderson K, Denton S, Oliver J, Catt M, Abell J, Kivimaki M, Trenell M, Singh-Manoux A (2015) A novel, open access method to assess sleep duration using a wrist-worn accelerometer. PLoS One. https://doi.org/10.1371/journal.pone.0142533
Varmuza K, Filzmoser P (2009) Introduction to multivariate statistical analysis in chemometrics. Taylor & Francis, New York. https://doi.org/10.1201/9781420059496
Wang H, Meng J, Tenenhaus M (2010) Regression modelling analysis on compositional data. In: Esposito Vinzi V, Chin WW, Henseler J, Wang H (eds) Handbook of partial least squares. Springer, Berlin
R Core Team (2021) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.r-project.org
Acknowledgements
This work has been partly supported by the Czech Science Foundation under reg. no. GA18-09188S (to N.Š., K.H., A.G. and J.D.) and no. GA22-02392S (to K.H., A.G. and J.D.), the Spanish Ministry of Science and Innovation (MCIN/AEI/ 10.13039/501100011033) and ERDF A way of making Europe [grant PID2021-123833OB-I00] (to J.P.A. and K.H.), the Scottish Government Rural and Environment Science and Analytical Services Division (to N.Š. and J.P.A.) and the Palacký University Grant Agency IGA PrF_2020_015 (to N.Š. and K.H.).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: On the relationships between PLS regression results from different logratio coordinate systems
The relationships between results obtained from PLS regression performed on different logratio coordinate systems, as presented in Sect. 3.1, can be easily deduced. Let us consider 3 different models (2):
where \({\textbf{C}}\) (\({\textbf{B}}^{(k)}\) and \({\textbf{B}}^{(l)}\) respectively) denotes a matrix of compositional data expressed in clr coefficients (balance coordinate systems k and l respectively) and \(\varvec{\beta }^{\star }\) (\(\varvec{\beta }^{(k)}\) and \(\varvec{\beta }^{(l)}\) respectively) denotes the respective vector of regression coefficients, with \(k, l = 1, \ldots , L\). For simplicity we do not include the additional non-compositional variables here.
The relationships between the vectors of regression coefficients \(\varvec{\beta }^{\star }\) \(\varvec{\beta }^{(k)}\) and \(\varvec{\beta }^{(l)}\) are straightforward. Since \({\textbf{C}} = {\textbf{B}}^{(l)} {\textbf{G}}^{(l)}\) and \({\textbf{B}}^{(k)} = {\textbf{B}}^{(l)} {\textbf{G}}^{(l)} \left( {\textbf{G}}^{(k)}\right) ^\top\), then
As to the relationships between scores and loadings, these can be established from e.g. the NIPALS algorithm as summarised in Sect. 3. Denoting the score (loading, respectively) vectors corresponding to the matrix \({\textbf{C}}\) by \({\varvec{t}}_j^{\star }\) (\({\varvec{p}}_j^{\star }\), respectively) and the score (loading, respectively) vectors corresponding to the matrix \({\textbf{B}}^{(l)}\) by \({\varvec{t}}_j^{(l)}\) (\({\varvec{p}}_j^{(l)}\), respectively), \(j=1, \ldots , a,\ l=1, \ldots , L\), we have
for all \(l=1, \ldots , L\),
and since
the analogous relationship can be deduced for the remaining components, i.e.
Appendix B: Comparing PLS-based results of the case study with other methods
See Figs. 2, 3, 4 and 5. See Tables 5 and 6.
Ternary diagrams using centred data of the 3-part composition (Sleep, SB, PA), with centre \((34.01, 46.80, 19.18) \%\) (upper figure), and of the 3-part subcomposition (LPA, MVPA, VPA), with centre \((85.06, 14.01, 0.93) \%\), (lower figure). The lighter the colour of the points, the higher the fat mass of the corresponding individual
PLS biplot based on pivot coordinates from five coordinate systems. The lighter the colour of the point, the higher the fat mass level of the corresponding individual. Statistically significant variables in positive (resp. negative) direction are coloured in red (resp. blue), grey refers to non-significant variables. The dashed lines indicate the origin for the first and second PLS component axes (PLS comp. 1 and PLS comp. 2). A \(92.22\%\) of the explanatory variables variance (resp. \(33.32\%\) of the response variable variance) is explained by the first two PLS components: \(88.50\%\) by PLS comp. 1 and \(3.72\%\) by PLS comp. 2 (resp. \(20.49\%\) by PLS comp.1 and \(12.83\%\) by PLS comp. 2)
PCA biplot based on pivot coordinates from five coordinate systems. The lighter the colour of the point, the higher the fat mass level of the corresponding individual. The dashed lines indicate the origin for the first and second PCA component axes (PC1 and PC2). A \(95.01\%\) of the data variability is explained by the first two PCs: \(88.58\%\) by PC1 and \(6.43\%\) by PC2
PCA biplot based on compositional balances from seven pivoting balance coordinate systems. The lighter the colour of the point, the higher the fat mass level of the corresponding individual. The dashed lines indicate the origin for the first and second PCA component axes (PC1 and PC2). A \(95.01\%\) of the data variability is explained by the first two PCs: \(88.58\%\) by PC1 and \(6.43\%\) by PC2
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Štefelová, N., Palarea-Albaladejo, J., Hron, K. et al. Compositional PLS biplot based on pivoting balances: an application to explore the association between 24-h movement behaviours and adiposity. Comput Stat 39, 835–863 (2024). https://doi.org/10.1007/s00180-023-01324-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-023-01324-w