1 Introduction

The creep-resistant steels of the family 9–12 wt% Cr steels are now used widely in modern power plant components [1]. Thermal efficiency and reduced CO2 emissions from power plants require more research on these steels [2]. The most commonly used 9–12 wt% Cr steels for power plant components are: P91, P122, E911, and P92 [1, 3]. These steels have become popular due to their excellent creep strength, weldability, creep resistance and fabricability [4, 5]. For example, P92 steel, which has ~ 30% higher creep strength than P91 steel [6], has replaced P91 steel and other older steel for power plant components such as turbine and boiler tubes and pipes. This steel can achieve a high steam temperature of up to 650℃ than the 9–12 wt% Cr steels [7].

The processing route for most components after casting involves rolling, forging, drawing, and extrusion [8]. The forming process can eliminate defects like voids formed during casting and cause grain refinement of the microstructure. The metal flow behaviour during forming is of great concern to the engineers and the designers [9]. To improve the mechanical properties of these steels, forming parameters must be controlled [10]. Constitutive equations provide information on metal flow patterns [11]. These equations can accurately describe the workability of any material under different forming conditions [12]. These equations act as input in the Finite Element Method (FEM) simulation codes for studying forming process [13]. However, FEM accuracy depends on the constitutive equations developed for the material [14]. Computer simulation reduces production costs and time, especially in metal processing [15]. Moreover, FEM modules provide a cost-effective way of designing and optimising metal forming techniques commonly used in the production industry [16].

Constitutive modelling of flow stress during hot forming is of great importance. Most works on the hot workability of metal have used the conventional Arrhenius equations to determine the material constants [17,18,19,20]. The hyperbolic sine-law Arrhenius model, as given in Eq. 1.1 [21], has been accepted widely as the constitutive model for analysing the metal flow pattern of most materials, such as P91steel [22] and P92 steel [17, 23, 24], and Titanium alloys [25]. This equation relates the deformation conditions and the flow stress as:

$$\dot{\varepsilon }=A{(\mathit{sin}h\left(\alpha \sigma \right))}^{n}exp\left[\frac{-Q}{RT}\right]$$
(1.1)

where A, α and n are material constants, Q is the thermal activation energy, \(\dot{\varepsilon }\) is the strain rate, σ is the flow stress, T is the deformation temperature, and R is the universal gas constant (8.314 kJ. mol−1). The constitutive constants obtained in Eq. 1.1 do not account for any internal microstructure evolution during deformation, thus referred to as apparent values [26]. The equation assumes that the microstructure remains constant during forming [27]. The obtained n and Q values are higher than 270 kJ.mol−1 for iron [28]. The deviation of activation energy is due to a variation of Young’s Modulus E (T) and self-diffusion coefficient, which varies with temperature [26]. Therefore, to account for these factors, Eq. 1.1 for the general physically-based equation (n = 5) is given as follows [27, 29, 30]:

$$\frac{\dot{\varepsilon }}{D(T)}=B{\left[sinh\left(\alpha\upsigma /E(T)\right)\right]}^{5}$$
(1.2)

where D(T) is determined using D(T) = D0 exp(Qsd/RT), D0 is the pre-exponential constant. Qsd and E(T) are self-diffusion activation energy, and temperature affected Young’s Modulus of the material, respectively. These values (D0 Qsd, E(T)) are obtained from the Ashby table [31].

However, the stress exponent n = 5 (Eq. 1.2) is an absolute value [32]. The equation assumes that no microstructure evolution such as DRX, DRV and dynamic precipitates occurs during forming, which affects the stress exponent. The n-value is, therefore, not a constant but a variable parameter [27, 33, 34], and the equation is as follows:

$$\frac{\dot{\varepsilon }}{D(T)}=B{\left[sinh\left(\alpha\upsigma /E(T)\right)\right]}^{n}$$
(1.3)

A few studies have reported results on using the physically-based model to analyse the flow stress behaviour of metals and alloys [27, 32, 33, 35, 36]. To this end, no study has reported on the applicability of the new physically-based constitutive equation in describing the deformation behaviour of creep-resistant steels. The novelty in this article refers to the effectiveness of the physically-based model in studying the workability of two P92 steels having variation in chromium and tungsten content, which is conspicuously missing in the literature. The present study aims to develop a suitable physically-based constitutive equation for evaluating and analysing the flow behaviour of P92 steel. The output of this study will provide more insight into this method for future applications in research and industrial application. Hot compression tests were conducted at different deformation conditions using Gleeble® 3500 equipment. The flow stress–strain curves were analysed to develop mathematical rate equations for predicting the flow stress behaviour of P92 steel under the investigated conditions.

2 Experimental procedure

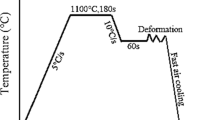
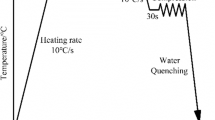
Table 1 shows the chemical composition (in wt%) of the two P92 steel with variations in chromium and tungsten content studied. Test specimens measuring 8 mm diameter and 12 mm height underwent a uniaxial compression test using the Gleeble-3500 simulator under vacuum. Experimental test conditions were: a temperature range of 850–1000°C at an interval of 50℃ and strain rates of 0.1, 1 and 10 s−1. These deformation temperatures were in the austenite region. Hence, the deformation tests in this study were in a single phase. These forming conditions have been used previously for this steel [37]. Thermocouples at the mid-height of the specimen assisted in monitoring temperature during testing. Nickel paste and graphite foil are applied between the sample and the anvil to reduce friction. Before testing, the samples were heated at a rate of 5°C/s to 1100°C and held for 180 s. Then, cooled at 10°C/s and soaked for 60 s at the deformation temperature before compression to a strain of 0.6. After deformation, samples were air-cooled rapidly to room temperature. At the austenitisation temperature (1100°C), the complete dissolution of most carbides, especially M23C6, occurs. Dissolution temperature of chromium carbide starts at 900°C and completely dissolves at 1100°C [1]. At 1100°C, the P92 steel transforms into the austenitic phase. At this temperature, deformation resistance is low due to the absence of carbides [2]. Carbide dissolution occurs below 920°C according to ThermoCalc calculations, as shown in Fig. 2 (also, Table 2) for the two steels. The information above justifies the selection of 1100°C as the austenitisation temperature during forming in this study.

Table 1 Chemical compositions (wt.%) of the two steels
Full size table
Table 2 Dissolution temperature of phase in the two steels investigated
Full size table

3 Results and discussion

3.1 Microstructure of as-received steels

Before being put into service, P92 steel undergoes normalisation and tempering conditions. The chemical composition of the two P92 steel (named steel A and B) are listed in Table 1 and have the following relative ‘amounts’ of Cr, W and Mo:

The optical micrographs (Fig. 1) show the tempered martensite microstructure of the as-received steels. The two steels had a tempered microstructure with well-defined prior austenite grain boundaries and triple points.

Fig. 1
figure 1

Optical microstructures of as-received samples

Full size image

After heat treatment, precipitation occurs along the grain and lath boundaries and in the matrix. M23C6 (M = Fe, Mo, W, Cr) carbides precipitate along the prior austenite grain boundaries PAGBs [38], while MX (M = V, Nb; X = C, N) precipitates are usually randomly distributed in the matrix [39]. The carbides along the prior austenite grain boundary hinder the movement of the PAG boundaries and the subgrain dislocations, thus improving the creep resistance [40]. M23C6 carbides improve the creep strength by pinning the grain boundary movement [41], while the MX precipitates impede dislocation movement during deformation [4].

Thermo-Calc software with the TCFe5 database predicted the equilibrium transformation and precipitate dissolution temperatures for the two steels investigated. Figure 2 shows the change in the phase volume (%) as a function of temperature predicted using ThermoCalc under equilibrium conditions for the commonly observed phases: M23C6 carbides, MX, and Laves phase. Dissolution of precipitates increases with an increase in temperature. The precipitate volume fraction increased as temperature decreased below the equilibrium dissolution temperature (Fig. 2).

Fig. 2
figure 2

Thermo-Calc predicted volume % of M23C6, MX and Laves phases vs. temperature under equilibrium condition for the two steels

Full size image

The ThermoCalc results show that MX precipitates have higher dissolution temperatures, as shown in Fig. 2. At higher austenitising temperatures, the precipitates will dissolve into the solid solution and precipitate during tempering. The ThermoCalc results (Fig. 2) provided the basis for choosing 1100℃ for austenitisation temperature during deformation.

3.2 Flow stress behaviour

In this study, the flow stress–strain curves were friction corrected. During the uniaxial compression test, deformation at a lower strain rate caused “sticking” friction. Hence, the study accounted for interfacial friction correction on flow stress. However, the study did not consider adiabatic heating during deformation. The temperature variation between the pre-set and measured temperature in all deformation conditions was approximately below 20°C. The temperature variation did not cause substantial variation in the flow stress values. Therefore, all the flow stress values used in this study were friction corrected. The relationship between the flow stress and temperature at a constant strain rate for the two steels is as given in Fig. 3. The plots show that the flow stress decreased as the deformation temperature increased at any strain rate. The decrease in flow stress is due to dynamic softening (dynamic recovery) [42], which is the dominant dynamic mechanism for P92 steel [18]. At higher deformation temperatures, the kinetic of atoms and dislocation movement increases, causing low flow stress [43]. The flow stress values are higher at a higher strain rate since the deformation time is shorter for dislocation and rearrangement to balance, resulting in work hardening and DRV as the dominant mechanisms. Table 3 shows the flow stress values obtained for the two steel at different deformation conditions. The flow stress results show that steel B had the highest flow stress values at 850℃ and in all strain rates investigated. High flow stress values at 850℃ were due to incomplete dissolution of carbides before deformation [18]. Hence, pinning dislocation results in an increase in flow stress values [44]. At higher temperatures (900–1000℃), the flow stress values for the two steels were relatively close. This deformation region (900–1000℃) lies in the austenitic zone for the two P92 steels. In this region, carbides dissolution of carbides occurs, causing low flow stress values. From the constitutive analysis, the stress exponent of the two steels was relatively the same, further suggesting less resistance to deformation under these conditions. The slight differences in flow stress values can be due to differences in Cr content. Higher Cr content in steel B causes more carbides to form, thus hindering dislocation and causing high flow stress [44].

Fig. 3
figure 3

Relationship between flow stress against temperature a) Steel-A, and b) Steel-B

Full size image
Table 3 Flow stress values obtained during forming
Full size table

3.3 The physically-based constitutive equation

The Young’s modulus and the self-diffusion affected by temperature incorporated in the physically-based model can describe the metal flow pattern [28]. Therefore, Eq. 1.1 then becomes [27]:

$$\frac{\dot{\varepsilon }}{D(T)}=B{\left[sinh\left(\alpha \sigma /E(T)\right)\right]}^{n}$$
(3.1)
$$D\left(T\right)={D}_{0}exp({-Q}_{sd}/RT)$$
(3.2)
$$E\left(T\right)={E}_{0}\left[1-\frac{{T}_{m}}{{G}_{0}}\frac{dG}{dT}\frac{\left(T-300\right)}{{T}_{m}}\right]$$
(3.3)

where Tm is steel absolute melting temperature, B, n, α are material constants and \(\dot{\varepsilon }\) is the strain rate (s−1), E0 and G0 are the Young’s modulus and the shear modulus at temperature of 300K respectively, the term Tm/G0.dG/dT is denoted as ƞ representing modulus as affected by temperature and D is the self-diffusion coefficient. The constants: D0, E0 and Qsd values are obtained from Ashby [31] tables, provided in Table 4. Then, α ≈ β′⁄n′.

Table 4 Data values obtained for P92 steel in Ashby tables [31]
Full size table

The unknown material constants in Eq. 1.2 are obtained by plotting graphs using Eqs. 3.5 and 3.6.

$$\frac{\dot{\varepsilon }}{D(T)}={B}_{1}{\left(\frac{\sigma }{E(T)}\right)}^{n\mathrm{^{\prime}}}$$
(3.5)
$$\frac{\dot{\varepsilon }}{D(T)}={B}_{2}exp\left(\frac{\beta \mathrm{^{\prime}}\sigma }{E(T)}\right)$$
(3.6)

n′ and β′ values were obtained from plots in Fig. 4 (Steel-A) and Fig. 5 (Steel-B) using linear regression analysis. Then, α ≈ β′/ n′. From Eq. 1.2, the slope and the intercept of the plots in Fig. 4c (Steel-A) and Fig. 5c (Steel-B) determined the stress exponent n (slope of the graph) and the ln B (slope intercept). Table 5 gives the calculated material constants for the two steels.

Fig. 4
figure 4

Plots for determining a) ln B, b) n′ and c) n for steel A

Full size image
Fig. 5
figure 5

Plots for determining a) ln B, b) n′ and c) n for steel-B:

Full size image
Table 5 Calculated consitutive constants of the two P92 steel
Full size table

By substituting material constants into Eq. 1.2, the resultant constitutive equations for the two steels is obtained as:

$$\dot{\mathrm{Steel}-\mathrm{A}:\varepsilon }\mathit{exp} \left(\frac{270000}{RT}\right)=Z=1.33\times {10}^{11}{\left(sinh(576.68{\sigma }_{ss}/E(T)\right)}^{9.8}$$
(3.7)
$$\mathrm{Steel}-\mathrm{B}:\dot{\varepsilon }\mathit{exp} \left(\frac{270000}{RT}\right)=Z=9.53\times {10}^{10}{\left(sinh(669.32{\sigma }_{ss}/E(T)\right)}^{10.3}$$
(3.8)

Then, Eq. 1.2 becomes:

$${\left(\frac{Z}{B}\right)}^\frac{1}{n}=\mathit{sin}h\left(\alpha \frac{{\sigma }_{ss}}{E\left(T\right)}\right)= \frac{{e}^{\alpha {\sigma }_{ss}/E(T)}}{2}-\frac{-{e}^{\alpha {\sigma }_{ss}/E(T)}}{2}$$
(3.9)

Solving Eq. 11 gives Eq. 12:

$${\sigma }_{ss}=\frac{E(T)}{\alpha }\mathit{ln}{\left[{\left(\frac{Z}{B}\right)}^\frac{1}{n}+\left({\left(\frac{Z}{B}\right)}^\frac{2}{n}+1\right)\right]}^\frac{1}{2}$$
(3.10)

Equation 3.10 can predict the flow stress under different forming conditions using \(Z=\dot{\varepsilon }exp\left(\frac{32475.34}{\mathrm{T}}\right)\). Therefore, α, B and n values from Table 5, the following equations can describe the flow stress:

$$For Steel-A: {\sigma }_{ss}=\frac{E(T)}{576.7}\mathit{ln}{\left[{\left(\frac{Z}{1.33\times {10}^{11}}\right)}^{\frac{1}{9.8}}+\left({\left(\frac{Z}{1.33\times {10}^{11}}\right)}^{\frac{2}{9.8}}+1\right)\right]}^\frac{1}{2}$$
(3.11)
$$For Steel-B: {\sigma }_{ss}=\frac{E(T)}{565.0}\mathit{ln}{\left[{\left(\frac{Z}{9.53\times {10}^{10}}\right)}^{\frac{1}{10.3}}+\left({\left(\frac{Z}{9.53\times {10}^{10}}\right)}^{\frac{2}{10.3}}+1\right)\right]}^\frac{1}{2}$$
(3.12)

From the above analysis, the calculated material constants of the two steels did not show any differences. Even though the two steels have a slight variation in the chemical composition (Cr Content), they have relatively the same stress exponent n values (difference of 4.7%). A study reported that n-values are affected by flow stress, which depends on the interaction between precipitates and mobile dislocations [45]. The carbides pin dislocation hence, hindering the deformation process. The stress exponent is temperature-sensitive. The stress exponent n-value increases with a decrease in the deformation temperature and vice-versa [46]. However, deformation temperatures were slightly higher than the Ac3 of the two steels. Therefore, the flow resistance during deformation should be relatively the same as most carbides might have dissolved. The results further show that the variation in the chemical composition had an insignificant effect on the stress exponent.

On the other hand, the B-value of steel A had one order of magnitude over steel B. Parameter B is proportional to the activation energy Q. Higher Q-value results in a higher B-value [47]. However, under the analysis method used, the Q-value was constant. Then, what might be the reason for this deference in B-value? B-value has no simple physical meaning [48]. Therefore, B-value is a function of forming conditions and microstructure orientation of the material [47]. The materials values given in Table 5 provide the necessary parameters to apply in the physically-based constitutive equation to determine precisely the flow stress behaviour during the deformation of this steel.

3.4 Comparison of Zener parameter and flow stress

The Zener parameter describes the combined effects of deformation temperature and strain rate on the flow stresses. Figure 6 shows the relationship between the flow stress and the lnZ. The plots showed a linear relationship between the flow stress and lnZ.

Fig. 6
figure 6

Comparison of the flow stress and lnZ of the two steels

Full size image

Figure 6 shows that at any given value of lnZ, the two steels experience different flow stress. This result shows the influence of the deformation conditions (temperature and strain rate) during deformation. Generally, the value of lnZ increases as the deformation temperature decreases with an increase in the strain rate. When comparing steel A and steel B, the latter had higher resistance to deformation. Steel B had the highest lnZ value, especially at higher strain rates, as shown in Fig. 6. Steel B also had higher flow stress than steel A at any given lnZ value (Eq. 3.12). These results indicate that steel B had higher resistance to deformation, which can be due to higher Cr content which contributes to a higher precipitation strengthening, hence hindering deformation. The Z-value also depends on the deformation temperature. Lower Z-values occur at higher forming temperatures. Higher Z-values show that work hardening is the dominant deformation mechanism, and the material undergoes severe plastic deformation. Lower Z-values indicate that DRX and DRV occurred due to an increased dislocation movement and reduced dislocation density. Work hardening and dynamic softening may simultaneously occur during forming, thus affecting the resultant dislocation density and influencing the flow stress behaviour [49]. Therefore, dynamic softening will occur depending on the initial thermal history of the sample subjected before deformation. For example, annealing before deformation can induce low dislocation density, which causes dislocation accumulation at the initial stages of deformation. As strain increases, a high generation of dislocation occurs, resulting in dislocation annihilation, hence initiating dynamic softening.

Equartion 3.12 gives the constitutive equations that can be used to predict the flow stress using the Zener parameter for the two steels investigated.

$$\mathrm{Steel}\;\mathrm A:\sigma_{sat}=17.41\mathrm{lnZ}-664.25$$
$$\mathrm{Steel}\;\mathrm B:\sigma_{sat}=14.55\mathrm{lnZ}-475.07$$
(3.12)

4 Model verification

The validity of the developed constitutive models (Eqs. 3.11 and 3.12) to accurately predict the flow stress behaviour of the two steels investigated was done using statistical parameters: correlation coefficient R (Eq. 4.1) and the average absolute relative error AARE (Eq. 4.2). These models are widely used to predict the linear relationship between two variables [14, 50, 51].

$$R=\frac{\sum_{i=1}^{N}\left({E}_{i}-\overline{E }\right)\left({C}_{i}-\overline{C }\right)}{\sqrt{\sum_{i=1}^{N}{\left({E}_{i}-\overline{E }\right)}^{2}\sum_{i=1}^{N}{\left({C}_{i}-\overline{C }\right)}^{2}}}$$
(4.1)
$$AARE\left(\mathrm{\%}\right)=\frac{1}{N}{\sum }_{i=1}^{N}\left[\frac{{E}_{i}-{C}_{i}}{{E}_{i}}\right]$$
(4.2)

where E is the flow stress values obtained form experimental data, C is the calculated flow stress and, \(\overline{E }\) is the mean values of experimental data and \(\overline{C }\) is the mean values caluculated flow stress.

Figure 7 shows the correlation of experimental and calculated (predicted) flow stress data. Table 6 shows the calculated statistical parameter values for the two steels investigated. The results indicate that the developed physically-based constitutive model has higher accuracy in predicting the flow stress of the two steels. The calculated flow stress values had an excellent correlation compared to the experimental flow stress values. The AARE values were 2.18% (P92-A) and 2.20% (P92-B), while the R values were the same for the two steels (0.99). These parameter values show that models have excellent predictability of flow stress behaviour. The analysis indicates that the physically-based model is applicable in determining the stress flow pattern of P92 steels for any given deformation conditions. Hence, it can be of use in most industrial metal-forming applications.

Fig. 7
figure 7

Comparison of the calculated and the experimental flow stress a) Steel-A, and b) Steel-B

Full size image
Table 6 Statistical parameters values
Full size table

5 Conclusion

The study observed the following:

  1. 1.

    The flow stress values increase with a decrease in the temperature or an increase in strain rate and vice versa. The results show that flow stress values depend on deformation conditions.

  2. 2.

    It is possible to obtain the material constants B, n, and α in the physically-based model using the self-diffusion activation energy of austenite iron during forming at different loading conditions.

  3. 3.

    The constitutive analysis results show that this model is accurate and reliable in analysing the flow stress behaviour of metals and alloys, hence an alternative technique to analyse metal flow patterns. From the results, the effect of the chemical composition of the two steels on the flow stress behaviour was insignificant.

  4. 4.

    The statistical analysis results show that the physically-based equations developed for the two steels exhibited high accuracy in predicting the metal flow pattern of the two P92 steel investigated. The predicted and experimental data had a good correlation.