1 Introduction

Soft sensor is a virtual inferential prediction method that uses easily measured variables to forecast process variables that are difficult to measure directly due to technological, economic constraints as well as a complex environment. Soft sensor attempts to construct a regression prediction method between easily measured variables as well as difficultly measured variables, which is used to address issue that hinders measurements from being used as feedback signals in quality control methods [1]. For at least 10 years, there has been a growing trend in use of data-driven AI (artificial intelligence) approaches to enhance machines, processes, and products across several industrial domains [2]. In recent years, reducing emissions as a result of stronger environmental restrictions has also been a major motivator [3]. However, gathering the data required for such approaches is fraught with difficulties, one of which is the long life of industrial gear. Official depreciation estimates range from (rarely) 6 to more than 30 years, depending on the country, type of machinery, and industrial sector [4]. Experience suggests that, particularly in small and medium-sized businesses, resilient equipment can last even longer in regular usage. Soft sensor approaches are used more widely in industrial processes, and they have become a key emerging trend in both academics as well as industry [5]. Early academics proposed model predictive control like generalized predictive control, dynamic matrix predictive control and model control method, in light of model prediction in industrial production process [6]. However, these soft sensor prediction approaches have several flaws. ANN (Artificial neural networks), rough set, SVM (support vector machine) and hybrid techniques are some AI and ML methods based on data-driven technologies that have been proposed to solve issues where it is difficult to measure key processes as well as quality variables for soft sensor methods as a result of DL in soft sensor control method as well as continuous progress in engineering technology [7].

The contribution of this research is as follows:

  • To design novel techniques in automation of manufacturing industry where the dynamic soft sensors are used in feature representation and classification of the data

  • To collect the data cloud storage and create the virtual sensors dataset based on gear fault detection, spindle fault detection, and bearing fault detection in automation industry

  • To represent the feature using fuzzy logic-based stacked data driven auto-encoder (FL_SDDAE) where the features of input data have been identified with general automation problems.

  • Then, the features have been classified using least square error backpropagation neural network (LSEBPNN) in which the mean square error while classification will be minimized with loss function of the data

  • Here the experimental results have been carried out in terms of QoS, measurement accuracy, RMSE, MAE, prediction performance, and computational time.

Research organization is as follows. In Section 2, related works are described. Section 3 gives details of proposed method. proposed method performance, and the results are present in Section 4. Finally, Section 5 concludes the work.

2 Related works

DL-based techniques are recently exhibited solid representation competency and success in a variety of computer science domains, including image processing, computer vision, NLP, and more [8]. Stack autoencoder (SAE) [9], DBN (deep belief network) [10], CNN [11], and LSTM [12] are some of widely utilized deep network architectures. Greedy layer-wise unsupervised pre-training, as well as supervised fine-tuning, are highly important for DL architectures like SAE. The SAE weights evaluated during unsupervised pre-training step are used in supervised fine-tuning stage, which is a more significant method than random weight initialization [13]. As a result, various industrial applications of soft sensors based on SAE [14] are presented. Same authors improved this result significantly by utilizing a TDNN in [15].Mean error dropped to just 1.14 to 1.32% and 1.65° to 3.08°, in the same conditions utilized in [16, 17]. As a result, the type of network used in these two papers had a significant impact on the algorithms’ performance. In [18], an RNN is presented that collects information regarding air–fuel ratio λ, ignition angle, and turbocharger boost pressure in addition to rotational speed signal. Focus was on neural network design, which had a significant impact on the algorithm’s performance. To estimate cylinder pressure curves, [19] uses a NN with RBF (radial basis functions) as well as consequently no recurrence. Authors of [20] presents a novel convolutional, BiGRU, and Capsule network-based deep learning model, HCovBi-Caps, to classify the hate speech and authors of [21] introduce BiCHAT: a novel BiLSTM with deep CNN and hierarchical attention-based deep learning model for tweet representation learning toward hate speech detection. Authors of [15] do not use raw rotational speed signal, but instead translate it into frequency domain as well as process only first 20 harmonics, to earlier research are used an RBF network. They also employ structure-borne sound signal’s 21st–50th harmonics. As a result, the preparation of the given data is the most important aspect of this project. The typical errors for pMax as well as its position in crank angle range are 3.4% and 1.5°, respectively. Using a multi-layer perceptron, [22] predicts combustion parameters directly from crankshaft’s rotational speed as well as acceleration data, in contrast to the previous studies (MLP). The mean error lies between 1.38° and 9.1°, with a range of 4.1 to 8.0%. A deep learning-based R2DCNNMC model is proposed for detection and classification of COVID-19 employed chest X-ray images data [23]. Privacy of data driven uses on the k-anonymity and l-diversity supervised models classifies the healthcare data [24]. Virtualization for dynamics on cloud for network operation and management is discussed in [25] and proposed hybrid model on cloud ensures the maximum benefits from virtualization.

The effective implementations of SAE-based DL listed above reveal a significant capacity to extract features. Deep structures exceed typical soft-sensing prediction performance thanks to unsupervised layer-wise pre-training as well as supervised fine-tuning processes. Proposed industrial soft sensors are static methods based on notion of a static process as well as steady-state. However, the inherently dynamic nature of industrial processes cannot be neglected. Chemical processes, for example, are highly dynamic, with current state being linked to earlier ones. As a result, time-related characteristics of time-series recorded data are important.

3 System model

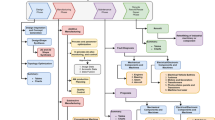
This section discusses the proposed design in automation of manufacturing industry based on dynamic soft sensors. Here the data has been processed to recognize the missing value and usual problems like hardware failures, incorrect readings, communication errors, process working conditions. Then their features have been represented in module 1 and the represented feature has been classified in module 2 using deep learning techniques. The overall research architecture is given in Fig. 1.

Fig. 1
figure 1

Overall Proposed diagram for virtual sensor-based fault detection in automation industry

Full size image

3.1 Feature representation using fuzzy logic based stacked data driven auto-encoder (FL_SDDAE)

ENotice is replaced Eq. (2) represents overall input–output transfer function about general autoencoder (AE) structure. The input \(\left({x}^{\left[\alpha \right]}\in {\mathcal{R}}^{d}\right)\) is supplied to hidden layer, whose output is utilized to reconstruct \(\left({\stackrel{\backprime}{x}}^{\left|\alpha \mathrm{\rfloor}\right.}\right)\) input through output layer (y) as shown in Eq. (1).

$${\stackrel{\backprime}{x}}^{\left[\alpha \right]}={y}_{\left({W}^{\mathrm{^{\prime}}},{b}^{\mathrm{^{\prime}}}\right)}\left({h}_{\left(W,b\right)}\left({x}^{\left[\alpha \right]}\right)\right)\equiv {x}^{\left[\alpha \right]}$$
(1)

An encoder or recognition model is another name for this approach. Optimize variational parameters φ such that as shown in Eq. (2):

$${q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\approx {p}_{\theta }\left(\left.\mathbf{z}\right|\mathbf{x}\right)$$
(2)

As stated in Eq. (3), inference models are any directed graphical model.

$${q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\left({\mathbf{z}}_{1},\dots ,\left.{\mathbf{z}}_{M}\right|\mathbf{x}\right)={\prod }_{j=1}^{M} {q}_{\phi }\left(\left.{\mathbf{z}}_{j}\right|Pa\left({\mathbf{z}}_{j}\right),\mathbf{x}\right)$$
(3)

In the directed graph, \(Pa\left({\mathbf{z}}_{j}\right)\) is set of parent variables of variable \({\mathbf{z}}_{j}\).

$$\mathrm{log}\;{p}_{\theta }\left(\mathbf{x}\right)={\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x}\right)\right]={\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\left[\frac{{p}_{\theta }\left(\mathbf{x},\mathbf{z}\right)}{{p}_{{\varvec{\theta}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\right]\right]={\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\left[\frac{{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)}{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\frac{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}{{p}_{{\varvec{\theta}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\right]\right]=\underset{={\mathcal{L}}_{\theta ,\phi }\left(\mathbf{x}\right)}{\underbrace{{\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\left[\frac{{p}_{\theta }\left(\mathbf{x},\mathbf{z}\right)}{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\right]\right]}}+\underset{={D}_{KL}\left(\left.\left.{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right|\right|{p}_{{\varvec{\theta}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)}{\underbrace{{\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\left[\frac{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}{{p}_{{\varvec{\theta}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\right]\right]}}$$
(4)

The non-negative Kullback–Leibler (KL) divergence between \({q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\) and \({p}_{{\varvec{\theta}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)\) is the second term in Eq. (5):

$${D}_{KL}\left(\left.\left.{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right|\right|{p}_{\theta }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)\ge 0$$
(5)

The variational lower bound, commonly known as ELBO, is the first term in Eq. (6):

$${\mathcal{L}}_{{\varvec{\theta}},\phi }(\mathbf{x})={\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\;{p}_{{\varvec{\theta}}}(\mathbf{x},\mathbf{z})-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right]$$
(6)

Because the KL divergence is non-negative, ELBO shows a lower bound on data’s log-likelihood, as demonstrated in Eq. (7).

$$\begin{array}{c}{\mathcal{L}}_{{\varvec{\theta}},\phi }\left(\mathbf{x}\right)=\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x}\right)-{D}_{KL}\left(\left.\left.{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right|\right|{p}_{{\varvec{\theta}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)\\\le \mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x}\right)\end{array}$$
(7)
$$\begin{array}{c}{\nabla }_{{\varvec{\theta}}}{\mathcal{L}}_{{\varvec{\theta}},\phi }\left(\mathbf{x}\right)={\nabla }_{{\varvec{\theta}}}{\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right]={\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathrm{x}\right)}\left[{\nabla }_{{\varvec{\theta}}}\left(\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)\right]\\\simeq {\nabla }_{{\varvec{\theta}}}\left(\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)={\nabla }_{{\varvec{\theta}}}\left(\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)\right)\end{array}$$
(8)

Because the ELBO’s expectation is taken \({q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\), which is a function of φby Eq. (9):

$${\nabla }_{\phi }{\mathcal{L}}_{\theta ,\phi }\left(\mathbf{x}\right)={\nabla }_{\phi }{\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right]\ne {\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[{\nabla }_{\phi }\left(\mathrm{log}{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)\right]$$
(9)

Apply a reparameterization approach to compute unbiased estimates of \({\nabla }_{\phi }{\mathcal{L}}_{\theta ,\phi }\left(\mathbf{x}\right)\), in case of continuous latent variables.

Replace an expectation w.r.t. \({q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\) with one w.r.t. \({p}_{{\varvec{\theta}}}\) via reparameterization given by Eq. (10).

$${\mathcal{L}}_{{\varvec{\theta}},\phi }\left({log}\mathbf{x}\right)={\mathbb{E}}_{{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)}\left[\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right]={\mathbb{E}}_{p\left({\varvec{\epsilon}}\right)}\left[\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right]$$
(10)
$${\varvec{\epsilon}}\sim p\left({\varvec{\epsilon}}\right)\mathbf{z}=\mathbf{g}\left({\varvec{\phi}},\mathbf{x},{\varvec{\epsilon}}\right){\stackrel{\backprime}{\mathcal{L}}}_{{\varvec{\theta}},{\varvec{\phi}}}\left(\mathbf{x}\right)=\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)\begin{array}{cc}{\mathbb{E}}_{p\left({\varvec{\epsilon}}\right)}\left[{\nabla }_{{\varvec{\theta}},\phi }{\stackrel{\backprime}{\mathcal{L}}}_{{\varvec{\theta}},{\varvec{\phi}}}\left(\mathbf{x};{\varvec{\epsilon}}\right)\right]& ={\mathbb{E}}_{p\left({\varvec{\epsilon}}\right)}\left[{\nabla }_{{\varvec{\theta}},{\varvec{\phi}}}\left(\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{{\varvec{\phi}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right)\right]\\ & ={\nabla }_{{\varvec{\theta}},{\varvec{\phi}}}\left({\mathbb{E}}_{p\left({\varvec{\epsilon}}\right)}\left[\mathrm{log}\;{p}_{{\varvec{\theta}}}\left(\mathbf{x},\mathbf{z}\right)-\mathrm{log}\;{q}_{{\varvec{\phi}}}\left(\left.\mathbf{z}\right|\mathbf{x}\right)\right]\right)\\ & ={\nabla }_{{\varvec{\theta}},{\varvec{\phi}}}{\mathcal{L}}_{{\varvec{\theta}},{\varvec{\phi}}}\left(\mathbf{x}\right)\end{array}$$
(11)

A simple factorized vGaussian encoder by Eq. (12)

$${q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)=\mathcal{N}\left(\mathbf{z};{\varvec{\mu}},\,\mathrm{diag}\left({{\varvec{\sigma}}}^{2}\right)\right):\left({\varvec{\mu}},\,\mathrm{log}{\varvec{\sigma}}\right)={\mathrm{EncoderNeuralNet}}_{{\varvec{\phi}}}\left(\mathbf{x}\right){q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)={\prod }_{i} {q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)={\prod }_{i} \mathcal{N}\left({z}_{i};{\mu }_{i},{\sigma }_{i}^{2}\right)$$
$$\mathbf{z}={\varvec{\mu}}+{\varvec{\sigma}}\odot{\varvec{\epsilon}}$$
(12)

The log determinant of the Jacobian is given by Eq. (13):

$$\mathrm{log}\;{d}_{\phi }\left(\mathbf{x},{\varvec{\epsilon}}\right)=\mathrm{log}\left|\mathrm{det}\left(\frac{\partial \mathbf{z}}{\partial{\varvec{\epsilon}}}\right)\right|=\sum\nolimits_{i} \mathrm{log}\;{\sigma }_{i}$$
(13)

and the posterior density is given by Eq. (14):

$$\begin{array}{cc}\mathrm{log}\;{q}_{\phi }\left(\left.\mathbf{z}\right|\mathbf{x}\right)=\mathrm{log}\;p\left({\varvec{\epsilon}}\right)-\mathrm{log}\;{d}_{\phi }\left(\mathbf{x},{\varvec{\epsilon}}\right)& ={\sum }_{i}\;\mathrm{log}\;\mathcal{N}\left({\epsilon }_{i};\mathrm{0,1}\right)-\;\mathrm{log}\;{\sigma }_{i}\end{array}\mathrm{when}\;z=g\left({\varvec{\epsilon}},\phi ,\mathbf{x}\right)$$
(14)

From Eq. (15)

$${\varvec{\Sigma}}={\mathbb{E}}\left[\left(\mathbf{z}-{\mathbb{E}}\left[\left.\mathbf{z}\right|\right]\right){\left(\mathbf{z}-{\mathbb{E}}\left[\left.\mathbf{z}\right|\right]\right)}^{T}\right]={\mathbb{E}}\left[\mathbf{L}{\varvec{\epsilon}}{\left(\mathbf{L}{\varvec{\epsilon}}\right)}^{T}\right]=\mathbf{L}{\mathbb{E}}\left[{\varvec{\epsilon}}{{\varvec{\epsilon}}}^{T}\right]{\mathbf{L}}^{T}={\mathbf{L}\mathbf{L}}^{T}$$
(15)

Let Gx be defined: X ⊂ Rn → R, that is, a function on compact set X = α1,1 × … × [αn,βn] and analytic formula of Gx be unknown.

Define \({N}_{j}\left(j=\mathrm{1,2},\dots ,n\right)\) fuzzy sets \({A}_{j}^{1},{A}_{j}^{2},\dots ,{A}_{j}^{{N}_{j}}\in \left[{\alpha }_{j},{\beta }_{j}\right]\), which are normal, consistent, and complete with triangular MFs \({\mu }_{{A}_{j}^{1}}\left({x}_{j};{a}_{j}^{1},{b}_{j}^{1},{c}_{j}^{1}\right),\dots ,{{\mu }_{{A}_{j}}}^{{N}_{j}}\left({x}_{j};{a}_{j}^{{N}_{j}},{{b}_{j}}^{{N}_{j}},{{c}_{j}}^{{N}_{j}}\right)\), and \({A}_{j}^{1}<{A}_{j}^{2}<\cdots <{A}_{j}^{{N}_{j}}\) with \({a}_{j}^{1}={b}_{j}^{1}={\alpha }_{j}\) and \({b}_{j}^{{N}_{j}}={c}_{j}^{{N}_{j}}={\beta }_{j}\), which,

  • \({e}_{1}^{1}={\alpha }_{1},{e}_{1}^{{N}_{1}}={\beta }_{1}\), and \({e}_{1}^{j}={b}_{1}^{j}\) for \(j=\mathrm{2,3},\dots ,{N}_{1}-1\), -\({e}_{2}^{1}={\alpha }_{2},{e}_{2}^{{N}_{2}}={\beta }_{2}\), and \({e}_{1}^{j}={b}_{2}^{j}\) for \(j=\mathrm{2,3},\dots ,{N}_{2}-1\),:\({e}_{n}^{1}={\alpha }_{n},{e}_{n}^{{N}_{n}}={\beta }_{n}\), and \({e}_{1}^{j}={b}_{1}^{\mathrm{^{\prime}}}\) for \(j=\mathrm{2,3},\dots ,{N}_{n}-1.\)

  • Construct \(I={N}_{1}\times {N}_{2}\times \dots \times {N}_{n}\) fuzzy if–then rules in following form:

  • \({R}_{X}^{{j}_{1}-{j}_{n}}:\mathrm{IF}{x}_{1}\) is \({A}_{1}^{{j}_{1}}\) and \({x}_{2}\) is \({A}_{2}^{{j}_{2}}\) and … and \({x}_{n}\) is \({A}_{n}^{{j}_{n}}\) Then \(y\) is \({B}^{{j}_{1}-{j}_{n}}\), where \({j}_{1}=\mathrm{1,2},\dots ,{N}_{1},{j}_{2}=\mathrm{1,2},\dots ,{N}_{2},\dots ,{j}_{n}=\mathrm{1,2},\dots ,{N}_{n}\), and center of the fuzzy set \({B}^{{j}_{1}\dots {/}_{n}}\), denoted by \({\overset{\leftharpoonup}{y} }^{{\mathrm{^{\prime}}}_{1}\cdots {/}_{n}}\), is chosen as Eq. (16):

  • \({\overset{\leftharpoonup}{y} }^{{j}_{1}\dots /n}=G\left({e}_{1}^{{j}_{1}},\dots ,{e}_{n}^{{j}_{n}}\right)\)

    $${\vartheta }_{l}=\tau \left({\mu }_{{A}_{1}^{1-j-in,i}}\left({x}_{1}\right),{\mu }_{{A}_{2}^{1-jn,i}}\left({x}_{2}\right),\dots ,{\mu }_{{A}_{n}^{j1-jn,i}}\left({x}_{n}\right)\right)$$
    (16)

Therefore, from \({\mu }_{\overline{{B }^{4}}}\left(y\right)=t\left({\vartheta }_{i},{\mu }_{{B}^{i}}\left(y\right)\right),\forall y\in R\), fuzzy inference produces fuzzy set of output by: \({\mu }_{\stackrel{-}{B/1-jn,A}}\left(y\right)=t\left({\vartheta }_{i},{\mu }_{{B}^{j1-jn,i}}\left(y\right)\right)\forall y\in R\).\(t\left({\vartheta }_{i},{\mu }_{{B}^{j1-jn,i}}\left(y\right)\right)\forall y\in R\). \({\mu }_{\overset{\leftharpoonup}{B}/1-/n}(y)=s\left({\mu }_{B/1-1n,1}(y),{\mu }_{B/1-jn,2}\left(y\right),\dots ,{\mu }_{B/1-jn,}(y)\right)\). , where \({a}_{j}^{i}\) are parameters, and are evaluated by LSM.

$$\left({\mu }_{{Q}_{IM}}\left(x,y\right)=\mathrm{min}\left[{\mu }_{{A}_{1}}\left(x\right),{\mu }_{{A}_{2}}\left(y\right)\right],{Q}_{IM}\in X\times Y\right){\mu }_{{B}^{\mathrm{^{\prime}}}}\left(y\right)={\mathrm{max}}_{\forall i} \left[{\mathrm{sup}}_{x\in X} \mathrm{min}\left({\mu }_{{A}^{\mathrm{^{\prime}}}}\left(x\right) ,{\mu }_{{A}_{1}^{\mathrm{^{\prime}}}}\left({x}_{1}\right),\dots ,{\mu }_{{A}_{n}^{t}}\left({x}_{n}\right),{\mu }_{{B}^{i}}\left(y\right)\right)\right]{\mu }_{{A}^{\mathrm{^{\prime}}}}\left(x\right) =\left\{\begin{array}{ll}1& \mathrm{ if }x={x}^{*}\\ 0& \mathrm{ otherwice }\end{array}\right.{y}^{*}=\frac{{\sum }_{i=1}^{l} {\overset{\leftharpoonup}{y} }^{i}{w}_{l}}{{\sum }_{i=1}^{I} {w}_{l}}$$
(17)

Since the fuzzy sets \({A}_{j}^{1},\dots ,{A}_{j}^{{N}_{j}}\) are complete at every \(x\in X\), then there exist \({j}_{1},{j}_{2},\dots ,{j}_{n}\) such that: \(\mathrm{min}\left({\mu }_{{{A}_{1}}^{^{\prime}}}\left({x}_{1}\right),{\mu }_{{A}_{2}^{\mathrm{^{\prime}}2}}\left({x}_{2}\right),\dots ,{\mu }_{{{A}_{n}}^{n}}\left({x}_{n}\right)\right)\ne 0.\) Let \(f\left(x\right)\) be fuzzy system in (13) and \(G\left(x\right)\) be unknown function in (18). If \(G\left(x\right)\) is continuously differentiable on \(X=\left[{\alpha }_{1},{\beta }_{1}\right]\times \left[{\alpha }_{2},{\beta }_{2}\right]\times \dots \times \left[{\alpha }_{n},{\beta }_{n}\right]\), then:

$${\left|\left|G-f\right|\right|}_{\infty }\le {\left|\left|\frac{\partial G}{\partial {x}_{1}}\right|\right|}_{\infty }{h}_{1}+{\left|\left|\frac{\partial G}{\partial {x}_{2}}\right|\right|}_{\infty }{h}_{2}+\cdots +{\left|\left|\frac{\partial G}{\partial {x}_{n}}\right|\right|}_{\infty }{h}_{n}.$$
(18)

where infinite norm \({\left|\left|.\right|\right|}_{\infty }\) is given as: \({\left|\left|d\left(x\right)\right|\right|}_{\infty }={\mathrm{sup}}_{x\in X} \left|d\left(x\right)\right|\) and \({h}_{j}={\mathrm{max}}_{1\le k\le {N}_{j}} \left|{e}_{j}^{k+1}-{e}_{j}^{k}\right|,(j=\mathrm{1,2},\dots ,n\). \(\underset{\_}{\mathrm{Let }{X}^{j1}\dots {/}_{n}}=\left[{e}_{1}^{{j}_{1}},{e}_{1}^{{j}_{1}+1}\right]\times \left[{e}_{2}^{{j}_{2}},{e}_{2}^{{j}_{2}+1}\right]\times \dots \times \left[{e}_{n}^{{j}_{n}},{e}_{n}^{{j}_{n}+1}\right]\), where \({j}_{1}=\mathrm{1,2},\dots ,{N}_{1}-1,{j}_{2}=\mathrm{1,2},\dots ,{N}_{2}-1,\dots\), \({j}_{n}=\mathrm{1,2},\dots ,{N}_{n}-1.\) Since \(\left[{\alpha }_{j},{\beta }_{j}\right]=\left[{e}_{j}^{1},{e}_{j}^{2}\right]\cup \left[{e}_{j}^{2},{e}_{j}^{3}\right]\cup \dots \cup \left[{e}_{j}^{{N}_{j}-1},{e}_{j}^{{N}_{j}}\right],j=\mathrm{1,2},\dots ,n.\) From Eq. (19):

$$f\left(x\right)=\frac{\sum_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum_{{k}_{n}={j}_{n}}^{{j}_{n}+1} {\overline{y} }^{{k}_{1}.{k}_{n}}\left(\mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),{\mu }_{{A}_{2}^{{k}_{2}}}\left({x}_{2}\right),\dots ,{\mu }_{{A}_{n}^{{k}_{n}}}\left({x}_{n}\right)\right)\right)}{\sum_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),{\mu }_{{A}_{2}^{{k}_{2}}}\left({x}_{2}\right),\dots ,{\mu }_{{A}_{n}^{{k}_{n}}}\left({x}_{n}\right)\right)}$$
(19)

From (20), (21), (22), we obtain:

$$f\left(x\right)=\sum\nolimits_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum\nolimits_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \left[\frac{\mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),\dots ,{\mu }_{{A}_{n}^{{k}_{n}}}\left({x}_{n}\right)\right)}{\sum_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \mathrm{m}\left({{\mu }_{{A}_{1}}}^{{k}_{1}}\left({x}_{1}\right),\dots ,{\mu }_{{A}_{n}^{{k}_{n}}}\left({x}_{n}\right)\right)}\right]*G\left({e}_{1}^{{k}_{1}},\dots ,{e}_{n}^{{k}_{n}}\right)$$
(20)
$$\sum\nolimits_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum\nolimits_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \left[\frac{\mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),\dots ,{\mu }_{{A}_{n}^{{k}_{n}}}\left({x}_{n}\right)\right)}{\sum_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),\dots ,{\mu }_{{A}_{n}^{{k}_{n}}}\left({x}_{n}\right)\right)}\right]=1$$
(21)
$$\begin{array}{cc}\left|G(x)-fx\right|& \le \sum_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \left[\frac{\mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),\dots ,{{\mu }_{{A}_{n}}}^{{k}_{n}}\left({x}_{n}\right)\right)}{\sum_{{k}_{1}={j}_{1}}^{{j}_{1}+1} \dots \sum_{{k}_{n}={j}_{n}}^{{j}_{n}+1} \mathrm{m}\left({\mu }_{{A}_{1}^{{k}_{1}}}\left({x}_{1}\right),\dots ,{\mu }_{{{A}_{n}}^{{k}_{n}}}\left({x}_{n}\right)\right)}\right]\\ & \underset{{k}_{1}={j}_{1}+1}{\mathrm{max}} \left|G\left(x\right)-G\left({e}_{1}^{{k}_{1}},\dots ,{e}_{n}^{{k}_{n}}\right)\right|\end{array}*\left|G\left(x\right)-G\left({e}_{1}^{{k}_{1}},\dots ,{e}_{n}^{{k}_{n}}\right)\right|$$
(22)

From the Mean Value \({}^{{k}_{n}={f}_{n}:{/}_{n}+1}\)

From the Mean Value model is given (23) as:

$$\left|G\left(x\right)-f\left(x\right)\right|\le \underset{{k}_{1}={1}_{1}{j}_{1}+1}{\mathrm{max}} \left({\left|\left|\frac{\partial G}{\partial {x}_{1}}\right|\right|}_{\infty }\left|{x}_{1}-{e}_{1}^{{k}_{1}}\right|+{\left|\left|\frac{\partial G}{\partial {x}_{2}}\right|\right|}_{\infty }\left|{x}_{2}-{e}_{2}^{{k}_{2}}\right|+\cdots +{\left|\left|\frac{\partial G}{\partial {x}_{n}}\right|\right|}_{\infty }\left|{x}_{n}-{e}_{n}^{{k}_{n}}\right|\right)$$
(23)

Since \(x\in {X}^{{j}_{1}-{j}_{n}}\), means that \({x}_{1}\in \left[{e}_{1}^{j1},{e}_{1}^{j1+1}\right],{x}_{2}\in \left[{e}_{2}^{j2},{e}_{2}^{j2+1}\right]\dots {x}_{n}\in \left[{e}_{n}^{jn},{e}_{n}^{jn+1}\right]\), have by Eq. (24),

$$\left|{x}_{1}-{e}_{1}^{{k}_{1}}\right|\le \left|{e}_{1}^{{j}_{1}+1}-{e}_{1}^{{j}_{1}}\right|,\left|{x}_{2}-{e}_{2}^{{k}_{2}}\right|\le \left|{e}_{2}^{{j}_{2}+1}-{e}_{2}^{{j}_{2}}\right|\dots ,\mathrm{ and }\left|{x}_{n}-{e}_{n}^{{k}_{n}}\right|\le \left|{e}_{n}^{{j}_{n}+1}-{e}_{n}^{{j}_{n}}\right|\mathrm{ for }{k}_{1}={j}_{1},{j}_{1}+1,{k}_{2}={j}_{2},{j}_{2}+1,\dots \mathrm{, and }{k}_{n}={j}_{n},{j}_{n}+1$$
(24)

Then, (25) becomes:

$$\begin{array}{lc}&\left|G\left(x\right)-f\left(x\right)\right|\leq{\left|\left|\frac{\partial G}{\partial x_1}\right|\right|}_\infty\left|e_1^{j_1+1}-e_1^{j_1}\right|+{\left|\left|\frac{\partial G}{\partial x_2}\right|\right|}_\infty\left|e_2^{j_2+1}-e_2^{j_2}\right|+\cdots+{\left|\left|\frac{\partial G}{\partial x_n}\right|\right|}_\infty\left|e_n^{j_n+1}-e_n^{j_n}\right|\\&\mathrm{Since}{\left|\left|d\left(x\right)\right|\right|}_\infty=\sup_{x\in X}\left|d\left(x\right)\right|\mathrm{then}{\left|\left|G-f\right|\right|}_\infty=\sup_{x\in X}\left|G-f\right|,\mathrm{we get:}\\&{\left|\left|G-f\right|\right|}_\infty\leq{\left|\left|\frac{\partial G}{\partial x_1}\right|\right|}_\infty\sum\max_{1\leq1\leq N_1-1}\left|e_1^{j_1+1}-e_1^{j_1}\right|+\cdots+{\left|\left|\frac{\partial G}{\partial x_n}\right|\right|}_\infty1\leq\max_{n\leq{\mathcal I}_n-1}\left|e_n^{j_n+1}-e_n^{j_n}\right|\\&\therefore{\left|\left|G-f\right|\right|}_\infty\leq{\left|\left|\frac{\partial G}{\partial x_1}\right|\right|}_\infty h_1+{\left|\left|\frac{\partial G}{\partial x_2}\right|\right|}_\infty h_2+\cdots+{\left|\left|\frac{\partial G}{\partial x_n}\right|\right|}_\infty h_n\end{array}$$
(25)

From (26), conclude that fuzzy systems in form.

\({\left|\left|\frac{\partial G}{\partial {x}_{1}}\right|\right|}_{\infty },{\left|\left|\frac{\partial G}{\partial {x}_{2}}\right|\right|}_{\infty },\dots ,{\left|\left|\frac{\partial G}{\partial {x}_{n}}\right|\right|}_{\infty }\) are finite numbers for any given \(\varepsilon >0\), select \({h}_{1},{h}_{2},\dots ,{h}_{n}\) small enough such that \({\left|\left|\frac{\partial G}{\partial {x}_{1}}\right|\right|}_{\infty }{h}_{1}+{\left|\left|\frac{\partial G}{\partial {x}_{2}}\right|\right|}_{\infty }{h}_{2}+\cdots +{\left|\left|\frac{\partial G}{\partial {x}_{n}}\right|\right|}_{\infty }{h}_{n}<\varepsilon\). Hence from (27):

$${\mathrm{sup}}_{x\in X} \left|G-f\right|={\left|\left|G-f\right|\right|}_{\infty }<\varepsilon$$
(27)

We can see from (28) that we need to know the boundaries of the derivatives of G(x) about \({x}_{1},{x}_{2},\dots ,{x}_{n}\) to represent a fuzzy system with a pre-specified accuracy.

$${\left|\left|\frac{\partial G}{\partial {x}_{1}}\right|\right|}_{\infty },{\left|\left|\frac{\partial G}{\partial {x}_{2}}\right|\right|}_{\infty },\dots ,{\left|\left|\frac{\partial G}{\partial {x}_{n}}\right|\right|}_{\infty }$$
(28)

Select a fuzzy method with a MIS, an SF, a CADand a Triangular MF, which then derive using Eq. (29).

$$f\left(x\right)=\frac{{\sum }_{i=1}^{l} {\overset{\leftharpoonup}{y} }^{i}\left({\mathrm{min}}_{\forall j} {\mu }_{{A}_{j}}\left({x}_{j}\right)\right)}{{\sum }_{i=1}^{l} \left({\mathrm{min}}_{\forall j} {\mu }_{{A}_{j}^{\mathrm{^{\prime}}}}\left({x}_{j}\right)\right)}=\frac{{\sum }_{i=1}^{l} {\overset{\leftharpoonup}{y} }^{i}\left[{\mathrm{min}}_{\forall j} \left(\mathrm{max}\left({\mathrm{min}}_{vj} \left(\frac{{x}_{j}-{a}_{j}^{i}}{{b}_{j}^{l}-{a}_{j}^{\mathrm{^{\prime}}}},\frac{{c}_{j}^{i}-{x}_{j}}{{c}_{j}^{l}-{b}_{j}^{l}}\right),0\right)\right)\right]}{{\sum }_{i=1}^{l} \left[{\mathrm{min}}_{vj} \left(\mathrm{max}\left({\mathrm{min}}_{\forall j} \left(\frac{{x}_{j}-{a}_{j}^{l}}{{b}_{j}^{l}-{a}_{j}^{i}},\frac{{c}_{j}^{i}-{x}_{j}}{{c}_{j}^{l}-{b}_{j}^{l}}\right),0\right)\right)\right]}$$
(29)

The more rules you have, the more parameters you will have and the more computation you will have to do, but you will get better accuracy. When initial parameters yi (0), aji (0), bji (0), cji (0) are specified, the fuzzy system becomes by Eq. (30).

$$f\left(x\right)=\frac{\sum_{{j}_{1}=1}^{{N}_{1}} \dots \sum_{{j}_{n}}^{{N}_{n}} {\overset{\leftharpoonup}{y} }^{{j}_{1}-{j}_{n}}\left(0\right)\left[\mathrm{m}\left(\mathrm{m}\left(\underset{\forall k}{\mathrm{min}} \left(\frac{{x}_{k0}^{p}-{a}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)}{{b}_{k}^{{j}_{1}{j}_{2}{j}_{3}}\left(0\right)-{a}_{k}^{{j}_{1}{j}_{2}{j}_{3}}{\left(0\right)}^{\mathrm{^{\prime}}}}\frac{{c}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)-{x}_{k0}^{p}}{{c}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)-{b}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)}\right),0\right)\right)\right]}{\sum_{{j}_{1}=1}^{{N}_{1}} \dots \sum_{{j}_{n}}^{{N}_{n}} \left[\mathrm{m}\left(\mathrm{m}\left(\underset{\forall k}{\mathrm{min}} \left(\frac{{x}_{k0}^{p}-{a}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)}{{b}_{k}^{{j}_{1},{j}_{n}}\left(0\right)-{a}_{k}^{{j}_{1}-{j}_{n}}{\left(0\right)}^{\mathrm{^{\prime}}}}\frac{{c}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)-{x}_{k0}^{p}}{{c}_{k}^{{j}_{1}-{j}_{n}}\left(0\right)-{b}_{k}^{{j}_{1},{j}_{n}}\left(0\right)}\right),0\right)\right)\right]}$$
(30)

for a sigmoid activation function, it gives by Eq. (31):

$$\begin{array}{c}{h}_{l}^{\left[\gamma \right]\left(t\right)}=\frac{1}{1+\mathrm{exp}-\left({\sum }_{u=1}^{{d}^{\mathrm{^{\prime}}}} {w}_{l,u}^{\mathrm{^{\prime}}}{x}_{\varphi (u)}^{\left(t\right)}+{b}_{l}^{\left[\gamma \right]}\left(t\right)\right)}{w}_{l,u}^{\mathrm{^{\prime}}}={\sum }_{f=1}^{{N}_{f}} {\sum }_{p=1}^{P} {\sum }_{q=1}^{Q} {K}_{p,q}^{f}{w}_{l,u}^{[\gamma ]}\\{Y}_{u}^{\left(t\right)}\equiv {Y}_{i,j}^{\left(t\right)}={\sum }_{f=1}^{{N}_{f}} {\sum }_{p=1}^{P} {\sum }_{q=1}^{Q} {K}_{p,q}^{f}{x}_{\varphi (u)}^{\left(t\right)}{h}_{l}^{\left[\gamma \right]\left(t\right)}=\sigma \left({\sum }_{u=1}^{{d}^{\mathrm{^{\prime}}}} {w}_{l,u}^{\left[\gamma \right]}{Y}_{u}^{\left(t\right)}+{b}_{l}^{\left[\gamma \right]\left(t\right)}\right),l\\\in \left\{1,\dots ,s\right\}{y}_{k}^{T}={\Psi }_{k}^{T}\left({h}^{\left[\gamma \right]\left(1\right)},\dots ,{h}^{\left[\gamma \right]\left(T\right)}\right),\;k\in \{1,\dots ,r\}\\{h}_{l}^{\left[\rho \right]}=\sigma \left(\sum\nolimits_{k=1}^{r} {w}_{l,k}^{\left[\rho \right]}{y}_{k}^{T}+{b}_{l}^{\left[\rho \right]}\right),l\in \left\{1,\dots ,{r}^{\mathrm{^{\prime}}}\right\}\end{array}$$
(31)

Thus, if consider \(\overset{\leftharpoonup}{X }={\left(0,\dots ,0\right)}^{^{\prime}},{b}_{l}^{\left[\gamma \right]\left(t\right)}=0\forall t\in \left\{1,\dots ,T\right\}\), the Taylor series expansion of \({h}_{l}^{\left[\gamma \right]\left(t\right)}\) is given by Eq. (32):

$${h}_{l}^{\left[\gamma \right]\left(t\right)}\approx {h}_{l}^{\left[\gamma \right]\left(t\right)}\left(\overset{\leftharpoonup}{X }\right)+\nabla {h}_{l}^{\left[\gamma \right]\left(t\right)}{X}^{\left(t\right)}=\frac{1}{2}+\sum_{u=1}^{{d}^{\mathrm{^{\prime}}}} \frac{\partial {h}_{l}^{\left[\gamma \right]\left(t\right)}\left(\overset{\leftharpoonup}{X }\right)}{\partial {x}_{\varphi \left(u\right)}^{\left(t\right)}}{x}_{\varphi \left(u\right)}^{\left(t\right)}=\frac{1}{2}+\sum_{u=1}^{{d}^{\mathrm{^{\prime}}}} {w}_{l,u}^{\mathrm{^{\prime}}}{x}_{\varphi \left(u\right)}^{\left(t\right)}$$
(32)

with w′ l u, given by Eq. (33), and \({X}^{\left(t\right)}={\left({x}_{\varphi \left(1\right)}^{\left(t\right)},\dots ,{x}_{\varphi \left(d,\right)}^{\left(t\right)}\right)}^{\mathrm{^{\prime}}}\) being a column vector of the input at time t. Let \(H={\left({h}^{\left[\gamma \right](1)},\dots ,{h}^{\left[\gamma \right]\left(T\right)}\right)}^{\mathrm{^{\prime}}},\mathrm{ for }X=\overset{\leftharpoonup}{X }\) then:

$$\overset{\leftharpoonup}{H }=H\left(\overset{\leftharpoonup}{X }\right)={\left\{{\left\{\frac{1}{2}\right\}}^{s},\dots ,{\left\{\frac{1}{2}\right\}}^{s}\right\}}^{T}$$
(33)

where s is number of hidden neurons. Taylor series expansion of Ψk T isgiven by Eq. (34):

$${y}_{k}^{T}={\Psi }_{k}^{T}\left(H\right)\approx {\Psi }_{k}^{T}\left(\overset{\leftharpoonup}{H }\right)\left(H-\overset{\leftharpoonup}{H }\right)={\Psi }_{k}^{T}\left(\overset{\leftharpoonup}{H }\right)+{\sum }_{t=1}^{T} {\sum }_{u=1}^{s} \frac{\partial {\Psi }_{K}^{T}\left(\overset{\leftharpoonup}{H }\right)}{\partial {h}_{u}^{\left[\gamma \left(k\right)\right.}}\left({h}_{u}^{\left[\gamma \right]\left(t\right)}-\frac{1}{2}\right)$$
(34)

By replacing \({h}_{u}^{\left[\gamma \right]\left(t\right)}\) of Eq. (35) with \({h}_{l}^{\left[\gamma \right]\left(t\right)}\) of Eq. (36):

$${\Psi }_{k}^{T}\left(H\right)\approx {\Psi }_{k}^{T}\left(\overset{\leftharpoonup}{H }\right)+\frac{1}{4}{\sum }_{t=1}^{T} {\sum }_{u=1}^{s} {\sum }_{\nu =1}^{{d}^{\mathrm{^{\prime}}}} \frac{\partial {\Psi }_{k}^{T}\left(\overset{\leftharpoonup}{H }\right)}{\partial {h}_{u}^{{\left[\gamma \right]}^{(t)}}}{w}_{l,\nu }^{\mathrm{^{\prime}}}{x}_{\varphi \left(v\right)}^{\left(t\right)}$$
(35)

Finally, by substituting

$$\begin{array}{c}h_l^{\left[\rho\right]}=\sigma\left(\sum\nolimits_{k=1}^rw_{l,k}^{\left[e\right]}\left[\Psi_k^T\left(\overset\leftharpoonup H\right)+\frac14\sum\nolimits_{t=1}^T\sum\nolimits_{u=1}^s\sum\nolimits_{\nu=1}^{d^{'}}\frac{\partial\Psi_k^T\left(\overset\leftharpoonup H\right)}{\partial h_u^{\left[\gamma\right]}\left(t\right)}w_{l,\nu}^{'}x_{\varphi\left(v\right)}^{\left(t\right)}\right]+b_l^{\left[\rho\right]}\right)\\h_l^{\left[\varrho\right]}=\sigma\left(\sum\nolimits_{k=1}^rw_{l,k}^{\left[\rho\right]}\Psi_k^T\left(\overset\leftharpoonup H\right)\right.+\frac14\sum\nolimits_{k=1}^r(\sum\nolimits_{\nu=1}^{d^{'}}\underbrace{\sum\nolimits_{u=1}^s\frac{\partial\Psi_K^T\left(H\right)}{\partial h_u^{\left(Y\right)\left(1\right)}}w_{l,\nu}^{'}w_{l,k}^{\lbrack\rho\rbrack}x_{\varphi\left(\nu\right)}^{\left(1\right)}}_{w_{l,\nu}^{\left(1\right)}}+,\dots\cdot\cdot\\+\sum\nolimits_{\nu=1}^{d^{'}}\underbrace{\sum\nolimits_{u=1}^s\frac{\partial\Psi\Psi_{\left(\right.}\left(\overset\leftharpoonup H\right)}{\partial h_u^{\left[\left|\left(T\right)\right.\right.}}w_{l,\nu}^{'}w_{l,k}^{\left[\rho\right]}x_{\varphi\left(v\right)}^{\left(T\right)}}_{w_{l,\nu}^{\left(T\right)}}+b_l^{\left[\rho\right]}\end{array}$$
(36)
$${{w}_{l,\nu }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}}^{\left(t\right)}={\sum }_{u=1}^{s} {\sum }_{f=1}^{{N}_{f}} {\sum }_{p=1}^{P} {\sum }_{q=1}^{Q} \frac{\partial {\Psi }_{k}^{T}\left(\overset{\leftharpoonup}{X }\right)}{\partial {h}_{u}^{\left[\gamma \right]\left(t\right)}}{K}_{p,q}^{f}{w}_{l,\nu }^{\left[\gamma \right]}{w}_{l,k}^{\left[\varrho \right]}$$
(37)

derived features \({{w}_{l,\nu }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}}^{\left(t\right)}\) through summations on indexes f, p, and q combine features \(\left(\left({w}_{l,\nu }^{\left[\gamma \right]}\right.\right.\) and \(\left.{w}_{l,k}^{\left[\rho \right]}\right)\) extracted from both Fuzzy based SAEs and gives compact representation of input over time.

3.2 Least square error back propagation neural network (LSEBPNN)

Let, training set in a C-class issue contains vector pairs \(\left\{\left(\stackrel{\backprime}{{x}_{1}},{y}_{1}\right),\left({{\varvec{x}}}_{2},{{\varvec{y}}}_{2}\right),\dots ,\left({{\varvec{x}}}_{P},{{\varvec{y}}}_{P}\right)\right\}\) where \({{\varvec{x}}}_{p}\in {\mathbb{R}}^{N}\) refers to pth input pattern and \({{\varvec{y}}}_{p}\in \left\{\left.{{\varvec{t}}}_{c}\right|,\stackrel{\backprime}{c}=\mathrm{1,2},\dots ,C;{{\varvec{t}}}_{c}\in {\mathbb{R}}^{c}\right\}\) refers to target output of c network corresponding to this input.

All weights and bias terms are included in LSEBPNN’s adaptive parameters. The training phase’s main aim is to establish the best weights and bias terms for minimizing difference between network output as well as target output. The difference is referred regarded as the network’s training error. MSE for pth input pattern in the traditional BP technique is \({E}_{p}=\frac{1}{2}{\sum }_{k=1}^{C} {\left({t}_{pk}-{o}_{pk}^{\circ }\right)}^{2}\). It shows that an input pattern’s target value could be several. To put it another way, any input pattern can have any target value with any membership value. To put it another way, the training problem can be thought of as a fuzzy constraint fulfillment problem.Suggested network modifies parameters throughout training phase to ensure that these limitations are overcome as efficiently as possible. The constraints for pth input pattern are stated mathematically as fuzzy MSE term, which is given by Eq. (38)

$${.}^{\mathrm{f}}=\frac{1}{2}{\sum }_{k=1}^{C} {\sum }_{c=1}^{C} {\mu }_{c}^{q}\left({{\varvec{x}}}_{p}\right){\left({t}_{ck}-{o}_{pk}^{\mathrm{o}}\right)}^{2}$$
(38)

The learning laws for networks are derived using same approach as traditional BP technique. Suppose that the weight update, Dw, happens after each input pattern has been presented. Assuming that all weight changes in network are made with same learning-rate parameter h, weight changes applied to weights w and w are k j ji determined according to the gradient-descent rules by Eq. (39), (40):

$$\Delta {w}_{kj}^{\mathrm{o}}=-\eta \frac{\partial {E}_{p}^{\mathrm{f}}}{\partial {w}_{kj}^{\mathrm{o}}}\;\mathrm{and}\;\Delta {w}_{ji}^{\mathrm{h}}=-\eta \frac{\partial {E}_{p}^{\mathrm{f}}}{\partial {w}_{ji}^{\mathrm{h}}}$$
(39)
$$\begin{array}{cc}\Delta {w}_{kj}^{\mathrm{o}}=& \eta \left[{\mu }_{k}^{q}\left({{\varvec{x}}}_{p}\right)-\sum_{c=1}^{C} {\mu }_{c}^{q}\left({{\varvec{x}}}_{p}\right){o}_{pk}^{\mathrm{o}}\right]\\ & \times {o}_{pk}^{\mathrm{o}}\left(1-{o}_{pk}^{\mathrm{o}}\right){o}_{pj}^{\mathrm{h}}\\ =& \eta {\delta }_{pk}^{\mathrm{o}}{o}_{pj}^{\mathrm{h}}\end{array}$$
(40)

where by Eq. (41)

$${\delta }_{pk}^{o}=\left[{\mu }_{k}^{q}\left({{\varvec{x}}}_{p}\right)-\sum\nolimits_{c=1}^{C} {\mu }_{c}^{q}\left({{\varvec{x}}}_{p}\right){o}_{pk}^{\mathrm{o}}\right]{o}_{pk}^{\mathrm{o}}\left(1-{o}_{pk}^{\mathrm{o}}\right)$$
(41)

Again, from Eq. (42),

$$\Delta w_{ji}^{\mathrm h}=\eta f_j^{\mathrm h}\left(\mathrm{net}_{pj}^{\mathrm h}\right)x_{pi}\sum\nolimits_{k=1}^C\left[\mu_k^q\left(({{\varvec{x}}}_p\right)-\sum\nolimits_{c=1}^C\mu_c^q\left(({{\varvec{x}}}_p\right)o_{pk}^{\mathrm o}\right]o_{pk}^{\mathrm o}\left(1-o_{pk}^{\mathrm o}\right)w_{kj}^{\mathrm o}=\eta f_j^{\mathrm h}\left(\mathrm{net}_{pj}^{\mathrm h}\right)x_{pi}\sum\nolimits_{k=1}^C\delta_{pk}^{\mathrm o}w_{kj}^{\mathrm o}=\eta\delta_{pj}^{\mathrm h}x_{pi},$$
(42)

where by Eq. (43)

$${\delta }_{pj}^{\mathrm{h}}={f}_{j}^{\mathrm{h}}\left({\mathrm{net}}_{pj}^{\mathrm{h}}\right)\sum\nolimits_{k=1}^{C} {\delta }_{pk}^{\mathrm{o}}{w}_{kj}^{\mathrm{o}}.$$
(43)

In many circumstances, the traditional BP technique may not converge quickly, when classes overlap. Because ambiguous vectors are assigned full weightage in one class, this is case. In suggested version, error to be back propagated is given more weight in the case of nodes with higher membership values.

The learning algorithm’s purpose is to reduce the squared error cost function, which is given by Eq. (44)

$${j}_{i}^{\left(s\right)}=\frac{1}{2}\sum\nolimits_{q=1}^{m} {\left({d}_{i,q}^{\left(s\right)}-{v}_{i}(s)\right)}^{2}$$
(44)

Equation (45), where m is total number of vectors in training data set given by

$${j}_{i}^{\left(s\right)}=\frac{1}{2}{\sum }_{q=1}^{m} {\left({d}_{i,q}^{\left(s\right)}-{w}_{i}\left(s\right)t.{x}_{out.q}^{(s-1)}\right)}^{2}$$
(45)

Partial derivative about w i (s) and equate it to zero to determine weight vector that minimizes cost function given by Eq. (46).

$$\frac{\partial {j}_{i}^{\left(s\right)}}{\partial {w}_{i}\left(s\right)}={\sum }_{q=1}^{m} \left(-{d}_{i,q}^{\left(s\right)}{x}_{\mathrm{out. }{q}^{\left(s-1\right)}}+{x}_{\mathrm{out. }{q}^{\left(s-1\right)}}{x}_{\mathrm{out. }{q}^{\left(s-1\right)}}{t}_{i}\left(s\right)\right)=0$$
(46)
$${c}_{i}^{\left(s\right)}={\sum }_{q=1}^{m} {x}_{\mathrm{out. }{q}^{(s-1)}}{x}_{\mathrm{out. }{q}^{(s-1)}}\mathrm{t}{p}_{i}^{(s)}={d}_{i,q}^{(s)}{x}_{{\mathrm{out.q }}^{(s-1)}}$$
(47)

In vector matrix form, Eq. (48) are rearranged as

$${c}_{i}^{\left(s\right)}{w}_{i}^{\left(s\right)}={p}_{i}^{\left(s\right)}$$
(48)

\({w}_{i}^{\left(s\right)}\) is weight vector to ith linear combiner in sth layer, Eq. (49) is given as deterministic normal equation

$${w}_{{i}^{\left(s\right)}}={\left[{c}^{\left(s\right)}\right]}^{-1}{p}_{i}^{\left(s\right)}$$
(49)

By equating partial derivative of performance index \({\mathbf{w}}_{i}^{\left(k\right)}(n)\) and setting it equal to zero, the performance index is minimised (50)

$$\frac{\partial J\left(n\right)}{\partial\mathbf w_i^{\left(k\right)}\left(n\right)}=\&2\sum\nolimits_{t=1}^n\lambda^{n-t}\times\sum\nolimits_{j=1}^{N_L}\left[\varepsilon_{j,R}^{\left(L\right)}\left(t\right)\frac{\partial\varepsilon_{j,R}^{\left(L\right)}\left(t\right)}{\partial\mathbf w_i^{(k)}\left(n\right)}+\varepsilon_{j,I}^{\left(L\right)}\left(t\right)\frac{\partial\varepsilon_{j,I}^{\left(L\right)}\left(t\right)}{\partial\mathbf w_i^{(k)}\left(n\right)}\right]=\&-2\sum\nolimits_{t=1}^n\lambda^{n-t}\times\sum\nolimits_{j=1}^{N_L}\left[\zeta_{j,R}^{\left(L\right)}\left(t\right)\varepsilon_{j,R}^{\left(L\right)}\left(t\right)\frac{\partial y_{j,R}^{\left(L\right)}\left(t\right)}{\partial\mathbf w_i^{\left(k\right)}\left(n\right)}+\zeta_{j,I}^{\left(L\right)}\left(t\right)\varepsilon_{j,I}^{\left(L\right)}(t)\frac{\partial y_{j,I}^{\left(L\right)}\left(t\right)}{\partial\mathbf w_i^{\left(k\right)}\left(n\right)}\right]=0$$
(50)

Equation (51), (52) is set to the following

$$\sum_{t=1}^{n} {\lambda }^{n-t}\left[\left\{{\psi }_{i,R}^{\left(k\right)}\left(t\right)-{y}_{i,R}^{\left(k\right)}\left(t\right)\right\}{\zeta }_{i,R}^{\left(k\right)}\left(t\right){f}^{\mathrm{^{\prime}}}\left({s}_{i,R}^{\left(k\right)}\left(t\right)\right)+\&\left.\left\{{\psi }_{i,I}^{\left(k\right)}\left(t\right)-{y}_{i,I}^{\left(k\right)}\left(t\right)\right\}{\zeta }_{i,I}^{\left(k\right)}\left(t\right){f}^{\mathrm{^{\prime}}}\left({s}_{i,I}^{\left(k\right)}\left(t\right)\right)\right]\times {\mathrm{x}}^{\left(k\right)*}(t)=0.\right.$$
(51)
$${\mathbf{r}}_{i}^{\left(k\right)}(n)={\mathbf{R}}_{i}^{\left(k\right)}(n){\mathbf{w}}_{i}^{\left(k\right)}(n)$$
(52)

where by Eq. (53)

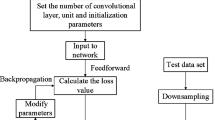
$$\begin{array}{ll}{\mathbf{r}}_{i}^{\left(k\right)}\left(n\right)=& \sum_{t=1}^{n} {\lambda }^{n-t}\\ & \times \left[{\zeta }_{i,R}^{\left(k\right)}\left(t\right){\psi }_{i,R}^{\left(k\right)}\left(t\right){f}^{\mathrm{^{\prime}}}\left({s}_{i,R}^{\left(k\right)}(n)\right)\right.\\ & \left.+\jmath {\zeta }_{i,I}^{\left(k\right)}\left(t\right){\psi }_{i,I}^{\left(k\right)}\left(t\right){f}^{\mathrm{^{\prime}}}\left({s}_{i,I}^{(k)}(n)\right)\right]\\ & \times {\mathbf{x}}^{\left(k\right)*}\left(t\right)\\ {\mathbf{R}}_{i}^{\left(k\right)}\left(n\right)=& \sum_{t=1}^{n} {\lambda }^{n-t}{\mathbf{x}}^{\left(k\right)*}\left(t\right)\\ & \times \left[{\zeta }_{i,R}^{\left(k\right)}(t){y}_{i,R}^{\left(k\right)}\left(t\right){f}^{\mathrm{^{\prime}}}\left({s}_{i,R}^{\left(k\right)}\left(t\right)\right)\right.\\ & \left.+\jmath {\zeta }_{i,I}^{\left(k\right)}(t){y}_{i,I}^{\left(k\right)}(t){f}^{\mathrm{^{\prime}}}\left({s}_{i,I}^{\left(k\right)}\left(t\right)\right)\right]\\ & \times {s}_{i}^{{\left(k\right)}^{-1}}(t){\mathbf{x}}^{{\left(k\right)}^{T}}\left(t\right).\end{array}$$
(53)

Now, define a matrix operation for simplicity \(A\odot B\doteq {A}_{R}{B}_{R}+\jmath {A}_{I}{B}_{I}\). The flow chart for LSEBPNN is represented in Fig. 2.

Fig. 2
figure 2

The flow chart for LSEBPNN

Full size image

4 Performance analysis

Proposed method is implemented into a prototype software system utilizing Python 3.7 to evaluate and assess potential contribution of proposed strategy for future real-world applications. Resources utilized to combine proposed method were an Intel i7 processor (Intel(R) Core(TM) i7-3770 CPU @3.40 GHz 3.80 Ghz) and an eight (8) gigabyte RAM (Intel, Santa Clara, CA, USA) (Samsung, Seoul, Korea). Microsoft Windows 10 was the operating system on which the suggested system was hosted and tested.

Table 1 shows comparative analysis for various fault situations for proposed and existing techniques. Here the fault situation has been detected by virtual sensor-based datasets of automation industry. The parametric analysis has been carried out in terms of QoS, measurement accuracy, RMSE, MAE, prediction performance, and computational time.\

Table 1 comparative analysis for various fault situation for proposed and existing technique
Full size table

Figures 3, 4, and 5 show comparative analysis for various virtual sensor-based datasets from automation industry. The dataset collected from cloud is based on spindle fault detection-based data, gear fault detection-based data, and bearing fault detection-based data. For spindle fault detection data, the proposed technique obtained computational time of 34%, QoS of 64%, RMSE of 41%, MAE of 35%, prediction performance of 94%, measurement accuracy of 85%.The proposed technique obtained computational time of 43%, QoS of 67%, RMSE of 43%, MAE of 39%, prediction performance of 79%, and measurement accuracy of 85% by gear-based fault detection dataset. For bearing fault detection data, the proposed technique obtained computational time of 49%, QoS of 68%, RMSE of 45%, MAE of 41%, prediction performance of 86%, and measurement accuracy of 84%. From the above analysis, proposed technique obtained optimal results for all the fault detection based on automation industry data.

Fig. 3
figure 3

Comparative analysis of spindle-based dataset in terms of a computational time, b QoS, c RMSE, d MAE, e prediction performance, f measurement accuracy

Full size image
Fig. 4
figure 4

Comparative analysis of gear-based dataset in terms of a computational time, b QoS, c RMSE, d MAE, e prediction performance, f measurement accuracy

Full size image
Fig. 5
figure 5

Comparative analysis of bearing-based dataset in terms of a computational time, b QoS, c RMSE, d MAE, e prediction performance, f measurement accuracy

Full size image

The fundamental challenge in dealing with soft sensor principles is a lack of understanding due to their novelty and, as a result, a lack of typical mathematical descriptions or structure. On the other hand, it allows for more creative expression. In general, vast arrays of statistics for calculations are required when working with soft sensors. It is vital to have a thorough understanding of the controlled process’s principles, physical characteristics, and the parameters’ relationships.

5 Conclusion

This research propose novel technique in virtual soft sensor-based fault detection in automation industry using deep learning technique integrated with cloud module. Here the aim is to design novel techniques in automation of manufacturing industry where the dynamic soft sensors are used in feature representation and classification of the data. The data has been collected from cloud storage and created the virtual sensors dataset based on gear fault detection, spindle fault detection, and bearing fault detection in automation industry. Then to represent the feature using fuzzy logic-based stacked data-driven auto- encoder (FL_SDDAE) where the features of input data have been identified with general automation problems. Then the features have been classified using least square error back propagation neural network (LSEBPNN) in which the mean square error while classification will be minimized with loss function of the data. Here the experimental results have been carried out in terms of computational time of 34%, QoS of 64%, RMSE of 41%, MAE of 35%, prediction performance of 94%, and measurement accuracy of 85% has been obtained by proposed technique. One is that nonlinear systems’ predictive control cannot be solved successfully. Another issue is that stability as well as resilience of multivariable predictive control algorithms must be addressed, and accurate principle models for complex systems are extremely difficult to construct. Despite the contributions made so far, there are still areas where future work might be improved. On the loss function, targeted-output regularizes would extract even better features, improving the suggested work. Another future intervention would be to use approaches on the unsupervised pre-training to identify dynamic-related aspects. In addition, industrial research scenarios were used to apply the proposed method, however developing a soft sensor proposal for a real-world industrial scenario could be challenging. Non-linearities, abnormalities, and highly complex ecosystems must all be taken into account. The industrial study cases have shown to be suitable and widely used in the implementation and evaluation of models, and they serve as the foundation for many contributions in this field of research.