1 Introduction

Tolerance allocation is the search for an optimal set of tolerance specifications. Parts are connected in an assembly, which establishes geometric relations between their features. Tolerances on part features should be as wide as possible to reduce manufacturing costs, yet tight enough to control the variation of some assembly-level geometric characteristics, here referred to as functional requirements (e.g., gaps, distances, or angles between features of different parts). For a candidate set of tolerances, the stackup of the allowed geometric deviations must be evaluated and compared with the allowable variation on each functional requirement; this task is called tolerance analysis and is carried out as a subtask of allocation. By solving a constrained optimization problem that has the tolerances as variables, it is possible to find the allocation that minimizes the manufacturing cost or alternative objective functions relating to tolerances (e.g., the reject rate or the expected quality loss).

Allocation problems were initially solved for dimensional tolerances. Only recently has attention been paid to the allocation of geometric tolerances, which are now widespread in design practice and extensively regulated in international standards [1, 2]. The main reason is the increasing availability of methods for geometric tolerance analysis, which are needed to verify the constraints of the optimization problem. In most assemblies, a functional requirement can involve both dimensional and geometric tolerances. The types of tolerances (e.g., orientation, position, profile) and their mutual relationships within the same part (datum system) must be chosen in a preliminary phase of tolerance specification; the allocation then finds the optimal values ​​of the specified tolerances (the two tasks are collectively referred to as geometric tolerance synthesis).

The allocation of geometric tolerances has an additional difficulty compared to the original problem with dimensional tolerances. Verifying the stackup constraint requires that the geometric tolerances are translated into statistical variables with suitable properties. For reasons that will be discussed later, an optimal solution expressed in these variables may not correspond to an optimal solution expressed in the original geometric tolerances. This occurs especially in allocation methods based on analytic optimization, which embed the stackup constraint in the objective function to avoid complex procedures of numerical simulation.

This paper proposes a way of handling the geometric tolerances in the stackup analysis, in order to allow the direct search for the optimal solution of the allocation problem. The main concept is the definition of the sensitivities of the functional requirement to the geometric tolerances (rather than to differently defined stackup variables). The approach is able to deal with one-dimensional stackup problems (or 1D dimension chains), the simplest allocation cases although very frequent in practice.

The paper is organized as follows. Section 2 recalls the allocation methods currently available for geometric tolerances. Section 3 discusses the difficulties of the problem, using a simple example to justify the proposed approach. Section 4 details the allocation procedure based on the sensitivities associated with geometric tolerances. Section 5 illustrates the application of the method to two 1D allocation cases that cover the main assumptions of this work. Section 6 compares the method with an alternative approach based on numerical search and simulation. Section 7 discusses the advantages and limitations of the proposed method.

2 Literature review

The progress in tolerance allocation literature has been documented in several reviews. Some of them discuss allocation within the broader framework of tolerancing, focusing on the major approaches at their time of writing: these include mathematical programming [3], design of experiments and numerical optimization [4], and estimation of cost-tolerance relationships [5]. Available worst-case and statistical allocation methods are described in [6,7,8]. Other reviews focus exclusively on allocation and recall the available methods [9] or discuss special formulations of the problem [10]. All these sources regard the allocation problem as limited to dimensional tolerances. Only a recent review [11], which provides an extensive classification of existing approaches, cites few studies where the allocation is extended to geometric tolerances; the apparent misalignment with standards is explained with the difficulty of representing geometric deviations as statistical variables for the purposes of optimization.

A first issue in the extension of the allocation problem is that manufacturing costs must now be related to all the standard geometric controls. Cost-tolerance functions have been proposed for various types of features and machining processes, considering position tolerances on holes [12] and profile tolerances [13]. To cover a wider range of cases, discrete cost-tolerance data have been published under given assumptions regarding machining and inspection processes [14,15,16].

Some allocation methods allow the use of geometric tolerances, but do not explain how they are treated. In one case, such detail is not addressed in a high-level description of assembly modeling software with tolerancing capabilities [17]. In another, the focus is on core aspects of geometric tolerancing such as datum systems [18], but formal details are expressed through constraint equations that are seemingly bound to the specific assembly example. Also difficult to generalize is the approach of [19,20,21], which optimizes an extended cost function including machining, rework, and assembly; the function is evaluated assuming a given process sequence for each geometric tolerance.

Some authors have studied elementary tasks as building blocks of a typical allocation problem. In [22], position tolerances are calculated without any optimization as a function of basic dimensions and IT tolerance grades (corresponding to alternative machining processes). For hole patterns, the definition of position tolerance with maximum material condition (MMC) is used to develop equations for such tasks as calculating process capabilities [23] or reconstructing datums and basic dimensions from inspection data [24]. In [25], the allocation of angularity tolerances on a dovetail joint is carried out by a solution search method using a graphical procedure for stackup analysis.

Among the full-fledged allocation methods proposed for geometric tolerances, some are limited to 1D tolerance stackups (the same assumption made in this paper). To allow tolerance analysis within the optimization procedure, geometric tolerances are translated into equivalent dimensional tolerances. For example, a position or profile tolerance is translated into a tolerance on one of the basic dimensions associated with the feature, while an orientation tolerance is translated into a tolerance on a zero nominal dimension. This is consistent with the simple tolerance analysis procedures described in handbooks [26, 27] and commonly used in practice. The same approach is used in allocation methods taking into account the uncertainty on cost-tolerance functions [28, 29] as well as in methods based on the optimization of objective functions including cost [30] and quality loss [31] by genetic algorithms.

When dealing with 2D or 3D tolerance stackups, the treatment of geometric tolerances is more complex and must rely on appropriate models or tools for tolerance analysis. One of the most popular choices is the use of commercial computer-aided tolerancing (CAT) software to verify stackup constraints for each candidate set of geometric tolerances. Software simulation is integrated with several optimization strategies; they include design-of-experiments (DOE) approaches such as full factorial plans [32, 33] or response surfaces [34, 35], solution search methods such as genetic algorithms [36, 37], and the improvement of an initial solution through interactive procedures [38, 39]. For an unusual formulation of the allocation problem without cost-based optimization [40], simulation drives the selection of solutions in a constraint space defined by applicable functional requirements.

While in CAT-based allocation the tolerance analysis task is “canned” within the optimization procedure, other allocation methods embed the formal details of available methods for the 3D analysis of geometric tolerances. For this purpose, geometric tolerances are translated into statistical variables associated with individual translational and rotational deviations allowed to toleranced features. Most studies are based on either the small displacement torsor method [41,42,43,44,45,46,47] or some of its variants such as Jacobian-torsor [48, 49] and DP-SDT [50]. Other analysis methods used for allocation include the vector loop [51, 52], variational geometric constraints [53], datum flow chains [54], virtual joints [55], and some methods based on skin model shapes to include form errors in the analysis [56, 57]. In [58], the allocation of geometric tolerances on deformable parts is carried out by integrating a finite-element model in the optimization procedure.

With the objective of covering a wider spectrum of cases and assumptions, a further step is the development of procedures based on advanced concepts and mathematical models for the representation of geometric tolerances. These include the actual mating envelope [59], vectorial tolerancing [60], quantifier and virtual boundary [61], and the T-maps in progressively more detailed definitions [62,63,64,65,66]. On the opposite end, other approaches try to reduce the complexity involved by geometric tolerances by special assumptions or approaches; examples include measurements on prototypes in the study of an electrical device [67] and the definition of variables with multivariate normal distributions in an allocation strategy considering designer’s preferences [68].

Related problems solved with similar methods include tolerance allocation on optical components [69] or CNC machine tools [70,71,72] and the allocation of geometric tolerances on machining processes [73,74,75,76,77,78,79].

In summary, any tolerance allocation method includes a tolerance analysis procedure. An optimization strategy generates solutions, i.e., sets of values ​​for the tolerances involved in a functional requirement. For each solution, it evaluates the objective function, e.g., the total machining cost of the toleranced features. Then it calls tolerance analysis to verify the stackup constraint, i.e., to estimate the statistical distribution of the functional requirement and compare it with assembly specifications. This applies to both dimensional and geometric tolerances. The treatment of geometric tolerances requires the use of more complex analysis methods, which translate the geometric tolerances into statistical parameters for properly defined variables describing elementary deviations on the features (small translations or rotations in/about different directions). Such variables are essential for the analysis, but create a difficulty: since there are unlikely to be as many deviations as there are geometric tolerances, translating back the former into the latter is generally impossible.

The lack of a one-to-one mapping with geometric tolerances implies that deviation variables cannot be directly used for optimization, because the optimal solution does not uniquely correspond to an optimal set of values for original unknowns of the allocation problem. Such condition does not actually affect many of the above methods, which are based on Monte Carlo stackup simulation (possibly implemented in CAT software) and numerical search strategies. These methods tackle allocation problems with possibly complex definitions and assumptions, but carry the price of a heavier computational burden as the simulation is to be repeated for a possibly high number of candidate solutions. Furthermore, it is not always clear and explicitly mentioned whether and how the results of the analysis (i.e., the individual contributions of the deviations to the variation of the functional requirement) can guide the search for the optimal solution.

The above difficulty is more critical for simpler allocation methods, discussed in the earlier reviews cited in this section. These methods use analytical optimization for a direct calculation of the solution, without the need to generate many candidate solutions. They have been widely used for dimensional tolerances with obvious computational advantages albeit with limitations on the assumptions of the allocation problem (e.g., on statistical distributions and cost-tolerance functions). However, their extension to geometric tolerances is not trivial, because they find an optimal solution in terms of deviation variables with no guarantee that it can be mapped to the unknown geometric tolerances. In the following, this issue is described in more detail for 1D allocation problems, and a method is proposed in order to avoid it.

3 Main concept

In a 1D stackup problem, an assembly-level functional requirement depends on a set of tolerances on different parts. For simplicity, however, we initially consider a simplified case involving different features of a single part. This limitation will be released in the next section.

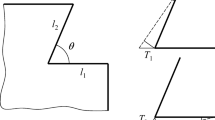
Figure 1a shows a flat rectangular plate with a hole. It is assumed that the functional requirement to be controlled is the distance Y between the edge of the hole and the right edge of the plate. Both features are subject to geometric tolerances, which reference datums A and B established on the bottom and left edges of the plate; some basic dimensions define the nominal positions of the two toleranced features. The values of the tolerances are assumed to be known, as candidate solutions (possibly not optimal) of the allocation problem. In detail, the three specified tolerances are (all dimensions in mm throughout the paper):

  • Ts =  ± 0.4: size tolerance on hole diameter

  • Tp1 = 0.6: position tolerance with MMC modifier on hole center with respect to datums A and B

  • Tp2 = 1: profile tolerance on the right edge with respect to datum B

Fig. 1
figure 1

Allocation example: a tolerances, b stackup dimensions

Full size image

To check whether the tolerance values satisfy the functional requirement, a tolerance analysis problem must be solved by calculating the resulting variation TY on the hole-edge distance and verifying that it is less than the specified variation (e.g., ± 1 mm). The calculation can be easily done using three stackup variables, each of which is associated with a dimensional tolerance. The defined variables and their tolerances are as follows:

  • H = 16 ± TH: hole diameter

  • A = 50 ± TA: distance between hole center and left edge

  • B = 70 ± TB: distance between left and right edges

The tolerances on the equivalent dimensions H, A, and B are set considering the definitions of the specified geometric tolerances:

$$\begin{array}{l} T_{H} = T_{{\text{s}}} = 0.4 \hfill \\ T_{A} = {{T_{{{\text{p1}}}} } \mathord{\left/ {\vphantom {{T_{{{\text{p1}}}} } 2}} \right. \kern-\nulldelimiterspace} 2} + T_{{\text{s}}} = 0.7 \hfill \\ T_{B} = {{T_{{{\text{p2}}}} } \mathord{\left/ {\vphantom {{T_{{{\text{p2}}}} } 2}} \right. \kern-\nulldelimiterspace} 2} = 0.5 \hfill \\ \end{array}$$
(1)

The expression of TA in (1) adds the maximum bonus 2Ts to the position tolerance as the hole departs from its MMC. A division by two is required whenever a geometric tolerance zone is converted into a semi-tolerance. The diagram in Fig. 1b provides the following functional equation:

$$Y = - {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-\nulldelimiterspace} 2} - A + B$$
(2)

The sensitivities of Y with respect to the three dimensions (in absolute values as required when composing deviations) are therefore

$$S_{H} = {1/2}{ , }\;S_{A} = 1{ , }\;S_{B} = 1$$
(3)

and can be used to estimate the maximum variation on Y under the assumption that all deviations are at the limits of their tolerance zones (worst-case stackup):

$$T_{Y} = S_{H} T_{H} + S_{A} T_{A} + S_{B} T_{B} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} \cdot 0.4 + 0.7 + 0.5 = 1.4$$
(4)

To account for the statistical compensation of deviations, the root sum square (RSS) equation can also be used to estimate the stackup of tolerances:

$$T_{Y} = \sqrt {S_{H}^{2} T_{H}^{2} + S_{A}^{2} T_{A}^{2} + S_{B}^{2} T_{B}^{2} } = \sqrt {{1 \mathord{\left/ {\vphantom {1 {4 \cdot 0.4^{2} + 0.7^{2} + 0.5^{2} }}} \right. \kern-\nulldelimiterspace} {4 \cdot 0.4^{2} + 0.7^{2} + 0.5^{2} }}} = 0.88$$
(5)

This estimate is more realistic than the worst-case stackup if the dimensions are statistically independent and have normal distributions. However, dimensions H and A are not independent because one of the specified tolerances (Ts) appears in the expressions of both tolerances TH and TA; if the hole has a larger diameter, it departs from MMC and can afford a higher position deviation. From a statistical point of view, an increase in the variance on H leads to an increase in the variance on A. Therefore the RSS equation, which corresponds to the sum of the variances under the assumption of equal process capabilities, is no longer valid and should be completed with an additional term involving the covariance between H and A.

Is there an alternative way to carry out the tolerance analysis task avoiding any dependence between variables? The proposed method consists in defining the sensitivities of Y with respect to the geometric tolerances. In the worst case, TY can be expressed as a function of the three specified tolerances:

$$\begin{aligned} T_{Y} & = {1/2} \cdot T_{{\text{s}}} + \left( {{{T_{{{\text{p1}}}} }/ {{2} + T_{{\text{s}}} }}} \right) + {{T_{{{\text{p2}}}} }/ {2}} \\ & = {3/2} \cdot T_{{\text{s}}} + {1/2} \cdot T_{{{\text{p1}}}} + {1/2} \cdot T_{{{\text{p2}}}} \end{aligned}$$
(6)

This gives the three sensitivities associated to the geometric tolerances

$$S_{{\text{s}}} = {3/2}{ , }\;S_{{{\text{p1}}}} = {1/2}{ , \;}S_{{{\text{p2}}}} = {1/2}$$
(7)

which can then be used for the RSS stackup:

$$T_{Y} = \sqrt {S_{{\text{s}}}^{2} T_{{\text{s}}}^{2} + S_{{{\text{p1}}}}^{2} T_{{{\text{p1}}}}^{2} + S_{{{\text{p2}}}}^{2} T_{{{\text{p2}}}}^{2} } = \sqrt {{9 \mathord{\left/ {\vphantom {9 {4 \cdot 0.4^{2} + {1 \mathord{\left/ {\vphantom {1 {4 \cdot }}} \right. \kern-\nulldelimiterspace} {4 \cdot }}0.6^{2} + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4} \cdot 1^{2} }}} \right. \kern-\nulldelimiterspace} {4 \cdot 0.4^{2} + {1 \mathord{\left/ {\vphantom {1 {4 \cdot }}} \right. \kern-\nulldelimiterspace} {4 \cdot }}0.6^{2} + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4} \cdot 1^{2} }}} = 0.71$$
(8)

This new estimate is likely to be more accurate than (5), because geometric deviations are independent: Ts limits the departure of hole diameter from MMC, while Tp1 limits the deviation from the nominal position of a corresponding hole at MMC. Furthermore, the geometric deviations associated to the three tolerances can be assumed to have normal distributions: this obviously applies to Ts (which is actually a dimensional tolerance on a feature of size), but also to Tp1 and Tp2. For the former, the normally distributed variable is the actual horizontal position of hole center at MMC; for the latter, it is the actual horizontal position of the right edge (for both, the mean of the distribution is the nominal position).

The above reasoning involves a transformation between two types of sensitivities of requirement Y:

  • The “dimensional” sensitivities seq = [SH, SA, SB]T, defined as the partial derivatives of the deviation on Y with respect to the deviations associated to the equivalent tolerances Teq = [TH, TA, TB]T

  • The “geometric” sensitivities s = [Ss, Sp1, Sp2]T, defined as the partial derivatives of the deviation on Y with respect to the deviations associated to the specified tolerances T = [Ts, Tp1, Tp2]T

The transformation can be expressed as

$${\mathbf{s}} = {\mathbf{M}} \cdot {\mathbf{s}}_{{{\mathbf{eq}}}}$$
(9)

where

$${\mathbf{M}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 \\ 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ \end{array} } \right]$$
(10)

is a matrix whose rows and columns correspond, respectively, to the specified geometric tolerances and to the equivalent dimensional tolerances. The element Mij of the matrix is the linear contribution of the i-th specified tolerance to the j-th equivalent tolerance. Such notation separates the two effects that determine the geometric sensitivities. The first one, expressed by seq, is the configuration of the dimension chain. The second one, expressed by M, is the meaning of the specified geometric tolerances. As will be described in the next section, M can be built using rules depending on tolerance types, datums, and possible MMC modifiers.

As already shown, s can be used instead of seq in the tolerance analysis task to get a more accurate estimate of the variation on Y. However, there is an even more important reason why it is useful to associate sensitivities to geometric tolerances. As recalled in Sect. 1, most tolerance allocation methods require the sensitivities as input data. In some cases, they are used to build a functional equation such as (2), which allows the statistical estimation of the deviations on Y by Monte Carlo simulation. In other cases, under given assumptions on statistical distributions, they appear in a constraint equation such as (5) for an optimization problem that is solved analytically or numerically. Suppose then that the equivalent sensitivities seq have been used to calculate an optimal set Teq of equivalent tolerances. To express the solution consistently with design specifications, the corresponding set T of specified tolerances is now to be calculated. Considering the definition of matrix M, it is easy to find that

$${\mathbf{T}}_{{{\mathbf{eq}}}} = {\mathbf{M}}^{{\text{T}}} \cdot {\mathbf{T}}$$
(11)

and therefore

$${\mathbf{T}} = \left( {{\mathbf{M}}^{{\text{T}}} } \right)^{ - 1} \cdot {\mathbf{T}}_{{{\mathbf{eq}}}}$$
(12)

In the above example, M is a square matrix, and its transpose has full rank. So there is one and only one back-transformation of the equivalent tolerances into the specified ones:

$$\left[ {\begin{array}{*{20}c} {T_{{\text{s}}} } \\ {T_{{{\text{p1}}}} } \\ {T_{{{\text{p2}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 1 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 \\ 0 & 0 & {1/2} \\ \end{array} } \right]^{ - 1} \cdot \left[ {\begin{array}{*{20}c} {T_{H} } \\ {T_{A} } \\ {T_{B} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ { - 2} & 2 & 0 \\ 0 & 0 & 2 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {T_{H} } \\ {T_{A} } \\ {T_{B} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{H} } \\ {2\left( {T_{A} - T_{H} } \right)} \\ {2T_{B} } \\ \end{array} } \right]$$
(13)

However, it is not guaranteed that the same conditions apply in any 1D allocation problem. The equivalent tolerances may not be as many as the original geometric tolerances. By solving the allocation problem on equivalent tolerances, an optimal solution Teq may correspond to no valid solution T, or to an infinite set of solutions. For example, the tolerancing scheme of the plate considered so far could be modified as shown in Fig. 2a, where the profile tolerance Tp2 references the hole center at MMC. According to the diagram in Fig. 2b, the requirement Y would depend on only two equivalent dimensions, H and A (now defined as the distance between hole center and right edge). The functional equation would be

$$Y = - {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-\nulldelimiterspace} 2} + A$$
(14)

and the sensitivities would transform as follows:

$$\left[ {\begin{array}{*{20}c} {S_{{\text{s}}} } \\ {S_{{{\text{p1}}}} } \\ {S_{{{\text{p2}}}} } \\ \end{array} } \right] = {\mathbf{M}} \cdot \left[ {\begin{array}{*{20}c} {S_{H} } \\ {S_{A} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 1 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ \end{array} } \right]$$
(15)
Fig. 2
figure 2

Alternative version of the allocation example: a tolerances, b stackup dimensions

Full size image
Fig. 3
figure 3

Geometric tolerances in relationship to an equivalent dimensional tolerance: a) size tolerance; b) tolerance with basic dimension; c) size tolerance of a feature toleranced at MMC; d) size tolerance of a datum feature referenced at MMC; e) tolerance on a feature with clearance fit

Full size image

Since the transpose of M is not square and therefore not invertible, it would not be possible to use Eq. (12) to transform an optimal allocation Teq back into T. Using the geometric sensitivities s to find the optimal allocation, this difficulty can be avoided by directly calculating the minimum-cost tolerances Ts, Tp1, and Tp2. As an extra benefit, the RSS stackup constraint can be verified more accurately than using the equivalent sensitivities seq.

4 Method

Now consider a full 1D stackup problem with its common assumptions. The parts of an assembly are connected through pairwise contact relations between features. The functional requirement is a linear distance between features of different parts, which is the result of a dimension chain possibly involving other parts. All the dimensions in the chain are parallel to the direction of the requirement. The part features involved in the dimension chain have random deviations due to manufacturing errors; the stackup of these deviations causes a deviation on the requirement, which must be controlled within a specified assembly tolerance.

It is assumed that, possibly using a formal method of tolerance specification [80], a tolerance scheme has been chosen for each part according to the ISO GPS [1] or ASME GD&T [2] standards. The scheme includes geometric tolerances of different types (form, orientation, position, profile) with possible MMC modifier. Size tolerances are also specified on features of size; they are always expressed as equal bilateral tolerances. A geometric tolerance on a feature can reference one or more datums established on other features of the same part; the MMC modifier can possibly be applied to a datum reference corresponding to a feature of size.

All specified geometric tolerances (including size tolerances) have unknown values, which are to be chosen in the tolerance allocation problem. According to the simplest and most widespread of the available formulations in literature [11], the allocation is the constrained optimization of the total manufacturing cost of the parts. The objective function is the sum of the cost-tolerance functions evaluated for the individual part features involved in the requirement. The constraint is the condition that the deviation on the requirement, i.e., the RSS stackup of the deviations on part features, is lower than the assembly tolerance.

The method chosen for the solution of the allocation problem is the optimal scaling procedure proposed in [81], which combines the Lagrange multiplier method [82] with an extended version of the reciprocal-power cost-tolerance function [83]. The procedure calculates tentative values ​​of the tolerances, which satisfy the optimal proportions between them; the tolerances are then scaled to satisfy the stackup condition. The initial value of each tolerance is calculated by the expression

$$F = f_{M}^{0.39} f_{F}^{0.39} f_{A}^{0.39} X^{0.072} S^{ - 0.78}$$
(16)

which includes the sensitivity S, the nominal dimension X [mm], the surface area fA of the feature [cm2], and two coefficients related to the material (fM) and to the type of feature (fF). These factors are described in detail in the Appendix. The optimal scaling method has been proposed for the allocation of dimensional tolerances, but can be easily extended to geometric tolerances by replacing nominal dimensions with appropriate basic dimensions included in the specified tolerance scheme.

All the data needed for the optimal scaling procedure are available in part drawings except for the sensitivities. As discussed in Sect. 3, these should be directly associated with the geometric tolerances. However, the method commonly used for 1D stackup analysis [26, 27] uses the sensitivities of the requirement to the equivalent dimensions of the chain. These dimensions are easily identified by following the chain of assembly relations between the two part features involved in the requirement. The chain may include dimensions with zero nominal value; examples include the displacement of an axis or midplane of a feature of size due to a position deviation and the displacement between the two mating features of a clearance fit (assembly shift).

In a 1D problem, the sensitivities seq associated with the equivalent dimensional tolerances are usually equal to 1 except in special cases (e.g., 1/2 when the equivalent dimension is half the diameter of a cylindrical feature). Setting seq is straightforward once the dimension chain has been described in a diagram. Then the sensitivities s associated with the specified geometric tolerances are calculated by Eq. (9). This requires constructing the transformation matrix M through a study of how the specified tolerances influence the dimension chain. The study includes three main steps as described below.

The first step is the identification of the geometric tolerances that are related with the equivalent dimensions. These may include the following:

  • Size tolerances corresponding to dimensions in the chain

  • Position tolerances on features of size, e.g., cylindrical shafts or holes, if the corresponding basic dimensions are in the chain

  • Profile tolerances on non-size features, e.g., planar surfaces, if the corresponding basic dimensions are in the chain

  • Orientation tolerances on datums involved in the dimension chain

According to the common assumptions in the analysis of tolerances (even in 2D/3D stackups, as in [84]), form tolerances are not considered in the study because they have usually little influence on the variation of the requirement. A basic dimension, which is usually the distance between the target feature and one of the datum features of a geometric tolerance, is assumed to correspond to the target feature because deviations on datum features do not cause further deviations at assembly level. In some cases, a basic dimension is identified as the sum or difference of basic dimensions specified in part drawing.

In the second step, the order of M is set, and its non-zero elements are identified. Each row of the matrix corresponds to one of the specified geometric tolerances, and each column to one of the equivalent dimensional tolerances. If it turns out that the matrix is not square, the proposed method is actually needed for an allocation based on sensitivities; without it, the optimization should be done with more computationally intensive methods based on Monte Carlo simulation (e.g., DOE, search algorithms, or sensitivity analysis).

Non-zero elements correspond to several possible relationships between the specified geometric tolerances and the equivalent dimensional tolerances. The following is a list of possible relationships:

  • Size tolerance on a feature of size corresponding to the equivalent dimension (Fig. 3a).

  • Position, profile, or (when these are not specified) orientation tolerance that has the equivalent dimension as a basic dimension (Fig. 3b).

  • Size tolerance on a feature of size subject to a position or orientation tolerance at MMC that has the equivalent dimension as a basic dimension; this relationship is due to the allowed increase (bonus) on the geometric tolerance when the feature size departs from its MMC (Fig. 3c).

  • Size, position, or (when the latter is not specified) orientation tolerance on a feature of size that is referenced as a datum at MMC in another geometric tolerance having the equivalent dimension as a basic dimension; this relationship is due to the additional bonus on the referencing tolerance (datum shift) that the datum feature allows when it departs from its MMC (Fig. 3d).

  • Size, position, or (when the latter is not specified) orientation tolerance on a feature of size involved in a clearance fit with another feature of size; in this case, the equivalent dimension is the assembly shift of the first feature with respect to the second one (Fig. 3e).

Regarding the last relationship, it is assumed that the minimum clearance between the two features (i.e., the difference between the MMC sizes of the hole and the shaft or fastener) is equal to the sum of the geometric tolerances specified at MMC for the two features. This is consistent with the fixed-fastener and floating-fastener rules recommended in geometric tolerancing (e.g., [26]). If a larger clearance is required for functional reasons, the extra-clearance is regarded as an additional equivalent dimension with zero tolerance.

The third step sets the values of the elements of M according to rules that are related with the standard definition of the geometric tolerances. For example, a position or profile tolerance defines the whole tolerance zone, so it must be multiplied by 1/2 to get an equal bilateral tolerance on an equivalent dimension. The possible cases under the assumptions made at the beginning of this section are listed in Table 1.

Table 1 Elements of the matrix for the transformation of sensitivities
Full size table

5 Results

The proposed method will now be applied to two examples of tolerance allocation on 1D stackups. The first is a simple block assembly, which includes the most common combinations of geometric tolerances and equivalent dimensional tolerances. The second is a more typical mechanical assembly, which requires the handling of additional situations such as part and feature patterns, stock parts, and composite tolerances.

5.1 Block assembly

Figure 4 shows three parts (base, pin, block) connected with simple contact relationships without any fastening or joining. The functional requirement Y is assumed to be the distance between the pin and the block in the free area above the base. The allowed variation on the requirement is Y0 ± TY = 5 ± 1 mm.

Fig. 4
figure 4

Block assembly

Full size image

As illustrated in the diagram of Fig. 5, Y can be analyzed as a stackup of equivalent dimensions along the horizontal direction. The functional equation is

$$Y = - {A / 2} + B + C + D + E$$
(17)

where:

Fig. 5
figure 5

Dimension chain for the block assembly

Full size image

  • A = 20 ± TA is the largest diameter of the pin.

  • B = 0 ± TB is the eccentricity between the two diameters of the pin.

  • C = 0 ± TC is the assembly shift between the pin and the hole in the base.

  • D = 15 ± TD is the distance between the axis of the hole and the step in the base.

  • E = 0 ± TE is the out-of-plane deviation of the vertical face of the block.

The following geometric tolerances have an influence on the equivalent dimensions:

  • Ts1: size tolerance on the largest diameter of the pin.

  • Tp1: position tolerance at MMC on the largest diameter of the pin.

  • Ts2: size tolerance on the smallest diameter of the pin.

  • To2: perpendicularity tolerance at MMC on the smallest diameter of the pin.

  • Ts3: size tolerance on the hole in the base.

  • To3: perpendicularity tolerance at MMC on the hole in the base.

  • Tp4: profile tolerance on the step in the base.

  • To5: perpendicularity tolerance on the vertical face of the block.

The nominal dimensions X02 and X03 of the features involved in the clearance fit are set with a common virtual condition of 10 mm:

$$\begin{array}{l} X_{02} = 10 - T_{{{\text{s2}}}} - T_{{{\text{o2}}}} \hfill \\ X_{03} = 10 + T_{{{\text{s3}}}} + T_{{{\text{o3}}}} \hfill \\ \end{array}$$
(18)

The allocation problem has 8 unknown geometric tolerances T = [Ts1, Tp1, Ts2, To2, Ts3, To3, Tp4, To5]T. If the optimal values of the 5 equivalent tolerances Teq = [TA, TB, TC, TD, TE]T could be found, they would correspond to an infinite set of solutions T. To find the optimal geometric tolerances directly, the sensitivities s of Y with respect to T have to be calculated; this is done by transforming the sensitivities seq of Y with respect to Teq, which appear in the functional equation:

$$\left[ {\begin{array}{*{20}c} {S_{{{\text{s1}}}} } \\ {S_{{{\text{p1}}}} } \\ {S_{{{\text{s2}}}} } \\ {S_{{{\text{o2}}}} } \\ {S_{{{\text{s3}}}} } \\ {S_{{{\text{o3}}}} } \\ {S_{{{\text{p4}}}} } \\ {S_{{{\text{o5}}}} } \\ \end{array} } \right] = {\mathbf{M}} \cdot \left[ {\begin{array}{*{20}c} {S_{A} } \\ {S_{B} } \\ {S_{C} } \\ {S_{D} } \\ {S_{E} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 1 & 0 & 0 & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 \\ 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 2 \\ 1 \\ 2 \\ 1 \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 1 \\ \end{array} } \right]$$
(19)

Matrix M in (19) is constructed by recognizing the following relationships between T and Teq:

  • Ts1 influences TA (size tolerance on diameter ∅20) and TB (bonus on the position tolerance Tp1 of the same diameter).

  • Tp1 influences TB (position tolerance on diameter ∅20).

  • Ts2 and To2 influence TB (datum shift on the position tolerance Tp1 of diameter ∅20) and TC (assembly shift between pin and hole).

  • Ts3 and To3 influence TC (assembly shift between pin and hole) and TD (datum shift on the profile tolerance Tp4 of the step at distance 15 mm to the hole).

  • Tp4 influences TD (profile tolerance of the step at distance 15 mm to the hole).

  • To5 influences TE (perpendicularity tolerance on the face of the block).

The non-zero elements of M are set according to Table 1.

Once the related sensitivities are known, the geometric tolerances are allocated by means of the optimal scaling procedure. All parts are assumed to be made of the same material (low-carbon steel). Table 2 lists the initial values F of the tolerances in optimal proportions, along with the data used for their calculation using Eq. (16). The data are collected pretty much as in the allocation of dimensional tolerances with few exceptions. When setting surface areas fA, the datum surface of a geometric tolerance may have to be considered in addition to the own surface of the feature; for consistency with the stackup constraint, this is done only when the datum is relevant to the position of the feature along the direction of the functional requirement. Among nominal dimensions X, the one corresponding to the orientation of a non-size feature is arbitrarily set to a value (in parentheses) representative of the machined feature.

Table 2 Tolerance allocation for the block assembly
Full size table

The optimal values Topt of the geometric tolerances in Table 2 are found by scaling the values of F on the assembly tolerance TY. From the procedure described in the Appendix, the scaling factor is

$$s = \frac{{T_{Y} }}{{c\sqrt {\sum\limits_{i} {S_{i}^{2} } F_{i}^{2} } }} = 0.073$$
(20)

where i = 1, … 8 is the index of the tolerance in T, and c = 1.5. Rounding the values of Topt and calculating the nominal sizes of the mating features from (18) yield the tolerance callouts shown in Table 2. For the sake of brevity, the callouts are described using the ISO text equivalents of tolerance types [85] to avoid showing them graphically on the final part drawings in a separate figure.

5.2 Bracket assembly

Figure 6 shows two brackets fastened to a baseplate by means of bolts and nuts. The distance Y between the vertical faces of the two brackets is to be controlled at Y0 ± TY = 20 ± 1 mm.

Fig. 6
figure 6

Bracket assembly

Full size image

The dimension chain in Fig. 7 corresponds to the functional equation

$$Y = - A + B - C + D + E + F + G$$
(21)

where:

Fig. 7
figure 7

Dimension chain for the bracket assembly

Full size image

  • A = 40 ± TA is the distance between the vertical face and the hole axes in the left bracket.

  • B = 100 ± TB is distance between the axes of the left and right holes in the baseplate.

  • C = 40 ± TC is the distance between the vertical face and the hole axes in the right bracket.

  • D = 0 ± TD is the assembly shift between the holes in the left bracket and the mating bolts.

  • E = 0 ± TE is the assembly shift between the left holes in the baseplate and the mating bolts.

  • F = 0 ± TF is the assembly shift between the right holes in the baseplate and the mating bolts.

  • G = 0 ± TG is the assembly shift between the holes in the right bracket and the mating bolts.

The following geometric tolerances have an influence on the above equivalent dimensions:

  • Tp3f: feature-relating tolerance at MMC on the holes in the baseplate; in the composite tolerance frame, the pattern-locating tolerance Tp3p is not related to the dimension chain as it references the edges of the baseplate.

  • Ts3: size tolerance on the holes in the baseplate.

  • Tp6p: pattern-locating tolerance at MMC on the holes in the bracket.

  • Tp6f: feature-relating tolerance at MMC on the holes in the bracket.

  • Ts6: size tolerance on the holes in the bracket.

  • Ts7: size tolerance on the diameter of the M8 bolt (which is assumed to be specified at 7.9 ± 0.1 mm on the stock part).

The nominal dimensions X03 and X06 of the holes in the baseplate and in the bracket are set according to the floating fastener rule with the same virtual condition of 8 mm as the bolt:

$$\begin{array}{l} X_{03} = 8 + T_{{{\text{s3}}}} + T_{{{\text{p3f}}}} \hfill \\ X_{06} = 8 + T_{{{\text{s6}}}} + T_{{{\text{p6f}}}} \hfill \\ \end{array}$$
(22)

A particular aspect of this allocation problem is that the left and right brackets are two random parts from the same manufacturing process. They have the same tolerances but different deviations and must be treated separately in the calculation of the RSS stackup for the functional requirement Y. Therefore the geometric tolerances specified for the two parts have separate sensitivities to take into account the statistical compensation between the corresponding deviations. Similarly, the geometric tolerances on the two pairs of holes in the baseplate have separate sensitivities. Based on these considerations, the vector of geometric tolerances is T = [Tp3f, Ts3, Tp6p_1, Tp6f_1, Ts6_1, Tp6p_2, Tp6f_2, Ts6_2, Ts7_1, Ts7_2]T, where the indices 1 and 2 refer to the left and right sides of the assembly. The corresponding vector of equivalent tolerances is Teq = [TA, TB, TC, TD, TE, TF, TG]T. The transformation of sensitivities from seq to s has the following result:

$$\left[ {\begin{array}{*{20}c} {S_{{{\text{p3f}}}} } \\ {S_{{{\text{s3}}}} } \\ {S_{{{\text{p6p\_1}}}} } \\ {S_{{{\text{p6f\_1}}}} } \\ {S_{{{\text{s6\_1}}}} } \\ {S_{{{\text{p6p\_2}}}} } \\ {S_{{{\text{p6f\_2}}}} } \\ {S_{{{\text{s6\_2}}}} } \\ {S_{{{\text{s7\_1}}}} } \\ {S_{{{\text{s7\_2}}}} } \\ \end{array} } \right] = {\mathbf{M}} \cdot \left[ {\begin{array}{*{20}c} {S_{A} } \\ {S_{B} } \\ {S_{C} } \\ {S_{D} } \\ {S_{E} } \\ {S_{F} } \\ {S_{G} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 3 \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 2 \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 2 \\ 2 \\ {2} \\ \end{array} } \right]$$
(23)

To construct matrix M, the following relationships are recognized between T and Teq:

  • Tp3f influences TB (position tolerance on the holes in the baseplate) as well as TE and TF (assembly shifts of the left and right holes with respect to the mating bolts).

  • Ts3 influences TB (bonus on the position tolerance Tp3f on the holes in the baseplate) as well as TE and TF (assembly shifts of the left and right holes with respect to the mating bolts).

  • Tp6p_1 influences TA (position tolerance on the holes in the left bracket).

  • Tp6f_1 influences TD (assembly shift of the holes in the left bracket with respect to the mating bolts).

  • Ts6_1 influences TA (bonus on the position tolerance Tp6p on the holes in the left bracket) and TD (assembly shift of the same holes with respect to the mating bolts).

  • Tp6p_2 influences TC (position tolerance on the holes in the right bracket).

  • Tp6f_2 influences TG (assembly shift of the holes in the right bracket with respect to the mating bolts).

  • Ts6_2 influences TC (bonus on the position tolerance Tp6p on the holes in the right bracket) and TG (assembly shift of the same holes with respect to the mating bolts).

  • Ts7_1 influences TD (assembly shift of the holes in the left bracket with respect to the mating bolts) and TE (assembly shift of the left holes in the baseplate with respect to the mating bolts).

  • Ts7_2 influences TF (assembly shift of the holes in the right bracket with respect to the mating bolts) and TG (assembly shift of the right holes in the baseplate with respect to the mating bolts).

Again, the non-zero elements of M are set according to Table 1.

The geometric tolerances (except the stock tolerance Ts7 =  ± 0.1 mm) are now allocated by the optimal scaling procedure. Tolerances are listed in Table 3 without separate consideration of left and right instances. Feature data are shown with similar assumptions as in the previous example: fM assumes that both parts are made of low-carbon steel; fF correspond to holes for all features; a datum feature is included in the surface area fA only for a pattern-locating tolerance; basic dimensions along the direction of Y are considered as nominal dimensions X for the appropriate geometric tolerances. The sensitivities S are extracted from vector s. Using Eq. (16), these data provide the listed initial values F of the tolerances in optimal proportions.

Table 3 Tolerance allocation for the bracket assembly
Full size table

Table 3 also lists the optimal values Topt of the geometric tolerances, which are calculated multiplying the corresponding F values by the following scaling factor:

$$s = \frac{{\sqrt {T_{Y}^{2} - 2S_{{{\text{s7}}}}^{2} T_{{{\text{s7}}}}^{2} } }}{{c\sqrt {S_{{{\text{p3f}}}}^{2} F_{{{\text{p3f}}}}^{2} + S_{{{\text{s3}}}}^{2} F_{{{\text{s3}}}}^{2} + 2S_{{{\text{p6p}}}}^{2} F_{{{\text{p6p}}}}^{2} + 2S_{{{\text{p6f}}}}^{2} F_{{{\text{p6f}}}}^{2} + 2S_{{{\text{s6}}}}^{2} F_{{{\text{s6}}}}^{2} } }} = 0.048$$
(24)

with c = 1.5. The numerator of (24) has a different expression from (20) as the variation specified on Y must be stripped of the contribution of the stock tolerance on the diameters of the two bolts (left and right side). This gives the actual variation to be distributed among the remaining dimensions.

The callouts shown in Table 3 are obtained by rounding the values of Topt and calculating the nominal sizes of the mating features from (22). Equal specifications are finally chosen for for the holes in the two parts although the optimal position tolerances would have been marginally different.

In the results of the allocation problem, it can be noted that the pattern-locating tolerance Tp6p is correctly optimized at a higher value than the feature-relating tolerance Tp6f of the same composite frame. Looking at Table 3, this is explained considering that it would cost more for the same allocated value, because it is associated with a larger area fA (as it also includes the datum surface) and with a larger nominal dimension X (as hole spacings are usually larger than hole diameters). Since the underlying cost-tolerance function takes these cost drivers into account, the optimal scaling procedure is able to loosen the tolerances having a greater impact on the total manufacturing cost.

6 Discussion

The method will now be compared with an alternative approach in order to validate its results and highlight differences in workflow and application potential.

The baseline method for the comparison is the numerical optimization of a cost function with stackup analysis by Monte Carlo simulation. This approach has the advantage of avoiding the issue mentioned in Sect. 3. As in the proposed method, it directly treats the geometric tolerances as optimization variables, avoiding to express the solution in terms of equivalent dimensional tolerances that would not be in one-to-one correspondence with valid geometric specifications.

The objective function for the optimization is the extended cost-tolerance function proposed in [81] and recalled in Eqs. (28) and (29) of the Appendix. Since the same function is embedded in the optimal scaling method, this choice makes the two methods consistent with respect to the assumed cost drivers (type and size of the feature, nominal dimension, material).

The tolerance analysis on each candidate allocation is done on a set of equivalent dimensions (A, B, C, …), which are linked to requirement Y by the functional equation. Given a set of geometric tolerances, a sample of geometric deviations is generated from a normal distribution with zero mean and standard deviation equal to 1/3 of the tolerance; the sample includes 5000 instances corresponding to simulated assemblies of manufactured parts. For each instance, the random deviations on the equivalent dimensions are calculated according the considerations made in Sect. 3; the functional equation then provides the random deviation on Y. Finally, the variation on Y is estimated as 3 times the standard deviation of the deviations on the sample. Again, the statistical assumptions are consistent with the proposed method although they would not be mandatory for Monte Carlo simulation.

To satisfy the stackup constraint, each candidate solution is scaled linearly to make the estimated variation on Y equal to the specified TY. This defines an unconstrained domain of input variables (the geometric tolerances) where the optimal solution is to be found. The search strategy was chosen considering the moderate dimension of the search space (8 and 5 variables for the cases of Sect. 5) and the likely occurrence of local minima; these properties suggest to avoid classical algorithms with proven efficiency (downhill simplex, direction set) and prefer local search algorithms where an initial solution is randomly perturbed until reaching a termination condition (maximum number of iterations). For a more reliable convergence, the search is guided by a heuristic related to the tendency of the optimal solution (cited in the reviews [9,10,11]) to avoid strong differences in the derivative of the cost-tolerance function. After selecting the tolerance to be perturbed, the direction and extent of the change are chosen based on the current derivative; to avoid being trapped in local minima, this criterion is alternated with a totally random perturbation.

For each of the two cases in Sect. 5, the above procedure was coded into a MATLAB script with 50,000 iterations, each including a stackup analysis and an evaluation of the objective function. The script was run 5 times, yielding slightly different optimal solutions due to the stochastic nature of Monte Carlo simulation. Each time, the optimal solution turned out to have a cost 30–40% lower than the initial solution with equal tolerances. Computing times were in the range of 10–15 min per run.

Figure 8 shows the optimal tolerances found with the simulation-based method, compared to the Topt values already listed in Tables 2 and 3 for the two cases. The optimal tolerances are in good agreement with the proposed method, as was expected given the consistency of the main assumptions. The difference in cost from the solution of the proposed method is within 2%, with the latter generally better as it derives from an analytical solution of the optimization problem.

Fig. 8
figure 8

Allocation results with the baseline method: a block assembly, b bracket assembly

Full size image

On the application side, the proposed method seems to have some advantages over an approach based on numerical search and Monte Carlo simulation. Specifically, it provides roughly the same optimal allocation in a much shorter time. This is not just about computing time, which might be reduced using a more efficient search algorithm and faster computing hardware or tuning the simulation parameters more carefully. Most of the time saved is in coding and testing the optimization procedure, whereas geometric sensitivities and optimal scaling involve simple calculations that can be done manually or with the help of a spreadsheet even when the problem involves a larger set of tolerances. Further benefits could derive from a software implementation that guides the user in the correct setting of geometric sensitivities.

On the other hand, the less computationally efficient approach has the advantage of flexibility, as it is not bound to any of the simplifying assumptions of the proposed method. In principle, it can be suitable to 2D and 3D problems without requiring a linearization of the dimension chain. It can allow a stackup analysis with statistical distributions and process capabilities consistent with the most likely production settings for individual parts. As already noted in the literature review, it can allow an integration with CAT software for stackup analysis in cases where the sensitivities are difficult to calculate due to the complexity of the assembly. The results of the tests reported in this section, however, suggest that long computing times could be required for the convergence of a CAT-based optimization procedure. In these cases, the proposed method could still be a useful support to numerical optimization if used as a means to get a quick initial solution close to the optimum.

7 Conclusions

The paper has proposed a different definition of sensitivities for geometric tolerance allocation. Traditionally used to allow the analysis of dimensional tolerances without resorting to Monte Carlo simulation, the sensitivities express the linear contribution of deviations from individual part dimensions to a functional requirement on the assembly. If geometric tolerances are specified on the parts, these must be translated into equivalent dimensions to analyze the stackup of geometric deviations. However, the same dimensions cannot be used as variables for the allocation, because an optimal solution could not be translated back into optimal values ​​of the original geometric tolerances. To solve this difficulty, the proposed method directly associates the sensitivities with the geometric tolerances and calculates them from the sensitivities related to the equivalent dimensions by means of a transformation matrix constructed with a rule-based procedure.

Some application examples prove that the use of “geometric” sensitivities solves allocation problems on one-dimensional tolerance stackups without excessive complications. In doing so, it drives designer’s attention to the correct relationships between specified tolerances and dimensions of the stackup model, removing another possible obstacle to the treatment of geometric tolerances in allocation. It also allows a slightly better accuracy in estimating the variation on the functional requirement, as it ensures statistical independence between the geometric deviations allowed by the tolerances.

The proposed approach is suitable for any optimization method available for linear stackup models. The optimal scaling method used in this work, previously proposed for the allocation of dimensional tolerances, is based on detailed feature data for a more accurate estimation of cost-tolerance relationships. It is easily extended to geometric tolerancing by additional rules dealing with datum features and basic dimensions.

Future studies will try to remove some limitations of the work. Additional controls provided in geometric tolerancing standards, such as the LMC modifier and the runout tolerance, will require additional rules for the transformation of sensitivities. More complex allocation problems will be addressed by integrating geometric sensitivities in available tolerance analysis methods for 2D/3D assemblies or under special assumptions on dimension chains and statistical distributions.

Although the method requires spreadsheet-like calculations on data that are easily obtained from engineering drawings, a CAD integration could greatly help its deployment in design practice especially for future 2D/3D extensions. For that purpose, tolerance schemes could be extracted from tolerance annotations with procedures generally available in the application interfaces of commercial modelers. Feature data for optimal scaling could be collected through procedural access to solid models with similarly available functions. Functional equations and sensitivities could be set up interactively, although their automatic recognition might be a realistic objective according to available research studies.