1 Introduction

Buffer Allocation Problem (BAP) is a well-known optimization problem in manufacturing systems design and operation, aiming at determining the optimal buffer sizes in a manufacturing system composed by various machines decoupled by buffers.

Typically, the BAP problem is addressed once most of the decisions involved in the design of production lines, including the definition of the number of workstations and their efficiency (processing rates and reliability parameters), have already been taken. The BAP problem is relevant because buffers have a double effect on the performance of unreliable production lines: (i) increasing the throughput by decoupling machines in the line and reducing the propagation of disruptions along the line in terms of starvation (no input available) and blocking (no space to move the output); (ii) increasing the total inventory and the average time parts spend inside the system [1, 2]. A larger buffer capacity helps to increase the effective production rate of the line, but buffers represent also an additional investment and operating cost, due to storage space and in-process inventory, respectively [3]. Therefore, the BAP deals with determining the right trade-off between the positive contribution to production rate and additional investments and costs.

The optimal buffer allocation and reallocation becomes even more relevant in automated manufacturing lines that are characterized by high reconfigurability to cope with evolving demand [4] and disruptive production scenarios [5]. The workstations are usually placed along a linear rail serving as buffer throughout the line [6]. Hence, the buffer capacity is given by the distance between stations and it is proportional to the pallet length. Since production managers tend to reduce the buffer sizes, linear rails can be equipped with proximity sensors used as stoppers to limit the buffer capacity between two consecutive stations. Moving the proximity sensors changes the buffer sizes according to the product type and pallet used. At the same time, even workstations may be moved along the linear rail in order to change the distance between them.

Herein, the attention is focused on automated multi-stage assembly systems that are characterized by deterministic or quasi-deterministic processing times, caused by the high repeatability of operations ensured by automation, high efficiency of the single workstations, and asynchronization of the operations [7]. These types of systems are employed in high-volume manufacturing sectors such as automotive, components for furniture, and electronics [8]. Technological advances enhanced automated multi-stage assembly systems with controllers and actuators that enable flexibility (i.e., reduced setups of the line to pass from one product type to another) together with frequent and fast reconfiguration [9].

In this work, a novel algorithm for optimally solving the BAP problem for unreliable asynchronous multi-stage serial lines is proposed. The algorithm integrates a stochastic performance evaluation model in a linear programming (LP) problem, by means of a surrogate model for linearized performance expressed as a combination of hyperplanes.

The work is organized as follows. Firstly, an overview of related literature is provided; secondly, the proposed methodology is described with respect to its building blocks. Then, numerical results are provided and the proposed methodology is applied in a real industrial case in the automotive sector. Finally, conclusions and future prospects close the work.

2 Buffer Allocation Problem

BAP is a well-established topic in the state of the art, drawing attention because of economic and strategical role of the required investment. Nevertheless, given technological and digital evolution for the modeling and optimization of manufacturing systems, contributions on this topic have been increasing lately.

Due to its relevance to real production systems, the buffer allocation problem has been studied for over 50 years, becoming one of the most popular research topics in industrial engineering and operative research fields (see the comprehensive reviews in Papadopoulos et al. [10], Demir et al. [11], and Weiss et al. [3]. The complexity of the problem is due to two main reasons: (1) it is a NP-hard combinatorial optimization problem (MacGregor Smith and Cruz [12]), in case of integrity constraint, and (2) no-closed formulas are available in order to calculate the main performance measures of production lines with more than two machines [13]. Consequently, as the total number of feasible solutions increases exponentially with the buffer size and the number of machines in the line, the complete enumeration through the whole solution space is unaffordable due to computational difficulty and numerical solutions are needed even for small-sized problems [14].

The buffer allocation problem can be classified according to (1) formulation of the objective function, and (2) procedure to solve BAPs, specifically the choice of the Evaluative Method and Generative Method. In literature, the Buffer Allocation Problem has been formulated mainly in three forms [11] according to the objective function:

  1. 1.

    Maximization of the production rate for a given fixed total buffer sizes (primal problem).

  2. 2.

    Minimization of total buffer size which guarantee a minimum throughput rate (dual problem).

  3. 3.

    Minimization of the average work-in-process inventory respecting defined level of total buffer size and desired production rate.

Generally, the last two formulations are appropriate in cases of specified demand and high floor space costs, high inventory, and work-in-progress (WIP) holding costs, respectively. Regarding solution procedures, due to the abovementioned complexity of the problem, the procedure to solve BAP generally consists in an iterative approach that combines evaluative methods, used to obtain the value of the objective function depending on a number of parameters, and generative methods that search for the optimal solution.

In literature, several approaches which leverage different evaluative and generative methods have been proposed. Evaluative methods exploit the characteristics and topologies of the production systems to estimate the system performance which the objective function depends on. If serial lines are considered, as in this work, the main distinctions with respect to the evaluative method and the system characteristics are the type of performance evaluation model (i.e., based on analytical or approximate analytical equations, or simulation as Discrete Event Simulation) and the line modeling assumptions (i.e.. synchronous/asynchronous, and reliable/unreliable lines). The advantage of using simulation is the flexibility in the modeling assumptions, despite requiring higher computational efforts than analytical methods. On the other hand, analytical methods may have quite restricted assumptions, hence the application capabilities of the optimization algorithm directly depend on the modeling technique. However, using analytical models allow evaluative methods to provide fast performance estimates, and to better exploit line properties. Indeed, when analytical methods are used, properties of the performance measures with respect to the buffer allocation are included in the optimization problem, according to the source of uncertainty characterizing the manufacturing line. For instance, in Shi and Gershwin [15], the manufacturing line is characterized by unreliable machines having the same deterministic processing rate (synchronous machines),hence, optimal buffer allocation solutions with respect to different reliability parameters are studied, according to varying cost functions for critical buffers. Properties of the system performance may be exploited also to derive adaptive optimization search algorithms as in Demir et al. [16]. Similarly, when the line assumptions allow it, as in reliable and synchronous manufacturing lines [17], extremely long serial lines can be optimized thanks to the analysis of system properties. An effective approach may combine analytical models and simulation models to enable multi-fidelity optimization approaches, as in Zhang et al. [18], by means of Mixed Integer Linear Programming (MILP). From the viewpoint of generative methods, sub-optimal algorithms as genetic algorithms (GAs) are among the most used, to overcome limitations in non-linearity and solution space complexity [19, 20].

In general, thanks to more accurate analytical models for performance evaluation of serial lines [14, 21], recent works focus on efficient algorithms for optimal buffer allocation based on the combination of analytical models and decomposition-based search algorithms. On the other hand, when more complex topologies or system characteristics are considered, simulation is generally used as evaluative method. It is worth mentioning that BAP is part of a larger manufacturing problem, dealing with the selection of optimal configurations for manufacturing systems. Hence, works in this field include also extended optimization problems with respect to decision variables and objective function, such as joint selection of machine and buffers with productivity performance [22], energy-efficient performance [23], transfer line [24, 25] and assembly line [26] balancing, CONWIP policies [27], and time buffers [28] for cost optimization. Since the proposed work deals with BAP in serial lines, a set of relevant works is classified in Table 1.

Table 1 Classification of selected related works from the literature
Full size table

2.1 Properties of the throughput function

In a multi-stage manufacturing system with K machines and K-1 buffers with finite capacity, the throughput function \(E=f\left({N}_{1},{N}_{2},{N}_{k},\dots ,{N}_{K-1}\right)\) represents the response curve of the throughput with respect to capacity of buffers in the line. For instance, Fig. 1 shows the throughput function of a three-machine two-buffer line as a function of the capacity of each buffer, where each machine \({M}_{k},k=\mathrm{1,2},3\) has parameters \(\mathrm{Mean Time to Failure }\left(\mathrm{MTTF}\right)=100 \left[\mathrm{t}.\mathrm{u}.\right],\) \(\mathrm{Mean Time to Repair }\left(\mathrm{MTTR}\right)=10 [\mathrm{t}.\mathrm{u}.],\) and cycle time \(\left(\mathrm{CT}\right)\) equal to \({\mathrm{CT}}_{1}=\mathrm{1,2 }[\frac{\mathrm{parts}}{\mathrm{t}.\mathrm{u}.}]\), \({\mathrm{CT}}_{1}=\mathrm{1,1 }[\frac{\mathrm{parts}}{\mathrm{t}.\mathrm{u}.}]\), and \({\mathrm{CT}}_{3}=1 [\frac{\mathrm{parts}}{\mathrm{t}.\mathrm{u}.}]\).

Fig. 1
figure 1

Throughput function in a three-machine two-buffer line

Full size image

The properties of the throughput function are fundamental for the implementation of the majority of methods used to solve the BAP, for both the evaluative and generative methods. An extensive study on the throughput function has been proposed in Gershwin and Schor [2]. The main properties that shall be exploited are the following ones:

  1. 1.

    Continuity. The throughput function can be considered a continuous differentiable function of buffer size \({N}_{k},k=1,\dots ,K-1\), as stated in [16]. Indeed, a small change in the buffer size causes a small change in the throughput.

  2. 2.

    Monotonicity. The throughput function of the system increases monotonically in each \({N}_{k}, k=1,\dots ,K-1\). Hence, a small change in the buffer size causes a small positive change in the throughput, until the limit is reached.

  3. 3.

    Concavity. The throughput function is concave with respect to all buffer sizes \({N}_{k},k=1,\dots ,K-1\).

  4. 4.

    Limitation. The throughput function is upper limited by the minimum production rate in isolation among the machines of the line.

These throughput function properties are exploited also by proposed method presented in the following section.

3 Method

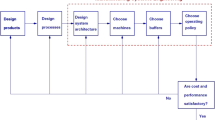
The proposed method is an iterative algorithm that integrates a stochastic analytical model for performance evaluation of serial manufacturing lines (Sect. 3.1) into a linear programming problem by means of performance linearization (Sect. 3.2). The reference manufacturing serial line of \(K\) machines and \(K-1\) buffers is shown in Fig. 2, based on the notation reported in Table 2.

Fig. 2
figure 2

Graphical representation of the multi-stage manufacturing line, where squares represent machines and circles represent buffers

Full size image
Table 2 Notation of the proposed algorithm
Full size table

Each machine \({M}_{k}\) is modeled as a continuous-time discrete-state Markov Chain, characterized by deterministic production rate \({m}_{k}\), failure rate \({f}_{k}\), and repair rate \({r}_{k}\). For each machine \({M}_{k}\) in the line, the efficiency in isolation \({e}_{k}\) is defined as:

$${e}_{k}=\frac{{r}_{k}}{{r}_{k}+{f}_{k}}$$
(1)

The production rate in isolation \({\rho }_{k}\) can be derived as:

$${\rho }_{k}=\frac{{r}_{k}}{{r}_{k}+{f}_{k}}\cdot {m}_{k}={e}_{k}\cdot {m}_{k}$$
(2)

Hence, given the upper limitation on the throughput function, the maximum possible throughput that can be obtained in the line is given by:

$$thmax=\mathrm{min}\left({\rho }_{1},{\rho }_{2},\dots ,{\rho }_{K}\right)$$
(3)

The proposed algorithm (represented in Fig. 3 and listed in Table 3) starts with the initialization (step 0), i.e., setting of the target throughput (th*), the maximum capacity of each buffer (\(maxca{p}_{k}\)) according the physical constraints of the manufacturing line, and calculating the maximum possible throughput (thmax) based on Formula (2). If the problem is feasible, then the algorithm starts the iterative loop that consists of solving an optimization model to obtain a candidate system configuration (step 1). The optimization model includes an estimate of the throughput thanks to an approximation based on linear constraints. The candidate system configuration obtained as result of the optimization model is given as input to the performance evaluation model for an accurate estimation of the throughput (step 2). The algorithm proceeds iteratively until convergence, i.e., when the throughput estimated by the performance evaluation is greater or equal to the target throughput, while considering a tolerance (ε). If convergence is not reached, then first-order derivatives are extracted from the performance evaluation model and used to generate a constraint (throughput cut) linearizing the performance that is added to the optimization model (step 3). The idea is to exploit the properties of the throughput function and iteratively calculate hyperplanes approximating the throughput function.

Fig. 3
figure 3

Graphical representation of the algorithm

Full size image
Table 3 Pseudo code of the algorithm
Full size table

In the following subsections, the evaluative method (Sect. 3.1) and generative method (Sect. 3.2) used in this approach to solve the BAP are presented. The tangent hyperplane formalization is included in an optimization problem to find the optimal buffer capacity allocation for a multi-stage serial production line.

3.1 Evaluative method: approximate analytical model

The stochastic analytical model for the performance evaluation of serial lines decoupled by finite-capacity buffers has been introduced in Magnanini et al. [6]. Decomposition equations based on the system dynamics model the propagation of effect, i.e., blocking and starvation, along the stages. A linear system of differential equations is solved by a numerical algorithm in order to evaluate the system performance in terms of throughput, average buffer level, and steady-state probabilities.

The advantage of using an analytical model is that the explicit relation between input parameters and output performance can be obtained. Based on this model, the first derivatives of the system throughput can be derived. The derivatives are then used to write the first-order approximation of the throughput with respect to the system parameters. In fact, as explained in the previous section, performance measures such as system throughput do not depend linearly on the system parameters. For instance, let us consider the throughput variation with respect to the buffer capacity \({N}_{1}\) and \({N}_{2}\) in a three-machine two-buffer line. If the first derivative of the throughput with respect to buffer capacity is known in a certain point corresponding to system configuration w \((t{h}^{w},{n}_{1}^{w},{n}_{2}^{w})\), the tangent hyperplane to a given point can be written as:

$$t{h}_{hyp}\left({n}_{1},{n}_{2}\right)=t{h}^{w}+{\left.\frac{\delta th}{\delta {n}_{1}}\right|}_{w}\cdot \left({n}_{1}-{n}_{1}^{w}\right)+{\left.\frac{\delta th}{\delta {n}_{2}}\right|}_{w}\cdot \left({n}_{2}-{n}_{2}^{w}\right)$$
(4)

More in general, in a serial line composed of \(K\) machines decoupled by \(K-1\) buffers, the tangent hyperplane of system configuration w \((t{h}^{w},{n}_{1}^{w},{n}_{k}^{w},\dots {n}_{K-1}^{w})\) is defined as:

$$t{h}_{hyp}\left({n}_{1},{n}_{k},\dots ,{n}_{K-1}\right)=t{h}^{w}+{\textstyle\sum }_{k=1}^{K-1}{\left.\frac{\delta th}{\delta {n}_{k}}\right|}_{w}\cdot \left({n}_{k}-{n}_{k}^{w}\right)$$
(5)

Moreover, considering the properties of the throughput function, it is possible to notice that the tangent hyperplanes are always over the given throughput function; hence:

$$\Delta th=t{h}_{hyp}\left({n}_{1},{n}_{k},\dots ,{n}_{K-1}\right)-th\left({n}_{1},{n}_{k},\dots ,{n}_{K-1}\right)\ge 0$$
(6)

As a consequence, if multiple hyperplanes are built based on an unknown throughput function, the accuracy of the linear approximation of the throughput function increases as additional hyperplanes are added to the envelope of already existing ones, as it is shown in Fig. 4 for the one-dimension case [6].

Fig. 4
figure 4

Throughput as a function of buffer capacity with first-order linearization [6]

Full size image

3.2 Generative method: linear programming problem

The optimization model is formulated as a MILP that includes the decision variables defined in Table 4. The optimization model returns the system configuration in terms of buffer capacities (nk) while considering the linear approximation of the throughput (thapp). The goal is to minimize the overall cost (7) given by the purchase of buffer capacity, while satisfying the target throughput (8 ). An upper bound for the throughput (9) can be calculated thanks to a preliminary analysis of the problem and exploiting the properties of the throughput function. Then, each buffer capacity cannot exceed a maximum value (10). Finally, constraint (11) represents the throughput cut that is added after each iteration based on the linearization of the throughput by means of hyperplanes (4).

Table 4 Formalization of the optimization model
Full size table

4 Numerical results

In this section, the proposed approach (from now on named hyperplane-based BAP, h-BAP) is validated against extensive research and analyzed with respect to the characteristics of various manufacturing systems. Then, the h-BAP is compared with the gradient-based BAP (g-BAP).

4.1 Experimental setting

The experimental results have been computed on small- and medium-sized multi-stage manufacturing systems, as defined in Demir et al. [16]. In particular, four-machine three-buffer (4M3B) and nine-machine eight-buffer (9M8B) systems have been analyzed with respect to varying experimental conditions.

For each manufacturing system size, four different system settings are considered:

  1. 1.

    Asynchronous homogeneous unreliable lines with identical machines, for which efficiency in isolation \({e}_{k}=e\) and production rate in isolation \({\rho }_{k}=\rho , \forall k=1,\dots ,K\).

  2. 2.

    Asynchronous homogeneous unreliable lines with machines characterized by decreasing efficiency in isolation \({e}_{1}>{e}_{2}>{e}_{k}>{e}_{K}\) and identical production rate in isolation \({\rho }_{k}=\rho , \forall k=1,\dots ,K\).

  3. 3.

    Asynchronous non-homogeneous unreliable lines with machines characterized by random efficiency in isolation \({e}_{K}\) and U-type production rate in isolation \({\rho }_{1}>{\rho }_{2}>{\rho }_{k}^{\mathrm{min}}<{\rho }_{K-1}<{\rho }_{K}\).

  4. 4.

    Asynchronous non-homogeneous unreliable lines with machines characterized by random efficiency in isolation \({e}_{K}\) and ∩ -type production rate in isolation \({\rho }_{1}<{\rho }_{2}<{\rho }_{k}^{\mathrm{max}}>{\rho }_{K-1}>{\rho }_{K}\).

Then, each system setting is further decomposed into two cases:

  1. (a)

    Low variability: in this case, each machine \({M}_{k}\) is characterized by frequent failures and fast repairs. Considering that failure rate and repair rate are exponentially distributed, this means that if their mean is small, also their variance is small. Therefore, the failures can be considered micro-stoppages along the line, with fast reaction to the stoppage hence low effect on blocking and starvation. In particular, for this case, the ratio between processing rate and repair rate is always included in the interval \(\frac{{m}_{k}}{{r}_{k}}\in \left[\mathrm{6,12}\right]\).

  2. (b)

    High variability: in this case, one machine \({M}_{k}\) is characterized by rare failures and long repairs. Hence, this means that also the variance is large. As a consequence, failures even if rare have serious effect when propagating along the line. The parameters for this set of experiments are obtained by scaling of a factor 10 the repair rate and failure rate parameters of case a). In particular, for this case, the ratio between processing rate and repair rate is always included in the interval \(\frac{{m}_{k}}{{r}_{k}}\in \left[\mathrm{60,120}\right]\).

As a consequence, experiments with the same system setting 1–4 but in different case (a)-(b) have the same efficiency in isolation and production rate in isolation. This guarantees that results can be pairwise compared to highlight the effect of variability in the availability parameters for machines characterized by similar performance in isolation.

For each experimental condition defined above, the dual problem, i.e., the minimization of allocated buffer spaces to reach a certain target throughput, is solved. Hence, the results are discussed according to the total buffer sizes identified by the algorithm, the actual throughput with respect to the target one (difference due to the integer constraint on the buffer capacity), and the number of iterations used for the optimal solution.

4.2 Results and discussion

Numerical results are presented according to various comments and analysis. First, an overview of the validation and results according to the defined experimental setting is provided. Then, the detailed analysis of iterations and explorative strategy used by the proposed algorithm is provided. Finally, some general considerations are derived according to the proposed experimental setting, with respect to the manufacturing system characteristics.

4.2.1 Overview of the results and validation

The proposed hyperplane-based approach has been validated with extensive search of the tested cases. In particular, for each experimental setting, the parameters have been randomly selected from the intervals defined in Table 5. Then, the optimality index has been computed as the percentage of the optimal solutions found by the algorithm with respect to the extensive search. Results are summarized in Table 5, showing a good efficacy of the proposed approach. When the optimal solution is not found, the difference with the optimal one is generally less than two buffer spaces, and may be due to calculation approximation.

Table 5 Overview of the tested cases and optimal results
Full size table

4.2.2 Analysis of iterations

This paragraph shows the analysis of the iterations for the proposed algorithm. In particular, the experimental condition 1a (i.e., experimental setting n.1 and case a) with medium-size manufacturing system (9M8B) is considered (\(m=1,f=0.011,r=0.125\)). The target throughput \(t{h}^{*}\) has been set to 90% of the production rate in isolation of the line \(\rho =0.9191\), hence \(t{h}^{*}=0.8276\).

For each iteration, the allocated capacity per buffer \({n}_{k},k=1,\dots ,K-1\), the total buffer capacity \({N}^{TOT}\), and the real throughput \(t{h}^{w}\) of the evaluated configuration \(w\) are shown in Figs. 5 and 6 respectively. The optimal solution \({n}^{OPT}=\left[8, 16, 22, 19, \mathrm{18,19}, 17, 9\right]\) is found in 52 iterations, hence by evaluating 52 different configurations.

Fig. 5
figure 5

Overview of the allocated buffer capacity in each iteration for 9M8B, case 1a

Full size image
Fig. 6
figure 6

Overview of the real throughput and total buffer capacity in each iteration

Full size image

As it can be noticed in Fig. 5, the algorithm tests quite different configurations at the beginning, while refining the solution later. Indeed, until iteration 17, there are peaks in the allocated buffer capacity since the algorithm tends to increase quickly the total amount of allocated buffer sizes, which can be noticed also in Fig. 6. At this point, the linear approximation obtained by the envelope of hyperplanes provides an accurate representation of the throughput function; hence, the algorithm moves carefully to identify the optimal configuration. After iteration 30, the total buffer capacity \({N}^{\mathrm{TOT}}\) remains almost constant, while the algorithm makes small changes in the capacity of each buffer to identify the correct buffer allocation guaranteeing the target throughput.

Hence, the algorithm tends to use the initial iterations to cut out areas of the throughput function which do not represent interesting solutions, either because unfeasible or because too expensive. Then, each throughput cut which is added iteratively refines the solution space in promising areas until the target throughput is found.

4.2.3 Effect of variability on BAP

In this paragraph, one detailed example from the medium-size manufacturing system (9M8B) is analyzed and commented, for each combination of setting (from 1 to 4) and case (a and b). For all the selected manufacturing systems, \({\rho }^{\mathrm{min}}=0.9191\), and the BAP with target throughput \({th}^{*}=0.75\cdot {\rho }^{\mathrm{min}}=0.6893\) is solved for the eight cases.

Figure 7 shows the optimal buffer allocation for the homogeneous lines (setting 1 and 2). When all machines are identical (case 1a), it is worth increasing the buffer capacity after the central machine, i.e., \({M}_{5}\), since it is the most affected by propagation of blocking and starvation phenomena descending from the downstream and upstream part of the line. This is a known result when dealing with buffer allocation in homogeneous lines. A similar reasoning can be found when one machine has a higher variability with respect to the other machines in the line: in case 1b, machine \({M}_{1}\) is characterized by the same performance in isolation than the corresponding machine \({M}_{1}\) in case 1a; however, the failure is rare and the repair rate is low, as defined previously. As a consequence, the optimal buffer allocation should increase the total number of buffer spaces, in order to mitigate the effect of propagating limitations from the upstream part of the line. However, given that the machines are still characterized by the same performance in isolation, i.e., a clear bottleneck cannot be identified, the largest buffer capacity still remains in the middle.

Fig. 7
figure 7

Optimal buffer allocation for homogeneous lines (settings 1–2)

Full size image

Setting 2 is characterized by decreasing efficiency in isolation within the line and same production rate in isolation among machines. Thus, faster but more unreliable machines are placed at the end of the line. Hence, more buffer capacity is allocated in this area, to cope with the effect of micro-stoppages within the line (case 2a) or is furtherly increased to mitigate the effect of rare, long, and also highly variable failures in machine \({M}_{1}\) (case 2b).

Figure 8 shows the optimal buffer allocation for the non-homogeneous lines (settings 3 and 4). In this case, the machines characterized by rare, long, and highly variable failures are the fastest ones, hence machine \({M}_{1}\) in case 3b and machine \({M}_{5}\) in case 4b. The goal of this analysis is to show that variability in the availability parameters can be only partially compensated by the production rate. It is interesting to notice that when rare and long failures occur, the buffer allocation strategy may change completely with respect to the same line having only micro-stoppages (cases 4a and 4b). This highlights the importance of such optimization problem in the design and operation of manufacturing systems, taking into account also its characteristics.

Fig. 8
figure 8

Optimal buffer allocation for non-homogeneous lines (settings 3–4)

Full size image

4.3 Comparison with gradient-based method

In this section, the proposed hyperplane-based method is compared with a gradient-based method. The gradient-based method defines the optimal direction to move given a starting configuration point, by iteratively selecting the buffer that provides a maximal increment in the production rate of the line. The gradient \({\varvec{g}}\) can be calculated either via finite difference or by analytically calculating the first-order derivatives. In the case of finite differences, Formula (11) is used, where \({g}_{i}\) are the \(K-1\) components of the gradient vector \({\varvec{g}}\).

$$\begin{aligned}&{g}_{k}=\frac{th\left({n}_{1},\dots ,{n}_{k}+\Delta {n}_{k},\dots , {n}_{K-1}\right)-th\left({n}_{1},\dots ,{n}_{k},\dots , {n}_{K-1}\right)}{\Delta {n}_{k}},\\& \forall k=1,\dots ,K-1\end{aligned}$$
(12)

Once the gradient has been determined, the step of the increment is estimated. Only the buffer \({B}_{k}\) with the maximal component of the gradient \({g}_{k}={g}_{\mathrm{max}}\) is incremented. Therefore, a new configuration point with buffer capacities \(\left({n}_{1}+\Delta {n}_{1},{n}_{k}+\Delta {n}_{k},{n}_{K-1}+\Delta {n}_{K-1}\right)\) is determined and the performance of the line can be evaluated with the analytical method. If the throughput is higher than the throughput requirement, then the optimal configuration has been found; if not, the incumbent configuration point becomes the new starting point for the iterative algorithm.

The comparison between the proposed hyperplane-based approach (\(h-\mathrm{BAP}\)) and the gradient-based approach (\(g-\mathrm{BAP}\)) is illustrated in Table 6, with respect to the number of iterations needed to find the optimum solution. For each manufacturing system size and experimental settings, the minimum and maximum numbers of iterations are provided. Moreover, the last column shows the mean difference in solution between the two approaches computed as follows, where \(m\) is the number of testes cases for each experimental set:

Table 6 Comparison between h-BAP and g-BAP
Full size table
$$\Delta {\overline{N} }^{TOT}=\frac{{\textstyle\sum }_{m}\left({N}_{h-\mathrm{BAP}}^{\mathrm{TOT}}\left(m\right)-{N}_{g-\mathrm{BAP}}^{\mathrm{TOT}}\left(m\right)\right)}{m}$$
(13)

This indicator points out if the optimal solution found by the two algorithms differs. If the difference is positive, it means that the h-BAP method found an optimal solution with a higher number of allocated buffer spaces, hence having a higher cost than the optimal solution found by the g-BAP.

Results shown in Table 6 highlights the efficiency of the proposed algorithm with respect to the gradient-based approach. Indeed, the number of iterations to reach the optimum is always lower in the h-BAP, for each experimental set. The difference in the number of iterations, hence in the algorithm efficiency, can be especially appreciated in those problems involving medium-sized manufacturing systems. The two methods find on average similar solutions (the indicator \(\Delta {\overline{N} }^{\mathrm{TOT}}\) is relatively small). Moreover, the \(\Delta {\overline{N} }^{\mathrm{TOT}}\) is always negative, thus indicating that the solutions found by the \(h-BAP\) method imply a smaller number of total buffer spaces, hence a lower cost. This difference, however, occurs quite rarely, in 4% of the cases.

Apparently, both the g-BAP method and the h-BAP method exploit the properties and characteristics of the throughput function. Moreover, the solution reached by the methods is in most of the cases similar. However, the iteration path is very different between the two methods. Figure 9 shows how the configurations tested in each iteration by the two methods perform in terms of throughput, represented by means of iso-throughput areas, in a small-scale problem with three machines and two buffers (3M2B). Parameters and the optimal solution for this example are provided in Table 7.

Fig. 9
figure 9

Comparison in the iterations between the gradient-based method and the hyperplane-based method

Full size image
Table 7 Parameters of the 3M2B example
Full size table

It can be noticed that the gradient-based method pushes the algorithm in testing configurations on the gradient, as expected (blue line). On the other hand, the hyperplane-based method selects configurations which may seem random, with respect to the selected parameters, but in fact they incrementally increase the accuracy of the linear approximation of the throughput function (red line). As a consequence, the hyperplane-based algorithm tests configurations very far between each other, enhancing the linear approximation of the throughput function in areas which guarantee a fair accuracy. In the end, the hyperplane-based algorithm guarantees a lower number of iterations with respect to the gradient-based method, thus ensuring higher computational efficiency. In addition, it must be stressed that the hyperplane-based algorithm offers a more flexible approach because the optimization model can be further complicated to take into account different types of decisions and planning horizons, while exploiting the linear approximation of the throughput function.

5 Industrial application

The proposed approach has been applied within a real industrial case, in the automotive sector. The company produces micro gear pumps with metallic bodies (Fig. 10a). The production is done based on lots according to the different product types.

Fig. 10
figure 10

Product (a) assembled in the manufacturing line (b)

Full size image

5.1 Description of the manufacturing system

The assembly line is composed by seven production areas, decoupled by linear rails serving as buffers, as in Fig. 10b, where arrows indicate the direction of the production flow. The first area (area 100 in Fig. 10b) loads and assembles the central body and driving gears, then other components such as bushings, magnets, and cups are assembled, as well as the front, rear body, and O-rings (toric joints) in area 200. Then the third area (area 300) is dedicated to the crimping process and test. The second part of the line is dedicated to testing and final operations, such as hydraulic test, pallet cleaning, laser marking, and finally unloading finished pumps (areas 400, 500, and 700). According to the pump variety, additional testing can be performed in the last area (area 600).

Due to many reconfigurations of the line within the years, linear rails are longer than needed; hence, proximity sensors (see Fig. 11) are used as stopper to limit the buffer capacity between stations thus limiting the work-in-progress (WIP) and reducing the lead time. Production planning is done weekly according to lots with varying lot sizes. According to setup time, planned maintenance within the week and other planned stoppages, as well as specific operations on the different product types, and availability of production time may vary; hence, the throughput required for alternative product types may differ. This results in the need of understanding the planned maximum production capacity for the given buffer configuration, or to modify it by means of the proximity sensors, in order to be able to achieve the required productivity.

Fig. 11
figure 11

Proximity sensor used as a stopper to limit buffer capacity on the linear rails

Full size image

5.2 Optimization problem and solution

The proposed algorithm for the BAP has been integrated in an automatic Decision Support System (DSS), internally developed by the research team, to help the company in identifying the correct positioning of the proximity sensors according to the target throughput.

Following the architecture proposed in Magnanini and Tolio [31], the h-BAP is used as plug-in module for the control and operations of the described manufacturing system. The modified architecture which has been used in the analyzed industrial case study is represented in Fig. 12. In particular, the performance evaluation model is parametrically implemented on the real multi-stage manufacturing system, and the configuration parameters are estimated from the real data gathered by means of the MES and the data analytics layer, to maintain the coherence between the evaluation model and the real system. According to the specific production plan, the target throughput \(t{h}^{*}\) is derived and provided as input to the DSS for h-BAP. This module corresponds to the proposed optimization algorithm for buffer allocation based on the linear approximation of the system performance by means of hyperplanes. Hence, the DSS uses the Performance Evaluation Model as evaluative model for the linearized performance to be included in the optimization problem.

Fig. 12
figure 12

Architecture of the DSS for h-BAP in the industrial case

Full size image

Once the solution is found, the DSS for h-BAP returns the optimal configuration in terms of allocated buffer spaces within the line and the actuation system of the proximity sensors acts on their position as indicated.

The advantages of the proposed approach are represented by the integration of an advanced and optimal solution method for the BAP within an operating manufacturing system, to support its responsive reconfiguration in different production scenarios. As it can be noticed in Table 8, the optimal buffer configurations may be quite different, leading to a difference of 40% in the total allocated buffer sizes to achieve the desired performance, and a difference of 25% in the circulating WIP. Moreover, the linear approximation of system performance increases the knowledge of the system with respect to the configuration parameters as the buffer capacities, thus allowing prompt reconfiguration actions when needed. The effectiveness of the optimized solution is ensured by the alignment between the performance evaluation model and the real system. Finally, the proposed architecture for the Decision Support in the operation of multi-stage asynchronous manufacturing systems can be easily extended to include more complex optimization problems related also to other configuration parameters.

Table 8 Optimal buffer capacity and related performance for alternative production plans
Full size table

6 Conclusion

Buffer Allocation Problem still represents an interesting research problem with respect to existing methodologies. In this work, BAP is solved for asynchronous unreliable multi-stage serial lines, by means of a novel algorithm based on the integration of linearized performance within a MILP. Linearized performances are obtained grounding on a stochastic approximate analytical model where the first-order derivative of the throughput with respect to the buffer capacities are used to define hyperplanes. These hyperplanes are then iteratively integrated as throughput cuts in the linear programming problem, to minimize the total costs while guaranteeing the target throughput.

The results show that the proposed methodology leads to optimal results in a limited number of iterations, thus guaranteeing a fair efficiency of the algorithm. Insights on optimal buffer allocation solutions are provided according to the variability affecting the manufacturing systems. Moreover, the proposed methodology is compared with a similar one in terms of evaluative and generative methods, i.e., the gradient-based approach. This comparison shows that the proposed hyperplane-based methodology outperforms in terms of efficiency of the gradient-based method, while also guaranteeing more flexibility in the overall approach.

Indeed, further developments are represented by the extension of the proposed methodology to large manufacturing systems, as well as the joint optimization of machine parameters together with buffer capacity. Challenging research developments are represented by the application of the proposed hyperplane-based approach to more complex system topologies as split and merge, parallel machine configurations, closed-loop networks. In these topologies, the throughput function may have different properties with respect to monotonicity and convexity; hence, the throughput cut based on the linearized performance should be adapted as a consequence. Moreover, the proposed approach can be further extended to consider multi-period decision problems, by means of stochastic programming, in which at the first stage the maximum buffer capacity is found, while at the second stage the actual buffer capacity for the specific demand scenario is obtained.