Robotic weld groove scanning for large tubular T-joints using a line laser sensor

Abstract

This paper presents a novel procedure for robotic scanning of weld grooves in large tubular T-joints. The procedure is designed to record the discrete weld groove scans using a commercially available line laser scanner which is attached to the robot end-effector. The advantage of the proposed algorithm is that it does not require any prior knowledge of the joint interface geometry, while only two initial scanning positions have to be specified. The position and orientation of the following scan are calculated using the data from two previous weld groove scans, so once initiated, the scanning process is fully autonomous. The procedure is a two-step algorithm consisting of the prediction and correction substeps, where the position and orientation of the sensor for the following scan are predicted and corrected. Such a procedure does not require frequent weld groove scanning for navigation along the groove. The performance of the proposed procedure is studied experimentally using an industrial-size T-joint specimen. Several cases of scanning motion parameters have been tested, and a discussion on the results is given.

1 Introduction

Robotic weld groove scanning (or weld groove tracking) is an automated process of moving a scanning device along the weld groove and obtaining the groove geometry and position. The collected groove data is essential for defining motion paths in the welding robot controller [1]. The application of robotic welding as a substitute for manual labor can be especially beneficial in the industries where a large amount of welding is done, such as the offshore industry. In the offshore industry, the application of large thick-walled tubular truss structures is widespread. Such truss structures contain a significant amount of T-joints, which constitute a considerable amount of welding needed to be done [2]. Robotic welding of such joints can significantly reduce the manufacturing time and improve welding quality, while robotic groove scanning is an initial step in the robotic welding procedure. It is noted that the term weld seam is often used in the literature, referring both to a finished weld and a weld groove before welding.

The sensors used in robotic welding are generally based on arc sensing or computer vision sensing technologies [1]. However, other approaches using ultrasound [3], infrared [4], and magneto-optical sensors [5] also exist. Arc sensing can be applied in cases when seam tracking is done while welding. In the case of weld groove scanning, structured light sensors with different projection patterns (lines, circles, triangles, grids) are often used [6, 7]. A structured light sensor with a line projection (i.e., a line laser scanner) is sufficient to perform weld groove tracking and scanning.

Line laser scanners have been broadly discussed in the literature as a tool for weld groove (or weld seam) tracking and scanning [7]. In general, seam tracking systems can be classified into three generations [1, 8]. In the first-generation systems, weld groove scanning is done in a separate pass before welding. The second and the third generations include real-time systems where scanning and welding are done simultaneously in the same pass. The work on the systems of the second or the third generations can be traced back to the 1980s [9], and most of the recent scientific publications cover such systems. In the sequence of papers [10, 11], a procedure for V-type and fillet weld seam tracking was proposed, which was experimentally tested to detect weld grooves in the presence of splash noises. The experimental verification was performed using straight welds in the horizontal plane. The same problem was addressed in [12], where an adaptive fuzzy controller was designed for tracking straight and curved weld seams in the horizontal plane. The authors had also suggested using three laser lines to add redundancy for handling the splash noise problems. Alternatively, in [13], the authors focused on the development of the shape-matching algorithm handling tracking of V (or U) grooves with varying geometry. Planar specimens were used in the experiments for verification. More examples of implementation of weld groove (or weld seam) tracking for planar specimens are given in the review papers [6, 7].

The review paper [7] revealed that most of the procedures in the field of seam tracking were developed and tested for planar specimens. Some work, however, has been done for weld groove tracking and scanning in 3-dimensional (3D) space. In [14], the authors proposed a trajectory-based control approach for robotic laser welding, where the experimental verification was done using a shell specimen with a sinusoidal welding path. Some more examples of weld seam scanning and tracking in 3D space using shell specimens were reported in [15,16,17].

The case of a more complex weld was investigated in [18], where a multiple segment scanning procedure was proposed and tested for a large tubular element with a sinusoidal lap weld around the pipe. The scanning was done in discrete sections, then the 3D geometry of the joint was reconstructed and processed for subsequent welding path generation. Tubular elements, however, can have more complex interfaces leading to more complex weld path geometries. For example, in [2], a joint of two large tubular sections was under investigation. The authors suggested a real-time seam tracking procedure which was verified experimentally using a 3D pen as a weld gun imitator. The experimental investigation involved the case of a one-pass weld, where a pipe joint of non-reflective surface material and without a weld groove was used.

In practice, an important challenge with large tubular joints used in the offshore industry is that the brace segment has to be welded entirely through the wall thickness (i.e., with a full penetration weld) for increasing fatigue lifetime of the welded connection [19]. The elements can be thick-walled, which requires deep pre-machined weld grooves and multi-pass welds. In addition, a weld groove has variable geometry, and the required number of weld layers and weld passes in each layer varies along the groove. In this case, the first-generation welding systems remain the most feasible (according to [1, 8] classification), as it is easier to define welding paths once the information about the entire groove is available. That is, a weld groove is first scanned, and then the obtained information is used for welding path generation for several weld layers. It is, however, reported relatively little results of robotic groove scanning for complex tubular 3D cases. The lack of the reported results for complex 3D cases was also highlighted in [2]. In fact, the majority of experimental results reported in the literature focus on robot welding path planning, and the scanning (or other data collection) step is not sufficiently described [20,21,22]. Alternatively, the robotic welding system is simulated, and the data is virtually generated, making a scanning algorithm unnecessary [23, 24]. From the industrial perspective, robotic scanning of T-joints with a line laser is a time-consuming manual operation when a robot is manually moved to all the scanning positions by a skilled operator. Therefore, automation of T-joint scanning and data parametrization for the eventual welding path planning is an important part of an autonomous welding system. The reported scanning and tracking approaches have, however, several deficiencies when seen in the perspective of application to T-joints:

• Planar or simple shell cases are covered;

• Seam tracking algorithms require high feedback update rate;

• Specific methods for complex 3D cases cover:

  • Test specimen cases with different types of grooves or without grooves;

  • Scanning paths are defined (or initial paths are pre-defined) by the CAD geometry.

To the best of authors’ knowledge, an experimentally verified method for robotic scanning of an industrial-scale steel T-joint with pre-machined weld grooves and reflective ground surfaces has not been reported in scientific literature before.

Alternatively, some commercial robot-integrated laser scanners are available. However, their functionality is limited to correction of pre-defined robot paths.

Therefore, in this work, we propose a method for robotic scanning of weld grooves in large tubular T-joints. The procedure considers the application of a commercially available line laser scanner, facilitating possible industrial implementations. In the proposed procedure, the scanning is done in discrete sections, which can be used to generate multi-pass welding paths. The main advantages of the proposed method are:

• The method can be used with less rigid robotic systems where vibration-induced errors is a problem, e.g., gantry-mounted robots;

• The method does not require a high rate of feedback updates;

• The method does not require a pre-defined scanning path, i.e., the robot navigates along the groove only using the sensor feedback;

• The method is experimentally verified using commercially available equipment and an industrial-size T-joint specimen.

The rest of this paper is organized as follows. In Sect. 2, a description of the system under consideration and the scope of the work are given. Section 3 presents the theoretical background of the proposed procedure, while the experimental results and discussion are given in Sect. 4. The conclusions are given in Sect. 5. In addition, the used laser calibration procedure is presented in Appendix 1, and the considerations for the reverse scanning are given in Appendix 2.

2 System description and problem formulation

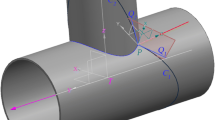
In this work, we consider a system where a weld groove in a large tubular T-joint is scanned by a robot-mounted structured light sensor. A T-joint is a type of stub joint where the elements are connected at a right angle. In the context of offshore truss structures (e.g., offshore platform jackets), the main element is referred to as a leg, and the connecting element is referred to as a brace, see Fig. 1. The brace is machined to match the leg and to form a weld groove at the interface. Since offshore structures are often welded with full penetration welds, the groove is made throughout the entire wall thickness of the brace. The elements are initially connected by a manually made one-pass root weld. A structured light sensor considered in this work has a line projection and will be further referred to as a line laser sensor or a line laser scanner.

A T-joint has a relatively complex interface geometry. Therefore, the groove geometry varies significantly along the interface line. It also means that the number of weld layers and beads in each layer is not constant. In that perspective, it is reasonable to perform scanning of the entire groove before the path planning for a welding robot starts. The groove is scanned in discrete sections, where the distance between groove sections depends on how fast the groove geometry changes. In an industrial setup, a welding robot (which is also used for groove scanning) is often mounted on a gantry. This introduces additional flexibility and vibrations to the robotic assembly. Therefore, in some configurations, it might be necessary to stop the robot while making a section scan. The procedure proposed in this work is developed accordingly, meaning that the robot stops before making a scan. In addition, parametrization of the scanned section (especially in the case of noisy data) can take significant computational time [25], and it might be challenging to implement continuous real-time robotic scanning algorithms. Moreover, the robot set-points in every step are defined in advance, and, therefore, this allows for early collision detection and better safety routines.

Fig. 1

A T-joint of two tubular elements

Consider a system where a commercial line laser sensor is rigidly fixed to the end-effector of a robot. The frame fixed at the base of the robot is Frame b (the inertial frame), while Frame f is fixed in the end-effector flange, and Frame s is fixed in the sensor. Frame f is oriented such that the $z_f$-axis is normal to the flange surface. Frame s is oriented such that the projected laser plane lies in the $x_sz_s$-plane. It is noted that both $\mathbf {R}^f_s$ (the rotation matrix from Frame f to Frame s) and $\mathbf {p}^{\; f}_{ \; fs}$ (the vector from the origin of f to the origin of s given in the coordinates of f) are constant. In addition to Frame s, we define another sensor frame denoted Frame $s'$. The transformation from Frame s to Frame $s'$ is $\mathbf {T}^s_{s'} = \{\mathbf {R}^s_{s'}, \mathbf {p}^s_{s,s'} \} \in \mathrm {SE(3)}$, which will be discussed in more details in Sect. 3.3. For more background information on homogeneous transformations in $\mathrm {SE(3)}$, see [26]. Each scanned groove cross-section i has a local fixed frame denoted Frame $g_i$. The local sensor and groove frames are shown graphically in Fig. 2.

Fig. 2

Definition of Frames s and $s'$, which are sensor-fixed, and Frame g, which is groove-fixed

3 Robotic weld groove scanning

3.1 Weld groove parametrization

Weld groove parametrization is a procedure of finding a minimal set of parameters sufficient to fully describe the geometry of the groove. In some literature, this procedure is also referred to as feature extraction. In this work, we will parameterize grooves by the coordinates of the corners points, as well as the coordinates of the end points.

The parametrization algorithm is based on RANSAC (random sample consensus) for sequential searching of line segments. The intersection points between the segments are used as the groove parameters. It is additionally implemented several correction and data noise detection steps in the algorithm. The details of the parametrization procedure are given in [25]. It is, however, important to note that the other parametrization procedures available in the literature can also be used [11, 27, 28], as long as they provide the same type of parameters as an output.

For the groove i in a T-joint, the parametrization gives a set of 5 points given in the coordinates of Frame s (the sensor frame) and relative to the origin of Frame s

$$\begin{aligned} \begin{aligned} \mathbf {S}^s_{g/si} = \begin{bmatrix} \mathbf {p}^s_{s,g1}&\cdots&\mathbf {p}^s_{s,g5} \end{bmatrix} \in \mathbb {R}^{3 \times 5} \end{aligned} \end{aligned}$$

(1)

where $\mathbf {p}^s_{s,gj}$ is a vector from the origin of Frame s to the corner point $\mathbf {p}_{gj}$. The points in Eq. (1) can be expressed in the coordinates of Frame b by the transformation

$$\begin{aligned} \begin{aligned} \mathbf {S}^b_{g/si} = \mathbf {R}^b_s \mathbf {S}^s_{g/si} \end{aligned} \end{aligned}$$

(2)

where $\mathbf {R}^b_s \in \mathrm {SO(3)}$ is a rotation matrix [26]. The matrix (1) can also be represented with the homogeneous points as

$$\begin{aligned} \begin{aligned} \mathbf {\tilde{S}}^s_{g/si} = \begin{bmatrix} \mathbf {\tilde{p}}^s_{s,g1}&\cdots&\mathbf {\tilde{p}}^s_{s,g5} \end{bmatrix} \in \mathbb {R}^{4 \times 5}. \end{aligned} \end{aligned}$$

(3)

Then the points in Eq. (3) can be expressed in the coordinates of Frame b and can be given relative to the origin of Frame b by the homogeneous transformation

$$\begin{aligned} \begin{aligned} \mathbf {\tilde{S}}^b_{g/bi} = \mathbf {T}^b_s \mathbf {\tilde{S}}^s_{g/si} \end{aligned} \end{aligned}$$

(4)

where $\mathbf {T}^b_s \in \mathrm {SE(3)}$ is a homogeneous transformation matrix [26]. The parametrization points are shown graphically in Fig. 3.

Fig. 3

Parametrization of a weld groove of a T-joint

The local coordinate frame for the groove i is denoted Frame $g_i$, see Sect. 2. The origin of Frame $g_i$ is obtained using the scanned data points and is defined as an intersection between the first and the last line segment in the groove model. In Fig. 3, it is an intersection between the lines along the vectors $\mathbf {v}_1$ and $\mathbf {v}_4$. The axes of Frame $g_i$ are defined as follows. The $x_{g_i}$-axis is defined by the normalized product $\mathbf {v}_{4}^\times \mathbf {v}_{1}$, the $y_{g_i}$-axis is defined as negative $\mathbf {v}_1$ of the groove i, and $z_{g_i}$-axis is found as the cross-product of $x_{g_i}$ and $y_{g_i}$.

Consider that the vectors $\mathbf {v}_i^b$ in Fig. 3 are given in the coordinates of Frame b and the Frame $g_i$ axes are also given as column vectors in the coordinates of Frame b, then the homogeneous transformation from Frame b to Frame $g_i$ is defined as

$$\begin{aligned} \begin{aligned} \mathbf {T}^b_{g_i} = \begin{bmatrix} \mathbf {x}^b_{g_i} &{} \mathbf {y}^b_{g_i} &{} \mathbf {z}^b_{g_i} &{} \mathbf {p}^b_{b,g_i} \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}. \end{aligned} \end{aligned}$$

(5)

3.2 Definition of stepwise motion

In this subsection, we present the mathematical derivations of the proposed stepwise scanning procedure. Such a scanning approach can be beneficial when a weld groove has to be scanned discretely in the sections of interest. The advantage of the procedure is that it does not require frequent scanning, which might be relevant when the groove parametrization algorithm is computationally expensive.

In this subsection, the theoretical background of the proposed procedure is derived for the counterclockwise scanning around the brace element (in the top view). Considerations for the clockwise scanning are given in Appendix 2.

As stated previously, the strategy for robotic weld groove scanning is to perform discrete scans along the groove with a defined distance $d_{st}$ between each scan. A step motion from the scanned groove section $i-1$ to the scanned groove section i is referred to as step i. Every step i consists of two control substeps: substep i1 referred to as the prediction substep, and substep i2 referred to as the correction substep. A new control set-point for Frame $s'$ is defined in every substep. After the substep execution, the frame is denoted $s'_{ij}$, where ij is a step stamp. It means that the frame is defined at substep j of step i. In this subsection, we will define the set-point for Frame $s'_{ij}$ as the homogeneous transformation matrix $\mathbf {T}^b_{s'_{ij}}$. The numbering convention for the weld groove scan frames is similar. The frame of the scan performed after execution of the prediction substep is denoted Frame $g_{i1}$, and the frame of the scan performed after execution of the correction substep is denoted Frame $g_{i2}$. The graphical representation of Frame $s'$ motion is given in Fig. 4.

Fig. 4

Schematic representation of the Frame $s'$ motion in the prediction and correction substeps of step i

Consider the configuration of the system when step $i-1$ has been finished, scan $i-1,2$ has been done, and Frame $g_{i-1,2}$ has been formulated. In this configuration, Frame $s'_{i-1,2}$ is in close vicinity with Frame $g_{i-1,2}$, that is $\mathbf {T}^b_{s'_{i-1,2}} \approx \mathbf {T}^b_{g_{i-1,2}}$.

The set-point for the prediction substep of step i is defined as

$$\begin{aligned} \begin{aligned} \mathbf {T}^b_{s'_{i1}} = \mathbf {T}^b_{s'_{i-1,2}} \mathbf {T}^{s'_{i-1,2}}_{s'_{i1}} \end{aligned} \end{aligned}$$

(6)

which alternatively can be formulated as

$$\begin{aligned} \begin{aligned} \mathbf {T}^b_{s'_{i1}} = \big ( \mathbf {T}^{s'_{i-1,2}}_{s'_{i1}} \big )_\mathrm {I} \mathbf {T}^b_{s'_{i-1,2}} \big ( \mathbf {T}^{s'_{i-1,2}}_{s'_{i1}} \big )_\mathrm {II} \end{aligned} \end{aligned}$$

(7)

where

$$\begin{aligned} \begin{aligned} \big ( \mathbf {T}^{s'_{i-1,2}}_{s'_{i1}} \big )_\mathrm {I}&= \begin{bmatrix} \mathbf {I} &{} \mathbf {p}^b_{s'_{i-1,2},s'_{i1}} \\ \mathbf {0}^{\mathrm T}&{} 1 \end{bmatrix}, \\ \big ( \mathbf {T}^{s'_{i-1,2}}_{s'_{i1}} \big )_\mathrm {II}&= \begin{bmatrix} \mathbf {R}^{s'_{i-1,2}}_{s'_{i1}} &{} \mathbf {0} \\ \mathbf {0}^{\mathrm T}&{} 1 \end{bmatrix}. \end{aligned} \end{aligned}$$

(8)

The advantage of formulation Eq. (7) instead of formulation Eq. (6) is that vector $\mathbf {p}^b_{s'_{i-1,2},s'_{i1}}$ appears in the coordinates of Frame b, which are the coordinates the vector is initially obtained in.

In this work, several strategies for the prediction of $\mathbf {T}^{s'_{i-1,2}}_{s'_{i1}}$ are discussed. Since the geometry of the weld groove is unknown, we propose to base this prediction on the results from the two previous scans, that is, the scans $i-1$ and $i-2$. Then, the rotation matrix in $(\mathbf {T}^{s'_{i-1,2}}_{s'_{i1}})_\mathrm {II}$ in Eq. (8) can be predicted as

$$\begin{aligned} \begin{aligned} \mathbf {R}^{s'_{i-1,2}}_{s'_{i1}}&= \mathbf {R}^{g_{i-2,2}}_{g_{i-1,2}} \\&=(\mathbf {R}^{b}_{g_{i-2,2}})^{\mathrm T}\mathbf {R}^{b}_{g_{i-1,2}} \end{aligned} \end{aligned}$$

(9)

which means that the prediction of the rotation from the initial $i-1$ to the next i scan orientation is assumed to be equal to the rotation between the two previous scans ($i-2$ and $i-1$). An alternative assumption could simply be $\mathbf {R}^{s'_{i-1,2}}_{s'_{i1}}=\mathbf {I}$, which disregards rotation in the prediction step. We will get back to the discussion on the choice of the rotation prediction in Sect. 4.

The position vector in $(\mathbf {T}^{s'_{i-1,2}}_{s'_{i1}})_\mathrm {I}$ in Eq. (8) can be predicted as

$$\begin{aligned} \begin{aligned} \mathbf {p}^{b}_{s'_{i-1,2},s'_{i1}}&= \mathbf {R}^{b}_{g_{i-2,2}} \mathbf {R}^{g_{i-2,2}}_{g_{i-1,2}} \mathbf {v}^{g_{i-2,2}}_{st} \\&= \mathbf {R}^{b}_{g_{i-2,2}} \mathbf {R}^{g_{i-2,2}}_{g_{i-1,2}} (\mathbf {R}^{b}_{g_{i-2,2}})^{\mathrm T}\mathbf {v}^{b}_{st} \\&= \mathbf {R}^{b}_{g_{i-1,2}} (\mathbf {R}^{b}_{g_{i-2,2}})^{\mathrm T}\mathbf {v}^{b}_{st} \end{aligned} \end{aligned}$$

(10)

where Eq. (9) is used and

$$\begin{aligned} \begin{aligned} \mathbf {v}^{b}_{st}= d_{st} \mathbf {\bar{p}}^{b}_{g_{i-2,2},g_{i-1,2}}. \end{aligned} \end{aligned}$$

(11)

Here, $\mathbf {\bar{p}}$ is the normalized form of a vector $\mathbf {p}$ and $d_{st}$ is the defined step length. The vector (11) defines the initial prediction of the Frame $s'$ location for the next scan. Although the assumption $\mathbf {p}^{b}_{s'_{i-1,2},s'_{i1}}=\mathbf {v}^{b}_{st}$ in Eq. (8) can be a reasonable prediction, especially for the small $d_{st}$ values, it will be demonstrated in Sect. 4 that Eq. (10) gives better results.

In the correction step, the position and orientation of Frame $s'$ are corrected to match the predefined scanning distance and angle. This leads to the new set-point

$$\begin{aligned} \begin{aligned} \mathbf {T}^b_{s'_{i2}}&= \begin{bmatrix} \mathbf {R}^{b}_{s'_{i2}} &{} \mathbf {p}^{b}_{b,s'_{i2}} \\ \mathbf {0}^{\mathrm T}&{} 1 \end{bmatrix} \\&= \begin{bmatrix} \mathbf {x}^b_{s'_{i2}} &{}\mathbf {y}^b_{s'_{i2}} &{}\mathbf {z}^b_{s'_{i2}} &{} \mathbf {p}^{b}_{b,s'_{i2}} \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned} \end{aligned}$$

(12)

where $\mathbf {p}^{b}_{b,s'_{i2}} = \mathbf {p}^{b}_{b,g_{i1}}$ and the Frame $s'_{i2}$ axes are defined by Frame $g_{i-1,2}$ and Frame $g_{i1}$ as follows

$$\begin{aligned} \begin{aligned} \mathbf {x}^b_{s'_{i2}}&= \mathbf {\bar{p}}^b_{g_{i-1,2},g_{i1}}, \\ \mathbf {y}^b_{t}&= (\mathbf {x}^{b \times }_{s'_{i2}} \mathbf {y}^b_{g_{i1}})^\times \mathbf {x}^{b}_{s'_{i2}}, \\ \mathbf {y}^b_{s'_{i2}}&= \mathbf {\bar{y}}^b_{t}, \\ \mathbf {z}^b_{s'_{i2}}&= \mathbf {x}^{b \times }_{s'_{i2}} \mathbf {y}^b_{s'_{i2}} \end{aligned} \end{aligned}$$

(13)

where $\mathbf {\bar{y}}^b_t$ is the normalized form of the vector $\mathbf {y}^b_t$. When the robot executes motion to Eq. (12), a new weld groove scan i is recorded, and Frame $g_{i2}$ is defined. Again, it is noted that after execution of the correction step, Frames $s'_{i2}$ and $g_{i2}$ have approximately the same location and orientation.

3.3 Definition of Frame $s'$

In Sect. 3.2, we defined a set-point for Frame $s'$ as the homogeneous transformation matrix $\mathbf {T}^b_{s'}$. Frame $s'$ was introduced as the second sensor-fixed frame in Sect. 2, but little was said on how it was defined. In this subsection, we discuss the definition of Frame $s'$, or, to be more precise, the definition of $\mathbf {T}^s_{s'}$. Note that we skip the step stamp ij in this subsection for simplicity of notations.

In the stepwise control sequence presented in the previous subsection, the control goal was to move Frame $s'$ to the desired location. The desired location was aligned with the predicted or corrected (depending on a substep) location of Frame g. In addition, transformation $\mathbf {T}^s_{s'}$ should be selected such that execution of a set-point for Frame $s'$ leads to reasonable scanning location and orientation of the laser, that is, reasonable location and orientation of Frame s. In a T-joint, the weld groove geometry is continuously changing, leading to varying reasonable location and orientation of Frame s. It means that the homogeneous transformation $\mathbf {T}^s_{s'}$ has to be redefined in every step of the procedure.

Assume that the homogeneous transformation $\mathbf {T}^s_{s'}$ is given as

$$\begin{aligned} \begin{aligned} \mathbf {T}^s_{s'}&= \begin{bmatrix} \mathbf {R}^s_{s'} \Delta \mathbf {R}^s_{s'} &{} \mathbf {p}^{s}_{s,s'} \\ \mathbf {0}^{\mathrm T}&{} 1 \end{bmatrix} \end{aligned} \end{aligned}$$

(14)

where $\mathbf {p}^{s}_{s,s'}$ is the distance between the origins of Frames s and $s'$, which, for smaller grooves, can be selected as $\mathbf {p}^{s}_{s,s'} = [0 \ 0 \ z_{s,s'}]^{\mathrm T}$. The rotation matrix in Eq. (14) is split into two parts for the convenience of derivations: the initial large rotation part and the local small rotation part. The initial rotation matrix $\mathbf {R}^s_{s'}$ is given as the sequence $\mathbf {R}_z(\phi )\mathbf {R}_x(\psi )$ [26] with $\phi = 90$ deg and $\psi = 180$ deg. The graphical representation of the initial rotation from Frame s to Frame $s'$ is given in Fig. 2. The local rotation matrix is given as

$$\begin{aligned} \begin{aligned} \Delta \mathbf {R}^s_{s'} = \mathbf {R}_y(-\alpha )\mathbf {R}_x(\beta ) \end{aligned} \end{aligned}$$

(15)

where $\alpha$ is referred to as a pull angle and $\beta$ is referred to as a work angle. The pull angle is an angle from the plane where the plane normal is parallel to the local weld groove direction vector. Optimally, the pull angle should be $\alpha = 0$ deg, which would result in the minimal (and the most precise) area of the scanned groove section. However, in practice, having a small pull angle helps to avoid problems with noise caused by the laser reflections. The work angle is introduced to ensure the correct positioning of the laser relative to the scanned groove section. An important aspect is that none of the scanned surfaces should be oriented at acute angles towards the laser rays, where the laser ray is a ray from the origin of Frame s to any scanned point. This gives low scanning resolution and potentially noisier data. A reasonable position of the laser is when the central laser ray is approximately in the middle of the groove opening angle. The groove opening angle is defined as an angle between $-\mathbf {v}_2$ and $\mathbf {v}_4$, see Fig. 3. A graphical demonstration of an incorrect and correct choice of the $\beta$ angle is shown in Fig. 5. In the a) case, $\beta = 0$ deg, which leads to an acute scanning angle towards the leg pipe surface. In the b) case, $\beta$ is selected such that the laser (and Frame s) is approximately located in the middle of the groove opening angle. The work angle is defined as follows

$$\begin{aligned} \begin{aligned} \beta = \frac{1}{2}(\gamma _1 - \gamma _2) \end{aligned} \end{aligned}$$

(16)

where $\gamma _i$ is given in Fig. 6, while the groove opening angle is $\gamma _1 + \gamma _2$.

Fig. 5

Graphical demonstration of incorrect (a) and correct (b) definition of $\mathbf {T}^s_{s'}$. Correct definition leads to the positioning of the laser sensor in the middle of weld groove opening angle after the execution of the correction substep. In comparison, incorrect positioning of the laser sensor leads to scanning of some surfaces at very acute angles, which gives lower scanning resolution and more noise

Fig. 6

Definition of the work angle $\beta$, where $\beta$ is shown being positive

The complete algorithm for the proposed robotic weld groove scanning procedure is presented in Algorithm 1.

4 Experimental results and discussion

The performance of the proposed robotic weld groove scanning procedure was studied experimentally. In this section, a description of the experiment as well as the experimental results is presented and discussed.

4.1 Experimental setup

The experimental setup is shown in Fig. 7. It consisted of the robotic manipulator Kuka KR5 Arc, the laser scanner Micro-epsilon scanCONTROL 2610-100 attached to the robot end-effector, and the T-joint test object. The test object was a tubular T-joint with a 90 deg angle between a brace and a leg. The two parts were welded together with a one-pass root weld. The leg segment was produced of the tubular profile 600$\times$20 mm, and the brace segment was produced of the tubular profile 457.2$\times$25.4 mm.

Fig. 7

Experimental setup for testing of the proposed scanning procedure. A commercial laser sensor is mounted on the robot end-effector and is projecting a line towards the weld groove of the tubular T-joint

The laser sensor was attached to the robot end-effector with a bracket. The calibration procedure for the determination of $\mathbf {T}^f_s$ transformation is derived and presented in Appendix 1.

The proposed procedure was implemented on an external control computer. The communication between the external computer, the robot, and the laser sensor was set up over a local network. The control computer generated the $\mathbf {T}^b_{s'}$ set-points, which were converted to the $\mathbf {T}^b_f$ set-points for the robot flange. The rotation matrix $\mathbf {R}^b_{f}$ was converted to ZYX Euler angles before the set-point $\mathbf {T}^b_f$ was sent to the robot controller. The laser sensor generated 2D point clouds, where points were given in the coordinates of Frame s (the laser sensor local frame). The robot pose was read as ZYX Euler angles and position of the robot flange (relative to the robot base), which were sent to the external computer and converted to the $\mathbf {T}^b_f$ transformation.

4.2 Experimental program

The scanning was done in the counterclockwise direction (in the plan view) over a groove segment of approximately 180 deg. Scanning of the entire groove was not possible due to the limitations of the robot’s operational space. The experimental program consisted of 36 tests, where different step lengths and parameters for the prediction substep were used. The following four cases of the prediction substep parameters were considered:

• 1. $\mathbf {R}^{s'_{i-1,2}}_{s'_{i1}} = \mathbf {I}$ and $\mathbf {p}^{b}_{s'_{i-1,2},s'_{i1}} = \mathbf {v}^b_{st}$,

• 2. $\mathbf {R}^{s'_{i-1,2}}_{s'_{i1}}$ is defined by Eq. (9) and $\mathbf {p}^{b}_{s'_{i-1,2},s'_{i1}}$ is defined by Eq. (10),

• 3. $\mathbf {R}^{s'_{i-1,2}}_{s'_{i1}} = \mathbf {I}$ and $\mathbf {p}^{b}_{s'_{i-1,2},s'_{i1}}$ is defined by Eq. (10),

• 4. $\mathbf {R}^{s'_{i-1,2}}_{s'_{i1}}$ is defined by Eq. (9) and $\mathbf {p}^{b}_{s'_{i-1,2},s'_{i1}} = \mathbf {v}^b_{st}$.

For each case of the prediction substep parameters, the following step lengths were considered: 10, 20, 30, 40, 50, 60, 70, 80, and 100 mm with corresponding 56, 28, 19, 14, 11, 9, 8, 7, and 5 steps in a test.

It is noted that scanning in the reverse (i.e., clockwise) direction was also tested outside the main experimental program. This was done for verification of the considerations given in Appendix 2.

4.3 Results and discussion

The scope of the robotic weld groove scanning operation is to automatically collect the groove geometrical data, which could be used for robotic welding path generation. Each executed scanning case generated discrete raw data points obtained directly from the laser scanner. An example of raw data points from the experiment with the 20-mm step length is shown in Fig. 8.

Fig. 8

Raw data points collected from the experiment with the 20-mm step length

The corresponding parametrization of the raw data is given in Fig. 9. The red dots indicate the root corners, and the black dots indicate all other points. The parametrization was done using the procedure presented in [25] with the groove parameter set described in Sect. 3.1.

Fig. 9

Groove corners and end points obtained by parametrization of raw data points collected from the experiment with the 20-mm step length. The red dots indicate the root corners and the black dots — all other points

As mentioned previously, the geometry of the groove is variable due to the relatively complex interface between the tubular sections. This is demonstrated by two examples of groove section scans given in Fig. 10, where the 1st and the 14th sections from Figs. 8 and 9 are plotted in the coordinates of Frame s.

Fig. 10

Sections 1 (to the left) and 14 (to the right) with the groove parameter points given in the coordinates of Frame s

In general, collecting the results presented above is the main practical goal of the robotic scanning procedure. From the perspective of the algorithm performance, it is important to discuss the precision and efficiency of the proposed procedure. As suggested in Sect. 2, discrete scanning of weld grooves in a large tubular T-joint is a good strategy for groove data collection. The quality of the groove parametrization itself is out of the scope in this work and is discussed in [25]. However, an important aspect of this work is that the parametrization results are of sufficient quality to be used with the proposed scanning algorithm. While the discrete scanning results obtained using the proposed algorithm are of good quality for all four parameter cases, the two-step structure of the procedure led to a slight zig-zag motion of the robot end-effector. An example of the robot end-effector path recorded from the experiment with the 50-mm step length is shown in Fig. 11.

Fig. 11

Path of the robot end-effector for all four substep parameter cases and the 50-mm step length. The colors are as follows: blue — case 1, orange — case 2, green — case 3, and purple — case 4

This 3D path plot can, for the sake of clarity, be transformed into the cylindrical coordinates $\theta , R, z$ and be shown with two plots, see Fig. 12. The origin of the cylindrical coordinates is moved to the center of the brace axis. From Fig. 12, it is seen that the paths in cases 1 and 3 deviate more in the $\theta R, R$ plot, while the paths in cases 2 and 4 deviate more in the $\theta R, z$ plot.

Fig. 12

Path of the robot end-effector for all four prediction substep parameter cases and the 50-mm step length, given in the cylindrical coordinates $\theta , R, z$. The colors are as follows: blue — case 1, orange — case 2, green — case 3, and purple — case 4

Therefore, in the following part of this section, we present an analysis of the optimality of the parameter choices for the different step lengths. Optimality is defined in terms of the step length precision, the total length of the robot end-effector path, and the total cumulative rotation of the robot end-effector.

The actual step length was collected during all the experiments as the distance between the origins of Frames $g_{i2}$. The mean step length values, as well as the standard deviations, are shown as a bar diagram in Fig. 13. The precision of the mean step length is important for planning the number of scanning steps for a weld groove of known length, while the standard deviation from the mean value is an important factor if step length consistency is a requirement for a weld path planner. The mean step length errors relative to the nominal values are shown in Fig. 14.

Fig. 13

Mean step length values (shown with bars) and the standard deviations (shown with black vertical lines). The colors are as follows: blue — case 1, orange — case 2, green — case 3, and purple — case 4

Fig. 14

Relative mean step length errors. The colors are as follows: blue — case 1, orange — case 2, green — case 3, and purple — case 4

The results show that for the 10-mm steps, the step lengths were of good precision for all four cases with the relative errors of 0.3–0.6 %. For the larger steps, the relative errors for parameter case 2 remained below 0.6 %, while for parameter case 3 — below 0.4 %. For parameter cases 1 and 4, however, the results looked differently. For parameter case 1, the relative mean errors increased up to 2.9 %, while for parameter case 4, the relative mean errors increased up to 13.5 %. The standard deviation was the lowest in all experiments for case 1, while the highest standard deviation was observed for case 4. The parameter cases 2 and 3 had insignificant standard deviation up to the 50-mm step length, and then it raised more rapidly for larger steps.

These results suggested that the step lengths for cases 2 and 3 are close to their nominal values and are preferable if the step length precision is important for the application case. If the step length consistency is the most important factor, parameter case 1 is the preferred choice. Parameter case 4 performed poorly both in terms of the mean step length and standard deviation.

The efficiency of the proposed scanning algorithm is evaluated in terms of the total end-effector travel distance and the cumulative rotation of the end-effector. Given constant end-effector translation and rotation speeds, this metric is equivalent to the scanning time. The efficiencies are compared for all four prediction parameter cases and all nine different scanning step lengths.

The results for the end-effector travel distances are shown as a bar diagram in Fig. 15. The lighter and darker colors indicate the cumulative travel distances of the prediction and correction substeps, respectively.

Fig. 15

Total travel distances of the end-effector. The colors are as follows: blue — case 1, orange — case 2, green — case 3, and purple — case 4. The lighter colors indicate the cumulative travel distances of the prediction substeps, while the darker colors — of the correction substeps

The obtained results suggested that the total travel distance for parameter cases 1 and 3 is shorter than the total travel distance for parameter cases 2 and 4. The difference was largest for the shortest 10-mm scanning step length, with the travel distances of 1945 mm for case 3 and 3344 mm for case 4. For the largest 100-mm step, the difference was practically negligible, with the travel distances of 1619 mm for case 3 and 1718 mm for case 2. For parameter cases 1 and 3, the cumulative travel distance during the prediction substeps was shorter than the travel distance during the correction substeps. The relative relation was opposite for parameter cases 2 and 4. This was due to the fact that in cases 1 and 3, no rotation prediction was used (i.e., $\mathbf {R}^{s'_{i-1,2}}_{s'_{i1}} = \mathbf {I}$), and all the correcting motion was made during the correction substep. For cases 2 and 4, the orientation of the following scan was predicted by (9), which means that a part of the correcting motion was already introduced in the prediction substep. Since the overall travel distance was consistently larger for cases 2 and 4, it can be concluded that the correction motion during the prediction substep was overestimating the orientation of the following scan. This led to the additional motion in the prediction substep and the additional correction motion in the correction substep. The parameter cases 1 and 3 performed nearly equally good with case 1 being marginally better for 20- and 30-mm steps, while case 3 was marginally better for all other step lengths.

The results for the cumulative rotation angle of the end-effector had a similar pattern as the results for the travel distance, see Fig. 16.

Fig. 16

Cumulative rotation angles of the end-effector. The colors are as follows: blue — case 1, orange — case 2, green — case 3, and purple — case 4. The lighter colors indicate the cumulative rotation angles of the prediction substeps, while the darker colors — of the correction substeps

The parameter cases 1 and 3 performed better for all the tested step lengths. Case 1 performed marginally better for all the step lengths except for the 10-mm step. Comparing cases 1 and 3 with 2 and 4, the difference was the largest for the 10-mm step length, with the cumulative rotation angle of 182 deg for case 3 and 402 deg for case 4. The difference was the smallest for the 100-mm step, with 133 deg for case 1 and 195 deg for case 2. The justification of why cases 2 and 4 performed worse is the same as in the travel distance analysis. The orientation of the next scanned section was overestimated, which led to an additional rotation of the robot end-effector during both the prediction and correction substeps.

It can be concluded that the prediction parameter cases 1 and 3 provided overall better performance than the parameter cases 2 and 4. Case 1 is recommended to use when the scanning step length consistency (low standard deviation) is important for a robotic welding path generator. Case 3 is recommended to use when the mean step length should be closer to the nominal step length value. However, for groove scanning with very large steps, it is recommended to use the prediction parameter cases 2 or 4. The reason is that for large steps, cases 1 and 3 resulted in rather acute scanning angles, which sometimes led to that the correction step scan was not obtainable. In the conducted experiments, this was observed for the 100-mm step length.

In an industrial setup, scanning of grooves in T-joints is still mostly a manual operation, where a robot operator manipulates the robot to the desired scanning positions. This is a time-consuming process, while the scanning step and laser angles towards the groove are of lower accuracy due to manual adjustment. The authors, for the sake of comparison, have performed several manual scanning operations. The next scanning step was possible to plan by measuring with a simple ruler, and it was, however, more challenging to measure and adjust the two angles towards the groove due to the lack of a good measurement reference. The average time used for one scan was about 1 min. Considering a case with the scanning step of 40 mm, this would result in the total scanning time of 14 min (i.e., 840 s). Alternatively, using the proposed robotic scanning procedure (with the parameter set 3) results in the total scanning time of 72 s, which is more than 10 times faster compared to manual scanning.

As mentioned previously, the precision of parametrization of each separate groove scan is out of the scope of this work and is discussed in [25]. It is, however, important to verify that the relative location of all groove scans of the T-joint has acceptable precision. This verifies that the obtained groove corners actually represent the groove geometry of the T-joint. The verification was done using the additional 3D data acquired using a high-precision Zivid Two ZVD2 structured light 3D camera. The point cloud of the T-joint used in the comparison is shown in Fig. 17.

Fig. 17

A point cloud from the Zivid camera plotted with the data points acquired by robotic scanning. The segment of comparison was reduced to 140 deg due to low quality of the Zivid point cloud at the edges

The raw point clouds acquired by the robotic scanning and Zivid camera had different reference coordinate systems, and, therefore, were fitted using the features of pipes and grooves. This allowed for obtaining the transformation between two coordinate systems. Then, the least-square error between the groove corners and the Zivid point cloud was found. It is noted that the comparison was done for one prediction parameter case and for a segment of around 140 deg due to limitations of the field of view in the Zivid camera. The average groove corner point error for all the tested step lengths in one parameter case was found to be 0.49 mm, which also includes the error from the groove parametrization itself, see [25]. The magnitude of the error is considered to be acceptable for welding applications.

5 Conclusions

In this work, a procedure for robotic scanning of weld grooves in large tubular T-joints was proposed, implemented, and studied experimentally. The scanning procedure is seen as an initial step in the robotic welding operation, where the groove geometrical data for weld path generation is automatically collected. The advantage of the proposed procedure is that it does not require a predefined scanning path, does not require frequent groove scanning, and can be used in the setups where a robot is mounted on a gantry, and the system is subjected to vibrations. Moreover, a commercially available line laser scanner was used to facilitate a more straightforward industrial implementation. The experimental study consisted of 36 tests with different parameter settings using an industrial-size tubular T-joint with a groove throughout the entire brace wall thickness. The proposed algorithm was integrated with the previously developed weld groove parametrization procedure, which allowed for obtaining good scanning results in the presence of laser reflections from the ground groove surfaces.

The scanning results obtained in all tests were of good quality, while the parameter cases with the best precision and efficiency were identified in the analysis of the results.

The analysis of the results was done using the data obtained by scanning only one tubular T-joint specimen. In order to get a better understanding of the performance of the proposed algorithm, it is recommended to conduct experiments with T-joint specimens of different sizes in future work. The possibility of using real-time robot controllers for groove scanning with reflection noise should be investigated. In addition, the results of this work should be used as an input for the development of the weld path planning algorithms as a part of an automated robotic welding system for T-joints.

Appendices

Sensor calibration

The presented technique is based on [29] with a difference that we implement the line constraints directly, instead of using points. In addition, we consider that the calibration plane can be measured using the robot TCP (tool center point) probe, which increases robustness of the procedure and does not require an iterative solution. The goal of the procedure presented in this section is to determine the rotation from Frame f to Frame s, i.e., $\mathbf {R}^f_s$, and the distance vector from the origin of f to the origin of s, i.e., $\mathbf {p}^{\; f}_{\; fs}$, given in the coordinates of Frame f.

Conditions for the line $\mathsf {L} = \{ \mathbf {a}, \mathbf {m} \}$ to be on the plane $\mathsf {P} = \{ \mathbf {u}, u_0 \}$ are $\mathbf {u}^\mathrm {T} \mathbf {a} = 0$ and $u_0 \mathbf {a} + \mathbf {u}^\times \mathbf {m} = \mathbf {0}$, which can be written for a given problem as

$$\begin{aligned} \begin{aligned} \mathbf {u}_c^\mathrm {b T} \mathbf {a}^b_{l_i}&= 0, \\ -u_{c0} \mathbf {a}^b_{l_i} + \mathbf {u}_c^{b\times } \mathbf {m}^b_{l_i/b}&= \mathbf {0} \end{aligned} \end{aligned}$$

(17)

where $\mathsf {P}_c^b = \{ \mathbf {u}_c^b, u_{c0} \}$ is the calibration plane given in the coordinates of Frame b, and $\mathsf {L}^b_{l_i/b} = \{ \mathbf {a}^b_{l_i}, \mathbf {m}^b_{l_i/b} \}$ is the measures laser Plücker line i given in the coordinates of Frame b and referenced to the origin of b. The line $\mathsf {L}^b_{l_i/b}$ is found as

$$\begin{aligned} \begin{aligned} \mathsf {L}^b_{l_i/b} = \mathbf {V}^{bs}_{bs} \mathsf {L}^s_{l_i/s} \end{aligned} \end{aligned}$$

(18)

where $\mathsf {L}^s_{l_i/s}$ is directly obtained from the sensor measurement and the screw transformation matrix [30] is

$$\begin{aligned} \begin{aligned} \mathbf {V}^{bs}_{bs} = \begin{bmatrix} \mathbf {R}^b_s &{} \mathbf {0} \\ \mathbf {p}^{b \times }_{bs} \mathbf {R}^b_s &{} \mathbf {R}^b_s \end{bmatrix}. \end{aligned} \end{aligned}$$

(19)

Then the first condition in Eq. (17) is explicitly written as

$$\begin{aligned} \begin{aligned} \mathbf {u}_c^\mathrm {b T} \mathbf {R}^b_f \mathbf {R}^f_s \mathbf {a}^s_{l_i}&= 0 \end{aligned} \end{aligned}$$

(20)

where it is noted that the y-coordinate of $\mathbf {a}^s_{l_i}$ is zero. Assuming that the first and the third columns of $\mathbf {R}^f_s$ are stacked in a vector $\mathbf {x}$, then (20) can be reformulated as a null space problem $\mathbf {A}\mathbf {x}=\mathbf {0}$, where

$$\begin{aligned} \begin{aligned} \mathbf {A} = \begin{bmatrix} \mathbf {u}_c^\mathrm {b T} \mathbf {R}^b_f a^s_{l_i,x} &{} \mathbf {u}_c^\mathrm {b T} \mathbf {R}^b_f a^s_{l_i,z} \\ \dots &{} \dots \\ \mathbf {u}_c^\mathrm {b T} \mathbf {R}^b_f a^s_{l_{nl},x} &{} \mathbf {u}_c^\mathrm {b T} \mathbf {R}^b_f a^s_{l_{nl},z} \end{bmatrix} \in \mathbb {R}^{n_l \times 6}. \end{aligned} \end{aligned}$$

(21)

The terms $a^s_{l_i,x}$ and $a^s_{l_i,z}$ are the x and z coordinates of $\mathbf {a}^s_{l_i}$ and $n_l$ is the number of scanned lines. The given null space problem can be solved using SVD (singular value decomposition). The the first column of $\mathbf {R}^f_s$ is $\mathbf {r}_1 = \mathbf {x}_{1:3}/ \Vert \mathbf {x}_{1:3} \Vert$ and the third column is $\mathbf {r}_3 = \mathbf {x}_{4:6} / \Vert \mathbf {x}_{4:6}\Vert$, while the second column is found as $\mathbf {r}_2 = \mathbf {r}_3^\times \mathbf {r}_1$. Then, SVD is applied again to find an $\mathrm {SO(3)}$ matrix which is the closest approximation of the initial solution for $\mathbf {R}^f_s$.

After the rotation $\mathbf {R}^f_s$ is determined, we can write the second condition of (17) explicitly as

$$\begin{aligned} \begin{aligned} -u_{c0} \mathbf {R}^b_s \mathbf {a}^s_{l_i} + \mathbf {u}_c^{b\times }(\mathbf {p}^{b \times }_{bs} \mathbf {R}^b_s\mathbf {a}^s_{l_i} +\mathbf {R}^b_s \mathbf {m}^s_{l_i/s})&= \mathbf {0} \end{aligned} \end{aligned}$$

(22)

where $\mathbf {R}^b_s= \mathbf {R}^b_f\mathbf {R}^f_s$ and $\mathbf {p}^{b}_{bs} = \mathbf {p}^{b}_{bf}\mathbf {p}^{b}_{fs}$. The line condition (22) can be further expanded as

$$\begin{aligned} \begin{aligned} -u_{c0} \mathbf {R}^b_s \mathbf {a}^s_{l_i}&+ \mathbf {u}_c^{b\times }(\mathbf {p}^{b \times }_{bf} \mathbf {R}^b_s\mathbf {a}^s_{l_i} +\mathbf {R}^b_s \mathbf {m}^s_{l_i/s}) \\&+ \mathbf {u}_c^{b\times } \mathbf {R}^b_f \mathbf {p}^{\; f \times }_{\; fs} \mathbf {R}^f_s \mathbf {a}^s_{l_i} = \mathbf {0} \end{aligned} \end{aligned}$$

(23)

where $\mathbf {p}^{b \times }_{fs} =\mathbf {R}^b_f \mathbf {p}^{\; f \times }_{\; fs}(\mathbf {R}^b_f)^\mathrm {T}$ is used. Equation (23) can be formulated as a linear least squares problem $\mathbf {A}_p \mathbf {p}^{\; f}_{\; fs} = \mathbf {b}$, where

$$\begin{aligned} \begin{aligned} \mathbf {A}_p = \begin{bmatrix} \mathbf {u}_c^\mathrm {b \times } \mathbf {R}^b_f [\mathbf {R}^f_s \mathbf {a}^s_{l_i}]^\times \\ \dots \\ \mathbf {u}_c^\mathrm {b \times } \mathbf {R}^b_f [\mathbf {R}^f_s \mathbf {a}^s_{l_{nl}}]^\times \end{bmatrix} \in \mathbb {R}^{(3 \cdot n_l) \times 3} \end{aligned} \end{aligned}$$

(24)

and the term $\mathbf {b} \in \mathbb {R}^{(3 \cdot n_l) \times 1}$ is

$$\begin{aligned} \begin{aligned} \mathbf {b} = \begin{bmatrix} - u_{c0} \mathbf {R}^b_s \mathbf {a}^s_{l_i} + \mathbf {u}_c^{b\times }(\mathbf {p}^{b \times }_{bf} \mathbf {R}^b_s\mathbf {a}^s_{l_i} +\mathbf {R}^b_s \mathbf {m}^s_{l_i/s}) \\ \dots \\ - u_{c0} \mathbf {R}^b_s \mathbf {a}^s_{l_{nl}} + \mathbf {u}_c^{b\times }(\mathbf {p}^{b \times }_{bf} \mathbf {R}^b_s\mathbf {a}^s_{l_{nl}} +\mathbf {R}^b_s \mathbf {m}^s_{l_{nl}/s}) \end{bmatrix} . \end{aligned} \end{aligned}$$

(25)

The result of the calibration is a constant transformation from Frame f to Frame s, which can be given as a homogeneous transformation matrix $\mathbf {T}^f_s= \{\mathbf {R}^f_s, \mathbf {p}^{\; f}_{\; fs} \} \in \mathrm {SE(3)}$.

In this work, the calibration was done using 12 laser line samples arranged in a circular pattern as discussed in [29]. The transformation $\mathbf {T}^f_s$ was found to be

$$\begin{aligned} \begin{aligned} \mathbf {T}^f_{s}&= \begin{bmatrix} 0.9999 &{} -0.0129 &{} -0.0002 &{} -0.749 \\ 0.0129 &{} 0.9999 &{} 0.0082 &{} -114.845 \\ 0.0001 &{} -0.0082 &{} 1 &{} 167.616 \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}. \end{aligned} \end{aligned}$$

(26)

Reverse scanning

The scanning procedure proposed in Sect. 3 was derived for the counterclockwise scanning about the brace axis (in the plan view). In this appendix, we propose a list of necessary modifications for the reverse scanning, that is the clockwise scanning with the $x_s$ axis pointing upwards:

• The rotation matrix in Eq. (9) is defined as

  $$\begin{aligned} \begin{aligned} \mathbf {R}^{s'_{i-1,2}}_{s'_{i1}}&=(\mathbf {R}^{b}_{g_{i-2,2}}\mathbf {R}_y(\pi ) )^{\mathrm T}\mathbf {R}^{b}_{g_{i-1,2}}\mathbf {R}_y(\pi ) \\&= \mathbf {R}_y^{\mathrm T}(\pi ) \mathbf {R}^{g_{i-2,2}}_{g_{i-1,2}} \mathbf {R}_y(\pi ) . \end{aligned} \end{aligned}$$

  (27)

• The local rotation matrix in Eq. (15) is defined as

  $$\begin{aligned} \begin{aligned} \Delta \mathbf {R}^s_{s'} = \mathbf {R}_y(\alpha )\mathbf {R}_x(-\beta ). \end{aligned} \end{aligned}$$

  (28)