Abstract
Recent years have seen the wide diffusion of composite materials in many manufacturing fields and the rapid evolution of additive manufacturing. Lately, these technologies have been combined practically allowing the fabrication of continuous-fiber reinforced polymer parts via 3D-printing. This topic is gaining attention both in the research community and among industrial users. Because of their novelty, such manufacturing methods are, however, still not thoroughly understood, and their performance limits have not yet been fully characterized. This study aims at analyzing the mechanical resistance of components made with continuous carbon fiber (CCF) thermoplastic materials by means of fused filament fabrication (FFF), focusing on the influence of the fiber orientation on such properties. In particular, both the tensile and the bending characteristics are evaluated according to the relative test standards, in specimens with both unidirectional and mixed-isotropic configurations. The experimental findings are compared with a set of reference specimens made with a base polymer filled with chopped “short” carbon fibers, allowing one to appreciate the advantages or limitations of the different fiber arrangements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, additive manufacturing (AM) of reinforced thermoplastics has seen a rapid growth, garnering increased interest among researchers and developers. What is attractive is the possibility of combining the wide range of composite materials available today with a versatile manufacturing process that also allows flexibility in the design of components. AM is indeed characterized by two pivotal features: direct manufacturing and layer-wise processing [1, 2], it being defined as the process of creating parts by depositing material layer upon layer, starting from digital 3D model data. Among all the AM technologies for fabricating polymer components, fused filament fabrication (FFF, also known as fused deposition modeling—FDM) is widely diffused [3]. FFF is advantageous thanks to its process flexibility, robustness and reliability, low material wastage, and relatively low cost of printers and consumables [4, 5].
In this scenario, 3D printing of thermoplastic-polymer composites is becoming a more and more promising solution for turning AM from a prototyping technology to a fabrication process to be implemented for real-world applications. As also recently pointed out by Fidan et al. [6], the developments in additive technologies have accompanied the evolution of the materials processable, progressively allowing the filling of thermoplastic filaments, such as nylon, polylactic acid (PLA), acrylonitrile butadiene styrene (ABS), polyether ether ketone (PEEK), with various filler-type reinforcements, such as short fibers including carbon fibers [7,8,9], glass fibers [10], carbon nanotubes [11], or even natural fibers [12].
Since 2015, several companies have started to develop systems for the fabrication of composite parts employing the technology commonly named continuous fiber additive manufacturing (CF-AM). This is substantially an evolution of FFF, whereby continuous high-resistance fibers are deposited together with a thermoplastic material acting as the matrix of the composite. This process yields components having remarkable mechanical properties in the direction of the reinforcement fibers [13].
Two systems employing fiber-laydown methods are used today: the first is based on the deposition of fibers utilizing a 6-DOF robot arm (e.g., Continuous Composites, Moi Composites); the second performs the deposition of fiber by means of a standard 3D printer (e.g., Markforged, Anisoprint, Desktop Metal). The present work concentrates on the latter type of systems.
Justo et al. [14] and Blok et al. [15] documented the enhancement of the mechanical properties of components manufactured via CF-AM, respectively, for the tensile and compressive case, and the bending and shear case. In both cases, the specimens were produced by using a MarkOne FDM 3D-printer (Markforged), limiting the analyses to a unidirectional alignment of the fibers. Over time, different authors have focused their attention on many aspects of interest related to the printing criteria/process parameters to adopt in AM of composites. Chacón et al. [16] performed extensive testing of specimens in tensile and three-point bending conditions to assess the effect of build orientation (i.e., “flat” or “on-edge,” with respect to the printing bed), layer thickness, and fiber volume content on the mechanical performance of components made via FFF. The influence of other process parameters such as the build orientation on the impact resistance of 3D-printed composites was investigated by Caminero et al. [17]. In a parallel study, the same authors also examined the interlaminar bonding performance of such materials, relating their behavior to process parameters such as layer thickness and fiber volume fraction [18]. Dickson et al. [19] compared different types of fibers (glass, carbon, and Kevlar), testing tensile and flexural specimens having a unidirectional arrangement of the fibers, by varying the number of built layers. Materials similar to the latter were also evaluated for creep and fatigue by Mohammadizadeh et al. [20]. The flexure behavior of 3D-printed specimens reinforced with continuous glass or carbon fibers, arranged unidirectionally, was then studied by Goh et al. [21]. Araya-Calvo et al. [22] specifically investigated the compressive and flexural response of CF-AM 3D-printed parts, focusing on the effect of factors such as the reinforcement type and its distribution inside the specimen bulk. Yu et al. [23] focused on the influence that the number of fiber layers and concentric Onyx rings has on mechanical properties. Al Abadi et al. [24] performed experimental testing and developed an analytical model to help to predict the elastic properties of CCF components.
The typical fabrication constraints of CF-AM systems imply that the fibers need to be cut at the end of each layer to allow the repositioning of the extrusion head. This constraint, in turn, translates to strongly orthotropic physical properties. Moreover, the fiber orientation with respect to the main loading direction has a profound impact on the final resistance of parts. In practical applications, it is rarely the case that the loads acting on a structure can be predicted with total certainty and provisions are typically made to ensure the structure withstands loads in other directions besides the principal ones. In composite components manufactured with traditional technologies, this issue is solved with mixed layups with up to four different fiber orientations. Stacking layers of fibers with varying orientations achieves the same effect in parts made via CF-AM.
Finding literature studies that comprehensively describe such situations is still difficult. Indeed, to the best of the authors’ knowledge, the only studies that considered such an aspect were those by Mei et al. [25], Pyl et al. [26], and Todoroki et al. [27]. Mei et al. [25] evaluated the tensile properties of mixed-isotropic 3D-printed composites after hot pressing. Pyl et al. [26] carried out studies on the effect of mixed fiber orientations (mainly focused on investigating aspects such as specimen geometry and tab configuration for tensile testing of CCF composites), but, once again, the data are to be considered as preliminaryFootnote 1. Similar tests were carried out by Todoroki et al. [27] with three fiber orientations, only for the tensile case.
The main results found in the literature are summarized in Table 1. Interestingly, a broad diversity of results can be observed, in the numerical values of the tensile and flexural strengths, and in the testing methodologies and testing approaches. Most tests were carried out with a limited number of samples (generally lower than or equal to three), and no comprehensive study with both tensional and flexural tests has yet been conducted. Moreover, nine out of the twelve works focused on CCF composites available in the literature only consider the case of the reinforcement fibers aligned to the loading direction.
This situation is problematic from a design standpoint because a clear indication of the ultimate strength of the given material is of utmost importance. Furthermore, this type of data is essential for structural simulations. The need to fully characterize the material properties, therefore, led us to conduct this study. More in detail, the current work aims at identifying how the change of fiber direction with respect to the main loading direction affects the mechanical properties of the resulting components, and at characterizing the effect of combining multiple layers of fibers with different orientations. This work concentrates on the use of carbon fiber as the reinforcing material.
2 Experimental set-up and mechanical evaluation
In this work, two types of filaments supplied by Markforged® (Watertown, MA, USA) were employed to build the specimens:
-
A Nylon filament reinforced with chopped carbon fiber, traded as Onyx, having a nominal diameter of 1.75 mm
-
And continuous carbon fiber (CCF) embedded in a Nylon matrix, which came in a diameter of 0.35 mm
Prior to their use, the filaments were stored in a protective dry box, to avoid ambient humidity absorption. For the same reason, before each test, all the specimens were further dried for 1.5 h at 80 °C.
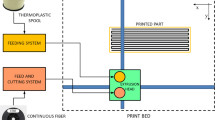
To print the carbon fiber reinforced thermoplastic (CFRT) composite specimens, a Mark Two (Markforged® Inc., Watertown, MA, USA) FFF desktop 3D-printer was used (Fig. 1). This device is equipped with two separate extrusion nozzles, one for Onyx and one for the CCF-reinforced wire. The temperature of the printing heads for the Onyx and the continuous-fiber reinforced filament was set to 265 and 270 °C respectively, whereas the printing bed was non-heated.
Markforged® Mark Two FFF desktop 3D-printer. a General view and b scheme of the printing process (adapted with permission from [17])
The accompanying slicing and pre-processing software, Eiger®, was used to set and adjust the most important printing parameters. Among these, the fiber type, fill mode and fiber orientation, number of layers, number of Onyx rings to generate the outer shell can be cited. The thickness of each layer was set to 0.125 mm for both Onyx and CCF, to make the results comparable between different builds.
The specimen geometries were specifically created via CAD software (SolidWorks 2016, Dassault Systems), exported as a stereolithography file (STL) and imported into Eiger®. Different configurations of test specimens were built to exhaustively characterize the 3D-printed composite parts and, specifically, evaluate the influence of the fiber orientation on their tensile and flexural resistance. Each set of samples was built on subsequent planes along the z-direction, each parallel to the printing bed (“flat” build mode): the CCF layers were laid down horizontally and continuously, with a fill type defined as “Isotropic”Footnote 2 within the Eiger® software. Hence, following the design rationale graphically summarized in Fig. 2, the fiber was at first arranged, layer by layer, according to unidirectional orientations: 0°, 90°, or 45° angle with respect to the longitudinal direction of the specimen. Various combinations of the previous orientations were then considered in order to increase progressively the isotropy of the test specimens. This was done to better characterize the specific contribution of each fiber orientation to the mechanical response of the multilayer material. Specifically, two sets of specimens having [0°/90°]n and [+45°/-45°]n sequences (repeated n-times to generate the desired thickness) were printed, and a mixed-isotropic fiber pattern [0°/90°/+45°/-45°]n, was also produced. Besides, a further set of samples made according to a CCF pattern [0°/+45°/90°/-45°]n was generated to evaluate whether the change of the lay-down base sequence affects the mechanical performance of the mixed-isotropic material.
The printing criteria followed by Eiger® obliges the user to print every component by adding an outer protective shell made exclusively with the Onyx material (with layers arranged at angles +45° and -45° alternatively with respect to the axial direction), the extent of which is defined as a set-up parameter. In particular, each specimen was built with four Onyx layers on the bottom (“floor”) and four Onyx layers on the top (“roof”). The floor layers avoided any fiber breakage while removing the specimen from the platform, whereas the roof layers were chosen for dimensional accuracy and symmetry. Furthermore, each layer built was made as a combination of two infill arrangements of the material: the infill made of CCF laid following one of the aforesaid sequences; and a concentric infill, consisting of two Onyx rings placed along the specimen perimeter (Fig. 3).
To assess the performance of the AM composite material, tensile and three-point flexural test specimens were built according to the geometries suggested by the related standards, following the testing scheme summarized in Table 2. Each configuration and testing condition was repeated five times (N = 5), to enhance the accuracy of the results. The mean resistance values are reported in the “Results” section, together with the related values of standard deviation.
An Instron 8802 universal testing machine (Instron, Norwood, MA, USA), equipped with a 50 kN load cell, was used to perform all the mechanical assessments.
Tensile testing was carried out on parallelepiped specimens of dimensions 157 mm × 16 mm × 3 mm, in accordance with the indications provided by ASTM D3039 [28]. To obtain a proper CCF/Onyx ratio, the thickness was achieved by superimposing a total of 24 layers, each 0.125 mm thick, arranged as follows: 4 floor layers of Onyx, 16 CCF core layers, and 4 roof layers made of Onyx. These tensile specimens were then tested to failure at a crosshead displacement rate of 2 mm/min, and the results were compared with those obtained from a set of reference specimens having the same geometry and size as the CCF-samples but made only of Onyx. Metallic tabs were bonded at the grip areas to avoid any crushing or shifts of the sample during the tests. Having defined F as the force measured by the load cell and A as the sample cross-sectional area, tensile stress was calculated as σ = F/A.
To determine the flexural properties of the material, specimens having dimensions 153.6 mm × 14 mm × 4 mm were built, following the indications provided by ASTM D7264 [29]. In this case, the thickness was obtained as a superposition of 32 layers—again 0.125 mm in thickness each—comprising 4 floor layers of Onyx, 24 core layers made of CCF, and 4 roof layers of Onyx. A three-point loading test method was carried out (Fig. 4). Thus, according to the aforesaid standard, the radius of both the loading nose and the two support rollers (bending dies) was 5.0 mm, and the specimens were tested guaranteeing a span-to-thickness ratio (L/t) of 32:1 (i.e., a span between the supports equal to 128 mm). The crosshead (loading nose) movement speed was set to 1.0 mm/min.
During bending, the test specimen behaves as a beam simply supported at two points and loaded at the mid-span. Thus, the bending moment increases from the support points to a maximum value at the mid-point: maximum stress occurs along a line at the center of the test specimen/beam, where the flexural stress, σf, is calculated with the following simplified equation [30, 31]:
where P is the load (N) corresponding to a deflection δ (mm), L is the length of the support span (mm), w and t are, respectively, width and thickness of the test specimen (mm), for a bending moment M equal to PL/4. However, when L/t exceeds 16:1 (as in this investigation), Eq. (1) has to include additional terms in order to take into account the significant end forces developed and relatively large deflections at the support noses [32]. It follows that, as also suggested by the ASTM D790 [33] standard, σf has to be calculated using the following equation:
where δ is the deflection of the centreline of the specimen at the mid-span (mm). The corresponding strain value at the outer surface is calculated as follows:
3 Results and discussion
3.1 Effect of the fiber arrangement on the tensile properties
Table 3 reports the results of the tests on the tensile performance of the specimens, having different fiber orientations with respect to the principal loading direction.
A set of Onyx-only specimensFootnote 3 was also included in the analysis to provide reference values for the mechanical properties of the base material. Specifically, Fig. 5 depicts the stress-strain curves acquired by testing five repetitions (from N01 to N05) of the reference Onyx sample.
3.1.1 Unidirectional configurations of the tensile specimens
Among all the unidirectional configurations examined (Fig. 6), the 0°-orientation of the CCF proved to be most efficient in providing resistance and stiffness to the composite material, since the fibers were aligned with the direction of the applied load. With the longitudinal arrangement, most of the overall strength was due to the carbon fibers alone rather than to the Nylon matrix, which did not seem to play a significant role in the specimen performance. This aspect is all the more evident by observing both the related stress-strain curves and typical failure modes, which make it clear that properties such as high strength and stiffness, along with little deformation capability, led to sudden, brittle rupture of the specimens as soon as breakage of the reinforcement fibers occurred.
The effectiveness of the 0°-configuration is particularly evident if compared with the other specimens with unidirectional fiber arrangements. Indeed, the variation of both strength, σ, and elastic modulus, E, was not linear with the angle between the load and fibers direction. Notably, when increasing the fiber angle to +45°, a rapid loss in mechanical resistance was observed, resulting in an average σ-value that was only 8.4% more than that of the Onyx-only samples. Also E reduced significantly, standing at 3.33 GPa on average, i.e., only three times higher than that of the reference and eight times lower than the 0°-CCF. Such a condition was further emphasized by the 90°-orientation of the CCF. The latter led to strength values that were just over half of those recorded by testing the reference Onyx specimens (42.3 MPa).
Comparing the +45°- and 90°-CCF cases, it is possible to note that they shared a similar failure behavior, characterized by matrix debonding as a consequence of the progressive distancing of fibers initially adjacent. The slight difference in performance between the two, of course, has to be related to the direction of the fibers embedded in the sample core relative to the load applied. In particular, with a 90°-orientation of the CCF (i.e., perpendicular to the load direction), the mechanical behavior of the specimen proved to be worse than that of a polymer reinforced with chopped fibers, since the CCF is not oriented in such a way as to explicate its role in the ultimate resistance of the composite material. Indeed, as also observable from the related failure mode, the fracture ran transversally to the principal specimen/load direction. As mentioned above, also the +45°-CCF specimens showed similar fractures but cracks developed diagonally, according to the fiber lay-down configuration. Thus, in both cases, the detachment of the two parts occurred as soon as the failure of the polymer matrix had taken place.
The reason for such a remarkable difference between the latter cases and the reference is twofold. Concerning mechanical strength, it should be taken into account that the short fibers embedded in the nylon matrix are directly involved in the mechanical performance of the Onyx-only specimen, these being oriented along the filament direction during extrusion. From a deformation point of view, it is worth noting that the presence of the CCF unavoidably increases the constraint grade within the material; it follows that the +45°- and, notably, 90°-orientations of the reinforcement alone are not only ineffectual but even detrimental since the fibers do not allow the matrix to deform. This greatly reduces the overall ductility of the so-loaded material and makes ultimate resistance of the specimen only dependent on the effectiveness of the matrix-to-fiber interfacial conditions on cross-sectional/diagonal planes.
3.1.2 Multidirectional configurations of the tensile specimens
Each tensile sample was designed with both a concentric and mixed isotropic infill, where the latter was made by superimposing 16 CCF layers, with the following base sequences: [0°/90°], [+45°/-45°], [0°/90°/+45°/-45°], or [0°/+45°/90°/-45°].
The stress-strain curves and failure modes of both the sets of samples built using bidirectional sequences of the fibers are shown in Fig. 7.
Given the symmetry of the layer number and orthogonality of the fibers, the specimens made according to the sequence [0°/90°] exhibited characteristics almost averaging those of the constituting base patterns. In particular, tensile strength stood at 308.9 MPa, namely, 45.4% lower than that of the 0°-CCF samples; similarly, the elastic modulus was 62.4%. In contrast, the maximum strain achieved by the multilayer samples stood at values (2% on average) that were almost comparable to those reached with the unidirectional 0°-CCF samples, suggesting that most of the deformation is related to that of the continuous fibers on the corresponding layers. Such behavior finds confirmation in the failure mode, which was mixed in type, involving fiber breakage at the 0°-CCF layers along with transversal matrix-to-fiber debonding at the 90°-CCF layers.
The [+45°/-45°] configuration was selected to evaluate the response of the previous configuration when subjected to a load applied diagonally with respect to the direction of the fibers. Compared with the +45°-CCF pattern alone, the adoption of a symmetric configuration enhanced toughness, improving both tensile strength (+41.4%) and maximum strain (+78.6%). Also, the failure behavior appeared to be different from the previous, since fractures mainly occurred on interlayer planes rather than at the diagonal section. This might explain the increased deformability shown by the material, presumably related to shear phenomena between subsequent layers, which made the fibers stretch with respect to the original orthogonality, causing them partly to break.
It is well known that, owing to the different possible loading modes and directions, most composite structures cannot be built following pre-defined orientation of the reinforcement fibers. Moreover, rigid design considerations have to be faced even when a prevalent direction of the fibers is to be defined, since it might lead to undesired loss of flexibility of the structure. This limitation pushes designers and manufacturers to build traditional CFRP parts by stacking the carbon plies to obtain a more isotropic behavior for the components. Transposing such considerations to additive manufacturing, a multidirectional set of specimens, characterized by a combination of the CCF orientations previously analyzed—[0°/90°/+45°/-45°]—was made. In Fig. 8, the stress-strain curves acquired during tensile testing are displayed, and a typical rupture zone of a multidirectional, quasi-isotropic test specimen is shown.
As expected, such a multilayer configuration seemed to mediate the tensile behavior of the unidirectional-CCF samples, summarizing the observations made on their two-by-two coupling. Indeed, the tensile strength of the mixed-oriented CCF set stood at 192.5 MPa on average, namely, 37% lower than the bidirectional [0°/90°]-CCF specimens, but almost three times higher than that obtained arranging the fibers according to a [+45°/-45°] pattern. Failure analysis demonstrated that each layer had contributed differently to the overall resistance of the additively built structure of the specimen: in accordance with the previous observations, transversal detachment of adjacent fibers occurred on layers having 90°-CCF laydown, whereas net fiber breakage was detected on the ±45°- and, notably, 0°-oriented layers. However, despite the presence of multiple-orientation patterns, one may reasonably deem that, even in this case, the layers having the fibers aligned with the load direction affected the overall resistance of the laminate most significantly. Indeed, longitudinal fibers enhanced the specimen stiffness and resistance, allowing it to bear load levels that were remarkably higher than those responsible for the failure of the 90°-CCF or ±45°-CCF specimens. Therefore, one believes that the ultimate resistance of the laminate was reached as soon as the 0°-oriented fibers alone (on the relative layers) failed, entailing the sudden, brittle rupture observed. Similarly to that concluded regarding the [0°/90°] case, this would explain why the strain values related to this mixed pattern appeared almost the same as those acquired testing the 0°-CCF configuration: the longitudinal fibers, preventing the other layers from deforming, limited the overall sample strain capability. It is also worth noting that such behavior was not affected by the base sequence adopted to print the mixed isotropic specimens; indeed, as reported in Table 3, tensile testing of specimens having a [0°/+45°/90°/-45°] pattern provided for σ, ε, and E values that were almost the same as those obtained from samples having base sequence [0°/90°/+45°/-45°].
3.2 Effect of the fiber arrangement on the flexural properties
The same various CCF orientations were adopted to build flexural samples having the dimensions described in Section 2, and a three-point flexure method was used to test them. Bending tests also highlighted how much the fiber orientation affects the mechanical response of the printed composite material, in terms of both flexural stress and strain capability. As a result, the stress-strain curves displayed in Figs. 9 and 10 were acquired, and the related maximum values of flexural strength, σf, and flexural elastic modulus, Ef, were extracted and summarized in Table 4.
3.2.1 Unidirectional configurations of the flexural specimens
The flexural stress-strain curves of the sets of samples printed using unidirectional arrangements of the fibers are displayed in Fig. 9. In accordance with the tensile findings, the 0°-oriented specimens resulted in a high stiffness, with average maximum flexural stress σf of 340.7 MPa. It was especially interesting to observe that, in this case, failure occurred as soon as maximum compression load was reached, owing to the sudden breakage of the carbon fibers.
Contrariwise, with the +45°-orientation, maximum σf registered stood at 92.0 MPa, whereas flexure elastic modulus, Ef, was equal to 3.32 GPa. It should be noted that the diagonal CCF disposition typical of this configuration introduced an unbalanced condition in the specimen, making it twist around its longitudinal axis during bending. Such behavior led to sudden sliding of the beams from their position, causing the test interruption, despite the sample still being intact. Nevertheless, although it was not possible to experimentally evaluate the deformability of such configuration from that point on, based on the similarity of their flexural modulus, one can reasonably believe that the +45°-CCF samples would have presented flexural behavior resembling that of the 90°-CCF samples. Concerning the latter case, the so-made material led to an average maximum value of σf equal to 51.8 MPa and Ef equal to 2.13 GPa. With the transversal configuration of the CCFs, the specimens showed completely ductile behavior, which in fact did not allow the test to complete before the loading nose had reached the end limit of the testing machineFootnote 4.
Since the samples of the two types above were still undamaged after flexure, they were further bent to 180° using a press to make them fail. In both cases, fracture occurred along the cross-section (transversal and diagonal, respectively), in accordance with that already observed on the corresponding tensile specimens.
3.2.2 Multidirectional configurations of the flexural specimens
From the flexural characterization of the multidirectional configurations considered, similar conclusions to those drawn after tensile testing were possible. In this regard, the reader is invited to refer to Fig. 10, which displays the flexural stress-strain curves acquired from bending tests performed in the four cases mentioned above.
The [0°/90°] sequence provided for stiff, high-resistant composite beams, the flexural strength and modulus of which stood at 241.2 MPa and 14.62 GPa on average, respectively. Also under such load conditions, failure occurred as a consequence of a mixed type fracture, from the observation of which it may be concluded that fibers arranged longitudinally affected the flexural resistance of the beam more.
In contrast, with the [+45°/-45°] orientation, maximum σf was −57.8% of that of the previous case. However, a remarkably higher ductility was observed (Ef stood at 3.25 GPa), and once again the test did not conclude with the specimen rupture. As previously done, the unbroken specimens were further bent to 180° using a press, but no failure occurred. Although qualitative, this result led us to reasonably conclude that a mixed-diagonal disposition of the fibers performs better than a single-diagonal one, providing for a more balanced structure of the beam core, contrasting its torque during bending.
The aforesaid observations converged when the quasi-isotropic [0°/90°/+45°/-45°] sequence was tested for bending (Fig. 11). As expected, the flexure-test results confirmed that the strength and stiffness of the material are significantly dependent on the CCF-laydown used to build each layer. An average flexural strength σf equal to 223.7 MPa was obtained, showing slightly higher deformation than that achieved before failure by the [0°/90°] configuration. This is presumably due to the further [+45°/-45°]-layer contribution. Also in this case, the modification of the base sequence with the [0°/+45°/90°/-45°] pattern did not determine significant variations in the flexural behavior of the specimens, providing for values of both σf and Ef that were almost comparable to those of the base layer sequence previously analyzed.
Hence, regardless of the layer sequence employed, the experimental findings lead one to conclude that the advantages of a mixed-CCF configuration are more emphasized in flexure rather than in traction. Indeed, in the latter, it was observed that the layers having longitudinal fibers were those bearing almost all of the load applied. Contrariwise, the flexural behavior of the beam was considerably improved by superposing layers with multiple, alternate orientations of the continuous fibers, which seemed to collaborate better with each other, providing the best balance between resistance and deformability of the beam.
3.3 Summary considerations: performance, current limitations, and future developments
The experimental results of both testing campaigns carried out are summarized in Fig. 12, in which the typical stress-strain curves acquired adopting the different CCF orientations previously described are compared with each other. It was also considered of remarkable interest to provide the relevant characteristics in the form of radar plots, in order to graphically transpose the unidirectional loading conditions of tests to a more representative situation in which multidirectional loads can occur on the printed laminate. Despite the latter still being an approximation of a real condition, such an on-plane representation emphasizes how a multi-oriented CCF composite exhibits a quasi-uniform response to the load applied. Therefore, starting from the typical fabrication criteria adopted for traditionally manufactured CFRP parts, the results confirmed that mixed orientations of the CCF may be successfully implemented as a practical and effective building criterion in additive manufacturing of composite structures. This helps designers to provide for more isotropic components able to be subjected to multiaxial stress states thanks to compromise features of strength and stiffness. However, it was noted that the advantages of such configurations (and, notably, of the quasi-isotropic layer sequence) reflect more on the flexural properties than on the tensile behavior, on the basis of the better collaboration between the differently oriented layers built observed during bending.
Summary of the results obtained from (a) tensile and (b) flexural testing. Specifically, a comparison between the average stress-strain curves of different fiber orientations is provided: the shaded areas represent the standard deviations of the results for each test condition. Besides, the radar plots graphically report, for each test, the related values of stress (left) and elastic modulus (right) relative to unidirectional, bidirectional or multidirectional arrangements of the CCFs
In view of such observations, additive manufacturing of continuous-fiber composite parts appears to have great potential for the realization of high-complexity structures in several fields, from aeronautics to motorsports, transport or robotics, which, in recent years, are starting to introduce this process into their own productions [13]. Nevertheless, although this method is being increasingly studied today, additive processes for the manufacturing of CFRT are still at an embryonic stage, and the achievement of appropriate characteristics for high-performing applications is often made difficult by some inherent process limitations. The latter are generally related to the fact that the out-of-oven, layer-by-layer fabrication procedure typical of FFF is affected by the cooling of the deposited layer below its glass transition temperature before the following layer is deposited [34]. This may limit the maximum strength achieved by the 3D-printed CCF composites, due to weak interlayer bonding, matrix-matrix or fiber-matrix interactions in portions that may be rich in porosities and voids [18]. The latter are intrinsically due to the printing procedure, in which neither pressure nor external heating is applied after the layer is laid down. In principle, this aspect defines the current performance threshold for the application of AM composites, especially when these are used to generate more complex geometries that may require assembly of different 3D-printed parts, e.g., adopting adhesive-bonding processes [35]. Therefore, further improvement in the mechanical performance of such materials might be obtained by implementing the process with a hot-press post-compaction of the laminates, currently subject of further investigation by the authors. This approach might be a promising solution for turning AM from a prototyping technology to a fabrication process to be widely implemented in industry, allowing the realization of composite materials having characteristics equivalent to those of the more conventional composites.
4 Conclusions
This study aimed at evaluating the influence of the orientation of continuous carbon fibers (CCF) on the mechanical response of composite materials 3D-printed via FFF technology. In particular, both the tensile and the flexural behavior was evaluated according to the relative test standards, building test specimens having various configurations: three unidirectional laydown patterns of the CCF (0°, +45°, and 90°) were set as references, and further mixed-oriented configurations ([0°/90°], [+45°/-45°], [0°/+45°/90°/-45°], and [0°/+45°/90°/-45°]) were considered to represent the more common building approaches adopted for most composite structures.
The experimental findings highlighted that:
-
In tensile conditions, the use of a unidirectional disposition of the continuous fibers is justified only if these are aligned with the load applied. In this condition (0°-oriented CCF), the composite exhibits high strength (σ=566 MPa) and stiffness (E=24.2 GPa). In turn, when varying the orientation of the CFF to a diagonal (45°-oriented CCF) or a transversal (90°-oriented CCF) one, the tensile strength obtained might be insufficient for most of the structural applications in which continuous carbon-fiber composites are used (respectively, only 8.2% and 4.2% of that of the 0°-CCF configuration). With respect to specimens only reinforced with chopped carbon fibers (Onyx), notably, only slight improvements were achieved by employing a +45°-CCF pattern (+9.2% in tensile strength), whereas the 90°-disposition of the fibers did not lead to any advantage, even resulting detrimental in terms of resistance (-44.0%) and deformability (-86.4%) of the laminate.
-
In flexural-load conditions, the highest resistance was achieved with a 0°-pattern of the CCF (σf = 340.7 MPa), at the expense of the deformation capability. The latter is instead a prerogative of the +45°-CCF and 90°-CCF configurations, for which no sign of failure was observed until the end of the standard flexural testing. It is also worth noting that +45°-CCF disposition led to an asymmetrical condition that caused beam torque during bending.
-
Adoption of mixed orientations of the CCF is recognized as a promising solution for the realization of balanced laminates able to be subjected to multiaxial stress states, thanks to compromise properties of strength and stiffness in both traction and flexure. However, it was noted that the advantages of such configurations (notably, of the quasi-isotropic layer sequences, [0°/90°/+45°/-45°] and [0°/+45°/90°/-45°]) reflect more on the flexural properties than on the tensile behavior, owing to a better collaboration between the different oriented layers built observed in the former case.
Data Avaialbility
Data can be made available upon request subject to approval of all parties involved in the research.
Notes
Describing the rationale of the experiment design, the authors state that “For these orientations, only a limited number of tests was performed as it was only for an initial estimation of the mechanical properties. More tests should be done for a full characterization.”
It should be noted that the term “Isotropic” is a label given to the fiber pattern by Markforged® and it does not define the mechanical properties of the final test specimen. In fact, an “isotropic” fill type determines the creation of a test specimen having a unidirectional laydown of the continuous fibers, thus resulting in anisotropic behavior of the specimen.
To make the results comparable, such control samples were manufactured by laying two concentric rings to generate the outer perimeter shell, filling the core of each specimen with Onyx
This also led us to consider it meaningless to adopt an Onyx-only configuration as a reference and, thus, not to test any specimen of this kind for flexure
References
Quan Z, Wu A, Keefe M, Qin X, Yu J, Suhr J, Byun JH, Kim BS, Chou TW (2015) Additive manufacturing of multi-directional preforms for composites: Opportunities and challenges. Mater Today 18:503–512. https://doi.org/10.1016/j.mattod.2015.05.001
Singh R, Singh S, Singh IP, Fabbrocino F, Fraternali F (2017) Investigation for surface finish improvement of FDM parts by vapor smoothing process. Compos Part B Eng 111:228–234. https://doi.org/10.1016/j.compositesb.2016.11.062
Suárez L, Domínguez M (2020) Sustainability and environmental impact of fused deposition modelling (FDM) technologies. Int J Adv Manuf Technol 106:1267–1279. https://doi.org/10.1007/s00170-019-04676-0
Urbanic RJ, Saqib SM (2019) A manufacturing cost analysis framework to evaluate machining and fused filament fabrication additive manufacturing approaches. Int J Adv Manuf Technol 102:3091–3108. https://doi.org/10.1007/s00170-019-03394-x
Parandoush P, Lin D (2017) A review on additive manufacturing of polymer-fiber composites. Compos Struct 182:36–53. https://doi.org/10.1016/j.compstruct.2017.08.088
Fidan I, Imeri A, Gupta A, Hasanov S, Nasirov A, Elliott A, Alifui-Segbaya F, Nanami N (2019) The trends and challenges of fiber reinforced additive manufacturing. Int J Adv Manuf Technol 102:1801–1818. https://doi.org/10.1007/s00170-018-03269-7
Ferreira I, Madureira R, Villa S, de Jesus A, Machado M, Alves JL (2020) Machinability of PA12 and short fibre–reinforced PA12 materials produced by fused filament fabrication. Int J Adv Manuf Technol 107:885–903. https://doi.org/10.1007/s00170-019-04839-z
Tekinalp HL, Kunc V, Velez-Garcia GM, Duty CE, Love LJ, Naskar AK, Blue CA, Ozcan S (2014) Highly oriented carbon fiber-polymer composites via additive manufacturing. Compos Sci Technol 105:144–150. https://doi.org/10.1016/j.compscitech.2014.10.009
Li Q, Zhao W, Li Y, Yang W, Wang G (2019) Flexural properties and fracture behavior of CF/PEEK in orthogonal building orientation by FDM: Microstructure and mechanism. Polymers (Basel) 11. https://doi.org/10.3390/polym11040656
Zhong W, Li F, Zhang Z, Song L, Li Z (2001) Short fiber reinforced composites for fused deposition modeling. Mater Sci Eng A 301:125–130. https://doi.org/10.1016/S0921-5093(00)01810-4
Pidcock GC, in het Panhuis M (2012) Extrusion printing: extrusion printing of flexible electrically conducting carbon nanotube networks (Adv. Funct. Mater. 22/2012. Adv Funct Mater 22:4789. https://doi.org/10.1002/adfm.201290133
Zandi MD, Jerez-Mesa R, Lluma-Fuentes J, Jorba-Peiro J, Travieso-Rodriguez JA (2020) Study of the manufacturing process effects of fused filament fabrication and injection molding on tensile properties of composite PLA-wood parts. Int J Adv Manuf Technol 108:1725–1735. https://doi.org/10.1007/s00170-020-05522-4
Saroia J, Wang Y, Wei Q, Lei M, Li X, Guo Y, Zhang K (2020) A review on 3D printed matrix polymer composites: its potential and future challenges. Int J Adv Manuf Technol 106:1695–1721. https://doi.org/10.1007/s00170-019-04534-z
Justo J, Távara L, García-Guzmán L, París F (2018) Characterization of 3D printed long fibre reinforced composites. Compos Struct 185:537–548. https://doi.org/10.1016/j.compstruct.2017.11.052
Blok LG, Longana ML, Yu H, Woods BKS (2018) An investigation into 3D printing of fibre reinforced thermoplastic composites. Addit Manuf 22:176–186. https://doi.org/10.1016/j.addma.2018.04.039
Chacón JM, Caminero MA, Núñez PJ, García-Plaza E, García-Moreno I, Reverte JM (2019) Additive manufacturing of continuous fibre reinforced thermoplastic composites using fused deposition modelling: Effect of process parameters on mechanical properties. Compos Sci Technol 181:107688. https://doi.org/10.1016/j.compscitech.2019.107688
Caminero MA, Chacón JM, García-Moreno I, Rodríguez GP (2018) Impact damage resistance of 3D printed continuous fibre reinforced thermoplastic composites using fused deposition modelling. Compos Part B Eng 148:93–103. https://doi.org/10.1016/j.compositesb.2018.04.054
Caminero MA, Chacón JM, García-Moreno I, Reverte JM (2018) Interlaminar bonding performance of 3D printed continuous fibre reinforced thermoplastic composites using fused deposition modelling. Polym Test 68:415–423. https://doi.org/10.1016/j.polymertesting.2018.04.038
Dickson AN, Barry JN, McDonnell KA, Dowling DP (2017) Fabrication of continuous carbon, glass and Kevlar fibre reinforced polymer composites using additive manufacturing. Addit Manuf 16:146–152. https://doi.org/10.1016/j.addma.2017.06.004
Mohammadizadeh M, Imeri A, Fidan I, Elkelany M (2019) 3D printed fiber reinforced polymer composites - Structural analysis. Compos Part B Eng 175:107112. https://doi.org/10.1016/j.compositesb.2019.107112
Goh GD, Dikshit V, Nagalingam AP, Goh GL, Agarwala S, Sing SL, Wei J, Yeong WY (2018) Characterization of mechanical properties and fracture mode of additively manufactured carbon fiber and glass fiber reinforced thermoplastics. Mater Des 137:79–89. https://doi.org/10.1016/j.matdes.2017.10.021
Araya-Calvo M, López-Gómez I, Chamberlain-Simon N, León-Salazar JL, Guillén-Girón T, Corrales-Cordero JS, Sánchez-Brenes O (2018) Evaluation of compressive and flexural properties of continuous fiber fabrication additive manufacturing technology. Addit Manuf 22:157–164. https://doi.org/10.1016/j.addma.2018.05.007
Yu T, Zhang Z, Song S, Bai Y, Wu D (2019) Tensile and flexural behaviors of additively manufactured continuous carbon fiber-reinforced polymer composites. Compos Struct 225:111147. https://doi.org/10.1016/j.compstruct.2019.111147
Al Abadi H, Thai HT, Paton-Cole V, Patel VI (2018) Elastic properties of 3D printed fibre-reinforced structures. Compos Struct 193:8–18. https://doi.org/10.1016/j.compstruct.2018.03.051
Mei H, Ali Z, Yan Y, Ali I, Cheng L (2019) Influence of mixed isotropic fiber angles and hot press on the mechanical properties of 3D printed composites. Addit Manuf 27:150–158. https://doi.org/10.1016/j.addma.2019.03.008
Pyl L, Kalteremidou KA, Van Hemelrijck D (2018) Exploration of specimen geometry and tab configuration for tensile testing exploiting the potential of 3D printing freeform shape continuous carbon fibre-reinforced nylon matrix composites. Polym Test 71:318–328. https://doi.org/10.1016/j.polymertesting.2018.09.022
Todoroki A, Oasada T, Mizutani Y, Suzuki Y, Ueda M, Matsuzaki R, Hirano Y (2020) Tensile property evaluations of 3D printed continuous carbon fiber reinforced thermoplastic composites. Adv Compos Mater 29:147–162. https://doi.org/10.1080/09243046.2019.1650323
ASTM International (2014) ASTM D3039 - Standard test method for tensile properties of polymer matrix composite materials. Annu B ASTM Stand. https://doi.org/10.1520/D3039
ASTM International (2007) ASTM D 7264 - Standard test method for flexural properties of polymer matrix composite materials. Annu B ASTM Stand. https://doi.org/10.1520/D7264
Hosseini Monazzah A, Pouraliakbar H, Bagheri R, Seyed Reihani SM (2014) Toughness behavior in roll-bonded laminates based on AA6061/SiCp composites. Mater Sci Eng A 598:162–173. https://doi.org/10.1016/j.msea.2014.01.014
Hosseini Monazzah A, Pouraliakbar H, Bagheri R, Seyed Reihani SM (2017) Al-Mg-Si/SiC laminated composites: Fabrication, architectural characteristics, toughness, damage tolerance, fracture mechanisms. Compos Part B Eng 125:49–70. https://doi.org/10.1016/j.compositesb.2017.05.055
Mehndiratta A, Bandyopadhyaya S, Kumar V, Kumar D (2018) Experimental investigation of span length for flexural test of fiber reinforced polymer composite laminates. J Mater Res Technol 7:89–95. https://doi.org/10.1016/j.jmrt.2017.06.010
ASTM (2017) D790 - Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM Stand 12. https://doi.org/10.1520/D0790-17.2
van de Werken N, Tekinalp H, Khanbolouki P, Ozcan S, Williams A, Tehrani M (2020) Additively manufactured carbon fiber-reinforced composites: State of the art and perspective. Addit Manuf 31:100962. https://doi.org/10.1016/j.addma.2019.100962
Pizzorni M, Parmiggiani A, Prato M (2021) Adhesive bonding of a mixed short and continuous carbon-fiber-reinforced Nylon-6 composite made via fused filament fabrication. Int J Adhes Adhes 107:102856. https://doi.org/10.1016/j.ijadhadh.2021.102856
Acknowledgments
The authors acknowledge prof. Carla Gambaro and her staff at the Department of Mechanical Engineering of the University of Genoa for valuable insights into experiment planning, mechanical testing and data interpretation, and Andrea Furlan for his technical support. The authors also acknowledge Dr. Marco Maggiali of the iCub Tech Facility of Istituto Italiano di Tecnologia (IIT) for helpful discussions.
Funding
Open access funding provided by Università degli Studi di Genova within the CRUI-CARE Agreement. This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.
Author information
Authors and Affiliations
Contributions
Alberto Parmiggiani: Conceptualisation, methodology, supervision, writing—review, validation, resources. Mirko Parto: Conceptualisation, supervision, validation, writing—review. Marco Pizzorni: Conceptualisation, methodology, formal analysis, investigation, data curation, writing, visualization.
Corresponding author
Ethics declarations
Ethical approval
No ethical approval was required for this research
Consent to participate
Not applicable.
Consent for publication
All authors have read and agreed to the published version of the manuscript.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Parmiggiani, A., Prato, M. & Pizzorni, M. Effect of the fiber orientation on the tensile and flexural behavior of continuous carbon fiber composites made via fused filament fabrication. Int J Adv Manuf Technol 114, 2085–2101 (2021). https://doi.org/10.1007/s00170-021-06997-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-021-06997-5