Abstract
During cryogenic turning of metastable austenitic stainless steels, a deformation-induced phase transformation from γ-austenite to α’-martensite can be realized in the workpiece subsurface, which results in a higher microhardness as well as in improved fatigue strength and wear resistance. The α’-martensite content and resulting workpiece properties strongly depend on the process parameters and the resulting thermomechanical load during cryogenic turning. In order to achieve specific workpiece properties, extensive knowledge about this correlation is required. Parametric models, based on physical correlations, are only partly able to predict the resulting properties due to limited knowledge on the complex interactions between stress, strain, temperature, and the resulting kinematics of deformation-induced phase transformation. Machine learning algorithms can be used to detect this kind of knowledge in data sets. Therefore, the goal of this paper is to evaluate and compare the applicability of three machine learning methods (support vector regression, random forest regression, and artificial neural network) to derive models that support the prediction of workpiece properties based on thermomechanical loads. For this purpose, workpiece property data and respective process forces and temperatures are used as training and testing data. After training the models with 55 data samples, the support vector regression model showed the highest prediction accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The surface morphology of a component is significantly influenced by the characteristics of the manufacturing process and has a decisive impact on the application behavior of the component [1, 2]. In order to tailor the surface morphology of a component to the demanded requirements, extensive knowledge regarding the causal correlations between the input variables of the manufacturing process, the acting mechanical, chemical and thermal loads, and their impact on the material properties is essential [3]. Especially for small batch sizes, the determination of suitable process parameters for new demanded requirements tends to be expensive due to a high number of required experiments. In this context, the application of machine learning can help to decrease the required amount of expensive experimental investigations. The presented case study on cryogenic turning focuses on the prediction of the martensite content generated during the process, which is decisive for the surface layer hardening.
1.1 Cryogenic turning of metastable austenitic stainless steels
During the cryogenic turning of metastable austenitic steels, a hardening of the subsurface material can be achieved which is caused by strain hardening mechanisms and deformation-induced phase transformation from metastable γ-austenite to ε- and α’-martensite. Hence, this finishing process allows to integrate surface layer hardening into the machining process and thus renders a separate hardening process such as shot peening obsolete, depending on the requirements on the component surface [4, 5]. It has already been proved that the wear resistance [6] and the fatigue strength [7] of stainless steel components manufactured in this way can be increased. The deformation-induced phase transformation and the resulting increase in microhardness are favored by low temperatures and increasing plastic deformation [8, 9]. During cryogenic turning, a pronounced plastic deformation can be achieved in the workpiece subsurface by applying high process forces, which can be realized by turning with high feed rates and the usage of tools with heavily chamfered or rounded cutting edges [10, 11]. Low temperatures can be ensured when turning with low cutting speeds and applying cryogenic coolants [12]. The impact of different input variables like the cutting parameters [13] or the tool properties [14] on thermomechanical load and the resulting α’-martensite content ξm and the microhardness is already well investigated. However, due to the complex interactions between the stress, strain, and temperature which are distributed inhomogenously depending on time and position and the resulting α’-martensite content ξm [15, 16], these correlations can only partially be determined with parametric models which are based on materials science fundamentals [17, 18]. Quantified models enable the indirect in-situ measurement of the α’-martensite content by measuring the process forces and the temperature. This soft sensor would allow the development of a closed-loop process control for the robust manufacture of stainless steel components with predefined surface morphologies [19, 20]. For these purposes, machine learning provides suitable data-based prediction methods.
1.2 Machine learning in context of manufacturing processes
Machine learning is one of the fundamental methods of artificial intelligence, which includes methods that allow to program computers in a way that they can learn from training data. That means, particular algorithms learn from a training data set and are able to apply the derived knowledge to data sets they have not handled before. This is also known as the process of converting experience into expertise. Machine learning can be grouped into three different learning categories: unsupervised learning, reinforcement learning, and supervised learning [21].
Unsupervised learning is mainly used in case a data set has no specific output value. In unsupervised learning, the algorithms try to reveal similarities or correlations between the input data. The algorithm categorizes data which has something in common with regard to a specific attribute [22]. Concerning reinforcement learning an algorithm or agent produces a sequence of actions. These actions cause a change in an environment which results in a reward or punishment. The goal for the algorithm is to maximize the utility over time; i.e., the agent has to “try out” different strategies to maximize its utility [23].
By using supervised learning, a training data set with input values (features) and corresponding output values (labels) is taken as a basis. An algorithm generalizes the connections and predicts the output when using other input data sets, the so-called test set. Supervised learning is also known as learning from examples [22]. The primary aim of supervised learning is therefore to maximize the accuracy of this prediction. Popular examples using supervised learning algorithms are spam filtering, face and speech recognition, machine translation, robot motion, or data mining [24]. These examples are either a task of data classification [22] or finding a function of a specific data set via regression [23]. An algorithm for solving a classification problem considers a data set (input vectors) and decides which of them belong to a specific class based on the training data set. The main aspect to point out regarding classification problems is the data discreteness; i.e., one example is typically part of one class and classes cover the entire output space [22]. Contrary to this, an algorithm for solving a regression problem generally handles continuous data. Different types of regression methods exist, addressing different forms of the fitted function: simple linear regression, multiple linear regression, or non-linear regression.
Wuest et al. give an overview of applications with regard to the different machine learning categories and consider supervised learning as the predominantly relevant method in manufacturing [25]. Widely used machine learning techniques following the supervised learning approach are for instance support vector machines, random forest algorithms, or artificial neural networks. Support vector machines (SVM) are useful for multidimensional regression problems. Support vector regression (SVR) uses a kernel function to map the problem from its original dimensionality to a higher dimensional space. The SVM algorithm finds the single hyperplane with maximum margins separating, e.g., two data sets [26]. Applications of SVM in machining are, e.g., given by Çaydaş et al. who compared artificial neural networks (ANNs) and SVR for surface roughness prediction in turning [27]. Yeganefar et al. applied ANN and SVR to predict and optimize surface roughness and cutting forces in milling [28]. Remesan et al. applied SVM for classification of thermal error in machine tools [29]. ANN are networks of perceptrons, which consist of a set of input nodes, (McCulloch-and-Pitts)-neurons and a weighted connection between input nodes and neurons. If more than one layer of neurons is used, the network is referred to as multi-layer perceptron (MLP) [22]. ANNs are widely used for the prediction of workpiece properties for machining: for instance, Das et al. examined the impact of different factors on the martensite content, i.e. stress, strain, temperature, chemical composition, and grain size, concluding that especially the applied stress and the temperature had the greatest impact on deformation-induced phase transformation [30, 31]. For this purpose, an ANN is used to solve the regression problems of martensite content within metal microstructures.
Random forest (RF) algorithms are defined as methods that build up a group of tree-structured classifiers with independent identically distributed random vectors. To find the most popular class at a certain input, each tree casts a unit vote [32]. RF are used, e.g., in condition monitoring of belt grinding [33], in quality assessment of resistance spot welding [34], or in microfabrication processes of stents in medical technology [35].
The predictions of these regression algorithms problems can suffer from overfitting, i.e., the model learned the data course of the given data set but not the relationship among the variables, which is why it would not been usable for unseen data sets [23]. The problem of overfitting is especially relevant while handling small data sets. Increasing the size of the data set is a possible measure to tackle this kind of problem. However, in the manufacturing domain, this is not always suitable. For example, the generation of a high amount of data can be hampered by costly experiments or small batch sizes. Besides adding more data, several methods to structure the training process can be used to lower the danger of overfitting: The test set method splits the data into training set and a test set. The model is trained using the training data set, and the performance is tested using the test data set. Other popular methods are the leave-one-out cross validation or the k-fold cross validation [23].
1.3 Research gap
Cryogenic turning enables to shorten process chains by combining the process of turning and subsequent heat treatment. However, current models can only partly describe the functional relationship between process parameters (e.g., forces and temperatures) and the resulting α’-martensite content that largely defines the resulting microhardness. Methods of machine learning are increasingly used in manufacturing to learn functional and often hidden knowledge from data sets. In the case of cryogenic turning, these methods bear potential to derive models from existing experimental data. This can be the foundation for improved predictions of the workpiece properties. Despite this potential, it is an open research question how the selection and configuration of suitable machine learning algorithms need to be carried out in order to deliver a high prediction accuracy in this specific use case.
To address this question, this paper is structured as follows: Section 2 describes the experimental setup that was used to generate a set of data, which is described in Section 3. Afterwards, the three machine learning algorithms are trained to model the relationship between the measured process data and the resulting α’-martensite content ξm (Section 3.2). The prediction performance of the respective models is compared in Section 3.3. Section 4 summarizes the findings and closes with an outlook on future investigations.
2 Experimental setup
The workpieces were turned on a CNC lathe to a final diameter of 14 mm over a feed travel of 18 mm. All experiments were conducted on one batch of metastable austenitic stainless steel AISI 347, because varying chemical composition and grain size influences the austenite stability [8, 37] and hence the amount of deformation-induced α’-martensite generated during cryogenic turning [38]. Bi-phase cryogenic CO2 was supplied with a total mass flow of 3.5 kg/min with a nozzle position that ensures a high cooling efficiency according to Becker et al. [39] (see Fig. 1a). A low cutting speed of 30 m/min and depth of cut of 0.2 mm were chosen, because these parameters ensure a low thermal load and thus a comprehensive phase transformation in the workpiece subsurfaces. Besides these constant cutting parameters, the feed rate, and the duration of precooling were varied in order to manipulate the thermomechanical load and hence the resulting α’-martensite content ξm. Cemented carbide inserts with the specification DNMA150416 were used. The cutting edge geometry and the tool coating were varied to further manipulate the thermomechanical load. The process forces were measured with a 3-component dynamometer. The temperature was measured with thermocouples inside the workpieces at a distance of 1 mm from the surface. A rotating radio unit which was clamped between the chucks was used to transfer the information to a computer. While these measurements do not take an inhomogeneous distribution of stress and temperature into account (see Fig. 1b), they give a good indication of the overall thermomechanical load acting in the workpiece subsurface during cryogenic turning. The α’-martensite content ξm was measured after the experiments with a magnetic sensor. This well-established integral measurement method also does not consider the phase distribution as a function of the distance from the surface but allows a fast and non-destructive estimation of the extent of the phase transformation [40,41,42,43].
3 Machine learning analysis
In this section, the performance of three machine learning algorithms to predict the α’-martensite content ξm based on the experimental data is analyzed.
3.1 Resulting data
The previously conducted experiments (see Hotz et al. [36] for more information) led to a data set with 55 instances, each containing four features (passive force Fp, cutting force Fc, feed force Ff, temperature T) and one label (α’-martensite content ξm). Figure 2 depicts the correlations of the respective features with respect to ξm in a scatter plot. The α’-martensite content ξm of the cryogenically turned workpieces was between 2.1 vol.-% and 12.4 vol.-%, representing a wide range of subsurface states. The measured values are in agreement with previous investigations ([10, 14]). As the figure reveals, trends can be seen regarding the influence of cutting force, passive force, and temperature on deformation-induced phase transformation. However, significant scatter can be observed. It can be assumed that this is a result of the fact that deformation-induced formation of α’-martensite cannot be explained solely by the mechanical or thermal load, but only by their superposition. To quantify the correlation intensity, the Pearson correlation coefficient r between each of the features and the label ξm is calculated. The cutting force shows the highest correlation with a value of 0.726, followed by the passive force (0.680) and then the temperature (− 0.628) which shows a negative trend as opposed to the other parameters. The feed force displays the minimum correlation coefficient (0.107) among the parameters. After investigating the correlations, three machine learning models were trained, which is described in the next subsection.
3.2 Machine learning analysis
The described problem can be interpreted as a regression problem. Furthermore, each feature vector in the data set contains a respective label (α’-martensite content ξm), thus supervised learning can be applied. There is no general approach that fits all supervised regression problems best, since every machine learning problem can be considered to be unique due to varying data set sizes, correlations, and feature characteristics. A common approach to find suitable machine learning models is to train and evaluate several machine learning regression methods with the goal of choosing the model that fits the real observations best. Firstly, to analyze the correlation characteristics in the data, a polynomial regression was performed with an 80 to 20 ratio between train and test data set. For this regression, L1 regularization (“lasso”) was applied to limit the complexity of the resulting model and to prevent overfitting. Root-mean-square error (RMSE) was selected as the corresponding loss function within the regularization. Figure 3 plots the resulting RMSE values that were achieved with polynomial regression models with varying degrees. As the figure indicates, the lowest RMSE results from a polynomial with a degree of 3. However, this RMSE of approximately 12.4% is considered too large to allow suitable predictions of material properties.
Polynomial regression revealed that the correlation between ξm and the measured process is characterized by non-linearities. Therefore, to derive models with a higher prediction accuracy, three major supervised learning algorithm classes that proved their applicability in previous studies (see Section 1.2) were considered for further analyses: SVM, RF, and ANN.
As the data set contains a comparably small number of instances, special attention had to be given to prevent overfitting. For this purpose, randomized sub-sampling (also known as Monte Carlo cross-validation) was used as the cross-validation method. This method was selected over k-fold cross validation, since randomized sub sampling does not affect the resulting ratio between training and testing set size. In consequence, this split ratio could be chosen independently. The data set is randomly split into sub-samples, of which the size can be chosen freely as opposed to k-fold cross validation [29]. According to the definition of randomized sub-sampling, 10 different randomized data set splits were created (see example in Fig. 4).
The same set of 10 randomized splits was then used for training within each algorithm class type. A train-test ratio of 80 to 20% was selected, so all randomized splits contained 44 training and 11 testing instances. For each of the three algorithms, a range of algorithm-specific hyperparameters was iteratively varied for the training processes: The small data set and the small number of hyperparameters being selected for optimization in each algorithm encouraged an exhaustive search or grid search over the selected hyperparameter space. The set of hyperparameters to be searched over for such an optimization was created by iteratively traversing over all possible hyperparameters or hyperparameter combinations over the given hyperparameter ranges, as described in Feurer et l. [44]. This grid search approach is suitable for smaller scale problems and has the advantage that all possible hyperparameter combinations are evaluated exhaustively.
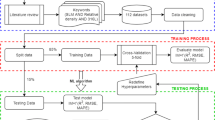
For each iteration, the prediction accuracy was evaluated using the arithmetic mean of the RMSE of the prediction of ξm over all 10 trained models. Afterwards, the hyperparameters that yielded the lowest RMSE values for each algorithm were selected. Additionally, all analyses were performed with as well as without considering the feed force Ff. This was done because reducing the number of features can help to prevent overfitting [45]. Furthermore, Ff showed a weaker correlation with ξm than Fc and Fp. Finally, the results of all three algorithms were compared using RMSE and the coefficient of determination R2 as performance indicators, calculated on the test set. The overview of the approach is shown in Fig. 5.
3.2.1 Support vector regression
The SVR module of the Python library scikit-learn [46] was applied for the analysis. Radial basis function (RBF) was chosen as the kernel function which in turn uses the Gaussian kernel as the kernel function. Using this kernel is common practice in cases of SVR. Since SVM algorithms are not scale invariant, the data was initially standardized.
For tweaking the hyperparameters, the kernel width σ and the regularization parameter C were varied. The other two hyperparameters, namely, the tolerance tol and the epsilon value ε were considered as default (tol = 0.001; ε = 0.1). The selected hyperparameters as well as the impact on RMSE and R2 is shown in Table 1. σ was varied from a range of 0.14 to 1.6 with a step of 0.001, and C was varied from a range of 0.6 to 3 with a step of 0.001.
3.2.2 Random forest regression
The RF algorithm was implemented using the Python library scikit-learn. The maximum number of trees ntrees and the maximum depth of the forest dmax were varied to find the best hyperparameters. ntrees was iterated over in the range of 1 to 200, and a depth equal to the number of features was chosen depending on the data set. The resulting hyperparameters as well as the corresponding results are shown in Table 2.
3.2.3 Artificial neural network
Furthermore, a MLP regression model was trained by implementing a three-layer MLP using the Python library keras [47]. The neurons in the input layer represent the features (Fc, Fp, T, and Ff in case of its consideration). They are connected to the neurons in the hidden layer that are assigned with a tanh activation function. Figure 6 depicts the architecture of the MLP.
The output layer neuron that yields the α’-martensite content ξm is activated by a rectified linear unit (ReLU) function. Several network architectures were evaluated by varying the number of hidden layer neurons from 10 to 100 in steps of 1. In case of Ff consideration, 35 hidden layer neurons were used, while 25 neurons were applied when Ff was neglected. The hyperparameter nEpochs, signifying the number of iterations used for training the MLP, was changed over values ranging from 500 to 5000 in steps of 50 epochs. The resulting minimum RMSE and the respective nEpochs are tabulated in Table 3. In this context, an epoch refers to one complete iteration over the entire train set which is fed to the network in a batch-wise manner. The batch size employed was 1 due to the small size of the data set. Values bigger than 5000 did not lead to better results, which led to the chosen interval. The optimizer used in both cases (with and without Ff) was Adam. Adam is a first-order gradient-based optimization algorithm mainly used for stochastic objective functions. The function principle of Adam is to minimize the training loss function by reducing the magnitude of the 1st order gradient to moving it towards zero. Based on this computation, the weights of the MLP are adjusted. Adam is considered to be very economical with regard to memory utilization and is one of the most widely used optimization algorithms in ANNs [48]. The loss function was the mean squared error (MSE). Table 3 lists the results for the ANN analysis.
3.3 Comparison of results
Figure 7 shows the results of all three algorithms. Overall, SVR that incorporates Ff provides the smallest RMSE value and the biggest coefficient of determination, so it delivers the best accuracy. The accuracy of ANN is slightly lower, while RF yields the least accurate results. It can be seen that considering Ff helps to generally achieve smaller RMSE values. Also, R2 is decreased in all algorithms when considering Ff. In case of ANN, R2 is likely to increase in case of increased data set size. The fact that including Ff improves the RMSE and R2 values lead to the conclusion that this force also has some importance when estimating the α’-martensite content ξm, although it is rather small in comparison to Fc and Fp. However, it is conceivable that the increase in Fp and Fc are of greater significance to the deformation-induced phase transformation, because these greater forces cause more deformation in the workpiece subsurface. This is also indicated by their higher correlation to the α’-martensite content ξm (see Fig. 2).
Regarding computational efforts for 10 iterations, SVR training required the least computing time (18 ms). RF needed 790 ms for training (ntrees = 200), while the ANN required 9 min and 46 s (nEpochs = 2000).
4 Conclusions and future work
Cryogenic turning of metastable austenitic stainless steels allows to integrate the processes of turning and surface layer hardening. In order to manufacture components with defined properties, extensive process knowledge regarding the correlations between input variables, thermomechanical load, and subsurface properties is required. In this work, three machine learning algorithms (SVR, RF, and ANN) were trained and their ability to predict the α’-martensite content as a function of the thermomechanical load was evaluated. The results indicate that in the described case of a low amount of available data (55 instances), SVR provides the most accurate results in terms of RMSE and R2. Randomized sub sampling was found to be a suitable technique to prevent the common risk of overfitting during training. Therefore, this approach can be adapted to other scenarios with small amounts of training data, which is rather common in industrial applications.
With the investigated correlations, it is now possible to determine the α’-martensite content already during machining by means of an indirect measurement of the process forces and the temperatures. Thus, when monitoring variations in the thermomechanical load, which can be caused by disturbance variables such as tool wear, a soft sensor based on the trained models now allows to estimate how this will impact the resulting α’-martensite content. Future investigations aim at developing a process control, which aims at ensuring the robust manufacture of workpieces with defined subsurface properties, despite the occurrence of disturbance variables. Necessities for developing such a process control on the one hand are the correlations between the thermomechanical load and the α’-martensite content, which was demonstrated in this study. The other prerequisite to this approach are correlations between the input machining parameters and the thermomechanical load, which were investigated in previous studies (e.g., [13] and [14]). As both correlations have now been investigated, the next step is the combination of these models and the development and implementation of a soft sensor-based control loop that can be used in industrial applications.
Change history
27 September 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00170-021-08117-9
References
Jawahir IS, Brinksmeier E, M'Saoubi R, Aspinwall DK, Outeiro JC, Meyer D, Umbrello D, Jayal AD (2011) Surface integrity in material removal processes: recent advances. CIRP Ann 60:603–626. https://doi.org/10.1016/j.cirp.2011.05.002
Jawahir IS, Attia H, Biermann D, Duflou J, Klocke F, Meyer D, Newman ST, Pusavec F, Putz M, Rech J, Schulze V, Umbrello D (2016) Cryogenic manufacturing processes. CIRP Ann 65:713–736. https://doi.org/10.1016/j.cirp.2016.06.007
Brinksmeier E, Meyer D, Heinzel C, Lübben T, Sölter J, Langenhorst L, Frerichs F, Kämmler J, Kohls E, Kuschel S (2018) Process signatures—the missing link to predict surface integrity in machining. Proc CIRP 71:3–10. https://doi.org/10.1016/j.procir.2018.05.006
Aurich JC, Mayer P, Kirsch B, Eifler D, Smaga M, Skorupski R (2014) Characterization of deformation induced surface hardening during cryogenic turning of AISI 347. CIRP Ann 63:65–68. https://doi.org/10.1016/j.cirp.2014.03.079
Hotz H, Kirsch B, Becker S, Müller R, Aurich JC (2019) Combination of cold drawing and cryogenic turning for modifying surface morphology of metastable austenitic AISI 347 steel. J Iron Steel Res Int 26:1188–1198. https://doi.org/10.1007/s42243-019-00306-x
Frölich D, Magyar B, Sauer B, Mayer P, Kirsch B, Aurich JC, Skorupski R, Smaga M, Beck T, Eifler D (2015) Investigation of wear resistance of dry and cryogenic turned metastable austenitic steel shafts and dry turned and ground carburized steel shafts in the radial shaft seal ring system. Wear 328-329:123–131. https://doi.org/10.1016/j.wear.2015.02.004
Smaga M, Skorupski R, Eifler D, Beck T (2017) Microstructural characterization of cyclic deformation behavior of metastable austenitic stainless steel AISI 347 with different surface morphology. J Mater Res 32:4452–4460. https://doi.org/10.1557/jmr.2017.318
Angel T (1954) Formation of Martensite in austenitic stainless steels: effect of deformation, temperature, and composition. J Iron Steel Inst 177:165–174
Zhang W, Wang X, Hu Y, Wang S (2018) Predictive modelling of microstructure changes, micro-hardness and residual stress in machining of 304 austenitic stainless steel. Int J Mach Tools Manuf 130-131:36–48. https://doi.org/10.1016/j.ijmachtools.2018.03.008
Hotz H, Kirsch B, Becker S, Harbou E, Müller R, Aurich JC (2018) Modification of surface morphology during cryogenic turning of metastable austenitic steel AISI 347 at different parameter combinations with constant CO2 consumption per cut. Proc CIRP 77:207–210. https://doi.org/10.1016/j.procir.2018.08.287
Hotz H, Kirsch B, Aurich JC (2020) Estimation of process forces when turning with varying chamfer angles at different feed rates. Proc CIRP 88C:300–305
Mayer P, Skorupski R, Smaga M, Eifler D, Aurich JC (2014) Deformation induced surface hardening when turning metastable austenitic steel AISI 347 with different cryogenic cooling strategies. Proc CIRP 14:101–106. https://doi.org/10.1016/j.procir.2014.03.097
Mayer P, Kirsch B, Müller C, Hotz H, Müller R, Becker S, von Harbou E, Skorupski R, Boemke A, Smaga M, Eifler D, Beck T, Aurich JC (2018) Deformation induced hardening when cryogenic turning. CIRP J Manuf Sci Technol 23:6–19. https://doi.org/10.1016/j.cirpj.2018.10.003
Hotz H, Kirsch B (2020) Influence of tool properties on thermomechanical load and surface morphology when cryogenically turning metastable austenitic steel AISI 347. J Manuf Process 52:120–131. https://doi.org/10.1016/j.jmapro.2020.01.043
Becker S, Hotz H, Kirsch B, Aurich JC, Harbou EV, Müller R (2018) A finite element approach to calculate temperatures arising during cryogenic turning of metastable austenitic steel AISI 347. J Manuf Sci Eng 140:165. https://doi.org/10.1115/1.4040778
Hotz H, Kirsch B, Becker S, von Harbou E, Müller R, Aurich JC (2018) Improving the surface morphology of metastable austenitic steel AISI 347 in a two-step turning process. Proc CIRP 71:160–165. https://doi.org/10.1016/j.procir.2018.05.090
Olson GB, Cohen M (1975) Kinetics of strain-induced martensitic nucleation. Metall Trans A 6:791–795. https://doi.org/10.1007/BF02672301
Hecker SS, Stout MG, Staudhammer KP, Smith JL (1982) Effects of strain state and strain rate on deformation-induced transformation in 304 stainless steel: part I. magnetic measurements and mechanical behavior. Metal Trans A 13:619–626. https://doi.org/10.1007/BF02644427
Hotz H, Ströer F, Heberger L, Kirsch B, Smaga M, Beck T, Seewig J, Aurich JC (2018) Konzept zur Oberflächenkonditionierung beim kryogenen Hartdrehen. Z Wirtsch Fabr 113:462–465. https://doi.org/10.3139/104.111951
Uebel J, Ströer F, Basten S, Ankener W, Hotz H, Heberger L, Stelzer G, Kirsch B, Smaga M, Seewig J, Aurich JC, Beck T (2019) Approach for the observation of surface conditions in-process by soft sensors during cryogenic hard turning. Proc CIRP 81:1260–1265. https://doi.org/10.1016/j.procir.2019.03.304
Shalev-Shwartz S, Ben-David S (2014) Understanding machine learning: from theory to algorithms. Cambridge University Press, Cambridge
Marsland S (2015) Machine learning: an algorithmic perspective, Second edn. Chapman & Hall / CRC machine learning & pattern recognition series. CRC Press, Boca Raton, FL
Neapolitan RE, Jiang X (2018) Artificial intelligence: With an introduction to machine learning. CRC Press, Florida
Lison P (2015) An introduction to machine learning. Language Technology Group (LTG). https://www.nr.no/~plison/pdfs/talks/machinelearning.pdf. Accessed 10 Dec 2019
Wuest T, Weimer D, Irgens C, Thoben KD (2016) Machine learning in manufacturing: advantages, challenges, and applications. Prod Manuf Res 4:23–45. https://doi.org/10.1080/21693277.2016.1192517
Schölkopf B, Smola AJ (2002) Learning with kernels: support vector machines, regularization, optimization, and beyond. Adaptive computation and machine learning. MIT Press, Cambridge
Çaydaş U, Ekici S (2012) Support vector machines models for surface roughness prediction in CNC turning of AISI 304 austenitic stainless steel. J Intell Manuf 23:639–650. https://doi.org/10.1007/s10845-010-0415-2
Yeganefar A, Niknam SA, Asadi R (2019) The use of support vector machine, neural network, and regression analysis to predict and optimize surface roughness and cutting forces in milling. Int J Adv Manuf Technol 105:951–965. https://doi.org/10.1007/s00170-019-04227-7
Remesan R, Mathew J (2016) Hydrological data driven modelling. Springer International Publishing, Cham
Das A, Chakraborti PC, Tarafder S, Bhadeshia HKDH (2011) Analysis of deformation induced martensitic transformation in stainless steels. Mater Sci Technol 27:366–370. https://doi.org/10.1179/026708310X12668415534008
Das A, Tarafder S, Chakraborti PC (2011) Estimation of deformation induced martensite in austenitic stainless steels. Mater Sci Eng A 529:9–20
Breiman L (2001) Random forests. Mach Learn 45:5–32. https://doi.org/10.1023/A:1010933404324
Lu Z, Wang M, Dai W, Sun J (2019) In-process complex machining condition monitoring based on deep forest and process information fusion. Int J Adv Manuf Technol 104:1953–1966. https://doi.org/10.1007/s00170-019-03919-4
Xing B, Xiao Y, Qin QH, Cui H (2018) Quality assessment of resistance spot welding process based on dynamic resistance signal and random forest based. Int J Adv Manuf Technol 94:327–339. https://doi.org/10.1007/s00170-017-0889-6
Maudes J, Bustillo A, Guerra AJ, Ciurana J (2017) Random Forest ensemble prediction of stent dimensions in microfabrication processes. Int J Adv Manuf Technol 91:879–893. https://doi.org/10.1007/s00170-016-9695-9
Hotz H, Kirsch B, Aurich JC (2020) Impact of the thermomechanical load on subsurface phase transformations during cryogenic turning of metastable austenitic steels. J Intell Manuf. https://doi.org/10.1007/s10845-020-01626-6
Nohara K, Ono Y, Ohashi N (1977) Composition and grain size dependencies of strain-induced martensitic transformation in metastable austenitic stainless steels. J Iron Steel Inst Jpn 63:772–782. https://doi.org/10.2355/tetsutohagane1955.63.5_772
Kirsch B, Hotz H, Müller R, Becker S, Boemke A, Smaga M, Beck T, Aurich JC (2019) Generation of deformation-induced martensite when cryogenic turning various batches of the metastable austenitic steel AISI 347. Prod Eng Res Devel 13:343–350. https://doi.org/10.1007/s11740-018-00873-0
Becker S, Hotz H, Kirsch B, Aurich JC, von Harbou E, Müller R (2018) The influence of cooling nozzle positions on the transient temperature field during cryogenic turning of metastable austenitic steel AISI 347. Proc Appl Math Mech 18. https://doi.org/10.1002/pamm.201800447
Talonen J, Aspegren P, Hänninen H (2004) Comparison of different methods for measuring strain induced α-martensite content in austenitic steels. Mater Sci Technol 20:1506–1512. https://doi.org/10.1179/026708304X4367
Ahmedabadi PM, Kain V, Agrawal A (2016) Modelling kinetics of strain-induced martensite transformation during plastic deformation of austenitic stainless steel. Mater Des 109:466–475. https://doi.org/10.1016/j.matdes.2016.07.106
Smaga M, Walther F, Eifler D (2008) Deformation-induced martensitic transformation in metastable austenitic steels. Mater Sci Eng A 483-484:394–397. https://doi.org/10.1016/j.msea.2006.09.140
Ishimaru E, Hamasaki H, Yoshida F (2015) Deformation-induced martensitic transformation behavior of type 304 stainless steel sheet in draw-bending process. J Mater Process Technol 223:34–38. https://doi.org/10.1016/j.jmatprotec.2015.03.048
Feurer M, Hutter F (2019) Hyperparameter optimization. In: Hutter F, Kotthoff L, Vanschoren J (eds) Automated machine learning. Springer International Publishing, Cham, pp 3–33
de Silva AM, Leong PHW (2015) Feature selection. In: de Silva AM, Leong PHW (eds) Grammar-based feature generation for time-series prediction, vol 17. Springer Singapore, Singapore, pp 13–24
Pedregosa F, Varoquaux G, Gramfort A et al (2011) Scikit-learn: machine learning in python. J Mach Learn Res 12:2825–2830
Chollet F (2015) Keras: The python deep learning API. Keras. https://keras.io. Accessed 10 Dec 2019
Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv cs.LG. http://arxiv.org/pdf/1412.6980v9
Funding
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—project number 172116086-SFB 926.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: Retrospective open access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Glatt, M., Hotz, H., Kölsch, P. et al. Predicting the martensite content of metastable austenitic steels after cryogenic turning using machine learning. Int J Adv Manuf Technol 115, 749–757 (2021). https://doi.org/10.1007/s00170-020-06160-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-020-06160-6