Abstract
In the field of material modeling, thermoplastic polymers are often studied because of their complex material behavior and their prevalence in industry applications due to their low cost and wide range of applications. Nowadays, where reusability becomes more and more important, materials which can undergo reversible thermomechanical deformations are appealing for, e.g., the construction of car body components. To predict such complex forming processes with multiple influencing factors, such as temperature, strain rate or underlying material morphology, model formulations are needed that account for these influences simultaneously and are validated against experimental data. Unfortunately, up to now only a few contributions are available which consider all these phenomena. In addition, the range of process parameters considered is often narrow due to the experimental effort required for testing. This usually results in limited predictive capabilities of the model. To overcome these limitations, in this work, a thermo-mechanically coupled material model is developed that accounts for the underlying morphology in terms of the degree of crystallinity (DOC). The model formulation is derived in a thermodynamically consistent manner, incorporating coupled nonlinear visco-elastic and elasto-plastic material behavior at finite strains. To characterize and further validate the model, mechanical as well as thermal experiments are conducted for polyamide 6 (PA6). Here, a blending strategy of PA6 together with an amorphous co-polymer is introduced during specimen production to achieve a wider range of stable DOCs(approximately 15%). The model formulation is successfully applied to experimental results and its predictions are in good agreement with experimental observations.
Similar content being viewed by others
1 Introduction
Polymers are macromolecules consisting of repeating units (monomers) with linear, branched or cross-linked structures. They are typically classified on the basis of their origin (synthetic, natural, modified natural), the origin of their resources (renewable, fossil), their biodegradability or their physiochemical properties (thermoplastics, thermosets, elastomers) in terms of their arrangement of monomers on the microlevel. The latter is of interest in industrial applications, for example, in automotive or aerospace industry, where polymers are used as engineering materials due to their beneficial high strength to weight ratio, as well as their eligibility for cost-effective mass-production. In contrast to three dimensional cross-linked network structures, highly pronounced in thermosets and less distinct in elastomers, thermoplastics primarily consist of long linear or branched polymer chains without cross-links. This underlying morphology allows for reversible thermoplastic deformations, needed for technical forming or molding processes, e.g., for car components. Thermoplastics can either be purely amorphous or semi-crystalline polymers (SCPs), depending on their chain morphology. Amorphous polymers mainly consist of disordered (coiled) chains that undergo a change from a glassy to a rubbery state around the glass transition temperature. In contrast, SCPs contain disordered (amorphous) and ordered (crystalline) regions, resulting in a recrystallization behavior during cool-down from the melt [1,2,3]. Hereby, the cooling rate and the production method (e.g., extrusion, injection molding, blow molding, compaction, etc.) have a crucial impact on the resulting degree of crystallinity (DOC). In industrial applications, the process stability is most important; therefore, additives such as softening agents, stabilizers, crystallization agents, dyes or fillers to enhance the mechanical properties are commonly used in plastics manufacturing. Nonetheless, these are not the only influencing factors on the resulting material behavior. Besides production parameters, temperature, heating or loading rate as well as moisture content or aging factors, such as UV radiation or other environmental factors, can alter the material characteristics. Hence, it is crucial to consider multiple influencing factors over a wide range when formulating and identifying a material model to reliably predict the material behavior of plastics.
Over the past decades, multiple models were proposed to simulate the material behavior of polymers under various influencing factors. Here, contributions for thermoplastic materials are of particular interest. Based on the modeling approach by [4] for glassy polymers and the idea of a split into a molecular network as well as an intermolecular resistance [5], several phenomenological models were developed for amorphous (e.g., [6,7,8]) and semi-crystalline (e.g., [9,10,11]) polymers. Within the class of phenomenological models, the approaches differ between purely visco-elastic formulations (e.g., [12, 13]) and models that cover the elasto-visco-plastic material behavior (e.g., [9, 11, 14]). Several works additionally account for the Bauschinger-like effect upon unloading (e.g., [15,16,17]).
Modeling the yielding behavior of thermoplastics requires the identification of an appropriate yield surface. Here, the well-known von Mises yield criterion, which depends on a single material parameter only (i.e., yield stress) and originates from the analysis of the inelastic behavior of metals, is not suitable, since it neglects the hydrostatic pressure dependence known for polymers, see, for example, [18, 19]. Possible alternatives are, for example, the Drucker–Prager yield surface [20] or the paraboloid yield surface by [21]. Both offer the possibility to consider tension–compression asymmetry in yielding, by introducing separate yield stresses in tension and compression. This effect is also visible in experiments. [22] showed, e.g., a tension–compression asymmetry in the onset of yielding for glassy polymers at room temperature, where the stiffer compressive response resulted from the effect of hydrostatic pressure. The temperature and strain rate sensitivity of yielding under compression were discussed in [23]. However, the ratio of the tensile and compressive yield stresses is not affected by the strain rate, as concluded by [24]. [25] investigated the mechanical response of various semi-crystalline polymers and found out that PA6, among others, shows a strain rate-dependent yielding together with a higher yield stress in compression. At higher temperatures, [26] tested the response of polyether-ether-ketone (PEEK) and compared the resulting yield stresses in tension and compression. Their difference decreased with increasing temperature, especially close to or above the glass transition. Further testing by [19] revealed that yield criteria based on the hydrostatic stress and second invariant of the deviatoric stress are not sufficient to predict biaxial stress states or shear banding. In these cases, the third invariant of the deviatoric stress needs to be considered as well. Another possibility are yield criteria derived from mechanical testing, see, e.g., [27]. These approaches are, however, tailored to a specific material and can therefore not be used for other cases.
Some works considered additional effects at the microlevel, for example, plastic flow occurring via crystallographic slip in the crystalline phase [28] or a change of the plastic flow depending on the glass transition [29]. Naturally, the morphology of the underlying microstructure, e.g., crystal configuration, lamellae thickness etc., has a significant influence on the overall material response. This motivated modeling formulations that take into account molecular dynamics or the microstructural constituents, employing analytical or FE-based homogenization schemes to arrive at the macroscopic material response, see, e.g., [30,31,32,33,34]. However, due to experimental limitations it is in general difficult and costly to obtain the required physical data for characterizing the microscopic material behavior. Especially semi-crystalline polymers prove to be difficult in terms of their different molecular arrangements. With the growing interest in artificial intelligence and machine learning, efforts have been made to use neural networks for describing the temperature dependence of mechanical properties of polyurethane [35] and the temperature and rate dependence of polypropylene in terms of a hybrid model approach, combining constitutive and data-based modeling [36]. Additional applications included material development, e.g., rubber blend optimization by tracing back targeted visco-elastic material properties [37] or polymer identification [38]. Similar to micromechanical approaches, the generation of experimental data sets remains cost and time intensive.
The influence of the internal microstructure on the macroscopic material response is only taken into account in a limited number of works. For example, the amount of crystal volume fraction was taken into account in [10, 39], who incorporated a two-phase representation of the intermolecular resistance, whereas in [40] and [41] mixture rules based on a crystallinity ratio were used to distinguish between the amorphous and the crystalline phase. [42] developed a micromechanics-based criterion for the yielding of SCPs, based on the amorphous volume fraction. In most cases, however, crystalline and amorphous phases are treated in a smeared manner and the degree of crystallinity serves as a constant input parameter, see, e.g., [11]. Several works additionally considered the evolution of the DOC as a stress-free pre-process, resulting during cool-down from the molten state [43], or elaborated a full coupling scheme (e.g., [44] based on [45, 46]). However, the validation of such approaches remains cumbersome, since the DOC cannot be measured directly during experimental testing and additional changes in the sample cannot be excluded, if tested afterward. Commonly, no further differentiation between fully extended (\(\alpha \)-form) and twisted (\(\gamma \)-form) polymer chains is made.
Thermal effects in semi-crystalline polymers need to be accounted for, due to the inherent structural changes occurring at the lamellae level. In the literature, multiple approaches exist for polymers that take into account a coupling with the temperature field (e.g., [15, 47]). Here, the approaches differ in terms of the treatment of thermal softening with increasing temperature. [48] and [49], for example, considered material degradation, whereas in the works of, e.g., [43, 50, 51], the material parameters themselves are dependent on the temperature. In regard to the considered temperature range, [52] identified the model framework below the glass transition, whereas [53] considered processing cases close to the glass transition. In contrary, [16] conducted a modeling framework that spans a wide temperature range independent of the phase change. Significant self-heating effects were visible in experiments from [24] for polyamide (PA66), polymethylmethacrylate (PMMA) and polycarbonate (PC) and in experiments from [54] for PA66 and polypropylene. In a recent publication, [55] studied the material behavior of PA6 under large deformations including the self-heating effect, prominent at high loading rates.
Other influencing factors were investigated in, for example, [56], who investigated the effects of a change in moisture content on the mechanical properties of PA6 by coupling a nonlinear diffusion model with a visco-elastic material model. In [57], the thermoviscoelastic behavior of PA6 is explored by means of dynamical mechanical analysis (DMA) under varying moisture contents. Further, [58] experimentally investigated the effect of UV-aging on polyethylene, whereas [59] incorporated the effect of thermal aging into a micromechanical constitutive model. Besides the influence of environmental factors, multiple attempts were made to model the failure regime of SCPs. [17] modeled, e.g., ductile damage in polypropylene, nylon 101 and high-density polyethylene, whereas [60] introduced a thermo-elastic-viscoplastic damage model for PA6. A gradient damage approach was used in [61] to overcome pathological mesh dependence issues in the simulation of PMMA and polycarbonate (PC) fracture.
Concluding from the review above, considerable efforts were made in the experimental and numerical analysis of SCPs. However, in most of these works the influencing factors on the material behavior are considered separately. Only a few works consider multiple influences at once. Especially regarding the temperature and process-induced morphology, as the degree of crystallinity, a strongly limited number of contributions is available that covers their correlations over a wide process range [11]. In these cases, mostly the mechanical model response is investigated, whereas the influence of the DOC on the thermal properties is neglected, in particular for temperatures above the glass transition. At the same time, the considered range of process parameters in experimental testing is often limited. Therefore, a broad overview of the material response is missing. As a result, material models identified from experimental data are often valid only for small regions, e.g., a small range of DOCs, limiting the predictive capability of the model for various applications and process-induced morphologies. Additionally, the production of temperature stable specimens with a significant range of crystallinities remains a challenge, since quenching during cool-down or post-production treatments, as for example, annealing, yield only small changes in the DOC that are unstable in temperature and time. Here, additives like crystallization agents or fillers are needed, to achieve significant and stable changes in the materials’ crystal content. Compounding such materials with designed properties is a separate research field in terms of identification of a suitable blend partner, blend composition, mixing technology, and chemical reactions initiated between the components that may require the use of compatibilizers, see, e.g., [62,63,64,65]. Further testing is required to validate the newly generated materials prior to mechanical testing, which increases the experimental effort.
The objective of this work is to evaluate the influence and interplay between strain rate, temperature and degree of crystallinity collectively over a wide range of process parameters and develop a corresponding thermo-mechanical constitutive theory. Therefore, in a first step (see Sect. 2) a thermodynamically consistent finite strain formulation is derived, where the temperature serves as an additional field variable. The degree of crystallinity is accounted as an additional constant input quantity. In line with previous works, a coupled visco-elastic, elasto-plastic model is developed that includes nonlinear kinematic hardening of Armstrong–Frederick type. The formulation is extended with a tension–compression asymmetry in yielding, necessitating experimental results in tension and compression to characterize the model. Further, the model is identified in a staggered manner with new experimental results from polyamide 6 cyclic-olefin-copolymer (COC) blends with a range of 15 % to 29% DOC (see Sect. 3). Tension, compression and relaxation tests are carried out for temperatures below and above the glass transition with an emphasis on a wide range of variation in the tested strains and strain rates. Here, several functions for a nonlinear relaxation time are tested and compared to experimental data. Additional thermal tests, for example, thermal conductivity measurements or specific heat capacity measurements, are carried out to identify the models’ thermal properties and their dependence on the underlying morphology. Following model verification, numerical examples are shown and discussed in Sect. 4. Finally, a conclusion and outlook are given in Sect. 5.
2 Constitutive modeling of semi-crystalline polymers
The experimental findings of, e.g., [11], imply that, to accurately represent the material behavior of SCPs, a coupled visco-elastic, elasto-plastic framework, incorporating nonlinear relaxation behavior as well as strain hardening, is required. To this end, the corresponding modeling strategy is presented in a schematic one dimensional rheological illustration (Fig. 1a to allow a better understanding of the following derivation.
a Schematic illustration of the constitutive model. b Multiplicative splits of the deformation gradient
2.1 Kinematics
In the finite strain regime, the previous assumptions lead to a multiplicative decomposition of the deformation gradient \({\varvec{F}}\) into an elastic (\({\varvec{F}}_{e1}\)) and a plastic (\({\varvec{F}}_{p}\)) part (see, e.g., [66,67,68]) as well as an elastic (\({\varvec{F}}_{e2}\)) and viscous (\({\varvec{F}}_{v}\)) contribution (see, e.g., [14, 69,70,71])
see Fig. 1. To model nonlinear kinematic hardening, an additional, physically motivated split of the plastic deformation gradient \({\varvec{F}}_p={\varvec{F}}_{pe} \, {\varvec{F}}_{pi}\) is introduced, according to [72, 73]. Naturally, the above decompositions of the deformation gradient result in the local intermediate configurations \(ic_1\), \(ic_{1} ^v\) and \(ic_2\) for plasticity, kinematic hardening and viscosity, respectively, with rc defining the reference and cc the current configuration (cf. Fig. 1).
2.2 Helmholtz free energy
The total Helmholtz free energy per unit mass, as the state potential of the model, is expressed in terms of physically reasonable deformation measures in the intermediate configurations. Therefore, next to the symmetric right Cauchy–Green tensor \({\varvec{C}} = {\varvec{F}}^\textrm{T} {\varvec{F}} \), the elastic and plastic Cauchy–Green-like tensors
are introduced, according to [74, 75]. Here, the general form of the total Helmholtz free energy \(\psi \) is additively decomposed, following the idea presented in Fig. 1
where \(\psi _1\) and \(\psi _2\) denote the energies related to the elasto-plastic and visco-elastic contributions, respectively. Analogously to [15, 43, 52, 76], the state potential is extended by a caloric contribution \(\psi _c\) in order to ensure flexibility regarding the function for the heat capacity \(c_T\) derived in Sect. 2.5. As indicated in (3), all energetic contributions jointly depend on the temperature field via the absolute temperature \(\theta \).
The first term \(\psi _1\) contains an elastic part \(\psi _{e1}\) based on the elastic right Cauchy–Green tensor \({\varvec{C}}_{e1}\) and the degree of crystallinity \(\chi \)
to account for the influence of the microstructural morphology. Note here that no distinction is made between the underlying crystal configurations and that the DOC in this framework serves as a constant input quantity. In addition, a defect energy \(\psi _p\) related to kinematic hardening is introduced, depending on \({\varvec{C}}_{pe}\) as well as \(\chi \). The energy related to viscous effects \(\psi _2\) is expressed in terms of the elastic right Cauchy–Green-like tensor \({\varvec{C}}_{e2}\) as the sole deformation measure.
2.3 Second law of thermodynamics: Clausius–Duhem inequality
To ensure non negative internal dissipation, the model equations need to fulfill the second law of thermodynamics. Therefore, the state relations are derived from the local form of the Clausius–Duhem inequality:
Here, \({\varvec{S}}\) is the second Piola–Kirchhoff stress tensor, \(\rho _0\) represents the material density per unit reference volume and \(\eta \) the entropy. The heat flux with respect to the reference configuration is introduced as \({\varvec{q}}_0\). Considering the assumed form of \(\psi _{1}\) and \(\psi _{2}\) in Eq. 3, the time derivative of the Helmholtz free energy is expressed as
The reader is kindly reminded that the derivatives with respect to \(\chi \) vanish, since the DOC is assumed to be constant in this constitutive framework. Now, using the chain rule of differentiation and additionally the relation \({\varvec{L}}_p = \dot{{\varvec{F}}}_p {\varvec{F}}_p^{-1}\) and \({\varvec{L}}_{pi} = \dot{{\varvec{F}}}_{pi} {\varvec{F}}_{pi}^{-1}\) for the velocity gradients, the derivatives of \({\varvec{C}}_{e1}\) and \({\varvec{C}}_{pe}\) can be reformulated as
Here, the identities \(\dot{{\varvec{F}}}_p^{-1}= -{\varvec{F}}_{p}^{-1} \, \dot{{\varvec{F}}}_p^{-1}\, {\varvec{F}}_{p}^{-1}\) and \(\dot{{\varvec{F}}}_p^{-T}= -{\varvec{F}}_{p}^{-T} \, \dot{{\varvec{F}}_p^{T}}\, {\varvec{F}}_{p}^{-T}\) have been used for the derivation of \(\dot{{\varvec{C}}}_{e1}\) and \(\dot{{\varvec{F}}_{pe}}^{-1}= -{\varvec{F}}_{pe}^{-1} \, \dot{{\varvec{F}}}_{pe}^{-1}\, {\varvec{F}}_{pe}^{-1}\) and \(\dot{{\varvec{F}}}_{pe}^{-T}= -{\varvec{F}}_{pe}^{-T} \, \dot{{\varvec{F}}}_{pe}^{T}\, {\varvec{F}}_{pe}^{-T}\) for the derivation of \(\dot{{\varvec{C}}}_{pe}\). The viscous deformation rate \(\dot{{\varvec{C}}}_{e2}\) is derived analogously using the corresponding inelastic velocity gradient \({\varvec{L}}_{v} = \dot{{\varvec{F}}}_v \, {\varvec{F}}_v^{-1}\). In the next step, \(\psi _{e1}\) is assumed to be an isotropic function of \({\varvec{C}}_{e1}\); therefore, coaxiality between \({\varvec{C}}_{e1}\) and \(\partial \psi _{e1} / \partial {\varvec{C}}_{e1}\) can be shown. Together with the relation for a scalar product of two second-order tensors (\({\varvec{A}}: {\varvec{B}} = \text {tr} ({\varvec{A}}^\textrm{T} {\varvec{B}}) = \text {tr} ({\varvec{A}}{\varvec{B}}^\textrm{T})\)), this results in the identity
Here, the velocity gradient \({\varvec{L}}_p\) can be replaced by its symmetric part \(\text {sym} {\varvec{L}}_p= {\varvec{D}}_p\), the plastic rate of deformation tensor, since the product of \({\varvec{C}}_{e1}\) and \(\partial \psi _{e1} / \partial {\varvec{C}}_{e1}\) is symmetric. Analogously, \(\psi _{p}\) and \(\psi _{e2}\) are assumed to be isotropic functions of \({\varvec{C}}_{pe}\) and \({\varvec{C}}_{e2}\), respectively. Thus, similar relations as in Eq. 8 are obtained for these quantities. Now, the reformulated energy rate \(\dot{\psi }\) is inserted back into Eq. 5
using the relation \(\dot{{\varvec{D}}}_p = \dfrac{1}{2} \, {\varvec{F}}_p^{-T} {\varvec{C}}_p {\varvec{F}}_p^{-1}\). For arbitrary \(\dot{{\varvec{C}}}\), the second Piola–Kirchhoff stress tensor \({\varvec{S}}\) is chosen according to the Coleman–Noll procedure [77] as
where \({\varvec{S}}_1\) and \({\varvec{S}}_2\) represent the second Piola–Kirchhoff stresses corresponding to the elasto-plastic and visco-elastic model, respectively
In addition, definitions for the Mandel stresses \({\varvec{M}}_{1}\) and \({\varvec{M}}_{2}\) in the intermediate configurations \(ic_1\) and \(ic_2\) are introduced
Moreover, the back stress \({\varvec{X}}\) related to kinematic hardening in \(ic_1\) and the Mandel stress corresponding to kinematic hardening \({\varvec{M}}_{1,\text {kin}}\) follow to
The entropy is specified as
to a priori fulfill the thermodynamic restrictions and a heat flux according to Fourier’s law in the reference configuration
is chosen with \(J = \text {det} {\varvec{F}}\) and \(\lambda _T(\theta )\) denoting the temperature dependent heat conductivity. Exploiting Eq. 9, together with Eq. 10–15 leads to a reduced form of the Clausius–Duhem inequality
2.4 Evolution equations and proof of thermodynamic consistency
2.4.1 Yield function and elasto-plastic evolution
Following [19, 21, 78], a Tschoegl-type or paraboloid yield criterion
is considered, which includes a tension–compression asymmetry in yielding. It depends on the first (\(I_{1} = \text {tr}({\varvec{\Sigma }})\)) and second (\(J_{2} = 1/2 \, \text {tr}(\text {dev} (({\varvec{\Sigma }}))^2 )\)) invariant of the relative stress \({\varvec{\Sigma }}= {\varvec{M}}_{1} - {\varvec{X}}\) and thus accounts for the effects of hydrostatic pressure on the yielding behavior. The tension–compression flow asymmetry is introduced via the ratio m
between the initial yield stresses in tension \(\sigma _t^0\) and compression \(\sigma _c^0\). Note here that both material quantities are assumed to depend independently on the degree of crystallinity and the temperature, resulting in a varying ratio m with temperature evolution. Under the assumption of associative plasticity, the evolution equation for the plastic strain rate follows to
where \(\dot{\lambda }_p\) denotes the plastic multiplier. The evolution equation for \({\varvec{D}}_{pi}\) is chosen to model nonlinear Armstrong–Frederick kinematic hardening according to [79]
with the corresponding material parameters b and c. Since the Mandel stress of kinematic hardening depends on c (Eq. 37,39), the ratio b/c is introduced for dimensional reasons. Finally, the Karush–Kuhn–Tucker conditions complete the constitutive equations for the elasto-plastic model part, i. e.
2.4.2 Visco-elastic evolution
The evolution equation for the visco-elastic part in the intermediate configuration \(ic_2\) is chosen according to [71]
where \(g({\varvec{M}}_2)\) is a potential introduced in [71]. Thereby, the bulk modulus \(K_2(\theta )\) as well as the shear modulus \(\mu _2(\theta )\) are temperature-dependent quantities related to the material stiffness defined in Sect. 2.7. The relaxation time \(\tau \) determines how fast the material releases stresses and must therefore be larger than zero. In this work, \(\tau ({\varvec{\tau }}_2, \theta )\) is chosen as a function of the Kirchhoff stress of the visco-elastic part (\({\varvec{\tau }}_2\)) as well as the temperature. For the specific function, the reader is referred to Sect. 3.
2.4.3 Note on thermodynamic consistency
For a more detailed derivation of the elasto-plastic part, the reader is kindly referred to [74, 75]. In these works, the classical von Mises yield criterion is exploited, in a framework considering isotropic and kinematic hardening, to derive the plastic flow rule and prove the thermodynamic consistency. The thermodynamic consistency of the constitutive model presented here can be shown in a similar manner, using the approach of [71] for the visco-elastic part.
2.5 First law of thermodynamics: energy balance
In the following section, the local form of the energy balance with respect to the reference configuration
is evaluated to derive the heat generation in a thermodynamically consistent manner. Therefore, the time derivative of the internal energy
is exploited. Subsequently, the rate of the total Helmholtz free energy (Eq. 6) is inserted in Eq. 23 and Eq. 14 is recalled to derive the entropy rate \(\dot{\eta }= - \partial \dot{\psi }/ \partial \theta \). Using the relations derived in Eq. 7- 13 as well as Eq. 16, the partial differential equation for the temperature field follows to
Here, the specific heat capacity was introduced as
From Eq. 29, it can be seen that the heat capacity in theory is a complex function of all internal variables. However, coming back to the definition of the total Helmholtz free energy in Eq. 3, a caloric energy term \(\psi _c\) was added to ensure flexibility regarding the function for the heat capacity which otherwise would be a priori defined. In reality it is hard to asses these energetic contributions experimentally for inelastic materials and thus derive the heat capacity in closed form [15, 52, 76]. Therefore, in this work, the heat capacity is approximated by a constant value \(c_T = c_T(\chi , \theta )\) for each DOC and test temperature according to cited literature. In Sect. 3, experiments are conducted to determine the specific heat capacity for the underlying morphology.
2.6 Representation of the constitutive equations in the reference configuration
In the preceding sections, the constitutive equations of the model were derived in a thermodynamically consistent manner, resulting in quantities in multiple configurations. However, since the intermediate configurations are non-unique, all quantities defined with respect to \(ic_1\), \(ic_{1}^i\) and \(ic_2\) can not be computed directly without further treatment [80]. Thus, several pull-back operations are needed to arrive at unique and therefore calculable quantities in the reference configuration. Simultaneously, this procedure allows the application of an exponential map algorithm [74] to integrate the evolution equations which automatically preserves the symmetry of the internal variables as well as the material’s incompressibility.
Since \(\psi _{e1}\) and \(\psi _{e2}\) are isotropic functions of \({\varvec{C}}_{e1}\) and \({\varvec{C}}_{e2}\), respectively, one can directly show that \({\varvec{S}}_1\) and\({\varvec{S}}_2\) are unique using the concept of invariants [81]. Now, the relations from Eq. 2 can be used to reformulate the Second Piola–Kirchhoff stresses in terms of \({\varvec{C}}\) and \({\varvec{C}}_p\) or \({\varvec{C}}_v\). A similar observation can be made for the back stress tensor in the reference configuration \(\bar{{\varvec{X}}}\). The rates of the plastic and viscous right Cauchy–Green-like tensors are defined as
Using the aforementioned relations together with Eq. 19, 20 and 22, the evolution equations can be represented in the reference configuration as
Next, the thermodynamic driving forces of the elasto-plastic part are pulled back to the reference configuration
showing that \({\varvec{M}}_1\) and \({\varvec{C}} \, {\varvec{S}}_1\) as well as \({\varvec{X}}\) and \({\varvec{C}}_p \, \bar{{\varvec{X}}}\) are similar tensorsFootnote 1 and share the same eigenvalues. Now, the relative stress can be reformulated as
Thus, since the yield function \(\Phi _p\) is an isotropic function of \({\varvec{\Sigma }}\), it can equally be expressed as \(\Phi _p = \Phi _p ({\varvec{\Sigma }}) = \Phi _p ({\varvec{Y}})\). In the same manner, pull-back operations for the visco-elastic part can be deduced (see Table 1), since it can be shown that \({\varvec{M}}_2\) and \({\varvec{C}} {\varvec{S}}_2\) are similar. Regarding the internal dissipative heat sources, pull-back operations need to be applied to \(r_p\) and \(r_v\) as well. Here, it is made use of Eq. 30-34, to arrive at the final form. Finally, all quantities are expressed in terms of \({\varvec{C}}\) and the internal variables \({\varvec{C}}_p\), \({\varvec{C}}_{pi}\) and \({\varvec{C}}_v\). An overview of the constitutive equations in the reference configuration is given in Table 1.
2.7 Specific choice of the Helmholtz free energy
Until this point, the constitutive framework has been presented in a quite general manner, to allow for a flexible adaption of the model to other polymeric materials. To proceed with the identification of the model using the experimental results in Sect. 3, however, a particular choice for the energetic contributions is required. Note, for consistency the subsequent energies are expressed in terms of the elastic right Cauchy–Green tensors \({\varvec{C}}_{e1}\) and \({\varvec{C}}_{e2}\) in the intermediate configurations. They can of course be equivalently reformulated in terms of the corresponding quantities of the reference configurations \({\varvec{C}}, {\varvec{C}}_{p}\) and \({\varvec{C}}_{v}\) as well.
For the elasto-plastic model part, the elastic contribution \(\psi _{e1}\) is chosen as a compressible Neo-Hookean-type energy
including the two Lamé constants \(\mu _1(\chi , \theta )\) and \(\Lambda _1(\chi , \theta )\) dependent on the DOC and temperature. Here, \(J_{e1} = \text {det}({\varvec{F}}_{e1})\) is the determinant of the elastic deformation gradient \({\varvec{F}}_{e1}\). The elastic energy is extended by a term related to volumetric thermal expansion with the elasto-plastic bulk modulusFootnote 2\(K_1(\theta )\), the coefficient of thermal expansion \(\alpha _T(\theta )\) and the temperature difference \(\Delta \theta = \theta -\theta _0\) between the current temperature \(\theta \) and the reference temperature \(\theta _0\). Alongside the elastic energy, a nonlinear plastic defect energy is introduced to account for kinematic hardening
where \(J_{pe} = \text {det}({\varvec{C}}_{pe})\) holds. Here, \(c (\chi , \theta )\) and the second dimensionless parameter \(b(\chi , \theta )\) that only shows up in the evolution equation of \({\varvec{D}}_{pi}\) or \(\dot{{\varvec{C}}}_{pi}\) are material parameters (cf. [79]). With Eq. (11) and (13), the second Piola Kirchhoff stress for the elasto-plastic part and the thermodynamic conjugate force for kinematic hardening in the reference configuration follow to
Similar to \(\psi _{e1}\), the visco-elastic energy contribution is defined as
where \(\mu _2(\theta )\) and \(\Lambda _2(\theta )\) are the viscous Lamé constants and \(K_2\) is the visco-elastic bulk modulus\(^{2}\). The determinant \(J_{e2}\) for volumetric thermal expansion is defined as \(J_{e2} = \text {det}({\varvec{F}}_{e2})\). Following Eq. 11, the inelastic second Piola–Kirchhoff tensor \({\varvec{S}}_{e2}\) takes the form
2.8 Numerical implementation
The presented thermo-mechanically coupled modeling framework is implemented as a user material subroutine UMAT and UMATHT into the commercial FEM software ABAQUS/Standard. During the solution of a thermo-mechanically coupled boundary value problem, at each Gaussian integration point, the deformation gradient \({\varvec{F}}\), the temperature \(\theta \) and the spatial temperature gradient grad(\(\theta \)) are passed down to the subroutine together with a vector containing all internal variables from the last converged time step. Here, for the time discretization of the local residuals of \(\dot{{\varvec{C}}}_p, \, \dot{{\varvec{C}}}_{pi}\) and \(\dot{{\varvec{C}}}_v\), the exponential map algorithm is exploited as an implicit time integration scheme. The starting point is a reformulation of the evolution equations from Table 1:
with the second-order tensors
To integrate equations (42)–(44), an exponential map algorithm proposed by [74, 82] is used. This leads to the final form of the discretized evolution equations, displayed in a residuum format together with the yield surface:
Here, the relations \(\Delta \lambda _p = \Delta t\, \dot{\lambda }_p, \, {\varvec{U}}_p = \sqrt{{\varvec{C}}_p}, \, {\varvec{U}}_{pi} = \sqrt{{\varvec{C}}_{pi}}\) and \({\varvec{U}}_v = \sqrt{{\varvec{C}}_v}\) are introduced. The index n refers to quantities from the last time step, whereas quantities without index n relate to the current time step. For a more detailed description of the time integration procedure, the reader is kindly referred to [74, 75]. Due to the symmetry of the internal variables, a system of 13 nonlinear equations, corresponding to the local plastic residual vector \({\varvec{r}}_{1,\text {loc}} = ({\varvec{r}}_{1, p}, {\varvec{r}}_{1, pi}, r_{1, \sigma }) ^\textrm{T} = {\varvec{0}}\), must be solved for the elasto-plastic part. Using the Newton–Raphson scheme, the plastic solution vector \({\varvec{x}}_{1,\text {loc}} = (\hat{{\varvec{U}}}_{p}^{-1}, \hat{{\varvec{U}}}_{pi}^{-1},{\Delta \lambda _p})^\textrm{T}\) is obtained. This procedure requires an additional linearization of the residuals (for constant \({\varvec{C}}\) and \(\theta \)) and the calculation of the Jacobian matrix \({\varvec{J}}_1 = \partial {\varvec{r}}_{1,\text {loc}}/ \partial {\varvec{x}}_{1,\text {loc}} \). The latter is obtained by automatic differentiation using the software AceGen (cf. [83]). Likewise, for the visco-elastic part a system of 6 nonlinear equations \({\varvec{r}}_{2,\text {loc}} = {\varvec{r}}_{2, v} = {\varvec{0}}\) is solved for \(\hat{{\varvec{U}}}_{v}^{-1}\).
After local convergence is achieved, ABAQUS requires the Cauchy stress tensor \({\varvec{\sigma }}\) and the volumetric heat generation r from the UMAT and the heat flux \({\varvec{q}}\) from the UMATHT together with the material sensitivities for the global Newton iteration. The rate of the right Cauchy–Green tensor needed for the calculation of the internal heat generation is approximated by \(\dot{{\varvec{C}}}\approx ({\varvec{C}} - {\varvec{C}}_n)/\Delta t\). Since the heat generation and the heat flux are derived with respect to the reference configuration (see Table 1), they firstly need to be related to the current configuration
In terms of the material sensitivities, ABAQUS requires the material tangent modulus \(\mathbb {C}_{{\varvec{D}}}^{{\varvec{\sigma }}} = 1/J \, \mathbb {C}_{{\varvec{D}}}^{{\varvec{\tau }}}\) (DDSDDE), which is related to the tangent modulus tensor \(\mathbb {C}_{{\varvec{D}}}^{{\varvec{\tau }}}\) for the Jaumann rate of the Kirchhoff stress tensor \({\varvec{\tau }}\). The linearized incremental form of the Kirchhoff stress can be expressed as
where \(\Delta {\varvec{D}}\) and \(\Delta {\varvec{W}}\) refer to the incremental symmetric and antisymmetric parts of the incremental velocity gradient \(\Delta {\varvec{L}}\), respectively. Further, the thermal tangent modulus \({\varvec{C}}_\theta ^{{\varvec{\sigma }}}\) (DDSDDT) and the derivatives of the internal heat sources with respect to the strain increment \({\varvec{C}}_{{\varvec{D}}}^r\) (DRPLDE) and the temperature \(C_\theta ^{{\varvec{\sigma }}}\) (DRPLDT) are needed:
These quantities are obtained in a consistent manner from the corresponding expressions in the reference configuration utilizing the algorithmic differentiation tool AceGen. Thus, quadratic convergence within the global Newton–Raphson iteration is achieved. The push forward operations are found in Appendix A.1 alongside a more detailed derivation of the tangent operators.
3 Parameter identification procedure
In this section, a staggered parameter identification scheme is described, to obtain a set of material parameters for each test temperature. Therefore, firstly the experimental data base is discussed (see Sect. 3.1), followed by a successive model characterization with a focus on the dependence on the degree of crystallinity and the temperature.
3.1 Experimental data base
3.1.1 Specimen preparation
All experimental results used in this work for model identification purposes were conducted at the Institute of Mechanics, University of the German Federal Armed Forces, Munich. To that end, the required test specimens were injection molded at Polymer Service GmbH Merseburg (PSM) as type 1A and 1BA specimens of DIN EN ISO 527-2:2012. In the following, 1BA specimens were used for monotonic tension as well as relaxation tests, whereas the 1A specimens were used to cut smaller specimens (\(10\times 4\times 50\) mm\(^3\)) from the middle section for compression tests in line with DIN EN ISO 604:2003. Prior to specimen production, the PA6 type B granulate, kindly provided by Bond Laminates (Lanxess), was compounded with an amorphous co-polymer (cyclic olefin copolymer (COC), type: Topas 9506F-500) in four different ratios PA6:COC (1:0, 0.85:0.15, 0.70:0.30, 0.55:0.45). The test specimens were then injection molded from the granulates. The idea of this blending technique is to achieve different thermally stable volume-crystallinities with a wide range of DOCs, where the change in DOC stems purely from the change in the PA6 mass content to the total compound mass. The resulting material behavior of the blends should therefore reflect the material behavior of pure PA6. Consequently, the blend partner COC was chosen to have a similar glass transition temperature compared to PA6, as well as a stiffness around 4 GPa which corresponds to the stiffness of the amorphous phase of pure PA6 below \(T_g\). Below the glass transition, the material behavior of the blends is influenced by both the amorphous and the crystalline phase. In this case, the similarity of the chosen blend partner to the amorphous PA6 phase should result in a comparable material behavior to pure PA6. Above the glass transition, the stiffness of the amorphous phase reduces to individual MPa; therefore, the crystalline phase is mainly responsible for the material performance. Here, the blending technique should enable testing on a broad variety of DOCs, while at the same time post-crystallization is avoided. Other methods that alter the DOC, for example, quenching at the end of the injection molding process or post-processing methods, like annealing, where the specimens are stored at high temperatures for several hours to enforce further crystallization, result in recrystallization when tested above the glass transition. Here, annealed specimens behave more thermally stable compared to quenched specimens; however, the change in DOC in annealed specimens is only minor and unpredictable. On the other hand, the use of blends should ensure a broad, predictable and most important controllable variety of DOCs, outweighing the complex manufacturing. After the production process, the specimens were stored in a dry chamber (MP Dry Cabinet IV ST) at \(40^\circ \) C, until the moisture content, obtained from an Aquatrack measurement, measured less than \(0.1 \, \%\).
3.1.2 Differential scanning calorimetry (DSC)
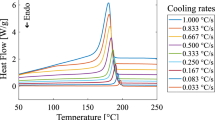
In a first step, the degree of crystallinity of each blend was determined by differential scanning calorimetry (DSC), using a Q2000 machine from TA instruments. Samples of between 5 and 8 mg were cut from the 1BA specimens and heated up from room temperature way above the melting point with a constant heating rate of 10 K/min, repeating the process for each blend. The heat absorption during the endothermic melting of the crystalline regime or, more specifically, the integrated heat flow over time of the melting peak yielded the change in specific enthalpy \(\Delta H_m\). Together with the specific fusion enthalpy for a hypothetical 100\(\%\) crystalline material as \(\Delta H_0 = 190 \, J/g\) from [84], the absolute DOC is obtained by
In this way, the four DOCs 0.29, 0.24, 0.18 and 0.15 (from highest to lowest PA6 content) were obtained, which will be used for model identification and verification. It should be noted that the DOC for pure PA6 multiplied by the respective blend ratio corresponds well with the measured DSC results for the three blends. Therefore, the authors conclude that the DOC of polyamide 6 blends can be approximated with the DSC results for pure PA6 together with the respective blend ratio leading to a possible reduction in experimental effort. Additional measurements conducted by PSM Merseburg GmbH in the first cooling and second heating run confirmed a predictable DOC based on blending ratios. The reproducible DOCs measured 0.4, 0.34, 0.28 and 0.24 from highest to lowest PA6 content. Further, a DSC measurement on pure COC showed a DOC lower then 1% which confirmed that the addition of the co-polymer does not change the resulting crystallization behavior in the specimens. An overview of the DSC results for all four PA6 blends as well as COC is found in Table 2. For model identification and verification, the DSC results from the first heating run are used. These results were obtained from samples untreated after injection molding and therefore contain the production history in terms of, e.g., cooling rate. Since no further (thermal) treatment is applied on the remaining test specimens, the DOC of the first heating run reflects the experimentally tested material morphology. In addition, the glass transition temperature was identified from DSC results. All specimens showed a glass transition temperature at around 58\(^\circ \)C, independent of the blend ratio, which supports the hypothesis of an unaltered caloric material behavior through the blending strategy.
Monotonic uniaxial extension: Experimental true strain and stress curves at \(\dot{\varepsilon }_{x} \approx 0.0005 \, \text {s}^{-1}\) for multiple degrees of crystallinity (DOC) and temperatures above the glass transition regime
Monotonic uniaxial extension: Experimental true strain and stress curves at \(\dot{\varepsilon }_x \approx 0.0005 \, \text {s}^{-1}\) for multiple degrees of crystallinity (DOC) and temperatures below the glass transition regime
3.1.3 Monotonic tension tests
For the mechanical tests, a Zwick/Roell Z020 machine with 2000 N and 500 N force sensors was used, together with a temperature furnace for the test temperatures above room temperature. Preliminary simulations by [85] identified the relevant magnitude of experimental inputs such as strain and strain rates. Concomitant, the specimens were subjected to displacement controlled loading at various loading rates between 0.05 and 1 % per second. Each loading procedure was repeated several times for all four blends at temperatures below and above the glass transition, namely at 23\(^\circ \) C, 50\(^\circ \) C, 100\(^\circ \) C, 130\(^\circ \) C and 150\(^\circ \) C.
In Fig. 2, the results of the monotonic uniaxial tension tests above the glass transition (\(T_g\)) for an exemplary loading rate of 0.05 % per second are shown for a stretch of approximately 20%. The true (Cauchy) stress over the logarithmic strain in the loading direction is determined under the assumption of incompressible material behavior, which is reasonable comparing the experimentally determined Poisson’s ratio (cf. Sect. 3.2). The interested reader is referred to Appendix A.3 for the conversion between engineering (1. Piola–Kirchhoff) and true (Cauchy) stress. In addition, the true stress relation allowed for the investigation of self-heating effects at higher loading rates, which generally lead to thermal softening in polymers. This effect cannot be accurately identified using the engineering (1. Piola–Kirchhoff) stress, since relating the current force to the reference area results in additional geometric softening at high strains. As a result, both effects overlap and no clear distinction can be made. Here, the dashed lines represent the mean values used in the following sections for identification (green) and validation (blue), whereas the deviation of the experimental results is plotted in terms of minimum and maximum values. Note here that the number of tests per DOC and temperature was too small for the calculation of further statistical measures (e.g., standard deviation) with a useful significance. As expected, a pronounced influence of the temperature and the degree of crystallinity on the material response is visible, in line with, e.g., [11, 23, 86, 87]. An increase in temperature led to a decrease in the overall material stiffness, whereas an increase in crystallinity resulted in a higher initial stiffness, hardening and yield stress. In addition, a gradual roll-over to yielding is apparent; therefore, the yield stress in tension cannot be determined directly from the peak in the stress–strain curve, nor from the intersection of the initial slope and the hardening slope (e.g., [26]). Hence, it is chosen as an additional fitting parameter for the identification of the plastic regime. Note here that a similar observation is made for the compressive yield stress, see Fig. 6. Below the glass transition, the influence of the DOC is less pronounced, see Fig. 3, which can be related to a lower chain mobility in the amorphous phase [11]. Interestingly, at 23\(^\circ \) C the blends of PA6 and COC failed earlier than the samples consisting of pure PA6 with a higher total stiffness. This effect can be related to the additional phase boundaries introduced by creating blends. Although binding agents were introduced during compounding to prevent this effect, the apparent heterogeneity of the blends contradicts the hypothesis of an unaltered material behavior below the glass transition temperature. To investigate the material behavior of PA6 for a wide range of crystallinities below the glass transition, other methods, for example, the addition of nucleation agents (see, e.g., [88,89,90]) to pure PA6 or different compatibilizers in the blends, could be tested to improve the results. At 50\(^\circ \) C, the experimental results showed the distinct influence of the crystallinity at large strains above 5%. Similar to the test results above \(T_g\), the total stress increased with increasing DOC. However, this trend was not visible in the elastic regime and equally during plastic yielding (see Fig. 3). Here, the results from the two blends with the highest COC content (\(\chi = 0.18\) and \(\chi = 0.15\)) differed severely from the results for \(\chi = 0.29\) and \(\chi = 0.24\) for all measured strain rates. Both curves showed a high initial stiffness and a first yield point, followed by a stress reduction and a second yielding around 10 % strain. This effect is similar to the double yield (DY) phenomenon, reported for amorphous polymers [5] and polyamide 6 in, e.g., [55, 87, 91]. The first yield point is related to the amorphous phase [28], whereas the second yield point corresponds to the crystalline regime [55]. At this point, it is unclear why this effect was only visible for the two lowest DOCs; however, the authors believe that it could be related to the higher amount of amorphous phase in these specimens. Nevertheless, micromechanical analysis as, for example, the determination of crystal configurations via X-ray diffraction and DSC [92] or additional density measurements, would be necessary, to further investigate whether the observed effects are related to the blend composition. In the elastic regime, the influence of the DOC on the initial stiffness differed from the observations made for the other test temperatures. Here, especially for \(\chi = 0.29\) and \(\chi = 0.24\) a softening in the elastic regime is visible, before the onset of yield is reached. To investigate this phenomenon, an additional dynamic mechanical analysis (DMA) was conducted to determine the storage modulus (stored elastic energy) over the temperature (see Appendix A.2). Here, the decrease in material stiffness started already at around 45\(^\circ \)C with a slightly later beginning with decreasing DOC. The glass transition temperature obtained from DMA lies around 58\(^\circ \)C as determined in the DSC tests. The authors therefore conclude that the tests at 50\(^\circ \)C were conducted in the glass transition regime of the specimens, where changes in the underlying morphology of the amorphous phase led to a change in the initial stiffness. Here, the glass transition started earlier for blends with a higher DOC; consequently, this effect was more pronounced for these blends since their stiffness degradation was further along.
Monotonic uniaxial extension: Results for \(\chi = 0.29\) at various temperatures and strain rates
The influence of the loading rate on the material behavior of PA6 is depicted in Fig. 4 for various temperatures and a DOC of \(\chi = 0.29\). Here, four different strain rates in the range of nearly two decades were tested. In line with findings from [11, 86], the initial elastic material response appeared to be mainly independent of the strain rate, especially below the glass transition. In the visco-elastic, elasto-plastic regime, an increasing velocity led to an increase in hardening, especially for temperatures below \(T_g\). In this temperature regime, the failure behavior is affected as well, with a premature failure at high loading rates, corresponding to the increase in the yield stress (cf. \(\chi = 0.29 \, \text {and}\, \dot{\varepsilon }_x = 0.01 \, \text {s}^{-1}\) ). Above the glass transition, the influence of the strain rate is less pronounced. These observations correspond with those of [86], who stated that the yield stress increased logarithmically with an increasing loading rate and that the influence of the velocity reduces in general with increasing temperatures. In addition, thermal softening due to dissipative effects related to material self-heating is observed at higher strain rates (see, e.g., [93]). This effect is mainly visible for temperatures below \(T_g\), where the slope of the stress–strain curve for \(\dot{\varepsilon }_x= 0.001 \, \text {s}^{-1}\) decreased, compared to the curve corresponding to a velocity of \(\dot{\varepsilon }_x= 0.0005 \, \text {s}^{-1}\). The curves intersect already at moderate strains of approximately 7%. For temperatures above \(T_g\), this intersection is slightly delayed to strains of around 15%; nonetheless, also here self-heating is prominent. To further investigate this effect, experiments using infrared thermography (IR) would be necessary, as done, for example, in [11].
3.1.4 Relaxation tests
Moreover, long-term relaxation test data was obtained at all test temperatures and various strains, to provide additional insight into the time dependent material response. To investigate the visco-elastic regime, relaxation tests at 1% strain were carried out, whereas the visco-elastic, elasto-plastic regime was tested at around 19% strain. The experimental results are shown in Fig. 5 for exemplary temperatures of 130 \(^\circ \)C and 150 \(^\circ \)C. Noteworthy, due to the extensive relaxation times (cf. Fig. 5), it was not possible to repeat this test with the current set of specimens. In contrast to, e.g., [11], the total relaxation time throughout all samples was very high, with a low initial relaxation time and therefore sudden stress reduction in the beginning of the relaxation step. Similar to the tension tests, a temperature dependence was present also in the relaxation tests, where the relaxation time decreased with increasing temperature (see also Sect. 3.3). Furthermore, the amount of stress relaxation in the beginning of the relaxation step increased notably at higher strains. This influence, as well as the impact of the degree of crystallinity that is not visible directly from the experimental results, is studied in detail in Sect. 3.3., where a post-processing method by [94] is applied to the experimental data.
Long-term stress relaxation: Experimental true stress over time curves for multiple degrees of crystallinity (DOC) at small strains and 150\(^\circ \) C and finite strains and 130\(^\circ \) C
3.1.5 Compression tests
To obtain insights into the deformation under compression, monotonic uniaxial compression tests were conducted at various temperatures for \(\chi = 0.29\) and \(\chi = 0.15\). Therefore, additional samples were cut with a cross section of approximately 3.77 \(\times \) 10 mm\(^2\) and tested at \(\dot{\varepsilon }_x = 0.0005 \, \text {s}^{-1}\) with a Zwick/Roell Z020 machine under 23\(^\circ \) C and 130\(^\circ \) C. Additional measurements were carried out at PSM for temperatures of 100\(^\circ \) C and 150\(^\circ \) C. However, no complete data set for all DOCs was available at the present point of time. The experimental results are displayed in Fig. 6. Here, a significant stiffening at high strains, typical for materials under compression, can be observed for all specimens, except for \(\chi = 0.15\) at 150\(^\circ \) C. Similar to the results in tension, no yield stress was directly detectable from the stress–strain curve for temperatures above the glass transition. The observed influence of temperature and degree of crystallinity is in agreement with the tensile results, where an increasing temperature led to a decrease in stiffness and an increasing DOC resulted in a generally stiffer material response. Further tests for the remaining blend ratios and test temperatures are necessary to confirm these findings in the future.
Compression tests for \(\chi = 0.29\) and \(\chi = 0.15\) at various temperatures below and above the glass transition
a Thermomechanical analysis (TMA): Thermal expansion over the temperature for all blends. b Specific heat capacity from DSC measurements for all blends. The trend lines are of the form \(c_T (\chi ) = c_1 \chi + c_2\)
3.1.6 Thermomechanical analysis (TMA)
To conclude the set of experimental results, additional measurements were conducted to obtain insights into the thermal properties of the material. A thermomechanical analysis (TMA) was conducted on a TMA/SDTA841e from Mettler Toledo to obtain the coefficient of thermal expansion (CTE) \(\alpha _T\). The results are shown in Fig. 7a, where the thermal expansion is plotted against the temperature for all DOCs. The corresponding plot of the evaluated CTE (gradient of the graph of dimensional change vs. temperature) plotted over the DOC is found in Sect. 3.5. The CTE generally depends on the glass transition, since thermal expansion is enforced by molecular motions and mobility which are low in the glassy state of the amorphous phase and higher in the rubbery state above the glass transition. This was also visible in the experimental results (cf. Fig. 7), where the thermal expansion increased significantly above the glass transition. The dependence of the CTE on the DOC was not pronounced below the glass transition, whereas above \(T_g\) a decrease of \(\alpha _T\) with increasing DOC was visible. In semi-crystalline polymers, the crystalline phases are interspersed with amorphous regions; therefore, their thermal expansion behavior is more complex as in purely amorphous polymers. For example, amorphous regions close or connected to the crystalline phases, the so-called rigid amorphous phase, show less thermal mobility than the bulk amorphous phase (e.g., [95, 96]). In addition, the amorphous blend partner COC adds separate amorphous regions with particular characteristics; therefore, the compatibility of the two materials was important during blend composition.
Thermal conductivity measurements: a for \(\chi = 0.29\) and various temperatures b for all blends at 130\(^\circ \) C. The linear trend line is of the form \(\lambda _T(\chi ) = c_1 \chi + c_2\)
3.1.7 Specific heat capacity
To determine the specific heat capacity and its dependence on temperature and DOC, the DSC measurements conducted at PSM Merseburg were evaluated further. To that end, the evolution of the specific heat capacity with increasing temperature is shown in Fig. 7b for all four blend ratios. The heat capacity can then be identified as the tangent to the experimental curve, with the remaining changes corresponding to structural changes associated with melting of the crystalline phase. There is no clear dependence on the DOC in the experimental results. However, the specific heat increases linearly with increasing temperature, with a lower total value below the glass transition (see Fig. 7).
3.1.8 Thermal conductivity measurement
The thermal conductivity \(\lambda _T\) was measured using the Hot-Disc method, in which a temperature sensor is placed between two samples that are subjected to a defined heating protocol. Subsequently, the thermal conductivity was derived from the temperature profile over the time as the average of several measurements. To that end, Hot-Disc measurements were taken for multiple test temperatures and a DOC of \(\chi = 0.29\), as well as all DOCs at a temperature of 130\(^\circ \) C, see Fig. 8. The experiments showed an inconclusive dependence of the thermal conductivity on the temperature (see Fig. 8a, where the thermal conductivity firstly increased with increasing temperature and then decreased for all temperatures above the glass transition. The thermal conductivity can be related to the product of thermal diffusivity, density and specific heat capacity (see, e.g., [97]). While the heat capacity increases with increasing temperature (cf. Fig. 7), the thermal diffusivity as well as the density decrease simultaneously (cf. [97, 98]). Consequently, the effect of the temperature on the thermal conductivity can be related to the change in the aforementioned quantities. Here, further measurements on the density and thermal diffusivity at various temperatures and for all other DOCs would be necessary to clearly explain the changes in the thermal conductivity. Since the changes in the thermal conductivity with increasing temperature are only small, the temperature dependence is neglected in this work. In terms of the crystal content, an increase with increasing DOC is visible. Consequently, for the identification procedure described in Sect. 3.5, the thermal conductivity is assumed to depend only on the DOC, hence \(\lambda _T(\chi )\).
3.1.9 Density measurements
Lastly, density measurements were carried out at room temperature, using a gas pycnometer by the company Anton Paar. The resulting density showed an increase with increasing DOC (see Fig. 9) which was expected due to the higher density of crystalline phases compared to amorphous regions.
Density measurements at room temperature. The linear trend line is of the form \(\rho (\chi ) = c_1 \chi + c_2\)
3.2 Elastic constants
The elastic constants, in terms of the Youngs’ modulus and the Poisson’s ratio, are obtained from the initial elastic response from uniaxial monotonic tension tests at all respective test temperatures. Here, the total Young’s Modulus \(E_{tot}(\chi , \theta )\) is determined for each blend, according to DIN EN ISO 527-2:2012, and plotted over the DOC in Fig. 10. Next, the dependence of \(E_{tot}\) on the DOC is examined; therefore; the Trust-Region algorithm in the software tool MATLAB is exploited. The data shows an exponential relation of the form
Here, \(C_1\) and \(C_2\) are temperature dependent material parameters. Interestingly, the nonlinear dependence of \(E_{\text {tot}}\) on the DOC is more pronounced for temperatures above the glass transition. As suspected, at 50\(^\circ \) C no trend is found, due to the differences in the elastic regime between the samples with different COC content (cf. Fig. 3), which is related to testing in the glass transition region. Therefore, during identification, for the temperature of 50\(^\circ \) C only two DOCs will be considered, i.e., \(\chi = 0.29\) and \(\chi =0.24\). From the experimentally identified \(E_{\text {tot}}\), the Youngs’ moduli \(E_1\) and \(E_2\) for the elasto-plastic and visco-elastic part, respectively, are determined using long-term relaxation data at small strains. With regard to [11], who conducted cyclic loading–unloading–recovery experiments at room-temperature for polyamide 6 with 23 % DOC, it can be concluded that at 1% strain the material still behaves visco-elastically and no plastic deformation has occurred yet. Hence, the equilibrium stress, measured at the end of the relaxation step, is assumed to correspond solely to the elastic spring of the elasto-plastic part of the model (see Fig. 1). Concomitant, \(E_1\), is determined using Eq. 38 and the relations for the Lamé constantsFootnote 3. Interestingly enough, the ratio \(m_E \) between the Young’s modulus of the elasto-plastic part \(E_1\) and the total Young’s modulus \(E_{\text {tot}}\) is found to be crystallinity dependent, with values ranging from 0.5 for \(\chi = 0.15\) to approx. 0.72 for \(\chi = 0.29\). This finding corresponds to the blend composition and, for example, the density measurements, where a lower DOC means a higher content of amorphous phase and therefore increased viscous behavior. A clear dependence on the temperature is not visible; therefore, this influence is neglected. The ratio \(m_E(\chi )\) is approximated by a linear function, and the Young’s modulus for the elasto-plastic term is determined according to \( E_1=m_E \, E_{\text {tot}}\). The Youngs’ modulus for the visco-elastic part followed from \(E_2 = E_{\text {tot}} - E_1\).
Crystallinity dependence of the total Young’s modulus below and above the glass transition temperature
To obtain the Poisson’s ratio, 2D measurements evaluated using digital image correlation (DIC) are necessary. The corresponding tests were conducted using a Limess Q400 system. Following Sect. 2 and the assumptions made therein, the Poisson’s ratio is chosen to be constant in this work, i.e., \(\nu _{tot}(\theta )=\nu _1 = \nu _2\). No trend on the DOC was visible in the experimental results; therefore, the dependence on the crystallinity is neglected. Furthermore, the dependence of the Poisson’s ratio on the temperature is observed to be relatively small above the glass transition; thus, a constant value of \(\nu _{\text {tot,Above Tg}} = 0.45\) is concluded, which is close to incompressible material behavior. For temperatures below \(T_g\), the experimentally determined Poisson’s ratio was lower compared to the results above the glass transition. However, the experimental data showed a pronounced strain rate dependence that is not yet clarified. Therefore, the Poisson’s ratio below the glass transition is approximated with \(\nu _{\text {tot,Below Tg}} = 0.35\).
3.3 Viscous quantities: nonlinear relaxation function
To represent the relaxation behavior of semi-crystalline polymers, a single Maxwell element in combination with a constant relaxation time \(\tau \) generally is not sufficient (see, e.g., [14, 48, 94]). Therefore, other approaches must be utilized, for example combining several Maxwell elements or employing a nonlinear relation for the relaxation time (e.g., [11, 49, 94]). In this work, the latter approach is chosen, since the addition of further Maxwell elements increases the number of material parameters significantly. With the governed elastic constants, a post-processing scheme, originally proposed by [94] for the identification of the viscosity and adapted for the relaxation time in the three-dimensional case by [11], is applied. Here, long-term relaxation test data at large strains (see Fig. 5) is used for identification purposes, whereas results at small strains and stepwise tests are utilized for model validation. The relaxation tests at small total strains were explicitly excluded from identification where possible, since [11] concluded that the nonlinearity of the relaxation time is more pronounced at finite strains. At 23\(^\circ \) C, only experimental data at small strains was available, due to early failure in three of the four blends.
To this end, a uniaxial tension test is conducted, where the loading direction coincided with the direction of the principal stretch \(\lambda _x\). The specimen is loaded until a maximum total strain of approximately 19% is reached, followed by a constant displacement (\({\varvec{u}} = \) constant) during the relaxation step. At the termination point of the experiment, stress equilibrium was assumed, where the remaining or equilibrium stress (\(\sigma _{1,x}\)) corresponded to the contribution of the elasto-plastic part of the model. Note here that a polynomial function is fitted to the results to reduce the oscillations in the experimental data, related to readjustments of the machine during testing. In general, experimental noise likely yields non-physical results and results in spikes when evaluating the relaxation time. During testing, DIC is used to obtain two-dimensional deformation data in terms of the stretches in the principal directions \(\lambda _x\) and \(\lambda _y\) to determine the deformation gradient \({\varvec{F}}\) for every experimental time step. In the third direction, the evolution of the stretch \(\lambda _z\) is assumed to be equal to \(\lambda _y\), according to [11]. Subsequently, the true (Cauchy) stress \(\sigma _x\) in loading direction is obtained by relating the machine force to the current area \(A= A_0 \, \lambda _y \, \lambda _z\), which is calculated using the reference area \(A_0\), as well as the corresponding stretches in y- and z-direction. The overstress \(\sigma _{2,x}\) in loading direction corresponding to the visco-elastic part is then calculated at each experimental time step by \(\sigma _{2,x}(t) = \sigma _x(t)- \sigma _{1,x}\) and used together with the deformation gradient \({\varvec{F}}\) as input data for the post-processing scheme. The associated coefficient matrices read:
From the experimental data, the second Piola–Kirchhoff stress during the relaxation step is obtained by a pull-back operation \({\varvec{S}}_2(t)=J\,{\varvec{F}}^{-1}{\varvec{\sigma }}_{2}(t){\varvec{F}}^{-T}\). Subsequently, Eq. 41 is solved for the viscous right-Cauchy–Green like tensor \({\varvec{C}}_v\) at each experimental time step. The corresponding evolution of the viscous stretch \(\lambda _{v,x}\) in loading direction over the time is shown in Fig. 11 exemplary for all DOCs at 100\(^\circ \) C. Exploiting the exponential map algorithm, Eq. 31 is integrated over the time
and further solved for the relaxation time \(\tau \). Here, the index \((*)_n\) indicates quantities from the last converged time step \(t_n\), whereas quantities from the current time step \(t_{n+1}\) are given without index. Since the coefficient matrices from the preceding time step are known and all tensor valued quantities commute, Eq. 61 can be solved in terms of a system of scalar-valued equations. The resulting relaxation time at each experimental time step is plotted in Fig. 11 over the Kirchhoff stress \(\tau _{2,x}\) for an exemplary temperature of 100\(^\circ \) C. Similar to [11, 94], a nonlinear relation of the relaxation time is observed, despite the slight noise in the data. However, no clear dependence of the relaxation time on the DOC is visible in the results of the post-processing procedure (see Fig. 11), the same holds for the other test temperatures. Thus, the relaxation time is concluded to be independent of the DOC. Furthermore, a significant decrease in the relaxation time with increasing temperature is observed as well as a nonlinear dependence on the overstress (see Fig. 11). These findings motivate the use of a nonlinear function for the relaxation time, depending on the temperature and the overstress.
Results of the visco-elastic post-processing procedure: Inelastic stretch over time and relaxation time over Kirchhoff stress at 100\(^\circ \) C for all DOCs
Following the findings from [99], who investigated various functions for the viscosity in the context of viscoelasticity models for rubber and brain tissue, several functions for the relaxation time are identified with the results from the post-processing method and compared to experimental data. Here, only functions are tested that showed an improvement in [99] for rubber compared to a constant viscosity and that have a relatively low number of material parameters (see Table 3). A constant relaxation time serves as the benchmark. Functions 2–4 depend purely on the stress in terms of the Kirchhoff overstress \({\varvec{\tau }}_2\), whereas in function 5 an additional dependence on the total deformation in terms of the left Cauchy–Green tensor \({\varvec{B}} = {\varvec{F}} {\varvec{F}}^\textrm{T}\) is introduced. From function 6 onwards, a dependence on the inelastic deformation is assumed. Here, it is made use of the equivalence of the norm \(||{\varvec{B}}_v || = || {\varvec{C}}_v ||\) and \(||{\varvec{B}}_v^{-1} || = || {\varvec{C}}_v^{-1} ||\) as well as the trace \(I_{1,v} = \text {tr} ({\varvec{B}}_v) = \text {tr} ({\varvec{C}}_v)\). Unlike all other functions, function 6 contains a dependence on the visco-elastic Mandel stress \({\varvec{M}}_2\) which can be related to the viscous Kirchhoff stress as \({\varvec{M}}_2 = {\varvec{F}}_{e2}^\textrm{T} {\varvec{\tau }}_2 {\varvec{F}}_{e2}^{-T}\). Therefore, \({\varvec{M}}_2\) and \({\varvec{\tau }}_2\) share the same eigenvalues and \(||{\varvec{M}}_2|| = || {\varvec{\tau }}_2 ||\) holds. Additionally, a modified version of the function from [14] is proposed in function 7, depending on the Kirchhoff stress \({\varvec{\tau }}_2\) and the inelastic deformation \({\varvec{B}}_v^{-1}\). An overview of the functions adapted for the relaxation time is given in Table 3. For a detailed description and investigation of further functions for the viscosity, the reader is kindly referred to [99] or the literature cited therein.
a Identification results for the nonlinear relaxation time functions from Table 3 at 100\(^\circ \) C normalized to a constant relaxation time. b Corresponding material parameters
To identify the function best suited to describe the present behavior of the relaxation time, the Trust-Region algorithm is exploited in MATLAB. A least squares problem is solved, where the residual is defined as the sum of the squared differences between the experimentally post-processed relaxation time \(\tau \) (see Fig. 11) and the corresponding function value (see Table 3). In accordance with [99], the range of feasible material parameter values for the identification procedure is chosen such that the second law of thermodynamics is satisfied (\(\tau > 0\)). The fitting results for all functions are shown in Fig. 12 together with the corresponding fitted material parameters. Note here that each function was identified simultaneously for all DOCs. Function 1 with a constant relaxation time clearly yielded an insufficient approximation of the nonlinear behavior of the relaxation time. Thus, it served as the reference solution for the comparison. In contrast, all other tested functions showed a significant improvement. The power law-type functions 2, 5 and 8 are, however, inferior to the exponential approaches as well as to the hyperbolic sine power law (function 4), which behaves like a power law for small stresses and as an exponential law for large stresses. Interestingly, the identified parameters for the relaxation time \(\tau _0\) in function 3, 4 and 6 (cf. Fig. 12) reflected the extrapolated value for the relaxation time at the termination point of the relaxation step, where the overstress is zero. Hence, this value could be determined during post-processing, reducing the number of material parameters during identification. The errors for function 3, 4 and 6 are almost identical (cf. Fig. 12); therefore, these approaches can be seen as equally suited to model the nonlinear relaxation time. In combination with the findings about the initial relaxation time \(\tau _0\) and considering the number of material parameters, functions 3 and 6 are best suited. However, function 7 shows an even lower error, compared to function 3 and 6. Here, the influence of the inelastic deformation is considered, depending on the exponent \(\gamma \), whereas function 6 assumed a constant ratio between overstress and viscous deformation.
For a temperature of 23\(^\circ \) C, long-term relaxation data were only available at a total strain of 0.5 %. Applying the post-processing scheme to the experimental data, a rather linear relation for the relaxation is visible (see Fig. 13), similar to the results of [11]. When comparing different nonlinear functions for the relaxation time, this resulted in a comparatively weaker improvement, compared to the constant relaxation time (see Fig. 13). Here, the use of multiple Maxwell elements with different relaxation time functions could improve the results. However, this investigation is beyond the scope of this paper. Function 8 performed worse than the benchmark test and is therefore excluded from the plot. In the case of small strains, function 7 yielded similar improvement, compared to function functions 3, 4 and 6. Finally, function 7 is identified for all remaining tests temperatures and further implemented in a ABAQUS user material subroutine UMAT. The comparison of the identification results at the other test temperatures is given in Appendix A.5, and the corresponding material parameters for function 7 are found in Table 4.
Results of the visco-elastic post-processing procedure: a Relaxation time over Kirchhoff stress at 23\(^\circ \) C for all DOCs. b Fitting results for the nonlinear relaxation time functions from Table 3
3.4 Plastic material parameters
In the final identification step for the mechanical parameters of the isothermal model, the remaining parameters related to plastic deformations are characterized. These are the parameters \(c(\chi , \theta )\) and \(b(\chi , \theta )\) that describe the nonlinear kinematic hardening behavior. Due to the inconclusive data for the yield stresses in tension and compression above the glass transition, also the parameters \(\sigma _t(\chi , \theta )\) and \(\sigma _c(\chi , \theta )\) are still undetermined. Therefore, a nonlinear multi-curve fitting procedure in MATLAB is used together with monotonic tensile data to identify these four parameters for all DOCs at each test temperature. A least squares problem is formulated, where the error is defined as the squared difference between the experimental true stress in loading direction and the Cauchy stress obtained from a single element test. Thus, in each iteration of the optimization, ABAQUS and the corresponding UMAT are called with the current set of plastic parameters. The boundary value problem for the single element test is displayed in Fig. 25 in Appendix. For the discretization in ABAQUS, a single C3D8T element is used together with isothermal boundary conditions. Concerning the optimization, the genetic algorithm is used in series with the Downhill-Simplex algorithm. This procedure is favorable, since the parameter range, apart from the yield stresses, is kept relatively large and for the Downhill–Simplex algorithm alone no restrictions can be applied to the parameter domain. Consequently, also negative, non-physical values are possible. Furthermore, convergence is unlikely if the initial parameters are too far away from their final values. The genetic algorithm therefore narrows down the range of possible solutions and its best fitted parameter set serves as the starting values for the Downhill–Simplex algorithm. In contrast to the gradient-based Levenberg–Marquardt algorithm or the closely related Trust-Region algorithm, the genetic algorithm as well as the geometrical Downhill–Simplex algorithm are gradient free and due to their construction not restricted in the direction of the iteration. Thus, in comparison they are more robust when used in combination with numerical simulations.
Results for the parameter identification from single curve fits at 100\(^\circ \) C. The linear trend line is of the form \((\bullet ) = c_1 \, \chi + c_2, \, \text {with} \, (\bullet )= \sigma _t^0, \sigma _c^0, c, b \)
Similar to [50], who investigated the thermo-viscoelastic material behavior of polyurethane and introduced temperature-dependent shift functions to relate the identified value at room temperature to higher temperatures, in this work a function for each material parameter depending on the DOC is identified. In this way, a parameter set for each test temperature is found. Therefore, in a first step single fits at each constant temperature and for each DOC need to be conducted using the aforementioned nonlinear optimization procedure. Besides the yield stresses, for which the parameter range can be restrained by identifying the intersection of the initial slope of the stress–strain curve with the inconclusive hardening slopes, the parameter range for the hardening parameters is kept large for the identification. The resulting plastic parameters for each blend are subsequently plotted against the degree of crystallinity (see Fig. 14). Now, the dependence of each parameter on the DOC can be determined as a post-processing step, by exploiting the Trust-Region algorithm in MATLAB. As done in all previous identification steps, the blend with \(\chi = 0.18\) is not considered for identification and serves for validation purposes. Here, a linear ansatz is chosen and the identified relation is visualized exemplary for a temperature of 100\(^\circ \) C in Fig. 14. For the identification, only experimental curves from three degrees of crystallinity (\(\chi = 0.15, 0.24, 0.29\)) are taken into account. Notably, the identified parameters for \(\chi = 0.18\) are overall in good agreement with the parameters of the other DOCs. Only for the kinematic hardening parameter c, a higher deviation is visible which is also apparent in the result for \(\chi = 0.15\). The results for the other temperatures above the glass transition are found in Appendix A.6. For the temperatures below \(T_g\), the fitting results are not visualized, since at 23\(^\circ \) C three of the four blends failed before significant plastification; therefore, the parameters, apart from the onset of yielding, are identified with a single fit for \(\chi = 0.29\). At 50\(^\circ \) C, the blends with \(\chi = 0.18\) and \(\chi = 0.15\) were excluded from identification, since inconclusive material behavior occurred, related to testing in the glass transition regime. Thus, only two blends remain for the characterization; therefore, the fitted linear trend line agrees perfectly with the results, leaving no possibility for validation. The identified parameters for the linear functions for all plastic parameters are listed in Table 4.
3.5 Thermal quantities
To obtain an expression for the coefficient of thermal expansion, it is calculated by \(\alpha _T = \Delta L /(L \Delta T )\) from the thermal expansion curve in Fig. 7 for every blend at each test temperature. Here, \(\Delta L\) is the thermal expansion, L is the initial length of the specimen, and \(\Delta T\) is the temperature difference. Next, the Trust-Region algorithm is exploited in the commercial software tool MATLAB to describe \(\alpha _T\) as a function of the degree of crystallinity for each test temperature separately. Again, \(\chi = 0.18\) is only used for validation purposes. The results are shown in Fig. 15, where it can be seen that the characterized curves are in good agreement with the experimental results. However, it is not clear as to why the behavior at 100\(^\circ \) C differs so much from the remaining temperatures above \(T_g\). A possible explanation could be changes in the ratio of the amorphous to the crystalline phase, related to post-crystallization.
Coefficient of thermal expansion at different temperatures and DOCs. The linear trend line is of the form \(\alpha _T (\chi ) = c_1 \chi + c_2\)
Concerning the specific heat capacity \(c_T\), the results of the identification procedure were already shown in Fig. 7. The corresponding material parameters are summarized in Table 5. Note here that no clear dependence on the DOC is present. For the thermal conductivity, a multifit using the Trust-Region algorithm in MATLAB is conducted, corresponding to Sect. 3.4. The results of the fitting procedure are visualized in Fig. 8. An overview of the thermal parameters including the density is given in Table 5.
3.6 Identification results
The results of the identification procedure are shown in Fig. 16 for all temperatures above the glass transition and in Fig. 17 for the temperatures below \(T_g\). Good agreement of the identification results with the experimental data can be observed, which is especially remarkable keeping in mind the extensive range of DOCs to be described by the model. The model prediction for \(\chi = 0.18\) also captures the experimental results well, especially the elastic regime and the onset of yielding. However, at large strains the deviation between model and experiment is notable. This can be traced back to the deviation between the function for each plastic parameter compared to the plastic parameters obtained in a single fit for \(\chi = 0.18\) (cf. Figures 14 and 27). For instance, at a temperature of 100\(^\circ \) C, the initial elastic response as well as the yield stress are accurately captured. However, the prediction of the hardening slope is inaccurate, since the hardening parameter c is not in good agreement with the single fit results (cf. Fig. 14). Similar observations can be made for the other temperatures above \(T_g\), though here, additionally the onset of yielding differs from the identified relation through the multifit.
Monotonic, uniaxial extension: Identification results for multiple degrees of crystallinity (DOC) and temperatures above the glass transition regime
Monotonic uniaxial extension: Identification results for multiple degrees of crystallinity (DOC) and temperatures below the glass transition regime
Below \(T_g\), the results for a temperature of 23\(^\circ \) C in Fig. 17 are in good agreement with the experimental data. Here, the elastic regime as well as the onset of yielding are accurately captured. Regarding the hardening slope, only results for one blend were available for identification; therefore, naturally, the hardening behavior is well represented. For a temperature of 50\(^\circ \) C, the model response already differs from the experimental results in the elastic regime, though the hardening behavior is well captured. This difference results from a material softening visible in the experimental data (see Sect. 3.1) and the DMA results in Appendix A.2, where the slope of the experimental curve flattens compared to the initial material stiffness before the onset of plastic yielding is reached at around 2.5 % strain. The authors believe that this behavior is related to testing in the glass transition regime. Since the gradual transition of the underlying morphology of the amorphous phase and its associated effect are, however, not incorporated in the model formulation, the difference is expected.
3.7 Model validation
In order to validate the proposed constitutive framework, further results are compared to the test data. Therefore, only experimental data that have not been used for identification are compared to the corresponding model response. The boundary value problem, in terms of a single element test, is given in Fig. 25 in Appendix. In a first step, the model prediction for the long-term relaxation behavior corresponding to Fig. 5 is shown for \(\chi = 0.18\) and all temperatures above the glass transition. It should be emphasized that the relaxation function was identified with experimental results for the other three blends only. Therefore, the specimens were loaded with \(\dot{\varepsilon }_x = 0.01 \, \text {s}^{-1}\) to a strain level of approximately \(\varepsilon _x = 0.19\) and subsequently relaxed for 32,000 s. The corresponding model response for \(\chi = 0.18\) is given in Fig. 18. Overall the model prediction is in good agreement with the experimental data, especially at 100\(^\circ \) C.
To validate the small strain regime, a stepwise loading–unloading test is carried out for a DOC of 29% at 130\(^\circ \) C. Here, the specimen undergoes a stepwise deformation of \(\varepsilon _x = 0.01\), until a maximum strain of \(\varepsilon _{\text {max},x}\) is reached (see Fig. 19). Subsequently, the specimen is unloaded at the same pace up into the compression regime. The corresponding loading rate was \(\dot{\varepsilon }_x = 0.0001 \, \text {s}^{-1}\), and the specimen was held at constant strain for 15,000 s in each step. In comparison with the experimental results, the model prediction underestimated the material behavior, especially at larger strains. However, the shape of the model curve corresponds well to the experimental data. The authors believe that this behavior results from the identification and characterization process to finite strain data only. As previously seen for small strain test data at 23\(^\circ \) (cf. Fig. 13), the nonlinear function for the relaxation time does not fit the linear relation between relaxation time and stress. As suggested in [99], the use of a second Maxwell element, identified with the relaxation behavior at small strains, could lead to an improvement. Moreover, it should be noted that the corresponding strain rate of \(\dot{\varepsilon }_x = 0.0001 \, \text {s}^{-1}\) has not been used for identification of either tensile, compressive or relaxation data and differs by two decades from the strain rate used for identification of the relaxation function (\(\dot{\varepsilon }_x = 0.01 \, \text {s}^{-1}\)).
Long-term stress-relaxation at finite strains for temperatures above \(T_g\). Experimental stress over time data and corresponding model predictions (\(\chi = 0.18\))
Stepwise long-term stress-relaxation at small strains for \(\chi = 0.29\) at 130\(^\circ \) C. Experimental strain and stress over time data and corresponding model predictions
Besides stepwise tests at small strains, also stepwise tests at large strains were conducted for \(\dot{\varepsilon }_x = 0.0001 \, \text {s}^{-1}\) (see Fig. 20). Therefore, the specimens were exposed to a maximum strain of \(\varepsilon _{\text {max},x}= 0.16\), distributed over four load steps of 4 % strain each. The holding period was 15,000 s per step. Again, the model predictions are less accurate, while the shape of the curves is in good agreement. Nevertheless, the predictions are good, keeping in mind that the strain rate is two decades lower than the one used for identification. Compared to the small strain case in Fig. 19 for the same strain rate, the experimental results for the large strain case are in better agreement with the test data. This supports the findings made in Sect. 3.3 that the chosen function for the relaxation time works best for finite strains. As mentioned earlier, the addition of further Maxwell elements could improve the model results.
The validation for the tensile tests is already given in Figs. 16 and 17 for \(\chi = 0.18\). Overall, as discussed in Sect. 3.6, the prediction is in good agreement with the experimental results. Especially the elastic regime and the onset of yielding are accurately captured, only the hardening behavior is underestimated. Unfortunately, it was not possible to validate the compression regime, since all available test data were used for identification. In the future, further compression tests on the remaining blends and temperatures are planned to close this gap.
Stepwise long-term stress-relaxation at large strains for multiple DOCs at 130\(^\circ \) C. Experimental strain and stress over time data and corresponding model predictions
4 Numerical example
To demonstrate the capabilities of the developed and validated constitutive framework in capturing the material response in multi-axial stress states, a structural example at ambient (\(\theta = 23^\circ \) C) and elevated (\(\theta = 100^\circ \) C) temperature is conducted. To this end, type 1BA (ISO 527-2:2012) specimens were modified by drilling a circular hole with approximately 1 mm diameter into the center of the measurement area (cf. Fig. 21). Here, various DOCs were tested to validate the model response. At room temperature, only the highest DOC (\(\chi = 0.29\)) was tested, since the other DOCs suffered from early failure (cf. Fig. 3). For a temperature of \(100^\circ \) C, three DOCs were tested, \(\chi = 0.29\) and \(\chi = 0.24\) which served for identification purposes and \(\chi = 0.18\) that is used for prediction only. The loading rate was controlled by the cross head speed of the Zwick/Roell Z020 machine and prescribed to \(\dot{\varepsilon }_x \approx 0.0005 \, \text {s}^{-1}\). During testing, the heterogeneous strain field around the hole was measured using the Q-4xx Istra 4D digital image correlation (DIC) system. The corresponding measurement area is highlighted in light blue in Fig. 21. Each experiment was repeated only two to three times due to good reproducibility and only small scatter in the recorded force over time data (cf. Fig. 21).
To reduce computation time, the symmetry of the specimen is exploited. Consequently, only one eighth of the specimen is modeled. The corresponding specimen dimensions were approximated from ISO 527-2:2012. Similar to [11], at the boundary of the measurement area, the evolution of the cross section was calculated from the initial cross section \(A_0= 5\cdot 2 \, \text {mm}^2\) and the measured mean stretch in y-direction by \(A(t) = \lambda _y (t)^2 A_0\). Note here that the assumption \(\lambda _y (t) \approx \lambda _z (t)\) is made in line with the findings from [11]. In this way, the evolution of the true stress in longitudinal direction could be computed from the recorded force data and the deformed cross section as \(\sigma _x(t)= F(t)/A(t)\). In the following, the respective true stress over time relation served as a traction boundary condition for the finite element model. In Fig. 21, the geometry for the FEM simulation is presented, where reduced eight-node solid elements (C3D8RT) from the ABAQUS/Standard element library are used for discretization. Note here that for visualization purposes a coarse mesh is shown. Prior to obtaining the simulation results, a mesh convergence study was conducted and a finer mesh distribution was chosen. The corresponding material parameters for each DOC are taken from Tables 4 and 5.
Top: Geometry and boundary value problem of type 1BA (ISO 527-2:2012) with circular hole, including DIC measurement area. Bottom: Recorded force data for various DOCs at room (\(\theta = 23^\circ \text {C}\)) and elevated (\(\theta = 100^\circ \text {C}\)) temperature. Note: The orange area indicates where the evaluation of the DIC measurement was not possible or only possible with the exclusion of larger areas around the hole, due to large deformations and flaked off DIC pattern
Figures 22 and 23 show the comparison of the true strain contours in longitudinal (x) and transverse (y) direction, obtained from both, the finite element simulation and the DIC images. For \(\chi = 0.29\) at room temperature, two time steps A (\(t= 25\) s) and B (\(t= 50\) s), highlighted in Fig. 21, are presented. At \(100^\circ \) C, the results are shown at \(t= 75\) s (point C) and \(t= 150\) s (point D) for all three DOCs and at \(t= 225\) s (point E) for \(\chi = 0.24\) only.
True strain contours in longitudinal and transverse direction: Comparison between experiment and model response for different temperatures and DOCs. Note here that the red and blue colored values correspond to the simulation extrema in the area close to the hole
Since the area close to the hole cannot be evaluated in the DIC data due to the chosen facet size and since therefore no strains are available, this area is excluded from the comparison with a light-gray patch. The size of the light-gray patch was chosen such that any area of the DIC where no strain data was available at that experimental time step was covered. Consequently, the patch size increased with increasing time (cf. Figs. 22 and 23). For the contour plots of the simulation, the chosen patch was mirrored at the x-axis and the legend of the DIC results was adopted for plotting. In the region close to the hole, however, the extreme values of the simulations occur. Thus, the extrema are included in red and blue color next to the legends.
True strain contours in longitudinal and transverse direction: Comparison between experiment and model response for different temperatures and DOCs. Note here that the red and blue colored values correspond to the simulation extrema in the area close to the hole
The predicted strain fields in longitudinal and transverse direction are in very good agreement with the experimental results. Considering the formation of a multi-axial strain field close to the hole, the prediction is especially impressive, since the constitutive model was identified with uniaxial test data only. In addition, for model identification no DIC data apart from the Poisson’s ratio was available and the true stress–strain data was obtained via the assumption of incompressibility. In terms of the results for \(\chi = 0.18\) (cf. Fig. 22) which is used purely for model validation, no big differences compared to the other DOCs can be observed, confirming the validity of the model for polyamide 6. For \(\chi = 0.24\) at \(100^\circ \) C, a third time step E at \(t= 225\) is evaluated. Here, the deformation of the specimen in the region close to the hole was already very large; therefore, a bigger area needed to be grayed out. To provide a better understanding, the resulting deformation of the specimen after testing is visualized in a photograph in Fig. 23. In addition, for this time step the temperature field is given as well, indicating a slight increase in temperature for the whole specimen originating from the area close to the hole, where large strains in longitudinal direction are present. Infrared thermography measurements during mechanical testing would be needed to validate this result in the future, which is caused by dissipative heating.
5 Conclusion and outlook
In this work, a thermo-mechanically coupled constitutive framework was presented to predict the material behavior of semi-crystalline polymers at finite strains. To this end, a visco-elastic and an elasto-plastic contribution were combined to capture the complex nonlinear material behavior. Hereby, the derivation of the model equations was carried out in a thermodynamically consistent manner. To account for the Bauschinger effect, nonlinear kinematic hardening of Armstrong–Frederick type was incorporated together with a tension–compression asymmetry in yielding. The corresponding yield surface incorporates a hydrostatic pressure sensitivity, typically observed in polymers. Besides the strain rate dependency, the temperature was considered as an influencing factor; therefore, the temperature field was fully coupled with the mechanical part of the model to account for self-heating effects. Moreover, the degree of crystallinity served as a constant input parameter to predict the effect of the underlying material morphology on the material behavior, as well as the interplay between the biphasic microstructure and applied thermal conditions. The implementation in the commercial FEM software ABAQUS/Standard, together with the use of the algorithmic differentiation tool ACEGEN, provided a flexible framework for current and future model adjustments.
To identify and validate the constitutive framework, an extensive experimental study was conducted, including a wide range of temperatures, finite strains as well as strain rates over two decades. Here, a novel blending technique was used during specimen production to achieve a wide range of degrees of crystallinities that were stable regarding time and temperature. In total, a range of approximately 15 % DOC, ranging from \(\chi = 0.15\) to \(\chi = 0.29\), was realized in the specimens. However, the addition of a co-polymer also had negative effects on the material response. Monotonic tensile tests revealed that the material strength below the glass transition regime is drastically reduced due to the increasing number of phase boundaries. Above \(T_g\), no such effects were visible. In order to investigate the complex visco-elastic, elasto-plastic material behavior, different loading procedures (i.e., monotonic tension, monotonic compression and relaxation tests) were conducted. The set of experimental data was completed by thermal experiments (i.e., TMA, DSC, Hot-Disc measurements, density measurements). The conducted experimental study provided important insights into the complex dependencies of temperature, strain rate and DOC and closed several gaps left in earlier works. Nonetheless, also further questions arose, especially related to the field of blend production. Here, further additives should be tested in the future. Especially the comparison of blends produced with a co-polymer or with crystallization agents could be of interest when it comes to producing specimens with a wide range of DOCs. In addition, the influence of adding different compatibilizers on the material response below the glass transition regime should be examined carefully.
Based on the experimental data base, a successive identification procedure for the proposed framework was presented to obtain a set of material parameters for each test temperature. At the same time, various functions for a nonlinear relaxation time were compared to a benchmark test to identify the best suited relation. Lastly, against the odds, the evaluation of the crystallinity dependence of the thermal quantities revealed that the influence was less pronounced as in the mechanical tests, apart from the thermal expansion coefficient.
Subsequently, validation studies were performed that showed good agreement with the experimental data in the case of monotonic tension. The prediction for the relaxation tests was, however, less accurate for strain rates that were not used during identification. Probably, this can be accounted to the range of two decades that were considered during experimental testing. Overall, the constitutive framework was able to predict the material behavior of PA6, as demonstrated in the structural examples, where experimental data for various DOCs and temperatures were considered. Here, the temperature field was visualized as well, demonstrating a slight increase in the overall specimen temperature due to dissipation.
In the future, forming experiments are planned, where large variations in temperature during the heating, consolidation and cooling steps will demonstrate the need for the thermo-mechanical coupling in a more elaborate way. Furthermore, the experimental data set will be completed with additional compression tests for the remaining blends and cyclic tension and compression tests to analyze the hysteresis loop. Further, experiments on more complex loading scenarios, for example, pure shear, are planned to validate the choice of the yield surface with respect to experimental findings. Finally, crystallization kinetics will be incorporated into the constitutive framework to study the effect of strain-induced crystallization as well as cold crystallization for further use in thermoforming simulations.
Notes
Two arbitrary tensors \({\varvec{A}}\) and \({\varvec{B}}\) are similar if \({\varvec{A}} = {\varvec{C}} \, {\varvec{B}} \, {\varvec{C}}^{-1}\) holds for invertible \({\varvec{C}}\). By evaluating the characteristic polynomial, it can be shown that \({\varvec{A}}\) and \({\varvec{B}}\) share the same eigenvalues and thus the same physical interpretation. Consequently, the invariants of \({\varvec{A}}\) and \({\varvec{B}}\) are interchangeable.
The bulk moduli \(K_*, *={1,2}\) are defined by the two Lamé constants \(\mu _*\) and \(\Lambda _*\) as \(K_* = \Lambda _* + \dfrac{2\mu _*}{3}\).
The 1. Lamé constant is calculated using the relation \(\lambda = (E_{\text {tot}}\nu _{\text {tot}})/((1+\nu _{\text {tot}})(1-2\nu _{\text {tot}}))\) and the shear modulus as (2. Lamé constant) \(\mu = E_{\text {tot}}/(2(1+\nu _{\text {tot}}))\).
Abbreviations
- a, A :
-
Scalar quantity
- \({\varvec{a}}\) :
-
First-order tensor
- \({\varvec{A}}\) :
-
Second-order tensor
- \({\varvec{I}}\) :
-
Identity tensor
- \(\mathbb {A}\) :
-
Fourth-order tensor
- \(\dot{(*)}\) :
-
Total derivative with respect to time
- \(({\varvec{A}})^\textrm{T}\) :
-
Transpose of \({\varvec{A}}\)
- \(({\varvec{A}})^{-1}\) :
-
Inverse of \({\varvec{A}}\)
- tr\(({\varvec{A}})\) :
-
Trace of \({\varvec{A}}\)
- \(\text {det}({\varvec{A}})\) :
-
Determinant of \({\varvec{A}}\)
- \(\text {sym}({\varvec{A}})\) :
-
\(\dfrac{1}{2}({\varvec{A}} + {\varvec{A}}^\textrm{T})\)
- \(\text {dev}({\varvec{A}})\) :
-
\({\varvec{A}} - \dfrac{1}{3} \, \text {tr}({\varvec{A}}) {\varvec{I}}\)
- \(\text {Grad}({\varvec{A}})\) :
-
Gradient of \({\varvec{A}}\) with respect to the reference configuration
- \(\text {Div}({\varvec{A}})\) :
-
Divergence of \({\varvec{A}}\) with respect to the reference configuration
- : :
-
Double contraction
- \(|{\varvec{A}}|\) :
-
\(\sqrt{\text {tr} ({\varvec{A}}^\textrm{T} {\varvec{A}})}\)
- \((*)_{n}\) :
-
Quantity from last converged time step
- \(\bar{(*)}\) :
-
Quantity in the reference configuration
- \(\hat{(*)}\) :
-
Quantity in Nye Notation \(\bigl ((11),(22),(33),(12),(13),(23)\bigr )^\textrm{T} \)
References
Strobl, G.R.: The Physics of Polymers, Vol. 2. Springer (1997)
Cowie, J.M.G., Arrighi, V.: Polymers: Chemistry and Physics of Modern Materials. CRC Press (2007)
Young, R.J., Lovell, P.A.: Introduction to Polymers. CRC Press, Boca Raton (2011)
Haward, R.N., Thackray, G.: The use of a mathematical model to describe isothermal stress-strain curves in glassy thermoplastics. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 302(1471), 453–472 (1968). https://doi.org/10.1098/rspa.1968.0029
Boyce, M.C., Parks, D.M., Argon, A.S.: Large inelastic deformation of glassy polymers. Mech. Mater. Part I: Rate Depend. Const. Model 7(1), 15–33 (1988). https://doi.org/10.1016/0167-6636(88)90003-8
Anand, L., Gurtin, M.E.: A theory of amorphous solids undergoing large deformations, with application to polymeric glasses. Int. J. Solids Struct. 40(6), 1465–1487 (2003). https://doi.org/10.1016/S0020-7683(02)00651-0
Mulliken, A.D., Boyce, M.C.: Mechanics of the rate-dependent elastic-plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 43(5), 1331–1356 (2006). https://doi.org/10.1016/j.ijsolstr.2005.04.016
Barriere, T., Gabrion, X., Holopainen, S.: A compact constitutive model to describe the viscoelastic-plastic behaviour of glassy polymers: comparison with monotonic and cyclic experiments and state-of-the-art models. Int. J. Plast. 122, 31–48 (2019). https://doi.org/10.1016/j.ijplas.2019.05.010
Boyce, M.C., Socrate, S., Llana, P.G.: Constitutive model for the finite deformation stress-strain behavior of poly(ethylene terephthalate) above the glass transition. Polymer 41(6), 2183–2201 (2000). https://doi.org/10.1016/S0032-3861(99)00406-1
Ayoub, G., Zaïri, F., Nait-Abdelaziz, M., Gloaguen, J.-M.: Modelling large deformation behaviour under loading-unloading of semicrystalline polymers: Application to a high density polyethylene. Int. J. Plast. 26(3), 329–347 (2010). https://doi.org/10.1016/j.ijplas.2009.07.005
Felder, S., Vu, N.A., Reese, S., Simon, J.-W.: Modeling the effect of temperature and degree of crystallinity on the mechanical response of Polyamide 6. Mech. Mater. 148, 103476 (2020). https://doi.org/10.1016/j.mechmat.2020.103476
Müller, S., Kästner, M., Brummund, J., Ulbricht, V.: A nonlinear fractional viscoelastic material model for polymers. Comput. Mater. Sci. 50(10), 2938–2949 (2011). https://doi.org/10.1016/j.commatsci.2011.05.011
Kästner, M., Obst, M., Brummund, J., Thielsch, K., Ulbricht, V.: Inelastic material behavior of polymers-experimental characterization, formulation and implementation of a material model. Mech. Mater. 52, 40–57 (2012). https://doi.org/10.1016/j.mechmat.2012.04.011
Lion, A.: On the large deformation behaviour of reinforced rubber at different temperatures. J. Mech. Phys. Solids 45(11–12), 1805–1834 (1997). https://doi.org/10.1016/S0022-5096(97)00028-8
Anand, L., Ames, N.M., Srivastava, V., Chester, S.A.: A thermo-mechanically coupled theory for large deformations of amorphous polymers. Part I: formulation. Int. J. Plast. 25(8), 1474–1494 (2009). https://doi.org/10.1016/j.ijplas.2008.11.004
Srivastava, V., Chester, S.A., Ames, N.M., Anand, L.: A thermo-mechanically-coupled large-deformation theory for amorphous polymers in a temperature range which spans their glass transition. Int. J. Plast. 26(8), 1138–1182 (2010). https://doi.org/10.1016/j.ijplas.2010.01.004
Krairi, A., Doghri, I.: A thermodynamically-based constitutive model for thermoplastic polymers coupling viscoelasticity, viscoplasticity and ductile damage. Int. J. Plast. 60, 163–181 (2014). https://doi.org/10.1016/j.ijplas.2014.04.010
Mears, D.R., Pae, K.D., Sauer, J.A.: Effects of hydrostatic pressure on the mechanical behavior of polyethylene and polypropylene. J. Appl. Phys. 40(11), 4229–4237 (1969). https://doi.org/10.1063/1.1657180
Ghorbel, E.: A viscoplastic constitutive model for polymeric materials. Int. J. Plast. 24(11), 2032–2058 (2008). https://doi.org/10.1016/j.ijplas.2008.01.003
Drucker, D.C., Prager, W.: Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 10(2), 157–165 (1952)
Tschoegl, N.W.: Failure surfaces in principal stress space. J. Polym. Sci. Part C: Polym. symposia 32, 239–267 (1971). https://doi.org/10.1002/polc.5070320113. (Wiley Online Library)
Nguyen, V.-D., Lani, F., Pardoen, T., Morelle, X.P., Noels, L.: A large strain hyperelastic viscoelastic-viscoplastic-damage constitutive model based on a multi-mechanism non-local damage continuum for amorphous glassy polymers. Int. J. Solids Struct. 96, 192–216 (2016). https://doi.org/10.1016/j.ijsolstr.2016.06.008
Richeton, J., Ahzi, S., Vecchio, K.S., Jiang, F.C., Adharapurapu, R.R.: Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: Characterization and modeling of the compressive yield stress. Int. J. Solids Struct. 43(7–8), 2318–2335 (2006). https://doi.org/10.1016/j.ijsolstr.2005.06.040
Ghorbel, E., Hadriche, I., Casalino, G., Masmoudi, N.: Characterization of thermo-mechanical and fracture behaviors of thermoplastic polymers. Materials 7(1), 375–398 (2014). https://doi.org/10.3390/ma7010375
Manaia, J.P., Pires, F.A., de Jesus, A.M.P., Wu, S.: Mechanical response of three semi crystalline polymers under different stress states: experimental investigation and modelling. Polym. Testing 81, 106156 (2020). https://doi.org/10.1016/j.polymertesting.2019.106156
Rae, P.J., Brown, E.N., Orler, E.B.: The mechanical properties of poly (ether-ether-ketone)(peek) with emphasis on the large compressive strain response. Polymer 48(2), 598–615 (2007). https://doi.org/10.1016/j.polymer.2006.11.032
Farrokh, B., Khan, A.S.: A strain rate dependent yield criterion for isotropic polymers: low to high rates of loading. Eur. J. Mech.-A/Solids 29(2), 274–282 (2010). https://doi.org/10.1016/j.euromechsol.2009.08.004
Van Dommelen, J., Parks, D.M., Boyce, M.C., Brekelmans, W.A.M., Baaijens, F.P.T.: Micromechanical modeling of the elasto-viscoplastic behavior of semi-crystalline polymers. J. Mech. Phys. Solids 51(3), 519–541 (2003). https://doi.org/10.1016/S0022-5096(02)00063-7
Richeton, J., Ahzi, S., Vecchio, K.S., Jiang, F.C., Makradi, A.: Modeling and validation of the large deformation inelastic response of amorphous polymers over a wide range of temperatures and strain rates. Int. J. Solids Struct. 44(24), 7938–7954 (2007). https://doi.org/10.1016/j.ijsolstr.2007.05.018
Nikolov, S., Doghri, I., Pierard, O., Zealouk, L., Goldberg, A.: Multi-scale constitutive modeling of the small deformations of semi-crystalline polymers. J. Mech. Phys. Solids 50(11), 2275–2302 (2002). https://doi.org/10.1016/S0022-5096(02)00036-4
Bouvard, J.-L., Ward, D.K., Hossain, D., Nouranian, S., Marin, E.B., Horstemeyer, M.F.: Review of hierarchical multiscale modeling to describe the mechanical behavior of amorphous polymers. J. Eng. Mater. Technol. 131(4), 1 (2009). https://doi.org/10.1115/1.3183779
Uchida, M., Tada, N.: Micro-, meso- to macroscopic modeling of deformation behavior of semi-crystalline polymer. Int. J. Plast. 49, 164–184 (2013). https://doi.org/10.1016/j.ijplas.2013.03.007
Popa, C.M., Fleischhauer, R., Schneider, K., Kaliske, M.: Formulation and implementation of a constitutive model for semicrystalline polymers. Int. J. Plast. 61, 128–156 (2014). https://doi.org/10.1016/j.ijplas.2014.05.010
Pisani, W.A., Radue, M.S., Chinkanjanarot, S., Bednarcyk, B.A., Pineda, E.J., Waters, K., Pandey, R., King, J.A., Odegard, G.M.: Multiscale modeling of peek using reactive molecular dynamics modeling and micromechanics. Polymer 163, 96–105 (2019). https://doi.org/10.1016/j.polymer.2018.12.052
Kopal, I., Harničárová, M., Valíček, J., Kušnerová, M.: Modeling the temperature dependence of dynamic mechanical properties and visco-elastic behavior of thermoplastic polyurethane using artificial neural network. Polymers 9(10), 519 (2017). https://doi.org/10.3390/polym9100519
Jordan, B., Gorji, M.B., Mohr, D.: Neural network model describing the temperature- and rate-dependent stress-strain response of polypropylene. Int. J. Plast. 135, 102811 (2020). https://doi.org/10.1016/j.ijplas.2020.102811
Román, A.J., Qin, S., Rodríguez, J.C., González, L.D., Zavala, V.M., Osswald, T.A.: Natural rubber blend optimization via data-driven modeling: The implementation for reverse engineering. Polymers 14(11), 2262 (2022). https://doi.org/10.3390/polym14112262
Rabiej, M., Rabiej, S.: Application of the artificial neural network for identification of polymers based on their x-ray diffraction curves. Comput. Mater. Sci. 186, 110042 (2021). https://doi.org/10.1016/j.commatsci.2020.110042
Ayoub, G., Zaïri, F., Fréderix, C., Gloaguen, J.-M., Naït-Abdelaziz, M., Seguela, R., Lefebvre, J.-M.: Effects of crystal content on the mechanical behaviour of polyethylene under finite strains: experiments and constitutive modelling. Int. J. Plast. 27(4), 492–511 (2011). https://doi.org/10.1016/j.ijplas.2010.07.005
Dusunceli, N., Colak, O.U.: Modelling effects of degree of crystallinity on mechanical behavior of semicrystalline polymers. Int. J. Plast. 24(7), 1224–1242 (2008). https://doi.org/10.1016/j.ijplas.2007.09.003
Regrain, C., Laiarinandrasana, L., Toillon, S., Saï, K.: Multi-mechanism models for semi-crystalline polymer: constitutive relations and finite element implementation. Int. J. Plast. 25(7), 1253–1279 (2009). https://doi.org/10.1016/j.ijplas.2008.09.010
Hachour, K., Zaïri, F., Naït-Abdelaziz, M., Gloaguen, J.-M., Aberkane, M., Lefebvre, J.-M.: Experiments and modeling of high-crystalline polyethylene yielding under different stress states. Int. J. Plast. 54, 1–18 (2014). https://doi.org/10.1016/j.ijplas.2013.06.004
Felder, S., Holthusen, H., Hesseler, S., Pohlkemper, F., Gries, T., Simon, J.-W., Reese, S.: Incorporating crystallinity distributions into a thermo-mechanically coupled constitutive model for semi-crystalline polymers. Int. J. Plast. 135, 102751 (2020). https://doi.org/10.1016/j.ijplas.2020.102751
Cundiff, K.N., Ayoub, G., Benzerga, A.A.: Modeling the viscoplastic behavior of a semicrystalline polymer. Int. J. Solids Struct. 254, 111920 (2022). https://doi.org/10.1016/j.ijsolstr.2022.111920
Doufas, A.K., McHugh, A.J., Miller, C.: Simulation of melt spinning including flow-induced crystallization: Part I. Model development and predictions. J. Nonnewton. Fluid Mech. 92(1), 27–66 (2000). https://doi.org/10.1016/S0377-0257(00)00088-4
Ahzi, S., Makradi, A., Gregory, R.V., Edie, D.D.: Modeling of deformation behavior and strain-induced crystallization in poly (ethylene terephthalate) above the glass transition temperature. Mech. Mater. 35(12), 1139–1148 (2003). https://doi.org/10.1016/S0167-6636(03)00004-8
Arruda, E.M., Boyce, M.C., Jayachandran, R.: Effects of strain rate, temperature and thermomechanical coupling on the finite strain deformation of glassy polymers. Mech. Mater. 19(2–3), 193–212 (1995). https://doi.org/10.1016/0167-6636(94)00034-E
Reese, S., Govindjee, S.: Theoretical and numerical aspects in the thermo-viscoelastic material behaviour of rubber-like polymers. Mech. Time-Depend. Mater. 1(4), 357–396 (1997). https://doi.org/10.1023/A:1009795431265
Lion, A.: A physically based method to represent the thermo-mechanical behaviour of elastomers. Acta Mech. 123(1–4), 1–25 (1997). https://doi.org/10.1007/BF01178397
Johlitz, M., Scharding, D., Diebels, S., Retka, J., Lion, A.: Modelling of thermo-viscoelastic material behaviour of polyurethane close to the glass transition temperature. ZAMM-J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik: Appl. Math. Mech. 90(5), 387–398 (2010). https://doi.org/10.1002/zamm.200900361
Johnsen, J., Clausen, A.H., Grytten, F., Benallal, A., Hopperstad, O.S.: A thermo-elasto-viscoplastic constitutive model for polymers. J. Mech. Phys. Solids 124, 681–701 (2019). https://doi.org/10.1016/j.jmps.2018.11.018
Ames, N.M., Srivastava, V., Chester, S.A., Anand, L.: A thermo-mechanically coupled theory for large deformations of amorphous polymers. Int. J. Plast. Part II: Appl. 25(8), 1495–1539 (2009). https://doi.org/10.1016/j.ijplas.2008.11.005
Shepherd, J.E., McDowell, D.L., Jacob, K.I.: Modeling morphology evolution and mechanical behavior during thermo-mechanical processing of semi-crystalline polymers. J. Mech. Phys. Solids 54(3), 467–489 (2006). https://doi.org/10.1016/j.jmps.2005.10.003
Krairi, A., Doghri, I., Schalnat, J., Robert, G., Van Paepegem, W.: Thermo-mechanical coupling of a viscoelastic-viscoplastic model for thermoplastic polymers: thermodynamical derivation and experimental assessment. Int. J. Plast. 115, 154–177 (2019). https://doi.org/10.1016/j.ijplas.2018.11.016
Hao, P., Laheri, V., Dai, Z., Gilabert, F.A.: A rate-dependent constitutive model predicting the double yield phenomenon, self-heating and thermal softening in semi-crystalline polymers. Int. J. Plast. 153, 103233 (2022). https://doi.org/10.1016/j.ijplas.2022.103233
Sharma, P., Sambale, A., Stommel, M., Maisl, M., Herrmann, H.-G., Diebels, S.: Moisture transport in PA6 and its influence on the mechanical properties. Continuum. Mech. Thermodyn. 32, 307–325 (2020). https://doi.org/10.1007/s00161-019-00815-w
Kehrer, L., Keursten, J., Hirschberg, V., Böhlke, T.: Dynamic mechanical analysis of PA 6 under hydrothermal influences and viscoelastic material modeling. J. Thermoplast. Compos. Mater. 08927057231155864. (2023). https://doi.org/10.1177/08927057231155864
Rodriguez, A.K., Mansoor, B., Ayoub, G., Colin, X., Benzerga, A.A.: Effect of UV-aging on the mechanical and fracture behavior of low density polyethylene. Polym. Degrad. Stab. 180, 109185 (2020). https://doi.org/10.1016/j.polymdegradstab.2020.109185
Bahrololoumi, A., Shaafaey, M., Ayoub, G., Dargazany, R.: Thermal aging coupled with cyclic fatigue in cross-linked polymers: Constitutive modeling & FE implementation. Int. J. Solids Struct. 252, 111800 (2022). https://doi.org/10.1016/j.ijsolstr.2022.111800
Shen, F., Kang, G., Lam, Y.C., Liu, Y., Zhou, K.: Thermo-elastic-viscoplastic-damage model for self-heating and mechanical behavior of thermoplastic polymers. Int. J. Plast. 121, 227–243 (2019). https://doi.org/10.1016/j.ijplas.2019.06.003
Narayan, S., Anand, L.: Fracture of amorphous polymers: a gradient-damage theory. J. Mech. Phys. Solids 146, 104164 (2021). https://doi.org/10.1016/j.jmps.2020.104164
Doshev, P., Tomova, D., Wutzler, A., Radusch, H.-J.: Morphology and mechanical properties of reactive and non-reactive COC/EOC blends. J. Polym. Eng. 25(5), 375–392 (2005). https://doi.org/10.1515/POLYENG.2005.25.5.375
Ozkoc, G., Bayram, G., Bayramli, E.: Effects of olefin-based compatibilizers on the morphology, thermal and mechanical properties of ABS/polyamide-6 blends. J. Appl. Polym. Sci. 104(2), 926–935 (2007). https://doi.org/10.1002/app.25848
Lin, X., Liu, Y., Chen, X., Wu, Y., Cui, L., Mao, L., Zheng, W., Lin, M.: Reactive compatibilization of polyamide 6/olefin block copolymer blends: Phase morphology, rheological behavior, thermal behavior, and mechanical properties. Materials 13(5), 1146 (2020). https://doi.org/10.3390/ma13051146
Perin, D., Dorigato, A., Pegoretti, A.: Thermoplastic self-healing polymer blends for structural composites: development of polyamide 6 and cyclic olefinic copolymer blends. J. Appl. Polym. Sci. 140(16), e53751 (2023). https://doi.org/10.1002/app.53751
Eckart, C.: The thermodynamics of irreversible processes. IV. The theory of elasticity and anelasticity. Phys. Rev. 73(4), 373 (1948). https://doi.org/10.1103/PhysRev.73.373
Kröner, E.: Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Ration. Mech. Anal. 4, 273–334 (1959). https://doi.org/10.1007/BF00281393
Lee, E.H.: Elastic-plastic deformation at finite strains. J. Appl. Mech. 36(1), 1–6 (1969). https://doi.org/10.1115/1.3564580
Sidoroff, F.: Un modèle viscoélastique non linéaire avec configuration intermédiaire. J. de mécanique 13, 679–713 (1974)
Lubliner, J.: A model of rubber viscoelasticity. Mech. Res. Commun. 12(2), 93–99 (1985). https://doi.org/10.1016/0093-6413(85)90075-8
Reese, S., Govindjee, S.: A theory of finite viscoelasticity and numerical aspects. Int. J. Solids Struct. 35(26–27), 3455–3482 (1998). https://doi.org/10.1016/S0020-7683(97)00217-5
Lion, A.: Constitutive modelling in finite thermoviscoplasticity: a physical approach based on nonlinear rheological models. Int. J. Plast. 16(5), 469–494 (2000). https://doi.org/10.1016/S0749-6419(99)00038-8
Dettmer, W., Reese, S.: On the theoretical and numerical modelling of Armstrong-Frederick kinematic hardening in the finite strain regime. Comput. Methods Appl. Mech. Eng. 193(1–2), 87–116 (2004). https://doi.org/10.1016/j.cma.2003.09.005
Vladimirov, I.N., Pietryga, M.P., Reese, S.: On the modelling of non-linear kinematic hardening at finite strains with application to springback—comparison of time integration algorithms. Int. J. Numer. Meth. Eng. 75(1), 1–28 (2008). https://doi.org/10.1002/nme.2234
Brepols, T., Wulfinghoff, S., Reese, S.: A gradient-extended two-surface damage-plasticity model for large deformations. Int. J. Plast. 129, 102635 (2020). https://doi.org/10.1016/j.ijplas.2019.11.014
Felder, S., Kopic-Osmanovic, N., Holthusen, H., Brepols, T., Reese, S.: Thermo-mechanically coupled gradient-extended damage-plasticity modeling of metallic materials at finite strains. Int. J. Plast. 148, 103142 (2022). https://doi.org/10.1016/j.ijplas.2021.103142
Coleman, B.D., Noll, W.: Foundations of linear viscoelasticity. Rev. Mod. Phys. 33(2), 239 (1961). https://doi.org/10.1103/RevModPhys.33.239
Melro, A.R., Camanho, P.P., Pires, F.M.A., Pinho, S.T.: Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part I-Constitutive modelling. Int. J. Solids Struct. 50(11–12), 1897–1905 (2013). https://doi.org/10.1016/j.ijsolstr.2013.02.009
Armstrong, P.J., Frederick, C.O. et al.: A mathematical representation of the multiaxial Bauschinger effect, volume 731 of CEGB Report RD/B/N731. Central Electricity Generating Board and Berkeley Nuclear Laboratories, Research & Development Department (1966)
Holthusen, H., Rothkranz, C., Lamm, L., Brepols, T., Reese, S.: Inelastic material formulations based on a co-rotated intermediate configuration - Application to bioengineered tissues. J. Mech. Phys. Solids 172, 105174 (2023). https://doi.org/10.1016/j.jmps.2022.105174
Spencer, A.J.M.: Part III. Theory of invariants. Continuum Phys. 1, 239–353 (1971)
Reese, S., Christ, D.: Finite deformation pseudo-elasticity of shape memory alloys-Constitutive modelling and finite element implementation. Int. J. Plast. 24(3), 455–482 (2008). https://doi.org/10.1016/j.ijplas.2007.05.005
Korelc, J.: Automation of primal and sensitivity analysis of transient coupled problems. Comput. Mech. 44, 631–649 (2009). https://doi.org/10.1007/s00466-009-0395-2
Campoy, I., Gomez, M.A., Marco, C.: Structure and thermal properties of blends of nylon 6 and a liquid crystal copolyester. Polymer 39(25), 6279–6288 (1998)
Kulkarni, S., Loos, K., Lion, A., Johlitz, M.: Thermoforming: Identification of process-relevant ranges for strain, strain rate, cooling rate, and degree of crystallinity through preliminary simulations. In: Lectures Notes on Advanced Structured Materials, pp. 303–314. Springer (2022). https://doi.org/10.1007/978-3-031-11589-9_20
Shan, G.-F., Yang, W., Yang, M., Xie, B., Feng, J., Fu, Q.: Effect of temperature and strain rate on the tensile deformation of polyamide 6. Polymer 48(10), 2958–2968 (2007). https://doi.org/10.1016/j.polymer.2007.03.013
Parodi, E., Peters, G.W.M., Govaert, L.E.: Prediction of plasticity-controlled failure in polyamide 6: influence of temperature and relative humidity. J. Appl. Polym. Sci. 135(11), 45942 (2018). https://doi.org/10.1002/app.45942
Mudra, I., Balázs, G.: Comparative study of efficiency of nucleating agents in PA-6. J. Therm. Aanal. Calorim. 52, 355–361 (1998). https://doi.org/10.1023/A:1010105825111
Nagarajan, K., Levon, K., Myerson, A.: Nucleating agents in polypropylene. J. Therm. Anal. Calorim. 59(1–2), 497–508 (2000). https://doi.org/10.1023/a:1010197609840
Menyhárd, A., Varga, J.: The effect of compatibilizers on the crystallisation, melting and polymorphic composition of \(\beta \)-nucleated isotactic polypropylene and polyamide 6 blends. Eur. Polymer J. 42(12), 3257–3268 (2006). https://doi.org/10.1016/j.eurpolymj.2006.09.003
Luo, H., Fu, Z., Jing, B., Shi, J., Zou, X., Dai, W.: Tensile behaviors of polyamide 6/UHLE blends. J. Mater. Sci. 44, 3694–3701 (2009). https://doi.org/10.1007/s10853-009-3494-8
Fornes, T.D., Paul, D.R.: Crystallization behavior of nylon 6 nanocomposites. Polymer 44(14), 3945–3961 (2003). https://doi.org/10.1016/S0032-3861(03)00344-6
Maurel-Pantel, A., Baquet, E., Bikard, J., Bouvard, J., Billon, N.: A thermo-mechanical large deformation constitutive model for polymers based on material network description: Application to a semi-crystalline polyamide 66. Int. J. Plast. 67, 102–126 (2015). https://doi.org/10.1016/j.ijplas.2014.10.004
Amin, A., Lion, A., Sekita, S., Okui, Y.: Nonlinear dependence of viscosity in modeling the rate-dependent response of natural and high damping rubbers in compression and shear: Experimental identification and numerical verification. Int. J. Plast. 22(9), 1610–1657 (2006). https://doi.org/10.1016/j.ijplas.2005.09.005
Menczel, J.D., Prime, R.B.: Thermal analysis of polymers: Fundamentals and applications. Wiley, Hoboken (2009)
Saba, N., Jawaid, M.: A review on thermomechanical properties of polymers and fibers reinforced polymer composites. J. Ind. Eng. Chem. 67, 1–11 (2018). https://doi.org/10.1016/j.jiec.2018.06.018
dos Santos, W.N., De Sousa, J.A., Gregorio, R., Jr.: Thermal conductivity behaviour of polymers around glass transition and crystalline melting temperatures. Polym. Testing 32(5), 987–994 (2013). https://doi.org/10.1016/j.polymertesting.2013.05.007
dos Santos, W.N., Mummery, P., Wallwork, A.: Thermal diffusivity of polymers by the laser flash technique. Polym. Testing 24(5), 628–634 (2005). https://doi.org/10.1016/j.polymertesting.2005.03.007
Ricker, A., Gierig, M., Wriggers, P.: Multiplicative, non-Newtonian viscoelasticity models for rubber materials and brain tissues: numerical treatment and comparative studies. Arch. Comput. Methods Eng. 1, 1–39 (2023). https://doi.org/10.1007/s11831-023-09889-x
Norton, F.H.: The creep of steel at high temperatures. McGraw-Hill, New York (1929)
Schmid, E., Boas, W.: Kristallplastizität mit besonderer Berücksichtigung der Metalle, vol. 17. Springer, Berlin (2013)
Garofalo, F.: An empirical relation defining the stress dependence to minimum creep rate in metals. Trans. Metall. Soc. AIME 227, 351 (1963)
Bergström, J.S., Boyce, M.C.: Constitutive modeling of the large strain time-dependent behavior of elastomers. J. Mech. Phys. Solids 46(5), 931–954 (1998). https://doi.org/10.1016/S0022-5096(97)00075-6
Stein, E., Sagar, G.: Convergence behavior of 3D finite elements for Neo-Hookean material. Eng. Comput. 25(3), 220–232 (2008). https://doi.org/10.1108/02644400810857065
Acknowledgements
The author gratefully acknowledges the experimental data base conducted by Sameer Kulkarni at the Institute of Mechanics, University of the Federal Armed Forces, Munich as well as the provision of PA6 type B granulate by Bond Laminates (Lanxess). Furthermore, financial support by the German Research Foundation (DFG) (RE 1057/52-1, project number 454873500) is gratefully acknowledged. In addition, S. Reese acknowledges the funding of the projects RE 1057/48-1 (DFG, project number 440959716) and IGF 21348 N/3 (Arbeitsgemeinschaft industrieller Forschungsvereinigungen, Otto von Guericke e.V. (AiF)).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Appendix
A Appendix
1.1 A.1 Consistent tangent operators
In this section, the computation of the consistent tangent operators required by ABAQUS (cf. Sect. 2.8) is discussed in more detail. Since all model quantities are computed in the reference configuration (cf. Sect. 2.6), push forward operations are needed before use in ABAQUS. Without further derivation, the linearization of the weak forms of the balance of linear momentum as well as the energy balance are given as
The Jaumann rate of the Kirchhoff stress tensor from Eq. 54 can be reformulated to
using the Lie derivative \((\mathring{*})\) of the Kirchhoff stress (cf. [104])
With the definition of the stress rate of the second Piola–Kirchhoff tensor \(\dot{{\varvec{S}}} = 1/2 \, \mathbb {K}_E [ \dot{{\varvec{C}}} ] \) and the rate of deformation \(\dot{{\varvec{C}}} = 2 {\varvec{F}}^\textrm{T} {\varvec{D}} {\varvec{F}}\), the material tangent modulus \( \mathbb {C}_{{\varvec{D}}}^{{\varvec{\tau }}} \) can now be calculated (Figs. 24, 25, 26, 27). The push forward operations for the remaining three material sensitivities are defined in the following
Here, the algorithmic tangents corresponding to the stress increment \(\Delta {\varvec{S}}\) and the derivatives related to the increment of the internal heat generation \(\Delta r\) are expressed as
To indicate which variables are held constant for the respective partial derivative, the set \(\Gamma = \{ {\varvec{C}}, {\varvec{U}}_p^{-1},{\varvec{U}}_v^{-1}, \theta \}\) was introduced for the stress. Likewise, for the internal heat generation the set \(\Upsilon = \{ {\varvec{C}}, {\varvec{U}}_p^{-1},{\varvec{U}}_{pi}^{-1}, \lambda _p, {\varvec{U}}_v^{-1}, \theta \}\) was introduced for brevity and a more clear representation. As discussed in detail in Sect. 2.8, the automatic differentiation tool AceGen is used to obtain the partial derivatives for the algorithmic tangents. Here, firstly the functions for the stress and the internal heat generation are implemented and \({\varvec{C}}, {\varvec{U}}_p^{-1},{\varvec{U}}_{pi}^{-1}, \lambda _p, {\varvec{U}}_v^{-1} \, \text {and} \, \theta \), as well as all internal variables from the last converged time step, serve as input quantities. Consequently, the derivatives of \({\varvec{S}}\) and r can be obtained rather easily after reaching local convergence. In the next step, the remaining derivatives of the two solution vectors \({\varvec{x}}_{1,\text {loc}} = (\hat{{\varvec{U}}}_{p}^{-1}, \hat{{\varvec{U}}}_{pi}^{-1},\lambda _p)^\textrm{T}\) and \({\varvec{x}}_{2,\text {loc}} = (\hat{{\varvec{U}}}_{v}^{-1})^\textrm{T}\) with respect to the global unknowns \({\varvec{x}}_{\text {glo}} = ({\varvec{C}}, \theta )^\textrm{T}\) are derived. For the elasto-plastic part, an additional linearization of the converged local residual vector \({\varvec{r}}_{1,\text {loc}} = ({\varvec{r}}_{1, p}, {\varvec{r}}_{1, pi}, r_{1, \sigma }) ^\textrm{T}\) is performed and implemented in AceGen.
Using the relation above, the incremental change of the local elasto-plastic variables \({\varvec{x}}_{1,\text {loc}}\) with respect to an incremental change of the global variables \({\varvec{x}}_{1,\text {glo}}\) can be expressed by \({\varvec{J}} = -{\varvec{J}}_{1}^{-1} {\varvec{J}}_{2}\). From this expression, the remaining derivatives for the elasto-plastic part can be extracted. The derivatives for the visco-elastic part are obtained in the same manner and therefore not further discussed.
1.2 A.2 Dynamical Mechanical Analysis (DMA)
The DMA tests were conducted on a TA instruments AR-G2 rheometer.
Dynamical mechanical analysis—storage modulus for various DOCs
1.3 A.3 Conversion between engineering and true stress
The engineering or nominal stress in terms of the 1. Piola–Kirchoff stress (\({\varvec{P}}\)) is converted to the true (Cauchy) stress (\({\varvec{\sigma }}\)) under the assumption of perfect incompressibility
Using Eq. 74, the deformation gradient for uniaxial monotonic tension or compression can be obtained by means of the experimentally measured stretch in loading (x-) direction
Now, the true (Cauchy) stress is calculated by a pushforward of the 1. Piola–Kirchhoff to the current configuration
Here, \({\varvec{P}}\) is the engineering or nominal stress,
which, in the case of uniaxial tension or compression, is the current experimentally measured force (F) in loading (x-) direction over the reference cross section (\(A_0\)).
1.4 A.4 Single element boundary value problem
Single element test—boundary value problem for a uniaxial monotonic tension/compression test
1.5 A.5 Results at remaining temperatures for the comparison of different nonlinear functions for the relaxation time
Fitting results for different nonlinear functions for the relaxation time: a and b above the glass transition regime c at 50\(^\circ \) C. Note here that due to the reduced set of experimental data (only \(\chi = 0.29\) and \(\chi = 0.24\) were considered at this temperature), a comparatively better fit is achieved
1.6 A.6 Results at remaining temperatures for the parameter identification from single curve fits
Results for the parameter identification from single curve fits for temperatures above \(T_g\). The linear trend line is of the form \((\bullet ) = c_1 \, \chi + c_2, \, \text {with} \, (\bullet )= \sigma _t, \sigma _c, c, b \). Note here that the fit for parameter b is weighted for both temperatures to avoid a function that leads to negative results for \(\chi = 0.15\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reuvers, MC., Kulkarni, S., Boes, B. et al. A thermo-mechanically coupled constitutive model for semi-crystalline polymers at finite strains: Mechanical and thermal characterization of polyamide 6 blends. Continuum Mech. Thermodyn. (2024). https://doi.org/10.1007/s00161-024-01288-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00161-024-01288-2