1 Introduction

Automotive industry is continuously developing and gradually implementing new materials used for the structural components. Despite the growing trend of using materials such as polymers, composites, aluminium or magnesium alloys, steels are still the main construction material used in automobile production. Medium manganese steels belonging to the newest, third-generation advanced high-strength steels (AHSS) are of particular interest of automotive industry due to their superior strength–ductility product (UTSxTEl = 20,000−30,000 MPa%) [1,2,3]. Due to beneficial mechanical properties of this type of steels, the reduction in car’s body-in-white weight is possible while maintaining high crash performance. The development of lightweight materials and technologies is crucial for the reduction in the amount of emissions emitted to the environment during production and vehicle life cycle [4, 5].

The microstructure of cold-rolled and intercritically annealed medium-Mn steels contains an ultrafine mixture of ferrite and austenite [1, 3], whereas the thermomechanically processed steel sheets of higher thickness (used for underbody elements) comprise a mixture of ferrite, bainite, martensite and some fraction of retained austenite (RA) [6]. This microstructural constituent controls the strain hardening behaviour and ductility of steels due to its gradual transformation into martensite during plastic deformation. This provides the transformation-induced plasticity (TRIP) effect related to the simultaneous strength and plasticity increase due to delaying necking during tensile deformation [2, 6]. RA may transform into martensite during sheet forming operations such as stamping, and bending, allowing the production of complex geometry elements [7, 8]. Moreover, the strain-induced martensitic transformation (SIMT) of RA may occur during vehicle crash events absorbing some part of kinetic energy, and as a result, enhanced crashworthiness can be obtained [9, 10]. The effectiveness of SIMT is closely related to the amount, morphology and stability of RA [11, 12]. The retained austenite present in steels showing the TRIP effect can be in a form of blocky grains or thin laths (films). For different morphological types of RA, the mechanism of martensitic transformation is different, which results in differences in mechanical properties of steel products. Experimental results obtained by Shen et al. [11] and Jimenez-Melero et al. [12] show that RA in the form of thin films is characterized by higher mechanical stability than in a form of blocky grains. Moreover, the small grains/laths of RA are more resistant against SIMT than the large ones. The tendency of retained austenite to SIMT is also dependent on its chemical composition. The RA is characterized by a carbon concentration gradient and resulting change in micromechanical behaviour inside its grains during straining [13, 14].

The optimization of the SIMT mechanism is crucial for obtaining high mechanical properties of medium-Mn steels [15, 16]. Estimation of the stability of retained austenite is possible through thermodynamic modelling, which is based on the calculated critical driving force for martensitic transformation of RA with a defined chemical composition. This approach allows to determine the martensite start \(\hbox {M}_{\textrm{s}}\) temperature of RA [17, 18]. Several reports concerning the application of representative volume element (RVE) modelling method [19,20,21] or digital material representation (DMR) approach [22,23,24] to monitor the microstructure evolution of dual phase (DP) and TRIP-aided steels with a microstructure composed on ferrite, bainite and retained austenite are available in the literature. This type of steels belongs to the first-generation AHSS. The numerical modelling and numerical simulations of SIMT belong to particularly difficult and complex tasks [25, 26]. Over the years the finite element method (FEM) has been developed but so far it is challenging to follow the changes in material properties during the numerical simulation process using commercial computer systems. These computer systems are usually dedicated for solving mechanical problems in macroscale such as designing light constructions as well as heavy duty machinery, in civil engineering, spacecrafts, etc. [27, 28]. Thus, applying such software for modelling the SIMT is rather cumbersome and unadjusted yet. However, special procedures can applied to overcome these difficulties using for example C++ language.

In a present study, the FEM method and thermodynamic calculations were used to predict the tendency of RA to SIMT during progressive tensile deformation. In the presented approach, the austenite properties have been adjusted to reflect in more detail the real situation. The gradient of carbon content inside austenite grains was taken into account during simulations. Hence, it was possible to analyse the micromechanical evolution inside individual grains with the focus on the SIMT details and corresponding stress–strain evolution as a function of increasing strain. The presented approach was not applied yet for advanced medium-Mn steels. Therefore, the study aims to complete this research gap combining modelling and experimental approaches.

2 Experimental

2.1 Material and processing route

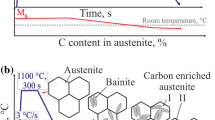
The investigated material with the chemical composition of Fe-0.17C-3.3Mn-1.7Al-0.22Si-0.23Mo (wt.%) was melted using a vacuum induction furnace under Ar atmosphere. After homogenization at \(1200 ^{\,\circ }\hbox {C}\) for 2 h, ingots were hot-forged (in a temperature range of \(1200 ^{\,\circ }\hbox {C}\)–\(900 ^{\,\circ }\hbox {C}\)) and air-cooled to room temperature. Afterwards, the ingots were hot-rolled in 4 passes to obtain the sheet samples with a thickness of 9 mm. Then, final thermomechanical rolling in 3 passes with a decreasing temperature range from \(1050^{\circ }\hbox {C}\) to \(850^{\circ }\hbox {C}\) was applied. The final sheet thickness was 4.5 mm. Following the hot rolling, the investigated steel sheet was directly cooled to the isothermal holding temperature of \(400^{\circ }\hbox {C}\) at the bainitic transformation range and held at this temperature for 300 s followed by air cooling. The detailed information about processing routes of investigated steel can be found in [29, 30].

2.2 Microstructure modelling

The micromechanical model of the microstructure was prepared based on the EBSD image of the sample after hot rolling (Fig. 1). This approach allows to preserving the complex geometry of individual RA grains. The microstructure at the initial state (after hot rolling) was composed of bainite matrix and some fraction of retained austenite (\(\sim \)8%) located between bainite laths. The blocky RA and lathy RA can be distinguished in the image, which are embedded in the bainitic (B) matrix. In order to monitor the strain-induced martensite formation, simulations of the deformation during interrupted static tensile test was carried out using FEM method and LS-DYNA software. The simulations were interrupted at defined strain values of: 0.02, 0.04, 0.06, 0.08 and 0.1. (The 0.1 strain corresponds to uniform elongation.) The strain-induced martensitic transformation (SIMT) also occurs after necking in the post-uniform elongation range (up to rupture). However, the most important from the industrial point of view is to monitor the mechanism of martensitic transformation in the uniform strain range. The gradual progress of SIMT in this deformation range ensures the high tensile strength and uniform elongation of formed sheet elements. The metal forming processes such as bending and stamping are conducted at the strain level corresponding to the uniform elongation range.

Fig. 1
figure 1

EBSD map of investigated steel in the initial state (after hot rolling) used for micromechanical modelling showing bainitic matrix (B) marked in red colour and retained austenite (RA) marked in green colour

Full size image

2.3 Description of the numerical model

The special procedure has been developed in order to simulate the SIMT using the C language. The steps were as follows:

  • \(\bullet \) conversion of bitmaps obtained from EBSD method into grey scale images and next into finite elements, nodes and material groups,

  • \(\bullet \) during the conversion the following restrictions have been imposed:

    • \(\bullet \) grains should be located inside the modelled region,

    • \(\bullet \) grains cannot be located at the boundary region of the modelled sample,

    • \(\bullet \) grains can touch the boundary regions but cannot cross them either be located beyond them,

    • \(\bullet \) grains can be in contact but cannot overlap one another.

The way of changing the mechanical properties during numerical simulations was as below:

  • \(\bullet \) input of all necessary data including the material properties especially for austenite and bainite structural constituents,

  • \(\bullet \) starting the main simulation, which contains four steps (four individual subsimulations),

  • \(\bullet \) if the pseudotime equals one-fifth of the total time of simulation (corresponding to 0.02 strain) then the simulation process is stopped and the following action takes place:

    • \(\bullet \) recording of the actual state of stress, strain and displacement,

    • \(\bullet \) after the above action, the change of mechanical properties occurs in the original file, where the task is already defined,

    • \(\bullet \) the earlier recorded state of stress, strain and displacement is treated as initial data in this particular step,

    • \(\bullet \) starting the subsequent subsimulation,

  • \(\bullet \) if the time equals two-fifths of the total time of simulation (corresponding to 0.04 strain), then the simulation process is stopped and repeated for four-fifths and five-fifths in loop according to the above subpoints.

The numerical simulations have been conducted using the finite element method and LS-DYNA software. On the basis of experimental images obtained by EBSD maps, the individual phases have been approximately mapped by appropriate modelling using finite element method. The microscale model has been developed in order to simulate the transformation of the retained austenite into martensite. The level of complexity relies on elaboration of many stages connected with the formation of the martensitic phase. In this particular case, as many as four different meshes of the same model have been generated. The corresponding calculations of state of stress and strain in the microstructure according to predetermined conditions of deformation and progress of SIMT have been performed. Conceptually, this can be taken to mean that each of the four modelling systems representing the successive stages of martensitic development and corresponding to them the individual meshes has been finally transformed into one highly complex finite element model.

The model of microstructure by means of computer system called LS PrePost has been elaborated, next the boundary conditions have been defined and the material models have been assumed. Then, the appropriate mesh using authors’ computer system elaborated in C language has been produced. Finally, the highly nonlinear physical phenomenon of martensitic phase formation has been solved numerically. The results are presented in the form of colourful contour maps illustrating the distribution of Huber Mises stresses in successive stages during the progressive tensile test.

The initial microstructure was composed of bainite (as a matrix) and islands of retained austenite (RA). The quantitative contribution of austenitic phase in bainitic matrix equals to 8% and the rest 92% is bainite, according to the real EBSD map in Fig. 1. The austenitic grains (islands) have been modelled in the shape of mirror images. The selected geometrical features are given in Table 1, and the dimensions of the modelled sample are given in Table 2. The total number of nodes in the model equals to 13,904, and the total number of plane state of strain elements is 13,650. In each node, there are two degrees of freedom along x and y axis, respectively. The sample has been fixed at the nodes belonging to the left utmost side of the model (Fig. 2). The displacement along x axis has been applied to all nodes belonging to the right utmost edge of the model and has been assumed as linear function of time, which varies from \({ u} = 0 \,\upmu \hbox {m}\) to \({ u} = \Delta \hbox {L} = 0.95\, \upmu \hbox {m}\), what is presented in detail in Fig. 2.

Table 1 Selected geometrical features of austenitic and bainitic structural constituents
Full size table
Table 2 Dimensions of the modelled sample
Full size table

The developed model of the SIMT is taking into account the various mechanical stability and yield strength of different areas located inside the RA grains. These areas correspond to the gradient of carbon content inside the individual RA grains. The carbon content is the lowest in the middle part of the grain, while the areas located near grain boundaries are characterized by the highest C content [13]. The higher carbon content means greater stability against SIMT [14, 31]. Therefore, three subareas of austenitic phases were included in the developed model (Table 1), which reflects the gradient of carbon content inside individual RA grains. Areas characterized by different mechanical stability of RA are represented by different colours in Fig. 2.

Fig. 2
figure 2

Boundary conditions, dimensions of the assumed modelled sample, boundary between bainite and randomly generated locations of the austenitic phases

Full size image

The modelling technique is intended for materials with composite microstructures, in which several phases have been modelled with different hardening behaviour. The bainitic phase constituted the matrix, in which there are two more phases: austenite which belongs to the softer one and newly generated martensitic phase, which is a hard microstructural constituent. All these phases have been modelled as deformable elastically as well as plastically until reaching the limited strain value corresponding to the uniform elongation of the sample, which has been established during experimental investigation on the level of 0.1 strain.

The material properties of bainitic ferrite, retained austenite and martensite were taken from the literature [32, 33] focused on the estimation of Young’s modulus for different phases: austenite, martensite and bainite in multiphase high-strength TRIP-aided steels based on the experimental results obtained in their previous study [34]. For most low-alloyed steels, the Young’s modulus is lower than that is presented in Table 3. In the present study, the investigated material was high-strength medium-Mn steel, which shows higher mechanical properties than low-alloyed steels. Therefore, the adopted Young’s modulus values for the analysed phases, i.e. austenite, bainite and martensite, are higher [32, 33] than usually occurring in the literature for conventional steels.

Table 3 Material parameters for individual phases which have been assumed similarly like in the literature [32, 33]
Full size table

The relationship between the true stress–strain curve for bainitic matrix, martensite and austenitic phases of different mechanical stability has been assumed according to the following mathematical formula [32]:

$$\begin{aligned} \sigma =R_{e}\cdot \left( 1+H\cdot \varepsilon \right) ^{n}, \end{aligned}$$
(1)

All aforementioned individual material phases described by Eq. (1) are additionally shown in Fig. 3.

Fig. 3
figure 3

Mechanical properties for individual structural constituents

Full size image
Fig. 4
figure 4

Process of the progressive austenite–martensite transformation; The subsequent stages of the process are shown from the initialisation a through evolutionary progression of martensitic phase corresponding to 0.02 strain b, 0.04 strain c and 0.08 strain d

Full size image

The four different meshes taking into account the accretion of the newly generated martensitic phase created at the expense of the austenitic one have been elaborated and are shown in Fig. 4. In the successive steps, the austenite–martensite transformation is presented showing the progress of the process beginning from the initialisation (0% of martensitic phase and 100% of austenite) to the total transformation reaching 75% of the martensitic phase (\(\sim \)25% of the retained austenitic phase remains untrasformed). A fraction of retained austenite transformed into martensite during simulations of incremental strain applied to the investigated steel is in good agreement with results presented in the literature [31, 35]. The highest fraction of RA transforms into martensite at low strain levels and decreases with increasing the strain level. During the real static tensile test, certain fraction of RA also remains unchanged even when uniform deformation level (0.1 strain) is achieved. The experimental results of the microstructural investigation of the progress of RA into SIMT as a function of strain is presented in Fig. 5.

Fig. 5
figure 5

Retained austenite change as a function of strain

Full size image

2.4 Thermodynamic calculations of retained austenite stability

The stability of RA depends on a combination of interrelated factors, such as austenite enrichment in carbon and manganese, temperature, stress state, yield strength of the matrix, particle size and morphology [36, 37]. All of these factors, except the last one, are included in the calculation of one parameter, the \(M_{s}^{\sigma }\) temperature which characterizes the stability of dispersed austenite under mechanically induced transformation. A mathematical model to determine the \(M_{s}^{\sigma }\) temperature was proposed by Haidemenopoulos and Vasilakos [17] by employing thermodynamically based calculations for the low-alloyed TRIP-aided multiphase steel. The mathematical relation to determining \(M_{s}^{\sigma }\) temperature is as follows [17]:

$$\begin{aligned} M_{s}^{\sigma }=T\Leftrightarrow \sigma _{\textrm{y}}=\sigma _{\textrm{t}}\left( T \right) =\frac{1}{\left[ -0.715-0.3206\left( \frac{\sigma _{\textrm{h}}}{\bar{\sigma }} \right) \right] }\left\{ {\begin{array}{c} \frac{{2\alpha \gamma _{\textrm{s}}} / \rho }{\textrm{ln}\left[ -\frac{\textrm{ln}\left( 1-f \right) }{N_{\textrm{v}}^{0}\cdot V_{p}} \right] }-{\Delta G}_{\textrm{chem}}^{\gamma \rightarrow \alpha ^{'}}\left( T,x^{C},x^{Mn} \right) + \\ -E^{\textrm{str}}-W_{\textrm{f}}\left( x^{C},x^{Mn} \right) \\ \end{array}} \right\} \end{aligned}$$
(2)

where T is the considered temperature of the system; \(\sigma _{\textrm{t}}\) is transformation stress at which the martensitic nucleation is activated; \(\sigma _{\textrm{y}}\) is the yield strength of the alloy; ratio (\(\sigma _{\textrm{h}}/\bar{\sigma })\) is defined as the stress state parameter (\(\sigma _{\textrm{h}}\) being the hydrostatic and \(\bar{\sigma }\) being the equivalent stress); \(\alpha \) is a constant; \(\gamma _{\textrm{s}}\) is the martensitic nucleus specific interfacial energy; \(\rho \) is the density of atoms in close-packed plane; f is the probability of finding at least one nucleation site in the particle; \(N_{\textrm{v}}^{0}\) is the total number of nucleation sites of all potencies; \(V_{p}\) is the average volume of the austenite particles, which is assumed to be spherical in case of blocky austenite and ellipsoid in case of lath austenite particles; \({\Delta G}_{\textrm{chem}}^{\gamma \rightarrow \alpha ^{'}}\) is the chemical driving force of the martensitic transformation; \(x^{C}\) and \(x^{Mn}\) are the mole fractions of carbon and manganese in austenite, respectively; \(E^{\textrm{str}}\) is the elastic–strain energy per unit volume associated with distortions in the nucleus; and \(W_{\textrm{f}}\) is the frictional work of the interfacial motion, which in current solution is determined according to linear expression. For more details about additional expressions and values of the parameters in Eq. (2), we refer the readers to the original article [17].

In the current work, the investigated TRIP-aided medium-Mn steel contains ultrafine-grained austenite with blocky and thin-film (lathy) morphologies of mean radius ranging between \(1~\upmu \hbox {m}\) to \(2~\upmu \hbox {m}\) and \(0.2~\upmu \hbox {m}\) to \(0.6~\upmu \hbox {m}\), respectively. Therefore, in our calculations, the parameter describing the total number of nucleation sites of all potencies was intentionally increased by two orders of magnitude (\(N_{\textrm{v}}^{0}=2\times {10}^{19})\). This change is justified by the fact that the average volume of the investigated RA particles (\(V_{p})\) is two orders of magnitude smaller than \(V_{p}\) considered in the original paper [17] with the \(M_{s}^{\sigma }\) temperature calculations. Primarily the result of the multiplication of \(N_{\textrm{v}}^{0}\) and \(V_{p}\) must be maintained at an appropriate level due to the logarithmic expression in Eq. 2. From a physical point of view, it can be explained that the total number of nucleation sites of all potencies increases when the average volume of the RA particles decreases with the same area fraction of austenite in the structure.

Note that the chemical driving force of the martensitic transformation (\({\Delta G}_{\textrm{chem}}^{\gamma \rightarrow \alpha ^{'}})\) is calculated at each step of temperature change using the dedicated computational thermodynamics program, which was developed based on the CALPHAD sublattice model [38] with the SGTE (Scientific Group Thermodata Europe) solution database [39]. Since the calculations of the chemical driving force of the martensitic transformation depend on temperature and are nonlinear, satisfying Eq. (2) cannot be obtained by analytical solution. Therefore, the iterative procedure was used to determine the \(M_{s}^{\sigma }\) temperature. Namely, a secant method was applied in the numerical code with the mathematical model. All mentioned procedures were implemented in C\(++\) programming language in a comprehensive computer program form.

2.5 Microstructure investigations

The scanning electron microscopy (SEM) and electron backscatter diffraction (EBSD) techniques were used for characterization of the microstructure of investigated steel in the initial state and after tensile test interrupted at particular strain level. The fraction of retained austenite was estimated using the EBSD method. The specimens for microstructural observations carried out by means of SEM were mechanically ground using SiC papers (up to 2000 grid), polished with diamond suspension (up to 1\(\upmu \)m) and etched using 3% nital. The microstructural details were revealed with a scanning electron microscope FEI Inspect-F operating at a voltage of 15 kV, working in a secondary electron (SE) detection mode. The EBSD measurements were performed using the high-resolution JEOL JSM 7200F scanning electron microscope with the TSL®OIM Data Collection 8.0 software. Specimens were prepared by mechanical grinding followed by electrolytic polishing using a TenuPol-5 device working at a voltage of 17 V for 30  s. The A3 electrolyte by Struers at temperature \(0\,^{\circ }\hbox {C}\) was used. Kikuchi patterns were collected at an accelerating voltage of 15 kV, a working distance of 15 mm and a step size of \(0.025~\upmu \hbox {m}\); sample tilt \(70^{\circ }\) was used.

3 Results and discussion

3.1 Numerical results

The finite element method has been used to generate the microstructure evolution as a function of strain as well as to initialise the modelling system according to an appropriate algorithm and finally to obtain the stress–strain distribution. In Fig. 4, four different meshes taking into account the accretion of the newly generated martensitic phase have been presented in order to show the results of deformation. The maps with effective plastic strain and equivalent Huber Mises stresses are shown in Figs. 6 and 7, respectively. Recapitulating, in the successive steps the progressive martensitic transformation is demonstrated reaching finally ca. 75% of total retained austenite loss.

Fig. 6
figure 6

Effective plastic strain distribution in the microstructural constituents during the progressive SIMT

Full size image
Fig. 7
figure 7

Equivalent Huber Mises stress distribution in the microstructural constituents during the progressive SIMT

Full size image

The simulation results of successive microstructure evolution steps during the SIMT in the form of maps with effective plastic strain distribution are shown in Fig.  6. Partitioning of local plastic strain between different structural constituents is observed at each step of deformation (Fig. 6b–e). The local plastic strain partitioning especially occurs in the vicinity of austenite particles. The increase in the global plastic strain during deformation strongly influences the degree of strain partitioning, which has also been observed in experimental work [40]. It can be seen that the high-strain areas are localized in small RA particles with the highest yield strength, whereas the low-strain regions mainly appear in the interiors of bainitic structures. Figure 6 shows that the character of local plastic strain partitioning in the simulated microstructure depends on the size and morphology of the RA particles.

Figure 7a shows the Huber Mises stresses for one-fifth of the total pseudotime of tensile test simulation (corresponding to 0.02 strain). The stress concentration may be observed within the region where the austenitic phase is in contact with the bainitic phase. In the austenitic phase the maximum values of stresses are within the range from 519 MPa to 673 MPa. Therefore, the stresses are high enough to initialise the formation of martensite. In the next stage for two-fifths of the total pseudotime (corresponding to 0.04 strain), the area of martensite zone relatively increases about 20% (Fig. 7b) in comparison with the previous stage, but the stress intensity grows from 673 MPa recorded in the previous stage to 1211 MPa and can be observed in the newly formed martensite. Moreover, at the borders between the martensite and austenite as well as austenite and bainite the stress concentration is still high. The difference in stresses between the same bainitic phase is at the level, which equals to ca. 200 MPa. For the stage corresponding to the three-fifths of the total pseudotime (Fig. 7c), the area of martensite zone relatively increases about 14.5% in comparison with the previous stage, but the stress intensity grows insignificantly from 1211 MPa recorded in the previous stage to 1307 MPa. Hence, the resulting change in stresses is rather small. The difference in stresses between the same bainitic phase still sustains at approximately the same level, which equals to about 200 MPa. In the remaining two stages corresponding to 0.08 and 0.1 strain (Fig. 7d and e), similar physical phenomena like further stress development can be observed but with increased level of stresses responsible for further formation of martensitic phase and depletion of austenitic one. The stress differences in microscale between the different phases such as the martensite and austenite as well as austenite and bainite are very high and reach approximately 600 MPa. These differences confirm the enhanced work hardening during the tensile straining, which has also been obtained in micromechanical simulations reported by other authors [41, 42].

In Fig. 8, the equivalent Huber Mises stress versus pseudotime for selected representative finite elements has been graphically shown. The chosen elements represent successive material phases such as bainite marked by letter A, austenite\(_{500}\) marked by letter B, austenite\(_{475}\) marked by letter C, and austenite\(_{450}\) marked by letter D, respectively. The bainite structural constituent (A) is as expected because there is no transformation of any kind. However, the austenite phases undergo the martensitic transformation, which is usually initiated by a certain minimum level of stress (equals to ca. 550 MPa). The mentioned transformation from the austenitic to martensitic phase occurred for the following successive pseudotimes: 0.2, 0.4 and 0.8 s, respectively (corresponding to 0.02, 0.04 and 0.08 strain). This can be observed on the curves described consecutively by letters: D, C and B. Summarising, the transformation (Fig. 8b) starts from the middle of the austenitic area (marked in green) and spreads out towards the outer boundary crossing successively the intermediate zone (marked in blue) and finally finishing at the outer boundary (marked in black). Such behaviour can be explained by the increasing content of carbon from the minimum amount in the middle zone and maximum at the outer layers, which is in agreement with the literature [13, 14].

Fig. 8
figure 8

Equivalent Huber Mises stress distribution versus pseudotime for the selected representative finite elements corresponding to the following initial phases: A bainite, B austenite\(_{500}\), C austenite\(_{475}\), D austenite\(_{450}\)

Full size image
Table 4 Juxtaposition of the maximum effective stress, strain, energy and maximum tensile force
Full size table

The most important physical quantities are gathered in Table 4: maximum effective plastic strain, maximum equivalent Huber Mises stress, maximum tensile force and total energy. The presented results give an idea of the potential stress distribution in the SIMT-aided multiphase steel containing austenite, bainite and martensite.

3.2 Thermodynamic stability of retained austenite

The results of the \(M_{s}^{\sigma }\) temperature calculations based on Eq. (2) are demonstrated in Fig. 9. It shows the effect of the mean RA particle size and the yield strength of the alloy on the \(M_{s}^{\sigma }\) temperature for different carbon concentrations in the initial chemical composition of RA particles. One can observe that increasing the mean austenite particle size as well as the yield strength of the alloy increases the \(M_{s}^{\sigma }\) temperature considerably. Increasing the carbon content of the RA decreases the \(M_{s}^{\sigma }\) temperature. These outcomes show a good agreement with the experimental and FEM micromodel simulation results. Austenite particles in the investigated TRIP steel, with a carbon content in the range of 0.9 to 1.2 wt.%, were detected using XRD measurements [25] as well observed by means of EBSD with a RA particle radius ranging from 0.2 to 2 \(\upmu \)m. Furthermore, Fig. 9 shows that RA particles containing 1.05 wt.% C and smaller than 0.5 \(\upmu \)m remain stable in a whole range of the alloy yield strength because the \(M_{s}^{\sigma }\) temperature is below room temperature. A similar effect can be observed in the FEM micromodel simulations, where RA particles with a high carbon content even under high stresses (around 1300 MPa) remain stable in the modelling sample (see Fig. 4d). In addition, thanks to the plotted plane (in grey) with a constant temperature of 20\(^{\circ }\hbox {C}\) in Fig. 9, it is easy to identify under what conditions (stress, particle size and carbon content) the retained austenite remains stable, i.e. below this temperature. The theoretical results of the \(M_{s}^{\sigma }\) temperature noticeably exhibit the influence of particle size, yield strength and chemical composition on retained austenite stability.

One should note that the approach used in the present study to determine the \(M_{s}^{\sigma }\) temperature was initially dedicated to low-alloyed steels [17]. In our case, this concept is used for medium manganese steels, which need a prudent interpretation of the results because of the high influence of manganese on the martensitic transformation and consequent calculations of the \(M_{s}\) temperature. For example, a lot of empirical formulas used for medium-Mn steels overestimate calculated \(M_{s}\) temperature and have to be adjusted [43]. Kaar et al. [43] proposed a new \(M_{s}\) formula for medium-Mn steels, which is the modification of \(M_{s}\) formulas proposed by Mahieu et al. [44] and Van Bohemen [45]. However, the accuracy of all formulas available in the literature for highly Mn-alloyed steels is still limited due to complex interactions between Mn, Al, Si alloying elements, which are a core of advanced high-strength steels.

Fig. 9
figure 9

Model predictions of \(M_{s}^{\sigma }\) temperature as a function of the mean retained austenite particle size, a yield strength of the alloy and a carbon content

Full size image

3.3 Experimental microstructural verification

The microstructure of investigated steel in the initial state was experimentally verified using SEM and EBSD techniques. The EBSD map presented in Fig. 1 was used for elaboration of the microstructure model. The initial microstructure is composed of bainite and retained austenite with various morphology (Figs. 1 and  10). The lath-type RA is dominant; however, some fraction of blocky grains of this phase can be also observed in the microstructure. Small fraction of martensite was also present in the initial microstructure. The amount of RA estimated using EBSD method was about 8%.

Fig. 10
figure 10

SEM micrograph of the specimen in the initial state (after hot rolling). RA retained austenite, B bainite, M martensite

Full size image

An analysis of the microstructure evolution during interrupted static tensile test allowed to characterize the tendency of RA to SIMT. The EBSD maps of the specimen deformed up to 0.04 strain were shown in Fig. 11. The most of large blocky RA grains transformed into martensite during deformation. Martensite can be observed in the darkest areas of image quality (IQ) map due to its highest dislocation density (Fig. 11a). Only small grains and thin laths of RA stayed untransformed. Results of thermodynamic calculations also confirm that the small grains of RA are more stable than the larger ones. It is expressed by their lower \(M_{s}^{\sigma }\) temperature (Fig. 9). Some fraction of martensite–austenite (MA) constituent was also observed. Some of the outer areas of RA stayed stable after deformation, while the areas located in the middle of RA transformed into martensite, which confirms the correctness of the FEM simulations. The lower stability of the central areas of RA is related to their lower carbon content. Such tendency was also observed by Krizan at al. [31]. The increased stability of RA caused by higher C content is expressed by lower \(M_{s}^{\sigma }\) temperature (Fig. 9). The amount of RA present in the microstructure after deformation up to 0.04 strain was estimated to about 4.9% (Fig. 11b). Figure 11c shows the local strain distribution in the specimens deformed up to 0.04 strain by means of the colour-coded kernel average misorientation (KAM) map. The highest strain localization (areas marked in yellow and green) can be observed in the laths and small grains of RA and also in the areas where martensite is located. Similar tendency was observed for FEM simulations of the microstructure evolution (Fig. 6).

Fig. 11
figure 11

EBSD maps of investigated steel deformed up to 0.04 strain: image quality map a, phase distribution map where retained austenite (RA) marked in red b, colour-coded kernel average misorientation maps displaying the local strain distribution c

Full size image
Fig. 12
figure 12

EBSD maps of investigated steel deformed up to 0.08 strain: image quality map a, phase distribution map where retained austenite (RA) marked in red b, colour-coded kernel average misorientation maps displaying the local strain distribution c

Full size image

Increasing the strain level up to 0.08 strain resulted in the lower fraction of RA stayed stable after deformation. The martensitic transformation occurred also in smaller austenite grains and thin laths of this phase (Fig. 12). The fraction of darker areas represented by martensite was higher when compared to the specimen deformed up to 0.04 strain (Fig. 12a). Some fraction of the thin outer areas of RA also stayed untransformed. The fraction of RA was estimated to about 2% (Fig. 12b). The observed tendency of RA to SIMT at particular strain level is consistent with the results obtained by FEM modelling (Fig. 4) and observations reported by other authors [46, 47] for TRIP-aided steels. FEM modelling results show that the fractions of RA stable after deformation up to 0.04 and 0.08 strain were about 5.24% and 2.0%, respectively. For higher deformation levels (corresponding to uniform elongation of 0.1), the change of RA fraction transforming into martensite is significantly hampered. It is related to high hydrostatic pressure introduced by significantly deformed bainite laths and newly formed martensite which contribute to the further increase in the mechanical stability of RA. FEM modelling results show that the stress values in RA areas observed in the specimen deformed up to 0.08 strain reached about 1300 MPa (Fig. 7). The amount of areas showing increased strain level observed in KAM maps is higher when compared to the sample deformed to 0.04 strain (Figs. 11c and  12c). The increased KAM value was also noted in some fraction of bainite laths. It is related to the significant degree of the microstructure deformation. The useful KAM data are sensitive to the dislocation density during deformation [12].

The tendency of RA to SIMT during incremental deformation level was validated using SEM method (Fig. 13). It was observed that martensite transformation was initiated in the middle part of blocky RA grains (Fig. 13a) and progresses towards the grain boundaries with increasing strain levels (Fig. 13b). The laths of larger thickness also transformed partially into martensite as a result of larger strain applied to the specimen.

Fig. 13
figure 13

SEM micrographs of the specimens deformed up to: 0.04 strain a, 0.08 strain b

Full size image

4 Conclusions

Modelling studies were performed to analyse the microstructure evolution of advanced medium-Mn multiphase steel during interrupted static tensile tests. The obtained results were compared to the calculations of the thermodynamic stability of retained austenite and verified with the real microstructures. The numerical simulations of the SIMT showed that martensitic transformation is initiated in the middle areas of large blocky RA grains. The lower stability of the central areas of RA was related to their lower carbon content, what was expressed by higher \(M_{s}^{\sigma }\) temperature. For the higher strain levels, a progress of SIMT towards the grain boundaries was observed in FEM simulations and microstructure observations. The micromechanical simulation results indicate that the local stress differences between martensite and austenite as well as austenite and bainite are very high and reach approximately 600 MPa. This confirms the strong work hardening of TRIP-aided medium-Mn steels.

The theoretical calculations to identify and quantify the primary stabilizing factors of RA were performed by using a thermodynamic model within the range of stresses which were registered in the microstructural FEM simulations. The model predictions of \(M_{s}^{\sigma }\) temperature corresponded well with the experimental and FEM micromodel simulation results. RA particles with a carbon content higher than 1.05 wt.% and smaller than 0.5 \(\upmu \hbox {m}\) even under high stresses (around 1300 MPa) remained stable. The microstructural study revealed that a fraction of this lath-type RA is about 2%.