1 Introduction

Arches are one of the main curved structures used in different engineering applications including civil and mechanical engineering. In civil engineering, arches have been employed for different construction purposes such as bridges and subway stations [1, 2] as it can carry greater loads compared to straight structures. As an application in the field of mechanical engineering, arch structures have been used in designing different types of energy harvesters to optimise the efficiency of the system [3,4,5,6]. For instance, in a study presented by Yang et al. [7], it was shown that by using arch structures, the total harvested power was 200% times more power compared to straight structures. As another example, shallow arches have also been used and examined for microelectromechanical systems (MEMS) [8].

During the last few years, researchers have studied the mechanical behaviour of both flat structures (including beams and plates) [9,10,11,12,13,14,15] and curved structures (including shells and arches) [16,17,18,19,20,21,22,23] to be able to use them efficiently for specific purposes. Focusing on arch structures, their behaviour in different engineering conditions has been examined lately. To name a few, Yang et al. [24] reinforced elastic arch structures using graphene nanoplatelets and studied the linear vibration behaviour of graphene-reinforced arches. Different fibre distribution was modelled using Halpin–Tsai micromechanics model and Hamilton’s principle showing that out-of-plane and in-plane linear frequencies of the elastic arch are highly affected by the fibre distribution and percentage. For dynamic instability analysis, Zhao et al. [25] studied the influence of having porosity in modelling graphene-reinforced elastic arches; it was shown that the best dynamic instability resistance can be seen in the symmetric porosity distribution model. The nonlinear mechanics of elastic shallow arches with nonuniform cross section made of functionally graded materials (FGMs) have been investigated by Ghayesh and Farokhi [26]. Coupled axial-transverse equations of motion were obtained using Euler-Bernoulli theory and Hamilton’s principle; it was shown that as the arch curvature increases, the maximum amplitude of transverse vibration decreases. For MEMS structures, Farokhi et al. [27] studied the pull-in phenomena in micro-scale arch structures. Using a high-dimensional reduced-order Galerkin model and generalised Hamilton’s principle, it was shown that by increasing the curvature of the arch, the DC voltage for pull-in phenomena increases.

The previous studies were mainly focused on linear-elastic structures under small strains. However, soft materials undergo large strains, which makes the classic linear modelling of the behaviour inaccurate for many hyper-elastic structures. There has been a significant attention on hyper-elastic structures in the past few years focusing on the statics [28,29,30,31] and dynamics [32,33,34,35]. In some recent studies, the anti-clastic bending of hyper-elastic beams in finite elasticity has been investigated by Lanzoni and Tarantino [36,37,38]. Khaniki et al. [39, 40] have examined the nonlinear vibration and mechanics of axially moving hyper-elastic structures and layered hyper-elastic beams. In another study, Khaniki et al. [41] investigated the effect of having porosity in hyper-elastic structures providing a porous-hyper-elastic strain energy model and modelling the vibration behaviour of porous soft beams. A detailed review on the nonlinear dynamic behaviour of different hyper-elastic structures can be found in Ref. [42].

However, since some soft structures show a combination of viscoelasticity and hyper-elasticity, researchers have developed different models for such structures [43,44,45,46,47]. In a recent study presented by Li et al. [48], a wide range of visco-hyper-elastic constitutive models were developed. The viscoelasticity was modelled via Maxwell and Kelvin–Voigt models, and the hyper-elasticity was modelled via neo-Hookean, Mooney–Rivlin, and Ogden models. It was shown that the proposed models are capable of modelling both hyper-elasticity and viscoelasticity of the biological structure. Since visco-hyper-elastic structures are widely applicable for modelling human body organs, soft robots and prosthesis, the visco-hyper-elastic constitutive models are useful for studying and manufacturing accurate mechanical and biomechanical structures in different environments.

Besides, since most of the hyper-elastic structures are significantly softer than linear-elastic structures, it is very likely to have them bent (like arches and shells) in real-life applications. Accordingly, in this study, visco-hyper-elastic thick soft shallow arches are examined in the framework of nonlinear bending and vibrations (with and without internal resonances). Since the soft arch is assumed to be thick, a third-order shear deformable theory is used and the visco-hyper-elasticity is modelled following Ref. [48] by using Mooney–Rivlin and Kelvin–Voigt models. The bending behaviour of the soft arch is formulated using the virtual work method and solved using the Newton–Raphson method. For the vibration analysis, the equations of motion are obtained using the force-moment balance method and solved using a dynamic equilibrium technique. The effect of having curvature in the structure is analysed, and the internal resonance phenomena caused by having this nonlinearity in the system are discussed. A detailed discussion of the influence of curvature term, the slenderness ratio and three-to-one internal resonance is given.

2 Bending of hyper-elastic thick arch formulation

For a thick, soft, shallow arch, using a higher-order shear deformation theory, by considering plane motion, von Kármán’s geometric nonlinearity, and curvature in the thickness direction, the nonlinear static strain terms are obtained as

$$\begin{aligned} \varepsilon _{11} \left( {x_{1} ,x_{3} } \right)= & {} \frac{\textrm{d}u_{1} \left( {x_{1} } \right) }{\textrm{d}x_{1} }+\frac{1}{2}\left( {\frac{\textrm{d}u_{3} \left( {x_{1} } \right) }{\textrm{d}x_{1} }} \right) ^{2}+\frac{\textrm{d}u_{3} \left( {x_{1} } \right) }{\textrm{d}x_{1} }\frac{\textrm{d}u_{30} \left( {x_{1} } \right) }{\textrm{d}x_{1} } \nonumber \\{} & {} +x_{3} \frac{\textrm{d}\phi \left( {x_{1} } \right) }{\textrm{d}x_{1} }+\Im _{1} \left[ {\frac{d^{2}u_{3} \left( {x_{1} } \right) }{\textrm{d}x_{1}^{2}}+\frac{\textrm{d}\phi \left( {x_{1} } \right) }{\textrm{d}x_{1} }} \right] , \end{aligned}$$
(1)
$$\begin{aligned} \varepsilon _{13} \left( {x_{1} } \right)= & {} \Im _{2} \left( {\frac{\textrm{d}u_{3} \left( {x_{1} } \right) }{\textrm{d}x_{1} }+\phi \left( {x_{1} } \right) } \right) , \end{aligned}$$
(2)
$$\begin{aligned} \varepsilon _{33}\ne & {} 0\,\,\,\,\,\left( {\hbox {should satisfy the incompressibility condition}} \right) \end{aligned}$$
(3)

with

$$\begin{aligned} \Im _{1} =-\frac{4}{3}\frac{x_{3}^{3}}{h^{2}},\,\,\,\,\,\,\,\,\,\,\,\Im _{2} =\frac{1}{2}\left( {1-4\frac{x_{3}^{2}}{h^{2}}} \right) , \end{aligned}$$
(4)

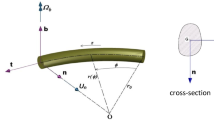
where \(u_{1}\) and \(u_{3}\) are the displacements of the arch in the \(x_{1}\) and \(x_{3}\) directions (shown in Fig. 1a), \(u_{30}\) is the curvature of the shallow arch, \(\varepsilon _{11}\) and \(\varepsilon _{33}\) are the axial strains in the \(x_{1}\) and \(x_{3}\) directions and \(\varepsilon _{13}\) is the shear strain. By considering plane motion and incompressible material, the right Cauchy-Green strain tensor is written as [49]

$$\begin{aligned} C=\left[ {{\begin{array}{ccc} {\left( {1+\varepsilon _{11} } \right) ^{2}+\varepsilon _{13}^{2}} &{} 0 &{}\quad {\varepsilon _{11} \varepsilon _{13} +2\varepsilon _{13} +\varepsilon _{33} \varepsilon _{13} } \\ 0 &{} 1 &{}\quad 0 \\ {\varepsilon _{11} \varepsilon _{13} +2\varepsilon _{13} +\varepsilon _{33} \varepsilon _{13} } &{} 0 &{}\quad {\left( {1+\varepsilon _{33} } \right) ^{2}+\varepsilon _{13}^{2}} \\ \end{array} }} \right] , \end{aligned}$$
(5)

which contains nonlinear higher-order strain terms since hyper-elastic structures undergo large strains and cannot be modelled by considering the linear part alone, as is undertaken for elastic structures.

Fig. 1
figure 1

Schematic figure of a visco-hyper-elastic thick shallow arch with simply supported boundary conditions

Full size image

The principle of virtual work is not only for linear elastic structures and can be applied for hyper-elastic structures [50]. To this end, by using the Mooney–Rivlin hyper-elastic strain energy density [51, 52] and the principle of virtual work, the variation of the energy term, due to the static applied forces, can be written in three variation terms for axial (PE1), transverse (PE2) and rotation (PE3) variations as

$$\begin{aligned} \int \limits _0^L {\left[ {F_{s1} \delta u_{1} +F_{s3} \delta u_{3} +F_{s2} \delta \phi } \right] \textrm{d}x_{1} } =\int \limits _0^L {\left[ {\left( {PE1} \right) \delta u_{1} +\left( {PE2} \right) \delta u_{3} +\left( {PE3} \right) \delta \phi } \right] \textrm{d}x_{1} } , \end{aligned}$$
(6)

where PE1, PE2, PE3 are given in Appendix A for the sake of brevity, with the moment of area coefficients defined as

$$\begin{aligned} I_{00}= & {} \int \limits _{A} {1d} A,\,\,\,\,\,\,I_{11} =\int \limits _{A} {u_{3} \textrm{d}} A,\,\,\,\,\,\,I_{22} =\int \limits _{A} {\Im _{1} \textrm{d}} A,\,\,\,\,\,\,I_{33} =\int \limits _{A} {\left( {u_{3} +\Im _{1} } \right) \textrm{d}} A,\,\,\,\,\,\,\nonumber \\ I_{44}= & {} \int \limits _{A} {\Im _{1}^{2}\textrm{d}} A,\,\,\,\,\,\,\,I_{55} =\int \limits _{A} {\Im _{2}^{2}\textrm{d}} A, \nonumber \\ \,I_{66}= & {} \int \limits _{A} {\Im _{1} \left( {u_{3} +\Im _{1} } \right) \textrm{d}} A,\,\,\,\,\,\,I_{77} =\int \limits _{A} {\left( {1-\Im _{2}^{2}} \right) \textrm{d}} A,\,\,\,\,\,\,\nonumber \\ I_{88}= & {} \int \limits _{A} {\left( {1-2\Im _{2}^{2}} \right) \textrm{d}} A,\,\,\,\,\,I_{99} =\int \limits _{A} {\left( {\Im _{1} +u_{3} } \right) ^{2}\textrm{d}} A, \nonumber \\ I_{1010}= & {} \int \limits _{A} {\Im _{1}^{3}\textrm{d}} A,\,\,\,\,\,\,I_{1111} =\int \limits _{A} {\Im _{1} \Im _{2}^{2}\textrm{d}} A,\,\,\,\,\,\,I_{1212} =\int \limits _{A} {\Im _{1} \left( {1-\Im _{2}^{2}} \right) \textrm{d}} A,\,\,\,\,\,I_{1313} =\int \limits _{A} {\Im _{2}^{2}\left( {\Im _{1} +u_{3} } \right) \textrm{d}} A, \nonumber \\ \,I_{1414}= & {} \int \limits _{A} {\Im _{1}^{2}\left( {\Im _{1} +u_{3} } \right) \textrm{d}} A,\,\,\,\,\,\,I_{1515} =\int \limits _{A} {\Im _{1} \left( {\Im _{1} +u_{3} } \right) ^{2}\textrm{d}} A,\,\,\,\,\,I_{1616} =\int \limits _{A} {\left( {\Im _{1} +u_{3} } \right) ^{3}\textrm{d}} A,\, \nonumber \\ I_{1717}= & {} \int \limits _{A} {u_{3} \left( {u_{3} +\Im _{1} } \right) \Im _{2} ^{2}\textrm{d}} A,\,\,\,\,\,\,I_{1818} =\int \limits _{A} {\Im _{2}^{3}\textrm{d}} A,\,\,\,\,\,I_{1919} =\int \limits _{A} {\left( {u_{3} +\Im _{1} } \right) \left( {\Im _{2}^{2}-1} \right) \textrm{d}} A . \end{aligned}$$
(7)

Using Eqs. (1–7), three equilibrium equations for the bending analysis are obtained by having homogeneity in the arch as

$$\begin{aligned}{} & {} -8C_{T} I_{00} u_{1x_{1} x_{1} } -8C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{30x_{1} } } \right) +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} }^{2}} \right) +24C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } u_{30x_{1} } } \right) \nonumber \\{} & {} \quad -4C_{T} I_{77} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}} \right) +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}u_{30x_{1} }^{2}} \right) +12C_{T} I_{44} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} }^{2}} \right) \,\, \nonumber \\{} & {} \quad +24C_{T} I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} } \phi _{x_{1} } \,} \right) +8C_{T} I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi } \right) +12C_{T} I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi _{x_{1} } ^{2}} \right) +4C_{T} \,I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi ^{2}} \right) \, \nonumber \\{} & {} \quad +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} }^{2}} \right) +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{30x_{1} } u_{3x_{1} }^{3}} \right) +3C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{4}} \right) =F_{S1} , \end{aligned}$$
(8)
$$\begin{aligned}{} & {} -8C_{T} I_{66} u_{3x_{1} x_{1} x_{1} } +8C_{T} I_{55} u_{3x_{1} } -8C_{T} I_{99} \phi _{x_{1} x_{1} } +8C_{T} I_{55} \phi \,+24C_{T} I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} x_{1} } } \right) -8C_{T} I_{55} u_{1x_{1} } u_{3x_{1} } \nonumber \\{} & {} \quad +24C_{T} I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } \phi _{x_{1} } } \right) -8C_{T} I_{55} u_{1x_{1} } \phi +24C_{T} I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} } u_{30x_{1} } } \right) -8C_{T} I_{55} u_{3x_{1} }^{2}u_{30x_{1} } \nonumber \\{} & {} \quad +24C_{T} I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi _{x_{1} } u_{30x_{1} } } \right) \,-8C_{T} I_{55} u_{3x_{1} } \phi u_{30x_{1} } +12C_{T} I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } ^{2}u_{3x_{1} x_{1} } } \right) -4C_{T} I_{55} u_{3x_{1} }^{3} \nonumber \\{} & {} \quad +12C_{T} I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}\phi _{x_{1} } } \right) \,\,-4C_{T} I_{55} u_{3x_{1} }^{2}\phi =F_{S2} . \end{aligned}$$
(9)
$$\begin{aligned}{} & {} -8C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{30x_{1} } } \right) -8C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{30x_{1} }^{2}} \right) \nonumber \\{} & {} \quad +8C_{T} I_{44} u_{3x_{1} x_{1} x_{1} x_{1} } -8C_{T} \,I_{55} u_{3x_{1} x_{1} } +8C_{T} I_{66} \phi _{x_{1} x_{1} x_{1} } -8C_{T} I_{55} \phi _{x_{1} } \nonumber \\{} & {} \quad +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} }^{2}u_{30x_{1} } } \right) -8C_{T} I_{77} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } } \right) \nonumber \\{} & {} \quad +24C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } u_{30x_{1} }^{2}} \right) \,-24C_{T} I_{44} \frac{d^{2}}{\textrm{d}x_{1} ^{2}}\left( {u_{1x_{1} } u_{3x_{1} x_{1} } } \right) \, \nonumber \\{} & {} \quad -24C_{T} I_{66} \frac{d^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{1x_{1} } \phi _{x_{1} } } \right) +8C_{T} I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } \phi } \right) \nonumber \\{} & {} \quad -12C_{T} I_{77} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } ^{2}u_{30x_{1} } } \right) +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}u_{30x_{1} }^{3}} \right) \nonumber \\{} & {} \quad +12C_{T} I_{44} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} }^{2}u_{30x_{1} } } \right) -24C_{T} I_{44} \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} } u_{3x_{1} x_{1} } u_{30x_{1} } } \right) +24C_{T} I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} } \phi _{x_{1} } u_{30x_{1} } \,} \right) \nonumber \\{} & {} \quad +16C_{T} I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi u_{30x_{1} } } \right) -24C_{T} I_{66} \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} } \phi _{x_{1} } u_{30x_{1} } } \right) \,\,\,\nonumber \\{} & {} \quad +12C_{T} I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi _{x_{1} }^{2}u_{30x_{1} } } \right) +4C_{T} I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi ^{2}u_{30x_{1} } } \right) \nonumber \\{} & {} \quad +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} }^{2}u_{3x_{1} } } \right) +36C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } ^{2}u_{30x_{1} } } \right) \,\nonumber \\{} & {} \quad -4C_{T} I_{88} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{3}} \right) +24C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{3}u_{30x_{1} }^{2}} \right) \nonumber \\{} & {} \quad +12C_{T} I_{44} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} }^{2}} \right) -12C_{T} I_{44} \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} }^{2}u_{3x_{1} x_{1} } } \right) \nonumber \\{} & {} \quad +24C_{T} I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} } \phi _{x_{1} } \,} \right) +12C_{T} I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}\phi } \right) \nonumber \\{} & {} \quad -12C_{T} I_{66} \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} } ^{2}\phi _{x_{1} } } \right) \,+12C_{T} I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi _{x_{1} }^{2}} \right) +4C_{T} I_{55} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi ^{2}} \right) +12C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} }^{3}} \right) \nonumber \\{} & {} \quad +15C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{30x_{1} } u_{3x_{1} } ^{4}} \right) +3C_{T} I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{5}} \right) =F_{S3} , \end{aligned}$$
(10)

It can be seen that the equilibrium equations are highly nonlinear in hyper-elasticity terms, with a high coupling between the axial, rotation and transverse motions. The equilibrium equations can be validated by comparing them to those presented in Ref. [40] by neglecting the curvature terms from these equations and unsymmetrical and time-dependant terms in the equations of motion of Ref. [40]. By employing the solution procedure given in Sect. 4, the bending behaviour of soft thick shallow arches will be obtained.

3 Dynamics of visco-hyper-elastic thick arch formulation via force-moment balance method

For the time-dependent analysis and modelling of soft thick shallow arches, using the same assumptions given in Sect. 2, the nonlinear strain terms are written as

$$\begin{aligned} \varepsilon _{11} \left( {x_{1} ,x_{3} ,t} \right)= & {} \frac{\partial u_{1} \left( {x_{1} ,t} \right) }{\partial x_{1} }+\frac{1}{2}\left( {\frac{\partial u_{3} \left( {x_{1} ,t} \right) }{\partial x_{1} }} \right) ^{2}+\frac{\partial u_{3} \left( {x_{1} ,t} \right) }{\partial x_{1} }\frac{\textrm{d}u_{30} \left( {x_{1} } \right) }{\textrm{d}x_{1} } \nonumber \\{} & {} +x_{3} \frac{\partial \phi \left( {x_{1} ,t} \right) }{\partial x_{1} }+\Im _{1} \left[ {\frac{\partial ^{2}u_{3} \left( {x_{1} ,t} \right) }{\partial x_{1} ^{2}}+\frac{\partial \phi \left( {x_{1} ,t} \right) }{\partial x_{1} }} \right] , \end{aligned}$$
(11)
$$\begin{aligned} \varepsilon _{13} \left( {x_{1} ,t} \right)= & {} \Im _{2} \left( {\frac{\partial u_{3} \left( {x_{1} ,t} \right) }{\partial x_{1} }+\phi \left( {x_{1} ,t} \right) } \right) , \end{aligned}$$
(12)
$$\begin{aligned} \varepsilon _{33}\ne & {} 0\,\,\,\,\,\left( {\hbox {should satisfy the incompressibility condition}} \right) . \end{aligned}$$
(13)

For visco-hyper-elastic structures, Li et al. [48] have shown that the visco-hyper Kelvin–Voigt model has a good accuracy in modelling visco-hyper-elastic structures while using Mooney–Rivlin, neo-Hookean and Ogden strain energy density models. The visco-hyper-elastic model (Fig. 2) is presented as [48]

$$\begin{aligned} \sigma _{\text {visco-hyper}} =\sigma _{\text {hyperelastic}} +\xi _{k} \dot{{\varepsilon }}, \end{aligned}$$
(14)
Fig. 2
figure 2

Constitutive model of Kelvin–Voigt visco-hyper-elasticity

Full size image

(Talk about the feasible applicability of the approach) For an element of the thick visco-hyper-elastic arch, shown in Fig. 2b, Newton’s law is applied for the rotational motion, as well as translational ones by having [53]

$$\begin{aligned} \frac{\partial N\left( {x_{1} ,x_{3} ,t} \right) }{\partial x_{1} }= & {} -\rho I_{00} u_{1tt} -\rho I_{22} u_{3xtt} -\rho I_{33} \phi _{tt} , \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial Q\left( {x_{1} ,x_{3} ,t} \right) }{\partial x_{1} }+F_{\text {external}} \left( {x_{1} ,x_{3} ,t} \right)= & {} \rho I_{22} u_{1xtt} +\rho I_{44} u_{3xxtt} +\rho I_{66} \phi _{xtt} -\rho I_{00} u_{3tt} , \end{aligned}$$
(16)
$$\begin{aligned} \frac{\partial M\left( {x_{1} ,x_{3} ,t} \right) }{\partial x_{1} }-Q\left( {x_{1} ,x_{3} ,t} \right)= & {} -\rho I_{33} u_{1tt} -\rho I_{66} u_{3xtt} -\rho I_{99} \phi _{tt} , \end{aligned}$$
(17)

where the stress resultants are defined as [54]

$$\begin{aligned} N= & {} \int \limits _{A} {\sigma _{\text {visco-hyper},x_{1} x_{1} } \textrm{d}A} , \end{aligned}$$
(18)
$$\begin{aligned} M= & {} \int \limits _{A} {x_{3}} {\sigma _{\text {visco-hyper},x_{1} x_{1} } \textrm{d}A} , \end{aligned}$$
(19)
$$\begin{aligned} Q= & {} \int \limits _{A} {\sigma _{\text {visco-hyper},x_{1} x_{3} } \textrm{d}A} , \end{aligned}$$
(20)

and the applied external periodic load with the magnitude of F is given as

$$\begin{aligned} F_{\text {external}} =F\cos \left( {\omega t} \right) . \end{aligned}$$
(21)

For isotropic visco-hyper-elastic shallow arches, by using force-moment balance method, one can reach the coupled equations of motions which are shown in Appendix B for the sake of brevity. By neglecting the viscoelasticity and the arch-related terms, the equations of motion can be validated through Ref. [40]. It can be seen that all three equations of motion are highly nonlinear in visco-elasticity and hyper-elasticity terms, with a high coupling between the axial, rotation and transverse motions. By using the solution procedure given in Sect. 5, the vibration behaviour of soft thick shallow arches will be obtained.

4 Solution procedure for hyper-elastic bending analysis

By assuming only transverse external load on the system (\(F_{{s}{1}} =F_{S2} = 0\) and \(F_{S3} = F)\) and defining nondimensional terms as

$$\begin{aligned} {x_{1}}^{*}= & {} \frac{x_{1} }{L},\,\,\,\,\,{u_{1}}^{*} =\frac{u_{1} }{h},\,\,\,\,{u_{3}}^{*} =\frac{u_{3} }{h},\,\,\,\,{u_{30}}^{*} =\frac{u_{30} }{h},\,\,\,\,\,{I_{00}}^{*} =\frac{I_{00} h^{2}}{I_{44} },\,\,\,\,\nonumber \\ {I_{55}}^{*}= & {} \frac{I_{55} h^{2}}{I_{44} },\,\,\,\,\,{I_{66}}^{*} =\frac{I_{66} }{I_{44} },\,\,\,\,\,{I_{77}}^{*} =\frac{I_{77} h^{2}}{I_{44} }, \nonumber \\ {I_{88}}^{*}= & {} \frac{I_{88} h^{2}}{I_{44} },\,\,\,\,\,{I_{99}}^{*} =\frac{I_{99} }{I_{44} },\,\,\,\,\,\eta =\frac{h}{L},\,\,\,\,\,F^{*} =\frac{FL^{4}}{C_{T} I_{44} h}, \end{aligned}$$
(22)

the nondimensional equilibrium equations are written as

$$\begin{aligned}{} & {} -8I_{00} \frac{1}{\eta ^{2}}u_{1x_{1} x_{1} } -8I_{00} \frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{30x_{1} } } \right) \nonumber \\{} & {} \quad +12I_{00} \frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} }^{2}} \right) +24I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } u_{30x_{1} } } \right) -4I_{77} \frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}} \right) +12I_{00} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}u_{30x_{1} }^{2}} \right) \nonumber \\{} & {} \quad +12\eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} }^{2}} \right) \,\,+24I_{66} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} } \phi _{x_{1} } \,} \right) +8I_{55} \frac{1}{\eta ^{2}}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi } \right) +12I_{99} \frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi _{x_{1} }^{2}} \right) +4I_{55} \frac{1}{\eta ^{3}}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi ^{2}} \right) \, \nonumber \\{} & {} \quad +12I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} }^{2}} \right) +12I_{00} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{30x_{1} } u_{3x_{1} }^{3}} \right) +3I_{00} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{4}} \right) =0, \end{aligned}$$
(23)
$$\begin{aligned}{} & {} -8I_{00} \frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{30x_{1} } } \right) -8I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{30x_{1} }^{2}} \right) +8u_{3x_{1} x_{1} x_{1} x_{1} } -8I_{55} \,\frac{1}{\eta ^{2}}u_{3x_{1} x_{1} } +8I_{66} \frac{1}{\eta }\phi _{x_{1} x_{1} x_{1} } -8I_{55} \frac{1}{\eta ^{3}}\phi _{x_{1} } \nonumber \\{} & {} \quad +12I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} }^{2}u_{30x_{1} } } \right) -8I_{77} \frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } } \right) +24I_{00} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } u_{30x_{1} }^{2}} \right) \,-24\eta \frac{\textrm{d}^{2}}{\textrm{d}x_{1} ^{2}}\left( {u_{1x_{1} } u_{3x_{1} x_{1} } } \right) \nonumber \\{} & {} \quad -24I_{66} \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{1x_{1} } \phi _{x_{1} } } \right) +8I_{55} \frac{1}{\eta ^{2}}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } \phi } \right) -12I_{77} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } ^{2}u_{30x_{1} } } \right) +12I_{00} \eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}u_{30x_{1} }^{3}} \right) \nonumber \\{} & {} \quad +12\eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} }^{2}u_{30x_{1} } } \right) -24\eta ^{2}\frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} } u_{3x_{1} x_{1} } u_{30x_{1} } } \right) +24I_{66} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} x_{1} } \phi _{x_{1} } u_{30x_{1} } \,} \right) \nonumber \\{} & {} \quad +16I_{55} \,\frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi u_{30x_{1} } } \right) -24I_{66} \eta \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} } \phi _{x_{1} } u_{30x_{1} } } \right) +12I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi _{x_{1} }^{2}u_{30x_{1} } } \right) \nonumber \\{} & {} \quad +4I_{55} \,\frac{1}{\eta ^{2}}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\phi ^{2}u_{30x_{1} } } \right) +12I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} }^{2}u_{3x_{1} } } \right) +36I_{00} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} }^{2}u_{30x_{1} } } \right) -4I_{88} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{3}} \right) \nonumber \\{} & {} \quad +24I_{00} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{3}u_{30x_{1} } ^{2}} \right) +12\eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} }^{2}} \right) -12\eta ^{2}\frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} }^{2}u_{3x_{1} x_{1} } } \right) \nonumber \\{} & {} \quad +24I_{66} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} } \phi _{x_{1} } \,} \right) +12I_{55} \,\frac{1}{\eta }\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}\phi } \right) -12I_{66} \eta \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {u_{3x_{1} }^{2}\phi _{x_{1} } } \right) \, \nonumber \\{} & {} \quad +12I_{99} \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi _{x_{1} }^{2}} \right) +4I_{55} \,\frac{1}{\eta ^{2}}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi ^{2}} \right) +12I_{00} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} }^{3}} \right) +15I_{00} \eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{30x_{1} } u_{3x_{1} }^{4}} \right) \nonumber \\{} & {} \quad +3I_{00} \eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{5}} \right) =F, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} -8I_{66} \eta u_{3x_{1} x_{1} x_{1} } +8I_{55} \frac{1}{\eta }u_{3x_{1} } -8I_{99} \phi _{x_{1} x_{1} } +8I_{55} \frac{1}{\eta ^{2}}\phi \,+24I_{66} \eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } u_{3x_{1} x_{1} } } \right) -8I_{55} u_{1x_{1} } u_{3x_{1} } \nonumber \\{} & {} \quad +24I_{99} \eta \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{1x_{1} } \phi _{x_{1} } } \right) -8I_{55} \frac{1}{\eta }u_{1x_{1} } \phi +24I_{66} \eta ^{3}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} } u_{30x_{1} } } \right) -8I_{55} \eta u_{3x_{1} }^{2}u_{30x_{1} } \nonumber \\{} & {} \quad +24I_{99} \eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } \phi _{x_{1} } u_{30x_{1} } } \right) \,-8I_{55} u_{3x_{1} } \phi u_{30x_{1} } +12I_{66} \eta ^{3}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} } ^{2}u_{3x_{1} x_{1} } } \right) -4I_{55} \eta u_{3x_{1} }^{3} \nonumber \\{} & {} \quad +12I_{99} \eta ^{2}\frac{\textrm{d}}{\textrm{d}x_{1} }\left( {u_{3x_{1} }^{2}\phi _{x_{1} } } \right) \,\,-4I_{55} u_{3x_{1} }^{2}\phi =0. \end{aligned}$$
(25)

where * is neglected from the parameters for the sake of brevity. By employing a series expansion, the degrees of freedom are written as

$$\begin{aligned} u_{1} \left( {x_{1} } \right)= & {} \sum \limits _{j=1}^M {\Re _{j} U_{j} } \left( {x_{1} } \right) , \end{aligned}$$
(26)
$$\begin{aligned} u_{3} \left( {x_{1} } \right)= & {} \sum \limits _{i=1}^N {\aleph _{i} W_{i} } \left( {x_{1} } \right) , \end{aligned}$$
(27)
$$\begin{aligned} \phi \left( {x_{1} } \right)= & {} \sum \limits _{i=1}^N {\kappa _{i} \psi _{i} } \left( {x_{1} } \right) , \end{aligned}$$
(28)
$$\begin{aligned} u_{30} \left( {x_{1} } \right)= & {} W_{0} \left( {x_{1} } \right) , \end{aligned}$$
(29)

and the equations of motion are discretised as

$$\begin{aligned}{} & {} K_{11}^{L} \Re +K_{12}^{L} \aleph +K_{11}^{NL} \Re ^{2}+K_{12}^{NL} \Re \aleph +K_{13}^{NL} \aleph ^{2}+K_{14}^{NL} \aleph \kappa \nonumber \\{} & {} \quad +K_{15}^{NL} \kappa ^{2}\,+K_{16}^{NL} \Re \aleph ^{2}+K_{17}^{NL} \aleph ^{3}+K_{18}^{NL} \aleph ^{4}=0, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} K_{21}^{L} \Re +K_{22}^{L} \aleph +K_{22}^{L} \kappa +K_{21}^{NL} \Re ^{2}+K_{22}^{NL} \Re \aleph +K_{23}^{NL} \Re \kappa \,+K_{24}^{NL} \aleph ^{2}+K_{25}^{NL} \aleph \kappa +K_{26}^{NL} \kappa ^{2}+K_{27}^{NL} \Re ^{2}\aleph \nonumber \\{} & {} \quad +K_{28}^{NL} \Re \aleph ^{2}+K_{29}^{NL} \aleph ^{3}+K_{210}^{NL} \aleph ^{2}\kappa \,+K_{211}^{NL} \aleph \kappa ^{2}+K_{212}^{NL} r\aleph ^{3}+K_{213}^{NL} \aleph ^{4}+K_{214}^{NL} \aleph ^{5}=F, \end{aligned}$$
(31)
$$\begin{aligned}{} & {} K_{32}^{L} \aleph \,+K_{33}^{L} \kappa +K_{31}^{NL} \Re \aleph +K_{32}^{NL} \Re \kappa +K_{33}^{NL} \aleph ^{2}+K_{34}^{NL} \aleph \kappa +K_{35}^{NL} \aleph ^{3}+K_{36}^{NL} \aleph ^{2}\kappa =0. \end{aligned}$$
(32)

The linear stiffness coefficients (\(K^{L}_{ij})\) of the bending equilibrium equations are defined as

$$\begin{aligned} K_{11}^{L}= & {} -8\frac{1}{\eta ^{2}}I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } {U}''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(33)
$$\begin{aligned} K_{12}^{L}= & {} -8\frac{1}{\eta }I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) W_{0} ^{\prime }\left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(34)
$$\begin{aligned} K_{21}^{L}= & {} -8I_{00} \frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(35)
$$\begin{aligned} K_{22}^{L}= & {} -8I_{00} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'^{2}_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} +8\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } W_{i}^{(4)} \left( {x_{1} } \right) \textrm{d}x_{1} \nonumber \\{} & {} -8I_{55} \,\frac{1}{\eta ^{2}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {W}''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(36)
$$\begin{aligned} K_{23}^{L}= & {} +8I_{66} \frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {\psi }'''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} -8I_{55} \frac{1}{\eta ^{3}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {\psi }'_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(37)
$$\begin{aligned} K_{32}^{L}= & {} -8I_{66} \eta \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'''_{i} \,\,\,\left( {x_{1} } \right) \textrm{d}x_{1} +8I_{55} \frac{1}{\eta }\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(38)
$$\begin{aligned} K_{33}^{L}= & {} +8I_{55} \frac{1}{\eta ^{2}}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \psi _{i} \left( {x_{1} } \right) \textrm{d}x_{1} -8I_{99} \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {\psi }''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(39)

and the nonlinear stiffness coefficients (\(K^{NL}_{ij})\) are defined as

$$\begin{aligned} K_{11}^{NL}= & {} +12\frac{1}{\eta }I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {U}'_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(40)
$$\begin{aligned} K_{12}^{NL}= & {} +24I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) W_{0}^{'}\left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(41)
$$\begin{aligned} K_{13}^{NL}= & {} -4\frac{1}{\eta }I_{77} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) W_{j} ^{\prime }\left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +12\eta I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) W_{j}^{'}\left( {x_{1} } \right) {W_{0}^{'2}}\left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +12\eta \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}''_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(42)
$$\begin{aligned} K_{14}^{NL}= & {} +24I_{66} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}''_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} +8\frac{1}{\eta ^{2}}I_{55} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( x \right) \psi _{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1},\nonumber \\ \end{aligned}$$
(43)
$$\begin{aligned} K_{15}^{NL}= & {} +12\frac{1}{\eta }I_{99} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{\psi }'_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} +4\frac{1}{\eta ^{3}}I_{55} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\psi _{i} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} ,\nonumber \\ \end{aligned}$$
(44)
$$\begin{aligned} K_{16}^{NL}= & {} +12I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) W_{k}^{\prime }\left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(45)
$$\begin{aligned} K_{17}^{NL}= & {} +12\eta I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) W_{k}^{\prime }\left( {x_{1} } \right) W_{0}^{'}\left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(46)
$$\begin{aligned} K_{18}^{NL}= & {} +3\eta I_{00} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) W_{k}^{\prime }\left( {x_{1} } \right) {W}'_{m} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(47)
$$\begin{aligned} K_{21}^{NL}= & {} +12I_{00} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {U}'_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(48)
$$\begin{aligned} K_{22}^{NL}= & {} -8I_{77} \frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} -24\eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {{U}'_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +24I_{00} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'^{2}_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(49)
$$\begin{aligned} \,K_{23}^{NL}&{=}&{-}24I_{66} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {{U}'_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} {+}8I_{55} \frac{1}{\eta ^{2}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(50)
$$\begin{aligned} K_{24}^{NL}= & {} -12I_{77} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +12I_{00} \eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'^{3}_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +12\eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}''_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} -24\eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {{W}'_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(51)
$$\begin{aligned} K_{25}^{NL}= & {} +24I_{66} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}''_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +16I_{55} \,\frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} -24I_{66} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {{W}'_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(52)
$$\begin{aligned} K_{26}^{NL}= & {} +12I_{99} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{\psi }'_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +4I_{55} \,\frac{1}{\eta ^{2}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {\psi _{i} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(53)
$$\begin{aligned} K_{27}^{NL}= & {} +12I_{00} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {U}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(54)
$$\begin{aligned} K_{28}^{NL}= & {} +36I_{00} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(55)
$$\begin{aligned} K_{29}^{NL}= & {} -4I_{88} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +24I_{00} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) {W}'^{2}_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +12\eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) {W}''_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} -12\eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}''_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(56)
$$\begin{aligned} K_{210}^{NL}= & {} +24I_{66} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) {\psi }'_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +12I_{55} \,\frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} -12I_{66} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}^{2}}{\textrm{d}x_{1}^{2}}\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {\psi }'_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(57)
$$\begin{aligned} K_{211}^{NL}= & {} +12I_{99} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) {\psi }'_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} +4I_{55} \,\frac{1}{\eta ^{2}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) \psi _{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(58)
$$\begin{aligned} K_{212}^{NL}= & {} +12I_{00} \eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) {W}'_{m} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(59)
$$\begin{aligned} K_{213}^{NL}= & {} +15I_{00} \eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) {W}'_{m} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(60)
$$\begin{aligned} K_{214}^{NL}= & {} +3I_{00} \eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) {W}'_{m} \left( {x_{1} } \right) {W}'_{n} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(61)
$$\begin{aligned} K_{31}^{NL}= & {} -8I_{55} \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {U}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) \textrm{d}x_{1} +24I_{66} \eta ^{2}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{j} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(62)
$$\begin{aligned} K_{32}^{NL}= & {} +24I_{99} \eta \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {\psi }'_{j} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} -8I_{55} \frac{1}{\eta }\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {U}'_{i} \left( {x_{1} } \right) \psi _{j} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(63)
$$\begin{aligned} K_{33}^{NL}= & {} +24I_{66} \eta ^{3}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}''_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} -8I_{55} \eta \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(64)
$$\begin{aligned} K_{34}^{NL}= & {} +24I_{99} \eta ^{2}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {\psi }'_{i} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \, \nonumber \\{} & {} -8I_{55} \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) \psi _{i} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(65)
$$\begin{aligned} K_{35}^{NL}= & {} +12I_{66} \eta ^{3}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}''_{k} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} -4I_{55} \eta \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {W}'_{k} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(66)
$$\begin{aligned} K_{36}^{NL}= & {} +12I_{99} \eta ^{2}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \frac{\text {d}}{\text {d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) {\psi }'_{k} \left( {x_{1} } \right) } \right) \text {d}x_{1} \nonumber \\ {}{} & {} -4I_{55} \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) {W}'_{j} \left( {x_{1} } \right) \psi _{k} \left( {x_{1} } \right) \text {d}x_{1} . \end{aligned}$$
(67)

which by solving the nonlinear polynomial equations of motion using the Newton–Raphson method, the static bending due to the external static force can be obtained.

5 Solution procedure for visco-hyper-elastic vibrations

Using the given nondimensional terms in Sect. 4 and additional nondimensional terms as

$$\begin{aligned} \,\Omega =\omega \sqrt{\frac{\rho I_{00} L^{4}}{C_{T} I_{44} }} ,\,\,\,\,\,t*=t\sqrt{\frac{C_{T} I_{44} }{\rho AL^{4}}} ,\,\,\,\,\,\xi _{k} =\frac{\xi _{k} }{C_{T} }*\sqrt{\frac{C_{T} I_{44} }{\rho AL^{4}}} , \end{aligned}$$
(68)

the nondimensional equations of motion are written as

$$\begin{aligned}{} & {} u_{1tt} -\xi _{k} I_{00} \frac{1}{\eta ^{2}}u_{1x_{1} x_{1} t} -\xi _{k} I_{00} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {u_{30x_{1} } u_{3x_{1} t} } \right) +2\xi _{k} I_{00} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{1x_{1} t} } \right) +2\xi _{k} I_{00} \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{30x_{1} } u_{1x_{1} t} } \right) \nonumber \\{} & {} \quad +2\xi _{k} I_{00} \frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{30x_{1} } u_{3x_{1} t} } \right) -\xi _{k} I_{77} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{3x_{1} t} } \right) \nonumber \\{} & {} \quad +2\xi _{k} I_{00} \eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{30x_{1} }^{2}u_{3x_{1} t} } \right) +2\xi _{k} \eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} x_{1} } u_{3x_{1} x_{1} t} } \right) \nonumber \\{} & {} \quad +2\xi _{k} I_{66} \frac{\partial }{\partial x_{1} }\left( {\phi _{x_{1} } u_{3x_{1} x_{1} t} } \right) +\xi _{k} I_{55} \frac{1}{\eta ^{2}}\frac{\partial }{\partial x_{1} }\left( {\phi u_{3x_{1} t} } \right) +2\xi _{k} I_{66} \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} x_{1} } \phi _{x_{1} t} } \right) +\xi _{k} I_{55} \frac{1}{\eta ^{2}}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } \phi _{t} } \right) \nonumber \\{} & {} \quad +2\xi _{k} I_{99} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {\phi _{x_{1} } \phi _{x_{1} t} } \right) +\xi _{k} I_{55} \frac{1}{\eta ^{3}}\frac{\partial }{\partial x_{1} }\left( {\phi \phi _{t} } \right) +\xi _{k} I_{00} \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{2}u_{1x_{1} t} } \right) +2\xi _{k} I_{00} \frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } u_{3x_{1} t} } \right) \nonumber \\{} & {} \quad +3\xi _{k} I_{00} \eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } ^{2}u_{30x_{1} } u_{3x_{1} t} } \right) +\xi _{k} I_{00} \eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{3}u_{3x_{1} t} } \right) -8I_{00} \frac{1}{\eta ^{2}}u_{1x_{1} x_{1} } -8I_{00} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{30x_{1} } } \right) \nonumber \\{} & {} \quad +12I_{00} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} }^{2}} \right) +24I_{00} \frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{3x_{1} } u_{30x_{1} } } \right) -4I_{77} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{2}} \right) +12I_{00} \eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{2}u_{30x_{1} }^{2}} \right) \nonumber \\{} & {} \quad +12\eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} x_{1} } ^{2}} \right) \,\,+24I_{66} \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} x_{1} } \phi _{x_{1} } \,} \right) +8I_{55} \frac{1}{\eta ^{2}}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } \phi } \right) \nonumber \\{} & {} \quad +12I_{99} \frac{1}{\eta }\frac{\partial }{\partial x_{1} }\left( {\phi _{x_{1} }^{2}} \right) +4I_{55} \frac{1}{\eta ^{3}}\frac{\partial }{\partial x_{1} }\left( {\phi ^{2}} \right) \, \nonumber \\{} & {} \quad +12I_{00} \frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{3x_{1} }^{2}} \right) +12I_{00} \eta \frac{\partial }{\partial x_{1} }\left( {u_{30x_{1} } u_{3x_{1} }^{3}} \right) +3I_{00} \eta \frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{4}} \right) =0, \end{aligned}$$
(69)
$$\begin{aligned}{} & {} \frac{I_{66} }{I_{00} }\eta ^{3}u_{3x_{1} tt} +\frac{I_{99} }{I_{00} }\eta ^{2}\phi _{tt} -\xi _{k} \eta I_{66} u_{3x_{1} x_{1} x_{1} t} +\frac{1}{2}\xi _{k} I_{55} \frac{1}{\eta }u_{3x_{1} t} -\xi _{k} I_{99} \phi _{x_{1} x_{1} t} \nonumber \\{} & {} \quad +\frac{1}{2}\xi _{k} I_{55} \frac{1}{\eta ^{2}}\phi _{t} +2\xi _{k} I_{66} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} x_{1} } u_{1x_{1} t} } \right) \nonumber \\{} & {} \quad -\xi _{k} I_{55} u_{3x_{1} } u_{1x_{1} t} +2\xi _{k} I_{99} \eta \frac{\partial }{\partial x_{1} }\left( {\phi _{x_{1} } u_{1x_{1} t} } \right) -\xi _{k} I_{55} \frac{1}{\eta }\phi u_{1x_{1} t} +2\xi _{k} I_{66} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{3x_{1} x_{1} t} } \right) \nonumber \\{} & {} \quad +2\xi _{k} I_{66} \eta ^{3}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} x_{1} } u_{30x_{1} } u_{3x_{1} t} } \right) -\xi _{k} I_{55} \eta u_{3x_{1} } u_{30x_{1} } u_{3x_{1} t}\nonumber \\{} & {} \quad +\xi _{k} 2I_{99} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {\phi _{x_{1} } u_{30x_{1} } u_{3x_{1} t} } \right) -\xi _{k} I_{55} \phi u_{30x_{1} } u_{3x_{1} t} \nonumber \\{} & {} \quad +2\xi _{k} I_{99} \eta \frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } \phi _{x_{1} t} } \right) +2\xi _{k} I_{99} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{30x_{1} } \phi _{x_{1} t} } \right) +2\xi _{k} I_{66} \eta ^{3}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} } u_{3x_{1} t} } \right) \nonumber \\{} & {} \quad +\xi _{k} I_{66} \eta ^{3}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{2}u_{3x_{1} x_{1} t} } \right) +2\xi _{k} I_{66} \eta ^{3}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{30x_{1} } u_{3x_{1} x_{1} t} } \right) \nonumber \\{} & {} \quad -\xi _{k} I_{55} \eta u_{3x_{1} } ^{2}u_{3x_{1} t} +2\xi _{k} I_{99} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } \phi _{x_{1} } u_{3x_{1} t} } \right) \nonumber \\{} & {} \quad -\xi _{k} I_{55} u_{3x_{1} } \phi u_{3x_{1} t} +\xi _{k} I_{99} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{2}\phi _{x_{1} t} } \right) -8I_{66} \eta u_{3x_{1} x_{1} x_{1} } +8I_{55} \frac{1}{\eta }u_{3x_{1} } -8I_{99} \phi _{x_{1} x_{1} } +8I_{55} \frac{1}{\eta ^{2}}\phi \nonumber \\{} & {} \quad +24I_{66} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } u_{3x_{1} x_{1} } } \right) -8I_{55} u_{1x_{1} } u_{3x_{1} } +24I_{99} \eta \frac{\partial }{\partial x_{1} }\left( {u_{1x_{1} } \phi _{x_{1} } } \right) \nonumber \\{} & {} \quad -8I_{55} \frac{1}{\eta }u_{1x_{1} } \phi +24I_{66} \eta ^{3}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } u_{3x_{1} x_{1} } u_{30x_{1} } } \right) \nonumber \\{} & {} \quad -8I_{55} \eta u_{3x_{1} }^{2}u_{30x_{1} } +24I_{99} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } \phi _{x_{1} } u_{30x_{1} } } \right) \,-8I_{55} u_{3x_{1} } \phi u_{30x_{1} } \nonumber \\{} & {} \quad +12I_{66} \eta ^{3}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} }^{2}u_{3x_{1} x_{1} } } \right) -4I_{55} \eta u_{3x_{1} } ^{3} \nonumber \\{} & {} \quad +12I_{99} \eta ^{2}\frac{\partial }{\partial x_{1} }\left( {u_{3x_{1} } ^{2}\phi _{x_{1} } } \right) \,\,-4I_{55} u_{3x_{1} }^{2}\phi =0. \end{aligned}$$
(70)
(71)

For time-dependant analysis, by employing the Galerkin’s procedure, the degrees of freedom are written as

$$\begin{aligned} u_{1} \left( {x_{1} ,t} \right)= & {} \sum \limits _{j=1}^M {U_{j} } \left( {x_{1} } \right) \Re _{j} \left( t \right) , \end{aligned}$$
(72)
$$\begin{aligned} u_{3} \left( {x_{1} ,t} \right)= & {} \sum \limits _{i=1}^N {W_{i} } \left( {x_{1} } \right) \aleph _{i} \left( t \right) , \end{aligned}$$
(73)
$$\begin{aligned} \phi \left( {x_{1} ,t} \right)= & {} \sum \limits _{i=1}^N {\psi _{i} } \left( {x_{1} } \right) \kappa _{i} \left( t \right) , \end{aligned}$$
(74)

and the equations of motion are discretised as

$$\begin{aligned}{} & {} M_{11} \ddot{{\Re }}+C_{11}^{L} \dot{{\Re }}+C_{12}^{L} \dot{{\aleph }}+C_{11}^{NL} \Re \dot{{\Re }}+C_{12}^{NL} \aleph \dot{{\Re }}+C_{13}^{NL} \Re \dot{{\aleph }}+C_{14}^{NL} \aleph \dot{{\aleph }}+C_{15}^{NL} \kappa \dot{{\aleph }}+C_{16}^{NL} \aleph \dot{{\kappa }}+C_{17}^{NL} \kappa \dot{{\kappa }} \nonumber \\{} & {} \quad +C_{18}^{NL} \aleph ^{2}\dot{{\Re }}+C_{19}^{NL} \Re \aleph \dot{{\aleph }}+C_{110}^{NL} \aleph ^{2}\dot{{\aleph }}+C_{111}^{NL} \aleph ^{3}\dot{{\aleph }}+K_{11}^{L} \Re +K_{12}^{L} \aleph +K_{11}^{NL} \Re ^{2}+K_{12}^{NL} \Re \aleph +K_{13}^{NL} \aleph ^{2} \nonumber \\{} & {} \quad +K_{14}^{NL} \aleph \kappa +K_{15}^{NL} \kappa ^{2}\,+K_{16}^{NL} \Re \aleph ^{2}+K_{17}^{NL} \aleph ^{3}+K_{18}^{NL} \aleph ^{4}=0, \end{aligned}$$
(75)
$$\begin{aligned}{} & {} M_{22} \ddot{{\aleph }}+M_{23} \ddot{{\kappa }}+C_{21}^{L} \dot{{\Re }}+C_{22}^{L} \dot{{\aleph }}+C_{23}^{L} \dot{{\kappa }}+C_{21}^{NL} \Re \dot{{\Re }}+C_{22}^{NL} \aleph \dot{{\Re }}+C_{23}^{NL} \kappa \dot{{\Re }}+C_{24}^{NL} \Re \dot{{\aleph }}+C_{25}^{NL} \aleph \dot{{\aleph }} \nonumber \\{} & {} \quad +C_{26}^{NL} \kappa \dot{{\aleph }}+C_{27}^{NL} \Re \dot{{\kappa }}+C_{28}^{NL} \aleph \dot{{\kappa }}+C_{29}^{NL} \kappa \dot{{\kappa }}+C_{210}^{NL} \Re \aleph \dot{{\Re }}+C_{211}^{NL} \aleph ^{2}\dot{{\Re }}+C_{212}^{NL} \Re \aleph \dot{{\aleph }}\,+C_{213}^{NL} \aleph ^{2}\dot{{\aleph }} \nonumber \\{} & {} \quad +C_{214}^{NL} \aleph \kappa \dot{{\aleph }}+C_{215}^{NL} \aleph ^{2}\dot{{\kappa }}+C_{216}^{NL} \aleph \kappa \dot{{\kappa }}+C_{217}^{NL} \aleph ^{3}\dot{{\Re }}+C_{218}^{NL} \Re \aleph ^{2}\dot{{\aleph }}\,+C_{219}^{NL} \aleph ^{3}\dot{{\aleph }}+C_{220}^{NL} \aleph ^{4}\dot{{\aleph }}+K_{21}^{L} \Re \nonumber \\{} & {} \quad +K_{22}^{L} \aleph +K_{22}^{L} \kappa +K_{21}^{NL} \Re ^{2}+K_{22}^{NL} \Re \aleph +K_{23}^{NL} \Re \kappa \,+K_{24}^{NL} \aleph ^{2}\nonumber \\{} & {} \quad +K_{25}^{NL} \aleph \kappa +K_{26}^{NL} \kappa ^{2}+K_{27}^{NL} \Re ^{2}\aleph +K_{28}^{NL} \Re \aleph ^{2} \nonumber \\{} & {} \quad +K_{29}^{NL} \aleph ^{3}+K_{210}^{NL} \aleph ^{2}\kappa \,+K_{211}^{NL} \aleph \kappa ^{2}+K_{212}^{NL} r\aleph ^{3}+K_{213}^{NL} \aleph ^{4}+K_{214}^{NL} \aleph ^{5}=F\cos \left( {\Omega t} \right) , \end{aligned}$$
(76)
$$\begin{aligned}{} & {} M_{32} \ddot{{\aleph }}+M_{33} \ddot{{\kappa }}\,+C_{31}^{L} \dot{{\aleph }}+C_{32}^{L} \dot{{\kappa }}+C_{31}^{NL} \aleph \dot{{\Re }}+C_{32}^{NL} \kappa \dot{{\Re }}+C_{33}^{NL} \Re \dot{{\aleph }}+C_{34}^{NL} \aleph \dot{{\aleph }}+C_{35}^{NL} \kappa \dot{{\aleph }}\,+C_{36}^{NL} \Re \dot{{\kappa }} \nonumber \\{} & {} \quad +C_{37}^{NL} \aleph \dot{{\kappa }}+C_{38}^{NL} \aleph ^{2}\dot{{\aleph }}+C_{39}^{NL} \aleph \kappa \dot{{\aleph }}+C_{310}^{NL} \aleph ^{2}\dot{{\kappa }}+K_{32}^{L} \aleph \,+K_{33}^{L} \kappa +K_{31}^{NL} \Re \aleph +K_{32}^{NL} \Re \kappa +K_{33}^{NL} \aleph ^{2} \nonumber \\{} & {} \quad +K_{34}^{NL} \aleph \kappa +K_{35}^{NL} \aleph ^{3}+K_{36}^{NL} \aleph ^{2}\kappa =0, \end{aligned}$$
(77)

with the mass coefficients (\(M_{ij})\) as

$$\begin{aligned} M_{11}= & {} \int \limits _0^1 {U_{p} \left( {x_{1} } \right) } U_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(78)
$$\begin{aligned} M_{22}= & {} +\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } W_{i} \left( {x_{1} } \right) \textrm{d}x_{1} -\frac{1}{I_{00} }\eta ^{2}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {W}''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(79)
$$\begin{aligned} M_{23}= & {} -\frac{I_{66} }{I_{00} }\eta \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {\psi }'_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(80)
$$\begin{aligned} M_{32}= & {} +\frac{I_{66} }{I_{00} }\eta ^{3}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(81)
$$\begin{aligned} M_{33}= & {} +\frac{I_{99} }{I_{00} }\eta ^{2}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \psi _{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(82)

and the linear visco-elastic coefficients (\(C^{L}_{ij})\) as

$$\begin{aligned}{} & {} C_{11}^{L} :-\xi _{k} I_{00} \frac{1}{\eta ^{2}}\int \limits _0^1 {U_{l} \left( {x_{1} } \right) } {U}''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(83)
$$\begin{aligned}{} & {} C_{12}^{L} :-\xi _{k} I_{00} \frac{1}{\eta }\int \limits _0^1 {U_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) W_{0}^{'}\left( {x_{1} } \right) } \right) \textrm{d}x_{1} , \end{aligned}$$
(84)
$$\begin{aligned}{} & {} C_{21}^{L} :-\xi I_{00} \frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{U}'_{i} \left( {x_{1} } \right) {W}'_{0} \left( {x_{1} } \right) } \right) \textrm{d}x , \end{aligned}$$
(85)
$$\begin{aligned}{} & {} C_{22}^{L} :+\xi \,\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } W_{i}^{(4)} \left( {x_{1} } \right) \textrm{d}x_{1} -\xi I_{00} \int \limits _0^1 {W_{l} \left( {x_{1} } \right) } \frac{\textrm{d}}{\textrm{d}x_{1} }\left( {{W}'_{i} \left( {x_{1} } \right) {W}'^{2}_{0} \left( {x_{1} } \right) } \right) \textrm{d}x_{1} \nonumber \\{} & {} \quad -\frac{1}{2}\xi I_{55} \frac{1}{\eta ^{2}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {W}''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(86)
$$\begin{aligned}{} & {} C_{23}^{L} :+\xi \,I_{66} \frac{1}{\eta }\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {\psi }'''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} -\frac{1}{2}\xi I_{55} \frac{1}{\eta ^{3}}\int \limits _0^1 {W_{l} \left( {x_{1} } \right) } {\psi }'_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(87)
$$\begin{aligned}{} & {} C_{31}^{L} :-\xi _{k} \eta I_{66} \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'''_{i} \,\left( {x_{1} } \right) \textrm{d}x_{1} +\frac{1}{2}\xi _{k} I_{55} \frac{1}{\eta }\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {W}'_{i} \left( {x_{1} } \right) \textrm{d}x_{1} , \end{aligned}$$
(88)
$$\begin{aligned}{} & {} C_{32}^{L} :-\xi _{k} I_{99} \int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } {\psi }''_{i} \left( {x_{1} } \right) \textrm{d}x_{1} \,+\frac{1}{2}\xi _{k} I_{55} \frac{1}{\eta ^{2}}\int \limits _0^1 {\psi _{l} \left( {x_{1} } \right) } \psi _{i} \left( {x_{1} } \right) \textrm{d}x_{1} . \end{aligned}$$
(89)

The nonlinear damping coefficients (\(C^{NL}_{ij})\) are shown in Appendix C for the sake of brevity, and the stiffness terms are defined in the previous sections. By solving the dynamic equilibrium equations [39, 41], the nonlinear vibration response of the system is obtained.

6 Results and discussions for bending and vibration

In this section, the nonlinear bending and vibration responses of thick visco-hyper-elastic shallow arches are modelled for different cases of curvature, slenderness ratio and internal resonances. The hyper-elastic properties are taken from Ref [55] for vulcanised rubbers with the Mooney–Rivlin coefficients as \(C_{1\, }=\) 0.28e6 Pa and \(C_{2\, }=\) 0.15e6 Pa and mass density \(\rho =\) 950 kg/m\(^{3}\).

6.1 Bending analysis

Study 1: Force-bending analysis

As the first part of the analysis, the nonlinear static deformation of thick hyper-elastic shallow arches is analysed following the solution procedure given in Sect. 4 and compared to those obtained using finite element software. The shallow arch is assumed to have the following geometrical properties: \(L =\) 0.3 m, \(h =\) 0.03 m, b \(=\) 0.03 m, with a simply supported boundary condition and assumed to undergo a static pressure (which is varied from \(-\) 1 to 1 kPa). The maximum transverse deformation is obtained and shown in Table 1 for different curvatures and external loads. By comparing the current results with those obtained from ANSYS [56], it is shown that the results are in very good agreement. Besides, it can be seen that by increasing the curvature term, the maximum deformation of the shallow arch decreases significantly especially for higher external loadings.

Table 1 Comparison of the maximum transverse deformation of the shallow arch for different loads
Full size table

Moreover, to understand the static behaviour of the shallow arch under different types of loadings, the curvature is assumed as following the first mode as \(W_{0}(x_{1}) = R_{0}W_{1}(x_{1})\) where \(R_{0}\) is the nondimensional curvature term assumed as 0.6. The nondimensional external applied static force (\(F_{\textrm{bending}})\) is modelled using a combination of sin functions as

$$\begin{aligned} F_{\textrm{bending}}^{\,} \left( x \right) :f_{1} \sin (\pi x)+f_{2} \sin (2\pi x),\,\,\,\,\,\,\,f_{1} =50\left( {n-1} \right) ,\,\,\,\,\,\,\,f_{2} =25\left( {n-1} \right) , \end{aligned}$$
(90)

where n is varied from 1 to 70. For the given function, the static force through the length of the arch is shown in Fig. 3a for different values of n. By solving the nonlinear bending equilibrium equations, the nondimensional deformations of the hyper-elastic thick arch are shown in Fig. 3b–d. It can be seen that there is a high coupling between the degrees of freedom; also, the force type and magnitude can change the deformations in the structure, significantly.

Fig. 3
figure 3

Nondimensional static force and nondimensional bending deformation response of the hyper-elastic arch a applied force, b axial deformation, c transverse deformation and d rotational deformation

Full size image

Study 2: Influence of the curvature on the bending behaviour

For the same shallow arch with the given properties in the previous subsection, the influence of the curvature in resisting deformation in the structure is analysed. To do this, an external static force following Eq. (93) is given to the structure with \(f_{1}\) and \(f_{2}\) as 1000 and \(-\) 500, respectively. Figure 4a–c shows the axial, transverse and rotation deformation of the shallow arch by varying the curvature term as \(R_{0} =\) 0.1, 0.3, 0.5, 0.7, 0.9, 1.0, and 1.5. It can be seen that increasing the shallow arch curvature leads to higher resistance against the transverse loading. Besides, as shown in Fig. 4a, the coupling between the axial and transverse deformations increases significantly by increasing the curvature term.

Fig. 4
figure 4

The nondimensional bending deformation response of the hyper-elastic shallow arch with different curvatures a axial deformation, b transverse deformation and c rotational deformation

Full size image

Study 3: Influence of considering the higher-order nonlinear terms

Since incompressible hyper-elastic structures show nonlinearity in their constitutive equation as well as large deformations, the importance of considering the higher-order nonlinear terms is discussed in this subsection. Accordingly, for the same shallow arch in previous sections with the curvature of \(R_{0} = 1.5\), bending behaviour is obtained using both linear and nonlinear models when subjected to an external static force following Eq. (93) with \(f_{1}\) and \(f_{2}\) as 10000 and \(-\) 2500. Figure 5a–c shows the axial, transverse and rotation deformation of the shallow arch by only considering the linear part of the equilibrium equations as well as considering the full equations. It can be seen that the linear simplification of the structure leads to underestimated bending deformations for the axial deformation and inaccurate transverse and rotation motions which indicates the importance of accurately modelling the nonlinear behaviour of the structure.

Fig. 5
figure 5

Comparison of the linear and nonlinear models for bending analysis of the hyper-elastic shallow arch with \(R_{0} =\) 1.5 a axial deformation, b transverse deformation, and c rotational deformation

Full size image

6.2 Internal resonance and vibration analysis

Study 1: Vibration in the hyper-elasticity framework with internal resonances

Since the curvature of the thick, soft shallow arch can change the linear frequencies of the structure, this section concentrates on detecting the internal resonance behaviour of the arch due to the curvature. For the same shallow arch model given in Sect. 6.1, the ratio of the second natural frequency to the fundamental natural frequency (\(\omega _{2}\)/\(\omega _{1})\) is shown in Fig. 6 by having different curvature terms. It can be seen that around \(R_{0} =\) 0.3, the ratio is equal to 3 and the three-to-one internal resonance in the system occurs. Accordingly, by having \(R_{0} =\) 0.3 (which leads to \(\omega _{2}\)/\(\omega _{1} \cong \)3), the frequency-amplitude responses of the system are shown in Figs. 7, 8 and 9 for the dominant vibration coordinates in the axial, transverse and rotational directions. It can be seen that a high coupling between modes it obtained, and the system shows a rich nonlinear behaviour, with a combination of hardening, softening and modal interactions.

Fig. 6
figure 6

The frequency ratio of a soft, thick shallow arch with respect to the curvature term

Full size image
Fig. 7
figure 7

First three axial nonlinear frequency responses of hyper-elastic thick, soft arches at the internal resonance a \(\mathfrak {R}_{11}\), b \(\mathfrak {R}_{21}\) and c \(\mathfrak {R}_{12}\)

Full size image
Fig. 8
figure 8

First three transverse nonlinear frequency responses of hyper-elastic thick, soft arches at the internal resonance a \(\aleph _{11}\), b \(\aleph _{12}\) and c \(\aleph _{21}\)

Full size image
Fig. 9
figure 9

First three rotation nonlinear frequency responses of hyper-elastic thick, soft arches at the internal resonance a \(k_{11}\), b \(\kappa _{21}\) and c \(\kappa _{12}\)

Full size image

Study 2: Vibration in the visco-hyper-elasticity framework with internal resonances

Many soft structures show visco-elastic behaviour together with hyper-elasticity (especially biological tissues). To see the influence of this combination on the nonlinear frequency response of the structure with an internal resonance, this section analyses the visco-hyper-elasticity behaviour of thick, soft, shallow arches. Since visco-elasticity is a function of many environmental parameters, such as temperature [57], this property of hyper-elastic structures should be measured for specific working environments. In this study, visco-elasticity is modelled using the Kelvin–Voigt visco-hyper-elastic model which has been shown that has a good accuracy in modelling visco-hyper-elastic materials [48]. The influence of the visco-elasticity on the three-to-one internal resonance of the structure is shown in Figs. 10, 11 and 12 for the axial, transverse and rotational directions by varying the viscoelastic parameter as \(\xi _{k} =\) [2e\(-\)3, 2e\(-\)4, 2e\(-\)5]. It can be seen that the visco-hyper-elasticity has a significant effect in changing the nonlinear frequency response, and increasing this term from 2e\(-\)5 to 2e\(-\)4 decreases the maximum amplitude. By increasing the viscous term to 2e\(-\)3, the complicated nonlinear internal resonance behaviour will be fully damped.

Fig. 10
figure 10

First three axial nonlinear frequency responses of visco-hyper-elastic thick, soft arches at the internal resonance a \(\mathfrak {R}_{11}\), b \(\mathfrak {R}_{21}\) and c \(\mathfrak {R}_{12}\)

Full size image
Fig. 11
figure 11

First three transverse nonlinear frequency responses of visco-hyper-elastic thick, soft arches at the internal resonance a \(\aleph _{11}\), b \(\aleph _{12 }\) and c \(\aleph _{21}\)

Full size image
Fig. 12
figure 12

First three rotation nonlinear frequency responses of visco-hyper-elastic thick, soft arches at the internal resonance a \(k_{11}\), b \(\kappa _{21}\) and c \(\kappa _{12}\)

Full size image

Study 3: Curvature sensitivity

One of the main concentrations of this paper is on considering the curvature modelling in soft thick shallow arches. To show the importance and influence of this term on the nonlinear vibration behaviour of the structure, the shallow arch is assumed to have the following geometrical properties given in Sect. 6.1 with a simply supported boundary condition and curvature term varied as \(R_{0} =\) [0.0, 0.1, 0.3, 0.5, 0.6, 0.8, 1.0].

The results for the amplitude-frequency response of the soft arch subjected to an external nondimensional load of \(F = 0.5\) are shown in Figs. 13, 14 and 15 for the dominant vibration coordinates in the axial, transverse and rotation directions, respectively. It can be seen that increasing the curvature term from 0 to 1.0 moves the amplitude responses to higher frequencies. For higher curvature terms, transverse dynamic equilibriums show a softening effect, while for lower curvature term a combination of hardening and softening behaviour is obtained. Furthermore, by increasing the curvature term, the maximum amplitude of the first transverse dynamic equilibrium coordinate decreases significantly.

Fig. 13
figure 13

Influence of the curvature term on the first three axial nonlinear frequency responses of thick, soft arches a \(\mathfrak {R}_{11}\), b \(\mathfrak {R}_{21}\) and c \(\mathfrak {R}_{12}\)

Full size image
Fig. 14
figure 14

Influence of the curvature term on the first three transverse nonlinear frequency responses of thick, soft arches a \(\aleph _{11}\), b \(\aleph _{12}\) and (c) \(\aleph _{21}\)

Full size image
Fig. 15
figure 15

Influence of the curvature term on the first three rotation nonlinear frequency responses of thick, soft arches a \(k_{11}\), b \(\kappa _{21}\) and c \(\kappa _{12}\)

Full size image

Study 4: Slenderness ratio sensitivity

Since a third-order shear deformable model has been used, different length-to-thickness models can be analysed. In this subsection, by assuming the same properties given in Sect. 6.1, the length of the arch is varied to \(L = S_{L}h\) where \(S_{L}\) is the slenderness ratio, which is varied as \(S_{L} =\) [10, 20, 30, 40, 50]. The results for varying the length-to-thickness ratio are shown in Figs. 16, 17 and 18 for the axial, transverse and rotation dynamic equilibrium directions. It can be seen that increasing the slenderness ratio increases the stiffness hardening behaviour in the transverse coordinates. The first axial and rotation coordinates’ amplitude decreases by increasing the slenderness ratio rate, which means the coupling between the axial and the transverse motion decreases and the rotation motion loses its importance.

Fig. 16
figure 16

Influence of the slenderness ratio on the first three axial nonlinear frequency responses of thick, soft arches a \(\mathfrak {R}_{11}\), b \(\mathfrak {R}_{21}\) and c \(\mathfrak {R}_{12}\)

Full size image
Fig. 17
figure 17

Influence of the slenderness ratio on the first three transverse nonlinear frequency responses of thick, soft arches a \(\aleph _{11}\), b \(\aleph _{12}\) and c \(\aleph _{21}\)

Full size image
Fig. 18
figure 18

Influence of the slenderness ratio on the first three transverse nonlinear frequency responses of thick, soft arches a \(\kappa _{11}\), b \(\kappa _{12}\) and c \(\kappa _{21}\)

Full size image

7 Summary and conclusions

The nonlinear bending and vibration behaviours of simply supported, thick, soft, visco-hyper-elastic shallow arches are examined in this study. The visco-hyper-elasticity was modelled using an incompressible Mooney–Rivlin’s hyper-elastic strain energy density model, together with Kelvin–Voigt visco-hyper-elasticity. A higher-order shear deformable model was used to model the axial, transverse and rotation motions. The curvature term was added to the model using von Kármán geometric nonlinearity, and the incompressibility condition was satisfied in the strain–displacement definition. The coupled nonlinear equations of motion were obtained and solved using force-moment balance method and the virtual work method for the vibration and bending analyses, respectively, showing that:

  1. (i)

    Increasing the shallow arch curvature leads to higher resistance against the transverse loading in all axial, transverse and rotation motions of the structure and changed the bending behaviour significantly.

  2. (ii)

    The linear simplification of the structure leads to underestimated bending deformations for all the axial, transverse and rotation motions which indicates the importance of accurately modelling the nonlinear behaviour of the structure.

  3. (iii)

    The coupling between the axial and transverse bending increases significantly by increasing the curvature term

  4. (iv)

    The curvature term can cause internal resonance in the system, leading to high coupling between modes, for which the system shows a rich nonlinear behaviour with a combination of hardening, softening and modal interactions.

  5. (v)

    The visco-hyper-elasticity has a significant effect in changing the nonlinear frequency response with a three-to-one internal resonance. By increasing the visco-hyper-elastic term to higher numbers, the complicated nonlinear internal resonance behaviour will be fully damped.

  6. (vi)

    For higher curvature terms, transverse dynamic equilibriums show a softening behaviour, while for lower curvature terms, a combination of hardening and softening behaviour is obtained.

  7. (vii)

    By increasing the curvature term, the maximum amplitude of the first transverse dynamic equilibrium coordinate decreases significantly.

  8. (viii)

    Increasing the slenderness ratio increases the stiffness hardening behaviour in the transverse coordinates.

  9. (ix)

    The dominant axial and rotation coordinates’ amplitude decreases by increasing the slenderness ratio rate, which means the coupling between the axial and the transverse motion decreases and the rotation motion loses its importance.