Mechanics of third-gradient continua reinforced with fibers resistant to flexure in finite plane elastostatics

Abstract

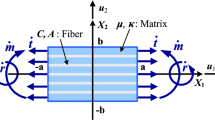
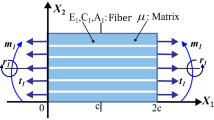
A third-gradient continuum model is developed for the deformation analysis of an elastic solid, reinforced with fibers resistant to flexure. This is framed in the second strain gradient elasticity theory within which the kinematics of fibers are formulated, and subsequently integrated into the models of deformations. By means of variational principles and iterated integrations by parts, the Euler equilibrium equation is obtained which, together with the constraints of bulk incompressibility, compose the system of the coupled nonlinear partial differential equations. In particular, a rigorous derivation of the admissible boundary conditions arising in the third gradient of virtual displacement is presented from which the expressions of the triple forces are derived. The resulting triple forces are, in turn, coupled with the Piola-type triple stress and are necessary to determine a unique deformation map. The proposed model predicts smooth and dilatational shear angle distributions, as opposed to those obtained from the first- and second-gradient theory where the resulting shear zones are either non-dilatational or non-smooth.

Appendix: Finite element analysis of the fourth-order coupled PDE

The resulting systems of PDEs (Eqs. (50)–(51)) are sixth-order differential equations with coupled nonlinear terms. The case of such less regular PDEs deserves delicate mathematical treatment as done similarly in [25, 37] and is of particular practical interest. Therefore, it is not trivial to demonstrate numerical analysis procedures regarding FE analysis.

For preprocessing, Eqs. (50)–(51) may be recast as

$$\begin{aligned} \mu \left( Q+\chi _{1,22}\right) -A\chi _{2,2} +B\chi _{2,1}-CQ_{,11}+AS_{,11}= & {} 0, \nonumber \\ \mu \left( R+\chi _{2,22}\right) +A\chi _{1,2} -B\chi _{1,1}-CR_{,11}+AT_{,11}= & {} 0, \nonumber \\ Q-\chi _{1,11}= & {} 0, \nonumber \\ R-\chi _{2,11}= & {} 0, \nonumber \\ S-Q_{,11}= & {} 0, \nonumber \\ T-R_{,11}= & {} 0, \nonumber \\ A-\mu (Q+\chi _{1,22})-CS= & {} 0, \nonumber \\ B-\mu (R+\chi _{2,22})-CT= & {} 0, \end{aligned}$$

(76)

where $Q=\chi _{1,11}$, $R=\chi _{2,11}$, $S=Q_{,11}$ and $T=R_{,11}$. Thus, we reduced the order of deferential equations from three coupled equations of sixth order to eight coupled equations of second order. In particular, the nonlinear terms (e.g., $A\chi _{2,2}$, $B\chi _{2,1}$, etc.) in the above equations can be systematically treated via the Picard iterative procedure;

$$\begin{aligned} -A_{\mathrm{initial}}\chi _{2,2}^{\mathrm{initial}}+B_{\mathrm{initial}}\chi _{2,1}^{\mathrm{initial}}&\Longrightarrow&-A_{0}\chi _{2,2}^{0}+B_{0}\chi _{2,1}^{0}, \nonumber \\ A_{\mathrm{initial}}\chi _{1,2}^{\mathrm{initial}}-B_{\mathrm{initial}}\chi _{1,1}^{\mathrm{initial}}&\Longrightarrow&A_{0}\chi _{1,2}^{0}-B_{0}\chi _{1,1}^{0}, \end{aligned}$$

(77)

where the values of A and B continue to be updated based on their previous estimations (e.g., $A_{1}$ and $B_{1}$ are refreshed by their previous pair of $A_{0}$ and $B_{0})$ as iteration progresses. Hence, we generalize the above expression for N number of iterations as

$$\begin{aligned} -A_{N-1}\chi _{2,2}^{N-1}+B_{N-1}\chi _{2,1}^{N-1}&\Longrightarrow&-A_{N}\chi _{2,2}^{N}+B_{N}\chi _{2,1}^{N}, \nonumber \\ A_{N-1}\chi _{1,2}^{N-1}-B_{N-1}\chi _{1,1}^{N-1}&\Longrightarrow&A_{N}\chi _{1,2}^{N}-B_{N}\chi _{1,1}^{N}, \end{aligned}$$

(78)

in which the number of iteration can be determined by a convergence criteria.

In addition, the weighted forms of Eq. (76) are obtained by

$$\begin{aligned} 0= & {} \int \limits _{\Omega ^{e}}w_{1}(\mu \left( Q+\chi _{1,22}\right) -A\chi _{2,2}+B\chi _{2,1}-CQ_{,11}+AS_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{2}(\mu \left( R+\chi _{2,22}\right) +A\chi _{1,2}-B\chi _{1,1}-CR_{,11}+AT_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{3}(Q-\chi _{1,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{4}(R-\chi _{2,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{5}(S-Q_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{6}(T-R_{,11})d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{7}(A-\mu (Q+\chi _{1,22})-CS)d\Omega , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{8}(B-\mu (R+\chi _{2,22})-CT)d\Omega . \end{aligned}$$

(79)

Applying integration by parts and Green–Stoke’s theorem (e.g., $\mu \int _{\Omega ^{e}}w_{1}\chi _{1,22}d\Omega =-\mu \int _{\Omega ^{e}}w_{1,2}\chi _{1,2}d\Omega +\mu \int _{\Omega ^{e}}w_{1}\chi _{1,2}Nd\Gamma$), we obtain from the above that

$$\begin{aligned} 0= & {} \int \limits _{\Omega ^{e}}(\mu w_{1}Q-\mu w_{1,2}\chi _{1,2}-w_{1}A_{0} \chi _{2,2}+w_{1}B_{0}\chi _{2,1}+Cw_{1,1}Q_{,1}-Aw_{1,1}S_{,1})d\Omega \nonumber \\&+\int \limits _{\partial \Gamma ^{e}}\mu w_{1}\chi _{1,2}Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}Cw_{1}Q_{,1}Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}Aw_{1}S_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(\mu w_{2}R-\mu w_{2,2}\chi _{2,2}+w_{2}A_{0} \chi _{1,2}-w_{2}B_{0}\chi _{1,1}+Cw_{2,1}R_{,1}-Aw_{2,1}T_{,1})d\Omega \nonumber \\&+\int \limits _{\partial \Gamma ^{e}}\mu w_{2}\chi _{2,2}Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}Cw_{2}R_{,1}Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}Aw_{2}T_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{3}Q+w_{3,1}\chi _{1,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{3}\chi _{1,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{4}R+w_{4,1}\chi _{2,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{4}\chi _{2,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{5}S+w_{5,1}Q_{,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{5}Q_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}(w_{6}T+w_{6,1}R_{,1})d\Omega -\int \limits _{\partial \Gamma ^{e}}w_{6}R_{,1}Nd\Gamma , \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{7}(A_{0}-\mu Q-CS-\mu w_{7,2}\chi _{1,2})d\Omega -\int \limits _{\partial \Gamma ^{e}}\mu w_{7}\chi _{1,2}Nd\Gamma \nonumber \\ 0= & {} \int \limits _{\Omega ^{e}}w_{8}(B_{0}-\mu R-CT-\mu w_{8,2}\chi _{1,2})d\Omega -\int \limits _{\partial \Gamma ^{e}}\mu w_{7}\chi _{2,2}Nd\Gamma , \end{aligned}$$

(80)

where $\Omega$, $\partial \Gamma$ and $\mathbf {N}$ are the domain of interest, the associated boundary, and the rightward unit normal to the boundary $\partial \Gamma$ in the sense of the Green–Stoke’s theorem, respectively. The unknowns, $\chi _{1}$, $\chi _{2}$, Q, R, S, T, A and B can be written in the form of Lagrangian polynomial as

$$\begin{aligned} (*)=\sum _{j=1}^{n=4}[(*)_{j}\Psi _{j}(x, y)]. \end{aligned}$$

(81)

Thus, the test function w is obtained by

$$\begin{aligned} w_{m}=\sum _{i=1}^{n=4}w_{m}^{i}\Psi _{i}(x, y)\quad {\text { and }}\quad m=1,2,3,\ldots ,8. \end{aligned}$$

(82)

Here, $w_{i}$ is weight of the test function and $\Psi _{i}(x,y)$ are the shape functions for the four-node rectangular elements such that

$$\begin{aligned} \Psi _{1}=\frac{(x-c)(y-d)}{cd},\Psi _{2}=\frac{x(y-d)}{-cd},~\Psi _{3} =\frac{xy}{cd}\quad {\text { and }}\quad \Psi _{4}=\frac{y(x-c)}{-cd}. \end{aligned}$$

(83)

By means of Eq. (81), Eq. (80) can be rewritten in terms of Lagrangian polynomial representation as

$$\begin{aligned} 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i}\Psi _{j} +C\Psi _{i,1}\Psi _{j,1})d\Omega \right\} Q_{j}\nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}} (\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{1j}-\sum _{i,j=1}^{n} \left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}A_{0}\Psi _{j,2}-\Psi _{i}B_{0}\Psi _{j,1})d\Omega \right\} \chi _{2j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(A\Psi _{i,1}\Psi _{j,1})d\Omega \right\} S_{j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{1,2})Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}(C\Psi _{i}Q_{,1})Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}A\Psi _{i}S_{,1}Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i}\Psi _{j} +C\Psi _{i,1}\Psi _{j,1})d\Omega \right\} R_{j}\nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{2j}+\sum _{i,j=1}^{n} \left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}A_{0}\Psi _{j,2}-\Psi _{i}B_{0}\Psi _{j,1})d\Omega \right\} \chi _{1j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(A\Psi _{i,1}\Psi _{j,1})d\Omega \right\} T_{j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{2,2})Nd\Gamma -\int \limits _{\partial \Gamma ^{e}}(C\Psi _{i}R_{,1})Nd\Gamma +\int \limits _{\partial \Gamma ^{e}}A\Psi _{i}T_{,1}Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} Q_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} \chi _{1j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}\chi _{1,1})Nd\Gamma ,\nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} R_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} \chi _{2j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}\chi _{2,1})Nd\Gamma ,\nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} S_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} Q_{j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}Q_{,1})Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} T_{j}+\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}\Psi _{i,1}\Psi _{j,1})d\Omega \right\} R_{j}-\int \limits _{\partial \Gamma ^{e}}(\Psi _{i}R_{,1})Nd\Gamma , \nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} A_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i} \Psi _{j})d\Omega \right\} Q_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(C\Psi _{i} \Psi _{j})d\Omega \right\} S_{j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{1j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{1,2})Nd\Gamma ,\nonumber \\ 0= & {} \sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\Psi _{i}\Psi _{j})d\Omega \right\} B_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i} \Psi _{j})d\Omega \right\} R_{j}-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(C\Psi _{i} \Psi _{j})d\Omega \right\} T_{j} \nonumber \\&-\sum _{i,j=1}^{n}\left\{ \int \limits _{\Omega ^{e}}(\mu \Psi _{i,2}\Psi _{j,2})d\Omega \right\} \chi _{2j}+\int \limits _{\partial \Gamma ^{e}}(\mu \Psi _{i}\chi _{2,2})Nd\Gamma . \end{aligned}$$

(84)

Now, for the local stiffness matrices and forcing vectors for each elements, we find

$$\begin{aligned} \left[ \begin{array}{cccc} K_{11}^{11} &{}\quad K_{12}^{11} &{}\quad K_{13}^{11} &{}\quad K_{14}^{11} \\ K_{21}^{11} &{}\quad K_{22}^{11} &{}\quad K_{23}^{11} &{}\quad K_{24}^{11} \\ K_{31}^{11} &{}\quad K_{32}^{11} &{}\quad K_{33}^{11} &{}\quad K_{34}^{11} \\ K_{41}^{11} &{}\quad K_{42}^{11} &{}\quad K_{43}^{11} &{}\quad K_{44}^{11} \end{array}\right] _{\mathrm{Local}}\left[ \begin{array}{c} \chi _{1}^{1} \\ \chi _{1}^{2} \\ \chi _{1}^{3} \\ \chi _{1}^{4} \end{array}\right] _{\mathrm{Local}}=\left[ \begin{array}{c} F_{1}^{1} \\ F_{2}^{1} \\ F_{3}^{1} \\ F_{4}^{1} \end{array}\right] _{\mathrm{Local}}, \end{aligned}$$

(85)

or alternatively, in a compact form,

$$\begin{aligned} \left[ K_{ij}^{11}\right] [\chi _{1}^{i}]=[F_{i}^{1}]\text { for }i, j=1,2,3,4, \end{aligned}$$

(86)

where

$$\begin{aligned} \left[ K_{ij}^{11}\right] =\int \limits _{\Omega ^{e}}(\mu \Psi _{i,2} \Psi _{j,2})d\Omega , \end{aligned}$$

(87)

and

$$\begin{aligned} {[}F_{i}^{1}]=-\mu \int \limits _{\partial \Gamma ^{e}}\Psi _{i} \chi _{1,2}Nd\Gamma +C\int \limits _{\partial \Gamma ^{e}}\Psi _{i}Q_{,1}Nd \Gamma -\int \limits _{\partial \Gamma ^{e}}A\Psi _{i}S_{,1}Nd\Gamma . \end{aligned}$$

(88)

Accordingly, the unknowns (i.e., Q, R, S, T, A and B) can be expressed as

$$\begin{aligned} Q_{i}=\{\chi _{1}^{i}\}_{,11}, R_{i}=\{\chi _{2}^{i}\}_{,11}, S_{i}=\{Q^{i}\}_{,11}\text { etc.} \end{aligned}$$

(89)

Finally, we repeat the same procedures for the rest of components (e.g., $\left[ K_{ij}^{21}\right] [\chi _{2}^{i}]=[F_{i}^{2}]$, etc.) and thereby obtain the following systems of equations (in the Global form) for each individual elements.

$$\begin{aligned} \left[ \begin{array}{cccccccc} \left[ K^{11}\right] &{}\quad \left[ K^{12}\right] &{}\quad \left[ K^{13}\right] &{}\quad \left[ K^{14}\right] &{}\quad \left[ K^{15}\right] &{}\quad \left[ K^{16}\right] &{}\quad \left[ K^{17}\right] &{}\quad \left[ K^{18}\right] \\ \left[ K^{21}\right] &{}\quad \left[ K^{22}\right] &{}\quad \left[ K^{23}\right] &{}\quad \left[ K^{24}\right] &{}\quad \left[ K^{25}\right] &{}\quad \left[ K^{26}\right] &{}\quad \left[ K^{27}\right] &{}\quad \left[ K^{28}\right] \\ \left[ K^{31}\right] &{}\quad \left[ K^{32}\right] &{}\quad \left[ K^{33}\right] &{}\quad \left[ K^{34}\right] &{}\quad \left[ K^{35}\right] &{}\quad \left[ K^{36}\right] &{}\quad \left[ K^{37}\right] &{}\quad \left[ K^{38}\right] \\ \left[ K^{41}\right] &{}\quad \left[ K^{42}\right] &{}\quad \left[ K^{43}\right] &{}\quad \left[ K^{44}\right] &{}\quad \left[ K^{45}\right] &{}\quad \left[ K^{46}\right] &{}\quad \left[ K^{47}\right] &{}\quad \left[ K^{48}\right] \\ \left[ K^{51}\right] &{}\quad \left[ K^{52}\right] &{}\quad \left[ K^{53}\right] &{}\quad \left[ K^{54}\right] &{}\quad \left[ K^{55}\right] &{}\quad \left[ K^{56}\right] &{}\quad \left[ K^{57}\right] &{}\quad \left[ K^{58}\right] \\ \left[ K^{61}\right] &{}\quad \left[ K^{62}\right] &{}\quad \left[ K^{63}\right] &{}\quad \left[ K^{64}\right] &{}\quad \left[ K^{65}\right] &{}\quad \left[ K^{66}\right] &{}\quad \left[ K^{67}\right] &{}\quad \left[ K^{68}\right] \\ \left[ K^{71}\right] &{}\quad \left[ K^{72}\right] &{}\quad \left[ K^{73}\right] &{}\quad \left[ K^{74}\right] &{}\quad \left[ K^{75}\right] &{}\quad \left[ K^{76}\right] &{}\quad \left[ K^{77}\right] &{}\quad \left[ K^{78}\right] \\ \left[ K^{81}\right] &{}\quad \left[ K^{82}\right] &{}\quad \left[ K^{83}\right] &{}\quad \left[ K^{84}\right] &{}\quad \left[ K^{85}\right] &{}\quad \left[ K^{86}\right] &{}\quad \left[ K^{87}\right] &{}\quad \left[ K^{88}\right] \end{array}\right] _{\mathrm{Global}}\left[ \begin{array}{c} \{\chi _{1}^{i}\} \\ \{\chi _{2}^{i}\} \\ Q_{i} \\ R_{i} \\ A_{i} \\ B_{i} \\ S_{i} \\ T_{i} \end{array}\right] _{\mathrm{Global}}{=}\left[ \begin{array}{c} \{F_{i}^{1}\} \\ \{F^{2}\} \\ \{F^{3}\} \\ \{F^{4}\} \\ \{F^{5}\} \\ \{F^{6}\} \\ \{F^{7}\} \\ \{F^{8}\} \end{array}\right] _{\mathrm{Global}}\!. \end{aligned}$$

(90)

In the simulation, the following convergence criteria are used for both nonlinear terms;

$$\begin{aligned} \left| A_{n+1}-A_{n}\right| =e_{1}\le \varepsilon , \left| B_{n+1}-B_{n}\right| =e_{2}\le \varepsilon \quad {\text { and }}\quad \varepsilon =\text {maximum error}=10^{-4}, \end{aligned}$$

(91)

which demonstrate fast convergence within 20 iterations (see Table 2).

Table 2 Maximum numerical errors with respect to the number of iterations