Abstract
Solving conjugate heat transfer design problems is relevant for various engineering applications requiring efficient thermal management. Heat exchange between fluid and solid can be enhanced by optimizing the system layout and the shape of the flow channels. As heat is transferred at fluid/solid interfaces, it is crucial to accurately resolve the geometry and the physics responses across these interfaces. To address this challenge, this work investigates for the first time the use of an eXtended Finite Element Method (XFEM) approach to predict the physical responses of conjugate heat transfer problems considering turbulent flow. This analysis approach is integrated into a level set-based optimization framework. The design domain is immersed into a background mesh and the geometry of fluid/solid interfaces is defined implicitly by one or multiple level set functions. The level set functions are discretized by higher-order B-splines. The flow is predicted by the Reynolds Averaged Navier–Stokes equations. Turbulence is described by the Spalart–Allmaras model and the thermal energy transport by an advection–diffusion model. Finite element approximations are augmented by a generalized Heaviside enrichment strategy with the state fields being approximated by linear basis functions. Boundary and interface conditions are enforced weakly with Nitsche’s method, and the face-oriented ghost stabilization is used to mitigate numerical instabilities associated with the emergence of small integration subdomains. The proposed XFEM approach for turbulent conjugate heat transfer is validated against benchmark problems. Optimization problems are solved by gradient-based algorithms and the required sensitivity analysis is performed by the adjoint method. The proposed framework is illustrated with the design of turbulent heat exchangers in two dimensions. The optimization results show that, by tuning the shape of the fluid/solid interface to generate turbulence within the heat exchanger, the transfer of thermal energy can be increased.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Solving conjugate heat transfer problems is relevant for various engineering applications. For systems operating at large or small scales, such as gas turbines or micro-electronic modules, an efficient thermal management is crucial to ensure reliable functionality. Heat exchangers are often added to systems to provide an efficient temperature control. They are made of highly conductive materials and are cooled or heated through natural or forced convection, i.e., a moving fluid is used to transport the heat to or away from the systems. By modifying the layout of heat exchangers, the flow path and the flow conditions can be altered which in turn influences the heat transfer between fluid and solid. Therefore, the performance in terms of heat transfer and dissipative losses can be improved by optimizing the geometry of the heating or cooling devices.
Since the seminal work of Bendsøe and Kikuchi (1988), topology optimization has become a popular tool to systematically address design problems and generate layouts with enhanced performance under specific requirements, see Sigmund and Maute (2013) and Deaton and Grandhi (2014). Originally introduced for structural designs, topology optimization was first applied to fluid problems by Borrvall and Petersson (2003). Considering Stokes flows, they introduced a porosity variable to represent the distribution of fluid and solid regions through the design domain. The method was extended to laminar Navier–Stokes models by Gersborg-Hansen et al. (2006). Following these pioneering works, various flow design problems have been solved by topology optimization, see Alexandersen and Andreasen (2020) for a comprehensive review.
While most designs are optimized assuming laminar flow, a wide range of fluid systems operate in the turbulent regime. Accurately modeling turbulence at an acceptable computational cost remains challenging, see Spalart (2000). High fidelity models, such as Direct Numerical Simulations (DNS) or Large Eddy Simulations (LES), are time-consuming and integrating them into an optimization loop remains impractical. Lower fidelity models based on time averaged velocity and pressure fields, such as the Reynolds Averaged Navier–Stokes (RANS) model, are commonly used. To represent the Reynolds stresses, they are generally coupled to eddy viscosity models, such as the Spalart–Allmaras (SA), the \(k-\varepsilon\), or the \(k-\omega\) model, see Spalart and Allmaras (1992) and Wilcox (1993). To date, the design of fluid systems for turbulent flows is mainly based on RANS models.
Working with finite volumes, Othmer (2008) proposed a continuous adjoint approach with respect to density design variables and studied turbulent flows in ducts under the assumption of frozen turbulence, i.e., the variations of the turbulence variables are not accounted for in the sensitivity analysis. Zymaris et al. (2009) extended the continuous adjoint approach with respect to shape parameters to account for the turbulence variations modeled by the SA equation. They showed that, considering frozen turbulence, sensitivities can exhibit erroneous signs. Philippi and Jin (2015) developed an adjoint sensitivity method where the turbulent flow in porous media is represented by a \(k-\varepsilon\) model. They used finite volumes to design channels for minimal mechanical energy loss under the assumption of frozen turbulence. Papoutsis-Kiachagias and Giannakoglou (2016) leveraged the continuous adjoint approach to perform shape and density-based topology optimization on aero- and hydrodynamic industrial applications. Working with finite elements, Yoon (2016) proposed a density-based optimization framework for the design of channels with minimal turbulent energy dissipation. The framework relies on a discrete adjoint sensitivity analysis of the RANS equations closed with the SA model. The approach was further extended to the \(k-\varepsilon\) turbulence model in Yoon (2020). Dilgen et al. (2018a) designed channels and manifolds for turbulent flows with minimal power dissipation using a density-based topology optimization approach. They used a finite volume approach and automatic differentiation to perform the discrete adjoint sensitivity analysis of the RANS equations with different eddy viscosity models. Sá et al. (2021) tackled the specific case of rotating flows with an adapted version of the SA model and using a density-based approach.
While all aforementioned studies rely on density-based approaches, other optimization techniques have also been applied to turbulent flow design problems. Kubo et al. (2021) proposed a level set-based approach with Ersatz material and finite volumes. They represented the turbulence with the \(k-\varepsilon\) and \(k-\omega\) models under the assumption of frozen turbulence. Picelli et al. (2022) used a binary topology optimization approach in combination with a geometry trimming procedure to design channels for minimum turbulent energy dissipation with the \(k-\varepsilon\) and \(k-\omega\) models. Alonso et al. (2022) extended the framework to the Wray–Agarwal turbulence model. To improve the predictive capabilities of the RANS equations, Hammond et al. (2022) used data-driven turbulence modeling and designed fluid systems with turbulent flows under the frozen turbulence assumption.
Along with the development of topology optimization approaches for fluid problems, multi-physics fluid problems gained in popularity, in particular conjugate heat transfer problems. Initial works on density-based methods considering conjugate heat transfer by Dede (2009) and Yoon (2010) focused on the design of channels for forced convection with laminar flows. Over the years, the complexity has increased to cover different heat transfer phenomena, different flow conditions, and to include multiple fluids. The interested reader is referred to Dbouk (2017) for an extensive overview.
As turbulence allows for increased heat transfer between fluid and solid phases as well as for an improved heat transport through the fluid, several research efforts have been devoted to the development of topology optimization frameworks for heat transfer with turbulent flows. Kontoleontos et al. (2013) extended the continuous adjoint approach of Zymaris et al. (2009) to account for turbulent heat transfer and generated channel layouts maximizing the energy transfer for a constrained pressure loss using density-based topology optimization. Koga et al. (2013) designed heat sinks for maximum heat transfer and minimum pressure loss considering Stokes flow discretized by finite volumes. In a post-design stage, they carried out validation simulations and considered turbulent flows with a \(k-\varepsilon\) model. Pietropaoli et al. (2017) used density-based topology optimization and a discrete adjoint approach to design internal channels heated at the outer walls. Turbulence was described by a \(k-\varepsilon\) model under the assumption of frozen turbulence. Dilgen et al. (2018b) extended their work on turbulent flow topology optimization to include thermal transport and design heat sinks for forced convection with turbulent flow modeled by the \(k-\omega\) model. Lee et al. (2020) developed a simplified non-exact adjoint sensitivity analysis for the design of aero-thermal systems including internal and external turbulent flows based on the SA model and finite volumes. Yaji et al. (2020) proposed a multi-fidelity design approach for thermal turbulent flow optimization problems. Zhao et al. (2021) used a multi-layer thermo-fluid model for the design of turbulent forced convective heat sinks using the SA model. Ghosh et al. (2022) focused on the design of internal cooling ducts for gas turbine blades using finite volumes and under the frozen turbulence assumption.
All previously cited works on turbulent conjugate heat transfer rely on density-based methods. As the key physics phenomenon, i.e., the heat transfer, happens at the fluid/solid interface and as the flow fields are strongly influenced by the shape of the fluid/solid interface, it is crucial that both the geometry and the physics responses across the interface are accurately resolved. Combining the level set method (LSM) with immersed finite element methods (IFEM) offers an elegant approach to tackle such problems. Several fluid design problems were studied using level set-based topology optimization with IFEM, such as hydrodynamic Boltzmann transport in Makhija et al. (2014), fluid-structure interactions in Jenkins and Maute (2016), heat transfers via natural convection in Coffin and Maute (2016), and species transport in Villanueva and Maute (2017). So far, design problems focusing on turbulent conjugate heat transfer have not been addressed using such techniques.
In this paper, a level set-based topology optimization framework for turbulent conjugate heat transfer problems is proposed. To obtain a crisp description of the fluid/solid interface, the design domain is immersed into a background mesh, and the design geometry is defined implicitly by one or multiple level set functions (LSF). For the first time, an eXtended Finite Element Method (XFEM) approach is used to predict the physical responses of the systems. To model turbulent conjugate heat transfer, the flow is described by the RANS equations for incompressible flows and stabilized by the Streamline Upwind Petrov-Galerkin (SUPG) and the Pressure Stabilizing Petrov-Galerkin (PSPG) formulations. Turbulence is described by the one-equation SA model. As the turbulence explicitly depends on the distance to the closest wall, a distance field is constructed based on the heat method, see Crane et al. (2017). The thermal energy transport in the fluid phase is predicted by an advection-diffusion equation. The temperature field in the solid phase is governed by a linear diffusion equation.
To discretize and solve conjugate heat transfer problems, an XFEM approach is adopted. This approach is similar to the XIGA approach presented in Noël et al. (2022) but is restricted to first-order approximations for the state variable fields. Higher-order B-spline functions are used for the geometry representation as was done in Noël et al. (2020). A generalized Heaviside enrichment strategy with multiple enrichment levels is used to ensure independent approximation on each connected fluid or solid subregion. Boundary and interface conditions are enforced weakly via Nitsche’s method, see Nitsche (1971). Additionally, the face-oriented ghost stabilization is used to mitigate numerical instabilities resulting from the creation of small integration subdomains, see Burman (2010) and Burman and Hansbo (2014).
Design problems are solved by a gradient-based optimization algorithm. The gradients of the objective and constraint functions are evaluated by the adjoint method. The optimization framework is applied to the design of heat exchangers considering turbulent flows to enhance heat transfer and thermal management with acceptable pressure losses.
The remainder of the paper is structured as follows. Section 2 is devoted to the geometry representation of the designs using one or several LSFs. In Sect. 3, the basic concepts of the XFEM approach such as the enrichment strategy, the face-oriented ghost stabilization, and the numerical integration scheme are briefly described. Section 4 details the physics model used to predict the solution of turbulent conjugate heat transfer problems. The handling of the governing equations using the XFEM approach is detailed. The ability of the proposed approach to solve turbulent conjugate heat transfer problems is demonstrated in Sect. 5 with benchmark problems, namely the backward facing step and the flow over a thick conducting plate. The formulation of the optimization problems is discussed in Sect. 6. In Sect. 7, the proposed optimization framework is illustrated with two dimensional heat exchanger design problems. Variations of the design problem are considered in terms of the outer geometry of the heat exchangers, of the imposed flow conditions, and of the formulation of the optimization problems. Finally, Section 8 draws conclusions on the developed framework and proposes extensions of the framework for future research.
2 Geometry representation
The LSM was introduced by Osher and Sethian (1988) to efficiently track propagating fronts. Soon after its introduction, the LSM has been used in combination with shape and topology optimization, see Sethian and Wiegmann (2000), Wang et al. (2003), Allaire et al. (2004), and van Dijk et al. (2013) for an overview. The method describes geometries implicitly by LSFs. The iso-level \(\phi _0\) of a LSF \(\phi (\mathbf {x})\) defines an interface or a boundary \(\Gamma _{\pm }\) that separates the domain \(\Omega\) into two subdomains, \(\Omega _{+}\) and \(\Omega _{-}\), such that:
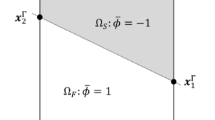
This paper follows the work by Vese and Chan (2002) on a multi-phase level set approach. One or multiple LSFs \(\phi ^i(\mathbf {x})\) with \(i=1,\dots , n\) are used to describe the design geometry. With n LSFs, \(2^n\) subregions can be identified within the domain \(\Omega\). Each subregion is characterized by a unique combination of the LSF signs, describing whether a point \(\mathbf {x}\) lies inside, outside, or on the interface. Each subregion is associated with the fluid, the solid, or the void phase, and their respective properties. An illustration of the geometry description of a fluid/solid/void problem is presented in Fig. 1. The design domain \(\Omega\) is defined by the dashed line. The fluid, the solid, and the void domains are represented in blue, grey, and white and are denoted by \(\Omega ^f\), \(\Omega ^s\), and \(\Omega^v\), respectively. The symbols \(\Gamma ^f\) and \(\Gamma ^s\) denote the interfaces of the fluid and solid domains with the void domain, respectively. The fluid/solid interface is denoted by \(\Gamma ^{fs}\), i.e., \(\Gamma ^{fs} = \Gamma ^f \cap \Gamma ^s\).
Geometric description of fluid/solid/void design domain \(\Omega\)
The level set description of the design domain geometry for a fluid/solid/void problem is shown in Fig. 2. Eight LSFs in green, \(\phi _1(\mathbf {x}),\dots ,\phi _8(\mathbf {x})\), are used to define the boundaries of the design domain that is fully immersed in a background analysis domain. The fluid/solid interfaces within the design domain are described by one LSF \(\phi _9(\mathbf {x})\) in red. The minus sign associated to each isoline \(\phi _i(\mathbf {x}) = \phi _0\) indicates the region where \(\phi _i(\mathbf {x}) < \phi _0\).
Geometric description of fluid/solid/void design domain \(\Omega\) using multiple LSFs
For numerical analysis, each LSF \(\phi ^{i}(\mathbf {x})\) is discretized on a mesh and approximated as:
where \(B_k(\mathbf {x})\) are B-spline basis functions and \((\phi _{i})_{k}\) are the coefficients associated with the LSF \(\phi ^i(\mathbf {x})\), similarly to Noël et al. (2022). In contrast to advancing the LSFs in the optimization process through the solution of the Hamilton–Jacobi equation, see approaches by Sethian and Wiegmann (2000), Wang et al. (2003), and Allaire et al. (2004), the coefficients of the LSFs are expressed as explicit functions of the design variables \(\mathbf {s}\). They are updated by mathematical programming methods driven by shape sensitivities.
3 XFEM formulation
IFEMs alleviate the need for generating conforming analysis meshes. IFEMs using enrichment functions enable the representation of discontinuities within a mesh element by augmenting the standard finite element approximation with enrichment functions. The XFEM was proposed by Moës et al. (1999) and Belytschko and Black (1999) to model crack propagation without remeshing. Over the years, the method has been successfully applied to various types of problems including the multi-phase problems considered here, see for example Burman and Hansbo (2014), Schott and Wall (2014), and Schott et al. (2015).
In this paper, an XFEM approach is adopted, which allows for accurate and efficient resolution of multi-phase problems with evolving interfaces and boundaries. The approach is similar to the XIGA proposed in Noël et al. (2022) but restricts the approximation of the state variable fields to first-order functions. The main ingredients of the XFEM approach are briefly recalled in this section. First, the enrichment strategy is described in Subsect. 3.1. Subsection 3.2 introduces the face-oriented ghost stabilization used to mitigate instabilities resulting from the generation of small integration subdomains. Finally, the numerical integration scheme used to accommodate elements occupied by multiple phases is explained in Subsect. 3.3.
3.1 Enrichment strategy
In this paper, the enrichment strategy described in Makhija and Maute (2014) is extended to enrich each individual basis function separately based on the topology of the phase layout within the basis function support as described in Noël et al. (2022). Considering a multi-phase problem, a state field \(\mathbf {a}(\mathbf {x})\) is approximated as:
where K is the number of background basis functions and \(L_k\) is the number of separate connected subregions \(\{ \Omega _k^{\ell } \}_{\ell =1}^{L_k}\) in the support of the background basis function \(B_k\). The coefficients \(a^{\ell }_{k}\) are the degrees of freedom (DOFs) associated with the basis function \(B_k\) and phase subregions \(\Omega _{k}^{\ell }\). The indicator function \(\varphi _k^{\ell }(\mathbf {x})\) determines whether a point \(\mathbf {x}\) belongs to a phase subregion \(\Omega _k^{\ell }\):
The selection of the enrichment levels is illustrated for a fluid/solid problem in Fig. 3. A basis function \(B_k\) spans both the fluid and the solid phases and its support is delimited by a red-dashed line. Five separate connected material subregions \(\Omega _k^{\ell }\) exist within the basis support. Each subregion is occupied by one and only one phase, such that \(\text{ supp }(B_k) = \bigcup _{\ell =1}^{5} \Omega _k^{\ell }\). Three subregions \(\Omega _k^{\ell =1}\), \(\Omega _k^{\ell =2}\), and \(\Omega _k^{\ell =3}\) are occupied by the fluid phase and two subregions \(\Omega _k^{\ell =4}\) and \(\Omega _k^{\ell =5}\) are occupied by the solid phase. As five subregions \(\Omega _k^{\ell }\) exist within the basis support, five enrichment levels \(L_k=5\) are necessary.
Enrichment strategy on a fluid/solid problem
3.2 Face-oriented ghost stabilization
Enriched IFEMs may suffer from numerical instabilities when boundaries and interfaces intersect the mesh such that small integration subdomains are generated. In this situation, the contributions of the basis functions approximating the state variable fields might vanish and lead to a poorly conditioned system of equations. To mitigate this issue, the face-oriented ghost stabilization penalizes the jump in state field gradients across so-called ghost facets, as proposed in Burman (2010) and Burman and Hansbo (2014). In this work, the approach of Noël et al. (2022) is adopted.
The set of ghost facets \(\mathcal {F}_{G}\) is the set of facets that lie inside the design domain and that are intersected by interfaces and boundaries. A ghost facet \(\mathcal {F}\) is shared between two adjacent elements \(\Omega _F^{+}\) and \(\Omega _{F}^{-}\), and is characterized by a normal \(\mathbf {n}_F\), defined so as to align with the outward normal to \(\Omega _F^{+}\) and \(\mathbf {n}_{F} = \mathbf {n}_{F}^{+} = - \mathbf {n}_{F}^{-}\). The elements adjacent to the facet \(\mathcal {F}\) are subdivided by the phase layout into \(N_{F}^{+}\) and \(N_{F}^{-}\) connected subdomains \(\Omega _{F,i}^{+}\) and \(\Omega _{F,j}^{-}\) with \(i = 1,\dots ,N_{F}^{+}\) and \(j=1,\dots ,N_{F}^{-}\). The jump in the state field gradients across the facet \(\mathcal {F}\) is penalized if \(\Omega _{F,i}^{+}\) and \(\Omega _{F,j}^{-}\) are occupied by the same phase, i.e., \(\Omega_{F,i}^{+}\) and \(\Omega_{F,j}^{-}\) are associated to the same material indices \(\mathcal{M}_{F,i}^{+} = \mathcal{M}_{F,j}^{-}\) corresponding to either fluid or solid, and meet along a portion of the facet with a non-zero measure. For a state field, denoted here by \(\mathbf {a}\), and the corresponding trial field \(\delta \mathbf {a}\), the ghost stabilization for facet \(\mathcal {F}\) is denoted \(\mathcal {G}_{F}^{\mathbf {a}}\) and is computed as:
where the set \(J_{F,i}\) defines the subdomains \(\Omega _{F,j}^{-}\) that with the subdomain \(\Omega _{F,i}^{+}\) satisfy the conditions for penalization. The parameter p is the degree of the considered approximation and the jump operator \(\llbracket \bullet \rrbracket\) is defined such that:
where \(\mathbf {a} _{F,i}^{+}\) and \(\mathbf {a}_{F,j}^{-}\) are the polynomial extensions of the fields \(\mathbf {a}|_{\Omega _{F,i}^{+}}\) and \(\mathbf {a}|_{\Omega _{F,j}^{-}}\) respectively to all of \(\mathbb {R}^{n_d}\) with \(n_d\) the spatial dimension. The jump is defined similarly for the trial field \(\delta \mathbf {a}\). The operator \(\partial _n^k(\bullet )\) is the \(k^{th}\) order normal derivative operator and \(\partial _n(\bullet ) = \nabla (\bullet ) \cdot \mathbf {n}_F\) with \(\nabla (\bullet )\) the spatial derivative operator. The ghost penalty parameters \(\gamma _{G}^{\mathbf {a}}\), used in this paper, are further described in Subsect. 4.6.
Figure 4 illustrates the subdivision of \(\Omega _{F}^{+}\) and \(\Omega _{F}^{-}\) into connected subdomains \(\Omega _{F,i}^{+}\) and \(\Omega _{F,j}^{-}\) and the associated indices \(\mathcal {M}_{F,i}^{+}\) and \(\mathcal {M}_{F,j}^{-}\) for a fluid/solid problem. The considered ghost facet \(\mathcal {F}\) and the adjacent background elements are marked using a red box. The background element \(\Omega _{F}^{-}\) is occupied by three connected subdomains \(\Omega _{F,1}^{-}\), \(\Omega _{F,2}^{-}\), and \(\Omega _{F,3}^{-}\) while the background element \(\Omega _{F}^{+}\) is divided into two connected subdomains \(\Omega _{F,1}^{+}\) and \(\Omega _{F,2}^{+}\). As \(\Omega _{F,2}^{-}\) and \(\Omega _{F,1}^{+}\) have the same material index \(\mathcal {M}_{F,2}^{-} = \mathcal {M}_{F,1}^{+}\) and meet along the facet, the jump in the associated field gradients is penalized across the facet. The same holds for the pairs \(\Omega _{F,1}^{-}\) and \(\Omega _{F,2}^{+}\), and \(\Omega _{F,3}^{-}\) and \(\Omega _{F,2}^{+}\).
Ghost stabilization on a fluid/solid problem
3.3 Numerical integration
The XFEM approach allows for the presence of multiple solid, fluid, and void phases within a single mesh element. The integration of the weak form of the governing equations is performed separately on each subdomain. For this purpose, a conforming integration mesh is built for each intersected element. A quadrangular intersected element is subdivided into triangular integration elements that align with the boundaries and interfaces described by the LSFs. It should be noted that the cost for generating the conforming XFEM models is negligible in comparison to the cost of the forward and sensitivity analyses. Standard quadrature is then performed on each triangular integration element and non-intersected background element. The reader is referred to Villanueva and Maute (2014) and Noël et al. (2022) for further details on the subdivision strategy.
4 Physics model
This section focuses on the physics models used to represent turbulent conjugate heat transfer problems. The governing equations and their weak formulations are detailed. The fluid flow is described by the incompressible Navier–Stokes equations. Subsection 4.1 details the implementation of these equations within the XFEM approach. The SA turbulence equation is used to model the eddy viscosity, as described in Subsect. 4.2. Subsection 4.3 is dedicated to the conjugate heat transfer and the associated diffusion-advection equation. As the SA turbulence model depends on the distance to the closest wall, the heat method is used to construct a distance field over the fluid domain, as explained in Subsect. 4.4. As advection-dominated problems may suffer from numerical instabilities, i.e., spurious oscillations of the state variable fields, subgrid stabilization is used as shown in Subsect. 4.5. Finally, the face-oriented ghost stabilization, introduced in Subsect. 3.2, is detailed for the particular case of turbulent conjugate heat transfer problems in Subsect. 4.6.
4.1 Incompressible Navier–Stokes equations
In this work, the fluid flow is governed by the incompressible Navier–Stokes equations. The residuals of the strong form of the momentum equilibrium equations \(\mathbf {r}_{\Omega }^{\mathbf {u}}\) and of the incompressibility condition \(r_{\Omega }^{p}\) are given as:
where \(\mathbf {u}\) is the fluid velocity, p is the pressure, and \(\rho\) is the constant fluid density. The Cauchy stress tensor is denoted by \(\varvec{\sigma }(\mathbf {u}, p)\) and is computed as:
where \(\mathbf {I}\) is the identity matrix, \(\mu\) is the fluid dynamic viscosity, and \(\varvec{\varepsilon }(\mathbf {u})\) is the strain rate tensor defined as:
The residuals of the weak form of the momentum equations and of the continuity condition within the fluid domain are given as:
where \(\mathbf {u}\) and \(\delta \mathbf {u}\) are the velocity field and test function, and p and \(\delta p\) are the pressure field and test function, respectively.
Boundary conditions on the fluid velocity field are imposed weakly via Nitsche’s formulation, see Nitsche (1971) and Bazilevs and Hughes (2007). To prescribe a velocity \(\mathbf {u}_{D}\) on \(\Gamma _D^f\), the following contributions are added to the velocity and pressure residuals:
where \(\beta ^{\mathbf {u}}_{N}\) and \(\beta ^{p}_{N}\) are parameters used to obtain a symmetric (\(\beta ^{\mathbf {u}}_{N} = 1\), \(\beta ^{p}_{N} = 1\)) or a skew-symmetric (\(\beta ^{\mathbf {u}}_{N} = -1\), \(\beta ^{p}_{N} = -1\)) Nitsche’s formulation. In this paper, a skew-symmetric formulation is adopted for both contributions. The Nitsche’s penalty parameter is denoted \(\gamma ^{\mathbf {u}}_{N}\) and is defined following Schott et al. (2015) as:
where \(\alpha _{N}^{\mathbf {u}}\) is a constant parameter chosen to achieve a desired accuracy in satisfying the boundary conditions. The first term accounts for viscosity-dominated flows and h is the length of the interface within an intersected element, while the second term accounts for convection flows. The operator \(\Vert \bullet \Vert _{\infty }\) is the infinite norm operator, such that \(\Vert \bullet \Vert _{\infty } = \max (\mathbf {u})\).
At the inflow, imposing inlet velocity conditions might cause inflow instabilities. To alleviate this issue, an additional up-winding term is added to the residual \(\mathbf {R}^{\mathbf {u}}_{\Gamma _{D}}\):
where \(\gamma ^{\mathbf {u}}_{up}\) is the up-winding parameter and is set to \(\gamma ^{\mathbf {u}}_{up} = 1\), as proposed in Schott and Wall (2014).
The pressure \(p_N\) can be imposed on the fluid boundaries \(\Gamma _{N}^{f}\). The weak form of the residual for the Neumann boundary condition is evaluated as:
4.2 Spalart–Allmaras turbulence model
In this paper, heat transfer with turbulent flows is considered. Turbulence introduces additional stresses in the fluid due to the presence of turbulent eddies in the flow. These eddies generate additional shear stress, i.e., the so-called Reynolds stress \(\varvec{\sigma }_t\). This stress is modeled based on the Boussinesq eddy viscosity assumption as:
where \(\mu _t\) is the turbulent dynamic viscosity. The stress tensor takes the form:
The RANS system of equations is closed using the turbulence model of Spalart and Allmaras (1992) and the turbulent dynamic viscosity is evaluated as:
where \(\tilde{\nu }\) is the so-called modified viscosity and is the additional state variable introduced in the SA model. The residual of the strong from of the SA equation is given as:
where P is the production term, D the wall destruction term, and K the diffusion coefficient. The modified velocity \(\tilde{\mathbf {u}}\) is defined as:
where the constants \(c_{b2}\) and \(\sigma\) are set to \(c_{b2} \,{=}\, 0.622\), and \(\sigma \,{=}\, 2/3\).
The original model presented in Spalart and Allmaras (1992) only admits non-negative values for the modified viscosity \(\tilde{\nu }\) given non-negative boundary and initial conditions. However, coarse grids and transient states may yield negative values. To handle these situations, a continuation model for negative turbulence values was proposed in Allmaras et al. (2012). The modified model recovers the original SA model for positive \(\tilde{\nu }\) values, while a negative value of the modified viscosity \(\tilde{\nu }\) produces zero eddy viscosity, i.e., \(\mu _{t} \,{=}\, 0\). The modified version of the model is adopted in this paper and is described hereunder in the context of the XFEM.
The turbulent dynamic viscosity \(\mu _t\) is evaluated as:
where \(\nu\) is the kinematic viscosity such that \(\mu = \rho \, \nu\), and \(c_{v1}\) is a constant set to \(c_{v1} \,{=}\, 7.1\).
The production term P is defined as:
where \(\beta _{f_{t2}}\) is a parameter that controls the use of the \(f_{t2}\) term, i.e., \(\beta _{f_{t2}} \,{=}\, 1\) to account for and \(\beta _{f_{t2}} \,{=}\, 0\) to exclude the \(f_{t2}\) term from the formulation. The \(f_{t2}\) term was initially introduced to control the laminar regions and to render solutions with \(\tilde{\nu } = 0\) stable. Rumsey (2007) showed that the \(f_{t2}\) term can be omitted for reasonably high Reynolds number. In this paper the influence of omitting the \(f_{t2}\) term on the optimization results is investigated. The constant parameter \(\alpha _P\) is used to enhance the numerical behavior of the model when \(\tilde{\nu }\) becomes negative and should be set such that \(\alpha _P \ge 1.0\), see Anderson et al. (2019). In this paper, the parameter is set to \(\alpha _P \,{=}\, 10.0\). The constants \(c_{b1}\), \(c_{t3}\), and \(c_{t4}\) are set to \(c_{b1} \,{=}\, 0.1355\), \(c_{t3} \,{=}\, 1.2\), and \(c_{t4} \,{=}\, 0.5\), respectively.
The wall destruction term D is defined as:
where d is the distance to the closest wall. The constants \(\kappa\) and \(c_{w3}\) are set to \(\kappa \,{=}\, 0.41\) and \(c_{w3} \,{=}\, 2\). The intermediate variable g is computed as:
where \(c_{w2}\) and \(r_{\lim }\) are constants set to \(c_{w2} \,{=}\, 0.3\) and \(r_{\lim } \,{=}\, 10.0\).
The diffusion coefficient K is defined as:
where \(c_{n1}\) is a constant set to \(c_{n1} \,{=}\, 16\).
The value of the modified vorticity \(\tilde{S}\) should always be positive and greater than \(0.3\, S\) for physically relevant configurations. Numerically, the model allows for zero or negative values of \(\tilde{S}\). To ensure the non-negativity of the modified vorticity \(\tilde{S}\), the following modifications were proposed in Allmaras et al. (2012):
where the magnitude of the vorticity S is evaluated as:
and the intermediate variable \(\overline{S}\) as:
Finally, the residual of the weak form of the SA equation is given as:
where \(\tilde{\nu }\) and \(\delta \tilde{\nu }\) are the modified viscosity field and test function, respectively.
As the flow at the fluid/solid interface is close to zero, i.e., it is laminar, the viscosity is prescribed to zero, i.e., \(\tilde{\nu } = 0\). A prescribed modified viscosity \(\tilde{\nu }_D\) is imposed weakly via Nitsche’s formulation as:
where \(\beta _N^{\tilde{\nu }}\) is a parameter used to obtain a symmetric (\(\beta _N^{\tilde{\nu }} \,{=}\, 1\)) or a skew-symmetric (\(\beta _N^{\tilde{\nu }} \,{=}\, -1\)) Nitsche’s formulation. In this paper, a skew-symmetric formulation is adopted. The Nitsche’s penalty parameter \(\gamma ^{\tilde{\nu }}_{N}\) is defined as:
where \(\alpha _{N}^{\tilde{\nu }}\) is a constant penalty parameter chosen to achieve a desired accuracy in satisfying the boundary conditions.
At the inflow, enforcing inlet viscosity conditions might cause instabilities. Similarly to Eq. (14), an additional up-winding term is added to the residual \(R^{\tilde{\nu }}_{\Gamma _{D}}\):
where the up-winding parameter \(\gamma ^{\tilde{\nu }}_{up}\) is set to \(\gamma ^{\tilde{\nu }}_{up} \,{=}\, 1.0\).
4.3 Advection–diffusion equation
The heat transfer in the fluid is described by an advection–diffusion equation where the velocity is governed by the flow model. The residual of the strong form of the advection–diffusion equation is given as:
where \(c_p\) is the heat capacity, and Q is the body heat load. The diffusive heat flux is denoted by \(\mathbf {q}\) and is computed as:
where \(\varvec{\kappa }\) is the isotropic diffusion tensor and \(\varvec{\kappa } = \kappa \, \mathbf {I}\) with \(\kappa\) the conductivity. The presence of turbulence results in an additional turbulent heat flux \(\mathbf {q}_t\) defined as:
where \(\varvec{\kappa _t}\) is the turbulent isotropic diffusion tensor and \(\varvec{\kappa }_t = \kappa _t\, \mathbf {I}\) with \(\kappa _t\), the turbulent conductivity. Finally, the diffusive heat flux takes the form:
The turbulent conductivity \(\kappa _t\) is evaluated as:
where \(\text{ Pr}_t\) is the turbulent Prandtl number and is set to \(\text{ Pr}_t \,{=}\, 0.9\).
The residual of the weak form of the advection-diffusion equation is given as:
where T and \(\delta T\) are the temperature field and test function, respectively.
For heat conduction in the solid, a linear diffusion model is used and can be obtained by omitting the advection term in Eqs. (32) and (53) and replacing the conductivity of the fluid, \(\kappa = \kappa ^{f}\), with the one of the solid, \(\kappa = \kappa ^s\).
Boundary conditions on the temperature field are prescribed weakly via Nitsche’s formulation:
where \(T_D\) is a prescribed temperature, \(\beta ^{T}_{N}\) is a parameter used to obtain a symmetric (\(\beta ^{T}_{N} \,{=}\, 1\)) or a skew-symmetric (\(\beta ^{T}_{N} \,{=}\, -1\)) Nitsche’s formulation. A skew-symmetric formulation is implemented in this paper. The Nitsche’s penalty parameter \(\gamma ^{T}_{N}\) is expressed as:
where \(\alpha _{N}^{T}\) is a constant parameter chosen to achieve a desired accuracy in satisfying the boundary conditions.
The continuity of temperature and heat flux at the fluid/solid interface \(\Gamma ^{fs}\) is imposed weakly via Nitsche’s formulation as follows:
where \(\beta ^{T}_{I}\) is a parameter used to obtain a symmetric (\(\beta ^{T}_{I} \,{=}\, 1\)) or a skew-symmetric (\(\beta ^{T}_{I} \,{=}\, -1\)) Nitsche’s formulation. The jump operator \(\llbracket \bullet \rrbracket\) computes the difference in the considered quantity between fluid and solid domains as \(\llbracket \bullet \rrbracket = \bullet ^{f} - \bullet ^{s}\). The mean operator \(\{ \bullet \}\) evaluates a weighted sum of the considered quantity over the fluid and solid domains as \(\{ \bullet \} = w^{f}\ \bullet ^{f} + w^{s}\ \bullet ^{s}\). The weights are defined following Dolbow and Harari (2009) and Annavarapu et al. (2012) as:
where \(\text{ meas }(\Omega ^{f})\) and \(\text{ meas }(\Omega ^{s})\) are the surface area of fluid and solid within the intersected element. The penalty parameter \(\gamma ^{T}_{I}\) is evaluated as:
where \(\text{ meas }(\Gamma ^{fs})\) is the length of the interface within the intersected element.
4.4 Wall distance through the heat method
The one-equation SA turbulence model requires the distance to the closest wall d. In this paper, the wall distance is constructed using the heat method, see Crane et al. (2017). First, a transient heat conduction problem for the additional state variable field \(\theta\) is solved over the design domain. The residual of the strong form of the conduction equation is written as:
where \(\rho ^{\theta }\), \(c_{p}^{\theta }\), and \(\varvec{\kappa }^{\theta }\) are the density, the specific heat capacity, and the isotropic diffusion tensor of the heat method. Zero initial boundary conditions, i.e., \(\theta \big |_{t=0} = 0.0\), are imposed on the design domain \(\Omega\) and a fixed temperature, i.e., \(\theta \big |_{\Gamma ^{fs}} = 1.0\), is enforced at the interface \(\Gamma ^{fs}\) between fluid and solid. The equation is solved in one single time step. The time step size is selected following the work by Geiss et al. (2019), i.e., just large enough to yield non-zero gradient over the design domain.
The distance \(\phi _{D}\) is constructed by solving a Poisson’s equation with a body heat load dependent on the normalized gradient of the additional temperature field \(\theta\). The strong form of the residual for the Poisson’s equation is expressed as:
A distance \(\phi _{D} \big |_{\Gamma ^{fs}} = 0.0\) is enforced on the interface \(\Gamma ^{fs}\) between fluid and solid.
The weak form of the residuals in Eqs. (43, 44) are formulated similarly to the advection-diffusion equations presented in Subsect. 4.3. It should be noted that building a wall distance field using the heat method requires the introduction of two additional state variable fields \(\theta\) and \(\phi _D\) and the solution of two additional scalar partial differential equations.
In the vicinity of and at the walls, the obtained distance field \(\phi _D\) might exhibit values close to machine precision and suffer from small spurious node-to-node variations. This issue results from the weak imposition of zero distance boundary conditions within the XFEM approach. The small variations might be amplified through the formulation of the SA source terms and lead to large node-to-node variations of the production and wall destruction coefficients, which in turn jeopardize the stability of the SA model. To mitigate this issue and regularize the distance field, a \(L^2\) projection scheme is used. First, a logarithmic function of the square of the distance \(\phi _D\) is projected to a intermediate distance variable \(\phi _P\), such that:
where \(\phi _P\) and \(\delta \phi _P\) are the intermediate distance field and the test function, respectively. Finally, the wall distance d is computed from the intermediate distance variable \(\phi _P\) as:
4.5 Subgrid stabilization
Spurious node-to-node velocity oscillations can arise from the convective terms in the incompressible Navier–Stokes equations, the SA turbulence equation, and the advection-diffusion equation, see Eqs. (7, 18, 32). Additionally, using approximations of the same order for both the velocity and the pressure fields may lead to spurious pressure oscillations. To mitigate these issues, the incompressible Navier–Stokes equations are augmented by the SUPG and the PSPG formulations of Tezduyar et al. (1992). The SUPG formulation introduced in Franca et al. (1992) is used to augment both the SA turbulence equations and the advection-diffusion equation.
The contribution of the SUPG/PSPG formulations to the weak form of the residuals of the incompressible Navier–Stokes equations is given as:
Following the approach of Taylor et al. (1998) and Whiting and Jansen (2001), the stabilization parameters \(\tau ^{\mathbf {u}}_{\mathrm{SUPG}}\) and \(\tau ^{p}_{\mathrm{PSPG}}\) are defined as:
where \(C_I\) is a constant set to 36.0 for linearly interpolated finite elements, see Whiting (1999). The operator \(\text{ tr }(\bullet )\) evaluates the trace as \(\text{ tr }(\bullet ) = \bullet _{ii}\) and the contravariant metric tensor \(\mathbf {G}\) is expressed as:
with \(\xi\) are the parametric coordinates in the background element.
The weak form of the residual for the turbulence equation is augmented with the SUPG formulation as:
The stabilization parameter \(\tau ^{\tilde{\nu }}_{\mathrm{SUPG}}\) is evaluated following Tezduyar and Osawa (2000) as:
where \(\Vert \bullet \Vert\) is the Frobenius norm and \(h_{\tilde{\mathbf {u}}}\) is a length measure defined as:
where \(|\bullet |\) is the absolute value operator and \(B_i\) are the basis functions used to approximate the velocity field.
Finally, the weak form of the residual for the advection-diffusion equation is augmented with the SUPG formulation as:
The stabilization parameter \(\tau ^{T}_{\mathrm{SUPG}}\) is formulated, similarly to Eq. (50), as:
where the length measure \(h_{\mathbf {u}}\) is defined as:
4.6 Face-oriented ghost stabilization
To counteract the effect of numerical instabilities related to small integration subdomains, the face-oriented ghost stabilization presented in Subsect. 3.2 is adopted in this work. The formulation of the residual of the weak form of the stabilization for a generic state field \(\mathbf {a}\) is given as:
where \(\mathcal {G}_{F}^{\mathbf {a}}\) is the ghost penalization for facet \(\mathcal{F}\) as presented in Subsect. 3.2.
A viscous ghost penalty term \(\mathbf {R}^{\mathbf {u},visc}_{F_{G}}\), as defined in Eqs. (5, 56), is added to the residual \(\mathbf {R}^{\mathbf {u}}_{\Omega }\). Following Burman and Hansbo (2014), the associated ghost penalty parameter \(\gamma _G^{\mathbf {u},visc}\) is given as:
where \(\alpha _G^{\mathbf {u},visc}\) is a constant penalty parameter, \(h_{F}\) is the length associated with ghost facet \(\mathcal{F}\), and p is the order of the considered approximation, as introduced in Eq. (5).
A convective ghost penalty term \(\mathbf {R}^{\mathbf {u},conv}_{F_{G}}\) acting on the first order gradient of velocity field \(\mathbf {u}\) only, as defined in Eqs. (56, 5) with \(p=1\), is added to the residual \(\mathbf {R}^{\mathbf {u}}_{\Omega }\) as proposed in Schott and Wall (2014). The associated ghost penalty parameter \(\gamma _G^{\mathbf {u},conv}\) is given as:
where \(\alpha _G^{\mathbf {u},conv}\) is a constant penalty parameter.
To control pressure instabilities, a ghost penalty term \(R^{p}_{F_{G}}\) is added to the pressure residual \(R^{p}_{\Omega }\), as proposed in Schott et al. (2015), and the associated ghost penalty parameter \(\gamma ^{p}_{G}\) is defined as:
where both viscous and convective flows are handled by the first and second term respectively and \(\alpha ^{p}_{G}\) is a constant penalty term.
Instabilities in the modified viscosity field \(\tilde{\nu }\) are mitigated by adding a ghost stabilization term to the viscosity residual \(R^{\tilde{\nu }}_{\Omega }\). The associated ghost penalty parameter is given as:
where \(\alpha _{G}^{\tilde{\nu }}\) is a constant penalty parameter.
Finally, a ghost penalization term is added to the temperature residual \(R^{T}_{\Omega }\) and the ghost penalty parameter \(\gamma _{G}^{T}\) is defined as:
where \(\alpha _{G}^{T}\) is a constant penalty parameter. Similar ghost penalization terms are introduced to stabilize the additional temperature \(\theta\), distance \(\phi _{D}\), and approximate distance \(\phi _{P}\) fields.
5 Validation examples
To validate the physics model presented in Sect. 4, two well-known academic examples are reproduced using our XFEM approach and are compared against numerical results from the literature. All verification examples are analyzed with the flow channels immersed in a background mesh to demonstrate the accuracy of the proposed numerical models for settings encountered in the optimization studies of Sect. 7.
Studying turbulent flows, the physics responses are often presented in terms of normalized quantities. In the following examples, the normalized distance to the wall \(y^{+}\), the normalized velocity \(u^{+}\), and the normalized temperature \(T^{+}\) are used and are expressed as:
The friction velocity \(u_{\tau }\) and the friction temperature \(T_{\tau }\) are defined as:
where \(\tau _w\), \(T_w\), \(q_w\) are quantities evaluated at the wall and are the wall shear, the wall temperature, and the wall heat flux, respectively. A normalized distance to the wall of approximately \(y^{+} \,{\approx }\, 1\) is recommended to accurately resolve boundary layer phenomena in turbulent flows.
The numerical studies presented in the paper are performed with a parallelized implementation of the XFEM approach into an in-house C++ code. The forward analysis uses a staggered solution strategy, i.e., the problem is solved successively for the heat method state variables, for the distance variables, followed by the flow and SA state variables, and finally the temperature variables. The flow-SA equations are solved staggered using a pseudo time stepping with a local CFL strategy and an increasing time step size are used to reach steady state, see Ceze and Fidkowski (2013) and Witherden et al. (2017). The fluid and SA subproblems are solved by Newton’s method. All linear and linearized systems of equations are solved by MUMPS, see Amestoy et al. (2001). Gauss quadrature rules are used to integrate the set of discretized governing equations on each integration subdomains. Working in two dimensions, a \(2{\times }2\)-point integration rule is used for quadrangular integration elements, a 7-point integration rule is used for triangular integration elements, and a 2-point integration rule is used for interface line elements.
5.1 Backward facing step
This subsection focuses on the validation of the XFEM formulation of the incompressible Navier–Stokes and SA models. The energy transport, in the fluid or solid phase, is not considered here. To this end, the backward facing step problem is investigated numerically using the approach proposed in Sect. 4. Following NASA Langley Research Center (2022a), the geometry of the backward facing step is illustrated in Fig. 5, where the dimension H is set to \(H\,{=}\,0.0127\) m. It should be noted that the geometry is not represented to scale.
Backward facing step: geometry (not drawn to scale) and boundary conditions
The fluid is chosen as water and is characterized by a density \(\rho ^f\,{=}\,1.18\) kg/m\(^3\) and a kinematic viscosity \(\nu ^{f}\,{=}\,1.57{\times }10^{-5}\) m\(^2\)/s at atmospheric conditions, and at a reference temperature of 300 K. The boundary conditions are presented in Fig. 5. The inflow conditions are represented in blue. A uniform inlet velocity with \(u_{\mathrm{x,in}}\,{=}\,41.5\) m/s and \(u_{\mathrm{y,in}}\,{=}\,0\) m/s is enforced corresponding to a Reynolds number of \(\text{ Re } \,{=}\, 33,570\). A uniform inlet viscosity is prescribed with \(\tilde{\nu }_{\mathrm{in}}\,{=}\,3\, \nu ^{f}\). Additionally, symmetry conditions, in green, are imposed close to the inlet, i.e., a zero tangent velocity \(u_{\mathrm{y,sym}}\,{=}\,0\) m/s and a prescribed viscosity \(\tilde{\nu }_{\mathrm{sym}}\,{=}\,3\, \nu ^{f}\). At the walls, colored in black, a no-slip condition is imposed on the velocity, i.e., \(u_{\mathrm{x,wall}}\,{=}\, u_{\mathrm{y,wall}}\,{=}\, 0\) m/s, and the modified viscosity is set to zero \(\tilde{\nu }_{\mathrm{sym}}\,{=}\,0\) m2/s. At the outlet, marked in red, the pressure is set to zero. The properties used for the heat method are chosen as \(\rho ^{\theta } \,{=}\, 1.0\) kg/m\(^3\), \(c_p^{\theta }\,{=}\,0.1\) J/kgK, and \(\kappa ^{\theta }\,{=}\,1.0\) W/mK. Finally, the different penalty parameters introduced in Sect. 4 are detailed in Table 1.
The ability of the proposed method to model turbulent flow is demonstrated by comparison against experimental results from Driver and Seegmiller (1985) and numerical results from NASA Langley Research Center (2022b). This study is performed on a refined mesh around the walls to allow for an accurate resolution of the wall distance field and of the boundary layer phenomena, as shown in Fig. 6. Mesh elements have an initial size \(h \,{=}\, H/5\) and are refined seven times around the walls leading to a mesh size of \(h \,{=}\, H/(5 {\times } 2^{7})\), 2,727,478 mesh elements, and 7,781,480 DOFs. This refinement leads to a normalized distance to the wall \(y^{+} \,{\approx }\, 3\) for the first element near the wall.
Backward facing step: mesh refinement around walls
Different settings of the SA model are considered. In particular, the use of the \(f_{t2}\) term in Eqs. (21, 22) and the use of the proposed approximated distance d in Eq. (46) instead of an exact analytical distance function are investigated. The solution obtained using the \(f_{t2}\) term and the exact wall distance is presented in Fig. 7.
Backward facing step: flow solution obtained using the \(f_{t2}\) term and the exact wall distance in the SA model
Figure 8 presents the velocity and turbulence profiles at different locations downstream of the step, i.e., \(x/H \,{=}\, 1.0, 4.0, 6.0\) and 10.0. Figure 8 shows that, regardless of the SA model configuration, the numerical results produced using the XFEM approach are in good agreement with both the numerical results from NASA Langley Research Center (2022b) and the experimental results from Driver and Seegmiller (1985) for all locations downstream of the step considered. Small discrepancies between all numerical models and the experimental results are only observed in the recirculation domain, here \(x/H \,{=}\, 1.0\). Using the approximated wall distance d or an analytical expression of the distance yields similar results, i.e., both the solid and dashed blue curves and the solid and dashed red curves overlap for all locations downstream of the step. These results indicate that the wall distance field is sufficiently resolved by the approximate wall distance proposed in Eq. (46). Therefore, this approximation will be used in subsequent simulations. Concerning the effect of the \(f_{t2}\) term, numerical results show that the term has a minor influence on the flow conditions at this Reynolds number. Small difference between velocity profiles with \(\beta _{f_{t2}} \,{=}\, 0\) (solid and dashed red curves) and \(\beta _{f_{t2}} \,{=}\, 1\) (solid and dashed blue curves) are only observed inside the channel. These results agree with the observations of Rumsey (2007). The influence of the \(f_{t2}\) term on topology optimization results is further studied in Sect. 7.
Backward facing step: comparison of velocity profiles at locations downstream the step with \(x/H \,{=}\, 1.0, 4.0, 6.0\) and 10.0 for numerical results from XFEM approach with \(f_{t2}\) term (\(\beta _{f_{t2}}\,{=}\,1\)) and with exact distance, without \(f_{t2}\) term (\(\beta _{f_{t2}}\,{=}\,0\)) and with exact distance, with \(f_{t2}\) term (\(\beta _{f_{t2}}\,{=}\,1\)) and with approximate distance d, without \(f_{t2}\) term (\(\beta _{f_{t2}}\,{=}\,0\)) and with approximate distance d, numerical results from NASA Langley Research Center (2022b), and experimental results from Driver and Seegmiller (1985)
5.2 Laminar and turbulent flow over a thick flat plate
In this subsection, the coupling of the flow model with the advection–diffusion equation is investigated. The problem of a laminar or a turbulent flow over a thick plate with a prescribed temperature at its bottom side is studied numerically using the proposed XFEM approach. Following Vynnycky et al. (1998), the geometry of the computational domain is presented in Fig. 9, where the dimensions are set with \(H \,{=}\, 1\) m.
Turbulent flow over a thick flat plate with a prescribed temperature at its bottom side: geometry and boundary conditions
The boundary conditions are illustrated in Fig. 9. The inflow conditions consist of a constant inlet velocity with \(u_{\mathrm{x,in}}\,{=}\,0.1\) m/s and \(u_{\mathrm{y,in}}\,{=}\,0\) m/s and an inlet temperature \(T_{\mathrm{in}}\,{=}\,300\) K. If a turbulent flow is considered, a uniform inlet viscosity \(\tilde{\nu }_{\mathrm{in}}\,{=}\,3\, \nu ^{f}\) is prescribed. Symmetry conditions are imposed along the edges in green. A zero tangent velocity \(u_{\mathrm{y,sym}}\,{=}\,0\) m/s and a zero viscosity \(\tilde{\nu }_{\mathrm{sym}}\,{=}\,0\) m2/s are imposed. On the surface of the plate and at the bottom of the fluid domain, represented in yellow, a no-slip condition is imposed, and the modified viscosity is set to zero. The plate is heated to a constant temperature \(T_{\mathrm{b}} \,{=}\, 310\) K at its bottom side colored in orange. The outflow conditions consist of a zero pressure at the outlet in red. Finally, the flow and heat transfer are governed by fixed adimensional numbers. For all simulations, a Reynolds number \(\text{ Re } \,{=}\, 10,000\) is used. Two different Prandtl numbers, \(\text{ Pr } \,{=}\, 0.01\) and 100 are investigated.
The solid plate has a density \(\rho ^s \,{=}\, 1.0\) kg/m\(^3\) and a conductivity \(\kappa ^s \,{=}\, 100.0\) W/mK. The fluid has a density \(\rho ^f \,{=}\, 1.0\) kg/m\(^3\), a kinematic viscosity \(\nu ^{f} \,{=}\,u_{x,in}\, H / \text{ Re }\), and a dynamic viscosity \(\mu ^{f} \,{=}\, \rho ^{f} \nu ^{f}\) related to the flow conditions. The thermal properties of the fluid are defined by a conductivity \(\kappa ^f \,{=}\, \kappa ^s / \kappa\), where \(\kappa\) is a prescribed conductivity ratio between the solid and the fluid, and a specific heat capacity \(c_p^f \,{=}\, \kappa ^f\, \text{ Pr } / \mu ^f\) J/kgK. When considering turbulence, the SA model is used with \(\beta _{f_{t2}} = 0\) and with the approximate wall distance. The properties used for the heat method are \(\rho ^{\theta } \,{=}\, 1.0\) kg/m\(^3\), \(c_p^{\theta }\,{=}\,0.1\) J/kgK, and \(\kappa ^{\theta }\,{=}\,1.0\) W/mK. Finally, the penalty parameters are set as detailed in Table 2.
The ability of the proposed method to model conjugate heat transfer is demonstrated by comparison against analytical results from Vynnycky et al. (1998) and numerical results from Yau (2016). The XFEM analysis is performed on a mesh refined near the plate to allow for an accurate resolution of boundary layer phenomena. Mesh elements have an initial size \(h \,{=}\, H/5\) and are refined six times near the plate, as shown in Fig. 10. The resulting mesh has a minimum element size of \(h \,{=}\, H/(5{\times }2^{6})\) with 143,844 quadrangular elements and 398,592 DOFs. For the turbulent case, this mesh refinement lead to a normalized distance to the wall \(y^{+}\,{=}\,0.87\).
Turbulent flow over a thick flat plate with a prescribed temperature at its bottom side: mesh refinement near the plate
Figure 11 presents the adimensional temperature contours in the fluid and solid domains obtained with the XFEM approach considering a laminar and a turbulent flow with a fixed Reynolds number of \(\text{ Re } \,{=}\, 10,000\) and for two Prandtl numbers, \(\text{ Pr } \,{=}\, 0.01\) and \(\text{ Pr } \,{=}\, 100\). The adimensional temperature \(T_{\mathrm{adim}}\) is defined as follows:
For a lower Prandtl number, a low ratio \(\kappa\) allows for a larger temperature drop within the solid. For a higher Prandtl number, the temperature drop is limited to the solid domain. The temperature profiles observed for the laminar and the turbulent flow are similar suggesting that turbulence has little effect on the thermal response and the problem is convection dominated.
Flow over a thick flat plate heated at its bottom side to a prescribed temperature: adimentional temperature \(T_{\mathrm{adim}}\) in the fluid and solid domains for a Reynolds number \(\text{ Re } \,{=}\, 10,000\) obtained with the XFEM approach
The evolution of the adimensional temperature in terms of the distance x along the plate is shown in Fig. 12. The numerical results obtained with the XFEM approach are compared against studies from Vynnycky et al. (1998) and Yau (2016) for a laminar flow over the plate. The obtained temperature profiles are in good agreement with both analytical results from Vynnycky et al. (1998) and numerical results from Yau (2016). This comparison verifies the ability of the proposed XFEM approach to accurately model conjugate heat transfer.
Turbulent flow over a flat plate with a prescribed temperature at its bottom side: adimensional temperature profile over the plate for conductivity ratios \(\kappa \,{=}\, 1, 5, 20\) considering laminar and turbulent results from the XFEM approach and laminar analytical results from Vynnycky et al. (1998) and numerical results from Yau (2016)
6 Optimization problems
In this paper, we consider optimization problems that can be formulated as follows:
where the vector \(\mathbf {s}\) contains the \(N_s\) design variables and \(\underline{s}\) and \(\overline{s}\) are the imposed lower and upper bounds, respectively. The vector \(\mathbf {y}(\mathbf {s})\) collects all state variables such that \(\mathbf {y}(\mathbf {s}) = [ \mathbf {u}\ p\ \tilde{\nu }\ T\ \theta \ \phi _D\ \phi _P ]^T\). Note that the state variables used in Eq. (65) satisfy the discretized governing equations for a given design \(\mathbf {s}\). The objective function is denoted by \(z(\mathbf {s}, \mathbf {y}(\mathbf {s}))\) and \(g_j(\mathbf {s}, \mathbf {y}(\mathbf {s}))\) is the j\(^{th}\) constraint function considered in the problem.
The objective function is defined as:
where \(\mathcal {F}(\mathbf {s}, \mathbf {y}(\mathbf {s}))\) is the quantity of interest to minimize; \(\mathcal {P}_p(\mathbf {s})\) and \(\mathcal {P}_{r}(\mathbf {s})\) are the perimeter penalty and the regularization penalty, as further defined in Subsect. 6.1. The parameters \(w_{f}\), \(w_{p}\), and \(w_{r}\) are weights associated with the terms in the objective function.
6.1 Regularization
Following Haber et al. (1996), the perimeter control penalization \(\mathcal {P}_{p}\) is added to the objective function to ensure the well-posedness of the optimization problem and to prevent the emergence of numerical artefacts, such as irregular geometric features:
where \(\mathcal {P}_0\) is the initial perimeter value.
To avoid spurious oscillations of the level set field that might deteriorate the stability and the convergence of the optimization problem, the regularization scheme proposed in Geiss et al. (2019) is adopted. The regularization promotes the convergence of the level set field \(\phi\) to a smooth target field \(\tilde{\phi }\) with advantageous properties, i.e., the convergence to an upper or lower bound \(\phi _{B}\) away from the interface and to a uniform gradient along the interface. The scheme is enforced by adding the penalty term \(\mathcal {P}_{r}\) to the objective function:
The weights \(w_{\phi }\) and \(w_{\nabla \phi }\) are evaluated as:
where the parameter \(\gamma _{\mathcal {P}_r}\) controls the regions of influence of the regularization, i.e., regions near and away from the interface. The weights \(w_{\phi _1}\), \(w_{\phi _2}\) control the mismatch between design and target LSF near and away from the interfaces, respectively. The weights \(w_{\nabla \phi _1}\) and \(w_{\nabla \phi _2}\) play the same role for the mismatch between design and target gradients of the LSF. The smooth target level set field \(\tilde{\phi }\) is built from the distance field \(\phi _{D}\), obtained by the heat method in Eq. (44), as:
where \(\beta _{\phi _B}\) is a parameter that is set to 1 or \(-1\) to select the upper bound \(\phi _B\) for the fluid domain or lower bound \(-\phi _B\) for the solid domain respectively.
6.2 Sensitivity analysis
In this paper, the update of the design variables is performed by mathematical programming techniques driven by shape sensitivity computations.
The derivative of a generic objective or constraint function \(\mathcal {F}(\mathbf {s}, \mathbf {y}(\mathbf {s}))\) with respect to a design variable \(s_i\) is computed as:
where the first and the second term in the right-hand side account for the explicit and the implicit dependency on the design variables, respectively. Using the adjoint approach, see Michaleris et al. (1994), the implicit term is evaluated as:
where \(\mathbf {R}\) is a collection of the residuals presented in Sect. 4 for the forward analysis and \(\varvec{\lambda }\) represents the adjoint responses, evaluated through:
The semi-analytical approach of Sharma et al. (2017) is used to evaluate the derivatives with respect to the design variables. During the sensitivity analysis, all the terms in the governing equations introduced in the forward analysis in Sect. 4 are accounted for, and all required derivatives with respect to the state variables are derived analytically following the approach of Zymaris et al. (2009) and Yoon (2016) to yield consistent sensitivities.
7 Numerical optimization examples
In this section, the features of the proposed XFEM level set-based optimization framework for solving turbulent conjugate heat transfer design problems are investigated. Two different optimization problem formulations are considered aiming at: (i) minimizing the maximum temperature, and (ii) maximizing the heat transfer within the heat exchangers, while maintaining an acceptable pressure drop. Additionally, two different heat exchanger geometric configurations are studied to demonstrate the flexibility of the approach.
Unless specified otherwise, all subsequent simulations are carried out using the following settings. By default, the \(f_{t2}\) term is omitted in the SA model. For specific configurations the analysis and optimization results are compared when using or omitting the \(f_{t2}\) term. The approximate distance field in Eq. (46) is used for the wall distance and the properties for the heat method are chosen as \(\rho ^{\theta } \,{=}\, 1.0\) kg/m\(^3\), \(c_p^{\theta }\,{=}\,0.1\) J/kgK, and \(\kappa ^{\theta }\,{=}\,1.0\) W/mK. The penalty parameters introduced in Sect. 4 are detailed in Table 3.
In the following examples, the state variable fields are approximated with linear B-spline functions, while the design variable field is approximated with quadratic B-spline functions, as they promote smoother designs, mitigate the development of spurious features, and limit the need for additional filtering techniques, see Noël et al. (2020). Filtering is achieved through a coarser and higher-order B-spline interpolation for the design variable field.
The set of discretized governing equations and adjoint sensitivity equations are built and solved following the approach described in Sect. 5, except that for the sensitivity analysis, the flow and the SA adjoints are solved for simultaneously using a monolithic formulation. The optimization problems are solved by the Globally Convergent Method of Moving Asymptotes (GCMMA) of Svanberg (2002). The initial, lower, and upper asymptote adaptation parameters in GCMMA are set to 0.5, 0.7, and 1.2, respectively. No inner iterations are used. The optimization problems are considered converged if the design is visually converged, if the objective function stagnates, and if the constraints are satisfied. The weights and parameters introduced in Sect. 6 are given in Table 4.
While adaptive mesh refinement is performed to resolve the boundary layer for the benchmark problems presented in Sect. 5, uniformly refined meshes are used for the optimization problems. This choice is made as the Reynolds numbers considered in this section are lower, and therefore sufficiently fine, uniform meshes can be used. This is verified in Subsect. 7.2 by solving the same optimization problem on a reference and a refined mesh.
7.1 Heat exchanger with single outlet
In this subsection, a heat exchanger with a single outlet is optimized for minimal average temperature in the solid subject to a constraint on the power dissipation. The problem is taken from Dilgen et al. (2018b) and the setup is presented in Fig. 13. The fluid is chosen as water and is used to cool a heated solid, here aluminum. The dimensions of the heat exchanger are described in terms of half the inlet size \(H \,{=}\, 0.1\) m. The inlet and outlet channels are extended, see red and blue dashed lines, to reduce the influence of the inlet and outlet conditions on the flow inside the heat exchanger.
Heat exchanger with a single outlet: geometry and boundary conditions
The working fluid is water with a density \(\rho ^{f} \,{=}\, 1.18\) kg/m\(^3\) and a dynamic viscosity \(\mu ^f \, {=}\, 1.77 {\times } 10^{-5}\) kg/ms. The fluid has a specific heat capacity \(c_p^f \,{=}\, 1004.9\) J/kgK and a conductivity \(\kappa ^f \,{=}\, 2.54 {\times } 10^{-2}\) W/mK. The turbulent Prandtl number is set to \(\text{ Pr}_{t} \,{=}\, 0.9\). The solid phase is aluminum with a thermal conductivity \(\kappa ^s \,{=}\, 237\) W/mK.
At the inlet \(\Gamma _{\mathrm{in}}\), boundary conditions are prescribed for the fluid. To obtain a developed flow at the inlet, a power law velocity profile is enforced, following Kubo et al. (2021), such that:
The magnitude \(u_{\mathrm{in}}\) is chosen to yield specific Reynolds numbers \(\text{ Re } \,{=}\, \rho ^f\, u_{\mathrm{in}}\, H/ \mu ^f\). A constant viscosity is prescribed at the inlet with a magnitude \(\tilde{\nu }_{\mathrm{in}} \,{=}\, 3\, \nu ^{f}\). The fluid enters the heat exchanger at a temperature \(T_{\mathrm{in}} \,{=}\,\) 300 K. At the outlet \(\Gamma _{\mathrm{out}}\), the pressure is prescribed to zero \(p_{out} \,{=}\, 0\) Pa. The solid is heated by a constant volumetric heat load \(Q \,{=}\, 10.0\) kW/m\(^2\).
To minimize the solid temperature, the objective function is formulated as:
where \(\mathcal {T}^{s}\) is the temperature integrated over the solid domain \(\Omega ^s\):
The reference temperature \(T_{\mathrm{ref}}\) is set to the inlet temperature, i.e., \(T_{\mathrm{ref}} \,{=}\, 300\) K. The volume \(\mathcal {V}^s\) of the solid domain \(\Omega ^s\) is evaluated as:
The parameters \(\mathcal {T}^s_{0}\) and \(\mathcal {V}^s_{0}\) are the integrals of the temperature over the solid domain and the volume of the solid evaluated for the initial design.
The power dissipation constraint is formulated as:
where
and \(\mathcal {D}_{\mathrm{in/out},0}\) is the dissipated power integrated over the inlet or the outlet for the initial design. The weight \(w_{d}\) controls the allowed power dissipation through the heat exchanger.
Finally, a volume constraint is enforced on the fluid domain to avoid a trivial solution with no solid and to control the amount of energy injected into the heat exchanger through the solid. The constraint is formulated as:
where \(\mathcal {V}^f\) is the volume of the fluid domain \(\Omega ^{f}\) evaluated as in Eq. (76), \(\mathcal {V}\) is the volume of the design domain, and \(w_{v}\) is the allowed fluid volume faction, here set to \(w_{v} = 0.55\).
The initial design is seeded with multiple solid inclusions, as shown in Fig. 14. The level set field is approximated by quadratic B-spline and is discretized on a coarse uniform background mesh with an element size \(h\,{=}\,H/5\), leading to 4284 design variables. The state variable fields are discretized on a finer uniform background mesh with an element size \(h \,{=}\, H/40\), leading to 251,264 quadrangular elements and 896,292 DOFs including 414,924 flow DOFs, 125,879 temperature DOFs, 251,758 DOFs for the heat method, and 103,731 DOFs for the construction of the approximate distance. This mesh size leads to normalized distances to the wall \(y^{+} \,{\approx }\, 2, 5,\) and 10 for Reynolds numbers \(\text{ Re } \,{=}\, 1000, 2500,\) and 5000, respectively, which is insufficient to fully resolve boundary layer phenomena, but offers a reasonable compromise between accuracy and computational cost.
Heat exchanger with a single outlet: initial design
The optimization problem is solved considering three different inlet velocities \(u_{\mathrm{in}} \,{=}\,0.15\), 0.375, and 0.75 m/s leading to the following Reynolds numbers, \(\text{ Re } \,{=}\,1000\), 2500, and 5000. The power dissipation is limited to a third of the dissipation observed for the initial design, i.e., the weight in Eq. (77) is set to \(w_d=0.33\). It should be noted that, as the inlet velocity changes, so does the initial power dissipation, and thus the allowed power dissipation in the heat exchanger. Therefore, comparison between the optimized designs and their performances should be made carefully.
The optimized designs and the corresponding level set fields are shown in Fig. 15. For all Reynolds numbers, the optimized design features a network of channels. Owing to the regularization, the level set fields converge to the upper and lower bounds in the bulk of the fluid and solid domains and have close to uniform spatial gradient along the fluid/solid interface.
Heat exchanger with a single outlet: optimized designs and level set fields for different Reynolds number \(\text{ Re } \,{=}\, 1000\), 2500, and 5000 at a fixed power dissipation with \(w_d\,{=}\,0.33\)
The solution fields over the optimized designs are presented in Fig. 16. For different Reynolds numbers, the velocity magnitude, the viscosity ratio, and the temperature over the optimized heat exchanger, as well as the performance of the designs in terms of average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\), are provided. Focusing on the geometry of the designs, a tendency to generate smooth straight channels that align with the flow is observed for all considered Reynolds numbers. For lower Reynolds numbers and thus lower power dissipation, smooth wide channels are created. As the Reynolds number is increased and a larger power dissipation is allowed, narrower channels with higher flow velocities are formed. These observations agree with the results presented in Dilgen et al. (2018b).
As expected, the heat transfer is enhanced for higher Reynolds numbers, allowing a larger dissipation in the heat exchanger. This is evident from the decrease of the maximum temperature in the solid phase, i.e., the adimensional maximum temperature reaches \(T_{\mathrm{max}}/T_{\mathrm{in}} \,{=}\,\) 2.4755, 1.5528, and 1.2997 for Reynolds numbers \(\text{ Re } \,{=}\,\) 1000, 2500, and 5000.
The contour plots of the viscosity ratio in Fig. 16 show that the optimized designs exhibit low or no turbulence in the channels within the heat exchanger. Interestingly, the maximum viscosity ratio decreases as the Reynolds number increases: \(\chi \,{=}\,5.9648\), 4.3823, and 3.7297 for Reynolds numbers \(\text{ Re } \,{=}\,1000\), 2500, and 5000, respectively. As the Reynolds number and the allowed power dissipation are increased, the optimized designs feature narrower channels which impede the development of turbulence.
Heat exchanger with a single outlet: optimized designs and performance in terms of average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\) for different Reynolds numbers \(\text{ Re } \,{=}\, 1000\), 2500, and 5000 at a fixed power dissipation with \(w_d\,{=}\,0.33\)
To separate the influences of increasing the Reynolds number and the allowed power dissipation on the generated design, the optimization problem is solved considering three different constraint weights \(w_d\,{=}\,0.25\), 0.33, and 0.50 at a fixed inlet velocity \(u_{\mathrm{in}} \,{=}\,\) 0.375 m/s leading to a Reynolds number \(\text{ Re } \,{=}\, 2500\). Figure 17 shows the velocity magnitude, the viscosity ratio, and the temperature over the optimized heat exchanger considering different allowed power dissipation. The performance in terms of average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\) is provided for each design.
As the allowed pressure drop is increased, a larger number of narrower channels through the heat exchanger is created. A larger pressure drop across the heat exchanger allows for the development of narrow channels with higher flow velocities, and advective energy transport, which in turns enhances the heat transfer and lowers the adimensional maximum temperature: \(T_{\mathrm{max}}/T_{\mathrm{in}} \,{=}\,\) 1.5985, 1.5528, and 1.4009 for constraint weights \(w_d\,{=}\,\) 0.25, 0.33, and 0.50, respectively. It should be noted that the distribution of the turbulence and the maximum viscosity ratios within the heat exchanger \(\chi \,{=}\,\) 4.1064, 4.3823, and 3.7496 are similar for all considered pressure drops.
Heat exchanger with a single outlet: optimized designs and performance in terms of average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\) for a Reynolds number \(\text{ Re } \,{=}\, 2500\) and different power dissipation constraint weights \(w_d\,{=}\,0.25\), 0.33, and 0.50
The influence of the \(f_{t2}\) term in the SA model is investigated by solving the optimization problem with and without the \(f_{t2}\) term, i.e., setting \(\beta _{f_{t2}}\) to 1 or 0. The velocity magnitude, the viscosity ratio, and the temperature distributions over the optimized heat exchangers, as well as the performance in terms of the average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\), are presented in Fig. 18 for \(\text{ Re } \,{=}\, 1000\) and \(w_d\,{=}\,0.50\) and in Fig. 19 for \(\text{ Re } \,{=}\,5000\) and \(w_d\,{=}\,0.33\). Reanalyses are performed on the designs, i.e., designs optimized with \(\beta _{f_{t2}}\,{=}\,0\) are reanalyzed setting \(\beta _{f_{t2}}\,{=}\,0\) and \(\beta _{f_{t2}}\,{=}\,1\), see Fig. 18a, and designs optimized with \(\beta _{f_{t2}}\,{=}\,1\) are reanalyzed setting \(\beta _{f_{t2}}\,{=}\,0\) and \(\beta _{f_{t2}}\,{=}\,1\), see Fig. 18b.
For a lower Reynolds number in Fig. 18, the designs generated with and without the \(f_{t2}\) term differ only slightly. Performing reanalyses shows that marginally lower mean temperatures over the heat exchanger are obtained when dropping the \(f_{t2}\) term, i.e., \(\mathcal {T}^s/\mathcal {V}^s \,{=}\,\) 1.6774 K for \(\beta _{f_{t2}}\,{=}\,0\) versus 1.6779 K for \(\beta _{f_{t2}}\,{=}\,1\) when optimizing designs with \(\beta _{f_{t2}}\,{=}\,0\), and \(\mathcal {T}^s/\mathcal {V}^s\,{=}\,\) 1.6880 K for \(\beta _{f_{t2}}\,{=}\,0\) versus 1.6886 K for \(\beta _{f_{t2}}\,{=}\,1\) for design obtained with \(\beta _{f_{t2}}\,{=}\,1\). Note that when predicting the thermal response with \(\beta _{f_{t2}}\,{=}\,1\), the design optimized without the \(f_{t2}\) term has a slightly lower mean temperature than the design optimized with the \(f_{t2}\) term. This issue is likely explained by the non-convexity of the problems solved.
For a higher Reynolds number in Fig. 19, similar observations can be made and reanalyses lead to \(\mathcal {T}^s/\mathcal {V}^s\,{=}\,\) 1.2063 K for \(\beta _{f_{t2}}\,{=}\,0\) versus 1.2064 K for \(\beta _{f_{t2}}\,{=}\,1\) when generating designs with \(\beta _{f_{t2}}\,{=}\,0\), and \(\mathcal {T}^s/\mathcal {V}^s\,{=}\,\) 1.2022 K for \(\beta _{f_{t2}}\,{=}\,0\) versus 1.2024 K for \(\beta _{f_{t2}}\,{=}\,1\) when generating designs with \(\beta _{f_{t2}}\,{=}\,1\). It should be noted that the effect of the \(f_{t2}\) term is less pronounced for Re = 5000 than for the lower Reynolds number case. In conclusion, while the design layout marginally changes, performances across designs optimized with and without the \(f_{t2}\) term differ insignificantly. In agreement with Rumsey (2007), the effect of including the \(f_{t2}\) term becomes negligible as the Reynolds number increases.
Heat exchanger with a single outlet: optimized designs and performance in terms of average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\) for a Reynolds number \(\text{ Re } \,{=}\, 1000,\) at a fixed power dissipation with \(w_d\,{=}\,0.50\)
Heat exchanger with a single outlet: optimized designs and performance in terms of average temperature in the solid domain \(\mathcal {T}^s/\mathcal {V}^s\) for a Reynolds number \(\text{ Re } \,{=}\, 5000,\) at a fixed power dissipation with \(w_d\,{=}\,0.33\)
7.2 Heat exchanger with split outlet
In this subsection, the versatility of the proposed optimization approach is illustrated by varying the design domain, the inflow conditions, and the heat loading. The influence of the formulation of the optimization problem is also investigated. A heat exchanger with a split outlet is optimized for maximum heat transfer under a mass flow constraint, see Fig. 20. Contrary to the single outlet case in Sect. 7.1, the geometry of the design domain prevents the development of a straight channel between the inlet and the outlet. In contrast to the previous example, a constant pressure is imposed at the inlet fixing the allowed pressure drop through the heat exchanger. In this example, the solid is heated up to a prescribed temperature and the design goal is to maximize the heat transfer between fluid and solid. The effects of these variations on the optimization process and the geometry of the optimized designs, i.e., the arrangement of the cooling channels within the heat exchanger, are investigated.
The problem setup is presented in Fig. 20. Water is used to cool heated aluminum. The dimensions of the design domain are described in terms of half of the inlet size \(H \,{=}\, 0.1\) m. The inlet and outlet channels are again extended, see red and blue dashed lines, to mitigate the influence of inlet and outlet conditions on the flow in the heat exchanger. The fluid and solid properties are identical to the ones described for the single outlet heat exchanger in Sect. 7.1.
Heat exchanger with a split outlet: geometry and boundary conditions
At the inlet \(\Gamma _{\mathrm{in}}\), the following boundary conditions are prescribed on the fluid flow. A constant inlet pressure \(p_{\mathrm{in}}\,{=}\, \rho ^f\, \tilde{u}_{\mathrm{in}}^{2}\) is enforced and is defined as a function of a nominal inlet velocity \(\tilde{u}_{\mathrm{in}}\) that corresponds to a desired Reynolds number \(\text{ Re } \,{=}\,\rho ^f\, \tilde{u}_{\mathrm{in}}\, H/ \mu ^f\). The inlet pressure increases with the Reynolds number as the dynamic viscosity remains constant. A constant viscosity is prescribed at the inlet with a magnitude \(\tilde{\nu }_{\mathrm{in}} \,{=}\, 3\, \nu ^{f}\). The fluid enters the heat exchanger at a temperature \(T_{\mathrm{in}} \,{=}\, 300\) K. At the outlet \(\Gamma _{\mathrm{out}}\), the pressure is prescribed to zero \(p_{out} \,{=}\, 0\) Pa. The solid is heated up to a temperature of \(T_{\mathrm{ref}} \,{=}\, 325\) K through a temperature dependent volumetric heat load \(Q(T) \,{=}\, h\, ( T - T_{\mathrm{ref}})\) W/m\(^2\) with \(h \,{=}\,14,583.3\) W/m\(^2\)K.
To maximize the heat transfer through the exchanger, the objective function is defined as:
where the convective flux \(\mathcal {Q}_{\mathrm{in/out}}\) at the inlet or the outlet is evaluated as:
and \(\mathcal {Q}_{\mathrm{in/out}, 0}\) is the convective flux evaluated at the inlet or the outlet for the initial design.
The mass flux constraint ensures a non-zero flow from the inlet to the outlet and that the solid does not obstruct the heat exchanger. The constraint is formulated as:
where the mass flux \(\mathcal {M}_{\mathrm{in/out}}\) through the inlet or the outlet is evaluated as:
and \(\mathcal {M}_{\mathrm{in/out},0}\) is the mass flux computed at the inlet or the outlet for the initial design. The weight \(w_{m}\) specifies the allowed mass flux through the heat exchanger and is set to \(w_{m} \,{=}\, 0.5\).
The initial design is seeded with multiple solid inclusions, as shown in Fig. 21. The level set field is discretized with quadratic B-spline on a coarse uniform background mesh with an element size \(h\,{=}\,H/10\), leading to 16,059 design variables. The state variable fields are discretized on a finer mesh with an element size \(h \,{=}\, H/40\), leading to 245,616 quadrangular elements and 875,477 DOFs including 405,640 DOFs for the turbulent flow, 122,809 DOFs for the temperature, 245,618 DOFs for the heat method, and 101,410 DOFs to build the distance field. This mesh size leads to normalized distances to the wall \(y^{+} \,{\approx }\, 2\), 5, and 10 for Reynolds numbers \(\text{ Re } \,{=}\, 1000\), 2500, and 5000, respectively, which is again insufficient to fully resolve boundary layer phenomena but offers a reasonable compromise between accuracy and computational cost, as further discussed later.
Heat exchanger with a split outlet: initial design
The influence of the inlet flow conditions on the optimized designs and their performances is investigated by solving the problem for three different inlet pressures corresponding to Reynolds numbers \(\text{ Re } \,{=}\, 1000\), 2500, and 5000. The optimized designs are shown in Fig. 22. For each design, the velocity magnitude, the viscosity ratio, the temperature, and the performance in terms of heat flux \(\Delta \mathcal {Q}\,{=}\, \mathcal {Q}_{\mathrm{in}}-\mathcal {Q}_{\mathrm{out}}\) are provided. Contrary to the single outlet case in Sect. 7.1, tortuous channels around multiple solid inclusions and recirculation areas are generated for all Reynolds numbers considered here. Such geometric features increase the area between fluid and solid, and in turn the heat transfer. With the increase in the Reynolds number, the large central channel tends to split into multiple narrow and tortuous channels.
As the Reynolds number increases, the turbulence distribution changes and areas with larger viscosity ratio move from the inlet to the core of the heat exchanger. Note that with increasing Reynolds number, the surface of the channels tends to be less smooth and presents a secondary oscillatory pattern, especially visible for the design at a Reynolds number \(\text{ Re }\,{=}\,5000\). In the following, these patterns are investigated to understand whether they are a numerical artifact or present a physical advantage. To this end, the maximum heat transfer optimization problem with \(\text{ Re }\,{=}\,5000\) is solved on a refined mesh with an element size of \(h\,{=}\,H/80\) and a normalized distance to the wall of approximately \(y^+\,{\approx }\,5\). Note that the level set field is represented with the same spatial discretization as used previously, i.e., a coarser mesh with an element size \(h\,{=}\,H/10\). The velocity magnitude, the viscosity ratio, and the temperature fields on the optimized designs, as well as the performance in terms of heat flux \(\Delta \mathcal {Q}\), for the reference and the refined mesh are shown in Fig. 23.
Heat exchanger with a split outlet: optimized designs and performance in terms of heat flux \(\Delta \mathcal {Q}\) for different Reynolds numbers \(\text{ Re } \,{=}\, 1000\), 2500, and 5000
While their geometry differs in their detailed layout, both designs present similar turbulence generating features, i.e., multiple narrow, tortuous channels and secondary patterns along the channels. The designs performance differs by less than one percent. The design optimized on the reference mesh achieves a slightly higher heat flux with \(\Delta \mathcal {Q}\,{=}\,25,959.9\) W/m\(^2\) compared to the design optimized on the fine mesh with \(\Delta \mathcal {Q}\,{=}\,25,029.3\) W/m\(^2\). The close-ups provided in Fig. 23 confirm that the finer mesh allows for an improved resolution of the boundary layer. The velocity profile and the temperature gradient close to the solid/fluid interface are represented across several elements, which yields a better accuracy. Nonetheless, the reference mesh provides a good compromise between accuracy and computational cost.
Heat exchanger with a split outlet: optimized design and performance in terms of heat flux \(\Delta \mathcal {Q}\) for a Reynolds number \(\text{ Re } \,{=}\, 5000\) comparison of a reference \(h\,{=}\,H/40\) and a refined mesh \(h\,{=}\,H/80\)
To gain insight into the reasons behind the development of oscillatory channel walls, the optimization problem at a fixed Reynolds number \(\text{ Re } \,{=}\, 5000\) is solved considering three different settings of the SA model namely, the presence of the \(f_{t2}\) term and the turbulent fluid conductivity \(\kappa _t\). Configuration (a) represents the setting used previously, i.e., the \(f_{t2}\) term is dropped and the turbulent fluid conductivity \(\kappa _t\) is accounted for. In Configuration (b), the \(f_{t2}\) term is accounted for, i.e., \(\beta _{f_{t2}}\,{=}\,1\), as well as the turbulent fluid conductivity \(\kappa _t\). Finally, for Configuration (c), the \(f_{t2}\) term is included, but the turbulent fluid conductivity is set to zero, i.e., \(\beta _{f_{t2}}\,{=}\,1\) and \(\kappa _t\,{=}\,0\).
The velocity magnitude, the viscosity ratio, and the temperature distributions over the optimized heat exchangers are presented in Fig. 24. For each configuration of the SA model, reanalyses are performed on each optimized design. The design generated with setting (a) is analyzed using settings (a), (b), and (c), see Fig. 24a. A similar procedure is followed for designs obtained with settings (b) and (c) as shown in Fig. 24b and c, respectively. For each analysis, the value of the heat flux \(\Delta \mathcal {Q}\,{=}\, \mathcal {Q}_{\mathrm{in}}- \mathcal {Q}_{\mathrm{out}}\) is provided.
From the results in Fig. 24a and b, similar conclusions to the study on the \(f_{t2}\) term presented in Subsect. 7.1 can be drawn. While the design geometry slightly changes, the performances of the designs generated including or neglecting the \(f_{t2}\) terms only differ marginally. However, omitting the turbulent diffusivity \(\kappa _t\) leads to noticeable drop in heat flux.
Figure 24c shows the design generated when omitting the turbulent diffusivity \(\kappa _t\). In this case, the design only features smooth channel surfaces, but the heat flux is significantly lower than the ones achieved when considering the turbulent conductivity \(\kappa _t\) as a result of increased turbulence. This study suggests that the development of oscillatory shapes along the channels is used to generate an increased turbulence within the heat exchanger, which in turn increases the total thermal conductivity in the fluid and leads to an enhanced heat transfer. Additional studies using different turbulence models are needed to confirm these results.
Heat exchanger with a split outlet: optimized design and performance in terms of heat flux \(\Delta \mathcal {Q}\) for a Reynolds number \(\text{ Re } \,{=}\, 5000\) considering three settings of the SA model: (a) \(\beta _{f_{t2}}\,{=}\, 0\) and \(\kappa _t\,{\ge }\,0\), (b) \(\beta _{f_{t2}}\,{=}\, 1\) and \(\kappa _t\,{\ge }\,0\), and (c) \(\beta _{f_{t2}}\,{=}\, 1\) and \(\kappa _t\,{=}\,0\)
8 Conclusions
In this paper, we proposed an XFEM level set-based topology optimization framework for turbulent conjugate heat transfer design problems. To achieve a crisp description of the fluid/solid interface, the geometry of the design is represented by one or multiple LSFs and the physical responses of the design are predicted using an IFEM, here the XFEM approach. The fluid flow is modeled by the RANS equations and the system is closed by the SA turbulence model. As the turbulence equation depends on the distance to the closest wall, a distance field is constructed using the heat method. The heat transfer in the fluid phase is described by the advection-diffusion equation and in the solid by linear isotropic diffusion. Boundary and interface conditions are enforced weakly with Nitsche’s method, and the face-oriented ghost stabilization is used to mitigate numerical instabilities associated with small integration subdomains. Verification cases are solved to show that the XFEM approach can reproduce benchmark results using an immersed geometry description. The ability of the proposed optimization framework to solve turbulent conjugate heat transfer problems is illustrated with the design of heat exchangers in two dimensions.
Numerical simulations show that the proposed XFEM approach is able to accurately predict the physics responses in turbulent flows. Using an immersed geometry description and an IFEM, benchmark results for the backward facing step and the turbulent flow over a thick conducting plate are reproduced. Additionally, the influence of the setting of the SA model on the numerical results is investigated and the numerical results with and without specific terms, such as the \(f_{t2}\) term, are in agreement with literature.
Numerical optimization examples demonstrate the ability of the proposed level set-based optimization framework to solve conjugate heat transfer design problems considering turbulent flows. The design of heat exchangers is performed under different flow conditions and for different geometries of the design domains. The optimized layouts achieve enhanced cooling or heat transfer under prescribed conditions. Furthermore, the versatility of the framework is illustrated by solving different optimization problems. The numerical examples show that the formulation of the optimization problem has a large influence on the optimized geometries. The optimization on the split outlet heat exchanger suggests that under particular flow conditions heat transfer can be enhanced through channel wall shapes that generate turbulence, and in turns increase the total conductivity of the fluid.
This work opens up several follow-up research tracks. As shown in the benchmark examples, an increased resolution of the fluid/solid interface is desirable, i.e., \(y^{+}\) around 1, to achieve a more precise description of the interface and a higher accuracy of the physics predictions. To this end, different strategies could be investigated: the use of hierarchical B-splines to carry out local mesh refinement, the use of wall functions for an improved description of the near-wall behavior, or the ability to generate a boundary layer mesh with immersed methods. The second optimization problem suggests that, using the SA model, oscillatory channel walls can be used to generate turbulence and increase the heat transfer. Additional studies relying on different turbulence models should be carried out to confirm this result and to understand the influence of turbulence models on the optimized topology and geometry. The extension of the framework to three dimensional optimization problems also presents various challenges. An overall increased efficiency of the computational strategy, including the use of local mesh refinement and iterative solvers, will be necessary to meet the mesh resolution requirements and to handle the sizes of the systems of discretized equations. Finally, including additional physics phenomena in the model, such as fluid/structure interaction or chemical reaction, would allow us to tackle a broader range of applications.
References
Alexandersen J, Andreasen CS (2020) A review of topology optimisation for fluid-based problems. Fluids. https://doi.org/10.3390/fluids5010029
Allaire G, Jouve F, Toader A-M (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194(1):363–393. https://doi.org/10.1016/j.jcp.2003.09.032
Allmaras SR, Johnson FT, Spalart PR (2012) Modifications and clarifications for the implementation of the Spalart-Allmaras turbulence model. In Seventh International Conference on ICCFD7-1902 Computational Fluid Dynamics (ICCFD7), https://www.iccfd.org/iccfd7/assets/pdf/papers/ICCFD7-1902_paper.pdfICCFD7-1902_paper
Alonso DH, Saenz JSR, Picelli R, Silva ECN (2022) Topology optimization method based on the Wray-Agarwal turbulence model. Struct Multidisc Optim 65:82. https://doi.org/10.1007/s00158-021-03106-8
Amestoy P, Duff IS, Koster J, L’Excellent J-Y (2001) A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J Matrix Analy Appl 23(1):15–41
Anderson WK, Wood SL, and Allmaras SR (2019) An initial exploration of improved numerics within the guidelines of the negative Spalart-Allmaras turbulence model. NASA Technical Memorandum. https://ntrs.nasa.gov/citations/20200000068NASA/TM-2019-220429
Annavarapu C, Hautefeuille M, Dolbow JE (2012) A robust Nitsche’s formulation for interface problems. Comput Meth Appl Mechan Eng 225–228:44–54. https://doi.org/10.1016/j.cma.2012.03.008
Bazilevs Y, Hughes TJ (2007) Weak imposition of Dirichlet boundary conditions in fluid mechanics. Comput Fluids 36(1):12–26. https://doi.org/10.1016/j.compfluid.2005.07.012
Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remeshing. Int J Numeric Method Eng 45(5):601–620. https://doi.org/10.1002/(sici)1097-0207(19990620)45:5<601::aid-nme598>3.0.co;2-s
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Meth Appl Mechan Eng 71(2):197–224. https://doi.org/10.1016/0045-7825(88)90086-2
Borrvall T, Petersson J (2003) Topology optimization of fluids in Stokes flow. Int J Num Meth Fluids 41(1):77–107. https://doi.org/10.1002/fld.426
Burman E (2010) Ghost penalty. Comptes Rendus Mathematique 348(21):1217–1220. https://doi.org/10.1016/j.crma.2010.10.006
Burman E, Hansbo P (2014) Fictitious domain methods using cut elements: III. A stabilized Nitsche method for Stokes’ problem. ESAIM Mathemat Model Numerical Analy 48(3):859–874. https://doi.org/10.1051/m2an/2013123
Ceze M, Fidkowski KJ (2013) Pseudo-transient continuation, solution update methods, and CFL strategies for DG discretizations of the RANS-SA equations. 21st AIAA Computational Fluid Dynamics Conference https://doi.org/10.2514/6.2013-2686
Coffin P, Maute K (2016) A level-set method for steady-state and transient natural convection problems. Struct Multidisc Optim 53(5):1047–1067. https://doi.org/10.1007/s00158-015-1377-y
Crane K, Weischedel C, Wardetzky M (2017) The heat method for distance computation. Commun. ACM 60(11):90–99. https://doi.org/10.1145/3131280
Dbouk T (2017) A review about the engineering design of optimal heat transfer systems using topology optimization. Appl Thermal Eng 112:841–854. https://doi.org/10.1016/j.applthermaleng.2016.10.134
Deaton JD, Grandhi RV (2014) A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct Multidisc Optim 49(1):1–38. https://doi.org/10.1007/s00158-013-0956-z
Dede EM (2009) Multiphysics topology optimization of heat transfer and fluid flow systems. In COMSOL Conference. https://www.comsol.com/paper/multiphysics-topology-optimization-of-heat-transfer-and-fluid-flow-systems-6282
Dilgen CB, Dilgen SB, Fuhrman DR, Sigmund O, Lazarov BS (2018) Topology optimization of turbulent flows. Comput Meth Appl Mech Eng 331:363–393. https://doi.org/10.1016/j.cma.2017.11.029
Dilgen SB, Dilgen CB, Fuhrman DR, Sigmund O, Lazarov BS (2018) Density based topology optimization of turbulent flow heat transfer systems. Struct Multidisc Optim 57:1905–1918. https://doi.org/10.1007/s00158-018-1967-6
Dolbow J, Harari I (2009) An efficient finite element method for embedded interface problems. Int J Numeric Method Eng 78(2):229–252. https://doi.org/10.1002/nme.2486
Driver DM, Seegmiller HL (1985) Features of a reattaching turbulent shear layer in divergent channel flow. AIAA Journal 23(2):163–171. https://doi.org/10.2514/3.8890
Franca LP, Frey SL, Hughes TJ (1992) Stabilized finite element methods: I. Application to the advective-diffusive model. Comput Method Appl Mech Eng 95(2):253–276. https://doi.org/10.1016/0045-7825(92)90143-8
Geiss MJ, Barrera JL, Boddeti N, Maute K (2019) A regularization scheme for explicit level-set XFEM topology optimization. Fronti Mechan Eng 14(2):153–170. https://doi.org/10.1007/s11465-019-0533-2
Gersborg-Hansen A, Bendsøe MP, Sigmund O (2006) Topology optimization of heat conduction problems using the finite volume method. Struct Multidisc Optim 31(4):251–259. https://doi.org/10.1007/s00158-005-0584-3
Ghosh S, Fernandez E, Kapat J (2022) Fluid-thermal topology optimization of gas turbine blade internal cooling ducts. Journal of Mechanical Design, Transactions of the ASME, 144, 2022. https://doi.org/10.1115/1.4053042
Haber RB, Jog CS, Bendsøe MP (1996) A new approach to variable-topology shape design using a constraint on perimeter. Struct Optim 11(1):1–12. https://doi.org/10.1007/bf01279647
Hammond J, Pietropaoli M, Montomoli F (2022) Topology optimisation of turbulent flow using data-driven modelling. Struct Multidisc Optim 65:49–65. https://doi.org/10.1007/s00158-021-03150-4
Jenkins N, Maute K (2016) An immersed boundary approach for shape and topology optimization of stationary fluid-structure interaction problems. Struct Multidisc Optim 54(5):1191–1208. https://doi.org/10.1007/s00158-016-1467-5
Koga AA, Lopes ECC, Villa Nova HF, de Lima CR, and Silva ECN (2013) Development of heat sink device by using topology optimization. International Journal of Heat and Mass Transfer, 64: 759–772, 2013. doi:10.1016/j.ijheatmasstransfer.2013.05.007
Kontoleontos EA, Papoutsis-Kiachagias EM, Zymaris AS, Papadimitriou DI, Giannakoglou KC (2013) Adjoint-based constrained topology optimization for viscous flows, including heat transfer. Eng Optim 45:941–961. https://doi.org/10.1080/0305215X.2012.717074
Kubo S, Koguchi A, Yaji K, Yamada T, Izui K, Nishiwaki S (2021) Level set-based topology optimization for two dimensional turbulent flow using an immersed boundary method. J Comput Phys. https://doi.org/10.1016/j.jcp.2021.110630
Lee JS, Ha MY, Min JK (2020) A finite-volume based topology optimization procedure for an aero-thermal system with a simplified sensitivity analysis method. Int J Heat Mass Trans. https://doi.org/10.1016/j.ijheatmasstransfer.2020.120524
Makhija D, Maute K (2014) Numerical instabilities in level set topology optimization with the extended finite element method. Struct Multidisc Optim 49(2):185–197. https://doi.org/10.1007/s00158-013-0982-x
Makhija D, Pingen G, Maute K (2014) An immersed boundary method for fluids using the XFEM and the hydrodynamic Boltzmann transport equation. Comput Methods Appl Mech Eng 273:37–55. https://doi.org/10.1016/j.cma.2014.01.020
Michaleris P, Tortorelli DA, Vidal CA (1994) Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications to elastoplasticity. Int J Numeric Method Eng 37(14):2471–2499. https://doi.org/10.1002/nme.1620371408
Moës N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numeric Method Eng 46(1):131–150. https://doi.org/10.1002/(sici)1097-0207(19990910)46:1<131::aid-nme726>3.0.co;2-j
NASA Langley Research Center. Turbulence modeling resource–2DBFS: 2D backward facing step. Accessed March 21 2022, 2022a. https://turbmodels.larc.nasa.gov/backstep_val.html
NASA Langley Research Center. Turbulence modeling resource–2D backward facing step validation case–SA model results. Accessed March 21 2022, 2022b. https://turbmodels.larc.nasa.gov/backstep_val_sa.html
Nitsche J (1971) Über ein variationsprinzip zur lösung von Dirichlet-problemen bei verwendung von teilräumen, die keinen randbedingungen unterworfen sind. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 36(1):9–15. https://doi.org/10.1007/bf02995904
Noël L, Schmidt M, Messe C, Evans JA, Maute K (2020) Adaptive level set topology optimization using hierarchical B-splines. Struct Multidisc Optim 62(4):1669–1699. https://doi.org/10.1007/s00158-020-02584-6
Noël L, Schmidt M, Doble K, Evans JA, Maute K (2022) XIGA: an eXtended IsoGeometric Analysis approach for multi-material problems. Comput Mech. https://doi.org/10.1007/s00466-022-02200-yarXiv:2202.05697
Osher S, Sethian JA (1988) Fronts propagating with curvature-dependent speed: Algorithms based on hamilton-jacobi formulations. J Comput Phys 79(1):12–49. https://doi.org/10.1016/0021-9991(88)90002-2
Othmer C (2008) A continuous adjoint formulation for the computation of topological and surface sensitivities of ducted flows. Int J Numeric Meth Fluids 58:861–877. https://doi.org/10.1002/fld.1770
Papoutsis-Kiachagias EM, Giannakoglou KC (2016) Continuous adjoint methods for turbulent flows, applied to shape and topology optimization: Industrial applications. Arch Comput Method Eng. https://doi.org/10.1007/s11831-014-9141-9
Philippi B, Jin Y. Topology optimization of turbulent fluid flow with a sensitive porosity adjoint method (SPAM). arXiv, 2015. arXiv:1512.08445
Picelli R, Moscatelli E, Yamabe PVM, Alonso DH, Ranjbarzadeh S, dos Santos Gioria R, Meneghini JR, Silva ECN (2022) Topology optimization of turbulent fluid flow via the TOBS method and a geometry trimming procedure. Struct Multidisc Optim. https://doi.org/10.1007/s00158-021-03118-4
Pietropaoli M, Ahlfeld R, Montomoli F, Ciani A, D’Ercole M (2017) Design for additive manufacturing: internal channel optimization. J Eng Gas Turbines and Power. https://doi.org/10.1115/1.4036358
Rumsey CL (2007) Apparent transition behavior of widely-used turbulence models. Int J Heat and Fluid Flow 28(6):1460–1471. https://doi.org/10.1016/j.ijheatfluidflow.2007.04.003
Schott B, Wall W (2014) A new face-oriented stabilized XFEM approach for 2D and 3D incompressible Navier-Stokes equations. Comput Meth Appl Mech Eng 276:233–265. https://doi.org/10.1016/j.cma.2014.02.014
Schott B, Rasthofer U, Gravemeier V, Wall WA (2015) A face-oriented stabilized Nitsche-type extended variational multiscale method for incompressible two-phase flow. Int J Numeric Meth Eng 104(7):721–748. https://doi.org/10.1002/nme.4789
Sethian J, Wiegmann A (2000) Structural boundary design via level set and immersed interface methods. J Comput Phys 163(2):489–528. https://doi.org/10.1006/jcph.2000.6581
Sharma A, Villanueva H, Maute K (2017) On shape sensitivities with heaviside-enriched XFEM. Struct Multidisc Optim 55(2):385–408. https://doi.org/10.1007/s00158-016-1640-x
Sigmund O, Maute K (2013) Topology optimization approaches-A comparative review. Struct Multidisc Optim 48(6):1031–1055. https://doi.org/10.1007/s00158-013-0978-6
Spalart P (2000) Strategies for turbulence modelling and simulations. Int J Heat and Fluid Flow 21(3):252–263. https://doi.org/10.1016/s0142-727x(00)00007-2
Spalart P, Allmaras S (1992) A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit, pages 1–22, 1992.https://doi.org/10.2514/6.1992-439
Svanberg K (2002) A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J Optimization 12(2):555–572. https://doi.org/10.1016/0021-9045(72)90080-9
Sá LF, Yamabe PV, Souza BC, Silva EC (2021) Topology optimization of turbulent rotating flows using Spalart-Allmaras model. Comput Meth Appl Mechanics Eng. https://doi.org/10.1016/j.cma.2020.113551
Taylor CA, Hughes TJ, Zarins CK (1998) Finite element modeling of blood flow in arteries. Comput Meth Appl Mech Eng 158(1):155–196. https://doi.org/10.1016/s0045-7825(98)80008-x
Tezduyar T, Mittal S, Ray S, Shih R (1992) Incompressible flow computations with stabilized bilinear and linear equal-order-interpolation velocity-pressure elements. Comput Meth Appl Mechan Eng 95(2):221–242. https://doi.org/10.1016/0045-7825(92)90141-6
Tezduyar TE, Osawa Y (2000) Finite element stabilization parameters computed from element matrices and vectors. Comput Method Appl Mechan Eng 190(3):411–430. https://doi.org/10.1016/S0045-7825(00)00211-5
van Dijk NP, Maute K, Langelaar M, van Keulen F (2013) Level-set methods for structural topology optimization: a review. Struct Multidisc Optim 48(3):437–472. https://doi.org/10.1007/s00158-013-0912-y
Vese LA, Chan TF (2002) A multiphase level set framework for image segmentation using the Mumford and Shah model. Int J Comput Vision 50(3):271–293. https://doi.org/10.1023/a:1020874308076
Villanueva CH, Maute K (2014) Density and level set-XFEM schemes for topology optimization of 3-D structures. Comput Mechan 54(1):133–150. https://doi.org/10.1007/s00466-014-1027-z
Villanueva CH, Maute K (2017) CutFEM topology optimization of 3D laminar incompressible flow problems. Comput Method Appl Mechan Eng 320:444–473. https://doi.org/10.1016/j.cma.2017.03.007
Vynnycky M, Kimura S, Kanev K, Pop I (1998) Forced convection heat transfer from a flat plate: the conjugate problem. Int J Heat and Mass Transfer 41(1):45–59. https://doi.org/10.1016/S0017-9310(97)00113-0
Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mechan Eng 192(1):227–246. https://doi.org/10.1016/s0045-7825(02)00559-5
Whiting CH (1999) Stabilized finite element methods for fluid dynamics using a hierarchical basis. PhD thesis, Rensselaer Polytechnic Institute
Whiting CH, Jansen KE (2001) A stabilized finite element method for the incompressible Navier-Stokes equations using a hierarchical basis. Int J Numeric Methods Fluids 35(1):93–116
Wilcox DC (1993) Turbulence modelling for CFD. DCW Industries, La Canada
Witherden FD, Jameson A, Zingg DW (2017) The Design of Steady State Schemes for Computational Aerodynamics, volume 18. Elsevier B.V., 1 edition, https://doi.org/10.1016/bs.hna.2016.11.006
Yaji K, Yamasaki S, Fujita K (2020) Multifidelity design guided by topology optimization. Struct Multidisc Optim 61:1071–1085. https://doi.org/10.1007/s00158-019-02406-4
Yau LC (2016) Conjugate Heat Transfer with the Multiphysics Coupling Library preCICE. PhD thesis, Technische Universität München
Yoon GH (2010) Topological design of heat dissipating structure with forced convective heat transfer. J Mechan Sci Technol 24:1225–1233. https://doi.org/10.1007/s12206-010-0328-1
Yoon GH (2016) Topology optimization for turbulent flow with Spalart-Allmaras model. Comput Method Appl Mechan Eng 303:288–311. https://doi.org/10.1016/j.cma.2016.01.014
Yoon GH (2020) Topology optimization method with finite elements based on the \(k-\varepsilon\) turbulence model. Comput Meth Appl Mechan Eng. https://doi.org/10.1016/j.cma.2019.112784
Zhao J, Zhang M, Zhu Y, Cheng R, Wang L (2021) Topology optimization of turbulent forced convective heat sinks using a multi-layer thermofluid model. Struct Multidisc Optim 64:3835–3859. https://doi.org/10.1007/s00158-021-03064-1
Zymaris AS, Papadimitriou DI, Giannakoglou KC, Othmer C (2009) Continuous adjoint approach to the Spalart-Allmaras turbulence model for incompressible flows. Comput Fluids 38:1528–1538. https://doi.org/10.1016/j.compfluid.2008.12.006
Acknowledgements
L. Noël and K. Maute received the support for this work from the Defense Advanced Research Projects Agency (DARPA) under the TRADES program (agreement HR0011-17-2-0022). L. Noël thanks the support of the Sectorplan Bèta & Techniek.
Author information
Authors and Affiliations
Contributions
The share of the author’s contributions in this paper is equal.
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Replication of Results
Upon request, the authors will provide the full set of input parameters and meshes for each validation problems and topology optimization problems presented in the paper.
Ethical approval
The opinions and conclusions presented in this paper are those of the authors and do not necessarily reflect the views of the sponsoring organizations.
Additional information
Responsible Editor: Joe Alexandersen
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Noël, L., Maute, K. XFEM level set-based topology optimization for turbulent conjugate heat transfer problems. Struct Multidisc Optim 66, 2 (2023). https://doi.org/10.1007/s00158-022-03353-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-022-03353-3