Reliability-based bottom-up manufacturing cost optimisation for composite aircraft structures

Abstract

A novel methodology is presented for the reliability-based manufacturing cost optimisation of composite aircraft structures. A comprehensive bottom-up costing approach is employed, enabling precise manufacturing cost estimation in terms of material, machine, labour, tooling, and indirect costs. This approach splits the manufacturing process into many individual activities, which can be combined in many different ways, allowing the proposed optimisation methodology to be applied to a wide range of composite aircraft structures. A genetic algorithm (GA) is coupled with a deep neural network (DNN) to efficiently determine the optimal composite ply stacking sequence for every part of an assembled structure. A numerical example featuring a composite-stiffened aircraft fuselage panel is investigated. The reliability of the panel is measured in terms of its buckling resistance, and its manufacturing cost is estimated based on the individual costs of over 20 activities. The labour times for each activity were estimated based on data collected from an aerospace company specialising in the manufacture of advanced composite aircraft structures. Results indicate that material, machine, labour, and tool costs can vary significantly depending on the level of structural reliability required, demonstrating the importance of accounting for non-material costs when designing composite aircraft structures.

1 Introduction

Cost estimation is vital for any aircraft part manufacturer. If a design can be manufactured at low cost, it can have a significant impact on the extremely competitive aviation market. It is therefore essential for manufacturers to accurately estimate the costs of their designs and have a good understanding of the many factors that influence these costs. Cost estimation is even more important for composite aircraft parts. Although composite materials have demonstrated their superiority, in terms of weight and mechanical properties, over more traditional materials, such as aluminium, their use is often limited due to their relatively high cost. For composites to become more widely used in the extremely competitive aviation market, accurate cost estimation of composite aircraft parts is essential.

Many examples can be found in the literature presenting methods for the comprehensive manufacturing cost estimation of composite aircraft parts (Sun et al. 2021; Muflikhun and Yokozeki 2021; Zabihi et al. 2020; Van Grootel et al. 2020; Clarke et al. 2020; Chen et al. 2020; Hueber et al. 2019; Hagnell 2019; Wang et al. 2018; Soares et al. 2018; Shama Rao et al. 2018; Aniruddha 2018; Al-Lami et al. 2018; Pinto 2017; Kalantari et al. 2016; Hueber et al. 2016; Hagnell et al. 2016; Hagnell and Åkermo 2015; Shehab et al. 2013; Schubel 2012; Weitao 2011; Song et al. 2009; Liu 2009; Mazumdar 2002; Haffner 2002). One notable example is a doctoral thesis by Haffner (2002) which provides a comprehensive overview of common methods used to manufacture composite aircraft parts, including detailed estimates for material, tool, machine, and labour costs. In a book authored by Mazumdar (2002), a thorough breakdown is provided In Chapter 11 for various costs involved in the manufacturing of composite aircraft parts. In a thesis by Liu (2009), detailed cost information was collected for a wide variety of materials and equipment used in composite manufacturing. In a thesis by Weitao (2011), detailed industry cost data were obtained from surveys of several composite aircraft part manufacturers, including key cost drivers and detailed breakdowns of material, tool, machine, labour, and indirect/fixed costs. Hagnell and Åkermo (2015) presented a cost model for several methods used for the manufacture of composite aircraft parts and demonstrated this model with an aircraft wing. Hagnell et al. (2016) later presented a detailed study of the costs associated with the full production of a composite aircraft wing box, including layup, bagging, curing, non-destructive testing (NDT), and assembly. Van Grootel et al. (2020) investigated the environmental impact of composite aircraft manufacturing. It was found that, by reducing manufacturing variability, the fuel consumption of aircraft could be significantly reduced.

Although it is important to take into account manufacturing cost when designing a composite part, the safety/reliability of the part is also a very important consideration to take into account as well, especially for parts used in aircraft. There are many examples in which the reliability of a structure is optimised under the presence of uncertainties (Farokhi et al. 2020; Yoo et al. 2020; Bacarreza et al. 2014; Lopez et al. 2016; Simoes et al. 2006; Hu et al. 2016). One notable example is (Farokhi et al. 2020) in which the geometric design of an aircraft mono-stringer composite-stiffened panel was optimised based on reliability. Reliability was estimated based on buckling behaviour and under the presence of uncertainties in composite material properties. Another notable example is (Yoo et al. 2020) in which a multi-fidelity modelling-based approach was taken to the reliability optimisation of another composite aircraft mono-stringer composite-stiffened panel. The multi-fidelity approach was found to significantly improve the efficiency of the optimisation process. Bacarreza et al. (2014) optimised the geometry and layup properties, such as the number of plies and the stacking sequence, of an aircraft composite-stiffened panel. The optimisation was performed under the presence of uncertainties, with the aim of improving the robustness of the stiffened panel to buckling loads.

Ideally, both manufacturing cost and reliability should be accounted for during the design stage. There are some examples of this in the literature (Dey et al. 2016; Fang et al. 2019; Chakri et al. 2017; Jiang et al. 2016; Beck and Gomes 2012; Dersjo and Olsson 2011; Strano 2010; Beck and Gomes 2010). One notable example is (Fang et al. 2019), where a time-variant methodology was developed for optimising the reliability and the welding cost of a beam structure. Chakri et al. (2017) developed a directional bat algorithm also for the reliability and welding cost of a beam structure. Jiang et al. (2016) developed a methodology for the reliability and re-manufacturing cost optimisation of a lathe bed. Beck and Gomes (2012) optimised the reliability and manufacturing cost, in terms of material and labour costs, of a three-bar structure, a plane truss structure, and a built-up column. Dersjo and Olsson (2011) optimised the reliability and the manufacturing cost, in terms of material and machining costs, of a drag link arm, a component of the steering gear of a heavy duty truck. Strano (2010) developed a methodology for the reliability and cost optimisation, in terms of material cost and cost of failure, of a sheet-metal stamping process.

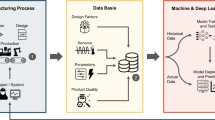
The above works have investigated the costs associated with very specific structures, and the developed methodologies for reliability and cost optimisation are often not applicable to other structures. Ideally, a reliability and cost optimisation methodology should be robust and comprehensive, allowing it to be applied to a wide range of different composite parts. This is achieved in this current work by the use of a bottom-up approach to cost estimation, splitting the manufacturing process into many different activities. These activities can be combined in many different ways, enabling the proposed optimisation methodology to be applied to a wide range of composite aircraft structures. The above works on reliability optimisation have also mainly considered only material costs. Although material costs account for a large percentage of the cost associated with manufacturing a composite aircraft part, typically 30–59% depending on production volume (Mazumdar 2002; Shehab et al. 2013; Weitao 2011), the remaining 41–70% can contribute significantly to the overall manufacturing cost and should not be disregarded. Based on composite part cost studies presented in the literature, labour costs can be in the range of 20–54%, machine costs in the range of 4–28%, tool costs in the range of 2–10%, and indirect/fixed costs typically around 10% (Mazumdar 2002; Shehab et al. 2013; Weitao 2011). Therefore, the designer should not only take into account material costs, but other costs as well when optimising the design of composite parts. Furthermore, reliability optimisation approaches typically involve optimising designs in terms of geometrical parameters such as length, width, thickness, area, and so on. The effect of these parameters on material costs is often clear. However, it is not often clear how these parameters can affect other costs, such as labour, machine, or tooling costs. This current work aims to address this issue.

In summary, this current work develops a novel comprehensive methodology for optimising the reliability and manufacturing cost of composite aircraft structures. The main novelties of this work are as follows:

• This work couples a comprehensive bottom-up approach for cost estimation with a structural reliability optimisation procedure. This bottom-up approach splits the manufacturing process into many individual activities, which can be combined in many different ways, enabling the proposed manufacturing cost and reliability optimisation methodology to be applied to a wide range of composite aircraft structures. The efficiency of this optimisation methodology is significantly improved through the use of a genetic algorithm (GA) and a deep neural network (DNN).

• Although material costs account for a large percentage of manufacturing costs, other costs contribute significantly to the overall manufacturing cost and should not be disregarded. The methodology developed in this work takes into account not only material costs, but also other costs such as machine, tooling, labour, and indirect costs. This work also investigates how these costs are influenced by various design parameters, and how these costs are distributed when different levels of structural reliability are desired.

The layout of the paper is as follows: The methodology for calculating reliability is described in Sect. 2.1. The methodology for the comprehensive bottom-up manufacturing cost estimation of aircraft composite structures is described in Sect. 2.2. When optimising a composite structure, the number of plies and ply thickness will need to be optimised, this means that the layup stacking sequence of the composite part will need to be optimised as well. This is achieved by coupling a genetic algorithm (GA) with a deep neural network (DNN) and is described in Sects. 2.3 and 2.4. Finally, a numerical example featuring a composite-stiffened panel from an aircraft fuselage subjected to buckling is presented in Sect. 3.

2 Methodology

2.1 Reliability analysis

Reliability analysis offers engineers many advantages when designing structures. It enables them to understand how uncertainties in various design parameters influence the reliability of their structure and allows them to focus on the most critical areas of their design and helps them identify ways of improving its overall reliability. This is especially important for aircraft structures.

In the field of reliability analysis, the boundary between succeeding or failing to meet a certain set of criteria can be represented mathematically by a limit state function (LSF) $g(\mathbf{Z })$. For example, if the goal is to investigate the probability of a structure failing due to load, the LSF will be:

$$\begin{aligned} g(\mathbf{Z }) = R - S(\mathbf{X }) \end{aligned},$$

(1)

where $\mathbf{Z }$ is a vector of random variables ($\mathbf{Z }\in {\mathbb {R}}^{n_r}$ where $n_r$ is the number of random variables), and $\mathbf{X }$ is a subset of $\mathbf{Z }$ if R is a random variable, where R is the resistance of the structure to some load S. If $S(\mathbf{X })>R$ then $g(\mathbf{Z })<0$ and the structure is considered to have failed, while if $S(\mathbf{X })\le R$ then $g(\mathbf{Z }) \ge 0$ and the structure is considered safe.

The probability that the set of criteria has failed to be met is termed the probability of failure $P_\mathrm{{F}}$, while the probability that the set of criteria has been successfully met is termed reliability $P_\mathrm{{R}}$. In the example outlined above, these probabilities would correspond to the probabilities of the structure failing or being safe under the load S, respectively. Reliability can be determined by evaluating the following integral:

$$\begin{aligned} P_\mathrm{{R}}=1-P_\mathrm{{F}}=P\{g(\mathbf{Z })>0\}=\int _{g(\mathbf{Z })>0} f_\mathbf{Z }(\mathbf{Z })\mathrm{{d}}\mathbf{Z } \end{aligned},$$

(2)

where $f_{\mathbf{Z }}(\mathbf{Z })$ is the joint probability density function (PDF) of $\mathbf{Z }$. $P_\mathrm{{R}}$ and $P_\mathrm{{F}}$ are obtained by integrating over the failure region ($g(\mathbf{Z })<0$) and the safe region ($g(\mathbf{Z })\ge 0$), respectively. All of the design variables are assumed to be mutually independent. The integral in Eq. (2) can be difficult to evaluate if there are many variables in $\mathbf{X }$ or if the boundary $g(\mathbf{Z })=0$ is non-linear. Therefore, several methods have been developed to evaluate the integral in Eq. (2). The most widely known are Monte Carlo simulations (MCS), the first-order reliability method (FORM), and the second-order reliability method (SORM). This work will focus on the FORM due to its efficiency.

The reliability $P_\mathrm{{R}}$ shown in Eq. (2) can be represented in terms of a reliability index $\beta$ as:

$$\begin{aligned} P_\mathrm{{R}}=1-P_\mathrm{{F}}=1-\Phi (-\beta )=\Phi (\beta ) \end{aligned},$$

(3)

while the probability of failure $P_\mathrm{{F}}$ can be represented as:

$$\begin{aligned} P_\mathrm{{F}}=1-P_\mathrm{{R}}=\Phi (-\beta )=1-\Phi (\beta ) \end{aligned},$$

(4)

where $\Phi$ denotes the cumulative distribution function (CDF) of the standard normal distribution. A large value for the reliability $P_\mathrm{{R}}$ corresponds to a large value for the reliability index $\beta$. $\beta$ can be found by rearranging the above equation to yield:

$$\begin{aligned} \beta =\Phi ^{-1}(P_\mathrm{{R}})=\Phi ^{-1}(1-P_\mathrm{{F}}) \end{aligned},$$

(5)

where $\Phi ^{-1}$ is the inverse of the CDF of the standard normal distribution.

2.2 Bottom-up manufacturing cost estimation for composites

This section presents a comprehensive general framework for estimating the manufacturing cost of composite parts using a bottom-up approach. The user is free to combine the activities as they wish and use whatever input values they desire.

The manufacturing cost of a part $C_{\mathrm{{part}}}$ can be calculated by adding up the cost of each of the individual activities used to manufacture the part:

$$\begin{aligned} C_{\mathrm{{part}}} = \sum _{i=1}^n C_{\mathrm{{act}}_i} + C_{\mathrm{{ind}}} \end{aligned},$$

(6)

where $C_{\mathrm{{act}}_i}$ is the direct cost associated with the ith activity used to manufacture the part and includes material, machine, tool, and labour costs. n is the total number of activities needed to manufacture the part. $C_{ind}$ is the indirect cost (also known as fixed costs) associated with the manufacturing of the part such as facility costs, indirect labour costs such as supervision costs, and process trouble-shooting costs and is typically calculated as a percentage of the total activity costs:

$$\begin{aligned} C_{ind} = \frac{\%_{ind}}{100} C_{\mathrm{{part}}} =\frac{\%_{ind}}{100-\%_{ind}} \bigg (\sum _{i=1}^n C_{\mathrm{{act}}_i} \bigg ) \end{aligned},$$

(7)

where $\%_{ind}$ is the indirect cost percentage. The indirect costs $C_{ind}$ typically account for around 10% of the total cost $C_{\mathrm{{part}}}$ associated with the manufacture of composite aircraft parts (Mazumdar 2002). Therefore, $\%_{ind}=10\%$ and

$$\begin{aligned} C_{ind} = 0.1 C_{\mathrm{{part}}} = 0.11\bigg (\sum _{i=1}^n C_{\mathrm{{act}}_i} \bigg ) \end{aligned},$$

(8)

The cost of an individual activity can be broken down in terms of material costs (e.g. purchasing composite prepregs), tool costs (e.g. mould costs), machine costs (e.g. autoclave costs), and labour costs:

$$\begin{aligned} C_{\mathrm{{act}}_i} = C_{\mathrm{{mat}}_i} + C_{\mathrm{{tool}}_i} + C_{\mathrm{{machine}}_i} + C_{\mathrm{{lab}}_i} \end{aligned},$$

(9)

where $C_{\mathrm{{mat}}_i}$ are the material costs, $C_{\mathrm{{tool}}_i}$ are the tool costs, $C_{\mathrm{{machine}}_i}$ are the machine costs, and $C_{\mathrm{{lab}}_i}$ are the labour costs for the ith activity.

2.2.1 Material costs

The material cost for the ith activity is:

$$\begin{aligned} C_{\mathrm{{mat}}_i} = \sum _{j=1}^m C_{\mathrm{{unit}}\_\mathrm{{mat}}_j} Q_{ij} (1+\%_{\mathrm{{waste}}_j}) \end{aligned},$$

(10)

where $C_{\mathrm{{unit}}\_\mathrm{{mat}}_j}$ is the unit cost of the jth material, $Q_{ij}$ is the quantity of the jth material used in the ith activity, $\%_{\mathrm{{waste}}}$ is the percentage of the jth material that is wasted, and m is the number of different materials used to manufacture the part. It is expected that there will be some material waste during the manufacturing process. Previous research studies concerning the bottom-up cost modelling of composites have considered waste percentages between 10 and 30% (Weitao 2011; Haffner 2002; Hueber et al. 2016; Hagnell and Åkermo 2015). Therefore, an average waste percentage of 20% is used for all the materials in this work.

The units costs, waste percentages, and descriptions of common materials used in the manufacture of composite parts can be seen in Table 1. There are a total of 9 materials, so $m=9$ in Eq. (10). The unit cost and waste percentage for each material are fixed and so do not change between activities. The only parameter in Eq. (10) that can change between activities is the quantity $Q_{ij}$, which can be zero for some activities and non-zero for others. The unit costs seen in Table 1 were chosen based on units costs found from a variety of sources: previous research studies concerning the manufacturing cost of aerospace composite parts, commercial websites, and information provided by our industry partner Plyform Composites Srl a company specialising in the manufacturing and assembly of advanced composite materials. The unit costs of the 7 materials from these sources can be seen in Table 2. These costs have been converted to Euros and adjusted for inflation.

Table 1 Common materials involved in composite manufacturing. Their typical unit costs and waste percentages are shown

Table 2 Unit costs of common materials involved in composite manufacturing from various references, including from our industry partner. The costs have been converted to Euros and adjusted for inflation

It can be seen in Table 2 that the unit costs for most materials have significant overlap, indicating the high reliability associated with these values. The unit costs from the research studies and commercial websites (Liu 2009; Haffner 2002; Aniruddha 2018; Carbon Composites 2017; Easycomposites; East coast fibre glass supplies) agree well with the unit costs from our industry partner. Differences in unit costs can be explained by differences in location, differences of the fibres and matrix, e.g. tow, tape (for the prepregs), and whether they were purchased in bulk, etc. Based on information provided by our industry partner, coverage levels of 25 m²/L were assumed for the mould cleaning fluids and the release agents. There do not seem to be any significant outliers in Table 2; therefore, the average of the unit costs for each of the materials seen in Table 2 was used as the unit costs seen in Table 1.

2.2.2 Tool costs

The cost of the kth tool for the ith activity can be calculated by dividing the total investment cost of the tool $\mathrm{{Investment}}_{\mathrm{{tool}}_k}$ by the number of parts the tool help manufacture over its life $N_{\mathrm{{tool}}\_\mathrm{{parts}}_k}$:

$$\begin{aligned} C_{\mathrm{{tool}}_{ik}}=\frac{\mathrm{{Investment}}_{\mathrm{{tool}}_k}}{N_{\mathrm{{tool}}\_\mathrm{{life}}\_\mathrm{{parts}}_k}} \end{aligned}.$$

(11)

A common tool used in composite part manufacturing is the mould. Akermo and Astrom (2000) provides investment cost data for aluminium moulds and steel moulds for various mould areas. Fitting a simple linear regression line to this data yields the following relationship for the investment cost of an aluminium mould:

$$\begin{aligned} \mathrm{{Investment}}_{\mathrm{{mould}}} = 3,820 + 79,210A_{\mathrm{{mould}}} \end{aligned}$$

(12)

where $A_{\mathrm{{mould}}}$ is the area of the mould. In this work, the area of the mould is assumed to be 20% higher than the surface area (one side only) of the part. For aluminium moulds, (Haffner 2002) suggested a minimum of 500 parts per mould, a number also used by Weitao (2011).

2.2.3 Machine costs

The cost of the lth machine for the ith activity can be calculated as:

$$\begin{aligned} C_{\mathrm{{mac}}_{il}} = \frac{C_{\mathrm{{mac}}\_\mathrm{{utilization}}_{il}} + C_{\mathrm{{mac}}\_\mathrm{{energy}}_{il}}}{N_{\mathrm{{mac}}\_\mathrm{{parts}}\_\mathrm{{worked}}_{il}}} \end{aligned},$$

(13)

where $C_{\mathrm{{mac}}\_\mathrm{{utilization}}_{il}}$ is the utilisation cost of the lth machine of the ith activity:

$$\begin{aligned} C_{\mathrm{{mac}}\_\mathrm{{utilization}}_{il}} = TDU_{\mathrm{{mac}}_{il}}t_{\mathrm{{mac}}\_\mathrm{{total}}_{il}} \end{aligned},$$

(14)

where $t_{\mathrm{{mac}}\_\mathrm{{total}}_{il}}$ is the total time for which the lth machine of the ith activity is used, and $TDU_{\mathrm{{mac}}_{il}}$ is:

$$\begin{aligned} TDU_{\mathrm{{mac}}_{il}} = \frac{\mathrm{{Investment}}_{\mathrm{{mac}}_{il}}}{N_{\mathrm{{years}}\_\mathrm{{dep}}}N_{\mathrm{{work}}\_\mathrm{{days}}}N_{\mathrm{{shifts}}}N_{\mathrm{{shift}}\_\mathrm{{length}}}} \end{aligned},$$

(15)

where $\mathrm{{Investment}}_{\mathrm{{mac}}_{il}}$ is the investment cost of the lth machine of the ith activity. For autoclaves, this cost can vary significantly depending on the size of the autoclave, typical values in the literature are between €450,000 and 1,300,000 (Liu 2009; Al-Lami et al. 2018; Weitao 2011; Mazumdar 2002) after converting to Euros and adjusting for inflation. Therefore, an average of €875,000 is used in this work for the autoclave. Based on the literature, the investment costs for the ultrasonic scanner used in NDT is between €124,000 and 143,000 (Weitao 2011; Hagnell et al. 2016). Therefore, an investment cost of €143,000 for the ultrasonic scanner is used in this work.

In Eq. (15), $N_{\mathrm{{years}}\_\mathrm{{dep}}}$ is the number of years in which the machine is depreciated. For autoclaves, this value can vary between 10 and 20 years (Weitao 2011; Liu 2009; Van Grootel et al. 2020). Therefore, an average of 15 years is used in this work. A value of 10 years is used for the ultrasonic scanner.

In Eq. (15) $N_{\mathrm{{work}}\_\mathrm{{days}}}$ is the number of work days per year in the company, $N_{\mathrm{{shifts}}}$ is the number of shifts per day, and $N_{\mathrm{{shift}}\_\mathrm{{length}}}$ is the length of each shift in hours. $t_{\mathrm{{mac}}\_\mathrm{{total}}_{il}}$ in Eq. (14) is the total machine time required for the lth machine of the ith activity per load. For autoclaves, this time can vary depending on the size of the load, but is typically 7–10 h (Mazumdar 2002; Hagnell and Åkermo 2015; Liu 2009; Haffner 2002). Therefore, a time of 8 hours is used in this work for $t_{\mathrm{{mac}}\_\mathrm{{total}}_{il}}$ and $N_{\mathrm{{shift}}\_\mathrm{{length}}}$ for the autoclave ($t_{\mathrm{{mac}}\_\mathrm{{total}}_{il}}=N_{\mathrm{{shift}}\_\mathrm{{length}}}=8$), so that there can be three shifts per day ($N_{\mathrm{{shifts}}}=3$). The number of work days per year is assumed to be 240 days ($N_{\mathrm{{work}}\_\mathrm{{days}}}=240$). It is assumed that the ultrasonic scanner uses the same values for $N_{\mathrm{{work}}\_\mathrm{{days}}}$, $N_{\mathrm{{shifts}}}$, and $N_{\mathrm{{shift}}\_\mathrm{{length}}}$ as the autoclave.

In Eq. (13), $C_{\mathrm{{mac}}\_\mathrm{{energy}}_{il}}$ is the total energy cost of the lth machine of the ith activity; it is a function of the energy cost per kWh $C_{\mathrm{{unit}}\_\mathrm{{energy}}}$ and the total energy required by the lth machine of the ith activity:

$$\begin{aligned} C_{\mathrm{{mac}}\_\mathrm{{energy}}_{il}} = C_{\mathrm{{unit}}\_\mathrm{{energy}}} t_{\mathrm{{mac}}\_\mathrm{{total}}_{il}} \end{aligned}.$$

(16)

For autoclaves, (Weitao 2011) gave an estimate of 10$/h. This equates to 10.6€/hr after converting to Euros and accounting for inflation. The ultrasonic scanner is assumed to have a power consumption of 3.35kW (Hagnell et al. 2016) and an energy cost of 0.1 €/kWh. The machining time is determined using Eq. (36).

It is worth pointing out that the bottom-up approach described in this section is general in nature and that the user is free to use different values for the above input parameters based on their own personal experience.

2.2.4 Labour costs

The labour cost of an activity is a function of the direct labour rate $C_{\mathrm{{unit}}\_\mathrm{{lab}}}$, the number of operators performing the activity $N_{operators}$, and the total time required to perform the activity $t_{\mathrm{{labour}}_i}$ (h):

$$\begin{aligned} C_{lab_i} = C_{\mathrm{{unit}}\_\mathrm{{lab}}} N_{\mathrm{{operators}}} t_{\mathrm{{labour}}_i} \end{aligned}.$$

(17)

Recent research studies concerning bottom-up cost modelling of composites have considered direct labour rates between 20 and 37 €/hr depending on location and expertise (Weitao 2011; Liu 2009). Therefore, an average labour rate of 28 €/hr is used in this work.

The total time required to perform the ith activity $t_{\mathrm{{labour}}_i}$ can be split into a variable time part $t_{\mathrm{{labour}}_i}^{\mathrm{{var}}}$ and a constant time part $t_{\mathrm{{labour}}_i}^{\mathrm{{const}}}$:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = t_{\mathrm{{labour}}_i}^{\mathrm{{const}}} + t_{\mathrm{{labour}}_i}^{\mathrm{{var}}} \end{aligned}.$$

(18)

The variable time part $t_{\mathrm{{labour}}_i}^{\mathrm{{var}}}$ includes the time required for tasks that can vary depending on part properties such as the area of the part, the area of the mould, number of plies, thickness of plies, and so on. The constant time part $t_{\mathrm{{labour}}_i}^{\mathrm{{const}}}$ includes the time required for tasks that do not depend on part properties, e.g. the time required to check for leaks in a vacuum bag.

Table 3 presents a list of common activities involved in the manufacture of composite parts, their descriptions, and the order in which they occur during the manufacturing process. The labour time relationships for each of these activities are detailed below. The labour times are given in hours.

The below activity labour time relationships were determined based on data collected by our industry partner. The time required for a worker to complete an activity was recorded multiple times for different values of the input parameters (such as mould area $A_{\mathrm{{mould}}}$ or number of plies $N_{\mathrm{{plies}}}$), and linear regression was used to create a relationship linking the value of the input parameters to labour time.

Table 3 The activities involved in composite manufacturing

Activity 1: Material withdrawal, inspection, and set-up The labour time required to issue, inspect, and set-up all the materials is assumed to be:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.5 \end{aligned}.$$

(19)

Activity 2: Mould inspection The labour time required for inspecting the mould is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 A_{\mathrm{{mould}}} \end{aligned},$$

(20)

where $A_{\mathrm{{mould}}}$ is the mould area ($m^2$) for the part.

Activity 3: Mould preparation The time required to apply cleaning fluid, release agent, and release film to the mould to prevent sticking of the part to the mould is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.16 + 0.05 A_{\mathrm{{mould}}} \end{aligned},$$

(21)

where $A_{\mathrm{{mould}}}$ is the mould area ($m^2$) for the part.

Activity 4: Manual ply cutting The labour time required to cut the composite prepregs to shape is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.25 + 0.015x \end{aligned},$$

(22)

where x is the total ply perimeter (m):

$$\begin{aligned} x = N_{\mathrm{{plies}}} * P_{\mathrm{{ply}}} \end{aligned},$$

(23)

where $N_{\mathrm{{plies}}}$ is the number of plies used to create the composite part, and $P_{\mathrm{{ply}}}$ (m) is the perimeter of each individual ply.

Activity 5: Manual layup The labour time required to place the composite prepregs by hand to create a layup is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 + 0.05 t_{\mathrm{{labour}}_i}^{\mathrm{{var}}} \end{aligned},$$

(24)

where $t_{\mathrm{{labour}}_i}^{\mathrm{{var}}}$ is depends on the geometric complexity of the composite part:

$$\begin{aligned} t_{\mathrm{{labour}}_i}^{\mathrm{{var}}}&= 0.04 A_{\mathrm{{ply}}} \hspace{1cm} \textup{Low complexity} \end{aligned},$$

(25)

$$\begin{aligned} t_{\mathrm{{labour}}_i}^{\mathrm{{var}}}&= 0.06 A_{\mathrm{{ply}}} \hspace{1cm} \textup{Medium complexity} \end{aligned},$$

(26)

$$\begin{aligned} t_{\mathrm{{labour}}_i}^{\mathrm{{var}}}&= 0.07 A_{\mathrm{{ply}}} \hspace{1cm} \textup{High complexity} \end{aligned},$$

(27)

where $A_{\mathrm{{ply}}},$ is the area of each ply.

Activity 6: Debulking The labour time required to conduct ‘debulking’ every 4 plies is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.3 x \end{aligned},$$

(28)

where x is:

$$\begin{aligned} x = (N_{\mathrm{{plies}}}/4)+1 \end{aligned},$$

(29)

Activity 7: Layup inspection The labour time required to inspect the layup for defects is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 N_{\mathrm{{plies}}} \end{aligned},$$

(30)

where $N_{\mathrm{{plies}}}$ is the number of plies in the layup.

Activity 8: Layup final vacuum bagging The labour time required to perform the final vacuum bagging of the layup is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.25 + 0.15 A_{\mathrm{{mould}}} \end{aligned},$$

(31)

where $A_{\mathrm{{mould}}}$ is the mould area ($m^2$) for the part.

Activity 9: Vacuum bag inspection The labour time required to check the final vacuum bag for leaks is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 \end{aligned}.$$

(32)

Activity 10: Autoclave cure As mentioned in Sect. 2.2.3, the total machining time required by the autoclave is estimated to be 8 h. Mazumdar (2002) gives estimates for the time required to complete various steps involved in the curing process. Only about  20% of the total time requires the presence of an operator. Therefore, the labour time required for the autoclave curing of the composite part is assumed to be 1.6hrs.

Activity 11: Demoulding The labour time required to remove the vacuum bag and breather materials, and then remove the composite part from the mould, is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.16 + 0.1 A_{\mathrm{{mould}}} \end{aligned},$$

(33)

where $A_{\mathrm{{mould}}}$ is the mould area (m$^2$) for the part.

Activity 12: Cure inspection The labour time required to inspect the laminate for obvious defects, such as resin starvation, edge delamination, or fibre break-out, and so on,. is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 \end{aligned}.$$

(34)

Activity 13: Manual trimming The labour time required to trim the edges of the laminate to the correct dimensions is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.25 + min(0.08; 0.05 P_{\mathrm{{part}}}) \end{aligned},$$

(35)

where $P_{\mathrm{{part}}}$ is the outer perimeter (m) of the part.

Activity 14: Non-Destructive Testing (NDT) The labour time required to inspect the part using a portable ultrasonic scanner is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.25 + A_{\mathrm{{part}}} / (3600 \times S_{\mathrm{{ins}}}) \end{aligned},$$

(36)

where $A_{\mathrm{{part}}}$ is the area of the part, and $S_{\mathrm{{ins}}}$ is the speed to the inspection and is assumed to be 0.2 m/s.

Activity 15: Dimensional inspection The labour time required to check for correct dimensions, such as length and thickness, is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 + N_{\mathrm{{dim}}} t_{\mathrm{{dim}}} \end{aligned},$$

(37)

where $N_{\mathrm{{dim}}}$ is the number of dimensions to inspect, and $t_{dim}=0.05$ is the time required to inspect each dimension (hrs per dimension).

Activity 16: Dynamic Mechanical Analysis (DMA) inspection The time required to perform the DMA inspection is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.55 + 1.0*N_{\mathrm{{specimens}}} \end{aligned},$$

(38)

where $N_{specimens}$ is the number of specimens to test.

Activity 17: Assembly The times required to assemble two or more components for various levels of complexity are:

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.05 N_{\mathrm{{components}}} \hspace{1cm} \textup{Low complexity} \end{aligned},$$

(39)

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.10 N_{\mathrm{{components}}} \hspace{1cm} \textup{Medium complexity} \end{aligned}$$

(40)

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.15 N_{\mathrm{{components}}} \hspace{1cm} \textup{High complexity} \end{aligned},$$

(41)

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.25 N_{\mathrm{{components}}} \hspace{1cm} \textup{Movement complexity} \end{aligned}$$

(42)

where $N_{\mathrm{{components}}}$ is the number of components to assemble.

Low complexity is for components that can be assembled easily , such as small components.

Medium complexity is for components that are more difficult to assemble, such as larger components or components that required fine adjustment.

High complexity is for components that are very difficult to assemble, such as very large components or components that provide limited accessibility to the workers.

Movement complexity is for parts that are difficult move, such as parts over 25kg in weight.

Activity 18: Lap shear test inspection The time required to perform the lap shear inspection is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.50 \end{aligned}.$$

(43)

Activity 19: Hole drilling The time required to drill holes in a component depends on the diameter of the holes and is:

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.010N_{HL} \hspace{1cm} \textup{Diameter} \le 4.8mm \end{aligned}.$$

(44)

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.015N_{HL} \hspace{1cm} \textup{Diameter} > 4.8mm \end{aligned},$$

(45)

where $N_{HL}$ is the number of holes to drill.

Activity 20: Fastener installation The time required to install fasteners depends on the diameter of the fasteners and is:

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.05N_{\mathrm{{Fasteners}}} \hspace{1cm} \textup{Diameter} \le 5mm \end{aligned},$$

(46)

$$\begin{aligned} t_{\mathrm{{labour}}_i}&= 0.078N_{\mathrm{{Fasteners}}} \hspace{1cm} \textup{Diameter} > 5mm \end{aligned},$$

(47)

where $N_{\mathrm{{Fasteners}}}$ is the number of fasteners to install.

Activity 21: Paint primer application The time required to apply the paint primer is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 + 0.39A_{\mathrm{{ToBePainted}}} \end{aligned},$$

(48)

where $A_{\mathrm{{ToBePainted}}}$ is the surface area to be painted (m$^2$).

Activity 22: Paint top-coat application The time required to apply the paint top coat is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05 + 0.50A_{\mathrm{{ToBePainted}}} \end{aligned},$$

(49)

where $A_{\mathrm{{ToBePainted}}}$ is the surface area to be painted (m$^2$).

Activity 23: Paint inspection The time required to perform a paint inspection is:

$$\begin{aligned} t_{\mathrm{{labour}}_i} = 0.05N_{\mathrm{{coats}}} \end{aligned},$$

(50)

where $N_{\mathrm{{coats}}}$ is the number of paint coats applied. For example, if one primer coat and one top coat are applied, then $N_{\mathrm{{coats}}}=2$.

2.3 Genetic algorithm

When optimising a composite structure, the number of plies and ply thickness can be design variables. Since the optimal stacking sequence will depend on the number of plies and ply thickness, the optimal stacking sequence of the composite part will need to be determined as part of the optimisation procedure. In this work, a genetic algorithm (GA) is used to optimise the layup stacking sequence of composite aircraft structures. In order to ensure good performance of a composite layup stacking sequence, several rules need to be followed, as suggested by Zein et al. (2016) and An et al. (2018):

• 1. The fibre orientations can take angles of 0, ± 45, and 90°.

• 2. Each ply in a layup has the same thickness.

• 3. The layup must be symmetric about the mid-plane.

• 4. The stacking sequence should be balanced, so it should have the same number of +$\theta$ plies as -$\theta$ plies (excluding 0° and 90° plies). For example, (0, 45, -45, 90)_s is allowed, but (0, 45, 45, 90)_s is not.

• 5. To alleviate matrix cracking, maximum four consecutive plies can have the same orientation. For example, (0, 0, 0, 0, 0, 45, − 45, 90)_s is not allowed because there are five 0° plies together, and (45, − 45, 90, 0, 0, 0)_s is also not allowed because there are six 0° plies together.

• 6. When bonding two composite parts, the orientation of the plies touching the bond line should be the same. For example, if part A has a stacking sequence of (0, 45, − 45, 90)_s, then the 0° ply is touching the bond line. Therefore, a stacking sequence of (0, 45, − 45, 90)_s is allowed for part B because the stacking sequence of part B starts with a 0° ply.

• 7. The stacking sequences of two composite parts bonded together can have different numbers of plies, as long as they follow the above rules. For example, if part A and part B are to be bonded together, and if part A has a stacking sequence of (0, 45, − 45, 90)_s, then part B can have a stacking sequence of (0, 90)_s.

• 8. Mechanical performance also needs to be considered as part of the design process. This could refer to the maximum stress in the structure, or resistance to fatigue etc., or a combination of these. As an example, this work considers the resistance of a composite aircraft structure to buckling, as buckling is a common problem encountered in aircraft parts.

Of the above rules, rules 1–3 can be easily enforced by changing the settings or the inputs of the GA. Rules 4–7 are more complex and require the application of penalties to the fitness function used to rate the performance of a design. The fitness function of the GA is based on the buckling performance of a design and is the inverse of the minimum buckling load $B_{\mathrm{{min}}}$, the minimum load required to cause buckling in the structure:

$$\begin{aligned} f = \frac{1}{B_{\mathrm{{min}}}} \end{aligned}.$$

(51)

A design that has a high minimum buckling load $B_{\mathrm{{min}}}$ will be more resistant to buckling. Therefore, a low value for the fitness function f indicates a good design. To enforce the above rules, a penalty is applied to the fitness function of a design. If a design breaks any of rules 4–7 above, the fitness function is set to a very large number, for example $f=100$. This rule-breaking penalty encourages the GA to avoid designs that break the above rules.

2.4 Deep neural network

The evaluation of the fitness function in Eq. (51) requires the use of a finite element method (FEM) model to evaluate the minimum buckling load $B_{\mathrm{{min}}}$. If the GA has a large population size and uses a large number of generations, the FEM model will need to be run 100s or 1000s of times. This can be very expensive, especially for buckling problems. To improve the efficiency of the GA, a deep neural network (DNN) can be created that acts as a surrogate model for the expensive FEM model. A DNN is defined as a neural network with multiple hidden layers. It is capable of modelling more complex behaviour than shallow neural networks that only use one or two hidden layers. There are many examples in the literature of DNNs being used as surrogate models in place of FEM models (Do et al. 2019, 2020; Lee et al. 2017; Truong et al. 2021) for different problems. Examples of shallow and deep neural networks can be seen in Figs. 1 and 2, respectively.

Fig. 1

A shallow neural network composed of an input layer of 3 nodes, a hidden layer of 5 nodes, and an output layer of 1 node

Fig. 2

A deep neural network (DNN) composed of an input layer of 3 nodes, 3 hidden layers of 5 nodes each, and an output layer of 1 node

Although the DNN will be significantly faster than the FEM model, a downside to this surrogate model approach is that it can require a significant amount of input data to achieve similar accuracy to the FEM model. This input data are in the form of FEM model responses, and the number of input data points required is dependent on the number of feasible stacking sequences. However, the number of feasible stacking sequences can be significantly reduced by the application of rules 4–7 in Sect. 2.3, reducing the amount of training data needed to create the DNN. Also, when running the GA, the DNN only needs to be run for designs that do not break rules 4–7, further improving computational efficiency.

The DNN takes as inputs the ply thickness t, the number of plies $N_{\mathrm{{plies}}}$, and the composite ply stacking sequence S. The output of the DNN is the minimum buckling load $B_{\mathrm{{min}}}$. This DNN can be written as:

$$\begin{aligned} B_{\mathrm{{min}}} = f(t,N_{\mathrm{{plies}}},S) \end{aligned},$$

(52)

where f is the DNN. This DNN is used to evaluate the fitness function seen in Eq. (51).

3 Numerical example

To demonstrate the proposed methodology, a numerical example featuring the composite-stiffened panel seen in Fig. 3 is investigated. The composite-stiffened panel is composed of three different parts: skin, five stiffeners, and three frames. It is subjected to a compressive load of 200 MPa on the right curved edge and is clamped on the left curved edge. The design of the panel is to be optimised in terms of manufacturing cost and probability of failure with respect to buckling. The design variables are the ply thickness in the three parts ($t_1$, $t_2$, and $t_3$), and the number of plies in the three parts ($N_{\mathrm{{plies}}_1}$, $N_{\mathrm{{plies}}_2}$, and $N_{\mathrm{{plies}}_3}$). The composite plies used in all three parts have the properties $E_1=138 GPa$, $E_2=E_3=9.5 GPa$, $G_{12}=G_{13}=5.2 GPa$, $G_{23}=1.45 GPa$, $\nu _{12}=\nu _{13}=0.28$, $\nu _{23}=0.40$, and mass density $\rho = 1400$ kg/m$^3$. The properties of the three parts can be seen in Table 3. A genetic algorithm (GA) is used to optimise the composite ply stacking sequences of these three parts: $S_1$, $S_2$, and $S_3$.

Fig. 3

The assembled stiffened panel composed of skin, five stiffeners, and three frames. The ply thickness t, number of plies $N_{\mathrm{{plies}}}$, and stacking sequence S for each of the three different parts are shown

Table 4 The properties of the three parts composing the stiffened panel

A finite element method (FEM) model was created of the composite-stiffened panel in Abaqus FEA and can be seen in Fig. 4. The FEM model is composed of 9016 nodes and 12718 elements, of which 8816 were linear triangular elements of type S3 and 3902 were linear quadrilateral elements of type S4, as this was found to provide convergence in the value of $B_{\mathrm{{min}}}$. The elements are concentrated at the edge that is subjected to the buckling load. The average time to complete an analysis was 117s on a computer with an 8-core 3.59 GHz processor.

Fig. 4

The FEM model of assembled stiffened panel

3.1 Multi-objective optimisation

The design of the stiffened panel is to be optimised such that both the probability of failure and the manufacturing cost of the panel are minimised. The optimisation problem is defined as:

$$\begin{aligned}&Minimise: \{Cost(\mathbf{d }), P_\mathrm{{F}}(\mathbf{d })\}\nonumber \\&Subject to: \mathbf{d }^L \le \mathbf{d } \le \mathbf{d }^U, \mathbf{d }\in {\mathbb {R}}^{n_d} \end{aligned},$$

(53)

where $\mathbf{d }=[t_1,t_2,t_3,N_{\mathrm{{plies}}_1},N_{\mathrm{{plies}}_2},N_{\mathrm{{plies}}_3}],$ is the vector of design variables, and $n_d=6$ is the number of design variables. The stacking sequences $S_1$, $S_2$, and $S_3$ for the three parts are not considered as design variables because they are calculated via a GA using the ply thicknesses $t_1$, $t_2$, and $t_3$ and numbers of plies $N_{\mathrm{{plies}}_1}$, $N_{\mathrm{{plies}}_2}$, $N_{\mathrm{{plies}}_3}$ for the three parts. The probability of failure is calculated with respect to the minimum buckling load of the panel $B_{min}$. The limit state function (LSF) is:

$$\begin{aligned} g(\mathbf{d }) = B_{\mathrm{{min}}}(\mathbf{d }) - B_{\mathrm{{load}}} \end{aligned},$$

(54)

where $B_{\mathrm{{load}}}$ is the compressive load applied to the panel $B_{\mathrm{{load}}}=200$ MPa. The details of the design variables $\mathbf{d }$, including their coefficients of variation (CoV), can be seen in Table 5. The ply thicknesses $t_1$, $t_2$, and $t_3$ are continuous random variables that follow Weibull distributions, while the numbers of plies $N_{\mathrm{{plies}}_1}$, $N_{\mathrm{{plies}}_2}$, and $N_{\mathrm{{plies}}_3}$ are discrete random variables that follow uniform distributions. The probability of failure $P_\mathrm{{F}}(\mathbf{d })$ in Eq. (53) is calculated using the methodology described in Sect. 2.1. $B_{\mathrm{{min}}}$ is the minimum applied load that causes buckling in the structure. In this example, mode-I buckling requires less applied load than the higher modes. Therefore, for the presented example, $B_{\mathrm{{min}}}$ is the minimum load that causes mode-I buckling. Since the higher buckling modes require larger applied loads, they are not considered in the reliability analysis. If $B_{\mathrm{{min}}}$ is less or equal to $B_{\mathrm{{load}}}$ ($B_{\mathrm{{min}}} \le B_{\mathrm{{load}}}$), the structure is considered to have failed by buckling. However, if $B_{min}$ is more than $B_{\mathrm{{load}}}$ ($B_{\mathrm{{min}}}>B_{\mathrm{{load}}}$), the structure is considered to be safe.

Table 5 The details of the input parameters of the DNN

The manufacturing cost of the panel $Cost(\mathbf{d })$ is calculated using the bottom-up methodology described in Sect. 2.2. In total, nine parts need to be manufactured: skin, five stringers, and three frames. The manufacture and assembly of these parts are carried out by the activities described in Sect. 2.2 and Table 3.

The optimisation technique NSGA2 (non-dominated sorting genetic algorithm) (Deb et al. 2002) is used to solve the multi-objective optimisation problem described in Eq. (53). In this technique, each objective is treated independently, and a Pareto front of designs is created at the end. The designer can use this Pareto front to determine the best combination of objective values. On a Pareto front, improving one objective is impossible without sacrificing the other objective. A flowchart showing the steps involved in the proposed multi-objective optimisation procedure can be seen in Fig. 5.

Fig. 5

Flowchart of the multi-objective optimisation

3.2 Genetic algorithm

The ply thickness t and the number of plies $N_{\mathrm{{plies}}}$ for each of the three parts are the design variables $\mathbf{d }$. Since the optimal stacking sequence of a part will depend on the number of plies and ply thickness of the part, the optimal stacking sequence of the part will need to be determined as part of the optimisation procedure. Therefore, once the optimisation procedure has chosen the values of the design variables $\mathbf{d }$ for an iteration, the optimal stacking sequence must be determined for that iteration. This can be achieved by the use of a genetic algorithm (GA), as described in Sect. 2.3. However, since the three different parts (skin, stringers, and frames) are to be joined together at the end of the manufacturing process, the stacking sequence of one part can influence the optimal stacking sequence of another. Therefore, the optimal stacking sequence of all three parts will need to be conducted at the same time. This can be accomplished in the GA by combining all three stacking sequences into a single chromosome. Therefore, the population of the GA would be:

$$\begin{aligned} Population= \begin{bmatrix} S_{11} &{} S_{12} &{}S_{13}\\ S_{21} &{} S_{22} &{}S_{23}\\ \vdots &{} \vdots &{}\vdots \\ S_{n1} &{} S_{n2} &{}S_{n3}\\ \end{bmatrix} \end{aligned},$$

(55)

where $S_{11}$ is the stacking sequence of the 1st chromosome for part 1, and $S_{n2}$ is the stacking sequence of the nth chromosome for part 2, etc. The flowchart for the GA used in the this work can be seen in Fig. 6.

Fig. 6

Flowchart of the genetic algorithm

The GA is stopped if the average relative change in the minimum fitness function is less than $1 \times 10^{-6}$ over 50 generations, or if the maximum number of generations, 200, is reached.

Given that each of the three parts can have 4, 6, or 8 plies, and that each ply can have an angle of 0°, -45°, +45°, or 90°, there are 37,933,056 possible unique combinations of the stacking sequences $S_1$, $S_2$, and $S_3$. However, after the rules shown at the beginning of Sect. 2.3 are implemented, the number of possible unique combinations of $S_1$, $S_2$, and $S_3$ drops to 27,436. This is still a significant number of possible unique combinations. Therefore, a large population of 400 chromosomes and an elite count of 40 (the 40 chromosomes with the best fitness function from the current populations are carried over to the next population) are needed to ensure good convergence in the minimum fitness function.

The convergence history of the GA for an extreme case where each of the three parts has 8 plies ($N_{\mathrm{{plies}}_1}=N_{\mathrm{{plies}}_2}=N_{\mathrm{{plies}}_3}=8$), and the thickness of each is 1.2 mm ($t_1=t_2=t_3=1.2$ mm) can be seen in Fig. 7. The GA was automatically stopped after 156 generations because the average relative change in the minimum fitness function was less than $1 \times 10^{-6}$ over the 50 generations 105–156. The minimum fitness function was 0.172. The average fitness function is initially close to 100; this is due to the rule-breaking penalty described in Sect. 2.3. The optimal stacking sequences found from the GA in this case are as follows: $S_1=[-45,45,90,90]_s$, $S_2=[-45,90,45,90]_s$, and $S_3=[-45,90,45,0]_s$. All three of these stacking sequences follow the rules shown in 2.3.

Fig. 7

The convergence history of the GA for an extreme case where each of the three parts has 8 plies, and the thickness of each ply is 1.2 mm

3.3 Deep neural network

The GA is run once per optimisation iteration, as shown in Fig. 5. Each generation of the GA contains 400 chromosomes, and there can, at most, be 200 generations. This means that, at most, 80,000 fitness functions need to be evaluated per optimisation iteration. Therefore, the finite element method (FEM) model of the stiffened panel seen in Fig. 3 would need to be evaluated 80,000 times per optimisation iteration. Given that the analysis time of the FEM model is on average 117s, this translates to 108 days per optimisation iteration, which is not practical. Therefore, an artificial neural network (ANN) is created to replace the expensive FEM model when evaluating fitness functions in the GA, as seen in Fig. 6. The Matlab Deep Learning Toolbox (Mathworks 2022) is used in this work to create the ANN.

Bayesian regularised artificial neural networks (BRANNs) are more robust than standard back-propagation neural networks and they are difficult to overtrain and overfit; they also do not require a validation dataset (Livingstone 2009). During preliminary testing for this work, BRANNs consistently demonstrated lower error with the test dataset than other types of ANNs. Therefore, the ANN created in this work is a BRANN. The BRANNs were created in the Matlab Deep Learning Toolbox via the training function ’trainbr’, which is based on the Levenberg–Marquardt training algorithm ’trainlm’. For the same reason, the hyperbolic tangent sigmoid transfer function, known as ’tansig’ in Matlab, is used in this work.

The ANN was trained using a train dataset of 7960 runs of the stiffened panel FEM model and tested with a test dataset consisting of a further 1405 runs, for a total of 9365 runs. The average time to complete an analysis using the FEM model is 117s. Therefore, the total time required to create the train and test datasets is $(7960+1405) \times 117 = 1.10 \times 10^6$s, or around 12 days. This is significantly less than the time to complete an optimisation iteration with the FEM model, which is estimated to be $80,000 \times 117 = 9.36 \times 10^6$ or 108 days. The train and test datasets were built by randomly sampling from the distributions of the thicknesses $(t_1,t_2,t_3)$ and the numbers of plies $(N_{{\mathrm{{plies}}}_1},N_{{\mathrm{{plies}}}_2},N_{{\mathrm{{plies}}}_3})$ seen in Table 5. Then the corresponding stacking sequences $(S_1,S_2,S_3)$ were found by picking random combinations from the list of 27,436 stacking sequence combinations that obey the rules shown in Sect. 2.3.

In this work, the performance of an ANN is based on its mean squared error (MSE). Ideally, an ANN should have an MSE that is as low as possible. To check if the performance of the ANN has converged, the gradient of MSE with respect to the network weights is calculated for each epoch. If this gradient reaches a value less than or equal to 1$\times 10^{-7}$, the performance of the ANN is considered to have converged and the training is stopped. Furthermore, to ensure that the performance of the ANN does not worsen during training, a limit is enforced for the Marquardt adjustment parameter $\mu$ used in the training of the ANN. When the MSE decreases during training, $\mu$ is small and large steps are taken in the training of the ANN, while if a tentative step would increase MSE, $\mu$ is large and small steps are taken. When $\mu$ reaches a value of 1$\times 10^{10}$, the training is topped. In addition to the previous stopping criteria, and to prevent overtraining, the training of the ANN is stopped if the number of epochs reaches 2000.

An incremental approach was taken to determining the optimal architecture of the ANN. A total of 24 different architectures were investigated to determine the optimal architecture of the ANN, and they can be seen in Table 6. To ensure that the performance of each architecture was accurately estimated, 100 ANNs with randomised initial weights and biases were trained and tested for each architecture, and the average MSE across these 100 ANNs when run with the train and test datasets was calculated. The average training time for each architecture was also calculated. Among the first group of architectures (Group 1), the best performing architecture was ’9-30-30-1’ which had an average MSE of 0.0025 with the test dataset. This indicated that a multi-layer ANN with an initial layer of 30 nodes could be the best architecture. Based on this assumption, a second group (Group 2) of multi-layer architectures with an initial layer of 30 nodes was tested. It was found that the best performing architectures were ’90-30-20-1’ and ’90-30-10-10-1’ which both had an average MSE of 0.0024 with the test dataset. Given that the architecture ’90-30-10-10-1’ demonstrated a shorter training time than ’90-30-20-1’, 1,902s vs. 2,756s, the architecture ’90-30-10-10-1’ was determined to be the best performing architecture of group 2. This indicated that a multi-layer ANN with an initial layer of 30 nodes and a 2nd layer of 10 nodes could be the best architecture. Based on this assumption, a third group (Group 3) of multi-layer architectures with an initial layer of 30 nodes and a 2nd layer of 10 nodes was tested. It was found that the best performing architectures were ’90-30-10-10-1’ and ’90-30-10-20-1’ which both had an average MSE of 0.0024 with the test dataset. Given that the architecture ’90-30-10-10-1’ demonstrated a shorter training time than ’90-30-10-20-1’, 1,902s vs. 5,910s, the architecture ’90-30-10-10-1’ was determined to be the best performing architecture of group 3. Therefore, the architecture ’90-30-10-10-1’ is used to create the ANN in this work.

Table 6 Average MSE with the train and test datasets for 24 different ANN architectures. 100 ANNs with randomised initial weights and biases were created for each architecture to determine an average MSE. Also shown is the average training time for each architecture

To prevent the overtraining of the ANN with the optimal architecture ’90-30-10-10-1’, a study was performed to determine a suitable size for the train dataset. Nine different sizes of the train dataset were investigated and 100 ANNs with the optimal architecture ’90-30-10-10-1’ and with randomised initial weights and biases were trained for each size of the train dataset. The test dataset was fixed at a size of 1405 data points. The results of this study can be seen in Fig. 8. It can be seen that the adjusted coefficient of determination $R_{\mathrm{{adj}}}^2$ and the mean absolute percentage error (MAPE) for the test dataset increases and decreases, respectively, as the size of the train dataset is increased. However, the MSE and the mean absolute error (MAE) increase. A size of 6369 data points for the train dataset offers a good compromise between the four error statistics and is therefore used in this work for training the ANN with the optimal architecture ’90-30-10-10-1’.

Fig. 8

Average error statistics of the optimal architecture ’90-30-10-10-1’ for different sizes of the train dataset including a MSE, b $R_{\mathrm{{adj}}}^2$, c MAPE, and d MAE

As stated previously, the optimal architecture is ’90-30-10-10-1’ and the optimal size of the train dataset is 6369 data points. To create the data seen in Fig. 8, 100 ANNs of the architecture ’90-30-10-10-1’ with randomised initial weights and biases were trained for each of the nine train dataset sizes, including for a train dataset of 6369 data points. Out of these 100 ANNs, the best performing ANN was found and its error statistics can be seen in Table 7. This ANN demonstrates excellent performance and is used in this work as part of the newly developed reliability-based bottom-up manufacturing cost optimisation procedure for composite aircraft structures. The design of this ANN can be seen in Fig. 9. The average time to complete a single run of the DNN is 0.0079s, this is over 13,000 times faster than the FEM model. Using the stopping criteria described earlier in this section, the convergence history for the train and test sets with respect to epoch is presented in Fig. 10. Convergence was achieved after 1337 epochs, when the Marquardt adjustment parameter $\mu$ exceeded the limit $1\times 10^{10}$, indicating that further training would worsen the performance of the ANN. The best epoch, in terms of performance, was epoch 1050.

Table 7 Error statistics for the best performing ANN with the optimal architecture ’9-30-30-10-1’

Fig. 9

The deep neural network (DNN) used to replace the expensive finite element method (FEM) model of the stiffened panel. It is composed of an input layer of 9 nodes, 3 hidden layers with 30, 10, and 10 nodes, respectively, and an output layer of 1 node

Fig. 10

Convergence history for the best performing ANN with the architecture ’90-30-10-10-1’. Convergence was achieved after 1337 epochs. The best epoch, in terms of performance, was epoch 1050

3.4 Bottom-up manufacturing cost estimation

The stiffened panel is assembled as shown in Fig. 11. The stiffener wet-layups are placed on the wet-layup of the skin and they are cured together to create a strong bonding. The frames are cured separately and assembled onto the skin. Holes are drilled through the frames and the skin, and fasteners are installed to securely attach the frames to the skin, thereby creating the final stiffened panel.

Fig. 11

Flowchart showing the assembly of the stiffened panel

Fig. 12

Flowchart of the bottom-up manufacturing cost estimation procedure for the stiffened panel using the activities described in Sect. 2.2

A more detailed breakdown of the activities involved in the manufacturing of the stiffened panel can be seen in the flowchart presented in Fig. 12. The activities in this flowchart correspond to the activities described in Sect. 2.2 and Table 3. It was assumed that each of the activities seen in Fig. 12 can be completed by one worker. The labour cost for each activity was calculated based on the equations seen in Sect. 2.2.4, with the input parameters seen in Table 4. The activity ’Material withdrawal, inspection, and set-up’ for each part included the costs associated with acquiring the composite prepreg material for that part. The activity ’Mould preparation’ for each part included the mould cost associated the part, as calculated in Eq. (11). The activity ’Dimensional inspection’ required the input $N_{\mathrm{{dim}}}$, the number of dimensions to inspect, and includes dimensions such as thickness, length, width, radius etc. For the frame, $N_{\mathrm{{dim}}}=8$, and for the stiffened panel without frames, $N_{\mathrm{{dim}}}=12$. For the stiffened panel, ’Dimensional inspection’ involved inspecting the quality of the hole drilling, specifically the distance between the holes. Since there are three frames, there will be three lines of holes, and therefore $N_{\mathrm{{dim}}}=3$. The paint involved in the activities ’Paint primer application’ and ’Paint top-coat application’ was only applied on the outside of the stiffened panel (the side without stiffeners and frames).

3.5 Results & discussion

A total of 3200 optimisation iterations were completed, the results of which can be seen in Fig. 13. Based on the Pareto front points, it is clear that the probability of failure $P_\mathrm{{F}}$ of the optimal designs decreases as the manufacturing cost increases. This suggests that for a design to have a low probability of failure $P_\mathrm{{F}}$, it is expected to be more expensive to manufacture, which is intuitive. The probability of failure decreases exponentially as indicated by the fact that the Pareto front points in Fig. 13a follow an almost straight line. A regression line can be plotted through these Pareto front points and is: $P_\mathrm{{F}} = 4.905 \times 10^3 \mathrm{{e}}^{-5.739 \times 10^{-4} \mathrm{{Cost}}}$. This regression line is plotted in Fig. 13. The two most extreme Pareto front designs in Fig. 13 are shown in Table 8. It is clear from these designs that reliability can be improved significantly by a magnitude of 3 by only doubling the manufacturing cost.

Fig. 13

Optimisation results of the composite-stiffened panel with a log-scale and b linear scale. The regression line $P_\mathrm{{F}} = 4.905 \times 10^3 e^{-5.739 \times 10^{-4} Cost}$ is plotted as a black dotted line through the Pareto front points

The distribution of costs between material, machine, labour, tool, and indirect costs for these two designs can be seen in Fig. 14. It can be seen that for the design with the lowest $P_\mathrm{{F}}$, the material costs are a much larger percentage of total costs. This is because to reduce the probability of failure of the stiffened panel, the ply thickness t and the number of plies $N_{\mathrm{{plies}}}$ need to be increased in the three parts, thereby increasing the quantity of composite pregregs needed and therefore increasing material costs. It can also be seen that the labour costs were higher for the design with the lowest $P_\mathrm{{F}}$, even though the labour cost percentage decreased. This is due to the fact that increasing the number of plies increases the time required for cutting the plies, laying-up the plies, and inspecting the plies. This is reflected by the fact that Eqs. (22), (30), and (28), are functions of $N_{\mathrm{{plies}}}$. The machine and tool costs, on the other hand, do not change between the two designs. The tool/mould costs depend on the surface area of the design, and since surface area was not a design variable during the optimisation procedure, tool/mould costs are not expected to change. The machine costs include costs associated with autoclave curing and the equipment needed for the NDT inspection. The cost of the NDT inspection is a function of the surface area of the design, as shown in Eq. (36). Therefore, since surface area was not a design variable, the cost of the NDT inspection is not expected to change. The cost associated with the autoclave curing is a function of the curing time and the investment cost of the autoclave.

Table 8 Details of the two most extreme Pareto front designs, in terms of manufacturing cost, from Fig. 13

Fig. 14

Pie charts showing the distribution of manufacturing costs between material, machine, labour, tool, and indirect costs for the two extreme Pareto front designs seen in Table 8

The cost percentages seen in Fig. 14a and b are within the ranges seen in the literature. Shehab et al. (2013); Weitao (2011), and Mazumdar (2002) give material cost percentages in the range of 30–59%. They also give labour costs in the range of 13–54%, machine costs in the range of 4–28%, tool costs in the range of 2–10%, and indirect/fixed costs typically around 10%. Many of the above cost percentages can vary depending on production volume (see Figure 11.16 in Mazumdar (2002)), and distinction is not often made between direct/indirect labour costs, so an exact comparison is not possible, but the percentages seen in Fig. 14a and b agree well with the literature. The tool costs given in Fig. 14a and b are within those found in the literature (2–10%).

The distribution of manufacturing costs between the different parts and assembly levels for the two designs can be seen in Fig. 15. It can be seen that the skin and the stiffeners account for larger percentages of the total cost for the design with the lowest $P_\mathrm{{F}}$, while the frames account for a smaller percentage. This suggests that the optimisation procedure considered the skin and stiffeners more important for increasing reliability. This makes sense, given the buckling load is applied parallel to the stiffeners. The costs associated with the stiffened panel and the stiffened panel without frames were the same for the two designs; this is because the activities involved in these assembly stages largely depend on non-design parameters such as the number of parts to assemble, the number of dimensions to inspect, and the surface area of the parts.

Fig. 15

Pie charts showing the distribution of manufacturing costs between the different parts and assembly levels for the two extreme Pareto front designs seen in Table 8

The distribution of manufacturing costs between all 23 activities for the two designs can be seen in Fig. 16a and b. It can be seen that the activity ’Material withdrawal, inspection, and set-up’ accounts for the majority of the total activity costs for both designs (65.7% and 81.3%). This is because this activity includes the cost of acquiring the composite prepreg material needed for all of the parts. The remaining 22 activities account for a smaller percentage of the total activity costs for both designs (34.3% and 18.7%). Of the remaining 22 activities, mould preparation is the largest (38.3% and 35.1%), followed by autoclave curing (19.4% and 17.8%). The costs for most of these 22 activities remain the same between the two designs because the costs of most of these activities are functions of non-design parameters such as the surface area of the parts. The activities that experience changes in cost are associated with the layup of the composite plies, these are the four activities: ’Manual ply cutting’, ’Manual layup’, ’Debulking’, and ’Layup inspection’. The costs of these four activities are almost doubled for the design with the lowest $P_\mathrm{{F}}$, compared with the design with the highest $P_\mathrm{{F}}$. This is because the amount of composite prepreg material, both in terms of ply thickness and number of plies, is significantly higher for the design with the lowest $P_\mathrm{{F}}$, increasing the labour time associated with layup of the composite plies.

Fig. 16

Pie charts showing the distribution of manufacturing costs between the activity ’Material withdrawal, inspection, and set-up’ and the remaining activities (left). Pie charts showing the distribution of manufacturing costs between all of the remaining activities (right)

It is difficult to find detailed activity cost breakdowns in the literature, and therefore exact comparisons cannot be easily made. However, a detailed cost breakdown of similar activities for the manufacture of a composite wing box can be found in Hagnell et al. (2016). It was determined that the activities associated with manual layup and autoclave curing were among those that contributed the most to the overall manufacturing cost, as is also the case in this work.

In summary, the results indicate that the proposed novel methodology for the reliability and manufacturing cost optimisation of composite aircraft structures agreed well with costing studies presented in the literature. The distribution of costs in terms of material, machine, labour, tool, and indirect costs showed good agreement, as did the distribution in terms of activity costs. This demonstrates the good level of accuracy associated with the proposed methodology, which is general and can be applied to a wide range of composite aircraft components.

Furthermore, the proposed novel methodology can optimise cost and structural reliability in one process, thus providing an excellent tool for the user and avoiding the need to balance the two features separately. It was shown that the distribution of material, machine, labour, and tool costs can vary significantly depending on the level of structural reliability required. It was also shown that machine, labour, tool, and indirect costs can contribute significantly to the total manufacturing cost. These non-material costs accounted for roughly 38.7% of the total manufacturing for a low-reliability structure and 25.4% for a high-reliability structure. This demonstrates the importance of accounting for non-material costs when designing composite parts.

Since the proposed novel methodology is based on bottom-up cost estimation with many individual unique activities, the cost estimates are very precise. This enables the user to examine the impact of both small and large design changes on the cost. It can also be easily be extended to a wide variety of structures and to both new and existing manufacturing procedures. For example, this current paper involves activities related to manual layup. New activities could be developed in the future for automated layup - extending the range of structures to which this newly developed methodology could be applied.

4 Conclusions

In conclusion, this work presented a novel comprehensive bottom-up methodology for the reliability-based manufacturing cost optimisation of composite aircraft structures. The proposed approach splits the manufacturing process into many individual activities, which can be combined in many different ways, allowing the proposed optimisation methodology to be applied to a wide range of composite aircraft structures. Furthermore, the proposed methodology takes into account not only material costs, but also other important costs such as machine, tooling, labour, and indirect costs, and investigates how these costs are influenced by the design parameters. As part of the optimisation procedure, a genetic algorithm (GA) was coupled with a deep neural network (DNN) to efficiently determine the optimal composite ply stacking sequence for every part of an assembled structure.

The proposed methodology was applied to a numerical example featuring a composite-stiffened panel from an aircraft fuselage composed of nine parts: skin, five stiffeners, and three frames. The structural reliability was based on buckling, a common mode of failure for aircraft structures. Results of the numerical example indicate that the proposed methodology for the reliability and manufacturing cost optimisation of composite aircraft structures agreed well with costing studies presented in the literature. It provided percentages for material, machine, labour, tool, and indirect costs, as well as percentages for activity costs, that are within ranges seen in the literature. It was shown that the material and labour costs can vary significantly depending on the level of structural reliability required. The proposed procedure is capable of providing an exact estimation of the influence of the two features, cost and reliability. For a low-reliability structure, material cost was 8750€ and constituted around 61.3% of total manufacturing costs, while for a high-reliability structure, this was 21,250€ and constituted around 74.6% of total manufacturing costs. The labour costs also increased from 1,850€ to 2,150€, due to the fact that more labour time is required to cut, layup, and inspect the additional prepreg material. This demonstrates the importance of accounting for non-material costs when designing composite parts.