Practical metamodel-assisted multi-objective design optimization for improved sustainability and buildability of wind turbine foundations

Abstract

In this work, we study the potential of using kriging metamodelling to perform multi-objective structural design optimization using finite element analysis software and design standards while keeping the computational efforts low. A method is proposed, which includes sustainability and buildability objectives, and it is applied to a case study of reinforced concrete foundations for wind turbines based on data from a large Swedish wind farm project. Sensitivity analyses are conducted to investigate the influence of the penalty factor applied to unfeasible solutions and the size of the initial sample generated by Latin hypercube sampling. A multi-objective optimization is then performed to obtain the optimum designs for different weight combinations for the four objectives considered. Results show that the kriging-obtained designs from samples of 20 designs outperform the best designs in the samples of 1000 designs. The optimum designs obtained by the proposed method have a sustainability impact 8–15% lower than the designs developed by traditional methods.

1 Introduction

Today, sustainable development considerations are becoming mainstream into most countries policies and legislation, as reflected by the United Nations’ 2030 Agenda for Sustainable Development. There is a need to tackle the economic, social, and environmental dimensions of sustainability in an integrated manner (UN 2015). This trend towards sustainability is of vital importance in the design of building and civil engineering structures, since the construction sector is one of the most important socio-economic sectors (Favier et al. 2018) at the expense of large negative environmental impacts (Taylor et al. 2006; Ramesh et al. 2010; Petek Gursel et al. 2014).

The importance of considering life-cycle sustainability criteria is being progressively recognized by stakeholders as appropriate choices in the early design stage are crucial to improve the sustainability of structures (Ek et al. 2019). Standards have been published in recent years to define the general principles and framework of the environmental, social, and economic sustainability assessment methods for civil engineering construction works (ISO 2019a; 2019b; CEN 2017). Yet, today, inclusive sustainability objectives are hardly ever used in real-world civil engineering projects to steer the structural design process towards more sustainable solutions. In addition, the number of design options considered is usually low as the structural engineer responsible for conducting the technical design, often, either inherits a design developed in a previous design stage or uses his/her past experience to come up with initial design parameters defining the geometry and properties of the structure. The structural design of reinforced concrete structures generally requires performing a large number of different checks, in accordance with design codes (e.g. the Eurocodes), in a supervised manner by the engineer, who commonly uses finite element (FE) analysis software to compute the load effects and to design the required quantities of concrete and steel reinforcement accordingly. In this context, achieving design improvements is a time-consuming process often conducted by trial and error, which limits the number of solutions that are evaluated (Boscardin et al. 2019). Different studies have previously shown how the solutions obtained in this traditional way may be suboptimal. Rempling et al. (2019) showed that the use of a set-based parametric design approach to calculate a larger number of design configurations could lead to reductions of material cost and CO₂ equivalent emissions of more than 20% for three studied types of bridges. This potential for improvement was corroborated by another study (Chalouhi et al. 2020) that showed that the use of heuristic optimization methods could reduce the material and labour costs and environmental impact of a multi-span reinforced concrete beam bridge by 10–15%. As described in Table 1, these different design approaches require different implementation efforts in terms of time and programming skills and allow different levels of exploration of the design space.

Table 1 Description of different design approaches and corresponding approximate number of design configurations considered

Additionally, assigning relative importance to the different objectives and aggregating them to find the solution that best fits the problem involve subjective judgements. This implies that the estimated optimal solution may change according to decision-making concerns as objectives are often competing. For this reason, a multi-objective optimization approach allowing the structural designer to find the set of most sustainable and feasible (i.e. fulfilling the constraints prescribed by design codes) solutions independently of the consideration of the different interests of decision makers would be of great value in practice and reduce the need for rework. The problem to be resolved can be mathematically formulated as follows:

$$\underset{x}{\mathrm{min}}\left({f}_{1}\left({\varvec{x}}\right),\dots ,{f}_{\mathrm{m}}\left({\varvec{x}}\right)\right),$$

(1a)

$${g}_{j}\left({\varvec{x}}\right)\le 0,$$

(1b)

$${\varvec{x}}\in {\mathbb{R}}^{D},$$

(1c)

where the variable ${\varvec{x}}$ is the vector of design parameters, ${f}_{i}, i=1, \ldots , m$ are objective functions and ${g}_{j}, j=1, \ldots , n$ are constraint functions that need to be fulfilled for a design to be considered feasible.

The structural optimization of concrete structures is commonly associated with high computational cost due to expensive structural analysis computations involving FE simulations and many load cases (e.g. for bridges and wind turbine foundations) (Mathern et al. 2020). Various evolutionary algorithms have been studied to optimize concrete structures (e.g. Jahjouh et al. 2013; Mergos and Mantoglou 2020). However, alternative methods need to be investigated to better address the expensiveness characteristic of the problem by reducing the number of calls of the FE procedure used in the structural design, which becomes even more relevant for multi-objective settings. The use of metamodels (or surrogate models) can reduce the computational cost by creating a mathematical response surface approximation that predicts the output from a set of inputs (Simpson et al. 2001). Kriging (Cressie 1990) is an increasingly popular metamodel, and despite more complex, it is more versatile and can provide more accurate results than other surrogate modelling methods such as polynomial models, moving least-squares, radial basis functions and support vector regression (Forrester and Keane 2009). Kriging also requires less training data than artificial neural networks, which makes it particularly interesting for applications where the training data are computationally expensive to generate (Simpson et al. 2001; García-Segura et al. 2017; Penadés-Plà et al. 2019). It was shown, on a concrete bridge design case that kriging-based heuristic optimization could reduce the computational time by more than 90% compared to conventional heuristic optimization without unduly affecting the quality of the obtained solutions (Penadés-Plà et al. 2019). Although kriging has often been applied in other fields, applications for structural optimization of civil engineering structures are still limited but have indicated good potential to handle the standard design constraints typical of structural engineering design problems (Lee and Kang 2006; Penadés-Plà et al. 2019). The selection of an adequate sampling plan is crucial to ensure a good prediction quality of the metamodel with only a few sample points (Forrester et al. 2008; Chang et al. 2016). One of the most widely used sampling methods is Latin hypercube sampling (LHS), which was first proposed by McKay et al. (1979).

Structural design optimization is of particular interest for wind turbine structures, as wind farm projects are especially capital-intensive and characterized by serial production of tens to hundreds of turbines. Minimizing the cost of wind energy is important to improve its competitiveness against non-renewable energy sources and support its current development in line with the ambitious energy and climate targets set by many countries. Although the largest part of the total investment costs of a wind farm project corresponds to the wind turbines (tower and rotor-nacelle assembly), the foundations required to support these very tall structures subjected to large and complex loads account for a significant share of the costs (5–7% of the total investment costs for the wind farm project considered in this study) and consume important amounts of materials. Foundations are typically designed on a project basis taking into account the loads from the previously selected wind turbine and the local geotechnical conditions of the site. This project-based design effort means that foundations are typically considerably less optimized than the high-end technology turbines they support, leaving a margin for improvement and reduction of their sustainability impact. The serial production of wind turbine foundations makes it particularly worthwhile to invest in the higher design effort required in the early planning and design stage to seek minimizing cost and maximizing sustainability and buildability. However, reaching this target requires the development of multi-objective optimization methods that are applicable in practice with appropriate sustainability objectives and to prove their potential. Such methods have been recently applied, e.g. for reinforced concrete beams (Mathern et al. 2020) and bridges (Rempling et al. 2019) but have not been studied before for onshore wind turbine foundations.

The main aim of this study is to examine the potential of using kriging to perform multi-objective design optimization of wind turbine foundations taking into account a comprehensive set of sustainability and buildability objectives. To do so, a case study based on data from a large Swedish wind farm project is considered. The study seeks to propose and evaluate an implementation procedure to determine designs with the best performance compatible with common structural engineering practice, i.e. according to design codes and based on the use of a common commercial FE analysis software. The design optimization process proposed in this work builds on the kriging-based heuristic optimization process presented in (Penadés-Plà et al. 2019). Their work was applied to bridges, whereas here the method is applied to wind turbine foundations. Additionally, we here expand their work by including structural design based on FE analysis and multiple sustainability objectives assessed in a life-cycle manner with buildability as a fourth dimension. In summary, this work brings three novel features to the design methods for optimization of structures. (1) It integrates objective functions based on more comprehensive life-cycle sustainability assessment than what is available in the current literature on sustainability-driven structural design optimization, i.e. the assessment covers multiple life-cycle impact categories in the three dimensions of sustainability over several life-cycle stages, as well as the additional dimension of buildability. (2) The kriging-based heuristic optimization process, previously developed in (Penadés-Plà et al. 2019), is here adapted for the first time to reduce the expensive computations associated with common FE calculations for the structural design of reinforced concrete structures. (3) In contrast with previous literature, structural design optimization is here applied to onshore wind turbine foundations. The proposed method is evaluated through a real-world case study based on industrial data from a Swedish wind farm project.

2 Material and methods

2.1 Design case definition

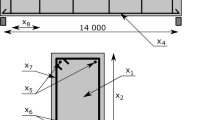
The design case considered in this work is based on the foundation design for the phase 1 of the Markbygden wind farm, located in the north of Sweden, which was built in 2017–2019. It comprises 314 turbines with a capacity of 3.6 MW, a hub height of 131 m, and a rotor diameter of 137 m. The turbines are supported by reinforced concrete gravity foundations based on a gravel base over glacial till. The static Young’s modulus of the soil is 50 MPa, which yields a modulus of subgrade reaction of 12 MN/m/m². The soil resistance, ${\sigma }_{\mathrm{Rd}}$, is 200 kPa. The foundations are designed for a service life of 30 years. The reinforcement bars have a characteristic yield strength of 500 MPa and are arranged in a radial and tangential layout, as illustrated in Fig. 1.

Fig. 1

Schematic view of foundation and reinforcement layout (in red, A radial reinforcement, B tangential reinforcement, C shear reinforcement) with indication of geometrical parameters used. (Color figure online)

In this study, the foundation was parametrized as described in Fig. 1. The design parameters are discretized, and their possible values are listed in Table 2, resulting in almost 300 million possible configurations. The diameter, ${d}_{\mathrm{r}}$, and width, ${w}_{\mathrm{r}}$, of the tower-base ring connecting the wind turbine tower to the foundation were determined previously by the turbine manufacturer in this project (${d}_{\text{r}}=5.16 \, \text{m}$ and ${w}_{\mathrm{r}}=0.5 \, \text{m}$). The chosen material parameter corresponded to various common concrete classes, characterized by different characteristic concrete strengths ${f}_{\mathrm{ck}}$.

Table 2 Design parameters and their possible values

2.2 FE analysis

FE analyses were conducted in Abaqus CAE 6.14-2 (Dassault Systèmes 2014) to determine the effects of the design loads to be used in the design process. The model consisted of shell elements with a linearly varying thickness from the edge of the foundation to the edge of the pedestal and a constant thickness on the pedestal, in accordance with the foundation geometry shown in Fig. 1. Such FE model based on shell elements is often used in practice to design reinforced concrete structures, and it is justified here by the fact that the foundations are relatively slender. Additionally, the model was built with a hole in the middle, see Fig. 2. This is a common workaround used in practice to take into account the fact that no reinforcement is placed at the centre of the foundation. Comparisons with a model without hole indicated that it is an assumption on the safe side and provides a more realistic load distribution around the tower base to enable the necessary transfer of forces from the radial to the tangential reinforcement.

Fig. 2

Triangular load applied in the model. The tower-base ring is marked in red. (Color figure online)

The concrete material was modelled as linear elastic according to the concrete class defined for each configuration. The concrete mechanical properties used in the analysis were derived from ${f}_{\mathrm{ck}}$ according to the Eurocode 2 (CEN 2004a), where the mean value of compressive strength is ${f}_{\mathrm{cm}}={f}_{\mathrm{ck}}+8 (\mathrm{MPa});$ the modulus of elasticity is ${E}_{\mathrm{cm}}=22\times {10}^{3}\times {\left(\frac{{f}_{\mathrm{cm}}}{10}\right)}^{0.3}(\mathrm{MPa})$; and the Poisson’s ratio is $\nu =0.2$. Using linear elastic analysis constitutes standard practice in design of reinforced concrete structures to keep computational time low and reduce modelling complexity; for instance, the use of nonlinear analysis is not accepted in Sweden for the design of transport infrastructures in reinforced concrete (Swedish Transport Agency 2018). Applied loads are described in Table 3. Design load cases and load values from the wind effects caused on the wind turbine rotor-nacelle assembly and tower are gathered in Appendix 1. These loads are applied in a partition made at the location of the tower-base ring, see Fig. 2. These are load cases for checking stability as well as structural integrity.

Table 3 Loads applied in the model

The boundary conditions were applied in a way that soil elasticity was taken into account. To do so, each node in the model was connected to a fixed point by a nonlinear spring, which acted only in compression with a stiffness in accordance with the modulus of subgrade reaction defined in Sect. 2.1.

The results were extracted as sectional forces and moments integrated in the shell section. As the coordinates system used was cylindrical, the output was obtained in the direction of the radial and tangential reinforcement. All the load effects were extracted in a path that followed the wind direction, see Fig. 3. This proved to yield maximum effects, except for shear forces, which were, therefore, also extracted along a path perpendicular to the wind direction.

Fig. 3

a Colour plot of moment about tangential direction (used to dimension radial reinforcement). The red line between the points A and B represents the path along which forces are extracted for the design in the wind direction. b Schematic representation of moment about tangential direction as function of the radial coordinate along the red extraction line in (a)

2.3 Structural design

The structural design was conducted according to regulations by the turbine manufacturer, the Eurocodes (CEN 2002, 2004a, b, 2005), the Swedish National Annex EKS 10 (Boverket 2015), and guidelines from DNV-GL (DNV/Risø 2002). Aspects to improve buildability were also taken into consideration according to project specifications (e.g. choice of design parameters values and limitation of top surface angle). The design constraints, ${g}_{i}$, considered are presented in Table 4, along with constraint violation factors, ${\eta }_{i}$ (larger than 1 if the constraint is violated).

Table 4 Summary of constraints, ${g}_{i}$, used in the foundation design, and constraint violation factors, ${\eta }_{i}$

The necessary amounts of bending and shear reinforcement were determined given the design criteria shown in Table 5. The bending reinforcement was estimated with an approximation often used in preliminary design. The calculation of shear reinforcement was done according to the design formula in the Eurocode 2, Sect. 6.2.3 (CEN 2004a). The load cases and design loads used for the check of the geotechnical constraints and for the design of reinforcement for Ultimate Limit State (ULS) are detailed in Appendix 1. Serviceability and fatigue limit states were not covered in this study. However, they could be included in the calculations in the same way as for the design for ULS, which may affect the reinforcement amounts obtained to a limited extent.

Table 5 Summary of criteria for design of reinforcement

2.4 Objectives definition

The proposed method of assessment encompassed all three dimensions of sustainability (economic, environmental, and social) based on life-cycle assessment (LCA) following the frameworks established by EN 15643-5:2017 (CEN 2017) and ISO 21931-2:2019 (ISO 2019b). Hence, the three corresponding objectives are evaluated using life-cycle cost (LCC), environmental LCA (E-LCA), and social LCA (S-LCA), respectively. In this work, a fourth dimension was included to complete the sustainability assessment, namely buildability, and evaluated in terms of construction time. The objective functions taken into account for each dimension are summarized in Table 6. They all correspond to negative impacts and need to be minimized.

Table 6 Objective functions considered in the assessment

This study focused on the optimization of the foundation for a preselected type of wind turbine and its associated loads. Hence, the object of assessment was the reinforced concrete foundation, which is why the wind turbine (i.e. the tower and rotor-nacelle assembly) and the tower-foundation connection (i.e. flanges and bolts) were not included in the assessment. A civil engineering works life cycle includes several stages, defined in EN 15643-5:2017 (CEN 2017). The relevant stages for the case study considered in this work are the product stage (A1–3) and the construction process stage (A4–5), but other stages could be integrated in a similar way when applying the method to a different case. The use and end-of-life stages were not included in the assessment as the foundations are buried under the ground and no control nor maintenance actions were planned during their service life, and what would happen with the foundation at the end of their service life (e.g. repowering, leaving them in place, recycling) was not yet defined. The pre-construction stage A0 was also excluded as it would have been identical for all designs. The materials, transport, and activities involved in the construction of the foundations were taken into considered in the assessment.

2.4.1 Economic

In this study, the objective function, ${f}_{1},$ associated with the economic impact was defined as the total cost, $C,$ associated with the production of the foundations:

$${f}_{1}\left({\varvec{x}}\right)=C\left({\varvec{x}}\right)={C}_{\mathrm{m}}\left({\varvec{x}}\right)+{C}_{a}\left({\varvec{x}}\right)+{C}_{\mathrm{tr}}\left({\varvec{x}}\right),$$

(2)

where ${C}_{\mathrm{m}}$ corresponds to the material cost, ${C}_{\mathrm{a}}$ to the cost of construction activities and ${C}_{\mathrm{tr}}$ to the cost of transport.

The material cost, ${C}_{\mathrm{m}}$, was calculated as the sum of the unit price (see Table 9 in Appendix 1), ${p}_{\mathrm{m},\mathrm{k}}$, for each material, $k$, times the respective material quantity, ${Q}_{\mathrm{m},\mathrm{k}}$, as follows:

$${C}_{\mathrm{m}}\left({\varvec{x}}\right)=\sum_{\mathrm{k}}{p}_{\mathrm{m},\mathrm{k}}\times {Q}_{\mathrm{m},\mathrm{k}}\left({\varvec{x}}\right).$$

(3)

The cost of construction activities, ${C}_{\mathrm{a}}$, is equal to the unit labour cost, ${p}_{\mathrm{a}}$, times the time required for construction activity, ${\mathrm{T}}_{\mathrm{a}}$,

$${C}_{\mathrm{a}}\left({\varvec{x}}\right)={p}_{\mathrm{a}}\times {T}_{\mathrm{a}}\left({\varvec{x}}\right),$$

(4)

in which the time of construction activity, ${T}_{a}$, was calculated as the sum of the unit time for the construction activity associated with each material times the respective material quantity, as follows:

$${T}_{a}\left({\varvec{x}}\right)=\sum_{k}{T}_{m,k}\times {Q}_{m,k}\left({\varvec{x}}\right),$$

(5)

where ${T}_{\mathrm{m},i}$ corresponds to the unit price for each construction activity k, as given in Table 10.

The cost of transport, ${C}_{\mathrm{tr}}$, is equal to the unit transport cost, ${p}_{\mathrm{tr},\mathrm{k}},$ for each material, $i$, times the corresponding distance, ${d}_{\mathrm{tr},\mathrm{k}}$, (as specified in Table 11), times the respective material quantity,

$${C}_{\mathrm{tr}}\left({\varvec{x}}\right)=\sum_{\mathrm{k}}{p}_{\mathrm{tr},\mathrm{k}}\times {d}_{\mathrm{tr},\mathrm{k}}\times {Q}_{\mathrm{m},\mathrm{k}}\left({\varvec{x}}\right).$$

(6)

2.4.2 Environmental and social

The evaluation of the environmental objective function, f₂, and social objective function, f₃, followed the same pattern as the economic one previously described:

$${f}_{2}\left({\varvec{x}}\right)=E\left({\varvec{x}}\right)={E}_{\mathrm{m}}\left({\varvec{x}}\right)+{E}_{\mathrm{a}}\left({\varvec{x}}\right)+{E}_{\mathrm{tr}}\left({\varvec{x}}\right),$$

(7)

where ${E}_{\mathrm{m}}$ corresponds to the material environmental impact, ${E}_{\mathrm{a}}$ to the environmental impact of construction activities and ${E}_{\mathrm{tr}}$ to the environmental impact of transport, and,

$${f}_{3}\left({\varvec{x}}\right)=S\left({\varvec{x}}\right)={S}_{\mathrm{m}}\left({\varvec{x}}\right)+{S}_{\mathrm{a}}\left({\varvec{x}}\right)+{S}_{\mathrm{tr}}\left({\varvec{x}}\right),$$

(8)

where ${S}_{\mathrm{m}}$ corresponds to the material social impact, ${S}_{\mathrm{a}}$ to the social impact of construction activities and ${S}_{\mathrm{tr}}$ to the social impact of transport.

The environmental assessment was conducted using the endpoint approach of the ReCiPe 2008 method and data of Ecoinvent database (Ecoinvent 2016). Each term ${E}_{j}$ of Eq. (7) was evaluated as in Eq. (9), by adding the three endpoint damage categories defined in the ReCiPe 2008 method, using the Europe H/H normalization and weight values to obtain the overall environmental impact. The damage categories are previously obtained by aggregation of 18 midpoint impact categories, e.g. climate change, human toxicity and mineral resource depletion (Goedkoop et al. 2009).

$${E}_{j}\left({\varvec{x}}\right)={E}_{j,\mathrm{EQ}}\left({\varvec{x}}\right)+{E}_{j,\mathrm{RC}}\left({\varvec{x}}\right)+{E}_{j,\mathrm{HH}}\left({\varvec{x}}\right),$$

(9)

where ${E}_{j,\mathrm{EQ}}$ represents the damage to ecosystem quality, ${E}_{j,\mathrm{RC}}$ the resources consumption, and ${E}_{j,\mathrm{HH}}$ the damage in human health.

In a similar manner, the social impact was obtained by adding the four stakeholders of the Social Impacts Weighting Method, using the PSILCA database (GreenDelta 2013), associated with the processes of the Ecoinvent database by means of an add-on called SOCA (Eisfeldt 2017). This procedure allowed performing the S-LCA using the same processes as the E-LCA to ensure the coherence of the overall assessment. Therefore, each term ${S}_{j}$ of Eq. (8) was evaluated as in Eq. (10),

$${S}_{j}\left({\varvec{x}}\right)={S}_{j,\mathrm{W}}\left({\varvec{x}}\right)+{S}_{j,\mathrm{VCA}}\left({\varvec{x}}\right)+{S}_{j,\mathrm{S}}\left({\varvec{x}}\right)+{S}_{j,\mathrm{LC}}\left({\varvec{x}}\right),$$

(10)

where ${S}_{j,\mathrm{W}}$ represents the social impact in workers, ${S}_{j,\mathrm{VCA}}$ the one in value chain actors, ${S}_{j,\mathrm{S}}$ in society, and ${S}_{j,\mathrm{LC}}$ in local community.

2.4.3 Buildability

As the different designs assessed in this study were based on the same concept and included the same type of construction activities, the buildability objective function, ${f}_{4}$, was measured in this study as the number of working hours required for the construction works, $T$, including construction activities, ${T}_{\mathrm{a}},$ and transport on site and to the site, ${T}_{\mathrm{tr}}$:

$${f}_{4}({\varvec{x}})=T\left({\varvec{x}}\right)={T}_{\mathrm{a}}\left({\varvec{x}}\right)+{T}_{\mathrm{tr}}\left({\varvec{x}}\right),$$

(11)

where ${T}_{\mathrm{a}}$ is calculated according to Eq. (5), and ${T}_{\mathrm{tr}}$ is calculated as the sum of the times necessary for transport for each material i, considering the respective unit transport times, ${t}_{\mathrm{tr},i}$, and distance, as defined in Table 10, in the following manner:

$${T}_{\mathrm{tr}}\left({\varvec{x}}\right)=\sum_{i}{t}_{\mathrm{tr},i}\times {d}_{\mathrm{tr},i}\times {Q}_{\mathrm{m},i}\left({\varvec{x}}\right).$$

(12)

2.4.4 Multi-criteria decision making

Converting the different objectives into a single quantifiable indicator constitutes a multi-criteria decision-making (MCDM) problem. To do so, weights need to be predefined for the objectives according to the stakeholders’ perception of their relative importance. Additionally, it is necessary to normalize the objective function values as economic, environmental, social, and buildability objectives are often measured in different units.

In this work, the indicator used was called sustainability index, $I$, and it was defined as follows:

$$I\left({\varvec{x}}\right)=\sum_{i}{w}_{i}\times {f}_{i,n}\left({\varvec{x}}\right),$$

(13)

with

$$\sum_{i}{w}_{i}=1,$$

(14)

where ${w}_{i}$ represents the different weights and ${f}_{i,n}$ the normalized values for the different objective functions assessed for each feasible design. The latter was calculated as the ratio of the objective function value, ${f}_{i}$, for this specific design, to the average, ${f}_{i,m},$ of the initial sample population considered:

$${f}_{i,n}\left({\varvec{x}}\right)=\frac{{f}_{i}\left({\varvec{x}}\right)}{{f}_{i,m}}.$$

(15)

2.5 Kriging-based heuristic optimization process.

Figure 4 shows the flow chart of the design optimization process used in this work. It builds on the metamodel-based heuristic optimization process presented in Penadés-Plà et al. (2019). The process is further developed here by integrating FE modelling for the structural analysis and design, and MCDM with a more comprehensive set of objectives assessed in a life-cycle manner.

Fig. 4

Flow chart of design optimization process

A purpose-written Python script was developed in this work to control the FE analysis and the structural design of the foundations. The computations were carried out on a single computer cluster node with 20 cores built on Intel Xeon E5-2650v3 (“Haswell”) CPU and 64 GB of RAM. The FE analysis was computationally expensive, taking approximately 60 s to complete for a single foundation, which called for the use of a metamodel to limit the number of FE simulations required in the optimization process.

In metamodel-based optimization, the optimization process is carried out from a response surface approximation derived from an initial sampling. In this work, initial samples were obtained by LHS using uniformly distributed intervals to guarantee that all the design parameters were represented along their respective ranges. LHS defines the position of the sample points according to the initial defined sample size. In this work, to study the influence of the sample size, the optimization process was carried out considering different sample sizes, N: 10, 20, 50, 100, 200, 500, and 1000.

The initial sampling covers the whole design space, and some of the designs in the samples were not feasible as they did not fulfil all the geometrical and geotechnical constraints defined in Table 4. To reduce computational time, the structural design step was interrupted for these designs after these preliminary checks. It was possible to do so for all the constraints considered here since they had known analytical expression. These constraints were chosen as they were the ones used in the design of the foundations for the industrial project that this case study is based on, to ensure the comparability of the results. If the problem had also included constraints of which evaluation relied on results from the FE analysis, the same design optimization process could have been followed by evaluating these constraints at a later stage of the structural design.

To maintain the sample size, a first kriging surface was used to predict the objective function’s values for the unfeasible designs. This kriging surface was built using the values obtained for the feasible designs in this sample (i.e. after conducting full structural design and MCDM). Before calculating the second kriging surface to be used in the optimization process, two alterations were applied to the imputed objective values of the unfeasible designs, with the aim of reducing the probability of getting optimum designs in non-feasible regions of the design space. First, a modification of the imputed values was done by setting a lower bound equal to the minimum value of all the feasible designs in the considered sample. Additionally, penalties were applied to the imputed values of the unfeasible designs by multiplying them by a penalty factor. Different penalty factors were investigated in this work: three constant penalty factors, p = 1 (no penalty), p = 1.25, p = 1.5, as well as a variable penalty factor, p = p_var, according to Eq. (16). This variable penalty factor ranges between 1 and 1.5, and it is a function of the constraint violation factors (see Table 4). Each of the four penalty factors was applied to all the different sample sizes considered in order to determine the influence of this parameter on the kriging model. The kriging code used in this work was developed based on the DACE kriging toolbox (Lophaven et al. 2002a, b), as described in more detail in Appendix 3.

$${p}_{\mathrm{var}}\left({\varvec{x}}\right)=\mathrm{min}\left[\underset{i}{\mathrm{max}}\left({\eta }_{i}\left({\varvec{x}}\right); 1\right);1.5\right].$$

(16)

The search for the optimal design was carried out using the metaheuristic simulated annealing (SA) algorithm (Kirkpatrick et al. 1983) applied to the kriging model. The use of SA was supported by its versatile acceptance criteria, which is the reason why it is used in many studies to carry out conventional heuristic optimization, e.g. (Medina 2001; Camp and Huq 2013). In each iteration of the optimization process, the design parameters were modified according to the chosen algorithm, and the value of the objective function was calculated using the mathematical approximation created by the kriging model. This value was then compared with the one of the previous iterations to determine if there was any improvement. The SA calibration was done according to the method proposed by Medina (2001), which suggests to halve the initial temperature when the percentage of acceptance is greater than 40% and to double it when the percentage of acceptance is lower than 20%. After that, the temperature decreases according to a coefficient of cooling k following the equation $T=k\times T$, when a Markov chain ends. In this work, the calibration revealed that a coefficient of cooling of 0.8 and a Markov chain length of 1000 were appropriate. The SA algorithm was terminated after three Markov chains showed no improvement.

In order to account for the variability of the process and obtain statistically significant results, nine different samples were generated by LHS for each initial sample size (i.e. N = 10, 20, 50, 100, 200, 500 and 1000) and used to create different kriging surfaces. In addition, a tenth sample was generated for each sample size N, to validate the accuracy of the kriging surfaces prior to conducting the optimization. For each sample size, the kriging surface error was defined as the average relative error between the calculated sustainability index values for the feasible designs of the tenth sample and the corresponding predicted values computed from each of the nine kriging surfaces. The error in the prediction of the objective function values provided insight into whether the model was adequate for subsequent optimization. Finally, once the optimization algorithm returned a prediction that was deemed optimal, the structural design and MCDM steps were repeated to verify its actual feasibility and sustainability performance.

2.6 Mono- and multi-objective settings

First, a mono-objective optimization was conducted to study the influence of different characteristics of the kriging-based optimization (sampling size and penalty factor). To do so, the four objectives (economic, environmental, social, and buildability) were considered equally important when calculating the sustainability index used as single objective function in the optimization process according to Eq. (1a), i.e. the relative weight associated with each one of these objectives was 0.25.

Once the best behaviour of the kriging-based optimization was determined, multi-objective optimization was done by performing the optimization process several times for different objective weight combinations to obtain a Pareto set of designs that forms a preferred trade-off between the sustainability and buildability objectives considered. For this purpose, the relative weights (${w}_{1}$, ${w}_{2}$, ${w}_{3}$, and ${w}_{4}$) were discretized into multiples of 0.05 (i.e. 0, 0.05, 0.1, …, 1), and combined such that they summed to one, leading to 266 possible weight combinations. In order to measure the quality of the set of Pareto solutions, the common hypervolume indicator was used (Zitzler and Thiele 1999). This indicator measures the volume of the space enclosed by the Pareto front and a reference point. The reference point used to calculate the normalized hypervolume was

$$r=\left[\mathrm{max}\left({f}_{1,n}\right), \mathrm{max}({f}_{2,n}),\mathrm{max}({f}_{3,n}),\mathrm{max}({f}_{4,n})\right],$$

(17)

where $\mathrm{max}\left({f}_{i,n}\right)$ corresponds to the maximum value reached by the objective function $i$ for all the initially generated designs.

As different initial sample sizes were considered and several runs were conducted for each of them in both the mono-objective and multi-objective settings, the normalized objective function value, ${f}_{i,n}$, for each objective i, was calculated as described in Eq. (15), using for ${f}_{i,\mathrm{m}}$ the average value of the feasible sample designs from the nine initial series with the largest sample size (i.e. N = 1000).

3 Results and discussion

3.1 Mono-objective optimization

As a first step, a mono-objective optimization was performed to study and choose the best way to carry out the kriging-based optimization. For this purpose, two different sensitivity analyses were performed: to study the influence of the initial sample size obtained by LHS and of the penalty factor applied to unfeasible solutions of the initial sample. In both cases, the goal was to determine the design with the lowest sustainability index considering all objectives to be equally important.

Figure 5 shows the average error and standard deviation (shaded areas), obtained from nine different kriging surfaces, for each initial sample size and penalty factor. Results showed that the kriging surfaces that best predicted the objective value were the ones obtained with p = 1.00 (i.e. without penalty) and with an initial sample size greater than N = 50, for which the error was about 5%. The fact that the best results were obtained when the kriging surface was not altered indicates that the alteration of the kriging surfaces using penalties considerably affects the accuracy of the predicted results. Although the average errors were similar between N = 50 and N = 1000 for a penalty p = 1, the standard deviation decreased between these sizes, i.e. the variability decreased when the sample size increased. The results do not reveal any significant improvement when using the variable penalty factor p = p_var (i.e. varying between 1 and 1.5) instead of the constant one of 1.5. For the problem considered with six design parameters, it appears necessary to create the kriging surface from initial samples consisting of at least 50 configurations to obtain good predictions.

Fig. 5

Influence of sample size (N) and penalty factor (p) on kriging surface error, and area within ± 1 standard deviation from the average (shaded areas). For each population and penalty factor, the kriging surface error corresponds to the average relative error between the predicted values using nine kriging surfaces of the sustainability index of the designs of a tenth surface and the calculated values for the designs of this tenth surface

Figure 6 shows the sustainability index of the kriging-obtained solutions for the different initial sample sizes and the influence of the penalty factor applied. The sustainability index obtained without penalty (p = 1) was marked by a sharp fall when the sample size increased from 10 to 20. Larger sample sizes seem to be required to reach similar sustainability performance with the penalty factor of 1.25. The sustainability of the solutions was poorer and the variability larger with the penalty factor of 1.5 and the variable one. These results can be explained by the larger kriging surface error observed for the series p = 1.5 and p = p_var in Fig. 5.

Fig. 6

Average sustainability index of kriging-obtained optimum solutions versus initial sample size (N) for different penalty factors (p)

Figure 7 shows a comparison between the sustainability index of the series without penalty (p = 1) and the average of the lowest sustainability index obtained for all the designs in the initial LHS-generated samples. The results showed that the designs obtained using a kriging surface based on a sample of 20 or more designs outperformed in average the best designs in the LHS-generated sample of 1000 designs. This result clearly highlights the potential of the kriging metamodel to reduce the computation time needed to obtain good-performance designs by limiting the extent of expensive FE analyses required.

Fig. 7

Average sustainability index of initial sample population and average sustainability index of kriging-obtained optimum solutions versus initial sample size (N) for penalty factor p = 1 (i.e. no penalty)

The results obtained here are in line with previous findings (Penadés-Plà et al. 2019) for kriging-based optimization of the embodied energy of concrete box-girder bridge designs. In both studies, the best performance was exhibited when no penalty was applied, and the kriging surface error was approximately 4–5% for N larger or equal to 50. In this previous study, little improvement of the results was observed for sample sizes larger or equal to 50, while this was already observed here from N = 20.

3.2 Multi-objective optimization

In a second phase, multi-objective optimization was performed to obtain the Pareto front of the most sustainable foundation designs for different combinations of weights for the four objectives considered. Based on the results from the mono-objective optimization, no penalty was used in this phase (p = 1).

Figure 8 shows the average normalized hypervolume values obtained for each sample size considered. It includes both the average hypervolume from the nine LHS initial samples and the one from the nine kriging generated sets of solutions to the multi-objective optimization problem based on the same initial samples.

Fig. 8

Normalized hypervolume as function of initial sample size (N) averaged over 9 runs without penalty (i.e. penalty factor of 1)

Similar to the mono-objective setting results, the normalized hypervolume calculated from the kriging solutions underwent a significant improvement when the kriging surface was interpolated from an initial sample with a size N = 20 or higher. These results revealed that the set of Pareto solutions obtained by the kriging metamodel based on 20 or more initial designs was better than the Pareto solutions obtained from 1000 LHS-generated designs. Although the normalized hypervolume of the kriging solutions did not improve significantly when using initial samples with more than 20 points, the spread of the results appeared to decrease for initial samples of 200 or more points.

Note that in this work a large number of weight combinations (i.e. 266 in total with the weight increment considered of 0.05) were calculated for the sake of accuracy and analysing the potential of the method. This number of combinations is rather large, given that each Pareto front was composed of one to five solution points. The reduced number of Pareto solutions in this case can be explained by the fact that the objectives taken into account are not conflicting a lot despite that they are related to very different aspects, similar to the results obtained for the two objectives of cost and CO₂ emissions in previous works (Camp and Assadollahi 2013; Yepes et al. 2015; Rempling et al. 2019). Finding the optimum design for each of these 266 combinations was done using the kriging metamodel, which does not involve the expensive structural analysis calculations using the FE method. What takes time instead is the verification of the solutions in the last step of the process. Therefore, in a practical application structural engineers could verify only the solutions corresponding to the expressed stakeholder’s preferences and possibly the ones in their immediate vicinity.

3.3 Influence of design approach

In the previous part, feasible designs obtained using kriging-based heuristic optimization were compared to the best designs from the initial LHS-generated sample. It should be noted that neither of these two approaches constitutes common practice today in design offices. An attempt is made here to evaluate the influence of the design approach on the performance of the developed designs on the case study at hand.

In the real-world industrial project on which the case study of this work is based, the technical design was first conducted using the design configuration developed in the predesign stage of the project due to limited time. This design was then refined in a trial-and-error manner inspired by engineering judgement in an attempt to reduce material quantities. In this second step, around ten solutions were investigated. However, the configuration used in the predesign had a definite influence on these results as the iterations started from it, which is mostly explained due to time limitations to select a design to be further developed (e.g. to produce the full technical design, the technical drawings and specifications, etc.). As a consequence, many possibly better-performing configurations were obviously disregarded at this stage. Using parametric design allows calculating a much larger number of design configurations, as was done in this work when calculating all the initial LHS-generated design configurations. Using metamodel optimization as was done with kriging in this work is a further development that allows to consider all possible design configurations. These four approaches require different design efforts (recall Table 1).

To put the results here obtained into context, the sustainability performances of the designs developed by the different design approaches are represented in Fig. 9. This comparison reveals that the optimum design obtained by kriging has a sustainability index 15% lower than the original predefined design and around 8% better than the best design obtained by trial-and-error improvement. This rate of improvement depends certainly on the quality of the predesign and of the engineer’s experience and judgment in the trial-and-error improvement process. However, it clearly appears that the use of kriging-based optimization can lead to further substantial improvement of the sustainability of the structure. In the case study investigated, satisfactory results were obtained, and therefore, it was not deemed necessary to include further complexity to the kriging metamodel. In more complex problems, it may be necessary to assess the need to update the kriging metamodel with infill points during the optimization process.

Fig. 9

Influence of design approach on sustainability of designs. The ranges for the sustainability index (SI) values cover all the considered improved designs obtained by trial and error, the best designs from each initial sample with a size of N = 1000 generated by Latin hypercube sampling (LHS) and the optimum designs obtained by kriging-based optimization without penalty (p = 1) using initial LHS-generated samples of sizes N = 20 to 1000

The parameter values, material quantities, and objective values for the designs with the lowest SI in Fig. 9 are detailed in Appendix 4. The best designs obtained by trial-and-error improvement and LHS have sensibly similar geometries to that of the unique predefined design. Interestingly, kriging-based optimization not only led to better designs with the same kind of geometry but also to an even better solution with a markedly different geometry (i.e. a thinner foundation with a larger diameter that is more heavily reinforced but using substantially less concrete). The analysis of the results reveals that this solution is characterized by the reduction of the concrete class and the quantity of concrete. Both these parameters impact the amount of cement required, which appears to be the dominant factor influencing the sustainability of the designs for wind turbine foundations.

4 Summary and conclusions

The aim of the present study was to investigate the potential of using metamodels for multi-objective structural design optimization in a manner compatible with real engineering practice. The proposed method integrates kriging-based heuristic optimization, FE analysis, and multi-criteria assessment. To verify the applicability and potential of the method, the optimization process developed was applied on a case study dealing with the design optimization of wind turbine foundations of a real-world project of a Swedish wind farm. This case study integrated FE analysis to compute the load effects on the structure and the verification of constraints in accordance with design codes.

The results shown in this paper indicate that a kriging model can be effectively used to find promising designs for a low number of calls of the expensive FE-based design procedure. The proposed method enabled us to generate designs that performed better in terms of the sustainability and buildability indicators considered, both in a mono-objective setting and in a multi-objective setting. This use of a metamodel is especially interesting for achieving multi-objective optimization and for uncoupling the determination of the relative importance of the objectives from the design and optimization process, which allows solving the MCDM problem in parallel or after the design stage. The findings of this study indicate that a kriging surface based on an initial sample size of only 20 designs results in good-quality designs. In the considered case study, the kriging-based optimization method led to an improvement by 8% to 15% of the sustainability index of the designs developed in practice.

Appendices

Appendix 1: Design loads

Load cases used for check of geotechnical design constraints are shown in Table 7, while load cases for design of reinforcement in ULS are presented in Table 8.

Table 7 Design loads for check of geotechnical design constraints

Table 8 Design loads for check of ULS, including partial safety factors, considering all applicable load cases (normal, abnormal and erection) according to the IEC 61400-1 design standard (IEC 2014)

The z-axis corresponds to the vertical axis and the r-axis corresponds to a radial axis in the acting wind direction.

Appendix 2: Data used for objectives assessment

A unit labour cost for construction activities of 69.8 €/h was taken into account according to (Wikells 2018). This cost includes direct costs (i.e. social security and payroll taxes) and indirect costs (e.g. site installation, equipment, transport, administrative and management costs, waste). The data have been retrieved from the Markbygden wind farm project and complemented with (Wikells 2018; Catalonia Institute of Construction Technology 2020). Unit costs, unit times, and transport distances used for criteria assessment, in the case study, at hand, are detailed in Tables 9, 10, and 11, respectively.

Table 9 Unit costs for construction materials and associated transport

Table 10 Unit times for construction activities and transport of materials

Table 11 Transport distances for different materials

Appendix 3: Kriging metamodel

Kriging is a spatial interpolation method that was originally developed for mining and geostatistical applications (Matheron 1963; Cressie 1990; Forrester et al. 2008). Kriging takes into account the spatial correlation of the data. The idea behind kriging is that the unknown deterministic response (of interest) $y\left({\varvec{x}}\right)$ can be described as in Eq. (17):

$$y\left({\varvec{x}}\right)=h\left({\varvec{x}}\right)+Z\left({\varvec{x}}\right),$$

(17)

where $h\left({\varvec{x}}\right)$ is the known approximation function that provides a global approximation of the design space, and $Z\left({\varvec{x}}\right)$ is a realization of a stochastic process with zero mean, variance ${\sigma }^{2}$ and non-zero covariance, which creates local deviations so that the kriging model interpolates the initial sample points, see Eq. (18).

$$cov\left[Z\left({x}^{i}\right),Z\left({x}^{j}\right)\right]={\sigma }^{2}\times R\left({x}^{i},{x}^{j}\right)$$

(18)

where the process variance ${\sigma }^{2}$ scales the spatial correlation function $R\left({x}^{i},{x}^{j}\right)$ between two data points. The kriging code used in this work was developed based on the DACE kriging toolbox (Lophaven et al. 2002a, b). The approximation function was considered constant in this work (i.e. the model becomes equivalent to ordinary kriging). The Gaussian correlation function, as defined in Eq. (19), was chosen for the stochastic process $Z\left({\varvec{x}}\right)$.

$$R\left({x}^{i},{x}^{j}\right)=\mathrm{exp}\left(-\sum_{k=1}^{q}{\theta }_{k}{\left|{x}_{k}^{i}-{x}_{k}^{j}\right|}^{2}\right).$$

(19)

This Gaussian correlation function, commonly used in engineering design, is defined by the unknown hyperparameters ${\theta }_{k}$ that fit the model to the data in hand by controlling the area of influence of nearby points (Simpson et al. 2001; Forrester and Keane 2009). The hyperparameters ${\theta }_{k}$ are determined by maximum likelihood estimation (Lophaven et al. 2002b).

Appendix 4: Details of the designs with the lowest SI in Fig. 9

Table 12 provides the details of the solutions with the lowest sustainability index for each design approach, as represented in Fig. 9.

Table 12 Details of solutions with lowest SI for each design approach in Fig. 9: input variables, ${x}_{1-6}$ objectives, ${f}_{1-4}$ sustainability index, SI and material quantities, including the volume of concrete, ${V}_{\mathrm{b}}$, and the mass of the bending and shear steel reinforcement (i.e. mass of radial top reinforcement, ${M}_{\mathrm{srt}}$ mass of radial bottom reinforcement, ${M}_{\mathrm{srb}}$ mass of tangential top reinforcement, ${M}_{\mathrm{stt}}$ mass of tangential bottom reinforcement, ${M}_{\mathrm{stb}}$ mass of shear reinforcement, ${M}_{\mathrm{sw}}$ and the total mass of reinforcement, ${M}_{\mathrm{s},\mathrm{tot}}$)