Topology optimization of periodically arranged components using shared design domains

Abstract

Building structures from identical components organized in a periodic pattern is a common design strategy to reduce design effort, structural complexity and cost. However, any periodic pattern will impose certain design restrictions often leading to lower structural efficiency and heavier weight. Much research is available for periodic structures with connected components. This paper addresses minimal compliance design for periodic arrangements of unconnected components. The design problem discussed here is relevant for many applications where a tightly nested, space-saving arrangement of identical components is required. We formulate an optimal design problem for a component being part of a periodic arrangement. The orientation and position of the component relatively to its neighbours are prescribed. The component design is computed by topology optimization on a design domain possibly shared by several neighbouring components. Additional constraints prevent components from overlapping. Constraint aggregation is employed to reduce the computational cost of many local constraints. The effectiveness of the method is demonstrated by a series of 2D and 3D examples with an ever-smaller distance between the components. Moreover, problem-specific ranges with only little to no increase in compliance are reported.

1 Introduction

A great number of technical products exhibit some level of periodicity by design. The reason behind is that reusing a certain component multiple times can save cost of manufacture, improve ease of assembly, facilitate maintenance, enhance modularity and, most importantly, lower the design effort and structural complexity of the entire product. The repeating pattern may extend along one or more spatial directions. Examples of one-dimensional periodicity include zippers and chains. Plywood, like many other composite materials, is produced from multiple layers arranged along a single stacking direction. Prominent examples of two-dimensional periodicity are honeycomb cores, isogrids and pin fin heat sinks. Structures with up to three-dimensional periodicity range from very large trusses to small-scale additively manufactured lattice structures. From a manufacturing point of view, usually the periodicity is achieved by appending additional components. However, the repeating topological feature can also be a cutout. Structural members receive a periodic structure by partly removing material or introducing perforations. For instance, beams with evenly spaced web openings are quite common in construction, architecture or shipbuilding. In the aviation and space industry the concept is often used in the form of so-called flanged lightening holes and can be seen in some structural parts such as floor beams, frames and formers. All the aforementioned structures have in common that they are built from a number of identical components which are organized in a spatially periodic arrangement. To achieve that the components act together as a single, macroscopic structure they are joint together or connected at discrete joint locations which enables mechanical load and heat transfer between them.

In this work we will focus on unconnected periodic arrangements. Each component is subject to the same set of design loads and has its own support. The periodic arrangement will be defined such that the components are placed with a potential to overlap. This induces a competition for available space during the design process. The gap between adjacent components may vanish, however there will be no contact forces. This particular design problem can be identified in many existing products. Shopping carts, nestable pallets or stackable chairs must be designed to provide a sufficient bearing load capacity while a close nesting is essential to reduce the area necessary for storage when not in use. Periodic Assemblies of components that must stay spatially separated can be found in mechanisms where moving structural parts are arranged close to each other. For example, in centrifugal clutches two or more hinged shoes are installed on the inner shaft following a cyclically symmetric positioning. The shoes are closely nested when the clutch is disengaged and start to swing outward when exceeding the engagement speed. Another example where the components are not even part of the same structural assembly is multi-part production. For instance, in sheet metal processing multiple copies of a 2D part are cut from a metal sheet. If the geometrical lay-out of the part allows for a closely nested, periodic arrangement of components without overlap and only a little gap in between overall material usage can be improved significantly. Similarly, in powder-bed-based additive manufacturing a dense packing of 3D parts leads to improved build space usage which is known to affect cost efficiency (Khorram and Nonino 2018). One may argue that a comparable nesting could alternatively be achieved by an irregular arrangement. However, in both sheet metal processing and additive manufacturing there exist certain preferential directions related to the direction of rolling and the movement of the recoater, respectively. Hence, a periodic arrangement will sometimes be preferred for the sake of similar, more reproducible mechanical properties among the components. Some of the previous examples are illustrated in Fig. 1.

Fig. 1

Examples of compact periodic arrangements of unconnected structural components found in existing products and industrial applications: dense packing of multiple parts on the build plate of a selective laser melting machine (left), confined spaces within a centrifugal clutch requiring closely nested shoes when disengaged (middle), stackable chair design combining load bearing capacity and space-saving functionality (right)

A straightforward design approach, suitable for both, periodic structures of connected components and periodic arrangements of unconnected components, may consist of two sequential steps. In the first step, a partitioning of the entire design domain into equal subdomains has to be determined. In the second step, a suitable design of the component has to be found within the subdomain. Regarding the case of unconnected components, the latter step equals a classical optimal design problem on a fixed design domain that can be addressed with readily available tools. In the case of connected components, the second step of the suggested design approach is also well investigated. Since the early 90s, researchers started applying topology optimization to find the yet unknown inner structural lay-out of the base component that maximizes some mechanical performance measure of a larger periodic structure. In fact, the concept of periodically repeating micro structures even was a key factor to the first successful implementation of the material distribution method described in Bendsøe and Kikuchi (1988) as it provided a physical model of a continuous density material as a composite consisting of an infinite number of microvoids periodically dispersed in a base material. The authors used a parametric material model based on a square unit cell of solid material with a square or rectangular hole in the middle to modify the overall density of a unit cell by adjusting edge length and orientation of the hole. In the limit of a periodic microstructure with infinitely small unit cells the macroscopic elastic properties can then be derived using homogenization theory assuming a separation of micro and macro scales. Sigmund (1994) was the first to use topology optimization in material design for finding the topology of a unit cell subject to periodic boundary conditions without making simplifying assumptions on the shape of void and solid regions. This technique is referred to as inverse homogenization and has subsequently been adopted by other authors to successfully solve microstructural design problems (Kikuchi et al. 1998; Neves et al. 2000).

If the cell size is not an order of magnitude smaller than the characteristic lengthscale of the entire structure, a macroscopic approach will be more appropriate as it resolves all structural details of the periodic pattern and also captures influences of inhomogeneous load distributions. One or two-dimensional translational periodicity has been studied in the context of cellular core design of sandwich structures (Zhang and Sun 2006; Huang and Xie 2008), bridges (Thomas et al. 2020; Huang and Xie 2008), roof frames (Rong et al. 2013) and thermo-elastic problems (Chen et al. 2010). Application of cyclic periodicity has been investigated for the design of car wheels (Zuo et al. 2011; Jiang et al. 2020), flywheels (Jiang and Wu 2017) and spur gears (Schmitt et al. 2019).

As outlined above, many researchers have focussed on the second step: finding an optimized topology within a fixed component design domain. In contrast, far less attention was paid to the first step, which is the partitioning of the entire design domain into equal subdomains each allowed to be occupied by a single component only. In the context of connected components, the application of polygonal unit cells has been studied for homogenization-based material design by Diaz and Bénard (2003). A similar investigation is currently missing for macroscopic cyclic and translational periodicity, where almost exclusively simple geometric shapes like rectangles or circular segments are used. In the case of arrangements of unconnected components the first step turns out to be the crucial part of the optimization problem. As illustrated in Fig. 1, the distance between the components is typically small to achieve a space-saving arrangement which is desirable for technical or economical reasons. If the design domain of the component is chosen improperly, a significant amount of material may be placed at its boundary suggesting that better designs could become accessible in the second step by reshaping the design domain of the component. Unfortunately, anticipating the design domain of the component which for a given periodic pattern finally leads to an optimal component design is not trivial and difficult to be achieved manually. This becomes even more evident from the numerical examples, see Section 4.

The sketched two-step procedure for the optimization of periodic arrangements of identical components bears similarities to the recent work of Previati et al. (2019) and Ballo et al. (2020). Using a SIMP-based approach, the authors minimize the summed compliance of two different, unconnected components with partly shared design domains. Overlapping regions are removed from the designs at the end of every iteration. The logic is to penalize the density field of a component where its local contribution to compliance minimization is smaller compared to the other overlapping component. Further modifications can still be necessary to establish connectedness of the updated component designs. Thus, the procedure ensures feasible designs before continuing with the next iteration, albeit it may also affect convergence. Note that without any further assumptions the concurrent optimization of two not necessarily equal components is a multi-objective optimization. The authors’ choice of using an unweighted sum of the individual compliances can be seen as just one possibility.

Furthermore, the problem of altering both the topology of a component and the shape of the design domain boundary also arises in other situations, most notably in the context of optimizing structures with contact interfaces. Promising results have been achieved using the level set method, see Lawry and Maute (2015), Lawry and Maute (2018) for bilaterial contact and Liu et al. (2016) for multi-material optimization with cohesive interfaces.

Our current work addresses the design of an infinite periodic arrangement of identical components with the aim of minimizing compliance. Hence, the problem naturally reduces to a single-objective optimization where the component design domain and its topology are sought. By means of the shared design domain approach we fully remain within the framework of topology optimization on a fixed mesh and avoid any shape optimization of the component design domain boundary. In contrast to Previati et al. (2019), the separation of the components is established by introducing a relaxed non-overlap constraint represented by a differentiable function that is directly handled by the optimizer. However, it is known that a large number of constraints makes optimization methods tailored for many design variables but only a few constraints inefficient. We address this issue using aggregation techniques to reduce the number of constraints necessary to satisfy the local non-overlap requirement.

The remainder of the present paper is organized as follows. In the following Section 2, we provide the mathematical formulation of the design optimization problem. Then, in Section 3, we present a new solution approach and elaborate on all its necessary ingredients including SIMP interpolation, constraint formulation, aggregation techniques, finite element discretization and sensitivity analysis. The proposed method has been applied to 2D and 3D problems, covering both translational and rotational periodicity. The results will be discussed in Section 4. We conclude with a short summary and perspectives on future work in Section 5.

2 Problem statement

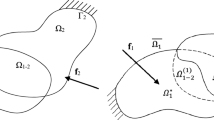
Our study addresses the minimum compliance design of an infinite periodic arrangement consisting of unconnected components. In Fig. 2 the problem set-up is illustrated schematically for a component i adjacent to its predecessor ($i-1$) and the following component ($i+1$). The design domain $\varOmega ^{(i)}$ is subdivided into a part $\varOmega ^{(i)}_{\star }$ exclusively allocated to the i-th component and the intersections with the design domains of the previous component and following component denoted as $\varOmega ^{(i)}_{-}=\varOmega ^{(i)}\cap \varOmega ^{(i-1)}$ and $\varOmega ^{(i)}_{+}=\varOmega ^{(i)}\cap \varOmega ^{(i+1)}$, respectively. Intersections of more than two component design domains are not explicitly considered here. However, the method we propose is not necessarily limited to only pairwise intersections, as we will discuss later. All components are related to the same linear elasticity problem. Each component i is subject to its individual load set $\varvec{f}^{(i)}$ and has its own support $\Gamma _u^{(i)}$. No contact interaction is considered between the components. We assume an infinite periodic arrangement ($i\in \mathbbm {Z}$) as opposed to the finite periodic case, where distinct first and last components exist. This assumption can be either exactly satisfied, as in the cyclic periodicity case, or it may be seen as a reasonable simplification if the number of components is in fact finite.

We seek a single, unique component design $\varOmega ^{(i)}_{mat}=\varOmega _{mat}$, thus restricting the yet unknown topologies of the components to be identical. We focus on the special case of one-dimensional periodicity where the distance and orientation between two consecutive components is specified by one single rigid motion $\varvec{\varphi }(\varvec{x})$. With these definitions, the optimization task can be formulated as:

$$\begin{aligned} \begin{aligned} \min _{\varvec{u \in U,\varOmega ^{(i)}_{mat}}}&~l(\varvec{u}) \\ \text {s.t.: }&a(\varvec{u},\varvec{v})=l(\varvec{v}), ~\forall \varvec{v} \in U,\\&\mathbbm {C}={\left\{ \begin{array}{ll} \mathbbm {C}_0 \qquad \text {on } \varOmega ^{(i)}_{mat},\\ {0} \qquad \text {on } \varOmega ^{(i)} ~\backslash ~\varOmega ^{(i)}_{mat}, \end{array}\right. }\\&\varOmega ^{(i)}_{mat} \subseteq \varOmega ^{(i)},\\&\text {Vol}(\varOmega ^{(i)}_{mat})\le V,\\&\varOmega ^{(i)}_{mat} \cap \varOmega ^{(i+1)}_{mat} = \emptyset ,\\&\varOmega ^{(i+1)}_{mat} = \{ \varvec{\varphi }(\varvec{x})~|~\varvec{x} \in \varOmega ^{(i)}_{mat} \}. \end{aligned} \end{aligned}$$

(1)

Here $\varvec{u}$ and $\varvec{v}$ are the fields of displacements and virtual displacements, respectively. U denotes the set of kinematically admissible displacements. The constitutive behaviour is described by the fourth order tensor $\mathbbm {C}$ which is equal to the linear elastic, isotropic stiffness tensor $\mathbbm {C}_0$ of the material within the final domain of the component $\varOmega ^{(i)}_{mat}$ and vanishes elsewhere. Also, we have introduced a constraint limiting the material volume of each component to a prescribed value V. The compliance function is $l(\varvec{u})=\int _{\varOmega ^{(i)}}\varvec{f}^{(i)}\varvec{u}~d\varOmega + \int _{\Gamma _\sigma ^{(i)}}\varvec{t}^{(i)} \varvec{u}~d\Gamma$ and the internal virtual work is given by the bilinear form $a(\varvec{u},\varvec{v})=\int _{\varOmega ^{(i)}} \varvec{\varepsilon }(\varvec{u}):\mathbbm {C}:\varvec{\varepsilon }(\varvec{v})~d\varOmega$. One may note that solving the minimization problem for one arbitrary component i is sufficient, as the entire periodic pattern can be concluded from the last equation of the optimization problem statement (1).

Fig. 2

Design domain, boundary conditions, loads (left) and optimized design (right) of three sequential components. The distance and the orientation of a component relative to its predecessor is described by the rigid motion $\varvec{\varphi }(\varvec{x})$

3 Solution approach

The structure we are seeking is supposed to be a periodic arrangement of multiple, macroscopic components. This allows us to further reduce the problem’s scope to the design of only a single component i. To simplify notation we drop the index in the following if not strictly necessary.

3.1 Density interpolation scheme

To solve the optimal topology problem we apply the Solid Isotropic Material with Penalization (SIMP) interpolation scheme introduced by Bendsøe (1989). The discrete 0–1 nature of the stiffness tensor is omitted and replaced by the common power-law approach

$$\begin{aligned} \mathbbm {C}(\varvec{x})=\rho (\varvec{x})^p\mathbbm {C}_0. \end{aligned}$$

(2)

In this way the local stiffness properties at any point $\varvec{x}$ are expressed with reference to the dense material via a smooth pseudo-density field $\rho (\varvec{x})$ which is defined on the entire design domain $\varOmega$ and subject to the simple bound constraints

$$\begin{aligned} \rho _{min}\le \rho (\varvec{x})\le 1. \end{aligned}$$

(3)

The power p is used to drive the optimization towards a solution with only a small fraction of areas having intermediate densities.

3.2 Spatial separation of components

Considering only $\varOmega _\star$, the part of the design domain which is unique to the component, the problem statement is not different to the classical one of compliance minimization on a fixed design domain. The difficulty lies in the treatment of the non-overlap requirement given by the second last equation in (1). The parts of a component design domain shared with the previous and the following components are related via

$$\begin{aligned} \varOmega _+= \{ \varvec{\varphi }(\varvec{x})~|~\varvec{x} \in \varOmega _- \}. \end{aligned}$$

(4)

In addition to (3), within $\varOmega _-$ and $\varOmega _+$ the density field of a component must be further constrained such that any overlap between the neighbouring components is avoided. Exploiting the periodic nature of the multi-component systems studied in this work, this non-overlap constraint can easily be established via a coupling of the mass distribution of a component within these two regions through

$$\begin{aligned} \rho (\varvec{x})\rho (\varvec{\varphi }(\varvec{x}))=0 \qquad \text {on } \varOmega _-. \end{aligned}$$

(5)

One possibility to satisfy (5) during an iterative solution procedure would be to reallocate the volume at a point $\varvec{x}$ in the shared design domain in every iteration to either $\varOmega _-$ or $\varOmega _+$. Here we take a different approach and account for the spatial separation of the components by directly introducing a non-overlap constraint function $g(\varvec{x})$ into the optimization problem. We propose the following relaxed form of (5) suited for a gradient-based solution method:

$$\begin{aligned} g(\varvec{x})=\rho (\varvec{x})\rho (\varvec{\varphi }(\varvec{x})) \le \rho _{min} \qquad \text {on } \varOmega _-. \end{aligned}$$

(6)

A graphical representation of (6) is shown in Fig. 3. The blue hyperbolae represent the equality cases $g(\varvec{x})=\rho _{min}$, feasible combinations of $\rho (\varvec{x})$ and $\rho (\varvec{\varphi }(\varvec{x}))$ are located below this graph. While the extreme case of two discrete overlapping components (top-right corner) is now far outside the feasible domain, it is still possible that $\varvec{x}$ is occupied by both components, especially in the low-density region with $\rho (\varvec{\varphi }(\varvec{x})),\rho (\varvec{x})\ll 1$. However, these intermediate combinations are ineffective and usually too uneconomical, as explained below.

The way how overlap between adjacent components is removed from the design during a typical optimization process is illustrated on the right of Fig. 4. Starting from an initial configuration (${{\textcircled {1}}}$) with distinct overlap, the topology changes more or less substantially to reduce and eliminate overlapping. Blurry areas of low-density may evolve within the shared part of the design domain $\varOmega _-^{(i)}=\varOmega _+^{(i-1)}$ where the placement of material is likewise efficient for both components (${{\textcircled {2}}}$). The optimizer will decide for every point of these highly competitive areas whether it should be allocated preferably to either component i or $i-1$, or, expressed in terms of a single component, whether material is placed at either $\varvec{x}$ or $\varvec{\varphi }(\varvec{x})$. This choice is based on the impact on compliance minimization and it can also change at a later stage of the optimization process. Once the density fields of neighbouring components are no longer overlapping and the topology has been adapted to compensate these imposed restrictions as far as possible, the solution finally converges towards to a 0-1 design exhibiting a sharp dividing line between the components (${{\textcircled {3}}}$).

A possible evolution of the densities at the fixed point $\varvec{x}$ can be tracked in the 3D plot on the left of Fig. 4. The horizontal plane is split by the graph of $g(\varvec{x})=\rho _{min}$ into two domains containing all feasible or infeasible combinations of $\rho (\varvec{\varphi }(\varvec{x}))$ and $\rho (\varvec{x})$. The respective penalized pseudo-densities are shown on the vertical axis. Just like in Fig. 3, it can be seen that feasible intermediate combinations with both $\rho (\varvec{\varphi }(\varvec{x}))$ and $\rho (\varvec{x})$ being non-negligible have low-density. As a consequence, large blurry areas could arise within the design which try to compensate for the low-density. However, this can be suppressed by means of a sufficient penalization by the SIMP interpolation (2) making the specific stiffness contribution of low-densities excessively small, see the surface plot in Fig. 4. For sake of clarity, a lower bound on the densities $\rho _{min}=0.1$ was chosen for the graph, although this is too large for practical use. In fact, the value of $\rho _{min}$ should be chosen relatively small to effectively inhibit the occurrence of overlapping regions in the sense that both $\rho (\varvec{\varphi }(\varvec{x}))$ and $\rho (\varvec{x})$ or at least one of them equals $\rho _{min}$. This is particularly relevant for larger problems where the use of constraint aggregation techniques becomes inevitable, see Subsection 3.3.

Fig. 3

Relaxed non-overlap constraint (6) for two different lower bounds $\rho _{min}$ on the pseudo-density. The area below the graphs is the feasible domain. When $\rho _{min}$ tends to zero, the blue curve approaches the orange-coloured graph of (5)

Fig. 4

Schematic visualization of three characteristic stages ${\textcircled {1}}$, ${\textcircled {2}}$ and ${\textcircled {3}}$ of a typical design optimization sequence: Detailed view of the topology in the vicinity of a point $\varvec{x}$ lying on the design domain shared by the blue and red components (right). Surface plot of the penalized densities ($p=3$) at $\varvec{x}$ showing the convergence from the infeasible domain towards a non-overlapping and nearly 0-1 solution (left)

3.3 Constraint aggregation

A pure compliance minimization problem can be seen as a special case of (1) with a priori separated design domains ($\varOmega _-=\emptyset$). In this situation, the global volume constraint is the only constraint function to be considered as against a number of design variables that is, depending on the problem size and the spatial descretization, in general very large. In the case of at least partly shared design domains, the number of constraints typically will reach the same order of magnitude as the number of design variables associated with the density field $\rho (\varvec{x})$. The reason is that the spatial separation of the components is a local requirement. Thus, in a discretized setting the non-overlap constraint (6) must be enforced for every design variable on $\varOmega _-$. These $N_-$ additional constraints, though linear with respect to the design variables, drastically increase the computational cost of commonly used dual optimization methods like the popular method of moving asymptotes (MMA) by Svanberg (1987) that would otherwise perform very efficiently.

A common approach to handle the known difficulties arising from imposing local constraints in topology optimization is the use of aggregation functions which has been studied in the context of local stress constraints by Yang and Chen (1996) and which we will also adopt here. The central idea is to satisfy a global constraint $\max {(g_1,\dots ,g_{N_-})} \le \rho _{min}$, where the maximum of the discretized non-overlap constraints function values $g_k$ is approximated by a suitable aggregation function $\tilde{g}(g_1,\dots ,g_{N_-})\approx \max {(g_1,\dots ,g_{N_-})}$.

The differentiability and the easy availability of gradient information are important advantages of aggregation functions. The main challenge is that aggregation functions only provide an estimation of the exact maxium. The accuracy of this approximation will become rather low if $N_-$ takes large values as it is the case for problems where the shared portion of the design domain is dominant. To address this, we apply a simple grouping strategy to improve the approximation inspired by the block aggregation technique suggested by París et al. (2010), i.e., we divide the $N_-$ constraint function values into $N_g$ groups each having its own scalar aggregation function $\tilde{g}_m$ that only merges the values of its group. For a compact notation, for every group $m=1,\dots ,N_g$ we define a set $\mathcal {N}_-^m$ storing its $N_-^m$ constraint functions numbers.

A popular type of aggregation function is the so-called KS-norm introduced by Kreisselmeier and Steinhauser (1979). In its original formulation, the KS-norm is an upper bound approximation and considerably overestimates the real maximum if all constraint function values are equal. For that reason, we use the following modified variant proposed by París et al. (2009):

$$\begin{aligned} \tilde{g}_m=\frac{1}{P}\ln \left( \sum _{k\in \mathcal {N}_-^m} \mathrm e^{Pg_k}\right) -\frac{1}{P}\ln \left( N_-^m\right) ,~~~ m=1,...,N_g, \end{aligned}$$

(7)

where P is a so-called aggregation parameter. The second term of the right-hand side in (7) has been chosen such that the approximation is now exact if all local function values of a group are equal, including the critical case $g_k=\rho _{min}\forall k\in \mathcal {N}_-^m$.

A large P in (7) is desirable as in the limit of $P\rightarrow \infty$ the KS-norm will always yield the exact maximum of any set. However, in practice P must be chosen carefully with respect to the possible range of local constraint function values. The reason is that the terms of the sum in (7) grow exponentially which might come along with very large gradients that can have a detrimental effect on the numerical stability. In fact, our numerical experiments have indicated that this issue becomes the limiting factor still well within the representable range of the floating-point format. For our implementation of the optimization problem at hand, an aggregation parameter of $P=8$ has proven to be a satisfactory choice. Another question is how to choose $N_g$. We found that limiting the group size $N_-/N_g$ to a value in the range of roughly $10^3...10^4$ was sufficient to solve the numerical examples presented in Section 4.

3.4 Finite element discretization of the optimization problem

To solve the equilibrium equations, to evaluate both the objective and the constraint functions and to provide the necessary sensitivities we use a geometrically linear finite element method. We use first order triangular elements to interpolate the nodal displacements $\varvec{u}$ inside the elements. Similarly, we choose a nodal-based representation of the density with the same standard $C^0$ shape functions on the common mesh so that the design variables of the problem are given by the global vector $\varvec{\rho }$ comprising the N nodal densities. Written in discrete form, the equilibrium equation is now given by the linear system

$$\begin{aligned} \varvec{K}(\varvec{\rho })\varvec{u}=\varvec{f}, \end{aligned}$$

(8)

where $\varvec{K}$ is the system stiffness matrix and $\varvec{f}$ is the vector of nodal forces. The stiffness matrix is generated in an assembly process $\varvec{K}= \textsf {A}^{N_e}_{e=1}\varvec{k}_e$ from $N_e$ element stiffness matrices defined as

$$\begin{aligned} \varvec{k}_e=\int _{\varOmega _e}\varvec{B}(\varvec{x})^T(\varvec{N}_e(\varvec{x})\varvec{\rho }_e)^p\varvec{C}_0\varvec{B}(\varvec{x})~d\varOmega . \end{aligned}$$

(9)

Here $\varvec{C}_0$ is the constitutive matrix of the material, $\varvec{B}(\varvec{x})$ denotes the usual operator matrix relating the nodal displacements to the strains, $\varvec{\rho }_e$ is the vector of element nodal densities and $\varvec{N}_e(\varvec{x})$ is the vector of shape functions to interpolate between the nodal densities on the element domain $\varOmega _e$.

Handling the simple bound constraints (3) in the discretized setting is trivial, as we impose them directly on the discrete design variables. The evaluation of the volume constraint is also easily accomplished by a local integration of the approximated density field over the element domain and adding up the contributions from all elements, i.e.,

$$\begin{aligned} g_0=\sum _{e=1}^{N_e}\left( \int _{\varOmega _e} \varvec{N}_e(\varvec{x})\varvec{\rho }_e~d\varOmega \right) =\varvec{h}^T\varvec{\rho }, \end{aligned}$$

(10)

where we have taken account of the linear relation between the actual volume and the nodal densities by introducing a constant vector $\varvec{h}$ that once assembled can be stored and reused throughout the optimization. Note that the derivative of the volume constraint with respect to the nodal densities is readily given by the entries of $\varvec{h}$. A detailed expression to compute them is given in the following Subsection 3.5.

Fig. 5

Illustration of the pointwise non-overlap constraint in the discretized setting: The nodal density at $\varvec{x}_k$ is compared with the interpolated density at $\varvec{\varphi }(\varvec{x}_k)$

A suitable discrete counterpart is to be formulated in the case of the relaxed non-overlap constraint (6). Here we follow an approach in the form of a point-wise constraint enforcement which is intuitive and easy to implement. As depicted in Fig. 5, we take the density at the nodal coordinates $\varvec{x}_k$, i.e., the nodal density $\rho _k$, and project it onto the density at $\varvec{\varphi }(\varvec{x}_k)$ interpolated from the nodal values $\varvec{\rho }_e$ of the element e, the element domain $\varOmega _e$ of which includes $\varvec{\varphi }(\varvec{x}_k)$. This leads to the following set of $N_-$ constraints:

$$\begin{aligned} g_k=\rho _k \varvec{N}_e(\varvec{\varphi }(\varvec{x}_k))\varvec{\rho }_e, \quad \varvec{\varphi }(\varvec{x}_k)\in \varOmega _e, \quad k\in \mathcal {N}_-. \end{aligned}$$

(11)

Here we have introduced a set $\mathcal {N}_-$ storing the $N_-$ constraint function numbers. As every constraint function $g_k$ corresponds to a node number k, the set $\mathcal {N}_-$ can equally be regarded as a node set containing the $N_-$ global node numbers of all the nodes lying on the shared part of the design domain $\varOmega _-$.

For the reason outlined in the previous Subsection 3.3, we will split the large number of constraint functions into smaller groups according to ${\mathcal {N}_-} = \bigcup _{m=1}^{N_g} {\mathcal {N}}_-^m$. It seems reasonable to keep the size of the groups balanced. Apart from that, we allocate the constraint function numbers to the individual groups simply in ascending order based on the corresponding node numbers assigned by the finite element routine. Thus, the groups do not necessarily have any geometrical meaning. The numerical performance can be affected by choosing a more sophisticated strategy to form the groups instead of assigning the constraints in random order. Different strategies have been suggested based on either geometrical considerations (París et al. 2010) or the current values of the constraint functions (Le et al. 2010; Holmberg et al. 2013). Although improvements have been reported, these findings may be very much problem dependent, which is why we do not examine this in more detail here.

Using these definitions, the discrete form of the optimization problem can be written as

$$\begin{aligned} \begin{aligned} \min _{\varvec{u} \in U,\varvec{\rho }}&~l\\ \text {s.t.: }&\varvec{f}^T\varvec{u}=l\\&\left( \textsf {A}^{N_e}_{e=1} \varvec{k}_e(\varvec{\rho }_e) \right) \varvec{u}=\varvec{f},\\&\rho _{min}\le \rho _j \le 1, \qquad j=1,\dots ,N,\\&g_0=\varvec{h}^T\varvec{\rho }\le V,\\&\tilde{g}_m(\varvec{\rho })=\frac{1}{P}\ln \left( \sum _{k\in \mathcal {N}^{m}_{-}} \frac{\mathrm e^{P\rho _k \varvec{N}_e(\varvec{\varphi }(\varvec{x}_k))\varvec{\rho }_e}}{N^m_-}\right) \le \rho _{min},\\&\varvec{\varphi }(\varvec{x}_k)\in \varOmega _e, \qquad m=1,\dots ,N_g. \end{aligned} \end{aligned}$$

(12)

3.5 Sensitivity analysis

The optimization problem (12) is to be solved by a gradient-based mathematical programming method. This section provides the necessary sensitivities with respect to the design variables.

By means of the adjoint method, the well-known expression for the derivative of the compliance $\frac{\partial l}{\partial \rho _j}=\frac{\partial ( \varvec{f}^T\varvec{u})}{\partial \rho _j} =-\varvec{u}^T\frac{\partial \varvec{K}}{\partial \rho _j}\varvec{u}$ can be obtained. Using the definition of the element stiffness matrices (9) we get

$$\begin{aligned} \begin{aligned} \frac{\partial l}{\partial \rho _j}&= -\sum _{e\in \mathcal {E}^j}\left( \int _{\varOmega _e}N_e^j\varvec{u}_e^T\varvec{B}^Tp(\varvec{N}_e\varvec{\rho }_e)^{p-1}\varvec{C}_0\varvec{B}\varvec{u}_e~d\varOmega \right) \\&= -\sum _{e\in \mathcal {E}^j}\left( \int _{\varOmega _e}N_e^j(\varvec{x}) w(\varvec{x})~d\varOmega \right) , \end{aligned} \end{aligned}$$

(13)

where $\mathcal {E}^j$ represents a set containing the element numbers of all elements that are connected to the j-th node and $N_e^j$ denotes the shape function associated to the nodal density at that node on the respective element. Moreover, we have introduced the specific strain energy density $w(\varvec{x})$ in the second line of (13). For further manipulation, the specific strain energy density is projected onto the linear FE space to obtain a discretized representation $w(\varvec{x})=\varvec{N}(\varvec{x})\varvec{w}$.

As investigated by Jog and Haber (1996), minimum compliance optimization using a finite element implementation with $C^0$ continuity of both the displacement and the density field suffers from numerical instability. Though not affected by the formation of checkerboard patterns known from element-density-based approaches (Matsui and Terada 2004), the optimal topology generated using such an implementation will also exhibit mesh-dependent anomalies, so-called “islanding” (Rahmatalla and Swan 2004). To suppress these artefacts, we apply a filterting of the sensitivities very similar to the heuristic procedure originately introduced by Sigmund (1994) for element-wise constant densities. This is done by smoothing the nodal values of the specific strain energy density in (13) through the following convolution:

$$\begin{aligned} \widehat{w}_j= \frac{1}{\int _{\varOmega }H_j(\varvec{x})~d\varOmega } \int _{\varOmega }H_j(\varvec{x})w(\varvec{x})~d\varOmega , \end{aligned}$$

(14)

where $H_j(\varvec{x})$ is a triangular kernel function defined as:

$$\begin{aligned} H_j(\varvec{x})={\left\{ \begin{array}{ll} r_{min}-\Vert \varvec{x}-\varvec{x}_j\Vert \qquad \text {for } \Vert \varvec{x}-\varvec{x}_j\Vert \le r_{min}, \\ 0\qquad\qquad\qquad\qquad~~ \text {else}. \end{array}\right. } \end{aligned}$$

(15)

Here $r_{min}$ has the meaning of a filter radius by controlling the support size of the kernel function. The filtered sensitivity expression then becomes:

$$\begin{aligned} \widehat{\frac{\partial l}{\partial \rho _j}}= -\sum _{e\in \mathcal {E}^j}\left( \int _{\varOmega _e}N_e^j(\varvec{x})\widehat{w}(\varvec{x})~d\varOmega \right) . \end{aligned}$$

(16)

In addition to the derivative of the objective function, we also need to provide the same for the constraints. The sensitivity of the volume constraint function is given as

$$\begin{aligned} \frac{\partial g_0}{\partial \rho _j}=\sum _{e\in \mathcal {E}^j}\left( \int _{\varOmega _e} N_e^j(\varvec{x})~d\varOmega \right) =h_j. \end{aligned}$$

(17)

For the sensitivities of the $N_g$ aggregated non-overlap constraints considered in (12) one needs to compute both the derivative of the aggregation function and the derivative of the constraint function itself. The former can be written as

$$\begin{aligned} \frac{\partial \tilde{g}_m}{\partial g_k}={\left\{ \begin{array}{ll} \frac{1}{N^m_-}\mathrm e^{P(g_k-\tilde{g}_m)} \quad \text {for } k\in \mathcal {N}^{m}_{-},\\ 0 \qquad\qquad\quad~~~ \text {else}, \end{array}\right. } \end{aligned}$$

(18)

and the derivative of the non-overlap constraint is given by

$$\begin{aligned} \frac{\partial g_k}{\partial \rho _j}={\left\{ \begin{array}{ll} \varvec{N}_e(\varvec{\varphi }(\varvec{x}_k))\varvec{\rho }_e \qquad \text {for } j=k,\\ \rho_k N_e^j(\varvec{\varphi }(\varvec{x}_k)) \qquad \text {for } j\in \mathcal {N}^{e},\\ 0 \qquad\qquad\qquad\quad~ \text {else}, \end{array}\right. } \end{aligned}$$

(19)

where $\mathcal {N}^e$ represents a set containing the global node numbers of the element e and we again assume that $\varvec{\varphi }(\varvec{x}_k)\in \varOmega _e$. By application of the chain rule, the sensitivities of the aggregated non-overlap constraints $\frac{\partial \tilde{g}_m}{\partial \rho _j}=\sum _k \frac{\partial \tilde{g}_m}{\partial g_k}\frac{\partial g_k}{\partial \rho _j}$ follow from (18) and (19).

4 Numerical examples

4.1 Implementation details

The proposed method described in the previous section has been implemented in Python. To solve the optimization problem we apply the method of moving asymptotes (MMA) by Svanberg (1987) which is accessed through the Python-based optimization package pyOpt (Perez et al. 2012). To compute function values and sensitivities for both objective and constraints we make use of the finite element analysis tools which are developed under the umbrella of the FEniCS project (Alnæs et al. 2015) with its core component DOLFIN (Logg and Wells 2010) providing major part of the functionality as well as a high-level Python interface. By default, we apply the sparse direct solver UMFPACK for the 2D problems. Due to the memory efficiency of iterative solvers, we switch to the minimal residual (MINRES) method paired with successive over-relaxation (SOR) preconditioning to solve the linear systems in 3D. We use the graphics package Matplotlib (Hunter 2007) for plotting the 2D topologies and a CAD program to visualize the 3D topologies.

4.2 2D plane stress cantilever with translational periodicity

To demonstrate the effectiveness of the proposed method we have solved a series of cantilever optimization problems where the shared part of the design domain is progressively increased. The first example is essentially two-dimensional and has also been chosen to illustrate how the optimal topology of the structure evolves when the spacing between the components is gradually reduced and to investigate how this affects its mechanical performance.

The problem set-up is given in Fig. 6. The design domain $\varOmega$ is rectangular with a fixed support in the left half of its lower boundary while a single point load F is acting on the midpoint of the right boundary in vertical direction. The design domain is discretized by a structured grid of triangular elements as illustrated in Fig. 7. The values of the parameters are summarized in Table 1. The value of the filter radius equals twice the element edge length such that the support of the filter kernel function comprises at least two layers of surrounding elements. We assume that the design problem has converged if the relative objective change falls below $10^{-6}$ for three consecutive iterations and the aggregated non-overlap constraints are satisfied. In every case, the optimization is started using a homogeneous material distribution $\rho =V/(2BH)$. This initial condition uses only half of the available amount of material V and is therefore compatible with the volume constraint. However, the non-overlap constraint is violated because $g_k=\rho (\varvec{x}_k)\rho (\varvec{\varphi }(\varvec{x}_k))=(\frac{V}{2BH})^2$ is larger than admissible limit $\rho _{min}$ for any node k on $\varOmega _-$.

Fig. 6

Design of a two-dimensional, infinite and translationally periodic arrangement of a single load cantilever using shared design domains: Schematic representation of the optimization problem

Fig. 7

Finite element discretization of the 2D plane stress cantilever problem with translational periodicity: Triangular cell mesh, Dirichlet boundary conditions and nodal point load

Table 1 2D plane stress problems: Dimensions, loads, material properties, volume limit and numerical parameters

To validate the basic functionality of the implementation we first compared the optimization results for the case $b=0$, i.e., essentially a pure minimal compliance problem without overlapping design domains, to those obtained by the popular 99-line Matlab code by Sigmund (2001). To ensure comparability we used identical parameters. The only exception refers to the sensitivity filter radius of the Matlab implementation, which we have set to $r_{min}/2$ to account for the ability of a nodal-based approach to resolve finer variations of the density compared to element-wise constant densities. However, note that the 99-line Matlab code shows further differences, primarily the use of rectangular finite elements, application of the optimality criteria method and a slightly different filtering technique. Nevertheless, the optimized material distributions obtained are similar, as it can be seen from Fig. 8. Moreover, the difference in compliance is found to be less than $1.5\%$.

Fig. 8

Cantilever problem with separated design domains: Optimal topology for $b=0$ (left) compared to the solution obtained using the 99-line Matlab code (right)

Increasing the portion of the shared design domain $\varOmega _{-}/\varOmega$ now initiates the transition from the classical topology optimization problem with its exclusive design domain to the case of shared design domains. The rectangular design domains are moved purely horizontally until they overlap the neighbouring design domains by b, which corresponds to the rigid motion $\varvec{\varphi }(\varvec{x})=\left( \begin{matrix}x+B-b\\ y\end{matrix}\right)$. The proposed method has been applied to solve this optimization task separately for a number of increasing values of the design domain overlap b/B. The optimizations are performed independently of each other. Each starts from the same initial condition and is directly solved for a predefined design domain overlap. It is noteworthy that for a given mesh the design domain overlap can still be chosen continuously as there is no need to ensure matching nodes on $\varOmega _+$ or $\varOmega _-$. A selection of the computed final designs is illustrated in Fig. 9. Note that we have included a design problem where $b/B>0.5$ which implies that parts of the design domain are shared by even more than two components. As mentioned earlier, we do not take measures to explicitly prevent any overlap between a component i and the component after next $i+2$. However, for the optimization problem at hand, this situation can not occur for any meaningful design, as demonstrated in Fig. 9.

Fig. 9

2D plane stress cantilever problem with translational periodicity: Optimal topologies obtained for increasing values of the design domain overlap b/B. To illustrate the infinite periodic arrangement, a series of three consecutive, identical components are shown by their density fields

The evolution of the structure’s topology may be divided into three phases. The first one is characterized by a formation of a unique topology that remains unaffected by the overlap between the design domains. By inspection of the optimal topology for $b/B=0$, one observes a considerable amount of empty space between the components. Thus, it is plausible that the topology does not change before the point of application of the force starts touching the diagonal member of the adjacent component at around $b/B\approx 0.15$. This assumption is also confirmed by the value of the objective shown in Fig. 10. The computed topology in the first phase is a discrete truss-like structure that resembles one of the famous Michell frames, namely the top half of the symmetric centrally loaded beam (Michell 1904). This is not surprising since both problem statements are almost equivalent, albeit differ in the direction of the force F and its point of application.

Fig. 10

Minimized compliance for different values of b/B. The black curve corresponds to the 2D plane stress cantilever problem with translational periodicity (values normalized by $l(b=0)=69.55$). The blue curve shows the results found for the similar 3D problem (values normalized by $l(b=0)=237.01$)

In the second phase, the components have already come close enough and the non-overlap constraints are activated locally to ensure feasibility. Hence, the modification of the density field itself leads to the formation of a curved dividing line between the components. Once the optimization has converged, the topology shows a distinct separation of the components, see Fig. 11. Despite the necessary adaption of the topology, the increase in compliance is small until $b/B\approx 0.25$. Thus, the second phase is of particular interest when a large b/B is for some reason economically desirable however one is willing to accept only very little losses of mechanical performance. As expected, the method does not preserve a minimum gap in the form of at least one single layers of void elements between the components. However, this could lead to unwanted contact between the components under operational loads or it might result in components being unintentionally bonded together during additive manufacturing. In a practical workflow, this could be solved by manually adding a small clearance to the design in a subsequent post-processing step.

Fig. 11

2D plane stress cantilever problem with translational periodicity: Detail view of the density fields (bottom) in a region where the clearance between two adjacent components vanishes. The location is indicated by the red circle (top)

For larger design domain overlap, feasibility reduces stiffness. This third phase is characterized by a rapid increase of the compliance, see again Fig. 10. Due to the tight spacing of the components the size of the design domain that can still effectively be occupied by a single component is narrowed down. This induces substantial structural modifications and the stiffness is compromised. The black graph in Fig. 10 indicates almost without exception that in the second and third phase the compliance is a strictly convex function of the design space overlap with a vertical asymptote at $b/B=1$.

The evolution of compliance and volume is plotted in Fig. 12 for the smallest, the largest as well as an intermediate design domain overlap. One observes a fast decrease of the compliance during the first twenty iterations largely irrespective of b/B. However, to finally converge to a stable configuration it takes a few tens of iterations more for the case of overlapping design domains compared to $b/B=0$. One also notices a decrease of the volume accompanied by an increase in compliance at $n=4$, which corresponds to the solution after three iterations. Interestingly, the classical minimum compliance problem with $b/B=0$ is slightly more affected than the two other optimization problems with $b/B=0.35$ and $b/B=0.55$. This effect is not related to the proposed method of handling shared design domains itself. It can rather be attributed to the fact that the largest and most fundamental structural modifications appear during the early optimization phase and that the design updates predicted by the optimizer seem to be somewhat too aggressive in the first three iterations. The fluctuation disappears for $n\ge 4$.

Fig. 12

2D plane stress cantilever problem with translational periodicity: Convergence of the compliance (values normalized by the initial compliance $l_1=2.4\cdot 10^4$) and the volume. The optimizations start at $n=1$ (initital condition) and terminate once the respective convergence criterion has been met

To verify, that the obtained results are in fact feasible, we compared the maximum among all the $\mathcal {N}_-$ nodal overlap values $\max (g_k)$ with the maximum of the $N_g$ constraint functions $\max (\tilde{g}_m)$, which is expected to be a sufficiently accurate approximation of the former. This comparison is shown in Fig. 13. Because of the particular formulation of (7), the approximation is exact for the homogeneous initial guess at $n=1$. Although the divergence of the graphs indicates a rather low quality of approximation during the following iterations, the constraint function value for $b/B=0.35$ is reduced or at least kept roughly constant while the design undergoes significant structural modifications. In principle, this is also true for the much more demanding optimization problem $b/B=0.55$, apart from the rise at $20\le n\le 30$. Once $\max (\tilde{g}_m)$ has finally dropped below $\rho _{min}$ the design becomes feasible and does no longer violate the non-overlap requirement. There are two observations in Fig. 13 that may warrant further discussion, the sudden drop of $\max (g_k)$ and the sharp peak at $n=70$ for the $b/B=0.55$ case. The reason for this becomes evident from Fig. 14. The graph shows that the number of violated constraints, which corresponds to the size of the overlap between the components, in fact monotonically decreases to zero. An even closer look reveals that for example in the case of $b/B=0.55$ there is only one remaining constraint at $n=38$ which the solution does not satisfy yet. This overlap is finally removed from the design in a single iteration, which makes plausible why the graph of $\max (g_k)$ in Fig. 13 suddenly drops. Likewise, the small increase at $n=70$, which appears as a sharp peak, is caused by a marginal overlap where again only a single $g_k$ is still larger than $\rho _{min}$. One may also note that the graph in Fig. 13 appears overly sensitive due to its log-log scale.

Fig. 13

2D plane stress cantilever problem with translational periodicity: Evolution of the maximum among the aggregated non-overlap constraints $\tilde{g}_m$ compared to the actual maximum among the nodal non-overlap constraints $g_k$. Note that the respective m and k possibly vary between iterations

Fig. 14

2D plane stress cantilever problem with translational periodicity: number of nodal non-overlap constraints for which $g_k>\rho _{min}$ holds. Numbers greater than zero indicate that a certain overlap between the components still remains

4.3 2D plane stress problem with rotational periodicity and single point load

The 2D example of translational periodicity from the previous Section 4.2 shall be supplemented by a complementary case study covering rotational periodicity. The problem set-up consists of a circular pattern of $n_c$ evenly distributed and identical components, as exemplified in Fig. 15. The distance and the relative orientation between two neighbouring components is given by the motion $\varvec{\varphi }(\varvec{x})=\left( \begin{matrix}\cos 2\pi /n_c&{}\sin 2\pi /n_c\\ -\sin2\pi /n_c&{}\cos 2\pi /n_c\end{matrix}\right) \Bigl (\begin{matrix}x\\ y\end{matrix}\Bigr )$, which describes a pure rotation about the origin. Besides the motion, the shape of the design domain, the support area, the vertical point load, the initial material distribution $\rho =V/(2BH)$, the convergence criterion and the values of the parameters (see Table 1) remain unchanged compared to the previous example.

As it can be seen from the optimization results illustrated in Fig. 16, the rotation angle $\frac{360^\circ }{n_c}$ leads to a closed periodic pattern where the identical topologies of component i and $i+n_c$ are congruent. This shows why it makes sense to use only integer numbers of components. For $n_c\le 3$ the designs are the same as in the translational periodicity problem for $b/B\le 0.15$, cf. the two topmost topologies in Fig. 9. The reason is that in these cases the design domains do not intersect at all or at least the intersection does not disturb the formation of an optimized topology. When the number of components equals four, one third of the support $\Gamma _u$ now reaches into the design domain of the neighbouring component leading to an interference of efficient potential load paths. Thus, the topology needs to be reorganized significantly to prevent overlapping. When the number of components is increased further, the structural modifications appear much less conspicuous. However, the structure is shifted more an more to the right so that it extends beyond the end of the supported edge causing an increase in compliance. Another interesting structural detail is the boundary shape of a component where it is directly bordering the neighbouring component. From Fig. 17, it can be seen that these particular sections of the boundary are not necessarily straight lines. In the rotationally periodic case, for instance, the boundary shape is a curve opening in anti-clockwise direction ($n_c=5$) and changes into a curve opening in clockwise direction ($n_c=7$). As opposed to this, in the translationally periodic case with a design domain overlap of $b/B=0.55$, the topology has a gentle s-shaped boundary.

A quantitative comparison of the topology optimization results obtained for different numbers of components is provided Fig. 18. Following the aforementioned idea of subdividing the evolution of the topology of the structure into three phases, one can easily identify the first phase as the interval $n_c\le 3$. A distinct second phase, where a larger number of components would be accompanied by only a modest increase in compliance, is not recognisable. Instead, one observes that the compliance quickly increases for $n_c\ge 4$.

This is contrary to the translational periodicity example presented in the previous Section 4.2. This shows that the non-overlap requirement has an influence on the compliance that is strongly dependent on the specific problem, for example the position and orientation of loads and supports and, in particular, the motion $\varvec{\varphi }$. The area of $\varOmega _-$ alone, does not necessarily indicate a poor mechanical performance of a component. For instance, the area of the shared part of the design domain $\varOmega _-$ is approximately the same for $n_c=7$ and $b/B=0.55$. Nevertheless, the compliances of the optimized designs, which also look quite comparable at first sight, differ by a factor of 3. It should be noted that the number of components $n_c$, and hence the extend of intersection of the design domains, can only be increased gradually and that these increments might be too large to resolve a visible second phase. This contrasts with the translational periodicity example, where the design domain overlap b/B is continuously variable.

A log-log plot of the objective and the volume is presented in Fig. 19 providing insights into the convergence behaviour. Based on the same convergence criterion used before, the iteration process is stopped when the design is feasible and the relative objective change has been smaller than $10^{-6}$ for the last three iterations. The number of iterations required for the solution to converge is roughly $2...4\cdot 10^{2}$. However, a satisfactory result with a compliance being close to that of the fully converged solution is already achieved after $n=4\cdot 10^{1}$, which is about an order of magnitude less.

The evolution of the constraint functions $\tilde{g}_m$ is illustrated in Fig. 20. For $n_c=4$ the initial design converges from an infeasible to a feasible solution in six iterations. In the more demanding case $n_c=7$, the maximum among the aggregated non-overlap constraints $\tilde{g}_m$ is also drastically reduced before it reaches a minimum at $n=11$. Until this point, the number of violated constraints ($g_k>\rho _{min}$) has been reduced to 6 as it can be seen from Fig. 21. All these constraints belong to nodes lying on a narrow strip where two neighbouring components are still slightly overlapping. Both components aim at occupying as much space as possible in this highly stressed area. It takes about twenty additional iterations before this localized overlap is removed and a sharp dividing line has been found, cf. the violet curve in Fig. 17.

With regard to the proposed method, it can be stated that the results found from this 2D case study on rotational periodicity resemble those obtained for the translational periodicity covered in the previous Subsection. This conclusion is also confirmed from a numerical perspective, as demonstrated by several convergence plots. Although the precise relation is problem-specific, both examples also exhibit the same expected behaviour whereby a closer arrangement leads to a less efficient design.

Fig. 15

Design of a two-dimensional structure with rotationally periodicity and signle point load consisting of $n_c$ identical components: Schematic representation of shared design domains, supports and loads for $n_c=5$

Fig. 16

2D plane stress problem with rotational periodicity and sinlge point load: Arrangement of optimal topologies for different numbers of components between $n_c=3$ (bottom) and $n_c=7$ (top)

Fig. 17

Comparison of the boundary shapes of different 2D topologies bordering each other: Results from the translational periodicity example (bottom) and the rotational periodicity example (top-left and top-right). The violet curves trace the imaginary dividing lines between adjacent components

Fig. 18

2D plane stress problem with rotational periodicity and single point load: Minimized compliance for increasing number of components $n_c$ (values normalized by $l(n_c=3)=69.55$)

Fig. 19

2D plane stress problem with rotational periodicity and single point load: Convergence of the compliance (values normalized by the initial compliance $l_1=2.4\cdot 10^4$) and the volume during design optimization

Fig. 20

2D plane stress problem with rotational periodicity and single point load: Evolution of the maximum among the aggregated non-overlap constraints $\tilde{g}_m$ compared to the actual maximum among the nodal non-overlap constraints $g_k$. Note that the respective m and k possibly vary between iterations

Fig. 21

2D plane stress problem with rotational periodicity and single point load: Number of nodal non-overlap constraints for which $g_k>\rho _{min}$ holds. Numbers greater than zero indicate that a certain overlap between the components still remains

4.4 2D plane stress problem with rotational periodicity and double point load

To further substantiate the method, we present another two-dimensional example with a rotationally periodic arrangement of $n_c=5$ components. The problem set-up is sketched in Fig. 22. The shape of the design domain, the support area, the vertical point load, the initial material distribution $\rho =V/(2BH)$, the motion $\varvec{\varphi }(\varvec{x})$ and the convergence criterion have been adopted from the previous example. We also use the same values of the parameters that can be gathered from Table 1. However, to make the problem more challenging and to promote a more sophisticated design, we have added a second point load of equal magnitude F acting on the midpoint of the left boundary in horizontal direction.

The optimization result is illustrated in Fig. 23. As expected, the computed final design shows a greater geometric complexity compared to the previous example. A considerable accumulation of material can be found at both ends of the supported edge $\Gamma _u$. While the structure at the left end is still truss-like with thick members, one observes a plate-like structure in the highly loaded region a the right end. Two larger and somewhat more filigree trusses are attached to these structures and carry the two applied forces. The contours of the two trusses are strongly interdependent as both lie mostly on the shared parts of the design domain $\varOmega _-$ and $\varOmega _+$, see Fig. 23. The tight periodic arrangement and the corresponding non-overlap requirement has a great influence on the optimal topology as the shared portion of the design domain is relatively large. Furthermore, especially important locations like supported edges and points of application of loads reach far into the design domains of adjacent components. This effect is best illustrated in Fig. 24, showing a visual comparison with the results of a classical topology optimization ($\varOmega =\varOmega _\star$) without shared design domains.

A convergence plot for the objective function and the volume constraint function is provided in Fig. 25. The result is similar to the previous example exhibiting fluctuations during the first four iterations followed by a smooth convergence behaviour. For completeness, we also provide a visualization of how the non-overlap constraint function evolves over iterations, see Fig. 26. It shows the maximum among the aggregated constraint function values $\max (\tilde{g}_m)$ contrasted with the maximum nodal overlap values $\max (g_k)$. The result is comparable to the previous example, too. This confirms once more that there is basically neither a conceptual nor a numerical difference between the problem with translational periodicity from Subsection 4.2 and the rotationally periodic case treated here.

Fig. 22

Design of a two-dimensional structure with rotationally periodicity and double point load consisting of five identical components: Schematic representation of shared design domains, supports and loads

Fig. 23

2D plane stress problem with rotational periodicity and double point load: Arrangement of five identical components with optimized topology

Fig. 24

Optimized topology from Subsection 4.4 considering rotational periodicity (grey) compared to the results from a classical topology optimization without shared design domains (blue). The compliance of the grey structure is 2.1 times larger than that of the blue structure

Fig. 25

2D plane stress problem with rotational periodicity and double point load: Convergence of the compliance (values normalized by the initial compliance $l_1=4.4\cdot 10^4$) and the volume during design optimization

Fig. 26

2D plane stress problem with rotational periodicity and double point load: Evolution of the maximum among the aggregated non-overlap constraints $\tilde{g}_m$ compared to the actual maximum among the nodal non-overlap constraints $g_k$. Note that the respective m and k possibly vary between iterations

4.5 3D cantilever with translational periodicity

In a fourth example, which is an extension of the plane stress example from Subsection 4.2 to three dimensions, we demonstrate the effectiveness of the proposed method also for larger 3D problems.

The problem set-up is sketched in Fig. 27. The design domain is cuboidal, the left half of its bottom face is fixed and the point load F is now acting on the center of the right side face. To make the optimization problem more demanding, we wish to obtain a design that is symmetric about the x-y-plane. The design domain is discretized by a structured mesh of tetrahedral elements. The values of all relevant parameters are summarized in Table 2. Each optimization is started using a homogeneous material distribution $\rho =V/(2BHD)$ as the initial condition.

Fig. 27

Design of a three-dimensional, infinite periodic arrangement of a single load cantilever using shared design domains: Schematic representation of the design domain, supports and loads (top), simplified problem set-up using half of the design domain with mirror symmetry about the x-y-plane (middle), and translationally periodic arrangement of three neighbouring components (bottom)

Table 2 3D cantilever problem with translational periodicity: Dimensions, loads, material properties, volume limit and numerical parameters

Similar to the 2D example, we consider a translationally periodic arrangement constituted by the motion $\varvec{\varphi }(\varvec{x})=\left( \begin{matrix}x+B-b\\ y\\ z\end{matrix}\right)$. A selection of the computed final designs corresponding to three different values of b/B is shown in Fig. 28. It is noteworthy, that the empty space between the components obtained from the conventional optimization with $b/B=0$ can be partly eliminated through a subsequent nesting along the x-axis. By this means, space savings can be achieved equivalent to $b/B\approx 0.3$ which marks the end of what we have earlier called the first phase. Beyond this point, an even closer arrangement of components can only be realized considering shared design domains during the topology optimization. The optimized compliance of ten different designs is plotted as a function of the design domain overlap, see the blue curve in Fig. 10. As expected, the compliance of the designs remains largely similar during the first phase. However, what is probably most striking is the small variation in compliance of about $\pm 2\%$ over the entire range investigated. Furthermore, one can observe a constant increase in compliance around $b/B=0.5$. This is likely due to the overlap of two areas of the design domains where the placement of material is particularly economical, namely the outmost parts of the fixed bottom face in the vicinity of $x=0$ and $x=B/2$.

From the above findings we draw the conclusion that in comparison to a 2D problem, a 3D problem allows to prescribe a closer spacing between the components before the loss of stiffness ultimately becomes unacceptable. We attribute this to the much greater flexibility in designing non-overlapping load paths within a three-dimensional rather than a two-dimensional design domain. One may think of two straight members belonging to different components that are initially intersecting. A trivial solution would be to move one of the members in the out-of-plane direction such that the members are now bypassing each other. While for a 3D problem this structural modification can most likely be realized and possibly even at low cost, it is impossible in a planar problem. This leads to comparatively less efficient designs in a 2D setting. On the contrary, it also has the convenient side-effect of a component acting as a barrier between its left and right neighbours. Thus, the overlap between components other than direct neighbours is often ‘naturally’ prevented in a meaningful 2D design while this is no longer true in 3D. In the current example, this needs to be considered for $b/B>0.6$. To solve this issue, the non-overlap constraint (6) must be generalized to more than two components. The larger design freedom in 3D also gives rise to another issue, namely the prediction of arrangements of interlocking component designs. If for example such an interlocking arrangement was manufactured using additive manufacturing, it would afterwards be impossible to separate the components from each other.

Fig. 28

3D cantilever problem: Optimal topologies obtained for three different values of the design domain overlap b/B portrayed from a front and a top-down perspective (top). To illustrate the infinite periodic arrangement, a series of three consecutive, identical components is shown using isometric projection (middle and bottom). Only elements with all their nodal densities exceeding a threshold of $\rho = 0.5$ are included

Finally we briefly present some numerical aspects of the proposed method applied to the described 3D problem. The evolution of the objective as well as the volume constraint can be studied in Fig. 29. The blue curves show a relatively smooth convergence behaviour for all three different optimizations. We found that, although the total number of degrees of freedom is more than six times larger, the number of iterations needed to meet a desired relative objective tolerance criterion does not increase significantly compared to the 2D example. Furthermore, we also reviewed the evolution of the constraint functions $\tilde{g}_m$ to assure compliance with the non-overlap requirement. The results are illustrated in Fig. 30. It can be observed, that the overlap between the components is continuously reduced until $\max (\tilde{g}_m)$ drops below $\rho _{min}$. Interestingly, there is almost no difference between the dashed ($b/B=0.4$) and the solid ($b/B=0.6$) blue curve.

Fig. 29

3D cantilever problem: Convergence of the compliance and the volume during design optimization

Fig. 30

3D cantilever problem: Evolution of the maximum among the aggregated non-overlap constraints $\tilde{g}_m$ compared to the actual maximum among the nodal non-overlap constraints $g_k$. Note that the respective m and k may vary between iterations

5 Conclusion

We have presented a novel approach to the optimal design problem of a structure that is part of an infinite periodic arrangement of identical, unconnected components. The difficulty is to find an optimized structural lay-out such that neighbouring components do not intersect. Depending on the arrangement of design domains, this leads to reduced design freedom and often to less efficient designs.

We address this optimization problem by allowing for shared design domains among the components and guide the optimization process towards non-overlapping designs. This is accomplished by local non-overlap constraints. The large number of local constraints is effectively reduced to a small fraction by an appropriate aggregation technique. The method is applied to a series of 2D as well as a large-scale 3D minimal compliance problems where the spacing between the components is gradually reduced. Starting from an infeasible, uniform initial material distribution, we demonstrate that the proposed method converges towards optimized designs where overlapping regions have been removed entirely.

The results reflect a sort of competition for available space between neighbouring components. This can be seen from the topologies that, to some degree, border each other and establish a curvilinear dividing line that is optimal with respect to the design goal. The competition does not only depend on the extend of intersection of their design domains but also on whether important regions such as supports are affected. The results are in clear contrast to those typically expected from a similar optimization problem considering connected structural components. In such a case the optimal topology incorporates members that enable mechanical load transfer between the components, and thus looks fundamentally different. The more specific differences will depend on the particular kind of load interface connecting the components, though.

Future work should include the development of a constraint that explicitly considers more than two potentially overlapping components, even though sometimes this is not necessary to achieve feasible designs, as demonstrated in our first and second 2D example. Furthermore, the treatment of interlocking, unseparable designs might warrant additional investigation. Another promising extension would be to generalize the mapping $\varvec{\varphi }(\varvec{x})$ to other linear transformations like scaling or reflection. For testing and validation, the proposed method should be applied to the design of a real product in an industrial application context. Insights gained from an industrial case study would also help to identify potential needs for improvement and directions for further development.