Overhang control in topology optimization: a comparison of continuous front propagation-based and discrete layer-by-layer overhang control

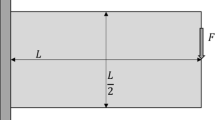
Abstract

Although additive manufacturing (AM) allows for a large design freedom, there are some manufacturing limitations that have to be taken into consideration. One of the most restricting design rules is the minimum allowable overhang angle. To make topology optimization suitable for AM, several algorithms have been published to enforce a minimum overhang angle. In this work, the layer-by-layer overhang filter proposed by Langelaar (Struct Multidiscip Optim 55(3):871–883, 2017), and the continuous, front propagation-based, overhang filter proposed by van de Ven et al. (Struct Multidiscipl Optim 57(5):2075–2091, 2018) are compared in detail. First, it is shown that the discrete layer-by-layer filter can be formulated in a continuous setting using front propagation. Then, a comparison is made in which the advantages and disadvantages of both methods are highlighted. Finally, the continuous overhang filter is improved by incorporating complementary aspects of the layer-by-layer filter: continuation of the overhang filter and a parameter that had to be user-defined are no longer required. An implementation of the improved continuous overhang filter is provided.

1 Introduction

Additive manufacturing (AM) is widely recognized for its capability to manufacture complex components. As the resulting designs of topology optimization (TO) are frequently geometrically complex, the combination of both methods has received significant interest. This interest is even further increased with the advent of metal AM, which opens the possibility to realize optimal functional components with high strength and toughness.

One of the most active research topics on combining TO and AM is the minimization of support structures required during manufacturing. Since AM is a layer-by-layer manufacturing process, in the majority of industrially relevant processes each layer requires a certain amount of support from the previously constructed layers, for a variety of reasons. For example, in fused deposition modeling, the support is mainly required because a new layer cannot be printed on air, and needs to be at least partly supported by the previous layer (Jiang et al. 2018). For metal powder bed fusion methods, each layer is built on either the already existing part or metal powder. Heat accumulation can be a major issue as the powder has low conductivity (Sih and Barlow 2004), obstructing the path for heat towards the base plate which acts as a heat sink. Here supports provide heat conduction as well as mechanical support to, among others, prevent distortions (Mercelis and Kruth 2006; Wang et al. 2013; Cloots et al. 2013).

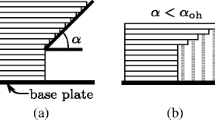
Since the production and removal of supports subsequent to printing is costly and time consuming, design rules have been set up to prevent the need for supports (Thomas 2009; Adam and Zimmer 2014; Kranz et al. 2015). For most AM processes, a critical overhang angle α_oh has been defined. The overhang angle is the angle between a down-facing surface and the base plate, as shown in Fig. 1. Surfaces with an overhang angle lower than α_oh are termed overhanging, and require supports. In order to attain support free optimized structures, numerous studies have proposed various methodologies to incorporate the minimum overhang angle as a design rule in TO. Based on the principle of overhang detection, these can be classified into three categories: overhang detection by (i) a processing of the geometry in printing sequence (e.g. Gaynor and Guest 2016; Langelaar 2016; van de Ven et al. 2018); (ii) inspection of the boundary orientation (e.g. Qian 2017; Guo et al. 2017; Allaire et al. 2017; Zhang et al.2019); and (iii) simulating the (simplified) physics of the printing process (e.g. Allaire et al. 2017; Amir and Mass 2018; Ranjan et al. 2018). For a comprehensive overview, the reader is referred to Liu et al. (2018).

Fig. 1

In order to print a given structure (left), it is discretized into layers (right). The overhang angle α_oh is defined as the angle between a down-facing surface and the base plate Ω₀

The focus of this study is on the methods in the first category: the filters that follow the printing sequence. Most methods in this category are presented as discrete filters, defined on a discretized geometry. However, the front propagation-based filter presented in van de Ven et al. (2018) is continuous in nature. This study investigates the differences and similarities between the discrete, layer-by-layer methods presented in Langelaar (2016, 2017), and the continuous, front propagation method presented in van de Ven et al. (2018). Due to similarities in implementation, it was suspected that the discrete layer-by-layer filter could be formulated using front propagation. In this paper it is shown that this is indeed the case. From this, it is concluded that the layer-by-layer filter cannot be used on unstructured grids as is. Furthermore, the front propagation-based filter is improved by using aspects of the layer-by-layer filter, which is enabled by the front propagation-based formulation of the layer-by-layer filter.

This paper is structured as follows. First, a brief overview of both methods is given in Section 2. Then, it is shown that the discrete method can also be formulated with front propagation discretized on a structured grid (Section 3). Next, the differences between both filters are examined (Section 4), and in Section 5 the continuous overhang filter is improved by using aspects of the layer-by-layer filter. Finally, the paper is concluded in Section 6. For clarity this paper focuses on 2D formulations, but the principles apply to the 3D case as well.

2 Overhang detection methods

For the sake of completeness, the overhang detection methods described in Langelaar (2017) and van de Ven et al. (2018) are summarized in this section. In the remainder of this work, the methods described in Langelaar (2017) and van de Ven et al. (2018) will be referred to as the layer-by-layer overhang filter, and the continuous overhang filter, respectively. Both methods are designed for density-based topology optimization, where the geometry is defined by a pseudo-density field ρ where 0 ≤ ρ ≤ 1. Void regions are indicated with ρ = 0, and regions of material with ρ = 1 (Bendsøe and Sigmund 2004). The overhang filter is typically applied directly after the density filter, to convert the density field ρ into a printable density field ξ. The overhang filter removes the overhanging regions: the geometry described by the printable density field ξ is thus directly printable without support structures. This field is then used evaluate the objective and constraints of the topology optimization. Note that the overhang filter can also be implemented as a constraint instead of a filter as demonstrated in van de Ven et al. (2018), which gives the possibility to relax the overhang constraint and balance printability with the impact on performance.

2.1 The layer-by-layer overhang filter

The layer-by-layer overhang filter described in Langelaar (2017) is defined on a structured rectangular grid. In a 2D setting, any element of a structured mesh can be identified by its row and column i, j. The filter can be summarized in two statements: for an element e_{i, j}, its supporting elements are the three elements e_{i− 1,j− 1}, e_i− 1,j and e_{i− 1,j+ 1} directly below it (see Fig. 2), and, the element’s printable density ξ_{i, j} cannot exceed the maximum printable density ξ of the elements that support e_{i, j}, i.e.

$$ \begin{array}{@{}rcl@{}} {{\varXi}}_{i,j} &=& \max(\xi_{i-1,j-1}, \xi_{i-1,j}, \xi_{i-1,j+1}) , \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} \xi_{i,j} &= &\min({{\varXi}}_{i,j}, \rho_{i,j}),, \end{array} $$

(2)

where the printing direction is assumed to be from the bottom to the top row. The filter can be propagated through a domain by initializing the bottom row of elements with ξ_1,j = ρ_1,j, and then evaluating (1) and (2) layer-by-layer in the printing direction. Evaluation of sensitivities is performed in the reverse order. For continuous differentiability and the use of gradient-based optimization, the non-smooth min and max operators are replaced by differentiable counterparts.

Fig. 2

Element i, j can be supported by the three elements directly below it

Note that the overhang angle is inherently linked to the grid. For instance, a square element implies α_oh = π/4. When a suitable structured finite element mesh is used, this filter can thus be applied directly to the elemental densities. In other cases, a mapping between FE mesh and a separate overhang grid must be used (Langelaar 2018). Alternatively, Hoffarth et al. introduce a search cone to define support relations on arbitrary meshes, instead of a mapping (Hoffarth et al. 2017).

2.2 Continuous overhang filter

The overhang filter presented in van de Ven et al. (2018) utilizes front propagation to detect overhanging regions. In a front propagation scheme, a front is initialized at a boundary, and propagated throughout the domain. The output is an arrival time field T(x), which indicates for each location the time at which the front reaches that location.

First, the concept of detecting overhang with front propagation is demonstrated on a given geometry, ignoring the dependence on the density field ρ. In order to detect overhang in a given geometry, such as the one shown in Fig. 3a, two arrival time fields are required. In the first arrival time field, T^layer, the arrival times are proportional to the height from the base plate Ω₀, and isosurfaces thus represent the printing sequence, as displayed in Fig. 3b. Assuming that the base plate coincides with the origin, it is given as

$$ \begin{array}{@{}rcl@{}} T^{\text{layer}}(\mathbf{x}) = \mathbf{b}\cdot\mathbf{x}/f_{0}, \end{array} $$

(3)

where b is a unit vector defining the build direction, and f₀ represents the default propagation speed in this build direction. The exact value of f₀ is not important as it is a scale factor whose effect is canceled, and is chosen as 1 ms^− 1. For the second arrival time field, T(x), a front propagation is performed in the design domain Ω, starting from the base plate Ω₀. This time, the propagation speed is chosen such that the arrival times are equal to T^layer(x), except when the front travels in a direction below the minimum overhang angle α_oh, i.e. when a region is not printable. This is achieved using a an anisotropic speed function, and the resulting arrival time field can be seen in Fig. 3c. Consequently, a delay field τ(x) between the two arrival time fields can be calculated as

$$ \begin{array}{@{}rcl@{}} \tau(\mathbf{x}) = T(\mathbf{x}) - T^{\text{layer}}(\mathbf{x}). \end{array} $$

(4)

In regions where τ(x) > 0, the propagation has been delayed, indicating that the structure is overhanging, as can be seen in Fig. 3d. Finally, the printable density field ξ(x) is attained from the delay field τ(x) with the delay-density relation h:

$$ \begin{array}{@{}rcl@{}} \xi(\mathbf{x}) = h(\tau(\mathbf{x})), \end{array} $$

(5)

where h is a monotonically decreasing differentiable function with h(0) = 1, such that zero delay results in full density, and 0 ≤ h(τ(x)) < 1 for τ(x) > 0. In (van de Ven et al. 2018), h is defined as

$$ \begin{array}{@{}rcl@{}} h(\tau(\mathbf{x})) = 2^{-k\tau(\mathbf{x})}, \end{array} $$

(6)

where k is a numerical parameter related to the element size: a high value for k will result in a short transition from full density to void as small delays will already result in low values for ξ. Therefore, for fine meshes, k is set to a higher value than for coarse meshes.

Fig. 3

The shaded overhanging region in the geometry given in (a) can be detected with front propagation by constructing the arrival time fields given in (b) and (c), and evaluating the difference (d). The vector b indicates the build direction

The first arrival time field, T^layer(x), can be obtained without performing an actual front propagation, as the arrival times are equal to the distance between the base plate Ω₀ and the point of interest x. However, in order to obtain the second arrival time field T(x), a front propagation is performed, which is governed by the Hamilton-Jacobi-Bellman equation:

$$ \begin{array}{@{}rcl@{}} &\underset{\mathbf{a} \in S_{1}}{\min} \left\{ (\nabla T (\mathbf{x}) \cdot \mathbf{a} ) f_{s}(\rho(\mathbf{x}),\mathbf{a},\alpha_{\text{oh}}) \right\} = 1, \quad \mathbf{x} \in {{\varOmega}}, \end{array} $$

(7)

where f_s anisotropic is the speed function that dictates the propagation speed, and a is a unit vector determining the direction of propagation: a ∈ S₁, $S_{1} = \{ \mathbf {a} \in \mathbf {R}^{2} | \| \mathbf {a}\|=1 \}$. It is in the speed function f_s where the original density field ρ is coupled to the arrival times T(x) and thus printable densities ξ(x). It is later shown that the speed function is simply scaled with the densities. Since all the densities are printable at the base plate Ω₀, it is required that

$$ \begin{array}{@{}rcl@{}} \xi(\mathbf{x}) = \rho(\mathbf{x}), \quad \mathbf{x} \in {{\varOmega}}_{0}. \end{array} $$

(8)

From this relation and (5), the initial condition for the front propagation can be derived as

$$ \begin{array}{@{}rcl@{}} T(\mathbf{x}) = h^{-1}(\rho(\mathbf{x})), \quad \mathbf{x} \in {{\varOmega}}_{0}, \end{array} $$

(9)

where h^− 1 is the inverse function of the delay-density relation h, such that h(h^− 1(ρ(x))) = ρ(x). For example, elements with ρ = 1 at the base plate are initialized at T = T_layer.

2.2.1 The speed function

For the sake of simplicity, the anisotropic speed function was scaled linearly with the density value ρ. As such, the speed function f_s can be decomposed into a part that depends on the density field, and a part that depends on the direction of propagation a and minimum overhang angle α_oh:

$$ \begin{array}{@{}rcl@{}} f_{s}(\rho(\mathbf{x}),\mathbf{a},\alpha_{\text{oh}}) &= g(\rho(\mathbf{x}))f(\mathbf{a},\alpha_{\text{oh}}). \end{array} $$

(10)

The function f(a, α_oh) relates the direction of propagation to speed. The speed function as used in van de Ven et al. (2018) is displayed in Fig. 4, where α represents the propagation direction defined by a. The top part of the speed function, where α_oh ≤ α ≤ 180^∘− α_oh, is defined by $f=f_{0}/\sin \limits {\alpha }$. When the propagation direction is equal to the build direction (α = 90^∘), the propagation speed is equal to that of the reference field T^layer, i.e. f = f₀. Moreover, in order to maintain a front parallel to the base plate, the propagation speed is increased to compensate for the larger distance travelled to the next printing layer. For example, for α = 45^∘, $f=\sqrt {2}f_{0}$. However, when the propagation direction is below α_oh, i.e. when α < α_oh or α > 180^∘− α_oh, the propagation speed is lowered, thereby a non zero value of τ(x) is attained. The anisotropic speed function capable of creating a delay in the overhanging regions is not unique. In van de Ven et al. (2018) a function resembling a rectangle is used, which is numerically efficient. The aspect ratio of the rectangle shown in Fig. 4 designates the minimum overhang angle α_oh.

Fig. 4

Polar plot of the rectangular speed function for α_oh = 45^∘, with propagation speed on the radial axis, and propagation direction on the tangential axis. A propagation direction of α = 90^∘ coincides with the build direction b

Finally, the speed function f_s also contains a geometry dependence in the speed-density relation g(ρ(x)). In the example shown in Fig. 3, the front propagated only through the structure. However, with topology optimization, this structure is determined by the density field ρ. In van de Ven et al. (2018), the propagation speed is linearly scaled with the density:

$$ \begin{array}{@{}rcl@{}} g(\rho(\mathbf{x})) = v_{\text{void}} + (1-v_{\text{void}}) \rho(\mathbf{x}), \end{array} $$

(11)

where v_void is the minimum propagation speed in the void regions, chosen such that 0 < v_void < 1. Consequently, the front will be delayed in void regions, leading to τ(x) > 0, and thus also void in the printable density field ξ (5).

2.2.2 Numerical implementation

The layer-by-layer overhang filter by Langelaar (2017) is defined on a discretized domain, hence its numerical implementation is straightforward (see Langelaar (2017) for details). Here, the numerical implementation of the continuous filter is briefly described in order to make a comparison between the two.

The front propagation can be efficiently executed using the Ordered Upwind Method (OUM) (Sethian and Vladimirsky 2003), on any mesh type in 2D as well as 3D. The necessary steps are briefly explained, while some details are omitted for brevity. In the OUM, nodes are labelled either Far, Candidate, or Accepted. All of the nodes are initialized as Far, with $T=\infty$. Then, the arrival times of nodes at the fixed boundary Ω₀ are initialized and are labelled Accepted. Finally, the nodes within a distance d of these Accepted nodes are labelled Candidate. Then, the following algorithm is executed:

• 1. Calculate the arrival times of the Candidate nodes.

• 2. Label the Candidate node with the lowest arrival time as Accepted, and label the nodes within a distance d of that node, that are not Accepted, as Candidate.

• 3. If there are any Candidate nodes left, go to Step 1.

The distance d is defined as

$$ \begin{array}{@{}rcl@{}} d= z F_{2}/F_{1}, \end{array} $$

(12)

where z is a typical element length, and F₁ and F₂ are the maximum and minimum values of f(a, α_oh), respectively. Thus, the more anisotropic the speed function, the larger this distance.

A crucial part of the algorithm is the calculation of the arrival times of Candidate nodes. Let us first consider the calculation of the arrival time of node i from a given point x_γ. This is simply the distance divided by the speed, plus the arrival time at point x_γ, defined as T_γ:

$$ \begin{array}{@{}rcl@{}} {T}_{\gamma}^{i} = \frac{\| \mathbf{x}_{i} - \mathbf{x}_{\gamma} \|}{f_{s}(\rho(\mathbf{x}_{i}),\mathbf{a},\alpha_{\text{oh}})} + T_{\gamma}, \end{array} $$

(13)

where a = (x_i −x_γ)/∥x_i −x_γ∥, and $T^{i}_{\gamma }$ denotes the arrival time at x_i when calculated from x_γ. In reality, the arrival time of the Candidate node i is calculated from, in 2D, two Accepted nodes, j and k. The point x_γ is then a point on the segment x_jx_k, as displayed in Fig. 5. The position and arrival time are linearly interpolated between nodes j and k, defined by parameter γ:

$$ \begin{array}{@{}rcl@{}} \mathbf{x}_{\gamma} &= \mathbf{x}_{j} (1-\gamma) + \mathbf{x}_{k} \gamma, \end{array} $$

(14)

$$ \begin{array}{@{}rcl@{}} T_{\gamma} &= T_{j} (1-\gamma) + T_{k} \gamma. \end{array} $$

(15)

The point from which x_i is updated is the point that results in the lowest arrival time:

$$ \begin{array}{@{}rcl@{}} {T}_{jk}^{i} = \underset{\gamma \in [0,1]}{\min} {T}_{\gamma}^{i} = \underset{\gamma \in [0,1]}{\min} \frac{\| \mathbf{x}_{i} - \mathbf{x}_{\gamma} \|}{f_{s}(\rho(\mathbf{x}_{i}),\mathbf{a},\alpha_{\text{oh}})} + T_{\gamma}, \end{array} $$

(16)

where ${T}_{jk}^{i}$ denotes the arrival time at x_i when calculated from the segment x_jx_k. Note that there is a dependency between the speed function f_s and γ through the propagation direction a. The final arrival time at x_i is the minimum arrival time that can be obtained from all the segments between adjacent Accepted nodes within a distance d:

$$ \begin{array}{@{}rcl@{}} T_{i} = \underset{\mathbf{x}_{j} \mathbf{x}_{k} \in \text{NF}(\mathbf{x}_{i})}{\min} {T}_{jk}^{i}, \end{array} $$

(17)

where NF(x_i) is the set of Accepted nodes that are within the distance d of x_i.

Fig. 5

Update of a node x_i from x_γ on the line segment x_jx_k. The position of x_γ is determined by γ ∈ [0,1]. The update direction is given by the unit vector a

In 3D the algorithm is unchanged, except that the propagation is based on tetrahedrons instead of triangles: the arrival time for a node i is calculated from three other nodes instead of two, where the point x_γ is now in the triangle spanned by these three nodes instead of a line segment.

Analogous to the layer-by-layer filter, the sensitivities are evaluated by following the reverse order in which the arrival times are evaluated. Since the order of the front propogation is already known, this reduces to a trivial loop over all the elements, as detailed in van de Ven et al. (2018).

3 Formulating the layer-by-layer filter with front propagation

Because the continuous filter is described in a continuous setting, it can be readily used in unstructured meshes while the maximum overhang angle can be adjusted independent of the mesh by simply modifying the speed function. However, in the previous section it became apparent that there is a considerable difference in complexity between the two methods: the layer-by-layer filter can be described by two equations while the continuous filter is much more involved. This is caused for a large part by the fact that the layer-by-layer filter is a discrete formulation, while the front propagation filter is continuous, which makes it difficult to compare both methods. Therefore, in this section, the layer-by-layer filter is cast into in an equivalent continuous formulation based on front propagation. To this end, the speed function (10) and the speed-density relation (11) have to be changed compared to the continuous filter, which is shown in the following.

3.1 Speed function for the continuous layer-by-later filter

In order to represent the layer-by-layer filter with front propagation, first, the speed function is adapted. The speed function utilized in van de Ven et al. (2018) allows propagation in all directions (Fig. 4). However, in the layer-by-layer filter, the printable density of an element only depends on either of the three elements directly below it (1). Therefore, the wedge-shaped speed function is chosen as displayed in Fig. 6 (its 3D equivalent is a cone). With this speed function, the propagation speed below the overhang angle is set to zero, and is given by

$$ \begin{array}{@{}rcl@{}} f(\mathbf{a}, \alpha_{\text{oh}}) &= \begin{cases} \frac{f_{0}}{\mathbf{b} \cdot \mathbf{a}} & \mathbf{b} \cdot \mathbf{a} \geq \sin(\alpha_{\text{oh}})\\ \hfil 0 & \mathbf{b} \cdot \mathbf{a} < \sin(\alpha_{\text{oh}}) \end{cases}, \end{array} $$

(18)

where, similar to the previous section, a and b are the propagation and build direction, respectively.

Fig. 6

Polar plot of the wedge-shaped speed function, with propagation speed on the radial axis, and propagation direction on the tangential axis, for α_oh = 45^∘. A propagation direction of α = 90^∘ coincides with the build direction b

This speed function can be propagated on a structured grid with ${{\varDelta }}\textit {y}/{{\varDelta }}\textit {x}=\tan (\alpha _{\text {oh}})$, where Δx and Δy are element width and height, and where the build direction coincides with the vertical axis, as displayed in Fig. 7. Because the propagation speed in (18) is zero for propagation directions below α_oh, a node can only be updated from nodes in a wedge below it, as indicated with the shaded green region in Fig. 7 where node i can only be updated from the red and yellow nodes. The same holds for the three red nodes directly below x_i, which can be updated from nodes in the region shaded red. Due to the overlap of the red and green regions, it can be seen that any yellow node that can update node i, can also update at least one of the three red nodes. Since the red nodes are closer to the yellow nodes than node i is, the front will pass the red nodes first. In order to propagate the speed function in Fig. 6, it is therefore sufficient to only check for updates from the three nodes directly below a given node.

Fig. 7

The node x_i can be updated from any node in the green area. The red nodes can be updated from nodes in the red area, covering all the yellow nodes. Due to the overlap, x_i only has to be updated by the red nodes

With only the three nodes directly below the node of interest required for the arrival time calculation, (17) simplifies to:

$$ \begin{array}{@{}rcl@{}} T_{i} = \min \left\{ {T}_{jk}^{i}, {T}_{kl}^{i} \right\}, \end{array} $$

(19)

where node i is the node of interest, and nodes j, k, and l are the three nodes below i, as displayed in Fig. 8. This means that node i is updated from a point on either x_jx_k or x_kx_l. Since for any position x_γ on both line segments ${\mathbf {b}\cdot \mathbf {a}\geq \sin \limits (\alpha _{\text {oh}})}$, the speed function in (18) reduces to f(a, α_oh) = f₀/(b ⋅a). Substituted into (13) this gives

$$ \begin{array}{@{}rcl@{}} {T}_{\gamma}^{i} = \frac{ \mathbf{b} \cdot (\mathbf{x}_{i} - \mathbf{x}_{\gamma} )}{g(\rho(\mathbf{x}_{i}))f_{0} } +T_{\gamma}. \end{array} $$

(20)

Since the build direction b is a unit vector and x_γ moves perpendicular to b with changing γ, b ⋅ (x_i −x_γ) = Δy (Fig. 8). This implies that the changing distance between x_i and x_γ has no influence on the final arrival time. Looking at the shape of the speed function in Fig. 6, this makes sense. As x_γ moves from x_k to x_j in Fig. 8, the distance x_ix_γ increases, but the speed increases proportionally, as the direction of propagation changes. This reduces (20) to

$$ \begin{array}{@{}rcl@{}} T^{i}_{\gamma} = \frac{{{\varDelta}}\textit{y}}{g(\rho(\mathbf{x}_{i}))f_{0} } +T_{\gamma}. \end{array} $$

(21)

In order to find the point x_γ that results in the lowest arrival time ${T}_{\gamma }^{i}$, this equation is differentiated w.r.t. γ:

$$ \begin{array}{@{}rcl@{}} \frac{\partial {T}_{y}^{i}}{\partial y} = T_{k} - T_{j}. \end{array} $$

(22)

As the right-hand side of (22) is a constant term, the minimum lies at the bounds of each segment. This reduces (19) to

$$ \begin{array}{@{}rcl@{}} T_{i} = \min \left\{ {T}_{j}^{i}, {T}_{k}^{i}, {T}_{l}^{i} \right\}, \end{array} $$

(23)

where ${T}_{X}^{i}$ represents the arrival time at node i when calculated from node X, as shown in (21).

Fig. 8

Update of a node x_i on a structured grid can occur only from the segments x_jx_k and x_kx_l

3.2 Delay-density and speed-density relation

The change of speed function was the first step to represent the layer-by-layer filter with a front propagation formulation. It can be seen that (23) already resembles (1), where the arrival time value of a node depends on the three nodes below it. The next step is to choose the speed-density relation (11) and the delay-density relation (5) such that the behaviour of the layer-by-layer filter is obtained. For this part, we ignore without loss of generality that each element can be supported by three elements, as this is now inherent to the specific speed function chosen, and we will be looking at single columns of elements only, as depicted in Fig. 9a.

Fig. 9

Demonstration of the conversion of densities ρ a to printable densities ξ b by the conventional layer-by-layer filter on a single column of elements

Let us first examine how the printable densities are related to original densities in the layer-by-layer filter. For a single column of elements, such as the one displayed in Fig. 9a, (1) and (2) reduce to

$$ \begin{array}{@{}rcl@{}} \xi_{i} &=& \min (\xi_{i-1},\rho_{i}), \end{array} $$

(24)

$$ \begin{array}{@{}rcl@{}} &=& \min (\rho_{1},\rho_{2},\ldots,\rho_{i}), \end{array} $$

(25)

where i is the index of each element, with i = 1 being the bottom element. Thus, the printable density of element i is equal to the lowest density encountered in elements 1 to i. This ensures that an element can only have full printable density if all the elements that support it also have full density. This can be seen in Fig. 9b, where the densities given in Fig. 9a have been processed according to (25). Here, e.g. elements 4 and 5 have ξ = 0.1, as ρ₄ = 0.1 is the lowest density in the set. The density of element 5 is reduced from 1 to 0.1 as it is not properly supported.

In order to describe the layer-by-layer filter with front propagation, the speed-density and delay-density relations need to be chosen such that (24) is obtained. Recall that with the front propagation formulation, the printable density is defined as (5)

$$ \begin{array}{@{}rcl@{}} \xi(\mathbf{x}) = h(\tau(\mathbf{x})) = h\left( T(\mathbf{x}) - T^{\text{layer}}(\mathbf{x})\right). \end{array} $$

(26)

In a discrete single column setting as in Fig. 9, and substituting (21) for the arrival time T(x), the printable density for an element i (26) reduces to

$$ \begin{array}{@{}rcl@{}} \xi_{i} = h \left( T_{i-1} + \frac{{{\varDelta}}\textit{y}}{g(\rho_{i})f_{0} } - T^{\text{layer}}_{i}\right). \end{array} $$

(27)

The terms between brackets are the following: the arrival time of the previous element, the distance to the current element divided by the propagation speed, and the arrival time of the reference field. In order to obtain the layer-by-layer filter, the speed-density relation g is chosen such that (24) is obtained from (27):

$$ \begin{array}{@{}rcl@{}} h \left( T_{i-1} + \frac{{{\varDelta}}\textit{y}}{g f_{0} } - {T}_{i}^{\text{layer}}\right) = \min (\xi_{i-1},\rho_{i}), \end{array} $$

(28)

where the arguments of the speed-density relation g are omitted for brevity. The arrival time of the previous element, T_i− 1, can be substituted by its printable density using (26):

$$ \begin{array}{@{}rcl@{}} h \left( h^{-1}(\xi_{i-1}) + {T}_{i-1}^{\text{layer}} + \frac{{{\varDelta}}\textit{y}}{g f_{0} } - {T}_{i}^{\text{layer}}\right) = \min (\xi_{i-1},\rho_{i}). \end{array} $$

(29)

Using ${T}_{i}^{\text {layer}} - {T}_{i-1}^{\text {layer}} = {{\varDelta }}\textit {y}/f_{0}$ (3), the following speed-density relation is derived:

$$ \begin{array}{@{}rcl@{}} g = \frac{{{\varDelta}}\textit{y}}{f_{0}\left( h^{-1}\left( \min (\xi_{i-1},\rho_{i})\right) - h^{-1}(\xi_{i-1})\right)+ {{\varDelta}}\textit{y}}. \end{array} $$

(30)

This can be interpreted as follows. If ρ_i > ξ_i− 1, the arrival time should be such that ξ_i = ξ_i− 1, or h(τ_i) = h(τ_i− 1). In other words, the delay should not increase, which is achieved when the front propagates with the same speed as with which T^layer increases over distance, i.e. when g = 1. This corresponds to (30), which reduces to 1 when ρ_i > ξ_i− 1.

For ρ_i < ξ_i− 1, the arrival time should ensure that ξ_i = ρ_i. Because ρ_i < ξ_i− 1, the delay should increase to lower the printable density ξ_i as compared to ξ_i− 1. With the speed-density relation given in (30), the speed is lowered exactly such that the new delay will result in ξ_i = ρ_i.

3.3 Comparison of front propagation and layer-by-layer formulation

With the speed-density relation in (30) and the speed function given in (18), the layer-by-layer AM filter can be described in a continuous setting with front propagation. For comparison of these formulations, both the layer-by-layer formulation as provided in Langelaar (2017) and its front propagation implementation described in this section are applied to a given density field displayed in Fig. 10a. The resulting printable density fields from the layer-by-layer filter and the front propagation implementation are shown in Fig. 10b and c, respectively. Although they appear visually similar, there are some differences, displayed in Fig. 10d. As can be seen, there is hardly a difference in printable regions (ξ = 1), but for intermediate density regions the printable density values differ. This is due to the different minimum approximations that are used. For the front propagation formulation, the minimum approximation are chosen as close as possible to the default settings given in Langelaar (2017). When the smooth minimum/maximum approximation are chosen more accurate and less smooth, the error between both implementations vanishes, and the layer-by-layer filter can be exactly reproduced with front propagation.

Fig. 10

Application of the layer-by-layer and front propagation formulation on the density field given in (a). The differences occur only in the intermediate density regions, as different minimum approximation are used (d). a Input density field ρ. b Printable densities ξ_lbl obtained with the layer-by-layer formulation. c Printable densities ξ_fp obtained with the front propagation formulation. d Absolute difference between ξ_lbl and ξ_fp

4 Comparison of layer-by-layer and front propagation-based overhang filters

In the previous section, it is shown that the layer-by-layer filter by Langelaar (2017) can be cast into a front propagation formulation. The front propagation formulation of the layer-by-layer filter enables a detailed comparison between the layer-by-layer overhang filter and the front propagation-based overhang filter presented in van de Ven et al. (2018). To avoid confusion of both methods, the front propagation implementation of the layer-by-layer filter, as shown in Section 3, is referred to as simply the layer-by-layer overhang filter. The original continuous, front propagation based, overhang filter, as introduced in Section 2.2, is referred to as the continuous overhang filter.

The two elements of the front propagation that differ between both filters are summarized in Fig. 11. First, the difference in the speed function f(a, α_oh) is discussed, followed by the differences in speed-density relation. Finally, the numerical implementations of the various minimum/maximum operators and their effect on the sensitivities are analysed.

Fig. 11

Differences in speed function and speed-density relation between the layer-by-layer and the continuous overhang filter

4.1 Differences in speed function

The speed functions of both implementations share a similar profile for propagation directions above the minimum allowable overhang angle, i.e. when ${\mathbf {b}\cdot \mathbf {a} \geq {\sin \limits } (\alpha _{\text {oh}})}$ (18). However, for other directions of propagation, the speed functions are different, as can be seen in Fig. 11 (both speed functions are displayed in more detail in Figs. 4 and 6). The rectangular speed function of the continuous filter allows propagation in all directions, even opposite to the build direction, and is only slightly anisotropic, with an anisotropy ratio, i.e. maximum speed divided by the minimum speed, of $\sqrt {2}$ for α_oh = 45^∘. The triangular speed function of the layer-by-layer filter on the other hand, only allows propagation when ${\mathbf {b}\cdot \mathbf {a} \geq \sin \limits (\alpha _{\text {oh}})}$ while the propagation speed is zero for other directions. It therefore has an infinite anisotropy ratio.

The layer-by-layer speed function has a close resemblance to the AM process, as it can only propagate in directions that are printable from its current position. It is therefore a more natural choice, and was investigated for the continuous filter as well, before adopting the rectangular speed function for numerical reasons further detailed in the following.

For practical applicability, one of the requirements for the continuous filter was that it should be applicable to unstructured meshes. On unstructured meshes, it is difficult to propagate a front with a highly anisotropic speed function. As mentioned in Section 2.2, a crucial part of the front propagation algorithm is the calculation of the arrival time for a node when updated from two other nodes. This update is executed several times per node, and is therefore the dominant factor in computational cost. Reducing the number of updates greatly reduces the computational cost.

The number of updates required per node depends on the distance d from which a node can be updated, which in turn depends on the anisotropy ratio of the speed function (12). Ideally, one would update a node only from its direct neighbours, as is the case for an isotropic speed function. However, for the speed function of the layer-by-layer filter, as the minimum speed equals zero, $d=\infty$, meaning a node can be updated from every other node in the mesh. This is demonstrated on the unstructured mesh given in Fig. 12a. Here, a front is propagated from the blue node with the wedge-shaped speed function as given in Fig. 6. If the front is propagated correctly, all the nodes in the gray area should be reached by the front. In order to do so, some nodes must be updated from a large distance. For example, due to the nature of the speed function, node x_i in Fig. 12b can only be updated from locations in the transparent green area. The only node that can provide the update is the blue node itself. Consequently, this front can only be propagated correctly when nodes are updated from a much larger distance than only the direct neighbours. This is shown in Fig. 12c, where the arrows indicate the closest node from which a node can be updated, such that the direction of the update is above the overhang angle.

Fig. 12

Front propagation from a single node (blue) with a speed function as displayed in Fig. 6 for unstructured (a, b, c) and structured meshes (d, e). Nodes in the gray domain are reachable by the front, while black nodes are not

For structured meshes, on the other hand, the wedge-shaped speed function can be propagated efficiently. If the overhang angle does not align with the mesh, as in Fig. 12d, the situation is similar to unstructured meshes, and updates from a large distance might be required, as illustrated. However, when $\tan (\alpha _{\text {oh}})={{\varDelta }}\textit {y}/{{\varDelta }}\textit {x}$, where dy and dx are the element height and width, a node only has to be updated from its direct neighbours, as displayed in Fig. 12e. That is because if a node i can be updated from a far away node j, at least one of the direct neighbours below i can also be updated from node j (Fig. 7). For the speed function as given in (18), it is therefore sufficient to only consider the three nodes directly below the node of interest.

Altogether, if the filter is required to function on an unstructured mesh, the anisotropic speed function used in the layer-by-layer filter cannot be used. Therefore, a different speed function is chosen that instead of having a zero propagation speed in the direction that are not printable, has a non-zero propagation speed in those directions. This requires a different processing of the resulting arrival times of the front propagation, which is discussed in Section 4.2.

4.1.1 Effect of the speed function on sensitivities

The speed function influences the direction in which the front propagates, which determines the order in which the nodes meet with the propagating front. This is important for the resulting sensitivities, as the sensitivity information spreads through the domain in exactly the opposite order as in which the front is propagated. This is shown in Fig. 13, where the layer-by-layer filter and the continuous filter have been applied to the same geometry shown in black-white. For every element, it is displayed from which other elements its arrival time has been calculated, indicated by the arrows. For one element, indicated with a light-blue circle, all the nodes that could have contributed to this node arrival time are highlighted with blue arrows.

Fig. 13

The arrows pointing from each element indicate which elements are used to calculate its arrival time. This indicates to which elements sensitivity information is passed. For one element, highlighted by a blue circle, all the dependencies of elements that are involved in the calculation of its arrival time are coloured blue. a Layer-by-layer filter. b Continuous filter with low υ_void. c Continuous filter with high υ_void

For the layer-by-layer filter (Fig. 13a), each element can only be updated from the three elements of the underlying layer (1). Since a smooth maximum is used to determine from which of the three lower elements it is updated, it can depend on up to three elements. This is usually the case when all the three underlying elements have the same printable density, for example for all the elements of the second row. On the other hand, in the implementation of the continuous filter as in van de Ven et al. (2018), no smooth minimum operator is used to select from which elements the arrival time is calculated (17). Therefore, each element depends strictly on two other elements: the two elements that define the line segment from which the element was updated (16), which can be seen in Fig. 13b. When multiple update directions result in a similar arrival time, a single direction is chosen. This can be seen in, for example, the elements on the second row. Most of them are updated from the elements below-left and below. An update from the elements below-right and below would have resulted in the same arrival time, but this is neglected due to the strict minimum operator. Furthermore, contrary to the layer-by-layer filter, the continuous filter allows propagation in all directions. Therefore, one can find elements that have been updated from elements in the same or even higher layers, as is the case for the element indicated with the light-blue circle.

As the sensitivities are propagated in opposite direction of the front propagation, these differences have a major effect on the sensitivities, albeit the resulting arrival times are similar. In Fig. 13, all the elements that have a blue arrow are in some way involved in the calculation of the arrival time of the element indicated with the light-blue circle. In other words, in order to increase the printable density of the indicated element, the density of the blue-arrowed elements should be increased. For the layer-by-layer filter, this results in the creation of a support column through the void region in the middle. For the continuous filter, the column to left of the indicated element will be expanded towards this element. In this case, the layer-by-layer filter is more likely to form support columns, while the continuous filter will expand or shift existing column for support.

For the continuous filter, the speed with which the front propagates through void can be increased, as can be seen in Fig. 13c. The higher void speed shifts the region for which it is faster to travel directly to the base upwards (i.e. where elements are updated from below, as in the layer-by-layer filter), as indicated by the dashed green line in Fig. 13c and b. This will result in a more similar behaviour to the layer-by-layer filter. Finally, a higher void speed also allows the front to “cut corners”, as can be seen by the corner indicated with the green circle, which can be beneficial for the sensitivities, as these corner elements are usually the only elements whose density can be further increased, as can be seen in Fig. 13b for the blue-arrowed elements.

4.2 Differences in speed-density relations

One of the most attractive features of the layer-by-layer filter as compared to the continuous filter, is that an element can be supported by an underlying element with a similar or higher density. For example, when the layer-by-layer filter is applied to a uniform density field of ρ = 0.5, the resulting printable density field is identical: ξ = 0.5, as displayed in Fig. 14a and b. With the continuous filter, the front will travel at half speed through the domain, and the delay will increase with increasing height, resulting in a printable density field that decays with height, as can be seen in Fig. 14c. Since only material at the bottom of the domain is usually an unfavourable starting condition, it is proposed in van de Ven et al. (2018) to activate the continuous filter after 10 iterations.

Fig. 14

Processing of a uniform intermediate density field (a), a typical initial condition of density-based topology optimization, by the layer-by-layer filter (b), and the continuous filter (c)

The layer-by-layer filter achieves its behaviour by a smart choice of speed-density relation. As explained in Section 3.2, the propagation speed is only lowered when the current element has a lower density than the printable density of the supporting element. Otherwise, g = 1, maintaining a propagation speed equal to f₀, the propagation speed used for the reference field T^layer. If the propagation speed is equal to f₀, the delay does not increase, and the printable density is equal to that of the supporting element, resulting in the desired behaviour described by (2).

For the continuous filter, the propagation speed is simply scaled with the element’s density: when the element has full density, g = 1, and for intermediate densities g < 1. This results in a stricter penalization of intermediate densities: for every intermediate density element, g < 1 and the delay increases.

Certainly, the layer-by-layer speed-density relation is preferable for better convergence. In Section 5 it is investigated if the speed function used in the layer-by-layer filter can be transferred to the continuous filter to improve its performance.

4.3 Smooth min/max approximations

The final difference between both methods that is compared in this work, is the implementation of the minimum/maximum operators of both methods to select which underlying element is the supporting element. For the layer-by-layer filter, this is the element with the highest printable density (1), and for the continuous filter the element with the lowest arrival time (17).

In Langelaar (2017), the discrete maximum operator is implemented as a penalized p-norm, to provide a smooth differentiable function. This enables the calculation of correct sensitivities when the arguments of the maximum operator are close to each other. In van de Ven et al. (2018), the minimum operator that selects the lowest arrival time is implemented as a discrete operator: only the lowest arrival time is used for the front propagation, and in the sensitivity analysis the adjoint is propagated only to the elements that provided the lowest arrival time. This leads to incorrect sensitivity information when the arrival time calculated from different nodes is equal, which is especially visible in the first iteration, where one starts with a uniform density field.

In order to investigate the effect of the discrete operator on the sensitivities, consider the volume constraint

$$ \begin{array}{@{}rcl@{}} f_{1} = \sum\limits_{i=1}^{N} \xi_{i} V_{\text{el}}/V_{\text{tot}} - V_{\text{frac}}, \end{array} $$

(31)

where V_el and V_tot are the element and domain volume, respectively, and N is the total number of elements. For the volume constraint on a structured mesh, the derivatives to the printable densities are equal for every element:

$$ \begin{array}{@{}rcl@{}} \frac{\text{d}f_{1}}{\text{d}\xi_{i}} = V_{\text{el}}/V_{\text{tot}}, \quad \forall i. \end{array} $$

(32)

The sensitivities towards the densities $\frac {\text {d} f_{1}}{\text {d}\rho _{i}}$ for a uniform density field are displayed in Fig. 15a. The finite differences show the expected result, where densities towards the bottom have a higher sensitivity value, since more printable densities (and thus a large volume) are influenced by the lower elements than by the higher elements, as the front propagates bottom to top.

Fig. 15

Comparison of finite differences and adjoint sensitivities for a the continuous filter applied to a uniform density field, b the continuous filter applied to a typical MBB beam result, and c the smoothed continuous filter applied to a uniform density field

Unfortunately, the adjoint sensitivity analysis is not able to capture the sensitivity behaviour accurately, as can be seen in Fig. 15a. Although for every element the three underlying elements provide equal arrival times in the uniform density field, the sensitivity information is propagated to only one of the underlying elements because of the discrete minimum operator. In this case, the sensitivities are transferred to the lower left element because it has the lowest index. This results in an aggregation of sensitivities in the leftmost column, as displayed in Fig. 15a.

Fortunately, this is a problem that only occurs for a perfectly uniform density field. For example, when a tiny random perturbation with a magnitude of 1 × 10^− 5 is added to the density field, the adjoint sensitivities and finite differences are virtually identical. This can be seen in Fig. 15b, where instead of a uniform density field, a density field resulting from an MBB beam optimization is used, similar to the density field shown in Fig. 10a. As can be seen, there is a good correspondence between the finite differences and adjoint sensitivities, with a maximum relative difference of less than 0.1%.

It is however possible to formulate the front propagation with a smooth minimum operator. The implementation is mainly an exercise in bookkeeping as, contrary to the layer-by-layer filter, it is not known a priori from how many elements an element is updated. This is determined during the front propagation, based on the order in which the elements are updated. Therefore, one needs to keep track of the number of updates an element receives, from which elements these updates are done, the resulting arrival times of these updates, and the corresponding sensitivity information. The resulting adjoint sensitivities are much closer to the finite differences for a uniform field, as shown in Fig. 15c. As the smoothed minimum operator is tedious to implement and did not result in a significant improvement in convergence, it was not implemented in van de Ven et al. (2018).

5 Improved continuous overhang filter

In the previous section, a detailed comparison between the layer-by-layer filter and the continuous filter was performed, enabled by the front propagation formulation of the layer-by-layer filter. In this section, an improved version of the continuous front propagation filter is proposed, by incorporating elements of the front propagation formulation of the layer-by-layer filter.

In Section 4.1 it was shown that the wedge-shaped speed function used by the layer-by-layer filter can only be used on a structured grid, and is therefore not eligible for use in the continuous filter. However, the speed-density relation g (30) can be applied to the rectangular speed function of the continuous filter. For this, only one alteration is required. For the layer-by-layer filter, the distance between two elements projected on the build direction is constant and appears as Δy in the speed-density relation (30). For the continuous filter, an element i is update from a location x_γ on a line segment between two other elements j and k, as displayed in Fig. 5. Therefore, the speed-density relation is formulated as:

$$ \begin{array}{@{}rcl@{}} g = \frac{|\mathbf{b} \cdot (\mathbf{x}_{i} - \mathbf{x}_{\gamma} )|}{f_{0}\left( h^{-1}\left( \min (\xi_{\gamma},\rho_{i})\right) - h^{-1}(\xi_{\gamma})\right)+ |\mathbf{b} \cdot (\mathbf{x}_{i} - \mathbf{x}_{\gamma} )|}, \end{array} $$

(33)

with

$$ \begin{array}{@{}rcl@{}} \xi_{\gamma} &= h(T_{\gamma} - {T}_{\gamma}^{\text{layer}}). \end{array} $$

(34)

In principle, this speed-density relation can be interpreted similar to the layer-by-layer version, as described in Section 3.2. Compared to the old speed-density relation, this speed function is not strictly anisotropic. When ξ_γ ≤ ρ_i on the whole line segment x_jx_k, the speed-density relation reduces to 1, and is isotropic (except for the edge case when |b ⋅ (x_i −x_γ)| = 0, in which case the speed function should be defined as g = 1). However, when ξ_γ > ρ_i, the speed-density relation tries to increase the delay such that ξ_i = ρ_i, which makes it dependent on x_γ and thus anisotropic. Therefore, one cannot use the same update algorithm as proposed in van de Ven et al. (2018). For this study, the minimization problem that has to be solved to find the minimal arrival time over the line segment x_jx_k (16) is solved with brute force by probing 10 locations along the line segment and accepting the minimum value. For practical applications, a similar solution as in van de Ven et al. (2018) should be constructed to speed up the front propagation.

Another effect of using the speed-density relation as given in (33), is that the choice of the delay-density relation h (34), as long as it is monotonically decreasing, is not relevant: the speed-density relation g will reduce the equation for printable densities to a minimum formulation (24), independent of h. Therefore, the parameter k that had to be set for the continuous overhang filter in van de Ven et al. (2018) (6) is no longer required. This simplifies the formulation and makes it more robust, as a user-defined parameter is eliminated.

5.1 Numerical results

First, the layer-by-layer filter and the conventional and improved continuous filter are compared on a 2D problem, after which the improved continuous filter is demonstrated in 3D.

5.1.1 2D case—comparison

The different overhang filters are compared on the compliance optimization of the MBB beam with 3:1 aspect ratio, with a volume constraint set to 50%. A density filter (Bruns and Tortorelli 2001; Sigmund and Petersson 1998) with a filter radius r = 2Δx is applied, intermediate densities are penalized with SIMP penalization (Bendsøe 1989; Bendsøe and Sigmund 1999) of p = 3, and the Method of Moving Asymptotes (Svanberg 1987) is used as optimization algorithm. The optimizations are terminated when the maximum change of printable densities is smaller than 0.01.

The printable densities at the iteration 0, iteration 20, and final designs for the three methods are displayed in Fig. 16. The initial condition is a uniform density field with ρ = 0.5. It can be seen that both the layer-by-layer filter and the improved continuous filter allow the stacking of intermediate densities, and thus have a resulting initial field of ξ = 0.5. The conventional implementation of the continuous filter does not allow this and therefore only the bottom layers remain. This is an unfavourable starting condition, as the design now has to grow from the bottom, as can be seen in the following snapshots. Eventually the optimization terminates in an suboptimal local minimum, as can be seen in Fig. 17. This behaviour is very similar to the overhang filter presented in Gaynor and Guest (2016).

Fig. 16

Initial, intermediate and final designs of the different overhang filters for the MBB beam optimization problem

Fig. 17

Convergence behaviour of the different overhang filters

The layer-by-layer filter and the improved continuous filter do not suffer from the poor initial condition, and can straight away put material at the top of the domain, as can be seen in Fig. 16. Both methods finalize in similar designs with similar objective values, as displayed in Fig. 17. Finally, the convergence behaviour of the conventional continuous filter with gradual activation after 10 iterations, as proposed in van de Ven et al. (2018), is also plotted in Fig. 17. As the filter is activated, the objective spikes, but converges to a lower objective than without continuation. However, the final objective is still higher than the layer-by-layer filter and the improved continuous filter.

5.1.2 3D case—bicycle pull brake

To fully demonstrate the capabilities of the improved continuous filter, it is demonstrated on a compliance case with a more challenging design domain, such as one might encounter in real-life problems. For the 3D case a linear pull brake for a bicycle is optimized for stiffness against a 10% volume constraint. The case will be optimized without an overhang constraint and with a 45^∘ overhang constraint. The 3D optimization is performed with an optimization code based on the Portable, Extensible Toolkit for Scientific Computing (PETSc) (Balay et al. 2017; Balay et al. 1997; Karypis and Kumar 1998), and visualized with ParaView (Ahrens et al. 2005). Isosurfaces of the printable density field at ξ = 0.5 are depicted for visualization. Finally, the PETSc-based MMA implementation presented in Aage and Lazarov (2013) and Aage et al. (2015) has been used as optimization algorithm.

The design domain for the pull brake is shown in Fig. 18. The red regions are fixed regions, while the gray region is the design domain. The pull brake is mounted to the bicycle with a bolt at the lowest fixed region in Fig. 18a. This is simulated by fixing the centre line of the bolted region in x- and y-direction, allowing rotation around the z-axis, and by fixing the back side in z-direction as indicated. When the brake is applied, a clamping force of F_clamp = 200N is exerted on the top fixed region, indicated by the two yellow arrows in x-direction. This will push the brake pad against the wheel. Therefore, the brake pad is fixed in x-direction, and the brake force exerted by the tire on the brake pad is applied in z-direction, indicated by the yellow arrows in z-direction. The force on the brake pad is proportional to the clamping force: due to the geometry of the lever mechanism, the clamping force is amplified by a factor 3.7, which gives F_brake = 3.7μF_clamp, where μ is the friction coefficient assumed to be 0.5. The mechanism is to be printed (without the brake pad) in the orientation shown in Fig. 18b. A small amount of support will be required to manufacture the curved section of the supported surface, but since metal components are generally already printed on a small layer of supports, this is not introducing a large amount of additional support material.

Fig. 18

The bicycle pull brake case. The fixed regions are shown in red, while the design domain is shown in gray. Applied forces are indicated by yellow arrows and fixed regions are indicated in (a). The domain is meshed with tetrahedral elements, of which a clipped section is shown in (b) and is to be printed in the orientation as shown in (b)

The irregular design domain of the pull brake shows the advantage of being able to restrict overhanging features on unstructured meshes. Standard meshing algorithms can be used to create a tetrahedral mesh, and fixed regions such as the brake pad can be meshed with a lower resolution to reduce the total number of nodes, as shown in Fig. 18b. In this case, the domain is meshed using Gmsh (Geuzaine and Remacle 2009), with 2.7 × 10⁵ nodes and 1.5 × 10⁶ elements.

The optimized geometries are shown in Fig. 20. It can be seen that the geometries optimized with overhang filter can be printed in the given orientation without support material, while the geometry without overhang constraint has some overhanging members. The optimizations ran for 300 iterations; however, after 90 iterations, there is little change in the design and the objective values of all three optimizations are within 1% of their final values. The convergence behaviour for the first 90 iterations is shown in Fig. 19. The convergence curve is smooth for the improved continuous filter, as there is no need for continuation. For the continuous filter which requires continuation there is some non-smooth behaviour between iterations 10 and 20 where the continuation is applied, but the impact on the final result is negligible. It can however happen that the continuation is too aggressive, and the design has to be built up from the bottom of the domain, as was the case in Fig. 16 for the continuous filter without continuation. Therefore, the improved filter is a more stable version of the continuous filter because it does not require continuation. The final objective values for the optimizations with the continuous improved filter and continuous filter with continuation are 0.6% and 1.0% higher than without overhang filter, respectively. It is however difficult to compare these values as the overhang filter slightly alters the length scale introduced by the density filter (Fig. 20).

Fig. 19

Convergence behaviour for the first 90 iterations of the 3D case

Fig. 20

Optimized geometries of the bicycle pull brake with: improved continuous filter (a), the old continuous filter with continuation (b), and without overhang filter (c). The geometry of the improved continuous filter is also shown with outlines of the original design domain, where the fixed density regions are shown in red (d)

6 Conclusion

In this paper, a detailed comparison is made between the layer-by-layer overhang filter as proposed in Langelaar (2017), and the continuous overhang filter as proposed in van de Ven et al. (2018). It is demonstrated that the layer-by-layer filter, originally formulated in a discrete setting, can be formulated in a continuous setting using front propagation. Similar to the continuous filter, the printable densities are based on a delay between two arrival time fields. As such, the layer-by-layer filter can be formulated using front propagation by only changing the speed function, and the speed-density relation.

The front propagation formulation of the layer-by-layer filter allows a component-level comparison between the two methods. It is shown that the speed function used by the layer-by-layer function cannot be applied to unstructured meshed due to the large anisotropy of the speed function. However, the speed-density relation of the layer-by-layer filter has the advantageous characteristic that it allows the support of intermediate density elements by elements of the same or higher density, improving convergence in the early stage of the optimization. Additionally, the different implementations of the minimum/maximum operators are investigated. As the continuous filter does not use a smooth minimum operator, the resulting sensitivities for a uniform density field are incorrect. It is possible to use smoothed operators, but in practice the difference is small, as the sensitivities are only inaccurate for a uniform density field: a minutely perturbed density field results in correct sensitivities.

Finally, the speed-density relation used by the layer-by-layer filter is transferred to the continuous overhang filter, resulting in an overhang filter with the advantageous characteristics of the layer-by-layer filter, but directly applicable to unstructured meshes.

A Matlab implementation of the continuous filter is provided with this work, to aide with the implementation of a front propagation-based overhang filter in any existing density-based topology optimization.