An interface-enriched generalized finite element method for level set-based topology optimization

Abstract

During design optimization, a smooth description of the geometry is important, especially for problems that are sensitive to the way interfaces are resolved, e.g., wave propagation or fluid-structure interaction. A level set description of the boundary, when combined with an enriched finite element formulation, offers a smoother description of the design than traditional density-based methods. However, existing enriched methods have drawbacks, including ill-conditioning and difficulties in prescribing essential boundary conditions. In this work, we introduce a new enriched topology optimization methodology that overcomes the aforementioned drawbacks; boundaries are resolved accurately by means of the Interface-enriched Generalized Finite Element Method (IGFEM), coupled to a level set function constructed by radial basis functions. The enriched method used in this new approach to topology optimization has the same level of accuracy in the analysis as the standard finite element method with matching meshes, but without the need for remeshing. We derive the analytical sensitivities and we discuss the behavior of the optimization process in detail. We establish that IGFEM-based level set topology optimization generates correct topologies for well-known compliance minimization problems.

1 Introduction

The use of enriched finite element methods in topology optimization approaches is not new; the eXtended/Generalized Finite Element Method (X/GFEM) (Oden et al. 1998; Moës et al. 1999; Moës et al. 2003; Belytschko et al. 2009; Aragón et al. 2010), for example, has been explored in this context. However, the Interface-enriched Generalized Finite Element Method (IGFEM) has been shown to have many advantages over X/GFEM (Soghrati et al. 2012a; van den Boom et al. 2019a). In this work, we extend IGFEM to be used in a level set–based topology optimization framework.

Topology optimization, first introduced by Bendsøe and Kikuchi (1988), has been widely used to obtain designs that are optimized for a certain functionality, e.g., minimum compliance. In the commonly used density-based methods, a continuous design variable that represents a material density is assigned to each element in the discretization. The design is pushed towards a black and white design by means of an interpolation function, e.g., the Solid Isotropic Material with Penalization (SIMP) (Bendsøe 1989), that disfavors intermediate density values (also referred to as gray values). A filter is then required to prevent checkerboard-like density patterns, and to impose a minimum feature size. However, due to the filter, gray values are introduced. Density-based topology optimization is straightforward to implement and widely available in both research and commercial software. However, because the topology is described by a density field on a (usually) structured mesh, material interfaces not only contain gray values but also suffer from pixelization or staircasing—staggered boundaries that follow the finite element mesh. Although a post-processing step can be performed to smoothen the final design, the analysis during optimization is still based on gray density fields and a staircased representation. This may be detrimental to the approximate solution’s accuracy, especially in cases that are sensitive to the boundary description, such as flow problems (Villanueva and Maute 2017). Furthermore, because the location of the material boundary is not well defined, it is difficult to track the evolving boundary during optimization, for example to impose contact constraints.

The aforementioned drawbacks could be alleviated by the use of geometry-fitted discretization methods, which have been widely used in shape optimization (Staten et al. 2012). In these methods, the location of the material interface is known throughout the optimization, and the analysis mesh is modified to completely eliminate the pixelization and gray values. Mesh-morphing methods such as the deformable simplex method (Misztal and Baerentzen 2012; Christiansen et al. 2014; Christiansen et al. 2015; Zhou et al. 2018), level set–based mesh evolution (Allaire et al. 2014), anisotropic elements (Jensen 2016), and r-refinement (Yamasaki et al. 2017) have been demonstrated for topology optimization. Nevertheless, adapting the mesh in every design iteration remains a challenge. Not only is it an extra computational step, the changing discretization also introduces another complication in the optimization procedure because design variables need to be mapped to the new discretization (van Dijk et al. 2013).

A more elegant option is to define material interfaces independently from the finite element discretization, e.g., implicitly by means of the zero-contour of a level set function. In level set methods, the material boundary is moved by evolving the level set function, and new holes can be nucleated by means of topological derivatives (Amstutz and Andrä 2006). Although the required mapping between the geometry and the discretization mesh can be done with an Ersatz method using material density interpolation (Allaire et al. 2004), this again introduces gray values and staircasing into the analysis. Similarly, NURBS-based topology optimization using the Finite Cell Method (FCM) (Gao et al. 2019) provides a higher resolution boundary description, that is however still staircased. Alternatively, there are methods that allow for a one-to-one mapping of the topology to the analysis mesh, resulting in a non-pixelized boundary description. These methods combine the advantages of clearly defined material interfaces with the benefits of a fixed discretization mesh used in density-based methods. In the literature, level set–based topology optimization has been established using for the analysis CutFEM (Villanueva and Maute 2017; Burman et al. 2018), where the basis functions are restricted to the physical domain, and X/GFEM (Belytschko et al. 2003; Villanueva and Maute 2014; Liu et al. 2016), where the approximation space is enriched.

In enriched finite element methods such as X/GFEM, the standard finite element space is augmented by enrichment functions that account for a priori knowledge of the discontinuity of the field or its gradient at cracks or material interfaces, respectively. Although X/GFEM has been shown to be advantageous in many applications, e.g., fluid–structure interaction (Mayer et al. 2010) and fracture mechanics (Fries and Belytschko 2010), the method has also weaknesses: degrees of freedom (DOFs) corresponding to original mesh nodes do not automatically retain their physical meaning, and non-zero essential boundary conditions mostly have to be prescribed weakly. Moreover, X/GFEM may result in ill-conditioned matrices, in which case Stable Generalized FEM (SGFEM) (Babuška and Banerjee 2012; Gupta et al. 2013; Kergrene et al. 2016) or advanced preconditioning schemes (Lang et al. 2014) are needed. Furthermore, the approximation of stresses can be highly overestimated near material boundaries (Van Miegroet and Duysinx 2007; Noël and Duysinx 2017; Sharma and Maute 2018). Finally, as the enriched functions are associated with original mesh nodes, the accuracy of the approximation may degrade in blending elements, i.e., elements that do not have all nodes enriched (Fries 2008).

The Interface-enriched General Finite Element Method (IGFEM) (Soghrati et al. 2012a) was first introduced as a simplified generalized FEM to solve problems with weak discontinuities, i.e., where the gradient field is discontinuous. The method overcomes most issues of X/GFEM for this kind of problems: In IGFEM, enriched nodes are placed along interfaces, and enrichment functions are non-zero only in cut elements, i.e., elements that are intersected by a discontinuity. Furthermore, enrichment functions are exactly zero at original mesh nodes. Therefore, original mesh nodes retain their physical meaning and essential boundary conditions can be enforced directly on non-matching edges (Cuba-Ramos et al. 2015; Aragón and Simone 2017; van den Boom et al. 2019a). It was shown that IGFEM is optimally convergent under mesh refinement for problems without singularities (Soghrati et al. 2012a, 2012b). Moreover, IGFEM is stable by means of scaling enrichment functions or a simple diagonal preconditioner (van den Boom et al. 2019a; Aragón et al. 2020), meaning it has the same condition number as standard FEM. The method has been applied to the modeling of fiber-reinforced composites (Soghrati and Geubelle 2012b), multi-scale damage evolution in heterogeneous adhesives (Aragón et al. 2013), microvascular materials with active cooling (Soghrati et al. 2012a, 2012b and 2012c, 2013), and the transverse failure of composite laminates (Zhang et al. 2019b; Shakiba et al. 2019). IGFEM was later developed into the Hierarchical Interface-enriched Finite Element Method (HIFEM) (Soghrati 2014) that allows for intersecting discontinuities, and into the Discontinuity-Enriched Finite Element Method (DE-FEM) (Aragón and Simone 2017), which provides a unified formulation for both strong and weak discontinuities (i.e., discontinuities in the field and its gradient, respectively). DE-FEM, which inherits the same advantages of IGFEM over X/GFEM, has successfully been applied to problems in fracture mechanics (Aragón and Simone 2017; Zhang et al. 2019a) and fictitious domain or immersed boundary problems with strongly enforced essential boundary conditions (van den Boom et al. 2019a). A drawback of IGFEM is that quadratic enrichment functions are needed when the method is applied to background meshes composed of bilinear quadrangular elements (Aragón et al. 2020). Another disadvantage of IGFEM, which is also shared by X/GFEM, is that it may yield inaccurate field gradients depending on how the enriched finite element space is constructed (Soghrati et al. 2017; Nagarajan and Soghrati 2018). Depending on the aspect ratio of integration elements, stresses may be overestimated, and the issue is more prominent near material interfaces. This is not an issue along Dirichlet boundaries, where a smooth reaction field can be recovered (van den Boom et al. 2019a; 2019b), nor along traction-free cracks where stresses are negligible (Zhang et al. 2019a).

In the context of optimization, IGFEM has been explored for NURBS-based shape optimization (Najafi et al. 2017), the shape optimization of microvascular channels (Tan and Geubelle 2017) and their combined shape and network topology optimization (Pejman et al. 2019), the optimization of microvascular panels for nanosatellites (Tan et al. 2018a), and optimal cooling of batteries (Tan et al. 2018b). Nevertheless, IGFEM has not yet been used for continuum topology optimization. In this paper, we show topology optimization based on a level set function, parametrized with Radial Basis Functions (RBFs) (Wendland 1995; Wang and Wang 2006), in combination with IGFEM. We demonstrate the method on benchmark compliance problems. The sensitivities are derived and the method is compared with density-based topology optimization and to the level set–based Ersatz method. It should be noted that no significant performance improvement is expected for these cases, as they are not sensitive to the way the boundaries are discretized. Cases that would benefit from our approach to topology optimization compared with density-based methods—and which may be shared among other methods that provide clearly defined interfaces—include those where the location of the boundary has to be known throughout the entire optimization. Examples include contact, problems where boundary conditions need to be enforced on evolving boundaries, or problems where an accurate boundary description is fundamental for resolving the fields at interfaces, such as fluid–structure interaction or wave scattering problems. Although no significant improvement in performance is expected for the compliance minimization cases in this paper, they should be seen as the necessary proof of concept before considering more complex cases.

2 Formulation

2.1 IGFEM-based analysis

In this work, we focus on elastostatics and heat conduction problems on solid domains, as represented in Fig. 1. A design domain $\varOmega \subset \mathbb {R}^{d}$ is referenced by a Cartesian coordinate system spanned by base vectors $\left \{ \boldsymbol {e}_{i} \right \}^{d}_{i=1}$. This domain is decomposed into a solid material domain and a void domain, denoted by Ω_m and Ω_v, respectively, such that the domain closure is $\overline {\varOmega } = \overline {\varOmega }_{\mathrm {m}} \cup \overline {\varOmega }_{\mathrm {v}}$, and Ω_m ∩Ω_v = ∅. The boundary of the design domain, $\partial \varOmega \equiv \varGamma = \overline {\varOmega } \setminus \varOmega$, is subjected to essential (Dirichlet) boundary conditions on Γ^D, and to natural (Neumann) boundary conditions on Γ^N, such that $\overline {\varGamma } = \overline {\varGamma }^{\mathrm {D}} \cup \overline {\varGamma }^{\mathrm {N}}$ and Γ^D ∩Γ^N = ∅. The material boundary, $\varGamma _{\mathrm {m}} = \left (\overline {\varOmega }_{\mathrm {m}} \cap \overline {\varOmega }_{\mathrm {v}} \right ) \setminus \varGamma$, is defined implicitly by a level set function, $\phi \left (\boldsymbol {x} \right ) = 0$, that is a function of the spatial coordinate x.

Fig. 1

Mathematical representation of a topology optimization design domain Ω. Essential and natural boundary conditions are prescribed on the part of the boundary denoted Γ^D and Γ^N, respectively. The material domain is referred to as Ω_m, while the void region is denoted Ω_v. The inset shows the discretization with a material interface, defined by the zero-contour of the level set function ϕ, that is non-matching to the mesh. Original mesh nodes and enriched nodes are denoted with black circles ∙ and ∘ white circles, respectively

For any iteration in the elastostatic optimization procedure, the boundary value problem is solved with prescribed displacements $\bar {\boldsymbol {u}} : \varGamma ^{\mathrm {D}} \to \mathbb {R}^{d}$, prescribed tractions $\bar {\boldsymbol {t}}: \varGamma ^{\mathrm {N}} \to \mathbb {R}^{d}$, and body forces b_i defined as the restriction of b to domain Ω_i as $\boldsymbol {b}_{i} \equiv \boldsymbol {b} \vert_{\varOmega _{i}} : \varOmega _{i} \to \mathbb {R}^{d}, \text {where} i = \mathrm {m}, \mathrm {v}$. Similarly, we denote the field u_i as the restriction of u to domain Ω_i, i.e., $\boldsymbol {u}_{i} \equiv \boldsymbol {u} \vert_{\varOmega _{i}}$. Note that here the field is defined on both material and void domains. However, following the techniques described in van den Boom et al. (2019a), it is also possible to completely remove the void regions from the analysis.

We define the vector-valued function space:

$$ \begin{array}{ll} \boldsymbol{\mathcal{V}}_{0} = \Big\{ \boldsymbol{v} \in \left[ \mathcal{L}^{2} \left( \varOmega \right) \right]^{d}, \boldsymbol{v} \vert_{\varOmega_{i}} & \in \left[ \mathcal{H}^{1}(\varOmega_{i}) \right]^{d}, \\ & \boldsymbol{v} \vert_{\varGamma_{i}^{\mathrm{D}}} = \boldsymbol{0}, i=\mathrm{m}, \mathrm{v} \Big\}, \end{array} $$

(1)

where ${\mathscr{L}}^{2} \left (\varOmega \right )$ is the space of square-integrable functions and ${\mathscr{H}}^{1}(\varOmega _{i})$ is the first-order Sobolev space. In this work we only focus on problems with homogeneous Dirichlet boundary conditions. For problems with non-homogeneous essential boundary conditions, the reader is referred to Aragón and Simone (2017). The weak form of the elastostatics boundary value problem can be written as: Find $\boldsymbol {u} \in \boldsymbol {\mathcal {V}}_{0}$ such that:

$$ B \left( \boldsymbol{u}, \boldsymbol{v}\right) = L \left (\boldsymbol{v} \right) \qquad \forall \boldsymbol{v} \in \boldsymbol{\mathcal{V}}_{0}, $$

(2)

where the bilinear and linear forms can be written as:

$$ \begin{array}{@{}rcl@{}} B \left( \boldsymbol{u}, \boldsymbol{v}\right) = \sum\limits_{i=\mathrm{m},\mathrm{v}} {\int}_{\varOmega_{i}} \boldsymbol{\varepsilon}_{i} \left( \boldsymbol{v}_{i} \right): \boldsymbol{\sigma}_{i} \left( \boldsymbol{u}_{i} \right) \textup{d}{\varOmega}, \end{array} $$

(3)

and

$$ \begin{array}{@{}rcl@{}} L \left (\boldsymbol{v} \right) = \sum\limits_{i=\mathrm{m},\mathrm{v}} {\int}_{\varOmega_{i}} \boldsymbol{v}_{i} \cdot \boldsymbol{b}_{i} \textup{d}{\varOmega} + {\int}_{{\varGamma^{\mathrm{N}}}} \boldsymbol{v}_{i} \cdot \bar{\boldsymbol{t}} \textup{d}{\varGamma}, \end{array} $$

(4)

respectively, where the stress tensor $\boldsymbol {\sigma }_{i} \equiv \boldsymbol {\sigma } \vert_{\varOmega _{i}}$ follows Hooke’s law for linear elastic materials, σ_i = C_i : ε_i, and C_i is the elasticity tensor. Small strain theory is used for the strain tensor, i.e., $\boldsymbol {\varepsilon } \left (\boldsymbol {u} \right )= \frac {1}{2} \left (\boldsymbol {\nabla } \boldsymbol {u} + \boldsymbol {\nabla } \boldsymbol {u}^{\intercal } \right )$.

For heat conduction, the variational problem is:

$$ B \left( u,v \right) = L \left( v \right) \qquad \forall v \in \mathcal{V}_{0}, $$

(5)

where trial and weight function are taken from the space $\mathcal {V}_{0} = \left \{ v \! \in {\kern -.5pt} {\mathscr{L}}^{2} \left (\varOmega \right ), v \vert_{\varOmega _{i}} \! \in {\mathscr{H}}^{1}(\varOmega _{i}), v \vert_{\varGamma _{i}^{\mathrm {D}}} = 0, i=\mathrm {m},\mathrm {v} \right \}$. For a prescribed temperature $u : \varGamma ^{\mathrm {D}} \to \mathbb {R}$, prescribed heat flux $q : \varGamma ^{\mathrm {N}} \to \mathbb {R}$, heat source $f_{i} : \varOmega _{i} \to \mathbb {R}$, and conductivity tensor $\boldsymbol {\kappa }_{i} \equiv \boldsymbol {\kappa } \vert_{\varOmega _{i}} \to \mathbb {R}^{d} \times \mathbb {R}^{d}$, the bilinear and linear forms for each iteration in heat compliance problems are given by:

$$ \begin{array}{@{}rcl@{}} B \left( u, v \right) = \sum\limits_{i=\mathrm{m},\mathrm{v}} {\int}_{\varOmega_{i}} \nabla v_{i} \cdot \left( \boldsymbol{\kappa}_{i} \cdot \nabla u_{i} \right) \textup{d}{\varOmega} \end{array} $$

(6)

and

$$ \begin{array}{@{}rcl@{}} L \left (v \right) = \sum\limits_{i=\mathrm{m},\mathrm{v}} {\int}_{\varOmega_{i}} v_{i} f_{i} \textup{d}{\varOmega} + {\int}_{{\varGamma^{\mathrm{N}}}} v_{i} \bar{q} \textup{d}{\varGamma}. \end{array} $$

(7)

It is worth noting that interface conditions that satisfy continuity of the field and its tractions (or fluxes) do not appear explicitly in (3) or in (6) because they drop out due to the weight function v (or v) being continuous along the interface.

The design domain is discretized without prior knowledge of the topology as $\overline {\varOmega }^{h} = \bigcup _{i \in \iota _{E}} \overline {e}_{i}$, where $\overline {e}_{i}$ is the i th finite element and ι_E is the index set corresponding to all elements in the original mesh. Similarly, we define the mesh nodes $\left \{ \boldsymbol {x}_{j} \right \}_{j \in \iota _{h}}$, where ι_h is an index set corresponding to all the original nodes of the mesh. A partition of unity is defined by standard Lagrange shape functions N_j, associated to the mesh nodes. The result is a mesh that is non-matching to material boundaries. The level set function, whose zero contour defines the interface between void and material, is then evaluated on the same mesh. This is done for efficiency, as the mapping needs to be computed only once, and results in discrete nodal level set values. New enriched nodes are placed at the intersection between element edges and the zero contour of the level set. As illustrated in Fig. 1, the locations of these enriched nodes, denoted x_n, are found by linear interpolation between two nodes of the original mesh. Given two mesh nodes x_j and x_k with intersecting supports (i.e., $\textup {supp} \left (N_{j}\right ) \cap \textup {supp} \left (N_{k}\right ) \neq \emptyset$) and level set values of different signs (i.e., $\phi \left (\boldsymbol {x}_{j} \right ) \phi \left (\boldsymbol {x}_{k} \right ) <0$), the enriched node is found as:

$$ \boldsymbol{x}_{n} = \boldsymbol{x}_{j} - \frac{ \phi_{j} }{ \phi_{k} - \phi_{j}}\left( \boldsymbol{x}_{k} - \boldsymbol{x}_{j} \right), $$

(8)

where we adopt the notation $\phi _{j} \equiv \phi \left (\boldsymbol {x}_{j} \right )$. The material interface Γ_m is defined as the piece-wise linear representation of the zero contour of the level set function, discretized with enriched nodes $\left \{ \boldsymbol {x}_{n} \right \}_{n \in \iota _{w}}$, where ι_w is the index set corresponding to all enriched nodes. Elements that are intersected by Γ_m, indexed by the index set ι_c, are then subdivided into integration elements by means of a constrained Delaunay algorithm. The index set referring to all integration elements is denoted ι_e. The complexity of finding intersections and creating integration elements is $\mathcal {O}\left (\left |\iota _{E}\right |\right )$, where $\left | \cdot \right |$ denotes set cardinality, since each element has to be processed only once per iteration.

Following a Bubnov-Galerkin procedure, the resulting finite dimensional problem is then solved by choosing trial and weight functions from the same enriched finite element space. The IGFEM approximation can then be written as:

$$ \boldsymbol{u}^{h}(\boldsymbol{x}) = \underbrace{\sum\limits_{i\in \iota_{h}} N_{i} \left( \boldsymbol{x} \right) \boldsymbol{U}_ i}_{\text{standard FEM}}+ \underbrace{\sum\limits_{i\in \iota_{w}} \mathit{\psi}_{i} \left( \boldsymbol{x} \right) \boldsymbol{\alpha}_{i}}_{\text{enrichment}}, $$

(9)

for elastostatics, or

$$ u^{h}(\boldsymbol{x}) = \underbrace{\sum\limits_{i\in \iota_{h}} N_{i} \left( \boldsymbol{x} \right) U_ i}_{\text{standard FEM}}+ \underbrace{\sum\limits_{i\in \iota_{w}} \mathit{\psi}_{i} \left( \boldsymbol{x} \right) \alpha_{i}}_{\text{enrichment}}, $$

(10)

for heat conduction problems. The first term in (9) and (10) corresponds to the standard finite element approximation, with shape functions $N_{i} \left (\boldsymbol {x}\right )$ and corresponding standard degrees of freedom U_i (or U_i), and the second term refers to the enrichment, characterized by enrichment functions $\psi _{i} \left (\boldsymbol {x}\right )$ and associated enriched DOFs α_i (or α_i). Enrichment functions ψ_i can be conveniently constructed from Lagrange shape functions of integration elements, as illustrated in Fig. 2, while the underlying partition of unity shape functions are kept intact.

Fig. 2

Schematic representation of enrichment function ψ_i corresponding to enriched DOFs α_i, where enriched nodes are shown with ∘ symbols. This enrichment function is constructed from standard Lagrange shape functions in integration elements

Subsequently, the local stiffness matrix k_e and force vector f_e are obtained numerically; elements that are not intersected follow standard FEM procedures. An isoparametric procedure is used in integration elements to obtain the local arrays. Figure 3 shows a schematic of a triangular integration element (shaded) within an original cut element—the parent element—in global coordinates. The reference triangular domains for both integration and parent elements are also shown. Each reference domain shows the master coordinate associated to a given global coordinate x. In elastostatics (heat conductivity follows an analogous procedure), k_e and f_e are computed on each integration element’s reference triangle ◺ as:

(11)

where $\mathbf{B} = [\mathbf{\Delta} N _{1}\quad \mathbf{\Delta} N _{2} \quad \ldots \quad \mathbf{\Delta} N _{n}\quad \mathbf{\Delta} \psi_{1} \quad \ldots \quad \mathbf{\Delta} \psi _{m}],$ and D is the constitutive matrix. The parental shape functions vector N and enrichment functions ψ are stacked together. Note that j_e is the determinant Jacobian of the isoparamatric mapping of the integration element. The isoparametric mapping is a standard procedure in FEM; however, as the steps are important for the derivation of the sensitivities in Section 2.3.1, it is explained in more detail in Appendix B. The differential operator Δ is defined as:

$$ \begin{array}{ll} \mathbf{\Delta}& \equiv \begin{bmatrix} \frac{\partial}{\partial x} & 0 & \frac{\partial}{\partial y} \\ 0 & \frac{\partial }{\partial y} & \frac{\partial}{\partial x} & \\ \end{bmatrix}^{\top}, \\ \mathbf{\Delta}& \equiv \begin{bmatrix} \frac{\partial}{\partial x} & 0 & 0 & 0 &\frac{\partial}{\partial z} & \frac{\partial}{\partial y}\\ 0 & \frac{\partial }{\partial y} & 0 & \frac{\partial}{\partial z} & 0 &\frac{\partial}{\partial x}\\ 0 & 0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial y} & \frac{\partial}{\partial x} & 0\\ \end{bmatrix}^{\top}, \end{array} $$

(12)

for elastostatics in 2-D and 3-D, respectively, and

$$ \mathbf{\Delta}\equiv \begin{bmatrix} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \\ \end{bmatrix}^{\top}, \mathbf{\Delta}\equiv \begin{bmatrix} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ \end{bmatrix}^{\top}, $$

(13)

for heat conductivity in 2-D and 3-D, respectively. The derivatives in global coordinates are computed from the derivatives in local coordinates as

$$\mathbf{\nabla}_{\text{x}} N_{i}= \mathbf{J}^{-1}\, \mathbf{\nabla}_{\mathbf{\xi}} N_{i}, \quad \mathbf{\nabla}_{\text{x}} \psi_{i}= \mathbf{J}^{-1}_{e}\, \nabla_{\xi} \psi_i$$

(14)

for standard and enriched shape functions, respectively, where J is the Jacobian of the intersected original element, and J_e is the Jacobian of the integration element.

Fig. 3

Schematic of an integration element (shaded), whose local arrays are obtained by using an isoparametric mapping. Integration points in integration elements (ξ_e) and parent elements (ξ_p) are mapped to global coordinate x

In this work, we are concerned with linear triangular elements, for which a single integration point in standard and integration elements is sufficient. The discrete system of linear equations KU = F is finally obtained through standard procedures, where:

(15)

where $\iota _{A} = \left (\iota _{E} \setminus \iota _{c} \right ) \cup \iota _{e}$ and denotes the standard finite element assembly operator.

For a more detailed description on IGFEM, the reader is referred to Soghrati et al. (2012a).

2.1.1 Relation to X/GFEM

IGFEM is closely related to X/GFEM: The general X/GFEM approximation can be written as:

$$ \boldsymbol{u}^{h}(\boldsymbol{x}) = \underbrace{\sum\limits_{i\in \iota_{h}} N_{i} \left( \boldsymbol{x} \right) \boldsymbol{U}_ i}_{\text{standard FEM}}+ \underbrace{ \sum\limits_{i\in \iota_{h}} N_{i} \left( \boldsymbol{x} \right) \sum\limits_{j\in \iota_{g}} E_{ij} \left( \boldsymbol{x} \right) \hat{\boldsymbol{U}}_{ij}}_{\text{enrichment}}, $$

(16)

where enrichment functions E_ij are associated to generalized DOFs $\hat {\boldsymbol {U}}_{ij}$—the latter assigned to nodes of the mesh. While the X/GFEM approximation uses partition of unity shape functions to localize the effect of enrichment functions, in IGFEM this is not necessary because enrichment functions are local to cut elements by construction. In addition, enriched nodes in IGFEM are collocated along the discontinuities, resulting in less DOFs than required by (16).

It is worth noting, however, that IGFEM is not only closely related to X/GFEM, it can actually be derived from it by means of a proper choice of enrichment functions E_ij and by clustering enriched DOFs (Duarte et al. 2006). Appendix A shows this with a simple 1-D example.

IGFEM has several benefits over X/GFEM:

• Enrichment functions in IGFEM are local by construction, i.e., they are non-zero only in elements cut by the interface and exactly zero elsewhere. Therefore, IGFEM has no issues with blending elements, which is an issue for X/GFEM for some choices of enrichment functions (Fries 2008);

• In IGFEM, the enrichment functions vanish at the nodes of background elements. Therefore, the original mesh node conserves the Kronecker property, and the DOFs associated to these nodes maintain their physical interpretation;

• In X/GFEM, prescribing non-zero Dirichlet boundary conditions is usually done weakly by means of penalty, Lagrange, or Nitsche methods (Cuba-Ramos et al. 2015). In IGFEM, on the contrary, these boundary conditions can be prescribed strongly, both on original nodes and, by means of a multipoint constraint, on enriched edges (Aragón and Simone 2017; van den Boom et al. 2019a);

• Smooth traction profiles can be recovered when Dirichlet boundary conditions are prescribed on enriched edges (Cuba-Ramos et al. 2015; van den Boom et al. 2019a; 2019b). This is currently not possible in X/GFEM even with stabilization techniques (Haslinger and Renard 2009);

• IGFEM is stable, i.e., the condition number of the system matrix grows as $\mathcal {O}\left (h^{-2} \right )$, which is the same order as that of standard FEM. This is accomplished by means of a proper scaling of enrichment functions or by using a simple diagonal preconditioner (Aragón et al. 2020);

• The computer implementation is simpler: data structures of standard FEM can be reused to store enriched DOFs, post-processing is required for enriched DOFs only, and no special treatment of Dirichlet boundary conditions is needed (Aragón and Simone 2017).

2.2 Radial basis functions

Although it is possible to directly use the level set values ϕ_j on original nodes of the finite element mesh as design variables, we choose to use compactly supported radial basis functions for the level set parametrization for a number of reasons (Wang and Wang 2006):

• (i) RBFs give control over the complexity of the designs, and as such, they act similarly to a filter in density-based topology optimization;

• (ii) By decoupling the finite element analysis mesh from the RBF grid, the design space can be restricted without deteriorating the finite element approximation. This can be used to mitigate approximation error discretizations that are too coarse; and

• (iii) By tuning the radius of support of RBFs, we can ensure that the influence of each design variable extends over multiple elements. This allows the optimizer to move the boundary further and therefore converge faster, while using fewer design variables. This effect is similar to that of a filter radius in standard density-based topology optimization.

Figure 4 illustrates a compactly supported RBF _i (Wendland 1995) described by:

$$ \theta_{i} \left( r_{i}\right) = \left( 1-r_{i}\right)^{4} \left( 4r_{i} + 1\right) , $$

(17)

where the radius r_i is defined as:

$$ r_{i} \left( \boldsymbol{x}, \boldsymbol{x}_{i} \right)= \frac{{\left \| \boldsymbol{x}- \boldsymbol{x}_{i} \right \|}}{r_{\mathrm{s}}}, $$

(18)

and r_s is the radius of support. In (18), $\left \| \cdot \right \|$ denotes the Euclidian norm, and x_i is the center coordinates corresponding to RBF _i.

Fig. 4

Compactly supported RBF given by (17) with coordinates $\boldsymbol {x} = [ 0 0]^{\intercal }$ and radius of influence r_s = 1

The scalar-valued level set function $\phi \left (\boldsymbol {x}\right )$ is found as a summation of every non-zero RBF _i, scaled with its corresponding design variable s_i:

$$ \phi \left( \boldsymbol{x} \right) = \boldsymbol{\Theta} \left( \boldsymbol{x}\right)^{\intercal} \boldsymbol{s} = \sum\limits_{i \in \iota_{s}} \theta_{i} \left( \boldsymbol{x}\right) s_{i}, $$

(19)

where ι_s is the index set corresponding to all design variables, and:

$$ \boldsymbol{s} \in \boldsymbol{\mathcal{D}} = \left\{ \boldsymbol{s} \vert \boldsymbol{s} \in \boldsymbol{\mathbb{R}}^{\left| \iota_{s} \right|}, -1 \leq s_{i} \leq 1 \right\} $$

(20)

is a vector of design variables, with lower and upper bounds − 1 and 1 that prevent the level set from becoming too steep. Finally, evaluating this function at the original nodes of the finite element mesh results in the level set vector:

$$ \boldsymbol{\phi} = \boldsymbol{\theta}^{\intercal} \boldsymbol{s} , $$

(21)

where is a matrix that needs to be computed only once, as the original mesh nodes do not move throughout the optimization.

2.3 Optimization

The optimization problem is chosen as a minimization of the compliance C with respect to the design variables s that scale the RBFs. It needs to be emphasized that compliance minimization is merely a demonstrator problem, and the method is not limited to it. The minimization problem is subject to equilibrium and to a volume constraint V_c. This problem can be written as:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{s}^{\star} =\underset{\boldsymbol{s} \in \boldsymbol{\mathcal{D}}}{\arg\min} & &C = \boldsymbol{U}^{\intercal} \boldsymbol{K} \boldsymbol{U},\\ \text{subject to} & & ~~~\boldsymbol{K} \boldsymbol{U} = \boldsymbol{F},\\ & &~~ V_{\varOmega_{\mathrm{m}}} \leq V_{c}. \end{array} $$

(22)

The Method of Moving Asymptotes (MMA) (Svanberg 1987), a method commonly used in density-based topology optimization, is employed to solve this optimization problem.

2.3.1 Sensitivity analysis

The compliance minimization problem is self-adjoint (Bendsøe and Sigmund 2004), resulting in the sensitivity of the compliance C with respect to the design variables s as:

$$ \frac{\partial C}{\partial \boldsymbol{s}} = -\boldsymbol{U}^{\intercal} \frac{\partial \boldsymbol{K}}{\partial \boldsymbol{s}} \boldsymbol{U} + 2 \boldsymbol{U}^{\intercal} \frac{\partial \boldsymbol{F}}{\partial \boldsymbol{s}} . $$

(23)

Applying the chain rule, the sensitivity of the compliance C with respect to design variable s_i can be written at the level of integration elements in terms of the nodal level set values ϕ_j:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial s_{i}} & = & \sum\limits_{j \in \iota_{i} } \sum\limits_{e \in \iota_{j}} \sum\limits_{n \in \iota_{n}} \left( - \boldsymbol{u}_{e}^{\intercal} \frac{\partial \boldsymbol{k}_{e}}{\partial \boldsymbol{x}_{n}} \frac{\partial \boldsymbol{x}_{n}}{\partial \phi_{j}} \boldsymbol{u}_{e} \right.\\ &&\quad\quad\quad\quad\quad\left.+ 2 \boldsymbol{u}_{e}^{\intercal} \frac{\partial \boldsymbol{f}_{e}}{\partial \boldsymbol{x}_{n}} \frac{\partial \boldsymbol{x}_{n}}{\partial \phi_{j}} \right)\frac{\partial \phi_{j}}{\partial s_{i}}. \end{array} $$

(24)

In (24), a summation is done over all the nodes in the index set ι_i which contains all the original mesh nodes that are in the support of the RBF corresponding to design variable s_i. Then, a summation is done over ι_j, which refers to the index set of all integration elements e in the support of original mesh node j, i.e., the region where the original shape function N_j is nonzero. Lastly, a summation is done over the index set ι_n, which contains all the enriched nodes n in integration element e. The location of these enriched nodes is denoted x_n. Note that a number of terms can be identified in the sensitivity formulation: the derivatives of nodal level set values with respect to the design variables, ∂ϕ_j/∂s_i, the design velocities ∂x_n/∂ϕ_j, and the sensitivity of the element stiffness matrix and force vector with respect to the location of the n th enriched node, ∂k_e/∂x_n and ∂f_e/∂x_n, respectively.

First, the sensitivity of the nodal level set values with respect to the design variables is simply computed by taking the derivative of (21) with respect to s as:

$$ \frac{\partial \boldsymbol{\phi}}{\partial \boldsymbol{s}} = \boldsymbol{\theta}^{\intercal} . $$

(25)

The design velocities ∂x_n/∂ϕ_j also remain straightforward as they are computed by taking the derivative of (8) as:

$$ \frac{\partial \boldsymbol{x}_{n}}{\partial \phi_{j}} = - \frac{\phi_{k}}{\left( \phi_{j} - \phi_{k}\right)^{2}} \left( \boldsymbol{x}_{j} - \boldsymbol{x}_{k}\right) . $$

(26)

Note that the enriched nodes remain on the element edges of the finite element mesh, and thus the direction of the design velocity is known a priori.

More involved is the sensitivity of the e th integration element stiffness matrix k_e with respect to the location of enriched node n, which can be computed on the reference domain as:

(27)

where $\mathbf{B} = [\mathbf{\Delta} N _{1}\quad \mathbf{\Delta} N _{2} \quad \ldots \quad \mathbf{\Delta} N _{n}\quad \mathbf{\Delta} \psi_{1} \quad \ldots \quad \mathbf{\Delta} \psi _{m}],$ as defined in Section 2.1. In this work, a single integration point is used for numerical quadrature, with $\boldsymbol {\xi }_{e} = \left [ 1/ 3, 1/3 \right ]$ and w_g = 1/2. Recall that the material within each integration element remains constant, and therefore ∂D/∂x_n = 0. The first term in (27) contains the sensitivity of the Jacobian determinant, and represents the effect of the changing integration element area; the second and third terms contain the sensitivity of the element B matrix, and represent the effect of the changing shape and enrichment functions. The latter is computed as:

$$ \frac{\partial \mathbf{B}}{\partial \mathbf{x}_{n}} = \begin{bmatrix} \mathbf{0} \quad \mathbf{0} \quad \ldots \quad \mathbf{0} & \frac{\partial \mathbf{\Delta} \psi_{l}}{\partial \mathbf{x}_{n}}\quad \ldots \frac{\partial \mathbf{\Delta} \psi_{m}}{\partial \mathbf{x}_{n}} \end{bmatrix}. $$

(28)

Observe that only the enriched part of the formulation has an influence, as for linear elements the background shape function derivatives are constant throughout the integration element, and do not change with enriched node location, and thus

(29)

The Jacobian of the parent element is not influenced by the enriched node location either (∂J/∂x_n = 0). Similarly to (29), the enrichment functions are constant throughout the integration element, so that:

(30)

Appendix C describes how to compute the derivative of the Jacobian inverse and determinant, $\partial \boldsymbol {J}_{e}^{-1} / \partial \boldsymbol {x}_{n}$ and ∂j_e/∂x_n, respectively, by straightforward differentiation.

Finally, the sensitivity of the design-dependent force vector f_e is evaluated. Due to the IGFEM discretization, enriched nodes whose support is subjected to a line or body load contribute to the force vector, implying that the derivatives of the force vector are nonzero for cases with line loads or body forces. Similarly to the sensitivity of the element stiffness matrix, each integral in the sensitivity of the element force vector consists of two terms: one related to the Jacobian derivative, and another containing the function derivatives:

(31)

In the second term of the integrals, only the parent shape functions have a contribution. This is because enrichment functions in reference coordinates are not influenced by the enriched node in global coordinates, i.e., ∂ψ/∂x_n = 0. However, as the mapping to the parent reference domain is influenced by the enriched node location, ∂N/∂x_n is nonzero, and can be evaluated as:

$$ \frac{\partial \boldsymbol{N}}{\partial \boldsymbol{x}_{n}} = \frac{\partial \boldsymbol{N}}{\partial \boldsymbol{\xi}_{p}} \frac{\partial \boldsymbol{\xi}_{p}}{\partial \boldsymbol{x}} \frac{\partial \boldsymbol{x}}{\partial \boldsymbol{x}_{n}} = \frac{\partial \boldsymbol{N}}{\partial \boldsymbol{\xi}_{p}} \boldsymbol{A}_{p}^{-1} \frac{\partial \boldsymbol{x}_{e}}{\partial \boldsymbol{x}_{n}} \boldsymbol{N}_{e} , $$

(32)

where $\boldsymbol {A}_{p}^{-1}$ is the inverse isoparametric mapping that maps global coordinates to the local master coordinate system of the parent element as explained in Appendix B.

Although the sensitivity analysis seems involved, the partial derivatives are relatively straightforward to compute on local arrays.

3 Numerical examples

The enriched method outlined above is demonstrated on a number of classical compliance optimization problems. The results generated by this approach are compared with those generated by open source optimization codes, and the influence of the design discretization is investigated. A 3-D compliance optimization case and a heat sink problem are also considered. It should be noted that no holes can be nucleated in the method presented in this paper. Therefore, initial designs containing a relatively large number of holes are used for the numerical examples. However, the method could be extended to also nucleate holes by means of topological derivatives (Amstutz and Andrä 2006).

In this section, no units are specified; therefore, any consistent unit system can be assumed. For the MMA optimizer (Svanberg 1987), the following settings are used unless otherwise specified:

• The lower and upper bounds on the design variables s_i are given by − 1 and 1, as defined in the design variable space in (20)

• The move limit used by MMA is set to 0.01;

• A value of 10 is used for the Lagrange multiplier on the auxiliary variables in the MMA sub-problem that controls how aggressively the constraints are enforced.

3.1 Numerical verification of the sensitivities

The analytically computed sensitivities ∂C/∂s_i are checked against central finite differences $C^{\prime }_{i}$ for a small test problem as illustrated in Fig. 5. This test problem consists of a beam of size 2L × L that is clamped on the left, and subjected to a downward force $\left |\boldsymbol {\overline {t}} \right | = 1$ on the bottom right. The material phase of this beam has Young’s modulus E₁ = 1. We consider the initial design with three holes, as shown in Fig. 5, with Young’s modulus E₂ = 10^− 6. The problem is solved on a symmetric mesh of 12 × 6 × 2 triangles. The RBFs are defined on a 13 × 7 grid, and have a radius of 0.15L.

Fig. 5

Test problem for the finite difference check of the analytical sensitivities. The relative differences δ_i as per (33) are illustrated in Fig. 6

The relative differences of the non-zero design variable sensitivities are computed as:

$$ \delta_{i} = \frac{C^{\prime}_{i} - \partial C /\partial s_{i} }{ \partial C /\partial s_{i}}, $$

(33)

and illustrated in Fig. 6 for different finite different step sizes Δs_i. For a step size of Δs_i = 10^− 5, the relative difference is minimized and takes a value of δ ≈ 5 × 10^− 6.

Fig. 6

Relative difference δ_i between the analytically computed sensitivities for node i and central finite differences, as a function of the step size Δs_i

3.2 Cantilever beam

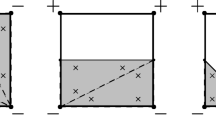
Our approach to enriched level set–based topology optimization is compared with the following open source codes: (i) the 99-line SIMP-based code by Sigmund (2001); (ii) an 88-line code for parameterized level set optimization using radial-basis functions and density mapping, proposed by Wei et al. (2018); and (iii) a code for discrete level set topology optimization with topological derivatives by Challis (2010).

The optimization problem for this comparison is the widely used cantilever beam problem, as illustrated in Fig. 7. It consists of a 2L × L rectangular domain that is clamped on the left and subjected to a downward point load $\bar {\boldsymbol {t}}$ in the middle of the right side. We set L equal to 1, the volume constraint to 55% of the design domain volume, and use $\left | \bar {\boldsymbol {t}}\right | = 1$. The material domain Ω_m is assigned a Young’s modulus E₁ = 1, whereas the void domain Ω_v has Young’s modulus E₂ = 10^− 6. Both domains have a Poisson ratio ν₁ = ν₂ = 0.3. Note that it is also possible to give the void regions a stiffness of exactly zero by removing DOFs (van den Boom et al. 2019a). However, this would entail extra overhead, and to ensure a fair comparison with the other models; in this work, it is chosen to use a small value for the void stiffness.

Fig. 7

Problem description and initial design for the cantilever beam example in Section 3.2. The domain is clamped on the left and a downward force is applied in the middle of the right side

Figure 7 shows the initial design that is used for the IGFEM-based optimization, which is the same as that used in the paper describing the 88-line code (Wei et al. 2018). The other two codes do not require an initial design, as they are able to nucleate holes. The optimization problem is solved on meshes defined on rectangular grids of 21 × 11, 41 × 21, 61 × 31, 81 × 41, and 101 × 51 nodes. Our proposed method makes use of triangular meshes, whereas the other methods use quadrilateral meshes. The RBF mesh used in the IGFEM-based solutions is the same as the analysis mesh, and a radius of influence of $r_{s} = \sqrt {2} \cdot a$ is used, where a is the distance between two RBFs.

The results for each code are illustrated in Fig. 8. For all methods, the design becomes more detailed when the mesh resolution is increased. Furthermore, the topologies obtained by each method are roughly the same. It is observed that the resulting designs are similar to those given by the code of Wei et al., especially for the finer meshes. Indeed, our proposed method yields results that have clearly defined (black and white) non-staircased boundaries. It should be noted, however, that the coarsest IGFEM result shows jagged boundaries. This zigzagging effect reduces with mesh refinement and is investigated in detail in Section 4.2. Figure 9a shows the convergence behavior of the different codes for the finest mesh. It is observed that our method leads to the lowest objective function value, which again is similar to that obtained by the code by Wei et al., while initially converging faster in the volume fraction.

Fig. 8

Final designs for a cantilever beam obtained by the proposed method and the other methods considered in this study, shown in the columns. The rows show designs obtained on meshes defined on grids of 21 × 11, 41 × 21, 61 × 31, 81 × 41, and 101 × 51 nodes, respectively

Fig. 9

Results of the cantilever beam problem for the different methods considered in Section 3.2; a shows the compliance and volume ratio convergence during optimization, b illustrates the final compliance as a function of the number of DOFs

Figure 9b shows the final compliance as a function of the number of DOFs. Initially, the different methods all find lower compliance values as the mesh is refined, but the method by Wei et al. and our method find slightly higher values for the finest mesh sizes. This may be explained by the optimizer converging to a local optimum. For each mesh size, the proposed method finds the lowest compliance value at the cost of adding some enriched DOFs.

3.3 MBB beam

The influence of the number of radial basis functions is investigated on the well-known MBB beam¹, which is illustrated in Fig. 10. The optimization problem consists of a 3L × L domain with symmetry conditions on the left. On the bottom right corner, the domain is simply supported, and a downward force $\bar {\boldsymbol {t}}$ is applied on the top left corner. As in the previous example, the volume constraint is set to 55% of the volume of the total design domain. The initial design is also indicated in Fig. 10, and the same material properties as in the previous example are used.

Fig. 10

Problem description and initial design for the MBB beam example in Section 3.3. Symmetry conditions are applied on the left of the domain, and the bottom-right corner is simply supported. A downward force is applied at the top-left side on the domain, in the middle of the beam

This optimization problem is solved on a triangular analysis mesh defined on a grid of 151 × 51 nodes, using a discretization of the design space consisting of 61 × 21, 91 × 31, 121 × 41, and 151 × 51 radial basis functions, so that only for the finest design space discretization, both resolutions match, and an RBF is assigned to every node in the analysis mesh. The support radius r_s is changed together with the design grid so that the overlap of RBFs is the same in each case: $r_{s} = \sqrt {2} \cdot a$, where a is again the distance between two RBFs.

Figure 11 shows the optimized designs. As expected, the level of detail in the design can be controlled by the RBF discretization. However, it is noted that in the finest RBF mesh, artifacts appear on the design boundary. This behavior will be further analyzed in Section 4.2. In Fig. 12a, the convergence behavior of the different RBF meshes is shown. Although the coarsest RBF mesh shows some initial oscillations, the overall convergence behavior is similar in all cases. Moreover, as shown in Fig. 12b, the compliance no longer significantly improves for the finest RBF discretization.

Fig. 11

Influence of the RBF mesh on the final design. Using symmetry conditions, only half of the MBB-beam is considered in the optimization. For each optimization, a structured mesh consisting of 150 × 50 × 2 triangular finite elements is used. From top to bottom, final designs are shown obtained with design meshes consisting of 61 × 21, 91 × 31, 121 × 41, and 151 × 51 RBFs

Fig. 12

Subfigure a shows the convergence of the compliance C and volume fraction $V_{\varOmega _{\mathrm {m}}} / V_{\varOmega }$ of the MBB beam using different discretizations of the design space; b shows the final compliance of the MBB beam as a function of the number of design variables

3.4 3-D cantilever beam

To show that the method is not restricted to 2-D, a 3-D cantilever beam example is also considered. The material properties are the same as those of previous examples. The size of this cantilever beam is 2L × L × 0.5L, and a structured mesh with 40 × 20 × 10 × 6 tetrahedral elements is used to discretize the model. The design space is discretized using a grid of 21 × 11 × 6 RBFs, with $r_{s} = \sqrt {2} \cdot a$. Figure 13 shows the initial design, along with the boundary conditions; the right surface is clamped, and a distributed line load with $\left | \bar {\boldsymbol {t}}\right | = 0.2$ per unit length is applied on the bottom-left edge. The move limit for MMA in this example is set to 0.001 to prevent the optimizer from moving the boundaries too fast, as only a small number of RBFs is used with a large r_s compared with the analysis mesh. The objective function is again the structural compliance, and the volume constraint is set to 40% of the total design domain.

Fig. 13

Initial design of the 3-D example with a schematic illustration of the boundary conditions: the right side is fixed and a vertical downward line load is applied on the bottom-left edge

Figure 14a displays the optimized design; the corresponding convergence plot is shown in Fig. 14b, where it can be seen that the volume satisfied the constraint, and the objective function converges smoothly.

Fig. 14

Optimized design for the 3-D cantilever beam optimization example (a), and the convergence of the compliance C and volume fraction $V_{\varOmega _{\mathrm {m}}} / V_{\varOmega }$ (b)

3.5 Heat sink

Lastly, we consider a heat compliance minimization problem, illustrated in Fig. 15. In this two-material problem, a highly conductive material (κ₁ = 1) is distributed within an L × L square domain with a lower conductivity (κ₂ = 0.01). The bottom-right corner of the domain has a heat sink, with u = 0, whereas the domain edges are adiabatic boundaries, i.e., $\bar q = 0$. The entire domain is subjected to uniform heat source f = 1. The problem is solved on a 41 × 41 node analysis mesh, using 31 × 31 RBFs with $r_{s} = \sqrt {2} \cdot a$.

Fig. 15

Problem description and initial design for the heat sink. A fixed temperature is applied to the bottom right corner, and a uniform heat source is applied throughout the entire square domain

As this problem considers a case with a body load, the load vector also contains enriched degrees of freedom that depend on the locations of the enriched nodes. Therefore, the right-hand side is design dependent, i.e., ∂F/∂s≠0, even though the body load is constant throughout the entire domain.

The results of this optimization problem are shown in Fig. 16. In the optimized design, narrow features can be distinguished that follow the edges of original elements in the background mesh. This is an effect caused by how the intersections are detected, and is investigated in more detail in Section 4.1. The convergence plot shows that, although there are initially some oscillations in both the objective and constraint (also investigated further in Section 4.1), they converge in the end.

Fig. 16

Subfigure a shows the optimized design of the heat sink problem, where narrow features are created along the edges of the original mesh element. The convergence plot in b shows initially some small oscillations that can be prevented by the use of a smaller move limit

4 Discussion

4.1 Oscillations: the level set discretization

Oscillations in the objective functions are visible in the convergence of the heat sink problem in Fig. 16, and in the coarsest RBF mesh of the MBB beam in Fig. 12. As these oscillations might point to inaccurate modeling or sensitivities, the phenomenon is discussed here in more detail.

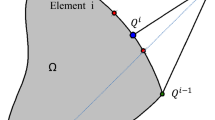
Recall that intersections between the zero contour of the level set function and element edges are found using a linear interpolation of nodal level set values. Because the level set function is discretized, no intersections can be found if two adjacent nodes have the same sign, as (8) does not hold for ϕ_jϕ_k ≥ 0. This effect is illustrated in Fig. 17. On the left, the zero contour of a level set function is shown in red, which defines a design shown in white/gray. The white arrows indicate the movement of the material boundary during the next design update. On the right, the updated level set contour is shown in red. As the level set values ϕ_j and ϕ_k on the two adjacent original nodes x_j and x_k now have the same sign, the two intersections between them, shown as cannot be found.

Fig. 17

Structure disconnecting due to level set discretization. White arrows (left) indicate the update of the level set in the next iteration (right), where the narrowest part of the zero contour lies within a single element, and the nodal level set values ϕ_j and ϕ_k have the same sign. The two intersections shown as are thus not found, and the structure disconnects

The sudden disconnection of the structure due to the level set discretization is a discontinuous event that cannot be captured by the sensitivity information. Therefore, as soon as such discontinuous event occurs, the sensitivities and the modeling deviate, and oscillations may occur.

This problem can be alleviated by using a smaller move limit, as was done in the 3-D MBB example. Another approach that could mitigate this issue is to evaluate the parametrized level set function on a finer grid, so that multiple intersections are found on an element edge. However, the procedure that creates integration elements would also need to allow for these more complex intersections. It should be noted that neither of these methods completely eliminates the problem of discontinuous events. Rather, the methods alleviate the problem by limiting their chance of occurrence. On the contrary, the use of a length scale control could eliminate this issue completely by enforcing material and void features to be larger than the element size. Besides eliminating the issue of numerical oscillations, length scale control can also ensure the mesh is sufficiently fine with respect to the design’s features to properly describe its physical behavior. Methods for length scale control in parametrized level set methods have recently been proposed (Dunning 2018; Jansen 2019).

A related observation can be made in the zigzagged features in the heat sink design of Fig. 16. As illustrated in Fig. 18, this pattern occurs when the optimizer tries to make a narrow diagonal feature in the opposite direction of the mesh diagonals. The red intersections cannot be detected; therefore, the structure is disconnected. As a result, the optimizer can only create diagonal narrow features by zigzagging them along element edges, as illustrated in Fig. 18 on the right.

Fig. 18

Illustration of the zigzagged pattern that appears in Fig. 16. When a narrow diagonal line is desired in the opposite direction of the diagonal lines of the mesh, the problem illustrated in Fig. 17 results in a disconnected line, as shown on the left. Instead, the optimizer will create narrow features along element edges, as illustrated on the right

4.2 Zigzagging: approximation error

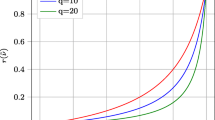
In the final designs of some of the numerical examples, zigzagging of the edges occurred where the zero contour of the level set function is not perfectly smooth, as detailed in Fig. 19. To investigate the cause of this artifact, the test problem of a clamped beam loaded axially shown in Fig. 20 was investigated. The compliance was computed for a varying zigzagging angle β while keeping the material volume constant.

Fig. 19

Detail of zigzagging that might occur when the design space is not reduced with respect to the FE mesh

Fig. 20

Schematic for the zigzagging approximation error. A beam with zigzagging angle β is clamped on the left, while a concentrated axial loading is applied on the right. The angle β is varied without changing the material volume, and the compliance is evaluated

The results in Fig. 21 show that the minimum compliance is not found at β = 0, as one would expect, but instead it is found at a negative value of β. Furthermore, the compliance is not symmetric with respect to β = 0 due to the asymmetry of the analysis mesh. The cause of this zigzagging is an approximation error, as the mesh is too coarse to accurately describe the deformations and stresses in the structure, similarly to the effect described for nodal design variables in Braibant and Fleury (1984). This effect can be resolved by reducing the design space with respect to the analysis mesh, for example with the use of RBFs, or by increasing the element order. Furthermore, as the non-smoothness is confined to a single layer of background elements, mesh refinement makes the issue less pronounced.

Fig. 21

The compliance of the test case, illustrated in Fig. 20, as a function of the zigzagging angle β. The compliance for this coarse test case is non-symmetric with respect to 0

5 Summary and conclusions

In this work we introduced a new enriched topology optimization approach based on the IGFEM. The technique yields non-pixelized black and white designs that do not require any post-processing. We have derived an analytic expression for the sensitivities for compliance minimization problems in elastostatics and heat conduction, and have shown that they can be computed with relatively low computational effort. Furthermore, the method was compared with a number of open source topology optimization codes, based on SIMP, the Ersatz approach, and discrete level sets. The influence of decoupling the design discretization from the analysis mesh was investigated using the classical MBB beam optimization problem. A 3-D cantilever beam and a heat sink problem were also demonstrated. The convergence behavior was provided for each numerical example. Any numerical artifacts, such as approximation errors and discretization errors of the level set, as discussed in Section 4, can be mitigated by means of suitable move limits and radial basis functions, where the latter serve as a sort of filter because they can control the design complexity.

A number of conclusions can be drawn from this work:

• The combination of IGFEM with the level set topology optimization based on RBFs results in crisp boundaries in both the design representation and the modeling. Because the RBF mesh and analysis mesh are completely decoupled, the resolution of the design and the modeling can be chosen independently, as is the case in any parametrized level set optimization. In addition, the radial basis functions help in reducing numerical artifacts, as they act like a black-and-white filter. Lastly, as the RBFs may extend over multiple elements, they allow the boundary to move further and the optimizer to converge faster;

• As only one intersection can be detected per element edge, due to the mapping of the level set to the original mesh nodes, features smaller than a single element might not be described correctly. As discussed in Section 4.1, this may lead to oscillations in the convergence. Using a finer grid for evaluating the level sets, more intersection may be found, allowing for narrower features. However, this will require a more involved procedure for creating integration elements. Similarly, the method may be extended to be used on quadrilateral elements, which also requires more involved integration element procedures. Furthermore, for quadrilateral elements, higher order enrichment functions are needed (Aragón et al. 2020);

• Due to approximation error, numerical artifacts may occur that may be exploited by the optimizer when the RBF mesh is too fine with respect to the analysis mesh. Another known issue in IGFEM and other enriched methods, which may be exploited by the optimizer, is the fact that the computation of stresses near material interfaces may yield inaccurate results (Soghrati et al. 2017; Nagarajan and Soghrati 2018);

• In this work, we chose to model the void together with the material domain for a number of reasons, including ease of implementation, and ease of comparing with other methods. However, we could have chosen to completely remove the void from the analysis (van den Boom et al. 2019a), which would reduce computation times and eliminate the artificial stiffness in the void.

Compared with the commonly used density-based methods, our proposed approach does not introduce staircasing nor gray values. The location of the boundary is therefore known throughout the entire optimization, and no post-processing of the design is required. However, additional complexity is introduced in the creation of integration elements. Furthermore, the extra enriched nodes slightly increase the size of system matrices, which is an effect that diminishes with mesh refinement. Lastly, in density-based methods for linear elasticity, the local element arrays can simply be scaled with the density, and need to be computed only once. In our approach, local arrays for integration elements have to be computed at every iteration.

In an optimization context, IGFEM has a number of advantages:

• (i) The IGFEM formulation provides a natural distinction between original mesh nodes, which are stationary and on which the level set is evaluated, and enriched nodes, which define the material boundary and are allowed to move during optimization. Enriched DOFs are directly related to the discontinuity in the gradient of the field;

• (ii) As the background mesh does not change during optimization, the mapping of the design variables to nodal level set values has to be computed only once; and

• (iii) As the location of enriched nodes is known to remain on the background element edges, and the enriched node location is computed as a linear interpolation between background mesh nodes, the direction of the design velocities is known a priori. This simplifies the sensitivity computations;

Regarding the benefits of IGFEM with respect to X/GFEM, in addition to those regarding the analysis phase described in Section 2.1.1, item (i) above must also be added. In X/GFEM, the distinction is less clear, as enrichments are associated to nodes of the background mesh.

As mentioned in Section 1, the benefits of using an enriched formulation are expected to be more pronounced for problems that rely heavily on an accurate boundary description, such as fluid-structure interaction and wave scattering. In fact, the optimization of the latter is the subject of an incoming publication.

Appendices

Appendix A: Derivation of IGFEM from X/GFEM

Here, we derive the IGFEM formulation from the X/GFEM approximation for a single 1-D linear finite element with nodes x₁ and x₂ that contain a weak discontinuity at x_n. For this element, the X/GFEM approximation can be written as:

$$ u^{h} \left( x \right) = \underbrace{ \sum\limits_{i= 1}^{2} N_{i} \left( x \right) U_{i} }_{\text{std. FEM}} + \underbrace{ \sum\limits_{i= 1}^{2} N_{i} \left( x \right) E_{i} \left( x \right) \hat{U}_{i} }_{\text{enrichment}}, $$

(33)

where E_i denotes the enrichment functions and $\hat {U}_{i}$ are the generalized DOFs. In order to derive the IGFEM formulation, the key is to select appropriate enrichment functions E_i. We use scaled heaviside enrichments, as shown in Fig. 22.

Fig. 22

Construction of IGFEM enrichment function from X/GFEM formulation

By clustering DOFs, i.e., $\hat {U}_{1} = \hat {U}_{2} = \alpha$, we reduce the number of enriched DOFs (Duarte et al. 2006). The enrichment term is then given by:

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i= 1}^{2} N_{i} E_{i} \hat{U}_{i} & = &\left( N_{1} E_{1} + N_{2} E_{2} \right) \alpha , \\ & = &\underbrace{ \left[ N_{1} c_{1} H \left( x - x_{n} \right) + N_{2} c_{2} H \left( x_{n} - x \right) \right]}_{\psi} \alpha \end{array} $$

(34)

where H is the heaviside function and the constants c₁ = 1/(1 − w) and c₂ = 1/w, with $w=x_{n}/ \left (x_{2} - x_{1} \right )$, yield a C⁰–continuous function that attains a maximum value of one regardless of the discontinuity location within the element.

The final approximation is therefore:

$$ u^{h} \left( x \right) = \sum\limits_{i= 1}^{2} N_{i} \left( x \right) U_{i} + \psi \alpha, $$

(35)

which is equivalent to the IGFEM approximation for a 1-D bar containing a weak discontinuity. Similar considerations can be made for higher dimensional problems.

Appendix B: Isoparametric mapping of integration elements

In order to make this manuscript self-contained, here we describe the isoparametric mapping and numerical integration of an IGFEM integration element, as explained in more detail in Section 2.1 and illustrated in Fig. 3.

The integration element’s stiffness matrix k_e can be computed in terms of the reference integration element as:

(36)

with $\mathbf{B} = [\mathbf{\Delta} N _{1}\quad \mathbf{\Delta} N _{2} \quad \ldots \quad \mathbf{\Delta} N _{n}\quad \mathbf{\Delta} \psi_{1} \quad \ldots \quad \mathbf{\Delta} \psi _{m}],$ and the element force vector f_e is computed in terms of the reference integration element as:

(37)

A global coordinate x, in terms of the isoparametric mappings of the integration and parent elements, can be written as:

$$ \boldsymbol{x} = \boldsymbol{x}_{e}^{\intercal} N_{e}(\boldsymbol{\xi}_{e}) = \boldsymbol{x}_{p}^{\intercal} N(\boldsymbol{\xi}_{p}) , $$

(38)

where N_e are the linear Lagrange shape functions associated to the nodes of the integration element, with global coordinates x_e. Similarly, N are the shape functions associated to the parent’s nodes with global coordinates x_p.

The Jacobians of these mappings and their determinants are computed as:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{J}_{e} =\frac{\partial \boldsymbol{x}}{\partial \boldsymbol{\xi}_{e}} = \boldsymbol{x}_{e}^{\intercal} \frac{\partial \boldsymbol{N}_{e}(\boldsymbol{\xi}_{e})}{\partial \boldsymbol{\xi}_{e}}, \qquad \quad j_{e} = \det\left( \boldsymbol{J}_{e} \right), \end{array} $$

(39)

and

$$ \begin{array}{@{}rcl@{}} \boldsymbol{J} = \frac{\partial \boldsymbol{x}}{\partial \boldsymbol{\xi}_{p}}= \boldsymbol{x}_{p}^{\intercal} \frac{\partial \boldsymbol{N}(\boldsymbol{\xi}_{p})}{\partial \boldsymbol{\xi}_{p}}, \qquad \quad j = \det\left( \boldsymbol{J} \right), \end{array} $$

(40)

respectively, where x_e contains the integration element nodes and x_p contains the parent element nodes.

Numerical integration is performed in the reference integration element by means of Gauss quadrature. Using (38), it is straightforward to map the Gauss integration point’s reference coordinates ξ_e to its corresponding global coordinates x. The inverse mapping from x to the location in the parent reference coordinate system ξ_p is more involved. For a 2-D triangular element, the procedure can be written as:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{x} & = & \left[\begin{array}{lll} x_{i,1} &x_{j,1} &x_{k,1} \\ x_{i,2} &x_{j,2} &x_{k,2}\end{array}\right] \left[\begin{array}{cll} 1-\xi_{1}-\xi_{2} \\ \xi_{1} \\ \xi_{2} \end{array}\right]\\ \boldsymbol{x} &=& \left[\begin{array}{l} x_{i,1} + \xi_{1}(x_{j,1}- x_{i,1}) + \xi_{2} (x_{k,1} - x_{i,1}) \\x_{i,2} + \xi_{1}(x_{j,2}- x_{i,2}) + \xi_{2} (x_{k,2} - x_{i,2}) \end{array}\right],\\ \boldsymbol{x}\! -\! \left[\begin{array}{l} x_{i,1} \\ x_{i,2} \end{array}\right] &=& \underbrace{\left[\begin{array}{ll} x_{j,1} - x_{i,1} & x_{k,1} - x_{i,1} \\ x_{j,2} - x_{i,2} & x_{k,2} -x_{i,2} \end{array}\right]}_{\boldsymbol{A} } \left[\begin{array}{l} \xi_{1} \\ \xi_{2} \end{array}\right]\\ \end{array} $$

(41)

Inverting this isoparametric mapping leads to the following equation for the integration point in parent coordinates ξ_p

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\xi}_{p} &= \left[\begin{array}{l}\xi_{1} \\ \xi_{2} \end{array}\right] &= \boldsymbol{A}^{-1} \boldsymbol{x} - \boldsymbol{A}^{-1} \left[\begin{array}{l} x_{i,1} \\ x_{i,2} \end{array}\right]. \end{array} $$

(42)

Appendix C: Derivatives of the Jacobian inverse and determinant

In the sensitivity computation discussed in Section 2.3.1, the derivative of the Jacobian inverse and determinant are required. According to Jacobi’s formula (Magnus and Neudecker 2007), the derivative of the determinant of a matrix can be computed as the trace of the adjugate of the matrix ($\textup {adj} \left (\boldsymbol {J}_{e} \right ) = j_{e} \boldsymbol {J}_{e}^{-\intercal }$), multiplied by the derivative of the matrix. For the Jacobian determinant j_e, the derivative can thus be computed as:

$$ \frac{\partial j_{e}}{\partial \boldsymbol{x}_{n}} = \textup{Tr} \left( \textup{adj} \left( \boldsymbol{J}_{e} \right) \frac{\partial \boldsymbol{J}_{e}}{\partial \boldsymbol{x}_{n}}\right) , $$

(43)

The sensitivity of the Jacobian inverse can be computed by realizing that $\boldsymbol {J}_{e} \boldsymbol {J}_{e}^{-1} = \boldsymbol {I}$:

$$ \frac{\partial \boldsymbol{J}_{e} \boldsymbol{J}_{e}^{-1}}{\partial \boldsymbol{x}_{n}} = \frac{\partial \boldsymbol{J}_{e}}{\partial \boldsymbol{x}_{n}} \boldsymbol{J}_{e}^{-1} + \boldsymbol{J}_{e} \frac{\partial \boldsymbol{J}_{e}^{-1}}{\partial \boldsymbol{x}_{n}} = \frac{\partial \boldsymbol{I}}{\partial \boldsymbol{x}_{n}} = 0, $$

(44)

and solving for $\partial \boldsymbol {J}_{e}^{-1} /\partial \boldsymbol {x}_{n}$:

$$ \frac{\partial \boldsymbol{J}_{e}^{-1}}{\partial \boldsymbol{x}_{n}} = - \boldsymbol{J}_{e}^{-1} \frac{\partial \boldsymbol{J}_{e}}{\partial \boldsymbol{x}_{n}} \boldsymbol{J}_{e}^{-1} . $$

(45)

For both (43) and (45), the sensitivity of the Jacobian is required; as the Jacobian of the integration element is computed as $\boldsymbol {J}_{e} = \boldsymbol {x}_{e}^{\intercal } \partial \boldsymbol {N}_{e} / \partial \boldsymbol {\xi }_{e}$, it can be computed as:

(46)

where ∂x_e/∂x_n is simply a selection array consisting of zeros except for a one on the entries of interest for enriched node n.