Stress and strain control via level set topology optimization

Abstract

This paper presents a level set topology optimization method for manipulation of stress and strain integral functions in a prescribed region (herein called sub-structure) of a linear elastic domain. The method is able to deviate or concentrate the flux of stress in the sub-structure by optimizing the shape and topologies of the boundaries outside of that region. A general integral objective function is proposed and its shape sensitivities are derived. For stress isolation or maximization, a von Mises stress integral is used and results show that stresses in the sub-structure can be drastically reduced. For strain control, a strain integral combined with a vector able to select the component of the strain is used. A combination of both can be used to minimize deformation of a prescribed direction. Numerical results show that strain can be efficiently minimized or maximized for a wide range of directions. The proposed methodology can be applied to stress isolation of highly sensitive non strain-based sensors, design for failure, maximization of mechanical strain and strain direction control for strain-based sensors and microdevices.

1 Introduction

Strains and stresses are mechanical quantities intrinsically present in a load carrying structure. Although directly related, strains and stresses can have different functionalities. In a statically loaded structure, low stress levels are generally preferred. On the other hand, higher stress or strain can be beneficial in certain microdevices or energy harvesters and in design for failure.

Stress isolation aims to minimize the stress levels in prescribed regions of a structure. This can be achieved by redirecting and attenuating the propagation of stresses from a base-structure ${\Omega }^{S}$ to a sub-structure ${\Omega }^{+}$ with the use of different materials or adding holes or cuts, see Fig. 1. In this sense, typical applications are in the design of sensors that are largely sensitive to mechanical stress, such as acceleration sensors (Tsuchiya and Funabashi 2004; Hsieh et al. 2011). Another example is the structural design for welding stress isolation, as patented by Gorard et al. (2011). In this case, the source of stress is in the sub-structure and the aim is to eliminate stress propagation to the base-structure.

Fig. 1

Scheme of a stress and strain control problem

The optimization of stress-based problems has long been a challenge for shape and topology optimization (Duysinx and Bendsøe 1998; Duysinx et al. 2008; Le et al. 2010). To the best of our knowledge, Li and Wang (2014) were the first authors to conduct stress isolation via shape and topology optimization by applying a level set method. In their work, different stress limits are imposed in the base and sub-structure, with the stress allowance in the sub-structure much smaller than the base one. Recently, Luo et al. (2017) used a similar idea but a density-based method and nonlinear finite elements to design stress-isolated hyperelastic composite structures. Both of these works, however, do not account for strain.

Strain control can be useful for a variety of applications. For example, piezoelectric vibration energy harvesters can obtain higher electrical charges by maximizing their strain (Lin et al. 2011; Kiyono et al. 2016; Thein and Liu 2017). One way of maximizing the strain in a piezoelectric component is to optimize the layout of the component itself (Silva et al. 1997; Silva 2003; Xia et al. 2013). The other approach can be the maximization of the mechanical strain of a base-structure where the piezoelectric device is attached. In this way, the applications can be broadened to other strain-based sensors.

The deformation of the structure can also be used to preserve the shape of a certain region of the structure, as showed by Zhu et al. (2016). The authors explored the minimization of the warping deformation to achieve a shape preserving effect. The same idea was applied to control the directional deformation behavior of the prescribed base-structure by Li et al. (2017). Very recently, Castro et al. (2018) carried out shape preserving design to minimized local deformation of vibrating structures. In other cases, prescribed displacements, deformation or motion are desired, such as in compliant mechanisms (Stanford and Beran 2012; Kim and Kim 2014; Zuo and Xie 2014). These works are all carried out under a density-based topology optimization approach.

This paper aims to develop a methodology to manipulate stresses and strains via level set topology optimization (LSTO). The shape of the structural boundaries are described via an implicit signed distance function and a fixed grid finite element analysis is used to evaluate the structural displacement field. A local von Mises stress measure can be used to minimize or maximize stresses in a prescribed sub-structure. The minimization of stress is applied as a stress isolation technique and its maximization as a design for failure procedure. A strain integral is introduced in order to maximize or minimize strains in a prescribed direction. A shape sensitivity analysis valid for both stress optimization and strain control is presented. We extend our previous work on stress-based topology optimization to achieve this (Picelli et al. 2018).

The remainder of the paper is organized as follows. Section 2 presents the structural description via a level set function and the finite element method. Section 3 describes the optimization formulation applied to stress and strain control. Section 4 briefly presents the level set topology optimization method. Section 5 shows numerical results and discussions and Section 6 concludes the paper.

2 Level set description and finite element method

Let ${\Omega }$ be a bounded design domain in $\text {I\!R}^{n}$ (n = 2, 3) occupied by a linear elastic isotropic structure defined by the domain ${\Omega }^{S}$. The structure is composed by a smooth boundary $\partial {\Omega }^{S}$ = ${\Gamma }_{D} \cup {\Gamma }_{N} \cup {\Gamma }_{H}$. Dirichlet boundary conditions are applied in ${\Gamma }_{D}$, while homogeneous Neumann conditions are applied in ${\Gamma }_{N}$. The free boundaries are defined as ${\Gamma }_{H}$. Herein, ${\Gamma }_{H}$ is divided in two different sets, the outer boundaries ${\Gamma }_{H_{0}}$ and the inner boundaries ${\Gamma }_{H_{0}}^{\ast }$ from the holes of the structures, see Fig. 2a. If the set of boundaries ${\Gamma }_{H_{0}}^{\ast }$ is allowed to change whilst keeping ${\Gamma }_{H_{0}}$ fixed, only the inner holes are subjected to optimization.

Fig. 2

a generic structure with a hole and b its description via an implicit level set function

In level set topology optimization, the structural boundaries are represented by an implicit function as

$$ \left\{ \begin{array}{cc} {\Phi} \left( \mathrm{x} \right) > 0 & \mathrm{x} \in {\Omega}^{S} \\ {\Phi} \left( \mathrm{x} \right) = 0 & \mathrm{x} \in \partial {\Omega}^{S} \\ {\Phi} \left( \mathrm{x} \right) < 0 & \mathrm{x} \notin {\Omega}^{S} \end{array} \right. \text{,} $$

(1)

where ${\Phi }$ is the level set function, $\mathrm {x}$ is the point inside the design domain ${\Omega }$ and ${\Omega }^{S} \subset {\Omega }$ (Allaire et al. 2004). In this work, the level set is defined as a signed distance function, as seen in Fig. 2b.

The analysis is conducted by the fixed grid finite element method with equivalent Ersatz material. In this approach, the domain ${\Omega }^{S}$ is projected onto a fixed grid that covers ${\Omega }$ and the boundary ${\Gamma }_{H}$ is discretized into a set of points coincident with the elements edges, as illustrated in Fig. 3. Cut elements are assigned with volume fractions between 0 and 1, according to the ratio of volume of solid material and the total volume of the element (Dunning et al. 2011).

Fig. 3

a projection of Ω^S onto a fixed grid and discretization of the boundary and b Ersatz material approximation

The structure ${\Omega }$ is in equilibrium when a displacement field $\mathbf {u}$ satisfies the equation,

$$ a\left( \mathbf{u}, \mathbf{v} \right) = l\left( \mathbf{v}\right) \text{,} $$

(2)

where the linear operators $a\left (\cdot ,\cdot \right )$ and $l\left (\cdot \right )$ represent the virtual work of internal and external forces, respectively,

$$ a\left( \mathbf{u},\mathbf{v}\right) = \int\limits_{{\Omega}} \boldsymbol{\sigma}\left( \mathbf{u} \right) \cdot \boldsymbol{\varepsilon}\left( \mathbf{v} \right) d{\Omega} \text{,} \qquad l \left( \mathbf{v} \right) = \int\limits_{{\Gamma}_{N}} \mathbf{t} \cdot \mathbf{v} d{\Gamma}_{N} \text{,} $$

(3)

where $\boldsymbol {\sigma }\left (\mathbf {u} \right )$ and $\boldsymbol {\varepsilon }\left (\mathbf {v} \right )$ are the stress and strain vectors, respectively, $\mathbf {t}$ is a constant and non-zero traction on ${\Gamma }_{N}$ and $\mathbf {v}$ is the field of virtual variations. No body forces are considered.

3 Problem formulation and sensitivity analysis

The stress objective and strain objective functions are defined, respectively, as

$$ f^{+}\left( \mathbf{u}; \mathrm{x} \right) = \int\limits_{{\Omega}^{+}} \sigma_{vm} d{\Omega}^{+} \text{,} \qquad f^{+}\left( \mathbf{u}; \mathrm{x} \right) = \int\limits_{{\Omega}^{+}} \boldsymbol{\alpha} \cdot \boldsymbol{\varepsilon} \left( \mathbf{u}\right) d{\Omega}^{+} \text{,} $$

(4)

where $\sigma _{vm}$ is the von Mises stress of the structure, $\boldsymbol {\varepsilon } \left (\mathbf {u}\right )$ is the strain with all components $\boldsymbol {\varepsilon }_{xx}$, $\boldsymbol {\varepsilon }_{yy}$ and $\boldsymbol {\varepsilon }_{xy}$ and $\boldsymbol {\alpha }$ is a vector to select the strain direction, when desired. For example, for the strain in the xx direction, $\boldsymbol {\varepsilon }_{xx} = \boldsymbol {\alpha } \cdot \boldsymbol {\varepsilon } \left (\mathbf {u} \right ) = \left (1, 0, 0\right )^{T} \cdot \boldsymbol {\varepsilon } \left (\mathbf {u} \right )$. Both stress and strain functions are integrals over the sub-structure control region ${\Omega }^{+}$.

The level set topology optimization requires the computation of shape sensitivities at the boundary points from Fig. 3a in order to update the implicit level set function. The shape sensitivity of a general function $f\left ({\Omega } \right )$ can be derived using the adjoint method. This technique is advantageous when using a large number of design variables, the typical case of topology optimization. An augmented integral function can be expressed with the aid of the equilibrium equation

$$ \mathcal{L} = f\left( {\Omega}\right) + a\left( \mathbf{u}, \boldsymbol{\lambda} \right) - l\left( \boldsymbol{\lambda}\right) \text{,} $$

(5)

where $\boldsymbol {\lambda }$ is the adjoint variable. The material derivative method is applied here (Wang and Li 2013; Choi and Kim 2005) and the derivative of the augmented functional $\mathcal {L}$ can be expressed as

$$ {\mathcal{L}^{\prime}} = {f^{\prime}}\left( {\Omega} \right) + {a^{\prime}}\left( {\mathbf{u},\boldsymbol{\lambda} } \right) - {l^{\prime}}\left( \boldsymbol{\lambda} \right) \text{,} $$

(6)

where,

$$ {f^{\prime}}\left( {\Omega} \right) = \int\limits_{{\Omega}} { \frac{\partial f\left( \mathbf{u} \right)}{\partial \mathbf{u}} \cdot {\mathbf{u}^{\prime}}d{\Omega} + \int\limits_{{\Gamma}} {f\left( \mathbf{u} \right){V_{n}}d{\Gamma}} } \text{,} $$

(7)

$$\begin{array}{@{}rcl@{}} {a^{\prime}}\left( {\mathbf{u},\boldsymbol{\lambda} } \right) = \int\limits_{{\Omega}} {\boldsymbol{\sigma} \left( {{\mathbf{u}^{\prime}}} \right) \cdot \boldsymbol{\varepsilon} \left( \boldsymbol{\lambda} \right)d{\Omega} + \int\limits_{{\Omega}} } \boldsymbol{\sigma} \left( \mathbf{u} \right) \cdot \boldsymbol{\varepsilon} \left( {{\boldsymbol{\lambda}^{\prime}}} \right)d{\Omega}\\ + \int\limits_{{\Gamma}} {\boldsymbol{\sigma} \left( \mathbf{u} \right) \cdot \boldsymbol{\varepsilon} \left( \boldsymbol{\lambda} \right)} {V_{n}}d{\Gamma} \text{,} \end{array} $$

(8)

$$ {l^{\prime}}\left( \boldsymbol{\lambda} \right) = \int\limits_{{\Gamma}_{N}} {\mathbf{t} \cdot {\boldsymbol{\lambda}^{\prime}}d{\Gamma}_{N}} \text{,} $$

(9)

in which $V_{n}$ is the normal velocity component of a boundary ${\Gamma }$ and $^{\prime }$ indicates the derivative with respect to this boundary.

Substituting (7), (8) and (9) into (6) and collecting all the terms that contain $\boldsymbol {\lambda }^{\prime }$, the weak form of the state equation is recovered, whose total sum is zero. By collecting all the terms that depend on $\mathbf {u}^{\prime }$ and letting their sum be zero, the following adjoint equation is obtained

$$ \int\limits_{{\Omega}} {\boldsymbol{\sigma} \left( {{\mathbf{u}^{\prime}}} \right) \cdot \boldsymbol{\varepsilon} \left( \boldsymbol{\lambda} \right)} d{\Omega} = - \int\limits_{{\Omega}} {\frac{\partial f\left( \mathbf{u} \right)}{\partial \mathbf{u}} \cdot {\mathbf{u}^{\prime}}d{\Omega}} \text{,} $$

(10)

where the right-hand side of (10) indicates the adjoint pseudo-load. Finally, collecting all the remaining terms, the shape derivative of the augmented functional with respect to the boundary points on ${\Gamma }$ can be written as

$$ {\mathcal{L}^{\prime}} = \int\limits_{{\Gamma}} {f\left( \mathbf{u} \right){V_{n}}d{\Gamma}} + \int\limits_{{\Gamma}} {\boldsymbol{\sigma} \left( \mathbf{u} \right) \cdot \boldsymbol{\varepsilon} \left( \boldsymbol{\lambda} \right)} {V_{n}}d{\Gamma} \text{.} $$

(11)

For the stress objective, the pseudo-load from (10) can be expressed as

$$ \int\limits_{{\Omega}} \frac{\partial f\left( \mathbf{u} \right)}{\partial \mathbf{u}} d{\Omega} = \int\limits_{{\Omega}^{+}} \frac{\partial \sigma_{vm}}{\partial \mathbf{u}} d{\Omega}^{+} = H\left( \mathrm{x} \right) \int\limits_{{\Omega}} \frac{\partial \sigma_{vm}}{\partial \mathbf{u}} d{\Omega} \text{,} $$

(12)

where $H\left (\mathrm {x} \right )$ is the Heaviside function

$$ H \left( \mathrm{x} \right) = \left\{ \begin{array}{cc} 1 & \text{if} \qquad \mathrm{x} \in {\Omega}^{+} \\ 0 & \text{if} \qquad \mathrm{x} \notin {\Omega}^{+} \end{array} \right. \text{.} $$

(13)

By using the Heaviside function, the pseudo-load is in the form of the general shape derivative and can be used to solve the adjoint problem from (10) and obtain $\boldsymbol {\lambda }$. For the strain objective, the pseudo-load is written as

$$ \int\limits_{{\Omega}} \frac{\partial f\left( \mathbf{u} \right)}{\partial \mathbf{u}} d{\Omega} = \int\limits_{{\Omega}^{+}} \boldsymbol{\alpha} \cdot \frac{\partial \boldsymbol{\varepsilon} \left( \mathbf{u} \right) }{\partial \mathbf{u}} d{\Omega}^{+} = H \left( \mathrm{x} \right) \int\limits_{{\Omega}} \boldsymbol{\alpha} \cdot \frac{\partial \boldsymbol{\varepsilon} \left( \mathbf{u} \right) }{\partial \mathbf{u}} d{\Omega} \text{.} $$

(14)

Substituting the objective function $f^{+}\left (\mathbf {u}; \mathrm {x} \right )$ in (11), one can rewrite it in terms of the boundary ${\Gamma }_{H_{0}}^{\ast }$ to be optimized

$$ {\mathcal{L}^{\prime}} = \int\limits_{{\Gamma}_{H}} f^{+}\left( \mathbf{u}; \mathrm{x} \right) V_{n} d{{\Gamma}_{H}} + \int\limits_{{\Gamma}_{H}} {\boldsymbol{\sigma} \left( \mathbf{u} \right) \cdot \boldsymbol{\varepsilon} \left( \boldsymbol{\lambda} \right)} {V_{n}}d{{\Gamma}_{H}} \text{.} $$

(15)

Both stress and strain objectives are defined within the space of ${\Omega }^{+}$. In this work, ${\Omega }^{+}$ is considered as a non-design domain to represent the sub-structure location of a sensor, thus, zero velocities are assigned in those points. Therefore, the first term of (15) is null and the shape sensitivities at the boundary points can be computed as

$$ {\mathcal{L}^{\prime}} = \int\limits_{{\Gamma}_{H}} {\boldsymbol{\sigma} \left( \mathbf{u} \right) \cdot \boldsymbol{\varepsilon} \left( \boldsymbol{\lambda} \right)} {V_{n}}d{{\Gamma}_{H}} \text{,} $$

(16)

For stress isolation, $\boldsymbol {\lambda }$ is obtained by solving the adjoint problem from (10) with the pseudo-load from (12), while for strain control the pseudo-load is computed as (14). The derivatives in both integrals from (12) and (14) are computed with respect to the displacement field.

As the results of our previous stress-based work suggest (Picelli et al. 2018), no regularization techniques (e.g. length scale or perimeter control) are needed in order to obtain smooth structural boundaries. However, in this work, a perimeter constraint is used in order to ensure the problem is well-posed, since volume is not constrained here. Differently from stress, the perimeter sensitivities are computed here via finite differences. One can efficiently compute perimeter sensitivities by locally checking the differences in the length of each point segment with a small perturbation of each boundary point coordinate in the normal direction. Our computational experience showed that the time for computing perimeter sensitivities is negligible if compared to solving the FEA equation using our open source code available at http://m2do.ucsd.edu/software/.

3.1 Computational procedure

In the finite element discretization, the shape sensitivity function from (16) is computed first at all Gauss integration points p’s in the finite element mesh as

$$ \frac{df}{d\mathrm{x}} = \left( \mathbf{C}\mathbf{B}\mathbf{u}\right)^{T}_{p} \left( \mathbf{B}\boldsymbol{\lambda}\right)_{p} \text{,} $$

(17)

where $\mathbf {B}$ is the strain-displacement matrix. The adjoint displacements vector $\boldsymbol {\lambda }$ is obtained for the stress objective by solving the equation

where $\mathbf {K}$ is the global stiffness matrix, $\mathbf {V}$ is the Voigt matrix

$$ \mathbf{V} = \left[\begin{array}{cccccc} 1 & -0.5 & 0 \\ -0.5 & 1 & 0 \\ 0 & 0 & 3 \end{array}\right] \text{,} $$

(19)

for 2D cases, and the operator is the finite element assembly of the load vector integral on the sub-structure ${\Omega }^{+}$, discretized into $ne^{+}$ elements with domain ${\Omega }_{e^{+}}$ (Helnwein 2001; Zienkiewicz and Taylor 2005). The right hand side of (10) is the discretized pseudo-load, which expression is the result of the derivative of the objective functional with respect to the displacement field given in (12). For strain control, the adjoint equation is

We employ isoparametric bilinear quadrilateral elements and stress is computed at four Gauss points per element. Although these elements present only one superconvergent point (the central one), the convergence properties of the integration points are still suggested to be used for sampling when the isoparametric element is not distorted (Zienkiewicz and Taylor 2005), which is the case of this paper. Based on the stress field at the Gauss points, the stresses at the boundary points are interpolated using the least squares method. This approach has been demonstrated in the context of both stress minimization and stress constrained level set topology optimization in our previous publication (Picelli et al. 2018).

4 Level set topology optimization

The level set topology optimization method used follows Picelli et al. (2018) and it is briefly described here for completeness. The structural boundary is optimized by updating the implicit level set function via an advection equation combined with the velocity field of motion. The discretized version of such equation can be expressed as

$$ \phi_{j}^{k + 1} = {\phi_{j}^{k}} - {\Delta} t | \nabla {\phi_{j}^{k}} | V_{n,j } \text{,} $$

(21)

where k is the iteration number, j is a discrete boundary point, ${\Delta } t$ is the time step and $V_{n}$ is the velocity at point j, considered as an advection velocity of the type $dx/dt = V_{n} \cdot \nabla \phi (x )$ (Osher and Fedkiw 2003). The velocities required for the level set update at every k-th iteration are obtained by solving the following discretized optimization problem:

$$ \begin{array}{llllll} & \underset{\beta^{k} , \lambda^{k}}{minimize} & & {\Delta} t \mathbf{S}_{f}^{k} \cdot \mathbf{V}_{n}^{k} (\beta^{k} , {\lambda}^{k}) \\ & \text{subject to} & & {\Delta} t \mathbf{S}_{i}^{k} \cdot \mathbf{V}_{n}^{k} (\beta^{k} , {\lambda}^{k}) \leq -\bar{g}^{k}_{i} \\ & & & \mathbf{V}_{n,{\min}}^{k} \leq \mathbf{V}_{n}^{k} \leq \mathbf{V}_{n,{\max}}^{k} \end{array} $$

(22)

where $\bar {g}^{k}_{i}$ is a relaxed change in the constraint function at every iteration and the velocities $\mathbf {V}^{k}_{n}$ are described in terms of a search direction $\mathbf {d}$ normal to the boundary and the actual distance $\beta > 0$, as

$$ \mathbf{V}_{n} {\Delta} t = \beta \mathbf{d} \text{.} $$

(23)

The Lagrangian function related to the problem given in (22) is expressed as

$$ \mathcal{L} (\beta^{k} , \mathbf{d}^{k} , {\lambda}^{k} , \boldsymbol{\mu}^{k}) = \beta^{k} \mathbf{S}_{f}^{k} \cdot \mathbf{d}^{k} + \sum\limits_{i = 1}^{ni} {\lambda}_{i}^{k} (\beta^{k} \mathbf{S}_{i}^{k} \cdot \mathbf{d}^{k} + \bar{g}_{i}^{k}) + \boldsymbol{\mu}^{k} ((\mathbf{d})^{T} \mathbf{d}^{k} - 1) \text{,} $$

(24)

where $\lambda ^{k}$ is a Lagrange multiplier and $\mathbf {S}_{f}^{k}$ and $\mathbf {S}_{i}^{k}$ are vectors containing integral coefficients computed with the shape sensitivities at the boundary points as

$$ \frac{\partial f }{\partial {\Omega}} \cdot {\Delta} {\Omega} = {\Delta} t {\int}_{{\Gamma}} s_{f} V_{n} d{\Gamma} \approx \sum\limits_{j = 1}^{nb} {\Delta} t V_{nj} s_{f,j} l_{j} = \mathbf{S}_{f} \cdot \mathbf{V}_{n} {\Delta} t \text{,} $$

(25)

$$ \frac{\partial g_{i} }{\partial {\Omega}} \cdot {\Delta} {\Omega} \,=\, {\Delta} t {\int}_{{\Gamma}} s_{gi} V_{n} d{\Gamma} \!\approx\! \sum\limits_{j = 1}^{nb} {\Delta} t V_{nj} s_{gi,j} l_{j} \,=\, \mathbf{S}_{gi} \cdot \mathbf{V}_{n} {\Delta} t \text{,} $$

(26)

for linearized objective f and i-th constraint functions $g_{i}$. The terms $s_{f}$ and $s_{g_{i}}$ are the shape sensitivity functions for the objective and constraint functions, respectively, and $l_{j}$ is the discrete length of the boundary associated with point j.

The optimization problem from (22) is solved at every iteration k. The optimal velocities are then substituted into (21) to update the level-set boundaries. The process is repeated until the objective function stops changing during five consecutive iterations under a certain relative tolerance of $10^{-3}$.

5 Numerical results

In this section numerical results and discussions are presented. First, the investigation of both stress and strain objectives is carried out for a square plane domain and optimization of the inner boundaries ${\Gamma }_{H_{0}}^{\ast }$. The method is then applied to stress isolation and stress maximization in a cantilever beam and directional strain control. In all examples, the structural perimeter is the only constraint applied.

5.1 Plane domain

A 200×200 nondimensional square domain as depicted in Fig. 4 is considered for optimization. A 20×20 square region ${\Omega }^{+}$ at the center is considered as the sub-structure for stress isolation and strain control. Plane stress condition is assumed. The Young’s modulus E of the solid material is considered to be 200× 10⁹ and the Poisson’s ratio $\mu = 0.3$. The Young’s modulus of the void material is 10^− 9.

Fig. 4

Square domain considered for optimization with a 20×20 sub-structure Ω⁺ in: a uni-directional in-plane tension and b bi-directional in-plane tension

The domain is discretized with 200×200 finite elements and two loading scenarios are considered, namely an uni-directional in-plane tension, Fig. 4a, and a bi-directional in-plane tension, Fig. 4b. The distributed force is 100. In this example, only the inner boundaries ${\Gamma }_{H_{0}}^{\ast }$ are subject to optimization.

5.1.1 Stress isolation

For the uni-directional in-plane tension scenario, stress minimization is applied to the integral of the von Mises stress inside the sub-structure region ${\Omega }^{+}$ (first expression in (4)). Figure 5 presents the initial hole configuration and the corresponding von Mises stress field. The black region in Fig. 5a indicates solid material and the gray region the initial holes with void material.

Fig. 5

Uni-directional in-plane tension optimization: a initial holes configuration and b corresponding von Mises stress field

Figure 6 presents the snapshots of the optimization iterations for the stress isolation of the uni-directional in-plane tension. The perimeter is constrained to 200. Stress flux is deviated from the sub-structure ${\Omega }^{+}$ with the changes in the hole shapes. Figure 7a–b presents the optimal hole configuration and its corresponding von Mises stress field, whilst Fig. 7c shows the convergence history of the stress minimization. The initial integral of the von Mises stress in ${\Omega }^{+}$ was 39374.24 and the final 4509.19, a reduction of almost 89%. The perimeter constraint is satisfied in the end of the optimization, as seen in Fig. 7c. Figure 8 presents the upper left quadrant of the same stress isolation solutions but starting with different initial holes and mesh sizes and all cases using the perimeter constraint of 200. The final topologies are similar, showing the perimeter control aids in reducing mesh dependency. The bi-directional in-plane tension case has a trivial solution when it comes to stress isolation, a circular hole around ${\Omega }^{+}$ which disconnects the base and sub-structure, case omitted herein.

Fig. 6

Topology optimization steps of the uni-directional in-plane tension for stress isolation, with final solution at iteration 304

Fig. 7

Corresponding (a) von Mises stress field and convergence history of (b) stress and c perimeter of the solution from Fig. 6

Fig. 8

Solutions (upper left quadrant) for the same stress isolation example from Fig. 6 with different initial holes and mesh sizes using perimeter constraint of 200

As discussed in the introduction of this paper, stress maximization of the integral in ${\Omega }^{+}$ can also be applied to concentrate stress flux in certain applications. This is limited to cases that do not violate the hypothesis of linear elastic behavior. Figure 9 presents the optimization results for both uni-directional and bi-directional loading cases, subject to perimeter constraint of 320. The stress flux is increased inside the sub-structure. The initial values of the integral of stress in ${\Omega }^{+}$ were 39374.24 and 56926.88 for the uni-directional and bi-directional tension scenarios, respectively. The final values were 89139.84, in the uni-directional tension, and 75987.4, in the bi-directional tension, representing an increase of 126% and 33%, respectively.

Fig. 9

Stress maximization in Ω⁺ for: a-b uni-directional in-plane tension optimal holes and stress field and c-d bi-directional in-plane tension optimal holes and stress field

5.1.2 Strain control

We consider the same initial holes configuration from Fig. 5a and the uni-directional in-plane tension scenario. The corresponding field of mechanical strains $\boldsymbol {\varepsilon } = \left (\boldsymbol {\varepsilon }_{xx}, \boldsymbol {\varepsilon }_{yy}, \boldsymbol {\varepsilon }_{xy}\right )^{T}$ is plotted in Fig. 10. It is observed that the strain $\boldsymbol {\varepsilon }_{xx}$ is predominant and positive due to the axial load applied. In these examples the perimeter is constrained to 600.

Fig. 10

Distributions of the mechanical strains (a) ε_xx, b ε_yy and c ε_xy of the initial solution

The mechanical strain objective function can be either positive or negative, as seen in Fig. 10. The sub-structure ${\Omega }^{+}$ is initially under tension, with a positive strain value $\boldsymbol {\varepsilon }_{xx}$ = 1.971× 10^− 7. The minimization of $\boldsymbol {\varepsilon }_{xx}$ leads to a mostly compressive strain field with only a few outer elements with positive xx strain, being the total integral valued $\boldsymbol {\varepsilon }_{xx}$ = -1.147× 10^− 7. The solution is presented in Fig. 11a. It can be seen that the application of the tension load in the optimized structure induces compression in ${\Omega }^{+}$ region, see Fig. 11b. Consequently, the sub-structure becomes under tension in the yy direction and $\boldsymbol {\varepsilon }_{yy}$ becomes positive, as seen in Fig. 11c. Similar effects are seen in the uni-directional in-plane tension case of which the optimum solution is when $\boldsymbol {\varepsilon }_{yy}$ is maximized, presented in Fig. 12.

Fig. 11

ε_xx minimization in the uni-directional in-plane tension scenario: a optimal shapes and plots of bε_xx and c ε_yy

Fig. 12

ε_yy maximization in the uni-directional in-plane tension scenario: a optimal shape, b ε_yy field plot and c convergence history

In the case of shear strain $\boldsymbol {\varepsilon }_{xy}$, the initial integral of the shear strain in the sub-structure is zero due to its symmetry. Figure 13 presents the results for both minimization and maximization of the shear strain where the shapes are antisymmetric because of the opposite shear strain sign. The integral objectives are the same for both cases and their absolute value is 1.856× 10^− 5.

Fig. 13

Solutions under uni-directional in-plane tension for shear strain ε_xy a–b minimization and c–d maximization

Optimization of strain in multiple directions is straightforward. For example, the objective for minimization of $\boldsymbol {\varepsilon }_{xx}+\boldsymbol {\varepsilon }_{yy}$ can be defined as $\boldsymbol {\varepsilon } = \boldsymbol {\alpha } \cdot \boldsymbol {\varepsilon } \left (\mathbf {u} \right ) = \left (1, 1, 0\right )^{T} \cdot \boldsymbol {\varepsilon } \left (\mathbf {u} \right )$ and its solution is presented in Fig. 14. The objective function decreased from 1.223× 10^− 7 to -1.967× 10^− 7, implying that the sub-structure ${\Omega }^{+}$ becomes mostly under compression, predominantly in yy direction.

Fig. 14

ε_xx + ε_yy minimization in the uni-directional in-plane tension scenario: a optimal shape, b convergence history and plots of cε_xx and d ε_yy fields

The same phenomena from all the previous examples are valid for other cases. Table 1 compiles four other different examples. Cases like minimization of $\boldsymbol {\varepsilon }_{yy}$ under bi-directional in-plane tension is omitted because it yields the same solution as minimization of $\boldsymbol {\varepsilon }_{xx}$ but rotated by 90^o.

Table 1 Compilation of four different cases of strain control optimization

5.2 Shape preserving and design for failure

This example shows the application of the proposed stress objective function to shape preserving and to design for failure. The minimization of deformation preserves the shape of a prescribed sub-structure ${\Omega }^{+}$ under the loading condition. For instance, Zhu et al. (2016) used a square measure of the strain in order to minimize the deformation energy in the sub-structure. In this work, this is achieved by stress isolation. The case of design for failure is the opposite. In such case, the stress in ${\Omega }^{+}$ should be maximized in order to ensure the structure will fail in the prescribed region, preserving the integrity of other parts.

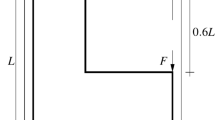
The cantilever beam model from Fig. 15 is used to carry out stress minimization of its sub-structure region ${\Omega }^{+}$ subject to a perimeter constraint of 400. The applied load is F = 1000, Young’s modulus E = 200× 10⁹ and the Poisson’s ratio $\mu = 0.3$. Figure 16 shows the initial stress field and the initial solution used in the level set optimization problem.

Fig. 15

Model considered for stress isolation and design for failure

Fig. 16

Structural example for stress isolation and design for failure: a initial solution and b stress field

Figure 17a shows the solution for stress isolation of the sub-structure ${\Omega }^{+}$ in the cantilever beam and Fig. 17b presents its stress field. The final stress integral in ${\Omega }^{+}$ is 1462.15, a decrease of $\approx$ 70% if compared with the value in the initial structure (4779.12). Figure 17c–d presents the solution for stress integral maximization in ${\Omega }^{+}$. The maximum stress point inside ${\Omega }^{+}$ ensures structural failure in that region or in its vicinity. The final integral on ${\Omega }^{+}$ for stress maximization is 97964.10, an increase of $\approx$ 1950%.

Fig. 17

Solutions and stress fields for a–b stress isolation and c–d stress maximization

The shape preserving effect can be observed by plotting the deformation of the sub-structure ${\Omega }^{+}$, as shown in Fig. 18a–c. It can be noticed that the warping deformation for the stress isolation solution is practically negligible if compared to its rigid body motion. The plotted displacements are scaled by 10⁸.

Fig. 18

Deformed sub-structure Ω⁺ for: a initial solution, b stress isolation and c stress maximization. The outline represents the initial position of the unloaded structure

5.3 Directional strain control

In Li et al. (2017), the directional strain behavior is controled by introducing artificial weak elements and a particular elastic matrix, where the diagonal of the direction of interest is assigned with a small positive value and the rest of the matrix is 0. The authors used a square measure of the strain. In this work we apply the stress isolation sensitivities with the particular elastic matrix with values depending on $\alpha$, previously defined for strain control. The elasticity matrix becomes

$$ \mathbf{C} = \left[\begin{array}{cccccc} \alpha_{1} & 0 & 0 \\ 0 & \alpha_{2} & 0 \\ 0 & 0 & \alpha_{3} \end{array}\right] $$

(27)

with $\alpha$ being 1 for the direction of interest and 0 for the other values.

Figure 19 presents the model used for directional strain control. The applied load is F = 1000, with Young’s modulus E = 200× 10⁹ and the Poisson’s ratio $\mu = 0.3$. The perimeter is constrained to 500. Figure 20 shows the solutions for $\boldsymbol {\varepsilon }_{xx}$ and $\boldsymbol {\varepsilon }_{yy}$ minimization, i.e., using $\alpha = \left \{1, 0, 0\right \}$ and $\alpha = \left \{0, 1, 0\right \}$, respectively. Notice that we are solving a stress isolation case, but with an unity value in the elasticity matrix to select the strain direction of interest. The same initial solution from Fig. 16a is used for this example.

Fig. 19

Model considered for directional strain control

Fig. 20

Solutions for: a ε_xx minimization and b ε_yy minimization

Figure 21 presents the $\boldsymbol {\varepsilon }_{xx}$ and $\boldsymbol {\varepsilon }_{yy}$ strain fields. Under the axial load, the domain ${\Omega }^{+}$ is initially stretched in the x direction and compressed in the y direction. The minimization of stress using $\alpha$ to select a prescribed direction leads to the minimization of deformation in that direction. Figure 22 presents the deformed ${\Omega }^{+}$ in the initial structure and for $\boldsymbol {\varepsilon }_{xx}$ and $\boldsymbol {\varepsilon }_{yy}$ minimization. The plotted displacements are scaled by 10⁸.

Fig. 21

Initial strain field ε_xx, (a), and final strain fields, ε_xx in (b), ε_yy in (c), for ε_xx minimization. Initial strain field ε_yy in (d), and final strain fields, ε_xx in (e), ε_yy in (f), for ε_yy minimization

Fig. 22

Deformed sub-structure Ω⁺ for: a initial solution, b ε_xx minimization and c ε_yy minimization. The outline represents the initial position of the unloaded structure

6 Conclusions

This paper presented a level set optimization method for stress and strain manipulation. The shape and topology modification of a base-structure ${\Omega }^{S}$ allowed the control of stress flux inside a sub-structure ${\Omega }^{+}$. A general integral objective function was proposed and the sensitivities were derived. For stress isolation, the von Mises measure was used. Numerical results show that stresses in ${\Omega }^{+}$ can be efficiently isolated in the presented examples via the optimization of the hole shapes in the base-structure, achieving the drastic reduction as much as 89% from the initial stress integral. The increase in the stress flux on the base-structure was also achieved by maximization of the stress integral. This may be applied when a failure needs to be designed in for prognosis. An increase of 126% was achieved in the bi-directional in-plane tension case.

It was shown that the solutions for strain control can be considerably different from those obtained for stress optimization. A strain objective function was proposed based on a vector $\boldsymbol {\alpha }$ able to select the strain component of interest. It was found that optimization explores the directionality of strain in the optimum solution, e.g., minimization of strain achieves a negative strain integral starting from a positive initial value (tension). A few other examples were briefly compiled.

The stress objective showed that it can also be used for shape preserving design and directional strain control. This paper therefore presents a level set optimization method that can manipulate stress and/or strain in a specified sub-structure. This can be used for stress isolation of highly sensitive non strain-based sensors, design for failure, maximization of mechanical strain, strain direction control and shape preserving design.