Level set topology optimization considering damage

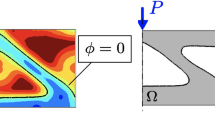
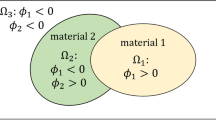
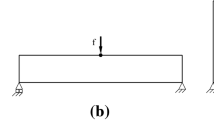
Abstract

This paper provides a level set based topology optimization approach to design structures exhibiting resistance to damage. The geometry of the structures is represented by the level set method. The design domains are discretized by the extended finite element method allowing for fixed non conforming meshes. The mechanical model represents quasi-brittle materials. Undamaged material behavior is assumed linear elastic while a loss of stiffness is introduced through a non-local damage model. Small strains are assumed. The sensitivities are evaluated by an analytical derivation of the discretized governing equations of the system and considering the adjoint approach. As the damage process is irreversible, the structural responses are path-dependent and this dependency is accounted for in the sensitivity analysis. The optimization problems are solved by mathematical programming algorithms, in particular using the GCMMA scheme. The proposed approach is illustrated with two dimensional examples that highlight the influence of degradation on the optimized designs.

Appendix :

A two dimensional validation example is provided as an extension of the one dimensional example presented in Noël et al. (2015). A perforated plate undergoing tension is studied considering a potential damage. The plate is loaded by imposing prescribed displacements on its left and right sides. The setting of the problem as well as the parameters used for the structural and sensitivity analyses are given in Fig. 12. Since the structure is symmetric, only a quarter of the plate is considered. Damage is modeled using the framework described in Section 3. An unstructured mesh with linear triangles T3 is used, as presented in Fig. 12c.

Fig. 12

Damaged perforated plate: description of the problem

The damage analysis is performed exploiting the path-following procedure presented in Section 4. The damage field over the structure at the last pseudo-time step as well as the evolution of the maximum damage in the structure are shown in Fig. 13a and b.

Fig. 13

Damaged perforated plate: structural and sensitivity analyses results using an unstructured T3 mesh

The hole is described by a level set function parametrized in terms of nodal values as explained in Section 2.1. The structural strain energy $\mathcal {C}$ is chosen as a design function and is given as:

$$ \mathcal{C} = \mathbf{u}^{T}\ \mathbf{K}(\mathbf{d})\ \mathbf{u}. $$

(35)

The sensitivity of the strain energy with respect to the design variables is evaluated for each pseudo-time step using the analytical sensitivity analysis proposed in Section 5. The obtained results are validated against finite differences. As no optimization problem is solved here, the nodal design values are not filtered as advised in (5), i.e. the filter radius is set to zero. The derivatives are only evaluated with respect to the design variables neighboring the interface. As shown in Fig. 12c, the design variables associated with nodes 1 to 13 are considered.

Figure 13c provides the evolution of the derivatives of the strain energy with respect to the considered design parameters. Analytical and finite differences results are in excellent agreement.