1 Introduction

Since the seminal paper regarding topology optimization of linearly elastic continuum structures by Bendsøe and Kikuchi (1988), the field of topology optimization has been subject to intense research. Today, material distribution topology optimization is applied to a range of different disciplines, such as linear and nonlinear elasticity (Clausen et al. 2015; Klarbring and Strömberg 2013; Park and Sutradhar 2015), acoustics (Christiansen et al. 2015; Kook et al. 2012; Wadbro 2014), electromagnetics (Elesin et al. 2014; Erentok and Sigmund 2011; Hassan et al. 2014; Wadbro and Engström 2015), and fluid–structure interaction (Andreasen and Sigmund 2013; Yoon 2010). A comprehensive account on topology optimization and its various applications can be found in the monograph by Bendsøe and Sigmund (2003) as well as in the more recent reviews by Sigmund and Maute (2013), and Deaton and Grandhi (2014).

In material distribution topology optimization, a material indicator function \(\rho :{\Omega }\subset \mathbb {R}^{d} \rightarrow \{0,1\}\) indicates presence (ρ = 1) or absence (ρ = 0) of material within the design domain Ω (Bendsøe and Sigmund 2003). To numerically solve the topology optimization problem, the domain Ω is typically discretized into n elements. The aim of the optimization is to determine element values ρ i ∈{0,1}, i∈{1,…, n}, that is, to determine if a given element contains material or not. The resulting nonlinear integer optimization problem is typically relaxed by allowing ρ i ∈[0,1], i∈{1,…, n}. This relaxation enables the use of gradient based optimization algorithms that are suitable for solving large-scale problems. In the continuum setting, such relaxation is often necessary to guarantee existence of solutions. To promote binary designs, penalization techniques are used. However, penalization typically makes the solutions of the optimization problem mesh-dependent. It is known that mesh dependency is sometimes due to lack of existence of solutions to the corresponding continuous problem. Several strategies have been proposed to resolve the issue of mesh-dependence and existence of solutions; Borrvall (2001) presents a systematic investigation of several common techniques.

Amongst the most popular techniques to achieve mesh-independent designs is to use a filtering procedure. Filtering procedures are commonly categorized as either sensitivity filtering (Sigmund 1994) or density filtering (Bourdin 2001; Bruns and Tortorelli 2001), where the derivatives of the objective function are filtered or where the design variables are filtered, respectively. When using a density filtering procedure, the design variables are no longer the “physical density”, that is, the coefficients that enter the governing equation. In a classic paper, Bourdin (2001) established existence of solutions to a continuous version of the linearly filtered penalized minimum compliance problem.

The primary drawback of the linear filter is that it counteracts the penalization by producing physical designs with relatively large areas of intermediate densities. More recently, a range of nonlinear filters, aimed at reducing the amount of intermediate densities while retaining mesh-independence, has been presented (Guest et al. 2004, 2011; Sigmund 2007; Svanberg and Svärd 2013). To harmonize the use of filters, we have recently introduced the class of generalized fW-mean filters that contains most filters used for topology optimization. Apart from providing a common framework for old as well as new filters, we also showed that filters from this class may be applied with O(n) computational complexity (Wadbro and Hägg 2015). To the best of our knowledge and perhaps due to the compelling numerical evidence of mesh-independence that has been accumulated over the years, the existence issue related to continuous nonlinearly filtered topology optimization problems has received little if any attention.

The main result of this paper is Theorem 1 of Section 2, which is a generalization of the result of Bourdin (2001), regarding the existence of solutions to an fW-mean filtered penalized minimum compliance problem. Section 3 provides a short discussion regarding desirable properties of a general filtering procedure in the discretized case, as well as a short summary on the fW-mean filters. Section 4 discusses various aspects on fast evaluation of filtered densities and their sensitivities. Finally, Section 5 presents large-scale numerical experiments utilizing cascaded nonlinear filters.

2 Existence of solutions to the fW-mean filtered continuous minimum compliance problem

In this section, we show that there exists a solution to a continuous version of the fW-mean filtered penalized minimum compliance problem.

Let \({\Omega }\subset \mathbb {R}^{d}\) be a bounded and connected domain in which we want to place our structure. The continuous fW-mean filtered density is, for x∈Ω, given by

$$ \big(F(\rho)\big)(x) = f^{-1}\left( \frac{1}{|\mathcal{N}_{x}|} \int \limits_{\mathcal{N}_{x}} (f\circ\rho)(y)\, \mathrm{d}y \right), $$
(1)

where f is a smooth and invertible function \(f:[0,1]\rightarrow [f_{{\min }},f_{{\max }}]\subset \mathbb {R}\) , \(\mathcal {N}_{x}\) is the neighborhood of x, and \(|\mathcal {N}_{x}|>0\) is the measure (area or volume) of \(\mathcal {N}_{x}\). We define the set of admissible designs \(\mathcal {A}\subset L^{\infty }({\Omega })\) as

$$ \mathcal{A} = \left\{ \rho \mid 0 \le \rho \le 1 \text{ a.e. on }{\Omega}, \int \limits_{\Omega} F(\rho) \le V \right\}. $$
(2)

Remark 1

Throughout the article we do not explicitly specify the measure symbol (such as dΩ, for instance) in the integrals, whenever there is no risk for confusion. The type of measure will be clear from the domain of integration.

Remark 2

To be able to apply the filter F on any design, we use a continuous bijective extension of f, \(\hat {f}:\bar {\mathbb {R}}\rightarrow \bar {\mathbb {R}}\), when evaluating expression (1). Assume (without loss of generality) that f is increasing, then the continuous and bijective extension \(\hat {f}:\bar {\mathbb {R}}\rightarrow \bar {\mathbb {R}}\) may, for instance, be defined as

$$ \hat{f}(x) = \left\{\begin{array}{ll} -\infty & \text{if}~x = -\infty,\\ f\left( 0 \right) + x & \text{if}~ x\in\left( -\infty,0 \right),\\ f(x) & \text{if}~ x\in\left[ 0,1\right],\\ f(1) + x-1 & \text{if}~ x\in\left( 1,\infty\right),\\ \infty & \text{if}~x = \infty. \end{array}\right. $$
(3)

Furthermore, for any Lebesgue measurable function \(\rho :{\Omega } \rightarrow \bar {\mathbb {R}}\), the composition \(\hat {f}\circ \rho \) is Lebesgue measurable. To simplify the notation below, whenever we write f it should be interpreted as a continuous and bijective extension of f.

We assume that the boundary ∂Ω is Lipschitz and that the structure is fixed at a nonempty open boundary portion Γ D ⊂∂Ω. The set of kinematically admissible displacements of the structure is

$$ \mathcal{U} = \left\{ u \in H^{1}({\Omega})^{d} \mid u|_{{\Gamma}_{D}} \equiv 0\right\}. $$
(4)

The equilibrium displacement of the structure is the solution to the following variational problem.

$$ \text{Find}~u \in \mathcal{U}~\text{such that} \enspace a(\rho;u,v) = \ell(v) \enspace \forall v \in \mathcal{U}. $$
(5)

The energy bilinear form a and the load linear form ℓ are defined as

$$\begin{array}{@{}rcl@{}} a(\rho;u,v) &=& \int \limits_{\Omega} {\tilde{\rho}(\rho)} E \epsilon(u):\epsilon(v), \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \ell(v) &= &\int \limits_{\Omega} b \cdot v + \int \limits_{{\Gamma}_{L}} t \cdot v , \end{array} $$
(7)

where b∈L 2(Ω)d and t∈L 2(Γ L )d represent the internal force in Ω and surface traction densities on the boundary portion \({\Gamma }_{L}=\partial {\Omega }\setminus \overline {{\Gamma }_{D}}\), respectively, 𝜖(u)=(∇u+∇u T )/2 is the strain tensor (or the symmetrized gradient) of u, the colon “:” denotes the scalar product of the two matrices, E is a constant forth-order elasticity tensor, and \(\tilde {\rho }(\rho )\) is the physical density. We define the physical density as

$$ \tilde{\rho}(\rho) = \underline{\rho} + (1-\underline{\rho}) P(F(\rho)), $$
(8)

where \(\underline {\rho }>0\) and P:[0,1]→[0,1] is a smooth and invertible penalty function. The above formulation includes the case when the problem is penalized using SIMP (Bendsøe and Sigmund 2003), that is, to use P(x) = x p in (8) for some p>1. The addition of a minimum physical density \(\underline {\rho }>0\) ensures that the bilinear form a(⋅;⋅,⋅) is coercive. That is, there exists a constant C>0 such that

$$ a(\rho;u,u) \ge C \|u\|_{H^{1}({\Omega})^{d}}^{2}. $$
(9)

Theorem 1

If \(\displaystyle |\mathcal {N}_{x}|>0\) for all x∈Ω, then there exists a solution to the following variation of the minimum compliance problem.

$$ \text{Find}~u^{\ast} \in \mathcal{U}^{\ast}~\text{such that}~\ell(u^{\ast}) = \inf_{u\in \mathcal{U}^{\ast}} \ell(u), $$
(10)

where

$$ \mathcal{U}^{*} = \left\{ u \in \mathcal{U} \mid\begin{array}{l} \exists \rho\in \mathcal{A} \text{ such that} \\ a(\rho;u,v)=\ell(v)\enspace \forall v\in \mathcal{U} \end{array}\right\}. $$
(11)

Proof

Let (u m ), \(u_{m}\in \mathcal {U}^{\ast }\) for all \(m\in \mathbb {N}\), be a minimizing sequence for ℓ; without loss of generality, we stipulate that (ℓ(u m )) is non-increasing. By the definition of \(\mathcal {U}^{\ast }\), there exists a sequence of designs (ρ m ) such that, for each \(m\in \mathbb {N}\), a(ρ m ;u m , v) = ℓ(v) for all \(v\in \mathcal {U}\). Since the bilinear form (6) is coercive, we have from (9) that

$$ C\|u_{m}\|^{2}_{H^{1}({\Omega})^{d}} \le a(\rho_{m};u_{m},u_{m}) = \ell(u_{m}) \le \ell(u_{1}). $$
(12)

That is, (u m ) is uniformly bounded in H 1(Ω)d. Thus there exists an element \(u^{\ast } \in \mathcal {U}\) and a subsequence, still denoted (u m ), such that u m converges weakly to u ∗ in H 1(Ω)d as m→∞.

For each \(m\in \mathbb {N}\), we define τ m = f∘ρ m . By construction, we have that f min≤τ m ≤f max almost everywhere in Ω. Since (τ m ) is bounded in L ∞(Ω), we can according to the sequential Banach–Alaoglu theorem find a subsequence, still denoted (τ m ), and a limit element τ ∗∈L ∞(Ω) so that τ m converges weak* to τ ∗ in L ∞(Ω) as m→∞. As a direct consequence of the weak star convergence, we have that for all x∈Ω

$$\begin{array}{@{}rcl@{}} &&\frac{1}{|\mathcal{N}_{x}|}\int \limits_{\mathcal{N}_{x}} \tau_{m}(y) \, \mathrm{d}y = \frac{1}{|\mathcal{N}_{x}|}\int \limits_{\Omega} \tau_{m}(y) \mathbb{1}_{\mathcal{N}_{x}}(y) \, \mathrm{d}y\\ &&\to \frac{1}{|\mathcal{N}_{x}|} \int \limits_{\Omega} \tau^{\ast} (y) \mathbb{1}_{\mathcal{N}_{x}}(y) \, \mathrm{d}y = \frac{1}{|\mathcal{N}_{x}|} \int \limits_{\mathcal{N}_{x}} \tau^{\ast} (y) \, \mathrm{d}y \end{array} $$
(13)

as m→∞, where \(\mathbb {1}_{\mathcal {N}_{x}}\in L^{1}({\Omega })\) is the characteristic function of \(\mathcal {N}_{x}\).

The sequential Banach–Alaoglu theorem also guarantees that f min≤τ ∗≤f max almost everywhere in Ω. We can thus define ρ ∗ = f −1∘τ ∗ and by construction 0≤ρ ∗≤1 almost everywhere in Ω. Since f −1 is continuous, we have that

$$\begin{array}{@{}rcl@{}} && F(\rho_{m})(x) = f^{-1}\left( \frac{1}{|\mathcal{N}_{x}|}\int \limits_{\mathcal{N}_{x}} \tau_{m}(y) \, \mathrm{d}y \right)\\ && \to f^{-1}\left( \frac{1}{|\mathcal{N}_{x}|}\int \limits_{\mathcal{N}_{x}} \tau^{\ast} (y) \, \mathrm{d}y \right) = F(\rho^{\ast})(x) \end{array} $$
(14)

as m→∞. So, the physical design converges pointwise. Moreover for all x∈Ω, we have that 0≤F(ρ ∗)(x)≤1 and 0≤F(ρ m )(x)≤1 for all m. Thus, by Lebesgue’s dominated convergence theorem,

$$ {\int}_{\Omega} F(\rho^{\ast}) = {\displaystyle \lim_{m\to\infty}} {\int}_{\Omega} F(\rho_{m}) \le V, $$
(15)

or in words, the physical design obtained by filtering ρ ∗ satisfies the volume constraint, so \(\rho ^{\ast } \in \mathcal {A}\). The pointwise convergence of the physical (filtered) design implies that the physical density converges pointwise and that for all x∈Ω, it holds that \(\underline {\rho }\le \tilde {\rho }(\rho ^{\ast })(x)\le 1\) and \(\underline {\rho }\le \tilde {\rho }(\rho _{m})(x)\le 1\) for all m.

Let v be an arbitrary function in \(\mathcal {U}\), then

$$\begin{array}{@{}rcl@{}} && \underbrace{a(\rho_{m};u_{m},v)}_{\ell(v)}-a(\rho^{\ast};u^{\ast},v) \\ &=& \int \limits_{\Omega} \big({\tilde{\rho}(\rho_{m})}-\tilde{\rho}(\rho^{\ast}) \big) E \epsilon(u_{m}):\epsilon(v)\\ &&+ \int \limits_{\Omega} \tilde{\rho}(\rho^{\ast}) E \big(\epsilon(u_{m})-\epsilon(u^{\ast}) \big): \epsilon(v). \end{array} $$
(16)

We have that \(\tilde {\rho }(\rho ^{\ast })\epsilon (v)\in L^{2}({\Omega })^{d\times d}\). In addition, since u m converges weakly to u ∗ in H 1(Ω)d as m→∞, we have that 𝜖(u m ) converges weakly to 𝜖(u ∗) in L 2(Ω)d×d as m→∞. Thus, the second term on the right hand side of expression (16) tends to 0 as m→∞. The absolute value of the first term on the right hand side of expression (16) is bounded by

$$ \sum\limits_{i,j,k,l} \int \limits_{\Omega} \left| \big({\tilde{\rho}(\rho_{m})} - \tilde{\rho}(\rho^{\ast}) \big) E_{ijkl} \epsilon_{ij}(u_{m}) \epsilon_{kl}(v) \right|. $$
(17)

Let A ijkl denote an arbitrary term in expression (17). We note that for a fixed v∈H 1(Ω)d, we have that \( L^{2}({\Omega })\ni |\tilde {\rho }(\rho _{m})-\tilde {\rho }(\rho ^{\ast })||\epsilon _{kl}(v)| \rightarrow 0\) almost everywhere on Ω when m→∞ since |𝜖 kl (v)| is finite almost everywhere on Ω. Moreover, \(|\tilde {\rho }(\rho _{m})-\tilde {\rho }(\rho ^{\ast })||\epsilon _{kl}(v)|\le |\epsilon _{kl}(v)|\). Hence, by using Cauchy–Schwartz’s inequality and Lebesgue’s dominated convergence theorem, we find that

$$\begin{array}{@{}rcl@{}} A_{ijkl}^{2} &\le& |E_{ijkl}|^{2} \|\epsilon_{ij}(u_{m})\|_{L^{2}({\Omega})}^{2} \\ &&\cdot \int \limits_{\Omega} | {\tilde{\rho}(\rho_{m})}-\tilde{\rho}(\rho^{\ast}) |^{2} |\epsilon_{kl}(v)|^{2} \to 0 \end{array} $$
(18)

as m→∞. Thus, \(a(\rho ^{\ast };u^{\ast },v) = \ell (v) \enspace \forall v \in \mathcal {U}\) so \(u^{\ast } \in \mathcal {U}^{\ast }\). Moreover, because u m converges weakly to u ∗ in H 1(Ω)d as m→∞ and ℓ is a bounded linear functional on H 1(Ω)d, we have that ℓ(u m )→ℓ(u ∗) as m→∞. Since u m is a minimizing sequence for ℓ(⋅), we have that

$$ \ell(u^{\ast}) = \inf_{u\in\mathcal{U}^{\ast}} \ell(u). $$
(19)

That is, u ∗ solves problem (10). □

Remark 3

All steps in the above proof also hold true if we replace the function f −1 in definition (1) by another smooth function g:[f min, f max]→[0,1]. In particular, this holds if we replace f −1 in definition (1) by a projected version h∘f −1 provided that h:[0,1]→[0,1] is smooth.

Remark 4

The proof also holds in the case with normalized but non-uniform weights within the neighborhoods. The only change required is to replace \(\mathbb {1}_{\mathcal {N}_{x}}(y)/|\mathcal {N}_{x}|\) in Eq. (13) by an L 1(Ω) function that describes the non-uniform weights.

Remark 5

Analogous reasoning may be used for proving existence of solutions to problems that are similar to the minimum compliance problem, for instance, the heat compliance problem described in Section 5.2.

Formulation (10) of the minimum compliance problem might at first seem obscure. However, as we now illustrate, formulation (10) is much related to the following more direct formulation of the minimum compliance problem.

$$\begin{array}{@{}rcl@{}} && \text{Find}~\rho^{\ast}\in\mathcal{A}~\text{and}~u^{\ast}\in\mathcal{U}~\text{such that} \\ &&\qquad\ell(u^{\ast}) \leq \ell(u)\enspace \forall u\in \mathcal{U}^{\ast},\\ &&\qquad a(\rho^{\ast};u^{\ast},v)=\ell(v)\enspace \forall v\in \mathcal{U}. \end{array} $$
(20)

Note that if ρ ∗ and u ∗ solve problem (20), then u ∗ solves problem (10). On the other hand, if u ∗ solves problem (10), then there exists \(\rho ^{\ast }\in \mathcal {A}\) such that ρ ∗ and u ∗ solve problem (20). Thus, existence of solutions to (20) implies existence of solutions to (10), and vice versa.

3 Filtering in the discretized case

3.1 Requirements on filters and their implications

The discussion below treats the discretized case, where the design domain Ω is partitioned into n elements and the aim of the optimization is to determine the design vector ρ = (ρ 1,…, ρ n )T∈[0,1]n. A general filter is any function F:[0,1]n→[0,1]n and the physical (filtered) design is F(ρ). Below, we discuss typical requirements on such filters.

The first requirement is already included in the definition of F, namely that we require that the range must be conforming, that is

$$ \boldsymbol{F}(\boldsymbol{\rho}) \in [0,1]^{n}. $$
(21)

In addition, we also require that the function F is coordinate- and component-wise nondecreasing. That is, for any i, j and any δ≥0, we require that

$$ F_{i}(\boldsymbol{\rho} + \delta \boldsymbol{e_{j}}) \ge F_{i}(\boldsymbol{\rho}), $$
(22)

where e j denotes the jth basis vector of \(\mathbb {R}^{n}\). Condition (22) stems from the idea that increasing a design variable should not decrease any value in the physical design. We note that, conditions (21) and (22) imply that

$$ F_{i}(\boldsymbol{0}_{\boldsymbol{n}}) \le F_{i}(\boldsymbol{\rho}) \le F_{i}(\boldsymbol{1}_{\boldsymbol{n}}), $$
(23)

where \(\boldsymbol {0}_{\boldsymbol {n}}=(0,\ldots ,0)^{T}\in \mathbb {R}^{n}\) and \(\boldsymbol {1}_{\boldsymbol {n}}=(1,\ldots ,1)^{T}\in \mathbb {R}^{n}\). Expression (23) shows that if we want each element in the physical design to be able to attain the values 0 or 1, then we must require that

$$\begin{array}{@{}rcl@{}} \boldsymbol{F}(\boldsymbol{0}_{\boldsymbol{n}}) &= \boldsymbol{0}_{\boldsymbol{n}},\\ \boldsymbol{F}(\boldsymbol{1}_{\boldsymbol{n}}) &= \boldsymbol{1}_{\boldsymbol{n}}. \end{array} $$
(24)

It is natural to require that the filtered density in element i is strictly increasing with the density in that element. A weaker assumption is to require that for each ρ∈[0,1)n there exists an i and a j such that F i (ρ) is strictly increasing in ρ j in the vicinity of ρ. That is, there exists 𝜖>0 such that

$$ F_{i}(\boldsymbol{\rho}+\delta\boldsymbol{e_{j}}) > F_{i}(\boldsymbol{\rho})\enspace\forall\, 0<\delta<\epsilon. $$
(25)

The reason to include a requirement of this type is to guarantee that the physical design is sensitive to changes in the design.

If we want to use gradient based optimization algorithms, then we need to require that F is differentiable. In this case, requirement (22) translates to

$$ \frac{\partial F_{i}}{\partial \rho_{j}} \geq 0. $$
(26)

Requirement (25) may be replaced by the more restrictive condition that for each ρ, there exists an i and a j such that

$$ \frac{\partial F_{i}}{\partial \rho_{j}}(\boldsymbol\rho) > 0. $$
(27)

Another desirable property that often is mentioned is volume preservation. A filter is volume-preserving if

$$ \boldsymbol{1}_{\boldsymbol{n}}^{T}\boldsymbol{F}(\boldsymbol{\rho}) = \boldsymbol{1}_{\boldsymbol{n}}^{T}\boldsymbol{\rho}\enspace\forall \boldsymbol{\rho}\in[0,1]^{n}. $$
(28)

The obvious benefit of using a volume-preserving filter is that the volume constraint can be applied directly to the design vector ρ.

For a linear filter F(ρ) = Aρ, where \(\boldsymbol {A} = [a_{ij}] \in \mathbb {R}^{n\times n}\), conditions (21) and (24) are equivalent to

$$ a_{ij} \geq 0\enspace \forall i,j \text{ and} ~\boldsymbol{A}\boldsymbol{1}_{\boldsymbol{n}} = \boldsymbol{1}_{\boldsymbol{n}}. $$
(29)

Furthermore, we find that volume preservation is equivalent to

$$ \boldsymbol{1}_{\boldsymbol{n}}^{T} \boldsymbol{A} = \boldsymbol{1}_{\boldsymbol{n}}^{T}. $$
(30)

Thus, a linear filter is both volume-preserving and has a conforming range if and only if A is a so-called doubly stochastic matrix.

3.2 fW-mean filters

Next, we present a short summary on fW-mean filters (Wadbro and Hägg 2015). For a given smooth and invertible function \(f:[0,1]\rightarrow \mathbb {R}\) with nonzero derivative, the fW-mean filter of a vector ρ∈[0,1]n is defined as

$$ \boldsymbol{F}(\boldsymbol{\rho}) = \boldsymbol{f}^{-1}\left( \boldsymbol{W}\boldsymbol{f}(\boldsymbol{\rho}) \right), $$
(31)

in which \(\boldsymbol {f}(\boldsymbol {\rho })=(f(\rho _{1}),f(\rho _{2}),\ldots ,f(\rho _{n}))^{T}\in \mathbb {R}^{n}\) and \(\boldsymbol {W} = [w_{ij}] \in {\mathbb {R}^{n\times n}}\) is a weight matrix with non-negative entries such that W1 n = 1 n .

We note that since

$$ w_{ij} > 0 \iff j\in{\mathcal{N}_{i}}, $$
(32)

the neighborhood \(\mathcal {N}_{i}\subset \{1,\ldots ,n\}\) of element i is implicitly defined by the weight matrix W. In topology optimization, it is common to use a neighborhood shape \(\mathcal {N}\subset \mathbb {R}^{d}\) to define the neighborhoods

$$ \mathcal{N}_{i} = \left\{ j:x_{j}-x_{i} \in \mathcal{N} \right\} , i\in\{1,\ldots,n\}, $$
(33)

where \(x_{i}\in \mathbb {R}^{d}\), i∈{1,…, n} are the element centroids. When equal weights are used within neighborhoods, W = D −1 G, where \(\boldsymbol {D} = \text {diag}(|\mathcal {N}_{1}|,\ldots ,|\mathcal {N}_{n}|)^{T}\) and G is the neighborhood matrix with entries g ij = 1 if and only if \(j\in \mathcal {N}_{i}\) and g ij = 0 otherwise.

All fW-mean filters map a vector with equal entries to itself, that is, if c∈[0,1], then F(c1 n ) = c1 n . Hence, the fW-mean filters satisfy conditions (24). However, the fW-mean filters are generally not volume-preserving, that is

$$ \exists \boldsymbol{\rho}\in[0,1]^{n} \text{ such that}~ \boldsymbol{1}_{\boldsymbol{n}}^{T}\boldsymbol{F}(\boldsymbol{\rho}) \neq \boldsymbol{1}_{\boldsymbol{n}}^{T}\boldsymbol{\rho}. $$
(34)

The ij entry of the Jacobian ∇F of the fW-mean filter is given by

$$ \frac{\partial F_{i}}{\partial \rho_{j}} = w_{ij}\frac{f^{\prime}(\rho_{j})}{f^{\prime}\left( F_{i}(\boldsymbol{\rho}) \right)} \geq 0, $$
(35)

where the inequality is strict provided w ij >0, that is, when j is in the neighborhood of i.

The fW-mean filter framework contains many filter types, such as the linear filters (Bruns and Tortorelli 2001), the morphology based filters introduced by Sigmund (2007), and the pythagoran mean based filters introduced by Svanberg and Svärd (2013), but not all. For example, the projection based filters (Guest et al. 2004; Wang et al. 2011) are not covered in the fW-mean filter framework. However, these filters can be fitted into the generalized fW-mean filter framework (Wadbro and Hägg 2015), in which the function f −1, used in definition (31), is replaced by a smooth function g:f([0,1])→[0,1] satisfying g(f(0))=0 and g(f(1))=1. That is, the generalized fW-mean filters are of the form

$$ \boldsymbol{\tilde{F}}(\boldsymbol{\rho}) = \boldsymbol{g}\left( \boldsymbol{W} \boldsymbol{f}(\boldsymbol{\rho}) \right). $$
(36)

4 Aspects of fast evaluation of filtered densities and sensitivities

4.1 On the computational complexity

In our previous paper (Wadbro and Hägg 2015), we showed that if the computational domain is discretized into n elements in a regular grid, the neighborhood shape is a polytope, and equal weighting within each neighborhood is used, then the fW-mean filter can be applied with computational complexity O(n). The O(n) algorithm is based on recursively adding and subtracting moving sums. Moreover, the computational complexity can be bounded independent of the size of the neighborhoods.

Non-equal weighting within neighborhoods can be achieved by sequentially applying the same equally weighted fW-mean filter twice (or more). More precisely, when applying an equally-weighted fW-mean filter twice, we have that

$$ \boldsymbol{F}(\boldsymbol{F}(\boldsymbol{\rho})) = \boldsymbol{f}^{-1}\left( \boldsymbol{W}^{2} \boldsymbol{f}(\boldsymbol{\rho}) \right). $$
(37)

The weight matrix W 2 has, in general and for each neighborhood, weights that decay from the neighborhood center. Figure 1 illustrates the weights corresponding to the first three powers of W = D −1 G, from top to bottom W, W 2, and W 3, for an octagonal (left column) and a rectangular neighborhood (right column). If the neighborhood shape is a convex polytope \(\mathcal {P}\subset \mathbb {R}^{d}\), then it can be shown that a neighborhood shape corresponding to W 2 is \(2\mathcal {P}\).

Fig. 1
figure 1

Illustration of the first three powers (from top to bottom) of the weight matrix, W = D −1 G, W 2, W 3, for an octagonal and a rectangular neighborhood (left and right column, respectively)

Full size image

We remark that, in general, evaluating the sums Gf(ρ) accounts for a significant portion of the computational cost of the filter application. Moreover, the computational effort required to evaluate these sums grows with the complexity of the neighborhood polytope. Thus, if one wishes to apply a filter with weights that decay with the distance from the neighborhood center, particularly in three space dimensions, one could save a great portion of the computational time by selecting a simple neighborhood. For example, the computational complexity for filtering over a box shaped neighborhood is approximately 10 times lower than the complexity for filtering over the significantly more complex rhombicuboctahedron (a polytope with 26 faces—twelve rectangular, six square, and eight triangular faces) neighborhood (Wadbro and Hägg 2015).

On the other hand, if one wishes to use one of the nonlinear filters that are designed to mimic min or max operators over the neighborhood, then the neighborhood shape is important. In this latter case, one cannot use the weighted version with a square or box shaped neighborhood to approximate a circular or spherical neighborhood, since the nonlinearity of the filtering process will essentially pick out the maximum/minimum of the element values in each neighborhood. However, by using neighborhoods of different but still relatively simple shapes, such as two square shaped neighborhoods (with a relative rotation of 45 degrees), one can get a filtering procedure where the neighborhood around each element is an octagon. A similar approach can also be used for the three dimensional case, where one can use four cubic neighborhoods (the scaled unit cube plus three other cubes, rotated 45 degrees in the x 1 x 2, x 1 x 3, and x 2 x 3 planes, respectively) to approximate a sphere. The use of a sequence of filters with simple neighborhood shapes streamlines the implementation. Moreover, the resulting memory access pattern can be made very regular, which paves the way for future highly efficient parallel implementations.

If the neighborhood shape and the weighting (possibly nonuniform) within each neighborhood is the same for all neighborhoods, then Wf(ρ) corresponds to a convolution. In this case fW-mean filters may be efficiently applied using an FFT based algorithm (Lazarov et al. 2016). The main idea behind FFT based filtering is that the convolution between the density and the filter kernel corresponds to elementwise multiplication in frequency domain. The application of an fW-mean filter can be performed as

$$ \boldsymbol{F}(\boldsymbol{\rho}) = \boldsymbol{f}^{-1}\left( \boldsymbol{\mathcal{F}}^{-1} \big\{ \boldsymbol{\mathcal{F}}\{\boldsymbol{w}\} \odot \boldsymbol{\mathcal{F}}\{\boldsymbol{f}(\boldsymbol{\rho})\} \big\} \right), $$
(38)

where \(\boldsymbol {\mathcal {F}}\) and \(\boldsymbol {\mathcal {F}}^{-1}\) represent the d-dimensional FFT and inverse FFT transform, respectively, ⊙ denotes the element-wise product, and w is a vector that represents the filter kernel. The asymptotic computational complexity of FFT based filters is O(nlogn) independent of the complexity of the neighborhood shape. For filtering using any given polygonal neighborhood, the FFT-based filters are hence asymptotically slower than the O(n) algorithm based on recursively adding and subtracting moving sums. For large-scale problems, with 105– 109 elements, the FFT based algorithm is 1.3–6.5 times slower than the moving sums based algorithm on a standard desktop equipped with an Intel Xeon E5-1650 v3 CPU. The FFT algorithm is potentially sensitive to round-off errors, similarly as the O(n) moving sums based algorithm (Wadbro and Hägg 2015). In many fields the FFT method is standard and there exists many highly optimized and parallel FFT routines, thus the FFT-based filters are a competitive alternative.

4.2 Sensitivity evaluation

The impact of the filter on the sensitivities is found by computing v T∇F(ρ) for some vector \(\boldsymbol {v}\in \mathbb {R}^{n}\). In practice, v is the gradient of the objective or a constraint function with respect to the filtered densities. By using expression (35) we find that

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{n} v_{i}\frac{\partial F_{i}(\boldsymbol{\rho})}{\partial \rho_{j}} &=& \sum\limits_{i=1}^{n} v_{i} w_{ij}\frac{f^{\prime}(\rho_{j})}{f^{\prime}\left( F_{i}(\boldsymbol{\rho}) \right)}\\ &=& f^{\prime}(\rho_{j})\sum\limits_{i=1}^{n} w_{ij}\frac{v_{i}}{f^{\prime}\left( F_{i}(\boldsymbol{\rho}) \right)}, \end{array} $$
(39)

that is, to modify sensitivities we need to carry out matrix multiplication by W T. In the special case of equal weighting within neighborhoods, multiplication by W T translates to multiplication by G T; or expressed differently, to perform summation over the transposed neighborhoods \(\mathcal {N}_{i}^{T} = \{j:i\in \mathcal {N}_{j}\} = \{j:g_{ji}=1\}\). If the neighborhoods are symmetric, then G T = G and the same summation algorithm can be used for both filtering and sensitivity calculation, which facilitates the implementation.

Assume that the neighborhoods are defined by a neighborhood shape \(\mathcal {N}\) so that \(\mathcal {N}_{i}= \{j:x_{j}-x_{i}\in \mathcal {N}\}\), where x i and x j denote the centroid of elements i and j, respectively. For each element \(j\in \mathcal {N}_{i}^{T}\), we have that \(i\in \mathcal {N}_{j}\) and by definition \(x_{i}-x_{j}\in \mathcal {N}\); that is, there exists \(y\in \mathcal {N}\) so that x i −x j = y or equivalently x j −x i = −y. Since all steps above are bidirectional, we have that \(\mathcal {N}_{i}^{T} = \{j:x_{j}-x_{i}\in - \mathcal {N}\}\); hence a neighborhood shape which defines the transposed neighborhoods is found by inversion of \(\mathcal {N}\) in the origin. Since \(\mathcal {P}\) and \(-\mathcal {P}\) are essentially the same polytope, this means that implementing the fast summation algorithm over \(-\mathcal {P}\) requires the same amount of work as implementing it over \(\mathcal {P}\).

If we work with a Cartesian grid and the design variables are stored using a standard slice/fiberwise numbering (row- or column-wise in the two dimensional case), then we can use that G T = PGP, where P is the flip or exchange matrix. That is, P is the matrix with ones along the anti-diagonal and zeros elsewhere. Hence, the same summation algorithm may be used both for filtering and sensitivity evaluation.

4.3 Cascaded fW-mean filters

It has already been established that sequential application of filters is a means to arrive at filters with desirable properties, see for instance the open and close filters introduced in topology optimization by Sigmund (2007).

Assume that we are given a family of N fW-mean filters,

$$ \boldsymbol{F}^{(K)}(\boldsymbol{\rho}) = \boldsymbol{f}_{K}^{-1}\left( \boldsymbol{W}^{(K)}\boldsymbol{f}_{K}(\boldsymbol{\rho}) \right), K\in\{1,\ldots,N\}. $$
(40)

For each K∈{1,…, N}, we define the cascaded filter function of order K, C (K):[0,1]n→[0,1]n, to be the composition

$$ \boldsymbol{C}^{(K)} = \boldsymbol{F}^{(K)} \circ \boldsymbol{F}^{(K-1)} \circ {\ldots} \circ \boldsymbol{F}^{(1)}, $$
(41)

and we define

$$ \boldsymbol{\rho}^{(K)} = \boldsymbol{C}^{(K)}(\boldsymbol{\rho}). $$
(42)

The cascaded filter is naturally applied sequentially

$$ \boldsymbol{\rho}^{(K)} = \boldsymbol{F}^{(K)}\left( \boldsymbol{C}^{(K-1)}(\boldsymbol{\rho})\right) = \boldsymbol{F}^{(K)}\left( \boldsymbol{\rho}^{(K-1)}\right), $$
(43)

where we set ρ (0) = ρ. If the prerequisites of the algorithm presented in Wadbro and Hägg (2015) are met for all N fW-mean filters in the cascade (41), then sequential application of the cascaded filter requires O(Nn) operations.

We proceed to show how to modify sensitivities in the case of a cascade of N fW-mean filters. That is, given a vector \(\boldsymbol {v}\in \mathbb {R}^{n}\), we want to compute v T∇C (N)(ρ). To this end, we assume that N≥2, let v (N) = v, combine expressions (42) and (43), and apply the chain rule

$$\begin{array}{@{}rcl@{}} && \sum\limits_{i=1}^{n} v_{i}^{(N)}\frac{\partial}{\partial \rho_{j}}C_{i}^{(N)}(\boldsymbol{\rho})\\ &&= \sum\limits_{i=1}^{n} v_{i}^{(N)}\frac{\partial}{\partial \rho_{j}}\left( F_{i}^{(N)}\left( \boldsymbol{C}^{(N-1)}(\boldsymbol{\rho})\right) \right) \\ &&=\sum\limits_{i=1}^{n} v_{i}^{(N)} \sum\limits_{k=1}^{n} \frac{\partial F_{i}^{(N)}}{\partial \rho_{k}}\bigg\rvert_{\boldsymbol{\rho}^{(N-1)}}\frac{\partial}{\partial \rho_{j}}C_{k}^{(N-1)}(\boldsymbol{\rho})\\ &&=\sum\limits_{k=1}^{n} \left( \sum\limits_{i=1}^{n} v_{i}^{(N)} \frac{\partial F_{i}^{(N)}}{\partial \rho_{k}}\bigg\rvert_{\boldsymbol{\rho}^{(N-1)}}\right) \frac{\partial}{\partial \rho_{j}}C_{k}^{(N-1)}(\boldsymbol{\rho})\\ &&=\sum\limits_{k=1}^{n} v_{k}^{(N-1)}\frac{\partial}{\partial \rho_{j}}C_{k}^{(N-1)}(\boldsymbol{\rho}), \end{array} $$
(44)

where we in the last step have defined

$$ v_{k}^{(N-1)} = \sum\limits_{i=1}^{n} v_{i}^{(N)}\frac{\partial F_{i}^{(N)}}{\partial\rho_{k}}\bigg\rvert_{\boldsymbol{\rho}^{(N-1)}}. $$
(45)

The first and last lines of expression (44) are similar in form. However, the order of the cascade in the last line is one less than that in the first line. The steps in expression (44) may be repeated until the order of the cascade in the last line is 1, that is, the cascade consists of just one filter. We conclude that evaluating v T∇C (N)(ρ) corresponds to sequentially computing the vectors v (K−1)

$$ v_{k}^{(K-1)} = \sum\limits_{i=1}^{n} v_{i}^{(K)}\frac{\partial F_{i}^{(K)}}{\partial\rho_{k}}\bigg\rvert_{\boldsymbol{\rho}^{(K-1)}}, $$
(46)

for K = N, N−1,…,1 and where as before v (N) = v. The sum on the right hand side of expression (46) is precisely of the form (39).

Hence, if we store the intermediate designs ρ (K), K∈{1,…, N} when sequentially applying the filter and if the prerequisites of the fast summation algorithm are fulfilled for all filters in the cascade, then modification of sensitivities requires O(Nn) operations. The low computational complexity for modifying sensitivities comes at the cost of O((N−1)n) memory used to store the intermediate designs ρ (K), K∈{1,…, N−1}.

Remark 6

Existence of solutions to the continuous penalized minimum compliance problem in the case when a cascade of fW-mean filters is applied can be proven by following the same reasoning as in the proof in Section 2.

4.4 Implementation of cascaded fW-mean filters

In the following section, we present numerical experiments performed in Matlab. For the cantilever beam experiments, we use a modified version of the 2D multigrid-CG topology optimization code by Amir et al. (2014). Below, we describe the major changes done to the code. First, we introduce a filter struct filterParam to hold all information needed to perform filtering and sensitivity modification, see Table 1. In the code excerpts, we have suppressed the struct name filterParam to increase the readability. For instance, we simply write N instead of writing filterParam.N. Listings 1–3 contain the new parts of code that needs to be included in order to use a filtering procedure composed of a cascade of generalized fW-mean filters. The Matlab code in Listing 1 computes the neighborhood sizes. The Matlab code in Listing 2 filters the vector rho by using the filterParam struct and the procedure outlined in Section 4.3. The observant reader notices that in fact it is not ρ (K) that is saved in the filtering, but (D (K))−1 G (K) f K (ρ (K−1)) since this enables the use of generalized fW-mean filters where \(g_{K} \neq f_{K}^{-1}\). The Matlab code in Listing 3 computes v T∇C (N)(ρ), as outlined in Section 4.3. We remark that filtering of densities must be moved inside the optimality criteria update whenever a non volume-preserving filter is used.

Table 1 The fields in the filterParam struct. Note that field N and index k corresponds to the variables N and K, respectively
Full size table
Listing 1
figure a

Matlab code that computes the neighborhood sizes

Full size image
Listing 2
figure b

Matlab code that filters the design variables by using a cascade of generalized fW-mean filters

Full size image
Listing 3
figure c

Matlab code that modifies the sensitivities with respect to the physical design following the description in Section 4.3

Full size image

5 Numerical experiments

5.1 Cantilever beam

As a first test problem, we consider the minimzation of compliance for the cantilever beam illustrated in Fig. 2. The beam is held fast at its left hand side, the boundary portion denoted Γ D in the figure and subject to a downward vertical force that is uniformly distributed over Γ F , the middle 10 % of the beam’s right side. We solve variational problem (5) by using bilinear finite elements, use the minimum physical density \(\underline {\rho }=10^{-9}\), and use SIMP as our penalization approach; that is, P(x) = x p in (8) with p = 3. To minimize the compliance we use the optimality criteria method with damping parameter η = 1/2.

Here, we use an open–close (open followed by close) filtering strategy over octagonal shaped neighborhoods as suggested by Sigmund (2007). However, instead of using exponential averaging, we use harmonic averaging as introduced in topology optimization by Svanberg and Svärd (2013). More precisely, the harmonic open–close filter is a cascade of four fW-mean filters defined by f 1(x) = f 4(x)=(x + α)−1, f 2(x) = f 3(x) = f 1(1−x), and \(g_{K}=f_{K}^{-1}\) for K = 1,…,4. In our experiment, we used the fixed parameter α = 10−4. Figure 3 shows the final physical design (not post processed nor sharpened!) from the optimization of the cantilever beam. The volume fraction used was 0.5 and the final measure of non discreteness (of the physical design) is 0.3 %.

To the best of our knowledge, previously no contribution has used an open–close or close–open filtering strategy to solve problems with more than a few tens of thousands degrees of freedom. Here, we capitalize on our fast filtering strategy (Wadbro and Hägg 2015) and solve a design problem with 7.96 million degrees of freedom. The size of the filter neighborhoods is 4,405 elements for the open step and 301 elements for the close step. The solution process required 111 iterations and took fourteen hours, the filtering and modification of sensitivities consumed about a quarter of this time, on a standard desktop equipped with an Intel Xeon E5-1650 v3 CPU. It should be noted that the fast summation algorithm was executed almost 24,000 times.

Figure 2
figure 2

Geometry for the cantilever beam problem

Full size image
Figure 3
figure 3

Filtered densities for a cantilever beam optimized by using 3456×2304 elements and a harmonic open filter over a “large” octagonal neighborhood followed by a harmonic close filter over a “small” octagonal neighborhood. The neighborhoods are indicated in the upper-right corner

Full size image

Recently, Schevenels and Sigmund (2016) demonstrated that an open–close filtering strategy in general does not guarantee minimum size control on both structure and void regions. Nevertheless, our numerical experiments suggest that for minimum compliance problems such a filtering strategy in combination with a gradient based optimization method results in physical designs that exhibit size control on both structure and void regions. By examination of Fig. 3, we note that the shape of the filter neighborhood is clearly visible in some of the corners of the internal void regions. More precisely, the resulting physical designs could be manufactured by using either a deposition tool or a punch in the shape of the neighborhood used in the open or close step, respectively. To illustrate that the bounds on the minimum sizes are dictated by the size of the neighborhoods used in the harmonic open–close filter, we present in Figs. 4 and 5 a series of cantilever beams optimized using different neighborhood sizes. In each sub-figure, the neighborhoods used in the filtering process are shown in the top right corner; the upper neighborhood corresponds to the open step that should impose a minimum size on the material regions and the lower neighborhood corresponds to the close step that should impose a minimum size on the void regions. The upper-right cantilever beam in Fig. 4 is a “coarse” version of the cantilever beam in Fig. 3 included to illustrate mesh-independence.

Figure 4
figure 4

Cantilever beams optimized by using 1536×1024 elements and different harmonic open–close filters. The octagonal neighborhoods are indicated in the upper-right corner of each sub-figure. Here, the relative ratio between the filter radii used in the open and close step is 4 for all experiments

Full size image
Figure 5
figure 5

Cantilever beams optimized by using 1536×1024 elements and different harmonic open–close filters. The octagonal neighborhoods are indicated in the upper-right corner of each sub-figure. Here, the relative ratio between the filter radii used in the open and closed step is 1 and 1/4 for the left and right beam respectively. The corresponding result with a ratio of 4 between the filter radii used in the open and close step are shown in Fig. 4

Full size image

5.2 Minimum heat compliance

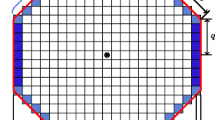
The second model problem that we consider is to minimize the heat compliance of a square plate that occupies the computational domain Ω, illustrated in Fig. 6, and is subject to uniform heating. The plate is held at zero temperature along the boundary portion Γ D and is insulated along the rest of the boundary Γ N . At thermal equilibrium, the temperature field u, satisfies the variational problem

Figure 6
figure 6

Geometry for the minimum heat compliance problem

Full size image

Find \(u\in \mathcal {V}\) such that

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega} \tilde \rho(\rho) \nabla u \cdot \nabla v = {\int}_{\Omega} v \enspace \forall v\in\mathcal{V}, \end{array} $$
(47)

where \(\tilde \rho (\rho )\) represents the physical heat conductivity that is inhomogeneous but isotropic and \(\mathcal {V}=\{u\in H^{1}({\Omega }) \mid u|_{{\Gamma }_{D}} \equiv 0 \}\). The physical conductivity is defined according to expression (8) with \(\underline {\rho }=10^{-3}\) and using SIMP for the penalization. The material distribution problem that we are interested in solving can be written as

$$ \min_{\rho \in \mathcal{A}} {\int}_{\Omega} u, $$
(48)

where \(\mathcal {A}\) is defined in expression (2) with V = |Ω|/2.

Variational problem (47) is solved by using bilinear finite elements. We use SIMP as our penalization approach, that is P(x) = x p in (8), and solve optimization problem (48) by using the optimality criteria method with damping parameter η = 1/8 coupled with a continuation approach for the penalty parameter. That is, we solve the problem for an increasing sequence of penalty levels p = 1,1.1,…,20. For the first penalty level we use a uniform initial guess and for the later levels, we use the final filtered conductivity from the previous level as starting guess. We remark that, similarly as observed by Lazarov et al. (2016) that using a single penalty level p = 3 for the SIMP parameter and damping parameter η = 1/2 in the optimality criteria update produces optimized designs with large regions with intermediate conductivities.

As in the cantilever beam examples in the previous section, we use a harmonic open–close filter over octagonal neighborhoods with different sizes for the open and the close steps. Figure 7 shows optimized physical designs for the heat compliance problem. The combination of the harmonic open–close filter and the proposed penalization scheme results in crisp physical designs with MNDs ranging between 0.2 % and 0.7 %. The lower left physical design, which contains a region of intermediate densities that is not located entirely on the boundary between the two materials, has the largest MND. Such a region of intermediate densities serves as an indication of insufficient penalization. (Since the filter is smooth some transitional region is always expected at an interface between high conductivity and low conductivity material.)

Figure 7
figure 7

Optimized results for the heat compliance problem using a resolution of 1024×1024 and 2048×2048 elements for the results in the top and bottom row, respectively. The octagonal neighborhoods are indicated in the upper-right corner of each sub-figure; the ratio between the filter radii in the open and close step was 3:2 for all results. The filter radii used for the results in the left column are twice as large as those used to obtain the results in the right column

Full size image

In all experiments the ratio between the filter radii of the open and close steps was 3:2. To illustrate the effect of the size of the filter neighborhoods the radii of the neighborhoods in the left column of Fig. 7 are twice as large as those in the right column. The results obtained using smaller filter radii exhibit finer details than those obtained with twice as large radii. Moreover, as is expected, the physical designs could be manufactured by using a deposition tool in shape of the larger neighborhood followed by a punch in the shape of the smaller neighborhood. We note that the same guarantee of manufacturability holds when replacing (in the open–close filter over different sized neighborhoods) the open by a dilate and the close by an erode filter (Svärd 2015). One reason to use the more complicated open and close filters is that these are closer to being volume-preserving than the dilate and erode filters (Sigmund 2007). Strictly speaking, the mentioned type of manufacturability can only be guaranteed for binary designs, and when the dilate and erode filters corresponds to max and min operators, respectively.

The bottom row of Fig. 7 shows designs optimized using twice the number of elements in each coordinate direction compared to those in the top row. Although the designs obtained for different mesh sizes are not identical, they are similar and share the same main features.

6 Concluding summary

In this paper, we have proven the existence of solutions to a continuous fW-mean filtered penalized minimum compliance problem. The existence of solutions is in accordance with previous experimental experience on mesh-independence gained by using nonlinear filters (Sigmund 2007; Svanberg and Svärd 2013). As was pointed out by Svanberg and Svärd (2013), the use of a different filter may give rise to a different solution. To facilitate switching between different filters, we recommend using a data structure similar to that found in Table 1. We have performed large-scale topology optimization in two space dimensions. The nonlinear nature of the filter together with a penalization technique results in physical designs that are almost black and white. A key to enable solutions of large-scale problems is our fast filtering algorithm (Wadbro and Hägg 2015), which enables us to filter densities and modify sensitivities with a computational cost proportional to the number of design variables. Filtering over complex neighborhood shapes can be achieved by cascading filters over simple neighborhood shapes, and doing so might considerably simplify the implementation of the filtering procedure. We have argued that uniform weighting within neighborhoods is the preferred choice when using filters designed to mimic max or min operators. It is important to keep in mind that using a nonlinear filter does not by itself ensure that the final designs are black–white; the filter must be paired with a properly chosen penalization strategy.